Basicsofhydrocarbons
1.1Introduction
Hydrocarbonstransportedbypipelinesystemsareusuallycomposed byalargenumberofcomponents;atambienttemperatures,someofthem arepresentinthegasphase,whileothersareliquids.Someheaviercomponentsmayalsoappearassolidinsomecriticaloperatingconditions(hydrates,waxes).Waterisoftenpresentinthetransported fl uidmixture, anditisusuallytreatedasaseparatephase,evenifahydrocarbonliquid ispresent.Thebehaviorofhydrocarbonmixturesdependsontheircompositionsaswellasthepressureandtemperatureconditionsencountered. Thethermodynamicsofmixturesisdeterminedbythecontributionsof singlecomponents;forthisreason,thepropertiesofsinglecomponents arecovered fi rst.Thetreatmentbeginswiththedescriptionoftheequationsofstate,de fi ningtherelationshipbetweenthemain fl uidproperties; startingwiththesimplestapproachbasedonidealgasmodel,morecomplexandrealisticmodelsareintroduced.Thermodynamicequilibrium conditionsarediscussedbyconsideringtherelevanttrendsofentropy
andfreeenergies,forspeci fi csystems.Stableequilibriumoccurswhenitis independentontimeanditsprevioushistory,anditisabletoresisttosmall thermodynamicparameter fl uctuations.Theseconceptsareappliedtothe analysisofvapor liquidphasetransformations,referredtobothsingle componentsandbinarymixtures.Thediscussionisfurtherextendedto multicomponentmixtures,astypicalofhydrocarbon fl uids.Thedescriptionoftheirpropertiesisdevelopedbytreatingtheinteractionofdifferent components,thephasebehaviorincludingavapor liquidcoexistence conditionoccupyinga fi niteregionofthepressure temperaturediagram, retrogradecondensationphenomena,thedifferentbehaviorsofreservoir fl uidasdependingontheirdominantcomponents,andtheinteraction withthewaterphase.
1.2Equationofstate
Thethermodynamicpropertiesofa fluidcanbedefinedbyusinga volumetricequationofstate,providinginformationabouttherelationship betweenpressure,temperature,andvolume(ordensity).
ThesimplerEoS(EquationofSate)isthatrelevanttotheidealgas model,whichassumesnointeractionamong fluidparticlesandneglectstheir volume.Itisexpressedbythefollowing:
where:
P ¼ fluidpressure
V ¼ fluidspecificvolume
R ¼ universalgasconstant
T ¼ fluidabsolutetemperature
Intermofcompressibilityfactor Z,definedinthisway,
theidealgasmodelisrepresentedbythecondition Z ¼ 1.
Thecompressibilityfactorisaparametergivingtheindicationofthe deviationofarealgasthermodynamicbehaviorfromtheidealgasapproximation;actually,therealsubstancescanbedescribedby Eq.(1.1) onlyina limitedrangeofconditions,i.e.,atlowpressuresandmoderatetemperatures.Hence,otherequationsofstatehavebeendevelopedonthebasis
ofexperimentaldataofreal fl uids;themostimportantfromahistorical pointofviewistheclassicalVanderWaalsequation,givenbythe following:
Inthisexpression,twoparametershavebeenintroducedtorepresentreal fluideffects,namely:
a ¼ itisaparameterrelevanttotheVanderWaalsintermolecularforces, whichareincludedasanequivalentpressuretermproportionaltotheinversesquareofthevolume
b ¼ itisaparameterrepresentingthe finitevolumeofmolecules
Eq.(1.3) isaso-calledcubicEoS,sinceacubicalgebraicequationmust besolvedinordertoobtainthevolume.
TheVanderWaalsequationisnotveryaccurate,butitwasthe first equationcapableofpredictingthetransitionbetweenvaporandliquid; furthermore,ithasalsobeentheprototypeformodern,moreaccurate equationsofstateasthePeng Robinsonone(PengandRobinson, 1976),givenby:
ortheSoave Redlich Kwong(Soave,1972):
Theparametersoftheaboveequationscanbeobtainedorby fittingthe equationsto PVT dataforthe fluidofinterestorbyusinggeneralrelations betweenthemandcriticalpointproperties(see Section1.4).
Alltheaboveexpressionscanbewritteninthefollowingform:
Thisisagainacubicalgebraicequationthatmustbesolvedtogetthe compressibilityfactor Z,asmustbeforthe fluidvolume.
Allcubicequationsofstateareapproximate;ingeneral,theyprovidea reasonabledescriptionofthermodynamicpropertiesofvaporandliquid phasesofhydrocarbons,andofvaporregiononlyformanyotherpure fluids. ThePeng RobinsonandSoave Redlich Kwongare,atpresent,among themorepopularcubicequationsofstateinoilandgasapplications.
Adifferenttypeofequationofstateisthevirialequation(Sandler,1999):
where BðT Þ and C ðT Þ arethetemperature-dependentsecondandthird virialcoefficients.Thisexpressionisoftheoreticalinterestsinceitcanbe derivedfromstatisticalmechanicswithexplicitformulationsofthevirial coefficientsintermsofparticleinteractions.Itisapowerseriesexpansionin specificvolumeabouttheidealgasresult.Withasufficientnumberofcoefficients,thevirialequationcanpredictthevaporphasepropertieswith goodprecision,butitisnotapplicabletotheliquidphase.However,evenin thecaseofthegases,itisnotrecommendedforpressureabove10bar.
1.3Otherreal fluidproperties
Oneofthequantitiesappearinginthefundamentalthermodynamic relationshipsistheheatcapacity.Itispossibletoshowthat,givenavolumetricEoS,andheatcapacitydataasafunctionoftemperatureatasingle valueofpressure P1 orvolume V1,thevalueoftheheatcapacityinanyother state(representedbypressure P2 orvolume V2)canbecomputedbythe following(Sandler,1999):
where CP and CV aretheconstantpressureandconstantvolumeheatcapacities,respectively.
Inpractice,heatcapacitydataareusuallycollectedforlowpressureconditionsorlargespecificvolumeswhereall fluidsareidealgases.Hence,if P1 or V1 aretakenas0and N,respectivelyin Eqs.(1.8)and(1.9) above,itis possibletowrite:
wheretheasteriskdenotestheidealgasheatcapacity.Usually,thetemperaturedependenceoftheidealgasheatcapacityisgiveninpolynomial formasfollows:
Otherthermodynamicvariablesthatallowtocalculatethedeviationsof thereal fluidbehaviorfromtheidealgasstatusarethe “Departure Functions.”
Inparticular,itispossibletoshowthat,forwhatconcernstheenthalpyH andtheentropyS,theirchangesforareal fluidareequaltothatofanideal gasundergoingthesametransformationplusthedepartureofthe fluidfrom theidealgasbehaviorattheendstatelessthedeparturefromtheidealgas behaviorattheinitialstate.These “DepartureFunctions” canbecomputed fromtheequationofstate,basedonthefollowing:
1.4Theprincipleofcorrespondingstates
Theanalysispresentedin Sections1.2and1.3 hasshownthatitis possibletocalculatethethermodynamiccharacteristicsofarealsubstance givenonlytheidealgasheatcapacityandthevolumetricEoS.However, thenecessaryinformationontheEoSisnotalwaysavailableforall fluids. Hence,itispossibletoresorttotheprincipleofcorrespondingstates,which allowstopredictthermodynamicpropertiesof fluidsfromgeneralizedpropertycorrelationsbasedonexperimentaldataforsimilar fluids.
WeconcentrateourattentiononavolumetricEoS,whichisdeterminedbytheintermolecularinteractions.Fromthestudyofmolecular behavior,ithasbeenfoundthatmoleculescanbegroupedintoclasses,
suchassphericalmolecules,nonsphericalmolecules,moleculeshavinga permanentdipole,andsoon,andthatwithinanyoneclassmolecularinteractionsaresimilar.
IthasbeenalsofoundthatallthemembersofaclassobeythesamevolumetricEoS,i.e.,thevolumetricdataofeachmemberare fittedbysimply changingtheparametersoftheEoS.Thefactthatseveraldifferentmolecular speciesmaybedescribedbyavolumetricEoSofthesameformsuggeststhat itmightbepossibletoconstructgeneralizedcorrelationsforboththeEoS anddensity-dependentcontributiontoenthalpy,entropy,andotherthermodynamicvariables.The firsthistoricalgeneralizedcorrelationarose fromthestudyoftheVanderWaalsEoS. Fig.1.1 showstheisothermsof thisequationina P versus V diagram,for fivevaluesoftemperature includingthecriticaltemperature TC,whichisdefinedasthemaximum temperatureatwhichaliquidphasecanexist.Tobenotedthatthisdefinitionholdsforasinglecomponent fluidonly.
Itcanbeobservedinthis figurethattheisothermswithtemperature belowthecriticaloneexhibitanon-monotonebehavior,withalocalminimumfollowedbyalocalmaximumoverpartofthespecificvolume pressurerange.Suchtrendisassociatedwithaliquid vaportransition. Whilethisbehaviorisabsentfor T > TC,insuchawaythattheliquidphase cannotexistinthisrange,inthecriticaltemperaturecurve,thetwoextremescoincide,andthispoint(calledcriticalpoint)isaninflectionpoint,
Figure1.1 IsothermsoftheVanderWaalsEOSinaplane(
wherethe firstandsecondderivativeof P withrespectto V vanishessimultaneously.Thisisexpressedanalyticallybythefollowingrequirements:
Byreplacing Eq.(1.3) intherelations(1.15),thefollowingexpressionsof theVanderWaalsparameters a and b areobtained:
Using (1.16) intheVanderWaals Eq.(1.3),itispossibletogetthepressure PC andthecompressibilityfactor ZC atthecriticalpoint:
Byusingtheaboveexpressionsandbydefiningthedimensionlessvariablescalledreducedtemperature Tr,reducedpressure Pr andreducedvolume Vr
thefollowingformoftheVanderWaalsequationofstateisobtained:
From (1.19) itisconcludedthatallthe fluidsobeyingtheVanderWaals equationofstatehavethesamenumericalvalueofreducedvolumeforgiven valuesof Pr and Tr.Two fluidshavingthesamevaluesofreducedpressure andtemperaturearesaidtobeincorrespondingstates.
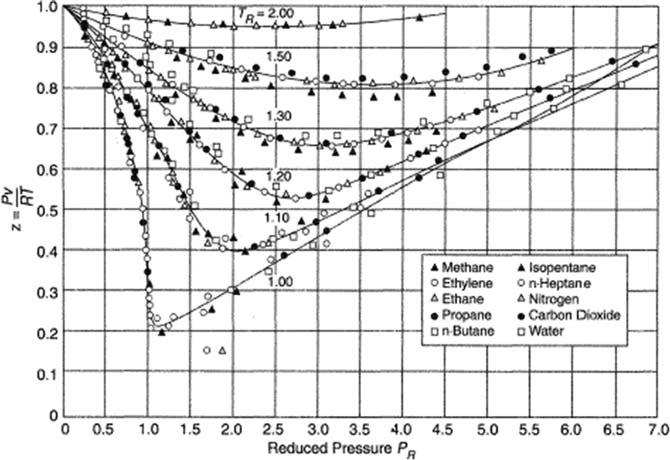
Theprincipleofthecorrespondingstateshasbeenhistoricallyrepresentedbydrawingthecompressibilityfactor Z asfunctionofreducedpressureandtemperature,asshownin Fig.1.2,wherethecompressibilitydata forseveral fluidshavebeenreported.
Fig.1.2 demonstratesthattheideaofthecorrespondingstatesisreasonable,sincethegeneraltrendofthedataconfirmsthesimilarityrepresented by (1.19).However,itcanbeobservedthatcompressibilityfactorsforinorganic fluidsarealmostalwaysbelowthoseforhydrocarbons.Furthermore,if (1.19) wereuniversallyvalid,all fluidswouldhavethesamevalueofthecriticalcompressibility ZC ¼ 0.375,asshownby (1.17),whileformost fluids, thecriticalcompressibilityisintherange0.23 0.31.
Figure1.2 Compressibilityfactorforseveral fluidsasafunctionofreducedpressure andtemperature. From SuandChang(1946).
Thesedeviationshaveledtothedevelopmentofmorecomplicatedcorrespondingstatesprinciples.Thesimplestgeneralizationisbasedonthe adoptionofafamilyofdifferentrelations Z ¼ Z(Pr,Tr),withdifferentvalues of ZC,i.e.,thecriticalcompressibilityfactorisusedasanadditionalparameterofthecompressibilitylaw:
Infact,otherquantitieshavebeenconsideredasadditionalcorrespondingstatesparameters,sincethecriticalcompressibilityfactor ZC isnot knownwithenoughaccuracyformanysubstances.
Pitzer(1995) hasproposedtheso-calledacentricfactor u asthirdcorrelativeparameter,whichisdefinedinthisway:
¼ 1:0 Log10 ðP vap ðTr ¼ 0:7Þ = PC Þ (1.21)
Here P vap ðTr ¼ 0:7Þ isthevaporpressureofthe fluidat Tr ¼ 0:7. Eventheseextensionsofthecorrespondingstateconcepthavebeen foundnotsuitabletorepresentthethermodynamicbehaviorofsomekinds ofmolecules,inparticularthathavingdipolesorquadrupoles.Hence,this applicationremainslimitedtosomeclassesofmoleculesonly,asincaseof mosthydrocarbons.
ThemodernversionofthecorrespondingstatesideaistheuseofgeneralizedEoS.
TheVanderWaalsequationisthe firstexampleofapplicationofthis approach.Infact,theexpressions (1.16),rewrittenintermsofthecritical pressureandtemperatureinthisway,
demonstratethatthethermodynamicpropertiesofaclassof fluidswith parameters a and b thathavenotbeenderivedfromasetofexperimentaldata canbedescribedbyknowingthe fluidcriticalpropertiesonly.Asitwassaid before,theVanderWaalsequationisnotaccurateenough,andothermore sophisticatedequationsareused.
Inparticular,weconsiderherethePeng Robinsonequationalreadypresentedin Section1.1,byshowingthatitsgeneralizedformisgivenbythe following:
TheaboverelationshipswereobtainedbyPengandRobinsoninorder toimprovethepredictionsoftheboilingpointpressureversustemperature, andthefunction aðT Þ waschosenby fittingthevaporpressurevaluesfor many fluids.WithrespecttotheVanderWaalsscheme,thegeneralized Peng Robinsonapproachusesoneparametermoreotherthan PC and TC,namelytheacentricfactor u
Thisequationcanbeusedtocalculatenotonlythecompressibilityfactor,butalsothedeparturefunctionsfortheotherthermodynamic properties.
AnotherverypopularcubicequationofstateusedintheoilandgasindustryistheSRK(Soave Redlich Kwong):
with:
Thecurrentindustrialpracticeisbasedontheapplicationofthecorrespondingstatesconcept,byassumingthatdifferent fluidsaredescribedby thesamegeneralizedequationsofstate,andthattheirthermodynamic behaviorinanextendedpressureandtemperaturerangeisdescribedby knowingthegeneralizedparametersonly.Suchkindofequationscan giveaveryaccuratethermodynamicpictureofmanysubstances,inparticularhydrocarbons.
1.5Equilibriumandstabilityofone-component fluids
Theequilibriumstateofaclosedthermodynamicsystemcanbe derivedbyusingtheenergyandentropybalancesderivedfromthe first andsecondprinciplesofthermodynamics:
where:
U ¼ specificinternalenergy _ Q ¼ heattransferrate
S irr ¼ rateofinternalgenerationofentropybyirreversibleprocesses 0 In (1.33) onlyworkduetodeformationofthesystemboundariesis considered.
Foranadiabatic( _ Q ¼ 0)andconstantvolumesystem,thesystemofenergyandentropybalancesequationsbecomes
Sincetheentropyfunctioncanonlyincreaseduringtheapproachto equilibriumdueto (1.36),theentropymustbeamaximumatequilibrium. Hence,theequilibriumcriterionforaclosedandisolatedsystemisas follows:
Thisprinciplecanbeillustratedbyreferringtothesimplesystemshown in Fig.1.3.
Thesystemiscomposedbytwosubsystemscontainingdifferentamounts ofthesamemolecularspeciesofparticlesofasingle-component fluid(N representsthenumberofmoles).Theyareconnectedbyachannelofinfinitesimalvolumeequippedbyanidealvalveopeninginstantaneously.The systemisassumedadiabaticandconstantvolume,exchangingneithermass neitherenergywiththeexternalenvironment.However,thetwosubsystemscanexchangeheatandmassacrossthecommunicationchannel whenthevalveisopen.Fortheglobalsystem,thetotalnumberofmoles
Figure1.3 Isolatednonequilibriumsystem.
N1, S1, U1, V1
N2, S2, U2, V2
N,thetotalinternalenergy U,thetotalvolume,andthetotalentropyare givenbytheadditionofthetwosubsystemscontributions:
Byusingthefundamentalthermodynamicrelationships,theentropy changeofeach i-thsubsystemaftercommunicationandmixingofparticles canbeexpressedasafunctionofchangesinthenumberofmoles,volumes, andinternalenergybythefollowing:
where Gi isthe i-thsubsystemmolarGibbsenergy.
Theentropychange dS oftheoverallsystemcanbeeasilyobtainedby summingthetwosubsystemscontributions,byconsideringthatthetotal quantitiesgivenby (1.38), (1.39),and (1.40) areconstant:
Sincetheentropymustbeamaximumatequilibrium,the (1.25) expressionmustvanishforsystemvariations,thusobtainingthefollowing:
Hence,theequilibriumconditionforanadiabaticisolatedsystemstates thatallitssubsystemsmusthavethesametemperature,thesamepressure, andthesamemolarGibbsenergy.
Theabovediscussionisbasedonthecondition dS ¼ 0,whichisnecessarybutnotsufficientforStoreachamaximumvalue.Thefurther
condition d 2 S 0assuresthatamaximumentropyvalue,givingatrue equilibriumstate,hasbeenidentified.Onthecontrary,aminimumofthe entropycorrespondstoanunstablestate.Therefore,thesignof d 2 S determinesthestabilityofthethermodynamicstatefoundfrom dS ¼ 0.
Itispossibletodeterminetheequilibriumandstabilityforotherkindsof systemsalso.
Forinstance,foraclosedsystemkeptatconstanttemperatureandvolume,theenergyandentropybalanceequationsbecome
Bycombiningtheaboveequations,thefollowingrelationship,writtenin termofthemolarHelmholtzfreeenergy F ,isobtained:
SincethemolarHelmholtzfreeenergy F canonlydecreaseduringthe approachtoequilibriumdueto (1.49),itmustbeaminimumatequilibrium. Hence,theequilibriumcriterionforaclosedsystemkeptatconstant temperatureandvolumeisthefollowing:
Foraclosedsystemkeptatconstanttemperatureandpressure,theenergy andentropybalanceequationsbecomethefollowing:
Bycombiningtheaboveequations,thefollowingrelationship,writtenin termofthemolarGibbsfreeenergy G ,isobtained:
whichleadstothefollowingequilibriumcriterion:
Table1.1
Equilibriumandstabilityconditionsforselectedsystems.
KindofsystemConstraints Equilibrium
Isolated,adiabatic systemwith constantvolume U ¼ constant, V ¼ constant S ¼ maximum, dS ¼ 0 d 2 S 0
Isothermal,closed systemwith constantvolume T ¼ constant, V ¼ constant F ¼ minimum, dF ¼ 0
Isothermal,isobaric closedsystem T ¼ constant, P ¼ constant
Actuallyforallthesystemsconsideredhere,theapplicationoftheequilibriumcriteriadeterminesthattheyareatuniformtemperature,pressure, andmolarGibbsfreeenergy.
Theequilibriumandstabilityconditionsforthesystemunderconsideration,writtenforasingle-component fluid,aresummarizedin Table1.1.It ispossibletoshowthattheyarealsovalidformulticomponent fluids.
Fromthestabilitycriterialistedin Table1.1,threefundamentalthermodynamicinequalitiescanbederivedforsystemsconsideredinastableequilibriumstate: CV > 0; vP vV T < 0; vU vT > 0(1.55)
1.6Vapor
fluids
liquidequilibriumforone-component
Nowwearegoingtoanalyzetheequilibriumoftwophases(vapor andliquid)onthebasisofthediscussionexposedin Section1.5.In Fig.1.4,someisothermalcurvesinaplane(P,V)areshown,asgivenbya typicalcubicEoS.Thesecurvesarerepresentedforincreasingtemperature (T1 < T2 < T3 < T4 < T5).Wecanobservethattheisothermslabeledby T1 and T2 donothaveamonotonetrend,buttheypresentaminimumfollowedbyamaximuminacertainregionofthe(P,V)diagram.Therefore, whileforthehigh-temperatureisothermsthestabilitycondition ð vP vV Þ T < 0isfulfilledeverywhere,thisisnottrueforthelow-temperatureisotherms. Actually,theregionsofthediagramwherethestabilityviolationoccursare notphysicallyrealizableandcannotbeobservedinpractice.Thus,inthis
particularthermodynamicregion,thecubicequationsofstatefailtopredict therealbehaviorofthe fluid,andtheirtrendmustbereplacedbyanother physicaldescription.Theisothermattemperature T3 hasasinglepointfor whichthe firstandsecondderivativesofpressurewhichrespecttovolume vanishsimultaneously:thisiscalledcriticalpointand T3 isthecriticaltemperature(usuallyidentifiedasTC).
Alow-temperatureisothermisrepresentedalonein Fig.1.5;itisshown thattheintersectionofahorizontallineatconstantpressurewiththecurve givesthreepossiblevaluesforthevolumeofthe fluid, V 0 , V 00 ,and V 000 .One ofthese, V 00 ,isonthepartoftheisothermthatisunphysicalfortheabove mentionedstabilityreasons.Theothertwovalueshaveaphysicalmeaning instead,andtheyrepresentthevolumesoftheliquidandvaporphase, respectively,atthespecifiedpressureandtemperature.
Thetruethermodynamicbehaviorintheregionbetween V 0 and V 000 is shownin Fig.1.6,whereaphasechangeoccursalongtheconsidered isothermisobarrepresentedbythehorizontalsectionwhichboundaryvolumesarethesingle-phaseliquidandvaporvolumeslabeledas V L and V V . Thisisthevapor liquidcoexistenceregion.Thetwo-phasemixturespecificvolume V M variesinthisregionsince,althoughthespecificvolumes ofthesinglephasesare fixed,thevaporfraction a inthemixturevaries from0to1,thusgivingthefollowing:
Figure1.4 Isothermsonaplane(P,V)predictedbyacubicequationofstate.
Isotherm T1 < T3
Line
Figure1.5 Low-temperatureisotherminaplane(P,V)predictedbyacubicEoS.
Isotherm T1 < T3
Figure1.6 Reallow-temperatureisotherminaplane(P,V)includingthevapor liquid phasetransition.
Thus,theisothermsectionpredictedbyacubicEoSinthetwo-phase regionofasingle-component fluidmustbereplacedbytheisobarichorizontallineshownin Fig.1.6
Thequestionthatremainsisthevalueofpressurecorrespondingtothe vapor liquidcoexistenceregion.Thecriteriontobeappliedinorderto findthispressureistheequalityofthetwophasesGibbsfreeenergies,as
derivedfrom Section1.5.Fromfundamentalthermodynamicrelationships, thefreeGibbsenergyvariation DG alonganisothermisgivenbythe followingintegral:
Thus,byusingtheequationofstatewhichprovidestherelationship among V and P ,thevalueofthephasechangepressure P f isobtained bythefollowing:
where P 0 and P 00 aretheminimumandmaximumpressurevaluesinthephase transitionregion.Graphically,thiscorrespondstotheequalitybetweenthe regions A and B of Fig.1.5,comprisedbetweenthehorizontaltransitionline andtheisothermcurvegivenbythecubicEoS. Fig.1.4 mustbereplacedby Fig.1.7,showingthetruethermodynamicbehaviorassociatedtothephase transition,inwhichthetwo-phasemixtureregionisincludedinsideadomeshapedenvelopecurvecrossingthelow-temperatureisotherms.For
Coexistence Region
Figure1.7 Realisothermsinaplane(P,V)includingthevapor liquidcoexistence region.
Critical Point (TC , PC )
temperaturesabovethecriticaltemperature,nophasetransitioncanoccur, andthe fluidissaidtobeinthesupercriticalconditionordensephasegas.
Atypicalphasetransitioncurveina(P,T)diagramhastheformshownin Fig.1.8,endingwiththecriticalpointidentifiedbythecouple(TC, PC). Again,fortemperaturesabovethecriticaltemperature,nophasetransition canoccur(supercritical fluid).Fortemperatures T < TC andpressures P > PC,the fluidisintheliquidphase,butitsthermodynamicproperties, closetothecriticalconditions,areverysimilartothatofthesupercritical gasinsuchawaytheyarepracticallyindistinguishable.
Theequation P ¼ P ðT Þ ofthephasetransitioncurvecanbederivedby applyingtheequalityoftheGibbsfreeenergiesrelevanttothetwophases:
From (1.59),itdescendsthatforsmallchangesofpressureandtemperaturethechangesoftheGibbsfreeenergiesaresmallandequal:
Fromfundamentalthermodynamicrelationships,thedifferentialsof (1.60) canbeexpressedintermsoftheotherthermodynamicquantitiesin thisway:
Liquid-Vapour Transition Curve
Figure1.8 Liquid vaportransitioncurveinaplane(P,T).
And,byindicatingwith DV ; DS thechangesinspecificvolumeandentropy whenpassingfromonephasetotheother,from (1.61),weobtainthe following:
where DH isthephasetransitionenthalpyvariation,alsocalledlatentheatof vaporization(orcondensation).The (1.62) isknownasClapeyronequation. Thepressureatwhichtheliquidandvaporphasesareinequilibriumis termedvapororsaturationpressure,hereindicatedas P vap .From (1.62), itstrendasfunctionoftemperature P vap ¼ f ðT Þ canbeobtained.At temperaturesforwhichthevaporpressureisnotveryhigh,itresultsthat V V >> V L and DV zV V .Furthermore,ifthevaporcanbetreatedas ideal,wehave DV ¼ V V ¼ RT P ,thusgivingthefollowing:
thatcanbewrittenalsoasfollows:
where DH vap ¼ H V H L isjustthelatentheatofvaporization.
Theintegrationof (1.64) givesthewantedvaporpressuretemperature function;ifitisassumedthatthetemperaturedependenceof DH vap isnegligible,wegetthefollowing:
where C isanintegrationconstant.
AcommoncorrelationusedtoreproducethevaporpressureastemperaturefunctionistheAntoineequation,whichisverysimilarto (1.65) andit isexpressedinthisway:
where D and E arecorrelatingparameters.
Thediscussionreportedsofarhasbeenconcernedwiththeanalysisof stableequilibriumstatesofasingle-component fluid.However,metastable statesasthesuperheatedliquidandthesubcooledvaporcanoccurin
Isotherm T1 < T3
Superheated Liquid
Subcooled Vapour
experiments.Infact,bysuitableexperimentalproceduresinwhichthethermodynamictransformationalonganisothermisrealizedveryslowly,by avoidingasmuchaspossibletheonsetofbubblenucleationincaseofliquid andofdropletnucleationincaseofvapor,theone-phaseisothermsections canbeprolongedoutsidethestabilityregionasshownin Fig.1.9.Theliquid belongingtotheextendedleftisothermportionissaidsuperheatedliquid andthevaporbelongingtotheextendedrightisothermportionissaidsubcooledvapor.Boththesestatesaremetastablesincetheyexistasone-phase fluidsinaregionwherethetwo-phasetransitionshouldhavehadoccurred, andifslightlyperturbed,the fluidexperiencesasuddentransitiontowardthe stablecondition.
Actually,inthestudyofliquid vaporequilibria,itiscommonpractice toutilizetheso-calledfugacityintheequilibriumequation,insteadofthe Gibbsfreeenergy.
Thefugacity f isdefinedinthisway:
Anotherquantitycorrelatedtothefugacityisthefugacitycoefficient
Figure1.9 Metastablestatesalonganisotherminaplane(P,V).