Contributors
RicardoAlmada-Monter InstitutodeQuı´mica, UniversidadNacionalAuto ´ nomadeMexico, MexicoCity,Mexico
OmarA.A ´ lvarez-Gonzaga EscuelaSuperiorde Fı´sicayMatema ´ ticas,InstitutoPolitecnico Nacional,MexicoCity,Mexico
JamesS.M.Anderson InstitutodeQuı´mica, UniversidadNacionalAuto ´ nomadeMexico, MexicoCity,Mexico
PaulW.Ayers DepartmentofChemistry, McMasterUniversity,Hamilton,Canada
JoseE.Barquera-Lozada InstitutodeQuı´mica, UniversidadNacionalAuto ´ nomadeMexico, MexicoCity,Mexico
YoshioBarrera InstitutodeQuı´mica, UniversidadNacionalAuto ´ nomadeMexico, MexicoCity,Mexico
GiovannaBruno DipartimentodiChimica, Universita ` degliStudidiMilano,Milano, Italy
PabloCarpio-Martı ´ nez InstitutodeQuı´mica, UniversidadNacionalAuto ´ nomadeMexico, MexicoCity,Mexico
JuliaContreras-Garcı ´ a Sorbonne Universite, CNRS, LaboratoiredeChimieTheorique,Paris, France
FernandoCortes-Guzma ´ n Institutode Quı´mica,UniversidadNacionalAuto ´ nomade Mexico,MexicoCity,Mexico
AuroraCostales DepartamentodeQuı´mica Fı´sicayAnalı´tica,FacultaddeQuı´mica, UniversidaddeOviedo,Oviedo,Spain
EmilianoDorantes-Herna ´ ndez EscuelaSuperiordeFı´sicayMatema ´ ticas,Instituto PolitecnicoNacional,MexicoCity,Mexico
MarkE.Eberhart DepartmentofChemistry, ColoradoSchoolofMines,Golden,CO,United States
AlbertoFerna ´ ndez-Alarco ´ n Institutode Quı´mica,UniversidadNacionalAuto ´ nomade Mexico,MexicoCity,Mexico
EvelioFrancisco DepartamentodeQuı´mica Fı´sicayAnalı´tica,FacultaddeQuı´mica, UniversidaddeOviedo,Oviedo,Spain
MarcoAntonioGarcia-Revilla Departmentof Chemistry,NaturalandExactSciencesDivision,UniversityofGuanajuato,Guanajuato, Mexico
CarloGatti CNR-SCITEC,IstitutodiScienzee TecnologieChimiche“GiulioNatta”;Istituto Lombardo,AccademiadiScienzeeLettere, Milano,Italy
RosaM.Go ´ mez-Espinosa CentroConjuntode Investigacio ´ n en Quı´micaSustentable UAEM-UNAM,Toluca,EstadodeMexico, Mexico
JoseM.Guevara-Vela Departamentode Quı´micaFı´sicaAplicada,Universidad Auto ´ nomadeMadrid,Madrid,Spain
Jesu ´ sHerna ´ ndez-Trujillo Departamentode Fı´sicayQuı´micaTeo ´ rica,FacultaddeQuı´mica, UNAM,MexicoCity,Mexico
Jesu ´ sJara-Cortes UnidadAcademicade CienciasBa ´ sicaseIngenierı´as,Universidad Auto ´ nomadeNayarit,Tepic,Mexico
SamanthaJenkins KeyLaboratoryofChemical BiologyandTraditionalChineseMedicine ResearchandKeyLaboratoryofResourceNationalandLocalJointEngineeringLaboratory forNewPetro-chemicalMaterialsandFine
UtilizationofResources,CollegeofChemistry andChemicalEngineering,HunanNormal University,Changsha,Hunan,People’s RepublicofChina
LaurentJoubert NormandyUniversity,COBRA UMR,UniversitedeRouen,INSARouen, CNRS,MontStAignanCedex,France
AiriKawasaki DepartmentofChemistry,GraduateSchoolofScience,TokyoMetropolitan University,Tokyo,Japan
StevenR.Kirk KeyLaboratoryofChemical BiologyandTraditionalChineseMedicine ResearchandKeyLaboratoryofResourceNationalandLocalJointEngineeringLaboratory forNewPetro-chemicalMaterialsandFine UtilizationofResources,CollegeofChemistry andChemicalEngineering,HunanNormal University,Changsha,Hunan,People’s RepublicofChina
BrunoLanderos-Rivera Departamentode Fı´sicayQuı´micaTeo ´ rica,FacultaddeQuı´mica, UNAM,MexicoCity,Mexico
CherifF.Matta DepartmentofChemistryand Physics,MountSaintVincentUniversity,Halifax,NovaScotia,Canada
HectorD.Morales-Rodrı ´ guez EscuelaSuperior deFı´sicayMatema ´ ticas,InstitutoPolitecnico Nacional,MexicoCity,Mexico
AmandaMorgenstern ChemistryandBiochemistryDepartment,UniversityofColorado, ColoradoSprings,CO,UnitedStates
AldodeJesu ´ sMortera-Carbonell Departamento deFı´sicayQuı´micaTeo ´ rica,Facultadde Quı´mica,UNAM,MexicoCity,Mexico
XingNie KeyLaboratoryofChemicalBiology andTraditionalChineseMedicineResearch andKeyLaboratoryofResourceNational andLocalJointEngineeringLaboratoryfor NewPetro-chemicalMaterialsandFine UtilizationofResources,CollegeofChemistry andChemicalEngineering,HunanNormal University,Changsha,Hunan,People’s RepublicofChina
EduardoOrozco-Valdespino Institutode Quı´mica,UniversidadNacionalAuto ´ nomade Mexico,MexicoCity,Mexico
A ´ ngel Martı ´ n Penda ´ s Departamentode Quı´micaFı´sicayAnalı´tica,FacultaddeQuı´mica, UniversidaddeOviedo,Oviedo,Spain
DavidI.Ramı´rez-Palma InstitutodeQuı´mica, UniversidadNacionalAuto ´ nomadeMexico, MexicoCity,Mexico
Toma ´ sRocha-Rinza InstitutodeQuı´mica, UniversidadNacionalAuto ´ nomadeMexico, MexicoCity,Mexico
JuanI.Rodrı ´ guez CICATA-Queretaro,Instituto PolitecnicoNacional,Queretaro,Mexico; EscuelaSuperiordeFı´sicayMatema ´ ticas, InstitutoPolitecnicoNacional,MexicoCity, Mexico
ShantShahbazian DepartmentofPhysics, ShahidBeheshtiUniversity,Tehran,Iran
DavidC.Thompson ChemicalComputing Group,Montreal,QC,Canada
VincentTognetti NormandyUniversity,COBRAUMR,UniversitedeRouen,INSARouen, CNRS,MontStAignanCedex,France
IsmaelVargas-Rodrı ´ guez Departmentof Chemistry,NaturalandExactSciencesDivision,UniversityofGuanajuato,Guanajuato, Mexico
TimothyR.Wilson DepartmentofChemistry, ColoradoSchoolofMines,Golden,CO,United States
TianlvXu KeyLaboratoryofChemicalBiology andTraditionalChineseMedicineResearch and KeyLaboratoryofResourceNational andLocalJointEngineeringLaboratoryfor NewPetro-chemicalMaterialsandFineUtilizationofResources,CollegeofChemistry andChemicalEngineering,HunanNormal University,Changsha,Hunan,People’s RepublicofChina
YongYang KeyLaboratoryofChemical BiologyandTraditionalChineseMedicine
ResearchandKeyLaboratoryofResourceNationalandLocalJointEngineeringLaboratory forNewPetro-chemicalMaterialsandFine UtilizationofResources,CollegeofChemistry
andChemicalEngineering,HunanNormal University,Changsha,Hunan,People’s RepublicofChina
Photochemistry:Atopological perspective
MarcoAntonioGarcia-RevillaandIsmaelVargas-Rodrı´guez DepartmentofChemistry,NaturalandExactSciencesDivision,UniversityofGuanajuato, Guanajuato,Mexico
1.Introduction
ThestudysubjectsofPhotochemistryarethephenomenaassociatedwiththeabsorption andemissionofelectromagneticradiationbychemicalsystems.Amongsuchprocessesare thefollowing [1]:
•Spectroscopicphenomenonasfluorescenceandphosphorescence.
•Luminescentchemicalreactions,asthecombustionandbioluminescence,forinstancethe planktonluminescenceandtheflashlightsoffireflies.
•Photopromotedchemicalreactions,asthephotosynthesis [1] andtheretinalreactionofthe humanvision [1].
•Nonlinearopticalproperties,relatedtothenonlinearbehavioroftheinducedpolarization ofthechargedistributionbytheinteractionofasubstancewiththeelectromagnetic radiation.Thisphenomenonhasbecomeofgreatimportanceintelecommunications, computing,opticaldevices,microscopy,amongothers.
Photochemicalreactions(PR)arechemicaltransformationsinwhichanexcitedstateis reachedbecauseoftheincidenceofelectromagneticradiation,inthesereactionstheexcitation degreeofreactantscanbeeasilycontrolledusingamonochromaticbeamoftherequired wavelength.Hence,PRarepreferredoverthethermalreactions,alsoknownasdark reactions.Besides,thermalreactionsdealwithaMaxwell-Boltzmandistributionofground stateenergiesoftranslational,vibrational,rotational,electronic,andnuclearcontributions, forthisreason,theprobabilityofcausingachemicalreactionislowerthaninthephotochemicalcase [2].Inaddition,therearemanynewsyntheticroutestoobtainorganiccompounds whicharenotpossibletobesynthesizedbythermalreactions [3].
TheStark-Einsteinlawofphotochemicalequivalencestablishesthatonelight-quantumis absorbedbyonemoleculepromotingachemicalreaction [4],andthatisall,thereisnotacontinuousmolecularabsorptionoflightduringaphotochemicaltransformation.Theefficient absorptionofalight-quantumcausesanelectronicexcitation,forthisreasonthecharacterizationofthegroundandexcitedstatesisfundamentalfortheunderstandingoftheeffectsof theelectromagneticradiationinasubstance.Anelectronicexcitedstateisasolutionofthe electronicSchr € odingerequationwithasuperiorenergythanthegroundelectronicstate [5],thequalityofthedescriptionoftheexcitedstateisrelatedtothechosenelectronicstructuremethod.Thefollowingareexamplesofprocessesinwhichexcitedstatesarereached fromgroundstates:
•Elementalparticlebombing.
•Alternatecurrentorfireheatingexposure.
•Electromagneticradiationexposure.
Theprocessesexperiencedbysubstancesinducedbyelectromagneticradiationcanbe viewedasthesuccessionoftwophenomena:theexcitationofthegroundstatereachingan excitedstate,andthedeactivationoftheexcitedstate.Somephotochemicalprocessesreturn tothestartingpoint,thegroundstateofthesubstance.Nevertheless,therearesomechemical transformationscausedbydeactivationofexcitedstates.
1.1Excitationofthegroundstate
Anexcitedstateisreachedaftertheabsorptionofelectromagneticradiation,fulfillingthe Frank-Condonprinciple [4] andtheselectionrules [4]. Fig.20.1 showstheJablonskidiagram, whichisageneralschemeoftheelectronicstructurerelatedtophotochemicalprocesses [4]. Themoleculeinitiallyreliesinthegroundstate,let’ssayasingletstate S0,abovethe S0 there aresuccessivesingletexcitedstates S1,S2, …, theconsecutivenumberingisrelatedtotheincreasingorderinenergy.Nevertheless,somemoleculesholdgroundstateswithdifferent multiplicity,thatisthecaseoftheoxygenmoleculeinthegasphaseat1atmand25°C displayingatripletgroundstate, 3Σ.Thesingletexcitedstatesareextremelyrelevantforphotochemicalprocesses,severalmoleculesofchemicalinterestdisplaysingletgroundstates.Besides,selectionrulesstablishedthatthepermittedexcitationsarethosewiththesame
FIG.20.1 Jablonskidiagram.
multiplicity [4].Meanwhile,excitedstateswithmultiplicitiesdifferentthansingletsarelocatedabovethegroundstate,amongsuchexcitedstatesarethetripletstates, T1, T2, , which areofspecialinterestbecauseofthecrucialroleoftripletstatesinphosphorescence.Forthis reason,acommonlyusedJablonskidiagramdisplayS0,S1,S2, …,and T1, T2, … electronic states.Besides,accordinglytoHundrules,thetripletstatesholdlowerenergythantheexcited singletstates.Inaddition,thequantizedvibrationalstructureisembeddedineachelectronic state,thevibrationalnormalmodesarerepresentedassublevelsofeachelectronicstate.
1.2Deactivationmechanismsofexcitedstates
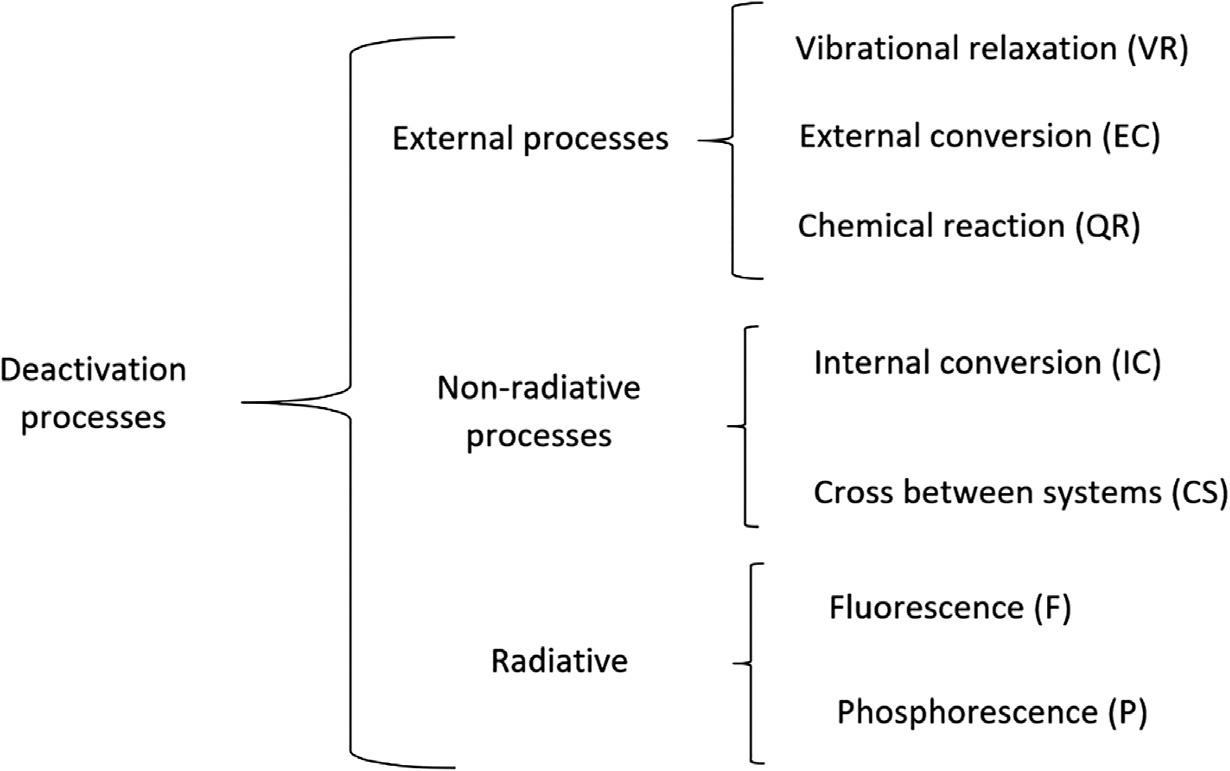
Onceanexcitedstateisreached,deactivationofsuchexcitedstatetakesplace.Deactivation processescanbeclassifiedasexternal(inducedbycollisions),nonradiative(isoenergetic)and radiative(luminescence)displayedin Scheme20.1.
Regardingexternalprocesses,thedeactivationprocesscouldhappenthrough:
I. Vibrationalrelaxation(VR),inwhichthemoleculesintheS1 excitedstatevibrateand collideeachotherdispersingtheenergyofthesystem,arrivingtothelowervibrational stateof S1.Thetimetoperformthisprocessisabout10 12 s.
II. Anexternalconversion(EC),inwhichthemoleculetravelsfromthelowervibrational modeof S1 tothefundamentalsingletstate.
III. ChemicalReaction(CR),inwhichthepotentialenergysurfaceprofileofthesingletand excitedstatechanges,causingbreakingandformingchemicalbonds.
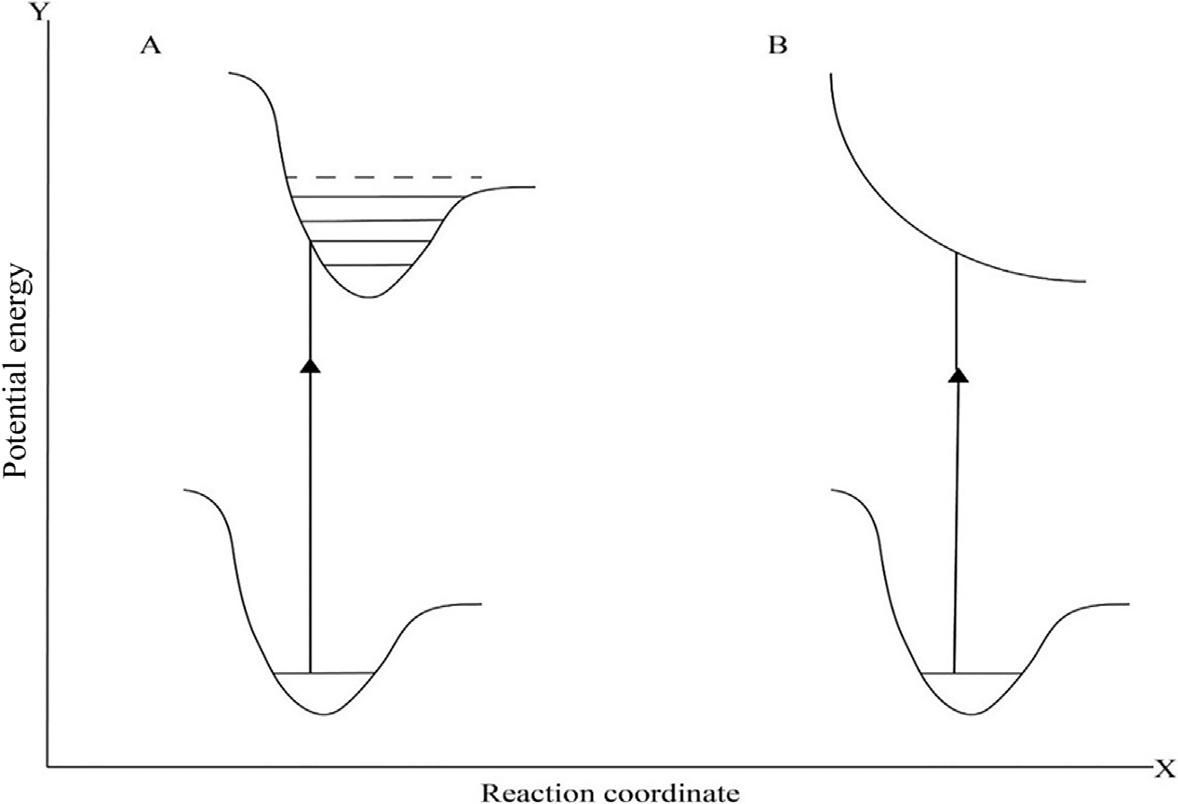
CRdeactivationprocesses,representedin Fig.20.2,showaverticalexcitationreachingan excitedstatewithavibrationalenergylargeenoughtoovercometheactivationenergyto reachasecondaryminimumintheexcitedstateprofile.Thiscoulddrivechangesintheconnectivity(moleculargraph),modificationsinbindingpropertiesandconsequentlychemical
SCHEME20.1 Deactivationprocessesclassification.
FIG.20.2 Energeticprofilesofphotochemicalprocessescausingchemicalreactions.
transformation. Fig.20.2Bshowsthecaseinwhichaverticalexcitationhitsanexcitedstate withnoenergybarrier,insuchcasethechemicaltransformationoccursstraightforward.
Anonradiativeprocesstakesplacethroughanisoenergeticenergytransference,suchprocessesareclassifiedas:
I. InternalConversion(IC),whichhappensthroughanisoenergetictransferencefromthe S1 excitedstatetoahighenergeticvibrationalmodeof S0,followedbyafullvibrational relaxationofthegroundstate.
II. IntersystemCrossing(ISC),whichisperformedthoughanisoenergetictransference fromavibrationalmodeof S1 excitedstatetoavibrationalmodeofatripledstate, let’ssaytothe T1 tripletstate.
Radiativeprocessesareclassifiedas:
I. NormalFluorescence,whichisobservedwhenafullvibrationalrelaxationalongtheS1 vibrationalmodesisfollowedbya S1 ➔ S0 emissivetransition.
II. ResonantFluorescence,whichisobservedthrougha S1➔ S0 emissivetransitionfrom theinitialvibrationalmodeof S1 tothe S0 groundstate. LifetimeofFluorescenceprocessesisabout10 7 s.
III. Phosphorescence,whichisobservedwhenaISCisfollowedbyatransitionbetween electronicstatesofdifferentmultiplicity, T1 ➔ S0.Lifetimeof T1 isabout10 5 sand thetransitionprobabilityto S0 islow.Thisisthereasonwhythisprocessisslowerthan thefluorescence.
Theradiativeprocessesdiscussedabovearethebasisofthefluorescencespectroscopyin instrumentalanalysis [6],greenfluorescentproteinasinvivomarkeringenetics [7],tumor markersinanticancertreatment [8],amongothers.
AnotherrelevantphenomenonistheChemiluminescence,whichisthelightemission causedbyachemicalreactionformingaexcitedstatefollowedbythedeactivationofthisexcitedstatetothegroundstate [9].Thebioluminescencephenomenaarethoseinwhichbiochemicalreactionsareinvolvedintheformationofthereferredexcitedstates,suchreactions arecommonlycatalyzedbyenzymes [10].Thereareseveralapplicationsofchemiluminescence,forinstance,theluminolreactioninforensicchemistry,theunderstandingofluciferase activityinfireflies,theuseofoxidationreactionsoftetraceneinlightbars,amongothers.
2.Theory
Asemiclassicalapproachisusefultostudythephotophysicalphenomenacausingchemicaltransformationsinasubstancebytheinteractionwithelectromagneticradiation.The mentionedapproachdealswiththesubstanceinquestionusingthequantummechanics, meanwhile,theelectromagneticradiationistreatedthroughtheclassicelectromagnetism theory.
Fromthewave-behaviorapproach,theelectromagneticradiationisdefinedasanelectromagneticoscillatingfieldwhichpropagatesasawave.Theclassicpicturestatesthat anelectromagneticradiationisproducedwhenacharge q experiencesacceleration,forinstance,analternatecurrentcircuitandtheco llisionofaprotonbeam.Theelectricandmagneticfieldsgeneratedbyanychargeandcurrentdistributionaredeterminedbythe Maxwellequations [4] ,
where F and B representtheelectricandmagneticvectors,respectively; E0 and μ0 arethepermittivity(E0¼ 8.85 * 10 12 C2N 1 m 2)andpermeability(μ0 ¼ 1.25 * 10 6 NS2C 2)vacuum constants,respectively.TheGausslawsforelectricandmagneticfieldsarepresentedin Eqs. (20.1)and(20.2).Eq. (20.1) showsthatanelectricfieldisproducedbyachargedistribution,meanwhile,Eq. (20.2) showsthatthenetmagneticfluxofaspaceenclosedbyasurfaceis zero.Theconsequenceofthislawisthattherearenotmagneticmonopoles,atvariancewhit electriccounterpartinwhichtheelectricmonopoleispossible.TheFaradayelectromagnetic inductionlawisplacedinEq. (20.3),whichstatesthatatemporaryvariationofamagnetic fieldgeneratesanelectricfield.Finally,Eq. (20.4) istheAmpereLaw,whichindicatesthat anelectriccurrentandthevariationofanelectricfieldgeneratesamagneticfield.ThesolutionsofthefourMaxwellequationsareelectromagneticwaves,inwhichtheenergyis transportedthroughthespace.Theelectricandmagneticfieldareperpendiculareachother andoscillateduringpropagationformingarightanglewiththepropagationdirection.
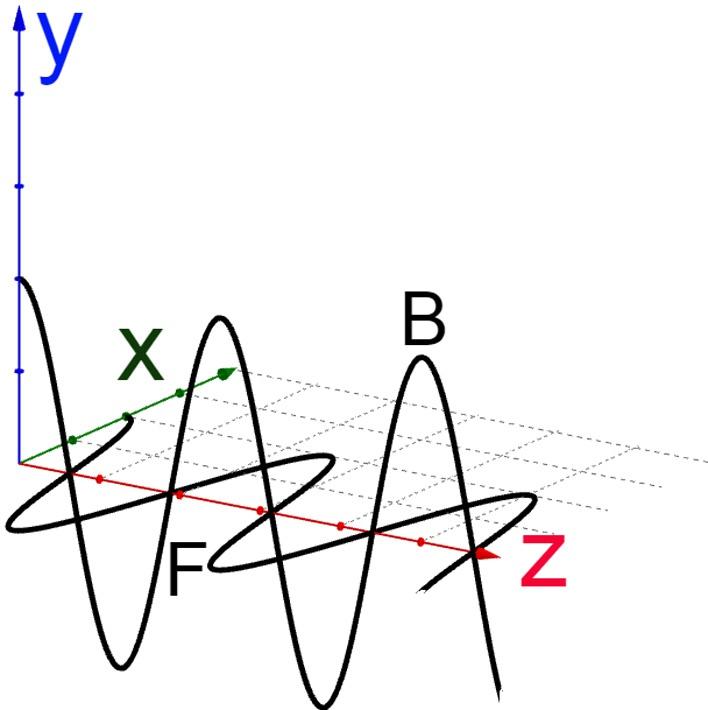
Electromagneticplanewaves(Fig.20.3)areofspecialinterestbecauseitssimplicity,they propagateinasingledirectionhavingaplanewavefront,thepointsofthewavepacket areinthesamephaseformingaplane.Inaddition,theelectricandmagneticfieldsoscillate eachoneinaplaneaswell,formingalinearpolarizedelectromagneticwave.
Theexpressionsfortheelectricandmagneticfieldofsuchawaveare
where F0x and B0y aretheamplitudesoftheelectricandmagneticfield,respectively,and w and k arethewavefrequencyandwavenumber,respectively.Anextrasimplificationcanbe made,thespatialcontributionoftheelectricfieldandtheentiremagneticcomponentcanbe neglected,
forthecaseofinteractionofelectromagneticwaveswithorganiccompounds.Suchapproximationisbasedon(a)thefactthatthemagnitudeoftheelectricfieldislargerthanthemagnitudeofthemagneticfield.Thecorrelationbetweenelectricandmagneticfieldmagnitudes isgivenby F(E) ¼ cB,wherecisthespeedoflight;and(b)thewavelengthsoftheelectromagneticradiationare3ordersofmagnitude,103 A ˚ ,largerthanthesizeofamolecularsystem. Nevertheless,suchapproximationisnotvalidformetallicsystems,inwhichtheelectric bands,andthereforetherespectivewavelengths,areclosetothesizeofthemetal.
Therearetwocorrelatedphenomenaexperiencedbyamoleculeduringtheinteraction withanelectromagneticwave:theverticalexcitation,andthechargedensitypolarization. QCTisausefultooltostudysuchphenomena.
Thequalityofthewavefunctiondescribingthegroundandexcitedstatesisrelatedtothe choiceoftheelectronicstructuremethodtosolvetheelectronicSchrodingerequation.There isalargevarietyofmethodstoaddresssuchissue.Asamatteroffact,themulticonfigurational(MC)methodsdisplaythebestagreementwithexperimentalmeasurements.
FEðÞ¼ iFx ¼ iF0x cos wt kz ðÞ,(20.5)
FEðÞ¼ iFx ¼ iF0x cos wt ðÞ,(20.7)
FIG.20.3 Planeelectromagneticwave.
Nevertheless,MCimplementationsscaling,andtheresultingcomputationalcostbecomes prohibitiveforthecharacterizationofsystemsofchemicalinterest,however,MCresults areusedasareference.Forlargesystemswithchemicalinterest,awaytoaffordthisproblem isusingtheTimeDependingDensityFunctionalTheory [11].
Twoissuesmustbestudiedduringaphotochemicalprocess:
1. Polarizationofthechargedensity.
2. Transitionprobabilitiesbetweenpossibleexcitedstates.
2.1Polarization
Theelectricfield, F,ofthephotonicincidentbeaminteractwiththesubstancechargedistributionandproducetheforces fi ¼ qiE [12],where q isthecharge.Theinducedpolarization duringtheelectricfieldinteractionisobservedin Fig.20.4A.Thepolarizationcanbedefined asthechangeinthechargedistributioninasubstanceduetotheinteractionwiththeelectromagneticradiation.Anymodificationinthechargeconfigurationbetweennucleiandthe electrondensityinamolecularsysteminducespolarization(Fig.20.4B).Therearetwotypes ofpolarizationthatcanbeobserved:linear(Fig.20.4),andnonlinear(Fig.20.5).Thelinear polarizationhappenswhenthepolarizationbehavesasalinearfunctionoftheelectricfield (Fig.20.4C).Besides,inducedpolarizationinmacroscopicscalecanbeexpressedas [12,13]:
,(20.8) where P istheinducedpolarization, F istheelectricfieldand χ (1) isthecoefficientoflinear susceptibility.
Linearpolarizationisobservedwhenamaterialinteractswithamoderateelectricfield, nevertheless,whentheintensityoftheelectricfieldisrelativelylarge,thepolarizationcould behaveinanonlinearlymanner.Observethenonlinearbehaviorininducedpolarizationasa functionoftime(Fig.20.5A),modificationsinthechargedistribution(Fig.20.5B)andinthe inducedpolarizationasafunctionoftheappliedelectricfield(Fig.20.5C),incomparisonwith thelinearcounterpart.
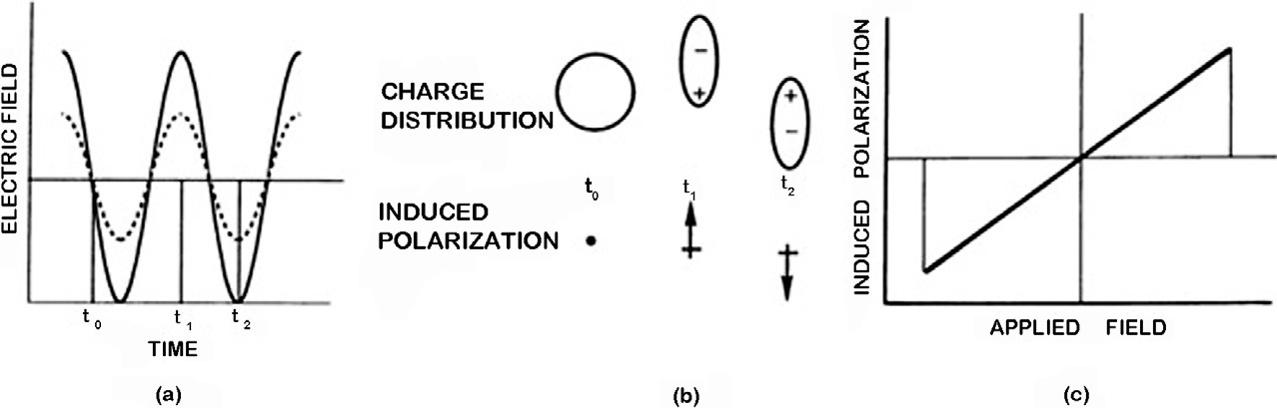
FIG.20.4 Linearpolarization,(A)lightbeamelectricfield(solidcurve)asafunctionoftime,inducedpolarization (solidcurve)asafunctionoftime,(B)polarizationofamaterialasafunctionoftime,(C)linearinducedpolarizationas afunctionoftheappliedelectricfield. ReprintedwithpermissionfromM.Pinnow,Materialsfornonlinearoptics:Chemical perspectives.ACSsymposiumseriesno.455.EditedbyS.R.Marder,J.E.SohnandG.D.Stucky.ISBN0-8412-1939-7.AmericanChemicalSociety,Washington,DC,1991.US $ 129.95.ActaPolym.44(1993)112–112. https://doi.org/10.1002/actp.1993. 010440216.Copyright2022AmericanChemicalSociety.
FIG.20.5 Nonlinearpolarization,(A)lightbeamelectricfield(solidcurve)asafunctionoftime,nonlinear-induced polarization(solidcurve)asafunctionoftime,(B)polarizationofamaterialwithnonlinearopticalactivityasafunctionoftime,(C)nonlinear-linearbehaviorofsecondorderinducedpolarizationasafunctionoftheappliedelectric field. ReprintedwithpermissionfromM.Pinnow,Materialsfornonlinearoptics:Chemicalperspectives.ACSsymposiumseries no.455.EditedbyS.R.Marder,J.E.SohnandG.D.Stucky.ISBN0-8412-1939-7.AmericanChemicalSociety,Washington, DC,1991.US $ 129.95.ActaPolym.44(1993)112–112. https://doi.org/10.1002/actp.1993.010440216.Copyright2022AmericanChemicalSociety.
Themathematicalexpressionofthemacroscopicnonlinearpolarizationisunknown.Nevertheless,thefollowingTaylorseriesexpansioncanbeusedbecausetheinducedpolarization isacontinuousfunctionoftheelectricfield [13],
where χ (1) , χ (2) and χ (3) arethesusceptibilitycoefficientsoffirst,secondandthirdorder,respectively. F istheelectricfield, P istheinducedpolarizationand P0 isthechargedistribution polarizationintheabsenceoftheelectricfield.Linearopticalproperties(refraction,reflection, andabsorption,amongothers)arerelatedtothemagnitudeof χ (1).Secondordernonlinear opticalproperties(secondharmonicgeneration,frequencymixing,amplification,electroopticeffect)arerelatedtothemagnitudeof χ (2).Third-ordernonlinearopticalproperties (thirdharmonicgeneration,frequencymixing,opticbio-stability)arerelatedtothemagnitudeof χ (3),andsoon.Someexamplesinwhichthenonlinearopticalpropertiesareapplied intechnologyfollow:lithiumniobatethirdorderpropertiesintelecommunications [14], processingofopticalsignaling [15],opticaldevices [16].Furthermore,inabiologicalsystem thephasechangesareproportionaltotheradiativeintensitychanges,gettingaclearcellimagingwithouttheuseofstainingsubstances [17],thisphenomenonisusedtovisualizethe heatwavesproducedbymaterials.
Fromthemicroscopicperspective,thequantumanalogtotheinducedpolarizationisthe induceddipolarmoment μ [12,13] givenbyaTaylorseriesexpansionas
,(20.10)
where μ istheinduceddipolarmoment, μ0 isthedipolarmomentinabsenceoftheelectric field F, α isdefinedasthepolarizability, β isthefirsthyperpolarizabilityand γ isthesecond hyperpolarizability.Comparingexpressionsofmacroscopicandmicroscopicframeworks, α, β and γ arethemicroscopicanalogstothefirst χ (1),second χ (2)andthird χ (3) ordersusceptibilitycoefficients,respectively.
TheapplicationoftheQuantumChemicalTopologytothecharacterizationofthelinear andnonlinearopticalpropertiesneedsadeepunderstandingofthemicroscopicpolarizabilitiesandhyperpolarizabilities.Theenergyoftheinteractionofachargedistribution ρ(r)with anelectricpotential Φ(r)canbecalculatedasfollows [18]:
Theelectricfield,definedas F ¼ ∂Φ ∂r ,isuniformatthemolecularframework,forthisreasontheenergycanbeexpressedbythemultipolarexpression
where q isthenetchargeormonopole, μ isthedipolarmomentand Q isthequadrupolemoment.Usingthelastequation,thedipolarmomentcanbeexpressedas
Intheabsenceofanexternalelectricfield,thedipolarandquadrupolemomentsarecalculatedfromthewavefunction |ψ i,
where r isthepositionvectorand r t isitstranspose.Moreover,thepresenceofanelectricfield conducestoaninduceddipolarmoment,whichisexpressedwithEq. (20.10).Besides,fora homogeneouselectricfieldthetotalenergyisexpressedasaTaylorseries,wherethederivativesareevaluatedin F ¼ 0.
thisexpressioncanbeusedtoevaluatetheinduceddipolarmomentas
ComparingwithEq. (20.10),thefollowingexpressionarededuced:
2.2Theoryoftransitionprobabilities
Theinteractionoftheelectricfieldofanelectromagneticradiationcanbestudiedasaperturbationofthetime-independentHamiltonian,suchperturbationisafunctionofthepositionandtime.Thisenablesustousethetime-independentSchr € odingerequationinthestudy ofthemater-radiationinteraction,atime-dependentphenomenon.Let
b H 0 ðÞ betheelectronic Hamiltonianofamoleculeand ψ n (0) thewavefunctionofthe nthstationarystateofsuchsystem,theresulteigenvaluesetofequationsare
where En(0) istheelectronicenergyofthe nthstate.ThezerosuperindexstablishestheequivalenceoftheelectronicHamiltonianwiththeunperturbedHamiltonianofthisapproach,for thisreason ψ n (0) isthewavefunctionofthe nthunperturbedsystemand En(0) theenergyofthe unperturbed nthstate.TheinclusionoftheperturbationgetstheHamiltonian
Ifthesysteminitiallyisinthestate ψ n (0)(r)and,overtheeffectofelectromagneticradiation representedbytheperturbation,evolvestoadifferentelectronicstate ψ m (0)(r)thetransition probability Pn!m(t)isarelevantquantitytocalculate,becausethemostprobabletransitions arethoseobservedinaspectroscopicexperiment.
Infirstplace,thesolutionofthetime-dependentSchrodingerequationforthisperturbed systemisneeded,usingawavefunction Ψ(r, t)theequationtosolveis
Expandingthewavefunction Ψ(r, t)asalinearcombinationoftheunperturbedsystems ψ n (0) ,
Andsolvingforaparticular m statewithasmallperturbationthetransitionprobabilityis
where b H 0 mn ¼ ψ 0 ðÞ m j b H 0 r, t ðÞjψ 0 ðÞ n DE and ωmn ¼
.Theperturbationconsideredintheinteractionofelectromagneticradiationwithmaterisjustthetemporalcontributionoftheelectric field,andtheinteractionofsuchelectricfieldisgivenby: V int ¼ μ F,(20.27) wherethe μ istheelectricdipolarmomentofthemolecule(μ ¼ P i qi ri )andFisthetemporal contributiontotheelectricfield(F ¼ Fox cos (wt)).Forthisreason,intheframeworkofthedipolarapproximation,theperturbativeHamiltonianiswrittenas
b H 0 t ðÞ¼ μx Fox cos wt ðÞ,(20.28)
where μx ¼ Pi qi xi .Substitutingthisexpressioninthetransitionprobability,weget
ItisofspecialinterestfortheQCTcommunitytocomputethefunctionalgroupcontributionsofsuchprobabilities.
3.QTAIM-photochemistry
3.1Polarizabilitiesandtransitionprobabilities
Baderandco-workers [19,20] addressthepartitionofthepolarizability,transitionprobabilitiesanddipolarmomentofdiatomicandpolyatomicmoleculesthroughtheQuantumtheoryofAtomsinMolecules.Suchworkisbasedontheperturbationtheoryapproach, demonstratingthatthepolarizability,transitionprobabilitiesanddipolarmomentcanbe expressedasafunctionofchargetransferenceandpolarizationcomponents.Inaddition, theshapeandvolumeoftheatomicbasinismodifiedfortheelectricfieldbecauseofthe chargetransference.Themainconclusionofthisworkisthatthetotalpolarizability,transitionprobabilitiesanddipolarmomentaredeterminedbytheatomicpolarizabilityandthe chargetransferencebetweentopologicalatoms.Furthermore,isdemonstratedthatafunctionalgroupcontributiontothetotalopticalpropertiesstudiedcanbedefined.Amoredetaileddescriptionofthiscontributionfollows.
Withinthedipoleapproximationandconsideringaweakfield,thetransition Pn!k probabilitybetween n and k statesisdefinedbyEq. (20.29),asimplerearrangementoftheequationis
wherethetime-independentcontributiontothetransitionprobabilityisthefirsttermofthe product, Pn!k.Followingwiththetime-independentterm,itcanbewrittenintheintegral form
where( eri)isthedipoleoperatorofthe ithelectronandthesumisoverallthe N electronsof thesystem.Duetothemultiplicativepropertiesofthedipolarmomentoperator,theprobabilitycanbewrittenas
wheretheintegrationisoverall N electroniccoordinates.Definingatransitiondensity
wheretheprimedintegrandmeansanintegrationoverallspinandspatialcoordinatesexcept forthespatialcoordinatesofelectron1.Theprobabilityiswrittenas
where Mnk isthetransitionmoment.
Consideringtheunperturbedandfirstperturbativecorrectiontothewavefunction, ψ n (0) and ψ n (1),respectively,theexpressionstothefirstandsecondenergycorrectionstoanatomic basin, Ω,energyare
where Hn(1)(r)and Hn(2)(r)arethefirst-andsecond-orderperturbationdensities,respectively. Thisperturbationmodifiestheinteratomicsurfaceofanatominamolecule,forthisreason itisimportanttoconsiderthisshiftinthesurface, δS,intheevaluationofthesecondorder energy.Whitthisregard,theenergycontributiontothesecondorderenergyduetothefirstorderchangedensityshouldbeevaluated,
Thefirst-orderchangeinthedensityisevaluatedby
Hence,thefirstpolarizability, αn(r),usingthedipolarapproximation,consideringtheperturbation b H 0 ¼ eF r,iswrittenintermsofthefirstorderchangeinthedensityas
Integrationofsuchpolarizabilityinanatomicbasingivestheatomicpolarizability α b n Ω ðÞ¼ ðΩ αn r ðÞdr,(20.41)
Thesumofallatomicfirstpolarizabilitiesisthemolecularpolarizability
n r ðÞ¼ X Ω α b n Ω ðÞ,(20.42)
Oneofthemainproblemsoftheatomicpolarizabilities, αn(r),istheorigindependencebecauseofthepositionvector r.Nevertheless,tosolvethisorigindependenceasubstitutionof r 5 rΩ +XΩ isusedtobuildthefollowingexpressionofthetotalfirstpolarizability α r ðÞ¼ X Ω e ð Ω drrΩ
wheretheatomicpolarizationisdefinedas
p Ω ðÞ¼ e ð Ω drrΩ ρ 1 ðÞ
Theintegrationofovertheatomicbasingives
wheretheatomicmoment Mnk(Ω)isobtainedwiththefollowingintegration:
Besides,itispossibletoregroupthenuclearcoordinatetermsintocontributionsproportionaltothechargetransferredfromanatomicbasing(Ω)toaneighboringatomicbasin(Ω0 ). Withthisregard,theatomicpolarizabilitygetstwocontributionsonethatcomesfromthe polarization, αp(Ω),andthesecondonebythechargetransferencebetweenneighboring atomicbasins, αc(Ω).
ThetransitionprobabilitydensitycanbeconstructedinanalogywithEqs. (20.38)and (20.44),
!k r ðÞ¼ Mnk Mkn r ðÞ¼ Mkn ∙ er ðÞρnk r ðÞ,(20.49)
where Mkn(r)isdeterminedbytherespectivetransitiondensity.Onceagain,thesubstitution of r 5 rΩ +XΩ andsubsequentintegrationgivestheexpression
where Mnk(Ω)istheatomictransitiondipole,and qnk Ω ðÞ¼ e Ð Ω dr ρnk r ðÞ istheinducedatomic
chargeproducedbychargedensitypolarization.Asinthecaseofthepolarization,itispossibletosolvetheorigin-dependentproblemreplacingthesumofnuclearcoordinatesbyaset oftermsdescribingthedipolarcontributiontothecharge, qnk(Ω),whichisinducedbythe polarizationbetweenaneighboringatomicbasin, Ω0
Atfirstorder,theelectronicpolarizabilityiswrittenintheform
Whichcanberearrangedas
Consideringasystemofasystemwithnuclearcharges Za andpositionvectors Xa thedipolemomentiswrittenas
ImposingtheQTAIMpartitioningthedipolarmomentiswrittenas
wherethe XΩ isthepositionvectorofthenuclearattractorofthetopologicalatom Ω, μc and μp arethechargetransferandpolarizationterms,respectively.Inaddition,theatomicchargeis definedas
andthefirstmoments M(Ω)arecalculatedwiththefollowingequation:
wheretheelectronicpositionvectorwithoriginatthenuclearattractorofthetopologicalatom Ω is rΩ 5r XΩ.Hence,thechangeinthedipolarmomentofsuchsystemiscalculatedby
wherethetopologicalexpressionof μ and 4μ areindependentofthechoiceoftheoriginfora neutralmolecule.WiththecorrespondingformusingtheQTAIMpartitioning
AsinthecaseofPolarizabilitiesandtransitionprobabilitiesitispossibletosolvetheorigin dependenceconsideringregroupingtermsinvolvingnuclearpositionvectors,asaresultthe dipolarmomentoriginindependentiscalculatedasthesumofatomicdipolarmomentcontributionsinthefollowingmanner:
4.QTAIMapplicationsinphotochemistry
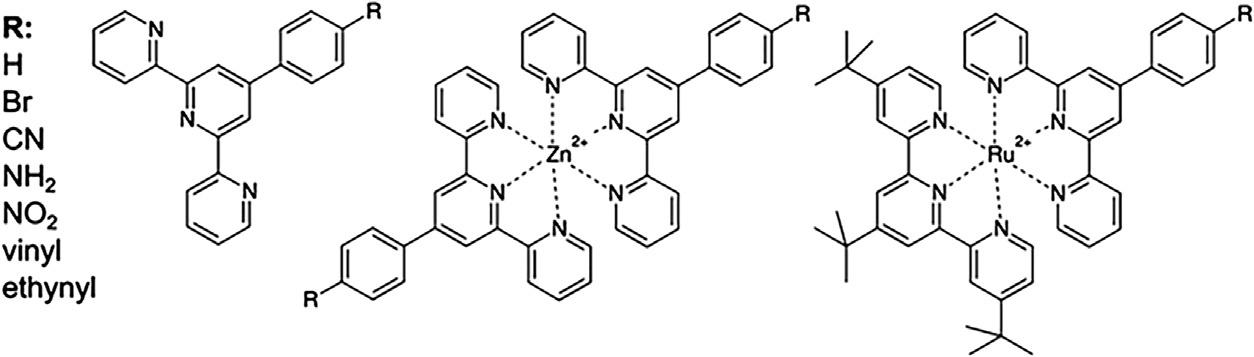
Arelevantcorrelationbetweentheellipticityandthephotophysicalpropertieswas reportedbyPresseltandco-workers [21],wheretherelationbetween π -conjugationandexcitationefficiencyisusedtostudyopticalefficiencyofPhenyl-TerpyridineRu(II)andZn(II) complexes(Fig.20.6).Presseltandco-workersanalyzedthecorrelationbetween π -conjugation,ellipticityandelectronictransitionenergiesofpyridyl-phenylligandsofsuchcomplexes,thelowesttransitionsarerelatedtoaMetal-to-ligandchargetransferdominatedby HOMO-LUMOexcitations.Thechangesintheellipticityareperformedchangingthesubstituent(R)atthe para positionofphenylgroup.TheconclusionwasthattheHOMO-LUMOenergygapdecreaseswithincreasingpyridyl-phenylellipticity,thereforeitispossibletogeta desirablephotophysicalpropertiestunningpyridyl-phenylellipticity.
In2012,J.N.Latosinskaandco-workers [22] analyzedthephotodegradationofnifedipine (NIF),anantihypertensivedrug,suchmoleculeishighlysensitivetotheelectromagneticradiationanddegradestonitrosoniphelipine(NO-NIF),whichisnotanantihypertensivemoleculebutanantioxidativeagent.Inacombinedexperimental-computationalstudy,
FIG.20.6 Schematicrepresentationoftheligands(tpy-ph-R,left),thehomolepticZn(II)complexes([Zn(tpy-phR)2]2+,middle),andtheheterolepticRu(II)complexes([(tert-butyl-tpy)Ru(tpy-ph-R)]2+,right)aswellasthevarious substituentsRinthe4-phposition. ReprintedwithpermissionfromM.Presselt,B.Dietzek,M.Schmitt,S.Rau,A. Winter,M.J € ager,etal.,Aconcepttotailorelectrondelocalization:applyingQTAIManalysistophenylterpyridinecompounds. J.Phys.Chem.A114(50)(2010)15163–74.Copyright2021AmericanChemicalSociety.
Latosinskaandco-workersdetectednifedipinephotodegradationproductsbymeansof 1H-14NNuclearQuadrupoleDoubleResonance(NQDR).Besides,aDFT/QTAIMstudy wasperformedtovalidatethecomputationalcapabilitytopredictsuchphotodegradation products.ThecomputationalreactivitycriterionwasbasedonthetopologicalQTAIM ChargesandtheLaplacianoftheelectrondensityatthebondcriticalpointr2 ρ(r)bcp,and theelectrondensityatthebondcriticalpoint ρ(r)bcp.Arelevantobservationisthat r2 ρ(r)bcp, ρ(r)bcp displaythelargestvaluesatthebondsthatbreakbecauseofirradiation.Hence, r2 ρ(r)bcp, ρ(r)bcp areproperdescriptorsofthebondsusceptibilitytobebrokenbyirradiation.
Inarecentpublication,Chavez-CalvilloandHerna ´ ndez-TrujillostudiedthetemporalevolutionoftheelectrondensitytopologicalpropertiesintheQTAIMframework [23].Themolecularweavefunctionisrepresentedasacombinationofelectronicstates,inagreementwith thesuperpositionofsatesprinciple,
where χ i(X, t)isthetime-dependentnuclearwavepacket,and χ i(X, t)isthe ithelectronicstate. Ψ(X, x, t)iscalculatedthroughthesolutionofthetime-dependentSchrodingerequation,at thesametimethesetofadiabaticstates{ψ i a}isobtainedtogetherwiththeirrespectiveeigenvalues,{Eia},andnuclearwavepackets{Xia}.ThetimeevolutionoftheaverageofsomepropertiesoftheelectrondensityischaracterizedbymeansoftheQTAIMpartitioning.Thetime evolutionoftheelectrondensityitselfcanbeexpressedas
where ρX ij (r)isthetransitiondensitybetween ithand jthstates.Inthesameway,thetimeevolutionoftheatomicchargeiscalculatedwiththeexpression
Thereactivescatteringof H3 + andthephotodissociationofLiFisstudiedbasedonthetime evolutionoftheatomiccharges.Animportantconclusionisthatthetimeevolutionofthe atomicchargesisconsistentwiththeadiabaticanddiabaticnatureofthestudiedprocesses.
5.Alternativetopologicalapproaches
AmoleculargraphMGisdefinedasthesetofcriticalpointsandfluxlinesconnectingthese criticalpoints [24],amongsuchsetisthebondpathwhichistheconjunctionofbondcritical points(BCP)andfluxlinesconnectingsuchBCPwithnonboringnuclei.Thecharacterization oftheevolutionofthemoleculargraphalongachemicaltransformationisacommonlyused tooltogetinsightofachemicalreaction.Besides,thequantityandtypeofcriticalpointsand
pathslinkingsuchcriticalpointsserveasaqualitativecharacterizationoftheconnectivityina molecule.Changesinmoleculargraphsalongachemicalreactiondisplayqualitativeinformationaboutbreakingandformingchemicalinteractions.Inaddition,inQTAIMitispossibletoquantitativelymeasurethebond-pathcurvature(BPC)separatingtwobondednuclei usingtheratio
whereBPListhebondpathlengthandGBListhegeometricbondlengthdefinedasthe internuclearseparation.Nevertheless,moleculargraphsandBPCdidnotshowsignificant changesduringelectronicstateexcitations,MGandBPCarequalitativelythesameinthe groundandexcitedstatesataparticularmolecularconfiguration.Forthisreason,molecular graphscannotbeusedtotracktheevolutionofamoleculethatexperiencesphotochemical transformations,asimilarsituationhappensforsomechemicaldescriptorsofQTAIM.For instance,theLaplacianoftheelectrondensityatthebondcriticalpoint(r2 ρ(r)bcp)getanaverageofthetotalcurvatureoftheelectrondensity,collapsinginascalartheinformationofthe chargeaccumulationofeachspatialdirection.So,2-D(MG)and1-D(r2 ρ(r)bcp)topological descriptorsareunsuccessinthestudyofphotochemicaltransformations,therearesomeapproachestosolvethisproblem:theNewGenerationQTAIMandthestresstensorapproaches. TheNewGenerationQTAIMmethods(NG-QTAIM)ispresentedasare-interpretationof topologicalaspectsofthechemicalbonding,a“bond-pathframeworkset” (B) isdefinedand itcanbeusedtodifferentiatethetopologyoftheelectrondensityofexcitedstatesfromthe groundstate.Suchsetisbuiltbythreelinkages p, q and r,whicharerelatedtotheeigenvalues ofthehessianmatrixe1,e2 ande3,respectively.Thepath r istheorthodoxQTAIMbondpath wheree3 istheeigenvectorwiththepositiveeigenvalue,thedirectionofdepletionofcharge density.Furthermore, e1, e2 arethesecondandfirstpreferreddirectionsinwhichthechargeis accumulated,respectively.The p and q pathsareconstructedasthecollectionoftippath pointsdefinedbytheexpressions
where ri isthe ithpointatthe r path, εi istheellipticityevaluatedin ri, e1, i and e2, i arethe eigenvectorsoftheaccumulativechargedensityat ri.Sucheigenvectorsareweightedby theellipticity εi,thispermittotrackthechangesinthechargeaccumulationpatternnotonly attheBCP,butinallthebondpath.Thereisnosensetodefinethepath r intermsoftheellipticitybecausetheeigenvector e3 isindependentoftheeigenvaluesdefiningtheellipticity. ThisapproachisanalternativetothecharacterizationoftheLaplacianoftheelectrondensity, inwhichtheinformationofeachcurvaturecollapsesatthemomentoftheevaluationofthe traceofthehessianmatrixattheBCPoratanypointalongthebondpath.Animportantobservationisthat p, q and r pathsareorthogonaleachotherbecauseareconstructedusingorthogonaleigenvectors e1,i, e2,i and e3,i.The p and q areusedtodefinethepathlengths
Thepathlengthsarerelatedtothebehaviorofthechargeaccumulationalongthebond path.Inthelimitofzeroellipticity, H pathlengthisequaltothebondpathlengthof r. Thesimplicityofthisapproachisusefultocharacterizebondinginexcitedstatesofphotochemicalprocesses.
Anusefulquantitytocharacterizethecovalencyofachemicalbondisthelocalenergydensitydefinedas [24]:
where G(rb)and V(rb)arethelocalkineticandpotentialenergydensitiesatthebondcritical point,respectively. H(rb) < 0ofclosedshellinteractions(r2 ρ(rb) > 0)showacovalentinteraction,forthesameclosedshellinteraction H(rb) > 0meansalackofcovalentcharacter.Astrong sharedshellinteractiondisplays r2 ρ(rb) < 0and H(rb) < 0,forexample,suchsituationcorrespondstoC CandC Hbonds.
5.1Stresstensor
Stresstensorconnects,throughVirialtheorem,thequantuminformationandtheclassicalpictureofmechanicalforcesequilibriainamolecularsystem.Suchforcesarethe Ehrenfestforcesexperiencedbyasystem,this approachgivesajustificationofthesmall frequenciesofthenormalmodesrelatedtointramolecularrearrangements [24] .Thecharacterizationoftheeigenvectorsofthestresstensorisausefultooltocharacterizethe changesintheelectrondistributionduringphotochemicalprocesses,suchchangesare notobservedintraditionalQTAIMapproaches(moleculargraph,Laplacianofelectron densityatthebondcriticalpoint,etc.).In theQTAIMframework,thestresstensorisdefinedas
,(20.70)
where γ (r, r0 )isthefirstorderdensitymatrix.Theprincipalelectronicstresses, Πxx, Πyy and Πzz,areobtainedbythediagonalizationof σ (r),whichareequivalenttothestresstensoreigenvalues λ1σ , λ2σ and λ3σ relatedtothecorrespondingeigenvectors e1σ , e2σ and e3σ .Anegative stresstensoreigenvalue λ1σ meansacompressioninthedirectionofthe e1σ eigenvector.Besides,thestresstensoreigenvectortrajectories Tσ (s)areconstructedasthesetofshifts dr(s) withstep s ataBCP [25].Theorderedsetofshiftsintheeigenvectorprojectionspace Uσ are directionvectorsdefinedby dr0 (s) ¼ {dr e1σ , dr e2σ , dr e3σ },relatedtothedirectionvectorsin therealspace dr(s) ¼ {dr e1, dr e2, dr e3}whicharerelatedtothefollowoftheIntrinsicReactionCoordinate(IRC)fromthetransitionstatetotherelatedminima.Therespectivetrajectory lengthinthestresstensorprojectionspace Uσ isdefinedas
σ ¼ X s¼0 dr0 s +1 ðÞ dr0 s ðÞ jj,(20.71)
HrbðÞ¼ GrbðÞ + VrbðÞ,(20.69)