





Dalle risorse online puoi scaricare la guida in formato PDF, per avere indicazioni generali sul Metodo Analogico e suggerimenti disciplina per disciplina.
Sfoglia il volume in versione digitale, in classe sulla LIM oa casa, e accedi direttamente alle risorse integrative.

Video di approfondimento
Inquadrando i QR code, o direttamente dal libro digitale, puoi accedere a risorse video che supportano la pratica didattica.
Inglese
Cliccando sull’icona all’interno del libro digitale puoi imparare, ascoltando e riascoltando, un agile repertorio di parole e frasi in inglese
Come accedere alle risorse digitali
– Collegati a risorseonline.erickson.it/mab – Se è la prima volta che accedi, seleziona Registrati; se invece hai già un account, clicca su Accedi ed effettua il login. – Una volta effettuato l’accesso, inserisci il codice di attivazione. Se sei già registrato, clicca su Riscatta un altro codice.





Calcolo mentale p. 4
Euro, decimali, frazioni p. 16
Problemi p. 28
Misure ed equivalenze p. 44
Problemi con le frazioni p. 62
Problemi proporzionali intuitivi p. 64
Calcolo in colonna p. 72
Geometria intuitiva p. 92
Tabelline p. 106
I bambini a casa risolvono problemi complicatissimi con una matematica senza parole e senza simboli. Il segreto, andando a scuola, è di non cancellare quel mondo di immagini e concretezza che si nasconde dietro il linguaggio freddo della disciplina.






Nel calcolo mentale non bisogna pensare ai numeri, ma a queste finestre disposte cinque a cinque… e il gioco è fatto!





Risultati: 501 600 750 760 510 601 800 910
Risultati: 901 700 710 760 781 920 861 711
4
Risultati: 312 620 850 800 300 610 311 301






100 + 100 + 100 + 100 + 100 +
500 + 100 + 100 + 100 + 100 + 100 =
500 + 300 + 200 + 100 + 100 + 100 =
Risultati:


500 + 500 + 500 =
500 + 500 + 200 =
500 + 500 + 800 =



+
=
=



















5000 – 1000 =
5000 – 1200 =
5000 – 2300 =
Risultati: 2700 4000 3800 999 400 1999
5000 – 3001 =
5000 – 4001 =
5000 – 4600 =
1000 + 1000 + 1000 + 1000 + 100 + 100 = 10 + 10 + 10 + 100 + 100 + 100 + 1000 = 2000 + 1000 + 100 + 100 + 100 + 100 =
3 + 50 + 100 + 100 + 1000 + 1000 + 1000 =
2 + 2 + 10 + 10 + 10 + 100 + 100 + 2000 =
Risultati: 3400 3253 4200 1330 2234
250 + 250 + 250 + 250 =
250 + 100 + 100 + 10 =
300 + 80 + 20 + 1000 =
600 + 600 + 100 + 100 =
400 + 600 + 400 + 600 =
– 80 =
– 90 =
– 201 =
– 1000 =
– 1100 =












10 000 – 5000 = 10 000 – 5500 = 10 000 – 6500 =




10 000 – 9 000 = 10 000 – 9 500 = 10 000 – 10 000 = 10 000 – 2 500 = 10 000 – 7 500 = 10 000 – 8 500 =
=
=

Sono divisioni che non hanno bisogno del calcolo in colonna, ma di strategie intuitive, come fare «metà della metà». es.








Sono moltiplicazioni intuitive che non hanno bisogno del calcolo in colonna, come, ad esempio «il doppio del doppio».

Consentire l’uso della calcolatrice. A volte è più veloce il calcolo mentale. L’importante è scoprire simmetrie tra gruppi e scrivere i risultati parziali.



Quanto denaro c’è nella cassaforte?
Sperimenta il percorso di calcolo più veloce.





Bisogna studiare a lungo come fare.


Avvisare che è un lavoro di strategia lungo e complesso, studiando le configurazioni in verticale o orizzontale.

Presentare queste due pagine come una sfida lasciando i bambini liberi di usare le strategie e gli strumenti che desiderano.



Denaro disponibile

Acquisti





3 avvitatori
3 annaffiatoi
3 barattoli di vernice
3 pennelli
vasi
colla
Quanto denaro gli rimane?
























Guardando le strisce puoi comprendere da solo la corrispondenza tra euro, numeri decimali e frazioni decimali.




Decimali
1 Scrivi il valore in numero decimale e in frazione













Evitare spiegazioni non richieste e lasciare spazio alle intuizioni dei bambini. Decimali e frazioni sono linguaggi.




2 Colora e completa € Frazione Colora l’immagine



















































































1 Colora
(Se ti aiuta, aggiungi uno zero ai centesimi)
Colora 1,2
Colora 1,02
Colora 2,5
Colora 2,05

2 Esegui le sottrazioni
(Se ti aiuta, aggiungi uno zero ai centesimi)
1,00 – 0,01 = 1,00 – 0,1 = 1,00 – 0,03 = 1,00 – 0,3 = 1,00 – 0,4 =
Colora 2,90

Nel terzo esercizio suggerire di osservare i disegni del primo esercizio.




Colora la frazione
Scrivi la frazione
Disegna la frazione







Focalizzare l’attenzione sulle immagini comparate facendo esercizi di confronto a voce.





Guardando le immagini confronta tra loro le varie frazioni.

e completa
mezzi terzi quarti
sesti
ottavi noni
Confronta le frazioni guardando la tabella sopra. In ogni bilancia cerchia la frazione maggiore
Colora in verde
Colora in rosa
Colora in verde
Colora in rosa
Colora in verde
Colora in rosa




Cerchia le bilance quando le frazioni hanno lo stesso valore, cioè sono equivalenti (sono 7 in tutto)



Completa le bilance, come nell’esempio
Ricopia sul tuo quaderno lo schema dell’esercizio 1 con le seguenti misure per ognuna delle 6 strisce





Cerchia in blu le frazioni che valgono metà intero

Cerchia in rosso le frazioni che valgono un intero
Cerchia in giallo le frazioni che valgono meno di metà intero
Cerchia in viola le frazioni che valgono più di metà intero




Colora
un mezzo
metà intero
un quarto
uno ogni quattro due ogni quattro

tre ogni quattro

Spiegare che bisogna risalire al valore di una parte dividendo per il denominatore.





Per calcolare la quantità di una frazione servono due operazioni come nell’esempio.
numeratore denominatore di 80 di

Prima dividi, poi moltiplichi.
80 : 4 = 20
20 × 3 = 60

valore di 1 4
valore di 3 4





Le frazioni complementari sono quelle che insieme formano un intero. Si completano.

Scrivi la frazione complementare in ogni puzzle

Le tesserine del puzzle sono un’immagine gancio familiare per spiegare il termine complementare.

L’uso della calcolatrice permette di concentrarsi sulla scelta delle operazioni, liberando i bambini dall’ansia esecutiva del calcolo.






ADDIZIONE
Significa aggiungere
Ora si tratta di saper scegliere le operazioni da fare. Il loro significato è semplice: pensa alla colla e alle forbici.

SOTTRAZIONE
Significa tagliare






MOLTIPLICAZIONE
Significa aggiungere tante volte (replicazione)


Significa tagliare tante volte (replicazione)
Quante palline in tutto ?





palline in tutto ?
palline in tutto ?








Tutte le palline devono essere suddivise nelle tre casse.


Tutte le palline devono essere suddivise nelle due casse.




Tutte le palline devono essere suddivise nelle quattro casse. 5 6 7 La calcolatrice consente di concentrarsi nella scelta delle operazioni.

Quante palline in ciascuna cassa?
Quante palline in ciascuna cassa?
Quante palline in ciascuna cassa?





Lasciare libertà di organizzare il calcolo. Poi è possibile condividere le scelte.
Qual è la differenza di quantità?
Quante sono le palline in tutto ?
Quante sono in totale le palline?





Segnalare l’importanza delle parole in grassetto.
Paolo prende 20 palline e Giovanna 32.
Francesca e Lisa prendono 23 palline per ciascuna .
Quante palline restano ?
Quante palline rimangono ? 11 12 13
Quante palline restano ?
Gianna e Lucia prendono 40 palline a testa .






Qual è il prezzo totale?
Far scrivere in riga le operazioni perché conta il procedimento.



Qual è il prezzo totale?



Qual è il prezzo totale?



Qual è il prezzo totale?




una risoluzione veloce anche senza calcolatrice.




Qual è il prezzo totale?




Qual è il prezzo totale?




Qual è il prezzo totale?




Qual è il prezzo totale?









Far osservare nel problema 24 che la calcolatrice opera in modo diverso dal calcolo in
Quanto costa ciascun borsellino?



Quanto costa lo zaino?


Quanto costano i calzini?






Quanto costa una palla?





Nella
26



Quanto costa il monitor?
Quanto costa la stampante?



Quanto costano tre tablet?










Quanto costano due proiettori?












Quanto costano quattro libri?
Quanto costano due vocabolari?















Quanto costano due mazzi di carte?
Quanto costa un temperamatite?





Quanto costano tre detersivi?




Quanto costa il burro?




Quanto costa una confezione di succo?




Quanto costa mezza torta?




































Quanto avrò di resto ?



Pago con 10 euro.






Compro tutto ma ho solo 10 euro.






Compro tutto e pago con 20 euro.





Compro tutto ma ho solo 5 euro.
Quanto avrò di debito ?
Quanto avrò di resto ?
Quanto avrò di debito ?





Ogni bicchiere costa 5 euro.
Tutti i bicchieri sono 36.



Ogni tazzina costa 3,50 euro.



Ogni bicchiere costa 6 euro.
Tutti i bicchieri sono 45.



Ogni tazza costa 5 euro.
Tutte le tazze sono 18.

Quanto costa una scatola?
Quanto costano tutte le tazzine?
Quanto costa una scatola?
Quanto costano due scatole?






PREZZO TOTALE (moltiplicazione)
Quantità (divisione) Prezzo unitario (divisione)

€ 25
Una penna costa 0,50 euro. Quante penne contiene la scatola?

€ 16,80
Ciascun pennarello costa 0,80 euro.
Quanti pennarelli sono contenuti nella scatola?

Un pacco di quaderni costa 32 euro.
Ciascuno costa 0,80 euro.
Quanti sono i quaderni ?
Cerca tra i seguenti i risultati


Questo schema, simile alle etichette dei prodotti, consente di organizzare i dati in modo utile per la risoluzione.
Completa l’etichetta
prezzo totale
quantità prezzo unitario
Operazione
prezzo totale
quantità prezzo unitario
Operazione
prezzo totale
quantità prezzo unitario
Operazione






Un pacco di merendine costa 6 euro.
Ciascuna costa 0,50 euro.
Quante ne contiene un pacco?

Ciascun pacchettino di biscotti costa 0,80 euro.
Quanti ne contiene la scatola?
cubetti
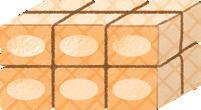
Ciascun cubetto di lievito costa 0,60
euro. Quanto costa la scatola intera?

Una scatola di yogurt costa 3,60 euro.
Ciascun vasetto costa 0,60 euro.
Quanti ne contiene la scatola?
prezzo totale
quantità prezzo unitario
Operazione
prezzo totale
quantità prezzo unitario
Operazione
prezzo totale
quantità prezzo unitario
Operazione
prezzo totale
quantità prezzo unitario
Operazione


Approfondire l’utilità di tutti gli strumenti, usandoli possibilmente in classe.




Per misurare ciò che ci circonda servono strumenti
sempre più evoluti.

metro snodabile

metro a nastro calibro


metro laser

metro da sartoria
Scrivi le misure
Lunghezza
Misura con il metro
Larghezza porta:
Altezza tavolo:
Altezza lavatrice:
Lunghezza quadro:



tanica

botte

caraffa graduata

bilancia elettronica

bilancia pesapersone

bilancia a molla

bilancia a mano

bilancia da orafo
Capacità
Cerca sulle confezioni
Olio:
Bibita:
Sciroppo:
Aceto: Peso
Cerco sulle confezioni
Zucchero:
Farina:
Pasta:
Caffè:




Leggi e memorizza tutti i nomi delle marche.








Presentare insieme. Osservare questa panoramica sia per le immagini sia per la costruzione dei termini.

Non si usa il chilolitro














La corona indica le unità di misura che servono per comporre le altre.






8 m 0,8 dam
Come usare le tabelle
1. Ritaglia una mascherina trasparente disegnando sopra una virgola, da trascinare sulle strisce durante le equivalenze.
2. Scrivi la misura nella casella giusta con la matita, così puoi cancellare e usare la tabella tutte le volte che vuoi.

Si chiamano equivalenze perché anche se cambia la marca il valore rimane lo stesso.

3. Osserva che trascinando la mascherina si trascina anche la virgola.
, 4 cm 2 cm

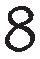
, ,




Scrivi quanto pesano e misurano, prima a stima e poi con gli strumenti.
Peso







Usando il metro laser o il metro a nastro con l’insegnante misura le pareti dell’aula .
Altezza Larghezza Lunghezza








Utilizzando la mascherina mobile con la virgola il risultato è immediato.




k h da u d c m
k h da u d c m k h da u d c m
5 = da 1 2 0 = h
k h da u d c m k h da u d c m
5 = k 1 2 0 = u
k h da u d c m k h da u d c m
5 = d 1 2 0 = d
k h da u d c m k h da u d c m 1 5 = c 2 8 = k
k h da u d c m k h da u d c m
1 5 = h 2 8 = h
k h da u d c m k h da u d c m
6 = m 8 0 0 = k
k h da u d c m k h da u d c m
6 = d 8 0 0 = da
k h da u d c m k h da u d c m
6 = c 8 0 0 = d
k h da u d c m k h da u d c m
1 2 5 = h 3 = u
k h da u d c m k h da u d c m
1 2 5 = k 3 = d






Qui mancano le marche e bisogna visualizzarle mentalmente oppure, se serve, farle riscrivere.
u c 1 2 = d 1 6 0 0 = u
u 2 4 0 = h 6 0 0 = k u d 1 2 0 0 = h 1 2 5 = da u u 3 0 = h 1 3 0 0 = h 3 2 0 u = h 3 4, 2 5 u = d
3 2 0 u = k 3 4, 2 5 u = da 3 2 0 u = da 3 4, 2 5 u = c
3 2 0 u = d 3 4, 2 5 u = h
2 0 u = c
4, 2 5 u = k

Spiegare che cambia il nome ma non la quantità.




hm dam m dm cm mm
km hm dam m dm cm mm
km hm dam m dm cm mm
hm dam m dm cm mm
hm dam m dm cm mm
4 = cm 4 = dam
km hm dam m dm cm mm km hm dam m dm cm mm
km hm dam m dm cm mm
hm dam m dm cm mm
0 = cm
hm dam m dm cm mm
0 = m km hm dam m dm cm mm
km hm dam m dm cm mm







Video dimostrativo sull’uso dello strumento per le equivalenze.
km hm dam m dm cm mm
km hm dam m dm cm mm
hm dam m dm cm mm 5 0 0 = dam
5 6 = m
km hm dam m dm cm mm km hm dam m dm cm mm 2





kg hg dag g dg cg mg
kg hg dag g dg cg mg
2 0 0 = dg 1 2 0 0 = dg
kg hg dag g dg cg mg
kg hg dag g dg cg mg
2 0 0 = dag 1 2 0 0 = hg
kg hg dag g dg cg mg
kg hg dag g dg cg mg 2 0 0 = mg 7 0 0 = g
kg hg dag g dg cg mg
kg hg dag g dg cg mg 2 0 0 = hg 2 5 = kg
kg hg dag g dg cg mg
kg hg dag g dg cg mg 4 5 6 = g 2 5 9 = dag g g 5 5 = dag 3 0 0 = dg g g 5 5 = dg 3 0 0 = cg g dg 1 2 5 5 = dag 3 0 8 = dag hg g 3 5 6 = kg 2 0 0 0 = hg




hl dal l dl cl ml

hl dal l dl cl ml
hl dal l dl cl ml
1 0 = dl 1 0 5 = l
hl dal l dl cl ml
hl dal l dl cl ml
1 0 = hl 1 0 5 = dal
hl dal l dl cl ml hl dal l dl cl ml
1 0 = cl 2 5 0 = dl
hl dal l dl cl ml hl dal l dl cl ml 1 0 2 = l
hl 8 = ml 7 = l
l











Quanti km di altezza?
Quanti cm di altezza?
Quanti m in totale?
Quanti m in totale?





La stoffa costa 6 €/m.
Quanto costano 12 metri?

Questa stoffa è lunga 4 metri.
È costata 48 euro.
Quanto costa al metro?

Queste bandierine sono lunghe 10 m.
Sono costate 2,50 €/m.
Qual è il prezzo totale?
Il filo elettrico è costato 36 euro.
Il prezzo al metro è 2 euro.
Quanto è lungo?

prezzo totale
quantità prezzo unitario
Operazione
prezzo totale
quantità prezzo unitario
Operazione
prezzo totale
quantità prezzo unitario
Operazione
prezzo totale
quantità prezzo unitario
Operazione





Quanti hg di peso?




Quanti kg ?
Quanti kg in totale?


Quanti kg in totale?






Quanto costa un hg?

Un kg costa 40 euro.
Cerca tra i seguenti i risultati corretti: 16 12 4 8 20
Quanto costano tre hg?
Quanto costa mezzo kg?
Un hg costa 3 euro.
Cerca tra i seguenti i risultati corretti: 1,50 30 20 15 3
Quanto costa mezzo kg?
Quanto costa un kg?
Quanto costa mezzo etto?
Un hg costa 5 euro.
Cerca tra i seguenti i risultati corretti: 25 65 75 30 50
Quanto costa un kg?
Quanto costa un kg e mezzo?
Quanto costa un kg e tre hg?
Mezzo kg
costa 20 euro.
Cerca tra i seguenti i risultati
Quanto costa un hg?
Quanto costa un kg?
Quanto costano due kg?





I commercianti usano queste parole per intendersi meglio sul peso.
Quanto pesa la cassa vuota (tara)?














Quanto pesano le mele (peso netto)?
Quanto pesa la cassa piena (peso lordo)?

















Quanto pesa la tara?
Qual è il peso netto?
Qual è il peso lordo?
Qual è il peso lordo?

Qual è il peso netto?
Quanto pesa la tara?


Qual è il peso lordo?
Quanto pesa la tara?
Qual è il peso netto?





es.
Una cassa di pere
diventa peso lordo
La cassa delle pere
diventa
Le pere contenute nella cassa
diventano

Un vasetto di marmellata =
Il vasetto della marmellata =
La marmellata nel vasetto

Una latta di olio =


L’olio nella latta =
La latta dell’olio =
Il cesto delle pere =
Le pere nel cesto =
Un cesto di pere =

Avvertire che si tratta di esercizi per familiarizzare con un linguaggio specifico.





25 1000 ml 5 l
Quanti l?
Quanti dl?
Quanti dal?
Cerca tra i seguenti i risultati corretti: 1 10 0,1 100

Cerca tra i seguenti i risultati corretti: 0,05 500 50 0,5




Cerca tra i seguenti i risultati corretti: 0,6 3 6 60




Cerca tra i seguenti i risultati corretti: 10 100 1 0,1
Quanti dal?
Quanti hl?
Quanti dl?
Quanti l?
Quanti dal?
Quanti dl?
Quanti l?
Quanti hl?
Quanti dal?





Il costo totale è 12 euro.
Quanto costa il detersivo al litro ?

Il vino contenuto nella botte costa 2 €/l.
Qual è il costo totale ?

Il costo totale è 48 euro.
Il prezzo dell’olio è 6 €/l.
Quanti litri contiene il recipiente?


Il prezzo al litro è 5 euro.
Qual è il prezzo complessivo ?
prezzo totale
quantità prezzo unitario
Operazione
prezzo totale
quantità prezzo unitario
Operazione
prezzo totale
quantità prezzo unitario
Operazione
prezzo totale
quantità prezzo unitario
Operazione


Far scrivere il risultato finale in rosso.




Pago solo 2 3 del prezzo.
€ 24 € 860

Pago solo 4 5 del prezzo.

Pago solo 3 5 del prezzo.
€ 640 € 1280

Pago solo 3 5 del prezzo.
Colora. 1 a operazione
2 a operazione 24 : 3 = 8 8 × 2 = 16

Colora.
1 a operazione
2 a operazione
Colora. 1 a operazione 2 a operazione
Colora. 1 a operazione 2 a operazione




Far osservare che scoprire l’unità frazionaria, cioè un quadratino, è fondamentale.

Maria ha pagato 2 3 .

Marco ha pagato 3 4 .
Colora.
12
1 a operazione
2 a operazione
Colora.
1 a operazione
2 a operazione

Lucia ha pagato 3 5 .

Luca ha pagato 3 5 .
Colora.
1 a operazione
2 a operazione
Colora.
1 a operazione
2 a operazione





Con queste tabelle si potenzia un approccio intuitivo alla risoluzione proporzionale dei problemi.
INTUITIVI
Completando queste tabelle dei prezzi puoi fare molte scoperte. La prima riga è il prezzo unitario .

















Invitare i bambini a confrontare i dati a destra o sinistra per risolvere intuitivamente i problemi.



























Presentare questa risoluzione come un gioco senza dare spiegazioni di significato delle operazioni.





Incrociando i dati non serve calcolare il prezzo unitario.

È un modo più veloce per risolvere questi problemi, che assomiglia a un gioco.




9,80 × 2 = 19,60 19,60 : 2,80 = 7

Risultati: 3 9 10,50 4
*










Si tratta di una procedura che anticipa le risoluzioni proporzionali della secondaria.



Lo schema aiuta a decodificare i dati e prepara alla risoluzione, che può avvenire tramite incrocio o risalendo al prezzo unitario.





Inserisci i dati e risolvi come piace a te.

Otto libri costano 120 euro.
Con 330 euro quanti ne compro?
2 4 3 5
libri €
In 30 giorni l’auto percorre 1500 chilometri.
Quanti giorni servono per fare 100.000 chilometri?
giorni km

Tre vasetti di marmellata costano 12,00 euro.
Quanto costano 10 vasetti?
Inserisci i dati
vasetti €
In sei giorni Laura percorre 120 chilometri.
Quanti chilometri percorre in 30 giorni?
giorni km
L’autobus in 7 giorni ha percorso 210 chilometri.
Quanti giorni impiega per fare 630 chilometri?
giorni km




Tre chilogrammi di arance
costano 4,50 euro.
Anna ha speso 18 euro
Quanti chilogrammi ha comprato?
kg €
stanze kg 8 6 10 9 7 11
Cinque metri di stoffa
costano 45,00 euro.
Irene ne acquista 7.
Quanto spende? m €

2,5 litri di olio costano 20,00 euro.
Quanto costano 6 litri dello stesso olio?
l €
Per imbiancare 3 stanze
sono serviti 5,4 chilogrammi di tempera.
Quanti chilogrammi per 4 stanze?
Con 12,00 euro compero 4 litri di vino.
Se spendo 120,00 euro quanti litri compro?
l €
Per fare 10 vestiti servono 45 metri di stoffa.
Quanti metri servono per farne 25? vestiti m

Queste operazioni sono presentate alla fine ma possono essere anche anticipate dato che il loro impegno è solo procedurale.







Concentrati sulle regole dell’algoritmo, cioè l’incolonnamento e il riporto.
1 2
Addizioni senza riporto
Risultati: 127 439 427 429 289
Addizioni con un riporto
Risultati: 927 384 978 729 375
3
Addizioni con due o tre riporti
Risultati:





4 Addizioni con vari riporti
6 Addizioni con vari riporti
Addizioni da incolonnare e risolvere nel quaderno










Ci sono due modi per eseguire la sottrazione. Guarda il video per scoprire la sottrazione dal basso.

Risultati: 341 245 204 331 243 213 162 361 415 263
1 2 Sottrazioni senza prestito (riporto)
Sottrazioni con un prestito (riporto)





4 5 Sottrazioni con un prestito Sottrazioni con due prestiti
























Per concentrarti sul procedimento, finché non ti senti sicuro puoi usare lo strumento Tabelline, che trovi a pagina 106. Poi, una volta esperto, potrai farne a meno.
1 Moltiplicazioni con uno o due riporti
2 Moltiplicazioni








































3 Moltiplicazioni con due o tre riporti
4 Moltiplicazioni con vari riporti
Risultati: 2639 1508 1131 1885 2262 3493 1497 1996 2994 2495 Risultati: 498 1440 830 2016 332 664 996 2304 1728 1152
Disegna e colora sul tuo quaderno una pagina intera di fiori.







6 Moltiplicazioni con difficoltà miste





Risultati: 1550 3600 520 3875 5125 3740 8080 6375 7625 8875 4 0 × 1 3 = 3 0 3 × 4 0 =
Moltiplicazioni con difficoltà miste
Risultati: 12120 6120 6528 12423
Completa e colora solo i rombi. Puoi usare la cornicetta per decorare il tuo quaderno.











Per eseguire le divisioni bisogna sapere le tabelline. Se hai difficoltà puoi utilizzare lo strumento Tabelline che trovi a pagina 106 con i pallini che rappresentano il resto.









Risultati: 8(1) 7 5(1) 4 6(1) 7(2) 9(2) 9
Divisioni con la tabellina del
Risultati: 9 5(3) 4(2) 3 3(3) 5 9(2) 8 Risultati: 6(1) 2(3) 2 4(2) 1(2) 5 5(4) 4 8 : 2 = 1 1 : 2 = 2 0 : 4 = 1 0 : 5 = 1 2 : 4 = 7 : 5 = 2 3 : 3 = 1
































Risultati: 3(2) 4(1) 3 5 8 7(3) 6(3) 5(4)
Risultati: 8(4) 8(2) 7(1) 7(1) 5(6) 5(1) 4 8(1)







Divisioni: prendo una cifra alla volta
Risultati: 23 14(2) 18(4) 32 22 16(3) 23 19(4)
Divisioni: prendo due cifre alla volta
Risultati: 53 56 80 97 32 68
= 9 Divisioni con difficoltà miste
Risultati: 40(4) 22 58(4) 20 57 31





Divisioni con difficoltà miste
Risultati: 48(4) 97(1) 62(6) 105 61(3) 102(6)
Divisioni con difficoltà miste
Risultati: 46(2) 56(2) 47(6) 93(4) 113(6) 40
Divisioni con difficoltà miste


Risultati: 50(2) 61(3) 72(8) 106 61(1) 95(1)

consiglia di





1230 × 2 = 1230 × 3 = 1230 × 4 =
× 5 =
Risultati: 4920 6150 8610 11070 3690 7380 9840 2460
× 2 =
× 3 =
× 4 =
× 5 =
Risultati: 22545 5010 10020 15030 20040 7515 12525 17535
× 20 =
× 30 =
× 40 =
× 50 =
Risultati: 16310 20970 4660 9320 13980 18640 6990 11650
× 12 =
× 13 =
× 14 =
× 15 =
Risultati:

× 6 =
× 7 =
× 8 =
× 9 =
× 6 =
× 7 =
× 8 =
× 9 =
× 60 =
× 70 =
× 80 =
× 90 =
× 16 =
× 17 =
× 18 =
× 19 =





× 11 =
× 21 =
× 31 =
× 41 =
× 22 =
× 44 =
× 55 =
× 21 =
× 31 =
× 41 =
× 51 =


× 51 =
× 61 =
× 71 =
× 81 =
×
×
×
=
=
=
× 101 =
× 102 =
× 103 =
× 104 =
×
×
×
×
=
=
× 105 =
×
× 107 =
× 108 =

Consentire di usare lo strumento Tabelline perché rinforza attraverso l’uso la loro memorizzazione.






: 2 =
Risultati:
: 3 =
: 3 =
: 3 =
Risultati:
: 5 =
: 5 =
Risultati:







1200 : 3 =
: 3 =
: 3 =
: 3 =
: 3 =
: 3 =
: 3 =
Risultati: 633(1) 400 433(1) 533(1) 566(2) 600 466(2) 500
: 3 = 2200 : 5 = 2300 : 5 = 2400 : 5 = 2500 : 5 =
: 5 =
: 5 =
: 5 = 2
Risultati: 520 500 440 480 540 460 560 580
: 5 =
3100 : 7 =
4300 : 7 = 5400 : 7 =
: 7 = 8700 : 7 =
: 7 = 9900 : 7 =
Risultati: 771(3) 900 1242(6) 614(2) 1414(2) 1085(5) 442(6) 1400
: 4 =
: 4 =
: 4 =
: 4 =
Risultati: 675 500 550 575 625 650 525 600
: 4 = 2300 : 4 = 3000 : 6 = 3100 : 6 = 3200 : 6 = 3300 : 6 =
: 6 =
: 6 = 3600 : 6 = 3700 : 6 =
Risultati: 616(4) 566(4) 533(2) 583(2) 600 516(4) 550 500
: 8 =
: 8 =
: 8 =
: 8 =
6300 : 7 = 2000 : 4 = 2100 : 4 =
: 8 = 8500 : 8 =
: 8 =
: 8 =
Risultati: 925 650 375 512(4) 1062(4) 1200 787(4) 1237(4)







Questi calcoli sono da fare a mente. Esercitati scoprendo per ognuno la strategia migliore.
1 Impara a moltiplicare per multipli di 10
30 × 10 =
40 × 10 =
50 × 10 =
×
×
×
=
=

×
×
×
=
2 Impara a moltiplicare per 5. Prima moltiplica per 10 e poi fai la metà
12 × 5 =
13 × 5 =
15 × 5 =
×
Risultati: 60 120 65 140 75 220 800 700 600
3 Impara a raddoppiare più volte
15 × 2 =
15 × 4 =
15 × 8 =
Risultati: 60 200 30 100 140 50 280 120 70
4 Impara a trovare la metà mentalmente Risultati:
120 : 2 = 130 : 2 =
: 2 =
Risultati: 210 65 75 85 60 95 80 315 480
× 5 =
× 5 =
× 2 =
× 4 =
× 8 =
: 2 =
: 2 =
: 2 =








Grazie a Francesca Moro per la cornicetta.






Esegui sul quaderno a quadretti le seguenti figure rispettando le misure indicate. Poi colorale come vuoi

Guarda il video per capire come usare bene il righello.







Guarda il video per capire come usare bene il goniometro.


Disegna un triangolo segnando i punti: 90 210 330.
Disegna un quadrato segnando i punti: 0 90 180 270.
Disegna una stella segnando i punti: 30 90 150 210 270 330.
3 4 5 6
Segna i punti: 30 90 150 210 270 330, poi disegna e colora la stella.
Disegna la girandola segnando i punti: 0 45 90 135 180 225 270 315.
Disegna i quadri intrecciati segnando i punti: 0 45 90 135 180 225 270 315.






Segna i punti: 18 90 162 234 306 e disegna un pentagono.
1 3 2 4
Segna i punti: 0 45 90 135 180 225 270 315 e disegna un ottagono.
Segna i punti 0 60 120 180 240 300 e disegna un esagono.
Segna i punti: 0 36 72 108 144 180 216 252 288 324 e disegna un decagono.
Segna i punti: 0 40 80 120 160 200 240 280 320 e disegna la stella.
5 6
Segna i punti: 0 30 60 90 120 150 180 210 240 270 300 330 e disegna la stella.








Apri il compasso di 6 cm e disegna una circonferenza. Mantenendo la stessa apertura punta sulla circonferenza e ottieni la seguente stella.
Con questi esercizi imparerai gradualmente a maneggiare il compasso per creare figure divertenti che potrai colorare a piacimento.
Costruisci una stella come quella precedente e poi, puntando sul punto intermedio tra due petali, costruiscine altri 6.
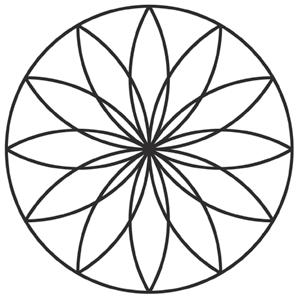
Con il raggio di 3 cm traccia una circonferenza. Poi, puntando sulla circonferenza con la stessa apertura, traccia tante altre circonferenze fino a ottenere il seguente fiore.
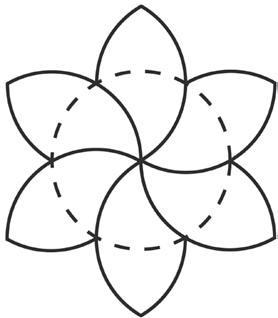
D






Con il raggio di 6 cm traccia
una circonferenza. Con un raggio di 3 cm puntando sulla circonferenza costruisci intorno i petali. Poi traccia tutti i raggi.
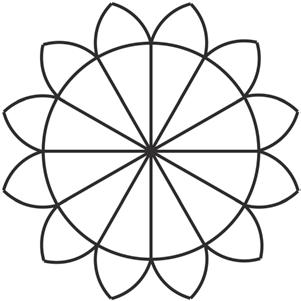
Disegna una circonferenza con raggio di 4 cm e i petali con raggio di 2 cm circa, come nel disegno precedente. Disegna poi le corone successive aumentando il raggio.
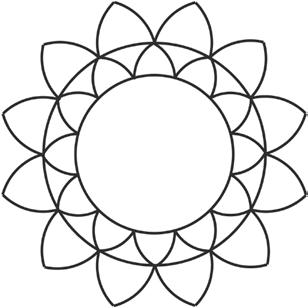
F
Costruisci un quadrato con lato di 5 cm e poi le semicirconferenze con raggio di 2,5 cm puntando sempre nel punto intermedio dei lati del quadrato. Poi aumenta il raggio per disegnare altri contorni.
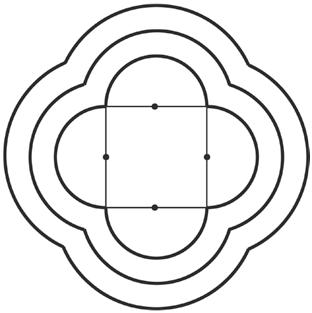








Disegnare triangoli equilateri .
Procedimento: disegna con la riga il lato di base AB, poi puntando in A e in B il compasso aperto di 10 cm trova l’incrocio C in alto. La base del primo triangolo come vedi poggia sulle righe del quaderno, la seconda è «in obliquo».
Disegnare triangoli isosceli .
Procedimento: dopo aver tracciato le basi, apri il compasso di 10 cm e trova l’incrocio in alto, puntando in A e in B.
Disegnare triangoli scaleni .
Procedimento: dopo aver tracciato le basi di 10 cm apri il compasso prima di 5 cm puntando in A e poi di 8 puntando in B per trovare l’incrocio in alto.
1 2 3






Disegnare due linee perpendicolari tra loro. A A
Prima Dopo
Procedimento: traccia un segmento di 10 cm (in obliquo).
Puntando su A e B il compasso aperto di 12 cm, trova gli incroci C e D. Uniscili. Osserva gli angoli al centro: sono di 90°.
Disegnare un quadrato .
Prima Dopo
Procedimento: disegna due linee perpendicolari come nell’esercizio precedente. Con il compasso aperto di 4 cm punta al centro e trova gli incroci. Se congiungi i punti ottieni un quadrato. Osserva gli angoli al centro: sono di 90°.
Disegnare un rettangolo .
Prima Dopo
Procedimento: disegna due segmenti «incidenti» di 15 cm circa. Punta al centro il compasso e traccia una circonferenza con raggio a tua scelta. Unisci i punti e otterrai un rettangolo. Come vedi al centro gli angoli non sono di 90°.





Ora sul tuo quaderno
imparerai a tracciare angoli con il goniometro e a classificarli con il loro nome.


Disegnare un angolo di 45°, cioè acuto .
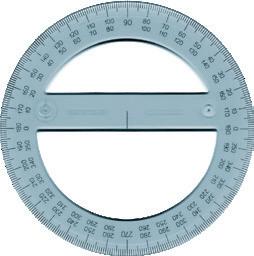

Traccia il segmento AB di 10 cm. Disponi il goniometro come vedi nella figura, con il centro in B. Segna il punto 45 e traccia il segmento.
Disegnare un angolo di 90°, cioè retto .

Traccia il segmento AB di 10 cm in obliquo. Disponi il goniometro come vedi nella figura, con il centro in B. Segna il punto 90 e traccia il segmento.
Disegnare un angolo di 120°, cioè ottuso .

Traccia il segmento AB di 10 cm in obliquo. Disponi il goniometro come vedi nella figura, con il centro in B. Segna il punto 120 e traccia il segmento.






Disegnare due angoli acuti di 60° e 80°.
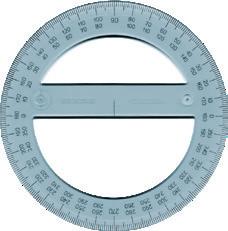

Traccia il segmento AB di 10 cm. Disponi il goniometro come vedi nella figura, con il centro in A. Segna i punti indicati e traccia i segmenti.
Disegnare due angoli retti.


Traccia il segmento AB di 10 cm in obliquo. Disponi il goniometro come vedi nella figura, con il centro in A. Segna i punti indicati e traccia i segmenti.
Disegnare due angoli ottusi di 130° e 160°.


Traccia il segmento AB di 10 cm in obliquo. Disponi il goniometro come vedi nella figura, con il centro in A. Segna i punti indicati e traccia i segmenti.







Quanto misura il perimetro?
Quanto misura il perimetro? (sposta mentalmente i lati corti)
Qual è il totale dei tre perimetri?
Qual è il totale dei tre perimetri?






Quanto misura il perimetro esterno?
Quanto misura il perimetro? (sposta mentalmente i lati corti)
Quanto misura il perimetro totale esterno?
Qual è il totale dei due perimetri?





Quanto misura ciascun lato del quadrato?

La somma dei due perimetri è 200 cm
La somma dei due perimetri è 120 cm
Quanto misura ciascun lato del quadrato?
La somma dei due perimetri è 190 cm
Quanto misura la base del rettangolo?
La somma dei due perimetri è 220 cm
Quanto misura ciascun lato dell’ottagono?






Usa il goniometro per costruire questa stella.
45°
Traccia una circonferenza con raggio di 4 cm e segna i punti.
Disegna 8 circonferenze con raggio 4 cm puntando su ognuno dei punti trovati prima.
Cancella le linee superflue e otterrai questo bellissimo fiore.









Grazie a Silvana Francese e Pina Messina per la cornicetta.
















Costruisci lo strumento Tabelline ritagliando le linee tratteggiate e sovrapponendo le varie strisce in ordine.
Poi, con una cucitrice pinza tutte le strisce.
Tieni lo strumento a portata di mano quando inizi lo studio delle moltiplicazioni e divisioni in colonna. Così ti aiuterà a concentrarti unicamente sulle procedure, che non sono semplici!

Istruzioni per la divisione con i puntini
1 Osserva le strisce.
2 Ogni striscia riporta una tabellina.
3 Contando i numeri si ottiene il quoziente.

Con lo strumento rinforzerai anche le tabelline senza accorgerti. Così poi non ti servirà più!

















4 Contando i puntini che avanzano si scopre il resto.










































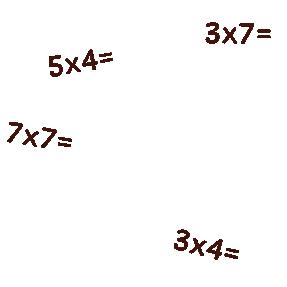
























1 pino 6 sedia 20 vaso 25 cicogna nel vaso




2 dadi 7 saetta 30 treno 35 cicogna sul treno




3 re 8 occhiali 40 quadro 45 quadro e cicogna




4 gatto 9 nido 50 cintura 54 cintura e gatto



5 cicogna 60 secchio 64 gatto nel secchio 56 cintura e sedia
✔ Nello strumento Tabelline compaiono alcuni di questi simboli che funzionano da «immagine gancio»: la forma dell’oggetto richiama la forma del numero scritto.
✔ Altri funzionano da «suono gancio»: il nome dell’oggetto richiama il nome del numero.
✔ Lasciare libertà di usare queste immagini senza prevedere un apposito studio.

Camillo Bortolato
Insegnante e pedagogista, autore di strumenti e materiali sul Metodo Analogico pubblicati con Erickson.
www.camillobortolato.it www.erickson.it
Un bambino quando è in difficoltà fa migliaia di supposizioni impiegando tutti i giga della mente. Poi scopre la banalità di quello che gli viene richiesto e si stupisce per la facilità: questa è la comprensione.
Supervisione editoriale
Giuseppe Degara
Progettazione / Editing
Tommaso Martino
Lucia Dorigatti
Collaborazione
Mariarosa Fornasier
Laura Bordignon
Direzione artistica
Enrico Bortolato
Giordano Pacenza
Progetto grafico
CHIALAB
Enrico Bortolato
Illustrazioni
Michela Nava
Illustrazioni di copertina
Enrico Bortolato
Michela Nava
Impaginazione
Mirko Pau
© 2025 Edizioni Centro Studi Erickson S.p.A.
Via del Pioppeto 24
38121 TRENTO
Tel. 0461 951500 www.erickson.it info@erickson.it
A scuola con Pitti 3 (Il mio libro di lettura, Il mio quaderno di scrittura, Il mio libro di matematica, Il mio libro di storia, geografia e scienze indivisibili)
ISBN: 978-88-590-4255-6
Kit A scuola con Pitti 3 + Gli strumenti del 1000
ISBN: 978-88-590-4256-3
Tutti i diritti riservati. Vietata la riproduzione con qualsiasi mezzo effettuata, se non previa autorizzazione dell’Editore.
Finito di stampare nel mese di aprile 2025 da Esperia S.r.l. – Lavis (TN)
Semplici regole per smaltire e riciclare gli imballaggi www.erickson.it/it/dove-lo-butto
A scuola con Pitti è una proposta completa per svolgere il percorso curricolare di classe terza in modo diretto e veloce, all’altezza delle aspettative dei bambini e delle bambine.
Proprio per questo, persegue il principio del fare di meno per imparare di più, rinnovando ogni materia all’insegna dell’essenzialità che si traduce in maggior efficacia.
Una scelta di cambiamento che nasce da decenni di esperienza nelle classi con il Metodo Analogico.



Il mio libro di LETTURA
Un «vero» libro di narrativa, al posto di tanti brani frammentati, che racconta le avventure di una volpe misteriosa e dei bambini che si mettono sulle sue tracce. Seguono storie tratte dalla tradizione, filastrocche e canzoni, per appassionare gli alunni al piacere della lettura.
Permette di perfezionare il corsivo e l’ortografia con esercizi confermativi che prevengono l’errore. Inoltre, sviluppa il testo personale grazie a una serie di modelli e, mediante la striscia dell’analisi grammaticale e l’armadio dei verbi, approfondisce al volo questi argomenti.

Il mio libro di MATEMATICA
Attraverso strumenti e rappresentazioni che veicolano le competenze, il volume consolida il calcolo mentale, per passare poi alla complessità dei problemi (centesimi, frazioni e misure) e alla fine affrontare senza timore moltiplicazioni e divisioni. Il tutto con il sorriso e senza paura di sbagliare.

Il mio libro di STORIA GEOGRAFIA e SCIENZE
Il libro propone le discipline in modo sintetico e chiaro, privilegiando, per presentare le informazioni, un approccio narrativo e ponendosi l’obiettivo principale di affascinare alunni e alunne con contenuti pregnanti.
Il volume è disponibile anche in formato digitale, con materiali e risorse aggiuntive. La guida online, inoltre, contiene le indicazioni per l’utilizzo del percorso durante tutto l’anno scolastico.