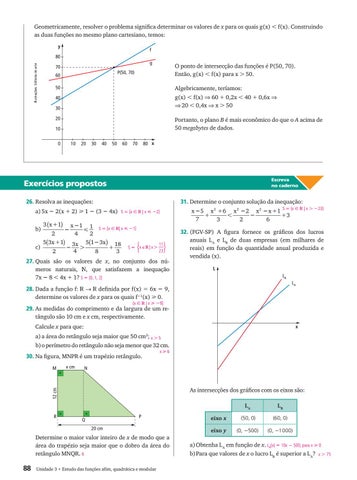
Geometricamente, resolver o problema significa determinar os valores de x para os quais g(x) f(x). Construindo as duas funções no mesmo plano cartesiano, temos: y
f
Ilustrações: Editoria de arte
80 g
70
O ponto de intersecção das funções é P(50, 70). Então, g(x) f(x) para x 50.
P(50, 70)
60 50
Algebricamente, teríamos:
40
g(x) f(x) Æ 60 0,2x 40 0,6x Æ Æ 20 0,4x Æ x 50
30 20
Portanto, o plano B é mais econômico do que o A acima de 50 megabytes de dados.
10 0
10
20
30
40
50
60
80 x
70
Escreva no caderno
Exercícios propostos 26. Resolva as inequações: a) 5x 2(x 2) 1 (3 4x)
31. Determine o conjunto solução da inequação: S {x R | x 2}
3 (x 1)
x 1 1 S {x R| x 1} < 4 2 2 5(3x 1) 3x 5(1 3x) 18 11 S x ∈ R | x c) 23 4 2 8 3
b)
27. Quais são os valores de x, no conjunto dos números naturais, N, que satisfazem a inequação 7x 8 4x 1? S {0, 1, 2}
x 5 x 2 6 x 2 2 x 2 x 1 S {x R | x 23} 3 7 3 2 6 32. (FGV-SP) A figura fornece os gráficos dos lucros anuais L A e LB de duas empresas (em milhares de reais) em função da quantidade anual produzida e vendida (x). L LB LA
28. Dada a função f: R é R definida por f(x) 6x 9, determine os valores de x para os quais f 1(x) 0. {x R | x 9}
29. As medidas do comprimento e da largura de um retângulo são 10 cm e x cm, respectivamente. Calcule x para que:
x
a) a área do retângulo seja maior que 50 cm2; x 5 b) o perímetro do retângulo não seja menor que 32 cm. 30. Na figura, MNPR é um trapézio retângulo. x cm
N
As intersecções dos gráficos com os eixos são:
12 cm
M
x 6
R
P
Q 20 cm
Determine o maior valor inteiro de x de modo que a área do trapézio seja maior que o dobro da área do retângulo MNQR. 6
88
Unidade 3
LA
LB
eixo x
(50, 0)
(60, 0)
eixo y
(0, 500)
(0, 1 000)
a) Obtenha L A em função de x. LA(x) 10x 500, para x 0 b) Para que valores de x o lucro LB é superior a L A?
x 75
Estudo das funções afim, quadrática e modular
CS-MAT-EM-3029-V1-U03-C04-070-091-LA.indd 88
5/6/16 11:23