Edición para estudiantes: Grado A1, Módulo 1, Copyright
Great Minds® is the creator of Eureka Math® , Wit & Wisdom® , Alexandria Plan™, and PhD Science® Published by Great Minds PBC. greatminds.org © 2024 Great Minds PBC. All rights reserved. No part of this work may be reproduced or used in any form or by any means—graphic, electronic, or mechanical, including photocopying or information storage and retrieval systems—without written permission from the copyright holder. Printed in the USA A-Print 1 2 3 4 5 6 7 8 9 10 XXX 28 27 26 25 24 ISBN 979-8-89191-194-9
Edición para estudiantes: Grado A1, Módulo 1, Título
Una historia de funciones®
Representar con funciones ▸ ÁLGEBRA I
APRENDER
Módulo
1 Expresiones, ecuaciones y desigualdades de una variable
2 Ecuaciones y desigualdades de dos variables
3 Las funciones y sus representaciones
4 Funciones cuadráticas
5 Funciones lineales y exponenciales
6 Representar con funciones
Edición para estudiantes: Grado A1, Módulo 1, Contenido
13
Resolver desigualdades lineales de una variable
Tema C
Enunciados compuestos que incluyen ecuaciones y desigualdades de una variable
Lección 14
Conjuntos de soluciones de enunciados compuestos
Lección 15
Usar el centro para comparar distribuciones de datos Lección
Usar la desviación estándar para describir la variabilidad de una distribución univariada Lección
Comparar distribuciones de datos univariados
2 A1 ▸ M1 EUREKA MATH2
Tema A 5 Sumar, restar y multiplicar
Lección 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
patrón creciente
Lección 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 Las propiedades conmutativa, asociativa y distributiva Lección 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 Polinomios Lección 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55 Sumar y restar polinomios Lección 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71 Multiplicar polinomios Lección 6 83 Identidades polinomiales Tema B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99 Resolver ecuaciones y desigualdades de una variable Lección 7 101 Las imprentas Lección 8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111 Conjuntos de soluciones para ecuaciones y desigualdades de una variable Lección 9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131 Resolver ecuaciones lineales de una variable Lección 10 147 Algunos riesgos posibles al resolver ecuaciones (opcional) Lección 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 159 Escribir y resolver ecuaciones de una variable Lección 12 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 169 Reorganizar fórmulas Lección
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Contenido Expresiones, ecuaciones y desigualdades de una variable
polinomios
El
de patos
185
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 203
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 205
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 225 Resolver y representar gráficamente desigualdades compuestas Lección 16 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 239 Resolver ecuaciones de valor absoluto Lección 17 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 255 Resolver desigualdades de valor absoluto Tema D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 273 Datos univariados Lección 18 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 275 Distribuciones y sus formas
19 289
20 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 307
21 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 323
Lección
Describir el centro de una distribución Lección
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 339
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 359
22
Estimar la variabilidad de distribuciones de datos Lección 23
© Great Minds PBC
3 EUREKA MATH2 A1 ▸ M1 Recursos Práctica mixta 1 . . . . . . . . . . . . . . . . . . . . . . . . . . 373 Práctica mixta 2 . . . . . . . . . . . . . . . . . . . . . . . . . . 379 Hojas extraíbles de Fluidez Rectas numéricas de la lección 15 . . . . . . . . . . . 385 Rectas numéricas de la lección 17 . . . . . . . . . . . 387 Práctica veloz: Sumar y restar fracciones . . . . 389 Práctica veloz: Aplicar la propiedad distributiva . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 393 Práctica veloz: Multiplicar y dividir fracciones . . . . . . . . . . . . . . . . . . . . . . . . . . 397 Práctica veloz: Operaciones con enteros 401 Práctica veloz: Resolver ecuaciones de uno y dos pasos . . . . . . . . . . . . . . . . . . . . . . . . 405 Práctica veloz: Resolver desigualdades de uno y dos pasos . . . . . . . . . . . . . . . . . . . . . . . . 409 Práctica veloz: Resolver ecuaciones de dos pasos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 413 Práctica veloz: Escribir expresiones equivalentes 417 Bibliografía 421 Créditos 422 Agradecimientos 423 © Great Minds PBC
Sumar, restar y multiplicar polinomios
Student Edition: Grade A1, Module 1, Topic A
Números en base x
Tengo una pregunta para ti: ¿Qué tiene en común esta imagen...
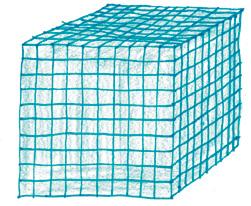
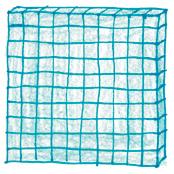














¿Líneas y recuadros?














¿Símbolos matemáticos?
¿Figuras mal dibujadas?
5
TEMA A
1347 103 102 102 102 101 101 101 101 1 1 1 1 1 1 1
con esta imagen? x3 + 3x2 + 4x + 7 x3 x2 x2 x2 x1 x1 x1 x1 1 1 1 1 11 1
…
Great Minds PBC
©
Sí, sí y sí. No importa si una imagen representa un número y la otra representa un polinomio, si una se usa en aritmética y la otra se usa en álgebra, o si una está llena de números 10 y la otra nada en una piscina de x. La realidad es que estas dos imágenes tienen prácticamente todo en común.
Un número es una suma de partes estándar: decenas, centenas, millares, y así sucesivamente. El nombre del número es una especie de lista de inventario breve: “Aquí tenemos 1 millar, 3 centenas, 4 decenas y 7 unidades”.
Lo mismo ocurre con un polinomio, salvo que las partes estándar incluyen x , x2 , x3, y así sucesivamente. El inventario se lee así: “Aquí tenemos 1 cubo, 3 cuadrados, 4 barras y 7 unidades”.
¿Qué es un polinomio? Es un número en base x.
A1 ▸ M1 ▸ TA EUREKA MATH2 6 PRESENTACIÓN DEL TEMA
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic A, Lesson 1
El patrón creciente de patos
1. Examina el patrón de patos.
a. Describe la organización de patos en la figura 1.
b. Describe la organización de patos en la figura 2.
EUREKA MATH2 A1 ▸ M1 ▸ TA▸ Lección 1 7
Figura 1
Figura 2
Figura 3
LECCIÓN 1
Fecha © Great Minds PBC
Nombre
c. ¿En qué se parece la organización de patos de la figura 2 a la organización de patos de la figura 1? ¿En qué se diferencia?
d. Describe la organización de patos en la figura 3.
e. ¿En qué se parece la organización de patos de la figura 3 a la organización de patos de la figura 2? ¿En qué se diferencia?
¿Cómo sigue creciendo?
2. Si el patrón continúa, ¿cuántos patos habrá en la figura 4? Describe la organización de patos.
A1 ▸ M1 ▸ TA ▸ Lección 1 EUREKA MATH2 8 L E CCIÓ N
© Great Minds PBC
3. Trabaja con tu grupo para hallar cuántos patos habrá en la figura 5, la figura 10 y la figura 100.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 1 9 L E CCIÓ N
Great Minds PBC
©
4. Describe cómo hallar el número de patos dado cualquier número de figura. Puedes usar palabras, símbolos, dibujos, expresiones o ecuaciones.
5. En tu hoja, registra dos expresiones diferentes de otros grupos. ¿En qué se parecen las expresiones? ¿En qué se diferencian?
A1 ▸ M1 ▸ TA ▸ Lección 1 EUREKA MATH2 10 L E CCIÓ N
Figura 1
Figura 2
© Great Minds PBC
Figura 3
Student Edition: Grade A1, Module 1, Topic A, Lesson 1
Nombre
Examina el patrón de calcetines.
1. Si el patrón continúa, ¿cuántos calcetines habrá en la figura 4? ¿En la figura 10? ¿En la figura 100?
2. Describe cómo hallar el número de calcetines dado cualquier número de figura.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 1 11
Figura 1
Figura 2
Figura 3
1 © Great Minds PBC
Fecha BOLETO DE SALIDA
Student Edition: Grade A1, Module 1, Topic A, Lesson 1
Nombre
El patrón creciente de patos
En esta lección:
• examinamos patrones visuales;
• escribimos expresiones numéricas para representar patrones visuales;
• describimos patrones visuales usando palabras y expresiones algebraicas.
Ejemplo
Examina el patrón de cebras.
a. ¿Cuántas cebras habrá en la figura 4?
En la figura 4, habrá 14 cebras.
En cada figura, hay 3 cebras más que en la figura anterior. En la figura 3, hay 11 cebras.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 1 13
Figura 3
Figura 1
Figura 2
1 © Great Minds PBC
Fecha RESUMEN
b. Describe cómo hallar el número de cebras dado cualquier número de figura. En cada figura, hay 3 grupos iguales de cebras y sobran 2. El número de cebras en cada grupo es el número de figura. Si n representa el número de figura, esto se podría representar como 3n + 2.
1
2
c. ¿Cuántas cebras habrá en la figura 10? ¿En la figura 100?
Figura 10: 32 cebras porque 3(10) + 2 = 32
Figura 100: 302 cebras porque 3(100) + 2 = 302
Figura 3
A1 ▸ M1 ▸ TA ▸ Lección 1 EUREKA MATH2 14 R ESUMEN
Figura
© Great Minds PBC
Figura
Student Edition: Grade A1, Module 1, Topic A, Lesson 1
Nombre Fecha
1. Examina el patrón de abejas.
a. ¿Cuántas abejas habrá en la figura 4? ¿En la figura 10? ¿En la figura 100?
b. Describe cómo hallar el número de abejas dado cualquier número de figura.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 1 15
Figura 1
Figura 2
Figura 3
© Great Minds PBC
PRÁCTICA 1
2. Examina el patrón de ratones.
a. ¿Cuántos ratones habrá en la figura 4? ¿En la figura 10? ¿En la figura 100?
b. Describe cómo hallar el número de ratones dado cualquier número de figura.
A1 ▸ M1 ▸ TA ▸ Lección 1 EUREKA MATH2 16 P RÁCTICA
Figura 1
Figura 2
© Great Minds PBC
Figura 3
3. Bahar y Nina examinan el patrón de tacos.
Bahar y Nina dividen las figuras en partes. Escriben expresiones para representar el número de tacos que hay en cada figura. Se muestra su trabajo.
Trabajo de Bahar:
EUREKA MATH2 A1 ▸ M1 ▸ TA▸ Lección 1 17 P RÁCTICA
Figura 1
Figura 2
Figura 3
Figura 4
1 12 + 12 + 2
Figura
2 22 + 22 + 2
Figura
3 32 + 32 + 2
Figura
4 42 + 42 + 2 © Great Minds PBC
Figura
Trabajo de Nina:
¿Representan las expresiones el mismo valor para cada figura? Explica cómo lo sabes.
A1 ▸ M1 ▸ TA ▸ Lección 1 EUREKA MATH2 18 P RÁCTICA
1
+ 2
Figura
2(12)
2
+ 2
Figura
2(22)
3
+ 2
Figura
2(32)
4
+ 2 © Great Minds PBC
Figura
2(42)
4. Examina el patrón de caracoles. Muestra dos maneras de representar el número de caracoles dado cualquier número de figura.
EUREKA MATH2 A1 ▸ M1 ▸ TA▸ Lección 1 19 P RÁCTICA
Figura 1
Figura 2
Figura 3
Figura 1
Figura 2
© Great Minds PBC
Figura 3
Recuerda
En los problemas 5 y 6, evalúa. 5.
7. ¿Qué ecuaciones son verdaderas? Elige todas las opciones que correspondan.
A. 72 + 45 = 9(8 + 5)
C. 24 + 6 = 6(4 + 1)
E. 48 + 28 = 4(12 + 7)
B. 80 + 60 = 8(10 + 60)
D. 39 + 27 = 3(19 + 9)
8. Ana cometió un error al resolver w − 16 = −25.
a. Identifica el error de Ana y explica qué debería haber hecho para resolver correctamente el problema.
b. Halla el valor de w.
A1 ▸ M1 ▸ TA ▸ Lección 1 EUREKA MATH2 20 P RÁCTICA
− 2.32
9.9 + 11.25 +
−12.14
6.
(−4)
w w w −= −+ =− =− 1625 16162516 41
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic A, Lesson 2
Nombre
Fecha
Las propiedades conmutativa, asociativa y distributiva
Tarea de emparejar expresiones
Empareja cada expresión de la tabla 1 con una expresión de la tabla 2. Explica por qué emparejaste cada par de expresiones.
Tabla 1
Tabla 2
A. (9 + p) + 6
B. 9p + 18
C. 9 ⋅ (p ⋅ 6)
D. 9(p + 6)
E. 2 ⋅ 9 ⋅ p
F. p + 9 + 2
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 2 21
1. 9 + p + 2 2. 9(p + 2) 3. 9 ⋅ 2 ⋅ p 4. (9 ⋅ p) ⋅ 6
9 +
+
5.
(p
6)
6. 9p + 54
LECCIÓN 2
© Great Minds PBC
Diagrama de árbol de las propiedades aritméticas
Completa los enunciados en el diagrama de árbol y proporciona ejemplos de cada propiedad.
Propiedades aritméticas
Distributiva
Conmutativa
Si a y b son números reales, entonces
Ejempl o
Si a , b y c son números reales, entonces
Asociativa
Si a y b son números reales, entonces
Si a , b y c son números reales, entonces
Si a , b y c son números reales, entonces
Ejemplo
Ejemplo
Ejemplo
A1 ▸ M1 ▸ TA ▸ Lección 2 EUREKA MATH2 22 L E CCIÓ N
Ejemplo Suma Multiplicación Suma Multiplicación
© Great Minds PBC
Definir expresiones equivalentes
Una expresión algebraica es un número, una variable o el resultado de colocar expresiones algebraicas previamente generadas en los espacios de uno de los cuatro operadores, ( ) + ( ), ( ) − ( ), ( ) ⋅ ( ), ( ) ÷ ( ), o en el espacio de la base de una potenciación con un exponente que es un número racional, ( )( ) .
7. Enumera algunos ejemplos de expresiones algebraicas.
Dos expresiones algebraicas son expresiones equivalentes si, al evaluarlas, dan como resultado el mismo número para todos los valores posibles de las variables.
Si podemos convertir una expresión en la otra mediante un determinado número de aplicaciones de las propiedades conmutativa, asociativa y distributiva y de las propiedades de los exponentes, entonces las dos expresiones son equivalentes.
8. Enumera dos expresiones equivalentes. Explica por qué son equivalentes.
9. Da un ejemplo erróneo de dos expresiones equivalentes. Explica por qué no son equivalentes.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 2 23 L E CCIÓ N
© Great Minds PBC
Demostrar la equivalencia
10. Muestra que −8(−5b + 7) + 5b es equivalente a 45b − 56 usando un diagrama de flujo y una tabla de dos columnas.
A1 ▸ M1 ▸ TA ▸ Lección 2 EUREKA MATH2 24 L E CCIÓ N
© Great Minds PBC
11. Completa el diagrama de flujo para mostrar que 3(y + 2) + 9x es equivalente a 3(3x + y) + 6. Escribe la propiedad o la operación que usaste en cada paso en la línea al lado de la flecha.
3(y + 2) + 9x 3y + 6 + 9x 9x + 3y + 6
(9x + 3y) + 6
3(3x + y) + 6
12. Completa la tabla de dos columnas para mostrar que (5y)(4 + y) − 12 es equivalente a 5y2 + 20y − 12. Escribe la propiedad o la operación que usaste en cada paso.
Expresión
(5y)(4 + y) − 12
5y ⋅ 4 + 5y ⋅ y − 12
5 ⋅ 4 ⋅ y + 5 ⋅ y ⋅ y − 12
5 ⋅ 4 ⋅ y + 5 ⋅ y2 − 12
20y + 5y2 − 12
5y2 + 20y − 12
Propiedad u operación usada
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 2 25 L E CCIÓ N
© Great Minds PBC
13. Muestra que 2(5a − 7 − 8 + 10a) es equivalente a 30(a − 1) escribiendo en la línea al lado de la flecha la propiedad o la operación usada en cada paso.
2(5a – 7 – 8 + 10a)
2(5a + 10a – 7 – 8)
10a – 14 – 16 + 20a
2(15a – 7 – 8)
2(15a – 15)
2 · 15(a – 1)
30(a – 1)
10a + 20a – 14 – 16
30a – 14 – 16
30a – 30
A1 ▸ M1 ▸ TA ▸ Lección 2 EUREKA MATH2 26 L E CCIÓ N
© Great Minds PBC
14. Muestra que 6d − d(d + 10) + 8(d + 10) es equivalente a d2 + 4d + 80. Organiza tu trabajo en un diagrama de flujo o en una tabla de dos columnas.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 2 27 L E CCIÓ N
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic A, Lesson 2
Nombre Fecha
Muestra que 6 + 5w + 3w(w + 2) y 3w2 + 11w + 6 son expresiones equivalentes indicando la operación o la propiedad usada en cada paso.
Expresión Propiedad u operación usada 6 + 5w + 3w(w + 2)
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 2 29
6 + 5
+ 3
2 + 6w 6 + 5w + 6w + 3w2 6 + 11w + 3w2 3w2 + 11w + 6
w
w
© Great Minds PBC
BOLETO DE SALIDA 2
Student Edition: Grade A1, Module 1, Topic A, Lesson 1
Nombre
Las propiedades conmutativa, asociativa y distributiva
En esta lección:
• usamos las propiedades conmutativa, asociativa y distributiva para reescribir expresiones algebraicas;
• aplicamos propiedades y operaciones para mostrar que dos expresiones algebraicas son equivalentes.
Propiedades de la aritmética
La propiedad distributiva
Si a, b y c son números reales, entonces
a(b + c) = ab + ac.
33234 (24)+= +
6630 (5) tt += +
La propiedad asociativa de la suma
Si a, b y c son números reales, entonces
(a + b) + c = a + (b + c).
(32)(24) ++ =+ + 43
(6)(5) ++ =+ + t 56 t
La propiedad conmutativa de la suma
Si a y b son números reales, entonces
a + b = b + a.
3223 += +
66 += + tt
Vocabulario
Una expresión algebraica es un número, una variable o el resultado de colocar expresiones algebraicas previamente generadas en los espacios de uno de los cuatro operadores,
( ) + ( ), ( ) − ( ), ( ) ( ), ( ) ÷ ( ), o en el espacio de la base de una potenciación con un exponente que es un número racional, ( )( ) .
Dos expresiones algebraicas son expresiones equivalentes si, al evaluarlas, dan como resultado el mismo número para todos los valores posibles de las variables.
Si podemos convertir una expresión en la otra mediante un determinado número de aplicaciones de las propiedades conmutativa, asociativa y distributiva y de las propiedades de los exponentes, entonces las dos expresiones son equivalentes.
La propiedad asociativa de la multiplicación
Si a, b y c son números reales, entonces
(a b) c = a (b c).
(32)(24) = 43 ⋅ ⋅ ⋅ ⋅
(6)(5) = tt 56 ⋅ ⋅⋅ ⋅
La propiedad conmutativa de la multiplicación
Si a y b son números reales, entonces
a ⋅ b = b ⋅ a.
3223 = ⋅ ⋅
66 = tt
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 2 31
⋅ ⋅
© Great Minds PBC
Fecha RESUMEN 2
Ejemplos
1. Muestra que 6x + 10x(2x − 3) es equivalente a 20x2 − 24x escribiendo al lado de la flecha la propiedad o la operación que mejor describe cada paso.
6x + 10x(2x – 3)
Las flechas tienen dos extremos con puntas para mostrar que las expresiones en cada extremo son equivalentes.
propiedad distributiva
6x + 20x2 – 30 x
propiedad conmutativa de la suma
6x – 30 x + 20x2
suma de términos semejantes
–24x + 20x2
propiedad conmutativa de la suma
20x2 – 24 x
A1 ▸ M1 ▸ TA ▸ Lección 2 EUREKA MATH2 32 R ESUMEN
© Great Minds PBC
2. Muestra que 2a(5a + 4) − 3(4a − 1) es equivalente a 10a2 − 4a + 3 escribiendo la propiedad o la operación usada en cada paso.
Expresión
2a(5a + 4) − 3(4a − 1)
10
10a2 − 4a + 3
Deja este recuadro en blanco, porque la expresión en esta fila es la expresión original.
Propiedad u operación usada
Multiplicación
Suma de términos semejantes
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 2 33 R ESUMEN
⋅
⋅
−
⋅ 4 ⋅
− 3 ⋅
⋅ 5 ⋅
2
⋅
⋅ a − 3 ⋅ 4 ⋅
− 3 ⋅ (−1)
⋅
2a ⋅ 5a + 2a ⋅ 4 − 3 ⋅ 4a − 3 ⋅ (−1) Propiedad distributiva 2 ⋅ 5 ⋅ a ⋅ a + 2
4
a
3
a
(−1) Propiedad conmutativa de la multiplicación 2
a
+ 2
4
a
Propiedad de los exponentes (ba
bc = ba + c)
a2 + 8a − 12a + 3
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic A, Lesson 2
En los problemas 1 a 4, escribe dos expresiones equivalentes para cada situación.
1. Longitud total de ambos segmentos
2. Área del rectángulo
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 2 35
01 1234567890
10 7
© Great Minds PBC
Nombre Fecha PRÁCTICA 2
En los problemas 5 a 10, identifica la propiedad que justifica por qué cada par de expresiones es equivalente.
A1 ▸ M1 ▸ TA ▸ Lección 2 EUREKA MATH2 36 P RÁCTICA 3. Volumen del prisma rectangular 5 6 8 4. Número de cuadrados en la figura
5. 3 + 5 + 2 y 3 + 2 + 5 6. 5 ⋅ (4 ⋅ 6) y (5 ⋅ 4) ⋅ 6 7. 9(2 + 5) y 18 + 45 8. 2x + 3x2 − 5 y 3x2 + 2x − 5 9. (y + 5)(y − 3) y (y + 5)y + (y + 5)(−3) 10. m2 + 2m − 6m − 12 y m2 + (2m − 6m) − 12 © Great Minds PBC
11. Muestra que 2x(3x + 2) − 4(3x + 2) es equivalente a 6x2 − 8x − 8 escribiendo la propiedad o la operación usada en cada paso.
Expresión
Propiedad u operación usada 2
12. Escribe la propiedad o la operación que usaste en cada paso para mostrar que
−8 + x(x + 3) + 4(y + 3) es equivalente a x2 + 3x + 4(y + 1).
Expresión
−8 + x(x + 3) + 4(y + 3)
−8 + x ⋅ x + 3x + 4y + 12
−8 + x2 + 3x + 4y + 12
x2 + 3x + 4y + 12 − 8
x2 + 3x + 4y + 4
x2 + 3x + (4y + 4)
x2 + 3x + 4(y + 1)
Propiedad u operación usada
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 2 37 P RÁCTICA
x(3x +
− 4(3x +
2x ⋅ 3x + 2x ⋅ 2 − 4 ⋅ 3x − 4 ⋅ 2 2 ⋅ 3 ⋅ x ⋅ x + 2 ⋅ 2 ⋅ x − 4 ⋅ 3 ⋅ x − 4 ⋅ 2 2 ⋅ 3 ⋅ x2 + 2 ⋅ 2 ⋅ x − 4 ⋅ 3 ⋅ x − 4 ⋅ 2
x2
4
− 8
2)
2)
6
+
x − 12x
6x2 − 8x − 8
© Great Minds PBC
13. Muestra que −4a + 3a(a + 2) es equivalente a 3a2 + 2a escribiendo en la línea al lado de la flecha la propiedad o la operación usada en cada paso.
–4a + 3a(a + 2)
A1 ▸ M1 ▸ TA ▸ Lección 2 EUREKA MATH2 38 P RÁCTICA
–4a + 6a + 3a2 2a + 3a2 3a2 + 2a –4a + 3a2 + 6a © Great Minds PBC
14. Completa el diagrama de flujo para mostrar que 2g + 8(g − 4) − 7g es equivalente a 3g − 32. Escribe en la línea al lado de la flecha la propiedad o la operación que usaste en cada paso.
2g + 8(g – 4) – 7g
2g + 8g – 32 – 7g
2g – 7g + 8(g – 4)
2g + 8g – 7g – 32
2g – 7g + 8g – 32
3g – 32
15. Muestra que 5p2 − 3 + 2(p2 − p3) es equivalente a −2p3 + 7p2 − 3 usando un diagrama de flujo o una tabla de dos columnas. Indica la propiedad o la operación que usaste en cada paso.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 2 39 P RÁCTICA
© Great Minds PBC
16. Muestra que 2(2 + n3) + n(5n2 + 2) es equivalente a 7n3 + 2n + 4. Indica la propiedad o la operación que usaste en cada paso.
Recuerda
En los problemas 17 y 18, evalúa.
17. 16.5 ⋅ 4.4
19. Evalúa 4x3 + 6x − 16 para x = 2.
18. 45 ÷ (−2.5)
A1 ▸ M1 ▸ TA ▸ Lección 2 EUREKA MATH2 40 P RÁCTICA
© Great Minds PBC
20. Halla la solución de g 7 = 8 usando cada método de la lista.
a. Usa diagramas de cinta.
b. Resuelve de manera algebraica.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 2 41 P RÁCTICA
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic A, Lesson 3
Nombre Fecha
Polinomios
En los problemas 1 a 3, completa la ecuación.
Evaluar expresiones en base x
En los problemas 4 a 6, evalúa la expresión para x = 10
43 EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 3
672100101 10101 2 =+ + =+ + 2. 89431000100101 101010 32 =+ ++ =+ ++ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ 1 3. 10548100001000100101 10 4 ,,=+ ++ + =+ ⋅ ⋅ ⋅ ⋅ ⋅ ++ 10101 2
1.
4. 6x2 + 7x + 2
5. 8x3 + 9x2 + 4x + 3
6. x4 + 5x2 + 4x + 8
LECCIÓN 3
© Great Minds PBC
Polinomios
Completa el mapa escribiendo ejemplos correctos y ejemplos erróneos, según corresponda, de cada definición. Usa los ejemplos correctos y los ejemplos erróneos de la actividad de clasificación de tarjetas.
Monomio
Grado de un polinomio
Grado del término que tiene el mayor grado
Término
Polinomio que se genera usando solo la multiplicación. No contiene los signos + ni −. Cada uno de los monomios diferentes de cero que componen un polinomio
El grado de un monomio de una variable es el exponente de su variable.
Polinomio
Expresión numérica o variable, o el resultado de sumar o multiplicar dos polinomios previamente generados
Forma estándar
Un polinomio está en la forma estándar si es una suma de un número finito de términos de la forma axn, donde cada n es un entero no negativo distinto, cada a es un número diferente de cero y los términos están ordenados por grado de forma descendente.
Trinomio
Polinomio con tres términos, en el que cada término tiene un grado distinto
Binomio
Polinomio con dos términos, en el que cada término tiene un grado distinto
A1 ▸ M1 ▸ TA ▸ Lección 3 EUREKA MATH2 44 L ECCIÓN
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic A, Lesson 3
Nombre
1.
a. Escribe la expresión en forma estándar e indica el grado del polinomio.
b. Evalúa la expresión para x = 10
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 3 45
Considera
3 − 5x2 + 2 + 8x + x3 + 7x2 − 5
el polinomio
3
Great Minds PBC
Fecha BOLETO DE SALIDA
©
Student Edition: Grade A1, Module 1, Topic A, Lesson 3
Nombre Fecha
Polinomios
En esta lección:
• comparamos números en base 10 con números en base x;
• identificamos polinomios;
• indicamos el grado de los polinomios;
• evaluamos polinomios;
• escribimos polinomios en forma estándar.
Ejemplos
En los problemas 1 y 2, indica si la expresión es un polinomio. Si es un polinomio, indica su grado. Si no lo es, explica cómo lo sabes.
1. +− + 4622 48 ww w
Sí; grado 8
2. 15215 x x -
El término con el mayor grado es − w8 .
No es un polinomio. No podemos sumar ni multiplicar ningún número o variable para obtener el término 15 x
Vocabulario
Un polinomio es una expresión numérica o variable, o el resultado de sumar o multiplicar dos polinomios previamente generados.
Un monomio es un polinomio que se genera usando solo la multiplicación. No contiene los signos + ni .
El grado de un monomio de una variable es el exponente de su variable.
Un término es cada uno de los monomios diferentes de cero que componen un polinomio.
El grado de un polinomio es el grado del término monomio de mayor grado.
Un binomio es un polinomio con dos términos, en el que cada término tiene un grado distinto.
Un trinomio es un polinomio con tres términos, en el que cada término tiene un grado distinto.
Un polinomio está en forma estándar si es una suma de un número finito de términos de la forma axn, donde cada n es un entero no negativo distinto, cada a es un número diferente de cero y los términos están ordenados por grado de forma descendente.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 3 47
© Great Minds PBC
RESUMEN 3
3. Considera el polinomio.
m2 − 10 + 7m5 + 6m2 + 5 − 2m5 + 9 + 8m3 + 2m
a. Escribe el polinomio en forma estándar.
b. Indica el grado del polinomio.
5
c. Evalúa el polinomio para m = 10. 51081051
Escribir un polinomio en base m en forma estándar es similar a escribir un número en base 10 en forma desarrollada.
A1 ▸ M1 ▸ TA ▸ Lección 3 EUREKA MATH2 48 R ESUMEN
5302104510000081000510021()2()()()(,)()()(++ ++ =+ ++ 0 04 5000008000500204 508524 ) , , + =+ ++ + =
++ +− ++ + =− +− ++ −+ + mm mm mm mmm mm m 25253 55322 107652982 728621059 = =+ ++ + 58524 532 mm mm © Great Minds PBC
Student Edition: Grade A1, Module 1, Topic A, Lesson 3
Nombre Fecha
En los problemas 1 y 2, completa cada ecuación.
1. 24351000100101 =+
1010101 32 ⋅ ⋅ ⋅ ⋅⋅
2. 21091061 320=+
En los problemas 3 y 4, evalúa el polinomio para x = 10.
3. 2x3 + 4x2 + 3x + 5
4. 2x3 + 9x2 + 6x
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 3 49
++ = ++ +
⋅ ⋅ ⋅
+ ⋅⋅
⋅
© Great Minds PBC
PRÁCTICA 3
En los problemas 5 a 9, escribe el polinomio en forma estándar.
5. 6x3 + 4x − 2x3 − 5
6. 2x2 − 8x + 6x + x2 + 1
7. 5 + 2x + 3x3 − 7 + 8x2 − x + 10 − 4x2
8. 3(x3 + 2x + 2) + 8x4 − 6
9. 0.2c(c3 − 3c) + 4 − 1.3 + 2c4 + 0.4c4 − 1.2c2
En los problemas 10 a 15, indica si la expresión es un polinomio. Si es un polinomio, indica su grado. Si no lo es, explica cómo lo sabes.
A1 ▸ M1 ▸ TA ▸ Lección 3 EUREKA MATH2 50 P RÁCTICA
10. y5 − 3y4 + y3 − y2 − 7y + 8 11. 0.8b2 − 0.2b3 © Great Minds PBC
En los problemas 16 a 19, usa la descripción para escribir un polinomio en forma estándar. 16. Tres términos;
a. Escribe el polinomio en forma estándar.
EUREKA MATH2 A1 ▸ M1 ▸TA ▸ Lección 3 51 P RÁCTICA
64 1 5 gg -
uu uu 7427 +− ++
21 22 1 3 1 2 1 6 cc cc +− −+
x x 351 −+
12.
13.
14.
15.
2
8
12
9
grado
17. Cuatro términos; grado
18. Tres términos; grado
19. Cinco términos; grado
x3 + 6x − 2x2 − 7 − x4 + 6x2 + x4
20. Considera el polinomio 9 +
© Great Minds PBC
b. Indica el grado del polinomio.
c. Evalúa el polinomio para x = 10
d. Describe cómo los polinomios en forma estándar pueden comportarse como enteros en forma desarrollada. Usa tu respuesta de la parte (c) para respaldar tu respuesta.
21. Considera la expresión 2x5 + + 7.
a. ¿Con qué término se puede completar el recuadro para convertir la expresión en un polinomio en forma estándar?
b. ¿Con qué término no se puede completar el recuadro para convertir la expresión en un polinomio?
c. ¿Con qué término se puede completar el recuadro para convertir la expresión en un polinomio que no esté en forma estándar?
A1 ▸ M1 ▸ TA ▸ Lección 3 EUREKA MATH2 52 P RÁCTICA
© Great Minds PBC
Lucas dice que la expresión 5a − 2a2 + 6a es un binomio disfrazado porque se puede reescribir como 11a − 2a2, con todos los términos distribuidos y los términos semejantes combinados.
En los problemas 22 a 25, determina si la expresión es un binomio disfrazado.
22. 2 ⋅ 5x5 − 12x4 + 3x5 + 2x4
23. t(t + 2) + 2(t + 2) − 4t
24. 5(b − 1) − 10(b − 1) + 100(b2 − 1)
25. (2πr − πr2) ⋅ r − (2πr − πr2) ⋅ 2r
Recuerda
En los problemas 26 y 27, evalúa.
26. 62.34 − (−5.66) + (−11.91)
27. −1.2 ⋅ 2.4 − 3.02
EUREKA MATH2 A1 ▸ M1 ▸TA ▸ Lección 3 53 P RÁCTICA
© Great Minds PBC
En los problemas 28 a 31, halla el producto.
28. m(m − 4)
30. n(10n2 − 7)
29. 6t(t + 3)
31. −2a2(1 − 5a)
En los problemas 32 y 33, resuelve la ecuación.
32. −3x − 12 = −18
33. 24 = 9 − 6x
A1 ▸ M1 ▸ TA ▸ Lección 3 EUREKA MATH2 54 P RÁCTICA
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic A, Lesson 4
Nombre Fecha
Sumar y restar polinomios
1. Evalúa las siguientes expresiones para x = −3, x = −2, x = −1, x = 0, x = 1, x = 2 y x = 3. a.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 4 55
3x
x − 3) + 2 + 2x − 5(x2 − 2x + 1) + 2(x2 − x + 2) + 1
(
b. x + 2
LECCIÓN 4
© Great Minds PBC
Hallar la suma o la diferencia
2. Escribe 125 en forma desarrollada.
3. Escribe 432 en forma desarrollada.
4. Suma las formas desarrolladas de los problemas 2 y 3 para hallar el total.
5. Halla la suma (x2 + 2x + 5) + (4x2 + 3x + 2). Combina los términos semejantes.
A1 ▸ M1 ▸ TA ▸ Lección 4 EUREKA MATH2 56 L ECCIÓN
© Great Minds PBC
6. Escribe 563 en forma desarrollada.
7. Escribe 251 en forma desarrollada.
8. Resta la forma desarrollada del problema 7 de la forma desarrollada del problema 6. Escribe la diferencia en forma estándar.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 4 57 L ECCIÓN
⋅⋅ ⋅⋅ ⋅
(5x2 + 6x + 3) − (2x2 + 5x + 1).
© Great Minds PBC
9. Halla la diferencia
Combina los términos semejantes.
Sumar y restar polinomios
En los problemas 10 a 20, halla la suma o la diferencia. Escribe tu respuesta como un polinomio en forma estándar.
10. (2x2 + 1) + (5x2 + 7)
11. (3x3 + 8x2) − (x3 + 6x2)
12. (3x5 + 4x2 + 6x) + (2x5 + 8x2 + 5x)
A1 ▸ M1 ▸ TA ▸ Lección 4 EUREKA MATH2 58 L ECCIÓN
© Great Minds PBC
13. (4x5 + 9x3 + 11) − (x4 + 7x3 + 10)
14. (9x2 − 1) + (5x2 + 10)
15. (−4x7 + 12x2) − (3x7 − 7x2)
16. (−3x3 + 4x4 + 6x) + (2x − x3 − 5x4)
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 4 59 L ECCIÓN
© Great Minds PBC
17. (12x2 − 8x5 + 1) − (−7 + 9x2 − 10x5)
18. (7x3 + 9x2 + 4) + (4x3 + 7)
19. (x9 + 3x8 + 6x7) − (2x7 + 5x8)
20. 3x(x − 3) + 2 + 2x − 5(x2 − 2x + 1) + 2(x2 − x + 2) + 1
A1 ▸ M1 ▸ TA ▸ Lección 4 EUREKA MATH2 60 L ECCIÓN
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic A, Lesson 4
Nombre Fecha BOLETO
Halla la suma o la diferencia. Combina los términos semejantes.
1. (w3 − 3w2 + 12w + 8) + (2w3 − 18w + 4)
©
2. (w3 − 3w2 + 12w + 8) − (2w3 − 18w + 4)
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 4 61
DE SALIDA 4
Great Minds PBC
Student Edition: Grade A1, Module 1, Topic A, Lesson 4
Nombre Fecha
Sumar y restar polinomios
En esta lección:
• comparamos la suma y la resta de polinomios con la suma y la resta de números de varios dígitos en forma desarrollada;
• sumamos y restamos polinomios.
Ejemplos
En los problemas 1 y 2, halla la suma. Combina los términos semejantes.
Sumar los dígitos de los términos que tienen el mismo valor posicional en un número de varios dígitos es similar a sumar los coeficientes de los términos que tienen el mismo grado en un polinomio.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 4 63
(5 ⋅ 102 + 2 ⋅ 10 + 3 ⋅ 1) + (1 ⋅ 102 + 4 ⋅ 10 + 5 ⋅ 1) 2. (5x2 + 2x + 3) + (x2 + 4x + 5) ()() ()()( 523452435 51243 2222 2 xx xx xx xx xx ++ ++ += ++ ++ + =+ ++ ++ 5 5 5) =+ + 668 2 xx ()() 510210311104105151011021 2204103 22 ++ ++ += ++ ++ 1 151 51102410351 61061081 2 2 + =+ ++ ++ =+ + ()()() ⋅⋅⋅⋅ ⋅⋅ ⋅⋅ ⋅ ⋅⋅ ⋅⋅ ⋅ ⋅
1.
RESUMEN 4 © Great Minds PBC
En los problemas 3 a 5, reescribe el polinomio en forma estándar.
3. (4p2 − 9p + 2) − (2p2 + 8p − 6)
()() 492286492286
429826 2222 22 pp pp pp pp pp pp −+ −+ −= −+
= 2 pp2178 −+
4. (w4 + 6 − w2) + (12 − w2 + 6w + 4w3)
()() ww ww ww ww ww ww w
Usa la propiedad distributiva para reescribir
−(2p2 + 8p − 6) como
−2p2 − 8p + 6
42234322 432 6126446612 426 +− +− ++ =+ ++ + =+ −+ w + 18
5. 1 3 1565362 ()() −+ +− yy y
Los polinomios son cerrados bajo la suma y la resta. La suma o la diferencia de dos polinomios es siempre un polinomio.
A1 ▸ M1 ▸ TA ▸ Lección 4 EUREKA MATH2 64 R ESUMEN
+ =− ++
1 3 22 2 2
62553 67 ()() −+ +− =− ++ −+ =+ +− =+ yy yy yy yy y yy 8
15653652536
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic A, Lesson 4
Nombre Fecha
En los problemas 1 y 2, escribe el número en forma desarrollada.
1. 306 2. 1042
En los problemas 3 a 7, halla la suma o la diferencia. Combina los términos semejantes.
3. 80,463 + 2510 4.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 4 65
104 + 4 102 + 6 10) + (2 103 + 5 102 + 1 10)
(4 ⋅ 103 + 2 ⋅ 102 + 9 ⋅ 10 + 5 ⋅ 1) − (3 ⋅ 103 + 2 ⋅ 102 + 5 ⋅ 10 + 3 ⋅ 1)
(8
5.
4 + 4x2 + 6x + 3) + (2x3 + 5x2 + 1x)
6. (8x
+ 2x2 + 9x + 5) − (3x3 + 2x2 + 5x + 3)
7. (4x3
PRÁCTICA 4 © Great Minds PBC
8. Describe en qué se parece sumar y restar polinomios a sumar y restar números enteros. Usa tus respuestas de los problemas 2 y 3 para respaldar tu respuesta.
9. Considera el polinomio (3n2 − 7n − 4) + (−4n + 9 + n2) + (8n + 5)
a. Evalúa la expresión para n = 10.
b. Reescribe la expresión en forma estándar.
c. Evalúa tu respuesta de la parte (b) para n = 10.
d. Explica por qué es útil combinar los términos semejantes en los polinomios. Usa las partes (a)–(c) para apoyar tu explicación.
En los problemas 10 a 14, reescribe el polinomio en forma estándar.
10. (2y2 + 6y − 4) + (−y2 − 4y + 7)
A1 ▸ M1 ▸ TA ▸ Lección 4 EUREKA MATH2 66 P RÁCTICA
© Great Minds PBC
15. Escribe un polinomio en forma estándar para el perímetro del triángulo, donde x > 2 3 . 3
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 4 67 P RÁCTICA
− 6
− 8q2) −
2 + 2)
dd d −+ +− +
232 3 4
2 3 2 5 312633 hh h −+ () +−()
11. (5
q
(14q
12. ()() dd
481632
13.
14. (6 − 3b2) − (5b5 − 9b + 2b2) − (2b − b2 + 7)
–2
x +8
x +6 A B C © Great Minds PBC
x
2
4
16. Halla un polinomio tal que, sumado a 8p3 + 4p − 7, dé como resultado una suma de 14p3 + 6p + 8
17. Considera la expresión (8x2 − 3x + 1) + (−8x + 2x − 4).
a. ¿Qué valores del exponente desconocido harían que sea un trinomio cuando se escribe en forma estándar?
b. ¿Qué valores del exponente desconocido, incluidos en el recuadro, harían que sea un polinomio con cuatro términos cuando se escribe en forma estándar?
c. ¿Qué valores del exponente desconocido harían que sea un binomio cuando se escribe en forma estándar?
A1 ▸ M1 ▸ TA ▸ Lección 4 EUREKA MATH2 68 P RÁCTICA
© Great Minds PBC
18. Emma escribió un polinomio de quinto grado. Tiah escribió un polinomio de tercer grado.
a. ¿Es la suma de sus expresiones un polinomio? Explica.
b. ¿Es la diferencia de sus expresiones un polinomio? Explica.
c. ¿Cuál es el grado de la suma de sus expresiones?
d. ¿Cuál es el grado de la diferencia de sus expresiones?
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 4 69 P RÁCTICA
© Great Minds PBC
Recuerda
En los problemas 19 y 20, evalúa.
21. Muestra que 7 + 2m + 6m(m + 3) y 6m2 + 20m + 7 son expresiones equivalentes. Indica la propiedad u operación usada en cada paso.
En los problemas 22 y 23, resuelve la ecuación.
A1 ▸ M1 ▸ TA ▸ Lección 4 EUREKA MATH2 70 P RÁCTICA
19. −+ 2 5 3 4 20. 4 9 2 3 1 27 +−()
22. −2(3x − 2) = 28
© Great Minds PBC
23. 5(2x + 4) − 12x = −6
Student Edition: Grade A1, Module 1, Topic A, Lesson 5
Nombre
Multiplicar polinomios
Notas y reflexiones
Del modelo de área al modelo tabular
Del modelo tabular al método algebraico
EUREKA MATH2 A1 ▸ M1 ▸TA ▸ Lección 5 71
LECCIÓN 5
© Great Minds PBC
Fecha
Elegir un problema
A1 ▸ M1 ▸ TA ▸ Lección 5 EUREKA MATH2 72 L ECCIÓN
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic A, Lesson 5
Nombre
Halla el producto. Escribe tu respuesta en forma estándar.
(a − 6)(3a + 4)
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 5 73
5 © Great Minds PBC
Fecha BOLETO DE SALIDA
Student Edition: Grade A1, Module 1, Topic A, Lesson 5
Nombre Fecha
Multiplicar polinomios
En esta lección:
• exploramos las conexiones entre la multiplicación de enteros usando el modelo de área y la multiplicación de polinomios usando el modelo tabular;
• describimos las conexiones entre el modelo tabular y el método algebraico para multiplicar polinomios;
• multiplicamos polinomios.
Ejemplos
En los problemas 1 a 3, halla el producto. Escribe la respuesta en forma estándar.
1. (x + 1)(x + 4)
Modelo tabular:
A menos que en un problema se especifique lo contrario, puedes elegir el método que prefieras para multiplicar polinomios.
Método algebraico:
Los polinomios son cerrados bajo la multiplicación. El producto de dos polinomios siempre es un polinomio. ()
En ambos enfoques se requiere la propiedad distributiva. Los términos x y 4 se multiplican por x y por 1.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 5 75
x2 x 44 x 4x x 1 5x x 2 4
(x + 1)(x + 4) = x2 + 5x + 4
xx xx x xx x xx +
54 2 2 += ++ + =+ ++ =+ +
()()()
14414 44
© Great Minds PBC
RESUMEN 5
2. (4m − 3)(5m + 2)
Modelo tabular:
Método algebraico:
20m2 –6
–7m
8m 4 m –3
43()()() 52452352
20m25m –62 –15m
(4m − 3)(5m + 2) = 20m2 − 7m − 6
3. (w − 8)(w2 − 4)
Modelo tabular: w3 w2 0w 0w –8w 2 0w2 w –8 w3
–8w2 –432–4 w
–4w 32
(w − 8)(w2 − 4) = w3 − 8w2 − 4w + 32
Método algebraico:
56
Al polinomio w2 − 4 le falta un término w Si usas el modelo tabular para multiplicar, es útil incluir un término 0w para alinear los términos semejantes correctamente en las diagonales.
A1 ▸ M1 ▸ TA ▸ Lección 5 EUREKA MATH2 76 R ESUMEN
mm
=+ −+ =+ =−
()
2081
2076 2 2 mm mm m mm m
−+
=− −+ =− −+
8432 222 32 32 © Great Minds PBC
()()()()ww ww w ww w ww w =−
84484 4832
Student Edition: Grade A1, Module 1, Topic A, Lesson 5
Nombre Fecha
En los problemas 1 a 6, halla el producto.
1. 9(7t4)
3. 8(3k5 + 2k2 + 11)
5. p( p − 5)
2. 1 2 126 3 () hh -
4. (7g3)(8g2)
6. (10s6 − 4s + 1) s
7. Halla el área del rectángulo. Escribe el área como un polinomio en forma estándar, donde b > 1
5b –5
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 5 77
3
© Great Minds PBC
PRÁCTICA 5
En los problemas 8 a 10, halla el producto.
8. 58 ⋅ 15
9. (50 + 8)(10 + 5)
10. (5x + 8)(x + 5)
11. Describe en qué se parece multiplicar polinomios a multiplicar enteros. Usa tus respuestas de los problemas 8 a 10 para respaldar tu respuesta.
12. Halla el área del triángulo. Escribe un polinomio en forma estándar para el área del triángulo, donde x > 0.
2x +6 3x
A1 ▸ M1 ▸ TA ▸ Lección 5 EUREKA MATH2 78 P RÁCTICA
© Great Minds PBC
En los problemas 13 a 17, halla el producto. Escribe tu respuesta en forma estándar.
13. (m + 2)(m + 5)
14. (a − 1)(a + 6)
15. (9 − v)(v − 3)
16. (7z − 2)(3z + 2)
17. nn + () + () 2 3 5 3
18. Escribe un polinomio en forma estándar para el área de un rectángulo con longitud d + 6 y ancho d + 9, donde d > −6
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 5 79 P RÁCTICA
© Great Minds PBC
19. Escribe un polinomio en forma estándar para el área del triángulo ABC, donde p > −2.
En los problemas 20 a 25, reescribe cada expresión como un polinomio en forma estándar.
26. Li Na escribió un polinomio de octavo grado y Lyla escribió un polinomio de segundo grado.
¿Será el producto de sus polinomios un polinomio? Explica.
A1 ▸ M1 ▸ TA ▸ Lección 5 EUREKA MATH2 80 P RÁCTICA
C AB p 1+1 6 p 1+1 2
20. (c + 6)(c2 + 1)
21. (w + 2)(w2 + 3w + 5)
22. (−2r + 7 + 3r2)(5r + 1)
23. 2( j − 5)( j + 3)
24. (0.2u2 + 1)(0.75u − 5) + 0.3
25. 7q2 + (2q − 7)(8q2 − 3) − 4
© Great Minds PBC
Recuerda
En los problemas 27 a 29, evalúa.
⋅
30. Considera el polinomio 7 − 8x2 − 4 + 2x2 − 6x + 4x3 − 1.
a. Escribe la expresión en forma estándar e indica el grado del polinomio.
b. Evalúa la expresión para x = 10.
31. Halla el valor de x en la ecuación −4(x − 6) = −2(3x + 2) − 8.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 5 81 P RÁCTICA
27.
2 3 5 6 28. − ÷−() 7 10 2 9 29. 5 8 18 35 () ⋅
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic A, Lesson 6
Nombre Fecha
Identidades polinomiales
En los problemas 1 a 5, halla el producto. Escribe tu respuesta como un polinomio en forma estándar.
1. (a + 3)(a + 3)
2. (w + 2)(w + 2)
3. (q − 7)(q − 7)
4. (n + 5)(n − 5)
5. (2y + 6)(2y − 6)
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 6 83
LECCIÓN 6
© Great Minds PBC
Cuadrados perfectos
Evan y Tiah observan que los problemas 1, 2 y 3 son binomios elevados al cuadrado. Se preguntan si elevar al cuadrado un binomio da un resultado especial. Deciden investigar el binomio a + b, donde a y b son números cualesquiera. Se muestra el trabajo de Evan.
Trabajo de Evan a2 + b2 ( a + b)2
6. ¿Es correcto el trabajo de Evan? ¿Por qué?
7. Tiah dice que elevar al cuadrado un binomio da el mismo resultado que multiplicar un binomio por sí mismo. Para comenzar, Tiah usa el modelo tabular para multiplicar (a + b) y (a + b). Completa su trabajo para hallar el producto (a + b)(a + b). (a + b)2 = (a + b)(a + b)
Trabajo de Tiah a b a b
A1 ▸ M1 ▸ TA ▸ Lección 6 EUREKA MATH2 84 L ECCIÓN
© Great Minds PBC
En los problemas 8 y 9, usa la multiplicación para reescribir la expresión como un polinomio en forma estándar.
8. (x + 3)2
9. ( y − 12)2
En los problemas 10 a 13, usa la identidad (a + b)2 = a2 + 2ab + b2 para reescribir la expresión como un polinomio en forma estándar.
10. (a + 12)2
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 6 85 L ECCIÓN
© Great Minds PBC
11. ( f − 6)2
12. (7r + 1)2
13. (3k − 4)2
Diferencia de cuadrados
14. Usa el modelo tabular para hallar el producto (a + b)(a − b).
A1 ▸ M1 ▸ TA ▸ Lección 6 EUREKA MATH2 86 L ECCIÓN
© Great Minds PBC
En los problemas 15 y 16, usa la multiplicación para reescribir la expresión como un polinomio en forma estándar.
15. (g + 4)(g − 4)
16. (10u + 5)(10u − 5)
En los problemas 17 a 20, usa la identidad (a + b)(a − b) = a2 − b2 para reescribir la expresión como un polinomio en forma estándar.
17. (m + 10)(m − 10)
18. (−h + 4)(−h − 4)
19. (2s + 12)(2s − 12)
20. (−5b + 1)(−5b − 1)
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 6 87 L ECCIÓN
© Great Minds PBC
Regresan los patos
21. Elige dos expresiones del problema El patrón creciente de patos de la lección 1 y verifica que sean equivalentes. Usa propiedades, identidades u operaciones para justificar tu razonamiento en cada paso.
A1 ▸ M1 ▸ TA ▸ Lección 6 EUREKA MATH2 88 L ECCIÓN
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic A, Lesson 6
Nombre Fecha
1. Halla el producto. Escribe tu respuesta en forma estándar.
(2t + 1)(2t − 1)
2. Escribe el polinomio (x − 4)2 en forma estándar.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 6 89
6 © Great Minds PBC
BOLETO DE SALIDA
Student Edition: Grade A1, Module 1, Topic A, Lesson 6
Nombre Fecha
Identidades polinomiales
En esta lección:
• multiplicamos polinomios;
• establecimos las identidades polinomiales (a + b)2 = a2 + 2ab + b2 y (a + b)(a − b) = a2 − b2 ;
• exploramos la utilidad de las identidades polinomiales.
Ejemplos
En los problemas 1 a 5, reescribe el polinomio en forma estándar.
1. (x + 2)2
()()()()
2. (m + 3)(m − 3)
Usa la identidad (a + b)(a − b) = a2 − b2 .
()()()()mm m m +− =− =− 333 9 22 2
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 6 91
2 .
Usa la identidad (a + b)2 = a2 + 2ab + b
() xx x xx xx += ++ =+ + =+ + 2222 ⋅ 224 44 222 2 2
RESUMEN 6 © Great Minds PBC
3. (3a − 4)(3a − 4)
Usa la identidad (a + b)2 = a2 + 2ab + b2 .
4. Usa la identidad (a + b)(a − b) = a2 − b2 . 66
El producto (3a − 4)(3a − 4) es equivalente a (3a − 4)2
Puedes aplicar la propiedad conmutativa de la multiplicación para reescribir el producto de la misma manera en que se escribe la identidad.
Expande (y − 8)2 primero.
Usa (a + b)2 = a2 + 2ab + b2
5. 7 + (y − 8)2 − 6y
7867288 222 + =+ + + ()()(())() yy yy
A1 ▸ M1 ▸ TA ▸ Lección 6 EUREKA MATH2 92 R ESUMEN
()()(())() () 343432344 921216 924 22 2 2 aa aa aa aa =+ + =+ + = + 16 ⋅
()
1 5 1 5 ()
()
666 36 36 1 5 1 5 21 5 2 1 25 2 1 25 2 + ()() = () () =− =− + ww w w w
+
ww
=+ + = ++ = + 6 716646 166764 2271 2 2 2 y yy y yy y yy ⋅ © Great Minds PBC
Student Edition: Grade A1, Module 1, Topic A, Lesson 6
Nombre
En los problemas 1 a 10, reescribe cada expresión como un polinomio en forma estándar.
EUREKA MATH2 A1 ▸ M1 ▸ TA ▸ Lección 6 93
1. (x + 3)(x + 3) 2. (h + 6)2 3. (8 + w)2 4. (p − 7)(p − 7) 5. (x − 5)2 6. x + () 1 3 2 7. (7x + 2)2 8. (8 − 3g)(8 − 3g) 9. 1 2 1 2 x + () 10. (0.7r − 1.1)2 11. Explica por qué (a + b)(a − b) = a2 − b2 se considera una identidad.
© Great Minds PBC
Fecha PRÁCTICA 6
12. La figura ABCD es un cuadrado. Escribe un polinomio en forma estándar para el área, donde x >− 4 3 3
13. Levi y Zara quieren hallar el producto (12 − d)2. Levi dice que la expresión (12 − d)2 es equivalente a 144 − d2. Zara dice que la expresión es equivalente a 144 + d2 .
a. ¿Quién está en lo correcto? Explica los errores que Levi y Zara pueden haber cometido.
b. Escribe el producto (12 − d)2 en forma estándar.
En los problemas 14 a 17, reescribe cada expresión como un polinomio en forma estándar.
A1 ▸ M1 ▸ TA ▸ Lección 6 EUREKA MATH2 94 P RÁCTICA
x +4 A BC D
14. (z + 1)(z − 1) 15. (4 + w)(4 − w) 16. (10 + 3a)(10 − 3a) 17. (1.2h − 0.6)(1.2h + 0.6) © Great Minds PBC
18. La figura IJKL es un rectángulo. Escribe un polinomio en forma estándar para el área, donde x > 10 7 .
7x –10
7x +10
19. KL es el radio del círculo. Escribe un polinomio en forma estándar para el área exacta del círculo, donde k > 1 9 .
9x –1
EUREKA MATH2 A1 ▸ M1 ▸TA ▸ Lección 6 95 P RÁCTICA
I K J L
K L © Great Minds PBC
20. Escribe un polinomio en forma estándar para el área del triángulo, donde x > 3.
En los problemas 21 a 25, reescribe cada expresión como un polinomio en forma estándar.
21. (6x + 3)2 + 20
23. −18k − 5k + (k + 5)2
22. 8x + (x − 1)2 − 8
25. 27c2 + (8c2 − 3)2 − 8
24. 8b2 − (4b + 6)(4b − 6) + 14
A1 ▸ M1 ▸ TA ▸ Lección 6 EUREKA MATH2 96 P RÁCTICA
–3
x +3 x
© Great Minds PBC
26. Escribe un polinomio en forma estándar para el volumen del prisma cuadrado, donde x > 3.
27. ¿Cuál es el grado del polinomio para el producto (ax3 + b)2, donde a y b son constantes y a ≠ 0?
Recuerda
En los problemas 28 y 29, evalúa.
EUREKA MATH2 A1 ▸ M1 ▸TA ▸ Lección 6 97 P RÁCTICA
x +3 x –3 x –3
28. 5 18 2 3 11 12 ÷ 29. − + () 7 8 1 4 3 4 © Great Minds PBC
En los problemas 30 y 31, halla la suma o la diferencia.
30. (−3p4 + 2p2 − 6p − 7) + (8p4 − 15p + 4)
31. (a3 − 6a2 − 4a + 10) − (−3a3 + 2a2 − 2)
32. ¿Qué enunciados pueden representarse mediante la desigualdad x >10? Elige todas las opciones que correspondan.
A. Hay más de 10 estudiantes en la clase.
B. La reunión durará al menos 10 minutos.
C. El valor de x es mayor que 10.
D. La donación mínima de la actividad para recaudar fondos es $10
E. El mayor valor de x es 10.
A1 ▸ M1 ▸ TA ▸ Lección 6 EUREKA MATH2 98 P RÁCTICA
© Great Minds PBC
Resolver ecuaciones y desigualdades de una variable
Edición para estudiantes: Grado A1, Módulo 1, Tema B
Los números buscan trabajo
En álgebra, cada enunciado es como un anuncio de empleo. Imagina que es un afiche matemático de REQUISITOS, donde se describe el papel a desempeñar y las cualificaciones necesarias. ¿Y quiénes se postulan?
Números, por supuesto.
A veces, todos los números se ajustan a la descripción. Estos trabajos son “identidades” y todos son contratados.

REQUISITOS:
2(x+3) = 2x+6


¡Cuántos candidatos calificados!




A veces, ningún número se ajusta a la descripción. Estos trabajos son imposibles, como requerir que se tengan 25 años o menos, con al menos 30 años de experiencia laboral.

REQUISITOS:
x+2 = x+3
Mmm... Creo que voy a tener que ofrecer un mejor salario.

Y a veces (de hecho, las más interesantes) ciertos números se ajustan a la descripción, y otros no. Estos anuncios son como los de los puestos de trabajo reales: selectivos, competitivos, interesantes de estudiar.

REQUISITOS:
x2 = 25
Felicitaciones. Están los dos contratados.



En todas las ciencias, buscamos números: el tamaño de una población, la concentración de una sustancia química, la velocidad de una montaña rusa. Aunque no sepamos qué número necesitamos, sabemos uno o dos datos al respecto. Ahí es donde entra en juego el álgebra: para describir las características del número y, luego, reclutar candidatos calificados.
Recuerda, la próxima vez que resuelvas una ecuación algebraica, tú serás la persona que contrata.
99 TEMA B
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 7
Nombre Fecha
Las imprentas
Lee el siguiente fragmento.
A principios del siglo XV, Johannes Gutenberg desarrolló la imprenta. Aunque los monjes chinos habían desarrollado una técnica de impresión alrededor del año 600 e. c., la tecnología no se usó ampliamente hasta que se inventó la imprenta de Gutenberg. Podía imprimir mucho más rápido que otras imprentas, lo que significaba que las personas que editaban podían producir más libros y folletos a un costo más bajo. Gracias a la imprenta de Gutenberg, ahora más personas podían permitirse comprar libros. Las nuevas ideas en ciencias y matemáticas se difundieron rápidamente.
Las imprentas
Un taller de impresión necesitaba imprimir el mismo número de ejemplares de una novela y de un libro de cocina. La novela tenía el doble de páginas que el libro de cocina. El primer día, todas las imprentas hicieron ejemplares de las novelas. El segundo día, las imprentas se dividieron en dos grupos de igual tamaño. El primer grupo continuó imprimiendo ejemplares de la novela. Terminaron al final del día. El segundo grupo imprimió ejemplares del libro de cocina. No terminaron al final del día. En su lugar, una imprenta trabajó durante dos días más para terminar de imprimir los ejemplares de los libros de cocina. Todas las imprentas imprimieron las páginas de ambos libros a la misma tasa constante. ¿Cuántas imprentas hay en el taller?
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 7 101
LECCIÓN LECCIÓN 7
© Great Minds PBC
Compartir ejemplos de trabajo
Registra tus notas y comentarios sobre los ejemplos de trabajo de la clase.
A1 ▸ M1 ▸ TB ▸ Lección 7 EUREKA MATH2 102 L ECCIÓN
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 7
Nombre Fecha
BOLETO DE SALIDA
Evan es 7 años menor que su hermana, Danna. La suma de sus edades es 37. Usa cualquier método para hallar sus edades.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 7 103
7
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 7
Nombre Fecha
Las imprentas
En esta lección:
RESUMEN 7
• resolvimos un problema al razonar cuantitativamente usando distintos métodos, como adivinar y comprobar o diagramas de cinta;
• resolvimos un problema de manera algebraica al crear una ecuación de una variable.
Ejemplo
En un partido de basquetbol, el número de boletos para personas adultas vendidos es 5 más que 2 veces el número de boletos para estudiantes vendidos. Se vende un total de 98 boletos. ¿Cuántos boletos para personas adultas se venden?
Resolver con un diagrama de cinta Número de boletos para estudiantes vendidos
Esta es una unidad. Representa el número de boletos para estudiantes vendidos.
de boletos para personas adultas vendidos
Dos unidades representan 2 veces el número de boletos para estudiantes vendidos.
Se venden 31 boletos para estudiantes.
Se venden 67 boletos para personas adultas.
=
98 − 31 = 67
Este es el número total de boletos vendidos.
Esta sección representa 5 boletos.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 7 105
Número
5 98
98 − 5 = 93 1unidad =
3unidades93 31
Great Minds PBC
©
Resolver de manera algebraica
Sea x el número de boletos para estudiantes vendidos. Entonces, 2x + 5 representa el número de boletos para personas adultas vendidos.
La suma del número de boletos para estudiantes vendidos y el número de boletos para personas adultas vendidos es el número total de boletos vendidos.
Se venden 31 boletos para estudiantes.
Sustituye x por 31 en 2x + 5 para hallar el número de boletos para personas adultas vendidos.
2315625 67 ()
Se venden 67 boletos para personas adultas.
A1 ▸ M1 ▸ TB ▸ Lección 7 EUREKA MATH2 106 R ESUMEN
xx x x x ++ = += = = ()2598 3598 393 31
+= + =
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 7
Nombre Fecha
PRÁCTICA
1 El más grande de dos números es 16 más que 3 veces el número más pequeño. La suma de los dos números es 62.
Lyla usó un diagrama de cinta para hallar los dos números. Halla el error en el trabajo de Lyla y corrígelo. Luego, halla los números.
Número más pequeño
Número más grande
16
62
2. Mason leyó 1 3 de su libro el lunes. El martes, leyó la mitad de las páginas restantes. El miércoles, leyó 54 páginas para terminar el libro. ¿Cuántas páginas tiene el libro de Mason? Usa un diagrama de cinta para resolver el problema.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 7 107
7
© Great Minds PBC
3. Una imprenta imprimirá un mismo número de libros de texto y novelas para completar un pedido.
a. Un libro de texto tiene 3 veces la cantidad de páginas que tiene una novela. Escribe expresiones para representar el número de páginas que tiene cada tipo de libro.
b. Si el pedido es de 2560 ejemplares de cada libro, escribe una expresión para el número total de páginas.
c. Se necesita imprimir un total de 1,925,120 páginas para completar el pedido. Usa tu expresión de la parte (b) para escribir y resolver una ecuación a fin de determinar el número de páginas que tiene cada libro.
A1 ▸ M1 ▸ TB ▸ Lección 7 EUREKA MATH2 108 P RÁCTICA
© Great Minds PBC
En los problemas 4 a 7, usa cualquier método para resolver.
4. Levi es 4 años mayor que el doble de la edad de su hermano menor. La suma de sus edades es 25. ¿Cuántos años tiene cada uno?
5. Tres multiplicado por la diferencia de un número y 5 es igual a la suma del número y 12. ¿Cuál es el número?
6. Danna, Evan y Mason combinan su dinero para comprar un regalo. Evan gasta $5.50 más que Danna. Danna gasta $3.00 menos que Mason. Gastan un total de $25. ¿Cuánto dinero gasta cada persona?
7. Ji-won y Emma escribieron el siguiente problema para la clase de Matemáticas. Resuelve el problema para ayudarles a crear la hoja de respuestas.
Ji-won tiene $68 y Emma tiene $18. ¿Cuánto dinero le tendrá que dar Ji-won a Emma de manera que Emma tenga cuatro veces la cantidad de dinero que tiene Ji-won?
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 7 109 P RÁCTICA
© Great Minds PBC
Recuerda
En los problemas 8 y 9, resuelve la ecuación.
10. Halla el producto. Escribe la respuesta en forma estándar.
(w + 4)(3w 7)
11. Escribe una desigualdad para cada oración de la tabla. Representa gráficamente el conjunto de soluciones de la desigualdad en la recta numérica. Oración Desigualdad Recta numérica Un
A1 ▸ M1 ▸ TB ▸ Lección 7 EUREKA MATH2 110 P RÁCTICA
2 5 4 += x 9. x 3 21=− .
8.
número x es menor que 20 025201510530 x Un número b es mayor que 5 025201510530 b Un número z es al menos 15. 025201510530 z © Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 8
Nombre Fecha
Conjuntos de soluciones para ecuaciones y desigualdades de una variable
En los problemas 1 a 18, determina si la oración es verdadera o falsa.
1. Estoy en la clase de Matemáticas.
2. El presidente de los Estados Unidos es un ciudadano de los Estados Unidos.
3. La presidenta de Francia también es la presidenta de México.
4. La Casa Blanca está en Washington D. C.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 8 111
8 LECCIÓN
5. 4 + 1 = 3 + 2 6. 3 + 2 = 4 − 9 7. 3 + 2 > 4 − 9 8. 1 2 5732()+= ⋅ © Great Minds PBC
A1 ▸ M1 ▸ TB ▸ Lección 8 EUREKA MATH2 112 L ECCIÓN 9. 4 3 1 3 5 3 += 10. 1 2 1 3 1 5 += 11. (7 + 9)2 = 162 12. (7 + 9)2 ≤ 162 13. (3 + 4)2 = 32 + 42 14. 32 + 42 = 72 15. 32 × 42 = 122 16. 32 × 43 = 126 17. π = 3.14 18. π > 3.14 © Great Minds PBC
Haz que sea verdadera
En los problemas 19 a 23, usa la ecuación o la desigualdad proporcionada para completar la tabla.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 8 113 L ECCIÓN
19. 3 + n = 4 − 9 Valor de n Oración numérica Verdadera ofalsa 0 1 © Great Minds PBC
A1 ▸ M1 ▸ TB ▸ Lección 8 EUREKA MATH2 114 L ECCIÓN 20. a2 = 25 Valor de a Oración numérica Verdadera ofalsa −5 0 1 5 21. 2(x − 6) = −12 + 2x Valor de x Oración numérica Verdadera ofalsa © Great Minds PBC
22. 3g = 2(g + 1) + g
Valor de g
Verdadera ofalsa ©
Oración numérica
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 8 115 L ECCIÓN
Great Minds PBC
A1 ▸ M1 ▸ TB ▸ Lección 8 EUREKA MATH2 116 L ECCIÓN 23. x + 1 ≥ 6 Valor de x Oración numérica Verdadera ofalsa −3 1 3 5 8 100 2 © Great Minds PBC
24. Resuelve la ecuación 3 + n = 4 − 9. Escribe el conjunto de soluciones usando la notación de conjuntos. Luego, representa gráficamente el conjunto de soluciones en la recta numérica.
Conjunto de soluciones:
25. Escribe el conjunto de soluciones de la ecuación usando la notación de conjuntos. Luego, representa gráficamente el conjunto de soluciones en la recta numérica.
a2 = 25
Conjunto de soluciones:
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 8 117 L ECCIÓN
© Great Minds PBC
Conjuntos de soluciones
Notación de conjuntos
Conjuntos infinitos
Conjuntos finitos
Conjuntos infinitos
Conjuntos finitos
Conjuntos infinitos {–5, 5} { a | a > 5}
Con palabras R epresentación gráfic a a = –5 o a =5 –5 05 a a > 5 a 05 10 e xtrem o a 05 10 e xtrem o e lementos (en orden creciente) lla ve s barra vertical se lee “tal que ”
Conjuntos finitos
a ≥ 5 ma yor que ma yor que o igual a
El conjunto de todos los números reales
Conjunto vacío
La ecuación 3 x = 3 x + 2 no tiene solución. –5 05 x a 2 = 25 tiene las soluciones 5 y –5 . a + 3 > 8 tiene como soluciones solo los valores de a que son ma yores qu e 5.
La ecuación 3 x + 2 = 3 x + 2 tiene infinitas soluciones que forman el conjunto de todos los números reales. –5 05 x {} ℝ
A1 ▸ M1 ▸ TB ▸ Lección 8 EUREKA MATH2 118 L ECCIÓN
© Great Minds PBC
Siempre verdadera y nunca verdadera
En los problemas 26 y 27, resuelve la ecuación. Escribe el conjunto de soluciones usando la notación de conjuntos. Luego, representa gráficamente el conjunto de soluciones en la recta numérica.
26. 2(x – 6) = –12 + 2x
Conjunto de soluciones:
27. 3g = 2(g + 1) + g
Conjunto de soluciones:
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 8 119 L ECCIÓN
Great Minds PBC
©
Desigualdad
En los problemas 28 y 29, resuelve la desigualdad. Escribe el conjunto de soluciones usando la notación de conjuntos. Luego, representa gráficamente el conjunto de soluciones en la recta numérica.
28. x + 1 ≥ 6
Conjunto de soluciones:
29. b – 6 < –3
Conjunto de soluciones:
A1 ▸ M1 ▸ TB ▸ Lección 8 EUREKA MATH2 120 L ECCIÓN
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 8
Nombre Fecha
BOLETO DE SALIDA
Resuelve cada ecuación o desigualdad. Escribe el conjunto de soluciones usando la notación de conjuntos y, luego, representa gráficamente el conjunto de soluciones en una recta numérica.
1. 8 + 2p = 2(p + 4)
2. 4 + x ≤ 7 ©
8
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 8 121
Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 8
Nombre Fecha
Conjuntos de soluciones para ecuaciones y desigualdades de una variable
En esta lección:
• determinamos si las ecuaciones y desigualdades son verdaderas para diferentes valores de la variable;
• representamos conjuntos de soluciones con palabras, usando la notación de conjuntos y mediante gráficas;
• resolvimos ecuaciones usando el cálculo mental.
Ejemplos
1. Escribe el conjunto de soluciones representado por la gráfica.
Vocabulario
Un elemento de un conjunto es cada una de las partes del conjunto.
Un conjunto vacío es un conjunto que no tiene elementos.
–1010 –8–7–9–6–5–4–3–2–10123456789 a {a | a ≤ 0}
El conjunto de soluciones de este problema es infinito; entonces, usamos la notación constructiva de conjuntos. Este conjunto de soluciones significa “el conjunto de todos los valores de a tales que a ≤ 0”.
2. Halla el valor de x que satisface la ecuación 9 + 3x = 6x. Escribe tu respuesta en notación de conjuntos. Resuelve el problema usando el cálculo mental.
Sé que 3x + 3x = 6x. Entonces, el 9 en el lado izquierdo de la ecuación debe ser igual a 3x.
Por lo tanto, x = 3. {3}
El conjunto de soluciones de este problema es finito; entonces, usamos la notación de conjuntos. Este conjunto de soluciones significa “el conjunto que consiste en el número 3”.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 8 123
8
© Great Minds PBC
RESUMEN
En los problemas 3 y 4, resuelve la ecuación usando el cálculo mental. Escribe el conjunto de soluciones y, luego, represéntalo gráficamente en una recta numérica.
3. 6x − 12 = 6(x − 12)
Puedo reescribir la ecuación como 6x − 12 = 6x − 72. Sé que 6x = 6x para todos los valores de x. Pero, como −12 no es igual a −72, no hay valores de x que hagan que la ecuación sea verdadera.
El conjunto de soluciones de este problema es el conjunto vacío. Esta notación significa “un conjunto sin elementos”.
–1010 –20123456789–4–1–6–3–8–5–9–7 x
4. 6x − 12 = 6(x − 2)
Una gráfica del conjunto vacío no muestra puntos ni sombreado.
Puedo reescribir la ecuación como 6x − 12 = 6x − 12. Todos los valores de x hacen que esta ecuación sea verdadera. ℝ
El conjunto de soluciones de este problema contiene cualquier valor de x. Esta notación significa “el conjunto de todos los números reales”.
–1010 –20123456789–4–1–6–3–8–5–9–7 x
Una gráfica del conjunto de todos los números reales muestra un sombreado en toda la recta numérica, incluidas las dos flechas.
A1 ▸ M1 ▸ TB ▸ Lección 8 EUREKA MATH2 124 R ESUMEN
{}
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 8
En los problemas 1 a 4, determina si la oración numérica es verdadera o falsa.
En los problemas 5 a 8, representa gráficamente el conjunto de soluciones. 5.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 8 125
8 Nombre Fecha PRÁCTICA
1. 18750 2 += 2. (24 + 16) ⋅ 5 = 24 + (16 ⋅ 5) 3. (5 + 4)2 = 52 + 42 4. 2 3 2 3 123−≥
3 4
Great Minds PBC
{8} 6. {}
7. ℝ ©
En los problemas 9 a 12, escribe el conjunto de soluciones representado por la gráfica. 9.
A1 ▸ M1 ▸ TB ▸ Lección 8 EUREKA MATH2 126 P RÁCTICA 8. xx < {} 1 2 |
0 x
p
n
© Great Minds PBC
–10–8–6–4–2024681
10.
–10–8–6–4–20246810 11.
q
–10–8–6–4–20246810 12.
–10–8–6–4–20246810
En los problemas 13 a 17, determina si la ecuación o la desigualdad es verdadera o falsa cuando x = 2
18. ¿Cuál es el conjunto de soluciones de una ecuación? Explica con tus palabras.
En los problemas 19 a 22, escribe una oración que interprete el conjunto de soluciones de la ecuación o la desigualdad.
19. 19 + x = 10; {−9}
21. c2 = 16; {−4, 4}
20. x − 3 = x − 5; {}
22. −6b + 4 < 10; {b | b > −1}
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 8 127 P RÁCTICA
13. 11 + 2x = 1 3x
+
1 − 3x
15. 3(x + 4) = 8(x + 1) − 3x 17. 8 − 3x + 4x
2 = 9 + 3x − 2(x + 1) 14. 11 + 2x ≥
16. 7x + 9 + 2x = 9(x + 1)
© Great Minds PBC
23. ¿Qué hace que una ecuación sea una identidad?
En los problemas 24 a 29, halla las soluciones de la ecuación. Escribe el conjunto de soluciones usando la notación de conjuntos. Intenta resolver el problema usando el cálculo mental.
En los problemas 30 a 32, resuelve la ecuación usando el cálculo mental. Escribe el conjunto de soluciones usando la notación de conjuntos. Luego, representa gráficamente el conjunto de soluciones en la recta numérica.
30. x2 = 36 31.
A1 ▸ M1 ▸ TB ▸ Lección 8 EUREKA MATH2 128 P RÁCTICA
24. x − 10.5 = 12 26. 3 416 = x 28. x2 = −9 25. 4x = 6 + 2x 27. 3 4 1 16 = + x 29. 3x + 5 = 6x + 5
5(x − 2) = 5x − 2
5(x − 2) = 5x − 10 © Great Minds PBC
32.
33. La ecuación A = l ⋅ a da el área de un rectángulo en unidades cuadradas con una longitud de l unidades y un ancho de a unidades.
a. Halla A cuando l = 10 y a = 15.5.
b. Halla l cuando A = 26 y a = 2.
c. Halla a cuando A = 9 y l = 1 2
En los problemas 34 a 39, halla la solución o las soluciones de la ecuación. Escribe tu respuesta usando la notación de conjuntos.
34. 3 − b + 8 = 16
36. 6b − (5 + 2b) = −5 + 4b
35. 8(b − 2) = 6b − 2 + 2b
37. 3b(b + 1) + 6 = 3(b2 + b + 2)
38. 24 10 2 5 b b + + =
39. b2 + 6b + 3 = b(b + 6)
40. Halla el valor de b si la ecuación b(y + 1) = 2(y + 1) es una identidad.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 8 129 P RÁCTICA
© Great Minds PBC
41. Crea una ecuación de una variable con una solución. Escribe el conjunto de soluciones usando la notación de conjuntos.
42. Corrige una expresión de la ecuación que creaste en el problema 41 de manera que el conjunto de soluciones de la nueva ecuación sean todos los números reales.
43. Corrige una expresión de la ecuación que creaste en el problema 41 de manera que la nueva ecuación no tenga solución.
Recuerda
En los problemas 44 y 45, resuelve la ecuación. 44.
46. Halla el producto. Escribe tu respuesta en forma estándar.
3)(2
En los problemas 47 y 48, resuelve la desigualdad.
A1 ▸ M1 ▸ TB ▸ Lección 8 EUREKA MATH2 130 P RÁCTICA
2 3 4 9 =− a
a +−() =− 1 4 3 8
45.
(n +
n2 − 3n + 4)
−13
47. x − 5 >
≤ 7 + x ≤ © Great Minds PBC
48. 2
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 9
Nombre Fecha
Resolver ecuaciones lineales de una variable
Dado que a, b y c son expresiones:
Si a = b, entonces a + c = b + c.
Si a = b, entonces ac = bc
En los problemas 1 a 3, identifica el conjunto de soluciones para cada ecuación. Usa las condiciones si... entonces al justificar cada paso de tu estrategia para hallar la solución. El problema 1 ya está empezado como ejemplo. Completa los enunciados.
1. 7345 x +=
7345
7 6 x x x +=
Conjunto de soluciones:
2. 54100 () v −=
Conjunto de soluciones:
3. 3 zz +=162 .
Conjunto de soluciones: ©
Si a = b, entonces a + c = b + c.
Si a = b, entonces
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 9 131
9 LECCIÓN
=
=
Great Minds PBC
Desarrollo de las propiedades
En los problemas 4 a 9, sin resolver, indica la propiedad o las propiedades que justifican por qué las dos ecuaciones deben tener el mismo conjunto de soluciones.
4. 5(v - 4) = 100 y (v - 4)5 = 100
5. 5(v - 4) = 100 y 5v - 20 = 100
6. 2[5(v - 4)] = 2(100) y (2 5)(v - 4) = 2(100)
7. v - 4 = 20 y 5(v - 4) = 100
8. v - 4 = 20 y v - 2 = 22
9. 5v - 20 = 100 y - 4 + v = 20
10. Aplica la propiedad de igualdad de la suma a la ecuación 1 − 9q = −19 para crear una ecuación con el mismo conjunto de soluciones.
11. Aplica la propiedad de igualdad de la multiplicación a la ecuación 1 − 9q = −19 para crear una ecuación con el mismo conjunto de soluciones.
A1 ▸ M1 ▸ TB ▸ Lección 9 EUREKA MATH2 132 L ECCIÓN
© Great Minds PBC
12. Considera la ecuación 3x = 3x + 2. Completa la tabla. Ecuación original Paso Ecuación resultante
Sumar −3x a ambos lados de la ecuación
Conjunto de soluciones de la ecuación resultante
Conjunto de soluciones de la ecuación original
3x = 3x + 2
Multiplicar ambos lados de la ecuación por un número diferente de cero
Multiplicar ambos lados de la ecuación por 0
Justificar los pasos
En los problemas 13 a 15, resuelve cada ecuación. Escribe la propiedad o la operación que usaste en cada paso. Escribe el conjunto de soluciones usando la notación de conjuntos.
13. 32 714 +=gg
Conjunto de soluciones: ©
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 9 133 L ECCIÓN
Great Minds PBC
14. 3x + 7 = 3 + 8x - 16
Conjunto de soluciones:
15. 6(2 + x) + 4x - 19 = - 18x - 3
Conjunto de soluciones:
A1 ▸ M1 ▸ TB ▸ Lección 9 EUREKA MATH2 134 L ECCIÓN
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 9
Nombre Fecha
BOLETO DE SALIDA
9
1. Resuelve la ecuación 2x − 3(x − 2) = 4x + 34. Indica la operación o la propiedad que usaste en cada paso y escribe el conjunto de soluciones usando la notación de conjuntos.
2. Sin resolver, explica por qué las ecuaciones 2 + 3x = 4x − 2 y 6x + 4 = 8x − 4 tienen el mismo conjunto de soluciones. Incluye referencias a las propiedades en tu respuesta.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 9 135
© Great Minds PBC
Resolver ecuaciones lineales de una variable
En esta lección:
• resolvimos ecuaciones lineales;
• verificamos que, con la excepción de multiplicar ambos lados de una ecuación por 0, aplicar las propiedades de la aritmética y la igualdad conserva el conjunto de soluciones de una ecuación;
• aplicamos las propiedades y las operaciones al justificar los pasos para resolver una ecuación.
Ejemplos
1. Explica por qué las ecuaciones −3(m − 5) = 8(m + 3) y −6(m − 5) = 48 + 16m tienen el mismo conjunto de soluciones.
Según la propiedad de igualdad de la multiplicación, puedo multiplicar ambos lados de la primera ecuación por 2. Esto conserva el conjunto de soluciones porque multipliqué por un número diferente de cero.
2 (−3(m − 5)) = 2 (8(m + 3))
Según la propiedad asociativa de la multiplicación, puedo reagrupar los factores. Esto conserva el conjunto de soluciones.
(())()()()
()() 235283 65163 =+ =+ mm mm ··
La propiedad asociativa de la multiplicación te indica que puedes reagrupar los factores para multiplicar primero 2 y −3.
Según la propiedad distributiva, puedo reescribir 16(m + 3) como 16m + 48. Esto conserva el conjunto de soluciones.
−6(m − 5) = 16m + 48 ©
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 9 137
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 9 9 Nombre Fecha RESUMEN
Great Minds PBC
Según la propiedad conmutativa de la suma, puedo reescribir 16m + 48 como 48 + 16m. El resultado es una ecuación que tiene el mismo conjunto de soluciones que la ecuación original.
−6(m − 5) = 48 + 16m
La ecuación original es
−3(m − 5) = 8(m + 3).
Las ecuaciones −3(m − 5) = 8(m + 3) y −6(m − 5) = 48 + 16m tienen el mismo conjunto de soluciones porque cada propiedad aplicada conserva el conjunto de soluciones.
En los problemas 2 a 4, halla el conjunto de soluciones. Indica la propiedad o la operación que usaste en cada paso.
2. 9x − 5 = 10x − 5
55 0 xx x x −= −= = {0}
95105
Propiedad de igualdad de la suma
Propiedad de igualdad de la suma
El conjunto de soluciones {0} significa que la ecuación es verdadera solo cuando x es igual a 0. El conjunto de soluciones {0} no es lo mismo que { }
3. 11x + 7(2 − x) − 8 = 4x + 6
1172846
11147846
1171
4846
4646 xx x xx x xx x xx +− −= + +− −= + −+ −= + += + ()
ℝ
Propiedad distributiva
Propiedad conmutativa de la suma
Suma de términos semejantes
Las expresiones resultantes son idénticas. Por lo tanto, los valores de las expresiones deben ser los mismos para todos los valores de x.
A1 ▸ M1 ▸ TB ▸ Lección 9 EUREKA MATH2 138 R ESUMEN
© Great Minds PBC
Propiedad de igualdad de la multiplicación
Multiplicación
Propiedad distributiva
Propiedad de igualdad de la suma
Propiedad de igualdad de la suma
Propiedad de igualdad de la multiplicación {−1}
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 9 139 R ESUMEN 4. x x = 2 3 451 24 () x x x x xx x = () = () −= −= 2 3 451 24 2 3 451 24 2424 82451 81620 () () ()() x x x x −= −= −= 4 16124 1212 1
© Great Minds PBC
En los problemas 1 a 4, escribe la propiedad o la operación que explica por qué las ecuaciones dadas tienen el mismo conjunto de soluciones. 1.
Sin resolver los problemas 5 y 6, explica por qué las dos ecuaciones tienen el mismo conjunto de soluciones. Incluye referencias a las propiedades en tu respuesta.
5. 3(a + 5) = −4a + 8 y 9(a + 5) = −12(a − 2)
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 9 141
Fecha
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 9 9 Nombre
PRÁCTICA
2x = 6 y 2x + 7 = 13
5y − 7y = 14 y −2y = 14
1 8 4 g = y 2g = 64 4. 3p − 8 = 21 y p −= 8 37
3.
2.
© Great Minds PBC
6.
7. En cada paso, escribe la propiedad o la operación que muestra por qué cada ecuación tiene el mismo conjunto de soluciones que la ecuación del paso anterior.
En los problemas 8 a 13, halla el conjunto de soluciones de la ecuación.
A1 ▸ M1 ▸ TB ▸ Lección 9 EUREKA MATH2 142 P RÁCTICA
3w +
w) + 2w
(8 + 6
= 180 y 11w = 172
9324834 93248244 92348244 111 xx x xx x xx x x −+ += −+ −+ += −+ +− += −+ += () 8 820 3120 321 7 x x x x += =− =−
4
− 9 = 5 9. 3m − 5 = 2(m + 6) − 17 + m 10. 32 618 += + xx 11. 52121023 2 ()xx xx +− =− () © Great Minds PBC
8.
x
En los problemas 14 y 15, resuelve la ecuación. Indica la propiedad o la operación que usaste en cada paso. Escribe el conjunto de soluciones usando la notación de conjuntos.
14. 5x + 7 = 4x + 7
15. 3(m − 2) = 5m + 4(2m + 1)
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 9 143 P RÁCTICA
xx++ = 6
238 20 ()
2 6 7 4 q q =
12.
5
13.
© Great Minds PBC
16. Nina y Ángel resolvieron una ecuación. Compararon sus estrategias para hallar la solución. Se proporcionan los pasos iniciales de cada estrategia.
a. Completa el trabajo de Nina y de Ángel. Escribe el conjunto de soluciones usando la notación de conjuntos.
b. Explica por qué Nina y Ángel obtendrán el mismo conjunto de soluciones. Usa las propiedades o las operaciones para justificar tu respuesta.
A1 ▸ M1 ▸ TB ▸ Lección 9 EUREKA MATH2 144 P RÁCTICA
Trabajo de Nina 1 5 4 5 3 5 1 5 3 5 4 5 3 5 3 ()xx x xx x += −+ + += −+ + Trabajo de Ángel 1 5 4 5 3 5 1 5 4 5 3 5 4 5 3 535 1355 () () () xx x xx x xx += ++ + () = ++ () += () + 3 5 5 + x
© Great Minds PBC
Recuerda
En los problemas 17 y 18, resuelve la ecuación.
17. 1.6 − m = 14.2
18. −5m = −22.5
19. Halla la diferencia. Escribe tu respuesta en forma estándar.
(5a + 2)2 −
(6a3 − 10a − 9)
En los problemas 20 y 21, resuelve la desigualdad.
20. −3x ≤ 42
21. x 2 5>− ©
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 9 145 P RÁCTICA
Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 10
Nombre Fecha
Algunos riesgos posibles al resolver ecuaciones (opcional)
Elevar ambos lados al cuadrado
1. Considera las ecuaciones x + 1 = 4 y (x + 1)2 = 16.
a. ¿Cuál es el conjunto de soluciones de x + 1 = 4? Explica.
b. ¿Cuál es el conjunto de soluciones de (x + 1)2 = 16? Explica.
c. Según tus resultados, ¿elevar ambos lados al cuadrado de una ecuación conserva el conjunto de soluciones de la ecuación original?
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 10 147
LECCIÓN
10
© Great Minds PBC
2. Considera las ecuaciones x − 2 = 0 y (x − 2)2 = 0.
a. ¿Cuáles son los conjuntos de soluciones de las dos ecuaciones?
b. Según tus resultados, ¿elevar ambos lados al cuadrado de una ecuación conserva el conjunto de soluciones de la ecuación original?
Propiedad de igualdad de la multiplicación
3. Considera la ecuación x − 3 = 5.
a. Multiplica ambos lados de la ecuación por una constante diferente de cero y verifica que el conjunto de soluciones de la nueva ecuación sea el mismo que el de la ecuación original.
b. Multiplica ambos lados de la ecuación por x y verifica que 8 es una solución de la nueva ecuación.
c. Demuestra que 0 también es una solución de la ecuación de la parte (b).
A1 ▸ M1 ▸ TB ▸ Lección 10 EUREKA MATH2 148 L ECCIÓN
© Great Minds PBC
d. Según tus resultados, ¿multiplicar ambos lados de una ecuación por una constante diferente de cero conserva el conjunto de soluciones de la ecuación original?
e. Según tus resultados, ¿multiplicar ambos lados de una ecuación por una expresión variable conserva el conjunto de soluciones de la ecuación original?
4. Halla el valor de x y, luego, comprueba la solución.
a. x xx 4 2 5 2 =
b. x xx + = 3 2 5 2
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 10 149 L ECCIÓN
© Great Minds PBC
5. Considera la ecuación x2 = 5x.
a. Ana multiplica ambos lados por 1 x para resolver la ecuación. ¿Qué solución obtiene? Verifica que sea una solución de la ecuación original.
b. Bahar dice que la ecuación en realidad tiene dos soluciones. ¿Cuál es la segunda solución de la ecuación?
6. Considera la ecuación (x − 1)(x − 5) = 2(x − 1).
a. El conjunto de soluciones de esta ecuación es {1, 7}. Demuestra que ambos números son soluciones de la ecuación.
b. Multiplicar ambos lados de la ecuación por 1 1 x - crea una nueva ecuación. ¿Qué valor no está incluido en el conjunto de soluciones de esta nueva ecuación?
c. Según tus resultados, ¿dividir ambos lados de una ecuación entre una expresión variable conserva el conjunto de soluciones de la ecuación original?
A1 ▸ M1 ▸ TB ▸ Lección 10 EUREKA MATH2 150 L ECCIÓN
⋅⋅
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 10
Nombre Fecha
BOLETO DE SALIDA
10
Considera la ecuación x + 3 = 10, que tiene el conjunto de soluciones {7}
En cada uno de los siguientes problemas, realiza la acción descrita en la ecuación x + 3 = 10 para crear una nueva ecuación. Luego, indica el conjunto de soluciones de la nueva ecuación.
1. Eleva ambos lados de la ecuación al cuadrado.
2. Multiplica ambos lados de la ecuación por x.
3. Suma x a ambos lados de la ecuación.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 10 151
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 10
Nombre Fecha
Algunos riesgos posibles al resolver ecuaciones
En esta lección:
• descubrimos que no todas las condiciones conservan el conjunto de soluciones al resolver una ecuación;
• exploramos condiciones conocidas que no garantizan que se conserve el conjunto de soluciones, como elevar ambos lados de una ecuación al cuadrado y multiplicar ambos lados de una ecuación por una expresión variable;
• descubrimos que ciertas condiciones al resolver una ecuación pueden dar como resultado una ecuación con un conjunto de soluciones diferente al de la ecuación original.
Ejemplos
1. Considera la ecuación 4x − 3 = x + 9.
a. Halla el conjunto de soluciones.
b. Demuestra que sumar x + 5 a ambos lados de la ecuación conserva el conjunto de soluciones.
Según la propiedad de igualdad de la suma, sumar una expresión variable a ambos lados de una ecuación conserva el conjunto de soluciones.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 10 153
10
RESUMEN
439 339 312 4 xx x x x −= + −= = = {4}
52214 3214 312 4 xx xx xx x x x −+ + () =+ ++() += + += = = {4}
43595
© Great Minds PBC
c. Demuestra que multiplicar ambos lados de la ecuación por x + 5 da como resultado una nueva ecuación con un conjunto de soluciones que también incluye el número −5
(4x − 3)(x + 5) = (x + 9)(x + 5)
Sustituyo x por −5 para verificar que −5 también es una solución.
Lado izquierdo: (4(−5) − 3)((−5) + 5) = (−23)(0) = 0
Lado derecho: ((−5) + 9)((−5) + 5) = (4)(0) = 0
2. Considera la ecuación 3x = x − 4.
a. Halla el conjunto de soluciones.
El conjunto de soluciones de la ecuación resultante es {−5, 4}. Entonces, multiplicar ambos lados de una ecuación por una expresión variable puede dar como resultado una nueva ecuación con un conjunto de soluciones diferente.
34
24 2 xx x x
{−2}
b. Eleva ambos lados de la ecuación al cuadrado. Demuestra que −2 es una solución de la ecuación resultante.
(3x)2 = (x − 4)2
Sustituyo x por −2 para verificar que −2 es una solución.
Lado izquierdo: (3(−2))2 = (−6)2 = 36
Lado derecho: ((−2) − 4)2 = (−6)2 = 36
c. Demuestra que 1 también es una solución de la ecuación resultante.
(3x)2 = (x − 4)2
Sustituyo x por 1 para verificar que 1 también es una solución.
Lado izquierdo: (3(1))2 = (3)2 = 9
Lado derecho: ((1) − 4)2 = (−3)2 = 9
El conjunto de soluciones de la ecuación resultante es {−2, 1} Entonces, elevar ambos lados de una ecuación al cuadrado puede dar como resultado una nueva ecuación con un conjunto de soluciones diferente.
A1 ▸ M1 ▸ TB ▸ Lección 10 EUREKA MATH2 154 R ESUMEN
=− =− =−
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 10
Nombre Fecha
PRÁCTICA
1. Considera la ecuación a = 3. Realiza la acción descrita en la ecuación para crear una nueva ecuación. Luego, indica el conjunto de soluciones de la nueva ecuación.
a. Eleva ambos lados de la ecuación al cuadrado.
b. Eleva ambos lados de la ecuación al cubo.
c. Multiplica ambos lados de la ecuación por a.
2. Considera la ecuación x + 4 = 3x + 2.
a. Halla el conjunto de soluciones.
b. Demuestra que sumar x − 4 a ambos lados de la ecuación crea una nueva ecuación con el mismo conjunto de soluciones.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 10 155
10
© Great Minds PBC
c. Demuestra que multiplicar ambos lados de la ecuación por x − 4 crea una nueva ecuación con un conjunto de soluciones diferente que incluye el número 4
3. Considera la ecuación x + 2 = 2x.
a. Halla el conjunto de soluciones.
b. Eleva ambos lados de la ecuación al cuadrado y verifica que tu solución satisface esta nueva ecuación.
c. Demuestra que2 3 también es una solución de la nueva ecuación.
A1 ▸ M1 ▸ TB ▸ Lección 10 EUREKA MATH2 156 P RÁCTICA
© Great Minds PBC
4. Considera la ecuación x(x − 3) = 5(x − 3).
a. Explica por qué es incorrecto dividir ambos lados entre x − 3 para hallar el valor de x.
b. ¿Cuál es el conjunto de soluciones de la ecuación?
En los problemas 5 a 7, halla el valor de x para resolver la ecuación.
5. 1 5 3 x =
6. x x = 5 5 3
7. x x = 5 5 1
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 10 157 P RÁCTICA
© Great Minds PBC
Recuerda
En los problemas 8 y 9, resuelve la ecuación. 8.
10. Halla la diferencia. Escribe tu respuesta en forma estándar.
(9y3 − 6y + 7) − (3y − 1)2
En los problemas 11 y 12, resuelve la desigualdad.
A1 ▸ M1 ▸ TB ▸ Lección 10 EUREKA MATH2 158 P RÁCTICA
−= 3 4 5 12 p 9. p − 4.7 =
−12.2
11. 5 − n > 35 12. −≤ 3 8 9 n © Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 11
Nombre Fecha
Escribir y resolver ecuaciones de una variable
Cuadrados de poliominó
Escribir y resolver ecuaciones
Escribe y resuelve una ecuación para resolver los problemas.
1. Ángel tiene $5.45 en quarters y dimes. Tiene 5 dimes menos que quarters. ¿Cuántas monedas de cada una tiene Ángel?
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 11 159
11 LECCIÓN
© Great Minds PBC
2. Dentro de dieciséis años, la edad de Tiah será el doble de la que tenía hace 12 años. ¿Cuál es la edad actual de Tiah, en años?
3. Bahar y Huan llenaron bolsas de palomitas de maíz para venderlas en un partido de beisbol.
• Huan llenó un 25 % más de bolsas de palomitas de maíz que Bahar.
• Después del partido, el 15 % del total combinado de sus bolsas no se había vendido.
• Cada bolsa se vendió a $0.75
• Bahar y Huan ganaron $114.75 por la venta de bolsas de palomitas de maíz.
¿Cuántas bolsas de palomitas de maíz llenó cada persona?
A1 ▸ M1 ▸ TB ▸ Lección 11 EUREKA MATH2 160 L ECCIÓN
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 11
Nombre Fecha
Nina vende boletos para la obra de teatro de la escuela. Los boletos para personas adultas cuestan $8 cada uno y los boletos para estudiantes cuestan $5 cada uno. Vende 15 boletos para estudiantes menos que boletos para personas adultas. Si el total de las ventas de boletos de Nina es $315, ¿cuántos boletos para estudiantes vende?
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 11 161
11
BOLETO DE SALIDA
© Great Minds PBC
Edición para estudiantes: 8.<superscript>o</superscript> grado, Módulo 1, Tema A, Lección 1
Nombre
Escribir y resolver ecuaciones de una variable
En esta lección:
• escribimos ecuaciones de una variable;
• usamos ecuaciones de una variable para resolver problemas.
Ejemplos
1. Un boliche tiene dos opciones de pago diferentes para jugar boliche:
• un costo de $5.75 por partida más una tarifa de alquiler de zapatos de $3.50 o
• una tasa fija por hora de $32.25 que incluye el alquiler de zapatos.
¿Cuántas partidas debe jugar una persona en una hora para que las dos opciones cuesten lo mismo?
Sea p el número de partidas.
5753503225
5752875 5 ... .. p p p += = =
Una persona debe jugar 5 partidas en una hora para que el costo sea el mismo.
2. La suma de la edad que tiene Ángel ahora y la edad que tiene su hermana ahora es 25. Hace tres años, la edad que tenía Ángel era 1 menos que 3 veces la edad que tenía su hermana en ese entonces. ¿Cuántos años tienen Ángel y su hermana ahora?
Sea e la edad que tiene Ángel ahora. Entonces, 25 − e representa la edad que tiene su hermana ahora. Además, e − 3 representa la edad que tenía Ángel hace 3 años y 22 − e representa la edad que tenía su hermana hace 3 años.
Edad que tenía Ángel hace 3 años
Hace tres años, la hermana de Ángel tenía (25 − e) −3, o 22 − e
Uno menos que 3 veces la edad que tenía su hermana en ese entonces
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 11 163
11
Fecha
RESUMEN
ee ee ee e 43 e e = () = = = = = 33221 36631 3653 65
17 46
8
© Great Minds PBC
Ángel tiene 17 años ahora.
Sustituyo e por 17 en 25 − e para hallar la edad que tiene su hermana ahora.
25 − (17) = 8
La hermana de Ángel tiene 8 años ahora.
A1 ▸ M1 ▸ TB ▸ Lección 11 EUREKA MATH2 164 R ESUMEN
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 11
1. El pentominó se puede colocar en la cuadrícula para cubrir un conjunto de números.
a. ¿Dónde se debería colocar el centro del pentominó de manera que la suma de los cinco números cubiertos sea 55? Escribe una oración numérica que verifique tu ubicación.
b. Escribe una expresión para representar la suma de cinco números cualesquiera cubiertos por el pentominó en la cuadrícula. Sea x el número cubierto por el centro del pentominó.
c. Usa tu expresión de la parte (b) para hallar x, el número cubierto por el centro del pentominó cuando la suma de los cinco números cubiertos es 75. Escribe una ecuación que verifique tu ubicación. 123456 789101112 131415161718 192021222324 252627282930
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 11 165
11
Nombre Fecha PRÁCTICA
© Great Minds PBC
d. Usa tu expresión de la parte (b) para hallar x, el número cubierto por el centro del pentominó cuando la suma de los cinco números cubiertos es 118. Escribe una ecuación que verifique tu ubicación.
2. Considera dos enteros. El primer entero es 3 más que el doble del segundo entero. Sumar 21 a cinco multiplicado por el segundo entero nos dará el primer entero. Halla los dos enteros.
3. La suma de la edad de un padre y la edad de su hijo es 53 años. En 9 años, la edad del padre será 8 años más que el doble de la edad de su hijo en ese entonces. Halla la edad actual de cada uno.
4. Una compañía de bajo costo que vende teléfonos celulares ofrece dos planes para enviar mensajes de texto.
• Opción A: Costo base de $10 más una tarifa de $0.10 por mensaje de texto enviado o recibido
• Opción B: Costo base de $25 y ninguna tarifa adicional por mensajes de texto enviados o recibidos
¿Cuántos mensajes de texto necesitaría enviar o recibir una persona para que los dos planes de servicio cuesten lo mismo?
A1 ▸ M1 ▸ TB ▸ Lección 11 EUREKA MATH2 166 P RÁCTICA
© Great Minds PBC
5. Ana vende camisetas y sudaderas para el equipo de futbol. El precio de una sudadera es $10 más que el precio de una camiseta. Vende 50 camisetas y 40 sudaderas por un total de $1480. ¿Cuál es el precio de una camiseta? ¿Cuál es el precio de una sudadera?
6. Un centro de rescate de mascotas crea un presupuesto mensual para alimentos. La cantidad de perros en el centro es dos tercios de la cantidad de gatos. Cada animal recibe 2 latas de alimento por día. El alimento para perros cuesta $0.68 por lata, mientras que el alimento para gatos cuesta $0.65 por lata. El centro de rescate ha presupuestado un total de $2581.80 para el alimento durante este mes de 30 días. ¿Cuántos perros hay en el centro de rescate?
Recuerda
En los problemas 7 y 8, resuelve la ecuación.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 11 167 P RÁCTICA
7. −6r + 8 = −28 8. 32 = 4 − 9r + 6r © Great Minds PBC
9. La edad del Sr. Wu es 7 años más que el doble de la edad de Ángel. La suma de sus edades es 79. ¿Cuántos años tiene Ángel?
10. ¿Qué ecuación representa correctamente el enunciado que establece que −30 está a 30 unidades de 0 en una recta numérica?
A. (−30) = 30
B. −30 = 30
C. |30| = −30
D. |−30| = 30
A1 ▸ M1 ▸ TB ▸ Lección 11 EUREKA MATH2 168 P RÁCTICA
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 12
Nombre Fecha
Reorganizar fórmulas
1. Se colocará una cerca alrededor de una porción rectangular de un parque para crear un patio de juegos. Una compañía de construcción donó un total de 117.5 pies de cerca. Según el espacio provisto para crear el patio de juegos, su longitud debe ser 35.5 pies. Usa la fórmula del perímetro de un rectángulo para determinar cuál debe ser el ancho del patio de juegos.
El ancho de cualquier rectángulo
2. Halla el valor de a para resolver la fórmula del perímetro P = 2(l + a).
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 12 169
12 LECCIÓN
© Great Minds PBC
Usar una fórmula para crear otra fórmula
3. La fórmula del área de un rectángulo es A = la, donde l representa la longitud y a representa el ancho.
a. Halla el valor de l
b. Halla el valor de a
4. Para hallar el volumen de un cilindro con radio r y altura h, usamos la fórmula V = πr2h
Halla el valor de la altura h para resolver la fórmula.
5. Ángel decidió memorizar tres fórmulas que relacionan la velocidad v, el desplazamiento d y el tiempo t recorrido por un objeto. v d t = t d v = d = vt
¿Necesita memorizar las tres fórmulas o puede memorizar solo una? Explica tu razonamiento.
A1 ▸ M1 ▸ TB ▸ Lección 12 EUREKA MATH2 170 L ECCIÓN
© Great Minds PBC
6. Dada una ecuación de una recta ax + by = c, halla el valor de y, donde b ≠ 0.
7. La fórmula del área de la superficie de un prisma rectangular con una base cuadrada es AS = 2a2 + 4ha, donde a representa la longitud del lado de la base cuadrada y h representa la altura del prisma. Halla el valor de h, donde a ≠ 0
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 12 171 L ECCIÓN
© Great Minds PBC

8. Si F representa la temperatura en grados Fahrenheit y C representa la misma temperatura en grados Celsius, entonces esta ecuación siempre es verdadera:
5F − 9C = 160.
Reescribe la fórmula de manera que sea más conveniente para las siguientes situaciones.
a. Una persona que viaja a los Estados Unidos procedente de un país que mide la temperatura en grados Celsius
b. Una persona que viaja desde los Estados Unidos a un país que mide la temperatura en grados Celsius
A1 ▸ M1 ▸ TB ▸ Lección 12 EUREKA MATH2 172 L ECCIÓN
© Great Minds PBC
c. ¿Por qué preferirían diferentes fórmulas las dos personas?
Números versus letras
En cada par de ecuaciones de los problemas 9 y 10, primero resuelve la ecuación que contiene más de una variable. Luego, resuelve la ecuación de una variable. Mientras trabajas, presta atención a las semejanzas y diferencias en cada paso de la resolución de las ecuaciones.
Ecuación que contiene más de una variable
9. Halla el valor de x para resolver ax + b = d − cx.
Ecuación relacionada de una variable
Halla el valor de x para resolver 3x + 4 = 6 − 5x.
10. Halla el valor de x para resolver
ax b cx d f += .
Halla el valor de x para resolver 2 57 3 xx+=
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 12 173 L ECCIÓN
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 12
Nombre Fecha
BOLETO DE SALIDA
12
La energía cinética Ec de un objeto depende de su masa m y su velocidad v. La fórmula de la energía cinética es mv = 1 2 2 Ec . Reorganiza la fórmula para escribir la masa m en términos de Ec y v, donde v ≠ 0
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 12 175
Great Minds PBC
©
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 12
Nombre Fecha
Reorganizar fórmulas
En esta lección:
• comparamos la resolución de ecuaciones con más de una variable y la resolución de ecuaciones con una variable;
• reorganizamos fórmulas para hallar el valor de una cantidad específica.
Ejemplos
1. Una fórmula del área de la superficie de un prisma rectangular con longitud l, ancho a y altura h es AS = 2la + 2(l + a)h. Las medidas están expresadas en pulgadas.
a. Halla la altura de un prisma rectangular cuando AS = 108, l = 6 y a = 4.
AS = 2la + 2(l + a)h
108264264
1084820
6020
La altura del prisma rectangular es 3 pulgadas.
Sustituye las variables por los valores conocidos en la fórmula. Luego, resuelve la ecuación.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 12 177
12
RESUMEN
=+ + =+ = =
h h h © Great Minds PBC
3
()()()h
b. Esta vez, comienza con la fórmula y reorganiza las variables para hallar el valor de h. Luego, sustituye las variables por los valores para hallar la altura de un prisma rectangular.
Recuerda que AS = 108, l = 6 y a = 4. Las medidas están expresadas en pulgadas.
En general, supón que las figuras como los prismas rectangulares tienen longitudes de lado positivas. Entonces, la posibilidad de dividir entre 0 no es algo que debe preocuparte en la fórmula reorganizada.
La altura del prisma rectangular es 3 pulgadas.
2. Halla el valor de n para resolver las ecuaciones.
Ecuación con una variable
La fórmula reorganizada es equivalente a la fórmula dada.
Obtenemos la misma respuesta independientemente de qué organización de la fórmula elijamos.
Ecuación relacionada con más de una variable
Aplica las mismas propiedades de igualdad para hallar el valor de n
3. Reescribe la ecuación en la forma pendiente-intersección: y = mx + b.
A1 ▸ M1 ▸ TB ▸ Lección 12 EUREKA MATH2 178 R ESUMEN
n = 6 10 4 n n n = −= = 6 10 4 640 46
na b c = donde b ≠ 0 na b c na bc nbca = −= =+
2 3 324 xy−= 2 3 2 3 2 9 324 324 8 xy yx yx −= −= −+ =−
() () () =
h
h h AS la l a =+ + + = + 22 22 2 − 2 108264 264 10848 20 60 20 3 + = = = =
() () h h h h
AS la la
AS la la
()
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 12
Nombre Fecha
1. La fórmula del perímetro de un rectángulo con longitud l y ancho a es P = 2(l + a)
a. Halla el ancho de un rectángulo cuando P = 92 y l = 13. Las medidas están expresadas en centímetros.
b. Usa la fórmula P = 2(l + a) para hallar el valor de a primero. Luego, sustituye las variables por los valores cuando P = 92 y l = 13.
2. La fórmula del volumen de un cilindro con radio r y altura h es V = πr2h
a. Halla la altura de un cilindro cuando r = 4 y V = 112π. El radio está medido en pulgadas y el volumen, en pulgadas cúbicas.
b. Usa la fórmula V= πr2h para hallar el valor de h primero. Luego, sustituye las variables por los valores cuando r = 4 y V = 112π para hallar la altura.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 12 179
12
PRÁCTICA
© Great Minds PBC
En los problemas 3 a 6, halla el valor de la variable que se indica para resolver la ecuación.
Ecuación con una variable
3. Halla el valor de m para resolver 32 5 = + m .
Ecuación relacionada con más de una variable
4. Halla el valor de m para resolver t mn s = + donde s ≠ 0.
5. Halla el valor de x para resolver 13 − 5x = 3x − 3
6. Halla el valor de x para resolver b − ax = cx − d
7. Usa los problemas 3 a 6 para comparar cada ecuación con una variable y su ecuación relacionada con más de una variable. Explica en qué se parecen y en qué se diferencian.
En los problemas 8 a 13, halla el valor de la variable que se indica para reescribir la fórmula.
8. La fórmula del perímetro de un cuadrado es P = 4l, donde l es la longitud de lado.
Halla el valor de l.
9. La fórmula de la circunferencia de un círculo con radio r es C = 2πr.
Halla el valor de r
A1 ▸ M1 ▸ TB ▸ Lección 12 EUREKA MATH2 180 P RÁCTICA
© Great Minds PBC
10. La fórmula de la fuerza de un objeto con masa m y aceleración a es F = ma.
Halla el valor de m.
11. La fórmula del perímetro de un triángulo con longitudes de lado a, b y c es P = a + b + c.
Halla el valor de b.
12. La fórmula del área de la superficie de un prisma es AS = 2B + ph, donde B representa el área de la base, p representa el perímetro de la base y h representa la altura del prisma.
Halla el valor de h.
13. La fórmula del área de un trapecio es .
Halla el valor de b
En los problemas 14 a 17, reescribe la ecuación en la forma pendiente-intersección, y = mx + b
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 12 181 P RÁCTICA
14. 2x + 4y = 8 16. 15. −3x + 7y = 14 17. 62 1 3 xy+= 3 4 520 xy−= h h a b Ah ab = () + 2 © Great Minds PBC
18. La fórmula usada para convertir la temperatura en grados Celsius a grados Fahrenheit es FC=+ 9 5 32
a. Reescribe esta fórmula para convertir la temperatura en grados Fahrenheit a grados Celsius.
b. Usa la fórmula de la parte (a) para convertir 72 grados Fahrenheit a grados Celsius.
19. Un granizado consiste en hielo aromatizado que llena un cono circular recto de papel y sobresale por la parte superior del cono en forma de hemisferio. El volumen de un granizado se estima con la fórmula
Vr hr=+ 1 3 2 3 23 ππ .
a. Halla el valor de h.
b. Usa la ecuación de la parte (a) para estimar la altura del cono circular recto de un granizado que tiene un volumen estimado de 17.08 pulgadas cúbicas y un diámetro de 3 pulgadas.
A1 ▸ M1 ▸ TB ▸ Lección 12 EUREKA MATH2 182 P RÁCTICA
© Great Minds PBC
h
20. ¿Cuándo es útil reorganizar una fórmula?
Recuerda
En los problemas 21 y 22, resuelve la ecuación.
21. 9 − 1.6t = −11
22. 4 3 2 9 2 tt−=
En los problemas 23 a 25, halla el valor de x para resolver la ecuación. Escribe el conjunto de soluciones usando la notación de conjuntos.
23. x2 = 36
25. x + 6 = x + 1
24. 2x + 5 = 5 + 2x
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 12 183 P RÁCTICA
© Great Minds PBC
26. Usa la recta numérica para responder las preguntas.
a. ¿Qué puntos, si hay alguno, corresponden a un número con un valor absoluto de 3? Explica.
b. ¿Qué puntos, si hay alguno, corresponden a un número con un valor absoluto que es mayor que 3? Explica.
c. ¿Qué puntos, si hay alguno, corresponden a un número con un valor absoluto de −7? Explica. –11–4 –1–9–8–7–6–50–3–2–103456129 78 AB
A1 ▸ M1 ▸ TB ▸ Lección 12 EUREKA MATH2 184 P RÁCTICA
© Great Minds PBC
CD EF
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 13
Nombre Fecha
Resolver desigualdades lineales de una variable
En los problemas 1 a 4, determina si el enunciado siempre, a veces o nunca es verdadero para cualquier valor de n. 1.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 13 185
13
LECCIÓN
3n + 1 > 3n + 5
3n + 8 > 3n + 5
4n − 12 > 3n + 5
1 2 38nn +> +
Great Minds PBC
2.
3.
4.
©
Identificar las propiedades de la desigualdad
Completa los enunciados en el organizador gráfico y proporciona ejemplos de cada propiedad.
Para los números reales
Multiplicación a, b y c :
Propiedades de la desigualdad
Para los números reales a, b y c : Si a b y c 0 , entonces > > Si a b y c 0 , entonces > <
Ejemplo
Suma
Para los números reales a, b y c : Si a > b , entonces
Ejemplo
Ejemplo
A1 ▸ M1 ▸ TB ▸ Lección 13 EUREKA MATH2 186 L ECCIÓN
© Great Minds PBC
Resolver desigualdades
En los problemas 5 a 9, halla el conjunto de soluciones de la desigualdad. Escribe el conjunto de soluciones usando la notación de conjuntos y, luego, representa gráficamente el conjunto de soluciones en una recta numérica.
5. 3(x − 4) > 18
Conjunto de soluciones:
6. 6 − 2x ≥ −4
Conjunto de soluciones:
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 13 187 L ECCIÓN
© Great Minds PBC
Conjunto de soluciones:
Conjunto de soluciones:
9. 2(x − 3) + x < 3(x + 4)
Conjunto de soluciones:
A1 ▸ M1 ▸ TB ▸ Lección 13 EUREKA MATH2 188 L ECCIÓN
2 3 1 3 5 3 3 gg −≥ +
7.
8. −6(x − 1) < 6 − 6x
© Great Minds PBC
10. Fin y Bahar resolvieron la desigualdad 8 − 5x > −10 en la clase de hoy. Hallaron diferentes conjuntos de soluciones.
a. ¿Qué conjunto de soluciones es correcto?
b. Usa las propiedades de la desigualdad para explicar el error.
Lograr la calificación deseada
11. Cada estudiante de la clase de Ciencias de Zara tendrá 5 calificaciones al final del periodo de evaluación. Zara se fija el objetivo de tener al menos un promedio de 90 durante el periodo de evaluación. Sus primeras cuatro calificaciones son 97, 85, 96 y 89. Escribe una desigualdad para hallar la calificación que necesita obtener Zara en su quinta evaluación para alcanzar su objetivo. Luego, resuelve la desigualdad.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 13 189 L ECCIÓN
de Fin 85 10 85 5105 81010105 18 5 18 5 1 5 1 5 18 5 > + > + +> + + > () > () > x xx x x x x x xx 18 5 > {} Trabajo de Bahar 8510 885108 518 51 18 5 1 5 18 5 −> >− −> () −> () > x x x x x ()() xx > {} 18 5
Trabajo
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 13
Nombre Fecha
BOLETO DE SALIDA
Halla el conjunto de soluciones de cada desigualdad. Escribe el conjunto de soluciones usando la notación de conjuntos y, luego, representa gráficamente el conjunto de soluciones en una recta numérica.
1. 6x − 5 < 7x + 4
2.
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 13 191
13
Great Minds PBC
10 − 3x ≤ −6(x − 2)
©
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 13
Nombre Fecha
Resolver desigualdades lineales de una variable
En esta lección:
• formalizamos las propiedades de desigualdad de la suma y la multiplicación;
• resolvimos desigualdades y representamos gráficamente los conjuntos de soluciones en rectas numéricas.
Ejemplos
1. Halla el conjunto de soluciones de la desigualdad 10 9w ≥ 28. Escribe el conjunto de soluciones usando la notación de conjuntos y, luego, representa gráficamente el conjunto de soluciones en una recta numérica.
Método 1:
1092
Invierte el signo de desigualdad al aplicar la propiedad de desigualdad de la multiplicación con un valor negativo.
Método 2: {w | w ≤ 2}
1092
Aplica la propiedad de desigualdad de la suma de manera que el coeficiente del término variable sea positivo. –1010
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 13 193
13
RESUMEN
2 −≥ −≥ ≤− w w w
8 918
10928
8 189 2 −≥ ≥+ −≥ −≥ w w w w
–6–3–8–5–9–7 w
Great Minds PBC
–20123456789–4–1
©
2. Un número es 5 menos que la mitad de otro número. Los números tienen una suma de como máximo 68. ¿Cuáles son los números más grandes que satisfacen estas condiciones?
La frase como máximo 68 indica que la suma de los números debe ser menor que o igual a 68
El número más grande que es menor que o igual a 42 es 42
Los números más grandes que satisfacen las condiciones dadas son 42 y 26.
A1 ▸ M1 ▸ TB ▸ Lección 13 EUREKA MATH2 194 R ESUMEN
n y
nn n n n +− ≤− −≤ ≤− ≤− 1 2 3 2 3 2 568 568 63 42 Sustituyo n por 42 en 1 25 n. 1 2 4252 ()1526 = −−=
Sean
1 25 n - los dos números.
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema B, Lección 13
Nombre Fecha
PRÁCTICA
En los problemas 1 y 2, representa gráficamente el conjunto de soluciones en la recta numérica.
1. {g | g > 4}
2. {m | 3 ≤ m}
En los problemas 3 a 5, escribe el conjunto de soluciones que representa la gráfica que se muestra en la recta numérica.
3. –6–3–5–4–1 –2 p 012345
4. n –6–3–5–4–1–25 01234
5. –10–8–9–7–5–6–4–3–2–1012345678910 h
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 13 195
13
Great Minds PBC
©
6. ¿Por qué es más útil representar gráficamente conjuntos de soluciones de desigualdades de una variable que representar gráficamente conjuntos de soluciones de ecuaciones de una variable?
En los problemas 7 a 10, coloca el signo de desigualdad correcto en el recuadro. Escribe la propiedad usada en cada caso.
7. Si y + 3 > 9, entonces y +−3393.
8. Si −2x ≤ 8, entonces2 2 x 8 2.
9. Si 17 3 > m , entonces 317 ()33m () .
10. Si −≤91 3 k , entonces 39() - 31 3 k ().
En los problemas 11 a 14, halla el conjunto de soluciones de la desigualdad. Escribe el conjunto de soluciones usando la notación de conjuntos y, luego, representa gráficamente el conjunto de soluciones en una recta numérica.
11. 2c > −9
Conjunto de soluciones:
12. h – 7 < 3
Conjunto de soluciones:
A1 ▸ M1 ▸ TB ▸ Lección 13 EUREKA MATH2 196 P RÁCTICA
© Great Minds PBC
13. 54 ≥ −6v
Conjunto de soluciones:
14. −≤93 4 f
Conjunto de soluciones:
15. Escribe y resuelve una desigualdad que represente el enunciado que establece que un número que aumenta 4 es mayor que 16
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 13 197 P RÁCTICA
© Great Minds PBC
En los problemas 16 a 18, halla el conjunto de soluciones de la desigualdad. Escribe el conjunto de soluciones usando la notación de conjuntos y, luego, representa gráficamente el conjunto de soluciones en una recta numérica.
16. –6b + 4 < 10
Conjunto de soluciones:
17. 2 5 1 4 2 u −>
Conjunto de soluciones:
18. 2(g – 8) > 2g – 16
Conjunto de soluciones:
19. Evan compra 3 yardas de tela que tiene el mismo precio por yarda. Necesita que le queden al menos $5 después de hacer la compra. Tiene un billete de $50. ¿Cuál es el precio máximo por yarda que puede pagar por la tela?
A1 ▸ M1 ▸ TB ▸ Lección 13 EUREKA MATH2 198 P RÁCTICA
© Great Minds PBC
En los problemas 20 a 22, halla el conjunto de soluciones de la desigualdad. Escribe el conjunto de soluciones usando la notación de conjuntos y, luego, representa gráficamente el conjunto de soluciones en una recta numérica.
20. 2g + (g + 5) ≥ 6g – 10
Conjunto de soluciones:
21. 3 5 1061 ()6 bb −≥
Conjunto de soluciones:
22. 2 5 2 3 49qq +<
Conjunto de soluciones:
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 13 199 P RÁCTICA
© Great Minds PBC
23. Un número es 8 más que el doble de otro número. Si los números tienen una suma de al menos −22, ¿cuál es el par de números más pequeño que cumple estas restricciones?
24. Doce más que cuatro multiplicado por un número es como máximo 42 más que el doble del número. Halla el conjunto de soluciones.
Recuerda
En los problemas 25 y 26, resuelve la ecuación.
25. −9n + 5n − 10 + 14n = 30
26. 1226 1 10 3 5 = nn
27. Escribe la propiedad o la operación que se usa en cada paso para resolver la ecuación
5(x + 4) + 6x = 11 − 3x. 546113 5206113
A1 ▸ M1 ▸ TB ▸ Lección 13 EUREKA MATH2 200 P RÁCTICA
14 ()xx
xx x xx x xx x ++ =− ++ =− ++ =− += + += =− =− 2011 149 9 14 x x © Great Minds PBC
5620113 1120113
x
28. La entrenadora de un equipo de futbol hizo un diagrama de puntos que muestra el número de goles anotados en cada partido de esta temporada.
Goles anotados en partidos de esta temporada
012345 6
Número de goles
a. ¿Cuántos partidos jugó el equipo de futbol esta temporada?
b. ¿En cuántos partidos de esta temporada anotó el equipo de futbol al menos 2 goles?
c. ¿Cuántos goles en total anotó el equipo esta temporada?
EUREKA MATH2 A1 ▸ M1 ▸ TB ▸ Lección 13 201 P RÁCTICA
© Great Minds PBC
Enunciados compuestos que incluyen ecuaciones y desigualdades de una variable
Edición para estudiantes: Grado A1, Módulo 1, Tema C
Astronomía de soluciones
¿Qué aspecto tienen las soluciones algebraicas?
Bueno, primero, ¿se parecen a algo? En cierto sentido, no. No son animales, ni planetas, ni frutas. Son números: sin color, sin pelo y sin rostro. No son en sí visuales.
Sin embargo, a las expertas y los expertos en matemáticas les encanta visualizarlas. Lo hacen con una recta numérica, que es una especie de pantalla de visualización matemática. En la recta numérica, los números aparecen como puntos. Se podría decir que la aritmética entra por nuestros ojos como lo hace la geometría.
Algunos conjuntos de soluciones (por ejemplo, para |x| = 2) forman puntos aislados, como estrellas en el cielo nocturno.



Otros (por ejemplo, para |x| ≤ 2) llenan regiones enteras, algo así como las estrellas de la Vía Láctea, que son tan numerosas que forman una mancha brillante a lo largo del cielo.



¿Qué pasa si hay más variables: y, z, y más allá? Entonces, las cosas se complican y las expertas y los expertos en matemáticas se entusiasman. Esta es la idea en la que se basa la geometría algebraica, una rama de las matemáticas avanzadas. Ha dado lugar a algunas imágenes asombrosas: primos lejanos de lo que vemos en nuestras rectas numéricas, que muestran cómo son los conjuntos de soluciones complicados. Son los cuásares, las nebulosas y los agujeros negros de las matemáticas, extrañas maravillas cósmicas que solo pueden ver los telescopios más avanzados.
203 TEMA C
-2 -1 0 1 2
-2 -1 0 1 2
© Great Minds PBC




Ahora, esta es la verdadera pregunta: ¿qué sabor tienen las soluciones algebraicas?
A1 ▸ M1 ▸ TC EUREKA MATH2 204
PRESENTACIÓN DEL TEMA © Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema C, Lección 14 LECCIÓN 14
Nombre Fecha
Conjuntos de soluciones de enunciados compuestos
En los problemas 1 a 4, usa una o más desigualdades para representar los requisitos de estatura de una persona sin acompañante para las atracciones del Parque Épico.
1. Montaña Rusa de la Oruga
2. Circuito Moebius
3. Río Salvaje
4. Montaña Rusa Little Dipper
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 14 205
© Great Minds PBC
Determinar la verdad
En los problemas 5 a 13, determina si el enunciado es verdadero o falso.
5. En este momento, estoy en la clase de Matemáticas y en la clase de Español.
6. En este momento, estoy en la clase de Matemáticas o en la clase de Español.
7. El hielo es frío y el fuego es caliente.
8. El hielo es frío o el fuego es caliente.
Un enunciado es una oración que es verdadera o falsa, pero no ambas a la vez.
Un enunciado compuesto consiste en dos o más enunciados conectados por modificadores lógicos, como y u o.
A1 ▸ M1 ▸ TC ▸ Lección 14 EUREKA MATH2 206 L ECCIÓN
© Great Minds PBC
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 14 207 L ECCIÓN 9. 3 + 5 = 8 y 5 < 7 − 1 10. 10 + 2 ≠ 12 y 8 − 3 > 0 11. 3 < 5 + 4 o 6 + 3 = 9 12. 16 20 > 1 o 5.5 + 4.5 = 11 13. 16 + 20 > 1 o 5.5 + 4.5 = 11 © Great Minds PBC
Representar conjuntos de soluciones gráficamente
En los problemas 14 a 16, resuelve cada enunciado compuesto. Escribe el conjunto de soluciones usando la notación de conjuntos. Luego, representa gráficamente el conjunto de soluciones en la recta numérica dada.
14. y + 8 = 3 o y 6 = 2
15. d 6 = 1 y d + 2 = 9
16. 2w 8 = 10 y w > 9
A1 ▸ M1 ▸ TC ▸ Lección 14 EUREKA MATH2 208 L ECCIÓN
© Great Minds PBC
17.
a. Con un lápiz de color, representa gráficamente la desigualdad x < 3.
b. Con un lápiz de color diferente, representa gráficamente la desigualdad x > −1.
c. Con un tercer lápiz de otro color, oscurece la sección de la recta numérica donde x < 3 y x > −1.
d. Escribe el conjunto de soluciones usando la notación de conjuntos.
e. ¿Cuántas soluciones tiene esta desigualdad compuesta? Explica.
f. ¿Hay una forma más eficiente de escribir este enunciado?
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 14 209 L ECCIÓN
x < 3 y x > −1
© Great Minds PBC
En los problemas 18 a 21, escribe el conjunto de soluciones del enunciado compuesto usando la notación de conjuntos. Luego, representa gráficamente las soluciones en la recta numérica.
18. f > 4 o f ≤ 0
19. g > −2 o g = −2
20. m > 2 o m > 6
21. x ≥ −5 o x ≤ 2
A1 ▸ M1 ▸ TC ▸ Lección 14 EUREKA MATH2 210 L ECCIÓN
© Great Minds PBC
En los problemas 22 y 23, reescribe como un enunciado compuesto conectado por y u o. Representa gráficamente el conjunto de soluciones en la recta numérica.
22. x ≤ 4
23. 1 < d < 3
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 14 211 L ECCIÓN
© Great Minds PBC
Aplicar nuestros conocimientos
24. Cada estudiante tiene que presentar un discurso en la clase de Español. Las normas establecen que el discurso debe durar al menos 7 minutos, pero no debe exceder los 12 minutos. Escribe una desigualdad compuesta para las posibles duraciones del discurso.
25. El elemento mercurio tiene un punto de congelación de −37.9 °F y un punto de ebullición de 673.9 °F. Es un líquido entre estas temperaturas. Escribe una desigualdad compuesta para las temperaturas a las que el mercurio es un líquido.
26. La temperatura interna de un filete cocinado debe ser de al menos 145 °F cuando está caliente o inferior a 40 °F cuando está refrigerado. A cualquier otra temperatura, las bacterias pueden crecer y hacer que el filete no sea seguro para comer. Escribe una desigualdad compuesta para la temperatura interna de un filete cocinado que sea seguro para comer.
A1 ▸ M1 ▸ TC ▸ Lección 14 EUREKA MATH2 212 L ECCIÓN
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema C, Lección 14
Nombre Fecha
1. Empareja cada enunciado compuesto con la gráfica de su conjunto de soluciones en la recta numérica.
a. x = 5 o x = −10
b. x < 5 y x > −10
c. x > 5 o x < −10
d. x ≥ 5 o x ≤ −10
e. x ≤ 5 y x ≥ −10
0510
f. El intervalo aceptable de niveles de cloro en las piscinas es de al menos 1 parte por millón y no más de 3 partes por millón. Escribe una desigualdad compuesta para el rango aceptable de niveles de cloro en una piscina.
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 14 213
–15–10–5 x 0510 –15–10–5 x 0510 –15–10–5 x 0510 –15–10–5 x
–15–10–5 x
0510
14 © Great Minds PBC
BOLETO DE SALIDA
Edición para estudiantes: Grado A1, Módulo 1, Tema C, Lección 14
Nombre Fecha
Conjuntos de soluciones de enunciados compuestos
En esta lección:
• describimos conjuntos de soluciones de dos ecuaciones o dos desigualdades unidas por y u o;
• representamos gráficamente conjuntos de soluciones de dos ecuaciones o dos desigualdades unidas por y u o en una recta numérica;
• escribimos enunciados compuestos para describir contextos.
Ejemplos
Vocabulario
Un enunciado es una oración que es verdadera o falsa, pero no ambas a la vez.
Un enunciado compuesto consiste en dos o más enunciados conectados por modificadores lógicos, como y u o.
En los problemas 1 a 3, representa gráficamente el conjunto de soluciones del enunciado compuesto.
1.
La palabra de conexión es o. Las soluciones deben hacer que sea verdadera al menos una parte del enunciado compuesto.
La gráfica del conjunto de soluciones consiste en ambas regiones.
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 14 215
x + 1 = 3 o x − 2 = 5
–10–2–9–8–7–6–5–4–3–110
x 8 012345679
2. w > 5 o w < −4
–10–2–9–8–7–6–5–4–3–110
w 8
012345679
14
Great Minds PBC
RESUMEN
©
3. c ≥ −7 y c ≤ 2
La palabra de conexión es y. Las soluciones deben hacer que sean verdaderas ambas partes del enunciado compuesto.
–10–2–9–8–7–6–5–4–3–110 c 8 012345679
La gráfica del conjunto de soluciones está donde las gráficas de c ≥ −7 y c ≤ 2 se superponen.
4. Escribe una desigualdad compuesta para la gráfica.
–10–2–9–8–7–6–5–4–3–110 m 8 012345679
−4 ≤ m ≤ 6
Otra forma de escribir esta desigualdad compuesta es m ≥ −4 y m ≤ 6.
5. Considera la desigualdad compuesta −5 < x ≤ 5.
a. Reescribe como un enunciado compuesto separado por y u o. x > −5 y x ≤ 5
b. Representa gráficamente la desigualdad compuesta.
–10–2–9–8–7–6–5–4–3–110 x 8 012345679
c. ¿Cuántas soluciones tiene la desigualdad compuesta?
La desigualdad compuesta tiene infinitas soluciones.
6. Escribe una desigualdad compuesta para representar la situación.
Se espera que la reparación del auto cueste al menos $100, pero no más de $150.
Sea r el costo de la reparación del auto en dólares.
100 ≤ r ≤ 150
Las frases al menos y no más de indican que la desigualdad debe incluir los valores
100 y 150.
A1 ▸ M1 ▸ TC ▸ Lección 14 EUREKA MATH2 216 R ESUMEN
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema C, Lección 14
Nombre Fecha
En los problemas 1 a 6, escribe si el enunciado compuesto es verdadero o falso.
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 14 217
1. 6 + 1 = 7 y 8 − 6
2 2. 5 > 3 o 7 < 1 3. 3 ⋅ 4 = 12 y 1 2 74 = ⋅ 4. 9 ⋅ 1 < 22 o 21 3 6 > 5. 1 3 93⋅≠ y 0.2 ⋅ 10 > 5 6. 4 − 10 > 6 o 1 4 163 ≤ ⋅
=
PRÁCTICA 14 © Great Minds PBC
En los problemas 7 a 16, representa gráficamente el conjunto de soluciones del enunciado en la recta numérica dada.
7. x = −2 o x = 8
8. w> 5
9. g ≤ 2
10. k > 5 o k < 2
11. m ≤ −8 o m ≥ −1
A1 ▸ M1 ▸ TC ▸ Lección 14 EUREKA MATH2 218 P RÁCTICA
© Great Minds PBC
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 14 219 P RÁCTICA 12. d < 9 y d > 7 13. v > −3 y v < 5 14. c £ 3 4 o c > 1 2 15. q ≤−21 4 o q ³ 21 4
x = −2 y x = 8 © Great Minds PBC
16.
En los problemas 17 y 18, escribe una desigualdad compuesta para cada gráfica.
17. b
18. p
19. Considera la desigualdad compuesta 0 < x < 3.
a. Reescribe la desigualdad compuesta como un enunciado compuesto conectado por y u o.
b. Representa gráficamente la desigualdad compuesta en una recta numérica.
c. ¿Cuántas soluciones tiene la desigualdad compuesta?
20. Considera la desigualdad compuesta −1.75 ≤ u < 4.
a. Reescribe la desigualdad compuesta como un enunciado compuesto conectado por y u o
b. Representa gráficamente la desigualdad compuesta en una recta numérica.
A1 ▸ M1 ▸ TC ▸ Lección 14 EUREKA MATH2 220 P RÁCTICA
–10–6–5–9–8–7–4–3–2–1021436589710
–10–6–5–9–8–7–4–3–2–1021436589710
© Great Minds PBC
21. Considera la desigualdad n ≤ 6.
a. Reescribe la desigualdad como un enunciado compuesto conectado por y u o.
b. Representa gráficamente la desigualdad en una recta numérica.
En los problemas 22 a 26, escribe una desigualdad simple o compuesta para la situación.
22. Las puntuaciones del último examen variaron de 65 % a 100 %.
23. Para subir a la montaña rusa, una persona debe medir al menos 48 pulgadas.
24. Las temperaturas corporales peligrosas son aquellas que son inferiores a 96 °F o superiores a 104 °F.
25. Para que un tiburón sobreviva en un acuario, el agua de su pecera debe tener al menos 18 °C y no más de 22 °C.
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 14 221 P RÁCTICA
© Great Minds PBC
26. Los niños, las niñas y las personas mayores reciben un descuento en las entradas del cine. El descuento se aplica a los niños y las niñas de 2 a 12 años y a los adultos de 60 años o más.
27. Considera los siguientes enunciados compuestos.
x < 1 y x > −1
x < 1 o x > −1
¿Cambiar la palabra y por o cambia el conjunto de soluciones? Explica y representa gráficamente las soluciones de ambos enunciados.
A1 ▸ M1 ▸ TC ▸ Lección 14 EUREKA MATH2 222 P RÁCTICA
© Great Minds PBC
Recuerda
En los problemas 28 y 29, resuelve la ecuación.
28. 3(x + 5) = −18
29. 7 = −4(2x − 1)
En los problemas 30 y 31, escribe el polinomio en forma estándar.
30. (a − 6)2
31. (m − 9)(m + 9)
32. Los datos muestran las alturas en centímetros de los saltos verticales de 18 jóvenes de un equipo de basquetbol.
Haz un diagrama de puntos con los datos.
Medidas de salto vertical
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 14 223 P RÁCTICA
13 15 17 13 15 18 15 15 14 13 15 15 13 16 14 15 13 13
10 11 12 13 14 15 16 17 18 19 20
Salto vertical (pulgadas)
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema C, Lección 15 LECCIÓN 15
Nombre Fecha
Resolver y representar gráficamente desigualdades compuestas Extremos
¿Cuál es mi entero?
En los problemas 1 a 4, halla el conjunto de soluciones de la desigualdad compuesta.
1. 2x + 1 < −3 o 2x + 1 ≥ 9
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 15 225
© Great Minds PBC
A1 ▸ M1 ▸ TC ▸ Lección 15 EUREKA MATH2 226 L ECCIÓN
−21 < 3(x −2) < 12
−+ < x 5 2 3 o −+ > x 5 2 4
−≤ −≤ 42 1 3 xx © Great Minds PBC
2.
3.
4.
Resuelve cada desigualdad compuesta. Escribe el conjunto de soluciones usando la notación de conjuntos. Luego, representa gráficamente el conjunto de soluciones en la recta numérica.
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 15 227
1. 9 + 2x > 15 o 7 + 4x < −9 2. 611 2 ££ x
Grado A1, Módulo 1, Tema C, Lección 15 Nombre Fecha
DE SALIDA 15 © Great Minds PBC
Edición para estudiantes:
BOLETO
Edición para estudiantes: Grado A1, Módulo 1, Tema C, Lección 15
Nombre Fecha
Resolver y representar gráficamente desigualdades compuestas
En esta lección:
• hallamos conjuntos de soluciones de desigualdades compuestas;
• representamos gráficamente conjuntos de soluciones de desigualdades compuestas.
Ejemplos
En los problemas 1 y 2, halla el conjunto de soluciones de la desigualdad compuesta. Escribe el conjunto de soluciones en notación de conjuntos. Luego, representa gráficamente el conjunto de soluciones en la recta numérica.
Resuelve cada parte de la desigualdad compuesta de manera individual.
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 15 229
5283 5103 210 5 xx xx x x −> + >+ > > 523 22 1 −> −> < x x x {x | x < 1 o x > 5}
1. 5x − 2 > 8 + 3x o 5 − 2x > 3
–10–2–9–8–7–6–5–4–3–110 x 8 012345679
RESUMEN 15
© Great Minds PBC
Reescribe como un enunciado compuesto usando y
{w | −8 ≤ w ≤ 6}
La notación −8 ≤ w ≤ 6 significa que w ≥ −8 y w ≤ 6
A1 ▸ M1 ▸ TC ▸ Lección 15 EUREKA MATH2 230 R ESUMEN
158 1 2 ≤+ ≤ w 1 2 51 w +≥ y 1 2 58 w +≤ 1 2 1 2 51 4 8 w w w +≥ ≥− ≥− 1 2 1 2 58 3 6 w w w +≤ ≤ ≤
2.
–10–2–9–8–7–6–5–4–3–110 w 8 012345679
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema C, Lección 15
Nombre
Fecha
En los problemas 1 a 4, elige las palabras y u o para la desigualdad compuesta, de manera que el conjunto de soluciones no sea ni el conjunto vacío ni el conjunto de todos los números reales.
1. x > −2 x < 12
3.
En los problemas 5 a 7, escribe cada desigualdad compuesta como un enunciado sin la palabra y. Luego, escribe una oración que describa todos los valores posibles de x.
5. x > −6 y x < −1
6. x ≤ 5 y x > 0
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 15 231
2. x > 4 x < −1
x
+ 1 > 3 x + 1 < −3
><
4. 1 3 1 3 04xx
15 © Great Minds PBC
PRÁCTICA
7. x ³ 1 2 y x < 1
En los problemas 8 a 10, halla el conjunto de soluciones de cada desigualdad compuesta. Escribe el conjunto de soluciones usando la notación de conjuntos. Luego, representa gráficamente el conjunto de soluciones en la recta numérica.
8. x − 2 < 6 o x 3 4 >
9. 5y + 2 ≥ 27 y 3y − 1 < 29
10. 2w > 8 o −2w < 4
A1 ▸ M1 ▸ TC ▸ Lección 15 EUREKA MATH2 232 P RÁCTICA
© Great Minds PBC
11. Considera la desigualdad compuesta 4p + 8 > 2p − 10 o 1 3 32 p −< .
a. Halla el conjunto de soluciones. Escribe el conjunto de soluciones usando la notación de conjuntos. Luego, representa gráficamente el conjunto de soluciones en la recta numérica.
b. Si las desigualdades están unidas por y en lugar de o, ¿cuál es el conjunto de soluciones?
Representa gráficamente el conjunto de soluciones en la recta numérica.
4p + 8 > 2p – 10 y 1 3 32 p −<
12. Considera la desigualdad compuesta 7 − 3x < 16 y x + 12 < −8
a. Halla el conjunto de soluciones. Escribe el conjunto de soluciones usando la notación de conjuntos. Luego, representa gráficamente el conjunto de soluciones en la recta numérica.
b. Si las desigualdades están unidas por o en lugar de y, ¿cuál es el conjunto de soluciones?
Representa gráficamente el conjunto de soluciones en la recta numérica.
7 − 3x < 16 o x + 12 < −8
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 15 233 P RÁCTICA
© Great Minds PBC
13. Considera la desigualdad compuesta −1 < g − 6 < 1.
a. Reescribe la desigualdad compuesta como un enunciado compuesto.
b. Halla el valor de g para resolver cada desigualdad de la parte (a).
c. Escribe el conjunto de soluciones usando la notación de conjuntos.
d. Representa gráficamente el conjunto de soluciones en la recta numérica.
A1 ▸ M1 ▸ TC ▸ Lección 15 EUREKA MATH2 234 P RÁCTICA
© Great Minds PBC
14. Considera la desigualdad compuesta −< ≤ 13 2 h .
a. Reescribe la desigualdad compuesta como un enunciado compuesto.
b. Halla el valor de h para resolver cada desigualdad de la parte (a).
c. Escribe el conjunto de soluciones usando la notación de conjuntos.
d. Representa gráficamente el conjunto de soluciones en la recta numérica.
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 15 235 P RÁCTICA
© Great Minds PBC
En los problemas 15 a 17, resuelve la desigualdad compuesta. Luego, representa gráficamente el conjunto de soluciones en la recta numérica.
15. 0 ≤ 4x − 3 ≤ 11
16. −8 ≤ −2(x − 9) ≤ 8
17. −< < + 63 1 4 x
A1 ▸ M1 ▸ TC ▸ Lección 15 EUREKA MATH2 236 P RÁCTICA
© Great Minds PBC
Recuerda
En los problemas 18 y 19, resuelve la ecuación.
18. 2 3 6912−+ () =− r
19. −+() = 5215 10 r
20. Sin resolver, usa las propiedades para explicar por qué las ecuaciones 5x + 6 = 3 − 4x y 18 + 15x = 9 − 12x tienen el mismo conjunto de soluciones.
21. Emma hizo una encuesta entre estudiantes de su clase y anotó el número de estados que cada estudiante ha visitado. Los números de estados visitados son 3, 8, 7, 6, 5, 4, 4, 5, 6, 4 y 5.
a. Halla la media del número de estados visitados por estudiantes de la clase de Emma. Redondea al décimo más cercano.
b. Halla la mediana del número de estados visitados por estudiantes de la clase de Emma.
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 15 237 P RÁCTICA
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema C, Lección 16
Nombre Fecha
Resolver ecuaciones de valor absoluto
Ecuaciones de valor absoluto
En los problemas 1 a 5, escribe la ecuación como un enunciado compuesto, si corresponde. Usa el enunciado compuesto para hallar el conjunto de soluciones. Comprueba tus soluciones en la ecuación original. Luego, representa gráficamente el conjunto de soluciones en la recta numérica dada.
1.|
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 16 239
x| = 5
2.|x| = −5
LECCIÓN 16
© Great Minds PBC
A1 ▸ M1 ▸ TC ▸ Lección 16 EUREKA MATH2 240 L ECCIÓN 3.|k − 2| = 7 4.|4y + 2| = 3 © Great Minds PBC
Una ecuación de valor absoluto es una ecuación de la forma, o equivalente a la forma, |bx − c| = d, donde b, c y d son números reales. La ecuación |bx − c| = d significa que bx − c es una distancia de d unidades desde 0 para algún valor o algunos valores de x y puede interpretarse mediante el enunciado compuesto bx − c = d o −(bx − c) = d.
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 16 241 L ECCIÓN 5.|2x − 3| = 0
© Great Minds PBC
Algo más que el valor absoluto
En los problemas 6 a 10, resuelve la ecuación. Escribe el conjunto de soluciones usando la notación de conjuntos.
6. |b − 5| + 2 = 10
7. 14 = 3 + |m + 6|
A1 ▸ M1 ▸ TC ▸ Lección 16 EUREKA MATH2 242 L ECCIÓN
© Great Minds PBC
8. 36 = 4|2 − h
9. −2|6x − 8| = −40 ©
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 16 243 L ECCIÓN
|
Great Minds PBC
A1 ▸ M1 ▸ TC ▸ Lección 16 EUREKA MATH2 244 L ECCIÓN 10. 8 + 2|3w + 8| = 4 © Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema C, Lección 16
Nombre Fecha
Considera la ecuación |2x + 5| = 3
a. Reescribe la ecuación como un enunciado compuesto.
b. Usa el enunciado compuesto para hallar el conjunto de soluciones de la ecuación original.
c. Usa la ecuación original para verificar las soluciones que hallaste en la parte (b).
d. Explica por qué la ecuación |2x + 5| = −3 no tiene solución.
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 16 245
© Great Minds PBC
BOLETO DE SALIDA 16
Edición para estudiantes: Grado A1, Módulo 1, Tema C, Lección 16
Nombre Fecha
RESUMEN
Resolver ecuaciones de valor absoluto
En esta lección:
• escribimos ecuaciones de valor absoluto como enunciados compuestos;
• resolvimos ecuaciones de valor absoluto;
• representamos gráficamente conjuntos de soluciones de ecuaciones de valor absoluto en una recta numérica.
Ejemplos
Vocabulario
Una ecuación de valor absoluto es una ecuación de la forma, o equivalente a la forma, |bx − c| = d, donde b, c y d son números reales. La ecuación
|bx − c| = d significa que bx −c es una distancia de d unidades desde 0 para algún valor o algunos valores de x y puede interpretarse mediante el enunciado compuesto bx − c = d o
−(bx − c) = d
En los problemas 1 y 2, escribe la ecuación como un enunciado compuesto, si corresponde. Luego, escribe el conjunto de soluciones en notación de conjuntos.
El enunciado compuesto significa que x es 7 o el opuesto de x es 7. Si el opuesto de x es 7, entonces x es −7
3. Considera la ecuación de valor absoluto |z − 6| = 2.
El valor absoluto representa la distancia desde 0, y la distancia nunca es negativa. Esta ecuación no es verdadera para ningún valor de m
a. Reescribe la ecuación de valor absoluto como un enunciado compuesto.
z − 6 = 2 o −(z − 6) = 2
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 16 247
x
7
1. |x| = 7 x = 7 o
=
{−7, 7}
= −9 {}
2. |m|
16 © Great Minds PBC
b. Halla el valor de z para resolver cada ecuación lineal.
z z −= = 62 8 = −= = () z z z 62 62 4
c. Escribe el conjunto de soluciones en notación de conjuntos.
{4, 8}
d. Representa gráficamente el conjunto de soluciones en la recta numérica. –10–2–9–8–7–6–5–4–3–110 z 8 012345679
4. Resuelve la ecuación de valor absoluto 4|6 − 4x| + 9 = 81. Escribe el conjunto de soluciones en notación de conjuntos.
Aplica las propiedades de igualdad para despejar primero el valor absoluto.
A1 ▸ M1 ▸ TC ▸ Lección 16 EUREKA MATH2 248 R ESUMEN
464981 46472 6418 || || || −+ = −= = x x x 6418 412 3 −= −= =− x x x o = −= −= = () 6418 6418 424 6 x x x x
{−3, 6}
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema C, Lección 16
Nombre Fecha
En los problemas 1 a 4, escribe la ecuación como un enunciado compuesto, si corresponde. Luego, representa gráficamente el conjunto de soluciones de cada ecuación en la recta numérica.
1. |p| = 10
2. |x| = 0
3. |t| = 1.5
4. |y| = −3
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 16 249
© Great Minds PBC
PRÁCTICA 16
5. Considera la ecuación de valor absoluto |x + 7| = 3.
a. Reescribe la ecuación de valor absoluto como un enunciado compuesto.
b. Halla el valor de x para resolver el enunciado compuesto. Escribe el conjunto de soluciones usando la notación de conjuntos.
c. Representa gráficamente el conjunto de soluciones en la recta numérica dada.
6. Considera la ecuación de valor absoluto d 2 41−= .
a. Reescribe la ecuación de valor absoluto como un enunciado compuesto.
b. Halla el valor de d para resolver el enunciado compuesto. Escribe el conjunto de soluciones usando la notación de conjuntos.
c. Representa gráficamente el conjunto de soluciones en la recta numérica dada.
A1 ▸ M1 ▸ TC ▸ Lección 16 EUREKA MATH2 250 P RÁCTICA
© Great Minds PBC
En los problemas 7 a 11, resuelve la ecuación de valor absoluto. Escribe el conjunto de soluciones usando la notación de conjuntos.
7. |x + 2| − 4 = 6
8. 2|2p − 11| = 66
9. 8 + |5x − 2| − 2 = 6
10. −2|2x + 25| = 14
11. 8|3 − 3x| − 5 = 91
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 16 251 P RÁCTICA
Great Minds PBC
©
12. ¿Por qué es necesario reescribir una ecuación de valor absoluto como un enunciado compuesto?
13. ¿Por qué no tiene solución una ecuación de valor absoluto cuando el valor absoluto es igual a un número negativo?
Recuerda
En los problemas 14 y 15, resuelve la ecuación.
14. 0 = −4(−6t + 3)
15. 2.5(8 − 2t) = 2
16. La fórmula del volumen V de un cono recto es Vr h = 1 3 2 π , donde r representa el radio de la base del cono y h representa la altura del cono. Reorganiza la fórmula para escribir la altura h en función de V y r.
A1 ▸ M1 ▸ TC ▸ Lección 16 EUREKA MATH2 252 P RÁCTICA
© Great Minds PBC
17. Un salvavidas contó y registró el número de personas que había en la piscina para niños y niñas cada media hora. Los datos se muestran en orden ascendente.
Haz un diagrama de caja con los datos.
Uso de la piscina para niños y niñas Número de personas
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 16 253 P RÁCTICA
0 0 0 1 1 1 1 2 2 2 2 3 3 3 4 4 5
2345 6
01
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic C, Lesson 17
Nombre Fecha
LECCIÓN 17
Resolver desigualdades de valor absoluto
Escribe la letra de la ecuación o desigualdad junto a la gráfica de su conjunto de soluciones.
Enunciado
Explica cómo emparejaste cada ecuación o desigualdad con la gráfica de su conjunto de soluciones.
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 17 255
Gráfica A. |x| = 7 –10–2–8–6–410 x 02468 B. x > 7 –10–2–8–6–410 x 02468 C. |x|< 7 –10–6–8–4–20246810 x D. x = 7 –10–6–8–4–20246810 x E.|x|> 7 –10–6–8–4–20246810 x
© Great Minds PBC
¿Está entre los valores?
En los problemas 1 a 6, escribe la desigualdad como un enunciado compuesto, si corresponde. Halla el conjunto de soluciones y escríbelo usando la notación de conjuntos. Luego, representa gráficamente el conjunto de soluciones en la recta numérica.
1. |x| < 4
2.
3.
4.
A1 ▸ M1 ▸ TC ▸ Lección 17 EUREKA MATH2 256 L ECCIÓN
|x| > 4
7
|k + 2|≤
3 © Great Minds PBC
|a − 5| >
Una desigualdad de valor absoluto es una desigualdad de la forma, o equivalente a la forma, |bx − c|> d, donde b, c y d son números reales y en la que se usa cualquier signo de desigualdad.
Completa cada enunciado con más o menos según la desigualdad de valor absoluto.
La desigualdad |bx − c|> d significa que el valor de la expresión bx − c es que d unidades desde 0.
La desigualdad |bx − c|< d significa que el valor de la expresión bx − c es que d unidades desde 0.
6.
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 17 257 L ECCIÓN
− 2|≥ 5
5. |6y
|10x + 1| < 11 © Great Minds PBC
En los problemas 7 a 10, halla el conjunto de soluciones. Escribe una breve justificación para tu respuesta.
7. |m| > −2
8. |m| < −2
9. |g − 4|≥ 0
10. |g − 4|≤ 0
A1 ▸ M1 ▸ TC ▸ Lección 17 EUREKA MATH2 258 L ECCIÓN
© Great Minds PBC
Algo más que el valor absoluto
En los problemas 11 y 12, resuelve la desigualdad. Escribe el conjunto de soluciones usando la notación de conjuntos.
11. |c + 4| − 8 < 20
12. −3|w + 12| + 10 ≤ −5
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 17 259 L ECCIÓN
© Great Minds PBC
13. Una máquina pesa bolsitas de harina. El peso de una bolsita llena de harina no debe estar a más de 0.04 libras del peso deseado de 5 libras. Escribe y resuelve una desigualdad de valor absoluto para hallar el rango de pesos aceptables.
14. Una fábrica está diseñando un sensor para el motor de un avión. La normativa permite que la altura no sea más de 0.001 pulgadas de la altura deseada de 6 pulgadas. Escribe y resuelve una desigualdad de valor absoluto para determinar el rango de alturas aceptables para el sensor. Escribe el conjunto de soluciones usando la notación de conjuntos.
A1 ▸ M1 ▸ TC ▸ Lección 17 EUREKA MATH2 260 L ECCIÓN Aplicar el valor
absoluto
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema C, Lección 17
Nombre Fecha
Considera la desigualdad |2x + 5|≤ 3
a. Reescribe la desigualdad como un enunciado compuesto.
b. Halla el conjunto de soluciones.
c. Representa gráficamente el conjunto de soluciones en una recta numérica.
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 17 261
BOLETO DE SALIDA 17 © Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema C, Lección 17
Nombre Fecha
Resolver desigualdades de valor absoluto
En esta lección:
• escribimos desigualdades de valor absoluto como desigualdades compuestas;
• resolvimos desigualdades de valor absoluto;
• representamos gráficamente conjuntos de soluciones de desigualdades de valor absoluto en una recta numérica.
Ejemplos
1. Considera la desigualdad de valor absoluto |4r + 3|< 7
a. Reescribe la desigualdad de valor absoluto como una desigualdad compuesta.
4r + 3 < 7 y −(4r + 3) < 7
b. Halla el valor de r para resolver cada desigualdad.
1
Vocabulario
Una desigualdad de valor absoluto es una desigualdad de la forma, o equivalente a la forma, |bx − c|> d, donde b, c y d son números reales y en la que se usa cualquier signo de desigualdad. La desigualdad |bx − c|> d significa que bx − c es una distancia de más de d unidades desde 0
La desigualdad |bx − c|< d significa que bx − c es una distancia de menos de d unidades desde 0
Si 4r + 3 y su opuesto son menos de 7 unidades desde 0, entonces el valor de 4r + 3 debe estar entre −7 y 7. Se usa y.
0 5 2 r r r r
c. Escribe el conjunto de soluciones usando la notación de conjuntos. rr
d. Representa gráficamente el conjunto de soluciones en la recta numérica. –5–3
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 17 263
437 44
r r r +< < < −+ < +> >− >− ()437 437 41
−<
{}
<
5 2 1
–4–2–1012345
r
© Great Minds PBC
RESUMEN 17
2. Considera la desigualdad de valor absoluto 2|6a − 10|≥ 4.
a. Despeja el valor absoluto.
26104
6102 || || a a −≥ −≥
b. Reescribe la desigualdad de valor absoluto como una desigualdad compuesta.
6a − 10 ≥ 2 o −(6a − 10) ≥ 2
Si 6a − 10 y su opuesto están al menos a 2 unidades desde 0, entonces el valor de 6a − 10 debe ser menor que o igual a 2 o mayor que o igual a 2. Se usa o
c. Halla el valor de a para resolver cada desigualdad.
6102
612 2 a a a −≥ ≥ ≥ ≥ −≤ ≤ ≤ ()
6102
6102 68 4 3 a a a a
d. Escribe el conjunto de soluciones usando la notación de conjuntos.
aa a ≤≥ {} 4 3 o2
e. Representa gráficamente el conjunto de soluciones en la recta numérica.
–4–3–2–101234 a
A1 ▸ M1 ▸ TC ▸ Lección 17 EUREKA MATH2 264 R ESUMEN
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema C, Lección 17
Nombre Fecha
1. Considera la desigualdad |x + 1|< 2.
a. Reescribe la desigualdad como un enunciado compuesto.
b. Halla el valor de x para resolver el enunciado compuesto. Escribe el conjunto de soluciones usando la notación de conjuntos.
c. Representa gráficamente el conjunto de soluciones en la recta numérica dada.
2. Considera la desigualdad |2b − 1|≥ 6.
a. Reescribe la desigualdad como un enunciado compuesto.
b. Halla el valor de b para resolver el enunciado compuesto. Escribe el conjunto de soluciones usando la notación de conjuntos.
c. Representa gráficamente el conjunto de soluciones en la recta numérica dada.
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 17 265
© Great Minds PBC
PRÁCTICA 17
En los problemas 3 a 9, halla el conjunto de soluciones de la desigualdad. Escribe el conjunto de soluciones usando la notación de conjuntos. Luego, representa gráficamente el conjunto de soluciones en la recta numérica dada.
3. |w + 2|< 10
4. |2m − 7|> 19
5. |3p + 5| + 20 ≤ 28
6. 1 2 421 d −<
A1 ▸ M1 ▸ TC ▸ Lección 17 EUREKA MATH2 266 P RÁCTICA
© Great Minds PBC
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 17 267 P RÁCTICA
|2r − 3|≥ 0
−5|4c + 25| + 7 ≥ −8
|5 − x| − 3 > 7
Great Minds PBC
7.
8.
9.
©
10. Compara y contrasta el conjunto de soluciones de |k − 2| = 3 con el conjunto de soluciones de |k − 2|≥ 3
En los problemas 11 a 14, crea una ecuación o desigualdad para la situación.
11. Una ecuación de valor absoluto que tiene dos soluciones
12. Una ecuación de valor absoluto que tiene una solución
13. Una desigualdad de valor absoluto que tiene una solución para todos los números reales
14. Una desigualdad de valor absoluto que no tiene solución
A1 ▸ M1 ▸ TC ▸ Lección 17 EUREKA MATH2 268 P RÁCTICA
© Great Minds PBC
15. En una fábrica de caramelos, se suele llenar cada bolsita con 362 caramelos. El recuento puede ser de hasta 12 caramelos por encima o por debajo de este número.
a. Escribe una desigualdad de valor absoluto que represente el rango aceptable de caramelos en una bolsita.
b. Resuelve la desigualdad de valor absoluto de la parte (a) para hallar el número aceptable de caramelos en cualquier bolsita.
Recuerda
En los problemas 16 y 17, resuelve la ecuación.
16. −2(d − 6) + 5d = 12
17. −= −+4289 4 d d
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 17 269 P RÁCTICA
© Great Minds PBC
18. Empareja cada desigualdad o ecuación compuesta con la gráfica de su conjunto de soluciones en la recta numérica.
A1 ▸ M1 ▸ TC ▸ Lección 17 EUREKA MATH2 270 P RÁCTICA
n > 4 o n < −2 –8–6–2–404628 n n ≤ 4 y n ≥ −2 –8–6–4–204628 n n = 4 o n = −2 –8–6–4–204628 n −2 < n < 4 –8–6–4–204628 n n ≥ 4 o n ≤ −2 –8–6–4–204628 n © Great Minds PBC
19. Se tomó una muestra aleatoria de todas las personas que compraron en la tienda A, y otra muestra aleatoria de todas las personas que compraron en la tienda B. Los diagramas de caja muestran las distribuciones del tiempo que las personas pasaron en cada tienda. ¿Qué enunciado es verdadero a partir de las distribuciones de datos mostradas en los diagramas de caja? Elige todas las opciones que correspondan.
Tiempo que pasaron en el supermercado
Tienda A
Tienda B
6121824303642485460667278
Tiempo (minutos)
A. Los rangos de los dos conjuntos de datos son iguales.
B. La mediana de la tienda A es menor que la mediana de la tienda B.
C. El rango intercuartil de la tienda B es mayor que el rango intercuartil de la tienda A.
D. La diferencia en las medianas de los dos conjuntos de datos es 1 2 veces el rango intercuartil de la tienda A.
E. La diferencia entre las medianas de los dos conjuntos de datos es 2 veces el rango intercuartil de la tienda B.
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 17 271 P RÁCTICA
© Great Minds PBC
Datos univariados
Edición para estudiantes: Grado A1, Módulo 1, Tema D
Grandes datos
Cuenta un segundo. Esa es aproximadamente la duración normal de un estornudo.
Ahora, en ese segundo, todo lo que sucedió en internet podría resumirse así:
5000
1000
5 publicaciones en Instagram horas de videos subidos a YouTube
70,000
¡Mira esos datos! ¡Son tan grandes!

Para que quede claro, el segundo que contaste no tenía nada de especial. Todos estos sucesos, más o menos, ocurren cada segundo, durante todo el día. Para cada publicación, las compañías registran la hora, el dispositivo, la cuenta que la publica, las etiquetas, las reacciones que provoca... y mucho más.
Multiplícalo por miles de publicaciones por segundo, 60 segundos por minuto, 1440 minutos por día, y podrás imaginar el asombroso tamaño y detalle de los conjuntos de datos.
273
D
TEMA
© Great Minds PBC
Son demasiados datos para que los examine una sola persona. Hay que resumirlos y seleccionar los aspectos importantes.
Ahí es donde intervienen las estadísticas. Una estadística es un resumen breve, información rápida acerca de un conjunto de datos.
¿Qué revelan las estadísticas? ¿Qué no revelan? ¿Quién debe tener acceso a estos datos y con qué fines? Estas preguntas no son solo matemáticas, sino también morales y sociales. Y, para responderlas sabiamente, necesitaremos comprender cómo funcionan las estadísticas.
A1 ▸ M1 ▸ TD EUREKA MATH2 274 PRESENTACIÓN DEL TEMA
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema D, Lección 18
Nombre Fecha
LECCIÓN 18
Distribuciones y sus formas
Comparar diagramas de puntos
Valores típicos
Conectarlo todo
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 18 275
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema D, Lección 18
Representaciones gráficas
Medidas de tendencia central
Datos cuantitativos univariados
Formas de distribuciones de datos
Medidas de dispersión
MATH2 A1 ▸ M1 ▸ TD ▸ Lección
▸ Organizador
277
EUREKA
18
gráfico de datos cuantitativos univariados
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema D, Lección 18
Nombre Fecha
El diagrama de puntos muestra los tiempos de demora redondeados a los cinco minutos más cercanos de 60 vuelos de Big Air en 2019.
Tiempos de demora de los vuelos de Big Air de 2019
a. ¿Cuál es la forma de la distribución?
b. ¿Fueron 70 minutos un tiempo de demora típico en los vuelos de Big Air? Justifica tu respuesta.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 18 279
30 120 40 50 60 70 80 90 100 110
Tiempo de demora (minutos) 01020
DE SALIDA 18 © Great Minds PBC
BOLETO
Edición para estudiantes: Grado A1, Módulo 1, Tema D, Lección 18
Nombre Fecha
Distribuciones y sus formas
En esta lección:
• describimos las formas de distribuciones de datos representadas mediante diagramas de puntos usando los términos simétrica, sesgada hacia la derecha, sesgada hacia la izquierda y con forma de campana;
• comparamos distribuciones de datos representadas mediante diagramas de puntos;
• estimamos valores típicos de distribuciones de datos.
Ejemplo
RESUMEN 18
Vocabulario
Datos cuantitativos univariados significa que hay una variable y que los valores de los datos son numéricos.
Una distribución de datos es aproximadamente uniforme cuando la mayoría de los valores tienen aproximadamente las mismas frecuencias.
Se detalla el número de gramos de proteína por porción en 20 diferentes variedades de cereales para el desayuno.
a. Crea un diagrama de puntos que muestre la distribución de los gramos de proteína por porción en los 20 cereales para el desayuno.
Cada punto representa un valor en el conjunto de datos.
Proteína por porción de cereales
012345 6 78 9
Proteína (gramos)
b. Describe la forma de la distribución. La distribución está sesgada hacia la derecha.
c. Usa el diagrama de puntos para estimar un número típico de gramos de proteína en una porción de cereales.
Un número típico de gramos de proteína en una porción es de aproximadamente 3 gramos.
Una distribución sesgada tiene cola en un lado. Esta distribución tiene una cola en el lado derecho.
El valor 3 gramos se sitúa en el centro del conjunto de datos, de manera que es una buena estimación de un valor de datos típico.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 18 281
1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 5, 5, 6, 6, 7, 8
1, 1, 1,
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema D, Lección 18
Nombre
1. Empareja cada diagrama de puntos con la descripción de su forma.
Número de mascotas que pertenecen a estudiantes
Aproximadamente simétrica
Número de mascotas
Medidas de longitud del pasillo este
Sesgada hacia la derecha
Antigüedad de los autos conducidos por maestras y maestros
Sesgada hacia la izquierda
012345 6 78
Antigüedad (años)
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 18 283
02 4 6 12 8 10
Longitud (metros) 8.2 8.3 8.4 8.5 8.6 8.7 8.8 8.9
18 © Great Minds PBC
Fecha PRÁCTICA
2. Ana registró la temperatura máxima diaria en grados Fahrenheit en su casa durante 10 días.
77, 85, 77, 79, 82, 84, 79, 78, 79, 80
a. Crea un diagrama de puntos que muestre la distribución de las temperaturas máximas en grados Fahrenheit para el periodo de 10 días.
b. ¿Cuál es la forma de la distribución?
A1 ▸ M1 ▸ TD ▸ Lección 18 EUREKA MATH2 284 P RÁCTICA
75 76 78 80 82 84 86 77 79 81 83 85 87
© Great Minds PBC
3. Hubo 25 personas que asistieron a un evento. Se indican las edades de las personas que asistieron.
a. Crea un diagrama de puntos que muestre la distribución de las edades en años de las personas que asistieron.
b. ¿Cuál es la forma de la distribución?
c. ¿Cuál es la edad típica de una persona que asistió al evento?
d. ¿Cuál podría haber sido el evento?
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 18 285 P RÁCTICA
3, 3, 4, 4, 4, 4, 5, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 10
6 7 9 8 11 12 13 14 10 15
012345
© Great Minds PBC
4. Se seleccionó una muestra aleatoria de 80 personas espectadoras de un programa de televisión. El diagrama de puntos muestra la distribución de las edades de esas personas en años.
Edades de las personas espectadoras de un programa de televisión
Edad de la persona espectadora (años)
a. ¿Cuál es la forma de la distribución?
b. Según el diagrama de puntos, ¿cuál es la edad típica de una persona espectadora?
c. ¿Dirías que este programa de televisión atrae a una amplia gama de edades? Explica.
5. ¿Cuándo no es eficiente representar un conjunto de datos usando un diagrama de puntos?
A1 ▸ M1 ▸ TD ▸ Lección 18 EUREKA MATH2 286 P RÁCTICA
020 30 10 40 50 60 70 80
© Great Minds PBC
6. Una médica midió el ritmo cardiaco en reposo de un gran grupo de personas adultas de mediana edad. De este grupo, la médica seleccionó al azar a 20 personas adultas que eran diestras y 20 personas adultas que eran zurdas. Las distribuciones se muestran en los diagramas de puntos.
a. En 2 o 3 oraciones, compara la distribución de los ritmos cardiacos en reposo de las personas adultas diestras con la distribución de los ritmos cardiacos en reposo de las personas adultas zurdas.
b. Basándote en los datos, ¿puede el hecho de que una persona adulta sea zurda o diestra influir en su ritmo cardiaco en reposo? Explica tu razonamiento.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 18 287 P RÁCTICA
Ritmo
44 48 50 46 52 54 56 58 60 62 64 66 68 72 74 70 76 82 78 80 84 Ritmo
(pulsaciones por minuto) Ritmos
zurdas 44 48 50 46 52 54 56 58 60 62 64 66 68 72 74 70 76 82 78 80 84
cardiaco (pulsaciones por minuto) Ritmos cardiacos en reposo de personas adultas diestras
cardiaco
cardiacos en reposo de personas adultas
© Great Minds PBC
Recuerda
En los problemas 7 y 8, resuelve la ecuación.
9. Encierra en un círculo cada polinomio.
10. Danna gana $114 por 8 horas de trabajo. Gana la misma cantidad de dinero cada hora. Escribe una ecuación que represente la relación entre los ingresos de Danna en dólares y y el número de horas que trabaja x.
A1 ▸ M1 ▸ TD ▸ Lección 18 EUREKA MATH2 288 P RÁCTICA
7. 16 = 7 − 2x − 5x 8. −+() −= 2 5 20915 x
(3x2 − 2x + 5) − (7x − 4) 15 5 3 4 x x 10 − 2 (3x + 1)(3x − 1) 9 4 3 x −+ ()xx x x 3 6 2 281
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema D, Lección 19
Nombre Fecha
LECCIÓN 19
Describir el centro de una distribución
Otro vistazo a Pon a prueba tu memoria
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 19 289
© Great Minds PBC
Traza un ejemplo de diagrama de puntos para cada caso y resume la información sobre la media y la mediana.
Medidas típicas de distribuciones de datos
Formas de la distribución
Simétrica o aproximadamente simétrica
Sesgada hacia la izquierda Sesgada hacia la derecha 012345012345012345
A1 ▸ M1 ▸ TD ▸ Lección 19 EUREKA MATH2 290 L ECCIÓN
© Great Minds PBC
Elegir una medida de tendencia central
La tabla muestra estimaciones del tamaño de la población, en miles, de 16 especies de pingüinos.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 19 291 L ECCIÓN
Especie Población (miles) Barbijo 8000 De Adelia 7560 Rey 4600 De penacho amarillo del sur 2500 Real 1700 De Magallanes 1300 Papúa 774 Emperador 595 Especie Población (miles) De penacho amarillo del norte 530 De cresta erguida 150 De Snares 63 Africano 50 De Humboldt 32 De Fiordland 6 De ojos amarillos 3.4 De Galápagos 1.2 © Great Minds PBC
1. Completa el diagrama de puntos.
2. ¿Cuál es la mediana del tamaño de la población?
3. Sin calcular, ¿cuál es mayor, la media o la mediana? ¿Por qué?
4. Para estimar el tamaño típico de la población de pingüinos, ¿es adecuado usar la media, la mediana o ambas? ¿Por qué?
A1 ▸ M1 ▸ TD ▸ Lección 19 EUREKA MATH2 292 L ECCIÓN
0 1000 2000 3000 4000 5000 6000 7000 8000
© Great Minds PBC
5. El tamaño de la población de la especie de pingüinos macaroni es aproximadamente 18,000,000. Si incluyéramos el tamaño de la población de pingüinos macaroni en el conjunto de datos, ¿cómo afectaría la media y la mediana? ¿Qué medida se vería más afectada?
Medidas de tendencia central a partir de un histograma
El histograma resume el número promedio de días despejados al año en las 48 ciudades más grandes de los Estados Unidos. Un día despejado se define como aquel en el que las nubes cubren como máximo el 30 por ciento del cielo durante las horas del día.
Días despejados en un año para ciudades de los EE. UU.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 19 293 L ECCIÓN
1 2 3 4 5 6 7 8 9 10 13 14 15 11 12 Frecuencia 16 50 65 80 95 110 125 140 155 170 185 200 215 0 Número promedio de días despejados en un año © Great Minds PBC
6. Estima la mediana y la media a partir del histograma.
7. ¿Cuál es el número típico de días despejados en un año para una de estas ciudades? Explica tu respuesta.
8. Construye un histograma de frecuencias relativas a partir del histograma del número promedio de días despejados.
9. Estima la mediana y la media de la distribución.
A1 ▸ M1 ▸ TD ▸ Lección 19 EUREKA MATH2 294 L ECCIÓN
0.2 0.1 0.3 0.4 0.5 0 50 65 80 95 110 125 140 155 170 185 200 215
© Great Minds PBC
1. Se preguntó a una muestra aleatoria de 10 estudiantes de noveno grado cuántos mensajes de texto enviaron el martes pasado.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 19 295
Estudiante Número de mensajes de texto enviados 1 285 2 15 3 37 4 3 5 11 6 56 7 22 8 32 9 71 10 28
para estudiantes: Grado A1, Módulo 1, Tema D, Lección 19 Nombre Fecha BOLETO DE SALIDA 19 © Great Minds PBC
Edición
Mensajes de texto enviados por estudiantes de noveno grado el martes pasado
Considera el diagrama de puntos que muestra el número de mensajes de texto enviados por cada estudiante. Número de mensajes de texto enviados
a. Calcula la media y la mediana del conjunto de datos.
b. Para describir un número típico de mensajes de texto que se enviaron el martes pasado, ¿usarías la media, la mediana o ambas? Explica tu respuesta.
A1 ▸ M1 ▸ TD ▸ Lección 19 EUREKA MATH2 296 B OLETO DE SALIDA
050 100 150 200 250 300
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema D, Lección 19
Nombre Fecha
Describir el centro de una distribución
En esta lección:
• determinamos la media y la mediana de una distribución a partir de un diagrama de puntos;
• estimamos la media y la mediana de una distribución a partir de un histograma;
• determinamos qué medidas de tendencia central son las más apropiadas para describir una distribución.
Ejemplos
1. El diagrama de puntos muestra el número de gramos de proteína por porción en 20 diferentes variedades de cereales para el desayuno.
Proteína por porción de cereales
012345 6 78 9
Proteína (gramos)
a. Halla la media y la mediana.
51423324252678
La media es 3.35 gramos.
La mediana es 3 gramos.
Como hay un número par de valores de datos, la mediana es la media de los dos valores del medio. 33 2
b. Determina si sería apropiado usar la media, la mediana o ambas para describir un número típico de gramos de proteína para una porción de cereales. Explica.
Sería más apropiado usar la mediana para describir un número típico de gramos de proteína para una porción de cereales porque la distribución está sesgada hacia la derecha.
En una distribución sesgada hacia la derecha, la media suele ser mayor que la mediana.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 19 297
20 67 20 33
. ++ ++ ++ + ==
()5 ()()()()()
3 + =
19 © Great Minds PBC
RESUMEN
Índices de audiencia de películas
2. El histograma muestra la distribución de los índices de audiencia (del 100 %) para una muestra de 100 películas. Índice
a. Describe la forma de la distribución.
La distribución es aproximadamente simétrica.
b. Usa el histograma para estimar la media y la mediana de la distribución.
La media de los índices de audiencia de películas es aproximadamente 65.
El punto de equilibrio está cerca del centro porque la distribución es aproximadamente simétrica.
La mitad izquierda de la distribución es casi un reflejo de la mitad derecha de la distribución.
La mediana de los índices de audiencia de películas está entre 60 y 70.
Un histograma no proporciona valores de datos exactos. La mejor estimación de la mediana se encuentra dentro de un intervalo.
c. Determina si sería apropiado usar la media, la mediana o ambas para describir un índice de audiencia típico de una película de esta muestra. Explica.
Tanto la media como la mediana son apropiadas para describir el índice de audiencia típico porque la distribución es aproximadamente simétrica.
En una distribución aproximadamente simétrica, la media y la mediana tienen aproximadamente el mismo valor.
A1 ▸ M1 ▸ TD ▸ Lección 19 EUREKA MATH2 298 R ESUMEN
de audiencia (porcentaje) 5 0 10 15 20 25 30 35 40 50 30 60 70 80 90 100 Frecuenci a
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema D, Lección 19
Nombre Fecha
1. Traza un diagrama de puntos de una distribución de datos que represente las edades de 20 personas y en la cual la mediana y la media tengan aproximadamente el mismo valor. Explica tu razonamiento.
2. Traza un diagrama de puntos de una distribución de datos que represente las edades de 20 personas y en la que la mediana sea claramente menor que la media. Explica tu razonamiento.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 19 299
19 © Great Minds PBC
PRÁCTICA
En los problemas 3 y 4, determina si es apropiado usar la media, la mediana o ambas para describir un valor típico. Explica.
3. Se preguntó a una muestra aleatoria de 70 personas que trabajan en varias compañías diferentes cuánto dinero gastaron en el almuerzo la semana pasada.
Gasto de las personas en el almuerzo la semana pasada (varios lugares de trabajo)
A1 ▸ M1 ▸ TD ▸ Lección 19 EUREKA MATH2 300 P RÁCTICA
(dólares) 5 0 10 15 20 25 10 20 30 40 0 50 Frecuenci a
Dinero
© Great Minds PBC
4. Se preguntó a otra muestra aleatoria de 70 personas, esta vez del mismo lugar de trabajo, cuánto gastaron en el almuerzo la semana pasada.
Gasto de las personas en el almuerzo la semana pasada (mismo lugar de trabajo)
5. El diagrama de puntos muestra la duración, en minutos, de las 8 películas nominadas a Mejor Película en los Premios Oscar de 2019.
Duración de las películas nominadas a Mejor Película en los Premios Oscar de 2019
Tiempo (minutos)
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 19 301 P RÁCTICA
Dinero (dólares) 5 0 10 15 20 25 30 10 20 30 40 0 50 Frecuencia
120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 © Great Minds PBC
La mediana de la duración de las películas es 133.5 minutos. Determina con el método de inspección si la media de la duración de las películas es mayor que, menor que o igual a la mediana de la duración de las películas. Explica tu razonamiento.
6. A un evento asistieron 40 personas. Las edades de las personas son las siguientes:
Crea un histograma de las edades usando los ejes que se proporcionan. Usa intervalos de 10 años.
A1 ▸ M1 ▸ TD ▸ Lección 19 EUREKA MATH2 302 P RÁCTICA
6 13 24 27 28 32 32 34 38 42 42 43 48 49 49 51 52 52 53 53 53 53 54 55 56 57 57 60 61 61 62 66 66 66 68 70 72 78 83 97
Edad (años) 2 0 4 6 8 10 12 14 50 60 70 80 0 10 20 30 40 90 100 Frecuenci a
© Great Minds PBC
Edades de las personas que asisten a un evento
a. ¿Describirías el histograma como simétrico o sesgado? Explica tu elección.
b. Usa el histograma para estimar la media y la mediana.
c. ¿La media, la mediana o ambas describirían apropiadamente la edad típica de una persona que asiste a este evento?
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 19 303 P RÁCTICA
© Great Minds PBC
7. El histograma de frecuencias relativas muestra la distribución de las estaturas de una muestra de 25 jugadoras de la Asociación Nacional de Basquetbol Femenino (WNBA, por sus siglas en inglés).
Estaturas de 25 jugadoras de la WNBA
a. Estima la media y la mediana.
b. Para describir la estatura típica de estas jugadoras de basquetbol, ¿es apropiado usar la media, la mediana o ambas? Explica.
A1 ▸ M1 ▸ TD ▸ Lección 19 EUREKA MATH2 304 P RÁCTICA
0.1 0 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 68 71 74 77 65 80 Frecuencia relativa
Estatura (pulgadas)
© Great Minds PBC
Recuerda
En los problemas 8 y 9, halla el valor de p para resolver la desigualdad.
8. 5p + 8 > 28
9. 3(p − 5) ≤ −18
10. El club de teatro vende ramos de flores en las representaciones musicales de primavera. Cada ramo pequeño se vende por $12 y cada ramo grande se vende por $20. El club de teatro vende 14 ramos pequeños más que ramos grandes. Si el club de teatro gana $552 en ventas totales, ¿cuántos ramos pequeños vende?
11. La entrenadora de futbol compró cintas para el pelo para el equipo. La gráfica muestra la relación entre el número de cintas compradas y el costo total. ¿Cuál es el costo por cinta?
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 19 305 P RÁCTICA
0 3 2 14 5 678 910 2 4 6 8 10 12 14 16 18 20 22 24 26 x y Costo total (dólares) Número
(2, 6) (4, 12)
24) © Great Minds PBC
de cintas para el pelo compradas
(8,
Edición para estudiantes: Grado A1, Módulo 1, Tema D, Lección 20
Nombre Fecha
Usar el centro para comparar distribuciones de datos
1. Se invitó a 100 personas a un restaurante a probar un nuevo sándwich y a dar su opinión completando una encuesta. Una de las preguntas de la encuesta se refería a cuál sería un precio razonable para el sándwich, al dólar más cercano. Los resultados se muestran en el histograma de frecuencias relativas.
Precio sugerido para el sándwich
Precio (dólares)
Escribe 2 o 3 oraciones que describan un valor típico para el conjunto de datos y lo que eso significa en términos del precio razonable sugerido para el sándwich.
Describe la distribución en términos de cuartiles y lo que significan los cuartiles en términos del precio razonable sugerido para el sándwich.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 20 307
0.05 0 0.1 0.15 0.2 0.25 5678 9 10 11 12 13 14 15 16 Frecuencia
relativa
LECCIÓN 20 © Great Minds PBC
Construir un diagrama de caja
2. Halla cada valor y crea un diagrama de caja que muestre la distribución del problema 1.
Mínimo:
C1:
Mediana:
C3:
Máximo:
Comparar distribuciones de datos
3. Los diagramas de caja resumen la esperanza de vida al nacer en países de Asia y Europa en 2017.
Esperanza de vida al nacer
a. ¿Cuál es la esperanza de vida más baja de cualquier país de Europa?
b. ¿Cuál es la esperanza de vida más alta de cualquier país de Asia?
A1 ▸ M1 ▸ TD ▸ Lección 20 EUREKA MATH2 308 L ECCIÓN
68 70 71 69 72 73 74 75 76 77 78 79 81 80 83 84 85 86 87 88 89 82 90
Edad (años)
Asia Europa
Precio (dólares) 5 6789 10 11 12 13 14 15 16 © Great Minds PBC
c. ¿Es verdadero que hay más países en Europa donde las personas tienen una esperanza de vida entre 76 y 80.5 años que entre 80.5 y 89 años? Explica.
d. Mason dice que el número de países de Asia donde las personas tienen una esperanza de vida entre 75 y 78 años es el mismo que el número de países de Europa donde las personas tienen una esperanza de vida entre 80.5 y 82 años. ¿Estás de acuerdo con Mason? Explica.
e. ¿Cómo se relacionan la esperanza de vida típica de las personas de un país de Asia y la esperanza de vida típica de las personas de un país de Europa?
f. Escribe varias oraciones en las que compares la esperanza de vida de las personas de un país asiático y la esperanza de vida de las personas de un país europeo.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 20 309 L ECCIÓN
© Great Minds PBC
4. Los diagramas de caja resumen el promedio de puntos por partido de dos grupos de jugadores de la NBA.
• El primer diagrama de caja muestra la distribución del promedio de puntos por partido de los 21 máximos anotadores en la historia de la NBA.
• El segundo diagrama de caja muestra la distribución del promedio de puntos por partido de los 21 máximos anotadores entre los jugadores de la NBA en actividad hasta junio de 2019.
Máximos anotadores de la NBA
A lo largo de la historia de la NBA
Jugadores en actividad
a. Completa cada oración.
16 18 20 22 24 26 28 30 32
Promedio de puntos por partido
El % de los máximos anotadores en la historia de la NBA tuvieron un promedio superior al 75 % inferior de los máximos anotadores en actividad hasta junio de 2019.
Aproximadamente el % de los máximos anotadores en la historia de la NBA tuvieron un promedio superior al 100 % de los máximos anotadores en actividad hasta junio de 2019.
b. Describe la forma de cada distribución de datos.
A1 ▸ M1 ▸ TD ▸ Lección 20 EUREKA MATH2 310 L ECCIÓN
© Great Minds PBC
c. Compara un valor típico del promedio de puntos por partido para los máximos anotadores en la historia de la NBA y los máximos anotadores en actividad hasta junio de 2019.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 20 311 L ECCIÓN
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema D, Lección 20
Nombre Fecha
Un bosque se divide en secciones iguales, y 100 de estas secciones se seleccionan al azar. Un científico pide a personas voluntarias que registren el número de ardillas y aves que se ven en cada sección. Los diagramas de caja muestran las distribuciones del número de ardillas y aves que se ven en cada sección.
Avistamientos de animales en 100 secciones del bosque
¿Es mayor el número típico de ardillas que se ven en cada sección del bosque que el número típico de aves que se ven? Justifica tu respuesta.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 20 313
0 56789 4 3 2 1 11 10 12 Número de ardillas
aves
ven Ardillas
y
que se
Aves
BOLETO
20 © Great Minds PBC
DE SALIDA
Edición para estudiantes: Grado A1, Módulo 1, Tema D, Lección 20
Nombre Fecha
Usar el centro para comparar distribuciones de datos
En esta lección:
• interpretamos información sobre una distribución a partir de un diagrama de caja;
• comparamos distribuciones representadas mediante diagramas de caja.
Ejemplo
Doce nadadoras nadaron cada una 1500 metros dos veces: una con traje de neopreno y otra sin traje de neopreno. Los diagramas de caja muestran las distribuciones de las velocidades máximas de las nadadoras en metros por segundo.
Velocidades de nado
Sin traje de neopreno
Con traje de neopreno
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 20 315
1 1.05 1.1 1.15 1.2 1.25 1.3 1.35 1.4 1.45 1.5 1.55 1.6 1.65 1.7 1.75 1.8 1.85 Velocidad
por segundo)
máxima (metros
20 © Great Minds PBC
RESUMEN
a. Determina si cada enunciado es verdadero o falso.
La mayoría de las velocidades máximas de las nadadoras cuando no llevan puesto un traje de neopreno son menores que 1.4 metros por segundo.
Falso
El rango de velocidades máximas de las nadadoras sin traje de neopreno es menor que el rango de velocidades máximas de las nadadoras con traje de neopreno.
Verdadero
Solo aproximadamente el 25 % de las velocidades pertenecen a esta categoría.
Aproximadamente el 50 % de las velocidades máximas de las nadadoras que llevaban traje de neopreno se sitúan entre 1.2 metros por segundo y 1.5 metros por segundo.
Verdadero
La velocidad máxima típica de una nadadora con traje de neopreno es menor que la velocidad máxima típica de una nadadora sin traje de neopreno.
Falso
La mediana de la velocidad de las nadadoras con traje de neopreno es 1.5 m/s La mediana de la velocidad de las nadadoras sin traje de neopreno es 1.45 m/s
b. ¿Alcanzaron un mayor porcentaje de nadadoras una velocidad máxima de al menos 1.45 metros por segundo cuando llevaban traje de neopreno o cuando no lo llevaban? Explica.
Un porcentaje mayor, aproximadamente el 75 %, de las nadadoras alcanzaron velocidades máximas de al menos 1.45 metros por segundo cuando llevaban un traje de neopreno. Este porcentaje es mayor que el de aproximadamente 50 % de nadadoras que alcanzaron esta velocidad máxima cuando no llevaban traje de neopreno.
A1 ▸ M1 ▸ TD ▸ Lección 20 EUREKA MATH2 316 R ESUMEN
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Tema D, Lección 20
Nombre Fecha
1. Ana registró la temperatura máxima diaria en grados Fahrenheit en su casa durante 10 días.
77, 85, 77, 79, 82, 84, 79, 78, 79, 80
Halla cada valor y crea un diagrama de caja que muestre la distribución de las temperaturas máximas diarias. Mínima:
C1:
Mediana: C3:
Máxima:
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 20 317
73 74 75 76 78 80 82 84 86 77 79 81 83 85 87 88
20 © Great Minds PBC
PRÁCTICA
2. El diagrama de caja muestra la distribución de las estaturas de una muestra de 25 jugadoras de la Asociación Nacional de Basquetbol Femenino (WNBA, por sus siglas en inglés). Determina si cada enunciado es verdadero o falso y justifica tu elección.
Estaturas de 25 jugadoras de la WNBA
a. La estatura mínima de las jugadoras de basquetbol es 66 pulgadas.
b. La mayoría de las jugadoras de basquetbol tienen una estatura de 73 pulgadas o menos.
c. Hay más jugadoras de basquetbol con una estatura entre 69 pulgadas y 73 pulgadas que entre 73 pulgadas y 76 pulgadas.
d. Aproximadamente el 25 % de las jugadoras de basquetbol miden entre 76 pulgadas y 78 pulgadas de alto.
A1 ▸ M1 ▸ TD ▸ Lección 20 EUREKA MATH2 318 P RÁCTICA
61 62 63 64 65 66 68 70 72 74 76 78 80 67 69 71 73 75 77 79 81 Estatura (pulgadas)
© Great Minds PBC
3. Se dio una prueba corta con límite de tiempo a 20 estudiantes. Al día siguiente, se les dio la misma prueba corta, pero sin límite de tiempo. Las distribuciones de las puntuaciones de las pruebas cortas se muestran en los diagramas de caja.
Puntuaciones de la prueba corta
Con límite de tiempo
Sin límite de tiempo
Puntuación
a. ¿Qué distribución tuvo un porcentaje más alto de puntuaciones que son 7 puntos o más? Explica.
b. Describe una puntuación típica en la prueba corta con límite de tiempo y una puntuación típica en la prueba corta sin límite de tiempo.
c. Basándose en los diagramas de caja, la maestra llega a la conclusión de que sus estudiantes obtuvieron resultados considerablemente mejores en la prueba corta sin límite de tiempo que en la prueba corta con límite de tiempo. Da tres ejemplos de evidencia que respalden esta conclusión.
d. ¿Puede concluir la maestra que sus estudiantes obtuvieron mejores puntuaciones en la segunda prueba corta porque no tenía límite de tiempo? Explica.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 20 319 P RÁCTICA
012345678 910111213
© Great Minds PBC
4. ¿Por qué son útiles los diagramas de caja para comparar dos conjuntos de datos univariados?
5. El diagrama de caja muestra la distribución de edades de 200 personas residentes de Kenia seleccionadas al azar. El histograma de frecuencias relativas muestra la distribución de edades de 200 personas residentes de los Estados Unidos seleccionadas al azar.
a. ¿En la distribución de qué país hay un mayor porcentaje de personas que tienen al menos 20 años? Explica.
b. Estima el porcentaje de personas en cada distribución que tienen al menos 50 años.
A1 ▸ M1 ▸ TD ▸ Lección 20 EUREKA MATH2 320 P RÁCTICA
020406080 100 Edad (años) Edades de personas residentes de Kenia Residentes de Kenia Edades de personas residentes de los EE. UU. 0.01 0.02 0.03 0.04 Frecuencia relativa 0.06 0.05 0.08 0.07 0153045 60 75 90 105 0 Edad (años)
© Great Minds PBC
Recuerda
En los problemas 6 y 7, halla el valor de c para resolver la desigualdad.
6. −34c + 18c ≤ 8
7. −4(2 c − 8) < −24
8. Considera la ecuación |3x − 5| = 4
a. Reescribe la ecuación como un enunciado compuesto.
b. Usa el enunciado compuesto de la parte (a) para hallar el conjunto de soluciones de la ecuación original.
9. Supón que Nina y Danna caminan cada una a una tasa constante. La ecuación dt = 16 5 representa la distancia de Nina d en millas para t horas de caminata. La gráfica representa la distancia de Danna durante el tiempo que camina. ¿Quién camina a una tasa mayor? Explica.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 20 321 P RÁCTICA
0 0.25 0.5 0.751 1.25 1.5 1.75 0.5 1 1.5 2 2.5 3 3.5 x y Distancia de Danna (millas) Tiempo (horas) © Great Minds PBC
Student Edition: Grade A1, Module 1, Topic D, Lesson 21
Nombre
Fecha
Usar la desviación estándar para describir la variabilidad de una distribución univariada
1. Una directora de escuela quiere saber cuánto duermen sus estudiantes cada noche. Selecciona al azar a 8 estudiantes de noveno grado y a 8 estudiantes de sexto grado y les pide que informen el número de horas que durmieron la noche anterior, redondeado a la hora más cercana. Los diagramas de puntos muestran los resultados.
de sueño (horas)
(horas)
A partir de las distribuciones, compara la cantidad típica de horas de sueño de quienes estudian en noveno grado con la cantidad típica de horas de sueño de quienes estudian en sexto grado.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 21 323
Horas
456789 11 10 12
Horas de sueño de estudiantes de sexto grado 456789 11 10 12
Cantidad
de sueño de estudiantes de noveno grado
Cantidad de sueño
21 © Great Minds PBC
LECCIÓN
Usar la desviación estándar para medir la dispersión
2.
Cantidad de sueño (horas)
Estudiantes de noveno grado
Desviación respecto de la media
Desviación respecto de la media al cuadrado
Suma de las desviaciones:
Suma de los cuadrados de las desviaciones:
Media:
Estima la desviación típica respecto de la media del conjunto de datos de estudiantes de noveno grado.
Varianza: la suma de las desviaciones respecto de la media elevadas al cuadrado dividida entre uno menos que el tamaño de la muestra
Desviación estándar: la raíz cuadrada de la varianza; puede usarse para medir la distancia típica desde la media
Varianza:
Desviación estándar:
¿Qué representa la desviación estándar en este contexto?
A1 ▸ M1 ▸ TD ▸ Lección 21 EUREKA MATH2 324 L ECCIÓN
6 7 7 8 8 8 10 10
© Great Minds PBC
Estudiantes de sexto grado Cantidad
Media:
Varianza:
Desviación estándar:
Interpreta la desviación estándar en este contexto.
Suma de los cuadrados de las desviaciones:
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 21 325 L ECCIÓN
3.
de sueño (horas) Desviación
de la media Desviación respecto de la media al cuadrado 7 8 8 8 8 8 8 9
respecto
Suma de las desviaciones:
© Great Minds PBC
Usar tecnología para calcular la desviación estándar
4. Los siguientes diagramas de puntos muestran una muestra aleatoria más grande de estudiantes de noveno grado y de sexto grado. Usa tecnología para hallar la desviación estándar de cada conjunto de datos.
Horas de sueño de estudiantes de noveno grado
456789 11 10 12
Cantidad de sueño (horas)
Horas de sueño de estudiantes de sexto grado
456789
11 10 12
Cantidad de sueño (horas)
Calcula la desviación estándar del conjunto de datos de estudiantes de noveno grado.
Calcula la desviación estándar del conjunto de datos de estudiantes de sexto grado.
Compara las desviaciones estándar de las muestras.
A1 ▸ M1 ▸ TD ▸ Lección 21 EUREKA MATH2 326 L ECCIÓN
© Great Minds PBC
Cambiar los valores y la desviación estándar
Determina si cada enunciado es verdadero siempre, a veces o nunca.
5. Disminuir el valor de un punto disminuirá la desviación estándar de un conjunto de datos.
6. Aumentar el valor de un punto aumentará la desviación estándar de un conjunto de datos.
7. Incluir un valor atípico en el cálculo aumentará la desviación estándar de un conjunto de datos.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 21 327 L ECCIÓN
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic D, Lesson 21
Nombre Fecha BOLETO DE SALIDA
1. El diagrama de puntos del conjunto de datos A muestra las puntuaciones en una prueba corta de matemáticas que incluía 4 preguntas con un valor de 2 puntos cada una. El diagrama de puntos del conjunto de datos B muestra las puntuaciones de una prueba corta de matemáticas que incluía 8 preguntas con un valor de 1 punto cada una.
¿Qué enunciado compara las medias y las desviaciones estándar de los conjuntos de datos A y B correctamente?
Puntuaciones de la prueba corta
A. El conjunto de datos A y el conjunto de datos B tienen la misma media y la misma desviación estándar.
B. El conjunto de datos A tiene una media y una desviación estándar mayores que las del conjunto de datos B.
C. El conjunto de datos A tiene una media mayor que la del conjunto de datos B, pero el conjunto de datos A y el conjunto de datos B tienen la misma desviación estándar.
D. El conjunto de datos A y el conjunto de datos B tienen la misma media, pero el conjunto de datos A tiene una desviación estándar mayor que la del conjunto de datos B.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 21 329
0 2 4 6 Conjunto de datos A Puntuaciones de la prueba corta 8 0 2 4 8 6
de datos B
Conjunto
21 © Great Minds PBC
2. El siguiente conjunto de datos indica el ahorro de combustible de 5 autos en millas por galón.
23.4, 24.7, 24.7, 24.9, 27.9
La media del conjunto de datos es aproximadamente 25.1 millas por galón y la desviación estándar es aproximadamente 1.7 millas por galón.
Un conjunto de datos diferente indica el ahorro de combustible de otros 6 autos en millas por galón.
22.9, 23.7, 23.7, 25.9, 26.5, 50.0
Sin calcular las desviaciones estándar, explica por qué la desviación estándar del segundo conjunto de datos es mayor que la desviación estándar del primer conjunto de datos.
A1 ▸ M1 ▸ TD ▸ Lección 21 EUREKA MATH2 330 B OLETO DE SALIDA
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic D, Lesson 21
Nombre Fecha
Usar la desviación estándar para describir la variabilidad de una distribución univariada
En esta lección:
• calculamos la varianza y la desviación estándar de una distribución, a mano y con tecnología;
• usamos la desviación estándar para comparar dos distribuciones;
• exploramos los efectos de cambiar valores de datos en la desviación estándar de una distribución.
Ejemplo
La lista muestra las edades en años de 5 estudiantes que juegan en los columpios de un patio de juegos.
6, 8, 8, 11, 12
a. ¿Cuál el rango del conjunto de datos?
12 − 6 = 6
6 años
b. ¿Cuál es la media de la distribución?
6881112 5 9 +++ + =
9 años
Vocabulario
La varianza es la suma de las desviaciones respecto de la media elevadas al cuadrado de un conjunto de datos dividida entre uno menos que el tamaño de la muestra. La varianza es una medida de la variación general respecto de la media en una muestra.
La desviación estándar es una medida de variabilidad apropiada para las distribuciones de datos que son aproximadamente simétricas. La desviación estándar se suele usar para describir la distancia típica desde la media y se calcula extrayendo la raíz cuadrada de la varianza de un conjunto de datos.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 21 331
21 © Great Minds PBC
RESUMEN
c. Registra las desviaciones respecto de la media y las desviaciones respecto de la media elevadas al cuadrado en la tabla.
Resta la media de cada valor de un dato.
Edad (años)
Desviación respecto de la media
d. ¿Cuál es la varianza de la distribución? 91149
Desviación respecto de la media elevada al cuadrado
La desviación respecto de la media es negativa cuando el valor de un dato es menor que la media. La desviación al cuadrado siempre es positiva.
e. ¿Cuál es la desviación estándar de la distribución? Redondea al décimo más cercano.
62449 ≈ . 2.4 años
Para calcular la varianza, divide entre 1 menos que el tamaño de la muestra. El tamaño de la muestra es 5. Entonces, divide entre 4 La desviación estándar es la raíz cuadrada de la varianza.
f. Interpreta la desviación estándar en contexto.
La distancia típica entre las edades del grupo de estudiantes y la media de las edades es aproximadamente 2.4 años.
A1 ▸ M1 ▸ TD ▸ Lección 21 EUREKA MATH2 332 R ESUMEN
6 −3 9 8 −1 1 8 −1 1 11 2 4 12 3 9
4 6
+ = 6
+++
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic D, Lesson 21
Nombre Fecha
1. Cada estudiante de noveno grado de una escuela secundaria debe correr una milla cronometrada como parte de un examen anual de estado físico. Cada conjunto de datos muestra los tiempos que tardaron 5 estudiantes de noveno grado que se seleccionaron al azar en correr una milla, redondeados al minuto más cercano.
Conjunto de datos 1: 9, 9, 9, 9, 9
Conjunto de datos 2: 7, 8, 9, 10, 11
a. Escribe una oración que compare los centros y las dispersiones de los conjuntos de datos.
b. Interpreta lo que significan los centros y las dispersiones en esta situación.
2. La persona encargada de un parque de trampolines registró la asistencia al parque cada día durante varios meses. La media del conjunto de datos es 85 personas y la desviación estándar es 6 personas.
a. Explica qué te indica la media de este conjunto de datos sobre el número de personas que asistieron al parque de trampolines.
b. Explica qué te indica la desviación estándar de este conjunto de datos sobre el número de personas que asistieron al parque de trampolines.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 21 333
21 © Great Minds PBC
PRÁCTICA
3. En la siguiente lista, se muestran las puntuaciones de una prueba corta de cinco estudiantes que se seleccionaron al azar.
6, 7, 9, 9, 9
a. ¿Cuál es el rango del conjunto de datos?
b. ¿Cuál es la media del conjunto de datos?
c. Registra las desviaciones respecto de la media y las desviaciones respecto de la media elevadas al cuadrado en la tabla.
Puntuación en la prueba corta
Desviación respecto de la media
Desviación respecto de la media elevada al cuadrado
d. ¿Cuál es la varianza de la distribución de datos?
e. ¿Cuál es la desviación estándar de la distribución de datos? Redondea al décimo más cercano.
f. Interpreta la desviación estándar en contexto.
A1 ▸ M1 ▸ TD ▸ Lección 21 EUREKA MATH2 334 P RÁCTICA
6 7 9 9 9
© Great Minds PBC
4. En una competencia de atletismo, se corren tres carreras masculinas de 100 metros. Los tiempos que tardaron los corredores en completar cada carrera se registran redondeados al 0.1 de segundo más cercano y se muestran en los diagramas de puntos.
a. Sin calcular, ordena las carreras de la menor desviación estándar a la mayor desviación estándar.
b. Explica cómo pudiste ordenar las desviaciones estándar de las distribuciones sin calcular.
c. ¿Qué estimación se acerca más a la desviación estándar de los datos de la carrera 1?
A. 0.1 segundos
B. 0.75 segundos
C. 1.15 segundos
D. 1.30 segundos
d. Usa tu calculadora para hallar la media y la desviación estándar de la carrera 1. Redondea cada valor al centésimo más cercano. ¿Cuán cerca del valor real estuvo tu estimación de la desviación estándar?
Media de la carrera 1:
Desviación estándar de la carrera 1:
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 21 335 P RÁCTICA
Carrera 1 Carrera 2 Tiempo (segundos) Carrera 3 10.5 11.0 11.5 12.0 13.0 12.5
© Great Minds PBC
5. El encargado de un supermercado se preguntó si había un número constante de manzanas en las bolsas de manzanas vendidas en el supermercado. Seleccionó al azar 20 bolsas de manzanas y registró el número de manzanas en cada bolsa. La media del número de manzanas en cada bolsa era 8 y la desviación estándar era aproximadamente 2 manzanas.
Bolsas de manzanas seleccionadas al azar
456789 10 11 13 12
Número de manzanas
a. ¿Cómo podría el encargado redistribuir las manzanas en bolsas de manera que la media de la distribución no cambie, pero la desviación estándar sea 0?
b. ¿Cómo podría el encargado redistribuir las manzanas en bolsas de manera que la media y el rango de la distribución no cambien, pero se maximice la desviación estándar?
c. Supón que se agrega otra bolsa de manzanas a la muestra original. Describe qué ocurriría con la desviación estándar si en la bolsa hubiera las siguientes cantidades de manzanas:
i. 9 manzanas
ii. 11 manzanas
iii. 3 manzanas
A1 ▸ M1 ▸ TD ▸ Lección 21 EUREKA MATH2 336 P RÁCTICA
© Great Minds PBC
Recuerda
En los problemas 6 y 7, resuelve la desigualdad.
6. 5341 5 −≤ m
7. −0.5(−4m − 6) > 4
8. ¿Qué ecuaciones o desigualdades no tienen solución? Elige todas las opciones que correspondan.
A. |x + 2| = −5
B. |x + 2| = 5
C. |x + 2| = −5
D. |x + 2|< −5
E. |x + 2|≥ −5
9. Halla la pendiente de la recta.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 21 337 P RÁCTICA
−612345678910−8−5 −10−7−4−3−2−1 −9 4 2 3 1 10 8 9 6 5 7 −6 −8 −9 −4 −7 −5 −2 −3 −1 −10 y x 0 © Great Minds PBC
Student Edition: Grade A1, Module 1, Topic D, Lesson 22
Nombre Fecha
Estimar la variabilidad de distribuciones de datos
1. Como parte de un proyecto, la clase de Álgebra I de la maestra Allen recopiló datos para determinar si la cantidad de tarea aumentaba a medida que aumentaba el nivel de grado. Un grupo encuestó a una muestra aleatoria de 50 estudiantes de noveno grado y a 50 estudiantes de undécimo grado y les preguntó cuántas horas a la semana dedicaban a hacer la tarea. Los diagramas de puntos muestran los resultados de la encuesta.
Horas semanales de tarea para estudiantes de noveno grado
Horas semanales de tarea para estudiantes de undécimo grado
Tiempo (horas)
Tiempo (horas)
Compara las dispersiones de las distribuciones. Explica tu razonamiento.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 22 339
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
22 © Great Minds PBC
LECCIÓN
Estimar la dispersión a partir de histogramas
Un equipo de control de calidad de productos está realizando un estudio de diferentes marcas de pilas. El equipo mide la duración de las pilas en una muestra aleatoria de 100 pilas de la marca D y una muestra aleatoria de 100 pilas de la marca E.
Duración de las pilas de la marca D
2. Estima la media de la distribución de la duración de las pilas de la marca D.
3. ¿Qué valor es más cercano al valor de la desviación estándar de la distribución de la duración de las pilas? Encierra en un círculo la mejor estimación.
3 horas
10 horas
30 horas
A1 ▸ M1 ▸ TD ▸ Lección 22 EUREKA MATH2 340 L ECCIÓN
0.10 0.20 0.30 0.40 Frecuencia relativa 85 95 105 115 125 135 145 155 165 0 Duración de las pilas (horas)
© Great Minds PBC
4. Estima la media de la distribución de la duración de las pilas de la marca E.
5. ¿Es la desviación estándar de esta distribución mayor que, aproximadamente igual a, o menor que la desviación estándar de la distribución de la duración de las pilas de la marca D? Explica tu razonamiento.
6. Compara la distribución de la duración de las pilas de la marca D con la distribución de la duración de las pilas de la marca E. Interpreta la comparación en contexto.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 22 341 L ECCIÓN 0.10 0.20 0.30 0.40 Frecuencia relativa 85 95 105 115 125 135 145 155 165 0 Duración de las pilas (horas) Duración de las pilas de la marca E
© Great Minds PBC
Medir la variación a partir de diagramas de caja
Velocidades máximas de las montañas rusas
De madera
De acero
Una compañía propietaria de parques de diversiones estaba estudiando las montañas rusas de madera y acero de la competencia. En una investigación, se seleccionó una muestra aleatoria de 75 montañas rusas de madera y 75 montañas rusas de acero y se registraron sus velocidades máximas. La distribución de los datos se muestra en los diagramas de caja. 0102030405060708090
Velocidad (millas por hora)
7. ¿Cuántos valores atípicos hay en cada distribución? Estima sus valores.
8. ¿Cuál es la diferencia aproximada entre las medianas de las velocidades de las distribuciones?
9. ¿Cuál es la diferencia aproximada entre los rangos de las distribuciones?
A1 ▸ M1 ▸ TD ▸ Lección 22 EUREKA MATH2 342 L ECCIÓN
100 110 120 130
© Great Minds PBC
10. ¿Cuál es la diferencia aproximada entre los rangos intercuartiles de las distribuciones?
11. ¿Qué medida compara con mayor precisión la variación de las distribuciones? Justifica tu razonamiento.
12. Compara las distribuciones de las velocidades máximas de las montañas rusas. Interpreta tus conclusiones en contexto.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 22 343 L ECCIÓN
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic D, Lesson 22
Nombre Fecha
1.
Pesos de los perros
¿Qué valor es la mejor estimación de la desviación estándar de la distribución?
A. 15 libras
B. 30 libras
C. 37.5 libras
D. 75 libras
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 22 345
2 6 10 4 8 12 14 16 Frecuenci a 18 015304560 75 0
(libras)
El histograma muestra la distribución de los pesos en libras de 50 perros en una exposición canina.
Peso
22
Great Minds PBC
BOLETO DE SALIDA
©
Ubicación 1
Ubicación 2
2. En dos ubicaciones distintas, hay un límite de velocidad de 70 kilómetros por hora. Ana usa un detector de velocidad para recopilar muestras aleatorias de las velocidades, en kilómetros por hora, de los autos que pasan por las dos ubicaciones en un día. Los diagramas de caja muestran las distribuciones de esas muestras aleatorias. 50
Supón que Ana afirma que la variación de las velocidades de conducción en la ubicación 1 es mayor que la variación de las velocidades de conducción en la ubicación 2.
a. A partir de los datos, proporciona un tipo de evidencia que respalde la afirmación de Ana.
b. A partir de los datos, proporciona un tipo de evidencia que refute la afirmación de Ana.
A1 ▸ M1 ▸ TD ▸ Lección 22 EUREKA MATH2 346 B OLETO DE SALIDA
60 70 80 90 100
(kilómetros por hora)
Velocidad
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic D, Lesson 22
Nombre Fecha
Estimar la variabilidad de distribuciones de datos
En esta lección:
• estimamos la media y la desviación estándar de una distribución a partir de un histograma;
• comparamos la dispersión de distribuciones en diagramas de caja y diagramas de puntos.
Ejemplos
1. El histograma muestra las edades de una muestra aleatoria de 100 personas suscritas a un servicio de streaming.
La distribución tiene forma de campana. Aproximadamente dos tercios de los valores de datos se encuentran dentro de una desviación estándar de la media de la distribución.
La media está ubicada aproximadamente en el centro de la distribución.
a. Estima la media de la edad de alguien que se haya suscrito al servicio de streaming. Márcala en el histograma con una línea vertical.
Aproximadamente 40 años
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 22 347
5 10 15 20 25 Frecuenci a 30 10 20 30 40 50 60 70 0 Edad (años)
RESUMEN 22 © Great Minds PBC
b. ¿Qué valor es más cercano al valor de la desviación estándar de la distribución de las edades? Encierra en un círculo la mejor estimación.
8 años
16 años
24 años
c. En el histograma, marca las ubicaciones que tengan aproximadamente una desviación estándar mayor que la media y una desviación estándar menor que la media.
2. El diagrama de caja resume el número de videos que la muestra aleatoria de quienes se suscribieron al servicio de streaming reprodujo durante el último mes.
Un dato separado del resto del diagrama en un diagrama de caja es un valor atípico.
Videos reproducidos el último mes
Número de videos
a. Identifica cualquier valor atípico en la distribución.
0 videos
b. ¿Cuál es el rango de la distribución?
30 videos
c. ¿Cuál es el rango intercuartil (RIQ) de la distribución?
8 videos
d. ¿Es el rango o el RIQ una mejor medida de la dispersión para esta distribución? Explica.
Incluye los valores atípicos cuando calcules las medidas de tendencia central y de dispersión. El valor mínimo en esta distribución es 0 videos, y no 13 videos.
30 − 0 = 30
El RIQ es la diferencia entre el C3 y el C1.
24 − 16 = 8
El RIQ es una mejor medida de dispersión para esta distribución. El valor atípico aumenta significativamente el rango de la distribución, pero tiene poco o ningún efecto en el RIQ. Entonces, el RIQ representa mejor la dispersión general de los datos.
A1 ▸ M1 ▸ TD ▸ Lección 22 EUREKA MATH2 348 R ESUMEN
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic D, Lesson 22
1. Se preguntó a cada miembro de un equipo de natación de una escuela secundaria cuántas horas estudió la semana pasada, estimadas a la media hora más cercana. El histograma resume los resultados.
Tiempo semanal dedicado a estudiar del equipo de natación A
a. ¿Qué valor estima mejor la media del tiempo de estudio?
A. 5 horas
B. 10 horas
C. 20 horas
b. ¿Qué valor estima mejor la desviación estándar del tiempo de estudio?
A. 2.5 horas
B. 5 horas
C. 10 horas
D. 20 horas
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 22 349
2 4 6 8 Frecuenci a 12 10 2.5 7.5 12.5 17.5 22.5 27.5 32.5 37.5 42.5 0 Tiempo de estudio (horas)
22 © Great Minds PBC
Nombre Fecha PRÁCTICA
2. Supón que se pregunta a cada miembro de un equipo de natación de otra escuela secundaria cuántas horas estudió la semana pasada, estimadas a la media hora más cercana. El diagrama de caja muestra la distribución de datos.
Tiempo semanal dedicado a estudiar del equipo de natación B
Tiempo de estudio (horas)
a. ¿Cuál es el rango de la distribución?
b. Interpreta el rango en este contexto.
c. Identifica cualquier valor atípico en la distribución.
d. ¿Cuál es el rango intercuartil (RIQ) de la distribución?
e. Interpreta el RIQ en este contexto.
A1 ▸ M1 ▸ TD ▸ Lección 22 EUREKA MATH2 350 P RÁCTICA
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40
© Great Minds PBC
3. Ahora, supón que se pregunta a cada miembro de un equipo de atletismo de una escuela secundaria cuántas horas estudió la semana pasada. El diagrama de caja muestra la distribución de datos.
Tiempo semanal dedicado a estudiar del equipo de atletismo
Tiempo de estudio (horas)
a. Identifica cualquier valor atípico en la distribución.
b. ¿Cuál es el rango de la distribución?
c. ¿Cuál es el RIQ de la distribución?
d. ¿Es el rango o el RIQ una mejor medida de la dispersión para la distribución? Explica tu razonamiento.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 22 351 P RÁCTICA
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40
© Great Minds PBC
4. La ciudad A organiza un maratón. Las edades de quienes corrieron el maratón se resumen en el histograma.
a. Estima la media de las edades de quienes corrieron el maratón de la ciudad A. Marca este valor en el histograma con una línea vertical.
Edades de quienes participaron del maratón de la ciudad A
Encierra en un círculo la mejor estimación de la desviación estándar de las edades de quienes corrieron el maratón en la ciudad A.
A1 ▸ M1 ▸ TD ▸ Lección 22 EUREKA MATH2 352 P RÁCTICA
2000 4000 6000 8000 10000 12000 14000 Frecuenci a 16000 18 28 38 48 58 68 78 0 Edad (años)
5 años 10 años 15 años © Great Minds PBC
b. En el histograma, marca con líneas verticales las ubicaciones que tengan aproximadamente una desviación estándar mayor que la media y una desviación estándar menor que la media.
Edades de quienes participaron del maratón de la ciudad A
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 22 353 P RÁCTICA
2000 4000 6000 8000 10000 12000 14000 Frecuenci a 16000 18 28 38 48 58 68 78 0 Edad (años) © Great Minds PBC
c. ¿Aproximadamente qué porcentaje de las edades de quienes corrieron se encuentra entre una desviación estándar menor que la media y una desviación estándar mayor que la media?
La ciudad B también organizó un maratón. Las edades de quienes corrieron el maratón se resumen en el histograma.
Edades de quienes participaron del maratón de la ciudad B
d. Estima la media de las edades de quienes corrieron el maratón de la ciudad B.
e. Encierra en un círculo la mejor estimación de la desviación estándar de las edades de quienes corrieron el maratón en la ciudad B.
5 años
10 años
15 años
f. ¿En qué distribución es mayor la desviación estándar de las edades de quienes corrieron el maratón? ¿Por qué es mayor?
A1 ▸ M1 ▸ TD ▸ Lección 22 EUREKA MATH2 354 P RÁCTICA
20 40 60 80 Frecuenci a 100 18 28 38 48 58 68 78 0 Edad (años)
© Great Minds PBC
5. Considera los diagramas de caja de las distribuciones de los tiempos de demora, en minutos, de 60 vuelos de la aerolínea Big Air seleccionados al azar en noviembre y diciembre de 2019.
Tiempos de demora de los vuelos de Big Air
Noviembre
Diciembre
0102030405060708090
100 110 120
Tiempo de demora (minutos)
Compara las distribuciones de los tiempos de demora en contexto usando la forma y las medidas de tendencia central y de dispersión.
6. Nina seleccionó a 10 estudiantes al azar de su clase de Español y a 10 estudiantes al azar de su clase de Matemáticas. Preguntó a cada estudiante cuántas películas había visto el mes anterior. Las respuestas se incluyen en las listas que se muestran.
Número de películas vistas por cada estudiante el mes pasado
Clase
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 22 355 P RÁCTICA
de Español 0, 0, 1, 1, 2, 2, 3, 4, 4, 6 Clase de Matemáticas 0, 0, 0, 1, 2, 2, 2, 4, 4, 16 © Great Minds PBC
a. Calcula la media y la mediana para los datos de cada clase.
Clase Media Mediana
Español
Matemáticas
b. Calcula la desviación estándar y el RIQ para los datos de cada clase. Redondea al décimo más cercano.
Clase
Español
Matemáticas
Desviación estándar
c. Identifica los valores atípicos en cada conjunto de datos.
Rango intercuartil (RIQ)
d. ¿Qué medidas de dispersión se ven más afectadas por el valor atípico? Explica tu razonamiento.
e. ¿Son diferentes el número típico de películas vistas el mes pasado en la clase de Español de Nina y el número típico de películas vistas el mes pasado en la clase de Matemáticas de Nina? Explica tu razonamiento.
A1 ▸ M1 ▸ TD ▸ Lección 22 EUREKA MATH2 356 P RÁCTICA
© Great Minds PBC
7. Los diagramas de puntos muestran tres conjuntos de datos.
Conjunto de datos A
Conjunto de datos B
Conjunto de datos C
20 21 22 23 24 25 26 27 28 29 30
a. Compara las distribuciones usando la forma y las medidas de tendencia central y de variación.
b. ¿Qué medidas de tendencia central y de variación elegiste comparar? ¿Por qué?
c. ¿De qué manera estos conjuntos de datos ejemplifican la importancia de medir la variación para describir una distribución de datos?
Recuerda
En los problemas 8 y 9, resuelve la desigualdad.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 22 357 P RÁCTICA
8. −> ()2583 3 t 9. 2 9 4 3 30 tt−≤ © Great Minds PBC
10. El diagrama de puntos muestra la distribución de las duraciones de los entrenamientos del martes para una muestra aleatoria de 40 miembros de un gimnasio. Los tiempos están redondeados a los 5 minutos más cercanos.
en el gimnasio
a. ¿Cuál es la forma de la distribución de las duraciones de los entrenamientos?
b. ¿Son 30 minutos una duración típica de un entrenamiento para esta muestra de miembros de un gimnasio? Justifica tu respuesta.
11. Escribe la ecuación de la recta en la forma pendiente-intersección.
A1 ▸ M1 ▸ TD ▸ Lección 22 EUREKA MATH2 358 P RÁCTICA
0 5 10 15 20 25 30 35 40 45 50 55 60 65 Tiempo
Tiempo (minutos)
4 2681 −8−60−10−4−2 4 2 10 8 6 −6 −8 −4 −2 −10 y x 0 © Great Minds PBC
Student Edition: Grade A1, Module 1, Topic D, Lesson 23
Nombre Fecha
Comparar distribuciones de datos univariados
Conjuntos de datos que te fueron asignados:
Describe el contexto de los conjuntos de datos que compararás con una oración.
Comparación informal de los conjuntos de datos:
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 23 359
23 © Great Minds PBC
LECCIÓN
Comparar conjuntos de datos univariados
Compararás los conjuntos de datos asignados a tu grupo completando las siguientes tareas:
• Determina qué medidas de tendencia central y de dispersión son apropiadas para comparar las distribuciones de datos.
• Calcula las medidas de tendencia central y de dispersión que seleccionaste, si es necesario.
• Compara la forma, el centro y la dispersión de los conjuntos de datos. Interpreta cualquier diferencia que halles en contexto.
Población
Home runs
A1 ▸ M1 ▸ TD ▸ Lección 23 EUREKA MATH2 360 L ECCIÓN
© Great Minds PBC
Precipitaciones
Gasolina
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 23 361 L ECCIÓN
Great Minds PBC
©
Student Edition: Grade A1, Module 1, Topic D, Lesson 23
Nombre Fecha
BOLETO DE SALIDA
El diagrama de puntos muestra la distribución del número de flexiones consecutivas realizadas por una muestra aleatoria de 20 personas.
de flexiones
El diagrama de caja muestra la distribución del número de flexiones consecutivas realizadas por una muestra aleatoria de 200 personas.
de flexiones
a. Compara las formas de las distribuciones de datos.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 23 363
Número
02468 10 12 14 16 18 20
02468 10 12 14 16 18 20 Número
© Great Minds PBC
23
b. Compara los centros de las distribuciones de datos en este contexto.
c. Compara la variación de las distribuciones de datos en este contexto.
A1 ▸ M1 ▸ TD ▸ Lección 23 EUREKA MATH2 364 B OLETO DE SALIDA
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic D, Lesson 23
Nombre
Fecha
Comparar distribuciones de datos univariados
En esta lección:
• comparamos distribuciones usando la forma, el centro y la variabilidad;
• interpretamos diferencias en distribuciones en contexto.
Ejemplo
Las gráficas muestran las distribuciones de los tiempos de vuelo en una muestra aleatoria de vuelos de Boston a San Francisco y en una muestra aleatoria de vuelos de San Francisco a Boston.
Tiempo de vuelo (minutos) Vuelos de Boston a San Francisco
Compara las distribuciones de los tiempos de vuelo en contexto usando la forma y las medidas de tendencia central y de dispersión.
Forma:
La distribución de los tiempos de vuelo de Boston a San Francisco parece aproximadamente simétrica, mientras que la distribución de los tiempos de vuelo de San Francisco a Boston parece estar sesgada hacia la derecha.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 23 365
325 330 335 340 345 350 355 360 365 370 375 380 385 390
Frecuenci
Tiempo
285 290 295 300 305 310 315 320 325 0 1 2 3 4 5 6 7
a
de vuelo (minutos) Vuelos de San Francisco a Boston
RESUMEN 23 © Great Minds PBC
Centro:
La mediana del tiempo de vuelo de Boston a San Francisco es aproximadamente 356 minutos.
La mediana del tiempo de vuelo de San Francisco a Boston está entre 295 minutos y 300 minutos.
El tiempo de vuelo típico de Boston a San Francisco es aproximadamente 55 a 60 minutos más largo que el tiempo de vuelo típico de San Francisco a Boston.
Dispersión:
El RIQ de la distribución de los tiempos de vuelo de Boston a San Francisco es aproximadamente 28 minutos. El RIQ de la distribución de los tiempos de vuelo de San Francisco a Boston está entre 10 y 20 minutos. La variación típica de los tiempos de vuelo de Boston a San Francisco es aproximadamente 10 a 20 minutos más que la variación típica de los tiempos de vuelo de San Francisco a Boston.
A1 ▸ M1 ▸ TD ▸ Lección 23 EUREKA MATH2 366 R ESUMEN
© Great Minds PBC
Student Edition: Grade A1, Module 1, Topic D, Lesson 23
Nombre Fecha
1. El siguiente diagrama de puntos representa las edades de 60 personas seleccionadas al azar en Japón en 2018.
Edades de las personas en Japón Edad
a. ¿Cuál es la forma de la distribución?
b. ¿Cómo nos ayuda la forma de una distribución a decidir qué medidas de tendencia central y de dispersión usar?
c. ¿Cuál es la edad típica de una persona de la muestra?
d. ¿Qué medida de tendencia central usaste para calcular una edad típica en la parte (c)? Justifica tu elección.
e. ¿Cuál es una estimación de la dispersión de la distribución?
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 23 367
(años) 0 10 20 30 40 50 60 70 80 100 90
23 © Great Minds PBC
PRÁCTICA
f. ¿Qué medida de dispersión usaste para calcular la dispersión en la parte (e)? Justifica tu elección.
2. El histograma de frecuencias relativas resume las edades de una muestra aleatoria de personas de Bangladés en 2018.
a. Compara las formas de las distribuciones de las edades en la muestra de Japón y la muestra de Bangladés.
b. ¿Qué medidas de tendencia central y de dispersión usarías para comparar las distribuciones? Justifica tu razonamiento.
c. Compara las distribuciones usando medidas de tendencia central y de dispersión apropiadas.
A1 ▸ M1 ▸ TD ▸ Lección 23 EUREKA MATH2 368 P RÁCTICA
Frecuencia relativa Edad (años) Edades de las personas en Bangladés 0 10 5152535455565758595 20 30 40 50 60 70 90 80 100 0 0.02 0.04 0.06 0.08 0.10 0.12
© Great Minds PBC
3. Un director seleccionó a 100 estudiantes de octavo grado al azar para que participen de un examen de fluidez en la lectura. Sus maestras y maestros registraron el número de palabras que cada estudiante leyó con precisión en un minuto. Los exámenes se llevaron a cabo en otoño y de nuevo en primavera. Los resultados de cada examen se resumen en los diagramas de caja.
del examen de fluidez en la lectura
Primavera
Otoño
Escribe dos o tres oraciones sobre los resultados del examen de lectura de octavo grado.
4. En las gráficas que siguen se muestran las distribuciones del número de carreras anotadas por partido en una muestra aleatoria de 30 partidos del equipo de beisbol Blue Socks y una muestra aleatoria de 30 partidos del equipo de beisbol Black Socks
Carreras anotadas por el equipo de beisbol Blue Socks
Carreras anotadas por el equipo de beisbol Black Socks
Número de carreras anotadas
Número de carreras anotadas
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 23 369 P RÁCTICA
60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 220 210 Fluidez (palabras por
minuto) Puntuaciones
10 9
012345678
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
© Great Minds PBC
Compara las distribuciones en contexto usando la forma y las medidas de tendencia central y de dispersión.
5. Los diagramas de caja resumen las distribuciones de las ventas semanales de galletas de chispas de chocolate en tres panaderías.
Ventas semanales de galletas de chispas de chocolate
Panadería A
Panadería B
Panadería C
de galletas vendidas
Compara las distribuciones en este contexto usando la forma y las medidas de tendencia central y de dispersión.
A1 ▸ M1 ▸ TD ▸ Lección 23 EUREKA MATH2 370 P RÁCTICA
30 50 70 90 110 130 150 170 190 210 230 250 Número
© Great Minds PBC
Recuerda
En los problemas 6 y 7, resuelve la ecuación.
6. 6a − 4a − 3(4a + 1) = 47
7. −8a + 2(−3a + 3) − a = 1
8. Se preguntó a una muestra aleatoria de estudiantes de noveno grado y de décimo grado de una escuela cuántas horas habían dedicado a tareas de voluntariado el mes pasado. Los diagramas de caja muestran las distribuciones del tiempo dedicado al voluntariado.
Horas de voluntariado
Décimo grado
Noveno grado
012345678
Tiempo (horas)
¿Es el número típico de horas de voluntariado de quienes estudian en noveno grado mayor que, menor que o igual al número típico de horas de voluntariado de quienes estudian en décimo grado, según la encuesta? Justifica tu respuesta.
EUREKA MATH2 A1 ▸ M1 ▸ TD ▸ Lección 23 371 P RÁCTICA
© Great Minds PBC
A1 ▸ M1 ▸ TD ▸ Lección 23 EUREKA MATH2 372 P RÁCTICA 9. Representa gráficamente yx=− 2 3 5 .
−60−8−5 −10−7−4−3−2−1 −9 4 2 3 1 10 8 9 6 5 7 −6 −8 −9 −4 −7 −5 −2 −3 −1 −10 y x 0 © Great Minds PBC
1234567891
3. Escribe un número que complete la ecuación para que tenga infinitas soluciones. 4(2x
EUREKA MATH2 A1 ▸ M1 373
Evalúa 41 1 2 x () para x =− 1 2 .
Halla el valor de x para resolver la ecuación 648 7 8 3 8 += ++xx .
1.
2.
=
x + 12
Fecha
+ _____)
8
Nombre
1 © Great Minds PBC
Práctica mixta 1 Edición para estudiantes: Grado A1, Módulo 1, Práctica mixta
4. Elige la solución del sistema de ecuaciones lineales que se muestra en la gráfica.
A. Punto F
B. Punto G
C. Punto J
D. Puntos F, G y J
5. Resuelve el sistema de ecuaciones lineales de manera algebraica.
A1 ▸ M1 ▸ Práctica mixta 1 EUREKA MATH2 374
yx yx =+ = 3 5 1 5 16 2 −313 −2−1 2 1 3 −3 −2 −1 y x 0 G F J © Great Minds PBC
6. Empareja cada gráfica con su descripción.
La gráfica muestra un valor atípico.
La gráfica muestra una asociación no lineal negativa.
La gráfica muestra una agrupación.
La gráfica muestra una asociación lineal positiva.
EUREKA MATH2 A1 ▸ M1 ▸ Práctica mixta 1 375
© Great Minds PBC
7. Cada estudiante de la escuela intermedia Sparks toma una clase optativa. Se preguntó a una muestra aleatoria de estudiantes qué clase optativa toman actualmente. La tabla de doble entrada muestra el número de estudiantes de la muestra por nivel de grado que toman cada clase optativa. Usa los datos de la tabla para calcular cada proporción en las partes (a) y (b).
Clases optativas
a. ¿Qué proporción de estudiantes de la muestra toman clases de Arte? Si es necesario, redondea la respuesta a dos decimales.
A. 0.27
B. 0.31
C. 0.36
D. 0.42
b. ¿Qué proporción de estudiantes de séptimo grado de la muestra toman clases de Anuario Escolar? Si es necesario, redondea la respuesta a dos decimales.
A. 0.21
B. 0.27
C. 0.30
D. 0.38
A1 ▸ M1 ▸ Práctica mixta 1 EUREKA MATH2 376
Banda Arte Anuario Escolar Total Nivel de grado 6.o grado 22 19 0 41 7.o grado 15 12 10 37 8.o grado 17 14 16 47 Total 54 45 26 125
© Great Minds PBC
8. Desde hace varios años, Tiah lleva un registro de cuántos peces pesca cada vez que va a pescar. Hoy planea ir a pescar de nuevo. La tabla muestra el número de peces que Tiah pescó en viajes anteriores y la probabilidad de que hoy pesque ese número de peces.
a. ¿Cuál es la probabilidad de que Tiah pesque exactamente 4 peces?
b. ¿Cuál es la probabilidad de que Tiah pesque al menos 3 peces?
EUREKA MATH2 A1 ▸ M1 ▸ Práctica mixta 1 377
Número de peces 0 1 2 3 4 5 6 o más Probabilidad 0.1 0.05 0.09 0.25 0.3 0.2 0.01
© Great Minds PBC
Práctica
mixta 2
Edición para estudiantes: Grado A1, Módulo 1, Práctica mixta 2 Nombre Fecha
A. 120,000
B. (1.0 × 106) + (2.0 × 105)
C. (2.0 × 103)(6.0 × 102)
D. 4810 4010 7 2 . ·
E. (2.0 × 105) − (8.0 × 104)
EUREKA MATH2 A1 ▸ M1 379
1. ¿Qué expresiones son equivalentes a 43 ⋅ 4 8? Elige todas las opciones que correspondan.
C.
D. 4 4 3 8E. 4 4 3 8 F. 1 4 5
A. 4 24 B. 4 5
411
2. ¿Qué expresiones son equivalentes a 1.2 × 105? Elige todas las opciones que correspondan.
© Great Minds PBC
3. Empareja cada enunciado con la desigualdad que lo representa. Una desigualdad puede emparejarse con más de un enunciado.
Cinco menos que 7 multiplicado por un número es al menos 21. 7x − 5 < 21
Cinco menos que 7 multiplicado por un número es menos de 21. 7x − 5 ≤ 21
Cinco menos que 7 multiplicado por un número es como máximo 21. 7x − 5 > 21
Cinco menos que 7 multiplicado por un número no es más de 21. 7x − 5 ≥ 21
Cinco menos que 7 multiplicado por un número es más de 21
4. Por una manguera fluye agua a una tasa constante de 14 galones por minuto.
a. Escribe una ecuación que represente el número de galones g que fluyen por la manguera en t minutos.
b. Completa la tabla.
Tiempo, t (minutos)
Número de galones, g 0
A1 ▸ M1 ▸ Práctica mixta 2 EUREKA MATH2 380
5 7 10 © Great Minds PBC
c. Representa gráficamente la relación entre el tiempo y los galones de agua.
5. Calcula la pendiente de la recta dos veces usando dos pares de puntos diferentes.
EUREKA MATH2 A1 ▸ M1 ▸ Práctica mixta 2 381
Tiempo (minutos) 0123456789 t 20 40 60 80 100 120 140 160 1011 g Número de galones −10−510 05 −5 5 10 −10 y x (0,6) (1,3) (2,0) (3,–3) © Great Minds PBC
6. La tabla representa una función. ¿Qué pares ordenados pueden agregarse a la tabla de manera que siga representando una función? Elige todas las opciones que correspondan.
A. (4, −13)
B. (1, −1)
C. (−4, −1)
D. (0, −1)
E. (6, −10)
F. (3, −12)
7. Un triángulo rectángulo tiene un cateto con una longitud de 12 cm y una hipotenusa con una longitud de 20 cm. ¿Cuál es la longitud del otro cateto?
A1 ▸ M1 ▸ Práctica mixta 2 EUREKA MATH2 382
x y 1 −4 2 −7 3 −10
© Great Minds PBC
8. Ji-won dice que una traslación es la única transformación de AB que dará como resultado una imagen con la misma longitud que AB . ¿Estás de acuerdo con Ji-won? Explica.
EUREKA MATH2 A1 ▸ M1 ▸ Práctica mixta 2 383
A B © Great Minds PBC
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 15 ▸ Rectas numéricas © 2024 Great Minds PBC 385 1. –10–6–5–9–8–7–4–3–2–1021436589710
–10–6–5–9–8–7–4–3–2–1021436589710 3. –10–6–5–9–8–7–4–3–2–1021436589710
–10–6–5–9–8–7–4–3–2–1021436589710 Edición para estudiantes: Grado A1, Módulo 1, Tema C, Lección 15
2.
4.
EUREKA MATH2 A1 ▸ M1 ▸ TC ▸ Lección 17 ▸ Rectas numéricas 387 1. –10–6–5–9–8–7–4–3–2–1021436589710 2. –10–6–5–9–8–7–4–3–2–1021436589710 3. –10–6–5–9–8–7–4–3–2–1021436589710 4. –10–6–5–9–8–7–4–3–2–1021436589710
–10–6–5–9–8–7–4–3–2–1021436589710
© Great Minds PBC
5.
Edición para estudiantes: Grado A1, Módulo 1, Tema C, Lección 17
Edición para estudiantes: Grado A1, Módulo 1, Práctica veloz: Sumar y restar fracciones
EUREKA MATH2 A1 ▸ M1 ▸ Práctica veloz ▸ Sumar y restar fracciones 389 Suma o resta. 1. 1 5 1 5 + 2. 1 5 3 5 + Práctica veloz
© Great Minds PBC
A1 ▸ M1 ▸ Práctica veloz ▸ Sumar y restar fracciones EUREKA MATH2 390 Suma o resta. 1. 1 7 1 7 + 2. 1 7 2 7 + 3. 1 7 3 7 + 4. 1 7 5 7 + 5. 8 11 1 116. 8 11 4 117. 8 11 5 118. 8 11 7 119. 8 11 8 1110. 1 5 1 10 + 11. 1 5 3 10 + 12. 1 10 3 5 + 13. 1 9 1 1814. 7 9 1 1815. 7 18 1 916. 9 20 1 10 + 17. 1 20 9 10 + 18. 9 10 1 2019. 5 9 2 3 + 20. 3 7 4 21 + 21. 5 9 4 2722. 3 4 9 16 + 23. 2 5 3 25 + 24. 3 4 7 2425. 9 24 2 3 + 26. 5 8 9 3227. 4 5 9 3528. 1 7 1 10 + 29. 1 7 1 1030. 5 8 2 9 + 31. 5 8 2 932. 7 20 7 8 + 33. 5 12 3 8 + 34. 5 6 4 2735. 4 25 9 10 + 36. 7 12 5 18Número de respuestas correctas:
© Great Minds PBC
A
BNúmero de respuestas correctas:
A1 ▸ M1 ▸ Práctica veloz ▸ Sumar y restar fracciones EUREKA MATH2 392
Progreso: Suma o resta. 1. 1 9 1 9 + 2. 1 9 3 9 + 3. 1 9 4 9 + 4. 1 9 6 9 + 5. 9 13 1 136. 9 13 4 137. 9 13 5 138. 9 13 7 139. 9 13 9 1310. 1 4 1 8 + 11. 1 4 3 8 + 12. 1 8 3 4 + 13. 1 7 1 1414. 5 7 1 1415. 5 14 1 716. 7 16 1 8 + 17. 1 16 7 8 + 18. 7 8 1 1619. 2 3 7 9 + 20. 5 21 4 7 + 21. 4 5 8 1522. 2 3 5 12 + 23. 2 7 3 35 + 24. 3 5 7 3025. 7 48 5 6 + 26. 2 7 3 2827. 2 3 4 2128. 1 9 1 10 + 29. 1 9 1 1030. 5 6 2 7 + 31. 5 6 2 732. 4 15 4 9 + 33. 7 16 5 6 + 34. 7 8 5 1235. 9 35 3 10 + 36. 7 12 4 15© Great Minds PBC
EUREKA MATH2 A1 ▸ M1 ▸ Práctica veloz ▸ Aplicar la propiedad distributiva
Edición para estudiantes: Grado A1, Módulo 1, Práctica veloz: Aplicar la propiedad distributiva
Práctica veloz
Aplica la propiedad distributiva y combina términos semejantes.
1. 1(x − 1)
2. 2(x + 3)
393
© Great Minds PBC
Número de respuestas correctas: A
A1 ▸ M1 ▸ Práctica veloz ▸ Aplicar la propiedad distributiva EUREKA MATH2 394
1. 1(x + 1) 2. 1(x + 2) 3. 1(x + 3) 4. 2(x − 1) 5. 2(x − 2) 6. 2(x − 3) 7. 3(2x + 1) 8. 3(2x + 2) 9. 3(2x + 3) 10. 4(2x − 1) 11. 4(2x − 2) 12. 3(3x + 6) 13. 3(3x − 6) 14. −3(3x − 6) 15. (−3x + 6)(−3) 16. 4(5x − 3) 17. −4(5x + 3) 18. −4(−5x − 3) 19. (−5x + 3)(−4) 20. (x − 10)(−1) 21. −(x + 10) 22. −(−x − 10) 23. x(x + 9) 24. x(x − 9) 25. (9 − x)x 26. x(5x + 2) 27. 5x(x − 2) 28. (−5x + 2)(−x) 29. 2x(6x − 1) 30. (−6x − 1)(2x) 31. −6x(2x + 1) 32. 4x(10 − 3x) 33. 10x(3x − 4) 34. −(6 + 5x) + 6 35. −(5x − 6) + 6 36. 6 − (−5x + 6) 37. 4(x + 3) + 2x 38. −4(x − 3) + 2x 39. 2x + 4(3 − x) 40. 2x − 4(−x + 3) 41. 2x(6x + 1) + 4x 42. 6x + 2x(4x − 1) 43. 4x(6x − 1) − 2x 44. 4x − 2x(6x − 1)
Aplica la propiedad distributiva y combina términos semejantes.
© Great Minds PBC
A1 ▸ M1 ▸ Práctica veloz ▸ Aplicar la propiedad distributiva EUREKA MATH2 396
1. 1(x + 4) 2. 1(x + 5) 3. 1(x + 6) 4. 2(x − 4) 5. 2(x − 5) 6. 2(x − 6) 7. 3(3x + 1) 8. 3(3x + 2) 9. 3(3x + 3) 10. 4(3x − 1) 11. 4(3x − 2) 12. 2(4x + 8) 13. 2(4x − 8) 14. −2(4x − 8) 15. (−4x + 8)(−2) 16. 3(6x − 4) 17. −3(6x + 4) 18. −3(−6x − 4) 19. (−6x + 4)(−3) 20. (x − 12)(−1) 21. −(x + 12) 22. −(−x − 12) 23. x(x + 5) 24. x(x − 5) 25. (5 − x)x 26. x(7x + 3) 27. 7x(x − 3) 28. (−7x + 3)(−x) 29. 2x(5x − 1) 30. (−5x − 1)(2x) 31. −5x(2x + 1) 32. 3x(10 − 4x) 33. 10x(4x − 3) 34. −(4 + 7x) + 4 35. −(7x − 4) + 4 36. 4 − (−7x + 4) 37. 3(x + 4) + 2x 38. −3(x − 4) + 2x 39. 2x + 3(4 − x) 40. 2x − 3(−x + 4) 41. 2x(3x + 1) + 2x 42. 3x + 2x(4x − 1) 43. 4x(3x − 1) − 5x 44. 4x − 5x(3x − 1) © Great Minds PBC
Número de respuestas correctas: Progreso: Aplica la propiedad distributiva y combina términos semejantes.
Edición para estudiantes: Grado A1, Módulo 1, Práctica veloz: Multiplicar y dividir fracciones
EUREKA MATH2 A1 ▸ M1 ▸ Práctica veloz ▸ Multiplicar y dividir fracciones 397 Multiplica o divide. 1. 1 4 1 3 2. 1 4 1 3 ÷
veloz
© Great Minds PBC
Práctica
A1 ▸ M1 ▸ Práctica Veloz ▸ Multiplicar y dividir fracciones EUREKA MATH2 398 Multiplica o divide. 1. 1 3 1 3 · 2. 1 3 1 5 3. 1 5 1 3 · 4. 31 5 5. 51 3 · 6. 1 3 1 3 ÷ 7. 1 5 1 5 ÷ 8. 1 3 1 5 ÷ 9. 1 5 1 3 ÷ 10. 1 3 2 5 11. 2 3 1 5 12. 1 3 2 5 ÷ 13. 31 5 ÷ 14. 3 4 1 7 15. 1 4 3 7 16. 3 4 1 7 ÷ 17. 71 4 ÷ 18. 1 7 3 ÷ 19. 4 7 3 5 20. 3 5 4 7 ÷ 21. 4 5 3 7 ÷ 22. 3 5 4 · 23. 35 7 ÷ 24. 5 9 4 7 · 25. 4 7 5 9 ÷ 26. 7 9 3 5 ÷ 27. 5 9 7 ÷ 28. 1 2 3 4 5 8 29. 1 4 3 8 7 10 ·· 30. 2 3 5 7 8 31. 2 5 3 7 4 5 32. 75 9 2 3 ·· 33. 2 3 4 5 1 2 ÷ 34. 2 3 3 5 1 7 ÷ 35. 34 5 1 7 ÷· 36. 2 3 4 5 3 ÷
correctas:
© Great Minds PBC
Número de respuestas
A
A1 ▸ M1 ▸ Práctica Veloz ▸ Multiplicar y dividir fracciones EUREKA MATH2 400
Progreso: Multiplica o divide. 1. 1 5 1 5 2. 1 5 1 7 3. 1 7 1 5 4. 51 7 5. 71 5 6. 1 5 1 5 ÷ 7. 1 7 1 7 ÷ 8. 1 5 1 7 ÷ 9. 1 7 1 5 ÷ 10. 1 5 2 7 11. 2 5 1 7 · 12. 1 5 2 7 ÷ 13. 51 7 ÷ 14. 5 4 1 9 15. 1 4 5 9 · 16. 5 4 1 9 ÷ 17. 91 4 ÷ 18. 1 9 5 ÷ 19. 3 7 2 5 20. 2 5 3 7 ÷ 21. 3 5 2 7 ÷ 22. 2 5 7 · 23. 53 7 ÷ 24. 4 5 3 7 25. 3 7 4 5 ÷ 26. 5 7 3 4 ÷ 27. 4 9 5 ÷ 28. 1 2 5 4 7 9 29. 1 4 3 5 7 10 30. 3 4 5 7 9 31. 3 5 4 7 4 5 ·· 32. 96 7 3 5 33. 4 5 2 7 1 3 ÷ 34. 3 7 2 3 1 5 ÷ 35. 32 7 1 5 ÷· 36. 4 7 2 5 3 ÷ © Great Minds PBC
Número de respuestas correctas:
Edición para estudiantes: Grado A1, Módulo 1, Práctica veloz: Operaciones con enteros
Práctica veloz
401
EUREKA MATH2 A1 ▸ M1 ▸ Práctica veloz ▸ Operaciones con enteros
Evalúa. 1. 3 − ( 3) 2. 3 ⋅ 3
© Great Minds PBC
A1 ▸ M1 ▸ Práctica veloz ▸ Operaciones con enteros EUREKA MATH2 402 Evalúa. 1. 1 + 1 2. 1 + ( 1) 3. 1 + ( 1) 4. 1 1 5. 1 ( 1) 6. 1 ( 1) 7. 1 ⋅ 1 8. 1 ( 1) 9. 1 ( 1) 10. 1 ÷ 1 11. 1 ÷ ( 1) 12. 2 + 3 13. 2 + ( 3) 14. 2 + ( 3) 15. 4 6 16. 4 ( 6) 17. 4 ( 6) 18. 10 5 19. 10 ( 5) 20. 10 ⋅ ( 5) 21. 14 ÷ 2 22. 14 ÷ ( 2) Número de respuestas correctas: A 23. 9 ⋅ ( 3) 24. 3 + ( 9) 25. 9 ÷ ( 3) 26. 9 ( 3) 27. 6 ( 12) 28. 12 ÷ 6 29. 6 + ( 12) 30. 12 ( 6) 31. 4 13 32. 13 ⋅ 4 33. 4 + ( 13) 34. 2 + 7 + ( 3) 35. 2 7 ( 3) 36. 2 7 ( 3) 37. 1(1 1) 38. 1 ⋅ 1 1 39. 5(2 − 6) 40. 5 2 − 6 41. ( 5 + 6) 2 42. 6 + 5 ⋅ ( 2) 43. ( 8 ⋅ 2) + ( 4 ⋅ 3) 44. (8 ⋅ ( 2)) ( 3 ⋅ 4) © Great Minds PBC
A1 ▸ M1 ▸ Práctica veloz ▸ Operaciones con enteros EUREKA MATH2 404
Progreso: Evalúa. 1. 2 + 2 2. 2 + ( 2) 3. 2 + ( 2) 4. 2 2 5. 2 ( 2) 6. −2 ( 2) 7. 2 2 8. 2⋅ ( 2) 9. 2 ⋅ ( 2) 10. −2 ÷ 2 11. 2 ÷ ( 2) 12. 4 + 5 13. 4 + ( 5) 14. 4 + ( 5) 15. 6 9 16. 6 ( 9) 17. 6 ( 9) 18. 20 ⋅ 4 19. 20 ( 4) 20. 20 ⋅ ( 4) 21. 18 ÷ 3 22. 18 ÷ ( 3) 23. 12 ⋅ ( 4) 24. 4 + ( 12) 25. 12 ÷ ( 4) 26. 12 ( 4) 27. 7 ( 21) 28. 21 ÷ 7 29. 7 + ( 21) 30. 21 ⋅ ( 7) 31. 6 15 32. 15 ⋅ 6 33. 6 + ( 15) 34. 1 + 9 + ( 4) 35. 1 9 ( 4) 36. 1 9 ( 4) 37. 2(2 2) 38. 2 2 2 39. 6(3 − 5) 40. 6 ⋅ 3 5 41. ( 5 + 6) ⋅ 3 42. 6 + 5 ⋅ ( 3) 43. ( 5 4) + ( 7 2) 44. (5 ⋅ ( 4)) ( 2 ⋅ 7) © Great Minds PBC
Número de respuestas correctas:
EUREKA MATH2 A1 ▸ M1 ▸ Práctica veloz ▸ Resolver ecuaciones de uno y dos pasos
Edición para estudiantes: Grado A1, Módulo 1, Práctica veloz: Resolver ecuaciones de uno y dos pasos
Práctica veloz
Resuelve las ecuaciones.
1. x + 4 = 7
2. 3x = 12
405
© Great Minds PBC
A1 ▸ M1 ▸ Práctica veloz ▸ Resolver ecuaciones de uno y dos pasos EUREKA MATH2 406 Resuelve las ecuaciones. 1. x + 2 = 6 2. x + 4 = 6 3. x + 6 = 6 4. x − 3 = 12 5. x − 5 = 12 6. x − 7 = 12 7. 8x = 16 8. 4x = 16 9. 2x = 16 10. 1 2 4 x = 11. 1 3 4 x = 12. 8 + x = −4 13. −8 + x = −4 14. x − 8 = −4 15. x − (−8) = 4 16. −5x = 10 17. 10x = −5 18. 2x = −6 19. −6x = 2 20. 1 2 6 x =− 21. −= 1 2 6 x 22. −= 1 6 2 x Número de respuestas correctas: A 23. 2x = 18 24. 2x + x = 18 25. 2x + x + 3 = 18 26. 2x + x + 6 = 18 27. 3x + 6 = 18 28. 18 = 3(x + 2) 29. 12 = −3x 30. 12 = −x − x − x 31. x − 3 − x − x = 12 32. −3x − 3 = 12 33. 12 = −3(x + 1) 34. () = 1 4 42 x 35. −+ = 1 4 12 x 36. −=21 1 4 x 37. 3 2 69 x += 38. 3 2 49() x += 39. 98 3 4 =+() x 40. −= + ()98 3 4 x 41. −+() =− 3 4 89 x 42. −+ = 2 3 11 x 43. = 2 3 11() x 44. 12 3 2 3 =− + x © Great Minds PBC
A1 ▸ M1 ▸ Práctica veloz ▸ Resolver ecuaciones de uno y dos pasos EUREKA MATH2 408
Número de respuestas correctas: Progreso: Resuelve las ecuaciones. 1. x + 3 = 7 2. x + 5 = 7 3. x + 7 = 7 4. x − 2 = 10 5. x − 4 = 10 6. x − 6 = 10 7. 9x = 18 8. 6x = 18 9. 3x = 18 10. 1 3 5 x = 11. 1 4 5 x = 12. 6 + x = −3 13. −6 + x = −3 14. x − 6 = −3 15. x − (−6) = 3 16. 8x = −24 17. −24x = 8 18. −6x = 12 19. 12x = −6 20. 1 3 4 x =− 21. −= 1 3 4 x 22. −= 1 4 3 x 23. 4x = 20 24. 4x + x = 20 25. 4x + x + 5 = 20 26. 4x + x + 10 = 20 27. 5x + 10 = 20 28. 20 = 5(x + 2) 29. 16 = −4x 30. 16 = −x − x − x − x 31. x − 4 − x − x − x = 16 32. −4x − 4 = 16 33. 16 = −4(x + 1) 34. () = 1 6 63 x 35. −+ = 1 6 13 x 36. −=31 1 6 x 37. 5 2 1015 x += 38. 5 2 415 x + () = 39. 1612 4 5 =+() x 40. −= + 1612 4 5() x 41. −+() =− 4 5 1216 x 42. −+ = 3 4 22 x 43. () = 3 4 22 x 44. 23 4 6 4 =− + x © Great Minds PBC
MATH2
▸ M1 ▸ Práctica veloz ▸ Resolver desigualdades de uno y dos pasos
Edición para estudiantes: Grado A1, Módulo 1, Práctica veloz: Resolver desigualdades de uno y dos pasos
Halla el valor de x para resolver cada desigualdad.
409
EUREKA
A1
1. x + 4 > 9 2. 6x < 12
Great Minds PBC
Práctica veloz ©
A1 ▸ M1 ▸ Práctica veloz ▸ Resolver desigualdades de uno y dos pasos EUREKA MATH2 410 Halla el valor de x para resolver cada desigualdad. 1. x + 2 > 10 2. x + 4 > 10 3. x + 6 > 10 4. x − 3 < 9 5. x − 5 < 9 6. x − 7 < 9 7. 2x < 18 8. 3x > 18 9. 10 + x > 15 10. 10 + x > −15 11. −10 + x > −15 12. −10 + x > 15 13. 4x > −4 14. 4x > 8 15. 4x > −16 16. 4x > 32 Número de respuestas correctas: A 17. 5x < −20 18. −4x < −20 19. 2x < −20 20. −2x < −20 21. x < −20 22. 1 2 2 x <− 23. −< 1 2 3 x 24. −> 1 3 2 x 25. 3(x + 3) > 18 26. −4(x + 3) > 24 27. −4x − 12 > 24 28. 2 3 612 x −< 29. < 6122 3 x 30. 2 3 912 x + () <− 31. <− 126 3 5 x 32. 3 5 206() x +< © Great Minds PBC
A1 ▸ M1 ▸ Práctica veloz ▸ Resolver desigualdades de uno y dos pasos EUREKA MATH2 412
1. x + 3 > 12 2. x + 5 > 12 3. x + 7 > 12 4. x − 2 < 8 5. x − 4 < 8 6. x − 6 < 8 7. 4x < 16 8. 8x > 16 9. 15 + x > 20 10. 15 + x > −20 11. −15 + x > −20 12. −15 + x > 20 13. 6x > −6 14. 6x > 12 15. 6x > −18 16. 6x > 36 17. 4x < −28 18. −7x < −28 19. 2x < −28 20. −2x < −28 21. x < −28 22. 1 4 3 x <− 23. −< 1 4 5 x 24. −> 1 5 4 x 25. 4(x + 2) > 16 26. −4(x + 2) > 20 27. −4x − 8 > 20 28. 2 5 614 x −< 29. < 6124 5 x 30. 2 5 1514 x + () <− 31. <− 189 3 7 x 32. 3 7 429 x + () < © Great Minds PBC
Número de respuestas correctas: Progreso: Halla el valor de x para resolver cada desigualdad.
EUREKA MATH2
A1 ▸ M1 ▸ Práctica veloz ▸ Resolver ecuaciones de dos pasos
Edición para estudiantes: Grado A1, Módulo 1, Práctica veloz: Resolver ecuaciones de dos pasos
Práctica veloz
Resuelve las ecuaciones.
1. 3x + 1 = 10
2. 3x − 4 = 8
©
413
Great Minds PBC
A1 ▸ M1 ▸ Práctica veloz ▸ Resolver ecuaciones de dos pasos EUREKA MATH2 414 Resuelve las ecuaciones. 1. 2x + 4 = 14 2. 2x + 5 = 15 3. 2x + 6 = 16 4. 2x + 7 = 17 5. 2x + 8 = 18 6. 2x − 2 = 6 7. 2x − 4 = 6 8. 2x − 6 = 6 9. 2x − 8 = 6 10. 2x − 6 = 14 11. 2x − 6 = 12 12. 2x + 4 = 18 13. 2x + 4 = 16 14. 2(x + 2) = 16 15. 2(x + 2) = 18 16. 2(x + 2) = 20 17. 2(x − 2) = 20 18. 2(x − 2) = 18 Número de respuestas correctas: A 19. 12 = 3(x + 2) 20. 3x + 6 = 12 21. 3x + 12 = 6 22. −6 = 3x + 12 23. 3x − 12 = −6 24. −3x − 6 = −12 25. −3(x − 2) = −12 26. 6 = −3(x − 2) 27. 3(x + 2) = −6 28. 1 3 63 x + () = 29. 32 1 3 =+ x 30. 1 3 23 x −= 31. 1 3 32 x −= 32. −+ = 1 3 32 x 33. −= ()29 1 3 x 34. = 1 3 93() x 35. 33 1 3 =− + x 36. −+ =− 1 3 33 x © Great Minds PBC
A1 ▸ M1 ▸ Práctica veloz ▸ Resolver ecuaciones de dos pasos EUREKA MATH2 416
Progreso: Resuelve las ecuaciones. 1. 3x + 4 = 10 2. 3x + 5 = 11 3. 3x + 6 = 12 4. 3x + 7 = 13 5. 3x + 8 = 14 6. 3x − 3 = 6 7. 3x − 6 = 6 8. 3x − 9 = 6 9. 3x − 12 = 6 10. 3x − 6 = 18 11. 3x − 6 = 15 12. 3x + 9 = 21 13. 3x + 9 = 18 14. 3(x + 3) = 18 15. 3(x + 3) = 21 16. 3(x + 3) = 24 17. 3(x − 3) = 24 18. 3(x − 3) = 21 19. 20 = 4(x + 3) 20. 4x + 12 = 20 21. 4x + 20 = 12 22. −12 = 4x + 20 23. 4x − 20 = −12 24. −4x − 12 = −20 25. −4(x − 3) = −20 26. 12 = −4(x − 3) 27. 4(x + 3) = −12 28. 1 4 84 x + () = 29. 42 1 4 =+ x 30. 1 4 24 x −= 31. 1 4 42 x −= 32. −+ = 1 4 42 x 33. −=2116 4() x 34. () = 1 4 164 x 35. 44 1 4 =− + x 36. −+ =− 1 4 44 x © Great Minds PBC
Número de respuestas correctas:
EUREKA MATH2 A1 ▸ M1 ▸ Práctica veloz ▸ Escribir expresiones equivalentes
Edición para estudiantes: Grado A1, Módulo 1, Práctica veloz: Escribir expresiones equivalentes
Práctica veloz
Reescribe cada expresión como una expresión equivalente en forma estándar.
1. 1 + (1 + 1)
2. x + (x + x)
417
Great Minds PBC
©
Reescribe cada expresión como una expresión equivalente en forma estándar.
A1 ▸ M1 ▸ Práctica veloz ▸ Escribir expresiones equivalentes EUREKA MATH2 418
1. 1 + 1 2. 1 + 1 + 1 3. (1 + 1) + 1 4. (1 + 1) + (1 + 1) 5. (1 + 1) + (1 + 1 + 1) 6. x + x 7. x + x + x 8. (x + x) + x 9. (x + x) + (x + x) 10. (x + x) + (x + x + x) 11. (x + x) + (x + x + x + x) 12. 2x + x 13. 3x + x 14. x + 4x 15. x + 7x 16. 2x + 7x 17. 7x + 3x 18. 10x − x 19. 10x − 5x 20. 10x − 10x 21. 10x − 11x 22. 10x − 12x Número de respuestas correctas: A 23. 4x + 6x − 12x 24. 4x + 6x − 4x 25. 4x + 6x + 4 26. (4x + 3) + x 27. (4x + 3) + 2x 28. 3x + (4x + 3) 29. 6x + (4x + 3) 30. 6x + (4 + 3x) 31. 6x + (4 − 3x) 32. 4x + (4 − 3x) 33. 2x + (4 − 3x) 34. (3x + 9) + (3x + 9) 35. (3x − 9) + (3x − 9) 36. (3x − 9) + (3x + 9) 37. (3x − 9) − (3x + 9) 38. (11 − 5x) + (4x + 2) 39. (5x + 11) + (2 − 4x) 40. (11 − 5x) − (2 − 4x) 41. (2x + 3y) + (4x + y) 42. (2x − 3y) + (4x − y) 43. (2x − 3y) + (3y − 4x) 44. (2x + 3y) − (2x − 3y) © Great Minds PBC
BNúmero de respuestas correctas:
Progreso:
Reescribe cada expresión como una expresión equivalente en forma estándar.
A1 ▸ M1 ▸ Práctica veloz ▸ Escribir expresiones equivalentes EUREKA MATH2 420
1. 1 + 1 + 1 2. 1 + 1 + 1 + 1 3. (1 + 1) + (1 + 1) 4. (1 + 1 + 1) + (1 + 1) 5. (1 + 1 + 1) + (1 + 1 + 1) 6. x + x + x 7. x + x + x + x 8. (x + x) + (x + x)
(x + x + x) + (x + x) 10. (x + x + x) + (x + x + x) 11. (x + x) + (x + x) + (x + x) 12. 4x + x 13. 5x + x 14. x + 8x 15. x + 11x 16. 3x + 11x 17. 11x + 5x 18. 9x – x 19. 9x − 5x 20. 9x − 9x 21. 9x − 10x 22. 9x − 11x 23. 3x + 5x − 10x 24. 3x + 5x − 3x 25. 3x + 5x + 3 26. (3x + 4) + x 27. (3x + 4) + 2x 28. 3x + (3x + 4) 29. 7x + (3x + 4) 30. 7x + (3 + 4x) 31. 7x + (3 − 4x) 32. 5x + (3 − 4x) 33. 3x + (3 − 4x) 34. (5x + 7) + (5x + 7) 35. (5x − 7) + (5x − 7) 36. (5x + 7) + (5x − 7) 37. (5x − 7) − (5x + 7) 38. (6 − 13x) + (8x + 3) 39. (13x + 6) + (3 − 8x) 40. (6 − 13x) − (3 − 8x) 41. (4x + 9y) + (8x + 3y) 42. (4x − 9y) + (8x − 3y) 43. (4x − 9y) + (9y − 8x) 44. (4x + 9y) − (4x − 9y) © Great Minds PBC
9.
Edición para estudiantes: Grado A1, Módulo 1, Bibliografía
Bibliografía
National Governors Association Center for Best Practices, Council of Chief State School Officers (NGA Center, CCSSO). Common Core State Standards for Mathematics. Washington, DC: NGA Center, CCSSO, 2010.
O’Connor, John J. and Edmund F. Robertson. “Abu Ja’far Muhammad ibn Musa Al-Khwarizmi.”
St. Andrews, Scotland: School of Mathematics and Statistics, University of St. Andrews. 2019.
http://mathshistory.st-andrews.ac.uk/Biographies/Al-Khwarizmi.html.
O’Connor, John J. and Edmund F. Robertson. “Arabic Mathematics: Forgotten Brilliance?”
St. Andrews, Scotland: School of Mathematics and Statistics, University of St. Andrews. 2019.
http://mathshistory.st-andrews.ac.uk/HistTopics/Arabic_mathematics.html#13.
Rashed, Rashdi. Al-Khwarizmi: The Beginnings of Algebra. London: Saqi Books, 2010.
421 EUREKA MATH2 A1 ▸ M1
© Great Minds PBC
Edición para estudiantes: Grado A1, Módulo 1, Créditos
Créditos
Great Minds® has made every effort to obtain permission for the reprinting of all copyrighted material. If any owner of copyrighted material is not acknowledged herein, please contact Great Minds for proper acknowledgment in all future editions and reprints of this module.
Common Core State Standards for Mathematics © Copyright 2010 National Governors Association Center for Best Practices and Council of Chief State School Officers. All rights reserved.
Cover, Georges Seurat, A Sunday on La Grande Jatte—1884, 1884–1886, Helen Birch Bartlett Memorial Collection, Art Institute of Chicago. Photo Credit: The Art Institute of Chicago/Art Resource, NY; page 273, (top left) TWITTER, TWEET, RETWEET and the Twitter logo are trademarks of Twitter, Inc. or its affiliates, (top right) and (bottom right), Facebook and Instagram are trademarks of Facebook and are used according to their brand guidelines, (bottom left) YouTube is a trademark of Google LLC and is used according to their brand guidelines; All other images are the property of Great Minds. For a complete list of credits, visit http://eurmath.link/media-credits.
422 A1 ▸ M1 EUREKA MATH2
© Great Minds PBC
Edición para el estudiante: Grado A1, Módulo 1, Agradecimientos

































