Vector 16

VECTOR

FEBRUARI 2023 - nummer 16

TIJDSCHRIFT voor wiskundeonderwijs

EEN TELPROBLEEM WAAR MUZIEK IN ZIT 7

TETRAËDER TORENS 25

MULTIVERZAMELINGEN 34

Met

medewerking van Uitwiskeling, VVWL (Vlaamse Vereniging van Wiskundeleraars), GeoGebra Instituut, Vlaamse Wiskunde Olympiade, Ars et Mathesis en Pythagoras

3 108 JAAR OUD DIPLOMATIEK TELEGRAM

EINDELIJK ONTCIJFERD

EEN TELPROBLEEM WAAR MUZIEK IN ZIT 7

11 EEN RODE DRIEHOEK

MEETKUNDE ZONDER COÖRDINATENSTELSEL 19

DE MEETKUNDE VAN COMPUTER GRAPHICS

23 EEUWENOUDE RAADSELS EN BAANBREKENDE INZICHTEN

TETRAËDER TORENS 25

30 BOEKBESPREKING

ZOEK BIJZONDER DEELBAAR GETAL 32

34 MULTIVERZAMELINGEN

EULER EN ZIJN PARTITIES 38

VECTOR

6e jaargang - nummer 16

REDACTIE Nicolas Ruys, Tom Harteel, Anke Oderij, Ellemijn Van Puymbroeck - die Keure, Kleine Pathoekeweg 3, 8000 Brugge, educatief@diekeure.be

EXTERNE AUTEURS die occasioneel of op geregelde basis een bijdrage willen leveren, kunnen contact opnemen met educatief@diekeure.be.

VECTOR Vector is gratis voor alle leerkrachten wiskunde in België.

VERANTWOORDELIJKE UITGEVER die Keure, Kleine Pathoekeweg 3, 8000 Brugge

VORMGEVING EN DRUK Isabelle Tilleman, Nathalie Hamelinckx - die Keure, Brugge REACTIES Al je reacties, suggesties en opmerkingen zijn welkom op educatief@diekeure.be

DIPLOMATIEK TELEGRAM EINDELIJK ONTCIJFERD

ARNOUT JASPERS

IN 1914 ONDERSCHEPTE DE COMMANDANT VAN DE NEDERLANDSE VREDESMISSIE IN ALBANÏE, LODEWIJK THOMSON, EEN GECODEERD TELEGRAM VAN EEN VERMOEDELIJKE DUBBELSPION, ESSAD PASHA. IN 2008 DOOK HET OP, EN SINDSDIEN HEBBEN CODEKRAKERS, WAARONDER DE MIVD, TEVERGEEFS GEPROBEERD DIT ALBANIË-TELEGRAM TE DECODEREN. FLORENTIJN VAN KAMPEN, COMPUTERWETENSCHAPPER AAN DE RADBOUD UNIVERSITEIT IN NIJMEGEN, IS HET NU WEL GELUKT.

In Pythagoras schreven we eerder over dit mysterieuze telegram (49ste jaargang, nr 4; https://pyth.eu/ uploads/user/ArchiefPDF/Pyth49-4.pdf). Het bestaat uit 736 decimale getallen onder de honderd, en het getal 119. In die tijd bestonden nog geen computers of codeermachines, en gebeurde al het coderen (cryptografen spreken van vercijferen) met pen en papier. Vercijfersystemen waren toen daarom veel simpeler dan nu. Voor het ontcijferen van zulke handmatige geheimschriften bestaan tegenwoordig ook computerprogramma's.

In zijn publicatie voor de Histocrypt conferentie, afgelopen juni in Amsterdam, schrijft Van Kampen echter: 'Geen van de beschikbare standaard gereedschappen leverde een oplossing op. We weten nu waarom: het telegram was geschreven in een oud Albanees dialect, en de cijfertekst zal vol met fouten'. Het telegram bevat 49 verschillende getallen, die tussen de 1 en 74 keer voorkomen, zie tabel 1. Dit aantal van 49 suggereert, dat elk getal staat voor één letter van een alfabet. Het was echter niet bekend in welke taal het bericht gesteld was. Dat had Nederlands

kunnen zijn, of Albanees, of een andere Europese taal. Ons – Latijnse - alfabet heeft slechts 26 letters, maar in andere talen komen daar nog speciale letters bij. Ook kennen talen vaste combinaties van twee letters, zoals in het Nederlands ng, eu, ie, die je met een apart getal zou kunnen vercijferen, waardoor het gebruikte alfabet in feite meer dan 26 letters zou hebben. Als een vercijferingssyteem iedere keer hetzelfde symbool (een letter, getal of speciaal teken) aan dezelfde letter in de brontekst toekent, heet dit een 'monoalfabetische substitutie'. Het is een van de simpelste manieren om een tekst te vercijferen: bijvoorbeeld A wordt C, B wordt D, C wordt E, en zo verder tot aan Y wordt A en Z wordt B. Uiteraard levert een meer willekeurige toekenning van de letters een sterkere vercijfering op.

Niettemin, de grote zwakte van elke monoalfabetische substitutie is, dat het de letterfrequenties intact houdt. De E komt in het Nederlands het vaakst voor, dus in een aldus vercijferde tekst zal de vaakst voorkomende codeletter voor de E staan. Hetzelfde geldt voor de op een na vaakst voorkomende letter, N, en in een stuk

Tabel 1 De frequenties van de twee-cijferige getallen in het Albanië-telegram. Bijvoorbeeld: het getal 28 komt 74 keer voor in het telegram. Het enige getal boven de honderd, 119, wordt in deze tabel vertegenwoordigd door vakje 99.

tekst van een paar honderd letters, zoals het Albaniëtelegram, zou je op die manier de vier of vijf meest voorkomende letters moeten kunnen identificeren. Met vier of vijf letters ingevuld, is het vaak al mogelijk om sommige woorden in de vercijferde tekst te raden, en dat geeft je meteen weer extra letters waarvan je de vercijfering weet, zodat het systeem als een kaartenhuis in elkaar stort.

Dit veronderstelt wel dat je de gebruikte taal kent, want dat bepaalt de letterfrequenties en of je woorden kunt raden waarvan maar een paar letters bekend zijn. De bestaande geautomatiseerde gereedschappen werkten hier niet, omdat die alleen toegesneden zijn op een beperkte set talen, niet op het Albanees.

EERSTE AANNAME: ZELDZAAM = FOUT

Nieuw was ook Van Kampens aanpak om mogelijke fouten uit het telegram te filteren. Omdat vercijferen toen handwerk was, werden er altijd fouten bij gemaakt, zeker als het onder grote tijdsdruk moest gebeuren. Van Kampen beperkte zijn analyse in eerste instantie simpelweg tot de getallen die 7 of meer keer voorkwamen (groen in tabel 1), er vanuit gaand dat de meeste zeldzame getallen het resultaat waren van fouten bij het vercijferen. Zo bleven nog maar 29 verschillende getallen over. Dat kwam aardig overeen met het feit dat het Albanese alfabet 36 tekens heeft.

Het 'kraken' van het telegram begon met het inscannen en digitaliseren van een flinke hoeveelheid Albanese tekst uit allerlei andere bronnen, in totaal ruim duizend pagina's. Een zogeheten corpus is nodig om de specifieke statistische eigenschappen en het vocabulaire van een taal tot in detail te kunnen identificeren.

Vervolgens schreef Van Kampen software om de score van een tekst te bepalen, gebaseerd op de frequenties van tetragrammen (vier opeenvolgende letters) in een tekst. Deze score geeft aan hoe goed de tetragram-frequenties overeen komen met die van zijn Albanese corpus. Er zijn heel veel mogelijkheden om in tabel 1 voor elk getal een letter in te vullen, en elke mogelijkheid genereert een andere 'ontcijferde' tekst. De aanname is nu, dat de echte, niet vercijferde tekst van het telegram de hoogste score zal hebben van alle uitgeprobeerde ontcijferingen.

Daarmee wordt het invullen van de tabel een optimalisatie-probleem, dat werd opgelost met een variant van het hill-climbing algoritme. Dat komt er op neer dat de computer, uitgaand van een willekeurige begintabel, telkens een kleine verandering doorvoert die de meeste winst in de score oplevert, om zo in het 'landschap' van alle scores stap voor stap naar de hoogste top te klimmen. Er is overigens geen garantie dat dit lukt; vaak zijn meerdere pogingen vanuit heel verschillende begintabellen nodig. Dat leverde onderstaande tabel op:

Verder nam Van Kampen aan, dat er een systematiek in de vele fouten in de vercijfering zou zitten: namelijk dat meestal degene die het bericht vercijferde zich alleen in de kolom of alleen in de rij vergiste, en er dan maar 1 naast zat. Dus dan vercijferde deze bijvoorbeeld de letter p niet als 46, maar als 56 of 47.

Bekijk bijvoorbeeld dit lange woord in de tekst: 54 45 33 63 48 58 45 56 38 42 56 38. Ontcijferd met tabel 2 levert dit op: kqyenjgjqithsith, wat geen Albanees woord is. Bij nader inzien blijken er maar liefst zes '1 ernaast'-fouten in te zitten, en er ontbreekt een letter:

54 (45=44) 33 63 (48=49) (58=59) (45=44) 56 (38=39) 62 42 56 (38=39)

kqyenjgjqithsith wordt dan: kryengritësit ofwel, in het Nederlands, 'opstandelingen'.

Het ontcijferen krijgt dan iets van een kruiswoordpuzzel oplossen, met als resultaat onderstaande tabel:

Tabel 2 De vercijfertabel op basis van het 'hill climbing' algoritme geeft een onvolledige, en naar later zou blijken niet geheel juiste oplossing. De hokjes 28 en 29 coderen voor een spatie in de tekst.

VEEL 'ÉÉN ERNAAST'-FOUTEN

Maar: met deze vercijfertabel leverde het telegram nog steeds geen leesbare tekst op. De computer had alles gedaan wat hij kon, en nu moest er ook nog menselijk taalgevoel aan te pas komen. Daarbij hielp enorm dat ook spaties vercijferd werden, zodat afzonderlijke woorden in de vercijferde tekst te onderscheiden waren.

Tabel 4 Gekraakt: de complete vercijfertabel die is gebruikt voor het Albanië-telegram. Het Albanese alfabet is simpelweg van rechtsonder naar linksboven in het diagram ingevuld.

Op deze manier heeft Van Kampen de hele tekst zo goed mogelijk gereconstrueerd, al blijven er een aantal vraagtekens in de tekst staan. Zelfs ontcijferd is het telegram lastig te begrijpen, omdat we zo weinig van de historische context weten, en het niet zeker is of Essad Pasha de afzender was. Het telegram is gericht aan ene Mustafa, waarschijnlijk Mustafa Ndroqi, een van de moslim leiders van de boerenopstand die toen gaande was, en het bevat een oproep om een paar honderd man versterking te sturen.

MAAR WAT STOND ER NOU IN DAT MYSTERIEUZE TELEGRAM?

Gjendur e ngjarjet e këtushme gjatë ngjare, ju kam diftue zotni ju.

Dje kryengritësit kane dërguar lajm dhe na thoshin poqe se nuk na pranoni propozimet tona do të jeni në rrezik se do te vijmë në githë këtyre trathorve.

I thashë qeverija sa të mundet do të kundërshtohet deri në fund tË jetës.

Mustafa Pashë i diftova fjalët te gjithë me dhanë bësen me vdes?? bej nje tradhëti?? ?? ?? ??

E vumë flamurin te Turqisë këtu ka rëndësie të madhe.

Ka mundësi që?? rrëzojshim?? po mundëm jam tu ju?? dhe disa këshillonjsve qi.

Çuen populli die me fjalë para ju.

Dhame pergjigje duke u thënë se do te vjimë vuë flamurin e turqiës.

Ju lutem një orë e më parë të dërgoni disa qindra njerëz, njerëz fuqishëm birbo.

Pashas të kam tregova me vehte punët janë njom ligësht.

Dat Van Kampen het Albanië-telegram heeft kunnen ontcijferen, nadat onder meer de militaire inlichtingendienst MIVD er zijn tanden op stuk gebeten had, had zeker ook te maken met het feit dat hij een Albanese in zijn directe omgeving had, Diana Zeneli, die hem heeft geholpen met het reconstrueren van de (in een dialect van het) Albanees geschreven tekst.

Het volledige artikel over de ontcijfering van het Albanië-telegram staat online: https://ecp.ep.liu.se/index.php/histocrypt/article/view/398/356

I have been in this situation here for a long time, I am telling you, sir.

Yesterday the insurgents sent news and told us if you do not accept our proposals you will be in danger that all these traitors will come.

I told him the government would oppose it as much as it could for the rest of its life.

Mustufa Pashe, I told him all that gave me the pledge to die before betrayal (?)

Placing here the Turkish flag is of great importance.

Maybe it is possible (?) to throw down (?) I can be your (?) and some counsellors. We responded by telling them that we would come to place the Turkish flag.

Please send as soon as possible a few hundred men, strong men without house or possession. Pasha, I told you that things are delicate.

EEN TELPROBLEEM WAAR MUZIEK IN ZIT

LUC VAN DEN BROECK, GILBERTE VERBEECK, REDACTIE UITWISKELING

AL JAREN VRAAG IK ME AF HOEVEEL AKKOORDEN MET DRIE VERSCHILLENDE NOTEN ER BESTAAN EN HOEVEEL MET VIER NOTEN. HET LIJKEN ME ER ONTZAGLIJK VEEL. MAAR IK BESEFTE PAS DAT IK HET MIS HAD TOEN IK (BOS, 2017) LAS. DE BEREKENING VAN DEZE AANTALLEN AKKOORDEN ZIJN IN HET ZEBRA-BOEKJE OPGENOMEN ALS EEN VRIJE EINDOPDRACHT VOOR DE LEERLINGEN. DIT ARTIKEL IS BEDOELD VOOR DE MUZIEKMINNENDE EN ARTISTIEKE LEERKRACHT EN LEERLING. MUZIEK EN WISKUNDE ZIJN INTERESSES DIE ELKAAR WEL EENS RAKEN.

DRIEKLANKEN

Een drieklank is een opeenstapeling van drie verschillende tonen. Om visueel te laten zien dat de drie noten tegelijkertijd moeten gespeeld of gezongen worden, noteren we ze boven elkaar op een notenbalk. In figuur 1 zie je de grote drieklank (of het grote tertsakkoord) do-mi-sol en de kleine drieklank (of het kleine tertsakkoord) do-mi b-sol. Elk akkoord heeft een eigen karakter. Het grote tertsakkoord klinkt vrolijk, het kleine klinkt droef. Als je de drie noten van een drieklank parallel verschuift over de notenbalk dan blijft het karakter behouden. Vrolijk blijft vrolijk. Droevig blijft droevig.

De grote en kleine drieklank klinken welluidend. De drie noten liggen immers niet vlak naast

elkaar. Deze klassieke akkoorden stralen rust uit. Het akkoord re-misol klinkt een beetje dissonanter omdat de re en mi tegen elkaar aan schuren. En het akkoord re-mi-fa klinkt heel wrang. De drie geclusterde noten genereren een geluidseffect dat goed zou passen bij een griezelfilm.

De onderlinge tussenafstanden van de noten van een drieklank bepalen de sfeer ervan. De oorspronkelijke vraag kan nu muzikaler vertaald worden. Hoeveel muzikale sferen kan men oproepen door drie noten samen te laten klinken? We tellen het zo meteen uit. Eerst iets over het wiskundige model achter de drieklanken.

Figuur 1 Twee drieklanken met een verschillende sfeer

DE HALVETONENCIRKEL

Als je een klavier van een piano of een orgel bekijkt, merk je dat de structuur zich elke twaalf halve tonen herhaalt. De afstand van 12 halve tonen noemen we een octaaf. De namen van de noten herhalen zich ook na elke cyclus van 12 halve tonen. Daarom kunnen we deze namen in een cirkel noteren, zoals in figuur 2.

we hadden net zo goed de notatie met de mollen kunnen gebruiken voor een verlaging met een halve toon. Onthoud wel: re# (re kruis) is gelijk aan mib (mi mol) en fa# (fa kruis) is gelijk aan solb (sol mol).

DRIEKLANKEN IN DE HALVETONENCIRKEL

Een drieklank kun je aanduiden in de halvetonencirkel door precies 3 van de 12 cirkeltjes in te kleuren. In de figuren 3 en 4 zie je de afbeelding van het kleine tertsakkoord do-mib-sol en die van het grote tertsakkoord do-mi-sol.

Ook al zouden er geen notennamen in de cirkeltjes staan, visueel zijn deze akkoorden makkelijk uit de posities van de gekleurde cirkeltjes op te maken. Het verschil zit in de tussenafstanden tussen de cirkeltjes die tot het akkoord behoren.

De toonhoogte stijgt in de richting van de pijlen. In het eenvoudigste geval beginnen we een toonladder bij de do en klimmen we op tot de si. Zo hebben we een heel octaaf doorlopen. Maar we kunnen ook op een andere plaats beginnen om het octaaf te doorlopen. We zullen nu verder redeneren op het model van de halvetonencirkel en niet meer op het pianoklavier.

Bij de benamingen van de noten zijn hier kruisen genoteerd voor een verhoging met een halve toon. Maar

Om cyclisch van de ene noot van het akkoord naar de volgende te hoppen, zijn er drie afstanden met pijlen te overbruggen. Kijk alleen naar de twee kleinste afstanden. De derde tussenafstand ligt immers vast wanneer de twee kleinste afstanden vast liggen. Bij het kleine tertsakkoord moeten er eerst 3 pijlen genomen worden (van do naar mib) en daarna 4 (van mib naar sol). Bij het grote tertsakkoord moeten er eerst 4 pijlen genomen worden (van do naar mi) en daarna 3 (van mi naar sol). Het temperament van een akkoord wordt zo gekarakteriseerd in

ROTEREN EN SPIEGELEN VAN EEN AKKOORD

We stellen ons nu de vraag of een akkoord verandert door de gekleurde cirkeltjes in de halvetonencirkel te roteren of te spiegelen. Kijken we eerst naar de rotatie.

Als we het grote tertsakkoord do-mi-sol over een twaalfde

twee kengetallen.

Figuur 2 Het octaaf, een cyclus van 12 halve tonen

Figuur 3 Het kleine tertsakkoord do-mib-sol

Figuur 4 Het grote tertsakkoord do-mi-sol

van een volledige omwenteling roteren naar het akkoord do#fa-sol#, klinkt het een halve toon hoger. Aan de sfeer is er niets veranderd. We kunnen dit akkoord beschouwen als een oude bekende en rekenen het niet mee in de telling van de verschillende drieklanken. De kengetallen van het akkoord blijven immers gelijk aan 4 en 3.

De spiegelingen zijn iets moeilijker. Stel dat we de gekleurde cirkeltjes van het grote tertsakkoord do-misol spiegelen rond de verticale door het middelpunt van de halvetonencirkel. Dan komen we uit bij het akkoord do-fa-sol#. Dit akkoord is wel degelijk verschillend van het grote tertsakkoord. De karakteristieke getallen zijn 3 en 4. De gespiegelde van het grote tertsakkoord klinkt als het kleine tertsakkoord.

Door te spiegelen rond een as krijgen we meestal een ander akkoord (een akkoord met andere kengetallen, een akkoord dat een andere sfeer oproept). Door te roteren blijft een akkoord altijd hetzelfde klinken (de kengetallen veranderen niet, de sfeer ook niet).

EN NU DE TELLING

Als je van de 12 cirkeltjes in de halvetonencirkel er precies 3 mag inkleuren, dan kunnen we het aantal inkleuringen berekenen met een combinatie: C 3 12 = 220. Deze inkleuringen zou je in groepjes per 12 moeten samennemen. Je krijgt telkens 12 akkoorden met dezelfde kengetallen maar met een andere positie op de halvetonencirkel. Groeperen per 12 lukt echter niet helemaal omdat het getal 220 is niet deelbaar door 12.

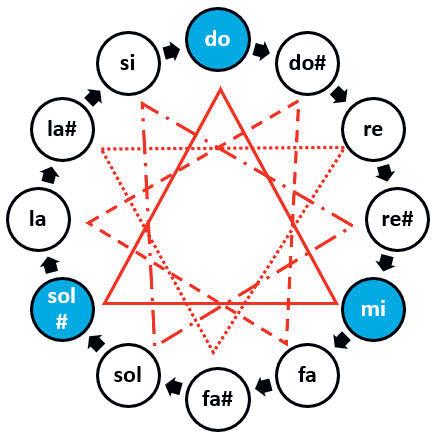
Sommige akkoorden kun je niet met 12 samennemen. Denk maar aan het akkoord do-mi-sol#, dat zijn bolletjes heeft op de hoekpunten van een gelijkzijdige driehoek.

We noemen dit merkwaardige akkoord een vergrote drieklank. De kengetallen zijn 4 en 4. In de halvetonencirkel van figuur 7 zie je vier vergrote drieklanken die aangegeven zijn door gelijkzijdige driehoeken van een verschillend lijntype. Deze vier akkoorden stralen dezelfde klanksfeer uit.

Een vergrote drieklank heeft de eigenschap invariant te zijn onder een rotatie over 120° en onder een rotatie over 240°. Alle andere drieklanken zijn enkel invariant onder de identieke transformatie. Deze opmerking geeft een aanwijzing in de richting van het lemma van Burnside. Maar ook zonder op dit lemma te steunen, vinden we het antwoord op de vraag.

Van de 220 oorspronkelijke kleuringen worden er 4 samengenomen tot 1. Dat zijn de vier vergrote drieklanken. De overige 216 worden in groepjes van 12 samengenomen. Dat zijn

Figuur 5 Het grote tertsakkoord geroteerd

Figuur 6 Het grote tertsakkoord gespiegeld

Figuur 7 Vier vergrote drieklanken

18 groepjes die bestemd zijn voor akkoorden zonder rotatiesymmetrie. We vinden dus 19 verschillende akkoorden.

Nu de berekening is gemaakt, is het nog een heel gedoe om al deze akkoorden op te sommen. We zetten ze hieronder netjes in een tabel. Links zie je de meest geclusterde drieklanken. Rechts de drieklanken met een wijdere spreiding. Uiterst rechts vind je

de merkwaardigste drieklank: de vergrote drieklank.

Wil je alle mogelijke drieklanken na elkaar horen, zet je dan maar achter de piano en speel de partituur uit figuur 8 ... of dan ga je naar de website van UW en klik je het bijbehorende audiobestand aan.

Als je nog zin hebt om de hele redenering over te doen voor

de berekening van het aantal vierklanken: het zijn er 43. Let op: er zijn symmetrische vierklanken die met drie moeten gebundeld worden (de bolletjes in de halvetonencirkel liggen op de hoekpunten van een vierkant), er zijn symmetrische vierklanken die je met zes moet samennemen (de bolletjes liggen op de hoekpunten van een rechthoek) en er zijn asymmetrische vierklanken die je met twaalf moet samennemen ...

BRONNEN

Bos, R., Tak, S. (2017). Symmetrie in telproblemen en puzzels. Amsterdam: Epsilon Uitgaven. ISBN 978-90-5041-116-0

Dit artikel verscheen in Uitwiskeling 35/3 als onderdeel van een groter artikel rond teltechnieken. Op www.uitwiskeling.be vind je alle info.

Figuur 8 Negentien verschillende drieklanken

EEN RODE DRIEHOEK

BENDEGEM

INLEIDING

Net zoals Wiskunde & Onderwijs hebben vele wetenschappelijke tijdschriften, gericht naar het welgekende ‘bredere’ publiek, een puzzelrubriek. Zo ook een van mijn vaste bladen, de New Scientist. De meeste puzzels zijn klassiekers in die zin dat er niet alleen een vrij systematische, zij het langdradige oplossing bestaat maar ook een kortere oplossing die handig gebruik weet te maken van een of andere ‘binnenweg’. Denk bijvoorbeeld aan een combinatorisch probleem waar je altijd kunt gaan voor een expliciete opsomming van alle mogelijkheden, maar waar een of andere symmetrie-eigenschap meteen het aantal mogelijkheden halveert. Net zoals voor de zoekersrubriek in dit tijdschrift, kan ik het niet laten ‘to have a go at it’. Meestal lukt het wel om de binnenweg te vinden. Maar lang niet altijd. Zoals met de puzzel die het onderwerp vormt van deze bijdrage. Het zou een beetje mager uitvallen indien ik mij daartoe zou beperken, wat ik dus niet zal doen. De slimme oplossing van de puzzel brengt mij naar een belangrijk historisch voorbeeld, met name naar de Principia Mathematica van Isaac Newton. Van daaruit is

het een kleine stap om enkele bedenkingen neer te schrijven rond creativiteit – ook het oplossen van een eenvoudig probleem vereist denkkracht – en daarvoor is het recente boek van Marcus Du Sautoy, De code van creativiteit, de bron om te raadplegen. Maar beginnen bij het begin.

EEN PUZZEL IN EEN TIJDSCHRIFT

De opgave in New Scientist luidt als volgt. Gegeven is de volgende figuur:

De figuur is correct in die zin dat het andere vierkant links van het bovenste vierkant ook oppervlakte 8 heeft, het grotere vierkant eronder 32 en het onderste vierkant (ongeveer) 53. Gek genoeg, zoals zal blijken, heeft die laatste maat niet zo veel belang! De lezer heeft allang begrepen wat er gevraagd wordt: wat is de oppervlakte van de rode driehoek?

Hoe begin je aan zoiets? Kiezen voor de lange weg is vrij eenvoudig. Coördinaten introduceren en je bent vertrokken. Het zijn uiteindelijk allemaal rechte lijnstukken en, als je het assenkruis goed weet te kiezen kan het allemaal nog vrij simpel uitvallen. In zekere zin was het goed om te weten dat ik die oplossing achter de hand had. Want één ding weet je zeker: het zal er wel op uitdraaien dat de oppervlakte een geheel getal is (wat ook zo is, het is en blijft een puzzel). Met de langdradige versie heb je tenminste al een idee. Ik heb het niet gedaan, omdat ik toch eerst een paar pogingen wilde wagen om de binnenweg te vinden.

Misschien is het wel een goed idee om de driehoek op de voor

PROF. EM. DR. JEAN PAUL VAN

de hand liggende manier in vier stukken op te delen. Je maakt van één probleem een verzameling van deelproblemen die elk apart misschien wel eenvoudiger op te lossen zijn en, zou dat zo zijn, dan moet je op het einde maar de som maken en je bent klaar. Alleen ogen die vier stukken niet ‘goed’, in die zin dat er drie driehoeken zijn en een vierhoek. Hoe begin je daaraan? Verschuiven, roteren, spiegelen… kan dat iets opleveren? Ook niet meteen omdat de vierkanten in drie formaten komen dus past een rood stukje uit een vierkant niet zomaar in een ander vierkant. Bovendien: als je kijkt naar het bovenste vierkant links dan is de driehoek bepaald door:

• de basis: dat is simpel, dat is een (deel van de) zijde van het vierkant zelf,

• de opstaande zijde aan de linkerkant: opnieuw heel eenvoudig, dat is de diagonaal van het vierkant,

• de opstaande zijde aan de rechterkant: dat is een probleem. Om de positie van die lijn te bepalen moet je kijken naar het grote vierkant onderaan want de lijn loopt door tot in het linker beneden hoekpunt van dat vierkant. Zodoende ben je toch verplicht om alle vierkanten mee in rekening te brengen (en dus ook voor de basis).

Een andere, welgekende aanpak is om niet het probleem zelf aan te pakken maar het ‘complement’ ervan. We kennen de totale oppervlakte van de vier vierkanten tezamen. Als we de oppervlakte van de witte stukken kunnen berekenen dan zijn we bijna thuis, want de vierkanten, minus de witte stukken, leveren bijna de rode stukken op. Er is namelijk dat rode stukje buiten de vierkanten dat voor problemen blijft zorgen. Maar is dat niet op te lossen door het onderste vierkant naar rechts te verschuiven zodat er aan de linkerkant verticaal een lijn ontstaat? Het uitsteeksel zit nu aan de rechterkant maar dat geeft niet. Helpt dat? Ja en neen. Ja, omdat we nu een rode driehoek hebben die netjes binnen de vierkanten zit, neen, omdat ik geen idee heb of door het verschuiven de oppervlakte van de rode driehoek wel dezelfde blijft. Ik had er een probleem bij. Ik heb die poging dan ook maar opgegeven. Nochtans was ik op de goede weg, niet per se voor de oplossing van het probleem maar om een belangrijk inzicht te verwerven, namelijk dat de positie van de vierkanten niet absoluut hoeft te zijn. Misschien kan je er wél mee schuiven. Ik mag er van uitgaan dat iedereen die situatie herkent. Had je volgehouden dan was er een kans dat je het cruciale inzicht gevonden (of bedacht) zou hebben. Maar omdat er niet meteen iets leek te komen, heb je de poging afgebroken.

Dit alles betekende dus wel dat de zeven dagen tussen het verschijnen van het nummer van New Scientist met de opgave en het daaropvolgende nummer met de oplossing voorbij zijn gegaan zonder een eurekamoment. En dan krijg je de oplossing te zien en, zoals de uitdrukking gaat, je vervloekt jezelf. “Had ik maar volgehouden, ik zou er zeker opgekomen zijn”, “Dat ik dat niet gezien heb” (maar dan bedenk je dat dat precies de bedoeling van dergelijke puzzels is), dat zijn jouw gedachten. Om de spanning niet onnodig op te drijven, laat ik eerst en vooral die oplossing presenteren. Of beter, eerst het inzicht dat leidt tot de oplossing.

Het inzicht is dit: de oppervlakte (Opp) van een driehoek is bepaald door de basis ( b) en de hoogte ( h) volgens de gekende bepaling:

Wat betekent dat twee driehoeken met dezelfde basis en dezelfde hoogte noodzakelijkerwijze dezelfde oppervlakte hebben. Klinkt dit niet allemaal behoorlijk triviaal? Misschien wel maar het betekent wel dat de twee driehoeken ∆ ABC en ∆ A’BC in de tekening hieronder dezelfde oppervlakte hebben, gegeven dat de twee horizontale rechten evenwijdig lopen. Ze hebben dezelfde basis en dezelfde hoogte. A’ mag zo ver als je wil naar rechts wegschuiven, de oppervlakte blijft dezelfde.

De ‘binnenweg’ maakt precies gebruik van deze eigenschap. Bij de oplossing stond deze figuur:

De cruciale stap is om in te zien dat de rode driehoek dezelfde oppervlakte moet hebben als de blauwgerande driehoek. Het is gemakkelijk in te zien dat de diagonaal van het bovenste linkse vierkant evenwijdig loopt met de diagonaal EC van het onderste vierkant. Beide driehoeken hebben dezelfde basis en dezelfde hoogte dus dezelfde oppervlakte. Daardoor kunnen we ons nu concentreren op de blauwe driehoek. En dat ziet er zeer goed uit. Eigenlijk ongelofelijk goed want je kan dezelfde eigenschap nog eens toepassen. Noem het punt in het midden helemaal bovenaan X, dan zijn AX en BX diagonalen van de bovenste vierkanten. BX is evenwijdig met AC en de driehoeken ABC en AXC (de blauwe driehoek) hebben dezelfde basis dus dezelfde oppervlakte. Dus nu mag ik kijken naar driehoek ABC, de helft van het vierkant ABCD en dus is de oppervlakte 32/2 = 16. Een noot hierbij is dat het merkwaardig is dat de figuur in New Scientist onvolledig werd voorgesteld.

Eigenlijk zou je dit verwacht hebben:

Waarom wel de diagonaal [EC] tekenen en de even cruciale diagonaal [XB] niet? Maar los daarvan had ik toch maar de oplossing niet gezien. Had ik ze kunnen zien? In zekere zin wel, want deze merkwaardige eigenschap was ik al eens tegengekomen, zij het in een

totaal andere context – het moge duidelijk zijn, ik ben mij hier aan het verontschuldigen en uitvluchten aan het bedenken.

NEWTON PRODUCEERT EEN BEWIJS

1

En zo komt Isaac Newton in beeld. Meer bepaald dat merkwaardige boek dat terecht als zijn magnum opus wordt beschouwd: de Philosophiae Naturalis Principia Mathematica, waarvan de eerste editie in 1687 verschenen is. Nog steeds verschijnen er boeken en artikels om dat boek te begrijpen met inbegrip van de bewijzen die soms op bijzonder ingenieuze wijze in elkaar steken. Ik beschouw mij in geen geval als een Newton-kenner maar omdat de opkomst, de bloei en het verdwijnen van de eerste formuleringen van de beruchtberoemde infinitesimalen2 mij altijd hebben gefascineerd, heb ik mij in functie hiervan ooit aan (delen van) de Principia gewaagd. Oneindig kleine grootheden die wel of niet nul kunnen zijn dagen het denkvermogen echt wel uit: is x oneindig klein dan is x + ɛ = x, maar is dan ɛ niet nul? Dat was, om het heel eerlijk te zeggen, hard labeur. Bijvoorbeeld bij de passage die volgt. (Noot: de oorspronkelijke versie was, zoals de titel het al verraadt, in het Latijn, maar ik heb zelf gebruik gemaakt van een recente Engelse vertaling en de Nederlandse versie die ik hier presenteer, is van eigen hand. Aan het Latijn heb ik mij zelfs niet durven te wagen, niettegenstaande een atheneumscholing in de afdeling Latijn-Wiskunde!)

We bevinden ons in het eerste boek, tweede sectie, getiteld ‘De bepaling van centripetale krachten’. In wat voorafgaat, zijn al een hoop definities en axioma’s gepresenteerd en in de eerste sectie zijn een aantal algemene beweringen aangetoond. Losjes gezegd, zou je kunnen stellen dat vanaf hier de zaak echt van start gaat. We krijgen een eerste stelling en een eerste bewijs met een figuur erbij. Om de lezer toch eens te laten proeven van het niveau waarop Newton zich vlot beweegt, volgen hier stelling en bewijs in detail, met de figuur afkomstig uit de oorspronkelijke tekst. Als ik het werkwoord ‘proeven’ heb gekozen dan is dat welbewust: wie iets proeft, hoeft niet meteen alle smaken thuis te brengen. Op dezelfde wijze hoeft niet alles in wat volgt meteen helder te zijn.

Stelling. De oppervlaktes die lichamen bewegend op een baan beschrijven door stralen die zijn getrokken naar een onbeweeglijk krachtcentrum toe, liggen in vaste vlakken en zijn evenredig met de tijd waarin ze doorlopen worden.

Bewijs. Laat de tijd in gelijke delen worden verdeeld, en laat in het eerste deel van de tijd een lichaam door zijn inertiekracht de rechte lijn AB beschrijven. In het tweede deel van de tijd, als niets het belemmerde, zou dit lichaam (volgens wet 1 – dat is uiteraard de wet van inertie, mijn toevoeging) rechtdoor gaan naar c en de lijn Bc beschrijven die gelijk is aan AB, zodat – wanneer de stralen

AS, BS en cS naar het midden werden getrokken – de gelijke gebieden ASB en BSc zouden worden beschreven. Maar als het lichaam naar B komt, laat dan een centripetale kracht werken met een enkele maar grote impuls en laat het lichaam afwijken van de rechte lijn Bc en verder gaan in de rechte lijn BC. Laat cC parallel aan BS worden getrokken en BC ontmoeten bij C; dan, wanneer het tweede deel van de tijd is voltooid, zal het lichaam (volgens gevolg 1 van de wetten – dit komt in moderne termen overeen met het optellen van vectoren, mijn toevoeging) worden gevonden op C in hetzelfde vlak als driehoek ∆ASB. Verbind SC. Omdat SB en Cc parallel zijn, zal driehoek ∆SBC gelijk zijn aan driehoek ∆SBc en dus ook aan driehoek ∆SAB. Door een soortgelijk argument, als de middelpuntzoekende kracht achtereenvolgens werkt op C, D, E, ..., waardoor het lichaam in elk van de individuele tijdsdelen de individuele rechte lijnen CD, DE, EF, ... beschrijft, zullen al deze lijnen in hetzelfde vlak liggen; en

driehoek ∆SCD zal gelijk zijn aan driehoek ∆SBC, ∆SDE aan ∆SCD en ∆SEF aan ∆SDE. Daarom worden in gelijke tijden gelijke gebieden beschreven in een onbeweeglijk vlak; en door samenstelling staan alle sommen SADS en SAFS van de gebieden tot elkaar zoals de tijden van hun beschrijving. Laat nu het aantal driehoeken worden vergroot en hun breedte onbepaald verkleind, en hun uiteindelijke omtrek ADF zal (door lemma 3, gevolg 4) een gebogen lijn zijn; en dus zal de middelpuntzoekende kracht waarmee het lichaam voortdurend wordt teruggetrokken van de raaklijn van deze curve ononderbroken werkzaam zijn, terwijl alle beschreven gebieden, SADS en SAFS, die altijd evenredig zijn met de beschreven tijden, ook evenredig zullen zijn met die tijden in dit geval. QED.

Gelukkig is het niet nodig om dit bewijs in detail door te nemen3 maar grosso modo is dit wel de ‘toon’ (of de ‘smaak’) van de Principia en die wou ik, zoals gezegd, de lezer toch even laten proeven. Het gaat mij hier enkel en alleen om de twee door mij gemarkeerde fragmenten omdat Newton daarin twee keer het idee toepast dat in de puzzel ter sprake kwam.

• Eerste fragment: dat ASB en SBc dezelfde oppervlakte moeten hebben volgt uit, één, het feit dat AB = Bc, want in gelijke tijden worden gelijke afstanden doorlopen, wat betekent dat de twee driehoeken dezelfde basis

hebben, twee, het toppunt S hetzelfde is voor beide driehoeken en, dus, drie, ook de hoogte omdat AB en Bc in elkaars verlengde liggen.

• Tweede fragment: dat SBC en SBc dezelfde oppervlakte moeten hebben, volgt uit de vaststellingen, één, dat ze dezelfde basis SB hebben en, twee, dat de hoogte voor beide dezelfde is omdat Cc evenwijdig is met SB

Ik herinner mij nog zeer goed, zovele jaren geleden, toen ik voor de eerste keer dit bewijs probeerde te begrijpen, dat ik een tijdje heb vastgezeten precies op die gemarkeerde passages (en daar niet alleen voor alle duidelijkheid!) tot mijn frank viel. Het is de moeite waard om, hierbij aansluitend, op te merken dat voor Newton zelf dit niet echt bijzonder was (en dus al zeker geen onderwerp voor een puzzel). In zijn dagen maakten de Elementen van Euclides namelijk deel uit van de basiskennis. En in boek I zegt stelling 38 precies dat driehoeken met gelijke basis en geplaatst tussen dezelfde parallelle lijnen gelijk zijn aan elkaar (te begrijpen als het hebben van dezelfde oppervlakte). Deze stelling behoorde dus tot de parate kennis. Dit bewijst dat hoe wiskunde wordt aangeleerd van fundamenteel belang is4. In mijn geval was de stelling na mijn “Newton-gevecht” tot mijn parate kennis gaan behoren en toch heb ik bij de New Scientist puzzel er niet aan gedacht om die eigenschap als deel van de oplossing te zien. Het heeft weinig zin om hier een

doorgedreven psychologische analyse te presenteren waarom mijn brein mij (even) in de steek heeft gelaten. Daarentegen is het wel interessant om even stil te staan bij de vraag of ik op een meer systematische manier toekomstige problemen/puzzels zou kunnen aanpakken zodat lichte irritatie opwekkende toestanden zoals met de rode driehoek mij bespaard blijven. Dat leidt vanzelf naar de vraag hoe we creativiteit kunnen begrijpen. Want, hoe bescheiden ook in het geval van een puzzel, ik ben creatief bezig geweest.

MARCUS DU SAUTOY KIJKT NAAR CREATIVITEIT

Op zijn beurt leidt deze vraagstelling meteen naar het recente boek van Marcus Du Sautoy – Britten zijn onverbeterlijk want spreek zijn naam niet op z’n Frans uit, iets wat klinkt als “Du Sootwa”, maar wel “Du Sotoj” (waarbij “toj” klinkt als het Engelse woord “toy”) – getiteld De code van creativiteit. De auteur is zelf professioneel wiskundige en schrijft ongelofelijk gepassioneerd over de koningin van de wetenschappen. Wat dat betreft is hij zeker vergelijkbaar met Ian Stewart die een omvangrijk oeuvre bij elkaar heeft geschreven met de bedoeling de wiskunde bij een breder publiek te brengen. Of, laat ik het zo zeggen, dit zijn het soort boeken die in een degelijke STE(A)M-opleiding zeker thuishoren.

Het hoofdthema van het boek is de creativiteitsvraag waarbij vooral gekeken wordt naar de

verwezenlijkingen van Artificial Intelligence of Kunstmatige Intelligentie. Dat klinkt zeer aannemelijk omdat, als er systematiek zit in het creatieve proces, een implementatie op een computer mogelijk moet zijn. En in die zin brengt het boek een mooi overzicht van alle pogingen tot nu toe, gaande van AlphaZero, het computerprogramma dat een grootmeester in het Japanse bordspel Go heeft verslagen over programma’s die muziekcomposities produceren zowel in popmuziek, jazz als klassiek, tot Mizar, een bibliotheek van wiskundige stellingen en bewijzen, herschreven in een uniforme taal tussen programma- en omgangstaal in. Dat muziek zo prominent aanwezig is, hoeft niet te verbazen, niet alleen vanwege de evidente wiskundige verbanden maar ook omdat Du Sautoy zelf musiceert en dus ook vertrouwd is met de muzikale praktijk. Kortom, meer dan het lezen waard. Speciaal voor deze bijdrage wil ik wat dieper ingaan op een elementaire classificatie die hij voorstelt in het inleidende deel van het boek met betrekking tot creativiteit. Hij onderscheidt hierbij drie types.

• Verkennende creativiteit: “betekent dat je uitgaat van wat er al is, en vervolgens de uiterste randen ervan onderzoekt en de grenzen van het mogelijke verlegt, terwijl je aan de regels gebonden blijft.” (p. 17)

• Combinerende creativiteit: “Denk aan een kunstenaar die twee totaal

verschillende concepten neemt en die probeert te combineren. De regels die in de ene wereld de dienst uitmaken, kunnen vaak een interessant nieuw kader bieden voor de andere wereld.” (p. 18)

• Transformationele creativiteit: “Dit zijn die zeldzame momenten die complete verschuivingen veroorzaken. … Het zijn net faseveranderingen, zoals wanneer water plotseling van een vloeistof in een gas verandert.” (p. 19)

Het is geen eenvoudige zaak om de kleine dosis creativiteit die ik bij het oplossen van de puzzel met weinig resultaat aan de dag heb gelegd te plaatsen in deze driedeling. Indien het toegelaten is om te spreken van een dosering dan lijkt het nog het meest op een vorm van transformationele creativiteit in een heel kleine dosis. Valt het niet te verdedigen dat de clou van de oplossing erin bestaat om de figuur op de ‘juiste’ manier te bekijken zodat (cruciale) hoofdzaak van (irrelevante) details onderscheiden wordt? Of is het toch eerder een verkennende vorm? En ben ik niet ver genoeg gegaan om al wat mogelijk is te exploreren? Zoals onder welke omstandigheden de oppervlakte van een driehoek constant blijft. Welke antwoorden we ook krijgen op deze vragen, wat het wel lijkt te suggereren is dat er sprake is van een zekere methodiek, dat je, met andere woorden, op een meer systematische manier een probleem kan aanpakken. Het is in die zin vrij onbegrijpelijk dat de naam van Georg Pólya in dit

boek niet wordt vermeld. In zijn nog steeds indrukwekkende boek How to solve it, daterend van 1945 (!), staan een aantal methodes opgelijst om een wiskundig vraagstuk aan te pakken en het is verrassend vast te stellen hoeveel van deze adviezen in onze tijd een nieuw leven zijn gaan leiden in digitale vorm.

Een zaak moet ik zeker nog vermelden vooraleer dit artikel af te ronden. Uiteraard schrijft Du Sautoy ook over vertaalprogramma’s en over software die zelf teksten kan genereren, op basis van een aantal trefwoorden en een minimale omschrijving. Dat de kwaliteit van de output in recente tijden duidelijk aan het verbeteren is – Google translate is de laatste jaren merkelijk verbeterd, om een bekender voorbeeld te vermelden – wil de auteur demonstreren door in het boek een passage op te nemen, ongeveer 350 woorden lang, die van een computer afkomstig is. Je komt niet te weten waar die staat zodat het bijna een mini-Turing test wordt: ben je in staat om het onderscheid te maken tussen mens en machine op basis niet van de interne werking maar van gedrag of output van dat gedrag zoals een tekstfragment? In een interview heeft hij wel weggegeven dat de passage in kwestie een spellingsfout bevat en ik moet bekennen dat dat stukje informatie mij heeft geholpen om die beruchte passage te vinden. (Er was nog een andere indicatie, namelijk dat de alinea’s ervoor en erna vanuit het ik-perspectief zijn geschreven terwijl de passage in kwestie volkomen

onpersoonlijk geformuleerd is.) Zoals te verwachten, vind je daarna nog tientallen andere indicaties maar dat mag als een cognitief-psychologisch neveneffect gezien worden. Ook wat je totaal verrast, heb je nadien zien aankomen!

EEN BEDENKING EN EEN NIEUWE PUZZEL

Nog even terug naar de drie vormen van creativiteit. In het begin van deze tekst had ik aangegeven dat de oppervlakte van het onderste vierkant niet zo veel belang had – ik schreef dat de oppervlakte ongeveer 53 is. Nu we de oplossing in handen hebben, zien we meteen in waarom dit effectief genegeerd mag worden. Waar het om gaat, is dat het onderste punt van de rode driehoek op een evenwijdige moet liggen met de diagonaal van het kleine vierkant bovenaan aan de linkerkant. Dus in de twee figuren hieronder heeft de roodgerande driehoek steeds dezelfde oppervlakte (in de figuur rechts is de basis van de driehoek in lengte gelijk aan de diagonaal van het vierkant linksboven):

Ondertussen is een volgend nummer van New Scientist in de bus gevallen en de puzzel doet deze keer beroep op de derde vorm van creativiteit. Een uurwerk – ronde schijf met alle getallen erop – valt uiteen in twee stukken (waarvan de vorm niet gespecifieerd wordt). Alle cijfers zijn op één van de twee stukken terug te vinden, anders gezegd, de scheur loopt niet door een cijfer. Blijkt dat de som van de getallen in het ene stuk even is, in het andere stuk oneven. Wat is de som van die twee getallen? Er komt wiskunde aan te pas om de onmogelijkheid te zien, dan te beseffen dat die onmogelijkheid

schijnbaar is om dan de oplossing te zien en meteen te begrijpen waarom de twee stukken gelijk welke vorm mogen hebben, op één detail na. Het is helemaal niet gezegd dat een computer met deze informatie de oplossing weet te vinden. Van een mens en een wiskundige in het bijzonder verwacht ik het eigenlijk wel. (Hint: het onderscheid tussen cijfer en getal is belangrijk.)

NOTEN

[1] Voor dit gedeelte van het artikel ben ik mijn collega aan de VUB, wetenschapshistoricus en -filosoof Steffen Ducheyne, zeer dankbaar omdat hij, als specialist van het werk van Newton en de verspreiding ervan, bijvoorbeeld in Nederland, mij op een aantal punten heeft gewezen die de kwaliteit van de tekst hebben verbeterd. Onder andere voetnoot 3 is daarvan getuige.

[2] Ik gebruik de uitdrukking “eerste formuleringen” omdat we vandaag een tweede formulering kennen die er wel in geslaagd is om infinitesimalen correct te formuleren. Dit is de verdienste geweest van Abraham Robinson die, gebruik makend van zogenaamde niet-standaard modellen, een niet-standaard analyse heeft uitgewerkt waarin infinitesimalen een plaats hebben gekregen. Vermeldenswaard is dat deze theorie aanleiding heeft gegeven tot handboeken, zoals het volumineuze werk van Keisler, die toelaten om deze niet-standaard analyse daadwerkelijk toe te passen. Newton zou verrukt geweest zijn!

[3] Dat een detailanalyse van dit bewijs voor interessante inzichten kan zorgen, wordt getoond door het artikel van Pourciau. Een grondige analyse laat zien dat de formulering van de stelling niet klopt. Dat de oppervlaktes in vaste vlakken liggen, is geen deel van de

alles door elkaar loopt. Straks maken we nog een uitstapje naar de meetkunde waarin meer kan.

22

We bewijzen (*) eerst met een berekening. In het parallellogram

een berekening. In het parallellogram geldt:

het parallellogram tot een vierkant via een afschuiving en een schaling. Omdat dit affiene afbeeldingen zijn, beelden ze de lijn af op een lijn en handhaven ze de genoemde verhoudingen. In het vierkant kunnen we gemakkelijker rekenen dan in het parallellogram. Bijna ongemerkt zijn we in de ‘gewone’, Euclidische meetkunde terechtgekomen. We kunnen immers alleen spreken van een vierkant als we de begrippen afstand en hoek tot onze beschikking hebben!

Opgave: Reken na dat (*) volgt uit het gelijkstellen van de bovenstaande twee uitdrukkingen voor C .

volgt uit het gelijkstellen van de bovenstaande twee uitdrukkingen voor C

OEFENING 4

voor (*). Wie bekend is met affiene meetkunde kan daarmee de opgave gemakkelijker op te lossen is. Vervorm het parallellogram tot een vierkant via schaling. Omdat dit affiene afbeeldingen zijn, beelden ze de lijn af op een lijn genoemde verhoudingen. In het vierkant kunnen we gemakkelijker rekenen dan in ongemerkt zijn we in de ‘gewone’, Euclidische meetkunde terecht gekomen. spreken van een vierkant als we de begrippen afstand en hoek tot onze

uitdrukkingen voor C de opgave een vierkant via op een lijn rekenen dan in terecht gekomen. tot onze het punt F

Er is ook een ander bewijs voor (*). Wie bekend is met affiene meetkunde kan daarmee de opgave omzetten in een vorm die gemakkelijker op te lossen is. Vervorm het parallellogram tot een vierkant via een afschuiving en een schaling. Omdat dit affiene afbeeldingen zijn, beelden ze de lijn af op een lijn en handhaven ze de genoemde verhoudingen. In het vierkant kunnen we gemakkelijker rekenen dan in het parallellogram. Bijna ongemerkt zijn we in de ‘gewone’, Euclidische meetkunde terecht gekomen. We kunnen immers alleen spreken van een vierkant als we de begrippen afstand en hoek tot onze beschikking hebben!

Figuur 4

7cm 4cm A 2 B 3 C 4 D 5 E 6

In figuur 4 doorsnijdt een lijn een parallellogram. De snijpunten verdelen twee van de zijden en de diagonaal elk in twee stukken in lengteverhoudingen die voldoen aan:

AB AE + AD AG = AC AF (*)

geldt. (Tip: Neem het eenheidsvierkant,

Opgave: Bewijs dat in het vierkant

Opgave: Bewijs dat in het vierkant (*) geldt. (Tip: Neem het eenheidsvierkant, AB = AD = 1 , AC = √ 2 , beschrijf de lijn in coördinaten (neem O = A ) en bedenk dat het punt F op de diagonaal van het vierkant ligt.)

vierkant (*) geldt. (Tip: Neem het eenheidsvierkant, beschrijf de lijn in coördinaten (neem O = A ) en bedenk dat het punt F vierkant ligt.)

, beschrijf de lijn in coördinaten (neem

op de diagonaal van het vierkant ligt.)

affiene stellingen affiene waar veel draait spannender vindt dan goed begrip van

Dit is een eenvoudige toepassing, maar er zijn er ook die verrassender zijn. Sommige affiene stellingen waren al in de klassieke oudheid bekend. Tegenwoordig, zo’n twee millennia later, wordt affiene meetkunde gebruikt in technieken achter computer graphics en computer aided design, waar veel draait om het verplaatsen en vervormen van personages of voorwerpen, wat je wellicht spannender vindt dan het bestuderen van eigenschappen van eenvoudige figuren. Maar de eerste stap is een goed begrip van de beginselen, en daarvan hebben we er hier een aantal behandeld.

Let wel, dit zijn verhoudingen tussen lijnstukken op dezelfde lijn. Zoals gezegd kent de affiene ruimte verhoudingen tussen gelijkgerichte lijnstukken, maar het is niet mogelijk lengten te meten en lijnstukken te vergelijken die niet in lijn liggen. Dit lijkt vreemd, maar veel wiskundige theorieën beogen met beperkte uitgangspunten een strak verhaal met krachtige stellingen te zijn en niet een onbestemde brij waarin van alles door elkaar loopt. Straks maken we nog een uitstapje naar de ‘gewone’, Euclidische meetkunde waarin meer kan.

) en bedenk dat het punt

Waarachtigewolvensprekenaltijddewaarheidenleugenachtigeluipaardenliegenaltijd.Tien zulkedierenzittenineenkring,zodatelkdiernegenandereziet. Vijfdierendoenelkeenuitspraak.

Dit is een eenvoudige toepassing, maar er zijn er ook die verrassender zijn. Sommige affiene stellingen waren al in de klassieke oudheid bekend. Tegenwoordig, zo’n twee millennia later, wordt affiene meetkunde gebruikt in technieken achter computer graphics en computer aided design, waar veel draait om het verplaatsen en vervormen van personages of voorwerpen, wat je wellicht spannender vindt dan het bestuderen van eigenschappen van eenvoudige figuren. Maar de eerste stap is een goed begrip van de beginselen, en daarvan hebben we er hier een aantal behandeld.

• E´endierzegt:“Ikzieprecies´e´enluipaard.”

We bewijzen (*) eerst met een berekening. In het parallellogram geldt: C

• E´endierzegt:“Ikziepreciesvijfwolven.”

• E´endierzegt:“Ikziedubbelzoveelluipaardenalswolven.”

• E´endierzegt:“Ikzieprecieszevenluipaarden.”

• E´endierzegt:“Ikziepreciesnegenwolven.”

Opgave: Reken na dat (*) volgt uit het gelijkstellen van de bovenstaande twee uitdrukkingen voor C

A 3 B 4 C 5 D 6 E 7

aangegevenhoekvormen.Hoeveelbruggensteekjeoverals jeopdiemaniervanAnaarBwilgaan? 90° A 150° 60° B 90° 90° 60° 90° 60° 90° 150° A 9 B 10 C 11 D 12 E 13 ©

Vlaamse Wiskunde Olympiade vzw, eerste ronde 2023

Er is ook een ander bewijs voor (*). Wie bekend is met affiene meetkunde kan daarmee de opgave omzetten in een vorm die gemakkelijker op te lossen is. Vervorm het parallellogram tot een vierkant via een afschuiving en een schaling. Omdat dit affiene afbeeldingen zijn, beelden ze de lijn af op een lijn en handhaven ze de genoemde verhoudingen. In het vierkant kunnen we gemakkelijker rekenen dan in het parallellogram. Bijna ongemerkt zijn we in de ‘gewone’, Euclidische meetkunde terecht gekomen. We kunnen immers alleen spreken van een vierkant als we de begrippen afstand en hoek tot onze beschikking hebben!

Opgave: Bewijs dat in het vierkant (*) geldt. (Tip: Neem het eenheidsvierkant, AB = AD = 1 , AC = √ 2 , beschrijf de lijn in coördinaten (neem O = A ) en bedenk dat het punt F op de diagonaal van het vierkant ligt.)

A 36 m2 B 42,25 m2 C 60,5 m2 D 72 m2 E 84,m2

A 36m2 B 42,25m2 C 60,5m2 D 72m2 E 84,5m2

Dit is een eenvoudige toepassing, maar er zijn er ook die verrassender zijn. Sommige affiene stellingen waren al in de klassieke oudheid bekend. Tegenwoordig, zo’n twee millennia later, wordt affiene meetkunde gebruikt in technieken achter computer graphics en computer aided design, waar veel draait om het verplaatsen en vervormen van personages of voorwerpen, wat je wellicht spannender vindt dan het bestuderen van eigenschappen van eenvoudige figuren. Maar de eerste stap is een goed begrip van de beginselen, en daarvan hebben we er hier een aantal behandeld.

3 19

OEFENING 3

EEUWENOUDE RAADSELS EN BAANBREKENDE INZICHTEN

HOE KRIJG JE VERSCHILLENDE AMBULANCES ZO SNEL MOGELIJK OP HUN PLEK? HOE PLAATS JE ACHT DAMES OP EEN SCHAAKBORD ZONDER

DAT TWEE VAN DIE DAMES ELKAAR AANVALLEN? HOE VERHOUDEN VERSCHILLENDE SOORTEN ONEINDIGHEDEN ZICH TOT ELKAAR?

WISKUNDE KOMT BIJ AL DIE VERSCHILLENDE PROBLEMEN VAN PAS.

VAN JAGEN OP PRIEMGETALLEN TOT FOTOGENIEKE KRIJTBORDEN EN KNOPENWISKUNDE; HET KOMT ALLEMAAL AAN BOD IN DE NIEUWE

WISKUNDESPECIAL VAN NEW SCIENTIST.

RECENSIE VAN KATINKA STEEN , UITGEVER VOOR HET SECUNDAIR ONDERWIJS BIJ DIE KEURE

De New Scientist heeft zijn tweede wiskundespecial uit, opnieuw een nummer vol prachtige wiskunde. Zo is de nieuwsrubriek bijzonder boeiend. In die rubriek lees je heel wat over de nieuwste wiskundemodellen en waarvoor ze praktisch worden ingezet. Ideaal om leerlingen de zin van wiskunde te duiden. Er zijn bijvoorbeeld meer dan 10 500 vogelsoorten, maar slechts 4 universele eivormen. Die eivormen zijn nu gevat in één formule. Handig voor biologen om de evolutie van het ei verder te onderzoeken, maar ook de voedingsindustrie, de kunst en architectuur zijn ermee gebaat.

Met wiskundige simulaties kan men nu ook aantonen dat het nut van bestrijdingsmiddelen op lange termijn vaak nihil is. Intuïtief zou je denken dat dit niet klopt doordat je natuurlijke vijanden een handje gaat helpen, maar een wiskundig model helpt in zo’n geval om meer inzicht te krijgen in het probleem. Wie gaat bestrijden, vermindert niet alleen de plaag maar ook de natuurlijke vijanden, daardoor

WIN EEN EXEMPLAAR VAN DE WISKUNDESPECIAL

kunnen de natuurlijke vijanden fel verminderen of zelfs uitgeroeid raken en gaat de plaag toch weer toenemen.

Verder werd ik geboeid door de vele interviews. De ene filosofischer van insteek en de andere dan weer wiskunde in een heel functionele context. Ook de fotoreportage deed me gniffelen, omdat ik me zo kan voorstellen dat veel wiskundigen in het Vlaamse onderwijslandschap hier tijdens hun lessen ook aan zouden kunnen bijdragen. Ben jij ook verknocht aan je krijtbord? In de fotoreportage vat de wiskundespecial samen dat wiskundigen wereldwijd nog altijd het liefst met krijt op een bord schrijven ondanks de vele technologische innovaties.

Kortom, 100 pagina’s vol lees-, kijk- en bovenal wiskundeplezier.

Bestel de wiskundespecial hier: www.newscientist.nl/wiskunde

Ben jij ook nieuwsgierig naar het boek? Stuur je naam, adres en e-mailadres naar info@newscientist.nl en wie weet sleep jij een exemplaar in de wacht! Deelnemen kan t.e.m. 31 maart 2023.

Waarachtigewolvensprekenaltijddewaarheidenleugenachtigeluipaardenliegenaltijd.Tien zulkedierenzittenineenkring,zodatelkdiernegenandereziet. Vijfdierendoenelkeenuitspraak.

• E´endierzegt:“Ikzieprecies´e´enluipaard.”

• E´endierzegt:“Ikziepreciesvijfwolven.”

• E´endierzegt:“Ikziedubbelzoveelluipaardenalswolven.”

• E´endierzegt:“Ikzieprecieszevenluipaarden.”

HET BOEK DENKWERELD BEVAT HEEL WAT CREATIEVE PUZZELS OVER LOGICA, TAAL EN WISKUNDE. DE PUZZELS VINDEN HUN INSPIRATIE IN ONDER MEER SPELLETJES, WISKUNDIGE PROBLEMEN, LITERATUUR EN TOPOGRAFIE. NA DE EERDERE DELEN DENKWAAR, DENKWERK EN DENKRAAM IS OOK DIT VIERDE BOEK IN DE REEKS GOED VOOR URENLANG PUZZELPLEZIER.

• E´endierzegt:“Ikziepreciesnegenwolven.”

DRS P DENKT MEE

Devijfdierendiezwijgen,zijnvandezelfdesoort.Devijfdierendiespreken,zijnnietvandezelfde soort.Hoeveelwolvenzittenerindekring?

Hoe kun je van het woord dame het woord heer maken, door telkens één letter te veranderen en enkel bestaande woorden te gebruiken? Drs P. denkt hierin mee! Waarom is 200 cc zo’n bijzondere inhoudsmaat? Welke Nederlandse woorden bevatten, net zoals denkwereld, precies alle drie de mogelijke e-klanken?

HOE ROND EEN VIERKANT IS

HetbloemenperkvanAndriesbestaatuittweecongruente vierkanten,afgebakendmetboordsteentjeszoalsindefiguur. Dedoorgangtussenbeidedelenis4mbreed.Alsdeomtrekvan hetbloemenperk44mis,watisdandeoppervlakteervan?

In Denkwereld ontdek je waarom ‘vier’ ook ‘6’ kan zijn en ‘tien’ ‘1’. Je zoekt uit hoe rond een vierkant is en wat het kleinste getal is dat je niet kunt maken met 2, 3, 7 en 12. Ook kun je aan de slag met rijmdrielingen – zo bestaat er slechts één woord dat rijmt op ‘hachelijk’ en ‘belachelijk’.

OVER DE AUTEUR

Jaap Klouwen is wiskundige. Hij is werkzaam aan de Hogeschool van Amsterdam, onder meer als docent statistiek en wiskunde bij diverse (bedrijfs-)economische opleidingen. Daarnaast schrijft hij hbo-studieboeken en artikelen voor het wiskundetijdschrift Pythagoras.

Bestel Denkwereld hier: www.newscientist.nl/denkwereld

Indebolletjesinhetonderstaandeschemamoetengetallenwordeningevuldzodatopelkvande zeslijneneenrekenkundigerijkomttestaan.Welkgetalkomtopdeplaatsvanhetvraagteken?

OEFENING 5

In de bolletjes in het onderstaande schema moeten getallen worden ingevuld zodat op elk van de zes lijnen een rekenkundige rij komt te staan. Welk getal komt op de plaats van het vraagteken?

Een1×6-blokjeishetkleinsteLEGO® -blokjedatschuinopeen rechthoekigeondergrondpast(metbehulpvan1×1-blokjesopdeuiteinden),zoalsindefiguur.Watishetopeennakleinsteblokjedatook schuinpastopeenrechthoekigeondergrond?

© Vlaamse Wiskunde Olympiade vzw, eerste ronde 2023

TETRAËDER TORENS

IN 1990 BESTOND MITO PRECIES

HONDERD JAAR ALS OFFICIËLE

JAPANSE STAD. OM DAT TE VIEREN

KREEG DE JAPANSE ARCHITECT

ARATA ISOZAKI OPDRACHT OM

EEN TOREN TE ONTWERPEN ALS

ONDERDEEL VAN EEN AANTAL CULTURELE VOORZIENINGEN

ZOALS EEN CONCERTZAAL, EEN THEATER EN EEN KUNSTGALERIE.

DEZE WEL HEEL BIJZONDERE

TOREN, VEELAL AANGEDUID ALS

ART TOWER MITO, IS 100 METER

HOOG EN WORDT GEVORMD DOOR

28 OP ELKAAR GESTAPELDE GROTE

REGELMATIGE VIERVLAKKEN. DEZE

BESTAAN UIT EEN STALEN FRAME

BEKLEEDT MET GELIJKZIJDIGE

DRIEHOEKIGE TITANIUM PLATEN. IN

TOTAAL BEVAT DE TOREN 57 VAN

DIE PLATEN.

Op een hoogte van 86,4 m is een klein plateau dat via een soort patrijspoorten uitzicht biedt over de stad en de omgeving. Daar is plaats voor maximaal 20 bezoekers. Dat plateau is bereikbaar met een glazen lift zodat je omhoog of naar beneden gaande ook zicht hebt op de interne structuur van de toren.

KLAAS LAKEMAN , ARS ET MATHESIS

TETRAËDERS STAPELEN

Zoals bekend bestaat een regelmatige viervlak dikwijls kortweg tetraëder genoemd, uit vier gelijkzijdige driehoeken. Het regelmatig viervlak is niet ruimte vullend. Met andere woorden door stapelen van regelmatige viervlakken kan de ruimte niet volledig worden opgevuld. Altijd blijven er kieren en gaten over. Ze kunnen echter wel in één richting bijvoorbeeld verticaal omhoog op elkaar worden gestapeld. Elke tetraëder wordt dan gedraaid over een hoek op zijn voorganger geplaatst. Dat levert een spiraalvormige keten.

Met de driehoeken van het alom bekende Trigo constructiespeelgoed (figuur 1) is dit goed te illustreren. Daarmee zijn 28 Trigo tetraëders op elkaar gestapeld. Ter verduidelijking zijn in figuur 2 driehoeken in drie verschillende kleuren gebruikt: rood, blauw en grijs.

Begin je met een viervlak en stapel je daar een tweede op dan kun je het zijvlak dat tot beide viervlakken behoort achterwege laten. Bij het ene viervlak is dat het ‘bovenvlak’ en het ‘ondervlak’ bij het viervlak dat daar op komt. Met het click-systeem

Figuur 1 Trigo’s, driehoeken en vierkanten met click-randen. Figuur 2 Trigo toren.

Figuur 3 Trigo torens met tegengestelde draaiingen.

van de Trigo’s is dat gemakkelijk te doen. Stapel je op de tweede vervolgens een derde tetraëder dan kan ook weer het gemeenschappelijke zijvlak achterwege worden gelaten, enzovoorts. Van het tweede en daaropvolgende viervlakken zijn dus steeds maar twee (opstaande) zijvlakken zichtbaar. Zo zie je van het tweede viervlak een rood en een blauw zijvlak, van het derde een blauw en een grijs zijvlak, van het vierde viervlak een grijs en een rood zijvlak, enzovoorts. Door bij het stapelen steeds de gemeenschappelijke zijvlakken weg te laten is het hele object hol en zie je van binnenuit steeds alleen maar driehoekige zijwanden.

HELICES

De opeenvolgende viervlakken zijn bij stapeling steeds iets gedraaid ten opzichte van elkaar. Het geheel vertoont een soort schroefvorm. Zo’n stapeling van regelmatige viervlakken leidt tot drie met elkaar verweven helices, gevormd door de randen die steeds tot maar één viervlak behoren. Zo’n helix wordt een Boerdijk-Coxeter-helix genoemd. In figuur 2 is dat mooi te zien. Een helix loopt tussen de grijze en rode zijvlakken, een tussen de grijze en blauwe en een tussen de rode en blauwe zijvlakken. Een stapeling van regelmatige viervlakken is niet roterend repetitief. Anders gezegd: al zou je de stapeling tot in het oneindige voort kunnen zetten dan zullen nog geen twee viervlakken dezelfde oriëntatie krijgen. De hoek waarover een tetraëder draait die aan de stapeling wordt toegevoegd, is namelijk geen rationaal deel van 360° (hele cirkel).

ANDERE DRAAIRICHTING

Naast de stapeling van figuur 2 is nog een zo’n verticale stapeling van regelmatige viervlakken mogelijk. Deze heeft een tegengestelde draairichting. Met andere woorden: de Boerdijk-Coxeter-helix heeft twee vormen. De ene heeft een schroefvorm die met de klok mee draait en de andere draait juist tegen de klok in. Ter vergelijking zijn in figuur 3 beide stapelingen naast elkaar afgebeeld.

TETRA-TOREN

De 5 meter hoge Tetra-toren van Jan Marcus bestaat uit een aaneenschakeling van gelijkzijdige driehoekige hylite platen die zijn ingeklemd tussen drie vloeiende helices (figuur 4). Ook dit zijn Boerdijk-Coxeter-helices. Figuur 4 is namelijk een stapeling van regelmatige viervlakken waarbij de gemeenschappelijke driehoeken van de opeenvolgende viervlakken worden weergegeven en de opstaande zijvlakken zijn weggelaten. Vergelijk de figuren 2 en 4 maar eens met elkaar. De drie helices ondersteunen het geheel en zorgen dat de toren niet in elkaar zakt. Hier zijn ze mooi vloeiend terwijl ze in figuur 2 uit een aaneenschakeling van rechte lijnstukken (randen van de viervlakken) bestaan. De hoek tussen twee opeenvolgende driehoekige vlakken is net als de hoek tussen de vlakken in een regelmatig viervlak, steeds 70° 31' 44".

ZELF AAN DE SLAG

Zoals Jan Marcus al aangaf is een Tetra-toren eenvoudig te maken door de drie spiralende staven te vervangen door een rechte staaf bijvoorbeeld een breinaald of een satéstokje. Neem de strook van figuur 5 - eventueel vergroot - over op stevig papier, karton of nog mooier op een strook aluminium. Knip de strook uit en maak er gaatjes in op exact dezelfde plaatsen als aangegeven in figuur 5 en met een diameter die 1,5 maal de diameter van de staaf is. De lengte van de staaf moet minimaal 0,8 maal die van de strook zijn. Vouw de strook met driehoeken langs de stippellijnen naar ‘achteren’ en langs de doorgetrokken lijnen naar ‘voren’. Steek de staaf door de gaatjes en prik hem op een voetstuk. Desgewenst is het bouwplaatje uit figuur 5 uit te breiden om een hogere Tetra-toren te verkrijgen.

Figuur 4 De Tetratoren.

TRIGO TETRA-TOREN

Dankzij de grote ronde gaten in de Trigo-driehoeken, is ook een Tetra-toren daarmee snel te maken. Click een aantal driehoeken tot een strook aan elkaar (figuur 6). Waar in de (papier)strook van figuur 5 de driehoeken naar beneden worden gevouwen en dus stippellijnen zijn, komen in figuur 6 de click-randen naar voren en waar de doorgetrokken lijnen zijn gaan de clickranden naar achteren. Vergelijk dat in figuur 7. Door de gaten kan bij voorbeeld een stuk bamboe worden gestoken dat gebruikt wordt om planten te ondersteunen. En klaar is de Trigo Tetra-toren (figuur 8). Steeds wijzen de click-randen van de driehoeken daarin naar binnen, dus naar de staaf toe. Minder fraai maar niet erg storend is dat de niet-gebruikte clickranden naar buiten wijzen en er wat los bij hangen.

Figuur 5 Strook voor een Tetra-toren.

Figuur 6 Trigo strook.

Figuur 7

Figuur 9 Trigo Tetra-toren met één helix.

Figuur 8 Trigo Tetra-toren.

Ook is goed te zien dat de bamboestaaf niet door het middelpunt van de grote ronde gaten in de Trigodriehoeken gaat.

In figuur 9 is de Trigo Tetra-toren nog op een voetstuk gezet en voorzien van slechts één helix in de vorm van een zwarte draad.

Net als de lange rechte staaf In de Trigo Tetra-toren is de Art Tower Mito voorzien van een grote rechte doorzichtige koker waarin dus een glazen lift op en neer kan bewegen.

Hieronder staan vijf sommen waarin de tien verschillende cijfers precies één keer voorkomen. In welke som zit een fout?

Hieronderstaanvijfsommenwaarindetienverschillendecijfersprecies´e´enkeervoorkomen.In welkesomziteenfout?

Hieronderstaanvijfsommenwaarindetienverschillendecijfersprecies´e´enkeervoorkomen.In welkesomziteenfout?

Hieronderstaanvijfsommenwaarindetienverschillendecijfersprecies´e´enkeervoorkomen.In welkesomziteenfout?

GETORDEERDE TETRAËDER

Hieronderstaanvijfsommenwaarindetienverschillendecijfersprecies´e´enkeervoorkomen.In welkesomziteenfout?

Hieronderstaanvijfsommenwaarindetienverschillendecijfersprecies´e´enkeervoorkomen.In welkesomziteenfout?

Hieronderstaanvijfsommenwaarindetienverschillendecijfersprecies´e´enkeervoorkomen.In welkesomziteenfout?

Opdeonderstaandedisplaystaandag,maand,jaar,uren,minutenensecondenaangegeven. Linskijktgedurende´e´enminuutenkelnaarhetcijferopdelaatstepositievandedisplay.Welk streepjeziethijindieminuuthetlangstaan´e´enstukdooroplichten?

Opdeonderstaandedisplaystaandag,maand,jaar,uren,minutenensecondenaangegeven. Linskijktgedurende´e´enminuutenkelnaarhetcijferopdelaatstepositievandedisplay.Welk streepjeziethijindieminuuthetlangstaan´e´enstukdooroplichten?

Opdeonderstaandedisplaystaandag,maand,jaar,uren,minutenensecondenaangegeven. Linskijktgedurende´e´enminuutenkelnaarhetcijferopdelaatstepositievandedisplay.Welk streepjeziethijindieminuuthetlangstaan´e´enstukdooroplichten?

In 1979 plaatste de Nederlandse architect en beeldhouwer Rudolf Wolf (1919 - 1989) in Zoetermeer zijn Getordeerde Tetraëder (figuur 10). Deze toren van roestvrij staal is 24 meter hoog en heeft een diameter van 3,5 meter. In feite is het een ‘model’ van het stalen frame van de Art Tower Mito, zij het dat hier geen 28 tetraëders op elkaar staan. Voorzie de min of meer verticale opstaande driehoekige frames van gelijkzijdige driehoekige platen en je hebt een aangeklede toren zoals de Art Tower Mito. Zoals gezegd waren er voor de Art Tower Mito met zijn 28 tetraëders 57 van die platen nodig. Namelijk twee bij elke tetraëder en nog een voor de bovenste tetraëder als afdichtend dak.

Opdeonderstaandedisplaystaandag,maand,jaar,uren,minutenensecondenaangegeven. Linskijktgedurende´e´enminuutenkelnaarhetcijferopdelaatstepositievandedisplay.Welk streepjeziethijindieminuuthetlangstaan´e´enstukdooroplichten?

Opdeonderstaandedisplaystaandag,maand,jaar,uren,minutenensecondenaangegeven. Linskijktgedurende´e´enminuutenkelnaarhetcijferopdelaatstepositievandedisplay.Welk streepjeziethijindieminuuthetlangstaan´e´enstukdooroplichten?

Opdeonderstaandedisplaystaandag,maand,jaar,uren,minutenensecondenaangegeven. Linskijktgedurende´e´enminuutenkelnaarhetcijferopdelaatstepositievandedisplay.Welk streepjeziethijindieminuuthetlangstaan´e´enstukdooroplichten?

7

Pauline heeft 20 speelgoedautootjes: 10 blauwe cabrio’s met een lengte van 4 cm en 10 rode bussen met een lengte van 7 cm. Door er een aantal bumper aan bumper te plaatsen, maakt zij een rij van 62 cm. Hoeveel bussen staan in die rij?

Paulineheeft20speelgoedautootjes:10blauwecabrio’smeteenlengtevan4cmen10rode bussenmeteenlengtevan7cm.Doorereenaantalbumperaanbumperteplaatsen,maaktzij eenrijvan62cm.Hoeveelbussenstaanindierij?

Paulineheeft20speelgoedautootjes:10blauwecabrio’smeteenlengtevan4cmen10rode bussenmeteenlengtevan7cm.Doorereenaantalbumperaanbumperteplaatsen,maaktzij eenrijvan62cm.Hoeveelbussenstaanindierij?

Paulineheeft20speelgoedautootjes:10blauwecabrio’smeteenlengtevan4cmen10rode bussenmeteenlengtevan7cm.Doorereenaantalbumperaanbumperteplaatsen,maaktzij eenrijvan62cm.Hoeveelbussenstaanindierij?

Paulineheeft20speelgoedautootjes:10blauwecabrio’smeteenlengtevan4cmen10rode bussenmeteenlengtevan7cm.Doorereenaantalbumperaanbumperteplaatsen,maaktzij eenrijvan62cm.Hoeveelbussenstaanindierij?

Paulineheeft20speelgoedautootjes:10blauwecabrio’smeteenlengtevan4cmen10rode bussenmeteenlengtevan7cm.Doorereenaantalbumperaanbumperteplaatsen,maaktzij eenrijvan62cm.Hoeveelbussenstaanindierij?

Paulineheeft20speelgoedautootjes:10blauwecabrio’smeteenlengtevan4cmen10rode bussenmeteenlengtevan7cm.Doorereenaantalbumperaanbumperteplaatsen,maaktzij eenrijvan62cm.Hoeveelbussenstaanindierij?

Defiguurhiernaasttoont12eilandenverbondenmetbruggen dievierkantenengelijkzijdigedriehoekenafbakenen.Op10 eilandenstaateenhoekaangegeven.Debruggenwaarlangs jeeeneilandbetreedtenverlaat,moetenonderlingsteedsdie aangegevenhoekvormen.Hoeveelbruggensteekjeoverals jeopdiemaniervanAnaarBwilgaan?

Defiguurhiernaasttoont12eilandenverbondenmetbruggen dievierkantenengelijkzijdigedriehoekenafbakenen.Op10 eilandenstaateenhoekaangegeven.Debruggenwaarlangs jeeeneilandbetreedtenverlaat,moetenonderlingsteedsdie aangegevenhoekvormen.Hoeveelbruggensteekjeoverals

Defiguurhiernaasttoont12eilandenverbondenmetbruggen dievierkantenengelijkzijdigedriehoekenafbakenen.Op10 eilandenstaateenhoekaangegeven.Debruggenwaarlangs jeeeneilandbetreedtenverlaat,moetenonderlingsteedsdie aangegevenhoekvormen.Hoeveelbruggensteekjeoverals jeopdiemaniervanAnaarBwilgaan?

Defiguurhiernaasttoont12eilandenverbondenmetbruggen

Defiguurhiernaasttoont12eilandenverbondenmetbruggen dievierkantenengelijkzijdigedriehoekenafbakenen.Op10 eilandenstaateenhoekaangegeven.Debruggenwaarlangs

Figuur 10 Getordeerde Tetraëder. (foto Collectiebeheer Beeldende Kunst, Afdeling Vrije Tijd, Gemeente Zoetermeer)

© Vlaamse Wiskunde Olympiade vzw, eerste ronde 2023

© Vlaamse Wiskunde Olympiade vzw, eerste ronde 2023

BOEK BESPREKING

MICKAËL LAUNAY, DE PARAPLU-STELLING.

VERRASSENDE INZICHTEN UIT DE WIS- EN NATUURKUNDE, UITGEVERIJ NOORDBOEK, 2021.

Wat een leuk boek! Oorspronkelijk geschreven in het Frans, in 2019 gepubliceerd bij Flammarion als Le Théorème du Parapluie, en dan in

2021 vertaald in het Nederlands. De auteur is een Frans wiskundige die een van de referenties is in Frankrijk wat betreft de popularisering van de wiskunde. Hij heeft een eigen YouTube-kanaal (MicMaths) en is dus met dit boek niet aan zijn proefstuk toe. Launay won al verschillende prijzen, o.a. de Prix d’Alembert van het Franse Wiskundige Genootschap. En in 2022 was De paraplu-stelling de grote winnaar van de Cosmos Boekenprijs, een prijs die in Nederland in het leven werd geroepen (in 2022) door de Nationale Wetenschapsagenda (NWA) en waarbij leerlingen en een vakjury het beste populairwetenschappelijke boek over natuurkunde, wiskunde of sterrenkunde kiezen van het voorbije jaar. De paraplu-stelling won beide prijzen.

Waar gaat het boek over?

Toegegeven, het gaat niet uitsluitend over wiskunde, er komt ook heel wat natuurkunde in voor. Er staat bijvoorbeeld een hoofdstuk in met als titel Over appels en manen, waarvan je zou kunnen

zeggen dat het in feite wel over de zwaartekracht gaat. En er is een hoofdstuk getiteld De afgronden van ruimte en tijd en daarin heeft de auteur het over de relativiteitstheorie van Einstein, maar ja, dat is natuurlijk ook vooral meetkunde, dus toch wiskunde.

Het begint allemaal met De wet van de supermarkten, een wet die zegt dat als je door een supermarkt loopt en van een heleboel willekeurige producten die daar te koop zijn het eerste cijfer van de prijs noteert, je dan als je later (thuis) al die cijfers even op orde zet, zal merken dat ongeveer 30% ervan een 1 is, ongeveer 18% is een 2, ongeveer 13% is een 3, en dat gaat zo verder, en de 9 komt het minst voor, ongeveer 5%. Dit is de beroemde wet van Benford, en in dit eerste hoofdstuk van De paraplu-stelling zal Launay verklaren waarom dit zo is. Daar komen getallen aan te pas en leren we wat over de geschiedenis van de getallen en over ons getalbegrip. We hebben ook logaritmes nodig, en zo komen we uit bij John Napier (de uitvinder

PAUL LEVRIE

van de logaritmes) en diens buurman Roslin, die duiven kweekte, en ook bij muziek. Een heel verhaal. Het tweede hoofdstuk, Over appels en manen, begint met de vraag: hoe meet je de hoogte van een berg? Meet je de afstand van de top van de berg tot het middelpunt van de aarde. Neen dus, want dan zou de Chimborazo, een vulkaan in Ecuador, de hoogste berg ter wereld zijn, en niet de Mount Everest, zoals iedereen weet. Dit heeft met meten te maken, en met schalen, maar ook met de zwaartekracht die de aardbol heeft afgeplat. Over de zwaartekracht gaat het in de titel van dit hoofdstuk, meer bepaald heeft Launay het hier over het feit dat de maan en een appel onder invloed van de zwaartekracht precies op dezelfde manier naar de aarde toe vallen. Ook dit hoofdstuk is doorspekt met verhalen, waarvan ik er een heel deel nog niet kende. In dit hoofdstuk wordt ook de titel van het boek aan de lezer uitgelegd.

Daarna komen we weer meer bij de wiskunde uit, in hoofdstuk 3: De kronkels van de oneindigheid

Dit hoofdstuk gaat over grote getallen, en oneindig, over de lengte van landsgrenzen, fractalen en dimensies. En hoofdstuk 4, De kunst van de vaagheid, voert ons via een inleiding op de euclidische en de niet-euclidische meetkunde met veel humor (zie bijvoorbeeld figuur 1 waar een wezen dat leeft op een Poincaré-schijf rechte lijnen aan het tekenen is, en figuur 2, de catalogus van een tegelwinkel in diezelfde wereld) naar het laatste hoofdstuk, De afgronden van ruimte en tijd, dat gaat over de relativiteitstheorie van Einstein.

Achteraf krijg je per hoofdstuk nog één formule die relevant is,

en enkele referenties naar boeken indien je nog meer wil weten over de behandelde onderwerpen.

Dit boek is een aanrader, vooral door de verhalende schrijfstijl van de auteur. Eens te meer blijkt dat wiskunde aanbrengen via verhalen een succesformule is, zeker als dit op een luchtige manier gebeurt!

De tekst gaat vergezeld van prachtig getekende, en vaak erg verduidelijkende illustraties (zie figuren 1 en 2) die allemaal van de hand zijn van Chloé Bouchaour, de partner van de auteur. Ze heeft ook een eigen website.

Figuur 1 p. 206, tekening © Chloé Bouchaour

Figuur 2 p. 212, tekening © Chloé Bouchaour

ZOEK BIJZONDER DEELBAAR GETAL

WILKO EMMENS

IK LAS OOIT IN EEN BOEK DE VOLGENDE OPDRACHT:

zet de cijfers 1 t/m 9 in zodanige volgorde dat:

- het getal gevormd door het eerste cijfer deelbaar is door 1,

- het getal gevormd door de eerste 2 cijfers deelbaar is door 2,

- het getal gevormd door de eerste 3 cijfers deelbaar is door 3,

- het getal gevormd door de eerste 4 cijfers deelbaar is door 4,

- het getal gevormd door de eerste 5 cijfers deelbaar is door 5,

- het getal gevormd door de eerste 6 cijfers deelbaar is door 6,

- het getal gevormd door de eerste 7 cijfers deelbaar is door 7,

- het getal gevormd door de eerste 8 cijfers deelbaar is door 8,

- het getal gevormd door de eerste 9 cijfers deelbaar is door 9.

Aan de eerste voorwaarde is uiteraard altijd voldaan, maar ook aan de laatste voorwaarde, want de som van de cijfers is 45 (9-voud).

OPLOSSING:

Noem het totale getal abcdefghi (schrijfwijze).

Het getal abcde moet deelbaar zijn door 5, dus is e 0 of 5, maar 0 komt niet voor dus: e = 5.

De getallen ab, abcd, abcdef en abcdefgh zijn deelbaar door resp. 2, 4, 6 en 8, zij zijn dus even. Dus de cijfers b, d, f en h zijn alle even en ongelijk, zij zijn samen de cijfers 2, 4, 6 en 8.

Daarom zijn de cijfers a, c, g en i de overgebleven oneven cijfers 1, 3, 7 en 9.

Het getal abc is deelbaar door 3, dus is de som van de cijfers a, b en c een drievoud.

Het getal abcdef is deelbaar door 6, dus ook door 3, dus moet ook de som van de cijfers d, e en f een drievoud zijn.

Het getal abcd is deelbaar door 4, dan moet ook cd een 4-voud zijn. Aangezien c oneven is, kan d alleen maar 2 of 6 zijn: cd = 12, 16, 32, 36, 72, 76, 92, 96 (52 en 56 kunnen niet).

Het getal abcdefgh is deelbaar door 8, dan moet ook fgh deelbaar zijn door 8. Aangezien f even is, is f00 een 8-voud, dus moet ook gh een 8-voud zijn. Aangezien g oneven is, kan h alleen maar 2 of 6 zijn: gh = 16, 32, 72 of 96 (56 kan niet).

Zowel d en h kunnen dus alleen maar 2 of 6 zijn, dus zijn b en f de getallen 4 en 8.

Het getal def = d5f is een 3-voud, dus is de som van de cijfers (d+f+5) een 3-voud. Met de gevonden beperkingen voor de waardes van d en f zijn er maar twee mogelijkheden: 258 en 654.

De moeilijkste eis is dat abcdefg een 7-voud is, hiervoor bestaan geen simpele checkmethoden.

geval A. Ga uit van def = 258, dan is b = 4 en h = 6; dan kan g alleen maar 1 of 9 zijn (gh = 16 of 96).

Het getal abc = a4c is deelbaar door 3, waarbij a en c allebei oneven zijn en ongelijk aan 5, dus a+c+4 is een 3-voud.

Als g = 1 zijn a en c twee getallen uit de combinatie 3, 7 en 9. Dit levert geen bruikbare waarde voor abc op. Als g = 9 zijn a en c twee getallen uit de combinatie 1, 3 en 7. Dit levert alleen een bruikbare combinatie op met 1 en 7. Dus abc = 147 of abc = 741.

Dus zijn er twee mogelijkheden voor abcdefg, nl. 1472589 en 7412589. Controle met een rekenmachine levert dat geen van beide een 7-voud is.

geval B. Ga uit van def = 654, dan is b = 8 en h = 2, dan kan g alleen maar 3 of 7 zijn (gh = 32 of 72).

Het getal abc = a8c is deelbaar door 3, waarbij allebei oneven en ongelijk aan 5 zijn. Nu zijn er meer mogelijkheden. Enig speurwerk op dezelfde manier als in geval A levert de volgende combinaties:

- abc = 189, 981, g = 3;

- abc = 789, 987, g = 3;

- abc = 189, 981, g = 7;

- abc = 183, 381, g = 7.

Voor abcdefg krijgen we nu 8 mogelijkheden:

- 1896543 en 9816543

- 7896543 en 9876543

- 1896547 en 9816547

- 1836547 en 3816547

Controle met een rekenmachine levert dat alleen 3816547 een 7-voud is (7 x 545221), dus moet het gevraagde totale getal zijn: 381 654 729

Nadere controle geeft aan dat dit inderdaad aan alle gestelde voorwaarden voldoet.

Zou de truc ook werken met minder cijfers? Dat valt tegen, zie de tabel, die geeft de combinaties aan van 1 t/m 8 cijfers die aan de voorwaarde voldoen. De laatste is makkelijk: omdat bij de combinatie met 9 cijfers de 9 achteraan staat kunnen we die gewoon weghalen. De getallen in de tabel zijn niet moeilijk te vinden, en computerberekeningen tonen aan dat er niet meer zijn.

UITWISKELING

MULTIVERZAMELINGEN

ANTONELLA PERUCCA , VOOR UITWISKELING

Het begrip verzameling speelde in de jaren 70 een belangrijke rol in ons wiskundeonderwijs. Met de nieuwe eindtermen is het terug van weggeweest. Onze leerlingen kennen de begrippen element, deelverzameling, unie, doorsnede en verschil. Deze begrippen worden in deze tekst uitgebreid naar algemenere begrippen.

In een verzameling komt elk element slechts één keer voor. We spreken bijvoorbeeld niet van de verzameling {3, 4, 4} Multiverzamelingen zijn een manier om een element toch meermaals te laten voorkomen. Het aantal keer dat een element voorkomt in een verzameling noemen we de multipliciteit. Elementen die niet in een multiverzameling voorkomen, hebben multipliciteit nul.

Stel dat je een multiverzameling A hebt met drie groene knikkers, twee rode en één blauwe. Dan is de multipliciteit van de groene knikker 3, die van rood 2 en die van blauw 1. Hou je van elke soort knikkers slechts eentje over, dan vind je de ondersteunende verzameling van de multiverzameling. In figuur 1 zie je een schematische voorstelling van de multiverzameling A en haar ondersteunende verzameling B.

De term multiset is in de jaren 70 geïntroduceerd door de Nederlandse wiskundige Nicolaas Govert De Bruijn (1918-2012). Multiverzamelingen zijn minder bekend dan de gewone verzamelingen maar ze zijn ook zinvol. Denk bijvoorbeeld aan de multiverzameling van de priemdelers van 5000. Je zou de priemdelers kunnen omschrijven met de ondersteunende verzameling {2, 5} maar er zit meer informatie in de multiverzameling

{2, 2, 2, 5, 5, 5, 5}. Denk bijvoorbeeld ook aan de voorraad van een apotheker. Hij is niet alleen

geïnteresseerd in welke medicijnen er nog in stock zijn maar ook in de multipliciteit van de voorradige medicijnen...

INCLUSIE, SOM, UNIE EN DOORSNEDE

Net zoals bij verzamelingen is er bij multiverzamelingen ook een inclusie gedefinieerd. Een multiverzameling C is omvat in een multiverzameling D als alle elementen van C ook in D zitten met minstens dezelfde multipliciteit. Zo is de multiverzameling C in figuur 2 omvat in de multiverzameling D. Ook kunnen we stellen dat elke multiverzameling haar ondersteunende verzameling omvat.

We geven hieronder nog enkele definities van begrippen die aan multiverzamelingen gerelateerd zijn. Nadien volgen er vragen die je kunt voorleggen aan leerlingen die meer interesse hebben in de theoretische grondslagen dan hun klasgenoten. Deze vragen stimuleren het abstracte denken en de taalvaardigheid.

De som van twee multiverzamelingen is de multiverzameling die je krijgt door de elementen van

Figuur 1 Een multiverzameling en haar ondersteuning

de gegeven multiverzamelingen samen te nemen met multipliciteiten die de som zijn van de gegeven multipliciteiten.

De unie van twee of meerdere multiverzamelingen is de kleinste multiverzameling die de gegeven multiverzamelingen omvat. De doorsnede van twee of meerdere multiverzamelingen is de grootste multiverzameling die omvat wordt door beide multiverzamelingen.

Twee of meerdere multiverzamelingen zijn disjunct als hun doorsnede ledig is. Een aantal multiverzamelingen kan ook paarsgewijs disjunct zijn. Dat betekent dat elk tweetal multiverzamelingen uit de gegeven multiverzamelingen disjunct is. Paarsgewijs disjunct zijn, is sterker dan disjunct zijn. Uit het paarsgewijs disjunct zijn van multiverzamelingen volgt disjunct zijn maar niet omgekeerd.

Tot slot, als een multiverzameling omvat is in een andere multiverzameling, dan definiëren we het verschil door alle elementen van de eerste multiverzameling uit de tweede multiverzameling weg te nemen. Ook voor twee willekeurige multiverzamelingen is het verschil gedefinieerd. Stel dat we het verschil D van M1 met M2 zoeken. Elk element van M1 dat in M2 voorkomt met een grotere multipliciteit, komt in D voor met multipliciteit 0. De andere elementen komen in D voor met een multipliciteit die het verschil is van de multipliciteiten in M1 en M2

Even een voorbeeld. Als je naar de kruidenier gaat met een boodschappenlijstje, dan zal de kruidenier na je aankoop het verschil in voorraad hebben van zijn oorspronkelijke stock en jouw boodschappenlijstje. Als je meer van een bepaald artikel nodig hebt dan er voorradig was, houdt de kruidenier niets meer over. Als je minder van een bepaald artikel nodig hebt dan de voorraad in de rekken, dan kun je kopen zoveel je wilt. De voorraad van de kruidenier wordt dan met zoveel eenheden verminderd als het aantal op je boodschappenlijstje.

In figuur 3 zie je een voorbeeld van multiverzamelingen A en B met hun som S, hun unie U, hun doorsnede D en hun verschil V.

Figuur 2 C is omvat in D

Figuur 3 Som, unie, doorsnede en verschil

EIGENSCHAPPEN VAN MULTIVERZAMELINGEN

De unie van (gewone) verzamelingen en de doorsnede zijn commutatief en associatief. Bovendien is de unie van (gewone) verzamelingen distributief ten opzichte van de doorsnede. De doorsnede is distributief ten opzichte van de unie. Voor willekeurige verzamelingen A, B en C kunnen we deze eigenschappen formuleren als:

4. Hoe bepaal je de multipliciteiten van de elementen van de som, de unie en de doorsnede van twee gegeven multiverzamelingen A en B? Voor de som nemen we de som van de multipliciteiten van elk element uit A en B. Voor de unie nemen we het maximum van de multipliciteiten van elk element in A en in B. Voor de doorsnede nemen we het minimum.

1. Welke van deze zes eigenschappen gelden ook voor multiverzamelingen?

Ze zijn allemaal geldig voor multiverzamelingen.

2. Wat is het verband tussen de multipliciteiten van de elementen van een multiverzameling en het totale aantal elementen van de multiverzameling?

De som van alle multipliciteiten is gelijk aan het aantal elementen van de multiverzameling.

3. Om een milkshake te maken heb je ofwel een kiwi en een banaan nodig, ofwel twee kiwi’s en drie aardbeien. Hoe bereid je je voor op het maken van één enkele milkshake als je nog niet beslist hebt welke je zult maken? Druk je antwoord uit met een bewerking op multiverzamelingen.

Je koopt alvast één banaan, twee kiwi’s en drie aardbeien. Deze multiverzameling is de unie van de multiverzamelingen A en B van de ingrediënten.

5. Wat kun je zeggen over de multipliciteiten van de elementen van een aantal disjuncte multiverzamelingen? En van een aantal paarsgewijze disjuncte multiverzamelingen?

Bij disjuncte multiverzamelingen is de doorsnede ledig. Dat betekent dat voor elk element het minimum van de multipliciteiten van een bepaald element in elke multiverzameling gelijk is aan nul. Bij paarsgewijze disjuncte multiverzamelingen komt elk element slechts in één multiverzameling voor. Dat betekent dat voor elk element alle multipliciteiten op eentje na gelijk aan nul zijn.

6. Is de som van drie disjuncte multiverzamelingen gelijk aan de unie?

Voor twee multiverzamelingen is de som gelijk aan de unie als ze disjunct zijn. Zo niet, dan zal de som de unie omvatten. Bij de som worden de elementen uit de doorsnede immers dubbel meegeteld. Voor twee of meer multiverzamelingen is de som gelijk aan de unie als en slechts als de multiverzamelingen paarsgewijs disjunct zijn. Dit is een nodige en voldoende voorwaarde. Inderdaad, beschouw de multipliciteiten van een bepaald element in alle multiverzamelingen. We willen dat hun som gelijk is aan hun maximum. Dit kan enkel indien al deze multipliciteiten nul zijn behalve eentje. Hieruit leiden we af dat de multiverzamelingen paarsgewijs disjunct zijn.

Dit artikel verscheen in Uitwiskeling 35/4. Op www.uitwiskeling.be vind je alle info.

Digisprong in de wiskunde

zaterdag 25 maart 2023

9 uur - 13 uur

Zebrastraat Gent

Programma:

Correlatie en regressie met GeoGebra Suite

Els Coussement

GeoGebra notitieblok en klaslokaal, didactiek in een online verhaal

Chris Cambré

GeoGebra-CAS een krachtig alternatief voor het grafisch rekentoestel

Ivan De Winne

Wijze wiskundelessen met GeoGebra

Karel Appeltans

Artificiële intelligentie (AI) en wiskunde

Natacha Gesquière

Oefeningen wiskunde online… het kan!

Paul Decuypere

Meer info en inschrijven via www.vvwl.be

Dit evenement wordt ondersteund door het departement Economie, Wetenschap en Innovatie binnen het actieplan Wetenschapsinformatie en Innovatie, een initiatief van de Vlaamse Gemeenschap.