asal_thinking_skills_sample_digital

Thinking Skills for

Cambridge International AS & A Level

John Chamberlain, Mark King & Andrew Roberts

Fourth edition with Digital access

SAMPLE

2.1

2.2

2.3

2.4

2.5

2.6

2.7

4 Arranging, searching and finding

4.1 Understanding timetables

4.2 Searching

4.3 Scheduling

4.4 Linked activity: Sharing a chocolate bar

5 Communicating reasoning and patterns in data

5.1 Summarising information

5.2 Justifying a solution to a problem

5.3 Checking all the possibilities

5.4 Making estimates and stating assumptions

5.5 Linked activity: Identifying errors in data

6 Logical relations and features in data

6.1 Logical relationships between pieces of information

6.2 Identifying features in data

6.3 Using patterns and other features found in data

6.4 Searching for solutions

6.5 Linked activity: Barcodes

7 More complex problems

7.1 Making and explaining more complex deductions

7.2 Complex models

7.3 Adapting solutions to problems in response to changes

7.4 Linked activity: Error detection

Section 2: Critical thinking

8 Evaluating reasoning (credibility)

8.1

8.3 Plausibility

8.4 Corroboration and consistency

8.5 Perspectives presented in evidence

9 Evaluate and use statistical evidence

9.1 Representativeness of samples

9.2 Design of questionnaires

9.3 Issues with the way data is presented

10 Use of

10.1

Assessing

11 Arguments

11.1 Distinguishing between arguments and other types of

Argument elements

11.3 Assumptions

11.4 Analysing the structure of

12 Evaluating reasoning

12.1 Fallacies (flaws)

12.2 Other potential

12.3

12.4 Analogies

12.5 Identifying

13 Constructing arguments and explanations

13.1

14 Preparing for assessment

14.5

SAMPLE

How to use this series

This suite of resources supports students and teachers following the Cambridge International AS & A Level Thinking Skills syllabus (9694). Both the components in the series are designed to work together and help students develop the necessary skills required for this subject.

Thinking Skills

The Digital Teacher’s Resource provides everything teachers need to deliver the course. Teaching notes provide information on essential background knowledge, tips on eliciting and overcoming misconceptions and extensive support on skill development and language. Each chapter comes with ready to use downloadable PowerPoint presentations and Worksheets, which can be used flexibly in the classroom or set as homework for additional practice. Supporting notes contain guidance on implementing this large array of additional materials to allow for differentiated teaching and assessment for learning.

The Coursebook is designed for students to use in class with guidance from the teacher. It is divided into two parts –the first section supports the Problem Solving strand and the second section supports the Critical Thinking strand of the syllabus. Six chapters within each section provide comprehensive support and practice of key skills of analysis, evaluation and reasoning. Each chapter provides plenty of opportunities to learn by doing a variety of activities involving group, pair and individual work to build confidence. Reflection feature promotes deep learning while the annotated Sample Answer section provides a framework to evaluate and improve own work.

A digital version of the Coursebook is included with the print version and is also available separately. This version contains videos that offer an engaging format to explain key concepts and provide strategies to understand and answer questions.

Thinking Skills for Cambridge International

How to use this book

Throughout this Coursebook, you will notice some features that are designed to help your learning. Here is a brief overview of what you will find.

LEARNING INTENTIONS

Learning intentions open each chapter. These help you with navigation through the Coursebook and indicate the important skills or topics in each chapter.

BEFORE YOU START

This provides a starter activity at the beginning of each chapter and it might involve an element of group work or class discussion. The activity will help you to get prepared for the skills or topics in the rest of the chapter.

TIP

Tips are provided throughout this Coursebook to help with your learning. The tips might cover how to avoid common errors or misconceptions, advice on answering questions or key skills for your course.

ACTIVITY

There are various activities throughout this Coursebook. These give you opportunities to practice skills or discuss topics for this course either individually, in pairs or in groups. Many of the activities are accompanied by commentaries or worked solutions which guide you through additional support or potential solutions for the questions.

A Level style questions in activities are marked with a blue line in the margin. A few of the activities are also accompanied by downloadable support sheets that you can use to complete the exercise.

REFLECTION

This feature enables you to look back at the topics or skills that you have covered in the chapter, and also think about your learning. You may reflect on and assess the process that you used to arrive at your answers.

KEY TERMS

Key vocabulary is highlighted in the Critical Thinking chapters when it is first introduced. An accompanying definition tells you the meanings of these words and phrases. You will also find definitions of these words in the Glossary at the back of this Coursebook. Please note that, due to the skills‑based nature of the Problem Solving content, there are no key terms in those chapters.

PROJECT

This offers a concluding activity for each chapter which often allows for an element of collaboration and group work. It will allow you the chance to apply your skills to a real world type of task, such as giving a presentation, taking part in a debate or writing a report.

SUMMARY

At the end of each chapter, you will find a list that brings together the key information you have learnt. This list can also be used as a useful revision aid.

Sample

answer

Each chapter provides a past paper question with a sample answer, and these are annotated with comments. Note: Chapter 13 has two sample questions and answers. These can be used to help you understand the success criteria that you are aiming for. The answers will show a range of levels and encourage you to learn how to evaluate your own work. Note that the sample answers have been written by the authors of this book.

Practice questions

Each chapter ends with a set of practice questions. These are a mixture of past paper questions and author-written practice questions. The questions give you an opportunity to consolidate the skills that you have learnt in the chapter. They relate to the assessment objectives that you will need for your course: use and evaluate information, and create and communicate reasoning.

A Level questions are marked with a blue line in the margin.

Videos

In order to provide you with further support, certain features within the Coursebook are accompanied by videos. These videos will help you to understand the concepts and skills that are needed for your course. They offer a mixture of walkthroughs that guide you through activities or practice questions, as well as videos offering analysis of key concepts or further practice with key skills.

Chapter 2 Understanding data in simple formats

LEARNING INTENTIONS

By the end of this chapter, you will be able to:

• identify the pieces of information that are needed to solve a problem

• identify the calculations that are needed to solve simple problems

• understand that rounding a final answer may not always be the correct decision

• understand information presented in text, tables, graphs and other diagrams

• use an identified method for representing some infor mation.

2 Understanding

Problem solving often involves making sense of some information. Sometimes this information is presented within some paragraphs of text, but often data is represented in tables, graphs or other diagrammatic representations. In this chapter you will explore some of the ways in which information might be presented.

SAMPLE

BEFORE YOU START

Nautical flags

Nautical flags provide a way for messages to be sent from ships. There is a standard international set of flags, representing letters and numbers, and the flags are arranged in a vertical line.

The flags are designed using different colours and layouts, so that they can be distinguished when there is little light or by people who are colour-blind. The first letter is the one at the top of the mast.

Since the wind could be blowing in any direction and the flags may be observed from different positions, it is possible that they could appear either to the left or right of the flagpole.

1 Working in groups, solve this problem: Each person in the group should create a word

made up of four different letters, so that you are using four of the flags. Draw a picture of the flags you have chosen. Next, swap the image of your flags with someone else in your group and work out what their word is.

It is inefficient to carry multiple copies of the same flag. Instead, there are pennants (triangular flags) used to show when a letter appears again in a message; you can see these pennants in the bottom row of the flag image. The pennants indicate the position of the flag that should be repeated. Since messages involve at most four flags, there are three positions that might need to be repeated, so three pennants are needed.

CONTINUED

For example, if the word SAGA needs to be sent, the flags for S, A and G are shown, followed by the pennant that indicates a repeat of the second flag. This is shown in the following figure.

2 How would you signal GGGG?

2.1 Understanding the information available

Problems usually involve some information. You might be provided with some data when you are given the problem, or you might need to do some research to obtain the data for yourself. In either case, once you have the data that you need, it may not be obvious what information is contained in the data or how you can use it.

You might think it is obvious that 2 + 2 = 4, but that is only the case if you are counting things. If you are measuring things then it is not so simple. In different situations the number 2 might mean different things, which will change what the answer to 2 + 2 is.

The length of something that has been made in a factory is likely to be very precise. For example, a two-inch screw is very close to 2 inches long (50.8 mm). A measurement of something natural as 2.0 units usually means between 1.95 units and 2.05 units. So, if you have two objects that have been measured as 2.0 cm long and you place them end to end, the total length might only be 3.9 cm (because it could be 1.95 + 1.95). Similarly, the total length could be as much as 4.1 cm (2.05 + 2.05). So, you can only really say that 2.0 + 2.0 gives an answer between 3.9 and 4.1 in this case.

ACTIVITY 2.1.1: 2 + 2

Here are some other situations where the number 2 might have a different meaning.

In pairs, discuss what the answer to 2 + 2 is for each situation.

a For sports like long jump, distances are rounded down, so 2.0 indicates not less than 2 but less than 2.1.

CONTINUED

b i A command for a robot is to turn right through 120 degrees. So, the number 2 indicates two turns through 120 degrees.

ii What if the turns are through 90 degrees each time?

Sometimes 2 + 2 might not even make sense at all. For example, numbers are sometimes just used as labels; a size 2 shoe plus another size 2 shoe does not make a size 4 shoe.

c Suggest two other situations in which 2 + 2 has an answer that is different from 4.

TIP

When working with numbers within a question you should make sure that you know whether they refer to things that are counted or things that are measured. If you are working with values that are measured, then you need to be sure that you understand the range of possible values a given number relates to.

Once you are sure that you understand what the information you have been given means, you need to work out how to reach the answer to the question you have been asked (and not a different question).

If there is a similar problem that you have solved before then it is not a surprise if the same approach worked again.

ACTIVITY 2.2.1: MARIO’S SALARY

Try this problem yourself, before reading the worked solution.

2.2 Working out the calculation that is needed SAMPLE

Mario’s monthly salary from work is $4000, but he pays $600 in local tax, $400 in federal tax, and $750 to repay his student loan. He also has money invested which gives him $100 (tax free). He pays $50 for fuel, and $60 for road tax and insurance for his car. He gets a small, untaxed, payment of $100 in royalties from blogging.

How much money does Mario have available to spend each month?

CONTINUED

WORKED SOLUTION

Each month Mario receives:

• $4000 salary from work

SAMPLE

• $ 100 from his investment

• $ 100 in royalties from blogging. This gives a total of $4200 per month. Mario makes payments each month:

• $600 in local tax

• $400 in federal tax

• $750 to repay his student loan

• $ 50 for fuel

• $ 60 for road tax and insurance for his car

This gives a total of $1860 per month.

So, the amount of money that Mario has available to spend each month is $4200 – $1860 = $2340

TIP

The calculation of Mario’s available money has a lot of components. If the calculation was completed in the order that the information is given it is: $4000 – $600 – $400 – $750 + $100 – $50 – $60 + $100

While this gives the same answer, it is often a good idea to group similar things together (in this case grouping the money in and the money out separately) to simplify the calculations and avoid errors.

ACTIVITY 2.2.2: WHAT3WORDS

What3words is a popular system that allows people to identify their location. It works by dividing the surface of Earth into squares with sides that are 3 m long. The sides of the squares are in the directions North–South and East–West. Each square has been allocated a list of three words (the choice of the three words for each square is essentially random).

For example, joke.scarcely.paints is next to farms.scared.rods.

The person who gets the code can see which square the other person is located in by looking up what3words.com/farms.scared.rods.

The system is also available in many different languages, so joke.scarcely.paints can also be referred to, for example, as repoblar.elegir.traga.

2 Understanding

CONTINUED

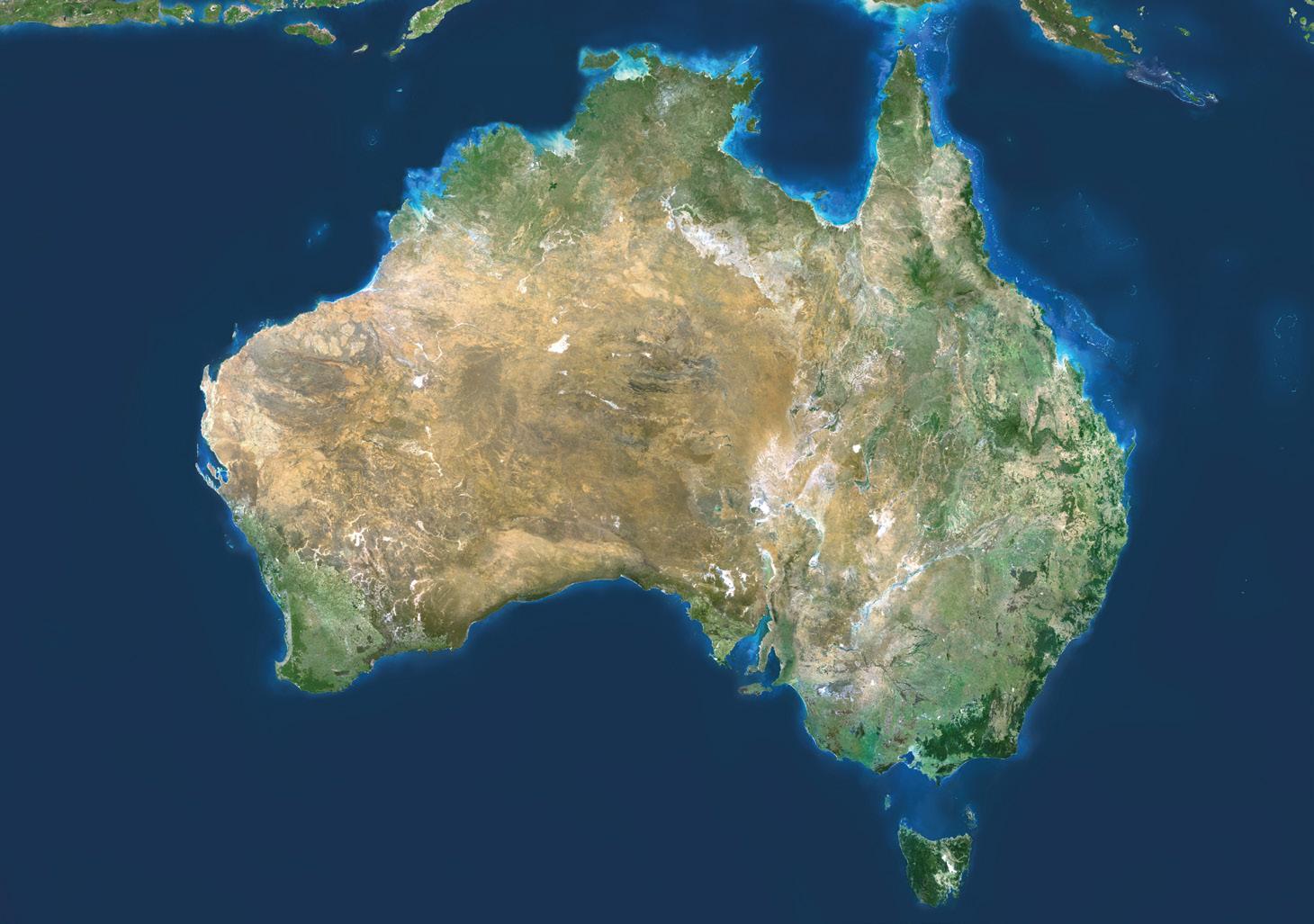
As a result of a natural process called ‘continental drift’ land masses are moving (very slowly). This means that the piece of land described by a particular set of three words today, will not be the same as the piece of land described by those words in a few years’ time.

In the case of Australia, the continent is moving due North at about 7 cm per year.

Try part (a) of this problem yourself, before reading the worked solution. Then answer part (b) before reading the commentary.

a How long will it be before half of the places in Australia have changed to a different three-word code?

b What is the range of possible actual answers?

WORKED SOLUTION

a The effect of continental drift is the same for all the squares that are currently in Australia, so it is sufficient to work with just one square. (The coast is tiny in comparison with the land area and can be ignored.)

SAMPLE

CONTINUED

Once the land represented by the square on the left has moved North by half the height of a square, half of the locations in the square will have changed to a different three-word code.

Since each square has a height of 3 metres, the time needed is how long it takes for Australia to move 1.5 metres.

At a speed of 7 cm per year, this takes 150 ÷ 7 = 21.4 years. The figure of 7 cm per year is an approximate value.

COMMENTARY

b The 3 m is already decided, so you can assume that this is an exact value. However, the figure of 7 cm per year is an approximate value, so you need to consider what the maximum and minimum values could be. In this case, the actual value should be between 6.5 and 7.5, which means that the two calculations become:

• 150 ÷ 7.5 = 20.0

• 150 ÷ 6.5 = 23.1

The actual answer could therefore be anywhere between 20.0 and 23.1.

ACTIVITY 2.2.3: ONLINE ENERGY

Solve all parts of this problem and then compare your solution with a partner.

There are many examples of online games played over a long period of time. Usually, there is some form of ‘energy’ system in place, where the amount of energy that the player has available will increase by one unit at regular intervals unless it has reached the maximum value allowed.

The player can use the energy that they have available to launch battles from which they will gain rewards. One of the rewards might be ‘in-game currency’ such as (virtual) gold coins, which can be used to buy items from a store. Such games will often have more than one type of energy and more than one type of in-game currency, with different types of items available to buy depending on the currency available.

Suppose that a game has just one type of energy:

• A player gains one unit of that energy every 10 minutes.

• A player can have a maximum of 100 units of energy.

• Each battle always uses 5 units of energy

a What is the longest amount of time that the player could be away from the game before they reach the maximum amount of energy?

b What is the largest number of battles that a player can launch if they play the game for a 20-minute period?

CONTINUED

Suppose also:

• there is only one in-game currency (gold coins)

• a player who wins a battle receives between 20 and 50 gold coins (the number of coins is deter mined randomly at the end of each battle). Suppose that you want to buy an item from the store that costs 500 gold coins and that you currently do not have any gold coins, but you have the maximum amount of energy.

c What is the smallest number of battles that you might need to launch to earn enough coins to buy the item that you want?

Someone asks you how long it will take you to buy the item that you want.

d Assuming you win any battles that you launch, what is the shortest amount of time that you could answer that guarantees that you had enough gold coins to buy the item?

TIP

The answers to parts (b) and (c) involve thinking about the extreme cases:

• In the first case you are thinking about what happens if you were lucky enough to get 50 gold coins for each battle.

• In the second case you are thinking about what happens if you only got 20 gold coins for each battle.

Although the answers that you obtain for each of these questions is based on a situation that it is not likely to occur, these kinds of ‘best-case’ and ‘worst-case’ scenarios can be very useful when making decisions.

2.3 Selecting which parts of the information are needed

Often the information available is more than you need to solve the problem. In these situations, you need to work out which pieces of information need to be used, and which should be ignored.

ACTIVITY 2.3.1: RARE CARDS

Try this problem yourself, before reading the worked solution.

Tomas enjoys playing a trading card game. The cards for the game are released in sets and are sold in packs of 9 cards. The sets of cards contain ‘common’, ‘uncommon’ and ‘rare’ cards. Each packcontains 5 common cards, 3 uncommon cards and 1 rare card. The latest set to be released contains 130 cards, of which 40 are common, 40 are uncommon and 50 are rare.

What is the smallest number of packs of cards that Tomas could buy to get at least one of each common and one of each uncommon card?

WORKED SOLUTION

The number of rare cards is irrelevant as the question only asks about Tomas getting the common and uncommon cards. The numbers of common and uncommon cards in the set are equal, so if Tomas buys enough packs of cards to get all the uncommon cards, he will have enough packs to get all the common cards (since there are more common cards in a pack than uncommon cards).

There are 40 uncommon cards in the set and 3 per pack, so he needs to buy at least 40 ÷ 3 = 13 1/3 packs.

The smallest number of packs that Tomas could buy is 14.

COMMENTARY

Note that the answer to the calculation rounds to 13, but in this context 13 packs are not enough. In situations where you need a whole number answer, but the calculation gives an answer that is not a whole number, always consider whether rounding is appropriate given the context.

2.4 Different ways to round numbers

If you see whole numbers in a problem, it is often useful to understand whether those numbers represent individual items or whether it is a measurement that has been rounded to a whole number.

In mathematics or statistics courses, it is common to have a fixed rule on how to round numbers (for example, round to the nearest whole number) and also a rule on how to handle something exactly halfway between the numbers (for example, round 3.5 up to 4). This simplification is often helpful in other subjects, but for real-world problems there are many different ways to round a number. For example, if a calculation has shown that 3.3 cans of paint are required to paint a wall, then 4 are actually needed; 3 are not enough.

ACTIVITY 2.4.1: ROUNDING

Discuss each of these questions in groups.

a How many one-dollar bills are needed to buy a $3.27 cake?

b How many $1 cakes can be bought with $5.78?

c If an average (mean) might be calculated with rounded-up data, how does it compare with the mean calculated using the data before rounding?

REFLECTION

Think about each of the examples in this section.

• How did you identify which parts of the information were important to solving the problem, and which parts did not need to be analysed any further?

• How confident are you that you could identify which pieces of infor mation to use when presented with similar problems?

2.5 Understanding information in tables

The problems that you have looked at so far have all been expressed using text. There are many examples of data that can be more clearly expressed by organising it in a table.

TIP

This book mostly uses international standard units such as litres and kilometres. These units may not be what you use every day, but it is worth learning the volume of a litre so you can check your answers are about right.

ACTIVITY 2.5.1: MUSEUM VISIT

Try this problem yourself, before reading the worked solution. The admission fees for a local museum are shown in the table.

(2 adults and 2 children)

(Up to 5 people)

A group of 6 adults and 5 children visited the museum on Wednesday.

a What was the cheapest total cost for the tickets? When buying tickets, it is possible to make a donation on top of the admission fee. The local government gives the museum an additional 20% of the amount donated.

A group of 2 adults and 3 children visited the museum on Saturday. They bought the cheapest possible tickets for their admission and made a donation. They paid a total of $25.

b How much was given to the museum by the local government as a result of this visit?

Adapted from Cambridge International AS & A Level Thinking Skills 9694 Paper 12 Q4 June 2024

WORKED SOLUTION

a The prices in the ‘Mon–Fri’ column of table are the ones that are relevant for this part of the question.

There are several ways to buy tickets for 6 adults and 5 children, so they need to be checked to find the cheapest option. When doing this there are some cases that can be ignored (for example, an option that includes 2 adult child and 2 child tickets isn’t worth checking, because the option that replaces these with a family ticket will always be cheaper).

The cheapest combination of tickets is to buy a group ticket (for 5 of the adults) and then 1 adult ticket and 5 child tickets.

The total cost is $17.50 + $4 + 5 × $2.50 = $34.00.

CONTINUED

b The prices in the ‘Sat’ column of the table are the ones that are relevant for this part of the question.

The cheapest combination of tickets is a family ticket and a child ticket, costing a total of $16.00 + $3.50 = $19.50.

The donation was therefore $5.50.

Since the local government gives an additional 20% of the donation amount, the local government gave $1.10 as a result of this visit.

ACTIVITY 2.5.2: PACKAGE HOLIDAY

Many people choose to buy all-inclusive package holidays (holidays where the amount that you pay covers all the costs of flights and accommodation).

Two holidays to the same destination and for the same length of time but on different dates might have different costs, though.

The following is the start of a table giving the per-person cost of all-inclusive packages, in the northern summer, to a holiday resort.

SAMPLE

Once you have chosen your holiday, you might want to know how the cost has been calculated, but you need more information than is given in the table.

Suppose that the following is true.

WORKED SOLUTION

You might be tempted to use algebra to solve these questions and start off by writing down many different equations with variables representing the accommodation cost and the prices of flights for each of the days. However, by thinking carefully about the information in the table, you can answer these questions without needing anything so complicated.

The price for each holiday is calculated by adding together:

• the weekly accommodation cost, which does not change from week to week

• the cost of the outward flight to get to the destination

• the cost of the retur n flight home.

On any given day, the price for an outward flight is the same as the price for a return flight, but the prices of flights change from day to day.

The prices of flights do not decrease as the season progresses.

Based on this information, discuss with a partner the approach you would take to answer these questions, before reading the worked solution.

a What is the weekly accommodation cost?

b What is the cost of a flight on 29 June?

c What is the cost of a one-week holiday starting on 29 June?

a The price for a one-week holiday starting on 1 June is the same as the price for a one-week holiday starting on 8 June. You know how these two prices are calculated:

• 1 June: flight price on 1 June + accommodation cost + flight price on 8 June

• 8 June: flight price on 8 June + accommodation cost + flight price on 15 June

CONTINUED

Since you know the accommodation cost is always the same, the only possible differences between the calculation are the flight costs. Since the price is the same, you know the flight costs on 1 June and 15 June must be the same.

You have also been told that the flight price never decreases, so it must be the same on 8 June as well.

Now you can consider the price of the two-week holiday starting on 1 June. This could be calculated as follows:

• flight price on 1 June + 2 × accommodation cost + flight price on 15 June

This table shows the components of the total charge for the three holidays.

componentoneweek holiday starting on 1 June oneweek holiday starting on 8 June twoweek holiday starting on 1 June

Flight on 1 June ✓

Accomm. w/b 1 June

Flight on 8 June

Accomm. w/b 8 June

Flight on 15 June

Flights

Accomm. charges

the charge for one week’s accommodation. The weekly accommodation cost is therefore $494 – $354 = $140.

SAMPLE

Since the prices for the flights are all the same and the accommodation charges are all the same, the difference between the total price for either of the one-week holidays and the two-week holiday are the same as

This table can also be used to work out the price of one of the flights without working out the accommodation charge. This is discussed in the commentary at the end of this activity.

b There are two holidays shown in the table for which the calculation of the price will include the price of a flight on 29 June:

• A one-week holiday starting on 22 June

• A two-week holiday starting on 15 June

In each case it is now known how much of the cost comes from the accommodation, but each calculation includes another flight price (in the first case the price of a flight on 22 June and in the second case the price of a flight on 15 June).

The two-week holiday is the one that is more useful, because you have already (in part (a)) worked something out about the price of flights on 15 June: since you know that it is the same as the price of a flight on 8 June.

The cost of a one-week holiday starting on 8 June is $354, and it is calculated by adding the prices of two flights which had the same cost as each other to the $140 accommodation costs. So, each flight must have cost half of $214, which is $107.

Now that you have that cost, you can use the price of a two-week holiday starting on 15 June to calculate the price of a flight on 29 June. It is $542 – $107 – 2 × $140 = $155.

c To work out the cost of a one-week holiday starting on 29 June you will need the price of the flight back on 6 July. You can get this price by applying a similar process to that used in part (b) to the price of a two-week holiday starting on 22 June (which also has a flight back on 6 July):

• The flight on 22 June must have cost $388 – $107 – $140 = $141.

• The flight on 6 July must have cost $595 – $141 – 2 × $140 = $174.

The price for a one-week holiday starting on 29 June is $155 + $140 + $174 = $469.

CONTINUED COMMENTARY

In part (a) a table was used to identify the different components of each of three different packages. If you want to know the price of one of the flights, you could use the accommodation figure calculated in the price for any one of the packages to work out the price of one of the flights. In fact, it is possible to reduce the amount of work needed if you notice the relationship between any two-week holiday and the two one-week holidays that cover the same period. The table used in part (a)is repeated here.

on 1 June

Accomm. w/b 1 June

Flight on 8 June

Accomm. w/b 8 June

Flight on 15 June

2 Understanding data in simple formats

If you buy both one-week holidays, you pay the same components as for the two-week holiday plus the price for two flights on the 8 June. Therefore, the price for a flight on 8 June costs:

($354 + $354 – $494) ÷ 2 = $107

The same reasoning applies to any other two-week period, so the price for a flight on 15 June costs:

($354 + $388 – $528) ÷ 2 = $107

Notice that this method does not require you to know that the accommodation prices were fixed, although that information is still needed to deduce the flight prices for the flights on 1 June or 29 June and later.

In addition to being able to work out the calculations that will help you to solve a given problem it is also important to be able to recognise when you don’t have enough information available.

d Suppose you had not been told that the accommodation price was fixed. Why is it not possible to calculate the accommodation price for the week beginning 1 June?

There are other figures that you cannot deduce from the table, such as the price of a two-week holiday starting on 29 June. You might be able to make a reasonable estimate for that price though based on some appropriate assumptions, as is explored in a later chapter.

REFLECTION

It is important to ensure that solutions to problems are easy to understand. In the worked solution to this question, there is much less detail in the solution to part c compared to the other parts, because it is following the same process. When answering problem-solving questions you will generally need to provide enough explanation so that someone reading the answer understands the steps that you have taken. How can you ensure that you have written enough?

TIP

It is sometimes possible to reduce the amount of calculation that you need to do, which can save you time and sometimes reduce the risk of errors (even if you are using a calculator, it is easy to press the wrong button by mistake!).

For example, if you have a calculation such as 45 + 68 + 83 – 45 then you could notice that the 45 that is subtracted at the end could pair with the 45 at the beginning and so it is only necessary to work out 68 + 83.

Similarly, if you have a calculation such as: 7 × 47 + 7 × 53, you could observe that this is the same as: 7 × (47 + 53) = 7 × 100 and so the answer is 700.

ACTIVITY 2.5.3: ROCKET LEAGUE

This activity refers to the time zone GMT. You might be more familiar with the standard UTC, which is similar. Do not worry if you are not familiar with GMT or the zone letters; as with many problems, all the information you need to solve the problem is included here.

Try this problem yourself, before reading the worked solution and commentary.

Pablo belongs to a group of online Rocket League players. The players come from countries all around the world. Pablo only plays with people living in countries where the time zone is similar to his own, as people generally play during the evening.

Everyone in the group lives in the Northern Hemisphere and in a country where the time zone differs from GMT by a whole number of hours. Some of the players live in countries where the clocks are put forward by one hour in the summer (daylight saving time) and others do not.

The table shows the number of players from the group in each time zone:

CONTINUED

How many of the players live in a country which has zone E in winter, but changes (to zone F, which is not shown in the table) in the summer?

WORKED SOLUTION

SAMPLE

For each zone the number of players listed on the ‘winter’ row will contain some that have the same zone in summer and some that have the next zone in summer. For example, there are 9 players who are in zone B during the winter and some of these are part of the 13 players who are in zone B in the summer. The others are in zone C in the summer.

Similarly, for each zone the number of players listed on the ‘summer’ row will contain some that have the same zone in winter and some that have the previous zone in winter.

To be able to start to solve this problem, notice that there are no players in zone N. This means that the 3 players in zone Z for the summer must also be in zone Z for the winter. The other 1 player who is in zone Z during the winter must be one of the players who is in zone A during the summer. You could then continue this process working across the table.

However, as the problem is about Zone E players, a quicker method is to notice that:

• all players identified in the numbers in the ‘summer’ row of the table are included in the numbers in the ‘winter’ row of the table

• all players identified in the numbers in the ‘winter’ row of the table are in one of the zones between Z and F during the summer.

Putting these two facts together, the difference between the totals must be the number of players who are in zone E during the winter and zone F during the summer.

The total of the numbers in the ‘winter’ row of the table is 45 and the total of the numbers in the ‘summer’ row of the table is 43, so the answer to the question is 2.

CONTINUED

COMMENTARY

Suppose there is an error in the table and one of the people who is in zone C in the Winter is recorded incorrectly as zone D. This means that the table is displayed as follows:

The shorter method for solving the problem still reaches the same answer of 2, but if you work through with the first suggestion you will discover a problem: If 1 moves from Z then it is one of the A summer ones, so there are 3 – 1 = 2 fixed in A and so 9 – 2 = 7 that move from A.

Repeating this process you get the table shown.

Once you have worked out that there are 5 fixed in C, the next step is to deduce that there is 4 – 5 = –1 person moving from C.

ACTIVITY 2.5.4: OLDER YOUNGER

Solve this problem on your own and then check your answer.

Since just the date of birth is generally used for age it is possible for a person to be legally older than someone born over 24 hours earlier in another part of the world. The local time at a particular point in the year can vary from 14 hours ahead of GMT (e.g. in Samoa) to 11 hours behind GMT (e.g. in American Samoa).

What is the greatest difference between the actual times of birth for two people with the same date of birth?

Cambridge International AS & A Level Thinking Skills 9694 Paper 13 Q4 November 2022

2 Understanding data in simple formats

2.6 Understanding information from graphs

Graphs are used in many contexts to provide information in such a way that it can be absorbed quickly and easily. For example, a graph may show variables (things that can vary), such as temperature, against time; financial data may be shown in bar charts. A particular challenge with graphs is that they are not always drawn in the most helpful or accurate way. The author might miss some essential elements of the graph (like labelling the axes). They might add the data incorrectly or might deliberately emphasise something that supports their argument. When problem solving you will need to work with the data you have been given, so it is important to be able to look at graphs critically.

ACTIVITY 2.6.1: EXAM SCORES

This problem involves studying some scatter plots, a type of diagram used to show patterns between two sets of data.

Working in a group choose one of the scatter plots and:

• decide which subject should be labelled for each axis

• for as many points as possible, identify the student that is represented.

Explain to other groups how you made your decisions.

Once you have identified as many students as possible for each scatter plot, work out the answers to the two questions.

The following graphs show the examination scores for 8 students in 3 school subjects.

CONTINUED

The head teacher tries to make a scatter plot for Maths and English, but neglects to label the axes.

He also accidentally interchanges one student’s Maths and English marks.

a Which student’s Maths and English marks have been interchanged on the scatter plot?

Next, the head teacher tries to make a scatter plot for Maths and Science, again neglecting to label the axes.

This time he accidentally interchanges two students’ Science marks.

b Which two students’ Science marks have been interchanged on this scatter plot?

Cambridge International AS & A Level Thinking Skills 9694 Paper 13 Q7 November 2022

ACTIVITY 2.6.2: EXCHANGE RATES

When changing money from one currency to another there is an exchange rate to determine the amount of the new currency that you obtain. This is usually expressed as the amount of one currency obtained for one unit of the other currency.

The exchange rate between two currencies changes many times during a day and this is often represented by a graph.

Here are two graphs and a table of the same information about the exchange rate between the US dollar ($) and the British Pound (£) (USD/GBP) one morning.

In groups, discuss the answers to the following questions. For each question consider all the different representations of the data (the two graphs and the table) and decide which representation makes the question easiest to answer.

a i Suppose that you want to change pounds (GBP £) to dollars (USD $). How would you identify the best time to make this exchange?

ii How would you identify the best time to change dollars to pounds?

Assume (to start with) that there is no cost for changing money.

Suppose that you had $1000 at the start of the day. You changed all the dollars into pounds at one point in the day and then changed all the pounds back into dollars later in the day.

Answer the following questions and discuss how you reached your answers with the other members of your group.

b i What is the best times to choose to make each exchange and how many dollars would you have at the end of the day?

ii Does the amount of money that you start with affect the choice of times that you make?

CONTINUED

Suppose instead that you had £1000 at the start of the day and changed to dollars, then back to pounds. c What is the best times to choose in this case?

Suppose that you were charged 1% of the total amount that you are exchanging for each transaction (so for example, if you want to exchange $1000, you

SAMPLE

TIP

Even if there is no commission, it is sensible to avoid the potential for errors that comes from switching into familiar units and back, unless that is the point of the question, as it was in Activity 2.6.2.

If you have a problem where the measurements are given in centimetres, it is better not to convert to (for example) millimetres or inches, unless you need to give an answer in one of those units.

2.7 Understanding information in diagrams

There are many other ways in which information might be provided. For example, if you are walking through a maze, you might have a map showing a view of the maze from above. Similarly, if you are analysing a position in a game you might be given a picture representing part of the board. As with any of the other representations that have been covered in this chapter, it is necessary to understand the information provided before you can apply the problem-solving strategies that is covered in later chapters. The activities in this section will illustrate some of these forms in which information might be provided.

2 Understanding data in simple formats

ACTIVITY 2.7.1: DRONE DELIVERY

In pairs solve all parts of this problem, then check your answers.

A drone is used to deliver medical supplies. It has a map with the location and heights above sea level of the tops of various features. It takes readings at regular intervals to track where it is and to ensure that it is high enough. For each reading it identifies the highest three points that are within range of its radar.

The diagram shows the locations marked A, B, C, D, E, F, G and H and circles that represent the range of the radar when three consecutive readings were taken as the drone moved across this region.

On the first reading the drone identified locations A, B and C.

On the third reading the drone identified locations C, D and E.

a In which direction was the drone moving?

b Which combinations of three locations might the drone have used on its second reading?

ACTIVITY 2.7.2: STRONG HAND

Solve this problem on your own before checking your solution. Bridge is a popular card game. In each round, each player is dealt 13 cards (there are four players, so all 52 cards in the pack are used for each hand). The first part of the round is called the ‘auction’, where players make bids based on how good the cards in their hand are (called ‘the strength of their hand’).

A common way to determine the strength of a hand is to count the ‘high card points’.

• Each Ace is counted as 4 points.

• Each King is counted as 3 points.

• Each Queen is counted as 2 points.

• Each Jack is counted as 1 point.

• No points are counted for any other card.

The following diagram shows the cards dealt in one round of a game of bridge. The players in a game are denoted by the four compass points (North, East, South and West). The hands are shown grouped in the four suits (Spades, Hearts, Diamonds, Clubs) as this is important for other aspects of the game.

According to the number of high card points, which player has the strongest hand?

ACTIVITY 2.7.3: BURIED TREASURE

Information is not just numbers or sentences. In this activity there are no numbers, just a diagram.

1 In pairs discuss how you would identify the areas required for this problem. Once you have agreed on the regions, read the commentary.

Blackbeard sailed due south across the ocean until he arrived at a beach on one of a small group of islands. Here he buried the treasure and then sailed off over the horizon due west into the sunset. Show, by using squared paper or Activity support sheet 2.7.3, all the parts of the coast or coasts where the treasure could be.

Question 1: Adapted from Cambridge International AS & A Level Thinking Skills 9694 Paper 13 Q3 November 2021

COMMENTARY

To find the places where the treasure might be you can expect to get the answer by excluding the places where it cannot be and by checking around the coast of each island whether the requirements are met.

There are two requirements: a clear path from the beach to the north (as Blackbeard was originally sailing southward) and one to the west. Remember that both requirements need to be met. Therefore, if you exclude a place when checking one requirement, you do not need to look again at that place when checking the other requirement.

Instead of starting with the coast another valid approach is to start from the western and northern edges and see where you can reach. Everywhere else ‘in the shadow’ can be ignored. Anywhere that is the first landfall from both directions is a possible place for the treasure.

2 Working in pairs, complete the next part of this activity

i Each draw a collection of islands from your imagination, preferably on squared paper. Think about any features that you can include to try to make it more difficult for your partner.

ii Challenge your partner to work out where the treasure might be, using the same instructions as in Question 1. Try to include the following features in your diagram:

CONTINUED

• more interesting shapes for the islands

• a bay, which could have the treasure on its shore.

Question 2: Please note that Question 2 of this activity is not derived from the Cambridge International AS & A Level Thinking Skills 9694 past paper referenced above and was written by the author.

REFLECTION

In each case, in which ways did the features the challenger set make it more difficult for the solver? What can you learn from any differences in the ways that you both tackled the problem?

ACTIVITY 2.7.4: SUDOKU

Sudoku is a popular game that is widely available in newspapers, puzzle books and apps. Simpler cases offer excellent exercises in logical deduction. In this section, the focus is on what parts of the puzzle are important. Although the numbers from 1 to 9 are used in many sudokus, you can think of the numbers simply as symbols. The aim of a sudoku puzzle is to fill all the squares and make sure that there are no repeated symbols in any row, any column or any of the nine 3 × 3 squares. Any nine letters or symbols could be used, as could the digits 0 to 8. Switching them around makes no essential difference to the puzzle.

Here are two different Sudoku puzzles. Although they look to be different, they are in fact equivalent puzzles.

In groups, discuss what it means to say that two puzzles are equivalent. Discuss the way in which these two puzzles are equivalent before reading the commentary.

CONTINUED COMMENTARY

When thinking about the way in which each puzzle is solved, you should be able to see that the same steps need to be taken with each puzzle to reach the solution. A useful approach in problem solving is to focus on one aspect at a time to build up a fuller picture. If you shade in the boxes (known as ‘cells’) that contain numbers, then you will obtain the following two patterns:

The second pattern is the reflection of the first pattern in the diagonal line that goes from the bottom left to the top right. This similarity between the two puzzles is the first step in showing that they are equivalent. However, you also need to know that the numbers match up in a similar way between the two puzzles.

Comparing the numbers in corresponding pairs of cells you can see that the pairing of the numbers is:

Number in left puzzle

Number in right puzzle

There doesn’t need to be a pattern to the way in which the replacements are made: in this case it might have looked like each number was replaced by its difference from 10, but this is not the case for 8 and 9. You should always be careful not to assume that there is a pattern when there doesn’t need to be one.

Find a Sudoku puzzle (or create one – you do not need to worry about whether it can be solved) and create a second puzzle that is equivalent to it. Discuss these questions with a partner.

a In what ways can you create an equivalent problem?

b For each of the following possible changes, decide if it gives an equivalent problem.

i Swapping the top row with the second row.

ii Swapping the top row with the bottom row.

iii Swapping two of the 3 × 3 boxes.

2.8 Further sources of information

SAMPLE

One way of showing numbers on electronic devices like digital clocks or calculators is known as a ‘seven element digital display’. Early seven element digital displays showed numbers as combination of short lines (the elements). Showing a time needs four of these displays, as shown in the following image.

0123456789

ACTIVITY 2.8.1: DIGITAL DISPLAYS 1

For the following problems, use the digits in the image above to see which elements are needed for each digit. You should assume that there are always 4 digits and that a 24-hour clock is being used.

In pairs agree on answers to all parts of this problem before checking your answers.

For some digital clocks the amount of power used depends on the number of elements lit up. The digit 8 has all 7 elements lit up, so requires 7 units of power, but the digit 3 takes only 5 units.

a At what time or times of day does the display use the most power, and what time(s) use the least?

When the time changes from 15:48 to 15:49, the amount of power that is needed is reduced by 2 units.

b Give an example where the amount of power that is needed does not change from one minute to the next.

There are 10 different digits in total. Therefore, if a digit is to be changed, there are 9 possible digits that it could change to. This means that there are 10 × 9 = 90 possible ways in which one digit could change to another.

c i Why are only 13 of the 90 possible changes ever seen when using a 24-hour clock?

ii How many different changes could be seen when using a 12-hour clock?

A similar display could be used to show the date, using two digits to represent the month and two digits to represent the day.

iii How many different changes could be seen when using a clock to represent the date in this way?

REFLECTION

What strategies did you use to identify the answers? Did you find any ways to reduce the amount of work that needed to be done for later parts of the problem based on what you had done in the earlier sections? Are the strategies that you applied in this activity ones that you could modify when attempting to solve other problems?

ACTIVITY 2.8.2: DIGITAL DISPLAYS 2

In groups discuss the approach that you should take to solve this problem. Once you have agreed on an approach, solve the problem before reading the worked solution.

In addition to the power requirement to light the elements, there is also a power requirement every time an element needs to be changed. For example, switching a digit from a ‘2’ to a ‘5’ requires 4 changes to elements, since there are two elements that need to be turned on and two elements that need to be turned off.

What time of day uses the most power to change from one minute to the next on a 24-hour clock?

WORKED SOLUTION

In most of the cases, only the final digit of the displayed number of digits will change. This could be a change from 0 to 1, from 1 to 2, and so on. The table shows the number of elements that need to be changed in each of these cases.

The largest requirement for the cases when only the last digit changes is 6 units (when a 6 changes to a 7).

However, it is possible that the last digit is a 9 changing to a 0 (which requires 3 units) and the digit that precedes it also changes, which means that a larger total requirement can be found when the minutes part of the time changes from 19 to 20 (5 + 3 changes) or when 59 changes to 00 (3 + 3 changes) as the number of minutes cannot start with a 6. But in this case the next digit will also change.

It is not a surprise if the most power is used when all four digits are changing. Since changing a 1 to a 2 uses more power than changing a 0 to a 1, it is worth considering the change from 19:59 to 20:00, which requires a total of 5 + 3 + 3 + 3 = 14 units of power.

Finally, there is one other case that needs to be checked: 23:59 to 00:00.

The ‘59’ changing to ‘00’ is the same for both cases, so you only need to check how much power is needed to change ‘23’ to ‘00’. This is 3 + 3 = 6 units (which is less than the 8 units needed to change ‘19’ to ‘20’).

The largest requirement is 14 units of power to change ‘19:59’ to ‘20:00’.

TIP

In many problems, the amount that needs to be checked initially appears to be very large. Thinking about the way in which the process works allows you to reduce the amount that needs to be checked so that you are only looking at the important cases.

ACTIVITY 2.8.3: BROKEN COMPONENTS

Solve this problem on your own before checking your solution.

Sometimes it is easier to explain what is happening by labelling the different components of a problem. In the case of the display for one digit, it helps to label the seven elements using the letters from ‘a’ to ‘g’ as shown below.

SAMPLE

If one of the elements of the display stopped working, some digits could then appear the same as a different digit. For example, if element g does not light up then the digit 8 appears the same as a 0.

Give another example where one element not working means that a digit appears to be a different digit.

ACTIVITY 2.8.4: CHARACTERS FROM BITS

In groups, solve all parts of this problem before checking your solutions. For the parts of the problem that involve completing parts of a table you may find it useful to allocate some of the rows to each member of the group; if you do this, make sure that there is more than one person working on each row so that you are able to compare your solutions.

Integrated circuits (chips) such as the 74LS47 convert digits into the 7 bits to control whether the 7 segments of a display are on or off.

Within circuits, information is transmitted in ‘bits’, which can only have one of two states (often denoted by 0 and 1). Four binary bits are needed to represent a digit that could be between 0 and 9. These bits are labelled A3, A2, A1 and A0

Each bit has a value associated with it which is a power of 2, so the rightmost bit (A0) has a value of 1, the bit to the left of it has a value of 2, and so on.

For example, the digit ‘6’ is represented by the four binary bits having values 0, 1, 1 and 0 (which corresponds to 0110, which is the binary representation of the number 6).

So, for each number there are two different representations – the binary inputs and the set of elements of the display that need to be lit. The information about the two representations can be put into a table like the one that is started here.

CONTINUED

Only the first four rows of the encoding have been shown. a Copy and complete the table. You will need to refer to the labelled image of an 8 from Activity 2.8.3 to complete the right hand column.

From the table you can work out some rules for when certain elements should be lit. For example, if the binary inputs A3 and A2 are both set to 0, then element b is lit (there may be other situations where this element is also lit). There are 6 more binary patterns that do not represent 0–9, and when you feed any one of them into the 74LS47 it produces a strange collection of outputs that are simply the result of doing the above conversion in the simplest way. What someone might want is a base 16 (hexadecimal) display with the letters A, B, C, D, E and F (although some will look like their lowercase equivalent on the display).

CONTINUED

b Copy and complete the table.

c What is the problem with doing this, and how could it be solved?

In other contexts, such as a display of temperature, it is more useful to have a space and a minus sign rather than letters.

TIP

d In groups discuss which inputs you would select for the inputs shown as ???? and why.

ACTIVITY 2.8.5: STARS ON US FLAGS

There are many famous examples of errors in films, including movies set in World War II that display the wrong version of national flags, such as the US flag. The current US ‘stars-and-stripes’ flag has 50 stars: one for each state. However, there were only 48 states in the 1940s as Alaska and Hawaii were not states yet.

The convention is that when a new state is added, the US flag is updated on the following 4 July to reflect the new total number of states. The current flag has five rows of six stars and four rows of five stars. Each row is centred and with the same gap between adjacent stars.

This is not a situation in which there is only one ‘correct’ answer; there are several different options and they each have different advantages. You should make sure that you have explained a reason to support the choice that you have made.

SAMPLE

CONTINUED

An easy way to denote the pattern of the stars on the US flag is to write the number on each row (starting from the top) separated by dashes. The World War II era flag simply had 6 rows of 8 stars, so this is denoted by 8–8–8–8–8–8

The table shows the last eight arrangements that have been used: number of starspattern of stars in rows 4th July to include

38 7–8–8–8–7 1877 Colorado

43 8–7–7–7–7–7 1890 Idaho, Montana, Washington, North Dakota, South Dakota

44 8–7–7–7–7–8 1891 Wyoming

45 8–7–8–7–8–7 1896 Utah

46 8–7–8–8–7–8 1908 Oklahoma

48 8-8-8-8-8-8 1912 Arizona, New Mexico

49 7-7-7-7-7-7-7 1959 Alaska

50 6–5–6–5–6–5–6–5–6 1960 Hawaii

Although there are defined proportions for the shape of the flag, there are no written rules for the size of the blue rectangle or the layout of the stars. In some of the earlier versions of the flag there were circular and other arrangements of the stars. So if you were asked how to arrange a different number of stars on the US flag, the best that can be done is to try to deduce what might be acceptable from the examples given.

Mathematicians might claim that the rectangle should approximate the golden rectangle (√5 +1 : 2 or approximately 1.618:1) in the way that photographic prints did before digital photography, e.g. 5 by 3 (inches 1.66:1), but the 7 by 7 square is nowhere near that.

Looking at the arrangements that have been used, you could deduce something about what is preferred:

There is never more than a difference of 1 between any rows in the flag, so arrangements such as 6–7–8–9–8–7–6 for 51 stars may not be useful. It does however have symmetry, which appears to be a feature of many of the patterns chosen.

In pairs, discuss how you would arrange the stars on the flag for each of these scenarios.

a What might it have been at a time where there were 47 states (if there had been a gap between Arizona and New Mexico joining)?

b What do you suggest for 51 stars if another state joins (or one state splits into two)?

c What do you suggest for 52 stars?

In non-digital photography there are several ways to affect the how dark or light the picture is. They are all based on something that is called the ‘stop’; changing the value of the stop by one unit changes the amount of light used by a factor of 2.

These pictures show the difference that one stop makes:

The three ways that a change can be made are by adjusting:

• the film sensitivity (how quickly the chemicals react to light)

• the shutter ‘speed’ (the time for which the shutter is open)

• the aperture (how big the opening is) and the scales for these are explored in that order.

Note that the mechanisms used in these cameras means that the numbers used are only values to a certain degree of accuracy. This means that occasionally some patterns might have small inconsistencies within them. This a feature of the way that many things work in the real world.

ACTIVITY 2.9.1: FILM SENSITIVITY

Two ways in which the sensitivity of film is indicated are:

2.9 Linked activity: Understanding the numbering used in photography SAMPLE

• A number defined by the American Standards Association (ASA). In this system, nor mal film was available as 100, 200, 400, or 800. Doubling the number indicates that the film is twice as sensitive to light. So if, for example, you use 200 rather than 100, a change of one stop (down) in speed or aperture would results in the same shade.

CONTINUED

• The German system (known as DIN) used a different scale, where adding 3 to the number indicates something is twice as sensitive.

This table shows some values where the two systems refer to film of the same sensitivity.

SAMPLE

To make a picture slightly darker or lighter, photographers under- or over-expose film, usually by a ‘third of a stop’.

Increasing the value of the stop by one unit corresponds to an increase of 3 units in the DIN system, so an increase of a third of a stop corresponds to an increase of 1 unit in the DIN system.

The difference between 100 and 200 is not the same as the difference between 200 and 400, so changing by one stop is not simply adding or subtracting some fixed number.

a If you have the ASA number of a film, and you want to get a film that is one stop faster, how do you calculate what its number is?

b If you want a film that is a third of a stop faster, how would you calculate its ASA number?

ACTIVITY 2.9.2: SHUTTER SPEED

The numbers used for shutter speed refer to the fractions of a second or the number of seconds for which the film is exposed, for example 1000 means 1/1000th of a second, and 2s means 2 seconds). Here are some common shutter speeds:

1000, 500, 250, 125, 64, 32, 16, 8, 4, 2, 1, 2s 4s.

a There is a pattern that applies for most of the sequence of numbers. At which point does this pattern not apply and how much is it out by?

b Why do you think that the pattern does not apply all the way through the sequence?

ACTIVITY 2.9.3: LENS APERTURE

The figures showing for aperture are, for example: 22, 16, 11, 8, 5.6, 4, 2.8, 2

Adjusting the value of lens aperture from one value to the next value in the list corresponds to a change of one stop.

a What is the pattern in these numbers?

b How much have they been rounded?

c What adjustment in lens aperture corresponds to a change of a ‘third of a stop’?

PROJECT: MORSE CODE

Morse code is a method for sending messages which makes use of sequences of marks (dots and dashes) to represent each letter of the alphabet. There is also a need for different types of gap.

• Within-character gaps – for example, the letter N is represented by the sequence dash, dot. The gap between the dash and dot is a within-character gap.

• Between-character gaps – for example, if the word ‘ON ’ is represented in morse code, the gap between the end of the sequence for ‘O’ and the start of the sequence for ‘N’ is a between-character gap.

• Between-word gaps – this has to be different from the between-character gap so that you can tell where one word has ended and the next word starts.

Measuring the length of a message in morse code requires the lengths of the different types of marks and gaps to be known.

This diagram shows the representation of each letter using Morse code. Start at the top and find the route that leads to the required letter. Each move to the left means that the mark is a dot and each move to the right means that the mark is a dash. Those that are not used for A–Z are shown as.

For example, G is reached by moving right, right, left, so the Morse code is dash dash dot.

The length of a G using morse code is 3 + 1 + 3 + 1 + 1 = 3 units.

a In groups, discuss why the letters might be arranged in this manner.

If the letters of the alphabet are ordered from the most frequent to least frequent in English, then the list (based on a recent count) is:

ETAOINSRHDLUCMFYWGBPVKXQJZ

b In your groups, create a short presentation to explain how you could improve the system if you know that all messages are in English.

SUMMMARY

This chapter explored some of the different forms in which data can be provided. It discussed the importance of identifying the correct aspects of the data to be able to solve simple problems, which might also involve identifying simple calculations that need to be performed.

Having read this chapter, you should be able to:

• understand the data that is provided in text, tables and graphs

• identify what data is relevant to the task

• be clear what any numbers represent

• avoid wasting time and effort on irrelevant data

• check that any numbers that you give as answers are credible.

Sample answer

Circular pond

The distance around a circle (the circumference) is the distance across the circle (the diameter) times a constant denoted by the Greek letter π (pi). If your calculator doesn’t have it, use the approximate value of 3.142.

A circular pond was described as 10 cubits across and 30 cubits around. (A cubit is supposed to be the distance from the elbow to the tip of the longest finger, and there have been many different ones in different places and times. The actual length is irrelevant for the question.)

These measurements are to the nearest cubit.

What is the possible range of values for the distance around the pond? [2]

If the distance across the pond is 10 cubits, then the distance around the pond must be

10 × 3.142 = 31.42 cubits.

It the distance across the pond was 9 cubits then the distance around the pond is

9 × 3.142 = 28.278 cubits.

31.42 is closer to 30 than 28.278, so the distance around the pond is probably more than 30 cubits. It can’t be more than 30.5 cubits, because that rounds to 31.

Answer: Somewhere between 30 and 30.5 cubits.

Analysis

This response identifies some of the important points:

• That the ‘10’ and the ‘30’ are approximations.

• That the ‘30’ could be as much as 30.5

However, the information hasn’t been put together correctly. The correct upper limit has been worked out, but the reasoning for the lower limit isn’t good enough. A full solution is now shown.

For the diameter to be recorded as 10 cubits, the actual diameter of the pond is between 9.5 cubits and 10.5 cubits which makes the circumference between 29.849 cubits and 32.991 cubits.

So, the two known facts about the circumference are:

This response has tried to deal with the inaccuracy that comes from the ‘10’ by comparing the value that is reached for the circumference by using 10 as the diameter with the value that comes from using 9. The important value to consider is 9.5 - this is the value at which the rounded value for the diameter changes from 9 to 10.

SAMPLE

• It is between 29.849 cubits and 32.991 cubits

• It is between 29.5 cubits and 30.5 cubits

Both must be true, so the circumference must be between 29.849 cubits and 30.5 cubits

This response correctly identifies that 30.5 is the highest possible value for the circumference as the value of 30 indicates that the circumference must be between 29.5 cubits and 30.5 cubits.

TIP

Only the 9.5 π needs to be calculated since (9.5 + 1) π will clearly be more than 30.5 (because it’s more than 28.9 + 3) and so will not be needed in the final answer.

Practice questions

1 The table shows the prices for admission to a theme park.

ticket (2 adults and up to 2 children)

How much does a family of 2 adults and 1 child save by using the family ticket instead of buying individual tickets? [1]

2 Tina sells cakes every Saturday in her town’s market. She makes 100 cakes every Saturday and sells them for $3 each, but she reduces the price to $2 for the final 2 hours that she is at the market. It costs her $1.50 to make each cake.

What is the smallest number of cakes that Tina could sell and make a profit? [1]

3 An organisation has two ways in which it raises money:

• A monthly subscription from members (a fixed amount of money that each member pays every month).

• Sales from the organisation’s online store.

The bar chart shows the total income for the organisation for each month last year.

$1,800.00

$1,600.00

$1,400.00

$1,200.00

$1,000.00

$800.00

$600.00

$400.00

$200.00

$0.00

The president of the organisation makes the following announcement: ‘The income from sales in the best month was three times the income from sales in the worst month.’

Assuming that the number of members has remained constant throughout the year, what is the total monthly income that the organisation receives from monthly subscriptions? [2]

4 The journey from Fred’s home to his caravan is a total distance of 150 km. Fred is travelling to his caravan this weekend. He expects to be able to travel at an average speed of 90 km/h, but has decided to visit a friend who lives along his route at a point 90 km from Fred’s house. He needs to arrive at the caravan by 21:00 and will leave home at 17:00.

What is the longest amount of time tha the can spend visiting his friend? [2]

Cambridge International AS & A Level Thinking Skills 9694 Paper 12 Q1 June 2020

5 The central sheet of paper in a newspaper contains the four page numbers 35, 36, 37 and 38.

a Which other three page numbers are on the sheet containing page 22? [2]

In a different newspaper, pages 52 and 90 are on the same sheet of paper.

b How many pages are there in this whole newspaper? [2]

Cambridge International AS & A Level Thinking Skills 9694

Paper 13 Q9 November 2020

6 The charges per night at the Windmill Hotel are shown in the following table. night of the week charge per night

Monday, Tuesday, Wednesday, Thursday or Friday $100 Saturday or Sunday $120 discounts

10% per night for any block of 3 consecutive nights*

15% per night for any block of 5 consecutive nights*

*Each night can be discounted only once

Pedro stays at the Windmill Hotel for 4 nights from Tuesday to Friday inclusive.

a What is the total charge for Pedro’s stay? [1]

Juan stays at the Windmill Hotel for 7 nights from Saturday to Friday inclusive.

b What is the least possible total charge for Juan’s stay? [2]

The hotel manager now decides that he will not allow any discount on the charges for a Saturday night stay. The discounts for 3 and 5 consecutive nights still apply, so long as the consecutive nights do not include a Saturday night.

Sasha arrives at the Windmill Hotel on a Tuesday and stays for 15 consecutive nights.

c What is the least possible charge for Sasha’s stay? [3]

Adapted from Cambridge International AS & A Level Thinking Skills 9694 Paper 12 Q9 June 2022

7

Eight of my friends each gave me a gift of some money for my birthday. The amounts are shown in the table below.

Jim$120Mike$155Rob$160Vicky$130 Chris$110Brian$280Geoff$105Oscar$140

My son made a chart to show the amount given by each friend.

One of the amounts was incorrect on the chart.

a Which friend’s amount was incorrect on the chart?

Brian telephoned me the next day to explain that his gift consisted of two gifts: one from himself and one from another friend, Phil, and that Phil’s gift was larger than his.

My son made a new chart to show the amount given by each friend. This time he made no mistake.

b How much was Phil’s gift? [2]

Cambridge International AS & A Level Thinking Skills 9694 Paper 12 Q5 June 2021

Chapter 8 Evaluating reasoning (credibility)

SAMPLE

LEARNING INTENTIONS

By the end of this chapter you will be able to:

• understand that credibility is a general term that can be subdivided into reliability, plausibility, corroboration and consistency

• understand that reliability is assessed using the criteria of reputation, ability to see, vested interest, expertise and neutrality/bias

• apply reliability criteria and assess the reliability and credibility of a source

• explain how reliability criteria can strengthen or weaken claims

• recognise the situations when it is not appropriate to discuss reliability criteria.

BEFORE YOU START

How do you spot fake news?

Figure 8.1: Vapour trails from a plane

It has been suggested that vapour trails from planes are the result of government experiments to stop climate change. The idea is that planes are spraying chemicals into the atmosphere to reflect sunlight back into space. This was widely seen as fake news, which lay behind a conspiracy theory. However, in April 2024, the Tennessee State House of Representatives voted to ban this activity. That suggests that the representatives believed the chemical spraying was happening or likely to happen. Senator Frank Niceley (Republican)

8.1 What is

commented: ‘For years they denied they were doing anything’. Assuming this bill becomes law ‘they won’t be doing it over Tennessee’.

Discuss as a class:

a How do you spot fake news?

b What other examples have you heard about where a government has been accused of trying to control the weather or the climate?

c Has AI made it harder to find the truth? Explain your answer.

‘evaluating evidence’?

Evidence and evaluate are two terms that you will see very frequently in this course, so it is important that you understand what they mean.

KEY TERMS

Evidence

SAMPLE

Evidence consists of statements that claim to be true and can support or undermine a conclusion. Almost any fact could support a conclusion, so evidence is a very broad concept. In practice, facts cannot be used unless someone remembers them, and preferably writes them down or records them digitally so they are available when needed.

evidence: claims that can support or undermine a conclusion. evaluate: to judge or calculate the quality, importance, amount or value of something.

Some facts may seem too unimportant to be worth using in evidence. However, even facts that seem trivial are potential evidence because these facts may later turn out to be important. For example, a common feature of crime novels is how the lead detective notices an unimportant detail that turns out to be the key to catching the criminal. In science too, advances sometimes come by chance observations.

ACTIVITY 8.1 THE DISCOVERY OF PENICILLIN

Alexander Fleming is the scientist who discovered the medication known as penicillin. This is a type of antibiotic. Research his discovery online and then answer these questions.

a What was the chance observation by Fleming that turned out to be important evidence?

b Search for other scientific discoveries made by chance. Choose the five you consider to be the most important.

There are several types of evidence. Although you are not required to classify evidence, it is useful to be aware of what sorts of evidence exist, as different types of evidence can be evaluated in different ways. Some of the different types of evidence are described in Table 8.1.

type description

Eye-witness testimonyA person reports what they have seen (or heard, etc.). This a common and important aspect of criminal cases and official enquiries.

Hearsay This is where a witness reports what someone else has told them.

Circumstantial If, for example, a suspect leaves the country shortly after a crime is committed, it doesn’t prove they are guilty, but guilt would be a motive for their departure, and if they are innocent it has to be a coincidence. If there are enough such coincidences, a suspect may be deemed to be guilty.

Documentary For events that took place a long time ago, eye-witnesses will not still be alive, and documents may well be the main evidence.

evaluation

It is generally evaluated by the credibility criteria discussed in this chapter.

In court, this is usually rejected as inadmissible. The ‘someone else’ who is being quoted should be called to speak for themselves.

For such evidence, the issue is not so much its credibility but rather its relevance.

SAMPLE

Reliability in part depends on the ability to access the documents, but also on reliability of the original author, and the extent to which we can be sure that the author is the person claimed (as opposed to the document being a forgery).

type description evaluation

Digital Digital evidence includes photos and videos (from smartphones, CCTV, and car and door cameras) and text (from social media, texts, emails, etc.). When police arrest someone, one of their first steps is to examine the contents of their phones and computers. Historians of the future looking back at the present day will be faced with numerous anonymous online claims and documents, and whose credibility is hard to assess even now, let alone in years to come.

Professional opinionThose who reach conclusions from physical forensic or medical evidence are not the only people who handle the evidence. Judges and juries will depend on professional accounts of when, where and how the physical evidence, such as finger prints or DNA samples, were obtained, and whether there is a match with the accused.

Physical In criminal trials, physical evidence is obtained by forensic examination and can consist of finger prints, footprints, and, increasingly DNA sequencing. Occasionally there will be exhibits in court, such as photos or video but with much forensic evidence, the court will accept an expert opinion from police that there is a match. Other professions that rely on physical evidence are archaeologists, geologists, doctors, accident investigators, etc.

Statistical Numbers derived from counting things or measuring things.

Whilst such evidence can be very useful, its credibility can be undermined by the increasing ability of AI to generate fakes.

Expert witnesses in court are generally seen as credible, though they have been known to make mistakes or change their mind.

Evaluation in the critical thinking sense doesn’t apply to physical objects. You could say, for example, that cliffs are evidence of coastal erosion, but you would not evaluate a cliff.

Numbers do not necessarily make evidence reliable.

The sort of evidence you need to evaluate are in the form of documents (called ‘sources’ at AS Level). A source or document could include photographs, charts or tables.

• Sources: these are shorter and the term is mainly used in the AS Level part of your course.

• Documents: these tend to be longer and this term is mainly used in the A Level part of your course.

KEY TERM

source: a person, organisation or document that provides information or evidence.

Table 8.1: Some types of evidence

Evaluation

To evaluate means to judge the quality and importance of something. Evaluating evidence involves deciding whether:

• claims or data are likely to be true or false/misleading

• claims are clear or vague/confusing

• opinions expressed are worth considering or of minor importance

• claims are widely accepted, or whether they represent a minority view.

This last bullet point raises the issue of whether a claim is always factually correct if a majority of people believe it. Often that is the case. For example, most people believe Earth is round and a minority believe it is flat. However, it is not always the case. For example, Galileo, a famous astronomer, was ordered to abandon his belief that Earth moves around the sun in 1616. Galileo’s view at that time was very much a minority view, but it turned out to be true.

There is another sense in which minority views can be viewed as right and that is when, with hindsight, we view them as morally right. For example, the abolition of slavery did not have majority support until the mid-19th century, giving women the vote did not have majority support till the early 20th century, and interracial marriage only became legal in southern USA in 1967 and in South Africa in 1985. However, the evaluation of statements about what policy is morally right is different from evaluating whether a claim is factually correct. For example, if someone says that young people should be entitled to vote from the age of 15 upwards, you may agree or disagree, but it is not a claim that is either true or false.

Claims

A claim is a general term for anything that is said or written which can be evaluated. It might help you to recognise claims by looking at some of the things that are not claims.

• Commands and instructions are things where you can choose whether you obey them or not. Like claims, they may be clear or confusing, but it makes no sense to say they are true or false, so they are not claims.

• Questions are things that you choose whether to answer them or not. Once again, they cannot be described as true or false, so they are not claims.

• Emotions can be expressed by exclamations, for example of surprise or annoyance. However, opinions are claims. If you agree with them, you could say that it is true. When someone begins a statement of opinion with ‘I’ (e.g. ‘I like country music’ or ‘I think those jeans suit you’), it is likely they are telling the truth. Although, of course, the person may just be saying it to please you.

TIP

One of the key things you need to do in this course is ‘use and evaluate information’. Evaluation is sometimes confused with summarising, but you should not just sum up the information from a document. Instead you need to judge the value of information in ways described here.

SAMPLE

When someone makes a claim that refers to themselves, it is possible that only they know whether it is true or not. If your friend says ‘I had a strange dream last night’, you have no reason to reply ‘No you didn’t!’. In the same way, if the friend says ‘I feel happy today’, it would be very odd to reply ‘No you don’t’. A more tactful way of questioning such a claim would be to reply ‘You don’t look very happy’. When you talk to someone face-to-face, their tone of voice and body language are said to matter more than the actual words.

KEY TERM

claim: a statement of a fact or an opinion that may or may not be true. It includes most of what is said or written apart from questions, instructions and exclamations.

There is a fine dividing line between claims that are stated and claims that are implied. Imagine your friend is hammering nails and accidentally hits their thumb. Your friend might say that it really hurt, which is a claim that is almost certainly true. On the other hand they might be more likely to utter a swear word, which is not a claim as such, but implies the claim that they are in pain.

There is a good deal of overlap between claims and evidence. A lot of statements that could be called evidence could also be called claims. However there are differences. Evidence refers to facts, whereas claims, as you have seen, include opinions. Evidence can also include physical objects; for example cliffs being evidence of coastal erosion, or fossils as evidence for the existence of dinosaurs. You would not say that cliffs or fossils are ‘claims’.

ACTIVITY 8.1.2: CLAIMS

a In pairs, decide which of the following statements are claims.

b When you have identified the claims, for each claim decide whether:

• the claim is true

• the claim is untrue, or

• it cannot be determined whether it is true or untrue.

A Lilongwe is the capital of Malawi.

B Do you like the taste of broccoli?

C Rio de Janeiro is the federal capital of Brazil.

D Call the police!

E I like vanilla ice cream.

F Make sure the electrical equipment is unplugged before attempting a repair.

G Billie Eilish is better than Dua Lipa.

H Can you fly direct from Santiago, Chili, to Sydney, Australia?

WORKED SOLUTION

Questions, exclamations and instructions are not claims, so we wouldn’t try to assess their credibility. That rules out B, D, F and H. The rest are claims: A is true, C is false (it should be Brasília). Whilst we could consider their credibility, when the truth or falsity is so well known we usually don’t need to. E and G are a matter of opinion, but they are still claims.

SAMPLE

Credibility

The general term for whether evidence or claims can be believed is credibility As shown in Figure 8.2, credibility is an overarching term that covers all the things you need to consider before you decide how likely it is that a claim is true.

Credibility Plausibility Reliability Corroboration and consistency

Reputation

Ability to see

Vested interest

Expertise

Neutrality

Figure 8.2: Credibility is an overarching term

When you have assessed credibility, you will still not be certain whether a claim is true or false, but you will understand better the likelihood that it is true. When it is certain that a claim is true or false, there is no further need to assess its credibility.

8.2 Reliability

If you describe a person as ‘reliable’ it implies that you trust their judgment, and that claims they make or documents they write are more likely to be truthful. (Trust has different aspects; for example, someone may trust that their partner loves them without necessarily trusting that they will make the best choice for the couple when it comes to buying a car.)

What is ‘reliability’?

If someone tells you a rumour and you are a critical thinker, you might well ask ‘Who told you?’ Reliability is about how much you can trust the person making or publishing claims. For example, in 2019 a conservative activist posted a claim on social media that Kamala Harris was raised in Canada and was therefore not eligible to run for President of the USA. Claims on social media, whether true or not, can get posted many times; this is known as ‘going viral’. The sort of questions you, as a critical thinker, need to ask are:

• Who stood to gain from spreading such a rumour?

• How would you go about investigating?

KEY TERM

credibility: the extent to which a claim or source is believable.

KEY TERM

reliability: the extent to which the person (or organisation) who makes a claim can be trusted.

ACTIVITY 8.2.1: FACT CHECK

In pairs, search online for the phrase ‘Where did Kamala Harris grow up –fact check’ (or use another a similar search term). You should then talk through the following questions:

a What do most websites say about whether Kamala Harris was eligible to run for president in 2024?

b Do all websites agree exactly? If the websites disagree, are the differences big or small?

c Are the websites neutral or are they clearly supporting one particular party?

WORKED SOLUTION

a The consensus seems to be that Kamala Harris was born in California in 1964, and moved to Canada at the age of 12 with her mother (so around 1976) and returned after completing school in 1981. Like many rumours, this one has a grain of truth, but it would not disqualify her from running as president.

b There are disagreements over details. For example, one website starts by saying Kamala Harris moved to Canada when she was about 5 years old, but later contradicts itself when it says her parents separated when she was 5 years old, and she moved to Montreal when she was 12. This appears to be a careless mistake rather than deliberately fake news and it may well have been corrected subsequently.

c The article mentioned in part a appears to be pro-Democrat. Some neutral websites also corroborate the claim she moved when she was 12.

Fact-checking claims to be a way of warning people against online claims that are not true. However, it only works well if the people doing the fact-checking are reliable. Opponents of fact-checking claim that when fact-checkers make a mistake they are limiting free speech. It is naïve to imagine that the truth will always prevail as in many parts of the world, that is not the case.

Some people’s evidence is more reliable than others. Being able to tell the difference is very important in many situations, such as serving on a jury or deciding what treatment to have when you are unwell.

When you are asked to assess the reliability of a source in your course, you will need to consider and name some or all of the criteria, remembered by the mnemonic ‘RAVEN’ (see Figure 8.2).

KEY TERM

SAMPLE

criteria (singular, criterion): standards or benchmarks used to measure or estimate something.

Figure 8.3: If you serve on a jury you need to judge which witnesses are reliable

TIP

If you are asked the question ‘How reliably can it be concluded that…?’, this is not asking you to assess the reliability of the source. It is about the use of evidence. Likewise if you are asked whether or how a source is significant, it is not asking you about reliability.

SAMPLE

Vested interest and neutrality/bias

Vested interest and neutrality (or bias) are the ‘V’ and ‘N’ of RAVEN. These terms are rather similar so it makes sense to consider them together. Bias is not a separate criterion, but just another name for a lack of neutrality. You will encounter these terms very often, so it makes sense to consider them first. Whenever anyone makes a claim, they almost always have a motive. When a company makes a claim in an advertisement, they want you to spend money on the goods or service they are advertising. When someone tells you ‘I love you’, if they mean it, they want to deepen their relationship with you, though if they don’t mean it, it could just be an attempt to manipulate you.

ACTIVITY 8.2.2: MOTIVES FOR CLAIMS

In pairs, consider any claims that you have made in the last few days and why you made them. For example:

• Have you tried to persuade your friends to do something or to believe something?

• Have you felt under pressure to say something?

• Did you tell a lie (make a false claim) as it helped to avoid an argument or made someone feel better?

Compare your answers with another pair. Then, in a class discussion, build up a list of why people make claims.

If you stand to gain something (or avoid making a loss) by making a claim, then you would have a vested interest. For example, advertisements make claims designed to encourage people to buy goods or services from those who place the adverts, as this will help to increase their profits. Bias, on the other hand, is an inclination to favour one view, or one person or category of persons, when other views are possible, and when you have a duty to treat different views and people with equality. Unlike vested interest, with bias, your attitude does not bring you direct benefit. For example, if someone says ‘I hate men with beards!’ then you can say they are biased. You could also say ‘prejudiced’. This is because you are not likely to be harmed by someone else’s beard. Not all opinions count as bias. If you say ‘I think athletics is boring’ you wouldn’t necessarily be described as biased because people are not under any moral obligation to enjoy all sports equally. However, if you have a job that involves an obligation to be fair to all sports (for example, distributing grants to sports organisations or scheduling televised sports), you would be biased if you said ‘Athletics is boring’.

KEY TERMS

vested interest: a motive of personal benefit (often financial) which may influence someone’s words or actions and thereby weaken their reliability. neutrality: an absence of bias. bias: an inclination to give particular weight to one view when other views are possible, based on personal prejudice, or organisational agenda.

Figure 8.4: Hating men with beards is an example of bias

People rarely admit that they are biased and bias can be subconscious. Bias leads to a desire to believe a particular interpretation of events and vested interest provides an incentive to present an interpretation from which you benefit. Even if a source is anonymous, you can sometimes spot bias if the author uses emotive language. Generalisations based on a person’s race, religion or gender are particularly harmful examples of bias and prejudice. Favouring one’s own family and friends when you are in a position of authority is called nepotism. This is a natural human instinct but it could even go against your vested interests. For example, if you run a small business and you only employ your own relatives, you may well miss out on the best person for the job. You can say that someone is neutral if they are not biased or prejudiced about an issue.

TIP

No one can avoid having vested interests, but you should try to avoid bias. Bias can lead to failing even to try to put yourself in the position of someone else.

SAMPLE

Eunice Newton Foote was a remarkable 19th century American climate scientist. Her story illustrates the sort of bias that was present at that time and for a long time afterwards. Foote’s experiments showed that carbon dioxide is heated more than other gases by sunlight and she was the first scientist to suggest that increases in the amount of carbon dioxide in the atmosphere could contribute to climate change. In 1856, Foote was the first woman to submit a paper to the American Association for the Advancement of Science (AAAS). Due to a bias against women and amateur scientists (women were not eligible for professional posts), her paper had to be read to the meeting by a man. The paper was also not included in the report of the meeting, but it was fortunately published in the 1856 edition of the American Journal of Science and Arts. Three years later, a similar conclusion was reached by an Irish

scientist, John Tyndall, and for the next 100 years or more he was given the credit for discovering what has come to be known as the greenhouse effect. Foote’s article was forgotten, due to a bias in Europe against American scientists, as well as bias against women scientists.

In the 1970s, historians researching early female scientists noted that Foote had been a member of the AAAS, but it was articles by Ray Sorenson (a retired geologist from Tulsa, Oaklahoma) in 2011 and by Katharine Hayhoe of Texas Tech University in 2016 which finally led to Foote being given the credit she deserved in time for the bicentenary of her birth in 2019. More information on Foote’s life story is available if you search online.

TIP

Choice of words can hint at a lack of neutrality. For example, those in favour of some particular public expenditure may say ‘The government should spend more’. Those who are against may say ‘Why should the taxpayer have to pay for this?’

Vested interest can either increase or decrease reliability. Most people tell the truth most of the time. You might think that someone wouldn’t suggest going to McDonald’s unless they genuinely wanted to go; although, it is possible they are just saying it to fit in with friends who like McDonald’s. Telling or publishing lies runs the risk of being found out. At the very least you look dishonest, and there may be legal consequences. Those who lie have a vested interest not to get caught. That means if someone makes a false claim that can easily be checked, they are likely to be found out, and so it is unlikely to be a deliberate lie. Such statements are therefore likely to be true or else a genuine mistake.

Figure 8.5: Eunice Newton Foote

Figure 8.6: A birthday surprise

However, there may be times when you hope to gain by telling a lie, or distorting the truth, or being selective in which facts you reveal and which you keep quiet about. This is likely to be the case if you have done something wrong, but it could be something quite innocent. For example, imagine that you are about to prepare a room for a friend’s surprise birthday party. If the friend walks in and asks you what you are doing, it would spoil the surprise if you tell the truth. When you have a vested interest to lie, your reliability is reduced.

However, if you stand to gain by saying one thing and in fact you say the opposite, your reliability is increased. Why would you say something that harms you if it isn’t even true? This is quite rare and often unintended, such as jokes that go wrong. For example, when the owner of a chain of British jewellery shops criticised his own merchandise (Gerald Ratner in 1991) or an actress criticised the products that she was paid to promote (Helen Mirren in 2017). A category of people who gain credibility by ignoring their vested interest are those who take part in street protests and demonstrations. They almost certainly will have sacrificed time and incurred costs to get to the venue. And they may even face arrest, fines or even imprisonment, often for causes that they feel strongly about but do not benefit them personally. Their vested interest would be to stay well away. Not everyone will agree with them, and their actions can inconvenience innocent people, but their actions show they feel strongly about the issue in question.

TIP

SAMPLE

When describing vested interest, you need to state what claim the person or organisation has a vested interest to make, and what they stand to gain (e.g. payment of money) from making it. You should indicate whether it is vested interest to tell the truth (enhancing reliability) or the opposite.

Most people who post something online have a vested interest in getting people to read it. People can also gain status, and may earn money, by having more followers. For tabloid news outlets, a common way of getting more hits is to provide a link that makes readers curious to know more, and in some cases it is quite misleading. Headlines designed to trick you into following a story online are called clickbait, and stories that are sensational at the expense of accuracy are called yellow journalism in the US. For example, a news item stating ‘All flights cancelled from Orlando International Airport’ looks like it is a story of a major disruption, but when you follow the link it might turn out to be a very short list of cancelled flights. Likewise, during the Olympic Games in 2024, a headline appeared saying ‘Olympian gets medal without competing – no one prepared to face him’. If you were curious enough to click on the link, you would find that the Olympian was a Greek wrestler from the games in 540 BCE.

Celebrities also sometimes like to keep people guessing. During a UK tour in 2024, Taylor Swift posted a picture on Instagram showing her with Prince William and Prince George. She added the caption ‘Happy Bday M8’ (Prince William’s birthday was on 21 June). People, especially in the US, wondered what ‘M8’ meant, so it achieved its goal of sparking interest and debate. (‘Mate’ is a British slang term used when talking to someone in a friendly way. It can be shortened to ‘M8’ in text messages. Taylor Swift and Prince William had met previously.)

SAMPLE

When it comes to court cases, many people assume that no one would plead guilty if they are innocent. The idea of reverse vested interest makes many people think that guilty pleas are generally reliable. If guilty pleas were always reliable there would be fewer miscarriages of justice. However, in order to ensure that guilty pleas are reliable, it is necessary that people are not pressured by circumstances or by the system to plead guilty when they are innocent.

KEY TERMS

reverse vested interest: a situation in which someone gives evidence contrary to their vested interest, e.g. because it incriminates them or costs them money. This strengthens their reliability.

Figure 8.7: Taylor Swift and Prince William met in 2013

ACTIVITY 8.2.3: PLEADING GUILTY

When someone is accused of a crime and the case comes to court, there are four possibilities:

a they are innocent and truthfully plead ‘not guilty’

b they are innocent but lie and plead ‘guilty’

c they are guilty and truthfully plead ‘guilty’

d they are guilty but lie and plead ‘not guilty’.

In pairs, consider possible vested interests which would explain each of the scenarios.

COMMENTARY

You may think the second situation in the list is the most surprising. If you need some hints about when and why it happens, do an online search for ‘why the innocent plead guilty’ or look for information about the Innocence Project.

Chiefs of businesses and organisations have a number of duties and vested interests which can sometimes conflict. They have a duty to employees and investors to do their best to ensure that the business or organisation survives and prospers. Company lawyers will generally advise them to avoid admitting any liability that damages the company’s reputation or profits. On the other hand, they have a moral duty to be honest and open in dealings with customers and the general public. Employees can face a similar conflict of interest: they may feel a moral duty to report when things are not as they should be (known as whistle-blowing), but they may well have signed a contract which prohibits disclosing anything about their work.

ACTIVITY 8.2.4: VESTED INTEREST

Imagine that you work for a large organisation, such as a manufacturer of airplanes. You discover that something dishonest or unsafe is going on in the organisation. If this information became public knowledge, it would seriously damage the organisation’s reputation and finances.

Research an example of where this happened (for example, the Boeing 737 MAX crashes). Then discuss your example with the rest of your class. You should consider the following questions:

a What are your vested interests for the following options: i to hush it up ii to admit it?

b How are your vested interests changed if you are the leader of theorganisation?

COMMENTARY

The first Boeing 737 MAX planes entered service in May 2017. The first 737 MAX plane to crash was 17 months later on an internal fight in Indonesia, and five months after that, a similar plane crashed soon after taking off in Ethiopia on a flight to Kenya. The entire fleet was grounded for the next 20 months as a result. Articles suggest that the whole episode cost Boeing US$20 billion in fines, compensation and legal fees by 2020, with further cases still going through the courts, and the loss of 1200 orders. In 2021 Boeing paid US$2.5 billion in penalties to settle the Department of Justice’s fraud conspiracy case against the company. Once the planes had crashed, the option to keep quiet about safety concerns was no longer open, so the significant aspect of the affair is what was known and what was done before the crashes.

If there is a significant chance that the truth will come out, then vested interest demands that the leader be open about it from the outset. It may help limit the harm done, and there is also a moral duty to the victims. Particularly in politics, if someone is found to have lied, they may lose their job or be forced to resign.

Many organisations have had their reputations damaged by publicity which is bad for them. This may lead you to think that honesty is best, because sooner or later any problems will become public knowledge. However, no one will ever know how many organisations have successfully covered up scandals, because if the cover-up is successful, it means no one will ever know about them. When scandals do become public, large organisations often spend large sums of money on attorneys in order to defend their reputation.

Figure 8.8: A protest by relatives of the victims of the Boeing 737 crash

ACTIVITY 8.2.5: PARTIAL TRUTHS

a In pairs, make a list of occupations where people are paid to present a one-sided argument and therefore have a vested interest to present partial truths rather than the whole truth. Compare your list with another pair. Next, in your pairs, discuss:

b Would you rather have a career in which you are paid to present alternative viewpoints or one in which you are paid to present a one-sided argument?

c What situations can you think of in which someone has a duty to do one thing and a vested interest to do the opposite (known as a conflict of interest)?

REFLECTION

Think about a time when your vested interest was to do or say one thing, and you said or did something different. Why did you choose to do that?

Expertise

The ‘E’ in ‘RAVEN’ stands for expertise

You can take someone’s claims more seriously if the person knows what they are talking about. The expertise of an individual can be judged by their qualifications (a degree or a doctorate, for example) or by their profession, since to enter a profession they will need to have qualifications. If the reliability of a claim or a document is to be boosted by expertise, then the expertise has to be relevant

ACTIVITY 8.2.6: EXPERTISE

SAMPLE

KEY TERMS expertise: the ability to make sound judgments using specialist knowledge or skills. relevant: having a close connection to the topic or claim.

Vitamin C is found in citrus fruit, such as lemons, and the juice from such fruit has been known for centuries to prevent scurvy. Historically, scurvy was a disease that was common in sailors, but it is now associated with people who are malnourished. Linus Pauling was a professor of chemistry at the University of California and later at Stanford University. In the decade from 1966 onwards, Pauling wrote about the benefits of large doses of Vitamin C in preventing the common cold and even cancer.

In pairs, look up the claims that Vitamin C can prevent common colds. You should then discuss whether the reliability of these claims was boosted by Pauling’s expertise. In particular, consider whether his expertise was relevant.

Figure 8.10: Citrus fruit

Figure 8.9: Linus Pauling

Expertise is also a reliability criterion that applies to organisations, such as universities and governments, because they employ people who are experts. Reports in academic journals also have their reliability increased because they cannot usually be published until other experts in the same area have read them and consider them to be reliable. This process is called peer review.

Students sometimes think the ‘E’ in RAVEN stands for experience. However, it is better to refer to expertise because that is the term used in this course. Although, it is true that experience and expertise usually go together. Even a newly qualified doctor, for example, will have gained a lot of experience during their training.

ACTIVITY 8.2.7: EXPERIENCE OR EXPERTISE?

In pairs, consider the following people and decide whether you would describe them as having experience, expertise, both or neither?

a A person who passed their driving test 40 years ago and has been driving regularly ever since

b A newly qualified doctor

c A taxi driver

d An astronaut who is being sent into orbit for the first time

e A parent who has raised six children

COMMENTARY

Expertise refers to specialist knowledge that only a few people have, so if you are experienced in some everyday activity like driving, commuting, using medication, sending emails or raising children, you probably would not be regarded as an expert.

Can you be an inexperienced expert? Certain degrees such as teaching, medicine, dentistry, etc. involve large amounts of practical experience, so in general it is hard to become an expert without at least some experience. In a few areas, no simulation is quite like the real thing; for example, an astronaut going into space for the first time, a pilot making their first solo fight or someone in the armed forces facing live combat for the first time. These people could be described as having expertise, but lacking experience.

Ability to see (or to hear, etc.)

The ‘A’ in RAVEN stands for ability to see. This can be associated with expertise, in that if somebody works in an organisation, they will have expertise in how it operates and also the ability to see what goes on in the organisation. This is an ongoing ability to see. However, ability to see sometimes refers to a particular event. In such a case, factors such as fog, darkness, intoxication, distraction, distance, etc. can reduce the ability of witnesses to see events accurately.

KEY TERM

ability to see (hear, perceive, etc.): presence as an eye-witness to a particular event, or an ongoing presence, e.g. as an employee in an organisation, gives someone this ability. Researchers and government departments also have the ability to see data.

Figure 8.11: In a foggy street it is harder to see

In describing ability to see, you should consider whether it is:

• first-hand evidence: used when someone is describing something that they really saw or heard

• second-hand evidence: used when someone is just reporting what another person told them (it is not admissible in court, because it could just be rumour or gossip). For historical events from long ago, first-hand witnesses will no longer be alive, so the ability to see documents written at the time will be the best available option.

The general term ability to perceive can be used as an alternative to ‘ability to see’ if you want to include the ability to hear or use any other of the senses.

Reputation

The ‘R’ of RAVEN stands for reputation, which means the generally held opinion about a person or organisation. Reputation could be regarded as the least useful reliability criterion. You cannot be expected to know whether a particular individual, organisation or publication has a good reputation. The generally held opinion about a person or organisation depends on who you ask. You could reasonably suggest that an organisation like the United Nations has a good reputation, but not everyone would agree. Whether or not you think your government has a good reputation is influenced by which political party you support. In countries that do not have an effective opposition, the leader may appear to enjoy a good reputation, but that could just be because people are afraid of making any criticism of their leader.

SAMPLE

The reputation of organisations, businesses, buyers and sellers is often displayed online. Customers are often invited to give a product or a service a rating of between 0 and 5 stars and the average number of stars is then displayed. The problem with such ratings is the difficulty of preventing comments that are biased and/or the result of vested interests. For example, a person caught shoplifting might get their revenge by giving the shop a bad review. Employees and business workers may leave fake bad reviews of their competitors, and fake good reviews of their own business. Similarly, the number of ‘likes’ on a social media post is not a good indication of the reputation of the person who posted. In part this is because social media platforms direct people to posts that express views that they agree with.

KEY TERM

reputation: the generally held opinion about the reliability of a person, group of people, or organisation.

Some people are famous because of their expertise, and in those cases it would be appropriate to name both expertise and reputation as relevant reliability criteria. You might think that someone is reliable because they would not want to damage their reputation by lying. Whilst that is usually the case, it is an example of the reliability criterion of vested interest rather than reputation

SAMPLE

TIP

When assessing reliability, always name the criterion, say why it applies, and say whether it increases or decreases reliability.

Look for factors on both sides. If you find them you can judge that the source is moderately reliable. If they are all on one side you can judge the source is very reliable or very unreliable.

ACTIVITY 8.2.8: THE PANAMA CANAL

In 1879 there was an international conference in Paris that had the aim of approving a plan for a canal in Panama connecting the Atlantic and Pacific Oceans. There were two proposals. The first was by Ferdinand de Lesseps who had studied law, become an expert horseman, and negotiated the construction of the Suez canal, completed in 1869. He had been a French diplomat in Egypt. His proposal was for a canal at sea level.

The second was by Adolphe de Lépinay, a civil engineer from a leading French Polytechnic, with experience of building railways in Algeria and Mexico, who proposed a canal involving dams and locks, which would require less excavation and be less costly to build.

De Lesseps had more influence and his plan was adopted. Work began in 1881, but the money ran out in 1889. Thousands of labourers, mainly from Jamaica, died from malaria and yellow fever. A new company was formed in 1894 and work resumed.

Figure 8.12: The Panama Canal

CONTINUED

8.13:

A major shareholder was a French man, Philippe-Jean Bunau-Varilla, who grew rich from the project as his company carried out much of the excavation. The region was at that time part of Colombia. Money again ran out with the work far from complete. Meanwhile the US became more interested in a canal for commercial and military reasons, but favoured a longer route through Nicaragua, which was seen as politically more stable than Colombia. Bunau-Varilla wanted to recoup some of his investment by selling the Canal Company to the Americans, so he lobbied US senators against the Nicaragua route by sending senators Nicaraguan stamps showing a volcano, Mount Momotombo, which he claimed would threaten a canal in Nicaragua (in fact the volcano is 150 km NW of the proposed route).

His campaign was successful and the US bought the French Canal Company for $40 million, much less than investors had invested, but better than nothing. Colombia was unhappy with the amount offered to them. Bunau-Varilla befriended Panamanian dissidents and in 1903 with US backing, they proclaimed independence from Colombia. Bunau-Varilla became Panama’s ambassador to the US, and the canal was completed in 1914, using a system of locks like those originally proposed by de Lépinay.

a In what ways did reputation, expertise, ability to see and vested interested of de Lesseps, de Lépinay and Bunau-Varilla contribute to the history of the construction of the Panama canal?

b In what ways did the vested interests of the US and Colombia contribute to the history of the Panama Canal?

Figure

Construction of Panama Canal

CONTINUED

WORKED SOLUTION

a Consider the 1879 conference and apply the RAVEN criteria. In terms of reputation, de Lesseps was more famous than de Lépinay because of his role in the construction of the Suez Canal, so his reputation and diplomatic skills got the investors on his side. However, as a civil engineer, de Lépinay had the more relevant expertise, and first-hand experience of the region. So he had the ability to see possible problems such as the fact that there was a lot of malaria and yellow fever in the area. De Lesseps’ expertise was in law, horse riding and diplomacy, which was less relevant. The fact that when the canal was finally built, the design resembled that proposed by de Lépinay shows with hindsight that he was right. (It has been suggested that if his plan had been adopted from the start, the canal would have been completed by the French 20 years earlier, on time and on budget.)

Bunau-Varilla, as a major shareholder in the French Canal Company and major contractor in the construction in the Panama site, had expertise and ability to see, which was not called into question by any of the parties involved. More significant was his vested interest. If the US had built the canal in Nicaragua, all his investment in the Panama site would be worthless, so it was in his interest to lobby against the Nicaragua route. The fact that the canal is where it is, and not in Nicaragua, is partly due to his vested interests. b Colombia had a vested interest in seeing the canal completed because as long as Panama was part of Colombia, it would be a valuable source of revenue. However, by refusing to agree to a deal with the US it gave the US a vested interest in considering an alternative route through Nicaragua, and once that idea was dropped, the US had a vested interest to encourage Panamanian dissidents. In return for US support, the new state of Panama agreed the deal with the US that Colombia had refused.

Use of sources

You might use sources (labelled A, B, C, etc.) to present an argument and you will therefore need to evaluate their reliability. If you evaluate a source that appears to support your argument, but you then conclude that it is unreliable, then it is not really helping to support your own argument. In this situation, you can mention features that make the source unreliable but you could then go on to say that whilst the source is not completely reliable in every respect, it is reliable enough to still support your conclusion.

TIP

SAMPLE

When using sources to argue to what extent you agree with a claim, it is best to structure your response in paragraphs. Each paragraph should relate to a single theme, and brief references to sources when they relate to the theme of the paragraph. The first time you mention a source, you should also comment on its reliability. It is less effective if you devote a paragraph to each source, and then go on to quote or paraphrase long sections of text from the source.

8.3 Plausibility

Reliability is purely about where a document or source is coming from. Plausibility focuses entirely on what claim or claims are being made within the document, irrespective of the reliability of the source.

• Plausible: a claim is said to be plausible if it is likely to be true.

• Implausible: a claim is described as implausible if it is unlikely to be true.

• Questionable: a claim is described as questionable if it is somewhere in between these extremes. When evaluating a document ‘reliance on a questionable claim’ is one of the weaknesses you can name and explain.

Plausibility is similar to probability, but not the same. Probability is a mathematical concept and applies to a future event for which there are a number of equally likely outcomes. For example, there are six equally likely outcomes when you throw a dice and the probability of each is 1/6. There is also a difference in the way the corresponding adjectives are used. If you say something is ‘probable’ it means that it is more likely to happen than not to happen. However if you say something is ‘plausible’ it means it could possibly happen. So when you throw a dice once it is plausible, but not probable, that it will show a 3. It is however both plausible and probable that the number shown will be 3 or more.

KEY TERM

plausibility: the likelihood that a claim is true.

Figure 8.14: Eugene Cernan; last man on the moon?

Plausibility is more often used for claims about the present or the past. Even without checking, you could say it is plausible that it rained in Miami yesterday. However it would not make sense to refer to the probability that it rained in Miami yesterday: either it did or it didn’t rain.

When you consider future events, you can refer to probability. For example, you can see on your phone the probability that it will rain in Orlando tomorrow or the probability that Miami Dolphins will beat Buffalo Bills, even while the match is being played. Insurance companies need to use their data to calculate probabilities in order to set insurance premiums. In this case, unlike throwing a dice, the different outcomes are not equally probable, so they are not calculated from pure mathematics, but from data from similar situations in the past. That is one reason why data is such a valuable commodity.

Whether or not a claim is plausible in part might seem to be down to gut-feeling (a feeling based on an emotional response rather than considered thought), and therefore rather subjective. However, even gut-feeling is often based on experience and context. When an experience is common to most people, it is possible to reach some agreement about what is plausible. If something happens very often, it is generally highly plausible to claim that it will happen again, but it doesn’t always follow. For example, when Eugene Cernan and Harrison Schmitt left the surface of the moon in December 1972, there had been six crewed moon landings over the past three and a half years, so it would have been very plausible to claim that there would be more before the end of the millennium. However, this did not happen. Claims referring to the future are sometimes called predictions and there is always a certain degree of uncertainty about future events.

ACTIVITY 8.3.1: SENDING HUMANS TO MARS

In pairs, research the cost and length of time it would take to send humans to Mars. You should then have a class discussion to discuss the plausibility of the claim that ‘Humans will land on Mars before the end of this century.’

SAMPLE

Figure 8.15: Unmanned landing on Mars, but when will people go there?

There is a danger that the world will be unprepared for events that have a low probability but could have extremely bad consequences. In 2019, many countries were unprepared for the effects of COVID-19. At the other extreme, there is a growing number of people called preppers or survivalists. These people sometimes go to great lengths to prepare for disasters that are plausible and they regard as near-certainties, but other people think are improbable.

When politicians make promises, they need to be able to come up with plausible estimates of the cost. The British politician, Diane Abbott, promised her party would recruit 10 000 extra police officers over four years. When asked the cost, at first she said £300 000. The interviewer spotted immediately that this was implausible as it means the officers would only be paid £30 (about $40) per year each. When challenged, she hesitated and then came up with a figure of £80 million. That is more plausible, as the cost per officer works out at £8000 (about $10 000) but still way below typical police salaries.

Plausibility does not need to be applied to claims that are true by definition (e.g. all triangles have three sides) or claims that can be proved mathematically (e.g. the internal angles of planar triangles add up to 180°). In critical thinking you should not apply the term to people (unlike reliability) but only to claims. So you would never say ‘The Chief Executive is plausible’ however much you might agree with them. However, you could say ‘The Chief Executive’s claims are plausible’.

SAMPLE

Figure 8.16: A survivalist outside his fallout shelter in Canada

ACTIVITY 8.3.2: CREDIBILITY

Assess the credibility of the following source.

Press release from a company supplying paper towels

SAMPLE

One of the world’s top polling companies conducted an opinion poll among 2048 US adults. 69% of respondents said they preferred to use paper towels rather than electric hot-air dryers when drying their hands in public washrooms.

Of those who preferred paper towels, the top five reasons given were:

• towels dry hands better – 70%

• towels dry hands faster – 69%

• towels can be used to open the washroom door – 52%

• air dryers blow bacteria – 24%

• air dryers are too loud – 22%.

WORKED SOLUTION

What are the steps you need to take?

Think about who the people or organisations are whose credibility needs to be assessed.

Answer: The polling company, the Paper Towel Company, that commissioned and published the poll, and possibly the people who responded (or failed to respond) to the poll.

What are the relevant aspects of credibility?

Answer: Reliability and plausibility. The former is divided reputation, ability to see, vested interest, expertise and neutrality/bias. Then apply each of these criteria to each of the organisations.

Answer:

The polling company: you are told it is ‘one of the world’s top’, which implies it has a good reputation and good level of expertise. The sample size of 2048 should be sufficient for them to have the ability to see/know the truth about the views of the population. All of these factors strengthen the reliability of the source. However, you are not told if 2048 was the number asked or the number who responded.

The Paper Towel Company: they have a vested interest to sell paper towels, therefore they are biased/not neutral in which bits of the survey results they choose to publish. This is shown by the fact that they have only published the reasons why the 69% prefer paper towels, and not the reasons why some or all of the other 31% prefer air dryers. This weakens the reliability of the source.

8.17: Are paper towels better than air dryers?

Figure

CONTINUED

The respondents: the reasons given for preferring paper towels are all plausible (it is not clear whether these were obtained from respondents’ answers to an open-ended question ‘Why do you prefer paper towels?’ or whether they were selected by respondents from a list provided by the pollsters). The topic is not a sensitive or embarrassing one, so respondents will not have had a vested interest to lie; moreover as almost everyone uses public washrooms, they have the ability to see the benefits of paper towels; their responses can be taken as reliable. These factors strengthen the reliability of the source.

What is your overall assessment (judgment)?

There are factors that increase reliability, and others that decrease it, so the overall judgment is that the source is moderately reliable.

8.4 Corroboration and consistency

Both corroboration and consistency refer to the extent that two (or more) claims agree with each other. The two claims could be found in the same source or document, in which case you would expect them to agree, but agreement is more significant when two independent sources agree with each other.

Corroboration

Two (or more) sources corroborate each other if they both make the same claim, or agree about an explanation. This enhances the credibility of both. An example would be witnesses in court whose statements agree with each other. The enhanced credibility only arises if the sources are independent; if one source simply copied the other, or, in the case of witnesses, if they came to an agreement about what to say, then it doesn’t increase credibility.

ACTIVITY 8.4.1: CORROBORATION

Look online for an account of the trial of Alex Murdaugh in South Carolina in 2023. This trial attracted a lot of attention at the time. You should make a list of pieces of evidence that do corroborate each other and pieces that do not. Next, consider the following questions:

KEY TERMS

corroboration: an additional independent source giving evidence supporting the original claim. consistency: when two or more claims are made and it is possible for both to be true at the same time.

SAMPLE

a Where there is a lack of corroboration, which witness is more credible and why?

b Why are alibis (a form of corroboration) not always reliable?

Consistency

Two claims are consistent with each other if it is possible they are both true. For example:

• John was seen in Poughkeepsie at 16:00 on Thursday 24 October 2024

SAMPLE

• John was seen boarding the 13:43 train from Grand Central Station, New York to Poughkeepsie on Thursday 24 October 2024.

These claims are consistent because the 13:43 train reached Poughkeepsie at 15.40 on that day as the records show it was on time, and that was when it was due to arrive.

If the first claim had said 15:00 instead of 16:00, the claims would be inconsistent with each other. A student might be tempted to say the claims contradict each other, but saying they are inconsistent is preferred.

ACTIVITY 8.4.2: CONSISTENCY

Since World War II, generations of people in the UK have been brought up to believe that eating lots of carrots enables you to see in the dark.

a Why might the fact that such advice appeared to be repeated by many sources not necessarily count as corroboration?

b Can you think of an example in your own country where a story that is repeated in many places can be traced back to a single source?

Figure 8.18: Alex Murdaugh during his trial

You have now learned about the criteria for assessing credibility and reliability of sources. Activity 8.4.3 is an opportunity to apply all of these criteria.

ACTIVITY 8.4.3: CREDIBILITY CRITERIA

In small groups, select one of the events A to E. Research the event online, in particular focusing on whether and how the event was influenced by credibility criteria.

Once your research is complete, your group should create a presentation and deliver it to the rest of your class.

A The prosecution of Clarens Desrouleaux in Miami in 2013 for burglary.

B The UK Post Office prosecution of William Quarm in 2010.

C The cross examination of Mandy Rice-Davies about her relationship with William Astor by James Burge at the trial of Stephen Ward in 1963.

D Tom Sawyer’s actions in class with Becky Sharp in the novel of the same name by Mark Twain (Chapter 20).

E The trials of Rosa Parks in Montgomery, Alabama in 1955 for refusing to give up her seat on a bus to white man and in 1956 for her part in organising the bus boycott that followed.

TIP

A key skill in this course and in life is listening to other people, and understanding the strengths and weaknesses in what people are saying. This is something you can practice during pair or group work in your course, and also when evaluating the sources when answering written questions. One way of practicing this skill is to discuss a topic in pairs and then feed back your responses to the rest of the class. You can take it in turns to summarise what each other has said.

REFLECTION

You have now learned about credibility. How has this helped you to re-evaluate claims that you have always believed? How can you now apply credibility criteria elsewhere in other subjects that you are studying, such as history, politics or economics?

ACTIVITY 8.4.4: RELIABILITY

Decide how many marks (out of a maximum of 3) you would give each of the following responses. When you have finished, compare your marks with a partner.

SOURCE A

Post by a mother on social media

My daughter has done far better in sport since I bought her this brand of trainers. Her PE teacher used to say that she wasn’t very talented at sport, but it was just because she was wearing cheap trainers. Now she has these amazing trainers, she is running much faster. Her friends can’t keep up with her any more.

Question Assess the reliability of Source A [3]

Source A has many factors to credit or hinder reliability, such as being opinion-based. The parent in the text makes claims highlighted by non-factual opinions. The reliability of this source can be truthful but since it is an opinion piece, it is low.

There is no statistical evidence so the source doesn’t have much to make it reliable. You don’t know who the person is, so you can’t tell if they have expertise or reputation. You don’t know what the website is so you can’t tell if it is reliable.

Source A is not reliable. It is a social media post, and social media has a reputation for spreading false or inaccurate information. The author of the post also has an extremely limited ability to see because they only have experience with one child, and a limited expertise because they do not seem to be a PE teacher. Finally, the author has a vested interest in viewing the trainers as successful because they want their daughter to do well in PE.

The reliability of Source A is not reliable because nothing in this source is reliable enough to back it up.

The source has some credibility. The mother is the only one who has seen this improvement.

Source A is not reliable because even though the child reports running faster, every child is different and the trainers might not be great for every child. And not everything you learn online is true.

8.5 Perspectives presented in evidence

The literal meaning of perspective refers to the way in which the image of an object or scene changes with the position of the observer. In critical thinking, however, different perspectives on a topic refer to the fact that the insights, assumptions and biases that people bring to an issue depend on their point of view or way of thinking about things. This will influence the way people select and describe the evidence that they present in support of an inference.

This can be illustrated by an example that will be familiar to anyone who watches the news. When the central bank of a country announces a change in interest rates, it makes the headlines of the financial news. The news coverage usually sees a rise in interest rates as a bad thing. This is because banks and other financial lenders generally follow the central bank’s lead and raise interest rates.

However, there is an important and different perspective. Many people in their working years will be paying in to a pension fund in order to make sure that they have an income when they retire. Pension funds depend not only on the contributions of members but also on the interest that these savings can earn. Higher interest rates are therefore a good thing for pension savings. Moreover the total amount of pension savings in a country is typically more than double the total amount of mortgage debt (this is the case for the US, the UK and many other countries). A likely reason why this perspective is more neglected is that most people are unaware and uninterested in how the value of their pension savings change month by month (especially young people, for whom retirement seems a long way away). On the other hand, people are immediately aware when their mortgage payments rise, and very quick to feel the impact.

There is an overlap between the idea of perspectives and the idea of vested interest. You could say that people with mortgages stand to gain from lower interest rates whereas people who have contributed to pension funds stand to gain from higher interest rates. Whilst that is true, the picture is made more complicated by the fact that many people are in both groups; they have a mortgage and pension savings.

KEY TERM

perspective: the point of view that a person has, which will influence the assumptions, insights and biases they bring to a topic.

PROJECT

Credibility of the evidence

In groups, choose a well-known trial. You could use one of the following examples.

• Ethel and Julius Rosenberg, 1951: found guilty of espionage.

• Patty Hearst, 1976: viewed as both victim and guilty. Patty was kidnapped by an extremist group in 1974, but was convicted of assisting them in a bank robbery, and then later pardoned.

• John Hinckley, 1982: accused of an attempted assassination of Ronald Reagan. He pleaded insanity and was committed to a psychiatric hospital.

Your group should consider the credibility of the evidence for the prosecution and for the defence. One member of the group should present the historical background to the rest of the class. One student should sum up for the prosecution and another should sum up for the defence. The rest of the group’s members should prepare notes for the rest of the class about how the trial raises issues of reliability, plausibility and corroboration/inconsistency.

SUMMARY

SAMPLE

• When considering the reliability of a source, (i) name some or all of the RAVEN criteria and (ii) explain how and why they apply to the source. Do not talk about plausibility, and do not simply summarise what the source says and why you agree or disagree with it.

• When you consider the credibility of a source, in addition to the details from the last bullet point, you can also talk about plausibility, and when comparing two sources you can consider corroboration and consistency

• When you describe the significance of a source, or whether a source supports a particular claim, do not talk about the credibility points in this chapter. Instead, you need to consider the use of evidence, which is described in the next chapters.

Figure 8.20: Patty Hearst

Sample answer

Study the evidence and then answer Question 1.

Source A: Post by a mother on social media

I have had far fewer behavioural problems with my 9-year-old son since I began homeschooling him. The teachers at his old school tried to make him learn subjects like maths, even though he just does not understand them. He can learn much more online. This morning, he gave me a piece of paper with something scribbled on it, which I couldn’t read, and he told me he had taught himself to write Arabic online.

Question

1 Assess the reliability of Source A.

Sample answer

Posts on social media have a reputation for being unreliable. 1 The mother has a vested interest to justify her decision to homeschool her son by claiming that it has been successful. 2 She is biased against school because her son got into trouble there. 3 She has some ability to see how her son spends his time, but not whether his claim to be able to write Arabic is true or not. She appears to lack expertise in teaching. 4, 5

3 If, as is likely, there are criteria that decrease reliability and others that increase it, it is advisable to include points on both sides.

4 This point may appear at first sight rather speculative. The source does not say that the parent has no training as teacher, but her comment is so dismissive of maths and is therefore unlikely to be something a trained teacher would say.

5 As there are three marks, you must make at least three points; if possible your points should be about different reliability criteria. If you can think of more than three points, give them all in case some of your points are not correct, as long as you don’t waste time by going into too much detail. This response has five distinct points.

1 A comment like ‘you can’t always believe what you read on social media’ is true, but it is advisable to use the term ‘reputation’ like in this sample answer, as it is one of the RAVEN criteria and this is a question about reliability.

2 This point and those that follow would be improved further if the student said whether this decreases the reliability, as it does in this case.

Practice questions

Study the evidence and then answer Question 1.

1 How reliable is Source A?

SOURCE A

Advertisement from private health clinic

PEACE OF MIND BECAUSE YOU ACTED IN TIME

Our Full Body Scan provides immediate insight into your health

[3]

A Full Body Scan is a complete physical examination, aimed at detecting how likely you are to develop specific medical conditions. If detected in time, treatment may be available, which will slow down the development of the condition or completely cure it. The key focus is on heart disease, cancer and dementia. We can also highlight hereditary factors that make you likely to develop these conditions. Recognising risk will mean effective action can be taken to safeguard your health.

Adapted from Cambridge International AS & A Level Thinking Skills 9694 Paper 23 Q1(a) June 2020

Study the evidence and then answer Question 2.

2 How reliable is Source B? [3]

SOURCE B

Retired teacher’s blog

Questions about the authorship of Shakespeare’s plays are being raised yet again. This reminds me of the time, more than 50 years ago, when I was studying 16th century English Literature in my first year at university. In my opinion, Christopher Marlowe was the only one of the authors we studied who could conceivably have gone on to write the plays attributed to Shakespeare.

Adapted from Cambridge International AS & A Level Thinking Skills 9694

Paper 21 Q1(e) Nov 2020

Study the evidence and then answer Question 3.

3 Assess the credibility of Source D. [3]

SOURCE C

Education News

For an experimental period, lessons for 16–18-year-old students at one school have begun at 13:30 and ended at 19:00. Lessons for younger pupils have remained at more traditional times. The school believes the experiment has been a success and has proved that the later working hours are more productive and less stressful for the students. The school has therefore decided to make this arrangement permanent. The headteacher commented that poor sleep routines had a “significant impact on teenage cognition and mental and physical health generally”. One student said, “I want to wake up in my bed, not in my maths lesson.”

SOURCE D

Comment on Source C

As a teacher, I hope that other schools will not imitate this ill-judged experiment. Teachers are people too, and we have the right to spend time with our own families. If students switch off their mobile phones and go to bed at a reasonable hour, they will be bright and alert in the mornings. Indulging their wishes in this way will not help them long-term, because they will soon find that employers will expect them to be at work on time, ready to put in a day’s work for a day’s pay.

Adapted from Cambridge International AS & A Level Thinking Skills 9694 Paper 21 Q1(e) June 2021

Study the evidence and then answer Question 4.

4 How useful is Source E in determining how Christopher Marlowe died? [3]

SOURCE E

Book Review, 2002

Mei Trow’s book, ‘Who killed Kit Marlowe?’, casts doubt on the official account of the death of Christopher Marlowe. Trow, a historical novelist, has discovered that Marlowe’s companions on the fatal day were all employed by the Government and were promoted soon after the death and inquest had taken place. Trow has studied documents written at the time of Marlowe’s death, which reveal that he was facing interrogation and trial as part of an investigation into illegal beliefs and practices amongst men in high positions; several other people had already been convicted and executed as a result of this investigation. If Marlowe had been interrogated under torture, he would probably have implicated powerful men in these crimes. Trow’s theory is that these political leaders paid Ingram Frizer to murder Marlowe and bribed the other two men to give false evidence at the inquest.

Adapted from Cambridge International AS & A Level Thinking Skills 9694 Paper 21 Q1(b) Nov 2020

Study the evidence and then answer Question 5.

5 a i What inconsistencies are there between these two accounts? [2]

ii In what way does Source G corroborate Source F? [1]

b Source G says Source F was ‘prompted by vested interests’. Explain whose vested interests might be served by press stories like Source A. [3]

c Assess the reliability of Source G. [2]

SOURCE F

Popular Newspaper Article

American fool sues McDonald’s for $2.9 million after spilling her coffee She bought a coffee from McDonald’s and whilst driving her car she spilt some on her lap, and sued McDonald’s for $2.9 million. She claimed the coffee was too hot. People bringing massive claims for damages over trivial incidents like this, which are their own fault, are costing us billions and changing the way we live according to organisations representing insurers. When businesses and their insurers end up paying ridiculous sums it forces them to put up their prices, so we all end up paying for other people’s stupidity.

SOURCE G

Comment by a lawyer

The media reports of this incident were highly misleading, and prompted by vested interests. The woman was a passenger in a car. The coffee she bought had been heated to over 80°C. The spillage caused 3rd degree burns, and she was given skin grafts in hospital for 8 days, disabled for the next 2 years, and permanently scarred. She didn’t originally sue, but just asked for reimbursement of her medical bills of $15 000. Only when McDonald’s offered her far less did she instruct a lawyer. At the trial it was claimed the firm knew the coffee was a hazard as there had been hundreds of previous complaints. The New Mexico jury recommended damages of $2.7 million, based on the estimated revenues for two days of coffee sales. The judge reduced the damages to $640 000. McDonald’s appealed and the case was finally settled out of court for an undisclosed smaller amount.

Study the evidence and then answer Question 6.

6 a Assess the credibility of the claims in Source H.

b Assess the credibility of the claims in Source I.

SOURCE

H

Online advertisement

[4]

[2]

SAMPLE

Energy companies don’t want you to know about this simple trick to heat your home, which will save you thousands of dollars on your heating bill this winter. The Magic-Heat is an ingenious way to heat your home without wasting money is sweeping the market. A clever student from Chicago University has destroyed the billion dollar heating industry by inventing a brilliant device that can heat any space at 90% less cost than conventional heaters. Brett developed the device in response to financial constraints that mean he could not afford to heat his room. With a knack for engineering and a strong desire to help his classmates, he cleverly figured out how to reverse engineer a basic air heater; he made a special device that creates a heating loop by reusing the heat that is produced so that none of it is wasted. He took this gadget to the university and the outcomes were fantastic. In carefully controlled conditions, the temperatures in almost freezing classrooms went from 10°C to 21°C in only two minutes. What’s even more impressive is that it used 85% less energy compared to regular heating systems. As news spread about his invention, investors came forward; a professor even predicted that Brett was destined to make history. However when a heating company offered him millions for the rights, Brett firmly declined. As a consequence he was expelled a few days later. This is when he truly grasped the significant impact his device could make. Brett partnered with top engineers in his field to prepare and enhance it for mass production. This innovation quickly warms rooms using minimum electricity, recycling warm air to minimise energy waste; its heating ability surpasses that of any standard system. It has ceramic heating technology that directs air over a meticulously engineered heating element. It can warm up rooms in minutes, costing only a few cents per day. It has been proved to be 97% more effective than traditional heating systems. Simply plug it into any power outlet in your home, set the temperature and the heater will warm up your room in just a few minutes. It’s effective in rooms up to 60 m2 in size. When Brett introduced the heater to the public, it quickly gained popularity, selling out in one day after going viral. The high demand resulted in a waiting list of over 79 000 orders. Brett is keen to share this ground-breaking technology with everyone, and to meet the demand he has tripled the production. For a limited time there’s a special 50% off welcome-back sale for anyone who orders it within the next 24 hours. This is a fantastic deal that may not last long, so it’s best to act now. My advice; secure yours before the price goes up. Click the link below to visit the official website and claim your discount today. This $70 heater warms up any room quickly without spending a fortune on heating.

SOURCE I

Online comments

This is clearly a scam. The Magic-Heat should be called the Mega-Cheat. Online platforms should not allow advertisements like this to trick people out of their money. AB

Any electric heater converts virtually 100% of the electrical energy you put in into heat. It is impossible to get more energy out that you put in, so there is nothing special about this device. CD

Heaters like this are made in the Far East for a few dollars. Someone in Eastern Europe has bought up a supply of these heaters and is selling them on with greatly inflated claims and greatly inflated prices. EF

You have only got to look at the reviews. Nearly all of them have given the firm the lowest possible star rating. GH

Avoid this. If you try to return the heater they do not reply and do not refund your money. JK

I got one from a friend yesterday who bought three from overseas. It warms the room effectively. LM