SC 6th Grade (Volume 1)

VOLUME 1

Grade 6 SOUTH

CAROLINA

ISBN: 979-8-893539-03-5

Math Nation 6-8 was originally developed by Illustrative Mathematics®, and is copyright 2019 by Illustrative Mathematics. It is licensed under Creative Commons Attribution 4.0 International License (CCBY 4.0).

The online curriculum resource platform offered at "mathnation.com", including the videos and practice questions are additions to the original Illustrative Mathematics content is copyright 2023 by Accelerate Learning, Inc.

The trademark "Math Nation" is owned by Accelerate Learning, Inc. All other trademarks and product names referred to in the Math Nation AGA curriculum are the property of their respective owners and used solely for educational purposes. Unless otherwise stated, Math Nation has no relationship with any of the companies or brands mentioned in the curriculum and does not endorse or have a preference for any of those companies or brands.

This curriculum includes public domain images or openly licensed images that are copyright by their respective owners. Openly licensed images remain under the terms of their respective licenses. See the image attribution section for more information. 00820231215

ManuscriptCopy

ManuscriptCopy

Unit 1: Area, Surface Area, and Volume

ManuscriptCopy

Unit 1, Lesson 1: Finding Area by Decomposing

and Rearranging

Warm-Up: Finding the Area of Rectangles and Squares

You may recall that the term area tells us something about the number of squares inside a two-dimensional shape.

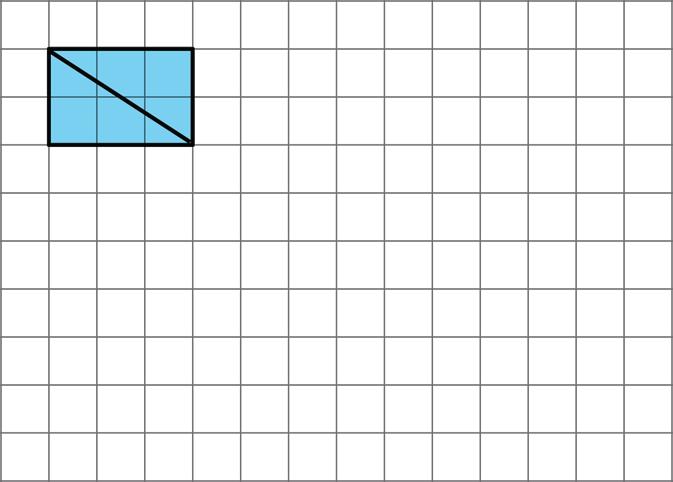
1. A rectangle is shown on the grid, where each grid line is 1 unit.

Determine the area of the rectangle. Show or explain your reasoning.

2. A drawing of a square is shown on the grid, where each grid line is 1 unit.

Explain whether your strategy for finding the area of a rectangle can be used for finding the area of a square. Note any similarities or differences.

3. Write a definition of area that includes all the information that you think is important.

ManuscriptCopy

Exploration Activity: Composing Shapes

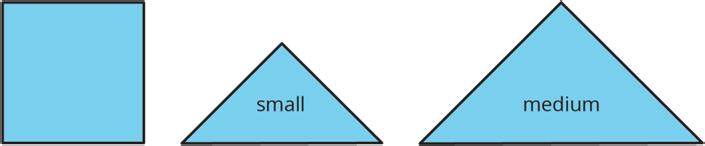
Your teacher will give you one square and some small, medium, and large right triangles. The area of the square is 1 square unit (sq. unit).

1. Notice that you can put together two small triangles to make a square. What is the area of the square composed of two small triangles? Be prepared to explain your reasoning.

2. Use your shapes to create a new shape with an area of 1 sq. unit that is not a square. Draw your shape on paper and label it with its area.

ManuscriptCopy

3. Use your shapes to create a new shape with an area of 2 sq. units. Draw your shape on paper and label it with its area.

4. Use your shapes to create a different shape with an area of 2 sq. units. Draw your shape on paper and label it with its area.

5. Use your shapes to create a new shape with an area of 4 sq. units. Draw your shape on paper and label it with its area.

Exploration Activity: Tangram Triangles

Recall that the area of the square you saw earlier is 1 sq. unit. Complete each statement and explain your reasoning.

1. The area of the small triangle is ____ sq. units. I know this because . . .

2. The area of the medium triangle is ____ sq. units. I know this because . . .

3. The area of the large triangle is ____ sq. units. I know this because . . .

Lesson Summary

There are 2 important principles to consider when finding area.

1. If 2 figures can be placed on top of one another so that they match up exactly, then they have the same area.

2. We can decompose a figure and rearrange the pieces to find its area.

Area is the measure, in square units, of the inside region of a closed two-dimensional figure.

To decompose means “take apart.” We use the word decompose to describe taking a figure apart to make more than one new shape.

To compose means “put together.” We use the word compose to describe putting more than one figure together to make a new shape.

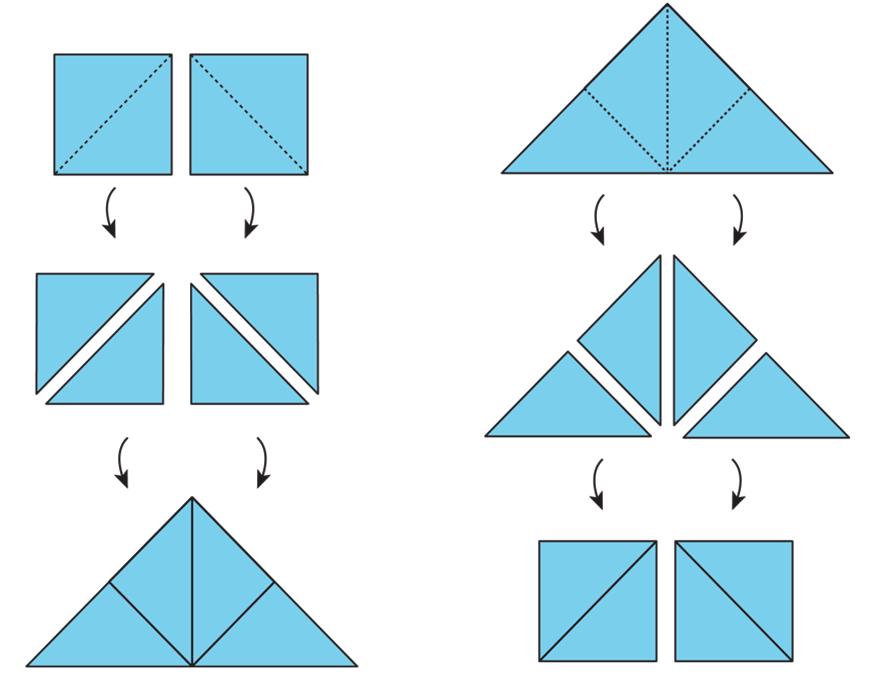
Illustrations of the two principles are shown.

• Each square on the left can be decomposed into 2 triangles. These triangles can be rearranged into a large triangle, so the large triangle has the same area as the 2 squares.

• Similarly, the large triangle on the right can be decomposed into 4 equal triangles. The triangles can be rearranged to form 2 squares. If each square has an area of 1 sq. unit, then the area of the large triangle is 2 sq. units. We can also say that each small triangle has an area of 1 2 sq. unit.

ManuscriptCopy

Practice Problems

1. The diagonal of a rectangle is shown.

a. Decompose the rectangle along the diagonal, and recompose the two pieces to make a different shape.

b. How does the area of this new shape compare to the area of the original rectangle? Explain how you know.

2. Priya decomposed a square into 16 smaller, equal-size squares and then cut out 4 of the small squares and attached them around the outside of original square to make a new figure.

How does the area of her new figure compare with that of the original square?

A. The area of the new figure is greater.

B. The two figures have the same area.

C. The area of the original square is greater.

D. We don’t know because neither the side length nor the area of the original square is known.

3. The area of the square is 1 sq. unit. Two small triangles can be put together to make a square or to make a medium triangle.

Which figure also has an area of 11 2 sq. units? Select all that apply. □ Figure A

Figure B

Figure C

Figure D

Review Problems

4. The area of a rectangular playground is 78 square meters (sq. m). If the length of the playground is 13 meters (m), what is its width?

5. A student said, “We can’t find the area of the shaded region because the shape has many different measurements, instead of just a length and a width that we could multiply.”

Explain why the student’s statement about area is incorrect.

ManuscriptCopy

Unit 1, Lesson 2: Reasoning to Find Area

Warm-Up: Comparing Regions

Is the area of Figure A greater than, less than, or equal to the area of the shaded region in Figure B? Be prepared to explain your reasoning.

Exploration Activity: On the Grid

Each grid square is 1 square unit (sq. unit). Find the area, in sq. units, of each shaded region without counting every square. Be prepared to explain your reasoning.

ManuscriptCopy

Exploration Activity: Off the Grid

Find the area of the shaded region(s) of each figure. Explain or show your reasoning.

ManuscriptCopy

A.

B.

C.

Lesson Summary

There are different strategies we can use to find the area of a region.

• Decompose it into shapes whose areas you know how to calculate. Find the area of each of those shapes, and then add the areas.

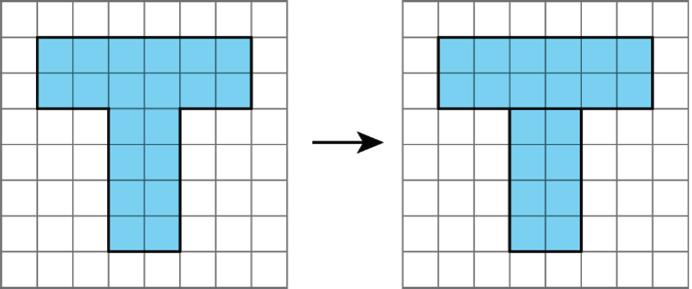
• Decompose it, and rearrange the pieces into shapes whose areas you know how to calculate. Find the area of each of those shapes, and then add the areas.

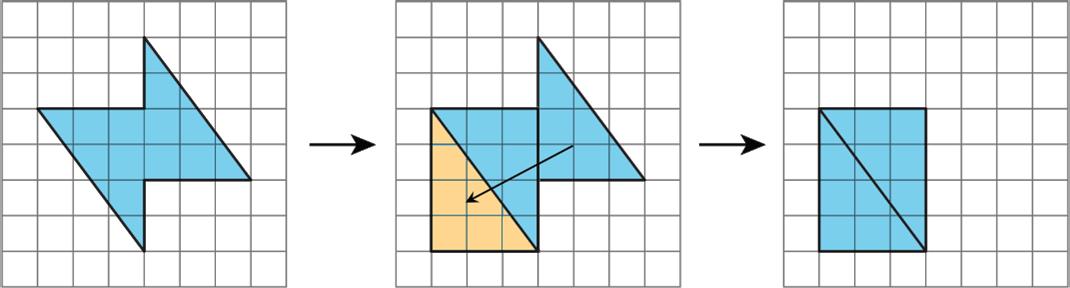
• Consider it as a shape with a missing piece. Calculate the areas of the shape and the missing piece, and then subtract the area of the piece from the area of the shape.

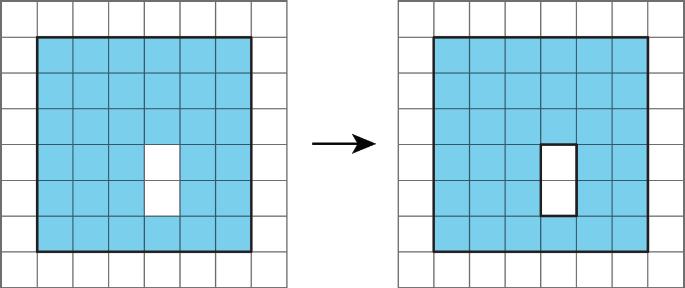
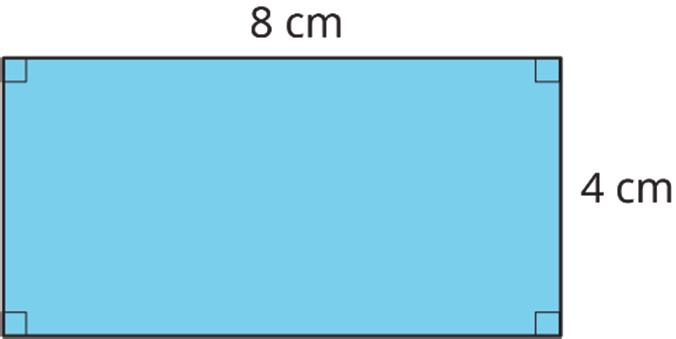
The area of a figure is always measured in square units. When both side lengths of a rectangle are given in centimeters (cm), the area is given in square centimeters (sq. cm).

The area of this rectangle is 32 sq. cm.

ManuscriptCopy

Practice Problems

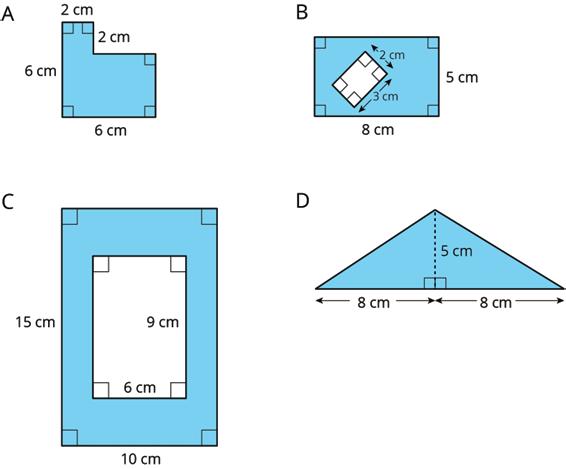
1. Find the area of each shaded region. Show your reasoning.

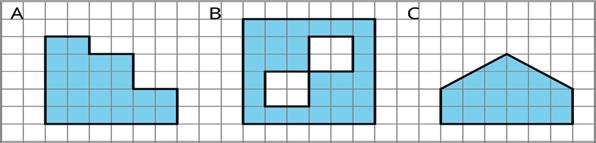
2. Find the area of each shaded region. Show or explain your reasoning.

ManuscriptCopy

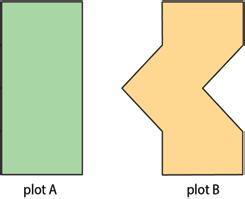
3. Two plots of land have very different shapes. Noah said that both plots of land have the same area.

Do you agree with Noah? Explain your reasoning.

Review Problem

4. A homeowner is deciding on the size of tiles to use to fully tile a rectangular wall in her bathroom that is 80 inches (in.) by 40 in. The tiles are squares and come in three side lengths: 8 in., 4 in., and 2 in. State if you agree with each statement about the tiles. Explain your reasoning.

a. Regardless of the size she chooses, she will need the same number of tiles.

b. Regardless of the size she chooses, the area of the wall that is being tiled is the same.

c. She will need two 2-in. tiles to cover the same area as one 4-in. tile.

d. She will need four 4-in. tiles to cover the same area as one 8-in. tile.

ManuscriptCopy

e. If she chooses the 8-in. tiles, she will need a quarter as many tiles as she would with 2-in. tiles.

ManuscriptCopy

Unit 1, Lesson 3: Parallelograms

Warm-Up: Features of a Parallelogram

Figures A, B, and C are parallelograms. Figures D, E, and F are not parallelograms.

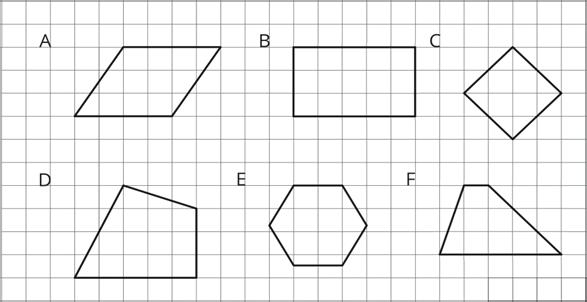
Study the examples and non-examples. What do you notice about:

1. the number of sides that a parallelogram has?

2. opposite sides of a parallelogram?

ManuscriptCopy

3. opposite angles of a parallelogram?

Exploration Activity: Lots of Parallelograms

Find the area of each parallelogram. Show your reasoning.

ManuscriptCopy

Exploration Activity: The Right Height?

Study the examples and non-examples of bases and heights of parallelograms.

• Examples: The dashed segment in each drawing represents the corresponding height for the given base.

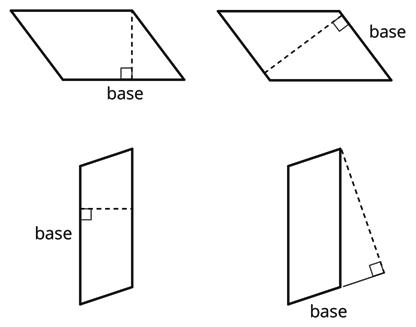
• Non-examples: The dashed segment in each drawing does not represent the corresponding height for the given base.

1. Select all statements that are true about bases and heights in a parallelogram.

□ Only a horizontal side of a parallelogram can be a base.

□ Any side of a parallelogram can be a base.

□ A height can be drawn at any angle to the side chosen as the base.

□ A base and its corresponding height must be perpendicular to each other.

□ A height can only be drawn inside a parallelogram.

□ A height can be drawn outside of the parallelogram, as long as it is drawn at a 90° angle to the base.

□ A base cannot be extended to meet a height.

2. Five students labeled a base �� and a corresponding height ℎ for each of these parallelograms. Are all drawings correctly labeled? Explain how you know.

Guided Activity: Digging Deeper into Area

1. A parallelogram is shown with a base, ��, and its corresponding height, ℎ, labeled.

a. Explain how the parallelogram can be decomposed and rearranged to form a rectangle.

b. Complete the statement.

The area of the resulting rectangle is _____ square units (sq. units). Therefore, the area of the original parallelogram is _____ sq. units.

Lesson Summary

A parallelogram is a quadrilateral, which means it has 4 sides. The opposite sides of a parallelogram are parallel. The properties shown are also true.

• The opposite sides of a parallelogram have equal length.

• The opposite angles of a parallelogram have equal measure.

A parallelogram is a quadrilateral containing two pairs of parallel sides.

Different strategies can be used to find the area of a parallelogram.

• Decompose and rearrange a parallelogram to form a rectangle. Three examples are shown.

• Enclose the parallelogram, and then subtract the area of the 2 triangles in the corners from the area of the enclosed parallelogram.

Both strategies will work for any parallelogram. However, for some parallelograms, the process of decomposing and rearranging requires more steps than if we enclose the parallelogram with a rectangle and subtract the combined area of the two triangles in the corners. One such example is shown.

ManuscriptCopy

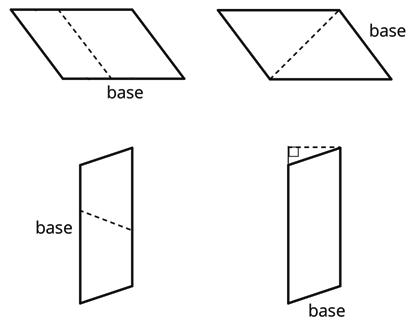
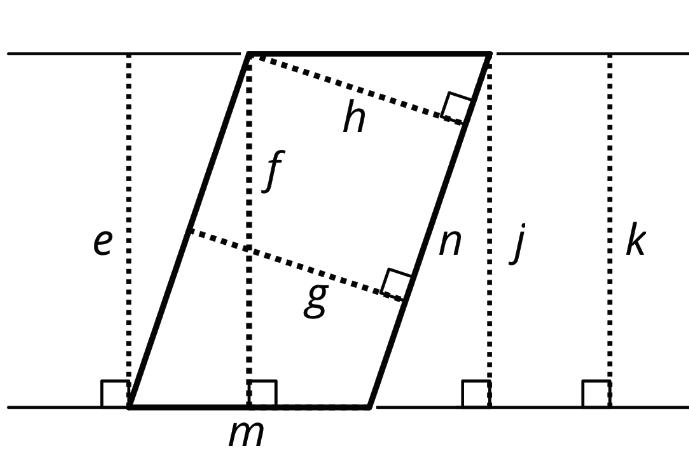
Different strategies can also be used to identify the base and height of a parallelogram.

• Choose any of the 4 sides of a parallelogram as the base. Both the side (the segment) and its length (the measurement) are called the base.

• Any perpendicular segment drawn from a point on the base to the opposite side of the parallelogram will always have the same length. This value is the height. There are infinitely many line segments that can represent the height.

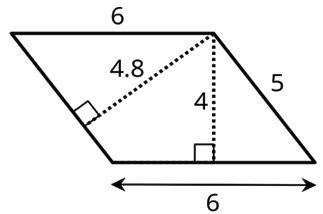
Two copies of the same parallelogram are shown. On the left, the side that is the base is 6 units long. Its corresponding height is 4 units. On the right, the side that is the base is 5 units long. Its height is 4.8 units. For both, three different segments are shown to represent the height.

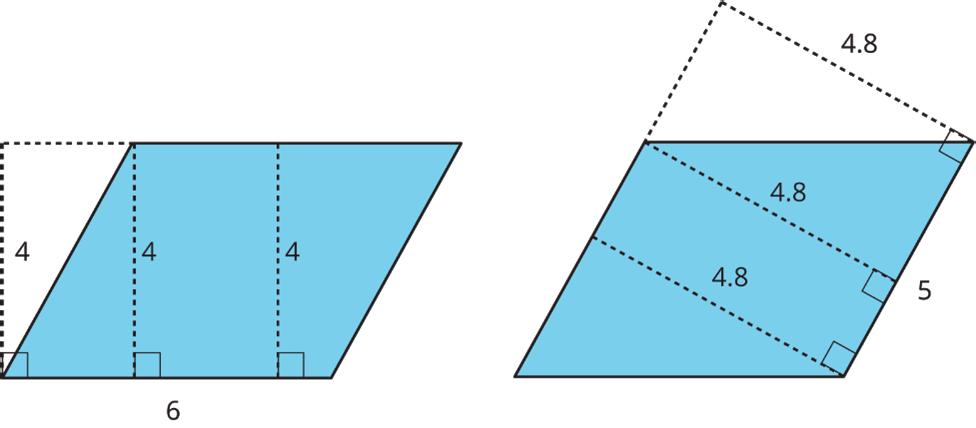
No matter which side is chosen as the base, the area of the parallelogram is the product of that base and its corresponding height.

4 × 6 = 24, and 4.8 × 5 = 24.

1.

Practice Problems

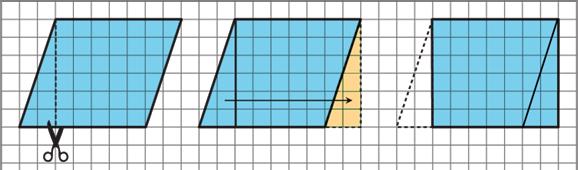
a. Decompose and rearrange this parallelogram to make a rectangle.

b. What is the area of the parallelogram? Explain your reasoning.

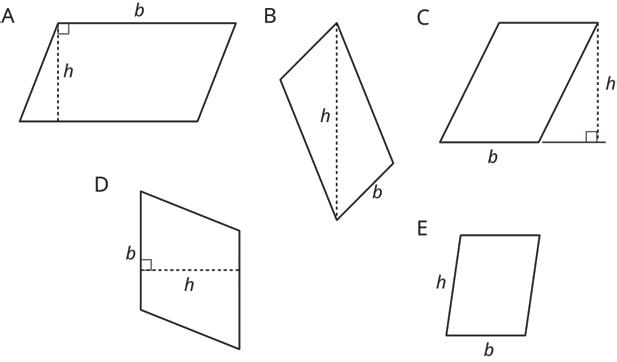
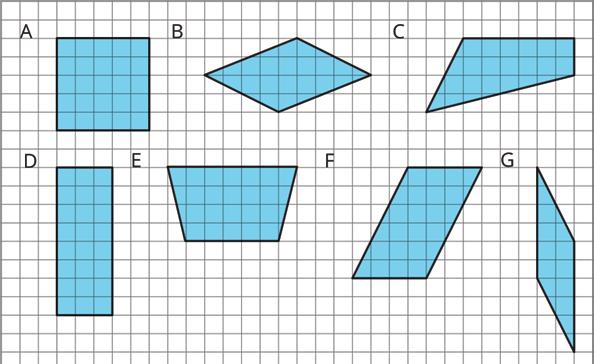
2. Select all of the parallelograms. For each figure that is not selected, explain how you know it is not a parallelogram.

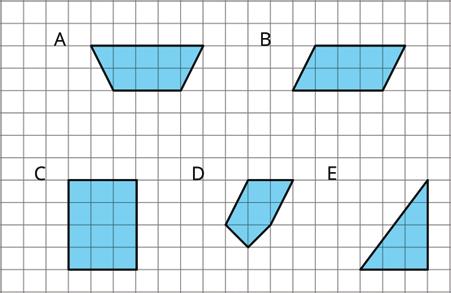
□ Figure A _________________________________________________________

□ Figure B _________________________________________________________

□ Figure C _________________________________________________________

□ Figure D _________________________________________________________

□ Figure E _________________________________________________________

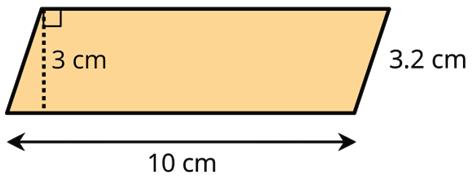
3. Find the area of the parallelogram.

ManuscriptCopy

4. The side labeled �� has been chosen as the base for this parallelogram.

Draw a segment showing the height corresponding to that base.

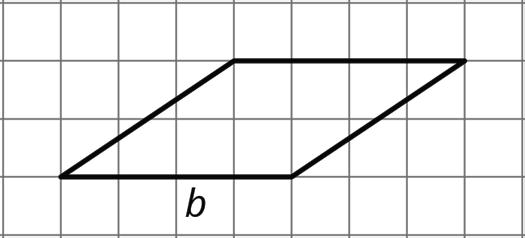
5. If the side that is 6 units long is the base of this parallelogram, what is its corresponding height?

A. 6 units

B. 4.8 units

C. 4 units

D. 5 units

Review Problem

6. Find the areas of the rectangles with the following side lengths.

a. 5 inches (in.) and 1 3 in.

b. 5 in. and 4 3 in.

c. 5 2 in. and 4 3 in.

d. 7 6 in. and 6 7 in.

Unit 1, Lesson 4: Area of Parallelograms

Warm-Up: A Parallelogram and Its Rectangles

Elena and Tyler were finding the area of this parallelogram:

Here is how Elena did it:

Here is how Tyler did it:

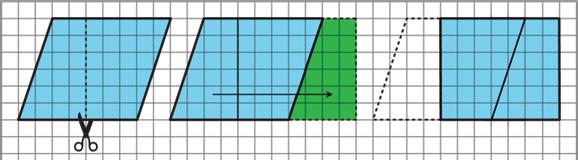
How are the two strategies for finding the area of a parallelogram the same? How are they different?

ManuscriptCopy

Exploration Activity: Finding the Formula for Area of Parallelograms

For each parallelogram:

• Identify a base and a corresponding height, and record their lengths in the table.

• Find the area and record it in the right-most column.

In the last row, write an expression using �� and ℎ for the area of any parallelogram.

ManuscriptCopy

Collaborative Activity: Area Using a Ruler

1. A parallelogram is shown.

a. Use a ruler to measure the lengths needed to find the area of the parallelogram in centimeters (cm). Round measurements to the nearest cm, and label the lengths on the image.

b. Find the area of the parallelogram in square centimeters (sq. cm).

Exploration Activity: More Area of Parallelograms

1. Find the area of each parallelogram. Show your reasoning.

ManuscriptCopy

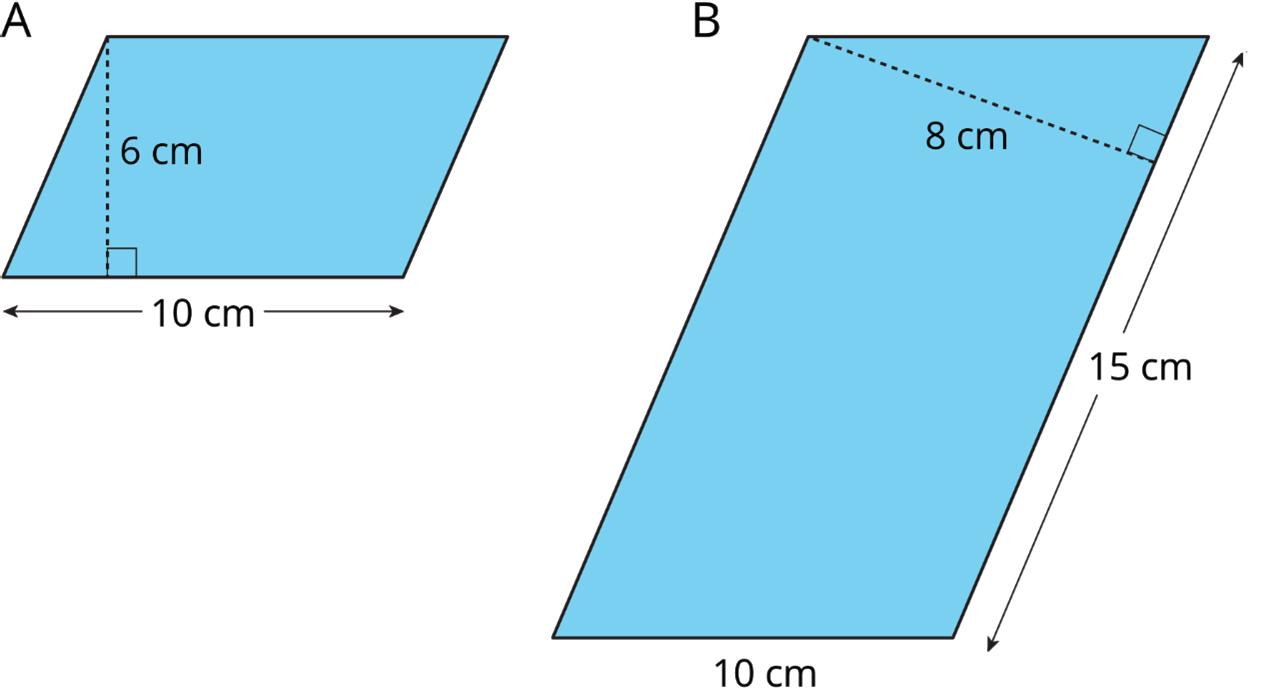
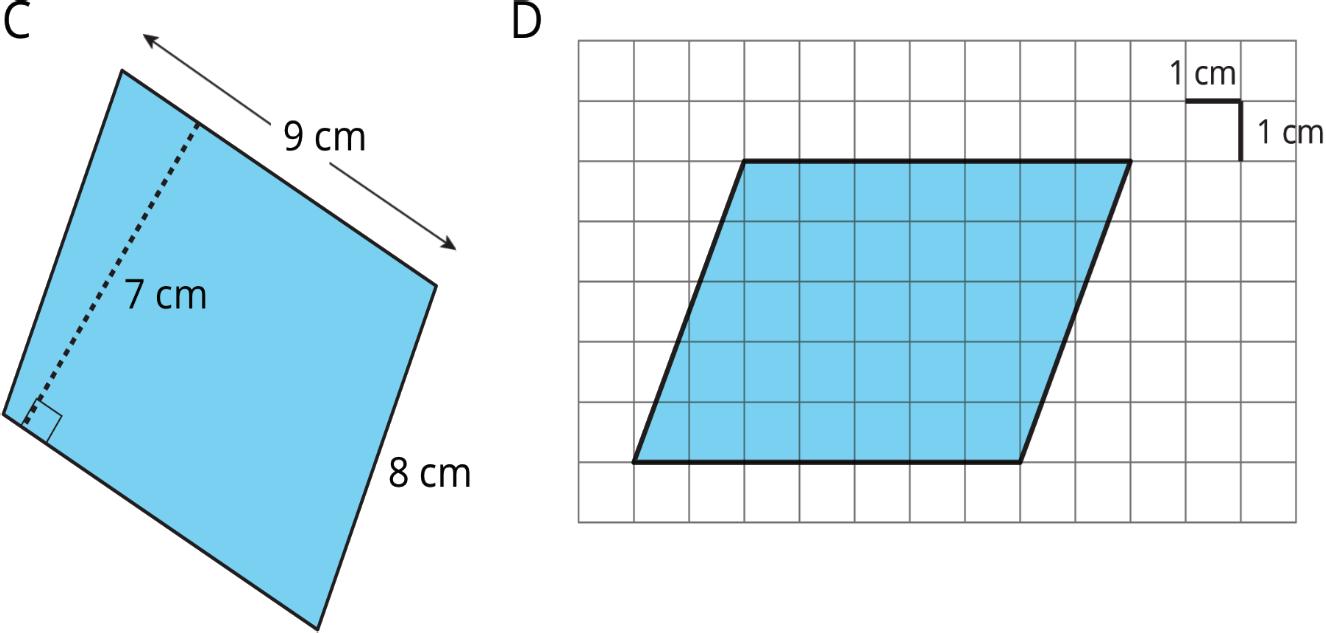
2. In Parallelogram B, what is the corresponding height for the base that is 10 cm long? Explain or show your reasoning.

3. Two different parallelograms P and Q both have an area of 20 sq. units. Neither of the parallelograms are rectangles.

On the grid, draw two parallelograms that could be P and Q.

ManuscriptCopy

Lesson Summary

We often use letters to stand for numbers. If �� is a base of a parallelogram, in units, and ℎ is the corresponding height, in units, then the area of the parallelogram, in square units (sq. units), is the product of these 2 numbers.

Notice that the multiplication symbol is written with a small dot instead of an × symbol. This is so that we don’t get confused about whether × means multiply or whether the letter �� is standing in for a number.

Any pair of base and corresponding height can be used to find the area of a parallelogram, but some base-height pairs are more easily identified than others.

When a parallelogram is drawn on a grid and has horizontal sides, a horizontal side can be used as the base. When it has vertical sides, a vertical side can be used as the base. The grid can then be used to find, or estimate, the lengths of the base and the corresponding height.

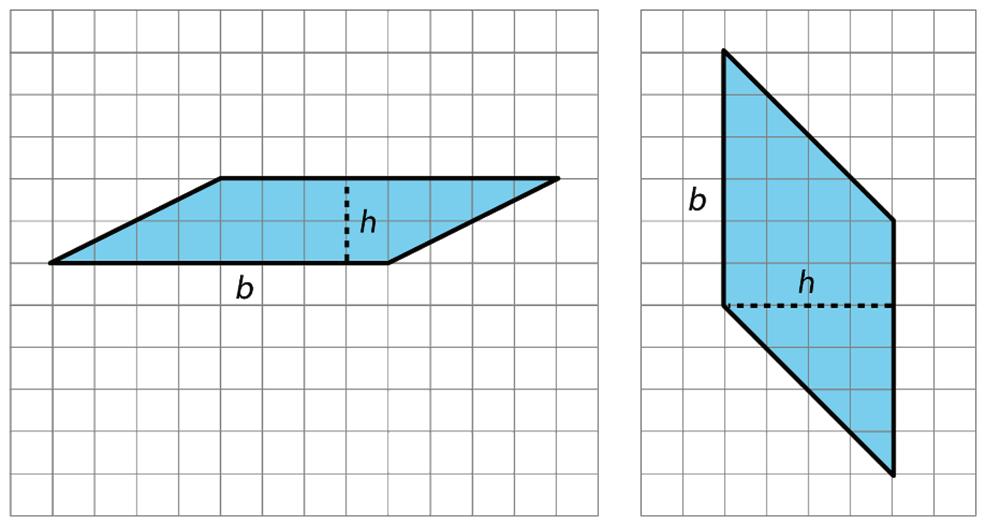
When a parallelogram is not drawn on a grid, if a base and a corresponding height are known, they can be used to find the area.

In the parallelogram shown, the corresponding height for the side that is 10 units long is not given, but the corresponding height for the side that is 8 units long is given. This baseheight pair can be used to find the area.

ManuscriptCopy

Regardless of their shape, parallelograms that have the same base and height will have the same area. The product of the base and height will be equal. Four parallelograms with the same pair of base-height measurements, and therefore the same area, are shown.

Practice Problems

1. Use a ruler to measure the dimensions of the parallelogram shown. Round measurements to the nearest cm and then find the area of the parallelogram in sq. cm.

2. Which of the following pairs of base and height produces the greatest area? All measurements are in cm.

A. �� = 4, ℎ = 3.5

B. �� = 0.8, ℎ = 20

C. �� = 6, ℎ = 2.25

D. �� = 10, ℎ = 1.4

3. Here are the areas of three parallelograms. Use them to find the missing length (labeled with a “?”) on each parallelogram. A: 10 sq. units B: 21 sq. units C: 25 sq.units

ManuscriptCopy

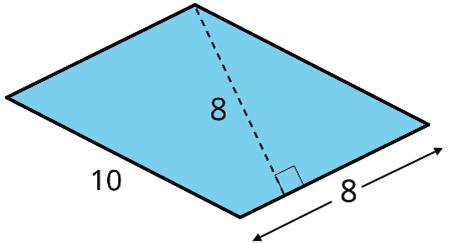
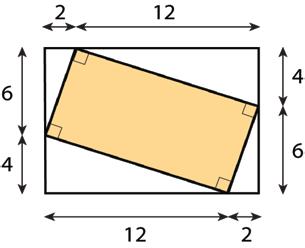
4. The Dockland Building in Hamburg, Germany is shaped like a parallelogram.

If the length of the building is 86 meters (m) and its height is 55 m, what is the area of this face of the building?

Review Problems

5. Select all segments that could represent a corresponding height if the side �� is the base.

6. Find the area of the shaded region. All measurements are in cm. Show your reasoning.

ManuscriptCopy

ManuscriptCopy

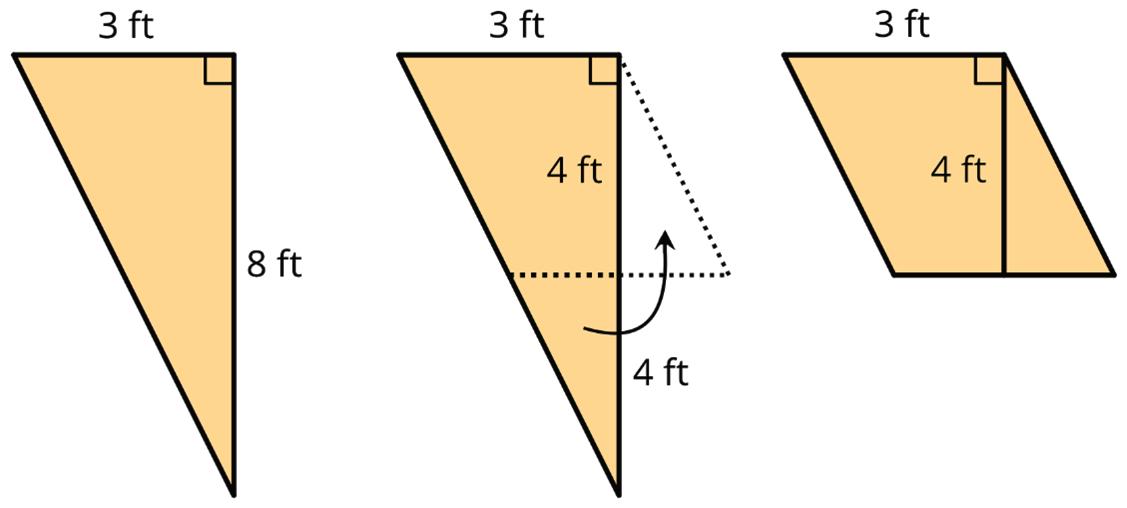
Unit 1, Lesson 5: From Parallelograms to Triangles

Warm-Up: Composing Parallelograms

Here is Triangle M.

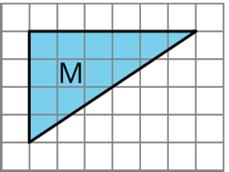
Han made a copy of Triangle M and composed three different parallelograms using the original M and the copy, as shown here.

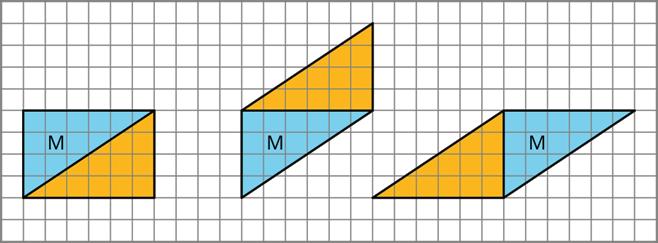
1. For each parallelogram Han composed, identify a base and a corresponding height, and write the measurements on the drawing.

2. Find the area of each parallelogram Han composed. Show your reasoning.

ManuscriptCopy

Exploration Activity: A Tale of Two Triangles (Part 1)

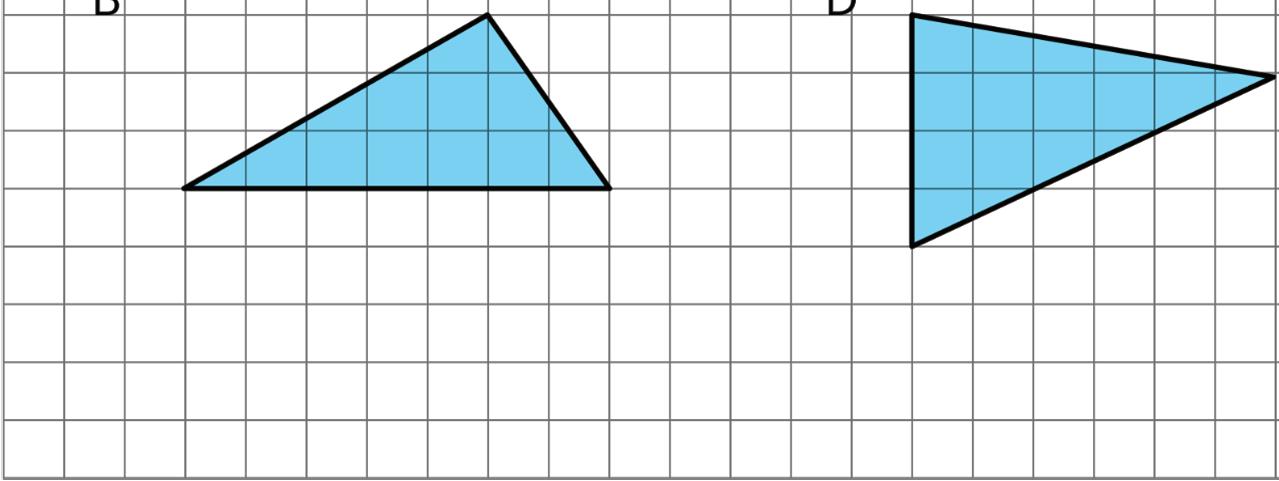
Two polygons are identical if they match up exactly when placed one on top of the other.

1. Draw one line to decompose each of the following polygons into two identical triangles, if possible. Use a straightedge to draw your line.

2. Which quadrilaterals can be decomposed into two identical triangles? Pause here for a small-group discussion.

3. Study the quadrilaterals that can, in fact, be decomposed into two identical triangles. What do you notice about them? Write a couple of observations about what these quadrilaterals have in common.

ManuscriptCopy

Exploration Activity: A Tale of Two Triangles (Part 2)

Your teacher will give your group several pairs of triangles. Each group member should take 1 or 2 pairs.

1. a. Which pair(s) of triangles do you have?

b. Can each pair be composed into a rectangle? A parallelogram?

2. Discuss your responses to the first question with your group. Then, complete each of the following statements with All, Some, or None. Sketch 1 or 2 examples to illustrate each completed statement.

a. ________________ of these pairs of identical triangles can be composed into a rectangle.

b. ________________ of these pairs of identical triangles can be composed into a parallelogram.

ManuscriptCopy

Collaborative Activity: More Triangles

1. Find the areas of at least two of these triangles. Show your reasoning.

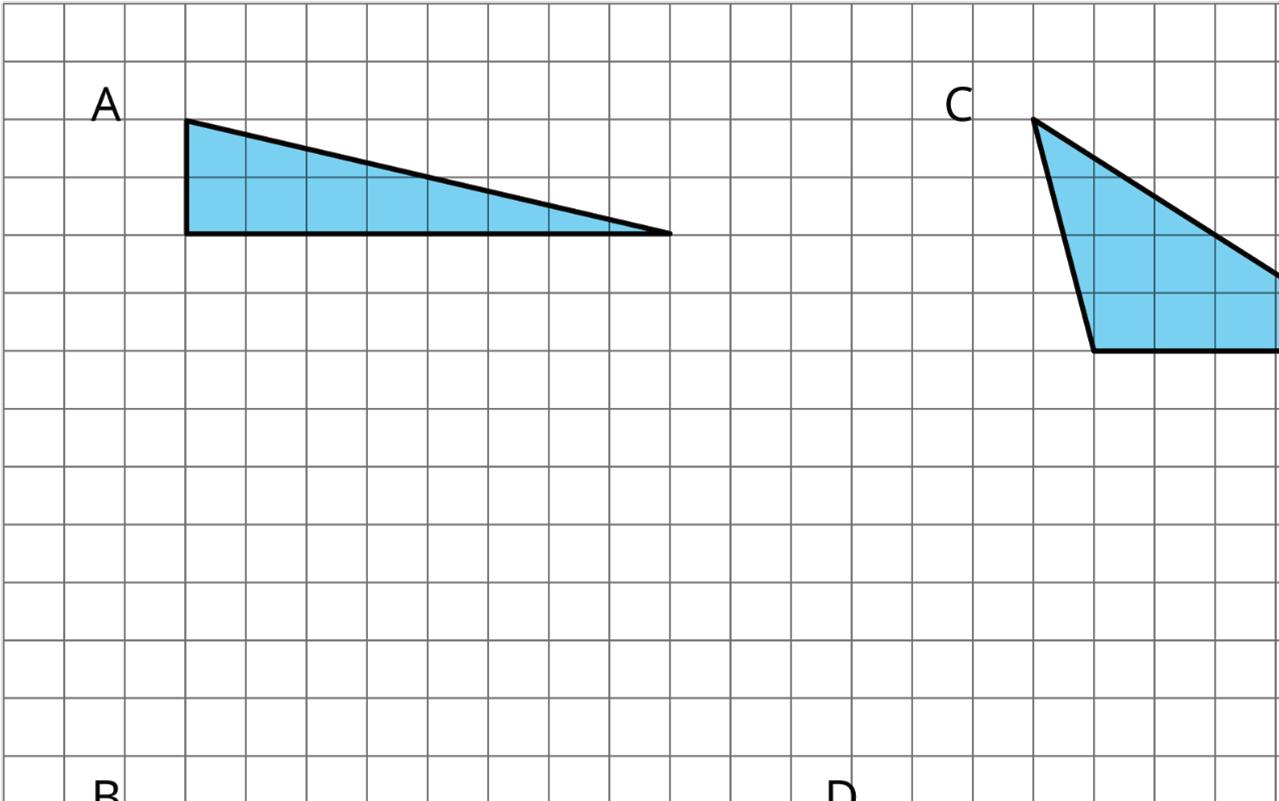
Lesson Summary

ManuscriptCopy

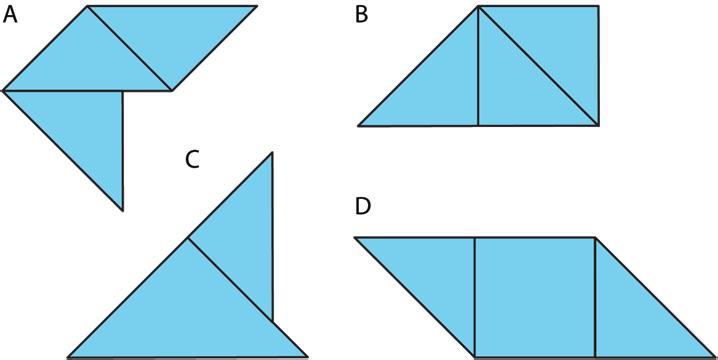
A parallelogram can always be decomposed into 2 identical triangles by a segment that connects opposite vertices.

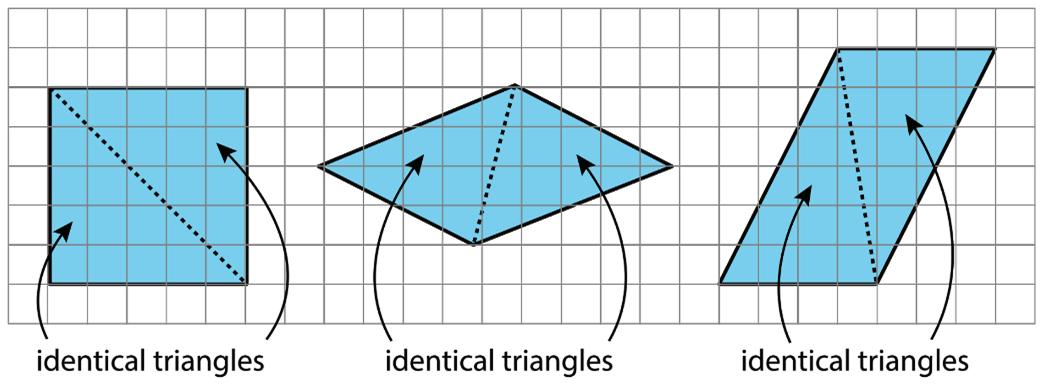
Going the other way around, 2 identical copies of a triangle can always be arranged to form a parallelogram regardless of the type of triangle being used.

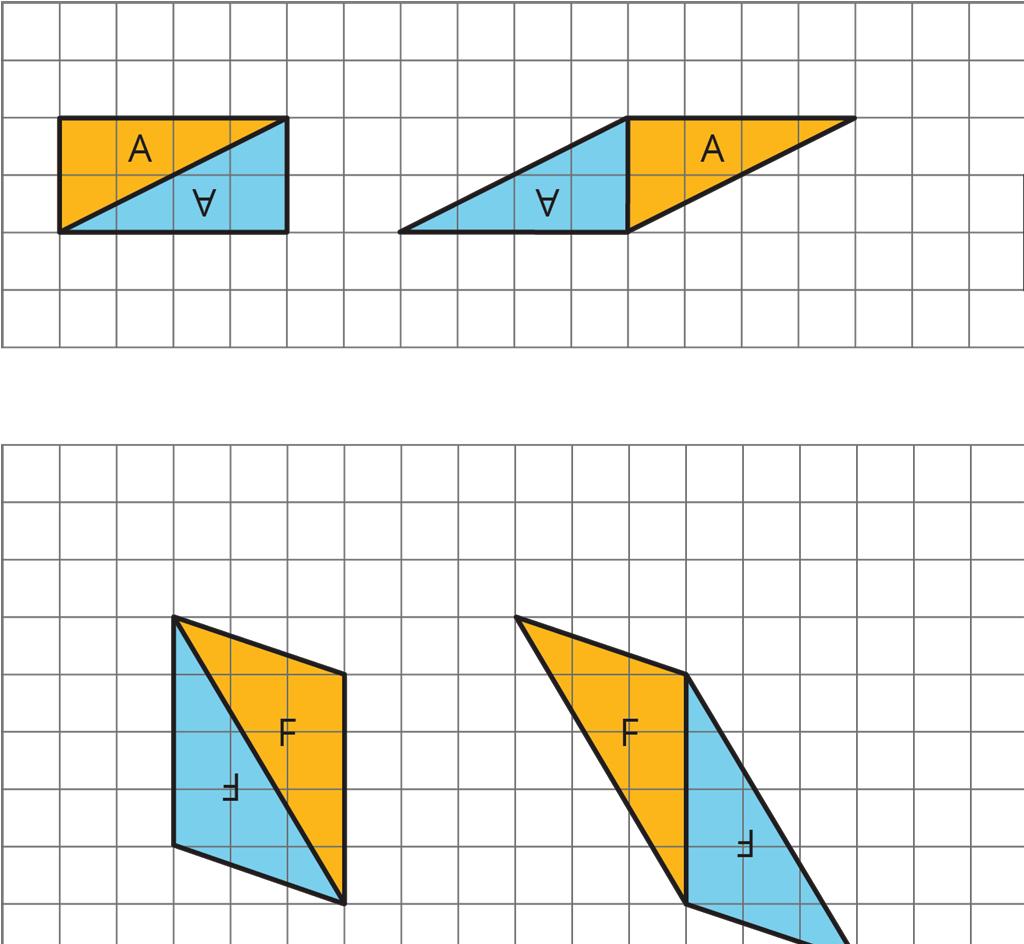
To produce a parallelogram, a triangle and its copy can be joined along any of the 3 sides, so the same pair of triangles can make different parallelograms.

Examples of how 2 copies of both triangle A and triangle F can be composed into 3 different parallelograms are shown.

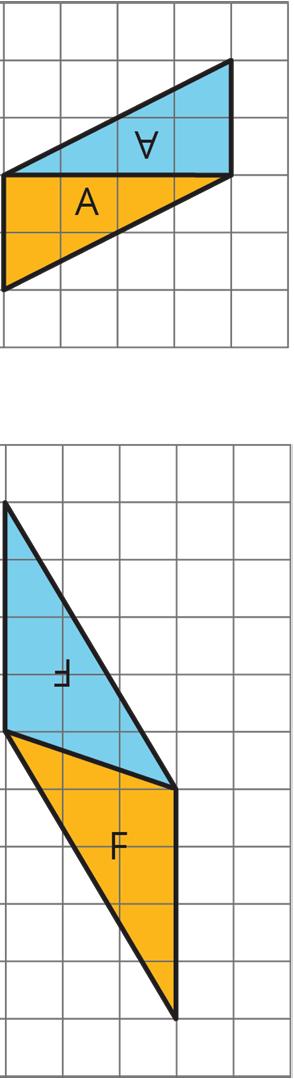
This special relationship between triangles and parallelograms can be used to reason about the area of any triangle.

Two additional strategies for reasoning about the area of a triangle are shown.

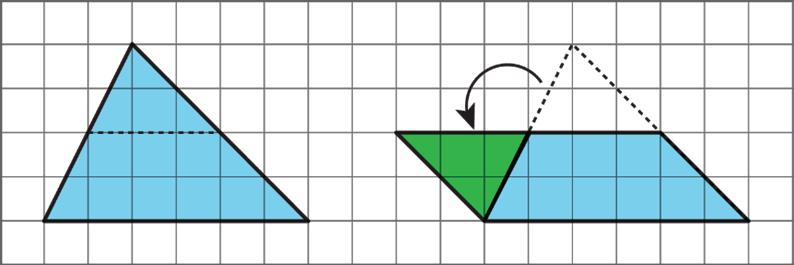
• Decompose the triangle into smaller pieces, and compose them into a parallelogram.

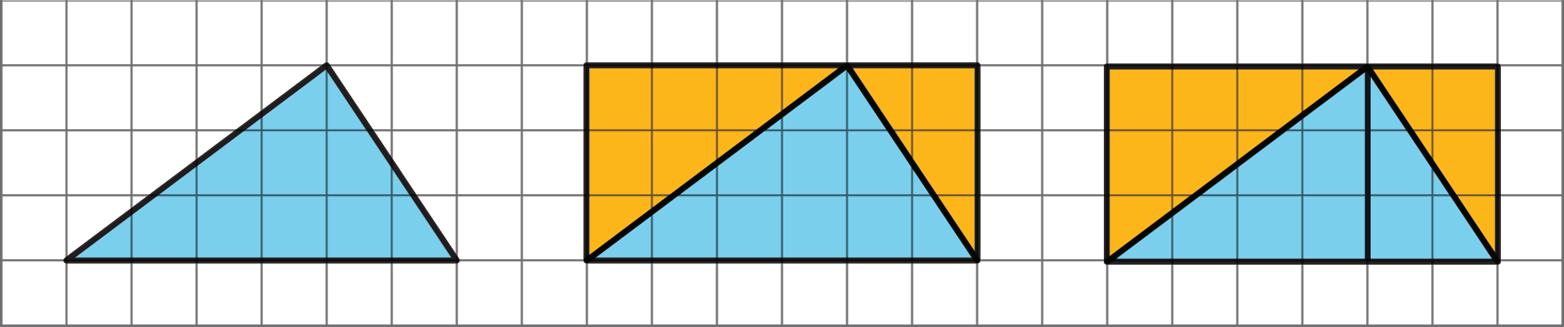
• Draw a rectangle around the triangle. The triangle has half of the area of the rectangle.

Practice Problems

1. To decompose a quadrilateral into two identical shapes, Clare drew a dashed line as shown in the diagram.

a. She said the that two resulting shapes have the same area. Do you agree? Explain your reasoning.

b. Did Clare partition the figure into two identical shapes? Explain your reasoning.

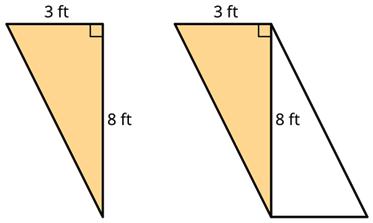
2. Triangle R is a right triangle. Can we use two copies of Triangle R to compose a parallelogram that is not a square?

If so, explain how or sketch a solution. If not, explain why not.

ManuscriptCopy

3.

a. On the grid, draw at least three different quadrilaterals that can each be decomposed into two identical triangles with a single cut (show the cut line). One or more of the quadrilaterals should have non-right angles.

b. Identify the type of each quadrilateral.

4. Find the area of each triangle. Explain or show your reasoning.

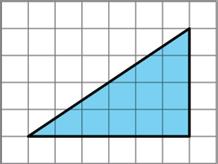
ManuscriptCopy

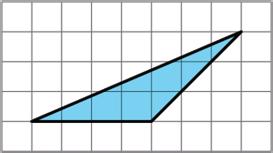
5. To find the area of this right triangle, Diego and Jada used different strategies.

Diego drew a line through the midpoints of the two longer sides, which decomposes the triangle into a trapezoid and a smaller triangle. He then rearranged the two shapes into a parallelogram.

Jada made a copy of the triangle, rotated it, and lined it up against one side of the original triangle so that the two triangles make a parallelogram.

a. Explain how Diego might use his parallelogram to find the area of the triangle.

b. Explain how Jada might use her parallelogram to find the area of the triangle.

Review Problem

6.

a. A parallelogram has a base of 3.5 units and a corresponding height of 2 units. What is its area?

ManuscriptCopy

b. A parallelogram has a base of 3 units and an area of 1.8 square units. What is the corresponding height for that base?

c. A parallelogram has an area of 20.4 square units. If the height that corresponds to a base is 4 units, what is the base?

Unit 1, Lesson 6: Areas of Triangles

Warm-Up: Bases and Heights of a Triangle

Study the examples and non-examples of bases and heights in a triangle.

• Examples: These dashed segments represent heights of the triangle.

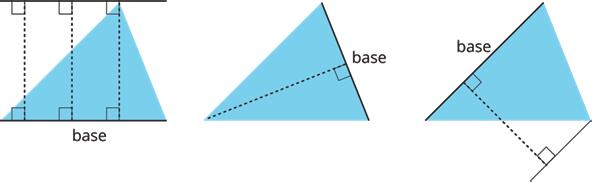
• Non-examples: These dashed segments do not represent heights of the triangle.

1. Select all the statements that are true about bases and heights in a triangle.

□ Any side of a triangle can be a base.

□ There is only one possible height.

□ A height is always one of the sides of a triangle.

□ A height that corresponds to a base must be drawn at an acute angle to the base.

□ A height that corresponds to a base must be drawn at a right angle to the base.

□ Once we choose a base, there is only one segment that represents the corresponding height.

□ A segment representing a height must go through a vertex.

Exploration Activity: Finding the Formula for Area of a Triangle

For each triangle:

• Identify a base and a corresponding height, and record their lengths in the table.

• Find the area of the triangle and record it in the last column of the table.

In the last row, write an expression for the area of any triangle, using �� and ℎ.

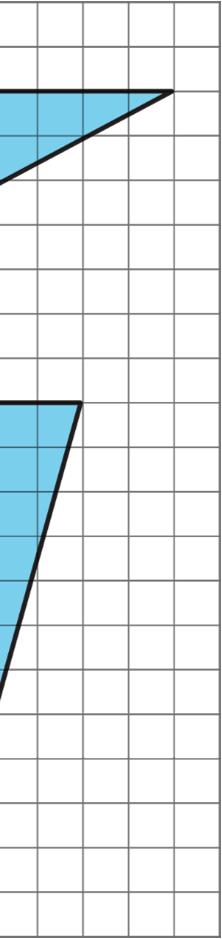
ManuscriptCopy

Exploration Activity: Applying the Formula for Area of a Triangles

For each triangle, circle a base measurement that you can use to find the area of the triangle. Then, find the area of any three triangles. Show your reasoning.

ManuscriptCopy

Collaborative Activity: Some Bases Are Better Than Others

For each triangle, identify and label a base and height. If needed, draw a line segment to show the height.

Then, find the area of the triangle. Show your reasoning. (The side length of each square on the grid is 1 unit.)

ManuscriptCopy

Lesson Summary

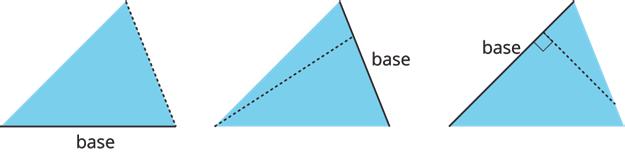
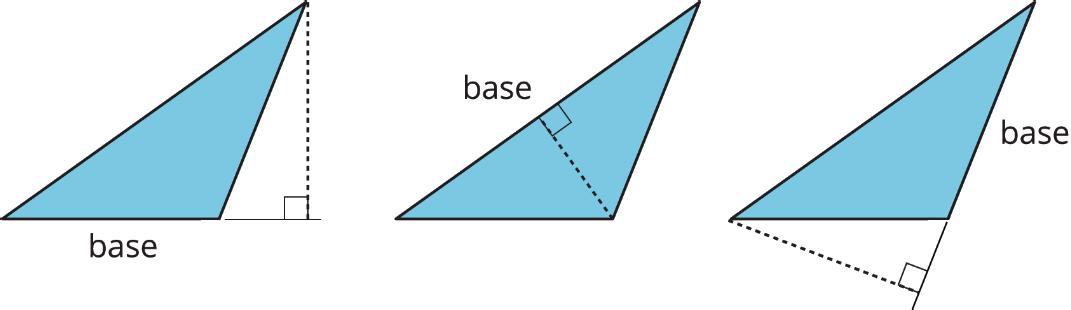
Different strategies can be used to identify the base and height of a triangle.

• Any of the 3 sides of a triangle can be chosen as the base. The term base refers to both the side (the segment) and its length (the measurement).

• The corresponding height is the length of a perpendicular segment from the base to the vertex opposite of it. The opposite vertex is the vertex that is not an endpoint of the base.

For each side of a triangle, there is one vertex that is not on that side. This is the opposite vertex.

Three pairs of bases and heights for the same triangle are labeled as shown. The dashed segments in the diagrams represent heights.

Sometimes, the line of the base must be extended to identify the height, such as when finding the height of an obtuse triangle or whenever the opposite vertex is not directly over the base. In these cases, the height segment is typically drawn outside of the triangle, as in the third example.

A segment showing a height must be drawn at a right angle to the base, but it can be drawn in more than 1 place. It does not have to go through the opposite vertex, as long as it connects the base and a line that is parallel to the base that goes through the opposite vertex, as shown.

ManuscriptCopy

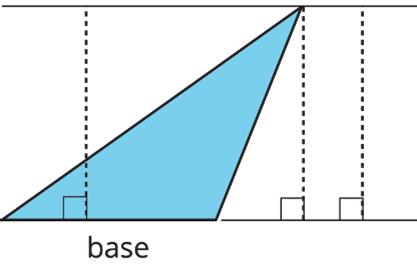
The base-height pairs in a triangle are closely related to those in a parallelogram. Recall that 2 copies of a triangle can be composed into 1 or more parallelograms. Each parallelogram shares at least 1 base with the triangle.

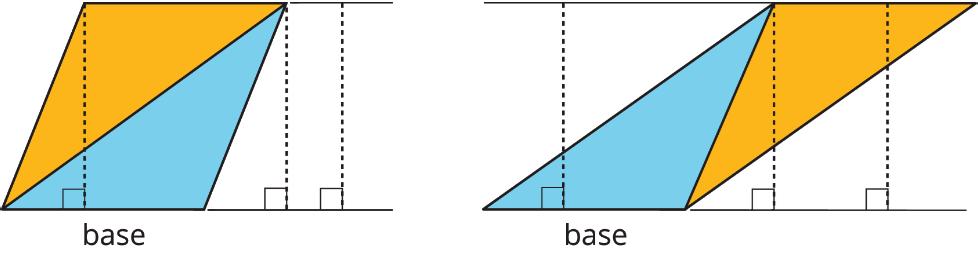
For any base that they share, the corresponding height is also shared, as shown by the dashed segments.

The base-height measurements and prior knowledge of parallelograms can be used to find the area of any triangle.

• The formula for the area of a parallelogram with base, ��, and height, ℎ, is �� ⋅ ℎ.

• A triangle takes up half of the area of a parallelogram with the same base and height. Therefore, the area, ��, of a triangle can be expressed as �� = 1 2 ⋅ �� ⋅ ℎ.

Triangle A

Triangle B Triangle C

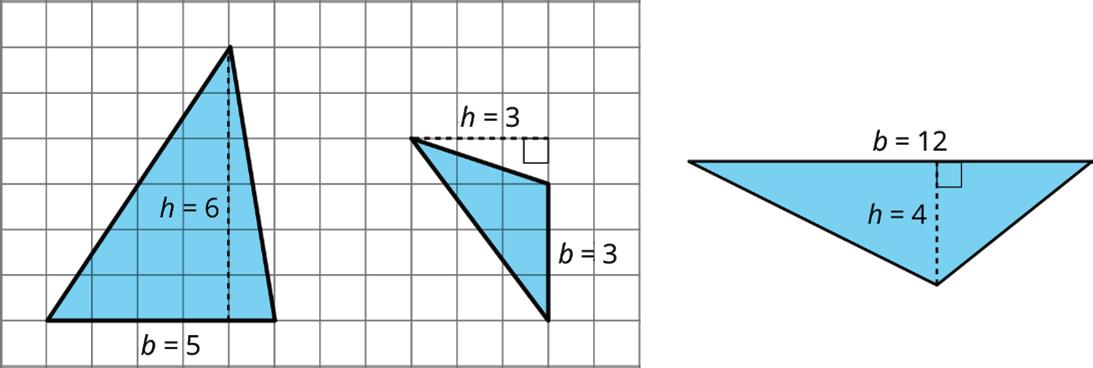
• The area of triangle A is 15 square units (sq. units) because 1 2 ⋅ 5 ⋅ 6 = 15.

• The area of triangle B is 4.5 sq. units because 1 2 ⋅ 3 ⋅ 3 = 4.5.

• The area of triangle C is 24 sq. units because 1 2 ⋅ 12 ⋅ 4 = 24.

In each case, 1 side of the triangle is the base, but neither of the other sides is the height. This is because the angle between them is not a right angle.

In right triangles, however, the 2 sides that are perpendicular can be a base and a height.

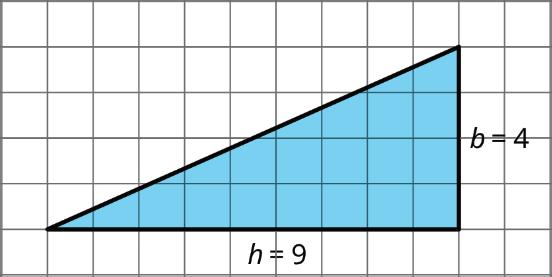
The area of the triangle shown is 18 sq. units whether we use 4 units or 9 units for the base.

Practice Problems

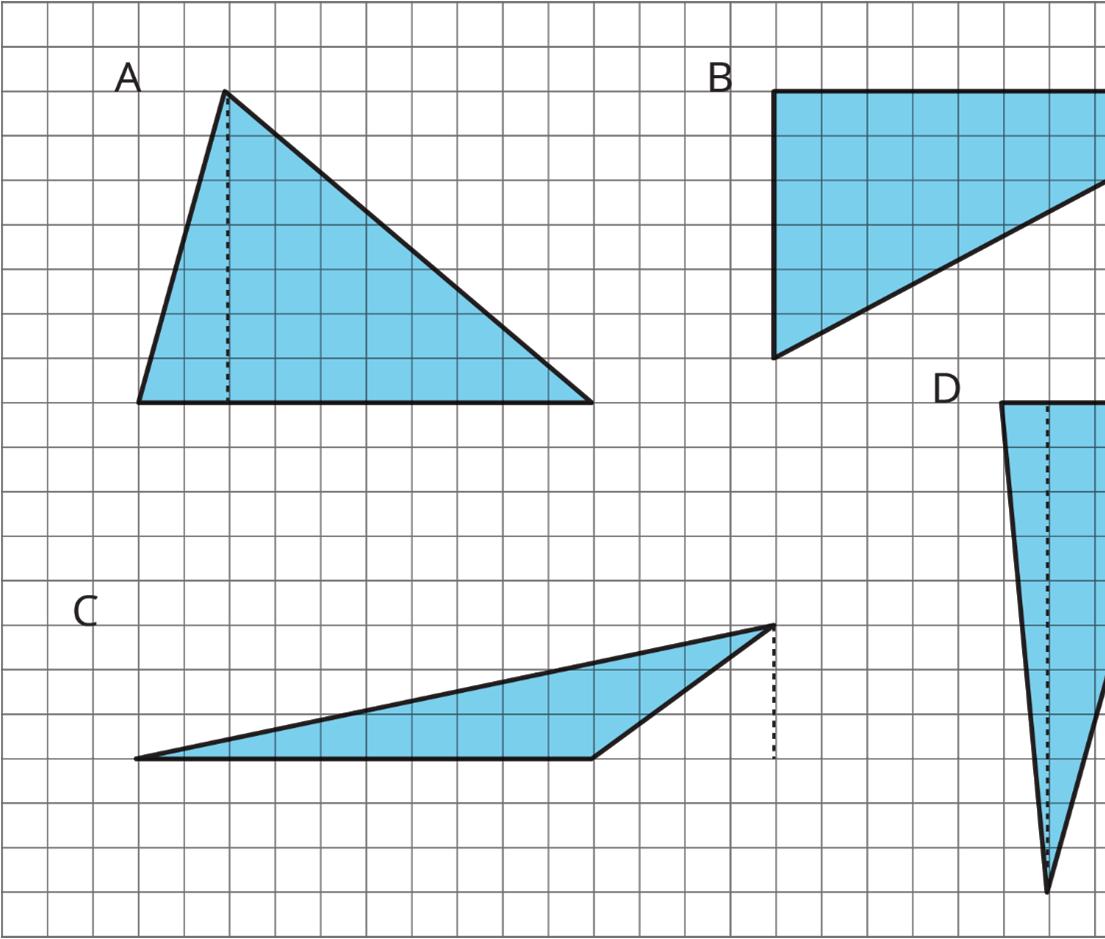
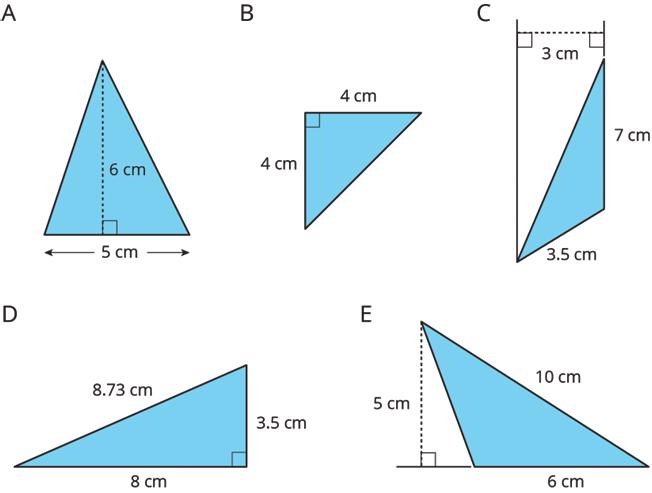
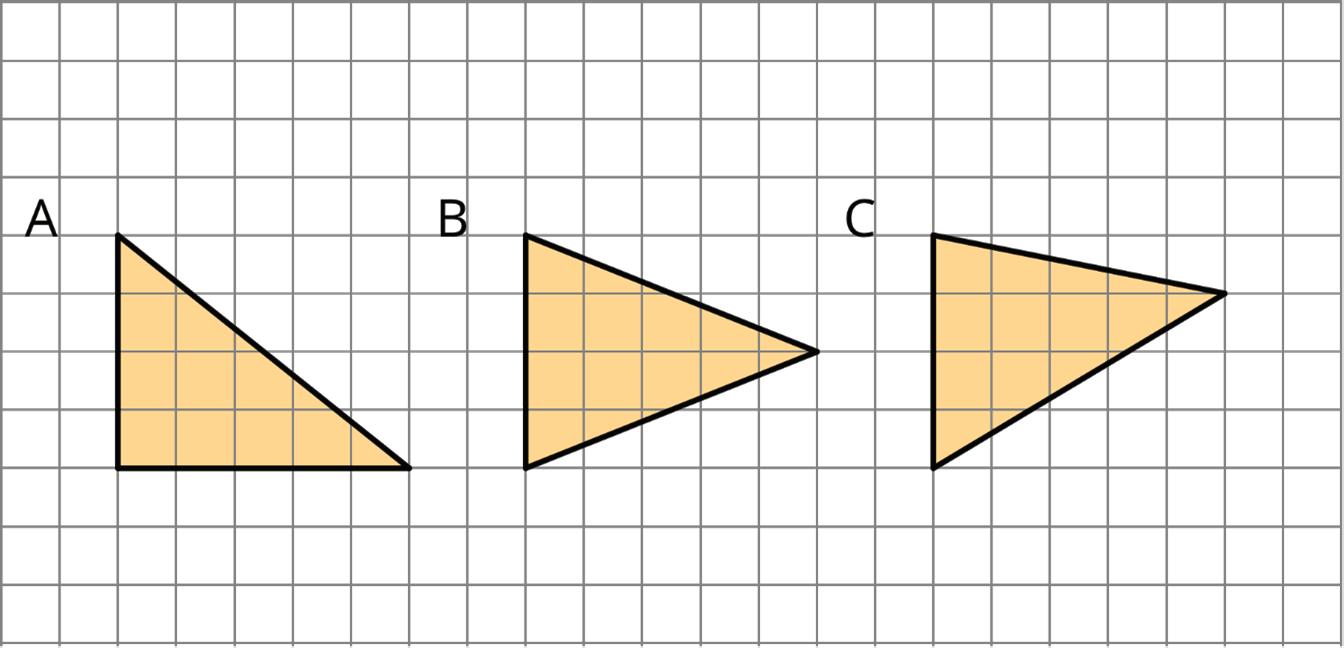
1. Which of the three triangles has the greatest area? Show your reasoning. If you get stuck, try using what you know about the area of parallelograms to help you.

2. Select all drawings in which a corresponding height, ℎ, for a given base, ��, is correctly identified.

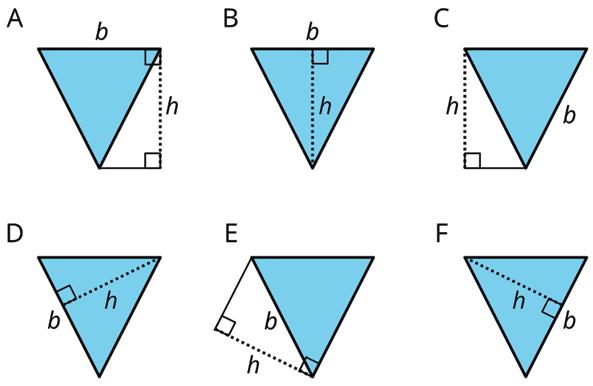
3. For each triangle, a base and its corresponding height are labeled.

a. Find the area of each triangle.

b. How is the area related to the base and its corresponding height?

ManuscriptCopy

4. Select all triangles that have an area of 8 sq. units. Explain how you know.

Review Problems

5. Here is an octagon.

a. While estimating the area of the octagon, Lin reasoned that it must be less than 100 square inches (sq. in.). Do you agree? Explain your reasoning.

ManuscriptCopy

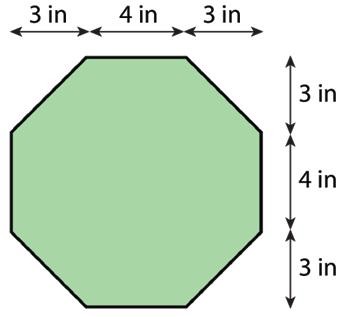
b. Find the exact area of the octagon. Show your reasoning.

6. On the grid, sketch two different parallelograms that have equal area. Label a base and height of each and explain how you know the areas are the same.

ManuscriptCopy

ManuscriptCopy

Unit 1, Lesson 7: Area of Trapezoids

Warm-Up: Notice and Wonder

Two figures are shown.

1. What do you notice about these two figures?

2. What do you wonder about the figures?

ManuscriptCopy

Figure 1

Figure 2

Exploration Activity: Decomposing a Trapezoid

A trapezoid is a quadrilateral with at least 1 pair of parallel sides.

Trapezoid A is shown on a grid with each grid line representing 1 unit.

Trapezoid A

Andi and Rogan decomposed trapezoid A to find its area. Their work is shown.

1. What do you notice about the ways Andi and Rogan decomposed the trapezoid? Note any similarities or differences in their work.

2. Find the area of the trapezoid. Show your reasoning.

Andi Rogan

Guided Activity: Deriving the Formula for the Area of a Trapezoid

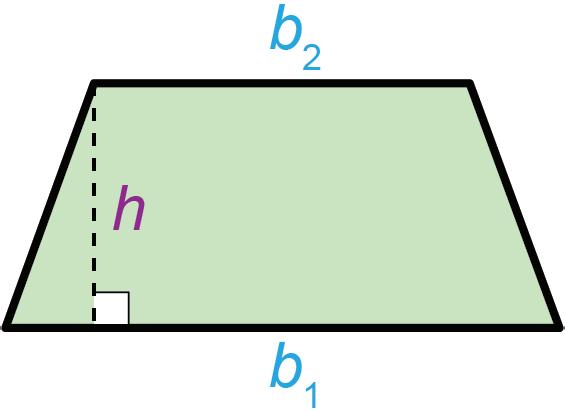
The two parallel sides of a trapezoid are both called bases. To distinguish between the two bases, one is named base 1, ��1, and the other base 2, ��2.

1. On trapezoid A, label the bases ��1 and ��2.

2. Complete the statements.

a. The length of ��1 of trapezoid A is _____ units.

b. The length of ��2 of trapezoid A is _____ units.

c. The height of trapezoid A is _____ units.

3. Trapezoid A is decomposed into two triangles, triangle M and triangle T, as shown.

a. Complete the statements.

Trapezoid A

Trapezoid A

b1 b2 Triangle M Triangle T

The base of triangle M, ��1, is _____ units, and its corresponding height is _____ units. The base of triangle T, ��2, is _____ units, and its corresponding height is _____ units. When a trapezoid is decomposed into 2 triangles by drawing a diagonal, the height of both triangles will always be the same.

b. Davita wrote a formula for the area of trapezoid A.

Davita’s Formula

Area trapezoid A = Area triangle M + Area triangle T �� = 1 2 ��1ℎ + 1 2 ��2ℎ

Explain how Davita determined her formula.

The formula Davita wrote can be rewritten as �� = 1 2 ℎ(��1 + ��2) using the distributive property. This formula can be used to find the area of any trapezoid.

4. Use Davita’s formula to find the area of trapezoid A. Show your work.

5. Compare your answer to question 4 with your answer to question 2 in the Exploration Activity. Make corrections, if necessary.

Collaborative Activity: Applying the Formula for Area of a Trapezoid

A trapezoid is shown.

1. Use a ruler to measure the dimensions of the trapezoid in centimeters (cm). Round to the nearest half cm. Complete the table.

2. Use the formula for the area of a trapezoid to determine the area. Show your work.

Lesson Summary

The lengths of the parallel bases and the height, the distance between the bases, can be used to find the area of a trapezoid.

A trapezoid is a quadrilateral with at least one pair of parallel sides.

When a trapezoid is drawn on a grid and has horizontal or vertical bases, the grid can be used to find the lengths of the height and bases. Two such examples are shown.

When a trapezoid is not drawn on a grid, the area can be found using the lengths of the bases and the corresponding height.

In the trapezoid shown, the parallel bases, ��1 and ��2, are 131 2 units and 41 2 units, and the distance between the bases, the height of the trapezoid, ℎ, is 5 units.

Different strategies can be used to find the area of a trapezoid.

• Decompose the trapezoid into other figures (such as rectangles, squares, parallelograms, and triangles) to determine its area.

ManuscriptCopy

• Enclose the trapezoid in a rectangle or parallelogram, and then subtract the area of the triangle(s) in the corner(s).

• Use the formula �� = 1 2 ℎ(��1 + ��2), where ��1 and ��2 are the bases and ℎ is the height.

Regardless of their shape, trapezoids with the same height whose bases have the same sum have the same area. Shown are two additional trapezoids with the same height whose bases have the same sum as the previous trapezoid.

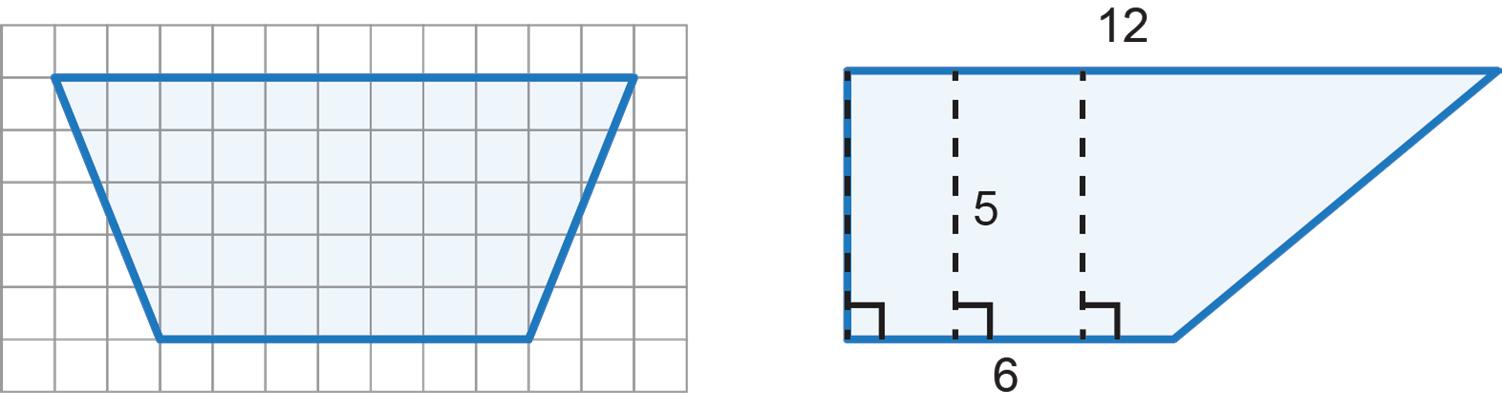
The area of all three trapezoids is 45 square units (sq. units). • 1 2 ⋅ 5�41 2 + 131 2 � = 45 sq. units • 1 2 ⋅ 5(11 + 7) = 45 sq. units

1 2 ⋅ 5(12 + 6) = 45 sq. units

Practice Problems

1. A trapezoid is shown on a grid where each grid square represents 1 square inch (sq. in.).

a. Show or explain how to decompose the trapezoid to find its area.

b. Determine the area of the trapezoid.

ManuscriptCopy

2. Four trapezoids are shown on a grid.

a. Circle the trapezoids that have the same area.

b. Explain your reasoning.

3. Which set of measurements represents the trapezoid with the greatest area?

A. ��1 = 4, ��2 = 10, ℎ = 7

B. ��1 = 7, ��2 = 10, ℎ = 4

C. ��1 = 8.5, ��2 = 3.5, ℎ = 10

D. ��1 = 10.5, ��2 = 3.5, ℎ = 8

4. A trapezoid is shown.

a. Use a ruler to find the lengths of the bases and height of the trapezoid in millimeters (mm). Round measurements to the nearest mm.

��1 = ______ mm ��2 = ______ mm

ℎ = ______ mm

b. Determine the area of the trapezoid.

A.

C.

Review Problems

5. Explain why this quadrilateral is not a parallelogram.

6. A square with an area of 1 square meter (sq. m) is decomposed into 9 identical small squares. Each small square is decomposed into two identical triangles.

a. What is the area, in sq. m, of 6 triangles? If you get stuck, consider drawing a diagram.

b. How many triangles are needed to compose a region that is 11 2 sq. m?

ManuscriptCopy

Unit 1, Lesson 8: Polygons

Warm-Up: Which One Doesn’t Belong – Bases and Heights

1. Which one doesn’t belong?

Exploration Activity: What Are Polygons?

Here are five polygons.

Here are six figures that are not polygons.

ManuscriptCopy

2. Circle the figures that are polygons.

3. What do the figures you circled have in common? What characteristics helped you decide whether a figure was a polygon?

Exploration Activity: Quadrilateral Strategies

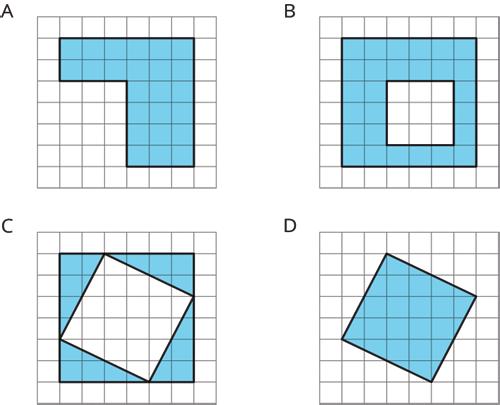
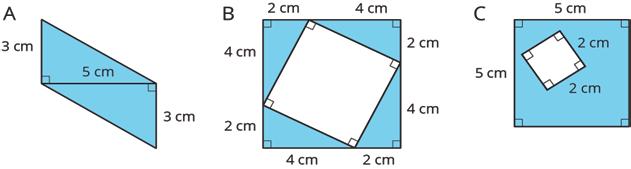
Find the area of two quadrilaterals of your choice. Show your reasoning.

ManuscriptCopy

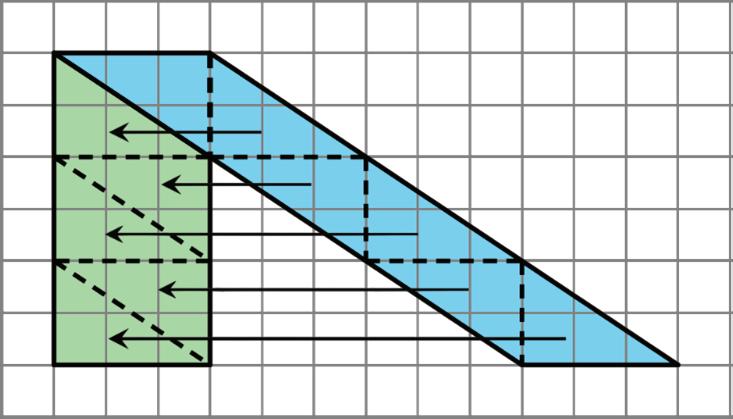
Collaboration Activity: Pinwheel

Find the area of the shaded region in square units. Show your reasoning.

Lesson Summary

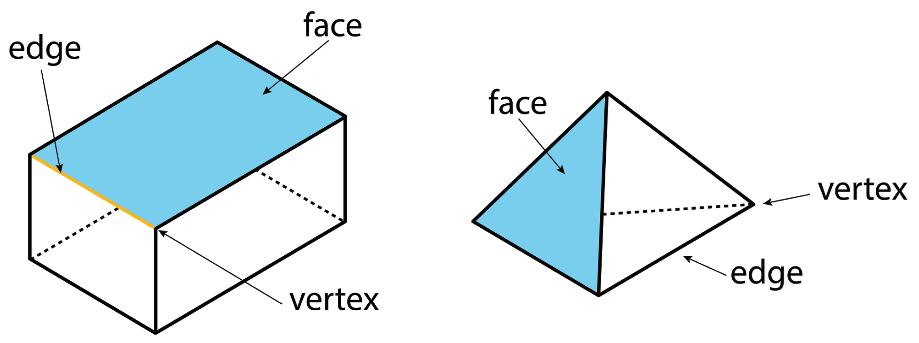
A polygon is a two-dimensional figure composed of straight line segments.

• Each end of a line segment connects to 1 other line segment. The point where 2 segments connect is a vertex. The plural of vertex is vertices.

• The segments are called the edges or sides of the polygon. The sides form the outer boundary of a polygon and do not intersect within the polygon. There are always an equal number of vertices and sides.

A polygon is a closed two-dimensional figured composed of at least three straight sides and three vertices.

The vertex (of a figure) is the point at which the rays or sides of an angle, the sides of a two-dimensional figure, or the edges of a three-dimensional figure meet.

In a figure, the segment or curve where two faces intersect is an edge.

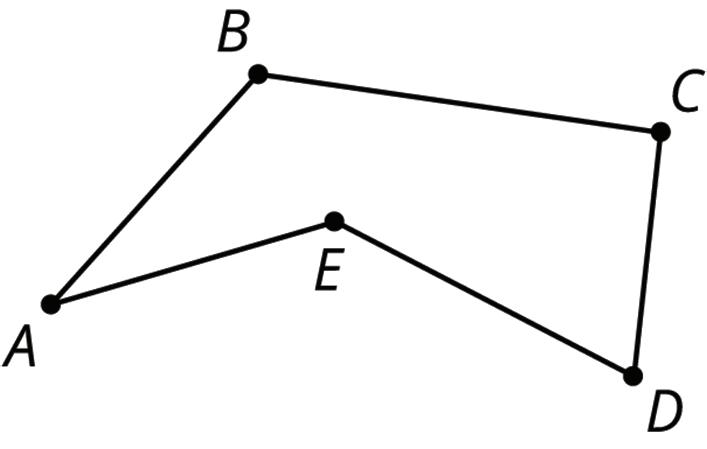
A polygon with 5 sides is shown. The vertices are labeled ��, ��, ��, ��, and ��.

A polygon encloses a region. To find the area of a polygon is to find the area of the region inside it.

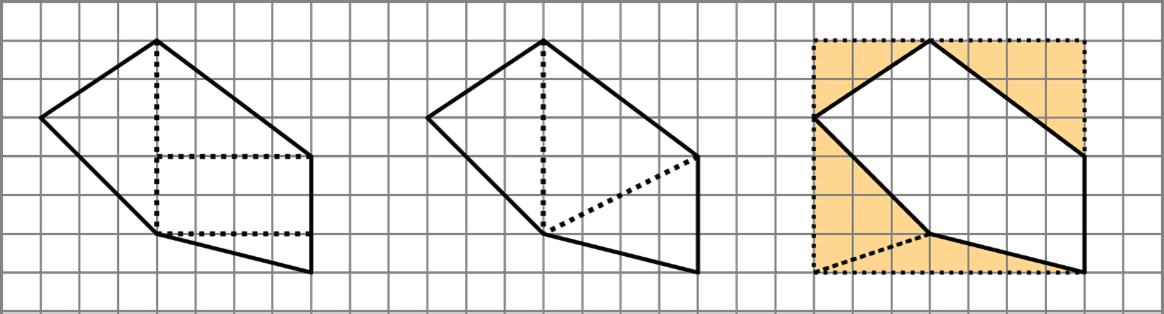
Find the area of a polygon by decomposing the region inside it into triangles and rectangles or composing the polygon into a rectangle. Three examples of strategies that can be used to find the area of the same polygon are shown.

• The first two diagrams show the polygon decomposed into triangles and rectangles. The sum of their areas is the area of the polygon.

• The last diagram shows the polygon enclosed in a rectangle. Find the area of the polygon by subtracting the areas of the triangles that are shaded from the area of the rectangle.

Practice Problems

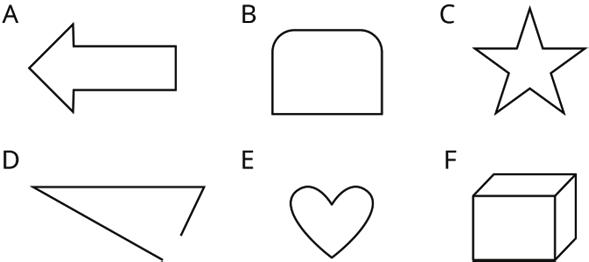
1. Select all the polygons.

2. Mark each vertex with a large dot. How many edges and vertices does this polygon have?

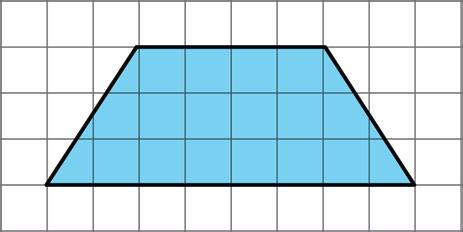
3. Find the area of this trapezoid. Explain or show your strategy.

4. Lin and Andre used different methods to find the area of a regular hexagon with 6-inch (in.) sides. Lin decomposed the hexagon into six identical triangles. Andre decomposed the hexagon into a rectangle and two triangles.

Find the area of the hexagon using each person’s method. Show your reasoning.

5.

a. Identify a base and a corresponding height that can be used to find the area of this triangle. Label the base �� and the corresponding height ℎ.

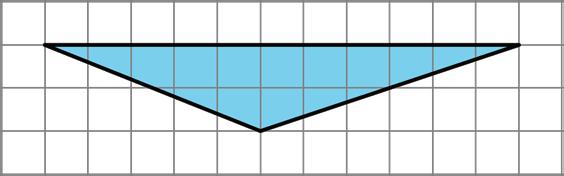
b. Find the area of the triangle. Show your reasoning.

ManuscriptCopy

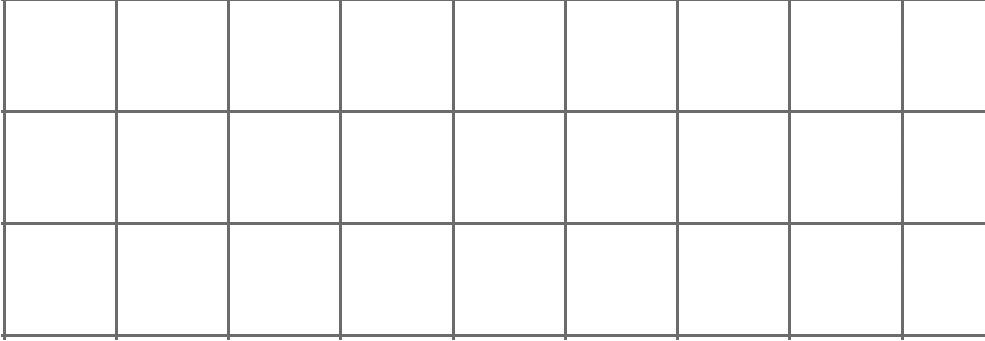
6. On the grid, draw three different triangles with an area of 12 square units. Label the base and height of each triangle.

Unit 1, Lesson 9: Solving Problems Involving Area of Composite Figures

Warm-Up: Covering the Pool

The Hollerbach family recently built a custom pool in the shape of a trapezoid. A representation of the pool is shown, with dimensions in feet (ft.).

During the cool months, the family will keep the pool covered. A cover will need to be designed to fit over the surface of the Hollerbach’s pool.

1. Explain how to decompose the figure to determine the area of the pool’s surface.

2. Determine the minimum area of a cover that will fit the Hollerbach’s pool.

ManuscriptCopy

Exploration Activity: Decomposing to Compose a Quilt

Mabel’s uncle is making her a quilt that resembles a soccer ball. In the quilt’s center, he is including a large, darker piece of fabric in the shape of a regular pentagon, as shown. The lengths are given in inches (in.).

1. Draw lines to decompose the pentagon into 5 congruent triangles.

2. Find the area of one congruent triangle. Include units.

3. What is the area of the entire darker piece of fabric Mabel’s uncle needs for the center of her quilt? Include units.

Collaborative Activity: Finding Area by Decomposing

A quadrilateral is shown. Lengths are shown in centimeters (cm). The quadrilateral can be decomposed into two triangles based on the dimensions given.

1. What are the bases and heights of the two triangles for which these dimensions are given in the figure?

2. Find the area of the original quadrilateral by finding the sum of the areas of the two decomposed triangles. Include units.

3. Discuss with your partner other ways to decompose the quadrilateral, and what measures you would need to find the area of the quadrilateral using a different decomposition.

Lesson Summary

To find the area of a composite figure, decompose the figure into quadrilaterals and/ or triangles. Then, find the sum of the areas of the smaller figures, and add them together for the total area.

A composite figure is a two- or three-dimensional figure that can be decomposed into smaller figures.

There is often more than one way to decompose a figure. Some options for decomposing a composite figure are shown. or or

ManuscriptCopy

Use information provided with the figure in a problem to help guide which decomposition works best. Calculate the area of each of the smaller parts, ensuring that the entire area of the original figure is accounted for. Add the areas to find the total area of the composite figure. Area is always measured in square units.

Practice Problems

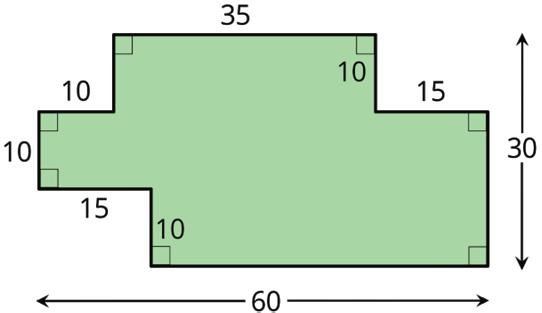
1. A composite figure is shown. The length of each square on the grid is 1 in.

Find the area of the composite figure.

2. Find the area of the figure in square feet (sq. ft.). Show your work.

3. Thomas has decided to put grass sod in his backyard. A drawing of this backyard is shown. The lengths are given in meters (m).

How much sod does Thomas need to buy, in square meters (sq. m)?

4. The floor plan of a store is shown with measurements in yards (yd.)

a. The store found 160 square yards (sq. yd.) of tile on sale. Based on the floor plan drawn, will the store have enough tiles to redo the flooring if they buy what is on sale?

b. Determine the amount of tile, in sq. yd., that the store is short or has left over.

Review Problems

5. Select all segments that could represent a corresponding height if the side �� is the base.

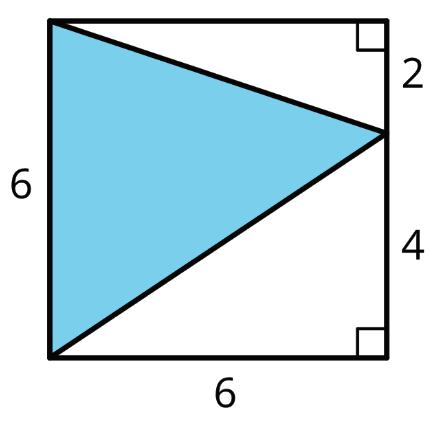
6. Find the area of the shaded triangle. Show your reasoning.

ManuscriptCopy

ManuscriptCopy

Unit

1,

Lesson

10: What Is Surface Area?

Warm-Up: Covering the Cabinet (Part 1)

Your teacher will show you a video about a cabinet or some pictures of it.

Estimate an answer to the question: How many sticky notes would it take to cover the cabinet, excluding the bottom?

Exploration Activity: Covering the Cabinet (Part 2)

Earlier, you learned about a cabinet being covered with sticky notes.

1. How could you find the actual number of sticky notes it will take to cover the cabinet, excluding the bottom? What information would you need to know?

2. Use the information you have to find the number of sticky notes needed to cover the cabinet. Show your reasoning.

Exploration Activity: Building with Snap Cubes

Here is a sketch of a rectangular prism built from 12 cubes.

It has six faces, but you can only see three of them in the sketch. It has a surface area of 32 square units (sq. units).

You have 12 snap cubes from your teacher. Use all of your snap cubes to build a different rectangular prism (with different edge lengths than shown in the prism here).

1. How many faces does your figure have?

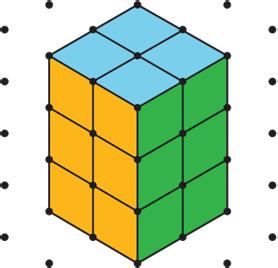
2. What is the surface area of your figure in sq. units?

3. Draw your figure on isometric dot paper. Color each face a different color.

ManuscriptCopy

Lesson Summary

The surface area of a figure (in sq. units) is the number of unit squares it takes to cover the entire surface without gaps or overlaps.

• If a three-dimensional figure has flat sides, the sides are called faces.

• The surface area is the total of the areas of the faces.

The surface area of a polyhedron is the number of square units that covers all the faces of the polyhedron, without any gaps or overlaps.

Each flat side of a polyhedron is called a face. For example, a cube has 6 faces, and they are all squares.

A rectangular prism, like the one shown, has 6 faces. The surface area of the prism is the total of the areas of the 6 rectangular faces.

The smaller cubes making up the prism shown have edge lengths of 1 centimeter (cm), so the rectangular prism has edge lengths of 2 cm, 3 cm, and 4 cm. The surface area of this prism is (2 ⋅ 3) + (2 ⋅ 3) + (2 ⋅ 4) + (2 ⋅ 4) + (3 ⋅ 4) + (3 ⋅ 4), or 52 square centimeters (sq. cm).

Practice Problems

1. What is the surface area of this rectangular prism?

A. 16 sq. units

ManuscriptCopy

B. 32 sq. units

C. 48 sq. units

D. 64 sq. units

2. Which description can represent the surface area of this trunk?

A. The number of square inches that cover the top of the trunk

B. The number of square feet that cover all the outside faces of the trunk

C. The number of square inches of horizontal surface inside the trunk

D. The number of cubic feet that can be packed inside the trunk

3. Which figure has a greater surface area?

4. A rectangular prism is 4 units high, 2 units wide, and 6 units long. What is its surface area in sq. units? Explain or show your reasoning.

ManuscriptCopy

Review Problems

5. Draw an example of each of these triangles on the grid.

a. A right triangle with an area of 6 sq. units.

b. An acute triangle with an area of 6 sq. units.

c. An obtuse triangle with an area of 6 sq. units.

6. Find the area of triangle ������ in sq. units. Show your reasoning.

ManuscriptCopy

7. Find the area of this shape. Show your reasoning.

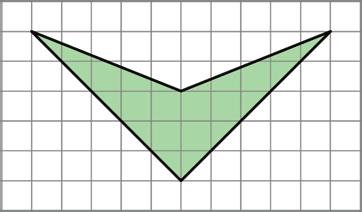
ManuscriptCopy

Unit 1, Lesson 11: Polyhedra

Warm-Up: What Are Polyhedra?

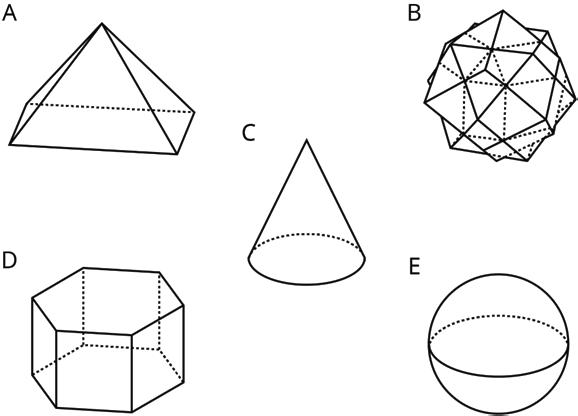
Here are pictures that represent polyhedra.

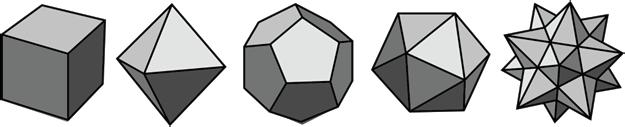
Here are pictures that do not represent polyhedra.

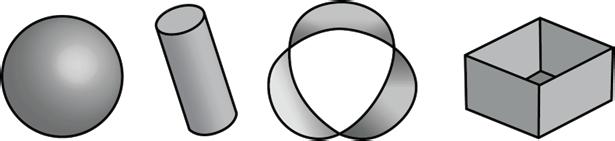
1. Your teacher will give you some figures or objects. Sort them into polyhedra and non-polyhedra.

2. What features helped you distinguish the polyhedra from the other figures?

ManuscriptCopy

Exploration Activity: Prisms and Pyramids

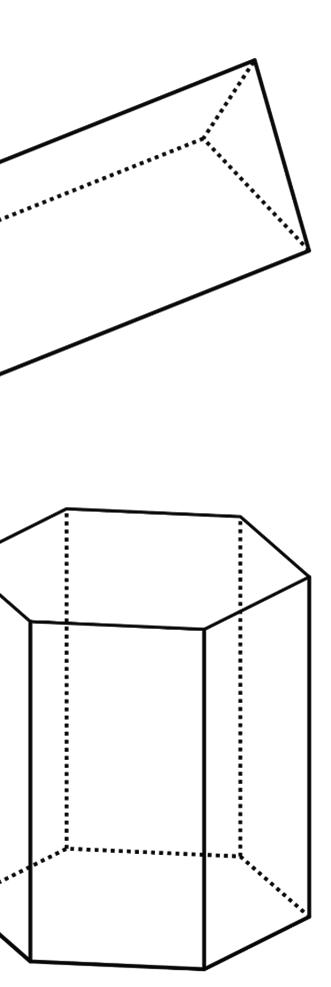
1. Here are some polyhedra called prisms.

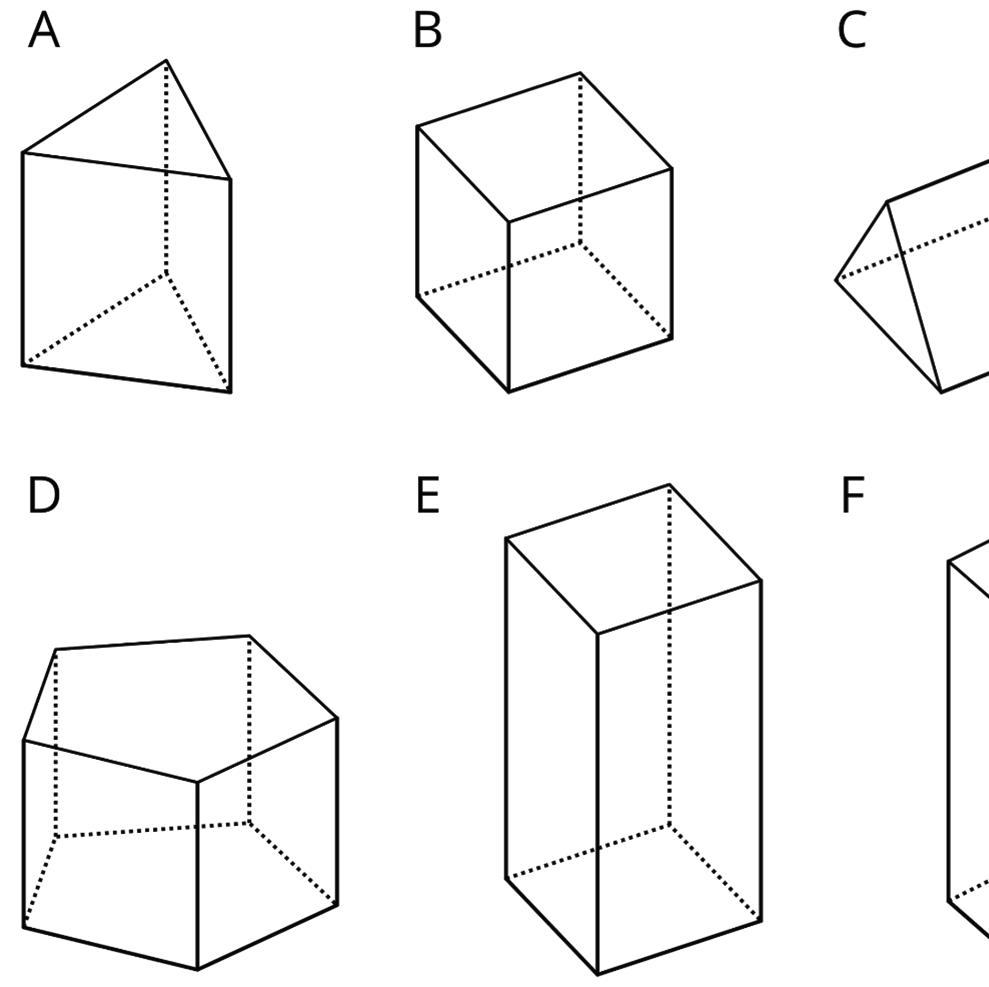
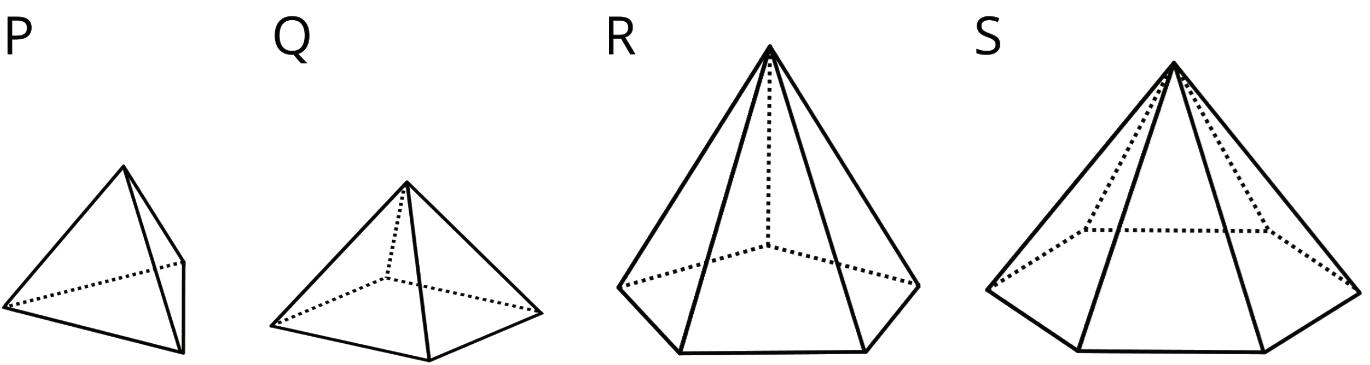
Here are some polyhedra called pyramids.

a. Look at the prisms. What are their characteristics or features?

b. Look at the pyramids. What are their characteristics or features?

ManuscriptCopy

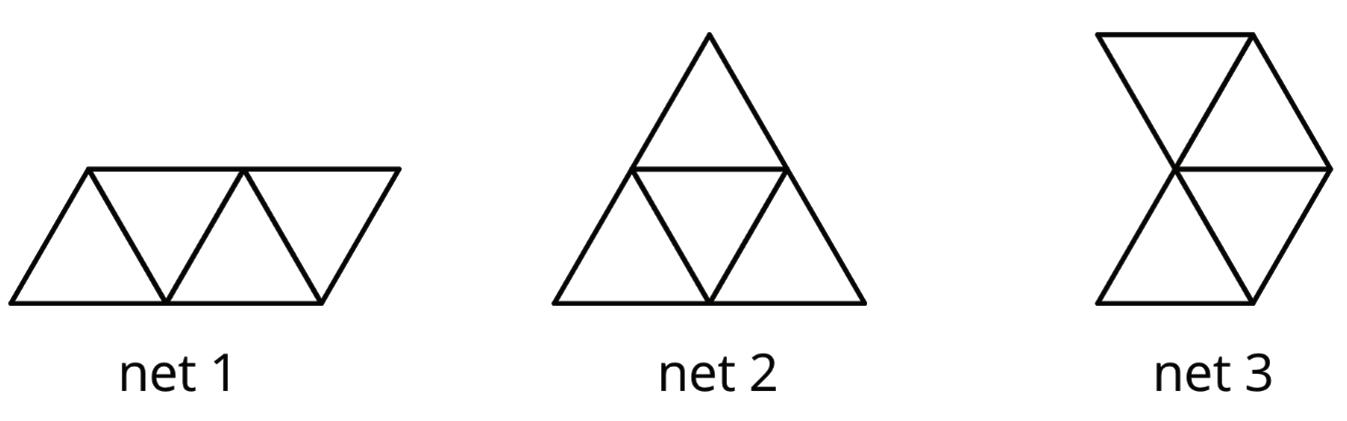
2. Which of these nets can be folded into Pyramid P? Circle all that apply.

3. Your teacher will give your group a set of polygons and assign a polyhedron.

a. Decide which polygons are needed to compose your assigned polyhedron. List the polygons and how many of each are needed.

b. Arrange the cut-outs into a net that, if taped and folded, can be assembled into the polyhedron. Sketch the net. If possible, find more than one way to arrange the polygons (show a different net for the same polyhedron).

ManuscriptCopy

Exploration Activity: Assembling Polyhedra

1. Your teacher will give you the net of a polyhedron. Cut out the net, and fold it along the edges to assemble a polyhedron. Tape or glue the flaps so that there are no unjoined edges.

2. How many vertices, edges, and faces are in your polyhedron?

Vertices: ______

Edges: ______

Faces: ______

Lesson Summary

A polyhedron is a three-dimensional figure composed of faces. Each face is a filled-in polygon and meets only 1 other face along a complete edge. The ends of the edges meet at points that are called vertices.

A polyhedron always encloses a three-dimensional region. Some drawings of different polyhedra are shown.

ManuscriptCopy

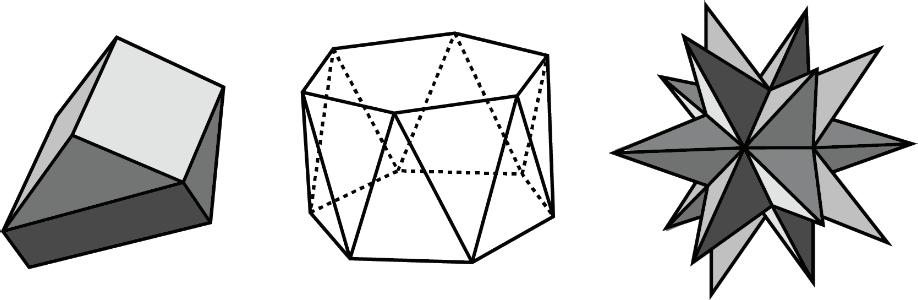
A polyhedron is a closed, three-dimensional shape with flat sides. When we have more than one polyhedron, we call them polyhedra.

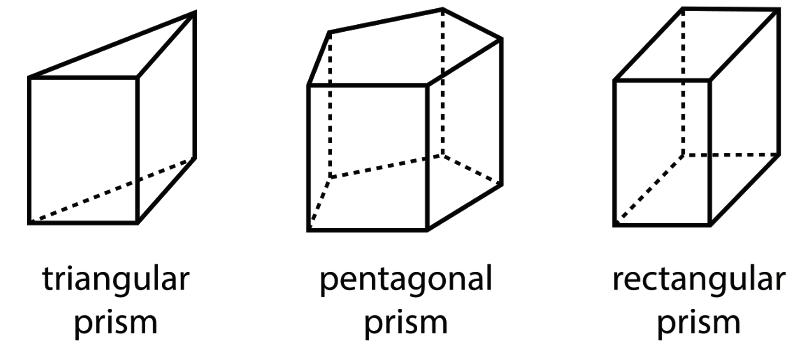
A prism is a type of polyhedron with 2 identical faces that are parallel to each other, which are called bases. The bases are connected by a set of rectangles or parallelograms.

A prism is a solid figure composed of two parallel, congruent faces (called bases) connected by parallelograms.

A prism is named for the shape of its bases. For example, if the base is a pentagon, then it is called a pentagonal prism.

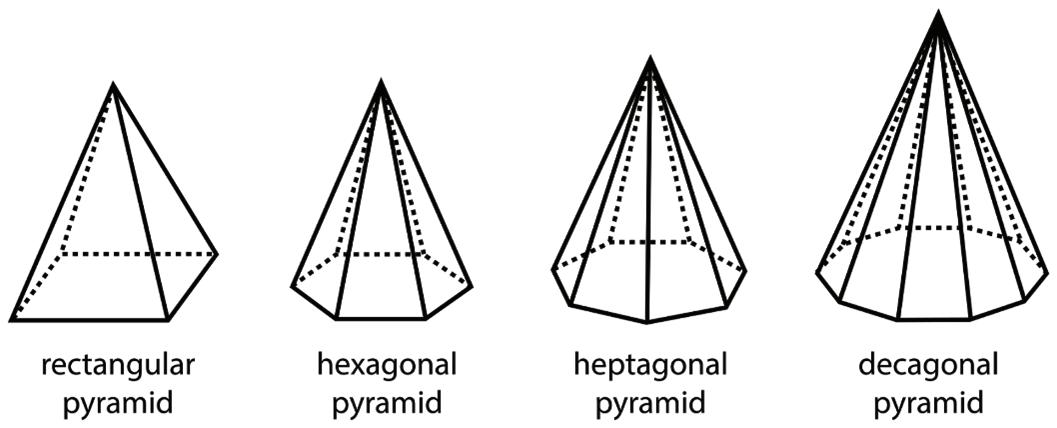
A pyramid is a type of polyhedron that has 1 special face called the base. All of the other faces are triangles that all meet at a single vertex.

A pyramid is a solid figure containing a polygonal base and triangular faces. The triangular faces have the same size and shape and they connect the sides of the base to a common point called the apex.

A pyramid is named for the shape of its base. For example, if the base is a pentagon, then it is called a pentagonal pyramid.

A net is a two-dimensional representation of a polyhedron. It is composed of the polygons that form the faces of a polyhedron.

A net is a two-dimensional diagram that can be folded or made into a three-dimensional figure.

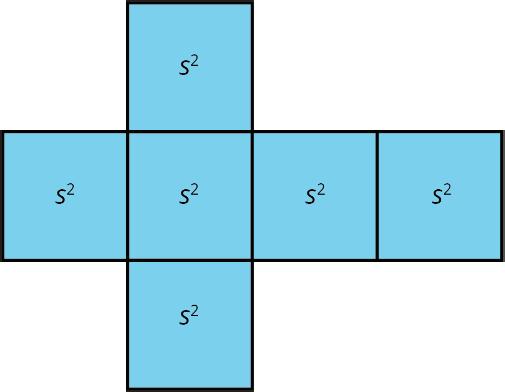
A cube has 6 square faces, so its net is composed of 6 squares, as shown.

A net can be cut out and folded to make a model of the polyhedron.

In a cube, every face shares its edges with 4 other squares. In a net of a cube, not all edges of the squares are joined with another edge. When the net is folded, however, each of these open edges will join another edge.

It takes practice to visualize the final polyhedron by just looking at the net.

Practice Problems

1. Select all the polyhedra.

2. A polyhedron is shown.

a. Is this polyhedron a prism, a pyramid, or neither? Explain how you know.

ManuscriptCopy

b. How many faces, edges, and vertices does it have?

Faces: ______

Edges: ______

Vertices: ______

3. Tyler said this net cannot be a net for a square prism because not all the faces are squares. Do you agree with Tyler? Explain your reasoning.

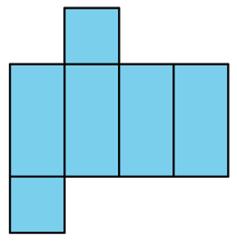
Review Problems

4. Explain why each of the following triangles has an area of 9 square (sq.) units.

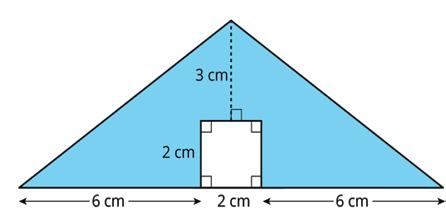
5. Find the area of the shaded region. Show or explain your reasoning.

ManuscriptCopy

a. A parallelogram has a base of 12 meters (m) and a height of 11 2 m. What is its area?

b. A triangle has a base of 16 inches (in.) and a height of 1 8 in. What is its area?

c. A parallelogram has an area of 28 square feet (sq. ft.) and a height of 4 ft. What is its base?

d. A triangle has an area of 32 square millimeters (sq. mm) and a base of 8 mm. What is its height?

ManuscriptCopy

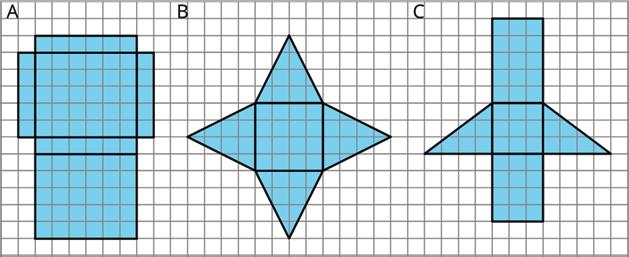
Unit 1, Lesson 12: Nets and Surface Area

Warm-Up: Matching Nets

Each of the nets can be assembled into a polyhedron. Match each net with its corresponding polyhedron, and name the polyhedron. Be prepared to explain how you know the net and polyhedron go together.

ManuscriptCopy

Exploration Activity: Using Nets to Find Surface Area

1. Name the polyhedron that each net would form when assembled.

Polyhedron A: _____________________________________________

Polyhedron B: _____________________________________________

Polyhedron C: _____________________________________________

2. Your teacher will give you the nets of three polyhedra. Cut out the nets and assemble the three-dimensional shapes.

3. Find the surface area of each polyhedron. Explain your reasoning clearly.

Polyhedron A:

Polyhedron B:

Polyhedron C:

Lesson Summary

A net of a pyramid has one polygon that is the base. The rest of the polygons are triangles. A net of a prism has 2 copies of the polygon that is the base.

In a rectangular prism, there are three pairs of parallel and identical rectangles. Any pair of these identical rectangles can be the bases, as shown.

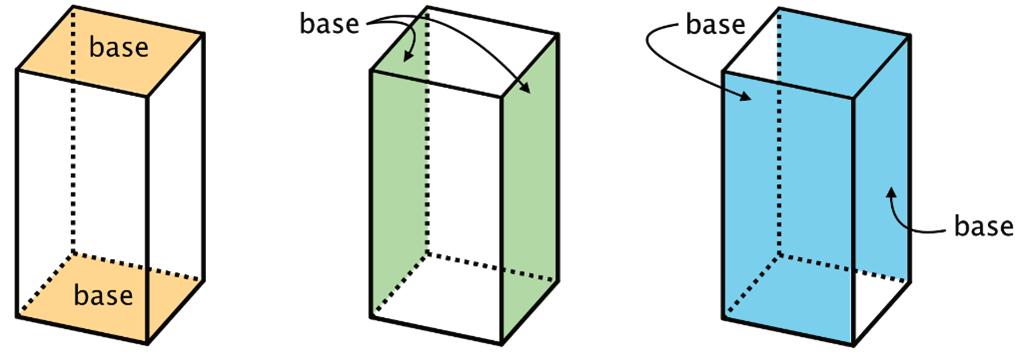
Because a net shows all the faces of a polyhedron, it can be used to find the polyhedron’s surface area.

The surface area of a polyhedron is the sum of the areas of all of the faces.

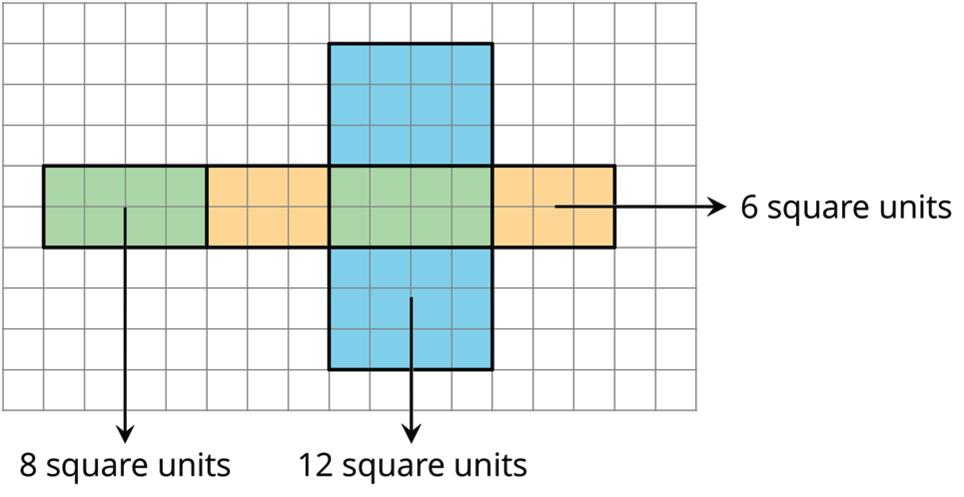
The net of a rectangular prism shows three pairs of rectangles. In the example shown, there are 2 rectangles that are 4 units by 2 units, 2 rectangles that are 3 units by 2 units, and 2 rectangles that are 4 units by 3 units.

The surface area of the rectangular prism is 52 square units because 8 + 8 + 6 + 6 + 12 + 12 = 52.

Practice Problems

1. A net is shown on a grid.

a. What polyhedron can be assembled from this net? Explain how you know.

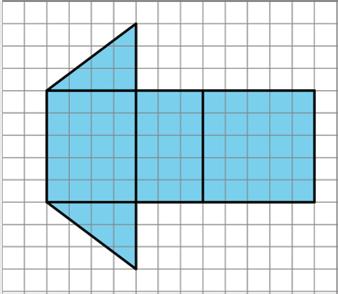
b. Find the surface area of this polyhedron. Show your reasoning.

2. Here are two nets. Mai said that both nets can be assembled into the same triangular prism. Do you agree? Explain or show your reasoning.

ManuscriptCopy

3. Jada drew a net for a polyhedron and calculated its surface area.

a. What polyhedron can be assembled from this net?

b. Jada made some mistakes in her area calculation. What were the mistakes?

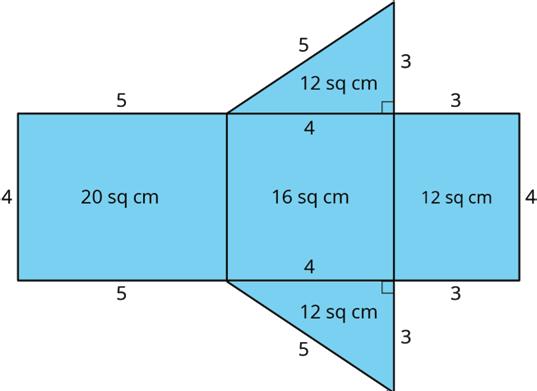
c. Find the surface area of the polyhedron. Show your reasoning.

Review Problems

4. Here are two polyhedra and their nets. Label all edges in the net with the correct lengths.

ManuscriptCopy

5. Here are two three-dimensional figures.

Tell whether each of the following statements describes Figure A, Figure B, both, or neither.

a. This figure is a polyhedron. ________________

b. This figure has triangular faces. ________________

c. There are more vertices than edges in this figure. ________________

d. This figure has rectangular faces. ________________

e. This figure is a pyramid. ________________

f. There is exactly one face that can be the base for this figure. ________________

g. The base of this figure is a triangle. ________________

h. This figure has two identical and parallel faces that can be the base. ________________

6. Find the area of this polygon. Show your reasoning.

ManuscriptCopy

Unit 1, Lesson 13: Surface Area of Prisms

Warm-Up: Wrapping Paper

Kiran is wrapping this box of sports cards as a present for a friend.

1. What do you notice?

2. What do you wonder?

Guided Activity: Finding Surface Area of Prisms

To find the surface area of a three-dimensional object, use the net of the shape to find the area of each face.

1. A tissue box is 9 inches (in.) long, 5 in. wide, and 6 in. tall.

a. Sketch the net of the tissue box.

b. Label the dimensions of each face on the net.

c. Find the area of each face. Include units.

d. Use the net to find the surface area of the tissue box. Include units.

2. A triangular prism is shown with dimensions given in inches (in.).

a. Sketch a net or individual faces of the prism.

b. Label the dimensions of each face in your sketch.

c. Find the area of each face of the prism. Include units.

d. Add the area of the faces to find the surface area of the triangular prism.

ManuscriptCopy

Collaborative Activity: Finding Surface Area of Prisms

1. Gretchen is preparing to paint a jewelry box but does not know how much paint she needs to buy.

a. What information about the jewelry box does Gretchen need to know in order to buy paint?

Gretchen measures the box to be 171 2 in. long, 111 2 in. wide, and 15 in. tall.

The net of the jewelry box is shown in the table.

b. Label the side lengths of the net. Then, complete the table to find the area of each face.

c. What is the surface area of the jewelry box? Include units.

2. Mateo is designing a tent for his next camping trip. A drawing of his tent is shown with dimensions given in feet (ft.).

How much fabric does Mateo need to buy to create the tent?

Lesson Summary

A given three-dimensional figure can be used to draw its net. Visualize each face of the figure, determine how they connect, and label the edge lengths on the net based on the dimensions given.

The nets of prisms should include 2 bases of the same size and a number of rectangular faces that matches the number of sides of the base.

To find the surface area of a three-dimensional object, use the net of the shape to find the area of each face. Then, add the areas of the faces together.

ManuscriptCopy

Practice Problems

1. Darsey wants to build trinket boxes made of wood to sell at the local craft festival. A drawing of her box is shown. How much wood does Darsey need to buy for each trinket box?

2. A carpenter is staining planks of wood to build the top of a long picnic table. The carpenter needs to determine the surface area of each plank in order to purchase the right amount of stain. Each plank is 3 4 in. thick, 51 2 in. wide, and 72 in. long. What is the surface area of each plank?

3. A triangular prism is shown with base side lengths of 6 centimeters (cm), 10 cm, and 113 5 cm. The prism has a height of 91 2 cm. What is the surface area of the triangular prism?

Review Problems

4. A net is shown on the grid.

a. What three-dimensional figure can be assembled from the net?

b. What is the surface area of the figure? (One grid square is 1 square unit.)

5. Select all units that can be used for surface area. □ square meters

feet

centimeters

cubic inches □ square inches □ square feet

6. Can this net be assembled into a cube? Explain how you know. Label parts of the net with letters or numbers if it helps your explanation.

ManuscriptCopy

Unit 1, Lesson 14: Surface Area of Pyramids

Warm-Up: Which One Doesn’t Belong?

1. Four figures are shown.

a. Which one doesn’t belong?

b. Justify your choice using mathematics.

Guided Activity: Finding Surface Area of Pyramids

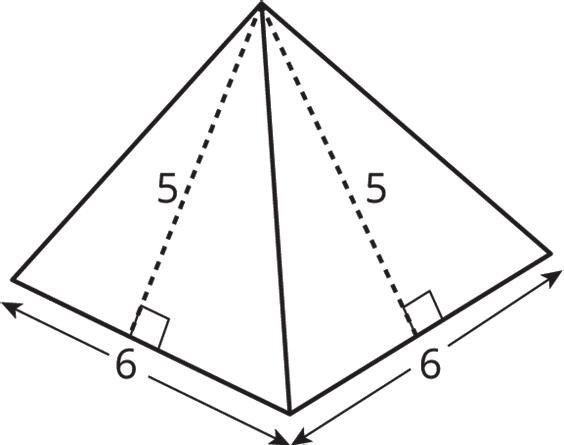
Around 2500 BCE, the Egyptians began building pyramids with intricate hallways and layouts to house the tombs of pharaohs and their families. One of the most famous is the Great Pyramid of Giza, also known as the Pyramid of Khufu, seen below. The Egyptians designed the pyramid to have a square base with approximate side lengths of 230 meters (m), a height of 1461 2 m, and a slant height of 1862 5 m, as shown.

1. Looking at the model of the pyramid, why is there a measurement called height and a measurement called slant height?

The slant height of the pyramid is the height of each triangular face that forms the pyramid.

2. A net of the Pyramid of Giza is shown.

a. Label the dimensions on the net.

ManuscriptCopy

b. Complete the table to determine the surface area of the pyramid.

Side Formula Area

Surface area:

3. Complete the statement.

To find the surface area of a rectangular pyramid, find the sum of the height area of the base and the area of one of all the lateral faces.

Collaborative Activity: Finding Surface Area of Rectangular Pyramids

1. Papier-mâché is a type of art that uses paper and glue. José is using papier-mâché to create a rectangular pyramid for his art project. José needs to determine the area that will be covered in newspaper. The dimensions of the figure that José is using are shown with dimensions given in feet (ft.).

a. Sketch and label the net of the pyramid.

b. Work with your partner to find the surface area of the pyramid.

2. A triangular pyramid is shown, where the base and all 3 faces are equilateral triangles with side lengths of 4 in. The slant height of the pyramid is 31 2 in.

a. Sketch and label the net of the pyramid.

b. Work with your partner to find the surface area of the pyramid.

Lesson Summary

A pyramid is a type of polyhedron that has 1 special face called the base. All of the other faces are triangles that meet at a single vertex, called an apex.

Pyramids are named for the shape of the base. A rectangular pyramid has a rectangular base and 4 triangular faces. A triangular pyramid has a triangular base and 3 triangular faces.

ManuscriptCopy

Pyramids have both a height and a slant height. The height represents the distance from the apex to the center of the base. The slant height represents the height of each triangular face on the lateral surface.

When finding the surface area of a pyramid, use the slant height to find the areas of the triangular faces.

A square pyramid and its net are shown.

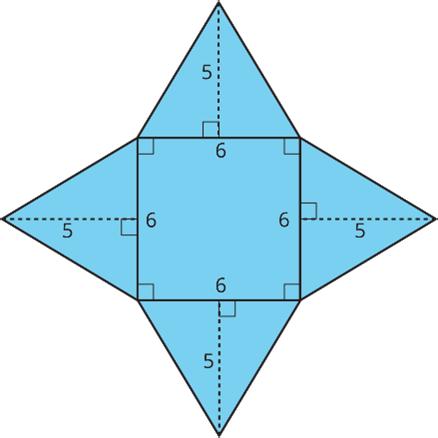
The square pyramid has a square and 4 triangles for its faces. Its surface area is the sum of the areas of the square base and the four triangular faces.

The surface area of this square pyramid is 96 square units.

Practice Problems

1. Calculate the surface area of the pyramid.

2. The net of a pyramid is shown, where the base is an equilateral triangle with side lengths of 2 inches (in.) and an area of 1.73 square inches (sq. in.). The slant height is 7 in. Find the surface area of the pyramid.

3. Find the surface area of a rectangular pyramid that has a rectangular base with a side length of 600 ft., which is the base of a triangle with a slant height of 545 ft., and another side length of 756 ft., which is the base of a triangle with a slant height of 5911 2 ft.

4. Do you agree with each of these statements? Explain your reasoning.

a. A parallelogram has six sides.

b. Opposite sides of a parallelogram are parallel.

c. A parallelogram can have one pair or two pairs of parallel sides.

d. All sides of a parallelogram have the same length.

e. All angles of a parallelogram have the same measure.

ManuscriptCopy

Unit 1, Lesson 15: Distinguishing Between Surface Area

and Volume

Warm-Up: Attributes and Their Measures

For each quantity, choose one or more appropriate units of measurement.

For the last two rows, think of a quantity that could be appropriately measured with the given units.

Quantities Units

1. Perimeter of a parking lot: _____________ i. millimeters (mm)

2. Volume of a semi truck: _____________ ii. feet (ft.)

3. Surface area of a refrigerator: _____________ iii. meters (m)

4. Length of an eyelash: _____________ iv. square inches (sq. in.)

5. Area of a state: _____________ v. square feet (sq. ft.)

6. Volume of an ocean: _____________ vi. square miles (sq. mi.)

7. ____________________: miles (mi.) vii. cubic kilometers (cu. km)

8. ____________________: cubic meters (cu. m) viii. cubic yards (cu. yd.)

Exploration Activity: Building with 8 Cubes

Your teacher will give you 16 cubes. Build two different shapes using 8 cubes for each. For each shape:

1. Give a name or a label (e.g., Mae’s First Shape or Eric’s Steps).

2. Determine the volume.

3. Determine the surface area.

4. Record the name, volume, and surface area on a sticky note.

Exploration Activity: Comparing Prisms without Building Them

Three rectangular prisms each have a height of 1 cm.

• Prism A has a base that is 1 cm by 11 cm.

• Prism B has a base that is 2 cm by 7 cm.

• Prism C has a base that is 3 cm by 5 cm.

1. Find the surface area and volume of each prism. Use the dot paper to draw the prisms, if needed.

2. Analyze the volumes and surface areas of the prisms. What do you notice? Write 1 or 2 observations about them.

ManuscriptCopy

Lesson Summary

Length is a one-dimensional attribute of a geometric figure. Lengths are measured using units like millimeters, centimeters, meters, kilometers, inches, feet, yards, and miles.

Area is a two-dimensional attribute. Area is measured in square units. For example, a square that is 1 centimeter on each side has an area of 1 square centimeter.

Volume is a three-dimensional attribute. Volume is measured in cubic units. For example, a cube that is 1 kilometer on each side has a volume of 1 cubic kilometer.

Surface area and volume are different attributes of three-dimensional figures. Surface area is a two-dimensional measure, while volume is a three-dimensional measure.

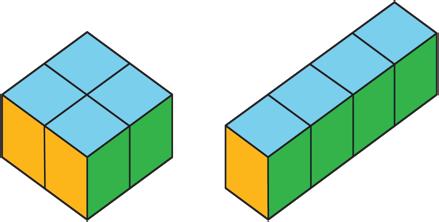
Two figures can have the same volume but different surface areas. Two examples are shown.

• A rectangular prism with side lengths of 1 cm, 2 cm, and 2 cm has a volume of 4 cu. cm and a surface area of 16 sq. cm.

• A rectangular prism with side lengths of 1 cm, 1 cm, and 4 cm has the same volume but a surface area of 18 sq. cm.

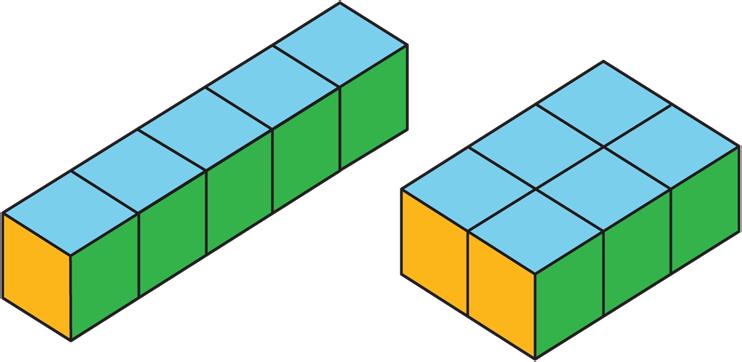
Similarly, two figures can have the same surface area but different volumes.

• A rectangular prism with side lengths of 1 cm, 1 cm, and 5 cm has a surface area of 22 sq. cm and a volume of 5 cu. cm.

• A rectangular prism with side lengths of 1 cm, 2 cm, and 3 cm has the same surface area but a volume of 6 cu. cm.

Practice Problems

1. Match each quantity with an appropriate unit of measurement.

A. The surface area of a tissue box i. sq. m

B. The amount of soil in a planter box ii. yards (yd.)

C. The area of a parking lot iii. cu. in.

D. The length of a soccer field iv. cu. ft.

E. The volume of a fish tank v. sq. cm

2. Here is a figure built from snap cubes.

a. Find the volume of the figure in cu. units.

b. Find the surface area of the figure in sq. units.

ManuscriptCopy

c. True or false: If we double the number of cubes being stacked, both the volume and surface area will double. Explain or show how you know.

3. Lin said, “Two figures with the same volume also have the same surface area.”

a. Which two figures suggest that her statement is true?

b. Which two figures could show that her statement is not true?

Review Problems

4. Draw a pentagon (five-sided polygon) that has an area of 32 sq. units. Label all relevant sides or segments with their measurements, and show that the area is 32 sq. units.

5. A rectangular prism is shown.

a. Draw a net for this rectangular prism.

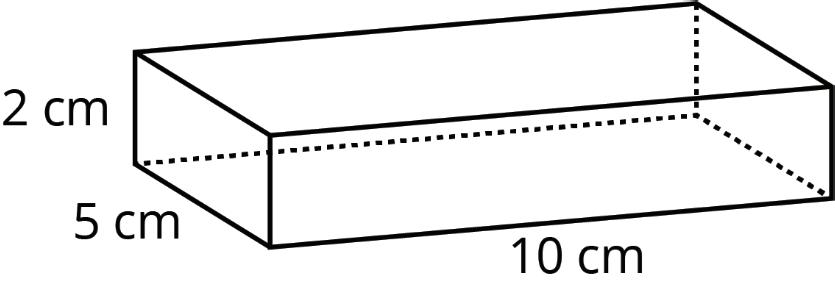
b. Find the surface area of the rectangular prism.

ManuscriptCopy

Unit 1, Lesson 16: Squares and Cubes

Warm-Up: Perfect Squares

1. The number 9 is a perfect square. Find four numbers that are perfect squares and two numbers that are not perfect squares.

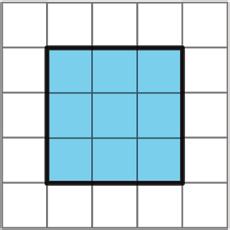
2. A square has a side length of 7 kilometers (km). What is its area?

3. The area of a square is 64 square centimeters (sq. cm). What is its side length?

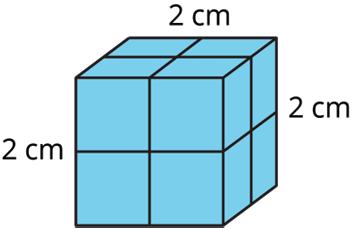
Exploration Activity: Building with 32 Cubes

Your teacher will give you 32 snap cubes. Use them to build the largest single cube you can. Each small cube has an edge length of 1 unit.

1. How many snap cubes did you use?

2. What is the edge length of the cube you built?

3. What is the area of each face of the built cube? Be prepared to explain your reasoning.

4. What is the volume of the built cube? Be prepared to explain your reasoning.

Exploration Activity: Perfect Cubes

1. The number 27 is a perfect cube. Find four other numbers that are perfect cubes and two numbers that are not perfect cubes.

2. A cube has side length 4 centimeters (cm). What is its volume?

3. A cube has side length 10 inches (in.). What is its volume?

4. A cube has side length �� units. What is its volume?

Guided Activity: Introducing Exponents

Make sure to include correct units of measure as part of each answer.

1. A square has side lengths of 10 cm. Use an exponent to express its area.

2. The area of a square is 72 square inches (sq. in.). What is its side length?

The area of a square is expressed using square units or units2. The volume of a cube is expressed using cubed units or units3.

3. Different units of length are given in the first column of the table. Complete the table by expressing the units of measure used for the area and volume of objects whose dimensions are in the given unit. Express each unit using exponents.

ManuscriptCopy

Feet (ft.)

Inches (in.)

Meters (m)

4. The area of a square is 81 m2. Use an exponent to express this area.

5. A cube has edge lengths of 5 in. Use an exponent to express its volume.

6. The volume of a cube is 63 cm3. What is its edge length?

7. A cube has edge lengths of �� units. Use an exponent to write an expression for its volume.

Lesson Summary

When two of the same number are multiplied together, such as 5 ⋅ 5, this is described as squaring the number. This is expressed as 52 and is equal to 25 because 5 ⋅ 5 = 25. The equation 52 = 25 is read, “5 squared is 25.”

We use the word squared to mean, “to the second power.” This is because a square with a side length �� has an area of �� ∙ ��, or ��2.

When three of the same number are multiplied together, such as 4 ⋅ 4 ⋅ 4, this is described as cubing the number. This is expressed as 43 and is equal to 64 because 4 ⋅ 4 ⋅ 4 = 64. The equation 43 = 64 is read, “4 cubed is 64.”

We use the word cubed to mean, “to the third power.” This is because a cube with a side length �� has a volume of �� ∙ �� ∙ ��, or ��3.

This exponent notation can also be used for square and cubic units.

• A square with side lengths of 5 in. has an area of 25 in.2.

ManuscriptCopy

• A cube with edge lengths of 4 cm has a volume of 64 cm3.

In expressions like 53 and 82, the 3 and the 2 are called exponents. They tell you how many factors to multiply.

For example, 53 = 5 ∙ 5 ∙ 5, and 82 = 8 ∙ 8.

The area 25 in.2 is read, “25 square inches.” Square inches are abbreviated as sq. in.

The volume 125 in.3 is read, “125 cubic inches.” Cubic inches are abbreviated as cu. in.

The area of a square with a side length of 7 km is 72 km2. The volume of a cube with an edge length of 2 millimeters (mm) is 23 mm3.

In general, the area of a square with side lengths of �� is ��2, and the volume of a cube with edge lengths of �� is ��3.

Practice Problems

1. What is the volume of this cube?

2. A list of numbers is shown.

16 20 25 100 125 144 225 10,000

a. Circle each number on the list that is a perfect square.

b. Write a sentence that explains your reasoning.

3. A list of numbers is shown.

1 3 8 9 27

a. Circle each number on the list that is a perfect cube.

b. Explain what a perfect cube is.

a. A square has side length 4 cm. What is its area?

b. The area of a square is 49 m2. What is its side length?

c. A cube has edge length 3 in. What is its volume?

Review Problems

5. Prism A and Prism B are rectangular prisms.

• Prism A is 3 in. by 2 in. by 1 in.

• Prism B is 1 in. by 1 in. by 6 in.

Select all statements that are true about the two prisms.

□ They have the same volume.

□ They have the same number of faces.

□ More inch cubes can be packed into Prism A than into Prism B.

□ The two prisms have the same surface area.

ManuscriptCopy

□ The surface area of Prism B is greater than that of Prism A.

6. A net is shown.

a. What polyhedron can be assembled from this net?

b. What information would you need to find its surface area? Be specific, and label the diagram as needed.

7. Find the surface area of this triangular prism. All measurements are in m.

ManuscriptCopy

Unit 1, Lesson 17: Surface Area and Volume of a Cube

Warm-Up: Exponent Review

Select the greater expression of each pair without calculating the value of each expression. Be prepared to explain your choices.

• 10 ⋅ 3 or 103

• 132 or 12 ⋅ 12

• 97 + 97 + 97 + 97 + 97 + 97 or 5 ⋅ 97

Exploration Activity: The Net of a Cube

1. A cube has edge length 5 inches (in.).

a. Draw a net for this cube, and label its sides with measurements.

b. What is the shape of each face?

c. What is the area of each face?

d. What is the surface area of this cube?

ManuscriptCopy

e. What is the volume of this cube?

2. A second cube has edge length 17 units.

a. Draw a net for this cube, and label its sides with measurements.

b. Explain why the area of each face of this cube is 172 square (sq.) units.

c. Write an expression for the surface area, in sq. units.

d. Write an expression for the volume, in cubic units (cu. units).

Exploration Activity: Every Cube in the Whole World

A cube has edge length ��.

1. Draw a net for the cube.

2. Write an expression for the area of each face. Label each face with its area.

ManuscriptCopy

3. Write an expression for the surface area. ______________

4. Write an expression for the volume. ______________

Lesson Summary

The volume of a cube with edge lengths of �� is ��3.

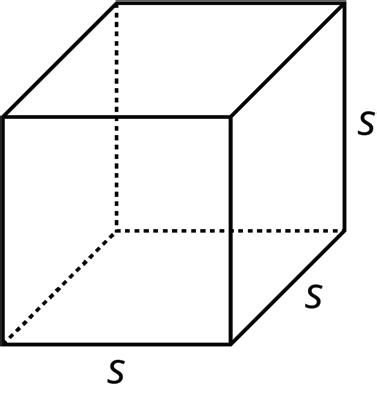
A cube has 6 faces that are all identical squares. The surface area of a cube with edge lengths of �� is 6 ⋅ ��2.

1.

Practice Problems

a. What is the volume of a cube with edge length 8 in.?

b. What is the volume of a cube with edge length 1 3 centimeters (cm)?

c. A cube has a volume of 8 ft.3. What is its edge length?

2. A net is shown.

a. What three-dimensional figure can be assembled from this net?

ManuscriptCopy

b. If each square has a side length of 61 cm, write an expression for the surface area and another for the volume of the figure.

a. Draw a net for a cube with edge length �� cm.

b. What is the surface area of this cube?

c. What is the volume of this cube?

Review Problems

4. Here is a net for a rectangular prism that was not drawn accurately.

a. Explain what is wrong with the net.

b. Draw a net that can be assembled into a rectangular prism.

c. Create another net for the same prism.

ManuscriptCopy

5. State whether each figure is a polyhedron. Explain how you know.

Figure A:

Figure B:

6. Here is Elena’s work for finding the surface area of a rectangular prism that is 1 foot (ft.) by 1 ft. by 2 ft.

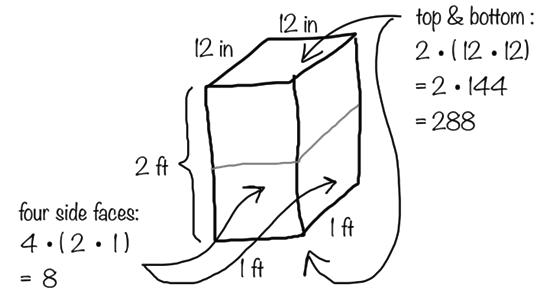
She concluded that the surface area of the prism is 296 square feet (sq. ft.). Do you agree with her? Explain your reasoning.

ManuscriptCopy

ManuscriptCopy

Unit 1, Lesson 18: Volume of Rectangular Prisms

Warm-Up: A Box of Cubes

Consider the box shown, with dimensions given in inches (in.).

1. How many unit squares with side lengths of 1 in. would it take to cover the bottom of the box?

2. What is the area of bottom of the box?

3. How many unit cubes with side lengths of 1 in. would it take to fill the box?

Guided Activity: A Study of Boxes

Boxes N, V, and R are rectangular prisms, with dimensions given in centimeters (cm). The base of each box is shaded, as shown.

1. Complete the table by identifying the dimensions and the area of the base of each box.

ManuscriptCopy

2. Discuss with your partner what you notice about the dimensions of the base of each of the boxes.

The volume, ��, of a prism is the number of cubic units that fill the prism without any gaps or overlaps. The volume of a rectangular prism can be determined using the methods described.

• Determine the number of unit cubes that can be packed inside the figure.

• Use the formula �� = ��ℎ, where �� is the area of the base and ℎ is the height of the prism.

3. Use the formula �� = ��ℎ to determine the volume of boxes N, V, and R.

Volume of Box N = ( ) × _______ = ________ cubic cm (cu. cm)

Volume of Box V = ( ) × _______ = ________ cu. cm

Volume of Box R = ( ) × _______ = ________ cu. cm

4. Discuss with your partner what you notice about the volume of each of the boxes. Summarize your discussion.

5. Consider a cube with side lengths of 3 in. What is the volume of the cube?

6. Determine the volume of a prism with a height of 7 in. and a square base with edge lengths of 5 in.

Collaborative Activity: Composite Prisms

1. Consider the prism shown.

a. Shade in the face of the prism that can represent the base of the prism.

b. What is the area of the base of the prism, in square units?

c. Use the formula �� = ��ℎ to determine the volume of the prism, in cubic units.

2. Two stacked rectangular prisms are shown.

With your partner, determine who will be partner A and who will be partner B.

a. Determine the volume of the prism using the stacked prisms. Show your work.

left.)

ManuscriptCopy

Partner A

(Use the prism on the

Partner B (Use the prism on the right.)

b. Compare your work with your partner’s work to verify that you both found the same volume. Discuss any errors, and make corrections as needed.

c. Discuss with your partner the different strategies used in the calculations.

3. Consider the composite prism shown.

a. Shade in the base of the composite prism.

b. Determine the area of the base of the composite prism.

c. Use the formula �� = ��ℎ to determine the volume of the composite prism.

d. Explain how the volume of the composite prism relates to the volumes of the stacked prisms found in question 2.

ManuscriptCopy

Lesson Summary

Area is a measurement of two dimensions. It represents how many square units are needed to cover a surface. Volume is a measurement of three dimensions that is built up from the base of a prism using a third dimension, height. Each unit of height represents a layer of unit cubes where the number of cubes in each layer is the same as the number of square units covering the area of the base.

Volume is the number of cubic units that fill a three-dimensional region, without any gaps or overlaps.

For example, the rectangular prism shown has base dimensions of 4 units by 4 units with a height of 5 units. The area of the base is shaded in gray. It is next shown that a layer of 4 unit cubes by 4 unit cubes can be used to cover the area of the base of 16 square units. To finish filling in the prism with a height of 5 units, 5 layers of 16 unit cubes are added to the prism to determine the volume of the prism is 80 cubic units.

The volume, ��, of a rectangular prism can be found using the formula �� = ��ℎ, where �� is the area of the base and ℎ is the height of the prism.

The strategies used to decompose a two-dimensional composite figure to find its area can be used to decompose a composite prism to find its volume. Break the composite prism apart into smaller rectangular prisms. Find the volume of each, and add them together to find the volume of the composite prism.

Practice Problems

ManuscriptCopy

1. The Washington family rented a moving truck, and the back of the truck is in the shape of a rectangular prism. The floor of the back of the moving truck is 12 feet (ft.) by 5 ft. The height of the back of the truck is 8 ft. What is the volume of the back of the moving truck? Show your work.

2. Find the volume of the rectangular prism shown.

3. Find the volume of the composite prism shown.

Review Problems

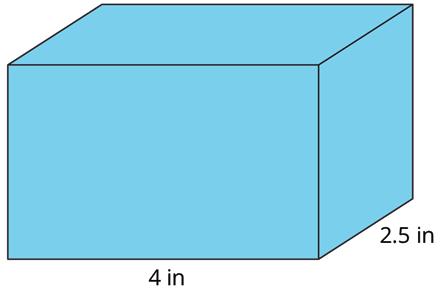
4. A cereal box is 8 in. by 2 in. by 12 in. What is its surface area? Show your reasoning. If you get stuck, consider drawing a sketch of the box or its net and labeling the edges with their measurements.

5. Twelve cubes are stacked to make this figure.

a. What is its surface area?

ManuscriptCopy

b. How would the surface area change if the top two cubes are removed?

Unit 2: Arithmetic in Base Ten

ManuscriptCopy

Unit 2, Lesson 1: Using Decimals in a Shopping Context

Warm-Up: Snack from the Concession Stand

Clare went to a concession stand that sells pretzels for $3.25, drinks for $1.85, and bags of popcorn for $0.99 each. She bought at least one of each item and spent no more than $10.

1. Could Clare have purchased 2 pretzels, 2 drinks, and 2 bags of popcorn? Explain your reasoning.

2. Could she have bought 1 pretzel, 1 drink, and 5 bags of popcorn? Explain your reasoning.

Exploration Activity: Planning a Dinner Party

You are planning a dinner party with a budget of $50 and a menu that consists of 1 main dish, 2 side dishes, and 1 dessert. There will be 8 guests at your party.

Choose your menu items and decide on the quantities to buy so you stay on budget. If you choose meat, fish, or poultry for your main dish, plan to buy at least 0.5 pound per person.

1. The budget is $ ___________ per guest.

2. Use the worksheet to record your choices and estimated costs. Then find the estimated total cost and cost per person. See examples in the first two rows.

3. Is your estimated total close to your budget? If so, continue to the next question. If not, revise your menu choices until your estimated total is close to the budget.

4. Calculate the actual costs of the two most expensive items and add them. Show your reasoning.

5. How will you know if your total cost for all menu items will or will not exceed your budget? Is there a way to predict this without adding all the exact costs? Explain your reasoning.

Lesson Summary

Decimals are often used when dealing with money. In these situations, sometimes rounding is used to make estimates. Other times, the numbers are calculated more precisely.

There are many different ways to add, subtract, multiply, and divide decimals. When you’re performing these computations, it’s helpful to understand the meanings of the digits in a number and the properties of operations, which will be investigated in the upcoming lessons.

ManuscriptCopy

Practice Problems

1. Mai had $14.50. She spent $4.35 at the snack bar and $5.25 at the arcade. What is the exact amount of money Mai has left?

A. $9.60

B. $10.60

C. $4.90

D. $5.90

2. A large cheese pizza costs $7.50. Diego has $40 to spend on pizzas. How many large cheese pizzas can he afford? Explain or show your reasoning.

3. Tickets to a show cost $5.50 for adults and $4.25 for students. A family is purchasing 2 adult tickets and 3 student tickets.

a. Estimate the total cost.

b. What is the exact cost?

c. If the family pays $25, what is the exact amount of change they should receive?

4. Chicken costs $3.20 per lb., and beef costs $4.59 per lb. Answer each question and show your reasoning.

a. What is the exact cost of 3 lb. of chicken?

b. What is the exact cost of 3 lb. of beef?

c. How much more does 3 lb. of beef cost than 3 lb. of chicken?

Review Problems

5. Find the area of the triangle. Show your reasoning.

If you get stuck, carefully consider which side of the triangle to use as the base.

ManuscriptCopy

6. Find the area of this shape. Show your reasoning.

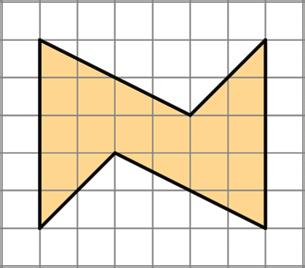
ManuscriptCopy

Unit 2, Lesson 2: Using Diagrams to Represent Addition and Subtraction

Warm-Up: Changing Values

1. A rectangle is shown.

Determine what number the rectangle represents if each small square within the rectangle has each value shown.

a. 1

b. 0.1 ________

c. 0.01 ________

d. 0.001 ________

2. A square is shown.

Determine what number the square represents if each small rectangle within the square has each value shown.

a. 10 ________

b. 0.1 ________

c. 0.001

ManuscriptCopy

Exploration Activity: Squares and Rectangles

You may be familiar with base-ten blocks that represent ones, tens, and hundreds. Here are some diagrams that we will use to represent base-ten units.

• A large square represents 1 one.

• A medium rectangle represents 1 tenth.

• A medium square represents 1 hundredth.

• A small rectangle represents 1 thousandth.

• A small square represents 1 ten-thousandth.

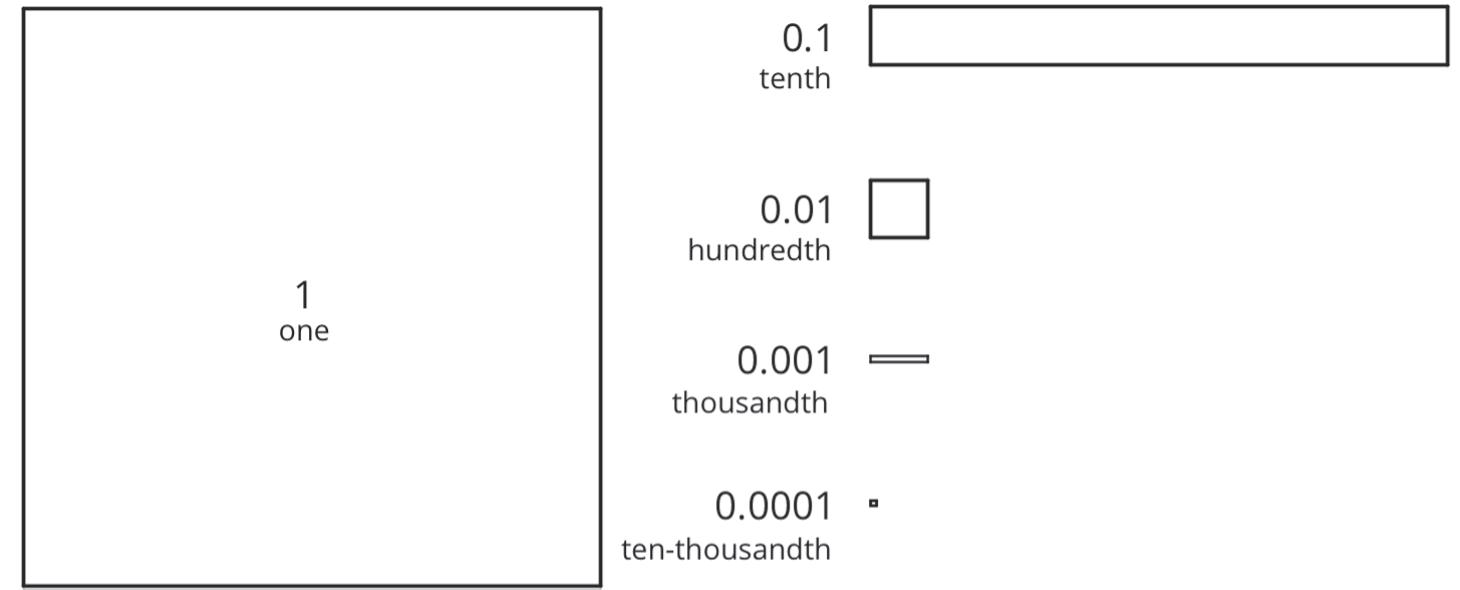
1. Here is the diagram that Priya drew to represent 0.13. Draw a different diagram that represents 0.13. Explain why your diagram and Priya’s diagram represent the same number.

2. Here is the diagram that Han drew to represent 0.025. Draw a different diagram that represents 0.025. Explain why your diagram and Han’s diagram represent the same number.

ManuscriptCopy

3. For each of these numbers, draw or describe two different diagrams that represent it.

a. 0.1

b. 0.02

c. 0.004

4. Use diagrams of base-ten units to represent each sum. Think about how you could use as few units as possible to represent each number.

a. 0.03 + 0.05

b. 0.006 + 0.007

ManuscriptCopy

0.4 + 0.7

c.

Collaborative Activity: Finding Sums in Different Ways

1. Two strategies for calculating the value of 0.26 + 0.07 are shown. In the diagram, each rectangle represents 0.1, and each square represents 0.01.

Use what you know about base-ten units and addition of base-ten numbers to answer each question about the strategies used.

a. Why can 10 squares can be “bundled” into a rectangle in the diagram?

b. How is this bundling reflected in the computation?

2. Consider the expression 0.38 + 0.67.

a. Draw a diagram that could be used to find the sum.

b. Explain whether bundling is needed to find the sum.

3. Calculate 0.38 + 0.67. Check your calculation against your diagram from the previous question.

4. Find each sum using the strategy shown.

a. The larger squares each represent 1. Complete the equation to represent the sum.

b. Complete the computation.

6. 0 3 + 0. 0 9 8

Exploration Activity: Representing Subtraction

1. Three diagrams representing differences are shown. Removed pieces are marked with Xs. For each diagram, write a numerical subtraction expression, and determine the value of the expression.

a.

ManuscriptCopy

b.

c.

2. Express each difference in words.

a. 0.05 – 0.02

b. 0.024 – 0.003

c. 1.26 – 0.14

3. Find each difference by drawing a diagram and by calculating with numbers. Make sure the answers from both methods match. If they don’t match, check your diagram and your numerical calculation.

a. 0.05 – 0.02

b. 0.024 – 0.003

c. 1.26 – 0.14

ManuscriptCopy

Lesson Summary

Base-ten diagrams represent collections of base-ten units: tens, ones, tenths, hundredths, etc. They can be used to understand sums and differences of decimals.

A diagram representing 0.008 and 0.013 is shown, where each square represents 0.001, and each rectangle, made up of ten squares, represents 0.01.

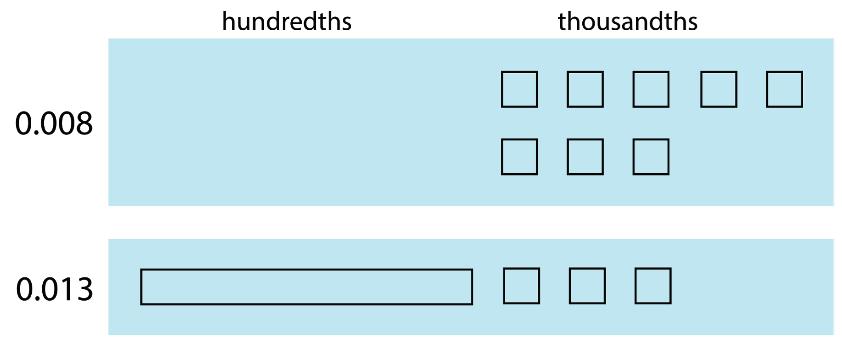
To find the sum, “bundle” (or compose) 10 thousandths into 1 hundredth.

The sum 0.008 + 0.013 = 0.021 is represented in this diagram, which shows the final result is 2 hundredths and 1 thousandth.

A vertical calculation can be also used to find 0.008 + 0.013. Notice that 10 thousandths are also bundled (or composed) into 1 hundredth.

ManuscriptCopy

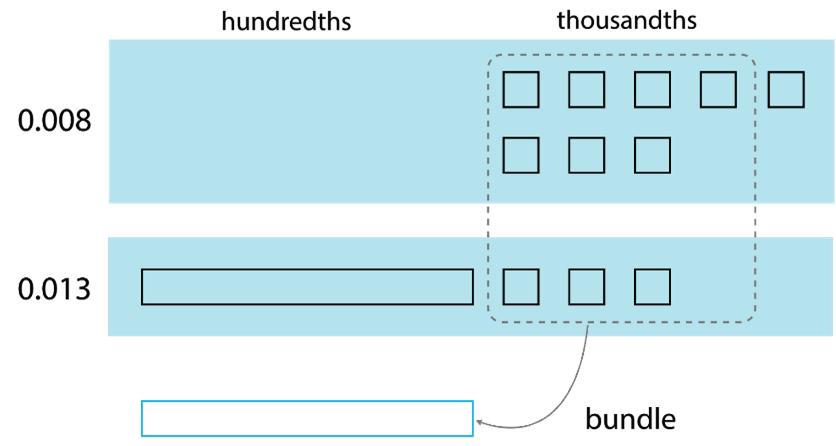
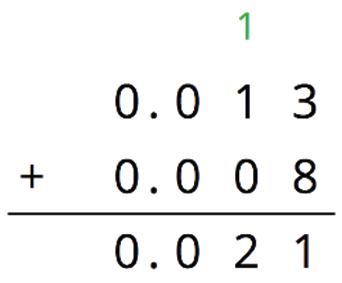
Both strategies can also be used for subtraction.

The diagram shown represents the difference of 0.25 and 0.12. The value 0.25 is represented by the base-ten blocks, and the value 0.12 is represented by the Xs to indicate what is being taken away.

A vertical calculatation can also be used to find 0.25 – 0.12. Both the diagram and the vertical calcuation show that the difference of 0.25 and 0.12 is 0.13.

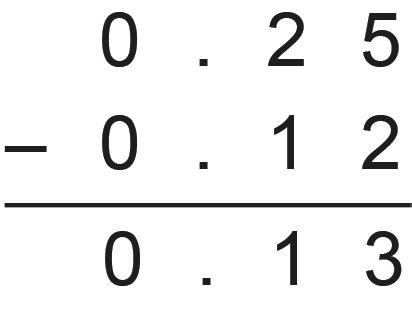
Practice Problems

1. Use the given key to answer the questions.

a. What number does this diagram represent?

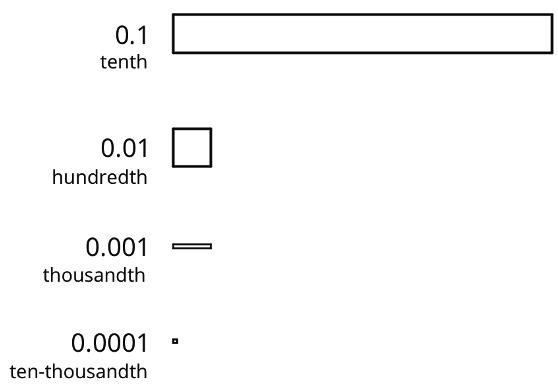
b. Draw a diagram that represents 0.216.

c. Draw a diagram that represents 0.304.

2. Here are diagrams that represent 0.137 and 0.284.

a. Use the diagram to find the value of 0.137 + 0.284. Explain your reasoning.

b. Calculate the sum vertically.

ManuscriptCopy

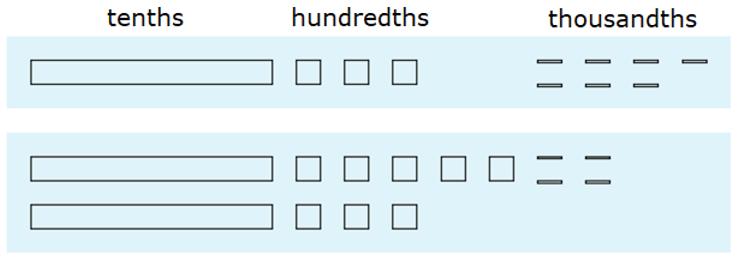
c. How was your reasoning about 0.137 + 0.284 the same with the two methods? How was it different?

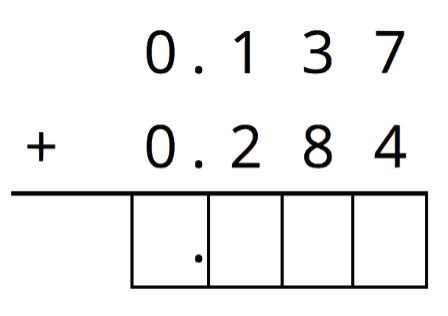
3. For the first two problems, circle the vertical calculation where digits of the same kind are lined up. Then, finish the calculation and find the sum. For the last two problems, find the sum using vertical calculation.

a. 3.25 + 1

0.5 + 1.15

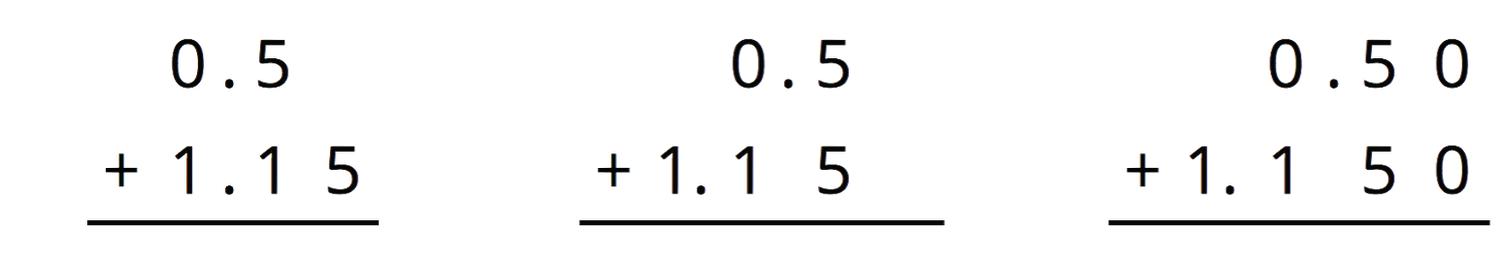
10.6 + 1.7

d. 123 + 0.2

4. Find each difference.

a. 0.09 – 0.05

b. 0.074 – 0.003

ManuscriptCopy

c. 1.57 – 0.25

b.

c.

Review Problem

5. Here is a right triangle. Name a corresponding height for each base.

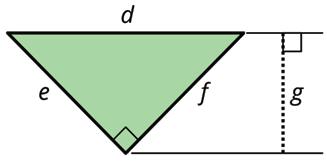
ManuscriptCopy

a. Side ��

b. Side ��

c. Side ��

Unit 2, Lesson 3: Adding and Subtracting Decimals with Non-Zero Digits

Warm-Up: Do the Zeros Matter?

1. Evaluate mentally: 1.009 + 0.391

2. Decide if each equation is true or false. Be prepared to explain your reasoning.

a. 34.56000 = 34.56

b. 25 = 25.0

c. 2.405 = 2.45

Collaborative Activity: Calculating Sums

1. Andre and Jada drew base-ten diagrams to represent 0.007 + 0.004. Andre drew 11 small rectangles. Jada drew only 2 figures: a square and a small rectangle.

a. If both students represented the sum correctly, what value does each small rectangle represent? What value does each square represent?

ManuscriptCopy

b. Draw or describe a diagram that could represent the sum 0.008 + 0.07.

2. Two calculations of 0.2 + 0.05 are shown.

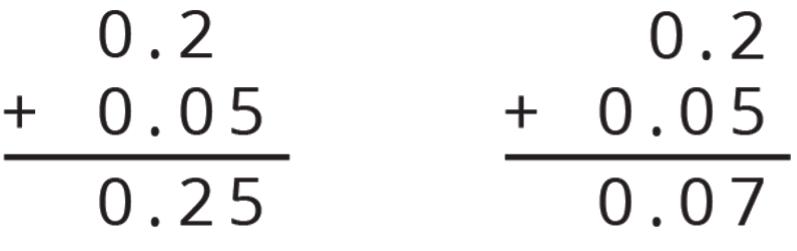
Explain which one is correct. Include why one is correct and the other is incorrect.

ManuscriptCopy

3. Compute each sum. Show your work. Consider drawing base-ten diagrams to help, if needed.

0. 1 1 + 0. 0 0 5

a.

b. 0.209 + 0.01

c. 10.2 + 1.145

Exploration Activity: Subtracting Decimals of Different Lengths

Diego and Noah drew different diagrams to represent 0.4 – 0.03. Each rectangle represented 0.1. Each square represents 0.01

• Diego started by drawing 4 rectangles to represent 0.4. He then replaced 1 rectangle with 10 squares and crossed out 3 squares to represent subtraction of 0.03, leaving 3 rectangles and 7 squares in his diagram.

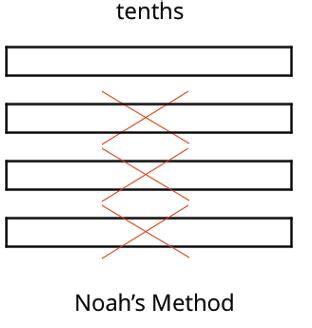
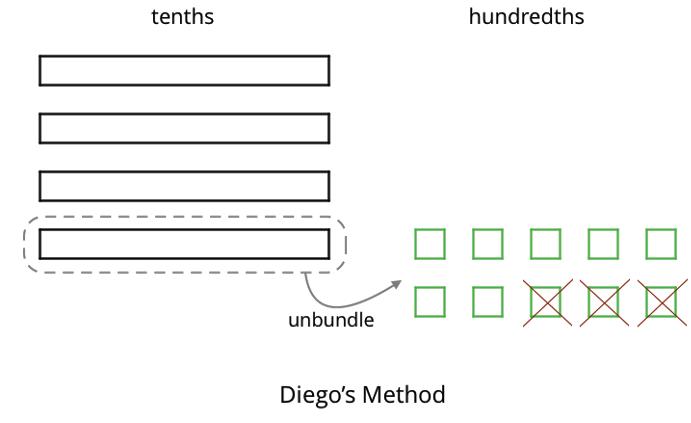
• Noah started by drawing 4 rectangles to represent 0.4. He then crossed out 3 rectangles to represent the subtraction, leaving 1 rectangle in his diagram.

1. Do you agree that either diagram correctly represents 0.4 – 0.03? Discuss your reasoning with a partner.

ManuscriptCopy

2. Elena also drew a diagram to represent 0.4 – 0.03. She started by drawing 4 rectangles. She then replaced all 4 rectangles with 40 squares and crossed out 3 squares to represent subtraction of 0.03, leaving 37 squares in her diagram. Is her diagram correct? Discuss your reasoning with a partner.

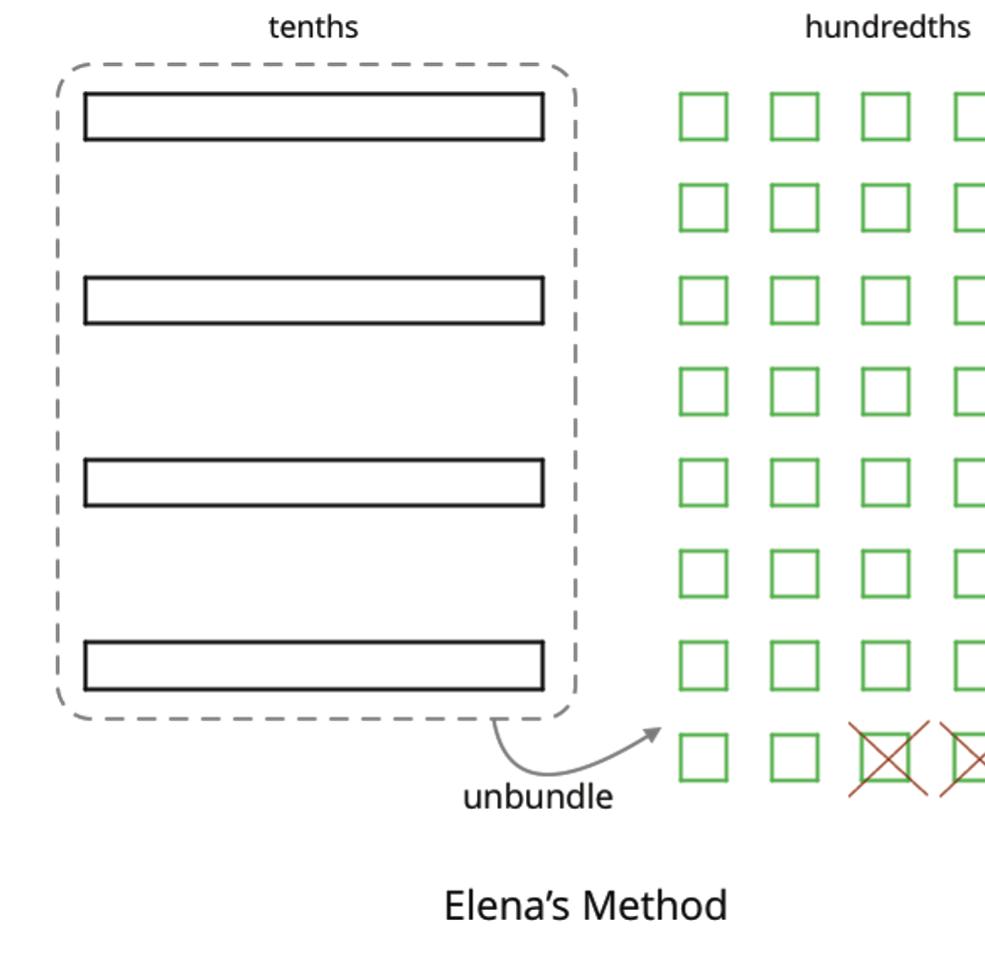
3. Find each difference. Explain or show your reasoning.

a. 0.3 – 0.05

b. 2.1 – 0.4

c. 1.03 – 0.06

d. 0.02 – 0.007

Collaborative Activity: Decimals All Around

1. Find the value of each expression. Show your reasoning.

a. 11.3 – 9.5

b. 318.8 – 94.63

ManuscriptCopy

c. 0.02 – 0.016

2. Discuss each question with your partner.

a. Which method(s) did you use in the previous question? Why?

b. In what ways was (were) your method(s) effective? Was there an expression for which your method(s) did not work as well as expected?

3. Lin’s grandmother ordered needles that were 0.325 inches (in.) long to administer her medication, but the pharmacist sent her needles that were 0.675 in. long. How much longer are these needles than the ones she ordered? Show your reasoning.

4. There are 0.162 liters (L) of water in a 1 L bottle. How much more water should be added to the bottle so it contains exactly 1 L? Show your reasoning.

Lesson Summary

Base-ten diagrams can be used to understand subtraction as well as addition. Consider the expression 0.023 – 0.007.

• The diagram shows 0.023, or 2 hundredths and 3 thousandths.

• Subtracting 7 thousandths means removing 7 small squares, but there are not enough small squares given. Since 1 hundredth is equal to 10 thousandths, “unbundle” (or decompose) 1 of the hundredths (1 rectangle) into 10 thousandths (10 small squares).

• Now, there is 1 hundredth and 13 thousandths, from which 7 thousandths can be removed.

• There is 1 hundredth and 6 thousandths remaining, so 0.023 – 0.007 = 0.016.

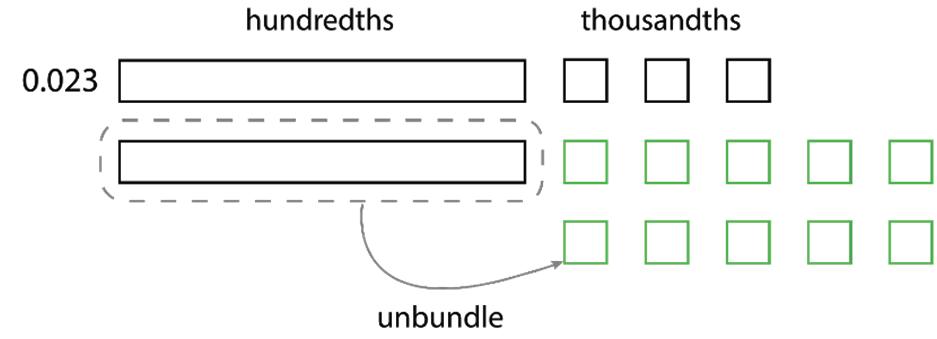
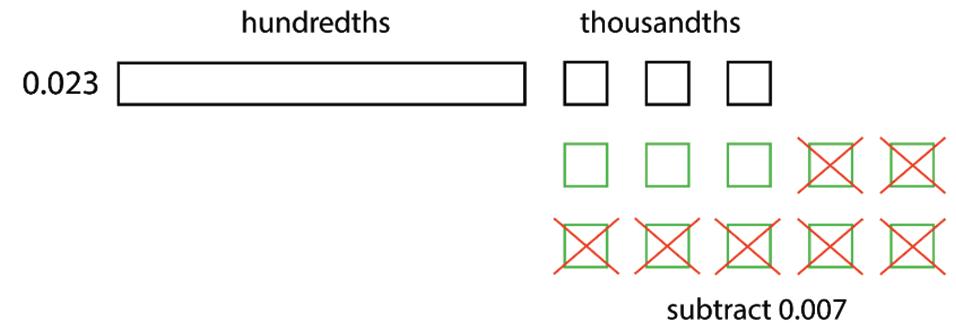
The vertical calculation of 0.023 – 0.007 is also shown.

ManuscriptCopy

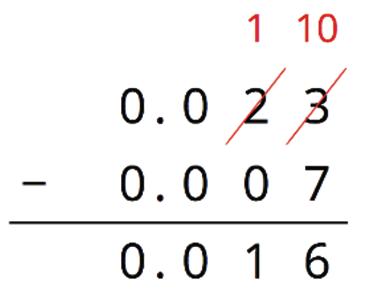
In both calculations, notice that a hundredth is unbundled, or decomposed, into 10 thousandths in order to subtract 7 thousandths.

Practice Problems

1. Here is a base-ten diagram that represents 1.13. Use the diagram to find 1.13 – 0.46. Explain or show your reasoning.

2. Decide which calculation shows the correct way to find 0.3 – 0.006 and explain your reasoning.

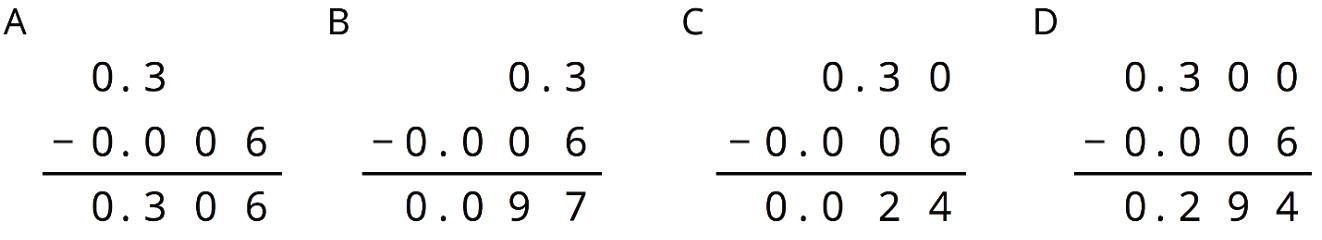
3. Complete the calculations so that each shows the correct difference.

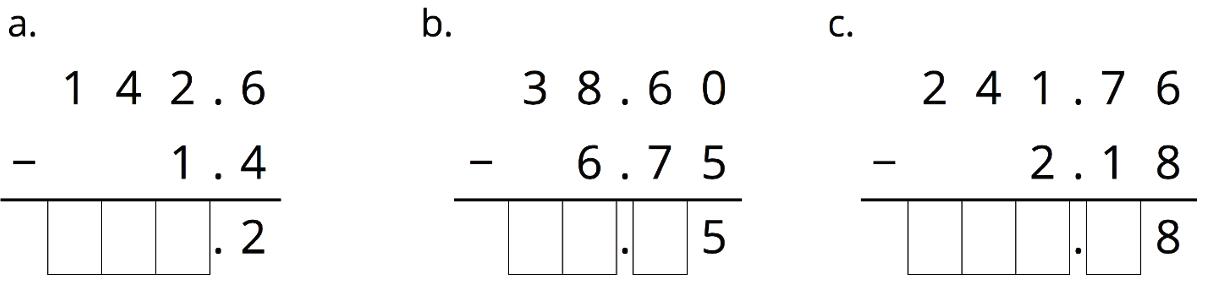
ManuscriptCopy

4. For each subtraction problem, circle the correct calculation.

a. 7.2 – 3.67

b. 16 – 1.4

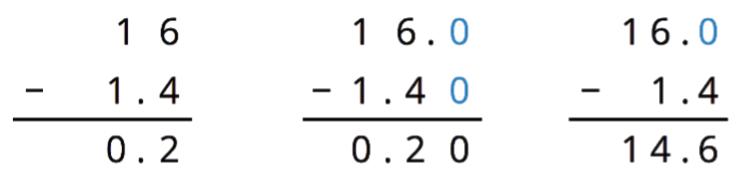
5. Complete the calculations so that each shows the correct sum.

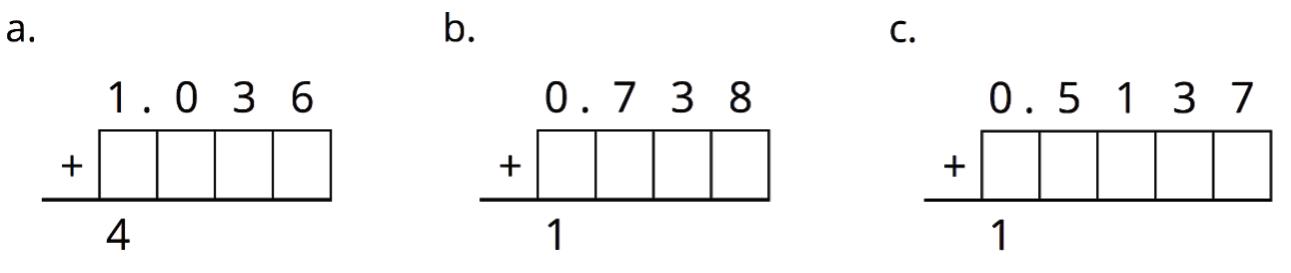
Review Problem

6. The school store sells pencils for $0.30 each, hats for $14.50 each, and binders for $3.20 each. Elena would like to buy 3 pencils, a hat, and 2 binders. She estimated that the cost will be less than $20.

a. Do you agree with her estimate? Explain your reasoning.

b. Estimate the number of pencils she could buy with $5. Explain or show your reasoning.

Unit 2, Lesson 4: Decimal Points in Products

Warm-Up: Multiply by 10

1. In which equation is the value of �� the largest?

A. �� ⋅ 10 = 810

B. �� ⋅ 10 = 81

C. �� ⋅ 10 = 8.1

D. �� ⋅ 10 = 0.81

2. How many times the size of 0.81 is 810?

ManuscriptCopy

Exploration Activity: Fractionally Speaking: Powers of 10

Work with a partner. One person solves the problems labeled “Partner A” and the other person solves those labeled “Partner B.” Then compare your results.

1. Find each product or quotient. Be prepared to explain your reasoning. Partner A

2. Use your work in the previous problems to find 720 ⋅ (0.1) and 720 ⋅ (0.01). Explain your reasoning.

Pause here for a class discussion.

3. Find each product. Show your reasoning.

a. 36 ⋅ (0.1)

b. (24.5) ⋅ (0.1)

c. (1.8) ⋅ (0.1)

d. 54 ⋅ (0.01)

e. (9.2) ⋅ (0.01)

4. Jada says, “If you multiply a number by 0.001, the decimal point of the number moves three places to the left.” Do you agree with her? Explain your reasoning.

ManuscriptCopy

Collaborative Activity: Fractionally Speaking: Multiples of Powers of 10

1. Select all expressions that are equivalent to (0.6) ⋅ (0.5). Be prepared to explain your reasoning.

□ 6 ⋅ (0.1) ⋅ 5 ⋅ (0.1)

□ 6 ⋅ (0.01) ⋅ 5 ⋅ (0.1) □ 6 ⋅ 1 10 ⋅ 5 ⋅ 1 10 □ 6 ⋅ 1 1,000 ⋅ 5 ⋅ 1 100

6 ⋅ (0.001) ⋅ 5 ⋅ (0.01) □ 6 ⋅ 5 ⋅ 1 10 ⋅ 1 10

□ 6 10 ⋅ 5 10

2. Find the value of (0.6) ⋅ (0.5). Show your reasoning.

3. Find the value of each product by writing and reasoning with an equivalent expression with fractions.

(0.3) ⋅ (0.02)

(0.7) ⋅ (0.05) ManuscriptCopy

a.

b.

Lesson Summary

Fractions like 1 10 and 1 100 can be used to reason about the location of the decimal point in the product of 2 decimals.

Consider 24 ⋅ (0.1) as an example. Here are three different ways to find the product

• Interpret the expression as 24 groups of 1 tenth, or 24 tenths, which is equal to 2.4.

• Think of the expression as 24 ⋅ 1 10 , which is equal to 24 10 , or 2.4.

• Since multiplying by 1 10 has the same result as dividing by 10, think of the expression as 24 ÷ 10, which is equal to 2.4.

Similar strategies can be used to multiply (0.7) ⋅ (0.09). The expression “7 tenths times 9 hundredths” can be rewritten as shown.

Rearrange the expression to group whole-number and fractional factors.

Rewritten as decimals, the result is (0.7) ⋅ (0.09) = 0.063.

To find (1.5) ⋅ (0.43), think of 1.5 as 15 tenths and 0.43 as 43 hundredths. Write the tenths and hundredths as fractions, and rearrange the factors, as shown.

Multiplying 15 by 43 results in 645, and multiplying 1 10 by 1 100 equals 1 1,000. Therefore, (1.5) ⋅ (0.43) is 645⋅ 1 1,000, which is 645 1,000 , or 0.645.

Practice Problems

1. Complete the following.

a. Find the product of each number and 1 100 .

i. 122.1

ii. 11.8

iii. 1350.1

iv. 1.704

b. What happens to the decimal point of the original number when you multiply it by 1 100 ? Why do you think that is? Explain your reasoning.

2. Which expression has the same value as (0.06) ⋅ (0.154)? Select all that apply. □ 6 ⋅ 1

⋅ 154 ⋅ 1

□ 6 ⋅ 154 ⋅ 1

□ 6 ⋅ (0.1) ⋅ 154 ⋅ (0.01) □ 6 ⋅ 154 ⋅ (0.00001)

□ 0.00924

3. Calculate the value of each expression by writing the decimal factors as fractions, then writing their product as a decimal. Show your reasoning.

a. (0.01) ⋅ (0.02)

b. (0.3) ⋅ (0.2)

c. (1.2) ⋅ 5

d. (0.9) ⋅ (1.1)

e. (1.5) ⋅ 2

Review Problems

4. Calculate each sum.

a. 33.1 + 1.95

b. 1.075 + 27.105

c. 0.401 + 9.28

5. Calculate each difference. Show your reasoning.

a. 13.2 – 1.78

b. 23.11 – 0.376

c. 0.9 – 0.245

6. On the grid, draw a quadrilateral that is not a rectangle that has an area of 18 square units (sq. units). Show how you know the area is 18 sq. units.

ManuscriptCopy

Unit 2, Lesson 5: Methods for Multiplying Decimals

Warm-Up: Equivalent Expressions

Write as many expressions as you can think of that are equal to 0.6. Do not use addition or subtraction.

Elena and Noah used different methods to compute (0.23) ⋅ (1.5). Both calculations were correct.

1. Analyze the two methods, then discuss these questions with your partner.

a. Which method makes more sense to you? Why?

ManuscriptCopy

Exploration Activity: Using Properties of Numbers to Reason about Multiplication

b. What might Elena do to compute (0.16) ⋅ (0.03)? What might Noah do to compute (0.16) ⋅ (0.03)? Will the two methods result in the same value? (0.23) ∙ 100 = 23 (1.5) ∙ 10 = 15

2. Compute each product using the equation 21 ⋅ 47 = 987 and what you know about fractions, decimals, and place value. Explain or show your reasoning.

a. (2.1) ⋅ (4.7)

b. 21 ⋅ (0.047)

c. (0.021) ⋅ (4.7)

Exploration Activity: Using Area Diagrams to Reason about Multiplication

1. In the diagram, the side length of each square is 0.1 unit.

a. Explain why the area of each square is not 0.1 square unit.

b. How can you use the area of each square to find the area of the rectangle? Explain or show your reasoning.

c. Explain how the diagram shows that the equation (0.4) ⋅ (0.2) = 0.08 is true.

ManuscriptCopy

2. Label the squares with their side lengths so the area of this rectangle represents 40 ⋅ 20.

a. What is the area of each square?

b. Use the squares to help you find 40 ⋅ 20. Explain or show your reasoning.

3. Label the squares with their side lengths so the area of this rectangle represents (0.04) ⋅ (0.02).

Next, use the diagram to help you find (0.04) ⋅ (0.02). Explain or show your reasoning.

Lesson Summary

Three strategies for calculating a product of 2 decimals, such as (0.04) ⋅ (0.07), are described and demonstrated.

• First, multiply each decimal by the same power of 10 to obtain whole-number factors.

(0.04) ⋅ 100 = 4 (0.07) ⋅ 100 = 7

4 ⋅ 7 = 28

Because 0.04 and 0.07 were each multiplied by 100 to get whole-number factors of 4 and 7, their product, 28, is (100 ⋅ 100) times the product of 0.04 and 0.07. So, 28 needs to be divided by 10,000.

28 ÷ 10,000 = 0.0028

• Second, write each decimal as a fraction, 0.04 = 4 100 and 0.07 = 7 100 , and then multiply them.

4 100 ⋅ 7 100 = 28 10,000 = 0.0028

• Third, use an area model. The product (0.04) ⋅ (0.07) can be thought of as the area of a rectangle with side lengths of 0.04 units and 0.07 units.

In this diagram, each small square has dimensions of 0.01 units by 0.01 units. The area of each small square, in square units (sq. units), is therefore � 1 100 ⋅ 1 100 �, which is equal to 1 10,000 .

Because the rectangle is composed of 28 small squares, the rectangle’s area, in sq. units, must be 28 ⋅ 1 10,000 = 28 10,000 = 0.0028 sq. units.

All 3 strategies show that (0.04) ⋅ (0.07) = 0.0028.

Practice Problems

1. Find each product. Show your reasoning.

ManuscriptCopy

a. (1.2) ⋅ (0.11)

b. (0.34) ⋅ (0.02)

c. 120 ⋅ (0.002)

2. You can use a rectangle to represent (0.3) ⋅ (0.5).

a. What must the side length of each square represent for the rectangle to correctly represent (0.3) ⋅ (0.5)?

b. What area is represented by each square?

c. What is (0.3) ⋅ (0.5)? Show your reasoning.

3. 1 gallon (gal.) of gasoline in Buffalo, New York, costs $2.29. In Toronto, Canada, 1 liter (L) of gasoline costs $0.91. There are 3.8 L in 1 gal.

a. How much does 1 gal. of gas cost in Toronto? Round your answer to the nearest cent.

b. Is the cost of gas greater in Buffalo or in Toronto? How much greater?

ManuscriptCopy

Review Problems

4. Calculate each sum or difference.

a. 10.3 + 3.7

b. 20.99 – 4.97

c. 15.99 + 23.51

d. 1.893 – 0.353

5. Find the area of the shaded region. All angles are right angles. Show your reasoning.

6. Consider the product of (1.05) ⋅ (2.8).

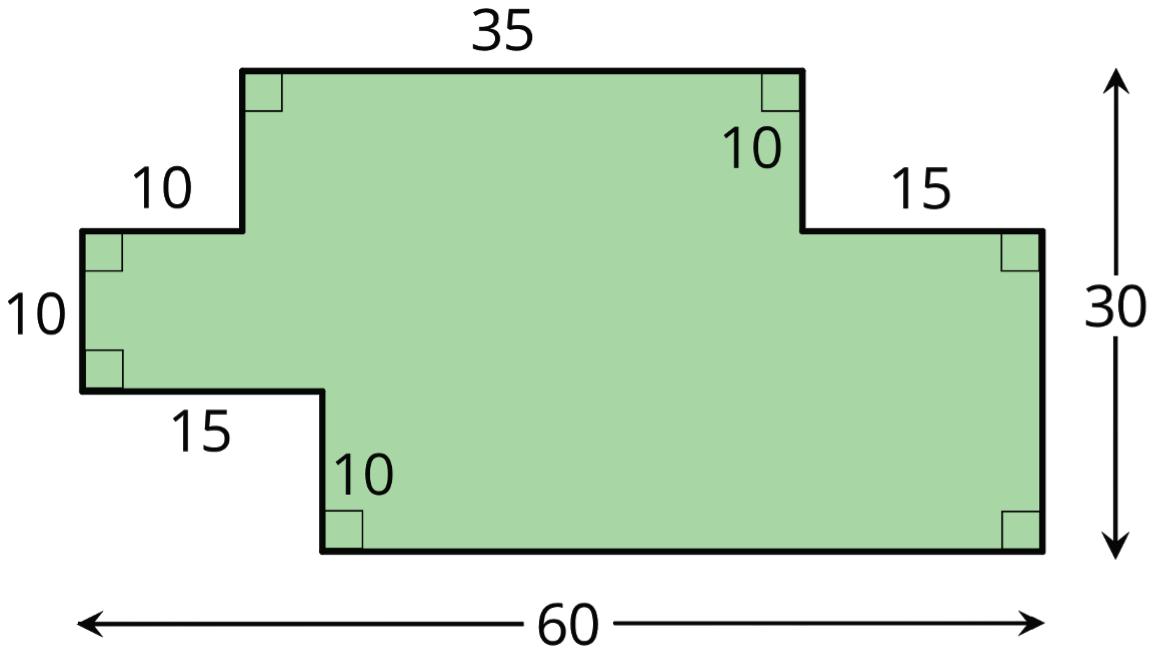
a. Priya finds (1.05) ⋅ (2.8) by calculating 105 ⋅ 28 and then moving the decimal point 3 places to the left. Explain why Priya’s method makes sense.

b. Use Priya’s method and the fact that 105 ⋅ 28 = 2,940 to calculate (1.05) ⋅ (2.8).

ManuscriptCopy

Unit 2, Lesson 6: Using Diagrams to Represent Multiplication

Warm-Up: Estimate the Product

ManuscriptCopy

For each of the following products, choose the best estimate of its value. Be prepared to explain your reasoning.

Exploration Activity: Connecting Area Diagrams to Calculations with Whole Numbers

1. Here are three ways of finding the area of a rectangle that is 24 units by 13 units.

a. What do the diagrams have in common? How are they alike?

b. How are they different?

c. If you were to find the area of a rectangle that is 37 units by 19 units, which of the three ways of decomposing the rectangle would you use? Why?

2. You may be familiar with different ways to write multiplication calculations. Here are two ways to calculate 24 times 13.

a. In calculation A, how are each of the partial products obtained? For instance, where does the 12 come from?

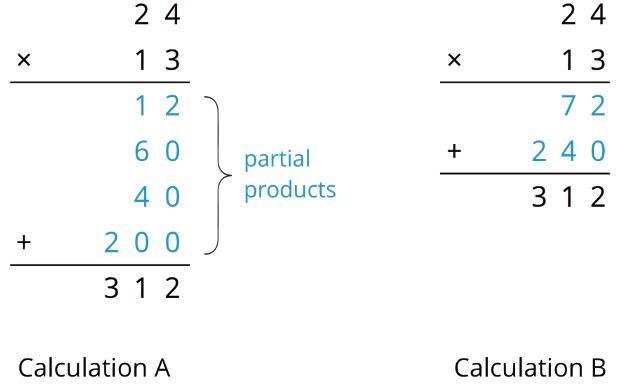
b. In calculation B, how are the 72 and 240 obtained?

c. Look at the diagrams in the first question. Which diagram corresponds to calculation A? Which one corresponds to calculation B?

d. How are the partial products in calculation A and the 72 and 240 in calculation B related to the numbers in the diagrams?

3. Use the two following methods to find the product of 18 and 14.

a. Calculate numerically.

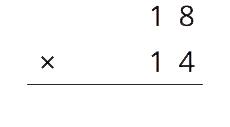
b. Here is a rectangle that is 18 units by 14 units. Find its area, in square units (sq. units), by decomposing it. Show your reasoning.

c. Compare the values of 18 ⋅ 14 that you obtained using the two methods. If they are not the same, check your work.

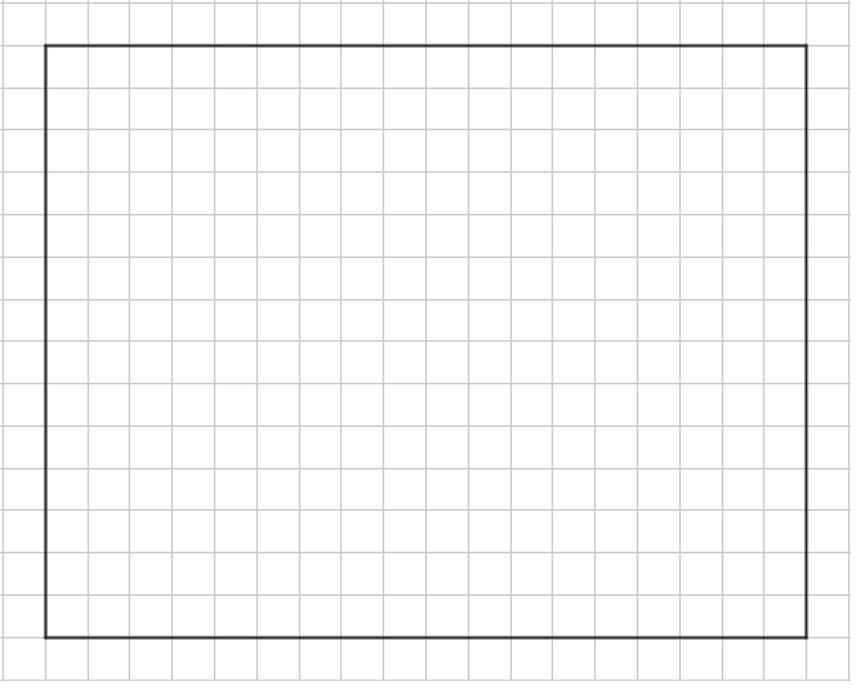
Guided Activity: Connecting Area Diagrams to Calculations with Decimals

1. You can use area diagrams to represent products of decimals. Here is an area diagram that represents (2.4) ⋅ (1.3).

a. Find the region that represents (0.4) ⋅ (0.3). Label that region with its area of 0.12.

b. Label each of the other regions with their respective areas.

c. Find the value of (2.4) ⋅ (1.3). Show your reasoning.

2. Here are two ways of calculating (2.4) ⋅ (1.3).

Analyze the calculations and discuss with a partner:

a. In calculation A, where does the 0.12 and other partial products come from?

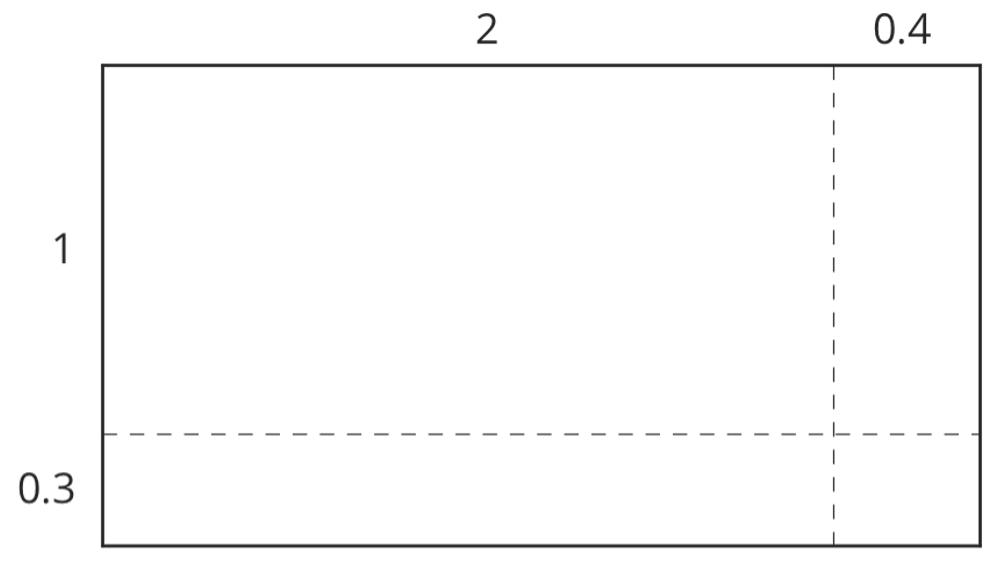
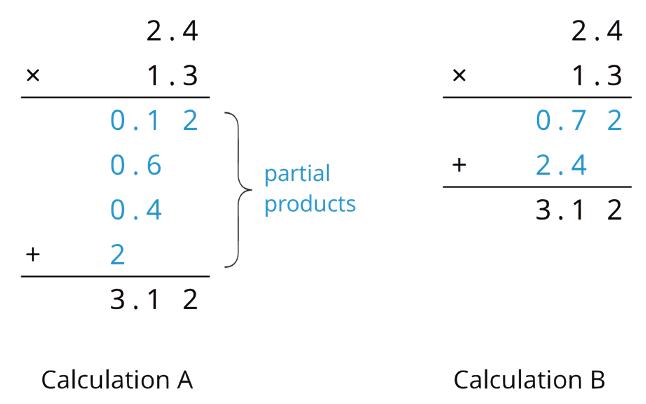
b. In calculation B, where do the 0.72 and 2.4 come from?

c. In each calculation, why are the numbers below the horizontal line aligned vertically the way they are?

3. Find the product of (3.1) ⋅ (1.5) by drawing and labeling an area diagram. Show your reasoning.

4. Show how to calculate (3.1) ⋅ (1.5) using numbers without a diagram. Be prepared to explain your reasoning. If you are stuck, use the examples in a previous question to help you.

Collaborative Activity: Using the Partial Products Method

1. Label the area diagram to represent (2.5) ⋅ (1.2) and to find that product.

a. Decompose each number into its base-ten units (ones, tenths, etc.) and write them in the boxes on each side of the rectangle.

b. Label Regions A, B, C, and D with their areas. Show your reasoning.

ManuscriptCopy

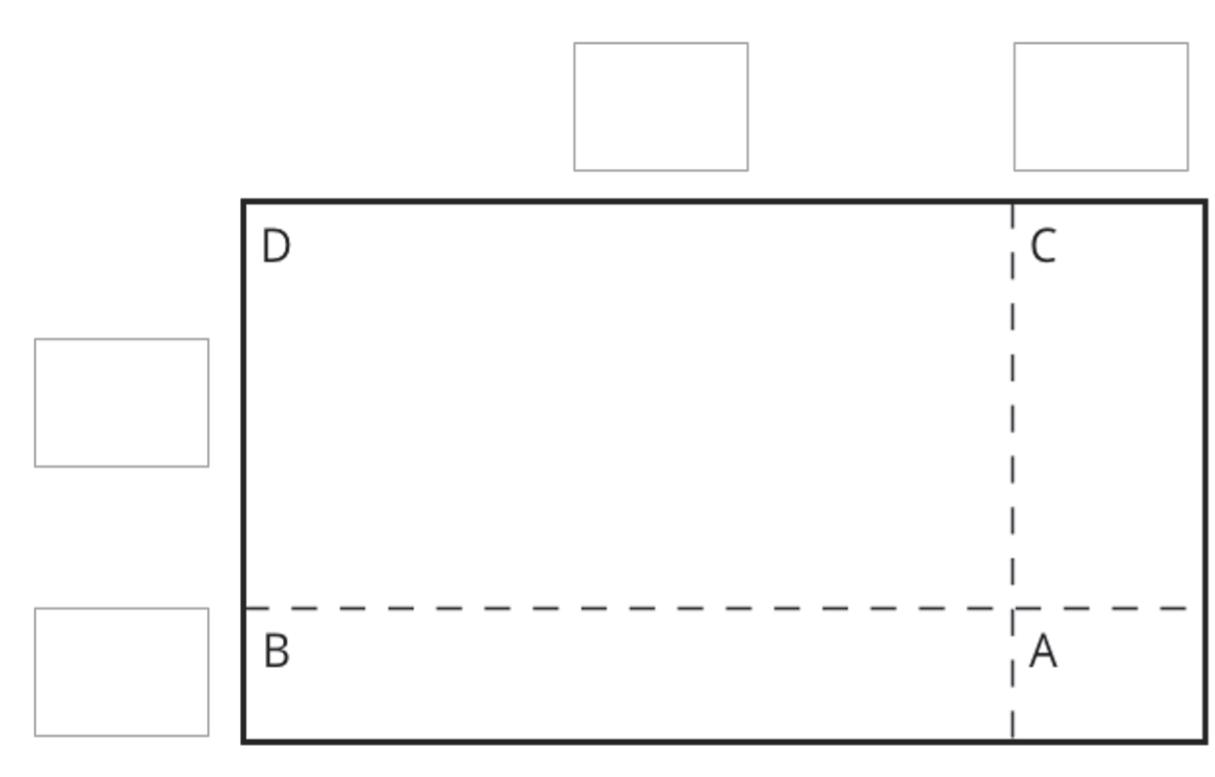
c. Find the product that the area diagram represents. Show your reasoning.

2. Here are two ways to calculate (2.5) ⋅ (1.2). Each number with a box gives the area of one or more regions in the area diagram.

a. In the boxes next to each number, write the letter(s) of the corresponding region(s).

b. In calculation B, which two numbers are being multiplied to obtain 0.5? Which two are being multiplied to obtain 2.5?

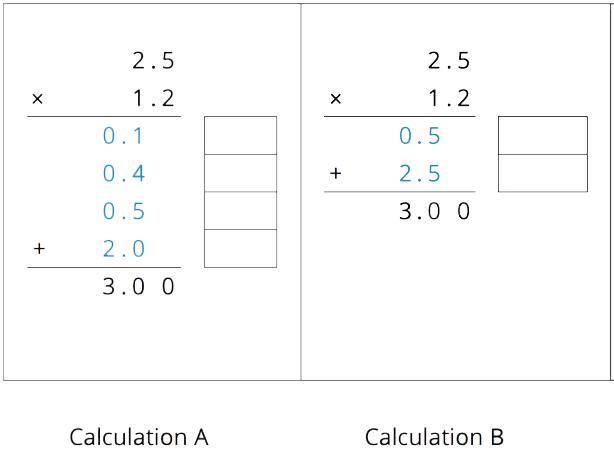
Lesson Summary

Calculating the product of 2 numbers that are written in base ten can be explained with base-ten numbers and areas of rectangles.

A diagram is shown of a rectangle with side lengths of 3.4 units and 1.2 units. Its area, in square units, is the product of (3.4) ⋅ (1.2). To calculate this product and find the area of the rectangle, decompose each side length into its base-ten units, 3.4 = 3 + 0.4 and 1.2 = 1 + 0.2, decomposing the rectangle into 4 smaller sub-rectangles.

To express this using base-ten numbers, rewrite the product, and then expand, as shown. (3.4) ∙ (1.2) = (3 + 0.4) ∙ (1 + 0.2) = (3 + 0.4) ∙ 1 + (3 + 0.4) ∙ 0.2 = 3

ManuscriptCopy

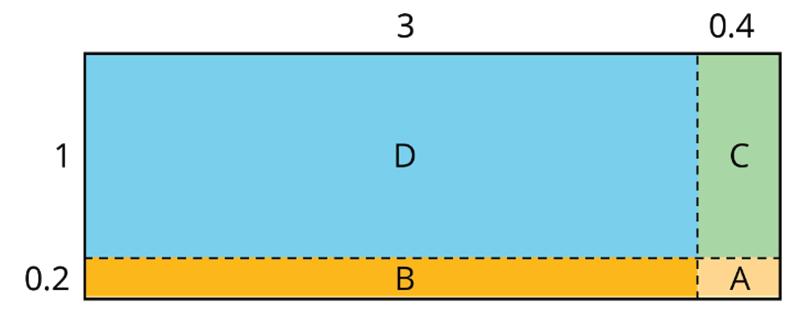
In the last expression, each of the 4 terms is called a partial product. Each partial product represents the area of a sub-rectangle in the diagram. The sum of the 4 partial products is the area of the entire rectangle.

The previous horizontal calculations can be rewritten as 2 vertical calculations.

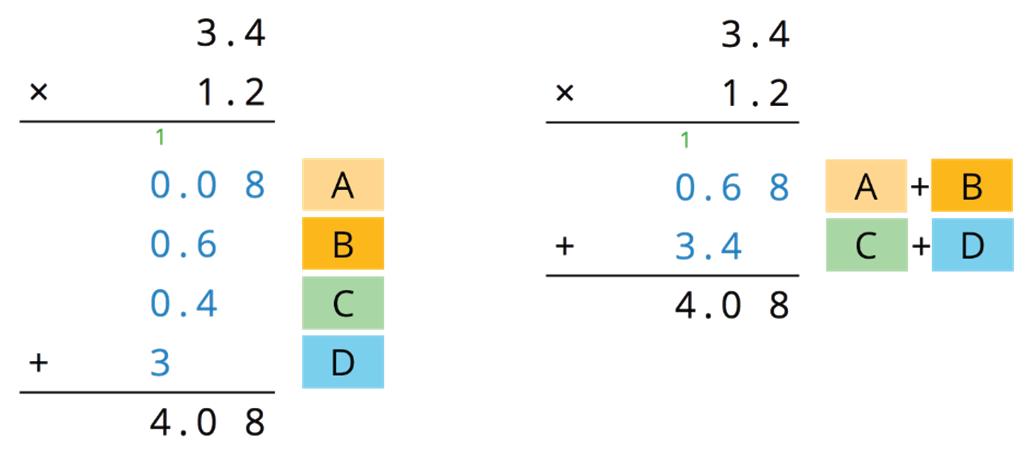
The vertical calculation on the left is an example of the partial products method. It shows the value of each partial product next to the name of the corresponding sub-rectangle. Each partial product represents an area of a sub-rectangle.

• A is 0.2 units by 0.4 units, so its area is 0.08 sq. units.

• B is 3 units by 0.2 units, so its area is 0.6 sq. units.

• C is 0.4 units by 1 unit, so its area is 0.4 sq. units.

• D is 3 units by 1 unit, so its area is 3 sq. units.

• The sum of the partial products is 0.08 + 0.6 + 0.4 + 3, so the area of the rectangle is 4.08 sq. units.

The calculation on the right shows the values of 2 products. Each value represents a combined area of 2 sub-rectangles.

• Regions A and B have a combined area of 0.68 sq. units; 0.68 is the value of (3 + 0.4) ⋅ 0.2.

• Regions C and D have a combined area of 3.4 sq. units; 3.4 is the value of (3 + 0.4) ⋅ 1.

ManuscriptCopy

• The sum of the 2 products is 0.68 + 3.4, so the area of the entire rectangle is 4.08 sq. units.

Practice Problems

1. Here is a rectangle that has been partitioned into four smaller rectangles.

For each expression, choose a sub-rectangle whose area, in square units, matches the expression.

a. 3 ⋅ (0.6)

b. (0.4) ⋅ 2

c. (0.4) ⋅ (0.6)

d. 3 ⋅ 2

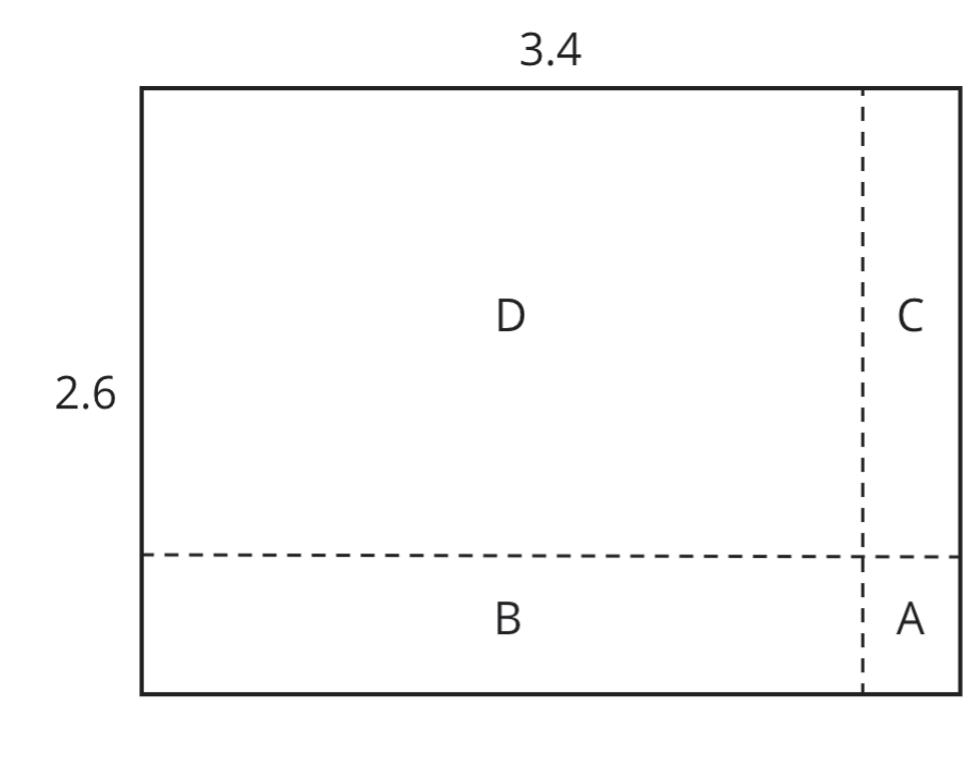
2. Here is an area diagram that represents (3.1) ⋅ (1.4).

a. Find the areas of sub-rectangles A and B.

b. What is the area of the 3.1 by 1.4 rectangle?

ManuscriptCopy

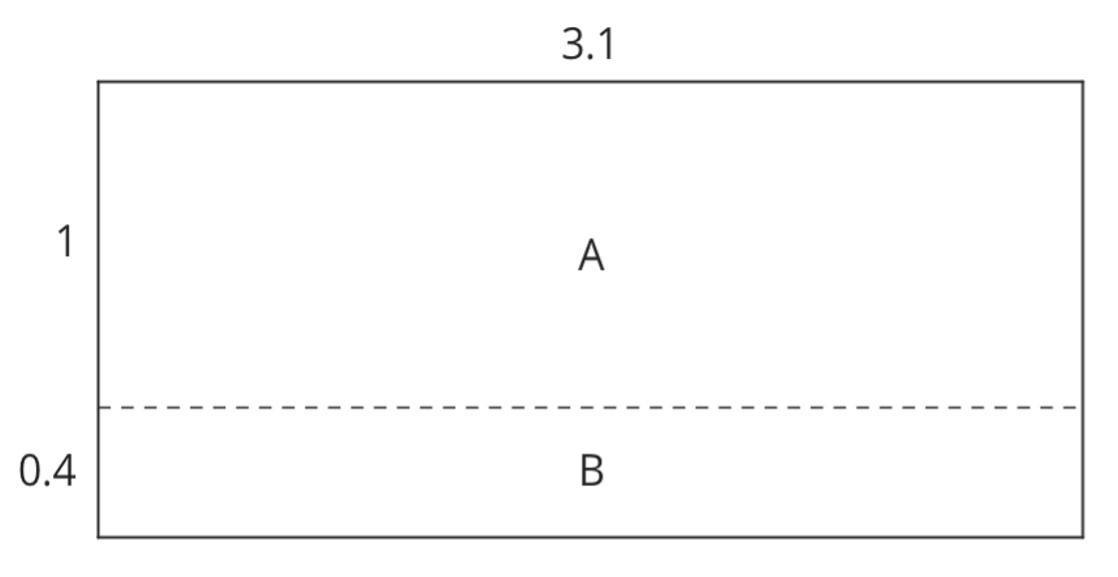
3. Draw an area diagram to find (0.36) ⋅ (0.53). Label and organize your work so that it can be followed by others.

4. Find each product. Show your reasoning.

a. (2.5) ⋅ (1.4)

b. (0.64) ⋅ (0.81)

Review Problems

5. Complete the calculations so that each shows the correct sum.

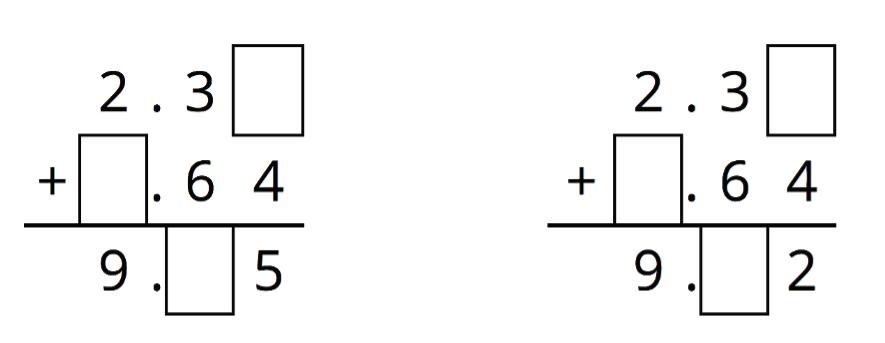
6. Which three of these parallelograms have the same area as each other?

ManuscriptCopy

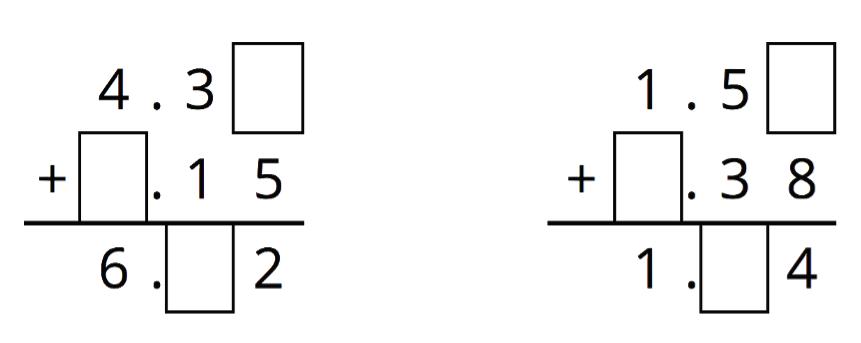
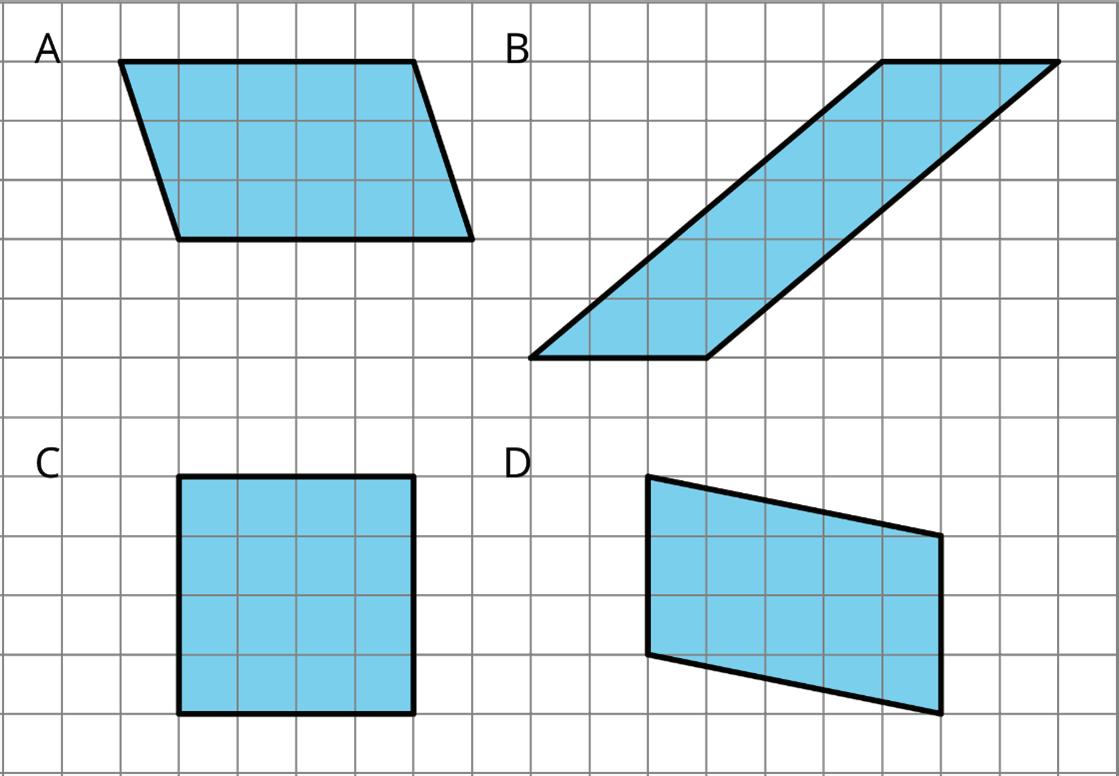
ManuscriptCopy

Unit 2, Lesson 7: Calculating the Products of Decimals

Warm-Up: Number Talk: 20 Times a Number

1. Evaluate mentally.

a. 20 ⋅ 5

b. 20 ⋅ (0.8)

c. 20 ⋅ (0.04)

d. 20 ⋅ (5.84)

Exploration Activity: Calculating Products of Decimals

1. A common way to find a product of decimals is to calculate a product of whole numbers, then place the decimal point in the product.

Here is an example for (2.5) ⋅ (1.2).

Use what you know about decimals and place value to explain why the decimal point of the product is placed where it is.

ManuscriptCopy

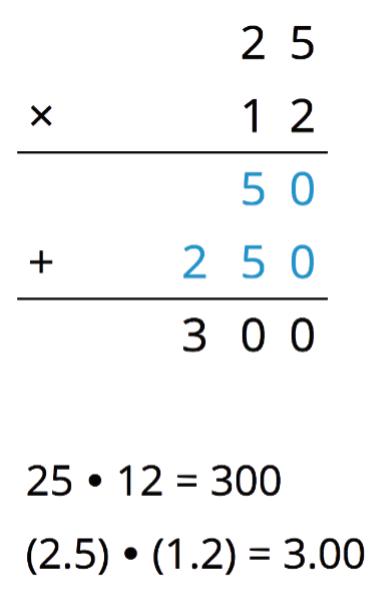
2. Use the method shown in the first question to calculate each product.

a. (4.6) ⋅ (0.9)

b. (16.5) ⋅ (0.7)

3. Use area diagrams to check your earlier calculations. For each problem:

• Decompose each number into its base-ten units and write them in the boxes on each side of the rectangle.

• Write the area of each lettered region in the diagram. Then find the area of the entire rectangle. Show your reasoning.

a. (4.6) ⋅ (0.9)

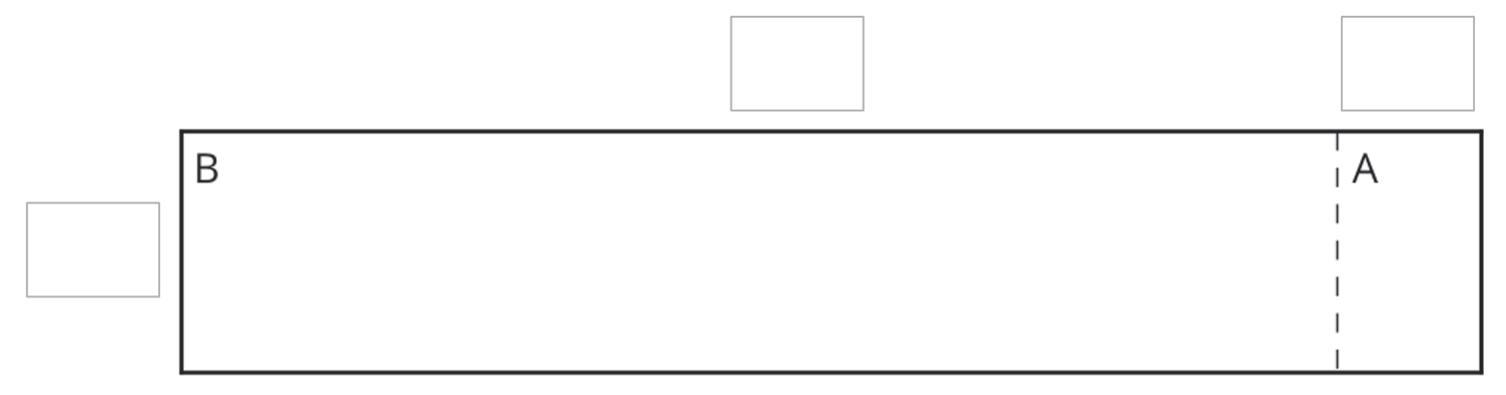
b. (16.5) ⋅ (0.7)

4. About how many centimeters (cm) are in 6.25 inches (in.) if 1 in. is about 2.5 cm? Show your reasoning.

Collaborative Activity: Muliplication of Decimals

1. Calculate each product. Show your reasoning. If you get stuck, consider drawing an area diagram to help.

a. (5.6) ⋅ (1.8)

b. (0.008) ⋅ (7.2)

2. A rectangular playground is 18.2 meters (m) by 12.75 m.

a. Find its area, in square meters (sq. m). Show your reasoning.

b. If 1 m is approximately 3.28 feet (ft.), what are the approximate side lengths of the playground in ft.? Show your reasoning.

Lesson Summary

Products of whole numbers can be used to determine products of decimals, using place value. For example, the product of 84 ⋅ 43 can be used to find (8.4) ⋅ (4.3).

If 8.4 is 84 tenths and 4.3 is 43 tenths, then: (8.4) ⋅ (4.3) = 84 10 ⋅ 43 10 (8.4) ⋅ (4.3) = 84 ⋅ 43 100

Therefore, to find (8.4) ⋅ (4.3), calculate 84 ⋅ 43 and then divide by 100. 84 ⋅ 43 = 3612 (8.4) ⋅ (4.3) = 36.12

Fractions such as 1 10 , 1 100 , and 1 1,000 can be used to find the product of 2 decimals using the following steps:

• Write each decimal factor as a product of a whole number and a fraction.

• Multiply the whole numbers.

• Multiply the fractions.

• Multiply the products of the whole numbers and the fractions.

Multiplying by fractions such as 1 10 , 1 100 , or 1 1,000 is the same as dividing by 10, 100, or 1,000, respectively. This means the decimal point in the whole-number product must be moved to the left the appropriate number of spaces.

ManuscriptCopy

Practice Problems

1. Here is an unfinished calculation of (0.54) ⋅ (3.8) and a 0.54-by-3.8 rectangle.

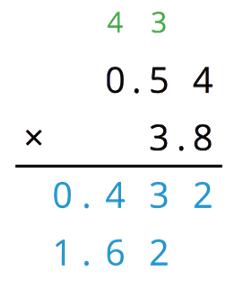
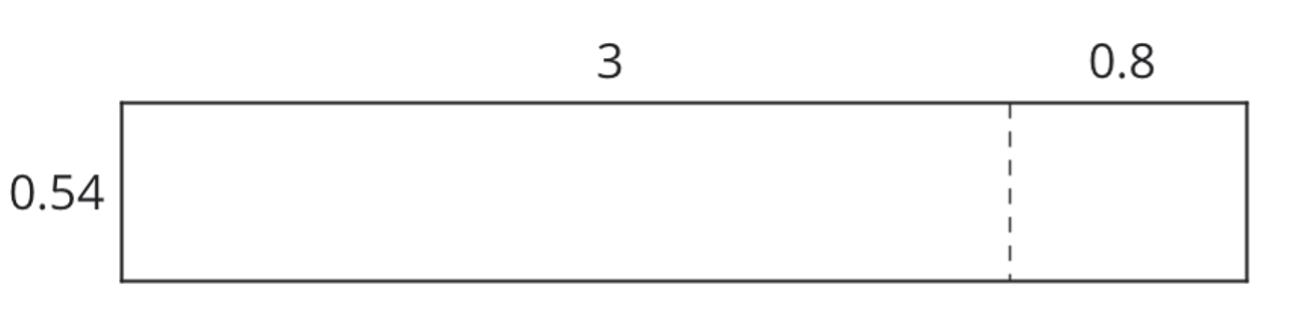
a. Which part of the rectangle has an area of 0.432? Which part of the rectangle has an area of 1.62? Show your reasoning.

b. What is (0.54) ⋅ (3.8)?

2. Explain how the product of 3 and 65 could be used to find (0.03) ⋅ (0.65).

3. Use vertical calculation to find each product.

a. (5.4) ⋅ (2.4)

ManuscriptCopy

b. (1.67) ⋅ (3.5)

4. 1 pound (lb.) of blueberries costs $3.98, and 1 lb. of clementines costs $2.49. What is the combined cost of 0.6 lb. of blueberries and 1.8 lb. of clementines? Round your answer to the nearest cent.

Review Problems

5. Complete the calculations so that each shows the correct sum or difference.

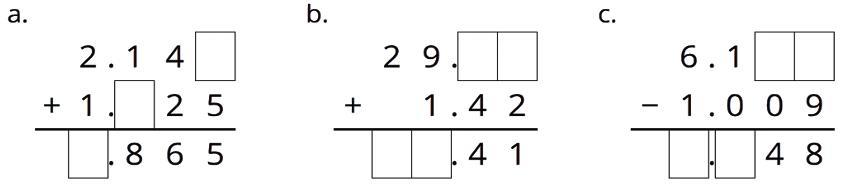
6. Draw an identical copy of each triangle such that the two copies together form a parallelogram. If you get stuck, consider using tracing paper.

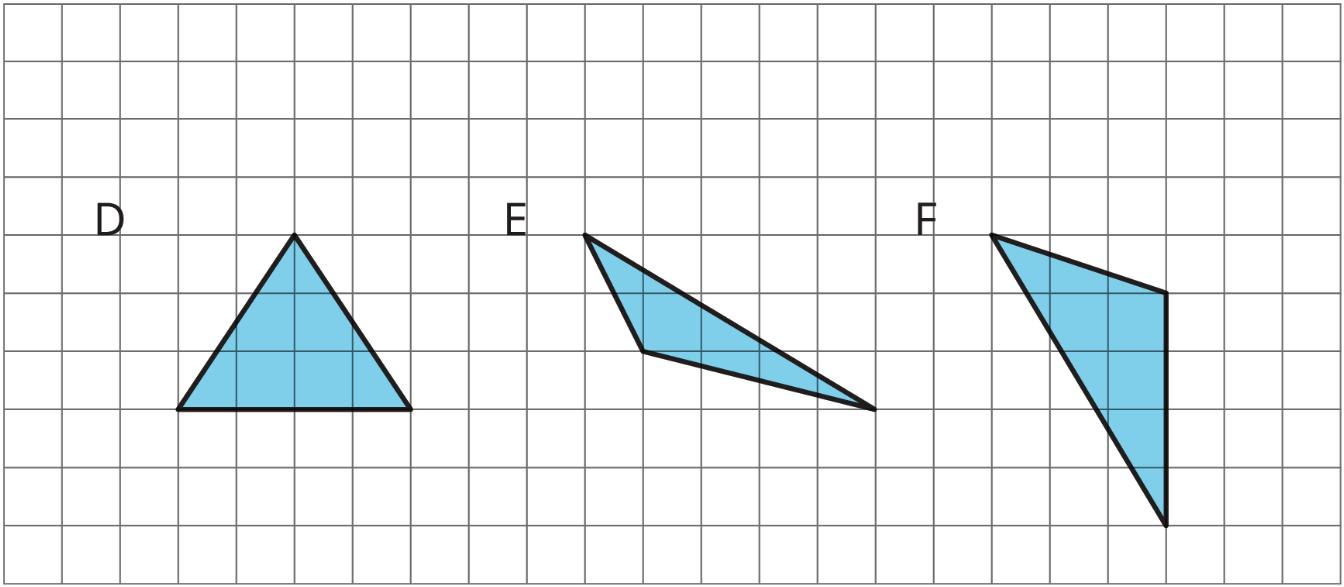
ManuscriptCopy

Unit 2, Lesson 8: Dividing Decimals by Whole Numbers

Warm-Up: Number Talk: Dividing by 4

1. Find each quotient mentally.

ManuscriptCopy

Exploration Activity: Using Diagrams to Represent Division

To find 53.8 ÷ 4 using diagrams, Elena began by representing 53.8.

She placed 1 ten into each group, unbundled the remaining 1 ten into 10 ones, and went on distributing the units.

This diagram shows Elena’s initial placement of the units and the unbundling of 1 ten.

1. Complete the diagram by continuing the division process. How would you use the available units to make 4 equal groups?

As the units get placed into groups, show them accordingly and cross out those pieces from the bottom. If you unbundle a unit, draw the resulting pieces.

2. What value did you find for 53.8 ÷ 4? Be prepared to explain your reasoning.

3. Use long division to find 53.8 ÷ 4. Check your answer by multiplying it by the divisor 4.

ManuscriptCopy

4. Use long division to find 77.4 ÷ 5. If you get stuck, you can draw diagrams or use another method.

Exploration Activity: Dividends and Divisors

Analyze the dividends, divisors, and quotients in the calculations, and then answer the questions.

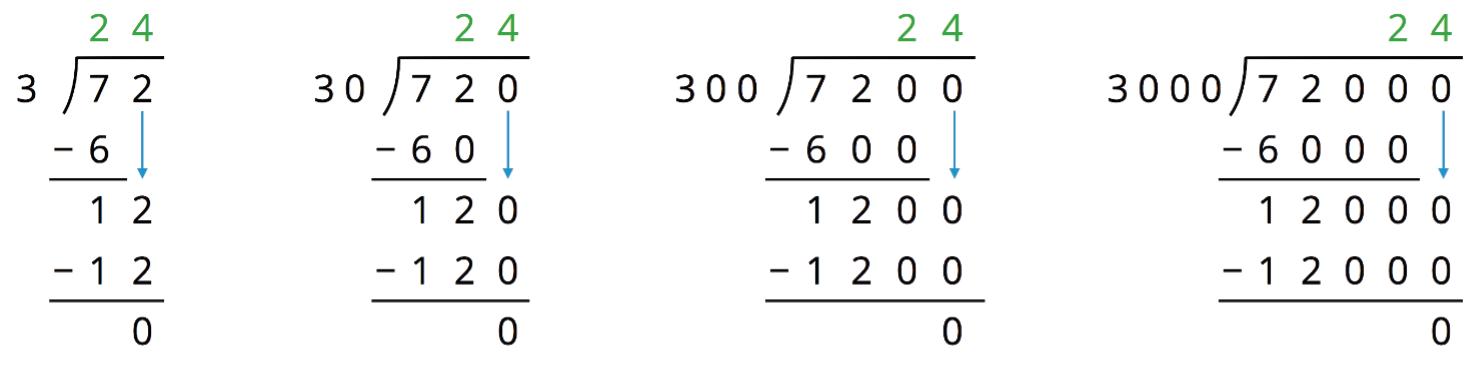
1. Complete each sentence. In the calculations shown:

a. Each dividend is ______ times the dividend to the left of it.

b. Each divisor is ______ times the divisor to the left of it.

c. Each quotient is _____________________ the quotient to the left of it.

2. Suppose we are writing a calculation to the right of 72,000 ÷ 3,000. Which expression has a quotient of 24? Be prepared to explain your reasoning.

A. 72,000 ÷ 30,000

B. 720,000 ÷ 300,000

C. 720,000 ÷ 30,000

D. 720,000 ÷ 3,000

3. Suppose we are writing a calculation to the left of 72 ÷ 3. Write an expression that would also give a quotient of 24. Be prepared to explain your reasoning.

4. Decide which of the following expressions would have the same value as 250 ÷ 10. Be prepared to share your reasoning.

□ 250 ÷ 0.1

□ 25 ÷ 1

□ 2.5 ÷ 1

□ 2.5 ÷ 0.1

□ 2,500 ÷ 100

□ 0.25 ÷ 0.01

Lesson Summary

Fractions such as 6 4 and 60 40 are equivalent. There are multiple ways to justify this fact:

• Both the numerator and denominator of 60 40 have a factor of 10, so the fraction can be rewritten as 6 4 .

• Both fractions can be simplified to 3 2 .

• 6 divided by 4 is 1.5, and 60 divided by 40 is also 1.5.

Just like fractions, division expressions can also be equivalent. For example, the expressions 540 ÷ 90 and 5,400 ÷ 900 are both equivalent to 54 ÷ 9 for the following reasons:

• All the expressions have a quotient of 6.

• The dividend and divisor in 540 ÷ 90 are each 10 times the dividend and divisor in 54 ÷ 9. Those in 5,400 ÷ 900 are each 100 times the dividend and divisor in 54 ÷ 90. In both cases, the quotient does not change.

This means that an expression such as 5.4 ÷ 0.9 also has the same value as 54 ÷ 9. The dividend and divisor of 5.4 ÷ 0.9 are each 1 10 of those in 54 ÷ 9.

In general, multiplying a dividend and a divisor by the same number does not change the quotient of the expression. Multiplying by powers of 10 (such as 10, 100, or 1,000) can be particularly useful for dividing decimals because of the relationship to place value in the base-ten system.

Practice Problems

1. Here is a diagram representing a base-ten number. The large rectangle represents a unit that is 10 times the value of the square. The square represents a unit that is 10 times the value of the small rectangle.

Here is a diagram showing the number being divided into 5 equal groups.

a. If a large rectangle represents 1,000, what division problem did the second diagram show? What is its answer?

2.

b. If a large rectangle represents 100, what division problem did the second diagram show? What is its answer?

c. If a large rectangle represents 10, what division problem did the second diagram show? What is its answer?

a. Explain why all of these expressions have the same value.

ManuscriptCopy

b. What is the common value? ____

3. Use long division to find each quotient.

a. 7.89 ÷ 2

b. 39.54 ÷ 3

c. 0.176 ÷ 5

4. Four students set up a lemonade stand. At the end of the day, their profit is $17.52. How much money do they each have when the profit is split equally? Show or explain your reasoning.

Review Problem

5. In this cube, each small square has side length 1 unit.

a. What is the surface area of this cube?

b. What is the volume of this cube?

ManuscriptCopy

ManuscriptCopy

Unit 2, Lesson 9: Dividing Decimals by Decimals

Warm-Up: Same Values

1. Use long division to find the value of 5.04 ÷ 7.

2. Select all of the quotients that have the same value as 5.04 ÷ 7. Be prepared to explain how you know.

5.04 ÷ 70

50.4 ÷ 70

504,000 ÷ 700

504,000 ÷ 700,000

ManuscriptCopy

Exploration Activity: Placing Decimal Points in Quotients

1. Think of one or more ways to find 3 ÷ 0.12. Show your reasoning.

2. Find 1.8 ÷ 0.004. Show your reasoning. If you get stuck, think about what equivalent division expression you could write.

3. Diego said, “To divide decimals, we can start by moving the decimal point in both the dividend and divisor by the same number of places and in the same direction. Then we find the quotient of the resulting numbers.”

Do you agree with Diego? Use the division expression 7.5 ÷ 1.25 to support your answer.

ManuscriptCopy

Exploration Activity: 2 Ways to Calculate Quotients of Decimals

1. Here are two calculations of 48.78 ÷ 9. Work with your partner to answer the following questions.

a. How are the two calculations the same? How are they different?

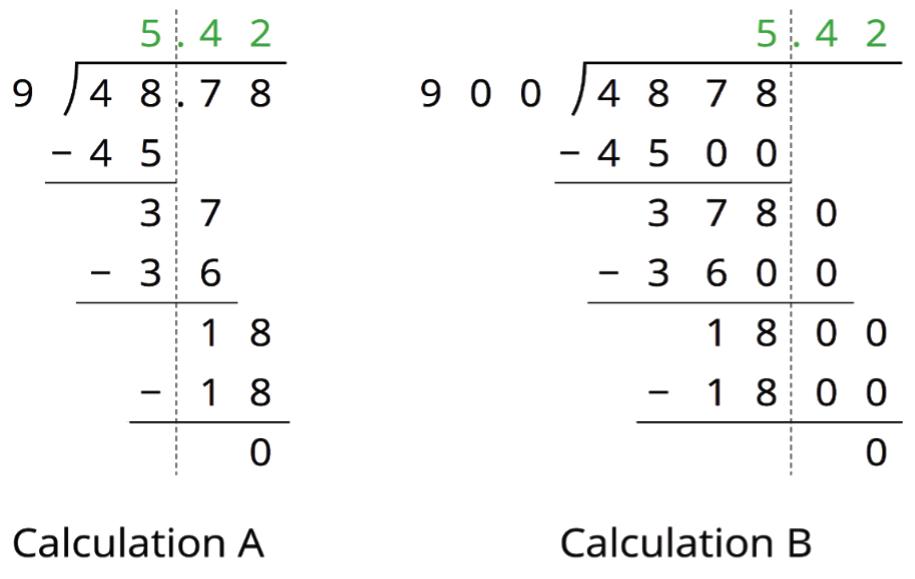
b. Look at calculation A. Explain how you can tell that the 36 means “36 tenths” and the 18 means “18 hundredths.”

c. Look at calculation B. What do the 3600 and 1800 mean?

ManuscriptCopy

d. We can think of 48.78 ÷ 9 = 5.42 as saying, “There are 9 groups of 5.42 in 48.78.” We can think of 4878 ÷ 900 = 5.42 as saying, “There are 900 groups of 5.42 in 4878.” How might we show that both statements are true?

a. Explain why 51.2 ÷ 6.4 has the same value as 5.12 ÷ 0.64.

b. Write a division expression that has the same value as 51.2 ÷ 6.4 but is easier to use to find the value. Then, find the value using long division.

Collaborative Activity: Practicing Division with Decimals

Find each quotient. Discuss your quotients with your group and agree on the correct answers. Consult your teacher if the group can’t agree.

ManuscriptCopy

1. 106.5 ÷ 3

2. 58.8 ÷ 0.7

3. 257.4 ÷ 1.1

4. Mai is making friendship bracelets. Each bracelet is made from 24.3 centimeters (cm) of string. If she has 170.1 cm of string, how many bracelets can she make? Explain or show your reasoning.

Lesson Summary

One way to find a quotient of 2 decimals is to multiply each decimal by a power of 10 so that both terms become whole numbers.

When both decimals are multiplied by the same power of 10, the value of the quotient remains unchanged. For example, the quotient of 7.65 ÷ 1.2 can be found by multiplying the 2 decimals by 10 or by 100 and instead finding 76.5 ÷ 12 or 765 ÷ 120.

To calculate 765 ÷ 120, which is equivalent to 76.5 ÷ 12, use base-ten diagrams, partial quotients, or long division. The calculation by long division is shown.

Practice Problems

1. A student said, “To find the value of 109.2 ÷ 6, I can divide 1,092 by 60.”

a. Do you agree with her? Explain your reasoning.

b. Calculate the quotient of 109.2 ÷ 6 using any method of your choice.

2. Here is how Han found 31.59 ÷ 13:

a. At the second step, Han subtracts 52 from 55. How do you know that these numbers represent tenths?

b. At the third step, Han subtracts 39 from 39. How do you know that these numbers represent hundredths?

3.

c. Check that Han’s answer is correct by calculating the product of 2.43 and 13.

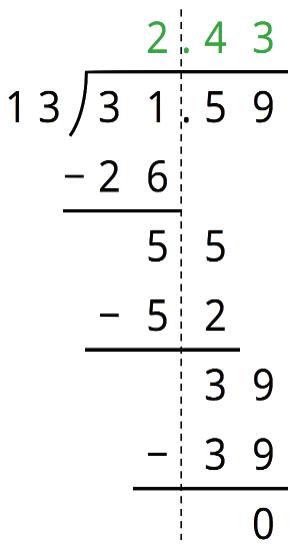
a. Write two division expressions that have the same value as 61.12 ÷ 3.2.

b. Find the value of 61.12 ÷ 3.2. Show your reasoning.

4. A bag of pennies weighs 5.1 kilograms. Each penny weighs 2.5 grams. About how many pennies are in the bag?

A. 20

B. 200

ManuscriptCopy

C. 2,000

D. 20,000

Review Problems

5. Find each difference. If you get stuck, consider drawing a diagram.

2.5 – 1.6

ManuscriptCopy

a.

b. 0.72 – 0.4

c. 11.3 – 1.75

d. 73 – 1.3

a. Draw a parallelogram that is not a rectangle that has an area of 24 square units. Explain or show how you know the area is 24 square units.

b. Draw a triangle that has an area of 24 square units. Explain or show how you know the area is 24 square units.

ManuscriptCopy

Unit 2, Lesson 10: Using Operations on Decimals to Solve Problems

Warm-Up: Close Estimates

For each expression, choose the best estimate of its value.

Collaborative Activity: Applying Division with Decimals

Your teacher will assign to you either Problem A or Problem B. Work together as a group to answer the questions. Be prepared to create a visual display to show your reasoning with the class.

Problem A: A piece of rope is 5.75 meters (m) in length.

1. If it is cut into 20 equal pieces, how long will each piece be?

2. If it is cut into 0.05 m pieces, how many pieces will there be?

Problem B: A tortoise travels 0.945 miles (mi.) in 3.5 hours (hr.).

1. If it moves at a constant speed, how many miles per hour (mph) is it traveling?

2. At this rate, how long will it take the tortoise to travel 4.86 mi.?

ManuscriptCopy

Collaborative Activity: Distance between Hurdles

There are 10 equally spaced hurdles on a race track. The first hurdle is 13.72 m from the start line. The final hurdle is 14.02 m from the finish line. The race track is 110 m long.

1. Draw a diagram that shows the hurdles on the race track. Label all known measurements.

2. How far are the hurdles from one another? Explain or show your reasoning.

ManuscriptCopy

3. A professional runner takes 3 strides between each pair of hurdles. The runner leaves the ground 2.2 m before the hurdle and returns to the ground 1 m after the hurdle. About how long are each of the runner’s strides between the hurdles? Show your reasoning.

Collaborative Activity: Examining a Tennis Court

A diagram of a tennis court is shown.

The full tennis court, used for playing doubles, is a rectangle. All of the angles formed by the line segments in the diagram are right angles.

1. The net partitions the tennis court into 2 halves. Explain whether each half is a square.

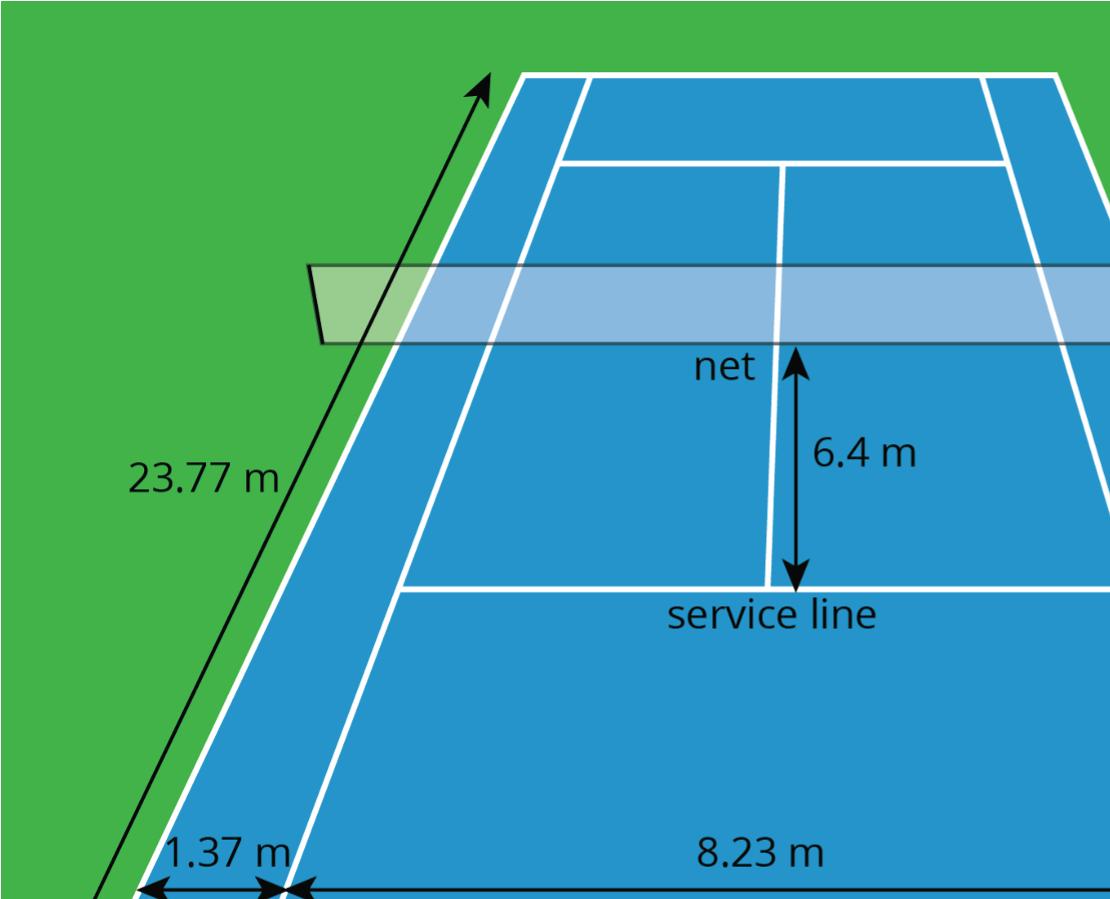
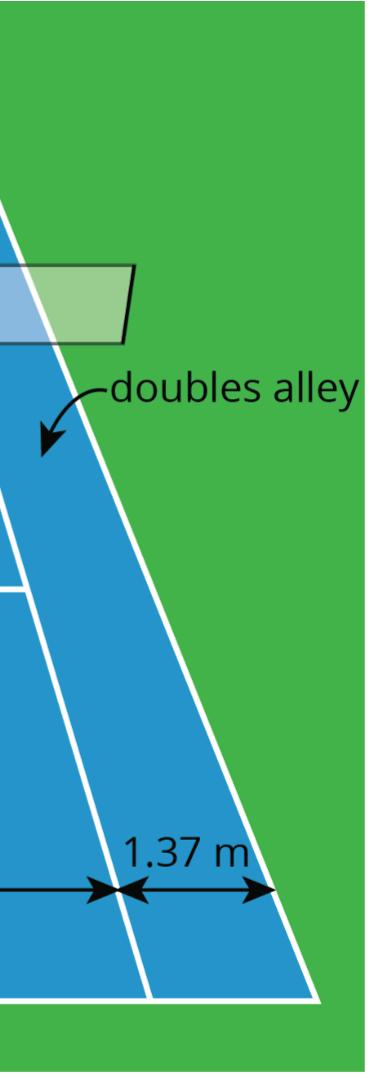
2. Explain whether the service line is halfway between the net and the baseline.

3. Lines painted on a tennis court are 5 centimeters (cm) wide, which is equivalent to 0.05 m. A painter made markings to show the length and width of the court, and then painted the lines to the outside of those markings.

a. Explain whether the painter’s mistake increased or decreased the overall size of the tennis court.

b. How many square meters (sq. m) did the court’s size change by? Explain your reasoning.

ManuscriptCopy

Lesson Summary

Diagrams can be helpful for communicating and modeling mathematics. A clearly labeled diagram helps to visualize what is happening in a problem and accurately communicate the information needed.

Sports offer great examples of how diagrams can be helpful for solving problems. For example, to show the placement of the running hurdles in a diagram, it would be necessary to know the meaning of the distances 13.72 m and 14.02 m, as well as the number of hurdles to draw. An accurate diagram is useful not only for setting up and solving the problem correctly, but also for visualizing that there are only 9 spaces between 10 hurdles.

To communicate information clearly and solve problems correctly, it’s also important to be precise with measurements and calculations, especially when they involve decimals. In tennis, for example, the length of the court is 23.77 m. Because the boundary lines on a tennis court have a significant width, it’s important to know whether this length is taken from inside the lines, the center of the lines, or the outside of the lines. Diagrams aid in attention to detail, as shown.

ManuscriptCopy

The accuracy of this measurement matters to the tennis players who use the court, so it matters to those who paint the boundaries as well. The tennis players practice their shots to be on or within certain lines. If the tennis court they play on is not precisely measured, their shots may not land as intended in relation to the boundaries. Court painters usually need to be sure their measurements are accurate within 1 100 m, or 1 cm.

Practice Problems

1. A roll of ribbon was 12 m long. Diego cut 9 pieces of ribbon that were 0.4 m each to tie some presents. He then used the remaining ribbon to make some wreaths. Each wreath required 0.6 m. For each question, explain your reasoning.

a. How many m of ribbon were available for making wreaths?

b. How many wreaths could Diego make with the available ribbon?

2. To get an A in her math class, Jada needs to have at least 90% of the total number of points possible. The table shows Jada’s results before the final test in the class.

a. Does Jada have 90% of the total possible points before the final test? Explain how you know.

b. Jada thinks that if she gets at least 92 out of 100 on the final test, she will get an A in the class. Do you agree? Explain.

3. Find each difference. Show your reasoning.

a. 0.151 – 0.028

b. 0.16 – 0.035

c. 3.57 – 2.604

4. Find these quotients. Show your reasoning.

a. 24.2 ÷ 1.1

ManuscriptCopy

13.25 ÷ 0.4

170.28 ÷ 0.08

b.

c.

ManuscriptCopy

ManuscriptCopy

Unit 3, Lesson 1: Introducing Ratios and Ratio Language

Warm-Up: What Kind and How Many?

Think of different ways you could sort the figures shown.

What categories could you use? How many groups would you have?

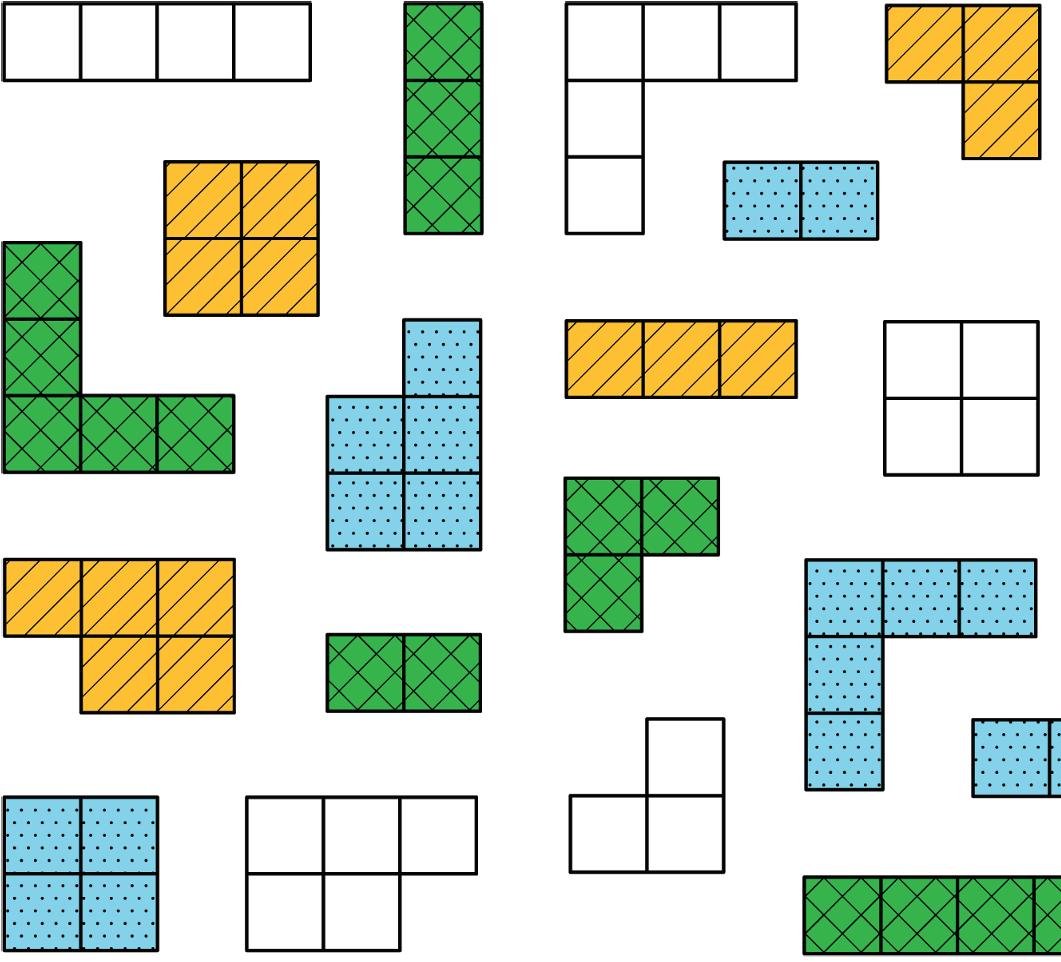
Exploration Activity: The Teacher’s Collection

1. Think of a way to sort your teacher’s collection into two or three categories. Count the items in each category, and record the information in the table.

Category

Pause here so your teacher can review your work.

ManuscriptCopy

2. Write at least two sentences that describe ratios in the collection. Remember, there are many ways to write a ratio.

• The ratio of one category to another category is ________ to ________.

• The ratio of one category to another category is ________ : ________.

• There are _______ of one category for every _______ of another category.

Exploration Activity: The Student’s Collection

1. Sort your collection into three categories. You can experiment with different ways of arranging these categories. Then, count the items in each category, and record the information in the table.

Category Name

Category Amount

2. Write at least two sentences that describe ratios in the collection. Remember, there are many ways to write a ratio.

• The ratio of one category to another category is ________ to ________.

• The ratio of one category to another category is ________ : ________.

• There are _______ of one category for every _______ of another category.

Pause here so your teacher can review your sentences.

3. Make a visual display of your items that clearly shows one of your statements. Be prepared to share your display with the class.

Lesson Summary

This lesson explored relationships between quantities, called ratios.

A ratio is an association between two or more quantities.

There are many ways to describe a situation in terms of ratios. For example, consider the collection shown.

Ratios can be written 3 different ways. The ratio of squares to circles is expressed all 3 ways in the table.

Regardless of the method used for writing the ratio, each is read the same way, “6 to 3.”

The order of the ratio is important because it relates specifically to the quantities being described. The order used in the written description must match the order of the values that are being compared. For example, the ratio of circles to squares is 3 ∶ 6.

Notice that the shapes can be arranged in equal groups, which can be used to represent the ratio using other numbers. Two examples are shown.

• There are 2 squares for every 1 circle.

• There is 1 circle for every 2 squares.

Practice Problems

1. In a fruit basket there are 9 bananas, 4 apples, and 3 plums.

a. The ratio of bananas to apples is ________: ________.

b. The ratio of plums to apples is ________ to ________.

c. For every ________ apples, there are ________ plums.

d. For every 3 bananas there is one ________.

2. Complete the sentences to describe this picture.

a. The ratio of dogs to cats is ____________.

b. For every _____ dogs, there are _____ cats.

3. Write two different sentences that use ratios to describe the number of eyes and legs in this picture.

ManuscriptCopy

Review Problems

4. Choose an appropriate unit of measurement for each quantity.

a. area of a rectangle ___________ • centimeters (cm)

b. volume of a prism ___________ • cubic centimeters (cu. cm)

c. side of a square ___________ • square centimeters (sq. cm)

d. area of a square ___________

e. volume of a cube ___________

5. Find the volume and surface area of each prism.

a. Prism A: 3 cm by 3 cm by 3 cm

b. Prism B: 5 cm by 5 cm by 1 cm

c. Compare the volumes of the prisms and then their surface areas. Does the prism with the greater volume also have the greater surface area?

6. Which figure is a triangular prism? Select all that apply.

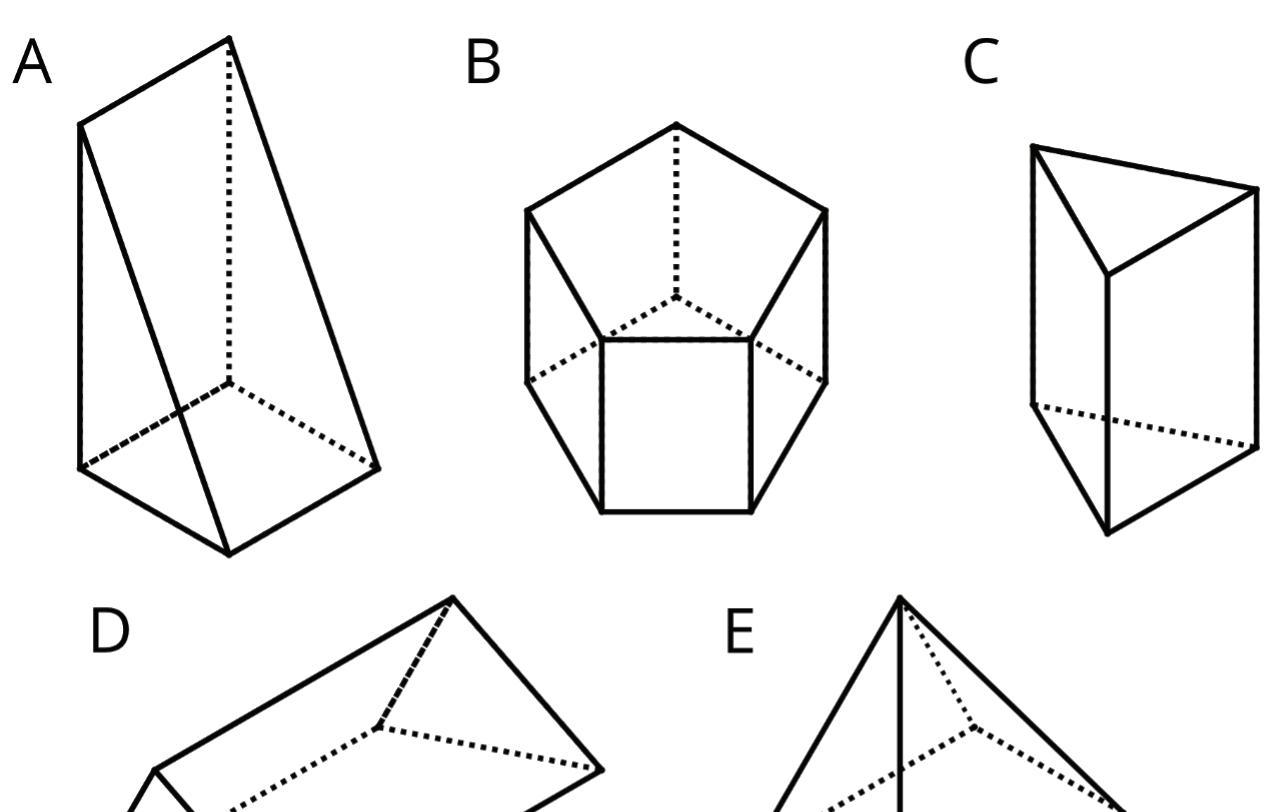
ManuscriptCopy

Unit 3, Lesson 2: Representing Ratios with Diagrams

Warm-Up: Dividing by 4 and Multiplying by 1 4

Find the value of each expression mentally.

Exploration Activity: A Collection of Snap Cubes

Here is a collection of snap cubes.

1. Choose two of the colors in the image, and draw a diagram showing the number of snap cubes for these two colors.

2. Trade papers with a partner. On their paper, write a sentence to describe a ratio shown in their diagram. Your partner will do the same for your diagram.

3. Return your partner’s paper. Read the sentence written on your paper. If you disagree, explain your thinking.

Exploration Activity: Blue Paint and Art Paste

Elena mixed 2 cups (c.) of white paint with 6 tablespoons (tbsp.) of blue paint.

Here is a diagram that represents this situation.

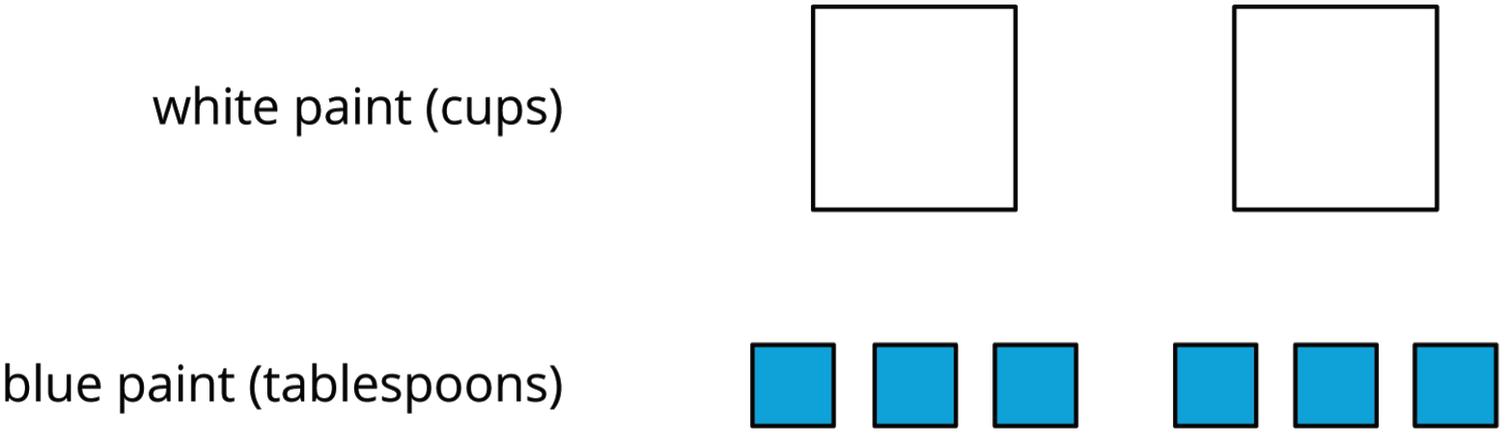
1. Discuss each statement, and select all those that correctly describe this situation. Make sure that both you and your partner agree with each selected answer.

□ The ratio of c. of white paint to tbsp. of blue paint is 2 : 6.

□ For every c. of white paint, there are 2 tbsp. of blue paint.

□ There is 1 c. of white paint for every 3 tbsp. of blue paint.

□ There are 3 tbsp. of blue paint for every c. of white paint.

□ For each tbsp. of blue paint, there are 3 c. of white paint.

□ For every 6 tbsp. of blue paint, there are 2 c. of white paint.

□ The ratio of tbsp. of blue paint to c. of white paint is 6 to 2.

2. Jada mixed 8 c. of flour with 2 pints (pt.) of water to make paste for an art project.

a. Draw a diagram that represents the situation.

b. Write at least two sentences describing the ratio of flour and water.

Collaborative Activity: Spaghetti Sauce

Your teacher will give you cards describing different recipes for spaghetti sauce. In the diagrams:

• a circle represents a c. of tomato sauce

• a square represents a tbsp. of oil

• a triangle represents a teaspoon (tsp.) of oregano

1. Take turns with your partner to match a sentence with a diagram.

a. For each match that you find, explain to your partner how you know it’s a match.

b. For each match that your partner finds, listen carefully to their explanation. If you disagree, discuss your thinking and work to reach an agreement.

2. After you and your partner have agreed on all of the matches, check your answers with the answer key. If there are any errors, discuss why and revise your matches.

3. There were two diagrams that each matched with two different sentences. Which were they?

• Diagram _______ matched with both sentences ______ and ______.

• Diagram _______ matched with both sentences ______ and ______.

4. Select one of the other diagrams and invent another sentence that could describe the ratio shown in the diagram.

ManuscriptCopy

Lesson Summary

Ratios can be represented using diagrams. The diagrams do not need to include realistic details. For example, a recipe for lemonade says, “Mix 2 scoops of lemonade powder with 6 c. of water.”

Both diagrams shown can be used to represent the recipe. Diagram A includes realistic details, but diagram B represents the same relationship using a more easily drawn representation.

ManuscriptCopy

Both diagrams show that the ratio of c. of water to scoops of lemonade powder is 6 to 2. The diagrams can also be used to show that for every scoop of lemonade powder, there are 3 c. of water.

Diagram A

Diagram B

Practice Problems

1. Here is a diagram that describes the c. of green and white paint in a mixture.

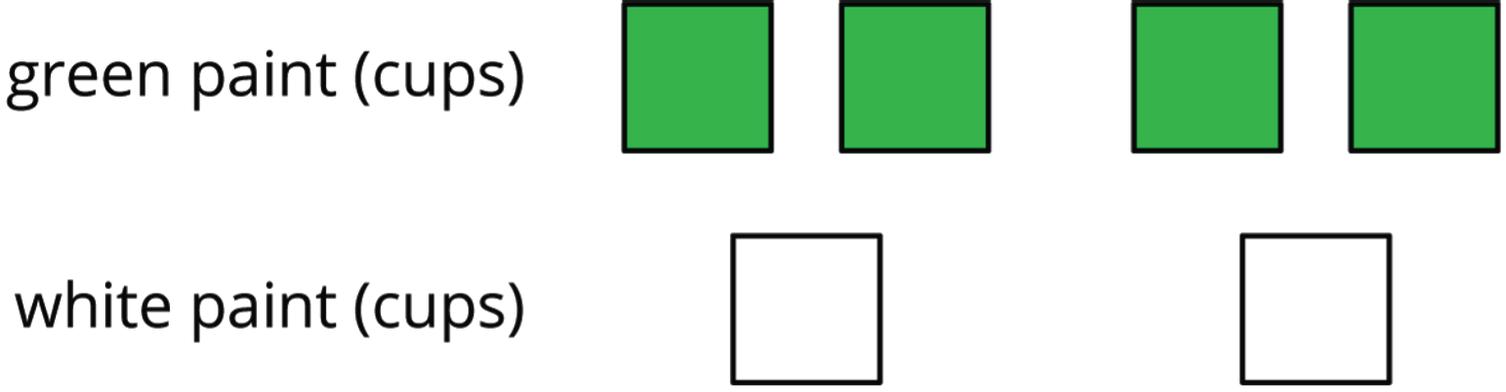
Select all the statements that correctly describe this diagram.

□ The ratio of c. of white paint to c. of green paint is 2 4 .

□ For every c. of green paint, there are 2 c. of white paint.

□ The ratio of c. of green paint to c. of white paint is 4 : 2.

□ For every c. of white paint, there are 2 c. of green paint.

□ The ratio of c. of green paint to c. of white paint is 2 : 4.

2. To make a snack mix, combine 2 c. of raisins with 4 c. of pretzels and 6 c. of almonds.

a. Create a diagram to represent the quantities of each ingredient in this recipe.

b. Use your diagram to complete each sentence.

ManuscriptCopy

• The ratio of ________________ to ________________ to ________________ is ________ : ________ : ________.

• There are ________ c. of pretzels for every c. of raisins.

• There are ________ c. of almonds for every c. of raisins.

3.

a. A square is 3 inches (in.) by 3 in. What is its area?

b. A square has a side length of 5 feet (ft.). What is its area?

c. The area of a square is 36 square centimeters (sq. cm). What is the length of each side of the square?

4. Find the area of this quadrilateral. Explain or show your strategy.

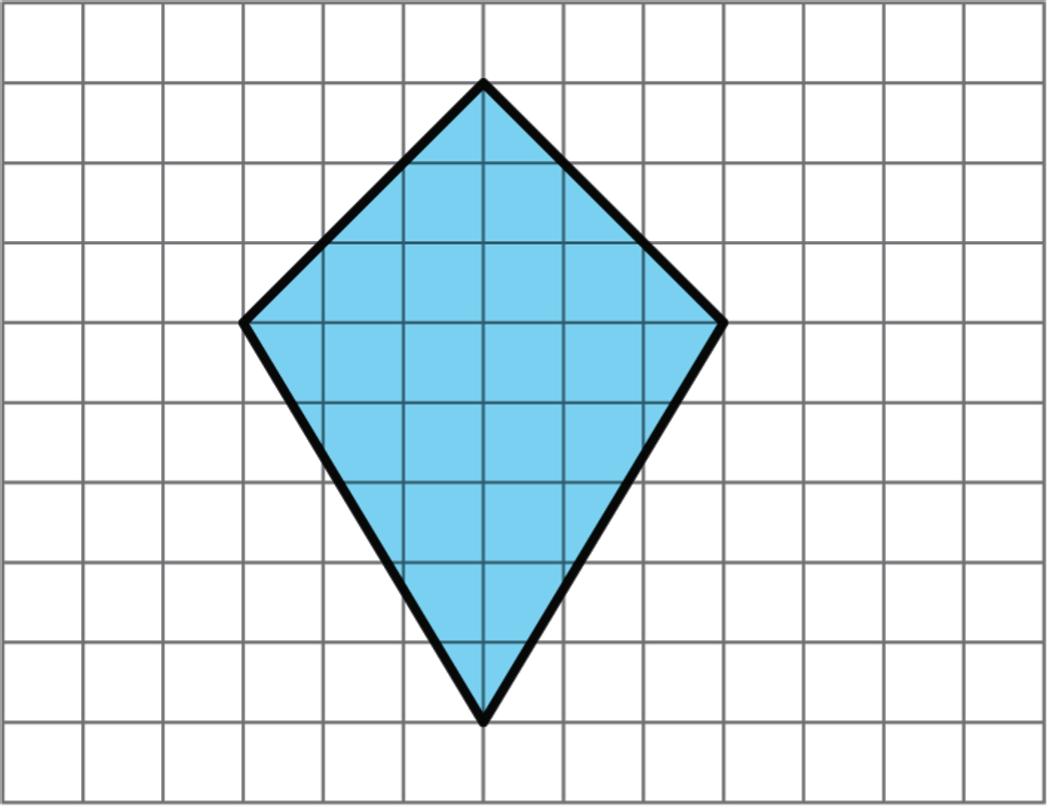
5. Complete each equation with a number that makes it true.

a. 1 8 ⋅ 8 = _______

b. 3 8 ⋅ 8 = _______ c. 1 8 ⋅ 7 = _______ d. 3 8 ⋅ 7 = _______

Unit 3, Lesson 3: Using Ratios in Recipes

Warm-Up: Flower Pattern

This flower is made up of yellow hexagons, red trapezoids, and green triangles.

1. Write sentences to describe the ratios of the shapes that make up this pattern.

2. How many of each shape would be in two copies of this flower pattern?

ManuscriptCopy

Exploration Activity: Powdered Drink Mix

Here are diagrams representing three mixtures of powdered drink mix and water.

Key:

= 1 teaspoon (tsp.) drink mix = 1 cup (c.) water

1. How would the taste of Mixture A compare to the taste of Mixture B?

2. Use the diagrams to complete each statement.

a. Mixture B uses ______ c. of water and ______ teaspoons tsp. of drink mix. The ratio of c. of water to tsp. of drink mix in Mixture B is ________.

b. Mixture C uses ______ c. of water and ______ tsp. of drink mix. The ratio of c. of water to tsp. of drink mix in Mixture C is ________.

3. How would the taste of Mixture B compare to the taste of Mixture C?

ManuscriptCopy

Collaborative Activity: Batches of Cookies

A recipe for one batch of cookies calls for 5 c. of flour and 2 tsp. of vanilla.

1. Draw a diagram that shows the amount of flour and vanilla needed for two batches of cookies.

2. How many batches can you make with 15 c. of flour and 6 tsp. of vanilla? Show the additional batches by adding more ingredients to your diagram.

3. How much flour and vanilla would you need for 5 batches of cookies?

4. Whether the ratio of cups of flour to teaspoons of vanilla is 5 ∶ 2, 10 ∶ 4, or 15 ∶ 6, the recipes would make cookies that taste the same. We call these equivalent ratios.

a. Find another ratio of cups of flour to teaspoons of vanilla that is equivalent to these ratios.

b. How many batches can you make using this new ratio of ingredients?

Exploration Activity: Drink Mix on a Double Number Line

Earlier, we made drink mixtures by mixing 4 tsp. of powdered drink mix for every c. of water. Here are two ways to represent multiple batches of this recipe.

drinkmix(tsp.)

water(c.)

drinkmix(tsp.) 04 01234 81216

water(c.)

1. How can we tell that 4 ∶ 1 and 12 ∶ 3 are equivalent ratios?

2. How are these representations the same? How are these representations different?

3. How many tsp. of drink mix should be used with 3 c. of water?

4. How many c. of water should be used with 16 tsp. of drink mix?

5. What numbers should go in the empty boxes on the double number line diagram? What do these numbers mean?

Lesson Summary

A recipe for fizzy juice says, “Mix 5 c. of cranberry juice with 2 c. of soda water.” To double this recipe, 10 c. of cranberry juice and 4 c. of soda water would be needed. To triple this recipe, 15 c. of cranberry juice and 6 c. of soda water would be needed.

The diagram shown represents a single batch, a double batch, and a triple batch of the recipe.

The ratios 5 ∶ 2, 10 ∶ 4, and 15 ∶ 6 are equivalent. Even though the amounts of each ingredient within a single, double, or triple batch are not the same, they would make fizzy juice that tastes the same.

A double number line diagram can be used to find equivalent ratios. The ratio of cranberry juice to soda water is 5 2 . Multiplying both ingredients by the same number creates an equivalent ratio.

A double number line diagram uses a pair of parallel number lines to represent equivalent ratios. The locations of the tick marks match on both number lines. The tick marks labeled 0 line up, but the other numbers are usually different.

This double number line shows that the ratio 20 8 is equivalent to 5 2 . Mixing 20 c. of cranberry juice with 8 c. of soda water makes 4 times as much fizzy juice that tastes the same as the original recipe. cranberry juice (c.)

Practice Problems

1. A recipe for 1 batch of spice mix says, “Combine 3 tsp. of mustard seeds, 5 tsp. of chili powder, and 1 tsp. of salt.” How many batches are represented by the diagram? Explain or show your reasoning.

mustard seeds (tsp.)

chili powder (tsp.)

salt (tsp.)

2. Priya makes chocolate milk by mixing 2 c. of milk and 5 tablespoons (tbsp.) of cocoa powder. Draw a diagram that clearly represents two batches of her chocolate milk.

3. In a recipe for fizzy grape juice, the ratio of c. of sparkling water to c. of grape juice concentrate is 3 to 1.

a. Find two more ratios of c. of sparkling water to c. of juice concentrate that would make a mixture that tastes the same as this recipe.

b. Describe another mixture of sparkling water and grape juice that would taste different than this recipe.

4. This double number line diagram shows the amount of flour and eggs needed for 1 batch of cookies.

Cups of flour

Number of eggs

0 5 0 3

a. Complete the diagram to show the amount of flour and eggs needed for 2, 3, and 4 batches of cookies.

b. What is the ratio of c. of flour to eggs?

c. How much flour and how many eggs are used in 4 batches of cookies?

d. How much flour is used with 6 eggs?

e. How many eggs are used with 15 c. of flour?

Review Problem

5. Diego estimates that there will need to be 3 pizzas for every 7 kids at his party. Select all the statements that express this ratio.

□ The ratio of kids to pizzas is 7 ∶ 3.

□ The ratio of pizzas to kids is 3 to 7.

□ The ratio of kids to pizzas is 3 7 .

□ The ratio of pizzas to kids is 7 to 3.

□ For every 7 kids there need to be 3 pizzas.

ManuscriptCopy

Unit 3, Lesson 4: Ratios and Color Mixtures

Warm-Up: Number Talk: Adjusting a Factor

Find the value of each product mentally.

Exploration Activity: Turning Green

Your teacher mixed milliliters (mL) of blue water and mL of yellow water in the ratio

5 ∶ 15.

1. Doubling the original recipe:

a. Draw a diagram to represent the amount of each color that you will combine to double your teacher’s recipe.

b. Use a marker to label an empty cup with the ratio of blue water to yellow water in this double batch.

c. Predict whether these amounts of blue and yellow will make the same shade of green as your teacher’s mixture. Next, check your prediction by measuring those amounts and mixing them in the cup.

d. Is the ratio in your mixture equivalent to the ratio in your teacher’s mixture? Explain your reasoning.

2. Tripling the original recipe:

a. Draw a diagram to represent triple your teacher’s recipe.

b. Label an empty cup with the ratio of blue water to yellow water.

c. Predict whether these amounts will make the same shade of green. Next, check your prediction by mixing those amounts.

d. Is the ratio in your new mixture equivalent to the ratio in your teacher’s mixture? Explain your reasoning.

3. Next, invent your own recipe for a bluer shade of green water.

a. Draw a diagram to represent the amount of each color you will combine.

b. Label the final empty cup with the ratio of blue water to yellow water in this recipe.

c. Test your recipe by mixing a batch in the cup. Does the mixture yield a bluer shade of green?

d. Is the ratio you used in this recipe equivalent to the ratio in your teacher’s mixture? Explain your reasoning.

Collaborative Activity: Perfect Purple Water

The recipe for Perfect Purple Water says, “Mix 8 mL of blue water with 3 mL of red water.”

Jada mixes 24 mL of blue water with 9 mL of red water. Andre mixes 16 mL of blue water with 9 mL of red water.

1. Which person will get a color mixture that is the same shade as Perfect Purple Water? Explain or show your reasoning.

2. Find another combination of blue water and red water that will also result in the same shade as Perfect Purple Water. Explain or show your reasoning.

ManuscriptCopy

Lesson Summary

When mixing a paint color, doubling or tripling the amount of each color in the mix will create the same result. In fact, the amount of each color in the mix can always can multiplied by the same number to create a different amount of the same mixed color.

For example, a batch of dark orange paint uses 4 mL of red paint and 2 mL of yellow paint.

• To make 2 batches of dark orange paint, mix 8 mL of red paint and 4 mL of yellow paint.

• To make 3 batches of dark orange paint, mix 12 mL of red paint and 6 mL of yellow paint.

The diagram represents 1, 2, and 3 batches of this recipe.

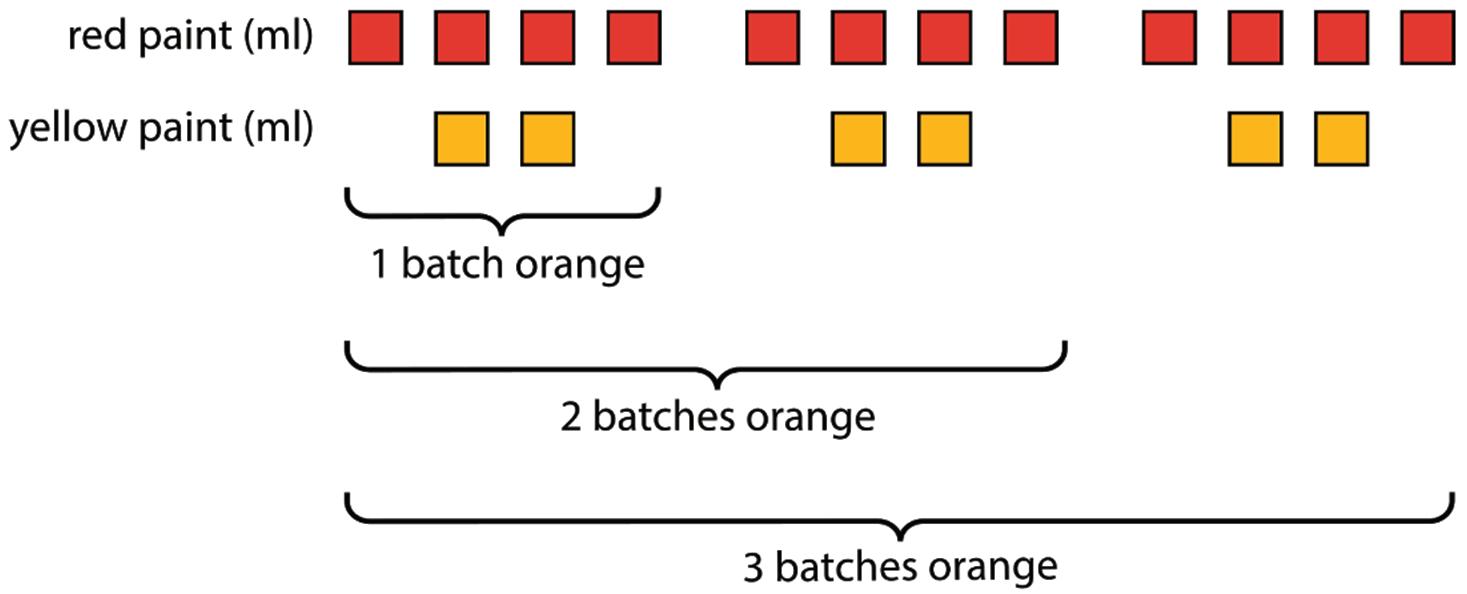
The ratios 4 ∶ 2, 8 ∶ 4, and 12 ∶ 6 are equivalent because they describe the same color mixture in different numbers of batches, and they make the same shade of orange.

ManuscriptCopy

Practice Problems

1. Here is a diagram showing a mixture of red paint and green paint needed for 1 batch of a particular shade of brown.

Add to the diagram so that it shows 3 batches of the same shade of brown paint.

2. Diego makes green paint by mixing 10 tablespoons (tbsp.) of yellow paint and 2 tbsp. of blue paint. Which of these mixtures produce the same shade of green paint as Diego’s mixture? Select all that apply.

□ For every 5 tbsp. of blue paint, mix in 1 tbsp. of yellow paint.

□ Mix tbsp. of blue paint and yellow paint in the ratio 1 : 5.

□ Mix tbsp. of yellow paint and blue paint in the ratio 15 to 3.

□ Mix 11 tbsp. of yellow paint and 3 tbsp. of blue paint.

□ For every tbsp. of blue paint, mix in 5 tbsp. of yellow paint.

3. To make 1 batch of sky blue paint, Clare mixes 2 cups (c.) of blue paint with 1 gallon (gal.) of white paint.

a. Explain how Clare can make 2 batches of sky blue paint.

b. Explain how to make a mixture that is a darker shade of blue than the sky blue.

c. Explain how to make a mixture that is a lighter shade of blue than the sky blue.

Review Problems

4. A smoothie recipe calls for 3 c. of milk, 2 frozen bananas, and 1 tbsp. of chocolate syrup.

a. Create a diagram to represent the quantities of each ingredient in the recipe.

b. Write 3 different sentences that use a ratio to describe the recipe.

5. Write the missing number under each tick mark on the number line.

6. Find the area of the parallelogram. Show your reasoning.

7. Complete each equation with a number that makes it true.

a. 11 ⋅ 1 4 = ____________

b. 7 ⋅ 1 4 = ____________

c. 13 ⋅ 1 27 = ____________

d. 13 ⋅ 1 99 = ____________

e. �� ⋅ 1 �� = ____________ (As long as �� does not equal 0.)

ManuscriptCopy

ManuscriptCopy

Unit 3, Lesson 5: Digging Deeper into Equivalent Ratios

Warm-Up: Nic’s Sweet Tea Lemonade

1. Nic prefers his sweet tea and lemonade to be mixed in a specific ratio to achieve his preferred taste. He made a mistake when mixing it because he wasn’t paying attention. The table shows what Nic should have mixed and what he actually mixed.

a. Describe what Nic did wrong.

b. How could Nic fix it so that the mixture contains his preferred balance of sweet tea and lemonade?

Collaborative Activity: Tuna Casserole

Here is a recipe for tuna casserole.

Ingredients

• 3 cups (c.) cooked elbow-shaped pasta

• 6 ounce (oz.) can tuna, drained

• 10 oz. can cream of chicken soup

• 1 c. shredded cheddar cheese

• 1 1 2 c. French fried onions

Instructions

Combine the pasta, tuna, soup, and half of the cheese. Transfer into a 9 inch (in.) by 18 in. baking dish. Put the remaining cheese on top. Bake 30 minutes (min.) at 350 degrees. During the last 5 min., add the French fried onions. Let sit for 10 min. before serving.

1. What is the ratio of the oz. of soup to the c. of shredded cheese to the c. of pasta in one batch of casserole?

2. How much of each of these 3 ingredients would be needed to make:

a. twice the amount of casserole?

b. half the amount of casserole?

c. five times the amount of casserole?

d. one-fifth the amount of casserole?

3. What is the ratio of c. of pasta to oz. of tuna in one batch of casserole?

4. How many batches of casserole would you make if you used the following amounts of ingredients?

a. 9 c. of pasta and 18 oz. of tuna?

b. 36 oz. of tuna and 18 c. of pasta?

c. 1 c. of pasta and 2 oz. of tuna?

Exploration Activity: What Are Equivalent Ratios?

The ratios 5 ∶ 3 and 10 ∶ 6 are equivalent ratios.

1. Is the ratio 15 ∶ 12 equivalent to these? Explain your reasoning.

2. Is the ratio 30 ∶ 18 equivalent to these? Explain your reasoning.

3. Give two more examples of ratios that are equivalent to 5 ∶ 3.

4. How do you know when ratios are equivalent and when they are not equivalent?

5. Write a definition of equivalent ratios.

Pause here so your teacher can review your work and assign you a ratio to use for your visual display.

6. Create a visual display that includes:

• the title “Equivalent Ratios”

• your best definition of equivalent ratios

• the ratio your teacher assigned to you

• at least two examples of ratios that are equivalent to your assigned ratio

• an explanation of how you know these examples are equivalent

• at least one example of a ratio that is not equivalent to your assigned ratio

• an explanation of how you know this example is not equivalent

Be prepared to share your display with the class.

ManuscriptCopy

Lesson Summary

All ratios that are equivalent to �� ∶ �� can be made by multiplying both �� and �� by the same number.

Two ratios are equivalent if you can multiply each of the numbers in the first ratio by the same factor to get the numbers in the second ratio.

For example, the ratio 18 ∶ 12 is equivalent to 9 ∶ 6 because both 9 and 6 are multiplied by the same number, 2.

3 ∶ 2 is also equivalent to 9 ∶ 6, because both 9 and 6 are multiplied by the same number, 1 3 .

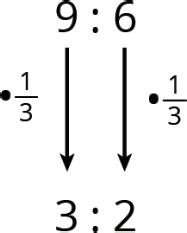
However, 18 ∶ 15 is not equivalent to 9 ∶ 6 because 18 is 9 ⋅ 2, but 15 is not 6 ⋅ 2.

1. Explain why 6 ∶ 4 and 18 ∶ 8 are not equivalent ratios. 9:6 18:15 ●2No.

Practice Problems

2. Each of these is a pair of equivalent ratios. For each pair, explain why they are equivalent ratios or draw a diagram that shows why they are equivalent ratios.

a. 4 ∶ 5 and 8 ∶ 10

b. 18 ∶ 3 and 6 ∶ 1

c. 2 ∶ 7 and 10,000 ∶ 35,000

3. Are the ratios 3 ∶ 6 and 6 ∶ 3 equivalent? Why or why not?

Review Problems

4. This diagram represents 3 batches of light yellow paint. Draw a diagram that represents 1 batch of the same shade of light yellow paint.

ManuscriptCopy

5. In the fruit bowl there are 6 bananas, 4 apples, and 3 oranges.

a. For every 4 __________________, there are 3 ________________.

b. The ratio of __________________ to __________________ is 6 : 3.

c. The ratio of __________________ to _________________ is 4 to 6.

d. For every 1 orange, there are ______ bananas.

6. Write fractions for points �� and �� on the number line.

ManuscriptCopy

ManuscriptCopy

Unit 3, Lesson 6: Creating Double Number Line Diagrams

Warm-Up: Ordering on a Number Line

1. Locate and label the following numbers on the number line.

2. Based on where you placed the numbers, locate and label four more fractions or decimals on the number line.

Exploration Activity: Just a Little Green

The other day, we made green water by mixing 5 milliliters (mL) of blue water with 15 mL of yellow water. We want to make a very small batch of the same shade of green water. We need to know how much yellow water to mix with only 1 mL of blue water.

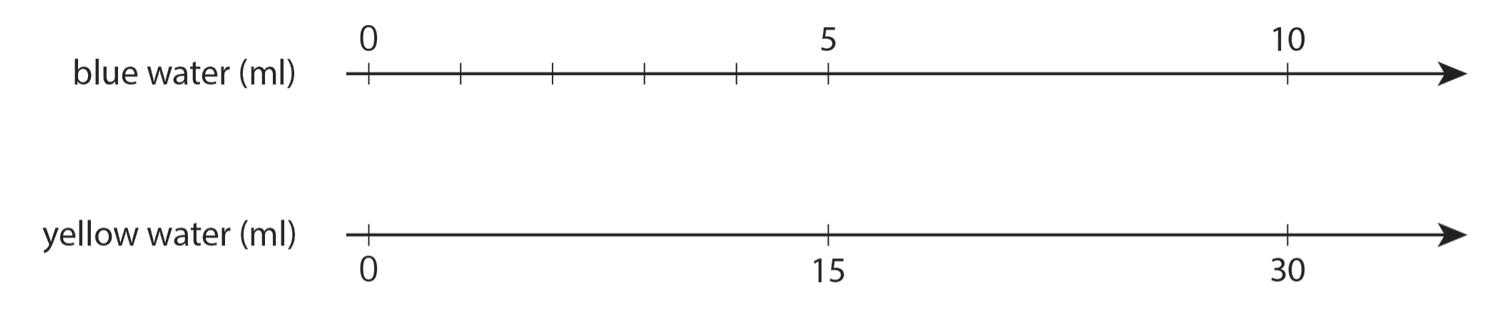
1. On the number line for blue water, label the four tick marks shown.

2. On the number line for yellow water, draw and label tick marks to show the amount of yellow water needed for each amount of blue water.

3. How much yellow water should be used for 1 mL of blue water? Circle where you can see this on the double number line.

4. How much yellow water should be used for 11 mL of blue water?

5. How much yellow water should be used for 8 mL of blue water?

6. Why is it useful to know how much yellow water should be used with 1 mL of blue water?

Guided Activity: Art Paste on a Double Number Line

A recipe for art paste says, “For every 2 pints (pt.) of water, mix in 8 cups (c.) of flour.”

1. Follow the instructions to draw a double number line diagram representing the recipe for art paste.

a. Use a ruler to draw two parallel lines.

b. Label the first line “pints of water.” Label the second line “cups of flour.”

c. Draw at least 6 equally spaced tick marks that line up on both lines.

d. Along the water line, label the tick marks with the amount of water in 0, 1, 2, 3, 4, and 5 batches of art paste.

e. Along the flour line, label the tick marks with the amount of flour in 0, 1, 2, 3, 4, and 5 batches of art paste.

2. Compare your double number line diagram with your partner’s. Discuss your thinking. If needed, revise your diagram.

3. Next, use your double number line to answer these questions:

a. How much flour should be used with 10 pt. of water?

b. How much water should be used with 24 c. of flour?

c. How much flour per pt. of water does this recipe use?

Collaborative Activity: Revisiting Tuna Casserole

The other day, we looked at a recipe for tuna casserole that called for 10 ounces (oz.) of cream of chicken soup for every 3 c. of elbow-shaped pasta.

1. Draw a double number line diagram that represents the amounts of soup and pasta in different-sized batches of this recipe.

2. If you made a large amount of tuna casserole by mixing 40 oz. of soup with 15 c. of pasta, would it taste the same as the original recipe? Explain or show your reasoning.

3. The original recipe called for 6 oz. of tuna for every 3 c. of pasta. Add a line to your diagram to represent the amount of tuna in different batches of casserole.

4. How many oz. of soup should you mix with 30 oz. of tuna to make a casserole that tastes the same as the original recipe?

Lesson Summary

When drawing a double number line diagram, use the following guidelines:

• The 2 parallel lines should have labels that describe what the numbers represent.

• The tick marks and numbers should be spaced at equal intervals.

• Numbers that line up vertically should make equivalent ratios.

For example, the ratio of the number of eggs to c. of milk in a recipe is 4 ∶ 1. The double number line diagram shown represents the situation.

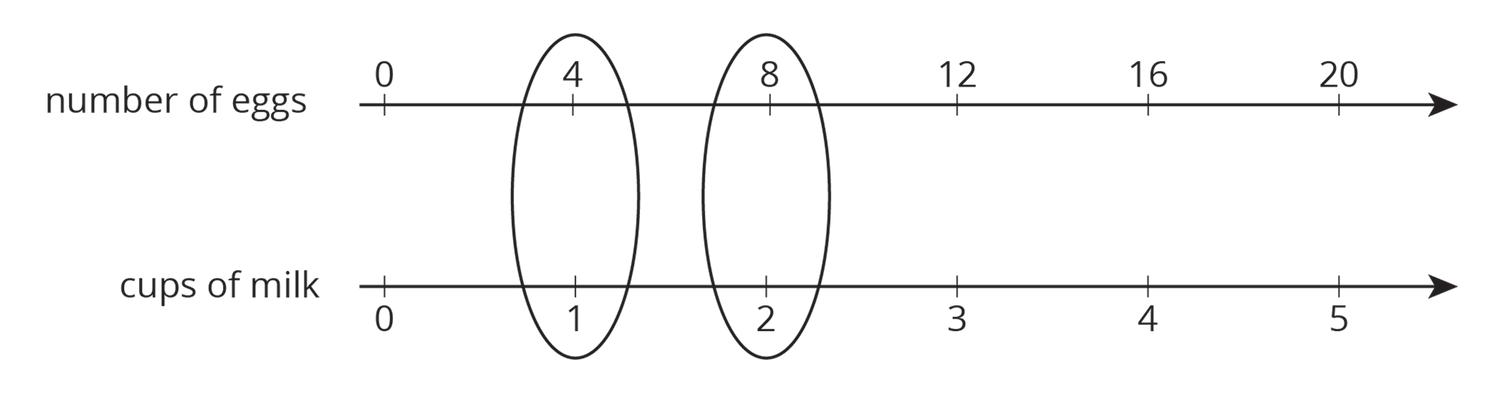
The word per means “for each,” so this recipe can also be described as using 4 eggs per c. of milk.

Practice Problems

1. A recipe for cinnamon rolls uses 2 tablespoons (tbsp.) of sugar per teaspoon (tsp.) of cinnamon for the filling. Complete the double number line diagram to show the amount of cinnamon and sugar in 3, 4, and 5 batches.

2. One batch of meatloaf contains 2 pounds of beef and 1 2 c. of bread crumbs. Complete the double number line diagram to show the amounts of beef and bread crumbs needed for 1, 2, 3, and 4 batches of meatloaf.

3. A recipe for tropical fruit punch says, “Combine 4 c. of pineapple juice with 5 c. of orange juice.”

a. Create a double number line showing the amount of each type of juice in 1, 2, 3, 4, and 5 batches of the recipe.

b. If 12 c. of pineapple juice are used with 20 c. of orange juice, will the recipe taste the same? Explain your reasoning.

c. The recipe also calls for 1 3 c. of lime juice for every 5 c. of orange juice. Add a line to your diagram to represent the amount of lime juice in different batches of tropical fruit punch.

Review Problems

4. One batch of pink paint uses 2 c. of red paint and 7 c. of white paint. Mai made a large amount of pink paint using 14 c. of red paint.

a. How many batches of pink paint did she make?

b. How many c. of white paint did she use?

5.

a. Find three different ratios that are equivalent to the ratio 3 ∶ 11.

b. Explain why your ratios are equivalent.

6. Here is a diagram that represents the pints of red and yellow paint in a mixture.

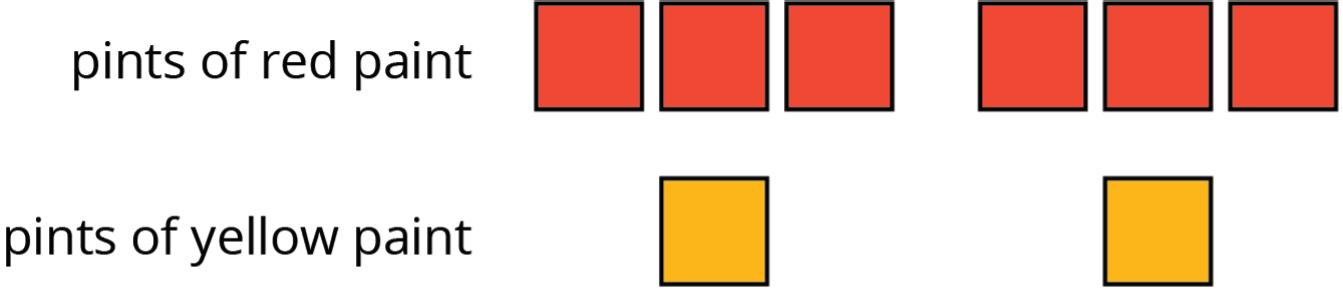
Select all statements that accurately describe the diagram.

□ The ratio of yellow paint to red paint is 2 to 6.

□ For every 3 pt. of red paint, there is 1 pt. of yellow paint.

□ For every pt. of yellow paint, there are 3 pt. of red paint.

ManuscriptCopy

□ For every pt. of yellow paint there are 6 pt. of red paint.

□ The ratio of red paint to yellow paint is 6 : 2.

Unit 3, Lesson 7: How Much for One?

Warm-Up: Remainders in Division

1. Find the quotient mentally. 246 ÷ 12

Exploration Activity: Grocery Shopping

Answer each question and explain or show your reasoning. If you get stuck, consider drawing a double number line diagram.

1. Eight avocados cost $4.

a. How much do 16 avocados cost?

b. How much do 20 avocados cost?

c. How much do 9 avocados cost?

ManuscriptCopy

2. Twelve large bottles of water cost $9.

a. How many bottles can you buy for $3?

b. What is the cost per bottle of water?

c. How much would 7 bottles of water cost?

3. A 10-pound (lb.) sack of flour costs $8.

a. How much does 40 lb. of flour cost?

b. What is the cost per lb. of flour?

Collaborative Activity: More Shopping

1. Four bags of chips cost $6.

a. What is the cost per bag?

b. At this rate, how much will 7 bags of chips cost?

2. At a used book sale, 5 books cost $15.

a. What is the cost per book?

b. At this rate, how many books can you buy for $21?

3. Neon bracelets cost $1 for 4.

a. What is the cost per bracelet?

b. At this rate, how much will 11 neon bracelets cost?

Pause here so your teacher can review your work.

ManuscriptCopy

4. Your teacher will assign you one of the problems. Create a visual display that shows your solution to the problem. Be prepared to share your solution with the class.

Lesson Summary

The unit price is the price of 1 thing, such as the price of 1 ticket, 1 slice of pizza, or 1 kilogram (kg) of peaches.

The unit price is the cost for one item or for one unit of measure.

If 4 movie tickets cost $28, then the unit price would be the cost per ticket. A double number line can be created to find the unit price.

This double number line shows that the cost for 1 ticket is $7.

The unit price can also be determined by dividing. For example, $28 ÷ 4 tickets = $7 per ticket. This can also be represented by multiplying 28 ⋅ 1 4 = 7 to show that 1 4 of the total cost of 4 tickets is equal to the cost of 1 ticket.

Practice Problems

1. In 2016, the cost of 2 ounces (oz.) of pure gold was $2,640. Complete the double number line to show the cost for 1, 3, and 4 oz. of gold.

ManuscriptCopy

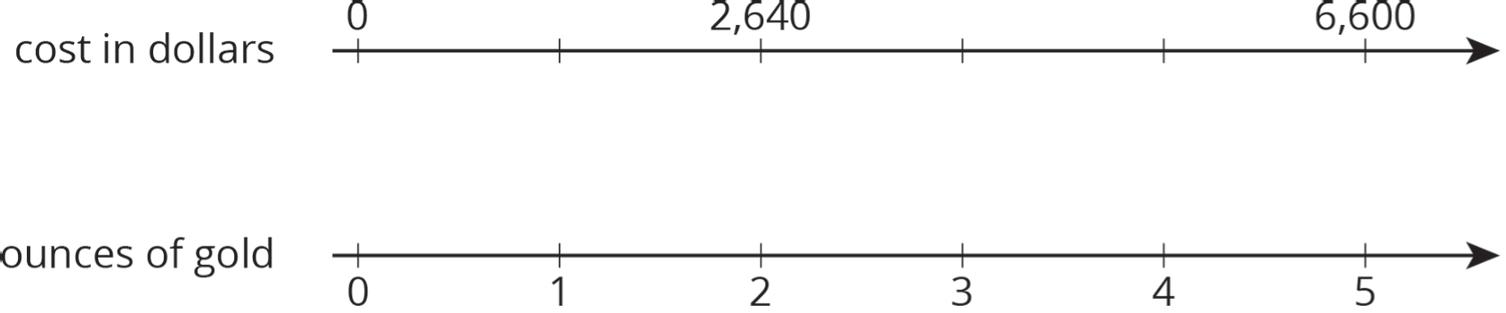
2. The double number line shows that 4 lb. of tomatoes cost $14. Draw tick marks and write labels to show the prices of 1, 2, and 3 lb. of tomatoes.

3. 4 movie tickets cost $48. At this rate, what is the cost of:

a. 5 movie tickets?

b. 11 movie tickets?

4. Priya bought these items at the grocery store. Find each unit price.

a. 12 eggs for $3. How much is the cost per egg?

b. 3 lb. of peanuts for $7.50. How much is the cost per lb.?

c. 4 rolls of toilet paper for $2. How much is the cost per roll?

d. 10 apples for $3.50. How much is the cost per apple?

Review Problems

5. Clare made a smoothie with 1 cup (c.) of yogurt, 3 tablespoons (tbsp.) of peanut butter, 2 teaspoons (tsp.) of chocolate syrup, and 2 c. of crushed ice.

a. Kiran tried to double this recipe. He used 2 c. of yogurt, 6 tbsp. of peanut butter, 5 tsp. of chocolate syrup, and 4 c. of crushed ice. He didn’t think it tasted right. Describe how the flavor of Kiran’s recipe compares to Clare’s recipe.

b. How should Kiran change the quantities that he used so that his smoothie tastes just like Clare’s?

6. A drama club is building a wooden stage in the shape of a trapezoidal prism. The height of the stage is 2 feet (ft.). Some measurements of the stage are shown here.

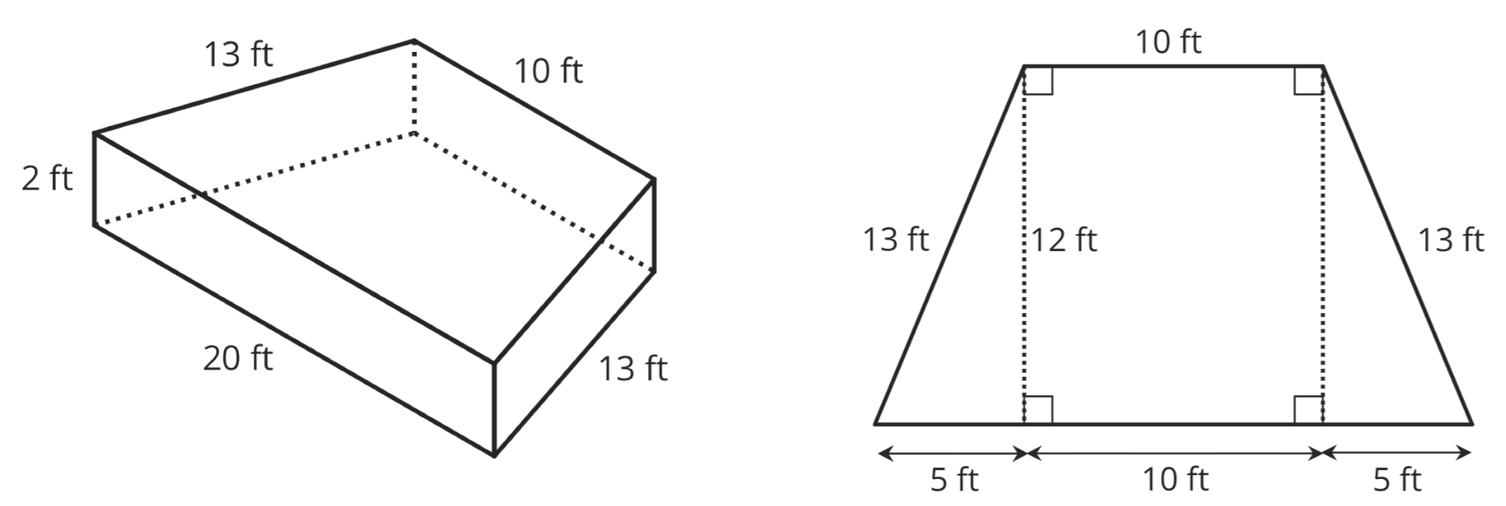
What is the area of all the faces of the stage, excluding the bottom? Show your reasoning. If you get stuck, consider drawing a net of the prism.

ManuscriptCopy

Unit 3, Lesson 8: Constant Speed

Warm-Up: Dividing by Powers of 10

1. Find the quotient mentally.

Exploration Activity: Moving 10 Meters

1. Your teacher will set up a straight path with a 1-meter (m) warm-up zone and a 10-m measuring zone. Follow the following instructions to collect the data.

a. The person with the stopwatch (the “timer”) stands at the finish line. The person being timed (the “mover”) stands at the warm-up line.

b. On the first round, the mover starts moving at a slow, steady speed along the path. When the mover reaches the start line, they say, “Start!” and the timer starts the stopwatch.

c. The mover keeps moving steadily along the path. When they reach the finish line, the timer stops the stopwatch and records the time, rounded to the nearest second (sec.), in the table.

d. On the second round, the mover follows the same instructions, but this time, moving at a quick, steady speed. The timer records the time the same way.

e. Repeat these steps until each person in the group has gone twice: once at a slow, steady speed, and once at a quick, steady speed.

2. After you finish collecting the data, use the double number line diagrams to answer the questions. Use the times your partner collected while you were moving.

Moving slowly:

Moving quickly:

a. Estimate the distance in m you traveled in 1 sec. when moving slowly.

b. Estimate the distance in m you traveled in 1 sec. when moving quickly.

c. Trade diagrams with someone who is not your partner. How is the diagram representing someone moving slowly different from the diagram representing someone moving quickly?

ManuscriptCopy

Collaborative Activity: Moving for 10 Seconds

Lin and Diego both ran for 10 sec., each at their own constant speed. Lin ran 40 m and Diego ran 55 m.

1. Who was moving faster? Explain your reasoning.

2. How far did each person move in 1 sec.? If you get stuck, consider drawing double number line diagrams to represent the situations.

3. Use your data from the previous activity to find how far you could travel in 10 sec. at your quicker speed.

4. Han ran 100 m in 20 sec. at a constant speed. Is this speed faster, slower, or the same as Lin’s? Diego’s? Yours?

ManuscriptCopy

Lesson Summary

Suppose a train traveled 100 m in 5 sec., moving at a constant speed. A double number line diagram can be created to find the train’s speed in meters per second (m/sec.).

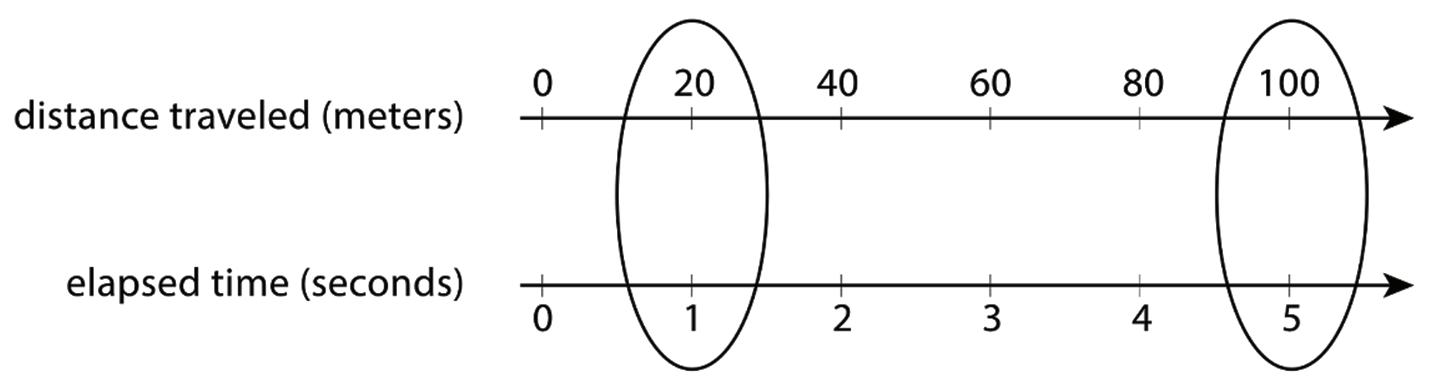
The double number line shows that the train’s speed was 20 m/sec. The constant speed can also be found by dividing the distance traveled by the elapsed time: 100 m ÷ 5 sec. = 20 m/sec.

Many questions about the situation become simpler to answer once the constant speed has been determined, because the constant speed can be multiplied by the elapsed time to get the distance traveled. For example, at this rate, how far would the train travel in 30 sec.? Since 20 ∙ 30 = 600, the train would travel 600 m in 30 sec. at this speed.

Practice Problems

1. Han ran 10 m in 2.7 sec. Priya ran 10 m in 2.4 sec.

a. Who ran faster? Explain how you know.

b. At this rate, how long would it take each person to run 50 m? Explain or show your reasoning.

2. A scooter travels 30 feet (ft.) in 2 sec. at a constant speed.

a. What is the speed of the scooter in ft. per sec.?

b. Complete the double number line to show the distance the scooter travels after 1, 3, 4, and 5 sec.

c. A skateboard travels 55 ft. in 4 sec. Is the skateboard going faster, slower, or the same speed as the scooter?

3. A cargo ship traveled 150 nautical miles in 6 hours (hr.) at a constant speed. How far did the cargo ship travel in 1 hr.?

Review Problems

4. A recipe for pasta dough says, “Use 150 grams (g) of flour per large egg.”

a. How much flour is needed if 6 large eggs are used?

b. How many eggs are needed if 450 g of flour are used?

5. The grocery store is having a sale on frozen vegetables. 4 bags are being sold for $11.96. At this rate, what is the cost of:

a. 1 bag?

b. 9 bags?

6. A pet owner has 5 cats. Each cat has 2 ears and 4 paws.

a. Complete the double number line to show the numbers of ears and paws for 1, 2, 3, 4, and 5 cats.

b. If there are 3 cats in the room, what is the ratio of ears to paws?

c. If there are 4 cats in the room, what is the ratio of paws to ears?

d. If all 5 cats are in the room, how many more paws are there than ears?

7. Each of these is a pair of equivalent ratios. For each pair, explain why they are equivalent ratios or draw a representation that shows why they are equivalent ratios. a. 5

1 and 15

3

ManuscriptCopy

5 and 10

Unit 3, Lesson 9: Representing Ratios with Tables

Warm-Up: How Is It Growing?

Look for a pattern in the figures.

1. How many total tiles will be in:

a. the 4th figure?

b. the 5th figure?

c. the 10th figure?

2. How do you see it growing?

ManuscriptCopy

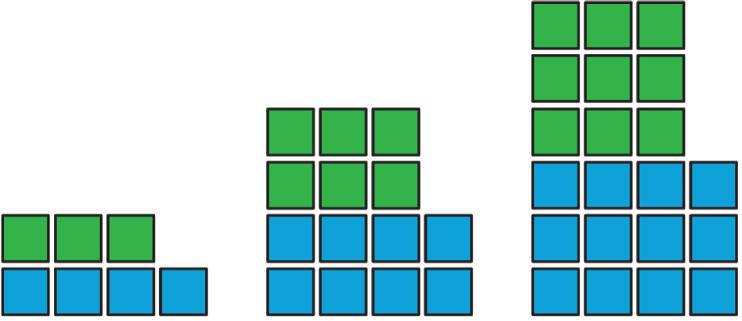
Exploration Activity: A Huge Amount of Sparkling Orange Juice

Noah’s recipe for one batch of sparkling orange juice uses 4 liters (L) of orange juice and 5 L of soda water.

1. Use the double number line to show how many L of each ingredient to use for different-sized batches of sparkling orange juice.

2. If someone mixes 36 L of orange juice and 45 L of soda water, how many batches would they make?

3. If someone uses 400 L of orange juice, how much soda water would they need?

4. If someone uses 455 L of soda water, how much orange juice would they need?

5. Explain the trouble with using a double number line diagram to answer the last two questions.

Exploration Activity: Batches of Trail Mix

A recipe for trail mix says, “Mix 7 ounces (oz.) of almonds with 5 oz. of raisins.” Here is a table that has been started to show how many oz. of almonds and raisins would be in different-sized batches of this trail mix.

1. Complete the table so that ratios represented by each row are equivalent.

2. What methods did you use to fill in the table?

3. How do you know that each row shows a ratio that is equivalent to 7 ∶ 5? Explain your reasoning.

Lesson Summary

A table is a way to organize information. Each horizontal set of entries is called a row, and each vertical set of entries is called a column.

A table organizes information into horizontal rows and vertical columns. The first row or column usually tells what the numbers represent.

The table shown has 2 columns and 5 rows. Like a double number line diagram, a table can be used to represent a collection of equivalent ratios.

Consider the situation “the price is $2 for every 3 mangos.” A double number line diagram and a table representing the situation are shown.

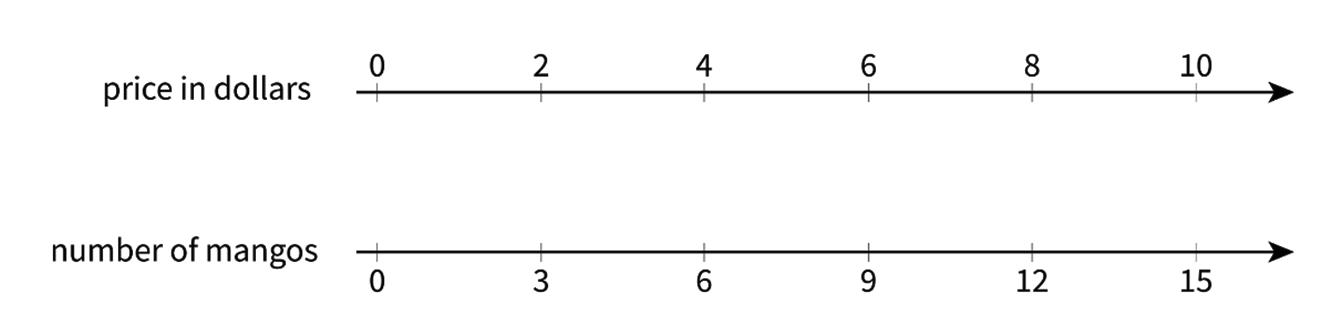
Equivalent ratios can be determined using a table by taking both values in the row (or column) representing a ratio and multiplying them by the same value. For example, to determine the price of 120 mangos, each value in the row showing the ratio 8 ∶ 12 can be multiplied by 10 to determine that the price of 120 mangos is $80.

Practice Problems

1. Complete the table to show the amounts of yellow and red paint needed for different-sized batches of the same shade of orange paint.

Explain how you know that these amounts of yellow paint and red paint will make the same shade of orange as the mixture in the first row of the table.

2. A car travels at a constant speed, as shown on the double number line.

How far does the car travel in 14 hours (hr.)? Explain or show your reasoning.

ManuscriptCopy

3. The olive trees in an orchard produce 3,000 pounds (lb.) of olives a year. It takes 20 lb. of olives to make 3 L of olive oil. How many L of olive oil can this orchard produce in a year? If you get stuck, consider using the table.

Review Problems

4. At a school recess, there needs to be a ratio of 2 adults for every 24 children on the playground. The double number line represents the number of adults and children on the playground at recess.

a. Label each remaining tick mark with its value.

b. How many adults are needed if there are 72 children? Circle your answer on the double number line?

5. While playing basketball, Jada’s heart rate goes up to 160 beats per minute (bpm). While jogging, her heart beats 25 times in 10 seconds (sec.). Assuming her heart beats at a constant rate while jogging, which of these activities resulted in a higher heart rate? Explain your reasoning.

6. A shopper bought the following items at the farmers’ market.

a. 6 ears of corn for $3. What was the cost per ear of corn?

b. 10 apples for $4. What was the cost per apple?

c. 8 tomatoes for $6. What was the cost per tomato?

Unit 3, Lesson 10: Tables and Double Number Line Diagrams

Warm-Up: Different Ways of Expressing Division

In many Latin American countries and other countries around the world, the colon (:) is used instead of ÷ to express division. Therefore, the expression “28 divided by 4” would be expressed as 28 ∶ 4 instead of 28 ÷ 4.

1. Using what you have learned about ratios, explain how 28 ∶ 4 and 28 ÷ 4 can be used to express the same value.

2. Write 1 question that comes to your mind after reading the above information.

Exploration Activity: Hourly Wages

Lin is paid $90 for 5 hours (hr.) of work. She used the table to calculate how much she would be paid at this rate for 8 hr. of work.

1. What is the meaning of the 18 that appears in the table?

2. Why was the number 1 5 used as a multiplier?

3. Explain how Lin used this table to solve the problem.

ManuscriptCopy

4. At this rate, how much would Lin be paid for 3 hr. of work?

Exploration Activity: Zeno’s Memory Card

In 2016, 128 gigabytes (GB) of portable computer memory cost $32.

1. Here is a double number line that represents the situation:

One set of tick marks has already been drawn to show the result of multiplying 128 and 32 each by 1 2 .

a. Label the amount of memory and the cost for these tick marks.

b. Next, keep multiplying by 1 2 and drawing and labeling new tick marks, until you can no longer clearly label each new tick mark with a number.

2. Here is a table that represents the situation. Find the cost of 1 GB. You can use as many rows as you need.

3. Did you prefer the double number line or the table for solving this problem? Why?

Collaborative Activity: The International Space Station

The International Space Station orbits around the Earth at a constant speed. Your teacher will give you either a double number line or a table that represents this situation. Your partner will get the other representation.

1. Complete the parts of your representation that you can figure out for sure.

2. Share information with your partner, and use the information that your partner shares to complete your representation.

3. What is the speed of the International Space Station?

4. Place the two completed representations side by side. Discuss with your partner some ways in which they are the same and some ways in which they are different.

5. Record at least one way that they are the same and one way they are different.

ManuscriptCopy

Lesson Summary

Finding a row containing a “1” is often a good way to work with tables of equivalent ratios. For example, the price for 4 pounds (lb.) of granola is $5. At that rate, what would be the price for 62 lb. of granola?

Tables are shown presenting 2 different approaches to solving this problem. Both of these approaches are correct. However, one approach is more efficient.

Less Efficient

More Efficient

Notice how the more efficient approach starts by finding the price for 1 lb. of granola.

Remember that dividing by a whole number is the same as multiplying by a unit fraction. In this example, 5 can be divided by 4 or multiplied by 1 4 to find the unit price.

Double number lines and tables both demonstrate how to use multiplication to create equivalent ratios, but there is an important difference between the 2 representations. The situation “a snail is moving at a constant speed down a sidewalk, traveling 6 centimeters (cm) per minute (min.)” is represented in 2 different ways.

On a double number line, the numbers on each line are listed in order. In a table, the ratios can be written in any order. For this reason, a table is sometimes easier to use to solve a problem.

Practice Problems

1. Kiran reads 5 pages in 20 min. He spends the same amount of time per page. How long will it take him to read 11 pages? If you get stuck, consider using the table.

2. Mai is making personal pizzas. For 4 pizzas, she uses 10 ounces (oz.) of cheese.

a. How much cheese does Mai use per pizza?

b. At this rate, how much cheese will she need to make 15 pizzas?

ManuscriptCopy

3. Clare is paid $90 for 5 hr. of work. At this rate, how many seconds (sec.) does it take for her to earn 25 cents?

4. A bread recipe uses 3 tablespoons (tbsp.) of olive oil for every 2 cloves of crushed garlic.

a. Complete the table to show different-sized batches of bread that taste the same as the recipe.

b. Draw a double number line that represents the same situation.

ManuscriptCopy

c. Which representation do you think works better in this situation? Explain why.

Review Problems

5. A car that travels 20 miles (mi.) in 1 2 hr. at constant speed is traveling at the same speed as a car that travels 30 mi. in 3 4 hr. at a constant speed. Explain or show why.

6. A sports drink recipe calls for 5 3 tbsp. of powdered drink mix for every 12 oz. of water. How many batches can you make with 5 tbsp. of drink mix and 36 oz. of water? Explain your reasoning.

ManuscriptCopy

Unit 3, Lesson 11: Solving Equivalent Ratio Problems

Warm-Up: What Do You Want to Know?

Consider the problem: A red car and a blue car enter the highway at the same time and travel at a constant speed. How far apart are they after 4 hours (hr.)?

What information would you need to be able to solve the problem?

Exploration Activity: Hot Chocolate and Potatoes

Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.

If your teacher gives you the problem card:

1. Silently read your card and think about what information you need to be able to answer the question.

2. Ask your partner for the specific information that you need.

3. Explain how you are using the information to solve the problem.

4. Continue to ask questions until you have enough information to solve the problem.

5. Share the problem card and solve the problem independently.

6. Read the data card and discuss your reasoning.

If your teacher gives you the data card:

1. Silently read your card.

2. Ask your partner “What specific information do you need?” and wait for them to ask for information.

3. If your partner asks for information that is not on the card, do not do the calculations for them. Tell them you don’t have that information.

4. Before sharing the information, ask “Why do you need that information?” Listen to your partner’s reasoning and ask clarifying questions.

5. Read the problem card and solve the problem independently.

6. Share the data card and discuss your reasoning.

Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.

Collaborative Activity: Comparing Reading Rates

• Lin read the first 54 pages from a 270-page book in the last 3 days.

• Diego read the first 100 pages from a 325-page book in the last 4 days.

• Elena read the first 160 pages from a 480-page book in the last 5 days.

If they continue to read every day at these rates, who will finish first, second, and third? Explain or show your reasoning.

Lesson Summary

To solve problems about something happening at the same rate, the following information is often needed:

• Two quantities that can be used to write a ratio that describes the situation

• A third piece of information that gives one number of an equivalent ratio (solving the problem often involves finding the other number in the equivalent ratio)

Suppose a recipe for fizzy juice says, “Mix 5 cups (c.) of cranberry juice with 2 c. of soda water.” The ratio of cranberry juice to soda water is 5 ∶ 2, and 2.5 c. of cranberry juice is needed per c. of soda water.

To make a large batch of the fizzy juice using 16 c. of soda water, determine what number goes with 16 to make a ratio that is equivalent to 5 ∶ 2. Steps in this process are shown in the table. To make this large batch taste the same as the original recipe, 40 c. of cranberry juice would need to be added.

ManuscriptCopy

Practice Problems

1. A chef is making pickles. He needs 15 gallons (gal.) of vinegar. The store sells 2 gal. of vinegar for $3.00 and allows customers to buy any amount of vinegar. Decide whether each of the following ratios correctly represents the price of vinegar.

a. 4 gal. to $3.00

b. 1 gal. to $1.50

c. 30 gal. to $45.00

d. $2.00 to 30 gal.

e. $1.00 to 2 3 gal.

2. A caterer needs to buy 21 pounds (lb.) of pasta to cater a wedding. At a local store, 8 lb. of pasta cost $12. How much will the caterer pay for the pasta there?

a. Write a ratio for the given information about the cost of pasta.

b. Would it be more helpful to write an equivalent ratio with 1 lb. of pasta as one of the numbers, or with $1 as one of the numbers? Explain your reasoning, and then write that equivalent ratio.

c. Find the answer and explain or show your reasoning.

3. Lin is reading a 47-page book. She read the first 20 pages in 35 minutes (min.).

a. If she continues to read at the same rate, will she be able to complete this book in under 1 hr.?

b. If so, how much time will she have left? If not, how much more time is needed? Explain or show your reasoning.

4. Diego can type 140 words in 4 min.

a. At this rate, how long will it take him to type 385 words?

b. How many words can he type in 15 min.?

If you get stuck, consider creating a table.

Review Problems

5. A train that travels 30 miles (mi.) in 1 3 hr. at a constant speed is going faster than a train that travels 20 mi. in 1 2 hr. at a constant speed. Explain or show why.

ManuscriptCopy

6. Find the surface area of the polyhedron that can be assembled from this net. Show your reasoning.

ManuscriptCopy

Unit 3, Lesson 12: Part-Part-Whole Ratios

Warm-Up: True or False: Multiplying by a Unit Fraction

1. True or false?

ManuscriptCopy

Exploration Activity: Cubes of Paint

A recipe for maroon paint says, “Mix 5 milliliters (mL) of red paint with 3 mL of blue paint.”

1. Use snap cubes to represent the amounts of red and blue paint in the recipe. Then, draw a sketch of your snap-cube representation of the maroon paint.

a. What amount does each cube represent?

2.

b. How many mL of maroon paint will there be?

3.

a. Suppose each cube represents 2 mL. How much of each color paint is there?

Red: _______ mL

Blue: _______ mL Maroon: _______ mL

b. Suppose each cube represents 5 mL. How much of each color paint is there?

Red: _______ mL

Blue: _______ mL Maroon: _______ mL

a. Suppose you need 80 mL of maroon paint. How much red and blue paint would you mix? Be prepared to explain your reasoning.

Red: _______ mL

Blue: _______ mL Maroon: 80 mL

b. If the original recipe is for one batch of maroon paint, how many batches are in 80 mL of maroon paint?

Guided Activity: Sneakers, Chicken, and Fruit Juice

Solve each of the following problems and show your thinking. If you get stuck, consider drawing a tape diagram to represent the situation.

1. The ratio of students wearing sneakers to those wearing boots is 5 to 6. If there are 33 students in the class, and all of them are wearing either sneakers or boots, how many of them are wearing sneakers?

2. A recipe for chicken marinade says, “Mix 3 parts oil with 2 parts soy sauce and 1 part orange juice.” If you need 42 cups (c.) of marinade in all, how much of each ingredient should you use?

3. Elena makes fruit punch by mixing 4 parts cranberry juice to 3 parts apple juice to 2 parts grape juice. If one batch of fruit punch includes 30 c. of apple juice, how large is this batch of fruit punch?

ManuscriptCopy

Collaborative Activity: Invent Your Own Ratio Problem

1. Invent another ratio problem that can be solved with a tape diagram and solve it. If you get stuck, consider looking back at the problems you solved in the earlier activity.

2. Create a visual display that includes:

• The new problem that you wrote, without the solution.

• Enough work space for someone to show a solution.

3. Trade your display with another group, and solve each other’s problem. Include a tape diagram as part of your solution. Be prepared to share the solution with the class.

4. When the solution to the problem you invented is being shared by another group, check their answer for accuracy.

Lesson Summary

A tape diagram is another way to represent a ratio. All the parts of the diagram that are the same size have the same value.

A tape diagram is a group of rectangles put together to represent a relationship between quantities.

For example, the tape diagram shown represents the ratio of ducks to swans in a pond, which is 4 ∶ 5.

• The first tape represents the number of ducks. It has 4 parts.

• The second tape represents the number of swans. It has 5 parts.

• There are 9 parts in all, because 4 + 5 = 9.

If there are 18 of these birds in the pond, then the 9 equal parts on the diagram need to represent 18 birds in all. This means that each part of the tape diagram represents 2 birds, because 18 ÷ 9 = 2.

ManuscriptCopy

The tape representing ducks has 4 parts, and 4 ⋅ 2 = 8, so there are 8 ducks in the pond.

Practice Problems

1. Here is a tape diagram representing the ratio of red paint to yellow paint in a mixture of orange paint.

a. What is the ratio of yellow paint to red paint?

b. How many total c. of orange paint will this mixture yield?

2. At the kennel, the ratio of cats to dogs is 4 ∶ 5. There are 27 animals in all. Here is a tape diagram representing this ratio.

a. What is the value of each small rectangle?

b. How many dogs are at the kennel?

c. How many cats are at the kennel?

3. Last month, there were 4 sunny days for every rainy day. If there were 30 days in the month, how many days were rainy? Explain your reasoning. If you get stuck, consider using a tape diagram.

Review Problems

4. A cashier worked an 8 hour (hr.) day, and earned $58.00. The double number line shows the amount she earned for working different numbers of hours. For each question, explain your reasoning.

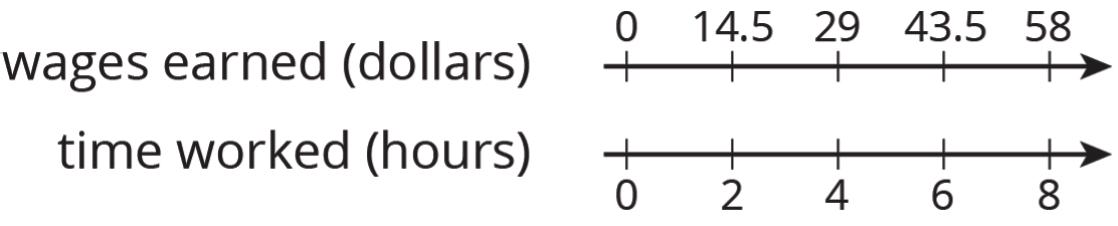
a. How much does the cashier earn per hr.?

b. How much does the cashier earn if she works 3 hr.?

5. A grocery store sells bags of oranges in two different sizes.

• The 3 pound (lb.) bags of oranges cost $4.

• The 8 lb. bags of oranges for $9.

Which oranges cost less per lb.? Explain or show your reasoning.

Unit 3, Lesson 13: Solving More Ratio Problems

Warm-Up: You Tell the Story

Describe a situation with two quantities that this tape diagram could represent.

ManuscriptCopy

Exploration Activity: A Trip to the Aquarium

Consider the problem: A teacher is planning a class trip to the aquarium. The aquarium requires 2 chaperones for every 15 students. The teacher plans accordingly and orders a total of 85 tickets. How many tickets are for chaperones, and how many are for students?

1. Solve this problem in one of three ways:

a. Use a triple number line.

b. Use a table. (Fill rows as needed.)

c. Use a tape diagram.

ManuscriptCopy

2. After your class discusses all three strategies, which do you prefer for this problem and why?

Collaborative Activity: Salad Dressing and Moving Boxes

Solve each problem, and show your thinking. Organize it so it can be followed by others. If you get stuck, consider drawing a double number line, table, or tape diagram.

1. A recipe for salad dressing calls for 4 parts oil for every 3 parts vinegar. How much oil should you use to make a total of 28 teaspoons (tsp.) of dressing?

2. Andre and Han are moving boxes. Andre can move 4 boxes every half hour (hr.). Han can move 5 boxes every half hr. How long will it take Andre and Han to move all 72 boxes?

ManuscriptCopy

Lesson Summary

When solving a problem involving equivalent ratios, it is often helpful to use a diagram. Any diagram is fine as long as it correctly shows the mathematics and you can explain it.

Three different ways of solving the same problem are shown.

Problem: The ratio of adults to kids in a school is 2 ∶ 7. If there are 180 people total, how many of them are adults?

• Tape diagrams are especially useful for this type of problem because both parts of the ratio have the same units (number of people) and the total number of parts can be represented.

This tape diagram has 9 equal parts, and they need to represent 180 people total. That means each part represents 180 ÷ 9, or 20 people.

Two parts of the tape diagram represent adults, so there are 40 adults in the school, because 2 ⋅ 20 = 40.

• Double number lines or triple number lines are useful for seeing how far apart the numbers are from one another. They are harder to use with very big or very small numbers, but they can be used to support reasoning, as shown.

ManuscriptCopy

• Tables are especially useful when the problem has very large or very small numbers.

The table shown can be used to pose the question “9 times what is 180?” The answer is 20. Therefore, 2 is also multiplied by 20 to get the total number of adults in the school.

Another reason to make diagrams is to communicate your thinking to others. Keep these tips in mind when making diagrams to represent problems.

• Label each part of the diagram with what it represents.

• Label important amounts.

• Make sure you read what the question is asking, and then answer it.

• Make the answer easy to find.

• Include units in your answer. For example, write “4 cups” instead of just “4.”

• Double-check that your ratio language is correct and matches your diagram.

Practice Problems

1. Describe a situation that could be represented with this tape diagram.

2. There are some nickels, dimes, and quarters in a large piggy bank. For every 2 nickels there are 3 dimes. For every 2 dimes there are 5 quarters. There are 500 coins total.

a. How many nickels, dimes, and quarters are in the piggy bank? Explain your reasoning.

ManuscriptCopy

b. How much are the coins in the piggy bank worth?

3. Two horses start a race at the same time. Horse A gallops at a steady rate of 32 feet (ft.) per second (sec.) and Horse B gallops at a steady rate of 28 ft. per sec. After 5 sec., how much farther will Horse A have traveled? Explain or show your reasoning.

Review Problems

4. Andre paid $13 for 3 books. Diego bought 12 books priced at the same rate. How much did Diego pay for the 12 books? Explain your reasoning.

5. Which polyhedron can be assembled from this net?

A. A triangular pyramid

B. A trapezoidal prism

C. A rectangular pyramid

D. A triangular prism

6. Find the area of the triangle. Show your reasoning. If you get stuck, consider drawing a rectangle around the triangle.

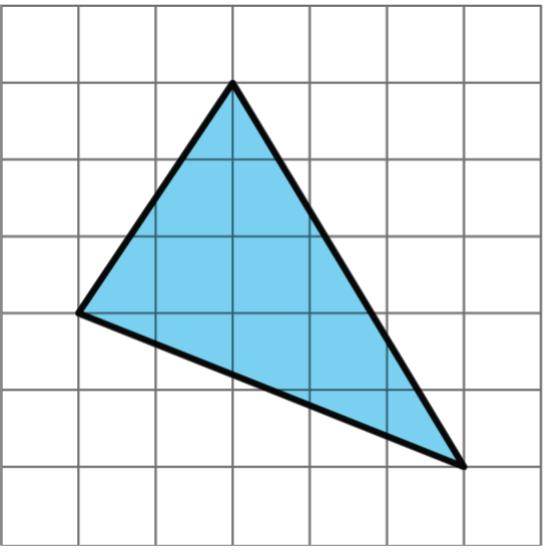
Unit 4: Unit Rates and Percentages

ManuscriptCopy

Unit 4, Lesson 1: Anchoring Units of Measurement

Warm-Up: Estimating Volume

Estimate the volume of the tiny salt shaker.

Exploration Activity: Cutting String

Your teacher will assign you one of the following lengths: 1 centimeter, 1 foot, 1 inch, 1 meter, or 1 yard.

Estimate and cut a piece of string as close to your assigned length as you can without using a measurement tool.

Exploration Activity: Card Sort: Measurement

Your teacher will give you some cards with the names of different units of measurement and other cards with pictures of objects.

1. Sort the units of measurement into groups based on the attribute they measure. Pause here so your teacher can review your groups.

2. Match each picture card that has “L” in the top right corner with the closest unit to the length of the object.

3. Match each picture card that has “V” in the top right corner with the closest unit to the volume of the object.

4. Match each picture card that has “WM” in the top right corner with the closest unit to the weight or mass of the object.

Your teacher will assign you a new group to discuss how you matched the objects. If you disagree, work to reach an agreement.

Lesson Summary

Two systems of measurement used throughout the world are the metric system and the customary system. Most countries use the metric system of measurement. In fact, only 3 countries still use the customary system: the United States, Liberia, and Myanmar.

Common units of measurement for mass, weight, length, and volume within each system are shown in the table.

Type of Measurement

Customary System Units Metric System Units

Mass or Weight ounces, pounds, tons milligrams, grams, kilograms

Length

Liquid Volume

Solid Volume

inches, feet, yards, miles millimeters, centimeters, meters, kilometers

fluid ounces, cups, pints, quarts, gallons milliliters, liters

cubic inches, cubic feet, cubic yards cubic centimeters, cubic meters

Everyday objects can be used to estimate standard units of measurement. It can be helpful to picture such objects when thinking about how big or small a unit is.

For units of length:

• 1 millimeter is about the thickness of a dime.

• 1 centimeter is about the width of a pinky finger.

• 1 inch is about the length from the tip of your thumb to the first knuckle.

• 1 foot is the length of a football.

• 1 yard is about the length of a baseball bat.

• 1 meter is about the length of a baseball bat and ball.

• 1 kilometer is about the distance the average person walks in ten minutes.

• 1 mile is about the distance the average person runs in ten minutes.

For units of volume:

• 1 milliliter is about the volume of a raindrop.

• 1 cup is about the volume of a school milk carton.

• 1 quart is about the volume of a large sports drink bottle.

• 1 liter is about the volume of a reusable water bottle.

• 1 gallon is about the volume of a large milk jug.

• 1 cubic centimeter is about the volume of a box that could fit a chocolate chip.

• 1 cubic inch is about the volume of a box that could fit a large grape.

• 1 cubic foot is about the volume of a box that could fit a watermelon.

• 1 cubic meter is about the volume of a box that could fit an armchair.

For units of mass and weight:

• 1 gram is about the mass of a raisin.

• 1 ounce is about the weight of a slice of bread.

• 1 pound is about the weight of a loaf of bread.

• 1 kilogram is about the mass of a textbook.

• 1 ton is about the weight of a small car.

Practice Problems

1. When this pet hamster is placed on a digital scale, the scale reads 1.5.

What could the units be?

2. Select the unit from the list that you would use to measure each object.

a. The length of a pencil _____

b. The weight or mass of a pencil _____

c. The volume of a pencil _____

d. The weight or mass of a hippopotamus _____

e. The length of a hippopotamus _____

f. The length of a fingernail clipping _____

g. The weight or mass of a fingernail clipping

h. The volume of a sink _____

i. The volume of a bowl _____

j. The length of a chalkboard or whiteboard _____

k. The weight or mass of a chalkboard or whiteboard _____

l. The length of the border between the United States and Canada _____

1. centimeters (cm)

2. cups (c.)

3. feet (ft.)

4. gallons (gal.)

5. grams (g)

6. inches (in.)

7. kilograms (kg)

8. kilometers (km)

9. liters (L)

10. meters (m)

11. miles (mi.)

12. milliliters (mm)

13. millimeters (mL)

14. ounces (oz.)

15. pounds (lb.)

16. quarts (qt.)

17. tons (t.)

18. yards (yd.)

3. Circle the larger unit of measure. Then, determine if the unit measures distance, volume, or weight (mass).

a. meter or kilometer

b. cup or quart

c. liter or milliliter

d. yard or foot

e. pound or ounce

f. gram or kilogram

4. Elena mixes 5 cups (c.) of apple juice with 2 c. of sparkling water to make sparkling apple juice. For a party, she wants to make 35 c. of sparkling apple juice. How much of each ingredient should Elena use? Explain or show your reasoning.

5. Lin bought 3 hats for $22.50. At this rate, how many hats could she buy with $60.00? If you get stuck, consider using the table.

Number of Hats Price in Dollars

6. Light travels about 180 million kilometers (km) in 10 minutes (min.). How far does it travel in 1 min.? How far does it travel in 1 second (sec.)? Show your reasoning.

ManuscriptCopy

Unit 4, Lesson 2: Converting Units Using Dimensional Analysis

Warm-Up: Number Talk: Fractions of a Number

Exploration Activity: Converti ng Units of Measure Using Conversion Factors

The United States uses the customary system of measurement. The table shows the unit conversions for units within this system.

1. Label each row with weight, length, or volume to indicate the type of measurement represented by each set of units.

Type of Measurement

Unit Conversions in the Customary System

1 foot (ft.) = 12 inches (in.)

1 yard (yd.) = 3 feet (ft.)

1 mile (mi.) = 5,280 feet (ft.)

1 mile (mi.) = 1,760 yards (yd.)

1 cup (c.) = 8 �luid ounces (�l.oz.)

1 pint (pt.) = 2 cups (c.)

1 quart (qt.) = 2 pints (pt.)

1 gallon (gal.) = 4 quarts (qt.)

1 pound (lb.) = 16 ounces (oz.)

1 ton (t.) = 2,000 pounds (lb.)

Each conversion rate represents a ratio. Double number lines can be used to convert measurement units.

2. Use the double number line shown to find how many ft. are in 4 yd.

There are _____ ft. in 4 yd.

Tables can also be used to convert units of measure.

3. The average weight of an African forest elephant is 6,000 lb. Use the unit conversion and the table to determine how many tons the average African forest elephant weighs.

Pounds (lb.) Tons (t.)

Collaborative Activity: Converting Units of Measure Using Dimensional Analysis

Rates can be used as factors to convert from one unit to another.

For example, the factor 4 quarts 1 gallon is equivalent to 1 because the numerator and denominator are equivalent values.

Multiplying by factors equivalent to 1 will result in equivalent values.

Kaluba determined how many quarts are in 2 gal. of milk using dimensional analysis. His work is shown.

gal. 1 × 4 qt. 1 gal. = 8 qt.

Kaluba explained, “In my calculation, the unit ‘gal.’ is in the numerator and the denominator. This means I can eliminate this unit, because it becomes 1, similar to when equivalent values are in the numerator and denominator. The result of the conversion is the number of qt.”

1. Comple te the calculation to find how many fl. oz. are in 6 c.

Most of the world uses the metric system of measurement. The table shows additional unit conversions for the metric system.

Type of Measurement

Length

Volume

Mass

Unit Conversions in the Metric System

1 meter (m) = 100 centimeters (cm)

1 meter (m) = 1,000 millimeters (mm)

1 kilometer (km) = 1,000 meters (m)

1 liter (L) = 1,000 milliliters (mL)

1 gram (g) = 1,000 milligrams (mg)

1 kilogram (kg) = 1,000 grams (g)

2. Use the conversion rates to find each value. Show your work.

a. 2.62 km = ____ m

b. 9 in. = ____ ft.

c. 9 c. = ____ pt.

3. Adrian weighed 7 lb. and 4 oz. when he was born. How many ounces did Adrian weigh when he was born?

4. Ibuprofen is a medicine sometimes used for pain relief, such as for a headache. It is not safe for an adult to take more than 3,200 mg of ibuprofen in a day. How many g of ibuprofen can an adult safely take in one day?

Lesson Summary

Measurements of the same object in 2 different units can be used to form a ratio. Equivalent ratios can be used to determine a rate, which is used as the conversion factor to convert measurements from one unit to another by dimensional analysis.

A rate is a ratio that compares two quantities of different units.

When converting units using dimensional analysis, multiply the given measurement by the conversion factor to determine its equivalent value in terms of another unit of measure. Be sure to use the conversion factor that correctly eliminates the original unit of measure and leaves only the new unit of measure. It can be helpful to write the original measurement as a fraction.

For example, to determine how many mi. are equivalent to 8,800 ft., use the conversion rate of 1 mi. = 5,280 ft.

With the unit “ft.” in the numerator and denominator, ft. ft. is equivalent to 1, so “ft.” can be eliminated, leaving only mi. as the unit of measure.

Practice Problems

1. Use the conversion rates to find each value.

a. 11,200 mL = ____ L

b. 3 1 2 pt. = ____ c.

c. 80 cm = ____ m

ManuscriptCopy

2. Malik plays football for his high school. Last Friday, he ran 94 yd. for a touchdown on a kickoff return. How many ft. did Malik run on the kickoff return?

3. About 727 pt. of milk are distributed each day in the cafeteria at a local middle school.

a. How many qt. of milk are distributed at the middle school each day?

b. Use your answer from part A to determine how many gal. of milk are distributed at the middle school each day.

Review Problems

4. An elevator travels 310 ft. in 10 seconds (sec.). At that speed, how far can this elevator travel in 12 sec.? Explain your reasoning.

5. Noah bought 15 baseball cards for $9.00. Assuming each baseball card costs the same amount, answer the following questions.

a. At this rate, how much will 30 baseball cards cost? Explain your reasoning.

b. At this rate, how much will 12 baseball cards cost? Explain your reasoning.

c. Do you think this information would be better represented using a table or a double number line? Explain your reasoning.

ManuscriptCopy

Unit 4, Lesson 3: Comparing Speeds and Prices

Warm-Up: Closest Quotient

Is the value of each expression closer to 1 2 , 1, or 1 1 2 ? 1. 20 ÷ 18 2. 9 ÷ 20 3. 7 ÷ 5

Exploration Activity: More Treadmills

Some students did treadmill workouts, each one running at a constant speed. Answer the questions about their workouts. Explain or show your reasoning.

• Tyler ran 4,200 meters (m) in 30 minutes (min.).

• Kiran ran 6,300 m in 1 2 hour (hr.).

• Mai ran 6.3 kilometers (km) in 45 min.

1. What is the same about the workouts done by:

a. Tyler and Kiran?

b. Kiran and Mai?

c. Mai and Tyler?

2. At what rate did each of them run?

3. How far did Mai run in her first 30 min. on the treadmill?

Collaborative Activity: The Best Deal on Beans

Four different stores posted ads about special sales on 15-ounce (oz.) cans of baked beans.

1. Which store is offering the best deal? Explain your reasoning.

ManuscriptCopy

2. The last store listed is also selling 28 oz. cans of baked beans for $1.40 each. How does that price compare to the other prices?

Collaborative Activity: Card Sort: Is It a Deal?

Your teacher will give you a set of cards showing different offers.

1. Find card A and work with your partner to decide whether the offer on card A is a good deal. Explain or show your reasoning.

2. Next, split cards B–E so you and your partner each have two.

a. Decide individually if your two cards are good deals. Explain your reasoning.

b. For each of your cards, explain to your partner if you think it is a good deal and why. Listen to your partner’s explanations for their cards. If you disagree, explain your thinking.

c. Revise any decisions about your cards based on the feedback from your partner.

3. When you and your partner are in agreement about cards B–E, place all the cards you think are a good deal in one stack and all the cards you think are a bad deal in another stack. Be prepared to explain your reasoning.

ManuscriptCopy

Lesson Summary

Diego ran 3 km in 20 min. Andre ran 2,550 m in 17 min. Since neither their distances nor their times are the same, there are 2 possible strategies for determining who ran faster:

• Find the time each person took to travel the same distance. The person who traveled that distance in less time is faster.

• Find the distance each person traveled in the same time. The person who traveled a longer distance in the same amount of time is faster.

It is often helpful to compare distances traveled in 1 unit of time (1 min., for example), which means finding the speed, in units such as m per min.

The tables shown represent Diego’s and Andre’s speeds in m per min.

Diego’s Speed

Both Diego and Andre ran 150 m per min., so they ran at the same speed.

Finding ratios that indicate how much of quantity �� there is per 1 unit of quantity �� is an efficient way to compare rates in different situations. Some familiar examples are given:

• Car speeds in miles per hour (mph)

• Vegetable prices in dollars per pound ($/lb.)

ManuscriptCopy

Knowing these ratios then helps in finding out how far a car will travel in periods of time other than 1 hr., or how much vegetables will cost for quantities other than 1 lb.

Practice Problems

1. Mai and Priya were on scooters. Mai traveled 15 m in 6 seconds (sec.). Priya travels 22 m in 10 sec. Who was moving faster? Explain your reasoning.

2. Here are the prices for cans of juice that are the same brand and the same size at different stores. Which store offers the best deal? Explain your reasoning.

Store X: 4 cans for $2.48

Store Y: 5 cans for $3.00

Store Z: 59 cents per can

3. Costs of homes can be very different in different parts of the United States.

a. A 450-square foot (sq. ft.) apartment in New York City costs $540,000. What is the price per sq. ft.? Explain or show your reasoning.

b. A 2,100-sq. ft. home in Cheyenne, Wyoming, costs $110 per sq. ft. How much does this home cost? Explain or show your reasoning.

ManuscriptCopy

4. This package of sliced cheese costs $2.97.

How much would a package with 18 slices cost at the same price per slice? Explain or show your reasoning.

Review Problems

5. Diego is 165 centimeter (cm) tall. Andre is 1.7 m tall. Who is taller, Diego or Andre? Explain your reasoning.

6. Here is a polygon.

a. Decompose this polygon so that its area can be calculated. All measurements are in cm.

b. Calculate its area. Organize your work so that it can be followed by others.

ManuscriptCopy

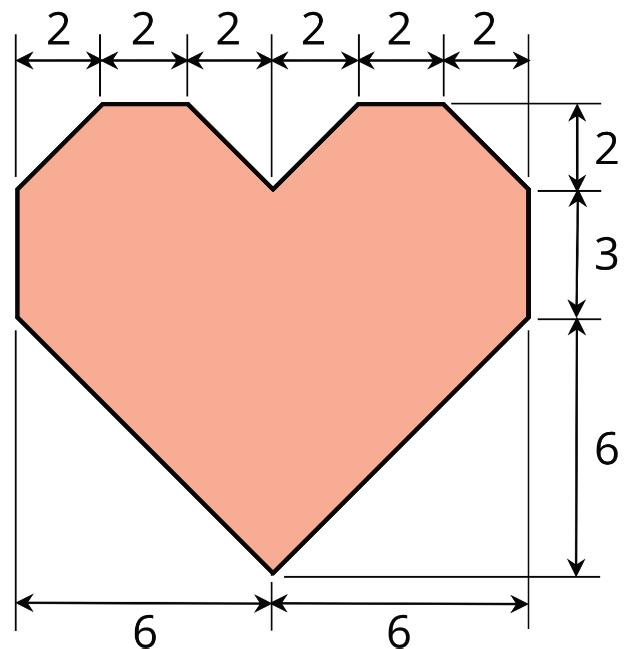
Unit 4, Lesson 4: Interpreting Rates

Warm-Up: Something per Something

1. Think of two things you have heard described in terms of “something per something.”

ManuscriptCopy

2. Share your ideas with your group, and listen to everyone else’s idea. Make a group list of all unique ideas. Be prepared to share these with the class.

Exploration Activity: Cooking Oatmeal

Priya, Han, Lin, and Diego are all on a camping trip with their families. The first morning, Priya and Han make oatmeal for the group. The instructions for a large batch say, “Bring 15 cups (c.) of water to a boil, and then add 6 c. of oats.”

• Priya says, “The ratio of the c. of oats to the c. of water is 6 ∶ 15. That’s 0.4 c. of oats per c. of water.”

• Han says, “The ratio of the c. of water to the c. of oats is 15 ∶ 6. That’s 2.5 c. of water per c. of oats.”

1. Who is correct? Explain your reasoning. If you get stuck, consider using the table.

2. The next weekend after the camping trip, Lin and Diego each decide to cook a large batch of oatmeal to have breakfasts ready for the whole week.

a. Lin decides to cook 5 c. of oats. How many c. of water should she boil?

b. Diego boils 10 c. of water. How many c.of oats should he add into the water?

ManuscriptCopy

3. Did you use Priya’s rate (0.4 c. of oats per c. of water) or Han’s rate (2.5 c. of water per c. of oats) to help you answer each of the previous two questions? Why?

Collaborative Activity: Cheesecake, Milk, and Raffle Tickets

For each situation, find the unit rates.

1. A cheesecake recipe says, “Mix 12 ounces (oz.) of cream cheese with 15 oz. of sugar.”

a. How many oz. of cream cheese are there for every oz. of sugar?

b. How many oz. of sugar is that for every oz. of cream cheese?

2. Mai’s family drinks a total of 10 gallons (gal.) of milk every 6 weeks.

a. How many gal. of milk does the family drink per week?

b. How many weeks does it take the family to consume 1 gal. of milk?

3. Tyler paid $16 for 4 raffle tickets.

a. What is the price per ticket?

b. How many tickets is that per dollar?

4. For each problem, decide which unit rate from the previous situations you prefer to use. Next, solve the problem, and show your thinking.

a. If Lin wants to make extra cheesecake filling, how much cream cheese will she need to mix with 35 oz. of sugar?

b. How many weeks will it take Mai’s family to finish 3 gal. of milk?

c. How much would all 1,000 raffle tickets cost?

Lesson Summary

Suppose a U-pick farm lets visitors pick 2 pounds (lb.) of blueberries for $5.00. This situation is represented in the table and can be described in 2 ways using rates.

• Visitors can pick 2 5 of a lb. of blueberries per dollar.

• The blueberries cost 5 2 dollars per lb.

The “cost per lb.” and the “number of lb. per dollar” are the 2 unit rates for this situation.

ManuscriptCopy

Every ratio relating 2 quantities can be expressed using 2 unit rates. Each of these unit rates is useful in different situations.

• To find out how much 8 lb. of blueberries will cost, it helps to know how much 1 lb. of blueberries will cost. This unit rate is shown in the first row of the table. Each quantity in the rate can be multiplied by 8 to determine the cost of 8 lb. of blueberries.

= $20

• To find out how many lb. of blueberries can be purchased for $10.00, it helps to know how many lb. can be purchased for $1.00. This unit rate is shown in the first row of the second table. Each quantity in the rate can be multiplied by 10 to determine the amount of blueberries that can be purchased for $10.00.

Which unit rate is most useful depends on the question being answered, so it is helpful to know how to find both for any given ratio.

Practice Problems

1. A pink paint mixture uses 4 c. of white paint for every 3 c. of red paint.

The table shows different quantities of red and white paint for the same shade of pink. Complete the table.

ManuscriptCopy

2. A farm lets you pick 3 pints (pt.) of raspberries for $12.00.

a. What is the cost per pt.?

b. How many pt. do you get per dollar?

c. At this rate, how many pints can you afford for $20.00?

d. At this rate, how much will 8 pt. of raspberries cost?

3. Han and Tyler are following a polenta recipe that uses 5 c. of water for every 2 c. of cornmeal.

• Han says, “I am using 3 c. of water. I will need 1 1 5 c. of cornmeal.”

• Tyler says, “I am using 3 c. of cornmeal. I will need 7 1 2 c. of water.”

Do you agree with either of them? Explain your reasoning.

ManuscriptCopy

4. A large art project requires enough paint to cover 1,750 square feet (sq. ft.). Each gallon (gal.) of paint can cover 350 sq. ft. Each sq. ft. requires 1 350 of a gal. of paint.

Andre thinks he should use the rate 1 350 gal. of paint per sq. ft. to find how much paint they need. Do you agree with Andre? Explain or show your reasoning.

Review Problems

5. Andre types 208 words in 4 minutes (min.). Noah types 342 words in 6 min. Who types faster? Explain your reasoning.

6. A corn vendor at a farmer's market was selling a bag of 8 ears of corn for $2.56. Another vendor was selling a bag of 12 for $4.32. Which bag is the better deal? Explain or show your reasoning.

ManuscriptCopy

ManuscriptCopy

Unit 4, Lesson 5: Equivalent Ratios Have the Same

Unit Rates

Warm-Up: Which One Doesn’t Belong: Comparing Speeds

Which one doesn’t belong? Be prepared to explain your reasoning.

A. 5 miles (mi.) in 15 minutes (min.)

B. 3 min. per mi.

C. 20 mi. per hour (hr.)

D. 32 kilometers (km) per hr.

Exploration Activity: Price of Burritos

1. Two burritos cost $14.00. Complete the table to show the cost for 4, 5, and 10 burritos at that rate. Next, find the cost for a single burrito in each case.

2. What do you notice about the values in this table?

ManuscriptCopy

3. Noah bought �� burritos and paid �� dollars. Lin bought twice as many burritos as Noah and paid twice the cost he did. How much did Lin pay per burrito?

4. Explain why, if you can buy �� burritos for �� dollars, or buy 2 ⋅ �� burritos for 2 ⋅ �� dollars, the cost per item is the same in either case.

Collaborative Activity: Making Bracelets

1. Complete the table. Then, explain the strategy you used to do so.

2. Here is a partially filled tabled from an earlier activity. Use the same strategy you used for the bracelet problem to complete this table.

3. Next, compare your results with those in the first table in the previous activity. Do they match? Explain why or why not.

Collaborative Activity: How Much Applesauce?

It takes 4 pounds (lb.) of apples to make 6 cups (c.) of applesauce.

1. At this rate, how much applesauce can you make with:

a. 7 lb. of apples?

b. 10 lb. of apples?

2. How many lb. of apples would you need to make:

a. 9 c. of applesauce?

ManuscriptCopy

b. 20 c. of applesauce?

Lesson Summary

The table shows different amounts of apples selling at the same rate, which means all of the ratios in the table are equivalent. In each case, the unit price, in dollars per lb., can be determined by dividing the price by the number of lb.

The unit price is always the same. Whether purchasing 4 lb. of apples for $10.00 or 8 lb. of apples for $20.00, the apples cost $2.50 per lb.

It is also possible to find the number of lb. of apples that can be purchased per dollar by dividing the number of lb. by the price.

The number of lb. per dollar is the same for every quantity of apples. Whether purchasing 4 lb. of apples for $10.00 or 8 lb. of apples for $20.00, 0.4 lb. can be purchased per dollar.

This is true in all contexts; when 2 ratios are equivalent, the 2 unit rates will always be equal, as shown in the table.

Practice Problems

1. A car travels 55 miles per hour (mph) for 2 hr. Complete the table.

2. The table shows the ounces (oz.) of onions and tomatoes in different sized batches of a salsa recipe.

Elena notices that if she takes the number in the tomatoes column and divides it by the corresponding number in the onions column, she always gets the same result.

What is the meaning of the number that Elena has calculated?

3. A restaurant is offering 2 specials: 10 burritos for $12, or 6 burritos for $7.50. Noah needs 60 burritos for his party. Should he buy 6 orders of the 10-burrito special or 10 orders of the 6-burrito special? Explain your reasoning.

4. Complete the table so that the cost per banana remains the same.

Review Problems

5. Two planes travel at a constant speed. Plane A travels 2,800 miles (mi.) in 5 hr. Plane B travels 3,885 mi. in 7 hr. Which plane is faster? Explain your reasoning.

6. A car has 15 gallons (gal.) of gas in its tank. The car travels 35 miles per gallon (mpg) of gas. It uses 1 35 of a gal. of gas to go 1 mi.

a. How far can the car travel with 15 gal.? Show your reasoning.

b. How much gas does the car use to go 100 mi.? Show your reasoning.

ManuscriptCopy

Unit 4, Lesson 6: More about Constant Speed

Warm-Up: Back on the Treadmill Again

While training for a race, Andre’s dad ran 12 miles (mi.) in 75 minutes (min.) on a treadmill. If he runs at that rate:

1. How long would it take him to run 8 mi.?

2. How far could he run in 30 min.?

Exploration Activity: Picnics on the Rail Trail

Kiran and Clare live 24 mi. away from each other along a rail trail. One Saturday, the two friends started walking toward each other along the trail at 8:00 a.m. with a plan to have a picnic when they meet.

Kiran walks at a speed of 3 miles per hour (mph) while Clare walks 3.4 mph.

1. After one hour (hr.), how far apart will they be?

ManuscriptCopy

2. Make a table showing how far apart the two friends are after 0 hr., 1 hr., 2 hr., and 3 hr.

3. At what time will the two friends meet and have their picnic?

4. Kiran says “If I walk 3 mph toward you, and you walk 3.4 mph toward me, it’s the same as if you stay put and I jog 6.4 mph.” What do you think Kiran means by this? Is he correct?

5. Several months later, they both set out at 8:00 a.m. again, this time with Kiran jogging and Clare still walking at 3.4 mph. This time, they meet at 10:30 a.m. How fast was Kiran jogging?

ManuscriptCopy

Collaborative Activity: Swimming and Biking

Jada bikes 2 mi. in 12 min. Jada’s cousin swims 1 mi. in 24 min.

1. Who was moving faster? How much faster?

2. One day Jada and her cousin line up on the end of a swimming pier on the edge of a lake. At the same time, they start swimming and biking in opposite directions.

a. How far apart will they be after 15 min.?

b. How long will it take them to be 5 mi. apart?

Lesson Summary

When 2 objects are each moving at a constant rate and their distance-to-time ratio is equivalent, they can be described as moving at the same speed. If their distance-totime ratio is not equivalent, they are not moving at the same speed.

Speed is described in units of distance per unit of time, like miles per hour or meters per second.

Speed is one way to describe how fast something is moving. Speed tells us how much distance the object travels in a certain amount of time.

ManuscriptCopy

• A snail that crawls 5 centimeters (cm) in 2 min. is traveling at a rate of 2.5 cm per min.

• A toddler who walks 9 feet (ft.) in 6 seconds (sec.) is traveling at a rate of 1.5 ft. per sec.

• A cyclist who bikes 20 kilometers (km) in 2 hr. is traveling at a rate of 10 kilometers per hour (kph).

Pace can also be described using distance and time. Pace is measured in units such as hours per mile or seconds per meter.

Pace is one way to describe how fast something is moving. Pace tells us how much time it takes the object to travel a certain distance.

• A snail that crawls 5 cm in 2 min. has a pace of 0.4 min per cm.

• A toddler who walks 9 ft. in 6 sec. has a pace of 2 3 of a sec. per ft.

• A cyclist who bikes 20 km in 2 hr. has a pace of 0.1 hr. per km.

Speed and pace are reciprocals. Both can be used to compare whether one object is moving faster or slower than another object.

• The object with a higher speed is faster than one with a lower speed because the former travels a greater distance in the same amount of time.

• The object with a greater pace is slower than one with a lesser pace because the former takes more time to travel the same distance.

Because speed is a rate per 1 unit of time for ratios that relate distance to time, the amount of time traveled can be multiplied by the speed to find the distance traveled.

Practice Problems

1. A kangaroo hops 2 km in 3 min. At this rate:

a. How long does it take the kangaroo to travel 5 km?

ManuscriptCopy

b. How far does the kangaroo travel in 2 min.?

2. Mai runs around a 400-meter (m) track at a constant speed of 250 m per min. How many min. does it take Mai to complete 4 laps of the track? Explain or show your reasoning.

3. At 10:00 a.m., Han and Tyler both started running toward each other from opposite ends of a 10-mi. path along a river. Han runs at a pace of 12 min. per mi. Tyler runs at a pace of 15 min. per mi.

a. How far does Han run after a half hour? After an hour?

Half hour: __________

Hour: __________

b. Do Han and Tyler meet on the path within 1 hr.? Explain or show your reasoning.

4. Two skateboarders start a race at the same time. Skateboarder A travels at a steady rate of 15 ft. per sec. Skateboarder B travels at a steady rate of 22 ft. per sec. After 4 min., how much farther will Skateboarder B have traveled? Explain your reasoning.

ManuscriptCopy

Review Problems

5. There are 4 tablespoons (tbsp.) in 1 4 cup (c.). There are 2 c. in 1 pint (pt.). How many tbsp. are there in 1 pt.? If you get stuck, consider drawing a double number line or making a table.

6. Two larger cubes are made out of unit cubes. Cube A is 2 by 2 by 2. Cube B is 4 by 4 by 4. The side length of Cube B is twice that of Cube A.

a. Is the surface area of Cube B also twice that of Cube A? Explain or show your reasoning.

b. Is the volume of Cube B also twice that of Cube A? Explain or show your reasoning

Unit 4, Lesson 7: What Are Percentages?

Warm-Up: Dollars and Cents

Find each answer mentally.

1. A sticker costs 25 cents. How many dollars is that?

2. A pen costs $1.50. How many cents is that?

3. How many cents are in one dollar?

4. How many dollars are in one cent?

ManuscriptCopy

Exploration Activity: Coins

1. Complete the table to show the values of these U.S. coins.

The value of a quarter is 25% of the value of a dollar because there are 25 cents for every 100 cents.

2. Write the name of the coin that matches each expression.

a. 25% of a dollar

b. 5% of a dollar

c. 1% of a dollar

d. 100% of a dollar

e. 10% of a dollar

f. 50% of a dollar

3. The value of 6 dimes is what percent of the value of a dollar?

4. The value of 6 quarters is what percent of the value of a dollar?

Exploration Activity: Coins on a Number Line

A $1 coin is worth 100% of the value of a dollar. Here is a double number line that shows this.

1. The coins in Jada’s pocket are worth 75% of a dollar. How much are they worth (in dollars)?

2. The coins in Diego’s pocket are worth 150% of a dollar. How much are they worth (in dollars)?

3. Elena has 3 quarters and 5 dimes. What percentage of a dollar does she have?

Collaborative Activity: Puppies Grow Up

1. Jada has a new puppy that weighs 9 pounds (lb.). The vet says that the puppy is now at about 20% of its adult weight. What will be the adult weight of the puppy?

2. Andre also has a puppy that weighs 9 lb. The vet says that this puppy is now at about 30% of its adult weight. What will be the adult weight of Andre’s puppy?

3. What is the same about Jada and Andre’s puppies? What is different?

ManuscriptCopy

Lesson Summary

A double number line can be used to solve problems about percentages.

A percentage is a rate per 100.

Percent means “for each 100.” The symbol for percent is %.

For example, percentages of $10 are represented on the double number line where 10 and 100% are aligned.

The double number line shows that $5.00 is 50% of $10.00 and that $12.50 is 125% of $10.00.

The double number line shown can be used to determine what 30% of 50 lb. is.

The distance between 0% and 100% and the distance between 0 and 50 lb. are each divided into 10 equal parts. The tick marks on the top line should be labeled in increments of 5 because 50 ÷ 10 = 5, and the tick marks on the bottom line should be labeled in increments of 10% because 100% ÷ 10 = 10%. A weight of 15 lb. is aligned with 30%, so 30% of 50 lb. is 15 lb.

ManuscriptCopy

Suppose that 140% of some amount of money is $28. The double number line shown can be used to determine what 100% of that amount is.

Divide the distance between 0% and 140% and the distance between $0 and $28 into 14 equal intervals. Label the tick marks on the top line in increments of 2 and on the bottom line in increments of 10%. The diagram then shows that 100% is $20.

Practice Problems

1. The United States government used to make coins of many different values. For each coin, state its worth as a percentage of $1.

a. 1 2 cent

b. 3 cents

c. 20 cents

d. $2 1 2

e. $5

2. Complete the double number to line show percentages of $50.

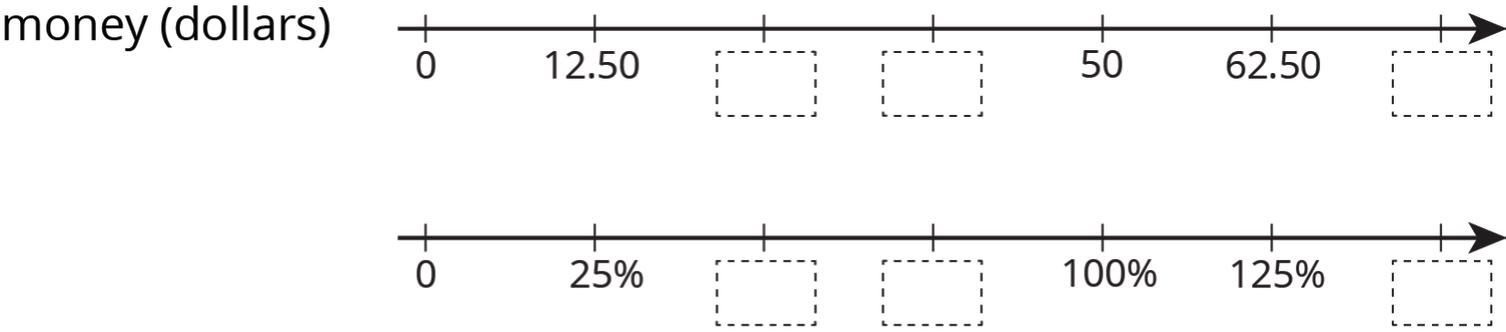
3. A 16 ounce (oz.) bottle of orange juice says it contains 200 milligrams (mg) of vitamin C, which is 250% of the daily recommended allowance of vitamin C for adults. What is 100% of the daily recommended allowance of vitamin C for adults?

4. Solve each problem. If you get stuck, consider using the double number lines.

a. During a basketball practice, Mai attempted 40 free throws and was successful on 25% of them. How many successful free throws did she make?

b. Yesterday, Priya successfully made 12 free throws. Today, she made 150% as many. How many successful free throws did Priya make today?

5. At a school, 40% of the sixth-grade students said that hip-hop is their favorite kind of music. If 100 sixth-grade students prefer hip hop music, how many sixth-grade students are at the school? Explain or show your reasoning.

6. A snail travels 10 centimeters (cm) in 4 minutes (min.). At this rate:

a. How long will it take the snail to travel 24 cm?

b. How far does the snail travel in 6 min.?

ManuscriptCopy

Unit 4,

Lesson

8: Percentages and Tape Diagrams

Warm-Up: Notice and Wonder: Tape Diagrams

What do you notice? What do you wonder?

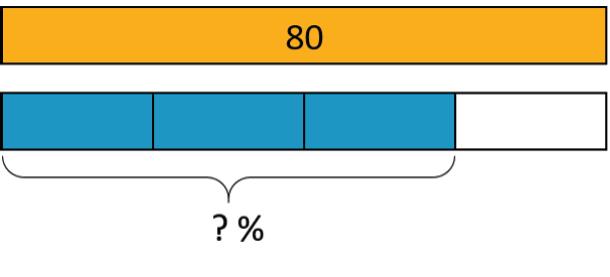
Exploration Activity: Revisiting Jada’s Puppy

Jada has a new puppy that weighs 9 pounds (lb.). It is now at about 20% of its adult weight.

1. Here is a diagram that Jada drew about the weight of her puppy.

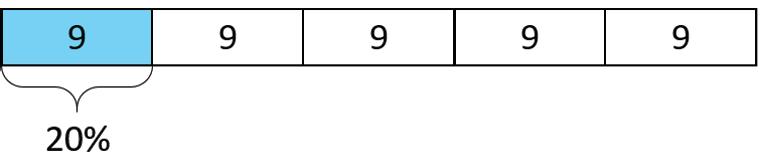
a. The adult weight of the puppy will be 45 lb. How can you see that in the diagram?

b. What fraction of its adult weight is the puppy now? How can you see that in the diagram?

2. Jada’s friend has a dog that weighs 90 lb. Here is a diagram Jada drew that represents the weight of her friend's dog and the weight of her puppy.

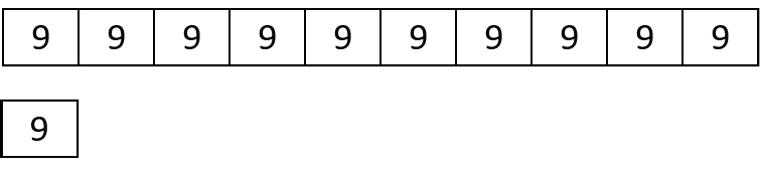
a. How many times greater is the dog’s weight than the puppy’s?

b. Compare the weight of the puppy and the dog using fractions.

c. Compare the weight of the puppy and the dog using percentages.

Collaborative Activity: 5 Dollars

Noah has $5.

1.

a. Elena has 40% as much as Noah. How much does Elena have?

b. Compare Elena’s and Noah’s money using fractions. Draw a diagram to illustrate.

a. Diego has 150% as much as Noah. How much does Diego have?

b. Compare Diego’s and Noah’s money using fractions. Draw a diagram to illustrate.

Collaborative Activity: Staying Hydrated

During the first part of a hike, Andre drank 1.5 liters (L) of the water he brought.

1. If this is 50% of the water he brought, how much water did he bring?

2. If he drank 80% of his water on his entire hike, how much did he drink?

ManuscriptCopy

Lesson Summary

Tape diagrams can be used to make sense of percentages.

Consider the 2 example problems solved in the previous lesson using double number lines. The problems and their solutions found using tape diagrams are shown.

Problem What is 30% of 50 lb.?

Tape Diagram

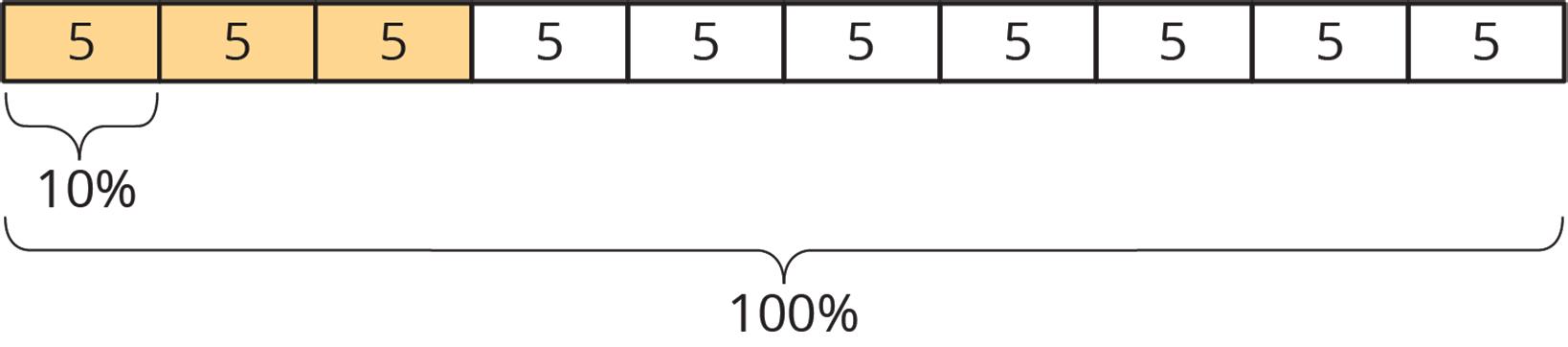
Solution

The tape diagram shows that 30% of 50 lb. is 15 lb.

Problem What is 100% of an amount of money if 140% of it is $28?

Tape Diagram

ManuscriptCopy

Solution

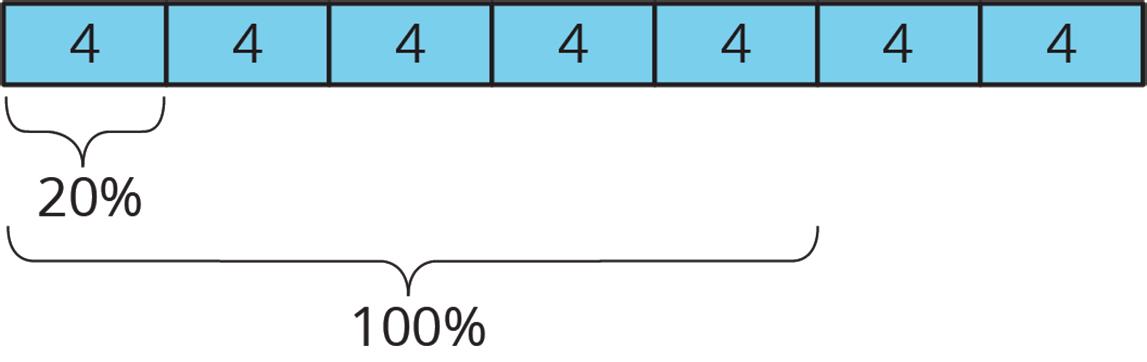
The tape diagram shows that if 140% of the amount is $28, then 100% of that amount must be $20.

Practice Problems

1. Here is a tape diagram that shows how far two students walked.

a. What percentage of Priya’s distance did Tyler walk?

b. What percentage of Tyler’s distance did Priya walk?

2. A bakery makes 40 different flavors of muffins. 25% of the flavors have chocolate as one of the ingredients. Draw a tape diagram to show how many flavors have chocolate and how many don’t.

3. There are 70 students in the school band. 40% of them are sixth graders, 20% are seventh graders, and the rest are eighth graders.

a. How many band members are sixth graders?

b. How many band members are seventh graders?

c. What percentage of the band members are eighth graders? Explain your reasoning.

4. Jada has a monthly budget for her cell phone bill. Last month she spent 120% of her budget, and the bill was $60. What is Jada’s monthly budget? Explain or show your reasoning.

5. Which is a better deal, 5 tickets for $12.50 or 8 tickets for $20.16? Explain your reasoning.

6. An athlete runs 8 miles (mi.) in 50 minutes (min.) on a treadmill. At this rate:

a. How long will it take the athlete to run 9 mi.?

b. How far can the athlete run in 1 hour (hr.)?

ManuscriptCopy

Unit 4, Lesson 9: Benchmark Percentages

Warm-Up: What Percent Is Shaded?

What percentage of each diagram is shaded?

ManuscriptCopy

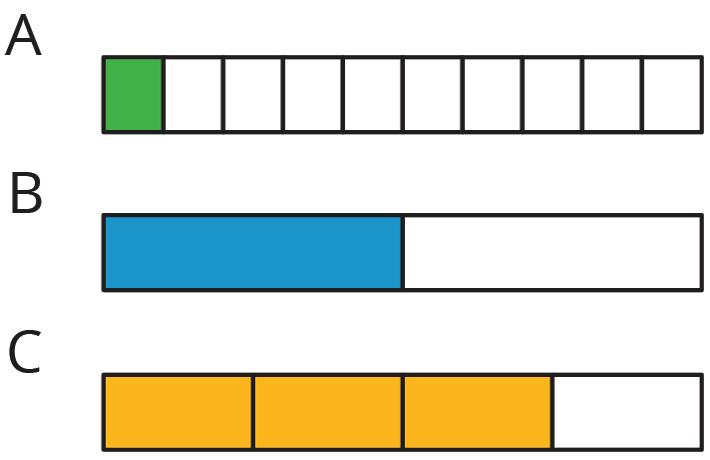
1.

Exploration Activity: Liters, Kilometers, and Hours

a. How much is 50% of 10 liters (L) of milk?

b. How far is 50% of a 2,000 kilometer (km) trip?

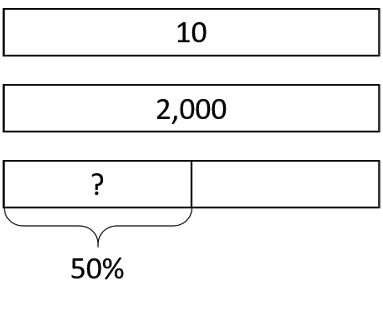
c. How long is 50% of a 24 hour (hr.) day?

d. How can you find 50% of any number?

2.

a. How far is 10% of a 2,000 km trip?

b. How much is 10% of 10 L of milk?

c. How long is 10% of a 24 hr. day?

d. How can you find 10% of any number?

a. How long is 75% of a 24 hr. day?

b. How far is 75% of a 2,000 km trip?

c. How much is 75% of 10 L of milk?

d. How can you find 75% of any number?

Explain how you can calculate each value mentally.

1. 9 is 50% of what number?

2. 9 is 25% of what number?

3. 9 is 10% of what number?

4. 9 is 75% of what number?

5. 9 is 150% of what number?

Collaborative Activity: Matching the Percentage

Match the percentage that describes the relationship between each pair of numbers. One percentage will be left over. Be prepared to explain your reasoning.

1. 7 is what percentage of 14? _____

2. 5 is what percentage of 20? _____

3. 3 is what percentage of 30? _____

4. 6 is what percentage of 8? _____

5. 20 is what percentage of 5? _____ A. 4% B. 10% C. 25%

Lesson Summary

Certain percentages are easy to think about in terms of fractions. The double number line shows an example of how to consider intervals of 25% in terms of fractions.

• 25% of a number is always 1 4 of that number. For example, 25% of 40 L is 1 4 ⋅ 40 or 10 L.

• 50% of a number is always 1 2 of that number. For example, 50% of 82 km is 1 2 ⋅ 82 or 41 km.

• 75% of a number is always 3 4 of that number. For example, 75% of 1 pound lb. is 3 4 lb.

• 10% of a number is always 1 10 of that number. For example, 10% of 95 meters (m) is 9.5 m.

Multiples of 10% can be found using tenths.

For example, 70% of a number is always 7 10 of that number, so 70% of 30 days is 7 10 ⋅ 30 or 21 days.

1.

Practice Problems

a. How can you find 50% of a number quickly in your head?

b. Andre lives 1.6 km from school. What is 50% of 1.6 km?

c. Diego lives 1 2 mile (mi.) from school. What is 50% of 1 2 mi.?

2. There is a 10% off sale on laptop computers. If someone saves $35 on a laptop, what was its original cost? If you get stuck, consider using the table.

ManuscriptCopy

3. Noah says that to find 20% of a number he divides the number by 5. For example, 20% of 60 is 12, because 60 ÷ 5 = 12. Does Noah’s method always work? Explain why or why not.

Review Problems

4. Diego has 75% of $10. Noah has 25% of $30. Diego thinks he has more money than Noah, but Noah thinks they have an equal amount of money. Who is right? Explain your reasoning.

5. Lin and Andre start walking toward each other at the same time from opposite ends of 22 mi. walking trail. Lin walks at a speed of 2.5 miles per hour (mph). Andre walks at a speed of 3 mph.

Here is a table showing the distances traveled and how far apart Lin and Andre were over time. Use the table to find how much time passes before they meet.

Unit 4, Lesson 10: Solving Percentage Problems

Warm-Up: Multiplication with Decimals

Find the products mentally.

6 ⋅ (0.8) ⋅ 2

(4.5) ⋅ (0.6) ⋅ 4

Guided Activity: Coupons

Han and Clare go shopping, and they each have a coupon. Answer each question and show your reasoning.

1. Han buys an item with a normal price of $15, and uses a 10% off coupon. How much does he save by using the coupon?

ManuscriptCopy

2. Clare buys an item with a normal price of $24, but saves $6 by using a coupon. For what percentage off is this coupon?

Collaborative Activity: Info Gap: Music Devices

Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.

If your teacher gives you the problem card:

1. Silently read your card and think about what information you need to be able to answer the question.

2. Ask your partner for the specific information that you need.

3. Explain how you are using the information to solve the problem.

Continue to ask questions until you have enough information to solve the problem.

4. Share the problem card and solve the problem independently.

5. Read the data card and discuss your reasoning.

If your teacher gives you the data card:

1. Silently read your card.

2. Ask your partner, “What specific information do you need?” and wait for them to ask for information.

If your partner asks for information that is not on the card, do not do the calculations for them. Tell them you don’t have that information.

3. Before sharing the information, ask, “Why do you need that information?” Listen to your partner’s reasoning and ask clarifying questions.

4. Read the problem card and solve the problem independently.

5. Share the data card and discuss your reasoning.

Lesson Summary

A pot can hold 36 liters (L) of water. What percentage of the pot is filled when it contains 9 L of water?

Two different ways are shown.

• Use a double number line:

Divide the distance between 0 and 36 into 4 equal intervals. This shows that 9 is 1 4 of 36, which means 9 is 25% of 36.

• Use a table:

Determine what to multiply by 36 for a result of 9, and then multiply 100% by the same factor to find the percentage.

Practice Problems

1. For each problem, explain or show your reasoning.

a. 160 is what percentage of 40?

b. 40 is 160% of what number?

c. What number is 40% of 160?

2. A store is having a 20% off sale on all merchandise. If Mai buys one item and saves $13, what was the original price of her purchase? Explain or show your reasoning.

3. The original price of a scarf was $16. During a store-closing sale, a shopper saved $12 on the scarf. What percentage discount did she receive? Explain or show your reasoning.

4. Select all the expressions whose value is larger than 100.

□ 120% of 100

□ 50% of 150

□ 150% of 50

□ 20% of 800

□ 200% of 30

□ 500% of 400 □ 1% of 1,000

Review Problems

5. An ant travels at a constant rate of 30 centimeters (cm) every 2 minutes (min.).

a. At what pace does the ant travel per cm?

b. At what speed does the ant travel per min.?

6. Name a unit of measurement that is about the same size as each object.

a. The distance of a doorknob from the floor is about 1 _____________________.

b. The thickness of a fingernail is about 1 _____________________.

c. The volume of a drop of honey is about 1 _____________________.

d. The weight or mass of a pineapple is about 1 _____________________.

e. The thickness of a picture book is about 1 _____________________.

f. The weight or mass of a buffalo is about 1 _____________________.

g. The volume of a flower vase is about 1 _____________________.

h. The weight or mass of 20 staples is about 1 _____________________.

i. The volume of a melon is about 1 _____________________.

j. The length of a piece of printer paper is about 1 _____________________.

ManuscriptCopy

ManuscriptCopy

Unit 4, Lesson 11: Finding This Percent of That

Warm-Up: Number Talk: Decimals

Find the value of each expression mentally.

⋅ 100

Collaborative Activity: Audience Size

A school held several evening activities last month: a music concert, a basketball game, a drama play, and literacy night. The music concert was attended by 250 people. How many people came to each of the other activities?

1. Attendance at a basketball game was 30% of attendance at the concert.

2. Attendance at the drama play was 140% of attendance at the concert.

3. Attendance at literacy night was 44% of attendance at the concert.

Collaborative Activity: Everything Is On Sale

During a sale, every item in a store is 80% of its regular price.

1. If the regular price of a T-shirt is $10, what is its sale price?

2. The regular prices of five items are shown here. Find the sale price of each item.

3. You found 80% of many values. Was there a process you repeated over and over to find the sale prices? If so, describe it.

4. Select all of the expressions that could be used to find 80% of ��. Be prepared to explain your reasoning.

Lesson Summary

Multiplication can be used to find the percentage of a number, along with tape diagrams or double number lines.

• To find 49% of a number, multiply the number by 49 100 or 0.49.

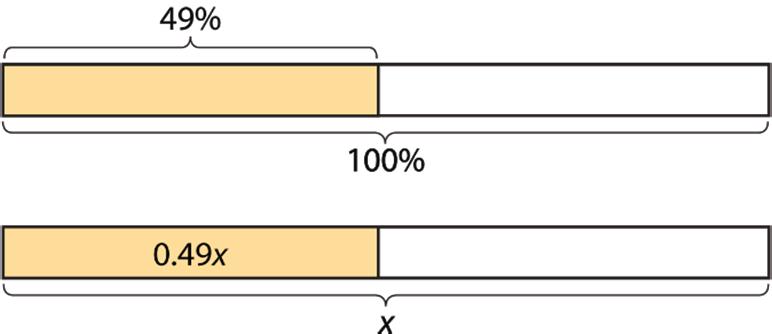
• To find 135% of a number, multiply the number by 135 100 or 1.35.

• To find 6% of a number, multiply the number by 6 100 or 0.06.

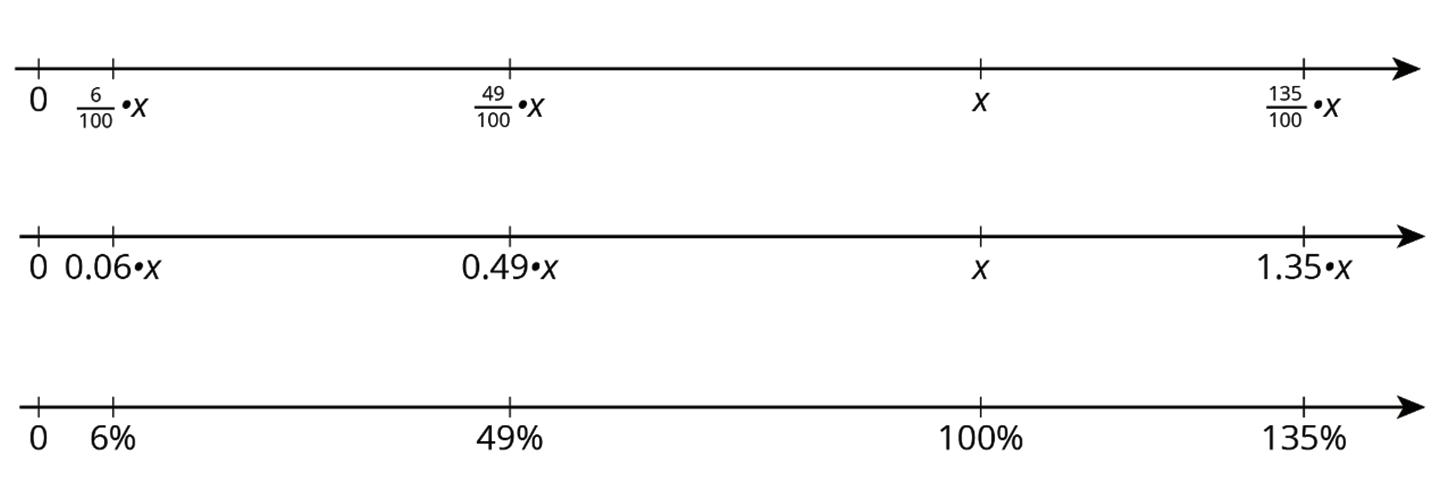
In general, to find ��% of ��, multiply

1.

ManuscriptCopy

Practice Problems

a. To find 40% of 75, Priya calculates 2 5 ⋅ 75. Does her calculation give the correct value for 40% of 75? Explain or show how you know.

b. If �� represents a number, does 2 5 ⋅ �� always represent 40% of that number? Explain your reasoning.

2. Han spent 75 minutes (min.) practicing the piano over the weekend. For each question, explain or show your reasoning.

a. Priya practiced the violin for 152% as much time as Han practiced the piano. How long did she practice?

b. Tyler practiced the clarinet for 64% as much time as Han practiced the piano. How long did he practice?

3. Last Sunday 1,575 people visited the amusement park. 56% of the visitors were adults, 16% were teenagers, and 28% were children ages 12 and under. Find the number of adults, teenagers, and children that visited the park.

4. Order from greatest to least:

• 55% of 180

ManuscriptCopy

• 300% of 26

• 12% of 700

5. Complete each statement.

a. 20% of 60 is ________.

b. 25% of ________ is 6.

c. % of 100 is 14.

d. 50% of 90 is ________.

e. 10% of ________ is 7.

f. 30% of 70 is ________.

6. A shopper needs 24 sandwich rolls. The store sells identical rolls in 2 differently sized packages. They sell a six-pack for $5.28 and a four-pack for $3.40. Should the shopper buy 4 six-packs or 6 four-packs? Explain your reasoning.

7. On a field trip, there are 3 chaperones for every 20 students. There are 92 people on the trip. Answer these questions. If you get stuck, consider using a tape diagram.

a. How many chaperones are there?

b. How many children are there?

ManuscriptCopy

Unit 4, Lesson 12: Finding the Percentages

Warm-Up: Percentages

Is each statement true or false? Be prepared to explain your reasoning.

1. 25% of 512 is equal to 1 4 ⋅ 500.

2. 90% of 133 is equal to (0.9) ⋅ 133.

3. 30% of 44 is equal to 3% of 440.

4. The percentage 21 is of 28 is equal to the percentage 30 is of 40.

ManuscriptCopy

Collaborative Activity: Jumping Rope

A school held a jump-roping contest. Diego jumped rope for 20 minutes (min.).

1. Jada jumped rope for 15 min. What percentage of Diego’s time is that?

2. Lin jumped rope for 24 min. What percentage of Diego’s time is that?

3. Noah jumped rope for 9 min. What percentage of Diego’s time is that?

4. Record your answers in this table. Write the quotients in the last column as decimals.

5. What do you notice about the numbers in the last two columns of the table?

Collaborative Activity: Restaurant Capacity

A restaurant has a sign by the front door that says, “Maximum occupancy: 75 people.” Answer each question and explain or show your reasoning.

1. What percentage of its capacity is 9 people?

2. What percentage of its capacity is 51 people?

3. What percentage of its capacity is 84 people?

ManuscriptCopy

Lesson Summary

What percentage of 90 kilograms (kg) is 36 kg? One way to solve this problem is to find what percentage 1 kg is of 90 and then multiply it by 36.

The table shows that 1 kg is � 1 90 ⋅ 100�%, so 36 kg is � 36 90 ⋅ 100�% or 40% of 90.

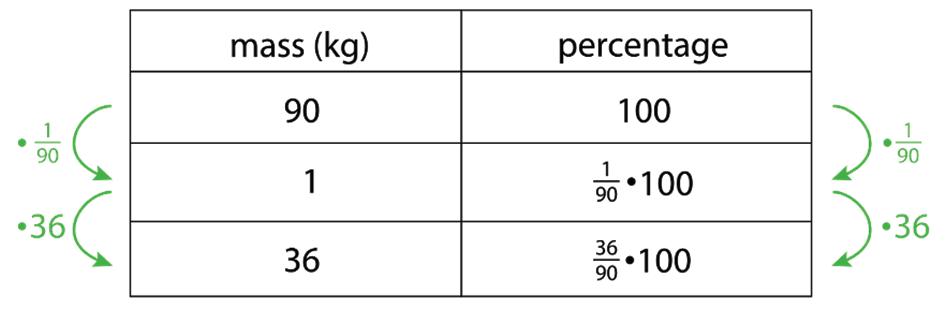
The answer can be confirmed using the double number line shown.

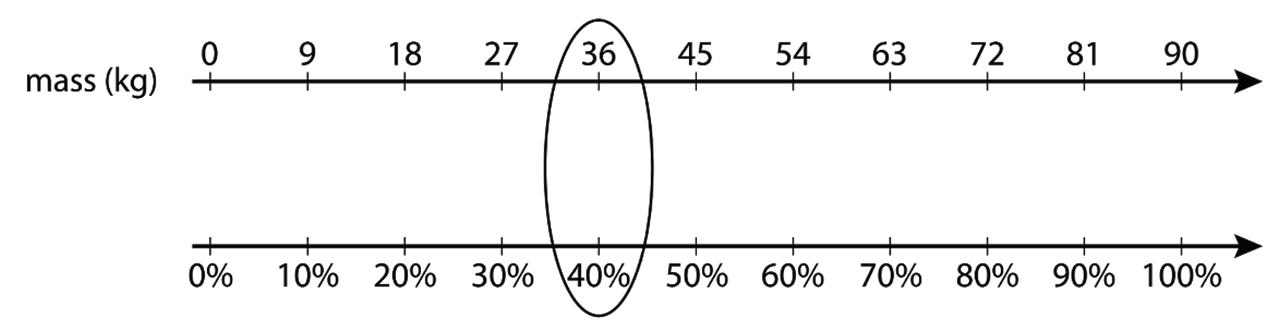
In general, to find what percentage a number �� is of another number �� is to calculate �� �� of 100%, for which the expression �� �� ⋅ 100 can be used.

Suppose a school club has raised $88 for a project but needs a total of $160. What percentage of its goal has the club raised?

To find what percentage $88 is of $160, find 88 160 of 100%, or 88

11 20 ⋅ 100 = 55, the club has raised 55% of its goal.

Practice Problems

1. A sign in front of a roller coaster says, "You must be 40 inches (in.) tall to ride." What percentage of this height is:

a. 34 in.?

ManuscriptCopy

b. 54 in.?

2. At a hardware store, a tool set normally costs $80. During a sale this week, the tool set costs $12 less than usual. What percentage of the usual price is the savings? Explain or show your reasoning.

3. A bathtub can hold 80 gallons (gal.) of water. The faucet flows at a rate of 4 gal. per min. What percentage of the tub will be filled after 6 min.?

Review Problems

4. The sale price of every item in a store is 85% of its usual price.

a. The usual price of a backpack is $30, what is its sale price?

b. The usual price of a sweatshirt is $18, what is its sale price?

c. The usual price of a soccer ball is $24.80, what is its sale price?

5. A shopper needs 48 hot dogs. The store sells identical hot dogs in 2 differently sized packages. They sell a six-pack of hot dogs for $2.10, and an eight-pack of hot dogs for $3.12. Should the shopper buy 8 six-packs, or 6 eight-packs? Explain your reasoning.

ManuscriptCopy

Unit

4,

Lesson

13: Equivalent Forms of Rational Numbers – Part 1

Warm-Up: Fractions Equal to 1

1. Place a digit in each blue box to make the statement true. Use only the digits 1 to 9, no more than once each. += 1

Guided Activity: Fraction and Decimal Conversions

1. Use the original number to fill in the missing digits and place values.

2. Consider the number 0.04.

a. In the number 0.04, what is the place value of the final digit?

b. What is the written description of the fraction 4 100 ?

c. Discuss with your partner any similarities or differences between the decimal 0.04 and the fraction 4 100 .

A fraction can be converted into its equivalent decimal form by dividing the numerator by the denominator.

3. To convert the fraction 1 4 to a decimal, divide 1 by 4 by completing the diagram below.

4 1 . 0 0

Number of ones, in groups of 4

Amount that remains

Number of tenths, in groups of 4

Amount that remains

Number of hundredths, in groups of 4

Amount that remains

Collaborative Activity: Fraction and Decimal Conversions

1. Complete the table by converting each decimal to an equivalent fraction. If possible, write the equivalent fraction so that the numerator and denominator have no common factors.

ManuscriptCopy

2. Complete the table by rewriting each fraction as its equivalent decimal. Show your work.

Guided Activity: Decimal and Percentage Conversions

Percentages can also be written as fractions with a denominator of 100, or as a decimal.

1. Write 66% as a fraction and as a decimal.

To convert a decimal to a percentage, multiply the decimal by 100.

2. Convert the decimal 0.16 to a percentage.

To convert a percentage to a decimal, divide the percentage by 100 or multiply by

3. Convert 16.2% to a decimal.

Collaborative Activity: Decimal and Percentage Conversions

1. Complete the table by converting each decimal to an equivalent percentage.

2. Rewrite each percentage into its equivalent decimal form to complete the table.

Lesson Summary

The place value of a number provides the numerical value that a digit has by virtue of its position in a number.

For example, in the number 278.493:

• The 8 is in the ones place.

• The 4 is in the tenths place.

• The 9 is in the hundredths place.

• The 3 is in the thousandths place.

When rewriting a decimal that is greater than 0 but less than 1 as an equivalent fraction, use the place value of the final digit to determine the denominator of the fraction. Decimal values greater than 1 are similar to mixed fractions, where the whole number portion is written to the left of the decimal.

Different strategies can be used to rewrite rational numbers in different but equivalent forms.

• To convert a fraction to a decimal, divide the numerator by the denominator.

• To convert a decimal to a percentage, multiply the decimal by 100.

• To convert a percentage to a decimal, divide the percentage by 100 or multiply by 1 100 .

Practice Problems

1. Rewrite each percentage as a decimal.

125.6%

2. Convert each decimal to an equivalent percentage.

0.008

3. Rewrite each fraction as a decimal.

1 2

b. 4.71

b. 2 1 10

4. Rewrite each decimal as an equivalent fraction. Simplify where applicable.

0.94 b. 1.7

a.

b. 3%

a.

a.

a.

Unit 4, Lesson 14: Equivalent Forms of Rational Numbers – Part 2

Warm-Up: Rewriting Rational Numbers

1. Rewrite 1 3 8 as a percentage.

2. Rewrite 88% as a fraction. Simplify if applicable.

Collaborative Activity: Relating Fractions and Percentages

1. The model represents a numerical value. Use the model to answer the questions that follow.

a. How many total squares are in the image?

b. How many of the squares are shaded blue?

c. What numerical value does the model represent, expressed as a fraction of blue shaded squares total squares ?

Recall that a percentage is a ratio expressed as a fraction of 100.

For example, 40% means “40 out of 100,” so 40% is equivalent to the fraction 40 100 .

2. What decimal value has the same value as 40% and 40 100 ?

One way to convert fractions to percentages is to generate an equivalent fraction with a denominator of 100 when possible.

3. Complete the table.

Guided Activity: Rewriting Rational Numbers in Equivalent Forms

Recall from the previous lesson that a fraction can be converted into its equivalent decimal form by dividing the numerator by the denominator.

1. Complete the table by rewriting the fraction into an equivalent decimal form.

2. Complete the table by rewriting the decimal into an equivalent percentage.

3. What is the equivalent decimal form of 5 8 ?

4. What is 0.625 rewritten as a percentage?

5. What is 5 8 rewritten as a percentage?

6. When rewriting a fraction as a percentage, why might it be helpful to first rewrite it in its equivalent decimal form?

7. Complete the table by rewriting each value in its equivalent forms.

ManuscriptCopy

Collaborative Activity: Strategies for Rewriting Rational Numbers

Working with your partner, use the words in the bank to complete each statement. Words can be used more than once.

Word Bank decimal numerator denominator percentage fraction place value

1. To convert a ________________ to a decimal, divide the ______________ by the _______________.

2. Multiply the _______________ by 100 to convert a ________________ to a ______________.

3. To rewrite a ________________ as a ________________, divide the ____________ by 100.

4. Use the _______________of the final digit to determine the denominator of the decimal when rewriting a ______________ as an equivalent ___________.

5. An equivalent fraction with a _____________ of 100 can be used to convert a _____________ to a percentage.

ManuscriptCopy

Lesson Summary

Rational numbers in the form of decimals, fractions, and percentanges can be rewritten, or converted, into equivalent forms.

• To convert a fraction to a decimal, divide the numerator by the denominator.

• To convert a decimal to a percentage, multiply the decimal by 100.

• To convert a fraction to a percentage, first rewrite the fraction in its equivalent decimal form, and then convert the decimal to a percentage.

• To convert a percentage to a fraction, use the value of the percentage as the numerator and 100 as the denominator. Simplify if applicable.

• To convert a decimal to a fraction, use the place value of the final digit to determine the denominator. Use the decimal value between 0 and 1 as the numerator. Simplify if applicable.

• To convert a percentage to a decimal, divide the percentage by 100 or multiply by 1 100 .

Practice Problems

1. Rewrite each fraction as an equivalent percentage.

2. Convert each percentage to a fraction. Simplify where applicable.

3. Complete the table by rewriting each value in its equivalent forms.

Review Problems

4. What percentage of a dollar is the value of each coin combination?

a. 4 dimes

b. 1 nickel and 3 pennies

c. 5 quarters and 1 dime

ManuscriptCopy

5. Andre sometimes mows lawns on the weekend to make extra money. Two weeks ago, he mowed a neighbor’s lawn for 1 2 hour and earned $10. Last week, he mowed his uncle’s lawn for 3 2 hours and earned $30. This week, he mowed the lawn of a community center for 2 hours and earned $30.

Which jobs paid better than others? Explain your reasoning.

6. The double number line shows how much water and how much lemonade powder to mix to make different amounts of lemonade.

Make a table that represents the same situation.

ManuscriptCopy

ManuscriptCopy

Unit 5, Lesson 1: Adding and Subtracting Fractions

Warm-Up: Solving Problems Using Fraction Models

Solve each problem. Support your thinking using each visual fraction model shown.

1. Yesterday, Daniel walked for 1 4 of an hour (hr.) in the morning and for 3 4 of an hr. in the afternoon.

What was the total amount of time Daniel spent walking yesterday?

2. A concession stand prepared a tray of sandwiches to sell at a game. Of all the sandwiches, 3 6 were ham, 2 6 were turkey, and the rest were tuna.

What fraction of the sandwiches were tuna?

HamHamHam

Exploration Activity: Adding and Subtracting Fractions with Unlike Denominators

While adding 3 4  + 2 5 , Kramer remembered that the first step in adding or subtracting fractions is to determine equivalent fractions with a common denominator.

1. Complete the table by listing the first 6 multiples of each fraction’s denominator.

2. What value should Kramer use for the common denominator?

3. Rewrite 3 4 + 2 5 using equivalent fractions with the common denominator identified in question 2. Show your work.

4. What is the value of 3 4 + 2 5 ?

5. What is the value of 157 200 –14 25 ?

Collaborative Activity: Keeping Fit

1. Each day, Grace swims 1 4 of a mile (mi.), and roller-skates 14 25 of a mi.

a. What is the combined distance that Grace swims and roller-skates each day? Simplify, if applicable.

b. How much farther does Grace roller-skate than she swims each day?

2. Each day, Liam jogs for 7 10 of a mi. and swims for 6 25 of a mi.

What is the combined distance that Liam jogs and swims each day? Simplify, if applicable.

3. Whose daily exercise covers more total distance?

4. What is the difference in the total daily distance covered by Grace’s and Liam’s exercise routines?

Lesson Summary

To add and subtract fractions with unlike denominators, the fractions need to be rewritten as equivalent fractions with a like, or common, denominator.

Use the steps shown to determine a common denominator.

• List several multiples of the denominators given in the problem. Identify a multiple that the denominators have in common. This will be the common denominator.

• Multiply each of the original fractions by a fraction equivalent to 1, using the factor needed to result in the common denominator in both the numerator and denominator.

• Then, add or subtract the resulting equivalent fractions to find the result.

• Simplify the answer, if applicable.

For example, to determine the value of 9 10 –4 25 , first determine multiples of 10 and 25, and identify a multiple they have in common, as shown. A common multiple of 10 and 25 is 50.

10: 10, 20, 30, 40, 50, 60 25: 25, 50, 75, 100, 125

The multiplicative identity property states that any number multiplied by 1 results in the number itself. This property can be used to create equivalent fractions for 9 10 and 4 25 using 50 in the denominator, as shown.

These fractions are equivalent to 1. Multiplying by 1 does not change the value of the original fraction.

Practice Problems

1. Determine the value of 2 5 + 1 2 .

2. Determine the value of 3 4 –21 200 .

3. Angelica completed 4 5 of her weekly homework on Monday and 2 15 of her homework on Wednesday.

a. How much more of her weekly homework did Angelica complete on Monday than on Wednesday?

b. How much of her weekly homework does Angelica have left to complete?

4. On his 11th birthday, Nigel planted a tree that was 1 2 of a meter (m) tall. On Nigel’s 12th birthday, the tree measured 9 10 of a m tall. How much did the tree grow in 1 year?

Review Problems

5. Calculate and express your answer in decimal form.

a. 1 2 ⋅ 17

b. 3 4 ⋅ 200

c. (0.2) ⋅ 40

d. (0.25) ⋅ 60

a. Three tacos cost $18. Complete the table to show the cost of 4, 5, and 6 tacos at the same rate.

b. If you buy t tacos for c dollars, what is the unit rate?

ManuscriptCopy

Unit 5, Lesson 2: Adding and Subtracting Fractions and Mixed Numbers

Warm-Up: True Statement

1. Place a digit in each blue box to make the statement true. Use only the digits 1 through 9, no more than once each.

ManuscriptCopy

Exploration Activity: Framing a Piece of Art

Claudia bought an art piece at a sidewalk art festival. She wanted to build her own frame for the art piece. The art piece has a height of 1 1 5 feet (ft.) and a width of 3 4 ft.

1. Claudia’s art piece is shown. Sketch a frame that Claudia could use. Label the width of the frame.

Three of Claudia’s classmates each sketched a frame for the art piece, as shown.

2. Which frame(s), when combined with the art piece, will result in a height that is 1 ft. taller than the original art piece?

3. Which frame(s), when combined with the art piece, will result in a width that is 1 4 ft. wider than the original art piece?

Eduardo Jahmelia Joshua

The frames drawn by Eduardo, Jahmelia, and Joshua show that the width of the frame can vary. Joshua’s frame shows that the frame does not have to be the same width on all 4 sides.

4. Claudia wants to determine the amount of material she needs to frame the piece of art. Since she is not sure of the widths of the frame, she labels the dimensions, as shown.

a. Work with your partner to write an expression that represents the width.

b. Work with your partner to write an expression that represents the height.

Guided Activity: Adding and Subtracting Fractions and Mixed Numbers

1. Determine a common denominator for 1 1 5 and 3 4 .

2. Rewrite 1 1 5 as an equivalent fraction using the common denominator found in question 1 by completing the fractions in the statement. Because 1 1 5 = 5 5 + 1 5 , the value 1 1 5 can be rewritten using the equivalent fractions 5 5 + 1 5 = +

3. Claudia’s art piece is shown.

a. What is the perimeter, in ft., of Claudia’s art piece?

Claudia decides to build a frame with the dimensions shown.

b. Write the numerical expression that represents the total width of the frame and art piece.

c. Find the total width, in ft.

d. Write the numerical expression that represents the total height of the frame and art piece.

e. Find the total height, in ft.

Lesson Summary

To add and subtract fractions and mixed numbers, the fractions and mixed numbers need to be rewritten as equivalent fractions with a common denominator. To find a common denominator, determine common multiples of the denominators in the problem.

Sometimes it can be helpful to rewrite mixed numbers as fractions greater than 1.

• Begin by rewriting the whole-number portion of the mixed number as an equivalent fraction with the same denominator as the fractional portion of the mixed number. An example of this step when rewriting 3 4 5 is shown.

• The sum of this fraction and the fractional portion of the original number is equivalent to the original mixed number represented as a fraction greater than 1.

When finding sums and differences using mixed numbers, it can be helpful to rewrite them as fractions greater than 1 before adding or subtracting the fractions. Whether you first rewrite mixed numbers as fractions greater than 1 or first find the common denominator is up to you. Simplify the answer, if applicable.

Practice Problems

Rewrite each of the following expressions as an equivalent expression with a common denominator. Then, add or subtract the values.

2  1 100 – 1  1 4  =

Review Problem

5. Fill in the blanks to make each equation true.

a. 3 ⋅  1 3  = _______

b. 10 ⋅  1 10 = _______

c. 19 ⋅  1 19 = _______

d. a ⋅  1 a  = ______ (As long as a does not equal 0.)

e. 5 ⋅ _______ = 1

f. 17 ⋅ _______ = 1

b ⋅ _______ = 1

g.

Unit 5, Lesson 3: Multiplying Fractions

Warm-Up: Patterns

The first 4 terms in 2 patterns are shown.

Pattern1

Pattern2

1. What do you notice about the terms in pattern 1?

2. What do you notice about the terms in pattern 2?

3. Write an expression to represent each pattern. Use �� for the term number.

Pattern 1

Pattern 2

Guided Activity: Multiplying Fractions

Alejandro took a trip to Louisville, Kentucky. While there, he ate 2 slices of Kentucky Derby Pie. He enjoyed the pie so much that he decided to make some pies for his family. The ingredients for the filling of one Kentucky Derby Pie are shown.

Kentucky Derby Pie Filling

1. Alejandro wanted to make 5 Kentucky Derby Pies to share with his family.

a. Write an expression that can be used to determine how much brown sugar Alejandro should buy.

b. Complete the statement.

Multiplication can be thought of as

repeated addition. repeated subtraction.

c. Rewrite your expression using the operation selected.

d. Draw a model to represent the expression.

ManuscriptCopy

2. Alejandro’s grandma, Camila, sliced her pie to share with her friends. She cut the pie into 8 slices.

a. Draw a model of the pie cut into 8 slices below.

b. Camila gave her friend Liliana 1 4 of the pie. Use your model to show how many slices Liliana received.

c. Complete a multiplication expression that has a value of the amount of pie that Liliana received.

d. How many slices of the pie are left?

e. Complete a multiplication expression that has a value representing the amount of pie that remains after Liliana received her slices.

3. Alejandro wants to make a sixth pie but realizes that he only has 1 2 of the amount of chocolate chips that he needs.

a. An incomplete model is shown that represents the amount of chocolate chips that Alejandro has. Shade in the model to represent the context. × =

b. The diagram of 3 figures shows the complete model that represents the amount of chocolate chips that Alejandro has. When the first 2 figures in the diagram are placed on top of each other, the result is the third figure. For the third figure, the denominator is represented by the total parts, and the numerator is represented by the number of parts where the shading overlaps. Fill in the fractions to complete the equation below the model.

c. What amount of chocolate chips does Alejandro have?

4. Complete the statements.

When multiplying fractions, the numerator of the first factor is multiplied by the numerator denominator of the second factor. The denominator of the first factor is multiplied by the numerator denominator of the second factor. Simply put, when multiplying fractions, multiply diagonally. straight across.

5. Alejandro knows he needs 7 1 2 cups of chocolate chips to make a batch of 10 pies. He wants to make 2 4 5 batches for an upcoming community bake sale.

Complete the statement.

ManuscriptCopy

To find the total number of cups of chocolate chips he needs, Alejandro should add multiply 2 4 5 10 with 7  1 2 because he needs 2 4 5 10 batches.

6. When multiplying using mixed numbers, an area model can be used.

a. Complete the left side of the area model with the missing factors, and then find the partial product in each box.

b. Add the partial products together to find the total number of cups of chocolate chips.

Collaborative Activity: Multiplying Fractions Greater Than 1 Using an Algorithm

When finding a product, such as 7 10 × 1 2 , the algorithm for multiplying, a b × c d , is used.

1. Work with your partner to complete the equation for the algorithm.

b × c d = × ×

2. Another way to represent multiplication is to use a dot.

ManuscriptCopy

3. Multiplication can also be represented using parentheses.

a b � � c d � = (______) (______) (______) (______)

4. Consider the product of 3 4 5 × 2  1 3 .

a. Write an equivalent expression by rewriting 3 4 5 and 2 1 3 as fractions greater than 1. 3 4 5 ×

b. Use the algorithm to find the product of 3 4

c. Verify your answer by completing the area model.

Lesson Summary

When multiplying fractions, multiply the numerators of the factors to find the numerator of the product, and multiply the denominators of the factors to find the denominator of the product. Then, simplify the product, if applicable.

The algorithm for multyiplying fractions is a b × c d =

An algorithm is a step-by-step way to solve a problem.

The algorithm does not account for mixed numbers. To multiply mixed numbers using the algorithm, first rewrite any mixed numbers as fractions greater than 1.

Practice Problems

1. Find each product.

a. 6 × 3 5

b. � 7 10 � � 1 2 �

c. 2  1 4 ∙ 4  4 5

2. Evaluate each of the expressions using the area model.

a. 2  3 5 × 4  1 3 b. 4  7 8 ∙ 6  1 4

ManuscriptCopy

Review Problems

3. Can side �� be the base for this triangle? If so, which length would be the corresponding height? If not, explain why not.

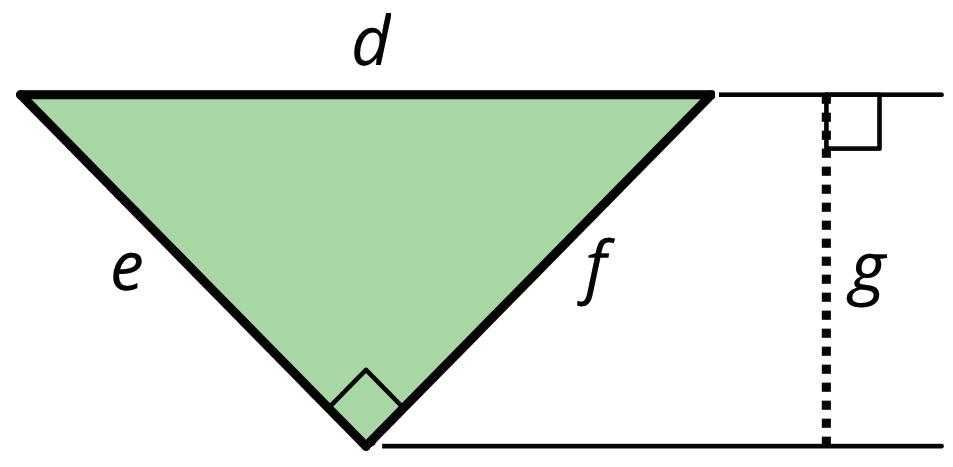
4. At a school, 460 of the students walk to school.

a. The number of students who take public transit is 20% of the number of students who walk. How many students take public transit?

b. The number of students who bike to school is 5% of the number of students who walk. How many students bike to school?

c. The number of students who ride the school bus is 110% of the number of students who walk. How many students ride the school bus?

ManuscriptCopy

Unit

5,

Lesson

4: How Many Groups?

Warm-Up: Reasoning with Fraction Strips

Write a fraction or whole number as an answer for each question. If you get stuck, use the fraction strips. Be prepared to share your reasoning. 1.

Exploration Activity: Reasoning with Pattern Blocks

Your teacher will give you pattern blocks as shown here. Use them to answer the following questions.

1. If a hexagon represents 1 whole, what fraction does each of the following shapes represent? Be prepared to show or explain your reasoning.

a. 1 triangle

b. 1 rhombus

c. 1 trapezoid

d. 4 triangles

e. 3 rhombuses

f. 2 hexagons

ManuscriptCopy

g. 1 hexagon and 1 trapezoid

2. Here are Elena’s diagrams for 2 ⋅  1 2 = 1 and 6 ⋅  1 3 = 2. Do you think these diagrams represent the equations? Explain or show your reasoning.

3. Use pattern blocks to represent each multiplication equation. Remember that a hexagon represents 1 whole.

a. 3 ⋅  1 6 = 1 2

b. 2 ⋅  3 2 = 3

4. Answer the following questions. If you get stuck, consider using pattern blocks.

a. How many 1 2 s are in 4?

b. How many 2 3 s are in 2?

c. How many 1 6 s are in 1  1 2 ?

Collaborative Activity: Representing Groups of Fractions with Tape Diagrams

To make sense of the question “How many 2 3 s are in 1?,” Antwan wrote 2 equations and drew a tape diagram. ? ∙ 2 3 = 1      1 ÷ 2 3 = ?

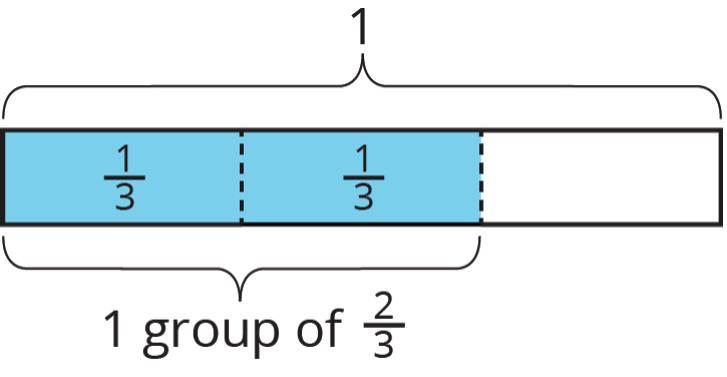
1. Explain how Antwan’s tape diagram can be used to solve the equation 1 ÷ 2 3 = ? .

2. Write a multiplication equation and a division equation for each question. Then, draw a tape diagram and find the answer.

a. How many 3 4 s are in 1?

b. How many 3 5 s are in 3?

c. How many 3 2 s are in 5?

Collaborative Activity: Draw Diagrams to Show Equal-Sized Groups

For each situation, draw a diagram for the relationship of the quantities to help you answer the question. Then write a multiplication equation or a division equation for the relationship. Be prepared to share your reasoning.

1. The distance around a park is 3 2 miles (mi.). Noah rode his bicycle around the park for a total of 3 mi. How many times around the park did he ride?

2. You need 3 4 yard (yd.) of ribbon for one gift box. You have 3 yd. of ribbon. How many gift boxes do you have ribbon for?

3. The water hose fills a bucket at 1 3 gallon (gal.) per minute (min.). How many min. does it take to fill a 2 gal. bucket?

4. How many groups of 1 2 pound (lb.) are in 2  3 4 lb.?

ManuscriptCopy

Lesson Summary

Some problems that involve equal-sized groups also involve fractions. For example, “How many 1 6 s are in 2?” can be expressed with multiplication and division equations.

⋅ 1 6 = 2      2 ÷ 1 6 =

Pattern block diagrams can be used to make sense of such problems. A set of pattern blocks is shown.

If the hexagon represents 1 whole, then a triangle must represent 1 6 because 6 triangles make 1 hexagon. The triangle can be used to represent the 1 6 in the problem.

Twelve triangles make 2 hexagons, which means there are 12 groups of 1 6 in 2.

Therefore, 12⋅ 1 6 = 2 and 2 ÷ 1 6 = 12.

Models can also be used to make sense of real-world problems.

A baker used 2 kilograms (kg) of flour to make several batches of a pastry recipe. The recipe called for 2 5 kg of flour per batch. How many batches did she make?

This question can be thought of as “how many groups of 2 5 kg make 2 kg?”

Represent the question with equations.

⋅ 2 5 = 2 or 2 ÷ 2 5 =

To help make sense of the question, draw a tape diagram. This diagram shows 2 kg, with each kg partitioned into fifths.

There are 5 groups of 2 5 in 2, so 2 5 ÷ 2 = 5.

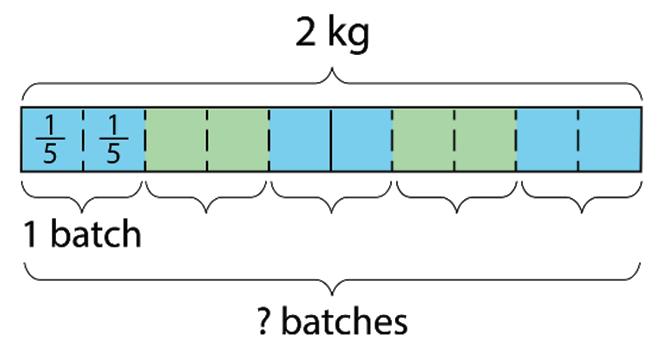
Multiplication can be used to check the answer. 5 ⋅ 2 5 = 10 5 and 10 5 = 2, so the answer is correct.

Notice that the number of groups that result from 2 ÷ 2 5 is a whole number. Sometimes the number of groups found from dividing may not be a whole number.

Suppose 1 serving of rice is 3 4 of a cup (c.). How many servings are there in 3 1 2 c. of rice?

⋅ 3 4 = 3 1 2    3 1 2 ÷ 3 4 = According to the diagram, there are 4 full groups of 3 4 , plus 2 fourths. If 3 fourths make a whole group, then 2 fourths make 2 3 of a group. Therefore, the number of servings is 4 2 3 because 3

this by multiplying

and

, which is equivalent to 3 1 2 .

Practice Problems

1. Which question can be represented by the equation? ⋅ 1 8 = 3?

A. How many 3s are in 1 8 ?

B. What is 3 groups of 1 8 ?

C. How many 1 8 s are in 3?

D. What is 1 8 of 3?

2. Write two division equations for each multiplication equation.

a. 15 ⋅  2 5 = 6

b. 6 ⋅  4 3 = 8

c. 16 ⋅  7 8 = 14

3. Use the tape diagram to find the value of 1 2 ÷ 1 3 . Show your reasoning.

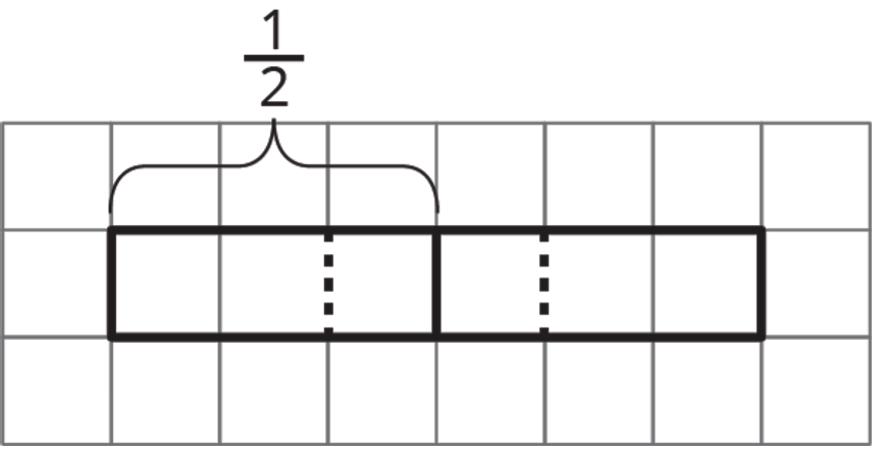
4. What is the value of 1 2 ÷ 1 3 ? Use pattern blocks to represent and find this value. The yellow hexagon represents 1 whole. Explain or show your reasoning.

5. We can think of 3 ÷ 1 4 as the question, “How many groups of 1 4 are in 3?” Draw a tape diagram to represent this question. Then find the answer.

Review Problem

6. At a farmer’s market, two vendors sell fresh milk. One vendor sells 2 liters (L) for $3.80, and another vendor sells 1.5 L for $2.70. Which is the better deal? Explain your reasoning.

ManuscriptCopy

Unit 5, Lesson 5:

What Fraction of a Group?

Warm-Up: Estimating a Fraction of a Number

1. Estimate each quantity.

a. What is 1 4 of 7?

b. What is 4 5 of 9 1 2 ?

c. What is 2 3 4 of 10 1 8 ?

2. Write a multiplication expression for each of the previous questions.

ManuscriptCopy

Exploration Activity: Fractions of Ropes

Here is a diagram that shows four ropes of different lengths.

1. Complete each sentence comparing the lengths of the ropes. Then, use the measurements shown on the grid to write a multiplication equation and a division equation for each comparison.

a. Rope B is _______ times as long as Rope A.

b. Rope C is _______ times as long as Rope A.

c. Rope D is _______ times as long as Rope A.

2. Each equation can be used to answer a question about Ropes C and D. What could each question be?

a. ? ⋅ 3 = 9 and 9 ÷ 3 = ?

b. ? ⋅ 9 = 3 and 3 ÷ 9 = ?

Guided Activity: Fractional Batches of Ice Cream

One batch of an ice cream recipe uses 9 cups (c.) of milk. A chef makes different amounts of ice cream on different days. Here are the amounts of milk she used.

• Monday: 12 c.

• Tuesday: 22 1 2 c.

• Thursday: 6 c.

• Friday: 7 1 2 c.

1. How many batches of ice cream did she make on these days? For each day, write a division equation, draw a tape diagram, and find the answer.

a. Monday

b. Tuesday

2. What fraction of a batch of ice cream did she make on these days? For each day, write a division equation, draw a tape diagram, and find the answer.

a. Thursday

b. Friday

3. For each question, write a division equation, draw a tape diagram, and find the answer.

a. What fraction of 9 is 3?

b. What fraction of 5 is 1 2 ?

Lesson Summary

It’s natural to think in groups when we have more than 1 group, but there can also be a fraction of a group.

To find the amount in a fraction of a group, multiply the fraction by the amount in the whole group.

For example, if a bag of rice weighs 5 kilograms (kg), 3 4 of a bag would weigh � 3 4 ⋅ 5� kg, as shown.

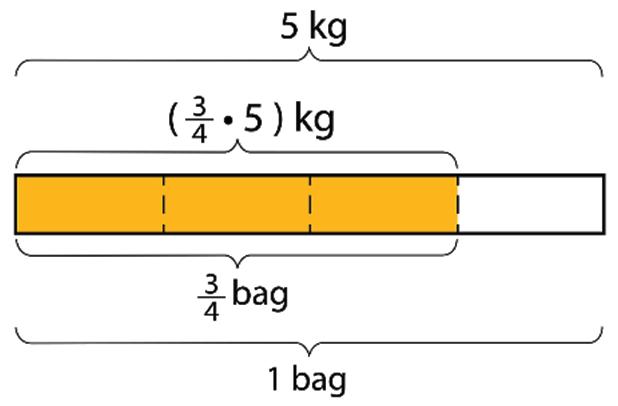
Sometimes it may be necessary to find what fraction of a group an amount is.

For example, suppose a full bag of flour weighs 6 kg, and a chef used 3 kg of flour. What fraction of a full bag was used? In other words, what fraction of 6 kg is 3 kg?

This question can be represented by a multiplication equation and a division equation, as well as by a diagram. ___ ⋅ 6 = 3 3 ÷ 6 = ___

The diagram can be used to show that 3 is 1 2 of 6, which can be checked using multiplication: 1 2 ⋅ 6 = 3.

A division equation can be used to find the answer in any situation where we want to know what fraction 1 number is of another number.

For example, “What fraction of 3 is 2 1 4 ?” can be expressed as ? ⋅ 3 = 2 1 4 , which can also be written as 2 1 4 ÷ 3 = ?.

The answer to “what is 2 1 4 ÷ 3?” is also the answer to the original question.

The diagram shows that 3 wholes contain 12 fourths, and 2 1 4 contains 9 fourths, so the answer to this question is 9 12 , which is equivalent to 3 4 .

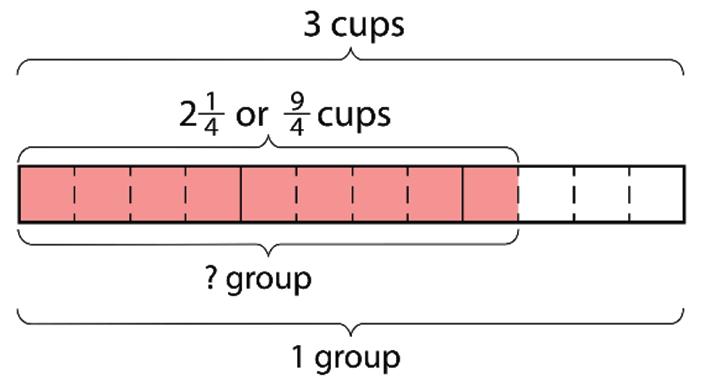
Diagrams can also be used to solve other division problems that require finding fractions of a group.

For example, the diagram shown can be used to answer the question “what fraction of 9 4 is 3 2 ?”

This question can also be expressed as 3 2 ÷ 9 4 = ?.

The diagram shows that the quotient is 6 9 , which is equivalent to 2 3 . Use multiplication to check this.

2 3 ⋅ 9 4 = 18 12 , and 18 12 is indeed equal to 3 2 .

Practice Problems

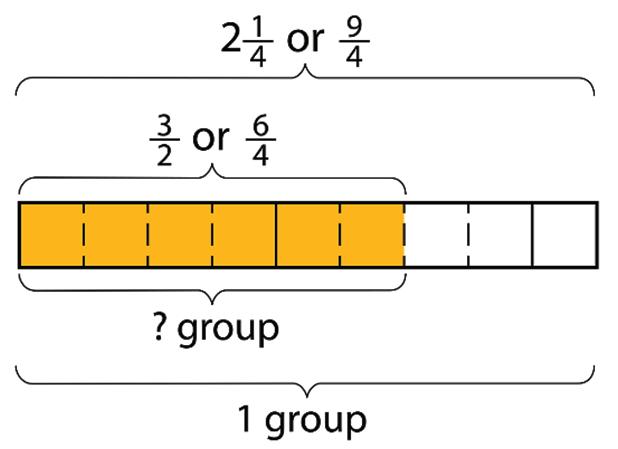
1. A recipe calls for 1 2 of a pound (lb.) of flour for 1 batch. How many batches can be made with each of these amounts of flour?

a. 1 lb

b. 3 4 lb.

c. 1 4 lb.

2. Whiskers and Piglio are cats. Whiskers weighs 2 2 5 kg, and Piglio weighs 4 kg. Determine how many times as heavy Whiskers is compared to Piglio. Include a multiplication equation and a division equation in your answer.

3. Isabella is walking from home to a festival that is 1 5 8 kilometers (km) away. She walks 1 4 km and then takes a quick rest. Which question can be represented by the equation ___ · 1 5 8 = 1 4 in this situation?

A. What fraction of the trip has Isabella completed?

B. What fraction of the trip is left?

C. How many more km does Isabella have to walk to get to the festival?

D. How many km is it from home to the festival and back home?

4. Draw a tape diagram to represent the question: What fraction of 2 1 2 is 4 5 ? Then find the answer.

Review Problem

5. How many groups of 3 4 are in each of these quantities?

Unit 5, Lesson

6: How Much in Each Group?

Warm-Up: Inventing a Situation

1. Think of a situation with a question that can be represented by the equation 12 ÷ 2 5 = ? Describe the situation and the question.

2. Trade descriptions with your partner, and answer your partner’s question.

ManuscriptCopy

Collaborative Activity: How Much in One Batch?

To make 5 batches of cookies, 10 cups (c.) of flour are required.

How many c. of flour does each batch require?

Two equations and a diagram representing this situation are shown.

5 ⋅ ? = 10 10 ÷ 5 = ?

The equations and diagram can be used to show that each batch requires 2 c. of flour.

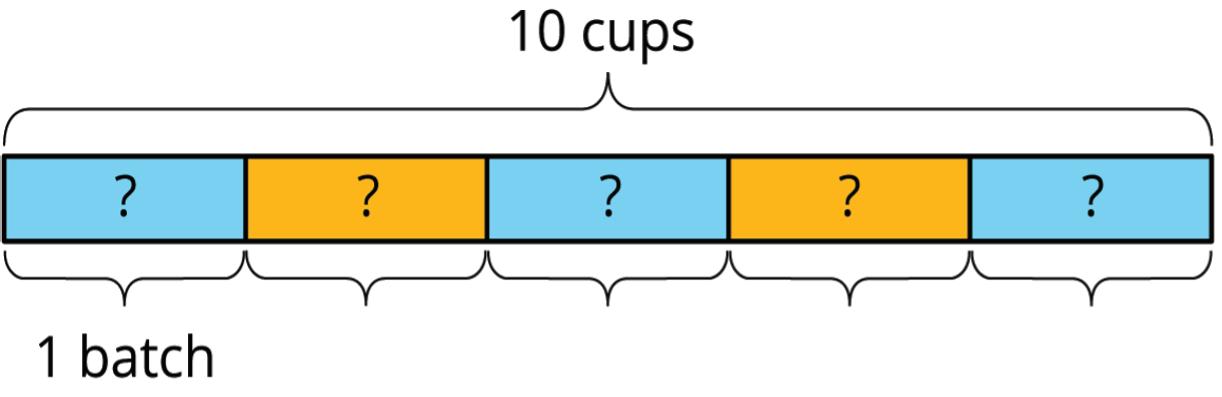
For each question, write a multiplication equation and a division equation, draw a diagram, and find the answer.

1. To make 4 batches of cupcakes, 6 c. of flour are needed. How many c. of flour are needed for 1 batch?

2. To make 1 2 of a batch of rolls, 5 4 c. of flour are needed. How many c. of flour are needed for 1 batch?

3. To make 2 5 of a batch of bread, 2 c. of flour are needed. How many c. of flour are needed for 1 batch?

Collaborative Activity: One Container and One Section of Highway

Here are three tape diagrams that represent situations about filling containers of water.

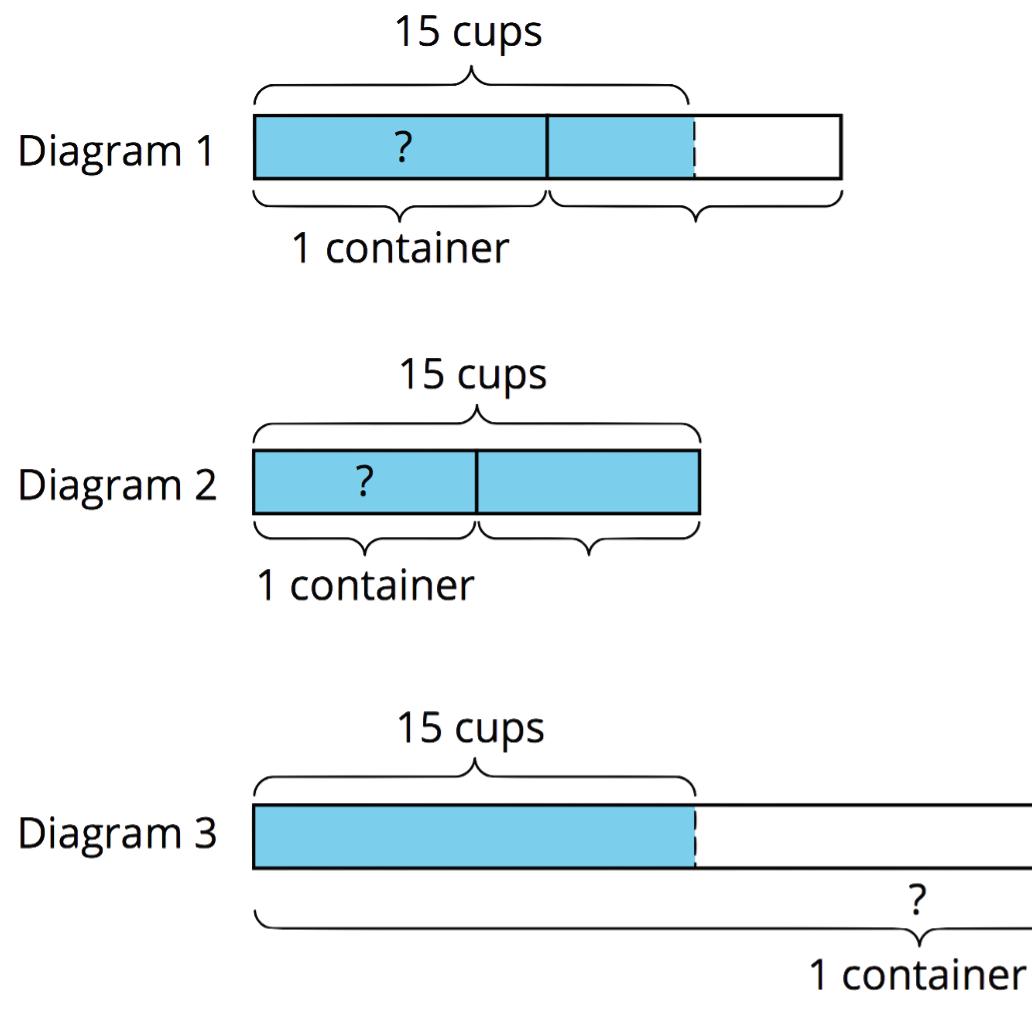
Match each situation to a diagram and use the diagram to help you answer the question. Then, write a multiplication equation and a division equation to represent the situation.

1. Tyler poured a total of 15 c. of water into 2 equal-sized bottles and filled each bottle. How much water was in each bottle?

2. Kiran poured a total of 15 c. of water into equal-sized pitchers and filled 1 1 2 pitchers. How much water was in the full pitcher?

3. It takes 15 c. of water to fill 1 3 pail. How much water is needed to fill 1 pail?

Here are tape diagrams that represent situations about cleaning sections of highway.

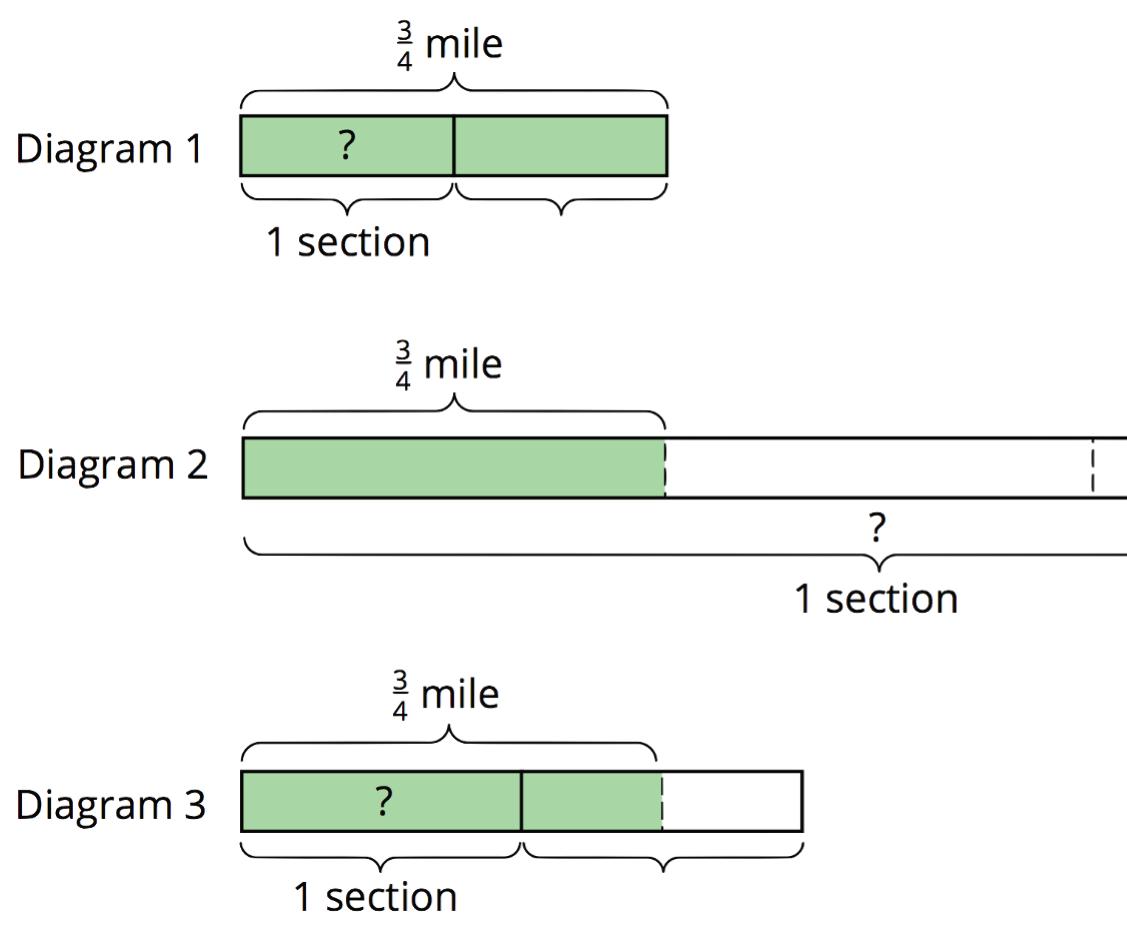
Match each situation to a diagram and use the diagram to help you answer the question. Then, write a multiplication equation and a division equation to represent the situation.

4. Priya’s class has adopted two equal sections of a highway to keep clean. The combined length is 3 4 of a mile (mi.). How long is each section?

5. Lin’s class has also adopted some sections of highway to keep clean. If 1 1 2 sections are 3 4 mi. long, how long is each section?

6. A school has adopted a section of highway to keep clean. If 1 3 of the section is 3 4 mi. long, how long is the section?

ManuscriptCopy

Collaborative Activity: Two Water Containers

1. After looking at these pictures, Lin says, “I see the fraction 2 5 .” Jada says, “I see the fraction 3 4 .” What quantities are Lin and Jada referring to?

2. Consider the problem: How many liters (L) of water fit in the water dispenser?

a. Write a multiplication equation and a division equation for the question.

b. Find the answer and explain your reasoning. If you get stuck, consider drawing a diagram.

c. Check your answer using the multiplication equation.

Lesson Summary

Division can be used to find how much is in 1 group when given an amount for multiple groups.

For example, if 5 people share 8 1 2 pounds (lb.) of cherries equally, how many lb. of cherries does each person get?

This situation can be represented using the diagram or the equations shown.

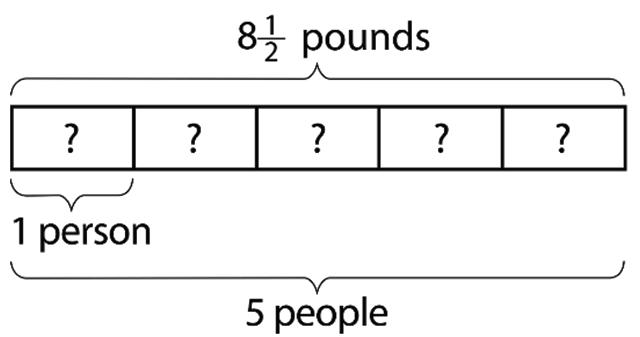
8 1 2 ÷ 5 can be rewritten as 17 2 ÷ 5. Dividing by 5 is equivalent to multiplying by 1 5 , and

17 2 ⋅ 1 5 = 17 10 . This means each person gets 1 7 10 lb. of cherries.

For other contexts, division can be used to find the size of 1 group when given the amount for a fraction of a group.

For example, suppose Jada poured 5 c. of iced tea in a pitcher and filled 2 3 of the pitcher. How many c. of iced tea fill the entire pitcher?

This situation can be represented using the diagram or the equations shown.

2 3 ⋅ 15 2 = 30 6 , and 30 6 = 5. ManuscriptCopy

The diagram can be used to reason about the answer. If 2 3 of a pitcher is 5 c., then 1 3 of a pitcher is half of 5, which is 5 2 . Because there are 3 thirds in 1 whole, there would be

⋅ 5 2 �, or 15 2 c., in 1 whole pitcher. Multiplication can be used to check the answer.

Consider another example: 3 4 of a lb. of rice fills 2 5 of a container.

There are 2 whole amounts to keep track of — 1 whole lb. and 1 whole container. Different equations and diagrams could be used depending on the question asked about this context.

Question Equations

How many lb. fill 1 container?

Reasoning and Answer

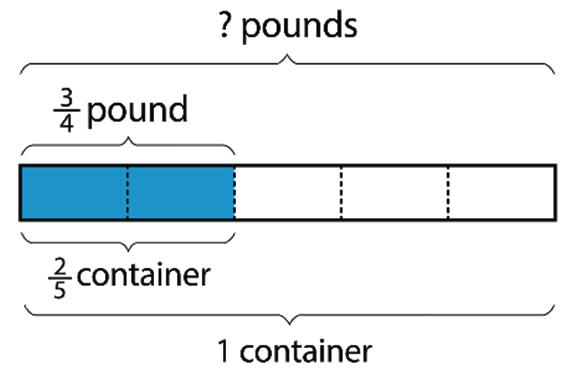
If 2 5 of a container is filled with 3 4 of a lb., then 1 5 of a container is filled with half of 3 4 , or 3 8 , lb. One whole container then has 5 ⋅ 3 8 , or 15 8 lb.

Question Equations Diagram What fraction of a container does 1 lb. fill? 3

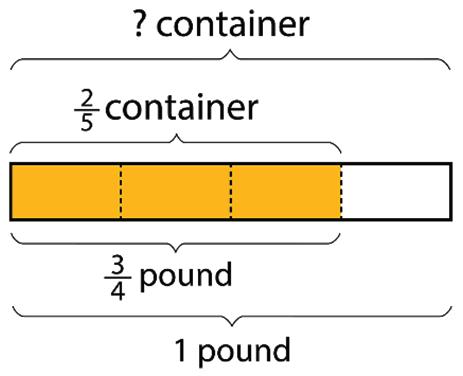
Reasoning and Answer If 3 4 of a lb. fills 2 5 of a container, then 1 4 lb. fills a third of 2 5 , or 2 15 , of a container. One whole lb. then fills 4 ⋅ 2 15 , or 8 15 of a container.

Practice Problems

1. For each situation, complete the tape diagram to represent and answer the question.

a. Mai has picked 1 c. of strawberries for a cake, which is enough for 3 4 of the cake. How many c. does she need for the whole cake?

b. Priya has picked 1 1 2 c. of raspberries, which is enough for 3 4 of a cake. How many c. does she need for the whole cake?

2. Consider the problem: Tyler painted 9 2 square yards (sq. yd.) of wall area with 3 gallons (gal.) of paint. How many gal. of paint does it take to paint each sq. yd. of wall?

a. Write multiplication and division equations to represent the situation.

b. Draw a diagram to represent and answer the question.

ManuscriptCopy

3. A group of friends is sharing 2 1 2 lb. of berries.

a. If each friend received 5 4 of a lb. of berries, how many friends are sharing the berries?

b. If 5 friends are sharing the berries, how many lb. of berries does each friend receive?

Review Problem

4. Without calculating, order the quotients from smallest to largest.

a. Explain how you decided the order of the three expressions.

b. Find a number n so that 56 ÷ n is greater than 1 but less than 7.

ManuscriptCopy

Unit 5, Lesson 7: Dividing by Unit and Non-unit Fractions

Warm-Up: Dividing by a Whole Number

1. Work with a partner. One person solves the problems labeled “Partner A,” and the other person solves those labeled “Partner B.” Write an equation for each question. If you get stuck, consider drawing a diagram in the space provided.

Partner A Partner B

How many 2s are in 16?

Division equation: What is 16 groups of 1 2 ?

Multiplication equation:

Diagram

How many 4s are in 16?

Division equation: What is 16 groups of 1 4 ?

Multiplication equation:

How many 8s are in 16?

Division equation: What is 16 groups of 1 8 ?

Multiplication equation:

2. What do you notice about the diagrams and equations? Discuss with your partner.

3. Complete this sentence based on what you noticed.

Dividing by a whole number a produces the same result as multiplying by

Exploration Activity: Dividing by Unit Fractions

To find the value of 6 ÷ 1 2 , Elena thought, “How many 1 2 s are in 6?” and then she drew this tape diagram. It shows 6 ones, with each one partitioned into 2 equal pieces.

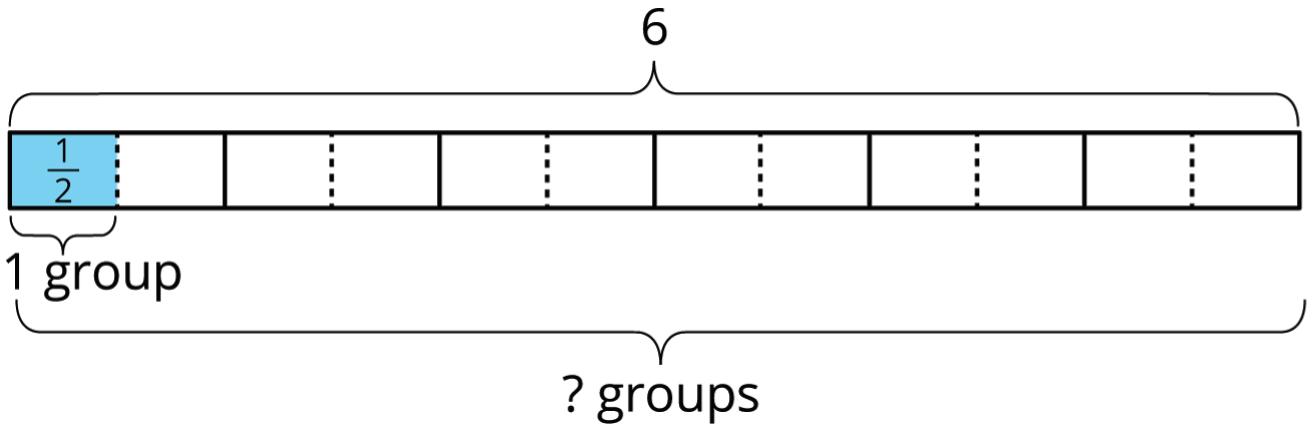
1. For each division expression, complete the diagram using the same method as Elena. Then, find the value of the expression.

6 ÷ 1 3

Value of the expression: ____________

b. 6 ÷ 1 4

Value of the expression: ____________

c. 6 ÷ 1 6

Value of the expression: ____________

ManuscriptCopy

2. Examine the expressions and answers more closely. Look for a pattern. How could you find how many halves, thirds, fourths, or sixths were in 6 without counting all of them? Explain your reasoning.

a.

3. Use the pattern you noticed to find the values of these expressions. If you get stuck, consider drawing a diagram.

4. Find the value of each expression.

Exploration Activity: Dividing by Non-Unit Fractions

1. To find the value of 6 ÷ 2 3 , Elena started by drawing a diagram the same way she did for 6 ÷ 1 3 .

a. Complete the diagram to show how many 2 3 s are in 6.

b. Elena says, “To find 6 ÷ 2 3 , I can just take the value of 6 ÷ 1 3 and then either multiply it by 1 2 or divide it by 2.” Do you agree with her? Explain your reasoning.

2. For each division expression, complete the diagram using the same method as Elena. Then, find the value of the expression. Think about how you could find that value without counting all the pieces in your diagram.

a. 6 ÷ 3 4

b. 6 ÷ 4 3

3. Elena examined her diagrams and noticed that she always took the same two steps to show division by a fraction on a tape diagram. She said:

“My first step was to divide each 1 whole into as many parts as the number in the denominator. So if the expression is 6 ÷ 3 4 , I would break each 1 whole into 4 parts. Now I have 4 times as many parts.

My second step was to put a certain number of those parts into one group, and that number is the numerator of the divisor. So if the fraction is 3 4 , I would put 3 of the 1 4 s into one group. Then I could then tell how many 3 4 s are in 6.”

Which expression represents how many 3 4 s Elena would have after these two steps? Be prepared to explain your reasoning.

4. Use the pattern Elena noticed to find the values of these expressions. If you get stuck, consider drawing a diagram.

Lesson Summary

Reasoning can be used to answer the question “how many 1 3 s are in 4?” or “what is 4 ÷ 1 3 ?”. There are 3 thirds in 1, so there are (4 ⋅ 3) thirds, or 12 thirds, in 4.

In other words, dividing 4 by 1 3 has the same outcome as multiplying 4 by 3. 4 ÷ 1 3 = 4 ⋅ 3

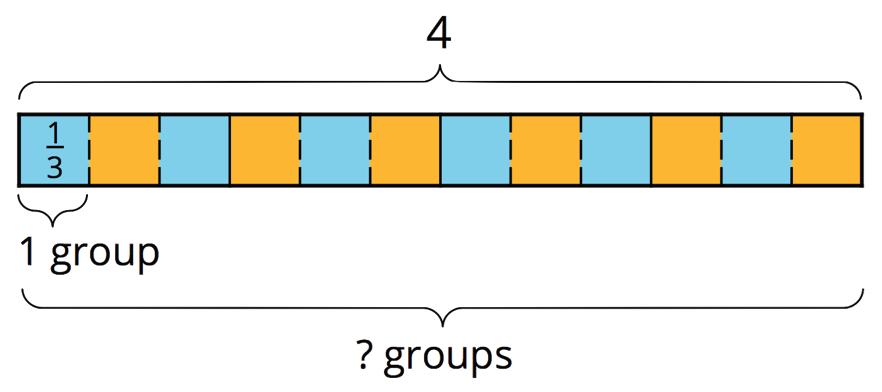
In general, dividing a number by a unit fraction 1 p is the same as multiplying the number by ��, which is the reciprocal of 1 p .

If p is a rational number that is not zero, then the reciprocal of p is the number 1 p .

Similar reasoning can be used to think about 4 ÷ 2 3 .

There are (4 ⋅ 3), or 12, 1 3 s in 4. To find how many 2 3 s are in 4, combine every 2 of the 1 3 s into a group. Doing this results in half as many groups, which is 6 groups. This thinking is represented by the diagram and equations shown.

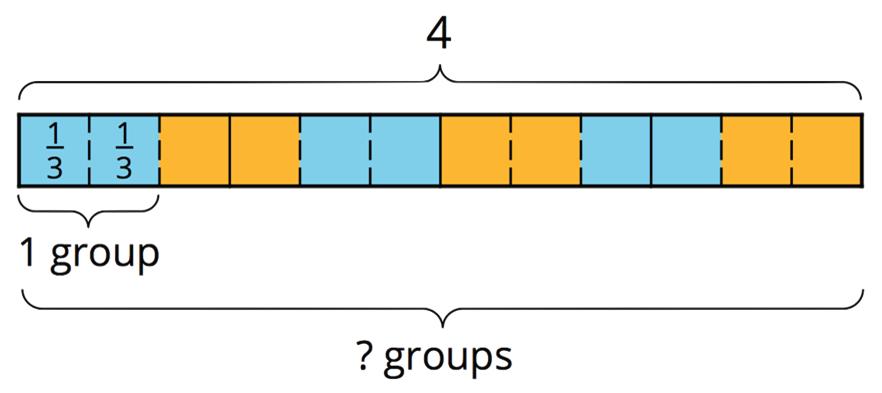
In general, dividing a number by a b is the same as multiplying the number by b and then dividing by ��, or multiplying the number by �� and then by 1 �� .

Practice Problems

1. Priya is sharing 24 apples equally with some friends. She uses division to determine how many people can have a share if each person gets a particular number of apples. For example, 24 ÷ 4 = 6 means that if each person gets 4 apples, then 6 people can have apples. Here are some other calculations:

a. Priya thinks the “?” represents a number less than 24. Do you agree? Explain or show your reasoning.

b. In the case of 24 ÷ 1 2 = ?, how many people can have apples?

2. Here is a centimeter ruler.

a. Use the ruler

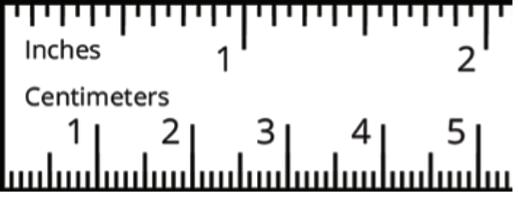
b. What calculation did you do each time?

c. Use this pattern

d. Explain how you

3. Find each quotient.

4. Use the fact that 2

. Explain or show your reasoning.

Review Problems

5. It takes one week for a crew of workers to pave 3 5 kilometer (km) of a road. At that rate, how long will it take to pave 1 km?

Write a multiplication equation and a division equation to represent the question. Then find the answer and show your reasoning.

6. Calculate each percentage mentally.

a. 25% of 400

b. 50% of 90

c. 75% of 200

ManuscriptCopy

d. 10% of 8,000

e. 5% of 20

Unit 5, Lesson 8: Using an Algorithm to Divide Fractions

Warm-Up: Multiply Fractions

Evaluate each expression.

Exploration Activity: Dividing a Fraction by a Fraction

Work with a partner. One person works on the questions labeled “Partner A,” and the other person works on those labeled “Partner B.”

1. Partner A: Find the value of each expression by completing the diagram.

a. 3 4 ÷ 1 8

How many 1 8 s in 3 4 ?

b. 9 10 ÷ 3 5

How many 3 5 s in 9 10 ?

Partner B:

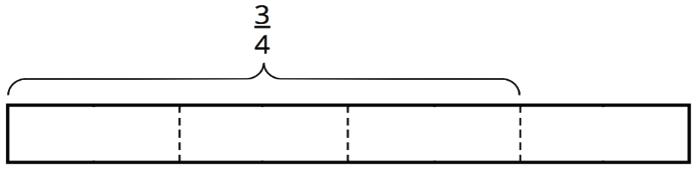
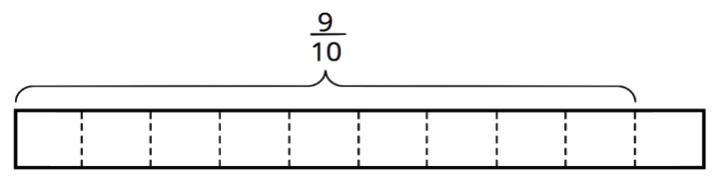
Elena said: “If I want to divide 4 by 2 5 , I can multiply 4 by 5 and then divide it by 2 or multiply it by 1 2 .”

Find the value of each expression using the strategy Elena described.

c. 3 4 ÷ 1 8 d. 9 10 ÷ 3 5

2. What do you notice about the diagrams and expressions? Discuss with your partner.

3. Complete this sentence based on what you noticed:

To divide a number n by a fraction a b , we can multiply n by ________ and then divide the product by ________.

4. Select all equations that represent the statement you completed.

Collaborative Activity: Using an Algorithm to Divide Fractions

Calculate each quotient. Show your work, and be prepared to explain your reasoning.

6. After biking 5 1 2 miles (mi.), Adriana has traveled 5 8 of the length of her trip.

a. Write an equation that can be used to determine the length, in mi., of her entire trip.

b. Determine the length of Adriana’s trip.

Lesson Summary

The equation a ÷ 3 4 = ? is equivalent to 3 4 ⋅ ? = a, so it can be interpreted as meaning “ 3 4 of what number is a?” The diagram can be used to represent the situation where the length of the entire diagram represents the unknown number. If 3 4 of a number is a, then, to find the number, first divide a by 3 to find 1 4 of the number, and then multiply the result by 4.

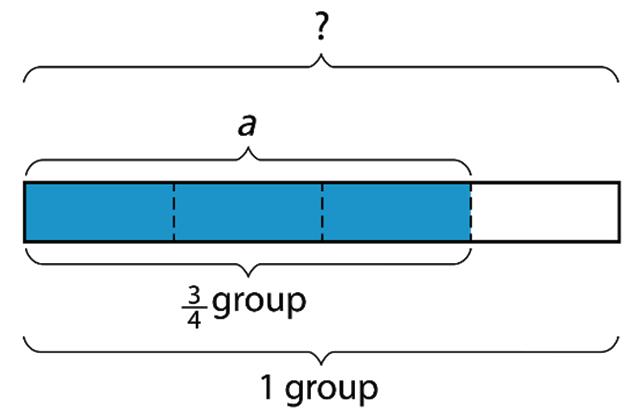
These steps can be written as a

. Dividing by 3 is the same as multiplying by 1 3 , so they can also be expressed as

In other words, a ÷

In general, dividing a number by a fraction c d is the same as multiplying the number by d c , which is the reciprocal of the fraction.

Practice Problems

1. Select all statements that show correct reasoning for finding 14 15 ÷ 7 5

□ Multiplying 14 15 by 5 and then by 1 7 .

□ Dividing 14 15 by 5, and then multiplying by 1 7 .

□ Multiplying 14 15 by 7, and then multiplying by 1 5 .

□ Multiplying 14 15 by 5 and then dividing by 7.

□ Multiplying 15 14 by 7 and then dividing by 5.

2. Clare said that 7 4 ÷ 5 2 is 35 8 . She reasoned: 7 4 5 = ⋅ 35 4 and 35 4 ÷ 2 = 35 8 .

Explain why Clare’s answer and reasoning are incorrect. Find the correct quotient.

3. Find the value of 35 4 ÷ 5 8 . Show your reasoning.

4. Kiran has 2 3 4 pounds (lb.) of flour. When he divides the flour into equal-sized bags, he fills 4 1 8 bags. How many lb. fit in each bag?

Write a multiplication equation and a division equation to represent the question Then, find the answer and show your reasoning.

5. Divide 4 1 2 by each unit fraction.

a. 1 8 b. 1 4

6. After charging for 1 3 of an hour (hr.), a phone is at 2 5 of its full power. How long will it take the phone to charge completely?

Decide whether each equation can represent the situation.

7. Elena and Noah are each filling a bucket with water. Noah’s bucket is 2 5 full and the water weighs 2 1 2 lb. How much does Elena’s water weigh if her bucket is full and her bucket is identical to Noah’s?

a. Write multiplication and division equations to represent the question.

b. Draw a diagram to show the relationship between the quantities and to find the answer.

Unit 5, Lesson 9: Fractional Lengths

Warm-Up: Multiplication Strategies

Find the product mentally.

19 ∙ 14

Collaborative Activity: How Many Times as Tall or as Far?

1. A 2nd-grade student is 4 feet (ft.) tall. Her teacher is 6 2 5 ft. tall.

a. How many times as tall as the student is her teacher?

b. What fraction of the teacher’s height is the student’s height?

2. Find each quotient. Show your reasoning and check your answer. a. 9 ÷ 3 5 b. 1 7 8 ÷ 3 4

3. Write a division equation that can help answer each of these questions. Then find the answer. If you get stuck, consider drawing a diagram.

a. A runner ran 1 4 5 miles (mi.) on Monday and 6 3 10 mi. on Tuesday. How many times her Monday’s distance was her Tuesday’s distance?

b. A cyclist planned to ride 9 1 2 mi. but only managed to travel 3 7 8 mi. What fraction of his planned trip did he travel?

Exploration Activity: Comparing Paper Rolls

The photo shows a situation that involves fractions.

1. Complete the sentences. Be prepared to explain your reasoning.

a. The length of the long tube is about ______ times the length of a short tube.

b. The length of a short tube is about ______ times the length of the long tube.

ManuscriptCopy

2. If the length of the long paper roll is 11 1 4 inches (in.), what is the length of each short paper roll?

Lesson Summary

Division can be used to solve comparison problems to determine how many times as large or as small 1 number is compared to another.

For example, a student is playing 2 songs for a music recital. The first song is 1 1 2 minutes (min.) long. The second song is 3 3 4 min. long.

Two different comparison questions can be asked for this context. Each can be represented by different multiplication and division equations.

• How many times as long as the first song is the second song?

• What fraction of the second song’s length is the first song’s length?

The algorithm can be used to calculate the quotient.

The algorithm can be used to calculate the quotient.

This means the second song is 2 1 2 times as long as the first song.

The first song is 2 5 as long as the second song.

Practice Problems

1. One inch is around 2 11 20 centimeters (cm).

a. How many cm long is 3 in.?

Show your reasoning.

b. What question can be answered by finding 10 ÷ 2 11 20 in this situation?

2. A zookeeper is 6 1 4 ft. tall. A young giraffe in his care is 9 3 8 ft. tall.

a. How many times as tall as the zookeeper is the giraffe?

b. What fraction of the giraffe’s height is the zookeeper’s height?

ManuscriptCopy

3. A rectangular bathroom floor is covered with square tiles that are 1 1 2 ft. by 1 1 2 ft. The length of the bathroom floor is 10 1 2 ft. and the width is 6 1 2 ft.

a. How many tiles does it take to cover the length of the floor?

b. How many tiles does it take to cover the width of the floor?

Review Problems

4. The Food and Drug Administration (FDA) recommends a certain amount of nutrient intake per day called the “daily value.” Food labels usually show percentages of the daily values for several different nutrients, like calcium, iron, vitamins, etc.

In 3 4 cup (c.) of oatmeal, there is 1 10 of the recommended daily value of iron. What fraction of the daily recommended value of iron is in 1 c. of oatmeal?

Write a multiplication equation and a division equation to represent the question. Then find the answer and show your reasoning.

5. Noah says, “There are 2 1 2 groups of 4 5 in 2.” Do you agree with him? Draw a tape diagram to show your reasoning. Use graph paper, if needed.

ManuscriptCopy

Unit 5, Lesson 10: Rectangles with Fractional Side Lengths

Warm-Up: Areas of Squares

1. What do you notice about the areas of the squares?

2. Kiran says, “A square with side lengths of 1 3 inch (in.) has an area of 1 3 square inches (sq. in.).” Do you agree?

Explain or show your reasoning.

Exploration Activity: Areas of Squares and Rectangles

Your teacher will give you graph paper and a ruler.

1. On the graph paper, draw a square with side lengths of 1 in. Inside this square, draw another square with side lengths of 1 4 in.

Use your drawing to answer the questions.

a. How many squares with side lengths of 1 4 in. can fit in a square with side length of 1 in.?

b. What is the area of a square with side lengths of 1 4 in.? Explain or show your reasoning.

2. On the graph paper, draw a rectangle that is 3 1 2 in. by 2 1 4 in.

For each question, write a division expression and then find the answer.

a. How many 1 4 in. segments are in a length of 3 1 2 in.?

b. How many 1 4 in. segments are in a length of 2 1 4 in.?

3. Use your drawing to show that a rectangle that is 3 1 2 in. by 2 1 4 in. has an area of 7 7 8 sq. in.

Collaborative Activity: Areas of Rectangles

Each of these multiplication expressions represents the area of a rectangle.

1. All regions shaded in light blue have the same area. Match each diagram to the expression that you think represents its area. Be prepared to explain your reasoning.

2. Use the diagram that matches

to show that the

Collaborative Activity: How Many Would It Take?

Noelle would like to cover a rectangular tray with rectangular tiles. The tray has a width of 11 1 4 in. and an area of 50 5 8 sq. in.

1. Find the length of the tray in inches.

ManuscriptCopy

2. If the tiles are each 3 4 in. by 3 4 in., how many would Noelle need to cover the tray completely, without gaps or overlaps? Explain or show your reasoning.

3. Draw a diagram to show how Noelle could lay the tiles. Your diagram should show how many tiles would be needed to cover the length and width of the tray, but your diagram does not need to show every tile.

Lesson Summary

If a rectangle has side lengths of a units and b units, the area is (a ∙ b) square units (sq. units). For example, for a rectangle with 1 2 in. side lengths, its area is 1 2 ⋅ 1 2 , or 1 4 sq. in.

This means that if the area and 1 side length of a rectangle are given, division can be used to find the other side length.

If 1 side length of a rectangle is 10 1 2 in. and the rectangle’s area is 89 1 4 sq. in., the relationship between the area and side lengths can be represented using the equation shown.

ManuscriptCopy

The other side length, in in., can be found using division.

Practice Problems

1. A rectangle is shown with an area of 16 1 2 square meters (sq. m) and a side length of 2 3 4 meters (m).

a. Find the unknown side length of the rectangle. Show your reasoning.

b. Check your answer using multiplication.

2. A worker is tiling the floor of a rectangular room that is 12 feet (ft.) by 15 ft. The tiles are square with side lengths of 1 1 2 ft. How many tiles are needed to cover the entire floor? Show your reasoning.

3. A television screen has length 16 1 2 in., width w in., and area 462 sq. in. Select all equations that represent the relationship of the side lengths and area of the television.

□ w ⋅ 462 = 16 1 2

□ 16 1 2 ⋅ w = 462

□ 462 ÷ 16 1 2 = w

□ 462 ÷ w = 16 1 2

□ 16 1 2 ⋅ 462 = w

4. The area of a rectangle is 17 1 2 sq. in. and its shorter side is 3 1 2 in. Draw a diagram that shows this information. What is the length of the longer side?

Review Problems

5. A bookshelf is 42 in. long.

a. How many books of length 1 1 2 in. will fit on the bookshelf? Explain your reasoning.

b. A bookcase has 5 of these bookshelves. How many ft. of shelf space is there? Explain your reasoning.

6. It takes 1 1 4 min. to fill a 3-gallon (gal.) bucket of water with a hose. At this rate, how long does it take to fill a 50-gallon (gal.) tub? If you get stuck, consider using a table.

Unit 5, Lesson 11: Fractional Lengths in Triangles and Prisms

Warm-Up: Area of a Triangle

Find the area of triangle A in square centimeters (sq. cm). Show your reasoning.

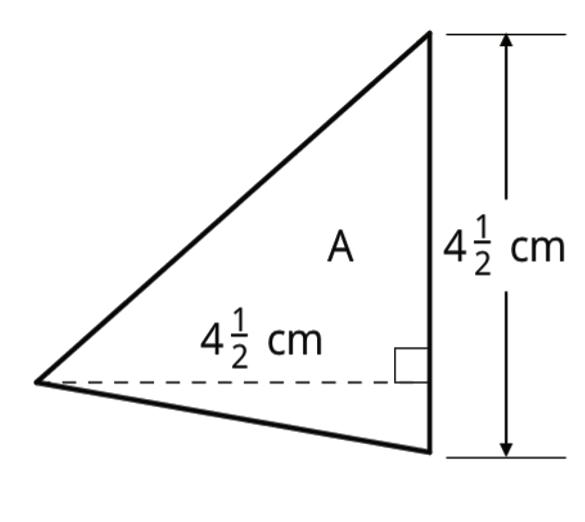
Collaborative Activity: Bases and Heights of Triangles

1. The area of triangle B is 9 square units (sq. units). Find the length of b. Show your reasoning.

ManuscriptCopy

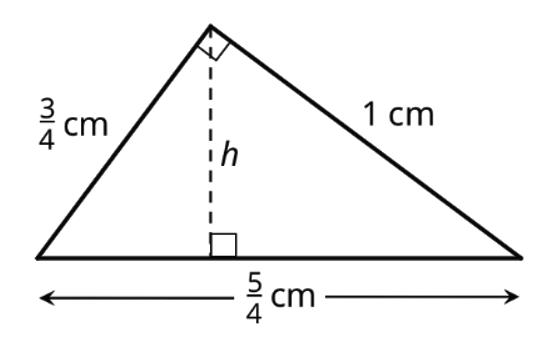
2. The area of triangle C is 54 5 sq. units. What is the length of h? Show your reasoning.

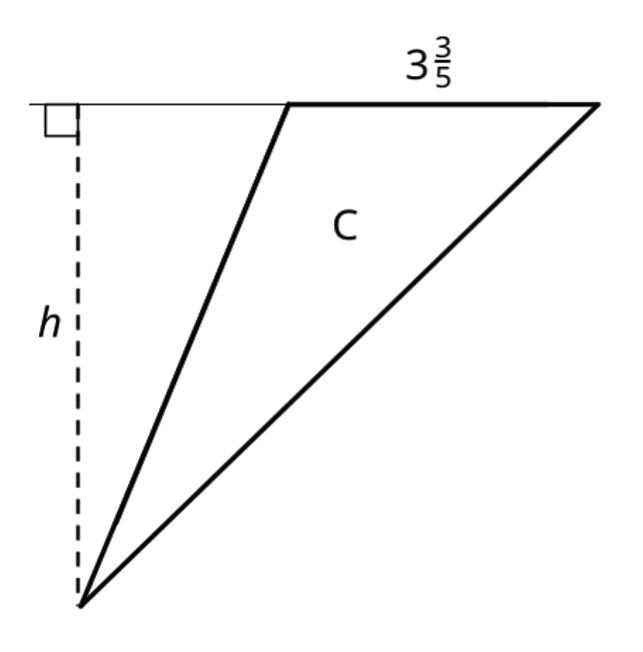
Collaborative Activity: Fish Tank and a Baking Pan

1. A nature center has a fish tank in the shape of a rectangular prism. The tank is 10 feet (ft.) long, 8 1 4 ft. wide, and 6 ft. tall.

a. What is the volume of the tank in cubic feet (cu. ft.)? Explain or show your reasoning.

b. The nature center's caretaker filled 4 5 of the tank with water. What was the volume of the water in the tank in cu. ft.? What was the height of the water in the tank? Explain or show your reasoning.

c. Another day, the tank was filled with 330 cu. ft. of water. The height of the water was what fraction of the height of the tank? Show your reasoning.

2. Clare’s recipe for banana bread won’t fit in her favorite pan. The pan is 8 1 2 inches (in.) by 11 in. by 2 in. The batter fills the pan to the very top, and when baking, the batter spills over the sides. To avoid spills, there should be about an inch between the top of the batter and the rim of the pan.

Clare has another pan that is 9 in. by 9 in. by 2 1 2 in. If she uses this pan, will the batter spill over during baking?

Lesson Summary

If a triangle has a base length of b units and a height of h units, the triangle’s area is the product of 1 2 , b, and h.

If the area and either the base or height are known, divide to find the missing dimension.

For example, if the area of a triangle is 5 5 8 sq. cm, the base is 9 4 cm, and the height is unknown, a multiplication equation can be written to to represent the situation.

Find the height using division.

If a rectangular prism has edge lengths of a units, b units, and c units, the volume is the product of a, b, and c.

If the volume and 2 edge lengths are known, divide to find the third edge length.

For example, if the volume of a rectangular prism is 400 1 2 cu. ft., one edge length is 11 2 ft., another is 6 ft., and the third edge length is unknown, a multiplication equation can be written to represent the situation.

Find the third edge length using division.

Practice Problems

1. The triangle has an area of 7 7 8 sq. cm and a base of 5 1 4 cm.

What is the length of h? Explain your reasoning.

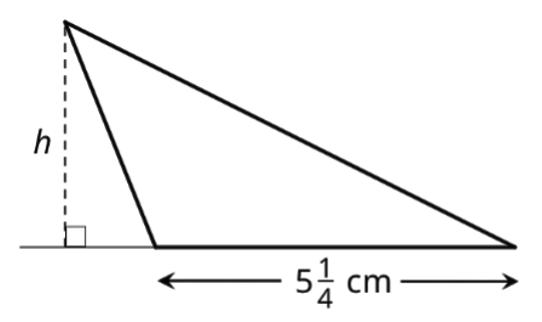
2. Here is a right triangle.

a. What is its area?

b. What is the height h for the base that is 5 4 units long? Show your reasoning.

ManuscriptCopy

3. A pool in the shape of a rectangular prism is being filled with water. The length of the pool is 24 ft., and the width of the pool is 15 ft. If the height of the water in the pool is 1 3 8 ft., what is the volume of the water, in cu. ft.?

Review Problems

4. A builder is building a fence with 6 1 4 in. wide wooden boards, arranged side-by-side with no gaps or overlaps. How many boards are needed to build a fence that is 150 in. long? Show your reasoning.

ManuscriptCopy

5. Here is a table that shows the ratio of flour to water in an art paste. Complete the table with values in equivalent ratios.

ManuscriptCopy

Unit 5, Lesson 12: Solving Problems Involving Fractions

Warm-Up: Operations with Fractions

Without calculating, order the expressions according to their values from least to greatest. Be prepared to explain or show your reasoning.

Exploration Activity: Situations with Three-Fourths and Halves

Here are four situations that involve 3 4 and 1 2 .

• Before calculating, decide if each answer is greater than 1 or less than 1.

• Write a multiplication equation or division equation for the situation.

• Answer the question. Show your reasoning. Draw a tape diagram, if needed.

1. There was 3 4 liter (L) of water in Andre’s water bottle. Andre drank 1 2 of the water. How many L of water did he drink?

2. The distance from Han’s house to his school is 3 4 kilometer (km). Han walked 1 2 km. What fraction of the distance from his house to the school did Han walk?

3. Priya’s goal was to collect 1 2 kilogram (kg) of trash. She collected 3 4 kg of trash. How many times her goal was the amount of trash she collected?

4. Mai’s class volunteered to clean a park with an area of 1 2 square mile (sq. mi.).

Before they took a lunch break, the class had cleaned 3 4 of the park. How many sq. mi. had they cleaned before lunch?

Collaborative Activity: Pairs of Problems

1. Write an equation for each question. Work with your partner so that 1 person works on the questions labeled Partner A and the other works on those labeled Partner B.

Partner A

A1: Natan’s bottle holds 3  1 4 cups (c.) of water. He drank 1 c. of water. What fraction of the water in the bottle did he drink?

A2: The area of a rectangle is 14 1 2 square centimeters (sq. cm), and one side is 4 1 2 cm. How long is the other side?

A3: A stack of magazines is 4 2 5 inches (in.) high. The stack needs to fit into a box that is 2  1 8 in. high. How many inches too high is the stack?

Partner B

B1: Natan’s bottle holds 3 1 4 c. of water. After he drank some, there were 1 1 2 c. of water in the bottle. How many c. did he drink?

B2: The side lengths of a rectangle are 4 1 2 cm and 2 2 5 cm. What is the area of the rectangle?

B3: A stack of magazines is 4 2 5 in. high. Each magazine is 2 5 in. thick. How many magazines are in the stack?

2. Trade papers with your partner, and check your partner’s equations. If you disagree, work together to reach an agreement.

3. For each question:

a. Estimate the answer before calculating it.

b. Find the answer, and show your reasoning.

ManuscriptCopy

Collaborative Activity: Baking Cookies

Nico, Katt, and Max are baking cookies together. They need 3 4 c. of flour and 2 5 c. of butter to make a batch of cookies. They each brought the ingredients they had at home.

• Nico brought 2 c. of flour and 1 4 c. of butter.

• Katt brought 1 c. of flour and 1 2 c. of butter.

• Max brought 1 1 4 c. of flour and 3 4 c. of butter.

If the students have plenty of the other ingredients they need (sugar, salt, baking soda, etc.), how many whole batches of cookies can they make? Explain your reasoning.

Lesson Summary

This unit focused on adding, subtracting, multiplying, and dividing with fractions. A summary of strategies for performing each operation with fractions is shown.

• To add or subtract fractions, look for a common denominator so the pieces involved are the same size. This makes it easy to add or subtract the pieces.

• To multiply fractions, multiply the numerators and the denominators.

• To divide a given number by a fraction, a b , multiply the given number by the reciprocal of that fraction, b a .

Where necessary, final answers can be simplified, or reduced, by dividing the answer by a fraction equal to 1. For example, 8 20 can be reduced as shown.

Practice Problems

1. An orange has about 1 4 c. of juice. How many oranges are needed to make 2 1 2 c. of juice? Select all equations that represent this question. □ ? ⋅ 1 4 = 2 1 2

2. Mai, Clare, and Tyler are hiking from a parking lot to the summit of a mountain. They pass a sign that gives distances.

• Mai says: “We are one third of the way there.”

• Clare says: “We have to go twice as far as we have already gone.”

• Tyler says: “The total hike is three times as long as what we have already gone.”

Do you agree with any of them? Explain your reasoning

3. Priya’s cat weighs 5 1 2 pounds (lb.) and her dog weighs 8 1 4 lb. First, estimate the number that would complete each sentence. Then, calculate the answer. If any of your estimates were not close to the answer, explain why that may be.

a. The cat is _______ as heavy as the dog.

b. Their combined weight is _______ lb.

ManuscriptCopy

c. The dog is _______ lb. heavier than the cat. Parking lot: 3 4 mi.

4. A school club sold 300 shirts. 31% were sold to fifth graders, 52% were sold to sixth graders, and the rest were sold to teachers. How many shirts were sold to each group: fifth graders, sixth graders, and teachers? Explain or show your reasoning.

5. Jada has some pennies and dimes. The ratio of Jada’s pennies to dimes is 2 to 3.

a. From the information given, can you determine how many coins Jada has?

b. If Jada has 55 coins, how many of each kind of coin does she have?

c. How much are her coins worth?

ManuscriptCopy

ManuscriptCopy

ManuscriptCopy

ManuscriptCopy