
HAND OUT MATERIAL

MATH - 1
Plug In
Make up numbers for the variables. Do the problem with your numbers until you get a number for an answer. Then see which answer choice gives you that same number.
Here are some common characteristics of Plug-In problems, with examples from problems we've seen:
• Any time you see a problem that has variables in the answer choices, you can definitely use Plug In. If the answer is x + 4, it will always be x + 4, no matter what x is.
• In particular, look out for questions that ask for "x in terms of y''. That's a big sign that Plug In is possible.
• Sometimes you can also use Plug In when there are variables in the question but not in the choices. Sometimes if you plug in for one variable you can figure out the other variables.
• You can use Plug In on problems with implicit variables. You can use Plug In any time there's some concept in the problem and:
1. You don't know its value.
2. There's no way to figure out its value.
3. They still expect you to get an answer.
4. So, it doesn't matter what that value is; you'll get the same answer no matter what.
27. Bob has 4 dollars more than Lisa does. If Lisa has x dollars, how much would Bob have if he doubled his money?
A. x + 4
B. x + 8
C. 2x
D. 2x + 4
E. 2x + 8
28. If x + 5 is 3 less than y, then x -2 is how much less than y?
A. 2
B. 3
C. 7
D. 8
E. 10
29. Scott drives to Bob's house at a speed of30 miles per hour and drives back at a speed of 50 miles per hour. If he takes the same route both ways, what was his average speed, in miles per hour, for the whole trip?
D. 35
G. 37.5
H. 40
J. 42.5
K. Cannot be determined from the given information

MATH - 2 Backsolve
Test the numbers in the answer choices. Start with the middle number, put it through the problem, and see if it matches what you know. If it doesn't, pick a bigger or smaller choice until you find one that works.
Some common characteristics of Backsolve problems:
• There are whole numbers in the answer choices. Any time you need to find some kind of single value or quantity, you've got five options for that value right here. Four of them are wrong, one of them is right. Test them.
• If they're asking you for the value of a variable (i.e., what number does x equal), you can usually use Backsolve. They want to know x? Well, here are five options. Try 'em until you find one that works.
33. Gerry's age is 5 more than three times Carol's age. If the sum of their ages is 45, how old is Carol?
A. 1 O
B. 12
C. 14
D. 16
E. 18
34. If a + b = 9 and a 2 + ab = 36 then b =
A. 3
B. 4
C. 5
J. 6
K. 7
Often, Backsolve questions have two pieces of information. When you test an answer choice, you run the choice through one piece of information and see if it matches the other. In #33 above, we started with "5 more than three times" and checked that the resulting sums were 45. In #42, we started with the first equation and checked that the second came out to 36.

MATH – 3
NUMBER CONCEPTS AND DEFINITIONS
Let's get some terminology out of the way to avoid confusion down the line. Integer: Any number that does not have a fraction or decimal part: . .. -3, -2, -1, 0, 1, 2, 3.
Factor: An integer that can be divided into another integer without a remainder. For example, 3 is a factor of 12 because 12 ÷ 3 = 4. We say the larger number "is divisible by" the smaller number, so here 12 is divisible by 3.'
Prime Number: A number that is divisible only by I and itself. 1 is not a prime number. The only even prime number is 2. Examples of prime numbers include 2, 3, 5, 7, 1 1, and 13.
Remainder: The integer left over when an integer is divided by an integer that is not its factor. For example: 13 ÷ 3 = 4 with a remainder of 1.
Say you wanted to find a number that gives a remainder of 3 when it’s divided by 4. Just take a multiple of 4 and add 3 to it. Any these numbers would fit:
4 + 3 = 7 8 + 3 = 11 12 + 3 = 15 16 + 3 = 19
Properties of Positive and Negative n umbers: Bigger digits give smaller negative numbers. That is, -1 0 is smaller than -2. (Pos) x (Pos) = Pos (Neg) x (Pos) = Neg (Neg) x (Neg) = Pos
Properties of Odd and Even Integers : (Even) x (Even) = Even (Even) x (Odd) = Even (Odd) x (Odd) = Odd
Decimal places: In the number 25.97 2 is in the "tens place" 5 is in the "units place"

In the number 379.045, what digit is in the units place?
Even + Even = Even Even + Odd = Odd
Odd + Odd = Even
9 is in the "tenths place 7 is in the "hundredths place",
If x is an odd positive integer, which of the following expressions must be even? I. 2x II. x + 2
If x has a remainder of 5 when divided by 6 and x > 10, what is the smallest possible value of x?
If j is the largest prime factor of 42, and k is the largest prime factor of 36, what is the value of j + k?


MATH – 6
Exercise #3
- Bob makes some fruit punch that contains apple juice and mango juice in a 1:5 ratio. If he uses 15 pints of the mango juice, how many pints of apple juice will he need?
- An animal shelter has 2 cats for every 3 dogs. If there are 45 animals in the shelter, how many dogs are there?
- At a certain school, the ratio of boys to girls in the seventh grade is 3 to 5. If there are 56 total seventh-graders, how many of them are girls?
- Two numbers x and y are in a direct proportion such that when x = 2,y = 9. What is the value of y when x = 7?

MATH - 7
Exercise #4:
- Mark can eat 20 hot dogs in 4 minutes. How many hot dogs can he eat in S hours?
- Elizabeth jogs for 2 hours each day. Her average jogging speed is 4 miles per hour. If she jogs 5 days a week, how far will she jog over 3 weeks?
- If a car is traveling at a speed of 90 kilometers per hour, how fast is it travelling in meters per second? (1 kilometer= 1,000 meters)
- A town is painting parking spots along the curbs of its streets. Each spot must be 20 feetlong, and each block is 300 feet long. What is the maximum number of parking spots that can fit on one side of a street that is 4 blocks long?
- Mark can eat 20 hot dogs in 4 minutes. Hot dogs are sold in packages containing 12 hot dogs, and packages cost $6 each. How much money will it cost if Mark buys enough hot dogs to eat for 3 hours continuously?

What is 42% of 50?
5 is what percent of 4?
21 is 35% of what number?
What is 15% of75% of80?
A school had 30 reported absences one week and 27 reported absences the following week. What was the percent decrease in the number of absences between the two weeks?

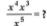

For all nonzero x and y

MATH - 10
Exercise #7
l 8 - 2 l =?
l 2 - 8 l = ?
l6 - 15 l - l 5(-4) l = ?
If l x - 2 l = 6, what are all possible values of x?
If Ix+ 11 I = 23, what are all possible values of x?

MATH - 10
Exercise #7
-If x = 5 and y = 4, what is the value of 3x -4y?
-If x = 3 and k = 12, what is the value of x2 + kx +6 ? 3b+4c
-If a= 3 b+4 c 2 , what is the value of a when b = 6 and c= 10?
-If j = 6km-n,what is the value of j when k= 100, m= 2and n = -10?
- What is the value of 8 x 9 x when x = 1 2

- If 4+(a-4)=9, a=?
- If = 5 x +6 6 = 11, x = ?
MATH - 12
Exercise #9
- If 4u + 11 = 3, u =?
If = 12 x +4 4 = 12, x=?
- If 13 - 3z = 15z + 4, z = ?
- If = 3 x x+5 = 4, x=?
If = 8 x + 2 3 =4 , x +?
- If P = 5(a + 8), what is a in terms of P?
- If = 2 3 x 6 = y , what is x ∈terms of y ?

- If = ab cd = e , what is b in terms of a, c, d, and e ?
MATH - 13
Exercise #10
- Freddie bought a flower for his garden. The equation h = 2.5d + 12 models the height, h, in inches of the flower d days after he purchased it. How much does the plant grow, in inches, every day?
- Sophie runs a lemonade stand and puts the money she makes in her piggy bank. This is modeled by the equation P = 21 + 14, where P is the amount of money in dollars in her bank and l is the number of cups of lemonade she has sold. How much money in dollars does Sophie get for each cup of lemonade?
- Lana got a box of donuts. The equation d = 120 - 5h shows the total number of donuts, d, remaining in the box after h hours. How many donuts were originally in the box?
- The equation c = 0.1 m + 0. 15t + 50 shows the total cost, c, in dollars, of Glenda's mobile phone service each month, where m is the number of minutes of phone calls and tis the number of text messages she sent. How much is Glenda charged each month, in dollars, for each text message?
- Andrew spent one day building a wall in his· backyard and has added to it every week since. The equation b = 25 (w + 10) models the total number of bricks in the wall w weeks after he started. How many bricks did he put in the wall on the first day?

- If j = 3x - 5 and k =6 x + 1, then 2j + 3k= ?
- If a b = 5 and 4a + 7b = 9, what is the value of b?
- If x-y = 10 and z= 3x-3y-8, then z=?
3x+y= 12
7x - y=18
- What is the solution (x, y) to the system of equations above?
4x-3y= 34
2x+5y=4
MATH - 14
Exercise #11
- What is the solution (x, y) to the system of equations above?
6x-7y= 36
2y-3x=-27
- What is the solution (x, y) to the system of equations above?
- If 5x + 2y= 41 and 3x + 2y= 271 then x=?
- If 3x + Sy = 58 and x + 2y = 12, then y = ?
- If 3p + 2q = 8 and 4p + 3q = 11, then 7p + 5q =?
- If 2x + y = 23 and x + 2y = 17, then 3x -3y =?

Solve these inequalities for x:
3(x+2) < 12
17-x > 23
5x + 6 < -3x -10
x+ 4
3 >¿ x 5
7 - 4x ¿ 35
MATH - 15
Exercise #12

- lf f{x) = x2 + 3x -10, then f (10) =?
- If f( x) = x2 + 3x -10, then f(7) =?
- If f(x) = x2 + 3x-10, then f(-3) =?
- If f(x) = x2 + 3x-10, then f(½) =?
- If f(x) = x2 + 3x- 10, then f(2x) =?
- If k(x) = x3 + 2x, what is k(-2)?
MATH - 16
Exercise #13
- If f(x) = 5x - 3 and f(a) = 12, what is the value of a?
- If f(x) = 2x + 2, then 2 f(x) + 2 =?
- If f(x) = 7x and g(x) = f(x) + 7, what is the value of g(10)?
- If f (x) = x2 - 2, what is the value of f(f(3 )) ?

2 + 2x + 5 + 4x2 = 3x – 7 = ?
( 3x2 - 7 x + 2) - ( 2x2+ 5x + 3) = ?
( 6x2 + 5x + 3) - 2( 2x2 - 3x - 3) = ?
3 + 3x2 + 2x + 1 – x3 +9x2 – 11x +8 = ?


- (x + 8)(x -3) = ?
- (a -7)(a -2) = ?
- (2y + 3)(y -4) = ?
- (x+y)2 = ?
- (x 2 + y)(3x2 +2y) =?

MATH 18
Exercise #15
Factor the following expressions:
X2 -2x-8
x2 -14x+24
2x2 +11x+5
9x2 -49
x4 -16

X__ =?
x2 +7x
MATH – 19
Exercise #16
MATH – 20
Exercise #16
_x+5_ = ?
X2-25
X2+6x-40 = ? x-4

- What are the solutions for x 2 - 12x = 0?
- What are the solutions for x 2 - 11x+ 30 = 0?
- What are the solutions for x 2 -7x -8 = 0?
- What are the solutions for x 2 - 81 = 0?
- What are the solutions for x 2 - 13x = -42?

Find these points on the graph provided
(-1) =?
(2) = ?
=?
Exercise #19

MATH – 23
Exercise #19
- What is the slope of the line that passes through the points (2,6) and (4,1)?
- What is the slope of the line that passes through the points (-2,-3) and (-1,5)?
- What is the slope of the line represented by the equation 2x - 6y = 7?
- What is the slope-intercept equation of the line that passes through the points (-1,2) and (1,6)?
- The equation of line/ is y = 3x + 5. If line k is perpendicular to line/ and passes through the point (0,-3), what is the equation of

Here are some other properties of parabolas:
MATH
- 24
- The vertex of the parabola is the point at the very bottom of the curve (or the very top, if the curve points down). This point is also called the maximum or minimum of the curve.
- Notice that this parabola is symmetrical-the left and right sides of the curve are mirror images of each other. That's because the square of a negative comes out positive (in our example: y = 4 when x = 2 and when x = -2.) All parabolas are symmetrical, though they may not be centered on the axis like this.
- If a (the number in front of x2) is positive, the parabola will open upwards. Ifa is negative, the parabola will open downwards.
- The value of a also gives the "squeeziness" of the parabola: a bigger a gives a thinner graph; a smaller a gives a wider graph.
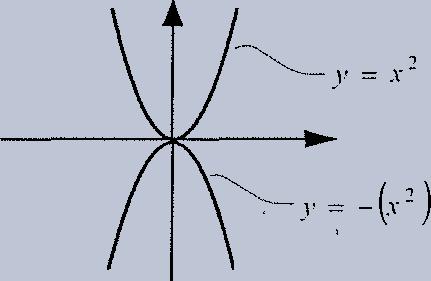
- The value of c (the number that doesn't have any x's next to it) will be the y-intercept of the parabola. Just like in a straight line, they-intercept is the value of y when x = 0. Because c is the only term in the equation that doesn't come with an x next to it, if x = 0, all that's left is c.*

- What is an equation of a circle that has center (2,1) and radius 6 coordinate units?
Exercise # 20
- What is an equation of a circle that has center (-4,0) and radius 5 coordinate units?
- What is an equation of a circle that has center (5,4) and is tangent to the x-axis?
- What is the center of a circle with equation (x+8) 2 +(y-2) 2 =9?

- What is the radius of a circle with equation (x-1) 2 +(y+2)2 =7?

Math - 26
{ 4, 6, 9, 17, 24}
- What is the average (arithmetic mean) _ o f the numbers in the set above?
- A set contains 3 consecutive integers that have a sum of 78. What is the median of the set?
- The 12 trees in John's backyard have an average height of 135 inches. lf7 of the trees have an average height of 100 inches, what is the average height of the other 5 trees?

The following questions all refer to the table below.
Hours of Sleep for 11th Grade Students at Cromwell High School
A survey asked all 70 students in the 11th grade class of Cromwell High School how many hours of sleep they got the previous evening. The results are shown in the provided .
- If a 15-year-old is chosen at random, what is the probability that he or she got 7 hours of sleep?
- If a student who got 7 hours of sleep is chosen at random, what is the probability that he or she is 15 years old?
- What is the probability that a student who is 16 or older got 6 hours of sleep?
- What is the probability that a student in the 11th grade class is 1.S years old?
- What is the probability that a student in the 11th grade class got 7 hours of sleep?
- If a student is chosen at random, what is the probability he or she is a 15-year old who got 7 hours of sleep or a 17-year-old who got 8 hours of sleep?
- What is the probability that someone in the class is 16 years old and got 8 hours of sleep?
- What is the probability that someone in the class is 16 years old and got at least 7 hours of sleep?
- What is the probability that someone in the class is 16 or younger and got less than 7 hours of sleep?
- If a student who got 7 hours of sleep or less is selected at random, what is the probability that he or she is 16 or younger?

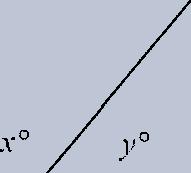
1.A straight line equals 180° .
2. A triangle equals 180° .
MATH – 28
What you need to know about angles
When angles form a straight line, the sum of their measures is 180 °. In this diagram, x + y = 180.
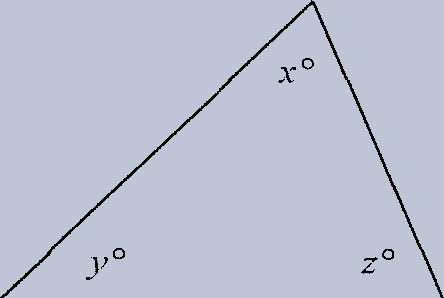
The three angles of a triangle acid up to 180 . In this diagram, x + y + z = 180.
Here's an example of using one rule to figure out another: An equilateral triangle has three equal sides and three equal angles. If all angles are equal, and they add up to 180 °, each angle of an equilateral triangle is 180/3 = 60° .
So we have a new rule: every equilateral triangle has three 60 ° angles. 2. An isosceles triangle has two equal sides and two equal angles.
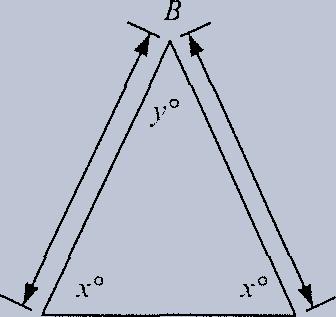
3. Vertical Angles are equal.
An isosceles triangle is one in which two of the sides are equal in length. The angles opposite the equal sides will also be equal to each other. (Similarly, an isosceles trapezoid has two pairs of equal angles.)
In this triangle, since we know that LBAC = LACB (both are x) we know AB= BC. Conversely, if we know that the sides AB and AC are equal, we can assume that the angles are equal.
When two straight lines cross, four angles are formed. The angles that are directly across from each other are called "vertical angles" and they are equal to each other.
In this diagram, the angles marked "x" are equal to each other, and the angles marked "y" are equal to each other.
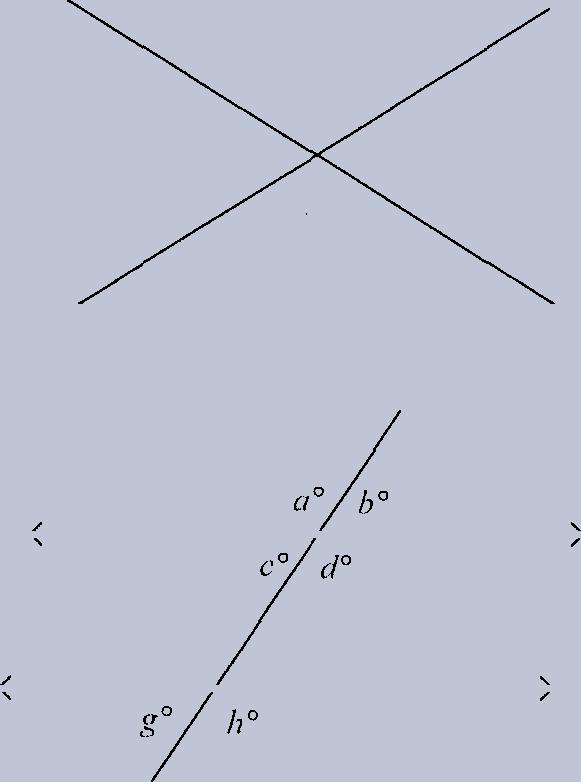
4. Parallel lines with a transversal produce a bunch of equal angles.
When a third line (a "transversal") cuts through two parallel lines, eight angles are formed. The four at the top are collectively the same as the four at the bottom. Basically, we've got two types of angles: big ones and little ones. All the big ones are equal, and all the little ones are equal. Any big one plus any little one is 180 . Here, a = d = e =hand b = c =f= g. Any of the big ones (a, d, e, h) plus any of the little ones (b, c, f, g) equals 180

MATH – 29
Fun Facts About Circles
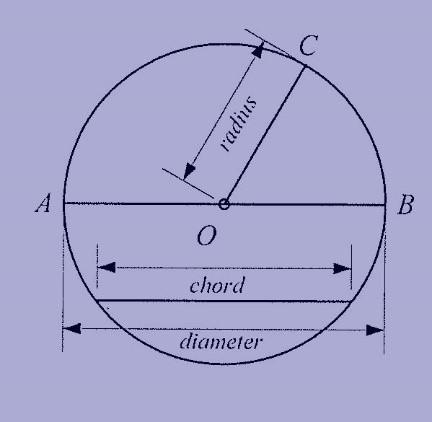
- A circle has 360 ° . In the figure to the left, all angles surrounding point O will add up to 360 °
-The diameter of a circle is a line segment from one end of the circle to the other, passing through the center. In the figure, AB is a diameter. The diameter by definition is the through a circle.
The radius of a circle is a line segment from the center to the end of a circle. The radius is half of the diameter. In the figure, OA, OB, and OC are all radii. All radii of a circle are equal.
A chord is any line segment from one end of the circle to the other. The longest chord in a circle is a diameter.

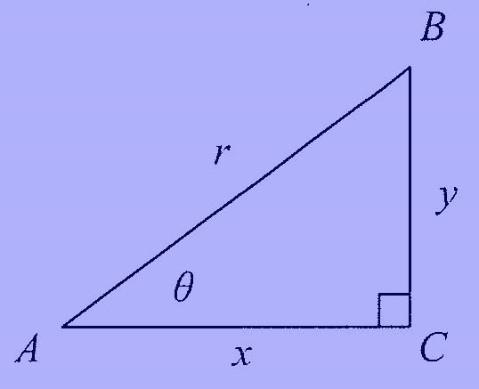
For any given angle of a triangle:
- the SINE of the angle is equal to the
sin Θ = Opposite Hypotenuse = y r length of the opposite side over the length of the hypotenuse.
- the COSINE of the angle is the length of cos Θ¿ Opposite Hypotenuse = x r the adjacent side over the hypotenuse.
- the TANGENT of the angle is the length of tan Θ= Opposite Adjacent = y x the opposite side over the adjacent.

What is the value of i18 ?
(5+8i)(4-6i)=?
(-2-7i)(2+3i)=?
(3- 2i)(3- 2i) =?
(4+3i)(4-3i)=?
MATH - 32 Exercise #26
