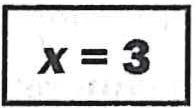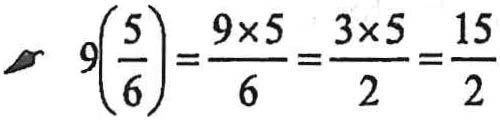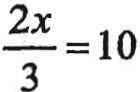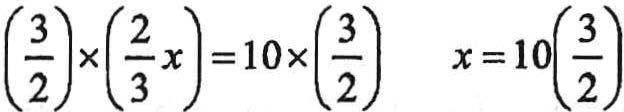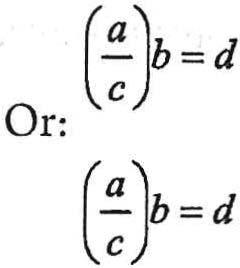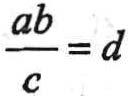The Ultimate Guide to the SAT Math

Introduction to Math

- Format

- Content

General Strategies

Guesstimate

Common Mistakes

Target Numbers

Plug In Backsolve

Using Techniques

Math Fundamentals

- Number Concepts and Definitions

- Fractions

- Ratios

Heart of Algebra

- Techniques - Solving an Equation - Writing Equations

- Rates and Units - Percents - Exponents

- Multiple Equations - Inequalities

Passport to Advanced Math

- F(x) Notation

- Polynomials

- Exponential Growth

Graphing

- The Coordinate Plane

- Lines - Parabolas

- Absolute Values - Circles - Transformation of Functions

Problem Solving and Data Analysis

- Proportions

- Figures

- Statistics

Additional Topics in Mathematics

- Angles

- Perimeter, Area and Volume

- Circles

- Triangles - Trigonometry - Imaginary and Complex Numbers

INTRODUCTION TO MATH

SATmathisnotexactlythesameasthemathyoudoinschool.Yes,alotofyouroldfavoriteswillshowuphere (ratios,two-variableequations,thePythagoreanTheorem,andmanymore!)butthequestionsarealittlebit different.Inschool,youlearncontent.Theyteachyousomethingandthentestyouonit.TheSATisareasoning test.Thatmeansit'slessaboutspecificrulesandmethodsthanaboutproblemsolving.Forexample,inschool, theyteachyoualgebraandthentestyouonhowwellyouusealgebra.OntheSAT,theygiveyouaproblemandask youtosolveitanywayyoucan.Thatcouldmeanalgebraoritcouldmeanarithmeticorgeometry.Onanygiven problem,there'snoonewaythat's"therightway"todoit.AlmosteveryproblemontheSATcanbedone severaldifferentways.Now,somewaysarefasterorsaferthanothers,soourjobistoshowyouthebestwaytodo agivenproblem.

Throughoutthenextfewchapters,we'llbetalkingabouttwotypesofthings:contentandtechniques.Contentis theliteralstuffyouneedtoknow(likethePythagoreanTheorem*).Techniquesaremethodsfordoinglotsof differentkindsofproblems(likePlugIn).Bothareequallyimportant.However,alotofthecontentyou'll alreadybefamiliarwithfromyouradventuresinschooliit'sthetechniquesthatwillbenewforyou,sothat's whereweshouldconcentrate.

*Actually,youdon'tevenneedtoknowthateither.

FORMAT

YouwillseetwomathsectionsontheSAT:

Module1:

Module2:

CalculatorOK

70 minutes

Somegeneralcommentsabouttheformat:

Questions

22questions:

20operationalquestions and2pretestquestions

22questions:

20operationalquestions and2pretestquestions

44 Questions

-CalculatorsareallowedthroughouttheMathsection.AsingleMathsectionreplacestheseparatelytimed no-calculatorandcalculator-allowedportionsofthepaperandpencilSATSuiteMathTests.Thischange allowstheMathsectiontomoreaccuratelyreflecthowcalculatorsareusedinschoolsandinthereal world.Italsoeasestestadministrationbyeliminatingseparatelytimedtestportionswithdifferentrules. Studentsmaycontinuetousetheirownapprovedcalculatorontestdayortakeadvantageofthegraphing calculatorbuiltdirectlyintothetestingapplication.Youmayusemostfour-function,scientificorgraphing calculators.Youwon'thavetoclearthememoryfromyourcalculator.

-AccordingtoCollegeBoardguidelines,youmaynotuse:

•cellphone,smartphone,orlaptopcalculators;

•calculatorsthatcanaccesstheInternet,havewireless,Bluetooth,cellular,audio/videorecording andplaying,camera,oranyothersmartphonetypefeature;

•modelsthathavetypewriter-likekeypad,pen-input,orstylus;

•modelsthatuseelectricaloutlets,makenoise,orhaveapapertape;

•calculatorsthataretoobigtofitonyourdesk,inthetestingroom,orinthetestingcenter;

•everythingelseisfine,though.

-Questionswithineachsectionareorderedbydifficulty.Thefirstquestionsare easy,thelastquestionsarehardandthetestisadaptivemeaningthesecond modulewilladjusttoyourperformanceonthefirstmodule.

-Eachsectionbeginswithmultiple-choicequestionsandendswithgrid-ins.

-Allfiguresaredrawntoscaleunlessotherwiseindicated.

Grid-ins

TheStudent-ProducedResponseQuestions(called"grid-ins"forshortaretheonlyquestionsontheSATthat arenotmultiple-choice.Here,youwillbeexpectedtocomeupwithyourownanswerandfillitintothegrid provided(thustheterm"grid-in").

Wedon'thaveanyspecifictechniquesorstrategiesforthegrid-insotherthanthosewehaveforalltheother mathquestions.Thecontentandstyleofthesequestionswillbejustliketherestofthesection;themath itselfisnodifferent.However,theymayseemabitweirdtothoseofyouwhoareunfamiliarwiththetest. Herearesomemiscellaneousnotesaboutthegrid-ins:

-Asmentionedabove,mathsectionsareorderedbydifficulty.However,gridinsareorderedbydifficultyseparately.Soonsection3,question#15(the lastmultiple­choicequestion)willbehard,whilequestion#16(thefirst grid-in)willbeeasy.

-Noticethatthegridhastwoelementstoit:spacesatthetoptowriteinyouranswer, andbubblesatthebottomtofillin(justlikewhenyoufilloutyournameatthe beginning).Youmustfillinthebubbles.Thespacesatthetoparenotscoredby themachine.Theyareonlythereforyourbenefitsoyoucaneasilyreadyour answerandcanfillinthebubblesmoreeasily.Ifyouwriteintheboxesbut don'tfillinthebubbles,themachinewillreaditasablank.*.*

-Youcanputyouranswerinanycolumn.Itdoesn'tmatterhowyoupositionit(tothe rightorleft).

-Noticethatthereisnonegativesymbolinthegrid-therewillneverbeanegative answeronthegrid-ins.Ifyougetanegativeanswer,youmessedup.Tryagain.

-Ifyouranswerisadecimal,youmustbeasaccurateaspossiblewhengriddingin youranswer.Forexample,iftherightansweris2/3(which,asadecimal,is.66666 repeating),.666wouldbeokay,and.667wouldbeokay,but.6and.66arenotokay.

*Conversely,thatmeansthatyoudon'thavetowriteanythingintheboxesatall.Youcoulddrawlittlepictures ofducksinthereorwritemessagestotheCollegeBoardandnoonewilleverknow.

Takethedecimalasfarasspaceallows.(Ofcourse,youcouldalsojustenter2/3and avoidthewholeissue).

-Youdonothavetoreducetothelowestpossiblefraction.Iftherightansweris2/3,an answerof4/6willstillgiveyoucredit.Ofcourse,ifyougetafractionthatdoesn'tfit intofourspaces,like10/15,thenyouwillhavetoreduce(orconverttoadecimal).

Calculator vs. No-calculator

Youwillwanttohaveacalculator.Butyoudon'thavetogooutandbuyafancycalculatorjustfortheSAT.A simplescientificwilldo.Frankly,mostofyourcalculatorusewillbesimpleaddingandmultiplying,soa cheap-afour-functiondrug-storecalculatorthat'smissingthe7-keywillbefine.*

Now,ifyoualreadyhaveafancygraphingcalculator,youmayseesomequestionsonwhichagraphing calculatorcanhelpyou.Beingabletographequationsorlookupvaluesinatablecansaveyousometime-if youknowhowtouseit.Butifyoudon'thaveone,orifyouhaveonebutbarelyknowhowtoturniton,don't sweatit.You'llbefine.

Using your calculator

Sometimesaquestionwillaskyoutounderstandsomedeepmathconcept,butacalculatorcanallowyouto doitbybruteforce.

Therewilloftenbesituationswhereyougetananswerthatisn'toneofthechoices.

* Well,okay,youprobablyneedthe7-key.

Usually,thatwillbebecauseyoudidsomethingwrong(ithappens).Butsometimesyouranswerisright,but thecorrectchoiceexpressesthatanswerinadifferentform.

OneofthegreatbenefitsofhavingacalculatoristheabilitytomanipulateUglyNumbers.Forexample,sayyou didaquestionandgotJwasyouranswer.Buthereareyourchoices:

A. 2✓5

B.4✓5

C. 5✓2

D.10✓2

Agh,youknowthere'ssomewaytosimplifyJwintooneoftheseterms,butyouforgotexactlyhow.Don't worryaboutit!JustpunchJwintoyourcalculatortogetabout4.47.Nowpunchoutallthechoicesandsee whichonecomesouttothesamething.It'schoiceA!

Therearealotofdifferentscenarioswhenyoumightwanttodosomethinglikethis-whenyougetradicalsin thedenominator,forexample.Don'tbeafraidtousethecalculatortoyourbenefit.

CONTENT

MathquestionsontheSATaresortedintofourcontentcategories.Youwillgetsubscoresfor . threeofthese categoriesbutnotthefourth.

Content Category

Algebra

AdvancedMath

ProblemSolvingandData

Analysis

AdditionalTopicsinMath(no subscore)

Algebra

Thesequestionsarethemostcommontype(thoughthemainthreetypesarefairlyevenlydistributed),andhave theseconddumbestname.Themainthemeofthesequestionsisalgebraoflinearequations.*Thesearesimple expressionsthathavenoexponentsandcanberepresentedasastraightlineinagraph.

- Writing,solving,andunderstandinglinearequations

- Writing,solving,andunderstandinglinearinequalities

-Graphinglines

-Solvingsystemsof2linearequations

AdvancedMath

Thesequestionsinvolvehigher-orderalgebraandhavethedumbestname.

-Writing,solving,andunderstandingquadraticequations

- Writing,solving,andunderstandingexponentialfunctions

- Manipulatingpolynomials

- Rationalfunctionsandlongdivision

- Graphingparabolas

-Functionnotation

* Thisisnottobeconfusedwith"linearalgebra"whichissomethingelseentirely.Linearalgebraiswhatyou takeincollegeafteryou'redonewithcalculus.Itinvolvesvectorspacesandhyperplanes.Letusnever speakofitagain.

ProblemSolvingandDataAnalysis

Thesequestionsfallintotwogeneralcontentareas:

-Proportions:fractions,ratios,unitconversions,percentages

-Statistics:datavisualization,tables,scatterplots,probability,averages

AdditionalTopicsin Math

Thisistheonlycategorythatdoesn'tgiveyouasubscore,andit'sbyfarthesmallest,withonly6totalquestions onthetest.Thesequestionsfallintothreegeneralcontentareas:

-Geometry:angles,triangles,circles,area,volume

-Trigonometry

-Imaginaryandcomplexnumbers

GENERAL STRATEGIES

We'llstartwithtwoquickandeasythingsyoucandotohelporganizeyourtime1 bemore efficient,andcutdownoncarelessmistakes:

1. Circle the Question

2. Show Your Work

Circle the Question

Thistakesalloftwosecondstodobutcansignificantlyhelpyou.

-Itcanhelpreducethenumberofcarelessmistakesyoumake(moreaboutthisinthe nextsection).

-Itwillhelpyouunderstandhowtodotheproblem.Byfocusingonthethingyou're tryingtofindratherthanthethingstheygiveyou,it'seasiertothinkaboutwhatyou needinordertofindit.

Dothisoneveryproblem.Noexceptions.

Show Your Work

You'reprobablytiredofhearingmathteacherstotellyouto"Showyourworld"Wel11 toobad.

SHOW YOUR WORK!

Wecanalreadyhearyoucomplaining: "Whybother?It'snotlikeyougetpartialcreditfordoingitcorrectly:'

True1 youdon'tgetpartialcredit,andthereisnosingle"correctmethod':Butthat'snotthepointatall.

Thepointisthatnotwritingdownyourstepsisthesinglegreatestreasonforstudents'carelessmistakes.Weare astoundedbyhowoftenweseestudentsdoanentiretestworthofmathproblemswithoutwritingathingonany page.Thesestudentsarenotgettingthescorestheywant.

Thisisnotamemorytest.Youcan'tpossiblykeeptrackofeverythinginyourhead1 andyoushouldneverhave morethanonestepinyourheadatanymoment.Byjustwritingdownwhatyou'redoingasyoudoit,youcanturn acomplexproblemintoaseriesofsmall,basicsteps.Andyoucansignificantlyreduceyouroddsofmakinga carelessmistake,likeaddinginsteadofsubtracting,orsolvingforthewrongvariable.

Furthermore,showingyourworkgivesyouarecordofwhatyou'vedone.Thismakesiteasiertofindmistakes whenyou'recheckingyourworkduringatest.Anditmakesiteasiertolookoveryourperformancewhenyou ' re reviewingapracticetestyoujustfinished.Thiswaywhenyouwanttoknowwhyyougot#1Owrong,you'llsee whatyoudidtogetyouranswer.

"ButIdon'tneedtowritestuffdown.I'mgoodatmathandcandoitallinmyhead:'

No1 youcan't.

"No,really,Ican:'

No1 really,youcan't.SATproblemsarecomplicated.Youcan'tholdeverystepinyourheadatonce.Andyou knowwhat?Youdon'thaveto!Ifyouwritestuffdown,youdon'thavetoremembereverything.

Andthesequestionsaredesignedtofoolyou.Manystudents'biggestproblemisn'tthattheydon'tknowenough math-it'sthatthey'remissingquestionsthatthey�lreadyknowhowtodo1 becausetheymakecareless,stupid mistakes.

"Thatjustslowsmedown.Idon'thavetimetoshowmywork:'

Youdon'thavetimetowritedownnumbers?That'sridiculous.What,areyouwritingwithacalligraphypen? We'renotaskingyoutowriteouteverysinglestepincompletesentencesandperfectpenmanship.Don'twrit� outannotatedEuclideanproofs;justkeeptrackofwhichvariableiswhich.

Seriously,we'renotkiddingaround.Justwritestuffdown.

Let'slookatasampleproblemtoseehowthisworks:

6. PointsA1 B, C, and D lie on a line in that order. The length ofAB is 8, and the length of CD is 7. Point C is the midpoint of segment 8D. What is the length of segment AD?

A} 7

B} 14

C} 15

D} 22

SATmathquestionsare numberedbydifficulty. Accordingly1 allsamplequestions throughoutthisbookare numberedasiftheywerepartofa 30-questionmultiplechoice section.Aquestion#6for exampleshouldberelatively simple.

Firstthingtodo:Focusonthequestion.Notthewholeproblem1 smartguy;justunderline thethingthatthey'reaskingyoutofind.

WRO�G

PointsA1 B, C, and D lie on a line in that order. The length ofAB is 8, and the length of CD is 7. Point C is the midpoint ofsegment __

BD. What is the length of segment AD?

RIGHT

PointsA, 8, C, and D lie on a line in that order. The length ofAB is 8, and the length of CD is 7. Point C is the midpoint ofsegment BD. Wtiat is the length of segment AD?

Okay1 nowwhat?

SATquestionsarecomplicated.There'softenalotgoingonwithinaquestion1 andit'seasytotakeyoureyeoff theball.Theremightbesomuchinformationthatyou'renotsurewhattodowithit.Ifyou'renotsurehowtoget started1 askyourselftwoquestions:

1.WhatdoIwant?Thatis,whatisthequestionaskingmefor?

2.WhatdoIknow?Thatis,whatinformationdoestheproblemgiveme?

Thenyourgoalistoconnectthesequestions.Lookatwhatyouwantandworkbackwardstoseewhat youneedinordertogetit.Orusewhatyoualreadyknowandseewhatelsethattellsyou.

Whatyouwant:Thelengthof AD. That'swhywecircledthequestion-tofindoutwhatwewant.

Whatyouknow:AB=81 CD=7,CismidpointofBD. Writedownwhatyouknow.Thisquestionisaboutaline,butnofigureisgiven.Sodrawthefigure.

Firstdrawthepointsinorder:

AndsinceCisthemidpointofBD,BC=CD: •

8

7 7

ADisthewholelength,sowehaveeverythingweneed:AD=8 + 7 + 7=22.

OuranswerischoiceD).

1hisisanadditiontoourruleaboutshowingyourwork:ifageometryproblemdoesntalreadyhaveapicture, DRAWAPICTURE!Itdoesn'thavetobeperfect;evenaroughsketchcanhelpyouunderstandtheproblem andcatchcarelessmistakes.

Noticethatwedidn'tknowwhereweweregoingwhenwestarted.Wejustplayedwiththestuffweknewuntilwe gotwhatweneeded.Thepointhereistonotbescared.1here'salwayssomethingthatyouknow,andsomething thatyoucanfigureout.Ifyouworkforwardfromwhatyouknoworbackwardsfromwhatyouwant,chancesare youcanconnecttheminthemiddle.Evenifyou'renotsurewhereyou'regoing,themoreyouwritedown,the easieritwillbetomakeaconnection.

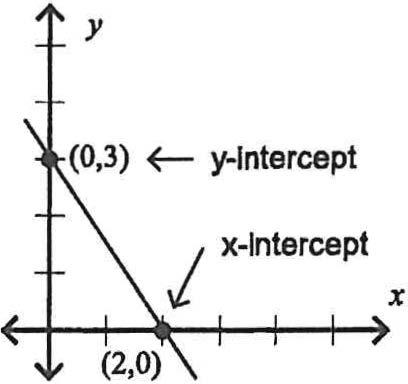
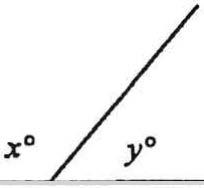
GUESSTIMATE

AsaruleoftheSAT,allfiguresaredrawntoscaleunlessotherwiseindicated.Soiftheproblemdoesn'tsay "notdrawntoscale",youcanassumethatitisdrawntoscale.Ifit'sdrawntoscale,youcanusethepictureto guessthevaluesyouneed.

1akealookatthisproblem:

C �------

29. In the figure above, c is equal to 5 less than twice b. What is the value of a+ b?

A) 60

B) 100

C) 135

D) 185

They'reaskingusfora+b.Solet'stakealookatthoseangles.Angleais

prettybig.Let'ssay...120?130?Let'ssay130.

-Anglebissmaller,maybeSOor60.Let'ssay60.

-Soa+bmustbeabout130+60orabout 190.Soouranswershouldbeprettyclose to190.

-Hmm,190isn'tachoice,but185is!That'sprettydarnclose.We'lltakeit.Theanswer isD).

Lookhoweasythatwas!Wedidn'tdoadarntllingotherthanjustlookingatthepicture.Igot#29inallof 10secondsandallIdidwasaddtwonumbers.

FrequentlyAsked Questionsabout Guesstimate

1. That's all well and good, but how do I know that's right? I Just made up those numbers could have been wrong.

That'strue,butyoudidn'trandomlymakeupthosenumbersyoumeasuredtheanglesintheproblem,the anglestheygiveyou.

Seriousl}'ijustlookattheotherchoicestheygiveyou.A)60?Coulda+_bbe60?Angleaisobtus�!Anglea alonehastobebiggerthan90!SoA)isoutrightaway.B)isstilltoosmall-angleaisstillprobablybigger than100,andwhenyouaddbtothemix,there'snowaythetwoofthemcomeoutthatsmall.C)stilllooks toosmall.

Andhere'sthething:ifyoudothisproblemalgebraicallytherearewaysyoucanmessitupthatwillmake youpickoneofthosewronganswers.Ifyouaddinsteadofsubtractorforgettodistributeacrossparentheses, youcould�hinkthatA)isaplausibleanswerbecauseofyourflawedalgebra.Butifyoulookatthepicture,it justdoesn'tmakesense.

2. Okay, I see that. But what's the real math way to do this problem?

Areyoukidding?Thisisrealmath.There'snothingmathematicallyillegitimateaboutdoingthis.Inmath,asin allthesciences,therearetwowaysofsolvinganyproblem:analytically,byusingpurelogicanddeducing (that'salgebra),orempirically,bygatheringevidenceandmeasuring(that'sGuesstimate).

Sayyouhaveadining-roomtableandyouwanttofigureouthowtallitis.Well,onewayIcouldfigureoutthe heightofthetableistoconstructalinefrommyeyetothetopofthetableandalinefrommyeyetothe bottomofthetable,measuretheangleofdeclination,andusethelawofcosinestofindthethirdsideofthe triangle.ORICOULDSIMPLY GETARULERANDMEASUREIT!

Hereareyourchoicesforhowtallthetableis:

A)2.5inches

B)3feet

C)60yards

D)7.8miles

ButhowdoIknowthetableisn't7.8milestall?Becauseit'sinmylivingroom.

1hisconcept,bytheway,istheentirepointofthexy-coordinateplane.Graphingisawaytovisualizethe relationshipbetweenvariables.Questionsinvolvingthecoordinateplaneoftenrequireyoutomakeconclusions basedonpictures.Sogetusedtoit.

3. Doesthis onlyworkwithangles?

Ofcoursenot!Youcanusethisonjustaboutanyproblemthathasapicture,aslongasit'sdrawntoscale.Takea lookatthisone:

0 p

27. In the figure above, STis a chord and OP connects the centers of the two circles with equal radii. If ST= 4 and OP= 4✓ , what is the radius of circle O?

A) 2

B) 2✓

C) 4

D) 4✓

H!hatdowewant?1heradiusof0.Hmm,wedon'thavearadiusthere.Solet'sdrawonein.Justdrawaline fromthecentertoanywhereontheside.

Sothatristhelengthwe'relookingfor.Let'scomparethattothelinesweknow.Well1 itdefinitelylookssmaller thanOP,whichweknowis4✓3 (orabout6.92).SoD)isout.Goodsofar.

WealsoknowthatSTis4,solet'scomparertoST.Hey,theylookthesame.Maybe r=4.Waitaminute-they'reexactlythesame!HowdoIknow?Measurethem.Takeapieceofpaper(tryyour answersheet)andlaythesideofthepaperagainstrandmarkoffitslength.Thenlaythatpaperyoumarkedoff againstST.Whatdoyoufind?They'rethesame!We'redone!Sotheradiusis4.SotheanswerisC).

Attheveryleast,ifwegopurelybyoureyes,weknowrightawaythattheradiusshouldbecloseto41 soonlyB) andC)makesense(2✓3isabout3.46,whichisclose).Ifweactuallymeasureitout1 wecanseethattheradiusis exactly4.Perfect.

4. Does Guesstimate always work?

Unfortunately,Guesstimateisn'talwaysgoingtoworkasbeautifullyasitdidonthesequestions.

-Ifthefiguresaysit'snotdrawntoscale,youcan'tGuestimate.Thenthepicture doesnothavetoactuallymeasurethewayitlooks.Thetwofiguresbelowdepict thesameshape,buttheoneontheleftisnotdrawntoscale,whiletheoneonthe rightis. 7 2□

Note:Figurenotdrawntoscale.

-Ifthechoicesaretooclosetogetherthere'snothingIcando.If,in#29above,my choiceswere175,1801 185,190,Ican'teliminateanything.I'mnotthatgoodofa guesser.

Guesstimatewon't workondrawingsof 3-Dfiguresbecause they'redrawnwith perspective.You maybeableto visualizethembut youcan'tmeasure them.

You'realsonotalwaysgoingtobeabletozeroinontherightanswerlikethis.However,youcanofteneliminate something,evenifit'sonlyonechoice.Andonceyoueliminatesomething,youroddsofgettingtheproblem increase.Evenifyoucan'tfigureoutanyothersolution1 youcanguessfromwhat'sleft.

Soanytimeyouseeaproblemwithadiagramthat'sdrawntoscale,tryGuesstimatefirst.Beforeyoudoanything else,trytogetaballparkfigureforthethingthey'reaskingfor.

COMMON MISTAKES

ThepeoplewhomaketheSATaren'tchumps.Theyknowhowhighschoolkidsthink.Moreimportantly,they knowhowhighschoolkidsmessup.Therefore,whentheywritethetesttheyintentionallyincludewronganswer choicesthatkidswhomakecertaincommonmistakeswillchoose.However,onceyouknowwhatthesemistakes areandhowtoavoidthem,youwillbemuchlesslikelytomakethem.

RTFQ_

Takealookatthisquestion:

8. A certain bookstore gets a shipment of 24 copies of a new book and sells 18 of them. What percentage of the books was NOT sold?

A) 75%

B) 67%

C) 33%

D) 25%

Okay,so18over24is0.75,whichis75%.That'schoiceA),right?

WRONG!That'sthenumberofbooksthatweresold;thequestionisaskingforthosethatwerenotsold. TheyevenputitinCAPITALLETTERS!Payattention!

WecallchoiceAtheRTFQchoice."RTF(Ystandsfor"Readthefullquestion:'It'swhathappenswhenallof yourmathwascorrect,butyoudidn'tsolveforthethingtheywereaskingfor.

RTFQchoicesshowupalloverthetest.Theycouldshowuponquestion#60oronquestion

#1.Itisaveryeasymistaketomake.Butit'salsoaveryeasymistaketoavoid:justreadthe question.Takeanextratwosecondstomakesurethatthenumberyou'rechoosingisthenumbertheywant.

Infact,we'vealreadygivenyoutwowaystohelpcutdownonRTFQmistakes:CircletheQuestionandShow YourWork.Bothofthesethingswillsignificantlyhelpyoukeeptrackofwhatyou'redoing.

Alotofpeopledon'tputenoughweightonthesemistakesonpracticetests."Oh;Iknewhowtodothatone," theysay."Ijustwrotedownthewronganswer:'What?That'ssomuchworse!Ifyoudon'tknowhowtodothe math,fine.We'llteachyouhowtodomath.Butyoudon't

knowhowtowritedownwhatthey'reaskingfor?Youarethrowingawaypointsbymissingquestionsthatyou alreadyknowhowtodo.Remember:eachmathquestionisworth10 points.IfyoumakejustthreeRTFQmistakes,that's30pointsyou'vetossedoutthe,window.Thesethingsadd up.

Here'saharderone.Giveitashot,andmakesureyourealeverywordofthequestion.

A= {1, 2, 3}

B= {3, 5, 7}

23. If a is a number selected from the setA and b is a number selected from set 8, how many different values for a+ bare possible?

A) 6

B) 78

C) 9

Fool's Gold

Takealookatthisproblem:

30. Scott drives to Bob's house at a speed of 30 miles per hour and drives back at � speed of 50 miles per hour. If he takes the same rou�e bQth w,ays, what was his average speed, in miles per hour, for the whole trip?

A) 37.5

B) 40

C) 42.5

D) ltcannot be determined from the information given.

Wewanttheaveragespeedforthetrip.Histwospeedsare30andSO.Sotheaverageis 30+SOdividedbytwo.That's40.ChoiceB).

Wow,thatwaseasy.Hmm.Alittletooeasy.

Waitaminute.Thisisquestionnumber30outof30.Questionsareorderedbydifficulty.Thatmeansthisis thehardestquestiononthetest.There'snowaythatthehardestquestion onthetestcanbedonepyjusttakingtheaverageoftwonumbersthattheygiveme!Thatcan'tpossiblyberight.

Lookatitthisway:

1.WeknowforafactthatSATMathTestquestionsareorderedbydifficulty.

2.Aquestion'sdifficultyisdeterminedbylookingatthepercentageofstudentswhogetitright.

3.MostkidsprobablyhadthesameinstinctIdid:taketheaverageofthespeeds.

4.ButIknowthatmostkidsgetitwrong.That1swhyit�number30.

5.Therefore,takingtheaverageof30and50iswrong.Ifitwereright,mostkidswouldgetitright.Soit wouldn'tbenumber30.

6.Therefore,Icaneliminateit.

WecallthisaFool'sGoldchoice.It'swhenahardquestionhasachoicethat'ssoeasyandsoobviousthatitcan't possiblyberight.Weknowthequestionmustbeharderthanthis.Itmustbeatrap.

Soifyouseeaneasychoiceonahardquestion-eliminateit.Youknowmostpeopleget itwrong.Sotheobviousanswercan'tberight.*Sometimesweseestudentswhoevenrecognizeachoiceasa Fool'sGoldchoice,andthenpickitanywaybecausetheycan'tthinkofanyotherwayofdoingtheproblem.They windupchoosingtheonechoicethattheyknowiswrong.That'smadness.Utter,uttermadness.

Let'sgobackandtakeanotherlookatthat#30above.WeeliminatedB)asFool'sGold.Hmm.Butifthat'snot right,howelsewouldyoudotheproblem?Allittellsusisthetwospeeds;wedon'tknowthedistancetraveledor thetimeittook.Somaybethereisntenoughinformation.That'sChoiceD).Right?

Wrong!"Cannotbedetermined"isaclassicFool'sGoldchoice.Number30isnotgoingtobeaseasyas,"Well, uhh,theydon'ttellmeanything,soIguessIdunno:'Don'tbeaquitter.

Sowe ' veeliminatedB)andD).Worst-casescenario,wecanguessfromthetworemainingchoices.Remember,no matterwhat,wemustpicksomething.Wemustneverleaveanythingblank.

Sohowdowedoactuallydothis?Thereasonyoucan'tjusttaketheaverageof30and50isbecausethoseare alreadyrates.Inordertofindtheaveragespeedforatrip,youhavetotaketherateofthetotaldistanceoverthe totaltime.Hmm.Ifweknewthedistancetraveled,wecouldfindthetimeittook,butwedon'tknoweither.But theanswercan'tbeD)-that'stooeasy.Soitprobablydoesn'tmatterwhatthedistanceisYouprobablygetthe sameanswernomatterwhat.

*Obviously,Fool'sGoldchoicesonlyoccuronthehardestquestions-aboutthelastthirdofthetest.If there'sachoiceonquestion#3thatlooksreallyeasy,itprobablyreallyisthateasy.

Solet'smakeupavalueforthedistance.Let'ssayit's150milesfromScott'shousetoBob'shouse.Sinced=rt, wecanusethedistancetofindthetimeeachlegofScott'striptook:

ToBob's:150=30t1 FromBob's:150=50t2 3hours=t2

5hours=t1

SoScott'striptook5hoursonewayand3hoursbackforatotalof8hours.Histotaldistancetraveledis 300 miles(twotrips,150each).So:

That'sChoiceA)!We'redone!Wait,butweonlygotA)afterusinganumberwemadeup.Howdoweknowwe won'tgetadifferentanswerifwechoseanothernumber?Well,tryit.Makethedistance300milesandseewhat youget.*

* You'vejustseenasneakpreviewofPlugIn,oneofourfundamentalMathTechniques.We'llseealotmore ofthisverysoon....

TARGET NUMBERS

Thisisoneofthemostpowerfulstrategiesthatwehave,somuchsothatitgetsitsownsection.Ifyouignore everythingelsewesay,atleastpayattentiontothis.

Oneofthebiggestproblemsthatstudentshaveonthetestistiming.You'vegotafiniteamountoftimetodo alotofquestions.Asaresult,moststudentsfeelrushedtryingtofinishthetest.Rememberthatthequestions arearrangedinorderofdifficulty-number1iseasy,number22ishard.Sokidsrushthroughtheearly questionsandmakealotofcarelessmistakes:theyaddinsteadofsubtract,theysolveforxinsteadofy,they misreadthequestion,etc.Thentheyspendalotoftimeonthehardonesandgetthosewrongtoo-because they'rereallyhard.

Buthere'sthething:theeasyquestionsareworththesamenumberofpointsasthehardones(mostly,at least;we’lltalkabouthowModule2isweighteddifferentlyinamoment).Thesolutionisincrediblysimple: DON'TDOTHEWHOLETEST.Youdon'thavetogeteveryquestioninordertogetthescorethatyou want.Thebiggestproblemmostkidshaveisn'tthattheydon'tknowenoughmath;it'sthatthey'remissing questionsthattheyalreadyknowhowtodo.

Whatdoesthismeanforyou?Itmeansthatbysettingatargetnumberofquestionsyoufocuson,andfocusing onlyonthosequestions,youendupgettingmorepointsoverallonthetestandthereforebringingyourscore up.Thinkaboutitthisway:ifIfocusonall44questionsbetweenthe2modulesbutonlyget20ofthem correct,I’mworseoffthanifIfocusedon30questionsbetweenthe2modulesandgot25ofthemcorrect. Ultimately,accuracyismoreimportantthanvolume.

Withthatsaid,theintroductionofadaptivetestinginthemodulesdoesmeanthateachquestionisweighted differentlyinthesecondmodule.Howthisworksisfairlysimple:onthefirstmodule,youhave22questions toanswer.Ifyouanswerabout16ormorecorrectly,yoursecondmodulewillincludeahigherpercentageof “difficult” questions.Ifyouanswerfewerthan16correctlyonthefirstmodule,yoursecondmodulewill includeahigherpercentageof “ easy ” questions.Yourfinalscoreisinpartdeterminedbythelevelofdifficulty ofyoursecondmodule.

Now,Iknowwhatyou’rethinking.Ihearthosewheelsturninginyourbrain. “Isitbettertoshootfortheeasier moduletotrytopickupmorepointsthere?” No.Letmesayitagain.NO.Thereasonforthisisthatifyou taketheeasiermoduleinModule2,yourmaximumscoreontheMathportionoftheSATisabouta600.If youtakethehardermoduleinModule2,yourmaximumscoreis800.Whatthismeansisthatthesecond moduleisweigheddifferentlydependingonthedifficulty,sothehigherscoreyouwant,themoreyouwantto reachthatmore “difficult” module.

Still,TargetScoresarehelpfulbecausenotallofusareshootingforan800ontheMathsectionoftheSAT. Fewofuscanevenachieveit,butregardlessofthat,evenfewerofusneedit.

Okay,you ’redoingfewerproblems,buthowdoyouknowyou ’lldobetteronthoseproblemsthanyouweredoingbefore?Because nowyou'vegotfewerquestions-inthesameamountoftime,soyoucanspendmoretimeoneachquestion.Themoretimeyou spendonaquestion,themoreconfidentyoucanbeofyouranswer.Thosecarelesserrorsyoufixwilltranslateintoahigherscore.

PeopletendtothinkaboutSATscoresinthewrongcontext.Peopletendtothinkofthemlikefigureskatingscores-there'sa perfecttenandthenpointsdeductedforyourflaws.*Instead,thinkofthemlikebasketballscores-you'rejusttryingtogetasmany pointsaspossible.Assuch,yourshootingpercentageismuchmoreimportantthanthenumberofshotsyoutake.

Thisstrategyisamazing.Youcangetascoreincreasebyliterallydoinglesswork.Youcangetahigherscorenotbylearningnew thingsbutbynailingallthethingsyoualreadyknowhowtodo.It'smiraculous.

Frequently Asked Questions about Target Numbers

1. Why are you.making me do this? What, you think I'm too dumb to get #30?

Let'ssaythisrightupfront:we'renotsayingyou'retoodumbtoget#30.Wefirmlybelievethatanyonecould get#30ifgivenenoughtimeforit.'Ibisisn'taboutskippingquestionsthataretoohardforyou.The goalhereissimplytodofewerquestions.That'sit.Soifwe'redoingfewerquestions,we'renotgoingto skiptheeasyones;we'regoingtoskipthehardones.That'sjustcommonsense.

Yes,ifyoudidthewholetest,youmightgetnumber#28.Butwhyworryabout#28whenyou'restill missing#3?Weknowyoucanget#3.That'sthegoalhere-tonailalltheeasyquestions.Whyworry aboutthehardst1;1ffwhenyou'restillmissingpointsontheeasystuff?Let'sgetthosedownpatbeforewe doanythingelse.

2. I finished my target numbers, but I've still got some time left. Should I move on to more questions?

NO!Ifyoufinishyourtargetnumbersandstillhavetime,gobackandcheckyourwork.Again,thepoint hereistomakesurethatyou'reassharpascanbeontheeasyquestions.Ifyouhavetimeleftover,don't keepgoing,anddon'tstareblanklyatthewallforfiveminutes.Gobackandcheckyourwork.

*Wait,isthathowfigureskatingisscored?Ihavenoidea.

3. I stuck to my target questions, but there·were still some hard ones In there, so I left them blank too.·1s that okay?

NO!Neverleaveanythingblank!Firstofall)there'snopenaltyforguessing.Secondly)thegoalhereisn'tto "skiphardquestions".We'retellingyouexactlyhowmanyquestionsyouneedtodotogetagoodscore increase.Thatmeansyouhavetodoallthequestionswithinyourtargetnumbers.

Yes)therewillstillbesomehardonesinthere.Theyaren'tallaseasyas#2.Butthat'swhywehavesevenmore chaptersaboutMath!Youdidn'tthinkwe'djuststophere,didyou?There'salotmorewehavetogothrough,and we'regoingtoshowyousomegreattechniquesthatwillhelpyouwiththosehardquestionsthatarewithinyour targetnumbers.

4. I'm supposed to stop at #24, but I don't know how to do it. But I think I can do #26. Can I skip #24 and do #26 instead?

Theveryfactthatyou'reaskingthisquestionmeansyou'vethoughtabouttwoquestions.Thattakestime,time youcould'vespentcheckingyourworkontheeasyquestions.Again,thepointhereistiming-wewantyouto spendtimemakingsureyougettheeasyquestions.WedoNOTwantyoutospendtimeontryingtofigureout whichquestionstodo.Wewantyourgameplantobesetbeforeyougotothetest.

Now,wedorealizethatthereisawidevarietyofquestiontypesonthet�st,andsomepeoplereallyarebetterat sometypesthanothers.Maybe#24isaweirdtrigonometryquestion,but#26isagraphingquestionandyou're reallygoodatgraphing.Orit'saquestionthatcanbereallyeasywithatechniquelikePlugIn.Thatseemsokay. Butbecareful:itmayonlylooklikeyo_ucando#26.Itmightbemorecomplicatedthanitseems.Maybethere's a

trickyoudidn'tsee.Maybethere'saFool'sGoldchoice.Whoknows? Butyouknowwhatwedoknow?Thatyouknowhowtodo.#2.Ifyou'vedoneeverythingyoucanon#24and stillcan'teveneliminateonechoice,GOBACKANDCHECKNUMBERTWO!!!Donotmoveon.Yes,there maybequestionsbeyondyourtargetnumbersthatyouarecapableofdoing.Butthegoalofthistechniqueisto makesureyougettheeasyquestions.Thequestionspastyourtargetnumbersarenotthere.Theydonotexist.

5. So those questions I skip, I should Just leave them blank? NO.FILLINRANDOMANSWERS.NEVERLEAVEANYTHINGBLANK.Youdon'tlosepointsfor wronganswers,sothere'snothingtolosebyguessingrandomly.Youshouldnotattemptthosequestions,but youshouldfillinrandombubblesforthoseyouskip,justincaseyoupickupsomepointsbychance.

6. I nailed my target numbers on this practice test. Can I do more on the next one?

Firstofall,ifyounailedallyourtargetnumbers,congratulations.Youprobablyhavea100-pointincreasein yourmathscore.Fantastic.Butforthenextpracticetest,keepthesamenumbers.Wewanttoseeyoudoit again.Oncemighthavebeenafluke-maybeyouwereinthezonethatdayorjusthappenedtogetalotof questiontypesthatyou'rereallygoodat.Ifyounailallyourtargetnumberstwiceinarow,thenwecanstartto talkaboutraisingthem.

Butthenagain,youmightnotwanttoraisethem.Ifyoureallydonailyourtargetnumbers,Ithinkyou'llbe pleasantlysurprisedbywhatthatdoesforyourscore.Youmightbehappywhereyouare.

7. I work really slowly and I never finish the test. What should I do?

Weweregoingtotellyounottofinishthetestanyway.Congratulations!You'reonestepaheadofus.Areyou psychic?.·

Again,thegoalhereistobeaccurateonthequestionsthatyoudo.Ifyou'renotquitemakingitthroughallof yourtargetnumbers,that'sokay-aslongasyou'vegotahighshootingpercentageontheonesyoudogetto. Plus,oncewegettoworkonthenutsandboltsofthemath,youshouldbeabletogetthroughthoseeasy problemsmuchfaster.

8. How do I split up my time between multiple-choice questions and gridins?

Rememberthateachsectioncontainsmultiple-choicequestionsfirstandgrid-insattheend.Rememberalso thatthesepartsareorganizedseparatelybydifficulty-insection3,number15(thelastmultiple-choice)will beahardquestion,while16(thefirstgrid-in)willbeeasy.It'sprobablyagoodideatoskipafewquestions fromeachpart.Ifyou'resupposedtoskipSquestionsinsection3,don'tjustskipallSgridins,becausethere areprobablysomeeasyonesinthere.

Onthetableweincludedsuggestionsforhowtosplityourtimebetweenthemultiple-

choiceandgrid-inquestions.Forexample,•ifyou'restartingwitha500and.goingfor a670,you'dskip6questionsinsection3.Youcansplitthatupasskipping4multiple­choiceand2grid-ins,thus you'ddoquestions1-11and16-18.

Butthisisjustasuggestion.Thetotalnumberofquestionsansweredandskippedismoreimportantthanhow youdividethattotaloverthe-questiontypes.

9.1 have extended/unlimited time for the SAT. Do I still have to do this? Hmm...areyoustillmakingcarelessmistakes,evenwithextratime?Thenyes.Yesyoudo.

10.Do I have to do this on the real test too? What?Ofcourseyoudo!Isthataseriousquestion?Whywouldwetellyoutodothisonlyonpracticetests? Forfun?Youthinkwe'rejustmessingwithyou?Everythingwetellyoutodointhisbookissomethingyou shoulddoontherealtest.

11. Should I do this on the Reading and Writing as well? Notexactly.Thereasonwedothisforthemathisquestionsarenumberedbydifficulty,soweknowthe firstquestionsaretheeasyquestions.Studentsmakecarelesserrorsonearlyquestions,questionstheyknow howtodo.QuestionsontheReadingandWritingtests,however,arenotorderedbydifficulty,sothere'sno guaranteethatskippingthelastquestionsmeansskippingthehardquestions.

Ontheotherhand,timingcertainlycanbeanissueontheothertests.Rememberthatthesameprinciple applieseverywhere:it'smoreimportanttobeaccurateonthequestionsyoudothantodoalotof questions.Soifyouarehavingtroublefinishingtheothertests,takeheart.Youcanstillgetagoodscorethere withoutansweringallthequestions,aslongasyou'reaccurateonthequestionsyoudo.

MATH TECHNIQUES

Thetechniquesarewaysofdoingproblems.Theycanbeusedorijustaboutanytypeofproblem:onhard problemsoreasyproblems,arithmeticoralgebra,withtrianglesorcircles,anywhere.Theyarepowerful,versatile, andvery,veryeasy.

We'regoingtoshowyoutwotechniquesforSATMathproblems:PlugInandBacksolve.Togethertheycanbe usedonabout40%ofthemathproblemsontheSAT.That'salot. Whileeachhasitsquirksandrelativestrengths,theyallhavethesamefundamentalprinciple-theyturn abstractproblemsintoconcreteproblems.Thegoalistoturneverythingintoarithmetic,togetridofvague unknowns,intangibleideas,andlongequationsandmakeeveryproblemintosimplestuffyoucanpunchinto yourcalculator.

PLUG IN

Let'stakealookatthisproblem:

9. Bob has 4 dollars more0than Lisa does. If Lisa has x dollars, how much would Bob have if he doubled his money?

A) x+4

B) 2x

C) 2x+4

D) 2x+8

Noticethatthisquestionisanumber9-nottoohard,butnottooeasy,justinthemiddleofthepack.We·can seewhattheywanttistodohere.Theygiveusawordproblemandexpectustotranslatefromsentencesinto mathematicalexpressions.Idon'twanttodothat.

Takealookattheanswerchoiceshere.Theyallhavex'sinthem,andxisavariable.Thatmeansitcanstandfor anynumber.Let'ssaytheanswerturnedouttobechoiceA).Well,iftheanswerisA),thenthat'stheanswer. That'showmuchmoneyBobhas:x+4dollars.Soitwillalwaysbex+4,nomatterwhatxis.IfxisS,ifxis10,if xis953,234,124.5255,theanswerwouldalwaysbeA).

Solet'spickanx.Iftheanswercomesoutthesamenomatterwhatnumberxis,wecanchooseanyvalueforx thatwelikeandwe'llalwaysgetthesamething.

ThisisPlugIn.Ithasthreesteps.

1. Pick a number.

Whatshouldwechoose?Somethingsmall,somethingmanageable,preferablysomethingthatisn'talreadyinthe problem(toavoidcon�usion).Try toavoidweirdnumbersthathavespecialpropertieslikeO,1,negatives,or fractions.Justaniceeasycountingnumber.Ilike3.Let'ssayxis3.

Onceyouchooseanumber,makesureyouwriteitdownandputaboxaroundit1soyourememberthat'sthe numberyoumadeup.

2. Do the problem with your number. Readtheproblemagain,butinsteadofx,use3.

9. Bob has 4 dollars more than Lisa does. If Lisa has 3 dollars, how much would Bob have if he doubled his money?

Lisahasxdollars,sonowwe'llsayLisahas3dollars.Bobhas4-more,soBobhas7dollars.SoifBob doubledhismoney,he'dhave14dollars.That'souranswer:14.Onceyouhaveananswer,circleit.

0Wait,but14isn'tananswerchoice.Ah1 onemorestep:

3. Putthe numbers Into the choices.

Ouranswerisn'tachoice,butallthechoiceshavex's.Aha!Wehaveanxnow.Let'sput3inforxinthechoices andseewhichonecomesoutto14.

OnlyD)works.That'souranswer.Wegottheproblembyaddingone-digitnumbers.

Thinkoftheproblemasalittlefunction,aseriesofsteps.IfIputinthisnumber,Igetoutthatnumber.WhenI putin3,Igot14.Therightanswerchoiceshouldgivemethesamefunction.WhenIputin3,Ishouldgetout 14.

Don'tbelieveme?Tryadifferentnumberfor x. .You shouldstillgetD)asyouranswer.

FrequentlyAsked Questions about Plug In·

1. Do I have to test every choice?

Yes,justtobesafe.Itispossiblethattwoanswerchoicesbothgiveyoutheansweryou'relookingfor.Thiscould happenifyouchooseanumberwithspecialproperties(like1)oranumberthatwasalreadyintheproblem.Or itcouldhappenpurelybychance.Soyoushouldcheckallthechoicestomakesuretherearen'ttwochoicesthat work.

2. So what do I do if I get two choices that work out?

Firstofall,eliminateeverythingelse.Youknowit'sgoingtobeoneofthosetwo.Worstcasescenario,guessone;you'vegota50-50chance.

Butbeforeyouguess,whynottryadifferentnumber?Iftwochoiceswork,it's probablybecauseyouhappenedtopickaweirdnumber.Pick�differentoneandtest thechoicesthatareleft.Trydifferentkindofnumber.Ifyoupickedasmallonebefore, tryabigonenow,andviceversa.

Ifyoukeepgettingthesametwoanswers,tryaweirdnumber,like0,1,afraction,ora negative.*Thesenumbershavespecialproperties,sotheycanhelpyounoticescenarios thatyoumightmissotherwise.

3. Why do I have to do this? That seemed like a lot of work for a #9.

Ifaquestionasks what"MUST"be truethat'sasign youmightwantto tryseveraldifferent numbers.

Firstofall,we'redemonstratingthetechniqueonaneasierproblemsoyoucanseehowitworks.Theproblems onlygetharderfromhere,yetPlugInisstilllittlemorethanaddingone-digitnumbers.Heck,wealreadysawa Plug-Inquestion-theFool'sGoldexampleaboutScottdrivingtoBob'shouse.Trydoingthatsuckerwith algebra.Itain'tpretty.

Second,PlugInmayseemweirdbecauseit'snewforyou.Themoreyoudoit,themoreyou'11getthehangofit. Prettysoon,you'llbeabletochurnoutproblemsinafractionofthetime.

*Conveniently,Eration,.Qne,Negative,andZerospellFONZ.

Third,algebraicmethodsarefraughtwithpossiblecarelessmistakes-evenon#9.

Let'strysomealgebraonthat#9justfor'kicks.Bobhas4morethanLisa,.soBobhas x+4.Multiplyitbytwo,you get2x+4right?That'sC),right?Ofcoursenot.It'snot 2x + 4iit's2(x + 4).Thatcomesoutto2x + 8,whichis D),justlikewegotwithPlugIn.Asbrilliantasweallarewithalgebra,it'sreallyeasytomakeasmallstupid mistakelikeforgettingtheparentheses.ButwithPlugIn,you'remuchlesslikelytorn,akethatmistakebecause you'reworkingwithconcretenumbers.Youunderstandwhatallthesetermsrepresentithey'renotjustabstract lettersonthepage.C)isnomoretemptingthananyotherwrongchoiceiit'sjustanotherchoicethatdoesn't comeoutto14.

The�eareotherwaysyoucanmess·thisup,too.Ify�uforgettodoubleBob'smoney,yougetA).Ifyoudouble Lisa'smoneyinsteadofBob's1 yougetB).NoneofthesemistakesarelikelywithPlugInbecauseallyou'redoingis simplearithmetic.

Soit'snotjustthatPlugInisfasteroreasierthanalgebra;it'salsosaferthanalgebra.You'remuchlesslikelyto makean·RTFQorFool'sGoldmistakewithPlugIn.

TypesofPlugIn Problems

1. ExplicitVariables

Aswe ' veah-eadyseen,havingavariableintheanswerchoicesisthefirstsignofaPlugInproblem.Butitalsoworks whenthereismorethanonevariable.

SometimesyoucanPlugInforeachvariableindependently: 15. How many hours are there ind days and hhours?

A) 24h+d

B) h+24d C) 24(h + d)

D) h+24

Becausethere'snorelationshipbetweenhanddhere,wecancomeupwithtotallydifferent numbersforeachofthem.Tomakethingseasy,l�t'sused=1andh=3.*Onedayhas24hours,plus3givesa totalof27hours.Whichchoicematches27?

*Picking1makesthingsniceandquickonaproblemlikethis.Butbecausemultiplyinganddividingby1 eachgiveyouthesameanswer,picking1cansometimesgiveyoutwochoicesthatwork.Therefore,ifyourquestionhasalotof divisioninthechoices,particularlyifyouseethevariableonthebottomofthefraction,youprobablyshouldn'tpick1Andanytime yougetmorethanonechoicethatworks,justeliminateandpickadifferentnumber.

A)24h+d B) h+24d C)24(h+d)

D)

h+d

24(3)+1=73X

3+24(1)=27✓

24(3+1)=96X

3+ 1 -X 24 24

Ontheotherhand,sometimestheproblemwillgiveyousomerestrictionsonthevariables.Inthesecases,you canPlugInfo�onevariable,andthenusethatvaluetofigureouttheothervariable:

14. Ifx + 5 is 3 less than y, then x- 2 is how much less than y?

A) 6 B) 7 C) 8 D) 10

Herewehavetwovariables,butthistime,ifwepickanx,wecanusethatnumbertofindy.Let'ssayx= 4. Read thebeginningoftheproblemwithournumberforx:"If4+Sis3lessthany.".4+S=9.Thatmeans"9is3less thany;'soyis3morethan9.Soy=12.Pickinganxallowedustofindy.

We'renotdoneyet.Thequestionasks" x-2ishowmuchlessthany?"4-2=2.So2ishowmuchlessthan12?

2is10lessthan12.That'schoiceD).

NoticealsothatwecouldstillusePlugIneventhoughthereweren'tanyvariablesintheanswerchoices.

2. lmplicitVariables

Takealookatthisproblem.It'sagrid-inquestion,sotherearenoanswerchoices:*

33. Larry cuts a piece of paper into two equal pieces. He takes one of those pieces and cuts it into three equal pieces. The area of one of the smallest pieces iswhat fraction of the area of the original piece of paper?

There'snovariableanywhereintheproblemortheanswerchoices,sowecan'tusePlugIn,right?

Wrong!Eventhoughnovariablewasexplicitlymentioned,thereisanimplicitvariable-thearea.There'snowayforus tofindtheareaoftheoriginalpieceofpaper,right?Itdoesn'ttellusthelengthorwidthoranynumbersatall(wedon't evenknowwhetherit'sarectangle!),butwe'restillexpectedtogetananswer.Soitmustnotmatterwhatthestartingarea is-we'llgetthesameanswernomatterwherewestart.There'snoactualletter,butwecouldassignitavariableifwe wanted.

Let'snot.Let'ssaytheoriginalpiecehasanareaof12.

-Hecutsitintotwopieces,soeachhasanareaof6.(12 7 6=2)

-Hecutsoneofthoseintothreepieces,soeachofthesmallerpieceshasanareaof2. (673=2)

-Soeachsmallerpieceis2-or�oftheoriginal. 126

WealreadysawaproblemwithimplicitvariablesintheFool'sGoldsection.Rememberthis?

30. Scott drives to Bob's house at a speed of 30 miles perhour and drives back at a speed of 50 miles perhour. If he takes the same route both ways, what washis average speed, in miles perhour, for the whole trip?

A) 37.5

B) 40

C) 42.5

D) It cannot be determined from the information given

*Thisisquestion#33,soitmightappearthatitshouldbehard,butrememberthatquestiondifficulty numberingresetswiththegrid-ins.So#31isthefirstgrid-inandshouldbeeasy.#33isthethirdoutof8.

Eventhoughtherearenovariablesatall,thedistanceisanimplicitvariable.Wecanmakeup avalueforthedistanceanddotheproblemwiththatnumber.That'sPlugIn.

3. Geometry

Takealookatthisproblem: z y �Figurenotdrawntoscale.

15. In the figure above, if y = 90-x, what is z in terms ofx?

A) 90+x

B) 90-x

C)180+x

D) 180-x

Wheneveraquestion containsthewords "in terms of"asin "whatiszinterms ofx•�youcanalmost alwaysusePlugIn.

Geometrycanbescaryforalotofkids,andwe'lltalkalotmoreaboutitinalaterchapter.Butlook:we'vegot variablesintheanswerchoices!ThatmeanswecanPlugInfor x, justlikeanyothernormalproblem.

Let'ssayx= 30.Weknowy=90-x, soy=60.

Wecantellfromthepicturethatzandymakeastraightline;thatmeansz +y=180.Since y= 60, weknowz= 120.Sowhenx=30, z=120.Put30inforxintheanswerchoicesand seewhichgivesyou120:

A) 90+x

B) 90-x

C)180 +x

D)180-x

90 + 30=120✓

90-30=60X

180 + 30=210X

180-30=150X

Don'tbescaredoffbyfigures.Ifyou'reconfused,don'tworry:we'lltalkaboutgeometryrulessoonenough.But atitsheart,thisproblemisnodifferentthananyotherPlugIn.Assoonasyouseeallthosevariablesinthe choices,youknowyoucanPlugIn.

AndkeepinmindthatGeometryPlugInscomeinallthesameflavorsthatwe'vealreadyseen:theremaybe explicitvariablesorimplicitvariables;sometimesyoupluginfordifferentvariablesseparately,sometimesyou pluginforoneandfigureouttheothers(aswejustdidin#10).

BACKSOLVE

Takealookatthisone.

17. Gerry's age is 5 more than three times Carol's age. Ifthe sum oftheir ages is 45, how old is Carol?

A) 10

B) 12

C) 14

D) 16

Here,wecan'tjustmakeupanumberforCarol'sagebecausethat'sthewholepointofthequestion.Thevalue doesmatter-there'sonlyonenumberthatworksforCarol'sage.SoPlugInisout.

However)likewedidwithPlugIn)wecanstillturnthisintoasimplearithmeticproblem.Butinsteadofpicking randomnumbers)let'susethenumbersintheanswerchoices.Weknowoneofthese4numbersisCarol'sage)so let'strythemuntilwefindonethatworks.

That'sBacksolve.Italsohasthreesteps.

1. Pick a choiceand make H theanswer.

It'softenbesttopickeitherB)orC).Whentherearenumbersintheanswerslikethis)theyalwaysputthe choicesinorder.SoifwetrychoiceC)anditdoesn'twork)wecanfigureoutifitwastoosmallortoobigand eliminatetwoanswerchoicesinonefellswoop.

Okay.Solet'ssaythatC)istheanswer.C)is14.Sowhatdoesthatmean?What's14?Well,14istheanswerto thequestion.Inthiscase,thequestionis"howoldisCarol?"ThatmeansifC)isright,thenCarolis14.

2. Dothe problem and see if it fits.

Whatelsedoweknow?WeknowthatGerry'sageis5morethanthreetimesCarol'sage.Again)we'resaying Carolis14,so:

C)Carol=14.

3X14=42

42+5=47=Gerry.

"Gerry'sageis5morethan3times14:' SoifCarolis14,thenGerryis47.

HowdoIknowifC)istherightanswer,then?Well,whatelsedoestheproblemtellus?Theiragesshouldaddup to45.Dothey?Ofcoursenot.Gerry'sagealoneisbiggerthan45.SoC)istoobig.

3. If it fails, figure out if you need a bigger or smaller number and repeat. Well,C)wasdefinitelytoobig,sowe'llneedasmallernumber.Sowe'llmoveontoB):

B)Carol=12.

12x3+5==41=Gerry.

12+41=53X

Stilltoobig.Theiragesshouldaddupto45.Let'smoveontoA):

A)Carol=10.

10x3+5=35=Gerry.

10+35=45✓

Bingo!A)isouranswer.

Thatwasawordproblem.JustlikewesawbeforewhenwewerediscussingPlugIn,thisproblemdidn'thaveany explicitvariablesmentioned,butitdidhaveimplicitvariables.TherewerenoactuallettersassignedtoCarolor Gerry'sage,butwecouldstillputnumbersinforthemallthesame.That'soneofthestrengthsofthese techniques.Wedon'tneedtoworryaboutvariables;wecanworkdirectlywiththeunderlyingconceptsinthe problem.ButBacksolveworksjustaswellwhenthereareexplicitvariables.Observe:

21. Ifj + k = 9 andj2 +jk = 36 then k = A) 3 B) 4 C) 5 D) 6

Anytimeaproblemasksforthevalueofavariable,wecanBacksolve.Justputthenumbersinthechoicesinfor thevariableandseeifitworks.

We'llstartwithC),that's5.They'reaskingfork,sowe'llsayk=5.Okay,fine.Weknowthatj+k= 9.Sincek= S,j= 4. Sofar,sogood.Nowlet'sputjandkintothatgiantequationandseeifitcomesoutto36.

j2 +jk = 42+4(5) = 16+20 = 36✓

Itworks!SinceC)worked,Idon'tevenhavetolookatanythingelse.TheanswerisC).I'mdone!

Let'stakeaminutetothinkabouthowtodothisproblemwithalgebra.Firstofall,youcouldsolveoneequation forj,andthensubstitute_thatintotheotherequation.Ugh.Iguesswecoulddothat,butit'salotofworkand easytomessup.Backsolveismuchquickerandeasier.Now,ifyou'vegotareallygoodeye,youmightnoticethis:

j + k=9andj2 +jk=36

j(j + k)=j1 +jk

j(9) =36

j=4

We'regiventwoequations.

Thesecondequationisjustthefirstequationtimesa.

Sowecanjustsubstitutethevaluesweknow,

Andouransweris4.That'sB).

Waitaminute:4?B)?Didn'twegetC)?Isn'tC)S?Aha!j=4;they'reaskingusfork.RTFQJSoevenifwe're reallycleverwithouralgebra,thealgebraeasilyleadstoanRTFQYou'remuchlesslikelytomakean RTFQmistakewithBacksolvebecauseyou'reworkingdirectlyfromthequestion.YoupickC),andthenmake C)theanswertothequestion.

Sotherearebasicallytwoalgebraicwaysofdoingthisproblem.Oneisslowandpainful.Theotheralmost inevitablyleadsyoutoanRTFQmistake.LikePlugIn,Backsolveisfaster,easier,andsaferthanalgebra..

FrequentlyAsked Questionsabout Backsolve

1. If the first choice I try works, should I try the other choices tobe safe?

No.UnlikePlugIn,withBacksolvethere'snowaythatmorethanonechoicewillworkout.Onceyoufinda choicethatworks,stop.That'syouranswer.

2. What if I'm not sure whether I want a higher or lower number?

Thenjustpickone!Don'tgocrazytryingtodeducewhichwaytogo.PartofthepointofBacksolveistowork quicklyandmethodically.IfC)failsandyou'renotsurewhetheryoushouldgotoB)orD),justpickone. You'rejustdoingsimplemathhere.Theworst-casescenarioisthatyougothewrongwayandwinduphaving totestallfourchoices.Butreally,that'snotverymuchwork.Andyouknowthateventuallyyou'llfindthe answer.

USING THE TECHNIQUES

It'sonethingtounderstandhowthesetechniqueswork.It'sanothertobeabletousethemandusethem effectivelyinareal-testsituation.It'sincrediblydifficulttochangeyourhabits.Thesetechniquesarea fundamentallydifferentapproachthanwhatyou'reusedtodoing inschool.Therefore,youhavetomakeaconsciousefforttousethemonyourpracticetests.Everytimeyoudoa problem,yourfirstthoughtshouldbe"CanIuseatechniquehere?"Evenifyouseeanotherwayofdoingthe problem.Evenifyouthi'nkthatotherwayisbetterthanthetechnique.Youmusttrytousethetechniques everychanceyouget.

Wecanalreadyhearyoucomplaining,buttrustus:it'sforyourowngood.Clearly,youroldwaysofdoing problemsaren'tworkingforyou-iftheywere,youwouldn'tbereadingthisnow.Youroldmethodshavegotten youthescoreyouhavenow.Ifyouwantadifferentscore,youhavetotrydifferentthings.

Ofcourse,youcan'tusethetechniquesoneverysingleproblemyousee.Andsometimes,therewillbeproblems wherethealgebraisn'tsobadandyoucangettheproblemwithoutthetechniques.But here'sthething:you'renotqualifiedtomakethatcallyet.Thetechniquesarestillnewforyou,soyoudon'tknow whetherornotthey'rethebestmethodonthisorthatproblem.Theonlyw�yyoucanbecomequalifiedisto trytou�ethetechniqueseverytimeyoupossiblycan.

Thisisnodifferentfromanytimeyoulearnsomethingnew.Insportsorinmusic,theonlywaytogetgoodat somethingistodoitathousandtimesinarowThemoreyoupractice,thebetteryoubecome.

Techniques and Target Numbers

Aswe ' veseenalready,thetechniquescanturnareallyhardproblemintoareallyeasyproblem.Buttechniques can'tbeusedoneveryquestion.Therewillbesomelegitimatelytoughquestionsthatcan'tbedonewithPlugIn orBacksolve.Luckily,alotofthosetoughquestionswillbepastyourtargetnumbers,soyou'llneverseethem. Butit'snotunusualforthelastquestioninyourtargetnumberstobealegitimatelytoughnon-technique question.Therefore,ifthelastquestioninyourassignedsetisnotatechniquequestion,andyousee aquestionpastyourtargetnumbersthat'sobviouslyatechniquequestion,youmaydothetechniquequestion insteadofoneofyourtargetquestions.

Thisexceptionisonlyfortechniquequestions.Ifyouseeanon-techniqueproblem-evenifyouthinkyoucan doit-it'snotworthyourtime.Rememberthatoneofthedangersoftheharderquestionsisthepossibilityofa Fool'sGoldchoice,awrongchoicethatlookslikeaneasyanswer.Butwe ' vealreadyseenthatusingthe techniquesactuallyreducesyourchancesofmakingthosemistakes.

Andthisdoesn'tmeanyoucandoalltechniquequestionspastyourtargetnumber�.Remember:thegoaloftarget numbersisdofewerquestions.Yourfirstgoalshouldstillbetodoyourtargetquestionsandonlyyourtarget questions.Butattheendofthesection,ifyounoticeaPlugInpastyourassignment,it'sokaytoswapitwith01:eof yourassignedquestions.

Sohowcanyoutellifyoucanuseatechniqueonaproblem?Gladyouasked.

IdentifyingTechniques

Circle the Question

Thisbearsrepeating.It'squiteremarkable,butasimpleactlikecirclingthequestion-thatis,thethingthey're �ctuallyasking'youtosolvefor�candowondersforyourperformance.

WealreadysawhowitcanhelpyouavoidRTFQmistakes.Circlingthequestionhelpsyourememberwhatthepoint oftheproblemis,andwillclearyourmindoneverythingyou do.Butmoreimportantly,itcanhelpyoudecidewhichtechnique,ifany,isapplicableonaquestion.

Here'sageneralruleofthumb:

If the question asks for a VALUE, try Backsolve. If the question asks for a RELATIONSHIP, try Plug In.

Whileitmayseemliketheyaskyouaboutamilliondifferentthingsonthetest,theyactuallyrepeatthesamekinds ofquestionoverandoveragain.Themorequestionsyoudo,theeasieritistospotthetechniques.

Let'srecapsomecommoncharacteristicsoftheThreeFundamentalTechniques:

PlugIn

Makeupnumbersforthevariables.Dotheproblemwithyournumbersuntilyougetanumberforananswer. Thenseewhichchoicegivesyouthatsamenumber.

MATH-1-PLUGIN

HerearesomecommoncharacteristicsofPlug-Inproblems,withexamplesfromproblemswe'veseen:

-Anytimeyouseeaproblemthathas variablesintheanswerchoices,youcan definitelyusePlugIn.Becauseifthe answerisx + 4,itwillalwaysbex + 4, nomatterwhatxis.

-Inparticular,lookoutforquestions thataskfor"xintermsofy':That'sa bigsignthatPlugInispossible.

-SometimesyoucanalsousePlug Inwhentherearevariablesinthe questionbutnotinthechoices. Sometimesifyoupluginforone variableyoucanfigureouttheother variables.

-YoucanusePlugInonproblemswith implicitvariables.YoucanusePlugIn anytimethere'ssomeconceptinthe problemand:

1.Youdon'tknowitsvalue

2.There'snowaytofigureoutits value

3.Theystillexpectyoutogetan answer

4.Soitdoesn'tmatterwhatthat valueis;you'llgetthesameanswernomatterwhat.

9.Bobhas4dollarsmorethanLisadoes. IfLisahasxdollars,howmuchwould Bobhaveifhedoubledhismoney?

x+4 B)2x C) 2x+4

14.Ifx+Sis3lessthany,thenx-2is howmuchlessthany?

30.ScottdrivestoBob'shouseataspeedof30milesperhour anddrivesbackataspeedofSOmilesperhour.Ifhetakes thesameroutebothways,whatwashisaveragespeed,in milesperhour,forthewholetrip? A)37.S

B)40 C)42.S D)Itcannotbedeterminedfromtheinformationgiven.

Backsolve

Testthenumbersintheanswerchoices.Startwiththemiddlenumber.Putitthroughthe•problem1 andseeif itmatcheswhatyouknow.Ifitdoesn't,pickabiggerorsmallerchoiceuntilyoufindonethatworks.

MATH-2-BACKSOLVE

SomecommoncharacteristicsofBacksolveproblems:

-Iftherearewholenumbersinthe answerchoicesyoucanusuallyuse Backsolve.Anytimeyouneedtofind somekindofsinglevalueorquantity1 you'vegotfouroptionsforthatvalue righthere.Threeofthemarewrong1 oneofthemisright.Testthem.

-Ifthey'reaskingyouforthevalueof avariable(i.e.1 whatnumberdoesx equal),youcanusuallyuseBacksolve. Theywanttoknowx?Well1 hereare fouroptions.Try' emuntilyoufind onethatworks.

17.Gerry'sageis5morethanthreetimes Carol'sage.Ifthesumoftheiragesis 45,howoldisCarol?

10

12

14

16

18.Ifj+k=9andj2+jk=36thenk=

3

4·

5

6

Often,Backsolvequestionshavetwopiecesofinformation.Whenyoutestananswerchoice1 yourunthechoice throughonepieceofinformationandseeifitmatchestheother.In#17above1 westartedwith"Smorethan threetimes"andcheckedthattheresultingsumswere45.In#21,westartedwiththefirstequationand checkedthatthesecondcameoutto36.

MATH FUNDAMENTALS

Themathtechniques-PlugInandBacksolve-canbeappliedtoalotofdifferent problems.However,thetechniqueswon'tworkoneveryproblem.Weneedtotalkabout content-theactualrulesofmathyouhavetoknowontheSAT.

Let'sbeginatthebeginning,asoneshould.Thischapterdealswiththenutsandboltsthat makeupthebasicrulesofmath.Muchofthecontentinthischapterisn'tdirectlytested somuchasitunderliesmanyoftheharderconceptswe'llseedowntheroad.Youcan't solveequationsdealingwithcomplicatedmulti-variablerationalfunctionsunlessyou knowalittlesomethingaboutfractions.

Sincewe'retalkingaboutthebasicshere,muchofthiswillprobablynotbenewtoyou. Therefore,youmaybetemptedtoskipoverthispart."Thisissoboring!Whydowehave totalkaboutfractions?Wedidthisin,like,seventhgrade!Ihateyou!"

Ah,butit'sbecausethisisstuffwe'veseenbeforethatwemustmakesureweknowitwell. Remember:moststudents'problemisn'tthattheydon'tknowenoughmath;it'sthat they'remissingquestionsthattheyalreadyknowhowtodo.Therefore,we'vegottomake sureweknowallthisstuffbackwardsandforwards.

MATH-3

NUMBER CONCEPTS AND DEFINITIONS

Let'sgetsometerminologyoutofthewaytoavoidconfusiondowntheline.

Integer:Anynumberthatdoesnothaveafractionordecimalpart:-3,-2,-1,O,1,2, 3...

Factor:Anintegerthatcanbedividedintoanotherintegerwithoutaremainder.For example,3isafactorof12because12+3=4.Wesaythelargernumber"isdivisibleby" thesmallernumber,sohere12isdivisibleby3.*

* Here'satricktohelpyoufindfactors:ifthesumofthenumber'sdigitsisdivisibleby3,thenthenumberis divisibleby3.12isdivisibleby3because1+2=3.And945isdivisibleby3because9+4+5=18, and18isdivisibleby3.Theruleistruefor9,too:ifthesumofthedigitsisdivisibleby9,the numberisdivisibleby9.

Conceptsinthis chapterthatdeal withproportions (likeratios,rates, andpercentages), aregenerally usedonProblem SolvingandData Analysisquestions. Therefore,they appearonlyonthe CalculatorOK section,notonthe NoCalculator section. Notethatzeroisan evenintegerbutitis neitherpositivenor negative.

Multiple:Anintegerthathasanotherintegerasafactor.Forexample,12isamultipleof3because3x4=12.

PrimeNumber:Anumberthathasexactlytwofactors:1anditself.1isnotaprimenumber.Theonlyeven primenumberis2.Examplesofprimenumbersinclude2,3,S,7,11,and13.

Remainder:Theintegerleftoverwhenanintegerisdividedbyanintegerthatisnotitsfactor.Forexample:13 -;-S=2witharemainderof3.Thatmeansyoucanfittwofivesin13,buttherewillbe3leftover:Sx2=10,and 10+3=13.

Remaindersarewholenumbers,NOTdecimals.Ifyoupunch"13-;-S"onyourcalculatoryou'llget2.6.The remainderisNOT6.

PropertiesofPositiveandNegativenumbers:Biggerdigitsgivesmallernegativenumbers.Thatis,-10is smallerthan-2.

EvenIntegers: (Pos)x(Pas)=Pas (Even)x(Even)= Even(Even)x(Odd)= Even(Odd)x(Odd)= Odd

Decimalplaces:Inthenumber25.97

(Neg)x(Pos)=Neg(Neg)x(Neg)=PosPropertiesofOddand

Even+Even=Even

Even+Odd=Odd

Odd+Odd=Even

•2isthe"tensdigit"andisinthe"tensplace"

•Sisthe"unitsdigit"andisinthe"unitsplace"

•9isthe"tenthsdigit"andisinthe"tenthsplace"

•7isthe"hundredthsdigit"andisinthe"hundredthsplace"

ScientificNotation:Becausedecimalnumbersarebasedonpowersoften(hundreds,tens,tenths, hundredths,etc),youcanexpressanynumberasadecimalmultipliedbyapoweroften.Sothenumber 43,500becomes4.35x 104 , and0.00S24becomes5.24x 10-3. Thisisjustawaytomakeiteasiertowritereally bigorreallysmallnumbers.Insteadof8,000,000,000wewrite8.0x 109 •

Youdon'thavetoknowmuchaboutthisnotation.SATquestionsmayaskyoutomanipulate

numbersinthisform,butusuallythat'seasytodoonyourcalculator.*Justrememberthattheexponentnextto the"10"hasthebiggesteffectonthevalueofthenumber:2x109ismuch, muchbiggerthan9x102

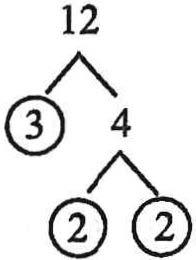
PrimeFactors

Aswesaidabove,integerscanbebrokendownintofactors,andaprimenumberisonethat can'tbebrokendownintofactors.Therefore,aprimefactorisafactorthatcan'tbebrokendownintosmaller factors.Anynumberthatisn'tprimecanbereducedtoauniquesetof primefactors.Andallthatnumber'sfactorsarejustdifferentcombinationsofitsprime factors.

- What are the prime factors of 12?

Allwehavetodoisbreak12upintoanyfactors,thenkeepsplittingupthefactorsuntilwecan'tanymore.

-Weknow3x4=12,so3and4arefactorsof12.

-3isprime,soitcan'tgoanyfurther.

-4isnotprime,sowecanbreakitupinto2and2.

-2isprime,soitcan'tgoanyfurther.

-Sotheprimefactorsof12are3,2,and2.(Becausewefoundtwo2's,welistbothof theminourlistofprimefactors.)

Ifwehadstartedwithadifferentpairoffactors-say,2and6-we'dstill getthesamesetofprimefactors.Allthefactorsof12canbeproducedby multiplyingtheprimefactorstogether:

Thebranchingdiagramshownheremakesiteasytofindtheprimefactorsofanyinteger. Splitupthenumberintoanyfactors.Ifoneofthefactorsisprime,circleit.Otherwise,keep factoring.Ithelpstostartwithasmallprimenumbersontheleft,soyouonlyhavetoexpand thetreeontherightbranch.Thediagramtotherightshowsthattheprimefactorsof180are 2,2,S,3,and3.

*Onsomecalculators,the"EE"buttonisshorthandforthisnotation.Typing"4.24EE4"givesyou4.24x104 (thoughit'softendisplayedwithone"E"as"4.24E4").

-Inthenumber379.045,whatdigitisinthe unitsplace?

- Ifxisanoddpositiveinteger,whichofthe followingexpressionsmustbeeven?

I.2x

II.x+2

III.3x+1

- Ifxhasaremainderof5whendividedby 6andx>IO,whatisthesmallestpossible valueofx?

- Ifjisthelargestprime-factorof42,andk isthelargestprimefactorof36,whatisthe valueofj+k?

-Ifxandyareintegerssuchthatxy=-12and x > O,whatisthegreatestpossiblevalueofy?

FRACTIONS

Afractionisnothingmorethanonenumberdividedbyanother.Assuch,toconvertafractiontoadecimal,just dividethenumbers.Thetopnumberiscalledthenumeratorithebottomnumberiscalledthedenominator.

3 -=3-i-4=0.75

Youmustknowhowtoadd,subtract,multiplyanddividefractions.

Toaddorsubtractfractions,youmustfindacommondenominator.Thisjustmeansthatyoucan'taddor subtractfractionsthathavedifferentnumbersonthebottom.

3 2 3x3 4x298 1 ---=-----=---=-

433x44x3121212

Tomultiplyfractions,youdon'thavetodoanypreparation.Justmultiplystraightacross:topxtop;bottomx bottom.

23(2 X3)61 -x--------

94(9 X4)366

Noticethatouranswercouldbereducedbecausethetopandbottomhadacommonfactor.Wealsocould havetakenoutthecommonfactorsbeforewemultiplied:

1 1 ,2'31'3..1111 -x-=-x---x-=---9ft''9...232(3x2)6 2 3

Todividefractions,youmusttakethereciprocalofthesecondfraction,andthenmultiply."Reciprocal"just meanstoflipthefractionover.

323,Y313 - : ---X---X-=105Nl.2224 2

Acompoundfractionisoneinwhichthenumeratorand/ordenominatorcontainfractions.Thisisequivalent todividingfractions.Remember:fractionsjustmean"divide".

4 1/3 1/2 - =- : -=-X-=11122 32313

Ifyoueverwanttocombineafractionwithawholenumber,rememberthatanywhole

numbercanbewrittenasafractionwithanumeratorof1:

Whenmultiplyingawholenumberbyafraction,thismeansthatthewholenumbercanmultiplystraightacross tothenumeratorandcancanceloutdirectlywiththedenominatorofthefraction:

Whenaddingorsubtracting,it'sbesttowriteinthedenominatorof1underthewholenumbertohelpfind thelowestcommondenominator.

Whenthenumeratorislargerthanthedenominatorlikethis,wecallthatanimproperfraction.Amixednumber containsawholenumberandafraction.

(Mixednumber) 4

(Improperfraction)

Manipulatingfractionsisalostart.Withtheadventofcalculators,alotofproblemsthatusedtorequire knowledgeoffractionscannowbedonequicklywithdecimals,sincefractionscanbeeasilyconvertedto decimalsonyourcalculator.

That'sfine.We'reallfordoingproblemsquickly.Butdon'tforgetaboutfractions.Often,usingfractions effectivelycanactuallymakeaproblemfasterthantypingtheproblemoutonyourcalculator.

-Firstofall,sometimesyou'renotallowedtouseacalculator,remember?

-Secondly,somefractionsbecomerepeatingdecimals,sothecalculatorwillgive approximateanswers-thiscanbedeadlyifyouhavealongcomputation.

-Third 1 youmustbecarefulofparentheses.Ifyoutrytodo(1/3)-:-(1/2)bytypingin "1-:-3-:-1-:-2'�you'llgetitwrong.Youmusttype"(1-:-3)-:-(1-:-2)':*

-Fourth,usingfractionsisofteneasierthanitseemsbecauseyoucanoftencancelout commonfactors1 thusturninghardmathintoeasymath.

*Funfact:thetechnicalnameforadivisionsymbol(+)isanobelus.

-Mostimportantly,fractionsarethebasisofalotofdifferentconceptsontheSAT. Ratios,rates,andpercentagesallrelyonfractions.You'llevenseesomealgebra problemswithfractionscomposedofvariables.Youwon'tbeabletodothoseonyour calculator,soyou'dbetterknowhowtodealwithfractions.

MATH -5

xercise #2

RATIOS

Aratioisjustarelationshipbetweentwoormorequantities.Ratiosare _usuallyexpressedasfractions1 butthere aremanywaysofdescribingthem.Allofthefollowingmeanthesamething:

Theratioofboystogirlsis2:3.

Theratioofboystogirlsis� 3 .

Takealookatthisproblem:

Theratioofboystogirlsis2to3.

Therearetwoboysforeverythreegirls.

- A recipe calls for 3 cups of sugar for every 7 cups of flour. If Bill uses 28 cups of flour, how many cups of sugar should he use?

Youcansetthisupastwofractionsequaltoeachother1 thensolvetheequationbycross­multiplyingthe termsacrosstheequalssign.*

xsugar3 sugar28flour 7flour

7x=28 X 3

7x=84

x= 12

Theonlytrickythingaboutratiosisthatyoumustmakesureyourunitsmatch.

- A certain park contains only maple and elm trees in a ratio of 2 to 3, respectively. If there are a total of 40 trees, how many maple trees are there in the park?

Youmaybetemptedtosetuptheratiolikethis:

X xmaple2maple 40totaltrees3elm

Butlook:theunitsinthedenominatorsdon'tmatch.Theleftratiois"maple"to"totaltrees"1

* Anotherwaytosolveequationslikethisistolookacrosstheequalssign.Noticethat28isfourtimes7, thereforexwillbefourtimes3.Whichis12.Itdoesn'talwaysworkthiseasily;butwhenitdoesit cansaveyousometime.

buttherightratiois"maple"to"elm".That'sbad.

Luckily,wecanfixtherightratiorathereasily-justadd.Ifthereare2mapletreesand3elmtrees,thenthere are5totaltrees.Sothereare2mapletreesforevery5totaltrees; ✓xmaple2maple =---=--

40totaltrees5totaltrees

Nowwecancross-multiply:

5x=2x40

5x=80

x= 16

Toavoidmismatchingunits,always writethefractionwiththequantity you'relookingforFIRST.Thenset upasecondfractionwithmatching units.

Onceagain,circlingthequestionwillhelpyouonratioproblems.Here,thequestionis"Ifthereareatotalof40 trees,howmanymapletreesarethereinthepark?"Thattellsustheratiowe'relookingforis"maple"to"total trees'�soweshouldsetupourfractionsusingthoseunits.

Directand Inverse Proportions

Ratiosliketheonesabovearealsocalleddirectproportions.Itjustmeansthatonequantitydividedbythe otheralwayscomesouttothesamenumber,sowecansettwofractionsequaltoeachother.Sayingone quantity"variesdirectly"withtheothermeansthesamething.

DirectProportionx=cy X -=c y

Inadirectproportion,thevariablesgointhesamedirection:asthevalueofxgoesup, thevalueofyalsogoesup.*Forexample1 considerthedirectproportion.=-=!: y 2

X yx/y=0.5

121+2=0.5

242 + 4=0.5 Asxincreases(1,2,3,...), yalsoincreases(2,4,6,...)

363+6=0.5

Ontheotherhand,youmayalsoencounter"inverseproportions':Thatmeansthatonequantitymultipliedby theotheralwayscomesouttothesamenumber,sowecansettwoproductsequaltoeachother.

InverseProportionxy= C

*Legaldisclaimer:it'sactuallytheabsolutevalueofthevariablesthatgointhesamedirection.Ifthefraction equalstoanegativeconstant,thevaluesgoinoppositedirections.Butyou'llneverseethatontheSAT,sodon'tworry.

Inaninverseproportion,thevariablesgoinoppositedirections:asthevalueofxgoesup, thevalueofygoesdown.Forexample,considertheinverseproportionxy=12.

X y 112 26 34 xy=-12

1 X 12=12

2 X 6=12

3 X 4=12

Asxincreases(1,2,3,...), ydecreases(12,6,4,...)

-Bobmakessomefruitpunchthatcontains applejuiceandmangojuiceina1:5ratio.If heuses15pintsofthemangojuice,howmany pintsofapplejuicewillheneed?

-Ananimalshelterhas2catsforevery3dogs. Ifthereare45animalsintheshelter,how manydogsarethere?

-Asif'slibraryhas3hardcoverbooksfor every8paperbackbooks.Ifhehas121 booksinhislibrary,howmanyofthem arepaperbacks?

-Atacertainschool,theratioofboystogirlsin theseventhgradeis3to 5. Ifthereare 56 total seventh-graders,howmanyofthemaregirls?

-Twonumbersxandyareinadirect proportionsuchthatwhenx=2,y=9.What isthevalueofywhenx=7?

RATES AND UNITS

OneofthemorecommonquestiontypesontheSATinvolveconversionofunits.Forexample:

- How many inches are in 3 feet? (1 foot= 12 inches)

Thisoneisprettyeasy.Mostofyoucanprobablyintuitivelyseewejustmultiply3by12toget36.

Butwecouldalsowritethisasmultiplicationoffractions:

3feetx(12-lfootinches)=36mches

Thatmayseemlikeunnecessarysetuphere1 butitshowsuswhywemultiplyby12instead ofdividingby12.Whenwetalkedaboutmultiplyingfractions1 wesawthatwecancancel outcommonfactorsacrossthetopandbottomofafraction:

Unitscanbecancelledoutjustlikenumberscan.The"feet"inthefirstnumbercancelsoutthe"feet"inthe denominatorofthesecond:*

-

Thisbecomesimportantwhenwewanttodomorecomplicatedconversions:

- How many seconds are there in 2 days?

2daysx(24---hours)x(60----minutes)x(60seconds)=2x24x60x60seconds=172,800seconds 1day1hour1mmute

Setupthefractionssothattheunitsyoudon'twantgetcancelledout.Dothatbymakingsurethoseunits appearbothinthetopofonefractionandinthebottomofanother. Thesameprincipleappliestoquestionsaboutrates:

*Remember:ifanumberdoesn'tlooklikeafraction,itcountsasanumerator(afractiontop)becausethere's animplied"7 l"underit.So"3feet"inourequationhereisanumerator,whichcancelsoutwiththe"lfoot"inthe denominatorofthefraction.

- If Molly can bake 3 pies in 2 hours, how many pies can she make in 10 hours?

Thiskindofquestioncanbesetuplikearatio,aswesawearlier: 3piesxpies2 hours10hours

Butifwetakethisequationandmultiplybothsidesby10hours,we'llseeit'sthesamesortofproblemasa unitconversion:

10�sx(;_;:;s)=xpies=5 x3pies= 15pies

It'seasyenoughtosolvethisparticularquestionbycross-multiplyingtheratio.Butratequestionscanget morecomplicated:

- Janelle is using a copy machine to make books for her class. Each book contains 120 pages, and the machine �an copy 100 pages per minute. How many hours will it take her to make 300 books?

That'salotofrates.Herearealltheratesweknow: lminute lbook 120pages l00pages

Let'sfocusonthequestionitself: minu 60lhourtes

- How many hours will it take her to make 300 books?

Basicallywewanttoconvert300booksintohours.Sowe'llstartwith300booksandwe'lladdonratesuntil wegettohours.

Doweknowanyratesthatuse"books"?Yes,1bookhas120pages:

300_.!)66ks X }20;:IS lb

Don'tdoitoutyet.Let'sfindalltheratesfirst.Nowthebookscanceloutandwe'releftwithpages.Dowehave anyratesthatuse"pages"?Yes,100pagesin1minute.

Thepagesca°:celoutandwe'releftwithminutes.Nowwejusthavetoconvertminutesto hours:

300Jx{oksx 120p�x �x 1hour 1� lOOpa� 60¥

We'releftwithhours.That'swhatwewant!Great!Nowthattheunitsarestraight,let'signoretheunitsandtry tocanceloutsomecommonfactorsinthenumbers:

Itmaytoughtoseehowtosetupthatonebigexpressionatthebeginning.Butwedon'thavetobeabletoseethe end;wecanjustaddonratesandkeepconvertinguntilwegettotheunitswewant.

-Markcaneat20hotdogsin4minutes.HowmanyhotdogscanheeatinS hours?

-Elizabethjogsfor2hourseachday.Heraveragejoggingspeedis4milesper hour.Ifshejogs5daysaweek,howfarwillshejogover3weeks?

-Ifacaristravelingataspeedof90kilometersperhour,howfastisit travellinginmeterspersecond?(1kilometer=1,000meters)

-Atownispaintingparkingspotsalongthecurbsofitsstreets.Eachspotmust be20feetlong,andeachblockis300feetlong.Whatisthemaximumnumber ofparkingspotsthatcanfitononesideofastreetthatis4blockslong?

-Markcaneat20hotdogsin4minutes.Hotdogsaresoldinpackages containing12hotdogs,andpackagescost$6each.Howmuchmoneywillit costifMarkbuysenoughhotdogstoeatfor3hourscontinuously?

PERCENTS

Bynow,weshouldallatleastbefamiliarwithpercents.Thesimplestwaytodopercentsisbypuredivision.

8 is what percent of 32?

Allyoudoisdivide1 thenmultiplyby100:

8 -=0.25 32 0.25X100=25%

Doyouwanttoknowasecret?Percentsarereallynothingmorethanglorifiedratios.Percentliterallymeans "outofonehundred':Soyou'rejustconvertingaratiointoanotherratiooutof100.Thisproblemisthesame thingascross-multiplying:

8X -=32100

"8outof32"isthesamethingas"25outof100'�or25"percent':

Ofcourse1 percentproblemsontheSATcangetmorecomplicatedthanthat.We'vedevisedthefollowing tableforpercentproblems: .Read

Wheneveryouseeoneofthewordsintheleftcolumn1 writethecorrespondingsymbolintherightcolumn.If youseeanumber1 justwrit�thenumber.Forexample:

12 is 40% ofwhat number?

becomes40 12=-xn 100

Youknow,alotofstudentsfreakoutaboutwordproblems.Butreally,thelanguageweusetodescribe problemsisexactlythesamestuffasallthesignsandsymbolsweuseinequations.Soaslongasyoucan speakEnglish1 youcanwriteequations;thewordsmeanexactlywhatyouthinktheymean.

Theadvantageofusingthetableisthatitmakespercentproblemsautomaticandrobotic.Yoticangodirectlyfrom wordstoanequationwithoutthinkingaboutanything.

Thereareothersimilarwaysofdoingpercentproblems(someofyoumayknowthe"is-over­of"method),butthis tableisparticularly�ffectiveonharderSATproblems.Takealookatthisproblem:

- If 25 percent of 12 percent ofs is 18, s = ?

Thiscanbereallynastywithotherwaysofdoingpercents.Butwiththetable,wedon'tcare.Doitrobotically; whenyouseeaword,writeitssymbol.Sothisquestionbecomes:

25 12 -x-xs=18

100 100

Nowwehaveaone-variableequationandwecansolvefors.Wedidn'thavetothinkaboutathing.Theequation camealmostinstantly.

Here'sanothertoughie: 1 - Ifx is 2 percent of 600, x = ?

Oh,wellhalfof600is300.Right?

WRONG!Itdoesn'tsayxishalfof600;itsaysxisone-halfpercentof600.Thatis,halfofonepercent.RTFQJ

Withthetable,wedon'tmakethismistakebecausewejustwritewhatwesee:

X= x600 100

Becausewearen'tthinkingabouttheproblem-we'rejustautomaticallywritingdownwhatweread-we're muchlesslikelytomaketheRTFQ

PercentIncreaseandDecrease

Apercentincreaseordecreasejustmeans:

The amount of the change is what percent of the original amount?

Or:

Change PercentChange=0rlglnalx100

- Joe made 150 dollars last week and 180 dollars this week. What was the percent increa�e in hi� p�y?

Inthisproblem,theamountofthechangeis30(that's180-150)andtheoriginalamountis150.Sothe questionis"30iswhatpercentof150?"Nowwecanjustusethetabletosetup anequation:

30=�xl50 100

Youcanalsothinkofpercentchangeasjustthechangedividedbytheoriginal.

301 20 0

-=-=0.2=-=201/o 150 5 100

Thereareseveraldifferentwaysofexpressingapercentincrease.Inthisproblem,we'resayingJoereceived 20%morethanthepastweek.Butforsomeproblems,itmaybeusefultowriteapercentincreaseinadecimal expressionintermsoftheoriginal.

Here,there'sa20%increaseovertheoriginal,whichweseecanalsobewrittenasthedecimal0.2.That20% wasaddedtotheoriginalamount,sothenewpriceis120%oftheoriginal,or1.2timestheoriginal.Inthis form,insteadofusingthechange,we'resaying:

The newamountIswhatpercentoftheoriginalamount.

180=�xl50 100 or 180 =�=1.2=120 150 5 100 or 120%

Whatis42%of50?

MATH - 8 Exercise #5

5iswhatpercentof4?

21is35%ofwhatnumber?

Whatis15%of75%of80?

Aschoolhad30reportedabsencesoneweek and27reportedabsencesthefollowing week.Whatwasthepercentdecreaseinthe numberofabsencesbetweenthetwoweeks?

EXPONENTS

1. Properties

Exponentstellyouhowmanytimestomultiplyanumberortermbyitself.Thenumberthatisbeingmultipliedis calledthe"base".Givinganumberanexponentisalsocalledtakingittothat"power".

base ➔42 �exponent

Hereareafewdefinitionsandpropertiesofexponentstoremember:

- Anexponenttellsyouhowmanytimestomultiplyanumberbyitself.

52 = 5 X 5 h4 = h X h X h X h

-Anegativebasetakentoanevenexponentwillbecomepositive. Anegativebasetakentoanoddexponentwillstaynegative.

(-2)2=(-2) X (-2)=4 (-2) 3 =(-2) X (-2) X (-2)=-8

-Whentakingapositivefractiontoapower,theresultissmallerthantheoriginal number.

-Anegativeexponentisthesameasthereciprocalofthebasewithapositive exponent(thatis,1dividedbythenumberwithapositiveexponent). -31 X =X3

-Anynumbertothezeropowerequalsone. x0=1

-Arootistheinverse(theopposite)ofitscorrespondingpower.Asquarerootisthe inverseofasquare,acuberootistheinverseofacube,thefourthrootistheinverse ofthefourthpower,etc.Thatmeansthatdoingbothatthesametimewillcancel themout. J;x..Jx=x N=x

-Afractionalexponentisthesameasaroot. I x2 = ✓x

A word about parentheses

Onexponentproblems,it'sespeciallyimportanttopayattentiontowhat'sinsideandoutsidetheparentheses.

Ifanexponentisnexttoparentheses,itappliestotheentireexpressioninsidethe parentheses.

Iftherearenoparentheses,theexponentappliesonlytothenumberorvariableright

(ab)2 :Bothaandbaresquared. nexttoit.

Onlybissquared,nota. Onlyxissquared.

-(2x)2 :2xissquared.Thisequals-4x2 •

(-2x)2 :-2andxarebothsquared.This equals4x2 •

2.Combiningexponents

Thereareafewrulesfordealingwithexponentialnumbersthatyoushouldknow:

1. To multiply exponential numbers with the same base, add the exponents.

25 X 23=25+3=28

2. To divide exponential numberswith the same base, subtractthe exponents.

�=2S-3 =22 23

3. To raise an exponential number to another exponent, multiply the exponents.

(25)3=25x3=215

Notethatforthese rules,thebasedoes notchange.

WARNING:Youcanaddvariableswiththesameexponent,butyoucannotaddbaseswithdifferentexponents:

OK: 2x2 +7x2 = 9x2

WARNING:Alltheserulesonlyapplytoexponentialnumberswiththesamebase.Ifyou'regivenexponential numbersindifferentbases,trytogettheminthesamebase.

Variables In exponents, Different bases

Ifanequationhasvariablesinitsexponents,youcanusuallysettheexponentsequaltoeachother.

If 2 a+10 = 2 30 , then a= ?

Bothsidesoftheequationhavethesamebase,sowecanjustsettheexponentsequaltoeachother:

a+ 10=3a 10= 2a S=a

Ifwe'regivennumbersthatdon'thavethesamebase,weshouldtrytoputtheminthesamebase:

If 3 x = 9 5 , then x = ?

'Wecan'tjustsetxequalto5becauseonebaseis3andtheotheris9.Butlook:9isapowerof3.If werewrite9as32 , we'llhavethesamebaseonbothsides. x= 10

{sxyJX3Y)

Forallnonzeroxandy, X y2 -2x _2=?

ABSOLUTE VALUE

Theabsolutevalueofanumberisitsnumericalvaluewithoutitssign.Thatmeansthatnegativenumbersbecome positiveandpositivenumbersstaypositive.

1s1=s I-SI=s

Whenyouwanttocomputeexpressionswithabsolutevalue,dowhateverisinsidethelinesfirst,thenstripaway anynegativesbetweenthelines:Let'slookatanexample:

110-81-15-111

110-s1-1s-111

=121- l-61

=2-6 =-4

Solvingfor

a variableTakealookatthis:

lxl =7

First,dothestuffinsidethelines.

Now,stripawaythenegativesinsidethelines,so-6 becomes6.

Thevariablexisinsidetheabsolutevaluelines,anditsabsolutevalueis7.Therearetwopossiblesolutions:

-Etherx=7andtheabsolutevaluekeepsitpositive7,

-orx=-7andtheabsolutevaluestripsitsnegativetomakeitpositive7.

Thekeytoabsolutevalueproblemsis:DON'TFORGETABOUTTHENEGATIVES.

- If In -121 =7, what is one possible value ofn?

If In -121=7,thenwehavetwooptions:

12 =7 n- or n-12=-7

n= 19 n=S

It'ssometimeshelpfultothinkofabsolutevalueasdistance:Theabsolutevalueofadifference

givesthedistancebetweenthetwopoints.Thatis:

IPointA-PointBI=distancebetweenpoints

Asimplesubtractionwillalwaystellusthedistance.Ifwewanttofindthedistancebetween19and12,we'd subtract19-12.ButifwewantthedistancebetweenSand12,subtractingS-12givesus-7,andwegenerally don'tliketousenegativedistances.Thenicethingabouttheabsolutevalueisthatitgivesusthedistancein eitherdirection.

Intheproblemabove,theexpression"In-12I=7"means"pointnisadistanceof7awayfrom12".Thatis,nis either7morethan12or7lessthan12.

12

Soanytimeyouhaveaproblemthatasksyouforarangelikethis,justrememberthisexpression: !variable-midpointI<halfthetotalrange

1s-21=?

l6-1s1-1s(-4)1=?

Ifjx-21=6,whatareallpossiblevaluesofx?

IfIx+11I =23,whatareallpossiblevaluesofx?

HEART OF ALGEBRA

Thischapterdiscusses.thebasicsofwhatwegenerallycallalgebra:solvingequations,substitutingvalues,andall sortsofotherfunstufflikethat.Ofcourse,intherealworldthere'salotmoretoalgebrathanwhat'sinthis chapter.We'llseesomemorecomplicatedproblemsinthenextchapter.Butagoodgroundinginthebasicsof algebraisnecessarytomoveontothenimblerbits.

TECHNIQUES!

Whilethischapterwillshowyouhowtosolvevarioustypesofalgebraproblems,don'tforgettheMath Techniques!PlugInandBacksolvewerecreatedtohelpyouavoidalgebra.OverhalfoftheHeartofAlgebra problemscanbedonewithtechniques,morethananyotherquestiontype.Sotheyshouldalwaysbeinyour mind,andyourheart.

Obviously,problemsthatareswimminginvariablesaregoodcandidatesforbothtechniques.Ifaquestionhas variablesinthechoices,itdoesn'tmatterwhattheirvaluesare,sowecanusePlugIn.Ifaquestionasksyoufor thevalueofavariable,youcanuseBacksolveandtestthechoicesforthatvariable.

Youwillstillneedtolearnsomealgebra;thetechniqueswon'tworkoneveryquestion,andonsomeproblems techniquesarepossiblebutalgebraisfaster.Inthischapterwe'regoingtoemphasizealgebraicsolutionsover techniquesolutions.Butdon'tforgetthatthetechniquesareheretohelpyou.

-Ifx=5andy=4,whatisthevalueof3x-4y?

-Ifx=3andk=12,whatisthevalueofx2+kx+6?

3b+4c

-Ifa=2,whatisthevalueofawhenb=6andc=10?

-Ifj=6km-n,whatisthevalueofjwhenk=100,m=2andn=-10?

-What1st.h eva1ueof 8x ---w 9henx=1-? X 2

SOLVING AN EQUATION

Mostoftheexamplesabovewereexpressions,notequations.Thatjustmeansthattheyhavenoequalssign.Buta lotofalgebrainvolvesequations.Whenanequationhasonevariableinit,therewillusuallybeonlyonevaluefor thevariablethatmakestheequationtrue.*

- If 3x+ 5 =23, x =?

Youcansolveanequationbygettingthevariablebyitselfononesideoftheequation.Thatmeanswe havetomoveallthestuffnextthextotheothersideoftheequalssign.Youcandothisbydoingthe oppositeofanythingyouseetobothsidesoftheequation:

3x+5=23

3x+S-5=23-5

3x= 18

3x 18 33 x=6

Tomove"+5'�subtract5frombothsides.

Tomove"x3'�dividebothsidesby3.

This,myfriend,istheheartofalgebra:togetxbyitself,dotheoppositeofanythingyouseetobothsides.We'll seemorecomplicatedconcepts,ofcourse,butthisisprettymuchit.Sometimesanequationmayseemmore complicated,butjustremembertodotheoppositetogetridofsomething:

.Jx-3 - If ---=4,x=? 2 .Jx-3 2 =4 .Jx-3 =8 x-3 =64

x=67

Toremove"-;-2",multiplybothsidesby2.

Toremovethesquareroot,squarebothsides.

Toremove"-3'�add3tobothsides.

*Whyisxalwaysthefirstvariableweuse?Thereareseveraltheories,butthisismyfavorite.Thisnotation startedin1637withtheFrenchmathematicianandphilosopherReneDescartesinhisbookLaGeometrie.Originally,hewantedto usezasthefirstvariable,yasthesecond,xasthethird,etc.Butwhenthebookwenttobepublished,thepublisherdidn'thave enough z's (backthen,bookswereprintedusingindividualblocksofmetalforeachletter).Hehadplentyofx'sthough-veryfew Frenchwordsusex.SoweusexasourvariablesbecausetheFrenchlanguageusestoomanyz's.

Howdoyouknowwhichoperationstodofirst?Thinkofanequationasapackagewithmanylayersofribbons, wrappingpaper,andboxes,andthevariableisyourbirthdaypresentinsidethepackage.*Tounwrapthe package,you'vegottostartwiththeoutermostribbon,thenthewrappingpaper,thentheboxunderneath. Eachlayeryouremoveiscoveringallthelayersbelowit.

Whensolvinganequation,startwiththeoperationsthatapplyto�verythingelseonthatsideof theequation.Inthefirstequationabove,3x+5,the"x3"onlyappliestothex)not the5.Butthe"+5"appliestoeverythingbeforeit,sowestartthere.Inthesecondequationabove,thesquare rootonlyappliestothe"x-3'�nottothe2.The"+2"appliestoeverythingelseonthatside,sowestartthere.

x in terms ofy

Noteveryalgebraproblemwilljustdealwithnumbers.Observe:

- Ify = Sx + 3, what is x in terms of y?

Rightnow,theequationgives"yintermsofx".Thatmeanstheequationdefinesyand usesx ' sinitsdefinition:yisbyitselfononesideoftheequation,anditsvalueis5x+ 3.Butwewant"xintermsofy':Thatmeansthatwewanttogetxbyitselfononeside oftheequationandnothingbuty'sandnumbersontheotherside.Wedothisexactly thesamewaywesolvedforxabove.Butnowinsteadofanumber,ouranswerwill haveabunchofy's.

y=5x+3

y-3 =5x+3-3

y-3 = Sx

y-3 5x = 5 5

Fractions

Subtract3frombothsides.

DividebothsidesbyS.

Manyquestionsthat askfor"xintermsof y"canbedonewith PlugIn.

Studentsoftengetconfusedabouthowtodealwithfractionsinalgebraproblems.Evenifyouhavenotrouble dealingwithfractionsthathavenumbers,theycansuddenlybecomedifficultwhentheyhavelettersinstead. Solet'stakeaminutetotalkaboutthedifferentwaystheycanshowup.

*Surprise!It'sjustwhatyouwanted!

1. Fraction times a variable

,First,afractionmayshowupasthecoefficientofavariable.Forexample: 2 x= 10

Whenavariableismultipliedbyafractionlikethis,youcanthinkofthevariableasbeinginthenumerator ofthefraction.Thatway,youcanseehowtobreakdownthestepstosolveit.

2 -x=lO 3 2x=1QX3 2x=30 x=l5

Afasterwaytodoitistoseethatitsimplymeansxtimes2/3.Tosolvef�rx,wecandotheopposite anddivideby2/3.Dividingbyafractionisthesamethingas.multiplyingbythereciprocal.So:

2 -x=lO 3 x=5x3 x = 15

Thesameprinciplesholdtruewhetherthefractioncontainsvariablesornumbers: ab=dc

2. Variable in denominator

Okay,sowhatdoyoudoifthevariableisinthedenominatorinsteadofthenumerator?

x 18=6, x=? x �=6.

Wewanttogetthevariableintothenumeratortosolveit.Howdowedothat?Let'sdothesamething!If somethingisonthebottom,multiplytogetittothetop.

18=6x 3=x

Thisprocesshasalotincommonwithcross-multiplying,amethodwesawwhenweweresolvingratio questionsintheFundamentalschapter.Ifweimaginethat6isactually6/1,wecanseethisisjusttwo fractionsmultipliedtogether:

Whentwofractionsaresetequal,wecancrossmultiplytosolve.Infact,wecaneventakeashortcut.The topofonesideandthebottomoftheothercanswitchplaces:

3. Adding and subtracting with variables

Allthesesituationssofarhaveinvolvedonlymultiplyinganddividing.Thingscangettrickierwhenaddition andsubtractionareinvolved.

Thefirstthingtokeepinmindistobecarefulwhensimplifyingfractions.Rememberthatwecancrossout commonfactorsfromthetopandbottomofafraction:

Butyoucanonlydothiswithmultipiication.Takealookatthisexpression: 2x+6 6

Itisverytemptingtotrytocanceloutthe6inthedenominatorwiththe6onthenumerator,leavinguswith 2x.Thatisnotallowed.Whynot?Becausethe6onthebottomisbeingdividedintothesixonthetopand the2x.Ifyoucancelitout,the2xdoesn'tgetthatsweetdivision.

Youcansplititupintotwofractions,eachdividedby6.Thenyoucansimplifyeachfraction:

Splittingthisfractionintotwofractionsissimplytheoppositeofwhatwenormallydowhenweadd fractions:

Noticethatinthealgebraproblemabove,wedividedeachofthetermsin2x+6by2.Wecouldalsopull outthat2firstbyfactoringthenumerator.Thenthenumeratorwillbetheproductoftwothings:2and (x+3).Soyoucandividethe2outofthetopandthebottom:

Notethatyoucanonlysplitupnumeratorsthisway,notdenominators.So x+3 CANNOTbesplitinto 2-+2.. Denominatorsmustremaintogether.There'snowayyou X cansimplify-x+3

Okay,sowhatdoyoudoifyouhavevariablesinthedenominatorandyouwanttoaddfractions?

3 4 - -+- =? X y

Rememberwhenweaddedfractionsbefore?Wejusthavetofindacommondenominator.Asbefore,the easiestwaytofindoneistomultiplythetwodenominatorstogether.Inthiscase,that'sxy.Sowe'llchange eachfractiontohaveaxyonthebottom:

4.A single unit

3y 4x =-+xy xy = 3y+4x xy

Finally,rememberthatyoucantreatanentirenumeratorordenominatorasasingleunit.Observe:

- If Y =5, what is yin terms ofx?

_ -.* x

Togetyintermsofx,weneedtogetybyitself.Todothat,wesimplymultiplybothsidesbyxtogety=Sx. Fine.Butwhataboutthis: 3x+20

- If y =5, �hatis yin terms ofx?

Aswesaw,wecannotsplitthedenominatortomaketwofractions.Butwecantreatthat wholedenominator,"3x+20•:asoneentityandcrossmultiplyitjustlikewedidbefore.

y=5(3x+20)

y=lSx+100

"'Whynot?PlugIntothinkaboutitintermsofnumbers.Sayx=1,soouroriginalexpressionis3/5or0.6. But3/2+3/3=1.5+1=2.5.Clearlynotthesameas0.6.

6-lf4+(a-4)=9,a=?

- If5x+6_11, X-_, • -If4u+11=3,u=?

-If13-3z=15z+4,z=? 3x x+S -If__=4,x=?

8 3 2 -If X -+-=5,x=?

. Ifp=S(a+8),whatisaintermsofP?

2 If3x-6=y,whatisxintermsofy?

-If::=e,whatisbintermsofa, c, d,ande?

WRITING EQUATIONS

Oftenquestionswillaskyoutowriteyourownequationsorexpressions.Youmaynotevenhavetosolvethem; they'rejusttestingyouifyouknowhowtosetthemup.

- Ifxis 3 less than twice y, what is xin terms of y?

HerewejusthavetoreadthequestionandtranslatetheEnglishwordsintomathematicalexpressionor algebraicequations.Let'stryit:

Words "."XIS "threeless "twicey" "

3

Therefore:"xisthreelessthantwicey"meansx=2y-3.

Notethatyoumust switchtheorderof termsfor"lessthan" It's2y-3not3-2y.

Translationproblemscanoftenbedonewithtechniques.Inproblemslikethis,it'softenmucheasiertousereal numbersandbypasstheequationsaltogether.WesawatonofquestionslikethisintheMathTechniques chapter,remember?

Bob has 4 dollars more than Lisa does. If Lisa hasx dollars, how much would Bob have if he doubled his money?

Lineartranslation

14. Ifx+ 5 is 3 less than y, then x-2 is how much less than y?

TI1ere'saspecialsubsetoftranslationquestionsinvolvinglinearequations.Alinear equationisanequationthatcanbedrawnasalineonthexy-coordinateplane.In algebraictermsthatmeans:

Anexpressionis likeonesideofan equationwithno equalssign.It'sjust agroupofvariables andnumbers connectedtoeach other.

•Ithastwovariables,usuallyxandy.(Ifit'sanexpressioninsteadofanequation,itwilloftenhavejust onevariable.)

•Neithervariableistakentoanypowerotherthan1.Thatis,theydonothaveanyexponents1 norare eitheroneinadenominatorofafraction.

WeseethatthistypeoffunctionshowupatonontheSAT;that'swhattheHeartofAlgebracategoryisallabout. Butit'snotenoughjusttobeabletoevaluateorsolvethem.Wehavetounderstandhowtheywork.Forexample:

- There are too many goats in the basement. Dad pays you a flat fee of $200 (for being brave enough to go down there at all) plus $50 for every goat you catch. Write an expression for the total amount of money you'll get if you catchxgoats.

Apaymentsituationisaclassiccontextforalinearfunction.There'saflatfeethatyougetnomatterwhatyou do,andaratethat'sdependentonhowwellyoudo(howmanyhoursyouwork,howmanythingsyousell, howmanygoatsyoucatch,etc.)

Let'sPlugIntoseehowthisworks.Sayx=3,soyoucatch3goats.You'llget$200plus3times$50.

200 + 50X3=200 + 150=350.

Nowlet'ssayx=10,soyoucatch10goats.You'llgetthat$200plus10times$50.

200 + 50X10=200 + 500=700.

Followingthatpattern,foreveryxgoatsyoucatch,youget

200+50x

That'sanexpression,notanequation.Ifwewantanequation,we'lljustsetitequaltosomething:

y=200+50x

Theyrepresentsthetotalmoneyyougetforeveryxgoatsyoucatch.

Thisisbasicallyhowalllinearfunctionswork.There'sanumberyoumultiplybyavariable­that'sthe rate-andanumberyouaddtoorsubtractfromit-that'sthestartingpoint.

- The equation g = 350 - 6h shows how many goats are remaining in the basement after you work for h hours. How many goats do you catch each hour? Whatdoyouthinkthesenumbersrepresent?Likebefore,there'sanumberbyitselfandanumberwitha variable.Likebefore,theyrepresentastartingpointandarate.Thestartingpointisthenumberbyitself.The rateisthenumbermultipliedbythevariable-inthiscase,howlongyouwork.Thefinalanswer,g,isin termsofgoats.Therefore,

• 350mustbetheinitialnumberofgoats,and

• 6 mustbethenumberofgoatsperhouryoucatch..

Thekeytothissortofquestionisthatyoumustunderstandthemeaningoftheequation,andwhateachterm represents.Butbecausetheseequationssooftentakethesamelinearform1 themoreyouseethemtheeasierit'll betopickup.

-Freddieboughtaflowerforhisgarden.The equationh=2.5d+12modelstheheight,h,in inchesoftheflowerddaysafterhepurchasedit. Howmuchdoestheplantgrow,ininches,every day?

-Sophierunsalemonadestandandputsthe moneyshemakesinherpiggybank.Thisis modeledbytheequationP=2l+14,wherePis theamountofmonerindollarsinherbankandl isthenumberofcupsoflemonadeshehassold. HowmuchmoneyindollarsdoesSophiegetfor eachcupoflemonade?

-Lanagotaboxofdonuts.Theequation d = 120-5hshowsthetotalnumberofdonuts, d,remainingintheboxafterhhours. Howmanydonutswereoriginallyinthe box?

-Theequationc=0.1m+0.lSt+50showsthe totalcost,c,indollars,ofGlenda'smobilephone serviceeachmonth,wheremisthenumberof minutesofphonecallsandtisthenumberoftext messagesshesent.HowmuchisGlendacharged eachmonth,indollars,foreachtextmessage?

-Andrewspentonedaybuildingawallinhis backyardandhasaddedtoiteveryweeksince. Theequationb=25(w+10)modelsthetotal numberofbricksinthewallwweeksafterhe started.Howmanybricksdidheputinthewall onthefirstday?

MULTIPLE EQUATIONS

Sofarwe'vebeendealingwithasingleequationatatime,butsomeproblemsmaygiveyoumultipleequations withmultiplevariables.Thereareseveralwaystodealwiththem:

Substitution

Oftenthemoststraightforwardwaytosolvetheseproblemsis substitution. Forexample:

- Ifa= 3x-6, and Sx+ a= 10, thenx= ?

We'regiventwoequationswithtwovariables, xanda. Noticethatthefirstequationhas aononesideof theequationbyitself.Since"a"isequivalentto"3x-6",wecansubstitute "3x-6"intothesecondequationwhereverweseean"a".

Sx+a= 10

Sx+(3x-6)= 10

Bx-6 =10

Bx= 16

x=2

Tryanother:

- Whenx+ y= 4, what is the valu� of S(x+ y) - 6?

Itmightseemlikewehavetosolveforxoryindividually,bµtwedon't.Thefirstequationgivesavaluefor"x + y",andthesecondequationalsocontains" x +y".Sowecansubstitute4forthatwholeexpression:

S(x+y)-6 =5(4)-6=20-6 = 14

Ifaproblemhastwoormorevariablesinit, don'tforgetthetechniques. Beingabletosolveintricatealgebra problemsisagoodskilltohave,butPlugInandBacksolvecanhelpturncomplicatedproblemsintosimple ones.

Systems

Othertimes,itmaybeeasiertoaddorsubtracttheequationsdirectly.Observe:

Sx+2y= 10

6x-2y=23

34. According to the system ofequations above, what is the value ofx?

Hereit'snoteasytosubstitutebecausewe'dhavetodoalittlebitofmaneuveringthegeteitherquestioninterms ofasinglevariable.Ugh.Butlook!Noticethattheywrotethetwoequationssothatthex'sandy'slineup.That's notanaccident.Theydidthattohelpyou:Andlook:oneequationhasa2yandtheotherhasa-2y.Ifweaddthe equationsthe2y'swillcancelout.

5x+2y= 10

+

6x-2y=23

llx=33 x=3

Systemsdon'talwaysworkoutsobeautifully.Sometimesyouhavetoworkforit:

2x-7y= 15

4x-2y= 18

35. According to the system ofequations above, what is the value ofx?

Nowwecan'tjustaddorsubtracttheequationsbecauseneithervariablewillcancelout.However,we canchangeoneoftheequationssothattheywilLLet'smultiplythefirstequationby2:

2(2x-7y)=2(15)

4x-14y=30

Nowbothequationsstartwith4x.Lasttime,onetermwaspositiveandtheothernegative,soadding themmadethemcancelout.Thistime,sincebothtermsarepositive,let'ssubtractthem.

4x-14y=30

[4x-2v= 18]. -12y=12 y=-1

Butwait!Don'tstop!We'renotdoneyet.That'sy.Wewantx.RTFQButgettingxiseasynow.Justputy=lintoeitherequationandsolveforx.

2x-7(-1)=15

2x+7=15

2x=8 x=4

4x-2(-1)=18

4x+2=18

4x= 16 x=4

Whensolvingasystem,weoftengivevaluesofbothvariablestogetherasanorderedpair(x,y).So thesolutiontothisproblemis(4, -1). Ifasystemcontainstwolinearequations,

therewillbeonepairofvalues-andonlyonepair-thatsolvethesystem:-onevalueforxandoneforythat togetherworkinbothequations.Youcanthinkofthetwoequationsasstraightlinesinthexy-coordinateplane. Theywillcrossatonepoint,andthatpoint (x1y)willbethesolutiontothesystem.(We'lltalkmoreaboutthecoordinateplanesoonenough...)

However,notalllinescross.Lookatthissystem:

2x-3y= 16

4x-6y= 32

Okay,let'sjustmultiplythefirstequationby21 andweget:

4x-6y=32

4x-6y=32

Hey,waitaminute.Thesecondequationisthefirstequationmultipliedbytwo.Thesearethesameequation. It'snottwolines;it'sthesameline,writtentwice.Soanypairofvaluesthatworkforthesecondequationwill alsoworkforthefirstequation.Sothereareinfinitely manysolutions.

Similarly,lookatthissystem:

3x+ y= 10

6x+2y= 14

Let'smultiplythefirstequationbytwosothey'scancelout:

6x+2y=20

- 6x+2y= 14

0=6

Huh?That'sweird.Ifltrytocanceloutthey'sIalsowindupcancellingoutthex's.Here,thelefthalvesofthe equationsareidenticalbuttherighthalvesarenot.Sothissystemhasnosolution.Thinkaboutit:both equationshave "6x+2y" ontheleft,butthey'resupposedtoequal2differentnumbers:20or14.Can'tequal20 and14atthesametime,sothere'snosetofnumbersthatwillsolvebothequations.Ifweweretographthese twolines,theywouldappearasparallellines,whichneverintersect.

Solving DirectlyforExpressions

Takealookatthisproblem:

- If4x - 3y = 13 and x+ 2y= 3, then Sx-y = ?

Therearesomeverypainfulwaystodothiswithnormalalgebra.Youcouldtrytosolveoneequation(orx,then substituteyouranswerinforxintheotherequation,solvefory,thenputybackintothefirstequationandsolve forx,thenstickxandyintotheexpressionthey'reaskingforandyou'redone:

Ugh.Imean,wecoulddoit,butitisn'tfun.Noonewantsthat.

Waitaminute-takeanotherlookatthisquestion.

- If4x- 3y= 13 and x + 2y= 3, then Sx-y= ?

They'renotaskingyouforxoryindividually;they'reaskingforanexpression:Sx-y.Insteadofsolvingforx ory,let'strytosolvedirectlyforSx-y.

Tomakeiteasier,let'swritetheequationsontopofeachothersothexandyvalueslineup:

4x-3y= 13

+ X . + 2v= 3

5x-y=16

Aha!Ifweaddtheequations,wegetSx-y!That'swhatwe'relookingfor.It'sjust13+3!It's16!

Wait,whataboutx?Howdowefindx?Forgetx!They'renotaskingmeforit,soIdon'tcare.Anytimetheyask youforanexpression,don'tsolveforindividualvariables;trytosolvedirectlyfortheexpression.Tryadding equations,multiplyingbytwo,whateverittakes.Trytoplaywithwhattheygiveyouuntilitlookslikewhat they'reaskingfor.Whydoyouthinkthey'reaskingforthatexpression,anyway?WhyspecificallySx-y?They didn'tcomeupwiththatrandomly;they'reaskingyouforthatbecausethat'swhatyougetwhenyouaddthe equations.

Onceagain,thisisanotherreasoncirclingthequestionwillhelpyou.Ifyouseethey'reaskingyouforan expression,don'tworryabouttheindividualvariables;trytosolvedirectlyfortheexpression.

-Ifj=3x-5andk=6x+1,then2j+3k=?

-If!!_=5and4a+7b=9,whatisthevalueofb? b

-Ifx-y=10andz=3x-3y-8,thenz=?

3x+y=12 7xy=l8

-Whatisthesolution(x,y)tothesystemof equationsabove?

4x-3y=34

2x+5y=4

-Whatisthesolution(x,y)tothesystemof equationsabove?

6x-7y=36

2y-3x=-27

-Whatisthesolution(x,y)tothesystemof equationsabove?

-If5x+2y=41and3x+2y=271 thenx=?

-If3x+Sy=58andx+2y=12,theny=?

-If3p+2q=8and4p+3q=11,then7p+5q =?

-If2x+y=23andx+2y=17,then3x-3y=?

INEQUALITIES

Inequalitiesworkjustlikeequationsforthemostpart.Youcansolveforvariablesjustlikeyoudowithequations. Theonlydifferenceisthatifyoumultiplyordividebyanegativenu�ber,youhavetoflipaieinequality.

Permitustodemonstrate:

7-3x> 16

7-3x;_7 > 16-7

-3x>9

-3x 9 -<-3 -3

x<-3

(-Watchouthere.Thisiswherethesignflips.

Morecomplicatedinequalityquestions-particularlythoseinvolvingmultiplevariables-areoftendifficultto solvewithalgebraicmanipulation.Don'tforget:techniqueslikePlugInandBacksolveareheretohelp!

MATH - 15

Exercsie

#12

Solvetheseinequalitiesforx: 3(x+2)<12

17-x>23

.Sx+6<-3x-10

X +4 X -->3 5

7-4x::.35

PASSPORT TO ADVANCED MATH

Phew!Sowejustdidalotofalgebrainthelastchapter.Butwhatifwedid...morealgebra?Wouldyouliketodo morealgebra?Ofcourseyouwould.

ThestupidlynamedPassporttoAdvancedMathquestionsarebasicallyjustFancyAlgebraquestions.You're goingtoseealotofvariablesandequationsjustlikewe'vealreadyseen.Thebiggestdifferenceisthatthis chapterwillhaveequationsandexpressionsthatarenotlinear.Thatmeansyou'llseesomeexponents,some polynomials,somequadraticequations,andtonsoffunstufflikethat.(You'llalsoseesomegraphingonthese questions,butwe'llsavethatforaseparatechapter.)

We'regoingtotalkalotaboutalgebraicmethodshere,butpleaserememberthatalotofproblemsthatseem liketheyneedalgebracanalsobedonewithourmathtechniques,PluginandBacksolve.Don'tforgetabout thetechniques!!

F(X) NOTATION

Lookatthis:

52

Whatdoesthatmean?Duh.Obviously:

52=5X5

Thelittle"2"tellsustomultiplythebignumbertimesitself.Weallknowthat. Similarly:

72 =7x7 {-23)2 =={-23)x{-23)

y2=yxy

D2 =DxD

PASSPORT TO ADVANCED MATH (donkey)2 =(donkey) x (donkey)

Thisshouldnotbenewstoyou.Anytimeyouseealittle"2"nexttoanything,multiplyitbyitself.

That'safunction.It'sasymbol(the"2")witharuleattachedtoit(multiplybyself).Everythingwedoinmathisa kindoffunction:asymbolwitharuleattachedtoit.

Wecanmakeupourownfunctions.Butinsteadofusingasymbollikethelittle2,we'llusetheletterf:

j(x) = 2x + S

Thexhereisjustaplaceholder;it'savariablethatstandsforanynumber,anexampleofhowtousethe function.Justasthelittle"2"meant"multiplythenumberbyitself':thefheremeans"multiplyby2andadds•:

Thatmeans: and: therefore: so: also: aswellas plusthis: thistoo: ergo: thus: whynot: onemore:

f(2)=2(2) + S

f(3)=2(3) + S

f(l8) =2(18) + S

J(1979):::::2(1979)+S

j(y) =2y + S

J(q) =2(q) + S

j(g(k)) =2(g(k)) + S

J(omg)=2(omg) + S

j(n) =2(n) + S

j(x2 + 1) =2(x2 + 1) + 5

J(©) =2(©) + S

f(flu.ffybabypandabear)= 2(jlu.ffybabypandabear)+5

Getthepoint?"f(x)"doesn'tmean"multiplyfbyx".Thefisn'tavariable;it'sthenameofafunction.Whatever youseenexttothef,stickitinforxin2x+5.

Wecandoalotwithfunctions,butitallcomesdowntosubstitution:

Take whatever you see inside the parentheses and stick it In for x.

Compositefunctions

- If/(x) = 3x + 4 and g(x) = x2 what is the value of/(g(3))?

We'regiventwofunctions,f(x)andg(x),andwehaveequationsforboth.Thismayseemscary,but itworksexactlythesamewaythepreviousproblemsdid.

Remember:takewhateveryouseefosidetheparenthesesandstickitinforx.Here,"g(3)"isinside theparenthesesnexttof,so"g(3)"willgoinforxintheequationforJ(x):

f(g(3))=3 X g(3)+4

Thatdoesn'thelp:whatdoesg(3)mean?Ah,that'sjustadifferentfunction.Wecanput3inforxintheequation forg(x):

g(3)=(3/=9.

Nowwe 'llsubstitute9backintothefirstfunction:

f(g(3))=j(9)=3 X 9+4=27+4=31

Notethattheorderisimportant:dothefunctioninsidetheparenthesesfirst.Here,gwasinsidethe parenthesesforf,sowedidgfirst.Ifthequestionhadaskedfor g(f(3))1 we'dfirstput3intotheequationforf, thenputtheresultintotheequationforg

g(r(3))=(r(3))2

.f{3)=3 X 3+4=9+4=13.

g(r(3))=g(13)

g(13)=132 =169

Multiplevariables

- If/(x, y)= 2x + 3y- xy, what is the value of/(5,-1)?

Thisfunctionhas two variablesinsidetheparentheses,butitalsohastwovariablesintheequation.Whenever weseetwonumbersinsidetheparentheses,we 'llmakethefirstnumberequaltoxandthesecondequaltoy.

j(5,-1)=2(5)+3(-1)-(5)(-1)=10+(-3)-(-5)=10-3+5=12

MATH - 16

Exercise#13

- lf./{x)= x2 + 3x-10, then./(10)=?

- Iff(x)= x 2 +3x-10,thenf(7)=?

- Ifj(x)= x 2 - Ifj(x)= x 2 + 3.x-10,thenf(-3)=? + 3.x-10,then1½) =?

- Ifj(x)= x 2 +3x-10,thenf(2x)=?

-Ifk(x)=x 3 +2x,whatisk(-2)?

- Ifj(x)=5x-3andf(a)=12,whatisthevalueofa?

- Ifj(x)=2x + 2,then2f(x) + 2=?

- Iff(x)=7xandg(x)=f(x)+7,whatisthevalueofg(lO)?

- Iff(x)=x 2 -2,whatisthevalueoff(/(3))?

POLYNOMIALS

1.What'sa polynomial?

Apolynomialisanymathematicalexpressionwithtermsthatareaddedorsubtractedtogether.Thesetermswill usuallycontainvariablestakentodifferentpowersmultipliedbyanumbercalleditscoefficient.Apolynomial containingtwotermsisabinomial.

Inthefollowingexpressions,allthetermscontainthesamevariabletakentothesamepower,sotheycanbe combineddirectlyintooneterm:

5+7=12

Sy+7y=12y Sx2 + 7x2=12x2

Butinthefollowingexpressions,thetermsarealldifferent,sotheycan'tbecombinedintooneterm:

Sx+7 Sx+7y

Tosimplifyalongpolynomialwithalotofdifferentterms,findanytermsthathavethesamecombinationof variablesandpowers:

x2 + 4x + 2xy + 7x2 - IOx+5 + 9xy-1

8x2 + 4x + 2xy-lOx + S + 9xy-l

8x2 -6x + 2xy + S + 9xy-l

8x2 -6x + llxy + 5-1

8x2-6x+llxy+4

(3x2 - 7x + 2)-(2x2 + 5x+3)=?

(6x2+5x+3)-2(2x2 - 3x-3)=?

Addthetermscontainingx 2 •

Subtractthetermscontainingx.

Addthetermscontainingxy.

Subtractthetermswithnovariables.

MATH 17 Exercise #14

3x2+ 8x

2.FOIL

Takealookatthis:

6(x+ S)

Herewehaveanumbermultipliedbyanentirebinomial.Todothis,justmultiply6byeachterminsidethe parentheses.Wesometimescallthisdistributingthe6insidetheparentheses.

6(x + 5) =6xx+6x5 =6x+30

Great.Sometimeswewanttomultiplytwo'binomialstogether:

· (x + 5 )(x + 4) = ?

Watchoutfornegatives!Ifyou multiplyapolynomialbya negativenumber,youmust distributethenegativeinside theparentheses.

Justlikewedidabove,wewanttomultiplyeachterminthefirstbinomialwitheachterminthesecond.To helpyoukeeptrackoftheterms,remembertheacronym"FOIL''.Multiply:

Firsttwoterms xxx

Outsideterms xx 4

Insideterms Sxx

Lastterms 5x4

Thenaddthemalltogetherandcombinesimilarterms: =x1 + 4x + Sx+ 20=x2 + 9x+20

MATH - 18 Exercise #15

(x+S)(x-3)=?

(a-7)(a-2)=?

(2y+3)(y-4)=?

3. Factoring

FOILinvolvesmultiplyingtwobinomialstogetalargerpolynomial.ButsomeSATproblemsmightwantyouto gotheotherway.Lookatthisexpression:

2x+6

Noticethateachterminthisexpressionisamultipleoftwo.Wecan"pullout"thattwoandputitofftotheside:

2x+6 =(2xx)+(2x3)=2(x+3)

Wecallthisprocessfactoring.It'stheoppositeofdistributing.Inthiscase,2wasafactorofeachterm,sowe "factoredout"the2.Wecandothesamethingwithvariables:

x1 -3x =(xxx)-(3xx) =x(x-3)

Whatifwewanttofactorapolynomialintotwobinomials?Lookatthisexpression: - What is the factored form of x2 +·1x +·12?

Weknowthattheremustbetwobinomialsthatmultiplytogethertomakethatexpression:

(?+?)(?+?)

Thefirsttermhere,x1 ,wastheresultofthefirsttwotermsofthebinomialsmultipliedtogether.Soeachof thebinomialsmuststartwithanx:

(x+?)(x+?)

Thelastterm,12,wastheresultofthelasttwotermsofthebinomialsmultipliedtogether.Soweknowthe productofourlasttwonumbersis12.Thatcouldbe1and12,2and61 or3and4.*

Themiddleterm,7x,wastheresultofeachofthelasttermsmultipliedbyxandthenaddedtogether.Sowe alsoknowthesumofthelasttwonumbersmustbe7.Whattwonumbershaveaproductof12andasumof7? Only3and4fitbothrequirements.

(x+3)(x+4) =x1+4x+3x+12=x1+7x+12

*That'sassumingalltermsareintegers,ofcourse.Thetermsmightalsobe24and0.5ifweallowdecimals.But SATproblemsusuallysticktointegers,soyoudon'thavetoworryaboutsuchmadness.

Thiscanbeeasierwhenyouhaveanswerchoices: - 2x- 15?

12. Which of the followin� expressions is equivalent tox2

A) (x -2)(x + 1)

B) (x -3)(x+S)

C) (x+3)(x-5)

!)) (x-3)( x-5)

OneoptionhereisBacksolve:It'softeneasiertoFOILthantofactor,soFOILouttheanswer choicesandseewhichoneequalsthepolynomialwewant: X

A) (x-2)(x+l)

B)(x-3)(x+5)

C) (�+3)(x-S)

D) (x-3)(x-5) =x2+x-2x-2 = x2+5x-3x-15 = x2 - Sx + 3x-1S = x2-Sx-3x +15 = x2 - Bx+ 15 X

Evenbetter,youcouldPlugInanumberforx.Sayx=6.

A)(6-2)(6+1)

B)(6-3)(6+5)

C) (6+3)(6-5)

(6)2-2(6)-15 = 36-12-15 =9 = (4)(7)=28 X = (3)(11) = 11 X = (9)(1) =9 ✓

D)(6-3)(6-5) = (3)(1)=3 X

(Notethatwepickedabiggishnumberheresothatmostofthechoicescameoutpositive.Butifyou startwithx=O,youcaneliminateA)andD)veryquickly.

DifferenceofSquares

Trythisproblem:

(x+y)(x-y) = ?

Bothbinomialscontainthesameterms,exceptonebinomialisasumandtheotherisadifference.To dothis,wecanjustFOILaswedidbefore:

(x+y)(x-y) = x2-xy+xy-y =x2-y2

Noticethatthemiddletermscanceledout,sotheresultwasjustthefirsttermsquaredminusthesecond termsquaredThisequationiscalledthedifferenceofsquaresidentity.An"identity"justmeansit'san equationthatshowsupalotthat'salwaystrueforanyvariables,soit'sgoodtorememberit.

x2-y2=(x+y)(x-y)

When you seetwosquaressubtractedfromeachother, youcan easilyfactorthe expression. For example:

X.2 - 64 =?

Bothtermsherearesquares,sowecanimmediatelyfactoritintothesumanddifference of theirroots: =(x+S)(x-8)

MATH 19

Exercise #16

Factorthefollowingexpressions:

2 x-2x-8

x2 -14x+24

9x2 -49

x4 -16

4. Dividing polynomials

Sofarwe'vebeenmultiplyingpolynomials,butwecandividepolynomials,too. x+3· ----=? x2+x-6

Whatdowedo?Rememberthatafractioncanbereducedwhenthetopandbottomhaveacommonterm:

22xl1 -=--=82x44

Thesameconceptappliestopolynomials.Let'sfactorthedenominatorandseeifwecan crossoutsometermscommontothetopandbottom.

Whenfactoring,ourultimategoaliscancelingoutterms.Dontfactorblindly:tryto factoroutthetermthat'sinthenumerator.Inthisproblem,wewanttocancelout"x+3'� sowe'lltrytoget"x+ 3"onthebottom.Thebottomendsin"-6":whattimes3gives-6? -2.Sotheothertermwillbe"x-2".Nowx + 3cancelsoutonthetopandbottom: x+3 x 2 +x-6 x+3 =---(x+3)(x-2)

We'regettinginto someconcepts thatonlyshowup onhardquestions. Ifyouhavelow targetnumbers, theseconceptsare probablynot importanttoyou.

PLEASENOTE:wheneveraprobleminvolvesdivisionbyabinomial,therewillbesomevaluesofxthatarenot allowed.Asarule,youcanneverdivideanythingbyzero.Anyvaluesthatmakethedenominatorzerowillnot beallowed.Thefancymathwayofsayingthatistosaytheexpressionisundefinedforthatvalueofx.Inthe problemabove,thedenominatoriszerowhenx+ 3 = 0orwhenx-2 = 0.Sotheexpressionisundefinedwhen

x= -3andwhenx= 2.

Longdivision

Butwhatifyouwanttodividebyapolynomialthatisn'tafactorofthenumerator?Canwedoanything?Yes!We canuselongdivision!

Let'stakearefresheronhowtodolongdivisionwithintegers.Let'stry172+S:

1.Howmanytimesdoes5gointo17?3times.

2.Multiply3x5toget15.Subtract15from 17toget2.

3.Bringdownthe2toget22.Howmany timesdoes5gointo22?4times.

4.Multiply4x5toget20.Subtract20from 22toget2.That'sasfarasyoucango,so yourremainderis2.

So172+5is34witharemainderof2.Butifwepunchthatoutonthecalculatorweget34.4That'sbecause ".4"isthesamethingas2/5: 172 5 170+2 = 1702 =-+5 5 2 =34+5

5

Basically,wesplitup172intoanumberthatwasdivisibleby5,plusabitthatgotturnedintoafraction.

Wecandothesamethingwithpolynomials!Let'slookatthisone: 3x-S --=? x+2

Here,x+2isnotafactorof3x-5.Solet'sfindsomethingthatdoeshavex+2asafactor.

I.Setitupaswedidbefore.Focusonthe firstterm.Howmanyx'sgointo3x?

2.Multiplyxby3toget3x. 3 x+2)3x-5

3.Multiply3byx+2andlineitup.

4.Subtracttogetaremainder·of-11

Youdon'thavetodothissoformally.Justthink:whatdoIhavetomultiply"x+2"byinordertogetananswer thatstartswith"3x"?Multiplyby3!Whichgetsyou3x + 6.Inotherwords: 3x-5 x+2 = (3x+6)-11 = 3x+6 + -11 =3(x+2)+-11 =311 x+2x+2x+2x+2x+2 x+2

Let'stryaharderone:

x2+4x+5 ----=? x+l

We'llstartthesameway:

1.Setitupaswedidbefore.Focusonthe firstterm.Howmanyx'sgointox2?

2.Multiplyxbyxtogetx2 •

3.Multiplyxbyx+landlineuptheresult. Subtract.

4.Bringdownthe"+S".Howmanyx'sgo into3x?

5.Multiply3byx+landlineuptheresult. Subtract.Ourremainderis2.

Likeinthelastone,think"whatcanImultiply"x+l"byinordertoget"x2+4x"atthestartofmy polynomial.Inotherwords:

Ifallthisscaresyou,don'tworry.Thiskindofdivisionisveryrareonthetest.Qµestionsthatdorequireitwill usuallybeharderquestionsattheendofasection,sochancesareyourTargetNumberswillhaveyouskipping themanyway.(Ofcourse,don'tforgetthatwhenthereareanswerchoices,problemslikethiscanbecome supereasywithPlugIn.)

Exercise#17

Dividethefollowingexpressions(assumingthedenominatorisnotzeroinallcases).

x+ 5 =?

x2-25

x 2 +6x-40 =? x-4

5. Quadraticequations

Allthepolynomialproblemswe'veseensofarhavebeenexpressions,notequations.Thatmeansalmostany valueofxwillmakeitwork.Butwemightalsoseepolynomialsinvolvedinequations,whereonlycertainvalues ofxwillmaketheequationtrue.

Anyequationintheform

isaquadraticequation-apolynomialcontainingonesquaredvariable,usuallysetequalto zero.*Sohowdowesolveit?

- For w,hat values ofx does x2 + 7x +12 = O?

Well,wealreadyfactoredthisexpressionbefore,solet'sdoitagain:

x2+7x+ 12=(x+3)(x+4)=0

Rememberthatzerohasaspecialproperty:anythingtimeszeroisequaltozero.Ifweknowab=0,thenwe knoweitheraorb(orboth)mustequalzero.Sinceweknowthat(x+3)times(x+4)equalszero,weknow thatoneorbothofthosetermsmustequalzero;

x+3=0 x=-3

Sooursolutionsare-3and-4.** or or

x+4=0 x=-4

Notethatyoumustsetaquadraticequationequaltozerotosolveit.

- Forwhat values ofx does x2 - 3x + 2 = 20?

Bewareofthe changeinsign!

Wefactoredthe expressiontox+3 andx+4,butthe solutionsforxare -3and-4.

*Ifthevariableisonlytakentothesecondpower,whyisitcalledquadratic?Doesn't"quad"mean"four"? Indeeditdoes.ThetermcomesfromtheLatinword"quadratus''.meaning"square"(asin"xsquared").Andasquarehasfoursides.** Noticethatthevalueofc-thenumberwithnovariable-isequaltotheproductofthesolutions (-3x-4=12),andthevalueofb-thenumbernexttoxintheoriginalequation-isequaltothesumofthenegativesofthe solutions(3+4)=12.Thisisjusttruebecauseoftherulesoffactoringthatwe'vealreadyseen(andbecausea=I),butbeingableto recognizethisfactcansometimessaveyousometime.(Whywetakethenegativeofthesumbutnottheproduct?Weactuallycan takethenegativesofthetermsintheproductaswell,it'sjustthat-3times-4comesoutthesameas3times 4.)

Herewehave20ontherightside.That'snogoodiwewantOthere.Sowe'lljustsubtract20frombothsides beforewefactor:

x2-3x+2-20=20-20

x2-3x-l8 = 0

(x-6)(x+3) = 0

x-6=0orx+3=0

x=6· orx=-3

The Quadratic Formula

Notallquadraticequationscanbehappilyfactored.Sometimesthesolutionsarenotintegers.Inyourmath classatschool,youmayhavebeenexposedtothequadraticformula.Thisisaspecialformulayoucanuseto findthesolutionsforaquadraticequation.Youcanuseitforanyquadraticequation,butit'sespeciallyusefulfor polynomialsthatcan'tbefactoredintohappyintegers.

Fortheequationax2+bx+c=01 thesolutionforxis:

x=----2a - What are the solutions forx2 + 2x-9 = O? =21 andc = -9.Let'sstick'eminthe

Theequationisintheformax2 +bx+c,wherea=l,b formulaandseewhatcomesout:

Thatmeanstherearetwosolutions:-1+✓10 and-1-✓10 .

Noticethatwegottwosolutionsthere.That'sbecauseofthenumberunderthesquarerootsign,calledthe disLTiminant.

discriminant=b2 - 4ac

Theformulaasksyoutobothaddandsubtracttherootofthediscriminant.Ifthediscrirninant_ispositive,like 10intheexampleabove,therootwillcomeouttoapositivenuII1-ber1 andyou'llgettwodifferentresults.

Butwhatifthediscriminantiszero?Thentherootwillcomeouttozero.Thenyou'llonlyget

oneresultbecauseaddingzeroandsubtractingzerogiveyouthesameanswer. Whatifthediscriminantcomesoutnegative?Thenyou'llhavetotakethesquarerootofanegative,butyou're notallowedtodothat.*Inthatcasetheresimplyisnorealsolutfon.Therefore:

-Ifthediscriminantispositive,yougettwosolutions.

-Ifthediscriminantiszero,yougetonesolution.

-Ifthediscriminantisnegative,yougetnosolution.

Ifallthisscaresyou,don'tworry.Youdon'thavetoworryaboutittoomuch.Therewillbesomequestionsthat requireyoutoknowthequadraticformula.However,suchquestionsarerare.Mostofthetimeyoushouldbe abletodoanyprobleminvolvingquadraticsbyfactoringorwithPlugInandBacksolve.**Furthermore, questionsthatdorequireitwillusuallybeharderquestionsattheendofasection,sochancesareyourTarget Numberswillhaveyouskippingitanyway.

* Technicallyyouareallowedtodothat,butyouwon'tgetrealsolutions.Onlyimagina,ysolutions.We'lltalk moreaboutimaginarynumbersintheAdditionalTopicschapter.

**Onewaytheformulacanhelpisifyouhaveagraphingcalculatorthatallowsprograms.Youcanprogramthe formulaintoyourcalculatorsothatyoujusthavetoinputa, b,andc,andtheprogramdoesthecalculationsforyou.Ifyouknow howtodothis,itcanbeniceandquick.Butifyoudon't,don'tworryaboutit.(Youcanalsofindthesolutionsbygraphingthe functionsandlookingwherethefunctioncrossesthex-axis.We'lltalkmoreaboutgraphinginthenextchapter.)

Exercise#18

-Whatarethesolutionsforx 2 -12x=m

-Whatarethesolutionsforx2 -1lx+30=O?

-Whatarethesolutionsforx2 - 7x-8=O?

-Whatarethesolutionsforx2 -81=O?

-Whatarethesolutionsforx2 - 13x=-42?

EXPONENTIAL GROWTH

We'veseenlotsofexamplesofequationsthathaveexponents.Butalltheoneswe ' veseenhavehadvariablesin thebaseofthenumber.Intheequationy=x2 , x?-isanexponentialnumber,xisthebase,and2istheexponent.

However,wecanalsomakefunctionsthathavevariablesintheexponents.Thesearecalledexponentialgrowth functions.Theyshowupmostfrequentlywhenyouwanttoapplyapercentmultipletimesinarow.Observe:

- Each year thepopulation ofgoats in the basementgrows by 20%. If the goat population starts at 125 goats, approximately how many goats will there be after 3 years?

Let'sjustdoitout.After1year,thepopulationwillgrowby20%.

1year: 125+20 X (125)100 =125+

0.2(125)

=125x(l+0.2)

=125X(1.2).= 150

That's125plus20%of125.

Wecanre-writethisbyfactoringout125.

150goatsafter1year

Tofindthenexttwoyears,repeattheprocess.Thetrickwithquestionslikethisisthatyouhavetore-calculate thepercenteveryyearusingthenewtotalforthepreviousyear.Sowhenwe'recalculatingyear2,we'llstartwith 150insteadof125.

2years:

3years: 20 150+- X (150)100

=150x(l.2) =180

180x(l.2) =216

That'safter2years.Onemore:

That'safter3years.

Butlookwhatwedid:togettoyearthree,westartedwith125andmultipliedby1.2threetimes.Looking backwardsfromyear3:

216 =(180)x1.2

After3years

That's2yearstimes1.2 ... = ([150] x1.2)x1.2whichinturnwas1yeartimes1.2...

= ( [ 125x1.2]x1.2)x�.2whichinturnwasthestartingvaluetimes1.2. =125x(1.2)3 Sowehavethestartingvaluetimesthreel.2's.

Ifthat'swhatwedidafterthreeyears1 wecangeneralizeitintoanequationforxyears:

G(x) =125X(1.2)xwherexisthenumberofyearspassed1 and125isthestartingvalue.

Wecanfurthergeneralizethatintoanequationforanykindofexponentialgrowth:

where:

- G(x) isthetotalquantityaftergrowth -a -r isthestartingtotal isthepercentgrowthratewithrespectto1(e.g.20%growthis1.21 while20%decreaseis0.8 )*- x isthetimepassed

Thismayseemintimidating1 butmostexponentialquestionswon'taskyoutodoalotofwork.Moreoftenthan not1 theysimplyaskyoutounderstandwhattheparts.Themoretimeyouspendwiththisequation1 themore you'llgettoknowhim1 maybeevenlovehim.

*InmostSATproblemstherateisexpressedasadecimalwithrespectto!likethis.Butsometimesthe equationmaybewrittenasa(l +r/l00)'instead.Here,with20%growth,theequationwouldhaver=20insteadofr=1.2).

GRAPHING

GraphiI?,gquestionswillshowupalloverthetest.Algebraquestions,dataquestions,evengeometryquestions mayinvolvethecoordinateplane.Sowe'regoingtobringallthoseconceptstogetherinoneplaceheresowecan seehowtheyconnect.

It'sokaytohategraphing.We'renotheretojudgeyou.*Butweareheretohelpyouunderstandafewofthebasic principlesbehindtheseproblems.Aswesawinalltheotherchapters,MathTestquestionsaskthesamethings overapd _overagain,soalittlebitofknowledgecangoalongway.

THE COORDINATE PLANE

A.Gettingto knowtheplane

1hisisthexy-coordinateplane(or"xygrid'�or"coordinateplane"orwhateveryouwanttocallit).

Alotofyouprobablyknowyourwayaround thisguy,butherearesomedefinitionsforthose whoareconfused:

Thex-axisisthehorizontalline;ittellsyouthe xvalueofapoint.Valuesofxarepositivetothe rightandnegativetotheleft.

They-axisistheverticalline;ittellsyouthey valueofapoint.Valuesofyarepositiveatthe topandnegativeatthebottom.

Thetwoaxes**dividethecoordinateplaneintofourquadrants,oftenlabeledwithRomannumerals.Thesignof thex-andy-valueofapointwilldeterminewhichquadrantthepointliesin.

*Well,maybealittle.

**Yes,thepluralof"axis"is"axes''.Itrhymeswith"taxis",notwith"faxes''.

Pointsonthegrapharegivenas(x)y).SopointPis(2,3)J sinceithasanxvalueof2andayvalueof3.Youcantell thexandyvaluesbylookingatwherethepointlieswithrespecttotheaxes.

Theoriginisthepointwheretheaxescross(labeled"O"here)iithasavalueof(0,0).

Beforewegoanyfurther,it'simportanttoemphasizethatgraphsarepictures.Therefore,youcanuseGuesstimate ongraphproblems.Infact)you'dbeastoundedhowmanygraphingproblemscanbe-donejustbylookingatthe picturetheygiveyou.Ifthislinelooksequaltothatline,thentheyareequal.

Infact,Guesstimateisofteneasieroncoordinategeometryquestionsbecausecoordinateshavevaluesyoucanuse asreferences.Onceyoubecomefamiliarwiththecoordinateplane,it'seasytoquicklyglanceatapointandsee"oh, thatpointhasanegativexandaybiggerthan7)soIcaneliminateA)andD):'Don'tforgetGuesstimate.

Distance

Ifyouwanttofindthedistancebetweentwopointsonagraph,justusethePythagoreanTheorem:

- What is the distance in coordinate units between P (2,2)an� Q (6,5)?

Wedon'thaveagoodwayofmeasuringdiagonallineslikethatdirectly.Butwe do haveagoodwayof measuringhorizontalandverticallines.Let'sdrawpointRtomakeatrianglethathasPQasitshypotenuse.We caneasilymeasureitslegsbecauseweknowthecoordinatesofthepoints.

PR=6-2=4QR=5-2=3

Thelegsofthetriangleare3and 4,sowecanusethePythagorean Theoremtofindthehypotenuse:* �Q(6,S) '�T2 P(2,2)�h6,2)

9+16=(PQ)2 S=PQ

Ifyouprefer,youcanuseTheDistanceFormula.Thedistance,d,betweenpoints(x1, y1) and(x2,y2)is

*Ifyoudon'tknowwhatthePythagoreanTheoremis,don'tworry.We'lltalkaboutitmoreinthePlane Geometrychapter.Someofyoumaybeabletoseerightawaythatit'sa3-4-5triangle.

or

Notethatthisisexactlythesamethingwejustdid.Thedistanceformulaisnothingmorethanthe PythagoreanTheorem.Anytwopointsonthecoordinategridcanformarighttriangle:(x2- x1)isonelegof thetriangle,(y2-y1)istheotherleg,andthedistancebetweenthepointsisthehypotenuse.

Midpoint

- What is the midpoint of (2,2) and (6,5)?

1hisquestionasksaboutthesamepointswejustlookedat.Tofindthecoordinatesofthemidpointbetween twopoints,taketheaverageofthexsandtheaverageoftheys.

Theaverageofthex-values,2and6,is=4.Theaverageofthey-values,2and5,is =3.5.

Sothecoordinatesofthemidpointare(4,3.5).

B. GraphingFunctions

Agraphonthecoordinateplaneisnothingmorethanapictureofafunction.

Taketheequationy=2x.Wecouldpluginanynumberwelikeforxandwe'llgetavalueforyasaresult.Below wehaveatableofx'sandtheirrespectivey's,alongwithagraphofthosepointsplottedonthegrid.

Wecanseethatthepointswechosestarttomakeastraightline.Ifwefillinallthepossiblex'sandtheir correspondingy's,includingallthenastydecimalnumbers,that'sexactlywhatwe'dget.Thegraphofy=2xisa pictureofallthepossiblesolutionstotheequation-everyxpairedwithitscorrespondingy.

Ratherthandefiningourequationasy = 2x,wecouldcallitf(x) = 2xandsaythaty=j(x)inthegraph.Don'tget boggeddownwithallthedifferentletters.

Themostimportantthingtorememberis:Ifapointliesonthegraphofafunction,thecoordinatesofthat pointwillsatisfythefunction'sequation;Andviceversa.Evenifyoudon'tknowtheequationofthefunction, youcanlearnalotjustfromthepicture.Forexample:

- The figure below shows the graph ofy=/(x). What is the value offt1)?

Ifthey'dgivenyouanequationforf(x),youcouldfindf(l) bysubstituting"1"for"x"intheformula.Noproblem.But herewedon'thaveanequation.Hmm.That's.acrazy,crazy lookingfunction.We'llneverbeabletowriteanequationfor it.

Butwedon'tneedanequationbecausewehaveagraphofthe function!Agraphisapictureofthefunction.Everypointon thatsquigglylineisasetofnumbersthatsatisfiesthe equation,whateverthatmaybe.

Wewantthevalueoff(1).Sowejusthavetofindthevalueofywhenx=1.That's3!Thesquigglyline crossespoint(1,3).Whenx = I,y = 3.SoJ(1) = 3..

Thisisanimportantpoint,soitbearsrepeating:

Ifthepoint(a,b)isonthegraphofj,thenJ(a)=b.IfJ(a) =b,thenthepoint(a,b)isonthegraphoff.

MATH - 22

Exercise #19

Findthesepointsonthewaphabove: f(-1)=? f(O)=? f(3)=?

Alotofpeoplegetconfusedbythisnotation,sohere'satricktohelpyouremember.Ifyoudrawinsome parentheses,theequationlooksjustlikeacoordinatepair.So:

f(1)=3 .r((1)=3) becomes f(x) =y _t((x)=y)

Intersection

Thisfactaboutpointsandfunctionshasaninterestingconsequence:Ifapointonagraphisasolutiontothat function'sequation,thenapointwheretwographsintersectisasolutiontobothfunctions'equations.

Forexample,considerthesefunctions:

y=2x+3

y= x+S

Whenwehavetwoequationstogetherlikethiswecallita "systemofequations':Eachequationhasaninfinitenumber of(x,y) pairsthatmaketheequationtrue.Butthere'sonly onepairthatmakesbothequationstrueatthesametime: (2,7).*

Thegraphofeachofthesefunctionsisastraightline.Ifwe drawbothlinesinthesameplane,wecanseethatthetwolinesintersectatthepoint(2,7).Point(2,7)isthe solutionforthesystemofequationsandtheplacewherethetwolinesintersect.

Inequalities

Mostgraphsyou'llseeontheSAThaveequationsthatdescribethem. Butyoucanalsographinequalities.Thegraphofaninequalitylooks justlikethegraphofthecorrespondingequation-alineoracurve ofsomekind-butwithashadedregionaboveorbelowtheline.

Forexample,thefiguretotherightshowsthegraphofy�2x.Notice thatthelinerunningthroughthemiddlelooksexactlyliketheline fory=2xthatwesawearlier,butnowtheregionabovethelineis

* Thereareseveralwayswecansolvethissystemalgebraically.Sincebothhaveybyitself,wecouldset thetwoequationsequaltoeachother:2x+3=x+S,thusx=2.OrwecouldsubtracttheequationsdirectlytogetO=x-2,thusx=2. Thenputx=2backintoeitherequationtogety=7.

shaded.Thatmeansthatallthepointswithintheshadedregionsatisfytheinequality.*

Forthisgraph,itshouldbeeasytounderstandwhytheareaabovethegraphisshaded.Thelineshowsallthe pointswhereyequals2x,soallthepointsabovethelinehaveay-valuegreaterthan2x.

Butifyou'renotsurewhichregionyouwanttoshade,youcanalways trysome testpoints. Pickapointabove thegraph,let'ssay(0,2).**Nowlet'splugx=0andy=2intotheinequalityy�2xandseeifitworks:

2�0✓Itworks!

Let'scheckapointfromtheothersideoftheline,say(0,-2),justtobesure. -2�2(0)-2�0xThatdoesn'twork!

Aftertryingthosepoints,wecanseewemustshadetheareaabovethegraph.(Hmm...usingrealnumberstotest analgebraicexpression.Haven'twedonethatbefore?Ohyeah!That's. PlugIn!)

Notethatifyouwanttosolvefortheintersectionoftwoinequalities,onlytheregionshadedbybothgraphswillbe thesolution.

*Becausetheinequalitysaysyisgreaterthanorequalto2x,thelineissolid.Iftheinequalitywerey>2xwithoutallowingthemtobe equal,thelinewouldbedashed.

**Pointsontheaxesaregenerallyeasiertotestbecauseit'seasytoplugOintoyourinequality.

LINES

RememberwhenwetalkedaboutlinearexpressionsandequationsintheHeartofAlgebrachapter?Youdon't? Jeez,itwasjust,like,twentypagesago.Fine.Gobackandlookagain,thencomebackhere.

Okay,you'reback.Wesaidtheycanbedrawninthecoordinateplaneaslines;andwesaidtheytwounique characteristics:theirrateandtheirstartingpoint.Wecanseethesecharacteristicsintheirgraphs.

1.Theirratecorrespondstoslope:

2.Theirstartingpointcorrespondstoy-intercept:

Thesetwofeaturesareallweneedtouniquelydefineanyline.Thesearethesamefeatureswetalkedaboutwhen wewerewritingequationsforwordproblemsabouthowmuchmoneyyou'regoingtoearn.

Equations

Wecanusetheslopeandy-interceptstowriteanequationofaline,calleda"linearequation".Anylinewillhave acorrespondingequationthatcontainsonexandoneywithnoexponents.*Thereareseveraldifferentwayswe canwritealinearequation.

Themostusefulformofalinearequationistheslope-interceptform: y=mx+b.The "m"standsfortheslope,the"b"standsforthey-intercept,andthe"x"and" y"standforthecoordinatesofany andallpointsontheline.

*Exception:anequationwithnox,likey=3,isahorizontalline.Ithasaslopeofzero.Similarly,anequation withnoy,likex=3,isaverticalline.Ithasanundefinedslope.

Slope

Asthenameimplies,slope(abbreviated "m" forsomereason*)isawaytomeasurethe "steepness"ofaline.Lookingfromlefttoright,apositiveslopegoes.YI2andanegativeslopegoesdown.Asyou canseefromtheexamplesbelow,themorethelinegoesup,thelargeritspositiveslope;themorethelinegoes down,thesmalleritsnegativeslope.

Youcanthinkofslopelikeastaircase:ifltakeonesteptotherightalongthex-axis,slope tellsyouhowmanystepsupordowntotake.Ifm=3,yputake3stepsupforeverystepto theright.Ifm=-1/3,youtakeathirdofastepdownforeverysteptotheright.

Thereare·:manywaystodefineslope,buttheyallmeanthesamething: changeiny changein x nse run

Whentheaxesof agraphmeasure distanceand time,theslopeof alinegivesthe speedofthe object.

Ifyoulmowtwopointsonaline,youcanfndtheslopeoftheline.Allyouhavetodoistakethedifferen!=eof they'soverthedifferenceinthex's:

Y2 -Yi 4-2

Q(6,4) 4 2 p(1,2) X 6

Don'tgetboggeddownbyallthoseletters.We'rejustpickingwhichpoint togofirstandwhichtogosecond.Infact,itdoesn'tmatterwhichpointwe usefirst.Wecouldsaythat (x1,y1) =(6,4)and (x2,y2) =(1,2) and... Y2-Yi 2-4 -2 2

- Xi 1-6 -5

...wegetthesamething.

Somethingstorememberwhencalculatingslope:

-Makesureyisontop.Werepeat:makesureYisontop.Youwillnotbegiventhe

* Nooneknowshow"m"becamethesymbolforslope.Overtheyears,differentpeopleindifferentcountries haveuseda,k,1,p,andsforslope.Descartes,whoinvented'.'x'�didnotuse"m''.Sometimesthisstuffisjustrandom.

formulaforslope.Youhavetorememberit.

-Beconsistentwiththexandy.Youcanstartwitheitherpoint,butyouhavetostart withthesamepointonthetopandthebottom.Intheexampleabove,whenweuse4 firstonthetop,wemustuse6firstonthebottom.

-Parallellineshaveequalslopes.

-Theslopesofperpendicularlinesarethe"negativereciprocals"ofoneanother.Take thefirstslope,makeitnegative,andflipthefractiontogetthesecondslope.

Intercepts

An"intercept"isjustthepointatwhichthelinecrossesoneoftheaxes.Sothex-interceptisthepointat whichthelinecrossesthex-axis.Andthey-interceptisthepointatwhichthelinecrossesthey-axis.

Inthefiguretotheright,thelinehasay-interceptof3,sinceit crossesthey-axisatthepoint(0,3).They-interceptalwayshasan x-valueofzero.

Inthefiguretotheright,thelinehasanx-interceptof2,sinceit crossesthex-axisatthepoint(2,0)Thex-interceptalwayshasa y-valueofzero.

Let'sseethisstuffatwork:

- Line e passes through the points {4,4) and (2,3) . What is the equation of line e?

Tofindtheequationoftheline,weneedtheslopeandthey-intercept.First,sinceweknowtwopoints,wecan findtheslope.

Nowweknow m, soourequationsofarisy=2x+b. Tofind b, let'sjuststickoneofthepoints

weknowinforxandy.Thenwecansolveforb.

Soourequationisy=2x+2.Thegraphofthelinecanbeseenbelow.

-Whatistheslopeofthelinethatpasses throughthepoints(2,6)and(4,1)?

-Whatistheslopeofthelinethatpasses 'throughthepoints(-2,-3)and(-1,5)?

-Whatistheslopeofthelinerepresentedby theequation2x-6y=7?

-Whatistheequationofthelinethatpassesthrough thepoints(-1,2)and(1,6)?

-Theequationoflineeisy=3x+5.Iflinekis perpendiculartolineeandpassesthrough thepoint(O,-3),whatistheequationoflinek?

PARABOLAS

Aparabolaisthegraphofaquadraticfunction-thatis, anequationcontainingthesquareofxandaywithno exponent.Shownhereisthegraphofy=x2 • Youcansee thatthemarkedpointsfittheequation:theyvalueof eachpointisthesquareofthexvalue:

Thestandardformofanequationofaparabolais y = ax2 +bx+c wherea, b,andcareconstants.*Fory=x 2 , a=I, b=0,andc=0.

Someofyoumayrecognizethisformaswhat'scalleda"quadraticequation".Someofyoumayalsoknowthat thereisacomplicatedformula(the"quadraticformula")thatyoucanusetosolvequadraticequations.Hmm. Didwetalkaboutthosealready?

Let'stakealookatthedifferentpartsoftheparabolaandhowtheyrelatetotheequation.Thefigurebelow showsthegraphofthefunctiony=x2 - 6x+8.

Intercepts

They-interceptisdeterminedbythevalueofc,thenumberbyitselfwithnovariableintheformulashown above.Inourequation,y=x1 - 6x+81 c=81 sothey-interceptis(0,8).

Justlikeinastraightline,they-interceptisthevalueofywhenx=0.Becausecistheonlytermintheequation thatdoesn'tcomewithanxnexttoit,ifx=0,allthat'sleftisc**

*Constantsarenumbersthatdon'tchangeatallwithinagivenequation.Youcanstickinanynumbersyou wantforxandyandit'llstillbethesameequation.Ifyouchangethevaluesofa,b,orc,it'snolongerconsideredthesameequation.

**Don'tbeconfusedbythefactthatcisthey-interceptforparabolas,whilebisthey-interceptforlines.The lettersareentirelyarbitrary.Wecouldcallthempandqforallitmatters.Heck,wedon'tevenhavetoputitlast;wecouldsayy=b + xm.Whatdoesmatteristhatit'sthenumberthatstandsbyitself.Ineachcase,they-interceptisthenumberthatdoesn'thaveanxnext toit.

Thex-interceptsarethezeroesorsolutions totheequation.Thatis1 theyarethevaluesof xwhen

y=0.Thesearethenumbersyou getwhenyoufactorthequadratic.Here1 our equationcanbefactoredintoy=(x-2) (x-4),sothe x-interceptsare(2,0)and(4,0).

NOTE:thefactoredformoftheequation showsthenegativevalueofthesolutions. Thatis,ifthefunction·canbefactoredinto y=(x+m)(x+n)

(0, 8) y-intercept y (3,-1) vertex

y=x 2 -6x+8

y= (x-2)(x-4) y = (x-3)2 -1 X

thenthesolutionsare-m and-n,andthex-interceptswillbe (-m, 0)and (-n, 0).*

Previously,wetalkedaboutquadraticequations.There,wehadanequationequaltozero insteadofequaltoy:therewereonlyoneortwovaluesofxthatsolvedtheequation.Here,wehaveafunction: wecanstickinanyvalueforxandgetoutay.Aquadraticequationisaquadraticfunctioninwhichy=0.An x-interceptisapointonthegraphwherey=0.Soyoucanquicklyfindthesolutionstoaquadraticequationby lookingatitsgraphandfindingtheplaceswhereitcrossesthex-axis.

NOTE:notallquadraticequationshavesolutions.Ifanequationhasnosolution,theparabolawillnotcrossthe x-axis.

Vertex

Thevertexisthepointattheverybottomofthecurve(ortheverytop,ifthecurvepointsdown).Thispointis alsocalledthemaximumorminimumofthecurve.Youcanactuallyrewriteaquadraticfunctionintoanother form:y-k=j(x-h)2 where(h,k)isthevertexoftheparabola.**

*Strictlyspeaking,thisisonlytruebecausethere'snocoefficientbeforethex'shere.Tofindtheintercepts,seteachfactorequalto zeroandsolveforx.Ifourequationfactoredinto(Sx+1)(3x-2),thex-interceptswouldbe-1/5and2/3.Butyouprobablywon't seethisontheSAT.

**Youcanconvertafunctionintothisformatusingaprocesscalled"completingthesquare':whichyoumay haveheardaboutinyourmathclass.Ifyouhave,great.Ifnot,don'tworryaboutit.Youlikelywon'tneedtodoitontheSAT.

Ifyou'relookingtofindthevertexofaparabola,youcandothatfromtheequation y=ax1+bx+c.Thex-valueofthevertexwillbeequalto-bThenputthatxvaluebackin 2a theoriginalequationtosolvefory.

Otherproperties

Noticethatbothparabolasshownabovearesymmetrical.That's becausethesquareofanegativecomesoutpositive.Inthefirst example:y = 4whenx = 2andwhenx=-2.Inthesecond,y = 0when x= 2andwhenx= 4.Allparabolasaresymmetrical,regardlessof whetherthey

Thevalueofa(thenumberinfrontofthex2) intheequationy=ax2 +bx+cwilltellyouwhichdirectionthe parabolawillpoint.Ifaispositive,theparabolawillpoint.lW·Ifaisnegative,theparabolawillpointdown.

MATH - 24

Exercise#21

-Whatisthey-interceptofthegraphofy=3x2 - 39x-24?

-Whatisthey-interceptofthegraphofy=(x-2)(x+7)?

-Whatisthey-interceptofthegraphofy=(x-3)2 ?

-Whatarethex-interceptsofthegraphofy=(x+7)(x-8)?

-Whatarethex-interceptsofthegraphofy=x2 +x-20?

CIRCLES

Sometimesyoumaywanttographcirclesonthexy-coordinateplane.Theequationofacircleisdefinedas: whereristheradius,and(a,b)isthecenterofthecircle.Ifthecircleiscenteredontheorigin(0,0),the"-a" and"-b"won'tbethere.Forthegrandmajorityofcirclegraphingquestions,allyouneedtoknowisthis equation,soLEARNIT!Let'slookatanexample:

- A circle in the standard (x,y) coordinate plane has center (3,2) and radius 5 coordinate units. What is the equation of the circle?

Usingtheformulaabove,weknowthe equationwillbe(x-3)2+(y-2)2=25

Doestheformofthisequationlook familiar?Itshould.It'sthePythagorean Theoremagain!

Thinkaboutit:whatisacircle?Acircleis definedasthesetofallpointsthatarea certaindistance(theradius)fromasingle point(thecenter).Inthiscase,thecurve willdefi�eallpointsthatareadistanceof 5awayfromthepoint(3,2).Howdowe findthedistancebetweenpoints?Withthedistanceformula: Here, (x1,y1)isthecenterofthecircle,(3,2)and (x2,Yi)isthegeneralpoint(x,y).Thatjustmeans(x,y) referstoanypointthat'sontheactualcircle.Sothedistancebetween(3,2)andanypointonthecircleis5.

y

y-2

P(3,2) r--x-3

Exercise #22

-Whatisanequationofacirclethathascenter(2,1)andradius6coordinate units?

-Whatisanequationofacirclethathascenter(-4,0) andradius5coordinate units?

-Whatisanequationofacirclethathascenter(5,4)andistangenttothe x-axis?

-Whatisthecenterofacirclewithequation(x+8)2 +(y-2)2 =9?

-Whatistheradiusofacirclewithequation(x-1)2+(y+2)2=7?

TRANSFORMATION OF FUNCTIONS

Herearesomeexamplesofhowfunctionscanmovedependingonwhatyoudotothem:

-ForanyJ(x), thegraphofJ(x) +cisthegraphoff(x) shiftedc.placesUP.

-Foranyf(x), thegraphoff(x) -cisthegraphoff(x) shiftedcplacesDOWN.

Subtractinganumberfromtheendmeansyou'lllowertheyvaluebythatnumber,sothegraphwillshiftdown. Addingwillincrease they value,sothegraphwillshiftup.Thisistrueofallfunctions,nomatterwhatthe equationlookslike.

Okay,thisnextoneisabitweird,sobearwithus.

y=f(x)+ I y=f(x)

y = f(x)-1

-Foranyf(x), thegraphofJ(x+c)isthegraphofj(x) shiftedcplacestotheLEFT .

-Foranyf(x), thegraph off(x-c)isthegraphofJ(x) shiftedcplacestotheRIGHT.

Before,wewereaddingtoorsubtractingfromtheendofthefunction.Here,we'readdingorsubtractingfrom insidetheparentheses.ThinkofthespaceinsidetheparenthesesasBizarroWorld:addingtothexmovesthe graphtowardthenegatives,subtractingfromthexmovesthegraphtowardthepositives.

Ifyouhaveagraphingcalculator1 youcantrythisoutyourself.Typetheseequationsinto "Y="

Youcanseethatthegraphofthesecondequationlooksjust likethatofthefirstequation,butshiftedtotheleftbyone space.*

Thiscanbeconfusing,anditisn'treallythatimportant1 soif you'restillconfused1 justmoveon.Butifyou'recuriousandreally mustknowwhythisistrue,let'sexplain.Takealookatthese: y=x2 y=(x+1)2

* We'vealreadyseenthisruleatworkinthevertexformofaparabola.Thegraphofy=(x-3)2-1isthegraph ofy=x2shiftedright3spacesanddown1space.That'swhythevertexmovesfrom(0,0)to(3,-1).

Man,that'safunny-lookingfunction.Wecertainlydon'tknowtheequationforit.Butnomatterwhatthe originalequationforf(x)is,weknowthatf(x+2)willmakethegraphshift2placestotheleft.

Tounderstand,let'slookatsomepoints.

y=1(2+2)=/(4)-5 J, J, I\ r y=j(x) I \....I I \ '--o/ t t -----i y=/(4+2)=/(6)=3 2 4 6

f(x + 2) (0,2) j(0+2)=f(2)

Whenxis0inj(x+2),theyvaluewillbethesameasJ(2)inthefirstgraph,whichis1.SoJ(0+2)=1,sothe graphwilltouch(0,1)Whenx=0, y=l

Whenxis2inf(x + 2),theyvaluewillbethesameasJ(4)inthefirstgraph,whichisS.Sof(2+2)=4,sothe graphwilltouch(2,5).Whenx=2,y=S.

SoeverypointinJ(x+2)takesitsyvaluefromthepointtwospacestotheright.ThatmeansJ(x+2)istwospaces totheleftofj(x).

PROBLEM SOLVING AND DATA ANALYSIS

We'realmostattheend.ProblemSolvingandDataAnalysisisthelastcategoryofmathquestionsforwhichyou willgetasubscore,andtheonewiththeleastdumbname.*Hereyou'llfindacollectionofdifferentconcepts thatareunitedbyaconnectiontotherealworld.

Mostofthemathwe'vebeendoinghasbeenpuremath.Thatmeanswe'vebeendealingwithequationsthatapply tonumbersintheabstractortheprinciplesofhownumberswork. ButtheSATalsohasalotofstatistics.Thisistherealmofappliedmath,workingwiththerealworldofrealthings. Andtherealworldcontainsdata,whenyou'vegotalotofdifferentnumbersthatyouhavetomakesenseof.

Youwillseeatotalof17ProblemSolvingandDataAnalysisquestionsontheSAT1aboutthesamenumberasthe othertwomaincategories.However1 notethatthesequestionsaredifferentfromtheothercategoriesinthatthey onlyappearonsection4, theCalculator OKsection.Theotherquestiontypesallappearonbothsections.If youhatedataquestions1thisisgoodnews.Itmeansthatyou'llhaveanentiresectionwithnoneofthesequestions. And itmeansyou'llalwaysgettouseyourcalculatoronthem.Ofcourse,theflipsideisthatsection4isgoingto seemlikeit'sheavyondataquestionsbecausethey'llmakeupalmosthalfthesection.

*Itisstillalittlebitdumb,mindyou.Afterall,everyquestionontheMathtestinvolvessomekindofproblem

solving.Andit'stoolong(thoughnotasbadas"Evidence-basedReadingandWriting").

PROPORTIONS

DoyourememberthechaptercalledMathFundamentals?RightafterTechniques,rightbeforeHeartofAlgebra? ThatchapterwaschockfullofconceptsthattheSATclassifiesasProblemSolvingandDataAnalysisconcepts. Thatincludes:

- Ratios -Ratesandunitconversion - Percentages

Alltheseconceptsaredifferentkindsofproportions.Basicallyalmostanyconceptinvolvingfractionsstrictly speaking.belongsinthischapter.Wedecidedtotalkaboutthemearlybecausetheyhaverelevancetosomeofthe conceptswetalkaboutinthealgebrachapters.Sincewetalkedaboutthemthere,we'renotgoi�gtotalkabout themhere.Feelfreetofipbackandreviewthosesections,though,astheymightshowuponsomepractice problemslateron.

Ifyou'reitchingforsomefractionwork,though,don'tworry.We'vegotsomeconceptscomingupinafew pages-averagesandprobability-thatareloadedwithfractionwork

FIGURES

Manydataanalysisproblemswillarrangedataintosomesortofgraphicalrepresentation,beitatable,linegraph, orsomethingelse.OverhalfoftheProblemSolvingandDataRepresentationquestionswillcontainafigureof somekind.Solet'sgettoknowthesefigures.

1. Tables

TablesarethemostcommonwayofpresentingdataontheSAT.Ingeneral,thetestwillhaveaboutasmany tablesasallotherfigurescombined.Youprobablyhavesomeexperiencewithtablesalready.Heck,we'veseena bunchoftheminthisbookalready.Mostofthemarestraightforward.Justmatchuptherowsandthecolumnsto findavalue:

inSpringfieldGardens

- Based on the table above, how many horse chestnut trees in Springfield Gardens are in fair condition?

Tofindout,findthe"Horsechestnut"rowandseewhereitcrossesthe"Fair"column:

Thereare10fairhorsechestnuts.

Subtotals

Aswecanseehere,tableswithmultiplerowsandcolumnslikethiswilloftenshowsubtotalsattheendofa roworcolumn.Inourexampleabove,thereareatotalofsixdifferentgroups:threetypesoftrees(intherows) andthreetypesofconditions(inthecolumns).Eachrowor

columnshowsthetotalofalltheitemsinthatcategoryattheend.

Forpinoaktrees1thereare23inGoodcondition,7inFaircondition1and2inPoorcondition.Addthemupto get23+7+2=32totalpinoaktrees.

Theboxintheverybottomright,then,isthetotalofthetotals:itshowsthetotalnumberofalltreesinall conditions.Noticethatit'sboththesumofthecolumntotalsandthesumoftherowtotals,sinceyou'llgetthe samenumberoftotaltreesnomatterhowyoucount.

32Pinoak

35Horsechestnut +20Baldcypress

87Totaltrees

Approximation

Sometimestableswillcomewithcrazyuglynumbers:

43Goodtrees

21Fairtrees +23Poortrees

87Totaltrees

PopulationofNewShelbyvillein2010 Ageinyears

10.According to the table above, approximately what fraction of residents 55 or older are female?

A) 1/3

B) 1/2

9 2/3

D) 3/4

"Phew,"youthink."Withallthosecrazynumbers,goodthingI'mallowedtousemycalculator:'WAIT, STOP!Don't.Don'tdothat.Lookatourchoices.Theseareallbasicfractions1 notcrazyfractions.Let'sdo somerounding.

We'retalkingabout55+resid�nts1 solet'slookatthatcolumnandrou�dtothenearestthousand:

GenderSSorolderRounded

Male 141807 15,000

Female1S1289 15,000

Total 30)096 30,000

Aha!Thereareabout30,000peopleSSorolder1andabout1S1000ofthemarefemale.That'saboutonehalf.

Grouping

Sofarwe'vebeendealingwithonlyonetablecellatatime.Butsometimeswemighthavetocombineparts ofthetable.Lookatthisone,stillaboutthesametableofresidentsofNewShelbyville:

11. According to the table above, approximately what fraction of residents 35 or older are female?

A) 1/2

B) 2/4

C) 3/8

D) 3/10

Thistimeit'saskingaboutresidentswhoare.3Sorolder.ThateD.compasses two columns:"3S-S4"and"SSandolder".Sowe'llhavetodealwithboththosecolumns together: Ageinyears

Let'sfocusonthosetwocolumnsandroundthem:

Gender3S-S455orolder

Male35,00015,000

Female15,00015,000

Total50,00030,000

Wewantthenumberofwomeninthesetwocolumnsasafractionofthetotalforthesetwo columns.

Totalwomen:15,000+15,000= 301000

Totalresidents: 501000 +301000=:=80,000

Sothefractionofwomenwouldbe30-,-80=3/8.

Frequencytables

Takealookatthistable:

- A survey asked 100 students'in school how many goats they own at home. The'results are shown in the table above.

Thisisa frequency table. Thestudycounted100studentsandaskedhowmanygoatstheyhaveathome. Everystudenthadsomewherefrom0to4goats.Thistableshowshowmanystudentsfallintoeachofthe ownershipcategories.Thatis:

-Therewere8studentswhohad0goats.

-Therewere14studentswhohad1goateach.

-Therewere22studentswhohad2goatseach.

Etcetera.Thisisaconvenientwaytoorganizedatawhenyouhavealotofthesamevaluesoverandover again.Insteadofwriting"3goats"forty-fivetimes1 youcansummarizeitinthistable.

2. Coordinate Planes

WejustspentatonoftimetalkingaboutthecoordinateplaneintheGraphingchapter,soyoushouldhavea decentsenseofhowitworksbynow.Butallthosequestionsdealtwithfunctions,linesorcurvesthatdescribe anequation.Butyoucanalsousetheplanetomapdata.

MASHA'SBIKERIDE

Thegraphshownabovelooksalotlikethekindsofgraphswe'veseenbefore,butthelinelooksdifferent.It's jaggedandblocky..We'reusedtoseeingsinglestraightlinesorsmoothcurves.Thisgraphinsteadshowsa relationshipthatchangesasitprogresses.There'snosingleequationthatdescribesthelineshown,butthe figureitselfbehavesthesameway�IIgraphsdo.Wecanlookuppointsbymatchingupthexandyaxes,andwe canseewhetherthelineincreases,decreases,orstaysthesame.

ThisgraphdescribesatripMashatakesonherbike.Wecansee:

-Shestartsathome(time=0,distancefromhome=0)

-After10minutesshe's4kmawayfromhome.

-After15minutes,she's5kmaway.

-ShestaysSkmawayforthenext10minutes.

-After30minutes,she's6kmaway.

-At40minutes,she's4.5kmaway.She'sstartingtocomebackhome.

-AfterSOminutes,she's3kmaway.

Allofthisjustinvolveslookingatthepictureandmatchinguptheaxes.

Wecanalsoseethevariousrelationshipsinthedata:

-FromOto15minutesherdistanceisincreasing.Notethatitincreasesatahigherrate fromOto10thanfrom10to15.Wecantellbecausethefirstparthasasteeperline­thatis,agreaterslope.

-From15to25minutesherdistancestaysthesame.Sheprobablytookabreak.Maybestoppedforadonut. Gottahavedonutsifyou'reonabikeride .

-From25to30minutesherdistancewasincreasingagain.

-From30toSOminutesherdistancewasdecreasing.Shestartedtoheadbackhome.

Graphsusingthexy-coordinateplanecancomeinallsortsofshapes.Theycanbejaggedlines,wigglylines,points connectedwithlines,orjustgroupsofunconnectedpoints.

3.Scatterplots

Speakingofgroupsofunconnectedpoints,lookatthesetwodatasets:

Thesegraphsarecalledscatterplots.Allthatmeansisthatthegraphshowspointsrepresentingdatathatwe collected.Ifyouhavedatawithtwocharacteristics,youcanputthosecharacteristicsonsomeaxesandshowthat dataonaplaneasajumbleofpoints.

Ineachofthesegraphsabove,wemeasuredtheheightofsometrees.Eachpointhererepresentsonetree.Inthe graphontheleft,wematchedeachtree'sheightwiththenumberofcicadaswefoundinit.Inthegraphonthe right,wematchedeachtree'sheightwiththecircumferenceofitstrunk.

Noticeadifference?Thegraphonthelefthaspointsthatseemrandomlyscatteredaroundthegraph.Thegraph ontheright,however,haspointsthatseemtomakeastraightline.Infact,wecantrytodrawthatline.*

*Wedon'thavetodrawitbyhand;therearemathematicallyrigorouswaysofcalculatingthisline.Butonthe SATyouwon'thavetodrawthematall.Ifyoucareaboutatrendline,itwillprobablyalreadybeon thefigure

Thegraphherehasatrendlineorlineofbestfit.

That'salinethatcloselyapproximatesthebehavior ofthepoints.Thelinedoesn'texactlydescribetheir behavior-youcanseethatnotallthepointsare ontheline.Butitcomesclose.

Whywouldwewantaline?First,inordertosee thatthereisastrongrelationshipbetweenour variables.Youcanseethelinehasapositiveslope. Thatmeansthatastreeheightincreases,trunk circumferencelikewiseincreases.Makessense.

Ofcourse,wesawthatpositiverelationshipwithouttheline.Havingthelinethere,however,allowsustomakea prediction.There'satrendintherateatwhichthecircumferencegrows..Theslopeofthelinetellsushowmany inchesofcircumferenceatreeexpectstogainforeverymeterofheightitgains.Wecanusethattofindthe expectedcircumferenceforanygivenheight.

Thatmaysoundfancy;butwhatwemeanistojustlookatthelineandfindnewpoints.

- According to the line of best fit, a tree that is 60 m tall can be predicted to have what trunk circumference?

Let'sjustfindthe60onthex-axis,followituptotheline,andlookupthevalueoftrunkcircumferenceontheyaxis:

Soatreewithaheightof60mwillhaveacircumferenceof40inches}right?

NO.Atreewithaheightof60mwillprobablyhaveacircumferenceofabout40inches. Rememberthatnotallpointslieexactlyontheline.They'reallprettyclose,sowecanbe

confidentthatthecircumferenceshouldbeprettycloseto40.*Butwedontknowforsurethatitwillbeexactly40 in.**

Incontrast1 thefirstdatasetwesawshowednorelationshipbetweentreeheightandnumberofcicadas.For example1 onetreethatwas40mtallhadaround7.cicadas1 whileanotherwasalso40mtallbuthad14cicadas.So wecan'tmakeanypredictionsatall.Atreethat's60mtallmighthave5cicadas1 mighthave20.Wedon'tknow.

Mindyou1 wecoulddrawalineofbestftforanycollectionofdata.It'sjustthatwhen thepointsareclosertothelinetherelationshipisstronger1 andthereforewecanbemoreconfidentinour predictions.

Ofcourse1 anincreasinglinearrelationshipisonlyonepossiblerelationship.Herearesome·more:

*Therearedifferentwaysformeasuringhowconfidentweareinourprojection,basedonhowwellthe pointsfittheline.Butyoudon'thavetoworryaboutsuchcalculationsontheSAT.

Decreasing relationships areoftencalled negativeassociations, andincreasing relationshipsare calledpositive associations.

**Andthat'stosaynothingofoutliers.Nomatterhowgoodourpredictionsare,therearesometimessome weirdosthatjustbuckwhatevertrendyouhave.Thismaybeforgoodreason.Forexample,youmay finda60-m-talltreewithacircumferenceof80in,becauseitusedtobe120mtallbutlosthalfits heightinastorm.Oritmightjustbeafreakishlyfattree.Therearelotsofreasonswhythingsmaynotturnoutaswe expect.Lifeisarichtapestry.

4. Bar Graphs

Bargraphsworkbasicallythesamewayasthexy-coordinateplane.*Youhavetwoaxesandyoumatchupthe data.Let'stryone.Let'ssayweleavehomeandstopevery10kmtocounthowmanygoatswesee:

Eachbarcorrespondstoadifferentdistancefromhome,matcheduptoanumberofgoats.Justlikeour scatterplot,butwithbarsinsteadofpoints.Infact,you·canoftenrepresentthesamedataseveraldifferentways. Here'sthesamedataasatableandasascatterplot:

Withabargraphyou'vegotalittlebitmore leewaywithwhattodowiththex-axis.You couldmakeitavaluejustlikewedidabove. Oryoucouldmakethebarsdifferentlabelsfor differentgroups:

*Somepeoplereservetheword"bargraph"forgraphswherethebarstretchhorizontally,andcallthesegraphs thathaveverticalgraphs"columngraphs".1heSATdoesnotcarewhatyoucallthem.

STATISTICS

Allright,-wetalkedaboutfigures.Nowlet'stalkaboutsomenumbers.Whatcanwedowithallthisdatawe have?

Averages

There'safancywordinstatisticscalledcentralityorcentraltendency)whichmeansthevalueatthecenterofa groupofnumbers.Thatis,onenumberthatbestrepresentsawholesetofnumbers.Thereareseveraldifferent waystofindthecenter.TwoinparticularareofinteresttousontheSAT:meanandmedian.

Arithmetic Mean

Thisiswhatweusuallymeanwhenwesay"average':Findtheaveragebytakingthesumofthenumbers dividedbythenumberofterms.

- Whatis the average.(arithmetic mean) of7, 18, 4, 9.and 2?

Thesumis7+18+4+9+2=40.

ThereareSterms,sotheaverageis40+S=8.

Median

Themedianisthemiddlenumber)whenyouputthetermsinorder.

- What is the median of7, 18, 4, 9 and 2?

Writetheminorder,youget2,4,7)9,18.Theoneinthemiddleis7,sothemedianis7.

Youmustputthe termsinnumerical orderbefore findingthemedian.

Notethatthevalueofthemediandoesn'tchangeifyoumakethehighesttermhigherorthelowesttermlower. Forexample)ifwechangedthesequenceaboveto2,4,7,9,157,themedianwouldstillbe7.

Ifthereareanevennumberofterms,suchthatthereisnoonenumberinthemiddle,themedianistheaverage ofthetwomiddlenumbers.

- Whatis the median of9, 2, 7, 8, 4 and 18?

Writetheminorderandyouget2,4,7,8)9,18.Thetwomiddlenumbersare7and8,sothemedianis7.5.

What's the difference?

Wejusttookthesamesetoffivenumbersandgottwodifferentcenters:themeanis8andthemedianis7. What'sthedifferencebetweenmedianandmean?Whybotherhavingdifferentcalculationslikethis?The differenceisthatthemedianisnotaffectedbyextremevalues}whilemeanis.Thismaybeimportant.

Let'ssayyou'reinabookclubwithsomepeoplefromyourneighborhood.Let'slookatthemedianandmeannet worthforev�ryoneinyourbookclub:*

Networth of book club members

Huh.That'sweird.ThereseemstobeadiscrepaIJ.cybetweenthemedianandmean.Youknowwhat?Let'slookat theindividualvaluesforthepeopleinthebookclubtotrytofigureoutthecause:

Member NetWorth Member NetWorth

You

Molly

Nihal

Jeanne

Yehuda

Gary

Steve

$0.00Jamelle $0.00

$0.00Audrey $0.00

$0.00Ariel $0.00

$0.00Colleen

$0.00Isabelle

$0.00MichaelJordan

$0.00Bob

$0.00

$0.00

$650,000,000.00

$0.00

Didyoucatchit?Mostofthemembersofthebookclubarehighschoolkidswhohavenojobs,assets,or money,sothey'reallworthnothing.ExceptforNBAHall-of-FarnerMichaelJordan,whoisalsointhebook clubforsomereasonandisworth$650million.Inthiscase,usingthemeandoesn'tactuallygiveyouanaccurate pictureofthegroupasawhole,becauseonememberisskewingtheaveragebysomuch.Butthemedianonly usestheterminthemiddleandistotallyunaffectedbyhowfarawaytheendpointsare.

Thatdoesn'tmeanthatmedianisalwaysbetter,ofcourse.Weusemeanalot!Incasesthataren'tasextremeas this,weoftendowanttoaccountforallthevalues,includingtheonesatthetopandbottom.There'snoone answerforwhichis"better"iitdependsonwhatyou'retryingtofigureout.

*"Networth"isbasicallyafancytermforthevalueofeverythingyouown.

Using the Sum

Let'stakeacloserlookatarithmeticmean(whichwe'lljustcall"average"fromhereonout).Weallknowpretty wellhowtotaketheaverageofalistofnumberstheygiveus.Ifyou'regivenalistofnumbers,justaddthemallup anddividebyhowmanythereare.

ButonSATquestionssometimeswedon'tknowwhattheindividualnumbersare.Let'slookatone:

- The average of 5 numbers is 15. Ifthe averag� of 3 of those numbers is 19, what is the averageofthe other two numbers?

Itlookslikewedon'thaveenoughinformation.Sincewedon'tknowtheterms,wecan'taddthemup.Whatdo wedo?

Ah,weknowmorethanwethink.Let'slookagainatthedefinitionofaverage: Average Swnofterms Howmanyterms

Ifwemultiplybothsidesofthisequationbythenumberofterms,weget:

(How many terms) x (Average) = Sum of the terms

Thisequationisveryimportant.Evenifwedon'tknowtheindividualnumbers,wecanstillworkdirectlywith theirsum.Inourproblem,weknqwwehave5numbersthathaveanaverageof15,sotheirsummustbe5x15= 75Regardlessofwhattheindividualnumbersare,theymusthaveasumof75,orelsetheywouldn'thavean averageof19.

Wecanfilloutacharttohelpusorganizethisinformation:

5numberswithanaverageof15,sotheirsum is5(15)=75 3'numberswithanaverageof19,sotheirsum is3(19)=57

Thereare2numberswedon'tknow,sotheir summustbe18.

Onceweknowthatthosetwonumbershaveasumof18,wecanfindtheaverage:

Sumofterms 18

Average = ------ = - =9

Howmanyterms 2

Butagain,youonlyneedtodothiswhenyoudon'tknowtheindividualtermsinvolved.Ifyou'regivenalistof numbers,justaddthemupanddividebyhowmanythereare.

Othercalculations

Mode

Themodeisthenumberthatoccursmostfrequently.

- What is the mode of 5, 2, 7, 2 and 9?

Eachnumberoccursonce,exceptfor2,whichoccurstwice.Sothemodeis2'.·

Standard deviation

Standarddeviationmeasureshowfarthedatacollectivelystraysfromthemean.Themorespreadoutthevalues are,thelargerthestandarddeviation.

Let'slookattwosetsofdata.

Cl�ss 1: {1, 2, 3, 3, 3, 3, 3, 3, 4, 5} Class 2: {1, 1, 2, 2, 3, 3, 4, 4, 5, 5}

- Mr. Lundqvist has two math classes, each with 10 students. He asked each student how many pets they own. The two sets above show the results. Which class has a larger standarddeviation?

Forboththesesets,theaverageis3.Bothclasseshadstudentswithasfewas1petandasmanyas5pets.Butfor class1,moststudentswereclusteredaroundtheaverage,whereasforclass2,thedatawasevenlydistributed acrossthevalues(eachvaluehad2students).Sinceclass2wasmorespreadout,class2willhavealargerstandard deviation.

Wouldyouliketoseethisdataasafrequencytable?No?Toobad,hereitis:

Calculatingstandarddeviationcanstarttogetverycomplexveryquickly-we'redippingourtoeintothepool ofCrazyMathhere.ButontheSAT,youwillonlyneedtoknowwhatthetermmeans.Nowletusneverspeak ofitagain.

Math - 26

Exercise#23

{ 4, 6, 9, 17, 24}

-Whatistheaverage(arithmeticmean)ofthenumbersintheset above?

-Asetcontains3consecutiveintegersthathaveasumof78.Whatisthe medianoftheset?

-The12treesinJohn'sbackyardhaveanaverageheightof135inches.lf7of thetreeshaveanaverageheightof100inches,whatistheaverageheightof theother5trees?

The next two questions refer to the following information: Asurveyasked30peoplehowmanyfloorstheirhousehas.Resultsareshowninthegraphbelow.

-Whatisthemediannumberoffloorsforthesehouses?

-Whatisthemeannumberoffloorsforthesehouses(roundyouranswertothe nearesttenth)?

Probability

"Probability"meansexactlywhatitsoundslike:how"probable"isthisevent.Theprobabilityofaneventis definedas:

numberof"winners" totalpossibleevents

Iftheprobabilityofwinningthelotteryis"oneinamillion'�thatjustmeansthere'sonewinningnumberoutofa millionpossiblenumbers.Sinceprobabilitiesarejustglorifiedfractions,youcanthinkofprobabilityasbasically thesamethingasapercentage.Peopletalkthiswayallthetime;whentheweathermansaysthere'sa60% chanceofrain1 that'sthesamethingasaprobabilityof3/5.Somostprobabilityquestionsjustboildownto: whatpartofthewholeisthethingyou'relookingfor?·

- A certainjar with 32 marbles contains only red marbles and blue marbles. If thejar contains 8 red marbles, whatis the probability that a marble chosen from thejar will be blue?

We'relookingfortheprobabilityofchoosingabluemarble.Soallwehavetofindis: bluenumberofbluemarbles totalnumberofmarbles 32

Weknowthereare32totalmarbles,so32willgoonthebottom.Wedon'tknowhowmanybluemarbles thereare,butwedoknowthereare8redmarbles,andthereareonlyredandbluemarbles.Soifwesubtract theredfromthetotal1 we'llbeleftwiththeblue.

32-8 24 3 --=-=32324

We'redone!Theprobabilityofchoosingablue marbleis3/4.

Notethatinsteadofsolvingforthebluemarbles,wecould'vefoundtheprobabilityofchoosingared marbleandsubtractedfrom1. red81 --=-=total324 1-..!.=i 44

There'sa1/4chanceofpickingaredmarble... ...sothere'sa3/4chanceofpickingablue marble.

Wecanseefromthisthattheprobabilitiesofalleventssurroundingagivenproblemmustaddupto1.Justlikeall percentsofawholeaddupto100%,allprobabilitiesaddupto1.

ProbabilityquestionsontheSAToftengetinvolvegettingdatafromtables.Thatmeansyou'llhavetofind andgroupdatajustlikewesawearlierwhenwewerediscussingtables.Infact1 questionswesawlikethis:

10. According to the table above, approximately what fraction of residents 55 or older are female?

...couldjustaseasilyhavebeenphrasedlikethis:

10. According to the tabl� above, what is the probabilit_y that a randomly selecied resident 55 or older will be female?

Becauseprobabilityandfractionsareoneandthesame.

Thefollowingquestionsallrefertothetablebelow.

Exercise #24

ofSleepfor11th GradeStudentsatCromwellHighSchooi

Asurveyaskedall70studentsinthe11thgradeclassofCromwellHighSchoolhowmanyhoursof sleeptheygotthepreviousevening.Theresultsareshowninthetableabove.

-Ifa15-year-oldischosenatrandom,whatistheprobabilitythatheorshegot7hoursofsleep?

-Ifastudentwhogot7hoursofsleepischosenatrandom,whatistheprobabilitythatheorsheis l.Syearsold?

-Whatistheprobabilitythatastudentwhois16oroldergot6hoursofsleep?

-Whatistheprobabilitythatastudentinthe11th gradeclassis1.Syearsold?

-Whatistheprobabilitythatastudentinthe11th gradeclassgot7hoursofsleep?

-Ifastudentischosenatrandom,whatistheprobabilityheorsheisa15-year­oldwhogot7hours ofsleepora17-year-oldwhogot8hoursofsleep?

-Whatistheprobabilitythatsomeoneintheclassis16yearsoldandgot8hoursofsleep?

-Whatistheprobabilitythatsomeoneintheclassis16yearsoldandgotatleast7hoursofsleep?

-Whatistheprobabilitythatsomeoneintheclassis16oryoungerandgotlessthan7hoursof sleep?

-Ifastudentwhogot7hoursofsleeporlessisselectedatrandom,whatistheprobabilitythathe orsheis16oryounger?

Sampling and Projection

Oneofthemainreasonspeoplecollectdataistogetasample.Mostofthetime1 Ican'tcounteverything.There aretoomanythings!Iflhaveaquestionabouttheworld,Ican'tgettotalknowledgeofeverything.ButIcan learnaboutasmallportionoftheworldandassumethattherestoftheworldissimilar.

Weseethisallthetimewithpolling.Let'slookatsomedata:

Survey Responses:-

. Doyousupport Proposition 409?

- The ta�le above shows the results ofa survey of 100 residents of Hartsville. Respondents were asked whether they support Proposition 409. Ifthe city of Hartsville has approximately 20,000 residents, roughly how many total residents can be expected to support Proposition 409?

Wecanseefromth�resultsthat60peopleoutofthe100whorespondedsaidyes,theysupportthe proposition.That's60%.Sowecouldexpectthat60%ofthewholepopulationsupportstheproposition.So

201000X(0.60)= 12,000 residentswouldsupporttheproposition.

Aprojectionisanotherkindofproportion.Wetakeasmallsamplewetaketoberepresentativeofthe wholegroup.Wecanthenprojectthatratioontotheentiregroup.If3/Softhesamplewouldvoteyes1 then 3/5ofthewholecitywillprobablyvoteyes.

MostSATquestionsaboutprojectionwillworkthatway.However1 wehadabigassumptionhere:howdo weknowthatthewholegroupwillbehavelikethesample?Wehavetobesurethatoursampleis representativeofthewholetown.Thatis1 thatitbehavesthesamewaythewholetownbehaves.

Firstofall1 samplesizewillmakeadifference.Themorepeopleyouask,themorereliableyoursampleis.I mean1 ifthiswastheresultofmysurvey:

Ican'tusethisdatatoprojectthat100%ofthetownwillvoteyes.Ionlyaskedtwopeople!Thisisnota representativesampleoftheentiretown.Thereareprobablyawiderrangeofopinionsthanthesetwopeople have.

Thatdoesn'tmeanweneedahugesampletobeaccurate.A100-personsampleisaperfectlyfinesamplesizefor ourcity.Buttheremaybeotherproblems.

Secondly,wecanlookforbias.Let'sgetmoreinformationaboutProposition409:

Proposition 409 is a bill to use taxpayer money to install fancy plush seats at Hartsville Stadium, home of the Hartsville Hounds football team.

Huh.That'sanoddbill.Andtellmemoreaboutthissurveywegave.Wherewasthissurveygivenexactly?

100 Hartsville residents were surveyed as they were leaving a Hartsville Hounds game.

Aha!Soallthepeoplewhorespondedtothesurveyhadjustbeentoafootballgame.Sothesepeoplearelikelyto befootballfans.That'simportantbecausethepropositionisaboutfootball.Peoplewhodon'tcareaboutfootball areprobablylesslikelytosupportusingtaxpayermoneyforfootball.Andthosepeoplewerelesslikelytotakethis survey.Sothissurveyisbiasedtowardspeoplewhowouldvoteyes.Soit'snotarepresentativesample.

Ifyouwantasampletoberepresentativeofalargegroup}thenithastobevariedinthesamewaythegroupis.It shouldbearandomsurvey.Ifallpeopleinthesampleshareaparticulartrait}itcouldbebiasedtowardthattrait.

Thelastthingtokeepinmindaboutsamplingisthateverythingwedoisanestimate.Evenifwe'recertainour sampleislargeandunbiased}wecan'tknowdefinitivelyhowall20,000residentsaregoingtovote.Wecanonlyget closetoknowinghowthey'relikelytovote.Thisisjustlikewhenweweretalkingabouttrendlinesinscatterplot graphs:thetrendlineisakindofprojectionthattellsuslikelyvalues.Thatdoesn'tmeanthatit'suselessandwe can'tknow

anythingaboutanything.Wecanstillbeconfidentinourprojection.Wecanevenbeveryconfidentinour projection.Butwewon'tbeabsolutelycertain.

Notethateverythingwe'retalkingabouthereisjustabriefglimpseintotheworldofsamplingandprojection.A quickinternetsearchwillshowyouthatthemathbehindthissortofthingcangetverycomplicatedveryquickly.* Therearewaysyoucancalculatehowconfidentyouareinyourprojections,waysyoucanmakeadjustmentsto correctforbias,andmore.

Iassureyou,youwillnothavetoknovyanyofthat.StatisticalquestionsontheSATtendtobeverydirect,only testingyouonwhetheryouunderstandtheunderlyingconcepts,notaskingyoutodoexcessivecomputation. Really,mostprojectionquestionsontheSATarejustglorifiedratios.

*Butbewarnedthatifyougoogle"sampling"youmaygetalotofresultsabouttheBeastieBoys.

ADDITIONAL TOPICS IN MATHEMATICS

ThesmallestportionoftheSATiscalledAdditionalTopicsinMath.Thisinvolvesafewdifferent concepts,butmostlyitmeansonething:GEOMETRY.Geometryisalove-it-or-hate­itworld.Some studentscan'tgetenoughofit.Somestudentsfreezeupandwetthemselvesattheverythoughtofit. You'regoingtohavetodosomegeometryontheSAT.

Butluckily,notthatmuch!Thereareonly6questionsonthetestcategorizedasAdditionalTopicsin Math,andusuallyatleastoneofthemisn'tonGeometry,s�we'rereallyonlytalkingabout5questions outof58-that'slessthan10percentofthetest.

We'regoingtoshowyouafewsimplerulesandnotmuchelse.Anyothertheoremsorrulesthatyou mayhaveheardaboutareonlytruebecauseofthestuffinthischapter.Forthemost part,thebasicrulesreallyareallyouneed.Butifyoudoneedamorecomplicatedrule,youcanfigure itoutfromthebasicrules.

Ofcourse,ifyouhaven'thadarigorousgeometryclassinschool!youneedtolearnthebasicrulesreally, reallywell.Butdon'tworry.Allyouneedisthestuffinthischapter.Learnit,andyou'regoodtogoon everygeometryquestionontheSAT.

INTRODUCTORY REMARKS

Afewquickremarksbeforewegetstarted:

A.Techniques

Seriously,thisisa tinypartofthetest. Don'tspendtime here.Gobackto Algebra.

Don'tforgetaboutGuesstimate.Ifyouseeaquestionwithapicture,beforeyoudoanythingelse,check thatit'stoscale,guessthevaluethey'reaskingfor,andtheneliminateanyimplausiblechoices.

Inthischapterwe'regoingtobetalkingaboutalotofstraightmathcontent(rulesandformulas).But thatdoesn'tmeanyoushouldforgetaboutthetechniques.AndnotjustGuesstimate,either.Youcan usePlugInandBacksolveongeometryproblems,too.Sostayalert.

B. Not sure of a formula?

We'regoingtotalkaboutalotoflittlerulesandformulasthroughoutthislecture.However,youdon'teven reallyhavetoknowalotofthem.Theytellyou manyofthefactsandformulasyou'llneed.Onthefirstpageof everymathsection,you'llseethis:

The Thenumber numberof of radians degrees of of arc arc in in a a circle circle is is 2n. 360.

Thesumofthemeasuresindegreesoftheanglesofatriangleisl80. It'sastoundinghowlittlemathyouactuallyhavetoknowonthistest.

Obviously,you'llworkafotmorequicklyifyouknowallthisstuffbyheart.Butifyou'reeverunsureofa formula,takeafewsecondstocheckthefront.Bettersafethansorry.

C. General Strategy for Geometry

Whilethenumberofrulesyouneedonthetestisrelativelysmall,itmaystillseemburdensometoyou.Imean, howdoyouknowwhichruletouseonwhichquestion?Wheredoyouevenbegin?

Justlikewesaidintheveryfirstmathchapter,therearetwoquestionstoaskyourself:

1.WhatdoIwant? 2.WhatdoIknow?

Thegoalofeverygeometryproblemistoconnectthesetwoquestions,tciplaywithwhatyouknowinorderto getwhatyouwant.

Takealookatthisproblem:

9. In the figure below, a circle is tangent to two sides of a 12 by 6 re·ctangle. What.is the area of the circle?

1. A) B) C) D) 6n 9n 12n 36n

I CJI

Whatdowewant?Theareaofthecircle.

TheformulafortheareaofacircleA=1rr2.Tofindthearea,we'llneedtheradiusofthe circle(orthediameter,whichisjustdoubletheradius).

2. Whatdoweknow?Thelengthoftherectangleis12andthewidthis6.

Sotherealkeytothisproblemis:howcanIusethelengthorwidthoftherectangletofindthe radiusordiameterofthecircle?

Aha!Thewidthoftherectangleisequaltothediameterofthecircle!HowcanItell?By Guesstimate!Don'tworryabouttheweird"tangent"stuff:theylookequal.

Ifageometry problemdoesn't alreadyhavea picture,DRAWA PICTURE!It doesn'thavetobe perfect;evena roughsketchcan helpyou understandthe problemandcatch carelessmistakes.

Thewidthoftherectangleis6,sothediameterofthecircleis6.Sotheradiusis3,andtheareaofthecircleis91r, whichischoiceB).*

Thepointhereisthatyoushouldneverbeabsolutelystuckonageometryquestion.There'salwayssomethingthatyou know,somethingthatyoucanfigureout.Don'tbescaredofthefigures,justputdownwhatyouknowandtryto connectittowhatyouwant.

*NotethatwecouldalsouseGuesstimatetogettheareaofthecircledirectly.Therectangleis12by6,soits areais72.Thecirclelookslikeabitlessthanhalftherectangle,soitsareashouldbeabitlessthan36.Alltheanswersareintermsof1C,so we'llmultiplythechoicesby3.14(orusethe"-,r'buttonifyourcalculatorhasone)andseewhichisclosest.C)andD)aremorethan36. A)is18.84,andB)is28.27.B)isclosest.Barn.

ANGLES

WhatyouneedtoknowaboutAngles

1. A straight line equals 180°. 2. A triangle equals 180°.

3. An isosceles triangle has two equal sides and two equal 4. Vertlcal Angles are equal. angles.

IfweknowthatLBAC=LACB}thenweWhenstraightlinescross,anglesacrossfromknowAB= BC.eachotherareequaltoeachother.

5. Parallel lines with a transversal produce a bunch ofequal angles.

Whenathirdline(a"transversal")cutsthroughtwoparallellines, eightanglesareformed.Thefouratthetoparecollectivelythe sameasthefouratthebottom.

Basically,we'vegottwotypesofangles:bigonesandlittle ones.Allthebigonesareequal,andallthelittleonesare equal.Anyofthebigones(a,d}e,h)plusanyofthelittleones (b}c}j,g)equals180° .

Ofcourse,thereareotherrulesthatexistaboutangles,butthey'reonlytruebecauseoftheserules.Forexample, takealookatthisproblem:

- What is the sum of the marked angles in quadrilateralABCD shown to the left?

What?Theydon'ttellusanythingaboutthisthing!Whatevershallwedo?'"

Fearnot.Wedidn'tlearnanyrulesaboutanglesofquadrilaterals.Butwe do knowthatatrianglehas180° . Let'ssplitthisguyupintotriangles!

1hequadrilateralismadeupoftwotriangles.Eachtriangle has180°Sothequadrilateralhas2x180= 360° . That'sit. We'redone!

Someofyoumayhavealreadyknownthattheanglesof anyquadrilateraladdupto360° .Butwecandothiswith anyshape.Drawtrianglesusingonlytheshape'sexisting

vertices.Wecanseethatapentagoncontains3triangles,soitsanglesaddupto:

3X180=540° .

Andahexagoncontains4triangles,soitsanglesaddupto

4 X 180=720° . H

Ourpointisnottogetyoutomemorizethenumberofdegreesineverypolygon.1hepointisthatyoudon'thave tomemorizeabunchofruleslikethat.Justknowthefivebasicanglerulesandyoucanfigureoutanythingelse youneedtoknowaboutangles.

* IfwehadanS\ver choices,this wouldbe agreat Guesstimateproblem.

** Ifyou'reinterestedhere'stheformula:theangles apolygonwithIIsideswilladdupto (11 -2)180degrees. 1hat'sbecause11 -2isthenumberoftrianglesyoucandrawintheshape.Whendrawingtriangles, remembertoonlyconnectpoints inthepolygon-don'tusethecenteroftheshapeasatriangle's vertex. 147 I Page

Youshouldneverbetotallystuckonaproblemthatdealswithangles,becausethere'salwayssomethingyou know.Moreoftenthannot,justputtingdownwhatyouknowbasedontheseruleswillleadyoutowhatyou're tryingtofind-evenifyoudon'tseewhereyou'regoingwithit."Okay,Ireallydon'tknowhowtofindwhatthey want,butIknowthat'satriangle,soitsanglesaddupto180.AndIknowthat'sastraightline,sothoseangles addupto180..."Etcetera.Justplaywiththeserulesandseewhereittakesyou.

Andremember:whenindoubt,drawtriangles.

PERIMETER, AREA & VOLUME

Let'sstartwithafewdefinitionsandformulas.NotethatthisisallyouneedtoknowfortheSATaboutperimeter, area,andvolume.Ifyouwanttofindtheareaorvolumeofashapethatisn'tlistedhere(likeapentagon),either:

A)youcanfinditbyusingsomecombinationoftheshapeslistedhere,or B)youdon'tactuallyneedthatarea(you'onlythinkyoudo).

A. Perimeter

Theperimeterofanyfigureisthesumofthelengthsofalltheoutsideedges.Okay?Okay.

2. Area

Somenotes:

Parallelogram: A=bh

-Inatriangle,thebaseisjustwhateversidehappenstobelyingflatontheground.The heightisalinefromthetopmostpointofthetriangleextendingperpendiculartothebase.Sometimes that'sjustasideofthetriangle,sometimesit'sinsidethetriangle,sometimesit'soutsidethetriangle.All threeofthefollowingtriangleshaveidenticalareas,becausetheyhavethesamebaseandheight:

-Theformulasforsquaresandrectanglessaythesamething.Asquareisjusta rectanglewithequalsides,sos=e=w.

-Noticethattheareaofatriartgleishalftheareaofarectangle.Imaginecuttinga rectangleinhalfalongthediagonal;you'dgettworighttriangles.Andforeachtriangle,thebaseand heightareequaltothelengthandwidthoftheoriginal

rectangle.

-Youcanalsousetrianglestofindtheareaofothershapes.Theareaofaparallelogram isbasetimesheight(that'stheheight;nottheside).Youcanseethisbydrawingin twotriangles,aswedobelow.Again,weusetherulesweknowtofigureouttherules wedon't.

Shaded Area Problems

Shadedareaproblemsarebestdonebysubtradion.Findtheareaofthewholefigureandtakeawaywhatyou don'tneed.

Takealookatthisone:

--'I� the figure below, a small'square is·inside a larger square. What is the �rea of theshaded region?

8

Note:Figurenotdrawntoscale.

Itmaybetemptingtotrytofindtheareadirectlybydividinguptheshaded regionintofourrectangles.Butwecan'tfindthoseareasbecausewedon't knowalloftheirdimensions.Plusit'skindoftedious.

Instead,let'sjustfindtheareaofthewholesquareandsubtracttheareaoftheunshaded square.Whatever's leftwillbetheareaoftheshadedregion

Aw/10/e=S2 =82 =64

A,mshaded= 5 2 =25

Ashaded=Awlwle-A,mshaded =64-25[= 39]

C.SurfaceArea

Wefindthe"surfacearea"byfindingtheareaofthesurface.*Thatmeanswehavetofindtheareasofallthe shapesontheoutsideofthebox.Aboxismadeupofabunchofrectangles;we'llfindtheareaoftherectangles andaddthemallup.1hat'sit.

Thisboxhasdimensions12,8,andS.Tofindthesurfacearea,we'lltaketheareasofalltherectanglesonthe outsideandaddthemup.

Wecanseethattherearethreetypesofrectanglesinthisbox:

A=12x8=96

A=12X5=60

=8X5=4O

BUT,eachofthesesidesshowsuptwiceinthebox(topandbottom,frontandback,sideandside.)

SA=2(A1+A 2 +A)

SA=2(96+60+40) = 2(196)

SA=392

Again,acubeisjustaspecialtypeofbox.Sinceit'smadeupof6squares,we'lljustfindtheareaofonefaceand multiplyby6.Thissquarehasedgesoflength4.

SA= 6(A0)

SA=6(s2) = 6(42)=6(16)

SA=96

*Brilliant.

D. Volume

A� .e

-Justastheareaofarectangleisfoundbymultiplyingitstwodimensions,thevolumeofaboxisfoundby multiplyingitsthreedimensions.*

-Justasasquareisarectanglewithequalsides,acubeisaboxwithequalsides.

-Noticethatthevolumeofacylinderworksunderthe sameprincipleasthevolumeofabox.Forabox,the baseisarectangle,soitsareaislengthtimeswidthi getthevolumebymultiplyingthatbytheheight.For acylinder,thebaseisacircle,soitsareaispr2 igetthe volumebymultiplyingthatbytheheight.

V=(lw)xhV=(nr2)xii

VOLUME:

Box:V=Ewh

Cylinder:V=m1h

Cone:V=.2._nr 1h 3 h 43 Spere:V=-n 3

Rectangular

Pyramid:V=.!...ewh 3

*Inasense,itdoesn'treallymatterwhichsideyoucalllength,width,orheight,sincethevolumecomesout thesamenomatterwhat(lx2x3=2x3xl),buttherearesomeconventionsaboutwhattocall them.Inarectangle,thelengthisusuallythelongersideandthewidthistheshorterone.Inabox,the heightwillalwaysbethesidethatgoesup,awayfromthefacelyingflatontheground.Thusifthebox is,say,atankfilledwithwater,theheightwillconespondtothedepthofthewater.

CIRCLES

Circlesareaweebitdifferentfromothershapes,sotheygettheirownsection .

A. Definitions

Somefuncirclefacts:*

MATH-29

-Acirclehas36D°. Inthefiguretotheright,angles surroundingpointOwilladdupto360°.**

-Thediameterofacircleisaline segmentfromoneendofthecircle theother,passingthroughthecenter.Inthefigure, isadiameter.Thediameterbydefinition thelongestsegmentyoucandrawthroughacircle. all B to is

-Theradiusofacircleisalinesegmentfromthecentertothee�dofacircle.The radiusishalfofthediameter.Inthefigure,DA,OB,andOCareallradii.Allradiiofa circleareequal.

Circlesarenamed fortheircenter points,sothiscircle iscircle0.Alotof circlesarenamed "O".Canyouguess why?

-Achordisanylinesegmentfromoneendofthecircletotheother.Thelongestchordinacircleisa diameter.

Almosteverythingwedowithacirclerequiresknowingitsradius(ordiameter,whichisjustdoublethe radius).ffyou'regivenacircleandyoudon'tknowitsra_dius,beforeyoudoanythingelsetrytofindthe radius.You'llprobablyneedit,evenifyoudon'tyetknowwhy.

-Whenalineistangenttoacircle,thatmeansittouchesthecircleat exactlyonepoint.Inthefiguretotheright,segmentABistangentto circleOatpointC.Notethatatangentlineisalwaysperpendicular totheradiusofthecircleatthepointofintersection.Here,radius OCisperpendiculartosegmentAB.

-Whenoneshapeisinscribedinsideanothershape, thatmeansitfitsexactlywithinthelargershape,

A circle inscribed Asquareinscribed in asquare in acircle *Well,notthatfun.

**Actually,wecanalreadyfigurethisoutfromouranglerules.Thediameterisastraightline,sotheanglesaboveitaddupto180° andtheanglesbelowitaddupto180°.Putthemtogetherandyou've,got360° .

touchingitsedgesatonepointoneachside.*Ifyouencounteraquestioninvolvingcirclesandinscribedshapes, theradiusordiameterofthecirclelikelycorrespondswithakeyelementoftheothershape.Inthefirstfigurehere, tl,iecircle'sdiameteristhesamelengthasthesideofthesquare.Inthesecond,thediameteristhesameasthe diagonalofthesquare.

B.Formulas

-Theperimeterofacircleiscalleditscircumference(C).Thecircumferenceisequal tothediametertimes n, whichisthesameastwotimestheradiustimesn (sincethediameterequalstwo radii).

-Notethatthedistanceawheeltravelsinonerevolutionisequaltothecircumference ·.ofthecircle.

-Theareadfacircleisequaltotheradiussquaredtimesn.

CIRCLE FORMULAS:

C=nd=2nr

A=nr2

-n(pronounced"pi")standsforaspecialnumberwhosevalueisapproximately3.14. FormostSATproblems,youdon'thavetocalculatethenumber;youcanjustleaveitasthesymboln.

Inthecircleshownhere1 theradiusis3,so

GC.Slices

C=2m- A=m-2

C=2n-(3) A=1r(32)

6,r A=91r I

Awedgeorsliceofacircleisnothingmorethanapartofacircle.Problemsdealingwiththemcanbedonewith simpleratios.Takealookatthiscircle:

Obviously,theshadedsectionisonefourthofthecircle.How canItell?Firstofall,becauseitlookslikeafourthofthecircle (Guesstimate!)

Thatcentralangle, LAOB, is90° .90isonefourthof360.Sothatcentral angleisonefourthofthewholeangle(360).

* Theoppositeofinsc1ibediscircumscribed.Tosaythatacircleisinscribedwithinasquaremeansthesame thingassayingthesquareiscircumscribedaboutthecircle..

Let'ssaythecirclehasaradiusof10.SoitsareaislO0rc.Theareaofthesliceisonefourthofthat:25rc Ifthecirclehasaradiusof10,itscircumferenceis20n.ThelengthofminorarcABisonefourthofit: Sn.

Thisisprettyeasytosee.Sincethatsliceisonefourthofthecircle1 everythingaboutthatsliceisonefourthofthe correspondingcharacteristicofthecircle:theangleisonefourthof360,theareaisonefourthofthecircle'sarea, andthearclengthisonefourthofthecircumference.

Thisistrueofallslices.Thesliceshowntotheleftis1/60ofthecircle, sothatangleis1/60of360°,thearcis1/60ofthecircumference,andtheareaofthesliceis1/60ofthewholearea.

Soifyouknowanyonethingaboutaslice,youcanfigureoutwhat fractionofthecircleitis.Onceyouknowwhatfractionofthecircleitis,youcanfind anythingelseaboutthatslice.

Youcansetupanysuchproblemwithaseriesofratios:

TRIANGLES

TrianglesarethekeytoalotofSATquestions.Infact,ifyou'reconfrontedwithanoddshapeyoudon't understand,trydrawinginatriangle.Trianglesareyourbestfriend.Trustus.

1.SimilarTriangles

Ifalltheanglesofonetriangleareequaltoallthecorrespondinganglesofasecondtriangle,thentheyare similartriangles.Thatmeansthatalltheirsidesareinthesameratiowitheachother.

Here,.6ABChasallthesameanglesas.6DEF,sotheyaresimilartriangles.AB=7andDE=14,soDE isdoubleAB.Sincethetrianglesaresimilar,eachsideof.6DEFwillbedoublethecorrespondingsideof .6ABC.SoEF= 2(10) = 20,andDF=2(12) = 24.

Whendealingwithsimilartriangles,it'simportanttokeeptrackofwhichsideiswhich.ABwillbe proportionaltoDEbecauseeachofthemisacrossfromthe"z"angle.

Similartrianglesdon'thavetobenexttoeachother.Often thesequestionswillfeatureatriangleinsideofatriangle.Inthe figuretotheleft,ifDEisparalleltoBC,thenLADE=LABC. Therefore.6ABCissimilarto.6ADEbecausealloftheir correspondinganglesareequal.

2.The

PythagoreanTheorem

ThePythagoreanTheoremisawaytofindthethirdsideofarighttriangle.* Thesumofthesquaresofthelegsofarighttriangleisequaltothe squareofthehypotenuse.·

Bytheway,ifyouforgetthePythagoreanTheorem,lookatthefrontofanymath section:theygiveittoyou.Youdon'tevenhavetoactuallyknowit!Thingswill obviouslygomoreswiftlyifyouknowitbyheart(andmanyofyouprobablydo),but evenifyou'reslightlyunsureaboutit,checkthefront.Bettersafethansorry.

Trythisone:

3 - If a right triangle has legs of length 3 and 4, what is the length of the hypotenuse?

32 + 42=x2

9+16=x2

25=x2

5=x

Arighttriangleis atrianglewitha rightangle(a90° angle).Theside oppositetheright angleiscalledthe hypotenuse.The twosidesnextto therightangleare calledlegs.

Someofyoumayhaverecognizedthetriangleintheproblemabove.It'sa"PythagoreanTriple".Becausethe PythagoreanTheoremhasallthose"squares"init,mostrighttrianglesdon'thaveintegervaluesforallthesides. Sothetrianglesthat do haveallintegersshowupalot.The3-4-5isacommonone.Ifyouseeatrianglethathas legs6flength3and4,youknowimmediatelythatthehypotenusemustbeS.

Beonthelookoutformultiplesofthe3-4-5,aswell.Forexample,a6-8-10triangleisjusta3-4-5trianglewith eachsidemultipliedbytwo.They'resimilartriangles:theyhavethesamesideratioswithdifferentvalues.

*ThetheoremisnamedfortheGreekphilosopherPythagorasandhiscult,thePythagoreans,butthe fundamentalsofthetheoremwereknownhundredsofyearsbeforehimbytheBabylonians,Indians,andChineseamongothers. Thereislittleevidencethatheorhisfollowerseverprovedthetheorem.Whyitwasnamedforhim,wehavenoidea.The Pythagoreansdidalotofimportantworkinmathematics,buttheyalsothoughteatingbeanswassinful.

3.SpecialRightTriangles

Thesimilartriangleruletellsusthattriangleswiththesamesetofangleswillhavethesame ratioofdimensions.Therearetwoparticularsetsofanglesthatshowupmorefrequentlythan others.

The

Isosceles Right Triangle (45-45-90).

Anisoscelesrighttrianglehastwolegsofequallength,apdtwo45°angles.*Thedi�ensionsof thesetrianglesarealwaysinthesameproportion:

Ifyoucan't rememberthese dimensions,look in thefrontofthe section.Theytell youthedimensions. Youdon'tevenhave torememberthem! They'rewrittenin thefront!

Thismeansthatifyouknowthelengthofalegofthetriangle1 youcanimmediatelyfindthehypotenuse-it'sjustthe legmultipliedby✓2

Whydoweknowallthesetriangleshavethesamedimensions?Theyallhavethesameangles1sothey're similartriangles!

Noticethatweknowallofthesetrianglesare45-45-90eventhoughtheydidn'ttellustheanglesare45°.That's becauseweknoweachhastwoequalsides-andthataloneisenoughtomakethemisosceles.

The 30-60-90 Triangle

Anytrianglewithanglesof30° 1 60° 1 and90°willalwayshavethesamedimensions. It'sthesameconceptasthe45-45-90triangle:iflknowjustafewthingsaboutthe triangle,Icanjustfillinallthevaluesfortherestofthetrianglewithoutdoingalotof calculationsorbotheringwiththe

*Plusa90°angle.Thus"righttriangle". X

PythagoreanTheorem.*Theyallhavethesameangles,sothey'resimilar�iangles!

Rememberingthesetriangles

Itcanbetoughtorememberallthesedimensions.The45-45-90isabiteasiersincetwoofthesidesarethesame. Butinthe30-60-90sinceeachsidehasadifferentvalueandit'seasytomixupwhereeverythinggoes.Here'satip forrememberingwhichangleandwhichlengthgoeswhere:

-The45-45-90triangleishalfasquare.Thediagonalofthe squarecutstworightanglesinto45°angles.Thetwox'sarethe x sidesofthesquareandthehypotenuseisthediagonal.

-The30-60-90triangleishalfanequilateraltriangle.Aline dividesoneofthe60°anglesintotwo30°angles,andthen cutstheoppositesideinhalfaswell.

Butagain,ifyou'renotsurewheretoputeverything-checkthefrontofthesection.Theygiveyouthis.Youdon't havetorememberit.

Sometimes,itmaynotbeobviousthatatriangleinaproblemis30-60-90or45-45-90.But

noticethatthesetrianglesinvolvetwohappymagicnumbers:✓2and✓.Thesenumbersdon'tshowup veryofteninothersituations.Infact,theyrarelyshowupinothersituations. Soifyou'redoingaproblemandnotice✓3intheanswerchoices,there'saprettygood chancethatthere'sa30-60-90triangleintheproblem.ThesamegoesforJi.i ifyouseeitin theanswers,there'sagoodchancethere'sa45-45-90triangleintheproblem.Ofcourse,this isn'talwaystrue.Butifyou'restuckonaproblem,lookforthesehappymagicnumbers.Theycouldhelpyou spotsomethingyouwouldhavemissedotherwise.**

*YoucouldprovethesedimensionswiththePythagoreanTheoremthesamewaywedidabovewiththe 45-45-90triangle.Wedidn't,becausewedon'tfeellikeitandwedon'tthinkanyofyoucare.Butifyoudo,goahead, knockyourselfout.

**.fi.iscertainlyamagicnumber.Itwasthefirst"irrationalnumber"-adecimalthatcan'tbeexpressedas afraction.ItwasfirstdiscoveredbyHippasusofMetapontum,aPythagoreanmathematician.Hewasatseawhenhediscoveredit, andsomeofhisPythagoreanshipmatesweresoangeredandoffendedbytheideaofanirrationalnumber,theythrewhimoverboard anddrownedhim.ThePythagoreanswerenuts.IfyouknowanyPythagoreans,don'tmention.fi.tothem.

TRIGONOMETRY

Trigonometrycanbeascarytopic.Someofyoumaynothavedoneanytrigonometryinschoolyet1 . sothiswill allbenew.Buttrigonometryisn'tsobad.Firstofall1 whilesometrigquestionsdoinvolvesometrickyconcepts1 mostofthemjusttestyourknowledgeofthedefinitionsofthebasictrigonometricfunctions.Onceyoulearn those1 youcanknockoutmosttrigonometryquestionswithoutbreakingasweat.Second1 becausetrigonometry questionsaredifficultforstudents1 theytendtoappearattheendofthetest.Thatmeansthatalotof trigonometryquestionswillbepastyourtargetnumbers1 soyouwon'tevenreadthematall.

Basic Functions

Whatistrigonometryandwhydoweneedit?Itallbeginswithrighttriangles.

Rememberwhenweweretalkingabout45-45-90triangles?Wesaidthateverytrianglewhoseanglesmeasure45° 1 45° 1 and90°havedimensionsinthesameproportion1 1:1:..fi.

Thesamewastrueofthe30-60-90triangle.Everytrianglewhose anglesmeasure30° 1 60° 1 and90°havesidesintheratio1:.Jj:2.We calltriangleslikethissimilartriangles-iftheiranglesareallthesame measure1 theirsideswillbeinthesameratio.

Ratherthanlookingattheratioofallthreesidesatthesametime1 it's easiertolookattwosidesatatime.Ifarighttrianglehasa45°angle1the ratioofthesideoppositetheangletothesidenexttoitwillbe1:1.Ifarighttrianglehasa60° angle1 theratioofthesideacrossfromittothehypotenusewillbe.Jj:2.

Theseratiosarethewholepointoftrigonometry.Therearethreebasictrigonometryfunctions: sine1 cosine,andtangent(abbreviated"sin'�"cos"1 and"tan").Thesefunctionsdoexactlywhat wejustdid:theytaketheratiosofthesidesofarighttriangleinrelationtoaspecificangle.

Herearethedefinitionsforthesefunctions:

For any given angle ofa triangle:

MATH - 30

- the SINE ofthe angle is equal to the length ofthe opposite side over the length ofthe hypotenuse.

sin 0= Opposite =2'..

Hypotenuse r

- the COSINE ofthe angle is the length ofthe adjacent side over thehypotenuse.

Adjacent x cos0 =-�--

Hypotenuse r

- the TANGENT ofthe angle is the length ofthe opposite side over the adjacent.

tan0 = Opposite = y Adjacent x

1he symbol "0" is the Greekletter "theta". It's often used to describe angles in trigonometry problems. Note that these functions onlyworkwithright triangles-triangles that contain right angle.

MEMORIZETHESEDEFINITIONS. Many trigonometry questions require nothing more than knowing these three definitions. You can remember these ratios via the acronym SoHCAHTOA:

Sine = Opposite over Hypotenuse

Cosine = Adjacent overHypotenuse

Tangent= Opposite overAdjacent

Calculating the ratios

Let's look at anexample:

-In .6.ABCto the right, what is the value ofsin A?

We know that sine is equal to the opposite side over the hypotenuse. 1heside oppositeangle A is 4, but we don'tknow the hypotenuse. We can use thePythagoreanTheoremto find it, or we can see that it's a 3-4-5 triangle, so the hypotenuse is S. Therefore, sin A=i. s

Infact,oncewehaveallthelengthsofthesides,it'seasytofindalltheratios:* 8

Let'stryonethathasanswerchoices: . B 3 SlD =4 17. If0° < X < 90° and tan X = � I what is cos x? 8

Sincethe hypotenuseis alwaysthelongest side,sinandcosare alwayslessthan1. Thiscanhelpyou eliminatechoices. . A 4 SlD =5 cosA=3 5 4

Thisquestiondoesn'tgiveusafigure,soweshoulddrawone.Itdoesn't havetobetoscale,justdrawatriangleandcalloneanglex.

Tangentisoppositeoveradjacent,sothesideoppositexis5andtheside nexttoxis 8. 3 tanBe:::-

Wewantcosx:that'sadjacentoverhypotenuse.Weknowthattheadjacentsideis81 butwe don'tknowthehypotenuse.WecouldusethePythagoreanTheoremtofindit.Butlook..:_all theanswerchoicescontaincombinationsofS,81 and./89.Sothehypotenusemustbe./89. Wedon'thavetodooutthework.Nice!

Thesideadjacenttoxis8,thehypotenus�is./891 socosxis8That'schoiceC).

*NoticethatsinA= cosB1 andcosA= sinB. That'sbecausethesidethat'soppositeoneangleisadjacentto theother.

Thesequestionsreferto.6ABCshownatriJ!ht -sin (LA)=? -tan (LB)=?

ATH 31 Exercise #25

-cos (LB)=?

Reciprocal functions

Thethreebasicfunctionsshowthreeratiosofsidesofarighttriangle.Butthosearenottheonlycombinationsof sides.Wecouldalsoflipthefractionstogetthereciprocalfunctions.Thesearecalledcosecant(csc),secant(sec), andcotangent(cot).

COSECANT:

SECANT:

COTANGENT:

csc0=_I_= Hypotenuse =!.... sin0 Opposite y

.sec0=_1 = Hypotenuse r cos0 Adjacent x

cot0=_I = Adjacent =� tan0 Opposite y B y A X C

It'seasytomixtheseupbecausethe"co-"sdon'tmatch:cosecantisthereciprocalofsine,andsecantisthe reciprocalofcosine.

Thereciprocalfunctionsdon'tshowupnearlyasmuchasthebasicfunctions,butyouwillseethemoccasionally, soit'sstillimportanttolearnthem.

Inverse functions

Sofarwe'vebeensolvingforlengthsortheratiosoflengths.Butwhatifwewanttosolvefortheangles?

- If0° <x < 90° , and sinx = 0.529, x =? .

Wecansolvethatdirectlyforxbyusinginversesine(abbreviatedsin-1).Thisisnotthesamethingasthe reciprocalfunctionsmentionedabove.It'spurelyawaytosolveanequationlikethisfortheangle.Itasks"the sineofwhatanglecomesto0.529?"Youcansolvethisbypunchingitoutonyourcalculator:*

sin X =0.529 x= sin-1(0.529) x:::::32.

Alltrigonometricfunctionshaveinversefunctionslikethis1 whichyoucanusetosolveforan angle.

Neitherthereciprocalfunctionsnortheinversefunctionsarelikelytoshowupoftenonthe SAT.Butit'sworthknowingthatthey'rethere.

Identities

Identitiesareequationsthatshowupfrequently(likethe"differenceofsquares"identity)so thatyoucanmemorizetheirformsanddothealgebraquickly.

Therearealotofrulesandidentitiesrelatedtotrigonometryfunctions.Theycanget complicatedandhardtoremember.However1 therearetwoidentitiesthatyoushould· remember: sinO =tan0 cosO (opp) (adj) (opp) (hyp) opp Tius1seasytoprove:-+-=h xd.=-=tan hyp hyp ryp a.J adj (sin0)2 +(cos0)2 =1 Sometimesthisiswritten"sin2 8+cos2 8= I"

Anytimeyoudo anytrigfunctions onyour calculator1besure tocheckwhether yourcalculatoris settoradiansor degrees.

Ifaquestionasksyoutoalgebraicallymanipulateanexpressionthatcontainsatrigfunction1chancesareyou'll needoneoftheseidentities.

Radians

Therearetwodifferentscalesformeasuringangles:degreesandradians.Radiansareadifferentwayofmeasuring anglesinsteadofdegrees1 usedmostlyinproblemsinvolvingtrigonometry.It'slikethedifferencebetweenmiles andkilometers.Youcanconvertdegreestoradiansusingthisformula:

2nradians=360°

*Justmakesurethatyourcalculatorissettodegrees,notradians.We'lltalkmoreaboutradiansinaminute.

Rememberwhenwesaidthateverypartofthesliceofacirclewasproportionaltoeveryotherpart?That'sthe ideawithradians.Imagineanangleasasliceofacirclewithradius1.Themeasureinradiansisthearclengthof theslice.360°is2nradiansbecause2nisthecircumferenceofthewholecircle.Similarly,nradiansishalfthe circumferenceand180°istheangleofasemicircle,etc.

Forexample,inthecircletotheright,thecentralangleofarc AB measures90° ,whichisequivalentton/2radians.Wecan seethatthesliceisone-fourthofthecircle.Theradiusis11 so thecircumferenceis2n,andthearclengthis2n-;-4orn/2.The measureinradiansisequivalenttothearclengthofasliceofa circlewithradius1.

IMAGINARY AND COMPLEX NUMBERS

ThisistheoneconceptinthissectionthathasnothingtodowithGeometry,butsomehowtheygetlumped togetherintotheAdditionalTopicscategory.Youwillnotseemanyquestionsinvolvingimaginarynumberson theSAT1buttheymaypopupeverynowandthen.

Youknowhowsometimesaproblemwillstartbysaying"Forallrealnumbers"?Whydotheysaythat?Arethere anynumbersthataren'treal?

Yesthereare!Imagi�arynumbersarenumbersthatcontaini,definedasi=�Questionsinvolvingimaginary numbersoftengivethedefinitionasi2 =-1,butthat'sthesamething.Usuallyyou'renotallowedtotakethe squarerootofanegative,whichiswhynumbersthatdosoarecalled "imaginary':Butdon'tbescaredbythename!Youcanmanipulateijustlikeyoudoanyvariable.

MostimaginarynumbersontheSATinvolvecomplexnumbers.Acomplexnumberisapolynomialintheform a + bi1 arealnumberplusorminusanimaginarynumber!Let'slookatanexample:

(3+2i)(S+3i)=?

ComplexnumbersworklikeanyotherpolynomialandcanbemultipliedusingFOIL: (3+2i)(S+3i) = 3(5)+9i+IOi+6i2 =15+19i+6i

We'renotdone.Rememberthati2=-1,sowecansubstitute-1inthelastterm: =15+19i+6(-1) = 9+19;

Occasionallyyoumaybeaskedabouthigherpowersofi.Ifyoumultiplyibyitselfabunch oftimes,you'llseethatthepowersofishowarepeatingpattern: I ., ,...-;1 =v-1=1 i6=i5xi=ixi=-l

etc...

* Actually;allrealnumbersaretechnicallyalsocomplexnumbers.Everynumberinthisbookcanbewrittenas a+ bi,it'sjustthatmostofthetimeb=0.

Whatisthevalueofi18?

(5+8i)(4-6i)=?

(-2-7i)(2+3i)=?

(3-2i)(3-2i)=?

(4+3i)(4-3i)=?