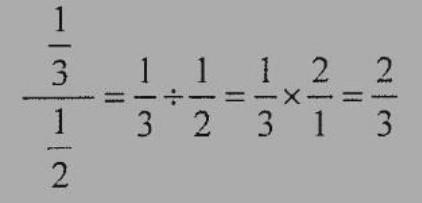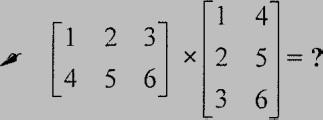THE ULTIMATE CAPSTONE GUIDE TO THE ACT MATH SE by 4cstrong

Introduction to Math

Math Techniques

Numbers and Quantity

Elementary Algebra

Intermediate Algebra

INTRODUCTIONTOACTMATH

WelcometoACTMath!Aswesaythat,Iamsureitcreatesanimmediatementalblockandinstantthoughtsof failureracethroughyourmind.However,Iencourageyoutocomeatitwithanopenmindandexploreways toovercomethisseeminglyinsurmountableobstacle.

ManypeopleconsidertheACTtobemuchmoreofacontent-basedtestcomparedtoitscousin,the SAT.WhileitistruethattheACTrequiresslightlymoreMathknowledgethantheSATdoes,itis stilla atheart.

ACTmathisnotexactlythesameasthemathyoudoinschool.Yes,manyofyouroldfavoriteswill showuphere(ratios,two-variableequations,thePythagoreanTheorem,andmanymore!)butthe questionsarealittlebitdifferent.Inschool,youlearnForexample,youlearn,then youlearnhowwellyouaretestedon

TheACTgivesyouaproblemandasks youtosolveitanywayyoucan.TheACTdoesnotcareifyouknowtheformulas,theysimplywantthe rightanswer.Ifyouneedaformulatofindtheanswerthenusealgebraicformulastofindtheright answer.But,ifyoucanusebasicarithmetictoansweraproblem,theydonotcarewhatstepsyoutake togetthere.Throughoutourclass,wewillfocusonhelpingyoufindthemostefficientandsuccessful waytofindtherightanswerwithinthetimeperiodgiven.

Throughoutthenextchapters,wewillbetalkingabouttwotypesofthings:contentandtechniques. istheliteralstuffyouneedtoknow(likethePythagoreanTheorem). aremethods fordoingmanydifferentkindsofproblems(likePlugIn).Bothareequallyimportant.However,much ofthecontentyouwilluseasarefreshercourseformaterialyouhavealreadylearnedfromyourmathclasses andteachers;thetechniqueswillbenewmaterialforyou,sothatiswherewewillfocusmost ofourtime.

GENERALFORMAT

HereareafewnotesabouttheformatoftheACTMathTest:

Thereare60multiplechoicequestionsin60minutes.Thistimingwillfeelveryrushed.Donotstresstoo muchaboutthis.Relax,takeadeepbreathandwewillhelptalkyouthroughitduringthecourse.

Allquestionsareorderedbydifficulty.Thismeanstheeasierquestionsareatthebeginningofthesection andtheendquestionsareharder.

Allquestionsareamultiplechoice.Thereare5choicesperquestionratherthan4.Thismeansyouhave a20%chanceofgettingaquestionrightratherthana25%chanceontheotherquestions.Thismeans youroddsofguessingarelowerthantheothersections.

Calculatorsareallowedbutnotrequired.Thismeansyoumaynotneedacalculatoronsomequestions especiallyifitslowsyoudown.However,onsomequestions,acalculatormayhelp[youarriveatthe rightanswermorequickly.

RememberthereisnopenaltyforguessingsoDONOTLEAVEANYANSWERSBLANK.Leavingananswer blankgivesyoua0%chanceofgettingitrightversusa20%chancewhenyouguess.Increaseyourodds byansweringeveryquestion!

TheACTtestinmathematicsisa60-minutetestdesignedtoevaluateyourmathematicalachievementincourses commonlytaughtinhighschool.Thistestincludesquestionsfromtheareasofpre-algebra,algebra,plane geometry,intermediatealgebra,coordinategeometry,andtrigonometry.

TheACTcoversseveralcategories.Therearequestionsbasedonbasicskillswhichcoverrecognitionandsimple applicationofelementaryconceptssuchassubsetsofrealnumbers,termsandrelationshipsconcerning operations,andaxiomsoftherealnumbersystem.Therearealsoapplicationquestionswhichrequireyouto applyoneortwoconceptstothesolutionofaproblem.Thequestionsintheanalysiscategoryusually requiretheapplicationofseveralconceptstoobtainthesolution.Frequentlythistypeofquestionis posedasatypical"wordproblem."

Theemphasisinthistestisonyourabilitytoreasonwithnumbersandmathematicalconcepts.No extremelycomplicatedformulasorprocedureswillbeinvolvedinthesolutionoftheproblems.

Foreachquestionfivepotentialanswersaregiven,onlyoneofwhichiscorrect.Theanswersmaybe designatedas or .Forsomequestions,thelastchoice(eitherormaybe"Noneofthe above."

QUESTIONTYPES

InadditiontoyouroverallMathscore(1-36),youwillgetthreesubscores(1-18)basedonthe differenttopicsthatappearinthemathquestions:

TheACTgroupsmathquestionsintosixcategories.Thenumberofquestionsinthesecategories isfixed,soeverytestwillalwayshavethesamenumberofquestionsofeachtype,thoughtheywill bemixedupinanyorder.Belowisanideaofthebreakdownofquestionsduringthetest.

PreparingforHigherMath-57-60%

oNumberandQuantity-7-10%

oAlgebra12-15%

oFunctions12-15%

oGeometry-23%

oStatisticsandProbability

IntegratingEssentialSkills-40-43%

Modeling-morethan27%

Here'sanoutlineoftheconceptsincludedinthroughoutthisbooktohelpcovereachoftheabove areasasdefinedbytheACT.Thisroughlycorrespondstotheorderinwhichtheyarepresented inthisonlinebook,thoughwemayhaveswitchedsomearoundtomakethingseasiertofollow.

Pre-Algebra

Pre-Algebraquestionsincludeanyquestionthatdealswithonlynumbers(notvariables),word problemswhichdonotrequirewritingequations,andsimpleequationswithonlyonevariable.Major topicsinclude:

One-variableequationsolving

Basicoperations

Manipulatingfractionsand decimals

Basicroots&exponents

Ratios&percents

ElementaryAlgebra

Multiples,factors,andprimes

Probabilityandcombinatorics

Mean,median,andmode

Datainterpretation

Basicmanipulationofabsolute value

ElementaryAlgebraquestionsinvolvemoreadvancedalgebraicmanipulation.Over40%ofthese questionscanbedonewithaMathTechniquelikePlugInorBacksolve.Majortopicsinclude:

Multi-variableequations

Moreadvancednonlinearequations

Translatingwordproblemsinto algebraicexpressions

Evaluatingequationswithagivenvalue

Substitutionofexpressions

FOIL,polynomials,and factoringexpressions

IntermediateAlgebra

IntermediateAlgebraquestionsinvolvehigher-levelalgebraquestionsandmoreadvancedtopics. Over50%ofthesequestionscanbedonewithaMathTechniquelikePlugInorBacksolve.Majortopics include:

Algebraicexpressionsusingexponents andexponentrules

Functions,j{x)format,combining functions

Quadraticmanipulationand quadraticinequalities

CoordinateGeometry

Absolutevalueequationsandinequalities

ArithmeticandGeometricsequences

Imaginarynumbers

Matrices

Logarithms

CoordinateGeometryquestionsincludeanythingandeverythingrelatedtographingandthexycoordinateplane.Majortopicsinclude:

Understandingthexy-coordinateplane anditsquadrants

Locatingcoordinatesofgeometrical figures

Slope&intercepts

Graphinglinearequations

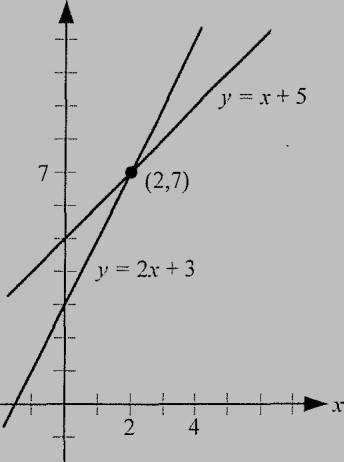
PlaneGeometry

Intersectionofgraphs

Equationsofcirclesandellipses

Graphsofinequalities

Midpoint&distanceformulas

Transformationoffunctions

PlaneGeometryquestionsincludeanythingandeverythingrelatedtogeometryandfigures,excluding figuresgraphedonthecoordinateplane(whichareincludedinCoordinateGeometry).Studentswill beexpectedtoknowsomebasicformulas(areaofatriangle,circumferenceofacircle,etc.)Some higher-levelformulas,whennecessary,willbegivenintheproblems.Majortopicsinclude:

Anglerulesandproperties

Pythagoreantheoremandspecial triangles(3-4-5,30-60-90,45-45-90 triangles)

Similartriangles&rulesofcongruence

Propertiesoftriangles, rectangles,parallelograms, trapezoids,circles

Trigonometry

Perimeterandlength

Area,shadedarea,andirregularshapes

Surfaceareaandvolume

Rotationandreflection

Logicandlogicalconsequence

Mosttrigonometryquestionswillrequireabasicunderstandingoftrigonometricterms.Somequestions mayinvolvehigher-levelformulas,suchasthelawofcosines,butinthosecasestheformulaswillbegiven toyouintheproblem.Majortopicsinclude:

Definitionsofbasictrigonometricratios (sin,cos,tan,sec,csc,cot)

Basicidentities

Graphingtrigonometricfunctionsand theirtransformations

Lawofsinesandlawofcosines

TheUnitCircle

Radiansanddegrees

Calculators

Yes!CalculatorsareallowedontheACT.OnlyontheMathTest,though.Youmaynotusea calculatorontheEnglish,Reading,orSciencetests(notthatyou'dneedone).

Forthemostpart.Youmayuseafour-function,scientific,orgraphingcalculators.Certain calculatorsarenotallowed.AccordingtotheACTguidelines,youmayuse: calculatorsoncellphonesorsmartphones calculatorswithbuilt-inalgebrasystems(liketheTI-89) handheld,tablet,orlaptopcomputers electronicwritingpadsorpen-inputdevices calculatorswithtypewriter-style("QWERTY")keypads.

Somecalculatorsareallowedwithmodifications:forexample,calculatorswithinfrared portsareallowedonlyifyoucoveruptheport.

Strictlyspeaking,calculatorsare Thatmeansthateveryquestion bedonewithoutacalculator.Mostofthetime,theonlyactualcalculationyou'llneedto doisbasicaddition,subtraction,multiplication,anddivision.

Ifaquestioninvolvesaconceptthatcan'tbedonebyhand,thequestionitselfwillgive youthenecessarycalculations.Infact,ifaquestionhassuchcalculations,that'sacluetelling youwhatyouneedtosolvetheproblem.Butyoumaynotneedeverycalculationtheygive you.

Thatsaid,justbecauseaquestionbedonebyhanddoesn'tmeanyouto. Calculatorsareusefulwhenyouhavebigcomputationstodo,and

Butdon'tleapforthecalculatortimeyouhavetodomath.Don'tuseacalculatorto do7+5.Thebetteryouareatdoingsimplemathinyourhead,thefasteryouwillwork. Thissoundscounterintuitive,butyes, Ipromise. Somepeoplehavenofaithintheirabilitiesandinsistonpunchingeverythingintotheir calculatorsbecause"thecalculatorisalwaysright."Thesepeoplearecowards.Andguess what?Whilethecalculatorisalwaysright,there'sachancemightmakeamistaketyping stuffintoyourcalculator.Especiallyifyouhavetroubledoing7+5inyourhead.

Youcertainlydon'tone.Again,thetestiscalculator-optional,soeverythingyouneed todocanbedonewithacheap-ofour-functiondrug-storecalculatorthat'smissingthe7key.

Now,therearesomequestionsonwhichagraphingcalculatorcanhelpyou,particularly CoordinateGeometryquestions.Thesequestionsarenotcommon,buttherearesome fancytoolsthatcansometimeshelpyou-ifyouknowhowtousethem.Ofcourse,ifyou don'tknowhowtousethem,theywon'tbehelpfulatall.

So,ifyoudon'talreadyhaveagraphingcalculator,youdon'thavetogooutandget one.Ifyouhaveone,sure,useit.Ifyouknowhowtouseitwell,itmightworktoyour advantageeveryonceinawhile.Butifnot,don'tsweatit.You'llbefine.Justlearn7+5. That'sallweask.Donotpurchaseonethedaybeforethetestandexpectittodoyouany good.

MOREINFOONCALCULATORS

Anycalculatormaybeusedwiththeexceptionofthefollowing: nopocketorganizersorelectronicnotepadswithpen-inputdevices nolaptoporsimilarcomputers nodevicewithastandardtypewriterkeyboard nocalculatorwithsymbolicalgebraability nocalculatorwiththeabilitytocommunicatewithanothercalculatorunlessthe communicationportisdisabled nocalculatorthatrequiresapowercord nocalculatorthathasasoundfunctionunlessthesoundfunctionisdisabled

Calculatorswithbuilt-inordownloadedcomputeralgebrasystemfunctionality,including:

Allmodelnumbersthatbeginwith TI-89orTI-92

TI-NspireCAS

Note:TheTI-Nspire(non-CAS)ispermitted.

HPPrime

HP48GII

Allmodelnumbersthatbeginwith HP40G,HP49G,orHP50G

fx-CP400(ClassPad400)

ClassPad300orClassPad330 Algebrafx2.0

Allmodelnumbersthatbeginwith CFX-9970G

MATHTECHNIQUES

Aswesaidbefore,therearetwoareasyouneedtobeconcernedwithontheACTMathTest.Thatis andSimplyput,thecontentisjustmath.Theseareallthethingsyourmathteachertellsyouinclass suchasmathterms,fractions,mathfacts,formulas,andalloftheotherthingsyouhavehypotheticallylearnedfrom yourmathteachersthroughyourlongmathcareerinschool.Inthis wewill talkaboutthetechniques, Theycanbeusedonjustaboutanytypeof problem:onhardproblemsoreasyproblems,arithmeticoralgebra,withtrianglesorcircles,anywhere.Theyare powerful,versatile,andvery,veryeasy.Ourgoalistohelpyoufindtheanswersasquicklyandefficientlyaspossibleso youcanmanageyourtimebetterthroughoutthetest.Techniquesaretrickandstrategiestohelpyoubeatthesystem. SincetheACTdoesnotbelievetheyhaveanyflawsintheirsystem,theytypicallywillnotteachyouthesetricksandtips. Theytendtofocusoncontentintheirtestprepmaterials.Therefore,thisisvaluableinformation!

GENERALSTRATEGIES

We'llstartwithsomequickandeasythingsyoucandotohelporganizeyourtime,bemoreefficient,andcut downoncarelessmistakes.

ACTquestionsarecomplicated.There'softenalotgoingonwithinaquestion,andit'seasytotakeyoureyeoff theprize.Theremightbesomuchinformationthatyou'renotsurewhattodowithit.Ifyou'renotsurehowto getstarted,therearetwoquestionstoaskyourself:

1.WhatdoI?Thatis,whatisthequestionaskingmefor?

2.WhatdoI?Thatis,whatinformationdoestheproblemgiveme?

Atthispointallyoumustdoisconnectthesequestions.Lookatwhatyouwantandworkbackwardstoseewhat youneedinordertogetit.Orusewhatyoualreadyknowandseewhatelsethattellsyou.

Let'slookatasampleproblemtoseehowthisworks:

Tofindoutwhatyouwant:Circlethequestion.Notthewholeproblem,justcirclethethingthat they'reaskingyoutofind.

ANOTHERWAYTOLOOKATIT

TobeinthebestpositiontodowellontheACTmathematicstest,areviewofthemathematicsmaterial coveredonthetestshouldbeplanned.Includedinthissectionisareviewthatshouldbereadwithapencil andscratchpaperinhand.Therearemanyexamplesofproblemswithdetailedcommentaryontheir solutions,aswellasmanypracticeexercises.Thepracticeexercisesalsohavecompletesolutionsand explanations.Thebestplanistoworkeachpracticeproblemonyourown,andthencheckyoursolution withtheoneinyourpracticeresults.Ifyouranswerthesame,youcanbereasonablysureyoudidthe problemcorrectly,eventhoughyourproceduremaybedifferent.Thereisnoclaimthatthereisonly onewaytodoanygivenproblem.Also,thechapterisintendedtobereview,notatextbookon mathematics.Noattemptismadetoprovemoststatements;theyaremerelypresentedasfacts.Ifyou wantjustificationforagivenstatementorifyouwantmorepracticeonaparticulartopic,consulta textbookthatcoversthematerialinanon-reviewmanner.

Areasonabletimeperiodtoreviewthematerialinthemathematicssectionofthisbookmaybe2or3months. Thiswouldleavetimetosearchforadditionalhelpifyoufindthatyouneedit.Thebestlong-rangestrategy forpreparationforthisoranyothertestistodowellinthecoursesthatyoutakeinschool.Althoughthe ACTtestisnotnecessarilyliketheteststhatyouhadinthesecourses,muchofthesamematerialiscovered; andifyouhaveretainedthefundamentalconcepts,youshouldbeabletodowellontheACTtest.Asin manyskills,however,thelevelofmathematicsabilitydecreaseswithtimeifyoudonotpracticecontinuously. Therefore,evenifyouhavedoneverywellincoursework,itwouldbewisetospendtimeonthisreview chapter.

Afteryouhavereviewedthemathematicschapteranddonethepracticeexercises,youshouldbereadyto taketheonlinemathematicstests.ThefollowingtechniqueswillbehelpfulintakingpracticeoractualACT mathematicstests:

1. TheACTmathematicstestisa60-question,60-minutetesttodeter-mineyour mathematicalachievement.Keepinmindasyoutakethetestthattheaverageamountoftimeallotted toeachquestionis1minute.Thismeansthatyoumustworkquicklyandusethetimethatremainsto trythemoredifficultquestionsagain.

2. Youmayassumethatgeometricfigureslieinaplaneandthattheword meansastraightline.Keepthesedirectionsinmindduringthetest.Markyouranswercarefullyonthe appropriateanswersheet.

3. Youshouldworkthrougheachquestion,takingeachstepinorder,ratherthantry toanswerthequestionbyworkingbackwardfromtheproposedanswers;usuallytoomuchtimeis requiredtoeliminateincorrectresponses.Onceyouhaveananswer,trytolocateitamongthe responsechoices.Ifitisthere,marktheanswersheetquicklybutaccuratelyandgoontothenext question.

Ifthesearchforacorrectanswertakestoomuchtime,markthequestionsothatyoucanreturntoitafter youhaveansweredalloftheothers.Then

Ifyoufindthataquestioninvolvesaverycomplicatedcomputationoraveryinvolved procedureforitssolution,youshouldre-evaluateyourmethod.TheproblemsontheACTdonotrequire lengthycomputationsorproofs.Inmanycasescomputationscanbedonemoreeasilyifproductsareleftin factoredformuntiltheverylaststepinordertomakeuseofcancellation.(Thisisparticularlytrueinthe evaluationofcombinationsandpermutations.)

Althoughthequestionsdonotrequiretheapplicationofcomplicatedformulas, youshouldknowcertainbasicformulassuchasthosefortheareasofsquares,rectangles,triangles,andso on,perimeters,simpleinterest,uniformmotionandthePythagoreantheorem.Youshouldalso knowthedefinitionsoftermsandoperations,suchasprimenumbers,compositenumbers,unionofsets, intersectionofsets,axiomsoftherealnumbersystem,theaxiomsofequalityandinequality(usedto solveequationsandinequalities),thetrigonometricfunctions,andsomeofthesimpleridentities.

Whenyoureturntoquestionsthatyouabandonedtemporarilybecausetheytook toomuchtime,considereliminatinganyresponsethatisnotrea-sonable,giventheproperinterpretationof theproblem.Ifthenthesolutionstilleludesyou,guess.Thereisnopenaltyforguessing.

Iftimeremainswhenyouhavefinishedthetesttoyoursatisfaction,gobacktoseethat youhaveansweredeachquestion,andcheckyouranswers.

ANOTHERWAYTOLOOKATIT

BecausetheACTtestwriterscaremoreaboutyourmathskillsthandotheSATtestwriters,theACTdoesnot provideanyformulasatthebeginningoftheMathtest.Beforeyoupanic,takeasecondlook.BecausetheACT issospecificaboutthetypesofquestionsitexpectsyoutoanswer,preparingtotackleACTMathtakesafew simplesteps.

handlepositive,negative,andfractionalexponents useparentheses graphsimplefunctions convertfractionstodecimalsandviceversa changealinearequationintoy=+form

IneachchapteroftheMathtest,you'llfindamixtureofreviewandtechnique,withasprinklingofACT-like problems.Attheendofeachchapter,thereisasummaryofthechapterandadrilldesignedtopinpoint yourmathtest-takingstrengthsandweaknesses.Inadditiontoworkingthroughtheproblemsinthisbook, westronglysuggestyoupracticeourtechniquesonsomerealACTpracticetests.Let'sbeginwithsomegeneral strategies.

Youget60minutesfor60questions.Thisseemsfairlystraightforward,butdon'tletthesymmetryofthesetwo numbersfoolyou;someproblemswilltakemuchlessthanaminute,andotherscouldtakeforeverifyoulet them.

Thefirstfewquestionsaredesignedtobeeasierthantherestofthetest,thenthequestionsgetabittougherfor theremainderofthetest-atleast,thisisACT'sintention.However,whatthepeopleatACTthinkiseasymaynot strikeyouthesameway.Similarly,youmayfindsomeoftheproblemsinthemiddleorendofthetesttobea pieceofcake.

Infact,ifyoutookaroomfullofhighschoolstudentsandaskedthemtovoteonwhichtypeofACTmath questiontheywouldprefertodo,youwouldalmostcertainlygetdifferentanswers:Whileonestudentmay preferalgebraquestions,anotherstudentwouldchoosegeometryquestionsinstead.Isoneofthestudentsmore justifiedinhisorherselection?Absolutelynot.OntheACT,establishinganorderofdifficultyforthequestionsisa process.OnlyyoucandeterminewhichquestionsaremostworthyourtimeinvestmentAgain,wecan usetriagetohelpplanourmathstrategy.

MATHTRIAGE

InChapter2,weintroducedtheconceptoftriage.Let'sapplythisconcepttoACTMath.Here'saproblem.

Cynthia,Peter,Nancy,andKevinareallcarpenters.Lastweek,eachbuiltthefollowing numberofchairs:

Cynthia-36Peter-45Nancy-74Kevin-13

Whatwastheaveragenumberofchairseachcarpenterbuiltlastweek?

WhentheaveragetesttakerbeginstheACTMathtest,whatdoyouthinktheperson'sfirstinstinctis?Ifyousaid, "Workquestions1through60asquicklyaspossibleuntiltimerunsout,"you're100percentcorrect.Afterall,isn't thatwhatwedoonourhighschoolmathtests?

TheproblemwithtakingsuchanapproachontheACTisthatyouareprobablyrobbingyourselfofpoints.Instead ofstartingwithquestionIandfinishingwithquestion60(ifyouevenmakeitthatfar),usethetriageapproachto activelyseekoutquestionsthatfityourPersonalOrderofDifficulty.Ifquestion5isaboutatopicwithwhichyou're notcomfortable,markitforreviewandseewhatelseliesahead.Thenextpagemayhaveseveralquestionsthat aremoreworthyofyourim-mediateattention.Attemptingeasierquestionsonyour"firstpass"willguarantee thatyourtimeinvestmentactuallyyieldspoints.Asyouconsistentlyidentifyandattemptquestionsthatfityour firstpasscriteria,yourconfidencewillincreaseaswell;you'llbesurprisedbyhowmucheasierthesecondpass questionswillseemonceyou'veestablishedasuccessfulpattern.Don'tgetcaughtupinthepsychologyofthetest. UseyourpracticetimetostudyACT'squestiontypesandcategorizethemaccording toyourPersonalOrderofDifficulty.

I'mAlmostDone...

Thetemptationtogetstubbornandstaywithaparticularproblemcanbeverystrong.Butifittakesyoufour minutestosolvequestion5,thenitmightmeanthatyoudon'thavethetimetodoseveralproblemslateronthat youmayhavefoundeasier.AswementionedinChapter2,youmighthavethe"oh,yeah!"revelationonthis problembeforeyoufinishthetest.

ThatWasanEasyOne

Ofcourse,tosolvetheproblemaboutthefourcarpenters,youwereprobablynotgoingtohavetodependona revelation.Didyouwanttodoitrightaway?Sure.It'samoderatelyeasyaverage problem.

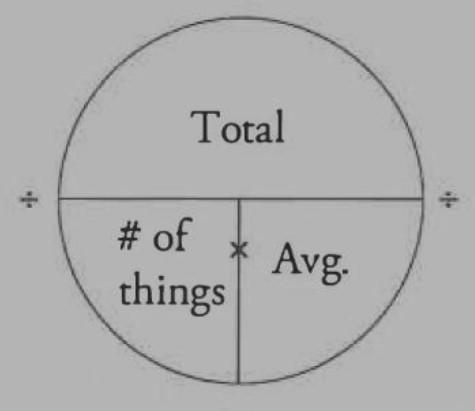
Tofindtheaverageofagroupofnumbers,addthenumberstogetheranddividebythenumber ofterms.

Inthiscase,thethingwedon'tknowistheaverage,butwedoknoweverythingelse,solet'sputthenumbers intoourformula.

(Bytheway,wecoveraverageproblemsmorefullylater.Theanswertothisquestionis(B).)

Youdistinguishaneasyproblemfromatoughoneinpartbydecidingwhetheritcanbedoneinoneortwostepsor whetheritwillrequirethreeormoresteps.

22.Fourcarpentersbuiltanaverageof42chairseachlastweek.IfCynthiabuilt36chairs,Nancybuilt74 chairs,andKevinbuilt13chairs,howmanychairsdidPeterbuild?

F.24

G.37

H.45

J.53

K.67

Thisisstillanaverageproblem,butitislessstraightforwardandrequiresanextrasteptogetthefinalanswer.Let's puttheinformationwehaveintothesameformulaweusedbefore.

36+74+13+Peter 4

=42

YoumightwanttosubstitutethevariablexforPeter.Mediumanddifficultaver-ageproblemsoftengiveyouthenumberof termsandtheaverage.Whattheydon'tgiveyou-andtheimportantthingtofigureoutisthesumofthenumberstobe averaged.

Ifwemultiplybothsidesby4,wegetthesumofallfournumbers.

36+74+13+Peter=168

TofindoutPeter'snumberofchairs,wejusthavetoaddtheothernumbersand subtractfrom168.168-123=45.Theansweris(H).

Here'saHardACTProblem

Fourcarpenterseachbuiltanaverageof42chairslastweek.Ifno chairswereleftuncompleted,andifPeter,whobuilt50chairs, builtthegreatestnumberofchairs,whatisthenumberof chairsoneofthecarpenterscouldhavebuilt,ifnocarpenterbuilt afractionalnumberofchairs?

Theconceptbehindthisquestionisreallynomoredifficultthaneitherofthefirsttwoproblems.Itisstillabout averages.Butnowthereareseveralmorestepsin-volved,includingasmallleapoffaith.Youcantellit'smoredifficult thanthefirsttwoquestionspartlybecauseofthelanguageituses:"Ifnochairswereleftun-completed"isclosinga potentialloophole.Easyproblemsareusuallytoosimpletohaveloopholes."Whatistheleast"impliestheneedfor reflection.

Let'sputwhatweknowintothesameformulawehaveusedtwicealready.

TheonlyindividualaboutwhomweknowsomethingspecificisPeter.We'verep-resentedtheotherthreecarpentersas y,andBecausethesumofallfourcarpenters'chairsaddsupto168,wenowhave

50++J+=168

Byitselfanequationwiththreevariablescan'tbesolved,sounlesswecangleanalittlemoreinformation fromtheproblem,we'restuck,andit'stimetoputacirclearoundtheproblemandmoveon.

Let'sassumeyouskippedtheproblemtemporarily,andyouhavenowcomebacktoitaftercompletingallthe problemsyouthoughtwereeasier.

Theproblemasksforthenumberofchairsonecarpentercouldhavebuilt.Tofigurethisout,let'shavethe othertwocarpentersbuildthenumberofchairstheycouldbuild.Accordingtotheproblem,Peter constructed50,andnooneelsebuiltasmanyashedid.Solet'ssaytwooftheothercarpentersconstructed 49each-thelargestpossibleamounttheycouldbuildandstillhavebuiltfewerthanPeter.Bymakingcarpenters andyconstructasmanychairsaspossible,wecanfindoutthe numberofchairscarpenterwouldhave tomake.

Nowtheproblemlookslikethis: 50+49+49+=168

Ifweadd50+49+49andsubtractitfrom168,then=20,andthecorrectansweris(C).

Writedownwhatyouknow.Thisquestionisaboutaline,butnofigureisgiven.So .

Firstdrawthepointsinorder:

Thenlabelthelengthsyou'regiven:

AndsinceCisthemidpointofCD: isthewholelength,sowehaveeverythingwe need:Ouransweris

AD=8+7+7=22.

Noticethatwehadnoideawhereweweregoingwhenwestarted.Allwedidwastakethethingswe knewandstartedworkingthrougheverythingfromthatpointuntilweendedupwhereweneededtobe. beintimidatedfromtheoverwhelminginformationatthebeginning.Youcanalwaysfindsomething youknowineveryproblemandusethatinformationtofigureoutthenextstep.Ifyouworkforwardfrom whatyouknoworbackwardsfromwhatyouwant,chancesareyoucanconnectsomewhereinthe middle.Evenifyou'renotsurewhereyou'regoing,themoreyouwritedown,theeasieritwillbeto startconnectingtheinformation.

Twothingsareworthrepeatinghere:

Thistakesalloftwosecondstodobutcansignificantlyhelpyou.

Itcanhelpreducethenumberofcarelessmistakesyoumake(moreaboutthisinthenext chapter).

Itwillhelpyouunderstandhowtodotheproblem.Byfocusingonthethingyou'retryingto findratherthanthethingstheygiveyou,it'seasiertothinkaboutwhatyouneedinorderto findit.

You'reprobablytiredofhearingmathteacherstotellyouto"Showyourwork!"Well,toobad.

Wecanheartheincessantwhiningandcomplaining:

Creditandmethodsarenotthepointhere.Thepointisthatnotwritingdownyoursteps forcarelessmistakes.Weareamazedatthenumberofstudentswhocompleteanentire testworthofmathproblemswithoutwritingasinglethingonthepage.Ineverycase,thesestudentsfall shortofachievingthescorestheyarecapableof.

TheACTisnotatestthatmeasureyourmemorizationskills.Theydonotcareifyoucanremember allofthestepsandnumberinyourheadwhileyougothroughthelonggruelingmathprocess.In

headthusthereasonyouarenotgettingthescoresyouwant.Byjustwritingdownwhatyou're doingasyoudoit,youcanturnacomplexproblemintoaseriesofsmall,basicsteps.More importantly,youcanlookbackatthosestepsatanytimeiftheyarewrittendown.Andyoucan reduceyouroddsofmakingacarelessmistake,likeaddinginsteadofsubtracting,or solvingforthewrongvariable.

Furthermore,showingyourworkgivesyouarecordofwhatyou'vedone.Thismakesiteasiertofind mistakeswhenyou'recheckingyourworkduringatest.Anditmakesithelpsyoutrackwhatyouhave donewrongduringapracticetestgivingyoutheopportunitytoviewit,makeadjustments,andcorrect yourmistakesbeforetakingthetest.Thisway,whenyouwanttoknowwhyyougot#10wrong,you'll seewhatyoudidtogetyouranswer.

Weknowyouthinkyouareinvincibleandhavespecialsuperpowersthatmostpeopledonothave.That iswhyyouwillarguewithusandsaythingslike:

"ButIdon'tneedtowritestuffdown.I'mgoodatmathandcandoitallinmyhead."

No,youcan't.

"No,really,Ican."

No,really,youcan't.ACTproblemsarecomplicatedandaredevelopedbypeoplewhoarepreyingon youroverinflatedegoinmath.Theyareliterallymathwolveswhoaresettingsnarestocaptureyouinto theirevilmathtrap.Youcan'tholdeverystepinyourheadatonce.Andyouknowwhat?Youdon'thave to!Ifyouwritestuffdown,youdon'thavetoremembereverything.

-it'sthatthey'remissingquestionsthattheyalreadyknowhowtodo, becausetheymakecareless,stupidmistakes.

"Thatjustslowsmedown.Idon'thavetimetoshowmywork."

Whatareyou,anoldEnglishscribewhousesilluminationandcalligraphytowritedownnumbers?That's ridiculous.We'renotaskingyoutowriteouteverysinglestepincompletesentencesandperfect penmanship.Don'twriteoutannotatedEuclideanproofs;justkeeptrackofwhichvariableiswhich. Similarly,justlikewesawintheproblemabove,ifageometryproblemdoesn'talreadyhaveapicture, DRAWAPICTURE!Itdoesn'thavetobeperfect;evenaroughsketchcanhelpyouunderstandthe problemandcatchcarelessmistakes.

****Seriously,Justwritestuffdown.***

CommonMistakes

MATHTECHNIQUES

ThepeoplewhomaketheACTaren'tchumps.Theyknowhowhighschoolkidsthink.More importantly,theyknowhowhighschoolkidsmessup.Therefore,whentheywritethetest,they intentionallyincludewronganswerchoicesthatkidswhomakecertaincommonmistakeswillchoose. However,onceyouknowwhatthesemistakesareandhowtoavoidthem,youwillbemuchlesslikely tomakethem

RTFQ(ReadtheFullQuestion)

Takealookatthisquestion

15.Acertainbookstoregetsashipmentof24copies ofanewbookandsells18ofthem.What percentageofthebookswasNOTsold? A.75% B.67%, C.50% D.33%

E.25%

Okay,so18over24is0.75,whichis75%.That'schoiceA,right?

WRONG!That'sthenumberofbooksthatwerethequestionisaskingforthosethatwere TheyevenputitinCAPITALLETTERS!Payattention!

WecallchoiceAtheRTFQchoice."RTFQ"standsfor"ReadtheFullQuestion."*It'swhathappens whenallofyourmathwascorrect,butyoudidn'tsolveforthethingtheywereaskingfor.

RTFQchoicesshowupthetest.Theycouldshowuponquestion#60oronquestion#1.Itisa veryeasymistaketomake.Butit'salsoaveryeasymistaketoavoid: Takean extratwosecondstomakesurethatthenumberyou'rechoosingisthenumbertheywant.

Infact,we'vealreadygivenyoutwowaystohelpcutdownonRTFQmistakes: and .Bothofthesethingswillsignificantlyhelpyoukeeptrackofwhatyou'redoing.

Here'saharderone.Giveitashot,andmakesureyou

44.Ifaisanumberselectedfromtheset{1,2,3}and bisanumberselectedfromtheset{3,5,7},how manydifferentvaluesfora+barepossible?

F.5

G.6

H.7

J.8

K.9

Takealookatthisproblem:

MATHTECHNIQUES

60.ScottdrivestoBob'shouseataspeedof30milesperhouranddrivesbackataspeedof50milesper hour.Ifhetakesthesameroutebothways,whatwashisaveragespeed,inmilesperhour,forthe wholetrip?

F.35

G.37.5

H.40

J.42.5

K.Cannotbedeterminedfromthegiveninformation.

Wewanttheaveragespeedforthetrip.Histwospeedsare30and50.Sotheaverageis30+50divided bytwo.That's40.ChoiceH.

Wow,thatwaseasy.Hmmm.Alittletooeasy.

Waitaminute.Thisisquestion

.Questionsareorderedbydifficulty.Thatmeans thisisthequestiononthetest.There'sthatthehardestquestiononthetestcanbe donebyjusttakingtheaverageoftwonumbers Thatcan'tpossiblyberight. lookattheinformationweknow:

WeknowforafactthatACTMathTestquestionsareorderedbydifficulty.

Aquestion'sdifficultyisdeterminedbylookingatthepercentageofstudentswhogetitright. MostkidsprobablyhadthesameinstinctIdid:taketheaverageofthespeeds. ButIknowthatmostkidsgetitwrong. Therefore,takingtheaverageof30and50iswrong.Ifitwereright,mostkidswouldgetitright. Therefore,IcaneliminatechoiceH.

MATHTECHNIQUES

So,ifyouseeaneasychoiceonahardquestioneliminateit.Youknowmostpeoplegetitwrong.So,the achoiceasaFool'sGold choice,andthenpickitanywaybecausetheycan'tthinkofanyotherwayofdoingtheproblem.Your That's madness.

Let'sgobackandtakeanotherlookat#60above.WeeliminatedHasFool'sGold. Hmm.Butifthat'snotright,howelsewouldyoudotheproblem?Allittellsusisthe twospeeds;wedon'tknowthedistancetraveledorthetimeittook.Somaybe thereisn'tenoughinformation.That'sChoiceK.Right?

Wrong!bedeterminedisaclassicGoldchoice.Number60isnotgoingto

So,eliminatedHandK.Worst-casescenario,wecanguessfromthethreeremainingchoices. Remember,

Sohowdowedoactuallydothis?Thereasonyoucan'tjusttaketheaverageof30and50isbecause thosearealreadyrates.Inordertofindtheaveragespeedforatrip,youhavetotaketherateofthe distanceoverthetime.Hmm.Ifweknewthedistancetraveled,wecouldfindthetimeit took,butwedon'tknoweither.Buttheanswercan'tbeK-that'stooeasy.Soitprobably whatthedistanceis.Youprobablygetthesameanswernomatterwhat.

So,let's

Let'ssayit's fromScott'shouseto Bob'shouse.SincewecanusethedistancetofindthetimeeachlegofScott'striptook:

ToBob's:150=301 5hours=1 FromBob's:150=302 3hours=

So,Scott'striptook5hoursonewayand3hoursbackforatotalofHistotaldistancetraveledis trips,150each).So:

AverageSpeed=TotalDistance= TotalTime 300 8

=37.5mph

That's We'redone!Wait,butweonlygotGafterusinganumberwemadeup.Howdo weknowwewon'tgetadifferentanswerifwechoseanothernumber?Well,tryit.Makethe distance300milesandseewhatyouget.

ANOTHER

Ofthe60problemsintheMathsection,severalwillcontainextrainformationthatisnot,strictlyspeaking, necessarytosolvetheproblems.Thetestwriterswanttoseeifyoucandistinguishimportantinformationfrom filler.Becausetherearesofewofthesequestions,itisn'tnecessarytoexamineeachnewpieceofinformation withamagnifyingglasstoseeifitmightbearedherring.InalmosteveryproblemontheACT,youwillneed theinformationgiventosolveit.However,ifyou'restaringataparticularnumberthatdoesn'tseemtohave anythingtodowiththesolutionofthequestionyou'redoing,itmightbearedherring.Here'sanexample.

5.Susan'stake-homepayis$300perweek,ofwhichshespends$80onfoodand$150onrent.Whatfractionofhertakehomepaydoesshespendonfood?

A. B. C.

Thelastlinetellsuswhatweneedtodo.Afractionisapartoverawhole.Inthiscase,thewholeis$300.The partistheamountofmoneyspentonfood.

$80 4 whichreducesto $300 15

Wheredoesthe$150fitin?Itdoesn't.Thequestionisn'taskingaboutrent.Thetestwritersjustthrewthat intoconfuseyou.Notethatifyougotconfusedandfoundthefractionofthetake-homesalarythatwaspaid inrent,$150/$300,youwouldpick(C).Thecorrectansweris(B).

TargetNumbers

MATHTECHNIQUES

Thisisoneofthemostpowerfulstrategiesthatwehave,somuchsothatitgetsitsownsection.If youignoreeverythingelsewesay,atleastpayattentiontothis.

MoststudentshavetroublewithtimingontheACT.You'vegot60questionstodoin60minutes. That'salotofquestionsinashortamounttimeandalotofstudentsfeelrushedtryingtofinish.But ACTMathTestquestionsareorderedbydifficulty-number1iseasy,andnumber60ishard.So,students rushthroughearlyquestions,makingalotofcarelessmistakesonquestionstheyshouldbe gettingright.Thentheyspendalotoftimeonhardquestions,whichtheygetwrongbecausethey're hard.So,they'regettingnailedonbothendsofthetest.

Buthere'sthething,theeasyquestionsareworththesamenumberofpointsasthehardones.

Thesolution?

It'sreallyeasytodo.It'sjustonerule

Youdon'thavetogetquestioninordertogetthescorethatyouwant.Thebiggestproblemmoststudents haveisn'tthattheydon'tknowenoughmath;it'sthat

Forthoselast15questionsyoudidn'tdo, Don'tleavethemblank.Itdoesn'tmatter whatyoupick,justpicksomething.Youdon'tlosepointsforwronganswers,soyou'llpickupafew pointsbychance.

Okay,soyou'redoingfewerproblems,buthowdoyouknowyou'lldoanybetteronthoseproblems thanyouweredoingbefore?Becausenowyou'vegot todo soyoucanspend Themoretimeyouspendonaquestion,theless likelyitisyou'llmakeacarelessmistake.

PeopletendtothinkaboutACTscoresinthewrongcontext.Peopletendtothinkofthemlike scores-there'saperfecttenandthenpointsdeductedforyourflaws.Instead, thinkofthemlike scores-you'rejusttryingtogetasmanypointsaspossible.Assuch, your ismuchmoreimportantthanthenumberofshotsyoutake.

Thisstrategyisamazing.Youcangetascoreincreasebyliterallydoingwork,notby learningnewthingsbutbynailingallthethingsyoualreadyknowhowtodo.It'smiraculous.

FrequentlyAskedQuestionsaboutTargetNumbers

Let'ssaythisrightupfront: We firmlybelievethatcouldget#60ifgivenenoughtimeforit. Thegoalhereissimplyto That'sit.So, ifwe'redoingfewerquestions,we'renotgoingtoskiptheeasyones;we'regoingtoskipthe hardones.That'sjustcommonsense.Yes,ifyoudidthewholetest,yougetnumber#58. Butwhyworryabout#58whenyou'restillmissing#3?Weyoucanget#3.That'sthegoal here-tonailtheeasyquestions.Whyworryaboutthehardstuffwhenyou'restillmissingpoints ontheeasystuff?Let'snailthosedownbeforewedoanythingelse.

Ifyoufinishyourtargetnumbersandstillhavetime, Again, Ifyouhavetimeleftover, don'tkeepgoing,anddon'tstareblanklyatthewallforfiveminutes.Gobackandcheckyourwork.

3.I

No!Neverleaveanythingblank!Firstofall,there'snopenaltyforguessing.Secondly,thegoalhere toskiphardquestions.We'retellingyouexactlyhowmanyquestionsyouneedtodotogeta goodscoreincrease.Thatmeansyouhavetodothequestionswithinyourtargetnumbers. Yes,therewillstillbesomehardonesinthere.Theyaren'tallaseasyas#2. Youdidn'tthinkwe'djuststophere,didyou?There'sa lotmorewehavetogothrough,andwe'regoingtoshowyousomegreattechniquesthatwill helpyouwiththosehardquestionsthatarewithinyourtargetnumbers. Ifyoucan'tdoaquestionwithinyourtarget,tryatechniquelikePlugInorBacksolve.Ifyou havewhattodo,don'tspendfiveminutesstaringatthepage.Guessrandomlyandmoveon. Buthonestly,thatshouldn'thappenveryfrequently.

Theveryfactthatyou'reaskingthisquestionmeansyou'vethoughtabouttwoquestions. timeyoucould'vespentcheckingyourworkontheeasyquestions.Again,the pointhereistiming-wewantyoutospendtimemakingsureyougettheeasyquestions.Wedo NOTwantyoutospendtimeontryingtofigureoutwhichquestionstodo.Wewantyourgame plantobesetbeforeyougotothetest.

Now,wedorealizethatthereisawidevarietyofquestiontypesonthetest,andsome peoplereallyarebetteratsometypesthanothers.Maybe#50isaweirdlogarithmquestion,but #53isafunctionquestionandyou'rereallygoodatfunctions.Orit'saquestionthatcanbe reallyeasywithatechniquelikePlugIn.Thatseemsokay.Butbecareful:itmayonlylike youcando#53.Itmightbemorecomplicatedthanitseems.Maybethere'satrickyoudidn't see.Maybethere'saFool'sGoldchoice.Whoknows?

Butyouknowwhatwedoknow?Thatyoucando#2.Ifyou'vedoneeverythingyoucanon #50andstillcan'teveneliminateonechoice, Yes,theremaybequestionsbeyondyourtargetnumbersthatyouarecapableofdoing.But thegoalofthistechniqueistomakesureyougettheeasyquestions.Thequestionspast yourtargetnumbersarenotthere.Theydonotexist.Wewouldtellyoutoripthosepages outofthetestbookifyouwereallowedtodothat.

Thisisn'taboutpickingwhichofquestionsyou'regoodorbadat.It'saboutdoing fewerquestions,period.Yes,youcertainlygetsomeofthelaterquestionsrightifyou hadthetime.Butyoudon't.Andyoucangettheeasyquestions.

Firstofall,ifyounailedallyourtargetnumbers,congratulations!Yourmathscorehas probablyincreasedsubstantially.Fantastic.Butforthenextpracticetest,keepthesame numbers.Wewanttoseeyoudoitagain.Oncemighthavebeenafluke-maybeyouwerein thezonethatdayorjusthappenedtogetalotofquestiontypesthatyou'rereallygoodat.If younailallyourtargetnumbersthenwecanstarttotalkaboutraisingthem.

Butthenagain,youmightnotwanttoraisethem.Ifyoureallydonailyourtargetnumbers, youmightbehappywhereyouare.Ithinkyou'llbepleasantlysurprisedbywhatitdoesfor yourscore.

Congratulations!Weweregoingtotellyounottofinishthetestanyway.You'reonestep aheadofus.Areyoupsychic?

Again,thegoalhereistobeonthequestionsthatyouIfyou'renotquite makingitthroughallofyourtargetnumbers,that'sokay-aslongasyou'vegotahighshooting percentageontheonesyougetto.Plus,oncewegettoworkonthenutsandboltsofthe math,youshouldbeabletogetthroughthoseeasyproblemsmuchfaster. Hmm...areyoustillmakingcarelessmistakes,evenwithextratime?Thenyes.Yes,youdo.

TECHNIQUES

What?Ofcourseyoudo!lsthataseriousquestion?Whywouldwetellyoutodothis onlyonpracticetests?Forfun?Youthinkwe'rejustmessingwithyou?Everythingwetellyou todointhisbookissomethingyoushoulddoontherealtest.

Notexactly.Thereasonwedothisforthemathisthatweknowthefirstquestionsarethe easyquestions.Studentsmakecarelesserrorsonearlyquestions,sothey'remissingquestions theyknowhowtodo.QuestionsontheEnglish,Reading,andSciencetestsarenotorderedby difficulty,sothere'snoguaranteethatskippingthelastquestionsmeansskippingthehard questions.

However,timingcertainlycanbeanissueonothertests(especiallytheReadingTest). Rememberthesameprincipleapplieseverywhere:it'smoreimportanttobeaccurateonthe questionsyoudothantodoalotofquestions.So,ifyouhavetroublefinishingtheother tests,takeheart.Youcanstillgetagoodscorewithoutansweringallthequestions,aslongas you'reaccurateonthequestionsyoudo.

ANOTHERWAYTOLOOKATIT

WhileonestudentmaypreferAlgebraquestions,anotherstudentcouldchooseGeometryquestionsinstead.Isone ofthestudentsmorejustifiedinhisorherselection?Absolutelynot!OntheACT,establishinganorderofdifficulty forthequestionsisapersonalprocess.Onlyyoucandeterminewhichquestionsareweremostworthyofyourtime investment.Workonyourstrengthsfirstnotyourweaknesses.Youcanworkonimprovingyourweaknessesduring practice. weakareas.

Ifquestion5isaboutatopicwithwhichyou'renotcomfortable,markitforreviewandseewhatelseliesahead. youhavecheckedeverythingelseorguessattheleast!Thenextpagemayhaveseveralquestionsthataremore willseemonceyou'veestablishedasuccessfulpass.Don'tgetcaughtupinthepsychologyofthetest.

Learnhowtoidentifyeasyquestions,mediumquestionsanddifficultquestions.

Aneasyproblemhasoneortwosteps

Animmediateproblemhastwoorthreesteps

Adifficultproblemhasmorethanthreesteps

THETECHNIQUES

Sofar,we'vetalkedaboutcommonmistakesandgeneralstrategies.Nowwe'regettingtothefunstuff: Ok,maybenotthatfunbutatleastitisproductive.

Collectively,thesethreetechniquescanbeusedonofallmathproblemsontheACT. Whileeachtechniqueisdifferent,theyallhavethesamefundamentalprinciple-they

Thegoalistoturneveryproblemintoarithmetic,togetridof vagueunknowns,intangibleideas,andlongequationsandmakeeveryproblemintosimplestuffyoucan punchinto rightanswer.Savethelongsteps,formulasandlongequationsforyourPreCalteacher.Dothesimplemath andgettherightanswerandgotothenextquestionwhenitcomestotheACT.

PlugIn

Let'stakealookatthisproblem:

27.Bobhas4dollarsmorethanLisadoes.IfLisahas dollars,howmuchwouldBobhaveifhedoubled hismoney? 8

Noticethatthisquestionisanumber27-nottoohard,butnottooeasy,justinthemiddleofthepack. Wecanseewhattheywantustodohere.Theygiveusawordproblemandexpectustotranslate fromsentencesintomathematicalexpressions.Idon'twanttodothat.

Takealookattheanswerchoiceshere.Theyallhavex'sinthem,andisavariable.

Let'ssaytheanswerturnedouttobechoiceA.Well,iftheanswerisA,then that'stheanswer.That'showmuchmoneyBobhas:+4dollars.So,itwillbe+4, Ifis5,ifis10,ifxis953,234,124.5255,theanswerwouldalwaysbeA.

So,let'spickanIftheanswercomesoutthesamenomatterwhatnumberis,wecanchoose anyvalueforthatwelikeandwe'llalwaysgetthesamething.

ThisisIthasthreesteps.

1.PickaNumber

Whatshouldwechoose?Somethingsmall,somethingmanageable,preferablysomethingthatisn't alreadyintheproblem(toavoidconfusion).Trytoavoidweirdnumbersthathavespecialproperties like0,1,negativesorfractions.Justaniceeasycountingnumber.

Onceyouchooseanumber,makesureyouwrite soyou rememberthat'sthenumberyoumadeup.

2.DotheProblemWithYourNumber

Readtheproblemagain,butinsteaduse3.

27.Bobhas4dollarsmorethanLisadoes.IfLisahas 3dollars,howmuchwouldBobhaveifhe doubledhismoney?

Lisahasdollars,sonowwe'llsayLisahas3dollars.Bobhas4more,soBobhas7dollars. So,ifBobdoubledhismoney,he'dhave14dollars.That'souranswer:14.Onceyouhave ananswer,

Wait,but14isn'tananswerchoice.Ah,onemorestep:

3.PuttheNumbersintotheChoices.

Ouranswerisn'tachoice,butallthechoiceshaveAha!Wehaveannow.Let'sput3infor inthechoicesandseewhichonecomesoutto14.

Onlyworks.That'souranswer.Wegottheproblembyaddingone-digitnumbers. Thinkoftheproblemasalittlefunction,aseriesofsteps.IfIputinthisnumber,Igetoutthatnumber. WhenIputin3,Igot14.Therightanswerchoiceshouldgivemethesamefunction.WhenIputin3,I shouldgetout14.

Don'tbelieveme?TryadifferentnumberforYoushouldstillgetEasyouranswer.

FrequentlyAskedQuestionsaboutPlugIn

Yes,justtobesafe.Itispossiblethattwoanswerchoicesbothgiveyoutheansweryou'relookingfor.This couldhappenifyouchooseanumberwithspecialproperties(like1)oranumberthatwasalreadyinthe problem.Oritcouldhappenpurelybychance.So,youshouldcheckallthechoicestomakesurethere aren'ttwochoicesthatwork.

Firstofall,eliminateeverythingelse.Youknowit'sgoingtobeoneofthosetwo.Worst-case gota50-50chance.

Butbeforeyouguess,whynottryadifferentnumber?Iftwochoiceswork,it'sprobablybecauseyou happenedtopickaweirdnumber.Pickadifferentoneandtestthechoicesthatareleft.

Firstofall,we'redemonstratingthetechniqueonaneasierproblemsoyoucanseehowitworks.The problemsonlygetharderfromhere,yetPlugInisstilllittlemorethanaddingone-digitnumbers.Heck,we alreadysawaPlug-Inquestion-theFool'sGoldexampleaboutScottdrivingtoBob'shouse.Trydoing badboywithalgebra.Itain'tpretty.

Second,PlugInmayseemweirdbecause Themoreyoudoit,themoreyou'llgetthe hangofit.Prettysoon,you'llbeabletochurnoutproblemsinafractionofthetime.

Third,algebraicmethodsarefraughtwithpossiblecarelessmistakes-evenon#27.Let'strysomealgebra onthat#27justforkicks.Bobhas4morethanLisa,soBobhas+4.Hedoubleshismoney, sothat's2times+4.That'sD,right?Twotimesplus4?Ofcoursenot.It'snot+4;it's+4).That comesoutto+8,whichisE,justlikewegotwithPlugIn.

Asbrilliantasweallarewithalgebra,it'seasytomakeasmallstupidmistakelikeforgettingthe ButwithPlugIn,you'relesslikelyto makethatmistakebecauseyou'reworkingwithconcretenumbers.Youunderstandwhatallthese termsrepresent;they'renotjustabstractlettersonthepage.ChoiceDisnomoretemptingthanany otherwrongchoice;it'sjustanotherchoicethatdoesn'tcomeoutto14.

Thereareotherwaysyoucanmessthisup,too.IfyouforgettodoubleBob'smoney,yougetA. IfyoudoubleLisa'smoneyinsteadofBob's,yougetC.NoneofthesemistakesarelikelywithPlug Inbecauseallyou'redoingissimplearithmetic.

So,it'snotjustthatPlugInisfasteroreasierthanalgebra;it'salsothanalgebra.You'remuch lesslikelytomakeanRTFQorFool'sGoldmistakewithPlugIn.

TYPESOFPLUGINPROBLEMS

Aswe'vealreadyseen,havinga isthefirstsignofaPlugInproblem.But italsoworkswhenthereis

SometimesyoucanPlugInforeachvariable 26.Howmanyhoursarethereindaysandhours?

F.+

G.+

H.24('1+)

J. 24

Becausethere'snorelationshipbetweenandhere,wecancomeupwithtotallydifferent numbersforeachofthem.Tomakethingseasy,let'suseandOnedayhas24hours,plus3 givesatotalofWhichchoicematches27? 1 24

Ontheotherhand,sometimestheproblemwillgiveyousome onthevariables.In thesecases,youcanPlugInforonevariable,andthenusethatvaluetofigureouttheother variable:

Herewehavetwovariables,butthistime,ifwepickanwecanusethatnumbertofind

Let'ssayJustreadtheproblemwithournumberforx:

4+5=9.Thatmeans9is3lessthanSo,yis3morethan9.So,y=Pickinganallowedustofind We'renotdoneyet.Thequestionasks-2ishowmuchlessthan4-2=2.So,2ishow muchlessthan12?2islessthan12.That's

NoticealsothatwecouldstillusePlugIneventhoughthereweren'tanyvariablesintheanswerchoices.

36.Larrycutsapieceofpaperintotwoequal pieces.Hetakesoneofthosepiecesandcutsit intothreeequalpieces.Theareaofoneofthe smallestpiecesiswhatfractionoftheareaof theoriginalpieceofpaper?

There'snovariableanywhereintheproblemortheanswerchoices,sowecan'tusePlugIn,right? Wrong!Eventhoughnovariablewasexplicitlymentioned,thereisanimplicitvariable-thearea. There'snowayforustofindtheareaoftheoriginalpieceofpaper,right?Itdoesn'ttellusthelength orwidthoranynumbersatall(wedon'tevenknowwhetherit'sarectangle!),butwe'restill expectedtogetananswer.So,it whatthestartingareaisgetthesame answernomatterwherewestart.There'snoactualletter,butweassignitavariableifwe wanted.

Let'snot.Let'ssaytheoriginalpiecehasanareaof12.

TECHNIQUESANDPLUGIN

Hecutsitintopieces,soeachhasanareaof6.(126=2) Hecutsoneofthoseintopieces,soeachofthesmallerpieceshasanareaof2.(6÷3=2) So,eachsmallerpieceisoroftheoriginal.choiceJ

WealreadysawaproblemwithimplicitvariablesintheFool'sGoldsection.Rememberthis?

60.ScottdrivestoBob'shouseataspeedof30 milesperhouranddrivesbackataspeedof 50milesperhour.Ifhetakesthesameroute bothways,whatwashisaveragespeed,in milesperhour,forthewholetrip?

F.35

G.37.5

H.40

J.42.5

K.Cannotbedeterminedfromthegiveninformation

Eventhoughtherearenovariablesatall,thedistanceisanimplicitvariable.Wecanmakeupa valueforthedistanceanddotheproblemwiththatnumber.That'sPlugIn.

3.Geometry

Takealookatthisproblem:

33.Inthefigurebelow,ify=whatisinterms

A.90+x

B.90-x

C.90-2x

D.180+x

E.180-x

Geometrycanbescaryforalotofstudents,andwe'lltalkalotmoreaboutitinalater chapter.Butlook:we'vegotvariablesintheanswerchoices!ThatmeanswecanPlugInfor justlikeanyothernormalproblem.

Let'ssay=Weknow=90Wecantellfromthepicturethatandmakeastraightline;thatmeans+=180. Since=60,weknow=So,when=30,=120.Put30inforintheanswerchoices andseewhichgivesyou120:

Don'tbescaredoffbyfigures.Ifyou'reconfused,don'tworry:we'lltalkaboutgeometryrules soonenough.Butatitsheart,thisproblemisnodifferentthananyotherPlugIn.Assoon asyouseeallthosevariablesinthechoices,youknowyoucanPlugIn.

AndkeepinmindthatGeometryPlugInscomeinallthesameflavorsthatwe'vealready seen:theremaybeexplicitvariablesorimplicitvariables;sometimesyoupluginfordifferent variablesseparately;sometimesyoupluginforoneandfigureouttheothers(aswejustdid in#32).

ANOTHERWAYTOLOOKATIT

Anytimeyouseevariablesinaquestionstemorintheanswerchoices,youcanPickNumbers.tryan examplequestion:

Thereare0totalintheclassroomtakingtheACT.nofthosestudentswillscoreabovethe90%percentile. WhichexpressionrepresentsthenumberofstudentswhowillNOTscoreinthe90thpercentile?

n(mn)

n+n m/n+n n(mn)/n mxn

Herewehavetwovariables:mandn.Wecanpicknumbersforthosevariablesaslongastheymakesense withinthecontextofthewordproblem.Weknowthatmmustbeabiggernumberthannsincemisthetotal numberofstudentsandnisaportionofthat.saym=4andn=2.Ichosethesenumbersbecausetheyare lowandeasytoworkwithrememberthatPickingNumbersshouldmakethemathsimpler.Whypick4,567 formwhenwecanpick4?

Ifm=4andn=2,weknowthat2studentswillNOTscoreinthe90thpercentile.pluginourpicked numbersintotheanswerchoicesandseewhichonceyields2!Theanswerhereis(D).

Nowlet'slookatthefollowingproblem:

1.Whatis5morethantheproductof4andacertainnumberx?

A.4x-5

B.4x

C.-x

D.5x-4

E.4x+5

Inthisproblem,thereisnoonevalueforx.Thevariablexcouldbe5or105or -317.Infact,theACTtestwritersareaskingyoutocreateanexpressionthatwill answerthisquestionnomatterwhatthe"certainnumber"is.

TECHNIQUESANDPLUGIN

Inotherwords,thisisacosmicproblem.Thecorrectanswerchoicewillbecorrect faranyvalueofx.Therearetwomethodsforapproachingcosmicproblems.

OntheACT,manywordproblemsrequireyoutotranslateEnglishtermsintotheirmathequivalents.In Chapter11,wediscussedusingtranslationtotacklewordproblemsdealingwithpercentages;onmanyof thealgebraicproblemsyou'retaskedwith,you'llwanttousethesamemethod.We'veexpandedthe percenttranslationtabletoincludesomeofthecommonphrasesyou'llfindinalgebraquestions.

Whiletranslationisafinewaytosolvethisproblem,wewantyoutotrythinkingaboutcosmicproblems inaslightlydifferentway.Ifaproblemistrulycosmic-ifthecorrectansweriscorrectforeveryvalueof"a certainnumber"-thenitshouldbecorrectforanyvalueyoucanthinkof,right?

TheOtherMethodIsPluggingIn.Whydon'twepickourownvalue?Let'smakex=7.(Why?Whynot? Wecouldjustaseasilyhavechosen5or12orwhateveryoulike.Tryitandsee.)Theadvantageofusinga specificnumberisthatourmindsdonotthinknaturallyintermsofvariables.Wedon'tgointoastore andaskforanx-packofsoda.Wehaveaspecificnumberinmind.

TherearethreestepsinvolvedinPluggingIn.

1.Picknumbersforthevariablesintheproblem(andwritethem down).

2.Usingyournumbers,findananswertotheproblem.

3.Plugyournumbersintotheanswerchoicestoseewhich choiceequalstheansweryoufoundinstep2.

Here'stheproblemagain.

1.Whatis5morethantheproductof4andacertainnumberx?

A.4x-5

B.4x

C.-x

D.Sx-4

E.4x+5

Let'smakex=7.Inthespaceoverthexintheproblemabove,writedown"7."Now,let'sfigureitout. Rereadthequestionwith"7"forthex.Theproductof4and7is28.5morethan28is33.So,ifx=7,then theanswertothequestionis33.We'redone.Allwehavetodonowischecktoseewhichoftheanswer choicesequals33.

-5=23.Nottheanswer.

Youmightbethinking,"Waitaminute.Itwaseasiertosolvethisproblemalgebraically.WhyshouldIplug in?"Thereareacoupleofreasons.

Thiswasaneasyproblem.PluggingInmakesevendifficultproblemseasy,soyoushouldlearnhowtodo itbypracticingontheeasyones,justasweadvisedwiththeWorkingBackwardtechniqueforparticular xproblems.TheACTtestwriterstrytoanticipatehowyoumightmessupthisproblemusingalgebra.If youmakeoneofthesecommonmistakes,youranswerwillbeamongtheanswerchoices;youwillpickit andgetitwrong.

StartlookingforopportunitiestoBacksolveandPickNumberswhenyoupracticeandremember,thesmartACT Mathtest-takerexcelsinbothtime-managementandstrategy!

Gerry'sageis5morethanthreetimes

Carol'sage.Ifthesumoftheiragesis45, howoldisCarol?

A.10

B.12

C.14

D.16

E.18

Here,wecan'tjustmakeupanumberforCarol'sagebecausethevaluematter-there'sonlyone numberthatworksforCarol'sage.So,PlugInwillnotworkonthisone.

However,wecanstillturnthisintoasimplearithmeticproblem.Insteadofpickingnumbers, let'susethenumbers

Weknowoneofthese5numbersisCarol'sage,solet's trythemuntilwefindonethatworks.

That'scalledItalsohasthreesteps.

Whentherearenumbersintheanswerslikethis,thechoicesarealwaysinorder,sochoiceCorH willbethemiddlenumber.Ifwetryitanditdoesn'twork,wecanfigureoutifitwastoosmallor toobigandeliminatethreeanswerchoicesinonefellswoop.

Okay.So,let'ssaythatCistheanswer.Cis14.So,whatdoesthatmean?What's14?Well,14isthe answertothequestion.Inthiscase,theis"howoldisCarol?"ThatmeansifCisright,thenCarolis14.

Whatelsedoweknow?WeknowthatGerry'sageis5morethanthreetimesCarol'sage.Again, we'resayingCarolis14,so:

C.Carol=14.

3xl4=42 42+5=47=Gerry.

"Gerry'sageis5morethan3times14" SoifCarolis14,thenGerryis47.

HowdoIknowifCistherightanswer,then?Well,whatdoestheproblemtellus?Theirages shouldaddupto45.Dothey?Ofcoursenot.Gerry'sageisbiggerthan45.So,Cistoobig.

Well,Cwasdefinitelytoobig,sowe'llneedasmallernumber.So,we'llmoveontoB. B.Carol=12.

12x3+5=36+5=41=Gerry. 12+41=53x

Stilltoobig.Theiragesshouldaddupto45.Let'smoveontoA.

A.Carol=10.

10x3+5=30+5=35=Gerry. 10+35=45

Bingo!ChoiceAisouranswer

Thatwasawordproblem.JustlikewesawbeforewhenwewerediscussingPlugIn,thisproblem didn'thaveanyexplicitvariablesmentioned,butitdidhavevariables.Therewerenoactual lettersassignedtoCarolorGerry'sage,butwecouldstillputnumbersinforthemallthesame. That'soneofthestrengthsof directlywiththeunderlyingconceptsintheproblem.

ButBacksolveworksjustaswellwhentherearevariables.Observe:

Anytimeaproblemasksforthevalueofavariable,wecanBacksolve.Justputthenumbersinthe choicesforthevariableandseeifitworks.

We'llstartwithH,that's5.They'reaskingforsowe'llsayWeknowthat=9.Since=5,= Sofar,sogood.Nowlet'sputandintothatbigequationandseeifitcomesoutto36.

a2+ab=42+4(5)=16+20=36

Itworks!Sinceworked,Idon'thavetolookatanythingelse.Theansweris I'mdone! Let'stakeaminutetothinkabouthowtodothisproblemwithalgebra.Firstofall,youcouldsolve oneequationforandthensubstitutethatintotheotherequation.Ugh.Iguesswecoulddothat, butit'salotofworkandeasytomessup.Backsolveismuchquickerandeasier. Now,ifyou'vegotareallygoodeye,youmightnoticethis:

=9and=36We'regiventwoequations.

Thesecondequationisjustthefirstequationtimes

a(9)=36

Sowecanjustsubstitutethevalueswe know,Andouransweris4.That'sChoiceG.

Waitaminute:4?G?Didn'twegetH:5?Aha!4,butthey'reaskingusforSoevenifwe're reallycleverwithouralgebra,thealgebraeasilyleadstoanRTFQerror.You'remuchlesslikelyto makeanRTFQmistakewithBacksolvebecauseyou'reworkingfromthequestion.Youpick H,andthenmakeH lt'sthefirststep!

So,therearebasicallytwoalgebraicwaysofdoingthisproblem.Oneisslowandpainful.Theother almostinevitablyleadsyoutoanRTFQmistake.LikePlugIn,Backsolveisfaster,easier,andthan algebra.

FrequentlyAskedQuestionsaboutBacksolve

No.UnlikePlugIn,withBacksolvethere'snowaythatmorethanonechoicewillworkout. Onceyoufindachoicethatworks,stop.That'syouranswer.

Thenjustpickone!Don'tgocrazytryingtodeducewhichwaytogo.Partofthepoint ofBacksolveistoworkquicklyandmethodically.IfCfailsandyou'renotsurewhetheryou shouldgotoBorD,justpickone.You'rejustdoingsimplemathhere.Theworst-case scenarioisthatyougothewrongwayandwinduphavingtotestallfivechoices.But really,that'snotverymuchwork.Andyouknowthateventuallyyou'llfindtheanswer.

ANOTHERWAYTOLOOKATIT

Backsolvingisanexcellentstrategytousewhentherearenumbersintheanswerchoices.Instead ofsettingupyourownequation,assumeeachanswerchoiceiscorrect.Thisisagreatstrategytousewhen youarestuckbecauseitletsyoucheckyourworkasyougo!

Clairetookafifty-questionalgebratestandansweredeveryquestion,scoringa10.Herteacher calculatedthescorebysubtractingthenumbercorrectfromthreetimesthenumberincorrect.Howmany questionsdidClaireanswercorrectly?

Sincethisisawordproblemandtherearenumbersintheanswerchoices,thisquestionisagreatcandidatefor arerankedfromsmallest togreatest,startingwithanswerchoice(C)willhelpuseliminatethreeanswersatonce.

IfClaireanswered36correctly,thenshemusthaveanswered14incorrectly(becauseitwasa50question-test). Threetimesthenumberincorrect(14)=42.Wethensubtractthenumbercorrect(36)togetascoreof6. However,theproblemtoldusthatherscorewasa10.A6istoosmall,sowecaneliminatechoices(A),(B)and (C).

Thenextlogicalchoicetotryis(D).Ifsheanswered40correctly,thenshemusthaveanswered10incorrectly. Threemultipliedby10=30.Thenwesubtract30fromthenumbercorrect(40).Ouransweris10,which matchesthescorementionedinthequestionstem,soweknowwehaveourcorrectanswer!

Algebraisawonderfuldiscipline,andwedowantyoutobeabletosolveproblemsliketheoneabove algebraically,particularlywhentheyareeasy.However,thereisanotherwaytodomostparticularxproblems-a waythatcan,insomecases,saveyouhugeamountsoftimeandtrouble.It'scalled"WorkingBackward."Ifwe askedyoutoguessthevalueofxinthisquestion,itmighttakeyoualong,longtime.Afterall,there'sonlygoing tobeonenumberinthewholeworldthatsatisfiesthisequation,andthereisalimitlesssupplyofnumbersfrom whichtochoose.Oristhere?Infact,ontheACTtherearealwaysjustfive-thefivepossibleanswerchoicesand oneofthemhastobethecorrectanswer.Let'strydoingtheproblembackward.

Todothis,youtaketheanswerchoicesoneatatimeandputthemintotheequationtoseewhichonemakes theequationwork.Withwhichchoiceshouldwebegin?

Theoneinthemiddle.Numericanswersarealwayspresentedinorderonthistest,fromleasttogreatest.There arethreestepstoWorkingBackward.

1.Startwiththemiddleanswer-(C)or(H).

2.Ifit'stoobig,gotothenextsmallerchoice.

3.Ifit'stoosmall,gotothenextlargerchoice. Here'saproblem.

1.If3x+7==28,whatisx?

Let'sstartwith(C):3(6)+7equalsonly25.Couldthisbetherightanswer?No,it'ssupposedtoequal28.Dowe needasmalleroralargerx?Becauseweneedalargernumber,wecanimmediatelyknockout(A)and(B).Let's try(D).3times(7)+7=28.Bingo!Wehaveouranswer.

Notethatif(D)hadstillbeentoosmall,theonlypossibleanswerwouldhavebeen(E),andyouwouldnothave hadtocheckit.Remember,ifyou'veeliminated4wronganswers,what'sleftmustberight.Oneofthegreat thingsaboutWorkingBackwardisthatyouwillusuallyhavetodoonlytwoactualcalculations.Youstartwith (C).If(C)iscorrect,you'redone.If(C)istoobig,thenyou'redownto(A)and(B).Nowyoutry(B).If(B)is correct,you'redone.Ifitisn't,you'restilldone.Theanswermustbetheonlyremainingchoice:(A).Nowwe knowthatmanyofyouarethinking,"Thistechniqueisawasteoftime.Itwouldhavebeenwayeasiertojust solveforx."Youknowwhat?You'reright.Onthisexample,solvingforxwouldhavebeeneasier,butifyou don'tlearnhowtodotheWorkingBackwardtechniqueoneasyquestions,youwon'tbeabletodoiteffectively onmorecomplexquestions(andbelieveus,thequestionsgetmuchmorecomplex).Sodoyourselfafavorand useWorkingBackwardontheseeasyquestionssothatyouhaveagoodfeelforitwhenit'stimetodothetough ones.

Sometimes,it'shardtotellwhichwaytoworkbackwardaftereliminating(C).Shouldyougohigherorlower? don'tfret;justpickadirectionandtry.Findachoicewithaneasy-tomanipulatenumber.Itmayturnouttobe wrong,butitwon'ttakelongtofindout.Itmayalsotellyouwhethertogohigherorlower.

Here'sanotherproblem.

2.If$600wasdepositedinabankaccountforoneyearandearned interestof$42,whatwastheinterestrate?

F.6.26%

G.7.00%

H.8.00%

J.9.00%

K.9.50%

Ofcourse,wecouldwriteanequation.Onthecontrary,oneoftheseanswerchoicesiscorrect,andallwehave todoisfindoutwhichoneitis.Whynotworkbackward?We'llstart,asalways,inthemiddle,thistimewith(H). Iftheinterestrateis8percent,then8percentof600shouldequal42.Usepercenttranslation(andyour 8calculator)tochecktheequation:Does-X600=42?Nope-itequals48,100whichmeansourpercentageis toolarge.Eliminate(H),(J),and(K),andtry(G).Does1?00X600=42?Itdoes,sowecircle(G)andcontinueon tothenextproblem.

HowDoYouKnowWhentoWorkBackward?

Youcanalwaysworkbackwardwhenyouseenumbersintheanswerchoicesandwhenthequestionaskedin thelastlineoftheproblemisrelativelystraightforward.Forexample,iftherearenumbersintheanswer choicesandthequestionasks,"Whatisx?"youcanworkbackward.However,ifthequestionasksinstead, "Whatisthedifferencebetweenxandy?"thenyouprobablydon'twanttoworkbackward.Inthiscase,the answerswon'tgiveusavaluetotryforeitherxory. Page

Guesstimate

Okay,thisisaprettyhardone.ThereareallsortsofGeometryrulesthatyoucouldusehereto setupequationsandcanceloutvariables.Thosecangetprettynasty,though.Plus,wehaven'ttalked aboutGeometryrulesyet.Let'snotdothat.Let'sfindaneasierway.

OneoftherulesgivenonthefirstpageofeveryACTMathTeststatesthat Thatmeansthatthelinesandanglesdon'tnecessarilyhavethe valuesthattheyappearto.Itmightlooklikeasquare,butmaybeitsdimensionsareactually8by97.

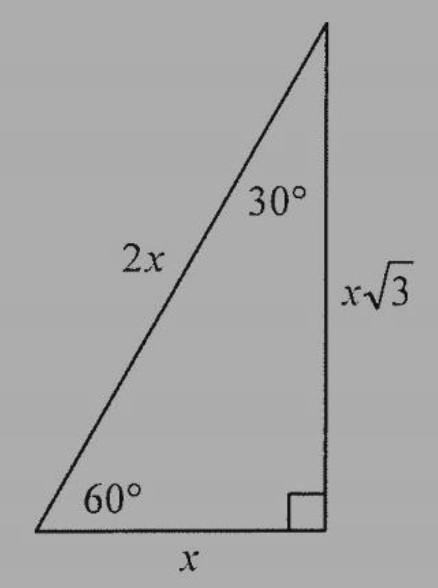
Figuredrawntoscale.

Thefirstdrawinglikeasquare,butit'snottoscale,sowecan'tassumeit'sasquare.Infact,we knowit'sdefinitelyasquarebecauseithasa60°angleand2by7dimensions.Thesecond drawingisthesamefiguredrawntoscale.Thatmeansthatifwemeasuredthatanglewithaprotractor, itwouldcomeoutto60°,andifwemeasuredthosesideswitharuler,theywouldbeina2to7ratio.

So,youcan'tusethesizeandshapeofthefiguretogetinformation.Youusethenumberstheytell you,butthepicturewon'tnecessarilylookright.

wehavediscoveredasecret.ThisrulejustmeansisthatACTfiguresnotbetoscale.It studyandfoundthatACTMATHFIGURESARE ALMOSTALWAYSDRAWNTOSCALE.

Thatmeansthatifitliketwolinesarethesamelength,thentheythesamelength.Ifit likeanangleis60°,thenit60°,oratleastreallycloseto60°.Thisis Ithasonestep:

Inourexampleabove,they'reaskingusforSo,let'stakealookatthoseangles.Angleisprettybig. Let'ssay...120?130?Let'ssay130.Angleissmaller,maybe50or60.Let'ssay60.So,must beabout130+60orabout190.So,ouranswershouldbeprettycloseto190.Hmm,190isn'tachoice,but 185is!That'sprettydarnclose.We'lltakeit.TheanswerisChoiceE.

Wedidn'tdoathingotherthanjustlookatthepicture.Igot#57inallof10secondsandallIdidwas addtwonumbers.

FrequentlyAskedQuestionsaboutGuesstimate

That'strue,butyoudidn't makeupthosenumbers;youmeasuredtheanglesinthe problem,theanglestheygiveyou.

Seriously,justlookattheotherchoicestheygiveyou.A?60?Couldbe60?AngleisAngle alonehastobebiggerthan90!So,AandBareoutrightaway.Cisstilltoosmall-angleisstill probablybiggerthanI00,andwhenyouaddtothemix,there'snowaythetwoofthemcomeoutthat small.ChoiceDseemsplausible,butit'sstilltoosmall.Look:theunmarkedanglenexttolookstobe aboutthesamesizeasThey'renotexactlythesamesize,butthey'reclose.Andmakesastraightline withthatunmarkedangle,sotogetherthey're180.So,+mustbeprettycloseto180.Noneofthese choicesmakesenseatall.OnlyChoiceEisplausible.

Andhere'sthething:ifyoudothisproblemalgebraically,therearewaysyoucanmessitupthatwill makeyoupickoneofthosewronganswers.Ifyouaddinsteadofsubtractorforgettodistribute acrossparentheses,youmightthinkthatchoiceAisaplausibleanswerbecauseofyourflawedalgebra. Butifyoulookatthepicture,youcanseethere'snowaythoseanglesaddupto60.Itjustdoesn't makesense.

Areyoukidding?

There'snothingmathematicallyillegitimateaboutdoingthis.In math,asinallthesciences,therearetwowaysofsolvinganyproblem: byusingpure logicanddeduction(that'salgebra),or bygatheringevidenceandmeasuring(that's Guesstimate).

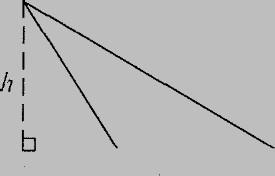
Sayyouhaveadining-roomtableandyouwanttofigureouthowtallitis.Well,onewayIcouldfigure outtheheightofthetableistoconstructalinefrommyeyetothetopofthetableandalinefrommy eyetothebottomofthetable,measuretheangleofdeclination,andusethelawofcosinestofind thethirdsideofthetriangle.

Hereareyourchoicesforhowtallthetableis:

ButhowdoIthetableisn't7.8milestall?Becauseit'sinmylivingroom.AndI'mlookingatit.

Ofcoursenot!YoucanuseGuesstimateonjustaboutanyproblemthathasapicture.Forexample, wecanuseittofindTakealookatthisone: ¯ 3

Hmm.That'satrickyone.Well,let'sthink.

Wewanttheradiusof0.Hmm,wedon'thavearadiusinthefigure.So,let's drawonein.Justdrawalinefromthecentertoanywhereontheside.

Sothatisthelengthwe'relookingfor.

Weknowis43(Notsurewhatthatmeans?Punchitoutonyourcalculator! It'sabout6.92.)Well,definitelylookssmallerthansoitmustbesmallerthan6.92.So.JandK areout.Goodsofar.

Wealsoknowthatis4,solet'scomparertoTheylookprettyclosetoeachother.ChoiceF,2,is ofST-that'sdefinitelytoosmall.ChoiceFisout.

So,we'redowntotwochoices-ifallelsefailsI'vegota50-50guess.ChoiceGwouldmeanis alittlelessthan(3isabout3.46)andchoicewouldmeanit'sequaltoHowcanItell?

Takeapieceofpaper(tryusingyouranswersheet)andlaythesideofthepaperagainst andmarkoffitslength.ThenlaythatpaperyoumarkedoffagainstWhatdoyoufind?

We'redone!So,theradiusis4andtheansweris

Attheveryleast,ifwegopurelybyoureyes,weknowrightawaythattheradiusshouldbeto 4,soonlyGandHmakesense.Ifweactuallymeasureitout,wecanseethattheradiusis4.Perfect. It'snotjustforanglesandlengths;itworksforquestionstoo.

Let'strytogetintheballparkofwhatwe'relookingfor.

Theonlyvaluewe'regivenisthatthesideofthesquareis4.

Wecanfindtheareaofthesquare:4x4=

Theshadedareaismuchsmallerthanthesquaresoour answermustbe Okay,let'seliminate.

Ah,butwait!What -it's So,wecanpunchallthosechoicesoutonour calculatorsandseewhichonescomeclosetowhatwewant. Look!istheonlyonethatmadesense.

Notexactly.Three-dimensionalfigureslikecubesaredrawnusing so wecan'tliterallymeasurethelinesasthey'redrawntoseewhichoneisbigger.In thecubeshownhere,segmentliterallyshorterthansegmentasthe figureisdrawn.Butweknowthatinacube,thetopfaceissupposedtobeasquare. Therefore,eventhoughthelinesonthepagearenotactuallyequal.

TECHNIQUESANDGUESSTIMATE

However,ifyouhaveagoodeye,youmightbeabletouseyourimaginationtofigurethisstuffout.Some ofyoumaybegoodatimagining3-Dobjectsinyourhead.Forexample,youmaybeabletoseethat eventhoughthey'renotequalinthedrawing.Ifyoucan,that'sgreat.Remember:thepointof Guesstimateistousewhatyouknowaboutthefigurealongwithyourcommonsense.

Unfortunately,Guesstimateisn'talwaysgoingtoworkasbeautifullyasitdidonthesequestions.You're notalwaysgoingtobeabletohoneinontherightanswerlikethis.Forexample,iftheanswerchoicesare tooclosetogether,youwon'tbeabletodistinguishthem.Yourguessprobablywasn'tthatexact. However,youcanusuallyeliminate evenifit'sonlyonechoice.Andonceyoueliminate something,youroddsofgettingtheproblemincrease.Evenifyoucan'tfigureoutanyothersolution,you canguessfromwhat'sleft.

So,youseeaproblemwithadiagram, Beforeyoudoanythingelse,tryto getaballparkfigureforthethingthey'reaskingfor,andanythingthatdoesn'tmakesense.

ANOTHERWAYTOLOOKATIT

YoucanfrequentlygetridofseveralanswerchoicesintheACTmathproblemswithoutdoinganycomplicatedmath.Narrow downthechoicesbyestimatingyouranswer.

A.0.9%

B.2.32%

C.9%

Thisisnotanadvancedproblem.ACTwantsyoutowriteasimpleequation.Butbeforewedoanyheavymath,let'ssee ifwecangetridofsomeanswerchoicesbyguesstimating.

Thequestionaskedustofindapercentageof600.Justtogetaroughfixonwhereweare,whatis10%of600?Ifyou said60,youareright.Tofind10%ofanything,yousimplymovethedecimalpointoveroneplacetotheleft.If60is 10%,then54mustbeslightlylessthan10%.Whichanswerchoicesmakesense?Choicesanddon'tworkbecause weneedsomethinglessthan10%.Onthecontrary,weneedsomethingonlyslightlylessthan10%.CouldtheAnswer beor?No.Onthisproblem,it'sjustaseasytoeliminatewronganswersasitistosolvefortherightanswer.The answeris

Ofcourse,yourcalculatoriscertainlyhandyfornarrowingdowntheanswerchoicesonquestionslikethis.Ifyou weretoenterandpressENTER,youwouldknowexactlywhichnumbersshouldappearintheanswerchoices. Afteryoueliminatetheanswerschatdon'tmatch,it'sjustamatteroftakingyourresultandmultiplyingby100to determinethepercentage.Wewilldiscussaccuratecalculatormethodsindetaillacerinthischapter,butthe processisassimpleastyping(54/600)X100andhittingENTER

OnmostACTproblemsyou'llbeabletoeliminateonlyoneortwoanswerschoicesbyguesstimatingbutit'svitalthat youalwaysthinkaboutwhatareasonableanswermightbeforaparticularproblembeforeyousolveit mathematically.ThisisbecausetheACThassometrapanswerswaitingforyou.

AvoidPartialAnswers

Sometimesstudentsthinktheyhavecompletedaproblembeforetheproblemisactuallydone.Thetest writersatACTliketoincludetrapanswerchoicesforthesestudents.Here'sanexample.

Abuslinecharges$5eachwaytoferryapassengerbetweenthehotelandanarchaeologicaldig.Onagiven day,thebuslinehasacapacitytocarry255passengersfromthehoteltothedigandback.Ifthebusline runsat90%capacity,howmuchmoneydidthebuslinetakeinthatday?

A.$1,147.50

B.$1,275

C.$2,295

J.$2,550

K.$2,625

Thefirststepinthisproblemistodeterminehowmuchmoneythelinewouldmakeifitranatotalcapacity.If therewere255passengers,eachofwhommade$10(rememberthebuscompanycharges$5eachway),that wouldbe$2,550.

Ifyouwereinahurryyoumightdecideatthispointthatyouwerealreadydoneandgostraighttotheanswer choices.Andthereis,beckoningseductively.Unfortunately,ofcourse,isnottherightanswer.Thebusline isrunningatonly90%ofcapacity.Togettherealanswer,wehavetofind90%of$2550.

Youalsohaveyoualsomayhavemissed,orputasidetemporarily,theinformationthateachpassengerhasto paycomingandgoing,inwhichcaseyoumayhavemultiplied255by5toget$1,275,andthenfound90%of that$1,147.50,whichjusthappenstobe

Both&werepartialanswers.Studentswhopickedoneoftheseanswersdidnotmakeamistakeintheir math,nordidtheymisunderstandtheoverallconceptoftheproblem;theysimplystoppedbeforetheywere finished.Allyouhadtodowith$1,147.50togettherightanswerwasdoubleitsothatyouincludedboth trips.Allyouhadtodowith$2,550togettherightanswerwastotake90%ofit.Theansweris

ArePartialAnswersFair?

YoumaydecidethatitisnotverysportingofACTtotrytotripupstudentswithpartialanswerchoices. However,ifthishadbeenashortanswertest,studentsmightwellhavemadeexactlythesamemistakeson theirown.Besides,ifpartialanswersrepresentthedownsideofmultiple-choicetesting,thereisa tremendousupsideaswell:Let'sseehowtakingbite-sizepiecescanhelpusonlongwordproblems.

TakingBite-SizedPieces

Asyouhaveprobablynoticedbynow,difficultyonmanyACTquestionsisdirectlyrelatedtothenumberof stepsrequiredtodeterminethecorrectanswer.Toavoidpartialanswersonmulti-stepproblems,breakdown lengthyquestionsintomanageablesteps.Youcanchewononebite-sizedpieceatatime.Let'swalkthrough anexample.

G.6

H.9

J.12

K.15

Althoughyourgutreactionmaybetojameverythingintoyourcalculatorandcirclewhateverpopsuponthescreen,think abouthowneatlytheinformationisdivided.Ifyouweretotranslateeachpartofthequestionintomathlanguageand writeeachstepintoyourtestbooklet,youbelesslikelytomakeamistake?Trythis.

1.Becausethequestionisdealingwithfractions,deletethestartwiththenumbermembersintheclub. scratchworkarea.

2.Nowworkthequestioninsteps.Thefirstthingwereadisofthememberschosetopickup outthat12peoplepickeduptrash,besuretolabeltheinformationsoyoudon'tforgetwhatthenumberis.

3.ThenextthingwereadisoftheremainingmemberschosetopaintBecarefulhere-wewanttotake¼ofthe remainingmembers,notoftheoriginal36.If12membersarealreadypickinguptrash,weknowthereare24people remaining.Writedowntheproperequationtoexpressthis:¼X24=6people.Againbesuretonotethat6isanumberof peoplepaintingfences.

4.What'snext?Wseealinesaying,ofthemembersstillwithouttaskchosetocleanschoolInthelaststepwe weredownto24members;if6arepaintingfences,howmanyareleftover?18.Theansweris 18.UsethistowriteyournextequationX18equals15people.Wenowknowthat15peoplearecleaningschoolbuses.

5.Almostthere...thenextlinesays,theremainingmemberschosetoplantWedon'tneedtodomuchmath here.If15outof18peopleendedupcleaningschoolbuses,thenweknowthereareonly3peopleleft.Those3are plantingtrees.

6.Finally,wearrivedatwhatthequestionisasking.Nowthatallthemathinvolvedisnicelymappedoutandlabeled,we shouldhavenoproblemfindingtheanswer.Thequestionasks,manyofthememberschosetoplantIfwe refertoourscratchwork,weseethat3peopleplantedtrees.WecansafelypickanswerchoiceFandmoveon.Your scratchworkforthisproblemshouldlooksomethinglikethis.

Bytakingamoremanageableapproach,youcanguaranteethatyouthatyouwon'tpickanyofthedistracteranswers.To illustratethepoint,takealookatthestepsaboveandcomparethemwiththeanswerchoices.Noticeanything?wasthe numberofpeoplepickinguptrash.Similarly,wasthenumberofpeoplepaintingfences,andwasanumberofpeople cleaningschoolbuses.Asyoucansee,beingtooquickonthedrawcangetyouintroubleonmultistepwordproblems.If youtakebite-sizedpiecesofwordproblems,you'llbeabletomovemanyoftheminyourfirstpastquestiongroup.

Evenifyouweren'tsurehowtodothatlastproblem,youmayhavebeenabletoeliminatetwoanswer choicesrightawayusingthemajortechniquewecallPOE.Remember,ACTdoesn'ttakeawayanypointsfor wronganswers,soitisinyourinteresttoguessoneveryquestionyoucan'tsolveusingothermethods.But yourguesseswillbemuchmorevaluableifyoucaneliminatesomeoftheanswerchoicesfirst.The problemsaidPeterbuiltthegreatestnumberofchairs-50ofthem.Therefore,couldanyoftheother carpentershavebuiltthanthat?No,so(E)doesn'tmakesense.Andbecausenocarpenterbuilta fractionalnumberofchairs,(D)doesn'tmakesense,either.

Atthispoint,you'redowntothreeanswerchoices.Butbeforeyouguess,youcantryafewmoretactics. Whatifyoudecidetotry(A)?If(A)isthecorrectanswerchoice,thenonecarpenter(theonewhomade theleastnumberofchairs)produced18chairs.So,whatdoyoudonow?Well,thatwouldleave100 chairsfortheothertwocarpenters,whicheithermeansthatbothofthemmade50chairsoronemade morethan50.However,thatcan'tbetruebecausePeter,whomadethemostchairs,madeonly50.So(A)is eliminated.Ifyoutry(B),you'llfindthatthesameholdstrue,andthus,only(C)remains.

CLICKHERETOACCESSTHEGUESSTIMATEDRILL

It'sonethingtounderstandhowthesetechniqueswork.It'sanothertobeabletousethemanduse themeffectivelyinareal-testsituation.It'sincrediblydifficulttochangeyourhabits.Thesetechniques areafundamentallydifferentapproachthanwhatyou'reusedtodoinginschool.Therefore,youhave tomakeaefforttousethemonyourpracticetests. Evenifyouseeanotherwayofdoingtheproblem. Evenifyouthinkthatotherwayisbetterthanthetechnique.Youmusttrytousethetechniquesevery chanceyouget.

Wecanalreadyhearyoucomplaining,buttrustus:it'sforyourowngood.Clearly,youroldwaysofdoing problemsaren'tworkingforyou-iftheywere,youwouldn'tbereadingthisnow.Youroldmethodshave gottenyouthescoreyouhavenow.Ifyouwantadifferentscore,youhavetotrydifferentthings.

Ofcourse,youcan'tusethetechniquesoneverysingleproblemyousee.Andsometimestherewill beproblemswherethealgebraisn'tsobadandyoucangettheproblemwithoutthetechniques.But here'sthething: Thetechniquesarestillnewforyou,soyou don'tknowwhetherornotthey'rethebestmethodonthisorthatproblem.Theonlywayyoucan qualifiedisto Thenwhenyougetto therealtest,youcandecidewhentousethetechniquesandwhennotto.

Thisisnodifferentfromanytimeyoulearnsomethingnew.Insportsorinmusic,theonlywaytoget goodatsomethingistodoitathousandtimesinarow.Themoreyoupractice,thebetteryoubecome.

TechniquesandTargetNumbers

Aswe'veseenalready,techniquescantumareallyhardproblemintoareallyeasyproblem.Buttechniques can'tbeusedoneveryquestion.Therewillbesomelegitimatelytoughquestionsthatcan'tbedone withPlugIn,Backsolve,orGuesstimate.Someofthosetoughquestionswillbepastyourtargetnumbers, soyou'llneverseethem.Butit'snotunusualforthelastquestioninyourtargetnumberstobea legitimatelytoughnon-techniquequestion.

Therefore,ifthelastquestioninyourassignedsetisatechniquequestion,andyouseeaquestion pastyourtargetnumbersthat's atechniquequestion,youmaydothetechniquequestion insteadofoneofyourtargetquestions.

Thisexceptionisfortechniquequestions.Ifyouseeanon-techniqueproblem-evenifyouthinkyou cando-it'snotworthyourtime.Rememberthatoneofthedangersoftheharderquestionsisthe possibilityofaFool'sGoldchoice,awrongchoicethatlookslikeaneasyanswer.Butwe'vealreadyseen thatusingthetechniquesactuallyyourchancesofmakingthosemistakes.

Andthisdoesn'tmeanyoucandotechniquequestionspastyourtargetnumbers.Remember: Yourfirstgoalshouldstillbetodoyourtargetquestions andyourtargetquestions.Butattheendofthesection,ifyounoticeaPlugInpastyour assignment,it'sokaytoswapitwithoneofyourassignedquestions.

Sohowcanyoutellifyoucanuseatechniqueonaproblem?Gladyouasked.

IdentifyingtheTechniques

Firstofall,itbearsrepeatingthatthesimpleactof is,thethingyou actuallyhavetosolvefor-candowondersforyourperformance.Wealreadysawhowitcanhelpyou avoidRTFQmistakes.Butthinkingaboutwhatthequestionisaskingyouforcanalsohelpyoudecide whichtechnique,ifany,youshoulduse.

Here'sageneralruleofthumb:

Whileitmayseemlikethetestasksyouaboutamilliondifferentthings,itactuallyrepeatsthesame kindsofquestionoverandoveragain.ThemoreyouusePlugInandBacksolve,theeasieritwillbeto spotthem.

Let'srecapsomecommoncharacteristicsoftheThreeFundamentalTechniques:

Did You Know That You Have Access to Free Test Prep Boot Camps? Through This Online Interactive Class,Live Capstone Instructors Will Show You All The Strategies You Need to Maximize You Test Score. Click Here To Register for Free!

Thethreefundamentaltechniques-PlugIn,Backsolve,andGuesstimate-canbeappliedtoalotof differentproblems.However,thetechniqueswon'tworkoneveryproblem.Weneedtotalkabout actualrulesofmathyouhavetoknowontheACT.

Let'sbeginatthebeginning,asoneshould.NumberandQuantityquestionsdealwithmostofthenuts andboltsthatmakeupthebasicrulesofarithmeticandalgebra.Sincewe'retalkingaboutthebasics here,muchofthiswillprobablynotbenewtoyou.Therefore,youmaybetemptedtoskipoverthis part."Thisissoboring!Whydowehavetotalkaboutfractions?Wedidthisin,like,seventhgrade!I hateyou!"

Ah,butit'sbecausethisisstuffwe'veseenbeforethatwemustmakesureweknowitwell.Thereare 14Pre-AlgebraquestionsoneveryACT-that'salmostaquarterofthetest.Remember:moststudents' problemthattheydon'tknowenoughmath;it'sthatthey'remissingquestionsthattheyalready knowhowtodo.Therefore,we'vegottomakesureweknowallthisstuffbackwardsandforwards.

NUMBERCONCEPTSANDDEFINITIONS

:Becausedecimalnumbersarebasedonpowersoften(hundreds,tens, tenths,hundredths,etc.),youcanexpress asadecimalmultipliedbyapoweroften.So thenumber43,500becomes4.35x104,and0.00524becomes5.24x10-3.Thisisjustawaytomakeit easiertowritereallybigorreallysmallnumbers.Insteadof8,000,000,000wewrite8.0x109. oudon'thavetoknowmuchaboutthisnotation.ACTquestionsmayaskyoutomanipulatenumbersin thisform,butusuallythat'seasytodoonyourcalculator.*Justrememberthatthe exponentnexttothe"10"hasthebiggesteffectonthevalueofthenumber:2x109ismuch,muchbigger than9x102

PrimeFactors

Aswesaidabove,integerscanbebrokendownintoanda one brokendownintofactors.Therefore,a isafactorthatcan'tbebrokendownintosmaller factors.Anynumberthatisn'tprimecanbereducedtoauniquesetofprimefactors.Andthat number'sfactorsarejustdifferentcombinationsofitsprimefactors.

Allwehavetodoisbreak12upintoanyfactors,thenkeepsplittingupthefactorsuntilwecan't

anymore.

Weknow3x4=12,so3and4arefactorsof12.

3isprime,soitcan'tgoanyfurther.

4isnotprime,sowecanbreakitupinto2and2.

2isprime,soitcan'tgoanyfurther.

Sotheprimefactorsof12are3,(Becausewefound

23 two2's,welistbothoftheminourlistofprimefactors.)

Ifwehadstartedwithadifferentpairoffactors-say,2and6-we'dstillgetthesamesetof primefactors.Allthefactorsof12canbeproducedbymultiplyingtheprimefactorstogether:

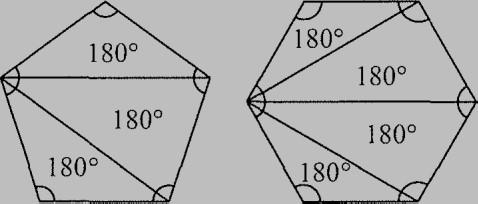
The branching diagram shown here makes it easy to find the prime factors of any integer. Split up the number into any factors. If one of the factors is prime, circle it. Otherwise, keep factoring. It helps to start with a small prime numbers on the left, so you only have to expand the tree on the right. This diagram shows that the prime factors of 180 are 2, 2, 5, 3, and 3.

ANOTHERWAYTOLOOKATIT

Itisimportanttobeabletoexpressawholenumberasaproductofprimefactors.Forexample, 12=2x2x3=22x3.Therearetwousefulmethodstoaccomplishthistask.MethodI:Factortree.Findtheprime factorizationof72.Firstnameanytwofactorsof72(notnecessarilyprime),say8and9.Eachofthesenumberscanbe factored.Continuethisuntilallfactorsareprime.Itisconvenienttoarrangethesenumbersinatree.

Method2:Repeateddivisionbyprimes.Determinetheprimefactorizationof120.Firstname anyprimenumberthatdivides120,andperformthedivision;thenrepeattheprocesswiththe quotientuntilthelastquotientisalsoprime.Thefactorizationconsistsofalltheprimedivisors andthelastquotient.

Therefore,theprimefactorizationis120=2x2x2x3x5=23x3x5.

Afractionisnothingmorethanonenumberdividedbyanother.Assuch,toconvertafractiontoa decimal,justdividethenumbers.Thetopnumberiscalledthe thebottomnumber iscalledthe

=3÷4=0.75

An isoneinwhichthenumeratorislargerthanthedenominator.A containsawholenumberandafraction.

3-(MixedNumber)=-+ (ImproperFraction)

Youmustknowhowtoadd,subtract,multiplyanddividefractions.

To fractions,youmustfinda Thisjustmeansthatyoucan'taddor subtractfractionsthathavedifferentnumbersonthebottom.

Tofractions,youdon'thavetodoanypreparation.Justmultiply topX top;bottomXbottom.

Noticethatouranswercouldbebecausethetopandbottomhada Wealso couldhavetakenoutthecommonfactorsbeforewemultiplied:

Tofractions,youmusttaketheofthesecondfraction,andthenmultiply. "Reciprocal"justmeanstoflipthefractionover.

A isoneinwhichthenumeratorand/ordenominatorcontainfractions.This isequivalenttodividingfractions.Remember:fractionsjustmean"divide".

Manipulatingfractionsisalostart.Withtheadventofcalculators,alotofproblemsthatusedtorequire knowledgeoffractionscannowbedonequicklywithdecimals,sincefractionscanbeeasilyconvertedto decimalsonyourcalculator.

That'sfine.We'reallfordoingproblemsquickly.Butdon'tforgetaboutfractions.Often,usingfractions effectivelycanactuallymakeaproblemthantypingtheproblemoutonyourcalculator.

Firstofall,somefractionsbecomerepeatingdecimals,sothecalculatorwillgive answers-thiscanbedeadlyifyouhavealongcomputation.

Secondly,youmustbecarefulofparentheses.Ifyoutrytodo(1/3)bytypingin you'llgetitwrong.Youmusttype

Third,usingfractionsisofteneasierthanitseemswhenyoucancanceloutcommonfactors,thus turninghardmathintoeasymath.

Finally,youmayseesomealgebraproblemswithfractionscomposedofvariables.Youwon'tbe abletodothoseonyourcalculator,soyou'dbetterknowhowtodealwithfractions.

ANOTHERWAYTOLOOKATIT

Thesetofrealnumbershasseveralveryimportantsubsets:

N={1,2,3,...}Natural(orcounting)numbers.

={0,1,2,3,...}Whole-numbers.

={...,-3,-2,-1,0,I,2,3,...}Integers.

=canbewrittenintheformand }RationalNumbers andQ)Irrationalnumbers.

=U/Realnumbers.

RATIONALNUMBERS

Thesetofrationalnumbersisthesetofallnumbersthatcanbewrittenasfractions.Theirrational numbersaretherealnumbersthatcannotbewrittenasfractions.Therealnumbersareall those,rationalandirrational,thatarefoundonanumberline.

ThefollowingVenndiagramshowstherelationshipsamongthesubsetsofrealnumbers:

Itisimportanttobeabletocategorizenumbersaccordingtothesubsetsabove.Allintegersarerational numbersbecauseanyintegercaneasilybewrittenasafractionbyplacingtheintegerinthenumerator andthenumber1inthedenominator.-3=-3/1

Realnumbersthatarewrittenindecimalformfallintotwobasictypes: 1.Therearethosethatterminate.(Onemaythinkofthistypeashavinganinfinitelylongstringofzeros afterthelastnonzerodigit.)Allsuchdecimalsrepresentrationalnumbers.Forexample,23.346is twenty-threeandthreehundredforty-sixthousandths. Therefore,anappropriatefractionwouldbe23or

Somedecimalsdonotterminate,andthesefallintotwotypes: a.Somenonterminatingdecimalsrepeat.Allrepeatingdecimalsrepresentrational numbers.Forexample:

=0.3333...=0.3

=0.83333...=0.83

=0.27272727...=0.27

b.Othernonterminatingdecimalsdonotrepeat.Anumberofthistypecannotbewritten asafractionandisthereforeirrational.Forexample:

=1.414213... =1.912931...

=3.1415926...

Arationalnumbercanalwaysbeexpressedasafractioninwhichthenumerator(thetopnumber) isanintegerandthedenominatorisanaturalnumber.(Noticethatzeroisnotanaturalnumber.) Iftheabsolutevalueofthenumeratorisgreaterthanorequaltothedenominator,the fractioniscalledotherwise,itisafraction.Twofractionsareifthey representthesamenumber.Aneasywaytotellwhethertwofractionsareequivalentistocross-multiply. Iftheproductsareequal,thenthefractionsareequivalentandtherationalnumbersare equal:

ifandonlyif 0

TheFundamentalPrincipleofFractionsstatesthatanyfractionisequivalenttoafraction obtainedbymultiplyingthenumeratoranddenominatorbythesamenonzeronumber:

Thispropertyisusedtoreducefractionstolowestterms:

Thissamepropertyisusedtorewriteafractionsothatithasaspecificdenominator:

Arationalnumbercanalwaysbeexpressedasafractioninwhichthenumerator(thetopnumber)isan integerandthedenominatorisanaturalnumber.(Noticethatzeroisnotanaturalnumber.)Iftheabsolute valueofthenumeratorisgreaterthanorequaltothedenominator,thefractioniscalled otherwiseitisafraction.Twofractionsareiftheyrepresentthesamenumber.Aneasy waytotellwhethertwofractionsareequivalentistocrossmultiply.Iftheproductsareequal,thenthe fractionsareequivalentandtherationalnumbersare equal:

ifandonlyif 0

TheFundamentalPrincipleofFractionsstatesthatanyfractionisequivalenttoafraction obtainedbymultiplyingthenumeratoranddenominatorbythesamenonzeronumber: Thispropertyisusedtoreducefractionstolowestterms:

Thissamepropertyisusedtorewriteafractionsothatithasaspecificdenominator:

Animproperfractioncanbechangedtoamixednumberorawholenumber.Amixednumber isaspecialformthatrepresentsthesumofawholenumberandaproperfraction: =1+=1

Todeterminethemixednumberthatisequivalenttoanimproperfraction,dividethedenominator intothenumerator.Thequotientbecomesthewholenumberpartofthemixednumber,andthe remainderbecomesthenumeratorofthefractionpartofthemixednumber.

AdditionandSubtraction

Therulesforadditionandsubtractionoffractionsareasfollows:

Toaddorsubtractfractionswiththesamedenominator,addorsubtractthenumeratorsand keepthesamedenominator.Theserulesareveryeasytoapply;however,difficultywiththese operationscomesinfourareas:

1.Ifthefractionsdonothavethesamedenominators,theymustfirstbechangedsothat thereisacommondenominator.Forexample:

Thelowestcommondenominator(LCD)isthelowestcommonmultipleofthe denominators.

TheLCMof12and16is48.

2.Ifthenumberstobeaddedorsubtractedaregivenasmixednumbers,therearetwo methodsofpe1formingtheoperations.Forexample:

Addthefractionpartsandwholenumberpartsseparately.

Sincethefractionpartisanimproperfraction,theanswermustbeexpressedin simplest form. or

Addthefractionpartsandwholenumberpartsseparately.

Writeeachmixednumberasanimproperfractionandthenaddaccordingtothe rule.

Changetheanswerbacktoamixednumber:

3.Theanswersmustnormallybeexpressedinsimplestform.

=Theanswerhasbeenreduced.

4.Insubtractionofmixednumbers,borrowingorregroupingmustbedonecarefully.

Borrow1fromthe5andaddittothefractionpartofthe mixednumber

Somecalculatorswillperformoperationswithfractions.

TEACHERNOTE:OntheACT,rationalanswersareexpressedinsimplestform.

Multiplication

Theruleformultiplicationoffractionsisasfollows: Tomultiplyanytwofractions,multiplythenumeratorsanddenominatorsseparately.

Division

Therulefordivisionisasfollows:

Thisrulestatesthat,todividefractions,onemustreplacethedivisorwithitsreciprocaland changetheoperationtomultiplication.Herearesomeexamples: = 2 x= 3

Mixednumbersmustbechangedtoimproperfractionsbefore multiplying. ) Thesamerulesofsignsapply.

Thereciprocalof.

ChangetoImproperFractions. Replacedivisorbyreciprocal,andchangeoperationto multiplication.

Itisimportanttorecallthatanexponentalwaysappliesonlytotheimmediatelyprecedingsymbol. Thus,toraiseanyfractiontoapower,parenthesesarenecessary.Forexample:

Ifthenumeratororthedenominator,orboth,themselvescontainfractions,theexpressionis calleda Therearetwomethodstosimplifycomplexfractions: 1.Treatthecomplexfractionasadivision-of-fractionsproblem.Forexample:

2.Multiplythenumeratoranddenominatorbythelowestcommondenominatorofthe fractionswithinbothnumeratoranddenominator.Forexample:

Thisisusuallythemoreefficientmethod.

ANOTHERWAYTOLOOKATIT

Yourcalculatorisanexcellenttooltoperformmanyofthebasicoperationsconcerningfractions.Manyof thecommoncalculatorerrors,however,involvefractions.Wehavefoundthatthebestwaytoavoidthese errorsistoknowhowtoperformbasicoperationsonfractionsbyhand.EvenifyouuseaTI-83/84onthe ACT,thenextfewpageswillprovideyouwithanunderstandingofwhatfractionsareandhowtheywork.

Fractionscanbethoughtofintwoways.Afractionisjustanotherwayofexpressingdivision.The expression1/2means1dividedby2.x/yisnothingmorethandividedbyAfractionismadeupofa numeratorandadenominator.The numeratorisontop;thedenominatorisonthebottom.Justthink, startswith"d,"justlike Theotherwaytothinkofafractionisasapartoverawhole.

Inthefraction1/2,wehaveonepartoutofatotaloftwoparts. Inthefractionwehavethreepartsoutofatotalofsevenparts.

Toreduceafraction,seeifthenumeratorandthedenominatorhaveacommonfactor.Itmaysavetimeto findthelargestfactortheyshare,butgettingthisinformationisn'tcrucial.Whateverfactortheysharecan nowbecanceled.Let'stakethefraction6/8.Isthereacommonfactor?Yes:2.

Getusedtoreducingallfractions(iftheycanbereduced)beforeyoudoanyworkwiththem.Itsavesalot oftimeandpreventserrorsthatcropupwhenyoutrytoworkwithlargenumbers.Useyourcalculator's [FRAC]functionunderthe MATHmenutoreduceaswell.

Sometimesaproblemwillinvolvedecidingwhichoftwofractionsislarger.Ifyourcalculatorcanconvert fractionstodecimalsatthetouchofabutton,that'sthewaytocomparethem.Ifnot,keepreading,and we'llexplainhowtodoitbyhand.

Whichislarger,2/5or4/5?Thinkoftheseaspartsofawhole.Whichisbigger,twopartsoutoffiveorfour partsoutoffive?4/5isclearlylarger.Inthiscase,itwaseasytotellbecausetheybothhadthesamewhole, orthesamedenominator.

Trythisone.Whichislarger,2/3or3/7?Todecide,weneedtofindacommonwhole,ordenominator.You changethedenominatorofafractionbymultiplyingitbyanothernumber.Tokeeptheentirefractionthe same,however,youmust multiplythenumeratorbythesamenumber.

Let'schangethedenominatorof2/3into21.

14/21stillhasthesamevalueas2/3(itwouldreduceto2/3)becausewemultipliedthefractionby7/7,or one.

Let'schangethedenominatorofinto21aswell.

9/21stillhasthesamevalueas3/7(itwouldreduceto3/7)becausewemultipliedthefractionby3/3,or one.

Nowwecancomparethetwofractions.Whichislarger,14/21or9/21?Clearly,14/21(or2/3)isbigger than9/21(or3/7).Whydidwedecideon21asourcommondenominator?Theeasiestwaytogeta commondenominatoristomultiplythedenominatorsofthetwofractionsyouwishtocompare:7X3=21.

Let'sdoitagain.Whichislargest?

Tocomparethesefractionsdirectly,youneedacommondenominator,butfindingacommondenominator thatworksforallthreefractionswouldbecomplicatedandtime-consuming.Itmakesmoresenseto comparethesefractionstwoatatime.Let'sstartwith2/3and4/7.Aneasycommondenominatoris21.

Because3islarger,let'scompareitwith5.Thistime,theeasiestcommondenominatoris15.

So,islargerthan1,whichmeansit'salsothebiggestofthethree.

YourteacherswantedyoutocalculatetheLeastCommonDenominator(LCD)ofafraction.Theyevenmade you"showyourwork."TheACTdoesn'tcare.ThisgivesyoutheluxuryoffindingtheEasiestCommon DenominatorbyusingtheCrossroadMethod.

Amorestreamlinedwaytodothisistousethe Let'scomparethelasttwofractionsagain.We getthecommondenominatorbymultiplyingthetwodenominatorstogether.

Wegetthenewnumeratorsbymultiplyingasshownbelow. So2/3islarger.

Nowthatwe'vereviewedfindingacommondenominator,addingandsubtractingfractionsissimple.Let's gototheCrossroadstoadd2/5and1/4.

Let'sgototheCrossroadstosubtract2/3from5/6.

Tomultiplyfractions,linethemupandmultiplystraightacross.

Wasthereanythingwecouldhavecanceledorreducedwemultiplied?Yes.Wecouldcancelthe5on top and the 5 on the bottom. What's left is 4/6, which reduces to 2/3

Sometimes students whose math skills are a bit rusty think they can cancel or reduce in the same fashion

Youcancelthe5sorreducethe4/6inthiscase.Whenthereisanequalsign,youhavetocrossmultiply,whichyields=24,sointhiscasewouldequal24/25.

Todivideonefractionbyanother,justinvertthesecondfractionandmultiply.

isthesamethingas

Anintegercanalwaysbeexpressedasafractionbymakingtheintegerthenumeratorand1the denominator.8=8/1

SometimestheACTgivesyounumbersthataremixturesofintegersandfractions(e.g.,31/2).Itisoften easiertoworkwiththesenumbersbyconvertingthemcompletelyintofractions.Becausethefractionis beingexpressedinhalves,let'sconverttheintegerintohalvesaswell.3=6/2.Nowjustaddthe1/2tothe 6/2.

AnACTfractionproblemcombinesseveraloftheelementswe'vejustdiscussed.Morecomplicatedfraction problemsmighttestyourabilitytorecognizethateveryfractionimpliesanotherfraction-what'sleftover.If aglassis3/5fullwhatpartoftheglassisempty?2/5.

OnFriday,Janedoesone-thirdofherhomework.OnSaturday,shedoesone-sixthoftheremainder.What fractionofher homeworkisstilllefttobedone?

C. D. E.

Janedid1/3onFriday.Howmuchisstilllefttobedone?That'sright:2/3.OnSaturdayshedid6 Inmath,theword"of"alwaysmeansmultiply,solet'ssetitup.

Ifwefindacommondenominator,wecanaddupwhatshe'sdone.Thenweget

Altogether,shehasdone4/9oftheassignment.Ifyouthoughtyouweredoneatthispoint,youmayhave picked(A),butthequestiondoesn'taskhowmuchwasdonebutratherhowmuchremainedHow muchisleft?5/9Theansweris(C).

Inthatlastproblem,(A)wasaanswerdesignedtocatchpeoplewhothoughttheyweredonebefore theyreallywere.Choice(G),onthecontrary,wasdesignedtocatchpeoplewhoslightlymisunderstoodthe question.Ifyoumissed thewords"oftheremainder"asyoureadthequestion,youprobablyadded1/6to1/3andgot1/2.

PERCENTS

CLICKHERETOACCESSTHEFRACTIONDRILL

Bynow,weshouldallatleastbefamiliarwithpercents.Thesimplestwaytodopercentsisbypure division.

Allyoudoisdivide,thenmultiplyby100:

Doyouwanttoknowasecret?Percentsarereallynothingmorethanglorifiedratios.Percent literallymeans"outofonehundred".So,you'rejustconvertingaratiointoanotherratiooutof100.This problemisthesamethingascross-multiplying:

"8outof32"isthesamethingas"25outof100",or25"percent".

Ofcourse,percentproblemsontheACTcangetmorecomplicatedthanthat.We'vedevisedthefollowing tableforpercentproblems:

Wheneveryouseeoneofthewordsintheleftcolumn,writethecorrespondingsymbolintheright column.Ifyouseeanumber,justwritethenumber.Forexample:

becomes12=Xn

Youknow,alotofstudentsfreakoutaboutwordproblems.Butreally,thelanguageweusetodescribe problemsisexactlythesamestuffasallthesignsandsymbolsweuseinequations.Soaslongasyoucan speakEnglish,youcanwriteequations;thewordsmeanexactlywhatyouthinktheymean.

Theadvantageofusingthetableisthatitmakespercentproblemsautomaticandrobotic.Youcan godirectlyfromwordstoanequationwithoutthinkingaboutanything.

Thereareothersimilarwaysofdoingpercentproblems(someofyoumayknowthe"is-over-of' method),butthistableisparticularlyeffectiveoncertaindifficultproblems.Takealookatthisproblem:

Thiscanbereallynastywithotherwaysofdoingpercents.Butwiththetable,wedon'tcare.Doit robotically;whenyouseeaword,writeitssymbol.Sothisquestionbecomes: XXs=18

Nowwehaveaone-variableequationandwecansolveforWedidn'thavetothinkaboutathing. Theequationcamealmostinstantly.

Here'sanothertoughie:

-Ifxispercentof600,x=?

Oh,wellhalfof600is300.Right?WRONG!Itdoesn'tsayxishalfof600;itsaysxisone-halfpercentof 600.Thatis,halfofonepercent.RTFQ!

Withthetable,wedon'tmakethismistakebecausewejustwritewhatwesee: Becausewearen'tabouttheproblem-we'rejustautomaticallywritingdownwhatwereadwe'remuchlesslikelytomaketheRTFQ.

Apercentincreaseordecreasejustmeans: Or:

Inthisproblem,theamountofthechangeis(that's180-150)andtheoriginalamountisSo thequestionis"30iswhatpercentof150?"Nowwecanjustusethetabletosetupanequation:

Youcanalsothinkofpercentchangeasjustthedividedbythe

ANOTHERWAYTOLOOKATIT

Thewordpercentliterallymeanshundredths,so25%means25/100,whichreducesto1/4.Since"hundredths" couldalsobeinterpretedasdividedby100,anddividingby100canmostefficientlybeaccomplishedbymoving thedecimalpointtwoplacestotheleft,25%isalso0.25.

Examples:

Changeeachpercenttobothafractionandadecimal.

1.78% Fraction:78/100=39/50

2.8% Fraction:8/100=2/25

Decimal:0.78

Decimal:0.08

3.2.5% Fraction:2.5/100=25/1000 Decimal:0.025 =1/40

4.3% Fraction: Decimal:3

Changeeachnumbertoapercent.

5.4/6 4/5(100%)=400/5%=80%

6.7

7.3/8

8.0.34

9.0.005 7(100)%=700%

3/8(100)%=3/8(100)%=3/2(25)%=75/2%=37½%or37.5%

0.34=0.34(100)%=34%

0.005=0.005(100)%=0.5%

Mostpercentapplicationsarevariationsofthissentence: AisPpercentofB.

Inthissentence,Aistheamount(orpercentage),Pisthepercent(orrate),andBisthebase.Thekeyto solvingapercentproblemistotranslatetheproblemintotheformofthesentenceabove.

Considerthefollowingexample:

Theenrollmentinanalgebraclassdroppedfrom30studentsto27.Whatpercentoftheclassdroppedout?

Inthisproblemweareaskedtofindthepercent,P.

Thebaseisalwaysthequantitybeforeanychange,30. Thenumberofstudentsthatdroppedoutistheamount(orpercentage),3.Sothesentenceis 3isPpercentof30.

Oncetheproblemhasbeenwrittenintheproperform,therearetwomethodsofsolvingtheproblem:

1.Anequationmaybewritten: A=(P%)B

Ofcourse,apercentsignisnotwrittenintheequation,sothepercentmustfirstbechangedtoeithera fractionoradecimal.

IftheunknownintheequationisA,multiply(P%)timesB. Iftheunknowniseither(P%)orB,divideAbytheotherquantity.

2.Aproportionmaybewritten.

P/100=A/B

Tosolveanyproportion,x/y=z/w,firstcross-multiply,andthendividebythecoefficientoftheunknown.

Intheproblemabove,P/100=30,30P=300andP=1010%ofthestudentsdropped.

Therearesomefractionsanddecimalswhosepercentequivalentsyoushouldknow.

Belowarethefourmainfraction/percentageequivalentsthatyoushouldknow:

1/5=0.2=20%

1/4=0.25=25% 331/3%

1/2=0.5=50%

Anotherfastwaytodopercentsistomovethedecimalplace.Tofind10percentofanynumber,movethe decimalpointofthatnumberoveroneplacetotheleft.

10%of500=50

10%of50=5

10%of5=.5

Tofind1percentofanumber,movethedecimalpointofthatnumberovertwoplacestotheleft.

1%of500=5

1%of50=0.5

1%of5=0.05

Youcanuseacombinationoftheselasttwotechniquestofindevenverycomplicatedpercentagesby breakingthemdownintoeasy-to-findchunks.

21.

Therefore,32percentof400=120+8=128

Youmayalsohavetoconvertadecimalintoapercentage.Thisissimilartoconvertingafractiontoa percentage,whichwejustreviewed.

Fouroutoffivedentistsrecommendapreferredbrandoftoothpasteoveranother.Whatpercentageofthe dentistrecommendthepreferredbrand?Ifyoudividefourbyfive,youget0.8.Toturnthatintoa percentage,takeittotwodecimalplacesandthenputitover100(removingthedecimalpoint).

0.8=0.80=80/100

That'sthesameas80percent,whichisthesameanswerwegotbefore(goodthing).

Here'swhatanACTpercentageproblemmightlooklike.

1.Atarestaurant,dinersenjoyan"earlybird"discountof10%offtheirbill.Ifadinerordersameal regularlypricedat$18andleavesatipof15%ofthediscountedmeal,howmuchdoeshepayintotal? A.$13.50

Acombinationofbite-sizepieces,percenttranslation,andcalculatorworkwillmakethisproblemeasyto tackle.Whenwetakefractionsorpercentagesofsomething,weneedtostartwiththeoriginalnumber.The firstthingwe'llhavetodoisfigureouthowmuchthediscountedmealcosts.Writeoutthesteps.

Discounttaken:(10/100)X18=$1.80

Discountedmealprice:$18-$1.80=$16.20

Tippaidformeal:(15/100)x16.20=$2.43

Totalmealprice:$16.20+$2.43=$18.63

Circle(C).Takeyourtimeandmakeitpainless.

RATIOS

Aratioisjustarelationshipbetweentwoormorequantities.Ratiosareusuallyexpressedasfractions,butthere aremanywaysofdescribingthem.Allofthefollowingmeanthesamething:

Theratioofboystogirlsis2:3.

Theratioofboystogirlsis2to3

Theratioofboystogirlsis

Therearetwoboysforeverythreegirls.

Takealookatthisproblem:

Youcansetthisupastwofractionsequaltoeachother,thensolvetheequationbycross-multiplying thetermsacrosstheequalssign.

Youmaybetemptedtosetuptheratiolikethis:

Butlook:theunitsinthedenominatorsdon'tmatch.Theleftratiois"maple"to"totaltrees",buttherightratiois "maple"to"elm".That'sbad.

Luckily,wecanfixtherightratiorathereasily-;justadd.Ifthereare2mapletreesand3elmtrees,thenthere are5totaltrees.So,thereare2mapletreesforevery5totaltrees.

Nowwecancross-multiply:

Onceagain,circlingthequestionwillhelpyouonratioproblems.Here,thequestionis"Ifthereareaof40trees, howmanytreesarethereinthepark?"Thattellsustheratiowe'relookingforis"maple"to"totaltrees", soweshouldsetupourfractionsusingthoseunits.

Ratiosliketheonesabovearealsocalled Itjustmeansthatonequantitydividedbytheotheralways comesouttothesamenumber,sowecansettwofractionsequaltoeachother.Sayingonequantity withtheothermeansthesamething.

AVERAGES

Therearethreetypesofcalculationsthatconcernushere:

ThisiswhatwemeanwhenwesayFindtheaveragebytakingthe dividedbythe

Thesumis2+4+7+9+18=40.Thereare5terms,sotheaverageis40/5=8.

Themedianisthenumber,whenyouputthetermsinorder. 7,

Writetheminorder,youget2,4,7,9,18.Theoneinthemiddleis7,sothemedianis7.

Ifthereareannumberofterms,suchthatthereisnoonenumberinthemiddle,themedianis

Writetheminorderandyouget2,4,7,8,9,18.Thetwomiddlenumbersare7and8,sothemedianis7.5.

Themodeisthenumberthatoccurs

Eachnumberoccursonce,exceptfor2,whichoccurstwice.Sothemodeis2.

Let'stakeanotherlookatArithmeticMean(whichwe'lljustcall"average").Thedefinitionofaverageis: Average= Sumoftheterms Howmanyterms

Ifwemultiplybothsidesofthisequationbythenumberofterms,weget:

Thisequationisveryimportant.Averagequestionscanbeabittrickierthantheyseem.Weallknowpretty wellhowtotaketheaverageofalistofnumberstheygiveus.ButACTaverageproblemscangetharder.

Let'slookatone:

Here,wedon'tknowwhattheindividualnumbersare.But,sinceweknowhowmanythereareandwhat theiraverageis,wecanworkdirectlywiththeirsum:

HowmanytermsAverageSumofterms

5numberswithanaverageof15,sotheirsumis5(15)=75

3numberswithanaverageof19,sotheirsumis3(19)=57

Therearenumberswedon'tknow,sotheirsummustbe

First,wemultipliedacrosseachrow.Thenumberoftermstimestheaveragegivesyouthesumoftheterms.

Then,aswecanseeinthefirstcolumn,weshouldsubtracttofindthetworemainingterms.Sincewe subtractedinthefirstcolumn,we'llsubtractthesumsaswell.(Don'ttrytosubtracttheaveragecolumn;justfocusonthe sum.)

Onceweknowthatthosetwonumbershaveasumof18,wecanfindtheaverage:

Average=

Sumofterms Howmanyterms

ANOTHERWAYTOLOOKATIT

ThestatisticthatmostpeoplerefertoastheaverageistheThemeanisfoundbydividingthesumofthedatabythe numberofitemsinthedataset.Forexample,themeanofthesampledatagivenaboveis

TheitemofdatathatoccursmostfrequentlyiscalledtheInoursampledata,thenumber4occursthreetimes,morethan anyotheritem,so4isthemode.Ifnooneitemofdataoccursmorethananyother,thesetofdatahasnomode.Iftwoitemsof dataoccurwithequalfrequency,greaterthananyother,thedatasetissaidtobebimodal.

ThenumberthatliesexactlyinthemiddleoftherankeddataiscalledtheIfthedatasetcontainsanoddnumberof items,themedianisthemiddlenumberattheposition,whereisthenumberofitemsofdata.Ifthedatasethasaneven numberofitems,themedianisthemeanofthetwodataitemsinthemiddle.Sinceoursampledatahastenitemsandthe twoitemsinthemiddleare4and7,themedianis=5.5.

Thereareonlythreepartstoanyaveragequestion.Fortunatelyforyou,theACTmusegiveyoutwooftheseparts,whichareall youneedtofindthethird.Theaveragepieisaneasywaytokeeptrackoftheinformationyougetfromquestionsdealingwith averages.Ifyouhavethecoral,youcanalwaysdividebyeithertheaverageorthenumberofthingsinthesec(whicheveryouare given)tofindthemissingpieceofthepie.Similarly,ifyouhavethenumberofthingsandtheaverage,youcanmultiplethetwo togethertoarriveatthetotal(thesumofalltheitemsintheset).

Forexample,ifyouwanttofindtheaverageof9,12,and6usingtheaveragepie,youknowyouhave3itemswithatotalof27. Dividingthetotal,27,bythenumberofthings,3,willyieldtheaverage,9.Yourpielookslikethis:

Althoughyouprobablycouldhavedonethatwithouttheaveragepie,moredifficultaveragequestionsinvolvemultiple calculationsandlendthemselvesparticularlywelltousingthepie.Let'stakealookatone:

Over9games,abaseballteamhadanaverageof8runspergame.Iftheaveragenumberofrunsforthefirst7gameswas 6runspergame,andthesamenumberofrunswasscoredineachofthelast2games,howmanyrunsdidtheteamscore duringthelastgame?

Let'susebite-sizepiecestoputtheinformationfromthefirstlineofthisproblemintoourtrustyaveragepie.

Whatisthesumofeverythingforthese9games?9X8,or72. Nowlet'sputtheinformationfromthesecondlineintotheaverageequation.

Whatisthesumofeverythingforthese7games?7X6,or42.

Ifall9gamesaddedupto72,and7ofthesegamesaddedupto42,thentheremaining2gamesaddedupto72-42,or30.In caseyouarefeelingsmugaboutgettingthisfar,theACTwritersmade30theanswerfor(D).

Butofcourse,ifyoureadthelastline,youknowthattheyonlywanttherunstheyscoredinthelastgame.Becausethesame numberofrunswasscoredineachofthelasttwogames,theansweris

ACTwritershaveaparticularfondnessfor"weightedaverage"problems.First,lee'slookataregularunweightedaverage question.

IfSallyreceivedagradeof90onatestlastweekandagradeof100onatestthisweek,whatisheraverageforthetwotests?

Pieceofcake,right?Theansweris95.Youaddedthescoresanddividedby2.Nowlet'sturnthesamequestionintoaweighted averagequestion.

IfSally'saveragefortheentireyearlastyearwas90,andheraveragefortheentireyearthisyearwas100,isheraverageforthe twoyearscombinedequalto95?

Theansweris"notnecessarily."IfSallytookthesamenumberofcoursesinbothyears,thenyes,heraverageis95.Butwhatif lastyearshetook6courseswhilethisyearshetookonly2courses?Canyoucomparethetwoyearsequally?ACTlikestotest youranswertothisquestion.Here'sanexample.

1.Thestartingteamofabaseballclubhas9memberswhohaveanaverageof12homerunsapiecefortheseason.The second-stringteamforthebaseballclubhas7memberswhohaveanaverageof8homerunsapiecefortheseason.What istheaveragenumberofhomerunsforthestartingteamandthesecond-stringteamcombined?

TheACTtestwriterswanttoseewhetheryouspotchisasaweightedaverageproblem.Ifyouthoughtthefirst-stringteamwas exactlyequivalenttothesecondstringteam,thenyoumerelyhadtotaketheaverageofthetwoaverages,12and8,toget10.In weightedaverageproblems,theACTtestwritersalwaysincludetheaverageofthetwoaveragesamongtheanswerchoices,and itisalwayswrong.10is(C).Crossoff(C).

Thetwoteamsarenotequivalentbecausetherearedifferentnumbersofplayersoneachteam.Togetthetrueaverage,we'll havetofindthetotalnumberofhomerunsanddividebythetotalnumberofplayers.Howdowedothis?Bygoingtothetrusty averageformulaasusual.Thefirstlineoftheproblemsaysthatthe9membersonthefirstteamhaveanaverageof12runs apiece.

Sothesumofeverythingis9X12,or108.

Thesecondsentencesaysthatthe7membersofthesecondteamhaveanaverageof8runseach. So,thetotalis7X8,or56.

Nowwecanfindthetrueaverage.Addalltherunsscoredbythefirstteamtoalltherunsscoredbythesecondteam:108+56= 164.Thisisthetruetotal.Wedivideitbythetotalnumberofplayers(9+7=16).

Theansweris10.25,or(D).

Combinatoricsisafancywordthatjustrefersto

Thereareseveral differentkindsofproblemsthatdealwithpossiblearrangements.

Takealookatthisproblem:

Therearefouroptionsfortheflavor,andeachofthosehasthreeoptionsforthetopping.Soallyouhavetodoto solvethisproblemis4x3.That's12.

Ifyougetconfusedbyproblemslikethis,itsometimeshelpstolistall thepossiblearrangementsthatcanbemade.Let'ssaytheflavorsare and Andlet'ssaythe optionsfortoppingsare andThe figuretotheleftshowsallthepossiblecombinations.

Foreachofthefourflavors,therearethreeoptionsfortoppings. Therefore,wecangetthetotalnumberofcombinationssimplyby multiplying4times3.

Soifyou'rejustpairingmembersofonegroupwithmembersof anothergroup,justmultiplythegroupstogethertogetthetotal numberofpossiblecombinations.

Here,insteadofpairingtogethertwogroups,we'reputtingasinglegroupofthingsintoacertainorder.Asinthelast problem,wecouldcountallthepossiblearrangements.Sincethepaintingsdon'thavenames,let'sjustcallthemA, B,andC.Writethemout:therearepossiblearrangements:

ThinkabouttheseproblemsaccordingtoTherearethree slotsthatwewanttofill:first,second,andthird.

Startwiththefirstslot.Thereare3possiblepaintingsforthefirst slot.

Let'ssayweputpaintingAinthefirstslot.Now,thereare leftforthesecondslot,BandC.

Let'sputpaintingBinthesecondslot.Now,there'sonly leftforthethirdslot,paintingC.

Wecanfigureouthowmanypossibleordersthereareby multiplyingtheoptionsforeachslot:3x2xI=6options. X X

Atheart,thisisthesameconceptastheicecreamproblem,wherewehad4optionsforthe"icecreamslot"and3 optionsforthe"toppingslot".Theonlydifferenceisthatnowwe'reusingthesamegrouptofillalltheslots,andonce weputapaintingintoaslot,it'snolongereligiblefortheotherslots.

Tryanotherone:

Thisproblemworksjustlikethelastone.Therearecandidatesforpresident.Oncewechooseapresi-dent,there arecandidatesforvicepresident.5x4=20.Therearetotalpossibilities.

Thisproblemisalotlikethelasttwo,butwithoneimportantdifference:

ThisisprettyeasytodoIfwejustwriteoutallthepossibleteams.Tomakethingseasier,let'sgivethemnames: and

Andre-Bob

Andre-Carlos

Andre-Dietrich

Bob-Carlos

Bob-Dietrich

Carlos-Dietrich

Thereare

Waitaminute.Six?Ifwedothemultiplicationwedidbefore,wewouldget4optionsforthefirstslotand3forthe second,and4x3is12.Howdidweget6?

Thisproblemisdifferentbecauseunlikethepaintingproblem, Inthepreviousproblem, havingAndreaspresidentandBobasvicepresidentwasdifferentthanhavingBobpresidentandAndrevicepresident, sowewanttocounteachscenarioseparately.Here,ateamofAndre-Bob asateamofBob-Andre,sowe don'twanttocountthemseparately.

Ifwemultiply4x3,thisiswhatwe'redoing:

Wearecountingeachteamwe'recountingAndre-BobBob-Andre.Sincethatgivesus12possibilities,if wedividethatbytwo,we'llgetouranswer.12/2=6.Thereare

ANOTHERWAYTOLOOKATIT

Combinationproblemsaskyouhowmanydifferentwaysanumberofthingscouldbechosenorcombined.Therulefor combinationproblemsontheACTisstraightforward.Thenumberofcombinationsistheofthenumberof thingsofeachtypefromwhichyouhavetochoose.

Here'sanexample.

At.theschoolcafeteria,studentscanchoosefrom3differentsalads,5differentmaindishes,and2differentdesserts. IfIsabelchoosesonesalad,onemaindish,andonedessertforlunch,howmanydifferentlunchescouldshechoose?

H.25

J.30

K.50

Isabelisgoingtochooseherlunchbychoosingoneofeachoftheitems.Thenumbersofitemsshehastochoosefrom foreachtypeofdishare3,5,and2.Thenumberofpossiblecombinationsshecouldchoosefromisalwaystheproduct ofthenumberofthingsofeachtypeshecanchoosefrom,sothereare3X5X2=30possiblelunchcombinations. Therefore,theansweris(J).Onamoredifficultproblem,youmayrunintoacombinationwithmorerestricted elements.Justbesuretoreadtheproblemcarefullybeforeattemptingit;ifthequestionmakesyourheadspin,pick yourLetteroftheDayandreturntoitlater.

Attheschoolcafeteria,2boysand4girlsareformingalunchline.Iftheboysmuststandinthefirstandlastplaces inline, howmanydifferentlinescanbeformed?

Let'sthinkabouttherestrictedspotsfirst.Ifonlyboyscanstandinthefirstspot,howmanypeopleinthequestioncan befirstinline?Becausethereareonly2boysavailable,thereareonlytwooptionsforspot#1.Now,whataboutthelast spotinline?Again,ifonlyboyscanstandthere,andifoneoftheboysisgoingtohavetostandinthefirstspot,thereis only1boylefttofilltheposition.Thespotsinthemiddlemustgotothegirls.Becausethequestiondoesnotsetany additionallimitsonthegirls,wecanassumetheycanbeplacedinanyofthe4remainingspots.Thus,anyofthe4girls canstandinspot#2,leaving3girlstostandinspot#3,2girlstostandinspot#4,andthelastgirltostandinspot#5. Nowallweneedtodoismultiplyallthepossibilitiestogether.Ifyoudrewapictureofthelineandwroteintheabove arrangements,itshouldlooklikethis.

Whenyoumultiplyeverything,you'llget48,whichisanswerchoice(C).

"Probability"meansexactlywhatitsoundslike:how"probable"isthisevent.Theprobabilityofaneventisdefinedas: Saytheprobabilityofwinningthelotteryis"oneinamillion".Thatjustmeansthere'swinningnumberoutof possiblenumbers.Sinceprobabilitiesarefractions,mostprobabilityquestionsjustboildowntothequestion:what isthethingyou'relookingfor?

We'relookingfortheprobabilityofchoosingabluemarble.Soallwehavetofindis:

Weknowthereare32totalmarbles,so32willgoonthebottom.Wedon'tknowhowmanybluemarblesthereare,but wedoknowthereare8redmarbles,andthereareonlyredandbluemarbles.Soifwesubtracttheredfromthetotal, we'llbeleftwiththeblue.

4 We'redone!Theprobabilityofchoosingabluemarbleis3/4.

Notethatinsteadofsolvingforthebluemarbles,wecould'vefoundtheprobabilityofchoosingaredmarble andsubtractedfrom1.

There'sa1/4chanceofpickingaredmarble...

...sothere'sa3/4chanceofpickingabluemarble.

Wecanseefromthisthat

I.Youcan thinkaboutprobabilityassimilartoIfthere'sa3/4chanceofpickingabluemarble,then75%ofthe marblesareblue.Justaspercentsaddupto100%,allprobabilitiesaddupto1.

ANOTHERWAYTOLOOKATIT

Probabilityisanumberassignedtothelikelihoodoftheoccurrenceofanevent.Theprobabilityofaneventthatissureto happenis1,andtheprobabilityofaneventthatissurenottohappenis0.Allotherprobabilitiesarenumbersbetween0and1. TheprobabilityofeventAisdenotedbyP(A).

Anexperimentisanyprocedurethathasarandomoutput,i.e.,theresultsoftheexperimentoccurrandomly.Thesamplespace ofanexperimentisthesetofallpossibleoutcomes.Forexample:

Thesamplespacefortheexperimentoftossingtwocoinsandnotingheads(H)ortails(T)ofeachcoinis: {HH,HT,TH,TT}

Thesamplespacefortheexperimentofrollingonedieandnotingthenumberofspotsontopis:

{l,2,3,4,5,6}

Theprobabilityofanyeventisthefractiona/bwhereaisthecountofthenumberofitemsinthesamplespacethatshowthe giveneventandbisthenumberofitemsinthesamplespace.

IfAistheeventofbothcoinsshowingheads(HH),thentheprobabilityofeventA,P(A)=¼(thenumberofoutcomesinthe samplespacethatshow2headsdividedbythenumberofitemsinthesamplespace).

IfBistheeventofanumberlessthan3showingwhenadieisrolled,thenP(B)=2/6=1/3.

Whilethischapterwillshowyouhowtosolvevarioustypesofalgebraproblems,don'tforgettheMathTechniques!Plug InandBacksolvewerecreatedtohelpyoualgebra.

sotheyshouldalwaysbeinyourmindandyourheart.Obviously,problemsthatareswimminginvariablesare goodcandidatesforbothtechniques.Ifaquestionhasvariablesinthechoices,itdoesn'tmatterwhattheirvaluesare,so wecanusePlugIn.Ifaquestionasksyouforthevalueofavariable,youcanuseBacksolveandtestthechoicesforthat variable.Techniquesarealsousefulon thatinvolve Thatis,theproblemwilldescribe mathematicalrelationshipsinnormalEnglishwordsandexpectyoutoturnthosewordsintoalgebraicequations.In problemslikethis,it'softenmucheasiertouserealnumbersandbypasstheequationsaltogether.Wesawatonof questionslikethisintheMathTechniqueschapter,remember?

Youwillstillneedtolearnsomealgebra;thetechniqueswon'tworkoneveryquestion,andonsomeproblems techniquesarepossiblebutalgebraisfaster.Inthischapter,we'regoingtoemphasizealgebraicsolutionsovertechnique solutions.Butdon'tforgetthatthetechniquesareheretohelpyou.

BASICMANIPULATION

Whenwetalkabout"algebra",wegenerallymeanproblemsthatinvolve thatcanstandforanunknown value.'ThesimplestalgebraproblemsontheACTwillgiveyouanexpressioncontainingavariableandaskyoutoevaluate theexpressionwhenthevariablehasacertainvalue.Observe,

Whatisthevalueoftheexpressionwhenx=7?

Weknowthatthevalueofxis7,sowecanreplaceeve1yxintheexpressionwitha7andsolve:

Problemslikethismayinvolvemorethanonevariable: -If

Substitutethevaluesforthecorrespondingletters.Justbecarefultoputthenumbersintherightspots: -(3)(8)-(3)(-4) =24-(-12)

Sometimethesequestionsmayseemcomplicated: =24+12=30

Waitaminute-whyarewelookingatageometryprobleminthealgebrachapter?Becausealltheproblemasksyou todoissubstitutevaluesintoagivenexpression.Don'tworryaboutwhataconeis;juststickthenumbersinforthe lettersintheformula:

= 30

Mostoftheexamplesabovewere not Thatjustmeansthattheyhavenoequalssign.Butalotof algebrainvolvesequations.Whenanequationhasonevariableinit,therewillusuallybeonlyonevalueforthevariablethat makestheequationtrue.

Youcansolveanequationby

Thatmeanswehavetomoveall thestuffnextthetotheothersideoftheequalssign.Youcandothisby ofanythingyouseeto

3x= 3x= 3x= X=6

This,myfriend,istheheartofalgebra:togetbyitself,dotheoppositeofanythingyouseetobothsides.We'llseemore complicatedconcepts,ofcourse,butthisisprettymuchit.Sometimesanequationmayseemmorecomplicated,butjust remembertodotheoppositetogetridofsomething:

Toremove"+2",multiplybothsidesby2.

Toremovethesquareroot,squareboth sides.Toremove"-3",add3tobothsides.

Howdoyouknowwhichoperationstodofirst?Thinkofanequationasapackagewithmanylayersofribbons,wrapping paper,andboxes,andthevariableisyourbirthdaypresentinsidethepackage.Tounwrapthepackage,you'vegottostart withtheoutermostribbon,thenthewrappingpaper,thentheboxunderneath.Eachlayeryouremoveiscoveringallthe layersbelowit.

Whensolvinganequation, Inthe firstequationabove,+5,the"x3"onlyappliestothenotthe5.Butthe"+5"appliestoeverythingbeforeit,so westartthere.Inthesecondequationabove,thesquarerootonlyappliestothe"x-3",nottothe2.The"+2"appliesto everythingelseonthatside,sowestartthere.

intermsof

Noteveryalgebraproblemwilljustdealwithnumbers.Observe: +

Rightnow,theequationgives"yintem1sofx".Thatmeanstheequationdefinesyandusesx'sinitsdefinition:yisbyitself ononesideoftheequation,anditsvalueis5x+3.Butwewant"xintem1sofy".Thatmeansthatwewanttogetxbyitself ononesideoftheequationandnothingbuty'sandnumbersontheotherside.Wedothis wesolved forxabove.Butnowinsteadofanumber,ouranswerwillhaveabunchofy's.

Subtract3frombothsides.

Dividebothsidesby5.

Eachproblemabovedealtwithasingleequation,butsomeproblemsmaygiveyoumultipleequationswithmultiple variables.Themoststraightforwardwaytosolvetheseproblemsis Forexample:

We'regiventwoequationswithtwovariables,andNoticethatthefirstequationhasononesideoftheequationby itself.Sinceisequivalentto-6",wecan -6"intothesecondequationwhereverweseean"a".

8x-6=10

8x=16

Tryanother:

Itmightseemlikewehavetosolveforxorindividually,butwedon't.Thefirstequationgivesavaluefor"x+and thesecondequationalsocontains"x+So,wecansubstitute4forthatwholeexpression: y)-=

Theseexampleswereprettysimple,butmorecomplicatedproblemscangetquiteintricate.Ifaproblemhastwoor morevariablesinit, Beingabletosolveintricatealgebraproblemsisagoodskilltohave,but PlugIn

ANOTHERWAYTOLOOKATIT

Anequationisalmostanymeaningfulmathematicalsentencethatcontainsanequalsign.Some equationsaretrue,somearefalse,andsomeareopenorconditional.

5=5 True

2/3=2/3True

X+1=x+1Trueforeveryreplacementofx

7=9 False

x+3=x+1Falseforeveryreplacementofx

x+2=5Open;trueifx=3only

Thesetofnumbersthatmakesanopenequationtruewhensubstitutedforthevariableiscalledthe Thenumbers themselvesarecalledthe(Thesolutionsetoftheequation+1=7is{3}.)

Equationsthathavethesamesolutionsetarecalledequations.Therearetwobasicrulestouseinordertosolve equations.Theapplicationofeitherruleguaranteesthatanequivalentequationwillresult.

1.Ifthen=+foranynumber

Ifthen=foranynumberc0.

Theprocessofsolvinganequationistoproduceasequenceofequivalentequations,thelastoneofwhichlookslike =constant fromwhichthesolutionsetcaneasilybefound.

Sincesubtractioncanbedonebyaddingtheoppositeofthesecondnumber,thereisnoneedforasubtractionaxiomof equality.Anddivisioncanbedonebymultiplyingbythereciprocalofthedivisor,sothereisnoneedforadivisionaxiomof equality.

Examples:

Solveeachofthefollowing:

1.9 Rule1.Add15tobothsidesofequation.

3x-1515915 3x=24

3x(1/3)24(1/3)Rule2.Multiplybothsidesof½ordivideby3. x=8

Thesolutionsetis{8}.

2.4z+2=-2(z+2)Firstusedistributivepropertytosimplify.

4z+2=-2z-4

4z+2+2z=-2z-4+2zAddtobothsides.

6z+2=-4

6z+2-2=-4-2 Add-2tobothsides.

6z=-6

6z(1/6)=-6(1/6)Multiplybothsidesby1/6,ordivideby6. z=-1

Thesolutionsetis{-1}.

3. Multiplybothsidesbythelowestcommondenominator,6.

2(2x-1)-+3)=3Simplify -2--3=3 -5=3

=8 Divideby3.

=Thesolutionsetis{

4.Solveforx:3x-2y=7

3x-2y+2y=7+2y 3x=7+2y

3x()=(7+2y)()

X= y

POLYNOMIALS

1.What'sapolynomial?

A isanymathematicalexpressionwithtermsthatareaddedorsubtractedtogether.Thesetermswill usuallycontainvariablestakentodifferentpowersmultipliedbyanumbercalledits Apolynomialcontaining twotermsisa

Inthefollowingexpressions,allthetermscontainthesamevariabletakentothesamepower,sotheycanbeadded togetherdirectly:

x2+4x+2xy+7x2-10x+5+9xy-1

8x2+4x+2xy10x+5+9xy-I

8x2-6x+2xy+5+9xy-1

8x2-6x+11xy+5-1

8x2-6x+11xy-4

ANOTHERWAYTOLOOKATIT

AdditionandSubtraction

Addthetermscontaining Subtractthetermscontaining Addthetermscontaining Subtractthetermswithnovariables.

Toaddorsubtractpolynomials,firstusethedistributivepropertyasneededtogetridofparenthesesandthencombinesimilar terms.Usually,thetermsofapolynomialarearrangedintheorderofdescendingdegreeinaspecifiedvariable.Forexample:

(3x2+5x-4)+(2x2-7x-3)=3x2+5x-4+2x2--7x-3 =5x2-2x-7

(2x26xy+3y2)-(x2-xy+2y2)=2x2-6xy+3y2-x2+xy-2y2 =X25xy+y2

Multiplication

Multiplicationofamonomialbyapolynomialofseveraltermsismerelyanextensionofthedistributive property.

8)=+-

Multiplicationoftwopolynomialsofmorethanonetermeachisalsoanextensionofthedistributive property.Itiseasier,however,tofollowtherule"Multiplyeachtermofonepolynomial byeachtermoftheotherpolynomialandthensimplify."

(a+b-c)(2a-b+c)=a(2a-b+c)+b(2a-b+c)-c(2a-b+e)

=2a2-ab+ac+2abb2+bc-2ac+bcc2

=2a2+ab-aceb2+2bcc2

Multiplicationoftwobinomialsissuchacommonoperationthataspecialprocedurehasbeendevisedtomakeiteasytodo mentallycalledFOILwhichwewilldiscussbelow.

ANOTHERWAYTOLOOKATIT

Hereisasimpleexampleofabasicequation.

+7=28

Thereisonlyonenumberintheworldthatwillsatisfythisequation.Tofindit,weneedtoisolatexononesideoftheequation andgetallofthenumbersontheotherside.Togetridofthe7chatisbeingaddedontheleftside,wemustdotheoppositeof additionandsubtract7fromtheleftside.However,toavoidchangingtheentireequation,wealsohavetosubtract7fromthe rightside.Whateverisdonetoonesidemustalsobedonetotheother.

3x+7=28

-7-7

3x=21

Togetridofthe3thatisbeingmultipliedontheleftside,wemustdotheoppositeofmultiplicationanddividetheleftsideby 3.Ifwearedividingtheleftsideby3,wemustalsodividetherightsideby3.

==7

x=7

Butinthislastproblem,weleftoutoneveryimportantthing:ACTquestionsalwayshavemultiple-choiceanswers.Let'slookat thisquestionthewayitwouldhaveappearedontheactualtest.

1.If+7=28,whatis?

A.4

B.5

C.6

D.7

E.8

Youmightsay,"Well,what'sthedifference?It'sthesameproblem."Butinfact,it'snotthesameproblematall.

Takealookatthis:

Herewehaveanumbermultipliedbyanentirebinomial.Todothis,justmultiply6byeach terminsidetheparentheses.Wesometimescallthisdistributingthe6insidethe parentheses.

6(x+5)=6X+6X5=6x+30

Great.Sometimeswewanttomultiplytwobinomialstogether:

(x+5)(x+4)=?

Justlikewedidabove,wewanttomultiplyterminthefirstbinomialwithtem1inthesecond.To

helpyoukeeptrackoftheterms,remembertheacronym"FOIL".Multiply:

Firsttwoterms

Outsideterms

Insideterms X X4 5X

Lastterms 5X4

Thenaddthemalltogetherandcombinesimilarterms: +4x+5x+20=x2+9x+20

FOILinvolvesmultiplyingtwobinomialstogetalargerpolynomial.ButsomeACTproblemsmightwantyoutogotheother way.Lookatthisexpression: -2x+6

Noticethateachterminthisexpressioncontainsamultipleoftwo.Wecan"pullout"thattwoandputitofftotheside:

2x+6=(2X)+(2X3)=2(x+3)

WecallthisprocessInthiscase,2wasafactorofeachte1111,sowe"factoredout"the2.Wecandothesame thingwithvariables:

x2-3x=(X)-(3X)=(-3)

Whatifwewanttofactorapolynomialintotwobinomials?Lookatthisexpression: 2

Weknowthattheremustbetwobinomialsthatmultiplytogethertomakethatexpression:

Thefirsttermhere,x2,wastheresultofthefirsttwo,termsofthebinomialsmultipliedtogether.Soeachof thebinomialsmuststartwithanx:

(x+?)(x+?)

Thelastterm,12,wastheresultofthelasttwotermsofthebinomialsmultipliedtogether.Soweknow theofourlasttwonumbersis12.ThatcouldbeIand12,2and6,or3and4.

Themiddleten11,wastheresultofeachofthelasttermsmultipliedbyandthenaddedtogether.So wealsoknowtheofthelasttwonumbersmustbe7.Whattwonumbershaveaproductof12and asumof7?Only3and4fitbothrequirements.

(x+3)(x+4)=x2+4x+3x+12

Thiscanbeeasierwhenyouhaveanswerchoices:

Whichofthefollowingexpressionsisequivalentto x2-2x-15?

A.(x-2)(x+1)

B.(x-3)(x+5)

C.(x+3)(x-5)

D.(x-3)(x-5)

E.(x-7)(x-8)

Oneoptionhereis It'softeneasiertoFOILthantofactor,soFOILouttheanswerchoicesandseewhichone equalsthepolynomialwewant:

A.(x-2)(x+1)= -2x-2

B.3)(x+5)=+5x-3x-15 +2x-15

D.(x-3)(x-5) =-5x+3x-15 =x25x3x+15-8x+15

E.(x-7)(x-8)=2-8x-7x+562+15x+56

Evenbetter,youcouldanumberforSay=

(6)2-2(6)-15=36-12-15

A.(6-2)(6+1)=(4)(7)=28

B.(6-3)(6+5)=(3)(11)=11 (6+3)(6-5)=(9)(1)

D.(6-3)(6-5)=(-3)(1)=-3

E.(6-7)(6-8)=(-1)(-2)=2

DifferenceofSquares

Trythisproblem: (x+y)(x-=?

Bothbinomialscontainthesameterms,exceptonebinomialisasumandtheotherisadifference.Todo this,wecanjustFOILaswedidbefore: + =x2-y2

Noticethatthemiddletermscanceledout,sotheresultwasjustthefirsttermsquaredminusthesecond termsquared.Thisequationiscalledthe Thatjustmeansit'sanequation thatshowsupalotthat'salwaystrueforanyvariables,soit'sgoodtorememberit. y2=+-

Whenyouseetwosquaressubtractedfromeachother,youcaneasilyfactortheexpression.Forexample: x2

Bothtermsherearesquares,sowecanimmediatelyfactoritintothesumanddifferenceoftheirroots: (x

ANOTHERWAYTOLOOKATIT

ManyACTproblemsinvolvefactoringofonekindoranother.Hereisthemostbasickindoffactoringproblem.

x2+7x12=?

Ifyourcalculatorcansolvequadratics,now'sthetimetomakesureyouknowhowtoputitthroughitspaces.To factorthisexpressionbyhand,putitintothefollowingformat,andstartbylookingforthefactorsofthefirstand lastterms.Notethatthefactorsforthelasttermhavetomeettwoconditions:Theirproductisthelasttermand theirsumisthecoefficientofthesecondterm.

x2+7x+I2= ()()= (x)(x)= (x3)(x4)= (x+3)(x+4)=

Toensurethatyou'vefactoredcorrectly,youcanalsousetheFOIL(First,Outer,Inner,Last)methodtocheckyour math.Let'stryitontheabovepolynomial.

1.First-multiplythefirsttwotermsineachpolynomial:Theresultshouldequalthefirsttermofyour quadraticexpression:

2.Outer/Inner-multiplytheoutertermsfromeachpolynomial:(x)(4).Dothesamewiththeinnerterms:(3)(x).Add thetwotermstoarriveatthemiddletermofyourquadraticexpression:3x+4x=7x.

3.Last-multiplythelasttermsineachpolynomial:(3)(4).Thisshouldbeequaltothelastterminyourquadratic expression:12.

4.WhenyouaddyourFirst,Outer,Inner,andLasttermstogether,you getbacktowhereyoustarted.

x2+7x+12

TheACTtestwritersmightusethatlastexpressiontomakeaproblemlikethis.

1.If

Thisisaspecificxquestion.Ifwefactorthetopexpressionaswedidamomentago,weget.

Nowwecancancelthe(x+4)s,withtheresultthatx+3=5.Togetridofthe3,wesubtractitfrombothsides.Now x=2,andtheansweris(B).

ANOTHERWAYTOLOOKATIT

Theprocessoffactoringinvolveschanginganexpressionfromadditionorsubtractiontomultiplication-creating factors.Thepropertyunderlyingallfactoringrulesisthedistributiveproperty:

ab+ac=a(b+c)

Ifanexpressionhasacommonfactorotherthan1inallofitsterms,usedistributivepropertytofactoritout.Here aresomeexamples:

2+2a2b=2ab(2b+a)

5y3-26x7y2+52x8y5=13x5y2(3y-2x2+4x3y3)Thecommonfactorchosenshouldbethegreatestcommon factoroftheterms.Choosetheexponentoneachvariabletobe thesmallestexponentonthatvariableintheexpression.

-25x3y2-20.x4y3+15x5y4-50x6y2=-5x3y2(5+4xy-3x2y2+10x3)Ifthefirsttermisnegative,chooseanegative commonfactor.

5)(x-6)+(x+5)(x-1)=(x+5)[(x-6)+(x-1)]Thecommonfactoristhebinomial(x+5). =(x+5)(2x-7)

rm=(pq+3rq)+(pm+3rm)Thetrickistogroupsothateachgrouphasacommonfactor. =q(p+3r)+m(p+3r) =(p+3r)(q+m)

2+6xy-12xy-9y2=(8x2+6xy)-(12xy+9y2)Beverycarefulofsigns. =2x(4x+3y)-3y(4x+3y) =(4x+3y)(2x-3y)

OperationsonPolynomials

AdditionandSubtraction

(3x2+5x-4)+(2x2-7x-3)=3x2+5x-4+2x27x-3 =5x2-2x-7

(2x26xy+3y2)-(x2-wy+2y2)=2x2-6xy+3y2x2+xy-2y2 =x2-5xy+y2

Multiplication

Multiplicationofamonomialbyapolynomialofseveraltermsismerelyanextensionofthedistributiveproperty.

-2a(3a2--5a+8)=-6a2+10a2-16a

Multiplicationoftwopolynomialsofmorethanonetermeachisalsoanextensionofthedistributiveproperty.Itiseasier, however,tofollowtherule"Multiplyeachtermofonepolynomialbyeachtermoftheotherpolynomialandthensimplify."

(a+b-c)(2a-b+e)=a(2a-b+e)+b(2a-b+e)-e(2a-b+e) =2a2-ab+ac+2abb2+bc-2ac+bcc2 =2a2+ab-acb2+2bcc2

Multiplicationoftwobinomialsissuchacommonoperationthataspecialprocedurehasbeendevisedtomakeiteasytodo mentally.Considertheproductoftwobinomials:

REMEMBERFOIL?

CallAandCtheEirsttermsofthebinomials. CallAandDtheQuterterms. CallBandCtheInnerterms. CallBandDtheLastterms.

Example,tomultiply(2x+3)(x+4); MultiplytheFirstterms:(2x)(x)=2x2 MultiplytheOuterterms:(2x)(4)= MultiplytheInnerterms:(3)(x)=3x. MultiplytheLastterms:(3)(4)=12. SincetheOuterproductandtheInnerproductaresimilarterms,combinetheinandwritetheanswer: 2x2+11x+12

Threeproductsoccurfrequentlyanddeservespecialattention:

Sumanddifferencebinomials:(A+B)(A-B)=A2B2 Squareofabinomial:(A±B)2=A2±2AB+B2 Cubeofabinomial:(A±B)3=A3±3A2B+3AB2±B3

Examples:

1.(3x-5)(3x+5)=9x2-25 (5x-2y)2=25x2-20xy+4y2 3.(x+4)3=x3+12x2+48x+64

DividingPolynomials

ELEMENTARYALGEBRA

Sofar,we'vebeenmultiplyingpolynomials,butACTquestionsmayaskyoutodividepolynomials,too.

Whatdowedo?Rememberthatafractioncanbereducedwhenthetopandbottomhaveacommonterm:

Thesameconceptappliestopolynomials.Let'sfactorthedenominatorandseeifwecancrossoutsometem1scommonto thetopandbottom.

Whenfactoring,ourultimategoaliscancelingoutterms.Don'tfactorblindly:

Inthisproblem,wewanttocancelout+3",sowe'lltrytoget+3"onthebottom.Thebottomendsin "-6":whattimes3gives-6?-2.Sotheothertermwillbe-2".Now+3cancelsoutonthetopandbottom:

ANOTHERWAYTOLOOKATIT

Wecaninterprettheruleforadditionandsubtractionoffractionsasamethodofdividingapolynomial byamonomial.

Thisrulemeansthateachtermofthepolynomialinthenumeratoristobedividedbythemonomial inthedenominator. Herearetwoexamples:

Sometimestherulefordivisionofexponentialexpressionsisneeded:

Theprocedurefordividingapolynomialbyabinomial(orotherpolynomial)issimilartothat forwholenumberdivision.Considerthedivisionproblem

x-3)2x2+5x-1

Dividethefirsttermofthedivisorintothefirsttermofthedividend,xinto2x2.Placethequotient abovethefirsttermofthedividend.

x-3}2x2+Sx-1

Multiply2xtimex-3,placetheproductunder2x2+Sx,andsubtract.Remembertofollow theruleforsubtraction;changethesignofthesubtrahend(thebottomexpression)andadd.

x-3J2x2+Sx-1

2x-6x

llx

Bringthenexttermdownfromthedividend,andrepeattheprocess.Dividexintollx.Then multiplyandsubtract.

2x+11

x-3)2x2+Sx-1

2x-6x

llx-1

llx-33

Theanswermaybewrittenaseither 2x+IIremainder32

2x2-2x-2

2x-1J4x3-6x2-2x+1

4x3-2x2

-4x2-2x -4x2+2x -4x+l -4x+2 ----=1

or2x+11+ll x-3

Theansweris2x2-1 -2x-2+2x_1.

WhenthedivisorinalgebraicdivisionisofdegreegreaterthanI,thesignaltostopthedivision processcomeswhenthedegreeoftheremainderissmallerthanthedegreeofthedivisor.

MathematicsReviewandPractice

Apolynomialcanbeeasilydividedbyafirst-degreebinomialofthetypex-abyaprocedure calledsyntheticdivision.Todemonstrate,wewillconsiderthefirstdivisionproblemdone above.Thecoefficientsofthedividendarealignedindescendingdegree.(Thevariablesarenot written.)Theconstanttermofthedivisoriswrittenwiththeoppositesigntotheleftofthecoefficients ofthedividend.Inthisproblem,3isplacedtotheleftoftherowofnumbers,25-1: 3I25-1

Theprocedureisasfollows:

1.Bringthefirstcoefficientofthedividenddowntothebottomrowundertheline.

2.Multiplythenumberontheleftofthetoprow,thatis,thedivisor,bythenumberonthe bottomrow.

Placethisproductabovethelineandunderthenextnumbertotheright.

Page 95

Addthenumbersinthatcolumn,placethesumundertheline,andrepeatsteps2,3, and4.

ELEMENTARYALGEBRA

Inthebottomrow,thelastnumberistheremainder,andtheothersarethecoefficientsofthe quotientinorderofdescendingdegree.

3I25-I

633

211322x+IIremainder32

Hereisanotherexample:(2x 5x+7)..,.(x+2). -212

2-4

l.(-48x2y3z)..,.(-16xy2z) 2.(25x3 -10x2+5x)..,.(5x) -85-67

3I2x2 -4x+3remainder1

QuadraticEquations

All the polynomial problems we've seen so far have been expressions, not equations. That means almost any value of x will make it work. But we might also see polynomials involved in equations, where only certain values of x will make the equation true.

- For what values of x does x2 + 7x + 12 = 0?

Any equation in the form ax2 +bx +c = 0 is a quadratic equation-a polynomial containing one squared variable, set equal to zero. So how do we solve it?

Well, we already factored this expression before, so let's do it again:

x2 + 7x + 12 = (x + 3)(x + 4) = 0

Remember that zero has a special property: anything times zero is equal to zero. If we know ab = 0, then we know either a orb (or both) must equal zero. Since we know that (x + 3) times (x + 4) equals zero, we know that one or both of those terms must equal zero:

x+3=0

x=-3

orx+4=0

orx=-4

Notethataquadraticequationmustbesetequaltozero.Ifit'snot,you'llhavetomake itequaltozero.

-Forwhatvaluesofxdoesx2-3x+2=20?

Herewehave20ontherightside.That'snogood;wewant0there.Sowe'lljustsubtract20sidesfrombothbeforewe factor:

x2-3x+2-20=20-20

x1-3x-I8=0

(x-6)(x+3)=0

x-6=0

x=6

TheQuadraticFormula

orx+3=0

orx=-3

Inyourmathclassatschool,youmayhavebeenexposedtothequadraticformula.Thisisaspecialformulayoucanusetofind thesolutionsforaquadraticequation.Youcanuseitforanyquadraticequation,butit'sespeciallyusefulforpolynomialsthat can'tbefactoredintohappyintegers.

For the equation ax2=+bx+c = 0, the solution for x is:

Generally, you will not need to know the quadratic formula on the ACT. You should be able to do any problem involving quadratics by factoring or with Plug In and Backsolve. If you really prefer the formula you can use it, but we generally don't recommend it. It's way too easy to mess it up.

INEQUALITIES

Numberlines numberlines.

Notethatthecirclearoundthe"2"markmeansthatcannot2.Incontrast,:S2lookslikethis:

Andyoucangraphmultipleinequalitiesonthesamenumberline.Thisgraphshows<1or2:3:

Algebraicmanipulation

youmultiplyordividebyanegativenumber,youhavetofliptheinequality.

Watchouthere.Thisiswherethesignflips.

INTERMEDIATEALGEBRA

Nowwe'regettingtotheinterestingstuff.IntermediateAlgebraproblemsstarttointroducesomemoredifficultmath conceptslikefunctions,exponents,andabsolutevalue.IntermediateAlgebradoesn'toccurasfrequentlyasthe previoustwocategories-only9questionspertest,comparedwith14Pre-Algebraand10ElementaryAlgebraquestions. Furthermore,sincetheseproblemstendtobeharder,theywillappearmoreoftenonthelaterquestionsonthetest.That meansthatifyou'vegotstrictTargetNumbers,you'IIbeskippingalotofthesequestions.So,theconceptsinthischapter arenotgoingtohaveaslargeaneffectonyourscoreasthoseinthepreviouschapters.However,ifyou'rehopingforahigher score,theseconceptswillbecrucial.

Keepinmind,again,thatthemathtechniquesarestillimportantandwidespread.Onaverage,65%ofIntermediate AlgebraquestionscanbedonewithPlugInorBacksolve.That'salot.Andthey'reparticularlyhelpfulondifficult questionsthatcanbeotherwiseconfusing.Sokeepaneyeoutforthem.

FUNCTIONS

1.FunnySymbols

Lookatthis:

Whatdoesthatmean?Duh.Obviously:

52=5x5

Thelittle"2"tellsustomultiplythebignumbertimesitself.Weallknowthat.Similarly: 72=7x7

(-23)2=(-23)x(-23)

y2=yxy 2=2x2

(donkey)2=(donkey)x(donkey)

Thisshouldnotbenewstoyou.Anytimeyouseealittle"2"nexttoanything,multiplyitbyitself.That's afunction.It'sasymbol(the"2")witharuleattachedtoit(multiplybyself).Everythingwedoin mathisakindoffunction:asymbolwitharuleattachedtoit.

OntheACT,sometimestherewillbenew,made-upsymbols.Takealookatthisproblem:

27.Theoperationisdefinedasx=2x+5.

Whatisthevalueof7-6?

A.1

B.2

C.6

D.7

E.9

Someofyouarethinking,"Huh?What'supwiththestar?I'veneverseenalittlestarsymbolbefore.SohowamI supposedtoknowwhatthestarmeans?"

Becausetheyjusttoldyouwhatitmeans!It'sthefirstthingtheysayintheproblem!Doyoureallythinkyou'reexpectedto knowwhatmeansbeforethetest?Canyoushowmethebuttononyourcalculator?Ofcoursenot.Theyjust madeitup.It'sarandom,arbitraryfunction,andtheytellyouexactlywhatitmeans.Theonlydifferencebetweenthisand 52isthattheexponentisacommonmathfunction,whileisjustonetheymadeuprandomly.

So.Thefunctiontheygiveusisdefinedas:

x2x+5

Thexhereisjustaplaceholder;it'savariablethatstandsforanynumber,anexampleofhowtousethefunction.Justasthe little"2"meant"multiplythenumberbyitself',thelittleheartheremeans"multiplyby2andadd5".

Thatmeans: and: therefore: so: also: ergo: thistoo: whynot: onemore:

2=2(2)+5

3=2(3)+5

18=2(18)+5

1979=2(1979)+5 y=2y+5

(omg)=2(omg)+5 =+5

()=2()+5

(fluffybabypandabear)=2(fluffybabypandabear)+5

Getthepoint?Whateveryouseenexttothe,stickitinforxin2x+5.

Now,let'sgetbacktotheoriginalproblem:

27.Theoperationisdefinedasx=2x+5. Whatisthevalueof7-6?

A.I

B.2

C.6

D.7

E.9

Solet'sjuststick7and6intothefunctionandsubtractouranswers.

7=2(7)+5=14+5=19

6=2(6)+5=12+5=17

7-6=19-17=W

Soouransweris2.That'sB.

We'vejustseensomeexamplesofnewfunctionsbeingdefinedwithfunnysymbols:

Butinreality,theydon'tusefunnysymbolsallthatoftenontheACT.Moreoften,theysimplyusealetter.

Thismeansexactlythesamethingasthelittleheartdid.Theonlydifferenceisthatheretheyusedan"f"insteadofa.The functionitselfbehavesinexactlythesameway.Thismeansthat:

{2)=2(2)+5

{-5)=2(-5)+5 =+5 =+5 1)+5

Yougetthepicture:doesn'tmean"multiplyfbyx."Thefisn'tavariable;it'sthenameofWecandoalot withfunctions,butitallcomesdownto

Let'slookatsomeexamples: Evaluation -=+-10,then{-4)=?

(-4)=-4)2+3(-4)-10=16-12-10=-6

Multiplevariables

-Iff(x,y)=1x+3y-xy,whatisthevalueoff(5,-1)?

Thisfunctionhastwovariablesinsidetheparentheses,butitalsohastwovariablesintheequation.Wheneverwe seetwonumbersinsidetheparentheses,we'llmakethefirstnumberequaltoxandthesecondequaltoy.

(5,-1)=2(5)+3(-1)-(5x-1)=4-3-(-5)

Compositefunctions =43+5

-Iff(x)=3x+4andg(x)=x2 ,whatisthevalueof . f(g(3))?

We'regiventwofunctions,f(x)andg(x),andwehaveequationsforboth.Thismayseemscary,butitworksexactlythe samewaythepreviousproblemsdid.Remember:takewhateveryouseeinsidetheparenthesesandstickitinforx. Here,"g(3)"isinsidetheparentheses,sothatwillgoinforx:

f(g(3))=3xg(3)+4

Thatdoesn'thelp:whatdoesg(3)mean?Ah,that'sjustadifferentfunction.Wecanput3inforxintheequationforg(x): g(3)=(3)2=9.

Nowwe'llsubstitute9backintothefirstfunction:

f(g(3))=f(9) =3x9+4=27+4=31

Notethattheorderisimportant:dothefunctioninsidetheparenthesesfirst.Here,gwasinsidetheparenthesesforf sowedidgfirst.Ifthequestionhadaskedforg(f(3)),we'dfirstput3intotheequationforf,thenputtheresultintothe equationforg:

g(f(3))=(f(3))2

f(3)=3x3+4=9+=13.

g(f(3))=g(13)=132=169

EXPONENTS

Youshouldbesomewhatfamiliarwithexponentsbynow.Exponentsinsomeformhaveshownupinthequestiontypes we'vealreadyseen-Pre-Algebraquestionsmayaskyoutocalculatethevalueofexponentialnumbers,and ElementaryAlgebraquestionsmayaskaboutpolynomialsthatcontainexponents.However,IntermediateAlgebra questionsintroducesomemorecomplexrulesandpropertiesaboutexponentialnumbers.

1.Properties

Exponentstellyouhowmanytimestomultiplyanumberortermbyitself.Thenumberthatisbeing multipliediscalledthe"base".Givinganumberanexponentisalsocalledtakingittothat"power".

Awordaboutparentheses

Onexponentproblems,it'sespeciallyimportanttopayattentiontowhat'sinsideandoutsidetheparentheses. Ifanexponentisnexttoparentheses,itappliesonlytotheexpressioninsidetheparentheses.If therearenoparentheses,theexponentappliesonlytothenumberorvariablerightnexttoit.

ab2 :Onlybissquared,nota. (ab)2 :Bothaandbaresquared.

2.Combiningexponents

-2x2 :Onlyxissquared. -(2x)2 :2xissquared.Thisequals-4x2 (-2x)2:-2andxarebothsquared.Thisequals4x2

Thereareafewrulesfordealingwithexponentialnumbersthatyoushouldknow:

OK:2x2+7x2=9x2

Variablesinexponents,Differentbases

Ifanequationhasvariablesinitsexponents,youcanusuallysettheexponentsequaltoeachother.

-If2a+10=23athena=?

Bothsidesoftheequationhavethesamebase,sowecanjustsettheexponentsequaltoeachother: a+10=3a10=2a5=a

Ifwe'regivennumbersthatdon'thavethesamebase,weshouldtrytoputtheminthesamebase:

-If3x=95,thenx=?

Wecan'tjustsetxequalto5becauseonebaseis3andtheotheris9.Butlook:9isapowerof3.Ifwe rewrite9as32,wehavethesamebaseonbothsides.

3x=(32)5=310 X=10

3.Logarithms

Alogarithmisjustawayofwritinganexponentprobleminadifferentorder.Usuallylogarithmproblemsjustrequireyouto understandthedefinitionofalogarithm:

logab=cmeansthatac=b

Aswithexponentialnumbers,the"a"hereiscalledthebase. Howaboutanexample?

-Whatisthevalueoflog39?

Let'ssetthatexpressionequaltoavariable,x.Usingthedefinitionabove, log39=xmeans3x=9

Thequestionisbasicallyasking:3takentowhatpowergivesyou9?Clearly,32isequalto9,sox=2.

Logarithmsdon'tappearoften,andwhentheydoappear,it'sonlyonthehardestquestions(thelastIOonthetest).Sothisis notaveryvaluableconcept-you'llseeaboutonelogarithmquestionforeverythreetestsyoutake.Ifyou'reshootingforavery highscoreontheACT,you'llwanttogetcovereveryconceptthatmightshowup.Otherwise,justworryaboutthebasicexponent rules.

Logarithmproblemsoftenjustrequireunderstandingthedefinitionshownabove.However,youmayalsoneedtoknowsome logarithmidentities,rulesforcombiningandsimplifyinglogarithms.Notethattheseidentitiesarejustlogicalconsequencesof theexponentrulesdiscussedintheprevioussection.

loga(mn)=logam+loganloga(a)=1loga(mn)=n(logam)

loga(m/n)=logam-loganloga(ax)=x

ABSOLUTEVALUE

Theabsolutevalueofanumberisitsnumericalvaluewithoutitssign.Thatmeansthatnegativenumbersbecomepositive andpositivenumbersstaypositive.Thesymbolforabsolutevalueistwostraightlinesoneithersideofthenumber:

Whenyouwanttocomputeexpressionswithabsolutevalue,dowhateverisinsidethelinesfirst,thenstripawayanynegatives betweenthelines:

First,dothestuffinsidethelines.

Now,stripawaythenegativesinsidethelines,so-6becomes6.

2-6=-4

Solvingforavariable

Takealookatthis:

Thevariablexisinsidetheabsolutevaluelines,anditsabsolutevalueis7.Therearetwopossiblesolutions: -Eitherxis7andtheabsolutevaluekeepsitpositive7, -orxis-7andtheabsolutevaluestripsitsnegativetomakeitpositive7.

Thekeytoabsolutevalueproblemsis:DON'TFORGETABOUTTHENEGATIVES.

-If ,whatisonepossiblevalueofn?

If ,thenwehavetwooptions:

n-12=7orn-12=-7 n=19 n=5

It'ssometimeshelpfultothinkofabsolutevalueasdistance:Theabsolutevalueofadifferencegivesthedistance betweenthetwopoints.Thatis: =distancebetweenpoints

Asimplesubtractionwillalwaystellusthedistance.Ifwewanttofindthedistancebetween19and12,we'dsubtract 19-12.Butifwewantthedistancebetween5and12,subtracting5-12givesus-7,andwegenerallydon'tliketouse negativedistances.Thenicethingabouttheabsolutevalueisthatitgivesusthedistanceineitherdirection. Intheproblemabove,theexpression""means"pointnisadistanceof7awayfrom12". Thatis,11iseither7morethan12or7lessthan12. n=5 12 n=19

Inequalities

Alotofabsolutevaluequestionsalsoinvolveinequalities.Takealookatthis: ,If,whatisthesolutionsetforx?

AswesawintheElementaryAlgebrachapter,inequalitiescanbesolvedjustlike equations.Liketheequationabove,thisinequalitywillhavetwosolutions, onepositiveandonenegative.Butthere'sonetricktosolvinginequalitieswith absolutevalues:youhavetofliptheinequalitysignforthenegativesolution:

,means2x-5>9 2x>14 x>7

or2x-5<-9

or2x<-4

orx<-2

Rememberwesaidthat,whensolvinginequalities,youhavetoflipthesignifyoumultiplyordividebya negative.Thisisthesameconcept.Here'sanotherwaytothinkaboutit:

,means2x-5>9or-(2x-5)>9.

Ifwedividethesecondequationby-1,weflipthesigntoget2x-5<-9.

CLICKHERETOACCESSTHE ABSOLUTEVALUEDRILL

You Can Receive a 70% Discount on our Full Length ACT Test Prep Class. Using This Link, You Pay Only $175. Our Normal Rate is $599This is a $424 Savings! Click Here Sign Up Today!

MISCELLANY

There are a few more concepts left that don't quite fit into any of the topics we've covered so far, so we threw them all together into a big grab bag of math. All of the following topics are at the bottom of the ACT Math totem pole: they don't appear often, maybe on one question for every three tests. If you're going for a 36, you'll want to know this stuff well. Otherwise, don't lose sleep over it.

1.Sequences

Asequenceisafancytermforalistnumbers(whichcontinuesinfinitely,unlessotherwisespecified) whereeachnexttermisobtainedbyapplyingsomesortofrule.Intheory,thisrulecanbeanything,but therearetwotypesofsequencesthatconcernusontheACT.

Arithmeticsequences

Anarithmeticsequence-isasequenceinwhicheachtermisobtainedby addingacertainnumbertothepreviousterm.Todefineasequence,youneed toknowwherethesequencestartsandwhatnumberisaddedtoeachterm (called"thecommondifference").Forexample: 5,8,11,14,17,20,23,26,29,32...

Thisarithmeticsequencestartswith5andthecommondifferenceis3.

-Thesecondtermofanarithmeticsequenceis31andthethirdtermis48.Whatis thefirsttermofthesequence?

Weknowtwoconsecutiveterms,sowecansubtractthemtofindthecommondifference.48-31=17. So,eachtermis17morethantheonebeforeit.So,thesecondterm,31,mustbe17morethanthe firstterm.Togetthefirstterm,subtractagain:31-17=14.

Butarithmeticsequencequestionscangetmorecomplicated:

-Thefirsttermofanarithmeticsequenceis5andthecommondifferenceis3.What isthe10thtermofthesequence?

Wecouldjustcountout10terms(whichwealreadydidabove,soweknowthe10thtermis32).But wecouldalsousethisformula:

an=a1+(n-1)d

anisthelasttermofthesequence(thetermwewant) a1isthefirsttermofthesequence nstandsforthenumberoftermswewant distheamountaddedtoeachterm

Inthisproblem,a1=5,d=3,andn=10.Therefore: an=5+(10-1)3=5+(9)3=5+27=32

Arithmeticsum

Sometimesaquestionwillaskusforthesumoftheterms,notjustthetermsthemselves.

-Thefirsttermofanarithmeticsequenceis3andthecommondifferenceis2.whatisthe sumofthefirst18termsofthissequence?

Wecouldliterallycountoutallthetermsandaddthemup.Thenumbersareprettysmall,sowecoulddoit: 3+5+1+9+11+n+15+11+19+21+n+25+21+29+31+33+35+37=360

Butthat'salotofnumbers,andthechancesofmakingacarelessmistakeareprettyhigh.Ifyouprefer,youcanremember anotherformula.Tofindthesumofthefirst11te1msofanarithmeticsequence: n(a1+an) sn::::: wheresnisthesumoffirstnterms.

To use this formula we need an the last term in the sequence. We can use the formula we learned before to find it: a,,=a1+(n-!)cl

Nowwecanstick37infora,,

=360

Wecouldalsocombinethesumequationwiththeequationforantoget:=n(2a1+(n-1)d) 2

Notethatthesumofconsecutivenumbersisjustanarithmeticsequencewhered=1.

Geometricsequences

Ageometricsequenceisasequenceinwhicheachtermisobtainedbymultiplyingacertainnumbertotheprevious term.Thenumberyoumultiplyeachtimeiscalledthe"commonratio".Here'sanexample: 1,2,4,8,16,32

Inthisgeometricsequence,thefirsttermis1,andthecommonratiois2.

Geometricsequencequestionsoftensimplyrequireyoutounderstandthisdefinition.

-Whatisthenexttermafter-1inthegeometricsequence27,-9,3,-1,...?

First,we'llfindthecommonratiobydividingthesecondtermbythefirstterm:

EachtermisobtainedbymultiplyingbyMultiply-1bytogetthenextterminthesequence:

2.Matrices

Thinkofamatrixasasetofdata.It'slikeatable,withnumbersorganizedintorowsandcolumns.Takeanytable,take awaythegridlinesandputinsomebigbrackets,andbarn!Youhaveamatrix.Unliketables,matricescanbedirectly added,subtracted,andmultiplied.Herearesomeexamplesofmatrices,withtheirdimensionslabeled:*

Additionandsubtraction

Toaddorsubtractmatricesofthesamedimensions,justaddorsubtractthecorrespondingentrieswitheachother. Forexample:

Multiplication

Multiplyingtwomatricesisamorecomplicatedprocessinvolvingsomeweirdrules.Let'stryone:

To multiply the matrices, take the entries in the first row of the first matrix, multiply each term with the corresponding entry in the first column of the second. Then add all those products. That gives you one entry in your new matrix. It goes in the first row and first column of the resulting matrix.

Dothiswitheveryrowandcolumnpair:

Dothissameprocessformatricesofanydimensions.Matchthefirstrowofthefirstmatrixtothefirstcolumnofthe secondmatrix:

3.ImaginaryandComplexnumbers

Youknowhowsometimesaproblemwillstartbysaying"Forallrealnumbers"?Whydotheysaythat?Arethereany numbersthataren'treal?

Yesthereare!Imaginarynumbersarenumbersthatcontaini,definedasi=Questionsinvolvingimaginarynumbers oftengivethedefinitionasi2=-l,butthat'sthesamething.Usually,you'renotallowedtotakethesquarerootofa negative,whichiswhynumbersthatdosoarecalled"imaginary".Oftenanimaginarynumberwillhaveacoefficient,such as"8i"or"3i".

MostimaginarynumbersontheACTinvolvecomplexnumbers.Acomplexnumberisapolynomialintheforma+bi,areal numberplusorminusanimaginarynumber.Let'slookatanexample: (3+2i)(5+3i)=?

ComplexnumbersworklikeanyotherpolynomialandcanbemultipliedusingFOIL: (3+2i)(5+3i)=3(5)+9i+l0i+6i2=15+19i+6i2

We'renotdone.Rememberthati2=-1,sowecansubstitute-1inthelastterm: =15+19i+6(-1)=9+19i

Occasionallyyoumaybeaskedabouthigherpowersofi.Ifyoumultiplyibyitselfabunchoftimes,you'llseethatthepowers ofishowarepeatingpattern:

4.Factorial(n!)

Very,veryrarelyaquestionmightaskyouaboutfactorials.Takingthefactorialofn(symbolis"n!")meansfindingthe productofalltheconsecutivenumbersupton.

3!=lx2x310!=1x2x3x4x5x6x7x8x9x10n!=1X2X(n-1)Xn

Youmightseeaquestionthatexpectsyoutoknowwhatthissymbolmeans.Othertimes,thedefinitionwillbegiventoyou inthetextofthequestion.Thisisatthebottomofthelistofimportantthingsforyoutoknow.

COORDINATEGEOMETRY

CoordinateGeometry,likePlaneGeometry,canbealove-it-or-hate-itfield.Somestudentsgeteasilyconfusedandscared byalltheselinesandformulas,andtheproblemstendbetowardthehardendofthetest.Otherstudentslovethelogicand consistencyoftheplane,andtheorderthatitbrings.

It'sokaytohateCoordinateGeometry.We'renotheretojudgeyou.Butweareheretohelpyouunderstandafew ofthebasicprinciplesbehindtheseproblems.Aswesawinalltheotherchapters,MathTestquestionsaskthesamethings overandoveragain,soalittlebitofknowledgecangoalongway.

Beforewegoanyfurther,it'simportanttoemphasizethatgraphsarepictures.Therefore,youcanuseGuesstimateon graphingproblems.You'dbeastoundedhowmanygraphingproblemscanbedonejustbylookingatthepicturetheygive you.Ifthislinelooksequaltothatline,thentheyareequal.Infact,Guesstimateisofteneasieroncoordinategeometry questionsbecausecoordinateshavevaluesyoucanuseasreferences.Onceyoubecomefamiliarwiththecoordinateplane, it'seasytoquicklyglanceatapointandsee"oh,thatpointhasanegativexandaybiggerthan7,soIcaneliminateA,B, andE."Don'tforgetGuesstimate.

THECOORDINATEPLANE

Thisisthestandard(x,y)coordinateplane(or"coordinateplane"or"grid"orwhateveryouwanttocallit):

Alotofyouprobablyalreadyknowyourwayaroundthisguy,but herearesomedefinitionsforthosewhoarenewtoit:

Thex-axisisthehorizontalline;ittellsyouthex-valueofapoint. Valuesofxarepositivetotherightandnegativetotheleft.

They-axisistheverticalline;ittellsyouthey-valueofapoint. Valuesofyarepositiveatthetopandnegativeatthebottom.

Thetwoaxesdividethecoordinateplaneintofourquadrants, oftenlabeledwithRomannumerals.Thesignofthex-andyvalueofapointwilldeterminewhichquadrantthepointliesin.

1.PlottingPoints

Pointsonthegrapharegivenas(x,y).PointPshownhereis(2,3), sinceithasanx-valueof2anday-valueof3.Youcantellthex-and y-valuesbylookingatwherethepointlieswithrespecttotheaxes. Theorigin(labeled"O"here)isthepointwheretheaxescross;ithas coordinates(0,0).

So,whatcanwedowiththesepoints?

Geometry

Coordinategeometryisstillgeometry-itdealswithshapesandpictures.Theonlydifferencebetween regulargeometryandcoordinategeometryisthatthecoordinateplanegivesspecificlocationsforevery point.You'llseecoordinategeometryquestionsthataskabouttraditionalshapeslikerectanglesand trianglesplottedontoacoordinateplane.Forexample:

-RectangleABCDhasverticesA(-3,6),B(4,6),C(4,l),andD(a,b).Whatarethe coordinatesofpointD?

Anytimeaquestionasksyouaboutpointswithoutgivingyouafigure,DRAW THEFIGURE.Itdoesn'thavetobeperfect;justsketchitout.

Inthisquestion,youcanseethatpointDwillhavethesamex-valueaspointAand thesamey-valueaspointC.SopointDmustbe(-3,1).

Youcanalsousethesepointstofigureoutlength.Andonceyouknowlengths, youcancalculateperimeter,area,andallthoseotherfunthingswe'lltalkaboutinthe nextchapter.Forexample:

-RectangleABCDhasverticesA(-3,6),B(4,6),C(4,l),andD(-3,1).Whatisthe perimeterofABCD?

Thisquestionasksusaboutthesamerectanglewejustlookedat.Butnowwewanttheperimeter.So,weneedthe lengthsofthesides.

Let'sstartbylookingatBC,therightsideoftherectangle.Itstwoendpointshavethesamex-valuebutdifferent y-values.So,wecancalculatethelengthbyjustsubtractingthey-values.6-1=5.

Nowlet'slookatAB,thetopoftherectangle.Itstwoendpointshavethesamey-value butdifferentx-values.So,wecancalculatethelengthbysubtractingthex-values. 4-(-3)=4+3=7.

Oppositesidesofarectangleareequal,sotheperimeteris5+5+7+7=24.

Youcaneasilyfindthelengthofhorizontalorverticallinesegmentsby subtractingtheirx-ory-values.That'sthewholepointofhavingagrid!Butwhatabout pointsthatdon'tshareavalue?Howdowefindtheirdistance?

Distance

Ifyouwanttofindthedistancebetweentwopointsonagraph,justusethePythagoreanTheorem:

-WhatisthedistanceincoordinateunitsbetweenP(2,2)andQ(6,5)?

Notethatthisisexactlythesamethingwejustdid.Thedistanceformulaisnothingmorethanthe PythagoreanTheorem.Anytwopointsonthecoordinategridcanformarighttriangle:(x2-x1)isone legofthetriangle,(y2-y1)istheotherleg,andthedistancebetweenthepointsisthehypotenuse.

Midpoint

Thisquestionasksaboutthesamepointswejustlookedat.Tofindthecoordinatesofthemidpoint betweentwopoints,

Theaverageofthex-values,2and6,is

So,thecoordinatesofthemidpointare

2.GraphingFunctions

.Theaverageofthey-values,2and5,is

Agraphonthecoordinateplaneisnothingmorethanapictureofafunction.Taketheequationy=2x.Wecouldplugin anynumberwelikeforxandwe'llgetavalueforyasaresult.Inthehandout,wehaveatableofx'sandtheirrespectivey's, alongwithagraphofthosepointsplottedonthegrid.

Wecanseethatthepointswechosestarttomakeastraightline.Ifwefillinallthepossiblex'sandtheircorrespondingy's, includingallthenastydecimalnumbers,that'sexactlywhatwe'dget.Thegraphofy=2xisapictureofallthepossible solutionstotheequation-everyxpairedwithitscorrespondingy.Ratherthandefiningourequationasy=2x,wecouldcall itf(x)=2xandsaythaty=f(x)inthegraph.Don'tgetboggeddownwithallthedifferentletters.

Themostimportantthingtorememberis:Ifapointliesonthegraphofafunction,thecoordinatesofthatpointwill satisfythefunction'sequation.Andviceversa.Evenifyoudon'tknowtheequationofthefunction,youcanlearnalotjust fromthepicture.Forexample:

-Thefiguretotherightshowsthegraphofy=f(x). Whatisthevalueof_f(1)?

Ifthey'dgivenyouanequationforf(x),youcouldfind.f(1)bysubstituting"1"for"x"in theformula.Noproblem.Butherewedon'thaveanequation.Hmm.That'sacrazy, crazylookingfunction.We'llneverbeabletowriteanequationforit.

Butwedon'tneedanequationbecausewehaveagraphofthefunction!Agraphis apictureofthefunction.Everypointonthatsquigglylineisasetofnumbersthat Wewantthevalueoff(1).So,wejusthavetofindthevalueofywhenx=1.That's3! Thesquigglylinecrossespoint(1,3).Whenx=1,y=3.Sof(1)=3. Thisisanimportantpoint,soitbearsrepeating:

Ifthepoint(a,b)isonthegraphoff,thenf(a)=b. Iff(a)=b,thenthepoint(a,b)isonthegraphoff Findthesepointsonthegraphabove: -f(-1)=? -f(2)=? -f(0)=? -f(3)=?

Alotofpeoplegetconfusedbythisnotation,sohere'satricktohelpyouremember.Ifyoudrawinsomeparentheses,the equationlooksjustlikeacoordinatepair.So:

f(1)=3

f((1)=3) becomes f(x)=Y f((x)=y)

Intersection

Thisfactaboutpointsandfunctionshasaninterestingconsequence:Ifapointona y graphisasolutiontothatfunction'sequation,thenapointwheretwographs intersectisasolutiontobothfunctions'equations.

Forexample,considerthesefunctions:

y=2x+3

y=x+5

Whenwehavetwoequationstogetherlikethiswecallita"systemofequations". Eachequationhasaninfinitenumberof(x,y)pairsthatmaketheequationtrue. Butthere'sonlyonepairthatmakesbothequationstrueatthesametime:(2,7).

Thegraphofeachofthesefunctionsisastraightline.Ifwedrawbothlinesinthe sameplane,wecanseethatthetwolinesintersectatthepoint(2,7).Point(2,7)isthe solutionforthesystemofequationsandtheplacewherethetwolinesintersect.

Inequalities

Mostgraphsyou'llseeontheACThaveequationsthatdescribethem.Butyoucanalsographinequalities.Thegraph ofaninequalitylooksjustlikethegraphofthecorrespondingequation-alineoracurveofsomekind-but withashadedregionaboveorbelowtheline. y

For example, the figure to the right shows the graph of y2> 2x. Notice that the line running through the middle looks exactly like the line for y = 2x that we saw earlier, but now the region above the line is shaded. That means that all the points within the shaded region satisfy the inequality.

For this graph, it should be easy to understand why the area above the graph is shaded. The line shows all the points where y equals 2x, so all the points above the line have ay-value greater than 2x.

But if you're not sure which region you want to shade, you can always try some test points. Pick a point above the graph, let's say (0,2). Now let's plug x = 0 and y = 2 into the inequality y>2x and see if it works:

2>2(0) 2 > 0 It works!

Let's check a point from the other side of the line, say (0,-2),just to be sure.

-2>2(0)-2>0xThatdoesn'twork!

Aftertryingthosepoints,wecanseewemustshadetheareaabovethegraph. (Hmm...usingrealnumberstotestanalgebraicexpression.Haven'twedonethat before?Ohyeah!That'sPlugIn!)

LINES

ThemostbasicfunctiononCoordinateGeometryquestions1sastraightline.Thereareseveral characteristicsthatdefinealine.

1.Slope

Asthenameimplies,slope,abbreviated"m"forsomereason,isawaytomeasurethe"steepness"ofa line.Lookingfromlefttoright,apositiveslopegoesupandanegativeslopegoesdown.Asyoucansee fromtheexamplesbelow,themorethelinegoesup,thelargeritsslope;themorethelinegoesdown,the smalleritsslope.

Thereareseveralthingstorememberwhencalculatingslope:

-Makesureyisontop.WerepeatmakesureYisontop.Youwillnotbegiventheformulafor slope.Youhavetorememberit.

-Beconsistentwithxandy.Youcanstartwitheitherpoint,butyouhavetostartwiththesame pointonthetopandthebottom.Intheexampleabove,whenweuse4firstonthetop,we must use6firstonthebottom.

-Parallellineshaveequalslopes.

-Theslopesofperpendicularlinesarethe"negative reciprocals"ofoneanother.Takethefirstslope,make itnegative,andflipthefractiontogetthesecond slope

2.Intercepts

An"intercept"isjustthepointatwhichthelinecrossesoneoftheaxes.Sothe interceptisthepointatwhichthelinecrossesthex-axis.And isthe pointatwhichthelinecrossesthey-axis.

Inthefiguretotheright,thelinehasay-interceptof3,sinceitcrossesthey-axisatthe point(0,3).

Inthefiguretotheright,thelinehasanx-interceptof2,sinceitcrossesthex-axisatthe point(2,0).

Wecanusetheslopeandinterceptstowriteanequationofaline,calleda"linearequation".Anylinewill haveacorrespondingequationthatcontainsoneandonewithnoexponents.Thereareseveral differentwayswecanwritealinearequation.

Slope-interceptform(y=mx+b)

Themostusefulformofalinearequationis y=+The"m"standsforthe slope,thestandsforthey-intercept,andthe"x"and''.,v"standforthecoordinatesofanyandall pointsontheline.

Let'sseethisstuffatwork:

Tofindtheequationoftheline,weneedtheand

First,sinceweknowtwopoints,wecanfind theslope.

Nowweknowm,soourequationsofarisy=1/2x+.Tofindlet'sjuststickoneofthepointsweknowinforandwe use(2,3)here-andthenwecansolvefor

So,ourequationis=½+2

Thegraphofthelinecanbeseenatright

Standardform(ax+c)

Theslope-interceptformisgreatbecausewecanimmediatelyfindtheslopeandy-interceptofthelinejustby lookingattheequation.Unfortunately,ACTproblemsoftenpresentlinesinthestandardform.Don'tworry aboutthename;that'sjustafancywordfortheform

Annoyingly,inthisformand(5,6,and7)don'tdirectlycorrespondtoanythingaboutthegraphoftheline,sothe equationdoesn'thelpusmuch.Ifwewanttheslope,wehavetoconvertittotheslope-interceptform.Todothat,just solvetheequationfor

CIRCLES

MostgraphfunctionsontheACTarelines.Ofcourse,intherealworld,linesarejustthetipofthegraphingiceberg. OntheACT,wewillmostlyjustseetwotypesofcurvedgraphs:circlesandparabolas.ThemostcommoncurveontheACT isacircle.Theequationofacircleisdefinedas:

whereristheradius,and(a,b)isthecenterofthecircle.Ifthecircleiscentered ontheorigin(0,0),the"-a"and"-b"won'tbethere.Forthegrandmajorityof CoordinateGeometrycirclequestions,allyouneedtoknowisthisequation,so LEARNIT!Let'slookatanexample:

Acircleinthestandard(x,y)coordinateplane hascenter(3,2)andradius5coordinateunits. Whatistheequationofthecircle?

We'lldiscusscirclesmoreinthePlaneGeometrychapter.Theonlyotherthingyou needtoknowforCoordinateGeometryisthetangentline.

Usually,ifyoudrawalinethroughacircle,itwillcrossthecircleintwopoints-once whereitentersthecircleandagainwhenitleaves.Atangentlineisalinethattouches thecircleatexactlyonepoint.Inthefiguretotheright,they-axisistangenttothe circleatthepoint(0,1),andthex-axisistangenttothecircleatthepoint(1,0).Note alsothatthetangentlinesareperpendiculartotheradiusofthecircle.

Ellipses

Anellipseislikeacirclethat'sbeenstretchedoutintwooppositedirections.Theequationofanellipseis definedby where(h,k)isitscenteroftheellipse,2aisthelengthofthehorizontal axis(alongthex)and2bisthelengthoftheverticalaxis(alongthey).

EllipseshaveshownupontheACT,butvery,veryrarely.Ifyoudon'talreadyknowhowtodealwithellipses, don'tworryaboutthem.Yourtimewouldbebetterspentmakingsureyouunderstandcircles.

PARABOLAS

IntheElementaryAlgebrachapter,wetalkedaboutquadraticequations.Previously,wehadanequationequal tozeroinsteadofy:therewereonlyoneortwovaluesofxthatsolvedtheequation.Here,wehaveafunction:wecan stickinanyvalueforxandgetoutay.Aquadraticequationisaquadraticfunctioninwhichy=0. Whatdoesthatmean?Itmeansthattherealsolutionstothequadraticequationcorrespondtothex-interceptsofthe parabola.Anx-interceptisapointonthegraphwherey=0.So,youcanquicklyfindthesolutionstoaquadraticequationby lookingatitsgraphandfindingtheplaceswhereitcrossesthex-axis.

Parabolascanalsobewritteninequationswithdifferentforms,suchasy-h=j(x-k)2where(h,k)isthevertexofthe parabola.Butmostparabolaequationswillbeexpressedasapolynomial,asshownabove. CLICKHERETOACCESSTHECOORDINATE

GEOMETRYDRILL

Want More Help? Why Not Schedule a Capstone Tutor. Who Better to Take You to the Next Level Than the Tutors Who Are Most Familiar With the Material? Click Here To Schedule

PLANEGEOMETRY

PlaneGeometryisabigpartoftheACTMath-itmakesupalmostaquarterofthetest.A"plane"isjustanytwo-dimensional surface,so"PlaneGeometry"iswhatwemeanwhenwetalkabout"geometry"ingeneral.Youwilloccasionallysee somethree-dimensionalsolidsontheACT,butit'smostlyflatstuff-triangles,squares,circles,andalltheirfriends.Wesawsomeof thisstuffintheCoordinateGeometrychapter,butnowwewon'thaveanyaxesorcoordinates.

Ifyou'vehadarigorousgeometryclassinschool,youprobablyhadtolearnalotoftheorems-littlerulesaboutanglesand lengthsandallsortsofweirdthings.OntheACT,youdon'tneedallthoserules.youneedisthestuffinthischapter. We'reonlygoingtoshowyouafewsimplerulesandnotmuchelse.Anyothertheoremsorrulesthatyoumayhaveheard aboutareonlytruethestuffinthischapter.Butifyoudoneedamorecomplicatedrule,youcanfigureitoutfrom thebasicrules.

Ofcourse,thatmeans Thatmeansmemorizingtheformulasand definitionsdiscussedinthischapter.Thebetteryouknowthem,theeasierlifewillbeforyou.

INTRODUCTORYREMARKS

Don'tforgetabout Ifyouseeaquestionwithapicture, checkthatit'stoscale, guessthevaluethey'reaskingfor,andtheneliminateanyimplausiblechoices.

Inthischapterwe'regoingtobetalkingaboutalotofstraightmathcontent(rulesandformulas).Butthatdoesn'tmeanyou shouldforgetaboutthetechniques.AndnotjustGuesstimate.YoucanusePlugInandBacksolveongeometryproblems, too.So,stayalert.

Whilethenumberofrulesyouneedonthetestisrelativelysmall,itmaystillseemburdensometoyou.Imean,howdoyou knowwhichruletouseonwhichquestion?Wheredoyouevenbegin?

Justlikewesawbefore,therearetwoquestionstoaskyourself: Iwant? Iknow?

Thegoalofeverygeometryproblemistoconnectthesetwoquestions,toplaywithwhatyouinordertogetwhat youTakealookatthisproblem:

Theareaofthecircle.

Aswe'llsoonsee,theformulafortheareaofacircle=m·2Tofindthearea,wewillneedtheradiusofthe circle(orthediameter,whichisjustdoubletheradius).

Thelengthoftherectangleis12andthewidthis6.

Sotherealkeytothisproblemis:

Aha!Thewidthoftherectangleisequaltothediameterofthecircle!HowcanItell?ByGuesstimate!Don'tworryabout theweird"tangent"stuff:theyequal.

Thewidthoftherectangleis6,sothediameterofthecircleis6.Sotheradiusis3,andtheareaofthecircleiswhichis c.

Thepointhereisthat

There'salwaysthatyouknow, somethingthatyoucanfigureout.Don'tbescaredofthefigures,justputdownwhatyouknowandtrytoconnect ittowhatyouwant.

Knowyourpolygons

isanyshapewithstraightedge.You'reprobablyalreadyfamiliarwithsomeofthem:

Aisapolygonwith3sides.

A isapolygonwith4sides.

Aisapolygonwith5sides. Aisapolygonwith6sides.

Polygonscanhavemanymoresideswithevenmorecomplexnames,butyouprobablywon'tseethoseontheACT. Quadrilateralsinparticularcomeinalotofdifferentshapes,andeachshapehasitsownfunnyname.SometimesanACT questionwilldefinethesetermsforyou,butit'sgoodtounderstandtheminadvance:

ANGLES

Therearefivethingsyouhavetoknowaboutangles.

Ofcourse,thereareotherrulesthatexistaboutangles,butthey'reonlytrue theserules.Forexample,takea lookatthisproblem:

-Whatisthesumofthemarkedanglesin quadrilateralshowtotheleft? What?Theydon'ttellusanythingaboutthisthing!Whatevershallwedo?

Fearnot.Wedidn'tlearnanyrulesaboutanglesofquadrilaterals.Butwe knowthatatrianglehas180°.Let'ssplitthisguyupintotriangles!

Thequadrilateralismadeupoftwotriangles.Eachtrianglehas180°.So,the quadrilateralhas2x180=That'sit.We'redone! B

Someofyoumayhavealreadyknownthattheanglesofanyquadrilateraladdup to360°.Butwecandothiswithanyshape.Drawtrianglesusingonlytheshape's existingvertices.Wecanseethatapentagoncontains3triangles,soitsangles addupto3x180=540°.Andahexagoncontains4triangles,soitsanglesaddup to4x180=720°.

Thepointisthatyoudon'thaveto memorizeabunchofruleslikethat.Justknowthefivebasicanglerulesandyoucanfigureoutanythingelseyouneedto knowaboutangles.

Youshouldneverbetotallystuckonaproblemthatdealswithangles,becausethere'salways youknow.More oftenthannot,justputtingdownwhatyouknowbasedontheseruleswillleadyoutowhatyou'retryingtofind-evenif youdon'tseewhereyou'regoingwithit."Okay,Ireallydon'tknowhowtofindwhattheywant,butIknowthat'sa triangle,soitsanglesaddupto180.AndIknowthat'sastraightline,sothoseanglesaddupto180..."Etcetera.Justplay withtheserulesandseewhereittakesyou.

Andremember:

TRIANGLES

TrianglesarethekeytoalotofACTquestions;you'llseealotmoretrianglesthananyothershape.Infact,ifyou're confrontedwithanoddshapeyoudon'tunderstand,trydrawinginatriangle.Wealreadysawanexampleofthatinthe quadrilateralprobleminthelastsection.Wedidn'tknowanythingaboutquadrilaterals,butweknowalotabout triangles,sowedrewsometriangles.Trianglesareyourbestfriend.Trustus.

1.ThePythagoreanTheorem

ThePythagoreanTheoremisawaytofindthethirdsideof Trythisone:

Someofyoumayhaverecognizedthetriangleintheproblemabove.It'sa"PythagoreanTriple".BecausethePythagorean Theoremhasallthose"squares"init,mostrighttrianglesdon'thaveintegervaluesforallthesides.Sothetrianglesthat haveallintegersshowupalot.The3-4-5isacommonone..Ifyouseeatrianglethathaslegsoflength3and4,you knowimmediatelythatthehypotenusemustbe5.

Beonthelookoutformultiplesofthe3-4-5,aswell.Forexample,a6-8-10triangleis justa3-4-5trianglewitheachsidemultipliedbytwo.

Beingabletospota3-4-5trianglecansaveyousometime.Ifyouseeatriangle withlegs6and8,youknowimmediatelythehypotenuseis10,withouthavingto doouttheTheorem.Butspottingthisisreallyjustabonus;ifyoucan'tseethe3-4-5 triangle,don'tworry.YoucanalwaysusethePythagoreanTheoremtofindthe dimensionsofarighttriangle.

Don'tbetooquicktodeclareatriangle3-4-5.Thehypotenusemustbethelargestsideofatriangle.If atrianglehasof4and5,thehypotenuseis3.

2.TheIsoscelesRightTriangle(45-45-90)

Anrighttrianglehastwolegsofequallength,andtwo45°angles.*Thedimensionsofthesetriangles arealwaysinthesameproportion:

Noticethatweknowallofthesetrianglesare45-45-90eventhoughtheydidn'ttellustheanglesare45°. That'sbecauseweknoweachhastwoequalsides-andthataloneisenoughtomakethemisosceles.

3.The30-60-90Triangle

Anytrianglewithanglesof30°,60°,and90°willalwayshavethesamedimensions,asshowninthe figuretotheleft.

It'sthesameconceptasthe45-45-90triangle:ifIknowjustafewthingsaboutthetriangle,Icanjustfill inallthevaluesfortherestofthetrianglewithoutdoingalotofcalculationsorbotheringwiththe PythagoreanTheorem.

Thisone'sabittrickiertoremember,sinceeachsidehasadifferentvalueand it'seasytomixupwhereeverythinggoes.Here'satipforrememberingwhich angleandwhichlengthgoeswhere:thistriangleissimplyhalfanequilateral triangle(seediagramtoright).Alinedividesoneofthe60°anglesintotwo30 angles,andthencutstheoppositesideinhalftoo.

Sometimes,itmaynotbeobviousthatatriangleinaproblemis30-60-90or45-45-90.Butnoticethatthesetrianglesinvolvetwo specialnumbers: Thesenumbersdon'tshowupveryofteninothersituations.So,ifyou'redoingaproblemand noticeintheanswerchoices,there'saprettygoodchancethatthere'sa30-60-90triangleintheproblem.Thesamegoesfor ifyouseeitintheanswers,there'sagoodchancethere'sa45-45-90triangleintheproblem.Ofcourse,thisisn't true.Butifyou'restuckonaproblem,lookforthesehappymagicnumbers.Theycouldhelpyouspotsomethingyouwould havemissedotherwise.

4.SimilarTriangles

Ifalltheanglesofonetriangleareequaltoallthecorrespondinganglesofasecondtriangle,thentheyare Thatmeansthatalltheirsidesareinthesameratiowitheachother.

Here,hasallthesameanglesassotheyaresimilartriangles.=7and14,soisdouble Sincethetrianglesaresimilar,eachsideofwillbedoublethecorrespondingsideofSo,2(10)=20, and2(12)=24.

Whendealingwithsimilartriangles,it'simportanttokeeptrackofwhichsideiswhich.willbeproportionalto becauseeachofthemisacrossfromtheangle.

This,bytheway,isexactlywhywecandothatstuffwiththe30-60-90triangleswejustsaw.All30-60-90triangleshavethe sameangles,thereforetheirsidesareinthesameratio-

Similartrianglesdon'thavetobenexttoeachother.Oftenthesequestionswill feature Inthefiguretotheleft,ifisparallel tothen=Therefore,issimilartobecauseall of theircorrespondinganglesareequal.

5.Lengthsofthesidesofatriangle

Thereareseveraladditionalpointstobemadeabouttherelationshipbetweensidesinatriangle.

Well,thatmakessense,sincethePythagoreanTheoremsaysaandtogethercontributetoc.So,ifsomeonetells youarighttrianglehassidesof7,24,25,youknowrightawaythatthehypotenuseis25andthelegsare7and24. Inarighttriangle,the90°anglemustalwaysbethelargestangle,sothesideopposite(thehypotenuse)mustbethe longestside.Butthissameruleholdsfortriangle:

Or,moregenerally,"thelargertheangle,thelargertheoppositeside."There'sadefiniterelationshipbetweenthe lengthsofthesidesofatriangleandtheanglesoppositethem.That'sexactlywhyanisoscelestrianglehastwoequalsides twoequalanglesoppositethem.

Let'slookatthisinaction:

Asyoucanseefromthesefigures,whenwemakeanglebigger,sideoppositeitalsobecomesbigger.Ditto,whenis smaller,issmaller.

Butaretherelimitstohowbigorsmallthatthirdsidecanget?Yes,thereare:

Thethirdsideofatrianglemustbethantheoftheothertwosides.

Let'sseehowfarwecanstretchthesetriangles.Ontheleft,we'llmakeanglebiggerandbigger;ontheright,we'llmake anglesmallerandsmaller.Let'sseewhathappenstoside

Wecankeepstretchingangleuntilitreaches180°-astraightline.Inthatcase,isexactlyequaltoandcombined. Butifwedothat, It'sjustastraightlinenow.So,ifwewantittobeatriangle,anglehastobelessthan 180°,sothethirdsidehastobelessthanthesumoftheothertwo.

Ontheright,wecanseethesamethinghappeningintheoppositedirection.Anglecankeepshrinkinguntilitgetsto0°. Nowwehaveastraightlineagain,thistimewithlyingontopofSo,isequaltothedifferenceoftheothertwo: -Butagain,ifwedothat, So,ifwewantittobeatriangle,anglehastobe greaterthan0°,sothethirdsidehastobegreaterthanthedifferenceoftheothertwo.

Similarly,wecanseethatifthethirdsidewerebiggerthanthesumoftheothertwo,thetwosmallersideswouldn'tbeable toreacheachother:

PERIMETER,AREA&VOLUME

Let'sstartwithafewdefinitionsandformulas.NotethatthisisyouneedtoknowfortheACTaboutperimeter,area, andvolume.Ifyouwanttofindtheareaorvolumeofashapethatisn'tlistedhere(likeapentagonorapyramid),either: or

Theperimeterofanyfigureisthesumofthelengthsofalltheoutsideedges. Okay?Okay.

SomeACTquestionswillgiveyouformulasinthequestions.Butyou'llbeexpectedtoknowtheformulasforbasicshapes Youhavetoknowthem.Ifyoudon't,

Noticethattheformulaforaparallelogramisbasetimesnotthe -Theformulasforsquaresandrectanglessaythesamething.Asquareisjustarectanglewithequal sides,s=l=w.Similarly,arectangleisjustaparallelogramwhoseheightisequaltooneside.

Noticethattheareaofatriangleishalftheareaofarectangle.Imaginecuttingarectangleinhalf alongthediagonal;you'dgettworighttriangles.Andforeachtriangle,thebaseandheightare equaltothelengthandwidthoftheoriginalrectangle.Thesameistrueforanyparallelogram:it ismadeupoftwoidenticaltriangles,soitsareaistwicetheareaofatriangle

Youcanalsousetrianglestofindtheareaofothershapesthataren'tshownhere.Forexample,the areaofatrapezoidistheheighttimestheaverageofthetwobases.Butyoucanalsoseethisby asseenbelow.Again,weuse therulesweknowtofigureouttheruleswedon't.

Shadedareaproblemsarebestdoneby Findtheareaofthewholefigureandtakeawaywhatyoudon'tneed.

Takealookatthisone:

Inthefigurebelow,asmallsquareisinsidealarger square.Whatistheareaoftheshadedregion?

Itmaybetemptingtotrytofindtheareadirectlybydividinguptheshadedregionintofour rectangles.Butwecan'tfindthoseareasbecausewedon'tknowalloftheirdimensions. Plus,it'skindoftedious.

Instead,let'sjustfindtheareaofthesquareandsubtracttheareaofthe square.Whatever'sleftwillbetheareaoftheshadedregion.

Awhole=s2=82=64

Aunshaded=52=25

Ashaded=AwholeAunshaded =64-25=39

3.SurfaceArea

Wefindthe"surfacearea"byfindingtheoftheThatmeanswehave tofindtheareasofalltheshapesontheoutsideofthebox.Aboxismadeupofabunch ofrectangles;we'llfindtheareaoftherectanglesandaddthemallup.That'sit. Thisboxhasdimensions12,8,and5.Tofindthesurfacearea,we'lltaketheareasofall therectanglesontheoutsideandaddthemup.

Wecanseethattherearethreetypesofrectanglesinthisbox:

=12x8=96

=12x5=60

=8x5=40

BUT,eachofthesesidesshowsupinthebox(topandbottom,frontandback,sideandside.)

SA=2(A1+A2+A3) =2(96+60+40)=2(196)

A=392

Again,acubeisjustaspecialtypeofbox.Sinceit'smadeupof6squares,we'll justfindtheareaofonefaceandmultiplyby6.Thissquarehasedgesoflength4. 6(A0

6(s2)=6(42)=6(16)

SA=96

Justlikewitharea,you'llbeexpectedtoknowsomeformulasforvolume,whilemorecomplicatedformulaswillbe giveninthequestion.

Learnthese:

CIRCLES

WealreadyspokeaboutcirclesabitintheCoordinateGeometrychapter.Let'stakeacloserlookatthem:

2.Formulas

-Theperimeterofacircleiscalleditscircumference(C).Thecircumferenceisequaltothe diametertimesTC,whichisthesameastwotimestheradiustimesTC(sincethediameterequalstwo radii).

-Notethatthedistanceawheeltravelsinonerevolutionisequaltothe circumferenceofthecircle.

-TheareaofacircleisequaltotheradiussquaredtimesTC.

-(pronounced"pi")standsforaspecialnumberwhosevalueisapproximately3.14.Formost ACTproblems,youdon'thavetocalculatethenumber;youcanjustleaveitasthesymbol. Thecircleshownherehasaradiusof3.Therefore:

Almosteverythingwedowithacirclerequiresknowingitsradius(ordiameter,whichisjustdoubletheradius).Ifyou're givenacircleandyoudon'tknowitsradius,beforeyoudoanythingelse You'llprobablyneedit, evenifyoudon'tyetknowwhy.

Awedgeorsliceofacircleisnothingmorethanaofacircle.Problemsdealing withthemcanbedonewithsimpleratios.Takealookatthiscircle: Obviously,theshadedsectionisonefourthofthecircle.HowcanItell?Firstofall, becauseitlikeafourthofthecircle(Guesstimate!)

Secondly,weknowcentralangle, °90isonefourthof360.Sothatcentral angleisonefourthofthewholeangle(360).

Let'ssaythecirclehasaradiusof10.So,itsareais100Theareaofthesliceisone fourthofthat:

Ifthecirclehasaradiusof10,itscircumferenceisThelengthofminorarcisonefourthofthat: Thisisprettyeasytosee.Sincethatsliceisonefourthofthecircle,everythingaboutthatsliceisonefourthof thecorrespondingcharacteristicofthecircle:theangleisonefourthof360,theareaisonefourthofthecircle's area,andthearclengthisonefourthofthecircumference.

TRIGONOMETRY

TrigonometrycanbethescariesttopicontheACTbecauseit'sthemostadvanced.Someofyoumaynothavedoneany trigonometryinschool,sothiswillbeentirelyunfamiliartoyou.TherearealotofweirdsymbolsandGreeklettersinvolved, anditcanbequiteintimidating.Buttrigonometryisn'tnearlyasbadasyouthinkit'sgoingtobe.

Firstofall,therewillonlybe4trigonometryquestionsoneachtest.That'sright:four.Thisisbyfartheleastsignificantofall themajortopicswe'vecovered.So,ifyoureallydon'tunderstandwhat'sgoingonhere,yourtimewouldprobablybebetter spentonsomeoftheotherconceptsandtechniquesthatappearmorefrequently.

Second,becausetrigonometryquestionsaresodifficultforstudents,theytendtoappearattheendofthetest.Thatmeans thatalotoftrigonometryquestionswillbepastyourtargetnumbers,soyouwon'tevenreadthematall.

Third,whilesometrigquestionsdoinvolvesometrickyconcepts,mostofthemjusttestyourknowledgeofthedefinitionsofthe basictrigonometricfunctions.Onceyoulearnthose,you'IIbeabletodomorethanhalfofallACTtrigonometryquestions withoutbreakingasweat.

TRIGONOMETRYFUNCTIONS

1.BasicFunctions

Whatistrigonometryand,whydoweneedit?Itallbeginswithrighttriangles. Rememberwhenweweretalkingabout45-45-90triangles?Wesaidthateverytrianglewhoseangles measure45 ° ,45°,and90°havedimensionsinthesameproportion,1:1:

Theseratiosarethewholepointoftrigonometry.Therearethreebasictrigonometryfunctions: sine,cosine,andtangent(abbreviated"sin","cos",and"tan").Thesefunctionsdoexactlywhatwejust did:theytaketheratiosofthesidesofarighttriangleinrelationtoaspecificangle. Herearethedefinitionsforthesefunctions:

Thesymbol""istheGreekletter"theta".It'softenusedtodescribeanglesintrigonometryproblems.Notethatthese functionsonlyworkwithrighttriangles-trianglesthatcontainarightangle.

MEMORIZETHESEDEFINITIONS.OverhalfofallACTTrigonometryquestionsrequirenothingmorethanknowingthese threedefinitions.YoucanremembertheseratiosviatheacronymSoHCAHTOA: Sine=OppositeoverHypotenuse,Cosine=AdjacentoverHypotenuse,Tangent=OppositeoverAdjacent

Calculatingtheratios

Let'slookatanexample:

-In.ABCtotheright,whatisthevalueofsinA?

Weknowthatsineisequaltotheoppositesideoverthehypotenuse.Thesideopposite angleAis4,butwedon'tknowthehypotenuse.WecanusethePythagoreanTheoremto findit,orwecanseethatit'sa3-4-5triangle,sothehypotenuseis5.Therefore, sinA= Infact,oncewehaveallthelengthsofthesides,it'seasytofindalltheratios:

SinA= cosA=tanA-=SinB=cosB=tanB= Let'stryonethathasanswerchoices

35.If0 ° <x<90 ° andtanx=,whatiscosx?

Thisquestiondoesn'tgiveusafigure,so Itdoesn'thavetobetoscale,justdrawatriangleandcall oneangle

Tangentisoversothesideoppositexis5andthesidenexttoxis8. Wewantcosx:that'sover Weknowthattheadjacentsideis8,butwe don'tknowthehypotenuse.WecouldusethePythagoreanTheoremtofindit.But look-alltheanswerchoicescontaincombinationsof5,8,and.Sothehypotenuse be..Wedon'thavetodooutthework.Nice!

Thesideadjacentto8,thehypotenuseis.,socosxis

Thesequestionsrefertoshownatright. sin tan

Usingtheratiostofindlengths

Herewedon'thavetoactuallyfindthevalueforWejusthavetosetupthesolution. Weknowouranswerwillinvolveatrigfunctionusingthe25°angle.Weknowthehypotenuseis12. Wewantwhichisthesidethe25°angle.Therefore,we'llneedatrigfunctionthatinvolvesthe sideandthe Whichonedoesthat?Sine!Wecansetuptheratiothisway: °

Tosolveformultiplybothsidesby12. That's

Let'stryanother:

35.Inbelow,lengthsaremeasuredininches. Whichofthefollowingisclosesttothelength,ininches,

(Note:sin65 ° 0.906,cos65 ° .423, tan65 ° 2.144)

Thistimewewanttofindanactualvalueforthelength.We'llstartthesamewaywedidbefore. Weknowouranswerwillinvolveatrigfunctionusingthe65°angle.Weknowthesideoppositeis20.

Wewantwhichisthesidetothe65°angle.Therefore,we'llneedatrigfunctionthatinvolvestheside andtheWhichonedoesthat?Tangent!Wecansetuptheratiothisway:

Reciprocalfunctions

Thethreebasicfunctionsshowthreeratiosofsidesofarighttriangle.Butthosearenottheonlycombinationsofsides. Wecouldalsoflipthefractionstogetthe Thesearecalled(csc),(sec),and (cot).

COSECANT:csc

SECANT:sec

COTANGENT:cot

It'seasytomixtheseupbecausethe"co-"sdon'tmatch:isthereciprocalofandisthe reciprocalof

OntheACT,thereciprocalfunctionsdon'tshowupnearlyasmuchasthebasicfunctions,butyouwillsee themoccasionally,soit'sstillimportanttolearnthem.

Sofar,we'vebeensolvingforlengthsortheratiosoflengths.Butwhatifwewanttosolvefortheangles? -If0° <x<x=x=?

Wecansolvethatdirectlyforbyusing (abbreviatedsin-1).Thisisthesamethingasthereciprocal functionsmentionedabove.It'spurelyawaytosolveanequationlikethisfortheangle.Itasks "thesineofwhatanglecomesto0.529?"Youcansolvethisbypunchingitoutonyourcalculator:

sinx=0.529 =sin-1(0.529)32.

All trigonometric functions have inverse functions like this. On the ACT these functions are not very useful-questions rarely ask you to solve for angle values like this. But the symbols may occasionally show up, so it's good to understand what they mean.

In the Elementary Algebra chapter, we spoke about identities. These are equations that show up frequently, like the "difference of squares" identity, so that you can memorize their forms and do the algebra quickly.

Thereareaofrulesandidentitiesrelatedtotrigonometryfunctions.Theycangetcomplicatedandhardtoremember. Luckily,ifanACTquestionrequiresoneoftheserules,itwillalmostalwaysbegiveninthe question.However,therearetwoidentitiesyouwon'tbegiventhatyoushouldremember:

Ifaquestionasksyoutoalgebraicallymanipulateanexpressionthatcontainsatrigfunction,chancesareyou'llneedoneof theseidentities.

Allthetrigfunctionswe'veseenonlyapplytorighttriangles.Butwhatifyouhaveatrianglethatcontainaright angle?Therearetwo"laws"thatcanhelpyou:theLawofSinesandtheLawofCosines.

Thenicethingabouttheselawsisthat

IfyouneedeitheroftheselawsonanACT question, Buteventhoughyoudon'tneedtotheformulas,it'sstillagoodideatobefamiliar withtheprinciples.

The statesthatintriangle,theratioofthesineofanangletothesideoppositeisalwaysconstant.Ifyou knowtwosidesandanangle,ortwoanglesandaside,youcansetupasimpleratiotosolveforanyothersideorangle. The givesarelationshipbetweenthreesidesandoneangleinanytriangle.Ifyouknowthreesides,you canusetheformulatosolveforanangle.Orifyouknowtwosidesandanangle,youcan useittosolveforthethirdside.

GRAPHINGTRIGONOMETRICFUNCTIONS

DomainandRange

Ifyoulookatthey-valuesofthegraphsabove,youcanseethattheynevergetabove1orbelow-1.Thefancywordforthisis Therangeofafunctiongivesallthepossiblevaluesofthatfunction.Here,therangeofy=sinxandy=cosxis

That'stherangefortheentirefunction,butwecanalsofindtherangeofapartofthefunctionifweonlyfocusonacertain groupvalues.Wecallthatselectionofx-valuestheForexample:

Whataretherangesofy=sinxandy=cosx inthedomain0o<x<180o?

Lookatthegraphsabovebutonlylookatx-valuesfrom0°to180°.Findthehighestandlowesty-valuesinthatspan.Theyvaluesofy=sinxgofrom0to1andbackto0.They-valuesofycosxgofrom1to0to-1.Sotherangeof=sinxis0<y<1 whiletherangeofy=cosxis-1<y<1

Radians

Thegraphaboveactuallyshowstwodifferentscalesforthex-axismappedontopofeachother: thetoplabelsareindegreesandthebottomlabelsareinGraphsoftrigfunctionsare oftenshowninradians-they'resimplyadifferentwayofmeasuringanglesinsteadof degrees.It'slikethedifferencebetweenmilesandkilometers.Youcanconvertdegreestoradians usingthisformula: o

Youwon't have to convert units often on the ACT, but you will seeanglesexpressed asradians,so it'simportant to understandwhattheymean.Ifyou just remember the values shown here, you'll be fine for most questions.

Degrees:90°180°270°360°

Radians:2 2

Periods

Youcanseethatthesineandcosinewavesrepeatthemselvesoverandoveragain.Thelengthofonewavefromstartto finish-bothatophumpandabottomhump--iscalledtheofthefunction.Bothsinandcoshaveaperiodof360°or radians.

Transformations

Thesegraphsshowthesimplestversionsofthefunctions,butthere'salotyoucandotothemtoaltertheirshapes.Wecall thesechanges ofthefunction.

Let'sseewhathappenswhenweacidormultiplythingstothefunction.We'lluse=sinxforourexamples,but theserulesholdequallytruefory=cosComparey=sin(x)toy=++d:

Ifyouforgettheserulesandyouhaveagraphingcalculator,youcanalwaystestthembygraphingthetransformedequation andtheoriginalfunctiontogetheronyourcalculator.Typetheseequationsinto"Y=" Y1=sin(x)Y2=sin(x+1)

Youcanseethatthegraphofthesecondequationlooksjustlikethatofthefirstequation,butshiftedslightlytotheleft.

TheUnitCircleisaconvenientwaytolookatallthesetrigonometricfunctions.Hereitis,inallitsglory:

Imagineacirclewithradius1plottedonthexy-coordinateplane,centeredontheorigin.AswesawintheCoordinate Geometrychapter,foranypointonthecirclewecandrawarighttriangle.Thelegsofthetrianglewillhavelengthxand andthehypotenusewillbe1.

Thetrianglemakesananglebetweenthex-axisandtheradius.Asgetsbigger,theanglemovescounterclockwise aroundthecircle.Ifwetakethenormaltrigratiosofthatangle,weget

Thatmeansthecoordinatesofanypointonthecircleareequalto

Theequationforthiscircleis+=1.Ifwesubstitutethetrigfunctionsforandweget

That'sthesameidentitywesawearlier!

Thisfigureshowsradiananglemeasures,thoughwecouldalsousedegrees.Butlook:theradianmeasureofanangleis simplyequalthelengthofthearcatthatpoint.

Therearelotsofwaystheunitcirclecanhelpyou.It'sperhapsmostusefulforfindingrangeofthefunctionsover variousdomains.Thatis,whichanglevaluesgivenegativeandpositivesineandcosine.Forexample:

Theunitcirclealsohelpsemphasizethenatureofthegraphs.Onthegraphswesawearlier,thewave repeatedthesameshapeinfinitelyasanglesgotbigger.Butitwasn'timmediatelyobvioushowbigtheperiodiswejusthavetoknowthatit'sOntheunitcircle,it'seasytoseethatsineandcosinehaveaperiodof360° becausethat'stheangleofonetriparoundthecircle.Foranglesbiggerthan360°,thetrigvaluescyclebackover themselves:sin450°givesthevalueassin=90°,because450-360=90.

arisefromgoinginsteadofcounterclockwise:givesthesamevalueas

Fromthiswecandeducethat and Anegativeanglemovesbelowtheaxis intoQuadrantIV.They-valuebecomesnegative,sothevalueofsineisnegative.ButthexvalueinQuadrantIV isstillpositive,socosineremainspositive,too.

Youdon'thavetoremembereverythingabouttheunitcirclefortheACT,butyoumayencountersome problemsthatuseit.Ifyoujustrememberthat ,),youshouldbe abletohandleanythingyousee.