
HAND OUT MATERIAL
MATH - 1
Use the chart above to find your target score and the number of questions you have to do to get that score. Do those questions, and those questions only. For example, let's say you're scoring around a 21 right now. From now on, you should do questions 1 to 45. Do all of these questions and only these questions; do not attempt the last 15 questions. If you get all or most of them right, you will get a 28 on the test. That's your target score. That's 7 points higher by doing less work! Sweet!

MATH - 2
Plug In
Make up numbers for the variables. Do the problem with your numbers until you get a number for an answer. Then see which answer choice gives you that same number.
Here are some common characteristics of Plug-In problems, with examples from problems we've seen:
• Any time you see a problem that has variables in the answer choices, you can definitely use Plug In. If the answer is x +4, it will always be x + 4, no matter what x is.
• In particular, look out for questions that ask for "x in terms of y''. That's a big sign that Plug In is possible.
• Sometimes you can also use Plug In when there are variables in the question but not in the choices. Sometimes if you plug in for one variable you can figure out the other variables.
• You can use Plug In on problems with implicit variables. You can use Plug In any time there's some concept in the problem and:
1. You don't know its value.
2. There's no way to figure out its value.
3. They still expect you to get an answer.
4. So, it doesn't matter what that value is; you'll get the same answer no matter what.

27. Bob has 4 dollars more than Lisa does. If Lisa has x dollars, how much would Bob have if he doubled his money?
A. x + 4
B. x + 8
C. 2x
D. 2x + 4
E. 2x + 8
28. If x + 5 is 3 less than y, then x -2 is how much less than y?
A. 2
B. 3 C. 7
D. 8 E. 10
29. Scott drives to Bob's house at a speed of30 miles per hour and drives back at a speed of 50 miles per hour. If he takes the same route both ways, what was his average speed, in miles per hour, for the whole trip?
D. 35
G. 37.5
H. 40
,J. 42.5
K. Cannot be determined from the given information
©2023 Capstone College and Career Advising LLC.MATH - 3 Backsolve
Test the numbers in the answer choices. Start with the middle number, put it through the problem, and see if it matches what you know. If it doesn't, pick a bigger or smaller choice until you find one that works.
Some common characteristics of Backsolve problems:
• Therearewholenumbers inthe answer choices.Anytimeyouneedto findsome kind of single value or quantity, you've gotfive optionsfor thatvalue righthere. Four of them are wrong, one of them is right. Test them.
• If they're asking you for the value of a variable(i.e., what numberdoes x equal), you can usually use Backsolve. They want to know x? Well, here are five options. Try 'em until you find one that works.
33. Gerry's age is 5 more than three times Carol's age. If the sum of their ages is 45, how old is Carol?
A. 1O
B. 12
C. 14
D. 16
E. 18
34. If a + b = 9 and a 2 + ab = 36 then b =
A.3
B. 4
C. 5
J. 6
K. 7
Often, Backsolve questions have two pieces of information. When you test an answer choice, you run the choice through one piece of information and see if it matches the other. In #33 above, we started with "5 more than three times" and checked that the resulting sums were 45. In #42, we started with the first equation and checked that the second came out to 36.

MATH - 4
Guesstimate
Look at the picture. Use the numbers you know to get an approximate value for the thing that you want. Eliminate any choices that don't make sense.
• Any timeyou see a problem that has a picture your first instinct should be Guesstimate. Obviously, there has to be apicture. Duh.
• Even though the ACT says the figures might not be to scale, 99% of the time they are to scale.
• You can dothis for any kind of value:angles, lengths, orareas.
• Try to eliminate as many implausible answers as you can. Maybe you can eliminate four choices, maybe only one. But get rid of any choice that doesn't make sense
• Don't worry about being too exact. Start with a broad guess and eliminate choices that are obviously wrong. Then try to get more precise with the choices that are left.
• Remember thatyouare guessinghere,soyou can'teliminatechoicesthat aretooclose together. If you guess an angle is 60 but 55, 57, 60, 63 and 65 are all choices, don't just pick 60. Those choices are too close to make a call; you're not that good at guessing.
• For three-dimensional figures, you can't literally measure the figure as it's drawn, though you may still be able to judge relative values if you have a good eye for figure

MATH – 5 NUMBER CONCEPTS AND DEFINITIONS
Let's get some terminology out of the way to avoid confusion down the line.
Integer: Any number that does not have a fraction or decimal part: -3,-2, -1, 0, 1, 2, 3.
Factor: An integer that can be divided into another integer without a remainder. For example, 3 is a factor of 12 because 12 ÷ 3 = 4. We say the larger number "is divisible by" the smaller number, so here 12 is divisible by 3.'
Prime Number: A number that is divisible only by I and itself. 1 is not a prime number. The only even prime number is 2. Examples of prime numbers include 2, 3, 5, 7, 11, and 13.
Remainder: The integer left over when an integer is divided by an integer that is not its factor. For example: 13÷ 3 = 4 with a remainder of 1.
Say you wanted to find a number that gives a remainder of 3 when it’s divided by 4. Just take a multiple of 4 and add 3 to it. Any these numbers would fit:
4 + 3 = 7 8 + 3 = 11 12 + 3 = 15 16 + 3 = 19
Properties of Positive and Negative numbers: Bigger digits give smaller negative numbers. That is, -1 0 is smaller than -2.
(Pos) x (Pos) = Pos (Neg) x (Pos) = Neg (Neg) x (Neg) = Pos
Properties of Odd and Even Integers :
(Even) x (Even) = Even (Even) x (Odd) = Even (Odd) x (Odd) = Odd
Decimal places: In the number 25.97
2 is in the "tens place" 5 is in the "units place"

Even + Even = Even
Even + Odd = Odd
Odd + Odd = Even
9 is in the "tenths place
7 is in the "hundredths place",
In the number 379.045, what digit is in the unitsplace?
MATH - 6
Exercise #1
If x isan odd positiveinteger,whichof the followingexpressionsmust beeven?
I. 2x
II. x +2
III. 3x + 1
If x has a remainder of 5 when divided by 6 and x > 10, what is the smallest possible value of x?
If j is the largest prime factor of 42, and k is the largest prime factor of 36, what is the value of j + k?


MATH – 8
Exercise #3
Reduce each fraction to lowest terms.
Rewrite each fraction so that it has the specified denominator.

MATH 9
Exercise #4
Change each improper fraction to a corresponding mixed number.
Change each mixed number to a corresponding improper fraction.

Whenever you see one of the words in the left column, write the corresponding symbol in the right column. If you see a number, just write the number. Read Write what n is = percent 100 of x (multiply)

MATH - 11
RULES WORTH MEMORIZING
1. To change a percent to a fraction, omit the percent sign, divide by 100, and reduce the fraction.
2. To change a percent to a decimal, omit the percent sign and move the decimal point two places to the left.
To change either a fraction or a decimal to a percent, the rules above are reversed:
1. To change a fraction to a percent, (do the division to get a decimal) multiply by 100 and attach a percent sign.
2. To change a decimal to a percent, move the decimal point two places to the right and attach a percent sign.

1. What is 22% of 1086?
A is unknown, P = 22%, and B = 1086. Substituting into the percent equation gives A= (0.22)(1086) = 238.92
2. Find 12% of 350.
A is unknown, P = 12%, and B = 350. Substituting into the percent proportion gives 12/100=A/350
100A=350 – cross multiply
A=42 – divide by 100
3. 4 is what percent of 80?
A= 4, P is unknown, and B = 80.
4 = P(80)
P = 4 ÷ 80 = 0.05 = 5%
4. What percent of 75 is 90?
A= 90, P is unknown, and B = 75.
P/100 = 90/75
75P=9000
P=120 – The answer is 120%
5. 35.1 is 78% of what number?
A= 35.1 P = 78%, and B is unknown.
35.1 = (0.78)B - Divide by 0.78.
B = 45
6. A student got a grade of 85% on a test in which she answered 3 questions incorrectly.
How many questions were on the test?
The 3 wrong answers represent 15% (100%-85%) of the questions on the test. Therefore, we have this question: 3 is 15% of what number?
A= 3, P = 15%, and B is unknown.
3 = (0.15)B - Divide by 0.15.
B=20
There were 20 questions on the test.

7. A house worth $120,000 is in an area where real estate is increasing in value at the rate of 8% per year. How much will the house be worth in l year?
The amount that the house will increase in value in 1 year is 8% of the original value of the house. Hence the amount of increase is 8% of $120,000.
A is unknown, P = 8%, and B = 120,000.
A= (0.08)(120,000) = 9600
The value of the house in 1 year will be $120,000 + 9600 = $ 129,600.
This problem could also be done by the following method:
The value in 1 year will be 108% of the present value. Hence the new value is 108% of $120,000.
A= 1.08(120,000) = 129,600
When approached in this manner, the problem is called a percent-increase type. If an amount decreases over time, the problem can be approached similarly, but it is then called a percent-decrease type. For example:
On a diet James's weight decreased 10%. If he now weighs 126 pounds, what was his original weight?
James's new weight is 90% (100% -10%) of his original weight. Therefore 126 is 90% of the original weight.
A= 126, P = 90%, and B is unknown.
90/100=126/B
90B = 12600
B=140
James originally weighed 140 pounds.

Exercise #5
- What is 42% of 50?
- 18 is what percent of 200?
- 5 is what percent of 4?
- 21 is 35% of what number?
- What is 15% of 75% of 80?
- A school had 30 reported absences one week and 27 reported absences the following week. What was the percent decrease in the number of absences between the two weeks?

MATH – 14
Exercise #6
- Bob makes some fruit punch that contains apple juice and mango juice in a 1:5 ratio. If he uses 15 pints of the mango juice, how many pints of apple juice will he need?
- An animal shelter has 2 cats for every 3 dogs. If there are 45 animals in the shelter, how many dogs are there?
- At a certain school, the ratio of boys to girls in the seventh grade is 3 to 5. If there are 56 total seventh-graders, how many of them are girls?
- Two numbers x andy are in a direct proportion such that when x = 2,y = 9. What is the value ofy when x = 7?

- A set contains 3 consecutive integers that have a sum of 78. What is the median of the set?
- The 12 trees in John's backyard have an average height of 135 inches. If 7 of the trees have an average height of 100 inches, what is the average height of the other 5 trees?
- In a certain class, a student's final grade is determined by taking the average of his or her scores on six tests, each of which is scored on a scale from 0 to 100. If Bob got an average score of 85 on his first 4 tests, what is the highest possible final grade he can get in the class?

MATH 16
Exercise #8
- Walter's cafe offers 3 different types of salad, 5 different entrees, and 2 different desserts. Walter's offers a dinner special that consists of a choice of exactly 1 salad, 1 entree, and 1 dessert. How many different dinner specials are possible?
- From the senior class, 1 boy will be chosen to be homecoming king and 1 girl will be chosen to be homecoming queen. If the senior class has 20 boys and 35 girls, how many different pairs of king and queen are possible?
- Four people live on a city block and each person has exactly one car. If there are four parking spots on the street, how many different assignments of cars to parking spots a1·e possible?
- A company assigns each employee a 4-digit ID number. The first digit of each number must be 3, the last digit must be either 0 or 1, and the 2 middle digits can each be any of the digits 0-9. How many different employee ID numbers are possible?

Exercise #9
- Freddy has only 4 green cars and 5 white cars. What is the probability that a car selected at random is green?
- A bag contains 3 fuchsia marbles, 7 hyacinth marbles, and 8 chartreuse marbles. What is r the probability that a marble selected fom the bag at random is hyacinth?
- A bag contains 24 cats, 3 of which are Siamese. What is the probability that a cat randomly selected from the bag is NOT Siamese?
- A bag contains 4 blueberry pancakes, 2 strawberry pancakes, and 6 blueberry waffles. If an item is drawn at random from the bag, what is the probability that it is blueberry flavored?
- An integer from 11 to 100, inclusive, is chosen at random. What is the probability that the number chosen has 9 as at least one digit?

MATH -18
Exercise #10
- If x= 5 and y = 4, what is the value of3x - 4y?
. - What is the value of 8�� 9 �� when x = 1 2 ?
- If x = 3 and k = 12, what is the value of x2 +kx+6 ?

- If 4u + 11 = 3, u = ?
- If 13 -3z =15z + 4, z =?
- If 5��+6 6 =11,�� =?
- If P = 5(a + 8), what is a in terms of P?
MATH – 19
Exercise #11
If 2 3 �� 6 = y, what isxin terms of y?

- If j = 3x - 5 and k = 6x + 1, then 2j + 3k = ?
- If a b 5 and 4a + 7b = 9, what is the value of b?
Exercise #12
- If x - y = 10 and z = 3x - 3y- 8, then z =?

- (x + 8)(x -3) = ?
- (a -7)(a -2) = ?
- (2y + 3)(y -4) = ?
- (x+y)2 = ?
- (x2 + y)(3x2 +2y) =?

MATH 21
Exercise #13
Factor thefollowing expressions:

MATH – 22
Exercise #14
X2 -2x-8 x2 -14x+24 2x2 +11x+5 9x2 -49 x4 -16X__ =?
x2 +7x
_x+5_ = ?
X2-25
X2+6x-40 = ? x-4

MATH – 23
Exercise #15
- What are the solutions for x 2 - 12x = 0?
- What are the solutions for x 2 - 11x+ 30 = 0?
- What are the solutions for x 2 -7x -8 = 0?
- What are the solutions for x 2 - 81 = 0?
- What are the solutions for x 2 - 13x = -42?

MATH 24
Exercise #16
- If f(x)= x2 +3x-10, then f(-4)=?
- If f(x) = x 2 +3x-10, then�� { 1 2}=? =?
MATH 25
Exercise #17
- If f(x) = x 2 + 3x -10, then f(2x) =?

Base 42 exponent
Here are a few definitions and properties of exponents to remember:
- An exponent tells you how many times to multiply a number by itself.
52 =5x5 h4 =h x h x h x h
- A negative base taken to an even exponent will becomepositive. A negative base taken to an odd exponent will stay negative.
(-2)2 = (-2)x(-2) = 4 (-2) 3 = (-2)x(-2)x(-2) = -8
- When taking apositive Fraction to apower the resultis smaller than theoriginal number. (1 2)2 = 1 4 1 2 > 1 4
- A negative exponent is the same as the reciprocal of the base with a positive exponent (that is, 1 divided by the number with a positive exponent).
- Any number to the zero power equals one.
x 0 = 1
- A root is the inverse (the opposite) of its corresponding power. A square root is the inverse of a square, a cube root is the inverse of a cube, the fourth root is the inverse of the fourth power, etc. That means that doing both at the same time will cancel them out.
- A fractional exponent is the same as a root.

MATH 27
Here are a few rules for dealing with exponential numbers that you should know:
1. To multiply exponential numbers with the same base, add the exponents.
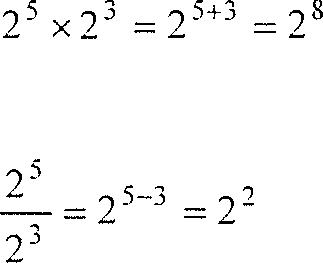
2. To divide exponential numbers with the same base, subtract the exponents.
3. To raise an exponential number to another exponent, multiply the exponents.
(2s )3 = 25x3 = 2 15
WARNING: You can add variables with the same exponent, but you cannot add bases with different exponents:
OK: 2x2 + 7x 2 = 9x 2

MATH 28
Exercise #18 (3

MATH – 29
Exercise #19
- Rectangle ABCD has vertices A(-1,7), B(6,7), C(x,y), and D(-1,1). What are the coordinates of vertex C?
- Triangle ABC has vertices A(-2,-2), B(7,10), and C(7,-2). What is the length of AB?
, What is the distance, in coordinate units, from (3,2) to (6,4) in the standard (x,y) coordinate plane?
- What is the midpoint of the line segment with endpoints (3,1) and (7,5) in the standard (x,y) coordinate plane?
- What is the midpoint ofthe line segment with endpoints (-2,-3) and (4,9) in the standard (x,y) coordinate plane?

Atable of x's and their respective y's, along with a graph of those points plotted on the grid.
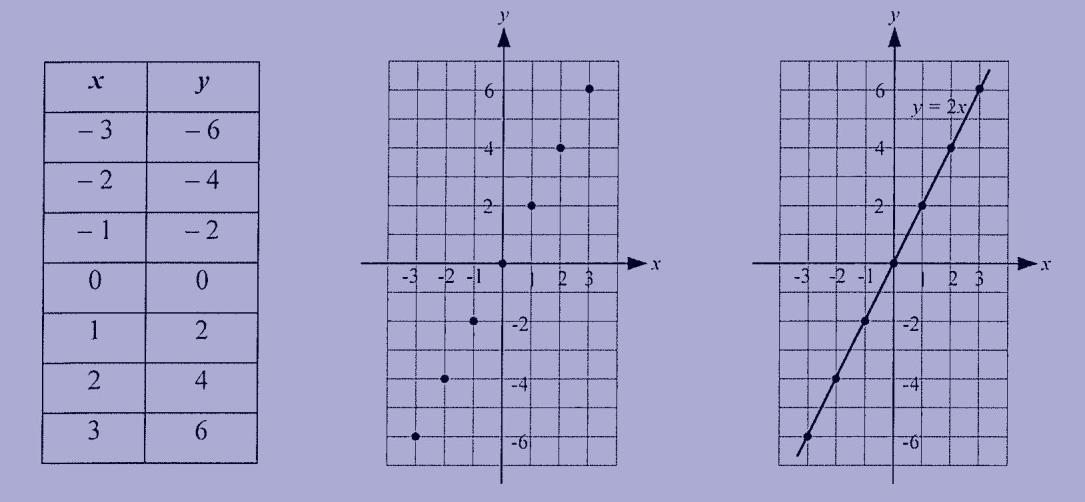

Exercise #20
- What is the slope ofthe line that passes through the points (2,6) and (4,1)?
- What is the slope of the line that passes through the points (-2,-3) and (-1,5)?
- What is the slope ofthe line represented by the equation 2x - 6y = 7?
- What is the slope-intercept equation of the line that passes through the points (-1,2) and (1,6)?
- The equation of line/ is y = 3x + 5. If line k is perpendicular to line/ and passes through the point (0,-3), what is the equation of line k?

- What is an equation ofa circle that has center (2,1) and radius 6 coordinate units?
MATH 32
Exercise # 21
- What is an equation ofa circle that has center (-4,0) and radius 5 coordinate units?
- What is an equation ofa circle that has center (5,4) and is tangent to the x-axis?
- What is the center ofa circle with equation (x+8) 2 +(y-2) 2 =9?
- What is the radius ofa circle with equation (x-1) 2 +(y+2)2 =7?

Here are some other properties of parabolas:
MATH - 33
- The vertex of the parabola is the point at the very bottom of the curve (or the very top, if the curve points down). This point is also called the maximum or minimum of the curve.
- Notice that this parabola is symmetrical-the left and right sides of the curve are mirror images of each other. That's because the square of a negative comes out positive (in our example: y = 4 when x = 2 and when x = -2.) All parabolas are symmetrical, though they may not be centered on the axis like this.
- If a (the number in front of x2) is positive, the parabola will open upwards. Ifa is negative, the parabola will open downwards.
- The value of a also gives the "squeeziness" of the parabola: a bigger a gives a thinner graph; a smaller a gives a wider graph.
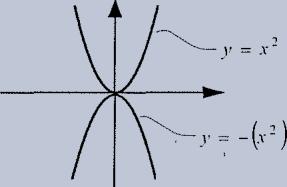
- The value of c (the number that doesn't have any x's next to it) will be the y-intercept of the parabola. Just like in a straight line, they-intercept is the value ofy when x = 0. Because c is the only term in the equation that doesn't come with an x next to it, if x = 0, all that's left is c.*


1. A straight line equals 180° .

2. A triangle equals 180° .
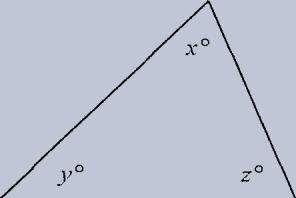
MATH – 35
What you need to know about angles
When angles form a straight line, the sum of their measures is 180 . In this diagram, x + y = 180.
The three angles of a triangle acid up to 180 ° In this diagram, x + y + z = 180.
Here's an example of using one rule to figure out another: An equilateral triangle has three equal sides and three equal angles. If all angles are equal, and they add up to 180 °, each angle of an equilateral triangle is 180/3 = 60°
So we have a new rule: every equilateral triangle has three 60 ° angles.
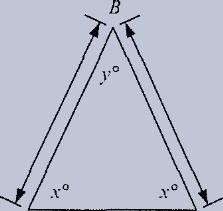
2. An isosceles triangle has two equal sides and two equal angles.
3. Vertical Angles are equal.
An isosceles triangle is one in which two of the sides are equal in length. The angles opposite the equal sides will also be equal to each other. (Similarly, an isosceles trapezoid has two pairs of equal angles.)
In this triangle, since we know that LBAC = LACB (both are x) we know AB= BC. Conversely, if we know that the sides AB and AC are equal, we can assume that the angles are equal.
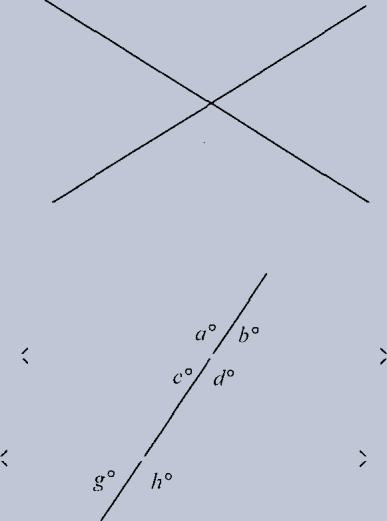
When two straight lines cross, four angles are formed. The angles that are directly across from each other are called "vertical angles" and they are equal to each other.
In this diagram, the angles marked "x" are equal to each other, and the angles marked "y" are equal to each other.
4. Parallel lines with a transversal producea bunch of equalangles.
When a third line (a "transversal") cuts through two parallel lines, eight angles are formed. The four at the top are collectively the same as the four at the bottom. Basically, we've got two types of angles: big ones and little ones. All the big ones are equal, and all the little ones are equal. Any big one plus any little one is 180 . Here, a = d = e =hand b =c =f=g. Any ofthe big ones (a, d, e, h) plus any of the little ones (b, c, f, g) equals 180

MATH – 36
Fun Facts About Circles
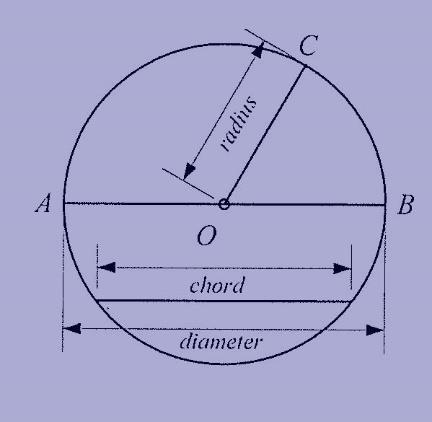
- A circle has 360 . In the figure to the left, all angles surrounding point O will add up to 360 °
-The diameter of a circle is a line segment from one end of the circle to the other, passing through the center. In the figure, AB is a diameter. The diameter by definition is the longest segment you can draw through a circle.
- The radius of a circle is a line segment from the center to the end of a circle. The radius is half of the diameter. In the figure, OA, OB, and OC are all radii. All radii of a circle are equal.
- A chord is any line segment from one end of the circle to the other. The longest chord in a circle is a diameter.

For any given angle ofa triangle:
MATH – 37
- the SINE of the angle is equal to the sin Θ = ���������������� �������������������� = �� �� length of the opposite side over the length of the hypotenuse.
- the COSINE ofthe angle is the length of cos Θ = ���������������� �������������������� = �� �� the adjacent side over the hypotenuse.
- the TANGENT ofthe angle is the length of tan Θ= ���������������� ���������������� = �� �� the opposite side over the adjacent.


MATH - 38
The graphs of y = sin x andy = cos x have distinctive wave -like shapes:
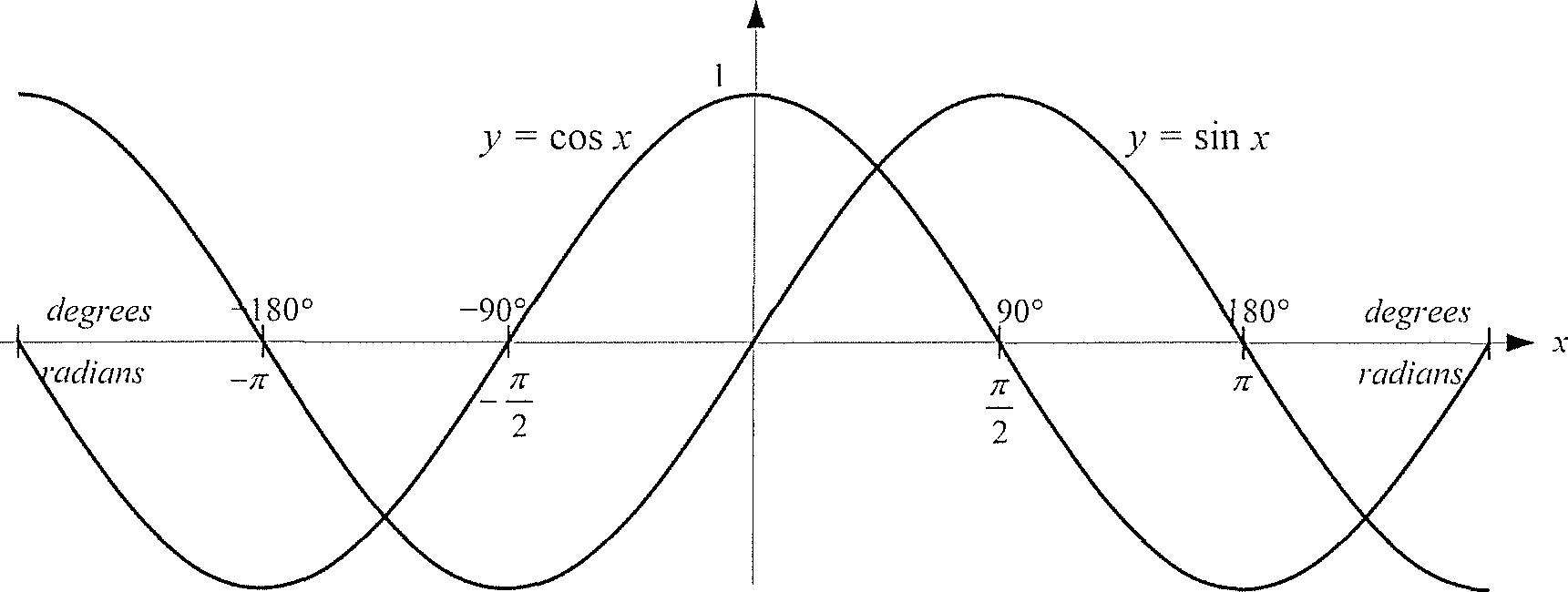
A few notable characteristics of these curves:
- The x-value gives the value of the angle, and they-value gives the value of the ratio of the sides.
- If you see a graph and you're not sure whether it shows sin x or cos x, check the y-intercept. In the graph of y = cos x the curve crosses the axis in the middle of a hump at (0, 1). The graph of Y = sin x crosses between humps at the origin.
- All the trig problems we've done so far have involved values of x between 0 ° and 90 ° But notice that both x and y can have negative values. That means that we can have negative values for the angle measures and that we can have negative values for the ratios themselves.

