ESTADO PLURINACIONAL DE BOLIVIA
MINISTERIO DE EDUCACIÓN
UNIVERSIDAD PEDAGÓGICA
DIPLOMADO EN EDUCACIÓN ECONÓMICAY MATEMATICAFINANCIERA
ESTADÍSTICAAPLICADAALAEDUCACIÓN
Participante : Ángel Rochin Escobar Herrera
Docente : Lic. Susana Vino Quisbert
CFP: ESFM : Rafael Chávez Ortiz
Grupo : 10

Actividad 2 : Elaborar una revista digital con ISSUU
Fecha actual : 13/08/2023
REGISTRO DE DATOS, ORGANIZACIÓN, REPRESENTACIÓN E
INTERPRETACIÓN EN GRAFICOS
ANALISIS HISTORICO DE LA ESTADISTICA
La enseñanza de la Estadística, se introduce en el año 1961 en el currículo de Inglaterra, se realiza de forma opcional para estudiantes con edades comprendidas entre 16 a 19 años, con el fin de que los estudiantes puedan especializarse en matemáticas, mostrando los diferentes tipos de aplicaciones.
El School Council Project mostró junto con Holmes y su equipo, que era posible la enseñanza desde la escuela primaria, iniciándola por las siguientes razones: La estadística es una parte de la educación general para los ciudadanos adultos, para adquirir la capacidad de interpretación y lectura de tablas y gráficos estadísticos. Es un recurso útil para la vida posterior, ya que se precisa en muchas profesiones y se aplican en problemas reales de la vida cotidiana.
Su estudio favorece el desarrollo personal, fomentando el razonamiento crítico.
Gal, (2002:2) afirma:
a) Capacidad para interpretar y evaluar críticamente la información Estadística, los argumentos apoyados en datos o los fenómenos estocásticos que las personas pueden encontrar en diversos contextos.
b) Capacidad para discutir o comunicar sus opiniones respecto a tales informaciones estadísticas cuando sea relevante.
Los estadísticos y educadores en los últimos años, consideran que la Estadística hoy en día es una herencia cultural necesaria para el ciudadano. De acuerdo con el análisis de (Ottoviani 1998:1, citado por Batanero 2002:2).
2 5 7 5 0 1 2 3 4 5 6 7 8
Nunca A veces Casi siempre Siempre
Estadistica en las finanzas personales
¿Qué estudia la estadística?
La estadística estudia el comportamiento de los fenómenos llamados de colectivo. Está caracterizada por una información acerca de un colectivo o universo, lo que constituye su objeto material; un modo propio de razonamiento, el método estadístico, lo que constituye su objeto formal y unas previsiones de cara al futuro, lo que implica un ambiente de incertidumbre, que constituyen su objeto o causa final.
Estadística descriptiva
La Estadística, en general, trata con información basada en ciertos datos de interés. La palabra “estadística”, ha sido referida ya sea a la información misma como a los métodos que tratan con la información.
Los métodos estadísticos se clasificanen cinco pasos:
1. Recopilación , datos estadísticos internos y externos

2. Organización, organizar datos es ordenar y corregir
3. Presentación, mediante enunciados o textos, tablas y gráficos estadísticos.
4. Análisis, análisis estadístico simple, inducción estadística series de tiempo y relación.
5. Interpretación, conclusión válida después de los resultados.
LA ESTADISTICA
Edades de estudiantes Cantidad 10 años 1 11 años 10 12 años 9 13 años 2 0 2 4 6 8 10 Cantidad 1 10 9 2 Edades estudiantes sexto de primaria
LA ESTADISTICA Y SUS APLICACIONES
Aplicación de la estadística
La estadística es una ciencia que tiene la finalidad de recoger información cuantitativa, con referencia a las personas, grupos, series de hechos, fenómenos sociales, para realizar la deducción, después del análisis de estos datos que se aproximan a la precisión, y lo más importante tomar las previsiones para el futuro de la familia, las instituciones y el Estado.
La estadística se aplica en diferentes áreas, campos, finanzas instituciones y el Estado
Educación,investigación pedagógica empírica

Psicología, técnicas de estadística, comportamiento, aptitudes, personalidad y la inteligencia.
Economía, índices de precio al consumo y el mercado
Administración pública
Y otros campos, las finanzas de la familia, las instituciones, salud y la investigación de la ciencia.
PRESENTACIÓN E INTERPRETACIÓN EN GRÁFICOS
Presentación de gráficos
Un gráfico en Excel es una representación de valores numéricos que mejora la comprensión de los datos que se encuentran en nuestra hoja. Los gráficos son una excelente herramienta para resumir la información e identificar fácilmente cualquier tendencia en los
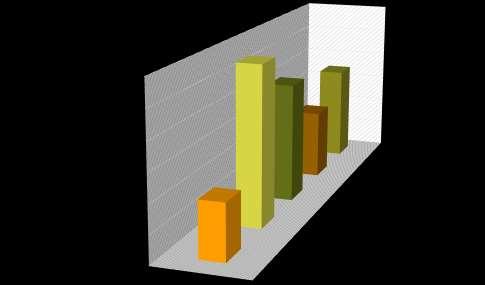
Un gráfico de barras apiladas sirve para mostrar el total o el promedio de cada categoría. Mientras más alta sea una barra, mayor será el volumen de los valores numéricos.
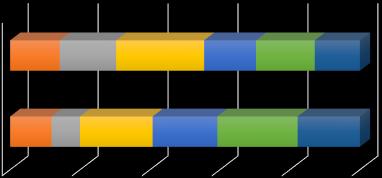
datos. Gráfico de columna horizontal 0% 20% 40% 60% 80% 100% Mujeres Varones 16 22 11 25 28 39 25 23 31 26 24 20 Estudiantes inscritos en la U.E. 2023 Primero segundo Tercero Cuarto Quinto Sexto Gráfico de barras apiladas 2019 2020 2021 2022 2023 270 280 290 300 310 320 330 Cantidad 290 327 313 295 305 Estudiantes inscritos en la U. E. en los 5 últimos años 2019 2020 2021 2022 2023
PRESENTACIÓN E INTERPRETACIÓN EN GRÁFICOS
Los gráficos de líneas permiten visualizar los cambios a lo largo de un rango continuo, como el tiempo o la distancia. La visualización del cambio con un gráfico de líneas permite ver de una sola vez la tendencia general y comparar simultáneamente varias tendencias.
Los gráficos circulares solamente se usan para representar una serie de datos que se muestran como una proporción respecto al total.
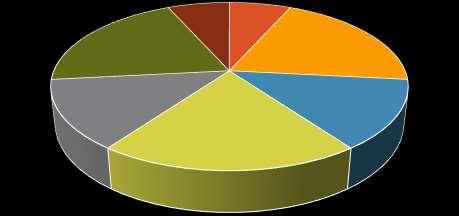
Gráfico en líneas Gráfico circular 0 10 20 30 40 50 60 70 2018 2019 2020 2021 2022 Estudiantes promovidos de sexto de primaria
2 7% 3 20% 4 13% 5 20% 6 13% 7 20% 8 7%
U. E. 1 2 3 4 5 6 7 8
Años de servicio de maestros/as en la
PRESENTACIÓN E INTERPRETACIÓN EN GRÁFICOS
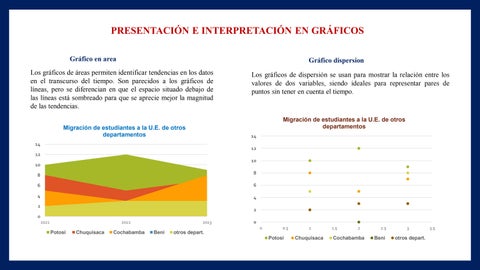
Gráfico en area
Los gráficos de áreas permiten identificar tendencias en los datos en el transcurso del tiempo. Son parecidos a los gráficos de líneas, pero se diferencian en que el espacio situado debajo de las líneas está sombreado para que se aprecie mejor la magnitud de las tendencias.
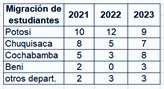
Migración de estudiantes a la U.E. de otros departamentos
Los gráficos de dispersión se usan para mostrar la relación entre los valores de dos variables, siendo ideales para representar pares de puntos sin tener en cuenta el tiempo.
Migración de estudiantes a la U.E. de otros departamentos
Gráfico dispersion
0 2 4 6 8 10 12 14 2021 2022 2023
Potosi Chuquisaca Cochabamba Beni otros depart.
0 2 4 6 8 10 12 14 0 0.5 1 1.5 2 2.5 3 3.5
Potosi Chuquisaca Cochabamba Beni otros depart.
ESTADÍGRAFOS DE POSICIÓN Y RESOLUCIÓN DE PROBLEMAS MATEMÁTICOS ESTADÍSTICOS APLICANDO
TABLAS Y GRÁFICOS
MEDIAARITMETICA
Cuando se habla de “media”, en la práctica se entiende “media aritmética”; y en ese sentido hablaremos de: salario medio, número medio de accidentes, rendimiento medio de un obrero, entre otros…
Cuadro 1: Edades del curso quinto y sexto de primaria
X = Eyi*fi/N = 555 / 50 = 11,1
Media aritmetrica = 11,1 años
MEDIA ARITMETICA DE LAS EDADES
Total 50 555
yi
yi*fi 10
140 11
231 12 13 156 14 2 28
fi
14
21
14 21 13 2 140 231 156 28 10 11 12 14
fi
yi*fi
ESTADÍGRAFOS DE POSICIÓN Y RESOLUCIÓN DE PROBLEMAS MATEMÁTICOS ESTADÍSTICOS APLICANDO TABLAS
Y GRÁFICOS
LAMEDIANA
La mediana de este conjunto de valores como aquel valor que no es superado ni supera a más de la mitad de las �� observaciones, arregladas en orden de magnitud creciente o decreciente.
Cuadro 3: frecuencia absoluta acumulada
Datos Tabulados. Cuando los datos están agrupados en clases, es decir, cuando existe una tabla de distribución de frecuencias, para determinar la mediana se sigue otro procedimiento. Se construye la tabal de distribución de frecuencias absoluta acumulada “menor que”
La mediana de edades de estudiantes
Total 50
Me = N / 2 = 50/2 = 25
La mediana = 11
Datos no Tabulados. En el cálculo de la mediana para datos no tabulados, hay que distinguir dos situaciones: número de observaciones impar y número de observaciones par. En impar es el dato que ocupa la parte central. En datos pares, tomar los dos datos centrales y dividir ente 2.

yi fi Fi 10 14 14 11 21 35 12 13 48 14 2 50
0 5 10 15 20 25 30 35 40 45 50 10 11 12 14
fi Fi
ESTADÍGRAFOS DE POSICIÓN Y RESOLUCIÓN DE PROBLEMAS MATEMÁTICOS ESTADÍSTICOS APLICANDO TABLAS Y GRÁFICOS
LAMODA
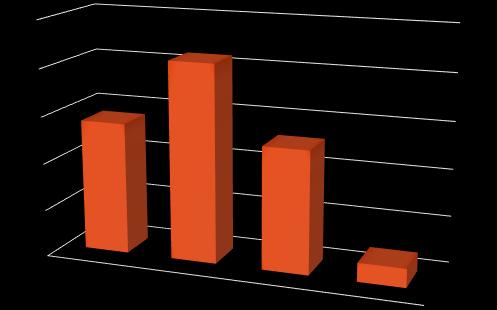
Definición. La moda de una muestra es aquel valor de la variable que se presenta con mayor frecuencia; es decir es el valor que más se repite.
Nota. La moda puede no existir para un conjunto de datos, incluso si existe puede no ser única.
Si el conjunto de datos tiene una sola moda se llama unimodal. Si tiene dos modas se llama bimodal. En general, si tiene más de dos modas, se llama multimodal.
yi fi 10 14 11 21 12 13 14 2 Cuadro 4: frecuencia absoluta Mo = 11 años 0 5 10 15 20 25 10 11 12 14 14 21 13 2
La moda de las edades
DISTRIBUCIONES BIDIMENSIONALES, TABLAS DE DOBLE
ENTRADAY,APLICACIONES ALAEDUCACIÓN ECONÓMICAY FINANCIERA
Distribuciones bidimensionales
Con frecuencia estamos interesados en investigar dos o más características de cada individuo o elemento. Por ejemplo, podemos observar la estatura y el peso de cada estudiante en una unidad educativa.
Características
1. Los dos caracteres cualitativos. Por ejemplo: nivel educacional y religión.
2. Uno cualitativo y otro cuantitativo, pueden ser:
Uno cualitativo, otro cuantitativo discreto. Ej. Nivel de educación y numero de hijos.
Uno cualitativo, otro cuantitativo continuo. Ej. Edad y estado civil.
3. Los dos cuantitativos
Los dos cuantitativos discretos
Uno discreto y otro continuo
Los dos continuos
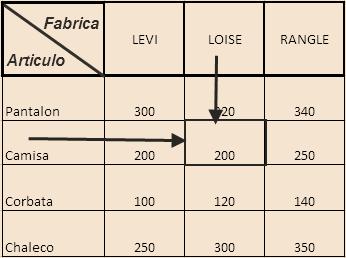
TABLA DE DISTRIBUCION DE FRECUENCIA BIDIMENSIONAL
La tabla estadística que describe las �� observaciones, es una TABLA DE DOBLE ENTRADA llamada Tabla de Distribución de Frecuencias Bidimensional, donde figuran en las filas las modalidades o valores de la característica ��, y en las columnas las modalidades o valores de la

TABLA DE DISTRIBUCION BIDIMENCIONAL DE FRECUENCIAS ABSOLUTAS
TABLAS DE DOBLE ENTRADA
característica.
Nº. hijos Nivel de estudios 0 1 2 3 4 o más Total Primaria o menos 2 5 14 29 35 85 Secundaria 5 24 37 40 30 136 Ed. Superior 10 15 30 6 2 63 Total 17 44 81 75 67 284
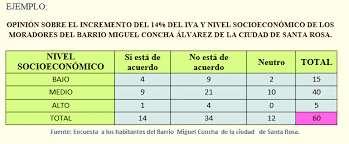
FRECUENCIAS RELATIVAS

Definición 1.1 Se llama frecuencia relativa o simplemente frecuencia de la pareja de valores o modalidades ���� e ���� (o bien frecuencia total) a la proporción de observaciones que presentan simultáneamente los valores o modalidades ���� e ����.
TABLA DE DISTRIBUCIÓN MARGINAL DE X

TABLAS DE DOBLE ENTRADA
DISTRIBUCIÓN MARGINAL X TABLA DE DISTRIBUCIÓN MARGINAL DE Y

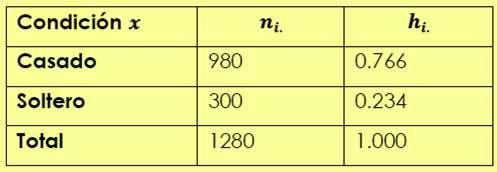
DISTRIBUCIÓN MARGINALY

TABLAS DE DOBLE ENTRADA
REPRESENTACIÓN GRÁFICA
Si las variables �� �� �� son cualitativas, se pueden hacer varias representaciones gráficas, dependiendo de que se quiere representar. Por ejemplo, si queremos representar: la distribución de uno de ellos respecto del otro o la distribución total de cada uno de ellos, se pueden usar las ya conocidas barras proporcionales.
Número de hijos y nivel de estudios
Nº. hijos Nivel de estudios 0 1 2 3 4 o más Total Primaria o menos 2 5 14 29 35 85 Secundaria 5 24 37 40 30 136 Ed. Superior 10 15 30 6 2 63 Total 17 44 81 75 67 284 Primaria o menos Ed. Superior 0 10 20 30 40 0 1 2 3 4 o más 2 5 14 29 35 5 24 37 40 30 10 15 30 6 2 CANTIDAD DE PERSONAS Nº. HIJOS
Primaria o menos Secundaria Ed. Superior
Universidad Pedagógica. 2023.Texto Académico (Semana 1). Módulo 2: EstadísticaAplicada a la Educación. Sucre, Bolivia.
Universidad Pedagógica. 2023.Texto Académico (Semana 2). Módulo 2: EstadísticaAplicada a la Educación. Sucre, Bolivia.
Universidad Pedagógica. 2023.Texto Académico (Semana 3). Módulo 2: EstadísticaAplicada a la Educación. Sucre, Bolivia.
Universidad Pedagógica. 2023.Texto Académico (Semana 4). Módulo 2: EstadísticaAplicada a la Educación. Sucre, Bolivia.
Bibliografía