EN MATEMÁTICA

Introducción
La aritmética es el área de las matemáticas centrada en los números y en las operaciones que se realizan con ellos Cabe recordar que los números son los signos que permiten expresar una cantidad.
En el proyecto presente vamos a encontrar elementos didácticos de la aritmética, que nos ayudarán a entender mejor los procesos que se realizan en el momento de desarrollar ejercicios y problemas en los que está implicada la aritmética, entre ellos conoceremos sobre los números decimales, lo que es la divisibilidad, múltiplos y sus múltiplos, las fracciones; de las cuales existe una variedad de ellas como son las propias, impropias, mixtas y más
Encontraremos también información sobre el sistema de numeración Maya y el sistema de numeración romano, los números enteros, y observaremos que cada uno de los temas que se presenta contiene una amplia información que nos ayuda a entender con mayor claridad el desarrollo de cada uno de ellos para encontrarles solución al momento de trabajar ejercicios que necesitan aplicación de la aritmética, estos que se pueden presentar como un gran problema en nuestra cabeza cuando desconocemos mucha información sobre ellos para poder darles una solución y así ampliar nuestros conocimientos en este gran mundo de la matemática.

Números Decimales
¿Qué son los números decimales?
Los números decimales se utilizan para representar números más pequeños que la unidad. Los números decimales se escriben a la derecha de las Unidades separados por una coma. Es decir: Centenas Decenas Unidades , Décimas Centésimas
Milésimas
En la imagen que aparece a continuación, el primer cuadrado representa la Unidad. Si esta unidad la dividimos en 10 partes iguales (segundo cuadrado), representaremos las Décimas. Si las décimas las dividimos en 10 partes iguales o la unidad en 100 partes iguales (tercer cuadrado), representaremos las Centésimas

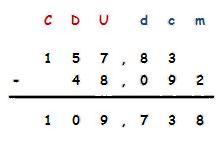
Suma y resta
Se acomodan los elementos de la operación en forma vertical con el punto decimal como referencia y se hacen coincidir las clases, para después efectuar las operaciones correspondientes
23. 9835
9. 654 + 293. 4545
335. 9920
Multiplicación
Se efectúa igual que la multiplicación de números enteros. Para ubicar el punto decimal se cuentan las cifras que contengan ambos factores a la derecha del punto decimal, lo que indica el lugar que debe ocupar el punto decimal, de derecha a izquierda, en el resultado.

División
Primero se divide la parte entera entre el divisor. Al llegar al punto decimal, éste se sube al cociente y se continúa la operación como si fueran números enteros. Las cifras subsecuentes del cociente quedarán después del punto decimal. Si la parte entera es menor que el divisor, entonces la mediatamente después del punto

Propiedad conmutativa, asociativa y distributiva en las operaciones con decimales.
Propiedad Conmutativa
Al cambiar el orden de los factores decimales se obtiene el mismo producto.
12 34 × 3 2
3.2 × 12.34
Propiedad asociativa
Al agrupar los factores decimales de diferente forma, se obtiene el mismo producto.
1.6 × 2.3 × 3.4
(1.6 × 2.3) × 3.4
Propiedad distributiva
Para multiplicar una suma indicada de números decimales por un número decimal, se puede multiplicar cada sumando por el número y, luego, sumar los productos indicados.
3 × (4.2 + 2.5)
Operaciones combinadas de números naturales y decimales.
Son expresiones numéricas en las que pueden aparecer varias operaciones (sumas, restas, multiplicaciones o divisiones) con paréntesis, corchetes, llaves o sin más.
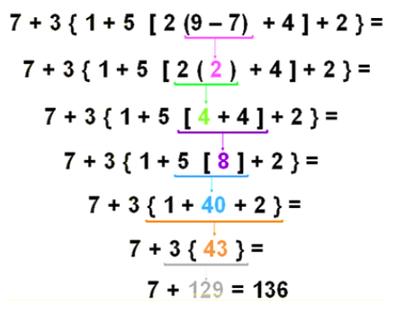

Múltiplos y divisores.

Los múltiplos de números que coinciden se llaman múltiplos comunes
Para obtener los múltiplos comunes de números: Escribe los múltiplos de cada número identifica y escribe los múltiplos que coinciden.
Ejemplo: determina los múltiplos comunes de 4 y 5. Múltiplos de cuatro:
4,8,12,16,20,24,28,32,36,40,44,48,52,56,60,64
Múltiplos de cinco:
5,10,15,20,25,30,35,40,45,50,55,60,65…
Los múltiplos comunes de 4 y 5 son 20 y 40 60... https://youtu.be/YW_04Esg4QQ

Cálculo de MCM Y MDC.
El menor de los múltiplos comunes se llama mínimo común múltiplo y su abreviatura es mcm.
para obtener el mcm de dos números:
Escribe los múltiplos de cada número.
1. identifica y escribe los múltiplos comunes.
3
2. identifica y escribe el menor de los múltiplos comunes.
Ejemplo: Determine el mcm de 4 y 5
1.
Múltiplos de 4: 4,8,12,16,20,24,28,32,36,40,44,48,52,56,60,64…
Múltiplos de 5: 5,10,15,20,25,30,35,40,45,50,55,60, 65…
2 Los múltiplos comunes de cuatro y cinco son 20,40,60
3 El mcm de 4 y 5 es 20
Cuando se encuentra el primer múltiplo común, no es necesario encontrar otros porque ese es el mcm.
El mayor de los divisores comunes se llama máximo común divisor y su abreviatura es mcd.
para obtener el mcd:
Escribe los divisores de cada número. identifica y escribe los divisores comunes. identifica y escribe el mayor de los divisores comunes.
Ejemplo: determina el mcd de 4 y 12
Divisores de 4: 1,2,4
Divisores de 12: 1,2,3,4,6, 12
Los divisores comunes de 4 y 12 son 1, 2 y 4
El mcd de 4 y 12 es 4
Relación de mcm y mcd.
Para dos números naturales se tiene que: El producto de los dos números es igual al producto del mcm y del mcd
Ejemplo: para los números 6 y 8.
El mcm de 6 y 8 es 24, mientras que el mcd de 6 y 8 es 2. el producto de los números de 6 y 8 es 6 x 8 = 48
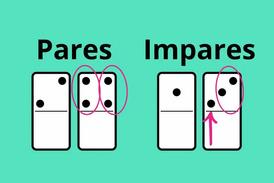
Números pares e impares.
Un número par es cualquier número entero que se puede dividir en dos grupos iguales. En otras palabras, son números que son exactamente divisibles por 2. Imagina que tienes cuatro rebanadas de pizza para ti y tu amigo. Si ambos comieran dos rebanadas, dirían que tenían una cantidad igual o par
Los números pares son múltiplos de 2. Por lo tanto, multiplicar cualquier número por 2 producirá un número par.
Ejemplos:
2 x 0 = 0
2 x 1 = 2
2 x 2 = 4
2 x 3 = 6
2 x 4 = 8
2 x 5 = 10
Como puedes notar en los ejemplos anteriores, los números pares se pueden identificar fácilmente porque el dígito de las unidades terminará en 0, 2, 4, 6 u 8.
No importa si el número es 168 o 922. Ambos son números pares porque ambos se pueden dividir por igual entre 2
Los números impares son números enteros que no son divisibles por 2. No se pueden dividir en dos grupos iguales.
Ahora, imagina que tú y tu amigo solo tienen 3 rebanadas de pizza para compartir. No sería igual si tu amigo comiera dos rebanadas y tú solo comieras una. El número 3 no se puede dividir por igual en dos grupos Por lo tanto, se llama un número impar
Los números impares no son múltiplos de 2. Los números impares son fáciles de reconocer porque el dígito de las unidades terminará en 1, 3, 5, 7 o 9. Sin embargo, lo mejor para estos casos es perfeccionar el conocimiento de los números pares. El motivo es que, si se identifican primero, al descartar los impares serán más visibles.
Los números impares son fáciles de reconocer porque el dígito de las unidades terminará en 1, 3, 5, 7 o 9.
Propiedades de los números pares e impares.
Los números pares e impares tienen muchas propiedades matemáticas interesantes.
La suma de dos números pares es un número par. Ejemplo: 4 + 4 = 8
La suma de dos números impares es un número par. Ejemplo: 7 + 7 = 14
La suma de un número par y un número impar es un número impar. Ejemplo: 5 + 4 = 9
Multiplicar un entero par por un entero par siempre dará como resultado un entero par Ejemplo: 4 x 4 = 16
Multiplicar un entero impar por un entero impar siempre dará como resultado un entero impar. Ejemplo: 5 x 5 = 25
Multiplicar un entero impar por un entero par siempre dará como resultado un entero par. Ejemplo: 3 x 4 = 12
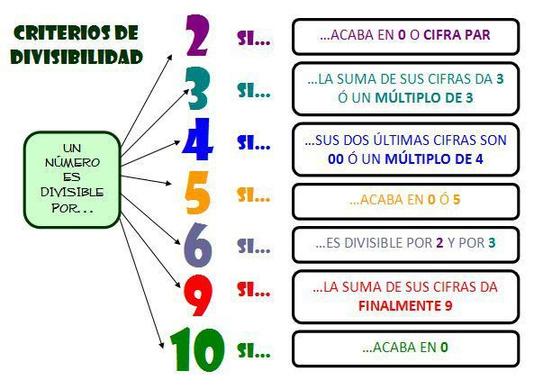
Criterios de divisibilidad por 2,3,5 y 10.
Un número natural es divisible por otro número natural si al dividirlos, el residuo es 0.
Los números pares son divisibles por 2, ya que al dividirlos entre 2 el residuo es 0.
Los números impares no son divisibles por 2, ya que al dividirlos entre 2 el residuo no es 0.
Ejemplo: 32 es divisible por 2.
45 no es divisible por 2
Un número es divisible por 2 si la cifra de las unidades es 0, 2, 4, 6 u 8.
Un número es divisible por otro si al dividirlos el residuo es 0
Un número es divisible por:
• 3, si al dividir por 3 el residuo es 0
• 5, si al dividir por 5 el residuo es 0.
• 10, si al dividir por 10 el residuo es 0
Un número es divisible por:
• 3, si la suma de sus cifras es divisible por 3
• 5, si la cifra de las unidades es 0 o 5
• 10, si la cifra de las unidades es 0
Fracciones.
Una fracción es un número, que se obtiene de dividir un entero en partes iguales. Por ejemplo cuando decimos una cuarta parte de la torta, estamos dividiendo la torta en cuatro partes y consideramos una de ellas.
Diferentes tipos de Fracciones
Fracciones
propias
Se llaman fracciones propias a aquellas que representan números menores que la unidad. Y ¿cómo son estas fracciones? Todas las fracciones que representan un número menor que la unidad se caracterizan por tener el numerador menor que el denominador. Por ejemplo:

Fracciones
impropias
Se llaman fracciones impropias a las que representan números mayores que la unidad. Y ¿cómo son estas fracciones? Todas las fracciones que representan un número mayor que la unidad se caracterizan por tener el numerador mayor que el denominador. Por ejemplo:

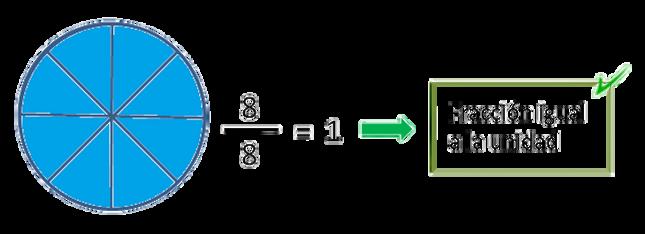
Fracciones iguales a la unidad
Son las que representan números iguales a la unidad Es decir, son las fracciones que representan el 1 y se caracterizan por tener el numerador y el denominador iguales.
Fracciones mixtas
Las fracciones mixtas se denominan así porque están formadas por un número entero y por una fracción. El número se llama número mixto, porque está formado por un número natural y una fracción propia m
Ejemplo: Toda fracción impropia mayor que la unidad se puede escribir como un número mixto.

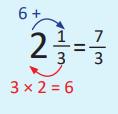
Conversión de número mixto a fracción impropia
Para convertir un número mixto en fracción impropia se puede hacer uso de la ubicación en la recta numérica. Otra forma de convertir un número mixto en fracción impropia:
① Multiplicar el denominador por el número natural y sumar el numerador, el resultado será el numerador de la fracción impropia.
② El denominador de la fracción propia en el número mixto es el denominador de la fracción impropia
Comparación de fracciones homogéneas
Las fracciones que tienen el mismo denominador se llaman fracciones homogéneas Las fracciones homogéneas se pueden comparar en la recta numérica de igual forma que los números naturales; las fracciones que están a la derecha son mayores y las que están a la izquierda son menores También se pueden comparar los numeradores; es menor la fracción homogénea que tiene menor numerador.
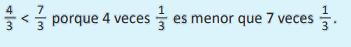
Fracciones equivalentes
Las fracciones que representan la misma cantidad se llaman fracciones equivalentes. La equivalencia se escribe utilizando el signo “=” . Ejemplo:
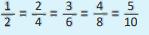
Cuando multiplicamos el numerador y denominador por el mismo número obtenemos fracciones equivalentes, a este procedimiento se le llama amplificación.

Obtencion de Fracciones equivalentes
Amplificación: consiste en obtener una fracción equivalente a una dada multiplicando sus términos por un mismo número
Simplificación: consiste en obtener una fracción equivalente a una fracción dada dividiendo sus términos entre un divisor común a ambos.
Suma y resta de fracciones
Para sumar (o restar) fracciones con el mismo denominador, se suman (o se restan) los numeradores y se mantiene el denominador.
Suma
Resta
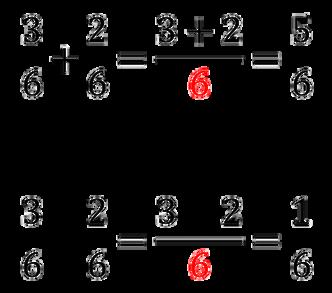
Para sumar (o restar) fracciones con distinto denominador:
1. Se reducen todas ellas a común denominador.
2. Se suman (o se restan) los numeradores, manteniendo el mismo denominador.
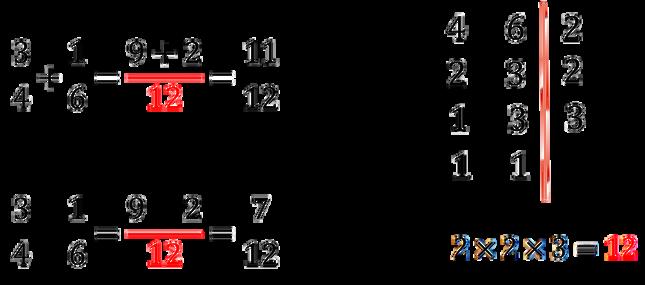
Multiplicación de fracciones
Para multiplicar fracciones se multiplican sus numeradores y se multiplican sus denominadores.

División de fracciones
Para dividir fracciones multiplicamos la primera por la inversa de la segunda

Resolución de prolemas
En una playa, 3/7 de los bañistas son españoles, 1/5 franceses y el resto de otras nacionalidades ¿Qué fracción del total representan estos últimos?

Sistemas de numeración
La numeración es la parte de la Aritmética que enseña a expresar y a escribir los números.
La numeración puede ser hablada y escrita.
Numeración hablada es la que enseña a expresar los números
Numeración escrita es la que enseña a escribir los números.
Numeración maya.

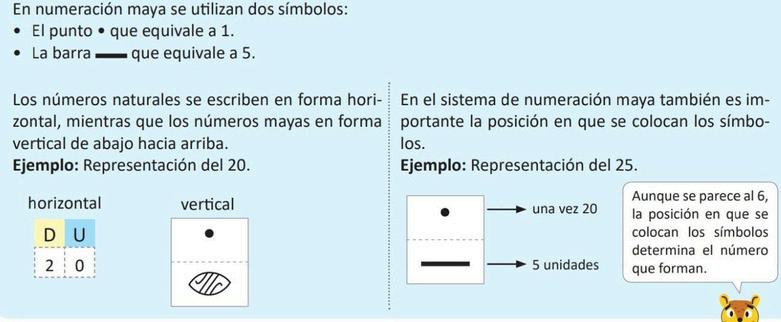

Los mayas crearon este sistema hace más de 2, 000 años Se cree que las primeras pruebas de numeración de esta cultura da tan de hace cientos de años a C
Los mayas fueron la primera cultura que re presentó en América el número 0, es decir, de alguna manera, los mayas ya entendían el concepto de “cero” y “nada”.
Los mayas no inventaron este sistema numérico para realizar operaciones matemáticas, sino para medir el tiempo.
Numeración romana.
La numeración romana es el sistema de representación de los números empleados por los romanos La numeración romana no utiliza el principio del valor relativo, Pues el valor de los símbolos siempre es el mismo, sin que influya el lugar que ocupa
La numeración romana parece ser resto de un sistema de numeración de base 5.
Se usa muy poco. Solamente se emplea para fechas, algunas veces; para numerar los capítulos de una obra; en algunos relojes, etc.
Los símbolos que emplea numeración romana son:

Además, una rayita colocada encima de una letra indica tantos millares como unidades tenga ese símbolo; dos rayitas encima de cualquier símbolo indican tantos millones como unidades en el símbolo; cuatro rayitas tanto billones como unidades indica el símbolo; seis rayitas tanto trillones como unidades tenga el símbolo.
Reglas para la representación de los símbolos.
1
Si a la derecha de una cifra colocamos otra igual o menor, el valor de la primera queda aumentado con el de la segunda.
Ej: LV equivale a L + V = 55
2 Si a la izquierda de una cifra colocamos otra menor, el valor de estas se resta de la anterior.
Ej: IV = equivale a V - I = 4
3 nunca se pueden emplear más de tres símbolos iguales seguidos a la derecha de otra cifra mayor, ni aislados; ni más de uno a la izquierda de otra mayor. Así, el 40 no se escribe XXXX, sino XL; el 9 no se escribe VIIII, sino IX; el 70 no se escribe XXXC, sino LXX.
https://youtu.be/IxxW4SFbWPM
Importancia del cero.
El uso del cero es reciente. En el transcurso de la historia, el uso de símbolos fue limitado para representar cantidades de objetos en un sentido positivo, es decir, pertenencia.
En el siglo VI después de Cristo en la India utilizaban 9 signos. Más tarde se adoptó el signo “cero” para indicar la ausencia de cantidad. (Boyer,1986)
La palabra cero proviene de la voz árabe ziffero, que significa lugar vacío. El cero recibe el nombre de cifra no significativa o cifra auxiliar.
El cero es un número pequeño y especial. Es un entero, pero no es positivo ni negativo. Sin embargo: Cero es par.
https://youtu.be/MdZmJ_wBo18

Números enteros
Los números enteros son el conjunto numérico que abarca la totalidad de los números naturales, sus inversos negativos y el cero Es decir, se trata de los números que se utilizan para contar, junto con sus opuestos de signo negativo (1 y -1) Normalmente, los enteros negativos se escriben con su signo (-), cosa que no hace falta para los positivos, pero puede hacerse en ocasiones para resaltar la diferencia (+1 y -1).

Valor absoluto de un números entero
El valor absoluto de un número entero es el número natural que resulta al suprimir su signo.
El valor absoluto lo escribiremos entre barras verticales
| 5| = 5
|+5| = 5
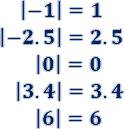
Por otro lado, con los números enteros es posible realizar las mismas operaciones que con los números naturales, es decir, se pueden sumar, restar, multiplicar o dividir. Sin embargo, en su caso, se debe atender siempre a las normas que determinan el signo del resultado.
Cuando se suman los números enteros, se debe prestar atención a los sumandos para calcular el resultado:
Si ambos números son positivos o uno de los dos es cero, se deberán sumar normalmente sus valores absolutos y se conservará el signo positivo. Por ejemplo: 1 + 3 = 4 ; 6 + 0 = 6.
Si ambos números son negativos o uno de los dos es cero, se deberán sumar normalmente sus valores absolutos y se conservará el signo negativo Por ejemplo: -1 + -1 = -2 ; -6 + 0 = -6
Si los números tienen signos diferentes, en cambio, se deberá restar el valor absoluto del menor al del mayor, y el resultado tendrá el signo del número mayor. Por ejemplo: -4 + 5 = 1 ; -8 + 4 = -4.
Resta
Cuando se restan los números enteros, se debe atender también a los signos del minuendo y el sustraendo, y a cuál de los dos tiene mayor valor absoluto, del siguiente modo:
Si tienen signo positivo:
Si el minuendo (positivo) es mayor que el sustraendo (positivo), se realizará la resta normalmente y la diferencia tendrá signo positivo
Por ejemplo: 8 – 5 = 3 ; 7 – 1 = 6.
Si el minuendo (positivo) es menor que el sustraendo (positivo), la resta será equivalente a la diferencia entre ambos números, pero tendrá signo negativo. Por ejemplo: 5 – 8 = -3 ; 2 – 9 = -7.
Si ambas cifras son positivas e iguales, el resultado será cero Por ejemplo: 5 – 5 = 0 ; 2 – 2 = 0
Si tienen signo negativo:
Si el minuendo (negativo) es mayor que el sustraendo (negativo), se realizará la resta normalmente y el resultado tendrá signo negativo. Por ejemplo: (-5) – (-3) = -2 ; (-9) – (-1) = -8.
Si el minuendo (negativo) es menor que el sustraendo (negativo), se considerará el sustraendo como un número positivo y se resolverá la operación como si fuera una suma. Por ejemplo: (-2) – (-3) = 1 ; (-5) – (-8) = 3.
Si ambas cifras son negativas e iguales, se sumarán sus valores absolutos y el resultado tendrá signo negativo.
Por ejemplo: (-1) – (-1) = -2 ; (-5) – (-5) = -10.
Si tienen signos distintos:
Si el minuendo (positivo) es mayor, igual o menor que el sustraendo (negativo), se sumarán normalmente sus valores absolutos y el resultado tendrá signo positivo
Por ejemplo: 9 – (-1) = 10 ; 5 – (-5) = 10 ; 1 – (-9) = 10
Si el minuendo (negativo) es mayor, igual o menor que el sustraendo (positivo), se sumarán normalmente sus valores absolutos y el resultado tendrá signo negativo.
Por ejemplo: -8 – 2 = -10 ; -2 – 2 = -4 ; -2 – 8 = -10.
Multiplicación
Cuando se multiplican los números enteros, se procede a multiplicar normalmente sus valores absolutos, y luego se calcula el signo del producto de acuerdo a lo siguiente:
Positivo por positivo es igual a positivo.
Por ejemplo: 2 x 2 = 4
Positivo por negativo es igual a negativo
Por ejemplo: 2 x -2 = -4
Negativo por positivo es igual a negativo
Por ejemplo: -2 x 2 = -4
Negativo por negativo es igual a positivo
Negativo por negativo es igual a positivo.
Por ejemplo: -2 x -2 = 4
División
Cuando se divide entre números enteros, se procede del mismo modo que en el caso de la multiplicación: se opera normalmente con los valores absolutos y se aplica el principio que determina el signo del resultado. Por ejemplo:
Positivo entre positivo es igual a positivo. Por ejemplo: 10 / 2 = 5
Positivo entre negativo es igual a negativo. Por ejemplo: 10 / -2 = -5
Negativo entre positivo es igual a negativo. Por ejemplo: -10 / 2 = -5
Negativo entre negativo es igual a positivo. Por ejemplo: -10 / -2 = 5
Propiedades distributivas del recíproco multiplicativos
La propiedad distributiva nos afirma que la multiplicación de un número por una suma es igual a la suma de las multiplicaciones de dicho número por cada uno de los sumandos.
Así, por ejemplo:
3 x (4 + 5) = 3 x 4 + 3 x 5
Pero también podemos aplicar la propiedad distributiva en el otro sentido, llamándolo entonces sacar factor común, y es así:
2 x 6 + 2 x 9 = 2 x (6 + 9)
Vamos a ver dos ejemplos más:
Distributiva: 8 x (13 – 1) = 8 x 13 – 8 x 1 = 8 x 13 – 8
Sacar factor común: 12 x 3 x 2 + 3 x 6 + 7 x 3 = 3 x (12 x 2 + 6 + 7)
Operaciones
combinadas
Son expresiones numéricas en las que pueden aparecer varias operaciones (sumas, restas, multiplicaciones o divisiones) con paréntesis, corchetes, llaves o sin más.
Resolver primero la operación o las operaciones que haya dentro de los paréntesis. 1.
2
Si hay varias operaciones seguidas, primero se hacen las multiplicaciones y divisiones y después las sumas y restas



Bibliografía
Colegio Nacional de Matemáticas (2009). Matemáticas Simplificadas Segunda edición Pearson Educación, México S.A. de C.V.
Baldor A. (1986). Aritmética. Ediciones Codice. Madrid, España
MINED (2019) Libro de texto de Cuarto Grado de Educación Básica. El Salvador.
MINED (2019) Libro de texto Quinto Grado de Educación Básica. El Salvador.
Artmann, P (2022) Números pares e impares Árbol ABC com Recuperado de 08 de febrero 2025 de https://arbolabc com/recursos/numeros-pares-e-impares
Editorial Etecé (2024). Números enteros. Concepto. Recuperado de 08 de febrero 2025 de https://concepto.de/numeros-enteros/
González D (2024) Números decimales Smartick Recuperado de 08 de febrero 2025 de https://www smartick es/blog/matematicas/decimales/losnumeros-decimales/
Diseñado por educadores, pensado para docentes (2021) Números decimales primaria. Smile and Learn. Recuperado de 07 de febrero de 2025 de https://www smileandlearn com/numeros-decimales-primaria/