ANÁLISE DE APLICABILIDADE DE UM SISTEMA DE REFRIGERAÇÃO CASCATA VERDE EM UM SUPERMERCADO NO CENÁRIO DO MUNICÍPIO DO RIO DE JANEIRO
Victor Assi Belfort Bastos
Projeto de Graduação apresentado ao Curso de Engenharia Mecânica da Escola Politécnica, Universidade Federal do Rio de Janeiro, como parte dos requisitos necessários à obtenção do título de Engenheira Mecânica.

Orientador:
Nísio de Carvalho Lobo Brum
Rio de Janeiro
Março de 2018
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO

DE ENGENHARIA MECÂNICA

ANÁLISE DE APLICABILIDADE DE UM SISTEMA DE REFRIGERAÇÃO CASCATA VERDE EM UM SUPERMERCADO NO CENÁRIO DO MUNICÍPIO DO RIO DE JANEIRO
PROJETO FINAL SUBMETIDO AO CORPO DOCENTE DO DEPARTAMENTO DE ENGENHARIA MECÂNICA DA ESCOLA POLITÉCNICA DA UNIVERSIDADE FEDERAL DO RIO DE JANEIRO COMO PARTE DOS REQUISITOS NECESSÁRIOS PARA A OBTENÇÃO DO GRAU DE ENGENHEIRA MECÂNICA.
Aprovado por:
Prof. Nísio de Carvalho Lobo Brum, D.Sc. (Orientador)
Prof. Hélcio Rangel Barreto Orlande, Ph.D.
Prof. Manuel Ernani de Carvalho Cruz, Ph.D.
RIO DE JANEIRO, RJ - BRASIL
MARÇO DE 2018
DEPARTAMENTO
DEM/POLITÉCNICA/UFRJ
Victor Assi Belfort Bastos
________________________________________________
________________________________________________
________________________________________________

iii
AGRADECIMENTOS
Agradeço ao meu orientador Nísio Brum pela paciência e pela assistência indispensável para a realização do projeto e aos professores Hélcio Orlande e Manuel Cruz por gentilmente aceitarem o convite para compor a banca.
Agradeço à minha família pelo esforço coletivo de gerações preocupadas com educação. Aos meus pais, Hector e Katia pelo amor e apoio incondicionais e aos meus primos Gustavo, Maria e Lara pelo companheirismo.
Agradeço aos amigos que fiz durante meu período no Colégio pH, sempre presentes, quando fugir um pouco dos estudos foi necessário.
Agradeço aos amigos que fiz durante meu período na UFRJ, em especial João Paulo, Lucas, Guido, Jessica, Letícia, Bruno, Rafael e Bruna pelos momentos de alegria compartilhados na Ilha do Fundão.
Finalmente, agradeço aos amigos que fiz durante o intercâmbio na Ulster University. Continuará sendo o período mais rico da minha vida.
iv
Resumo do Projeto de Graduação apresentado à Escola Politécnica/ UFRJ como parte dos requisitos necessários para a obtenção do grau de Engenheira Mecânica.
ANÁLISE DE APLICABILIDADE DE UM SISTEMA DE REFRIGERAÇÃO CASCATA VERDE EM UM SUPERMERCADO NO CENÁRIO DO MUNICÍPIO DO RIO DE JANEIRO
Belfort Bastos
Orientador: Nísio de Carvalho Lobo Brum, D.Sc.
Curso: Engenharia Mecânica
Esse projeto visa a realização de uma análise abrangente da aplicação em supermercadodeumsistemaderefrigeraçãotipocascata,usandoCO comorefrigerante noestágiodebaixatemperatura.Umdosfocosdoestudoseráaavaliaçãodausabilidade desse sistema no cenário da cidade do Rio de Janeiro. Como critério de análise serão usadasaPrimeiraeaSegundaLeidaTermodinâmica.
Palavras-chave: refrigeração cascata, dióxido de carbono, ciclo subcrítico.
v
Victor Assi
Março/2018
Abstract of Undergraduate Project presented to POLI/UFRJ as a partial fulfillment of the requirements for the degree of Mechanical Engineer.
ANALYSIS OF APLICABILITY OF A GREEN CASCADE REFRIGERANT SYSTEM IN THE CITY OF RIO DE JANEIRO
Victor Assi Belfort Bastos/2018
Advisor: Nísio de Carvalho Lobo Brum, D.Sc.
Course: Mechanical Engineering
This undergraduate final project aims to accomplish a wide analysis of the application in a supermarketofacascaderefrigerationsystem,usingCO astherefrigerantinthelowtemperature stage.OneofmainobjectivesistoevaluateitsusabilityinthecityofRiodeJaneiro.Asacriteria forthisanalysistheFirstandSecondLawofThermodynamicswillbeused.
Keywords: cascade refrigeration, carbon dioxide, subcritic cycle.
vi
seus
de
SistemadeReferência
deprimeira
dosistema
Vazõesmássicase
Análisedesegundaleitermodinâmica
sistema
Comportamentodosistemaderefrigeraçãoeosparâmetrosdeoperação
V.1OsistemaderefrigeraçãoeatemperaturadeevaporaçãonoEBT
OsistemaderefrigeraçãoeatemperaturadeevaporaçãonoEMT
V.3Osistemaderefrigeraçãoeaaproximaçãotérmicanotrocadordecalor2
Osistemaderefrigeraçãoeaaproximaçãotérmicanotrocadordecalor1
VIComportamentodosistemaderefrigeraçãoecargatérmica
dosistemaderefrigeraçãoeoregimedetemperaturasnoRJ
vii SUMÁRIO IIntrodução.......................................................................................................................1 I.1Contexto ......................................................................................................................1 I.2OCO e
ciclosusuais ..........................................................................................2 IISistema
Refrigeração ...............................................................................................3 II.1
................................................................................................5 IIIAnálise
leitermodinâmicanosistema ....................................................10 III.1Pontos
esuascaracterísticasdeoperação .............................................10 III.2
coeficientedeperformance ......................................................14 IV
no
....................................................20 V
.................31
.........................31 V.2
........................37
............44 V.4
............48
....................................53 VIIComportamento
......65 VIIIConclusão ...............................................................................................................68 IXBibliografia ................................................................................................................70
ÍNDICEDEFIGURAS
FiguraI.1–GráficopxhparaCO ,mostrandoumciclotranscrítico
FiguraI.2–GráficopxhparaR134a,mostrandoumciclosubcrítico
2
3
FiguraII.1–Diagramadosistemaderefrigeraçãocascatac/CO noestágiodeBT ......4
FiguraII.2–Limitestécnicosdeoperaçãodocompressor4NSL-30K-40P ....................8
FiguraII.3–LimitestécnicosdeoperaçãodocompressorW6FA ..................................9
FiguraIII.1–GráficopxhparaoestágiocomR744nosistemadereferência ............10
FiguraIII.2–GráficopxhparaoestágiocomR717nosistemadereferência ............12
FiguraIII.3–GráficopxhparaoestágiocomR718nosistemadereferência ............13
FiguraIV.1–Gráfico pizza deproporçãodeirreversibilidadeporaparelho .................29
FiguraIV.2–Gráficoembarrasdorendimentodesegundaleip/cadaaparelho .........30
FiguraV.1–Limitesdeoperaçãoeavariaçãodatemperaturadeevaporação .............32
FiguraV.2–Gráficodaeficiênciaisentrópicavariandoc/temperaturadoEBT ..........33
FiguraV.3–Gráficodavazãomássicavariandoc/temperaturadoEBT .....................34
FiguraV.4– GráficodaCOPvariandocomatemperaturadoEBT .............................34
FiguraV.5–Gráficoderend.desegundaleivariandocomatemp.doEBT ................35
FiguraV.6–Gráficodeirreversibilidadeporaparelhovariandocomat.doEBT .......36
FiguraV.7–Gráficodairreversibilidadetotaldosist.variandocomat.doEBT ........36
FiguraV.8–Limitesdeoperaçãoeavariaçãodatemperaturadecondensação ...........38
FiguraV.9–Limitesdeoperaçãoeavariaçãodatemperaturadeevaporação .............38
FiguraV.10–GráficodaeficiênciaisentrópicavariandocomtemperaturadoEMT ...39
FiguraV.11–Gráficode�� variandocomatemp.deev.doestágiocomamônia .........40
FiguraV.12–GráficodavazãomássicavariandocomatemperaturadoEMT ............41
FiguraV.13–GráficodoCOPvariandocomatemperaturadoEMT
41
viii
............................
..........................
...........................
FiguraV.14–Gráficoderendimentodesegundaleivariandocomat.doEMT..........42
FiguraV.15–Gráficodeirreversibilidadeporaparelhovariandoc/at.doEMT ........43
FiguraV.16–Gráficodeirreversibilidadetotalvariandoc/atemperaturadoEMT ....43
FiguraV.17–Gráficodevazãomássicavariandocomaaprox.térmicanoTC2 .........45
FiguraV.18–Gráficodocoef.deperf.variandocomaaprox.térmicanoTC2 ...........46
FiguraV.19–Gráficodorend.de2 leivariandocomaprox.térmicanoTC2 ...........47
FiguraV.20–Gráficodairreversibilidadevariandocomaprox.térmicanoTC2.........47
FiguraV.21–Gráficodairreversibilidadetotalvariandoc/aprox.térmicanoTC2 ....48
FiguraV.22–Gráficodevazãomássicavariandocomaaprox.térmicanoTC1 .........50
FiguraV.23–Gráficodocoef.deperf.variandocomaaprox.térmicanoTC1 ...........50
FiguraV.24–Gráficoderend.desegundaleivariandocomaprox.térmicanoTC1 ...51
FiguraV.25–Gráficodairrev.poraparelhovariandocomaaprox.térmicanoTC1 ..52
FiguraV.26–Gráficodairrev.totalvariandocomaaprox.térmicanoTC1 ...............52
FiguraVI.1–Gráficodavazãomássicaecargatérmicadecongelamento
FiguraVI.2–Gráficodavazãomássicaeacargatérmicaderesfriamento
FiguraVI.2–Gráficodecontornoparaavazãomássicatotaldeglicol
FiguraVI.4–Gráficodecontornoparacoeficientedeperformance
FiguraVI.5–Gráficodecontornoparaairreversibilidade
FiguraVI.6–Gráfico3Ddesuperfíciedairreversibilidade
FiguraVI.7–�� eatemperaturano
FiguraVI.8–�� eatemperaturanoEBT
FiguraVI.9–�� eaaproximaçãonoTC1
FiguraVI.10–�� eaaproximaçãonoTC2
FiguraVI.11–Comparaçãoentreostesteseirreversibilidadetotal
55
55
56
57
ix
...................
..................
........................
.............................
...........................................60
..........................................61
EMT .......................................................................62
........................................................................62
.......................................................................63
.....................................................................63
..............................63
FiguraVII.1–Perfildetemperatura
debulboúmidoanual
FiguraVII.2–Variaçãoanualdacargatérmicaderesfriamento
FiguraVII.3–Variaçãoanualdacargatérmicadecongelamento
FiguraVII.4–VariaçãoanualdoCOP
x
média
................................65
...................................66
................................66
..........................................................................67
ÍNDICEDETABELAS
TabelaI.1–Comparaçãodoimpactoambientaldosrefrigerantes
TabelaII.1–Temperaturasindicadasnaexposiçãodosprodutos
TabelaII.2–Temperaturasdereferênciaparaoperação
TabelaII.3–Capacidadetérmicafrigoríficadereferênciaparaoperação
TabelaIII.1–EstadodoR744nospontosdeoperaçãodoseuciclo
TabelaIII.2–EstadodoP-Glicolnospontosdeoperaçãodoseuciclo
TabelaIII.3–EstadodoR717nospontosdeoperaçãodoseuciclo
TabelaIII.4–EstadodoR718nospontosdeoperaçãodoseuciclo
TabelaIII.5–EstadodoArnoEBTnospontosdeoperaçãodoseuciclo
TabelaIII.6–EstadodoArnoEMTnospontosdeoperaçãodoseuciclo
TabelaIII.7–Vazõesmássicasediâmetrosnosistemaderefrigeraçãodereferência
TabelaIV.1–Equaçõesdeirreversibilidadeparacadatipodeequipamento
TabelaV.1–TemperaturasdeevaporaçãodoEBTtestadas
TabelaV.2–Eficiênciaisentrópicaeavariaçãodatemperaturadeevaporação
TabelaV.3–TemperaturasdeevaporaçãodoEMTtestadas
TabelaV.4–�� domodelo4NSL-30K-40Peavariaçãodatemp.decondensação
TabelaV.5–�� domodeloW6FAeavariaçãodatemperaturadeevaporação
TabelaV.6–VariaçãodeparâmetrosnoTC2
TabelaV.7–VariaçãodaaproximaçãonoTC2
TabelaV.8–VariaçãodosparâmetrosparaoTC1
TabelaV.9–VariaçãodaaproximaçãonoTC1
TabelaVI.1–Relaçãoentrecargatérmicabásicaeirreversibilidade
11
12
13
14
14
18
24
xi
..................................1
...................................6
...................................................7
.......................7
.............................11
.........................
.............................
.............................
.....................
....................
...
................
.........................................32
...........33
........................................37
.......39
..............40
...............................................................44
............................................................47
........................................................49
............................................................49
............................61
LISTADEABREVIATURASESÍMBOLOS
CO DióxidodeCarbono
CFC Clorofluorcarbono
HFC Hidroclorofluorcarbono
NH Amônia
BC1
Bombadecirculação1
BC2 Bombadecirculação2
C1 Compressor1
C2 Compressor2
Cd Condensador
VE1 Válvuladeexpansão1
VE2 Válvuladeexpansão2
TC1 Trocadordecalor1
TC2 Trocadordecalor2
EMT Evaporadordemédiatemperatura
EBT Evaporadordebaixatemperatura
T
TemperaturadorefrigeranteYnoponton
PressãodorefrigeranteYnoponton
Entalpiadorefrigerante
Entropiadorefrigerante
Volumeespecíficodorefrigerante
Fraçãomássicadevapordorefrigerante
T Temperaturaambiente
CT Capacidadetérmicanoevaporadordemédiatemperatura
xii
��
ℎ
��
��
��
CT Capacidadetérmicanoevaporadordebaixatemperatura
Energianovolumedecontrole
Taxadecalortrocada
Potêncianovolumedecontrole
Vazãomássica
Velocidadedofluido
Aceleraçãodagravidade
Altura
Potência
Rendimentodabombaderecirculação
A Áreadaseçãodotubo
Diâmetrodotubo
Coeficientedeperformance
Irreversibilidade
Rendimentodesegundaleidatermodinâmica
Eficiênciaisentrópicadocompressor
TBH Temperaturadebulboúmido
xiii
��
��
��
��
v
��
��
��
��
d
��
I
��
��
Introdução
I.1 Contexto
DeacordocomapudSilva(2009),ousodoCO emsistemasderefrigeraçãoestá intimamenteligadoàhistóriadaproduçãodefrioapartirdaRevoluçãoIndustrial.Se,em 1805, o engenheiro americano Oliver Evans foi um dos primeiros a publicar uma descriçãodeumsistemaderefrigeraçãomoderno,já,45anosdepois,oinventorbritânico AlexanderTwiningpropõeumsistemaderefrigeraçãoavaporcomDióxidodeCarbono.
Ainda,segundoGrantz,atéadécada de40doséculo XXo CO continuousendo utilizado largamente até ser substituído por gases mais “seguros” do ponto de vista de toxicidadeeoperação,osClorofluorcarbonosouCFCemabreviação.Todavia,em1973, osquímicosFrankRowlandeMarioMolinadescobriramosimpactosnocivosqueesses gases possuem sobre a camada de ozônio. Essa descoberta, que lhes rendeu o prêmio Nobel da química em 1995, acabou culminando na Protocolo de Montreal de 1987 que temcomoobjetivoreduzirousodegasesquepossamdegradaracamadadeozônio.
Esse processo culminou na ascensão dos Hidrofluorcarbonos ou HFC que não reagem com o ozônio. Por outro lado, como mostra a Tabela I.1, esses gases são 3000 vezes mais intensos que o CO na contribuição para o aumento do aquecimento global. Dessemodo,abriu-seespaçoparaareintroduçãodessegáscomorefrigerante.Em1993, o professor sueco Gustav Lorentzen propôs o uso do CO para o caso subcrítico em cascataetranscrítico.
TabelaI.1:ComparaçãodoImpactoAmbientaldosRefrigerantes(Silva.2009)

1 I
I.2 O������ eseusCiclosUsuais
OssistemasderefrigeraçãocontemporâneosqueusamDióxidodeCarbonofazem o refrigerante transcrever um ciclo transcrítico ou subcrítico ao longo de sua operação. Essaclassificaçãofazreferênciaàmaneiracomoocicloestárelacionadoaopontocrítico da substância que é a condição de temperatura e pressão que elimina a distinção entre a faselíquidaeagasosa(Borgnakke&Sonntag,2013).
FiguraI.1:GráficopxhparaCO ,mostrandoumciclotranscrítico(Silva,2009)
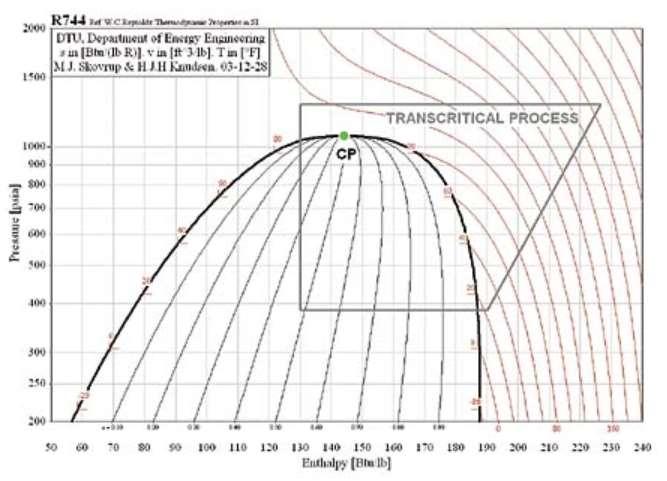
O ciclo que exibe pontos de estado acima do que é delimitado pelo ponto crítico édenominadocomoumciclotranscrítico(FiguraI.1).NasituaçãopráticadousodoCO , aaplicaçãodessetipodecicloacarretaempressõesdeoperaçãoelevadas,entre10.000e 15.000 kPa, assim sendo, demandam compressores e outros acessórios especialmente construídospararesistiraessasituação.Alémdisso,elaeliminaanecessidadedeseusar condensador,umavezqueésubstituídoporumresfriadorgasoso.
Essas restrições construtivas fazem com que o ciclo subcrítico (Figura I.2) seja mais usado em aplicações comerciais e industriais. Esse tipo de ciclo tem natureza mais usual, neleos pontos de estado estão abaixo do ponto crítico, dando lugar ao tradicional conjuntodeequipamentos:evaporador,condensador,válvuladeexpansãoecompressor. No entanto, secomparado com outros refrigerantes, as pressõesde operação com o CO aindasãomuitoaltas.Isso,naprática,obrigadividirosistemaderefrigeraçãoemestágios
2
para que os compressores não sejam sobrecarregados com uma diferença de pressão exagerada.Essetipodesistemarecebeonomedecascata(daSilva,2009).
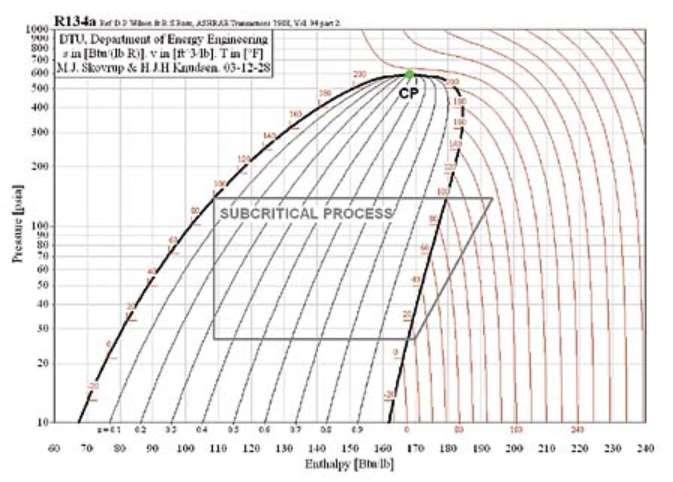
FiguraI.2:GráficopxhparaR134a,mostrandoumciclosubcrítico(Silva,2009)
Como o foco do trabalho será na aplicação de um sistema de refrigeração para supermercado, optou-se pelo subcrítico, uma vez que é potencialmente mais viável do pontodevistaeconômico.
3
II SistemadeRefrigeração
Além de se optar por um sistema cascata, outro critério relevante para sua escolha foi o conjunto de refrigerantes usados nos diferentes estágios. Todos eles deveriam possuir a mesma característica não degradante da camada de ozônio que o CO e não contribuir para o efeito estufa mais que dióxido de carbono, desse modo, podendo-se classificar esse sistema de refrigeração como “verde”. Ademais, deveria ter natureza construtiva aplicável no cenário de um supermercado e já ter aplicação prática comprovada.Poressesmotivos,osistemaderefrigeraçãodaFiguraII.1foiescolhido.
FiguraII.1:Diagramadosistemaderefrigeraçãocascata comCO noestágiodeBT
Essesistemapossuinadireçãoanti-horáriaumestágiodecondensaçãocomágua que possui uma torre de resfriamento e a bomba de circulação 1 (BC1) para garantir a vazão do líquido. Esse estágio permite o funcionamento do condensador (Cd) acoplado noestágiocomamônia(NH ),queemumestadolíquidoéexpandidanumaválvula(VE1) atingindo o estado bifásico líquido-vapor, já numa temperatura mais baixa. A amônia, então, absorve calor no trocador de calor 1 (TC1) que serve como um evaporador para

4
esseestágioe,comovapor,érepressurizadapelocompressor1(C1)e,novamente,segue paraocondensador.
Ocalor queaamônia absorvenoTC1 éextraídodoglicolquecircula emfunção de uma bomba (BC2). Uma parte da vazão é encaminhada para o evaporador de média temperatura (EMT) que atende as câmaras de alimento refrigerado como laticínios, carnes, aves, pescado, embutidos e alimentos processados. A outra parte é encaminhada para o trocador de calor 2 (TC2) que absorve calor do estágio com CO , servindo como um condensador para o mesmo. Dióxido de Carbono líquido é, então, levado para a válvuladeexpansão2(VE2),ondeperdepressãoetemperaturaatéchegarnoevaporador de baixa temperatura (EBT). Esse resfriará o ar insuflado nas câmaras de congelamento e, eventualmente, será evaporado e seguirá para o compressor 2 (C2), onde terá pressão e temperatura aumentadas novamente e será encaminhado, mais uma vez, para o TC2, fechandoociclo.
Do ponto de vista construtivo, essesistema pode sermontado em um rack house noestacionamentodoestabelecimento.Nocasodeumvazamentodaamônia,acargade gásseriadescarregadanabaciadatorrederefrigeraçãoe,posteriormente,amisturaáguaamôniaseriaremovidaatravésdeumdreno(daSilva,2009).
II.1 SistemadeReferência
Para o prosseguimento do trabalho, foi necessário determinar uma condição de operaçãodereferência,tantoparaastemperaturasnosdiversosequipamentoscomopara acargatérmicaderefrigeraçãonascâmarasderefrigeraçãoecongelamento.
O critério para a escolha dessas temperaturas envolveu valores propostos por da Silva(2009), anecessidadede atender àAssociaçãoBrasileirade Normas Técnicas e as restriçõesdeoperaçãoestabelecidaspelosmodelosdecompressoresutilizados.
5
TabelaII.1Temperaturasindicadasnaexposiçãodosprodutos(ABNT,2013)
Daconfiguraçãoselecionadafoiretiradaatemperaturadecondensaçãonoestágio com amônia (T = 40℃) e a temperatura do EBT (T = -35℃). Já da tabela II.1 foram determinadastemperaturasparaoEMT(T = -4℃e T =-7℃)suficientepara refrigeraroitemmaisconservadordatabela.Tomandoumaaproximaçãodetemperaturas de 6℃ no TC2 e 5℃ no TC1, pode-se estabelecer a temperatura de condensação do estágio de alta pressão (T = 0℃) e a temperatura de evaporação do estágio de baixa pressão (T = -11℃). Levando ainda em consideração uma temperatura ambiente de 20℃ e que o ar sofre um aquecimento de 5K ao passar pelos produtos armazenados nas câmarasfriforíficas,podemoscomessesdadosdeterminartodosospontosdosistemade refrigeraçãoestudado.Atabelaabaixoresumeessesparâmetrosdereferência.

6
PropilenoGlicol
II.2
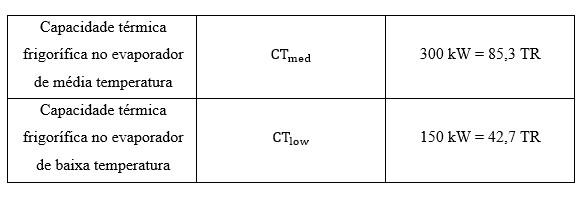
dereferênciaparaoperação
noEMT
noEBT
Paraascargastérmicasfrigoríficas,tantonocasodacâmaraderefrigeração comoparaocasodocongelamento,serãousadosvalorestípicosnaaplicaçãodeum supermercadodegrandeporte(Silva&Euzébio,2013).
TabelaII.3Capacidadetérmicafrigoríficadereferênciaparaoperação
Para conferir maior realismo à análise é fundamental realizar a seleção dos compressoresusadosnosistemaderefrigeração.Paraisso,lançou-semãodocatálogoda BITZER,umafabricantereconhecidapelomercado.Aempresaforneceumsoftwarepara facilitaressaescolhadeequipamento,nelebastaindicartemperaturaecapacidadetérmica de operação – estabelecidas na tabela II.2 e II.3 – para se obter uma recomendação de modeloeaeficiênciaisentrópicadocompressorparaocasodelimitado.
ParaoestágiocomCO ,omodelorecomendadofoio4NSL-30K-40Pnacategoria de compressores com pistões semi-herméticos. Outrossim, é importante notar que esse
7 Tabela
Temperaturas
Ambiente �� 20℃ ���� �� 40℃ �� -11℃ ���� �� 0℃ �� -35℃
�� -4℃ �� -7℃ Ar
�� 0℃ �� -5℃ Ar
�� -15℃ �� -20℃
modelo impõe uma temperatura de superaquecimento mínima de 5K e que as temperaturas de evaporação e condensação devem se manter contidas no limite imposto pelafiguraII.2.
FiguraII.2Limitestécnicosdeoperaçãodocompressor4NSL-30K-40P(Bitzer)
Analisando a figura, percebe-se que o ponto vermelho – indicador do par temperatura de evaporação e temperatura de condensação – está dentro dos limites de operação impostos pelo modelo. Além disso, obteve-se uma temperatura de descarga igual à62,3℃,oque,porsuavez,implicanumaeficiênciaisentrópicade68%paraesse compressor.
Já no caso do estágio com amônia, o modelo proposto pelo software da BITZER foi o W6FA na categoria de compressores com pistões abertos. Assim como no caso do compressorparaoR744,essemodelodemandaumsuperaquecimentomínimo,agora,no valorde1K.OslimitestécnicosdeoperaçãodessemodeloseguemnafiguraII.3:

8
FiguraII.3LimitestécnicosdeoperaçãodocompressorW6FA(Bitzer)
A área com hachura indica a necessidade de resfriamento no cabeçote. A temperatura de descarga nesse caso é igual a 155,6℃. Isso implica numa eficiência isentrópicade71%.
Levanto em conta todos os parâmetros estabelecidos no capítulo 2, podemos realizar uma análise termodinâmica do sistema de refrigeração. Isso permitirá inferir aspectos ligados ao coeficiente de performance e as eficiências exergéticas dos equipamentoscontidosnosistemadereferência.

9
III Análisedeprimeiraleidatermodinâmicanosistema
III.1 Pontosdosistemaesuascaracterísticasdeoperação
Paracompletaratabelatermodinâmicasnosdiferentesestágioscompreendidosno sistema de refrigeração estudado, precisa-se conhecer as propriedades dos fluidos refrigerantes em cada um desses pontos de operação. O CoolPack, um software livre desenvolvidopela Danish Energy Agency,vaiserutilizadoparamontarosgráficospxh emcadaumdosestágios.
Aplicando-se astemperaturasdeevaporaçãoecondensação, osuperaquecimento indicado e o rendimento isentrópico desse compressor, teremos o seguinte gráfico p x h paraoestágiocomCO ,expostonafigura3.1:
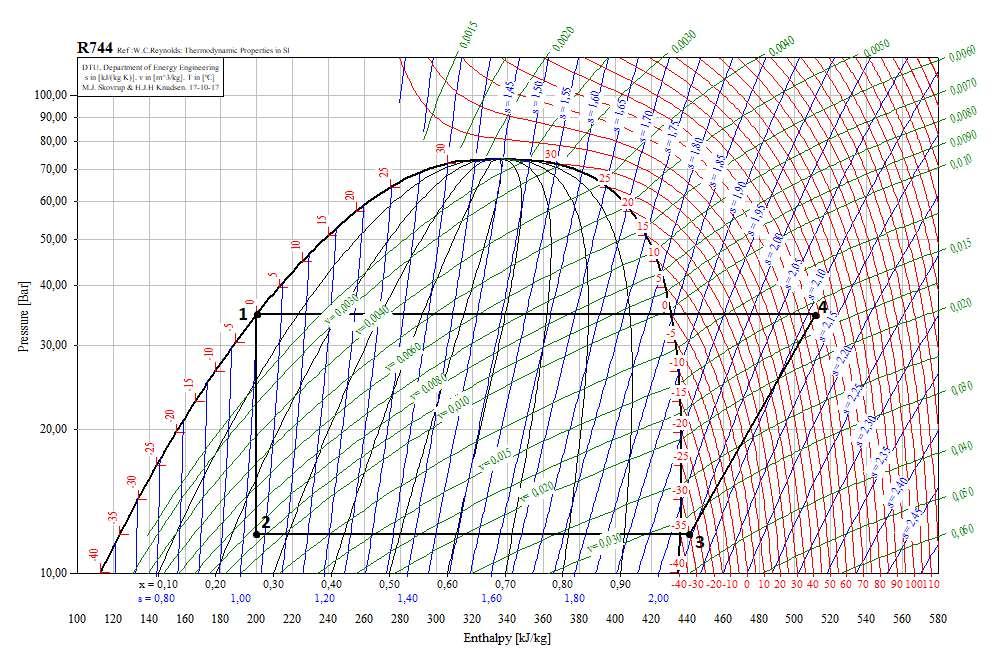
FiguraIII.1GráficopxhparaoestágiocomR744nosistemadereferência(CoolPack)
Essegráficoviabilizacompletarosvaloresdeentalpia,entropia,pressão,volume específicoefraçãomássicadevaporparaospontosde1a4dociclocomCO
10
CO
TabelaIII.1EstadodoR744nospontosdeoperaçãodoseuciclo
T(˚C) p (bar)
x
1 0,0 34,857 200,00 0,9990 0,001080 0
2 -35,0 12,048 200,00 1,0300 0,008490 0,24
3 -30,0 12,048 441,33 2,0439 0,033058 SuperAq
4 63,2 34,857 511,49 2,1128 0,011596 SuperAq
No caso do estágio de MT que possui como refrigerante o propileno glicol com 30% deconcentração, usou-se aferramenta Heat Transfer Calculator do CoolPack para se calcular o calor e o volume específico médio desse refrigerante. Ademais, lançou-se mãodaexpressãoabaixoparaseestimaravariaçãodaentalpianesseestágio.
Dessa forma, é possível determinar os parâmetros dos pontos desse estágio, estandocontidosnatabelaaseguir:
TabelaIII.2EstadodoP-Glicolnospontosdeoperaçãodoseuciclo
P-Glicol
T(˚C) p (bar)
1e3 -4,0 4,942 3,790 0,000964 11,358 LSR
2 -7,0 4,942 3,782 0,000963 LSR Med 3,786 0,000964
Já para a amônia – ou R717 – e com o rendimento isentrópico de 71%, tem-se o seguintegráficocontidonafiguraIII.3.
11
h s ��
∆ℎ= �� ∆��
�� �� ∆ℎ x
FiguraIII.2GráficopxhparaoestágiocomR717nosistemadereferência(CoolPack)
Apartirdográfico,pode-sedeterminaratabelatermodinâmicaparaesseestágio, definindo-seospontosdeoperaçãodesseciclo.

TabelaIII.3EstadodoR717nospontosdeoperaçãodoseuciclo
NH
T(˚C) p (bar) h s �� x
1 40,0 15,549 386,43 1,6280 0,002280 1
2 -11,0 2,791 386,43 1,7130 0,079790 0
3 -10,0 2,791 1450,59 5,7753 0,436156 SuperAq
4 155,6 15,549 1810,33 6,0306 0,129303 SuperAq
Ademais, tem-se a água – ou R718 – queservecomo condensador do sistema de refrigeração. Para se estimar suas propriedades ao longo do estágio, deve-se usar o processodescritopelográficoabaixo:
12
FiguraIII.3–GráficoparadeterminaçãodaspropriedadesdoR718
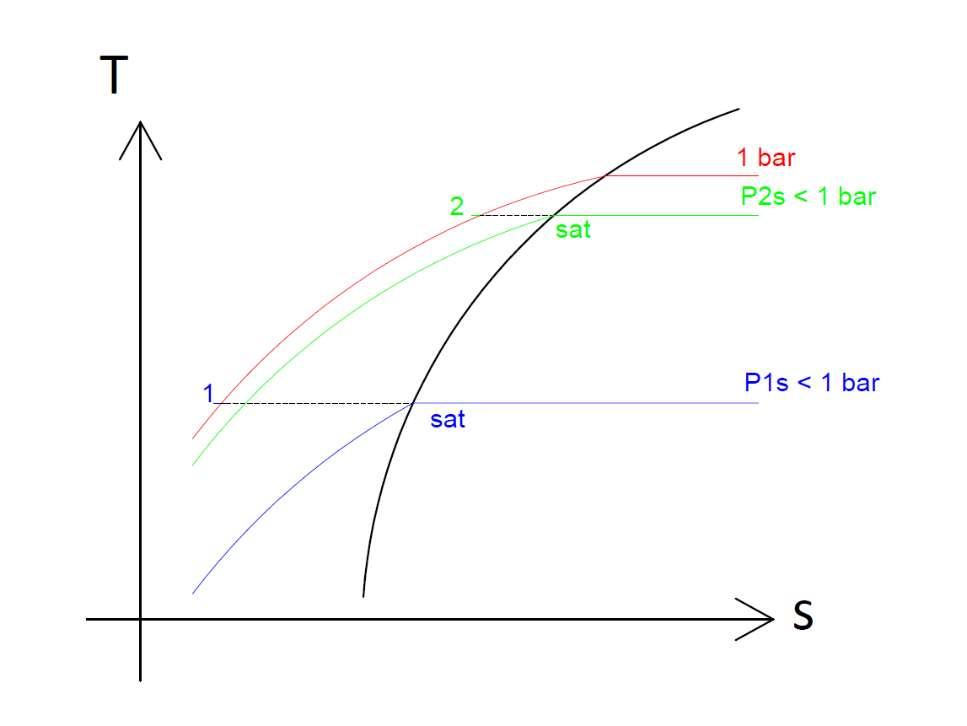
Seguindo a isotérmica entre o ponto 1 e o ponto saturado, pode-se determinar a variaçãodeentalpiacomo:
Osvaloresde
Refrigerant Calculator doCoolPack
Comisso,pode-seestabelecerosvaloresnatabelatermodinâmicaparaesseciclo condensante.
III.4EstadodoR718nospontosdeoperaçãodoseuciclo
20,0
95,0
LSR
LSR
Por último, a mesma ferramenta usada para definir a tabela acima pode ser aplicadaparasedefinircomooar,tantonoEMTquantonoEBTsecomportará:
13
∆ℎ=��∆�� ℎ −ℎ =��(�� − �� ) ℎ =ℎ +��(�� − �� )
ℎ ,��e�� serãoextraídosdo
Tabela
H2O T(˚C) p (bar) h �� �� ���� ������ x 1
1,000 82,97 0,001000 4,18
2
1,000 398,74 0,001040 4,18
TabelaIII.5EstadodoArnoEBTnospontosdeoperaçãodoseuciclo
ArnoEBT
T(˚C) p (bar)
-15,0 1,000 486,81 0,74049 1,0085 3,799
-20,0 1,000 481,76 0,72604 1,0085 3,780
TabelaIII.6EstadodoArnoEBTnospontosdeoperaçãodoseuciclo
ArnoEBT
T(˚C) p (bar)
0,0 1,000 501,93 0,78376 1,0085 3,856
-5,0 1,000 496,89 0,76515 1,0085 3,836
Tendodefinidoospontosdeoperaçãoparatodososestágiosépossívelaplicaros conceitos da Primeira Lei Termodinâmica para inferir valores para as diferentes vazões mássicasecoeficiente deperformancedosistemaderefrigeração.
III.2 Vazõesmássicasecoeficientedeperformance
Dobalançodedeenergiaparaumvolumedecontrole,tem-se:
1
Contudo, os aparelhos analisados estão sempre no regime permanente o que implicaque =0eque
.Alémdisso,variaçõesemalturaevelocidadeserão desconsideradas. Desse modo, pode-se determinar uma equação simplificada de energia ligada ao tipo de equipamento em questão. Para trocadores de calor, evaporadores ou condensadoresotrabalho novolume decontroleserázero.Jánoscompressoresteremos ataxadecalornosistemaigualàzero.
14
h �� �� ���� ������ s 1
2
h �� �� ���� ������ s . 1
2
���� ���� = �� − �� + �� ℎ + 1 2 v +���� − �� ℎ +
2 v +����
�� =��
Compressores:
Para as bombas de circulação, será usada a equação abaixo. Ela permite inferir a potênciarequeridaporessesequipamentos
basenavazãomássicadefluido,volume específicodomesmo,perdadepressão
rendimento
bomba.
Agora, basta aplicar essas expressões nos diversos estágios do sistema de refrigeração para se obter vazões mássicas, potência das bombas e dos compressores –fundamentaisparaocálculodocoeficientedeperformance.
com
pelo EBT e levando em conta que a taxa de calor absorvido por esse equipamento corresponde à capacidade térmica frigorífica no EBT, deve-se utilizar a expressão3.1parasecalcularavazãomássicanesseestágio.
dióxidodecarbono,pode-se
pelocompressor
15 -Trocadoresdecalor,evaporadoresoucondensadores: �� = ��(ℎ ℎ ) (III.1) -
�� = ��(ℎ ℎ ) (III.2)
com
e
da
�� = ����(�� �� ) �� (III.3)
Estágio
������ Iniciando
�� =CT = �� (ℎ − ℎ ) �� = CT (ℎ − ℎ ) �� =0,62���� �� Agora,fazendousodaexpressãoIII.2entreospontos3e4edavazãomássicade
estabelecerapotênciademandada
2. �� = �� = �� (ℎ − ℎ ) �� =43,61����
estimar
expressão
trocado
trocador de calor 2, basta usar novamente
ciclo
EstágiocomPropileno-Glicol
Nesseestágio,éimportantenotarquehaverásangramentodavazãomássica.Parte delaseráencaminhadaparaoevaporadordemédiatemperaturaeoutraparteseráenviada para o trocador de calor 2 e funcionará como condensador para o estágio com R744. A expressãoabaixogaranteaconservaçãomássica
problema:
ovalordataxadecalortrocadonotrocadordecalor2eospontos2e 3 desse ciclo, pode-se estimar a vazão mássica para a parte de fluido que passa por esse equipamento.
calcular avazãomássica
outraporçãode fluidorefrigerante,necessita-se somenteaplicaraexpressão
Dessemodo,nointuitodesecalcularavazãomássicatotalnesseestágio,deve-se somenteaplicaraexpressão
16 Já para
a taxa de calor
no
a
III.1,lançandomãodospontos4e1do
comCO . �� = �� (ℎ − ℎ ) �� =193,61����
no
�� = �� + �� ′′ (III.4) Usando-se
�� = �� ′(ℎ − ℎ ) �� ′= �� (ℎ − ℎ ) �� =0,50���� �� Para
da
anteriorparaoEMT. CT = �� ′′(ℎ − ℎ ) �� ′′= CT (ℎ − ℎ ) �� =0,78���� ��
III.4:
rendimento
seusodataxadecalortrocado
modo,
possível calcular
requerida
compressor 1, usando avazãomássicadeamônia,aspropriedadesdofluidonospontos4e3eaexpressãoIII.2:
taxadecalortrocado
17 �� = �� + �� =0,50+078 �� = 1,28���� �� Alémdisso,pode-seusaraequação3.3,aliadaàspropriedadesdofluidoextraídas no CoolPack eseestipulandoumaquedadepressãodemeiaatmosferaeum
debombade0,6paraestimarapotênciarequeridapelabombadecirculação2. �� = �� �� (�� − �� ) �� �� =0,21���� Finalmente,aexpressãoIII.1podesermaisumavezutilizadaparaestimarovalor dataxadecalortrocadanotrocadordecalor1. �� = �� (ℎ − ℎ ) �� =493,61���� Estágiocom������ Paraseencontraravazãomássicanesseciclo,aplica-seaexpressãoIII.1,fazendo-
noTC1. �� = �� (ℎ − ℎ ) �� =0,46���� �� Desse
é
a potência
pelo
�� = �� (ℎ − ℎ ) �� =166,87���� Ademais,bastalançarmãodessamesmaequaçãonospontos4e1paraseestimar a
docondensador. �� = �� (ℎ − ℎ )
Para se calcular a vazão mássica de água, precisa-se unicamente da expressão acimaaliadaaospontos
e1desuatabelatermodinâmica.
Antesdedarcontinuidade
análise,
importanteressaltarqueosvaloresobtidos paravazãomássicaestãodentrodoesperado,levandoemcontarestriçõesimpostaspelos diâmetrosdostubosqueeventualmenteseriamusadosemumprojeto.Paraisso,usa-sea expressãoabaixoeanaturezacilíndricadostubos.
Supondo ainda uma velocidade de2 m/s para os fluidos, teremos seguinte tabela comosdiâmetrosdostubosempolegadas:
TabelaIII.7Vazõesmássicasediâmetrosnosistemaderefrigeraçãodereferência
Diâmetro
Refrigerante Vazãomássica
CO –R744 0,68 4,5’’
P-Glicol–R1270 1,28 1,6’’
NH –R717 0,46 6,0’’
H O R718 2,01 1,4’’
Esses valores estão em sintonia com o esperado para as dimensões dos tubos. Todavia, em uma situação prática se deverá escolher diâmetros de tubo dentro dos padrõesdomercado.
18 �� =660,47���� Estágiocom������
2
�� = �� (ℎ − ℎ ) �� =2,01���� ��
a
é
v= ���� �� �� ��= �� �� 4 ��= 4���� ��v
Coeficientede Performance
Por conseguinte, finda-se a análise de primeira lei usando a equação abaixo para ocálculodocoeficiente deperformance(Borgnakke&Sonntag,2013).
dessesistemaderefrigeraçãoserconsideradaviávelnumcenáriorealista.
19
��= ∑�� ∑�� ��= CT + CT P + P + P + P (3.5) ��=3,2 Essevalorparacoeficientedeperformanceestádentrodafaixaquefazaaplicação
IV Análisedesegundaleitermodinâmicanosistema
Parafundamentaressaanálise,seráutilizado,principalmente,oconceitodeexergia – potencialmáximodegerartrabalhodeumadeterminadamassadefluido–eoconceito deirreversibilidade–diferençaentreessetrabalhomáximoeotrabalho,defato,utilizado. Dessa forma, poder-se-á comparar os diversos equipamentos existentes no sistema de refrigeração para sedeterminarqual deles tem maiorimpacto na destruição de exergia –ounacapacidadedegerartrabalho–paraessesistema.Comisso,ficaráevidenteondese devemfocarosesforçosparamelhorarosistemaemquestão(apudKiliç,2012).
Aexergiaespecíficaemumamassaderefrigerantepodeserconhecidapelaequação abaixo:
��
)
Em que ℎ e �� fazem referência, respectivamente, à uma entalpia e entropia de referência.
Todavia,pode-selevaremcontaqueaexergiafísicaédesprezível,logoaexpressão acimaficará:
O interesse maior do trabalho no uso do conceito da exergia é no tocante a uma análisedecadaequipamentocomovolumedecontrole.Portanto,buscar-se-á,naverdade, um valor queexpresse a diferençaentre exergiade entrada e exergiade saída. Paraisso, bastalançarmãodaequação
Agora, para se estimar a exergia total em um determinado ponto do sistema de refrigeração,segueumaequaçãorecomendada:
A exergia proveniente da taxa de calor é descrita, aliada ao rendimento de Carnot, conformeestáindicadoabaixo:
20
��=(ℎ− ����)+ 1 2 v +����−(ℎ −
��
��=(ℎ− ����) −(ℎ − ���� )
acima: �� − �� =(ℎ − ���� ) −(ℎ − ���� )− (ℎ − ����)+(ℎ − ���� ) �� �� =(ℎ ℎ ) ��(�� ��) (IV.1)
Ψ= ���� (IV.2)
Jáaexergiacausadapelataxadetrabalho,édescritasimplesmentepor:
(IV.4)
Finalmente, para se estimar a irreversibilidade de cada equipamento que compõe o sistemaderefrigeração,deve-seutilizaraexpressãoabaixousandoosvaloresdeentrada esaídadeexergia:
(IV.5)
Levando em conta as expressões IV.2, IV.3 e IV.4, o fato de que em todos os equipamentos haver apenas uma fonte para cada tipo de exergia e a hipótese de regime permanente,pode-sereescreveraequação4.5daseguinteforma:
(IV.6)
Com a expressão 4.6, pode-se compor genericamente equações para se estimar o valordairreversibilidadeparacadaaparelhoeaeficiênciadesegundaleicorrespondente.
Compressores
No caso dos compressores, leva-se em conta a hipótese de ser um equipamento adiabático(��=0)equeataxadetrabalhocorrespondeàpotênciadocompressoreterá um valor negativo na expressão (��<0). Além disso, como temperatura e pressão de entradasãomenoresqueasmesmasnasaídateremosque�� < ��
Manipulando a expressão acima para que apenas valores positivos apareçam, teremos:
21 Ψ = 1 �� �� �� (IV.3)
Ψ = ��
��= Ψ + Ψ Ψ Ψ
��= 1 �� �� ��+ ��(�� ��) ��
. ��= −( ��)+��(�� − ��)
��+ ��(�� − �� ) = ��
Dessa forma, fica clara a natureza do compressor no qual a potência recebida pelo equipamentoérepartidaentreoobjetivodoequipamento –aumentaraexergia dofluido –eairreversibilidadeaqualsedesejaseramenorpossível.
Parafinalizar,aplica-seaexpressãoIV.1naequaçãoacima:
(IV.7)
valor para rendimento de segunda lei da termodinâmica,bastacompor
Da expressão IV.7 surge naturalmente
fração
desejadopelorequerido.
(IV.8)
EvaporadoreseCondensadores
Nesses equipamentos, não há trabalho sendo realizado sob o volume de controle (��=0),então,aplicando-seaexpressão IV.6e IV.1earranjandoseustermosparaque todossejammaioresquezero,ter-se-á:
(IV.9)
Noqualorendimentodesegundaleipodeserdescritocomo:
(IV.10)
TrocadoresdeCalor
Esse equipamento pode ser compreendido como adiabático (��=0) e não possui trabalho sendo exercido no ou pelo sistema (
=0). Além disso, em um trocador
22
��+ ��[(ℎ ℎ ) ��(�� �� )] = ��
o
uma
do
�� = ��[(ℎ ℎ ) ��(�� �� )] ��
��+ �� / [ ℎ / ℎ / �� �� / ℎ / ] = ��[(ℎ ℎ ) ��(�� ��)]
�� / = = �� / [ ℎ / ℎ / �� �� / ℎ / ] ��[(ℎ −ℎ ) − ��(�� − ��)]
��
dois fluidos
fluidos
expressão
essaexpressãoàequação
controle trocando calor entre
frio(C). Dessemodo,
sejampositivosficará:
orendimentodesegundaleiparaostrocadoresserá:
VálvulasdeExpansão
Assimcomonocasodostrocadoresdecalor,esseequipamentopodeserconsiderado comoadiabáticoecomtrabalhonulo(
=0).Ademais,oprocessorealizadoporesse equipamentonãotemalteraçãonaentalpia.Porconseguinte,aplicando-seaexpressão4.6 nessasituação,ter-se-ácomoresultado:
Nesse caso, não faz sentido se falar em rendimento de segunda lei uma vez que, comomostraaexpressão,todaaexergiaétransformadaemirreversibilidade.Issoindica aperdadacapacidadederealizartrabalhodofluidoaopassarporesseequipamento.
A tabela a seguir reúne as expressões obtidas para serem analisadas com mais clareza.
23 haverão
entrando e saindo do volume de
si. Esses
serãodenominadoscomofluidoquente(H)efluido
a
IV.6dispostadeformaemquetodososcomponentes
��+ �� (�� − �� ) = �� (�� − ��) Aliando
4.1: ��+ �� [(ℎ ℎ ) ��(�� �� )] = �� [(ℎ ℎ ) ��(�� �� )] (IV.11) Já
�� = �� [(ℎ ℎ ) ��(�� �� )] �� [(ℎ ℎ ) ��(�� �� )] (IV.12)
��,��
��=����(�� �� ) (IV.13)
Trocadorde Calor
Válvulade Expansão
irreversibilidade das bombas de circulação não será calculada, uma vez que possuem valores desprezíveis para destruição da capacidade de gerar trabalho (Kiliç, 2012). Agora, basta aplicar as expressões acima para cada equipamento específico do sistemaderefrigeração:
24 TabelaIV.1Equaçõesdeirreversibilidadeparacadatipodeequipamento Compressor I ��+ ��[(ℎ ℎ ) ��(�� �� )] = �� �� ��[(ℎ ℎ ) ��(�� �� )] �� Evaporador/ Condensador I ��+ �� / [ ℎ / ℎ / �� �� / ℎ / ] = ��[(ℎ −ℎ ) − ��(�� − ��)] �� �� / [ ℎ / ℎ / �� �� / ℎ / ] ��[(ℎ ℎ ) ��(�� ��)]
I ��+ �� [(ℎ ℎ ) ��(�� �� )] = �� [(ℎ −ℎ ) − ��(�� − �� )] �� �� [(ℎ ℎ ) ��(�� �� )] �� [(ℎ ℎ ) ��(�� �� )]
I ��=����(�� �� ) �� Nãohá A
Compressor2:
Lançando mão da expressão
pode-se estabelecer a seguinte relação de irreversibilidadeparaesseequipamento:
paraocálculodorendimento,usar-se-á
equação4.8:
VálvuladeExpressão2
Paraestimara perda de exergia promovida poresse equipamento, deve-se aplicara expressão4.13:
EvaporadordeBaixaTemperatura
ter-se-á como valor de irreversibilidade para esseequipamento:
Levando em conta a expressão
E, agora, para estimar o rendimento de segunda lei da termodinâmica com a expressãoIV.10:
25 Estágiocom������
IV.7,
�� + �� [(ℎ −ℎ ) − ��(�� − �� )] = �� �� + 31,06 = 43,61 �� = 12,55���� Já
a
�� = �� [(ℎ −ℎ ) − ��(�� − �� )] �� �� =71,23%
�� =�� ��(�� − �� ) �� =5,65����
IV.9,
�� + �� [(ℎ −ℎ ) − ��(�� − ℎ )] = �� [(ℎ −ℎ ) − ��(�� − �� )] �� + 15,36= 34,65 �� =19,29����
TrocadordeCalor2
opropileno-glicol
logo
aexpressãoacima
orendimento,então,
IV.12:
26 �� = �� [(ℎ −ℎ ) − ��(�� − ℎ )] �� [(ℎ −ℎ ) − ��(�� − �� )] �� =44,32%
Com a equação IV.11, pode-se escrever uma expressão para estimar a irreversibilidadenesseequipamento: �� + �� [(ℎ −ℎ ) − ��(�� − �� )] = �� ′[(ℎ −ℎ ) − ��(�� − �� )] Todavia,
podesertomadocomo líquidoincompressível,
a exergianospontospodeserreescritascomo: �� = �� (�� − ��)− ������ �� �� + �� (�� − �� ) �� = �� (�� − ��)− ������ �� �� + �� (�� − �� ) ∆��= �� (�� − ��)− ������ �� �� Logo
resultaráem: �� + �� [(ℎ −ℎ ) − ��(�� − �� )] = �� ′ �� [(�� − ��)− ������ �� �� ] �� + 9,23= 28,60 �� =19,37���� Para
usa-seaexpressão
�� = �� [(ℎ −ℎ ) − ��(�� − �� )] �� ′ �� [(�� − ��)− ������ �� �� ] �� =32,28%
EvaporadordeMédiaTemperatura
TrocadordeCalor1
para estimar
propileno-glicol
se usar a
27 EstágiocomGlicol
Novamente,usandoaexpressãoIV.9eoglicolcomolíquidoincompressível,ter-seá: �� +�� [(ℎ −ℎ ) − ��(�� − ℎ )] = �� ′′ �� [(�� − ��)− ������ �� �� ] �� + 18,46= 30,77 �� =12,32���� Jácomaequação IV.10paraorendimentodesegundalei: �� = �� [(ℎ −ℎ ) − ��(�� − ℎ )] �� ′′ �� [(�� − ��)− ������ �� �� ] �� =59,98%
Mais uma vez, aplicando a equação IV.11 e tomando o
como líquidoincompressível: �� + �� �� [(�� − ��)− ������ �� �� ] = �� [(ℎ −ℎ ) − ��(�� − �� )] �� + 47,06=58,49 �� =11,43���� Agora,
o rendimento de segunda lei datermodinâmica, basta
expressãoIV.2: �� = �� �� [(�� − ��)− ������ �� �� ] �� [(ℎ −ℎ ) − ��(�� − �� )] �� =80,46%
irreversibilidade
aparelho
lançando-se mão, novamente, da equaçãoIV.7:
orendimentodesegundalei
Condensador
serestimando,usando-seaequaçãoIV.8:
Para se estimar a exergia
por esse aparelho, basta usar a expressão IV.9 nospontos4e1desseestágioeofatodaáguaserconsideradaumlíquidoincompressível:
Maisumavez,orendimentodesegundaleipodesercalculadopelaexpressãoIV.10:
VálvuladeExpansão
para esseaparelho,usa-sea expressãoIV.3:
parase estimar
28 Estágiocom������ Compressor2 A
desse
é calculada,
�� + �� [(ℎ −ℎ ) − ��(�� − �� )] = �� �� + 132,17 = 166,87 �� = 34,70���� Já
vai
�� = �� [(ℎ −ℎ ) − ��(�� − �� )] �� �� =79,21%
destruída
�� + �� [(ℎ −ℎ ) − ��(�� − �� )] = �� �� [(�� − ��)− ������ �� �� ] �� + 62,13= 71,88 �� = 9,75����
�� = �� [(ℎ −ℎ ) − ��(�� − �� )] �� �� [(�� − ��)− ������ �� �� ] �� = 86,43%
1 Finalmente,
ovalordairreversibilidade
�� =�� ��(�� − �� )
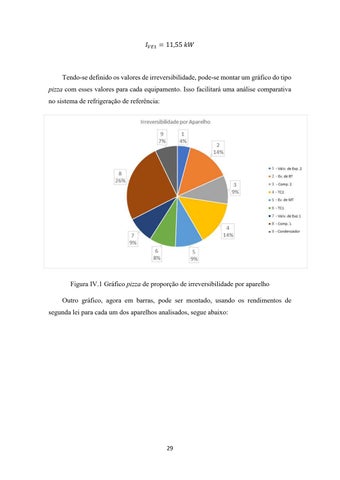
Tendo-sedefinidoosvaloresdeirreversibilidade,pode-semontarumgráficodotipo pizza com esses valores para cada equipamento. Isso facilitará uma análise comparativa nosistemaderefrigeraçãodereferência:

FiguraIV.1Gráfico pizza deproporçãodeirreversibilidadeporaparelho
Outro gráfico, agora em barras, pode ser montado, usando os rendimentos de segundaleiparacadaumdosaparelhosanalisados,segueabaixo:
29 �� =11,55����
FiguraIV.2Gráficoembarrasdorendimentodesegundaparacadaaparelho
Essesgráficosindicamqueocompressor1–aqueleusadonoestágiocomamônia–é o equipamento que mais destrói capacidade útil de realizar trabalho no sistema de refrigeração. Ele corresponde à quase um terço da exergia gasta com irreversibilidade entreosequipamentosutilizados.Issoimplicaqueosesforçosparamelhoraressesistema deveriam se concentrar principalmente nesse aparelho. Todavia, não há muito o que se fazer nesse sentido para o compressor. Seus parâmetros de operação são definidos pelas temperaturas no evaporador e condensador que no caso específico desse estágio equivalem ao trocador de calor 1 e o condensador com água como fluido frio, respectivamente.
Outrossim,maisumaparelhochamaatenção,quandoseobservaosegundográfico. Oequipamentocommenorrendimentodesegundaleidatermodinâmicaéotrocadorde calor2.IssocolocatambémoTC2nalistaprioritáriadeaparelhosaseremalterados.










Dessa forma, surge naturalmente como meio mais simples de se modificar os resultados obtidos nesses equipamentos críticos a mudança de seus parâmetros de operação.Ademais,nãoéofocodessetrabalhoaanálisedeaspectosconstrutivosdecada equipamento que, eventualmente, também poderiam ser alterados para promover melhorias no sistema de refrigeração. Logo, o próximo capítulo focará na modificação das temperaturas e aproximações térmicas dos trocadores para se compreender como se dáocomportamentodessesistemaemdiferentessituaçõesdefuncionamento.

30
44,32 71,23 32,28 59,98 80,4679,21 86,43 0,00 10,00 20,00 30,00 40,00 50,00 60,00 70,00 80,00 90,00 100,00 1 % Ev.deBT Comp.2 TC2 Ev.deMT
V Comportamento do sistema de refrigeração e os parâmetrosdeoperação
No intuito de se obter uma análise abrangente, foram variados quatro parâmetros importantesparaadefiniçãodosistemaderefrigeraçãodereferência:
-Temperaturadeevaporaçãodoevaporadordebaixatemperatura
-Temperaturadeevaporaçãodoevaporadordemédicatemperatura
-Aproximaçãotérmicadotrocadordecalor2
-Aproximaçãotérmicadotrocadordecalor1
Em cada um desses casos, as situações de operação foram redefinidas e o software daBITZERfoiutilizadotantoparaconstatarseessesparâmetrosestãodentrodoslimites de operação do compressor, quanto para extrair um valor realista para o coeficiente isentrópico. Em seguida, usou-se o software COOPACK para refazer a tabela de estado termodinâmico do fluido em cada ponto de operação. Dessa forma, pôde-se realizar novamente as análises de primeira e segunda lei da termodinâmica, obtendo-se novos valoresparacoeficientedeperformanceeirreversibilidadedosaparelhos.
V.1OsistemaderefrigeraçãoeatemperaturadoEBT
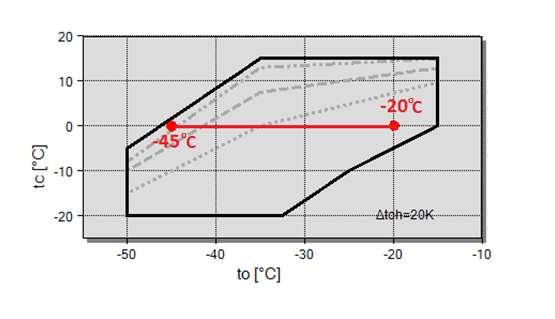
Inicialmente,deve-sedefinirodomíniodeinteressedastemperaturasdeevaporação do EBT. Para isso, leva-se em conta as temperaturas de congelamento definidas por normatécnica,jáexpostasnessetrabalhopelatabelaII.1.AnormaNBR16255estabelece que itens congelados devemser mantidos entre -15℃e -35℃a depender do produto em questão.Logo,levandoemcontaqueaaproximaçãotérmicadeveficarentre-5Ke-10K para um trocador usual, selecionaram-se para análise as temperaturas de evaporação indicadasnatabelaabaixo:
31
Teste T
-20
-25
-30
-35
V.1TemperaturasdeevaporaçãodoEBTtestadas
T T T T
Agora,deve-seusarosoftwareda Bitzer paradeterminarseessasnovas temperaturasdeevaporaçãoestãodentrodoslimitesdeoperaçãodomodelode compressorescolhido(4NSL-30K-40P).
FiguraV.1Limitesdeoperaçãoeavariaçãodatemperaturadeevaporação(Bitzer)
Comopodeservistoacima,alinhavermelharepresentaodomíniodastemperaturas de evaporação testadas. Essa linha está totalmente contida nos limites de operação do modelodecompressorselecionadooquesignificaquesãovaloresválidosparatestenesse aparelho.
Alémdisso,domesmosoftwareda Bitzer,opolinômiocaracterísticoparaoaparelho foiusadoparaseobteraseficiênciasisentrópicasparacadaumdessescasos.
32 Tabela
T
1
℃ 0℃ -7℃ -4℃ -11℃ 40℃ 2
℃ 0℃ -7℃ -4℃ -11℃ 40℃ 3
℃ 0℃ -7℃ -4℃ -11℃ 40℃ 4
℃ 0℃ -7℃ -4℃ -11℃ 40℃ 5 -40℃ 0℃ -7℃ -4℃ -11℃ 40℃ 6 -45℃ 0℃ -7℃ -4℃ -11℃ 40℃
TabelaV.2Eficiênciaisentrópicaeavariaçãodatemperaturadeevaporação
Teste T =T / ��
-20℃ 0,7101
-25℃ 0,7067
-30℃ 0,6963
-35℃ 0,6788
-40℃ 0,6582
-45℃ 0,6398
Umgráficopodesermontadocomosvaloresacimaparaseencontrareventualmente eficiênciasisentrópicasemtemperaturasintermediárias.
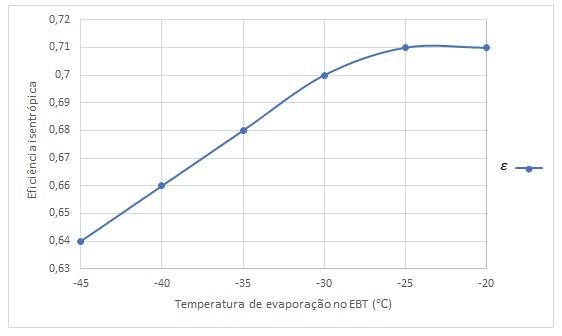
FiguraV.2GráficodaeficiênciaisentrópicavariandocomtemperaturadoEBT
Agora, lançando mão da mesma análise de primeira lei do capítulo 3 para cada um dos testes expostos na tabela V.1, ter-se-á a seguinte variação para a vazão mássica dos refrigerantesdosistema:
33
1
2
3
4
5
6
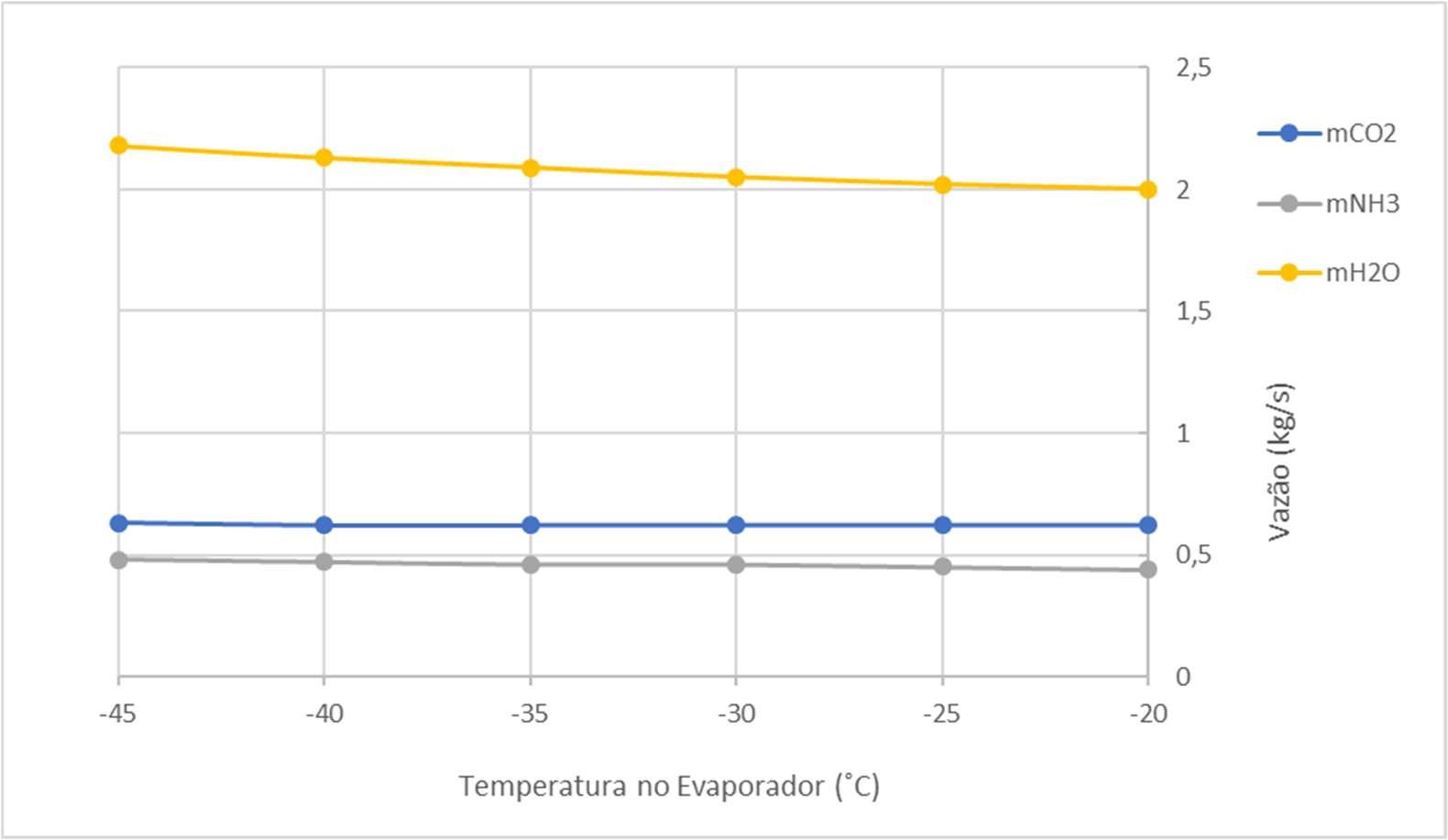
FiguraV.3GráficodavazãomássicavariandocomatemperaturadoEBT
Observando-seográfico,pode-sedizerqueaalteraçãodesseparâmetrodeoperação não altera significativamente as vazões mássicas. Isso atribui flexibilidade ao sistema, uma vez que, caso se queira modificar a temperatura no EBT depois da instalação, não serianecessáriaqualquermudançanostubosquecompõeosistemaderefrigeração.
Outrossim,tambémsepodeestabelecerumgráficosemelhanteparaocoeficientede performance:
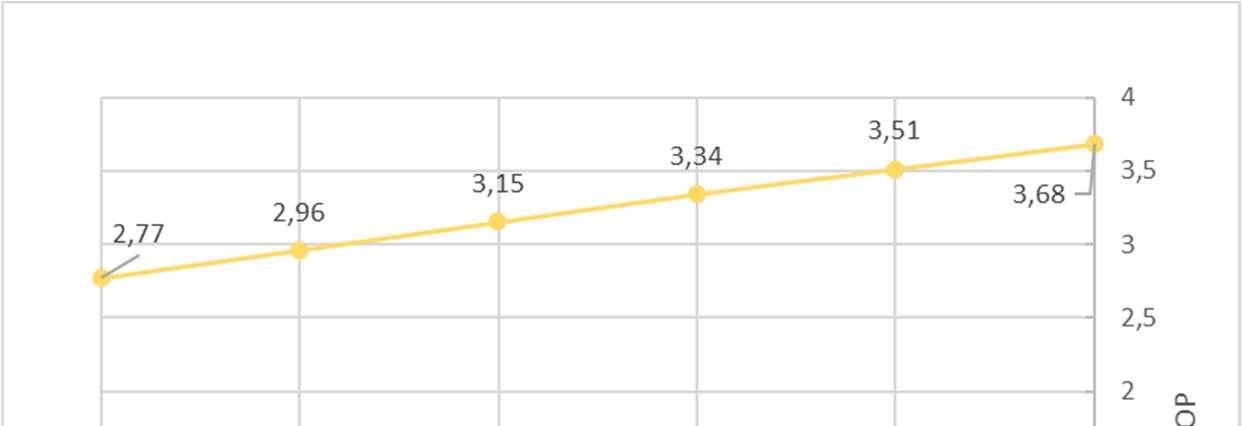
FiguraV.4GráficodaCOPvariandocomatemperaturadoEBT
34
Desse gráfico, percebe-se que o coeficiente de performance muda consideravelmentecomatemperaturadeevaporaçãonoEBT.Setomarmoscomocritério deaplicabilidade dosistemadeperformance,terumvalordeCOPmaior quetrês,devese, então, estabelecer como limitede operaçãouma temperaturade -40℃. Além disso, a performance do sistema melhora (máx. 9,2%), na medida em que se aumenta a temperaturadeevaporação.
Jánessemomento,pode-seusaramesmaanálisedescritanocapítuloIV–segunda leitermodinâmicanosistema–parasecalcularorendimentoexergéticodecadaaparelho emcadaumdostestesdescritosnatabelaV.1:
FiguraV.5GráficoderendimentodesegundaleivariandocomatemperaturadoEBT
Como pode ser percebido, o equipamento mais suscetível às mudanças na temperatura de evaporação é o trocador de calor 2. Esse equipamento foi um dos considerados como crítico por ter baixa eficiência de segunda lei. Dessa forma, surge naturalmentecomoalternativaparamelhorarseurendimento,aumentaratemperaturade evaporaçãonoEBT.
Outro gráfico que foi montado, é o de valores absolutos de irreversibilidade. Ele é importante, pois permite acompanhar como a destruição da capacidade de trabalho útil docompressordoestágiocomamônia–outroequipamentodefinidocomocríticoparaa análise.

35
IrreversibilidadeporEquipamento
40,00
35,00
30,00
25,00
20,00
15,00
10,00
5,00
0,00
TemperaturanoEvaporador(˚C)
(kW)
EdVE EdEvBT
EdCpBT EdTC2 EdEvMT EdTC1 EdVE
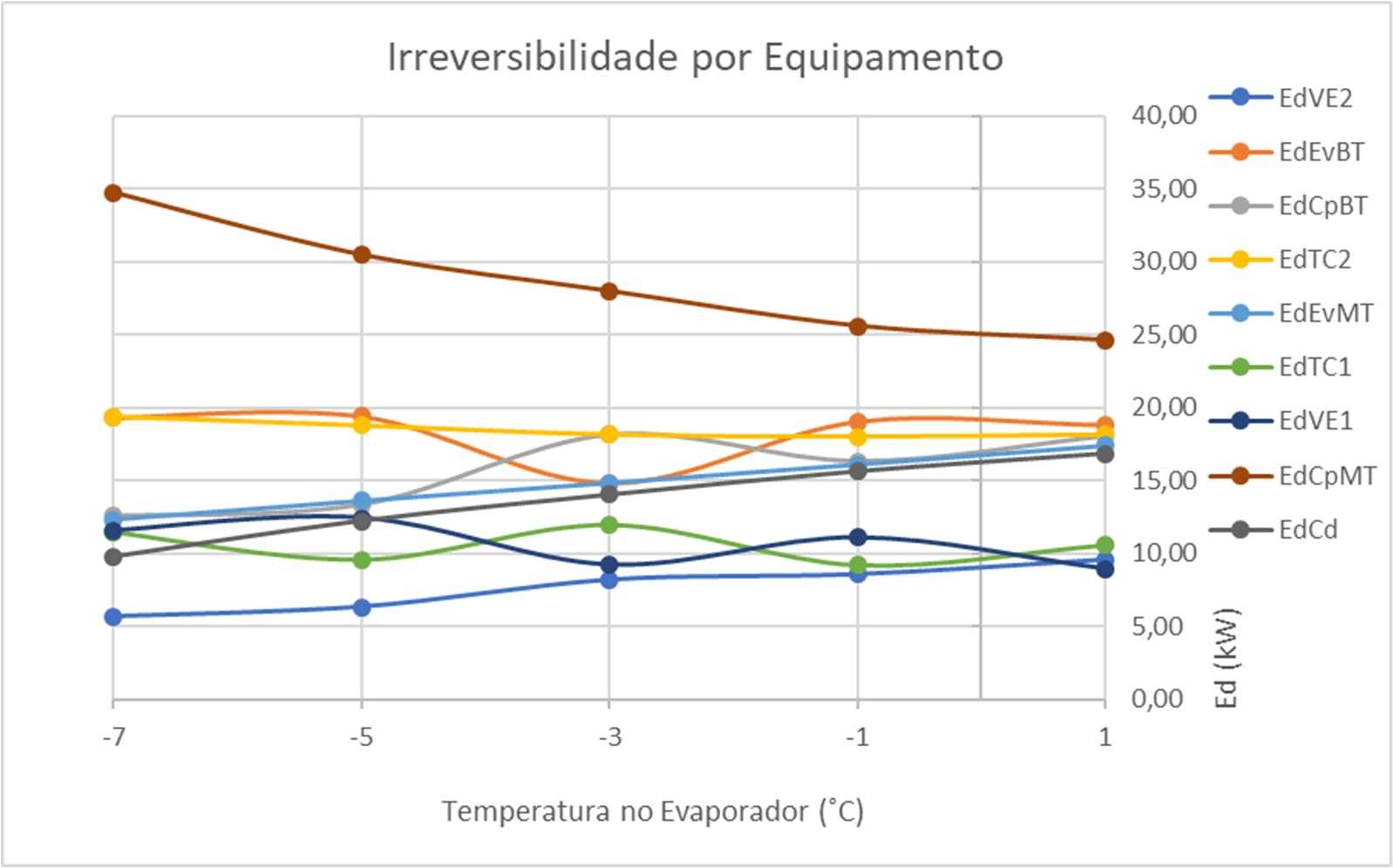
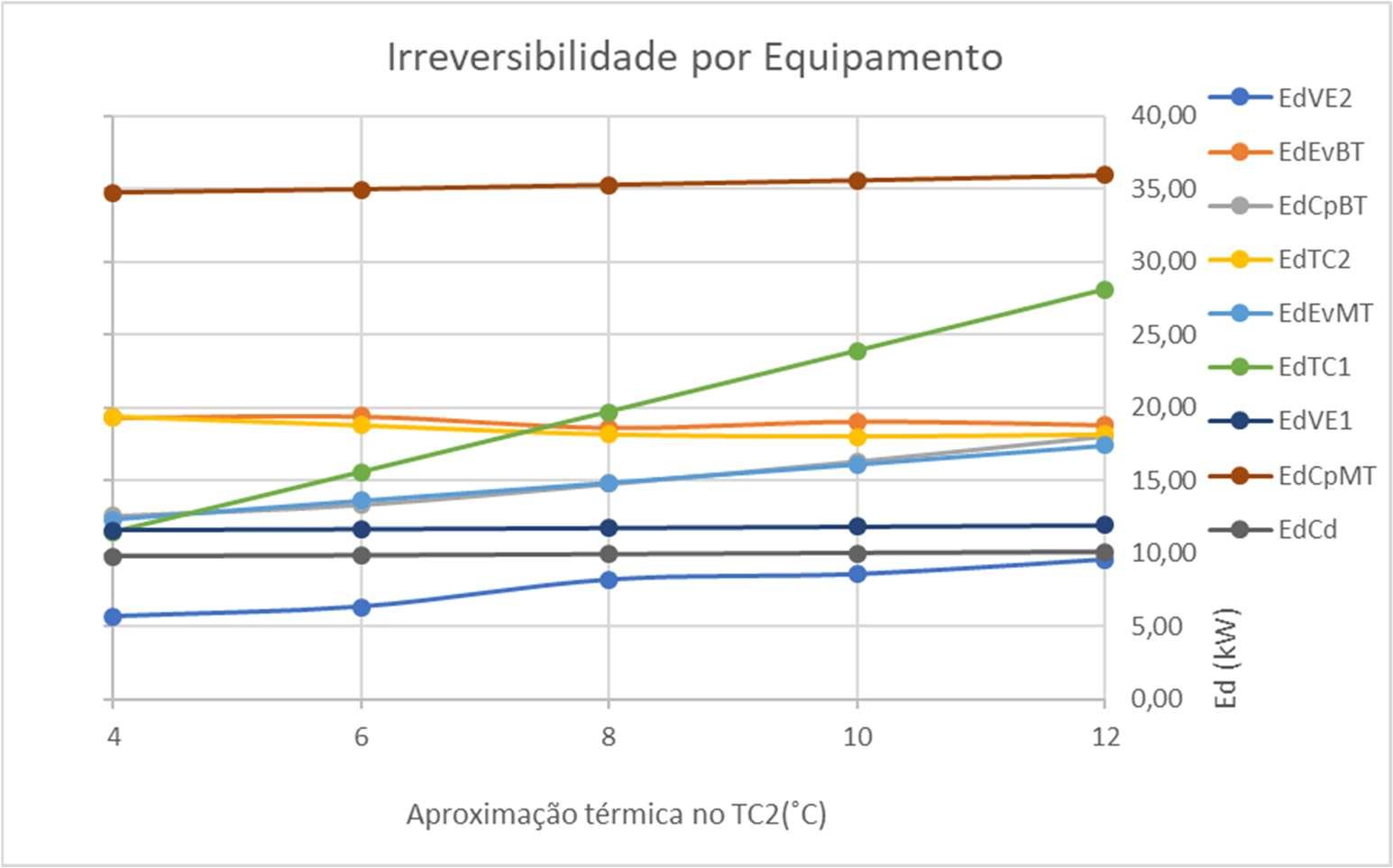
FiguraV.6Gráficodeirreversibilidadeporaparelhovariandocomatemp.doEBT
O gráfico indica que a irreversibilidade do compressor no estágio com amônio teve redução considerável (4,6%, se comparado a situação de referência com o melhor caso: o teste 1). Já o TC2, tem redução mais expressiva, 9,2%. Outros equipamentos interessantessão:oC2(53,0%deredução)eoEBT(57,7%).
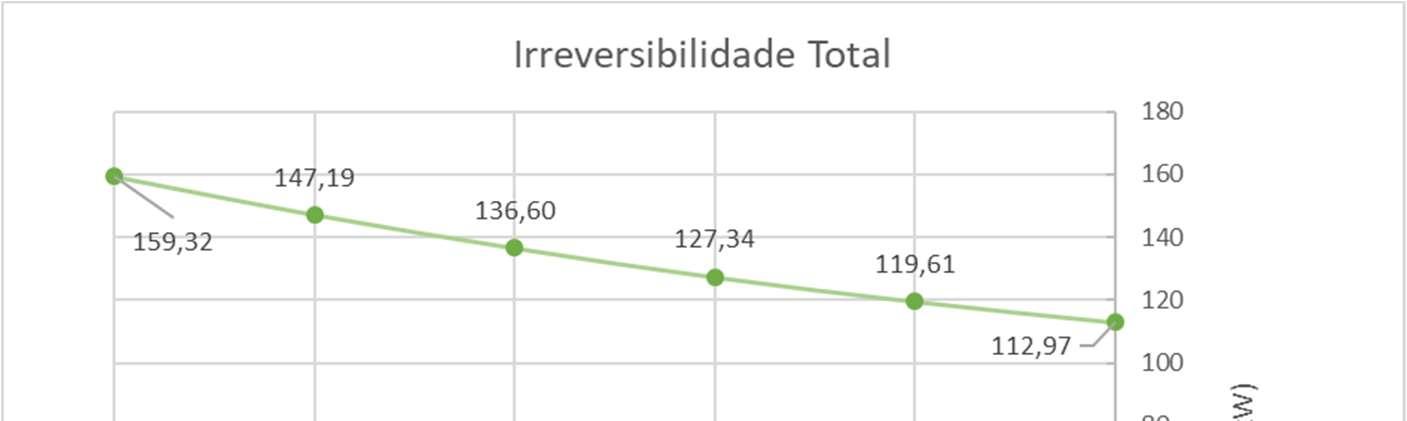
Finalmente,umnovográficocomvaloresparaairreversibilidadetotaldosistema serátraçadoparaquesecompreendacomoelasecomportaglobalmente.
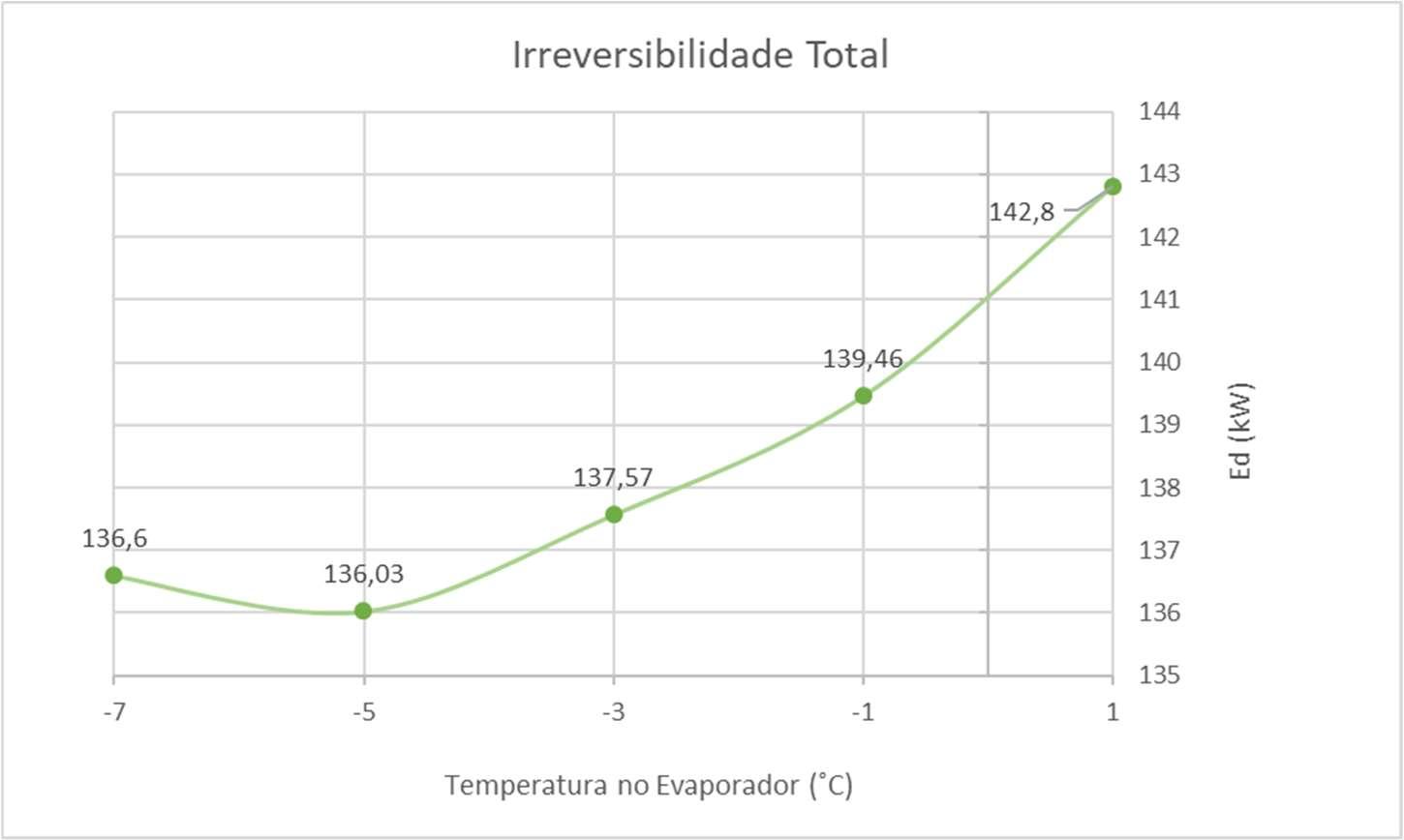
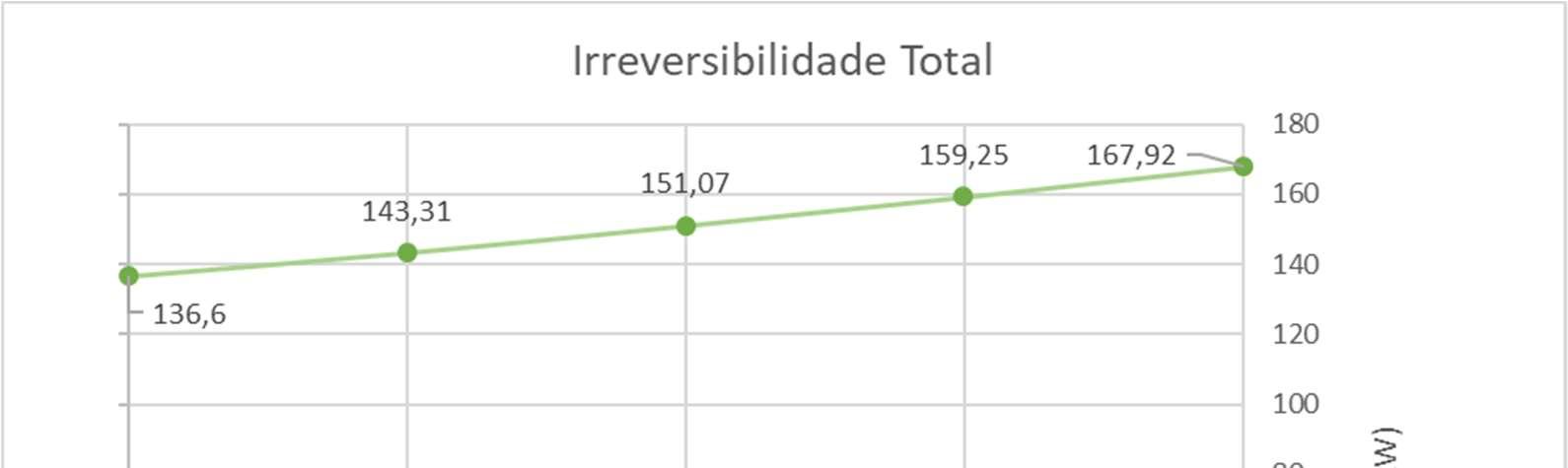
FiguraV.7Gráficodairreversibilidadetotaldosistemavariandocomatemp.doEBT
36
-45-40-35-30-25-20 Ed
Como esperado, há uma redução da irreversibilidade total do sistema de refrigeraçãonamedidaemqueseaumentaatemperaturadeevaporaçãodoEBT.Todavia, isso não significaque o melhorteste poderásempreserusado, uma vez queos produtos congeladosdeumsupermercadopodemdemandartemperaturasdearmazenamentomais baixas.
V.2OsistemaderefrigeraçãoeatemperaturadoEMT
Assim como foi feito no subcapítulo V.1, deve-se definir um domínio para as temperaturas de evaporação do EMT dentro dos limites impostos pelos equipamentos. Como o objetivo desse subcapítulo é a análise exclusiva do impacto da temperatura do EMTnosistema,osestágioscomamôniaegáscarbônicotambémtiveramquemudarde modoanãoalteraraaproximaçãotérmicanostrocadores.Atabelaabaixoindicaostestes aseremrealizados:
TabelaV.3TemperaturasdeevaporaçãodoEMTtestadas
Teste T T T T T T
1 -35℃ 0℃ -7℃ -4℃ -11℃ 40℃
-35℃ 2℃ -5℃ -2℃ -9℃ 40℃
-35℃ 4℃ -3℃
-35℃
-35℃
-1℃
℃ -7℃ 40℃
-5℃ 40℃
-3℃ 40℃
Agora, deve-se verificar se essas temperaturas estão dentro dos limites de operaçãotantodocompressorcomamônia,quantocomaquelecomR744.Paraomodelo 4NSL-30K-40Pteremososeguintedomíniodetrabalho:
37
2
3
0
4
6℃
2℃
5
8℃ 1℃ 4℃
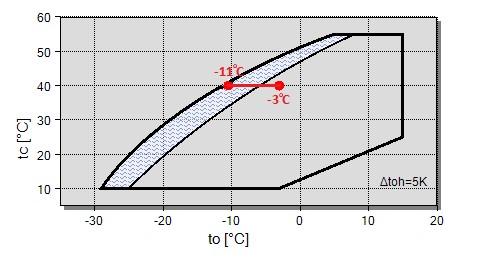
FiguraV.8Limitesdeoperaçãoeavariaçãodatemperaturadecondensação(Bitzer)
Já no caso do modelo W6FA, o compressor no estágio com amônia teremos a representação gráfica a seguir para indicar se os testes estão compreendidos nos limites domodelo.
FiguraV.9Limitesdeoperaçãoeavariaçãodatemperaturadeevaporação
Agora, lançando mão dos polinômios característicos para cada um desses modelos, deve-se extrair os valoresde eficiência isentrópicados dois compressorespara cada um dos testes estabelecido na tabela V.3. Para o modelo no estágio com gás carbônico,ter-se-á:

38
V.4��
modelo
variação
temperaturadecondensação
comavariaçãodosparâmetrosdeoperação,ográficoabaixofoimontado:
FiguraV.10GráficodaeficiênciaisentrópicavariandocomtemperaturadoEMT
O mesmo pode ser feito para o modelo W6FA de compressor com amônia, resultandonaseguintetabeladevaloresparaaeficiênciaisentrópica:
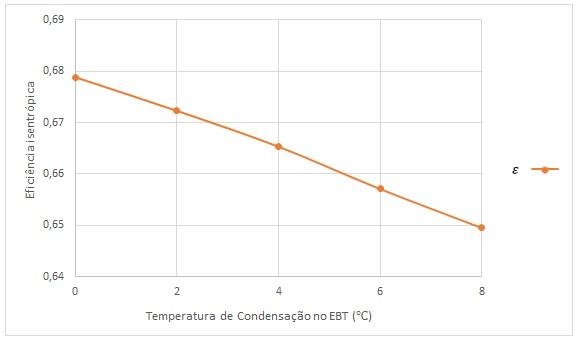
39 Tabela
do
4NSL-30K-40Pea
da
Teste T = T �� 1 0℃ 0,6788 2 2℃ 0,6723 3 4℃ 0,6653 4 6℃ 0,6571 5 8℃ 0,6495 Nointuitodeseterumamelhorvisualizaçãodaevoluçãodaeficiênciaisentrópica
TabelaV.5�� domodeloW6FA
Teste
avariaçãodatemperaturadeevaporação
0,7255
0,7368
0,7458
0,7538
Da mesma forma que foi estabelecido um gráfico na página anterior para se compreender a evolução da eficiência isentrópica com a sua aproximação, outro será realizadoaseguir:

FiguraV.11Gráficode�� variandocomatemp.deev.doestágiocomamônia
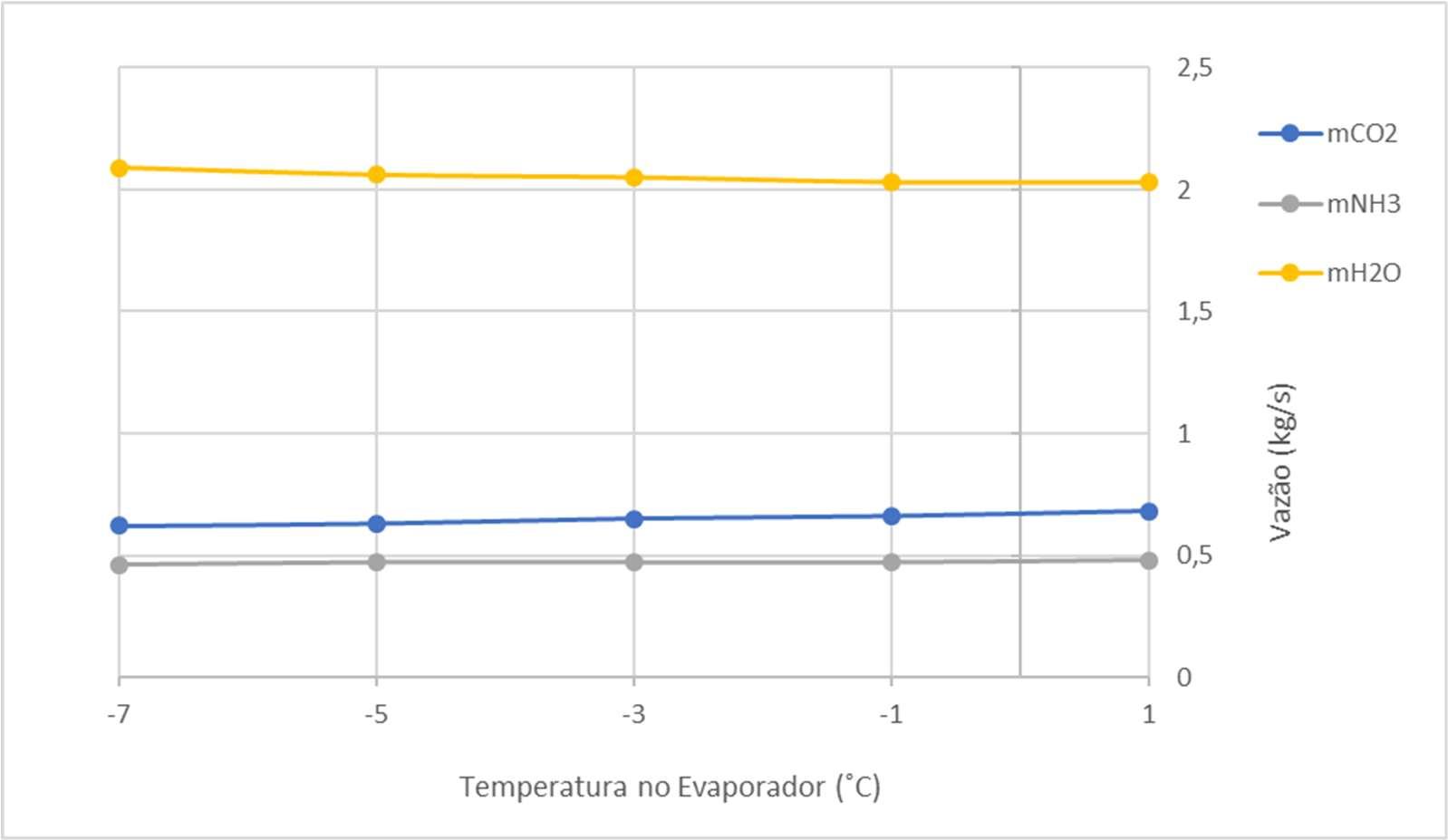
Comoobjetivodeanalisarcomoasvazõesmássicasdecadarefrigeranteevoluem ao longo dos testes expostos natabela V.3, basta-se usar oprocesso descrito no capítulo 3comprimeiraleidatermodinâmica.
Umgráficoparaessasvazõessegueabaixo:
40
e
T = T / �� 1 -11℃ 0,7126 2 -9℃
3 -7℃
4 -5℃
5 -3℃
FiguraV.12GráficodavazãomássicavariandocomatemperaturadoEMT
Assimcomonocasodavariaçãodatemperaturadeevaporaçãodoevaporadorde baixa temperatura, a mudança do parâmetro de operação desse subcapítulo não altera significativamente as vazões mássicas envolvidas no processo de refrigeração. Isso atribui flexibilidade ao sistema estudado, uma vez que eventuais ajustes na temperatura derefrigeraçãonãoexigemmodificaçõesestruturais.
Jáparaocoeficientedeperformance,teremosaseguinterepresentaçãográfica:
FiguraV.13GráficodoCOPvariandocomatemperaturadoEMT
Como esperado, o coeficiente de performance aumenta (máx. 9,4%) na medida em que a temperatura no evaporador de média temperatura cresce. Todavia, é evidente
41
3,48 3,293,373,45 3,15 0 0,5 1 1,5 2 2,5 3 3,5 4 -7-5-3-11 COP TemperaturanoEvaporador(˚C)
que os itens a serem resfriados imporão limites nessas temperaturas, seguindo o que é determinadopelaAssociaçãoBrasileiradeNormasTécnicasnatabela II.1.
A partir daqui, deve-se aplicar a segunda lei da termodinâmica da mesma forma emquefoiusadaparaosistemadereferêncianocapítulo4.Dessaforma,pode-semontar um gráfico que expõe como o rendimento de segunda lei evolui para cada aparelho ao longodavariaçãodatemperaturaderefrigeração.
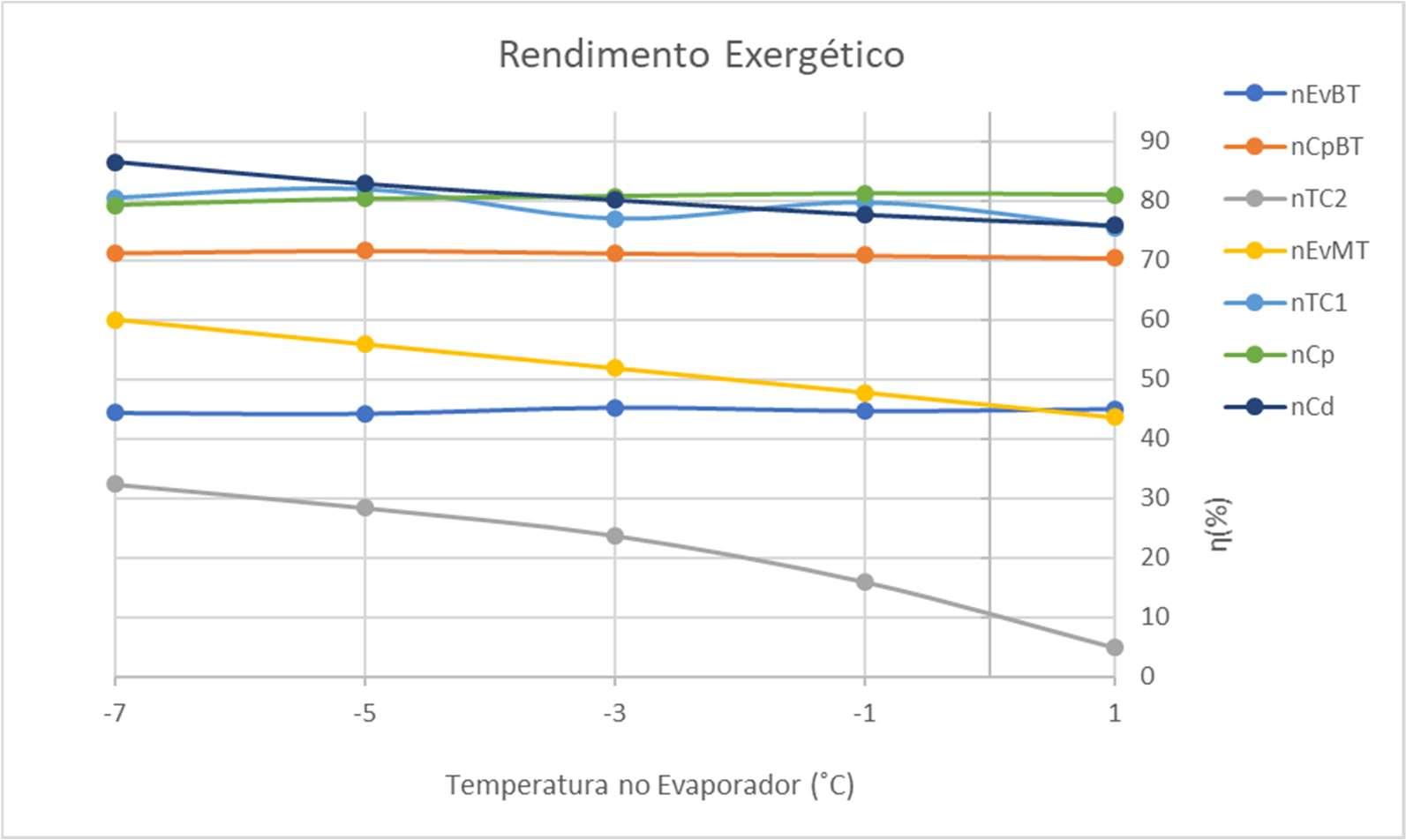
FiguraV.14GráficoderendimentodesegundaleivariandocomatemperaturadoEMT
Aoanalisararepresentaçãográficaacima,percebe-secertaflutuaçãodosvalores de rendimento de segunda lei da termodinâmica provavelmente em função da natureza contrária no desenvolvimento da eficiência isentrópica para os dois compressores do sistema de refrigeração demonstrados nos gráficos V.10 e V.11. Ademais, destaca-se o trocadordecalor2que,diferentedosoutrosaparelhos,sofrequedanamedidaemquese aumenta a temperatura de evaporação no EMT. Isso descaracteriza a variação desse parâmetrodeoperaçãocomoalternativaparasemelhorarorendimentodoTC2.
Também foram calculados valores absolutos das irreversibilidades para cada aparelhoesuadinâmicaaolongodosdiversostestesrealizadossegueabaixo:
42
FiguraV.15Gráficodeirreversibilidadeporaparelhovariandoc/atemperaturado EMT
Nota-se uma redução expressiva da irreversibilidade no compressor 1 (29,1%) e no condensador, algo dentro do desejado uma vez que esse aparelho foi um dos considerados como crítico no capítulo IV. Ademais, tem-se também uma redução da destruiçãodacapacidadederealizartrabalhoporpartedocondensador(42,1%).Poroutro lado, alguns aparelhos tiveram aumento na sua irreversibilidade. O compressor 2, por exemplo, teveincremento de30,0%. Jáo trocador de calor 2 teve aumento de 36,1%na suairreversibilidade.
FiguraV.16Gráficodeirreversibilidadetotalvariandox/atemperaturadoEMT
43
Nota-se que o valor da irreversibilidade total atinge seu mínimo quando a temperaturanoevaporadoré-5℃,fazendodesseopontomaisindicadoparatrabalho.
A aproximação térmica de um trocador de calor corresponde à diferença de temperatura entre um fluido entrando no aparelho e outro saindo. Esse fator tem forte influência sobre a área de troca do trocador e na sua eficiência de segunda lei (Kern, 1965).
A seguinte tabela foi montada paramostrar como os parâmetros de operaçãosão alteradosnosistemaderefrigeraçãoestudado.Alinhagrifadaemvermelhocorresponde aosistemadereferência.
TabelaV.6VariaçãodeparâmetrosnoTC2
Teste T T T T T T
1 -35℃ 0℃ -7℃ -4℃ -11℃ 40℃
2 -35℃ 2℃ -7℃ -4℃ -11℃ 40℃
3 -35℃ 4℃ -7℃ -4℃ -11℃ 40℃
4 -35℃ 6℃ -7℃ -4℃ -11℃ 40℃
5 -35℃ 8℃ -7℃ -4℃ -11℃ 40℃
A aproximação térmica nesse caso será a diferença entre a temperatura de condensaçãonoestágiocomCO eatemperaturadeevaporaçãonoevaporadordemédia temperatura.Atabelaabaixoindicaessefatoraterseuimpactonosistemaestudado.
Segundo Silva (2009), o critério para se definir os valores para a aproximação térmicaaseremtestadosforamdefinidossebuscandodiferençadetemperaturamaiorque 5℃-jáque,sefossemenor,issoimplicariaemumtrocadorcom grande área detrocae, por sua vez, muito caro. Por outro lado, esse valor deve ser menor que 15℃ para que a eficiênciadoaparelhonãosejademasiadamentebaixa.
44
V.3Osistemaderefrigeraçãoeaaproximaçãotérmicano trocadordecalor2
operação é aquele no estágio com CO . Essa variação se dá nos mesmos moldes que aquela exposta na figura V.8, logo, está dentro dos limites de operação exigidos pelo modelo 4NSL-30K-40P. Já a evolução da eficiência isentrópica com a mudança da aproximaçãotérmicadotrocadordecalor2,estáestabelecidanatabelaV.4.
Desse modo, usando o mesmo processo de cálculo contido no capítulo III que lança mão da primeira lei de termodinâmica, pode-se realizar uma análise de como as vazõesmássicasdosdiversosrefrigerantessecomportamcomaalteraçãodaaproximação térmicanoTC2.
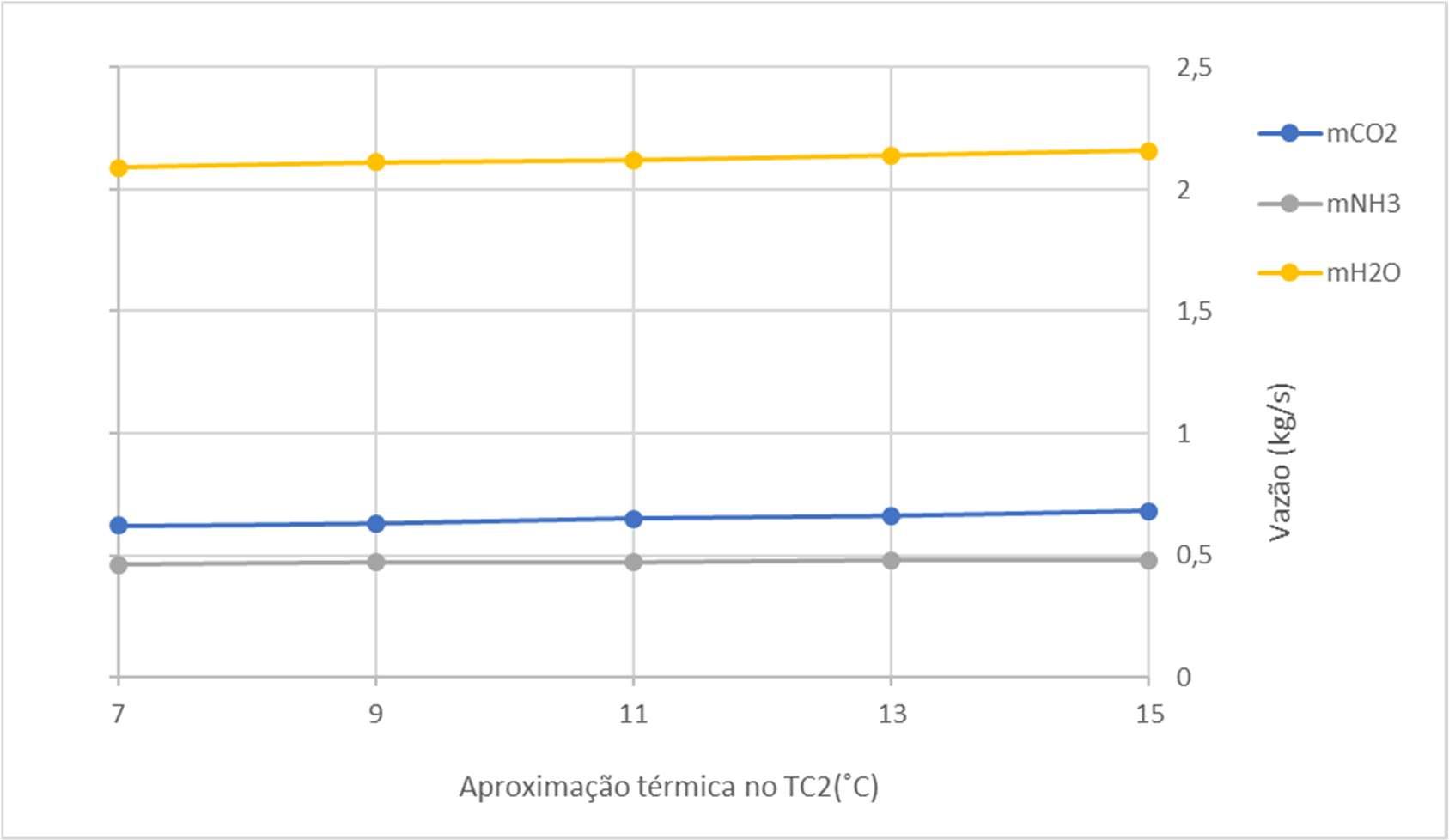
FiguraV.17Gráficodevazãomássicavariandocomaaprox.térmicanoTC2
45 TabelaV.7VariaçãodaaproximaçãonoTC2 Teste Aprox.=T T / 1 7℃ 2 9℃ 3 11℃ 4 13℃ 5 15℃ Nessesubcapítulo,oúnicocompressorquesofrealteraçãonosseusparâmetrosde
Assim como nos subcapítulos anteriores, a vazão mássica não sofre alteração relevante com o aumento da aproximação térmica. Isso significa que esse fator pode ser alterado sem a preocupação com o seu impacto nos tubos que compõe o sistema de refrigeração.
Outrossim, também é importante acompanhar o desenvolvimento do coeficiente deperformancedosistemaderefrigeração,expostonarepresentaçãográficaabaixo:
FiguraV.18Gráficodocoef.deperformancevariandocomaaprox.térmicanoTC2
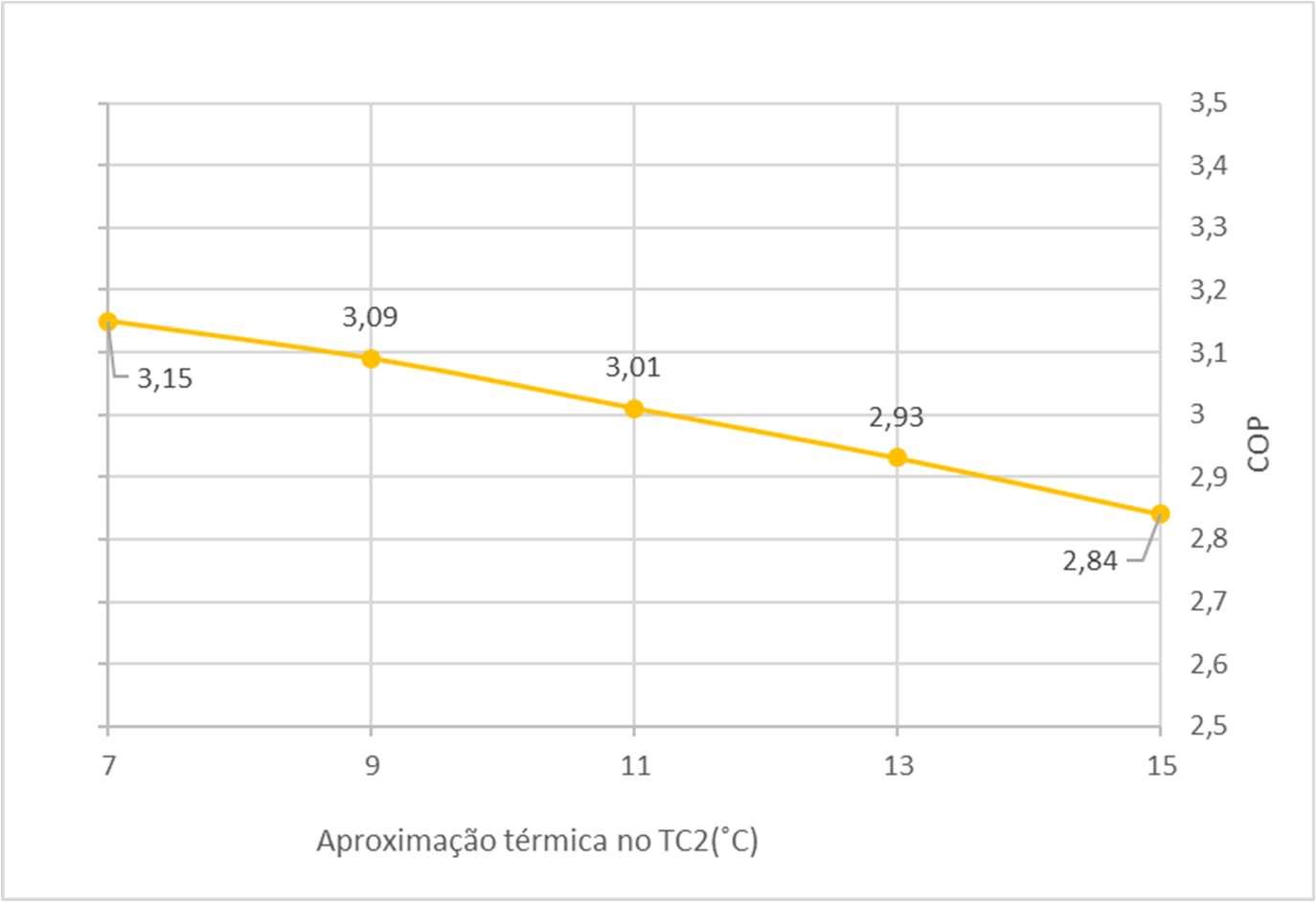
Como esperado, o coeficiente cai na medida em que a aproximação térmica diminui, ou melhor, quando a diferença entre a temperatura de condensação do estágio com CO e a temperatura de evaporação no EMT aumenta. Usando-se o mesmo critério restritivoparaaaplicabilidadedosistema–terumcoeficientedeperformancemaiorque três – deve-se descartar valores de aproximação menores que 11℃ como possibilidades realistasdeoperaçãodosistema.
Agora, levando em conta a análise exergética desenvolvida no capítulo IV, é possível determinar os valores referentes a irreversibilidade para cada aparelho que compõeo sistema de refrigeração. O rendimento desegundalei da termodinâmicae sua evoluçãocomaaproximaçãotérmicaestáexpostanarepresentaçãográficaaseguir:
46
FiguraV.19Gráficodorendimentodesegundaleivariandocomaprox.térmicanoTC2
Nota-se que a mudança desse fator não gera repercussão no rendimento de segundaleiparaamaioriadosaparelhosdosistema.Aexceçãoflagrantedessacolocação é o trocador de calor 2 que sofre grave redução com o aumento da aproximação. Isso é justamenteoopostoqueodesejadonotocanteaosaparelhosdefinidoscomocrítico.
Outro gráfico que pode ser montado é o de irreversibilidade para cada aparelho emvaloresabsolutos:

FiguraV.20Gráficodairreversibilidadevariandocomaprox.térmicanoTC2

47
Jáadestruiçãototaldacapacidadederealizartrabalhopodeserrepresentadapelo gráficoaseguir:

FiguraV.21Gráficodairreversibilidadetotalvariandoc/aprox.térmicanoTC2
Mais uma vez, com esse gráfico, reforça-se a ideia de que o sistema de refrigeração estudado piora em todos os sentidos na medida em que se aumenta a aproximação térmica. Isso indica que mudar esse parâmetro não é uma alternativa interessante para a produção de melhora nesse sistema. Desse modo, fica a cargo de questões unicamente ligadas ao projeto do trocador de calor 2 e financeiras para se realizaraseleçãodesseaparelho.
Seguindo o modelo definido no subcapítulo V.3, será estudado e efeito da aproximaçãotérmica,todavia,agora, referenteaotrocadordecalor1.Esse equipamento reside entre o estágio com glicol e aquele com amônia. Logo, tanto a temperatura de evaporação no EMT quanto a temperatura de condensação no estágio com CO serão gradualmente aumentadas de forma que mantenham a aproximação térmica no TC2. A tabelaabaixoindicaosdiversostestespropostos:
48
V.4 O sistema de refrigeração e a aproximação térmica do trocadordecalor1
V.8VariaçãodosparâmetrosparaoTC1
Teste T T T T T T
-35
-35
-35
-35
-35
-11℃ 40℃
-11℃ 40
-11
-11
40
40
-11℃ 40
Aaproximaçãotérmicadotrocadordecalorseráobtidaapartirdadiferençaentre a temperatura de evaporação no EMT e a temperatura de evaporação no estágio com amônia.Essadiferençaestádispostanográficoaseguir:
V.9VariaçãodaaproximaçãonoTC1
Teste Aprox.=T T /
5℃
10℃
Agora, para se estimar o comportamento das vazões mássicas dos refrigerantes que compõe o sistemade refrigeração aolongo dos testes propostos natabelaV.8, basta lançarmãodaanálisedeprimeiraleidatermodinâmicadescritanocapítuloIII:
49 Tabela
Tabela
1 4℃ 2
3 8℃ 4
5 12℃
1
℃ 0℃ -7℃ -4℃
2
℃ 2℃ -5℃ -2℃
℃ 3
℃ 4℃ -3℃ 0℃
℃
℃ 4
℃ 6℃ -1℃ 2℃
℃
℃ 5
℃ 8℃ 1℃ 4℃
℃
FiguraV.22Gráficodevazãomássicavariandocomaaprox.térmicanoTC1
Mais uma vez, mostra-se que a variação desse fator não tem repercussão significativa nas vazões mássicas envolvidas no sistema de refrigeração. Portanto, sua eventual variação não exigirá mudanças em aspectos construtivos do sistema como o diâmetrodostubos.
Outrográficodeinteresseéoqueindicaadinâmicadocoeficientedeperformance frente asalteraçõesnaaproximaçãotérmicanotrocadordecalor1.
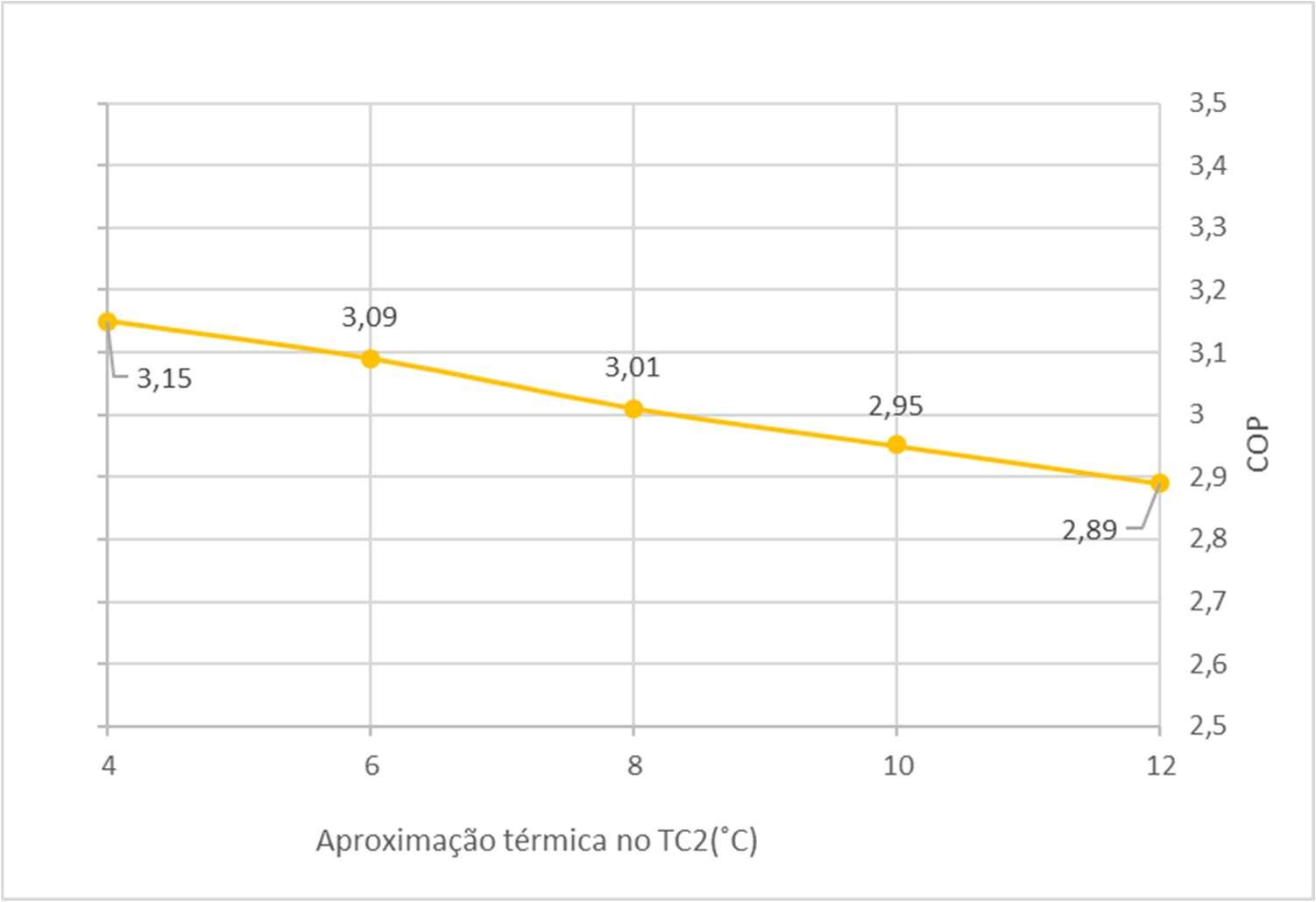
FiguraV.23Gráficodocoef.deperformancevariandocomaaprox.térmicanoTC1

50
Essegráficomostracomoocoeficientedeperformancecainamedidaemque se diminui a aproximação térmica. Seguindo o critério que propõe um valor mínimo de três para coeficiente de performance, devem-se descartar os testes com aproximação menorque9℃
Agora, pode-se usar o mesmo processo descrito no capítulo IV em cada um dos testes propostos para se avaliar o comportamento dos aparelhos envolvendo suas irreversibilidades inerentes. Abaixo segue um gráfico que mostra o rendimento de segundaleidatermodinâmicaparacadaequipamento:
FiguraV.24Gráficoderendimentodesegundaleivariandocomaprox.térmicanoTC1
Essa representação gráfica mostra como existe uma forte redução do rendimento do trocador de calor 2 na medida em que se reduz a aproximação térmica do TC2. Também é importante ressaltar a queda desse mesmo valor para o EMT e uma queda significativanoTC1.
Nesse momento, para se compreender como se comporta o valor absoluto da irreversibilidadeporaparelhofoiestabelecidoográficoabaixo:
51
FiguraV.25Gráficodairrev.poraparelhovariandocomaaprox.térmicanoTC1
Analisando o gráfico, percebe-se aumento da irreversibilidade por aparelho na maioria dos equipamentos. No trocador de calor 1 o aumento máximo é de 59%, já o trocador de calor 2 tem incremento de 6,3%, o compressor do estágio com amônia de 3,3%eocompressor2teveaumentode30,4%.
Finalmente,podeserestabelecidoumgráficoexpressandoairreversibilidadetotal dosistemaaolongodostestesefetuados:
FiguraV.26Gráficodairreversibilidadetotalvariandocomaaprox.térmicanoTC1
52
Dessemodo,ficaevidentequediminuiraaproximaçãotérmicadessetrocadorde calor não é uma boa alternativa para obter qualquer melhoramento no sistema de refrigeração.Logo,pararealizaraseleçãodesseaparelhodevemserobservadosaspectos ligadosàsquestõesfinanceirasedeprojetodetrocadordecalor.
53
VI Comportamento do sistema de refrigeração e carga térmica
Nessa etapa do trabalho, retorna-se para o sistema de refrigeração de referência, porém o valor da carga térmica de refrigeração será alterado no intuito de ter seu efeito sob o sistema avaliado. Esse parâmetro de operação é definido pelo espaço a ser refrigerado, portanto, a alteração da carga térmica indica uma alteração do próprio supermercado.
No supermercado estudado existem duas demandas por carga térmica: uma a ser destinadaparao congelamentodeprodutos (que ficoudenominada como CT )eoutra para resfriamento de produtos (que ficou denominada como CT ). Isso implica que, para definir um supermercado específico, deve-se indicar os valores desse par CT /CT .Alémdisso,paraacompanharcomocaracterísticasimportantesdosistema derefrigeraçãocomo coeficientedeperformance,vazãomássicaeirreversibilidadetotal mudam com a alteração desse par pode ser montado um gráfico de contorno bidimensional,mapeandoessesvalores.
Todavia, para se dizer que o sistema de refrigeração permanece inalterado na medida em que o par de cargas térmicas é modificado, é importante se determinar uma faixa de operação em que os equipamentos permaneçam os mesmos. Observando-se o softwaredaBITZER,percebe-sequeambososmodelosutilizadosparacompressor,tanto aquele aplicado no estágio com gás carbônico, o 4NSL-30K-40P, tanto aquele instalado no estágio com amônia, o W6FA, são selecionados para cargas térmicas frigoríficas maioresque80kW.
Dessa forma, esse valor será usado como limite inferior para a análise. Caso surgissem valoresmenoresque 80kW, o compressor selecionado teria que ser diferente, o que alteraria, dentre outros itens, sua eficiência isentrópica. Isso acabaria com a linearidadedoestudoaserdesenvolvidonessecapítulo.Poroutrolado,parasedeterminar um limite superior foi fixado um valor de 400kW, uma vez que, na lista de sistemas de refrigeraçãoqueserãoinstaladosnoBrasil,constamapenasvaloresmenoresque400kW (Silva & Euzébio, 2013). Essas restrições implicam na prática que os supermercados analisadosterãoportedetamanhomédioagrande.
Primeiramente, pode-se estimar como a vazão mássica de gás carbônico e da porçãodeglicolquepassapeloTC2variacomoaumentodacargatérmicafrigoríficade congelamento,lançando-semãodaequação3.1:
54
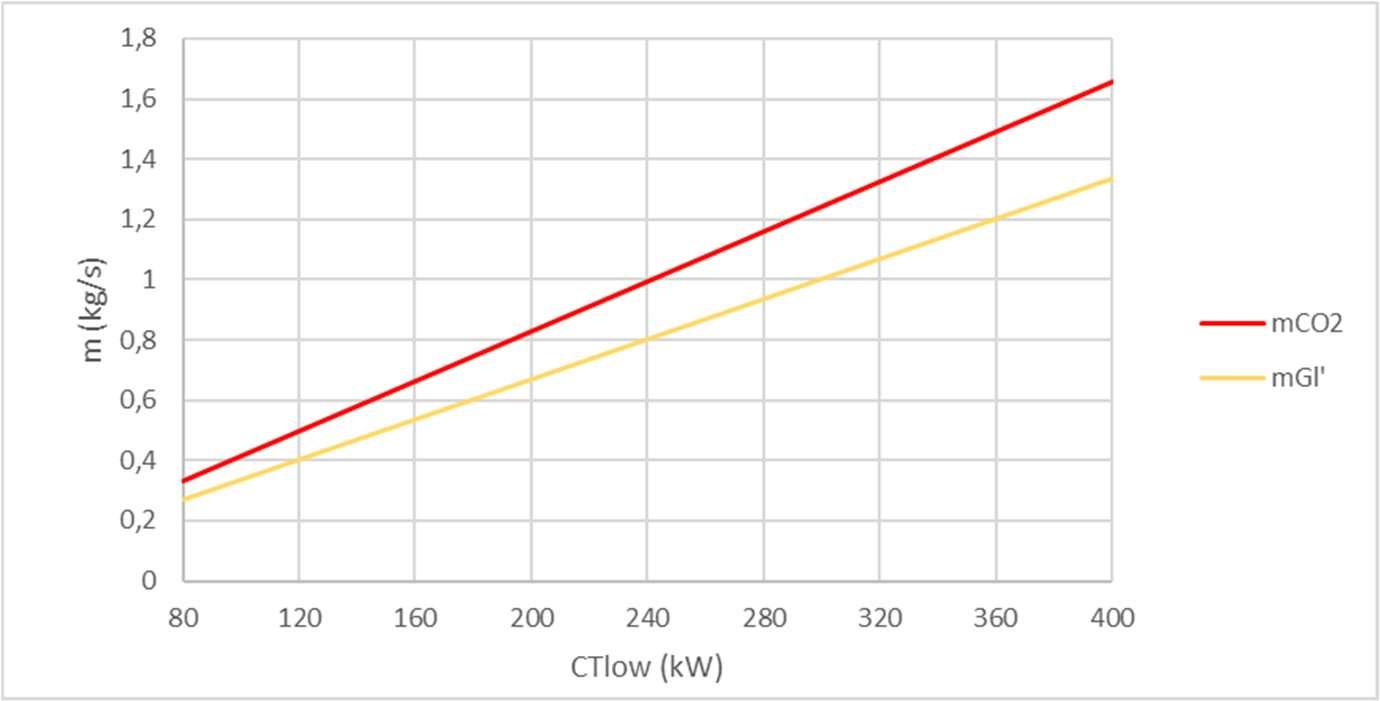
FiguraVI.1Gráficodavazãomássicaecargatérmicadecongelamento
Percebe-se que, com o incremento da demanda de potência, há um aumento da vazão mássica de refrigerante para atende-la. Isso implica que certas questões de ordem construtiva como diâmetro dos tubos terão que mudar de acordo com o porte do supermercadoquesedesejaconstruir.
Já a porção da vazão de glicol que segue para o evaporador evoluirá coma carga térmicaderefrigeraçãodessemodo:
FiguraVI.2Gráficodevazãoeacargatérmicaderesfriamento
Portanto, levando em conta que a vazão mássica total de glicol é estimada pela soma de suas porções, definida na equação III.4, um gráfico de contorno bidimensional pode ser produzido para se mapear seu valor com a alteração do par de cargas térmicas dosistema.

55
FiguraVI.3Gráficodecontornoparaavazãomássicatotaldeglicol
Essegráficomostracomclarezaanaturezalineardoproblema,oqueestá dentro do esperado já que as equações da primeira lei da termodinâmica possuem essa característica e a análise está restrita a valores de carga térmica frigorífica que não acarretamnatrocadoscompressoresindicadospelosoftwaredaBITZER.
Também seguindo a expectativa, nota-se que o valor da vazão mássica aumenta namedidaemqueopardecargastérmicassofreomesmoprocesso.
O mesmo tipo de gráfico pode serobtido para os vários componentes do sistema derefrigeraçãodefinidosnocapítuloIII,vazãomássicadaamônia,daágua,calortrocado nos trocadores de calor e no condensador e potência dos compressores e das bombas de circulação. Tudo isso, permite realizar um gráfico bidimensional de contorno para expressar como o coeficiente de performance se comporta em função do par CT /CT
56
Figura6.4Gráficodecontornoparacoeficientedeperformance
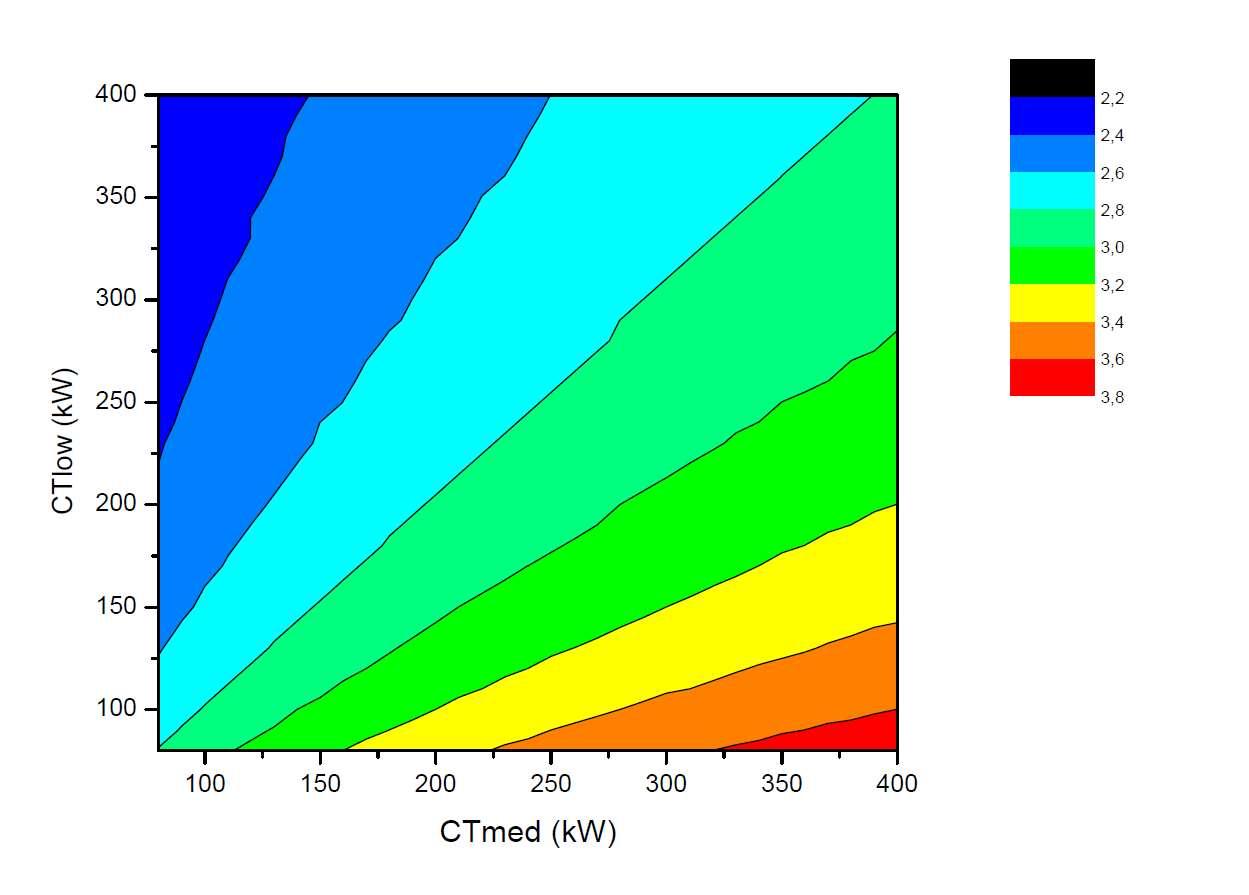
Essegráficotambémressalta anaturezalineardo problema.Alémdisso,pode-se dizerqueparesdecargatérmica“retangulares”(quandoarelaçãoentre CT eCT é desigual)comoladomaiorcorrespondendoàdemandadepotêncianoresfriamento,são beneficiados com valores melhores para o coeficiente de performance. Ademais, é possível dizer que as linhas vistas no gráfico são de “iso-performance”. Se se tomar o critério já estabelecido para a usabilidade do sistema de refrigeração ter um coeficiente maior que três, pode-se usar a linha de isso-performance entre os tons de verde para se determinarpreviamente a viabilidade do uso desse sistema de refrigeração de referência paraumdeterminadorequisitoestabelecidonoprojetodosupermercado.
Uma equação da reta pode ser rapidamente proposta nesse sentido aplicada na linhadeiso-performanceigualàtrês:
CT = CT .��+��
Onde �� é o coeficiente angular e �� o coeficiente linear. Levando ainda em conta que,quandoseestendeessalinha,ela corta oeixoCT nopar(0,0), a equação dareta podeserreescritadessaformacom��=0:
57
Logo,parasedefinirocoeficienteangular,bastaescolherumdosparesdecargas térmicas nessa linha de iso-performance e encontrar a razão entre a carga de congelamentoeacargaderesfriamento.
Dessa forma, para se ter um valor de coeficiente de performance maior que três nosistemaderefrigeraçãodereferência,oseguintecritériotemqueseratendido:
No intuito de se encontrar o valor desse coeficiente angular para cada um dos testesexplicitadosnocapítuloV,bastariarealizaressemesmoprocessoemtodoseles.
Além do impacto da variação do par de cargas térmicas nos elementos extraídos ao se realizar a análise de primeira lei da termodinâmica no sistema, também é interessanteestudarsuainfluênciasobaquelesavaliados,quandoseaplicaasegundalei.
Aprimeira informaçãorelevantequese obteve ao sevariaro par CT /CT é que, desde queessa variação se dê dentro da faixa jáestabelecida nessecapítulo, nãohá qualqueralteraçãono rendimento de segunda leinos aparelhos estudados. Isso é reflexo danaturezalineardessasequaçõeseseráprovadoalgebricamente.
Paraoscompressoressetomaaequação4.8e3.2:
ter-se-á
58 CT = CT ��
��= CT CT = 100 140=0,7143
CT CT ≤0,7143
��= ��[(ℎ −ℎ ) − ��(�� − �� )] �� �� = ��(ℎ −ℎ ) Logo,
que: ��= [(ℎ −ℎ ) − ��(�� − �� )] (ℎ −ℎ )
Portanto fica claro que, para esse equipamento, o rendimento de segunda lei é indiferente a qualquer mudança na carga térmica
desde que ela não implique emalteraçãonosparâmetrosquedefinemessesistemacomoaeficiênciaisentrópica.
Paraevaporadoresoucondensadores,perceber-se-áalgosemelhante,tomando-se asequaçõesIV.10
Então:
Que também independe da carga térmica. Por último, os trocadores de calor são damesmaformaindependentesdacargatérmica.Dasequações4.12e3.1,tem-seque:
Isso implica que mudar o par de cargas térmicas não é uma alternativa para se buscar qualquer tipo de melhoramento do rendimento de segunda lei dos aparelhos que compõeosistemaderefrigeração.Ele,portanto,éexergeticamenteindiferente.
Por outro lado, também foi constatado que os valores absolutos para a irreversibilidade total variam linearmente com a alteração do par de cargas térmicas, seguindo o mesmo raciocínio empregado para estabelecer o gráfico 6.4, pode-se criar a representaçãográficaabaixo:
59
frigorífica
eIII.1: ��= 1− �� �� �� ��[(ℎ −ℎ ) − ��(�� − ��)] ��= ��(ℎ −ℎ )
��= 1− �� �� (ℎ −ℎ ) [(ℎ −ℎ ) − ��(�� − ��)]
��= �� [(ℎ −ℎ ) − ��(�� − �� )] �� [(ℎ −ℎ ) − ��(�� − ��)] ��= ��(ℎ −ℎ ) ��= (ℎ −ℎ ) .[(ℎ −ℎ ) − ��(�� − �� )] (ℎ −ℎ ) .[(ℎ −ℎ ) − ��(�� − ��)]
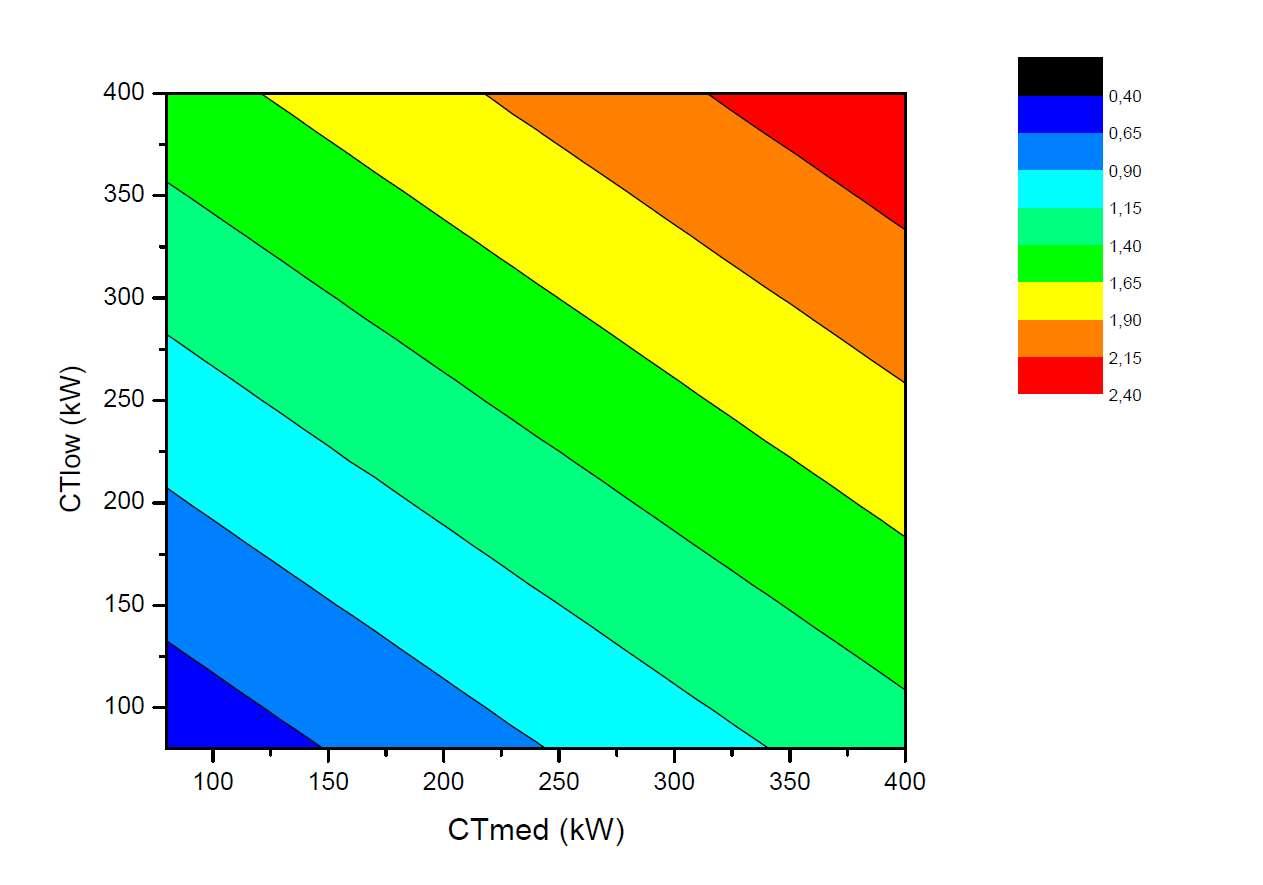
FiguraVI.5Gráficodecontornoparaairreversibilidade
Nesse gráfico, as linhas podem ser compreendidas como linhas de “isoirreversibilidade”.Comoesperado,adestruiçãodacapacidadedegerartrabalhoaumenta na medida em que há incremento no par CT /CT . Da mesma forma como foi feito no gráfico de contorno do coeficiente de performance, é possível usar a equação da reta paradefinirocomportamentodessaslinhasdeiso-irreversibilidade.
CT = CT .��+��
Todavia, como nesse gráfico as restas em questão são paralelas pode ser definir que o coeficiente angular �� é na verdade um número característico para esse sistema de refrigeração, portanto será substituído pela letra grega ��. Outrossim, o coeficiente linear �� correspondeaopontoemqueessalinhacortaoeixoCT .Paralinhasintermediárias, não mostradas no gráfico VI.5, basta se observar a representação tridimensional dessa superfície para que se chegue a conclusão de que as linhas de iso-irreversibilidade são retas:
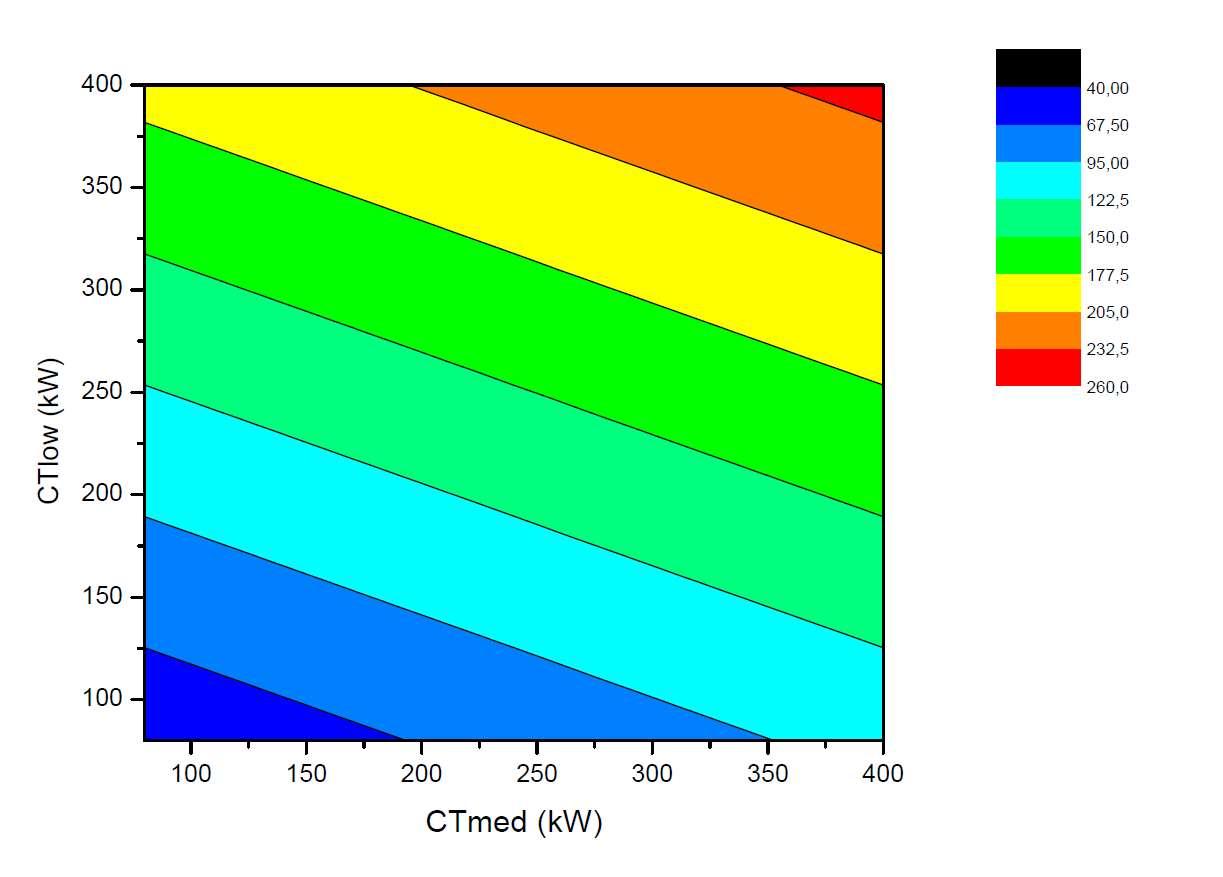
60
FiguraVI.6Gráfico3Ddesuperfíciedairreversibilidade
Dessemodo,ocoeficientelinearseráoelementoquevariaentreasdiversaslinhas deiso-irreversibilidade.Cadaumadessaslinhasestáevidentementeligadaàumvalorde destruiçãodacapacidade degerartrabalho. Logo,encontrarovalordocoeficiente linear se torna uma forma fácil de determinar a irreversibilidade total do sistema, desde que estejamos munidos do par de cargas térmicas desejado e do valor do número característico. Pela sua grande relevância �� passará a ser chamado de carga térmica de congelamentobásica,ouCT .
CT = CT ��+ CT
Selecionando, então, dois pontos pertencentes de uma dessas linhas, pode-se estimarovalordonúmerocaracterísticodessesistemadereferência:
��= −0,4820

Agora,seisolandoacargatérmicabásica,ter-se-á:
CT = CT +0,4820.CT
Assimsendo,bastaescolherumpardecargastérmicaqualquer(desdequecontido nodomíniodelimitadopor80e400kW)paraseestimarovalordacargatérmicabásica.
61
Finalmente, sabe-se que cada valor de carga térmica básica está vinculado a um determinado valor para irreversibilidade. Usando o próprio conjunto de dados que fundamentou o gráfico da figura 6.5, basta usar a primeira coluna de números (quando CT =0), para formular uma tabela que relaciona diretamente a carga térmica básica e o valor da irreversibilidade. Caso este seja intermediário, uma simples interpolação forneceovalordesejado,umavezqueoproblemaélinear.
TabelaVI.1Relaçãoentrecargatérmicabásicaeirreversibilidade
CTlow0 Sist.Ref. CTlow0 Sist.Ref. CTlow0 Sist.Ref. CTlow0 Sist.Ref.
6,00958 110 48,90747 210 91,80536 310 134,703249
10,29937 120 53,19726 220 96,09515 320 138,993038
14,58916 130 57,48705 230 100,3849 330 143,282827
18,87895 140 61,77684 240 104,6747 340 147,572616
23,16874 150 66,06663 250 108,9645 350 151,862405
27,45852 160 70,35641 260 113,2543 360 156,152194
31,74831 170 74,6462 270 117,5441 370 160,441983
36,0381 180 78,93599 280 121,8339 380 164,731772
40,32789 190 83,22578 290 126,1237 390 169,021561
44,61768 200 87,51557 300 130,4135 400 173,31135
Ademais,épossívelsubmetertodosostestespropostosnocapítulo5aessamesma análise e, dessa forma, encontrar os números característicos para cada um deles. Os gráficosabaixoindicamcomo�� secomportacom aalteraçãodosparâmetros dosistema derefrigeração.


FiguraVI.7�� eatemperaturanoEMT
FiguraVI.8�� eatemperaturanoEBT
62
10
20
30
40
50
60
70
80
90
100
FiguraVI.9�� eaaproximaçãonoTC1
FiguraVI.10�� eaaproximaçãonoTC2
Desse modo, para se extrair valores intermediários de números característicos, basta buscar no gráfico adequado. Além disso, é importante notar que cada um desses testesproduziráuma tabela decargatérmica básicasemelhante àquela expostanatabela VI.1. Com isso, pode-se produzir um gráfico responsivo que compara os valores de irreversibilidade total de todos os testes para qualquer par de cargas térmicas. Um exemplosegueabaixoparaopar(125,100)kW.
FiguraVI.11Comparaçãoentreostesteseirreversibilidadetotal
Nesse gráfico, a linha tracejada vermelha denominada linha de referência indica justamente o valor de irreversibilidade do sistema de referência. Cada uma das curvas explicita como as mudanças de parâmetro repercutem na destruição da capacidade de gerartrabalhodosistema.Portantoográficopodeserusadocomocritériodeescolhados



63
parâmetros de operação, ainda mais se forem levados em conta os requisitos de um determinadoprojeto.
64
VII Comportamento do sistema de refrigeração e o regime detemperaturasnoRiodeJaneiro
Atéagoranaanálisetomou-secomotemperaturadoambienteumvalorarbitráriode 20℃. Para atribuir maior realismo a análiseseria interessante estudar o comportamento do sistema de refrigeração, quando é levado em conta o perfil de temperatura anual na cidadedoRiodeJaneiro.
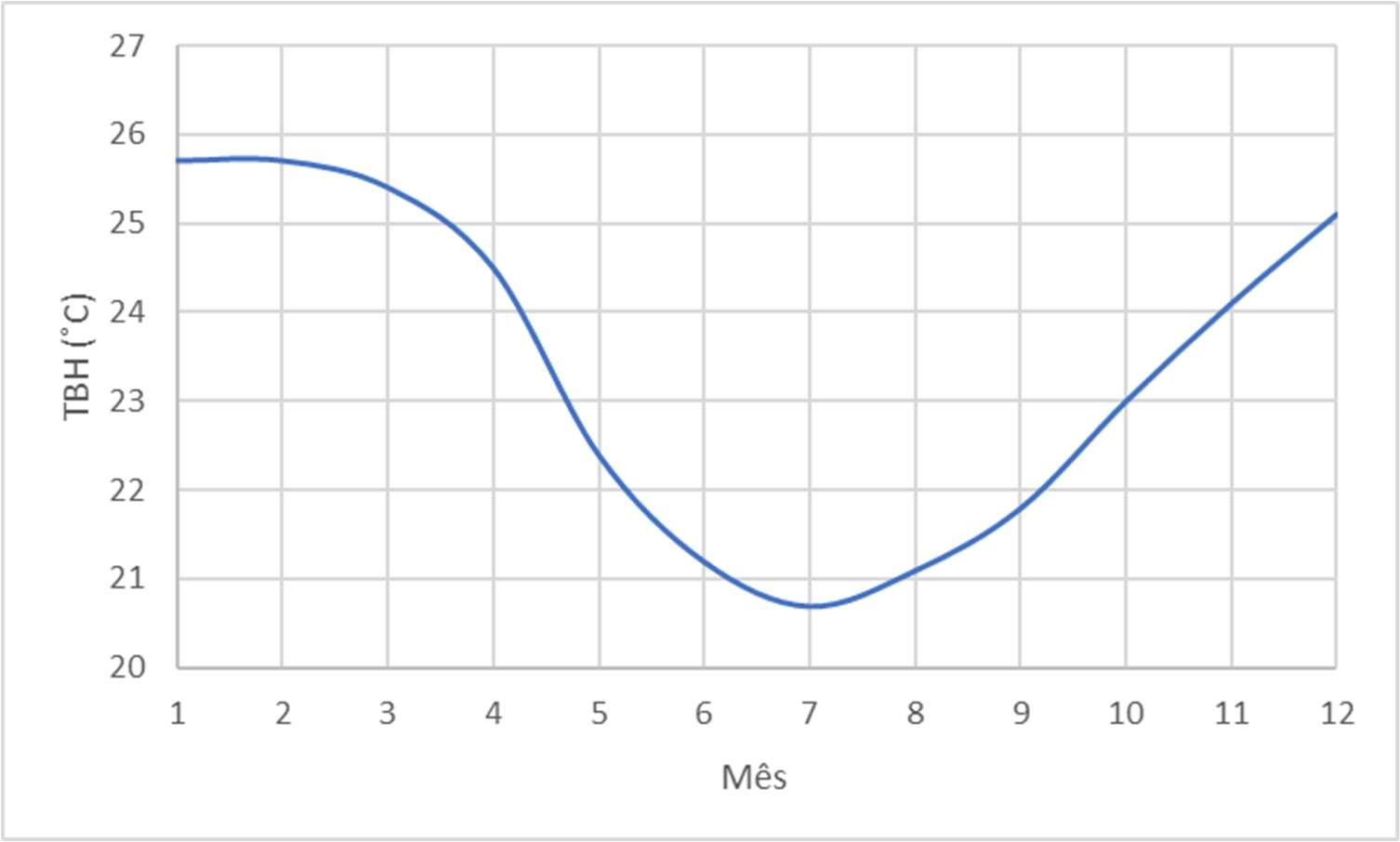
Uma vez que o condensador é um sistema com água operando com uma torre de refrigeração,atemperaturadoambientedeinteresseparaaanáliseseráatemperaturade bulbohúmido.Umperfilmédioanualdessatemperaturapodeserextraídodomanualde dadosclimáticosdaASHRAEeseguenográficoabaixo:
FiguraVII.1Perfildetemperaturamédiadebulboúmidoanual
Nota-seclaramenteocomportamentosazonaldevariaçãodessatemperatura.Para se estimar como as cargas térmicas serão alteradas com o passar dos meses, deve-se somente lançar mão da avaliação proposta no capítulo 3, substituindo-se o valor de temperaturadeambientearbitrárioporesseperfil, acrescendo-se4℃,umvalortípicode aproximaçãotérmicaemtorresderefrigeração.
65
FiguraVII.2Variaçãoanualdacargatérmicaderesfriamento
FiguraVII.3Variaçãoanualdacargatérmicadecongelamento
Observando-se esses gráficos, percebe-se que as cargas térmicas têm comportamento oposto ao perfil de temperatura de bulbo húmido. Isso está dentro do esperado, já que, ao se reduzir a temperatura ambiente, aumenta-se a redução de temperatura do estágio com água o que incrementa sua capacidade de absorver energia térmica.
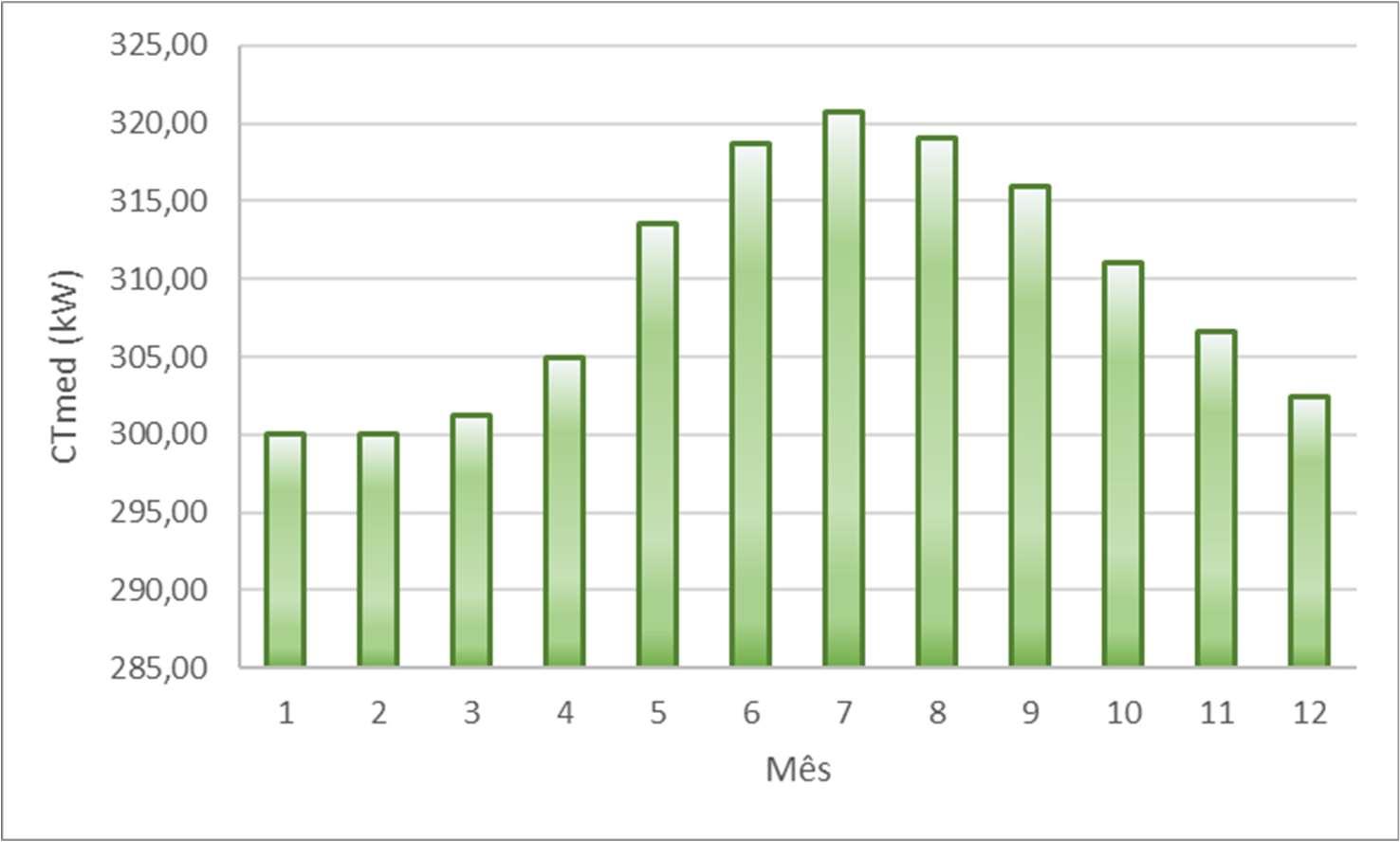
A demanda de energia do sistema de referência é o par de cargas térmicas (300,150) kW. Desse modo, caso se desejasse fazer com que esses valores se mantivessem estáveis ao longo do ano, poder-se-ia reduzir as vazões mássicas dos
66
refrigerantes o que acarretaria na redução do consumo de energia de compressores e bombasdecirculação.
Finalmente, também tem relevância a forma como o coeficiente de performance evoluicomopassardosmeses.Ográficoabaixoomostra:


FiguraVII.4VariaçãoanualdoCOP
Nota-sequenãoháalteraçãosignificativanocoeficientedeperformanceselevado em conta a dinâmica anual da cidade do Rio de Janeiro. Todavia, deve-se ter em mente que essa análise é limitadauma vez queo impacto da alteração da temperatura aolongo doanonaenergiarequeridaparaascâmarasfrigoríferasnãofoicontabilizado.
67
Conclusão
Ademandaporumsistemaderefrigeração“verde”–quetemimpactozerosobre a destruição da camada de ozônio – no contexto da cidade do Rio de Janeiro foi o que norteou esse trabalho. Nele, um sistema de refrigeração do tipo cascata com amônia, proprileno-glicol e dióxido de carbono indicado por Silva (2009) foi testado sob três diferentesângulos.
Primeiramente, foi analisado como a mudança dos seus parâmetros internos de operação como temperatura nos evaporadores e aproximação térmica nos trocadores de calorimpactamseucoeficientedeperformanceerendimentodesegundaleiparacadaum dosequipamentosquecompõeosistemaderefrigeração.
Depois, foi variado a carga térmica demandada em ambos os evaporadores. Isso permitiu estabelecer a linearidade desse problema demonstrada pelas linhas de “isoperformance” e “iso-irreversibilidade”. Essa última foi utilizada para se definirem equaçõescaracterísticasparacadaumadasalternativasestudadasnafasedavariaçãodos parâmetros internos do sistema. Compôs-se, então, uma forma de realizar preliminarmente uma comparação qualitativa entre essas alternativas no intuito de se encontraramelhorparaumadeterminadademanda.
Finalmente,oregimedetemperaturasdebulbohúmidoanualfoiutilizadoparase compreender como o sistema de refrigeração responde às alterações climáticas ao longo do ano na cidade do Rio de Janeiro. A partir dessa análise, pode-se dizer que essas alterações não apresentam impacto significativo na alteração do coeficiente de performance do sistema de refrigeração. Por outro lado, deve-se ter em mente que essa análise tem caráter limitado uma vez que não foi contabilizado a alteração na demanda deenergiatrazidapelavariaçãodetemperaturaambiente.
Por conseguinte, parece ser viável o uso de um sistema de refrigeração cascata com dióxido de carbono no cenário do Rio de Janeiro. Para fortalecer essa afirmação, poder-se-ia realizar a seleção dos equipamentos como trocador de calor, condensador, válvula de expansão, bombas de circulação e evaporadores. Além disso, também seria interessante realizar a análise de “iso-irreversibilidade” para sistemas de refrigeração diferentes paraque se possa criar uma espécie de banco dedados para ajudarprojetistas
68 VIII
em uma seleção preliminar do sistema de refrigeração ideal para uma determinada demanda
69
IX Bibliografia
DASILVA,A.Dióxido deCarbono(������)emSistemasdeRefrigeraçãoComercial eIndustrial.1sted.SãoPaulo:NovaTécnicaEditorial,2009
SILVAA.;EUZEBIOM.Umavisãogeraldaexperiênciaobtidadaaplicaçãodo CO2narefrigeraçãodesupermercadosnoBrasil.SãoPaulo:XIIIConbrava,17-20 Setembro,2013
KILIÇ,B.Exergyanalysisofvaporcompressionrefrigerationcyclewithtwo-stage andintercooler.HeatandMassTransfer.Sitz:SpringerVerlag,v.48,n.7,p.1207–1217,2012
ASHRAE.FundamentalsHandbook. Georgia,Atlanta:ASHRAE,2009
MATTOS, E.; DE FALCO, R. Bombas Industriais. 2nd ed. Rio de Janeiro: Editora Interciência,1998
BORGNAKKE, C.; SONNTAG, R. Fundamentos da Termodinâmica. 8th ed. John Wiley&Sons,INC.,2013
ABNT, Sistema de refrigeração para supermercados – Diretrizes para o projeto, instalaçãoeoperaçãoNBR16255.1sted.ABNT,2014
GRANTZ, C. Refrigeration: A History. 1st ed. Jefferson: McFarland & Company, INC.,2015
70