Simplificando el mundo

Simplificando el Mundo

I n f e r e n c i a P r o b a b i l í s t i c a

En inteligencia artificial, a menudo queremos modelar las relaciones entre varios eventos no deterministas. Si el clima predice un 40% de probabilidad de lluvia, ¿debo llevar mi paraguas? ¿Cuántas bolas de helado debo tomar si cuantas más bolas tenga, es más probable que se me caiga todo? Si hubo un accidente hace 15 minutos en la autopista de camino al estadio para ver el partido de la Selección, ¿debo irme ahora o en 30 minutos? Todas estas preguntas (y muchas más) pueden responderse con i n f e r e n c i a p r o b a b i l í s t i c a .

La semana pasada, modelamos el mundo como si existiera en un estado específico que siempre se conoce. Durante esta semana, utilizaremos un nuevo modelo en el que cada posible estado del mundo tiene su propia probabilidad. Por ejemplo, podríamos construir un modelo meteorológico, donde el estado consiste en la estación, la temperatura y el clima. Nuestro modelo podría decir que P(invierno, 35°, nublado) = 0,023. Este número representa la probabilidad del resultado específico de que sea invierno, 35° y el cielo este nublado.

Más precisamente, nuestro modelo es una d i s t r i b u c i ó n c o n j u n t a , es decir, una tabla de probabilidades que captura la probabilidad de cada posible r e s u l t a d o , también conocida como a s i g n a c i ó n de variables (PDF). Como ejemplo, considere la siguiente tabla:

T e m p o r a d a ( S )

T e m p e r a t u r a ( T )

C l i m a ( W )

P r o b a b i l i d a d

verano caliente sol 0.30

verano caliente lluvia 0.05

verano frío sol 0.10

verano frío lluvia 0.05

invierno caliente sol 0.10

invierno caliente lluvia 0.05

invierno frío sol 0.15

invierno frío lluvia 0.20

Este modelo nos permite responder preguntas que pueden ser de nuestro interés, por ejemplo:

! ¿Cuál es la probabilidad de que haga sol? P(W = sol)

! ¿Cuál es la distribución de probabilidad del clima, dado que sabemos que es invierno? P(W|S = invierno)

! ¿Cuál es la probabilidad de que sea invierno, dado que sabemos que llueve y hace frío? P(S = invierno|T = frío, W = lluvia)

! ¿Cuál es la distribución de probabilidad para el clima y la estación en la que sabemos hace frío?

P(S,W|T = frío)

Inferencia por enumeración

Dada una PDF conjunta, podemos calcular trivialmente cualquier distribución de probabilidad deseada P(Q1 ...Qk|e1 ... ek) usando un procedimiento simple e intuitivo conocido como i n f e r e n c i a p o r e n u m e r a c i ó n , para el cual definimos tres tipos de variables que trataremos:

1. V a r i a b l e s d e c o n s u l t a Qi, que son desconocidas y aparecen en el lado izquierdo del condicional (|) en la distribución de probabilidad deseada.

2. V a r i a b l e s d e e v i d e n c i a ei, que son variables observadas cuyos valores se conocen y aparecen del lado derecho de la condicional (|) en la distribución de probabilidad deseada.

3. V a r i a b l e s o c u l t a s , que son valores presentes en la distribución conjunta general pero no en la distribución deseada. En Inferencia por Enumeración, seguimos el siguiente algoritmo:

1. Recopile todas las filas consistentes con las variables de evidencia observadas.

2. Sumar (marginar) todas las variables ocultas.

3. Normalice la tabla para que sea una distribución de probabilidad (es decir, los valores sumen 1)

Por ejemplo, si quisiéramos calcular P(W|S = invierno) usando la distribución conjunta anterior, seleccionaríamos las cuatro filas donde S es invierno, luego sumaríamos sobre T y normalizaríamos. Esto produce la siguiente tabla de probabilidad:

sol Invierno 0.10+0.15=0.25 0.25/(0.25+0.25)=0.5 lluvia invierno 0.05+0.20=0.25 0.25/(0.25+0.25)=0.5

Por lo tanto, P(W=sol|S=invierno)=0.5 y P(W=lluvia|S=invierno)=0 5, y aprendemos que en invierno hay un 50% de probabilidad de sol y un 50% de probabilidad de lluvia.

Siempre que tengamos la tabla PDF conjunta, se puede usar la inferencia por enumeración (IBE) para calcular cualquier distribución de probabilidad, incluso para múltiples variables de consulta Q1...Qk.

Representación de Redes Bayesianas

Si bien la inferencia por enumeración puede calcular probabilidades para cualquier consulta que deseemos, representar una distribución conjunta completa en la memoria de una computadora no es práctica para problemas reales, si cada una de las n variables que deseamos representar puede tomar d valores posibles (tiene un dominio de tamaño d),

entonces nuestra distribución conjunta la mesa tendrá dn entradas, ¡exponencial en el número de variables y bastante poco práctico para almacenar!

Las redes bayesianas evitan este problema aprovechando la idea de probabilidad condicional. En lugar de almacenar información en una tabla gigante, las probabilidades se distribuyen a través de una serie de tablas de probabilidad condicional más pequeñas junto con un g r á f i c o a c í c l i c o d i r i g i d o (DAG) que captura las relaciones entre variables. Las tablas de probabilidad locales y el DAG juntos codifican suficiente información para calcular cualquier distribución de probabilidad que podríamos haber calculado dada toda la distribución conjunta grande.

Definimos formalmente una Red Bayesiana en que consiste de:

! Un gráfico acíclico dirigido de nodos, uno por variable X.

! Una distribución condicional para cada nodo P(X|A1...An), donde Ai es el i-ésimo padre de X, almacenado como un t a b l a d e p r o b a b i l i d a d

c o n d i c i o n a l o CPT. Cada CPT tiene n+2 columnas: una para los valores de cada uno de los n variables padre A1...An, una para los valores de X y otra para la probabilidad condicional de X dada sus padres.

La estructura del gráfico de la Red Bayesiana codifica relaciones de independencia condicional entre diferentes nodos.

Estas independencias condicionales nos permiten almacenar varias tablas pequeñas en lugar de una grande.

Es importante recordar que los bordes entre los nodos de la red bayesiana no significan que haya específicamente una relación causal entre esos nodos, o que las variables son necesariamente dependientes unas de otras. Eso solo significa que puede haber algunarelación entre los nodos.

Como ejemplo de una Red Bayesiana, considere un modelo donde tenemos cinco variables aleatorias binarias descritas:

! B : Ocurre un robo.

! A : La alarma suena.

! E : Ocurre un terremoto.

! J : Juan llama a emergencia.

! M : María llama a emergencia.

Suponga que la alarma puede sonar si ocurre un robo o un terremoto, y que María y Juan llamarán a emergencia si oyen la alarma. Podemos representar estas dependencias con el gráfico que se muestra a continuación.

En esta Red de Bayes almacenaríamos las tablas de probabilidad !"#$% !"&$% !"'(#% &$% !")('$ y !"*('$.

Dados todos los CPT para un gráfico, podemos calcular la probabilidad de una asignación dada usando la siguiente regla: + ",! % ," % - % ,# $ . / + ",$ (012345 ",$ $$ # $ %!

Para el modelo de alarma anterior, podemos calcular la probabilidad de una probabilidad conjunta de la siguiente manera: + " 7 % 4 % 81 % 89% :$ . + "67 $ < + "64 $ < + "81 ( 6 7 % 64 $ < + "89( 8 1 $ < + "6:( 8 1 $=

Como verificación de la realidad, es importante internalizar que las Redes de Bayes son solo un tipo de modelo. Los modelos intentan capturar la forma en que funciona el mundo, pero

debido a que siempre son una simplificación, siempre están equivocados. Sin embargo, con buenas opciones de modelado, aún pueden ser aproximaciones lo suficientemente buenas como para ser útiles para resolver problemas reales en el mundo real.

En general, es posible que un buen modelo no tenga en cuenta todas las variables o incluso todas las interacciones entre variables. Pero al hacer suposiciones de modelado en la estructura del gráfico, podemos producir técnicas de inferencia increíblemente eficientes que a menudo son más útiles en la práctica que los procedimientos simples como la inferencia por enumeración.

Estructura de las Redes Bayesianas

En esta clase, nos referiremos a dos reglas para las independencias de las redes bayesianas que se pueden inferir observando la estructura gráfica de la Red Bayesiana:

! Cada nodo es condicionalmente independiente de todos sus nodos antecesores (no descendientes) en el gráfico, dado todos sus padres.

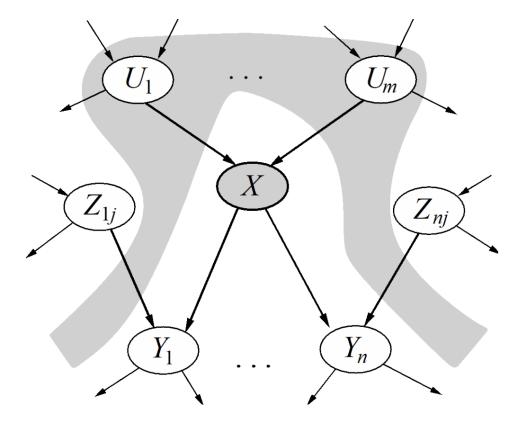
! Cada nodo es condicionalmente independiente de todas las demás variables dada su manta de Markov. La manta de Markov de una variable que consta de padres, hijos y otros padres de los hijos.

Usando estas herramientas, podemos volver a la afirmación de la sección anterior: que podemos obtener la distribución

conjunta de todas las variables uniendo los CPTs de la Red Bayesiana. + ",! % ," % - % ,# $ . / + ",$ (012345 ",$ $$ # $ %!

Esta relación entre la distribución conjunta y los CPT de las redes Bayes funciona debido a las relaciones de independencia condicional dadas por el gráfico. Probaremos esto usando un ejemplo.

Repasemos el ejemplo anterior. Tenemos los CPTs !"#$% !"&$% !"'(#% &$% !")('$ y !"*('$ , y el siguiente gráfico:

Para esta red de Bayes, estamos tratando de probar la siguiente relación: !"#% &% '% )% *$ . !"#$!"&$!"'(#% &$!")('$!"*('$(1)

Podemos expandir la distribución conjunta de otra manera: usando la regla de la cadena. Si ampliamos la distribución

conjunta con ordenación topológica (padres antes que hijos), obtenemos la siguiente ecuación:

!"#% &% '% )% *$ .

!"#$!"&(#$!"'(#% &$!")(#% &% '$!"*(#% &% '% )$ (2)

Note que en la Ecuación (1) cada variable está representada en un CPT !">?@(!?A@BC">?@$, mientras que en la Ecuación (2), cada variable se representa en un CPT !">?@(!?A@BC">?@$% 'DEBCF@GC">?@$$. Confiamos en la primera relación de independencia condicional anterior, que c a d a n o d o e s c o n d i c i o n a l m e n t e i n d e p e n d i e n t e d e t o d o s s u s n o d o s a n t e p a s a d o s e n e l g r á f i c o , d a d o s t o d o s s u s p a d r e s 1

Por lo tanto, en una red de Bayes, !">?@(!?A@BC">?@$% 'DEBCF@GC">?@$$ . !">?@(!?A@BC">?@$$, entonces la Ecuación (1) y La ecuación (2) son iguales. Las independencias condicionales en una Red Bayesiana permiten múltiples tablas de probabilidad condicionales más pequeñas para representar toda la distribución de probabilidad conjunta.

Inferencia exacta en redes bayesianas

La inferencia es el problema de encontrar el valor de alguna distribución de probabilidad P(Q1...Qk|e1...ek), como se detalla en la

! "#!$%&'!('&%)*!+'!,-($,./.0#!(-)1)!1)2.#.&,)!/$3$!4-#!#$1$!),!/$#1./.$#'+3)#%)!.#1)()#1.)#%)!1)! ,-,!#$!1),/)#1.)#%),!1'1$,!,-,!('1&),45 6.)3(&)!7-)&)3$,!8'/)&!+'!,-($,./.0#!39#.3'!($,.:+)!;! (&$:'&!+$!7-)!#)/),.%'3$,*!',9!7-)!-,'&)3$,!+'!,-($,./.0#!1)!+$,!'#%)(','1$,5

sección de Inferencia Probabilística al comienzo de la clase. Dada una Red de Bayes, podemos resolver esto ingenuamente formando el PDF conjunto y usando Inferencia por Enumeración. Esto requiere la creación de una iteración sobre una tabla exponencialmente grande.

Eliminación de Variables

Un enfoque alternativo es eliminar las variables ocultas una por una. Para e l i m i n a r una variable X, hacemos lo siguiente:

1. Unir (multiplicar juntos) todos los factores que involucran a X.

2. Sume X.

Un f a c t o r se define simplemente como una probabilidad no normalizada . En todos los puntos durante la eliminación de variables, cada factor será proporcional a la probabilidad a la que corresponde, pero la distribución subyacente para cada factor no necesariamente sumará 1 como debería hacerlo una distribución de probabilidad. El pseudocódigo para la eliminación de variables es:

f u n c t i o n Eliminacion(X, e , bn ) r e t u r n s una distribucion en X i n p u t s : X, variable consulta e , valores observados para variables E bn , una red Bayesiana especificando una distribucion conjunta P(X1,…,Xn) factores! []

f o r e a c h var i n Ordenar(bn.Var)d o factores! [Hacer-Factor(var , e )|factores ]

i f var es una variable oculta t h e n factores!

Suma(var , factores )

r e t u r n Normalizar(Produto-Punto(factores))

Hagamos estas ideas más concretas con un ejemplo. Supongamos que tenemos un modelo como el que se muestra a continuación, donde T, C, S y E pueden tomar valores binarios. Aquí, T representa la posibilidad de que un aventurero tome un tesoro, C representa la probabilidad de que una jaula caiga sobre el aventurero dado que toma el tesoro, S representa la posibilidad de que se liberen serpientes si un aventurero toma el tesoro, y E representa la posibilidad de que el aventurero escape dada la información sobre el estado de la jaula y las serpientes.

En este caso, tenemos los factores !"H$% !"I(H$% !"J(H$ y !"&(I% J$. Supongamos que queremos calcular!"H( 8 B$. El enfoque de inferencia por enumeración sería formar la PDF conjunta de 16 filas !"H% I% J% &$ , seleccionar solo las filas correspondientes a 8B , y luego sumar I y J para finalmente normalizar.

El enfoque alternativo es eliminar I, luego J, una variable a la vez. Procederíamos de la siguiente manera:

! Unir (multiplicar) todos los factores que involucran a I , formando K! "I% 8B(H% J$ . !"I(H$ < !"8B(I% J$.

! Sumar I a partir de este nuevo factor, dejándonos con un nuevo factor K" "8B(H% J$.

! Une todos los factores que involucran a J , formando K& "8B% J(H$ . !"J(H$ < K" "8B(H% J$.

! Sumar J, dando K' "8B(H$.

! Une los factores restantes, lo que da K( "8B% H$ . K' "8B(H$ < !"H$.

Una vez que tenemos K( "8B% H$ , podemos calcular fácilmente !"H( 8 B$ mediante la normalización.

Si bien este proceso es más complicado desde un punto de vista conceptual, el tamaño máximo de cualquier factor generado es solo 8 filas en lugar de 16 como sería si formáramos el PDF conjunto completo.

Una forma alternativa de ver el problema es observar que el cálculo de !"H( 8 B$ puede hacerse a través de la inferencia por enumeración de la siguiente manera:

L M M + "N$+ "5 (N$+ "O (N$+ "84 (O % 5$ ) *

o por eliminación de Variables de la siguiente manera:

L!"H$ M + "5(N $ M + "O (N $+ "84 (O % 5$ ) *

¡Podemos ver que las ecuaciones son equivalentes, excepto que en la eliminación de variables hemos movido términos que son irrelevantes para las sumas fuera de cada suma!

Como nota final sobre la eliminación de variables, es importante observar que solo mejora la inferencia por enumeración si somos capaces de limitar el tamaño del factor más grande a un valor razonable.

Ejercicio: Redes Bayesianas

Supongamos que un paciente puede tener un síntoma (S) que puede ser causado por dos enfermedades diferentes (A y B). Se sabe que la variación del gen G juega un papel importante en la manifestación de la enfermedad A. La Red de Bayes y las tablas de probabilidad condicional correspondientes para esta situación se muestran a continuación. Para cada pregunta, puede dejar su respuesta como una expresión aritmética.

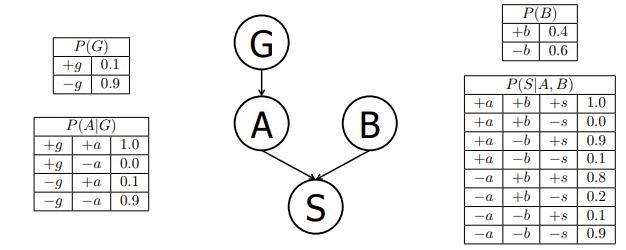
(a) Calcule la siguiente entrada de la distribución conjunta:

!"8P% 8?% 8Q% 8C$ .

!"8P$!"8?( 8 P$!"8Q$!"8C( 8 Q% 8?$ . "R=S$"S=R$"R=T$"S=R$ . R=RT

(b) ¿Cuál es la probabilidad de que un paciente tenga la enfermedad A?

!"8?$ .

!"8?( 8 P$!"8P$ 8 !"8?( P$!" P$ . "S=R$"R=S$ 8 "R=S$"R=U$ . R=SU

!"8?( 8 Q$ .

!"8?$ . R=SU

La primera igualdad se cumple ya que A VV B, lo que se puede inferir del gráfico de la red de Bayes.

(d) ¿Cuál es la probabilidad de que un paciente tenga la enfermedad A dado que tiene el síntoma S y la enfermedad B?

!"8?( 8 C% 8Q$ .

!"8?% 8Q% 8C$

!"8?% 8Q% 8C$ 8 !" ?% 8Q% 8C$ .

!"8?$!"8Q$!"8C( 8 ?% 8Q$

!"8?$!"8Q$!"8C( 8 ?% 8Q$ 8 !" ?$!"8Q$!"8C( ?% 8Q$ . "R=SU$"R=T$"S=R$

"R=SU$"R=T$"S=R$ 8 "R=WS$"R=T$"R=W$ . R=RXY

R=RXY 8 R=Z[UZ \ R=ZZYX

(e) ¿Cuál es la probabilidad de que un paciente tenga la enfermedad portadora de la variación genética G dado que tiene la enfermedad A?

!"8P( 8 ?$ .

!"8P$!"8?( 8 P$

!"8P$!"8?( 8 P$ 8 !"6P$!"8?( 6 P$ . "R=S$"S=R$

"R=S$"S=R$ 8 "R=U$"R=S$ . R=S R=S 8 R=RU . R=[ZY]

Ejercicio: Eliminación de Variables

Usando la Red Bayesiana que se muestra a continuación, queremos calcular !"^( 8 _$ . Todas las variables tienen

d o m i n i o s b i n a r i o s . Nosotros ejecutamos la eliminación de variables, con el siguiente orden de eliminación de variables: X, T, U, V, W.

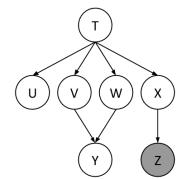
Después de insertar evidencia, tenemos los siguientes factores para comenzar:

!"H$% !"`(H$% !"a (H$% !"b(H$% !"c(H$% !"^ (a% b$% !"8_(c$

Al eliminar X generamos un nuevo factor f1 de la siguiente manera,

d! "8e (N $ . M + "f (N$+ "8e(f $ +

lo que nos deja con los factores:

!"H$% !"`(H$% !"a (H$% !"b(H$% !"^ (a% b$% K" "8_(H$

(a) Al eliminar H generamos un nuevo factor K" de la siguiente manera, lo que nos deja con los factores:

K" "`% a% b% 8_$ . M !"F$!"`(F$!"a (F$!"b(F$d! "8_(F$ , !"^ (a% b$% K" "`% a% b% 8_$

(b) Al eliminar ` generamos un nuevo factor K& de la siguiente manera, lo que nos deja con los factores:

K& "a% b% 8_$ . M d" "g% a% b% 8_$!"^ (a% b$% K& "a% b% 8_$

Tenga en cuenta que ` podría haberse eliminado del gráfico original, porque h !"`(F$ . S - Podemos ver esto en el gráfico: podemos eliminar cualquier nodo hoja que no sea una variable de consulta o una variable de evidencia.

K' "b% ^% 8_$ . M d& ">% b% 8_$!"^(>% b$ .

K' "b% ^% 8_$

(d) Al eliminar b generamos un nuevo factor K( de la siguiente manera, lo que nos deja con los factores:

K( "^% 8_$ . M d' "i% ^% 8_$ / K( "^% 8_$

(e) ¿Cómo obtendría !"^ ( 8 _$ a partir de los factores anteriores?

Simplemente vuelva a normalizar K["^% 8_$ para obtener !"^ ( 8 _$. Concretamente,

!"j(8_$ . d( "k% 8e$ h d( "k 0 % 8e$ 10

(f) ¿Cuál es el tamaño del factor más grande que se genera durante el proceso anterior?

K" "`% a% b% 8_$ . Este contiene 3 variables no condicionadas, por lo que tendrá 23 = 8 entradas (`% a% b son variables binarias, y solo necesitamos almacenar las entradas para 8_ para cada configuración posible de estas variables).

(g) ¿Existe un mejor orden de eliminación (uno que genera factores más pequeños y más grandes)?

Sí. Una de esas ordenaciones es c% `% H% a% b . Todos los factores generados con esta ordenación contienen como máximo 2 variables no condicionadas, por lo que las tablas tendrán como máximo 22 = 4 entradas (ya que todas las variables son binarias).

Conclusión

Para resumir, las redes bayesianas son una poderosa representación de distribuciones de probabilidad conjunta. Su estructura topológica codifica la independencia y las relaciones de independencia condicional, y podemos usarla para modelar distribuciones arbitrarias para realizar inferencia y muestreo.

En esta clase, cubrimos dos enfoques de la inferencia probabilística: la inferencia exacta y la inferencia probabilística (muestreo). En la inferencia exacta, se nos garantiza la probabilidad correcta exacta, pero la cantidad de cálculo computacional puede ser prohibitiva.

Los algoritmos de inferencia exactos cubiertos fueron:

! Inferencia por enumeración

! Eliminación de Variables