Aprendizaje Reforzado

En esta presentación

! Aprendizaje Reforzado

! Aprendizaje basado en modelos

! Aprendizaje sin modelos

! Evaluación Directa

! Aprendizaje de diferencias temporales

! Q-learning

! Funciones de Exploración

! Representaciones basdas en Características

Procesos de decisión de Markov (MDP) - Offline

! Un MDP se define por:

! Un conjunto de estados

! un conjunto de acciones

! Un modelo de transición

! Probabilidad de que

! Una función de recompensa

! Un estado de inicio

! Posiblemente un estado terminal

! Función de utilidad que es recompensas adicionales (con descuento)

! Los MDP son problemas de búsqueda totalmente observables pero probabilísticos

Aprendizaje reforzado Online

! Todavía suponga un proceso de decisión de Markov (MDP):

! Un conjunto de estados s ! S

! Un conjunto de acciones (por estado) A

! Un modelo T(s,a,s')

! Una función de recompensa R(s,a,s')

! Sigo buscando una politica !(s)

! Nuevo giro: no sé T o R

! decir, no sabemos qué estados son buenos o qué hacen las acciones.

! En realidad debe probar acciones y estados para aprender

estado: s

Recompensa: r

Aprendizaje reforzado

Agente

Acciones: a

Ambiente

! Idea básica:

! Reciba retroalimentacion en forma de recompensas

! La utilidad del agente está definida por la función de recompensa

! Debe (aprender a) actuar para maximizar las recompensas esperadas

! ¡Todo el aprendizaje se basa en muestras observadas de resultados!

Aprendizaje reforzado

Ideas básicas:

! Exploración: tiene que probar acciones desconocidas para obtener información

! Explotación: eventualmente, tiene que usar lo que sabe

! Muestreo: es posible que deba repetir muchas veces para obtener buenas estimaciones

! Generalización: lo que aprende en un estado también puede aplicarse a otros

Aprendizaje basado en modelos

! Idea basada en modelos

Aprende un modelo aproximado basado en experiencias

Ejemplo: aprendizaje basado en modelos

Política de entrada !

Episodios observados (entrenamiento)

Episodio 1

B, este, C, -1

C, este, D, -1

D, salida, x, +10

Suponga: ! = 1

Episodio 3

E, norte, C, -1

C, este, D, -1

D, salida, x, +10

Pros y contras

! Pro: ! Hace un uso eficiente de las experiencias.

! Con:

! No se puede escalar a grandes espacios de estado.

! Aprende a modelar un par estado vez (pero esto se puede arreglar

! No se puede resolver MDP para un |S| muy grande.

¿Por qué funciona esto? Porque eventualmente aprendes el modelo correcto.

Analogía: edad esperada

Meta: Calcular la edad esperada de los estudiantes

P(A) conocido

Sin P(A), recolecte muestras [a1 , a2 , … aN ]

P(A) desconocido: “Basado en modelo”

P(A) desconocido: “Modelo libre”

¿Por qué funciona esto? Porque las muestras aparecen con las frecuencias adecuadas.

Aprendizaje sin modelo

Aprendizaje por refuerzo pasivo

! Tarea simplificada: evaluación de políticas

! Entrada: una política fija "(s)

! No conoces las transiciones T(

! No sabes las recompensas R(

! Objetivo: aprender los valores del estado

! En este caso:

! El alumno está “yendo con la corriente"

! No hay elección sobre qué acciones tomar

! Simplemente ejecute la política y aprenda de la experiencia

! ¡Esto NO es una planificación offline! Realmente tomas acciones en el mundo.

Evaluación Directa

! Meta: Calcular valores para cada estado bajo !

! Idea: promedio de los valores de muestra observados juntos

! Actuar de acuerdo con "

! Cada vez que visite un estado, anote cuál resultó ser la suma de las recompensas con descuento

! Promediar esas muestras

! Esto se llama evaluación directa.

Ejemplo: Evaluación Directa

Política de entrada "

Suponga: ! = 1

Episodios observados (entrenamiento) Valores de salida V(s)

Episodio 1

B, este, C, -1

C, este, D, -1

D, salida, x, +10

Episodio 2

B, este, C, -1

C, este, D, -1

D, salida, x, +10

Episodio 3

E, norte, C, -1

C, este, D, -1

D, salida, x, +10

episodio 4

E, norte, C, -1

C, este, A, -1

A, salida, x, -10

Si B y E van a C bajo esta política, ¿cómo pueden ser diferentes sus valores?

Problemas con la evaluación directa

! ¿Qué tiene de bueno la evaluación directa?

! es fácil de entender

! No requiere ningún conocimiento de T, R

! Eventualmente calcula los valores promedio correctos, usando solo transiciones de muestra

! ¿Qué tiene de malo?

! Desperdicia información sobre conexiones de estado.

! Cada estado debe aprenderse por separado.

! Entonces, lleva mucho tiempo aprender

Si B y E van a C bajo esta política, ¿cómo pueden ser diferentes sus valores?

! Según la ecuación de Bellman, esto significa que tanto B como E deberían tener el mismo valor bajo !.

! Sin embargo, de las 4 veces que nuestro agente estuvo en el estado C, hizo la transición a D y cosechó una recompensa de 10 tres veces y pasó a A y cosechó una recompensa de −10 una vez.

! Fue pura casualidad que la única vez que recibió la recompensa de -10 comenzara en el estado E en lugar de B, pero esto distorsionó severamente el valor estimado para E.

! Con suficientes episodios, los valores de B y E convergerán a sus valores reales, pero casos como este hacen que el proceso tarde más de lo que nos gustaría.

! Este problema se puede mitigar eligiendo utilizar nuestro segundo algoritmo de aprendizaje por refuerzo pasivo, el aprendizaje por diferencia temporal.

Aprendizaje de diferencias temporales

Ejemplo: aprendizaje de diferencias temporales

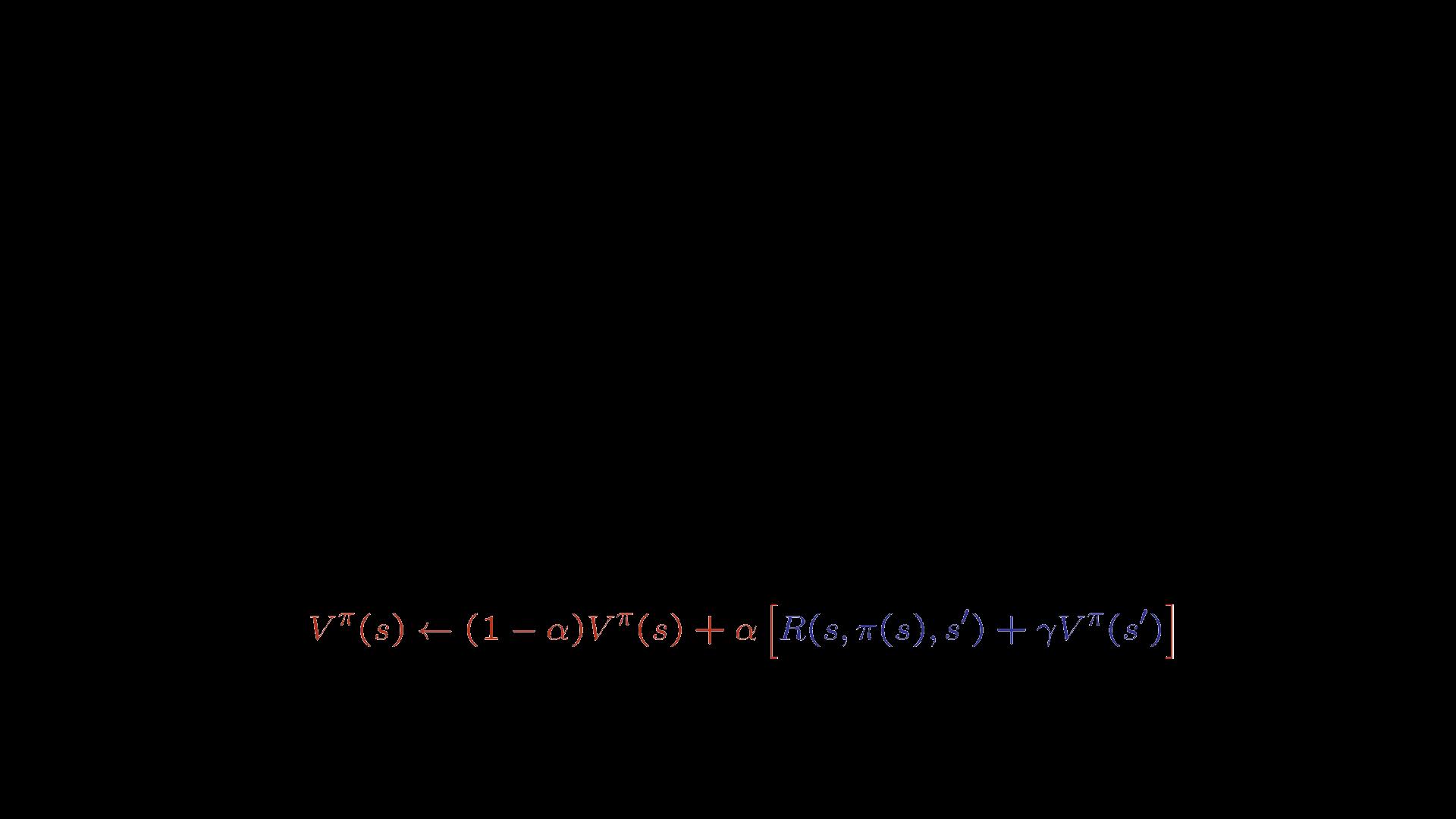
Suponga: ! = 1, ! = 1/2

Problemas con TD Value Learning

Q-learning

! Q-Learning: iteración de valor Q basada en muestras

! valores de Q( s,a ) sobre la marcha

! Recibir una muestra ( s,a,s',r )

! Considere su estimación anterior:

! Considere su nueva estimación de muestra:

! Incorpore la nueva estimación en un promedio móvil: ¡ya no hay evaluación de políticas!

Aprendizaje por refuerzo activo

! Aprendizaje por refuerzo pasivo:

! Un agente de aprendizaje pasivo tiene una política fija que determina su comportamiento.

! Aprendizaje por refuerzo activo:

! Un agente de aprendizaje activo puede decidir qué acciones tomar

Q-Learning:

actuar según el óptimo actual (y también explorar …)

! Aprendizaje de refuerzo completo: políticas óptimas (como iteración de valor)

! No conoces las transiciones T( s,a,s ‘).

! No sabes las recompensas R( s,a,s ‘).

! Tú eliges las acciones ahora.

! Objetivo: conocer la política/los valores óptimos.

! En este caso:

! ¡El programa toma decisiones!

! Compensación fundamental: exploración frente a explotación.

! ¡Esto NO es una planificación fuera de línea! De hecho, tomas acciones en el mundo y descubres lo que sucede.

Propiedades de Q-Learning

! Resultado sorprendente: Q-learning converge en una política óptima, ¡incluso si está actuando de manera subóptima !

! Esto se llama aprendizaje fuera de la política.

! Advertencias:

! Tienes que explorar lo suficiente

! Tienes que eventualmente hacer la tasa de aprendizaje lo suficientemente pequeña

! … pero no lo disminuyas demasiado rápido

! Básicamente, en el límite, no importa cómo seleccione las acciones

Aprendizaje por refuerzo activo

Aprendizaje basado en modelos

Política de entrada "

actuar de acuerdo con la política óptima actual Y también explora!

Exploración vs. Explotación

¿Cómo explorar?

! Varios esquemas para forzar la exploración

! Más simple: acciones aleatorias ( #-voraz)

! Cada paso de tiempo, lanza una moneda

! Con (pequeña) probabilidad !, actuar al azar

! Con (gran) probabilidad 1- !, actuar sobre la política actual

! ¿Problemas con acciones aleatorias?

! Eventualmente exploras el espacio, pero sigues dando vueltas una vez que terminas de aprender.

! Una solución: reducir ! con el tiempo

! Otra solución: funciones de exploración

Funciones de exploración

Mejor idea: explorar áreas cuya maldad no esta (todavía) establecido, eventualmente dejar de explorar

Toma un valor estimado u y un recuento de visitas n, y devuelve una utilidad optimista, por ejemplo,

Nota: ¡esto propaga la "bonificación" a los estados que también conducen estados desconocidos!

! ¡Incluso si aprende la política óptima, aún comete errores en el camino!

! El arrepentimiento es una medida del costo total del error: la diferencia entre recompensas (esperadas), incluida la subóptima juventud y las recompensas óptimas (esperadas).

! Minimizar el arrepentimiento va más allá de aprender a ser óptimo: requiere un aprendizaje óptimo para ser óptimo.

! Ejemplo: la exploración aleatoria y las funciones de exploración terminan siendo óptimas, pero la exploración aleatoria tiene un mayor arrepentimiento

Q-Learning aproximado

Generalizando a través de los estados

! Q-Learning básico mantiene una tabla de todos los valores-

! ¡En situaciones realistas, no podemos aprender sobre cada estado!

! Demasiados estados para visitarlos todos en entrenamiento

! Demasiados estados para mantener las tablas memoria.

! En su lugar, queremos generalizar:

! Aprenda sobre una pequeña cantidad de estados de entrenamiento a partir de la

! Generalizar esa experiencia a situaciones nuevas y similares.

! Esta es una idea fundamental en el aprendizaje automático.

Digamos que descubrimos por experiencia que este estado es malo:

Ejemplo: Pacman

En q-learning ingenuo, no sabemos nada sobre este estado:

¡O incluso este!

Representaciones basadas en características

! Solución: describe un estado usando un vector de características (propiedades).

! Las características son funciones de estados a números reales (a menudo 0/1) que capturan propiedades importantes del estado

! Características de ejemplo:

! Distancia al fantasma más cercano

! Distancia al punto más cercano

! número de fantasmas

! 1 / (distancia al punto) 2

! ¿ Pacman está en un túnel? (0/1)

! …… etc.

! ¿Es el estado exacto en esta diapositiva?

! También puede describir un estado q (s, a) con características (p. ej., la acción acerca a Pacman a la comida)

Funciones de valor lineal

Resumen: MDP y RL

MDP conocido: solución fuera de línea

Calcular V*, Q*, ! *

Evaluar una política fija !

MDP desconocido: basado en modelos