CAPITULO 2: REVISIÓN DE LITERATURA
INTERPOLACIÓN DE PRECIPITACIONES
Entre las variables utilizadas en estudios hidrometeorológicos, la precipitación es la más importante debido a su función como dato de entrada en diversos modelos hidrológicos. Por esta razón, contar con registros y bases de datos de dicha variable es de suma importancia. Enel caso deBolivia,el país cuenta con estaciones pluviométricas que capturaninformación desde la década de 1980. Sin embargo, debido a que estas estaciones generan datos puntuales, es necesario realizar un proceso de interpolación para su uso en estudios a mayor escala
La interpolación se entiende como una herramienta que permite generar superficies continuas a partir de información puntual (Alzate Velásquez et al., 2017). Así, la interpolación ofrece una representación descriptiva de cualquier variable en el espacio y facilita la predicción de su distribución (Garcia Calabrese et al., 2022)
En el proceso de interpolación espacial, existen diversas metodologías que permiten generar esquemas predictivos.Algunas de estas incluyen:
1.1.1.POLÍGONOS DE THIESSEN
Los polígonos de Thiessen utilizan una cobertura de puntos para su generación, lo que permite que la forma de cada polígono esté influenciada por la ubicación de los puntos de muestreo (Cuza-Sorolla et al., 2021) En el contexto de las estaciones pluviométricas, esta metodología crea polígonos basados en la altura de precipitación registrada de manera constante, de modo que cada polígono generado representa la influencia de la estación sobre la zona de estudio (Oliveira Diodato et al., 2021)
La generación de estos polígonos se realiza mediante la creación de triángulos entre los puntos de medición, y posteriormente, se traza una mediatriz a lo largo de cada línea que conecta estos puntos. Las mediatrices forman los lados de los diferentes polígonos, y las intersecciones de estas mediatrices indican los límites entre ellos. En la Figura 1, se presenta el resultado de la generación de estos polígonos.
Figura 1 Generación de Polígonos de Thiessen
Fuente: ESRI, 2023
Esta metodología de estudio fue utilizada para el análisis de datos de precipitación en la cuenca del río Rocha a escala mensual (Vallejos et al., 2016) y en la cuenca Katari a escala diaria en Bolivia (Ureña et al., 2018). Ambos estudios se centraron en la comparación entre datos pluviométricos y productos de precipitación satelital en donde, la implementación de los polígonos permitió representar la precipitacion de una manera poco precisa debido a la poca cantidad de estaciones disponibles en ambas aras de estudio. Otros estudios que aplicaron esta metodología para el análisis de datos de precipitación incluyen la cuenca del río Sabinal en México (Aragón Hernández et al., 2019) y la zona denominada 'La Terraza' en Arizona, Estados Unidos (Oliveira Diodato et al., 2021) En estos casos, ambos estudios favorecieron el uso de polígonos de Thiessen en comparación con otros métodos de interpolación
1.1.2.KRIGING
La interpolación kriging ordinario que utiliza “métodos geoestadísticos surgió con el propósito de predecir valores de las variables en sitios no muestreados” (Aragón Hernández et al., 2019, p.4), basándose en la reducción del error cuadrático medio de la base de datos introducida. El método kriging utiliza diferentes modelos, como el lineal, gaussiano, esférico, exponencial, entre otros (Garcia Calabrese et al., 2022). Esto dio como resultado que, en la región occidental del Paraguay, el modelo lineal de kriging mostró el menor valor de suma cuadrática ponderada.
En comparación con otros métodos de interpolación, como Thiessen e IDW, tanto el modelo lineal como el “Ajuste Automático” de kriging presentaron mejores resultados en términos de error cuadrático medio.
1.1.3.DISTANCIA
INVERSAPONDERADA(IDW)
El método de interpolación del inverso ponderado a la distancia (IDW) se basa en el análisis de la distancia entre los puntos a interpolar, asignando un peso a cada punto en función de su distancia, de modo que a mayor distancia, menor es el peso (Aragón Hernández et al., 2019; Liu et al., 2020) A diferencia de kriging, el método IDW se centra menos en enfoques probabilísticos y más en cálculos geométricos.
Este método se empleó en el análisis comparativo del río Sabinal en México, donde fue comparado con la interpolación kriging y el método de Thiessen, mostrando resultados estadísticos aceptables, similares a los de kriging. Sin embargo, al examinar las láminas de lluvias, se observa que los métodos IDW y Thiessen presentan diferencias de hasta un 50% en comparación conlos datos de control. En el contexto de estudios hidrológicos, esto podría generar dificultades en la estimación del escurrimiento a nivel de subcuenca (Aragón Hernández et al., 2019)
1.1.4.REGNIE
La interpolación mediante el modelo REGNIE es un método exclusivo para variables hidrometeorológicas, ya que considera factores geográficos y fisiográficos en su desarrollo, tales como elevación, pendiente y exposición del terreno, los cuales se obtienen a partir de modelos digitales de elevación (DEM, por sus siglas en inglés). Este enfoque se basa en modelos de regresión lineal e IDW.
El modelo REGNIE fue aplicado en los departamentos de las regiones Andina, Pacífica y Caribe de Colombia, utilizando un total de 1,440 estaciones durante un período de 31 años (1980-2011).Enel estudioseobservóquelaintegración delasvariables topográficas mejoró la generación de los mapas interpolados. Con una correlación de 0.81, en comparación con el valor de 0.80 obtenido mediante el método IDW, el modelo REGNIE demostró un mejor rendimiento en la generación de superficies en zonas montañosas (Alzate Velásquez et al., 2017)
1.2. SEMIVARIOGRAMA
En el manejo de los procesos de interpolación mediante kriging, el semivariograma se define como una función que describe la variabilidad espacial de los componentes de un fenómeno de interés, permitiendo su representación a través de una ecuación (Gallardo, 2007).
Dicha ecuación surge de la representación gráfica de la varianza entre los componentes del fenómeno a analizar, caracterizándose en función de los elementos que la componen. Para el caso, los componentes que definen gráficamente y en la ecuación de un semivariograma son: Distancia (Distance): Extensión total acumulada que existe entre los componentes del fenómeno a analizar
• Distancia (Distance): Extensión total acumulada entre los componentes del fenómeno a analizar.
• Rango (Range): Valor de la distancia que alcanza el umbral del modelo.
• Umbral (Sill): También conocido como meseta, es un valor (dependiente del fenómeno analizado) en el cual las varianzas de los elementos se estabilizan.
• Nugget: Representa la variabilidad más pequeña que se puede encontrar entre los componentes del fenómeno.
• Umbral Parcial (Partial Sill): Es la diferencia entre el valor de varianza estable y la menor varianza detectada.
Estos elementos son visibles en la Figura 2.
Fuente: ESRI (2024b)
No obstante, la definición de un semivariograma no puede asemejarse a lo presentado anteriormente. Debido a las combinaciones entre la distancia y el valor del fenómeno, la forma de un semivariograma puede adquirir características únicas que no se pueden aplicar directamente en software de interpolación kriging. A este tipo de semivariograma se le conoce como “empírico”.
La mejor manera de tratar con los semivariogramas empíricos es ajustarlos a través de un modelo que se aproxime a su forma real. Estos modelos corresponden a diferentes
Figura 2. Componentes de un Semivariograma
ecuacionesbasadas en fenómenosquepermitenestandarizarla forma. Entre los modelos que se destacan se encuentran: Lineal, Gaussiano, Exponencial y Esférico. Dependiendo de la forma del semivariograma empírico, es posible que uno o más de estos modelos se ajusten adecuadamente (Gallardo, 2007).
1.3. PRODUCTOS DE PRECIPITACIÓN SATELITAL
Dentro del manejo de alternativas para los datos de precipitación, se encuentran los denominados productos de precipitación satelital (SBP, por sus siglas en inglés). Estos productos son el resultado de la implementación de diversos sensores a bordo de satélites que registran diferentes variables atmosféricas. Los datos obtenidos son introducidos en complejos algoritmos para la generación de mapas de precipitación.
No obstante, estos datos presentan la característica de ser "estimaciones" en el proceso de su generación, ya que se basan en la posible cantidad de agua que se acumula en las nubes
Entre los diferentes productos disponibles se encuentran:
1.3.1.GSMAP
“Global Satellite Mapping of Precipitation” (GSMaP) es un proyecto internacional desarrollado por la Agencia Japonesa de Exploración Aeroespacial (JAXA) que se dedica a proporcionar estimaciones globales de precipitación utilizando datos satelitales. El objetivo principal de GSMaPes crear conjuntos de datos de precipitación de alta calidad y resolución a nivel global, utilizando información recopilada de diversas fuentes satelitales (Kubota et al., 2007)
GSMaP emplea una combinación de sensores a bordo de satélites, denominados receptores de microondas, para el procesamiento de datos mediante su algoritmo. Utiliza información de múltiples satélites, como el TRMM y el GPM (“Global Precipitation Measurement”), para estimar la precipitación en todo el mundo (Kubota et al., 2020).
Con una resolución espacial de 0.1° (aproximadamente 10 km de grilla) y una resolución temporal mínima de una hora, GSMaP ofrece varias versiones y subproductos. La línea GSMaP incluye tres productos procesados a nivel diario: GSMaP_MVK, GSMaP_Gauge y GSMaP_GREV (disponible únicamente en la versión 6 del producto). El producto “MVK” utiliza exclusivamente datos de los sensores satelitales en su algoritmo. Por su parte, “Gauge” integra los datos de los satélites TRMM y GPM en su algoritmo de generación.
Finalmente, el producto “GREV” es una mejora del algoritmo utilizado en “Gauge”, y su
denominativo deriva de los términos “Gauge REVised” (Kubota et al., 2007, 2020). Actualmente, están disponibles cuatro versiones del producto GSMaPa escala diaria: v5, v6, v7 y v8
1.3.2.CHIRPS
“Climate Hazards Group InfraRed Precipitation with Station Data” (CHIRPS) es un producto de precipitación desarrollado por el Grupo de Peligros Climáticos (“Climate Hazards Group”, CHG) de la Universidad de California en Santa Bárbara. La característica distintiva de CHIRPS es su capacidad para combinar datos de satélites con observaciones de estaciones terrestres, lo que permite generar estimaciones de precipitación de alta resolución tanto espacial como temporal (Funk et al., 2015).
CHIRPS utiliza información de sensores infrarrojos en satélites geoestacionarios para capturar patrones de nubes y lluvia en tiempo real. Además, incorpora datos de estaciones meteorológicas para calibrar y mejorar la precisión de las estimaciones (Funk et al., 2020). Este producto presenta una resolución espacial de 0.05° (aproximadamente 5 km de grilla) y una resolución temporal mínima diaria. Debido a su integración con estaciones, se utilizará la versión 2 de este producto.
1.3.3.PERSIANN
“Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks” (PERSIANN) es una línea de productos de estimación de precipitación desarrollada por el Centro de Ciencias delAgua (“Center for Hydrometeorology and Remote Sensing”, CHRS) de la Universidad de California en Irvine. Estos productos emplean técnicas avanzadas de inteligencia artificial y análisis de imágenes satelitales para estimar la precipitación en diversas regiones (Nguyen et al., 2019)
Debido a los avances de algunos de sus productos se decidió manejar dos versiones:
• PERSIANN-CCS: El “Cloud Classification System (CCS)” combina información de varios sensores y satélites para generar estimaciones de precipitación en tiempo real y de alta resolución espacial. Entre los componentes clave de PERSIANN-CCS seincluyen: InteligenciaArtificial(IA)y redes neuronalesartificiales,datos denubes y clasificación denubes,así como imágenes satelitales demicroondas (Nguyenet al., 2019)
• PERSIANN-CCS-CDR: El “Cloud Classification System - Climate Data Record” (CCS-CDR) es una extensión del producto PERSIANN-CCS, que se centra en la creación de un registro climático de estimaciones de precipitación a largo plazo y de alta calidad (Sadeghi et al., 2019, 2021).
Ambos productos ofrecen una resolución espacial de 0.04° (aproximadamente 4 km de cuadrícula) y una resolución temporal mínima de 3 horas
1.3.4.IMERG
“Integrated Multi-satellitE Retrievals for GPM” (IMERG) es un producto de datos de precipitación generado por la misión GPM, cuyo objetivo es medir de manera precisa y global la precipitación y la nieve mediante una red de satélites y sensores. IMERG cuenta con diversas versiones que han ido mejorando el algoritmo de generación del producto (Wang et al., 2017) y permiten el reanálisis de los datos, generando variantes para cada versión, incluidas versiones tempranas, tardías y finales (early, late y final) como se presentan en su repositorio) (Pradhan et al., 2022). IMERG presenta una resolución espacial de 0.1° (aproximadamente 10 km de cuadrícula) y una resolución temporal horaria y diaria
1.3.5.CMORPH
El “Climate Prediction Center (CPC) morphing technique” (CMORPH) es producto de precipitación satelital desarrollado por el National Oceanic and Atmospheric Administration (NOAA). Utiliza sensores infrarrojos, microondas pasivas y un vector de propagación derivativo para generar una cuadrícula de 8 km de resolución temporal de 30 minutos, así como una cuadrícula de 0.25° con resoluciones horarias y diarias (Joyce et al., 2004)
Debido a su naturaleza de estimación en los datos de precipitación, CMORPH puede corregirse a través del análisis de su sesgo en relación con datos de pluviómetros para su versiónde30minutos.Esteprocesodecorrección varíasiseaplicaaocéanosoaextensiones terrestres, pero en ambos casos, se observa una mejora significativa al utilizar el producto corregido en lugar del producto en bruto (Xie et al., 2017).
1.3.6.TRMM
El “Tropical Rainfall Measuring Mission” fue uno de los primeros productos de precipitación satelital, resultado de los proyectos de exploración espacial enfocados en la climatología. Este proyecto, llevado a cabo en cooperación entre organizaciones de Estados Unidos y Japón, tuvo como objetivo realizar mediciones sistemáticas y cuantitativas de las
precipitaciones en latitudes tropicales y medias. El producto satelital TRMM presenta una resolución espacial de 0.25° y una resolución temporal mensual (Kozu et al., 2001)
1.3.7.ERA5
El “Copernicus Climate Change Service” (C3S) de la Comisión Europea, con apoyo de “European Centre for Medium-Range Weather Forecasts” (ECMWF) desarrollaron el “Eurpean ReAnalysis” de quinta generación (ERA5) Este producto de análisis climático global se encarga de describir las anomalías detectadas en el ciclo del agua y la energía a lo largo del tiempo (Muñoz-Sabater et al., 2021). El producto presenta un amplio abanico de variables climatológicas obtenidas mediante la integración de información satelital y sistemas de estaciones terrestres, a través de un proceso de reanálisis de variables.Además, ofrece una resolución temporal nativa horaria y un tamaño de grilla de 0.25°.
1.4. METODOLOGÍA
DE CORRECCIÓN DE DATOS DE PRECIPITACIÓN
1.4.1.CORRECCIÓN DE “BIAS” MEDIANTE “MACHINE LEARNING”
El método de corrección del sesgo (bias en inglés) entre datos de tierra y datos satelitales es una metodología estandarizada que ha sido perfeccionada a medida que las diferentes tecnologías han avanzado. Una de estas tecnologías es el uso de “machine learning” (ML), una herramienta que emplea inteligencia artificial para aprender distintas operativas a través de ejemplos y luego replicar lo aprendido en nuevos casos (Li et al., 2023).
De acuerdo con Iqbal et al. (2022), la corrección del sesgo entre precipitaciones pluviométricas y satelitales, se pueden utilizar modelos como “Random Forest” (RF) o “KNearest Neighbors” (KNN). En ambos casos, la integración de sus ecuaciones incluye un factor de aleatoriedad debido a sus fundamentos:
• Random Forest (RF): Este método se basa en algoritmos flexibles que se adaptan a diferentes enfoques para la clasificación y regresión de datos, permitiendo la generación de árboles de decisión para realizar la corrección del sesgo. Gracias a la implementación de tecnología de ML, el software puede desarrollar un criterio predictivo suficiente para seleccionar la mejor ruta
• K-Nearest Neighbors (KNN): Este enfoque utiliza algoritmos no paramétricos que agrupan el conjunto de datos en “vecindades” basadas en condiciones aleatorias que varían con cada consulta. Como resultado, se obtienen diferentes soluciones para una misma base de datos inicial.
En una aplicación en la Península de Malasia, que involucró 364 estaciones, se demostró que la implementación de este método pudo corregir varios productos que inicialmente presentaban correlaciones menores a 0.7, alcanzando valores cercanos a 0.95. En este estudio, el método RF mostró los mejores resultados (Iqbal et al., 2022).
1.4.2.CORRECCIÓN DE “BIAS” MEDIANTE “QUANTILE MAPPING”
En el caso de la corrección del sesgo mediante el método de mapeo de cuantiles (quantile mapping en inglés), se trata de un enfoque no paramétrico que implementa transformaciones estadísticas. Esta metodología utiliza datos mensuales para generar funciones de distribución, permitiendo transformar datos no corregidos en datos corregidos. Después de este proceso, se generan coeficientes de desagregación para convertir datos mensuales en datos diarios (Cannon et al., 2015)
Según Blanco et al. (2023), en la región pampeana de Argentina, que cuenta con 22 estaciones pluviométricas, se observaron correlaciones menores a 0.75 en relación con productos de precipitación satelital. Tras la implementación de la corrección por cuantiles, las correlaciones mejoraron ligeramente, alcanzando valores cercanos a 0.8. Sin embargo, el sesgo que inicialmente oscilaba entre ±100% con respecto a los datos observados se redujo a valores cercanos a -5%
1.4.3.MÉTODO DE COMBINACIÓN ITERATIVA
De acuerdo a Saavedra y Ureña (2022), el proceso de generación utiliza el error relativo entre la base de datos pluviométrica y el producto de precipitación satelital como indicador a tratar. La metodología establece que el cálculo de este error debe basarse en un mapa de unidades hidrológicas, el cual se emplea en procesos de modelación hidrológica.
Una vez obtenidos los valores promedio, se generan factores de ajuste que permiten reducir el error relativo. Sin embargo, dado que este factor puede adquirir un valor demasiado alto, se limita el error a rangos de ±95%. Después de obtener el valor de ajuste, este se multiplica por los valores iniciales del producto satelital. Al tratarse de una metodología iterativa, el nuevo producto generado reemplaza al producto satelital, y se repite el proceso (Ureña et al., 2021).
Los resultados de su aplicación indican que el proceso de generación del producto combinado produce una base de datos aceptable en su quinta iteración. Como resultado de su implementación, productos de precipitación satelital que inicialmente mostraban
correlaciones inferiores a 0.5 mejoraron su precisión, alcanzando valores de correlación entre 0.86 y 0.9. Sin embargo, el sesgo relativo que inicialmente indicaba sobrestimaciones de hasta 10% fue sustituido por subestimaciones del 30% (Saavedra y Ureña, 2022)
1.5. INDICADORES ESTADÍSTICOS
Para la evaluación de los datos de precipitación, es fundamental utilizar diferentes métodos matemáticos que faciliten la comparación entre los datos observados (provenientes de estacionespluviométricas)ylos datos generados porlos productos deprecipitación.Algunos de los indicadores comúnmente empleados en hidrología son:
1.5.1.COEFICIENTE
DE DETERMINACIÓN
El coeficiente de determinación (R²) indica la proporción de la variabilidad de una variable explicada por un modelo de regresión. Este coeficiente presenta valores que varían entre 0 y 1; un valor de 0 indica una alta variabilidad, mientras que un valor de 1 indica una baja variabilidad (Palma, 2022). La ecuación correspondiente a este coeficiente es la siguiente:
Donde:
• X representa los valores observados
• Y representa los valores a comparar o simulados
• Ẍ representa el promedio de los valores observados
• n representa el número de observaciones
1.5.2.COEFICIENTE
DE CORRELACIÓN
El coeficiente de correlación lineal de Pearson, o simplemente coeficiente de correlación (R), es un indicador estadístico que mide el grado de asociación lineal entre dos variables. Este coeficiente varía entre -1 y 1, donde un valor de -1 indica una correlación perfecta inversa,los valores entre -1y 0indican unacorrelación inversa,unvalorde 0 indicaausencia de correlación, los valores entre 0 y 1 indican una correlación positiva, y un valor de 1 indica una correlación perfecta (Dagnino, 2014). La ecuación correspondiente a este indicador estadístico es la siguiente:
Donde:
• X representa los valores observados
• Y representa los valores a comparar o simulados
• Ẍ representa el promedio de los valores observados
• Ÿ representa el promedio de los valores a comparar o simulados
• n representa el número de observaciones
1.5.3.SESGO
RELATIVO
El sesgo se entiende como la diferencia entre un dato observado y un dato de referencia o simulado. Sin embargo, esta diferencia se limita a ese único par de datos. Por lo tanto, el sesgo relativo se define como un valor que engloba la diferencia general entre una serie de datosobservadosyunaseriededatosdereferencia,expresadocomounporcentajequepuede ser positivo o negativo; en este caso, los valores cercanos a 0 son considerados los resultados esperados (Pedraza Triviño et al., 2020). La ecuación correspondiente a este indicador es la siguiente:
Donde:
• X representa los valores observados
• Y representa los valores a comparar o simulados
• Ẍ representa el promedio de los valores observados
• Ÿ representa el promedio de los valores a comparar o simulados
• n representa el número de observaciones
1.5.4.RAÍZ DELERROR CUADRÁTICO MEDIO (RMSE)
La raíz del error cuadrático medio, también conocida como RMSE (del inglés Root Mean Square Error), es una medida que representa la magnitud promedio de la diferencia entre los datos observados y los datos simulados, elevando dicho valor al cuadrado para ofrecer una mejor perspectiva del mismo (Mentaschi et al., 2013). La ecuación correspondiente a este indicador es la siguiente:
Donde:
• X representa los valores observados
• Y representa los valores a comparar o simulados
• n representa el número de observaciones
1.5.5.ERRORABSOLUTO MEDIO (MAE)
El error absoluto medio, conocido como MAE (del inglés Mean Absolute Error), es un indicador que calcula la diferencia entre los datos observados y los datos simulados, obteniendo posteriormente el valor absoluto de esta operación (Toro Trujillo et al., 2015)
La ecuación correspondiente a este indicador es la siguiente:
Donde:
• X representa los valores observados
• Y representa los valores a comparar o simulados
• n representa el número de observaciones
1.5.6.EFICIENCIADE NASH & SUTCLIFFE (NSE)
La eficiencia de Nash y Sutcliffe (NSE, derivada de Nash & Sutcliffe Efficiency) es un indicador que evalúa la precisión de los valores simulados en relación con los valores observados (Valencia-Gonzalez et al., 2022) Este indicador presenta varios escenarios de resultados: cuando el NSE es igual a 1, los valores simulados son idénticos a los observados; si el NSE es igual a 0, los valores simulados muestran muchas diferencias y es recomendable utilizar los valores observados; y si el NSE es negativo, los datos simulados presentan demasiados errores y no se asemejan a los datos observados. La ecuación de este indicador es la siguiente:
Donde:
• X representa los valores observados
• Y representa los valores a comparar o simulados
• Ẍ representa el promedio de los valores observados
• n representa el número de observaciones
CAPITULO 3: METODOLOGÍA
2.1. ÁREADE ESTUDIO
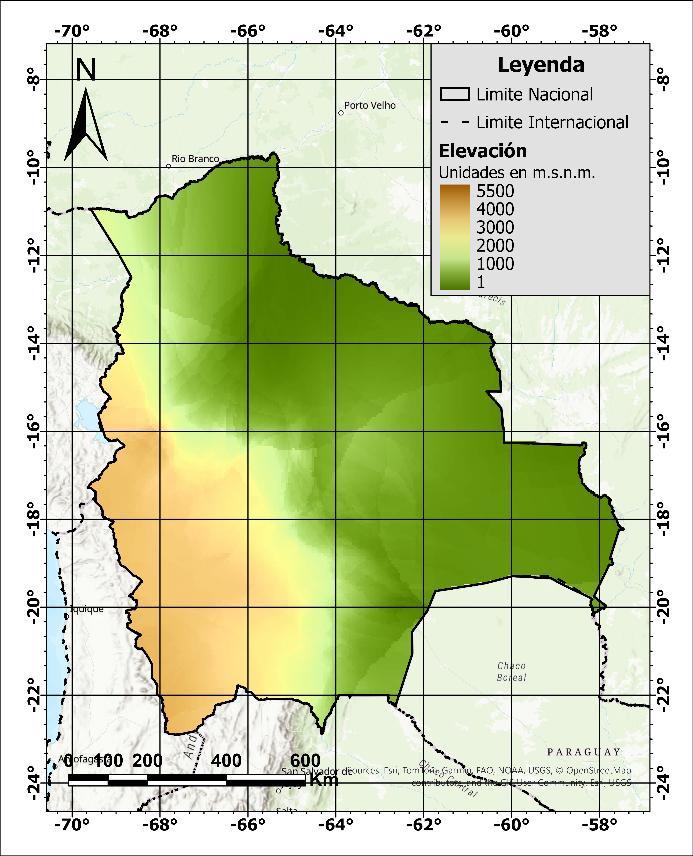
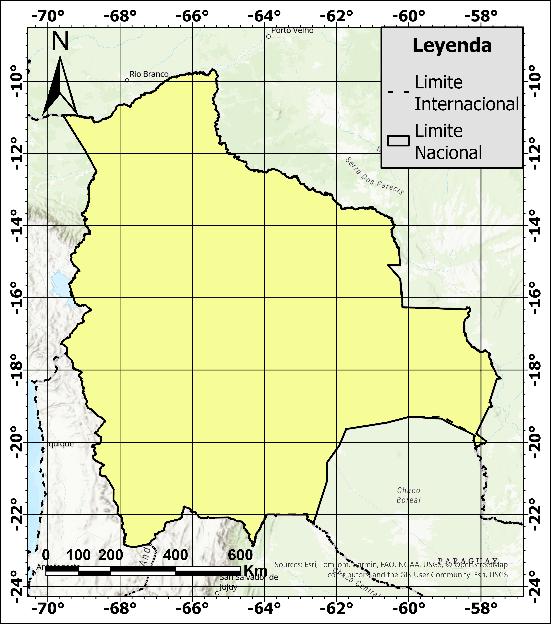
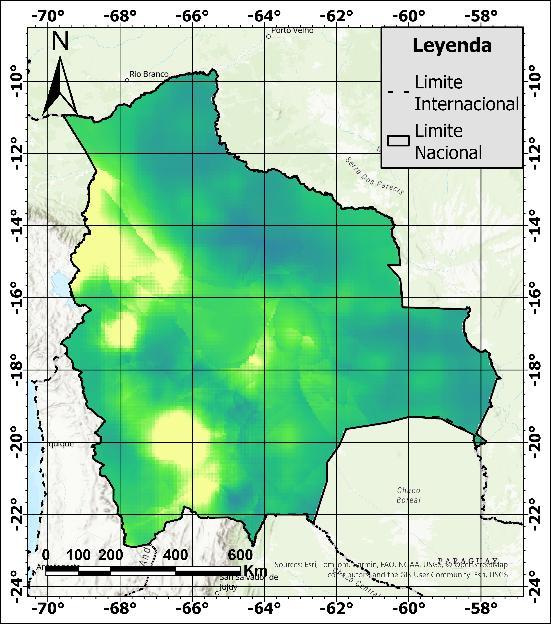
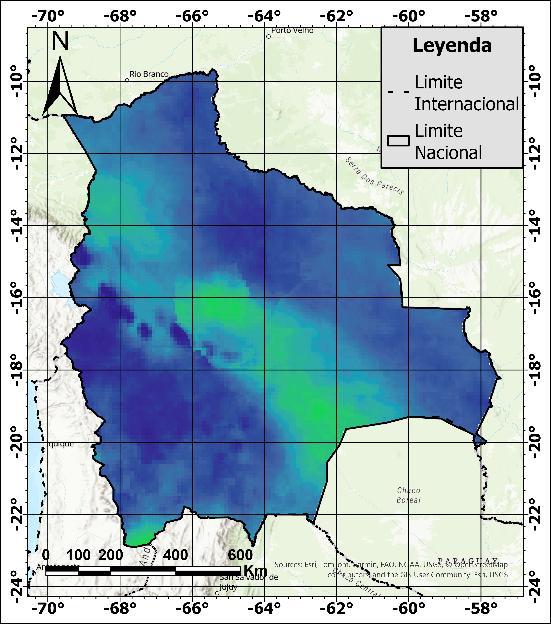
Bolivia presenta una superficie terrestre de aproximadamente 1,098,000 km², con elevaciones promedio que oscilan entre los 200 y 5,000 metros sobre el nivel del mar (m.s.n.m.), incluyendo algunos picos que superan este rango. En función de la elevación, el país se divide en tres regiones ecológicas: el altiplano y las montañas (oeste y suroeste del país), los valles y yungas (región media) y los llanos y laAmazonía (norte y este) (Embajada de Bolivia en Alemania, s. f.). Estas regiones se pueden apreciar en la Figura 3.
Figura 3. Mapa de elevación y ríos
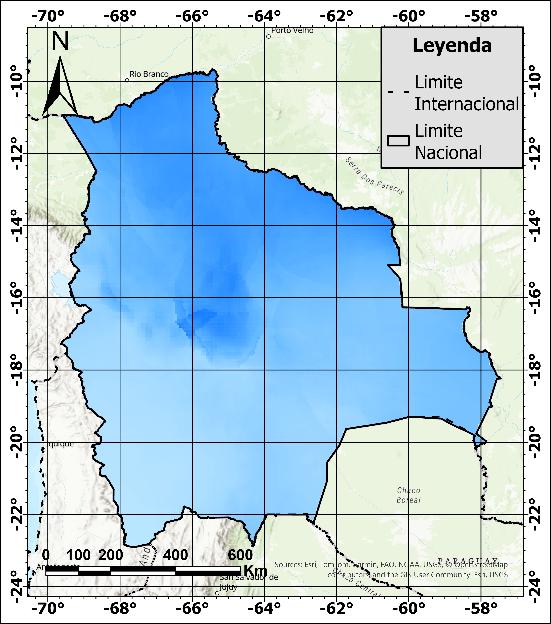
En cuanto al aspecto hidrográfico, Bolivia está formada por tres cuencas principales: el Altiplano, el Amazonas y la Plata (Figura 4). La cuenca del Altiplano, con una superficie aproximada de 145,100 km², presenta características de una cuenca endorreica y contiene una región ecológica montañosa a lo largo de su extensión. La cuenca del Amazonas cubre 724,000 km² y presenta tres regiones ecológicas: montañosa en el sureste, valles en la región media y llanos en el noreste. Esta cuenca desemboca en el Océano Atlántico. Por otro lado, la cuenca del Plata tiene una superficie de 229,500 km². Al igual que la cuenca del Amazonas, la cuenca del Plata desemboca en el Océano Atlántico y se compone de tres regiones ecológicas: montañas en la zona oeste, valles en la zona central y tierras bajas en la zona este (Villegas, 2016; Saavedra y Ureña, 2022)
Figura 4. Mapa de división de macrocuencas
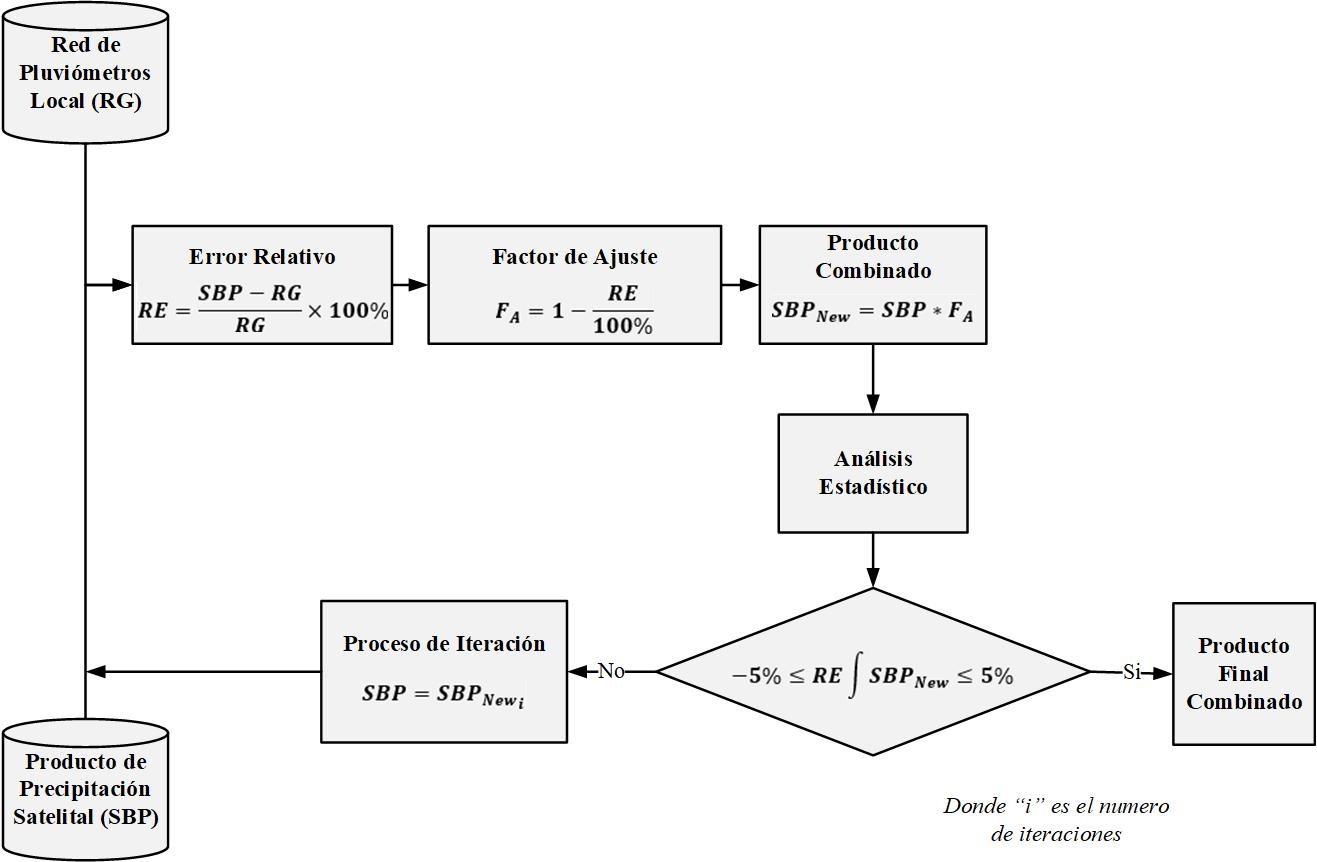
2.2. FLUJOGRAMADE TRABAJO
Con base en las diferentes metodologías de corrección de precipitación satelital presentadas, se optó por emplear el método iterativo en este estudio. Esta selección se justifica por la posibilidad de mejora que ofrece, gracias a su cualidad única de manejar subcuencas para generar factores de ajuste (Ureña et al., 2021)
La selección de este método se debe a su potencial para generar mejoras. Dicha mejora proviene de la cualidad única que posee esta metodología, que a su vez puede limitarla: el manejo de subcuencas para generar factores de ajuste. Las metodologías de corrección de sesgo basadas en Machine Learning y Cuantiles abordan la corrección de los valores de precipitación de manera directa, operando en función de la posición de los datos pluviométricos y sus equivalentes satelitales (Blanco et al., 2023; Iqbal et al., 2022) Además, si se utiliza una cuadrícula de precipitación basada en datos observados, es posible realizar la corrección para cada píxel del producto satelital que coincida con el dato observado
Ante ello, se busca que la metodología iterativa adquiera la capacidad de manejarse a nivel de píxel, generando un factor de ajuste para cada uno y determinando si dicha condición mejora los resultados observados en la metodología La mejora de este enfoque se basa en tres actividades clave, resumidas en la Figura 5.
En este proceso, la recopilación de datos de precipitación, tanto pluviométricos como satelitales, desempeñará un papel clave, ya que será la base para procedimientos como la interpolación de datos pluviométricos y la combinación de información. Para ello, la elección de una resolución temporal y espacial adecuada es fundamental para generar una base de datos uniforme
En los procesos de interpolación de precipitación, es necesario considerar el factor de elevación de las estaciones. Por ello, se realizará un análisis para determinar los valores de semivariogramas de elevación, que serán utilizados en kriging (Garcia Calabrese et al., 2022) Asimismo, el método IDW se considera una alternativa eficaz en entornos con distintos rangos de distancia entre puntos de interpolación (Aragón Hernández et al., 2019). Finalmente, se plantea el uso de REGNIE como otra opción, ya que integra la elevación y un modelo digital de elevación para generar mapas interpolados (Alzate Velásquez et al., 2017).
METODOLOGÍACOMBINATORIAITERATIVAENTREPRODUCTOSDEPRECIPITACIÓNPUNTUALYSATELITALENBOLIVIA,PERIODO1980-2016
Recopilación de Datos de Precipitación Combinación de Datos de Preciptación
Proceso de Interpolación
Inicio
Procesode Interpolación
Datosde Precipitación porOrigen
Validacion de Productos Combinados
Procesode Combinación Iterativo
Métodos
Considerandola Elevación
Datos Satelitales
Formateode Datos
Datos Pluviométricos
Procesode Generacionde Indicadores Estadisticos
Kriging
MétodosSin Considerar Elevación IDW
Mapasde Error Relativo
Mapasde Factorde Corrección
No
Indicadores Estadísticos Promedios
Semivariograma deElevación
Extensión TamañodePixel
Resolución Temporal
Selección Métodode Interpolación
Nuevo Producto Combinado ErrorRelativo entre±5%
Mapasde Indicadores Estadísticos Generación deResumen
Conclusión
Datos Satelitales Formateados
Datos Pluviométricos Interpolados
Datosde Precipitación Combinado Si
REGNIE
Figura 5. Flujograma de Trabajo
2.3.
ADQUISICIÓN DE DATOS
Para el proceso de adquisición de datos, se decidió utilizar las siguientes bases de datos:
2.3.1.Datos Pluviométricos
En el caso de la recopilación de datos de precipitación pluviométrica para Bolivia, la principal fuente de datos disponibles es el Servicio Nacional de Meteorología e Hidrología (SENAMHI). Este organismo cuenta con un listado de estaciones que realizan diversas funciones y recopilan diferentes variables. Sin embargo, estos datos requieren un trabajo adicional de selección, depuración y completado para poder generar una base de datos adecuada para desarrollar el trabajo. Ante la necesidad de contar con una gran cantidad de datos de precipitación, se decidió emplear una base de datos de precipitación utilizada para el Balance Hídrico Superficial de Bolivia, correspondiente al período 1980-2016.
Esta base de datos fue tratada por el Instituto de Medio Ambiente de Estocolmo (SEI, por sus siglas en inglés). Su objetivo era la generación de un nuevo producto de precipitación en formato grillado basado en las 295 estaciones rellenadas, destinado a desarrollar el proceso de modelación hidrológica, conocido como GMET (Wickel et al., 2019). Esta base de datos se utilizó, junto con el producto GMET, en el análisis de la metodología de combinación de productos de precipitación por iteración en Saavedra y Ureña (2022)
2.3.2.Productos CHIRPS
En el caso de la base de datos de CHIRPS, esta fue descargada desde la página oficial del CHG1 . En dicha página, se presentan varias versiones de sus productos de precipitación, las cuales corresponden a cambios en las regiones o en la resolución espacial. Para este estudio, se utilizó la base de datos global con una resolución espacial de 0.05° y en formato TIFF.
2.3.3.Productos GSMaP
Los productos de precipitación GSMaPpresentan una amplia gama de versiones, que varían según el tiempo de procesamiento de sus imágenes, la introducción de un mayor número de sensores, revisiones de algoritmos, entre otros aspectos.Además de estos elementos, se debe considerar el manejo de las versiones y la resolución temporal. Para el presente documento, se optó por las versiones horarias de los productos GSMaP_MVK, GSMaP_Gauge y GSMaP_Grev, en sus versiones 6 y 8. Esta selección de versiones se basa en dos factores:
1 Acceso a datos CHIRPS: https://data.chc.ucsb.edu/products/CHIRPS-2.0/
• La comparación con el producto utilizado en otros estudios
• El uso de la versión más reciente del producto.
Elprocesodedescargarequirióelusodeunnombredeusuarioyunacontraseñaparaacceder a sus servidores. Según Aryastana et al. (2021), el acceso a dichos servidores se realiza a través de un enlace compartido en su estudio2 .
2.3.4.Productos IMERG
En el caso de los productos IMERG, estos al ser un producto derivados y continuación del “Tropical Rainfall Measuring Mission” (TRMM), se encuentran a disposición en la base de datos de la NASA. Para el acceso y descarga de estos datos, es necesario poseer una cuenta en esta institución que es posible crear en minutos. Por otro lado, el proceso de descarga se realizó desde la página de “GIOVANNI”, un visor de datos de la NASA3. No obstante, fue necesario la implementación de un gestor de descargas para acelerar el proceso de compilación y descarga de los datos.
2.3.5.Productos PERSIANN
Para los productos PERSIANN, a diferencia de otros, solo se requiere un correo electrónico para acceder a su base de datos4 Esto se debe a que su página oficial permite el recorte y la selección del período de datos requeridos.
Debido a la diversidad de formatos, así como a las distintas resoluciones temporales y espaciales de todos estos productos, surge la necesidad de uniformizar estos valores a los requeridos parael análisis, lo quetambiéncontribuiráalareducción del espacio enmemoria:
• Resolución Espacial: 0.05° (aprox. 5 km)
• Resolución Temporal: Diaria
2.4.
PROCESOS DE INTERPOLACIÓN
Para el proceso de interpolación, se considerarán dos variables: la elevación y la precipitación. Esto se debe a que se desea utilizar la elevación como una condición para la interpolación de la precipitación, basándose en resultados positivos de otros estudios (Liu et al.,2020;Songet al.,2019) Enestecontexto,sedecidióanalizarinicialmentelosmétodos de interpolación IDW, kriging ordinario y kriging universal, disponibles en ArcGIS Pro, y
2 Acceso a datos GSMaP.v7: ftp://rainmap:Niskur+1404@hokusai.eorc.jaxa.jp/standard/v7/hourly/
3 Acceso de datos IMERG: https://giovanni.gsfc.nasa.gov/giovanni/
4 Acceso a datos PERSIANN: https://chrsdata.eng.uci.edu/
añadir el método REGNIE, desarrollado en R (Alzate Velásquez et al., 2017), mediante su paquete RegRAIN (Alzate, 2018)
Dentro del análisis de los métodos de interpolación de la precipitación con influencia de la altura, surgió la necesidad de determinar los valores de las variables y el tipo de semivariograma teórico a utilizar. Para ello, se debe analizar inicialmente de manera independiente la variable de la elevación, empleando definiciones y ecuaciones para el diseño de un semivariograma empírico que represente el comportamiento de esta variable en la zona de estudio. Una vez obtenido este semivariograma, se aplican las ecuaciones de los semivariogramas teóricos para determinar cuál de estos se asemeja al empírico
Paraesto, seempleóel modelodigitaldeelevación “Advanced Spaceborne Thermal Emision and Reflection Radiometer Global Digital Elevation Model” (ASTER GDEM) como la base de este componente. Dicho producto fue seleccionado debido a su accesibilidad desde la página de Infraestructura de Datos Espaciales del Estado Plurinacional de Bolivia (IDEEPB)5 y su portal GeoBolivia6 En esta, se describe al modelo ASTER GDEM como información topográfica de buena calidad, para un manejo en diversas áreas de estudio (Historico GeoBolivia, 2023).
A partir de las variables obtenidas, se generará ráster a través de los diferentes métodos de interpolación: REGNIE, IDW, kriging ordinario lineal, kriging ordinario gaussiano, kriging universal lineal con deriva lineal y kriging universal lineal con deriva cuadrática.
Para ello, se empleará las herramientas de ArcGIS Pro, con la configuración que incluye a la elevación para analizar su comportamiento. Se establecerá escenarios considerando diferentes valores de puntos para el proceso, con valores de 6, 12 y 18. Por otro lado, se configuraron dos escenarios, uno considerando los valores de semivariogramas y otro utilizando la configuración por defecto de la herramienta.
2.5. PROCESO DE COMBINACIÓN DE DATOS
La propuesta del presente documento es la eliminación del concepto del mapa de subcuencas, permitiendo obtener un nuevo diagrama de procesos como el mostrado en la Figura 6 En esta, el proceso de generación inicia obteniendo el error relativo del producto
5 Enlace a IDE-EPB: https://ideepb.geo.gob.bo/
6 Enlace GeoBolivia: https://geo.gob.bo/#/
de precipitación pluviométrico interpolado y un producto satelital de precipitación. Dicho proceso se realizará a espacialmente.
Una vez obtenido este valor, se calculará el factor de ajuste restando el error relativo a 1 y eliminando su porcentaje. Es importante establecer límites de ±95% como valores de control antes del cálculo del factor de ajuste.
Luego, este factor se multiplicará por el producto satelital para generar un nuevo mapa de precipitaciones, que se evaluará mediante indicadores estadísticos como coeficientes de correlación, determinación, eficiencia y error relativo. Este último es clave: si el promedio general del nuevo producto está entre ±5 %, se considerará definitivo. De lo contrario, se reemplazará la base de datos del producto satelital por la versión ajustada, repitiendo el proceso hasta cumplir esta condición.
Figura 6. Flujograma Propuesto de Generación de Producto Combinados
CAPITULO 4: RESULTADOS Y DISCUSIÓN
3.1. RESULTADOS
3.1.1.Interpolación
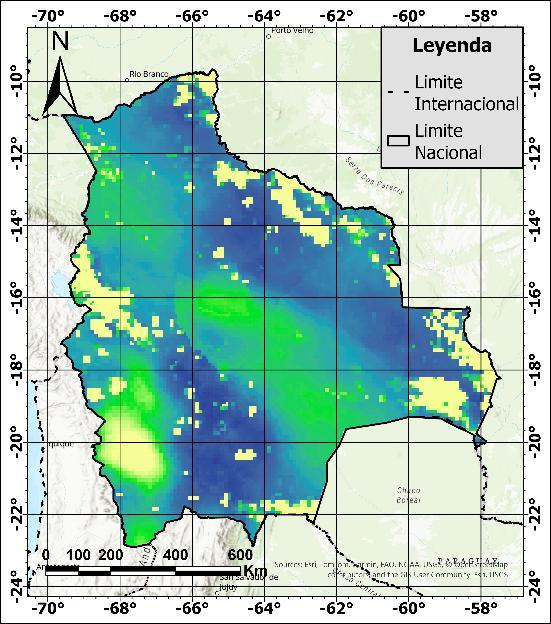
Dentro del componente de interpolación del presente documento, se puede observar en la Figura7queelsemivariogramaempíricodesarrolladoatravésdelasalturas delasestaciones seleccionadas, muestra un comportamiento inicial casi lineal para distancias menores. No obstante, este comportamiento comienza a oscilar a medida que la distancia aumenta. Por otro lado, los semivariogramas teóricos gaussiano y lineal son los que mejor simulan el comportamiento del semivariograma empírico
Figura 7. Semivariograma empírico y teóricos para la variable de elevación.
Con base en el comportamiento de los semivariogramas teóricos en relación con el empírico, se pudieron obtener las variables requeridas para generar una interpolación orientada a la variable. Para ello, se sintetizaron las variables en la Tabla 1. En el caso de la variable de tamaño de “Lag Size”, esta se obtuvo a través de la herramienta “Average Nearest Neighbor” deArcGIS Pro (ESRI, 2024a).
Tabla 1. Variables de Interpolación basada en datos de elevación para Bolivia
Apartir de los componentes del semivariograma empírico seleccionado, se generó las grillas interpoladas usando: REGNIE, IDW, kriging ordinario lineal, kriging ordinario gaussiano y kriging universal lineal con deriva lineal. Los resultados estadísticos de estos se encuentran en la Tabla 2. Se identificó que cinco combinaciones de interpolación presentan estadísticas similares al archivo DEM utilizado como referencia. Las interpolaciones son las siguientes: REGNIE, kriging ordinario lineal con SV-6 puntos, kriging ordinario gaussiano con SV-18 puntos, y kriging universal lineal con deriva lineal con SV-6 puntos.
Tabla 2. Estadísticas de rasters generados a partir de interpolación de datos de elevación
Métodos De Interpolaciones
En la Figura 8 y 9, se observan los mapas de interpolación obtenidos y comparados con el DEM de la zona de estudio (Panel a de cada figura). En el caso de los datos de kriging universal, ambos modelos presentan el mismo mapa
Figura 8. Mapas de Interpolación de elevación por diferentes métodos: (a) Modelo digital de elevación (DEM), (b) Modelo REGNIE y (c) Kriging ordinario lineal con SV-6puntos
9. Mapas de Interpolación de elevación por diferentes métodos: (a) Modelo digital de elevación (DEM), (b) Kriging ordinario gaussiana con SV-18 puntos y (c) Kriging universal con derivada lineal y cuadrática con SV-6puntos
Figura
En base de los resultados del análisis, la interpolación en elevación se procedió a generar mapas interpolados de precipitación para los años 1982, 1992, 1998, 1999 y 2016. Como se muestra en la Tabla 3, se observa que la interpolación de kriging ordinario lineal es la más adecuada en las tres cuencas, con la adición de la interpolación REGNIE en la cuenca del Amazonas al comparar sus valores con relación a datos puntuales. Sin embargo, las diferencias entre las metodologías de interpolación son mínimas y se encuentran en el orden de milésimas, siendo válido el manejo de cualquier de estos métodos desde el aspecto estadístico.
Tabla 3. Indicadores Estadísticos de los datos interpolados diarios con relación a los datos puntuales de pluviómetros por macrocuencas de Bolivia.
Cuenca
Método de Interpolación
Coef. Determinación (R2)
Coef. Correlación
Por otro lado, al analizar las características de los archivos ráster, se observa en la Tabla 4 que el comportamiento de REGNIE difiere considerablemente de los otros métodos de interpolación en las cuencas del Altiplano y La Plata. Aspectos como valores mínimos, promedio, mediana, suma de valores y percentiles presentan un alejamiento critico a los observados por otros métodos de interpolación. Esto puede deberse a la orografía de estos sistemas que, al presentar regiones con cambios abruptos en la altura, impiden que el método REGNIE puede ejecutarse de manera correcta, a pesar de poseer una mayor densidad de estaciones. Por otro lado, la interpolación mediante kriging universal presenta variaciones significativas en el valor máximo del ráster en las cuencas deAmazonas y La Plata.
Tabla 4. Estadísticas de promedio diario de interpolación de precipitación en Bolivia
Con los resultados previos, es posible discernir que los métodos de kriging ordinario gaussiano y lineal serían los más adecuados para la interpolación en el área de estudio. Para ello, se generó mapas de precipitación del periodo completo de estudio (Figura 10). En estos, se observan que el método Gaussiano presenta un mejor suavizado en la zona de alta precipitación. Por otro lado, el método lineal muestra un cambio de valor más rápido en una distancia corta dentro de la misma área de mayor precipitación, a pesar de que previamente demostró un mayor acercamiento estadístico a valores puntuales.
En consecuencia, se determinó que el método a emplear para el desarrollo del proceso de combinación será kriging ordinario gaussiano con SV–18 puntos, siendo un producto que no resultó estadísticamente, pero teniendo un mejor comportamiento desde el aspecto espacial del proceso.
Figura 10. Mapas de interpolación de precipitación promedio diario por diferentes métodos: (a) Modelo REGNIE, (b) Kriging ordinario linear con SV-6puntos, (c) Kriging ordinario gaussiana con SV-18 puntos, (d) Kriging universal con derivada lineal y cuadrática con SV-6 puntos
(a)
(b)
(c)
(d)
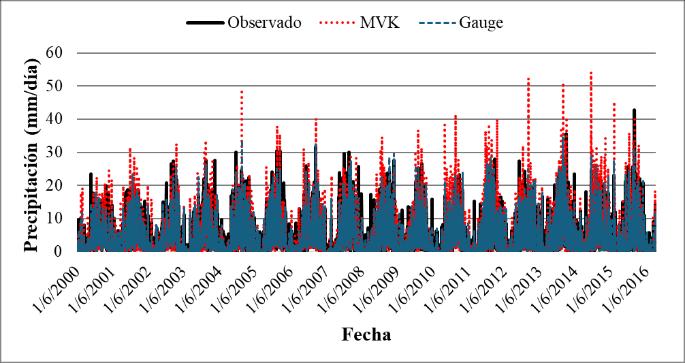
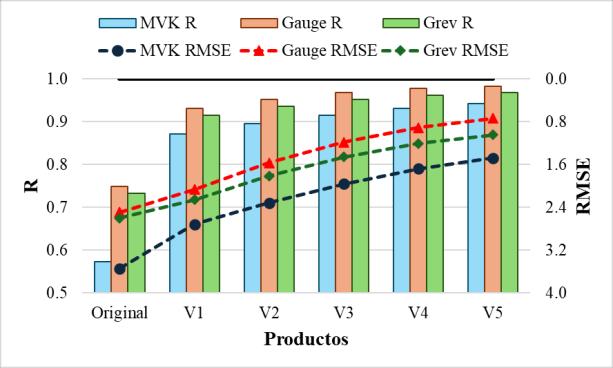
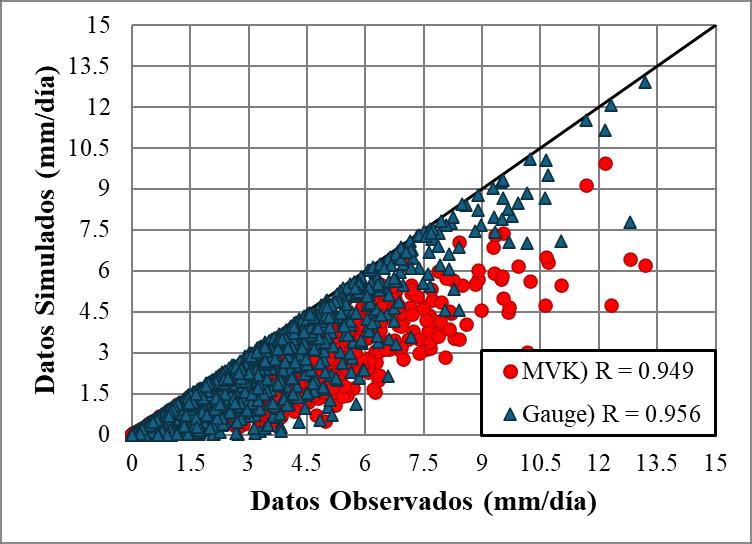
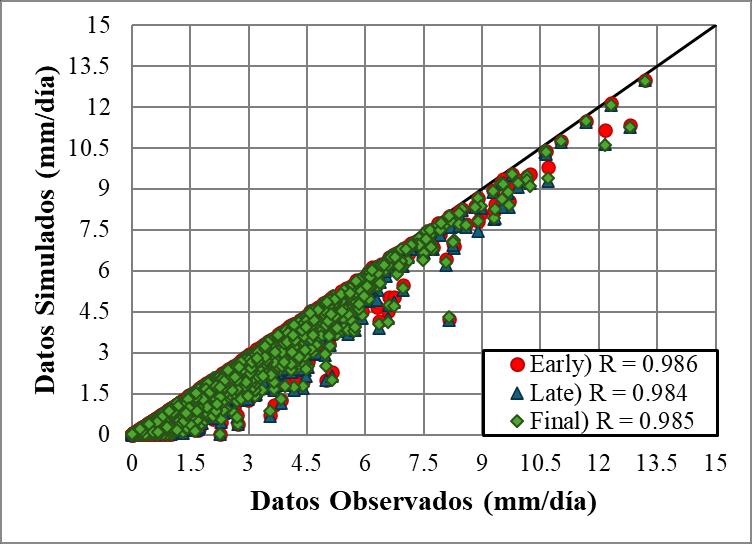
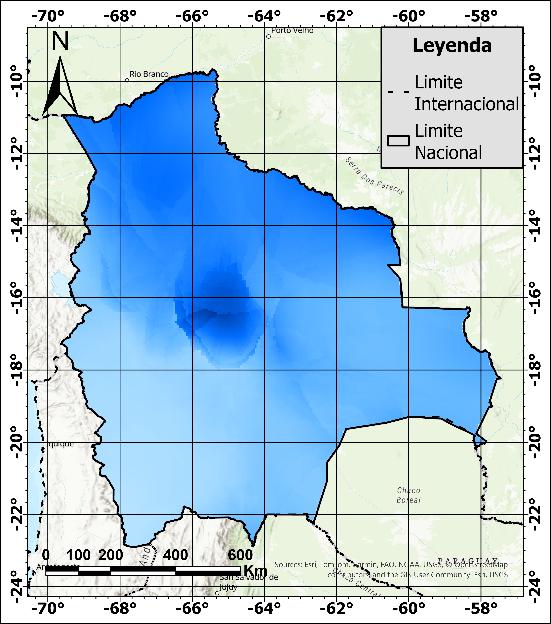
3.1.2.Análisis de Productos de Precipitacion Satelital Los productos de precipitacion satelital seleccionados se agrupan en cinco categorías según su procedencia o versión: CHIRPS (producto único), GSMaP.v6 (MVK, Gauge y Grev), GSMaP.v8 (MVK y Gauge), IMERG.v6 (Early, Late y Final) y PERSIANN CCS-CDR (producto único).
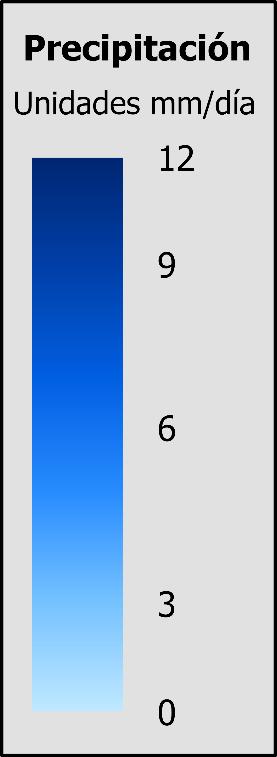
Enlas Figura11 y12, seobservan lasdiferenciasy similitudes deestos productos enrelación con la precipitación interpolada en Bolivia. En esta figura, los productos GSMaP.v6_Gauge (Fig. 11d), GSMaP.v6_Grev (Fig. 11e) y GSMaP.v8_Gauge (Fig. 12b) no registran precipitaciones mayores a 6 mm/día en la zona central del país. En contraste, los productos GSMaP.v8_MVK (Fig. 11f), IMERG.v6_Early (Fig. 12c) e IMERG.v6_Late (Fig. 12d) muestran valores de precipitación de hasta 12 mm/día en esa misma zona, en comparación con los 6 mm/día de los datos interpolados (Paneles a). Otro aspecto notable es el cuadriculado más evidente que presenta el producto GSMaP.v6_Grev en comparación con los otros productos satelitales.
Leyenda (d) (e) (f) Leyenda
Figura 11. Mapas de Precipitación promedio diaria del periodo marzo 2000 a agosto 2016 para productos satelitales: (a) Estaciones pluviométricas interpoladas, (b) CHIRPS, (c) GSMaP.v6_MVK, (d) GSMaP.v6_Gauge, (e) GSMaP.v6_Grev y (f) GSMaP.v8_MVK
Figura 12. Mapas de Precipitación promedio diaria del periodo marzo 2000 a agosto 2016 para productos satelitales: (a) Estaciones Pluviométricas Interpoladas, (b) GSMaP.v8_Gauge, (c) IMERG.v6_Early, (d) IMERG.v6_Late, (e) IMERG.v6_Final y (f) PERSIANN CCS-CDR
Leyenda
Leyenda
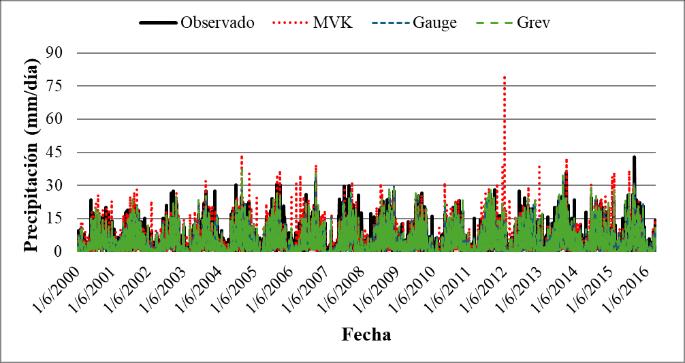
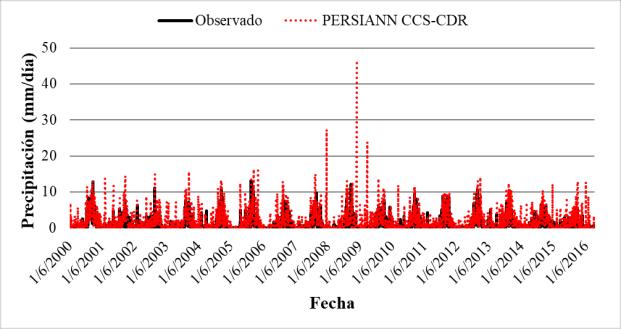
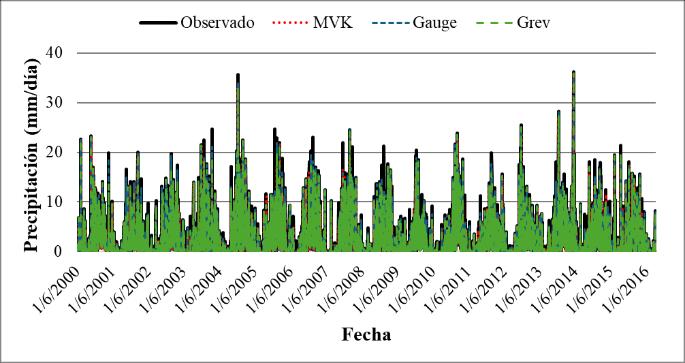
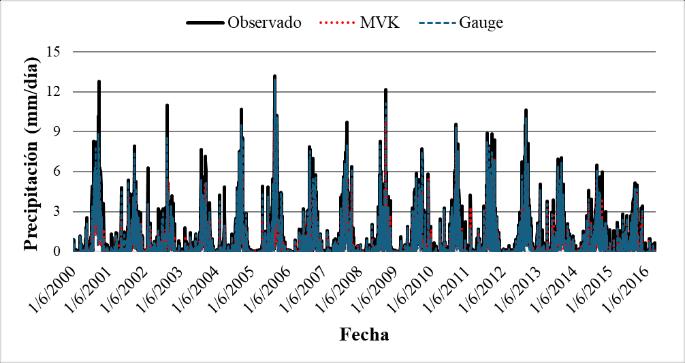
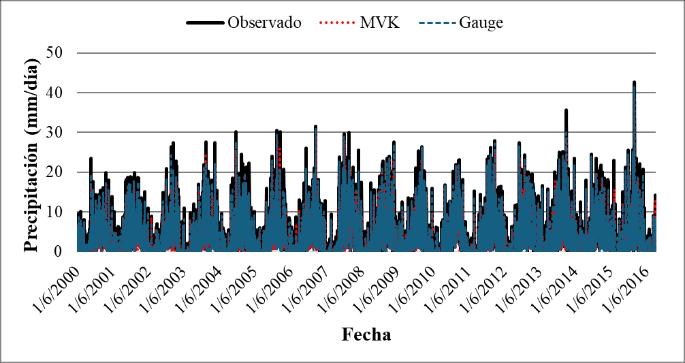
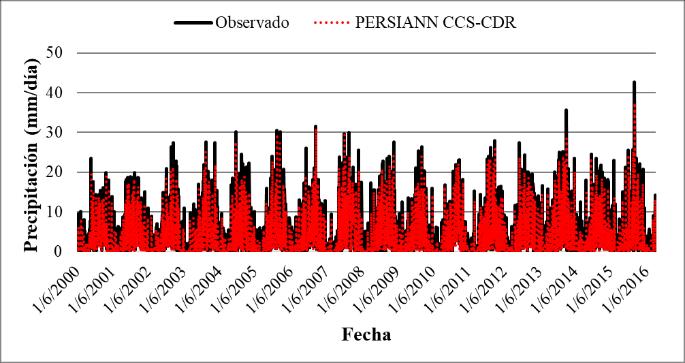
Debido al uso de promedios, no se logra apreciar la verdadera naturaleza de los diferentes productos de precipitación satelital en comparación con los datos interpolados. Por ello, se generaron series de tiempo de los distintos productos, utilizando el mapa de macrocuencas de Bolivia como referencia. En la Figura 13 se observan las series de tiempo de los datos promedio para la macrocuenca del altiplano, comparadas con los datos de CHIRPS. En esta figura, se nota que el producto satelital presenta sobreestimaciones a partir de 2010, especialmente durante la temporada de lluvias.
Figura 13. Series de tiempo para el producto CHIRPS en el periodo Marzo 2000 a Agosto 2016 para las macrocuencas del altiplano.
Debido a la gran cantidad de gráficos generados para cada producto y macrocuenca, estos se agruparon en el Anexo 6.1 Allí, los gráficos se presentan en una tabla de tres columnas: la columna izquierda corresponde a la macrocuenca del Altiplano, la columna central a la macrocuenca Amazonas, y la derecha a la macrocuenca de La Plata. En la mayoría de los casos, los productos satelitales muestran sobreestimaciones de precipitación en cada macrocuenca. Los casos más críticos corresponden a GSMaP_MVK, tanto en su versión 6 como 8, donde los valores superan los observados, alcanzando alrededor de 50 mm/día en la cuenca delAltiplano y hasta 90 mm/día en las cuencas del Amazonas y La Plata.
Sin embargo, el análisis de las series de tiempo permite únicamente comparar el comportamiento estándar de las bases de datos, destacando los periodos y variaciones de los datos satelitales en relación con los observados. Para analizar con mayor detalle la relación entre los productos satelitales y los datos observados, el uso de diagramas de dispersión es una alternativa adecuada
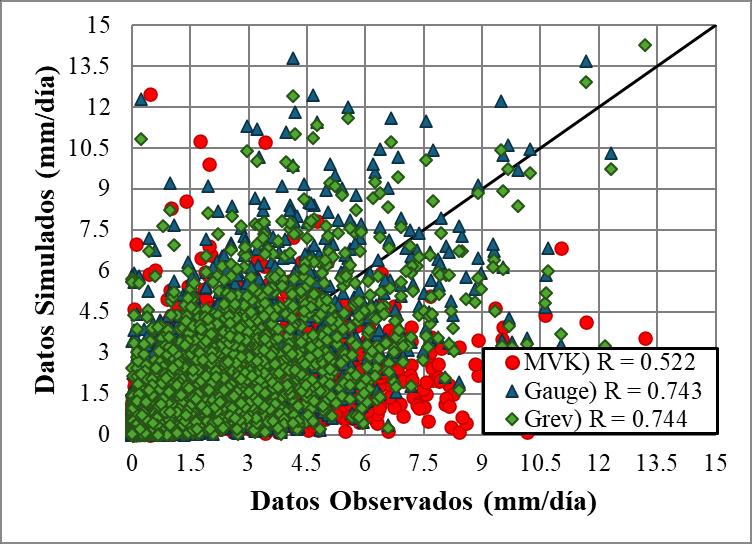
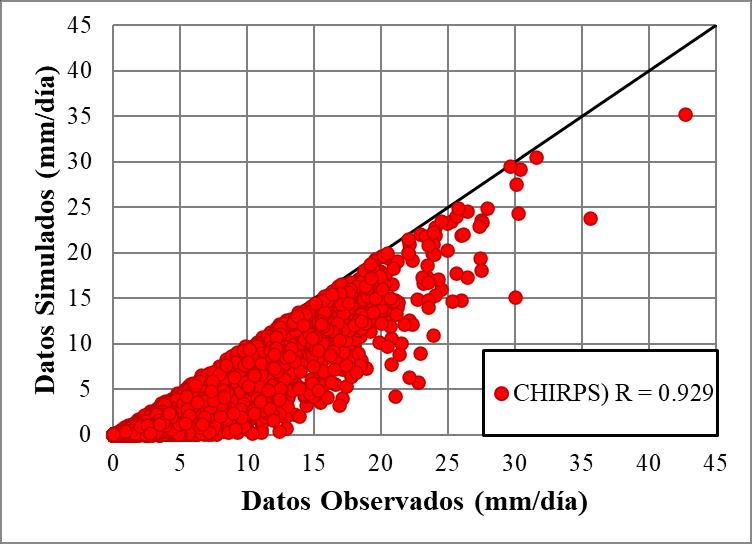
En la Figura 14 se muestra la relación entre los datos observados promedios y los datos de CHIRPS para la macrocuenca del Altiplano. En este gráfico, se observa que la variación es menor para valores inferiores a 6 mm/día, incrementándose a medida que la precipitación aumenta. Los datos de CHIRPS presentan una correlación de 0.806 con respecto a los datos observados, lo cual indica una similitud aceptable entre ambas bases de datos
Figura 14 Diagrama de Dispersión para el producto CHIRPS en el periodo marzo 2000 a agosto 2016 para las macrocuencas del altiplano.
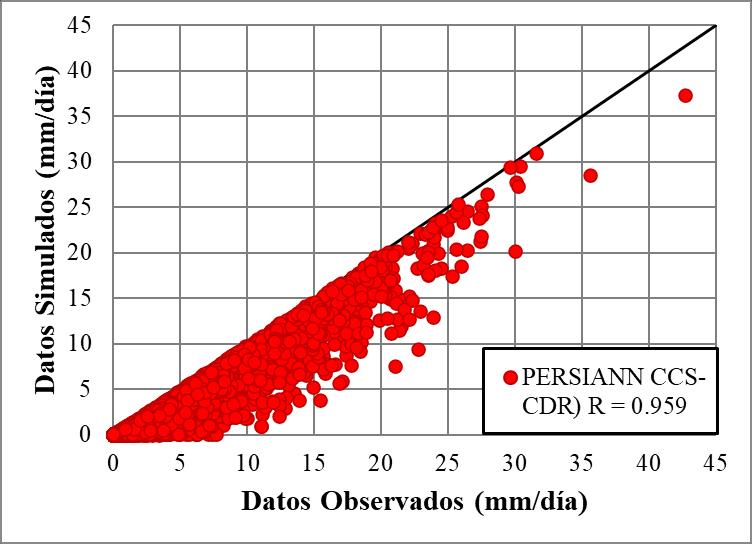
Al igual que en el caso anterior, los gráficos correspondientes a las demás macrocuencas y productos se encuentran en el Anexo 0. En estos, se confirma la tendencia a sobreestimaciones significativas de los productos GSMaP_MVK en sus versiones 6 y 8 para las tres macrocuencas. Por otro lado, los productos IMERG.v6 muestran una mayor tendencia a la sobrestimación, en comparación con los pocos casos de subestimación observados en las tres macrocuencas. En el caso del producto PERSIANN-CCS-CDR, la tendencia a la sobrestimación de valores se manifiesta principalmente en la macrocuenca del Altiplano
Dada la variabilidad de los diferentes productos satelitales, se analizó la relación entre estos productos y los datos observados mediante diversos indicadores estadísticos. En la Tabla 5 seobservaquelosproductospresentancorrelacionesentre0.5y0.85,destacandoelproducto IMERG.v6_Final con la mejor correlación de 0.8480. Sin embargo, el indicador de sesgo relativo muestra que GSMaP.v6_Gauge tiene una ligera sobrestimación de 0.3 en comparaciónconlosdatosobservados.Encontraste,losproductosMVKdeambasversiones de GSMaP presentan eficiencias menores a 0.2.
Además, la tabla muestra que el producto PERSIANN CCS-CDR presenta los mayores sesgos y errores, lo cual indica que sus estimaciones son notablemente altas en comparación con los datos observados. Su eficiencia negativa adicionalmente sugiere que la base de datos de este producto no guarda relación con los datos de precipitación obtenidos a partir de pluviómetros
Tabla 5. Indicadores estadísticos de productos satelitales para la macrocuenca del Altiplano
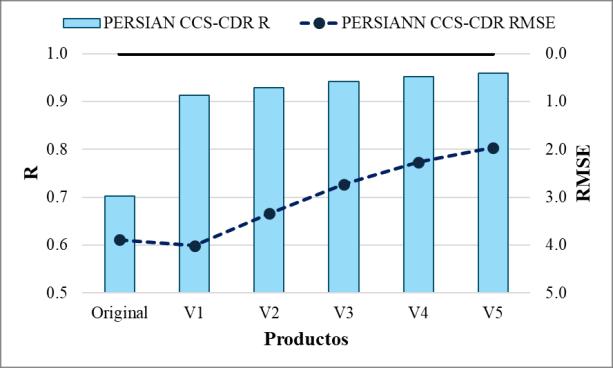
Para la macrocuenca del Amazonas (Tabla 6), el producto GSMaP.v6_Gauge es el que presenta la mejor correlación, los menores errores y la mayor eficiencia del conjunto. Aunque todos los productos muestran correlaciones superiores a 0.65, lo que indica un nivel aceptable, las eficiencias de ambas versiones de GSMaP_MVK y de toda la línea de IMERG.v6 son muy bajas, con valores entre 0.15 y 0.32. Esto sugiere que es muy poco probable que sus bases de datos puedan reemplazar los datos interpolados. Finalmente, el producto PERSIANN CCS-CDR muestra mejores indicadores al compararse con los datos de la macrocuenca del Amazonas, en relación con los datos delAltiplano.
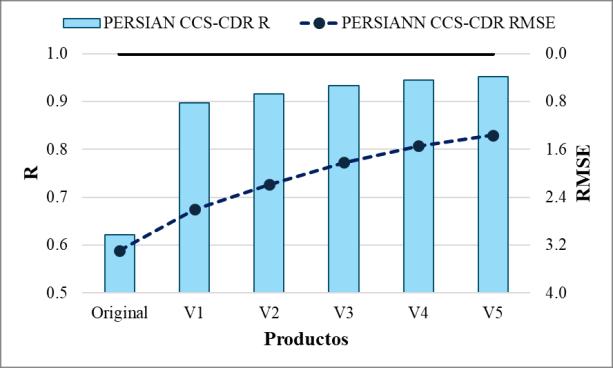
En el caso de la macrocuenca de La Plata (Tabla 7), los indicadores muestran que el producto GSMaP.v6_Gauge presenta la mejor correlación y eficiencia, con los menores errores de
todos los productos, al igual que en la macrocuenca anterior. Por otro lado, los productos
GSMaP_MVK presentan una baja correlación y eficiencia, lo que indica una escasa posibilidad de ser empleados como sustitutos de los productos observados, siendo la versión 6 la más crítica.
Tabla 6 Indicadores estadísticos de productos satelitales para la macrocuenca del Amazonas
Al igual que en la macrocuenca anterior, los indicadores con valores críticos están dispersos en varios productos. Por ejemplo, IMERG.v6 muestra una mejora en sus indicadores al acercarse a la versión Final de sus productos, lo que resulta en un rendimiento superior al procesar los datos.
Con base en estos resultados, se puede observar la relación entre los promedios y los datos observados. Sin embargo, la importancia de especializar este tipo de información permitiría comprender mejor la realidad de los datos satelitales. Dada la variedad de opciones en el manejodelainformación,seoptóporseleccionarlaeficienciacomoindicadoraespacializar, ya que este indicador permitirá determinar las áreas con mayores diferencias entre ambas bases de datos.
Tabla 7. Indicadores estadísticos de productos satelitales para la macrocuenca de La Plata
En la Figura 15 y 16, se pueden observar los diferentes mapas de los productos satelitales en relación con los datos observados interpolados. En este tipo de mapas, la tendencia de los colores debe inclinarse hacia los tonos azules, lo que indica un alto grado de similitud y la posibilidad de sustituir los datos satelitales por los datos observados. En el caso de los tonos amarillos, estos indican una eficiencia cercana o menor a 0, lo que sugiere que el dato satelital no posee una semejanza o completamente diferentes a los datos observados Respecto a los productos satelitales seleccionados, todos presentan regiones en tonos amarillos, en mayor o menor medida, seguidas por tonos verdes en las regiones norte y sureste de los mapas. Los productos CHIRPS (Fig. 15b), GSMaP.v6_Gauge (Fig. 15d), GSMaP.v6_Grev (Fig. 15e) y GSMaP.v8_Gauge (Fig. 16a) destacan en cuanto a eficiencia, mostrando zonas con extensión de verde y azul; lo que indica una posible sustitución en las zonas de estudio en las macrocuencas del Amazonas y La Plata, principalmente. GSMaP.v8_Guage presenta el mejor resultado inicial.
Leyenda
Leyenda
Figura 15. Mapas de eficiencia diaria con relación a la precipitacion pluviométrica interpolada (a) del periodo marzo 2000 a agosto 2016 para productos satelitales: (b) CHIRPS, (c) GSMaP.v6_MVK, (d) GSMaP.v6_Gauge, (e) GSMaP.v6_Grev y (f) GSMaP.v8_MVK
Leyenda (d) (e) (f) Leyenda
Figura 16. Mapas de eficiencia diaria con relación a la precipitacion pluviométrica interpolada (a) del periodo marzo 2000 a agosto 2016 para productos satelitales: (b) GSMaP.v8_Gauge, (c) IMERG.v6_Early, (d) IMERG.v6_Late, (e) IMERG.v6_Final y (f) PERSIANN CCS-CDR
3.1.3.Combinación de Datos
Basado en los datos satelitales analizados previamente, se implementó una metodología de combinación de datos a través de métodos iterativos, utilizando datos observados interpolados y datos satelitales como fuente de resultados. A partir de estudios previos, se generaron nuevos productos mediante cinco interpolaciones para cada producto satelital.
Cada uno de estos productos mostró mejoras constantes, aunque en mayor o menor medida, dependiendo del producto específico
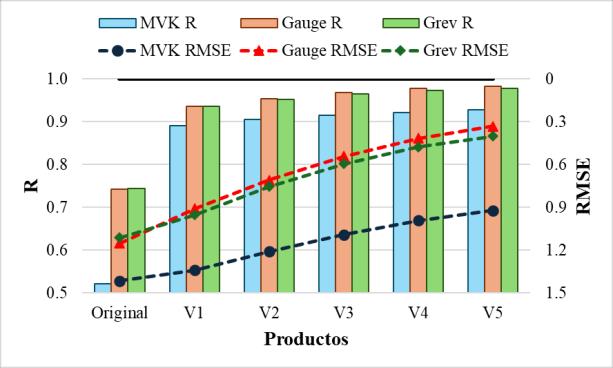
En la Figura 17, se puede observar un ejemplo de la mejora para el producto CHIRPS en la macrocuenca del Altiplano. En este caso, la correlación inicial, que rondaba 0.8, mejora drásticamente al generar la primera versión del producto combinado, superando la correlación de 0.9, lo cual representa un valor óptimo al acercarse al ideal de 1. A medida que se generaban las demás versiones a través de la iteración, el producto continuó mejorando ligeramente, manteniéndose alrededor de 0.95 a partir de la tercera versión del producto hasta alcanzar la quinta versión del producto combinado
Un caso similar se observa con la RMSE, que mantiene su valor en 0.95 desde la versión original al iterar por primera vez, y luego va reduciendo su valor hasta alcanzar aproximadamente 0.65 en la cuarta versión, manteniéndose en ese nivel en las iteraciones posteriores. Esto indica que la metodología de combinación no solo mejora la correlación, sino que también reduce el error en las estimaciones, lo que sugiere que la integración de datos observados y satelitales resulta efectiva para optimizar los productos de precipitación
Figura 17. Indicador de coeficiente de correlación y error cuadrático medio para cada producto generado a partir del producto CHIRPS en la macrocuenca del Altiplano
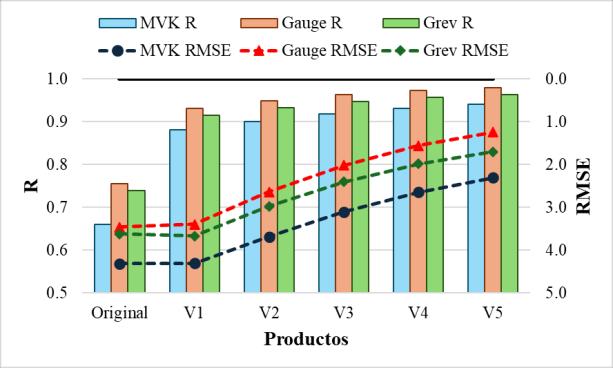
En el caso de las demás macrocuencas y productos generados, estos se encuentran en el Anexo 6.3 Los resultados mantienen la tendencia de mejora observada en el caso de CHIRPSparalamacrocuencadelAltiplano.Elproductomejoradrásticamentesucoeficiente de correlación, superando el valor de 0.9, aunque el porcentaje de mejora tiende a reducirse a medida que se generan nuevas versiones del producto. Por su parte, la raíz del error cuadrático medio puede aumentar ligeramente en la primera iteración del producto, pero se reduce drásticamente en versiones posteriores
Sinembargo,apesardequevariosindicadoresmuestranunamejoraamedidaquesegeneran nuevas versiones, el sesgo relativo es el único indicador que “empeora” su valor en comparación con el valor inicial. Este indicador presenta una característica particular: los nuevos productos generados tienden a subestimar los datos pluviométricos, aunque esta subestimación mejora ligeramente al acercarse a la quinta iteración.
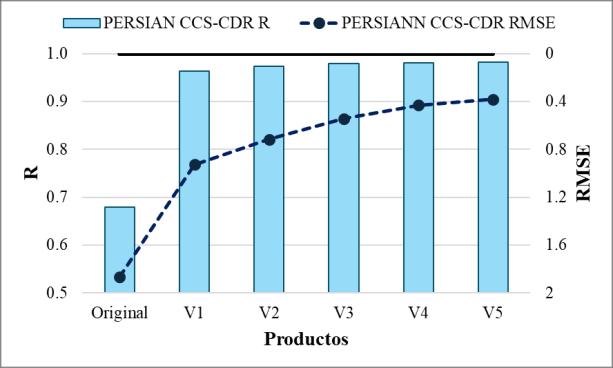
En la Tabla 8 se puede observar la evolución del sesgo en la macrocuenca del Guadalquivir, que muestra en su totalidad subestimaciones que superan el 50% al iniciar el proceso de combinación (primera versión), las cuales eventualmente se van reduciendo al generar nuevos productos. De la lista de productos, GSMaP.v6 Gauge, Grev, GSMaP.v8, IMERG.v6 y PERSIANN CCS-CDR son los que presentan un valor menor al 25% en la quinta versión del producto. Sin embargo, solo el producto PERSIANN CCS-CDR muestra una mejora significativa respecto a su versión original, pasando de una sobrestimación del 73% a una subestimación del 22%.
Tabla 8. Variación del sesgo en la generación de productos para la macrocuenca del Altiplano
En el caso de la macrocuenca delAmazonas, se observa un comportamiento similar al de la macrocuenca del Altiplano. Sin embargo, de acuerdo con la Tabla 9, los valores de subestimación inicial alcanzan el 70% y se reducen al 30% en la quinta iteración. En esta iteración, los productos GSMaP.v6 Gauge, GREV, GSMaP.v8 Gauge, IMERG.v6 y PERSIANN-CCS-CDR presentan los mejores resultados, siendo GSMaP.v6 Gauge el único que muestra una mejora real en comparación con el producto original
Tabla 9. Variación del sesgo en la generación de productos para la macrocuenca del Amazonas
En el caso de la macrocuenca de La Plata (Tabla 10), el sesgo relativo presenta un comportamiento similar al de los casos anteriores. Los productos originales muestran sesgos con valores que oscilan entre -14% y 17%; sin embargo, este aumenta drásticamente, alcanzando valores entre -67% y -47% en la primera versión del producto. A lo largo del proceso de generación de los productos, el sesgo se va reduciendo, llegando a valores entre -12% y -44% en los diferentes productos de precipitación. En este contexto, los mejores productos generados fueron GSMaP.v6 Gauge y GREV, ambos con valores menores a -20%.
Sin embargo, para esta cuenca, no existe un producto generado que haya mejorado en comparación con su versión inicial.
Tabla 10. Variación del sesgo en la generación de productos para la macrocuenca de La Plata
3.1.4.Análisis de Productos Combinados
Tras el proceso decombinación dedatos através decincoiteracionesdel producto, seobtuvo una nueva base de datos para cada uno de los productos satelitales analizados. En las Figuras 18 y 19, se puede apreciar el promedio de precipitación de los nuevos productos. En esta figura, todos los nuevos productos (paneles b hasta e de ambas figuras) muestran características espaciales similares a los datos interpolados (panel a). Sin embargo, el valor de precipitación en la región central del país es subestimado por todos los productos. Otro aspecto que destacar es que GSMaP.v6_MVK (Figura 18d) presenta regiones con valores de precipitación de cero en la zona norte del país, una región que se caracteriza por tener precipitaciones constantes.
Figura 18. Mapas de Precipitación promedio diaria del periodo Marzo 2000 a Agosto 2016 para productos generados a partir de: (a) Estaciones Pluviométricas Interpoladas, (b) CHIRPS, (c) GSMaP.v6_MVK, (d) GSMaP.v6_Gauge, (e) GSMaP.v6_Grev y (f) GSMaP.v8_MVK
Leyenda
Leyenda
Leyenda
Leyenda
Figura 19. Mapas de Precipitación promedio diaria del periodo Marzo 2000 a Agosto 2016 para productos generados a partir de: (a) Estaciones Pluviométricas Interpoladas, (b) GSMaP.v8_Gauge, (c) IMERG.v6_Early, (d) IMERG.v6_Late, (e) IMERG.v6_Final y (f) PERSIANN CCS-CDR
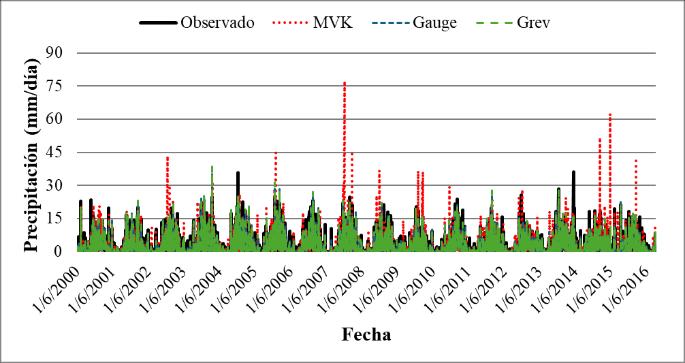
Para analizar los resultados desde otra perspectiva, en la Figura 20 se puede observar la serie de tiempo de los datos observados y del nuevo producto basado en CHIRPS para la macrocuenca del Altiplano. En esta figura, se evidencia que el nuevo producto se aproxima a los datos observados de los datos interpolados. Sin embargo, en varios de los picos registrados, el nuevo producto generado presenta subestimaciones que oscilan entre 0.5 y 3 mm/día. Por otro lado, las precipitaciones que registran valores menores a 3 mm/día muestran un mayor grado de subestimación en comparación con los picos de la serie de tiempo
Figura 20. Series de tiempo para el producto combinado basado en CHIRPS en el periodo marzo 2000 a agosto 2016 para las macrocuencas del altiplano.
Al igual que en el caso anterior, las gráficas de las otras macrocuencas y productos se encuentran en el Anexo 0. En estas gráficas, se puede observar que la mayoría de los nuevos productos generados presentan un comportamiento similar al de los productos anteriores. Entre las características notables se encuentran la subestimación, con diferentes variaciones con relación a los picos, y una subestimación general en precipitaciones bajas. Debido a la semejanza de los valores, resulta complicado determinar alguna diferencia o comportamiento drástico en comparación con los datos observados.
Por lo tanto, el uso de diagramas de dispersión permite analizar la relación basada en la tendencia. En la Figura 21, se puede observar la dispersión de los valores del nuevo producto basado en CHIRPS para la macrocuenca del Altiplano. En esta figura, se aprecia que el producto presenta tendencias a la subestimación, donde los valores más bajos muestran un mayor alejamiento de los datos observados, y esta diferencia se va reduciendo a medida que aumenta el valor de precipitación, con algunas excepciones.
Figura 21. Diagrama de Dispersión para el producto combinado basado en CHIRPS en el periodo marzo 2000 a agosto 2016 para las macrocuencas del altiplano.
Para el caso de los demás productos y macrocuencas, estos se encuentran en el Anexo 0. En elcasodelproductoCHIRPS,seobservaquelamacrocuencadeLaPlatapresentaunamayor subestimación en comparación con las otras zonas de estudio, manteniendo la misma característica que se mostró en la macrocuenca delAltiplano. Por otro lado, en el caso de los productos de GSMaP, se puede notar que los productos MVK presentan una mayor subestimación con relación a los datos observados y en comparación con sus otras versiones (Gauge y Grev).Además, el producto MVK muestra una mayor subestimación a medida que aumenta el valor de la precipitación
En cuanto a los productos de IMERG, estos presentan leves variaciones entre ellos, que dependen de la macrocuenca analizada; mostrando ligeras diferencias en sus coeficientes de correlación de ±0.003. Para el producto PERSIANN CCS-CDR, la subestimación es mayor en la macrocuenca de La Plata
Al analizar los diferentes indicadores estadísticos, se observa una mejora drástica en varios de ellos, excepto en el sesgo relativo, como se explicó previamente. Por ejemplo, en laTabla 11, que corresponde a la macrocuenca del Altiplano, se puede ver que la correlación de los productos supera el valor de 0.9 en todos los casos, siendo el producto generado a partir de GSMaP.v6_Gauge el mejor del conjunto. Además, este producto presenta el menor sesgo, menores errores y mejor eficiencia entre los nuevos productos. Por otro lado, los productos generados a partir de GSMaP_MVK (ambas versiones) presentan los valores más bajos en sus indicadores dentro del conjunto
Tabla 11. Indicadores estadísticos de productos combinados para la macrocuenca del Altiplano
En el caso de la macrocuenca del Amazonas, las correlaciones tienen valores superiores a 0.9, como se observa en la Tabla 12. El producto generado a partir de CHIRPS resulta ser el que presenta los indicadores más bajos del conjunto, mostrando una correlación de 0.9285 y una eficiencia de 0.7174. Por otro lado, el producto basado en GSMaP.v6_Gauge destaca por tener los mejores indicadores del grupo, siendo el único en alcanzar correlaciones superiores a 0.98 y eficiencias mayores a 0.93
Tabla 12. Indicadores estadísticos de productos combinados para la macrocuenca del Amazonas
EnelcasodelamacrocuencadeLaPlata,el productogeneradoapartirdeGSMaP.v6_Gauge presenta los mejores resultados en términos de sesgo, errores y eficiencia del grupo, como se observa en laTabla 13. Por otro lado, el producto CHIRPS muestra indicadores dentro del conjunto de nuevos productos generados, alcanzando valores de 0.91 en correlación y 0.72 eneficiencia.LosproductosGSMaP_GaugeyGSMaP.v6_Grevsonlosúnicosquepresentan eficiencias superiores a 0.9. El resto de los productos, a excepción de CHIRPS, presentan eficiencias entre 0.8 y 0.9.
Tabla 13. Indicadores estadísticos de productos combinados para la macrocuenca de La Plata
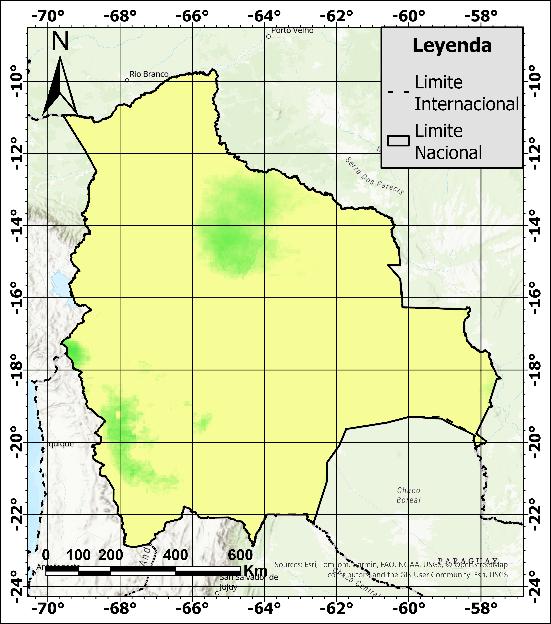
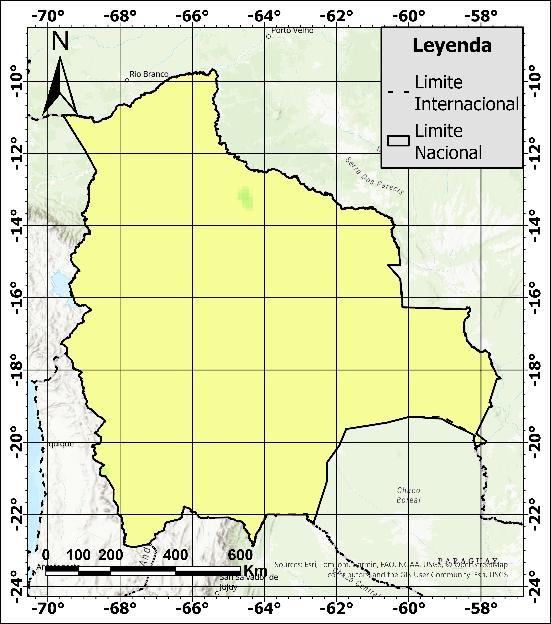
Con base en las tablas anteriores, la presentación espacial de la eficiencia permitirá analizar las regiones con mayor o menor nivel de corrección o ajuste con respecto a los datos observados. En las Figura 22 y 23, se presentan los mapas de eficiencia de Nash & Sutcliffe para cada uno de los productos generados. El primer mapa que resalta es el del producto basado en GSMaP.v6_MVK (Figura 22c), donde se observan varios segmentos en tonos amarillos que indican una eficiencia nula (igual a 0). Otro de los productos que presenta una baja eficiencia es GSMaP.v8_MVK (Figura 22f), que se ubica en la región suroeste del país.
El producto basado en CHIRPS (Figura 22b) muestra eficiencias entre 0.4 y 0.6 de manera general a lo largo del país, formando una franja diagonal que recorre desde la zona noroeste hasta la región sureste. Este mismo fenómeno se repite en mayor o menor medida en todos los mapas generados, siendo la zona con mayor precipitación observada la que presenta menor eficiencia en todos los casos.
Por otro lado, algunos productos muestran resultados óptimos, como GSMaP.v6_Gauge (Figura 22d), GSMaP.v6_Grev (Figura 22e) y GSMaP.v8_Gauge (Figura 23b), que presentan altas eficiencias en las regiones norte y sur del país (ignorando la diagonal descrita), con valores entre 0.75 y 1, siendo el primero mencionado el mejor de este grupo. Adicionalmente, los productos IMERG.v6 (Figura 23c, 23d y 23e) y PERSIANN CCS-CDR (Figura 23f) presentan resultados aceptables, con eficiencias entre 0.7 y 0.85.
Leyenda
Leyenda
Figura 22. Mapas de eficiencia diaria con relación a la precipitacion pluviométrica interpolada (a) del periodo marzo 2000 a agosto 2016 para productos generados a partir de: (b) CHIRPS, (c) GSMaP.v6_MVK, (d) GSMaP.v6_Gauge, (e) GSMaP.v6_Grev y (f) GSMaP.v8_MVK,
Leyenda
Figura 23. Mapas de eficiencia diaria con relación a la precipitacion pluviométrica interpolada (a) del periodo marzo 2000 a agosto 2016 para productos generados a partir de: (b)
GSMaP.v8_Gauge, (c) IMERG.v6_Early, (d) IMERG.v6_Late, (e) IMERG.v6_Final y (f) PERSIANN CCS-CDR
Leyenda
3.2. DISCUSIÓN
3.2.1.Interpolación
Para el desarrollo del presente estudio, se consideró unos pocos de los métodos de interpolación tradicionales como pueden ser IDW y kriging; adicionalmente se integró el método REGNIE como una innovación para su consideración en territorio boliviano. Dentro de las consideraciones de kriging, se analizó un semivariograma que permitiese la integración de la altura al proceso de interpolación de precipitaciones, teniendo como resultados que modelos teóricos como el lineal y el gaussiano presentan un mayor acercamiento a los datos observados.
Todo este proceso inicial se desarrolló con el fin de mejorar los resultados presentados por Ureña et al. (2021), donde solo se describe la implementación de un modelo kriging para la representación de los datos de precipitaciónAdicionalmente, la incorporación de la altura en los procesos de interpolación representa un importante avance en la mejora de la calidad de los datos. Al comparar interpolaciones que consideraron la integración del semivariograma de altura con aquellas que no se obtuvieron mejores resultados, tanto numéricos como espaciales, en aquellos que lo incorporaban, confirmando así los resultados presentados por Song et al. (2019). Por su parte, REGNIE mostro resultados óptimos en su comparación con el DEM.
Tras el proceso de validación de los métodos kriging usando semivariogramas lineales y gaussianos para precipitacion, se observó que los productos generados a través de kriging ordinario lineal presentaron un mejor resultado desde la perspectiva numérica. Sin embargo, especialmente el producto presenta regiones con cambios abruptos de valor siendo susceptibles a la orografía del país. Por su parte, kriging ordinario gaussiano presento un mejor desenvolvimiento espacialmente, teniendo cambios con una menor intensidad de la presentada por los otros métodos.
Por último, el modelo REGNIE presentó mapas muy alejados a los presentados por método kriging, presentando datos de precipitacion mínima de 6 mm/día. Esto se debe a la poca presencia de estaciones pluviométricas para este estudio, siendo que en el estudio presentado por Alzate Velásquez et al. (2017) se implementó 1,440 estaciones para una extensión de 481,312 km2 y para el presente estudio se usó 295 estaciones en 1,098,000 km2; marcando una dependencia de la metodología a la presencia de estaciones, haciéndole inviable en un estudio macro dentro del territorio boliviano.
3.2.2.Análisis de Productos de Precipitacion Satelital
Para el análisis de productos de precipitacion satelital, se seleccionó diferentes productos de 4 familias: GSMaP, IMERG, CHIRPS y PERSIANN, siendo un total de 10 productos usados; en relación a los 2 usados por Saavedra y Ureña (2022). Al analizar ambos estudios relacionados a sus productos en común (GSMaP.v6_Gauge y CHIRPS), ambos estudios presentan los mismos resultados relacionados a su comportamiento con la base de datos.
La cantidad de familias de productos empleados en este estudio representa una cantidad similar a otros estudios dentro de la zona. En el caso de Blacutt et al. (2015), el estudio comprendido 3 familias de productos y un método de combinación multi-producto para analizar el comportamiento de los mismos en condiciones extremas en territorio boliviano, siendo MERRA, TRMM y CFSR los productos empleados.
3.2.3.Combinación de Datos
Para el presente estudio se seleccionó el método de combinación por iteraciones ante los métodos por cuantiles y la implementación de ML debido a un aspecto importante, no era comparable en su estado inicial con los otros métodos. Estos métodos presentan características que permitían la generación de mapas combinados a través del manejo de ecuaciones estadísticas y estocásticas para el desarrollo de mapas a nivel de píxel.
La metodología de combinación por iteraciones consiste en corregir el error relativo entre datos observados y datos satelitales a nivel de subcuenca. Está orientada al uso en estudios con modelos hidrológicos semi-distribuidos, según lo propuesto por Saavedra y Ureña (2022), y puede adaptarse a diferentes zonas de estudio para generar productos con un tamaño de grilla adecuado. En el caso de la cuenca Guadalquivir, al sur del territorio boliviano, se empleó una grilla de 250 metros, siendo más fina que la grilla de 5 km usada a nivel nacional (Saavedra et al., 2023). Sin embargo, a pesar de su utilidad orientada a modelos semi-distribuidos, los resultados espaciales del producto dejan mucho que desear, debido a la clara presencia de líneas que cortan el mapa de precipitación resultante de la combinación.
Debido a ello, el presente estudio decidió retirar el manejo de las subcuencas como unidad de ajuste y cálculo del error relativo para ser sustituida por un cálculo directo a nivel de píxel; dando como resultado mapas espacialmente más detallados, manteniendo las características de ajuste y el número de iteraciones requeridas en la metodología de
combinación original; teniendo como resultados valores similares a los obtenidos por Saavedra y Ureña (2022)
3.2.4.Análisis de Productos Combinados
Dentro de los productos obtenidos, los mapas de precipitacion muestran entre ellos ligeras diferencias en base a la cantidad de precipitación diaria interpolada; sin embargo, algunos de estos productos mantienen características y tendencias de precipitacion de sus productos satelitalesdelos quefuerongenerados. Porsu parte,los productos combinados por Saavedra y Ureña (2022) presentan regiones de precipitaciones delimitadas según al mapa de subcuencas que se usó para su generación pero mantiene ligeramente los valores de precipitacion correspondiente.
Dentro del análisis estadísticos, la correlación de los productos comparables GSMaP.v6_Gauge y CHIRPS muestran valores similares entre ambos estudios, siendo los productos generados con la nueva metodología los mejores al contar con valores de 0.98 y 0.94, respectivamente. Por su parte, el otro estudio obtuvo valores de 0.97 y 0.93 respectivamente. Este mismo comportamiento se llega a apreciar con los otros indicadores: coeficientes de terminación, errores y eficiencias; mostrando que la eliminación de las subcuencas dentro de la metodología tiende a mínimas mejoras estadísticas.
Sinembargo,elaspecto máscrucialdelprocesoradicaenlaanalíticadelaeficienciaespacial endondelos productosdesarrollados apartirdelanuevameteorologíapresentanunesquema de distribución con mayor eficiencia que los presentados por Saavedra y Ureña (2022) en su versión delametodología decombinación. Dentro desus mapas, seobserva quela eficiencia del producto depende de la cuenca que se desee mostrar, terminando de generar mapas de eficiencias con cambios abruptos de un píxel a otro en base a su delimitación; siendo las subcuencas deAmazonas las que presentan una mayor área de subcuenca y las que presentan una menor eficiencia La nueva metodología, al incluir la corrección de pixeles, muestra que los productos desarrollados presentan una gran eficiencia de la cuenca del Amazonas.
3.2.5.Respuestas a Preguntas de Investigación
Ante el desarrollo de todo el presente documento se puede responder a las preguntas de investigación:
• ¿Qué método de geoestadística para la interpolación se ajusta mejor a distribución de datos pluviométricos en el país de Bolivia?
Para los 295 pluviómetros utilizados en esta investigación, el método que mejor se adapta es el kriging ordinario gaussiano, empleando un semivariograma basado en la elevación de los pluviómetros.Aunque este método es el segundo mejor en términos estadísticos, ofrece un mejor suavizado espacial en los valores pico.
• ¿Cuáles son los productos de precipitación satelital con mejor performance al momento con relación a las estaciones interpoladas?
Los productos de precipitación satelital con mejor performance corresponden a GSMaP.v6_Gauge, GSMaP.v8_Gauge, IMERG.v6_Final, CHIRPS y PERSIANN
CCS-CDR, en ese orden. Estos productos alcanzaron correlaciones máximas que llegan a la correlación de 0.76, mostrando una similitud alta con los datos interpolados. Sin embargo, al analizar la eficiencia de estos productos, los valores llegan a 0.61 indicando solo un buen grado de sustitución a la base interpolada.
• ¿Cuál es el efecto en cuestión de los resultados al cambiar la subcuenca, unidad decontroldelametodología,porunmanejoporpíxelenlosaspectosestadísticos y visuales?
Al cambiar el manejo de subcuencas por pixeles, desde una perspectiva estadística, los resultados obtenidos con relación a la metodología original muestran una mejora entre 1 a 5% en algunos productos; traducido en un incremento de 0.97 a 0.98 en cuestión a la correlación.
No obstante, dentro del apartado visual, la sustitución de la unidad de control presenta un mapa de precipitacion mucho más detallado con relación a la metodología original, donde el mapa presentaba “divisiones” drásticas debido a la influencia de las subcuencas.
• ¿Cuál de los productos combinados presenta un mayor grado de mejora con relación a su base satelital?
Desde la perspectiva de mejora, el peor producto satelital para su empleo dentro de Bolivia era GSMaP.v6_MVK. Sin embargo, tras el proceso de combinación, paso a de tener correlaciones máximas de 0.65 a correlaciones cercanas a 0.95, desde la perspectiva estadística. No obstante, dentro aspecto visual, aun puede mejorar ante la presencia de zonas con eficiencias nulas.
3.2.6.Análisis Crítico de la Metodología
La metodología propuesta para la generación de productos combinados mediante la implementacióndelpíxelcomounidaddecontrolrepresentaunavancequemejoralacalidad del producto tanto estadísticamente como visualmente. Sin embargo, aún no es completamente precisa.
De los 10 productos evaluados, 9 mostraron resultados óptimos desde ambas perspectivas.
No obstante, en el caso de GSMaP.v6_MVK, los mapas generados aún presentan errores visuales, lo que sugiere que la metodología podría tener falencias en algunas de sus condiciones, las cuales deben ser abordadas.
Otro aspecto que mejorar es la gestión del espacio. Originalmente, el uso de mapas basados en subcuencas reducía el tamaño de los archivos al considerar 329 subcuencas, es decir, 329 valores de error relativo. Sin embargo, al cambiar la unidad de control al píxel, el tamaño de los mapas aumentó drásticamente debido al mayor número de componentes. Para optimizar el almacenamiento, será necesario desarrollar herramientas que mejoren el rendimiento, como el uso de archivos NetCDF como bases de datos.
CAPITULO 5: CONCLUSIONES Y RECOMENDACIONES
4.1. CONCLUSIONES
El presente estudio tuvo como objetivo el análisis y mejoramiento de la metodología de combinación a través de interpolaciones de datos de precipitación pluviométrica y productos de precipitación satelital, considerando la metodología de interpolación para la especialización de datos pluviométricos y el cambio de unidades de control de subcuencas a píxeles.
Dentro del análisis de la metodología de interpolación, se decidió integrar la variable de la altura de las estaciones mediante el manejo de semivariogramas, lo que permitió generar escenarios específicos para la región. Para el caso de Bolivia y sus 294 estaciones, se ajustó un semivariograma del tipo gaussiano, aplicando la metodología kriging con 18 puntos de consideración para el proceso de interpolación. En el aspecto estadístico, los semivariogramas gaussiano y lineal presentaron resultados similares, siendo el último el mejor bajo este aspecto. Sin embargo, la selección del método gaussiano se debió a los resultados mostrados en la espacialización, ya que presenta una cuadrícula mejor tratada y con menos quiebres abruptos de valores de un píxel a otro
Con respecto al estado inicial de los productos de precipitación satelital, se observan casos de sobreestimación en la zona con mayor valor en productos como GSMaP.v6_MVK, GSMaP.v8_MVK, IMERG.v6_Early y IMERG.v6_Late, en comparación con los datos observados. Otros productos, como GSMaP.v6_Gauge, GSMaP.v6_Grev y GSMaP.v8_Gauge, presentan casos de subestimación en la misma región. La influencia y manejo de las diversas tecnologías generan diferentes mapas en las versiones de los productos.
El análisis de productos de precipitación indica que su desempeño varía según las macrocuencas. Para el Altiplano, el producto más confiable es IMERG.v6_Final, con alta correlación (0.8480) y eficiencia (0.6174), adecuado para estudios hidrológicos. En las macrocuencas del Amazonas y La Plata, GSMaP.v6_Gauge se destaca con correlaciones de 0.7554 y 0.7494, respectivamente, y eficiencias superiores a 0.52. Mientras IMERG.v6 tiene mejores resultados en zonas altas, GSMaP ofrece mayor precisión en áreas medias y bajas, siendo su versión Gauge la más eficiente. Por su parte, CHIRPS presenta resultados aceptables en todas las macrocuencas, y PERSIANN CCS-CDR muestra un rendimiento limitado, especialmente en elAltiplano.
El proceso de mejora mediante iteraciones reduce errores y mejora indicadores como MAE, RMSE y NSE, alcanzando en la quinta iteración correlaciones superiores a 0.9 y eficiencias mayores a 0.65, aunque persisten subestimaciones con sesgos entre -46% y -12.3%. Los productos combinados a partir de GSMaP.v6_Gauge sobresalen por su rendimiento en todas las macrocuencas, mientras que los basados en CHIRPS son los menos efectivos en Amazonas y La Plata. Un error en GSMaP.v6_MVK genera áreas con eficiencia nula, reflejandoproblemas enel procesamiento. Lametodologíalograunéxitodel90%engenerar productos de precipitación mejorados.
El resultado de ello es una metodología sencilla de generación de productos de combinación de datos que permite, a través de un concepto de corrección del error relativo en base a diferentes productos de precipitacion satelital, para generar un producto de precipitación de gran aproximación a los datos observados; con capacidades de adaptabilidad a diferentes tamaños de áreas de estudios y para enfoques de trabajos relacionados a la climatología e hidrología. Para el caso de Bolivia, el producto GSMaP.v6_Gauge se caracteriza por tener el mejor producto combinado tanto para las cuencas delAltiplano y elAmazonas.
4.2. RECOMENDACIONES
Apartir del desarrollo de esta tesis, se recomienda:
• El proceso de análisis y selección del método de interpolación deprecipitaciónpuede mejorarse mediante la inclusión de otras metodologías que consideren la elevación comounavariable.Estotienecomoobjetivomejorarlacalidaddelosmapasenzonas con altas diferencias de relieve
• Elprocesodeselección deproductosdeprecipitaciónsatelitalsebasóprincipalmente en su resolución temporal diaria. Se pueden incluir otros productos con resoluciones temporales más pequeñas (horarias o menores), que podrían estar sujetos a correcciones dependiendo de la franja horaria de la zona de interés, mejorando así los datos de entrada del producto
• La metodología de generación de productos a través de iteraciones tiene un límite para restringir los errores relativos de ±95%, con el fin de evitar valores excesivamente altos. Dicho valor podría ajustarse para analizar los efectos en el proceso de generación de los valores.
• Durante el proceso de generación, se determinó que con 5 iteraciones se podía generar un producto aceptable, según la revisión bibliográfica. Sin embargo, el sesgo
relativo hasta ese punto se mantiene alto, con valores entre -15% y -45%. Se podría incrementar el número de iteraciones para tratar de reducir el sesgo, analizando sus efectos en el resto de los indicadores estadísticos
REFERENCIAS BIBLIOGRÁFICAS
Achá, N. A., Saavedra, O. C., y Ureña, J. E. (2022). MODELACIÓN HIDROLÓGICA EN LA CUENCA DEL RÍO ROCHA INCORPORANDO LINEAMIENTOS DE CAUDAL ECOLÓGICO. Revista Investigación & Desarrollo, 22(1). https://doi.org/10.23881/idupbo.022.1-5i
Alzate, D. F. (2018). RegRAIN 0.1.0.tar [Dataset]. [object Object]. https://doi.org/10.13140/RG.2.2.29799.19361
Alzate Velásquez, D. F., Araujo Carrillo, G. A., Rojas barbosa, E. O., Gomez Latorre, D. A., y Martínez Maldonado, F. E. (2017). Interpolacion REGNIE para lluvia y temperatura en las regiones andina, caribe y pacífica de Colombia. Colombia forestal, 21(1), 102. https://doi.org/10.14483/2256201X.11601
Aragón Hernández, J. L., Aguilar Martínez, G. A., Velázquez Ríos, U., Jiménez Magaña, M. R., y Maya Franco, A. (2019). Distribución espacial de variables hidrológicas. Implementación y evaluación de métodos de interpolación. Ingeniería Investigación y Tecnología, 20(2), 1-15.
https://doi.org/10.22201/fi.25940732e.2019.20n2.023
Aryastana, P., Liu, C.-Y., Jou, B. J.-D., Cayanan, E., y Punay, J. P. (2021). Objective Evaluation of Satellite Precipitation Datasets for Heavy Precipitation Events Caused by Typhoons in the Philippines. https://doi.org/10.21203/rs.3.rs-684518/v1
Blacutt, L. A., Herdies, D. L., De Gonçalves, L. G. G., Vila, D. A., y Andrade, M. (2015). Precipitation comparison for the CFSR, MERRA, TRMM3B42 and Combined Scheme datasets in Bolivia. Atmospheric Research, 163, 117-131. https://doi.org/10.1016/j.atmosres.2015.02.002
Blanco, M., Demaria, E., Cazenave, G., y Zimmermann, E. (2023). Validación y corrección de estimaciones de precipitación satelital utilizando observaciones en superficie en la región pampeana argentina. Tecnología y ciencias del agua, 14(2), 110-168. https://doi.org/10.24850/j-tyca-14-02-04
Cannon, A. J., Sobie, S. R., y Murdock, T. Q. (2015). Bias Correction of GCM Precipitation by Quantile Mapping: How Well Do Methods Preserve Changes in Quantiles and Extremes? Journal of Climate, 28(17), 6938-6959. https://doi.org/10.1175/JCLI-D-14-00754.1
Cuza-Sorolla, A., Hernández-Aguilar, M. L., y Barrera-Rojas, M. Á. (2021). Aplicación de polígonos Thiessen para la definición y análisis de áreas de influencia del sistema de salud en ciudades costeras del estado de Quintana Roo. Quivera. Revista de Estudios Territoriales, 23, 49-71.
Dagnino, J. (2014). Coeficiente de correlación lineal de Pearson. Revista Chilena de Anestesia, 43(1), 150-153.
Embajada de Bolivia en Alemania. (s. f.). Datos Generales. Botschaft Des Plurinationalen Staates Belivien in Deutschland. Recuperado 24 de agosto de 2024, de http://www.bolivia.de/es/bolivia/datos-generales/
ESRI, Environmental Systems Research Institute. (2023). Crear polígonos de Thiessen (Análisis) ArcGIS Pro | Documentación Recuperado 18 de agosto de 2023, de https://pro.arcgis.com/es/pro-app/latest/tool-reference/analysis/create-thiessenpolygons.htm
ESRI, Environmental Systems Research Institute. (2024a). Choosing a lag size ArcMap | Documentation Recuperado 9 de abril de 2024, de https://desktop.arcgis.com/en/arcmap/latest/extensions/geostatisticalanalyst/choosing-a-lag-size.htm
ESRI, Environmental Systems Research Institute. (2024b). Funciones de semivariograma y covarianza ArcGIS Pro | Documentación. Recuperado 5 de octubre de 2024, de https://pro.arcgis.com/es/pro-app/latest/help/analysis/geostatisticalanalyst/semivariogram-and-covariance-functions.htm
Funk, C., Peterson, P., Landsfeld, M., Davenport, F., Becker, A., Schneider, U., Pedreros, D., McNally, A., Arsenault, K., Harrison, L., y Shukla, S. (2020). Algorithm and Data Improvements for Version 2.1 of the Climate Hazards Center’s InfraRed Precipitation with Stations Data Set. En V. Levizzani, C. Kidd, D. B. Kirschbaum, C. D. Kummerow, K. Nakamura, & F. J. Turk (Eds.), Satellite Precipitation Measurement (Vol. 67, pp. 409-427). Springer International Publishing. https://doi.org/10.1007/978-3-030-24568-9_23
Funk, C., Peterson, P., Landsfeld, M., Pedreros, D., Verdin, J., Shukla, S., Husak, G., Rowland, J., Harrison, L., Hoell, A., y Michaelsen, J. (2015). The climate hazards infrared precipitation with stations A new environmental record for monitoring extremes. Scientific Data, 2(1), 150066. https://doi.org/10.1038/sdata.2015.66
Gallardo, A. (2007). Geostadística. Ecosistemas - Revista Científica y Tecnica de Ecología y Ecosistema, 15(3), 48-58.
Garcia Calabrese, M. V., Paniagua, M. T., y Chicaiza, E. (2022). Análisis de la distribución espacial de la precipitación anual (1979-2014) aplicando métodos de interpolación en la Región Occidental del Paraguay. Revista Geográfica, 164, 6381. https://doi.org/10.35424/regeo.164.2022.1067
Historico GeoBolivia. (2023). Indice de escenas del Modelo Digital de Elevación de ASTER (30 metros) para Bolivia. GeoBolivia. https://geo.gob.bo/catalogue/#/dataset/1125
Iqbal, Z., Shahid, S., Ahmed, K., Wang, X., Ismail, T., y Gabriel, H. F. (2022). Bias correction method of high-resolution satellite-based precipitation product for Peninsular Malaysia. Theoretical and Applied Climatology, 148(3-4), 1429-1446. https://doi.org/10.1007/s00704-022-04007-6
Joyce, R. J., Janowiak, J. E., Arkin, P. A., y Xie, P. (2004). CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. Journal of Hydrometeorology, 5(3), 487-503. https://doi.org/10.1175/1525-7541(2004)005<0487:CAMTPG>2.0.CO;2
Kozu, T., Kawanishi, T., Kuroiwa, H., Kojima, M., Oikawa, K., Kumagai, H., Okamoto, K., Okumura, M., Nakatsuka, H., y Nishikawa, K. (2001). Development of precipitation radar onboard the Tropical Rainfall Measuring Mission (TRMM) satellite. IEEE Transactions on Geoscience and Remote Sensing, 39(1), 102-116. https://doi.org/10.1109/36.898669
Kubota, T., Aonashi, K., Ushio, T., Shige, S., Takayabu, Y. N., Kachi, M., Arai, Y., Tashima, T., Masaki, T., Kawamoto, N., Mega, T., Yamamoto, M. K., Hamada, A., Yamaji, M., Liu, G., y Oki, R. (2020). Global Satellite Mapping of Precipitation (GSMaP) Products in the GPM Era. En V. Levizzani, C. Kidd, D. B. Kirschbaum, C. D. Kummerow, K. Nakamura, & F. J. Turk (Eds.), Satellite Precipitation Measurement (Vol. 67, pp. 355-373). Springer International Publishing. https://doi.org/10.1007/978-3-030-24568-9_20
Kubota, T., Shige, S., Hashizume, H., Aonashi, K., Takahashi, N., Seto, S., Hirose, M., Takayabu, Y. N., Ushio, T., Nakagawa, K., Iwanami, K., Kachi, M., y Okamoto, K. (2007). Global Precipitation Map Using Satellite-Borne Microwave Radiometers by the GSMaP Project: Production and Validation. IEEE Transactions on Geoscience and Remote Sensing, 45(7), 2259-2275. https://doi.org/10.1109/TGRS.2007.895337
Li, H., Zhang, Y., Lei, H., y Hao, X. (2023). Machine Learning-Based Bias Correction of Precipitation Measurements at High Altitude. Remote Sensing, 15(8), 2180. https://doi.org/10.3390/rs15082180
Liu, D., Zhao, Q., Fu, D., Guo, S., Liu, P., y Zeng, Y. (2020). Comparison of spatial interpolation methods for the estimation of precipitation patterns at different time scales to improve the accuracy of discharge simulations. Hydrology Research, 51(4), 583-601. https://doi.org/10.2166/nh.2020.146
Mentaschi, L., Besio, G., Cassola, F., y Mazzino, A. (2013). Problems in RMSE-based wave model validations. Ocean Modelling, 72, 53-58. https://doi.org/10.1016/j.ocemod.2013.08.003
MMAyA, Ministerio de Medio Ambiete y Agua (Ed.). (2018). Balance hídrico superficial de Bolivia (1980 2016): Documento de difusión. Ministerio de Medio Ambiente y Agua.
Muñoz-Sabater, J., Dutra, E., Agustí-Panareda, A., Albergel, C., Arduini, G., Balsamo, G., Boussetta, S., Choulga, M., Harrigan, S., Hersbach, H., Martens, B., Miralles, D. G., Piles, M., Rodríguez-Fernández, N. J., Zsoter, E., Buontempo, C., y Thépaut, J.N. (2021). ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth System Science Data, 13(9), 4349-4383. https://doi.org/10.5194/essd-13-4349-2021
New, M., Todd, M., Hulme, M., y Jones, P. (2001). Precipitation measurements and trends in the twentieth century. International Journal of Climatology, 21(15), 1889-1922. https://doi.org/10.1002/joc.680
Nguyen, P., Shearer, E. J., Tran, H., Ombadi, M., Hayatbini, N., Palacios, T., Huynh, P., Braithwaite, D., Updegraff, G., Hsu, K., Kuligowski, B., Logan, W. S., y Sorooshian, S. (2019). The CHRS Data Portal, an easily accessible public repository for PERSIANN global satellite precipitation data. Scientific Data, 6(1), 180296. https://doi.org/10.1038/sdata.2018.296
Oliveira Diodato, J., Shinma Galbetti, T. A., Galbetti, M. V., De Oliveira Ribeiro, V., y Dante, M. (2021, diciembre 31). Comparação dos métodos da Média Aritmética, dos Polígonos de Thiessen e do IPD na avaliação espacial de dados pluviométricos. Revista EIA, 19(37). revistas.eia.edu.co/index.php/reveia/article/view/1500
Palma, R. P. (2022). Análisis crítico del coeficiente de determinación (R2), como indicador de la calidad de modelos lineales y no lineales. Matemática, 20(2).
Pedraza Triviño, A. F., Téllez Piñerez, C. F., y Trujillo Oyola, L. (2020). Estimación de los resultados en matemáticas y ciencias de las pruebas TIMSS 2015: Un nuevo enfoque desde la metodología de áreas pequeñas. Comunicaciones en Estadística, 13(2), 62-77. https://doi.org/10.15332/2422474x.6209
Pradhan, R. K., Markonis, Y., Vargas Godoy, M. R., Villalba-Pradas, A., Andreadis, K. M., Nikolopoulos, E. I., Papalexiou, S. M., Rahim, A., Tapiador, F. J., y Hanel, M. (2022). Review of GPM IMERG performance: A global perspective. Remote Sensing of Environment, 268, 112754. https://doi.org/10.1016/j.rse.2021.112754
Saavedra, O., y Ureña, J. (2022). Generation of Combined Daily Satellite-Based Precipitation Products over Bolivia. Remote Sensing, 14(17), 4195. https://doi.org/10.3390/rs14174195
Saavedra, O., Ureña, J., y Perales, M. (2023). Implementation of HydroBID Model with Satellite-Based Precipitation Products in Guadalquivir Basin, Bolivia. Water, 15(18), 3250. https://doi.org/10.3390/w15183250
Sadeghi, M., Lee, J., Nguyen, P., Hsu, K. L., Sorooshian, S., y Braithwaite, D. (2019). Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks-Cloud Classification System-Climate Data Record (PERSIANN-CCSCDR). 2019, H13P-1964. AGU Fall Meeting Abstracts.
Sadeghi, M., Nguyen, P., Naeini, M. R., Hsu, K., Braithwaite, D., y Sorooshian, S. (2021). PERSIANN-CCS-CDR, a 3-hourly 0.04° global precipitation climate data record for heavy precipitation studies. Scientific Data, 8(1), 157. https://doi.org/10.1038/s41597-021-00940-9
SENAMHI Bolivia, Servicio Nacional de Meteorología e Hidrología. (2023). Administración y Revisión de Estaciones. Servicio Nacional de Meteorología e Hidrología. Recuperado 17 de agosto de 2023, dehttps://senamhi.gob.bo/index.php/are
Song, L., Chen, M., Gao, F., Cheng, C., Chen, M., Yang, L., y Wang, Y. (2019). Elevation Influence on Rainfall and a Parameterization Algorithm in the Beijing Area. Journal of Meteorological Research, 33(6), 1143-1156. https://doi.org/10.1007/s13351-019-9072-3
Toro Trujillo, A. M., Arteaga Ramírez, R., Vázquez Peña, M. A., y Ibáñez Castillo, L. A. (2015). Relleno de series diarias de precipitación, temperatura mínima, máxima de la región norte del Urabá Antioqueño. Revista mexicana de ciencias agrícolas, 6(3), 577-588.
Ureña, J. E., Vallejos, A. G., Saavedra, O. C., y Escalera, A. C. (2018). EVALUACIÓN DE LA PRECIPITACIÓN DISTRIBUIDA EN LA CUENCA KATARI BASADO EN TECNOLOGÍA SATELITAL Y PRODUCTOS DERIVADOS. INVESTIGACION & DESARROLLO, 18, 35-51.
Ureña, J., y Saavedra, O. (2020). Evaluation of Satellite Based Precipitation Products at Key Basins in Bolivia. Asia-Pacific Journal of Atmospheric Sciences, 56(4), 641655. https://doi.org/10.1007/s13143-020-00184-4
Ureña, J., Saavedra, O., y Kubota, T. (2021). The Development of a Combined SatelliteBased Precipitation Dataset across Bolivia from 2000 to 2015. Remote Sensing, 13(15), 2931. https://doi.org/10.3390/rs13152931
Valencia-Gonzalez, J. N., Arteaga-Ramírez, R., Vázquez-Peña, M. A., y QuevedoNolasco, A. (2022). Modelos de evapotranspiración de referencia diaria en la zona arrocera del Valle del Cauca, Colombia. Tecnología y ciencias del agua, 13(1), 246-291. https://doi.org/10.24850/j-tyca-2022-01-06
Vallejos, A. G., Ancalle, S. A., Escalera, A. C., y Saavedra, O. C. (2016). ANALYZING AREAL PRECIPITATION AT KEY BASINS IN COCHABAMBA USING SATELLITE-BASED PRECIPITATION. INVESTIGACION & DESARROLLO, 1, 25-38.
Villegas, I. (2016). Hidrografia. Embajada de Bolivia en Francia. Recuperado 24 de agosto de 2024, de https://www.emboliviafrancia.fr/index.php/es/para-saber-mas/111hidrografia.html
Wang, Z., Zhong, R., Lai, C., y Chen, J. (2017). Evaluation of the GPM IMERG satellitebased precipitation products and the hydrological utility. Atmospheric Research, 196, 151-163. https://doi.org/10.1016/j.atmosres.2017.06.020
Wickel, A., Ghajarnia, N., Yates, D., Newman, A., Escobar, M., Purkey, David, Lima, Nilo, Escalera, Ana Cecilia, y Kaenel, Manon von. (2019). Developing a gridded high-resolution gauge based precipiation product for Bolivia. Geophysical Research Abstracts (Vol. 21)..
WMO, World Meteorological Organization (Ed.). (2008). Guide to hydrological practices (6th ed). World Meteorological Organization.
Xie, P., Joyce, R., Wu, S., Yoo, S.-H., Yarosh, Y., Sun, F., y Lin, R. (2017). Reprocessed, Bias-Corrected CMORPH Global High-Resolution Precipitation Estimates from 1998. Journal of Hydrometeorology, 18(6), 1617-1641. https://doi.org/10.1175/JHM-D-16-0168.1
Zubieta, R., Saavedra, M., Espinoza, J. C., Ronchail, J., Sulca, J., Drapeau, G., y Martin‐Vide, J. (2019). Assessing precipitation concentration in the Amazon basin from different satellite‐based data sets. International Journal of Climatology, 39(7), 3171-3187. https://doi.org/10.1002/joc.6009
ANEXOS
6.1. SERIE DE TIEMPO DE PRODUCTOS DE
PRECIPITACIÓN SATELITAL
Producto CHIRPS
Macrocuenca delAltiplano
Macrocuenca delAltiplano
Macrocuenca delAmazonas
Productos GSMaP.v6
Macrocuenca delAmazonas
Macrocuencas de La Plata
Macrocuencas de La Plata
Productos GSMaP.v8
Productos IMERG.v6
Macrocuenca delAltiplano
Macrocuenca delAmazonas
Macrocuencas de La Plata
Macrocuenca delAltiplano
Macrocuenca delAmazonas
Macrocuencas de La Plata
Producto PERSIANN CCS-CDR
Macrocuenca delAltiplano
6.2. DIAGRAMADE DISPERSIÓN DE PRODUCTOS DE PRECIPITACIÓN SATELITAL
Producto CHIRPS
Macrocuenca delAltiplano
Macrocuenca delAmazonas
Macrocuencas de La Plata
Macrocuenca delAmazonas
Macrocuencas de La Plata
Productos GSMaP.v6
Macrocuenca delAltiplano
Macrocuenca delAltiplano
Macrocuenca delAmazonas
Productos GSMaP.v8
Macrocuenca delAmazonas
Macrocuencas de La Plata
Macrocuencas de La Plata
Productos IMERG.v6
Macrocuenca delAltiplano
Macrocuenca delAltiplano
Macrocuenca delAmazonas
Macrocuenca delAmazonas
Macrocuencas de La Plata
Macrocuencas de La Plata
Producto PERSIANN CCS-CDR
6.3. TENDENCIADE MEJORAEN ELPROCESO DE PRODUCTOS DE PRECIPITACIÓN COMBINADOS
Producto CHIRPS
Macrocuenca delAltiplano
Macrocuenca delAltiplano
Macrocuenca delAmazonas Macrocuencas de La Plata
Productos GSMaP.v6
Macrocuenca delAmazonas Macrocuencas de La Plata
Productos GSMaP.v8
Productos IMERG.v6
Macrocuenca delAltiplano
Macrocuenca delAmazonas
Macrocuencas de La Plata
Macrocuenca delAltiplano
Macrocuenca delAmazonas
Macrocuencas de La Plata
Producto PERSIANN CCS-CDR
Macrocuenca delAltiplano
Macrocuenca delAmazonas
6.4. SERIE DE TIEMPO DE PRODUCTOS DE PRECIPITACIÓN COMBINADOS
Producto CHIRPS
Macrocuenca delAltiplano
Macrocuenca delAmazonas
Macrocuencas de La Plata
Macrocuencas de La Plata
Productos GSMaP.v6
Productos GSMaP.v8
Macrocuenca delAltiplano
Macrocuenca delAmazonas
Macrocuencas de La Plata
Macrocuenca delAltiplano
Macrocuenca delAmazonas
Macrocuencas de La Plata
Productos IMERG.v6
Macrocuenca delAltiplano
Macrocuenca delAmazonas
Macrocuencas de La Plata
Producto PERSIANN CCS-CDR
Macrocuenca delAltiplano
Macrocuenca delAmazonas
Macrocuencas de La Plata
6.5. DIAGRAMADE DISPERSIÓN DE PRODUCTOS DE PRECIPITACIÓN COMBINADOS
Producto CHIRPS
Macrocuenca delAltiplano
Macrocuenca delAltiplano
Macrocuenca delAmazonas Macrocuencas de La Plata
Productos GSMaP.v6
Macrocuenca delAmazonas Macrocuencas de La Plata
Productos GSMaP.v8
Productos IMERG.v6
Macrocuenca delAltiplano
Macrocuenca delAmazonas Macrocuencas de La Plata
Macrocuenca delAltiplano
Macrocuenca delAmazonas Macrocuencas de La Plata