LOGISTICA,
TRANSPORTE Y DISTRIBUCIÓN
Análisis y comparativa de modelos. Toma de decisiones
Introducción a la gestión de la distribución
Análisis y comparativa de modelos. Toma de decisiones
Exposición de modelos
Cuadro comparativo
Método de decisión
Exposición de modelos
Algoritmo de caminos críticos de Dijkstra
Es un algoritmo de búsqueda con el que se pretende establecer la ruta más corta entre los pares de vértices de nuestros sistema.
Es un método basado en las iteraciones por lo que solo es adecuado para sistemas simples con tamaños de red pequeños.
Valor de distancia o tiempo o coste
Etiqueta de nodo
La ruta más corta entre el nodo 1 y el nodo seis es 1 -2 -4 -5 -6
Con un total de 23 km
Algoritmo de Floyd - Warshall
Es un algoritmo de búsqueda con el que se pretende establecer la ruta más corta desde un nodo origen hasta cualquier nodo de la red. Es un método basado en las iteraciones por lo que solo es adecuado para sistemas simples con tamaños de red pequeños.
Basado el desarrollo por decantación en cada iteración se va puliendo hasta llegar a la mejor solución
Matriz C: conjunto de distancias entre cada par de puntos
Matriz Z de nodos antecesores: de rutas mínimas en las que cada nodo es el punto directo anterior de distancia más corta en el conjunto de nodos antecesores
i,j: representa la ubicación concreta de un elemento representando i a la fila y j a la columna. Cada par es la distancia entre i y j. Atención la distancia es finita si hay camino e infinita si no hay camino
k: es la iteración que se está realizando
Para C=
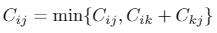
Para Z=
Algoritmo de Prim o Jarnik o DJP
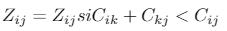
Es un algoritmo de árbol recubridor con el uso de un conexo (no hay puntos sin conexión en el grafo), y no dirigido con aristas etiquetadas. Consiste en ir formando un árbol desde un nodo escogido al azar (habitualmente nuestro Cedis).
El árbol se va creando uniendo siempre las arista con el valor menor. El valor representa km o bien coste o bien tiempo.
Algoritmo de Voguel
Método para resolver problemas de transporte con una solución que, sin ser la solución perfecta, es una solución aproximada y aplicable.
Procedimiento:
1.Tener los valores de coste de envíos desde cada origen a cada destino tabulados (matriz de costes). En caso de que la matriz no este equilibrada (el Nº de filas es diferente al Nº de columnas), se debe agregar una fila o columna de ceros según corresponda. Es decir, sea el caso se creara un origen o un destino ficticio.
2.Realizar el cálculo de las penalizaciones para cada fila y columna. Las penalizaciones se calculan restando los dos valores más pequeños de cada fila y cada columna. Las penalizaciones tienen valor absoluto.
3.Identificar la fila o columna con la mayor penalización (en caso de que exista un empate en las penalizaciones, se puede elegir cualquiera de las que tiene el mayor valor), y asignar la mayor cantidad de material posible a la casilla con el menor costo en esa fila o columna.
4.Se sombrean (eliminan) las filas o columnas que hayan sido satisfechas, reduciendo así la matriz.
5.Se repite el procedimiento desde en paso 2.
6.Una vez satisfechos todos los orígenes y destinos (sombreadas todas las filas y columnas) se puede proceder a calcular el costo del programa de envió encontrado mediante este método (cabe resaltar que la solución factible encontrada con este método no es necesariamente la optima).
Algoritmo de Voguel
Matriz inicial
Repetimos el cálculo de las penalizaciones
Coste de enviar una unidad entre el origen 1 y el destino 4
Tenemos 2 máximas penalizaciones y las realizaremos por separado.
La oferta de 150 del origen 1 satisface toda la demanda del destino 2 (valor 150).
Finalmente la oferta del origen 2 satisface las demandas de los destinos 3 y 4 (valor 150 + 100 = 250)
calculamos las penalizaciones
Repetimos
el cálculo de las penalizaciones
Ahora tomamos el valor de penalización de la columna. Repetimos el proceso para satisfacer las demandas de destinos 3 y 4 pendientes.
Asignamos la demanda en el punto de menor coste
La oferta del origen 3 cubre la demanda del destino 1 (valor 50).
Dado que la demanda y la oferta están ambas completas marcamos las celdas.
Comparación de coste 1 y 2
Coste 1= 50(0) + 150(0) + 150(90) + 100(200)
C1= 33500
Coste 2= 50(0) + 50(0) + 100(70) + 150(90) + 100(110)
C2= 31500
Algoritmo de La esquina noroeste (similar al algoritmo de Voguel)
Método para resolver problemas de transporte con una solución que, sin ser la solución perfecta, es una solución aproximada y aplicable. Es más rápido de ejecutar que el método de Voguel, si bien los resultados pueden no ser tan buenos.
Procedimiento:
1. En la celda seleccionada como esquina Noroeste se debe asignar la máxima cantidad de unidades posibles, cantidad que se ve restringida ya sea por las restricciones de oferta o de demanda. En este mismo paso se procede a ajustar la oferta y demanda de la fila y columna afectada, restándole la cantidad asignada a la celda.
2. En este paso se procede a eliminar la fila o destino cuya oferta o demanda sea 0 después del «Paso 1», si dado el caso ambas son cero arbitrariamente se elige cual eliminar y la restante se deja con demanda u oferta cero (0) según sea el caso.
3. Una vez en este paso existen dos posibilidades, la primera que quede un solo renglón o columna, si este es el caso se ha llegado al final el método, «detenerse».
La segunda es que quede más de un renglón o columna, si este es el caso iniciar nuevamente el «Paso 1».
Asignamos la mayor cantidad posible en la esquina noroeste
Matriz inicial
La siguiente esquina NO es destino 2 y asignamos el resto de oferta 1 A continuación completamos la demanda de 2 con la oferta de 2 en la que queda disponible 200 Completamos la demanda del destino 4 con las ofertas de 3 (restante) y 3
Algoritmo del
coste
mínimo(similar
al algoritmo de Voguel y al de la esquina noroeste)
Método para resolver problemas de transporte con una solución optimizada de coste. Es el método más sencillo.
Procedimiento:
1. De la matriz se elige la ruta (celda) menos costosa (en caso de un empate, este se rompe arbitrariamente) y se le asigna la mayor cantidad de unidades posible, cantidad que se ve restringida ya sea por las restricciones de oferta o de demanda. En este mismo paso se procede a ajustar la oferta y demanda de la fila y columna afectada, restándole la cantidad asignada a la celda.
2. En este paso se procede a eliminar la fila o destino cuya oferta o demanda sea 0 después del «Paso 1», si dado el caso ambas son cero arbitrariamente se elige cual eliminar y la restante se deja con demanda u oferta cero (0) según sea el caso.
3. Una vez en este paso existen dos posibilidades, la primera que quede un solo renglón o columna, si este es el caso se ha llegado al final el método, «detenerse».
La segunda es que quede más de un renglón o columna, si este es el caso iniciar nuevamente el «Paso 1».
Matriz inicial
Coste de enviar una unidad entre el origen 1 y el destino 4
Asignamos la mayor cantidad posible en la celda de menor coste
Vamos asignando las cargas en la celda de menos coste sucesivamente
Cuadro comparativo
La comparación entre diferentes modelos de ruteo puede realizarse de diversas formas, si bien el empleo de cuadros comparativos permite tener una visión completa de las diferentes alternativas. Por ellos es una de las técnicas más utilizadas.
Lo importante es que el diseño del cuadro nos permita tener esta visión y, por lo tanto su estructura debe contener todos los elementos que se consideren de importancia para realizar dicha comparativa.
Un cuadro comparativo se presenta como una matriz de doble entrada en la de disponemos bien en las columnas, bien en las filas los elementos a comparar, en nuestro caso los modelos de algoritmo. Si a los Ítems utilizados vamos a darle valor es conveniente situar los modelos a comparar en las columnas, de esta forma tendremos sumatorios de puntuación para cada uno al final de cada columna / modelo. Lógicamente, en función de la cantidades de elementos a comparar y de Ítems a valorar podemos invertir el orden (columnas / filas) para ajustarlo a una hoja de visión completa.
caminos críticos o Dijkstra
A continuación nos toca decidir cuales van a ser los Ítems de valoración. Podemos crear dos tablas (una con Ítems cuantitativos y otra con cualitativos) y posteriormente integrarlas. Lo más sencillo es crear una sola tabla, al fin y al cabo vamos a darle valores numéricos a todos lo Ítems por lo que la comparativa tendrá en sí un carácter de decisión inicial cuantitativo.
El resultado se presentará mediante puntuación, si bien la comparación no tiene que representar una decisión directa como veremos en el siguiente apartado.
Floyd - Warshall
Prim o Jarnik o DJP Voguel esquina noroeste
coste mínimo
Cuando hablamos de modelos para la gestión operativa los Ítem más habituales suelen se:
El resultado obtenido. Es decir el nivel de optimización que el modelo consigue con su desarrollo.
El tiempo de ejecución. Es decir el nivel de dedicación que requiere (recordemos que las rutas se gestionan diariamente, pero es cierto que no todas las empresas tienen cada día entregas totalmente dispares en cuanto a volumen y dispersión. Pueden darse casos – de hecho es muy común - en los que una parte importante de la distribución sea estable y rutinaria y no necesite diariamente generar el modelo para optimizar las rutas.) También cabe añadir que en muchas ocasiones el tamaño de las entregas puede completar vehículos con los que la salida y el retorno no tiene paradas intermedias, a excepción del aprovechamiento para recogidas, por lo que las rutas carecen de interés en la búsqueda de combinatoria de menor recorrido.
La complejidad del sistema. Es decir, si para poderlo completar necesitamos una base compleja de cálculo que además requiera mucha información de alimentación diaria.
La facilidad de la carga de datos. Es decir, si una vez estructurado el modelo, por ejemplo en Excel, podemos importar los datos desde nuestra base de datos sin necesidad de manipularlos. Esto significa que nuestros ficheros maestros de clientes, pedidos y proveedores deben estar configurados con esa posibilidad.
Ítem caminos críticos o
resultado tiempo complejidad
Facilidad datos
Dijkstra FloydWarshall
Prim o Jarnik o DJP Voguel esquina noroeste
coste mínimo
A partir de este punto podemos añadir otros Ítem que el caso particular de cada empresa se consideren de interés.
También se puede entender que no todos los ítem tiene la misma importancia, y en este caso podremos aplicar una factores de ponderación para cada uno.
Ítem ponderació n caminos críticos o
resultado tiempo complejidad
Facilidad datos
Suma
Dijkstra
FloydWarshall
Prim o Jarnik o DJP Voguel esquina noroeste
coste mínimo
Método de decisión
Este apartado solo pretende llamar la atención de que un valor numérico de puntuación no siempre es el único elemento valorable para la toma de decisiones. Pude simplemente formar parte del análisis.
Por ejemplo podríamos, a partir de un resultado dado, preguntarnos como evolucionaremos a futuro, como serán nuestras necesidades de distribución y si en ese futuro el modelo con mayor puntuación funcionará bien.
También podemos plantearnos si para el modelo con mayor puntuación tenemos personas con el conocimiento para ponerlo en práctica.
Para concluir remarcar que un dato no es por sí mismo un elemento de decisión directa. La Toma de decisión es el máximo ejercicio de responsabilidad de un directivo y por tanto debe sopesar todas la variables, pros y contras, para tomar la correcta.
Conclusiones
Los modelos manuales sirven cuando la red de distribución y puntos de entrega tienen un volumen reducido. Se hacen impracticables con grandes cantidades de entrega o flota de vehículos.
Lo habitual hoy en día es utilizar alguno de los numerosísimos softwares de gestión de rutas que existen en el mercado.
Algunas de estas herramientas las encontraremos de forma gratuita
