Sbírka úloh z matematiky 8

8 SBÍRKA ÚLOH Z MATEMATIKY

pro základní školy

ALGEBRA

I. ÚVODNÍ OPAKOVÁNÍ

1. Zlomky

2 Početní operace s celými čísly

3. Poměr a postupný poměr

4. Úměra a trojčlenka

MOCNINA A ODMOCNINA

1 Druhá mocnina bez užití tabulek a

2. Určování

III. PYTHAGOROVA VĚTA A jEjÍ UžITÍ

1 Pythagorova věta

2. Výpočet délek

IV. MOCNINA S PŘIROZENÝM MOCNITELEM

1. Třetí mocnina

6. Základy statistiky

7. Pravděpodobnost

GEOMETRIE

I. ÚVODNÍ OPAKOVÁNÍ

1 Úhly včetně úhlů trojúhelníku

2. Shodnost

3 Čtyřúhelníky

4. Souměrnost

5. Hranoly

II.

KRUžNICE A KRUH

1. Zobrazení kružnice a kruhu

2 Kružnice, přímka a tětiva

3. Vzájemná poloha dvou kružnic

4 Thaletova věta

5. Tečny kružnice procházející daným bodem

6. Délka kružnice a obvod kruhu .

7 Obsah kruhu

8. Části kružnice a kruhu (rozšiřující učivo)

III. VÁLEC

1. Základní pojmy

2 Povrch a objem válce

3. Válcová tělesa kolem nás

4. Souhrnná cvičení k tématům Kružnice, Kruh a Válec

IV. KONSTRUKČNÍ ÚLOHY

1. Jednoduché konstrukce

2 Množiny bodů dané vlastnosti

3. Konstrukční úlohy řešené pomocí množin bodů dané vlastnosti

V. ZÁVĚREČNÉ OPAKOVÁNÍ

1. Čtyřúhelníky

3. Válec

II. DRUHÁ MOCNINA A ODMOCNINA

1. Druhá mocnina bez použití tabulek a kalkulaček

1. Zapište ve tvaru druhé mocniny: a) 3 · 3 b) 65 · 65 c) k · k d) (a + b) · (a + b)

2. Vypočítejte: a) 42 b) 702 c) 102 d) 1002

3. Ověřte, zda následující zápisy představují správné rovnosti: a) 62 + 82 = 102 b) 22 + 62 + 92 = 112 c) 52 + 62 + 82 + 102 = 152 d) 22 52 = 82 + 62 e) 37 = 32 + 72 – 3 7 f) 102 – 42 = 22 + 42 + 82

4. Vypočítejte:

5. Vypočítejte:

6. Jsou dány následující součty druhých mocnin přirozených čísel: a) 12 + 22 +

II.

II. Čím jsou tyto součty zajímavé? II. Který z těchto součtů je dělitelný číslem: ,,,,,,, ?

7. Daná čísla vyjádřete ve tvaru druhých mocnin prvočísel, nebo součinu prvočísel: a) 25 b) 49 c) 225 d) 5 929

8. Vynikající švýcarský matematik Leonhard Euler [leonhart ojler] (viz foto), žijící dlouhá léta 18. století v carském Petrohradě, zjistil, že pro mnoho přirozených čísel n se hodnota výrazu n2 + n + 41 rovná prvočíslu. Ověřte, zda pro n = 1, 2, 8 a 20 je toto tvrzení pravdivé. (Prvočísla od 2 do 1 000 najdete v některých vydáních školních tabulek.)

9. Nahraďte obdélníčky v následujících zápisech jedním ze znaků rovnosti nebo nerovnosti (= , > , <) tak, abyste získali pravdivý výrok: a) –42  (– 4)2 b) 102  – 102 c) –72  (– 7)2 d) 22  (+ 2)2 2 3 4 5 6 7 9 11

2. Určování druhých mocnin převážně pomocí tabulek a kalkulaček

1. Určete: a) 682 b) 3,42 c) 0,752 d) 2572 e) 12 0002 f) 132 + 564 g) 16 42 h) 122 : 6

2. Vypočítejte: a) 4,22 b) 36,072 c) – 538,312 d) 6,3762 e) f) g) h) 6,42 · 102

0,9 0,8 22 2

4. Rozhodněte, pro která čísla se jejich druhá mocnina rovná: a) 0,09 b) 0,36 c) –81 d) 0 + 

3. Určete, kolikrát se zvětší obsah čtverce, jestliže délku jeho strany zvětšíme: a) dvakrát b) třikrát c) pětkrát d) xkrát

krovy AC a BC na dvě trojice stejně dlouhých dílů Vypočítejte s přesností na centimetry délky a) krovů AC a BC, b) vzpěr EF, JK, a GD, IL.

9. Odvěsny AC a BC pravoúhlého trojúhelníku mají délky 12 cm a 5 cm. Vypočítejte: a) délku kružnice k opsané tomuto trojúhelníku, b) obsah kruhu ohraničeného kružnicí k

3. Pythagorova věta kolem nás

1. Stavební pozemek má tvar rovnoramenného lichoběžníku. Vzdálenost jeho základen se rovná 24 m. Boční rameno má délku 30 m a kratší základna je dlouhá 27 m. Na tomto pozemku stojí dům a garáž. Jejich půdorysy mají tvary obdélníků s rozměry 14 m × 16 m a 7 m × 4 m (viz obr.). a) Vypočítejte výměru tohoto pozemku v arech. b) Kolik procent pozemku zaujímá zastavěná plocha?

2. Na obrázku A je znázorněn zemědělský pozemek tvaru čtyřúhelníku MNOP o rozměrech: |MN| = 72 m, |NP| = 210 m, |NO| = 264 m. |∢OPN| = |∢MNP| = 90°. Vypočítejte jeho: a) obvod v metrech, b) výměru v hektarech.

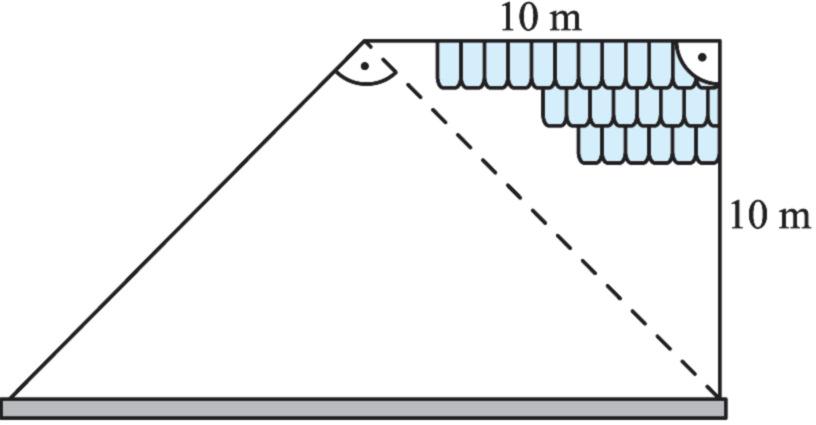
3. Na obrázku B vidíte kresbu severní strany střechy, na které je třeba vyměnit všechny tašky a v její dolní části i okapový žlab. Vypočítejte: a) počet tašek na její překrytí, víte­li, že na 1 m2 se jich spotřebuje 17 a tvarovou úpravou se jejich spotřeba zvýší o 4 %, b) délku okapového žlabu, který je o 2 % delší, než je dolní okraj střechy.

4. Před opravou selské usedlosti památkáři požadovali výměnu všech střešních krovů (na obrázku to jsou úsečky XC a YC) is příčkou (DE). Vypočítejte:

a) šířku (AB) půdní podlahy, b) výšku (CC2) půdy, c) vzdálenost (C1C2) příčky od půdní podlahy (zároveň zdůvodněte, proč byla větší než 2 metry).

(Poznámka: Krov i příčku z důvodu zjednodušení výpočtu považujte za úsečky.)

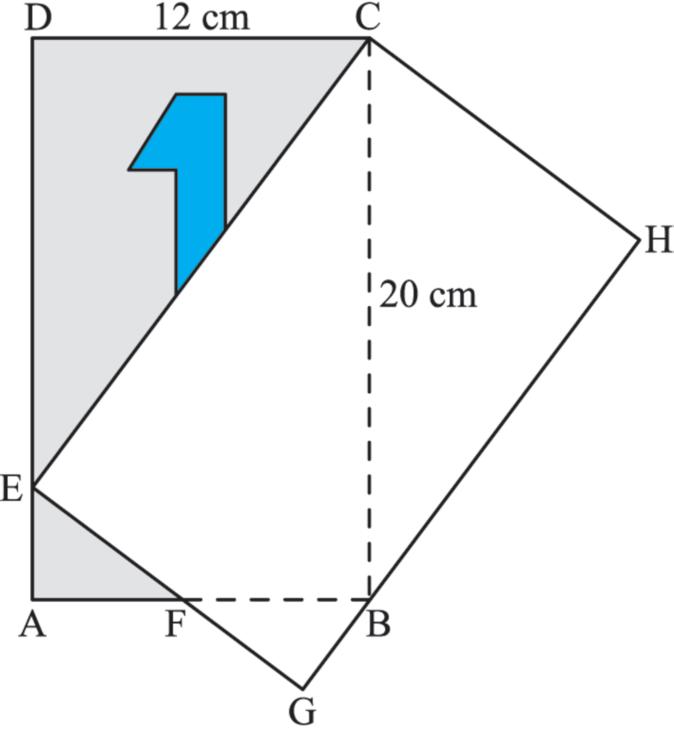
5. Na obrázku je obdélníkový list kalendáře s rozměry 20 cm x 12 cm částečně zakryt listem určeným k odtržení (viz zmenšený obrázek kalendáře).

II. Vypočítejte poměr a) obvodů, b) obsahů trojúhelníku ECD a pravoúhlého lichoběžníku BCEA

II. Bez výpočtu rozhodněte, která část listu ABCD je větší, zda odkrytá, nebo zakrytá.

1. Rozhodněte, které z tří daných délek vyjadřují velikosti stran pravoúhlého trojúhelníku:

a) 2 cm; 4,8 cm; 5,2 cm b) 8 m; 6 m; 4 m c) 16 mm; 30 mm; 34 mm d) 9,2 dm; 10 dm; 13 dm e) 3,5 km; 12 km; 12,5 km f) cm; 36 mm; 1,11 dm g) dm; 3 dm; 6,3 dm h) 12 709 mm; 13 500 mm; 18 541 mm

2. Měla vydlážděná podlaha chodby tvar obdélníku, jestliže dlaždič zjistil, že je dlouhá 4,5 m, široká 2,4 m a její úhlopříčka měla délku 5,1 m?

4. Obrácená Pythagorova věta

47. Do přespolního běhu se zapojilo 144 žáků jedné venkovské základní školy Ti byli rozděleni do 13 družstev, a to desetičlenných dívčích a dvanáctičlenných chlapeckých. Kolik dívčích a kolik chlapeckých družstev bylo vytvořeno?

48. Oceláři dostali za úkol vyrobit 50 t betonářské oceli s hustotou 7 800 (7,8 ).

K její výrobě mohli použít ocel A s hustotou 7 400 (7,4 ) a ocel B s hustotou

8 000 (8 ). Kolik tun oceli s uvedenými hustotami k výrobě požadované oceli

použili? kg m 3 t m 3 t m 3 kg m 3

4. Souhrnná cvičení

1. Ověřte, zda číslo na pravé straně zápisu rovnosti se rovná hodnotě výrazu na jeho levé straně:

a) (–1) 9 + 8 + 5 = 4 b) 1 – 9 + 8 + 5 = 5 c) 1 · 9 – 8 + 5 = 6 d) 1 + 9 – 8 + 5 = 7 e) f)

g) h) 63 · (16 200 : 600 + 15) = 2 646

2. Určete chybějící členy (barevné čtverečky) rovností: a) 10 : 5 = 2 –  b) 4,8 :  = 4,8 – 0,8 c) –2 · (6x – 7) = – 12x +  d) · 6 =  –3

3. Řešte rovnice a správnost získaných kořenů ověřte zkouškami: a) x – 1 = 3x – 6 b) 0,6y – 1,02 = 0 c) 7z + 8 = 6z – 15 d) 5 · (r + 2) + 9 = 54 e) 2s + 1 – (6

VI. LINEÁRNÍ

6. Cestovní kancelář WEST prodala loni 432 zahraničních zájezdů, z toho připadly na prázdninové období. Kolik zájezdů připadlo na období červenec až srpen?

7. Vstupenky do akvaparku v Žamberku si 15 července zaplatilo 190 osob Platících

žen bylo o 10 více než platících mužů.

Dětí bylo o 14 méně než platících dospělých. Kolik žen, mužů a dětí si v uvedený den koupilo vstupenky?

8. Pan Zámečník nakupoval v Londýně ve třech obchodních domech A, B, C. Jeho útrata v obchodním domě B byla o 3 ₤ vyšší než v obchodním domě A a v obchodním domě C byla o 5 ₤ nižší než v obchodním domě A Jeho celková útrata včetně DPH ve všech třech obchodních domech byla 61 ₤. Vypočítejte útratu pana Zámečníka v jednotlivých obchodních domech v librách i korunách (směnný kurz v době nákupu byl 1 ₤ = 29,80 Kč).

9. Vypočítejte obsah parketové podlahy, víte­li, že její délka je 1,2krát větší než její šířka a že délka lišty po jejím obvodu se rovná 22 m.

10. Obdélníkový pozemek osázený bramborami je 184 m dlouhý a má výměru 2,76 ha. Vypočítejte jeho obvod.

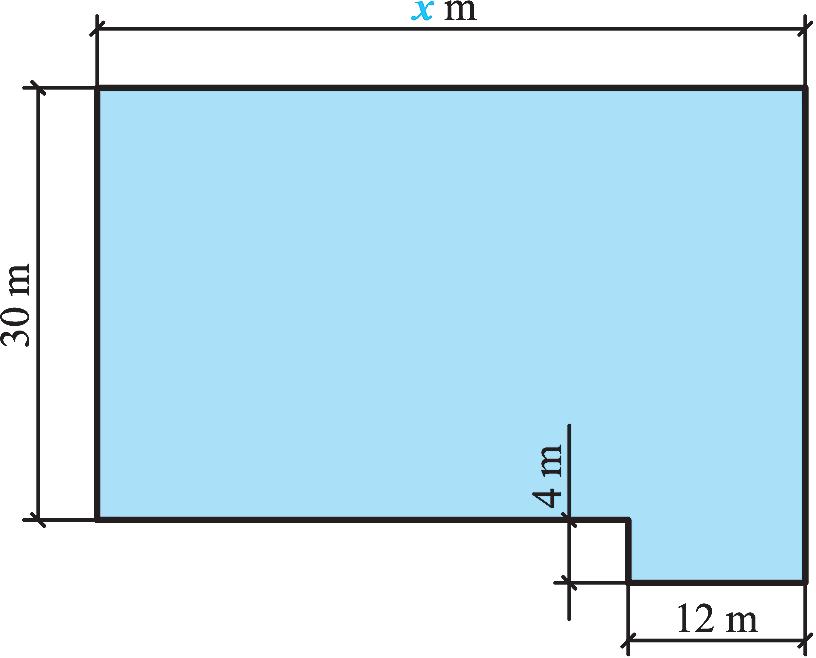
11. Na obrázku je náčrt stavební parcely s výměrou 15,48 arů Vypočítejte velikost neznámé kóty x v metrech.

12. V jednom z mnoha autobazarů bylo v letošním jarním období nabídnuto k prodeji 96 osobních automobilů. Z tohoto počtu jich byla značky Ford Mondeo a z této čtvrtiny byly červené barvy. Kolik červených automobilů Ford Mondeo autobazar nabízel k prodeji?

PŘEHLED

VYBRANÝCH POJMŮ A ZÁPISŮ UČIVA GEOMETRIE V 8. ROČNÍKU

Kružnice a kruh

Kružnice je množina všech bodů X dané roviny, které mají od pevného bodu S stálou vzdálenost |SX| = x. Bod S se nazývá střed kružnice, r je poloměr kružnice, jeho velikost vyjadřujeme kladným číslem.

Zápis kružnice: k(S; r) čteme: kružnice k se středem S a poloměrem r

Zápis: X ∈ k čteme: bod X náleží kružnici k

Kruh je množina všech bodů X dané roviny, pro jejichž vzdálenost od pevného bodu S platí |SX| ≤ r. Bod S se nazývá střed kruhu, r je poloměr kruhu. Zápis kruhu: K(S; r) čteme: kruh K se středem S a poloměrem r

Zápis: X ∈ K čteme: bod X náleží kruhu K

Tětiva AB, která prochází středem kružnice (kruhu), je nejdelší tětivou kružnice (kruhu). Nazývá se průměr kružnice (kruhu) a označuje se d.

Výpočet délky kružnice (obvodu kruhu) podle vzorce: o =2πr

Výpočet obsahu kruhu podle vzorce: SK =πr2

Thaletova věta: Množina vrcholů všech pravých úhlů dané roviny, jejichž ramena procházejí dvěma jejími různými body A, B, je kružnice s průměrem AB (kromě bodů A, B). Viz obrázek.

Válec

Válec je těleso (čili prostorový geometrický útvar), který je vymezen obdélníkem otáčejícím se kolem šířky, nebo délky.

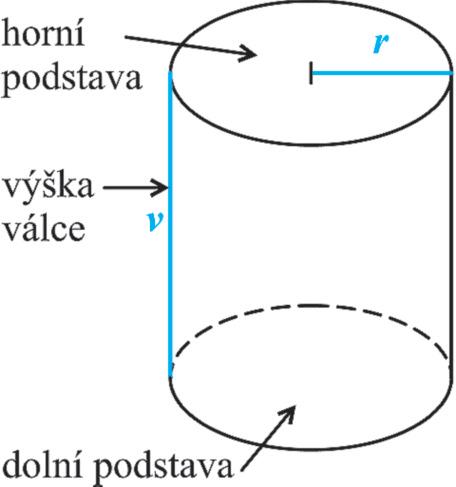
Otáčející se strany obdélníku vytvoří shodné kruhy, kterým říkáme horní a dolní podstava válce Viz obrázek

Vzdálenost obou podstav, se nazývá výška válce.

Výpočet povrchu válce podle vzorce: S =2πr(r + v)

Výpočet objemu válce podle vzorce: V =πr2v

Konstrukční úlohy

Konstrukční úlohy požadují sestrojení matematických objektů (například úseček, trojúhelníků, kružnic aj ); rozlišujeme:

• jednoduché konstrukční úlohy,

• složité konstrukce, při nichž obvykle využíváme množiny všech bodů daných vlastností.

Při řešení úloh obvykle používáme následující postup:

1 Rozbor, při kterém stanovíme kostrukční postup

2 Konstrukce, při níž stanovený postup provedeme,

3. Důkaz (zdůvodnění) konstrukce pomocí množin všech bodů daných vlastností, matematických vět a definic matematických pojmů.

4 Diskuse, při níž rozhodujeme o počtu řešení dané úlohy

I. ÚVODNÍ OPAKOVÁNÍ

1. Úhly včetně úhlů trojúhelníku

1. Na vedlejším obrázku je úhel β třikrát větší než úhel α Určete velikosti obou úhlů.

2. Přímka p protíná rovnoběžky a, b v průsečících A, B (A ∈ a, B ∈ b) tak, že jeden ze vzniklých úhlů s vrcholem A má velikost 47°

Určete a zapište velikosti zbývajících sedmi úhlů

3. Na obrázku protíná přímka c rovnoběžky a, b. Dva ze vzniklých úhlů jsou označeny ε a ω; pro jejich velikosti platí: ε = 54°30´, ω = 126°30´ Je tvrzení o velikostech úhlů ε a ω pravdivé?

Svou odpověď zdůvodněte.

4. Přímka MN protíná rovnoběžky AB a CD v bodech O, P. Vypočítejte velikost úhlu AOM, víte-li, že pro velikost úhlu OPD platí: |∢OPD| = 62°.

5. Přímka c = ↔ GH procházející bodem B (B ∈ b) je kolmá k přímce a, kterou protíná v bodu C. Přímka d = ↔ EF procházející též bodem B protíná přímku a v bodu D tak, že pro velikost úhlu BDC platí: |∢BDC| = δ = 30° Vypočítejte velikost úhlu β = |∢CBD| a úhlu DCB.

10. Tmavý okraj ciferníku hodin na obrázku A považujte za kružnici Vypočítejte její délku, je-li její průměr 22 cm.

AB

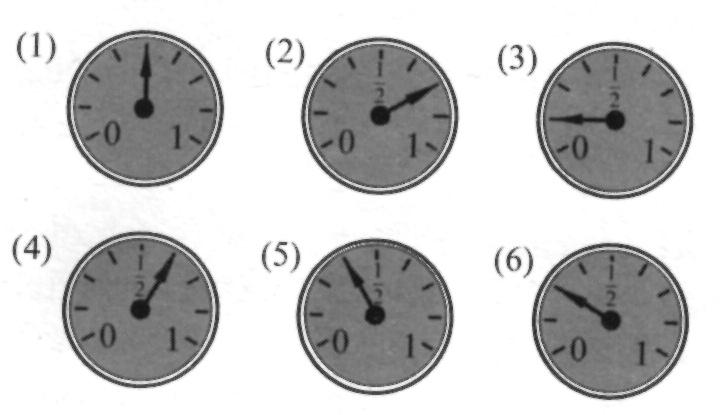
11. Byty nového sídliště jsou vytápěny ústředním topením napojeným na jeden kotel. Objem topného oleje v nádrži kotle ukazuje kruhové měřidlo, na jehož obvodu jsou rysky, k nimž směřuje ukazatel v podobě ručičky. Jestliže ručička měřidla směřuje k jedničce, znamená to, že je nádrž plná oleje Blíží-li se k nule, je třeba nádrž urychleně doplnit Nádrž je zcela naplněna, jestliže je do ní natankováno 8 000 litrů oleje Prohlédněte si na obrázku B všech 6 poloh ručičky měřidla a uveďte počet litrů (m3) oleje, který je při jednotlivých polohách ručičky v nádrži.

7. Obsah kruhu

kruh K a) b) c) d)

jeho průměr d(∅) 5,2 m

jeho poloměr r 16 cm 2,9 km

jeho délka SK 52,81 dm

2. Vypočítejte ve čtverečných centimetrech obsahy obrazců na obrázcích a), b), c). (Rozměry jsou v mm.)

1. Vypočítejte údaje, které chybějí v jednotlivých sloupcích tabulky. a) b) c)

3. Vypočítejte v arech výměru hřiště u základní školy (viz obr. – rozměry jsou v cm)

4. Na plánu pozemku mateřské školy s měřítkem 1 : 4 000 se průměr kruhového dětského hřiště rovná 1,8 cm. Vypočítejte jeho obvod v metrech a výměru v arech.

5. Kruh K1 má obsah 120 cm2 a kruh K2 má obsah 106 cm2 Který z kruhů K1 nebo K2 je možné vystřihnout z obdélníkové čtvrtky s rozměry 5,9 cm a 8 cm?

6. Z dřevotřískové desky tvaru čtverce se stranou délky 1 m vyrobil truhlář co největší možnou kruhovou desku konferenčního stolku Vypočítejte procento odpadu dřevotřísky při výrobě desky stolu.

7. Obvody kruhu a čtverce jsou stejné, rovnají se 25 dm. Který z nich má větší obsah ao kolik decimetrů čtverečných?

8. Uprostřed trojúhelníkové části parku je kruhový bazén lemovaný cestičkami (viz obr.).

Průměr jeho vodní plochy je 8 m. V jeho středu je vodotrysk. Betonový okraj bazénu, podobající se při pohledu shora mezikruží, je široký 20 cm a je od každé cestičky vzdálen 1 m

a) Jaká je vzdálenost středu roury vodotrysku od okraje každé okolní cestičky?

b) Vypočítejte obsah vodní plochy bazénu. Plochu, kterou zabírá vodotrysk, neberte při výpočtu v úvahu.

c) Jak se nazývá kružnice na okraji bazénu vzhledem k trojúhelníku, jehož obvod je naznačen čárkovanou čarou?

9. O kolik metrů je třeba zmenšit poloměr kruhu r = 6 m, aby se jeho obsah zmenšil o 25 %?

10. Vypočítejte obvod kruhu, jehož obsah se rovná obsahu mezikruží ohraničeného kružnicemi k(S; 3,5 cm) a h(S; 2 cm).

11. Při archeologických vykopávkách bylo odhaleno základové zdivo kruhové románské kaple. Vnitřní průměr zdiva byl původně 6 láter a zdivo bylo široké látra. Vypočítejte:

a) obsah podlahové dlažby kaple v celých m2, b) vnější obvod kaple v metrech po zaokrouhlení na desetiny.

(1 staročeské látro 2,4 m) 5 4 1 3 

19. Jsou dány body M, N tak, že |MN| = 7 cm Narýsujte přímku p procházející bodem N tak, aby měla od bodu M vzdálenost: a) 2 cm b) 7 cm c) 8 cm

20. Sestrojte čtverec ABCD s úhlopříčkou AC délky 7 cm

21. Narýsujte kružnici k1(S1; 1,8 cm) a vyznačte bod S2 tak, že |S1S2| = 3,6 cm. Jakou hodnotu má poloměr r2 kružnice k2 se středem S2, jestliže a) kružnice k1 a k2 mají vnější dotyk, b) kružnice k2 prochází bodem S1 kružnice k1, c) kružnice k1 a k2 mají vnitřní dotyk?

22. Při budování studně používají dosud někteří studnaři rumpál (válcový naviják lana s nádobou, který lze otáčet klikou – viz obr ) Jeden ze studnařů při vyvážení vykopané zeminy otočil klikou rumpálu 13krát, a tím navinul lano na válec také 13krát. Do jaké hloubky od válce navijáku byla studna v dané chvíli vykopána, víte-li, že průměr válce se rovnal 20 cm?

23. Studnaři provedli válcový výkop pro studnu a posléze ho zpevnili 14 betonovými skružemi tvaru dutého válce s výškou m a vnitřním průměrem 1 m. Nad poslední skruží, která celá vyčnívala nad povrch okolního terénu, dali kryt s pumpou. Po dvou dnech sahala hladina nateklé podzemní vody až k počátku sedmé skruže. Vypočítejte objem této vody.

24. Do strojírenského závodu je dodávána mazací vazelína ve válcových plechovkách s držadly tvaru „půlkružnice“ Vnitřní hloubka plechovky se rovná 30 cm a průměr jejího dna je 28 cm. Vypočítejte:

a) objem vazelíny v jedné plechovce v litrech, b) spotřebu plechu na výrobu 50 plechovek ve čtverečných metrech (na spojové „švy“ připočítejte 20 % plechu navíc),

c) délku držadla po zaokrouhlení na centimetry

25. Na korbu nákladní vozu o nosnosti 3 tuny naložil před první jízdou závozník 1 000 ocelových „prutů“. Každý z nich měl hmotnost 3 kg. Před druhou jízdou naskládal „pruty“ s kruhovými průřezy, které měly průměry 2 cm a délky 4 m. Byly vyrobeny z oceli, která měla hustotu ρ=.

7600 kg m 7,6 g cm 33

a) Byla při první jízdě „třítunka“ přetížena?

b) Kolik ocelových prutů směl závozník na korbu „třítunky“ naložit, jestliže ji nechtěl přetížit?

IV. KONSTRUKČNÍ ÚLOHY

Zopakujme si:

Řešení konstrukčních úloh provádíme obvykle některou z těchto metod:

• pomocí množin dané vlastnosti

Příklad 1

Sestrojte ∆ABC s velikostí stran |AB| = c = 6 cm, |BC| = a = 4 cm a výšky vc = 3 cm. Řešení:

a) Umístění žádného z daných prvků není textem příkladu dáno, proto se rozhodneme pro umístění jednoho z daných prvků – úsečky AB.

b) Vrchol C má od bodu B vzdálenost 4 cm a od přímky AB 3 cm. Leží proto na – kružnici k(B; 4 cm), – na přímkách m nebo n, pro které platí: m || ↔ AB, n || ↔ AB

Ze zmenšeného obrázku konstrukce je zřejmé, že v rovině existují čtyři různé trojúhelníky splňující dané podmínky Platí pro ně:

∆ABC ≅ ∆ABC1

∆ABC´ ≅ ∆ABC2

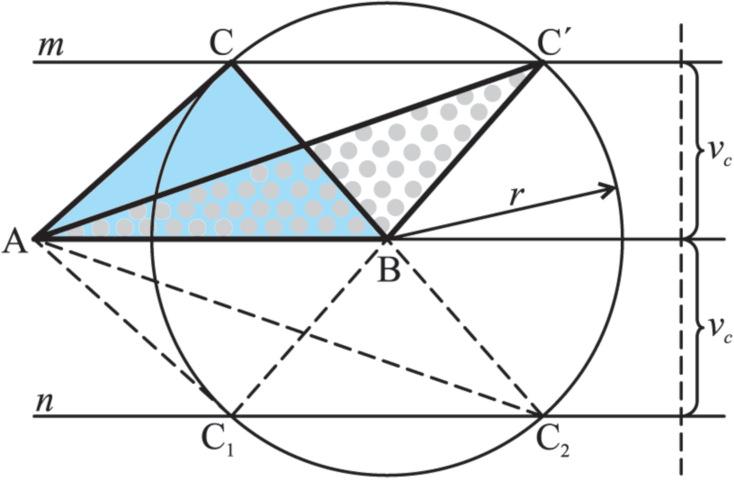
Každé dva trojúhelníky jsou souměrně sdružené podle osy AB. Matematici se domluvili, že každá konstrukce se bude provádět jen v jedné z polorovin, a proto příklad 1 má jen dvě řešení – trojúhelníky ABC a ABC´, které nejsou shodné

• na základě výpočtu

Tato metoda se pro svoji náročnost provádí jen na středních a vysokých školách.

• pomocí zobrazení –v osové souměrnosti

Příklad 2:

Je dána kružnice k(S; 3 cm) a bod P tak, že |PS| = 7 cm. Sestrojte tečny kružnice k procházející bodem P.

Řešení: (viz obr )

Z obrázku je zřejmé, že příklad 2 má 2 řešení.

Tato sbírka slouží učitelům k rozšíření námětů procvičovacích úloh využitelných přímo při vyučování, nebo za domácí úkol. Je rozdělena na část algebraickou a geometrickou. V závěru sbírky najdete klíč k řešení všech úloh. Řazení tematických celků odpovídá struktuře učebnic matematiky pro 8. ročník (algebra a geometrie) vydaných naším nakladatelstvím. Univerzálnost sbírky však zajišťuje její využití nezávisle na těchto učebnicích.

Ve zmíněné řadě učebnic jsou pro každý ročník určeny dvě učebnice, z nichž jedna je věnována aritmetice (algebře), druhá geometrii. Praktickým a užitečným doplňkem učebnic jsou pracovní sešity ke každé z nich.

Koncepce učebnic vychází z osvědčené praxe škol, vyhovuje záměrům Rámcového vzdělávacího programu pro základní vzdělávání. O tom svědčí mimo jiné i udělená schvalovací doložka MŠMT.

Celou řadu učebnic matematiky pro 6.–9. ročník ZŠ tvoří:

Matematika pro 6. ročník ZŠ – aritmetika (učebnice a pracovní sešit)

Matematika pro 6. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Sbírka úloh z matematiky pro 6. ročník ZŠ

Matematika pro 7. ročník ZŠ – aritmetika (učebnice a pracovní sešit)

Matematika pro 7. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Sbírka úloh z matematiky pro 7. ročník ZŠ

Matematika pro 8. ročník ZŠ – algebra (učebnice a pracovní sešit)

Matematika pro 8. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Sbírka úloh z matematiky pro 8. ročník ZŠ

Matematika pro 9. ročník ZŠ – algebra (učebnice a pracovní sešit)

Matematika pro 9. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Sbírka úloh z matematiky pro 9. ročník ZŠ

Pro výuku matematiky na 1. stupni ZŠ je určena obdobná ucelená řada učebnic. (blíže viz www.spn.cz)