Sbírka úloh z matematiky 6

6 SBÍRKA ÚLOH Z MATEMATIKY

pro základní školy

OBSAH

I. ÚVODNÍ OPAKOVÁNÍ

1. Přirozená čísla ..............................................................................................................7

2. Rovnosti a nerovnosti mezi přirozenými čísly .............................................................9

3. Zápisy a porovnávání přirozených čísel........................................................................9

4. Zaokrouhlování přirozených čísel ..............................................................................10

5. Sčítání a odčítání přirozených čísel ............................................................................12

6. Násobení a dělení přirozených čísel ...........................................................................13

7. Zlomky – rozšiřující učivo .........................................................................................16

II. DĚLITELNOST

1. Násobek, dělitel a jiné pojmy......................................................................................18

2. Dělitelnost deseti, pěti a dvěma ..................................................................................20

3. Dělitelnost třemi a devíti.............................................................................................21

4. Prvočísla a čísla složená..............................................................................................23

5. Společní dělitelé a společné násobky .........................................................................24

III. DESETINNÁ ČÍSLA

1. Zápis desetinných čísel ...............................................................................................26

2. Porovnávání desetinných čísel ...................................................................................28

3. Zaokrouhlování desetinných čísel ..............................................................................30

4. Sčítání a odčítání desetinných čísel

IV. JEDNOTKY DÉLKY, OBSAHU A HMOTNOSTI

1. Násobení a dělení desetinného čísla deseti, stem a tisícem ........................................33

2. Jednotky délky ............................................................................................................35 3. Jednotky obsahu .........................................................................................................36 4. Jednotky hmotnosti

V. NÁSOBENÍ A DĚLENÍ DESETINNÝCH ČÍSEL

1. Násobení desetinného čísla přirozeným číslem ..........................................................39

2. Násobení desetinného čísla desetinným číslem ..........................................................40

3. Dělení desetinného čísla přirozeným a desetinným číslem

4. Opakování násobení a dělení

VI. ZÁVĚREČNÉ OPAKOVÁNÍ

1. Dělitelnost ..................................................................................................................45

2. Desetinná čísla ............................................................................................................

3. Jednotky délky, obsahu a hmotnosti

GEOMETRIE

I. PROSTOR A JEHO ZOBRAZENÍ

1. Různá zobrazení prostoru – prostorových útvarů .......................................................53

2. Zjednodušování tvarů a poloh prostorových útvarů a jejich umístění .......................55

3. Zobrazujeme, zapisujeme a počítáme .........................................................................56

II. ÚHEL

1. Úhel, přenášení úhlů...................................................................................................61

2. Osa úhlu......................................................................................................................63

3. Velikost úhlu............................................................................................................... 63

4. Grafické sčítání a odčítání úhlů..................................................................................66

III. OSOVÁ SOUMĚRNOST

1. Shodné útvary.............................................................................................................68

2. Osová souměrnost......................................................................................................69

3. Osově souměrné útvary..............................................................................................71

IV. TROJÚHELNÍK

1. Úhel a trojúhelník .......................................................................................................74

2. Rovnoramenné a rovnostranné trojúhelníky ..............................................................75

3. Výšky trojúhelníku .....................................................................................................77

4. Těžiště a těžnice trojúhelníku .....................................................................................78

5. Kružnice opsaná a vepsaná trojúhelníku ....................................................................79

6. Opakování učiva o trojúhelníku .................................................................................80

V. KRYCHLE A KVÁDR

1. Zobrazení krychle a kvádru ........................................................................................83

2. Povrch kvádru a krychle .............................................................................................84

3. Objem kvádru a krychle .............................................................................................85

4. Jednotky objemu .........................................................................................................87

5. Opakování učiva o kvádru a krychli ..........................................................................88

VI. ZÁVĚREČNÉ OPAKOVÁNÍ

1. Prostor a jeho zobrazení .............................................................................................89

2. Úhly ............................................................................................................................90

3. Osová souměrnost ......................................................................................................92

4. Trojúhelník .................................................................................................................93

5. Krychle a kvádr ..........................................................................................................94

VÝSLEDKY ...................................................................................................................103

II. DĚLITELNOST

1.Násobek, dělitel a jiné pojmy

1. Nejdřívesi zopakujme:

Jestliže například pro čísla 3, 4, 12 platí 12 = 3 · 4, pak říkáme:

přesněji trojnásobkem čísla 4

číslo 12 je násobkem

přesněji čtyřnásobkem čísla 3 nebo

číslem 4 (12 : 4 = 3)

číslo 12 je dělitelné dělenec dělitel podíl číslem 3 (12 : 3 = 4)

Určete: a) aspoň dva násobky čísel 2; 3; 5; 7; 11; 13, které jsou větší než 10, b) trojnásobek čísla 12, c) sedminásobek čísla 6.

2. Napište pět násobků čísla 10 počínaje jeho jednonásobkem, pak pokračujte dvojnásobkem, trojnásobkem atd.

3. Rozhodněte, zda první číslo číselné dvojice je dělitelné jejím druhým číslem: a) 18; 3 b) 35; 7 c) 93; 7 d) 684; 18

4. Určete největší číslo, které je násobkem prvního čísla zdvojice aje menší než druhé číslo zdvojice: a) 7; 60 b) 5; 73 c) 13;70 d) 32; 165

5. Napište všechny násobky čísla 17, které jsou větší než 40 amenší než 90.

6. Doplňte čísla do prázdných rámečků, víte-li, že jsou pokračovateli násobků čísla: a) 5 ... 35; 40; ; 50; 55; ; ; ... ; 130; . b) 9 ... 72; ; 90; 99; 108; ... ; 252; ; ; ... ; 999; .

7. Určete, která zčísel 18; 23; 36; 45; 51; 60; 63; 88; 90; 108 jsou násobky čísla: a) 2b) 3 c) 5 d) 8 e) 9 f) 10

8. Čím je zajímavý zápis čísla, které se rovná součtu sedminásobku čísla 131, dvojnásobku čísla 47 astonásobku čísla 101?

9. Určete aspoň tři dělitele každého znásledujících čísel kromě dělitele 1: a) 20 b) 32 c) 40 d) 64 e) 72 f) 100

10. Která zčísel 96; 207; 6 283; 5536 jsou dělitelná číslem a) 2; b) 3; c) 4; d) 8?

11. Najděte všechna dvojciferná čísla menší než 20, která mají jen dva samozřejmé dělitele, ato číslo 1 asamo sebe.

12. Napište všechna přirozená čísla, která jsou děliteli (včetně samozřejmých dělitelů) čísla: a) 72 b) 84

13. Tečky nahraďte souslovím „je (není) násobkem“, „je (není) dělitelem“, „je (není) dělitelné“: a) Číslo 5 ............. 15.b) Číslo 33 ............. 11. c) Číslo 20 ............. 8. d) Číslo 80 .......... 20.e) Číslo 7 ................ 42. f) Číslo19 ............ 19.

14. Určete všechna čísla, která jsou a) násobky čísla 6 azároveň děliteli čísla 48, b) násobky čísla 5 azároveň děliteli čísla 60.

15. Při přespolním běhu závodilo několik družstev, která učitel tělocviku vytvářel z24 chlapců dvou šestých tříd. Na kolik stejně početných družstev mohli být všichni chlapci rozděleni? (Jedinec netvoří družstvo.)

16. Po prohlídce ZOO šlo 30 žáků 6. třídy spolu spaní učitelkou na oběd. Ukaždého stolu vedle oken restaurace byly 3 židle, ukaždého ze zbývajících stolů bylo po 4 židlích. Všichni se posadili ke stolům tak, že žádná židle obsazeného stolu nebyla volná. Kolik stolů se třemi akolik se čtyřmi židlemi bylo jimi obsazeno?

17. Lištu dlouhou 280cm rozřezal truhlář na stejné díly tak, že délku každého dílu bylo možné vyjádřit počtem celých decimetrů (tedypřirozeným číslem). Jaké délky mohly jednotlivé díly mít?

18. Zahradník Jonatán uvažoval: „Budu-li vázat kytice po 7 růžích, žádná mi nezbude.“ Po skončení vázání kytic přišel na to, že by mu žádná růže též nezbyla, kdyby kytice vázal po 9 růžích. Kolik růží pan Jonatán nařezal, víte-li, že jich bylo více než 120 améně než 130?

19. Blanka bydlí vnovém paneláku s24 byty. Tlačítka zvonků ke všem bytům mohl elektrikář umístit na obdélníkový panel alespoň do dvou sloupců apříslušný počet řádků tak, aby všechny sloupce iřádky byly těmito tlačítky rovnoměrně zaplněny. Kolika způsoby mohl elektrikář všechna zvonková tlačítka na panel umístit?

10. Prázdné obdélníčky nahraďte jedním ze znaků = , ≠ , který do nich patří:

a) 3,2 3,20 b) 4,8 4,08 c) 9,802 9,01 d) 327,014 327,140 e) 6 786 6786,000 f) 5000005,5 500000,5

1. Uspořádejte:

2.Porovnávání desetinných čísel

a) sestupně čísla: 0,71; 0,55; 0,39; 0,72; 0,03, b) vzestupně čísla: 2,101; 2,110; 2,011; 2,010; 2,001.

2. Obdélníčky nahraďte jedním ze znaků >, <, = :

a) 0,17 0,16 b) 4,007 4, 070 7c) 9, 002 9,003 d) 4,03 4, 30 e) 0,5 1 2 f) 0,250 1 4 g) 0,555 555 1 000 h) 0,505 0,55 i) 0,173 0,163 7 j) 0,898 9 0,900 3 k) 2,009 2,011 0 l) 545,000 545

3. Vyhledejte a) nejmenší, b) největší zčísel: 0,58; 0,508; 0,85; 0;580.

4. Zčíslic 4; 0; 2; 1 vytvořte zápis a) co největšího, b) co nejmenšího desetinného čísla.

5. Porovnejte podle velikosti:

a) 0,28m a 1 4 mb) 2,2m a232cm c) 3 1 000 m a0,03m

d) 2,305m a2315mme) 5,4dm a54cmf) 1 2 cm a6mm

g) 1,1kg a1,3kg h) 3,04kg a3,1kg i) 7,001kg a7,1kg

j) 4,8t a480kg k) 1 2 t a5,0kg l) 0,5 q a5t

6. A) Určete, na kolikátém místě za desetinnou čárkou vlevo či vpravo je číslice vyjadřující číslo desetkrát a) menší než 100 b) větší než 1 000 c) větší než 1 d) menší než 1 e) menší než 0,1 f) větší než 0,001

B) Určete, počet kterých čísel vyjadřuje číslice na druhém místě a) vpravo od desetinné čárky, b) vlevo od desetinné čárky.

7. Rozhodčí okresního kola plaveckého závodu vkraulu oznámil jména plavců ačasy, kterých dosáhli, spřesností na setiny sekundy:

Bednář 50,25 sDouša 50,79 s

Hamáček 51,21 sJireš 50,84 s

Janák 50,87 sProcházka 50,74 s

Seřaďte jména plavců podle jejich výkonnosti počínaje vítězem.

8. Prodavačka nakrájela porce tvrdého sýru, zabalila je do papíru anapsala na ně jejich hmotnost (viz obr.).

Která ztěchto porcí byla a) nejlevnější, b) nejdražší?

9. Staročeské jednotky –rozšiřující učivo

jednotka délky

český palec

její přibližná velikost

0,025 m

píď 0,197 m

stopa

0,296 m

loket 0,59 m

kročej 1,183 m

sáh 1,774 m

látro

jednotka hmotnosti

2,37 m

její přibližná velikost

hřivna 0,257 kg

česká libra 0,514 kg

jednotka obsahu

jitro

korec

její přibližná velikost

5754,6 m2 = · (0,6 ha)

2877,3 m2 = (0,3 ha)

jednotka objemu její přibližná velikost

žejdlík

holba

0,358 l (litru)

0,7 l (litru)

máz 1,4 l (litru)

Pro porovnávání jejich velikostí svelikostmi dnes užívaných jednotek nahraďte obdélníčky znaky > , < , = :

a) 1 č.palec 3cm b) 1 píď 197mm c) 1 stopa 3dm

d) 1 loket 0,5m e) 1 kročej 2m f) 1 sáh 2m

g) 1 látro 2,5m h) 1 hřivna 0,5kg i) 1 č.libra 0,5kg j) 1 jitro 0,5 ha k) 1 korec 0,5 ha l) 1 žejdlík 0,5 litru

m) 1 holba 1 litr

n) Vjedné staré české písničce se zpívá:

„Pějme píseň dokola okolo stola. Komu píseň schází,zaplatí dva mázy.“

Vypočítejte objem piva, který by měl být podle textu písně zaplacen.

4.Jednotky hmotnosti

1. Zopakujte si používané převodní vztahy mezi jednotkami hmotnosti:

Poznámka: Víte, že základní jednotka soustavy SI prohmotnost je 1 kilogram

Vedlejšíschéma převodních vztahů naznačuje vytváření násobků adílůzákladní jednotky.

Metrický cent (q) jako jednotka hmotnosti vsoustavě SInení uvedena. Přesto se unás občaspoužívá. Hovorový výraz „metrák“ můžete občas slyšet, například ve spojitostech: „Vzimě jsme spálili dvacet metráků uhlí.“ – „Pekaři zpracovali za týden osm metráků mouky.“ –„Koupím si půl metráku cementu.“ atd.

2. Vypočítejte:

a) 12,3t – 4,8t

d) 6500g – 2,3kg

g) 2,8kg · 10kg

b) 8,7t – 2500kg

e) 3,9kg – 300g

h) 13,5 q · 100 (q i t)

3. Zaokrouhlete na celé kilogramy:

a) 23,745kg

d) 1303,8kg

b) 930g

e) 206,1kg

c) 1,4kg + 780g

f) 4000mg + 2000g

i) 2,5t : 1000kg

c) 7,876 q

f) 8345g

4. Pan Kadlec je vytrvalostní běžec. Před posledním maratonským závodem (42km 195m) apo jeho skončení si zjistil svou tělesnou hmotnost. Dospěl khodnotám: 76,2kg a 72,8kg.

a) Zaokrouhlete délku maratonu na desetinu kilometru. b) Vypočítejte rozdíl mezi oběma hodnotami tělesné hmotnosti pana Kadlece apokuste se to zdůvodnit.

V. NÁSOBENÍ A DĚLENÍ DESETINNÝCH ČÍSEL

1. Vynásobte písemně:

1.Násobení desetinného čísla přirozeným číslem

a) 0,49 · 5 b) 27,4 · 73 c) 1,268 · 205 d) (41,5 + 2,38) · 2 e) (213,865 – 13,065) · 35 f) (86,7 – 5,24) · (19,9 – 0,9) g) 5,62 · 10 h) 0,836 · 100 i) 752,4 · 1000

2. Vyjádřete nejkratším možným zápisem čísla: 1,050 0 2,160 50,410 00 0,750 000 a pak je postupně vynásobte čísly: a) 3 b) 67 c) 138 d) 10

3. a)Kčíslu 23,8 přičtěte jeho trojnásobek.

b) Kdvojnásobku čísla 5,6 přičtěte čtyřnásobek čísla 8,7.

c) Od pětinásobku čísla 23,8 odečtěte trojnásobek čísla 4,75.

4. Vypočítejte: a) 5 · 0,7 · 4 b) 8 · 3,9 · 52 c) 64 · 23,5 · 12

5. Vobchodě prodávali minerální vodu vplastových lahvích sobjemem 0,5 litru a 0,75 litru.Kolik litrů minerální vody zůstalo ve 2 malých a 5 velkých neprodaných lahvích?

6. Paní Vávrová koupila 12 krabic polotučného mléka po 14,50 Kč a 6 housek po 2,50Kč. U pokladny platila bankovkou vhodnotě 200 Kč. Kolik korun dostala nazpět?

7. Určete hmotnost nákladu na přepravních kamionech se 3 a 5 osobními automobily (viz obrázek), jestliže hmotnost jednoho převáženého automobilu je 0,75 t.

3. Proveďte náčrty předmětů (věcí), které jsou na následujících obrázcích: a) k danému pohledu zepředu načrtněte pohled shora, b) k danému pohledu zepředu načrtněte pohled shora, c) k danému pohledu zleva načrtněte pohled zprava.

4. Na obrázku je pohled na průčelí dvojdomku. Načrtněte pohled na tento dvojdomek zepředu.

5. Na obrázku jsou vánoční svíčky. Některé z nich se svým tvarem blíží kouli, válci nebo kvádru se čtvercovou podstavou. Načrtněte pohled shora na tyto svíčky.

6. Na obrázku je rotunda sv. Jiří na hoře Říp. Načrtněte přibližně pohled shora (jako byste se na tuto rotundu dívali z velké výšky, např. z letadla).

7. a) Na obrázku vidíte tělesa A, B, C, D, E, F složená ze dvou částí. Načrtněte, jak vypadají při pohledu shora. Poznámka: Obrysy či hrany těchto těles, které jsou při tomto pohledu neviditelné, rýsujte čárkovanými čarami, ostatní plnými. Viditelné vrcholy kuželů vyznačte plnými kroužky, neviditelné prázdnými kroužky. Viditelné vrcholy krychle (tělesa B) a viditelný vrchol kuželu (těleso F) se při pohledu shora kryjí s neviditelnými vrcholy. Rýsujte je jako viditelné.

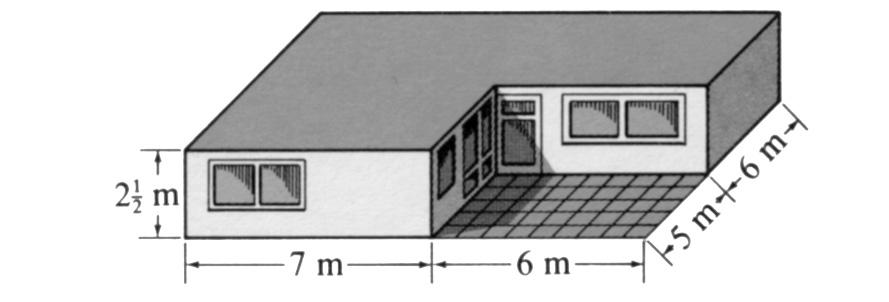
8. Na obrázku je zobrazena šatna dětského koupaliště. Načrtněte pohled na tuto šatnu: a) shora b) zepředu c) zprava

Poznámka: Všechny uvedené rozměry šatny, a to i při pohledu zprava, jsou skutečné (nezkrácené). Při tvorbě náčrtku použijte vztah: 1 metr ve skutečnosti = 1 cm v náčrtku

2.Zjednodušování tvarů a poloh prostorových útvarů a jejich umístění

1. Blanka připravila jídelní obdélníkový stůl se čtyřmi židlemi a s prostíráním pro čtyři osoby na slavnostní oběd k 35. maminčiným narozeninám. Načrtněte zmenšený pohled shora na tuto Blančinu slavnostní tabuli. Židle a příbory zobrazte jako úsečky, dvojice talířů na obdélníkových ubrouscích a nápojové skleničky na čtvercovém podnosu vyjádřete příslušnými geometrickými obrazci odpovídajících tvarů a zmenšených velikostí. Potřebné rozměry si zvolte.

B)Jsou obrazy chrousta (sdélkou 3,5 cm) a kancelářské sponky také osově souměrné útvary?

3. Na obrázcích a), b), c) jsou tři kružnicové ornamenty. Představují osově souměrné útvary? Pokud ano, uveďte u jednotlivých ornamentů počet jejich os souměrnosti.

4. Jsou útvary na obrázcích a), b), c), d) osově souměrné? Pokud ano, uveďte počet jejich os souměrnosti.

5. Prohlédněte si obrazy státních vlajek Dánska, Francie, Japonska a Kanady na obrázku a rozhodněte, zda jsou osově souměrné. Pokud ano, určete počet jejich os souměrnosti. (Poznámka: Při osové souměrnosti různobarevných útvarů vyžadujeme, aby vzor a obraz měly nejen shodné tvary, ale i stejnou barevnost. U vlajky b) je ve skutečnosti levá třetina modrá a pravá třetina červená.)

6. Na obrázku jsou obrazy několika dopravních značek.

A)Na co řidiče upozorňují, nebo co mu přikazují či zakazují?

B)Které ztěchto značek

a) nejsou osově souměrné, b) jsou osově souměrné a podle kolika os?

7. Na obrázku vidíte Salisburskou katedrálu (postavenou ve Velké Británii v 1. polovině 13. století). Tato katedrála je typickým příkladem gotické architektury, která se vyznačovala souměrností staveb. Rozhodněte, zda průčelí katedrály je osově souměrné. Pokud ano, naznačte hranou pravítka, kudy na obrazu průčelí prochází osa souměrnosti.

5.Opakování učiva o kvádru a krychli

1. A)Zobrazte kvádr srozměry 4,2 cm, 5,6 cm a 8 cm.

B)Vypočítejte: a) v dm2 jeho povrch,b) v litrech jeho objem.

2. A)Zobrazte krychli sobsahem jedné stěny 36 cm2.

B)Vypočítejte: a) v dm2 její povrch,b) v dm3 její objem.

3. Veterinární lékař vozí ve skladovacím prostoru svého automobilu plechovou bednu tvaru kvádru srozměry 110 cm, 60 cm, 65 cm. Převáží vní ke zvířecím pacientům mimo jiné nezbytné chirurgické náčiní, léky, především anestetika, tj. léky na znecitlivění aj. (viz obr.). Vypočítejte její objem vkrychlových metrech.

4. Pan Šafařík naplnil benzinem na počátku roku 2010 pětilitrový kanystr (viz obr.). Jeho vnitřní prostor měl tvar kvádru se stejnou délkou i hloubkou 25 cm.

Vypočítejte: a) jeho vnitřní šířku, b) cenu 5 l benzinu po 36 Kč za 1 litr.

5. Vypočítejte objemy (Vš) šedých i objemy (Vf) fialových částí těles A, B, C, D, která jsou zobrazena na obrázku v centimetrové čtvercové síti (zmenšené na polovinu). Poznámka: Šedá část tělesa A má výšku 1,2 cm, šedá část tělesa B má výšku 0,6 cm. Délka šikmo narýsované úsečky (rozměr b) se ve skutečnosti (z důvodu názornosti) také rovná 1 cm.

VI. ZÁVĚREČNÉ

VI. ZÁVĚREČNÉ OPAKOVÁNÍ

1.Prostor a jeho zobrazení

1. Na obrázku je těleso, které můžeme nazvat kvádr svýřezem. Narýsujte toto těleso při pohledu: a) zleva ashora b) zepředu c) shora d) zdola

Neviditelné hrany při pohledu zdola narýsujte čárkovanými čarami.

2. Na obrázku je zjednodušená kresba staršího typu venkovského domu sněkolika základními rozměry. (Chybějící rozměry oken, dveří aj. odhadněte.)

Načrtněte pohled na tento dům: a) shora, b) zepředu, c) zprava.

Poznámka: V náčrtu zachovejte vztah: 1m ve skutečnosti = 1cm vnačrtnutém obrázku

Tato sbírka slouží učitelům k rozšíření námětů procvičovacích úloh využitelných přímo při vyučování, nebo za domácí úkol. Je rozdělena na část aritmetickou a geometrickou. V závěru sbírky najdete klíč k řešení všech úloh. Řazení tematických celků odpovídá struktuře učebnic matematiky pro 6. ročník (aritmetika a geometrie) vydaných naším nakladatelstvím. Univerzálnost sbírky však zajišťuje její využití nezávisle na těchto učebnicích. Ve zmíněné řadě učebnic jsou pro každý ročník určeny dvě učebnice, z nichž jedna je věnována aritmetice, druhá geometrii. Praktickým a užitečným doplňkem učebnic jsou pracovní sešity ke každé z nich.

Koncepce učebnic vychází z osvědčené praxe škol, vyhovuje však i záměrům

Rámcového vzdělávacího programu pro základní vzdělávání. O tom svědčí mimo jiné i udělená schvalovací doložka MŠMT.

Celou řadu učebnic matematiky pro 6. – 9. ročník ZŠ tvoří:

Matematika pro 6. ročník ZŠ – aritmetika (učebnice a pracovní sešit)

Matematika pro 6. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Sbírka úloh z matematiky pro 6. ročník ZŠ

Matematika pro 7. ročník ZŠ – aritmetika (učebnice a pracovní sešit)

Matematika pro 7. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Sbírka úloh z matematiky pro 7. ročník ZŠ

Matematika pro 8. ročník ZŠ – algebra (učebnice a pracovní sešit)

Matematika pro 8. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Sbírka úloh z matematiky pro 8. ročník ZŠ

Matematika pro 9. ročník ZŠ – algebra (učebnice a pracovní sešit)

Matematika pro 9. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Sbírka úloh z matematiky pro 9. ročník ZŠ

Pro výuku matematiky na 1. stupni ZŠ je určena obdobná ucelená řada učebnic. (blíže viz www.spn.cz)