Matematika 8 - Geometrie

pro základní školy

RPZ A COVÁNO V SOULAD U S RVP PRO ZÁKLADNÍ VZDĚLÁVÁNÍ V = � r 2 v A T S M T' C B v r

8MATEMATIKA geometrie

Zpracovali: prof. RNDr. Zdeněk Půlpán, CSc., Mgr. Michal Čihák, Ph.D., Mgr. Josef Trejbal

Lektorovali: PaedDr. Eva Kučinová, RNDr. Václav Sýkora, CSc., Mgr. Barbora Stušová

Schválilo MŠMT č. j. MSMT-26392/2021-5 dne 23. 11. 2021 k zařazení do seznamu učebnic pro základní vzdělávání jako součást ucelené řady učebnic pro vzdělávací obor Matematika a její aplikace s dobou platnosti šest let.

Tato učebnice je třetí částí ucelené řady učebnic pro výuku matematiky na 2. stupni základních škol. Věnuje se algebraické části učiva 8. ročníku ZŠ, je přehledná, důkladně vysvětluje učivo a je vybavena dostatečným množstvím úloh k procvičení a upevnění probraného učiva. Doplňuje ji pracovní sešit.

Koncepce celé řady matematik vychází z osvědčené praxe škol. Respektuje však také doporučení a záměry Rámcového vzdělávacího programu pro základní vzdělávání. O tom svědčí mimo jiné i udělená schvalovací doložka MŠMT.

Celou koncepční řadu učebnic tvoří tyto publikace:

Matematika pro 6. ročník ZŠ – aritmetika (učebnice a pracovní sešit)

Matematika pro 6. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Matematika pro 7. ročník ZŠ – aritmetika (učebnice a pracovní sešit)

Matematika pro 7. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Matematika pro 8. ročník ZŠ – algebra (učebnice a pracovní sešit)

Matematika pro 8. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Matematika pro 9. ročník ZŠ – algebra (učebnice a pracovní sešit)

Matematika pro 9. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Vhodným doplňkem učebnic je řada sbírek cvičení a příkladů z matematiky (viz www.spn.cz).

ISBN 978-80-7235-653-9

OPAKOVÁNÍ

I. KRUŽNICE A KRUH

1. Zobrazení kružnice a kruhu ...........................................................................................12

2. Kružnice a přímka .........................................................................................................16

3. Vzájemná poloha dvou kružnic

4. Thaletova věta ...............................................................................................................24

5. Tečny kružnice procházející daným bodem ..................................................................28

6. Délka kružnice a obvod kruhu ......................................................................................31

7. Obsah kruhu ...................................................................................................................34

8. Části kružnice a kruhu (rozšiřující učivo)

II. VÁLEC

1. Základní pojmy ..............................................................................................................40

2. Povrch a objem válce ....................................................................................................41

3. Válcová tělesa kolem nás..............................................................................................46

4. Souhrnná cvičení k tématům Kružnice, Kruh a Válec ..................................................49

III. KONSTRUKČNÍ ÚLOHY

1. Jednoduché konstrukční úlohy ......................................................................................57

2. Množiny bodů dané vlastnosti .......................................................................................60

3. Konstrukční úlohy řešené pomocí množin bodů dané vlastnosti .................................66

4. Souhrnná cvičení ...........................................................................................................78

IV. ZÁVĚREČNÉ

3

OBSAH

Úhly .....................................................................................................................................5 Shodnost ..............................................................................................................................5 Čtyřúhelníky ........................................................................................................................7 Souměrnost

Hranoly ..............................................................................................................................10

..........................................................................................................................9

.....................................................................................21

.....................................................................36

OPAKOVÁNÍ ....................................................................................80 VÝSLEDKY ....................................................................................................................87

2. II.Podle následujícího obrázku a) sestrojte do dvoucentimetrové sítě obrazec ohraničený čtyřmi shodnými čtvrtkružnicemi avyznačte všechny jeho osy, popřípadě středy souměrnosti. Kolik má os souměrnosti akolik středů souměrnosti?

II.Podle obrázku b) sestrojte ve svých sešitech geometrický útvar adoplňte ho tak, aby byl souměrný podle středu S.Pokud existují ijeho osy souměrnosti, narýsujte je. Vkladném případě uveďte jejich počet.

Hranoly

1. Vypočítejte povrch pravidelného čtyřbokého hranolu stělesovou výškou vt = 2,3dm apodstavou tvaru

a) kosočtverce se stranou a = 1,4dm avýškou kní příslušnou va = 1,1 dm, b) pravoúhlého trojúhelníku sodvěsnami délek 28 cm, 45cm apřeponou délky 53cm. (Trojúhelník suvedenými délkami stran je určitě pravoúhlý.)

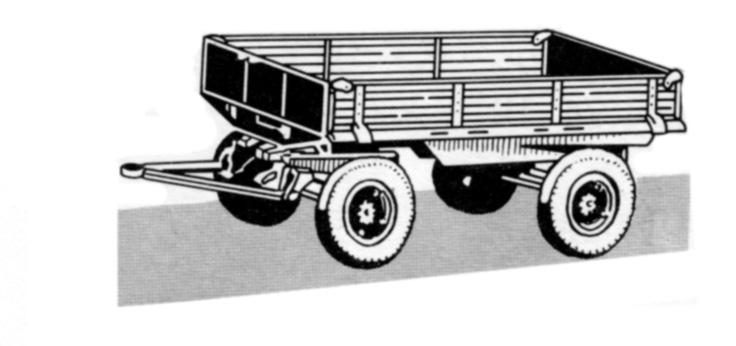
2. Na obrázku je přívěs za traktor.

a)Kterému geometrickému tělesu se blíží vnitřní prostor jeho korby?

b)Vypočítejte objem této korby, víte-li, že má rozměry 4,5 m, 2,4m a0,65m.

10

? OPAKOVÁNÍ E a) b) c) d) e) f) g) h) i) B´ B A´ S b) a)

c)Jakou hmotnost má naložený písek na této korbě, jestliže průměrná výška

vrstvy písku je 0,37m ahustota

písku ρ = 1500?

✽ 3. Psí bouda (viz obrázek) je zhotovena zprken. Vypočítejte jejich spotřebu ve čtverečných metrech spředpokladem, že vdůsledku jejich tvarové úpravy se zvýšila jejich spotřeba asi o8 %.

(Podlaha boudy má tvar obdélníku srozměry 0,9m a0,8m.)

4. Otvory vděrované cihle na obrázku zaujímají 10 % objemu plné cihly srozměry 30 cm, 15cm a7,5cm. Vypočítejte

a)hmotnost jedné děrované cihly, víte-li, že hustota vypáleného cihlového materiálu

je ρ = 1800 , (1,8)

kg m3 kg dm3 kg m3

b)počet děrovaných cihel, který smí řidič naložit na korbu nákladního auta snosností 5 tun, nemá-li být toto auto přetíženo.

5. Akciový zemědělský podnik vybudoval na svých pozemcích nádrž na vodu určenou kzavlažování zeleniny. Voda do ní přitékala odbočkou zmístního potoka. Tvar arozměry vodní nádrže jsou na obrázku. Vypočítejte její objem.

11

OPAKOVÁNÍ ?

3. ✽ 5.

Jaká je vzdálenost bodu A od přímky p?

Je to |AX| ?

Je to |AP| ?

Je to |AZ| ?

Všimněte si:

Vzdálenost bodu A od přímky p měříme na kolmici vedené bodem A kpřímce p.

Bod P je pata kolmice.

Vzdálenost bodu A od přímky p zapíšeme |Ap|.

Cvièení B1

1. Určete vzdálenost průsečíku úhlopříček čtverce o velikosti strany 5 cm od některé zjeho stran. Načrtněte obrázek.

2. Rozhodněte, zda vzdálenost bodu Sod přímky p je větší než poloměr kružnice k(S; 4 cm), je-li p její: a) sečnou, b) tečnou, c) vnější přímkou. (Načrtněte si obrázek.)

3. Je dán obdélník ABCD, pro jehož strany platí |AB| = 5 cm, |BC| = 3 cm. Určete vzdálenost bodu A od přímky BC.

4. Sestrojte kružnici k(S; 2,5 cm).

a) Narýsujte libovolnou přímku v, která bude vnější přímkou této kružnice.

b) Sestrojte s přímkou v rovnoběžnou přímku t, která bude tečnou kružnice k.

c) Pak narýsujte přímku s, která bude soběma předchozímipřímkami rovnoběžná a bude sečnou kružnice k. Označte její dva průsečíky skružnicí k písmeny A, B.

d) Sestrojte osu úsečky AB. Kterým bodem prochází?

5. Jsou dány dva body X, Y (X ≠ Y) kružnice k. Je vzdálenost úsečky XY od středu této kružnice rovna jejímu poloměru?

Tečna kružnice

Zvolte bod S a narýsujte kružnici k(S; 2,5 cm).

Dále narýsujte sečnu s kružnice k; sečna s protne kružnici k vbodech A, B.

Pak se snažte co nejpřesněji sestrojit jednu tečnu t kružnice k tak, aby platilo t || s.

Budete-li dost pečliví, dostanete bod dotyku, který označte T.

18

I. KRUŽNICE A KRUH B

C

Je-li vámi narýsovaná přímka skutečně tečnou kružnice k, pak:

a) přímka t je kolmá na poloměr TS kružnice k, b) trojúhelník ABT je rovnoramenný: |AT| = |BT|, c) trojúhelník ASB je také rovnoramenný: |AS| = |BS|, d) přímka o je osou souměrnosti ΔABT i ΔBAS.

Jak sestrojit tečnu kružnice?

Sestrojení tečny t kružnice k vdaném bodě T

Postup: 1. a) k(S; r) 2. c) přímka ST (↔ ST) 3. d) t; t ⊥↔ ST b) T; T ∈ k

Tečna kružnice je kolmákpřímce, která prochází bodem dotyku a středem kružnice. kk k

Sestrojení tečny t kružnice k, rovnoběžné s danou přímkou p

Postup: 1. a) k(S; r) 2. c) m; m ⊥ p, S ∈ m 3. d) T; T ∈ m ∩ k b) p e) t; t || p, T ∈ t

Cvièení C1

1. Narýsujte kružnici k(S; 3 cm), vyznačte na ní bod T a sestrojte tečnu t, která tímto bodem prochází.

2. Na obrázcích je narýsována vrůzných polohách přímka t a na ní bod T. Překreslete si je do sešitů a narýsujte kružnice k o poloměru 3 cm tak, aby přímka t byla vždy tečnou kružnice k vbodě T.

19

I. KRUŽNICE A KRUH

Příklad 2:

a) Sestrojmetečny t1, t2 kružnice k, k(S; r = 1,4 cm), procházející bodem M (|SM| = 5 cm).

Dotykové body tečen t1, t2 označíme písmeny T1, T2.

(Pozor: Dotykové body vždy musíme určit konstrukcí, ne zkusmo!)

Všimněte si:

↔ T1T2 ⊥↔ SM;

↔ SM je osourovnoramenného

ΔT1T2M i ΔT1T2S; přímka SM je osou úhlu T1MT2.

b) Vpravoúhlém trojúhelníku SMT1 známe velikosti dvou stran: |ST1| = r = 1,4 cm

a |SM| = 5 cm. Podle Pythagorovy věty tedy můžeme určit velikost strany třetí:

|SM|2 = |ST1|2 + |MT1|2

25 = 1,96 + |MT1|2

|MT1|2 = 23,04

|MT1| = 4,8

|MT1| = 4,8 cm

O správnosti konstrukce tečen t1, t2 kružnice k se můžeme přesvědčit výpočtem.

Vzhledem ktomu, že ΔT1T2M je rovnoramenný, je |MT1| = |MT2| = 4,8 cm.

CCvièení

1. Je dána kružnice k(S; 2,5 cm) a bod M, |SM| = 7 cm.

a) Sestrojte tečny t1, t2 kružnice k, které procházejíbodem M. b) Dotykové body tečen skružnicí k označte T1, T2 c) Vypočítejte velikosti úseček MT1, MT2.

2. Bodem M prochází tečna kružnice k(S; r = 1,5 cm) sdotykovým bodem T. Určete vzdálenost bodu M od středu kružnice k, víte-li, že |MT| = 5 cm.

Obdélníku ABCD, |AB| = 5 cm, |BC| = 3 cm, byla opsána kružnice. Vjaké vzdálenosti od středu této kružnice leží bod M, kterým procházejí tečny ktéto kružnici : Bod M sestrojte a vzdálenost středu kružnice od bodu M změřte.)

Thaletova věta

První, kdo zformuloval tento poznatek jako matematickou větu, byl nepochybně Thales zMilétu (asi 624 – 543 př. n. l.). Patřil mezi nejvýznamnější řecké filozofy, matematiky a astronomy. Předpokládal kulový tvar Země. Výšky pyramid určoval pomocídélek jejich stínů. Pověstná prý byla i Thaletova soustředěnost na řešení vědeckých problémů. Traduje se, že jednou vnoci při sledování hvězdné oblohy spadl do hluboké jámy. Pokřikem si přivolal pomoc. Někteří lidé mu pak posměšněpředhazovali: „Jak bys moh‘, Thalete, poznat nebeské hvězdy, když ani nevíš, co je na zemi.“ Thales zMilétu

30

I. KRUŽNICE A KRUH

6. Délka kružnice a obvod kruhu

Ze čtvrtky si vystřihneme kruhy různých poloměrů, např. 5 cm, 6 cm, 8 cm. Budeme zkoumat, kolikrát je obvod kruhu (o) větší než jeho průměr (d):

Poměr je pro všechny kruhy stejný. Přesnou hodnotu poměru však takto nezjistíme, proto ho jen označíme řeckým písmenem π [pí]:

Ztabulky vidíme, že číslo π můžeme odhadnout a zapsat číslem 3,14. Pro naše výpočty tento odhad sice postačuje, ale vtechnice se musí použít jeho přesnější přibližná hodnota. Číslo π vypočítal roku 1615 dokonce na 35 desetinných míst Ludolf van Ceulen [kélen], proto se mu říká Ludolfovo číslo.

Na číselné ose je zobrazované číslo π bodem, jehož souřadnice se musí zapsat nekonečným počtem číslic; vyjadřuje se proto často jeho dolním a horním odhadem:

dolní odhad ... 3,1415 < π < 3,1416 ... horní odhad

Číslo π bylo odhadováno již ve starověku. Staří Egypťané užívali odhad π ve tvaru zlomku , Babyloňané ve tvaru . Archimedes dospěl kpoměrně přesnému odhadu čísla π: 3 + < π < 3 + .

31

I. KRUŽNICE A KRUH

A d o 5 cm 15,7 cm 3,14 6 cm 18,8 cm 3,14 8 cm 25,1 cm

d o d 22 7 28 8 10 71 10 70 o d o d = π o

π . d o

πr 01234 π

3,14 o

=

= π . 2r = 2

Postup konstrukce:

Sestrojíme obdélník srozměry o = 11,3cm, a v = 3,2cm.

Narýsujeme dvě shodné kruhové podstavy spoloměry r = 1,8cm tak, aby se dotýkaly stran obdélníku. Jako body dotyku kruhů (podstav) sobdélníkem můžeme zvolit kterékoli body dvou jeho stran sdélkou 11,3cm.

Zpravidla je sestrojujeme tak, aby přímka S1S2, která prochází body dotyku, byla kolmá ke stranám obdélníku sdélkou o (viz obr.).

Úkol 1:

Sestrojte síť válce, je-li: a) r = 2 cm, v = 3 cm, b) d = 42 mm, v = 0,5dm.

Příklad 2:

Spolupracujte při odvození vzorce pro výpočet povrchu válce, který je ivzorcem pro výpočet obsahu jeho sítě (viz obr. nahoře).

Odvození:

Po označenía) obsahu podstavy válce Sp platí: Sp = πr2 (podstava je kruh)

b) obsahu pláště válce Spl platí: Spl = o v (plášť je obdélník)

c) povrchu válceS platí: S = 2Sp + Spl

Můžeme pak pro výpočet povrchu válce napsat vzorec: S = 2πr2 + 2πrv, a po algebraické úpravě

S=2πr (r + v)

Příklad 3:

Vypočítejte povrch válce spoloměrem podstavy r = 2,4cm avýškou v = 6,5cm.

Řešení (viz obr.):

r = 2,4cm

v = 6,5 cm

S = ? cm2

S = 2πr2 + 2πrvS=2πr . (r + v)

S = . 6,28 . 2,42 + 6,28 . 2,4 . 6,5 S = . 6,28 . 2,4 . (2,4 + 6,5)

S = 6,28 . 5,76 + 15,072 . 6,5 S = 15,072 . 8,9

S = 36,172 8 + 97,968

S = . 134,140 8

S = . 134,14

S = 134,14 cm2

S = 134,140 8

S = . 134,14

S = . 134,14 cm2

Povrch válce se po zaokrouhlení rovná 134,14 cm2.

v = 6,5 cm r =2,4 cm

42

II. VÁLEC

r o

πr v S2 S1

= 2

Úkol 2:

Vypočítejte povrch válce, je-li dáno: a) r = 7cm , v = 8cm b) d = 9,6 m, v = 4 m

Příklad 4:

Výška válce se rovná 14cm. Jeho plášť má obsah 264 cm2. Vypočítejte a) obvod, b) obsah podstavy válce. (Pro snazší výpočet užijte hodnotu π = . .)

Řešení (viz obr.): a) Spl = 2πrv

264 = 2 . 3,14 . 14 . r

264 = 88r |:88,L za P

r = 3

r = 3cm

b) Sp = πr2

Sp = . 32

Sp = . 9

Sp =

o= 2πr

o = 2 .. 3

o =

o = 9 (= . 9,4)

o= 9 cm (= 9,4 cm)

v =14cm

Sp = 28 (= . 28,29)

Sp = 28 cm2 (= 28,29 cm2)

Spl = 264 cm2

Obvod podstavy válce se přibližně rovná 9,4cm.

Obsah podstavy má přibližnou hodnotu 28,29 cm2

Úkol 3:

Výška válce se rovná 2,1m ajeho plášť má obsah 18,48 m2. Svyužitím hodnoty

π = vypočítejte obvod aobsah podstavy válce.

Objem válce

Pro pochopeníodvození vzorce pro výpočet objemu válce je důležitá ta část válce, které říkáme výseč válce. Je to část válce podobající se klínu, jejíž hrana tvaru úsečky leží vose válce (viz obr. a). Podstavou tohoto tělesa je kruhová výseč.

43

a)b)c) II. VÁLEC 2 3 22 7 22 7 22 7 22 7 66 7 198 7 22 7 2 7 2 7 3 7 3 7 B v r v S1 S2

π

v

r r

Příklad 5:

Na obrázku jsou kružnice srůznými středy aodlišnými poloměry. Všechny procházejí dvěma různými body A, B. Jednu znich, ato kružnici k1, lze zapsat: k1(S1; r1).

Úkol:

Zapište obdobně zbývající dvě kružnice avyslovte názor na danou vlastnost středů všech kružnic na obrázku.

Množinou středů Svšech kružnic k, které procházejí dvěma různými body A, B, je osa o úsečky AB.

Příklad 6:

Vkapitole oPythagorově větě jste řešili příklad, který si nyní připomeňme (viz obr.).

Narýsujte si do svých sešitů obrázek kružnice k sprůměrem AB, sbody X1, X2, X3 asvyznačenými konvexními úhly AX1B, AX2B, AX3B. Pomocí úhloměrů pak určete a potom zapište velikosti těchto tří úhlů. Co zjišťujete?

Množina vrcholů X všech pravých úhlů vrovině, jejichž ramena procházejí dvěma různými body A, B, je kružnice sprůměrem AB. Body A, B do této množiny nepatří

Tento poznatek se nazývá Thaletova věta. (Žáci si tuto větu občas nesprávně zestručňují: „Všechny úhly nad průměrem kružnice jsou pravé.“)

Poznámka: S Thaletovou větou jste se seznámili již v kapitole Kružnice a kruh. Nyní ji máte zformulovanou jako množinu všech bodů dané vlastnosti.

64

III. KONSTRUKČNÍ ÚLOHY

Úkoly:

1. Prohlédněte si následující obrázky. Na každém znich je barevně zvýrazněna množina bodů dané vlastnosti. Vyslovte stručně společnou danou vlastnost každé ztěchto množin. Nejdříve si samozřejmě jednotlivé obrázky narýsujte do svých sešitů adoplňte chybějící část popisu týkající se množiny bodů dané vlastnosti.

Nápověda: Za rovinný pás považujeme společnou část dvou různých polorovin, jejichž hraniční přímky jsou rovnoběžné, navzájem různé akaždá znich patří oběma polorovinám. Na obrázku jde opoloroviny mM, nN arovnoběžky m, n.

2. Na obrázku jsou kružnice k1, k2, k3, k4 se stejným poloměrem r, které se dotýkají přímky p vbodech T1, T2, T3 aT4.

Slovně vyjádřete barevně zvýrazněnou množinu aurčete danou vlastnost jejích bodů.

4. Na obrázku je konvexní úhel AVB akružnice k1, k2 a k3, které jsou částmi tohoto úhlu adotýkají se jeho ramen VA aVB.

Odpovězte na otázku: Které všechny body tvoří konvexní úhel AVB?

3. Coje množinou všech středů S1, S2, S3, ... kružnic k1, k2, k3 ..., které se dotýkají kružnice l(O; r) vdaném boděT(T ∈ l)? (Viz obr.)

65

III. KONSTRUKČNÍ ÚLOHY

3.

Tato učebnice je třetí částí řady dvoudílných učebnic matematiky pro 2. stupeň základní školy a případně pro nižší ročníky víceletých gymnázií.

Pro každý ročník jsou vždy určeny dvě učebnice, z nichž jedna je věnována aritmetice (algebře), druhá geometrii. Praktickým a užitečným doplňkem učebnic jsou pracovní sešity ke každé z nich. Další materiály k procvičení a upevnění učiva přinášejí rovněž sbírky úloh a cvičení z matematiky, které jsou spolu s učebnicemi k dispozici.

Koncepce učebnic vychází z osvědčené praxe škol, vyhovuje však i záměrům

Rámcového vzdělávacího programu pro základní vzdělávání. O tom svědčí mimo jiné i udělená schvalovací doložka MŠMT.

Celou řadu učebnic matematiky pro 6.–9. ročník ZŠ tvoří: