Engineering Economy 8th edition by Blank Tarquin ISBN 0073523437
9780073523439
Download solution manual at:
https://testbankpack.com/p/solution-manual-for-engineeringeconomy-8th-edition-by-blank-tarquin-isbn-00735234379780073523439/
Solutions to end-of-chapter problems
th Engineering Economy, 8 edition
Leland Blank and Anthony Tarquin
Chapter 8
Rate of Return Analysis: Multiple Alternatives
Understanding Incremental ROR
8.1 Alternative B is preferred if the rate of return on the increment of investment between A and B is ≥ MARR.
8.2 (a) The rate of return on the increment is less than 22%per year.
(b) Overall ROR = 150,000(0.25) + 50,000(i*X-Y) = 200,000(0.22)
i*X-Y = 13%
8.3 The rate of return on the increment is less than 0%
8.4 By switching the position of the two cash flows, the interpretation changes completely. The situation would be similar to receiving a loan in the amount of the difference between the two alternatives if the lower cost alternative is selected. The rate of return would represent the interest paid on the loan. Since it is higher than what the company would consider attractive (i.e., 15% or less), the loan should not be accepted. Therefore, select the alternative with the higher initial investment, that is, A.
8.5 The company should select the lower cost infrared model because the rate of return on the increment of investment for the microwave model has to be lower than 19%
8.6 (a) The rate of return on the increment has to be larger than 18%.
(b) The rate of return on the increment has to be smaller than 10%
8.7 There is no income associated with a cost alternative. Therefore, the only way to obtain a rate of return is based on the increment of investment and annual cost estimates.
8.8 Overall ROR = [30,000(0.20) + 70,000(0.14)]/100,000 = 0.158 (15.8%)
8.9 Overall ROR: 100,000(i*) = 30,000(0.30) + 20,000(0.25) + 50,000(0.20)
i* = 0.24 (24%per year)
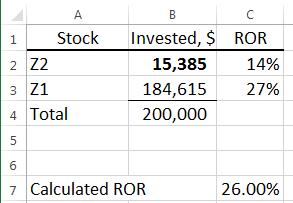
8.10 (a) 40,000(0.14) + (200,000 – 40,000)(i*Z1) = 200,000(0.26)
i*Z1 = 0.29 (29%per year)
(b) Goal Seek results are shown. Thresehold investment in Z2 is $15,385. Any more than $15,385, and the overall ROR falls below 26%.
8.11 200,000(0.28) + 100,000(0.42) + 400,000(0.19) = 700,000(x)
x = 0.249 (24.9%)
8.12 (a) Size of investment in Y = 50,000 – 20,000 = $30,000
(b) 30,000(i*) + 20,000(0.15) = 50,000(0.40)
i* = 0.567 (56.7%)
8.13 (a) Incremental investment analysis is not required. Alternative X should be selected because the rate of return on the increment is known to be lower than 20%
(b) Incremental investment analysis is not required because only Y has ROR greater than the MARR
(c) Incremental investment analysis is not required. Neither alternative should be selected because neither one has a ROR greater than the MARR.
(d) The ROR on the increment is less than 25%,but an incremental investment analysis is required to determine if the rate of return on the increment equals or exceeds MARR = 20%
(e) Incremental investment analysis is not required because it is known that the ROR on the increment is greater than 22% Select Y
8.14 (a) Incremental CF, year 0: -25,000 – (-15,000) = $-10,000
(b) Incremental CF, year 3: -400 - (-1600 – 15,000 + 3000) = $+13,200
(c) Incremental CF, year 6: (-400 + 6000) – (-1600 + 3000) = $+4200
8.15 Year System X, $ System Z, $ (Z – X), $
Sum of CF for (Z – X) = -111,000 - (-140,000) = $29,000
8.16 (a) - First costP - (-30,000) = -53,000 First costP = $-83,000
(b) -11,000 – (-M&OA) = 21,000 M&OA = $-32,000
(c) ResaleP – 4000 = 8000 ResaleP = $12,000
8.17 The incremental cash flow equation is 0 = -65,000 + x(P/A,25%,4),where x is the difference in the AOC.
0 = -65,000 + x(2.3616)
x = 65,000/2.3616 = $27,524
AOCB = 60,000 – 27,524 = $32,476
Incremental ROR Comparison (Two Alternatives)
8.18 Solve for ∆i* by trial and error or spreadsheet
∆i* = 18.0%per year
Any MARR value greater than 18%favors X
Function: = RATE(10,9000,-40000,-2000) displays 18.05%
8.19 (a) Find rate of return on incremental cash flow
0 = -5500 + 600(P/A,∆i*,3) + 6390(P/F,∆i*,3)
∆i* = 15.5% (spreadsheet)
(b) Incremental ROR is less than MARR; select Ford Explorer
8.20 0 = - (2,300,000 – 1,200,000) + {[(360,000 + 56,000 -125,000] – [(270,000 –105,000)]}(P/A,∆i*,10)
= -1,100,000 + {[(291,000] – [(165,000)]}(P/A,∆i*,10)
= -1,100,000 + 126,000(P/A,∆i*,10)
(P/A,∆i*,10) = 8.7302
From interest tables, ∆i* is between 2 and 3%
∆i* = 2.55%per year (spreadsheet)
∆i* = 2.55%< MARR of 5%, Select Alternative B
8.21 Write ROR equation for increment between B and A
0 = -50,000 + 20,000(P/A,∆i*,5)
(P/A,∆i*,5) = 2.5000
Solve for ∆i* by interpolation or spreadsheet
∆i* = 28.6%> MARR = 20% Select B
Function: = RATE(5,20000,-50000) displays 28.65%
8.22 Write PW-based incremental ROR equation using CFVS – CFDS
0 = -25,000 + 4000(P/A,∆i*,6) + 26,000(P/F,∆i*,3) – 39,000(P/F,∆i*,4) + 40,000(P/F,∆i*,6)
∆i* = 17.4% (spreadsheet)
∆i* > MARR of 15%;select Variable Speed (VS)
8.23 By hand, in $1000 units
(a) X vs. DN: i*X: 0 = -84 + (96 - 31)(P/A,i*X,3) + 40(P/F, i*X,3) i*X = 67.9%
Y vs DN: i*Y: 0 = -146 + (119 - 28)(P/A,i*Y,3) + 47(P/F, i*Y,3) i*Y = 47.8%
Both X and Y have i* values > MARR = 15%;select robot X
Copyright © 2018 McGraw-Hill Education All rights reserved
prior
consent of McGraw-Hill Education
(b) Incremental CF amounts for (Y-X)

Incremental first cost = $-62,000
Incremental M&O = $3000
Incremental revenue = $23,000
Incremental salvage = $7,000 0 = -62,000 + 3000(P/A,∆i*,3) + 23,000(P/A ∆i*,3) + 7000(P/F,∆i*,3)
Solve for ∆i* by trial and error
∆i* = 16.8%> MARR = 15%
Select robot Y. Different selection than that based on ROR values
(c) Incremental ROR is the correct basis; selecting robot X in part (a) is incorrect
By spreadsheet
(a) Select robot X since i*X is larger and both exceed MARR
(b) Select robot Y since ∆i* = 16.83%> MARR = 15%
(c) Incremental ROR is the correct basis; selecting robot X in part (a) is incorrect
8.24 (a) 0 = -10,000 + 1200(P/A,∆i*,4) + 12,000(P/F,∆i*,2) + 1000(P/F,∆i*,4)
Solve for ∆i* by trial and error or spreadsheet
∆i* = 30.31% > MARR = 20% (spreadsheet)
Select Model 200
(b) If n105 = 4 years, the incremental ROR equation changes to 0 = -10,000 + 1200(P/A,∆i*,4) + 1000(P/F,∆i*,4)
∆i* = -17.22%
Select Model 105; the incremental investment is definitely not economical
8.25 (a) 0 = -17,000 + 400(P/A,∆i*,6) + 17,000(P/F,∆i*,3) + 1700(P/F,∆i*,6)
Solve for ∆i* by trial and error or spreadsheet
Copyright © 2018 McGraw-Hill Education All rights reserved
∆i* = 6.84%< MARR = 10%
Select alternative P
(b) AWP = -18,000(A/P,10%,3) - 4000 + 1000(A/F,10%,3)
= -18,000(0.40211) - 4000 + 1000(0.30211)
= $-10,936
AWQ = -35000(A/P,10%,6)– 3600 + 2700(A/F,10%,6)
= -35,000(0.22961) – 3600 + 2700(0.12961)
= $-11,286
Select P, though neither option makes MARR = 10%
8.26 Revenue projects; determine i* first. Monetary units are in $1000
Treated vs. DN: 0 = -5000 + (2500 - 1000)(P/A,i*,5) + 100(P/F,i*,5)
= -5000 + 1500(P/A,i*,5) + 100(P/F,i*,5)
i*Trt = 15.7% (spreadsheet)
Impregnated vs. DN: 0 = -6500 + (2500 - 650)(P/A,i*,5) + 200(P/F,i*,5)
= -6500 + 1850(P/A,i*,5) + 200(P/F,i*,5)
i*Imp = 13.7%
Reject treated and impregnated since i* < MARR = 25%
Select DN
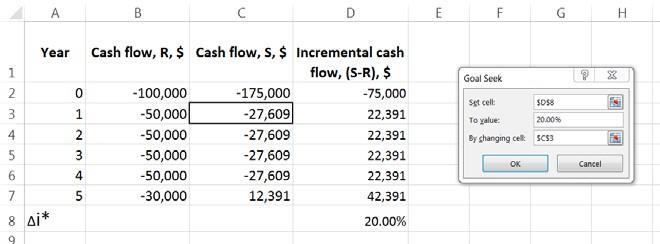
8.27 By hand: Let x = M & O costs. Perform an incremental cash flow analysis.
0 = -75,000 + (-x + 50,000)(P/A,20%,5)+ 20,000(P/F,20%,5)
0 = -75,000 + (-x + 50,000)(2.9906) + 20,000(0.4019)
x = $27,609
M & O cost for S = $27,609
By spreadsheet: Enter any number for M&O in cell C3 and use Goal Seek to display 20.00%in cell D8. If RATE is used, different cash flow values must be entered repeatedly into cell C3.
8.28 (a) Breakeven ROR is the ∆i* for a perpetual investment
0 = -500,000(∆i*) + 60,000
∆i* = 60,000/500,000 = 0.12 (12%per year)
(b) ∆i* = 12%> MARR = 10%;select design 1B
8.29 Sample further information items to request before saying ‘yes”:
• What about multiple ∆i* values?
• Basis of negative CF in years 5 and 10
• Basis and percentage of increased savings from year 7 forward
• Required extra savings of FS to reach MARR of 20%
Multiple Alternative ( > 2) Comparison
8.30 Select the one with the lowest initial investment cost because none of the increments were justified.
8.31 (a) A vs DN: 0 = -30,000(A/P,i*,8) + 4000 + 1000(A/F,i*,8)
Solve for i* by trial and error or spreadsheet
i* = 2.1% (spreadsheet)
Method A is not acceptable
B vs DN: 0 = - 36,000(A/P,i*,8) + 5000 + 2000(A/F,i*,8)
i* = 3.4%
Method B is not acceptable
C vs DN: 0 = - 41,000(A/P,i*,8) + 8000 + 500(A/F,i*,8)
i* = 11.3%
Method C is acceptable
D vs DN: 0 = - 53,000(A/P,i*,8) + 10,500 - 2000(A/F,i*,8)
i* = 11.1%
Method D is acceptable
(b) Revenue alternatives; compare to DN initially
A vs DN: 0 = -30,000(A/P,i*,8) + 4000 + 1000(A/F,i*,8)
Solve for i* by trial and error or spreadsheet
i* = 2.1% (spreadsheet)
Eliminate A; retain DN
B vs DN: 0 = - 36,000(A/P,i*,8) + 5000 + 2000(A/F,i*,8)
i* = 3.4%
Eliminate B; retain DN
C vs DN: 0 = - 41,000(A/P,i*,8) + 8000 + 500(A/F,i*,8)
i* = 11.3%
Eliminate DN; retain C
D vs DN: 0 = - 53,000(A/P,i*,8) + 10,500 - 2000(A/F,i*,8)
i* = 11.1%
Eliminate DN; retain D
D vs C: 0 = - 12,000(A/P,∆i*,8) + 2,500 - 2500(A/F,∆i*,8)
∆i* = 10.4%
Eliminate D
Select method C
8.32 Rank cost alternatives by increasing initial investment: 1, 3, 4, 2
3 to 1: 0 = -4000 + 1000(P/A,∆i*,5)
∆i* = 7.93%< MARR of 25% Eliminate 3
4 to 1: 0 = -5000 + 2000(P/A,∆i*,5)
∆i* = 28.65%> MARR of 25% Eliminate 1
2 to 4: 0 = -18,000 + 6000(P/A,∆i*,5)
∆i* = 19.86%< MARR of 25% Eliminate 2
Select machine 4
8.33 These are revenue alternatives; add DN
(a) 8 vs. DN: 0 = -30,000(A/P,i*,5) + (26,500 – 14,000) + 2000(A/F,i*,5)
Solve for i* by trial and error or spreadsheet
i* = 31.7% (spreadsheet)
Eliminate DN
Copyright © 2018
10 vs. 8: 0 = -4000(A/P,∆i*,5) + (14,500 – 12,500) + 500(A/F,∆i*,5)
∆i* = 42.4%
Eliminate 8
15 vs. 10: 0 = -4000(A/P,∆i*,5) + (15,500 – 14,500) + 500(A/F,∆i*,5)
∆i* = 10.9%
Eliminate 15
20 vs. 10: 0 = -14,000(A/P,∆i*,5) + (19,500 – 14,500) + 1000(A/F,∆i*,5)
∆i* = 24.2%
Eliminate 10
25 vs. 20: 0 = -9000(A/P,∆i*,5) + (23,000 – 19,500) + 1100(A/F,∆i*,5)
∆i* = 29.0%
Eliminate 20
Purchase 25 m3 truck
(b) For second truck, purchase truck that was eliminated next to last: 20 m3
8.34 (a) Select all proposals with overall ROR ≥ 17%
Select B and C
(b) Compare alternatives incrementally after ranking: DN, A, B, C, D
A to DN: ∆i* = 11.7%< 14.5% Eliminate A
B to DN: ∆i* = 22.2%> 14.5% Eliminate DN
C to DN: ∆i* = 17 9%> 14.5% Eliminate DN
D to DN: ∆i* = 15.8%> 14.5% Eliminate DN
Retain B, C, D
C vs. B: ∆i* = 10.0%< 14.5% Eliminate C
D vs. B: ∆i* = 10.0%< 14.5% Eliminate D
Select alternative B
(c) Compare alternatives incrementally after ranking: DN, A, B, C, D
A to DN: ∆i* = 11.7%> 10.0% eliminate DN
B to A: ∆i* = 43.3%> 10.0% eliminate A
C to B: ∆i* = 10.0%= 10.0% eliminate B
D to C: ∆i* = 10.0%= 10.0% eliminate C
Select alternative D
Copyright © 2018
8.35 (a) Select all projects whose ROR ≥ MARR of 15%.Select A, B, and C
(b) Eliminate all alternatives with ROR < MARR; compare others incrementally: Eliminate D and E
Rank survivors according to increasing first cost: B, C, A
C vs B: ∆i* = 800/5000 = 0.16 (16%) > MARR Eliminate B
A vs C: ∆i* = 200/5000 = 0.04 (4%) < MARR Eliminate A
Select alternative C
8.36 Proposals are independent; compare each against DN only
Product 1: 0 = -340,000 + (180,000 – 70,000)(P/A,i*,5)
i* = 18.52%> MARR = 15% Accept
Product 2: 0 = -500,000 + (190,000 - 64,000)(P/A,i*,5)
i* = 8.23%< MARR = 15% Reject
Product 3: 0 = -570,000 + (220,000 - 48,000)(P/A,i*,5)
i* = 15.49%> MARR = 15% Accept
Product 4: 0 = -620,000 + (205,000 - 40,000)(P/A,i*,5)
i* = 10.35%< MARR = 15% Reject
Company should introduce products 1 and 3
8.37 (a) Proposals are independent; Select A and C
(b) Alternative A is justified. B vs. A yields 1%,eliminate B; C vs. A yields 7%, eliminate C; D vs A yields 10%,eliminate A. Select D
(c) Alternative A is justified. B vs A yields 1%,eliminate B; C vs A yields 7%, eliminate C; D vs A yields 10%,eliminate D. Select A
8.38 (a) Initial cost, Machine 1: - 60,000 - (-16,000) = $-44,000
Overall ROR, Machine 2: 0 = -60,000 + 16,000(P/A,i*,10); i* = 23.41%
Incremental investment, 3 vs. 2: -72,000 - (-60,000) = $-12,000
Incremental cash flow: 4 vs. 3: 24,000 – 19,000 = $5000
Incremental ROR 3 vs. 2: 0 = -12,000 + 3000(P/A,∆i*,10); ∆i* = 21.41%
Incremental ROR 4 vs. 3: 0 = -26,000 + 5000(P/A,∆i*,10); ∆i*= 14.08%
(b) Machines are ranked according to initial investment: 1, 2, 3, 4; MARR = 18%
Compare 1 to DN: i* = 18.6%> MARR eliminate DN
Compare 2 to 1: ∆i* = 35.7%> MARR eliminate 1
Compare 3 to 2: ∆i* = 21.41% > MARR eliminate 2
Compare 4 to 3: ∆i* = 14.08%< MARR eliminate 4
Select Machine 3
8.39 (a) Find ROR for each increment of investment using the general relation
AW
1 + AWII = AW2 where II = incremental investment
E vs F: 20,000(0.20) + 10,000(∆i*) = 30,000(0 35)
∆i* = 65%
E vs G: 20,000(0.20) + 30,000(∆i*) = 50,000(0.25)
∆i* = 28.3%
E vs H: 20,000(0.20) + 60,000(∆i*) = 80,000(0.20)
∆i* = 20%
F vs G: 30,000(0.35) + 20,000(∆i*) = 50,000(0.25)
∆i* = 10%
F vs H: 30,000(0.35) + 50,000(∆i*) = 80,000(0.20)
∆i* = 11%
G vs H: 50,000(0.25) + 30,000(∆i*) = 80,000(0.20)
∆i* = 11.7%
(b) Revenue = A = Pi
E: A = 20,000(0.20) = $4000
F: A = 30,000(0.35) = $10,500
G: A = 50,000(0.25) = $12,500
H: A = 80,000(0.20) = $16,000
(c) Conduct incremental analysis using results from part (a) with MARR = 16%
E vs DN: i* = 20% > MARR eliminate DN
E vs F: ∆i* = 65% > MARR eliminate E
F vs G: ∆i* = 10% < MARR eliminate G
F vs H: ∆i* = 11% < MARR eliminate H
Copyright © 2018 McGraw-Hill Education
Therefore, select Alternative F
(d) Conduct incremental analysis using results from part (a) with MARR = 11%
E vs DN: i* = 20% > MARR, eliminate DN
E vs F: ∆i* = 65% > MARR, eliminate E
F vs G: ∆i* = 10% < MARR, eliminate G
F vs H: ∆i* = 11% = MARR, eliminate F
Select alternative H
(e) Conduct incremental analysis using results from part (a) with MARR = 19%
E vs DN: i* = 20% > MARR, eliminate DN
E vs F: ∆i* = 65% > MARR, eliminate E
F vs G: ∆i* = 10% < MARR, eliminate G
F vs H: ∆i* = 11% < MARR, eliminate H
Select F as first alternative; compare remaining alternatives incrementally.
E vs DN: i* = 20% > MARR, eliminate DN
E vs G: ∆i* = 28.3% > MARR, eliminate E
G vs H: ∆i* = 11.7% < MARR, eliminate H
Therefore, select alternatives F and G Spreadsheet Exercises
8.40 (a) The i* values show that both alternatives are justified for MARR = 5% Incremental ROR analysis results in ∆i* = 5.85 %,which exceeds MARR = 5% Select Model 1000. Develop plot of AW vs. ∆i values to show ∆i* = 5.85%per year.
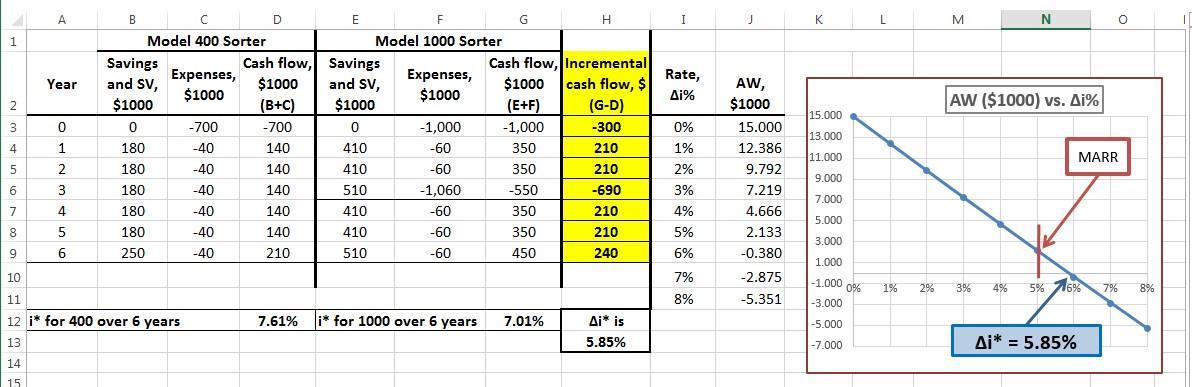
(b) Ranking inconsistency is present. Based on AW analysis over 6 years, select Model 400 (at the higher i* of 7.61%),which is different than incremental analysis result.
8.41 (a) Determine if methods are economically justified. From row 14,
i*B = 6.25%> MARR = 5%;justified
i*I = 4.52%< MARR = 5%,not justified
Incremental ROR is not needed; select method B
(b) Neither method is justified at MARR = 8%.Since one of the methods must be installed, reduce the MARR expectation; select B with the larger i* and small ∆i* = 2.55%per year
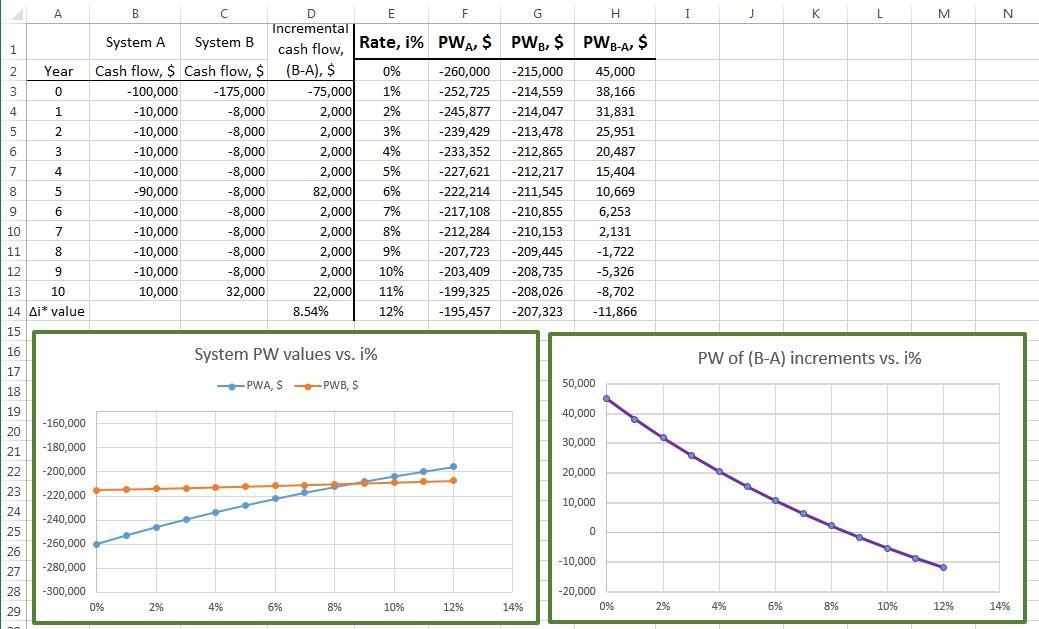
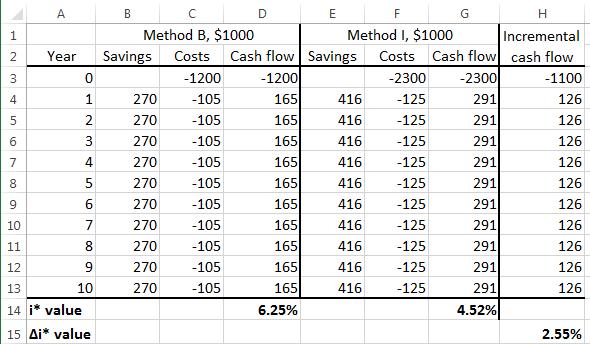
8.42 (a) Graph of breakeven ROR is approximately 8.5%per year in both renditions.
(b) If MARR > approximately 8.5%,the lower-investment system A is selected.
8.43 (a) Select C and D with i* values exceeding MARR (rows 21 and 22).
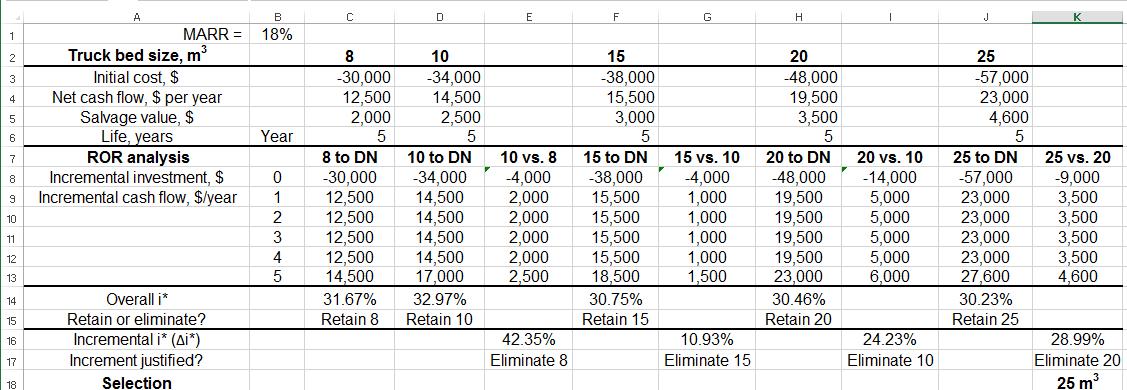
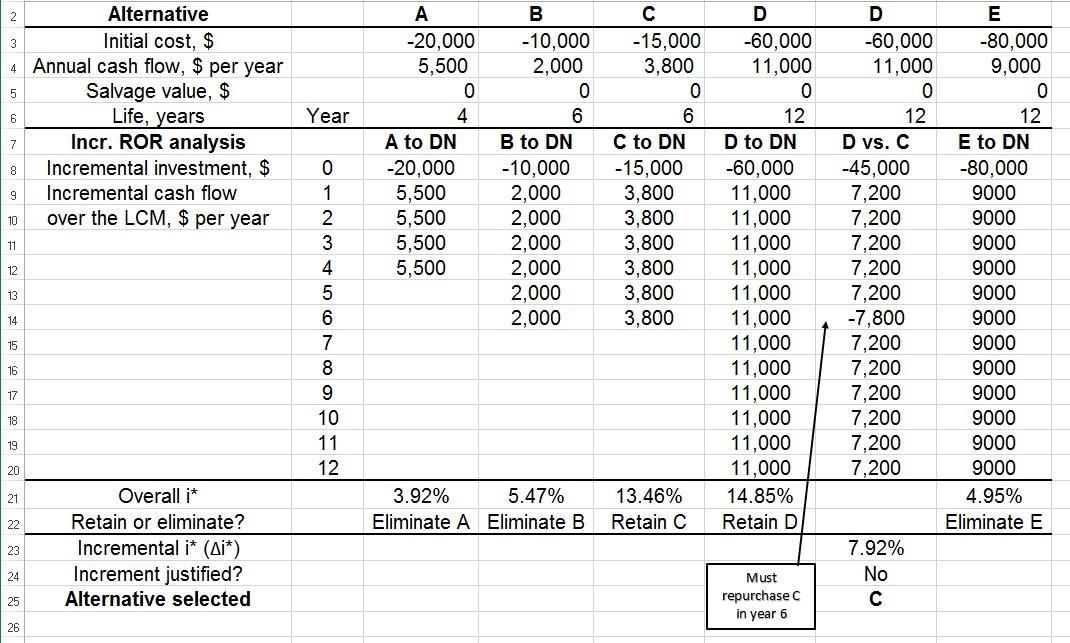
(b, c) Select C. It is the alternative with the largest investment that has the extra investment justified over another acceptable alternative, DN, in this case
8.44 (a) Spreadsheet analysis results in selection of 25 m3 truck bed size.
(b) Purchase truck that was eliminated next to last: 20 m3
Additional Problems and FE Exam Review Questions
8.45 Answer is (b)
8.46 Answer is (c)
8.47 20,000(0.40) + 80,000(x) = 100,000(0.25) x = 21.3% Answer is (c)
8.48 Answer is (c)
8.49 Answer is (a)
8.50 Answer is (b)
8.51 Answer is (d)
8.52 Diesel - Gasoline = -40,000
Diesel - (-150,000) = -40,000
Diesel = -190,000 Answer is (a)
8.53 i* for B, D, and E > MARR Answer is (c)
8.54 Rank alternatives in terms of increasing first cost: DN, A, B, C, D, E
Eliminate alternatives A and C because i* < MARR =15%
B to DN: i* = 15.1% i* > MARR eliminate DN
D to B: ∆i* = 38.5% ∆i* > MARR eliminate B
E to D: ∆i* = 26.8% ∆i* > MARR eliminate D; select E
Answer is (d)
8.55 Rank alternatives in terms of increasing first cost: DN, A, B, C, D, E
Eliminate alternatives A, B, C and E because i* < MARR = 25% Only D remains; select D
Answer is (b)
8.56 Rank alternatives in terms of increasing first cost: DN, A, B, C
Eliminate alternative B because i* < MARR =16%
A to DN: i* = 23.4% i* > MARR eliminate DN
C vs. A: ∆i* = 12 0% ∆i* < MARR eliminate C; select A
Answer is (a)
8.57 Rank Alternatives: C, A, B. D, E; perform incremental ROR analysis for n = ∞
A vs. C: -2000(∆i*) + 400 = 0; ∆i* = 400/2000 = 20% > MARR; eliminate C
B vs. A: -1000(∆i*) + 100 = 0; ∆i* = 100/1000 = 10% < MARR; eliminate B
D vs. A: -3000(∆i*) + 300 = 0; ∆i* = 300/3000 = 10% < MARR; eliminate D
E vs. A: -4,000(∆i*) + 700 = 0; ∆i* = 700/4000 = 17.5% > MARR; eliminate A
Select E
Answer is (d)
Copyright © 2018 McGraw-Hill Education All rights reserved
Solution to Case Study 1, Chapter 8
Sometimes, there is not a definitive answer to a case study exercise Here are example responses.
PEFORMING ROR ANALYSIS FOR 3D PRINTER AND IIoT TECHNOLOGY
1. PW at 12%is shown in row 29. Select server #2 (n = 8) with the largest PW value.
2. #1 (n = 3) is eliminated. It has i* < MARR = 12%.Perform an incremental analysis of #1 (n = 4) and #2 (n = 5). Column H shows ∆i* = 19.5%. Now perform an incremental comparison of #2 for n = 5 and n = 8. This is not necessary since no extra investment is necessary to expand cash flow by three years. The ∆i* is infinity. It is obvious: select #2 (n = 8).
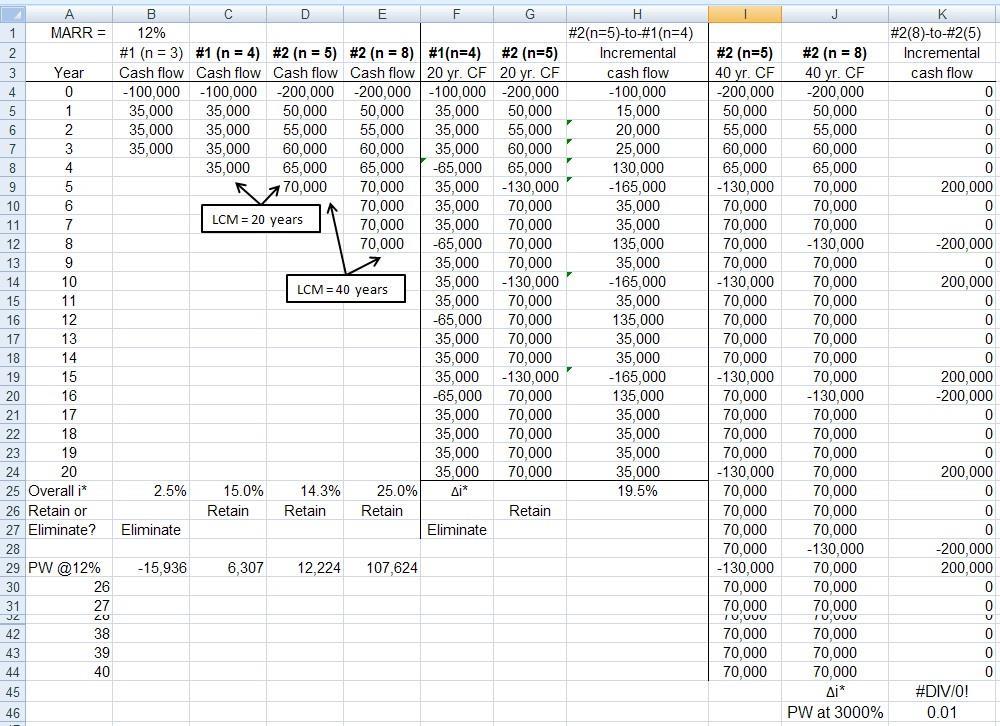
3. PW at 2000% > $0.05. ∆i* is infinity, as shown in cell K45, where an error for IRR(K4:K44) is indicated.
Some rows hidden
Solution to Case Study 2, Chapter 8
Sometimes, there is not a definitive answer to a case study exercise Here are example responses. HOW A NEW ENGINEERING GRADUATE CAN HELP HIS FATHER
1. Cash flows for each option are summarized at top of the spreadsheet. Rows 9-19 show annual estimates for options in increasing order of initial investment: 3, 2, 1, 4, 5.
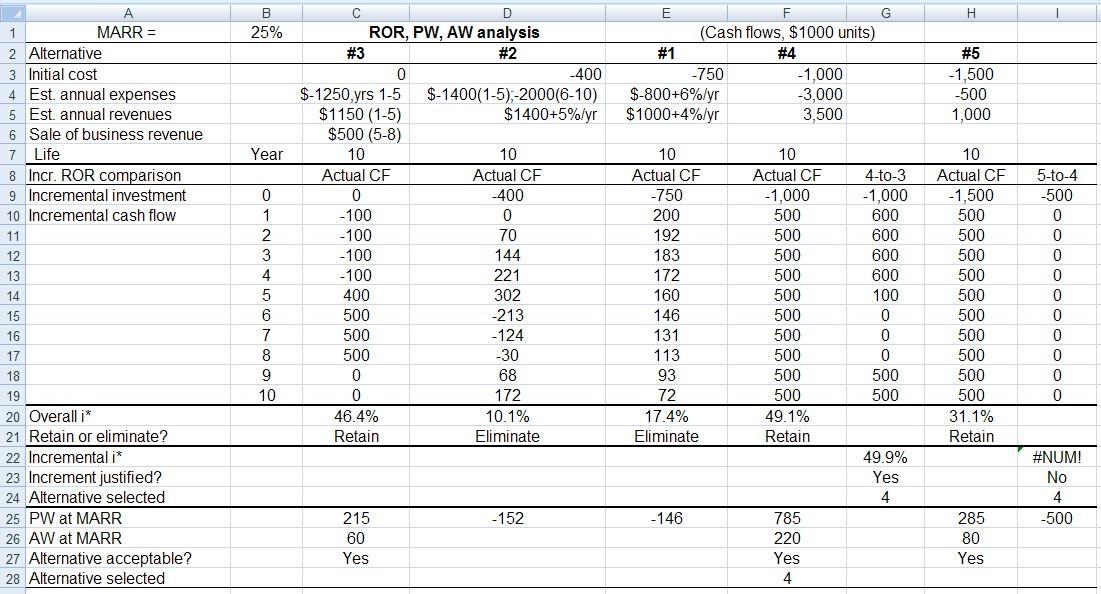
2. Multiple i* values: Only for option #2; there are 3 sign changes in cash flow and cumulative cash flow series. No values other than 10.1%are found in the 0 to 100%range.
3. Do incremental ROR analysis after removing #1 and #2. See row 22. 4-to-3 comparison yields 49.9%,5-to-4 has no return because all incremental cash flows are 0 or negative. PW at 25%is $785 for #4, which is the largest PW. Aw is also the largest for #4.
Conclusion: Select option #4 – trade-out with friend.
4. PW vs. i charts for all 5 options are on the spreadsheet.
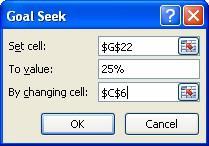
5. Force the breakeven rate of return between options #4 and #3 to be equal to MARR = 25%. Use trial and error or Goal Seek with a target cell of G22 to equal 25% and changing cell of C6 (template at right). Make the values in years 5 through 8 of option #3 equal to the value in cell C6, so they reflect the changes. The answer obtained should be about $1090, which is actually $1,090,000 for each of 4 years.

Required minimum selling price is 4(1090,000) = $4.36 million compared to the current appraised value of $2 million.