MERA FAVORIT MATEMATIK 6B
Elevpaket – Tryckt + Digitalt
MERA FAVORIT MATEMATIK 6B
Elevpaket – Tryckt + Digitalt
Elevpaketen till Favorit matematik 4–6 ger dina elever de bästa förutsättningarna för ett varierat lärande då de kombinerar det digitala läromedlet med en tryckt elevbok.
ELEVBOK
Elevboken består av 4 kapitel som alla är indelade i lektioner. Till varje lektion finns det fyra sidor. Det obligatoriska uppslaget och uppslaget för att träna extra ÖVA och PRÖVA. I elevboken tränar eleven på egen hand men den gemensamma kommunikativa undervisningen leder du med hjälp av lärarhandledningens resurser.
DIGITALT LÄROMEDEL
I det digitala läromedlet är alla instruktioner inlästa. Dessutom finns genomgångsfilmer av lektionens innehåll. Till vissa statistikövningar kan eleverna välja att arbeta med eller utan digitalt verktyg. Eleverna hittar också digitala programmeringsövningar. Det finns interaktiva TRÄNA-rutor till nästan varje lektion. Eleverna får även tillgång till den populära matteordlistan med matematiska ord och begrepp för åk 1-6.
Interaktiv version av boken, inläst med autentiskt tal och textföljning
BEDÖMNING FÖR LÄRANDE
Bedömning för lärande är en möjlighet för dig som vill göra eleverna medvetna om sitt eget lärande. I häftet finns proven med koppling till kunskapskraven och elev- och lärardokumentation.
LABORATIVT MATERIAL
De laborativa materialen finns i ett kuvert som medföljer elevpaketet. Aktiviteter där det laborativa materialet används hittar du både i lärarhandledningen och elevboken.
TOMOYO
Tomoyo ger eleven lustfylld färdighetsträning på webben.
Interaktiva övningar
Fungerar på dator, surfplatta och mobiltelefon
Favoritmatematik 6B
Studentlitteratur AB
Box 141
221 00 Lund
Besöksadress Åkergränden 1
Telefon 046-31 20 00 studentlitteratur.se
Bilder:
homydesign/Shutterstock.com 35a vvoe/Shutterstock.com 123
Övriga bilder: Shutterstock.com
Kopieringsförbud
Detta verk är skyddat av upphovsrättslagen. Det är ett engångsmaterial och får därför, vid tillämpning av Bonus Copyright Access skolkopieringsavtal, överhuvudtaget inte kopieras för undervisningsändamål. Inte ens enstaka sida får kopieras, dock får enstaka fråga/övning kopieras för prov/skrivning. För information om avtalet hänvisas till utbildningsanordnarens huvudman eller Bonus Copyright Access.
Vid utgivning av detta verk som e-bok, är e-boken kopieringsskyddad.
Den som bryter mot lagen om upphovsrätt kan åtalas av allmän åklagare och dömas till böter eller fängelse i upp till två år samt bli skyldig att erlägga ersättning till upphovsman eller rättsinnehavare.
Studentlitteratur har både digital och traditionell bokutgivning.
Studentlitteraturs trycksaker är miljöanpassade, både när det gäller papper och tryckprocess.
Art.nr 45962
ISBN 978-91-44-16695-7
Upplaga 2:1
© 2023, 2017 Författarna och Studentlitteratur AB Originalets titel: Tuhattaituri 6b
© 2011 Otava Publishing Company Ltd, Helsingfors
Asikainen, Nyrhinen, Rokka, Vehmas
Illustrationer: Maisa Rajamäki
Översättning: Cilla Heinonen
Printed by Pozkal/BESTingraphics, Poland 2023
HEJ SJÄTTEKLASSARE!
I Mera Favorit matematik 6B övar vi på decimaltal, procenträkning samt uträkningar med tid. Det finns också ett stort antal lektioner som repeterar tidigare moment. Favoritsidorna är en kul variation till de vanliga lektionerna. Boken är full av olika intressanta extrauppgifter, allt från enkla repetitionsuppgifter till utmanande problemlösningsuppgifter.
Du hittar säkert uppgifter som passar och inspirerar just dig!
Vi önskar dig lycka till med matematiken!
Läroboksförfattarna
VÄLKOMMEN TILL FAVORIT MATEMATIK!
Boken har fyra kapitel som är indelade i lektioner. Varje lektion har två uppslag i boken. Varje kapitel innehåller:
Lektioner
På det första uppslaget finns basuppgifterna. På det andra uppslaget finns extrauppgifterna öva och pröva
Lektionens innehåll.
Lektionens namn.
Lektionens mål.
Träna-rutan används i Finland som läxa. Den övar det som varit nytt.
Favoritsidor Favoritsidorna innehåller aktiviteter som stöder en mångsidig matematikinlärning. Här lär sig eleverna matematik genom spel och aktiviteter som övar problemlösning och olika matematiska resonemang. Flera av spelen kan även spelas på nytt hemma.
Vad har jag lärt mig? I slutet av varje kapitel finns en diagnos. Genom att ställa frågan ”Vad har jag lärt mig?” får eleven och läraren möjlighet att formativt utvärdera arbetet.
Öva-sidan innehåller övningar som passar de elever som behöver repetera och befästa ytterligare.
På prÖva-sidan finns uppgifter för de elever som kan pröva något nytt.
Sammanfattning / repetition Sist i kapitlet får eleven repetera de begrepp och moment som kapitlet handlat om.
Digitala övningar I boken finns länkar ( ) till övningar och extramaterial i det digitala läromedlet. Här finns berättelser, filmer och fler övningar som tränar det matematiska innehållet. Till varje kapitel finns även matteordlistor som innehåller tio ord och begrepp med tillhörande bilder, förklaringar och övningar.
INNEHÅLL
KAPITEL 1
1.
3. Vardagliga
4.
5.
6. Multiplikation
7.
I
KAPITEL 1 Tal i decimalform
• Sambandet mellan bråkform och decimalform
• Avrunda tal i decimalform
• Beräkningar med tal i decimalform i de fyra räknesätten
KAPITEL 2 Procent
• Sambandet mellan bråkform, decimalform och procentform
• Procenträkning
• Vardagliga beräkningar med procent
KAPITEL 3 Tid
• Mätning av tid och tidsintervall
• Omvandla tidsenheter
• Klockan, analog och digital
• Hastighet
KAPITEL 4 Repetition
• Negativa tal
• Tal i decimalform
• Tal i bråkform
• Procent
• Algebra
• Mätning
• Geometriska objekt, omkrets och area med och utan digitalt verktyg
• Volym
• Sannolikhet och simulering av sannolikhet
• Statistik med och utan digitalt verktyg
• Koordinatsystem
• Problemlösning och programmering
1. Från bråkform till decimalform
Storleksjämförelser med decimaltal
• Jämför först heltalen.
• Om heltalen är lika många, jämför tiondelarna.
• Om tiondelarna är lika många, jämför hundradelarna.
• Om hundradelarna är lika många, jämför tusendelarna.
1. Skriv bråket som ett decimaltal.
a. 2 10 =
b. 6 100 = c. 25 100 = d. 449 1 000 = e. 2
2. Skriv talet som ett bråk i blandad form med nämnaren 10, 100 eller 1 000.
a. 0,75 =
b. 0,35 =
c. 2,10 = d. 3,04 = e. 4,921 = f. 6,025 = g. 3,405 = h. 0,012 =
Film Film: Förklara
3. Skriv det tal som pilen pekar på.
4. Skriv <, = eller >.
a. 2,38 2,279
b. 7,85 6,900
c. 2,8 2,800
d. 3,45 3,098 e. 6,001 5,999 f. 0,463 0,401 g. 9,346 9,436 h. 2,09 2,078
5. Skriv bokstäverna i storleksordning enligt talen. Börja med det minsta. a. b. c. 2,890 O 2,908 N 2,098 H 2,009 P 2,998 E
Metod – placerar decimaltal på tallinjen – storleksordnar tal i decimalform
sätt; i decimalform och bråkform
ÖVA
TRÄNA
1. Skriv bråket som ett decimaltal.
a. 5 10 =
b. 6 10 =
Kan du förklara?
Hur vet du att 0,7 är mindre än 0,87?
c. 42 100 = d. 16 100 = e. 70 100 = f. 3 100 = g. 14 1 000 = h. 105 1 000 = i. 33 1 000 =
2. Skriv <, = eller >.
a. 2,678 2,768
b. 3,98 3,099
6. Dra streck.
7. Skriv som ett decimaltal.
a. noll hela sju hundradelar
b. två hela sex tusendelar
c. noll hela sexton hundradelar
d. sju hela elva tusendelar
e. hundra hela sju tiondelar
f. nio hela åttiofem tusendelar
8. Använd räknare för att omvandla bråket till ett decimaltal. Hitta bokstaven.
a. 1 4 = b. 6 4 = c. 1 5 = d. 4 25 =
9. Det stora kugghjulet snurrar ett varv. Åt vilket håll pekar de röda linjerna i kugghjulen a till c efter det?
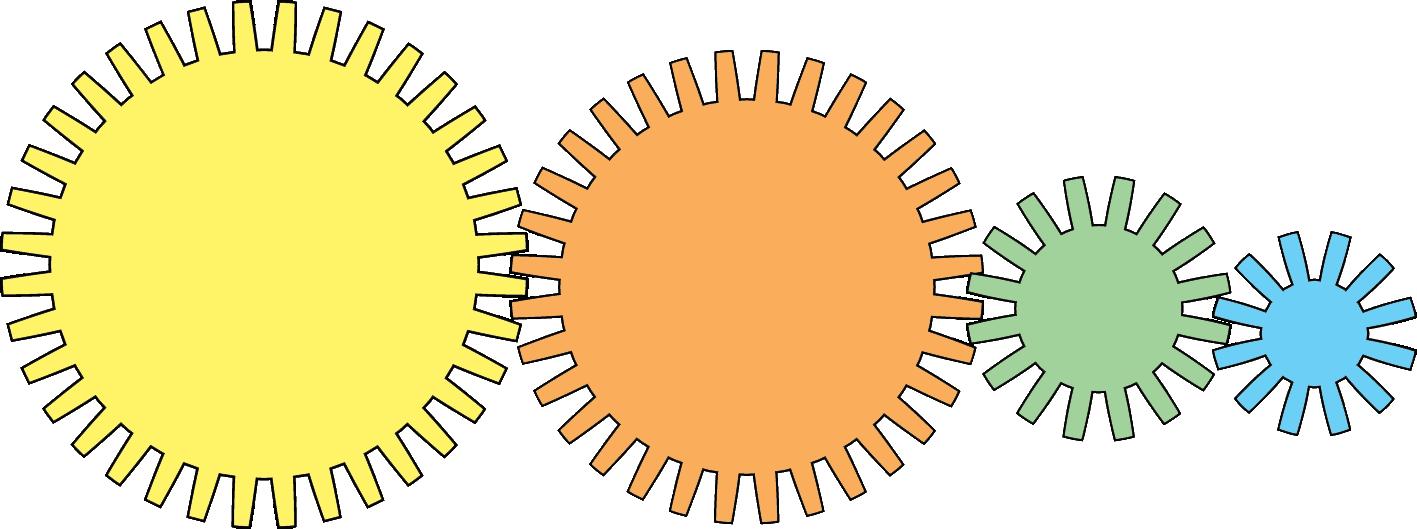
Antal kuggar: 36 32 16 12
10. Lös sudokut. I varje lodrät och vågrät rad, och varje markerat område ska det finnas en siffra av varje (1, 2, 3, 4, 5, 6).
2. Avrunda tal i decimalform
E = ental Td = tiondel Hd = hundradel Tud = tusendel
• När du avrundar till närmaste ental tittar du på tiondelarna.
• När du avrundar till närmaste tiondel tittar du på hundradelarna.
Avrundningsregeln: 0, 1, 2, 3, 4 5, 6, 7, 8, 9 nedåt uppåt
• När du avrundar till närmaste hundradel tittar du på tusendelarna.
1. Ringa in rätt alternativ. Vi avrundar talet till närmaste a.
2. Avrunda talet till närmaste ental. till närmaste tiondel. till närmaste hundradel.
a. 4,734
b. 5,091
c. 7,095
d. 8,998
3. Avrunda talet till närmaste ental.
a. 5,7 ≈
b. 8,2 ≈
c. 6,4 ≈
d. 3,56 ≈
e. 7,43 ≈
f. 0,91 ≈
4. Avrunda talet till närmaste tiondel.
a. 6,33 ≈
b. 2,15 ≈
c. 4,03 ≈
d. 5,09 ≈
e. 0,98 ≈
f. 3,97 ≈
5. Avrunda talet till närmaste hundradel.
a. 3,444 ≈
b. 1,256 ≈
c. 6,865 ≈
d. 7,009 ≈
e. 0,899 ≈
f. 3,796 ≈
g. 0,825 ≈
h. 4,906 ≈
i. 2,501 ≈
g. 6,981 ≈
h. 0,237 ≈
i. 7,042 ≈
g. 9,999 ≈
h. 6,999 ≈
i. 3,025 ≈
Metod – avrundar decimaltal Kommunikation – använder ungefär lika med-tecknet (≈) korrekt E Td E TdHd E TdHdTud E TdHd E TdHd E TdHdTud E TdHdTud E TdHdTud E TdHdTud
ÖVA
TRÄNA
Kan du förklara?
Varför ska du titta på hundradelarna när du avrundar till närmaste tiondel?
1. Avrunda talet till närmaste ental. till närmaste tiondel. till närmaste hundradel.
a. 3,872
b. 6,045
c. 8,514
d. 9,995
6. Skriv <, = eller >.
7. Skriv det största och det minsta talet som du kan bilda av korten.
Du måste använda alla kort i varje tal. Det ska vara minst ett sifferkort före och efter decimaltecknet.
största: minsta:
största: minsta:
8. Använd räknare och omvandla bråk till decimaltal. Avrunda svaret till närmaste tiondel, hundradel och tusendel.
a. 2 11
b. 3 14
c. 7 19
d. 6 17
e. 18 27
f. 14 26
9. Vem äger mobilen, vad har den för ringsignal, färg och vem talar mobilägaren med?
A
Namn: Färg: Talar med:
B
C
• Den ena pojken talar i en svart mobil.
• Annas ringsignal heter Nostalgia.
• Från den guldfärgade mobilen ringde någon till den röda mobilen.
• Josefs ringsignal heter Elefantmarschen.
• Jonas har en röd telefon.
• Josef står till höger om Siri på bilden, från vårt håll sett.
• Den guldfärgade mobilen har ringsignalen X-files och tillhör Siri.
• Från den svarta mobilen ringde någon till den blå mobilen.
• Josefs grannes mobil har James Bond-musik som ringsignal. tiondel hundradel tusendel
D
tal i decimalform
På måndagen skickar Milo sms för 10,65 kronor och på tisdagen för 20,85 kronor. Hur mycket kostar måndagens och tisdagens sms sammanlagt?
Isa räknar så här: 10,65 kr + 20.85 kr = = 10,65 kr + 20 kr + 0,85 kr = = 30,65 + 0,85 kr = = 31,50 kr
Siri räknar så här:
10,65 kr + 20,85 kr = = (10 kr + 20 kr) + (0,65 kr + 0,85 kr) = = 30 kr + 1,50 kr = = 31,50 kr
Svar: 31,50 kr
1. Räkna. Hitta bokstaven.
a. 1,10 + 3,10 =
b. 2,40 + 5,55 =
c. 3,05 + 4,95 =
d. 0,60 + 3,10 =
e. 2,75 + 1,75 =
f. 9,85 − 5,15 =
g. 8,85 − 4,65 =
h. 9,15 − 1,05 =
i. 9,65 − 6,55 =
j. 8,20 − 3,75 =
k. 6,10 − 1,40 =
Film: Förklara
Nora har ett kontantkort på 200 kronor. Hur många kronor har Nora kvar att använda, om hon har använt 137,50 kronor?
Charlie räknar så här:
200 kr − 137,50 kr = = 200 kr − 130 kr − 7,50 kr = = 70 kr − 7,50 kr = = 62,50 kr
Adnan räknar så här:
200 kr − 137,50 kr = = 200 kr − 140 kr + 2,50 kr = = 60 kr + 2,50 kr = = 62,50 kr
Svar: 62,50 kr
2. Skriv uttrycket i ditt häfte och räkna. Ringa in svaret i rutan.
mobilskal 77,45 kr
mobilsmycke 34,20 kr
a. Hur mycket dyrare än mobilsmycket är mobilmaskoten?
mobilmaskot 54,90 kr
hörlurar 188,85 kr
b. Hur mycket dyrare än mobilmaskoten är mobilskalet?
c. Hur mycket kostar hörlurarna, mobilsmycket och mobilskalet sammanlagt?
e. Emma köper en mobilmaskot och ett par hörlurar. Hur mycket får hon tillbaka om hon betalar kontant med 400 kr?
d. Hur mycket mer än den sammanlagda kostnaden för mobilsmycket och mobilmaskoten kostar hörlurarna?
f. Liam köper hörlurar och ett mobilskal. Han får 35 kronor rabatt. Hur mycket kostar inköpen efter rabatten?
Metod – använder fungerande metoder för att utföra beräkningar med tal i decimalform vid huvudräkning och överslagsräkning – väljer och använder
ÖVA
TRÄNA
1. Räkna.
a. 5,85 + 5,05 =
b. 6,75 + 3,35 =
c. 8,05 + 7,75 =
Kan du förklara? Hur räknar du uppgiften 5,85 + 5,05?
d. 7,75 − 4,45 =
e. 9,65 − 7,25 =
f. 8,35 − 3,45 =
2. Titta på bilderna till uppgift 2 på s. 15. Skriv uttrycket i ditt häfte och räkna.
a. Hur mycket mer än mobilskalet kostar hörlurarna?
b. Amina köper ett mobilskal och en mobilmaskot. Hur mycket får hon tillbaka på 200 kronor när hon betalar kontant?
3. Skriv siffran som saknas. Kontrollera med räknare.
a. 3, + 2,0 = 5,4
b. 1,8 + ,0 = 4,8
c. 4,8 − ,0 = 0,8
d. 3, − 1,1 = 2,2
e. 4, + ,2 = 5,7
f. 3, + ,4 = 4,1
g. 2, 1 + ,43 = 6,74
h. 5, 8 − ,02 = 2,06
i. ,00 − 3, 5 = 1,15
j. , 2 + , 6 = 0,95
k. 0, 67 − ,3 1 = 0,066
l. 3,4 8 − ,38 = 2,026
4. Skriv tal i rutorna så att summan av talen i varje vågrät och lodrät rad är
a. 2 b. 7,8 c. 1,49
0,15 0,80
0,70 0,95
5. Ta hjälp av de fyra ledtrådarna för att hitta den hemliga kombinationen.
– Ingen av cirklarna på raden är på rätt plats.
– Bara en av cirklarna på raden är på rätt plats.
– Bara en av cirklarna på raden är på rätt plats.
– Två av cirklarna på raden är på rätt plats.
6. Lös sudokut. I varje lodrät och vågrät rad, och varje markerat område ska det finnas en siffra av varje (1, 2, 3, 4, 5, 6).
2 5 3 5 1 4 5 6 6 2 2 1 6
4. Addition och subtraktion med tal i decimalform, uppställning
87,50 + 76 + 12,781
Svar: 176,281 145,23 − 87,563
Förklara Film
8 7 5 0 0
Svar: 57,667 1
• Skriv talen så att decimaltecknen är under varandra.
• Lägg vid behov till nollor i slutet av talet så att varje tal har lika många decimaler. Exempel: 76 = 76,000
• Skriv ett decimaltecken i svaret på samma plats som i de uppställda talen.
1. Räkna med uppställning. Hitta bokstaven.
7 6 0 0 0 + 1 2 7 8 1 1 7 6 2 8 1 , , , , 1 1 4 5 2 3 0 8 7 5 6 3 5 7 6 6 7 , , , 10 10 10 10 10 Taluppfattning och tals användning
FASTA AVGIFTER nov O9–dec O8
dec O9–jan O8
jan O9–feb O8
till mobil
till fast telefon
2. Undersök räkningen. Skriv uttrycket i ditt häfte och räkna.
a. Vilken är räkningens slutsumma? Det vill säga, hur mycket kostar fasta avgifter, samtal, sms och mms sammanlagt?
b. Vilken blir räkningens nya slutsumma när du subtraherar en kampanjrabatt på 226,65 kronor?
c. Hur mycket mer än samtalen kostade sms:en?
d. Hur mycket mindre än 200 kronor kostade samtalen?
e. Hur mycket kostade sms:en och mms:en sammanlagt?
f. Hur mycket högre blir den fasta avgiften för tre månader, om den stiger med 1,17 kr/månad?
ÖVA
TRÄNA
1. Räkna med uppställning i ditt häfte.
a. 32,6 + 19,08
b. 28,075 − 6,9
Kan du förklara? Hur räknar du 32,6 + 19,08 med uppställning?
c. 72,1 − 48,68
d. 52 − 16,843
2. Skriv uttrycket i ditt häfte och räkna.
a. Johans mobilsamtal kostar 29,76 kronor och Leos mobilsamtal kostar 3,98 kronor mindre. Hur mycket kostar samtalen tillsammans?
e. 17,43 + 28,729 − 16,43 f. 36,01 − 19,586 − 7,3
b. Siri skickar sms för 85,60 kronor och ringer för 179,80 kronor. Från början hade Siri 300 kronor på sitt kontantkort. Hur mycket finns kvar efter att kostnaderna för sms och samtal dragits bort?
3. Skriv decimaltecken så att svaret på uträkningen stämmer.
a. 2 6 8 0 + 1 5 0 = 4,18
b. 2 6 8 0 + 1 5 0 = 28,3
c. 2 6 8 0 + 1 5 0 = 17,68 d. 2 6 8 0 + 1 5 0 = 41,8
4. Räkna ut vilka orden är med hjälp av nyckelordet. Varje siffra i nyckelordet motsvaras av en bokstav. I nästa ord hittar du några av bokstäverna från nyckelordet men också några bokstäver som du får räkna ut/leta upp. Vilka ord kan det vara? En ledtråd är att orden går att hitta i en mobiltelefon.
5. Räkna med räknare. Skriv <, = eller >.
a. 12,747 + 3,287 8,46 + 7,368
b. 39,38 − 14,561 17,32 + 9,46
c. 26,57 + 14,815 15,982 + 26,1
d. 37,6 − 18,45 8,15 + 11
e. 89,075 + 29,9 50,975 + 68,768
f. 76,8 − 34,08 26,78 + 18,96
6. Ta hjälp av de tre ledtrådarna för att hitta den hemliga kombinationen. Kom på två lösningar.
– Bara en av cirklarna på raden är på rätt plats.
– Två av cirklarna på raden är på rätt plats.
– Bara en av cirklarna på raden är på rätt plats.
7. Vilket tal motsvarar den fjärde bilden?
eller
17. Räkna procent med räknare
Hur många procent är 3 av 7?
3
7 = 0,42 8571…≈ 0,43
0,43 = 43 %
Film
Film: Förklara
Talet i decimalform avrundas med en hundradels noggrannhet och det avrundade talet omvandlas till procent.
1. Avrunda med en hundradels noggrannhet. Omvandla till procent.
a. 0,271964… ≈ =
b. 0,369251… ≈ =
c. 0,815201… ≈ =
d. 0,067189… ≈ =
e. 0,1348917… ≈ = f. 0,927705… ≈ =
2. Man frågade 135 av eleverna i årskurs sex vilket klädesplagg de senast fått. Svara med hjälp av cirkeldiagrammet. Hur många procent av eleverna fick senast
a. en kjol? Svar:
b. en mössa? Svar:
c. en t-shirt? Svar:
d. ett par jeans? Svar:
e. ett par skor? Svar:
Kläderna som eleverna i årskurs sex senast fått t-shirt 33 elever jeans 37 elever
mössa 6 elever skor 16 elever kjol 29 elever
f. en halsduk? Svar: halsduk 14 elever
Taluppfattning och tals användning – centrala metoder för beräkningar med räknare – metodernas användning i olika situationer
3. Omvandla till procentform. Hitta bokstaven.
a. 6 8 =
b. 3 12 =
c. 111 300 =
d. 18 24 =
e. 432 600 =
f. 56 140 =
g. 40 500 =
h. 42 210 = i. 144 200 = j. 37 148 = k. 18 150 = l. 74 200 =
m. 49 196 = n. 45 1 500 =
4. Räkna ut hur många procent av bollarna som är röda. Avrunda till heltal.
a. Svar:
d. Svar: g. Svar: b. Svar:
Svar:
ÖVA
TRÄNA
Kan du förklara?
Berätta allt du kan om begreppet procent.
1. Omvandla till procentform. Du kan använda räknare.
a. 72 300 = b. 126 600 = c. 256 800 =
2. Hur många procent av paraplyerna är uppfällda?
a. b. c.
5. Räkna med räknare.
a. 5 av de 25 eleverna i Johannas klass spelar innebandy. Hur många procent spelar innebandy?
Svar:
b. 10 av de 25 eleverna i Johannas klass har vita gymnastikskor. Hur många procent har vita gymnastikskor?
Svar:
6. Rektangeln är indelad i sex månghörningar. Rita en rak linje i rektangeln så att det blir flera månghörningar och trianglarna utgör
a. 75 % av antalet månghörningar. b. 50 % av antalet månghörningar.
7. Räkna med räknare.
a. Av de 23 eleverna i Charlie och Isas klass har sju glasögon. Hur många procent av eleverna har glasögon?
Svar:
c. Av skolans 223 elever brukar 110 cykla till skolan. Hur många procent av eleverna brukar cykla till skolan?
Svar:
e. Av de 52 eleverna i årskurs ett har 16 stycken fyllt 8 år. Hur många procent av eleverna i årskurs ett är 8 år?
Svar:
b. Av skolans 18 lärare dricker 11 kaffe. Hur många procent av lärarna dricker kaffe?
Svar:
d. Ahmena går 300 meter av sin 3,7 kilometer långa skolväg. Resten av vägen åker hon skolbuss.Hur många procent av skolvägen går Ahmena?
Svar:
f. Skolans gård har en area på 2 000 m2. 300 m2 av gården är asfalt. Hur många procent av skolgården är asfalterad?
Svar:
8. Räkna för varje person ut hur många procent av sträckan som är kvar. Avrunda till en procents noggrannhet.
9. Använd räknare för att räkna ut vilket talet är när
a. 30 är 50 %.
b. 20 är 20 %.
c. 100 är 8 %.
d. 24 är 16 %.
e. 300 är 40 %.
f. 600 är 30 %.
Asta Milo Joar Vera
Asta: Milo: Joar: Vera:
18. Hur du räknar ut en procent
Hur mycket är 1 % av 250 kronor, alltså hur mycket är en hundradel av 250 kronor?
Eftersom en procent är en hundradel så dividerar du talet med hundra.
250 kr 100 = 2,50 kr
• När du vill räkna ut 1 % av ett tal dividerar du talet med hundra.
Förklara
1. Skriv uttrycket och räkna. Hur mycket är en hundradel, alltså 1 % av
a. talet 100?
b. talet 500?
c. talet 1 000?
d. talet 200?
e. talet 750?
f. talet 6 000?
g. talet 400?
h. talet 930?
i. talet 8 400?
2. Skriv uttrycket och räkna. Hur mycket är 1 % av
a. 300 kronor?
b. 6 000 kronor?
c. 35 kronor?
d. 250 kronor?
e. en krona?
f. 1 250 kronor?
g. 1 000 kronor?
h. fem kronor?
i. 10 000 kronor?
Taluppfattning och tals användning – tal i procentform och deras samband med tal i bråk- och decimalform
Samband och förändring – procent
3. Visa hur du löser uppgiften.
a. Det finns 300 kg äpplen. 1 % av dem har blivit dåliga. Hur många kg äpplen har blivit dåliga?
b. I bageriet finns 62 kg bröd. 1 % av bröden är baguetter. Hur många kg bröd är baguetter?
Svar:
c. Det finns 30 kg vindruvor. 1 % av vindruvorna innehåller inga kärnor. Hur många kg vindruvor innehåller inga kärnor?
Svar:
d. Fiskaffären beställer 256 kg fisk. 1 % av fisken är abborre. Hur många kg fisk är abborre?
Svar:
e. I affärens köttdisk finns 70 kg kött. 1 % av köttet är lamm. Det finns 6,5 kg mer nötkött än lammkött. Hur många kg nötkött finns det i köttdisken?
Svar:
f. Det finns 60 kg godis. Av dem är 1 % choklad och 6,5 kg saltlakrits. Hur många kg av godiset är varken choklad eller saltlakrits?
Svar:
Svar:
Metod – visar och använder centrala metoder för beräkningar av procent som del av helhet, del av antal och del av värde – utför beräkningar med procent i vardagliga situationer
Problemlösning – förstår frågan i en textuppgift, använder olika strategier, avgör om ett svar är rimligt, löser problem själv eller i grupp
ÖVA
TRÄNA
1. Skriv uttrycket och räkna. Hur mycket är 1 % av
a. talet 600?
b. talet 8?
d. talet 40?
2. Skriv uttrycket och räkna.
e. 150 kronor?
a. Man får 1 % rabatt på en bil som kostar 47 000 kronor. Hur stor är rabatten?
Svar:
Kan du förklara?
Hur räknar du ut 1 % av 250 kr?
c. 18 kronor? f. 100 000 kronor?
b. Ett år sålde en affär 1 200 cyklar. Nästa år ökade försäljningen med en procent. Hur många fler cyklar sålde man då?
Svar:
4. Hur många procent av figuren är färgad i varje del?
= B = C = D =
=
= C =
= B = C =
= E =
= B = C =
5. Lös uppgiften.
a. Hur stor del av bilden är färgad?
b. Hur många procent av bilden är vit?
6. Räkna ut rätt siffra eller siffror.
a. När du skriver siffran med bokstäver utgör varje bokstav 25 %.
b. När du skriver siffran med bokstäver finns det 50 % av en bokstav.
c. När du skriver siffran med bokstäver utgör bokstaven å 33,3… %.
d. När du skriver siffran med bokstäver utgör bokstaven t 66,6… %.
7. Lös uppgiften.
Samuel Svensson har två förnamn. I hela hans namn utgör bokstaven s 25 %. Kom på ett lämpligt andranamn till Samuel.
Favoritmatematik
Favorit matematik är ett basläromedel i matematik med en gedigen, välfungerande och tydlig struktur. Materialet kommer från Finland där det är uppskattat för strukturen och de goda resultaten.
I sällskap med Isa, Charlie och deras klasskamrater byggs en stabil matematisk grund utifrån vardagliga situationer. Det är så matematiken blir en favorit!
Tillsammans med den tryckta elevboken får eleverna ett digitalt läromedel som ger stöd och möjliggör en varierad undervisning. I det digitala läromedlet finns alla elevbokens instruktioner inlästa. Det innehåller även filmer, övningar och matteordlistor samt det spelifierade läromedlet Tomoyo för digital färdighetsträning.
Favorit matematik för skolår 6 består av elevböckerna 6A och 6B i två nivåer. Till varje elevbok medföljer laborativt material samt häftet Bedömning för lärande med prov, självbedömning och lärardokumentation. Lärarhandledningarna 6A och 6B kan kompletteras med Favorit matematik – Utökat stöd för klasslärare och Favorit matematik – Special för speciallärare.