







MATEMATICA 4





PROVE D’INGRESSO
ED. CIVICA E MOTORIA
INGLESE E CLIL
INVALSI - STEM
MAPPE DI RIPASSO

A cura di Erica Zampieri

DIGITA IL CODICE PER ATTIVARE
LA VERSIONE DIGITALE DEL LIBRO!


CODICE DI ATTIVAZIONE UNICO





RAFFAELLO PLAYER
RISORSE DIGITALI e SOLUZIONI con l’app RAFFAELLO PLAYER









VERSIONE ONLINE www.raffaelloplayer.it
VERSIONE MOBILE









ATTIVITÀ INTERATTIVE GRATUITE
ATTIVITÀ INTERATTIVE GRATUITE con l’app GLI ANTIRUGGINE
ITALIANO e MATEMATICA
























VERSIONE ONLINE www.gliantiruggine.it
VERSIONE MOBILE



Ti serve aiuto? Leggi le F.A.Q. o richiedi assistenza collegandoti all’indirizzo supporto.raffaellodigitale.it oppure scrivi una e-mail a supporto@raffaellodigitale.it

MATEMATICA al CENTRO ESTIVO VA A E C N Z



Indica le pagine svolte con una .
2 IL CENTRO ESTIVO
4 REGOLE MAPPE e
52 Prodotti tipici
54 Zaini e borracce


IN CITTÀ
13 Benvenuti!
14 Allenamenti numerici
56 Problemi di montagna
58 Passatempi per la pioggia
60 Giochi di logica
62 Uno sciame di frazioni


AL MARE
16 Poligoni in spiaggia
18 Gabbiani e numeri
20 Pesci e boe
22 In colonna tra le onde
24 Sui pedalò
26 Problemi al mare
28 Gocce di mare
30 Castelli di operazioni
32 A tutta vela
64 Acquisti montani


IN CITTÀ
66 In mongolfiera sulla città
68 Il treno dei decimali
70 Tragitti in terra e cielo
72 Al parco acquatico
74 Poligoni gustosi
76 Picnic al parco
78 PROVE MODELLO INVALSI


IN CAMPAGNA
34 Vola, vola farfallina
36 Ulivi centenari
38 Piante e frutti
40 Gara di cucina
42 Frazioni al lago
44 Fra i campi
46 Figure di campagna
48 Figure nei campi







IN MONTAGNA
50 Operazioni fra i monti


4 CLASSE
Inquadra per attivare le RISORSE DIGITALI TROVI LE SAGOME DI ANIMATORI E ANIMATRICI DA RITAGLIARE

CENTRO

QUESTA È LA CASA BASE.


CON IL PULMINO FAREMO MOLTE GITE!
IL
ESTIVO
2 JULY
LUCA
VALE
ANNA ROBY



IL CAMPETTO È ADATTO PER MOLTI SPORT DI GRUPPO ALL’APERTO!









Questa è una tabella “magica”: se sommi i numeri di ogni riga orizzontale, di ogni riga verticale o delle diagonali, il risultato è sempre lo stesso. Osserva il disegno del Centro e scrivi i numeri che corrispondono alle definizioni, poi completa con quelli che mancano.
I mezzi di trasporto del centro estivo.
Il numero di palline.
Il numero di animatrici.
Il numero di animatori.
Il numero di palloni.
Il numero di ambienti in cui si svolgono le gite.


6
3
3
7 1
4




IL SISTEMA DI NUMERAZIONE

Il nostro sistema di numerazione usa 10 cifre:

è un sistema:
• DECIMALE, perché per contare si raggruppano le quantità di dieci in dieci, cioè in base dieci;
• POSIZIONALE, perché ogni cifra ha valore diverso a seconda della posizione che occupa nel numero.
Dieci unità di qualsiasi ordine formano un’unità dell’ordine immediatamente superiore.


La cifra 0 sembra non valere niente e invece è importantissima: in un sistema di numerazione posizionale occorre un simbolo per indicare la posizione vuota.
Osserva:
1 u= 1 10 u= 1 da 10 da= 1 h
10 h= 1 uk 10 uk= 1 dak 10 dak= 1 hk


Ogni periodo è formato da 3 ordini.


REGOLE MAPPE e 4 MATEMATICA
1 2 3 4 5 6 7 8 9
0
Secondo periodo o delle unità di migliaia Primo periodo o delle unità semplici centinaia di migliaia decine di migliaia unità di migliaia centinaia decine unità hk dak uk h da u 100 000 10 000 1 000 100 10 1





NUMERI
ADDIZIONE
L’addizione si usa per unire, per mettere insieme due o più quantità.
345 + addendo
236 = addendo 581 somma
Nell’addizione lo 0 è l’elemento neutro: ogni numero sommato a zero dà come risultato il numero stesso.
7 + 0 = 7 0 + 5 = 5

SOTTRAZIONE


La sottrazione si usa quando si deve calcolare quanto resta, la differenza o la parte mancante. Nei numeri naturali è possibile calcolarla solo quando il minuendo è maggiore o uguale al sottraendo.
765 – minuendo
37 = sottraendo
728 resto o differenza
Per eseguire la prova della sottrazione si esegue un’addizione.
392 –147 = 245
245 + 147 = 392

Proprietà commutativa: se si cambia l’ordine degli addendi, la somma non cambia.
Questa proprietà viene utilizzata per eseguire la prova dell’addizione.
36 + 410 = 446
410 + 36 = 446
Proprietà associativa: se a due o più addendi si sostituisce la loro somma, il risultato non cambia.
36 + 14 + 45 = 95
50 + 45 = 95


Proprietà invariantiva: se si aggiunge o si toglie dai termini di una sottrazione lo stesso numero, il risultato non cambia.
356 – 174 = 182
352 – 170 = 182 – 4 – 4


MAPPE e 5 MATEMATICA
REGOLE




La moltiplicazione è l’operazione che ripete più volte la stessa quantità.

14 x moltiplicando o 1° fattore
35 = moltiplicatore o 2° fattore
70 1° prodotto parziale
420 2° prodotto parziale
490 prodotto finale

Lo 0 è l’elemento assorbente della moltiplicazione: se si moltiplica qualsiasi numero per 0, il prodotto è sempre uguale a 0.


L’1 è l’elemento neutro: se si moltiplica qualsiasi numero per 1, il prodotto è sempre uguale al numero stesso.

Proprietà commutativa:

se si cambia l’ordine dei fattori il prodotto non cambia.
Questa proprietà si applica per eseguire la prova.
32 x 54 = 1728
54 x 32 = 1728
Proprietà associativa: se a due o più fattori si sostituisce il loro prodotto, il risultato non cambia.
40 x 3 x 8 = 960
120 x 8 = 960
Proprietà distributiva: se a un fattore si sostituiscono due addendi la cui somma è uguale al fattore considerato, il risultato non cambia.
28 x 14 = 28 x (10 + 4) = (28 x 10) + (28 x 4) = 280 + 112= 392

REGOLE MAPPE e 6 MATEMATICA
NUMERI MOLTIPLICAZIONE




DIVISIONE

La divisione è l’operazione che distribuisce quantità o indica quante volte un numero è contenuto in uno più grande.
: = 48 dividendo 4 divisore 12 quoziente







Proprietà invariantiva: se si dividono o si moltiplicano i termini di una divisione per lo stesso numero, diverso da 0, il risultato non cambia.
640 : 80 = 8 45 : 15 = 3


64 : 8 = 8 90 : 30 = 3


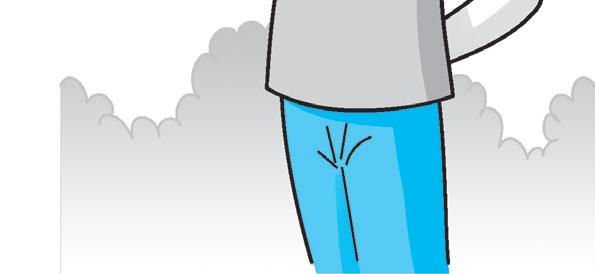

2 7 numeratore: indica quante parti sono state considerate linea di frazione: indica che l’intero viene diviso in parti uguali denominatore: indica in quante parti è stato diviso l’intero
Le frazioni possono essere:
• proprie: quando sono minori di un intero; hanno il numeratore minore del denominatore.
• improprie: quando sono maggiori dell’intero; hanno il numeratore maggiore del denominatore e non multiplo del denominatore.
• apparenti: quando indicano uno o più interi; hanno il numeratore multiplo del denominatore.

11
13 3 4 1 2 ; ; 9 5 23 8 7 4 ; ;
11 9 9 2 2 ; ;


REGOLE MAPPE e 7 MATEMATICA
FRAZIONI
NUMERI
x 2 : 10 x 2
: 10
22





Le frazioni possono essere:

• complementari, quando sommandole formano un intero.
3 5 2 5 5 5 = +
• equivalenti, quando frazioni differenti rappresentano la stessa parte dell’intero o indicano la stessa quantità.
Le frazioni equivalenti si ottengono moltiplicando o dividendo il numeratore e il denominatore per lo stesso numero diverso da 0.



Per calcolare la frazione di un numero si deve dividere quel numero per il denominatore e poi moltiplicare il risultato per il numeratore.
3 4 di 24 = 24 : 4 = 6 poi 6 x 3 = 18 quindi 3 4 di 24 è 18.
FRAZIONI DECIMALI
Le frazioni che hanno come denominatore 10, 100 e 1000 si chiamano frazioni decimali.
Le frazioni decimali possono essere trasformate in numeri decimali.
NUMERI DECIMALI
Un numero decimale
è formato da una parte intera e una parte decimale separate dalla virgola. 2,50


REGOLE MAPPE e 8 MATEMATICA
2 5 3 5 1 2 1 2 2 4 4 8 2 4 4 8 FRAZIONE COMPLEMENTARE
VIRGOLA PARTE INTERA PARTE DECIMALE
NUMERO
NUMERI = 0,003 3 1000 = 0,02 2 100 = 0,7 7 10
FRAZIONE DI UN
FRAZIONI
x 2 x 2 x 2 x 2




NUMERI
OPERAZIONI CON I NUMERI DECIMALI
5
• Incolonna i numeri, rispettando il valore posizionale delle cifre.
• Inserisci la virgola nel risultato.
• Pareggia le cifre decimali se necessario.
Moltiplicazione
24 x
• Esegui la moltiplicazione come se i fattori fossero numeri interi e calcola il prodotto finale.
• Metti la virgola nel prodotto finale contando, a partire da destra, tante cifre quante quelle delle cifre decimali dei fattori.
Divisione
Con il dividendo decimale: procedi come nella divisione con i numeri interi. Metti la virgola al quoziente quando abbassi la prima cifra decimale.
Con il divisore decimale: rendi intero il divisore moltiplicandolo per 10, 100 o 1000. Fai lo stesso con il dividendo.
2,352 : 1,2
23,52 : 12 x 10 x 10
A questo punto procedi come sai già fare.


REGOLE MAPPE e 9 MATEMATICA
6, 2 7 + 3, 4 0 =
9, 6 7 3 4, 0 0 –5, 6 7 = 2 8, 3 3
5
Addizione e sottrazione
1,2
28,8 6,55 x 2,7 = 17,685
=



MOLTIPLICARE PER 10, 100 E 1 000
Con i numeri interi:

19 x 10 = 190 19 x 100 = 1 900 19 x 1 000 = 19 000
Con i numeri decimali:
5,768 x 10 = 57,68
5,768 x 100 = 576,8 5,768 x 1 000 = 5 768
Quando si moltiplica un numero per 10, 100 o 1 000 ogni cifra aumenta il suo valore di 10, 100 o 1 000 volte. Si sposta la virgola verso destra di uno, due o tre posti e, se necessario, si aggiungono gli zeri.
DIVIDERE PER 10, 100 E 1 000
Con i numeri interi:

5 000 : 10 = 500
Con i numeri decimali:
956 : 10 = 95,6
5 000 : 100 = 50
956 : 100 = 9,56
5 000 : 1 000 = 5

956 : 1 000 = 0,956
Quando si divide un numero per 10, 100 o 1 000 ogni cifra diminuisce il suo valore di 10, 100 o 1 000 volte. La virgola si sposta di uno, due o tre posti verso sinistra e, se necessario, si aggiungono gli zeri.
MISURA
Per passare da un’unità di misura maggiore a una minore si deve moltiplicare per 10, 100 o 1 000.

15 da = 150
14 m = 1 400 cm
21 kg = 21 000 g x 10 x 100 x 1 000
Per passare da un’unità di misura minore a una maggiore si deve dividere per 10, 100 o 1 000.
11 m = 1,1 dam
8 = 0,08 h


21 g = 0,021 kg
: 10 : 100 : 1 000



10 MATEMATICA
REGOLE MAPPE e
NUMERI





REGOLE MAPPE e
SPAZIO E FIGURE
PERIMETRI E AREE

Quadrato
P = x 4
A = x

Triangolo isoscele
P = + ( 1 x 2)
A = (b x h) : 2
Trapezio
P = b + B + 1 + 2
A = (B + b) x h 2
Rettangolo

Triangolo equilatero
P = x 3
A = (b x h) : 2

P = (b + h) x 2
A = b x h

Romboide
Triangolo scaleno
P = (b + ) x 2
A = b x h
P = 1 + 2 + 3
A = (b x h) : 2
Rombo

P = x 4
A = (D x d) 2

11 MATEMATICA
1 1 1 1
2
3 2
B D b b b d h
spore
IL FUNGO
cappello



REGOLE MAPPE e
SCIENZE
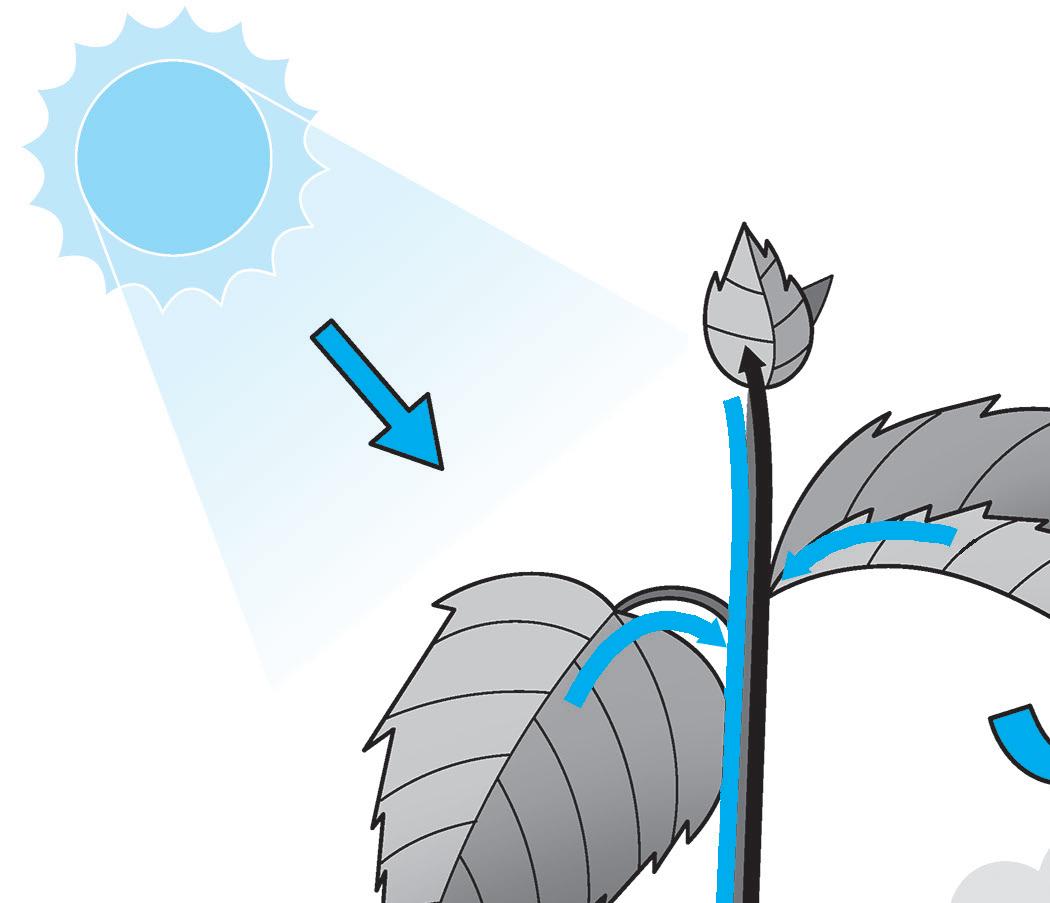
LA FOTOSINTESI
ife
lamelle
ossigeno
gambo
micelio
INGLESE luce
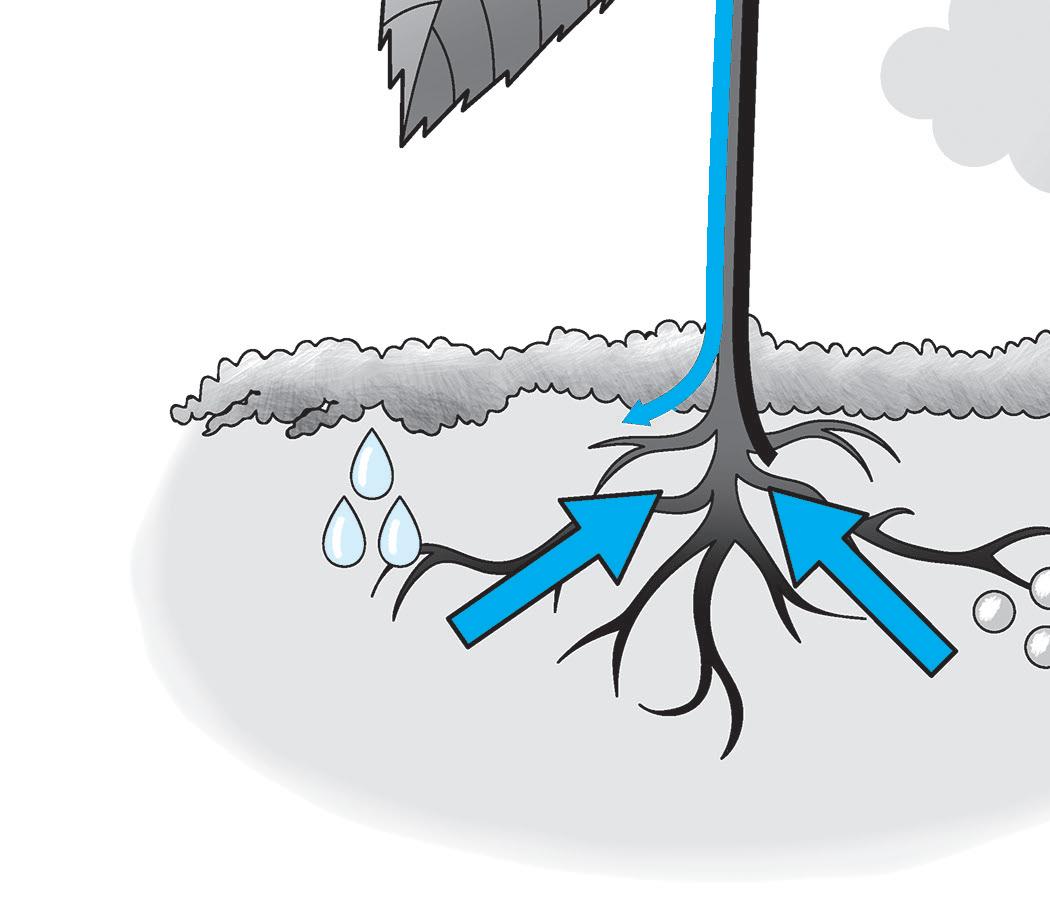
anidride carbonica

linfa elaborata linfa grezza acqua
sali minerali
THOUSANDS (migliaia)


HUNDREDS (centinaia)

TENS (decine)
UNITS (unità) NUMBERS



12 SCIENZE INGLESE
















1 Anna, Luca, July, Vale e Roby saranno i vostri cinque animatori e, davanti all’entrata, danno alcune indicazioni per frequentare il centro estivo. Leggi le informazioni e scrivi i numeri al posto giusto.

5 • 32 • 7:30 • 38 • 45 • 348



L’orario di ingresso al centro estivo è dalle alle 8:30. Ogni bambino riceverà la maglietta del centro estivo. Le taglie sono 36, ............ , 40, 42.
Se la temperatura supererà i °C, i bambini giocheranno al chiuso, in un locale dotato di aria condizionata.


I bambini saranno divisi in gruppi, ogni gruppo avrà un animatore di riferimento.

Il costo a settimana è di euro. Il numero di telefono per le comunicazioni è ................/4333678


















BENVENUTI!

ALLENAMENTI NUMERICI
1 Quest’anno le nostre gite saranno al mare, in campagna, in montagna e in città. Prima però, allenati con i calcoli veloci. Calcola a mente e scrivi i risultati sui puntini.

877 – 99 =
68 + 99 =
52 – 9 =
45 + 9 = ..............

15 x 0 =
7 x 0 x 1 = ..............
0 x 8 x 4 = ..............

34 : 0 = A C B
7 x 0 x 1 =
58 + 11 =
322 – 11 =
876 – 11 =
980 + 11 = ..............
20 : 5 =
15 : 15 = ..............
36 : 9 = ..............

14 MATEMATICA
D





FOLLOW THE SEQUENCE!
2 Look and complete. Then say the sequences.











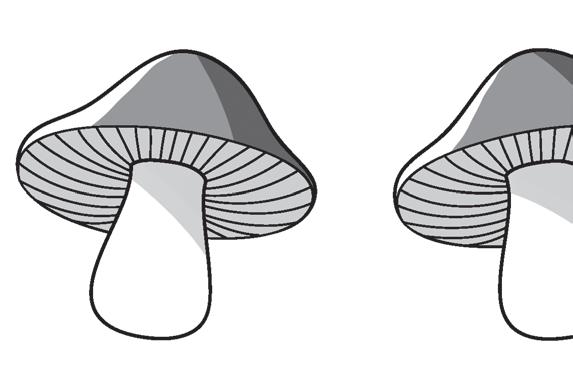
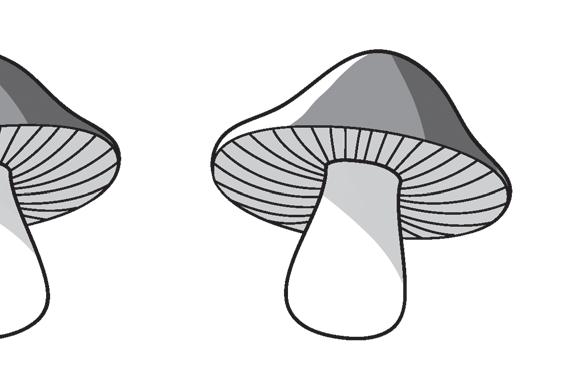
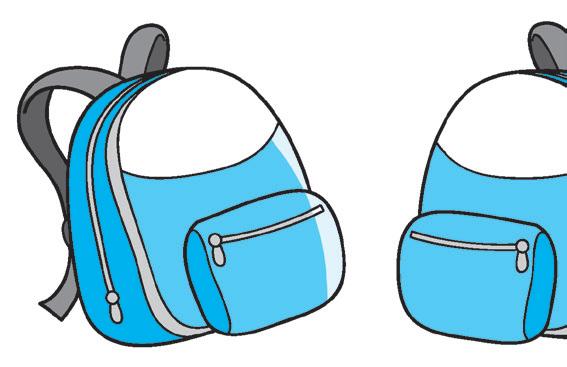

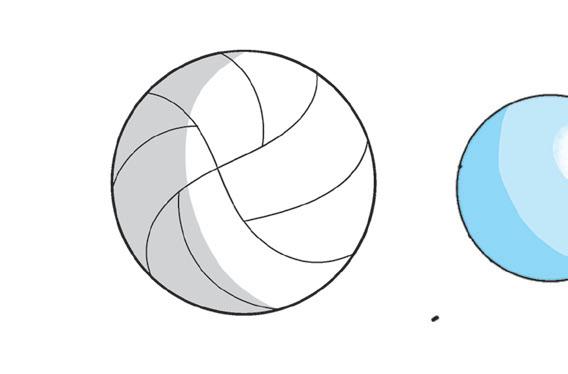






15 INGLESE
IMPARIAMO L’INGLESE con July D 28 42 56 E 3 9 27 F 3125 625 125 A 25 50 75 B 128 64 32 ....... C 900 750 600 .......








Quest’anno le gite del Centro estivo cominciano al mare!




POLIGONI IN SPIAGGIA












1 Che bel posto! In spiaggia e nel mare sono nascosti 5 poligoni diversi. Cerchiali.













16 MATEMATICA


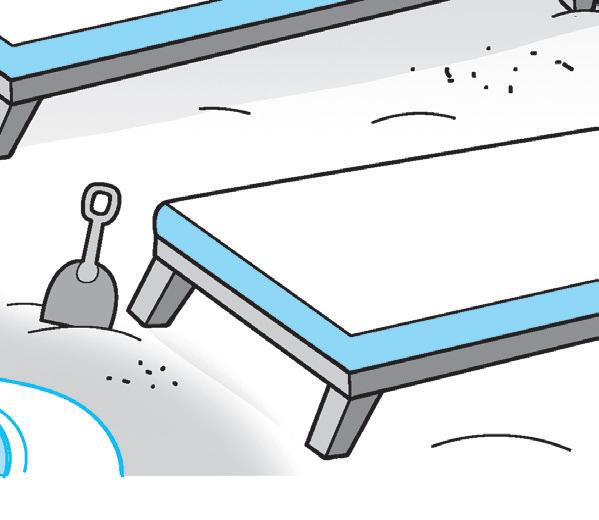
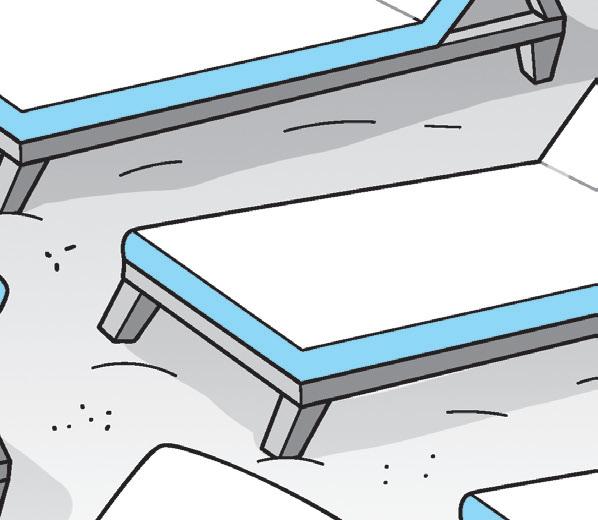

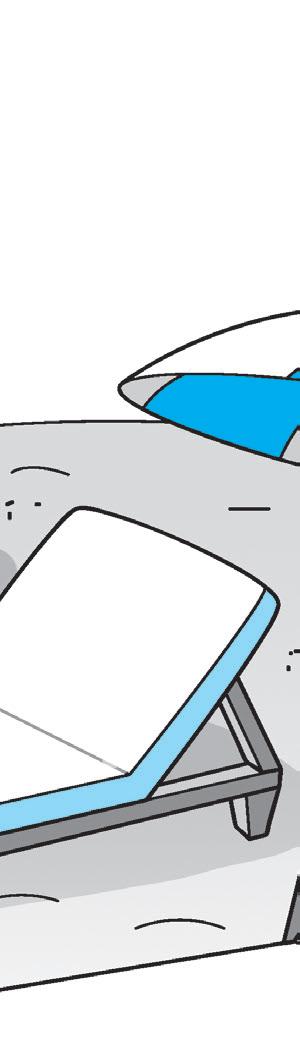








































23 000 2 h 3 da 7 u 3 uk 8 h 5 hk 6 dak 560 000 237 3 800 23 uk 17 MATEMATICA
2 Colora in giallo i lettini con i numeri minori di 10 000 e in azzurro i lettini con i numeri maggiori di 10 000.
3 Completa
>). 457 031 499 876 560 897 45 731 562 315 53 421 15 780 4 321 509 421 31 243 43 298 764 213 863 215 89 007 897 000 799 407 8 652 985 320 6 uk 5 h 5 da 7 dak 5 uk 3 h 3 da 8 u 2 dak 3 uk 7 uk 2 h 3 da 1 u 9 uk 5 h 4 da 3 u 1 hk
4 Colora nello stesso modo le conchiglie che contengono numeri uguali.
con il segno corretto (<,
0 dak 3 uk

GABBIANI E NUMERI
1 Abbiamo visto dei gabbiani che facevano a gara per pescare i pesci! Registra negli abachi i numeri rappresentati.


2 Collega i numeri scritti in lettere a quelli corrispondenti in cifre

3 I gabbiani inseguono la nave. Osserva l’esempio e determina il valore della cifra 3 in ogni numero.


18 MATEMATICA
k h da u k h da u k h da u k h da u k h da u k h da u milleduecentocinquanta 5 122 duemilasettecento 2 700 cinquemilacentoventidue 1 250 1 350 3 450 1 213 5 731 300 , .................. , , .................. , , , .................. , , .................. , , 3 h 300
4 Rappresenta i numeri sull’abaco e registra.


5 Componi e scomponi.

19 MATEMATICA
hk dak
...... ...... ...... ...... ...... ...... hk dak uk h da u hk dak uk h da u hk dak uk h da u ...... ...... ...... ...... ...... ...... hk dak uk h da u hk dak uk h da u 8 310 22 916 32 066 64 091 7 258 157 131 8 hk + 6 dak + 9 uk + 5 h + 1 da + 7 u = 2 h + 6 d + 6 u = ................. 2 dak + 8 h + 4 u = 6 hk + 1 uk + 7 h + 1 da = ................. 12 340 = 71 018 = 30 648 = ........................................................... 18 826 =
uk h da u

1 Aiuta il polpo a formare in tanti modi il numero 10 000 e scrivilo negli spazi.


10000
1 0 0 0 0 dak uk h d u Ricordi?
2 Collega i numeri scritti in lettere a quelli scritti in cifre
diecimilaquattrocentosei
quindicimiladuecentodue
99 009
tredicimilaquaranta
diecimilaquarantasei novantanovemilanove


15 202
10 046

3 Confronta e scrivi i segni giusti nelle boe (>,<, =).
10 406
13 040

20 MATEMATICA
PESCI E BOE
1 dak 2 uk 0 h 7 da 1 u 6 uk 4 h 2 da 9 u 1 dak 7 uk 4 h 1 da 1 u 8 uk 2 h 5 da 3 u 5 dak 7 uk 4 h 7 da 8 u 1 271 6 429 17 411 9 874 9 874 ....................................... .......................................


4 Completa seguendo le istruzioni.


5 Scopri gli operatori da seguire nella successione e scrivili.


6 Scrivi i numeri dal minore




21 MATEMATICA
– 10 numero + 10 2 000 3 409 ......................... 5 672 ......................... – 99 (– 100 + 1) numero + 99 (+ 100 – 1) ..................................... 5 600 ..................................... 242 000 75 001 – 999 (– 1 000 + 1) numero + 999 (+ 1 000 – 1) 67 999 10 000 ..................................... 999 000 ..................................... 8 200 10 000 100 000 5 000 500 000 100 000 111 111 999 999 + 1 800 .............. .............. .............. .............. • • • • 43 683 • 9 561 • 530 842 • 555
al maggiore.



IN COLONNA TRA LE ONDE
1 Quante conchiglie! Calcola in colonna le addizioni e le sottrazioni.
1 832 + 20 418 =
4 323 – 1 216 =
5 616 + 1 946 =
1 8 462 – 1 482 =

13 148 + 27 196 =
2 596 – 1 412 =
1 902 + 11 098 =
20 018 – 12 026 =




2 Calcola in colonna su un foglio e fai la prova seguendo gli esempi.


Per l’addizione applica la proprietà commutativa
2 418 +
1 104 = 3 522
126 + 1 919 + 30 014 =
96 + 8 129 + 12 016 =
1 104 +


Per la sottrazione usa l’operazione inversa
4 714 +
8 120 – 4 117 =
38 819 – 5 612 =


22 MATEMATICA
6 126 –1 412 = 4 714
2 418 = 3 522
1 412 = 6 126

3 Esegui le addizioni e le sottrazioni in colonna. Poi ordina i risultati in ordine crescente
5 678 + 42 720 =
46 518 – 32 206 =
43 281 + 19 088 =
61 263 – 50 480 =


4 Roby si diverte a inventare indovinelli numerici: risolvi questo.


704 050 + 121 993 =
709 000 – 610 455 =
122 467 + 509 342 =
820 400 – 301 062 =


Qual è la diff erenza tra la somma di 1 h e 3 da e la somma di 5 da e 8 u?

Indicala con una .
188 62
72 70



23 MATEMATICA
< < < < < < <

SUI PEDALÒ
1 Luca, Anna e Vale hanno affittato i pedalò. Calcola applicando le proprietà dell’addizione, come gli esempi.
associativa
130 + 2 + 8 = 130 + (2 + 8) = 130 + 10 = 140
189 + 11 + 49 = =
550 + 150 + 31 =
commutativa
68 + 99 + 12 = 68 + 12 + 99 = 179
395 + 100 + 15 =
17 + 88 + 33 =
strategia
1 480 + 2 100 + 3 300 =
3 218 + 5 400 + 1071 =


2 Calcola applicando la proprietà invariantiva della sottrazione.
9 256 – 455 =
6
3 Completa le tabelle.


24 MATEMATICA
=
=
............
............................................................... =
6
000
100 +
50
40
6 150 + 1 040 + 309 =
000 + 1
+
300 +
+
+ 9 = ............
=
600
600)
(750
600)
5 000
150
= 5 600 – 750 = (5
–
–
–
=
–
=
=
(33 625 + 25)
(375 + 25)
33 650
400
33 625 – 375 =
–
=
–
=
=
860 – 999 =
+ 50 500 5 000 50 000 3 244 10 277 250 200 + 10 100 1 000 10 000 99 486 564 881 480 900

4 Osserva le proprietà che caratterizzano le quattro operazioni.

Proprietà commutativa






Proprietà associativa










5 Le due proprietà sono applicate all’operazione giusta? Rispondi con una e, se l’operazione è possibile, scrivi il risultato.
Proprietà distributiva Proprietà invariantiva + –x : proprietà commutativa proprietà invariantiva
20 + 40 = 40 + 20 sì no
10 x 2 = 2 x 10 sì no ............
70 – 5 = 5 – 70 sì no
8 : 2 = 2 : 8 sì no

8 + 2 = (8 + 3) + (2 + 3) sì no
8 x 2 = (8 + 3) x (2 + 3) sì no ............
4 – 2 = (4 + 3) – (2 + 3) sì no
6 : 3 = (6 : 3) : (3 : 3) sì no
6 Applica la proprietà distributiva alle seguenti moltiplicazioni.
25 x (11 + 4) = ( .............. x .............. ) + ( .............. x .............. ) = .............. + .............. = ..............
35 x (6 + 2) = ( x ) + ( x ) =
7 Applica la proprietà associativa e completa.
38 + 45 + 5 = + = 20 + 14 + 5 =





25 MATEMATICA
+ =
+ =

PROBLEMI AL MARE
1 Leggi i testi dei problemi, analizza i dati e risolvi.
a. A maggio, Carlo ha acquistato un paio di scarpe al costo di 123 euro, una camicia al costo di 56,99 euro e una cintura al costo di 15,50 euro. Quanto ha speso Carlo? Se precedentemente aveva speso 197 euro in costumi, ciabatte e telo mare, a quanto ammonta la sua spesa complessiva?
Dati
Operazioni
Risposte

b. L’estate scorsa Gaia ha collezionato 1 089 figurine. Quest’anno ne ha acquistate 1 378 e 107 le sono state regalate dai bambini del centro estivo. Quante figurine ha in tutto Gaia?
Dati
Operazioni
Risposta

26 MATEMATICA
........................................................................................
........................................................................................
Dati

a. Oggi in un tratto di spiaggia ci sono 228 adulti. I bambini sono 80 in meno rispetto agli adulti. Quanti sono i bambini? Il personale che lavora alla spiaggia è composto da 46 persone. Quante persone ci sono in tutto in spiaggia?

b. Una squadra di operatori ecologici ha raccolto in un sacco i rifiuti lasciati su un tratto di spiaggia. In tutto 74 bottigliette di plastica, 24 stecchini di legno e 31 cartacce. Il sacco è forato e fuoriescono 18 oggetti. Quanti ne rimangono nel sacco?
• Per andare dall’ombrellone alla sua bicicletta Roby ha fatto 350 passi nel primo tratto e 215 nel secondo tratto. Per arrivare gli mancano ancora 118 passi. Qual è la distanza, in passi, fra il suo ombrellone e la sua bici?


27 MATEMATICA
2 Risolvi i problemi.
3 Risolvi il problema sul quaderno.
........................................................................................
........................................................................................ Operazioni ........................................................................................ ........................................................................................ Operazioni ........................................................................................
Dati Risposte Risposta

1 Scrivi nelle gocce d’acqua l’operatore corretto in modo da ottenere il risultato indicato.
2 Calcola in colonna le moltiplicazioni scritte sugli scogli.

118 x 26 =
138 x 14 = ..................
125 x 32 = 146 x 46 = ...................
138 x 143 = 226 x 319 =
2 816 x 132 =
1 948 x 312 =
3 Completa la regola: scrivi sui puntini i termini mancanti.
interi • decimali • destra • virgola
Le moltiplicazioni con i numeri ............................................. si eseguono come se i fattori fossero numeri Poi, nel prodotto finale, si rimette la , contando da tante cifre quante sono le cifre decimali dei due fattori.

28 MATEMATICA
10 000 = 10 850 000 = 8 500 .............. 500 = 500 000 7 462 = 746 200 7 560 64 800 = 75 600 = 6 480 .............. ..............
GOCCE DI MARE
4 Scrivi in colonna e calcola sul quaderno.
12,6 x 18,2 =
23,5 x 16,2 = ..............
3,84 x 2,7 =
428 x 0,12 = ..............
5 Completa la regola: scrivi sui puntini i termini mancanti.


dividendo • decimale • intero • invariantiva • quoziente




Le divisioni con il decimale si eseguono come le altre, ma si
deve mettere la virgola al ............................................. prima di dividere la parte decimale.
Se il divisore è ............................................. devi applicare la proprietà ................................................ e moltiplicare x 10, 100 o 1 000 i termini della divisione.
Se dividendo e divisore sono decimali, applica la proprietà invariantiva per rendere il divisore.
6 Applica la proprietà invariantiva per rendere intero il divisore ed esegui in colonna, come nell’esempio.
326 : 3,2=
3260 32
456,18 : 0,9=
642,8 : 4,6=
52,82 : 0,62=
385:0,242=
7 Scrivi in colonna e calcola sul quaderno.
648,32 : 28 =
546 : 6,7 =
13,2 : 0,14=
83,24 : 6,7 =

29 MATEMATICA
x
x 10
10
x x
x ....... x .......
x x
x ....... x .......
x x

CASTELLI D I O PERAZIONI








Che bello costruire castelli di sabbia tutti insieme!
1 Esegui le operazioni nei castelli.







zeri • destra • sinistra • virgola • decimale
2 Completa le regole (attenzione: dovrai usare alcune parole più di una volta).

- Per moltiplicare un numero ...................................... per 10, 100, 1 000, devi spostare la di tanti posti, verso quanti sono gli del divisore. Se mancano delle cifre aggiungi degli
- Per dividere un numero per 10, 100, 1 000, devi spostare la di tanti posti, verso quanti sono gli del divisore. Se mancano delle cifre aggiungi degli ................................... .
3 Trasforma le frazioni nel numero decimale corrispondente.
30 MATEMATICA = = = = = =
0,3 0,87 1,245 0,56 .............. 0,283 .............. 2,07 .............. 0,017 1,1 0,9 0,04 .............. 0,104 .............. 0,607.............. 0,4 0,2 823,6 0,8 15,4 1 258,2 0,25 50,1 3 499,1 11,3 .............. 3,75 .............. 66 .............. x 10 : 10 x 100 : 100 x 1 000 : 1 000
3 10 56 10 155 1 000 9 100 23 100 3 455 1 000 = = = = = = 3 : 10 0,3

4 Scopri come si costruisce il castello di sabbia perfetto. Sottolinea le informazioni principali.
1) Un elemento chiave è la giusta quantità di acqua. Ogni otto secchi di sabbia bisogna usare un secchio di acqua.

2) Sabbia troppo asciutta provocherà lo sgretolamento dell’edificio, mentre troppa acqua farà “liquefare” il castello sotto i vostri occhi. La resistenza di un castello di sabbia dipende da come i grani di sabbia interagiscono tra loro. Qui entra in azione una proprietà dell’acqua: la tensione superficiale. Ogni granello di sabbia bagnata è avvolto da una sottile pellicola che, tutta insieme, dà compattezza al castello. Dato che si utilizza acqua di mare, bisogna considerare anche l’effetto del sale, che si comporta come una colla, rafforzando la tenuta del castello e garantendo stabilità all’intera costruzione.

3) Ciottoli, conchiglie, frammenti di legno e ghiaia renderanno più bella la struttura, ma soprattutto più solida.
4) Per gli strumenti di lavoro da usare: i secchielli migliori sono quelli semplici senza decorazioni in rilievo, perché disegni e forme tendono a franare rapidamente. Pale, palette e rastrelli devono essere di dimensione adeguata: la dotazione ottimale è costituita da un insieme di misure differenti.
5) La sabbia migliore è quella né troppo fine né troppo grossa. Rid e adatt da www.Focus.it


5 Completa il significato di questi concetti con le parole chiave giuste.


- Il passaggio di stato da aeriforme a liquido si chiama ................................................. . In questo testo è usato non proprio correttamente come sinonimo di fusione, per indicare che la sabbia (cioè un solido) è diventata liquida.
- La superficie dell’acqua sembra tenuta insieme da una pellicola trasparente. Questo fenomeno si chiama e accade perché le molecole esterne dell’acqua tendono a restare più vicine le une alle altre.

31 MATEMATICA
superficiale • liquefazione SCIENZE
tensione



A TUTTA VELA
1 A Roby e July piace andare in barca a vela. Classifica i triangoli delle vele, in base ai lati e agli angoli, scrivendo nella tabella le lettere corrispondenti.



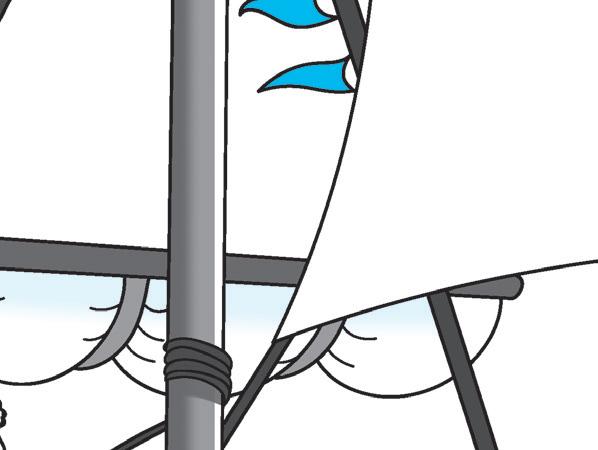






2 Completa le definizioni.
equilatero
isoscele A
scaleno A B C D E F G
acutangolo rettangolo ottusangolo


- Il triangolo è un poligono avente tre , tre , tre .
- L’altezza di un triangolo è il segmento perpendicolare che unisce un al suo lato opposto.
- Il triangolo scaleno ha tutti e tre i lati
- Un triangolo con una coppia di lati uguali, è un triangolo ................................................ .
- Se uno dei tre angoli del triangolo è retto, allora è un triangolo
- La somma dei tre angoli interni di un triangolo è di °: un angolo
3 Misura con il righello e calcola il perimetro dei triangoli. Poi per ciascun triangolo traccia l’altezza relativa al lato evidenziato.
32 MATEMATICA
P = P = P =

4 Collega ogni triangolo al quadrilatero che contiene la misura del suo perimetro e completa la formula
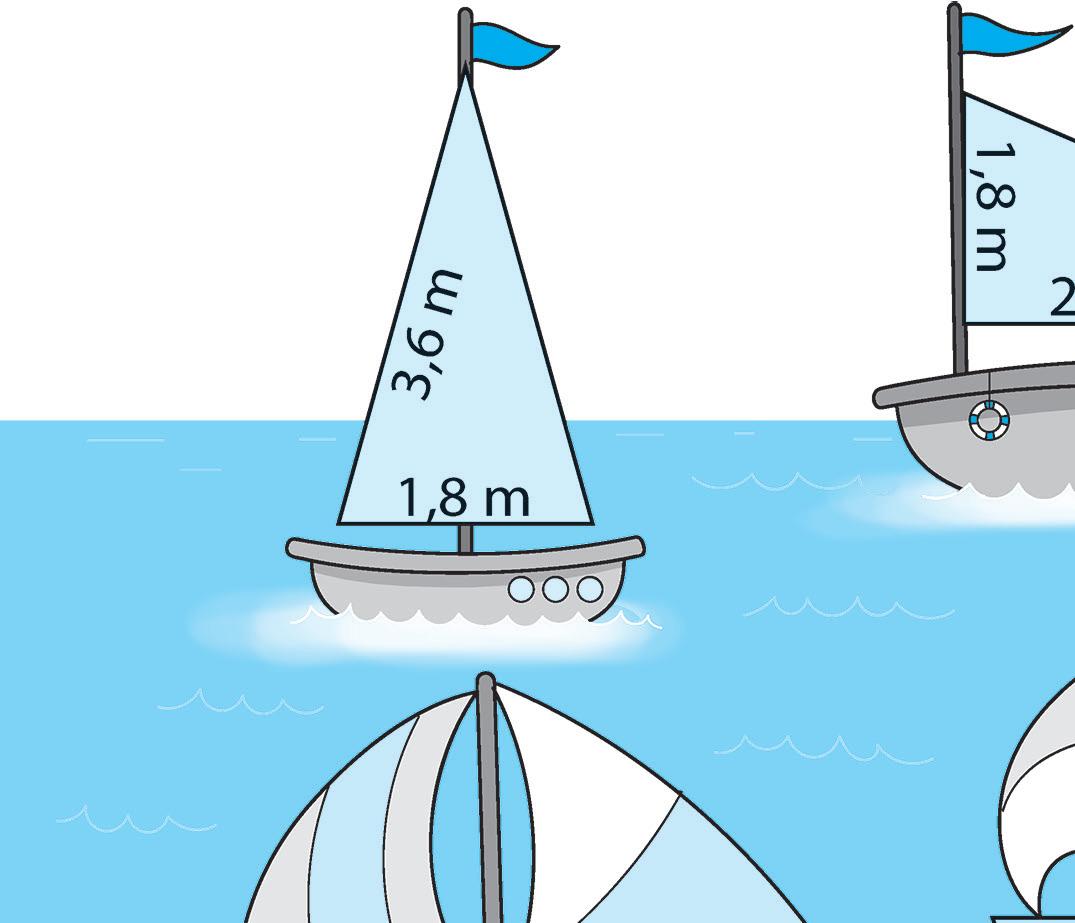
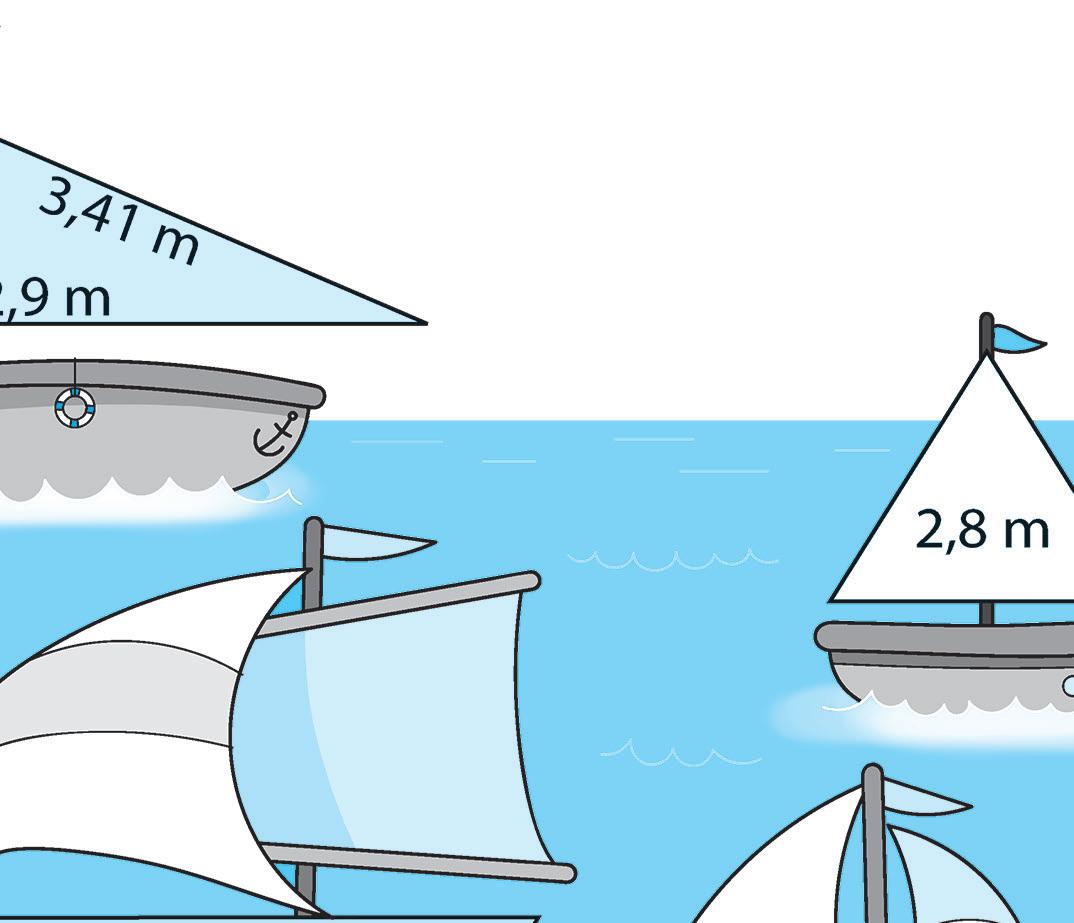
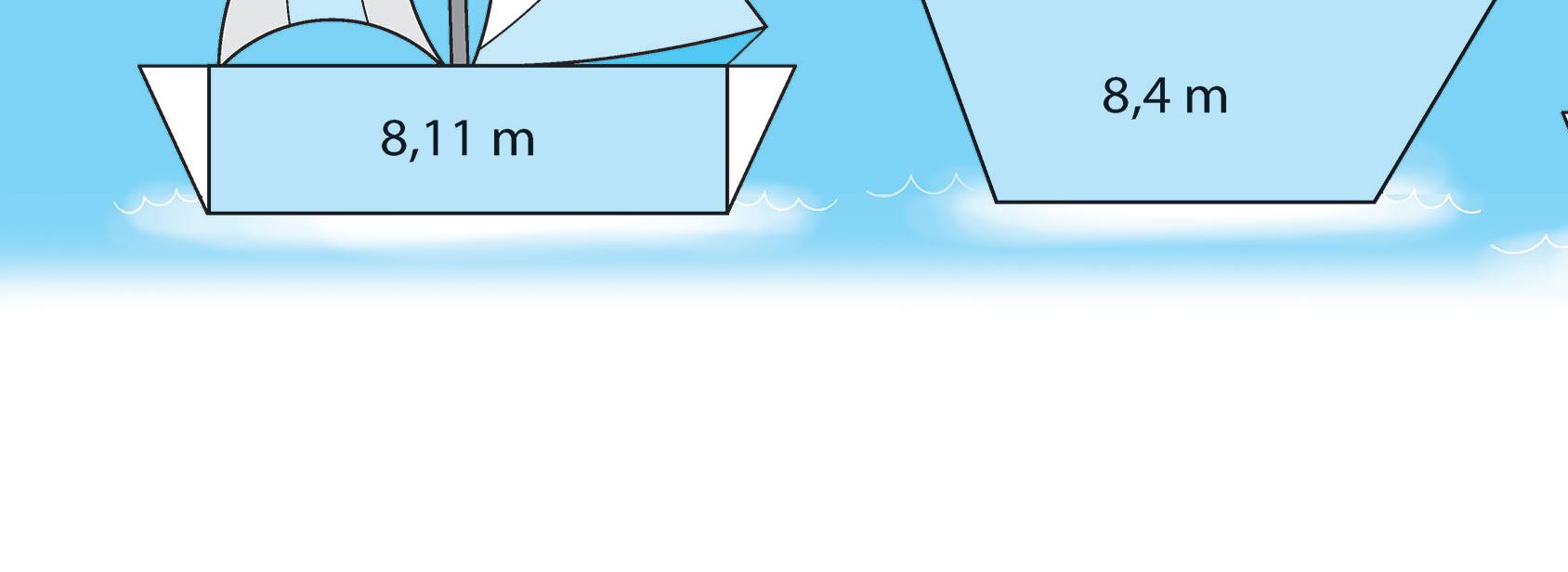
P = somma dei lati E se il triangolo è equilatero?
P = l x
5 Completa la formula, poi calcola l’area delle vele triangolari.
A =
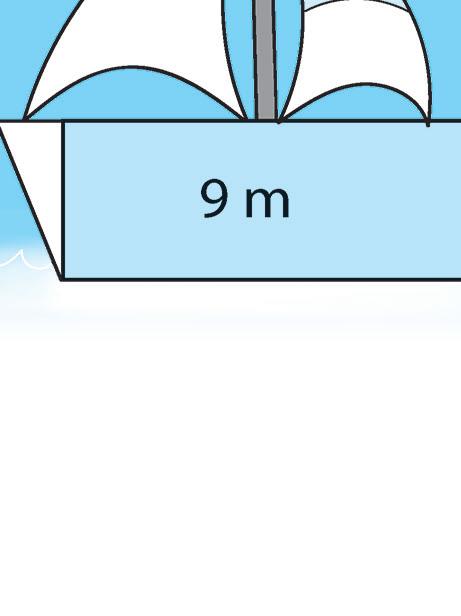
3,5 m
1,8 m
1,8 m
2,9 m
6 Risolvi i problemi.
a. Anna ha comprato un telo parasole triangolare alto 1,80 m e con la base di 1,20 m. Calcola l’area del telo in metri quadrati.

2,8 m 2,4 m


b. In mare ci sono 10 barche a vela triangolare. Ogni vela ha la base di 3,4 m e l’altezza di 8 m. Qual è l’area di ogni vela? Quanti metri quadrati di stoffa servono per tutte le vele?

33 MATEMATICA





Da oggi le nostre gite si spostano in campagna!




VOLA, VOLA FARFALLINA
1 ln campagna è pieno di farfalle, che si spostano di fiore in fiore. Esegui le moltiplicazioni in colonna.
















34 MATEMATICA
225 x 6=
109 x 8= 87x 9=
1542 x 4=
3472 x 5= 2654 x 3=
3620 x 2=
8483 x 7=
4286 x 4=
6649 x 7=
7218 x 3=
641 x 5=








35 MATEMATICA
2 Segui i voli delle farfalle ed esegui le divisioni in colonna.
8953 : 7=
67344 : 6=
1469 : 4=
152396 : 2=
427459: 8=
12168 : 9=
71325 : 5=
942876 : 3=
35749 : 4=

ULIVI C E N TENARI



Oggi abbiamo visitato il parco degli ulivi centenari!





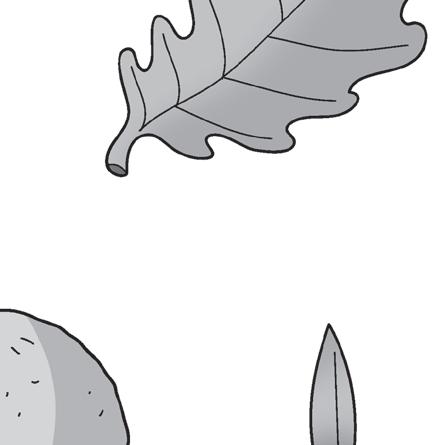
1 Leggi le spiegazioni. Poi cerchia le foglie e i frutti dei disegni giusti.
L’olivo (o ulivo) è una pianta da frutto, sempreverde che cresce sulle colline soleggiate e vive moltissimi anni. Ha un tronco nodoso e contorto che diventa grigio con il passare degli anni. Le foglie dell’olivo hanno la forma della punta di una lancia; hanno due diverse sfumature di verde nella pagina superiore e in quella inferiore. Il fiore dell’olivo è piccolo, di color bianco crema e ha quattro petali. Il frutto dell’olivo si chiama oliva. È di forma ovale, ha un nocciolo e una buona polpa ricca. L’oliva dapprima è di colore verde poi, maturando, diventa viola.


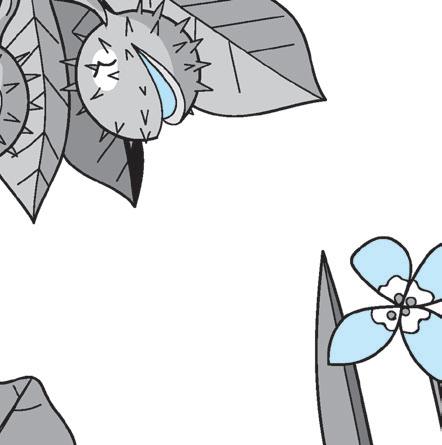
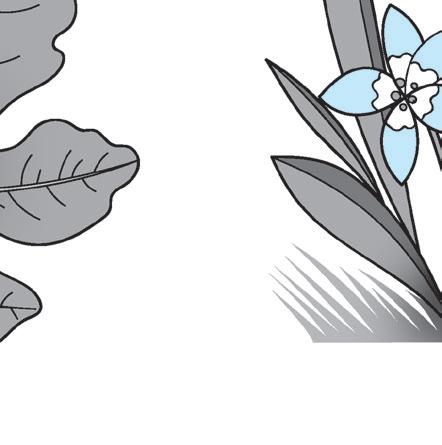




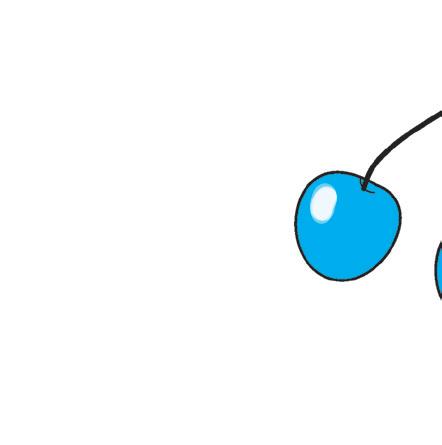






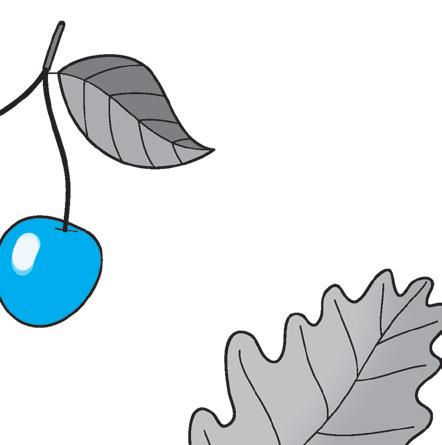







36
SCIENZE



ATTIVITÀ CREATIVE con Vale






SPILLOLIVA
Crea una o più spille a forma di oliva da indossare o regalare a chi vuoi tu!
Ti servono: • una spilla da balia • pinzatrice • ago e filo
• un foglio di pannolenci (o tessuto) verde • 3 batuffoli di cotone
• due bottoni neri e due bianchi • pennarello nero Come si fa?

1. Disegna due quadrati di 5 cm sul panno e ritagliali arrotondando le punte.
2. Imbottiscili di cotone, poi pinza i due panni lungo i bordi.
3. Con l’aiuto di un adulto, cuci i bottoni per formare gli occhi e le guance.

4. Disegna la bocca e applica dall’altro lato la spilla da balia.




2 Per misurare la durata di un evento si usano le misure di tempo. Osserva lo schema e scrivi le parole al posto giusto.












3 Registra sugli orologi le ore indicate: disegna le lancette al posto giusto. secondo mese settimana lustro decennio millennio ora
















37 MATEMATICA
x 60 x 30 x 60 x 12 x 24 x 5 x 7 x 2 x 10 x 10 giorno •
•
•
•
8 e 45 11 e 30 6 e 20 14 e 10 ATTIVITÀ CREATIVE
anno
secolo
minuto
giorno





PIANTE E FRUTTI
1 ln campagna si vedono molti alberi carichi di frutti. Disegna la parte simmetrica della pera rispetto all’asse.




Prima rotazione
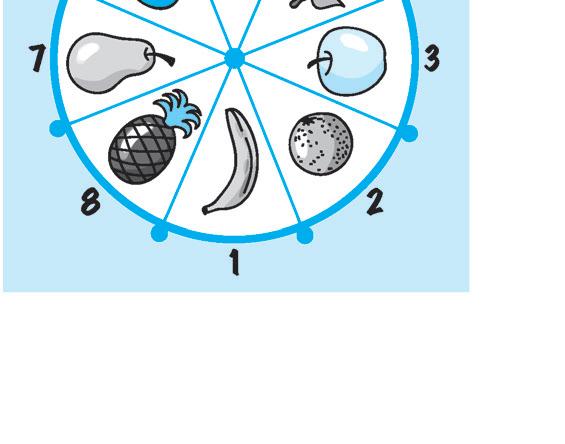
Prima rotazione

- Quale numero ha la casella con la mela? .............
- Il tavolo ha ruotato di 90°, 180° o 360°?
- La rotazione è avvenuta in senso orario o antiorario?


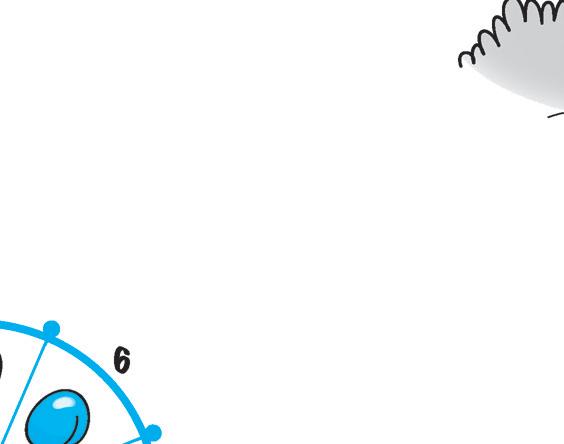
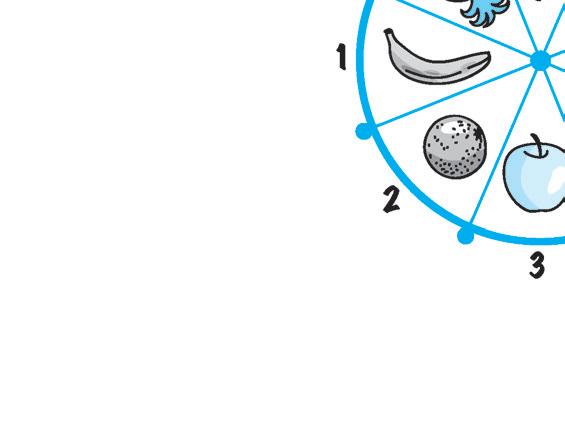
2 Il tavolo che vedi può girare intorno al proprio centro. Osserva le rotazioni e rispondi.
Seconda rotazione
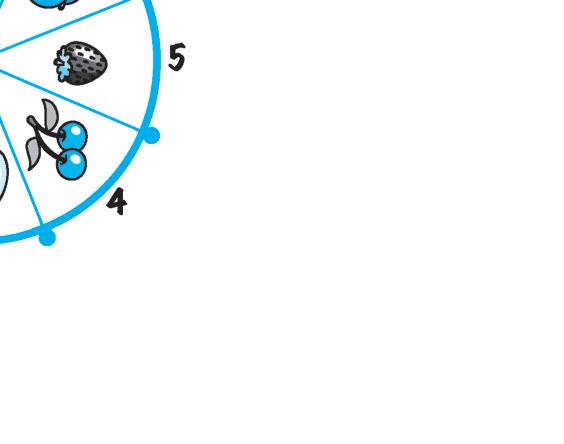
Seconda rotazione

- Quale frutto c’è nella casella 3?
- Il tavolo ha ruotato di 90°, 180° o 360° rispetto alla posizione iniziale?


- La rotazione è avvenuta in senso orario o antiorario? vettore

3 Esegui la traslazione dei fiori secondo il comando del vettore.






38 MATEMATICA


4 Scrivi le parole nel posto giusto.
radici • fotosintesi • ossigeno • zuccheri • linfa grezza • nutrimento • linfa elaborata
Le piante sono organismi in grado di fabbricarsi da sole il loro .........................................
Acqua e sali minerali sotto forma di giungono alle foglie.

Con le assorbono dal terreno acqua e sali minerali.

Nelle foglie avviene il processo di ..................................... clorofilliana.
Acqua e anidride carbonica attraverso l’energia del Sole, diventano e
Gli zuccheri, cioè la viene poi portata nei luoghi di accumulo da dove saranno prelevati all’occorrenza per nutrire tutta la pianta.
5 Quale funzione svolge ogni parte della pianta? Collega correttamente.
Traspirazione
Ancoraggio della pianta al suolo

Trasporto di linfa grezza ed elaborata

Assorbimento sali minerali e acqua



39 MATEMATICA SCIENZE

GARA DI CUCINA
1 Gli animatori hanno partecipato a una gara di dolci, organizzata dall’agriturismo
Luna Piena e i bambini del Centro estivo li hanno votati. Osserva il grafico.




Legenda
Vale Anna Luca Roby July n. voti = 1 voto






2 Rispondi in base al grafico dell’esercizio 1.
- Se ogni membro della giuria ha espresso un solo voto, quanti bambini hanno partecipato alla votazione?
- Chi ha vinto la gara? Scrivi il suo nome nel cappello.
- Chi ha ricevuto meno voti? ..........................................

3 Leggi le regole e segna quella corretta.
La media di una serie di dati si ottiene sommando tutti i dati e dividendo il risultato per il numero dei dati stessi.
La media di una serie di dati si ottiene sommando tutti i dati e moltiplicando il risultato per il numero dei dati stessi.
4 Calcola la media dei voti totalizzati da ogni partecipante alla gara di dolci.
( + + + + ) : =


• Quanti voti ha preso in media ogni cuoco/a? ............

40 MATEMATICA
Prove d'ingresso
Alunno Classe
Più e meno
1 Esegui in colonna sul quaderno e verifica con la prova .
1 342 + 997 + 130 =
174 + 815 + 27 =
3 561 + 667 + 1 789 =
943 + 2 175 + 1 118 =
368 + 2 586 + 451 =
24 291 – 23 196 =
2 Applica la proprietà associativa per risolvere le addizioni.
7 845 – 4 298 =
5 800 – 459 =
28 932 – 13 356 =
90 + 25 + 210 + 75 = (90 + 210) + (25 + 75) = + =
430 + 120 + 70 + 80 =
1 250 + 3 260 + 240 + 250 =
3 Applica la proprietà invariantiva per rendere più semplice il calcolo.
170 – 48 = (170 + 12) – (48 + 12) = 182 – 60 =
210 – 35 =
175 – 19 =
4 Trova il minuendo .
– 75 = 90
– 149 = 200
– 190 = 290
5 Numera per 3 da 958 a 1 018.
958 • 961
6 Numera per 7 da 2 010 a 1 870.
2 010 • 2 003
– 61 = 80
– 230 = 300
– 1 450 = 1 600
– 56 = 100
– 89 = 100
– 240 = 500
1
Matematica
Alunno Classe
Per e diviso
1 Esegui in colonna sul quaderno e verifica con la prova .
138 x 45 =
483 x 86 =
791 x 69 =
968 x 73 =
1 067 x 64 =
5 600 x 65 =
3 002 x 36 =
4 098 x 58 =
8 756 : 85 =
8 540 : 58 =
7 268 : 43 =
9 999 : 48 =
2 Applica la proprietà associativa della moltiplicazione.
3 x 2 x 5 = 3 x (2 x 5) = 3 x 10 = 30
3 x 6 x 2 =
8 x 2 x 5 =
3 Usa la proprietà distributiva per calcolare il prodotto.
5 x 16 = 5 x (10 + 6) = (5 x 10) + (5 x 6) = 50 + 30 = 80
7 x 13 =
9 x 14 =
4 Applica la proprietà invariantiva alle divisioni.
420 : 60 = (420 : 10) : (60 : ) = : 6 =
270 : 90 = (270 : 10) : ( : ) = : =
56 743 : 94 =
34 120 : 18 =
56 309 : 62 =
64 754 : 75 =
250 : 25 = ( : 25) : ( : ) = : =
5 Di quali numeri sono multipli ? Completa. 6 Colora i divisori dei numeri al centro.

18 1 1 32 12 36 45 6 7 9 3 5 6 15 9 8 7 3 2
Matematica Prove d'ingresso
Alunno Classe
Problemi in città
1 Risolvi il problema .
Vengono spedite 192 bottiglie di vino confezionate in 8 casse. Quante bottiglie contiene ogni cassa? Quanto costa ogni cassa, se una bottiglia è venduta a € 11?
DATI
192 =
8 =
€ 11 =
? =
? = ESPRESSIONE
11 x (192 : 8) = =
2 Risolvi su un foglio.
11 192 8
RISPOSTE
In una famiglia vengono spesi ogni mese € 52 per giornali e riviste, € 56 per libri, € 48 per ricariche telefoniche e € 32 per il cinema. Quanto spende la famiglia per la lettura? Quanto spende per gli spettacoli cinematografici? Quanto spende complessivamente?

Mohammed raccoglie i punti al supermercato per ricevere in regalo uno smartphone. Ce ne vogliono 2 450. Mohammed ne ha 1 876. Quanti gliene mancano?
Kim si diverte a contare le ruote dei veicoli posteggiati nel parcheggio del supermercato: ci sono 43 auto, 25 motorini e 37 biciclette. Quante ruote in tutto?

3
Matematica Prove d'ingresso
Alunno Classe
Frazioniamo
1 Collega con una freccia ogni tipo di frazione al suo valore.
Frazione propria
Frazione impropria
Frazione apparente

È maggiore dell’intero
Indica uno o più interi
È minore dell’intero
2 Cerchia di verde le frazioni proprie , di rosso quelle improprie e di azzurro quelle apparenti .
3 Calcola il valore delle seguenti frazioni .
4 Risolvi sul quaderno i seguenti problemi .
A. A una gara di corsa si iscrivono 595 persone.
I 3 7 degli iscritti sono donne.
Quanti sono gli uomini?
B. Su una bancarella del mercato sono esposti 315 kg di agrumi: 3 5 sono arance, 2 7 sono mandarini, i rimanenti sono limoni.
Quanto pesano i limoni?
4
4 7 7 4 5 8 2 10 3 5 32 24 25 16 11 3 16 4 18 9 4 7 di 210 7 9 di 99 6 13 di 169 8 9 di 189 6 7 di 49 3 5 di 125
Matematica Prove d'ingresso




LA CAMERA OSCURA



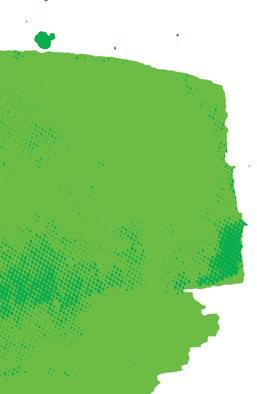

Un principio molto semplice
Gli antichi Greci conoscevano già la legge fisica che avrebbe portato alla nascita delle prime macchine fotografiche nel XIX secolo. Questo principio è chiamato “camera oscura”. Il grande filosofo greco Aristotele lo conosceva già nel IV secolo a.C.

Se fai un piccolo buco su una scatola completamente nera e chiusa, l’immagine posta davanti alla scatola viene “proiettata” all’interno. In realtà, essa risulta capovolta, come puoi vedere nel disegno. Se sulla parte interna della scatola inserisci una pellicola sensibile alla luce, ottieni una macchina fotografica!


Ora rispondi alle domande.
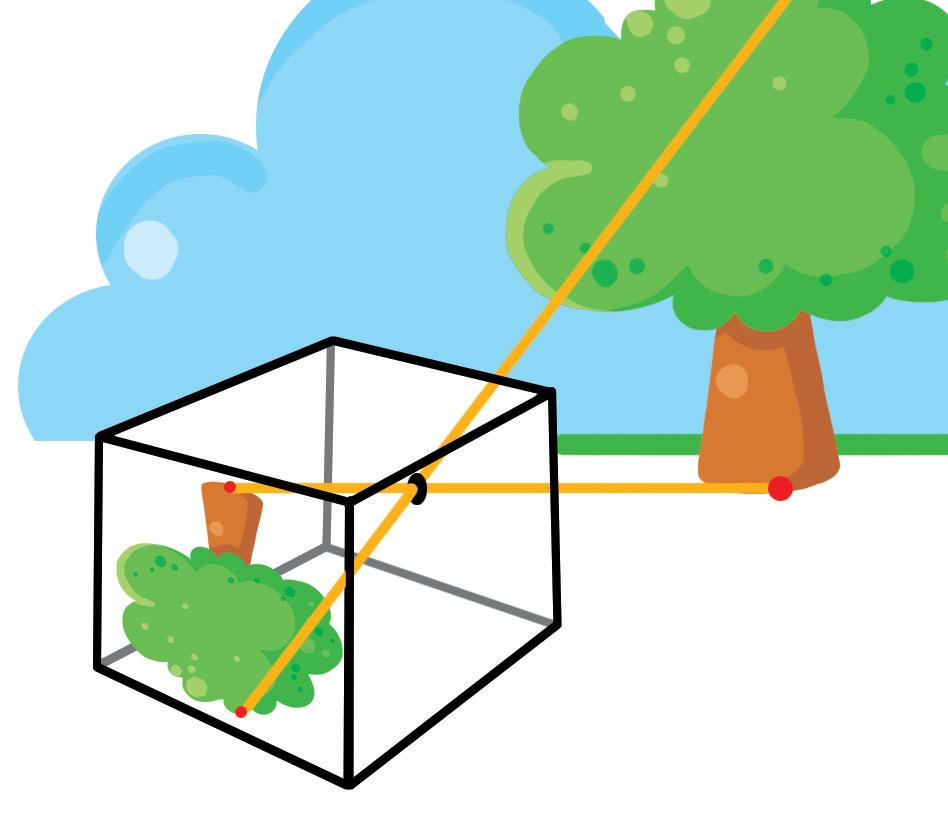
Una foto “senza foto”

Le pellicole fotografiche sono state inventate circa due secoli fa. Prima di allora le immagini non potevano essere “fermate” sulla pellicola e ci si doveva accontentare di vedere le immagini proiettate su uno schermo. Il principio della camera oscura è stato utilizzato anche da molti artisti. Alcuni, per esempio, praticavano un foro nelle tende nere di una stanza per proiettare su una parete il paesaggio. In questo modo, il pittore poteva copiare in tutta calma l’immagine proiettata.
• Cos’è una camera oscura? .........................................................................................................................................................
• Perché viene praticato un foro in una scatola?.......................................................................................................
• Quali caratteristiche deve avere il foro? ..........................................................................................................................
• Perché gli artisti utilizzavano la pratica della camera oscura?
.......................................................................................................................................................................................................................................
.......................................................................................................................................................................................................................................
COSTRUIRE UNA CAMERA OSCURA
Mettiamoci al lavoro.
COSA TI SERVE
• cartoncino bristol nero;
• carta oleata da forno;
• nastro adesivo;
• elastici
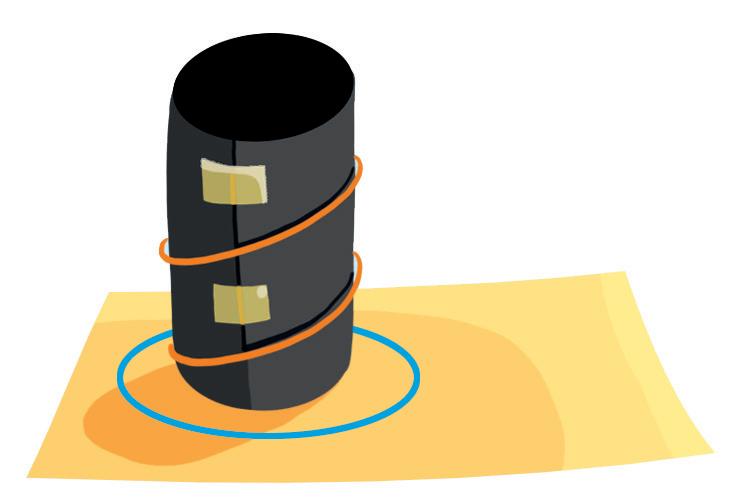
2 Ora appoggialo su un foglio di carta oleata e disegna un cerchio un po’ più grande della base del cilindro. Ritaglia il cerchio che hai ottenuto.


1 Costruisci un cilindro con il cartoncino bristol e fermalo con degli elastici. Poi fissa il cilindro con del nastro adesivo.




3 Trasforma il cerchio in una specie di stella, come nella figura. In questo modo, potrai incollare agevolmente la carta oleata al cartoncino. Fai la stessa operazione per l’altra estremità utilizzando, però, del cartoncino nero. Sul cerchio di cartoncino nero pratica un piccolo foro con la punta di un compasso.
4 Punta il forellino nero verso una fonte di luce: una lampada non troppo forte o una candela. Se è una giornata molto soleggiata, puoi provare a guardare fuori dalla finestra. Attenzione a non fissare il sole!!!







































BUONE VACANZE!
































Alunno Classe
Metri, grammi, litri, ore, gradi
1 Scrivi ogni cifra nella casella corrispondente. 2 Completa le equivalenze.
km hm dam m dm cm mm

0,11 km
32,29 hm
126 dam
11,18 m
132 dm
55 cm
127 mm
h l da l l d l c l m l
3,04 h l
11,6 da l
224,2 l
31,4 c l
6,7 d l
126 m l
0,06 h l
4 Completa la tabella.
kg hg dag g
35 83 10
3 Rispondi alle domande.
a) Se devi indicare il peso di un chiodo, usi i kg o i cg?
b) Se vuoi indicare la distanza tra Milano e Roma, usi i m o i km?
c) Il farmacista, se ti deve indicare la quantità di sciroppo necessaria, usa i c l o i da l ?
5 Scrivi il nome dell’ angolo formato dalle lancette degli orologi.
5
90° MIN. DI 90° MAG. DI 90° NOME Matematica Prove d'ingresso
Alunno Classe
Figure e grafici
1 Collega con una freccia ogni termine alla sua definizione.
Trapezio
Quadrato
Rettangolo
Rombo

È un parallelogramma con i lati e gli angoli uguali.
È un quadrilatero con una coppia di lati paralleli che si chiamano basi.
2 Risolvi su un foglio i seguenti problemi
È un parallelogramma con gli angoli tutti retti e i lati opposti uguali.
È un parallelogramma con i lati tutti uguali e gli angoli opposti uguali.
A. Si vuole recintare un orto a forma di triangolo isoscele con la rete metallica. Se la base misura 18 m e il lato obliquo 23,5 m, quanta rete metallica occorre?
B. Davanti a una scuola c’è un’aiuola che ha la forma di un trapezio isoscele. La base minore, uguale al lato obliquo, misura 3,8 m e la base maggiore 4,2 m. Calcola il perimetro.
3 Il direttore della multisala ha registrato in una tabella quanti film ha proiettato ogni giorno della settimana. Completa l’ istogramma e rispondi.
Lunedì 2
Martedì 3
Mercoledì 3
Giovedi 3
Venerdì 5
Sabato 6
Domenica 6
6 5 4 3 2 1
LUNEDÌMARTEDÌMERCOLEDÌGIOVEDÌVENERDÌSABATODOMENICA
• Qual è la media dei film proiettati in una settimana?
• Qual è la moda?
LEGENDA: 1 film
6
Matematica Prove d'ingresso
Alunno Classe A pieni polmoni
1 Che cosa conosci dell’ aria che respiri? Mettiti alla prova: indica con una X la risposta corretta e completa le frasi.
L’aria non ha odore, non ha sapore, non ha colore ma c’è!
Tutti gli esseri viventi ne hanno bisogno per vivere.
• Da che cosa è composta l’aria?
Da un solo gas, l’ossigeno.
Da un solo gas, l’idrogeno.
Da un miscuglio di gas.
• L’aria occupa uno spazio, cioè:
ha delle dimensioni, come una figura geometrica. scorre sopra le nostre teste come un fiume. esercita una pressione e ha un volume.
• Che cos’è un gas?
È un insieme di particelle invisibili a occhio nudo (gli atomi e le molecole) che sono strettamente legate tra loro.
È un insieme di particelle invisibili a occhio nudo (gli atomi e le molecole) che si muovono liberamente nello spazio perché non sono legate tra loro.
È un insieme di particelle leggerissime che assumono una forma ben definita. L’aria è composta principalmente da tre gas.
• Quali sono i gas principali che compongono l’aria?
Azoto, ossigeno, anidride carbonica.
Azoto, elio, idrogeno. Azoto, ossigeno, ozono.

Scienze

• L’ossigeno presente nell’aria è prodotto: dall’uomo. dall’acqua.
dai vegetali.
7
Prove d'ingresso
Alunno Classe
I nostri amici alberi
1 È importante che l’aria si mantenga ricca di ossigeno. Gli alberi sono nemici dell’inquinamento! Osserva e indica con una X la risposta esatta.
Ossigeno

Ac ua
Glucosio
• La foglia è come un laboratorio chimico, cioè:
trasforma l’anidride carbonica in ossigeno e zuccheri. trasforma l’ossigeno in anidride carbonica e zuccheri.
• Quali elementi consentono questa trasformazione all’interno della foglia?
La pioggia e gli amidi.
La clorofilla e la luce solare.
• Come si chiama il processo di trasformazione?
Fotosintesi clorofilliana.
Combustione.
• È molto importante:
proteggere boschi e parchi da chi li vorrebbe tagliare o da chi non ne ha cura.
passeggiare di notte nei boschi respirando a pieni polmoni.

Luce Anidride carbonica
Amidi
8
21PV01423
Prove d'ingresso
Scienze

5 Il proprietario dell’agriturismo svolge un’indagine statistica sui dolci preferiti dai bambini del Centro estivo. I bambini sono in tutto 100. Osserva le percentuali riportate nell’areogramma a torta, poi rappresentale nell’areogramma quadrato e nell’ideogramma (come nell’esempio).
Dolci preferiti
Torta al cioccolato
Torta di mele
Crostata di marmellata
Tiramisù
Legenda
Areogramma quadrato Ideogramma Numero bambini e bambine
Legenda
= 1 bambino/a
A = 10 bambini

6 Completa.
- La moda è







- Il dolce che piace meno ai bambini del centro estivo è


7 Completa la regola: cancella il termine sbagliato.


In un insieme di dati, la moda / media è il dato che si presenta con la frequenza maggiore, cioè il maggior numero di volte.



41 MATEMATICA
10% 30% 20% 40%

FRAZIONI AL LAGO
1 Oggi abbiamo fatto una gita a piedi e siamo arrivati a un laghetto. Osserva le zattere che abbiamo costruito e colora la parte indicata dalle frazioni.




2 Rappresenta con il disegno le seguenti frazioni.

3 Calcola il valore delle frazioni indicate.




42 MATEMATICA
6 14 5 6 8 8 3 4 6 10 1 9 7 10 3 9 9 12 1 3 7 7 8 10 4 6 2 7 9 12 6 8 12 15 9 11 8 9 di 15 = (15 : ) x 1 = di 35 = di 50 = di 72 = di 21 = di 24 = di 72 = ................................................................ di 30 = ................................................................. di 33 = ................................................................ di 54 = .................................................................
4 Leggi e risolvi i problemi.
a. Lungo il lago ci sono 288 persone che partecipano a una gara podistica. Se i 2 3 dei partecipanti sono tesserati, quanti sono i non tesserati? Trova la frazione complementare e calcola.



b. La prima parte del percorso di gara è segnalata con 432 bandierine, di cui 4 9 sono rosse. Quante sono le bandierine NON rosse?
c. Gli spettatori della gara sono 112 : 1 4 degli spettatori sono parenti dei partecipanti. Quanti sono i parenti degli iscritti alla gara?

Dati
Risposta
Operazioni
Risposta
Dati
Operazioni
Risposta
Dati


43 MATEMATICA
.................................................................................... ....................................................................................
= ............................................. = .................................
= =
: x
Operazioni

1 Completa la regola.
equiestese • congruenti • perimetro • area • isoperimetriche
• La misura del contorno di una figura si chiama ..............................................................................
• La misura della superficie di una figura si chiama
• Le figure che hanno lo stesso perimetro si dicono
• Le figure con la stessa area si dicono o equivalenti.
• Le figure che hanno lo stesso perimetro e la stessa area e se sovrapposte combaciano si dicono
2 Vicino all’agriturismo Luna Piena un contadino ha arato i campi formando delle figure geometriche. Scrivi quanto vale il perimetro e quanto misura la superficie di ogni figura. Usa come unità di misura le unità indicate. Infine indica con una se le frasi sono vere o false.
• Le figure 1, 2 e 3 sono isoperimetriche. V F
• Le figure 1 e 2 sono isoperimetriche. V F
• Le figure 1 e 3 sono isoperimetriche. V F
• Le figure 4, 5 e 6 sono equivalenti. V F
• Le figure 4 e 7 sono equivalenti. V F
• Le figure 4 e 6 sono equivalenti. V F
3 Scegli una delle figure dell’esercizio 2 e disegna una figura congruente (uguale), poi colorala come vuoi.


44 MATEMATICA
FRA I CAMPI
6 7 5 4 3 2 1 P = ....... P = P = ....... A = A = ....... A = A =
4 Leggi e completa la tabella con le misure di superficie.

chilometro quadrato ettometro quadrato decametro quadrato metro quadrato decimetro quadrato centimetro quadrato millimetro quadrato

5 Completa il testo.
• Ogni misura è volte più piccola di quella che la precede e 100 volte più di quella che la segue. Per scrivere ogni misura si usano due cifre, quella delle e quella delle
136,83 m2 si legge 1 36 e 83
6 Scomponi, come nell’esempio.
50,25 m2
116,35 m2
28,05 dm2
246,06 dam2
2 128,05 cm2
7 Nelle misure di superficie si procede di 100 in 100. Componi in base alla marca.


45 MATEMATICA
MULTIPLI UNITÀ fondamentale SOTTOMULTIPLI
km2 hm2 dam2 m2 dm2 cm2 mm2 m2 m2 m2 1 m2 di m2 di m2 di m2 ...................... 1 1000
000
7 m2 e 50 dm2 .................................................................. m2 4 dam2 e 35 m2 m2 15 km2 e 30 hm2 km2 0 m2 e 30 dm2 .................................................................. m2 128 dm2 e 60 cm2 dm2
...............................................................................
............................................................................... 50 m 2, 25 dm 2 1 100





FIGURE DI CAMPAGNA
1 Scrivi sotto ogni poligono il suo nome.







I lati obliqui non sono congruenti (uguali).
È un trapezio





I lati obliqui non sono congruenti (uguali), ma uno di essi è perpendicolare alla base.

È un trapezio



I lati obliqui sono congruenti (uguali).
È un trapezio



2 Indica con una i trapezi a cui si riferiscono le seguenti affermazioni.

I due lati obliqui hanno la stessa lunghezza.
Ha angoli retti.
Ha assi di simmetria.

3 Osserva i trapezi e classificali nella tabella.




scaleno rettangolo isoscele , , , , trapezio scaleno trapezio rettangolo trapezio isoscele
trapezio
46 MATEMATICA

Misure: b = 7 cm; h = 5,5 cm
4 Completa le formule e calcola il perimetro di ogni quadrilatero presente negli scaffali dell’agriturismo. P = ( + ) x =


Misure: b = 9,5 cm; = 3,5 cm

Misure: B = 11 cm; b = 7 cm; = 15 cm; = 16 cm
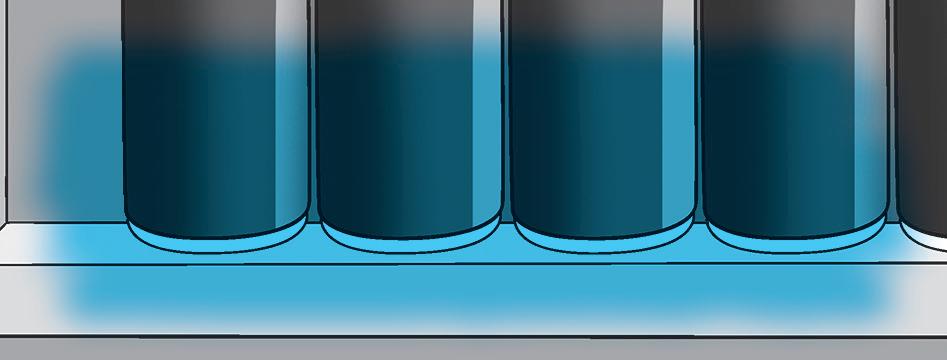


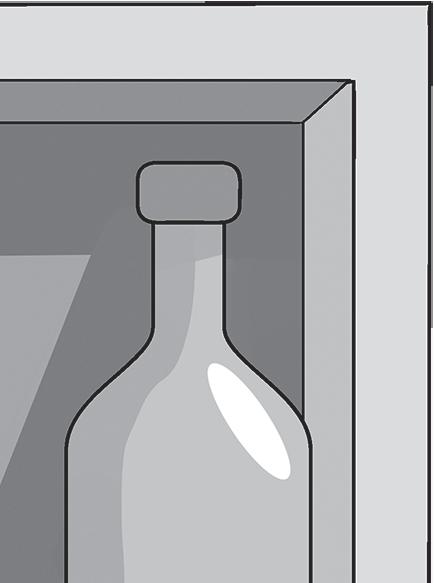
Misure: = 6,7 cm

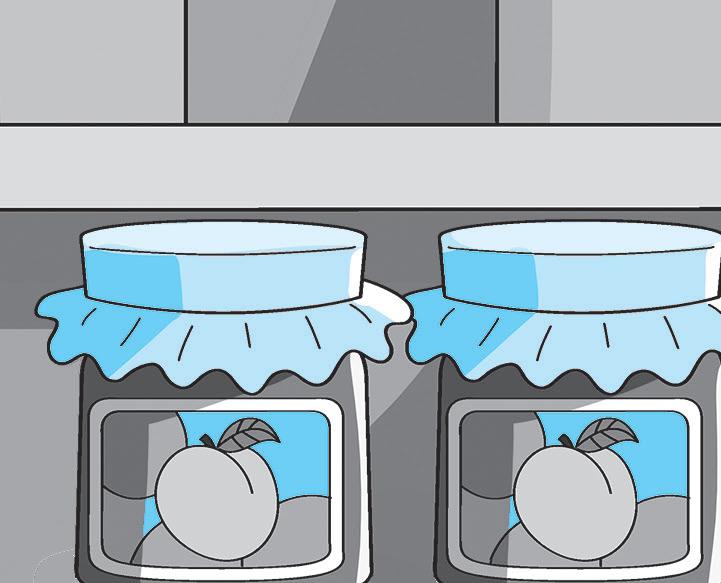

Misure: h = 12 cm; b = 4,5 cm
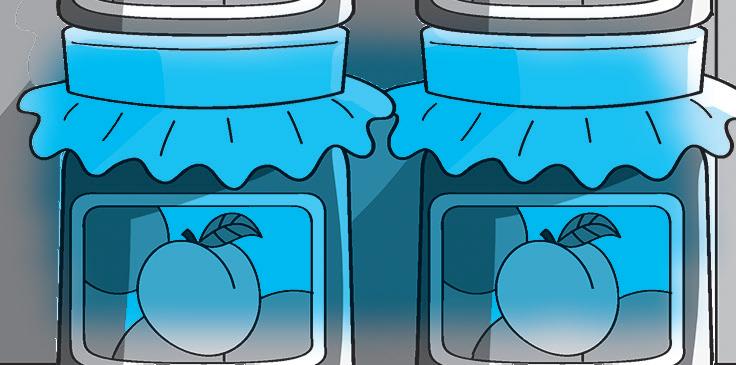
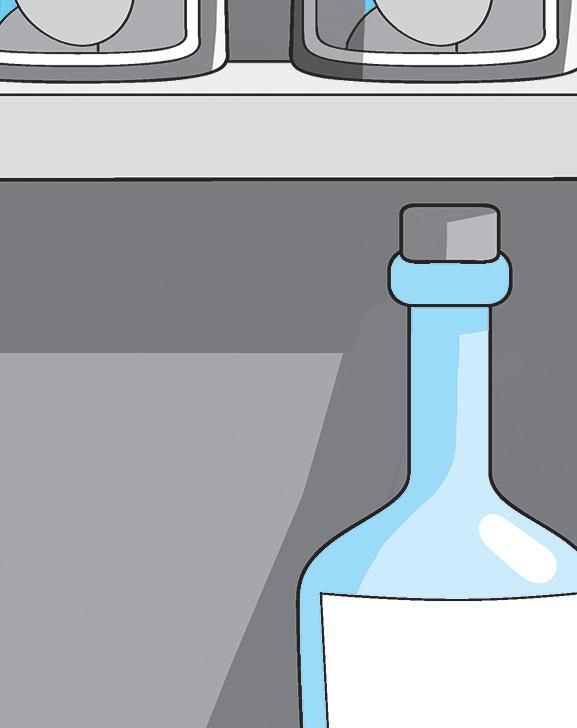

Misure: B = 16 cm; b = 8 cm; = 15 cm

47 MATEMATICA
+ ....... ) x .......
P
+ ....... + ....... + .......
.................
+ + + = P = + + + =
P = (.......
= ................. P = x =
= .......
=
P =
a c d e f b

FIGURE NEI CAMPI
1 Collega con una freccia ogni formula ai poligoni corrispondenti e calcola le area.
b = 12 cm
h = 9 cm
A = cm2
h = 2 cm
b = 5 cm
A = b x h
A = (D x d) : 2
A = (B + b) x h : 2
B = 8 cm
A = cm2
h = 5 cm
b = 14 cm
A = x
A = (b x h) : 2
A = .............................................. cm2
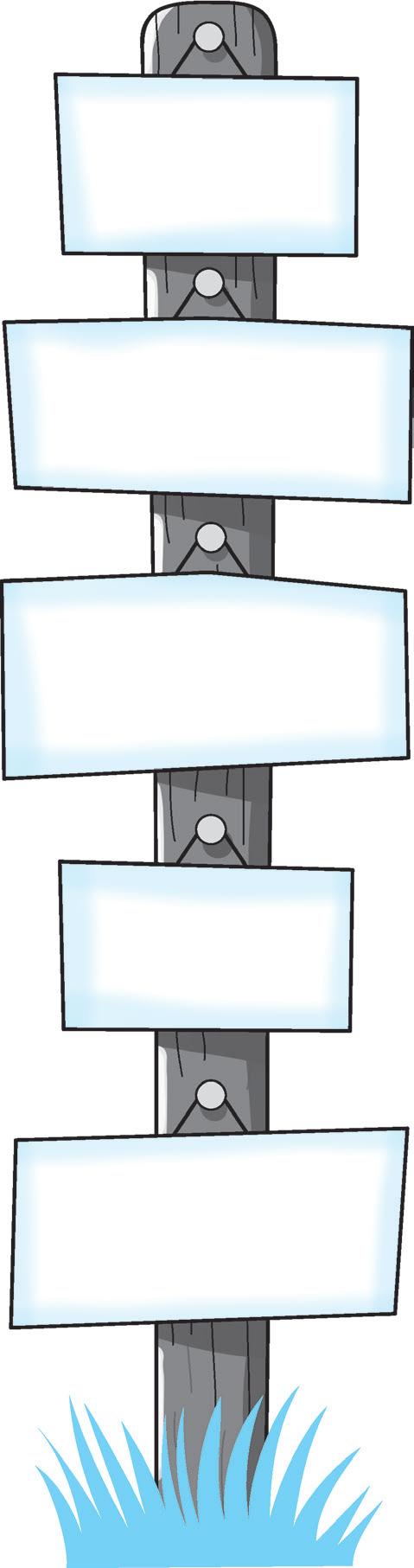
2 Calcola l’area dei seguenti triangoli, poi rispondi.
A = cm2
- Le due figure sono equiestese? sì no
Perché?

= 20 cm
A = cm2
d = 5 cm
D = 10 cm
A = cm2
h = 16 cm
b = 13 cm
A = .............................................. cm2
A = cm2
48 MATEMATICA
3 Inserisci le misure nella tabella, poi esegui l’equivalenza.
1. 3 m2 e 2 dm2 e 4 cm2
2. 12 km2 e 500 m2
3. 154 m2 e 20 dm2
4. 1,32 dam2 e 0,8 dm2
5. 13 dm2 e 44 mm2
6. 51 hm2 e 7 dam2
7. 63 km2 e 1 hm2
8. 4,62 hm2 e 7 m2


km2 hm2 dam2 m2 dm2 cm2 mm2 da u da u da u da u da u da u da u

1 = ............................. dm2
2 = ............................. hm2
3 = dm2
4 = m2
5 = mm2
6 = hm2
7 = hm2
8 = dam2
4 Scomponi le misure di superficie.
1
152 m2
800 cm2
92 350 mm2
326 dm2
1 148 m2
111 dam2
2 460 hm2
33 859 dam2
271 dm2
246 hm2

49 MATEMATICA
....................................................
....................................................
dam 2 , 52 m 2





Da oggi le nostre gite si spostano in montagna!







OPERAZIONI FRA I MONTI




1 Esegui le operazioni in colonna.






749 x 26 =
414 x 132 =
7 436 : 24 =
7 515 : 15 =
253 x 62 =
563 x 245 =
5 816 : 12 =
25 123 : 37 =
386 x 42 =
379 x 428 =
88 436 : 48 =
403 875 : 25 =





50 MATEMATICA

2 Calcola applicando la proprietà invariantiva della sottrazione per semplificare i calcoli. Osserva l’esempio.

























3 Calcola applicando la proprietà invariantiva della divisione per semplificare i calcoli. Osserva l’esempio



































51 MATEMATICA
187 344 198 251 566 750 180 350 200 27 34 38 26 27 150 20 40 40 ........... ........... – 7 + 6 + 2 ........ – 7 + 6 + 2 ........ ––––––––––––= = = = = = = = = = = = 50 42 24 100 14 5 6 2 10 2 ........... x 2 : 3 x 2 : 3 : : : : : : = = = = = = 120 60 280 10 6 40 ........... ........ ........ : : : : : : = = = = = = 36 2 500 9 100 : : : : = = = = 160 160 10





PRODO T T I TIPICI

Oggi all’agriturismo

abbiamo assaggiato nocciole, miele e frutti di bosco.


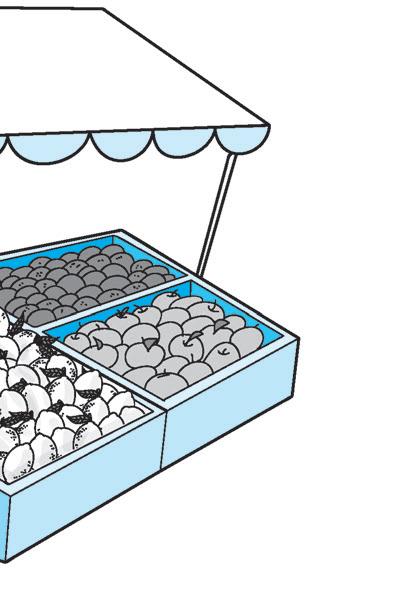
1 Cerchia in rosso i multipli di 4 e in verde i multipli di 5, poi rispondi alle domande.
• Ci sono multipli comuni di 4 e di 5? Quali?
• Tutti i multipli di 4 sono anche multipli di Essi sono: pari. dispari.
2 Cancella con una i numeri che non sono multipli del numero scritto sul vasetto di miele.
3 Sulle foglie dei frutti di bosco ci sono alcuni divisori del numero scritto sul frutto, ma uno è sbagliato, cancellalo con una . Aggiungine altri, se è possibile.





52 MATEMATICA
55 15 14 42 45 12 66 36 28 18 30 24 32 25 20 40
6 3 17 10 2 24 11 30 2 7 3 5 23 56 14 28 49 63 70 37 29 18 3 21 9 23 15 33 34 53 40 35 55 25 50 21 18 100 30 36 21 20 15 7 7 30 4 9 3 2 10 3 2 3 ...... ...... ...... ...... ...... 8 2

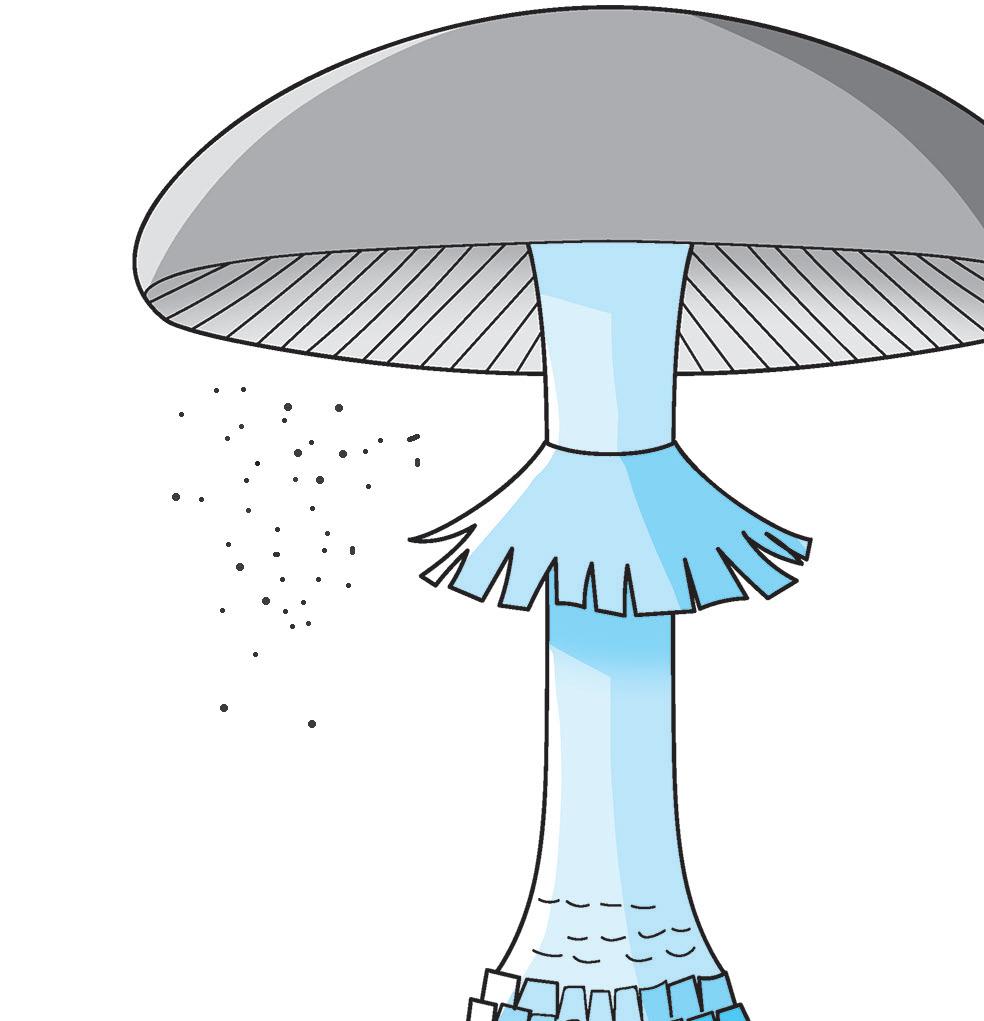
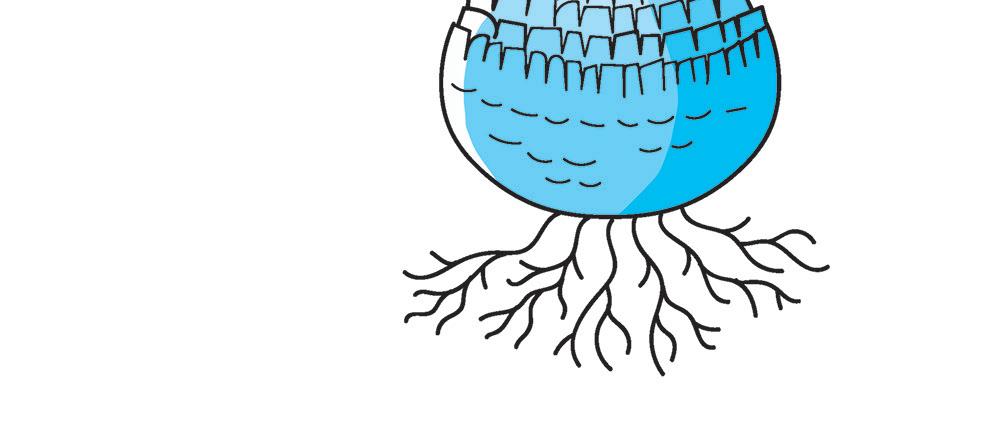
4 Leggi la spiegazione, poi scrivi nelle targhette le parole evidenziate.
I funghi a cappello sono i più conosciuti e si raccolgono nei boschi tagliandone il gambo Sotto il cappello di questi funghi ci sono delle sottili lamine disposte a coltello unite al margine col gambo, chiamate lamelle In realtà, quelli che chiamiamo funghi sono il frutto di una pianta, il micelio. Il micelio è il vero fungo ed è formato da sottili filamenti di cellule, detti ife, che si diffondono sul terreno o si attaccano su un vegetale. Il micelio si sviluppa dalle spore, delle piccole cellule che cadono dalle lamelle. Alcuni funghi svolgono l’importante funzione di decomporre gli organismi morti, cioè li trasformano e li riducono in sostanze che possono essere riassorbite dal terreno, rendendolo così più fertile. I funghi vanno raccolti da persone esperte, perché possono essere molto pericolosi.
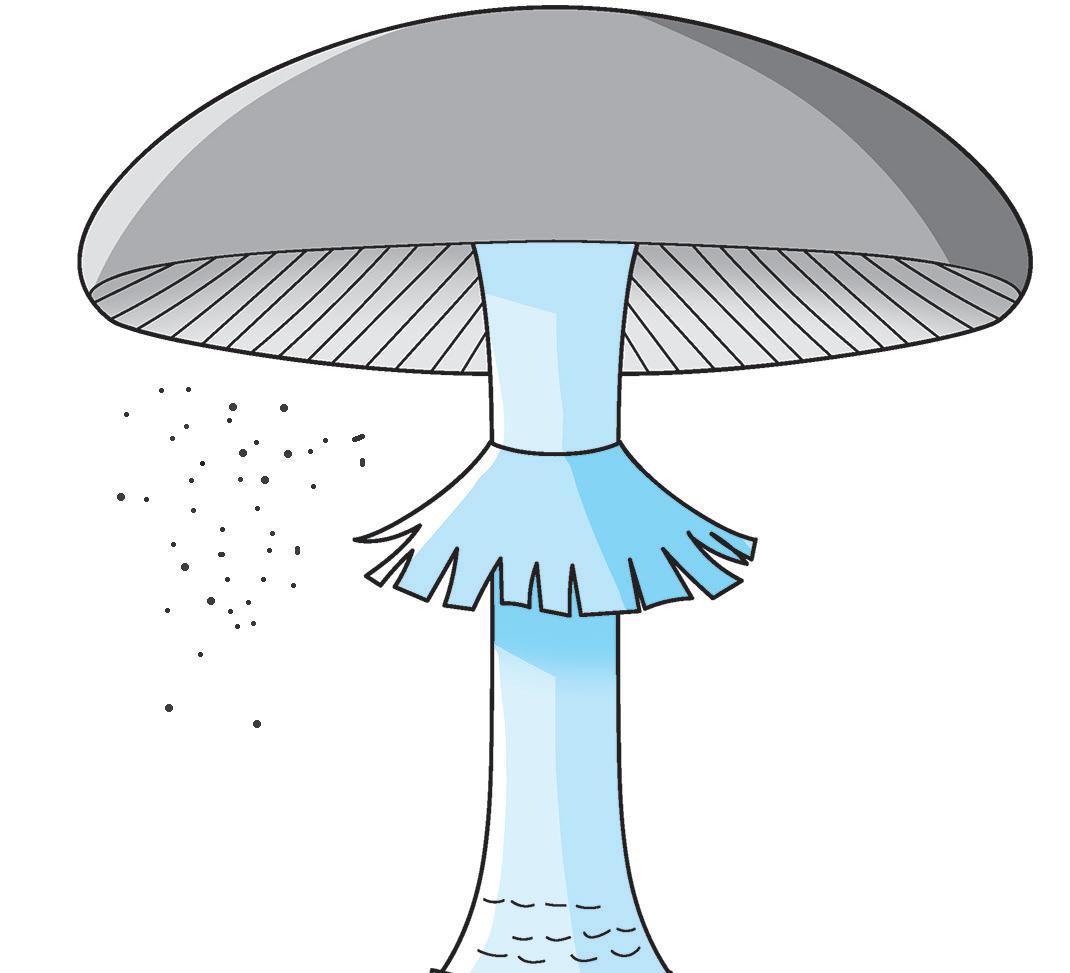
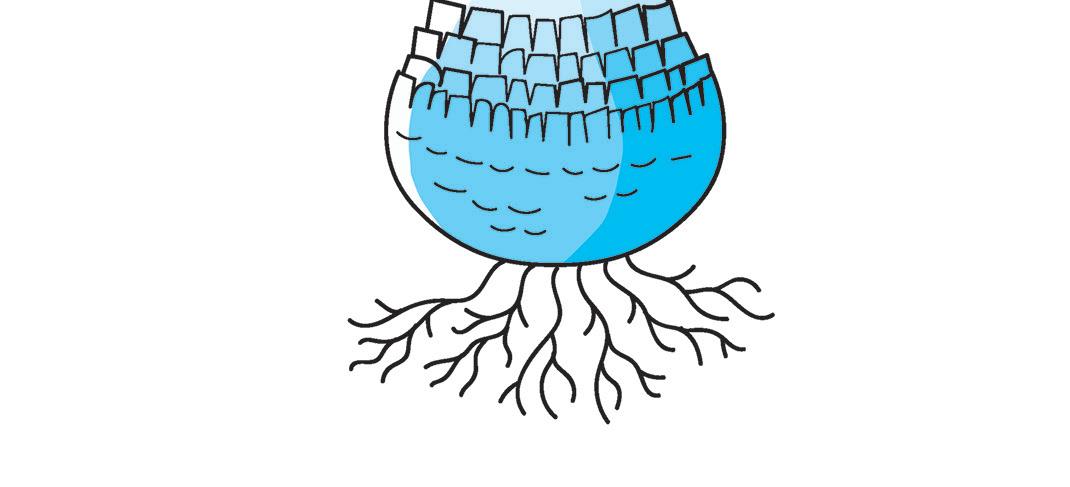




IMPARIAMO L’INGLESE con July

PARTS OF A MUSHROOM




5 Osserva e leggi come si chiamano le parti del fungo in inglese. Aiutati con pag. 12.











53 SCIENZE
INGLESE .................................. .................................. .................................. ..................................
GILLS
CAP STEM SPORES MYCELIUM HYPHAE

ZAINI E BORRACCE
1 Come sono pesanti questi zaini da trekking! Trasforma tutte le misure in hg.


2 Completa le tabelle.










3 Scomponi le misure e indica il valore di ogni cifra.






4 Indica il valore della cifra 2 in ogni misura.


54 MATEMATICA
kg hg dag 355,2 920 ...................... 46 ...................... 9,09 ...................... ...................... g dg cg 960 0,02 ...................... 67,7 ...................... 83 ...................... ...................... 472 g hg 970 dg hg 0,7 kg hg 6 700 g hg 2,6 dag .......... hg 5 400 g .......... hg 731 g .............................................................. 428 mg .............................................................. 53 cg .............................................................. 75 dag .............................................................. 600 cg .............................................................. 460 dag .............................................................. 1 384 mg .............................................................. 96 hg .............................................................. 52 g .............................................................. 5 082 g .............................................................. 7 hg, 3 dag, 1 g 1 234 g 2 305 mg 2 087 g 2,2 cg ............ ............ ............ ............ ............
5 Rispondi alle domande sui puntini.


Quanti d ci sono in 1 ?
Quanti corrispondono a 1 h ?







Quanti c corrispondono a 1 h ? ...............

Quanti ci sono in 1 da ? 33

6 Indica con una la quantità di liquido che si avvicina di più alla misura indicata in ciascuna roccia.

La quantità di acqua contenuta in una borraccia.
La quantità di aranciata contenuta in una lattina.
7 Esegui le equivalenze
0,12
La quantità di olio contenuta in una bottiglia.
La quantità di vino contenuta in una botte.

La quantità di acqua contenuta in un secchiello.

La quantità di acqua contenuta in una bottiglietta.


55 MATEMATICA
c 1 1 2
=
3,5 h = da 78 da = ...................... 3,4 d = ...................... 62 c = d 600 c = 40 d = ...................... 255 m = ...................... d 8,2 d = c 12 da = h 3,47 da = ...................... h 1,73 da = ...................... c
d

PROBLEMI DI MONTAGNA
1 Risolvi i problemi con le misure di peso e capacità. Attenzione alle equivalenze!
a. Dentro uno zaino che pesa 7 hg vengono messi 24 barattoli di miele dal peso di 200 g ciascuno. Quanti chilogrammi pesa lo zaino pieno?

Risposta:
b. Anna ha comprato 6 confezioni di marmellata. Ogni confezione pesa 300 g. Quanti chili di marmellata ha comprato Anna?

Risposta:


Risposta:

Dati
Dati
c. Samir ha bevuto 2 borracce di acqua al giorno. Se ogni borraccia contiene 1,5 di acqua, quanti litri di acqua ha bevuto Samir in una settimana? Dati
56 MATEMATICA
.................................................................................... ....................................................................................
.......................................................................................................................................................................................... Risposta: Operazioni ............................................. = ................................. ............................................. = ................................. Operazioni =
= =
Operazioni

2 Completa la regola con i termini che mancano e gli schemi con il segno + oppure –
- Il peso della merce insieme al contenitore si chiama peso
- Il peso della sola merce si chiama peso
- Il peso del contenitore vuoto si chiama ..................................................
peso netto
peso lordo tara
peso lordo tara
peso lordo
peso netto
peso netto
3 Completa la tabella. Attenzione alle equivalenze necessarie!




tara



4 Completa il diagramma, poi scrivi il testo di un problema adatto
peso lordo: 850 g
tara: peso netto: 790 g



57 MATEMATICA
PESO LORDO TARA PESO NETTO 540 g g 500 g kg 1 000 g 4,6 kg .............. kg 0,5 kg 2 kg 250 g g 22 dag
............................................................................................................... ............................................................................................................... ............................................................................................................... ...............................................................................................................

PASSATEMPI P E R LA PIOGGIA


Quando piove è bello stare al calduccio nel rifugio a giocare!

1 Anna e Luca lanciano in aria una moneta da 1 euro e cercano di indovinare se, cadendo, la faccia della moneta sarà testa o croce. Leggi la domanda e rispondi vero V o falso F.
• Qual è la probabilità che esca testa?
- Poiché la moneta ha due facce, i casi possibili sono due.
- I casi favorevoli sono due.
- Il caso favorevole è uno (quello in cui esce testa).
- Il caso favorevole è uno (quello in cui esce croce).
- C’è una probabilità su due che esca testa.
- La probabilità non si può esprimere con una frazione.
V F
V F
V F
V F
V F
V F
2 Osserva le dieci carte. Completa i calcoli delle probabilità che esca ogni tipo di carta.
casi favorevoli
casi possibili
casi favorevoli
casi favorevoli casi possibili
casi possibili casi favorevoli
3 Leggi e rispondi.
casi possibili = = = =
• Gli animatori hanno portato un sacchetto con 5 palline nere e 3 palline blu. Estraendo una pallina, qual è la probabilità che essa sia blu?
I casi possibili sono
I casi favorevoli sono su
La frazione che indica la probabilità che esca una pallina blu è 5 3 o 3 8 ?
58 MATEMATICA

4 Completa la tabella con tutte le possibili combinazioni che si possono ottenere tirando due dadi.





5 Nella tabella dell’esercizio 4 cerchia le somme uguali, poi riportale nel grafico.
somme possibili
6 Rifletti e rispondi.
- Quante probabilità ci sono che esca il 6? ....................
- Qual è il numero che ha la maggiore probabilità di uscita? ....................

59 MATEMATICA
1 • 1 1 • 2 1 • 3 2 • 1 2 • 2 2 • 3 3 • 1 3 • 6 4 • 3 6 • 1 6 • 5 2 3 4 5 6 7 8 9 10 11 12 6 5 4 3 2 1 0

GIOCHI DI LOGICA
1 Conosci il gioco del Sudoku? Ogni quadratino di nove caselle deve contenere tutte le cifre dall’1 al 9 (escluso lo 0). In ogni riga e colonna dello schema non devono mai comparire due cifre uguali. Risolvi questo Sudoku.

2 Fai le somme attribuendo a ogni lettera il giusto valore

A + B + B = 7
A = B = C =
4 Questa addizione è sbagliata: per correggerla hai a disposizione altri tre fiammiferi che dovrai mettere al posto giusto.
3 Quanti quadrati ci sono dentro allo sfondo colorato?

• Ci sono quadrati.
5 Scrivi fra i cinque 7 quattro segni matematici per fare in modo che il risultato sia 13.
60 MATEMATICA
2 3 6 6 5 9 4 8 1 5 2 4 9 6 3 8 7 1 1 4 9 1 6 2 7 2 8 4 4 1 8 7
A + B + C = 6
A + C + C = 5 B + C + C = 7
x + - : 7 7 7 7 7 = 13
Adatt. da Focus junior

6 Vale conosce molto bene il mondo degli animali. Leggi che cosa ci ha spiegato poi sottolinea le informazioni principali e rispondi.
Come si comportano gli animali con la pioggia? Quasi tutti gli insetti si nascondono appena sentono le prime gocce, per loro che sono così piccoli, una goccia d’acqua può essere molto pericolosa! Per evitare le gocce, a pesci e anfibi basta immergersi in acqua. Gli oranghi e altre scimmie usano le foglie di banano, proprio come noi usiamo gli ombrelli! Gli animali sentono prima l’arrivo del brutto tempo?
Sì. Le mucche, prima dell’arrivo del cattivo tempo, diventano irrequiete e agitano la coda, cercando un posto riparato dove sdraiarsi. Le pecore si riuniscono in un gruppo compatto.

Quando le farfalle smettono di svolazzare tra le aiuole il maltempo è in arrivo. Se le rondini volano più vicine al suolo, sta per piovere, perché l’alterazione della pressione atmosferica causata dall’arrivo del maltempo, rende più faticoso volare in alto. E se il gracidare delle rane si fa più forte, ricordatevi l’ombrello! Prima dell’arrivo della pioggia, i gatti hanno l’abitudine di grattarsi con la zampa l’orecchio, perché è sensibile all’aumento di umidità nell’aria.
- Come si comportano gli animali evidenziati nel testo? Scrivilo nel quaderno.





IMPARIAMO L’INGLESE con July
ANIMALS
7 Osserva le immagini e collega ogni animale al nome giusto.










61
SCIENZE INGLESE
fish • monkey • cat • cow • goat • butterfly • swallow • frog

UNO SCIAME DI FRAZIONI
1 Colora le parti indicate dalle frazioni e completa le definizioni.
La frazione propria indica una quantità ................................................. dell’intero. La frazione impropria indica una quantità ................................................. dell’intero.
2 Scrivi nei quadratini P (propria), I (impropria) o A (apparente).
La frazione apparente indica una quantità ................................................. all’intero. 6 8

















3 Ricordi? Due o più frazioni si dicono equivalenti quando, pur sembrando diverse, rappresentano la stessa quantità. Collega con una freccia le frazioni equivalenti.
4 Colora secondo le indicazioni date dalle frazioni e scrivi nei quadratini i segni >, <, =






62 MATEMATICA
3 4 1 3 1 4 2 4 2 5 4 8 1 6 8 12 1 2 6 8 2 3 3 18 3 4 10 25 3 8 6 16 2 6 1 3 1 7 7 14 9 5 12 6 3 3 2 15 14 9
5 Leggi e risolvi i problemi.

2 8
a. Se un piccolo sciame è composto da 16 api e i tornano all’alveare, quante api tornano all’alveare?

2 10 2 6

b. Un altro sciame è composto da 30 api. I si posano su fiori di tiglio, i su fiori di castagno e i 2 15 su fiori di acacia. Quante api volano sui fiori di tiglio? Quante su fiori di castagno? Quante su fiori di acacia?
Operazioni
Risposta
Operazioni

c. Alla fine della giornata, l’apicoltrice ha preparato 48 barattoli di miele. I sono già stati venduti. Quanti barattoli di miele ha venduto l’apicoltrice? Quanti gliene restano da vendere? 2 12
Risposte

Operazioni
Risposte


63 MATEMATICA
.................................................................................... ....................................................................................
....................................................................................
.................................................................................... ....................................................................................
(16 : ) x = x =
....................................................................................
......... .........

ACQUISTI MONTANI
1 Completa le formule scrivendo spesa e ricavo al posto giusto.
guadagno
guadagno + – –
guadagno

2 Rispondi con una .


• Quando si verifica una perdita?
Quando la spesa è uguale al ricavo.
Quando la spesa è superiore al ricavo.
Quando la spesa è inferiore al ricavo.
3 Scrivi spesa, ricavo e guadagno al posto giusto.
Una negoziante ha acquistato una forma di formaggio per 30 euro. Rivenderà la forma di formaggio a 38 euro.

30 euro .....................................
38 euro
8 euro
4 Osserva il cartellino dei prezzi dei due oggetti, poi indica con quale dei due può essere acquistato spendendo tutti (o quasi) gli euro rappresentati.


















64 MATEMATICA

5 Risolvi i problemi con il diagramma e le operazioni in colonna.
a. Roby ha accompagnato alcuni bambini del centro estivo a comprare i panini per l’escursione. Hanno comprato 2 panini al costo di 4,70 euro ciascuno e 2 panini al costo di 3,20 euro ciascuno.
Quanto hanno speso in tutto?


Operazioni in colonna
Risposta


b. È il compleanno di Roby e gli altri 4 animatori decidono di fargli un regalo. Ognuno versa 6,50 euro. Con il denaro raccolto comprano un libro da 18 euro e una scatola di cioccolatini. Quanto è costata la scatola di cioccolatini?


Operazioni in colonna
Risposta

65 MATEMATICA
......... ......... .............. ..............
















IN MONGOLFIERA









Le gite del Centro estivo si spostano in città! Oggi siamo saliti su una mongolfi era e abbiamo visto la nostra città dall’alto.



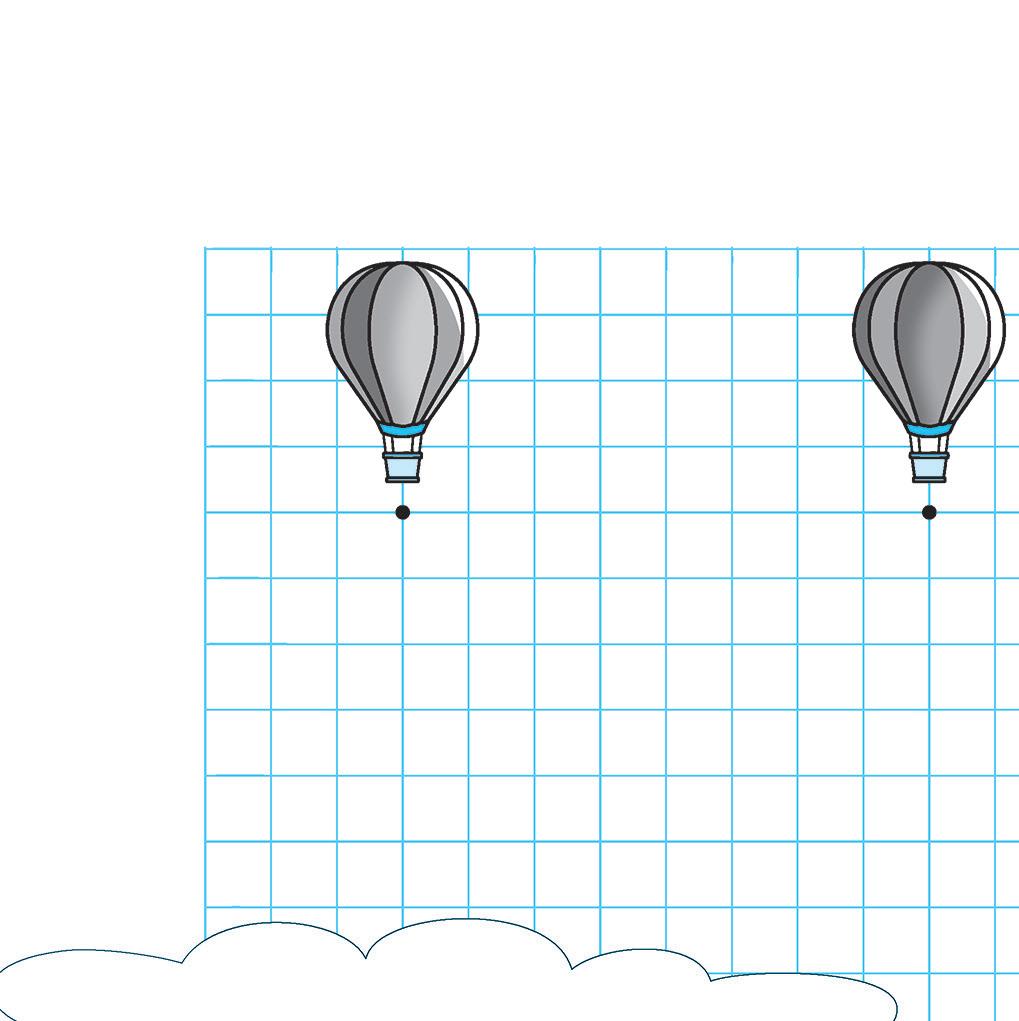
= 1 quadretto
1o spostamento da A1 a A2 = 8

















1 La mongolfiera si sposta varie volte in questo cielo quadrettato. Segui le indicazioni e muovi la mongolfiera.




2o spostamento da A2 a A3 = 4 e 6
3o spostamento da A3 a A4 = 4 e 1
4o spostamento da A4 a A5 = 5
2 Completa l’intreccio del cesto della mongolfiera rispettando questo ritmo.













66 MATEMATICA
A1 A2





IMPARIAMO L’INGLESE con July
THOUSANDS, HUNDREDS, TENS, UNITS
3 Leggi come si dicono migliaia, centinaia, decine e unità in inglese.


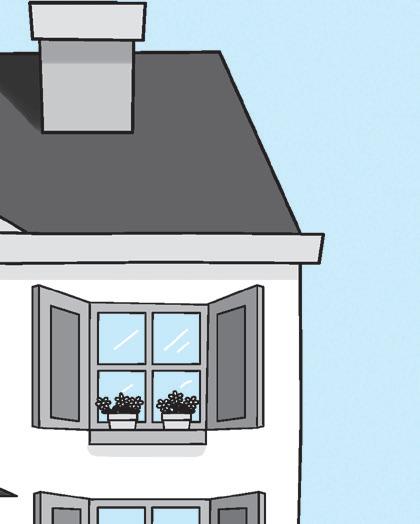





The number on this door is 5 267.
That is:
• 5 thousands
• 2 hundreds
• 6 tens
• 7 units
But we say the number:
five thousands, two hundreds, and sixty-seven.

4 Ora osserva le immagini e completa.
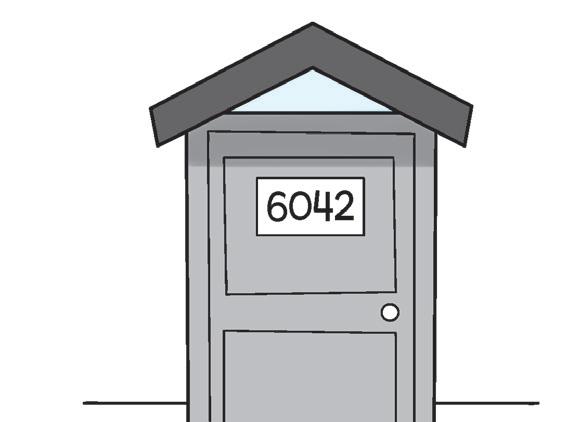


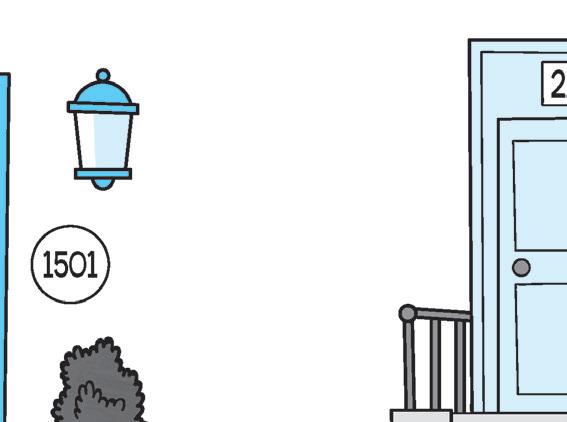





thousands
hundreds

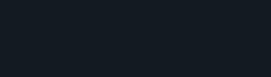

tens
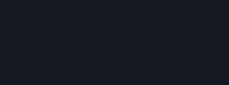
USED CARS
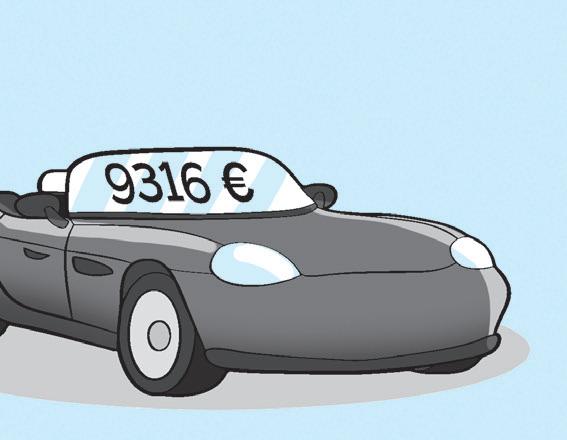
thousands hundreds ten units












67 INGLESE
..............
..............
..............
..............
............................... ............................... ............................... .............. ...............................
.............. ..............











68 MATEMATICA
1 Completa la tabella.
uk h da u d c m 204,86 1 8 6 .............................. 7 4 3 3 5 5 6 233,128 0,071 ........... ........... ........... ........... ........... ........... ........... 3,9 27,18 ........................................................................ ................................................................................................ 10,3 27,7 1,3 , , , , , , 16,2 9,8 33,3 3,1 33,03 12,6 0,25 6,2 20,05 2,6 8,13 + 0,4 + 0,3 12,31 1,231 123,1 1 231 0,17 44,58 4,458 445,8 445 3,7 12 u 3 c 2 da 5 m 45 da 1 d 23 m 1 h 8 da 2 c 1 uk 5 u 86 m 2 uk 8 u 33 m
2 Riscrivi i numeri decimali in ogni serie, in ordine decrescente.
IL TRENO DEI DECIMALI
4 Scrivi sotto forma di numero decimale
a. c. b. d.
3 Calcola a mente.

5 Esegui le operazioni in colonna.

6 Completa le operazioni con il termine mancante.



69 MATEMATICA
85,42 + 9,72
........... 36,87 – 13,48 = 480,35 + 38,01 = ........... 517,91 – 66,49 = 653,2 + 87,84 = ........... 125,02 – 24,38 = 6,8 + = 7 5,34 + = 6 4,400 – = 4 7,38 – = 5 7,35 + = 8 2,91 + = 3 3,18 – = 3 11,5 – = 0,5 35,72 + = 36 13,05 + = 14 9,88 – = 9,8 33,7 – = 10,7 5,99 + = 6 49,1 + = 50 19,80 – = 10 50,1 – = 40
=
6,5 + 3,5 = 9,10 V F 10 – 6,125 = 4,875 V F 9,74 + 7,26 = 17 V F 20,8 – 4,21 = 16,59 V F 1,096 + 3,405 = 3,401 V F 39,1 – 0,628 = 38,472 V F
7 Vero (V) o falso (F)?

TRAGITTI IN TERRA E CIELO
1 Completa il paesaggio seguendo le indicazioni e aggiungendo quello che manca.
• Vai in via delle Linee Parallele e disegna un taxi vicino alla Casa delle Magnolia.


• Prosegui fino all’incrocio delle rette incidenti… Oh, oh! Chi ha rubato il semaforo? Disegnalo.
• Sali sul ponte perpendicolare al Fiume Azzurro e disegna un cagnolino bianco e nero.





• Prosegui e gira a destra… finalmente sei al Giardino della fontana: colora con i colori dell’arcobaleno il recinto dei segmenti.
 VIA DELLE LINEE PARALLELE
VIA DELLE LINEE PARALLELE
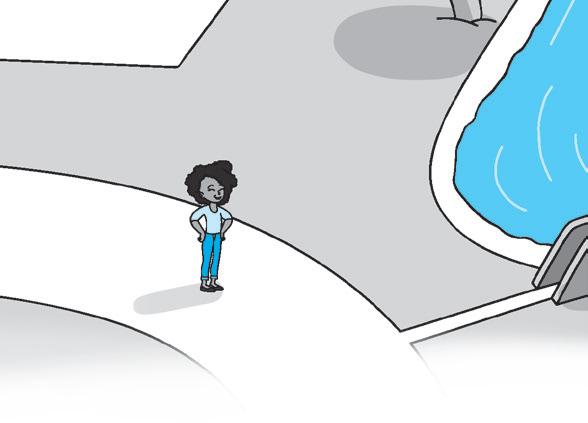
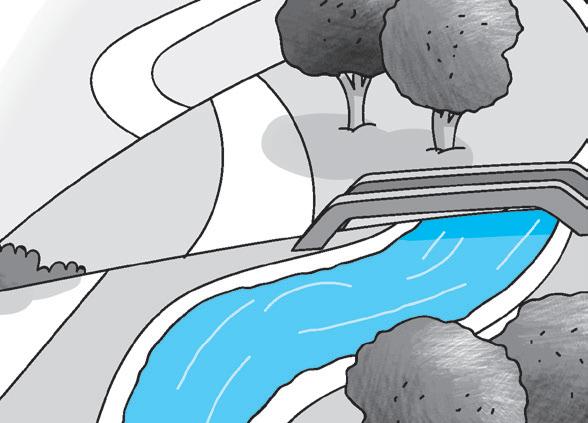

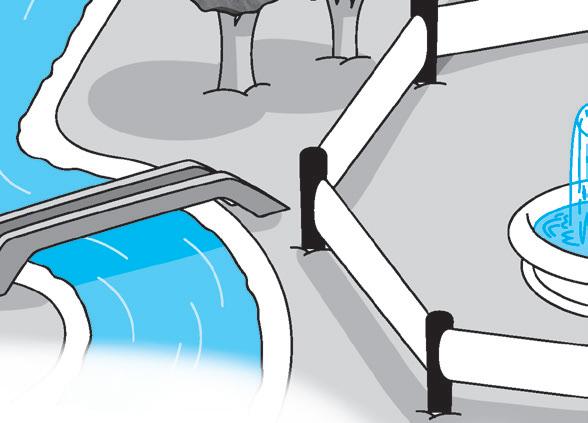
2 Collega ogni definizione alle linee corrispondenti.
Il segmento è una parte di retta compresa tra due punti.
Due rette incidenti perpendicolari formano 4 angoli retti. Due rette sono incidenti se si incontrano in un punto.
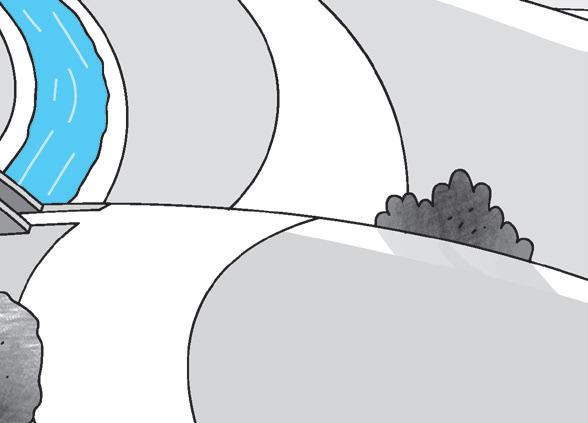


VIADELLE RETTE INCIDENTI
CASA DELLA MAGNOLIA
FIUME AZZURRO
70 MATEMATICA
GIARDINO DELLA FONTANA
B
A

3 Quante rondini sui fili! Ordina gli angoli dal più ampio al meno ampio e scrivi la successione delle sillabe corrispondenti. Scoprirai il nome della rondine più giovane.

















Disegna




























4 Le rondini volano sul cielo della città. Ordina l’ampiezza degli angoli dal meno ampio al più ampio, poi registrali nella tabella.






71 MATEMATICA
1 3 2 D B A 4 > > > ....... ....... ....... ....... < < < to piu la met
1 ° 2 ........................ ° 3 ° 4 ........................ °
C
angolo ampiezza
5
un angolo ampio la metà di un angolo retto
.

AL PARC O A CQUATICO

Oggi giornata di tuffi , ginnastica e divertimento!
1 Quanti dei 10 ingressi per gli scivoli ha già effettuato ogni bambino?
Scrivili nella tabella in frazione decimale, in lettere e in numero decimale



2 Calcola e collega la cuffia di ogni bambino agli occhialini con lo stesso valore
3 Scrivi le cifre sotto forma di numero decimale.


72 MATEMATICA
FRAZIONE DECIMALE FRAZIONE IN LETTERE NUMERO DECIMALE Marco Gaia ................................. ................................. Amina ................................. ................................. Lidia 5 100 4 100 7 10 62 1000 9 1000 0,009 0,05 0,04 0,062 0,7 ........... ........... 25 unità 4 decimi da u d c m 0 unità 5 centesimi u d c m 8 unità 4 decimi 2 centesimi u d c m 0 unità 7 decimi 1 millesimo u d c m 19 unità 4 millesimi da u d c m
BAMBINI - BIGLIETTI



GINNASTICA con Roby
LA POSTURA CORRETTA


4 Osserva il disegno e le diverse posture. Poi completa ed esegui gli esercizi.
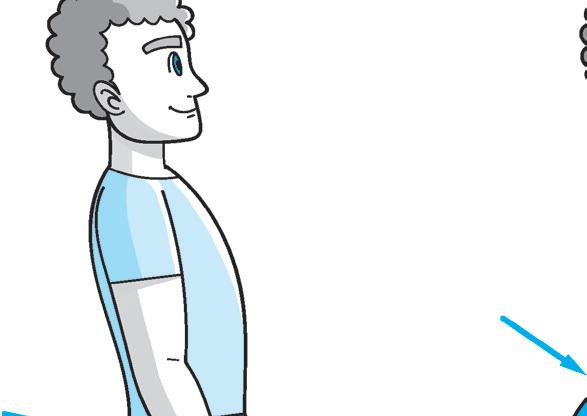
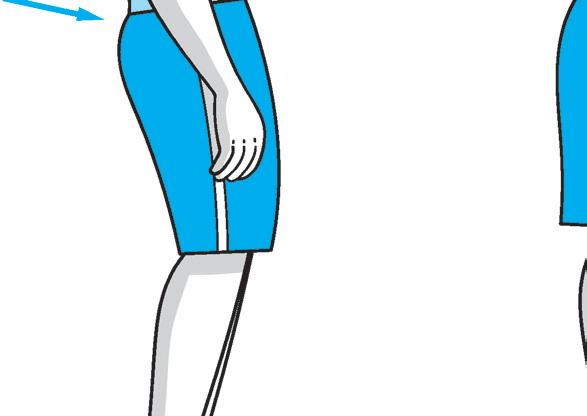

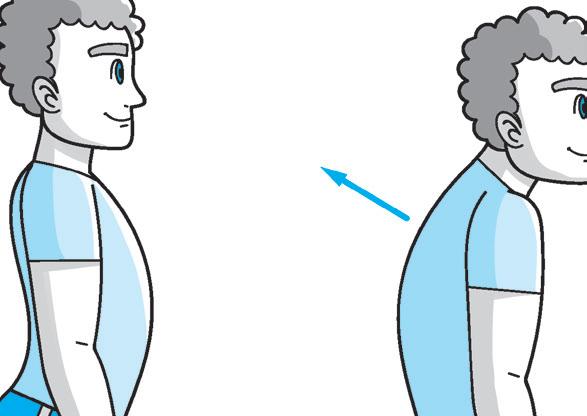
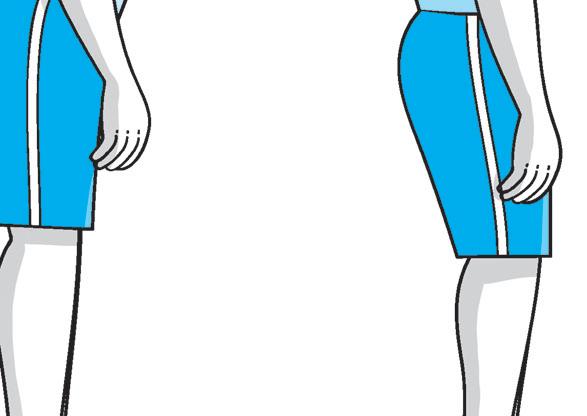
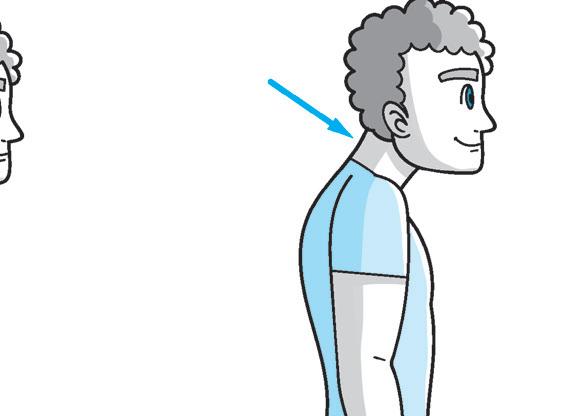
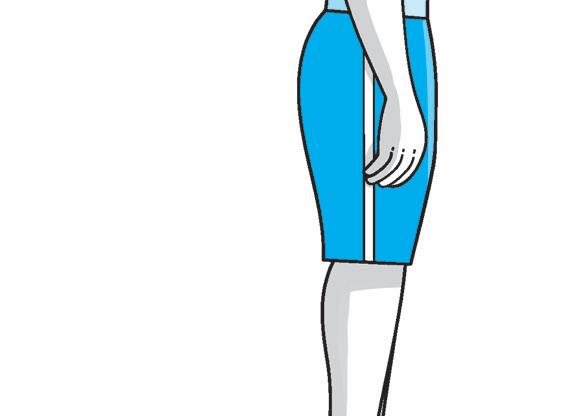
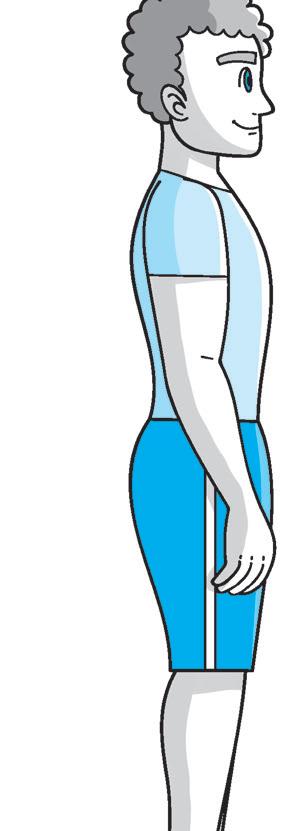
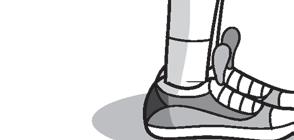

La postura corretta è quella della figura ............. , cerca di imitarla per almeno un minuto.
Dopo aver fissato bene la posizione corretta 5, prova a modificarla imitando le posture “scorrette” (senza sforzarti) e mantenendo sempre le posizioni per almeno 10 secondi. Dopo ogni modifica ritrova sempre la posizione corretta.
Al termine di ogni postura annota qui sotto le sensazioni che hai provato e quali movimenti e muscoli hai dovuto utilizzare per modificare la postura “corretta” originaria.





73
MOTORIA
1 2 3 4 5 • • • •

POLIGON I G USTOSI






Oggi merenda con pizza e gelati!


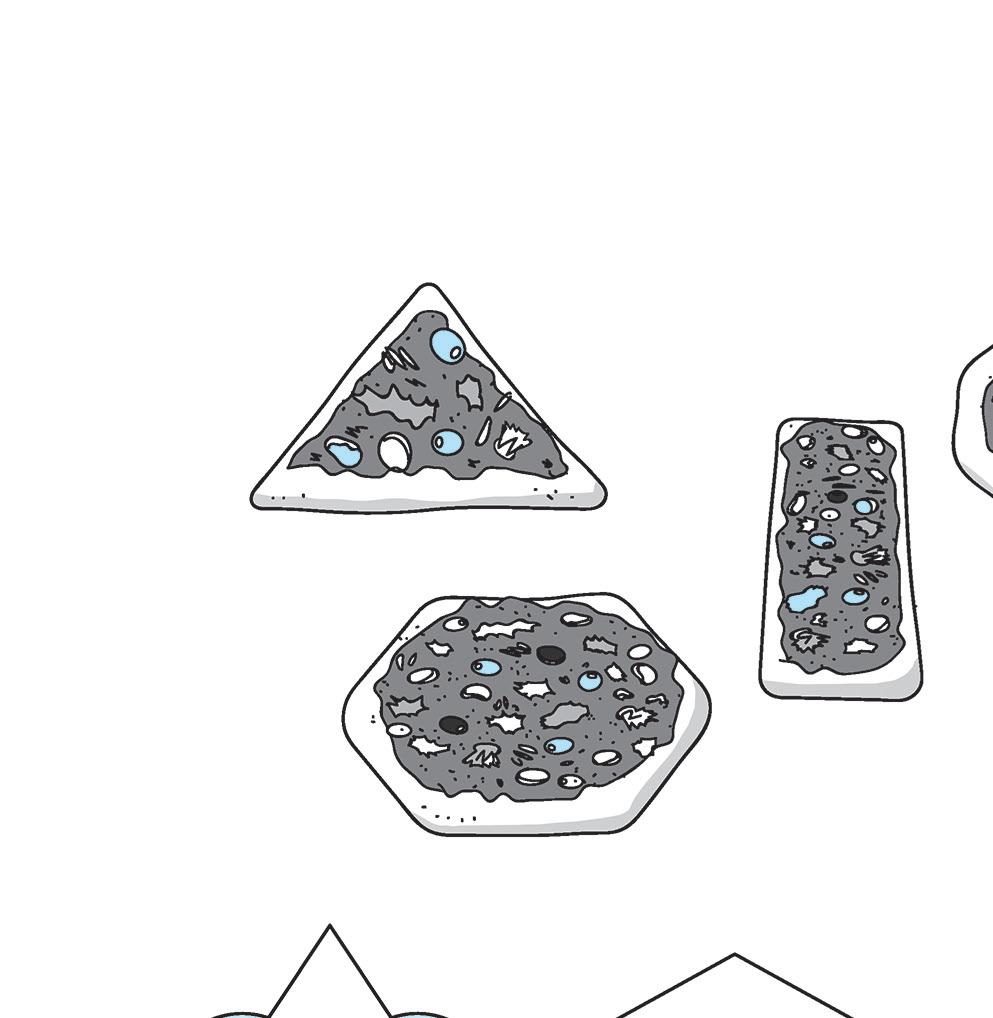
1 Collega i pezzi di pizza ai vassoi che ne indicano la forma.
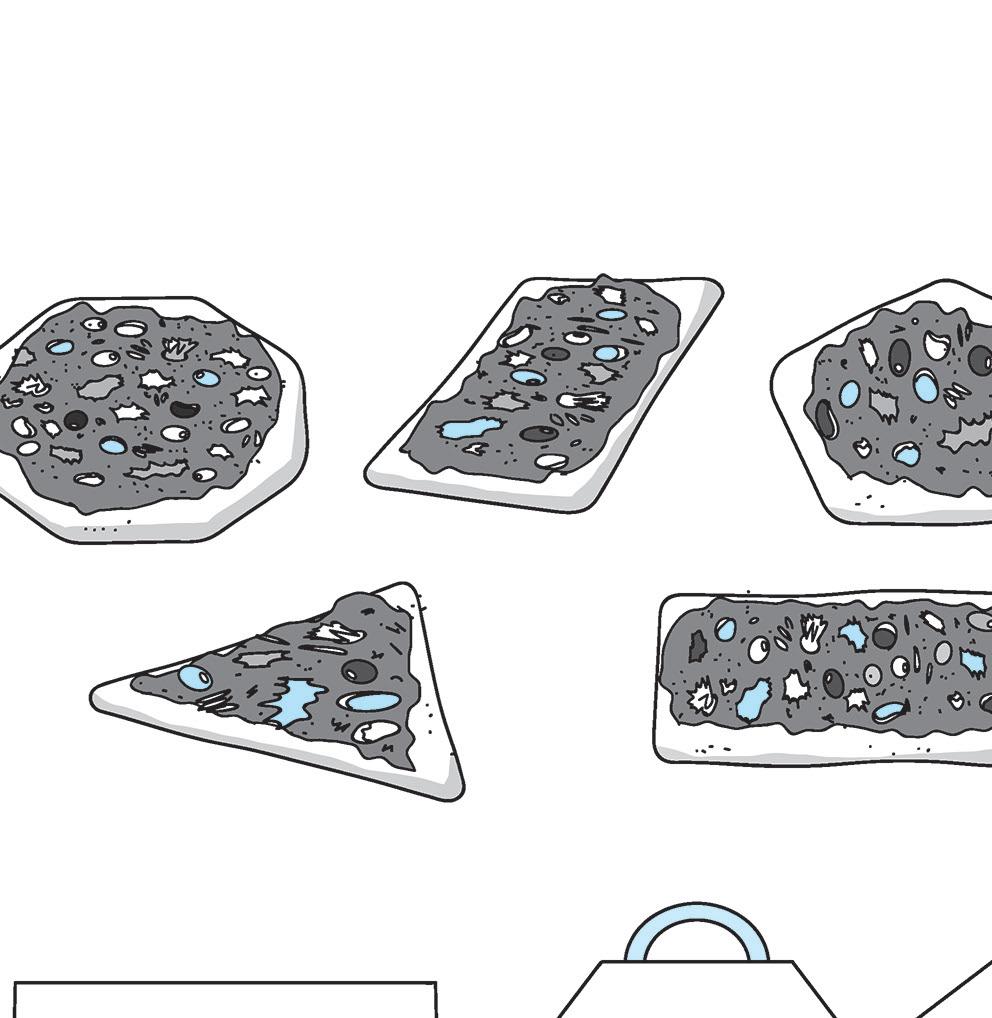

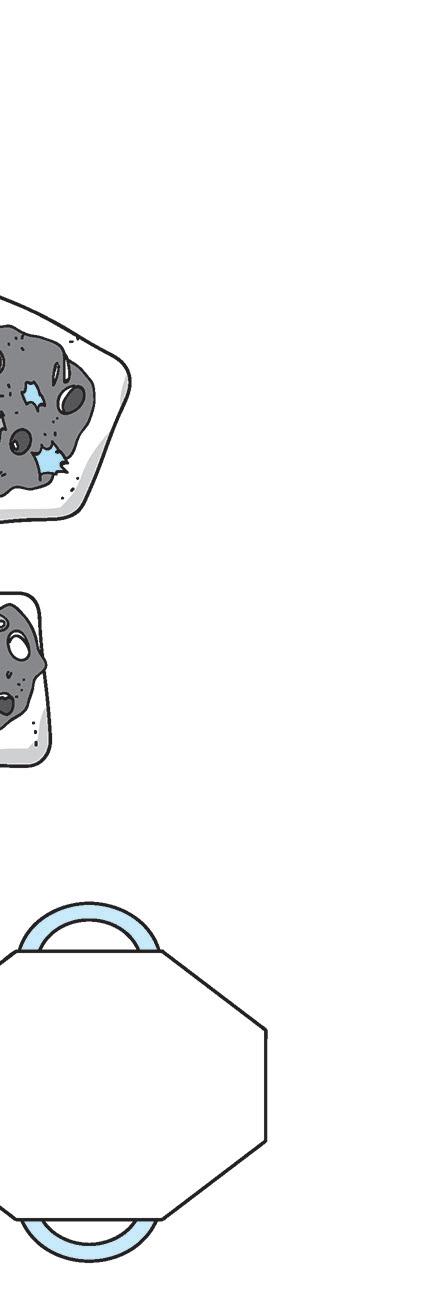
TRIANGOLI
PENTAGONI ESAGONI QUADRILATERI
OTTAGONI
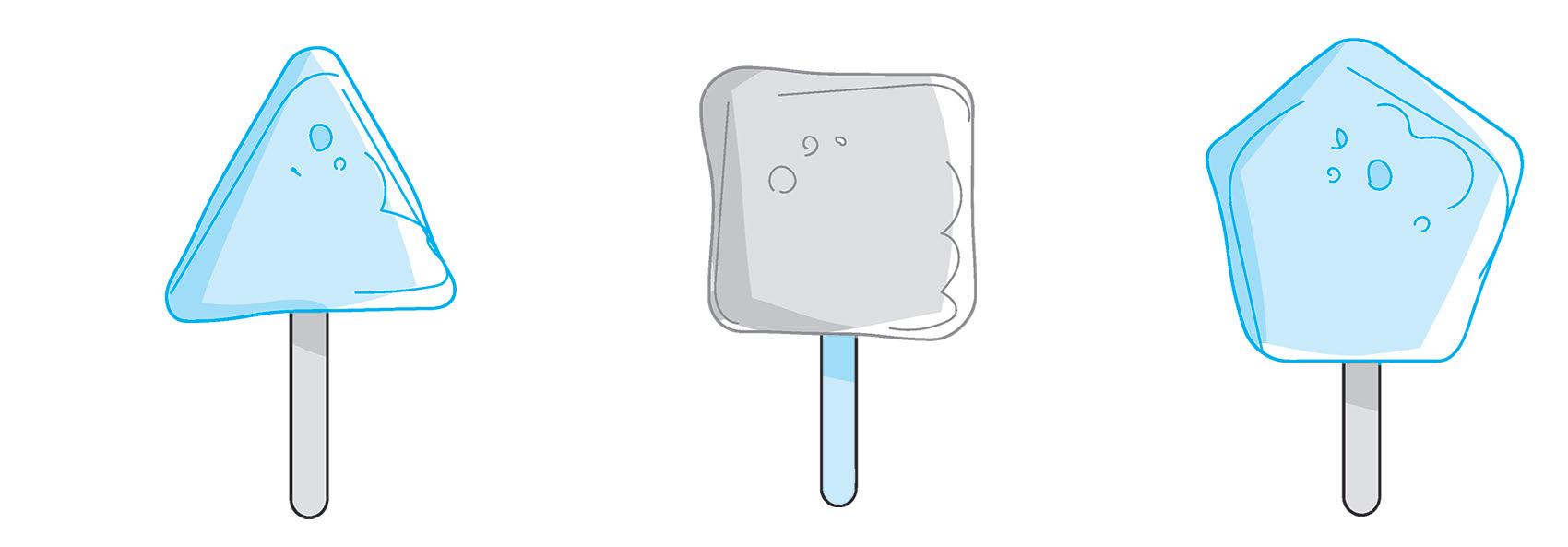
2 Non trovi che questi ghiaccioli siano simili a figure piane? Scrivi sui puntini i loro nomi.
3 Scrivi al posto giusto nei cartellini gli elementi che formano un poligono.
angolo diagonale lato

74 MATEMATICA
.................................. ...............................................
4 Collega ogni definizione al poligono giusto, usando le frecce.
Poligono convesso
Poligono concavo
5 Osserva le figure, poi completa.

• Almeno 2 prolungamenti dei segmenti di confine (lati) entrano nella figura.
• I prolungamenti dei lati non entrano nella figura.
• Percorrendo i segmenti di confine, i cambi di direzione non sono sempre nello stesso senso.
• Percorrendo i lati, i cambi di direzione sono sempre nello stesso senso.






Non sono poligoni: Sono poligoni concavi: Sono poligoni convessi:



6 Disegna un poligono… concavo di 5 lati. convesso di 7 lati.

75 MATEMATICA
A C E B D

PICNIC AL PARCO
1 Gli animatori vanno a comprare merende e bibite. Leggi i grafici e rispondi.
Merenda
Pizza
Focaccia
Biscotti
Panino
Gelato

Legenda
= 5 bambini

• Quante pizze e focacce devono prendere gli animatori? .............................
• Quale tipo di merenda piace di più: dolce o salata?
• Quanti bambini in più preferiscono la focaccia alla pizza?

Bibite
Acqua
Succo di frutta
Tè freddo
• Qual è la differenza tra i bambini che bevono l’acqua e quelli che preferiscono il succo di frutta?
• Quanti bambini bevono il tè?


Legenda
= 20 preferenze

76 MATEMATICA
2 Leggi, poi inserisci i nomi dei bambini nell’insieme giusto.
I bambini che hanno mangiato i biscotti hanno scelto così:
• Lucia, Roberto, Agnese, Yili biscotti quadrati
• Lorenzo, Assan, Veronica biscotti al cioccolato


• Marta, Sonia biscotti rotondi al cioccolato
• Sofia, Marco, Giulio biscotti quadrati al cioccolato

Bambini che mangiano biscotti quadrati





Bambini che mangiano biscotti quadrati al cioccolato




Bambini che mangiano biscotti al cioccolato



3 Ora disegna i biscotti come indicato nel diagramma ad albero.

77 MATEMATICA
A B
................................................... ....................................... A C B
C
BISCOTTI NON al cioccolato quadrati quadrati NON quadrati NON quadrati al cioccolato

VALUTIAMO LE COMPETENZE
1. Quale delle seguenti scritture corrisponde al numero cinquecentosessantaquattromilatrecentoventinove?
A. 500 000 + 40 000 + 6 000 + 300 + 29
B. 500 000 + 60 000 + 4 000 + 500 + 20 + 9
C. 500 000 + 60 000 + 4 000 + 300 + 20 + 9
D. 600 000 + 60 000 + 4 000 + 300 + 20 + 9
2. Quale dei seguenti numeri corrisponde a 9 da?
A. 90 B. 0,9 C. 0,09 D. 9
3. Il numero 365 692 deve essere arrotondato alle unità di migliaia. Qual è l’arrotondamento esatto?
A. 365 690 B. 365 000 C. 365 600 D. 366 000
4. Quale numero è rappresentato su questo abaco?
A. 251 102
B. 250 102
C. 251 120
D. 205 102
h k da k u k h da u
5. Qual è il risultato esatto della divisione 80 350 : 25?
A. 3 116
B. 3 214
C. 3 213
D. 3 316

SITUAZIONE NON NOTA 78 MATEMATICA PROVE MODELLO INVALSI

6. Qual è il numero che indica la media della seguente successione di numeri?
19 • 9 • 16 • 25 • 13 • 44
A. 24
B. 15
C. 12
D. 21
7. Nella seguente serie manca l’ultimo numero. Qual è?
5 • 15 • 45 • 135 • 405 •
A. 1 135
B. 910
C. 525
D. 1 215
8. Per acquistare un computer nuovo che costa 1 200 € , Ahmed ha risparmiato 80 € al mese per un anno.
Quanto deve ancora risparmiare per poter acquistare quel computer?
A. (1 200 + 80) x 12
B. 1 200 – (80 x 12)
C. 1 200 + (80 + 12)
D. (1 200 – 80) x 12
9. Qual è il risultato della moltiplicazione 1,2 x 100?
A. 12
B. 120
C. 0,12
D. 1,200
10. Quanto vale il perimetro di un quadrato che ha un lato lungo 10 cm?
A. 30 cm
B. 20 cm
C. 50 cm
D. 40 cm

SITUAZIONE NON NOTA 79 MATEMATICA PROVE MODELLO INVALSI

11. Quattro bicchieri e una bottiglia pesano come due bottiglie e un bicchiere. Quanti bicchieri pesano come due bottiglie? Aiutati disegnando le bottiglie e i bicchieri indicati.
A. 6
B. 7
C. 5
D. 3
12. Quale dei seguenti numeri è il successivo di 899 999?
A. 899 000
B. 800 000
C. 900 000
D. 890 000
13. Qual è la capacità totale di una confezione da 6 bottiglie d’acqua da 1,5 litri?
A. 15
B. 9
C. 20
D. 18
14. Come si calcola il perimetro di un triangolo equilatero?
A. x 4
B. b + ( x 2)
C. x 3
D. (b + h) x 2
15. In un barattolo ci sono 32 caramelle: 17 alla panna e 15 alla menta. Qual è la frazione che indica la probabilità di estrarre una caramella alla panna?
A. 15 32
B. 17 32
Autovalutazione
C. 0 32 D. 17 15
Sei soddisfatta/o del tuo lavoro?

SITUAZIONE NON NOTA 80 MATEMATICA PROVE MODELLO INVALSI
SCEGLI TRA LE TANTE

IL MULINO A VENTO
Per far crescere l’abitudine e il piacere della lettura.








L’ISOLA DEL TESORO
Avventure, viaggi, esplorazioni, tesori nascosti.
Pagine: 176 - Prezzo: € 8,50
ISBN: 978-88-472-4082-7








IL MULINO A VENTO



Pagine: 48 - Prezzo: € 8,90
ISBN: 978-88-472-3985-2

Coordinamento e redazione: Corrado Cartuccia
Progetto grafico e impaginazione: Marco Mancini
Copertina: Licinia Tozzi, Marco Mancini
Illustrazioni: Michele Bizzi
Coordinamento digitale: Paolo Giuliani
Referenze fotografiche: Istock, Archivio Raffaello
Stampa: Gruppo Editoriale Raffaello


GIOCHI





CHIEDI ALLE STELLE
I bellissimi sogni dei ragazzi del mondo.
Pagine: 144 - Prezzo: € 9,00
ISBN: 978-88-472-4083-4



- FUMETTI STICKERS ATTIVITÀ DI LOGICA E INTELLIGENZA CON CON
Storie per tenere in allenamento corpo e mente!




















Il progetto SIAMO PARI del Gruppo Editoriale Ra aello sostiene e promuove il codice POLITE (Pari Opportunità nei LIbri di TEsto) per la formazione di una cultura delle pari opportunità e del rispetto di tutte le di erenze.









Pagine: 48 - Prezzo: € 8,90


ISBN: 978-88-472-3986-9

2024
Raffaello Libri S.p.A. Via dell’Industria, 21 60037 - Monte San Vito (AN) www.ra aelloscuola.it - info@gruppora aello.it Ristampa:


Per esigenze didattiche alcuni testi sono stati ridotti e/o adattati. L’Editore è a disposizione per eventuali omissioni o inesattezze nella citazione delle fonti. Tutti i diritti sono riservati. È vietata la riproduzione dell’opera o di parti di essa con qualsiasi mezzo, compresa stampa, fotocopia, micro lm e memorizzazione elettronica, se non espressamente autorizzata dall’Editore.
5 4 3 2 1 0 2029 2028 2027 2026 2025 2024 ©
PROPOSTE DEI CATALOGHI
PER CONSOLIDARE CONOSCENZE E ABILITÀ ,
MAPPE DI RIPASSO FACILITATE per lavorare in autonomia.
PROVE D’INGRESSO per la nuova classe.




L’ambientazione al centro estivo è super motivante con:








































Questo volume, sprovvisto del talloncino a fronte (o opportunamente punzonato o altrimenti contrassegnato), è da considerarsi copia di SAGGIO-CAMPIONE GRATUITO, fuori commercio (vendita e altri atti di disposizione vietati: art. 17, c. 2 L. 633/1941). Esente da I.V.A. (D.P.R. 26-10-1972, n° 633, art. 2 lett. d). Esente da bolla di accompagnamento (D.P.R. 6-10-1978, n° 627, art.4. n° 6). VACANZE ALCENTROESTIVO Matematica4 ISBN978-88-472-4297-5 € 4,50
VERSO LE COMPETENZE
E IN PIÙ... ANIMATORI E ANIMATRICI RITAGLIABILI
DIPLOMA DI FINE CORSO + GIOCO ROBY VALE





























































































































































































































































































































































































































































































































































































































































































































































































































































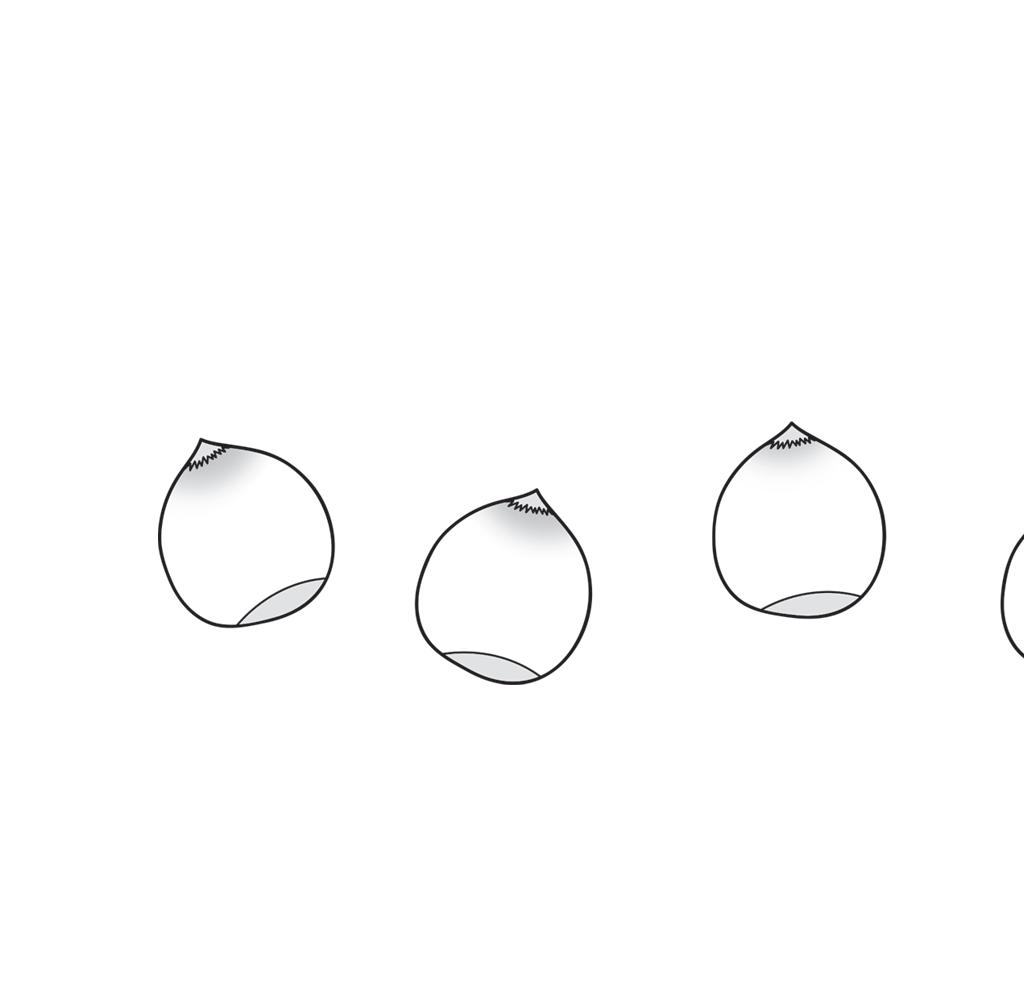































































































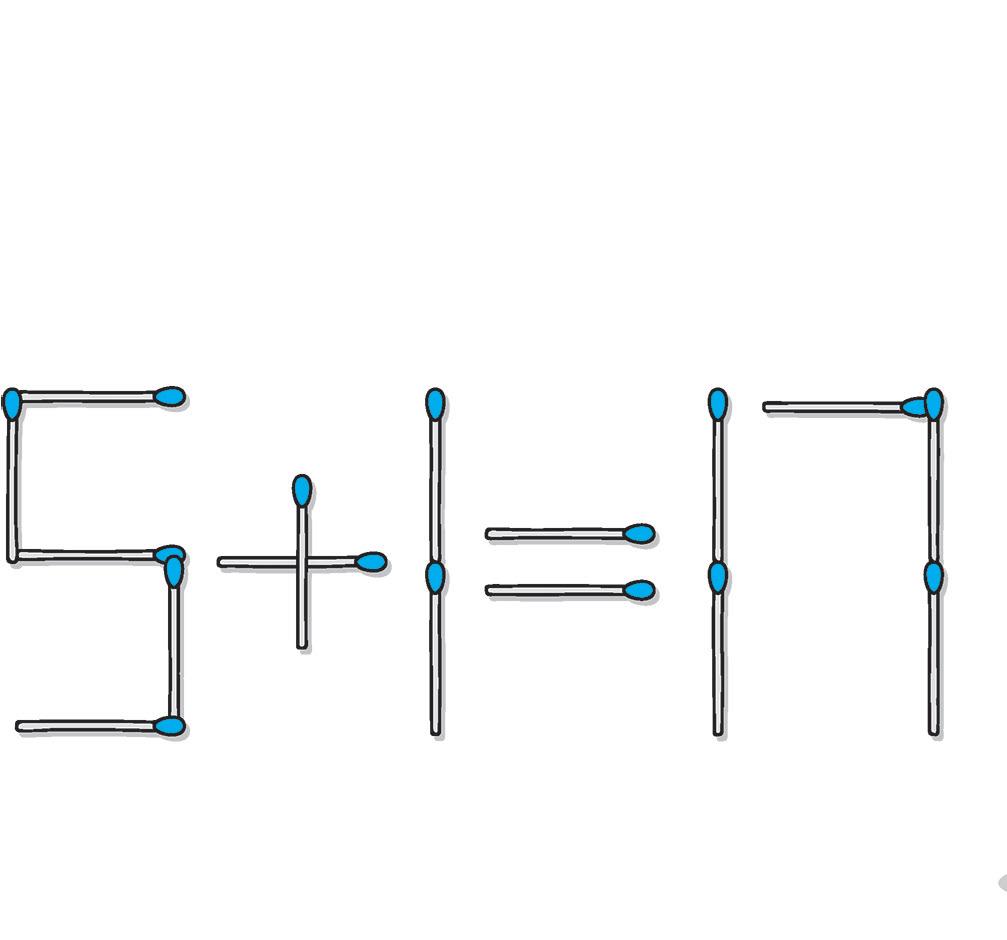

























































































































































 VIA DELLE LINEE PARALLELE
VIA DELLE LINEE PARALLELE










































































































































































































