

Guida pratica
Raffaello
Percorsi didattici e operativi per la
Scuola Primaria



2



Alessandra Furnari • Angela Mattiello
Michela Mori
Simona Savarino
CONTENUTI DIGITALI CON L’APP R AFFAELLO PLAYER
Per attivare i contenuti digitali, registrati sul sito raffaellodigitale.it. Successivamente scarica, installa e avvia l’applicazione Raffaello Player: effettua il login, seleziona il titolo e inserisci il codice di attivazione riportato sotto.

Collegandoti a raffaellodigitale.it puoi scaricare l’applicazione.
Digitando raffaelloplayer.it puoi utilizzare l’applicazione senza effettuare nessuna installazione.
Inquadra e installa.


CODICE DI ATTIVAZIONE
Ti serve aiuto? Leggi le F.A.Q. o richiedi assistenza collegandoti all’indirizzo supporto.raffaellodigitale.it oppure scrivi un'e-mail a supporto@raffaellodigitale.it
Alessandra Furnari • Angela Mattiello • Michela Mori
Simona Savarino
Guida pratica
Raffaello
Percorsi operativi per la valutazione nella
Scuola Primaria
Matematica
I numeri da 50 a
I numeri da 60 a 70
I numeri fino a 70
INDICE Matematica 2
I
I numeri da 90
I numeri fino a 99
PERCORSO 4 CLASSIFICAZIONI
UNITÀ 1 E RELAZIONI
Gli insiemi
Appartiene o non appartiene 229
Un elemento in più
Gli insiemi 231
Le classificazioni: l’intersezione 232
Le classificazioni: il sottoinsieme 233
I quantificatori 234 - 235
Le relazioni 236 - 237
HO IMPARATO Classificazioni e relazioni 238
HO IMPARATO Classificazioni e relazioni
PERCORSO 4 PROBLEMI
UNITÀ 2
Ho un problema? 241
Se ho un problema, che cosa faccio? 242
Il problema matematico 243
Una domanda per ogni problema 244
Che cosa mi serve per trovare una soluzione? 245
L’informazione nascosta 247
L’informazione mancante 248
La rappresentazione: una strategia per risolvere i problemi 249
La tabella: una strategia per risolvere i problemi 250
Dalla rappresentazione al problema 251
Dall’immagine al problema 252 Problemi con le addizioni 253
Problemi con le sottrazioni 254
Contenuti digitali
L’educazione che utilizza le nuove tecnologie, miscelandole con i metodi canonici, dota docenti e studenti di strumenti che possono portare a una vera innovazione, necessaria allo sviluppo sociale e tecnologico.
All’interno di questa guida scolastica è stato scelto di proporre delle attività digitali interattive inerenti ai percorsi didattici, che offrono strumenti di lavoro, di condivisione e cooperazione, oltreché di inclusione. Questa scelta segue le indicazioni del PNRR per l’adozione delle pedagogie innovative. Attraverso le attività proposte, i docenti possono favorire la motivazione e l’impegno attivo delle bambine e dei bambini, utilizzando modelli educativi progettati a misura della loro inclinazione naturale verso il gioco, la creatività, la collaborazione e la ricerca, in coerenza con il più recente quadro di riferimento europeo delle competenze digitali dei cittadini.
• La guida è fruibile anche in versione digitale, proiettabile sulla LIM e Smart Board o da dispositivi mobile grazie all’applicazione RaffaelloPlayer.
• Allegati scaricabili in formato PDF.
• Soluzioni delle schede, scaricabili e stampabili per l’autocorrezione.
• Laboratori e attività interattive e auto-valutative.
Inquadra il seguente QR-code per accedere ai contenuti digitali del volume

Presentazione
La scuola oggi si trova ad operare in un contesto nuovo, vario, in continua evoluzione, caratterizzato da molteplici bisogni e culture che s’incontrano diventando occasione di confronto, scambio e arricchimento continuo. La società attuale è diventata globale, multiculturale e questo offre opportunità alle nuove generazioni di acquisire saperi e competenze specifiche anche al di fuori delle classi con nuovi strumenti e possibilità.
In questo scenario, la scuola, agenzia educativa per eccellenza, è chiamata a diventare “comunità educante” intesa come setting che accoglie e stimola ogni alunno e ogni alunna a costruire la propria identità, con le proprie caratteristiche in uno scambio continuo tra pari e territorio.
Gli insegnanti assumono, quindi, un ruolo privilegiato all’interno del percorso educativo e formativo. Essi veicolano e favoriscono l’attuazione di un ambiente di apprendimento rinnovato che valorizzi le specificità degli studenti, che sappia avvalorare le diverse situazioni individuali e garantire il successo formativo di ogni alunno. In quest’ottica, si attesta di fondamentale rilevanza l’uso di metodologie e di elementi innovativi che promuovono sempre di più la costruzione e la progettazione di una didattica per competenze, poiché è solo attraverso la competenza che ogni alunno e ogni alunna potrà essere in grado di mobilitare conoscenze, abilità, comportamenti ed emozioni in situazioni nuove e reali.
Per rispondere ai bisogni dei nuovi scenari è stata ideata la Guida Pratica Raffaello. La guida è stata progettata per gli insegnanti a supporto di una didattica efficace, inclusiva e per competenze. Nell’ottica di promuovere il pieno successo formativo degli alunni e delle alunne è stata elaborata una progettazione per obiettivi di apprendimento, divisa in percorsi, in ognuno dei quali vengono proposte strategie didattiche mirate a supporto dell’azione dell’insegnante. L’impianto valutativo è stato strutturato per promuovere un monitoraggio continuo degli apprendimenti.
La guida, inoltre, è arricchita da una serie di risorse digitali disponibili, anche in forma editabile, a integrazione del lavoro del docente.

Schema Guida Pratica Matematica 2
OSSERVAZIONE IN INGRESSO
Permette di effettuare una ricognizione sulle conoscenze e sulle abilità a inizio anno delle alunne e degli alunni che diventano la necessaria premessa per una progettazione funzionale ed efficace.
La Guida propone di osservare gli ambiti relativi ai nuclei tematici.
Numeri
Dati e Previsioni
Spazio e Figure
Relazioni e Funzioni
PROGETTAZIONE
La progettazione si articola in obiettivi relativi all’apprendimento logico-matematico riferito ai quattro ambiti sottoindicati.
A supporto delle attività proposte, è possibile usufruire anche di risorse digitali.
Numeri
Relazioni, dati e previsioni
Spazi e figure
Risorse digitali
VALUTAZIONE FORMATIVA
A sostegno del processo di apprendimento è stato predisposto un percorso valutativo che pone lo studente al centro dell’azione didattica.
Valutazione per l’apprendimento Griglie valutative
Le Verifiche in itinere
Valutazione come processo di apprendimento
Autovalutazione
VALUTAZIONE DELLE COMPETENZE
La valutazione delle competenze pone lo studente nelle condizioni di mobilitare il patrimonio delle risorse personali e quelle acquisite.
Compito autentico Prova stile INVALSI
OSSERVAZIONE IN INGRESSO
Nei primi giorni della classe seconda della scuola primaria il docente è chiamato a porre particolare attenzione alle conoscenze e alle abilità acquisite da ogni bambino e da ogni bambina durante la classe prima. La Guida propone una serie di schede per osservare alcune dimensioni relative all’apprendimento logico-matematico. Il riferimento è ai quattro ambiti declinati ognuno in obiettivi di apprendimento.
NUMERI
• Contare entro il 20;
• Raggruppare per 10;
• Ordinare e confrontare i numeri entro il 20;
• Eseguire addizioni e sottrazioni entro il 20.
DATI E PREVISIONI
• Saper classificare e mettere in relazione;
• Interpretare un grafico e raccogliere i dati.
SPAZIO E FIGURE
• Riconoscere le linee e le figure geometriche piane;
• Eseguire e descrivere percorsi sul piano quadrettato.
RELAZIONI E FUNZIONI
• Misurare e confrontare più elementi.
L’osservazione della classe, che all’interno della Guida è definita “Per cominciare”, rappresenta uno strumento per effettuare un bilancio iniziale delle conoscenze e delle abilità di ogni componente della classe. Attraverso l’osservazione, l’insegnante acquisisce una maggiore consapevolezza della situazione di partenza, raccoglie le evidenze emerse e registra i risultati in una tabella predisposta a una facile lettura, da allegare alla documentazione di classe.
L’insegnante può trovare la tabella predisposta all’interno delle risorse digitali.
PROGETTAZIONE
Terminata la fase dell’osservazione, l’insegnante elabora la propria progettazione tesa a maturare i traguardi per lo sviluppo delle competenze.
A partire dalle Indicazioni Nazionali e in coerenza con il curricolo d’Istituto, l’insegnante opera scelte sugli obiettivi di apprendimento operativi e sulla valutazione, tenendo conto del contesto classe.
La guida propone una progettazione per l’acquisizione del pensiero logico matematico attraverso il raggiungimento degli obiettivi di apprendimento in riferimento agli ambiti funzionali per l’attuazione dei nuclei tematici: numeri, spazio e figure, relazioni e funzioni, dati e previsioni. A supporto della progettazione didattica, inoltre, sono state sviluppate delle attività interattive che l’insegnante può ritrovare all’interno delle risorse digitali. Particolare attenzione è stata posta al valore dell’inclusione rispettando il principio della gradualità sia nella strutturazione dei contenuti che nella richiesta della prestazione.

VALUTAZIONE
La valutazione rappresenta uno strumento del corpo docente in cui si costruisce un dialogo tra insegnante e allievo/a finalizzato a sviluppare l’identità personale, le risorse e le potenzialità di ciascun alunno/a affinché possa esprimere, con sempre maggiore sicurezza, le proprie abilità, capacità e competenze traducendosi nel pieno successo formativo. Per raggiungere tale traguardo il team docente agisce cooperando con strumenti diversi e vari. I docenti operano quindi non solo per stimolare ed esprimere le potenzialità personali delle alunne e degli alunni, ma insegnano e offrono strategie e modalità per saperle perfezionare e trasformare in competenze agite anche attraverso l’esercizio, i laboratori, il recupero e l’orientamento. La valutazione, pertanto, assume una chiara connotazione formativa (valutazione “per l’apprendimento” e valutazione “come apprendimento”) in quanto consente di riprogettare l’azione didattica in maniera efficace, valorizzando i punti di forza emersi. La scelta degli obiettivi in chiave operativa, pertanto, può e deve essere rappresentativa del percorso di apprendimento degli studenti.
LE VERIFICHE IN ITINERE
L’impianto valutativo della Guida è coerente con le prescrizioni del curricolo ministeriale: accompagna e sostiene il docente nella progettazione didattica. In ogni percorso sono presenti delle verifiche, denominate “Ho imparato”, progettate secondo i criteri della gradualità e dell’inclusione sia nella presentazione degli argomenti da verificare sia andando incontro ai bisogni educativi di ogni bambino e bambina. In alcune verifiche è presente la “situazione non nota”, un quesito che ha lo scopo di attivare ulteriori processi cognitivi, fin a quel momento non messi in atto dagli alunni e dalle alunne.
GRIGLIE VALUTATIVE

L’elaborazione del giudizio periodico e finale richiede l’utilizzo di una pluralità di strumenti, differenziati in relazione agli obiettivi e alle situazioni di apprendimento, che consentono di acquisire, per ciascun obiettivo disciplinare, una varietà di informazioni funzionali alla formulazione del giudizio e a una riprogettazione efficace delle attività didattiche.
• una griglia relativa alle registrazioni delle evidenze emerse durante le verifiche in itinere (vedi l’esempio 1);
• una griglia, che raccoglie le evidenze rilevate in ogni fase dell’apprendimento di ciascun alunno/a, che orienta l’insegnante nella riprogettazione delle attività e può essere usata come sintesi ragionata per attribuire il livello ad ogni alunno/a nel documento di valutazione (vedi l’esempio 2);
• una griglia degli esiti per monitorare il livello degli apprendimenti degli alunni e delle alunne dell’intera classe (vedi l’esempio 3).
Di seguito si riportano gli esempi delle griglie che l’insegnante può trovare tra le risorse digitali. Nella griglia relativa alla registrazione delle evidenze (esempio 1) è presente la colonna dedicata al feedback, un’azione didattica orientata a promuovere e a garantire un apprendimento efficace. Il feedback non è una semplice correzione, un rinforzo o l’attribuzione di apprezzamenti, ma una risorsa che guida lo studente a compiere azioni per superare le difficoltà e raggiungere l’obiettivo.
LA GUIDA PROPONE:
Esempio 1 – Griglia per la verifica del percorso 1 unità 1
Verifica di MATEMATICA Data
Obiettivo di apprendimento: Contare entro il numero 99. Scritta
Aree osservabili
Nome
EvidenzeEvidenzeEvidenze
Scrivere in modi diversi lo stesso numero.
Contare progressivamente i numeri.
Individuare i numeri maggiore e minore. NOTA NON NOTA
Esempio 2 – Sintesi delle verifiche effettuate alla fine del secondo quadrimestre.
Nome: Classe:
OBIETTIVI DI APPRENDIMENTO
I NUMERI contare fino a 999.
I NUMERI
Eseguire addizioni sulla linea dei numeri, in tabella e con tre addendi.
I NUMERI eseguire sottrazioni con rappresentazione grafica, in colonna con cambio e senza cambio.
SPAZIO E FIGURE riconoscere le figure solide, piane e i tipi di linee.
RELAZIONI, DATI E PREVISIONI
stabilire i criteri di classificazione; mettere in relazione due o più elementi.
Disciplina: MATEMATICA
Aree osservabili
Esempio 3 – Griglia degli esiti conseguiti dalla classe alla fine del primo quadrimestre.
DISCIPLINA: MATEMATICA
OBIETTIVO DI APPRENDIMENTO 1
NOME
OBIETTIVO DI APPRENDIMENTO 2
OBIETTIVO DI APPRENDIMENTO 3
OBIETTIVO DI APPRENDIMENTO 4
* La recente O.M. n°3 del 09/01/2025 individua delle aree osservabili dai docenti per orientare il percorso di apprendimento di alunne ed alunni e per determinare il giudizio sintetico da apporre nel documento di valutazione. La Guida Pratica Raffaello recepisce le recenti indicazioni e presenta una varietà di griglie per registrare le evidenze emerse dall’osservazione in maniera semplice ed efficace. Le griglie sono uno strumento essenziale per monitorare l’apprendimento degli alunni in modo oggettivo e strutturato, consentono di raccogliere dati concreti sul continuo progresso, individuando punti di forza e aree di miglioramento. Sono, inoltre, funzionali a un continuo adattamento della didattica ai bisogni di ciascuno, favorendo un percorso di apprendimento inclusivo.

AUTOVALUTAZIONE
Nel rapporto insegnamento-apprendimento, la valutazione si pone come uno strumento capace di portare al centro della didattica ogni bambino e bambina nell’ottica del miglioramento continuo. In questa prospettiva assume un ruolo privilegiato l’autovalutazione, intesa come un momento in cui ogni studente e ogni studentessa sviluppa un approccio riflessivo sul proprio modo di apprendere e una consapevolezza delle proprie capacità e dei propri limiti, così come delineato nelle Indicazioni Nazionali del 2012 e nel profilo delle competenze al termine del primo ciclo. Con l’autovalutazione, gli alunni e le alunne monitorano le fasi dei processi che mettono in atto durante l’apprendimento. Pertanto, l’insegnante può usare il modello fornito dalla Guida per effettuare l’autovalutazione, un questionario composto da semplici domande che consente allo studente di fare un’analisi sulla comprensione della consegna, sulla scansione temporale e sulla valutazione del risultato. Il modello proposto nasce dalla consapevolezza che l’autovalutazione debba iniziare fin dalla classe prima, pertanto, si presenta con una struttura semplice e ricorre a una rappresentazione grafica che esprime la percezione che ogni bambino e ogni bambina può avere del proprio processo di apprendimento. La metafora del seme che diventa un fiore (vedi figura 1) rappresenta in maniera chiara e immediata il processo di crescita degli apprendimenti. L’insegnante avrà cura di condividere con gli alunni e le alunne gli obiettivi, i traguardi attesi, i processi coinvolti e di esplicitare bene il significato della rappresentazione grafica in uso. Il modello per l’autovalutazione è fruibile nelle risorse digitali.

◀ figura 1
AUTOVALUTAZIONE per la verifica di MATEMATICA
Esempio di un obiettivo di apprendimento: risolvere una situazione problematica.
HO COMPRESO LA CONSEGNA DEL COMPITO?
COLORA IL DISEGNO CHE TI RAPPRESENTA
HO LAVORATO CON IMPEGNO?

HO SVOLTO IL COMPITO IN TUTTE LE SUE PARTI?
HO RISPETTATO IL TEMPO?


VALUTAZIONE DELLE COMPETENZE
PROVA STILE INVALSI
Gli alunni e le alunne delle classi seconde sono chiamati nel mese di Maggio a sostenere la prova standardizzata INVALSI. Nell’ottica di costruire un atteggiamento positivo verso la matematica attraverso esperienze significative, che permettano di far comprendere come gli strumenti matematici appresi siano utili per interpretare la realtà che ci circonda, la Guida propone una prova stile INVALSI composta da venti quesiti. Questa è finalizzata alla valutazione “delle competenze matematiche secondo tre dimensioni denominate Risolvere problemi, Argomentare e Conoscere all’interno di tre ambiti di contenuto: relazioni, dati e previsioni, spazio e figure e numeri” come riportato dal Quadro di riferimento delle Prove INVALSI.
IL COMPITO AUTENTICO
Uno strumento completo per la rilevazione degli apprendimenti è il compito autentico; una prestazione assegnata per fare in modo che gli alunni e le alunne utilizzino in modo attivo e consapevole abilità, saperi acquisiti e la creatività per affrontare e trovare soluzioni pertinenti in una situazione di vita reale. Questi costituisce la situazione non nota per eccellenza, in quanto consente di manifestare diverse operazioni come evidenze degli articolati processi cognitivi. Il compito autentico è prezioso perché mette in luce il “come” si apprende e rivela tutta quella serie di attività sommerse che altrimenti non verrebbero fuori: l’impegno, la motivazione, la sensibilità al contesto, le strategie metacognitive, la reazione alla risposta, la pianificazione, la
gestione del tempo. Tutte abilità e atteggiamenti funzionali all’ambito traguardo per lo sviluppo delle competenze. Le attività proposte come compito possono essere diverse: orali, scritte, visive. In ognuna di queste, bisogna soddisfare dei requisiti, gli alunni devono interpretare un ruolo credibile che abbia un significato per loro; devono essere indicati dei destinatari anche questi verosimili, è necessario creare una situazione che richieda un’applicazione al mondo reale e un prodotto da eseguire.
All’interno della Guida vengono fornite due prove di competenza, consigliate alla fine di ogni quadrimestre, che consentono di osservare il livello di autonomia, le abilità e gli atteggiamenti con i quali gli alunni e le alunne sono chiamati a lavorare in gruppo o individualmente. Le due prove a conclusione del primo e del secondo quadrimestre proposte guida consistono nella realizzazione di giochi matematici.
L’insegnante per procedere a una valutazione del compito può contemplare l’uso delle griglie di osservazione integrate dalle rubriche valutative fornite dalla Guida in formato digitale ed editabile (vedi griglia per la verifica).
Di seguito viene riportata la rubrica valutativa del compito autentico di fine primo quadrimestre. L’insegnante troverà la versione editabile della rubrica tra le risorse digitali.
RUBRICA DI PRESTAZIONE COMPITO AUTENTICO FINE PRIMO QUADRIMESTRE
Organizzazione complessiva delle fasi del lavoro
Uso corretto del materiale a disposizione
Eseguire addizioni e sottrazioni entro il 50.
Affronta il compito solo se guidato dal compagno o dall’insegnante.
L’utilizzo del materiale a disposizione deve essere sempre guidato e organizzato dall’insegnante.
Esegue le operazioni solo se guidato dal compagno o dall’insegnante. Non ha ancora consolidato le procedure del calcolo.
Rispetto dei tempi di esecuzione
I tempi di esecuzione sono rispettati solo se è affiancato dall’insegnante.
Partecipazione con spirito d’iniziativa
Partecipa solo se guidato dall’insegnante.
Organizza le fasi del compito richiedendo talvolta il supporto dell’insegnante.
L’utilizzo del materiale a disposizione deve essere orientato dall’insegnante.
Esegue le operazioni talvolta con il supporto dell’insegnante. Non è ancora sicuro nelle procedure del calcolo.
I tempi di esecuzione sono rispettati solo se è sollecitato dall’insegnante.
Partecipa ma necessita di stimoli per essere coinvolto nell’attività.
Organizza le fasi del compito in modo autonomo ma non sempre corretto e funzionale alla richiesta.
L’utilizzo del materiale è corretto.
Organizza le fasi del compito in modo autonomo, personale e funzionale alla richiesta.
L’uso materiale è corretto e funzionale alla richiesta del compito.
Esegue le operazioni in modo autonomo. Si dimostra sicuro nelle procedure del calcolo.
Esegue correttamente le operazioni e applica le strategie di calcolo mentale.
In autonomia rispetta parzialmente i tempi di esecuzione.
Partecipa ma non sempre con spirito di iniziativa.
Rispetta ampiamente i tempi di esecuzione.
Partecipa attivamente, apportando i propri contributi personali.
Nome Cognome Classe Data
È IL TUO MOMENTO...
Per la manifestazione ricreativa ed educativa rivolta ai bambini, Il Borgo Dei Ragazzi, la scuola chiede alle classi seconde di realizzare il gioco Memory Matematico da usare in occasione dell’evento.

L’attività prende spunto dal gioco da tavolo Memory. Lo scopo del Memory Matematico è trovare coppie di carte che rappresentano lo stesso valore numerico.
I bambini associano un numero naturale a un’operazione di addizione o di sottrazione che abbia lo stesso valore numerico.
Nome Cognome Classe Data
La classe viene divisa in 4 o 5 gruppi. Ogni gruppo
1 Avrà a disposizione cartoncini e materiale per ritagliare, scrivere e decorare.
2 Dovrà scegliere 4 o 5 numeri, compresi tra il 10 e il 50, e scegliere l’operazione di addizione o di sottrazione con lo stesso valore numerico
IL COMPITO È COSTITUITO DA:
Realizzare un gioco didattico
Matematica, arte, tecnologia DELLE DISCIPLINE
Gruppi di alunni e alunne DELLE MODALITÀ
TEMPO PREVISTO PER LA REALIZZAZIONE DEL COMPITO:
• ½ ora in cui l’insegnante in circle time spiega che cosa fare, come bisogna realizzare le coppie di tessere e suddivide la classe in 4 o 5 gruppi;
• 2 ore per realizzare le coppie di tessere e decorarle.
METODOLOGIA:

• circle time
• brainstorming
• Cartoncino;
• pennarelli e matite;
• cooperative learning
• riflessione metacognitiva
STRUMENTI:
• forbici.
COMPETENZE CHIAVE DI RIFERIMENTO:
• Competenza matematica
• Personale, sociale, e capacità di imparare a imparare
• Competenza in materia di cittadinanza
VALUTAZIONE FORMATIVA:
Durante la prestazione del compito autentico, l’insegnante può osservare le evidenze del processo di apprendimento e può registrarle con le griglie in dotazione alla guida.
Le evidenze del processo di apprendimento sono:
• ascoltare le indicazioni dei docenti;
• decodificare la richiesta del compito;
• interagire con i compagni e le compagne per sviluppare un progetto di lavoro;
• eseguire operazioni numeriche entro il 50, usando le addizioni e le sottrazioni;
• verificare la coerenza tra la richiesta del docente e il prodotto da realizzare;
• portare a termine il lavoro.
AUTOVALUTAZIONE:
Compilare il questionario in allegato alla Guida.
Nome Cognome Classe Data
È IL TUO MOMENTO...
La scuola, a fine anno, organizza i Giochi Senza Frontiere della Matematica. Ogni classe progetta e realizza un gioco da proporre ai concorrenti dei Giochi Senza Frontiere. Gli alunni e le alunne della classe seconda si occuperanno di creare il gioco “Apri il Lucchetto”.

I partecipanti del gioco “Apri il Lucchetto” devono riuscire ad aprire il maggior numero di lucchetti entro un tempo stabilito. Per aprire i lucchetti numerati è necessario trovare la chiave con l’etichetta che riporta l’operazione il cui risultato è corrispondente al numero indicato sul lucchetto.
Fine 2° quadrimestre
COMPITO
Nome Cognome Classe Data
La classe viene divisa in 4 o 5 gruppi. Ogni gruppo
1 avrà a disposizione lucchetti, chiavi e portachiavi con etichetta, materiale per scrivere;
2 dovrà scegliere 4 o 5 numeri da scrivere sui lucchetti, compresi tra il 10 e il 100, e scegliere l’operazione di addizione, o di sottrazione, o di divisione, o di moltiplicazione, da riportare sull’etichetta della chiave. Il risultato dell’operazione deve corrispondere al numero scritto sul lucchetto.
IL COMPITO È COSTITUITO DA:
Realizzare un gioco
DEI DESTINATARI
I partecipanti dei Giochi Senza Frontiere della Matematica
DELLE DISCIPLINE IN PICCOLI GRUPPI DELLE MODALITÀ
MATEMATICA, TECNOLOGIA, EDUCAZIONE CIVICA

TEMPO PREVISTO PER LA REALIZZAZIONE DEL COMPITO:
• ½ ora in cui l’insegnante in circle time spiega che cosa fare per realizzare il gioco e suddivide la classe in 4 o 5 gruppi;
• 2 ore per scegliere le operazioni, per riportarle sulle etichette dei portachiavi e per scrivere i risultati sui lucchetti.
METODOLOGIA:
• circle time
• brainstorming
• cooperative learning
• riflessione metacognitiva
COMPETENZE CHIAVE DI RIFERIMENTO:
• Competenza matematica
• Personale, sociale, e capacità di imparare a imparare
• Competenza in materia di cittadinanza
VALUTAZIONE:
Durante la prestazione del compito autentico, l’insegnante può osservare le evidenze del processo di apprendimento e può registrarle con le griglie in dotazione alla guida.
Le evidenze del processo di apprendimento sono:
• decodificare in maniera appropriata la richiesta del compito;
• interagire con i compagni e le compagne per sviluppare un progetto di lavoro efficace;
• eseguire le quattro operazioni entro il 100;
• verificare la coerenza tra la richiesta del docente e il prodotto da realizzare;
• portare a termine il lavoro.
Questionario in allegato alla Guida
AUTOVALUTAZIONE:

Progettazione didattica
Obiettivi di apprendimento
Contare entro il 20.
Raggruppare per 10.
PER COMINCIARE
Contenuto Guida
Conteggio e associazione di una quantità 26
Raggruppamenti per identificare le decine e le unità 27
Ordinare e confrontare i numeri entro il 20. Ordine crescente e decrescente 28
Eseguire addizioni entro il 20. Le addizioni 29
Eseguire le sottrazioni entro il 20. Le sottrazioni 30
Misura e confrontare più elementi.
Riconoscere le linee;
Riconoscere le figure geometriche piane; Eseguire e descrivere percorsi sul piano quadrettato.
Saper classificare e mettere in relazione; Interpretare un grafico e raccogliere i dati.
Confronto fra grandezze 31
Le linee
Le figure piane I percorsi sul piano quadrettato 32
Le classificazioni e le relazioni
Dalla rappresentazione grafica ai dati 33
NUCLEO TEMATICO: NUMERI
Traguardi per le competenze Obiettivo di apprendimento Contenuto Guida
Contare entro il numero 30.
Contare e scrivere i numeri entro il 40.
Costruisce semplici ragionamenti formulando ipotesi, sostenendo le proprie idee e confrontandosi con il punto di vista di altri.
Contare e comporre i numeri entro il 40.
Contare e scrivere i numeri entro il 50.
Raggruppamenti di decine e di unità per identificare il numero.
Corrispondenza tra i diversi modi di scrivere un numero.
Numero precedente e successivo. Conteggio progressivo dei numeri.
Rappresentazione numerica sull’abaco. Scrittura dei numeri in lettere.
Contare entro il numero 50.Confronto e ordinamento.
38
39
40
Contare entro il numero 60.Conteggio progressivo dei numeri. 41
Contare e conoscere la successione numerica entro il 60.
Riconosce ed utilizza rappresentazioni diverse di oggetti matematici (numeri naturali e retta dei numeri...).
Contare entro il numero 70.
Contare entro il numero 70. Conoscere i numeri pari e dispari
Contare e scomporre entro l’80.
Contare entro il numero 80.
Conteggio progressivo dei numeri. Numero precedente e successivo. Calcolo ragionato. Ordine crescente e decrescente.
Rappresentazione numerica sull’abaco. Scrittura dei numeri in lettere.
Confronto numerico. Catene numeriche I numeri pari e dispari
Raggruppamenti di decine e di unità per identificare il numero.
Scomposizione numerica.
Rappresentazione numerica sull’abaco. Ordine crescente e decrescente.
42
43
44
45
46
Sviluppa un atteggiamento positivo rispetto alla matematica, attraverso esperienze significative, che gli hanno fatto intuire come gli strumenti matematici che ha imparato ad utilizzare siano utili per operare nella realtà.
Si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali.
Contare entro il numero 90.
Contare entro il numero 99.
Raggruppamenti di decine e di unità per identificare il numero.
Composizione del numero 90.
Conteggio progressivo dei numeri.
Rappresentazione numerica sull’abaco.
Scrittura dei numeri in lettere.
Scomposizione numerica.
Corrispondenza tra i diversi modi di scrivere un numero.
Conteggio progressivo dei numeri.
Acquisire il concetto di centinaio. Il cambio
Acquisire e operare con il concetto di centinaio.
Acquisire e operare con il centinaio.
Conoscere i numeri entro il 300. Comporre e scomporre il numero.
Conoscere e confrontare i numeri entro il 300.
Conoscere e confrontare i numeri entro il 600.
Conoscere e confrontare i numeri entro il 700.
Conoscere e confrontare i numeri entro il 999.
Comporre, scomporre e ordinare i numeri entro il 999.
Scomporre e confrontare i numeri entro il 999.
Conoscere e confrontare i numeri entro il 999.
Comprendere il concetto di addizione con il supporto della rappresentazione.
Eseguire addizioni sulla linea dei numeri.
Raggruppamenti di decine e per identificare il centinaio.
Scomposizione
Conteggio progressivo dei numeri. Composizione, scomposizione e ordinamento
Confronto numerico.
Rappresentazione numerica sull’abaco.
Confronto numerico.
Ordinamento.
Scomposizione e composizione numerica.
Confronto numerico.
Corrispondenza tra i diversi modi di scrivere un numero.
Ordinamento.
Numeri precedenti e successivi. Composizione e scomposizione.
Corrispondenza tra i diversi modi di scrivere un numero. Conteggio progressivo per decine.
Conteggio progressivo dei numeri.
Confronto numerico.
Rappresentazione grafica dell’addizione.
Addizioni sulla linea dei numeri.
Eseguire addizioni in sequenza. Addizioni in sequenza
Applicare strategie di calcolo.
Eseguire addizioni a mente.
Calcolo ragionato.
47
48
49
50
54
55
56
57
58
59
60
61
62
63
64
68
69
70
71-7273
74
Eseguire addizioni in tabella. Addizioni in tabella. 75
Eseguire addizioni con l’abaco. Addizioni con l’abaco.
Eseguire addizioni in colonna. Addizioni in colonna.
76
77
Eseguire addizioni in colonna con il cambio. Addizioni in colonna con il cambio. 78
Eseguire addizioni in colonna con la prova. Addizioni in colonna con la prova.
Eseguire addizioni con le centinaia. Addizioni con le centinaia.
79
80
Eseguire addizioni con tre addendi. Addizioni con tre addendi. 81
Comprendere e risolvere problemi con l’addizione. Problemi. 82
Operare con la sottrazione in situazioni rappresentate graficamente.
Eseguire sottrazioni sulla linea dei numeri
Eseguire sottrazioni con l’ausilio della rappresentazione grafica.
Eseguire calcoli a mente.
Rappresentazione grafica della sottrazione 86
Sottrazioni sulla linea 87
Sottrazioni con materiale strutturato88
Calcolo ragionato
Eseguire sottrazioni in tabella. il “quanto manca”
Eseguire calcoli a mente. Calcolo ragionato
89
90
91
Completare sequenze di numeri. Sottrazioni in sequenza. 92
Eseguire sottrazioni con rappresentazione grafica.
Sottrazioni con l’abaco.
Eseguire sottrazioni in colonna senza cambio. Sottrazioni in colonna.
93
94
Eseguire sottrazioni in colonna con il cambio. Sottrazioni in colonna con il cambio.95-96
Eseguire sottrazioni in colonna con la prova. Sottrazioni in colonna con la prova.
Discriminare e operare con addizione e sottrazione.
97
Operazioni inverse. 98
Operare con la sottrazione in tabella. Sottrazioni in tabella
Eseguire la sottrazione con le centinaia. Sottrazioni con le centinaia.
Comprendere e risolvere problemi con la sottrazione. Problemi.
Operare con l’addizione ripetuta.
Rappresentazione grafica dell’addizione ripetuta.
Riconoscere la moltiplicazione come cardinalità̀ del prodotto cartesiano. Le combinazioni.
Eseguire moltiplicazioni sulla linea dei numeri. Le moltiplicazioni sulla linea.
Riconoscere e utilizzare la moltiplicazione come schieramento.
Gli schieramenti.
Riconoscere la moltiplicazione come schieramento e simbolizzazione dell’operazione. Gli incroci.
Conoscere la tabellina del 2-3-4-5-6-7-8-9-10Le tabelline.
99
100
101
105
106
107
108
109
110-112-115-117119-121-123-125 -127
Traguardi per le competenze
Riconosce, rappresenta forme del piano e dello spazio, relazioni e strutture che si trovano in natura o che sono state create dall’uomo.
Descrive, denomina e classifica figure in base a caratteristiche geometriche.
Conoscere ed utilizzare la tabellina del 2-3-4-56-7-8-9-10
Gioco delle tabelline.
111-113-116118-120-122124-126-128
Comprendere e utilizzare il concetto di doppio e triplo. Il doppio e il triplo. 114
Moltiplicare in colonna.
Moltiplicazioni in colonna. 129
Moltiplicare in colonna con il cambio. Moltiplicazioni con il cambio. 130
Moltiplicare in colonna con le centinaia. Moltiplicazioni con le centinaia.131
Operare con la divisione in situazioni rappresentate graficamente.
Operare con la divisione in situazioni rappresentate graficamente.
Eseguire divisioni in riga senza resto.
Risolvere problemi con divisioni in riga senza resto.
Rappresentazione grafica della divisione. 135
Diversi modi per dividere: distribuzione; raggruppamento.
Gli schieramenti e gli incroci. Divisioni sulla linea.
con le dita.
Eseguire divisioni in riga con il resto. Divisioni con il resto.
Risolvere problemi eseguendo divisioni in riga con il resto.
Riconoscere i numeri pari e i numeri dispari. Pari e dispari.
Comprendere e applicare il concetto di doppio e metà.
Comprendere e applicare il concetto di triplo e di terzo, di quadruplo e quarto. Il triplo, il terzo, il quadruplo e il quarto.
Riconoscere e utilizzare la moltiplicazione la divisione come operazioni inverse. 16
Leggere, comprendere e risolvere problemi con la divisione e con la moltiplicazione.
Operare
Obiettivo di apprendimento
Riconoscere le linee in base alle loro caratteristiche principali. Le linee. La classificazione delle linee. 211-212
Individuare forme geometriche solide nell’ambiente quotidiano. I solidi nella realtà.
213
Riconoscere le caratteristiche delle forme geometriche solide. I solidi e le loro caratteristiche.214-216-218-220
Riconoscere le caratteristiche delle forme geometriche piane.
Dai solidi alle figure piane.215-217-219-221
Riconoscere e rappresentare forme del piano e dello spazio. Le costruzioni
222
Costruire figure simmetriche. La simmetria. 223-224
Contenuto Guida Pagina
Traguardi per le competenze
NUCLEO TEMATICO: DATI E PREVISIONI
Obiettivo di apprendimento
Contenuto Guida Pagina
Misurare lunghezze con unità arbitrarie. I campioni di misura.
159
Misurare lunghezze con l’unità convenzionale. L’unità di misura della lunghezza.160
Risolvere semplici situazioni problematiche con le misure.
Misurare le lunghezze.
Misurare la massa con unità arbitrarie. La bilancia.
Misurare la massa con l’unità convenzionale. L’unità di misura della massa.
Risolvere semplici situazioni problematiche con le misure.
Confronto tra pesi.
Misurare la capacità con unità arbitrarie. La capacità.
161
162
163
164
165
Misurare la capacità con l’unità convenzionale. L’unità di misura della capacità.166
Risolvere semplici situazioni problematiche con le misure.
Ricerca dati per ricavare informazioni e costruisce rappresentazioni (tabelle e grafici). Ricava informazioni anche da dati rappresentati in tabelle e grafici.
Riesce a risolvere facili problemi in tutti gli ambiti di contenuto.
Misurare la capacità.
Confrontare misure con unità arbitrarie. Gli oggetti e le misure.
Conoscere strumenti di misura convenzionali.
Misurare intervalli di tempo con strumenti convenzionali.
Ore e minuti.
Conoscere i giorni della settimana. La settimana.
Conoscere il calendario. Il calendario.
Conoscere i mesi dell’anno. I mesi dell’anno.
Risolvere situazioni problematiche relative al tempo. Problemi.
Conoscere il valore di monete e banconote. Monete e banconote.
167
168
170
171-172173-174
175
176
177
178-179
183
Comporre il valore delle monete. Forma le monete. 184
Comporre il valore delle banconote. 185
Risolvere situazioni problematiche con l’uso del denaro. Fare spesa. Il resto. 186-187-188189-190-191
Individuare le coordinate all’interno di un reticolo. Orientamento con le coordinate.195-196
Individuare le coordinate all’interno di un reticolo a incroci Individuazione delle coordinate.197-198
Eseguire e descrivere percorsi sul piano quadrettato. I percorsi numerati. 199-200
Riconoscere e descrivere il percorso in un piano quadrettato nel rispetto delle caratteristiche date. Descrizione del percorso. 201-202
Seguire le indicazioni delle frecce numerate in un reticolo. Il disegno nascosto. 203-204
Leggere e rappresentare il codice di un’immagine in pixel. Pixel Art 205-206
Riconoscere gli oggetti dai vari punti di vista. Il punto di vista. 207
Classificare elementi in base a una proprietà̀. Gli insiemi. Appartiene o non appartiene. 228-229-230
Riconoscere il criterio di classificazione. Il criterio di classificazione. 231
Legge e comprende i testi che coinvolgono aspetti logici e matematici.
Classificare elementi utilizzando la rappresentazione ad intersezione.
Classificare elementi utilizzando la rappresentazione per sottoinsiemi.
L’intersezione.
I sottoinsiemi.
Comprendere il significato dei quantificatori. I quantificatori.
Stabilire relazioni tra due elementi. Le relazioni.
Discriminare una situazione reale problematica da una non problematica.
Individuare le soluzioni per le situazioni problematiche reali.
Riconosce e quantifica in casi semplici le situazioni di incertezza.
Individuazione di una situazione problematica reale.
Risoluzione di una situazione problematica reale.
Riflettere sul problema matematico. Il problema matematico.
Individuare la domanda pertinente alla situazione problematica. La domanda del problema. 244
Analizzare una situazione problematica per trovare la soluzione.
Risolvere i problemi con l’utilizzo di rappresentazioni schematiche.
Risolvere i problemi con l’utilizzo di tabelle.
Risolvere i problemi con l’utilizzo di immagini.
Risolvere situazioni problematiche.
Individuare l’operazione corretta per risolvere il problema.
Leggere e interpretare i dati.
La soluzione del problema. L’informazione nascosta.
L’informazione mancante.
Le diverse rappresentazioni schematiche per risolvere un problema.
Dall’immagine al problema
I problemi con le quattro operazioni.
Dalla tabella al grafico.
Leggere ed interpretare un istogramma. Dall’istogramma alla tabella.
261
Leggere ed interpretare un ideogramma. Dall’ideogramma all’istogramma. 263
Ricavare le informazioni per realizzare un istogramma.
La realizzazione di un istogramma. 267
Comprendere il significato di certo, probabile, impossibile. Certo, probabile, impossibile.
Riconoscere la probabilità di un evento.
Rappresentare delle situazioni che corrispondono a specifiche probabilità. Le probabilità
NUCLEO TEMATICO: EDUCAZIONE CIVICA
268
269
270
Traguardi per le competenze Obiettivo di apprendimento Contenuto Guida Pagina
Conoscere gli articoli 2,3 e 9 della Costituzione. Gli articoli 2,3 e 9 della Costituzione.273
Conoscere l'Agenda 2030. Agenda 2030.
Conoscere i 17 Goals per lo sviluppo sostenibile. Gli obiettivi dell’agenda 2030.
Conoscere i valori della cittadinanza digitale. Le relazioni.
I valori della cittadinanza globale.
274
275
276 - 277
Prerequisiti Percorso 0
La Guida propone un percorso iniziale volto a consolidare le competenze matematiche fondamentali per gli studenti della classe seconda. Il volume è organizzato in sezioni, ognuna dedicata a specifiche competenze.
Scheda 1: Conteggio e rappresentazione visiva
Sono presenti esercizi per contare e rappresentare graficamente quantità entro il numero 20.
Scheda 2: Raggruppamento e uso dell’abaco
Gli studenti imparano a raggruppare per dieci e a registrare i numeri. L’utilizzo dell’Abaco graduato favorisce il consolidamento di una rappresentazione mentale chiara delle quantità, migliorando la loro capacità di associare quantità concrete a simboli numerici. Questa modalità supporta anche il passaggio dal conteggio all’elaborazione dei numeri in termini di decine e unità.
Scheda 3: Ordinamento dei numeri

Attività per ordinare i numeri in modo crescente e decrescente, utile anche per consolidare il valore posizionale delle cifre.
Schede 4 e 5: Addizioni e sottrazioni
Attività costituite da schede operative che rendono l’apprendimento visivo e pratico, coinvolgendo i bambini attraverso disegni e situazioni della vita quotidiana come ombrelloni, oggetti di spiaggia, dolci, ecc. Questa impostazione facilita il coinvolgimento degli studenti e favorisce un apprendimento contestualizzato. Sono presenti calcoli sulla linea dei numeri, addizioni e sottrazioni entro il 20.
Scheda 6: Misurazioni e confronti
Esercizi per ordinare elementi in base a lunghezza, altezza e peso.
Scheda 7: Riconoscimento di figure geometriche
Esercizi per migliorare la distinzione visiva e concettuale tra linee aperte e chiuse, promuovere la conoscenza delle figure geometriche piane e rafforzare la capacità di seguire istruzioni e movimenti pianificati su un tracciato quadrettato.
Scheda 8: Classificazione e interpretazione di grafici
Esercizi che mirano a sviluppare nei bambini la capacità di organizzare dati, riconoscere relazioni e interpretare rappresentazioni visive.
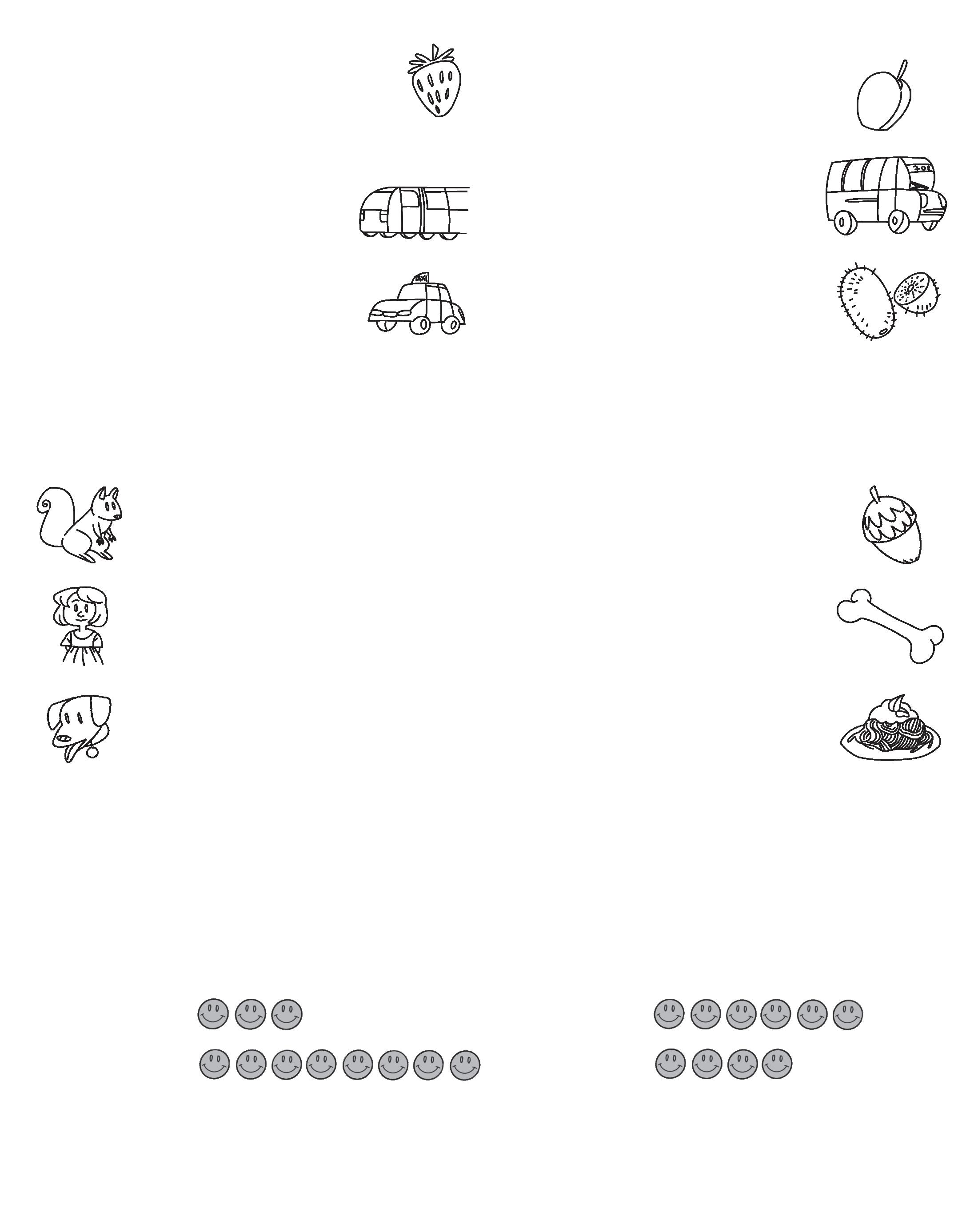
Classificazione: gli alunni devono inserire elementi negli insiemi di appartenenza, rafforzando la capacità di categorizzare oggetti o concetti secondo criteri dati.
Relazioni: un esercizio prevede di collegare elementi secondo le indicazioni date da frecce, per evidenziare le relazioni logiche o funzionali tra di essi. Questo supporta lo sviluppo del pensiero logico e la comprensione dei legami tra concetti.
Grafici: i bambini osservano un grafico che mostra le preferenze degli alunni e delle alunne per gli animali domestici (coniglio, gatto, cane, criceto).
1 CONTA E REGISTRA IN TABELLA.

2 DISEGNA TANTE PALLINE QUANTE SONO INDICATE NEL CARTELLINO.
3 COMPLETA CON I NUMERI MANCANTI. 14 18
RAGGRUPPA
1 CERCHIA 10 ELEMENTI, E CONTA. REGISTRA SULL’ABACO E SCRIVI IL NUMERO IN LETTERE. da u .................................. da u


In spiaggia ci sono 8 ombrelloni e 6 sdraio. Quanti elementi sono in tutto?
CONFRONTA
1 ORDINA DALLA PIÙ CORTA ALLA PIÙ LUNGA. USA I NUMERI DA 1 A 5.
2 ORDINA DAL PIÙ BASSO AL PIÙ ALTO. USA I NUMERI DA 1 A 5.
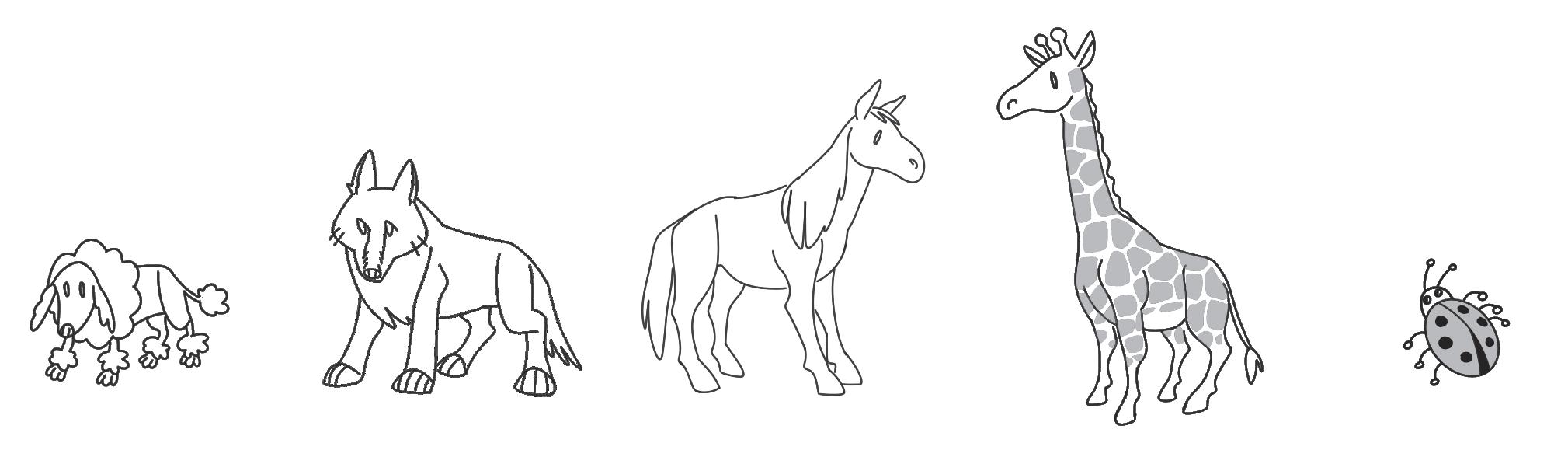
2 ORDINA DAL PIÙ LEGGERO AL PIÙ PESANTE. USA I NUMERI DA 1 A 5.
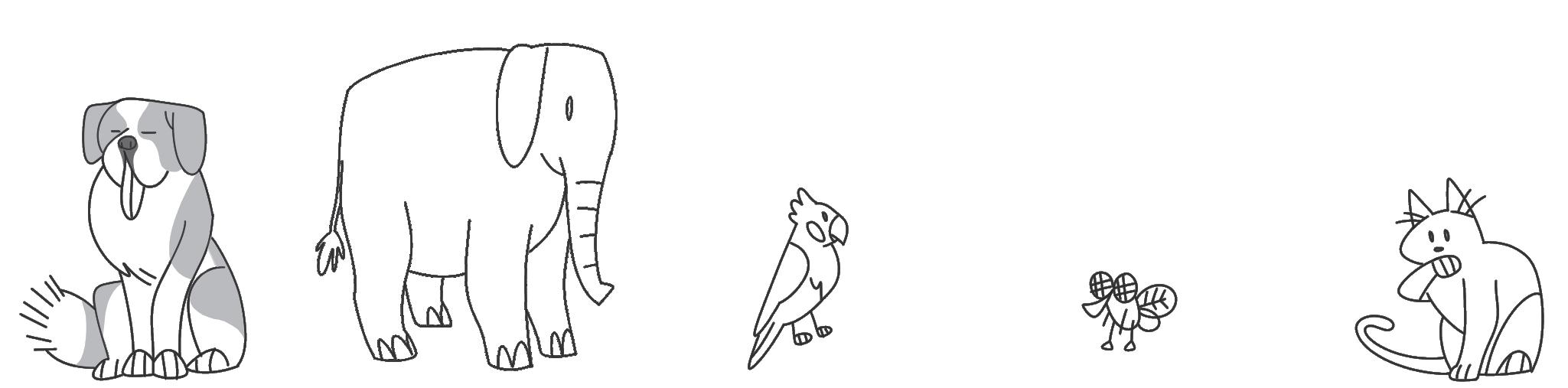
ODA: misurare e confrontare più elementi.
PERCORSI E FIGURE
1 RIPASSA DI ROSSO LE LINEE APERTE, DI BLU LE LINEE CHIUSE.
2 COLORA IL CONIGLIO RUFUS E IL TRENINO. SEGUI LE INDICAZIONI.
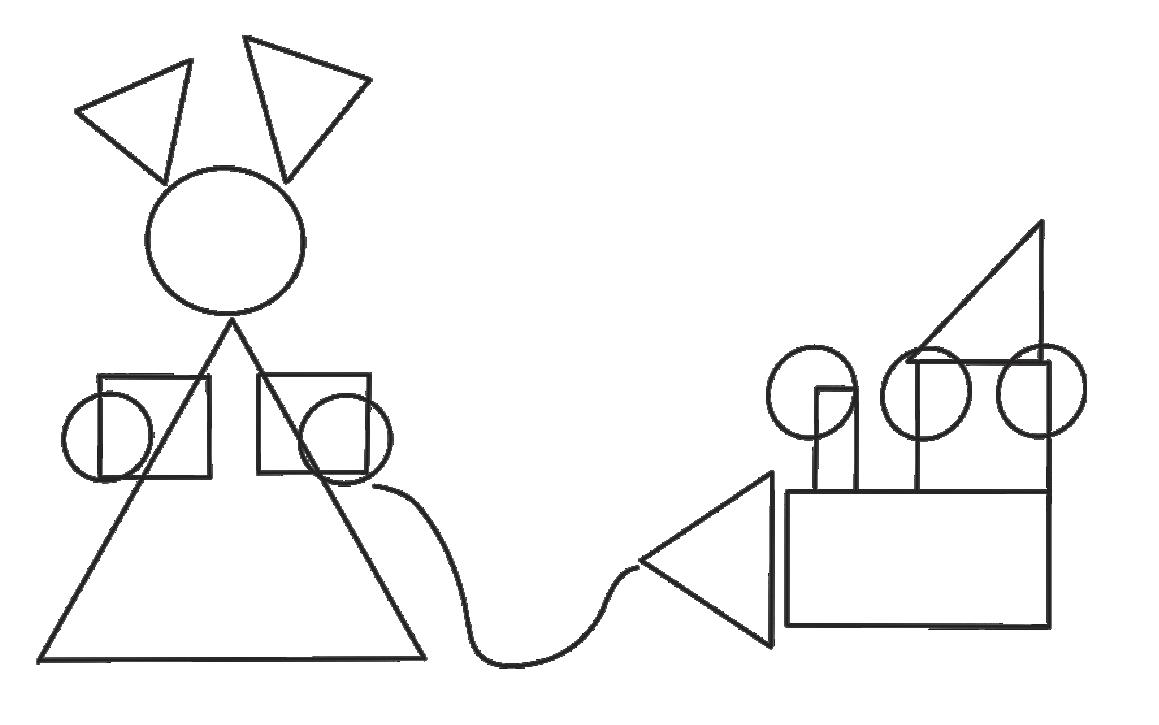
3 AIUTA RUFUS A RAGGIUNGERE IL SUO TRENINO USA . POI COMPLETA.

1 passo Rufus ha fatto ............................ passi.
ODA: riconoscere le linee. Riconoscere le figure geometriche piane. Eseguire e descrivere percorsi sul piano quadrettato.
CLASSIFICAZIONE, RELAZIONI, GRAFICI
1 COLLEGA GLI ELEMENTI AGLI INSIEMI DI APPARTENENZA.
Percorso 1
UNITÀ 1
I numeri fino a 99
Il Percorso 1 è progettato per sviluppare la comprensione numerica nei bambini della classe seconda, concentrandosi sulla capacità di operare con numeri fino a 99. Si focalizza sul conteggio, la scrittura dei numeri, la loro composizione e scomposizione in decine e unità, e sulla capacità di confronto e ordinamento.
Ogni scheda offre attività interattive e pratiche che incoraggiano e stimolano il coinvolgimento diretto degli alunni, rendendo l’apprendimento dei numeri dinamico, visivo e partecipato. I materiali scelti per la rappresentazione dei numeri: bastoncini, abaco graduato, pop it, supportano il subitizing, cioè la capacità di distinguere in modo rapido ma accurato la quantità di un ridotto numero di elementi.
Schede 1 e 2: I Numeri da 20 a 30
Attività in cui i bambini possono contare e registrare i numeri, scrivendoli in cifre e lettere con l’obiettivo di introdurre i numeri oltre il 20, consolidando l’uso di decine e unità. Unione di puntini numerati fino a 30 e scomposizione dei numeri in decine e unità con il focus su conteggio visivo e comprensione della scomposizione numerica.
Schede 3 e 4: I Numeri da 30 a 40
Schede operative in cui gli alunni possono contare e scrivere numeri, riconoscendo le unità e le decine con l’obiettivo di introduzione dei numeri fino a 40, con esercizi che aiutano a padroneggiare la loro composizione. Ordinamento dei numeri in sequenza crescente e decrescente e completamento di serie numeriche con l’intento di sviluppare abilità di ordinamento e riconoscimento delle successioni numeriche.
Schede 5 e 6: I Numeri da 40 a 50
Attività in cui gli studenti possono utilizzare l’abaco per rappresentare e scrivere i numeri, identificando decine e unità con l’obiettivo di rinforzare la comprensione dei numeri fino a 50. Utilizzo dei segni >, < e = per confrontare i numeri e ordinamento in sequenze diverse al fine di sviluppare abilità di confronto numerico, migliorando la comprensione delle relazioni tra i numeri.
Schede 7 e 8: I Numeri da 50 a 60
Schede operative in cui gli studenti possono ampliare la padronanza numerica fino a 60, consolidando il concetto di decine e unità. Esercizi di completamento dei numeri in sequenze.

Schede 9 e 10: I Numeri da 60 a 70 Esercizi di conteggio dei numeri entro 70, rappresentando i numeri sull’abaco con l’obiettivo di consolidare la comprensione dei numeri fino a 70 e il riconoscimento delle unità e decine. Esercizi per sviluppare abilità di ordinamento.
Schede 11-16: Numeri da 70 a 99 Serie di attività in cui gli alunni lavorano con i numeri rappresentandoli sull’abaco e completando esercizi di confronto, composizione e scomposizione con l’obiettivo di arrivare alla soglia dei 100 con una solida comprensione del valore posizionale delle cifre.
I NUMERI DA 20 A 30
SEGUI L’ESEMPIO.
I NUMERI FINO A 30
I NUMERI DA 30 A 40
1 CONTA E COMPLETA. SEGUI L’ESEMPIO.
da u 3 3 da u .......... .......... da u .......... ..........
2 COMPLETA. SEGUI L’ESEMPIO.
• 3 da e 2 u = 32
• 3 da e 9 u = ..........
• 3 da e 3 u =
• 3 da e 7 u = ..........
• 3 da e 4 u = ..........
• 4 da e 0 u =
3 SCRIVI IL NUMERO IN LETTERE.
• 3 da e 5 u = ..........
• 3 da e 1 u = ..........
• 3 da e 0 u =
• 3 da 4 u = ..............................................................................................................................................
• 3 da 6 u = ..............................................................................................................................................
• 3 da 2 u = ..............................................................................................................................................
• 3 da 3 u =
• 3 da 8 u =
I NUMERI DA 40 A 50
1
I NUMERI FINO A 50
3
I NUMERI FINO A 60
I NUMERI DA 60 A 70
1 CONTA E REGISTRA. SEGUI L’ESEMPIO.
I NUMERI FINO A 70
1 IN OGNI GRUPPO COLORA DI ROSSO IL NUMERO MAGGIORE.
2 IN OGNI GRUPPO COLORA DI BLU IL NUMERO MINORE.
3 COMPLETA LE CATENE DI NUMERI. SEGUI L’ESEMPIO.
I numeri che terminano con 0, 2, 4, 6, 8 sono PARI. I numeri che terminano con 1, 3, 5, 7, 9 sono DISPARI. OSSERVA!
4 SCRIVI LA CATENA DI NUMERI DA 40 A 70 . POI COLORA DI VERDE I NUMERI PARI E DI GIALLO I NUMERI DISPARI
I NUMERI DA 70 A 80
PERCORSO
I NUMERI FINO A 80
1 COMPLETA GLI ABACHI, POI CONFRONTALI E METTI I SEGNI >, <, = .
2 RISCRIVI I NUMERI IN ORDINE CRESCENTE.
3 RISCRIVI I NUMERI IN ORDINE DECRESCENTE.
I NUMERI FINO A 90
1 FORMA IL 90 AGGIUNGENDO LA DECINA CORRETTA.
3 COMPLETA CON I NUMERI MANCANTI E CERCHIA DI ROSSO I NUMERI PARI.
3 COLLEGA OGNI SCOMPOSIZIONE AL NUMERO CORRISPONDENTE.
I NUMERI FINO A 99
2 COMPLETA LA CATENA. SEGUI LE INDICAZIONI.
3
3
Percorso 1
UNITÀ 2
I numeri fino a 999
Il Percorso introduce e consolida il concetto di centinaio, guidando i bambini alla scoperta di questa nuova unità numerica e delle sue applicazioni pratiche. Attraverso attività semplici e graduali, gli studenti imparano a contare, scomporre e rappresentare il centinaio, acquisendo padronanza del sistema decimale. Ogni scheda operativa propone attività interattive per stimolare il coinvolgimento degli alunni attraverso la visualizzazione, la manipolazione e il colore, favorendo un apprendimento concreto e partecipato.
Scheda 1: Il centinaio
Introduce il centinaio come nuova unità numerica, spiegando che 100 unità equivalgono a 10 decine o a 1 centinaio. Gli studenti imparano a rappresentare graficamente il numero 100, scrivendo il numero precedente e successivo, e utilizzando il simbolo h per indicare il centinaio.
Scheda 2: Il centinaio
Attraverso esercizi pratici, i bambini possono contare gruppi formati da 10 bastoncini per arrivare a 100 e verificare le combinazioni di decine che formano il numero, consolidando la comprensione del passaggio tra decine e centinaia ed eseguendo calcoli a completamento del numero 100.
Scheda 3: Il centinaio
Gli studenti rappresentano i numeri sull’abaco, imparando a distinguere l’assenza di unità, decine o centinaia attraverso la cifra 0. Inoltre, completano sequenze numeriche per raggiungere il 100, rafforzando il calcolo e il concetto di quantità numerica.
Schede 4 e 5: Numeri fino a 300
In queste schede operative i bambini iniziano a lavorare con numeri più grandi, fino a 300. Completano esercizi di composizione e scomposizione, consolidando come i numeri si articolano in centinaia, decine e unità, e scrivendo numeri in ordine crescente e decrescente. Gli studenti confrontano ancora numeri entro il 300 utilizzando i simboli <, > e =. Scrivono, inoltre, i numeri precedenti e successivi rispetto a un dato valore, sviluppando la capacità di posizionare i numeri in sequenza esatta.
Schede 6 e 7: Numeri fino 700
Queste schede operative estendono il lavoro fino ai numeri fino a 700. Gli studenti ordinano numeri crescenti e decrescenti, identificano numeri maggiori o minori rispetto a un riferimento centrale e colorano valori secondo specifiche indicazioni. (Scheda 6) I numeri vengono composti e confrontati fino a 700. Gli studenti imparano a scomporre numeri partendo dalle cifre date e scrivono i risultati in lettere. Completano inoltre somme che portano al 600, applicando operazioni semplici per consolidare i numeri di base.
Schede 8 e 9: Numeri fino a 999
Si lavora con numeri fino a 999, scomponendoli in centinaia, decine e unità. Gli studenti ordinano i numeri in sequenze crescenti e decrescenti e completano tabelle che rappresentano i numeri in maniera completa, rafforzando il collegamento tra rappresentazione numerica e scomposizione. LA scheda 9 propone esercizi di completamento di sequenze numeriche e un crucinumero che combina numeri, parole e scomposizione, unendo creatività e matematica per consolidare quanto appreso fino ad ora.
Schede 10 e 11: Confronti Verificati
Gli studenti si esercitano a confrontare numeri e a verificare se relazioni matematiche tra di essi (per esempio 573 > 274) sono vere o false. Questo li aiuta a sviluppare una comprensione più approfondita dei numeri e delle loro proprietà. I bambini imparano a combinare cifre per formare numeri maggiori e minori e rispondono a domande relative ai valori ottenuti. Questo esercizio stimola la logica e la flessibilità mentale, incoraggiando il ragionamento e la riflessione sui numeri
IL CENTINAIO • 1
1 OSSERVA I PASSAGGI PER FORMARE IL NUMERO 100.
Proviamo ad aggiungere 1 al 99
2° cambio
RICORDA
Il centinaio si indica con la lettera h.
2 COMPLETA.
h da u
1° cambio 1 h = 100 0 da 0 u
• 100 unità = ............................ decine = ............................ centinaio
• 100 u = ............................ da = ............................ h
3 REGISTRA IN TABELLA IL NUMERO 100.
4 SCRIVI IN LETTERE IL NUMERO PRECEDENTE E IL NUMERO SUCCESSIVO.
IL CENTINAIO • 2
1 OSSERVA I GRUPPI E RISPONDI ALLE DOMANDE.
• Quanti bastoncini ci sono in ogni gruppo?
• Quanti gruppi osservi? ....................................................................................................
• Quanti bastoncini ci sono in tutto? ...............................................................
2 COMPLETA CON LA DECINA CORRETTA.
IL CENTINAIO • 3
1 COLORA I POP-IT E RISPONDI.
• Quante bolle ci sono? .......................................................................................................
2 RAPPRESENTA I NUMERI SULL’ABACO.
Ricorda sull’abaco la cifra 0 indica l’assenza di unità, decine o centinaia!
RICORDA
I NUMERI ENTRO 300 • 1
1 COMPLETA CON I NUMERI CHE MANCANO.
2 COMPONI I NUMERI. SEGUI L’ESEMPIO.
• 3 h 0 da 0 u = 300 + 0 + 0 = 300
• 2 h 5 da 3 u = =
• 1 h 6 da 7 u = .................................................................................... = .....................................
• 2 h 4 da 1 u = .................................................................................... = .....................................
• 1 h 8 da 0 u = .................................................................................... = .....................................
3 SCOMPONI I NUMERI. SEGUI L’ESEMPIO.
• 285 = 2 h 8 da 5 u = 200 + 80 + 5 • 176 = ............................................................................................................... = ..................................... • 108 = ............................................................................................................... = ..................................... • 144 = ............................................................................................................... = ..................................... • 243 = ...............................................................................................................
4 RISCRIVI I NUMERI IN ORDINE DECRESCENTE.
1
I NUMERI ENTRO 300 • 2
>, < O = .
2 COMPLETA CON I NUMERI PRECEDENTE E SUCCESSIVO.
3 RAPPRESENTA I NUMERI SULL’ABACO.
4
I NUMERI ENTRO 600
2 COLORA DI BLU I NUMERI MINORI DI QUELLO AL CENTRO.
1
I NUMERI ENTRO 700
3
3
2
Il progetto SIAMO PARI del Gruppo Editoriale Raffaello sostiene e promuove il codice POLITE (Pari Opportunità nei LIbri di TEsto) per la formazione di una cultura delle pari opportunità e del rispetto di tutte le differenze.
Coordinamento di redazione: Corrado Cartuccia
Coordinamento grafico: Marco Mancini
Redazione: Corrado Cartuccia, Cecilia Barletta
Laboratori digitali: Anna Conforti
Progetto grafico: Marco Mancini
Impaginazione: Marco Mancini, Be Orange s.r.l.
Illustrazioni: Isabella Cacciabaudo, Claudia Schembari, archivio Raffaello
Copertina: Mauro Aquilanti
Referenze fotografiche: iStock, Shutterstock
Coordinamento digitale: Paolo Giuliani
Supervisione contenuti digitali: Anna Conforti
Redazione digitale: Bianca Sagretti
Stampa: Gruppo Editoriale Raffaello
Per esigenze didattiche alcuni testi sono stati ridotti e/o adattati. L’Editore è a disposizione per eventuali omissioni o inesattezze nella citazione delle fonti. Tutti i diritti sono riservati. È vietata la riproduzione dell’opera o di parti di essa con qualsiasi mezzo, compresa stampa, fotocopia, microfilm e memorizzazione elettronica, se non espressamente autorizzata.
Raffaello Libri S.p.A.
Via dell’Industria, 21 60037 - Monte San Vito (AN) www.raffaelloscuola.it
Ristampa: 5 4 3 2 1

La Raffaello Guida pratica accompagna
e supporta il lavoro dell’insegnante, dai primi giorni fino alla valutazione finale.
Nel volume:
• Progettazione
• Griglie e rubriche valutative
• Percorsi operativi
• Attività per i primi giorni
• Verifiche intermedie, finali e inclusive
• Proposte per situazioni NON NOTE
• Autocorrezione
• Compiti autentici
• Educazione civica
• Prove modello INVALSI

CONTENUTI DIGITALI CON L’APP RAFFAELLO PLAYER

Nella collana:
• Italiano
• Matematica
• Storia
• Geografia
• Scienze e Tecnologia
• Religione
• Educazione motoria

Inquadra il QR code: scopri il progetto e gli aggiornamenti
