Matematica e Scienze
Guida didattica mista con CD-Rom
Claudia Ricciardi, Eva Pigliapoco e Ivan Sciapeconi
nella Scuola Primaria
Il progetto
Insegnare.LIM presenta un percorso integrato che coinvolge sia Matematica che Scienze. I materiali presenti in Insegnare.LIM sono stati organizzati su base mensile, per consentire ai docenti il pieno controllo dell’andamento della programmazione didattica.
Le novità introdotte dal legislatore con l’ultima riforma, infatti, hanno accentuato il concetto di “docente prevalente” della classe. Una prevalenza che può disorientare, se non opportunamente organizzata. Per quanto scandito mese per mese, il percorso si compone di schede che possono essere utilizzate indipendentemente dalla collocazione pensata dagli autori.
I materiali (le schede e gli oggetti digitali presentati nelle prossime pagine) vengono forniti anche su CD-Rom in modo da poter sfruttare la massima flessibilità del digitale.
Ciascun mese è introdotto da una breve descrizione delle attività proposte e degli obiettivi da raggiungere. Anche se può sembrare ridondante presentare le attività mensili, è però importante che il docente condivida l’impostazione di fondo del lavoro. Potrà poi, se lo ritiene necessario, operare su questo sfondo con scelte personali e integrazione di materiali. Le pagine introduttive hanno lo scopo di fornire una mappa con la quale orientarsi tra le schede e le indicazioni operative.
Il curricolo di quinta
Nella prima parte dell’anno si propongono attività legate alla lettura, scrittura e composizione dei grandi numeri, si rafforza il concetto di divisione e si consolida la conoscenza delle potenze e dei numeri decimali. In Geometria si presentano i poligoni regolari; in Scienze il Sistema Solare e le caratteristiche della luce e del suono. Nel secondo quadrimestre si presentano i concetti di percentuale e interesse, le divisioni con i numeri decimali e le espressioni aritmetiche, si scoprono i numeri relativi e il sistema di numerazione dei Romani. In Geometria si lavora sulle figure piane e sui solidi, si affrontano le misure di superficie e di volume e si individuano strategie per la soluzione dei problemi. In Scienze si studiano il corpo umano e tutti i suoi apparati.
Le vacanze e i compiti
I periodi di vacanza sono assolutamente necessari, ma è indubbio che possano avere delle ricadute negative sugli apprendimenti dei bambini. Normalmente, al ritorno a scuola dopo un periodo più o meno lungo di assenza, i docenti rilevano la necessità di recuperare una parte degli apprendimenti. All’interno di Insegnare.LIM sono previste due diverse sezioni, relative ai compiti di Natale e Pasqua, che il docente potrà fotocopiare in tutto o in parte e distribuire ai bambini. I compiti ricalcano il percorso didattico della Guida, quindi gli alunni potranno contare su una sostanziale unitarietà di percorso didattico.
I materiali per la verifica e la valutazione
Un altro importante materiale di lavoro, presente in Insegnare.LIM, è rappresentato dalle schede per la verifica e la valutazione delle competenze.
Al termine del primo e del secondo quadrimestre, vengono fornite: • pagine per la verifica delle attività svolte; • pagine per la registrazione e la sintesi dei dati.
Il docente potrà decidere se avvalersi in tutto o in parte dei materiali proposti. È anche possibile partire da essi per personalizzarli sulle esigenze e sulle caratteristiche della classe.
Il materiale digitale
Negli ultimi anni, i materiali didattici tradizionali sono stati accompagnati da prodotti digitali: principalmente CD-Rom e risorse online.
Nel caso di Insegnare.LIM la scelta è stata quella di pensare ad un percorso integrato. Nel CD-Rom non sono stati inseriti materiali digitali genericamente aggiuntivi, rispetto al percorso didattico delineato nella Guida. Il Web è pieno di risorse digitali che, in questo senso, possono supportare il lavoro del docente.
I materiali messi a disposizione sono, invece, funzionali alla conduzione di vere e proprie lezioni con la Lavagna Interattiva Multimediale o con un normale videoproiettore. Le lezioni sono scandite secondo una metodologia precisa e una presentazione “step by step”, che ha lo scopo di facilitare i docenti meno esperti.
Una descrizione più accurata di questa distinzione, tutt’altro che sottile, viene articolata nelle pagine seguenti.
Gli strumenti digitali
Negli ultimi tempi, le proposte di strumenti didattici digitali sono aumentate notevolmente. È importante, però, saper riconoscere cosa realmente è utile alla didattica.
Negli ultimi anni, l’inserimento delle Lavagne Interattive Multimediali nelle aule della Scuola Primaria ha segnato un importante segno di svolta.
Dopo aver inserito l’Informatica nei laboratori, limitando in modo sostanziale il suo apporto alla didattica, finalmente le nuove tecnologie entrano nelle discipline e nel fare scuola di tutti i giorni.
Anche per questo motivo, sul versante delle opportunità metodologiche, Insegnare.LIM propone una soluzione integrata tra materiale cartaceo e digitale. A supporto di questa scelta, c’è la convinzione che le risorse per la LIM, da sole, non possano innovare la didattica o fornire aiuti di rilievo agli apprendimenti dei bambini.
In questa Guida non verranno proposti giochi animati o prodotti multimediali caratterizzati da una forte incidenza di “effetti speciali”. Ai docenti verrà fornito qualcosa di tecnologicamente molto più semplice, ma enormemente più interessante e produttivo sotto il profilo del rapporto fra insegnamento e apprendimento: idee e strategie didattiche.
È utile ricordare che tutte le soluzioni proposte possono essere utilizzate, rinunciando ad una pur significativa interattività, con un videoproiettore collegato ad un computer.
Cosa aspettarsi dalla LIM
Indubbiamente, la Lavagna Interattiva Multimediale rappresenta una innovazione significativa nel panorama delle tecnologie per la didattica.
Essa si basa su un’idea sostanzialmente semplice: espandere le funzioni della lavagna collegandola al computer. O, volendo, espandere le caratteristiche del computer portandolo ad assumere l’aspetto di una lavagna.
Al di là dei giochi di parole, però, è fondamentale che i docenti sappiano cosa aspettarsi da questa come qualsiasi altra innovazione.
Appiattire la didattica su un versante tutto incentrato sugli aspetti ludici e multimediali potrebbe non essere una prospettiva condivisibile, per molti docenti.
Gran parte dei prodotti software attualmente in circolazione e destinati alla LIM si possono dividere in due grandi categorie:
• gli Edutainment, ovvero i programmi che coniugano insegnamento e intrattenimento (Education e Entertainment). Sono i software che, sotto una impostazione molto simile a quella dei videogiochi, nascondono degli intenti didattici;
• i Learning Object, che sono percorsi di apprendimento strutturati. Un insieme di istruzioni e verifiche che dovrebbero consentire agli alunni, autonomamente, di costruire i propri apprendimenti.
I materiali contenuti in Insegnare.LIM partono da tutt’altro punto di vista ed hanno ambizioni ben diverse.
I materiali di Insegnare.LIM: i Teaching Object
Insegnare.LIM è un progetto che si basa in modo sostanziale sul potenziamento della relazione di insegnamento-apprendimento. Le risorse didattiche non sono pensate per intrattenere i bambini o per catturare genericamente la loro attenzione. Esse sono, piuttosto, costruite intorno alla necessità del docente di strutturare una lezione completa ed efficace.
Volendo anticipare la loro descrizione con un nome, si potrebbero definire Teaching Object: oggetti utili al docente per fare lezione.
Contrariamente ai Learning Object, espressamente pensati per far lavorare gli alunni in modo autonomo (con il rischio, spesso, di perdere i più deboli o i meno motivati), i Teaching Object di Insegnare. LIM sono pensati come risorse per condurre la lezione, per attivare tutti gli alunni, per scandire le tappe del lavoro.
Per questo, prima di utilizzare i materiali digitali contenuti nel CD-Rom, si consiglia un’attenta lettura delle indicazioni metodologiche.
Le risorse abbinate alla Guida possono essere utilizzate solo in abbinamento alle schede e alle procedure descritte nelle pagine seguenti. Diversamente, non avrebbero alcuna utilità.
L’organizzazione
Per una maggior chiarezza espositiva, le lezioni con la LIM sono state raggruppate alla fine di ogni quadrimestre. Questa scansione non è l’unica possibile, tanto più che il docente potrà proporre le attività con gli strumenti digitali in qualsiasi periodo dell’anno e gestirle con la dovuta flessibilità. In realtà, la scansione quadrimestrale serve solo per consentire una facile consultazione, in base alla programmazione mensile delle attività.
Da un punto di vista tecnico, le attività digitali richiedono competenze informatiche minime. Tutte le risorse multimediali (immagini, suoni, animazioni) sono già contenuti nei singoli file. Sarà sufficiente lanciare lo strumento digitale desiderato per essere immediatamente operativi.
Le risorse digitali presenti nel CD-Rom
Il CD-Rom allegato a Insegnare.LIM contiene una serie di risorse digitali facilmente identificabili nella schermata principale.
• Prove nazionali: prove INVALSI in formato PDF.
• Libro sfogliabile: è un vero e proprio libro digitale, sfogliabile tramite l’apposito player.
• Materiale per la LIM. Sono i materiali digitali sicuramente più interessanti. I materiali interattivi consentono di integrare le normali attività di classe con strumenti digitali di approfondimento o consolidamento. All’interno del menu, sono presenti:
– le schede in formato PDF. Le pagine operative di Insegnare.LIM sono presentate anche in forma digitale, per essere proiettate sulla LIM. In questo modo risulterà agevolata, ad esempio, la spiegazione dell’esercizio o la correzione collettiva dei lavori. Le schede in formato PDF possono essere gestite con il software caratteristico del modello di LIM in dotazione (ad esempio per sottolineare, scrivere o cancellare).
– attività digitali divise tra I e II quadrimestre. Si tratta di attività che possono essere condotte con l’aiuto di risorse presenti nel CD-Rom allegato, pensate in stretto collegamento con le attività del primo e del secondo quadrimestre, utilizzabili con la LIM o con un videoproiettore.
Anche nel
CD, i materiali interattivi sono organizzati con la stessa scansione della Guida.
Come già accennato nelle pagine precedenti, tutte le attività con la LIM fanno riferimento e si integrano alle soluzioni proposte in cartaceo. Per questo motivo, le descrizioni delle attività digitali faranno costante riferimento al contenuto della Guida e alle schede operative. Tutte le schede operative, inoltre, sono accompagnate da un sistema di icone che segnala la presenza di risorse aggiuntive sul CD-Rom.
Icona digitale: la scheda fa parte di uno dei percorsi legati alla LIM ed è accompagnata da risorse digitali. Per sapere come utilizzare la scheda in abbinamento all’attività per la LIM, si può fare riferimento alle pagine di descrizione dell’attività, raccolte al termine di ogni quadrimestre.
Programmazione Matematica
Classe quinta
Competenze alla fine della classe quinta
L’alunno:
• sviluppa un atteggiamento positivo rispetto alla Matematica, anche grazie a molte esperienze in contesti significativi, che gli hanno fatto intuire come gli strumenti matematici di cui si è impossessato siano utili per operare nella realtà;
• si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali e sa valutare l’opportunità di ricorrere a una calcolatrice;
• percepisce e rappresenta forme, relazioni e strutture che si trovano in natura o che sono state create dall’uomo, utilizzando, in particolare, strumenti per il disegno geometrico (riga, compasso, squadra) e i più comuni strumenti di misura;
• utilizza rappresentazioni di dati adeguate e le sa sfruttare in situazioni significative per ricavare informazioni;
• descrive e classifica figure in base a caratteristiche geometriche;
• affronta i problemi con strategie diverse, rendendosi conto che, in molti casi, possono ammettere più soluzioni;
• riesce a risolvere facili problemi mantenendo il controllo sia sul processo risolutivo sia sui risultati e spiegando a parole il procedimento seguito;
• riconosce situazioni di incertezza e ne parla con i compagni utilizzando le espressioni “è più probabile”, “è meno probabile”.
SETTEMBRE – OTTOBRE
Conoscenze
Il nostro sistema di numerazione: decimale e posizionale
L’addizione
La moltiplicazione
Obiettivi
Leggere, scrivere e scomporre i numeri naturali
Ordinare e confrontare i numeri naturali
Comprendere il valore posizionale delle cifre
Comporre e scomporre i numeri naturali
Conoscere e saper applicare le proprietà dell’addizione
Leggere, completare e compiere osservazioni sulla tabella dell’addizione
Schede operative di riferimento
Pag. 17
Pag. 18
Pag. 19 Pag. 20
Pag. 21
Pag. 22
Eseguire addizioni in tabella e compiere le relative osservazioni Pag. 23
Saper applicare strategie di calcolo mentale Pag. 24
Risolvere problemi di tipo additivo Pag. 25
Eseguire moltiplicazioni e applicare la proprietà commutativa e associativa
Pag. 26
Eseguire moltiplicazioni e applicare le relative proprietà Pag. 27
Leggere, completare e compiere osservazioni sulla tabella della moltiplicazione Pag. 28- 29
Eseguire moltiplicazioni in colonna Pag. 30
Risolvere problemi di tipo moltiplicativo Pag. 31
La sottrazione
La sottrazione
Lo spazio e le figure: i poligoni
La statistica
Conoscenze
La divisione
Il nostro sistema di numerazione: decimale e posizionale.
L’addizione
La sottrazione
Lo spazio e le figure: i poligoni
Le classificazioni e le relazioni logiche.
La statistica
Conoscenze
Il nostro sistema di numerazione: decimale e posizionale
Le frazioni
Applicare la proprietà invariantiva della sottrazione
Leggere, completare e compiere osservazioni sulla tabella della sottrazione
Eseguire sottrazioni in tabella e compiere le relative osservazioni
Risolvere problemi di tipo sottrattivo
Riconoscere i poligoni
Interpretare e descrivere grafici
NOVEMBRE
Obiettivi
Leggere, completare e compiere osservazioni sulla tabella della divisione
Identificare i divisori di un numero
Eseguire divisioni sull’abaco con due cifre al divisore
Eseguire divisioni in colonna
Risolvere problemi con la divisione
Pag. 32
Pag. 33
Pag. 34
Pag. 35
Pag. 36 – 37- 38
Pag. 39
Schede operative di riferimento
Pag. 45-46
Pag. 47
Pag. 48
Pag. 49
Pag. 50-51
Comporre e scomporre numeri “grandi” Pag. 52
Rappresentare con l’abaco numeri “grandi” Pag. 53
Ordinare e confrontare numeri “grandi” Pag. 54
Scrivere i numeri come somma di prodotti Pag. 58
Comprendere il significato delle potenze Pag. 59
Eseguire addizioni in colonna con la prova Pag. 55
Eseguire sottrazioni in colonna con la prova Pag. 56
Saper applicare strategie di calcolo mentale Pag. 57
Riconoscere i triangoli
Pag. 60–61
Individuare angoli interni nei poligoni Pag. 62
Classificare secondo due o tre criteri usando connettivi e quantificatori
Consolidare l’uso degli indici statistici: moda, mediana, media
Pag. 63-64
Pag. 65
Interpretare, descrivere e progettare grafici Pag. 66
DICEMBRE
Obiettivi
Comprendere il significato delle potenze
Conoscere le potenze di 10 e la scrittura polinomiale
Schede operative di riferimento
Pag. 73
Pag. 74
Scrivere i numeri in forma di polinomio Pag. 75
Risolvere i problemi con l’elevazione a potenza
Trovare la frazione corrispondente a parti di una figura
Pag. 76
Pag. 77
Comprendere la frazione complementare Pag. 78
Le frazioni
I numeri decimali
Lo spazio e le figure: i poligoni
La misura: le misure monetarie
Conoscenze
L’addizione con i numeri decimali
La sottrazione con i numeri decimali.
La moltiplicazione con i numeri decimali
Comprendere le frazioni proprie, improprie, apparenti Pag. 79
Calcolare il valore di una frazione e l’intero Pag. 80
Confrontare frazioni Pag. 81-82-83-84
Completare e compiere osservazioni sulla tabella delle frazioni Pag. 85
Trasformare una frazione propria o impropria in numero decimale Pag. 86-87
Leggere e scrivere numeri decimali Pag. 88
Confrontare e ordinare numeri decimali Pag. 89
Costruire poligoni con riga e compasso Pag. 90
Classificare i quadrilateri. Pag. 91
Riconoscere i quadrilateri Pag. 92
Conoscere e operare con l’euro Pag. 93
GENNAIO
Obiettivi
Eseguire addizioni in colonna con i numeri decimali
Le frazioni e le percentuali
Lo spazio e le figure: i poligoni regolari
La misura: le misure monetarie per il calcolo di spesa, guadagno, ricavo.
Le classificazioni e le relazioni logiche
Le classificazioni e le relazioni logiche
Schede operative di riferimento
Pag. 105
Saper applicare strategie di calcolo mentale Pag. 106
Risolvere problemi di tipo additivo Pag. 107
Eseguire sottrazioni in colonna con i numeri decimali Pag. 108
Saper applicare strategie di calcolo mentale Pag. 109
Eseguire moltiplicazioni per 10 Pag. 110
Eseguire moltiplicazioni per 100 Pag. 111
Eseguire moltiplicazioni per 1000 Pag. 112
Eseguire moltiplicazioni con i numeri decimali Pag. 113-114
Individuare i multipli di un numero Pag. 115
Comprendere e usare la frazione come percentuale Pag. 116-119
Confrontare e ordinare numeri decimali, Pag. 117
Risolvere problemi con il calcolo della percentuale Pag. 118
Individuare i poligoni regolari e le loro caratteristiche Pag. 120
Individuare le diagonali nei poligoni Pag. 121-122
Individuare assi di simmetria Pag. 123
Individuare gli assi di simmetria di un poligono Pag. 124
Calcolare spesa, ricavo, guadagno, perdita Pag. 125
Risolvere problemi sulla compravendita Pag. 126
Classificare secondo due o tre criteri usando connettivi e quantificatori Pag. 127
Trovare le proprietà di una classificazione, dato un diagramma Pag. 128
La statistica Interpretare, descrivere e progettare grafici Pag. 129
Conoscenze
Il nostro sistema di numerazione: posizionale e decimale
L’addizione e la sottrazione
La moltiplicazione e la divisione
Le frazioni
La risoluzione dei problemi
Lo spazio e le figure: i poligoni
Conoscenze
La misura: le misure monetarie per il calcolo di interesse, IVA
La moltiplicazione
VERIFICHE QUADRIMESTRALI
Obiettivi
Comprendere il sistema posizionale di rappresentazione dei numeri
Saper applicare strategie di calcolo mentale
La divisione
Lo spazio e le figure: il perimetro dei poligoni
La misura:il sistema di misura convenzionale per le lunghezze, le capacità e i pesi.
Le classificazioni e le relazioni logiche
La statistica
Schede operative di riferimento
Pag. 135
Pag. 136
Eseguire moltiplicazioni e divisioni per 10-1001000 Pag. 137
Confrontare frazioni
Pag. 138
Risolvere problemi con le quattro operazioni Pag. 139
Risolvere problemi con i concetti di sconto, IVA, interesse Pag. 140
Individuare le caratteristiche dei triangoli Pag. 141
Individuare le caratteristiche dei quadrilateri Pag. 142
FEBBRAIO
Obiettivi
Comprendere e utilizzare l’interesse
Schede operative di riferimento
Pag. 157-158
Comprendere e saper utilizzare l’IVA Pag. 159
Riconoscere numeri quadrati, rettangolari, primi Pag. 160
Saper individuare i numeri primi Pag. 161
Stimare il prodotto di una moltiplicazione Pag. 162
Eseguire divisioni con il dividendo decimale e il divisore a una cifra Pag. 163
Eseguire divisioni con il dividendo decimale e il divisore a due cifre Pag. 164
Stabilire i criteri di divisibilità di un numero Pag. 165-166
Eseguire divisioni con dividendo intero e quoziente con cifre decimali
Eseguire divisioni con dividendo minore del divisore
Calcolare il perimetro del triangolo
Calcolare il perimetro di un quadrilatero
Calcolare il perimetro dei poligoni regolari
Conoscere e operare con le unità di misura di lunghezza
Risolvere problemi con le unità di misura di lunghezza
Conoscere e saper operare con le unità di misura di peso/massa
Risolvere problemi con le unità di misura di peso/massa
Risolvere situazioni problematiche mediante l’uso di diagrammi
Interpretare, descrivere e progettare grafici
Pag. 167-168
Pag. 169
Pag. 170
Pag. 171
Pag. 172
Pag. 173
Pag. 174
Pag. 175
Pag. 176
Pag. 177-178
Pag. 179
Conoscenze
La divisione
Le espressioni aritmetiche
MARZO
Obiettivi
La misura: il sistema di misura convenzionale per le lunghezze, le capacità , i pesi, le superfici
La misura: le misure monetarie
Lo spazio e le figure: l’area dei poligoni
La risoluzione dei problemi
La probabilità
Conoscenze
Le espressioni aritmetiche
Lo spazio e le figure: l’area dei poligoni
Il cerchio e la circonferenza
Schede operative di riferimento
Eseguire divisioni per 10; 100; 1000 Pag. 189-190-191
Comprendere e applicare la proprietà invariantiva Pag. 192-193-194
Eseguire divisioni con divisore decimale Pag. 195
Risolvere espressioni aritmetiche Pag. 196
Comprendere le regole di esecuzione di un’espressione Pag. 197
Calcolare peso lordo, peso netto, tara Pag. 198
Risolvere problemi con peso lordo, peso netto e tara Pag. 199
Conoscere e operare con le unità di misura di capacità Pag. 200
Risolvere problemi con le unità di misura di capacità Pag. 201-202
Conoscere e operare con le misure di superficie Pag. 204-205
Risolvere problemi sulla compravendita Pag. 203
Calcolare l’area del quadrato e del rettangolo Pag. 206
Calcolare l’area del romboide e del rombo Pag. 207
Calcolare l’area del triangolo Pag. 208
Calcolare l’area del trapezio Pag. 209
Conoscere le formule per calcolare l’area dei poligoni Pag. 210
Risolvere problemi con le misure di superficie Pag. 211
Riflettere ed esaminare i dati di un problema Pag. 212
Comprendere la procedura e risolvere un problema. Pag. 213
Introdurre il concetto di probabilità Pag. 214
APRILE
Obiettivi
Schede operative di riferimento
Costruire un’espressione partendo da un diagramma Pag. 223
Comprendere la risoluzione di un problema mediante l’espressione Pag. 224
Risolvere problemi con un’espressione aritmetica Pag. 225-226
Calcolare l’area del pentagono Pag. 227
Calcolare l’area dell’esagono Pag. 228
Utilizzare formule inverse nei poligoni Pag. 229-230
Costruire la circonferenza e individuarne il raggio e il diametro
Costruire la circonferenza e individuarne il raggio, il diametro, la corda e l’arco
Pag. 231
Pag. 232
Calcolare la circonferenza Pag. 233-234
Calcolare l’area del cerchio Pag. 235-236-237
La misura: le unità di misura di tempo
La statistica
La probabilità
Conoscere le unità di misura di tempo
Eseguire operazioni con le unità di misura di tempo
Ricavare dati e informazioni da una tabella
Introdurre il concetto di probabilità
MAGGIO – GIUGNO
Conoscenze
I numeri relativi
Il sistema di numerazione romano
Lo spazio e le figure: i poliedri
La misura: le unità di misura di volume.
Conoscenze
I numeri naturali e i numeri decimali
Lo spazio e le figure: l’area e il perimetro
Lo spazio e le figure: il cerchio e la circonferenza.
La misura: le unità di misura di peso, capacità, lunghezza, superficie e monetarie.
Le classificazioni e le relazioni logiche.
La statistica
Pag. 238
Pag. 239-240
Pag. 241
Pag. 242
Obiettivi
Scoprire l’uso dei numeri interi relativi nella realtà
Conoscere, comprendere ed operare con il sistema di numerazione romano
Descrivere i poliedri in termini di facce, spigoli, vertici
Classificare i solidi
Consolidare il concetto di facce parallele
Comprendere e saper usare la formula di Eulero
Individuare gli sviluppi piani dei solidi
Calcolare la superficie dei solidi
Calcolare il volume dei solidi
Operare con i volumi
Conoscere le misure di volume e operare con esse
Risolvere problemi con le misure di volume
Risolvere problemi con le misure di volume e superficie
VERIFICHE FINALI
Obiettivi
Saper operare con i numeri naturali e i numeri decimali
Calcolare il perimetro e l’area dei poligoni
Calcolare la circonferenza e l’area del cerchio
Operare con diverse misure
Classificare secondo due o tre criteri usando connettivi e quantificatori
Interpretare e completare i grafici
Schede operative di riferimento
Pag. 257-258
Pag. 259- 260
Pag. 261
Pag. 262
Pag. 263
Pag. 264
Pag. 265
Pag. 266-267
Pag. 268-269
Pag. 270-271
Pag. 272-273
Pag. 274
Pag. 275
Schede operative di riferimento
Pag. 285
Pag. 286
Pag. 287
Pag. 288
Pag. 289
Pag. 290
Programmazione Scienze
Classe quinta
Competenze alla fine della classe quinta
L’alunno:
• ha capacità operative, progettuali e manuali, che utilizza in contesti di esperienzaconoscenza per un approccio scientifico ai fenomeni;
• si pone domande esplicite e individua problemi significativi da indagare a partire dalla propria esperienza, dai discorsi degli altri, dai mezzi di comunicazione e dai testi letti;
• formula ipotesi e previsioni, osserva, registra, classifica, schematizza, identifica relazioni spazio/ temporali, misura, argomenta, deduce, prospetta soluzioni, prevede alternative, ne produce rappresentazioni grafiche e schemi di livello adeguato;
• analizza e racconta in forma chiara ciò che ha fatto e appreso;
• ha atteggiamenti di cura verso l’ambiente scolastico in quanto ambiente di lavoro cooperativo e finalizzato e di rispetto verso l’ambiente sociale e naturale, di cui conosce e apprezza il valore;
• ha cura del proprio corpo con scelte adeguate di comportamenti e di abitudini alimentari.
Conoscenze
L’Universo: il Sistema Solare
Conoscenze
L’Universo: il Sistema Solare
La luce e le sue caratteristiche
Conoscenze
La luce e le sue caratteristiche
Il suono e le sue caratteristiche
SETTEMBRE – OTTOBRE
Obiettivi
Schede operative di riferimento
Conoscere e descrivere le caratteristiche dei pianeti Pag. 40
Conoscere e descrivere le caratteristiche della Luna Pag. 41
Conoscere e descrivere le fasi della Luna Pag. 42
NOVEMBRE
Obiettivi
Schede operative di riferimento
Conoscere le principali caratteristiche del Sole Pag. 67
Osservare e descrivere corpi luminosi e corpi illuminati Pag. 68-69
Scoprire come avviene la propagazione della luce Pag. 70
DICEMBRE
Obiettivi
Schede operative di riferimento
Osservare, scoprire e descrivere il fenomeno della riflessione della luce Pag. 94
Osservare , scoprire e descrivere il fenomeno della rifrazione della luce Pag. 95
Descrivere le caratteristiche del suono Pag. 96
GENNAIO
Conoscenze
Il suono e le sue caratteristiche
Il mondo degli esseri viventi al microscopio
Conoscenze
L’Universo e il Sistema Solare
Conoscenze
Il mondo degli esseri viventi al microscopio
Il corpo umano
Conoscenze
Il corpo umano
La tutela dell’ambiente
Obiettivi
Descrivere le caratteristiche del suono
Conoscere e descrivere la riflessione del suono
Conoscere le caratteristiche comuni degli esseri viventi
Conoscere e descrivere le caratteristiche dei batteri
Conoscere e descrivere la cellula
VERIFICHE QUADRIMESTRALI
Obiettivi
Conoscere e descrivere alcune caratteristiche delle stelle
FEBBRAIO
Obiettivi
Conoscere e descrivere la cellula e l’organizzazione del corpo umano
Conoscere la struttura e le funzioni del sistema scheletrico
Conoscere e descrivere le principali caratteristiche delle ossa e delle articolazioni
Conoscere e descrivere le principali caratteristiche del sistema muscolare
Conoscere, denominare e classificare i muscoli
Conoscere e descrivere la struttura, le funzioni e la fisiologia dell’apparato digerente
MARZO
Obiettivi
Conoscere e descrivere la struttura, le funzioni e la fisiologia dell’apparato digerente
Conoscere la struttura e la funzione dei denti
Conoscere i principi nutritivi e le loro funzioni
Conoscere la struttura, le funzioni e la fisiologia dell’apparato respiratorio
Saper mettere in sequenza ordinata gli organi coinvolti nell’atto della respirazione
Identificare le cause di inquinamento dell’aria e i relativi comportamenti corretti per prevenire le malattie respiratorie
Schede operative di riferimento
Pag. 130
Pag. 131
Pag. 132
Pag. 133
Pag. 134
Schede operative di riferimento
Pag. 143
Schede operative di riferimento
Pag. 180
Pag. 181
Pag. 182
Pag. 183
Pag. 184
Pag. 185-186
Schede operative di riferimento
Pag. 215
Pag. 216
Pag. 217
Pag. 218
Pag. 219
Pag. 220
APRILE
Conoscenze Obiettivi
Conoscere la funzione e la composizione del sangue
Comprendere la funzione dei diversi vasi sanguigni
Il corpo umano
Il corpo umano
Comprendere la funzione e la struttura del cuore
Comprendere la funzione di grande circolazione e di piccola circolazione
Conoscere e denominare le parti principali del sistema nervoso
Conoscere e descrivere le parti e le funzioni del sistema nervoso centrale
Conoscere e descrivere le parti e le funzioni del sistema nervoso periferico
Conoscere le caratteristiche principali della vista e la struttura dell’occhio
MAGGIO-GIUGNO
Conoscenze Obiettivi
Conoscere le caratteristiche principali della vista e la struttura dell’occhio
Identificare comportamenti corretti per mantenere una buona capacità visiva
Conoscere il funzionamento dell’olfatto e le funzioni del naso
Schede operative di riferimento
Pag. 243
Pag. 244
Pag. 245
Pag. 246
Pag. 247
Pag. 248
Pag. 249
Pag. 250
Il corpo umano
La tutela dell’ambiente
Conoscenze
Il corpo umano
Conoscere il funzionamento dell’udito e la struttura dell’orecchio
Conoscere il funzionamento del gusto e la struttura della lingua
Conoscere il funzionamento del tatto e la struttura della pelle
Conoscere e descrivere le parti principali dell’apparato escretore
Conoscere le cause di inquinamento acustico
VERIFICHE QUADRIMESTRALI
Obiettivi
Descrivere l’organizzazione del corpo umano
Schede operative di riferimento
Pag. 276
Pag. 277
Pag. 278
Pag. 279-280
Pag. 282
Pag. 283
Pag. 284
Pag. 281
Schede operative di riferimento
Pag. 291
Settembre Ottobre
Le prime proposte didattiche si riferiscono alla revisione del concetto di numero, attraverso attività legate alla lettura, scrittura e scomposizione dei numeri naturali e al loro ordinamento e confronto. In Scienze, il percorso didattico inizia con la conoscenza dei Pianeti del Sistema Solare.
Presentazione
Il percorso didattico si apre affrontando attività di consolidamento sul numero, utili per una buona accoglienza del gruppo classe e per un buono avvio di Anno Scolastico.
Prima di affrontare i numeri “grandi” è infatti importante lavorare sulla scrittura, la lettura e la scomposizione dei numeri naturali conosciuti in classe quarta (figura 1) per rafforzare così le conoscenze e le abilità necessarie a comprendere la scrittura polinomiale dei numeri in base 10, grande obiettivo finale della classe quinta.
Utile sarà reintrodurre le operazioni di addizione, moltiplicazione e sottrazione mediante le loro proprietà e la compilazione delle relative tabelle; la risoluzione di alcuni problemi aritmetici completerà il percorso sul numero.
In Geometria si partirà dal riconoscimento dei poligoni, consolidandone il concetto (figura 2); si presenterà una scheda sull’interpretazione e la descrizione di un grafico per un ripasso degli indici statistici ”moda”, “media” e “mediana”.
Per quanto riguarda Scienze, il percorso didattico inizia affrontando un tema da sempre ricco di fascino e interesse per l’uomo, fin dai tempi più antichi: la conoscenza del Sistema Solare. Nel primo periodo scolastico si guideranno gli alunni a conoscere e descrivere i Pianeti del Sistema Solare, la Luna e le sue fasi (figura 3) attraverso la lettura, la comprensione e il completamento di testi con termini adeguati e connessioni logiche.
Fig. 1
Fig. 2
Fig. 3
NUMERI E CITTÀ
Scrivi in cifre i seguenti numeri.
• Ventiduemila
• Cinquemilaottocentosessanta ...................................................................................................................
• Cinquantanovemilatrecentoquattro ......................................................................................................
• Novantaseimilasettecento
• Centoquattromilanovecentoventisette
• Trecentomiladuecentoquaranta ...............................................................................................................
Scrivi in parole il numero degli abitanti di ciascuna città.
• Brescia 192 749 ...................................................................................................................................
• Pavia 71 345 ...................................................................................................................................
• Modena 183 889
• Ferrara 135 168
• Siena 52 774 ...................................................................................................................................
• Ancona 102 759 ...................................................................................................................................
• Macerata 41 625
• Urbino 15 202
Scomponi i seguenti numeri, come nell’esempio.
• 95 324 = 90 000 + 5 000 + 300 + 20 + 4
• 167 583 = ...................................................................................................................................................................
• 304 631 = ...................................................................................................................................................................
• 462 897 =
• 31 745 =
• 206 384 = ...................................................................................................................................................................
ORDINA I NUMERI
Completa la tabella inserendo il numero precedente e il numero successivo di ogni numero dato.
Confronta le seguenti coppie di numeri inserendo i segni >, <, =.
Ordina in senso crescente i seguenti numeri.
Ordina in senso decrescente i seguenti numeri.
NUMERI SUL TABLET
Inserisci nella tabella che vedi sul tablet i seguenti valori, come nell’esempio.
• 1 725 unità semplici
• 8 unità di migliaia
• 20 decine semplici
• 4 centinaia di migliaia
• 100 decine semplici
• 50 centinaia semplici
• 6 centinaia di migliaia
• 3 decine di migliaia
• 15 738 unità semplici
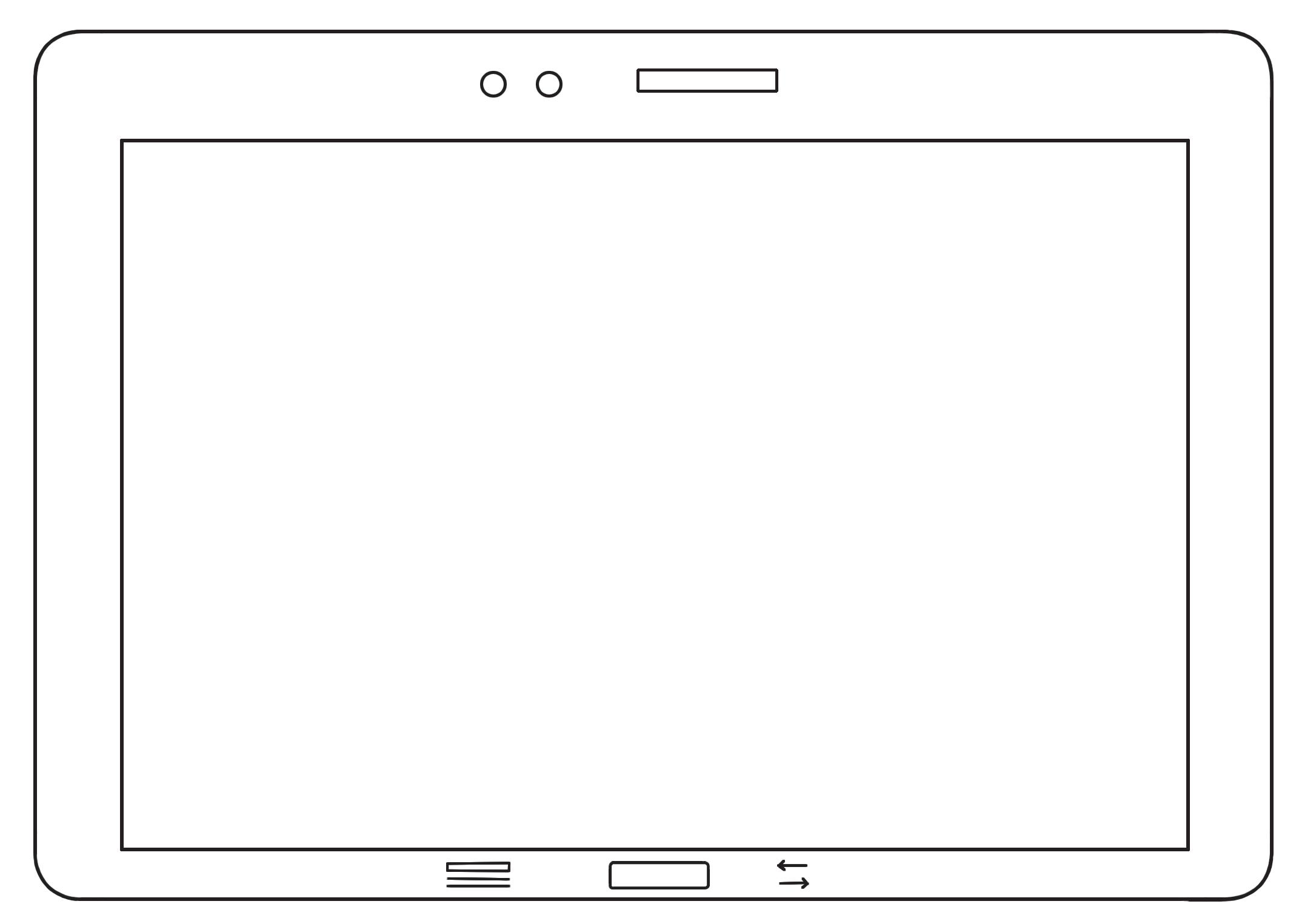
PERIODO UNITÀ DI MIGLIAIA PERIODO UNITÀ SEMPLICI
Scrivi i numeri formati dai seguenti valori.
Cerchia le unità di migliaia in rosso, le decine di migliaia in blu e le centinaia di migliaia in verde.
148 736 54 061 528 634 1 348 107 342
NUMERI SULL’ABACO
Rappresenta sull’abaco i numeri indicati.
hk dak uk h da u
275 329
hk dak uk h da u
806 481
hk dak uk h da u 17 362
hk dak uk h da u
Scrivi in cifre il numero che compare in ogni tabella.
hk dak uk h da u
hk dak uk h da u
42 975
hk dak uk h da u
Cerchia in ogni numero la cifra 3 solo quando ha valore di decine di migliaia (dak).
LE PROPRIETÀ DELL’ADDIZIONE
25 + 12 = 37 Ricorda
1° addendo 2° addendo somma o totale
Esegui le addizioni in colonna, poi applica la proprietà commutativa per verificarne l’esattezza.
168 142 + 1 375 =
172 965 + 12 621 = 853 343 + 106 098 =
Applica la proprietà associativa, come nell’esempio.
35 + 1 165 + 43 = (35 + 1 165) + 43 = 1 200 + 43 = 1 243
2 384 + 16 + 458 = .......................................................................................................................................................
560 + 40 + 3 370 + 30 =
Indica con una crocetta se le seguenti affermazioni sono vere (V) o false (F).
• La somma di due numeri naturali è sempre maggiore di ognuno di essi. V F
• Quando la somma di due numeri naturali è zero, uno di questi è uguale a zero. V F
• La somma di due numeri naturali non può mai essere minore di ognuno di essi. V F
LA TABELLA DELL’ADDIZIONE
Completa la tabella e le osservazioni che ne puoi ricavare.
• La tabella dell’addizione è tutta perché l’operazione con i numeri naturali è ..................................................... possibile.
• Nella prima riga, sotto l’intestazione, che cosa puoi osservare?
• Nella prima colonna, a destra dell’intestazione, che cosa osservi? ..........................................................
Quindi, nell’addizione il numero zero è
• Quali numeri trovi sulla diagonale?
Sono la somma di due ...............................................................................................................................................
• Nella tabella puoi osservare una proprietà dell’addizione? ...................................................................... Quale?
Scrivi alcuni esempi:
• Dove si trovano le coppie additive di un numero? .....................................................................................
ADDIZIONI IN TABELLA
Completa le seguenti tabelle dell’addizione.
Esegui i seguenti calcoli.
TUTTO A MENTE
Completa le catene di numeri seguendo il comando dato dalle frecce.
Indica con una crocetta se le seguenti relazioni sono vere (V) o false (F). Correggi le relazioni errate.
4 PROBLEMI E UN TESORO
Risolvi i problemi che ti permettono di raggiungere il forziere con il tesoro.
• Un negoziante di abbigliamento sportivo ha acquistato dei giubbotti spendendo ? 4 200 e dei pantaloni spendendo ? 1 850. Inoltre ha dovuto pagare ? 145 per il trasporto. Quanto ha speso in tutto?
Operazioni: ........................................................
3 2 4
• Simone possiede nel suo salvadanaio ? 385, suo fratello Alessandro ha ? 248 più di Simone e sua sorella Claudia possiede ? 132 più di Alessandro. Quale somma di denaro hanno in tutto i tre fratelli?
Operazioni: ........................................................
Risposta: ..........................................................
Risposta: ..........................................................
• Il papà di Andrea ha acquistato un’auto nuova. Ha pagato subito ? 12 000 e pagherà il resto in 36 rate da ? 300 ciascuna. Quanto gli costerà l’automobile?
Operazioni: ........................................................
• Una famiglia composta dai genitori e da 3 figli vuol trascorrere un pomeriggio al cinema. Sapendo che il biglietto adulti costa ? 6,50 e che il biglietto bambini costa ? 4,50, quanto spenderà la famiglia?
Operazioni: ........................................................
Risposta:
Risposta:
LA MOLTIPLICAZIONE E LE SUE PROPRIETÀ
Esegui le seguenti moltiplicazioni in colonna applicando la proprietà commutativa per verificarne l’esattezza.
149 × 9 =
268 × 7 = 36 × 43 = ..............
516 × 28 =
3 × 5 = 5 × 3
Le proprietà della moltiplicazione
4 × 3 × 2 = 4 × (3 × 2) = 4 × 6
7 × 12 = 7 × (10 + 2) = (7 × 10) + (7 × 2)
Ora esegui le moltiplicazioni applicando la proprietà associativa.
6 × 5 × 4 = × (5 × 4) =
8 × 3 × 5 =
× 4 × 3
2 × 10 × 9 =
2 × 4 × 15 =
× 8 × 6 =
TANTE PROPRIETÀ
Risolvi queste moltiplicazioni applicando la proprietà distributiva.
9 × 52 = 9 × (......... + 2) = (9 × 50) + (......... × 2) = 450 + ......... =
113 × 4 = (100 + ) × 4 = (100 × ) + (13 × ) = + =
75 × 6 = (70 + ) × 6 = ( × ) + ( × ) = + =
× 3 = (
8 × 420 =
× 384
3 × 508
Indica con una crocetta quali proprietà sono state applicate.
15 × 3 = 3 × 15
16 × 5 = (10 + 6) × 5
7 × 8 × 3 = 7 × (8 × 3) = 7 × 24
125 × 14 = 14 × 125
9 × 33 = 9 × (30 + 3)
24 × 3 × 2 = 24 × (3 × 2) = 24 × 6
Commutativa Associativa Distributiva
Applica le proprietà per facilitare il calcolo.
5 × 17 × 2 =
25 × 14 × 2 = ...............................
6 × 31 × 5 =
5 × 43 × 4 =
4 × 39 × 25 = ...............................
× 5 × 4 =
× 12 × 8 = ...............................
× 33 × 5 =
× 6 × 2 = 2 × 78 × 50 = .............................
LA TABELLA DELLA MOLTIPLICAZIONE
Completa la tabella e le osservazioni che ne puoi ricavare.
• La tabella della moltiplicazione è tutta perché la moltiplicazione è un’operazione .................... possibile.
• Che cosa osservi nella prima colonna dopo l’intestazione? ................................ Perché? .................................... .....................................................
• Che cosa osservi nella prima riga sotto l’intestazione? .............................................................................
Perché?
Lo zero nella moltiplicazione è ..............................................................................................................................
• Nella seconda colonna a destra dell’intestazione osservo che .............................................................. perché
Nella seconda riga sotto l’intestazione osservo che ............................................ perché ..................................................................................................................................
Nella moltiplicazione l’uno è ..................................................................................................................................
• Sulla diagonale sono disposti i numeri : sono prodotti di fattori
OSSERVO LA TABELLA DELLA MOLTIPLICAZIONE
Completa osservando la tabella della moltiplicazione.
• La diagonale è asse di simmetria della tabella? ............................................................................................. Perché? ..............................................................................................................................................................................
• Nella tabella puoi osservare la proprietà commutativa della moltiplicazione?
Scrivi alcuni esempi: ...................................................................................................................................................
• Scrivi i multipli dei numeri 0, 1, 2, 3,
• Ogni numero ha un numero di multipli finito o infinito? .........................................................................
• Lo zero è multiplo di
• Osserva in tabella i numeri primi: quante volte compaiono? multipli ¿di
Ora completa le seguenti tabelle.
MOLTIPLICAZIONI IN COLONNA
Esegui le moltiplicazioni in colonna con la prova.
PROBLEMI E MOLTIPLICAZIONI
Risolvi i problemi con le operazioni e la risposta.
1 In una Scuola Primaria ci sono 4 classi prime, ciascuna di 22 bambini, 3 classi seconde ciascuna di 24 bambini, 5 classi terze ciascuna di 18 bambini, 4 classi quarte ciascuna di 25 bambini e 5 classi quinte ciascuna di 21 bambini. Quanti bambini ci sono nella scuola?
• Operazioni: ............................................................................. .............................................................................
• Risposta: .............................................................................
2 Un negozio di elettrodomestici ha venduto 54 frigoriferi a ? 899 l’uno, 74 forni microonde a ? 475 l’uno e 30 lavatrici a ? 1 200 l’una. Quanto ha incassato il negozio?
• Operazioni: ....................................................
• Risposta: ......................................................... .............................................................................
3 Un pasticciere ha preparato 18 torte alla crema guarnendole con 12 fragole ciascuna e 24 torte al cioccolato guarnendone ciascuna con 4 fragole in meno. Quante fragole ha utilizzato?
• Operazioni: .................................................... .............................................................................
• Risposta: .........................................................
.............................................................................
SOTTRAZIONI E PROPRIETÀ
Esegui le seguenti sottrazioni, applicando la proprietà invariantiva, dopo aver osservato l’esempio.
LA TABELLA DELLA SOTTRAZIONE
Completa la tabella della sottrazione e le relative osservazioni.
• La tabella della sottrazione non è perché la sottrazione con i numeri naturali non è sempre
• Che cosa osservi nella prima colonna a destra dell’intestazione?
Perché?
• Che cosa osservi nella prima riga sotto l’intestazione?
Perché?
• Lo zero, nella sottrazione, è elemento neutro solo quando è
• Sulla diagonale troviamo . ........................................................................................................................................: si ottengono ...................................................................................................................................................................
• La diagonale è asse di simmetria della tabella? Perché?
• Dove si trova il numero 2 come risultato/differenza? ............................................................................... E il numero 4? ................................................................................................................................................................
SOTTRAZIONI IN TABELLA
Completare le seguenti tabelle della sottrazione.
PROBLEMI E SOTTRAZIONI
Leggi e risolvi i seguenti problemi.
1 Martina, Federico ed Eleonora confrontano le loro collezioni di figurine: Martina ne ha 184, Federico ne ha 17 in meno di Martina ed Eleonora ne ha 29 in meno di Federico. Quante figurine hanno Federico ed Eleonora?
• Operazioni: .................................................... .............................................................................
• Risposta:
2 In un frutteto ci sono meli, peschi e albicocchi. Le piante di mele sono 85, 12 in più delle piante di pesche; le piante di albicocche sono 25 in meno delle piante di pesche. Quanti sono i peschi e gli albicocchi?
• Operazioni: ............................................................................. .............................................................................
• Risposta: .........................................................
3 Al Museo di Scienze Naturali sono entrate in sette giorni 1 580 persone. Lunedì sono entrati 424 visitatori, martedì 39 in meno e mercoledì 28 in meno di martedì. Quante persone sono entrate in tutto negli altri quattro giorni?
• Operazioni: .................................................... .............................................................................
• Risposta:
POLIGONI E NON POLIGONI
Osserva le figure, colora le regioni che hanno il confine formato solo da segmenti e completa.
• Un poligono è una figura geometrica piana formata da una linea
Ora colora con lo stesso colore i poligoni che hanno lo stesso numero di lati.
Prova a disegnare un paesaggio utilizzando solo poligoni.
POLIGONI CONCAVI E POLIGONI CONVESSI
Osserva i poligoni e rispondi.
• Quale caratteristica hanno in comune i poligoni A e C?
• Quale caratteristica hanno in comune i poligoni B e D?
Nell’insieme universo individua l’insieme dei poligoni convessi e l’insieme dei poligoni concavi.
GRUPPI DI POLIGONI
Conta il numero degli angoli e dei lati di ogni poligono, poi ricopia le lettere corrispondenti nel relativo diagramma.
TRIANGOLI
QUADRILATERI
PENTAGONI ESAGONI
OTTAGONI
• Il nome dei poligoni dipende dal numero dei ............................... e degli ...................................
• Il poligono con il minor numero di lati è il
• In un poligono il numero dei lati e il numero degli angoli è .............................................................
GRAFICI E INFORMAZIONI
Osserva l’istogramma che si riferisce al numero di allievi iscritti ai corsi di musica della scuola “Settenote” nei 7 anni di attività. Poi rispondi.
• In quale anno ci sono stati più iscritti? ................................ Quanti sono stati? ................................
• In quale anno ci sono stati meno iscritti? ................................ Quanti in meno rispetto all’anno con più allievi?
• Qual è la media degli allievi?
• Qual è la moda? ................................
• Qual è la mediana? ................................
Ora registra gli stessi dati con un ideogramma.
= 5 allievi
I PIANETI DEL SISTEMA SOLARE
Leggi il testo e inserisci in modo opportuno le parole date.
Intorno al Sole ruotano otto . I Pianeti hanno un’origine simile al ............................................., ma si sono raffreddati e non brillano di luce ....................................
Alcuni Pianeti sono luminosi semplicemente perché ............................................. la luce solare.
Venere, Mercurio, la Terra e Marte sono i quattro Pianeti più al Sole e sono chiamati Pianeti perché la loro superficie è solida e rocciosa. Giove, Urano, Nettuno e Saturno si trovano a grande .................................................... dal Sole, sono costituiti da ............................................. e hanno dimensioni enormi.
Molti Pianeti sono circondati da , corpi celesti simili a loro, ma di ridotte dimensioni.
Ora osserva il disegno e collega i nomi dei Pianeti in modo opportuno.
LA LUNA
Completa le frasi cancellando con una ✗ i riquadri sbagliati.
• La Luna è il nostro…
• La Luna ruota intorno…
• La Luna è il corpo celeste più…
• Sulla Luna non ci sono piogge, venti, nubi perché…
• Il paesaggio lunare presenta…
• I cosiddetti “mari” sono…
• La superficie lunare è ricca di…
• La Luna è luminosa e visibile dalla Terra grazie…
• Quando la superficie lunare è esposta ai raggi del Sole può raggiungere i… ... Satellite. ... Pianeta. ... a luce propria. ... ai raggi del Sole. ... al Sole. ... 40° C. ... 100° C. ... 2 000° C. ... lontano dalla Terra ... vicino alla Terra ... non c’è acqua. ... grandi laghi. ... grandi pianure. ... lunghi fiumi e colline. ... alte montagne e immense pianure. ... crateri prodotti dal ghiaccio. ... crateri prodotti dall’impatto con meteoriti. ... non c’è atmosfera. .... alla Terra
LA LUNA NEL CIELO
Leggi e completa il testo inserendo le parole date in modo opportuno.
La Luna compie tre movimenti contemporaneamente: ruota su se stessa mentre ruota intorno alla Terra, compiendo così un moto di ; la Terra, a sua volta, la “trascina” nella .......................................... intorno al Sole.
Noi vediamo sempre la stessa faccia della Luna perché ruota su se stessa nello stesso tempo che impiega a compiere un giro intorno alla . Questo tempo è chiamato e corrisponde a 29 giorni.
Nel corso del mese lunare, l’aspetto della Luna cambia periodicamente: questi cambiamenti prendono il nome di ...........................................
Ora collega ogni “fase lunare” con la propria descrizione.
Luna nuova o novilunio
Luna crescente
Luna piena o plenilunio
Ultimo quarto
