2.1.3 Gaussian Mixture Models (GMM

Figure 1. The Potential Effects of Centroid Initialisation on Final Clustering ��-means++ (left) randomised (right)

��-means++ finds optimal centroid locations by endeavouring to cover as much of the feature space as possible with the probabilistic spreading out of centroids. The first centroid’s position is randomly chosen whilst the positions of the following centroids are initialised at the farthest data point ���� from their nearest preceding centroid ���� (Arthur and Vassilvitskii, 2007).

Algorithm 2. ��-means++ centroid initialisation 1. Randomly assign the first centroid ���� 2. Compute distance of all data points ���� from the nearest previously chosen centroid ���� 3. Assign new centroid to the farthest point ���� from the nearest previously chosen centroid ���� 4. Repeat steps 2 & 3 until all k centroids are initialised

Thiruvengatanadhan (2015) evaluated the performance of ��-means clustering on Power Normalised Cepstral Coefficients (PNCC) features for the separation of speech and music. The study achieved 87% cluster accuracy for 10-second audio durations. Also in 2015, Bello and Salamon applied the spherical ��-means algorithm to feature learning on an urban sound dataset, yielding improved results compared against Mel Frequency Cepstral Coefficients (MFCC) features when configured to capture the temporal dynamics of urban sounds.

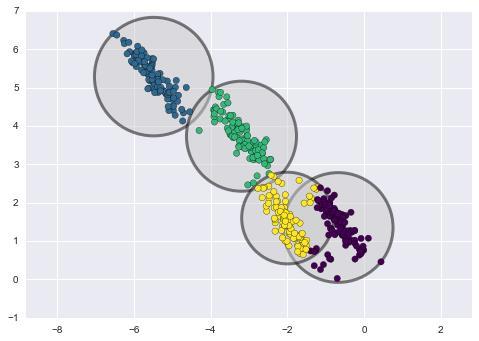
Although k-means is a common choice for multivariate data segmentation, it is not without its limitations, most notably, the fixed circular cluster model (spherical in higher dimensions) relies on circular cluster allocations and can cause data points to be incorrectly clustered if the clusters present in non-circular distributions (fig 2).

Figure 2. Incorrect Cluster Assignments Caused by ��-means Circular Cluster Models

Gaussian Mixture Models (GMM) are presented in the literature as a more flexible alternative to ��means due to their probabilistic nature and ability to model arbitrary shaped clusters. The underlying algorithm of GMM is very similar to k-means, however, due to small differences in the way cluster probability is quantified, GMM can tackle the drawbacks of the k-means algorithm (Everitt et al., 2011). Whilst k-means performs what is referred to as ‘hard classification’ meaning it makes final specifications regarding which data belong to which cluster, it doesn’t achieve what GMM ‘soft