Propiedadesdelasdesigualdadesypasospara resolverinecuaciones
¿Qu´eesunintervalo?
Enmatem´aticas,un intervalo esunsubconjuntodelosn´umerosrealesqueincluyetodoslosn´umeros comprendidosentredosextremosdados.Seutilizaparaexpresarsolucionesdeinecuaciones,dominios defunciones,rangosyrestricciones.
Losintervalosseclasificanseg´unsiincluyenoexcluyensusextremos:
• Abierto: (a,b)= {x ∈ R : a<x<b} —noincluyelosextremos.
• Cerrado: [a,b]= {x ∈ R : a ≤ x ≤ b} —incluyeambosextremos.
• Semiabiertoalaizquierda: (a,b]= {x ∈ R : a<x ≤ b}
• Semiabiertoaladerecha: [a,b)= {x ∈ R : a ≤ x<b}
Tambi´enexistenintervalosinfinitos:
• (a, +∞)= {x ∈ R : x>a}
• (−∞,b)= {x ∈ R : x<b}
• [a, +∞)= {x ∈ R : x ≥ a}
• (−∞,b]= {x ∈ R : x ≤ b}
Ejemplos:
• Losvaloresmayoresque5seescribencomo(5, +∞).
• Losn´umerosentre2y4,incluyendoambosextremos,seescribencomo[2, 4].
• Lasoluci´onde1 <x ≤ 3serepresentacomo(1, 3].
Parasaberm´as: https://youtu.be/3hoeBMp0cQw?si=qYhfV2Meh2wigYYI
Representaci´ongr´aficadeintervalos
Losintervalospuedenrepresentarsesobrelarectanum´erica.Paraelloseusan:
• C´ırculosabiertos (◦)paraextremosnoincluidos.
• C´ırculoscerrados ()paraextremosincluidos.
• Flechas parase˜nalarqueelintervaloseextiendehaciainfinito.
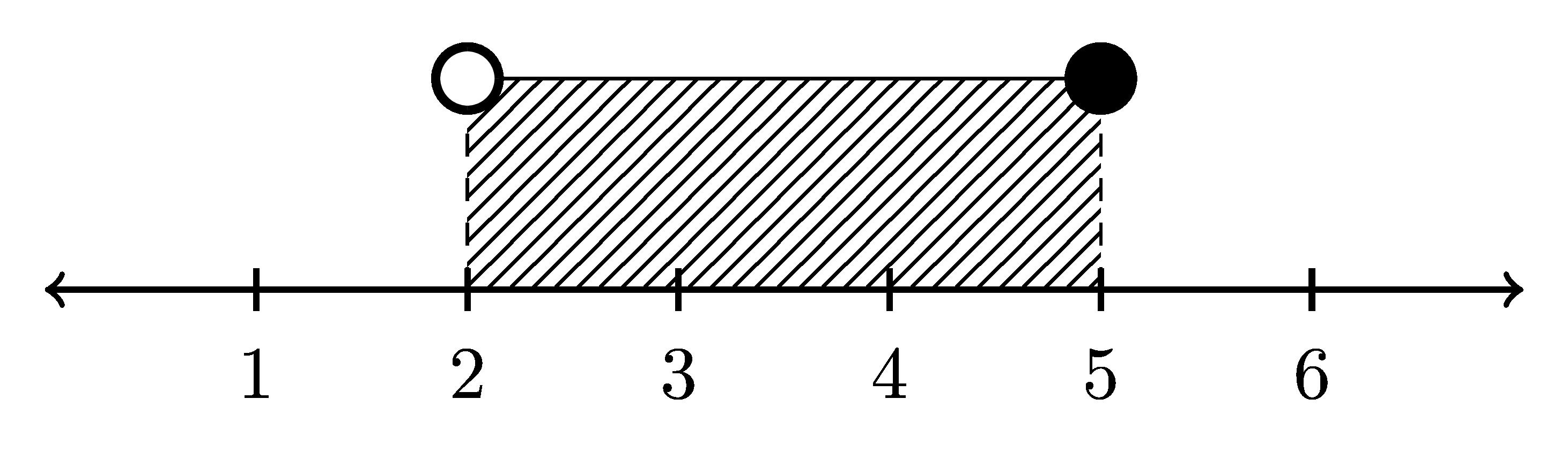
Ejemplo1: Elintervalo(2, 5]serepresentaconunc´ırculoabiertoen2ycerradoen5.
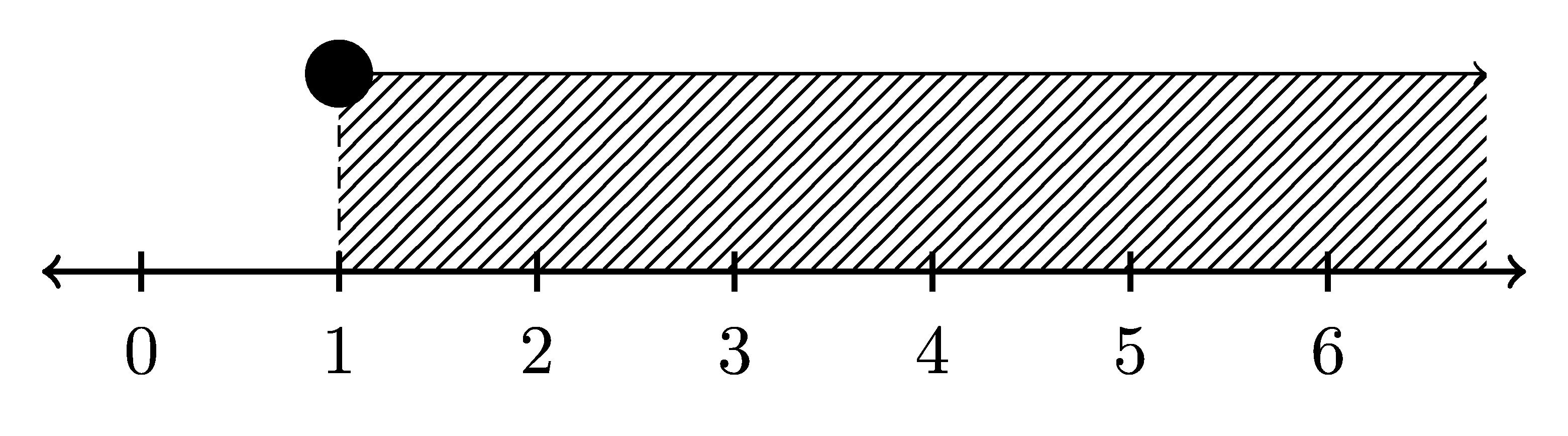
Ejemplo2: Elintervalo[1, +∞)serepresentaconunpuntocerradoen1yunaflechahacialaderecha.
Parasaberm´as: https://youtu.be/tyt6T1Ukq3w?si=GaGqDEjowc92xeVq
¿Qu´eesunainecuaci´on?
Una inecuaci´on esunadesigualdadalgebraicaquecontieneunavariable.Adiferenciadeunaecuaci´on, susoluci´onnoesun´unicovalor,sinounconjuntodevaloresquesatisfacenladesigualdad.
S´ımbolosutilizados: <, >, ≤, ≥
Ejemplo: Lainecuaci´on x +2 < 5secumpleparatodoslos x< 3.Soluci´on:(−∞, 3)
Parasaberm´as: https://youtu.be/y9vDsarVxtg?si=2iPVsN9IECS9_orq
Propiedadesdelasdesigualdades
Lasinecuacionespuedenresolverseaplicandotransformacionesv´alidas,similaresalasdelasecuaciones:
1. Sumaoresta: Sepuedesumarorestarelmismon´umeroenambosladossinalterarelsentido.
x +3 > 5 ⇒ x> 2
2. Multiplicaci´onodivisi´onporn´umeropositivo: Elsignodeladesigualdadsemantiene.
4x ≤ 12 ⇒ x ≤ 3
3. Multiplicaci´onodivisi´onporn´umeronegativo: Seinvierteelsentidodeladesigualdad.
3x ≤ 12 ⇒ x ≥−4
Parasaberm´as: https://youtu.be/yPSuv-CoZ3g?si=Qf3Yzgmsc9dIGW0X
Inecuacionescuadr´aticas
Una inecuaci´oncuadr´atica esunadesigualdaddondeapareceuntrinomiodesegundogrado.
Pasospararesolver:
• Llevarlaexpresi´onalaformaest´andar:desigualdadconcero.
• Factorizareltrinomio.
• Analizarlossignosdelaexpresi´onenlosintervalosdefinidosporlasra´ıces.
Ejemplo: x 2 4 < 0 ⇒ (x 2)(x +2) < 0
Lasra´ıcesson x = 2y x =2.Analizamoslossignos:
• En(−∞, 2):(+)( )= → nocumple
• En( 2, 2):( )(+)= → s´ıcumple
• En(2, +∞):(+)(+)=+ → nocumple
Soluci´on: ( 2, 2)
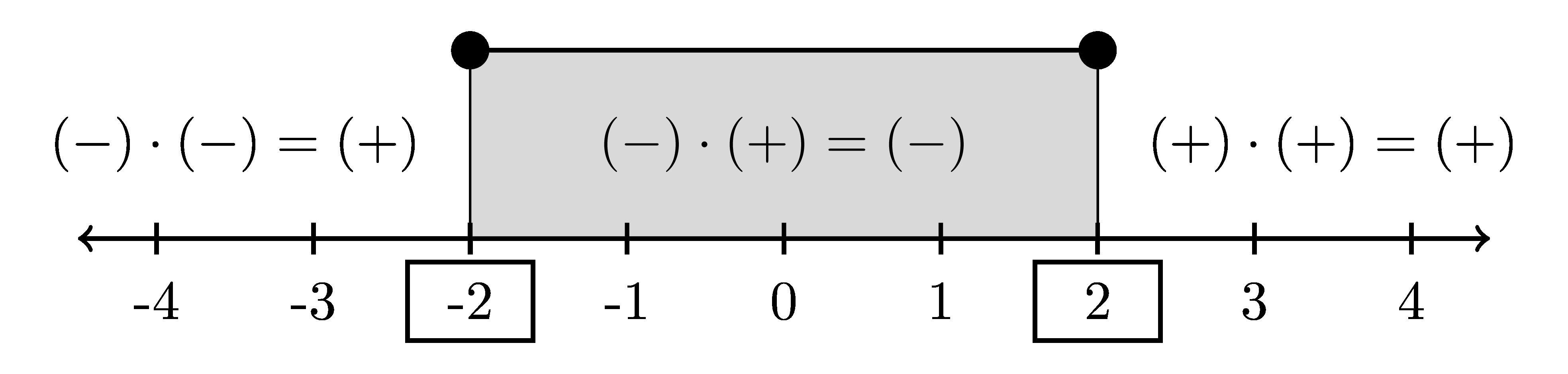
Parasaberm´as: https://youtu.be/h8pcBJEFemc?si=UB3QIKCMloEmsFPB
Consejosclave
• Representalasoluci´onenlarectanum´ericaparamayorclaridad.
• Eninecuacionescuadr´aticas,nobastaconencontrarlasra´ıces:analizaelsignoencadaintervalo.
• Simultiplicasodividesporunn´umeronegativo,recuerdacambiarelsignodeladesigualdad.
ReferenciasBibliogr´aficas Stewart,J.,Redlin,L.,&Watson,S.(2013). Prec´alculo:Matem´aticaspara elc´alculo (6.ª ed.).CengageLearning.
