The finite element method: fundamentals and applications in civil, hydraulic, mechanical and aeronautical engineering Zhu B.
Visit to download the full and correct content document: https://textbookfull.com/product/the-finite-element-method-fundamentals-and-applicati ons-in-civil-hydraulic-mechanical-and-aeronautical-engineering-zhu-b/

More products digital (pdf, epub, mobi) instant download maybe you interests ...

Biota
Grow 2C
gather 2C cook Loucas
https://textbookfull.com/product/biota-grow-2c-gather-2c-cookloucas/

Fundamentals of the Finite Element Method for Heat and Mass Transfer 2nd Edition Perumal Nithiarasu
https://textbookfull.com/product/fundamentals-of-the-finiteelement-method-for-heat-and-mass-transfer-2nd-edition-perumalnithiarasu/

The finite element method : basic concepts and applications with MATLAB, MAPLE, and COMSOL Third Edition Heinrich
https://textbookfull.com/product/the-finite-element-method-basicconcepts-and-applications-with-matlab-maple-and-comsol-thirdedition-heinrich/

Harmonic Balance Finite Element Method: Applications in Nonlinear Electromagnetics and Power Systems 1st Edition Junwei Lu
https://textbookfull.com/product/harmonic-balance-finite-elementmethod-applications-in-nonlinear-electromagnetics-and-powersystems-1st-edition-junwei-lu/

A First Course in the Finite Element Method Si Edition
Martin
https://textbookfull.com/product/a-first-course-in-the-finiteelement-method-si-edition-martin/

The Finite Element Method for Boundary Value Problems: Mathematics and Computations 1st Edition Reddy
https://textbookfull.com/product/the-finite-element-method-forboundary-value-problems-mathematics-and-computations-1st-editionreddy/

Engineering Applications of Discrete Element Method: Operation Analysis and Optimization Design of Coal and Agricultural Machinery Xuewen Wang
https://textbookfull.com/product/engineering-applications-ofdiscrete-element-method-operation-analysis-and-optimizationdesign-of-coal-and-agricultural-machinery-xuewen-wang/

Basic Civil and Mechanical Engineering 1st Edition G. Shanmugam
https://textbookfull.com/product/basic-civil-and-mechanicalengineering-1st-edition-g-shanmugam/

Extended Finite Element Method Tsinghua University Press Computational Mechanics Series 1st Edition Zhuo Zhuang
https://textbookfull.com/product/extended-finite-element-methodtsinghua-university-press-computational-mechanics-series-1stedition-zhuo-zhuang/

TheFiniteElementMethod
TheFiniteElementMethod
FundamentalsandApplicationsinCivil,Hydraulic,Mechanicaland AeronauticalEngineering
BofangZhu Professor,ChinaInstituteofWaterResourcesandHydropowerResearch and Academician,ChineseAcademyofEngineering Beijing,China
Thiseditionfirstpublished2018byJohnWiley&SonsSingaporePte.Ltdunderexclusivelicencegrantedby TsinghuaUniversityPressforallmediaandlanguages(excludingsimplifiedandtraditionalChinese) throughouttheworld(excludingMainlandChina),andwithnon-exclusivelicenseforelectronicversionsin MainlandChina.
©2018TsinghuaUniversityPress
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedinaretrievalsystem,or transmitted,inanyformorbyanymeans,electronic,mechanical,photocopying,recordingorotherwise, exceptaspermittedbylaw.Adviceonhowtoobtainpermissiontoreusematerialfromthistitleisavailable athttp://www.wiley.com/go/permissions.
TherightofBofangZhutobeidentifiedastheauthorofthisworkhasbeenassertedinaccordancewithlaw.
RegisteredOffices
JohnWiley&Sons,Inc.,111RiverStreet,Hoboken,NJ07030,USA
JohnWiley&SonsSingaporePte.Ltd,1FusionopolisWalk,#07-01SolarisSouthTower,Singapore138628
EditorialOffice
1FusionopolisWalk,#07-01SolarisSouthTower,Singapore138628
Fordetailsofourglobaleditorialoffices,customerservices,andmoreinformationaboutWileyproducts visitusatwww.wiley.com.
Wileyalsopublishesitsbooksinavarietyofelectronicformatsandbyprint-on-demand.Somecontentthat appearsinstandardprintversionsofthisbookmaynotbeavailableinotherformats.
LimitofLiability/DisclaimerofWarranty
Whilethepublisherandauthorshaveusedtheirbesteffortsinpreparingthiswork,theymakeno representationsorwarrantieswithrespecttotheaccuracyorcompletenessofthecontentsofthisworkand specificallydisclaimallwarranties,includingwithoutlimitationanyimpliedwarrantiesofmerchantabilityor fitnessforaparticularpurpose.Nowarrantymaybecreatedorextendedbysalesrepresentatives,written salesmaterialsorpromotionalstatementsforthiswork.Thefactthatanorganization,website,orproductis referredtointhisworkasacitationand/orpotentialsourceoffurtherinformationdoesnotmeanthatthe publisherandauthorsendorsetheinformationorservicestheorganization,website,orproductmayprovide orrecommendationsitmaymake.Thisworkissoldwiththeunderstandingthatthepublisherisnotengaged inrenderingprofessionalservices.Theadviceandstrategiescontainedhereinmaynotbesuitableforyour situation.Youshouldconsultwithaspecialistwhereappropriate.Further,readersshouldbeawarethat websiteslistedinthisworkmayhavechangedordisappearedbetweenwhenthisworkwaswrittenandwhen itisread.Neitherthepublishernorauthorsshallbeliableforanylossofprofitoranyothercommercial damages,includingbutnotlimitedtospecial,incidental,consequential,orotherdamages.
LibraryofCongressCataloging-in-PublicationDataappliedfor HardbackISBN:9781119107316
Coverdesign:Wiley
CoverImage:©Magnilion/Gettyimages
Setin10/12ptWarnockProbySPiGlobal,Chennai,India 10987654321
Contents
Preface xxiii
AbouttheAuthor xxv
1IntroductiontoFiniteElementMethodandMatrixAnalysisof Truss 1
1.1IntroductiontoFiniteElementMethod 1
1.2TrussAnalysisOverview 5
1.3StiffnessMatrixofHorizontalBarElement 8
1.4StiffnessMatrixofInclinedBarElement 10
1.5CoordinateTransformation 11
1.6NodalEquilibriumEquationandGlobalStiffnessMatrix 14
1.7TreatmentofBoundaryConditions 15 Bibliography 23
2PlaneProblemsinTheoryofElasticity 25
2.1DiscretizationofContinuousMedium 25
2.2DisplacementFunction 28
2.3ElementStrain 30
2.4InitialStrain 31
2.5ElementStress 32
2.5.1IsotropicBody:PlaneStress 32
2.5.2IsotropicBody:PlaneStrain 33
2.5.3AnisotropicBody 34
2.6EquivalentNodalForceandElementStiffnessMatrix 35
2.7NodalLoads 40
2.7.1EquivalentNodalLoadsofDistributedBoundaryForces 41
2.7.2NodalLoadsofUniformVolumeForce 41
2.7.3NodalLoadsDuetoPotentialofVolumeForce 42
2.7.4NodalLoadsCausedbyInitialStrain 43
2.8NodalEquilibriumEquationandGlobalStiffnessMatrix 43
2.9EstablishtheGlobalStiffnessMatrixbytheCodingMethod 48
2.10CalculationExample 51
2.10.1StressConcentrationneartheCircularHole 51
2.10.2StressAnalysisofIBeamwithaHoleinWeb 51
2.10.3StressAnalysisoftheConcreteGravityDam 51 Bibliography 51
3ElementAnalysis 53
3.1PrincipleofVirtualDisplacement 53
3.2ElementDisplacement 56
3.3ElementStrainandStress 57
3.4NodalForceandElementStiffnessMatrix 57
3.5NodalLoad 59
3.5.1DistributedVolumeForce 60
3.5.2DistributedSurfaceForce 60
3.5.3InitialStrainandInitialStress 61
3.6ApplicationExamplesofthePrincipleofVirtualDisplacements:Beam Element 61
3.7StrainEnergyandComplementaryStrainEnergy 64
3.8PrincipleofMinimumPotentialEnergy 65
3.9MinimumComplementaryEnergyPrinciple 69
3.10HybridElement 70
3.11HybridElementExample:PlaneRectangularElement 73
3.12MixedEnergyPrinciple 75
3.13CompositeElement 77 Bibliography 79
4GlobalAnalysis 81
4.1NodalEquilibriumEquation 81
4.2ApplicationofthePrincipleofMinimumPotentialEnergy 82
4.3TheLowLimitPropertyoftheSolutionofMinimumPotentialEnergy 84
4.4TheConvergenceofSolutions 85
4.5AnalysisoftheSubstructure 88
4.5.1MultipleSubstructures 89
4.5.2CondensationoftheInternalDegreesofFreedomofSubstructures 90
4.5.3CoordinateTransformation 90 Bibliography 91
5High-OrderElementofPlaneProblem 93
5.1RectangularElements 93
5.2AreaCoordinates 97
5.3High-OrderTriangularElement 100
5.3.16-NodeQuadraticTriangularElement 100
5.3.210-Node3-OrderTriangularElement 101
5.3.33-Node18DOFTriangularElement 102 Bibliography 104
6AxisymmetricalProblemsinTheoryofElasticity 105
6.1StressesDuetoAxisymmetricalLoads 105
6.1.1DisplacementFunction 105
6.1.2ElementStrains 106
6.1.3ElementStress 108
6.1.4ElementStiffnessMatrix 109
6.1.5NodalLoads 110
6.2AntisymmetricalLoad 110 Bibliography 114
7SpatialProblemsinTheoryofElasticity 115
7.1ConstantStrainTetrahedralElements 115
7.1.1DisplacementFunction 115
7.1.2ElementStrain 117
7.1.3ElementStress 118
7.1.4StiffnessMatrixoftheElement 119
7.1.5NodalLoad 120
7.2VolumeCoordinates 121
7.3High-OrderTetrahedralElements 122
7.3.110-NodeLinearStrainTetrahedralElements 122
7.3.220-NodeTetrahedralElement 123 Bibliography 124
8ShapeFunction,CoordinateTransformation,Isoparametric Element,andInfiniteElement 125
8.1DefinitionofShapeFunctions 125
8.2One-DimensionalShapeFunctions 126
8.3Two-DimensionalShapeFunction 127
8.4Three-DimensionalShapeFunction 130
8.5CoordinateTransformation 136
8.5.1PlaneCoordinateTransformation 142
8.5.2SpatialCoordinateTransformation 144
8.6DisplacementFunction 145
8.7ElementStrain 147
8.8StiffnessMatrix 151
8.9NodalLoads 153
8.10DegradationofIsoparametricElements 155
8.10.1Degradationof4-NodePlaneIsoparametricElements 155
8.10.2Degradationofan8-NodeSpaceIsoparametricElement 158
8.10.3DegradationofHigh-OrderElements 160
8.11NumericalIntegration 161
8.11.1One-DimensionalGaussQuadratureFormula 162
8.11.2Two-DimensionalandThree-DimensionalGaussQuadrature Formulas 163
8.12SelectionoftheNumericalIntegrationOrder 164
8.12.1ConditionsforNonsingularityoftheGlobalStiffness Matrix[K ] 164
8.12.2IntegralOrderEnsuringtheCalculationPrecision 165
8.12.3ReducedIntegrationandSelectedIntegration 167
8.13StressRefinementandStressSmoothing 168
8.13.1StressRefinement 168
8.13.2StressSmoothing 169
8.14ElementalFormandLayout 173
8.14.1EffectoftheElementalShapeonStrain 173
8.14.2EffectofEdgeNodeSpacingonStrain 175
8.14.3IntensificationofComputingMeshofIsoparametricElements 175
8.15InconsistentElements 176
8.16PatchTest 179
8.17Triangular,Tetrahedral,andPrismaticCurved-SideElements 183
8.18VectorComputationinIsoparametricElements 187
8.18.1DirectionCosine 188
8.18.2ScalarProduct 188
8.18.3VectorProduct 188
8.18.4InfinitesimalAreainCurvilinearCoordinateSystem 189
8.18.5InfinitesimalAreaofSpatialCurvedSurface 190
8.18.6SpatialInfinitesimalVolumes 191
8.19NumericalExamplesofIsoparametricElements 191
8.20InfiniteElements 192
8.20.1Two-DimensionalInfiniteElements 192
8.20.2Three-DimensionalInfiniteElements 196 Bibliography 199
9ComparisonandApplicationInstancesofVariousPlanarand SpatialElements 201
9.1ComparisonandSelectionofVariousPlanarElements 201
9.2ComparisonandSelectionofVariousSpatialElements 205
9.3AnalysisofStressesinArchDam 209
9.3.1ComparisonofDifferentComputationMethods 210
9.3.2TheEffectofFoundationDeformationontheDisplacementandStressof ArchDam 212
9.4AnalysisofStressinButtressDam 215
9.5AnalysisofSpatialEffectofGravityDam 217
9.6AnalysisofSpatialEffectofEarthDam 217
9.7AnalysisofStressonTunnelLining 220 Bibliography 221
10ElasticThinPlate 223
10.1BendingofElasticThinPlate 223
10.2RectangularThinPlateElement 228
10.2.1DisplacementFunction 229
10.2.2StiffnessMatrix 231
10.2.3NodalLoad 232
10.2.4Example 233
10.2.4.1SquareThinPlateSupportedbyFourEdges 233
10.2.4.2SquareThinPlateSupportedbyCornerPoints 233
10.3TriangularThinPlateElement 235
10.3.1DisplacementFunction 235
10.3.2StiffnessMatrixandNodalLoad 238
10.3.3SmoothingCurvature 238
10.3.4Example 239
10.3.4.1TheSquarePlateBearingConcentratedandDistributedLoads 239
10.3.4.2TheDistortionoftheSquarePlate 239
10.4PlateElementwithCurvedBoundaryandDeflectionandRotationDefined Respectively 241
10.4.1BeamElementConsideringtheShearingDeformation 241
10.4.2CurvedPlateElementwiththeDeflectionandRotationInterpolated Respectively 245
10.5ThePlateonElasticFoundation 248
10.5.1PlateonWinklerFoundation 248
10.5.2PlateonElasticHalfSpace 249 Bibliography 252
11ElasticThinShell 255
11.1ElementStiffnessMatrixinLocalCoordinateSystem 255
11.2CoordinateTransformation:GlobalStiffnessMatrix 259
11.3DirectionCosineofLocalCoordinate 261
11.4Curved-SurfaceShellElement 264
11.5ShellSupportedorReinforcedbyCurvedBeam 268
11.6Example 271 Bibliography 271
12AxisymmetricShell 273
12.1LinearElement 273
12.2CurvedElement 277 Bibliography 280
13ProblemsinFluidMechanics 281
13.1RelationbetweenStressandStrainforNewtonianFluids 281
13.1.1Stress–StrainRelationsforSolids 281
13.1.2Stress–RateandStrainRelationsforFluid 282
13.2EquationofMotion 283
13.3ContinuityEquation 284
13.4EnergyEquation 284
13.5StateandViscosityEquations 284
13.6FundamentalEquationsforSteadySeepageFlowandTheir Discretization 285
13.6.1GeneralizedDarcyLaw 285
13.6.2FundamentalEquations 287
13.6.3DiscretizationoftheProblems 287
13.7FreeSurfaceCalculationforSeepageAnalysis 290
13.7.1MethodofMeshRevision 290
13.7.2MethodofRevisionoftheConductivityMatrix 290
13.7.3ResidualVelocityMethod 291
13.7.4InitialVelocityMethod 294
13.8SubstitutionoftheCurtainofDrainageHolesbytheSeepingLayerfor SeepageAnalysis 296
13.9UnsteadySeepageFlow 300
13.10DynamicWaterPressureduringEarthquake 301
13.11InviscidFluidFlowFormulatedbyPotentialFunction Φ 303
13.11.1BasicEquations 303
13.11.2TheFlowaroundObjectswithoutLift 306
13.11.3TheFlowaroundObjectswithLift 307
13.12PotentialFlowFormulatedbyStreamFunction �� 307
13.12.1BasicEquations 307
13.12.2TheFlowaroundObjectswithoutLift 308
13.12.3TheFlowaroundObjectswithLift 310
13.13FlowontheFreeSurface 312
13.14ViscousandNon-NewtonianFlow 316
13.14.1SolutionoftheStokesEquation 316
13.14.2SolutionoftheNavier–StokesEquations 317 Bibliography 318
14ProblemsinConductionofHeatinSolids 321
14.1DifferentialEquation:InitialandBoundaryConditionsforConduction ofHeatinSolids 321
14.2VariationalPrincipleforConductionofHeatinSolids 322
14.2.1Euler’sEquation 322
14.2.2VariationalPrincipleofProblemofHeatConduction 322
14.3DiscretizationofContinuousBody 323
14.4FundamentalEquationsforSolvingUnsteadyTemperatureFieldby FEM 324
14.5Two-DimensionalUnsteadyTemperatureField,TriangularElements 327 14.6IsoparametricElements 329
14.6.1Two-DimensionalIsoparametricElements 329
14.6.2Three-DimensionalIsoparametricElements 331
14.7ComputingExamplesofUnsteadyTemperatureField 331
14.8TemperatureFieldofMassConcretewithPipeCooling 332
14.8.1ConcreteCylinderCooledbyWaterPipe 332
14.8.2MassConcreteCooledbyWaterPipe 334
14.8.3MassConcreteCooledbyWaterPipewithPrecise �� (�� ) 334 Bibliography 335
15MethodsforNonlinearFiniteElementAnalysis 337
15.1IncrementalMethod 338
15.1.1MethodofStartingPointStiffness 338
15.1.2MethodofMidpointStiffness 339
15.2IterativeMethod 342
15.2.1DirectIterativeMethod 342
15.2.2NewtonMethod 343
15.2.3ModifiedNewtonMethod 344
15.2.4Quasi-NewtonMethod 345
15.2.5TheCalculationof {Ψn } andInitialStressMethodandInitialStrain Method 347
15.3MixedMethod 349
15.4ApplicationofSubstructureMethodinNonlinearAnalysis 349 Bibliography 351
16ProblemsinTheoryofPlasticity 353
16.1One-DimensionalStress–StrainRelation 353
16.2DecomposeofStressTensorandStressInvariant 355
16.3Haigh–WestergaardStressSpace 357
16.3.1GeometricCharacteristicsofStressSpace 357
16.3.1.1TheHydrostaticStressAxis 357
16.3.1.2 �� Plane 358
16.3.1.3Line L′ ParalleltotheLine L358
16.3.1.4ThePlaneParallelto �� Plane 358
16.3.2TheGeometricExpressionofAnyPoint 358
16.3.3PrincipalStresses 361
16.4DecomposeofStrainTensor 362
16.5CriterionofYield 363
16.5.1TrescaYieldCriterion 364
16.5.2MisesYieldCriterion 365
16.5.3Mohr–CoulombYieldCriterion 367
16.5.4Drucker–PragerYieldCriterion 368
16.5.5LadeYieldCriterion 370
16.5.6Bresler–PisterYieldCriterion 370
16.5.7OttosenYieldCriterion 371
16.5.8Hsieh–Ting–ChenFour-ParameterCriterion 371
16.5.9Mohr–CoulombCriterionwiththeMaximumTensileStress 372
16.5.10Willam–WarnkeCriterionwithThreeandFiveParameters 373
16.5.10.1Willam–WarnkeCriterionwithThreeParameters 374
16.5.10.2Willam–WarnkeCriterionwithFiveParameters 376
16.5.11Zhang–LuYieldCriterion 378
16.6StrainHardening 379
16.6.1IsotropicStrainHardeningModel 380
16.6.2FlowingStrainHardeningModel 381
16.6.3MixedStrainHardeningModel 381
16.7CriterionofLoadingandUnloading 382
16.7.1LoadingandUnloadingofIdealPlasticMaterial 382
16.7.2LoadingandUnloadingofStrainHardenedMaterials 382
16.7.3StrainSoftening,BrittleFailure,andResidualStrength 383
16.8TheFiniteElementMethodinElastic–PlasticIncrementalTheory 384
16.8.1TheElastoplasticMatrixofIncrementalTheory 384
16.8.2SymmetricExpressionofNonassociatedElastic–PlasticStiffness Matrix 386
16.8.3TheCalculationof { �� F ���� } 387
16.8.4EffectiveStress,EffectivePlasticStrain,andCalculationof �� F /���� 389
16.8.4.1TheEffectiveStress ��i 389
16.8.4.2TheEffectivePlasticStrain ��i 389
16.8.4.3TheCalculationof �� F /���� 390
16.8.5SingularPointsontheYieldSurface 391
16.8.6NumericalCalculationMethod 392
16.8.6.1TheDisplacementIncrement 392
16.8.6.2TentativeStress 392
16.8.6.3TheScaleFactor 393
16.8.6.4ThePlasticStressIncrement 394
16.8.6.5StressBacktotheYieldSurface 395
16.8.6.6CalculationSteps 396
16.8.7Example 396
16.9FiniteElementMethodintheFullVariableTheoryofPlasticity 397
16.9.1BasicAssumptionofFullVariableTheory 397
16.9.2TheStress–StrainRelationshipofYiliuxin 398
16.9.3TheElastic–PlasticMatrixofFullVariableTheory 399
16.10PracticalSimplifiedModelsforNonlinearProblemofMaterial 399
16.10.1IsotropicModelContainingOne-VariableModulus E (t ) 400
16.10.2IsotropicModelContainingTwo-VariableModulus K (t )and G(t ) 400
16.10.3OrthotropicModelandtheEquivalentUniaxialStrain 401
16.10.3.1OrthotropicConstitutiveRelations 401
16.10.3.2EquivalentUniaxialStrain 403
16.10.4TheApproximateCalculationofStrainSoftening 404 Bibliography 404
17CreepofConcreteanditsInfluenceonStressesandDeformations ofStructures 407
17.1Stress–StrainRelationofConcrete 407
17.1.1Stress–StrainRelationofConcreteunderActionofStressinOne Direction 408
17.1.2Stress–StrainRelationUnderComplexStressConditions 411
17.1.3ModulusofElasticityofConcrete E (�� ) 413
17.1.4UnitCreepofConcrete 414
17.1.5FormulaforPreliminaryDesign 416
17.2InfluenceofCreeponStressesandDeformationsofLinearElastocreeping Body 416
17.3AnalysisofElastocreepingStressesofConcreteStructure 419
17.3.1TheCalculationofStrainIncrementunderUniaxialStress 420
17.3.1.1TheElasticStrainIncrement 420
17.3.1.2TheIncrementofCreepStrainWhen C (t ,�� )= ��(�� )[1 e r (t �� ) ] 420
17.3.1.3TheIncrementofCreepStrainWhen C (t ,�� )= ∑ ��j (�� )[1 e rj (t �� ) ] 422
17.3.2TheCalculationofStrainIncrementsunderComplexStress Conditions 423
17.3.3EquilibriumEquations 423
17.4CompoundLayerElementfortheSimulationAnalysisofConcrete Dams 424 Bibliography 429
18StressAnalysisforViscoelasticandVisco-PlasticBodies 431
18.1TheStress–StrainRelationofViscoelasticBodyundertheActionof UnidirectionalStress 431
18.1.1TheStress–StrainRelationofIdealElasticBody(HookeBody) 431
18.1.2TheStress–StrainRelationofIdealPlasticBody:TheDashpot 431
18.1.3MaxwellBody 431
18.1.4KelvinBody 432
18.1.5Standardthree-ComponentViscoelasticBody 433
18.1.6KelvinChain 433
18.1.7TheStress–StrainRelationWhenStressChangeswithTime 434
18.2TheStress–StrainRelationundertheActionofComplexStresses 434
18.2.1TheStress–StrainRelationWhenPoisson’sRatioIsConstant 434
18.2.2DifferentLawforVolumeDeformationandShearDeformation 435
18.3StressAnalysisofViscoelasticBody 436
18.3.1StressAnalysisofViscoelasticBodywithConstantPoisson’sRatio 437
18.3.2StressAnalysisofViscoelasticBodywithDifferentLawsforVolume DeformationandShearDeformation 437
18.4EffectiveModulusMethodandEquivalentTemperatureMethodforSimple HarmonicTemperatureCreepStressAnalysisofConcreteatLateAgesand ViscoelasticBody 439
18.5StressAnalysisforVisco-PlasticBodies 441
18.5.1Viscoelastic–PlasticProblemsunderActionofOne-Dimensional Stress 441
18.5.2Viscoelastic–PlasticProblemswithComplexStressStates 444
18.5.3Visco-PlasticStrainIncrement 446
18.5.4StressAnalysisofViscoelastic–PlasticBodies 446
18.5.5TheChoiceofTimeInterval Δtn 448
18.6CombinedViscoelastic–PlasticModels 449 Bibliography 451
19ElasticStabilityProblem 453
19.1GeometricalStiffnessMatrixoftheBeamElement 453
19.2GeometricalStiffnessMatrixofPlateElements 457
19.3GlobalAnalysis 459
19.4CasesofBeamSystem 461
19.5ComputingExamplesofElasticStabilityofThinPlateSystem 462
19.5.1RectangularThin-PlateElement 462
19.5.2TriangularThin-PlateElements 464 Bibliography 465
20ProblemsinAnalysisofStructureswithLargeDisplacement 467
20.1TheBasicMethodforGeometricalNonlinearProblems 467
20.1.1BasicFormulas 467
20.1.2TheSolution 469
20.1.3TheElasticStabilityProblem 470
20.2ThePlateElementofLargeDeflection 471
20.3Three-DimensionalSolidElementofLargeDisplacement 476
20.4DoubleNonlinearity:ElastoplasticLargeDisplacementProblem 478 Bibliography 478
21ProblemsinFractureMechanics 481
21.1Introduction 481
21.2DirectMethod 484
21.2.1DisplacementMethod 484
21.2.2StressMethod 486
21.3 J-Integral Method 486
21.4EnergyMethod,FlexibilityMethod,andBuecknerFormula 490
21.4.1EnergyReleaseRate G andtheRelatedFormulas 490
21.4.2FlexibilityMethod 491
21.4.3EnergyMethod 492
21.4.4BuecknerFormula 492
21.5StiffnessDerivativeMethod 494
21.5.1PlaneProblem 494
21.5.2AxialSymmetricalProblem 495
21.5.3SpaceProblem 497
21.6SingularElementoftheCrackTip 499
21.6.1TriangularSingularElement 499
21.6.2CircleSingularElement 500
21.6.3HybridSingularElement 500
21.7SingularIsoparametricElement(1/4LengthMidpointMethod) 502
21.7.1RectangularSingularIsoparametricElement 502
21.7.2TriangularDegeneratedSingularIsoparametricElement 503
21.8BluntCrackZoneModel 506
21.9Elastic–PlasticFracture 509
21.10ExtendedFiniteElementMethodforFractureAnalysis 512 Bibliography 514
22ProblemsinStructuralDynamics 515
22.1EquationsofMotion 515
22.2MassMatrix 516
22.2.1ConsistentMassMatrix 517
22.2.2LumpedMassMatrix 517
22.2.3SeveralTypicalElementMassMatrices 518
22.2.3.1BeamElement 518
22.2.3.2PlaneConstantStrainTriangularElements 518
22.2.3.3RectangularPlateElement 520
22.2.4ComparisonofTwoMassMatrices 520
22.3DampingMatrix 522
22.3.1DampingofSingleFreedomSystem 522
22.3.2DampingofSystemofMultidegreeofFreedom 523
22.4NaturalFrequencyandVibrationModeofStructure 526
22.4.1NaturalFrequencyandVibrationMode 526
22.4.2OrthogonalityofModes 529
22.4.3FreeVibrationEquationofStructureRepresentedbyFlexibility Matrix 531
22.4.4EffectsofZeroMass 532
22.4.5StaticCondensation 532
22.5ModeSuperpositionMethodforAnalyzingtheStructureofForced Vibration 535
22.6DynamicResponseofStructureundertheActionofEarthquakeSolvingby VibrationModeSuperpositionMethod 536
22.7VectorIterationMethodforComputingtheNaturalFrequencyand VibrationMode 538
22.7.1InverseIterationMethod:TheCalculationofLowestFrequencyand VibrationMode 539
22.7.2ModeClearance:CalculationofOtherFrequenciesandModes 541
22.7.3Shifting:ToImprovetheConvergenceSpeed 544
22.7.4PositiveIterativeMethod:CalculationoftheMaximumFrequencyand VibrationMode 545
22.8EnergyMethodforComputingtheNaturalFrequenciesofStructure 545
22.8.1RayleighEnergyMethod 546
22.8.2RitzEnergyMethod 547
22.9SubspaceIterationMethodforComputingtheNaturalFrequenciesand VibrationModesofStructure 548
22.9.1SubspaceIterationMethod 549
22.9.2ModifiedSubspaceIterationMethod 553
22.10RitzVectorSuperpositionMethodforSolvingForcedVibrationof Structure 554
22.11ModifiedRitzVectorSuperpositionMethod 556
22.12DynamicSubstructureMethod 557
22.13DirectIntegrationMethodforSolvingtheEquationof Motion 560
22.13.1LinearAccelerationMethod 561
22.13.2WilsonMethod(�� Method) 563
22.13.3NewmarkMethod 564
22.13.4CalculationStability,Precision,andtheSelectionofTimeStep 566
22.13.4.1ComputationalStability 567
22.13.4.2CalculationAccuracy 567
22.13.4.3TheSelectionoftheTimeStep Δt569
22.14CoupledVibrationofSolidandFluid 570
22.15SeismicStressofGravityDam 571
22.16SeismicStressofButtressDam 574
22.17VibrationofArchDam 575
22.18SeismicStressofEarthDam 575
22.19SeismicStressesofCylindricalShell 577
22.20NonlinearDynamicResponsesofUndergroundStructures 578 Bibliography 580
23ProblemsinRockMechanics 581
23.1StructureofRock 581
23.1.1RockBlock 582
23.1.2Fault 582
23.1.3SoftLayer 582
23.1.4Joint 582
23.1.5Crack 583
23.2EquivalentDeformationModulus 583
23.3Two-DimensionalLinearJointElement 584
23.3.1StiffnessMatrixofElement 584
23.3.2NodalForceDuetoInitialStress 587
23.4StiffnessCoefficientsofJointElement 587
23.5LayerElement 591
23.6Two-DimensionalHigh-OrderJointElement 593
23.6.16-NodeQuadraticJointElement 593
23.6.26-NodeCurvedJointElement 595
23.7Three-DimensionalJointElement 597
23.7.16-NodeThree-DimensionalJointElement 597
23.7.2Three-DimensionalCurvedJointElement 599
23.8InfiniteJointElement 602
23.8.1InfiniteJointElementinPlaneProblem 603
23.8.2InfiniteJointElementinSpatialProblem 604
23.9ChoiceofMethodforStressAnalysisinRock 605
23.9.1TheObjectiveandImportanceofAnalysis 606
23.9.2CharacterofRock 606
23.9.3BuriedDepthoftheProject 606
23.9.4OriginalData 606
23.10ElasticIncrementMethodforNonlinearStressAnalysis 606
23.10.1FractureandSlideofRock 607
23.10.2FractureandSlideofJointandSoftLayer 608
23.11InitialStressMethodandNoTensionMethod 608
23.11.1NoTensionMethod 609
23.11.2FractureandSlideofStratifiedRock 609
23.11.3FractureandSlideofJointandSoftLayer 611
23.12Elastic–PlasticIncrementMethod 612
23.12.1Elastic–PlasticComputationforIntegralRock 612
23.12.2Elastic–PlasticComputationforRockwithWeakSurface 613
23.12.3Elastic–PlasticCalculationforJointElement 614
23.13Viscoelastic–PlasticMethod 616
23.14ComputationofAnchorBoltinRockFoundation 618
23.15ComputingExamplesinRockMechanics 621
23.15.1ComputingofRockSlope 621
23.15.2AntislidingStabilityofGravityDamonRockFoundation 623 Bibliography 626
24ProblemsinSoilMechanics 627
24.1NonlinearElasticModel 627
24.2Elastic–PlasticModelwithTwoYieldSurfaces 633
24.2.1YieldFunctionandElastic–PlasticMatrix 634
24.2.2PlasticCoefficient 636
24.3InteractionbetweenSoilandStructure:ContactElement 637
24.4ConsolidationofSoil 640
24.4.1Terzaghi’sConsolidationTheory 640
24.4.2Biot’sConsolidationTheory 643
24.4.3NonlinearConsolidationProblem 647
24.4.3.1NonlinearElasticConsolidationProblem 648
24.4.3.2Elastic–PlasticConsolidationProblem 648
24.4.3.3ViscoelasticConsolidationProblem 648
24.4.3.4Viscoelastic–PlasticConsolidationProblem 648
24.5Stress,Deformation,andStabilityofEarthDam 648
24.6ComputationofRockfillDamwithConcreteFaceSlab 649
24.7LimitAnalysisinRockandSoilMechanics 652
24.7.1ComputationMethods 652
24.7.1.1FiniteElementStrengthDiscountMethod 653
24.7.1.2FiniteElementIncrementLoadingMethod 654
24.7.2FailureCriteria 654
24.7.3AdvantageofFiniteElementLimitAnalysisMethod 655
24.7.4CalculationExamples 655 Bibliography 657
25PlainandReinforcedConcreteStructures 659
25.1ConstitutiveModelsofConcrete 660
25.1.1UniaxialStress–StrainRelationshipofConcrete 660
25.1.2ConstitutiveModelsofConcreteinBiaxialStressState 662
25.1.3ConstitutiveModelsofConcreteinTriaxialStressState 666
25.1.4EquivalentUniaxialStrainandOrthotropicModelforConcrete 668
25.2FiniteElementModelsforCracksinConcrete 672
25.2.1CrackInducementinConcrete 672
25.2.2DiscreteCrackModel 673
25.2.3SmearedCrackModel 675
25.2.4Thin-LayerElementforCrack 677
25.2.5No-TensionCrackModel 679
25.2.6FractureMechanicsModel 680
25.2.6.1TheSharpCrackModel 680
25.2.6.2TheBluntCrackBandModel 681
25.2.6.3ComparisonofConcreteCrackModels 681
25.3TheCalculationoftheSmearedCrackModel 682
25.3.1ModesoftheConcreteFailureandConstitutiveRelationsBeforeandAfter Failure 682
25.3.2ConcreteCrushing 684
25.3.3TheSplitofConcreteUnderthePlaneStress 684
25.3.4ConcreteSplitUnderthePlaneStrainState 685
25.3.5TheSplitofConcreteoftheSpatialProblems 685
25.3.6TheBehaviorofConcreteAfterSplit 686
25.3.7TheStressAdjustmentandtheCalculationProcedurewhenConcrete Splits 686
25.4TheConstitutiveRelationandtheStressCalculationoftheSteel 691
25.4.1TheConstitutiveRelationoftheSteelBar 691
25.4.1.1TheIdealElastic–PlasticModel 691
25.4.1.2TheTrilinearModel 691
25.4.1.3TheCompleteModel 691
25.4.2TheCalculationoftheStressoftheSteelBar 692
25.5TheFiniteElementModeloftheSteelBar 692
25.5.1LineElement 692
25.5.2SolidElement 693
25.5.3ThinMembraneElement 693
25.6TheConnectionoftheSteelBarandConcrete 693
25.6.1FixedConnection 693
25.6.2TheLinkingSpringElement 693
25.6.3TheContactElement 695
25.7TheBondStressbetweentheSteelBarandConcrete:TheStiffness CoefficientoftheLinkingSpringandtheContactElement 696
25.7.1TheBondStressbetweentheBarandtheConcrete 696
25.7.2TheStiffnessCoefficientoftheLinkingSpring 697
25.7.3TheStiffnessCoefficientoftheContactElement 698
25.8TheStiffnessMatrixoftheReinforcedConcreteStructure 698
25.9TheCalculationofSteelBarintheIsoparametricElement 698
25.9.1PlaneProblem 699
25.9.2TheAxisymmetricProblems 701
25.9.2.1TheCalculationoftheBarintheRadialPlane 702
25.9.2.2TheCalculationoftheCircumferentialBar 702
25.9.2.3TheCalculationoftheSteelPlateLining 703
25.9.2.4TheCircumferentialPointElement 703
25.9.2.5TheSpatialProblems 703
25.10TheLayeredElementoftheReinforcedConcretePlatesandShells 706 Bibliography 709
26BackAnalysisofEngineering 711
26.1GeneralPrinciplesofBackAnalysis 711
26.2BackAnalysisoftheSeepageField 712
26.2.1TheOptimizationMethod 713
26.2.2TheApproximateReanalysis 713
26.2.3ApplicationoftheSubstructureMethod 715
26.3ElasticDisplacementBackAnalysisofHomogeneousBodyand ProportionalDeformationHeterogeneousBody 716
26.3.1InversionofElasticModulus 717
26.3.2TheInversionofInitialGroundStressinaSmallArea 717
26.3.2.1 E IsKnown:Inversionof q and p718
26.3.2.2 q IsKnown:Inversionof p and E718
26.3.2.3Inversionof E, p,and q attheSameTime 719
26.3.3BackAnalysisofInitialGroundStressinaWideRange 720
26.3.3.1TheFirstMethod 720
26.3.3.2TheSecondMethod 721
26.4BackAnalysisofMaterialParametersofHeterogeneousElasticBody 722
26.4.1TheDifferenceStateandItsInverseAnalysis 722
26.4.2TheStiffnessMatrixDecompositionMethod 723
26.4.3OptimizationMethod 725
26.4.4ImprovementoftheOptimizationMethod 725
26.5BackAnalysisofInteractionofElasticStructurewiththeSurrounding Medium 728
26.5.1TheDisplacementMethod 728
26.5.2TheHybridMethod 731
26.6NonlinearSolidBackAnalysis 733
26.6.1TheSolvingMethod 733
26.6.1.1TheDirectSearchMethod 733
26.6.1.2TheFirst-OrderTaylorExpansion 734
26.6.1.3TheSecond-OrderTaylorExpansion 734
26.6.2TheConstitutiveModel 734
26.6.2.1TheNonlinearElasticModel 735
26.6.2.2Elastic–PlasticModel 735
26.6.2.3ViscoelasticandViscoelastic–PlasticModel 735
26.6.2.4PartitionCompositeModel 736 Bibliography 737
27AutomaticMeshGeneration,ErrorEstimation,and Auto-adaptationTechnique 739
27.1AutomaticGenerationofComputingGrid 740
27.1.1IsoparametricTransformationMethod 740
27.1.2CompositeFunctionMethod 740
27.2ErrorEstimation 742
27.3Auto-adaptationTechnique: h Method 745
27.4Auto-adaptationTechnique: p Method 746 Bibliography 748
28Matrix 751
28.1DefinitionofMatrix 751
28.2PrincipalTypesofMatrix 752
28.2.1SquareMatrix 752
28.2.2RowMatrix 752
28.2.3ColumnMatrix 752
28.2.4Scalar 752
28.2.5TriangularMatrix 752
28.2.6DiagonalMatrix 753
28.2.7UnitMatrix 753
28.2.8ZeroMatrix 753
28.2.9TransposeMatrix 754
28.2.10SymmetricMatrix,AntisymmetricMatrixandSkewSymmetric Matrix 754
28.2.11BandMatrix 755
28.3Equality,Addition,andSubtractionofMatrices 755
28.3.1TheEqualityofMatrices 755
28.3.2TheAdditionandSubtractionofMatrices 756
28.4MatrixMultipliedbyaNumber 756
28.5MultiplicationofMatrices 757
28.5.1CompatibleMatrix 757
28.5.2RulesofMatrixMultiplication 757
28.5.3PropertiesofMatrixMultiplication 758
28.5.4ThePositivePowerofSquareMatrix 760
28.6Determinant 760
28.6.1DefinitionofDeterminant 760
28.6.2MinorsandCofactors 761
28.6.3PrincipalMinors 761
28.6.4ExpansionoftheDeterminantbyOneRow(Column) 762
28.6.5PropertiesofDeterminant 763
28.7InverseMatrix 763
28.7.1TheDefinitionofInverseMatrix 763
28.7.2TheAdjointMatrix 764
28.7.3InverseMatrix 764
28.7.4TheInverseMatrixoftheDiagonalMatrix 765
28.7.5ThePropertiesoftheInverseMatrix 766
28.8PartitionedMatrix 766
28.8.1DefinitionofthePartitionedMatrix 766
28.8.2AdditionandSubtractionofthePartitionedMatrix 766
28.8.3TheMultiplicationofthePartitionedMatrix 767
28.8.4TheInverseofthePartitionedMatrix 768
28.9OrthogonalMatrix 770
28.10PositiveDefiniteMatrix 771
28.11DerivativeofMatrix 772
28.12IntegrationofMatrix 774 Bibliography 775
29LinearAlgebraicEquationSet 777
29.1LinearAlgebraicEquationSet 777
29.2SimpleIterativeMethod 778
29.3SeidelIterativeMethod 780
29.4Over-RelaxationIterativeMethod 781
29.5BlockOver-RelaxationIterativeMethod 781
29.6DirectSolutionMethod 783
29.7ConjugateGradientMethod 788
29.8ComparisonofSeveralKindsofCommonlyUsedMethod 790
29.9HomogeneousLinearEquations 791 Bibliography 792
30VariationalMethod 793
30.1TheExtremaofFunctions 793
30.1.1TheExtremaofOne-VariableFunctions 793
30.1.2TheExtremaofaFunctionwithSeveralVariables 794
30.2TheExtremaofFunctionals 795
30.3PreliminaryTheorems 796
30.4Euler’sEquationofOne-DimensionalProblems 797
30.5Euler’sEquationforPlaneProblems 800
30.6Euler’sEquationsofSpatialProblems 803
30.7RitzMethodforSolvingVariationalProblems 806
30.8FiniteElementMethodforSolvingtheVariationalProblems 809 Bibliography 811
31WeightedResidualMethod 813
31.1IntroductiontoWeightedResidualMethod 813
31.2WeightFunctionforInternalResidualMethod 814
31.2.1CollocationMethod 814
31.2.2LeastSquaresMethod 816
31.2.3MomentMethod 817
31.2.4GalerkinMethod 818
31.3EstablishFundamentalEquationsofFiniteElementMethodbyWeighted ResidualMethod 820
31.4TwistofElasticColumn 824
31.5UnsteadyTemperatureField 828
31.6DynamicResponseofStructure 832 Bibliography 834
AppendixA 835
AppendixB 839
Index 841
Preface
Thefiniteelementmethod(FEM)issopowerfulthatmanyverycomplicatedengineeringproblemscanbesolvedbyit.Thisbookisprimarilywrittenforengineers.ItintroducesthebasicprinciplesandapplicationsofFEM.Itmayalsobeusedastextbookin universitiesandcolleges.
Thefirstpurposeofthisbookistomakeaneasyreadforengineers,sothephysical ideasareenhancedandthebasicprinciplesandcomputingmethodsareintroducedin aneasybutaccurateway.
Thesecondpurposeofthisbookistobeofpracticalvaluetoengineers,sotheformulas thatcanbeusedtoanalyzeproblemsinpracticalengineeringaregivenindetail.
Thus,therearethreedistinguishingcharacteristicsofthisbook:(1)itiseasytoread; (2)thetheoryandcomputingformulasoffiniteelementmethodarecomplete;(3)itisof practicalusetoreaders,especiallytoengineersandprofessorsandengineeringstudents.
BeforethepublicationofthefirsteditionofthisbookinChinesein1979,thepredicted readerswereengineers,butafterpublicationitwasnoticedthatitwaswellreceivednot onlybyengineersbutalsobyprofessorsandstudentsinuniversitiesandcolleges.Itis nownotonlyawidelyacceptedreferencebookforengineersbutalsowidelyusedas textbookforprofessorsandstudentsinuniversitiesandcollegesinChina.
AccordingtotheInformationCenterofChineseAcademyofScience TheFiniteElementMethod,Theory,andApplications (inChinese)isoneofthemostwell-received10 booksinChinainwaterresourcesandhydropowerdomain.
NowthenewbookinEnglishwillbepublished,Ihopeitwillbewellreceivednot onlybyengineersworkinginpracticalengineeringprojectbutalsobyprofessorsand students.
AbouttheAuthor
BofangZhu,anacademicianoftheChineseAcademyofEngineeringandafamousscientistofhydraulicstructuresandsolidmechanicsinChina,wasbornonOctober17, 1928,inYujiangCounty,JiangxiProvince.In1951,hegraduatedincivilengineering fromShanghaiJiaoTongUniversityandthenparticipatedinthedesignofthefirstthree concretedamsinChina(Fozilingdam,Meishandam,andXianghongdiandam).In1957, hewastransferredtotheChinaInstituteofWaterResourcesandHydropowerResearch wherehewasengagedintheresearchworkofhighconcretedams.Hewasawarded ChinaNationalOutstandingYoungScientistin1984andwaselectedtheacademician oftheChineseAcademyofEngineeringin1995.HeisnowtheconsultantofthetechnicalcommitteeoftheMinistryofWaterResourcesofChina,amemberoftheconsultant groupofthethreeveryhighdamsintheworld:theXiaowandam,theLongtandam, andtheBaihetandam.HewasamemberoftheeighthandtheninthChinesePeople’sPoliticalConsultativeConference,theboardchairmanoftheInstituteofComputer ApplicationofChinaCivilEngineeringSociety,andamemberofthestandingcommitteeoftheChinaCivilEngineeringSocietyandthestandingcommitteeoftheChina HydropowerEngineeringSociety.
Heisthefounderofthetheoryofthermalstressesofmassconcrete,theshapeoptimizationofarchdams,thesimulatingcomputationofconcretedam,andthetheoryof creepofmassconcreteintheword.
Hehasestablishedaperfectsystemofthetheoryofthermalstressandtemperature controlofmassconcrete,includingtwobasictheoremsofcreepofnonhomogeneous concretestructures;thelawofvariationandthemethodsofcomputationofthethermalstressesofarchdams,gravitydams,docks,sluices,tunnels,andvariousmassive concretestructures;themethodofcomputationoftemperatureinreservoirsandpipe cooling,thermalstressinbeamsonfoundation,coldwave,heighteningofgravitydam; andthemethodsandcriteriaforcontroloftemperatures.Heproposedtheideaof“longtimethermalinsulationaswellascomprehensivetemperaturecontrol”thatendedthe historyof“noconcretedamwithoutcrack”andsomeconcretedamswithoutcrackthat hadbeenfirstconstructedinChinainrecentyears,includingtheSanjiangheconcrete archdamandthethirdstageofthefamousThreeGorgesconcretegravitydam.
Heproposedthemathematicalmodelandmethodsofsolutionforshapeoptimization ofarchdams,whichwasrealizedforthefirsttimeintheworldanduptonowhadbeen appliedtomorethan100practicaldams,resultingin10–30%savingofdamconcrete, andtheefficiencyofdesignwasraisedagreatdeal.
Hehadaseriesofcontributionstothetheoryandapplicationsofthefiniteelement method(FEM).
Heproposedalotofnewmethodsforfiniteelementanalysis,includingthecompoundelement,differenttimeincrementsindifferentregions,theequivalentequation ofheatconductionforpipecooling,andtheimplicitmethodforcomputingelastocreepingstressesbyFEM.
HedevelopedthemethodofsimulatingcomputationofhighconcretedamsbyFEM. Allfactors,includingthecourseofconstruction,thevariationofambienttemperatures, theheathydrationofcement,thechangeofmechanicalandthermalpropertieswithage ofconcrete,andthepipecooling,precooling,andsurfaceinsulationcanbeconsidered intheanalysisofthestressstate.Ifthetensilestressislargerthantheallowablevalue,the methodsoftemperaturecontrolmustbechangeduntilthemaximumtensilestressis notbiggerthantheallowablevalue.Thuscrackswillnotappearinthedam.Experience showsthatthisisanimportantcontributionindamtechnology.
HeproposedtheequivalentstressforFEManditsallowablevaluesthathadbeen adoptedinthedesignspecificationsofarchdamsinChina;thustheconditionforsubstitutingthetrialloadmethodbyFEMisprovided.
Theinstrumentalmonitoringcangiveonlythedisplacementofsomeparticularpoints butcannotgivethestressfieldandthecoefficientofsafetyofconcretedams.Inorderto overcomethisdefect,heproposedanewmethodofnumericalmonitoringbyFEMthat cangivethestressfieldandthecoefficientofsafetyandraisethelevelofsafetycontrol ofconcretedamandthathadbeguntobeappliedinpracticalprojectsinChina.
Anewideaforsemimatureageofconcretehasbeenproposedbyhim.Thecrackresistanceofconcretemaybepromotedbychangingitssemimatureage.
Avastamountofscientificresearchworkshadbeenconductedunderhisdirectionfor aseriesofimportantconcretedamsinChina,suchasThreeGorges,Xiaowan,Longtan, Xiluodu,Sanmenxia,Liujiaxia,Xing’anjiang,andsoon.Fourteenresultsofhisscientific researchwereadoptedinthedesignspecificationsofgravitydams,archdams,docks, andhydraulicconcretestructures.
Hehaspublished10books: TheoryandApplicationsoftheFiniteElementMethod (1sted.in1979,2nded.in1998,3rded.in2009), ThermalStressesandTemperature ControlofMassConcrete (1sted.in1999,2nded.in2012), ThermalStressesandTemperatureControlofHydraulicConcreteStructures (1976), TheoryandApplicationsof StructuralOptimization (1984), DesignandResearchofArchDams (2002), Collected WorksonHydraulicStructuresandSolidMechanics (1988), SelectedPapersofAcademicianBofangZhu (1997), NewDevelopmentsinTheoryandTechnologyofConcreteDams (2009),and ThermalStressesandTemperatureControlofMassConcrete(inEnglish) (2014).Hehaspublishedmorethan200scientificpapers.
HewasawardedthetitleofChinaNationalOutstandingYoungScientistin1984,the ChinaNationalPrizeofNaturalSciencein1982forhisresearchworkinthermalstresses inmassconcrete,theChinaNationalPrizeofScientificProgressin1988forhisresearch workintheoptimumdesignofarchdams,andtheChinaNationalPrizeofScientific Progressin2001forhisresearchworksinsimulatingcomputationandthermalstresses. HebecameICOLD(InternationalCommissiononLargeDams)HonoraryMember.
IntroductiontoFiniteElementMethodandMatrix AnalysisofTruss
Thischapterfirstintroducesthebasicconceptionoffiniteelementmethod.Thebasic principlesoftrussanalysisaresimilartofiniteelementmethodbuteasiertobeunderstood,sothematrixanalysisoftrussisintroducedlaterasanintroductiontothefinite elementmethod.
1.1IntroductiontoFiniteElementMethod
AtrussisshowninFigure1.1(a)withallnodespinjointedandeachelementisamember onlybearingaxialforce.AframeisshowninFigure1.1(b)withallnodesrigidjointed andeachelementisamemberbearingbendingmoment,shearingforce,andaxialforce.
AbeamisshowninFigure1.1(c).Alloftheabovethreetypesofstructuresmaybe analyzedbystructuralmechanicsandthetheoryofstrengthofmaterials.Thebasic assumptionofthemistheplanesectionassumption;inotherwords,theplaneperpendiculartothecentralaxisofthememberbeforedeformationremainstobeaplane afterdeformation.Forarectangularhighbeamwithrelativelyhighratiooftheheight H tolength L (H /L),asshowninFigure1.1(d),theplanesectionassumptioncannot beapplied.Thecalculationmustbemadeaccordingtothetheoryofelasticitythatis actuallyacomplicatedproblemeventhoughtheshapeissimple.
Figure1.2showssomeengineeringstructures.Figure1.2(a)showsagravitydamon therockfoundation.Thedambodyisnearlyatriangle.However,thereareslopesonboth upstreamanddownstreamboundaries.Themechanicalandthermalpropertiesofthe dambodyandthebaserockaredifferent.Figure1.2(b)showsadouble-curvaturearch dam,whichisaparabolicshellwithvariedcurvatureandthickness,supportedonthe baserock.Figure1.2(c)showsanundergroundcaverninrockfoundation.Figure1.2(d) showsamassiveconcreteblockintheconstructionoftheconcretedam.Theblockis greatinvolumewithconcreteplacedlayerbylayer.Generally,alayerofconcretewith thicknessof1.5–3.0misplacedevery6–10days.Duetodifferentages,themodulusof elasticity,creep,andheatofhydrationarealldifferentineachlayer.
ForthevarioustypesofactualengineeringstructuresshowninFigure1.2,itisobviouslyimpossibletoworkoutthetheoreticalsolutionsbymeansoftheoryofelasticity. Numericalmethodisprobablytheonlysolutionforstresscalculation.Previously, attemptshavebeenmadetoanalyzesuchcomplicatedstructuresbyfinitedifference method.Forexample,forplaneproblems,thestructuralsectionsaredividedinto
TheFiniteElementMethod:FundamentalsandApplicationsinCivil,Hydraulic,MechanicalandAeronauticalEngineering, FirstEdition.BofangZhu. ©2018TsinghuaUniversityPress.Allrightsreserved.Published2018byJohnWiley&SonsSingaporePte.Ltd. Companionwebsite:www.wiley.com/go/zhufem17
Truss,frame,beam,andhighbeam.

Practicalengineeringstructures. rectangularmeshes,andthedifferentialequationsofequilibriumaretransformedinto finitedifferenceequations.Buttherectangularcomputingmeshisdifficulttoadapt totheboundaryofthetruestructure,soitisrarelyappliedintheanalysisofpractical complicatedstructures.
Thefiniteelementmethoddividestheoriginalstructureintofiniteelements,asshown inFigure1.3.
Theelementsareaseriesoftrianglesofdifferentsizeandshape;thusthecomputing meshcanadapttotheboundaryofthetruestructure.Furthermore,differentelements
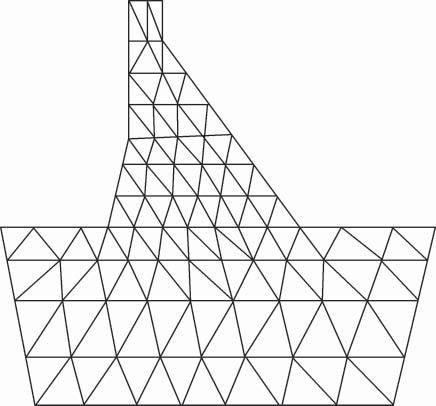
Figure1.3 Crosssectionofgravitydamdiscretedintotriangularelements.
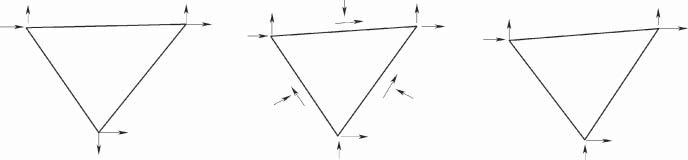
Nodal displacements
Figure1.4 Nodaldisplacements,equivalentnodalforces,andnodalloadsofanelement.
maypossessdifferentmaterialproperties,forexample,someelementsrepresentconcreteandothersrepresentrockorsoil.Thus,thefiniteelementmethodcanbeusedto analyzepracticalcomplicatedstructuresinengineeringoncomputers.Itisnowwidely appliedincivil,hydraulic,mechanical,andaeronauticalengineering.
Forexample,agravitydamontherockfoundationshowninFigure1.3isanalyzedas planeproblem.Itmaybedividedintodefinitenumberoftriangularelements,asshown inFigure1.4.Eachelementhasthreenodes,andeachnodehastwodisplacementcomponents(horizontaldisplacement ui andverticaldisplacement vi ).Soeachelementhas sixnodaldisplacements:
�� }e = [ui vi uj vj um vm ]T
Iftheelementissufficientlysmall,thevariationofthedisplacementsintheelement maybeexpressedapproximatelyasfollows:
where N i isthelinearfunctionof x and y;atnode i, Ni = 1and Nj = Nm = 0;atnode j, Nj = 1and Ni = Nm = 0;and ui and vi are,respectively,thehorizontalandvertical displacementofnode i.Thestraincomponentsare
WithstraincomponentsavailableandbythegeneralizedHooke’slaw,thestresscomponentsintheelementmaybecomputedandexpressedby
ThestressesareactingontheboundariesoftheelementasshowninFigure1.4(b).By theprincipleofvirtualwork,theactionofthestressesontheboundaryofanelement canbereplacedbythenodalforces U i , V i , U j , V j , U m , V m andexpressedby
{F }e =[Ui , Vi , Uj , Vj , Um , Vm ]T
AsshowninFigure1.4,asstrainisexpressedbythedisplacementoftheelementnode, thenodalforcemayalsobeexpressedbynodaldisplacementsas {F }e =[k ]e {�� }e (1.4)
Theloadsundertakenbytheelementsuchasboundaryforce,volumeforce,andtemperaturevariationmayalsobetransferredintonodalloads X i , Y i onnode i basedon virtualworkprinciple,asshowninFigure1.4(c).
Assumingthatthetotalnumberofelementsaroundnode i is“m”,theequilibrium equationofnode i maybegivenasfollows:
where U i isthehorizontalnodalforceofeachelement, X i isthehorizontalnodalload, and ∑ e referstothesumoftheelementsaroundnode i.
ExpressingthenodalforceinEq.(1.5)bynodaldisplacementsasEq.(1.4),wegetthe nodalequilibriumequationexpressedbynodaldisplacementsasfollows:
where[K ]referstothestiffnessmatrixand{P }referstotheloadvector.Theinverseofthe previousformulafornodaldisplacementis {�� }=[K ] 1 {P }.Withnodaldisplacement available,thestrainandstressofeachelementmaybecomputed.
Thefiniteelementmethodpossessesthefollowingsuperiorities:
1)Theoriginalcontinuousmediumisprovidedwithinfinitedegreesoffreedomand isimpossibletobesolvedoncomputers.Afterbeingdividedintofiniteelements, thenodaldisplacementsaretakenasunknownquantities.Thenumberofunknown quantitiesisfiniteanditmaybesolvedoncomputers.
2)Itmaybeusedtoanalyzevarioustypesofstructureswithcomplicatedshapesin actualengineering.
3)Differentmaterialsmaybeusedfordifferentelements.
4)Thenonlinearproblemsmaybecalculated,includingmaterialnonlinearityandgeometricalnonlinearity(greatdeformation)problems.
Thefiniteelementmethodisnowthemostpowerfulnumericalmethodthatcanbe usedtoanalyzeanycomplicatedstructureinengineering.Figure1.5showsthefinite elementmeshofafighteraircraft[1];ofcourse,itisnotcomputedbythetriangular planeelements,anditiscomputedbythecomplexelementsthatwillbedescribedin Chapters7,10,and11.
Thoughthefiniteelementmethodisoriginallydevelopedtosolvestructuralproblems, duetoalotofresearches,itisnowavailabletosolvevariousfieldproblemssuchas temperaturefields,flowfields,andelectromagneticfields.

1.2TrussAnalysisOverview
Withtheinventionofcomputers,inordertomakeuseofthisinnovativeandpowerful computationtool,matrixmethodisfirstappliedontrussandframe[2,3]andthengeneralizedintocontinuousmedium.Thecontinuousmediumistransformedintoagroup offiniteelements,withthenodaldisplacementsasunknownvariables.Anequilibrium equationsetwithfinitenumberofdegreesoffreedomisderived,whichcanbesolved bycomputer.Thisisfiniteelementmethod[4–6]inanarrowsense.Thefiniteelement methodofcontinuousmediumandthematrixanalysisoftrussandframesharethe samebasicconceptions,thatis,regardingastructureastheintegrationoffiniteelementsandconnectingsuchelementsonfinitenodes.Theonlydifferenceisthat,for trussandframe,theoriginalmemberssuchasbars,beams,andpillarsmaybedirectly takenaselements,buttherearenosuchnaturalelementsforcontinuousmediums. Therefore,theoriginalstructuremustbeartificiallydividedintofiniteblocks,which aretakenastheelementsforcalculation.Withtheassistanceoftruss,theconceptionof finiteelementmethodmaybeexplainedinarelativelyvividmanner.Therefore,inthe followingpartofthischapter,theanalysisoftrussbymatrixmethodisintroducedfirst asanintroductiontotheanalysisofcontinuousmediumbythefiniteelementmethod. Ofcourse,theframedstructurematrixanalysisitselfisofgreatapplicationvaluesin actualengineering.
Whensolvinganymechanicalproblemsrelatedtostaticallyindeterminatestructures,itisnecessarytoconsiderequilibriumconditions,deformationconditions,and physicalconditions.Thekeyforsolutionisusuallytheaccurateanalysisofdeformation conditions.
Another random document with no related content on Scribd:
gana por el valor y merecimiento de las personas ó la que procede en los hombres por la dependencia de sus pasados. Es colloquio muy provechoso para descubrir el engaño con que las gentes están ciegas en lo que toca á la honra �������� �������� en que un pastor llamado Torcuato cuenta á otros dos pastores llamados Filonio y Grisaldo los amores que tuvo con una pastora llamada Belisia. Va compuesto en estilo apacible y gracioso y contiene en sí avisos provechosos para que las gentes huyan de dexarse vencer del Amor, tomando enxemplo en el fin que tuvieron estos amores y el pago que dan á los que ciegamente los siguen, como se podrá ver en el proceso deste colloquio
�������� �������� en que se tratan los amores de un pastor llamado Torcato con una pastora llamada Belisia; el cual da cuenta dellos á otros dos pastores llamados Filonio y Grisaldo, quexándose del agravio que recibió de su amiga. Va partido en tres partes. La primera es del proceso de los amores. La segunda es un sueño. En la tercera se trata la causa que pudo haber para lo que Belisia con Torcato hizo
548
549
