IntelligentSystemsReferenceLibrary
Volume124
Serieseditors
JanuszKacprzyk,PolishAcademyofSciences,Warsaw,Poland
e-mail:kacprzyk@ibspan.waw.pl
LakhmiC.Jain,UniversityofCanberra,Canberra,Australia; BournemouthUniversity,UK; KESInternational,UK
e-mail:jainlc2002@yahoo.co.uk;jainlakhmi@gmail.com URL:http://www.kesinternational.org/organisation.php
AboutthisSeries
TheaimofthisseriesistopublishaReferenceLibrary,includingnoveladvances anddevelopmentsinallaspectsofIntelligentSystemsinaneasilyaccessibleand wellstructuredform.Theseriesincludesreferenceworks,handbooks,compendia, textbooks,well-structuredmonographs,dictionaries,andencyclopedias.Itcontains wellintegratedknowledgeandcurrentinformationinthe fieldofIntelligent Systems.Theseriescoversthetheory,applications,anddesignmethodsof IntelligentSystems.Virtuallyalldisciplinessuchasengineering,computerscience, avionics,business,e-commerce,environment,healthcare,physicsandlifescience areincluded.
Moreinformationaboutthisseriesathttp://www.springer.com/series/8578
ComputationalGeometry,VisualImage
StructuresandObjectShapeDetection
JamesF.Peters
ElectricalandComputerEngineering
UniversityofManitoba
Winnipeg,MB
Canada
ISSN1868-4394ISSN1868-4408(electronic)
IntelligentSystemsReferenceLibrary
ISBN978-3-319-52481-8ISBN978-3-319-52483-2(eBook) DOI10.1007/978-3-319-52483-2
LibraryofCongressControlNumber:2016963747
© SpringerInternationalPublishingAG2017
Thisworkissubjecttocopyright.AllrightsarereservedbythePublisher,whetherthewholeorpart ofthematerialisconcerned,specificallytherightsoftranslation,reprinting,reuseofillustrations, recitation,broadcasting,reproductiononmicrofilmsorinanyotherphysicalway,andtransmission orinformationstorageandretrieval,electronicadaptation,computersoftware,orbysimilarordissimilar methodologynowknownorhereafterdeveloped.
Theuseofgeneraldescriptivenames,registerednames,trademarks,servicemarks,etc.inthis publicationdoesnotimply,evenintheabsenceofaspecificstatement,thatsuchnamesareexemptfrom therelevantprotectivelawsandregulationsandthereforefreeforgeneraluse.
Thepublisher,theauthorsandtheeditorsaresafetoassumethattheadviceandinformationinthis bookarebelievedtobetrueandaccurateatthedateofpublication.Neitherthepublishernorthe authorsortheeditorsgiveawarranty,expressorimplied,withrespecttothematerialcontainedhereinor foranyerrorsoromissionsthatmayhavebeenmade.Thepublisherremainsneutralwithregardto jurisdictionalclaimsinpublishedmapsandinstitutionalaffiliations.
Printedonacid-freepaper
ThisSpringerimprintispublishedbySpringerNature TheregisteredcompanyisSpringerInternationalPublishingAG Theregisteredcompanyaddressis:Gewerbestrasse11,6330Cham,Switzerland
Thisbookisdedicatedto AnnaDiConcilio,ArturoTozziandsweet P forthemanyshapesandpullbacksthey havegiventome
Preface
Thisbookintroducesthefoundationsofcomputervision.Theprincipalaimof computervision(also,calledmachinevision)istoreconstructandinterpretnatural scenesbasedonthecontentofimagescapturedbyvariouscameras(see,e.g., R.Szeliski[191]).Computervisionsystemsincludesuchthingsassurveysatellites, roboticnavigationsystems,smartscanners,andremotesensingsystems.Inthis studyofcomputervision,thefocusison extractingusefulinformationfromimages (see,e.g.,S.Prince[162]).Computervisionsystemstypicallyemulatehuman visualperception.Thehardwareofchoiceincomputervisionsystemsissomeform ofdigitalcamera,programmedtoapproximatevisualperception.Hence,thereare closetiesbetweencomputervision,digitalimageprocessing,optics,photometry andphotonics(see,e.g.,E.StijnsandH.Thienpont[188]).
Fromacomputervisionperspective, photonics isthescienceoflightinthe captureofvisualscenes. Imageprocessing isthestudyofdigitalimageformation (e.g.,conversionofanalogueopticalsensorsignalstodigitalsignals),manipulation (e.g.,image filtering,denoising,cropping),featureextraction(e.g.,pixelintensity, gradientorientation,gradientmagnitude,edgestrength),description(e.g.,image edgesandtexture)andvisualization(e.g.,pixelintensityhistograms).See,e.g.,the mathematicalframeworksforimageprocessingbyB.Jähne[87]andS.G.Hoggar [82],extendingtoanumberofpractitionerviewsofimageprocessingprovided, forexample,byM.SonkaandV.HlavacandR.Boyle[186],W.Burgerand M.J.Burge[21],R.C.GonzalezandR.E.Woods[58],R.C.GonzalezandR.E. WoodsandS.L.Eddins[59],V.Hlavac[81],andC.SolomonandT.Breckon [184].Thisusefulinformationprovidesthebedrockforthefocalpointsofcomputer visionists,namely,imageobjectshapesandpatternsthatcanbedetected,analyzed andclassified(see,e.g.,[142]).Ineffect, computervision isthestudyofdigital imagestructuresandpatterns,whichisalayerofimageanalysisabovethatof imageprocessingandphotonics.Computervisionincludesimageprocessingand photonicsinitsbagoftricksinitspursuitofimagegeometryandimageregion patterns.
Inaddition,itishelpfultocultivateanintelligentsystemsviewofdigitalimages withaneyetodiscoveringhiddenpatternssuchasrepetitionsofconvexenclosures
ofimageregionsandembeddedimagestructuressuchasclustersofpointsinimage regionsofinterest.Thediscoveryofsuchstructuresismadepossiblebyquantizers. A quantizer restrictsasetofvalues(usuallycontinuous)toadiscretevalue.Inits simplestformincomputervision,aquantizerobservesaparticulartargetpixel intensityandselectsthenearestapproximatingvaluesintheneighbourhoodofthe target.TheoutputofaquantizeriscalledacodebookbyA.GershoandR.M.Gray [55, §5.1,p.133](see,also,S.Ramakrishnan,K.RoseandA.Gersho[164]).
Inthecontextofimagemeshoverlays,theGersho–Grayquantizerisreplacedby geometry-basedquantizers.A geometry-basedquantizer restrictsanimageregion toitsshapecontourandobservesinanimageaparticulartargetobjectshape contour,whichiscomparedwithothershapecontoursthathaveapproximatelythe sameshapeasthetarget.Inthefoundationsofcomputervision,geometry-based quantizersobserveandcompareimageregionswithapproximatelythesame regionssuchasmeshmaximalnucleusclusters(MNCs)comparedwithother nucleusclusters.A maximalnucleuscluster (MNCs)isacollectionofimagemesh polygonssurroundingameshpolygoncalledthenucleus(see,e.g.,J.F.Petersand E. İnanonEdelsbrunnernervesinVoronoï tessellationsofimages[150]).An imagemeshnucleus isameshpolygonthatisthecentreofacollectionofadjacent polygons.Ineffect,everymeshpolygonisanucleusofaclusterofpolygons. However,onlyoneormoremeshnucleiaremaximal.
A maximalimagemeshnucleus isameshnucleuswiththehighestnumberof adjacentpolygons.MNCsareimportantincomputervision,sincewhatwewillcall aMNCcontourapproximatestheshapeofanunderlyingimageobject.A Voronoï tessellation ofanimageisatilingoftheimagewithpolygons.AVoronoï tessellationofanimageisalsocalledaVoronoï mesh.Asampletilingofamusician imageinFig. 0.1.1isshowninFig. 0.1.2.Asamplenucleusofthemusicianimage tilingisshowninFig. 0.2.1.Thered dotsinsideeachofthetilingpolygonsare examplesofVoronoï region(polygon)generatingpoints.Formoreaboutthis,see Sect. 1.22.1.Thismusicianmeshnucleusisthecentreofamaximalnucleuscluster showninFig. 0.2.2.ThisistheonlyMNCinthemusicianimagemeshinFig. 0.1.2. ThisMNCisalsoanexampleofaVoronoï meshnerve.ThestudyofimageMNCs takesustothethresholdofimagegeometryandimageobjectshapedetection.For moreaboutthis,seeSect. 1.22.2.
Each imagetilingpolygon isaconvexhulloftheinteriorandvertexpixels. A convexhull ofasetofimagepointsisthesmallestconvexsetofthesetofpoints. Asetofimagepoints A isa convexset,providedallofthepointsoneverystraight linesegmentbetweenanytwopointsintheset A iscontainedintheset.Inother words,knowledgediscoveryisattheheartofcomputervision.Bothknowledgeand understandingofdigitalimagescanbeusedinthedesignofcomputervision systems.Invisionsystemdesigns,thereisaneedtounderstandthecomposition andstructureofdigitalimagesaswellasthemethodsusedtoanalyzecaptured images.
Thefocusofthisvolumeisonthestudyofrasterimages.Thesequeltothis volumewillfocusonvectorimages,whicharecomposedofpoints(vectors),lines andcurves.Thebasiccontentofeveryrasterimageconsistsofpixels
(e.g.,distinguishedpixelscalledsitesormeshgeneratingpoints),edges(e.g., common,parallel,intersecting,convex,concave,straight,curved,connected, unconnected),angles(e.g.,vectorangle,anglebetweenvectors,pixelangle),image geometry(e.g.,Voronoï regions[141],Delaunaytriangulations[140]),colour, shape,andtexture.Manyproblemsincomputervisionandsceneanalysisare solvedby findingthemostprobablevaluesofcertainhiddenorunobservedimage variablesandstructures(see,e.g.,P.KohliandP.H.S.Torr[96]).Suchstructures andvariablesincludethetopologicalneighbourhoodofapixel,convexhullsofsets ofpixels,nearness(andapartness)ofimagestructuresandpixelgradientdistributionsaswellasfeaturevectorsthatdescribeelementsofcapturedscenes.
Othercomputervisionproblemsincludeimagematching,featureselection, optimalclassi fierdesign,imageregionmeasurement,interestpointidentification, contourgrouping,segmentation,registration,matching,recognition,imageclustering,patternclusteringinF.Escolono,P.Suau,B.Bonev[45]andinN.Paragios, Y.Chen,O.Faugeras[138],landmarkandpointshapematching,imagewarping,
0.2.1: Musician mesh nucleus
0.2.2: Musician maximal nucleus cluster
Fig.0.2 Maximalnucleusclusteronmusicianimage
0.1.1: Muscian
0.1.2: Muscian tiling
Fig.0.1 Voronoï tessellationofmusicianimage
shapegradients[138],falsecolouring,pixellabelling,edgedetection,geometric structuredetection,topologicalneighbourhooddetection,objectrecognition,and imagepatternrecognition.
Incomputervision,thefocusisonthedetectionofthebasicgeometricstructures andobjectshapescommonlyfoundindigitalimages.Thisleadsintoastudyofthe basicsofimageprocessingandimageanalysisaswellasvectorspaceandcomputationalgeometryviewsofimages.Thebasicsofimageprocessinginclude colourspaces, filtering,edgedetection,spatialdescriptionandimagetexture. DigitalimagesareexamplesofEuclideanspaces(both2Dand3D).Hence,vector spaceviewsofdigitalimagesareanaturaloutcomeoftheirbasiccharacter. A digitalimagestructure isbasicallyageometricoravisualtopologicalstructure. Examplesofimagestructuresareimageregions,linesegments,generatingpoints (e.g.Lowekeypoints),setofpixels,neighbourhoodofapixel,halfspaces,convex setsofpixelsandconvexhullsofsetsofimagepixels.Forexample,suchstructures canbeviewedintermsofimageregionsnearestselectedpointsorcollectionsof imageregionswithaspeci fiedrangeofdiameters.An imageregion isasetof imagepoints(pixels)intheinteriorofadigitalimage.The diameter ofanyimage regionisthemaximumdistancebetweenapairofpointsintheregion).Such structurescanalsobefoundinlinesegmentsconnectedbetweenselectedpointsto formtriangularregionsin2Dand3Dimages.
Suchstructuresarealsocommonlyfoundin2Dand3Dimagesintheintersectionofclosedhalfspacestoformeitherconvexhullsofasetofpointsorwhat G.M.Zieglercalls polytopes [221].An imagehalfspace isthesetofallpoints eitheraboveorbelowaline.Inallthreecases,weobtainaregionalviewofdigital images.Formoreaboutpolytopes,seeAppendixB.15.
Everyimageregionhasashape.Someregionshapesaremoreinterestingthan others.Theinterestingimageregionshapesarethosecontainingobjectsofinterest. Theseregionalviewsofimagesleadstovariousformsofimagesegmentationsthat havepracticalvaluewhenitcomestorecognizingobjectsinimages.Inaddition, detectionofimageregionshapesofinterestviewsleadtothediscoveryofimage patternsthattranscendthestudyoftexelsinimageprocessing.A texel isanimage regionrepresentedbyanarrayofpixels.Formoreaboutshapes,seeAppendixB.18 onshapeandshapeboundaries.
Imageanalysisfocusesonvariousdigitalimagemeasurements(e.g.,pixelsize, pixeladjacency,pixelfeaturevalues,pixelneighbourhoods,pixelgradient,closenessofimageneighbourhoods).Threestandardregion-basedapproachesinimage analysisareisodatathresholding(binarizingimages),watershedsegmentation (computedusingadistancemapfromforegroundpixelstobackgroundregions), andnon-maximumsuppression(findinglocalmaximabysuppressingallpixelsthat arelesslikelythantheirsurroundingpixels)[212].
Inimageanalysis,objectandbackgroundpixelsareassociatedwithdifferent adjacencies(neighbourhoods)byT.Aberra[3].Therearethreebasictypesof neighbourhoods,namely,Rosenfeldadjacencyneighbourhoods[171,102], Hausdorffneighbourhoods[74,75]anddescriptiveneighbourhoodsinJ.F.Peters [142]andinC.J.Henry[77,76].Usingdifferentgeometries,anadjacency
neighbourhoodofapixelisdefinedbythepixelsadjacenttoagivenpixel.An image Rosenfeldadjacencyneighbourhood ofapixel p isasetofpixelsthatare adjacentto p.Adjacencyneighbourhoodsarecommonlyusedinedgedetectionin digitalimages.
A Hausdorffneighbourhood ofapoint p isdefinedby findingallpixelswhose distancefrom p islessthatapositivenumber r (calledtheneighbourhoodradius).
A descriptiveneighbourhood ofapixel p (denotedby N(img (x, y), r)isthesetof pixelswithfeaturevectorsthatmatchoraresimilartothefeaturevectorthat describes img(x, y)(theneighbourhood ‘centre’ ofadigitalimage img)andwhich arewithinaprescribedradius r.
Unlikeanadjacencyneighbourhood,adescriptiveneighbourhoodcanhave holesinit,i.e.,pixelswithfeaturevectorsthatdonotmatchtheneighbourhood centreandarenotpartoftheneighbourhood.Othertypesofdescriptiveneighbourhoodsareintroducedin[142,Sect.1.16,pp.29–34].
Thechaptersinthisbookgrewoutofmynotesforanundergraduateclassin ComputerVisiontaughtoverthepastseveralyears.Manytopicsinthisbookgrew outmydiscussionsandexchangeswithanumberofresearchersandothers, especially,S.Ramanna(thosemanyshapes,especiallyincrystals),AnnaDi Concilio(thoseproximities,region-freegeometry,andseascapeshapeslikethosein Fig. 0.3),ClaraGuadagni(those flowernervestructures),ArturoTozzi(those Borsuk-UlamTheoreminsightsandGibsonshapes,Avenariusshapes),Romy Tozzi(remember8, ∞),ZdzisławPawlak(thoseshapesinpaintingsofthePolish countryside),LechPolkowski(thosemereological,topologicalandroughset structures),PiotrArtiemjew(thosedragonflywings),GiangiacomoGerla(thosetips (points)–vertices–ofUNISAcourtyardtrianglesandspatialregions),GeraldBeer (thosemomentsinSomNaimpally’slife),GuiseppeDiMaio(thoseinsightsabout proximities),Somashekhar(Som)A.Naimpally(thosetopologicalstructures), ChrisHenry(thosecolourspaces,colourshapesets),MacekBorkowski(those3D viewsofspace),HomaFashandi,DanLockery,IrakliDochviri,Ebubekir İnan (thosenearnessrelationsandneargroups),MehmetAli Öztürk(thosebeautiful algebraicstructures),MustafaUçkun,NickFriesen(thoseshapesofdwellings), ÖzlemUmdu,DoungratChitcharoen, ÇenkerSandoz(thoseDelaunaytriangulations),SurabiTiwari(thosemanycategories),KyleFedoruk(applicationofcomputervision:SubaruEyeSight®),AmirH.Meghdadi,ShabnamShahfar,Andrew Skowron(thoseproximitiesatBanacha),AlexanderYurkin,MarcinWolksi(those sheaves),PiotrWasilewski,LeonSchilmoeler,JerzyW.Grzymala-Busse(those insightsaboutroughsetsandLATEXhints),ZbigniewSuraj(thosemanyPetrinets), JarosławStepaniuk,WitoldPedrycz,RobertThomas(thoseshapesoftilings), Marković G.oko(polyforms),MiroslawPawlak,PradeepaYahampath,Gabriel Thomas,Anthony(Tony)Szturm,SankarK.Pal,DeanMcNeill,Guiseppe(Joe)Lo Vetri,WitoldKinsner,KenFerens,DavidSchmidt(settheory),WilliamHankley (time-basedspecifi cation),JackLange(thosechalkboardtopologicaldoodlings), IrvingSussman(goldnuggetsintheoremsandproofs)andBrianPeters(those fleetingglimpsesofgeometricshapesonthewalls).

Anumberofourdepartmenttechnologistshavebeenveryhelpful,especially, Mount-FirstNg,KenBiegun,GuyJonatschickandSinisaJanjic.
Andmanyofmystudentshavegivenimportantsuggestionsconcerningtopics coveredinthisbook,especially,DrewBarclay,BradenCross,BinglinLi,Randima Hettiarachchi,EnochA-iyeh,Chidoteremndu(Chido)ChinonyelumUchime, D.Villar,K.Marcynuk,MuhammadZubairAhmad,andArminaEbrahimi.
Chapterproblemshavebeenclassifi ed.Thoseproblemsthatbeginwith are thekindyoucanrunwith,andprobablywillnottakemuchtimetosolve.Problems thatbeginwith arethekindyoucanprobablysolveinaboutthetimeittakesto drinkacupofteaorcoffee.Theremainingproblemswillneedvaryinglengthsof timetosolve.
Winnipeg,CanadaJamesF.Peters
Fig.0.3 SeascapeshapesalongthecoastlineofVietri,Italy
2.7.1ComplementingandLogicalnotofPixelIntensities
2.7.2XorOperationonPairsofBinaryImages
2.8SeparatingImageForegroundFromBackground
2.9ConjunctionofThresholdedColourChannels
3.1.5WireframeSurfacePlot
3.2Isolines
4.4LinearConvolutionFiltering
4.5SelectingaRegion-of-Interest
4.6AddingNoisetoImage
5.3DoublePrecisionLaplacianFilter
5.4EnhancingDigitalImageEdges
5.5GaussianKernel
5.6GaussianFilter
5.7GaussianFilterandImageRestoration
5.8LaplaceofGaussianFilterImageEnhancement
5.12DetectingImageCorners
5.13ImageCorner-BasedVoronoï MeshesRevisited
5.13.1Voronoï TessellationDetails
5.13.2SitesforVoronoï Polygons
5.14StepstoConstructaCorner-BasedVoronoï
5.15ExtremeImageCornersinSetofMeshGenerators
5.16Voronoï MeshonanImagewithExtremeCorners ............
5.17ImageGradientApproachtoIsolatingImageEdges
5.18Corners,EdgesandVoronoÏ Mesh ........................
6.1DelaunayTriangulationGeneratesaTriangularMesh
6.2TriangleCircumcircles
6.3ConstructingaCorner-BasedDelaunayMesh
6.4Centroid-BasedDelaunayImageMesh .....................
6.4.1FindingImageCentroids .........................
6.4.2FindingImageCentroidalDelaunayMesh............
6.4.3FindingImageCentroidalVoronoï Mesh ............
6.4.4FindingImageCentroidalVoronoï Superimposed onaDelaunayMesh
7VideoProcessing.AnIntroductiontoReal-Time andOfflineVideoAnalysis
7.1BasicsofVideoProcessing
7.1.1FramePointProcessing
7.1.2ImageAcquisition
7.1.3Blobs
7.1.4FrameTilingandFrameGeometry
7.2Voronoï TilingofVideoFrames
7.3DetectionofShapesinVideoFrames ......................
7.4MeasuringShapeSimilarityandtheVoronoï VisualHull
.........................................
7.5MaximalNucleusClusters ..............................
7.8WeightFunctionforEdgelets
7.9MaximumEdgelets ....................................
7.9.1CoarseContourEdgelets
7.9.2ConnectedMeshRegionsthatareMNCs
8LoweKeypoints,MaximalNucleusClusters,Contours
8.5ShapeTheoryandtheShapesof2DImageObjects: TowardsImageObjectShapeDetection
8.6ImagePixelGradientOrientationandMagnitude
8.7Difference-of-Gaussians
8.8ImageKeypoints:D.G.Lowe’sSIFTApproach
8.9Application:KeypointBoundariesofImageMeshNuclei
8.10Supra(Outer)NucleusContours
8.11QualityofaMNCContourShape
8.12CoarseS2PandS3P(Levels2and3)MNCContours
8.13ExperimentingwiththeNumberofKeypoints
Chapter1 BasicsLeadingtoMachineVision
Fig.1.1 Voronoïgeometricviewsofimagestructures
©SpringerInternationalPublishingAG2017 J.F.Peters, FoundationsofComputerVision,IntelligentSystems ReferenceLibrary124,DOI10.1007/978-3-319-52483-2_1
Delaunaygeometricviewsofimagestructures
p , q ∈ S , ( pqr ) = Delaunaytriangle
1.1WhatIsComputerVision?
Theprincipalaimofcomputervisionistoreconstructandinterpretnaturalscenes basedonthecontentofimagescapturedbydigitalcameras[190].A naturalscene isthatpartofvisualfieldthatiscapturedeitherbyhumanvisualperceptionorby opticalsensorarrays.
Fig.1.2
Fig.1.3
Aopticalsensorarray-basednaturalsceneiseitherasasingledigitalimage capturedbycameraorasvideoframeimagecapturedbyavideocamerasuchasa webcam.
Thebasiccontentofeveryimagesceneconsistsofpixels(e.g.,adjacent,nonadjacent),edges(e.g.,common,parallel,intersecting,convex,concave,straight, curved,connected,unconnected),angles(e.g.,vector,betweenvectors,pixels),image geometry(e.g.,Voronoïregions[141],Delaunaytriangulations[140]),colour,shape, andtexture.
1.2DivideandConquerApproach
Thereconstructionandinterpretationofnaturalscenesismadeeasierbytiling(tessellating)asceneimagewithknowngeometricshapessuchastriangles(Delaunay triangulationapproach)andpolygons(Voronoïdiagramapproach).Thisisadivideand-conquerapproach.Examplesofthisapproachincomputervisionarefoundin
Shapedetection:VideoframeshapedetectionusingDelaunaytriangulationis giveninC.P.Yung,G.P.-T.Choi,K.ChenandL.M.Lui[214](see,e.g.,Fig. 1.4). Silhouettes:Usesilhouettestofindepipolarlinestocalibrateanetworkofcameras,anapproachusedbyG.Ben-Artzi,T.Halperin,M.WermanandS.Pelegin [14].Thebasicgoalhereistoachievebinocularvisionanddeterminethescene positionofa3Dobjectpointviatriangulationonapairof2Dimages(whateach singlecamerasees).Pointscalledepipolesareusedtoextract3Dobjectsfrom apairof2Dimages.An epipole isthepointofintersectionofthelinejoining opticalcenterswithanimageplane.Thelinebetweenopticalcentersiscalleda baseline.An epipolarplane istheplanedefinedbya3Dpoint m andtheoptical
Fig.1.4 Triangulatedvideoframefrom[214]
Fig.1.5 Epipolesandepipolarlines
Fig.1.6 StagesoftheVoronoïsegmentationmethodfrom[79]
centers C and C .See,forexample,thepairofepipolesandepipolarlinesin Fig. 1.5.
Videostippling:Stipplingrendersanimageusingpointsets,elementaryshapes andcolours.ThecoretechniqueinvideostipplingisVoronoïtessellationofvideo frames.ThisistheapproachbyT.HouitandF.Nielsenin[85].Thisarticlecontain agoodintroductiontoVoronoïdiagramssuperimposedonvideoframeimages(see [85,Sect.2,pp.2–3]).Voronoïdiagramsareusefulinsegmentingimages.This leadstowhatareknownasDirichlettessellatedimages,leadinganewformofkmeansclustersofimageregions(seeFig. 1.6 forstepsintheVoronoïsegmentation method).Thisformofimagesegmentationusesclustercentroidproximityto findimageclusters.ThisisapproachusedbyR.HettiarachchiandJ.F.Petersin
1.2DivideandConquerApproach5 [79].VoronoïmanifoldsareintroducedbyJ.F.PetersandC.Guadagniin[146]. A manifold isatopologicalspacethatislocallyEuclidean,i.e.,aroundeverypoint inthemanifoldthereisanopenneighbourhood.Anonemptyset X withatopology τ onit,isa topologicalspace.Acollectionofopensets τ onanonemptyopen set X isa topology on X ,providedithascertainproperties(seeAppendixB.19 forthedefinitionsofopensetandtopology).An openset isanonemptysetof points A inspace X containsallpointssufficientlycloseto A butdoesnotinclude itsboundarypoints.
Fig.1.7 Openset A = { , , , , , }
Example1.1 Sampleopensets
applepulp Applewithoutitsskin. egginterior Eggyokewithoutitsshell. wall-lessroom Roomwithoutitswalls. OpenSubimage Asubimagethatdoesincludeitsboundarypoints.Asample2 × 3 subimage A inatiny4 × 5digitalimage Img isshowninFig. 1.7.Theset A is open,sinceitcontainsonlyblacksquares anddoesnotcontainthegraypixels alongitsboundaryrepresentedby
Amanifold M isa Voronoïmanifold,provided M isaVoronoïdiagram.Any digitalimageorvideoframeimagewithatopologydefinedonit,isaVoronoï manifold.Thisisimportantincomputervision,sinceimagesthatareVoronoï manifoldshavegeometricstructuresthatareanaidinthestudyofthecharacter ofimageshapesandobjects.
CombinedGeodesicDelaunayandVororonïTessellation:DelaunaytriangulationandVoronoïdiagramsarecombinedinthestudyofgeodesiclinesandgraphs isintroducedbyY.-J.Lin,C.-XuXu,D.FanandY.Hein[112].Agraph G isa
geodeticgraph,provided,foranytwovertices p , q on G ,thereisatmostone shortestpathbetween p and q .A geodeticline isastraightline,sincetheshortest pathbetweentheendpointsofastraightlineisthelineitself.Formoreaboutthis, seeJ.Topp[195].Forexamples,seeAppendixB.7.
ConvexHulls:A convexhullofasetofpoints A (denotedbyconvh A )isthe smallestconvexsetcontaining A .Anonemptyset A inan n -dimensionalEuclideanspaceisa convexset (denotedbyconv A ),providedeverystraightlinesegment betweenanytwopointsinthesetisalsocontainedintheset.Voronoïtessellation ofadigitalimageresultsinimageregionclustersthatarehelpfulinshapedetectionandtheanalysisofcomplexsystemssuchasthecosmicweb.Thisapproach isusedbyJ.Hidding,R.vandeWeygaert,G.Vegter,B.J.T.JonesandM.Teillaud in[80].Forapairof3Dconvexhulls,seeFig. 1.8.Formoreaboutconvexhulls, seeAppendixB.3.
Fig.1.8 Sample3Dconvexhullsofasetof89points
Thesemethodsuseimageareasinsteadofpixelstoextractimageshapeandobject information.Inotherwords,weusecomputationalgeometryintheinterpretationand analysisofsceneimages.
1.3VoronoïDiagramsSuperimposedonImages
Let S beanysetofselectedpixelsinadigitalimageandlet p ∈ S .Thepixelsin S arecalled sites (or generatingpoints)todistinguishthemfromotherpixelsinan image.RecallthatEuclideandistancebetweenapairofpoints x , y intheEuclidean planeisdenotedby x y anddefinedby
Voronoïregion of p ∈ S (denoted V p )isdefinedby
Everysitein S belongstoonlyoneVoronoïregion.Adigitalimagecoveredwith Voronoïregionsiscalleda tessellatedimage.NoticethateachVoronoïregionis a convexpolygon.Thismeansthatallofthepointsonastraightedgeconnecting anypairofpointsinaVoronoïregionbelongstotheregion.Andacompletesetof Voronoïregionscoveringanimageiscalleda Voronoïdiagram or Voronoïmesh.
Example1.2 SampleVoronoïandDelaunayImageMeshes
SampleVoronoïregionsonanfMRIimageareshowninFig. 1.1.1withtheextracted VoronoïmeshshowninFig. 1.1.2.Inthiscase,eachVoronoïregionisaconvex polygoninthemeshthatsurroundsanimagecorner.ADelaunaytriangleisformed byconnectingthesitepointsofneighbouringVoronoïregions.AsampleDelaunay triangulationmeshisshowninFig. 1.2.1.ThisgivesusanotherviewofimagegeometryformedbytheinteriorpointssurroundingameshgeneratorofeachDelaunay triangle.TheextractedDelaunaytriangulationisshowninFig. 1.2.2.
Manyproblemsincomputervisionandsceneanalysisaresolvedbyfindingthe mostprobablevaluesofcertainhiddenorunobservedimagevariablesandstructures[96].SuchstructuresandvariablesincludeVoronoïregions,Delaunaytriangles,neighbourhoodsofpixels,nearness(andapartness)ofimagestructuresand pixelgradientdistributionsaswellasvaluesofencodeddesiredpropertiesofscenes. Othercomputervisionproblemsincludeimagematching,featureselection,optimalclassifierdesign,imageregionmeasurement,interestpoint,contourgrouping, segmentation,registration,matching,recognition,imageclustering,patternclustering[45, 138],landmarkandpointshapematching,imagewarping,shapegradients[138],falsecolouring,pixellabelling,edgedetection,geometricstructure detection,topologicalneighbourhooddetection,objectrecognition,andimagepatternrecognition.Typicalapplicationsofcomputervisionareindigitalvideostabilization[49,Sect.9,startingonp.261]andinrobotnavigation[93,Sect.5,starting onp.109].
Theterm camera comesfromLatin cameraobscura (darkchamber).Manydifferentformsofcamerasprovideaplaygroundforcomputervision,e.g.,affinecamera,pinholecamera,ordinarydigitalcameras,infraredcameras(alsothermographic camera),gamma(tomography)cameradevices(in3Dimaging).Anaffinecamera isalinearmathematicalmodelthatapproximatestheperspectiveprojectionderived fromanidealpinholecamera[218].Apinholecameraisaperspectiveprojection device,whichisaboxwithlight-sensitivefilmonitsinteriorbackplaneandwhich admitslightthroughapinhole.
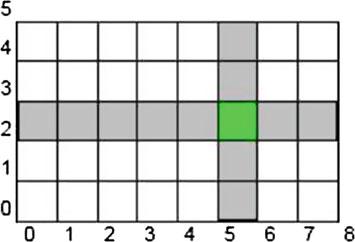
Inthiswork,thefocusisonthedetectionofthebasiccontentandstructures indigitalimages.Aninterestin imagecontent leadsintoastudyofthebasicsof imageprocessingandimageanalysisaswellasvectorspaceandcomputational geometryviewsofimages.Thebasicsofimageprocessingincludecolourspaces, filtering,edgedetection,spatialdescriptionandimagetexture.Thestudyof image structures leadstoacomputationalgeometryviewofdigitalimages.Thebasicidea istodetectandanalyzeimagegeometryfromdifferentperspectives. DigitalimagesareexamplesofsubsetsofEuclideanspaces(both2Dand3D). Hence,vectorspaceviewsofdigitalimagesareanaturaloutcomeoftheirbasic character.Digitalimagestructuresarebasicallygeometricstructures.Suchstructures canbeviewedintermsofimageregionsnearestselectedpoints(see,e.g.,thetiny regionnearestthehighlightedpixelcenteredat(5.5,2.5)inFig. 1.9).Suchstructures canalsoviewedwithrespecttolinesegmentsconnectionbetweenselectedpoints toformtriangularregions.Botharegionalviewandatriangulationviewofimage structuresleadstovariousformsofimagesegmentationsthathavepracticalvalues whenitcomestorecognizingobjectsinimagesandclassifyingimages.Inaddition, bothregionalandtriangleviewsleadtothediscoveryofpatternshiddenindigital images.
BasicApproachinImageComputationalGeometry
Thebasicapproachistodescribeadigitalimageobjectwithaknown geometricstructure.
1.4ABriefLookatComputationalGeometry
Toanalyzeandunderstandimagescenes,itisnecessarytoidentifytheobjectsin thescenes.Suchobjectscanbeviewedgeometricallyascollectionsofconnected edges(e.g.,skeletonizationsoredgesbelongingtoshapesoredgesinpolygons)or
Fig.1.9 Pixelcenteredat(5.5,2.5)inaverysmallimagegrid
imageregionsviewedassetsofpixelsthatareinsomesenseneareachotherorsetof pointsnearafixedpoint(e.g.,allpointsnearasite(also,seedorgeneratingpoint)ina Voronoïregion[38]).Forthisreason,itishighlyadvantageoustoassociategeometric structuresinanimagewithmesh-generatingpoints(sites)derivedfromthefabricof animage.Imageedges,corners,centroids,criticalpoints,intensities,andkeypoints (imagepixelsviewedasfeaturevectors)ortheircombinationsprovideidealsources ofmeshgeneratorsaswellassourcesofinformationaboutimagegeometry.
ComputationalgeometryisthebrainchildofA.Rosenfeld,whosuggested approachingimageanalysisintermsofdistancefunctionsinmeasuringthe separationbetweenpixels[168]andimagestructuressuchassetsofpixels[169, 170].Rosenfeld’sworkeventuallyledtotheintroductionoftopologicalalgorithms usefulinimageprocessing[99]andtheintroductionofafull-scaledigitalgeometry inpictureanalysis[94].
FoundationsofSceneAnalysis
ThefoundationsfordigitalimagesceneanalysisarebuiltonthepioneeringworkbyA.Rosenfeldworkondigitaltopology[98, 168–172](later calleddigitalgeometry[94])andothers[39, 99, 102, 104, 105].The workondigitaltopologyrunsparallelwiththeintroductionofcomputationalgeometrybyM.I.Shamos[175]andF.P.Preparata[158, 159], buildingontheworkonspatialtessellationsbyG.Voronoï[201, 203] andothers[27, 53, 64, 103, 124, 196].
Computationalgeometry (CG)isanalgorithmicapproachinthestudyof geometricstructures.InCG,algorithms(step-by-stepmethods)areintroducedto constructandanalyzethelinesandsurfacesofobjects,especiallyrealworldobjects. ThefocusinCGisonhowpoints,lines,polygons,smoothcurves(in2D)and polyhedraandsmoothsurfaces(in3D)areeitherconstructedordetectedandanalyzed byacomputer.ForamoregeneralviewofCPfromalinegeometryperspective,see, forexample,H.PottmannandJ.Wallner[157].
Inthecontextofdigitalimages,computationalgeometryfocusesontheconstructionandanalysisofvarioustypesofmeshoverlaysonimages.Ontheground floor,thetwomaintypesofmeshesresultfromDelaunaytriangulationsandVoronoï tessellationsonsetsofimagepixels.A Delaunaytriangulation isacoveringofa digitalimagewithtriangleswithnon-intersectinginteriors.WithDelaunaytriangulation,thefocusisonconstructingmeshesoftrianglesderivedfromselectedsetsof pixelscalledsitesorgeneratorsandwhichcovereithera2Dor3Ddigitalimage. Aprincipalbenefitofimagetriangulationsisthedetectionofimageobjectshapes coveredbymeshtriangles.Thankstotheknownpropertiesoftriangles(e.g.,uniform shape,sumoftheinteriorangles,perimeter,area,lengthsofsides),objectshapes canbedescribedinaveryaccuratefashion.FormoreaboutDelaunaytriangulation, seeJ.A.Baerentzen,J.Gravesen,F.AntonandH.Aanaes[8,Sect.14].
ImageobjectshapescanalsobecloselyapproximatedbycollectionsofVoronoï polygons(alsocalledVoronoïregions)inaVoronoïtessellationofanimage.A 2D Voronoïdiagram representsatessellationoftheplaneregionbyconvexpolygons. A 3DVoronoïdiagram representsatessellationofa3Dsurfaceregionbyconvex polygons.
Aconvexpolygonisanexampleofaconvexset.A convexset ofpoints A (denoted byconv A )hasthepropertythat,foreachpairofpoints p , q inconv A ,allofthepoints onthestraightlinesegmentconnectedbetween p and q alsobelongtoconv A .For moreaboutconvexsets,seeAppendixB.3.
Sinceobjectshapestendtoirregular,thevaryingshapesofpolygonsinatypical Voronoïimagecoveringanimagegiveamorepreciseviewoftheshapesofimage objects.ItisimportanttonoticethatDelaunaytriangleshaveemptyinteriors(only thesidesofthetrianglesareknown).Bycontrast,Voronoïpolygonshavenon-empty interiors.ThismeansthatweknowboththesidesaswellasthecontentoftheinteriorofeachVoronoïpolygon.AprincipalbenefitofimageVoronoïtessellationisthe detectionofimageobjectshapescoveredbymeshpolygons.Thankstotheknown propertiesofVoronoïpolygons(e.g.,shape,interiorangles,edgepixelgradientorientation,perimeter,diameter,area,lengthsandnumberofsides),objectshapescan bedescribedinaveryaccuratefashion.Forthisreason,Voronoïpolygonsthatcover animageneighbourhoodcontaininganobjectprovideaverydetailedviewofimage objectshapesandcontent.
AsampledigitalimagegeometryalgorithmusefulineithertriangulatingortessellatingadigitalimageisgiveninAlgorithm1.
Algorithm1:DigitalImageGeometryviaMeshCoveringImage
Input :Readdigitalimage img .
Output :Mesh M coveringanimage.
MeshSite ← MeshGeneratingPointType ; 1 img −→ MeshSitePointCoordinates ; 2
S ← MeshSitePointCoordinates ; 3
/* S containsMeshSitePointTypecoordinatesusedasmeshgeneratingpoints(seedsor 4 sites).*/;
MeshType ← MeshChoice ; 5
/* MeshType identifiesachosenformofmesh,e.g.,Voronoï,Delaunay,polynomial.*/; 6
S −→ MeshType M ; 7
MeshType M −→ img ; 8
/*Use M togaininformationaboutimagegeometry.*/; 9
Algorithm1leadstoameshcoveringadigitalimage.Imagemeshescanvary considerably,dependingonthetypeofimageandthetypemeshgeneratingpointsthat arechosen.Imagegeometrytendstoberevealed,wheneverthechoiceofgenerating pointsaccuratelyreflectstheimagevisualcontentandthestructureoftheobjectsin animagescene.Forexample,cornerswouldbethelogicalchoiceforimagescenes containingbuildingsorobjectswithsharplyvaryingcontourssuchashandsorfacial profiles.
Fig.1.10 Huntinggroundsforsceneinformation:corner-basedDelaunayandVoronoïmeshes
Example1.3 MeshesCoveringaSalernoPosteAutoScene Acorner-basedVoronoïmeshcoveringanimagescenecontainingaPosteautoparked outsidethetrainstationinSalerno,ItalyisshowninFig. 1.10.1.ThisVoronoïmesh isalsocalleda Dirichlettessellation.Usingthesamesetofcornergeneratingpoints, aDelaunaytriangulationcoverinthePosteautosceneisshowninFig. 1.10.2.For
aDelaunaytriangulationviewoffMRIs(functionalMagneticResonanceImages), seeFig. 1.2.FormoreaboutDelaunaytriangulation,seeSect. 6.1.
ForaVoronoïtessellationofthesamefMRIs,seeFig. 1.1.Oneimportantthing tolookforinVoronoïtessellationofanimageisthepresenceofclustersofmesh polygons,eachwithacentralpolygonthathasamaximumnumberofadjacent polygons.Thecentralpolygonofameshclusteriscalledthe clusternucleus.Inthat case,theclusteriscalleda maximalnucleuscluster (MNC).ImagemeshMNCs approximatetheshapeoftheunderlyingimageobjectcoveredbytheMNC.For moreaboutMNCs,seeSect. 7.5
1.5FrameworkforDigitalImages
A digitalimage isadiscreterepresentationofvisualfieldobjectsthathavespatial (layout)andintensity(colourorgreytone)information. Fromanappearancepointofview,a greyscaledigitalimage1 isrepresentedby a2Dlightintensityfunction I ( x , y ),where x and y arespatialcoordinatesandthe valueof I at ( x , y ) isproportionaltotheintensityoflightthatimpactedonanoptical sensorandrecordedinthecorrespondingpictureelement(pixel)atthatpoint. Ifwehaveamulticolourimage,thenapixelat ( x , y ) is1 × 3arrayandeacharray elementindicatesared,greenorbluebrightnessofthepixelinacolourband(or colourchannel).Agreyscaledigitalimage I isrepresentedbyasingle2Darrayof numbersandacolourimageisrepresentedbyacollectionof2Darrays,oneforeach colourbandorchannel.Thisishow,forexample,Matlabrepresentscolourimages. A binaryimage consistsentirelyofblackpixels(pixelintensity = 0)andwhite pixels(pixelintensity = 1).Forsimplicity,weusetheterm binaryimage toreferto ablackandwhiteimage.Bycontrast,a greyscaleimage isanimagethatconsists entirelyofpixelswithvaryingshadesofblack,greytonesandwhite(greytones). Binaryimagesandgreyscaleimagesare2-dimensionalintensityimages.Bycontrast,anRGB(redgreenblue) colourimage (isa3-dimensionalor multidimensionalimage)image,sinceeachcolourpixelisrepresentedby3colourchannels, onechannelforeachcolour.RGBimagesliveinawhatisknownasanRGBcolour space.Therearemanyotherformsofcolourspaces.Themostcommonalternative toanRGBspaceistheHSV(Hue,Saturation,Value)spaceimplementedbyMatlab ortheHSB(Hue,Saturation,Brightness)spaceimplementedbyMathematica.
1 A greyscaleimage isanimagecontainingpixelsthatarevisibleasblackorwhiteorgreytones (intermediatebetweenblackandwhite).
Another random document with no related content on Scribd:






































