

The Griffin
A student-led publication.
Introduction
The Humanities Corner
The Changing Nature of Spinosaurus: Earth’s Most Mysterious
Predator
Harry Tiffen
Secrets of the Select: The Mystical and Esoteric Patterns of Religion
Mr. Harman
The Strategic Importance of the Suez Canal
Sarah Ellingworth
Medea: Victim or Villain?
Calliope Psylla
The STEM Corner
Mastery Learning in Education: Is AI the Missing Link?
Mr. Britton
The Collatz Conjecture: A Simple Maths Problem No-One Can Solve - Can You?
Harry Wilson
Autism: An Overview
Oluwatamilore Adeola




Welcome to the third edition of The Griffin! This is a student-led journal, published every half-term, which hopes to provide a platform for students, staff, and alumni to write about absolutely any topic that interests and excites them. This half-term’s issue includes yet another wonderful variety of entries, ranging from exploration of ‘The Mystical and Esoteric Patterns of Religion’, to discussion of the ‘Macroeconomic Outlook for 2025’ ; hopefully, something to pique everyone’s interest!
As ever, I would like to extend a huge thank you to all of those who wrote an article! The ongoing support for and interest in this initiative from students, teachers, and alumni has been fantastic! It would also be remiss of me not to give special thanks to Mr Goulding, who was, once again, indispensable in the editorial process.
If you – students, alumni, staff, or parents – are interested in contributing to the next half-term’s edition, please do get in contact at: maximilian.pietrzak@newhallstudent.co.uk
Any feedback on the journal is also warmly welcome and encouraged – it is your opinion that matters!
I hope that you enjoy your reading of the articles!
Max.
The Changing Nature of Spinosaurus: Earth’s Most Mysterious Predator
Harry Tiffen, Y12.

Cast your minds back to 1912. You just found a pile of bones in the Egyptian desert and are wondering: ‘What on earth is this?’. That is exactly what Australian palaeontologist Richard Markgraf was thinking after discovering what we now know as the Spinosaurus in the Bahariyya oasis. It has since become an icon, featuring in (objectively the best) Jurassic Park film, countless documentaries and in the hearts of children everywhere. However, the road to where we are now, in terms of our knowledge about Spinosaurus, was a very rocky one. Countless setbacks, disasters, and advances in science have constantly changed the image of this ancient predator, an image that is changing even as I write this article.


The bones found by Richard Markgraf (left), and a reconstruction of the bones circa 1936.
Ernst Stromer von Reichenbach’s Spinosaurus
The bones discovered by Markgraf back in 1912 caught the attention of palaeontologists all over the globe, and for good reason. The remains found included a strangely shaped (even for a dinosaur) lower jaw, crocodile-like teeth and, most remarkably, a series of vertebrae sporting large spines, some of which were up to 2 metres tall. It was the German palaeontologist Ernst Stromer von Reichenbach who took up the task of studying the partial skeleton, the spines of which were so remarkable that he named the dinosaur after them: Spinosaurus aegypticus. The fossil was revolutionary, making palaeontologists rethink their ideas of what a dinosaur could look like (‘now they could have spines?!’). However, due to the limited number of bones found and the limits of early 20th century technology, not much was really known about Spinosaurus. When it was first discovered, many believed it to look like a T-Rex, but with a sail on its back. The way in which it used its sail was much debated then, and it is still debated now; some believe it was for show, while others believe it was used for thermal regulation. But, during an air raid on Munich on the 24th of April 1944, all of Stromer’s fossils, including Spinosaurus, were destroyed. For over 60 years no more significant remains of this dinosaur were found, with palaeontologists only having scans of Stromer’s original fossils to use in order to research more into what Spinosaurus may have been like.
Spinosaurus and The Late 20th Century
A few small bones were found throughout the 20th century, and the image of Spinosaurus went through some – let’s say – growing pains. As some fossils belonging to the arms were found, it was believed that Spinosaurus had remarkably long forelimbs, a theory that was reflected in reconstructions from the 70s which saw it walking on all fours. That image had worn off by the 90s, which saw Spinosaurus lose weight and get longer; it was now believed it could grow up to 20 metres long, making it the largest known predator to walk the earth. A key part of Spinosaurus, its long and slender jaw, was missing from reconstructions until the late 90s and early 2000s. It was in 2001 when arguably the most iconic reconstruction of the Spinosaurus was made – that of Universal’s Jurassic Park III.
Nizar Ibrahim’s Chance Encounter
In an event, the cause of which can only be down to the stars aligning, the Spinosaurus-shaped hole in palaeontology was filled. In the late 2000s, palaeontologist Nizar Ibrahim was conducting research in the Kem Kem beds in Morocco, an area extremely rich in fossils. He met a Bedouin fossil hunter there who led him to a rock formation made up of purple sediment with yellow stripes (this is important), within which were a series of dinosaur bones. Nizar then went on a trip to Milan’s natural history museum a year later to examine a newly discovered fossil, thought to be a Spinosaurus. He noticed that the same purple and yellow sediment was clinging to this fossil as the ones from Morocco, and immediately set out to find the Bedouin fossil hunter. He didn’t have much to go on, however – only the fossil hunter’s moustache and white shirt. He had just about given up until four years later, when sitting in a café, Nizar caught sight of a man with a moustache and a white shirt: the Bedouin fossil hunter! He managed to convince him to return to the fossil bed, after a lengthy catch-up. After confirming that they had come from the
same dinosaur as the fossil in Milan, he was able to deduce where Spinosaurus might have hunted: around rivers and marshy plains.
The Present Day
We know more about Spinosaurus now than ever before. New technology has made it possible to examine the remaining bones in extreme depth; in 2008, the top half of its jaw was put through a CT scanner, revealing a collection of holes and sinuses in its snout, just like a modern-day crocodile. This, in combination with its nostrils being set high on its skull, allowed palaeontologists to discern that Spinosaurus was an aquatic predator (it also had a diet consisting mainly, but not exclusively, of fish). The knowledge that it spent most of its time in the water led to what we now think of as the ‘most accurate reconstruction of Spinosaurus to date’ (looking pretty cool, if you ask me).

The most accurate reconstruction of Spinosaurus, circa 2021.
Secrets of the Select: The Mystical and Esoteric Patterns of Religion
Mr. Harman, Teacher of Theology.
If mysticism is defined as ‘the emphasis on religion as subsisting in experience as opposed to teaching and dogma’, it is certainly true that this was the kind of religion in which I was raised. I grew up with the traditional Latin liturgy of the Church, whose emphasis on ancient language, incense, and strict ritual impressed upon me the belief that what I partook of was something secret, esoteric, and hidden. My classical studies further intrigued the situation with mention of Bacchic rituals (as described by Euripides), Eleusinian Mysteries (Homer), and Mithraism (Plutarch and Porphyry); all of these promoted a notion of ‘mystical knowledge for initiated’, and, I should be ashamed to admit, this rather attracted me. My academic study of religion, however, painted a picture of creed, dogma, and institution. Are the organised faiths of today indeed guilty of amnesia when it comes to their mystical ancestry? Are we mistaken in our attempts to institutionalise and systematise the divine? A ‘deep dive’ of the great mystery cults of history appears necessary.
The first rule of the Eleusinian Mysteries, it appears, is that you do not talk about the Eleusinian Mysteries. Tradition tells us that a chap did try – Diagoras of Milos –but was soon charged with impiety and a bounty was put on his head: the Edward Snowden of 5th century Athens. The rituals themselves are definitionally shrouded in mystery, but we are informed of a particularly enjoyable brew, kykeon, whose psychoactive property, Cicero reports, offered the experience of ‘death and rebirth’. The removal of a ‘fear of death’, common also to modern ceremonies of psilocybin mushroom ingestion (hence the emerging hypothesis of ancient ritualistic usage of this fungus), was to Cicero fascinating: ‘They have refined and ennobled human nature and initiated us into true principles of life, teaching us not only how to live joyfully but also to die with a better hope’. I am reminded of the critique of Marx that religion is the ‘opium of the people’.

The notion of mystical death is maintained by an Islamic example of mystical practice, namely the radical 13th century Qalandariyya order (roughly, ‘group of ascetics’) and their objective of fana’a, or ‘self-annihilation’. This is to be achieved (naturally) through dancing and the drinking of wine, the latter of which broke Islamic law. Described as ‘hippies’, these men shaved their heads and wore ragged clothing – sometimes nothing at all – to lead a simple, unattached life. Their ecstatic rituals of detachment parallel young Tobit’s scholarly impression that unity with God is achieved neither through adherence to laws, nor the employment of reason, but through radical, countercultural experiences. The ‘self’ is ‘annihilated’ and the human ‘I’ and divine ‘Him’ become a mystical ‘Us’, the language not just of Sufis like al-Hallaj and Rumi but indeed reflective of Christian authors Meister Eckhart and Teresa of Ávila.
A further mystery cult reflective of Christian theology is Mithraism, the worship of Mithras, a Persian god of light, popular with Roman soldiers of the 1 st-4th centuries AD. The myth follows Mithras, ordered to slay a bull representing some primordial life-force, who chases the beast to a cave, where the slaughter finally occurs; the resulting liquid discharge of the animal itself produces new life – animals, grains, vines – and a feast is called to celebrate. It does not take the symbolic drunkenness of Peterson or Pageau to appreciate the common motifs of light-bringer, cosmic battle, a cave-based victory, new life, and celebratory feast all shared with the Christian narrative tradition. In a Eucharistic style, participants of Mithraism honoured the god with a regular feast, which was but one of the seven levels or instances of knowledge available to followers. Sacraments, anyone?!

As far as Christianity is concerned, ‘mystery’ is the concept to which the teacher appears to refer when the questions become too exposing. ‘Mysticism’, therefore, might exist as the official, practical acceptance of this surrender. Jesus – whom we are in danger of sidelining in the dogmatic dance of academic theology – did allude to levels of knowledge and mystery, rather explicitly: (speaking to his apostles) “To you has been given the secret of the Kingdom of God, but for those outside everything is in parables, so that they may indeed see but not perceive, and may indeed hear but not
understand…” A common mic-drop at the end of Christ’s parables in the Gospels is, “He who has ears, let him hear”. We find here the suggestion that there existed deeper truths, reserved for an inner circle of initiates alone, much like the examples above of the Eleusinian Mysteries or Mithraism: “Do not case your pearls before swine”, Jesus remarks in Matthew’s Gospel, which further motivated polymath and friend of The Griffin, Albert Schweizer (see Issue I) to label Paul a mystic himself in describing Christians as the ‘stewards of the mysteries of God’ (1 Cor 4). Entering the waters of Baptism is portrayed by Paul as a dying and rising with Christ, dying to your old self and rising in glory, that one might say “It is no longer I who live, but Christ who lives in me” (Gal 2), imagery resonant with the delectable dram of Eleusis.
The central image of Catholic Christianity is the Eucharist, the sacred meal which remembers (that is, the opposite of ‘dismembers’) the sacrifice of Jesus on Calvary. It, too, fulfils the criteria outlined above with the motifs of life and initiation caught neatly in a claim of John: ‘unless you eat the flesh of the Son of Man and drink his blood, you have no life in you’ . Crikey. I am left rather scratching my head at what occurred to take the rich mystery of the Jesus Movement and transform it into an official, universal state structure; from secretive sect to a universally Tweeting (X-ing?) pope. It was probably the Romans – the Brussels bureaucrats of their day – but my conscience forces me – as well as the liberalism of our dear Editor – to acknowledge the universality of the Church as befitting the universality of Christ’s sacrificial love. So, perhaps we’re not too far gone.
Any further talk on my part of amnesia or abandonment of early Christianity or indeed Christ’s ‘intentions’ is unproductive and near schismatic. It is probably also intellectually dishonest. I argue that Christianity, in its evolution, is not a departure but a fulfilment. Organisation need not come at the expense of mystery, for that is what is fundamental to God’s nature. The Church, described by Pius XII as the ‘mystical body of Christ’ is a continuation of the Mysterion to which Paul referred above: a guardian of sacred truths – of salvation, of spiritual transformation, of participation in the divine, all available in the saving embrace of faith in Christ –interpreted in, but not for, our changing world. I will continue to embrace traditional, sensory liturgy, because that is what feeds me; yet, this is not a practice reserved for a distinguished few. With the Kingdom presented paradoxically in Scripture as both hidden and revealed, we can only assume – rather spurred-on by the Great Commission – that this knowledge is meant to be gradually revealed, as the mustard seed of the Gospels. Diagoras likely had it right – as with Snowden – in inadvertently fulfilling the instruction of Jesus: “What I tell you in the dark, say in the light; what you hear whispered, proclaim on the housetops”. The intrigue of mystery subsists, therefore, not in its concealment, but in its endless discovery.
The Strategic Importance of the Suez Canal
Sarah Ellingworth, Y12.
Overview
The Suez Canal is located in Egypt, connecting the Red Sea and Mediterranean Sea, utilising several lakes: Lake Manzala, Lake Timush, and the Bitter Lakes. It a strategically important maritime choke point, measuring 193.3km long, 205m wide and 24m deep. It can handle larger ships than other canals, however it still has restrictions on the vessels passing through it. After an expansion in 2014, it now allows regulated two-way traffic. The timings are carefully executed to ensure that when ships pass each other, they are in an area which has been widened and is safe to do so.
Historical and political context
The idea of creating a canal in Egypt was explored by Linant de Bellefonds, who discovered that the Mediterranean and Red seas were at the same altitude, making the construction of the canal significantly easier. Construction of the Suez Canal began in 1859, involving around 1.5 million people working on the project. However, it was not a particularly safe environment: tens of thousands of people died while working on the construction of the canal.
It was officially opened on 17th November 1869. At the time, Egypt was under colonial rule from Great Britain and France, and so most of the shares in the Suez Canal Company were owned by Britain and France. Great Britain in particular maintained control over the canal by stationing troops in Egypt.
In 1956, however, Britain agreed to withdraw their troops from Egypt, after years of negotiations. This handed control of the canal over to the Egyptian government, led by Gamal Abdel Nasser, who immediately nationalised the canal. He justified this by saying that the money would be used to fund the Aswan Dam Project. This caused political tensions, and the U.S and Great Britain withdraw their support for funding the canal and other infrastructure projects.
In response to Nasser, France, Britain, and Israel formed a secret alliance to take military action. Israel began by invading the Sinai Peninsula, which followed with widespread criticism, particularly from the U.S, who were focused on stopping the spread of Soviet influence and did not want any disruptions or conflicts in the Middle East. The U.S helped to influence a ceasefire, and British and French forces were forced to retreat. This exposed the limitations of French and British military power, whilst marking an end to colonial rule.
Currently, the Suez Canal is owned by the Suez Canal Authority, an Egyptian stateowned authority.
Economic significance
The Suez Canal is still today a major maritime choke point. Approximately 12% of global trade and 30% of global container traffic travel through the canal. This is equivalent to about USD $1 trillion per year. The strategic location of the Suez Canal, cutting between Asia and Africa, saves ships the long, alternative journey around the bottom of Africa, and shows it to be a faster, cost-effective route. Typically, the journey from one end of the canal to the other takes around 13-15 hours, whilst the alternative journey around the Cape of Good Hope can take around 6-14 days, depending on the type of ship, and the cargo that it is transporting. This significant difference in transport times shows how beneficial the canal is to journey times, as well as fuel costs, having a significant impact upon trade between Asia and Europe.
Many countries have a high dependence on the Suez Canal for trade, so when a blockage occurs, this can result in major economic losses. As a lot of oil is transported, many nations will have energy dependence upon the canal. Some countries are more reliant than others, and the graph below outlines the dependence of certain nations on oil transports through the canal:
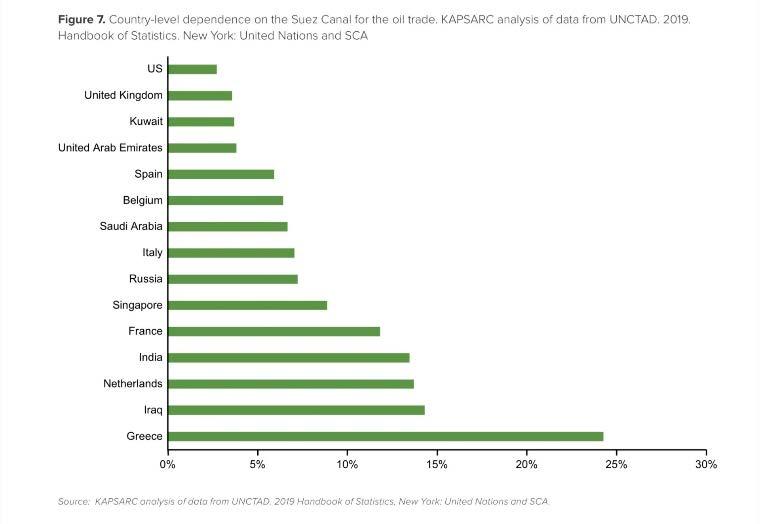
Disruptions to oil movements can cause knock on effects with the entire oil supply chain. As a result of disruptions to trade, expanded trade relations may form. For example, some European countries may form trade relations with countries that do not rely on the Suez Canal.
Blockages and disruptions
However, despite the Suez Canal being a strategic route, it can still cause problems, due to being narrow and having large container ships passing through it. As many nations are heavily dependent on the canal, this can cause major issues if problems with the canal occur.

Disruptions and conflicts which have historically occurred in the Suez Canal emphasise the dependence that many nations have upon it, as a major transport route. We have been able to see the severe economic costs of any delays, and the inconvenience of re -routing. For example, in March 2021, the Suez Canal was blocked for 6 days, caused by the grounding of Evergreen’s ‘Ever Given’ containership, loaded with over 18,000
containers from China, heading to the Netherlands. This ended up lodged horizontally in a 265m wide stretch of the canal, stopping any other vessels from travelling through the canal. The companies that were affected had to decide on whether to wait until the blockage was cleared, with uncertainty, or choose to reroute around Africa. Rerouting would have increased fuel costs, and delayed cargo, which may have resulted in certain food being spoilt, for example. Some companies chose to use air freight instead, which had much higher economic costs. Even once the container ship was dislodged, there was still congestion at major global trade hubs, due to disruptions in schedules. The major consequences arising from this incident have enlightened us about the fragility of marine transportation methods and their routes.
Conclusion
The Suez Canal plays a significant role in trade between Europe and Asia. It brings great economic benefits, through saving the transportation costs of alternative routes, as well as being a significantly faster route. It is evident that many nations are reliant on the Suez Canal, and any disruptions to this are seen to have major consequences.
Medea: Victim or Villain?
Calliope Psylla, Y12.

The character of Euripides’ Medea can be read in at least two dramatically contrasting ways. According to one, she is a feminist icon whose actions (including murder and infanticide) are somehow justified as a response to her circumstances; according to another, Medea is a vindictive and deceitful woman whose behaviour was wildly irrational and completely detached from the behaviour of women typical of the Greek world. How can both be valid responses to the same character?
In order to formulate a valuable opinion, we must begin to unravel the complex layers which are embodied by Medea, and we need to be aware that, although she endures a significant amount of suffering, the way in which she reacts to that suffering must be considered carefully. I am making the assumption that most of you reading this might not be aware of Euripides’ tragedy Medea, and I therefore ask you the following: how would you react if you were
a) madly in love with someone to the point of an infatuation so severe that you b) betray your family to aid your lover and then c) become exiled from your home, the only place you knew, and are forced to seek refuge in a foreign in city and d) build a family with your lover in that city
only for them to provide you with a pathetic excuse as to why they are abandoning you and your children to marry someone else? And then, as this news has been delivered to you, you find out that you are being exiled from this new city and must accept this betrayal while moving without your children to another unknown city. And, on top of all this, you are expected to behave meekly after being deserted by someone you trusted and loved.
If you would react with intense anger, you would feel the same as Medea did.
The events that occur throughout Euripides’ tragedy may need some explanation. In simple terms, before the start of the play, Medea (the princess of Colchis) meets Jason who must take the Golden Fleece from Colchis to regain his position for the throne of Iolcus in Thessaly. Through various enchantments and magical endeavours, Medea betrays her family who were in possession of the Golden Fleece by helping Jason complete seemingly impossible tasks and allowing him to take the Golden Fleece. Once their plan was complete, Medea waylays her father (King Aeëtes of Colchis) by helping Jason murder her brother (Absyrtus), and she shows a lack of remorse when strewing the remains of her brother as a technique of distraction, allowing her and Jason to escape capture by her father as the latter works to collect his son’s remains. The pair then flees to Corinth where Medea bears two sons and, as seen in the opening of the play, it is at this point that the audience is told of Jason’s arrangements to abandon Medea and his sons to wed the princess of Corinth (Glauce) under the pretence of providing his children with a better life as they would have royal half-siblings.
Considering Medea has committed deplorable acts against her family to aid Jason in his mission, all while having been promised a happy life together, I think it is plausible for us to pity her and foster a more-than-slight dislike towards Jason. The feeble excuse Jason provides Medea for his betrayal of her exposes his spineless nature and shows how his actions in the play are founded solely on his self-interest, making it quite insulting to Medea and undermining everything she did for Jason. At the beginning of the play, we are definitely inclined to side with Medea, and the first impression we have of Jason is defined by his callous and insensitive nature. Medea is described by the Nurse as ‘calling out on her father’s name, and her land, and her home betrayed when she came away with a man who is now determined to dishonour her’. The Nurse acknowledges also that ‘she herself helped Jason in every way’. These are two examples of how a reliable witness to the action before the play starts views the sacrifices Medea has made for Jason. Medea’s upset with Jason leaving her for another woman is also evident when the Chorus describe hearing ‘a shriek … laden with sorrow. Shrilling out her hard grief she cries out upon him who betrayed both her bed and her marriage.’
Medea now has two options:
a) either she leaves Corinth and does not partake in any revenge (as is expected of her by the male characters in the play), b) or she can make Jason suffer for the dishonour he has brought upon her.
Judging by the fact that I’m writing about a tragedy, you can predict that Medea chooses option (b) and decides to make Jason suffer in way she feels is commensurate with the way he has made her suffer. Medea, being a cunning and skilful woman asks Creon, king of Corinth, if she may remain in the city for one more day, which is the time it takes her to carry out her plan. She seeks asylum in Athens by promising to use her magic to help the king Aegeus (of Athens) with his fertility issues. The next step in her revenge plan is to eliminate Glauce (Jason’s future bride) and her father, Creon. She pretends to have come to terms with Jason’s betrayal and offers a coronet and dress for Glauce. Unbeknownst to the other characters, both items are poisoned and will end up killing Glauce and her father.
She then kills both her children to ensure Jason’s torment and rides away in the dragon-pulled chariot that belongs to her grandfather, Helios (the god of the Sun).
Stripping away contemporary Athenian expectations of women, and looking solely at her emotions and how she acted in response to them, we can perhaps understand the actions of Medea, something which, prima facie, seems impossible when you remember that she is responsible for a quadruple murder.
Through the killing of the king of Corinth and his daughter and then her own children, it is evident that Medea’s behaviour, although irrational and violent, can be understood as a response to the maltreatment she endured as a result of Creon’s (a king’s) and Jason’s (a powerful man’s) hands. For a play performed in 431 BC, written for a predominantly male audience who will have had certain views on the expected and socially-acceptable behaviour of women, we can imagine the character of Medea would be a jarring contrast to the women of this time. Athenian women were expected to focus primarily on domestic duties and to manage their household. The cunning and scheming nature of Medea would have been a difficult thing for the male audience to come to terms with, as their view of women was that, when confronted with a situation determined in the political and public world of men, they should accept the circumstances and behave in a passive and compliant way.
So, by the contemporary standards of expected behaviour of women, Medea would be deemed an immoral and malevolent woman who committed a depraved and unjustifiable act. However, if we analyse the situation through a more sympathetic lens, although murder, and especially infanticide, is abhorrent and inexcusable, we can understand that her murderous urges stem from her being used, abused, and deprived of an outlet for her rage in a society where women were forced to accept their fate. And this woman, who betrayed her own family for a man, would have received little to no sympathy for her situation.
Attempting to excuse Medea’s actions is extremely difficult, as that would essentially entail me suggesting murder as a reasonable response to (albeit significant) wrongdoing. However, it is necessary to try to understand the depth of a character such as Medea. The betrayal she faced cannot be fathomed unless we were in a similar position, and the grief she endured led her to react in such a way. The way society viewed women prohibited her from expressing her feelings and therefore forced her into taking an extreme route to do so. Medea is aware of the expectations women are bound by “Surely, of all creatures that have life and will, we women/ Are the most wretched”, and, although she acknowledges the oppression of women, she still desperately feels the need to carry out her revenge regardless of the consequences.
In this tragedy, I find that trusting our own judgement and how we feel towards the characters of Medea and Jason changes quite significantly, and this leaves me with a discomfort that is difficult to express. Jason is seemingly the villain at the beginning of the play, but when we see his desperation and misery at the end, our feelings towards him change. The same applies to Medea: we pity her and sympathise with her but then we realise how manipulative and despicable her actions were. How can
I feel sorry for a murderer, as I (and the Nurse and Chorus) did at the start of the play? How can I feel anger towards a man who has lost everything, his children, and his bride, as I (and the Nurse and the Chorus) did at the start of the play?
The play has quite a strange ending where we try to comprehend everything that occurred whilst also trying to decide whose side we are on, which is arguably impossible. We cannot fully side with one character as they both did things with the intention of hurting the other. We feel sympathy for both Medea and Jason, but, at the same time, we feel that we should not. Therefore, we are left simply to digest and ponder every word we have just consumed: a tragedy of human events taken to inhuman extremes.
Mastery Learning in Education: Is AI the Missing Link?
Mr. Britton, Head of Physics.
The following draws heavily from a 2017 TED talk given by Sal Khan, creator of Khan Academy, on the topic of mastery learning in education. I have updated the argument to include the impact of new developments in Artificial Intelligence.
Mastery learning is an old idea in education which rests on two core principles: aiming for true proficiency and believing our abilities can grow through effort. When students approach any subject with the conviction that they can improve, they open themselves to deeper understanding. Yet, in a traditional educational setting, gaps in knowledge often unintentionally go unaddressed. These gaps accumulate until, upon facing advanced topics, learners conclude they are ‘not good’ at Maths, Science, or some other subject. In truth, the problem usually lies not in a lack of ability, but in a system that overlooks mastery and pushes everyone ahead at a rigid pace.
Observing how people learn reveals the pitfalls of moving on too quickly. A student might struggle with algebra because they never fully absorbed parts of pre -algebra, or find calculus intimidating due to weak algebra skills. This pattern is often misread by students as innate inability, when in fact it usually stems from unaddressed gaps. Many who believe they lack a ‘maths gene’ later discover that, by systematically filling in missing pieces, they can succeed at once-daunting topics, reinforcing the idea that ability is shaped by perseverance and proper support.
In martial arts, students must master white-belt skills before advancing to the yellow belt. Similarly, in music, one practises foundational pieces until they are secure, then tackles more complex compositions. Traditional schooling, however, seldom follows this model. Instead, students are grouped by age or perceived ability, study a topic like exponents for a few weeks, take a test, and move on, regardless of whether they have truly mastered the material. Over time, these gaps resurface when new concepts build on these shaky foundations.
To illustrate how absurd a method for learning this is, imagine constructing a house in this way. You hire a building company and say “we have two weeks to build a foundation, what is the best you can do?” If the foundation is incomplete, poured with inadequate time or materials, an inspector might rate it at 75%, yet the project advances anyway. After the second and third floors are complete, those weaknesses inevitably cause the structure to fail.
Unfortunately, current education mirrors this exact same process. If a student scores 75% on an exponent test, it indicates a 25% gap. Forcing the student into logarithms without fixing that gap almost guarantees future confusion. Soon, the learner concludes that they are inherently bad at the subject, when the system’s pace – not their potential – has sabotaged them.
Mastery learning offers a more sensible approach. Instead of limiting how long students spend on a topic and accepting variable results, this model fixes the outcome – i.e., true comprehension – and varies the time in which this is achieved. If
someone struggles with exponents, they keep practising until they genuinely understand them before moving on. By ensuring a solid foundation, students build confidence and resilience. Under this model, mistakes become cues for further learning, rather than permanent labels of inadequacy.
The historical-practical impediment to this approach was obvious. Scaling mastery learning to the level of a whole class or even of a whole school was clearly impractical in the non-digital age. Tailoring lessons, resources, or feedback for each individual student would exceed the limited resources that teachers and institutions had at their disposal.
However, modern technology has begun to solve these logistical barriers. Ondemand videos let students learn at their own pace, and digital platforms can offer immediate feedback. Teachers can thus devote class time to deeper engagement and individualised support. Now, artificial intelligence, especially large language models, elevates this further. It is now possible for students to simulate AI tutors which can deliver custom explanations in real time, adapting to each learner’s personal struggles. Students can instantly generate fresh variations of a problem to verify mastery before proceeding. Teachers, meanwhile, can harness AI to create and recreate resources aimed at each student’s needs, tracking progress at a finegrained level.
This kind of personalised learning aligns with society’s shift from an industrial to an information-based economy. Automation and computerisation already handle a lot of manual labour and many routine tasks. By enabling more people to master advanced skills, AI-driven, mastery-based education can help invert the old pyramid structure, where only a small elite thrived, and create a broader creative class. The question is whether we use these tools to expand opportunity or allow them to benefit only a privileged few.
Centuries ago, even in relatively advanced parts of the world, perhaps 15% of the population could read. If you had asked someone then, perhaps a literate member of the clergy, what percentage of humanity was even capable of literacy, they might have guessed 20–30%. Today, near-universal literacy is a norm in most societies. Perhaps, under a mastery framework, the same will prove true for advanced mathematics, science, or other complex fields. Bolstered by AI -driven support, what once seemed beyond most people’s reach may become achievable by far more learners, so long as they are allowed to fill their knowledge gaps and proceed at a pace that fosters true understanding.
For decades, the dream of mastery learning was hampered by the difficulty of providing individualised instruction at scale. Breakthroughs in AI now promise to eliminate many of these barriers. By offering on-demand tutoring, continuous problem generation, and instant feedback, AI can let each student solidify foundations before progressing. Teachers remain indispensable, but with the menial tasks of resource creation, manual assessment, and personalised feedback now being handled skilfully by AI, they could now focus on arguably the more important part of education – the part that AI cannot do – namely guiding,
mentoring, and, most importantly, inspiring their students to see the beauty and joy that exploring their subject can bring.
It is important to recognise that, like all new paradigm-shifting technologies, there are dangers associated with improper use. AI is not perfect – it has inherent bias, and there is a risk of data security. If used inappropriately, it could foster an overreliance and risk students not cultivating some foundational skills, including critical thinking and the interpersonal skills demanded of them when interacting with their teachers and peers. However, if used appropriately, these risks could easily be mitigated.
Legitimate questions also remain: Is this practically implementable in schools? Can students rise to the task of being the masters of their own education, and at what age? Are there limitations to the kinds of subjects for whichh this framework is suitable? And will students actually enjoy this method of learning? These are all legitimate questions and require further consideration.
However, at the heart of this switch is the idea that the shift to mastery learning recognises that initial struggles simply signal a need for further work, not a permanent limitation on students’ ability. With AI as the missing practical link, some version of mastery-based learning becomes not only feasible, but the most logical way to educate every learner in a new era that demands adaptability, creativity, and lifelong growth for each newly educated member of society.
The
Conjecture:
Harry Wilson, Y11.
What is the Collatz Conjecture?
The Collatz Conjecture, also known as 3� + 1, or the Syracuse Problem, is a famous and unsolved mathematical problem, so simple that mathematicians have become infuriated that they cannot solve it. In fact, it is so difficult to solve that a Japanese company has offered 120 million yen (equivalent to about £628,000!) to anyone who can either prove or disprove it. The Conjecture (a mathematical term for a theory proposed by someone that has neither been proven nor disproven), first devised by Lothar Collatz in 1937, states that if you take any positive integer, and repeatedly apply these rules...
• if the number is odd, then triple it then add 1
• if the number is even, then divide it by 2
...then you will always end up with 1.
For example, take the number 3:
• 3 (is odd so we triple it then add 1): 3 × 3 + 1 = 10
• 10 (is even so we divide it by 2): 10 ÷ 2 = 5
• 5 (is odd...): 3 × 5 + 1 = 16
• 16 (is even...): 16 ÷ 2 = 8
• 8 (is even...): 8 ÷ 2 = 4
• 4 (is even...): 4 ÷ 2 = 2
• 2 (is even...): 2 ÷ 2 = 1 (so for the number 3, we do indeed end up with 1).
Reader, I challenge you to take any number, any number you can think of, and apply the rules mentioned above. I guarantee that you will always end up with 1! It seems so simple, but how can we prove that it is always true? Or how can we be sure that no ‘magic number’ exists for which this does not work?
Why is the conjecture seemingly impossible to solve?
The difficulty in solving the problem lies in the recursive and piecewise nature of it (in other words, the fact that you have to apply rules repeatedly, and that the rules change). For instance, if we have to notate the Conjecture mathematically, then I think that the most succinct way to do it would be as follows.
Let's define the 0th iteration as:
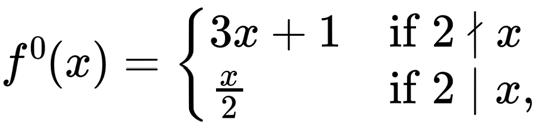
and then define the (� + 1)th iteration recursively by:
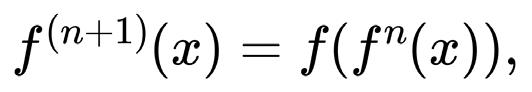
Then the conjecture states that there exists a positive integer value � such that the recursion must reach the value 1.

From this, we can clearly see the two main issues . One of them is that that the function is piecewise or conditional; what happens to the number � depends on the value of � itself, meaning that it is impossible to place into an algebraic equation that could be solved.
Another issue is that it is recursive, meaning that we don't initially know how many times we will have to apply the rules, as this number will change depending on the value of � , so, again, we cannot put this into a single expression or equation.
How could this ever be solved?
Some people have tried to graph the function, looking for patterns. Here is a graph below of Stopping Time against the Starting Number (note that the ‘Stopping Time’ refers to the number of steps � it takes for the value to reach 1):
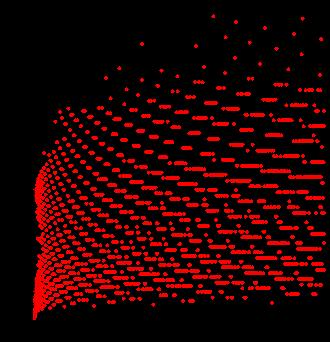
However, it is difficult to graph for a few reasons: firstly, some numbers take only a few steps to reach 1, for example 2 and 4, whilst other numbers like 9663 climbs as high as ~2.7 × 10! – this means that it is very difficult to find a good scale for the graph, so it is hard to visualise any patterns. Also, no patterns can discernibly be found! Mathematicians have studied these graphs for decades and cannot find any patterns yet, describing the graphs as 'chaotic' and 'unpredictable'.
As proving the Conjecture is seemingly impossible, mathematicians have thought about trying to disprove it. They have thought about 2 ways:
1. An unbounded loop:
It has been speculated that there may exist some number which gets stuck in an infinite cycle that shoots straight to infinity, whether directly (by constantly applying 3� + 1) or indirectly (for example, by periodically applying 3� + 1 some number of times, then " # some number of times). I will leave it as a simple exercise to the reader to show that no number � exists which can have 3� + 1 repeatedly applied. The periodic unbounded loop, meanwhile, is (so far) impossible to prove/disprove, and is still an open problem.
2. An enclosed loop:
Mathematicians have known for a very long time about the 4-2-1 loop (if you apply the rules to 4, it will get stuck in this infinite loop) and they have also attempted to find a loop that numbers may get stuck in other than the 4-2-1. However, none have been found so far.
Will someone ever solve the Conjecture?
Unfortunately, it is unlikely that it will ever be solved by a human alone. For one, I highly doubt it will be disproven by humans: computers have recursively checked through the numbers from 1 to 2.95 × 10#$ , and all these numbers have followed the Conjecture so far. As numbers this huge have been tested already (by the way, 2.95 × 10#$ is 295 thousand million billion!), no human will ever find the exception (if one is ever found). Also, mathematicians love to know why, not just how, so even if some ‘magic number’ is found, it will be a very long time I think before we ever come up with a satisfactory reason for it. For now, proving the Conjecture is seeming as impossible as ever, so perhaps it will remain forever the simplest unsolved problem in Mathematics!
Something to think about...?
Have a think: you might want to have a look yourself into the Conjecture and see what problems you encounter. Who knows, maybe it could be you who solves the problem and wins £628,000!
Also, does the Conjecture seem to hold for 0? What about negative numbers? What are the patterns you can see (if any!) and why is this the case? Feel free to email me with any findings at harry.wilson@newhallstudent.co.uk.
Bonus Riddle: I start with the number 5. I add a 1 (and do not change it in any way afterwards). The result is 3. How is this possible?
(This riddle was written by me, so please do email me (see email above) if you think you have the answer or need a hint!)
Autism: An Overview
Oluwatamilore Adeola, Y12.
What is Autism?
Autism, or Autism Spectrum Disorder (ASD), is a neurodevelopment condition that affects how a person perceives and interacts with the world. It is called a ‘spectrum’ because it varies widely in how it presents, ranging from mild to more significant challenges.
Autism Spectrum Disorder is characterised by differences in social communication, repetitive behaviours, sensory sensitivities, and unique strengths. Individuals with autism may struggle with understanding social cues, maintaining conversations, or forming relationships, with some preferring solitude and others desiring connection but finding typical social norms challenging. Repetitive behaviours, such as handflapping or rocking, and a strong preference for routines are common, with changes causing distress. Sensory sensitivities vary, with some highly sensitive to sounds, lights, or textures, while others seek sensory input through touch or deep pressure. Many autistic individuals exhibit unique strengths, including intense interests in specific topics, exceptional pattern recognition, strong memory, and creative problem-solving skills.
Autism Spectrum Disorder is a complex neurodevelopment condition caused by a combination of genetic and environmental factors. Genetic influences play a significant role, as autism often runs in families, with certain gene mutations and conditions like Fragile X syndrome increasing risk. Environmental factors that may contribute include advanced parental age, prenatal exposure to specific medications or chemicals, pregnancy or birth complications (such as low birth weight or prematurity), and maternal infections during pregnancy. Thanks to extensive research, vaccines have conclusively been shown not to cause autism, and parenting style or emotional deprivation are not contributing factors. While the exact cause remains unclear, the interaction between genetic predisposition and environmental triggers is believed to be central to the development of ASD.
Misconceptions & Realities
One common misconception about autistic people is that they lack emotions or empathy. In reality, autistic individuals do feel emotions deeply and can be highly empathetic. However, they may express emotions differently from neurotypical people. Some might struggle to show emotions in conventional ways, such as through facial expressions or tone of voice, while others may experience ‘hyperempathy’, feeling emotions so intensely that it becomes overwhelming.
This misunderstanding often comes from differences in communication styles rather than a lack of feeling. Many autistic people care deeply about others but may struggle with social cues or expressing their emotions in ways that are easily recognised by neurotypical individuals.
Autism is a different way of experiencing the world, and with the right understanding and support, autistic individuals can thrive in their own unique ways.
The way autistic people are viewed in the world varies widely, depending on cultural beliefs, awareness, and societal attitudes. In modern, progressive societies, there is growing awareness and acceptance of autism as a natural neurodivergence rather than a disorder that needs to be ‘fixed’. However, in more traditional communities, perceptions of autism can be more complex and sometimes challenging.
How Traditional Communities View Autism
In many traditional communities, autism is often misunderstood and stigmatised due to limited awareness. Autistic traits may be misinterpreted as bad behaviour, stubbornness, or signs of poor parenting or mental illness. These misconceptions can lead to social exclusion, as traditional cultures often prioritise conformity, making autistic individuals - who may struggle with eye contact, verbal communication, or traditional social cues - appear ‘different’ or ‘difficult’. Families may face judgment or shame, prompting some to hide their child’s condition rather than seek help. In certain cultures, spiritual beliefs surrounding disabilities lead families to turn to healers, religious rituals, or traditional medicine instead of medical or therapeutic support.
Limited access to diagnostic services, therapy, and inclusive education in traditional or rural areas further hinders support for autistic individuals. Schools and workplaces often lack accommodations, resulting in discrimination and exclusion. However, perspectives are gradually changing with global awareness campaigns, advocacy, and the efforts of autistic self-advocates and families educating their communities. Social media and international initiatives are promoting neurodiversity, enabling even conservative societies to better understand and accept autism as a different way of being rather than a problem.
Conclusion
Autism Spectrum Disorder is a neurodevelopment condition characterised by diverse traits, including social communication differences, repetitive behaviours, and unique strengths. It arises from a combination of genetic and environmental factors, with misconceptions - such as a lack of empathy - stemming from misunderstandings of autistic communication styles. While progressive societies increasingly embrace neurodiversity, autistic people in traditional communities often face stigma and limited support. However, global awareness, advocacy, and autistic voices are driving positive change, promoting acceptance and enabling autistic individuals to thrive in their own ways.
Macroeconomic Outlook for 2025: Why we can be optimistic about
dealmaking themes
Alice McLeish, Class of 2019. Alice is currently an Investment Banking Analyst at UBS, having graduated from the University of Surrey with a BSc in Economics.
Macroeconomic and political shifts going into 2025 have created a supportive environment for dealmaking across Mergers & Acquisitions (M&A), Equity Capital Markets (ECM), and Leveraged Capital (financing) Markets (LCM). 2024 was a year of great political change, with elections taking place across major economies; regardless of expected outcomes, the uncertainty of the global political landscape led to a risk-off approach by investors which subdued market activity in 2024. Whilst there are some mitigating factors which could hinder the expected bullish economic backdrop, I’ll discuss a few key drivers that make it an exciting year.
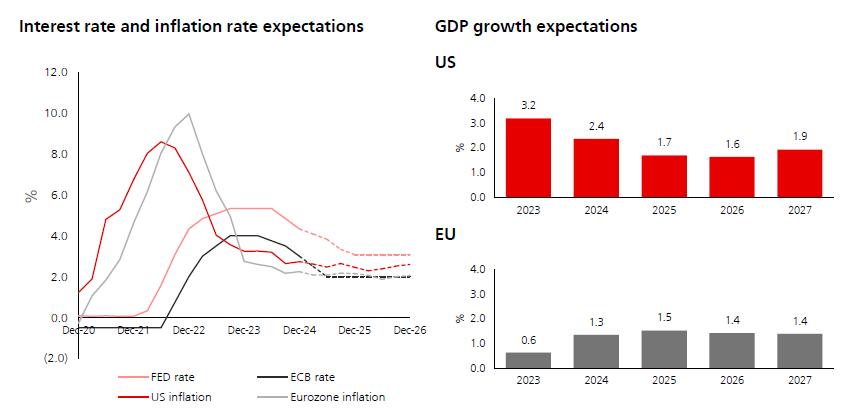
Global inflation has been a pressing issue in the recent cycle, peaking at double-digit figures in the UK at the end of 2022. By December 2022, the Bank of England had raised interest rates multiples times in one of the most aggressive monetary-policytightening cycles in history, with similar stabilization policies implemented globally to curb inflation. Entering 2025, inflation continues to trend downwards towards targets for a host of reasons, such as steady monetary policy adjustments, supply chain recovery since Covid-19 disruption, and falling prices of energy and commodities. In addition, global economic slowdown in many countries has reduced demand for goods and services, which has aided control of inflation. With inflation levelled off, it is expected that interest rates will decline further, reducing the cost of capital and cost of investment, boosting global inflow of capital and creating constructive financing markets.
In addition to lower interest rates, on a corporate level, the Trump administration victory in the US elections suggests a more business-friendly environment, with less
regulation and lower taxes. Despite the chaos of Trump’s first term from the perspective of foreign and domestic policy, it was a period of economic success, and he looks to bring the same success in higher magnitude. On the flip side, despite catalysed markets, policy-related unknowns (e.g., tariffs) could have very negative economic implication and increase market volatility. For example, they may hike inflation as consumers are forced to pay higher prices for domestic goods, or pay higher prices for imported tariffed goods.
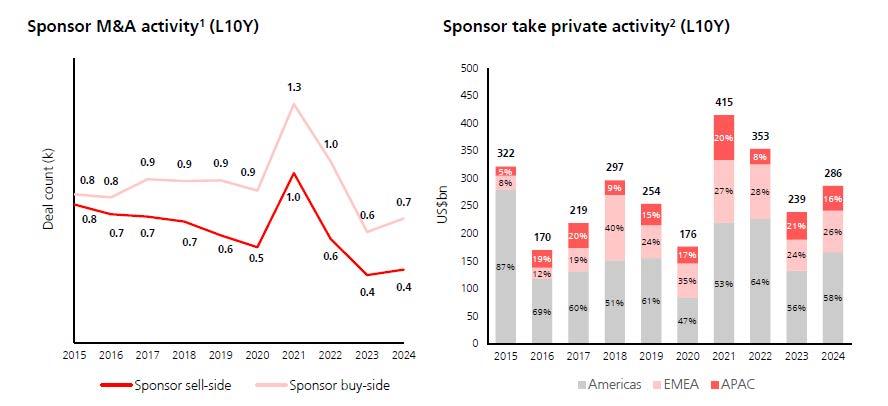
Moving onto M&A markets in particular, the fundamentals for corporate and sponsor (Private Equity and the like) deal flow have improved in recent months. Very low deal count in 2023-24 saw sponsors facing distribution and deployment pressure, so in 2025 we can expect activity and exits to pick up. Entering this year, the investment capacity is underpinned by a huge level of dry-powder (funds raised for investment yet to be deployed), at an industry-wide level of $3.9 trillion, up 24% over the last 3 years as a result of recently depressed buy-side activity. A key driver of the next wave of deal activity is technological transformation, as the world is becoming increasingly digitalised, with AI, cybersecurity, and fintech rapidly on the rise. Bullish sentiment towards generative AI buildout and investment is likely to be a focus area for Private Equity investors and for corporates looking to keep up with competitive advancements.
Constructive financing markets are providing funding optionality for M&A, further fuelling the rebound in activity. Equity markets have been trading close to all-time highs across industries and geographies, which enables corporate acquirers to use their high-value shares as consideration and to benefit from attractive valuations in capital raising opportunities. Debt issuance was strong in 2024 and is expected to rise across sectors, ratings, and maturities, with both public and private lending markets in support of accelerated M&A activity. A reduction in loan pricing results in higher leverage ratios and purchase price valuations, all contributing to a strong financing backdrop, spurred by the wider macro-outlook.
Finally, along with touching on tariffs, there are a number of other headwinds facing the macroeconomy in 2025 to be considered. Geo-political factors, such as ongoing conflicts in the Middle East and the Russia-Ukraine war, bring uncertainty for energy prices and effects on commodities, which will remain until a ceasefire is reached. Deficit concerns also continue, with 1/3 of countries facing deficit increases, the US being the furthest from debt stabilization, and many countries not stabilized since the pandemic. High government debt reduces an economy’s ability to respond to future crises and increases interest payments, which puts a strain on public spending and reduces confidence in financial markets. Last, but certainly not least, slow growth in China, weakened further by tariffs, will lead to some ripple effects, particularly for emerging economies closely tied to China through trade and investment, e.g., through exporting commodities and raw materials to China.
To conclude, political shift in 2025 brings rise to a number of key themes for dealmaking in 2025, and the macroeconomic environment is favourable to bring a strong year. Time will tell how this will be counteracted by potential headwinds, but there is plenty to be excited about.
Gödel’s Incompleteness Theorem
Edward Broderick, Y12.

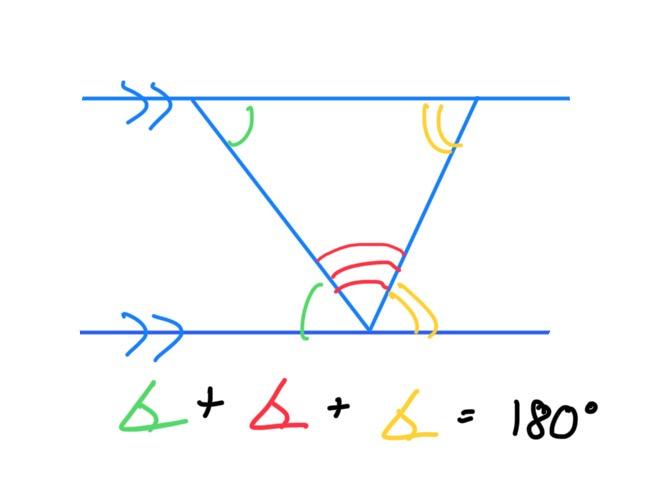
Assume for a moment that there is a way to prove every true statement in maths, as long as you have enough axioms. An axiom is a statement we assume to be true because it is clearly so from observation (such as: we can form a straight line joining up any two points). Ideally these are as limited in number as possible to avoid making unfair assumptions. Only the clearest, such as ‘if a=b then b=a’, are allowed (even this one was later proven by Bertrand Russell). We then use logical proof to show other new facts are true from these ones. For example, if we take Euclid’s 5 geometric axioms for flat 2D space, we can prove that the sum of the angles in a triangle adds to 180°, or perhaps the beloved Pythagorean theorem that for a right-
For many years, it was assumed that we could prove every true statement in maths with a given special set of axioms. Indeed, if, for some reason, we ever found something that was definitely true but couldn’t be proven with our axioms, that
idea could be added as an axiom, thus covering all bases. However, in 1931, Kurt Gödel published what will likely remain one of the most revolutionary pieces of mathematics in all its history, proving this idea to be absolutely, unequivocally false. Observe the following word game:
Assumption: every true mathematical statement is provable given all the necessary axioms.
Let us take this perfect set of axioms:
The key idea: There does not exist a set of axioms such that our axioms may be used to prove this statement.
For ease we could label this statement g, and g says: there does not exist a proof of g.
Any statement is either provable, or not provable. So, we have 2 cases:
Case 1: g is provable, so we can prove that g (which says there does not exist a proof of g) is true – this is a contradiction so must be false.
Case 2: g is not provable, so g is provably not provable (see the assumption that every true statement can be proven), so we can prove that g is not provable, so there exists a proof of g (that g is not provable). This is a contradiction, so must be false.
Both cases fail, so the only logical conclusion is that our first assumption is false, giving us the new knowledge that not every true statement is provable.
Many would quite justifiably dismiss this as a silly word game. It does not have any real bearing on logic, much like the statement ‘This statement is false’. Is it true or false? The answer is neither, and we can dismiss this as a nonsense born out of the limitations of the English language; our language is not designed for writing logical statements, and so not all statements have to be true or false – they can be nonsensical. The image below works in a similar fashion, taking advantage once more of the limits of our language. Gödel, however, wanted to try something else.

As a mathematician, Gödel loved numbers, and so had the idea of assigning unique numbers to logical statements. The statements would first be written in PM – a formal way of writing logical proofs established in Principia Mathematica, a book made famous for its eventual proof that 1+1=2, followed by the amusing comment that ‘The above proposition is occasionally useful.’ There are a limited number of characters used in PM (see below an example of part of an argument written in PM)
and so each individual character can be assigned a unique number, e.g. ∃ (which means ‘there exists’ in logic) might be assigned the number 6 Gödel then used the idea that any integer greater than two (2, 3, 4, 5…) may be expressed as a product of primes (e.g. 6 = 2*3 OR 18 = 2*3*3 = 2*32). He realised that you could write any unique statement like ‘abc’ as a unique product, like 2a * 3b * 5c – a product of primes with the powers as each successive character. We know each character can itself be expressed as a number, so if we wanted to write ‘there exists x… ’ OR ‘∃x…’, where ∃ has number 6 and x has number 17, we could rewrite this as ‘26 * 317 * …’ Since any product of primes provides a unique number, and any logical statement can be written in PM, any logical statement can be written in PM and then as a product of primes (like the above), which = a single unique number.

Gödel had managed to find a way to reduce any logical statement down to a single number. After doing a lot of complex mathematics, he then formulated two functions: sub() and dem()1 , and using these was able to write a non-self-referential statement very similar to ‘This statement cannot be proved’. Indeed, he did this in such a manner that the Gödel number for any set of axioms x is unique. So, were we to account for these unprovable statements by adding them to our list of axioms to accommodate for this unusual result, the new set of axioms y would have a different Gödel number to x, and thus an almost identical statement could be rewritten, but with a different Gödel number in place of the previous one for our axioms, such that the same problem arises. Ultimately, the only conclusion is that, for any given set of axioms, there will always exist at least one true statement (but quite possibly more) which cannot be proven.
Many mathematicians were terrified by this prospect as it suggested that many ideas (such as the Goldbach Conjecture) might be true but just never provable, ruining the idea that we could one day prove every true statement in maths. It became the Ancient Greek hydra of Mathematics, and despite the many successful mathematicians attempting to disprove this new idea, none have succeeded in over 90 years. That said, many have embraced this new idea happily; there will always be new problems to solve and ideas to consider. Many have looked at the further philosophical results that stem from this: are there true philosophical ideas which, while true, cannot be proven? Perhaps this is something to think about.
1 understanding how these functions actually work requires very complex university maths which I do not yet understand, however in essence dem(x, y) is a function that takes Gödel numbers x and y and calculates whether the axioms x can be used to prove y, and sub(x, v, y) takes every instance of v in x and replaces it with y
