Determinación

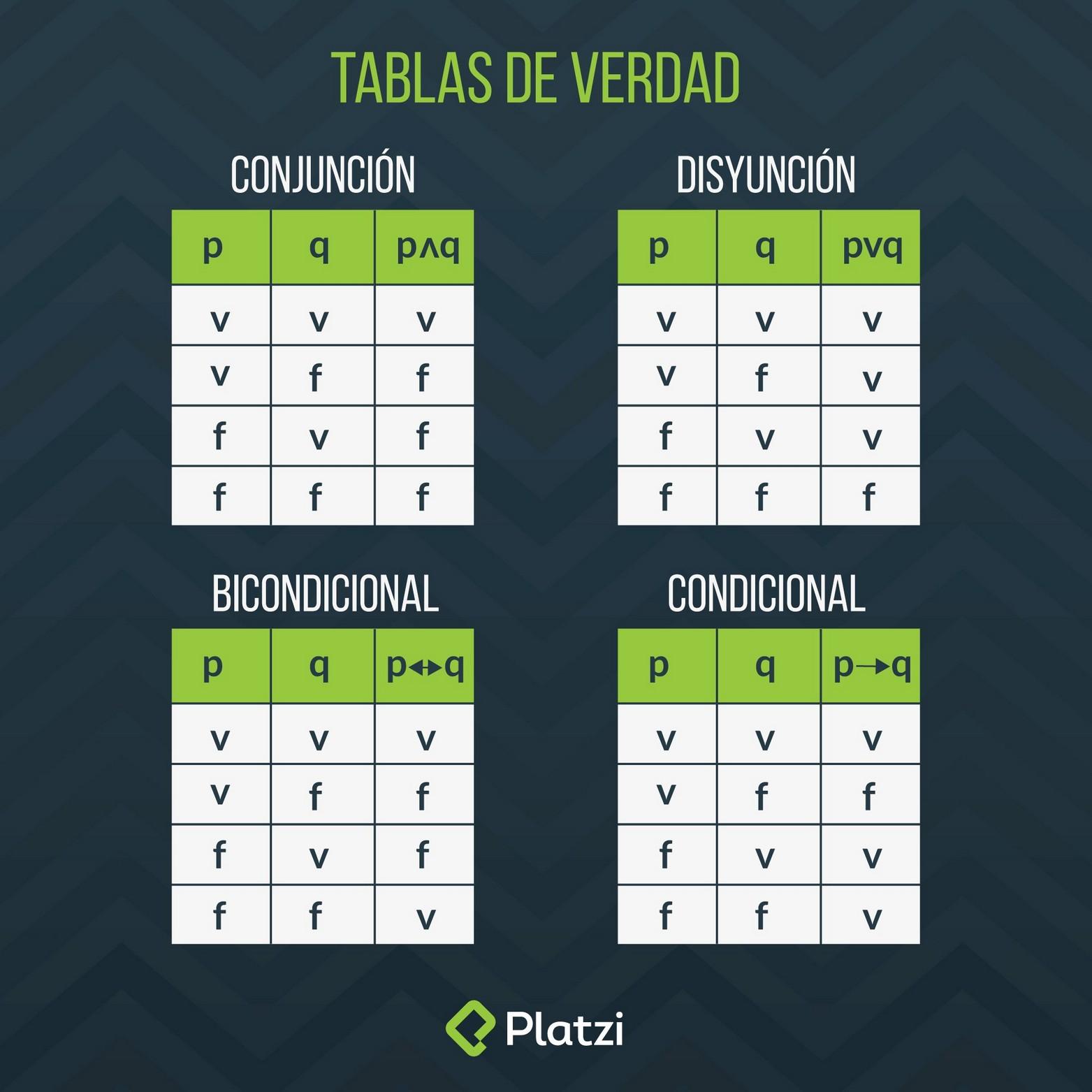
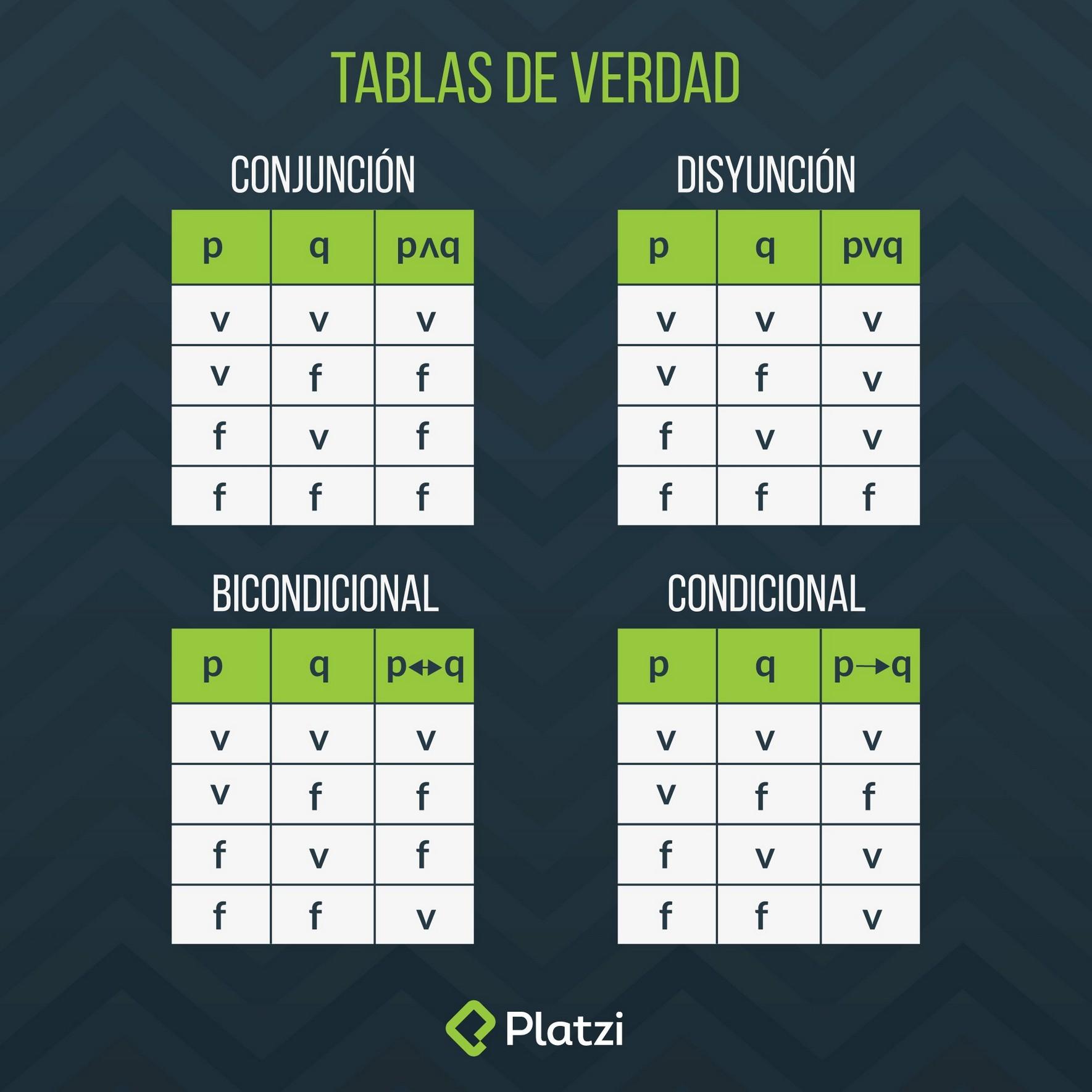
Determinación de la validez de un argumento utilizando tablas de verdad

Es un método formal para evaluar la validez lógica de un razonamiento deductivo. Se basa en construir una tabla que muestra todas las posibles combinaciones de verdad de las proposiciones involucradas en el argumento y luego examinar si la conclusión es verdadera en todas las filas en las que todas las premisas son verdaderas.

Aquí tienes los pasos para determinar la validez de un argumento utilizando tablas de verdad:

1. Identifica las premisas y la conclusión del argumento.

2. Asigna letras proposicionales a cada una de las proposiciones involucradas en el argumento. Puedes usar letras como p, q, r, etc., para representar proposiciones.

3. Construye una tabla de verdad con columnas para cada proposición y para las premisas y la conclusión.

4. Completa la tabla de verdad asignando los valores de verdad posibles (verdadero o falso) a las proposiciones involucradas. Asegúrate de considerar todas las combinaciones posibles.

• 5. Evalúa el valor de verdad de cada premisa y la conclusión en cada fila de la tabla de verdad. Utiliza las reglas de lógica para determinar el valor de verdad de las proposiciones compuestas (mediante el uso de conectivos lógicos como negación, conjunción, disyunción, implicación, etc.).

• 6. Examina las filas en las que todas las premisas son verdaderas y verifica si la conclusión también es verdadera en esas filas. Si la conclusión es verdadera en todas las filas en las que todas las premisas son verdaderas, el argumento se considera válido. De lo contrario, se considera inválido.

Como se aplican las leyes de la inferencia y las leyes de equivalencia lógica, para probar la validez de los argumentos

Para probar la validez de un argumento utilizando las leyes de inferencia y las leyes de equivalencia lógica, se sigue un enfoque deductivo. Aquí tienes los pasos generales a seguir:

1. Identificar las premisas y la conclusión del argumento.

2. Representar las premisas y la conclusión utilizando proposiciones simbólicas. Asignar letras proposicionales como p, q, r, etc., a cada proposición.

3. Utilizar las leyes de equivalencia lógica para simplificar las premisas y la conclusión. Utilizar las leyes de negación, conjunción, disyunción, implicación, etc., para transformar las proposiciones y reducir la complejidad del argumento. Puedes utilizar tablas de verdad, equivalencias conocidas o técnicas de simplificación para aplicar estas leyes.

4. Aplicar las leyes de inferencia para realizar inferencias válidas. Utilizar las leyes de Modus Ponens, Modus Tollens, Silogismo Hipotético, Silogismo Disyuntivo, entre otras, para derivar nuevas proposiciones a partir de las premisas simplificadas. Asegurarse de aplicar las reglas de inferencia de manera correcta y precisa.

5. Continuar aplicando las leyes de inferencia y las leyes de equivalencia lógica de manera sistemática hasta llegar a la conclusión o hasta que no se puedan realizar más inferencias. Realizar todas las inferencias posibles y utilizar todas las reglas lógicas pertinentes para analizar la validez del argumento.

6. Si se puede llegar a la conclusión utilizando las premisas y las reglas lógicas aplicadas, entonces el argumento es válido. Si en algún punto se llega a una contradicción o no se puede llegar a la conclusión utilizando las premisas y las reglas lógicas aplicadas, entonces el argumento es inválido.