Método de los Multiplicadores de Lagrange

“https://rua.ua.es/dspace/bitstream/10045/16373/8/Microsoft%20Word%20%208.%20INTRODUCCION%20A%20LA%20OPTIMIZACION%20NUMERIC A-1.pdf”.

8. Método de los Multiplicadores de Lagrange.

Lagrange (1736,1813) fue un físico, matemático y astrónomo italiano, y el desarrollador del presente método. El método de los multiplicadores de Lagrange es un procedimiento para encontrar los máximos y mínimos de funciones de múltiples variables sujetas a restricciones.

El método reduce el problema restringido con n variables a uno sin restricciones de n + k variables, donde k es igual al número de restricciones, y cuyas ecuaciones pueden ser resueltas más fácilmente. Estas nuevas variables escalares desconocidas, una para cada restricción, son llamadas multiplicadores de Lagrange.

Este método afirma que los puntos donde la función tiene un extremo condicionado con k restricciones, están entre los puntos estacionarios de una nueva función sin restricciones construida como una combinación lineal de la función y las funciones implicadas en las restricciones, cuyos coeficientes son los multiplicadores. La demostración usa derivadas parciales y la regla de la cadena para funciones de varias variables. Se trata de extraer una función implícita de las restricciones, y encontrar las condiciones para que las derivadas parciales con respecto a las variables independientes de la función sean iguales a cero.

Paz. D. (2013). Metodo lagrange & kuhn tucker - Optimizacion de sistemas y funciones. Slideshare. Recuperado “https://es.slideshare.net/danielpaz01/metodo-lagrange-kuhn-tucker- optimizacin-de-sistemas-y-funciones”. de

Este método tiene aplicaciones en el área de economía y en teoría de control. La técnica de los multiplicadores de Lagrange te permite encontrar el máximo o el mínimo de una función multivariable, f(x, y,…), cuando hay alguna restricción en los valores de entrada que puedes usar. Esta técnica solo se puede aplicar a restricciones del tipo: g(x, y,…)=c. Donde g es otra función multivariable con el mismo espacio de entrada que f, mientras que c es constante.

La idea principal sería buscar puntos en donde las curvas de nivel de f y g sean tangentes entre sí. Lo cual es igual que encontrar puntos en donde los vectores de los gradientes de f y g sean paralelos entre sí. Todo el proceso puede reducirse a hacer el gradiente de una cierta función, llamada el lagrangiano, igual al vector cero.

A continuación se presentará un problema que puede ser resuelto mediante la aplicación de los multiplicadores de Lagrange:

Una fabrica produce muebles de madera, los costos por mano de obra son 30$ por hora para los trabajadores, la medera cuesta 100$ por tonelada. Suponiendo que los ingresos R se modelan por la siguiente ecuación:

Donde h representa las horas de trabajo y s las toneladas de madera. Si el presupuesto es de 20 000$ ¿Cuál es el ingreso máximo posible?

Los costos de 30$ por hora de trabajo y de 100$ por tonelada de madera, nos dice que el costo total de producción, en términos de h y es:

Por lo tanto, el presupuesto de 20 000$ se traduce en:

L (h, s, )=300h2/3s1/3 -

Derivadas respecto a h: (30h+100s-20000)

Derivadas respecto a s:

Derivada respecto a

De forma que el sistema de ecuaciones a resolver es:

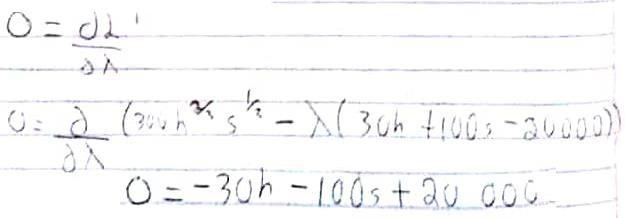
Solo queda resolver el sistema de ecuaciones, sin embargo para resolver sistemas como este, casi siempre es recomendable y necesario usar una computadora. Según la aplicación web Wolfram Alpha, el resultado sería:

Por tanto: