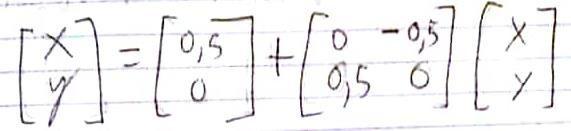Método Jacobiano

Y=-0.2+1.2 (1)=1;

El procedimiento puede repetirse, convergiendo a la solución analítica x=2, y=1.

2. Método Jacobiano.

El método de Jacobi o jacoviano es el método iterativo para resolver sistemas de ecuaciones lineales más simple, sin embargo este solo puede aplicarse a sistemas cuadrados, es decir a sistemas con tantas incógnitas como ecuaciones. Dicho algoritmo toma su nombre en honor al matemático alemán Carl Gustav Jakob Jacobi.

Para realizar este método, primeramente se ha de determinar la ecuación de recurrencia. Para esto, se ordenan las ecuaciones y las incógnitas. De la ecuación i se despeja la incógnita i. En notación matricial se escribirse como:

x = c + B x (1)

Donde x vendría a ser el vector de incógnitas. Luego, se toma una aproximación para las soluciones y a esta se le designa por xo. Para luego iterar en el ciclo que cambia la aproximación:

Xi +1 = c + Bxi

Es importante tener en cuenta que uno de los principales inconvenientes presentes en los métodos iterativos es la garantía de que el método convergerá, Para determinar si el método de Jacobi converge hacia una solución, se evalúan las siguientes condiciones de convergencia:

La matriz sea estrictamente dominante diagonalmente por filas (E.D.D. por filas), es decir, para todo i desde 1 hasta n que es el tamaño de la matriz A:

Es decir, el elemento de la diagonal correspondiente a la fila i debe ser mayor a la suma de los elementos de esa fila i.

A partir de la siguiente identidad:

Donde D corresponde a la matriz formada por los elementos de la diagonal de A (D=diag(a11, a22, ann)), -L corresponde a la matriz triangular inferior obtenida de la parte triangular estrictamente inferior de A, y -U corresponde a la matriz triangular superior obtenida de la parte triangular estrictamente superior de A, se puede deducir la fórmula vectorial de este método:

, k = 1, 2,...

De donde BJ (conocida como la matriz de iteración de Jacobi) es D1(L+U). Para que el método de Jacobi converja hacia una solución

, para una norma matricial inducida.

ρ(BJ), que corresponde al máximo de los valores absolutos de

las raíces de la ecuación característica de la matriz BJ (det(BJ - λI)) es menor que 1.

López, D. (2016). MÉTODO DE JACOBI. Aprende en Línea. Recuperado de “http://aprendeenlinea.udea.edu.co/lms/moodle/mod/page/view.php?id=2449 0”.

A continuación se explicará un ejercicio del actual método:

Partiendo de (x=1, y=2), aplique tres iteraciones del método Jacoviano para resolver el sistema:

Se despeja la ecuación con la incógnita correspondiente:

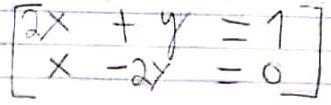
Quedando en notación vectorial como:

Aplicando la primera iteración partiendo de x0=1 y y0=2: