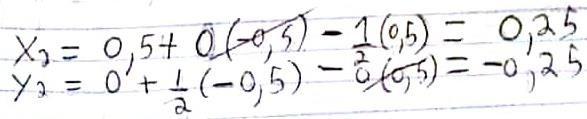
2 minute read
Método y Condiciones de Kuhn Tucker
Aplicando la segunda iteración partiendo de x1=-0.5 y y1=0.5
Aplicando la tercera iteración partiendo de x1=-0.5 y y1=0.5
Advertisement
De forma que, representándolo de mejor forma:

Di vendría a ser el margen de error conforme a la aproximación. Este también puede ser utilizado como criterio de paro. Si se quisiera se podría seguir iterando hasta obtener un error igual o menor a 0.001.

3. Método y Condiciones de Kuhn Tucker.
Las condiciones que deben satisfacer los óptimos de los problemas de optimización no lineal con restricciones de desigualdad fueron publicadas por
primera vez en 1939, en la tesis de Maestría de William Karush (Minima of Functions of Several Variables with Inequalities as Side Constraints), aunque fueron renombradas tras un artículo en una conferencia de Harold W. Kuhn y Albert W. Tucker en 1951. Las condiciones de Karush-Kuhn-Tucker (KKT) son una generalización del método de los multiplicadores de Lagrange para restricciones de desigualdad.
Las condiciones establecidas en el Teorema KKT, permiten abordar la resolución de modelos de programación no lineal que consideran tanto restricciones de igualdad como desigualdad. Las condiciones de KuhnTucker son necesarias solamente si se satisface una disposición específica llamada hipótesis de cualificación de la restricción (h.c.r.), que impone una condición sobre las funciones de restricción con el fin de descartar ciertas irregularidades en la frontera del conjunto factible, que invalidarían la condiciones de Kuhn- Tucker como necesarias, dándose la posibilidad de la existencia de puntos que siendo óptimos del problema, no verifiquen dichas condiciones. Esta disposición h.c.r. es en general difícil de comprobar, por ello en la práctica, se exige el cumplimiento de la condición de regularidad, que es una condición suficiente para que se verifique la h.c.r.
La condición de regularidad por otra parte, implica que un punto (X, Y) es regular si no satura ninguna de las restricciones, o bien, en el caso de saturar alguna de ellas, los gradientes de las restricciones saturadas en dicho punto son vectores linealmente independientes. A continuación se presentará un ejercicio utilizando este método:

La función a maximizar se encuentra sujeta a g(x,y); por otra parte las condiciones de primer orden son:
La condición de holgura complementaria es:

Queremos hallar todos los posibles (x,y) que verifiquen estas condiciones para un valor adecuado de

Habiendo dos posibilidades: =-2 o x=0.

x=0. Si =-2 entonces L2 da 1=0, lo cual es una contradicción, por lo tanto,
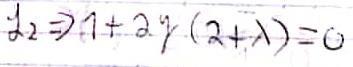
Si y=1:
De forma que
=-5/2. Verificando la condición de holgura complementaria, por tanto (0, 1) con =-5/2, es un candidato, por lo que se satisfacen las condiciones L2 y de holgura.

Si y=-1:
con Verificando la condición de holgura complementaria, por tanto (0, -1) =-3/2 es otro candidato óptimo.
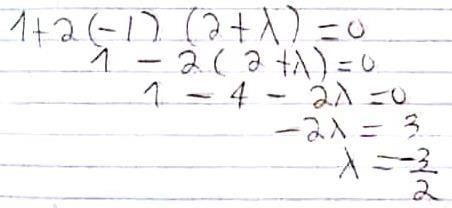
Considerando el caso en que x=0 y x2+y2<1, esto es: -1<y<1.
La holgura complementaria implica que =0 y L2 da y=-3/2 por tanto,
(0, -3/2) con
es candidatos óptimos: un candidato a óptimo. Concluyendose así con 3








