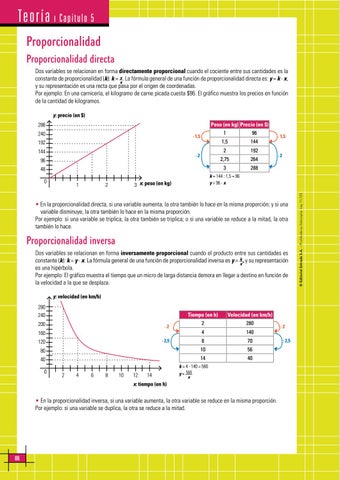
Teoría ı Capítulo 5 Proporcionalidad Proporcionalidad directa Dos variables se relacionan en forma directamente proporcional cuando el cociente entre sus cantidades es la constante de proporcionalidad (k): k = xy . La fórmula general de una función de proporcionalidad directa es: y = k · x, y su representación es una recta que pasa por el origen de coordenadas. Por ejemplo: En una carnicería, el kilogramo de carne picada cuesta $96. El gráfico muestra los precios en función de la cantidad de kilogramos. y: precio (en $) Peso (en kg) Precio (en $)
288 240
∙ 1,5
192 144
∙2
96 48 0
1
96
1,5
144
2
192
2,75
264
3
288
∙ 1,5
∙2
k = 144 : 1,5 = 96 y = 96 ∙ x
3 x: peso (en kg)
2
1
• En la proporcionalidad directa, si una variable aumenta, la otra también lo hace en la misma proporción; y si una variable disminuye, la otra también lo hace en la misma proporción. Por ejemplo: si una variable se triplica, la otra también se triplica; o si una variable se reduce a la mitad, la otra también lo hace.
Proporcionalidad inversa Dos variables se relacionan en forma inversamente proporcional cuando el producto entre sus cantidades es constante (k): k = y · x. La fórmula general de una función de proporcionalidad inversa es y = kx , y su representación es una hipérbola. Por ejemplo: El gráfico muestra el tiempo que un micro de larga distancia demora en llegar a destino en función de la velocidad a la que se desplaza. y: velocidad (en km/h) 280 240 200
Tiempo (en h)
Velocidad (en km/h)
2
280
4
140
∙2
160
∙ 2,5
120 80 40 0
2
4
6
8
10
12
14
8
70
10
56
14
40
k = 4 ∙ 140 = 560 y = 560 x
x: tiempo (en h)
• En la proporcionalidad inversa, si una variable aumenta, la otra variable se reduce en la misma proporción. Por ejemplo: si una variable se duplica, la otra se reduce a la mitad.
86
:2 : 2,5