h-7-al-me by sloven

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

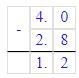
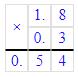
3. Обчисліть значення виразу: 1) 3,8 + (- 2,5) = 3,8 – 2,5 = 1,3; 2) - 4,8 +4,8 = 0; 3)

6. Знайдіть значення виразу: 1) 2х – 3 при х = 4; 0; -3:

1) 0,4у + 1 при у = -0,5; 8; -10:

0,4 · (-0,5) + 1 = -0,2 + 1 = 0,8

0,4 · 8 + 1 = 3,2 + 1 = 4,2

0,4 · (-10) + 1 = -4 + 1 = -3

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Ця

числом. Отже,

2) a + bc

Це сума числа

(6 – 8)³ = (-2)³ = -8

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) (b – a) (км) – на стільки за 1

2) s : (b – a) (год) – велосипедистка

3) 12 : (12 – 4) = 12 : 8 = 1,5 (год)

Відповідь: s : (b – a) годин; 1,5 годин.

17. Запишіть у вигляді виразу:

1) потроєний добуток різниці чисел а і b та їхньої суми: 3(a – b)(a + b)

2) суму трьох послідовних натуральних чисел,

n + (n + 1) + (n + 2)

3) добуток трьох послідовних

(2k – 4)(2k – 2) · 2k

4) число, у якому а тисяч, b сотень і с

1000a + 100b + c

5) кількість сантиметрів

(100x + y) см

6) кількість

хв =

с (3600m + 60n + p) с

18. Запишіть у

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

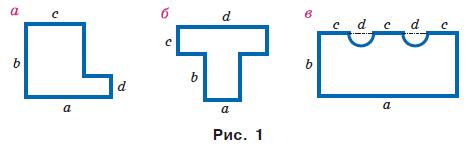
b + c + (b – d) + (a – c) + d = a + b + c + b

2a + 2b; ab – (a – c)(b – d).

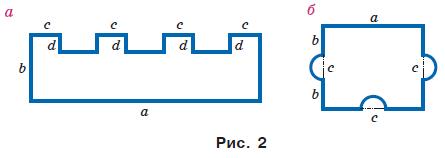
b) + 2(c + d) – 2a = 2a + 2b + 2c + 2d – 2a = 2(b + c + d).

ab + cd. Відповідь: 2(b + c + d); ab + cd.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

5 8

1) 64 · 5 8 = 40 (кг) – маса моркви.

2) 40 · 1,8 = 72 (кг) – маса картоплі.

3) 64 + 40 + 72 = 176 (кг) – маса овочів.

Відповідь: 176 кг.

25. Відомо, що а і b –

стверджувати, що:

1) a – b > 0: Нерівність a – b > 0

3) �� > �� : Нерівність

рівняння 3х + 1 = 21 – х:

х = 5, то: 3х + 1 = 3 · 5 + 1 = 16; 21 – х

рівняння х(х + 4) = 4:

Якщо х = -2, то х(х + 4) = -2 · (-2 + 4) =

27. Розв’яжіть рівняння:

1) 0,3х = 9

х = 9 : 0,3 х = 30 2) -2х = 3 х = 3 : (-2) х = -1,5 3)

дужки: 1) 2(х – 3у + 4z) = 2z – 6y + 8z 2) -0,4(-5 + 1,5у) = 2 – 0,6y

= -2 3) -7х + 2 = 3х – 1 -7х – 3х = -1 – 2 -10х = -3 х = 0,3 4) 10 – 2х = 12 + х -2х

38. Знайдіть корінь рівняння:

1) 3х + 6 = 2х – 1

3х – 2х = -1 – 6

х = -7

2) 10х + 7 = 8х – 9

10х – 8х = -9 – 7

2х = -16

х = -8

3) 20 – 3х = 2х – 45

39. Розв’яжіть рівняння:

1) -3(х – 4) = 5х – 12

-3х + 12 = 5х – 12

-3х – 5х = -12 – 12

-8х = -24

х = 3

2) (16х – 5) – (3 – 5х) = 6

16х – 5 – 3 + 5х = 6

16х + 5х = 6 + 5 + 3

21х = 14

х = 2 3

0,2х + 3,4 = 0,6 –

– 0,6х = -2,6 – 3,4 -0,4х = -6 х = 15

-3х – 2х = -45 – 20 -5х = -65 х = 13

4) 2,7 + 1,9х = 2х + 1,5 1,9х – 2х = 1,5 – 2,7 -0,1х = -1,2 х = 12

3) 26 – 4х = 3х – 7(х – 3) 26 – 4х = 3х – 7х + 21 -4х – 3х + 7х = 21 – 26

0х = -5

Коренів немає 4) -2(3 – 4х) + 5(2 – 1,6х) = 4 -6 + 8х + 10 – 8х = 4

0х = 4 + 6 – 10

0х = 0

-яке число

(5 + 6x) = 8,

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

9 – 4x – 5 + 6x = 8;

2x = 8 + 9 – 5;

2x = 12; x = 6.

Знайдіть помилки в цьому «розв’язуванні».

1) Василь неправильно розкрив дужки.

2) Неправильно зведені подібні члени (повинен

доданків).

3) Неправильно знайдено значення x.

41. Розв’яжіть рівняння:

1) 4(13 – 3х) – 17 = -5х

52 – 12х – 17 = -5х

-12х + 5х = 17 – 52

х = 5

2) (18 – 3х) – (4 + 2х) = 10 18 – 3х – 4 – 2х = 10

-5х = 10 – 18 + 4

х = 0,8

42. Доведіть, що:

3) 14 – х = 0,5(4 – 2х) + 12 14 – х = 2 – х + 12 -х + х = 2 + 12 – 14

0х = 0

Будь-яке число 4) 4х – 3(20 – х) = 10х – 3(11 + х)

4х – 60 + 3х = 10х – 33 – 3х

4х + 3х – 10х + 3х = -33 + 60

0х = 27 Коренів

1) коренем рівняння 4 (x – 5) = 4x – 20 є будь-яке число;

4(х – 5) = 4х – 20

4х – 20 = 4х – 20

4х – 4х = -20 + 20

0х = 0

Будь-яке число

2) рівняння 2y – 8 = 4 + 2y не має коренів.

2у – 2у = 4 + 8

0у = 12

Коренів немає

43. Розв’яжіть рівняння:

1) 0,8 – (1,5х – 2) = -0,8 + 4,5х

0,8 – 1,5х + 2 = -0,8 + 4,5х -1,5х – 4,5х = -0,8 – 0,8 – 2 -6х = -3,6

х = 0,6 2) 0,6х – 5(0,3х + 0,2) = 0,5(х – 1) – 0,8 0,6х – 1,5х – 1 = 0,5х – 0,5х – 0,8 0,6х – 1,5х – 0,5х = -0,5 – 0,8 + 1 -1,4х = -0,3 х = 3 14 3) 1 7 �7 8 у +7

0,3х + 1,8 = 0,4х – 2,6

0,3х – 0,4х = -2,6 – 1,8 -0,1х = -4,4

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

х = 44

2) -0,4(3х – 1) + 8(0,8х – 0,3) = 5 – (3,8х + 4)

-1,2х + 0,4 + 6,4х – 2,4 = 5 – 3,8х – 4

5,2х – 2 = 1 – 3,8х

5,2х + 3,8х = 1 + 2

9х = 3

х = 1 3

3) 4 7 (0,56 − 4,2у) +0,4= 5 13 (0,52 − 6,5у)

0,32 – 2,4у + 0,4 = 0,2 – 2,5у

-2,4у + 2,5у = 0,2 – 0,32 – 0,4

0,1у = -0,52

у = -5,2

45. Розв’яжіть рівняння:

1) 8(7х – 3) = -48(3х + 2)

7х – 3 = -6(3х + 2)

7х – 3 = -18х – 12

7х + 18х = - 12 + 3

25х = -9

х = -0,36

46. Чому дорівнює корінь рівняння:

1) -36(6х + 1) = 9(4 – 2х)

-4(6х + 1) = 4 – 2х

-24х – 4 = 4 – 2х

-24х + 2х = 4 + 4

-22х = 8

х = 4 11

47. Розв’яжіть рівняння:

1) (4х – 1,6)(8 + х) = 0

4х – 1,6 = 0 або 8 + х = 0

4х = 1,6 або х = -8

х = 0,4 або х = -8

3) (3х − 2) �4+ 1 3 х� =0

3х – 2 = 0 або 4+ 1 3 х =0

3х = 2 або 1 3 х = 4

х = 2 3 або х = -12

48. Розв’яжіть рівняння: 1) (1,8 – 0,3у)(2у + 9) = 0

1,8 – 0,3у = 0 або 2у + 9 = 0 -0,3у = -1,8 або 2у = -9 у = 6 або у = -4,5

49. Розв’яжіть рівняння: 1) 5х−4 2 = 16х+1 7

7(5х – 4) = 2(16х + 1)

35х – 28 = 32х + 2

2) 4,5(8х + 20) = 6(6х + 15)

18(2х + 5) = 18(2х + 5)

2х + 5 = 2х + 5

2х – 2х = 5 – 5

0х = 0

2) 3,2(3х – 2) = -4,8(6 – 2х)

2(3х – 2) = -3(6 – 2х)

6х – 4 = -18 + 6х

6х – 6х = -18 + 4

0х = -14 Коренів немає

2) х(5 – 0,2х) = 0

х = 0 або 5 – 0,2х = 0

х = 0 або -0,2х = -5

х = 0 або х = 25

4) (2х + 1,2)(х + 1)(0,7х – 0,21) = 0

2х + 1,2 = 0 або х + 1 або 0,7х – 0,21 = 0

2х = -1,2 або х = -1 або 0,7х = 0,21

х = -0,6 або х = -1 або х = 0,3

2) (5у + 4)(1,1у – 3,3) = 0 5у + 4 = 0 або 1,1у – 3,3 = 0 5у = -4 або 1,1у = 3,3 у = 0,8 або у = 3

35х – 32х = 2 + 28

3х = 30 х = 10

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2) 4у+33 3 = 17+у 2

2(4у + 33) = 3(17 + у)

8у + 66 = 51 + 3у 8у – 3у = 51 – 66 5у = -15 у = -3

50. Знайдіть корінь рівняння: 1) 3��+5 4 = 5��+1 3

3(3m + 5) = 4(5m + 1)

9m + 15 = 20m + 4

-11m = -11 m = 1

51. Чому дорівнює корінь рівняння: 1) 2х 3 + 5х 4 = 23

8х + 15х = 276

23х = 276

х = 12

52. Розв’яжіть рівняння: 1) 7х

= 14 х =4 2 3 4

5х+3 5 = х−5 8 8(5х + 3) = 5(х – 5)

40х + 24 = 5х – 25

40х – 5х = -25 – 24

35х = -49 х = -1,4

53. При якому значенні змінної: 1) значення виразу 4x – 0,2 (8x – 7) дорівнює –22,6; 4х – 0,2(8х – 7) = -22,6

4х – 1,6х + 1,4 = -22,6

4х – 1,6х = -22,6 – 1,4

2,4х = -24

х = -10

2) вирази 0,2 (3 – 2y) і 0,3 (7 – 6y) + 2,7 набувають рівних значень;

0,2(3 – 2у) = 0,3(7 – 6у) + 2,7

0,6 – 0,4у = 2,1 – 1,8у + 2,7 -0,4у + 1,8у = 2,1 + 2,7 – 0,6

1,4у – 4,2

у = 3

3) значення виразу 0,6y на 1,5 більше

0,6у = 0,3(у – 4) + 1,5

0,6у = 0,3у – 1,2 + 1,5

0,6у – 0,3у = -1,2 + 1,5

0,3у = 0,3

у = 1

5(5х – 1) = 6,5 + 2х

25х – 5 = 6,5 + 2х

25х – 2х = 6,5 + 5

23х = 11,5

х = 0,5

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) вирази 6 – (2x – 9) і (18 + 2x) – 3 (x – 3) набувають рівних

6 – (2х – 9) = (18 – 2х) – 3(х – 3)

6 – 2х + 9 = 18 + 2х – 3х + 9

15 – 2х = 27 – х

-2х + х = 27 – 15

-х = 12

х = -12

2) значення виразу –(2y – 0,9) на 2,4 менше від значення виразу 5,6 – 10y?

-(2у – 0,9) + 2,4 = 5,6 – 10у

-2у + 0,9 + 2,4 = 5,6 – 10у

-2у + 3,3 = 5,6 – 10у

-2у + 10у = 5,6 – 3,3

8у = 2,3

у = 0,2875

55. Розв’яжіть рівняння:

1) ǀхǀ + 6 = 13

ǀхǀ = 7

х = 7 або х = -7

2) ǀхǀ - 7 = -12

ǀхǀ = -5

Коренів

3) 7ǀхǀ - 3 = 0 7ǀхǀ = 3

56. Розв’яжіть рівняння: 1) ǀхǀ - 8 = -5

ǀхǀ = 3

х = 3 або х = -3

4) ǀ8 – 0,2хǀ = 12

8 – 0,2х = 12 або 8 – 0,2х = -12 -0,2х = 4 або -0,2х = -20

х = 20 або х = 100

5) ǀ10х - 7ǀ - 32 = -16

ǀ10х - 7ǀ = 16

10х + 7 = 16 або 10х – 7 = -16

10х = 23 або 10х = -9

х = 2,3

= 9 або х = 1 5) ǀ9 + хǀ = 0 9 + х = 0

ǀхǀ + 5 = 2

= -3

3) ǀх + 12ǀ = 3 х + 12 = 3

х + 12 = -3

= -9 або х = -15

х = -0,9 6) ǀǀхǀ - 2ǀ ǀхǀ - 2 = 2 або ǀхǀ - 2 = -2 ǀхǀ = 4 або ǀхǀ = 0 х = 4 або х = -4 або х = 0 57. При якому значенні a рівняння:

1) 5ax = –45 має

5а · 3 = -45

15а = -45

а = -3

2) (a – 4) x = –5a + 4x – 7

(а – 4) · (-6) = -5а + 4 · (-6) – 7 -6а + 24 = -5а – 24 – 7 -6а + 5а = -24 – 7 – 24

–6?

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

-а = -55 а = 55

58. При якому значенні a рівняння:

1) 3ax = 12 – x

3а · (-9) = 12 – (-9) -27а = 21 а = 7 9

2) (5a + 2)x = 8 – 2a має корінь, що дорівнює числу 2? (5а + 2) · 2 = 8 – 2а

10а + 4 = 8 – 2а

10а + 2а = 8 – 4

12а = 4 а = 1 3

59. Укажіть яке-небудь

1) 0,1x = b. Наприклад, якщо b = 1, то 0,1х = 1; х = 10 – ціле число.

2) bх = 21. Наприклад, якщо b = 3, то 3х = 21; х = 7 –

3) 1 6 х =b. Наприклад, якщо

4) bх = 1 6. Наприклад, якщо b = 1 6, то 1 6 х = 1 6; х = 1 –

60. Складіть рівняння, яке: 1) має єдиний корінь, що дорівнює числу –4;

2х = -8

2) має безліч коренів; 2х = х + х

3) не має коренів.

2х + 2 = х + х

61. Знайдіть усі цілі значення

1) mx = 3;

х = 3 : m

Частка 3 : m

2) (m + 4) x = 49.

х = 49 : (m + 4)

Частка 49 : (m + 4)

коли m = -5; -3; -11; 3; -53; 45. 62.

1) nx = –5;

= -5 : n

-5 : n

2) (n – 6) x = 25.

= 25 : (n – 6)

25 : (n – 6)

n = 7; 11; 31. 63.

1) 7 – 3x = 6x

7 – 3х = 6х – 56 -3х – 6х = -56 – 7 -9х = -63

n =

х = 7

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

- 3b = -35

2) 2y – 9b = 7 і 3,6 + 5y = 7 (1,2 – y)?

3,6 + 5у = 7(12 – у)

3,6 + 5у = 8,4 – 7у

5у + 7у = 8,4 – 3,6

12у = 4,8

у = 0,4

Коренем рівняння 2у - 9b = 7

-9b = 6,2; b = − 31 45 .

1) (4x + 1) – (7x + 2) = x і 12x – 9 = c + 5;

(4х + 1) – (7х + 2) = х

4х + 1 – 7х – 2 = х

4х – 7х – х = -1 + 2 -4х = 1

х = -0,25

12х

-3 – 9 = с + 5; с = -17.

2) 1 7 cx = + x + с і 6 – 3 (2x – 4) = –8x + 4?

6 – 3(2х – 4) = -8х + 4

6 – 6х + 12 = -8х + 4

-6х + 8х = 4 – 6 – 12

2х = -14

х = -7

Коренем рівняння 1 7 cx = + x + с

; -с = -7 + с; -2с = -7; с = 3,5.

65. При якому значенні a не має

рівняння: 1) ax = 6;

Рівняння не має коренів, якщо а = 0 2) (3 – a) x = 4;

Рівняння не

3) (a – 2) x = a + 2?

Рівняння не має

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

має єдиний корінь, якщо: а + 7 ≠ 0, тобто, якщо а ≠ -7

68. Розв’яжіть рівняння: 1) (b + 1) x = 9;

Якщо b + 1 ≠ 0, тобто, якщо b ≠ -1, то х = 9 : (b + 1)

Якщо b + 1 = 0, тобто, якщо b = -1, то: 0х = 9 – рівняння коренів не має

2) (b² + 1)х = -4.

х = -4 : (b² + 1)

69. Розв’яжіть рівняння (m + 8) x = m + 8.

Якщо m + 8 ≠ 0, тобто, якщо m ≠ -8, то х = (m + 8) : (m + 8); х = 1.

Якщо m + 8 = 0, тобто, якщо m = -8, то: 0х = 0 – будь-яке число є коренем рівняння.

70. Яким виразом можна замінити

рівняння, яке:

6x + 8 = 4x + *

6х – 4х = * -8

2х = * - 8

1) не має коренів;

2) має безліч коренів; Рівняння 2х = * - 8

3) має один корінь?

Рівняння 2х = * - 8 завжди має

71. У рівності 2 (1,5x – 0,5) = 7x + *

рівняння, яке:

2 (1,5x – 0,5) = 7x + *

3х – 1 = 7х + *

3х – 7х = * + 1 -4х = * + 1

1) не має коренів;

Рівняння -4х = * + 1 має

2) має безліч коренів;

Рівняння -4х = * + 1 не може

3) має один корінь.

Рівняння -4х = * + 1 завжди має

72. Розв’яжіть рівняння:

1) | x | + 3x = 12;

Нехай х ≥ 0, тоді: х + 3х = 12; 4х = 12; х = 3

-4

Нехай х < 0, тоді: -х + 3х = 12; 2х = 12; х = 6

2) | x | – 4x = 9;

Нехай х ≥ 0, тоді: х – 4х = 9; -3х = 9; х = -3. Число -3

є коренем рівняння. Нехай х < 0, тоді: -х – 4х = 9; -5х = 9; х = -1,8 3) 2 (x – 5) – 6 | x | = –18.

х ≥ 0, тоді: 2х – 10 – 6х = -18; -4х = -8; х = 2

х < 0, тоді: 2х – 10 + 6х = -18; 8х = -8; х = -1

рівняння: 1) 2x – | x | = –1;

х ≥ 0, тоді: 2х – х = -1; х = -1. Число -1

рівняння.

задовольняє умову х ≥ 0, тому -3

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Нехай х < 0, тоді: 2х + х = -1; 3х = -1; х = 1 3 . 2) 7 | x | – 3 (x + 2) = –10.

Нехай х ≥ 0, тоді: 7х – 3х – 6 = -10; 4х = -4; х = -1. Число -1 не задовольняє умову х ≥ 0, тому -1 не є коренем рівняння.

Нехай х < 0, тоді: -7х – 3х – 6 = -10; -10х = -4; х = 0,4. Число 0,4 не задовольняє

74. При яких цілих значеннях a

1) x – 2 = a;

х = а + 2

Число а + 2 ділиться націло на 2, якщо

–

число 2) x + 7a = 9;

х = 9 – 7а

Число 9 – 7а

3) 2x – a = 4;

2х = 4 + а

х = 2 + а : 2

Число 2 + а : 2 ділиться націло

4) x + 2a = 3

х = 3 – 2а

Число 3

числом,

1) x + 3 = b

х = b – 3

Число

2) x – 2 = b

х = b + 2

Число b + 2

3) x – 3b = 8

х = 8 + 3b

Число 8 + 3b

1) 3x = b;

х = b : 3

Число b : 3

2) x = 2b?

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

(х + 6) + х = 24

2х + 6 = 24

2х = 18

х = 9 – зошитів у

9 + 6 = 15 – зошитів у

Відповідь: 9; 15.

х + (х + 12,6) = 65,4

2х + 12,6 = 65,4

2х = 52,8

х = 26,4 – зібрали з першого дерева.

26,4 + 12,6 = 39 (кг) –

Відповідь: 26,4 кг; 39 кг.

86. Периметр

сторони прямокутника.

Нехай менша сторона прямокутника

(х + х + 1,3) · 2 = 7,8

2х + 1,3 = 3,9

2х = 2,6

х = 1,3 (см) – менша сторона

1,3 + 1,3 =

Відповідь: 1,3 см; 2,6 см.

87. Одна зі сторін

менша

12х = 72 х = 6 (см)

3х – 70 = 6113

3х = 6183

х = 2061 (м) –

2061 – 29 = 2032 (м)

7,8

2061 –

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

(х + 115)

х + (х + 115) + (х – 30) = 1285

3х + 85 = 1285

3,2х = 1900

х = 400 (м) – Каскадна.

400 + 115 = 515 (м) – Солдатська.

400 – 30 = 370 (м) – Нахімовська.

Відповідь: 400 м; 515 м; 370 м.

90. У

х + 24, тоді:

Скільки

х + 2х + (х + 24) = 160

4х + 24 = 160

4х = 136

х = 34 – однокімнатних.

2 · 34 = 68 – двокімнатних.

34 + 24 = 58 – трикімнатних.

Відповідь: 34; 68; 58.

91. Троє робітників

кожний робітник? Нехай

робітник

(х + 16) деталей, тоді:

3х + х + (х + 16) = 96

5х + 16 = 96

5х = 80

х = 16 (д.) –

3 · 16 = 48 (д.)

16 + 16 = 32 (д.)

48; 16; 32.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

х + 1,2х + 0,8х = 270

3х = 270

х = 90 (км) Відповідь:

6(х + 6) + 8х = 232

6х + 36 = 8х = 232

14х + 36 = 232

14х = 196

х = 14 (кг) – яблук у

14 + 6 = 20 (кг)

+ 4) місць, тоді:

12(х + 4) + 15х = 534

12х + 48 + 15х = 534

27х + 48 = 534

27х = 486

х = 18

12(18 + 4) = 12 · 22 = 264 (м.) –

0,8(х + 48) = 4х

0,8х + 38,4 = 4х

3,2х = 38,4

х = 12 (км/год)

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

12 + 48 = 60 (км/год) – швидкість

Відповідь: 12 км/год; 60 км/год.

дорівнює (х + 24) грн, тоді:

3(х + 24) = 3,5х

3х + 72 = 3,5х

0,5х = 72

х = 144 (грн) – другого виду.

144 + 24 = 168 (грн) – першого виду.

Відповідь: 168 грн; 144 грн.

98. Кілограм огірків

3,6(х – 8) = 3,2х

3,6х – 28,8 = 3,2х

0,4х = 28,8

х = 72 (грн)

Відповідь: 72 грн.

+ 80)

3х + 16 = х + 80

3х – х = 80 – 16

2х = 64

х = 32 (л) – у другому

3 · 32 = 96 (л)

26 + х = 5(2 + х)

26 + х = 10 + 5х

4х = 16

х = 4 (р.)

Відповідь: 4 роки.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

від матері?

Нехай

15х + 24(40 – х) = 690

9х = 270

х = 30 – орфографічних.

40 – 30 = 10 – тлумачних.

Відповідь: 30; 10. 104.

– (х – 200) т, тоді:

5(х – 680) = х – 200

5х – 3400 = х – 200

4х = 3200

х = 800 (т) –

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

x – 180 = 2(x − 270)

x – 180 = 2x –

−180 + 540 = 2x –

= x

5 7 (5х 12) = х + 12

5(5х – 12) = 7(х + 12)

25х – 60 = 7х + 84

25х – 7х = 84 + 60

18х = 144

х = 8 (кг) – у другому мішку.

5 · 8 = 40 (кг) – у першому

В одному

90 – 4х = 2(60 – 5х)

90 – 4х = 120 – 10х

6х = 30

х = 5

Відповідь: 5 днів.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

3,5(200 – х) = 640 – 2х

700 – 3,5х = 640 – 2х

-3,5х + 2х = 640 – 700

-1,5х = -60

х = 40 (л) – з першої цистерни.

2 · 40 = 80 (л) – з другої цистерни.

Відповідь: 40 л; 80 л. 112. Із двох міст,

50х + 80(х + 4) = 385

50х + 80х + 320 = 385

130х = 65

х = 0,5 (год)

0,5 + 4 = 4,5 (год)

16х

20х

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

швидкість теплохода

швидкість автобуса – (х + 30) км/год.

Теплохід подолав 6х км, а автобус – 3,5(х + 30) км, тоді:

3,5(х + 30) – 6х = 55

3,5х + 105 – 6х = 55 -2,5х = -50

х = 20 (км/год) – швидкість теплохода.

20 + 30 = 50 (км/год) – швидкість автобуса.

Відповідь: 20 км/год; 50 км/год.

115. Теплохід

(х + 2,5) км/год, а проти течії –

(х + 2,5) · 4 км, а

(х + 2,5) · 4 – (х – 2,5) · 3 = 48

4х + 10 – 3х + 7,5 = 48

х + 17,5 = 48

х = 30,5 (км/год)

Відповідь: 30,5 км/год.

(24 – х) км/год.

(24 – х) · 1,5 – 5х = 23

36 – 1,5х = 23

-6,5х = -13

х = 2 (км/год)

Відповідь: 2

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

0,3х + 0,25х + 0,3х – 26 + 0,25х + 10 = х

1,1х – 16 = х

0,1х = 16

х = 160 (л)

Відповідь: 160 л.

деталей, тоді:

28(х – 2) – 20х = 8

28х – 56 – 20х = 8

8х = 64

х = 8 (дн.)

Відповідь:

10х – 14(х – 3) = 2

10х – 14х + 42 = 2 -4х = -40

х = 10

10 · 10 = 100 (з.)

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

11х 2=1 3 4 (11х 20)ǀ ·4

44х – 8 = 7(11х – 20)

44х – 8 = 77х – 140

33х = 132

х = 4

11 · 4 – 20 = 24 – дане двоцифрове число.

Відповідь: 24.

127. Із двох

становить (х – 10) км/год. Перший

км, тоді:

2х + 2(х – 10) = 270 – 30

2х + 2х – 20 = 240

4х = 260

х = 65 (км/год) – швидкість першого автомобіля.

65 – 10 = 55 (км/год) –

Відповідь: 65 км/год; 60 км/год.

128. Компанія складається із

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2; n = 3k – 1; n = 3k,

1. Нехай n = 3k – 2, тоді n + 26 = 3k – 2 + 26 = 3k + 24 = 3(k + 8) –

2. Нехай n = 3k – 1, тоді n – 2 = 3k – 1 – 2 = 3k – 3 = 3(k – 1). Число 3(k – 1) для усіх

3 + 2 = 5 є

числом. Якщо n = 5, то значення виразів n + 24 і n + 26 відповідно

числами.

3. Нехай n = 3k, тоді n + 24 = 3k + 24 = 3(k + 8)

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

5. Знайдіть корінь рівняння 7x + 2 = 3x – 6. А) 2; Б) 1; В) –2; Г ) –1.

7х + 2 = 3х – 6

7х – 3х = -6 – 2

4х = -8

х = -2

6. Яке з рівнянь є лінійним?

Лінійне рівняння має форму ax + b = 0, де a і b – константи, а x – змінна.

А) 2x = –3;

Це рівняння можна переписати у вигляді 2x + 3 = 0, що є лінійним рівнянням. Б) 1 х =0 ; Це рівняння не має розв'язків,

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

x + 2x + 2x + 10 = 70; Б) x + 2x + x + 10 = 70;

більше, ніж перший, тобто x +

х + 2х + (х + 10) = 70

х + 2х + х + 10 = 70

4х + 10 = 70

4х = 60

х = 15

2 (4x – 12) = x + 12; Б) 2 (4x + 12) = x – 12;

2(х + 12) = 4х – 12

2х + 24 = 4х – 12

24 + 12 = 4х – 2х

36 = 2х х = 18

x + 2x + 2x – 10 = 70; Г) x + 2x + x – 10 = 70.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

5) Рівність не є тотожністю, бо, наприклад, якщо а = 1, b = 1, то (a + b) · 0 = (1 + 1) · 0 = 0? a + b = 1 + 1 = 2 і 0 ≠ 2.

6) Перетворю ліву частину рівності: (a – a)(b + b) = 0 · 2b = 0 – рівність є тотожністю.

7) Рівність не є тотожністю, бо, наприклад, якщо а = 0, то 3а – а = 0 – 0 ≠ 3.

8) Перетворю ліву частину рівності: 4х + 3х = (4 + 3)х = 7х – рівність є тотожністю.

9) Рівність не є тотожністю, бо, наприклад, якщо а = 1, b = 1, c = 1, то a – (b + c) = 1 – (1 + 1) = -1, a – b + c = 1 – 1 + 1 = 1 і -1 ≠ 1.

10) Перетворю ліву частину рівності: m + (n – k) = m + n – k – рівність є тотожністю.

11) Перетворю ліву частину рівності: 4а – (3а – 5) = 4а – 3а + 5 = а + 5 – рівність є тотожністю.

12) Рівність не є тотожністю, бо, наприклад, якщо а = 1, то (а – 5)(а + 3) = (1 – 5)(1 + 3) =16, (5 – а)(3 + а) = (5 – 1)(3 + 1) = 16 і -16 ≠ 16.

141. Чи є тотожно рівними вирази:

1) 8(a – b + c) = 8a – 8b + 8c – вирази є тотожно рівними.

2) Вирази не є тотожно рівними, бо, наприклад, якщо х = 1, то -2(х – 4) = -2(1 – 4) = 6, -2х – 8 = -2 · 1 – 8 = -10 і 6 ≠ -10.

3) Вирази не є тотожно рівними, бо, наприклад,

– 7) = 3, 3а – 11 = 3 · 0 – 11 = -11 і

а = 2, то а² = 4, ǀаǀ = 2 і 4 ≠ 2. 143.

–4a – 3b; 2) –3a + 3b; 4) –3a – 3b?

-3а + 8b – a – 11b = -4a – 3b

Відповідь: 3).

144. Серед виразів –10a + 7; –10a – 7; –14a +

дорівнює виразу –12a + (7 – 2a). -12а + (7 – 2а) = -12а + 7 – 2а = -14а + 7

Відповідь: -14а + 7

145. Доведіть тотожність:

1) -5х – 6(9 – 2х) = -5х – 54 + 12х = 7х – 54 – тотожність

3(7 –

доведена.

5) 3(2,1m – n) – 0,9(7m + 2n) = 6,3m – 3n – 6,3m – 1,8n = -4,8n – тотожність доведена.

3) 5(0,4х – 0,3) + (0,8 – 0,6х) = 2х – 1,5 + 0,8 – 0,6х = 1,4х – 0,7 – тотожність доведена.

1 9 (

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

ǀа + 5ǀ = а + 5 не є тотожністю, бо, наприклад, якщо а = -6, то ǀа + 5ǀ = ǀ-6 + 5ǀ = ǀ-1ǀ = 1, а + 5 = -6 + 5 = -1 і 1 ≠ -1.

4) ǀа - bǀ = ǀ-(b – a) ǀ = ǀb - aǀ - рівність є тотожністю.

5) ǀа² + 4ǀ = а² + 4, бо а² + 4 > 0 для усіх

рівність ǀа² + 4ǀ = а² + 4 є тотожністю.

6) Рівність ǀa + bǀ = ǀaǀ + ǀbǀ не є тотожністю, бо, наприклад, якщо а = 6, b = -5, то ǀa + bǀ = ǀ6 - 5ǀ = 1, ǀaǀ + ǀbǀ = ǀ6ǀ + ǀ-5ǀ = 6 + 5 =

- 1² = 4 – 1 = 3? (a – b) ² = (2 – 1) ² = 1² = 1 і 3 ≠ 1. 148. Запишіть у вигляді рівності твердження:

1) сума протилежних чисел дорівнює нулю; а + (-а) = 0

2) добуток даного числа та числа 1 дорівнює 1; а · 1 = 1

3) добутком даного числа та числа –1 є число, протилежне даному; а · (-1) = -а

4) модулі протилежних чисел рівні; ǀаǀ = ǀ-аǀ

5) різниця протилежних чисел дорівнює нулю.

а – (-а) = 0

Які із цих рівностей є тотожностями? – 1), 3), 4).

149. Доведіть тотожність:

1) 4(2 – 3m) – (6 – m) – 2(3m + 4) = 8 – 12m – 6 + m – 6m – 8 = -17m – 6 – тотожність

доведена.

2) a + b – 10ab = 2a (3 – b) – 3b (a – 2) – 5 (ab + a + b) = 2a(3 – b) – 3b(a – 2) – 5(ab + a + b) = 6a – 2ab – 3ab + 6b – 5ab – 5a – 5b = a + b – 10ab – тотожність доведена.

3) 6(5а – 3) + (10 – 20а) – (6а – 4) = 30а – 18 + 10 – 20а – 6а + 4 = 4а – 4 5а – (3а – (2а – 4)) = 5а

тотожність: 1) (3m – 7) · 0,6 – 0,8(4m – 5) – (-1,7 + 1,4m) = 1,8m – 4,2 – 3,2m + 4 +

доведена.

Доведіть, що не

бо, наприклад, якщо b = 1, то (b –1)(b + 1) = (1 – 1)(1 + 1) = 0, (b – 1)b + 1 = (1 – 1) · 1 + 1 = 1 і 0 ≠ 1.

3) Рівність (с + 1)³ = с³ + 1 не є тотожністю, бо, наприклад, якщо с = 1, то (с + 1)³ = (1 + 1)³ = 2³ =

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) 981

2) 591 : 1130 = 0,523 = 52,3%

3) (−х) ⋅ (−х) … ⋅ (−х) =(−х)19 4) (�� + �� ) ⋅

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

10 ⋅ 1 2�2 = �10 2 �2 =5 ⋅ 5= 25

2,55 ⋅ 104 =2,55 ⋅ 10000 = 25500

Відповідь: 25 500 км².

169.

1,495 ⋅ 1011 =1,495

Відповідь: 149 500 000 000 м.

170.

1) 1,49 ⋅ 108 =1,49

171. Обчисліть: 1) 82 110 = 64 1= 63

2) 0,3 ⋅ 24 =0,3 ⋅ 16 =4,8 3)(4,2 3,8)4 ⋅ 252 =0,44 ⋅ 252 =0,4 ⋅ 0,4

⋅ (0,4 ⋅ 25) =0,16 ⋅ 10 ⋅ 10 = 16

172. Обчисліть:

1) 43 +35 = 64 + 243 = 307

2) 0,63 0,43 =0,216 0,064 =0,152 3) 0,12 ⋅ 54 =0,12 ⋅ 625 = 75 173. Знайдіть значення виразу: 1) Якщо х =

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

3) ( 12)7 <( 6)4 , бо число ( 12)7 <0 (показник

число ( 6)4 >0 (показник

4) −88 <(−8)8 , бо число −88 <0 (спочатку

число ( 8)8 >0 (показник

5) ( 17)6 = 176 , протилежні числа

6) ( 34)5 >( 39)5 . 176. Не

1) 0<( 1,9)10

2) 0>( 76)15 3) ( 0,1)12 >( 12)25 4) �−4 7 9�9 > �−5 8 11�9 177. Чи є правильною рівність:

1) 32 +42 =9+ 16 = 25;72 = 49; 25 ≠ 49. Рівність неправильна.

2) 52 + 122 = 25 + 144 = 169; 132 = 169; 169 = 169. Рівність правильна.

3) 12 +32 +52 +72 +92 =1+9+ 25 + 49 + 81 = 165; 132 = 169; 165 ≠ 169.

неправильна.

4) (1+2+3)2 62 = 36;13 +23 +33 =1+8+ 27 = 36; 36 = 36.

178. Доведіть, що:

12 +22

= 121

2 =0,09;0,33 =0,027

Порядок зростання: 0,027; 0,09; 0,3. 2) 0,4; ( 0,4)2 =0,16; ( 0,4)3 = 0,064

Порядок

182. (Домашня

-0,4; -0,064; 0,16.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) ( 2)14 ∙ ( 3)15 ∙ ( 4)16

( 2)14 >0,( 4)16 >0,( 3)15 <0

( 2)14 ∙ ( 3)15 ∙ ( 4)16 <0

2) ( 5)17 ∙ ( 6)18 ∙ ( 7)19 ( 5)17 <0,( 7)19 <0,( 6)18 >0

( 5)17 ∙ ( 6)18 ∙ ( 7)19 >0

185. Запишіть: 1) числа 16; 64; 256 у

4; 2) числа 0,09; 0,027; 0,00243 у

1) 16 =4 ∙ 4=42

4=44

2) 0,09 =0,3 ∙ 0,3=0,32 0,027 =0,3 ∙ 0,3 ∙ 0,3=0,33

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2) 1 км/с = 1000 м/с

192.

1) 1 м² = 100 дм² = 10² дм²

- 2,28 ∙ 108 км

1) х4 = 16

х = 2 або х = -2

24 =2 ∙ 2 ∙ 2 ∙ 2= 16

( 2)4 = ( 2) ∙ ( 2) ∙ ( 2)

2) х5 = 243 Показник

2х – 3 = 0 2х = 3

значень.

Отже, рівняння

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) х2 +7

х2 =0, х =0

207. При

1) 10 −х2

х2 =0, х =0

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2) (х− 1)4 + 16 (х− 1)4 =0, х− 1=0, х =1

2) 24 (х +3)6 (х +3)6 =0, х +3=0, х = 3 208.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

-6х + х = 60 – х

-6х + х = 60 – 160

-5х = -100

х = 20

першого мішка взяли 3 ∙ 20 = 60 (кг) цукру.

Відповідь: 60 кг; 20 кг.

215. Розв’яжіть рівняння:

1) 9(2х – 1) – 5(11 – х) = 3(х + 4)

18х – 9 – 55 + 5х = 3х + 12

18х + 5х – 3х = 12 + 9 + 55

18х + 2х = 21 + 55

20х = 76

х = 76 20 = 38 10 =3,8

216.

2) 5х – 26 = 12х – 7(х – 4)

5х – 26 = 12х – 7х + 28

5х – 26 = 5х + 28

5х – 5х = 28 + 26

0х = 54 – коренів не має

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

у9 = у3+5+9 = у17

6) с8 с9 с = с8+9+1 = с18

7) (��−�� )10 (��−�� )6 =(��−�� )10+6 =(��−�� )16

8) 112 ∙ 114 ∙ 116 = 112+4+6 = 1112

9) х4 х11 х2 = х4+1+11+2 = х18

10) (��)5 (��)15 =(��)5+15 =(��)20

11) (2х + 3у)6 (2х + 3у)14 =(2х + 3у)6+14 =(2х + 3у)20

12) ( ху)2 ( ху)7 ( ху)9 =( ху)2+7+9 =( ху)18

220. Подайте у вигляді степеня

1) а5 а8 = а5+8 = а13

2) а2 а2 = а2+2 = а4

3) а9 а = а9+1 = а10

4) аа2 а3 = а1+2+3 = а6

5) (�� + ��)13 (�� + ��) =(�� + ��)13+1 =(�� + ��)14

6) (�� )8 (�� )18 (�� ) =(��)8+18+1 =(�� )27 221.

1) а6 а8 = а6+8 = а14

2) аа6 = а1+6 = а7

3) а10 а6 а2 = а10+6+2 = а18

2) (−х)2

= х2 ∙х = х3 3) −х∙ (−х)2 = −х∙х2 = −х3 4) (−х) ∙ (−х)2 ∙ (−х) = х∙х2 ∙х = х4

236. Спростіть вираз:

1) (−а)2 ∙а3 = а2 ∙а3 = а2+3 = а5

2) −а2 ∙а3 = −а2+3 = −а5

3) а2 ∙ (−а)3 = а2 ∙ (−а3 )= (а2 ∙а3 )= −а2+3 = −а5

4) −а2 ∙ (−а)3 = −а2 ∙ (−а3 ) = а2 ∙а3 = а2+3 = а5

237. Спростіть вираз:

1) (−а5 )2 =(а5 )2 = а5∙2 = а10

2) (−а3 )3 = (а3 )3 = (а3 )3 = −а3∙3 = −а9

3) (−а4 )7 ∙ (−а2 )6 = (а4 )7 ∙ (а2 )6 = −а4∙7

238. Спростіть вираз:

1) ((а6 )5 )9 =(−а30 )9 = −а270

2) ((−а11 )2 )3 =(а22 )3 = а22∙3 = а66

1) (с5 )4 = с5∙4 =

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) х7 =614

х7 =62∙7

х7 =(62 )7 х =62

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

625 + 625 + ⋯ + 625 =5101

625х = 5101

54 ∙х =5101

х =5101 ∶ 54

х =5101−4

х =597

Відповідь:

1) 4100 =(42 )50 =(16)50 . Оскільки

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) 178 + 19 =(172 )4 + 19.

які закінчуються цифрою 6, у

2) 2004171 + 1712004 . Число 2004171 у

1712004 =(1712) 1002

5, тобто

2004171 + 1712004

267. Доведіть, що 4825 < 34417 .

4925 =(72 )25 =750

34317 =(73 )17 =751

750 <751 , значить,

4925 < 34317

Оскільки 4825 < 4925 < 34317 < 34417 , то

4825 < 34417

Що і треба

шкільного

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

= 9,6

Відповідь: 9,6 км. 272. Розв’яжіть рівняння: 1) 2,5 – 3х = 3 (х – 2,5) – 2

2,5 – 3х = 3х – 7,5 – 2

2,5 – 3х = 3х – 9,5 -3х – 3х = -9,5 – 2,5 -6х = -12

х = 2

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

квиток 239601 отримає в пару квиток 760398.

Очевидно, парою до кожного

цьому жоден квиток не отримає в пару себе (цифра не може доповнювати

сама себе, оскільки 9 – непарне число).

Таким чином, ми отримали розбиття усіх «щасливих» квитків

2) 1,5�� 3 �� 4 ∙

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

3) (

4) (6�� 6 �� 7 �� 8 )2 = 36�� 12 �� 14

2) (0,5��12 ��14 )2 =0,25�� 24 �� 28

3) (3�� 4 �� 5 )4 = 81�� 4 ��16 �� 20

293. Чи є правильним

1) Ні, бо 6х2 ≥ 0, при х = 0 6х2 =0

2) Так, а4 ≥ 0, �� 6 ≥ 0 → 0,4�� 4 �� 6 ≥ 0 3) Ні, бо при а = 3, а3 =0 і 1 3

4) Ні, 5�� 2 ≤ 0 набуває недод.

3) ( 2��3 )3 ∙ (3��4 ��)2 = 72��8 ��11

4) (�� 2 �� 3 �� 2 )2 ∙ (2�� 5 �� 3 ��)5 = 32�� 29 �� 21 �� 9

304. Значення

5х2 у4 =6 1) 1,5х2 у4 =0,3 ∙ 5х2 у4 =1,8 2) 25х4 у8 =(5х2 у4

Нехай

= 0,9х.

0,9х + 0,2 ⋅ 0,9х = 1,08х

1,08х – х = 48

0,08х = 48

х = 600

Відповідь: 600.

310. Замініть зірочки

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) Ні; 2) Так; 3) Ні; 4) Так; 5) Ні; 6)

2) Так; 3) Так; 4) Ні. 321.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

10 м ± 0,8%

10 ∙ 0,008 = 0,08 м

10 м + 0,08 м = 10,08 м 10 м – 0,08 м = 9,92

210 + 285(1 – х) = 240 –

-75х = -45

х = 0,6 (кг) –

1 – 0,6 = 0,4 (кг) – іншого

Відповідь: 0,6 кг; 0,4 кг.

За зняття готівкових

1). 334. Спростіть вираз: 1) (2a + b) – (b – 2a) = 2a + b – b + 2a = 4a

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2) (3a – 4) + (3 – 5a) = 3a – 4 + 3 – 5a = -2a – 1 3) (m + n) – (2m + n) – (m – 4n) = m + n – 2m – n – m + 4n = -2m + 4n

4) (5c – 2) – (6c + 1) + (c – 8) = 5c – 2 – 6c – 1 + c – 8 = -11 335.

1) a + b + (-a -b) = a + b – a – b = 0;

2) a – b + (-a + b) = a – b – a + b = 0; двочлен (-a + b)

3) -a – b + (a + b) = -a – b + a + b = 0; двочлен (a + b)

Розв’яжіть рівняння:

1) 10 (7 4х х2 ) = х2 + 8х 9

10 7+ 4х + х2 −х2 8х = 9

-4х = -3 – 9 -4х = -12

х = 3

3) 6 + х3 − (2х − 9 + х3 ) = 5

6+ х3 2х +9 −х3 =5 -2х = 5 – 15 -2х = -10

(5х2 3) (2х + 5) = 5х2 5х2 3 2х 5= 5х2 -2х = 8 х = -4

х = 5 4) 12 − (6 − 9х − х2 ) = х2 + 5х − 14 12 6+ 9х + х2 = х2 + 5х 14 9х – 5х = -14 – 6

5) 3х2 − (2х2 − 8х) − (х2 − 3) = х

3х2 2х2 + 8х −х2 +3= х

8х – х = -3

4х = -20 х = -5

7х = -3 х = 3 7 6) 4у3 − (4у3 − 8у) − (6у + 3) = 7 4у3 4у3 + 8у 6у 3=7 8у – 6у = 7 + 3 2у = 10 у = 5

7) (у2 4у 17) (6у2 3у 8) = 1 у 5у2 у2 4у 17 6у2 + 3у +8=1 −у− 5у2 -4у + 3у + у = 1 – 9

0 ∙ у = -8 - Коренів немає 346. Розв’яжіть рівняння:

1) 5у3 (6у + 1) = 19 2у + 5у3

5у3 6у 1= 19 2у +5у3

-6у + 2у = 19 + 1

-4у = 20

у = -5

2) 7х 2х2 (10 2х2 ) = 11

7х 2х2 10 +2х2 = 11

7х = 10 + 11

7х = 21

х = 3

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

3) 8х2 + 6х (2х + 8х2 12) = 4

8х2 + 6х − 2х − 8х2 + 12 =4

4х = 4 – 12

4х = -8

х = -2

х2 (х + 1) (х2 7х + 32) = 3

−х− 1

= 3 + 33 6х = 36 х = 6 5) (у3 + 3у 8) (5у у3 + 7) = 2у3 2у 15 у3 + 3у 8 5у + у3 7=2у3 15 -2у + 2у = -15 + 15 0 ∙ у = 0

+ 7х − 32 =3

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

�� 3 = 20�� 4 +5�� 2

357. Подайте у вигляді многочлена число, яке складається: 1) із 4 сотень, x десятків і y одиниць:

400 + 10х + у = 10х + у + 400

2) з a тисяч, b сотень, 5 десятків і c одиниць: 1000а + 100b + 50 + c = 1000a + 100b + c + 50

358. Подайте у вигляді многочлена вираз:

1) cba = 100c + 10b + a

2) abc – ab = 100a + 10b + c – (10a + b) = 100a + 10b + c – 10a – b = 90a + 9b + c

3) a0c + ac = 100a + c + 10a + c = 110a + 2c

359. Подайте у вигляді многочлена вираз:

1) cab + ca = 100c + 10a + b + 10c + a = 11a + b + 110c

2) abc + bca = 100a + 10b + c + 100b + 10c + a = 101a + 110b + 11c

3) ab9 + 7a = 100a + 10b + 9 + 70 + a = 101a + 10b + 79

360. Доведіть, що значення

n. (9 – 18n) – (6n

7) = 9 – 18n

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

n + (n + 1) + (n + 2) + (n + 3) = n + n + 1 + n + 2 + n + 3 = 4n + 6 – 4(n + 1) + 2.

4(n + 1)

n + (n + 1) + (n + 2) + (n + 3) + (n

376. Доведіть, що: 1)

3: n + (n + 1) + (n + 2) = n + n + 1 + n + 2 = 3n + 3 = 3(n + 1). Оскільки

остачі на 3, то твердження

3) сума чотирьох

2n + (2n + 2) + (2n + 4) + (2n + 6) = 2n + 2n + 2 + 2n + 4 + 2n + 6 = 8n + 12 = 4(n + 3).

4(n + 3)

4) сума п’яти

10: 2n + (2n + 2) + (2n + 4) + (2n + 6) + (2n + 8) = 2n + 2n + 2 + 2n + 4 + 2n + 6 + 2n + 8 = 10n + 20 = 10(n + 2). Оскільки 10(n + 2) ділиться

377. Доведіть, що:

1) сума чисел ab, bc і ca ділиться націло на 11: ab + bc + ca = 10a + b + 10b + c + 10c + a = 11a + 11b + 11c = 11(a + b + c). Оскільки 11(a + b + c) ділиться без остачі на 11, то твердження

2) різниця чисел abc і cba ділиться націло на 99:

abc – cba = 100a + 10b + c – (100c + 10b + a) = 100a + 10b + c – 100c – 10b – a = 99a – 99c = 99(a – 1). Оскільки 99(a – c) ділиться

Доведіть, що:

1) сума чисел abc, bca і cab кратна 111: abc + bca + cab = 100a + 10b + c + 100b + 10c + a + 100c + 10a

2) різниця числа abc

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

15%, 115% = 1,15 1,15

⋅ 22 000 = 25 300 (грн) –

90% = 0,9. 0,9 ⋅ 25 300 = 22 770 (грн) – з 15 грудня.

Відповідь: вигідніше купувати

382. На діаграмі (рис. 6)

протягом 6 місяців.

(150 + 300 + 270 + 210 + 180 + 210) : 6 = 220 (р.)

Відповідь: у середньому щомісячно продавали

на 5 %. Якою стала нова ціна пальто?

Знизили на 5%, 95% = 0,95

0,95 ⋅ 4000 = 3800 (грн)

Підвищили на 5%, 105% = 1,05 1,05 ⋅ 3800 = 3990 (грн)

Відповідь: нова ціна пальто 3990

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) 4(2a – 3b) = 8a –

2) 0,3(9х – 5у + 7) = 2,7х – 1,5у

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

= 32 +7= 39.

400. Розв’яжіть рівняння: 1) 5х(3х – 2) – 15х(4 + х) = 140

15х2 10х 60х 15х2 = 140

-70х = 140

х = 140 : (-70)

х = -2 2) 1,2х(4 + 5х) = 3х(2х + 1) – 9 4,8х +6х2 =6х2 + 3х 9 4,8х – 3х = -9 1,8х = -9

18х = -90

2х = -10

х = -5

3) 6х(7х – 8) – 2х(21х – 6) = 3 – 30х

42х2 48х 42х2 + 12х =3 30х

-36х + 30х = 3

-6х = 3

х = 0,5

5) 7х2 х(7х 5) 2(2,5х + 1) 3 = 0

7х2 7х2 + 5х 5х 2 3=0

0 ∙х =5

4) 12х – 3х(6х – 9) = 9х(4 – 2х) + 3х

12х 18х2 + 27х = 36х 18х2 + 3х

39х – 39х = 0

0 ∙х =0

х – будь-яке значення.

6) 8(х2 4) 4х(3,5х 7) = 20х 6х2 8х2 32 14х2 + 28х = 20х 6х2 −6х2 + 28х − 20х +6х2 = 32

8х = 32 х = 4 401. Знайдіть корінь рівняння:

1) 0,4х(5х – 6) + 7,2 = 2х(х + 0,6)

2х2 2,4х +7,2=2х2 +1,2х

2х2 2х2 2,4х 1,2х = 7,2 -3,6х = -7,2

х = 2 2) х(3х + 2) 9(х2 7х) = 6х(10 х) 3х2 + 2х − 9х2 + 63х = 60х − 6х2

65х – 60х = 0

5х = 0

х = 0

3) 12(х3 2) 7х(х2 1) =5х3 + 2х +6 12х3 − 24 − 7х3 + 7х =5х3 + 2х +6

5х3 5х3 + 7х 2х =6+ 24

5х = 30

х = 6

402. Доведіть тотожність:

аbc = abc

Вирази тотожні

3) a(a + 2b) + b(a + b) = b)2ª + b) + a(a + b) �� 2 +2�� + �� + �� 2 =2�� + �� 2 + �� 2

Вирази тотожні

4) a(b +c – bc) – b(a + c – ac) = (a – b)c ab + ac – abc – ab – bc + abc = ac – bc

ac – bc = ac – bc

Вирази тотожні

403. Доведіть тотожність:

тотожні

(12х + 11) −х2 (х2 +8) −х(11 +

ab + bc = ab + bc

3(7х + 1) = 6(4х + 3)

– 21х – 3 = 24х + 18 -21х = 21 х = -1

2y (4y – 10,5)?

8у(у – 7) – 15 = 2у(4у – 10,5)

8у2 56у 15 =8у2 21у

-56у + 21у = 15

-35у = 15

у = − 3 7

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

у(у + 14) – у(у + 8) = 72

у2 + 14у −у2 8у = 72

6у = 72

у = 12

у + 8 = 12 + 8 = 20

Р = 20 ∙ 2 + 12 ∙ 2 = 64 (см)

Відповідь: 64 см.

413. Замініть зірочки такими одночленами, щоб

1) ∗∙ (��−�� + �� ) = �� + �� 2 ��−�� 2 �� (��−�� + �� ) = �� + �� 2 ��−�� 2

Відповідь: -bc

2) ∗∙ (�� −�� 2 ) = �� 3 ��−�� 2 �� 2 �� 2 ∙ (�� −�� 2 ) = �� 3 ��−�� 2 �� 2

Відповідь: а2

3) 3а2 (∗−∗) =6а3 + 15а4

3а2 ( 2а 5а2 ) =6а3 + 15а4

Відповідь: −2а − 5а2

414. Замініть зірочки такими

1) (х−у) ∙∗= х2 у2 −х3 у

(х−у)(−х2 ∙у) = −х3 у2 + х2 у2 = х2 у2 −х3 у2

Відповідь: −х2 у

2) ( 9х2 +∗) ∙у =∗ +у4 ( 9х2 + у2 ) ∙у = 9х2 у + у4

Відповідь: у3 ; 9х2 у

3) (1,4х −∗) ∙ 3х =∗−0,6х3

(1,4х 0,2х2 ) ∙ 3х =4,2х2 0,6х3

Відповідь: 0,2х2 ;4,2х2

4) ∗ (∗−х2 у5 +5у6 ) =8х3 у3 +5х3 у8

5ху3 ( 1,6х2 −х2 у5 +5у6 ) =8х3

Відповідь: 5ху3 ; 1,6х2 ; 25ху9 415. Доведіть, що коли: 1) a(bc – 1) + b(ac

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) 6х 7 5 − 3х+1 6 = 11 х 15

60 ∙ �6х−7 5 3х+1 6 � = 60 ∙ 11−х 15

12(6х – 7) – 10(3х + 1) = 4(11 – х)

72х – 84 – 30х – 10 = 44 – 4х

42х + 4х = 44 + 94

46х = 138

х = 3 2) 5х 3 9 4х+3 6 = х− 1 18 ∙ �5х−3 9 4х+3 6 � = 18 ∙ (х− 1)

2(5х – 3) – 3(4х + 3) = 18(х – 1) 10х – 6 – 12х – 9 = 18х – 18 -2х – 18х = -18 + 15 -20х = 3

4(8х – 5) – 3(4х + 3) + 6(2 – 9х) = -36

32х – 20 – 12х – 9 + 12 – 54х = -36 -34х = -36 + 17 -34х = -19 х

2(2х + 3)

(5х + 13) + 3(5 – 2х) = 36 4х + 6 – 5х – 13 + 15 – 6х = 36 -7х = 28 х

х2 3х) 4(6х2 +1) = 48 24х2 − 9х − 24х2 − 4= −48 -9х = -44

= 44 9 =4 8 9

тоді третя бригада

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

3 7 (2х + 12) деталей,

деталей. Маємо рівняння: х + (х + 12) + 3 7 (2х + 12) = 80

Домножимо обидві частини на 7, отримуємо:

7х + 7(х + 12) + 3(2х + 12) = 560

7х + 7х + 84 + 6х + 36 = 560

20х = 560 – 120

20х = 440

х = 22

Перша

3 7 (2 ∙ 22 + 12) = 3 7 ∙ 56 = 24 деталі.

Відповідь: 22 деталі; 34 деталі; 24 деталі.

423. Остача

натурального числа b

націло на 3. З умови випливає, що a = 3n + 1, b = 9m + 7, n і

4a + 2b = 4(3n + 1) + 2(9m + 7) = 12n + 4 + 18m + 14 = 12n + 18m + 18 Кожен

ділиться на 3.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

х +2 2 9 х + 256 450 х = 1364,8

450 �х + 20 9 х + 256 450 х� = 1364,8 ∙ 450

450х + 1000х + 256х = 614 160

1706х = 614 160

х = 360 (км²) – площа лиману «Дністровський» 20 9 ∙ 360 = 800 (км²) – площа лиману «Дністровсько-Бузький».

256∙360 450 = 256∙4 5 = 1024 5 = 204,8 (км²) – площа лиману «Сасик».

Відповідь: 800 км²; 360 км²; 204,8 км². 428.

3х = 24

х = 8 (д.)

Відповідь: 8 днів. 431.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

= 7�� 2 19�� + 16 4) (4��− 1)(4��− 3) (2��− 10)(8�� +1) = =4�� 2 12��−

= 55 + 21

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

-38х = 76

х = -2

3) 21х2 (3х 7)(7х 3) = 37

21х2 21х2 + 9х + 49х 21 = 37

58х = 37 + 21

58х = 58

х = 1

4) (х + 1)(х + 2) – (х – 3)(х + 4) = 12

х2 + 2х + х +2 −х2 4х + 3х + 12 = 12

2х = 12 – 14

2х = -2х

х = -1

5) (-4х + 1)(х – 1) – х = (5 – 2х)(2х + 3) – 17

4х2 + 4х + х− 1 −х = 10х 4х2 + 15 6х 17

4х – 10х + 6х = -2 + 1

0 ∙ х = -1

Рівняння не має розв’язків

439. Розв’яжіть рівняння:

1) (2х – 1)(15 + 9х) – 6х(3х – 5) = 87

30х + 18х2 − 15 − 9х − 18х2 + 30х = 87

51х = 87 + 15

51х = 102

х = 2

2) (14х – 1)(2 + х) = (2х – 8)(7х + 1)

28х + 14х2 2 −х = 14х2 56х + 2х 8

27х + 54х = -8 + 2

81х = -6

х = −6 81 = 2 27

3) (х + 10)(х – 5) – (х – 6)(х + 3) = 16 х2 5х + 10х 50 −х2 + 6х 3х + 18 = 16

8х = 16 + 32

8х = 48

х = 6

4) (3х + 7)(8х + 1) = (6х – 7)(4х – 1) + 93х

24х2 + 3х + 56х +7= 24х2 28х 6х +7+ 93х

59х – 59х = 0

0 ∙ х = 0

Розв’язком є

1) (х +2)(х− 1)(х− 4) = (х2 −х + 2х 2)(х− 4) = (х2 + х− 2)(х− 4) = = х3 4х2

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

За умовою: n : (n + 6) = (n + 1) : (n + 8).

n(n + 8) = (n + 6)(n + 1)

n² + 8n = n² + n + 6n + 6 тобто n² + 8n = n²+ 7n + 6 Звідси 8n − 7n = 6

n = 6

6, 7, 12, 14.

+ 4 + 6 = n +

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

добутків: n(n + 10) = (n + 4)(n + 4)

Розв’яжемо це рівняння: n² + 10n = n² + 4n + 4n + 16

тобто n² + 10n = n² + 8n + 16

Звідси 10n − 8n = 16

2n = 16

n = 8

Отже, перше число дорівнює 8,

Відповідь: 8, 12, 18.

447. Знайдіть чотири послідовних

другого із цих чисел на 17 більший

За умовою (n + 3)(n + 1) на 17 більший за (n + 2)n.

Отримуємо рівняння: (n + 3)(n + 1) – 17 = (n + 2)n

Розкриємо дужки:

n² + n + 3n + 3 – 17 = n² + 2n

спростимо:

n² + 4n – 14 = n² + 2n

Звідси: 4n − 2n = 14

2n = 14

n = 7

Отже, перше число

число дорівнює 10. Відповідь: 7, 8, 9, 10. 448. Знайдіть три

n² + 2n +

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

= (х + 3)(х – 5).

х² - 45 = х² - 5х + 3х – 15

2х = 30

х = 15

Сторона

Відповідь: 15 см.

нового прямокутника буде дорівнювати (х

цього прямоткуника буде дорівнювати (х – 5)(33 – х) см². За умовою

прямокутника зменшиться на 21 см². Маємо рівняння:

х(30 – х) = (х – 5)(33 – х) + 21

30х - х² = 33х - х² - 165 + 5х + 21 -8х = -144

х = 18

Сторони даного прямокутника 18 і 12 см.

Відповідь: 18 см; 12 см. 451.

– (х + 4)(х – 4) = 40

х² + 2х = х² - 4х + 4х – 16 + 40

2х = 24

х = 12

Сторони даного

8х +7= х2 7х −х +7

− 8х +7= х2 − 8х +7

доведено. 2) у2 (у 7)(у + 2) = у4 5у3

3) а3 8 = (а 2)(а2 + 2а + 4)

а3 8= а3 +2а2 + 4а 2а2 4а 8

а3 − 8= а3 − 8

Тотожність доведено.

4) (а 1)(а + 1)(а2 + 1) = а4 1

(а2 + а−а− 1)(а2 +1) = а4 1

(а2 − 1)(а2 +1) = а4 − 1

а4 + а2 −а2 1= а4 1

а4 1= а4 1

Тотожність доведено.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

5) (а4 −а2 +1)(а4 + а2 +1) = а8 + а4 +1

а8 −а6 + а4 + а6 −а4 + а2 + а4 −а2 +1= а8 + а4 +1

а8 + а4 +1= а8 + а4 +1

Тотожність доведено.

453. Доведіть тотожність:

1) 3а2 + 10а +3=3(а +3) �а + 1 3�

3а2 + 10а +3= (3а +9) �а + 1 3�

3а2 + 10а +3=3а2 + 9а + а +3

3а2 + 10а +3=3а2 + 10а +3

Тотожність доведено

2) (а +1)(а2 + 5а +6) =(а2 + 3а +2)(а +3)

а3 +5а2 + 6а + а2 + 5а +6= а3 +3а2 +3а2 + 9а + 2а +6

а3 +6а2 + 11а +6= а3 +6а2 + 11а +6

Тотожність доведено

3) (а +1)(а4 −а3 + а2 −а +1) = а5 +1

а5 −а4 + а3 −а2 + а + а4 −а3 + а2 −а +1= а5 +1

а5 +1= а5 +1

Тотожність доведено 454. Чи при всіх натуральних

12?

20�� + 99 ��2 5�� 3�� 15

Маємо 24n : 8, 80 : 8. Відповідь: значення

456.

1) (а – 2)(* + 6) = а² + **

(а – 2)(а + 6) = а² + 6а – 2а – 12

(а – 2)(а + 6) = а² + 4а – 12

Відповідь: а, 4а, 12.

457. Замініть

1) (х + 3)(* + 5) = 3х² + * + *

(х + 3)(3х + 5) = 3х² + 5х + 9х + 15

(х + 3)(3х + 5) = 3х² + 14х + 15

Відповідь: 3х, 14х, 15.

2) (2а + 7)(а - *) = * + * - 14

(2а + 7)(а – 2) = 2а² - 4а + 7а – 14

(2а + 7)(а – 2) = 2а² + 3а – 14

Відповідь: 2, 2а², 3а.

щоб утворилася тотожність:

2) (х – 4)(х + *) = * + * + 24

(х – 4)(х – 6) = х² - 6х – 4х + 24

(х – 4)(х – 6) = х² - 10х + 24

Відповідь: -6, х², -10х.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

6. За умовою х = 6n + 3; y = 6m + 2 (n i m –

= 36mn + 12n + 18m + 6.

6).

462.

+ 9)(11b + 5) = 11k + 1

–

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) 100% - 18% = 82%

2) 19 680 : 0,82 = 24 000 (грн)

Відповідь: було нараховано 24 000 грн.

466. Після

1) 100% + 20% = 120% = 1,2

2) 2760 : 1,2 = 2300 (грн) Відповідь: ціна

4 х + 1 5 х + 1 3 х + 13 = х

15х + 12х + 20х + 780 = 60х

47х – 60х = -780 -13х = -780

х = 60

Отже, Демохар прожив 60 років. Відповідь: 60 років.

472. Обчисліть, використовуючи

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) 4b + 16c = 4(b + 4c)

3) –8a – 18b = –2(4a + 9b)

5) 10mx – 15my = 5m(2x – 3y)

7) 3d2 – 3cd = 3d(d – c)

9) a6 – a3 = a3(a3 – 1)

11) 7p3 – 5p = p(7p2 – 5)

13) 14x2y + 21xy2 = 7xy(2x+ 3y)

15) 8a4b2 – 36a3b7 = 4a3b2(2a – 9b5)

480. Знайдіть

1) 4a + 4 = 4(a + 1)

2) 12x – 15y = 3(4x – 5y)

4) 24x + 30y = 6(4x + 5y)

6) x2 + xy = x(x + y)

8) 4a2 + 16ab = 4a(a + 4b)

10) b2 + b8 = b2(1 + b6)

12) 15c2d – 3cd = 3cd(5c – 1)

14) –2x9 + 16x6 = –2x6(x3 – 8)

2) 6ab – 3b = 3b(2a – 1)

3) -5x – 10y = -5(x + 2y) 4) x6 – x4 + x2 = x2(x4 – x2 + 1)

481. Розкладіть на множники:

1) За + 6b = 3(а + 2b); 2) 12m – 16n = 4(3m – 4n);

3) 10сk – 15ср = 5с(2k – 3р); 4) 8ах + 8а = 8а(х + 1);

5) 5b – 25bс = 5b(1 – 5с); 6) 14х2 + 7х = 7х(2х + 7);

7) n10 – n5 = n5(n5 – 1); 8) m6 + m7 = m6(1 + m);

9) 9х – 27х4 = 9х(1 – Зх3); 10) 18y5 + 12y4 = 6y4(3y + 2)

11) 56а10b6 – 32а4b8 = 8а4b6(7а6 – 4b2); 12) 36mn5 + 6Зm2n6 = 9mn5(4 + 7mn).

482. Обчисліть, використовуючи

1) 1732 + 173 ∙ 27 = 173 ∙ (173 + 27) = 173 ∙ 200 = 34600; 2) 214 ∙ 314 – 2142 = 214 ∙ (314 – 214) = 214 ∙ 100 = 21400; 3) 0,43 + 0,42 ∙ 0,6 = 0,42 ∙ (0,4 + 0,6) = 0,16 ∙ 1 = 0.16.

483. Знайдіть значення виразу:

1) 5162 – 516 ∙ 513 = 516 ∙ (516 – 513 = 516 ∙ 3 = 1548;

2) 0,73 + 0,7 ∙ 0,51 = 0,7 ∙ (0,72 + 0,51) = 0,7 ∙ (0,49 + 0,51) = 0,7; 3) 0,24 – 0,23 ∙ 1,2 = 0,23 ∙ (0,2 – 1,2) = –0,008.

484. Обчисліть значення виразу, попередньо розклавши його

1) 6,32x – х2 = х(6,32 – х).

Якщо х = 4,32, то х(6,32 – х) = 4,32 ∙ (6,32 – 4,32) = 4,32 ∙ 2 = 8,64; 2) а3 + а2b = а2(а + b).

Якщо а = 1,5, b = –2,5, то а2(а + b) = 1,52 ∙ (1,5 + (–2,25)) = 2,25 ∙ (–1) = –2,25; 3) m3p – m2n2 = m2(mp – n2).

Якщо m = 3, p = 1 3, n = –3, то m2(mp – n2) = 32 ∙ (3 ∙ 1 3 – (–3)2) = 9 ∙ (1 – 9) = 9 ∙ (–8) = –72.

485. Знайдіть значення виразу: 1) 0,74x2 + 26x = x(0,74x + 26).

Якщо х = 100, то x(0,74x + 26) = 100 ∙ (0,74 ∙ 100 + 26) = 100 ∙ (74 + 26) = 10000; 2) x2y3 – x3y2 = x2y2(y – x).

Якщо х = 4, у = 5, то x2y2(y – x) = 42 ∙ 52(5 – 4) = 16 ∙ 25 = 400.

486. Розв’яжіть рівняння: 1) у2 – 6у = 0; у(у – 6) = 0; у = 0 або y – 6 = 0; у = 0 або у = 6.

Відповідь: 0 або 6; 3) 4m2 – 20m = 0; 4m(m – 5) = 0; m = 0 або m – 5 = 0; m = 0 або m = 5.

Відповідь: 0 або 5; 5) 9х2 – 6х = 0; 3х(3х – 2) = 0; х = 0 або Зх – 2 = 0; х = 0 або х = 2 3

Відповідь: 0 або 2 3

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2) х2 + х = 0;

х(х + 1) = 0;

х = 0 або х + 1 = 0;

х = 0 або х = – 1.

Відповідь: 0 або –1;

487. Розв’яжіть рівняння:

1) х2 – х = 0;

х(х – 1) = 0;

х = 0 або х – 1 = 0;

х = 0 або х = 1.

Відповідь: 0 або 1.

2) р2 + 15р = 0;

p(p + 15) = 0;

р = 0 або р + 15 = 0; p = 0 або p = –15.

Відповідь: 0 або –15.

4) 13х2 + х = 0; x(13х + 1) = 0;

х = 0 або 13х + 1 =0; х = 0 або х = –1 13

Відповідь: 0 або х = –1 13

6) 12х – 0,3х2 = 0; 0,3х(40 – х) = 0;

х = 0 або 40 – х = 0; х = 0 або х = 40. Відповідь: 0 або 40.

3) 5х2 – 30х = 0;

5х(х – 6) = 0;

х = 0 або х – 6 = 0;

х = 0 або х = 6.

Відповідь: 0 або 6.

4) 14х2 + 18х = 0;

2х(7х + 9) = 0;

х = 0 або 7х + 9 = 0;

х = 0 або х = –12 7 .

Відповідь: 0 або –12 7 .

488. Закінчіть розкладання на множники:

1) 3a (x – y) + b (x – y) = (x – y) (3a + b).

2) b(c – 2) + (c – 2) = ( c – 2) (b + 1).

3) x(y – 6) + z (6 – y) = x(y – 6) – z(y – 6) = (y – 6) (x – z).

4) m(8 – n) – 5 (n – 8) = m(8 – n) + 5(8 – n) = (8 – n) (m + 5).

489. Закінчіть розкладання на множники:

1) a (b – c) – (b – c) = (b – c) (a – 1).

2) 2x(3c –y) + 7y(y –3c) = 2x(3c –y) – 7y(3c –y) = (3c – y) (2x – 7y).

490. Розкладіть на множники:

1) 2х(a + b) + у(a + b) = (a + b)(2x + y)

2) (а – 4) – b(а – 4) = (а – 4)(1 – b)

3) 5а(m – n) + 7b(m – n)= –(m – n)(5а + 7b)

4) а(с – d) + b(d – с) = а(с – d) – b(c – d) = (с – d)(a – b)

5) х(х – 6) – 10(6 – х) = х(х – 6) + 10(х – 6) = (х – 6)(х + 10) 6) b(b – 20) + (20 – b) = b(b – 20) – (b – 20) = (b – 20)(b – 1)

491. Подайте вираз у

1) c(x – 3) – d(x – 3 ) = (x – 3)(c – d)

2) m(p – k) – (p – k) = (p – k)(m – 1)

3) m (x – y) –n(y – x) = m(x – y) + n(x – y) = (x – y)(m + n)

4) x(2 – x) + 4(x – 2) = x(2 – x) – 4(2 – x) = (2 – x)(x – 4)

5) 4x(2x – у) – 5y(y – 2x) = 4x(2x – y) + 5y(2x – y) = (2x – y)(4x+ 5y)

492. Розкладіть на множники:

1) 2a5b2 – 4a3b + 6a2b3 = 2a2b(a3b – 2a + 3b2) 2) mn3 + 5m2n2 – 7m2n – mn(n2 + 5mn – 7m)

3) xy2 + x2y – xy = xy(y + x – 1) 4) 9x3 + 4x2 – x = x(9x2 + 4x – 1)

5) –6m4 – 8m5 – 2m6 = –2m4(3 + 4m + m2) 6) 42a4b – 28a3b2 – 70a5b3 = 14a3b(3a – 2b – 5a2b2)

493. Винесіть за дужки спільний множник:

1) m2n + mn + n = n(m2 + m + 1);

2) Зх6 + 6х5 – 15x4 = 3x4(x2 + 2x – 5);

3) 7a4b3 – 14a3b4 + 21a2b5 = 7а2b3(а2 – 2ab + 3b2;

4) 20b6c5 – 45b5c6 – 30b5c5 = 5b5c5(4b – 9c – 6).

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

n + n2 = n(n + 1)

495.

1) (m – 9)2 – 3(m – 9) = (m – 9)(m – 9 – 3) = (m – 9)(m – 12);

2) a(a + 5)2 + (a + 5) = (a + 5)(a(a + 5) + 1) = (a + 5 )(a2 + 5a + 1); 3) (m2 – 3) – n(m2 – 3)2 = (m2 – 3)(1 – n(m2 – 3)) = (m2 – 3)(1 – nm2 + 3n);

4) 8c(p – 12) + 7d(p – 12)2 = (p – 12)(8c + 7d(p – 12)) = (p – 12) (8c + 7dp – 84d).

5) a(2a + b)(a + b) – 4a(a + b)2 = a(a + b)(2a + b – 4(a + b)) = a(a + b)(2a + b – 4a – 4b) = = a(a + b)(–2a – 3b) = –a(a + b)(2a + 36);

6) 3m2(m – 8) + 6m(m – 8)2 = 3m(m – 8)(m + 2(m – 8)) = 3m(m –8) ∙ (m + 2m – 16) = = 3m(m – 8)(3m – 16);

7) (2a + 3)(a + 5) + (a – 1)(a + 5) = (a + 5)(2a + 3 + a – 1) = (a + 5)(3a + 2);

8) (3x + 7)(4y – 1) – (4у – 1)(2x + 10) = (4у – 1)(3x + 7 – (2x + 10)) = = (4y – 1)(3x + 7 – 2x – 10) = (4y – 1)(x – 3);

9) (5m – n)3(m + 8n)2 – (5m – n)2(m + 8n)3 = (5m – n)2(m + 8n)2(5m – n – (m + 8n)) = = (5m – n)2(m + 8n)2(5m – n – m – 8n) = (5m – n)2 ∙ (m + 8n)2(4m – 9n).

496. Подайте у

1) (у + 1)2 – 4y(y + 1) = (y + 1)(y + 1– 4y) = (y + 1)(1– 3y);

2) 10(a2 – 5) + (a2 – 5)2 = (a2 – 5)(10 + a2 – 5) = (a2 – 5 )(a2 + 5);

3) (a – 2)2 – 6(a – 2) = (a – 2)(a – 2 – 6) = (a – 2)(a – 8).

4) (x – 6)(2x – 4) + (x – 6)(8 – x) = (x – 6)(2x – 4 + 8 – x) = (x – 6)(x + 4);

5) (x2 – 2)(3у + 5) – (x2 – 2)(y + 12) = (x2 – 2)(3у + 5 – (у + 12)) = = (x2 – 2)(2y – 7);

6) (4a – 3b)(5a + 8b) + (3b – 4a)(2a + b) = (4a – 3b)(5a + 8b) – (4a – 3b)(2a + b) = = (4a – 3b)(5a + 8b – (2a + b)) = (4a – 3b)(3a + 7b); 7) (p – 9)4(2p + 1)3 + (p – 9)3(2p + 1)4 = (p – 9)3(2p + 1)3(p – 9 + 2p + 1) = = (p – 9)3(2p + 1)3 ∙ (3p – 8).

497. Розв’яжіть рівняння, використовуючи

1) (х – 3)(х + 7) – (x + 7)(х – 8) = 0;

(х + 7)(х – 3 – (х – 8)) = 0;

(х + 7)(х – 3 – х + 8) = 0; 5(х + 7) = 0; х = –7.

Відповідь: –7;

3) 0,2х(х – 5) + 8(х – 5) = 0;

(х – 5)(0,2х + 8) = 0;

х – 5 = 0 або 0,2х + 8 = 0;

х = 5 або 0,2х = –8;

х = 5 або х = –40.

Відповідь: –40 або 5;

на множники:

2) (4х – 9)(х – 2) + (1 – х)(х – 2) = 0;

(х – 2)(4х – 9 + 1 – х) = 0;

(х – 2)(3х – 8) = 0;

х – 2 = 0 або 3х – 8 = 0;

х = 2 або х = 8 3 .

Відповідь: 2 або 8 3 .

4) 7(х – 7) – (х – 7)2 = 0;

( х – 7)(7 – (х – 7)) = 0;

( х – 7)(14 – х ) = 0;

х – 7 = 0 або 14 — х = 0;

х = 7 або х = 14.

Відповідь: 7 або 14. 498. Розв’яжіть рівняння, використовуючи розкладання на множники:

1) (2х – 9)(х + 6) – х(х + 6) = 0; (х + 6)(2х – 9 – х) = 0; (х + 6)(х – 9) = 0;

х + 6 = 0 або х – 9 = 0;

х = –6 або х = 9.

Відповідь: –6 або 9;

2) (3х + 4)(х – 10) + (10 – х)(х – 8) = 0;

(х – 10)(3х + 4 – (х – 8)) = 0; (х – 10)(2х + 12) = 0;

х – 10 = 0 або 2х + 12 = 0;

х = 10 або х = –6.

Відповідь: –6 або 10.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

3) 3(3х + 1)2 – 4(3х + 1) = 0; (3х + 1)(3(3х + 1) – 4) = 0; (3х + 1)(9х + 3 – 4) = 0; (3х + 1)(9х – 1) = 0;

3х + 1 = 0 або 9х – 1 = 0;

х = –1 3 або х = 1 9 .

Відповідь: –1 3 або 1 9;

499. Винесіть за дужки спільний множник:

1) (2х – 6)2 = (2(х – З))2 = 4(х – З)2; 2) (5у + 5)2 = (5(у + 1))2 = 25(у + 1)2; 3) (36х + 30у)2 = (6(6х + 5у))2 = 36(6х + 5у)2;

4) (2х + 4)4 = (2(х + 2))4 = 16(х + 2)4;

5) (6х – 9у)3 = (3(2х – 3у))3 = 27(2х – 3у)3;

6) (а2 + ab)2 = (а(а + b))2 = а2(а + b)2;

7) (–7а – 14ab)2 = (–7а(1 + 2b)2 = 49а2(1 + 2b)2;

8) (Зс4 – 6с3)4 = (Зс3(с – 2))4 = 81с12(с – 2)4.

500. Винесіть за дужки спільний множник:

1) (4х – 4у)2 = (4(х – у))2 = 16(х – у)2;

2) (18а + 27b)2 = (9(2a + 3b))2 = 81(2а + 3b)2;

3) (8m – 10n)3 = (2(4m – 5n))3 = 8(4m – 5n)3;

4) (а2 – 9а)2 = (а(а – 9))2 = а2(а – 9)2;

4) (9х – 12) – х(9х – 12) = 0; (9х – 12)(1 – х) = 0;

9х – 12 = 0 або 1 – х = 0; 9х = 12 або –х = –1; х = 4 3 або х = 1.

Відповідь: 4 3 або 1.

5) (16х2у + 40xy2)2 = (8ху(2х + 5у))2 = 64х2у2(2х + 5y)2;

6) (22х4 – 28х2у3)5 = (2х2(11х2 – 14у3))5 = 32x10(11х5 –

501. Доведіть, що значення виразу:

1) 195 + 194 = 194(19 + 1) = 20 ∙ 194 —

2) 810 – 89 – 88 = 88(82 – 8 – 1) = 55 ∙ 88 — кратне 11

2) 164 + 85 – 47 = (24)4 + (23)5 – (22)7 = 216 + 215 – 214 = 214(22 + 2 – 1) = 5

націло на 10;

3) 365 + 69 = (62)5 + 69 = 610 + 69 = 69(6 + 1) = 7 ∙ 69 —

на 42; 4) 105 – 57 = (2 ∙ 5)5 – 57 = 25 ∙ 55 – 57 = 55(25 – 52) = 7 ∙ 55 —

націло на 7.

503. Доведіть, що коли: 1) а2b + аb2 – 2аb = аb(а + b – 2).

Якщо а + b = 2, то аb(а + b – 2) = аb(2 – 2) = 0; 2) 12a3b + 16а2b2 + 32a2b = 4a2b(За + 4b + 8).

Якщо За + 4b = –2, то 4а2b(За + 4b + 8) = 4a2b(–2 + 8) = 24а2b.

504. Доведіть, що коли:

1) а3b3с2 + а2b4с2 + а2b3с3 = а2b3с2(а + b + с).

Якщо а + b + с = 0, то маємо: а2b3с2 ∙ 0 = 0; 2) а6b4 – 2а5b5 – а4b6 = а4b4(а2 – 2аb – b2) = а4b4(a2 – b2 – 2аb).

Якщо а2 – b2 = 2аb + 1, то а4b4(а2 – b2 – 2аb) = а4b4(2аb + 1 – 2аb) = а4b4

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

505. Розв’яжіть рівняння:

1) 8х2 – 3(х – 4) = 12;

8х2 – 3х + 12 – 12 = 0;

8х2 – 3х = 0;

х(8х – 3) = 0;

х = 0 або 8х – 3 = 0;

х = 0 або x = 3 8 .

Відповідь: 0 або 3 8;

3) 4х – 0,2х(х + 20) = x3;

4х – 0,2х2 – 4х – х3 = 0; –0,2x2 – х3 = 0; –

х2(0,2 + х) = 0;

х2 = 0 або х + 0,2 = 0;

х = 0 або х = –0,2.

Відповідь: 0 або –0,2.

506. Знайдіть корені рівняння:

1) (Зх – 2)(3х + 2) – (2х – 5)(8х – 3) = 4х – 19;

2) 5x3 – х(2х – 3) = 3х;

5х3 – 2х2 + 3х – 3х = 0;

5х3 – 2х2 = 0;

х2(5х – 2) = 0;

х2 = 0 або 5х – 2 = 0;

х = 0 або х = 0,4.

Відповідь: 0 або 4;

4) 9х(х – 3) + (х – 4)(х – 5) = 20;

9х2 – 27х + х2 – 5х – 4х + 20 – 20 = 0;

10х2 – З6х = 0;

х(10х – 36) = 0;

х = 0 або 10х – 36 = 0; х = 0 або х = 3,6.

Відповідь: 0 або 3,6.

9х2 + 6х – 6х – 4 – (16х2 – 6х – 40х + 15) – 4х + 19 = 0;

9х2 + 6х – 6х – 4 – 16х2 + 6х + 40х – 15 – 4х + 19 = 0; –

7х2 + 42х = 0;

–7х(х – 6) = 0;

х = 0 або х – 6 = 0;

х = 0 або х = 6.

Відповідь: 0 або 6; 2) 1 3 (12 + х3) = 1 9 х2 + 4 |∙ 9;

3 – х2 = 0; х2(3х – 1) = 0; х2 = 0 або 3x – 1 = 0; х = 0 або х = 1 3 . Відповідь: 0 або 1 3 .

1) (а – 1)(a + 2) – (a – 2)(a + 2) + (а – 3)(a + 2) – (a – 4)(а + 2) = (а + 2)(a

(a – 4)) = (a +

+ 10) = (3a

= 2b(3a – 2) = 6аb

– b2)) = (4а – 7b)(2a2 – 4ab + b2 – 2b2 + 4аb + b2) = 2b2(4а – 7b) = 8аb

1) аb(a2 + аb + b2) – аb(а2 – ab + b2) = аb(а2

2) (а + b)(a + 1) – (a + b)(1 – b) + (b + a)(b – а) = (a + b)(а + 1– 1 + b + b – а) = = 2b(а + b) = 2ab + 2b2

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) 5y2 – 20у + 10 = 5(у2 – 4у + 2). Якщо y2 – 4у + 2 = 6, то 5(у2 – 4у + 2) = 5

6 = 30; 2) у2(y2 – 4у + 2) – 4у (у2 – 4у + 2) = (у2 – 4у + 2)(у2 – 4у) = (у2 – 4у + 2)(y2 – 4у + 2 – 2). Якщо y2 – 4у + 2 = 6, то (у2 – 4у + 2)(y2 – 4у + 2 – 2) = 6 ∙ (6 – 2) = 24; 3) Зy2 – 12у + 8 = 3y2 – 12у + 6 + 2 = 3(y2 – 4у + 2) + 2.

Якщо y2 – 4у + 2 = 6, то 3(y2 – 4у + 2)

1) –2а2 – 4а + 10 = –2(a2 + 2а –5). Якщо а2 + 2а – 5 = –4, то

2) a2(а2 + 2а – 5) + 2а(а2 + 2а – 5) = (а2 + 2a – 5)(a2

а2 + 2а – 5 = –4, то (a2 + 2a – 5)(a2 + 2а – 5 + 5) = –4 ∙ (–4 + 5) = –4;

3) 4а2 + 8a – 16 = 4(a2 + 2a – 4) = 4(a2 + 2a – 5 + 1).

Якщо а2 + 2a – 5 = –4, то 4(a2 + 2a – 5 + 1) = 4 ∙ (–4 + 1) = –12.

513. При якому

1) (x + 1)(x – 3) – x(x – 3) = ax;

(x – 3)(x + 1 – x) = ax;

x – 3 – ax = 0;

(1 – a)x = 3 — рівняння не має

2) х(5х – 1) – (х – а) (5х – 1) = 4х – 2а;

(5х – 1)(х – х + а) = 4х – 2а;

а(5х – 1) – 4х + 2а = 0; 5ax – а – 4х + 2а = 0;

(5а – 4)х + а = 0;

(5а – 4)х = –а — рівняння не

3) (2х – 5)(х + а) – (2х + 3)(х + 1) = 4;

якщо а = 1;

2x2 + 2ах – 5х – 5а – 2x2 – 2х – 3х – 3 = 4;

2ах – 10х = 5а + 3 + 4; (2а – 10)х = 5а + 7 — рівняння

514. При якому значенні

1) (х – 4)(х + а) – (х + 2)(х – а) = –6; х2 + ах – 4х – 4а – х2 + ах – 2х + 2а = –6; 2ах – 6х – 2а = –6; (2а – 6)х = 2а – 6 —

= 0,8;

= 5.

= 3; 2) х(3х – 2) – (х + 2а)(3х + 2) = 5а + 6;

2 – 2х – 6ах – 4а = 5а + 6;

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) 1200 ∙ 8 = 9600 (ар.) – на 6 тижнів.

2) 9600 : 500 = 19,2 (пачок).

Відповідь:

Нехай потрібно

519.

дорівнює 27?

1) 3m + 3n + mx + nx = (3m + 3n) + (mx + nx) = 3(m + n) + x(m + n) = (m + n)(3 + x).

2) 8c – 8 – ac + a = (8c – 8) + (–ac + a) = 8(c – 1) – a(c – 1) = (с – 1)(8 – a).

3) 4ab + 8b + 3a + 6 = (4ab + 8b) + (3a + 6) = 4b (a + 2) + 3(a + 2) = (а + 2)(4b + 3).

4) a2b + 2c2 – abc – 2ac = a2b – abc + 2c2 – 2ac = (a2b – abc) + (2c2 – 2ac) = = ab(a – c) + 2c(c – a) = (a – c)(ab – 2c).

523. Закінчіть

1) 5a + 5c – ab – bс = (5a + 5c) + (–ab – bc) = 5(a + c) – b(a+ c) = (a + c) (5 – b).

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2) xy + 2y – x – 2 = (xy + 2y) + (–x – 2) = y(x + 2) – 1(x + 2) = (х + 2)(y–1).

3) x3 + x2 + x + 1 = x2(x + 1) + (x + 1) = (x + 1) (x2 + 1).

524. Подайте у вигляді добутку многочленів вираз:

1) a(b + c) + 4b + 4c = (b + c) (a + 4).

2) x(y – 8) + 6y – 48 = (y – 8) (x + 6).

3) m(n –2) + n – 2 = (n – 2) (m + 1).

4) x(m – n) + n – m = (m – n) (x – 1).

525. Розкладіть на множники:

1) b(p – k) + cp – ck = (p – k) (b + c).

2) a(b + 9) + b + 9 = (b + 9) (a + 1).

3) a(c – 6) + 5c – 30 = (c – 6)(a + 5).

4) 7 – x + y (x – 7) = (x – 7) (y – 1).

526. Розкладіть на множники многочлен:

1) mа + mb + 4а + 4b = m(а + b) + 4(а + b) = (а + b)(m + 4);

2) Зх + су + cх + Зу = (Зх + Зу) + (су + сх) = 3(х + у) + с(у + х) = (х + у)(3 + с);

3) 5а – 5b + ар – bр = 5(а – b) + р(а – b) = (а – b)(5 + р);

4) 7m + mn + 7 + n = (7m + 7) + (mn + n) = 7(m + 1) + n(m + 11) = (m + 1)(7 + n);

5) а – 1 + аb – b = (а – 1) + b(а – 1) = (a – 1)(1 + b);

6) ху + 8у – 2х – 16 = (ху – 2х) + (8у – 16) = х(у – 2) + 8(у – 2) = (у – 2)(х + 8);

7) аb + ас – b – с = а(b + с) – (b + с) = (b + с)(а – 1);

8) Зр – Зk – 4ар + 4аk = 3(р – k) – 4а(р – k) = (р – k)(3 – 4а).

527. Подайте

1) ау – Зу – 4а + 12 = (ау – 3у) – (4а – 12) = у(а – 3) – 4(а – 3) = (а – 3)(у – 4);

2) 9а + 9 – nа – n = (9а + 9) – (na + n) = 9(а + 1) – n(а + 1) = (а + 1)(9 – n);

3) 6х + ау + 6у + ах = (6х + 6у) + (ау + ах) = 6(х + у) + а(х + у) = = (х + у)(6 + а);

4) 8х – 8у + хz – уz = 8(х – у) + z(х – у) = (х – у)(8 + z);

5) mn + m – n – 1 = (mn + m) – (n + 1) = m(n + 1) – (n + 1) = (n + 1)(m – 1);

6) аb – ас – 2b + 2с = а(b – с) –

1) 8с3 – 2с2 + 4с – 1 = 2с2(4с – 1) + (4с – 1) = (4с – 1)(2с2

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2) ху + у2 – 12х – 12у = у(х + у) – 12(х + у) = (х + у)(у – 12).

Якщо х = 10,8,у = – 8,8, то (х + у)(у – 12) = (10,8 + (–8,8))(–8,8 – 12) = 2 ∙ (–20,8) = –41,6;

3) 27x3 – 36х2 + 6х – 8 = 9х2(Зх – 4) + 2(3х – 4) = (Зх – 4)(9x2 + 2)

Якщо х = –1 1 3, то (Зх – 4) ∙ (9x2 + 2) = (3 ∙ (–1 1 3) – 4)(9(–1 1 3)2 + 2) = (–3 ∙ 4 3 – 4)(9(–4 3)2 + 2) = =(–4 – 4)(9 ∙ 16 9 + 2) = –8(16 + 2) = –8 ∙ 18 = –144.

531. Знайдіть значення виразу: 1) 2а + b + 2а2 + ab = (2а + b) + а(2а + b) = (2а + b)(1 + а).

Якщо а

2) 3х3 – х2 – 6x + 2= х2(3х – 1) – 2(3х – 1) = (3х – 1)(x2 – 2). Якщо х = 2 3, то (Зх

532. Закінчіть

1) 38,14 ∙ 12,26 + 12,26 ∙ 11,86 – 24,37 ∙ 2,26 – 2,26

– 2,26 ∙ (24,37 + 25,63) = 12,26 ∙ 50 – 2,26 ∙ 50 = = 50(12,26 – 2,26) = 50 ∙ 10 = 500. 2) 0,7 ∙ 2,48 – 0,3

1,62) = 2,48(0,7 – 0,4) + 0,3 ∙ (3,14 – 1,62) = 2,48 ∙ 0,3 + 0,3 ∙ 1,52 = 0,3 (2,48 + 1,52) =

1) 3,742 +

+ (а + b + 3) = ab(a + b + 3) + (а + b + 3 ) = = (аb + 1)(а + b + 3);

3) x3 – х2 + х2у + х – ху

2 – х + 1) + у(х2 – х + 1) = = (х + у)(х2 – х + 1); 4) m2n + mn – 5 – 5m + n – 5m2 = (m2n + mn + n) – (5 + 5m + 5m2) = = n(m2 + m + 1) – 5(m2 + m + 1) = (n – 5)(m2 + m + 1);

5) х6 – 2x5 + 4x3 – 8x2 + 5х –10 = x5(х – 2) + 4х2(х – 2) + 5(х – 2) = (х5 + 4х2 + 5)(х –2); 6) a3b + ab2 – abc3 – a2с – bc + с4 = a2(ab – c) – c3(ab – c) + b(ab – c) = (ab – c)(a2 – c3 + b).

1) ab + ас + ad + bx + сх + dх = a(b + с + d)+ x(b + с + d) = (а + x)(b + c + d); 2) 7p – 7k – рх + kх + k – p = 7(p – k) – x(p – k) – (p – k) = (p – k)(7 – x – 1); 3) x3y3 –

+ 6ху) + (ху – 6) = = (ху – 6)(х2у2 – ху+ 1);

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

4) а5 – a4b + a3b2 – а2b3 + аb4 – b5 = а4(а – b) + a2b2(a – b) + b4(a – b) = (a – b)(a4 + a2b2 + b4).

537.

1) x2 + 8x + 12 = x2 + 2x + 6x + 12= x(x + 2) + 6(x + 2) = (x + 2)(x + 6); 2) x2 – 5x + 4 = x2 – x – 4x + 4 = x(x – 1) – 4(x – 1) = (x – 1)(x – 4);

3) x2 + 7x – 8 = x2 – x + 8x – 8 = x(x + 8) + (x + 8) = (x + 8) (x – 1); 4) x2 – 4x – 5 = x2 – 5х + x – 5 = x(x – 5) + (x – 5) = (x – 5)(x + 1).

538. Розкладіть на множники тричлен:

1) x2 + 4x + 3 = x2 + x + 3x + 3 = x(x + 3) + (x + 3) = (x + 3)(x + 1);

2) x2 – 10x + 16 = x2 – 2x – 8x + 16 = x(x – 2) – 8(x – 2) = (x – 2)(x – 8);

3) x2 + 3x – 18 = x2 + 6x – 3x – 18 = x(x + 6) + 3(x + 6) = (x + 6)(x – 3); 4) x2 – 4x – 32 = x2 – 8x + 4x – 32 = x(x – 8) + 4(x – 8) = (x – 8)(x + 4).

539.

націло на 6.

n3 + Зn2 + 2n = n(n2 + 3n + 2) = n(n2 + n + 2n + 2) = n(n(n + 1) + 2(n + 1)) = n(n + 1)(n + 2).

(кратне 3).

Висновок. Значення даного виразу

540. Розкладіть на множники многочлен.

а2 + b2 + с2 + 2ab + 2bс + 2ас = а2 + b2 + с2 + ab + bс + ас + ab + bс + ас = = (a2 + ab) + (ас + bc) + (b2 + ab) + (с2 + bс + ас) = а(а + b) + с(а + b) + b(b + а) + с(с + b + а) = (а + b)(a + с + b) + с(с + b + а) = (а + b)(a + b + с) + с(а + b + с) = (а + b + с) ∙ (а + b + с) = = (а + b + с)2 . 541. Доведіть, що при будь–якому

Відповідь:

л.

Рівняння: 2 3

1) (2a)2 = 4a2;

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

маємо

Якщо маємо n фіналістів (n — натуральне число), то ігр буде (n − 1).

Аналогічно при виході до півфіналу, чвертьфіналу кількість фіналістів

учасників), або непарна (7 учасників).

Якщо n = 8, то ігр 4 + 2 + 1 = 7, (8 – 1 ).

Якщо n = 7, то ігр 3 + 2 + 1 = 6, (7 – 1).

Взагалі кількість матчів = (n − 1).

Відповідь: (n − 1) матчів. ЗАВДАННЯ № 3 «ПЕРЕВІРТЕ

у вигляді многочлена вираз 3y2 (y3 + 1).

А) 3y6 + 1; Б) 3y6 + 3y2; В) 3y5 + 1; Г) 3y5 + 3y2.

3y2 ⋅ y3 + 3y2 ⋅ 1 = 3y2 + 3 + 3y2 = 3y5 + 3y2

2. Спростіть вираз –9y (y – 3) + 4,5y (2y – 4).

А) 45y; Б) –45y; В) –9y; Г) 9y. –9y (y – 3) + 4,5y (2y – 4)

−9y(y − 3) = −9y2 + 27y

4,5y(2y − 4) = 9y2 − 18y

(−9y2 + 27y) + (9y2 − 18y) = −9y2 + 9y2 + 27y −18y = 9y.

3. Якому многочлену дорівнює вираз (x – 3) (x + 7)? А) x2 + 4x – 21; Б) x2 – 4x – 21; В) x2 + 10x – 21; Г) x2 – 10x – 21. (x − 3)(x + 7) = x2 + 7x − 3x – 21 = x2 + 4x – 21

4. Спростіть вираз (3x + 2) (2x – 1) – (5x – 2) (x – 4). А) x2 – 23x – 10; Б) x2 + 23x – 10; В) x2 – 21x + 6; Г) x2 + 21x + 6. (3x + 2)(2x − 1) − (5x − 2)(x − 4) = (6x2 + x − 2) − (5x2 − 22x + 8) = = 6x2 + x – 2 − 5x2 + 22x – 8 = (6x2 − 5x2) + (x + 22x) + (−2 − 8) = x2 + 23x – 10

спільний множник за дужки: 3mn – 4mk. А) n (3m – 4k); Б) m (3n – 4k); В) n (4m – 3k); Г) m (4n – 3k). 3mn − 4mk = m(3n − 4k)

6. Розкладіть на множники вираз m2n + mn2

А) m (m + n); Б) n (m + n); В) mn (m + n); Г) m2n2 (m + n). m2n + mn2 = mn(m + n)

7. Розкладіть вираз mn – mn2 на множники.

А) mn (1 – n); Б) mn (1 + n); В) m (1 – n) (1 – n); Г) n (1 – m) (1 – m). mn − mn2 = mn(1 − n)

А) 2x2 (1 – 2x3);

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2x2 – 4x6

Б) 2x2 (1 – 2x4);

В) 2x2 (2 – x3); Г) 2x2 (2 – x4).

2x2 − 4x6 = 2x2(1 − 2x4)

9. Розв’яжіть рівняння x2 – 2x = 0.

А) 0; Б) 0; –2; В) 0; 2; Г ) 2.

x2 – 2x = 0

x(x − 2) = 0

x = 0 або x – 2 = 0

x = 0 або x = 2

10.

многочлен ax – ay + 5x – 5y. А) (x – y) (a + 5); Б) (x – y) (a – 5); В) (x + y) (a – 5); Г) (x + y) (a + 5).

ax – ay + 5x – 5y = (ax − ay) + (5x − 5y) = a(x − y) + 5(x − y) = (a + 5)(x − y)

11. Розв’яжіть рівняння х−1 2 х+1 3 =1. А) 11; Б) 1;

2 х+1 3 =1

3(х – 1) – 2(х + 1) = 6

3х – 3 – 2х – 2 = 6

х – 5 = 6

х = 6 + 5

х = 11

a2 − 7a + 3 = 2

a2 − 7a + 3 – 2 = 0

a2 − 7a + 1 = 0

a2 − 7a = −1

7; Г ) 5.

2a2 − 14a + 10 = 2(a2 − 7a) + 10 = 2(−1) + 10 = −2 + 10 = 8

1) (c – 8)(c + 8) = c2 – 82 = c2 – 64. 2) (5x – 7y2)(5x + 7y2) = (5x)2 – (7y2)2 = 25x2 – 49y4 . 3) (a4 + b3)(b3 – a4) = (b3 + a4)(b3 – a4) = (b3)2 – (a4)2 = b6 – a8. 4) (–9хy – z)(9xy – z) = –(9xy + z)(9xy – z) = ((9xy)2 – z2) =

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

554.

1) (2ab + 3)(2ab – 3) = (2ab)2 – 32 = 4a2b2 – 9.

2) (6m2 – 11p5)(11p5 + 6m2) = (6m2 – 11p5)(6m2 + 11p5) = (6m2)2 – (11p5)2 = 36m4 – 121p10.

555. Виконайте

1) (m – n)(m + n) = m2 – n2;

2) (х – 1)(х + 1) = х2 – 12 = х2 – 1;

3) (9 –y)(9 + у) = 92 – у2 = 81 – у2; 4) (3b – 1)(3b + 1) – (3b)2 – 12 = 9b2 – 1; 5) (10m – 7)(10m + 7) = (10m)2 – 72 = 100m2 – 49;

6) (4а – b)(b + 4a) = (4а – b)(4a + b) = (4a)2 – b2 = 16a2 – b2; 7) (5b + 1)(1 – 5b) = (1 + 5b)(1 – 5b) = 12 – (5b)2 = 1 – 25b2; 8) (3x – 5y)(3x + 5y) = (3x)2 – (5y)2 = 9x2 – 25y2; 9) (13c – 10d)(13c + 10d) = (13c)2 – (10d)2 = 169c2 – 100d2;

10) (8m + 11n)(11n – 8m) = (11n + 8m)(11n – 8m) = (11n)2 – (8m)2 = 121n2 – 64m2

556. Подайте

1) (c – 2)(c + 2) = c2 – 22 = c2 – 4; 2) (12 – x)(12 + x) = 122 – x2 = 144 – x2; 3) (3x + y)(3x – y) = (3x)2 – y2 = 9x2 – y2; 4) (6x – 9)(6x + 9) = (6x)2 – 92 = 36x2 – 81; 5) (x + 7)(7 – x) = (7 + x)(7 – x) = 72 – x2 = 49 – x2; 6) (5a – 8b)(5a + 8b) = (5a)2 – (8b)2 = 25a2 – 64b2; 7) (8m + 2)(2 – 8m) = (2 + 8m)(2 – 8m) = 22 – (8m)2 = 4 – 64m2; 8) (13c – 14d)(14d + 13c) = (13c – 14d)(13c + 14d) = (13c)2 – (14d)2 = 169c2 – 196d2.

557. Виконайте множення:

1) (a2 – 3)(a2 + 3) = (a2)2 – 32 = a4 – 9; 2) (5 + b2)(b2 – 5) = (b2 + 5)(b2 – 5) = (b2)2 – 52 = b4 – 25; 3) (3x – 2у2)(3х + 2y2) = (3x)2 – (2y2)2 = 9x2 – 4y4; 4) (10p3 – 7k)(10p3 + 7k) = (10p3)2 – (7k)2 = 100p6 – 49k2; 5) (4x2 – 8y3)(4x2 + 8y3) = (4x2)2 – (8y3)2 = 16x4 – 64y6;

6) (11a3 + 5b2)(5b2 – 11a3) = (5b2 + 11a3)(5b2– 11a3) = (5b2)2 – (11a3)2 = 25b4 – 121a6; 7) (7 – xy)(7 + xy) = 72 – (xy)2 = 49 – x2y2; 8) (8a3b –1 3ab2)(8a3b + 1 3ab2) = (8a3b)2 – (1 3ab2)2 = 64a6b2 –1 9 a2b4.

558. Виконайте множення: 1) (x3 + 4)(х3 – 4) = (х3)2 – 42 = х6 – 16; 2) (аb – с)(аb + с) = (ab)2 – с2 = а2b2 – с2; 3) (x – y2)(y2 + х) = (х – у2)(х + у2) = x2 – (у2)2 = х2 – у4; 4) (3m2 – 2с)(3m2 + 2с) = (3m2)2 – (2с)2 = 9m4 – 4с2; 5) (6а3 – 8b)(6а3 + 8b) = (6а3)2 – (8b)2 = 36a6 – 64b2; 6) (5n4 – m4)(5n4 + m4) = (5n4)2 – (m4)2 = 25n8 – m8

559. Спростіть вираз: 1) (2а – b)(2а + b) + b2 = (2а)2 – b2 + b2 = 4а2; 2) 10x2 + (у – 5х)(у + 5х) = 10х2 + у2 – (5х)2 = 10х2 + у2 – 25х2 = у2 – 15х2; 3) 64m2 – (8m + 9)(8m – 9) = 64m2 – ((8m)2 – 92) = 64m2 – 64m2 + 81 = 81; 4) 3а(а – b) – (3а + 2b)(3а – 2b) = 3а2 – 3аb – ((3а)2 – (2b)2) = 3а2 – 3аb – 9а2 + 4b2 = = –6а2 – 3ab + 4b2.

560. Спростіть вираз: 1) (9а – 2)(9а + 2) – 18а2 = (9а)2 – 22 – 18а2 = 81а2 – 4 – 18а2 = 63a2 – 4; 2) 25m2 – (5m – 7)(5m + 7) = 25m2 – ((5m)2 – 72) = 25m2 – 25m2 + 49 = 49;

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

3) 4х(3х– 10y) – (4х + у)(4х – у) = 12х2 – 40ху – ((4х)2 – у2) = 12х2 – 40ху – 16х2 + у2 = = –4х2 – 40ху + у2 .

561.

0,3x3 – xy2,

0,09x6 – x2y4? (0,3х3 – хy2)(0,Зх3 + ху2) = (0,3х3)2 – (хy2)2 = 0,09х6 – х2у4

562.

49t8 – 81p10? (7t4 + 9p5)(7t4 – 9р5) = (7t4)2 – (9р5)2 = 49t8 – 81р10 .

563. Які одночлени треба

1) (3b – 12а)(3b + 12а) = (3b)2 – (12а)2 = 9b2 – 144а; 2) (4d – 5с)(4d + 5с) = 16d2 – 25с2;

7t4 + 9p5, щоб

3) (0,7p + 1 3m4)(1 3 m4 – 0,7p) = (1 3 m4 + 0,7p)( 1 3 m4 – 0,7p) = 1 9 m8 – 0,49p2;

4) (3m2 + n3)(3m2 – n3) = 9m4 – n6.

564. Поставте

1) (8а2b – 5с3)(8а2b + 5с3) = 64а4b2 – 25с6;

2) ( 1 15 a2 –1 12 x4y5)( 1 15 a2 + 1 12 x4y5) = 1 225 a4 –1 144 x8y10 .

565. Подайте у

1) а(а – 2)(а + 2) = а(а2 – 4) = а3 – 4а;

2) –3(х + 3)(х – 3) = –3(х2 – 9) = –За2 + 27;

3) 7b2(b + 4)(4 – b) = 7b2(4 + b)(4 – b) = 7b2(16 – b2) = 112b2 – 7b4;

4) (с – d)(c + d)(с2 + d2) = (с2 – d2)(c2 + d2) = c4 – d4;

5) (2а – 1)(2а + 1)(4а2 + 1) = (4а2 – 1)(4а2 + 1) = 16a4 – 1; 6) (с3 – 5)(с3 + 5)(с6 + 25) = (с6 – 25)(с6 + 25) = с12 – 625.

566. Виконайте множення:

1) 5b(b – 1)(b + 1) = 5b(b2 – 1) = 5b3 – 5b; 2) (с + 2)(с – 2) ∙ 8с2 = (с2 – 4) ∙ 8с2 = 8с4 – 32с2;

тотожність:

3) (m – 10)(m2 + 100)(m + 10) = (m – 10)(m + 10)(m2 + 100) = (m2 – 100)(m2 + 100) = = m4 – 10000;

4) (а2 + 1)(а2 – 1)(а4 + 1) = (а4 – 1)(a4 + 1) = а8 – 1.

567. Виконайте множення двочленів (n — натуральне число):

1) (an – 4)(аn + 4) = (аn)2 – 42 = а2n – 16; 2) (b2n + с3n) (b2n – с3n) = (b2n)2 – (с3n)2 = b4n – с6n; 3) (х4n + yn+2)(yn+2 – х4n) = (yn+2 +

= (y

– (x4n)2 = y2n+4 – x8n; 4) (an+1 – bn–1)(аn+1 + bn–1) = (аn+1)2 – (bn–1)2 = а2n+2 – b2n–2.

568. Спростіть вираз:

1) (4х – 7у)(4х + 7у) + (7х – 4у)(7х + 4у) = (4х)2 – (7у)2 + (7х)2 – (4y)2 = = 16y2 – 49у2 + 49х2 – 16y2 = 65х2 – 65y2; 2) (а – 2)(а + 3) + (6 – а)(а + 6) = а2 + За – 2а – 6 + (6 – а)(6 + а) = а2 + а – 6 + 62 – а2 = = а – 6 + 36 = а + 30; 3) (8а – 3)(8a + 3) – (7а + 4)(8а – 4) = (8а)2 – З2 – (56а2 – 28а + 32а – 16) = = 64а2 – 9 – 56а2 + 28а – 32а + 16 = 8а2 – 4а + 7; 4) 0,6m(2m – 1)(2m + 1) + 0,3(6 + 5m)(6 – 5m) = 0,6m(4m2 – 1) + + 0,3(36 – 25m2) = = 2,4m3 – 0,6m + 10,8 – 7,5m2 = 2,4m3 – 7,5m2 – 0,6m + 10,8; 5) (7 – 2х)(7 + 2х) – (х – 8)(х + 8) – (4 – 3х)(5 + 3х) = = 49 – 4х2 – (х2 – 64) – (20 + 12x – 15х – 9x2) = 49 – 4x2 – х2 + 64 – 20 – 12х + 15х + 9х2 = = 4х2 + 3х + 93; 6) –b2с(4b – с2)(4b + с2) + 16b4с = –b2с(16b2 – с4) + 16b4с = –16b4с + b2с5 + 16b4с = b2с5

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

569. Спростіть вираз: 1) (b + 7)(b – 4) + (2b – 6)(2b + 6) = b2 – 4b + 7b – 28 + (2b)2 – 62 = = b2 + 3b – 28 + 4b2 – 36 = 5b2 + 3b – 64; 2) (х + 1)(х – 1) – (х + 5)(x – 5) + (х + 1)(х – 5) = х2 – 1 – (x2 – 25) + х2 – 5х + х – 5 = = х2 – 1 – х2 + 25 + х2 – 5х + х – 5 = х2 – 4х + 19; 3) 81а8 – (За2 – b3)(9а4 + b6)(3а2 + b3) = 81а8 – (За2 – b3)(За2 + b3)(9а4 + b6) = = 81а8 – (9а4 – b6)(9а4 + b6) = 81а8 – (81а8 – b12) = 81а8 – 81а8 + b12 = b12.

570. Розв’яжіть рівняння:

1) 8х(3 + 2х) – (4х + 3)(4х – 3) = 9х – 6;

24х + 16х2 – 16х2 + 9 = 9х – 6; 24х + 16х2 – 16х2 – 9х = –6 – 9; 15x = –15;

х = –1.

Відповідь: –1.

3) (6х + 7)(6х – 7) + 12х = 12х(3х + 1) – 49;

36х2 – 49 + 12х = З6х2 + 12х – 49;

36х2 + 12х – З6х2 – 12х = –49 + 49;

0х = 0 — коренем є будь–яке число.

Відповідь: Коренем рівняння є будь–яке число.

2) 7х – 4х(х – 5) = (8 – 2х)(8 + 2х) + 27х;

7х – 4x2 + 20х = 64 – 4x2 + 27х; 7х – 4х2 + 20х + 4х2 – 27х = 64;

0х = 64 — рівняння не має коренів.

Відповідь: Рівняння коренів

4) (х – 2)(х + 2)(х2 + 4)(х4 + 16) = х8 + 10х; (х2 – 4)(х2 + 4)(х4 + 16) = х8 + 10х; (х4 – 16)(х4 + 16) = х8 + 10х; х8 – 256 = х8 + 10х; х8

10х = 256; х = –25,6.

Відповідь: –25,6. 571. Розв’яжіть рівняння:

1) (х – 17)(х + 17) = х2 + 6х – 49;

х2 – 289 = х2 + 6х – 49;

х2 – х2 – 6х = –49 + 289; –6х = 240;

х = –40.

Відповідь: –40. 2) (1,2х – 4)(1,2х + 4) – (1,3х – 2)(1,3х + 2) = = 0,5х(8 – 0,5х); 1,44х2 – 16 – (1,69х2 – 4) = 4х – 0,25x2; 1,44х2 – 16 – 1,69х2 + 4 = 4х – 0,25x2; 1,44x2 – 1,69x2 – 4х + 0,25х2 = 16 – 4; –4х = 12;

х = –3.

Відповідь: –3.

572. Доведіть, що

1) (х – 9)(х + 9) – (х + 19)(х

2) (2а – b)(2а + b) + (b – с)(b + с) + (с

573. Доведіть, що

+ 10) (5n – 10)

12. (7n + 8)(7n – 8) – (5n + 10)(5n

= 24n2 + 36 = 12(2n2+ 3)

(4n + 3) (9n – 4) – (6n – 5) (6n + 5) – 3 (n – 2)

(4n + 3)(9n – 4) – (6n – 5)(6n + 5) – 3(n –

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

(5 + 2817)(5 – 2817) + 1434 ∙ 234 = 52 – (2817)2 + (14 ∙ 2)34 = 25 – 2834 + 2834 = 25; 3) 736 ∙ 812 – (1418 + 3)(1418 – 3) = 736 ∙ (23)12 – ((1418)2

232 = (22 – 1)(22 + 1)(24 + 1)(28 + 1) (216 + 1) –

(28 – 1)(28 + 1)(216 + 1) – 232 = (216 – 1)(216 + 1) –

1) 8115 ∙ 820 – (630 + 1 )(630 – 1) = (З4)15 ∙ (23)20 – ((630)2 – 1) =

= 660 – 660 + 1 = 1;

2) 524 – (53 – 2)(53 + 2)(56 + 4)(512 + 16) = 524 – (56 – 4)(56 + 4)(512 + 16) = = 524 – (512 – 16)(512 + 16) = 524 – (524 – 256) = 524 – 524 + 256 = 256.

578.

1) 415 ∙ 425 = (420 – 5)(420 + 5) = 4202 – 52;

426 ∙ 414 = 414 ∙ 426 = (420 – 6)(420 + 6) = 4202 – 62.

Отже, 4202 – 52 > 4202 – 62.

2) 1234567 ∙ 1234569 = (1234568 – 1)(1234568 + 1) = 12345682 – 1.

Отже, 1 234 5682 – 12 < 1 234 5682 579.

1) 253 ∙ 259 = (256 – 3)(256 + 3) = 2562 – З2;

252 ∙ 260 = (256 – 4)(256 + 4) = 2562 – 42.

Отже, 2562 – З2 > 2562 – 42.

2) 987 646 ∙ 987 662 = (987 654 – 8)( 987 654 + 8) = 987 6542 – 82.

Отже, 987 6542 > 987 6542 – 82.

580. Олеся

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

60 – х = 2(100 – 4х);

60 – х = 200 – 8х;

8х – х = 200 – 60;

7х = 140;

х = 20.

16 807 ∙ 80 = 1 344 560

кішкам.

Відповідь: 16 807 жмень або 1,34 т. 585. Розв’яжіть

2(4х –

–

+ 1)

– 2 – 9х – 3 = 24х + 24; 8х – 9х – 24х = 24 + 2 + 3; –25х = 29; x = –1 4 25 . Відповідь: –1 4 25 .

586. Подайте

+ 1);

│∙18; 2(3х – 2) – 3(2х + 1) = 6(5 – х); 6х – 4 – 6х – 3 = 30 – 6х; 6х – 6х + 6х = 30 + 4 + 3; 6х = 37; x = 6 1 6 .

Відповідь: 6 1 6

1) x6 = (x3)2; 2) y4 = (y2)2; 3) 4x2 = (2x)2; 4) 1 9 x4 = (1 3 x2)2; 5) a8b10 = (a4b5)2; 6) 0,36x2y12 = (0,6xy6)2; 7) 1,21m10n20 = (1,1m5n10)2; 8) 1 9 16 a14b16 = 2 5 16 a14b16 = (5 4a7b8)2.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) a2 – 16b2 = a2 – (4b)2;

2) 25с2 + 9b2 —

3) 100b4 – 25с6 = (10b2)2 – (5с3)2;

4) –64 + a10 = a10 – 64 = (a5)2 – 82; 5) –a12 – 49с8 = (а12 + 49с8) — цей

6) –0,01а4 + 0,04b4 = 0,04b4 – 0,01а4 = (0,2b2)2 – (0,1а2)2

588. Для

4 + 8 ⋅ 1 = 44; 44 = 44. Отже, треба 4-тонних

дві, 7-тонних вантажівок

Відповідь: 2, 4, 1.

589. Яким

а2 – 144 = а2 – 122 = (а – 12)(а + 12).

590. Яка з даних рівностей є тотожністю: –49 + b2 = b2 – 49 = (b – 7)(7 + b). Тотожністю є рівність 2).

591. Чи можна, застосовуючи формулу

то

1) а2 – 9 = a2 – З2 = (а – 3)(a + 3);

2) b2 + 1 — не можна;

3) 4 – с2 = 22 – с2 = (2 – с)(2 + с);

4) 25 + х2 — не можна;

5) 1 – y2 = 12 – y2 = (1 – y)(1 + y);

6) 16a2 – b2 = (4a)2 – b2 = (4a – b)(4а + b);

7) 81 + 100p2 — не можна;

8) 81 – 100р2 = 92 – (10р)2 = (9 – 10р)(9 + 10р);

9) m2n2 – 25 = (mn)2 – 52 = (mn – 5)(mn + 5); 10) –m2n2 – 25 = –(m2n2 + 25) — не можна.

592. Розкладіть на множники:

1) b2 – d2 = (b – d)(b + d);

2) х2 – 1 = x2 – 12 = (x – 1)(х + 1);

3) –х2 + 1 = 12 – х2 = (1 – x)(1 +х);

4) 36 – с2 = 62 – с2 = (6 – с)(6 + с);

5) 4 – 25а2 = 22 – (5a)2 = (2 – 5а)(2 + 5а);

6) 49a2 – 100 = (7а)2 – 102 = (7a – 10)(7a + 10);

7) 900 – 81k2 = 302 – (9k)2 = (30 – 9k)(30 + 9k);

8) 16x2 – 121y2 = (4х)2 – (11y)2 = (4х – 11у)(4х + 11у);

9) b2с2 – 1 = (bс)2 – 12 = (bс – 1)(bс + 1);

10) 1 4 x2 –1 9y2 = (1 2x)2 – (1 3y)2 = (1 2 x –1 3y)(1 2 x + 1 3y);

11) –4а2b2 + 25 = 52 – (2аb)2 = (5 – 2ab)(5 + 2ab);

12) 144х2у2 – 400 = (12ху)2 – 202 = (12ху – 20)(12ху + 20);

13) а2b2с2 – 1 = (аbс)2 – 12 = (аbс – 1)(аbс + 1);

14) 100а2 – 0,01b2 = (10а)2 – (0,1b)2 = (10а – 0,1b)(10а + 0,1b);

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

15) а4 – b2 = (а2)2 – b2 = (а2 – b)(а2 + b);

16) р2t2 – 0,36k2d2 = (pt)2 – (0,6kd)2 = (рt – 0,6кd)(рt + 0,6kd);

17) у10 – 9 = (у5)2 – 32 – (у5 – 3)(у5 + 3);

18) 4x12 – 111 25y16 = (2x6)2 –36 25y16 = (2x6)2 – (6 5y8)2 = (2x6 –6 5y8)(2x6 + 6 5y8).

593. Розкладіть на множники:

1) 16 – b2 = 42 – b2 = (4 – b)(4 + b);

2) с2 – 49 = с2 – 72 = (с – 7)(с + 7);

3) 0,04 – а2 = 0,22 – а2 = (0,2 – а)(0,2 + а);

4) x2 –4 9 = x2 – (2 3)2 = (x –2 3)(x + 2 3);

5) 4х2 – 25 = (2х)2 – 52 = (2х – 5)(2х + 5);

6) 81с2 – 64d2 = (9с)2 – (8сd)2 = (9с – 8сd)(9с + 8d);

7) 0,09x2 – 0,25y2 = (0,3x)2 – (0,5у)2 = (0,3х – 0,5у)(0,3х + 0,5у);

8) а2b4 – c6d8 = (аb2)2 – (с3d4)2 = (аb2 – с3d4)(аb2 + с3d4);

9) 4а2с2 – 9х2у2 = (2ас)2 – (3xу)2 = (2ас – 3xу)(2ас + 3ху);

10) х24 – у22 – (х12)2 – (у11)2 = (х12 – у11)(х12 + у11);

11) –1600 + а12 = а12 – 402 = (а6)2 – 402 = (а6 – 40)(а2 + 40);

12) a18 –49 64 = (a9)2 – (7 8)2 = (a9 –7 8)(a9 + 7 8).

594. Обчисліть,

1) 862– 762 = (86 – 76)(86 + 76) = 100 ∙ 162 = 1620.

2) 1072 – 932 = (107 – 93)(107 + 93) = 14 ∙ 200 = 2800.

3) 7,322 – 6,322 = (7,32 – 6,32)(7,32 + 6,32) = 1 ∙ 13,64 = 13,64.

4) 19,42 – 19,32 = (19,4 – 19,3)(19,4 + 19,3) = 0,1 ∙ 38,7 = 3,87.

5) 8,542 – 1,442 = (8,54 – 1,44)(8,54 + 1,44) = 7,1 ∙ 9,98 = 70,858.

595. Знайдіть значення виразу x2 – y2 , якщо:

1) 752 – 252 = (75 – 25)(75 + 25) = 50 ∙ 100 = 5000.

2) 10,52 – 9,52 = (10,5 – 9,5)(10,5 + 9,5) = 1 ∙ 20 = 20. 3) 5,892 – 4,112 = (5,89 – 4,11)(5,89 + 4,11) = 1,78 ∙ 10 = 17,8.

4) 3,042 – 1,952 = (3,04 – 1,95)(3,04 + 1,95) = 1,08 ∙ 5 = 5,4.

596. Розв’яжіть рівняння:

1) х2 – 49 = 0;

(х –7)(х + 7) = 0;

х – 7 = 0 або х + 7 = 0;

х = 7 або х = –7.

Відповідь: –7 або 7; 2) 1 4 – z2 = 0; (1 2 – z)( 1 2 + z) = 0; 1 2 – z = 0 або z = –1 2 . Відповідь: –1 2 або 1 2;

З) x2 + 36 = 0;

х2 = –36.

Відповідь: Коренів немає; 4) х2 – 0,01 =0; (х – 0,1)(х + 0,1) = 0; х – 0,1 = 0 або х + 0,1 = 0; х = 0,1 або х = – 0,1. Відповідь: –0,1 або 0,1;

5) 9x2 – 4 = 0;

(3х – 2)(3х + 2) = 0;

3х – 2 = 0 або 3х + 2 = 0; 3х = 2 або 3х = –2;

х = 2 3 або x = –2 3 Відповідь: –2 3 або 2 3 .

6) 0,04x2 – 1 = 0; (0,2х – 1)(0,2х + 1) = 0; 0,2х – 1 = 0 або 0,2х + 1 = 0; 0,2х = 1 або 0,2х = –1; х = 5 або х = –5.

Відповідь: –5 або 5.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

597. Розв’яжіть рівняння:

1) с2 – 0,25 = 0;

(с – 0,5)(с + 0,5) = 0;

с – 0,5 = 0 або с + 0,5 = 0; с = 0,5 або с = –0,5.

Відповідь: –0,5 або 0,5; 2) 81x2 – 121 = 0; (9х – 11)(9х + 11) = 0; 9х – 11 = 0 або 9x + 11 = 0; x =

3) –0,09 + 4х2 = 0; 4x2 – 0,09 = 0; (2х – 0,3)(2х + 0,3) = 0; 2х – 0,3 = 0 або 2х + 0,3 = 0; 2х = 0,3 або 2х = –0,3; х = 0,15 або х = –0,15. Відповідь: –0,15 або 0,15.

598. Розкладіть на множники, користуючись формулою різниці квадратів:

1) (х + 2)2 – 49 = (х + 2 – 7)(х + 2 + 7) = (х – 5)(х + 9); 2) (х – 10)2 – 25y2 = (х – 10 – 5у)(х – 10 + 5у) – (х – 5у – 10)(х + 5у – 10);

3) 25 – (у – З)2 = (5 – (у–3))(5 + (у – 3)) = (5 – у + 3)(5 + у – 3) = (8 – у)(2 + у);

4) (а – 4)2 – (a + 2)2 = (а – 4 – (а + 2))(а – 4 + (a + 2)) = (а – 4 – a – 2)(а – 4 + а + 2) =

= –6(2a – 2) = –12(a – 1);

5) (m – 10)2 – (n – 6)2 = (m – 10 – (n – 6))(m – 10 + (n – 6)) = = (m – 10 – n + 6)(m – 10 + n – 6) = (m – n – 4)(m + n – 16);

6) (8у + 4)2 – (4у – З)2 = (8у + 4 – (4у – 3))(8у + 4 + (4у – 3)) = = (8у + 4 – 4у + 3)(8у + 4 + 4у – 3) = (4у + 7)(12у + 1); 7) (5a + 3b)2 – (2a – 4b)2 = (5а + 3b – (2а – 4b))(5а + 3b + (2а – 4b)) = = (5a + 3b – 2а + 4b)(5a + 3b + 2a – 4b) = (За + 7b)(7a – b);

8) 4(a – b)2 – (а + b)2 = (2(a – b))2 – (a + b)2 = (2(a – b) – (a + b))(2(a – b) + (а + b)) = = (2а – 2b – а – b)(2а – 2b + а + b) = (a – 3b)(3а – b); 9) (х2 + х + 1)2 – (х2 – х + 2)2 = (х2 + х + 1 – (х2 – х + 2))(х2 + х +1 + (х2 – х + 2)) = = (х2 + х + 1 – х2 + х – 2)(х2 + х + 1 + х2 – х + 2) = (2х – 1)(2х2 + 3); 10) (–Зх3 + у)2 – 16х6 = (–Зх3 + у)2 – (4х3)2 = (–Зх3 + у – 4х3)(–Зх3 + у + 4х3) = = (–7x3 + у)(х3 + у).

599. Подайте у вигляді добутку

1) (х – 2)2 – 4 = (х – 2 – 2)(х – 2 + 2) = х(х – 4); 2) (b + 7)2 – 100с2 = (b + 7 – 10с)(b + 7 + 10с) = (b – 10с + 7)(b + 10с + 7); 3) 121 – (b + 7)2 =(11 – (b + 7))(11 + b + 7) = (11 – b – 7)(b + 18) = (4 – b)(b + 18);

4) а4 – (7b – a2)2 = (a2 – (7b – а2)) (а2 + (7b – a2)) = (а2 – 7b + a2)(a2 + 7b – а2) = 7b(2а2 – 7b);

5) (4х – 9)2– (2х + 19)2 = (4х – 9 – (2х + 19))(4х – 9 + (2х + 19)) = = (4х – 9 – 2х – 19)(4х – 9 + 2х + 19) = (2х – 28)(6х + 10);

6) (а + b + с)2 – (a – b – с)2 = (а + b + с – (а – b – с))(а + b + с + а – b – с) = = (a + b + с – a + b + с))(a + b + с + а – a – с) = 2а(2b + 2с) = 4а(b + с).

600. Знайдіть значення виразу: 1) (9х – 4)2 – (7х + 5)2 = (9х – 4 – (7х + 5))(9х– 4 + (7х + 5)) = = (9х – 4 – 7х – 5)(9х – 4 + 7х + 5) = (2х – 9)(16x + 1).

Якщо х = 1,5, то(2x – 9)(16х + 1) = (2 ∙ 1,5–9)(16 ∙ 1,5 + 1) = (3 – 9)(24 + 1) = –6 ∙ 25 = –150; 2) (5х + 3у)2 – (3х + 5у)2 = (5х + 3у – (3х + 5у))(5х + 3у + (3х + + 5у)) = = (5х + 3у – 3х – 5у)(5х + 3у + 3х + 5у) = (2х – 2у)(8х + 8у) = 16(x – у)(х + у).

Якщо х = 2,1; у = 1,9, то 16(х – у)(х + у) = 16 ∙ (2,1 – 1,9)(2,1 + 1,9) = 16 ∙ 0,2 ∙ 4 = 12,8.

(2,5а – 1,5b)2 – (1,5а – 2,5b)2 = (2,5а – 1,5b – (1,5а –2,5b))(2,5а – 1,5b + (1,5а – 2,5b)) = = (2,5а – 1,5b – 1,5а + 2,5b)(2,5а – 1,5b + 1,5а – 2,5b) = (а + b)(4а – 4b) = 4(а + b)(а – b). Якщо а = –1,5; b = –3,5, то 4(а + b)(а – b) = 4(–1,5 + (–3,5))(–1,5 – (–3,5)) = 4 ∙ (–5) ∙ 2 = –40. 602.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Sф = а2 – b2 = (а – b)(а + b). Якщо а = 7,4 см, b = 2,6 см, то

SФ = (а – b)(а + b) = (7,4 – 2,6)(7,4 + 2,6) = 4,8 ∙ 10 = 48.

603. Два кола, радіуси

R = 5,1 см, r = 4,9 см.

shkola.in.ua

r (R > r),

Sф = πR2 – πr2 = π(R2 – r2) = π(R – r)(R + r).

Sф = π(R – r)(R + r) = π(5,1 – 4,9)(5,1 + 4,9) ≈ 3,14 ∙ 0,2 ∙ 10 = 6,28.

604. Подайте у

1) m4 – 625 = (m2)2 – 252 = (m2 – 25)(m2 + 25) =(m – 5)(m + 5) ∙ (m2 + 25); 2) х16 – 81 = (х8)2 – 92 = (х8 – 9)(х8 + 9) = ((х4)2 – 32)(х8 + 9) = (х4 – 3)(х4 + 3)(х8 + 9);

605. Розкладіть на множники:

1) а8 – b8 = (а4)2 – (b4)2 = (а4 – b4)(а4 + b4) = (а2 – b2)(а2 + b2) ∙ (а4 + b4) = = (а – b)(а + b)(а2 + b2)(а4 + b4); 2) а16 – 256 = (а8)2 – 162 = (а8 – 16)(а8 + 16) = (а4 – 4)(а4 + 4)(а8 + 16) = = (а2 – 2)(а2 + 2)(а4 + 4)(а8 + 16).

606. Розв’яжіть рівняння:

1) (3х – 5)2 – 49 = 0;

(3х – 5 – 7)(3х – 5 + 7) = 0; (3х – 12)(3х + 2) = 0;

3х – 12 = 0 або 3х + 2 = 0; x = 4 або х = –2 3 .

Відповідь: 4 або –2 3; 2) (4х + 7)2 – 9х2 = 0; (4х + 7 – 3х)(4х + 7 + 3х) = 0; (х + 7)(7х + 7) = 0; х + 7 = 0 або 7х + 7 = 0;

3) (а – 1)2 – (2а + 9)2 = 0; (а – 1 – 2а – 9)(а – 1 + 2а + 9) = 0;

(–а – 10)(3а + 8) = 0; –

а – 10 = 0 або За + 8 = 0;

а = – 10 або а = –8 3

Відповідь: –10 або –8 3;

607. Розв’яжіть рівняння: 1) 16 – (6 – 11х)2 = 0; (4 – 6 + 11х)(4 + 6 – 11х) = 0; (11х – 2)(10 – 11х) = 0; 11х – 2 = 0 або 10 – 11х = 0; x = 2 11 або х = 10 11 .

Відповідь: 2 11 або 10 11 .

х = –7 або х = –1

Відповідь: –7 або –1;

4) 25(3b + 1)2 – 16(2b – 1)2 = 0; (5(3b+ 1) – 4(2b – 1))(5(3b + 1) + 4(2b – 1)) = 0; (15b + 5 – 8b + 4)(15b + 5 + 8b – 4) = 0; (7b + 9)(23b + 1) = 0; 7b + 9 = 0 або 23b + 1 = 0; b = –9 7 або b = –1 23

Відповідь: –9 7 або –1 23 .

2) (7m – 13)2 – (9m + 19)2 = 0; (7m – 13 – 9m – 19)(7m – 13 + 9m + 19) = 0; (–2m – 32)(16m + 6) = 0; –2m – 32 = 0 або 16m + 6 = 0; m = –16 або m = –0,375.

Відповідь: –16 або –0,375.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Відповідь: 2 11 або 10 11 .

націло на 7; 2) (8n +1)2 − (3n −1)2

націло на 24; 4) (7n +6)2 − (2n −9)2

2) (7m – 13)2 – (9m + 19)2 = 0; (7m – 13 – 9m – 19)(7m – 13 + 9m + 19) = 0; (–2m – 32)(16m + 6) = 0; –2m – 32 = 0 або 16m + 6 = 0; m = –16 або m = –0,375.

Відповідь: –16 або –0,375.

1) (7n + 4)2 – 9 = (7n + 4 – 3)(7n + 4 + 3) = (7n + 1)(7n + 7) = 7(7n + 1)(n + 1) —

націло на 7;

2) (8n + 1)2 – (3n – 1)2 = (8n + 1 – 3n + 1)(8n + 1 + 3n – 1) = 11n(5n + 2) —

на 11;

3) (3n + 7)2 – (3n – 5)2 = (3n + 7 – 3n + 5)(3n + 7 + 3n – 5) = 12(6n + 2) = 24(3n + 1) —

націло на 24;

4) (7n + 6)2 – (2n – 9)2 = (7n + 6 – 2n + 9)(7n + 6 + 2n – 9) = (5n + 15)(9n – 3) = = 15(n + 3)(3n – 1) — ділиться націло на 15. 609.

на 80; 2) (9n +10)2 − (9n + 8)2

націло на 12. 1) (5n + 4)2 – (5n – 4)2 = (5n + 4 – 5n + 4)(5n + 4 + 5n – 4) = 8 ∙ 10n —

2) (9n + 10)2 – (9n + 8)2 = (9n + 10 – 9n – 8)(9n + 10 + 9n + 8) = 2(18n + 18) = 36(n + 1) — ділиться націло на 36; 3) (10n + 2)2 – (4n – 10)2 = (10n + 2 – 4n + 10)(10n + 2 +

(n + 2) ∙ 2 ∙ (7n – 4) = 12(n + 2)(7n – 4)

1) (2n + 2)2 – (2n)2 = (2n + 2 – 2n)(2n + 2 + 2n) = 2((2n + 2) + 2n).

+ 2) + 2n); 2) (2n + 1)2 – (2n – 1)2 = (2n + 1 – 2n + 1)(2n + 1 + 2n – 1) = 2

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

(10m + n)2 – (10n + m)2 = (10m + n – 10n – m)(10m + n + 10n + m) = (9m – 9n)(11m + 11n) = = 99(m – n)(m + n).

Рівняння: 99(m – n)(m + n) = 693; (m – n)(m + n) = 7; m – n = 1 і m + n = 7; m = 4 і n = 3.

Відповідь: 43 і 34.

614. Остача

2) рівняння (b – 2)(b + 2)х = b –

616. При якому значенні a рівняння

3) має один корінь? (a2 – 25)х = a + 5; (а – 5)(а + 5)х = а + 5.

1) Рівняння

2) рівняння (а – 5)(а + 5)х = а + 5

2,4(х + 2,5) – 3,6(х– 2,5) = 5,4; 2,4х + 6 – 3,6х + 9 = 5,4; –1,2х = –9,6; х = 8. Відповідь: 8 км/год. 619. За 3

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

третій — (x + 4 9x) кг.

Рівняння:

х + 4 9х + (х + 4 9х) = 130| ∙ 9;

9х + 4х + 9х + 4х = 1170; 26х = 1170;

х = 45.

Відповідь: 45 кг.

620. У послідовності ..., a, b, c, d, 0, 1, 1, 2, 3, 5, 8, ...

попередніх. Чому дорівнює число a?

d + 0 = 1; d = 1;

с + d = 0; с + 1 = 0; с = –1; b + c = d; b + (–1) = 1; b = 2; а + b = с; а + 2 = –1; а = –3.

621. Розв’яжіть рівняння:

1) 2х 1 8 х+2 4 = x│∙ 8;

2х – 1 – 2х – 4 = 8х; –5 = 8х;

х = –0,625.

Відповідь: –0,625;

622. Для пари

усі

2) 3(2х + 3) – 2(3х + 5) = –1; 6х + 9 – 6х – 10 = –1; 0х = 0. Відповідь: Будь-яке число.

626. Чи є

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) так; 2) нi; 3) так; 4) нi; 5) так; 6) нi.

627. Якому

(5а + 3)2 = 25а2 + 30а + 9.

628. Яка з даних рівностей є тотожністю:

1) (12а – b)2 = 144а2 – 24аb + b2 ≠ 144а2 – b2 —

2) (12а – b)2 = 144а2 – 24аb + b2 ≠ 144а2 + 24аb + b2 — нетотожність;

3) (12а – b)2 = 144а2 – 24аb + b2 — тотожність;

4) (12а – b)2 = 144а2 – 24аb + b2 ≠ 12а2 – 24аb + b2 — не тотожність.

629. Подайте у вигляді многочлена вираз:

1) (а + х)2 = а2 + 2ах + х2; 2) (х + 2)2 = х2 + 4х + 4;

3) (у – 1)2 = y2 – 2у + 1; 4) (5 – р)2 = 25 – 10р + р2; 5) (у – 13)2 = y2 – 26у + 169; 6) (13 – у)2 = 169 – 26у + y2

630. Виконайте піднесення до квадрата:

1) (а + 8)2 = а2 + 16а + 64; 2) (b – 2)2 = b2 – 4b + 4;

3) (7 + с)2 = 49 + 14с + с2; 4) (4 + k)2 = 16 + 8k + k2;

5) (6 – d)2 = 36 – 12d + d2; 6) (d – 6)2 = d2 – 12d + 36.

631. Закінчіть піднесення двочлена до квадрата:

1) (3x + 5y)2 = (3x)2 + 2 ∙ 3x ∙ 5y + (5у)2 = 9х2 + 30ху + 25у2 .

2) (1 2a + 6b)2 = (1 2a)2 + 2 ∙ 1 2a ∙ 6b + (6b)2 = 1 4 a2 + 6ab + 36b2

3) (1 3 x4 + 0,6y)2= (1 3 x4)2 + 2 ∙ 1 3 x4 ∙ 0,6y5+ (0,6y5)2 = 1 9 x8 + 0,4x4y5 + 0,36y10 .

632. Закінчіть піднесення двочлена до

1) (ab – 9)2 = (ab)2 – 2ab ∙ 9 + 92 = a2b2 – 18ab + 81.

2) (4a2 – a3)2 = (4a2)2 – 2 ∙ 4a2a3 + (a3)2 = 16a4 – 8a5 + a6.

633. Подайте у

1) (3a – 2)2 = 9a2 –12a + 4.

3) (8x + 4y)2 = 64x2 + 64xy + 16y2 .

5) (3a + 1 3b)2 = 9a2 + 20ab + 1 9 b2

7) (a2 + 4b)2 = a4 + 8a2b + 16b2

9) (3b2 – 2b5)2 = 9b4 – 12b7 + 4b10.

634. Виконайте піднесення до квадрата:

1) (2m + 1)2 = 4m2 + 4m + 1.

3) (10c + 7d)2 = 100c2 + 140cd + 49d2 .

5) (0,3a + 0,9b)2 = 0,09a2 + 0,54ab + 0,81b2.

6) (c2 – 6)2 = c4 – 12c2 + 36.

2) (7b + 6)2 = 49b2 + 84b + 36.

4) (0,4m – 0,5n)2 = 0,16m2 – 0,4mn + 0,25n2.

6) (b2 – 11)2 = b4 – 22b2 + 121.

8) (a2 + a)2 = a4 + 2a3 + a2

2) (4x – 3)2 = 16x2 – 24x + 9.

4) (4x –1 8y)2 = 16x2 – xy + 1 64y2 .

7) (m2 – 3n)2 = m4 – 6m2n + 9n2.

8) (m4 – n3)2 = m8 – 2m4n3 + n6. 9) (5a4 – 2a7)2 = 25a8 – 20a11 + 4a14.

635. Спростіть

(4х + 5)2 – 40х = 16х2 + 40х + 25 – 40х = 16х2 + 25; 3) 50а2 – (7а – 1)2 = 50а2 – (49а2 – 14а + 1) = 50а2 – 49а2 + 14а – 1 = а2 + 14а – 1;

с2 +

5) (х – 2)2 + х(х + 10) = х2 – 4х + 4 + х2 + 10х = 2x2 + 6х + 4;

6) 3m(m – 4) – (m + 2)2 = 3m2 – 12m – (m2 + 4m + 4) = 3m2 – 12m – m2 – 4m – 4 = = 2m2 – 16m – 4.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

636. Спростіть вираз:

1) (x – 12)2 + 24x = x2 – 24x + 144 + 24x = x2 + 144; 2) (x + 8)2 – x(x + 5) = x2 + 16x + 64 – x2 – 5x = 11x + 64; 3) 2x(x + 2) – (x – 2)2 = 2x2 + 4x – (x2 – 4x + 4) = 2x2 + 4x – x2 + 4x – 4 = x2 + 8x – 4; 4) р(р – 7) – (р + 7)2 = р2 – 7р – (р2 + 14р + 49) = р2 – 7р – р2 – 14р – 49 = –21р – 49.

637. Доведіть тотожність (a – b)2 = c2 – 2ab + b2; (b – a)2 = b2 – 2ba + a2 = a2 – 2ab + b2. Тотожність доведена.

638. Спростіть вираз:

1) (y – 9)2 + (4 – y)(y + 6) = y2 – 18y + 81 + 4y + 24 – y2 – 6y = –20y + 105; 2) (x –4)(x + 4) – (x – 1)2 = x2 – 16 – (x2 – 2x + 1) = x2 – 16 – x2 + 2x – 1 = 2x – 17; 3) (2a – 3b)2 + (3a + 2b)2 = 4a2 – 12ab + 9b2 + 9a2 + 12ab + 4b2 = 13a2 + 13b2;

4) (x – 5)2 – (x – 7)(x + 7) = x2 – 10x + 25 – (x2 – 49) = x2 – 10x + 25 – x2 + 49 = –10x + 74.

639. Спростіть вираз:

1) (y + 7)2 + (y + 2)(y – 7) = y2 + 14y + 49 + y2 – 7y + 2y – 14 = 2y2 + 9y + 35; 2) (a + 1)(a – 1) – (a + 4)2 = a2 – 1 – (a2 + 8a + 16) = a2 – 1 – a2 – 8a – 16 = –8a – 17; 3) (x – 10)(9 – x) + (x + 10)2 = 9x – x2 – 90 + 10x + x2 + 20x + 100 = 39x + 10. 4) (x – 4)(3 + х) – (x – 3)2 = 3х + x2 – 12 – 4х – (x2 – 6x + 9) = x2 – х – 16 –

25.

640. Розв’яжіть рівняння:

1) (x – 8)2 – x(x + 6) = –2; x2 – 16x + 64 – x2 – 6x = –2; –22x = –2 – 64; – 22x = – 66; x = 3.

Відповідь: 3;

3) (2x + 1)2 – (2x – 1)(2x + 3) = 0;

4x2 + 4x + 1 – (4x2 + 6x – 2x – 3) = 0;

4x2 + 4x + 1 – 4x2 – 6x + 2x + 3 = 0; 4x2 + 4x – 4x2 – 6x + 2x = –1 – 3; 0x = –4.

Відповідь: Коренів немає;

2) (x + 7)2 = (x – 3)(x + 3); x2 + 14x + 49 = x2 – 9; x2 + 14x + x2 = –9 – 49; 14x = –58; x = –29 7 .

Відповідь: –29 7 .

4) x(x – 2) – (x + 5)2 = 35;

x2 – 2x – (x2 + 10x + 25) = 35;

x2 – 2x – x2 – 10x – 25 = 35;

x2 – 2x – x2 – 10x = 35 + 25; –12x = 60;

x = –5.

Відповідь: –5. 641. Розв’яжіть рівняння:

1) (x + 9)2 – x(x + 8) = 1; x2 + 18x + 81 – x2 – 8x = 1; x2 + 18x – x2 – 8x = 1 – 81; 10x = –80; x = –8;

Відповідь: –8;

3) (x – 4)(x + 4) – (x + 6)2 = –16;

x2 – 16 – (x2 + 12x + 36) = –16;

x2 – 16 – x2 – 12x – 36 = –16;

x2 – x2 – 12x = –16 + 16 + 36; –12x = 36;

x = –3.

Відповідь: –3;

2) (x – 11)2 = (x – 7)(x – 9); x2 – 22x + 121 = x2 – 9x – 7x + 63; x2 – 22x – x2 + 9x + 7x = 63 – 121; –6x = –58;

x = 29 3 .

Відповідь: 29 3 ;

4) (1 – 3x)2 – x(9x – 2) = 5; 1 – 6x + 9x2 – (9x2 – 2x) = 5; 1 – 6x + 9x2 – 9x2 + 2x = 5; –6x + 9x2 – 9x2 + 2x = 5 – 1; –4x = 4;

x = –1.

Відповідь: –1.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

642.

1) (2a + b)2 = 4a2 + 4ab + b2; 2) (4x – 10y)2 = 16x2 – 80xy + 100y2;

3) (2b2 – 5c)2 = 4b4 – 20b2c + 25c2; 4) (7a2 + 3b3)2 = 49a4 + 42a2b3 + 9b6.

643. Замініть

1) (2a + 6b)2 = 4a2 + 24ab + 36b2; 2) (3m2 – 7n8)2 = 9m4 – 42m2n8 + 49n16

644. Перетворіть у многочлен вираз:

1) (–x + 1)2 = (x – 1)2 = x2 – 2x + 1;

2) (–m – 9)2 = (m + 9)2 = m2 + 18m + 81;

3) (–5a + 3b)2 = (5a – 3b)2 = 25a2 – 30ab + 9b2;

4) (–4x – 8y)2 = (4x + 8y)2 = 16x2 + 64xy + 64y2;

5) (–0,7c – 10d)2 = (0,7c + 10d)2 = 0,49c2 + 14cd+ 100d2;

6) (–4a2 + 1 8ab)2 = (4a2 –1 8ab)2 = 16a4 – a3b + 1 64 a2b2

645. Виконайте піднесення до квадрата:

1) (–3m + 7n)2 = (3m – 7n)2 = 9m2 – 42mn + 49n2;

2) (–0,4x– 1,5y)2 = (0,4x + 1,5y)2 = 0,16х2 + 1,2xy + 2,25y2;

3) (–x2 – y)2 = (x2 + y)2 = x4 + 2x2y + y2;

4) (–a2b2 + c10)2 = (а2b2 – c10)2 = a4b4 – 2a2b2c10 + c20 .

646. Виконайте піднесення до квадрата:

1) (10a2 – 7ab2)2 = 100a4 – 140a3b2 + 49a2b4; 2) (0,8b3 + 0,2b2c4)2 = 0,64b6 + 0,32b5c4 + 0,04b4c8;

3) (1

4) (21 3 x3y2 –9 14y8x)2 = (7 3 x3y2 –9 14y8x)2 = 49

647. Перетворіть у многочлен вираз:

1) 6(1 – 2c)2 = 6(1 – 4c + 4c2) = 6 – 24c + 24c2; 2) –12(x + 1 3y)2 = –12(x

3) a(a – 6b)2 = a(a2 – 12ab + 36b2) = a3 – 12a2b + 36ab2;

4) 5b(b2 + 7b)2 = 5b(b4 + 14b3 + 49b2) = 5b5 + 70b4 + 245b3; 5) (a + 3)(a – 4)2 = (a + 3)(a2 – 8a + 16) = a3 – 8a2 + 16a + 3a2 –

–

6) (2x + 4)2(x – 8) = (4x2 + 16x + 16)(x – 8) = 4x3 – 32x2 + 16x2 – 128x + 16x – 128 = = 4x3 – 16x2 – 112x – 128;

7) (a – 5)2(a + 5)2 = ((a – 5)(a + 5))2 = (a2 – 25)2 = a4 – 50a2 + 625; 8) (3x + 4y)2(3x – 4у)2 = ((3х + 4y)(3x – 4y))2 = (9x2 – 16y2)2 =

648. Подайте

1) (0,02р3k + 20p2k4)2 = 0,0004p6k2 + 0,8p5k5 + 400р4k8; 2) (11 6 mn –4 21m2n5)2 = (7 6

3) –15(

4) 7x(х3 – 2х)2 = 7x(x6 – 4х4 + 4х2) =

3; 5) (5у – 2)2(2y + 1) = (25y2 – 20у + 4)(2у + 1) = 50y3 +

–

4 .

–

+ 4 = = 50y3 – 15y2 – 12у + 4; 6) (10p – k)2(10p + k)2 = ((10р – k)(10р + k))2 = (100p2 – k2)2 = 10000p2 – 200p2k2 + k4 649. Спростіть вираз і знайдіть

значення: 1) (a + 3)2 – (a – 9)(a + 9) = a2 + 6a + 9 – (a2 – 81) = a2 + 6a + 9 – a2 + 81 = 6a + 90. Якщо а = –2,5, то 6a + 90 = 6 ∙ (–2,5) + 90 = –15 + 90 = 75; 2) (5х – 8)2 – (4х– З)2 + 26х = 25х2 – 80х + 64 – (16х2 – 24х + 9) + 26х = = 25x2 – 80х + 64 – 16х2 + 24х – 9 + 26х = 9х2 – 30х + 55.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Якщо х = –1 3, то 9х2 – 30х + 55 = 9 ∙ (–1 3)2 – 30 ∙ (–1 3) + 55 = 9 ∙ 1 9 + 10 + 55 = 66;

3) (3y2 + 4)2 + (3y2 – 4)2 – 2(1 – 3y2)(1 + 3y2) = = 9y4 + 24y2 + 16 + 9y4 – 24y2 + 16 – 2(1 – 9y4) = 18y4 + 32 – 2 + 18y4 = 36y4 + 30.

Якщо у= 1 2, то 36y4 + 30 = 36 ∙ (1 2)4 + 30 = 36 ∙ 1 16 + 30 = 21 4 + 30 = 321 4

650. Спростіть

1) 2m(m – 6)2 – m2(2m – 15) = 2m(m2 – 12m + 36) – 2m3 + 15m2 = = 2m3 – 24m2 + 72m – 2n3 + 15m2 = –9m2 + 72m = –9m(m – 8).

Якщо m = –4, то –9m(m – 8) = –9 ∙ (–4) ∙ (– 4 – 8) = 36 ∙ (–12) = –432;

2) (2х – 5)2 – 4(х + 1)(х – 7) = 4x2 – 20х + 25 – 4(х2 – 7х + х – 7) = = 4x2 – 20х + 25 – 4x2 + 28х – 4х + 28 = 4х + 53.

Якщо х = –3,5, то 4х + 53 = 4 ∙ (–3,5) + 53 = –14 + 53 = 39.

651. При якому

відповідне значення квадрата двочлена x – 13?

Значення квадрата

х – 13

(х + 12)2 – (х – 13)2 = 225;

(х + 12 – х + 13)(х + 12 + х – 13) = 225;

25(2х – 1) = 225;

2х – 1 = 9;

х = 5.

652. Розв’яжіть рівняння:

1) (х – 12)(х + 12) = 2(х – 6)2 – х2;

х2 – 144 = 2(х2 – 12х + 36) – х2;

х2 – 144 = 2х2 – 24х + 72 – х2;

х2 – 2x2 + 24х + х2 = 72 + 144; 24х = 216;

х = 9.

Відповідь: 9;

3) 5(x + 2)2 + (2x – 1)2 – 9(x + 3)(x – 3) = 22; 5(x2 + 4x + 4) + 4x2 – 4x + 1 – 9(x2 – 9) = 22; 5x2 + 20x + 20 + 4x2 – 4x + 1 – 9x2 + 81 = 22; 5x2 + 20x + 4x2 – 4x – 9x2 = 22 – 20 – 1 – 81; 16x = –80;

x = –5.

Відповідь: –5. 653. Розв’яжіть рівняння: 1) (3x + 2)2 + (4x – 1)(4x + 1) = (5x – 1)2; 9x2 + 12x + 4 + 16х2 – 1 = 25x2 – 10x + 1; 9x2 + 12x + 16х2 – 25x2 + 10x = 1 – 4 + 1; 22x = –2; x = –1 11 .

2) (3х – 1)2 + (4х + 2)2 = (5х – 1)(5х + 1); 9х

– 4; 10х = –6;

х = –0,6.

Відповідь: –0,6;

Відповідь: –1 11; 2) 2(m + 1)2 + 3(m – 1)2 – 5(m + 1)(m – 1) = –4; 2(m2 + 2m + 1) + 3(m2 – 2m + 1) – 5(m2 – 1) = –4; 2m2 + 4m + 2 + 3m2 – 6m + 3 – 5m2 + 5 = –4; 2m2 + 4m + 3m2 – 6m – 5m2 = – 4 – 2 – 3 – 5;

– 2m = –14; m = 7.

Відповідь: 7.

654.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

квадрата дорівнює (х + 5) см,

Рівняння:

(х + 5)2 – х2 = 95;

(х + 5 – х)(х + 5 + х) = 95;

5(2х + 5) = 95;

2х + 5 = 19;

2х = 14;

х = 7.

Відповідь: 7 см.

655. Якщо сторону

Рівняння:

х2 – (х – 8)2 = 352;

(х – х + 8)(х + х – 8) = 352; 8(2х – 8) = 352;

2х – 8 = 44;

2х = 52;

х = 26.

Відповідь: 26 см.

Рівняння:

2(n + 1)2 – ((n – 1)2 + n2) = 79; 2(n2 + 2n + 1) – (n2 – 2n + 1 + n2) = 79; 2n2 + 4n + 2 – n2 + 2n – 1 – n2 = 79; 6n = 79 – 2 + 1; 6n = 78; n = 13.

12; 13;

((n + 1)2 + (n + 3)2) – (n2 + (n + 2)2) = 82; (n + 1)2 + (n + 3)2 – n2 – (n + 2)2 = 82; n2 + 2n + 1 + n2 + 6n + 9 – n2 – n2 – 4n – 4 = 82;

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

4n = 82 – 1 – 9 + 4; 4n = 76; n = 19.

Друге число дорівнює: n + 1 = 19 + 1 = 20, третє

— n + 3 = 19 + 3 = 22.

Відповідь: 19; 20; 21; 22.

658. При яких значеннях a і b є правильною рівність: 1) (а + b)2 = а2 + b2; a2 + 2ab + b2 = а2 + b2; а2 + 2ab + b2 – а2 – b2 = 0; 2ab = 0.

Рівність (а + b)2 = а2 + b2 буде правильною лише тоді, коли а = 0 або b = 0;

659. Доведіть тотожність:

n + 2 = 19 + 2 = 21, а

2) (а – b)2 = (а + b)2;

а2 – 2аb + b2 = а2 + 2ab + b2; а2 – 2ab + b2 –а2 – 2ab – b2 = 0; –4аb = 0.

Рівність (а – b)2 = (a + b)2 буде правильною лише тоді, коли а = 0 або b = 0.

1) (a + b)2 + (a – b)2 = a2 + 2ab + b2 + a2 – 2ab + b2 = 2a2 + 2b2 = 2(a2 + b2) — тотожність

доведена;

2) (a + b)2 – (a – b)2 = a2 + 2ab + b2 – (a2 – 2ab + b2) = a2 + 2ab + b2 – a2 + 2ab – b2 = 4ab —

тотожність доведена; 3) (a + b)2 – 2ab = a2 + 2ab + b2 – 2ab = a2 + b2 — тотожність доведена;

4) (a2 + b2)(c2 + d2) = a2c2 + a2d2 + b2c2 + b2d2 = (a2c2 + b2d2) + (a2d2 + b2c2) = = (a2c2 + 2abcd + b2d2) + (a2d2 – 2abcd + b2c2) = (ac + bd)2 + (ad – bc)2 — тотожність доведена.

660. Доведіть тотожність:

1) (a – b)2 + 2ab = a2 – 2ab + b2 + 2ab = a2 + b2 = — тотожність доведена; 2) (a – b)2 + (ab + 1)2 = a2 – 2ab + b2 + a2b2 + 2ab + 1 = a2 + b2 + a2b2 + 1 = = (a2 + a2b2) + (b2 + 1) = a2(1 + b2) + (b2 + 1) = (a2 + 1) ∙ (b2 + 1) — тотожність доведена. 661. Доведіть, що

(x – 3)2 + (x + 3)2 – 2(x – 6)(x + 6)

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

(а + b + c)2 = a2 + b2 + с2 + 2ab + 2bc + 2ac доведена.

1) (а + b – c)2 = (а + b + (–c))2 = а2 + b2 + (–c)2 + 2ab + 2b(–c) + 2а(–с) = = a2 + b2 + с2 + 2ab – 2bc – 2ac; 2) (а – b + 4)2 = (а + (–b) + 4)2 = a2 + (–b)2 + 42 + 2а ∙ (–b) + 2 ∙ (–b) ∙ 4 + 2а ∙ 4 = = а2 + b2 + 16 – 2ab – 8b + 8a.

667. Давньогрецький учений

shkola.in.ua

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

(11n + 6)2 = 121n2 + 132n + 36 = 121n2 + 132n + 33 + 3 = 11(11n2 + 12n + 3) + 3 —

673. Використовуючи

1) (а + b + с)(а + b – с) = ((а + b) + с))((а + b) – с)) = (а + b)2 – с

3) (а + b + c + d)(a + b – c – d) = ((a + b) + (с + d))((a + b) – (c + d)) =

2) (а – b + с + d)(a – b – c – d) = ((a – b) + (c + d))((a – b) – (c + d)) =

= a2 – 2ab + b2 – c2 – 2cd – d2.

675. При якому значенні a рівняння

(6x – a)2 + (8x – 3)2 = (10х – 3)2;

36х2 – 12xa + a2 + 64x2 – 48x + 9 = 100x2 – 60x + 9; 36x2 – 12xa + 64x2 – 48x – 100x2 + 60x = 9 – a2 – 9; –12xa + 12x = –a2; –12x(a – 1) = –a2.

Рівняння –12x(a – 1) = –a2 не має коренів при а = 1.

676. При якому значенні a рівняння

коренів? (2а – 3х)2 + (х – 1)2 = 10(х – 2)(х + 2); 4а2 – 12ах + 9х2 + х2 – 2х + 1 = 10x2 – 40; –12ax + 9х2 + х2 – 2х – 10x2 = –40 – 4а2 – 1;

–12aх – 2х = –41 – 4а2;

–2х(6а + 1) = –41 – 4a2;

2х(6а + 1) = 41 + 4а2 .

Рівняння 2х(6а

(2n + 1)2 + (2n2 + 2n)2 = (2n2 + 2n + 1)2

(a2 + b2 + с2)(m2 + n2 + k2) – (аm + bn + сk)2 = а2m2 + а2n2 + a2k2 + b2m2 + bn2 + b2k2 + с2m2 + с2n2 + с2k2 – а2m2 – b2n2 – с2k2 – 2аbmn – 2acmk – 2bcnk = (а2n2 – 2аbmn + b2m2) + (a2k2 –2асmk + с2m2) + (b2k2 – 2bсnk + с2n2) + а2m2 + b2n2 + с2k2 – а2m2 – b2n2 – с2k2 = (аn – bm)2 + (ak – сm)2 + (bk – сn)2 .

(а2 + b2 + с2)(m2 + n2 + k2) – (аm + bn + сk)2 = (an – bm)2 + (аk – сm)2 + (bk – сn)2 доведена.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

3,4х + х + 1 + х = 28;

5,4х = 27;

х = 5. Відповідь:

х 10 + 740−х 5 = 80|∙ 40;

4х + 5(740 – х) = 3200;

4х + 3700 – 5х = 3200; –х = 3200 –3700; x = 500.

Відповідь: 500 кг.

2) 13300

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

12 – ( х – 1)2 + 20

(х – 1)2 + (х + 1)2 = –

2) рівність (х – 1)2 + (х + 1)2 = 0 не

3) (х2 – 1)2 + (х + 1)2 = 0; ((х – 1)(х + 1))2 + (х + 1)2 = 0; (х + 1) ∙ ((х – 1)2 + 1)2 = 0.

Рівність (х + 1)((х – 1)2 + 1)2 = 0 виконується, якщо х = –1.

1) Рівність (х + 2)2 + (у – 6)2 = –1 не виконується ні при яких значеннях змінних, бо сума двох невід’ємних чисел не може

(х + 2)2 + (у – 6)2 =

m = 10n

2 – 18а + 81 = а2 – 2 ∙ а ∙ 9 + 92 = (а – 9)2

691. Яка з даних рівностей є тотожністю: а2 + 8аb + 16b2

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) y2 – 8у + 16 = (у – 4)2. Якщо у = –4, то (у – 4)2 = (–4 – 4)2 = (–8)2 = 64;

2) с2 + 24с + 144 = (с + 12)2. Якщо с = –10, то (с + 12)2 = (–10 + 12)2 = 22 = 4;

3) 25x2 – 20ху + 4y2 = (5х – 2у)2. Якщо х = 3, у = 5,5, то (5х – 2у)2 = (5 ∙ 3 –

5,5)2 = = (15 – 11)2 = 42 = 16; 4) 49а2 + 84аb + 36b2 = (7а + 6b)2. Якщо а = 1

= (7 ∙ 8 7 + 6 ∙ 17 6 )2 = (8 + 17)2 = 252 = 625.

697. Знайдіть значення виразу: 1) b2 – 30b + 225 = (b – 15)2. Якщо b = 6, то (b – 15)2 = (6 – 15)2 = (–9)2 = 81; 2) 100а2 + 60аb + 9b2 = (10а + 3b)2. Якщо а = 0,8, b = –3, то (10а + 3b)2 = = (10 ∙ 0,8 + 3 ∙ (–3))2 = (8 – 9)2 = (–1)2 = 1.

698. Який

двочлена вираз: 1) * – 56а + 49 = * –

2b2

2b4)2; 6) 1,44х2у4 – *у + 0,25у6 = (1,2ху2)2 – *у + (0,5у3)2.

*y = 2 ∙ 1,2xy2 · 0,5y3; *y = 2 · 1,2xy2 · 0,5y3 : y; * = 1,2xy4;

7) 64 – 80у20 + *у40 = 82 · 2 · 8 · 5у20 + *y40. Отже, *у40 = (5y20)2; *y40 = 2540; * = 25;

8) 9 25 a6b2 – a5b5 + * = (3 5a3b)2 – 2 · 3 5 a2b · 5 6 a2b4 + *. Отже, * = (5 6a2b4)2 = 25 36 a4b8.

699. Замініть

1) n2 + 60n + 900 = (n + 30)2; 2) 25с2 – 80сk + 64k2 = (5с – 8k)2;

3) 225a2 – * + 64b4 = (15а)2 – * + (8b2)2; 225а2 – 240аb2 + 64b4 = (15a – 8b2)2; 4) 0,04x2 + 0,12xу3 + 0,09у6 = (0,2x + 0,3у3)2.

700. Подайте, якщо це

протилежного

1) –8х + 16 + х2 = х2 – 8х + 16 = (х – 4)2; 2) а8 + 4а4b3 + 4b6 = (a4 + 2b3)2; 3) 2х – 25 – 0,04х2 = –0,04х2 + 2х – 25 = –(0,04x

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

5) 80ху + 16х2 + 25у2 = 16х2 + 80ху + 25у2 = (4х)2 + 2 ∙ 4x ∙ 5у ∙ 2 + (5у)2 —

6) b10 –1 3 b5c + 1 9 c2 = (b5)2 – b5 ∙ 1 3c + (1 3c)2 –

702. Подайте у

1) (4а + 3b)2 – 8b(4а + b) = 16а2 + 24аb + 9b2 – 32аb – 8b2 = 16а2 – 8аb + b2 = (4а – b)2; 2) (10x + 3у)2 – (8x + 4у)(8x – 4у) = 100x2 + 60xу + 9у2

+ 25у2 = (6х + 5у)2 .

703. Перетворіть у

1) (3m – 2n)2 + 5m(4n – m) = 9m2 – 12mn + 4n2 + 20mn –

2) (9х + 2у)2 – (8х + 3у)(4х – 4у) = 81х2 + 36ху + 4y2 – 32x2 + 32ху – 12ху + 12у2 = = 49x2 + 56ху + 16у2 = (7x + 4у)2 .

704. Користуючись

1) 1,022 – 1,02 ∙ 1,96 + 0,98

705. Обчисліть:

1) 2032 – 406 ∙ 103 + 1032 = 2032 – 2 ∙ 203 ∙ 103 +

706.

додати число –4.

708. Розв’яжіть рівняння:

1) х2 – 16x + 64 = 0;

(х – 8)2 = 0;

х – 8 = 0;

х = 8.

Відповідь: 8;

709. Розв’яжіть рівняння:

1) х2 + 12х + 36 = 0; (х + 6)2 = 0;

х + 6 = 0;

х = –6.

Відповідь: – 6;

710. Чи є тотожністю рівність

рівність (а –

2) 81x2 + 126x + 49 = 0; (9x + 7)2 = 0; 9х + 7 = 0; x = –7 9 .

Відповідь: –7 9 .

2) 25x2 – 30x + 9 = 0; (5x – 3)2 = 0;

5х – 3 = 0;

х = 0,6.

Відповідь: 0,6.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

3) (а – 8)2 + 2(а – 8)(3 – a) + (а – 3)2 = (a – 8)2 – 2(a – 8)(a – 3) + (а – 3)2 = ((a – 8) – (a – 3))2 = (a – 8 – a + 3)2 = (–5)2 = 25 — тотожність

4) (хn – 2)2 – 2(хn – 2)(хn + 2) + (хn + 2)2 = ((xn – 2) – (xn + 2))2 = (xn – 2 – xn – 2)2 = (–4)2 = 16 — тотожність доведена.

712. Доведіть, що значення виразу

значення змінної: 1) (3x + 8)2 – 2(3x + 8)(3x – 8) + (3x – 8)2 = ((3х + 8) – (3х – 8))2 = (3х + 8 – 3х + 8)2 = = 162 = 256; 2) (4х – 7)2 + (4х – 11)2 + 2(4х – 7)(11 – 4х) = (4х – 7)2 – 2(4х –7)(4х – 11) + (4x – 11)2 = = ((4х – 7) – (4х – 11))2 = (4х – 7 – 4х + 11)2 = 42 = 16.

713. Доведіть, що рівняння не має коренів: 1) x2 – 14x + 52 = 0; x2 – 14x + 49 + 3 = 0; (x – 7)2 + 3 = 0.

Відповідь: Коренів немає. 2) 4x2 – 2x + 1 = 0; (2x)2 – 2x + 1 4 –1 4 + 1 = 0; (2x –1 2)2 + 3 4 = 0. Відповідь: Коренів немає.

714. Доведіть, що даний вираз

2) 16х2 + 24х + 25 = (4х)2 + 24х +

716.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

5) х2 + 5у2 + 4ху – 4у + 4 = (х2 + 4ху + 4у2) + (у2 – 4у + 4) = (х + 2у)2 + (у – 2)2; 6) 2а2 + 2b2 = (a2 + 2аb + b2) + (а2 – 2аb + b2) = (а + b)2 + (а – b)2 723.

+ 4)2 + (у – 5)2 = 0;

= –4; у = 5;

726.

існують такі

1) х2 + 4y2 + 2х – 4у + 2 = 0;

x і y,

(х2 + 2х + 1) + (4y2 – 4у + 1) = 0; (х + 1)2 + (2у – 1)2 = 0;

= –1; у = 0,5; 2) 9х2 + у2 – 12х + 8у

+ 37у

+ 12ху – 2у + 1= 0; (x2 + 12ху + 36у2) + (у2 – 2у + 1) = 0; (х + 6у)2 + (у – 1)2 = 0; у = 1, х + 6 ∙ 1 = 0; х = –6.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

728.

виразу a + b.

Якщо а2 + b2 = 34, аb = 15, то (а +

729. Від’ємні

a + b.

Якщо а2 + b2 = 68, аb = 16, то (а + b)

730.

1) 72 + 264 = 336 (ос.) – всього; 2) 336 : 60 = 5 (ост.36) Відповідь: 6 човнів.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Рівняння:

0,4х + 0,4x + 20 = х; 0,8x – х = –20; –0,2x = –20;

х = 100.

Відповідь: 100 км.

738. Загальна площа

Рівняння:

90х – 80(100 – х) = 2200;

90х – 8000 + 80х = 2200;

170х = 10200;

х = 60.

Площа другої ділянки

Відповідь: 60 га, 40 га.

739. Розкладіть на множники:

1) 2ab – 3аb2 = ab(2 – 3b);

2) 8х4 + 2х3 = 2х3(4х + 1);

100 – 60 = 40 (га).

3) 11а2b2 + 6a2b3 + 12аb3 = 6ab2(2a + ab + 2b);

4) 2а – 2b + ас – bс = 2(а – b) + с(а – b) = (а – b)(2 + с);

5) m2 – mn – 4m + 4n = m(m – n) – 4(m – n) = (m – n)(m – 4);

6) ах – ау + су – сх – х + у = а(х

(х

1) (у2)3 = y6; 2) (2х3)3 = 8x9; 3) (3a2b4)3 = 27а6b12; 4) (0,1mn5)3 = 0,001m3n15; 5) (1 6 b6c7)3 = 1 216 b18c21; 6) (2 7p10k15)3 = 8 343p30k45.

744.

1) а3b6 = (аb2)3;

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2) 8х3y9 = (2xу3)3;

3) 1 64 c9 = (1 4 c3)3; 4) 125m12n21 = (5m4n7)3; 5) 0,216k15p24 = (0,6k5p8)3; 6) 0,008а9b18с27 = (0,2a3b6с9)3.

745. Чи можна

Відповідь: Не можна.

1. Виконайте множення:

(3n + 1)(3n – 1) = 9n2 – 1.

Відповідь: В).

2. Якому многочлену дорівнює вираз?

(4х – 1)2 = 16х2 – 8х + 1.

Відповідь: Б).

3. Розкладіть на множники вираз

4а2 – 25 = (2a – 5)(2a + 5).

Відповідь: В).

4. Подайте у вигляді

–0,09x4 + 81y16 = 81y16 – 0,09x4 = (9y8)2 – (0,3х2)2 = (9y8 – 0,3x2) ∙ (9у8 + 0,3х2).

Відповідь: Б).

5. Який із даних двочленів

a2 – 4b2 = (a – 2b)(a + 2b).

Відповідь: В).

a2 – 8a + 16 = (a – 4)2

Відповідь: Б).

7. Відомо, що (1 2 х

Б).

8. Спростіть вираз (х +

Б). 11.

+ 4))2 = (–8)2 = 64.

А).

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Відповідь: Г).

різниці: 1) повний квадрат суми; 2) не є; 3) неповний квадрат суми; 4) не є; 5)

різниці; 6) повний квадрат різниці.

747. Чи є тотожністю рівність: 1) Ні; 2) Так; 3) Так; 4) Ні.

748. Якому з даних виразів тотожно дорівнює многочлен a3 −27: Многочлен a3 – 27 тотожно дорівнює виразу 4) (a – 3)(a2 + 3а + 9).

749. Розкладіть на множники:

1) a3 + 8 = (а + 2)(a2 – 2a + 4);

2) с3 – 64 = (с – 4)(с2 + 4с + 16);

3) 125 – b3 = (5 – b)(25 + 5b + b2);

4) 1 + х3 = (1 + х)(1 – х + х2);

5) a3 + 1000 = (а + 10)(a2 – 10a + 100);

6) 27a3 – 1 = (3а – 1)(9a2 + 3а + 1);

7) 1000с3 – 216 = (10с – 6)(100с2 + 60с + 36);

8) a3b3 – 1 = (ab – 1)(a2b2 + аb + 1);

9) m3n3 + 0,001 = (mn + 0,1)(m2n2 – 0,1mn + 0,01).

750. Розкладіть на множники:

1) x3 – 1 = (x – 1)(x2 + x + 1);

2) 27 + a3 = (3 + a)(9 – 3a + a2)

3) 216 – y3 = (6 – y)(36 + 6y + y2);

4) 1 8 a3 + b3 = (1 2a + b)(1 4 a2 –1 2 ab + b2);

5) 0,001m3 + 8n3 = (0,1m + 2n)(0,01m2 – 0,2mn + 4n2);

6) a3b3 – c3 = (ab – c)(a2b2 + abc + c2).

751. Яка з даних рівностей є тотожністю:

3) m3 + 8n3 = (m + 2n2)(m2 – 2mn2 + 4n4).

752. Закінчіть розкладання на множники:

1) 64х6 – 0,027у9 = (4х2)3 – (0,3у3)3 = (4х2 – 0,3у3) (16х4 + 1,2х2у3 + 0,09у6).

2) b12 + 216c15 = (b4)3 + (6c5)3 = (b4 + 6c5)(b8 – 6b4c5)(b8 – 6b4c5 + 36c10).

3) 1 8p18 –1 27 b21 = (1 2p2)3 – (1 3b7)3 = (1 2p6 –1 3b7)( 1 4p12 + 1 6p6b7 + 1 9b14).

753. Розкладіть на множники:

1) a12 + b9 = (a4)3 + (b3)3 = (a4 + b3)(a8 – a4b3 + b6).

2) x18 – y27 = (x6)3 – (y9)3 = (x6 – y9)(x12 + x6y9 + y18) = (x

3) m6n3 – p12 = (m2n)3 – (p4)3 = (m2n – p4)(m4n2 + m2np4 + p8).

4) a24b33 + 1 = (a8b11)3 + 13 = (a8b11 + 1)(a16b22 – a8b11 + 1).

5) 8m6 + 27n9 = (2m2 + 3n3)(4m4 – 6m2n3 + 9n6).

6) 0,027x21 + 0,125y24 = ( 3 10 x7)3 + (1 2y8)3 = ( 3 10 x7 + 1 2y8)( 9 100 x14 –3 20 x7y8 + 1 4y16).

7) 0,216 – 8c27 = (0,6)3 – (2c9)3 = (0,6 – 2c9)(0,36 + 1,2c9 + 4c18).

8) 1000a12b3 + 0,001c6d15 = (10a4b)3 + (�� 2 �� 5 10 )3 = (10a4b + �� 2 �� 5 10 )(100a8b2 – a4bc2d5 + �� 4 �� 10 100 ).

754. Подайте у вигляді добутку вираз: 1) a6 – 8 = (a2)3 – 23 = (a2 – 2)(a4 + 2a2 + 4).

+ y18).

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2) m12 + 27 = (m4)3 + 33 = (m4 + 3)(m8 – 3m4 + 9).

3) a3 – b15c18 = a3 – (b5c6)3 = (a3 – b5c6)(a6 + a3b5c6 + c12).

4) 1 – a21b9 = 13 = (a7b3)3 = (1 – a7b3)(1 + a7b3 + a14b6).

5) 125c3d3 + 0,008b3 = (5cd)3 – (0,2b)3 = (5cd – 0,2b).

6) 64 729 x3 –27 1000y6 = (4 9 x –3 10y2)( 16 81 x2 + 2 15xy2 + 9

755. Знайдіть,

виразу: 1) 93 +73 32 = (9+7)(92 −63+72 ) 32 = 16(81−63+49) 32 = (81−63+49) 2 = 67 2 = 33 1 2;

2) 163 −103 24 = (16+10)(162 +160+102 ) 24 = 6(256+160+100) 24 = 516 2 = 258.

756. Подайте

: 1) (x – 2)(x2 + 2x + 4) = х3 – 23; 2) (2a – 1)(4a2 + 2a + 1) = 8a3 – 1;

3) (a2 – 1)(a4 – a2 + 1) = a6 + 1; 4) (0,5xy – 2)(0,25x2y2 – xy + 4) = 0,125x3y3 + 8.

757. Виконайте множення:

1) (b – 4)(b2 + 4b + 16) = b3 – 64; 2) (2a + 3b)(4a2 – 6ab + 9b2) = (2a)3 + (3b)3 = 8a3 + 27b3; 3) (x3 + 6y2)(x6 – 6x3y2 + 36y4) = (x3)3 + (6y2)3 = x9 + 216y6;

4) (1 4 a –1 5b)( 1 16 a2 + 1 20 ab + 1 25b2) = 1 64 a3 –1 125 b3.

758. Спростіть вираз і знайдіть його значення:

1) (9a2 + 3a + 1)(3a – 1) = (3a – 1)(9a2 + 3а + 1) = (3а)3 – 1 = 27a3 – 1.

Якщо a =

2) (5y – 2)(25y2 + 10y + 4) + 8 = (5y)3 – 8 + 8 = 125y3 . Якщо y = –1 5, то: 125y3 = 125 ∙ (–1 5)3 = –125 ∙ 1 125 = –1.

759. Знайдіть

1) (1 – b2)(1 + b2 + b4) = 1 – (b2)3 = 1 – b6.

2) 2x3 + 7 – (x + 1)(x2 – x + 1) = 2x3 + 7 – (x3 + 1) = 2x3 +

Якщо x = –1, то: x3 + 6 = (–1)3 + 6 = – 1 + 6 = 5.

760. Розкладіть на множники:

1) (a + 6)3 – 27 = (a + 6)3 – 33 = (a + 6 – 3)((a + 6)2 + 3(a + 6) + 9) = (a + 3)(а2 + 12a + 36 + 3a + 18 + 9) = (a + 3)(a2 + 15a + 63);

2) (2x – 1)3 + 64 = (2x – 1)3 + 43 = (2x – 1 + 4)((2x – 1)2 – 4(2x – 1) + 16) = (2x + 3)(4x2 – 4x + 1 – 8x + 4 + 16) = (2x + 3)(4x2 – 12x + 21);

3) 8a6 – (4a – 3)3 = (2a2)3 – (4a – 3)3 = (2a2 – (4a – 3))((2a2)2 + 2a2(4a – 3) + (4a – 3)2) = (2a2 –

4a + 3)(4a4 + 8a3 – 6a2 + 16a2 – 24a + 9) = (2a2 – 4a + 3)(4a4 + 8a3 + 10a2 – 24a + 9);

4) 1000 + (y – 10)3 = 103 + (y – 10)3 = (10 + y – 10)(102 – 10(y – 10) + (y – 10)2) = y(100 – 10y + 100 + y2 – 20y + 100) = y(y2 – 30y + 300);

5) (x + y)3 – (x – y)3 = (x + y – x + y)((x + y)2 + (x + y)(x – y) + (x – y)2) = 2y(x2 + 2xy + y2 + x2 – y2 + x2 – 2xy + y2) = 2y(3x2 + y2);

6) (a – 2)3 + (a + 2)3 = (a – 2 + a + 2)((a – 2)2 – (a – 2)(a + 2) + (a + 2)2) = 2a(a2 – 4a + 4 – a2 + 4 + a2 + 4a + 4) = 2a(a2 + 12).

761. Подайте у

1) (b – 5)3 + 125 = (b – 5)3 + 53 = (b – 5 + 5)((b – 5)2 – 5(b – 5) + 25) = b(b2 – 10b + 25 – 5b + 25 + 25) = b(b2 – 15b + 75); 2) (4 – 3x)3 – 8x3 = (4 – 3x)3 – (2x)3 = (4 – 3х – 2х)((4 – 3х)2 + 2х(4 – 3а) + (2х)2) = (4 – 5х)(16 – 24х + 9х2 + 8х – 6х2 + 4х2) = (4 – 5x) ∙ (7х2 – 16х + 16);

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

3) (а – b)3 + (а + b)3 = (а – b + а + b)((a – b)2 – (a – b)(a + b) + (а + b)2) = 2а(а2 – 2аb + b2 – а2 + b2 + а2 + 2аb + b2) = 2а(а2 + 3b2);

4) (с + 3)3 – (с – 3)3 = (с + 3 – с + 3)((с + 3)2 + (с + 3)(с – 3) + (с – 3)2) = 6(с2 + 6с + 9 + с2 – 9 + с2 – 6с + 9) = 6(3с2 + 9) = 18(с2 +3).

762. Спростіть вираз:

1) (х + 1)(х2 – х + 1) + (2 – х)(4 + 2х + х2) =

2) (х – 4)(х2 + 4x + 16) – х(х – 5)(x + 5) = х3 – 64 – х(х2 –

3) а(а – 3)2 – (а + 3)(а2 – 3а + 9) = а(а2 – 6а +

= –6а2 + 9а – 27; 4) (а – 1)(а + 1)(а2 – а + 1)(а2 + а

вираз:

(а

+ 9) = = у3 – 27 – у3 + 9у – у2 – 6у – 9 = –у2 + 3у – 36; 3) (а – b)(а + b)(а4 + а2b2 + b4) = (a2 – b2)(а4 + а2b2 + b4) = а6 – b6.

764. Поставте

1) (7k – р)(49k2 + 7kр + р2) = 343k3 – р3; 2) (5а2 + 6b)(25а4 – 30а2b + 36b2) = 125а6 + 216b3; 3) (mn + k3)( m2n2 – mnk3 + k6) = m3n3 + k9.

765. Розв’яжіть рівняння:

1) (3х – 1)(9x2 + 3х + 1) – 9х(3х2 – 4) = 17;

27х3 – 1 – 27х3 + 36х = 17; 36x = 18;

х = 0,5.

Відповідь: 0,5;

2) (х + 4)(х2 – 4х + 16) – х(х – 7)(х + 7) = 15;

х3 + 64 –х(х2 – 49) = 15; х3 + 64 – х3 + 49х = 15;

49х = –49; х = –1.

Відповідь: –1;

3) (х + 6)(х2 – 6х + 36) – х(х – 9)2 = 4х(4,5х – 13,5);

х3 + 216 – х(х2 – 18х + 81) = 18х2 – 54х;

х3 + 216 – х3 + 18х2 – 81х = 18х2 – 54х;

х3 – х3 + 18x2 – 81х – 18х2 + 54х = –216; –27х = –216; х = 8.

Відповідь: 8.

766. Розв’яжіть рівняння: 1) (7 – 2х)(49 + 14х + 4х2) + 2x(2x – 5)(2х + 5) = 43;

343 – 8х3 + 2x(4x2 – 25) = 43; 343 – 8х3 + 8х3 – 50x = 43; –50х = –300; х = 6.

Відповідь: 6; 2) 100(0,2x + 1 )(0,04x2 – 0,2x + 1) = 5х(0,16х2 – 4);

100(0,008х3 + 1) = 0,8х3 – 20х;

0,8х3 + 100 – 0,8x3 + 20x = 0; 20x = –100;

х = –5.

Відповідь: –5.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

3) 176 – 1 = (173)2 – 1 = (173 – 1)(173 +

на 35. 1) 3413 + 1093 = (341 + 109)(3412 –

= 5 ∙ 90 ∙ (3412 – 341 ∙ 109

націло на 35.

769. Укажіть найменше

на 4. (2n – 1)3 + (2n + 1)3 = (2n – 1 + 2n + 1)((2n – 1)2 – (2n

1)(2n + 1) + (2n + 1)2) = = 4n((2n – 1)2 – (2n – 1)(2n + 1) + (2n + 1)2)

на 4. 773. Доведіть,

на 9. (3n + 1)3 + (3n + 2)3 = (3n + 1 + 3n + 2)((3n + 1)2 – (3n + 1) ∙ (3n + 2) + (3n + 2)2) = = (6n + 3)(9n2 + 6n + 1 – (9n2 + 6n + 3n + 2) + 9n2 + 12n + 4) = = 3(2n + 1)(9n2 + 6n + 1 – 9n2 – 6n – 3n – 2 + 9n2 + 12n + 4) = 3(2n + 1)(9n2 + 9n + 3) = = 9(2n + 1)(3n2 + 3n + 1)

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

776. Доведіть, що коли 2a – b = 1, то 8a3 – b3 = 6ab + 1. 8а3 – b3 = (2а – b)(4а2 + 2ab + b2). Якщо 2a – b = 1, то (2а –b) ∙ (4a2 +

2 + 2аb + b2 = 4а2 – 4ab + b2 + 6ab=(2а – b)2 + 6ab = 1 + 6ab.

777. Доведіть, що коли a + 3b = 2, то a3 + 27b3 = 8 − 18ab. а3 + 27b3 = (а + 3b)(а2 – 3аb + 9b2). Якщо а + 3b = 2, то (а + 3b)(а2 –

+ 9b2) = 2((а2 + 6ab + 9b2) – 9аb) = 2((а + 3b)2 – 9аb) = 2(22 – 9аb) = 8 – 18ab.

778.

1) 600 ⋅ (1 – 0,6) = 600 ⋅ 0,4 = 240 (грн) –

2) 600 + 240 = 840 (грн) – ціна

3) 550 ⋅ (1 – 0,4) = 550 ⋅ 0,6 = 330 (грн) – ціна

4) 550 + 330 = 880 (грн) – ціна

ящика

х + 12 – 4 = (х + 8) (кг).

Рівняння:

х + 4 = 5 7 (х + 8)│ ∙ 7;

7(х + 4) = 5(х + 8);

7х + 28 = 5х + 40;

7х – 5x = 40 – 28;

2х= 12;

х = 6.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Якщо а = –1, то аа2а3a4 ∙...

782. Розкладіть на множники:

1) 3х2 + 12ху = 3х(х + 4у);

2) 10m5 – 5m = 5m(2m4 – 1);

3) аb – ас + 7b – 7с = а(b – с) + 7(b – с) = (b – с)(а + 7);

4) 6х – ху – 6у + у2 = х(6 – у) – у(6 – у) = (6 – у)(х – у);

5) 49b2 – с2 = (7b – с)(7b + с);

6) р2 + 12рk + 36k2 = (р + 6k)2;

7) 100a4 –1 9 b2 = (10a2)2 – (1 3b)2 = (10a2 –1 3b)(10a2 + 1 3b);

8) 25а2 – (а – 3)2 = (5a – a + 3)(5a + а – 3) = (4а + 3)(6а – 3).

783. Розв’яжіть рівняння:

1) (х – 4)(х + 3) = 0;

х – 4 = 0 або х + 3 = 0;

х = 4 або х = –3.

Відповідь: 4; –3;

3) 7х2 + 21х = 0;

7х(х + 3) = 0;

х = 0 або х + 3 = 0;

х = 0

або х = –3.

Відповідь: 0; –3;

5) х(х + 7)(3х – 2) = 0;

х = 0 або х + 7 =0, або 3х –2 = 0;

х = 0 або х = –7, або х = 2 3 .

Відповідь: 0; –7; 2 3;

2) х2 – 81 = 0; (х – 9)(х + 9) = 0; x – 9 = 0 або х + 9 = 0; х = 9 або х = –9.

Відповідь: –9; 9;

4) 9х2 – 6х + 1 = 0; (3х – 1)2 = 0; 3х – 1 = 0;

х = 1 3 .

Відповідь: 1 3;

6) 12х3 – 2х2 = 0; 2х2(6х – 1) = 0; х = 0 або 6х – 1 = 0; х = 0 або x = 1 6 .

Відповідь: 0; 1 6 .

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

785. Закінчіть

1) 7a2 – 7b2 = 7(a2 – b2) = 7(a – b)(a + b).

1) x4 – 16 = (x2 – 4)(x2 + 4) = (x – 2)(x + 2)(x2 + 4); shkola.in.ua

2) 3y3 – 27y = 3y(y2 – 9) = 3y(y – 3)(y + 3).

3) m5 – m3 = m3(m2 – 1) = m3(m – 1)(m + 1).

4) 49 64 x2y3z6 – 0,04yz8 = yz6(49 64 x2y2 – 0,04z2) = yz6(7 8xy + 0,2z).

786. Розкладіть на множники многочлен:

1) 2а2 – 2b2 = 2(а2 – b2) = 2(а – b)(а + b);

2) сх2 – су2 = с(х2 – y2) = с(х – у)(х+ у);

3) 3х2 – 3 = 3(х2 – 1) = 3(х – 1)(х + 1);

4) 3аb2 – 21а = 3а(b2 – 9) = 3а(b – 3)(b + 3);

5) х3 – 4х = х(х2 – 4) = х(х – 2)(х + 2);

6) 2y3 – 18y = 2у(y2 – 9) = 2у(у – 3)(у + 3);

7) х4 – х2 = х2(х2 – 1) = х2(х – 1)(х + 1);

8) 0,09t4 – t6 = t4(0,09 – t2) = t4(0,3 – t)(0,3 + t2);

9) 16 49 a2b4c5 – b2c3 = b2c3(16 49 a2b2c2 – 1) = b2c3(4 7 abc – 1)( 4 7abc + 1).

787. Подайте у вигляді добутку многочлен:

1) 12b2 – 12с2 = 12(b2 – с2) = 12(b – с)(b+ с);

2) 2а2с – 2b2с = 2с(а2 – b2) = 2с(а – b)(а + b);

3) 5а2 – 20 = 5(а2 – 4) = 5(а – 2)(а + 2);

4) 3mn2 – 48m = 3m(n2 – 16) = 3m(n – 4)(n + 4);

5) 7у3 – 7у = 7y(y2 – 1) = 7y(y – 1)(у + 1);

6) а3 – а5 = а3(1 – а2) = а3(1 – а)(1 + а).

788. Закінчіть розкладання на множники:

1) 9a2b2 – 6ab + b2 = b2 (9a2 + 6a + 1) = b2(3a – 1)2.

2) 4b2c – 20abc + 25a2c = c(4b2 – 20ab + 25a2) = c(2b – 5a)2.

3) –3m3 + 6m2n – 3mn2 = –3m(m2 – 2mn + n2) = –3m(m – n)2.

789. Розкладіть на множники:

1) 3а2 + 6ab + 3b2 = 3(а2 + 2ab + b2) = 3(а + b)2; 2) 5m2 + 5n2 – 10mn = 5(m2 – 2mn + n2) = 5(m – n)2; 3) –3х2 + 12х – 12 = –3(х2 – 4х + 4) = –3(х – 2)2;

4) –7b2 – 14bс – 7с2 = –7(b2 + 2bс + с2) = –7(b + с)2; 5) х2у + 14ху2 + 49у3 = y(х2 + 14ху + 49у2) = у(х + 7y)2; 6) –8а3b + 56а2b2 – 98ab3 = –2ab(4a2 – 28аb + 49b2) = –2аb(2а –7b)2.

790. Розкладіть на множники:

1) 8х2 + 16ху + 8y2 = 8(х2 + 2ху + у2) = 8(х + у)2; 2) –2а2 + 24аb – 72b2 = –2(а2 – 12аb + 36b2) = –2(а – 6b)2;

3) –12b3 – 12b2 – 3b = –3b(4b2 + 4b + 1) = –3b(2b + 1)2;

4) 48m3n – 12m2n + 21mn = 3mn(16m2 – 24m + 9) = 3mn(4m – 3)2.

791. Закінчіть розкладання на множники:

1) a4 – 10000 = (a2)2 – 1002 = (a2 – 100)(a2 + 100) = (a – 10)(a + 10)(a2 + 100).

2) m8 – n4 = (m4)2 – (n2)2 = (m4 – n2)(m4 + n2) = (m2 – n)(m2 + n) ∙ (m4 + n2).

792. Подайте у

1) а4 – b4 = (а2 – b2)(a2 + b2) = (а – b)(a+ b)(a2 + b2); 2) c4 – 81 = (c2 – 9)(c2 + 9) = (c – 3)(c + 3)(c2 + 9).

793. Розкладіть на множники:

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2) y8 – 1 = (y4 – 1)(y4 + 1) = (y – 1)(y2 + 1)(y + 1) = (y – 1)(y + 1)(y2 + 1)(y4 + 1).

794. Закінчіть розкладання

1) 16x – 2x4 = 2x(8 – x3) = 2x(2 – x)(4 + 2x + x2).

2) 3a5 + 375a2 = 3a2(a3 + 125) = 3a2(a + 5)(a2 – 5a + 25).

795. Розкладіть на множники:

1) 4a3 – 4b3 = 4(a3 – b3) = 4(a – b)(a2 + ab + b2);

2) 2m3 – 16 = 2(m3 – 8) = 2(m – 2)(m2 + 2m + 4);

3) 7 + 7b3 = 7(1 + b3) = 7(1 + b)(1 – b + b2);

4) –x4 + 27x = –x(x3 – 27) = –x(x – 3)(x2 + 3x + 9);

5) 2a4 – 250a = 2a(a3 – 125) = 2a(a – 5)(a2 + 5a + 25);

6) 9a5 – 9a2 = 9a2(a3 – 1) = 9a2(a – 1)(a2 + a + 1).

796. Подайте у вигляді добутку многочлен:

1) 3х3 + 3y3 = 3(x3 + y3) = 3(x + x)(x2 – xy + y2);

2) 5m4 – 320mn3 = 5m(m3 – 64n3) = 5m(m – 4n)(m2 + 4m + 16n);

3) 6c5 – 6c8 = 6c5(1 – c3) = 6c5(1 – c)(1 + с + с2).

797. Розкладіть на множники:

1) а7 + ab6 = a(a6 + b6) = a(a2 + b2)(a4 – a2b2 + b4);

2) x8 – y8 = (x4 – y4)(x4 + y4) = (x2 – y2)(x2 + y2)(x4 + y4) = (x – y)(x + y)(x2 + y2)(x4 + y4);

3) c6 – 1 = (c2 – 1)(c4 + c2 + 1) = (c – 1)(c + 1)(c4 + c + 1).

798. Розкладіть на множники:

1) с6 + с9 = c6(1 + с3) = c6(1 + c)(1 – с + с2);

2) m9 – n9 = (m3 – n3)(m6 + m3n3 + n6); 3) a8 – b4 = (a4 – b2)(a4 + b2) = (a2 – b)(a2 + b)(a4 + b2).

799. Подайте у вигляді добутку многочлен:

1) 3аb + 15b – 3a – 15 = 3b(a + 5) – 3(a + 5) = (a + 5)(3b – 3); 2) 84 – 42y – 7xy + 14x = 42(2 – y) + 7x(2 – y) = (2 – y)(42 + 7x);

3) abc + 6ac + 8ab + 48а = ac(b + 6) + 8a(b + 6) = (b + 6)(ac + 8a);

4) m3 – m2n + m2 – mn = m(m2 – mn + m – n) = m(m(m – n) + (m – n)) = m(m – n)(m + 1);

5) a3 + а2 – a – 1 = a2(a + 1) – (a + 1) = (a + 1)(a2 – 1) = (a + 1)(a – 1)(a + 1) = (a – 1)(a + 1)2;

6) 2x3 – 2хy2 – 8x2 + 8y2 = 2x(x2 – y2) – 8(x2 – y2) = (x2 – y2)(2x – 8) = 2(x – y)(x + y)(x – 4);

7) 5a2 – 5b2 – 15a3b + 15ab3 = 5(a2 – b2) – 15ab(a2 – b2) = (a2 – b2)(5 – 15ab) = = 5(a – b)(a + b)(1 – 3аb);

8) a2b2 – 1 – b2 + a2 = a2b2 – b2 + a2 – 1 = b2(a2 – 1) + (a2 – 1) = (a2 – 1)(b2 + 1) = = (a – 1)(a + 1)(b2 + 1).

800. Розкладіть на множники:

1) 15cx + 2су – cxy – 30c = c(15x + 2y – xy – 30) = c((15x – 30) + (2y – xy)) = = c(15(x – 2) – y(x – 2)) = c(x – 2)(15 –y);

2) 35a2 – 42ab + 10a2b – 12ab2 = а(35а – 42b + 10аb –12b2) = а(7(5а – 6b) + 2b(5а – 6b)) = = а(5а – 6b)(7 + 2b);

3) x3 + х2у + х2 + ху = х(х2 + xy + x + у) – х(х(х + у) + (х + у)) = х(х + у)(х + 1); 4) mn4 – n4 + mn3 – n3 = n3(mn – n + m – 1) = n3(n(m – 1) + (m – 1)) = n3(m – 1)(n + 1).

801. Розкладіть на множники: 1) (а2 + b2)2 – 4а2 = (а2 + b2 – 2а)(а2 + b2 + 2а);

2) 81 – (х2 + 6х)2 = (9 – (х2 + 6х))(9 + (х2 + 6х)) = (9 – х2 – 6х)(9 + х2 + 6х) = = (9 – x2 – 6х)(х + 3)2 .

802. Подайте у

добутку вираз: 1) (m2 – 2m)2 – 1 = (m2 – 2m – 1 )(m2 – 2m + 1) = (m2 – 2m –1) ∙ (m – 1)2;

2) 16 – (m2 + 4m)2 = (4 – m2 – 4m)(4 + m2 + 4m) = (4 – m2 – 4m)(2 + m)2.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

803. Розкладіть на множники: 1) x2(x – 2) – 18x(x – 2) + 81(x – 2) = (x – 2)(x2 – 18x + 81) = (x – 2)(x – 9)2;

2) 4x(y2 – 9) + 4x2(y2 – 9) – 9 + y2 = 4x(y2 – 9) + 4x2(y2 – 9) + y2 – 9 = (y2 – 9)(4x + 4x2 + 1) = (y – 3)(y + 3)(2x + 1)2;

3) b2(a + 1) – a2(b + 1) = ab2 + b2 – a2b – a2 = (ab2 – a2b) + (b2– a2) = ab(b – a) + (b – a)(b + a) = (b – a)(ab + b + a); 4) (a – b)(b2 – c2) – (b – c)(a2 – b2) = (a – b)(b – c)(b + c) – (b – c)(a – b)(a + b) = = (a – b)(b – c)(b + c – a – b) = (a – b)(b – c)(c– a).

804. Подайте у вигляді добутку вираз:

1) x2(x + 4) – 20x(x + 4) + 100(x + 4) = (x + 4)(x2 –20x + 100) = (x + 4)(x – 10)2; 2) a2 – 36 – 2a(36 – a2) – a2(36 – a2) = a2 – 36 + 2a(a2 – 36) + a2(a2 – 36) = (a2 – 36)(1 + 2a + a2) = (a – 6)(a + 6)(1 + a)2; 3) a2(b – 1) – b2(a – 1) = a2b – a2 – ab2 + b2 = (a2b – ab2) – (a2 – b2) = ab(a – b) – (a – b)(a + b) = (a – b)(ab – a – b); 4) (m – n)(n3 – p3) – (n – р)(m3 – n3) = (m – n)(n – p)(n2 + np + p2) – (n – p)(m – n)(m2 + mn + n2) = (m – n)(n – p)(n2 + np + p2 – m2 – mn – n2) = (m – n)(n – p)(np + p2 – m2 – mn) = (m – n)(n – p)((np – mn) + (p2 – m2)) = (m – n)(n – p)(n(p – m) + (p – m)(p + m)) = (m – n)(n – p)(p – m)(n + p + m).

805. Розв’яжіть рівняння: 1) х3 – 4х = 0;

х(х2 – 4) = 0;

х(х – 2)(х + 2) = 0;

х = 0 або х – 2 = 0, або х + 2 = 0;

х = 0 або х = 2, або х = –2.

Відповідь: 0; –2; 2; 2) х4 – х2 = 0; х2(х2 – 1) = 0; х2(х – 1)(х + 1) = 0; х = 0 або х – 1 = 0, або х + 1 = 0; х = 0 або х = 1, або х = –1.

3) х5 – 36х3 = 0;

х3(х2 – 36) = 0;

х3(х – 6)(х + 6) = 0;

х = 0 або х – 6 = 0, або х + 6 = 0;

х = 0 або х = 6, або х = –6.

Відповідь: 0; –6; 6;

5) х3 – 10х2 + 25х = 0;

х(х2 – 10х + 25) = 0;

х(х – 5)2 = 0;

х = 0 або х – 5 = 0;

х = 0 або х = 5.

Відповідь: 0; 5;

7) х3 – 5х2 + 4х – 20 = 0;

х2(х – 5) + 4(х – 5) = 0;

(х – 5)(х2 + 4) = 0;

х – 5 = 0;

х = 5.

Відповідь: 5;

Відповідь: 0; –1; 1;

4) 9х3 – х = 0;

х(9х2 – 1) = 0;

х(3х – 1)(3х+ 1) = 0;

х =0 або 3х –1 = 0, або 3х + 1= 0;

х = 0 або х = 1 3, або х = –1 3 .

Відповідь: 0; –1 3; 1 3;

6) х3 + 2х2 – 9х – 18 = 0;

х2(х + 2) – 9(х + 2) = 0;

(х + 2)(х2 – 9) = 0;

(х + 2)(х – 3)(х + 3) = 0;

х + 2 = 0 або х – 3 = 0, або х + 3 = 0;

х = –2 або х = 3, або х = –3.

Відповідь: –3; –2; 3;

8) х5 – х4 – х + 1 = 0;

х4(х – 1) – ( х – 1) = 0;

(х – 1)(х4 – 1) = 0;

(х – 1)(х2 – 1)(х2 + 1) = 0; (х – 1)(х – 1)(х + 1)(х2 + 1) = 0;

х – 1 = 0 або х + 1 = 0; х = 1 або х = –1.

Відповідь: –1; 1.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

806. Розв’яжіть рівняння:

1) х3 – х = 0;

х(х2 – 1) = 0;

х(х – 1)(х + 1) = 0;

х = 0

або х – 1 = 0, або х + 1 = 0;

х = 0 або х = 1, або х = –1.

Відповідь: 0; –1; 1;

3) х4 – 8х3 = 0;

х3(х – 8) = 0;

х3 = 0 або х – 8 = 0;

х = 0 або х = 8.

Відповідь: 0; 8;

5) х3 + х2 – х – 1 = 0;

(х3 – 1) + (х2 – х) = 0;

(х – 1)(х2 + х + 1) + х(х – 1) = 0;

(x – 1)(x2 + x + 1 + x) = 0;

(x – 1)(x2 + 2x + 1) = 0;

(x – 1)(x + 1)2 = 0;

x = – 1

або x = 1.

Відповідь: –1; 1;

2) х4 + х2 = 0;

х2(х2 + 1) = 0;

х2 = 0 або х2 + 1 = 0; х = 0 коренів немає

Відповідь: 0;

4) 49х3 + 14х2 + х = 0;

х(49х2 + 14х + 1) = 0;

х(7х + 1)2 = 0;

х = 0 або 7х + 1 = 0; х = –1 7 .

Відповідь: –1 7; 0;

6) х3 – 4х2 – 25х + 100 = 0;

х2(х – 4) – 25(х – 4) = 0;

(х – 4)(х2 – 25) = 0;

(x – 4)(x – 5)(x + 5) = 0; x – 4 = 0 або х – 5 = 0, або х + 5 = 0; х = 4 або х = 5, або х = –5.

807. Чи є тотожністю рівність: 1) (a – 1)3 – 9(a – 1) = (a – 1)((a – 1)2 – 9) = (a – 1)((a – 1 – 3)(a –1 + 3) = = (a – 1)(a – 4)(a + 2) – рівність є тотожністю; 2) (x2 + 1)2 – 4x2 = (x2 + 1 – 2x)(x2 + 1 + 2x) = (x2 – 2x + 1)(x2 + 2x + 1) = = (x – 1)2(x + 1)2 – рівність є тотожністю.

808. Доведіть тотожність: 1) (a + 2)3 – 25(a + 2) = (a + 2)((a + 2)2 – 25) = (a

1) a) (ab + 1)2 – (a + b)2 = (ab + 1 – a – b)(ab + 1 + a + b) = (ab –

= (a(b – 1))((a(b + 1) + (b + 1)) = (b – 1)(a – 1)(b + 1)(a + 1); б) (ab + 1)2 – (a + b)2 = a2b2 + 2ab + 1 – a2 – 2ab – b2 = a2b2 – a2 –b2 + 1 = a2(b2 – 1) – (b2 – 1) = (b2 – 1)(a2 – 1) = (b – 1)(b + 1)(a – 1)(a + 1); 2) a) (a + 2b)2 – (ab + 2)2 =(a + 2b – ab – 2)(a + 2b + ab + 2) = = (–ab + a + 2b – 2)(ab + a + 2b + 2) = (–a(b – 1) + 2(b – 1))((a(b + 1)) = = (b – 1)(–a + 2)(b + 1)(a + 2); б) (a + 2b)2 – (ab + 2)2 = a2 + 4ab + 4b2 – a2b2 – 4ab – 4 = a2 + 4b2 – a2b2 – 4 = = a2 – a2b2 + 4b2 – 4 = a2(1 – b2) – 4(1 –b2) = (1– b2)(a2 –4) = (1 – b)(1 + b)(a – 2)(a + 2).

810. Розкладіть на множники: 1) а2 + 2ab + b2 – с2 = (а + b)2 – с2 = (а + b – c)(a + b + c); 2) c2 + 4c + 4 – k2 = (c + 2)2 – k2 = (c + 2 – k)(c + 2 + k); 3) 9а2 + с2 + 6ас – 9 = (9a2 + 6ac + c2) – 9 = (3а + c)2 – 9 = (3а + с – 3)(3а + c + 3);

4) a2 – b2 – 10b – 25 = a2 – (b2 + 10b + 25) = a2 – (b + 5)2 = (a – b –5) ∙ (a + b + 5);

5) 49 – y2 + x2 – 14x = (x2 – 14x + 49) – y2 = (x – 7)2 – y2 = (x – 7 –y) ∙ (x – 7 + y); 6) mn2 – m3 – 12m2 – 36m = m(n2 – m2 – 12m – 36) = m(n2 – (m2 + 12m + 36) = = m(n2 – (m + 6)2) = m(n – m – 6)(n + m + 6).

811. Подайте у

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) x2 – 18ху + 81y2 – z2 = (х – 9у)2 – z2 = (х – 9у – z)(x – 9у + z);

2) 64х2 + 48ху + 9y2 – 144 = (8х + 3у)2 – 144 = (8х + 3у – 12)(8х + 3у + 12);

3) с2 – а2 + 22а – 121 = с2 – (а2 – 22а + 121) = с2 – (а – 11)2 = (с – а + 11)(с + а – 11);

4) 100 –25y2 – 60х2у – 36х4 = 100 – (36х4 + 60х2у + 25y2) = 100 – (6х2 + 5у)2 = = (10 – 6х2 – 5у)(10 + 6х2 + 5у).

812. Розкладіть на множники:

1) а2 – b2 – а – b = (а – b)(а + b) – (a + b) = (а + b)(a – b – 1);

2) x – у – x2 + y2 = (х – у) – (х2 – у2) = (х – у) – (х – у)(х + у) = (х – у)(1 – х – у);

3) 4m2 – 9n2 + 2m + 3n – (2m – 3n)(2m + 3n) + (2m + 3n) = (2m + 3n)(2m – 3n + 1);

4) с2 – d2 + 4с – 4d = (с – d)(c + d) + 4(с – d) = (с – d)(c + d + 4);

5) 5х2у – 5ху2 – x2 + у2 = 5ху(х – у) – (х – у)(х + у) = (х – у)(5ху – х – у);

6) а2 – 10а + 25 – ab + 5b = (а – 5)2 – b(а – 5) = (а – 5)(а – 5 – b);

7) 8mр + 8nр – m2 – 2mn – n2 – 8р(m + n) – (m + n)2 – (m + n)(8р –m – n);

8) а3 + b3 – a2b – ab2 = (а3 – a2b) + (b3 – ab2) = а2(а – b) – b2(а – b ) = (а – b)(а2 – b2) = = (а – b)(а – b)(а + b) = ( а – b)2(а + b);

9) m3 – 8n3 – m2 + 4mn – 4n2 = (m3 – 8n3) – (m2 – 4mn + 4n2) = = (m – 2n)(m2 + 2mn + 4n2) – (m – 2n)2 = (m – 2n)(m2 + 2mn + 4n2 – m + 2n);

10) a3 – 4a2 + 4a – 1 = а3 – 1 – (4а2 – 4а) = (а – 1)(а2 + а + 1) – 4а(а – 1) = = (а – 1)(а2 + а + 1 – 4а) = (а – 1)(а2 – 3а + 1).

813. Розкладіть на множники:

1) m2 – n2 – m + n = (m – n)(m + n) – (m – n) = (m – n)(m + n – 1);

2) с + d – c2 + d2 = с + d – (с2 – d2) = с + d – (с – d)(c + d) = (с + d) ∙ (1 – с + d);

3) 16х2 – 25у2 – 4х – 5y = (4х – 5у)(4х + 5у) – (4х + 5у) = (4х + 5у) ∙ (4х – 5у – 1);

4) 12a2b3 + 3a3b2 + 16b2 – a2 = 3a2b2(4b + a) + (4b – a)(4b + a) = (4b + a)(3a2b2 + 4b – a);

5) 49с2 – 14с + 1 – 21ас + 3а = (7с – 1)2 – 3а(7с – 1) = (7с – 1)(7с –1 – 3а);

6) ах2 + ay2 + x4 + 2х2y2 + y4 = а(х2 + у2) + (х2 + у2)2 = (х2 + у2)(а + х2 + у2);

7) 27с3 – d3 + 9с2 + 3cd + d2 = (3с – d)(9c2 + 3cd + d2) + (9c2 + 3cd + d2) = = (9c2 + 3cd + d2)(3c – d + 1); 8) b3 – 2b2 – 2b + 1 = (b3 + 1) – (2b2 + 2b) = (b + 1)(b2 – b + 1) – 2b(b + 1) = = (b + 1)(b2 – b + 1 – 2b) = (b + 1)(b2 – 3b + 1).

814. Подайте у

1) a3 + 3a2 + 3a + 1 = (a3 + 1) + (3a2 + 3a) = (a + 1)(a2 – 2 + 1) + 3a(a + 1) = = (a + 1)(a2 – a + 1 + 3a) = (a + 1)(a2 + 2a + 1) = (a + 1)2 = (a + 1)3; 2) b3 – 6b2 + 12b – 8 = (b3 – 8) – (6b2 – 12b) = (b – 2)(b2 – 2b + 4) – 6b(b – 2) = = (b – 2)(b2 + 2b + 4 – 6b) = (b – 2)(b2 – 4b + 4) = (b – 2)(b – 2)2 = (b – 2)3.

815. Доведіть тотожність:

1) (a + b + c)3 – a3 – b3 – c3 = ((a + b + c)3 – a3) – (b3 + c3) = = (a + b + c – a)((a + b + c)2 + (a + b + c)a + a2) – (b + c)(b2 – bc + c2) = = (b + c)(a2 + b2 + c2 + 2ab + 2ac + 2bc + a2 + ab + ac + a2) – (b + c)(3a2 + 3ab + 3ac + 3bc) = = 3(b + c)(a2 + ab + ac + bc) = 3(b + c)(a(a + b) + c(a + b)) = 3(a + b)(b + c)(a + c); 2) (a – b)3 + (b – c)3 – (a – c)3 = (a – b + b – c)((a – b)2 – (a – b)(b – c) + (b – c)2) – (a – c)3 = = (a – c)((a – b)2 – (a – b)(b – c) + (b – c)2) – (a – c)3 = = (a – c)((a – b)2 – (a – b)(b – c) + (b – c)2 – (a – c)2) = = (a – c)(a2 – 2ab + b2 – ab + ac + b2 – bc + b2 – 2bc + c2 – a2 + 2ac – c2) = = (a – c) ∙ (–3ab + 3b2 + 3ac – 3bc) = (a – c)(–3b(a – b) + 3c(a – b)) = = (a – c)(a – b)(–3b + 3c) = –3(a – b)(b – c)(a – c).

816. Розкладіть

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

вираз: 1) (x – y)(x + y) + 2(x + 3y) – 8 = x2 – y2 + 2x + 6y – 8 = (x2 + 2x + 1) – (y2 – 6y + 9) = = (x + 1)2 – (y – 3)2 = (x + 1 – y + 3)(x + 1 + y – 3) = (x – y + 4)(x + y – 2); 2) (2a – 3b)(2a + 3b) – 4(a + 3b) – 3 = 4a2 – 9b2 – 4a – 12b – 3 = (4a2 – 4a + 1) – (9b2 + 12b + 4) = (2a – 1)2 – (3b + 2)2 = (2a – 1 – 3b – 2) ∙ (2a – 1 + 3b + 2) = (2a – 3b – 3)(2a + 3b + 1).

817. Подайте у вигляді добутку вираз:

1) (5x – y2)(5x + y2) – 2(15x – 7y2) – 40 = 25x2 – y4 – 30x + 14y2 – 40 = = (25x2 – 30x + 9) – (y4 – 14y2 + 49) = (5x – 3)2 – (y2 – 7)2 = (5x – 3 – y2 + 7)(5x – 3 + y2 – 7) = =(5x – y2 + 4)(5x + y2 – 10); 2) (3m – 2n)(12m + 5n) + 3m(3n + 4) – 2(3n2 – 20n + 12) = = 36m2 + 15mn – 24mn – 10n2 + 9mn + 12m – 6n2 + 40n – 24 = = 36m2 – 16n2 + 12m + 40n – 24 = (36m2 + 12m + 1) – (16n2 – 40n + 25) = = (6m + 1)2 – (4n – 5)2 = (6m + 1 – 4n + 5)(6m + 1 + 4n – 5) = = (6m – 4n + 6)(6m + 4n – 4) = 4(3m – 2n + 3)(3m + 2n – 2). 818. Розкладіть

1) x2 – 10x + 24 = (x2 – 10x + 25) – 1 = (x – 5)2 – 1 = (x – 5 – 1) ∙ (x – 5 + 1) = (x – 6)(x – 4);

2) a2 + 4a – 32 = (a2 + 4a + 4) – 36 = (a + 2)2 – 36 = (a + 2 – 6)(a + 2 + 6) = (a – 4)(a + 8);

3) b2 – 3b – 4 = (b2 – 3b + 2,25) – 6,25 = (b – 1,5)2 – 6,25 = (b – 1,5 – 2,25)(x – 1,5 + 2,25) = = (b – 3,75)(x + 0,75);

4) 4a2 – 12a + 5 = (4a2 – 12a + 9) – 4 = (2a – 3)2 – 22 = (2a – 3 – 2)(2a – 3 + 2) = = (2a – 5)(2a – 1);

5) 9x2 – 24xy + 7y2 = (9x2 – 24xy + 16y2) – 9y2 = (3x – 4y)2 – 9y2 = = (3x – 4y – 3y)(3x – 4y + 3y) = (3x – 7y)(3x – y);

6) 36m2 – 60mn + 21n2 = (36m2 – 60mn + 25n2) – 4n2 = (6m – 5n)2 – 4n2 = = (6m – 5n – 2n)(6m – 5n + 2n) = (6m – 7n)(6m – 3n) = 3(6m – 7n)(2m – n).

819. Розкладіть на множники многочлен:

1) x2 – 4x + 3 = (x2 – 4x + 4) – 1 = (x – 2)2 – 1 = (x – 2 – 1)(x –2 + 1) = (x – 3)(x – 1); 2) a2 + 2a – 24 = (a2 + 2a + 1) – 25 = (a + 1)2 – 25 = (a + 1 – 5)(a + 1 + 5) = (a – 4)(a + 6); 3) y2 + 12y + 35 = (y2 + 12y + 36) – 1 = (y + 6)2 – 1 = (y + 6 – 1)(y + 6 + 1) = (y + 5)(y + 7); 4) x2 + x – 6 (x2 + x + 0,25) – 6,25 = (x + 0,5)2 – 6,25 = (x + 0,5 – 2,5)(x + 0,5 + 2,5) = = (x – 2)(x + 3); 5) c2 + 8cd + 15d2 = (c2 + 8cd + 16d2) – d2 = (c + 4d)2 – d2 = (c + 4d + d) = (c + 3d)(c

6) 9x2 – 30xy + 16y2 = (9x2 – 30xy + 25y

= (3x – 5y – 3y)(3x – 5y + 3y) = (3x – 8y)(3x – 2y). 820. Значення змінних x1 і x2 є такими, що

1 – x2)2 + 2x1x2

Якщо x1 – x2 = 8, x1x2 = 5, то (x1 – x2)2 + 2x1x2 = 82 + 2 ∙ 5 = 64 + 10 = 74; 3) (x1 + x2)2 = x1 2 + 2x

= (x

x2)2 + 4x1x2. Якщо x1 – x2 = 8, x1x2 = 5, то (x1 – x2)2 + 4x1x2 = 82 + 4 ∙ 5 = 64 + 20 = 84; 4) x1 3 – x2 3 =

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) x3y2 + x2y3 = x2y2(x + y) = (xy)2(x + y).

Якщо x + y = 6, xy = –3, то (xy)2(x + y) = (–3)2 ∙ 6 = 9 ∙ 6 = 54; 2) (x – y)2 = x2 – 2xy + y2 = (x2 + 2xy + y2) – 4xy = (x + y)2 – 4xy.

Якщо, x + y = 6, xy = –3, то (x + y)2 – 4xy = 62 – 4 ∙ (–3) = 36 + 12 = 48; 3) x4 + y4 = (x4 + 2x2y2 + y4) – 2x2y

+ y)2 – 2xy)2. Якщо x + y = 6, xy = –3, то ((x

4) x5 + x + 1 = (x5 –

= х2(х – 1)(х2 + х + 1) + (х2 + х + 1) = (х2 + х + 1)(х2(х – 1) + 1) = (х2 + х + 1)(х3 – х2 + 1);

5) х4 + 4 = (х4 + 4х2 + 4) – 4х2 = (х2 + 2)2 – (2x)2 = (х2 + 2 – 2х)(х2 + 2 + 2х);

6) х8 + х4 – 2 = (х8 – 1) + (х4 – 1) = (х4 – 1)(х4 + 1) + (х4 – 1) = (х4 – 1)(х4 + 1 + 1) = = (х2 – 1)(х2 + 1)(х4 + 2) = (х – 1)(х + 1)(х2 + 1)(х4 + 2).

824. Подайте у вигляді добутку вираз:

1) х4 + 5х2 + 9 = (х4 + 6х2 + 9) – х2 = (х2 + 3)2 – х2 = (х2 + 3 – х)(х2 + 3 + х); 2) х4 – 8х2 + 4 = (х4 – 4х2 + 4) – 4х2 = (х

n + 4.

n(n + 4) – (n – 4)(n + 4) = 88; n2 + 4n – n2 + 16 = 88; 4n + 16 = 88; 4n = 72; n = 18.

18 – 4 = 14; 18; 18 + 4 = 22.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

х 2,5 + х+3 4 = 4│∙ 20;

8х + 5(х + 3) = 80;

8х + 5х + 15 = 80; 13х = 65; х = 5.

Загальний шлях, пройдений, пройдений Петром, становить: 5 + (5 + 3) = 13 (км).

Відповідь: 13 км.

829. Розв’яжіть рівняння:

1) |7х – 3| = 4;

7х – 3 = 4 або 7х – 3 = –4;

7х = 7 або 7х = –1; х = 1 або х = –1 7 .

Відповідь: 1; –1 7;

3) 4(х – 2) + 5|х| = 10.

а) Нехай х ≥ 0. Маємо: 4(х – 2) + 5х = 10;

4х – 8 + 5х = 10; 9х = 18; х = 2;

Відповідь: –18; 2; б) нехай х < 0. Маємо: 4(х – 2) – 5х = 10;

4х – 8 – 5 х = 10; –х = 18; х = –18.

830. Доведіть, що сума трицифрового

2) ||x| – 10| = 8;

|х| – 10 = 8 або |х| – 10 = –8;

|х| = 18 або |х| = 2; х = 18 або х = –18, х = 2 або х = –2.

Відповідь: –18; –2; 2; 18;

4) |x| = 3х – 8. a) Нехай x ≥ 0. Маємо: х = 3х – 8; х – 3х = –8; –2х = –8; х = 4;

Відповідь: 4. б) нехай х < 0. Маємо: –х = 3x – 8; –х – 3х = –8; –4х = –8; х = 2 не підходить.

831. Обчисліть

2) якщо х = –3, то у = 0,2x – 3 = 0,2 ∙ (–3) – 3 = –0,6 – 3 = –3,6. 832. Знайдіть координати точок A, B, C, D, E, F, K, M, N, зображених на рисунку 7. А(2; 2), В(5; 1), С(0; –5), D(2; –3), E(–1 ; –1), F(–5 ; 0), K(–4; 3), М(–3; 2), N(–4; –3). 833. На координатній площині позначте точки: A (2; 3), B (4; 5), C (–3; 7), D (–2; 2), K (–2; –2), M (0; 2), N (–3; 0), P (1; –6), F (–4; –2).

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

якщо A (–5; –2), B (1; 4), C (–3; 2), D (2; –3).

1) A (2; 6)

2) А (–3; 1) — розміщена

(–4; –5)

4) А (–3; 0) —

(0; 0), (0; 4), (4; 0), (4; 4)

(0; 0), (0;

(–2; 1).

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

shkola.in.ua

1. Подайте у вигляді многочлена вираз. (x − 6)(x2 + 6x + 36) = x3 – 63 = x3 − 216.

Відповідь: В).

2. Знайдіть многочлен M, якщо y3 – 64 = (y − 4) ⋅ M. y3 – 64 = (y − 4)(y2 + 4x + 16). Отже, M = y2 + 4x + 16.

Відповідь: Г).

3. Спростіть вираз. (a2 + 2b3)(a4 − 2a2b3 + 4b6) = (a2)3 + (2b3)3 = a6 + 8b9.

Відповідь: Г).

4. Розкладіть на множники многочлен.

3c2 – 48 = 3(c2 − 16) = 3(c − 4)(c + 4).

Відповідь: Б).

5. Розкладіть на множники вираз.

7a2 − 42a + 63 = 7(a2 − 6a + 9) = 7(a − 3)2

Відповідь: Б).

6. Розкладіть на множники многочлен. a8 − a6 = a6(a2 − 1) = a6(a − 1)(a + 1).

Відповідь: Б).

7. Розкладіть на множники вираз.

m2 + n2 + m + n = (m – n)(m + n) + m + n = (m + n)(m – n + 1).

Відповідь: А).

8. Подайте у вигляді добутку вираз.

х2 – у2 + 14у – 49 = х2 – (у2 – 14у + 49) = х2 – (у – 7)2 = (х – у + 7)(х + у – 1).

Відповідь: В).

9. Розкладіть на множники многочлен.

81а4 – 1 = (9а2)2 – 1 = (9а2 – 1)(9а2 + 1) = (3а – 1)(3а + 1)(9а2 + 1).

Відповідь: А).

10. Розв’яжіть рівняння.

49х – х2 = 0

х(49 – х) = 0

х = 0 або 49 – х = 0

х = 0 або х = 49

Відповідь: В).

11. Розв’яжіть рівняння.

х3 + 3х – х – 3 = 0

х2(х + 3) – (х + 3) = 0

(х2 – 1)(х + 3) = 0

(х – 1)(х + 1)(х + 3) = 0

х – 1 = 0, або х + 1 = 0, або х + 3 = 0

х = 1, або х = -1, або х = -3

Відповідь: Г).

12. Подайте у вигляді добутку вираз.

(х2 – 2)2 – 4(х2 – 2) + 4 = ((х2 – 2) – 2)2 = (х2 – 4)2 = (х – 2)2(х + 2)2 .

Відповідь: Б).

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

848. Кожному раціональному числу, відмінному

число. Чи є таке правило функцією? Правило: «Кожному

нього число» є функцією.

849. Користуючись

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

турист витратив 3 год;

3) турист був на відстані 8 км від

4) до зупинки турист йшов зі швидкістю 4

5) останні дві

1) g(7) = 9, g(3) = 9, g(1)

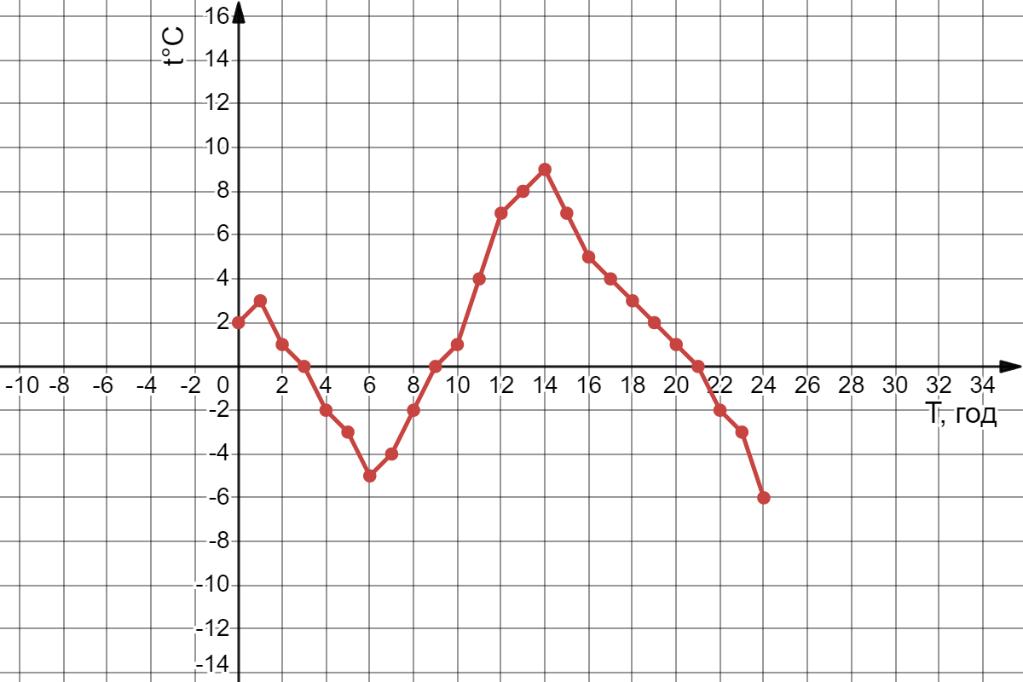
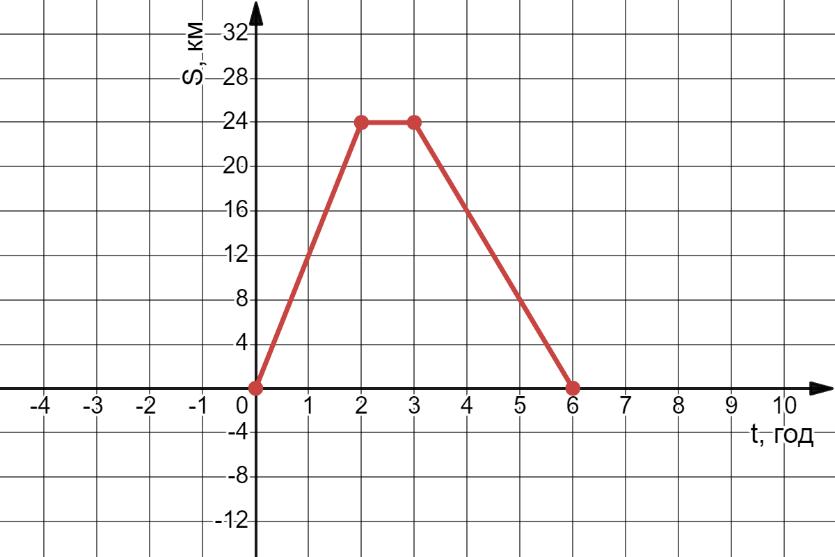
https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

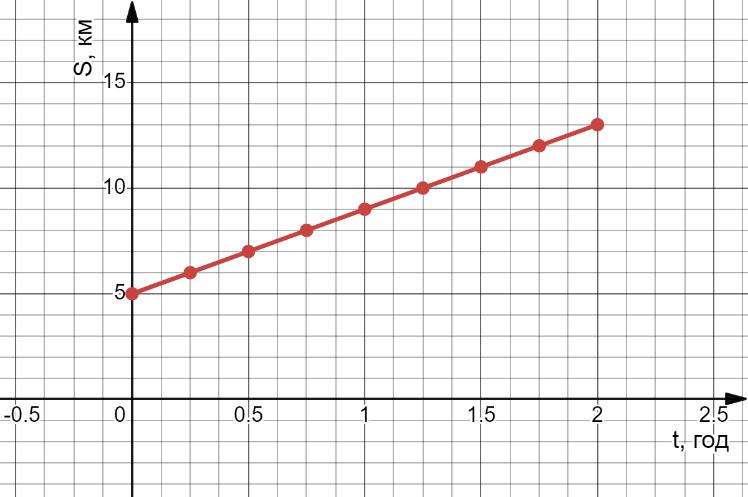
1) –1,2х + 7,2 = 0; –1,2х = –7,2; х = 6.

Відповідь: 6;

3) 3х + 1,5 = –2,5; 3х = –4; х = –11 3 .

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2) –1 3 х – 6 = 0 | ∙ 3; –х – 18 = 0; x = –18.

Відповідь: –18;

870. Розкладіть на множники вираз:

4) 6 – 0,5х = 16; –0,5х = 10; x = –20.

Відповідь: –20.

1) –9 64 b6 + 16m2n4 = 16m2n4 –9 64 b6 = (4mn2)2 – (3 8b3)2 = (4mn2 –3 8b3)(4mn2 + 3 8b3);

2) 20z2 + 3ху – 15xz – 4уz = 20z2 – 15хz + 3xz – 4уz = 5z(4z – 3х) + у(3х – 4z) = = 5z(4z – 3х) – у(4z – 3x) = (4z – 3х)(5z – у);

3) 0,027а12 + b9 = (0,3а4)3 + (b3)3 = (0,3а4 + b3)((0,3а4)2 – 0,3а4 b3 + (b3)2) = = (0,3a4 + b3)((0,09а8 – 0,3а4b3 + b6).

871. Доведіть, що при

1) (n + 25) (n + 3) – (n + 6) (n + 4) – 6 : 9.

Доведення: (n + 25) (n + 3) – (n + 6) (n + 4) – 6 = n2 + 3n +

= 18n + 45 = 9 (2n+ 5) : 9.

Доведено.

2) (13n – 24) (13n + 24) – (12n – 26) (12n + 26) : 25

Доведення: (13n – 24) (13n + 24) – (12n – 26) (12n + 26) = (169n2 – 576) – (144n2 – 676) = = 169n2 – 576 – 144n2 + 676 = 25n2 + 100 = 25 (n2 + 4) : 25.

Доведено.

3) (9n + 2)2 – (3n – 2)2 : 24.

Доведення: (9n + 2)2 – (3n – 2)2 = (9n + 2 – 3n + 2) (9n + 2 + 3n – 2) = (6n + 4) 12n = = 2 ∙ 12n (3n + 2) = 24n (3n + 2) : 24.

Доведено. 872. Відомо,

1) s(t ) = 70t —

2) y(x) = –2х + 4 —

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

4) ƒ(х) = х2 – 4

— х, залежна змінна — ƒ. 877. Функцію задано формулою y = 10x + 1.

y, якщо:

1) Якщо х = –1, то у = 10 ∙ (–1) + 1 = –10 + 1 = –9;

2) якщо х = 3, то у = 10 ∙ 3 + 1 = 30 + 1 = 31;

3) якщо х = –1 5, то у = 10 ∙ (1 5) + 1 = –2 + 1 = – 1;

4) якщо х = 7, то у = 10 ∙ 7 + 1 = 70 + 1 = 71. 878. Функцію задано формулою y = 3 – 4х. Чи є правильною рівність:

1) f(–2) = –5 – не є правильною рівність, оскільки f(–2) = 3 – 4

2) f (1 2) = 1 – правильна рівність, оскільки

3) f(0) = –1 – не є правильною рівність, оскільки

4) f(–1) = 7 – правильна рівність, оскільки f(–1) = 3

879. Функцію задано формулою f (x) = 7x – 5. Знайдіть:

1) f(2) = 7 ∙ 2 – 5 = 14 – 5 = 9; 2) f(0) = 7 ∙ 0 – 5 = –5;

3) f(–3) = 7 ∙ (–3) – 5 = –21 – 5 = – 26. 4) f(200) = 7 ∙ 200 – 5 = 1400 – 5 = 1395.

880. Функцію задано формулою f (x) = 2x2 – 1. Чи

1) f(1) = 1 – правильна рівність.

f(1) = 2 ∙ 12 – 1 = 1.

2) f (4) = 2 ∙ 42 – 1 = 2 ∙ 16 – 1 = 32 – 1 = 31.

3) f(–2) = –9 – не є правильною рівність. f(–2) = 2 ∙ (–2)2 – 1 = 2 ∙ 4 – 1 = 7.

4) f(0) = 2 ∙ 02 – 1 = –1 – не є

правильною рівність:

5) f(–1) = 1. f(–1) = 2 ∙(–1)2 – 1 = 1 – правильна рівність. 6) f(–5) = 19. f(–5) = 2 ∙ (–5)2 – 1 = 50 – 1 = 49 –

881. Функцію задано формулою y = x2 - 3.

рівність.

значення y, якщо:

1) x = 5; у = 52 – 3 = 22. 2) x = –4; у = (-4)2 – 3 = 13.

3) x = 0,1; у = (0,1)2 – 3 = -2,99. 4) x = 0; у = 02 – 3 = -3.

882. Функцію задано формулою f (x) = 3 + 4x.

значення x, при якому: 1) f(x) = 19; 3 + 4x = 19; 4x = 19 – 3; 4x = 16; x = 4.

2) f(x) = –3; 3 + 4x = –3; 4x = –3 – 3; 4x = –6; x = –1,5.

3) f(x) = 0; 3 + 4x = 0; 4x = –3; x = – 0,75.

4) f(x) = 323; 3 + 4x = 323; 4x = 320; x = 80.

883. Функцію задано формулою f (x) = –0,1x – 2. Знайдіть значення x, при якому: 1) f(x) = 1; –0,1x – 2 = 1; 0,1x = 3; x = 3: (–0,1); x = –30.

2) f(x) = –100; –0,1x – 2 = –100; –0,1x = –100 + 2; –0,1x = –98; x = –98 : (–0,1); x = 980.

3) f(x) = –43,6; –0,1x – 2 = –43,6; –0,1x = 2 – 43,6; –0,1x = –41,6; x = –41,6 : (–0,1); x = 416.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

ƒ(3), ƒ(–4), ƒ(0), ƒ(–0,5), ƒ(3,2). 2) Знайдіть значення

правильною рівність: ƒ(5) = 9, ƒ(0,3) = 0,4, ƒ(–3) = –7? 1) ƒ(3) = 2 ∙ 3 – 1 = 6 – 1 = 5; ƒ(–4) = 2 ∙ (–4) – 1 = – 8 – 1 =

9; ƒ(0) = 2 ∙ 0 – 1 = 0 –1 = –1; ƒ(–0,5) = 2 ∙ (–0,5) – 1 = –1 – 1 = –2; ƒ(3,2) = 2 ∙ 3,2 – 1 = 6,4 – 1 = 5,4.

2) якщо ƒ(х) = 7, то: 7 = 2х – 1; 2х = 8; х = 4; якщо ƒ(х) = –9, то: –9 = 2х – 1; 2х = –8; х = –4; якщо ƒ(х) = 0, то: 0 = 2х – 1; 2х = 1; х = 0,5; якщо ƒ(х) = –2,4, то: –2,4 = 2х – 1; 2х = –1,4; х = –0,7;

3) ƒ(5) = 2 ∙ 5 – 1 = 10 – 1 = 9 — рівність ƒ(5) = 9 правильна;

ƒ(0,3) = 2 ∙ 0,3 – 1

–3) = 2 ∙ (–3) – 1 = –6 – 1 = –7 — рівність ƒ(–3) = –7 правильна. 886. Функцію задано

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

y(–3) = (–3)2 + (–3) + 1 = 9 – 3 + 1 = 7.

y(–2) = (–2)2 + (–2) + 1 = 4 – 2 + 1 = 3.

y(–1) = (–1)2 + (–1) + 1 = 1.

y(0) = 02 + 0 + 1 = 1.

y(1) = 12 + 1 + 1 = 3.

y(2) = 22 + 2 + 1 = 7.

y(4) = 42 + 4 + 1 = 16 + 4 + 1 = 21.

y(7) = 72 + 7 + 1 = 49 + 7 + 1 = 57. х

889.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

898. Дано функції g(x) = 20 х −3 і h (x) = 8 – 3x.

1) g(1) = 20 1 – 3 = 17. h(1) = 8 – 3 ∙ 1 = 5. g(1) > h(1);

2) g(5) = 20 5 – 3 = 1. h(2) = 8 – 3 ∙ 2 = 2. g(5) < h(2);

3) g(–2) = 20 −2 – 3 = –13. h(6) = 8 – 3 ∙ 6 = –10. g(–2) < h(6).

899. Дано функцію. Знайдіть: 1) ƒ (–3); 2) ƒ (–2); 3) ƒ (2); 4) ƒ (3); 5) ƒ (2,9); 6) ƒ (8,1).

�� (�� ) �

2х +1, якщо х≤ 2, х2 , якщо 2 < х <3, 6, якщо х≥ 3.

1) ƒ(-3) = -2 ∙ (-3) + 1 = 7;

2) ƒ(-2) = -2 ∙ (-2) + 1 = 5;

3) ƒ(2) = 22 = 4;

4) ƒ(3) = 6;

5) ƒ(2,9) = 2,92 = 8,41; 6) ƒ(8,1) = 6.

900. Знайдіть

у = � 2х +4, якщо х >0; 0,1х 5, якщо х≤ 0.

1) у(3) = -2 ∙ 3 + 4 = -2;

2) у(0,001) = -2 ∙ 0,001 + 4 = -0,002 + 4 = 3,998;

3) у(0) = 0,1 ∙ 0 – 5 = -5;

4) у(-8) = 0,1 ∙ (-8) – 5 = -0,8 – 5 = -5,8.

901.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

якщо: х2 – 8х = 4 – 8х; х2 = 4; х = –2 або х = 2. 904. Функцію задано формулою ƒ (x) = 3x +

дорівнює значенню аргументу?

Значення функції ƒ(х) = 3х + 5 дорівнює значенню

якщо: х = 3х + 5; х – 3х = 5; –2x = 5; х = –2,5. 905. Функцію задано формулою y = x2 + 2x − 1.

дорівнює подвоєному значенню аргументу?

Значення функції

2х = х2 + 2х – 1; х2 – 1 = 0; х2 = 1; х = –1 або х = 1.

906. Функцію

ƒ (–2,8).

ƒ(3,7) = 3, ƒ(0,64) = 0, ƒ(2) = 2, ƒ(0) = 0, ƒ(

908. Яке

жодного кореня: 1) 3,4(1 + 3х) – 1,2 = 2(1,1 + 5,1х);

3,4 + 10,2х – 1,2 = 2,2 + 10,2x; 10,2x – 10,2x = 2,2 – 3,4 + 1,2;

0х = 0 — рівняння має безліч

Відповідь: Рівняння

3) 3(|x – 1| – 6) + 21 = 0;

3(|x – 1| – 6) = – 21; |x – 1| – 6 = –7; |х – 1| = –1 —

кореня.

Відповідь: Рівняння

кореня;

2) |2х – 1| = 17,3; 2x – 1 = 17,3 або 2x – 1 = –17,3; 2х = 18,3 або 2х = –16,3; х = 9,15 або x = –8,15 — рівняння має два корені.

Відповідь: Рівняння має два корені;

4) 0,2(7 – 2x) = 2,3 – 0,3(x – 6); 1,4 – 0,4x = 2,3 – 0,3x + 1,8; –0,4x + 0,3x = 2,3 + 1,8 – 1,4 ; –0,1x = 2,7; x = –27

+ 10) + 10 = n + 20.

(n + 20)(n + 10) – n(n + 20) = 320; n2 + 10n + 20n + 20 – (n2 + 20n) = 320; n2 + 10n + 20n + 20 – n2 – 20n = 320; 10n + 20 = 320; 10n = 300; n = 30.

n + 10 = 30 + 10 = 40, а третє — n + 20 = 30 + 20 = 50.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Відповідь: 30; 40; 50. 910.

2 – 4b2 + 4bс – с2 = a2 – (4b2 – 4bс + с2) = a2 – (2b – с)2 = (а – 2b + с)(а + 2b – с) = (а + с –

= 0.

911. Відомо, що x + y = а2 4 , y + z = –a, x + z = 1. Доведіть, що вираз x + y + z

невід’ємних значень. (x + y) + (x + y) = а2 4 + (–a) + 1; x + y + y + z + x + z = а2 −4а+4 4 ; 2x + 2y + 2z = (а−2)2 4 ; x + y + z = (а−2)2 8 –

912.

913.

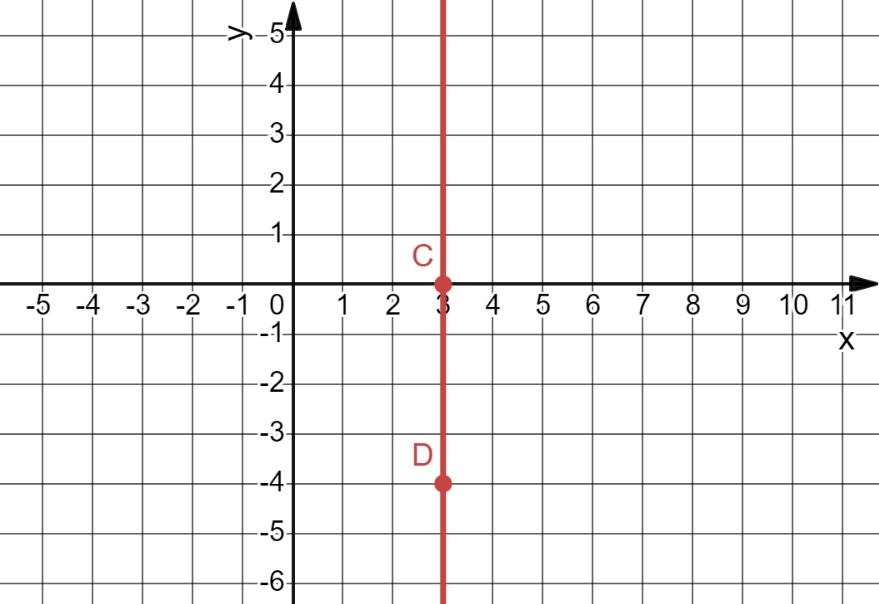
https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

рисунку 30. а) Д(у): -1 ≤ x < 4;

≤ y < 1; г) Д(у): -3 < x < 4; E(y): y = 2; ґ) Д(у): x = 1; x = 2; E(y): y = 1; y = -2. 918. Знайдіть

рисунку 31.

а) Д(у): -2 ≤ x < 2; E(y): 4 ≤ y < -1; б) Д(у): -2

2; Е(у): 4 ≤ у ≤ 1; в) Д(у): -2 ≤ х < 3; E(y): 1 ≤ y < 4; г) Д(у): -3 < x < 2; E(y): y = -2; ґ) Д(у): x = -3; x = 4; E(y): y = 3; y = -1. 919. Користуючись

1) значення аргументу, при яких y = 3; у = 3 при х = –3, х = 2, х = 6,5.

2) значення

у = 0 при х = –5, х = 3, х = 6.

3) область визначення функції; Д(у): [–5; 7].

4) область значень функції; Е(у): [–2; 5].

5) значення аргументу,

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

: Д(у): [–6; 6].

2) область значень функції: Е(у): [–5; 5].

3) координати точок

Ох: (–5; 0); (–3; 0); (3; 0) (5; 0).

4) координати точки перетину

Оу: (0; 5)

5) значення аргументу, при яких функція

у < 0 при х ϵ (–5; –3) ∪ (3; 5).

6) значення аргументу, при яких функція

у > 0 при х ϵ [–6; –5) ∪ (–3; 3) ∪ (5; 6].

922. На рисунку 34 зображено

функції y = ƒ(x). Користуючись графіком,

1) ƒ(–4); ƒ(–2,5); ƒ(0,5); ƒ(2); 2) значення x, при яких ƒ(x) = 2,5; ƒ(x) = 1; ƒ(x) = 0; 1) ƒ(–4) = 3,5; ƒ(–2,5) = 2; ƒ(0,5 ) = 0; ƒ(2) = 0,5;

2) ƒ(x) = 2,5, коли х = –3,5; ƒ(х) = 1, коли х = –2 або х = 1, або х = 4; ƒ(x) = 0, коли х = –0,5 або х = 0,5, або х = 2,5, або х = 3,5; 3) область визначення функції: усі х такі, що –4 ≤ х ≤ 4,5;

область значень функції: усі у такі, що –1 ≤ у ≤ 3,5; 4) значення функції додатне, якщо значення аргументу, наприклад, дорівнює: –4; –3; 1; 2; 5) значення функції від’ємне, якщо значення аргументу, наприклад, дорівнює: –0,5; 0; 3. 923. Чи належить графіку функції y = x2 + 2 точка:

1) точка А(0; 2) належить графіку функції у

2 = 02 + 2; 2 = 2

2) точка В (–1; 1) не

1 = (–1)2 + 2; 1 = 3 неправильна

3) точка С(–2; 6) належить

6 = (–2)2 + 2; 6 = 6

4) точка D(–3; –7)

бо –7 = (–3)2

1) у = 7х – 4. Якщо х = 0, то у = 7 ∙ 0 – 4 = – 4; якщо а = –1, то у = 7 ∙ (–1) – 4 = –11; якщо х = 2, то у = 7 ∙ 2 – 4 = 10; якщо х = 4, то у = 7 ∙ 4 – 4 = 24. Графіку функції у = 7а – 4 належать точки (0; –4); (–1; –11); (2; 10); (4; 24); 2) у = а2 + 1. Якщо х = 0, то у = 02 + 1 = 1; якщо х = –1, то у = (–1)2 + 1 = 2; якщо x = 2, то у = 22 + 1 = 5; якщо x = 4, то у = 42 + 1 = 17. Графіку функції у = х2 + 1 належать точки (0; 1); (–1; 2); (2; 5); (4; 17); 3) у = 4 – |x|. Якщо х = 0, то у = 4 – |0| = 4; якщо х = –1, то у = 4 – |–1| = 3; якщо х = 2, то у = 4 – |2| = 2; якщо а = 4, то у = 4 – |4| = 0. Графіку функції у = 4 – |x| належать точки (0; 4); (–1; 3); (2; 2); (4; 0).

926. Графікам

1) у = 1 – 2х; 2 = 1 – 2 ∙ 1; 2 = 1 – 2; 2 = –1. не належить.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2) у = х2 + 1; 2 = 12 + 1; 2 = 2; належить. 3) у = 2 х 2 = 2 1 2 = 2. належить.

927. Чи належить графіку

4) у = 0,3х + 0,7; 2 = 0,3 ∙ 1 + 0,7; 2 = 1; не належить.

х?

Графіком

1; 1)

shkola.in.ua

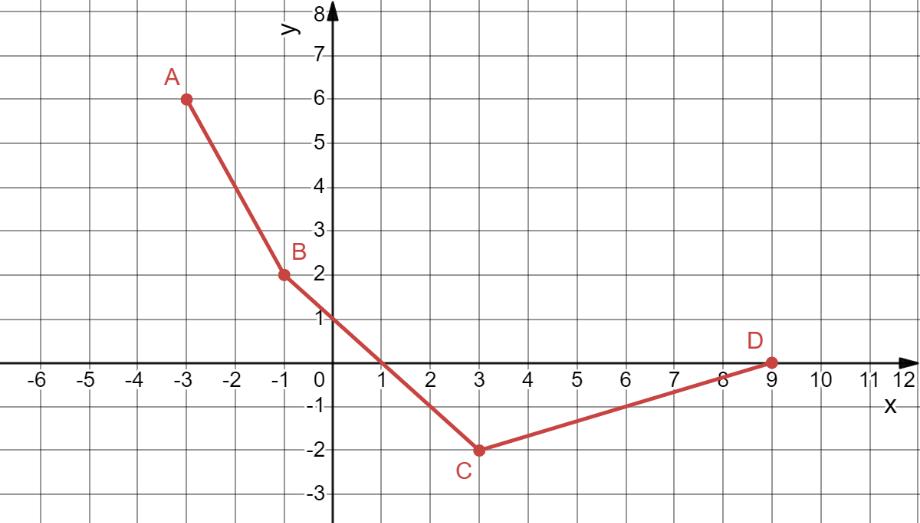
2) якщо x = якщо x = 0, то у = 1; якщо x = 2, то у

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

і (4; 0).

графіка функції:

1) у = х2 – 16х. а) х2 – 16х = 0; х(х – 16) = 0;

(0; 0);

2) у = |х| – 2. а) |х| – 2 = 0; |х|

віссю

(–2; 0); (2; 0); б) |0| – 2 = –2. Координати

2);

3) у = х3 – 9х.

а) х3 – 9х = 0; х(х2 – 9) = 0; х(х – 3)(х + 3) = 0; х =

б) 03 – 9 ∙ 0 = 0.

Координати

4) у = 0,8х.

а) 0,8х

1) у = 36 – 9x.

а) 36 – 9х

віссю абсцис (4; 0);

б) 36 – 9

0 = 36.

(0; 0); (16; 0);

(0;

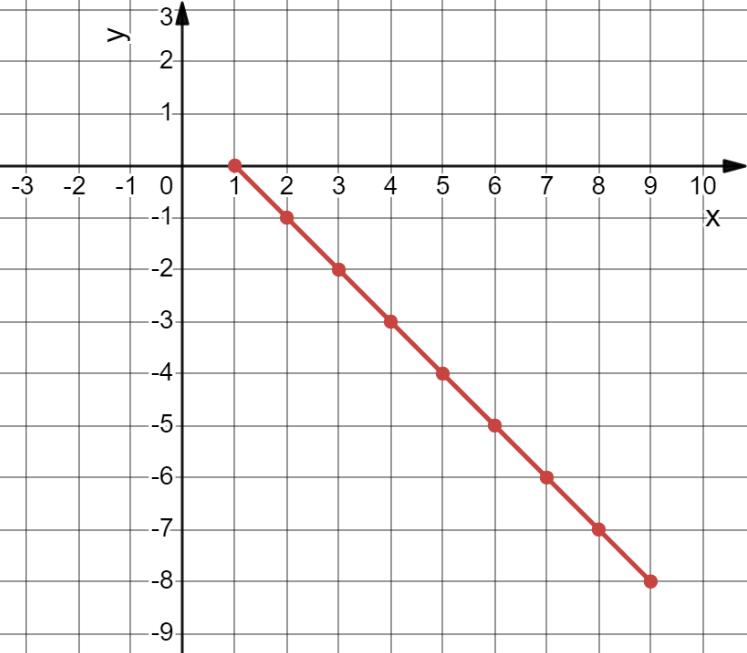
28у – 2 = –70y2 – 112у + 173.

944. Доведіть тотожність: 1) (4а2 + 3)2 + (7 – 4а2)2 – 2(4a2

тотожність доведена; 2) (а2 – 6аb + 9b2)(a2

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1 5 x + 1 3х + 3 ∙ (1 3 x –1 5x) + 1 = х|∙ 15;

3х + 5х + 15х – 9х + 15 = 15х; 14х + 15 = 15x; x = 15.

Відповідь: 15 бджілок. 948. У таблиці

прямо пропорційними. 1)

х 2 5 7 9

у 6 15 21 27

Величини

6 : 2 = 15 : 5 = 21 : 7 = 27 : 9 = 3;

9,6 : 3,2 = 3; 0,3 ∙ 3 = 0,9; 8 ∙ 3 = 24; 2,7 : 3 = 0,9; 42 : 3 = 14.

х 0,3 8 3,2

= –4; 9) у = 0, k = 0, b = 0. 952.

дорівнює: 9; –5; 0.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

y = –2x + 5.

–4; 3,5; 0; 2) значення

1) Якщо х = –4, то у = –2 ∙ (–4) + 5 = 8 + 5 = 13; якщо х = 3,5, то у = –2 ∙ 3,5 + 5 = –1 + 5 = –2; якщо х = 0, то .у = –2 ∙ 0 + 5 = 5;

2) якщо у = 9, то: 9 = –2х + 5; 2х = –4; х = –2; якщо у = –5, то: –5 = –2х + 5; 2х = 10; х = 5;

якщо у = 0, то: 0 = –2х + 5; 2х = 5; х = 2,5.

955. Функцію задано формулою y = 0,4x + 3.

+ 3 = –

5; –2; 0; 2)

1; –11; 0,8. у = 0,3х – 2.

1) Якщо х = 5, то у = 0,3 ∙ 5 – 2 = 1,5 – 2 = –0,5; якщо х = –2, то у = 0,3 ∙ (–2) – 2 = –0,6 – 2 = –2,6;

якщо х = 0, то у = 0,3 ∙ 0 – 2 = –2; 2) якщо у = 1, то: 1 = 0,3х – 2; 0,3х = 3; х = 10; якщо у = –11, то: –11 = 0,3х – 2; 0,3х = –9; х = –30; якщо у = 0,8, то: 0,8 = 0,3х – 2; 0,3х = 2,8; 3х = 28; х = 28 3 957. Заповніть таблицю

1) у = х + 3 2) у = 1 3 х – 5 0 3

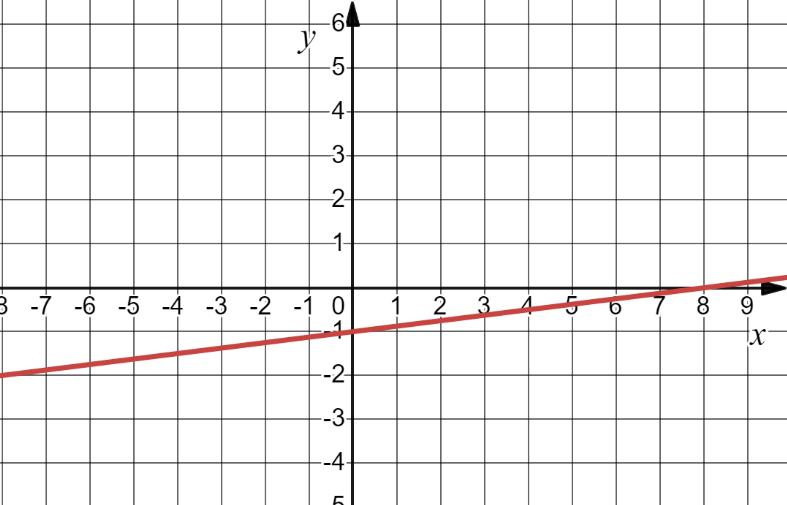
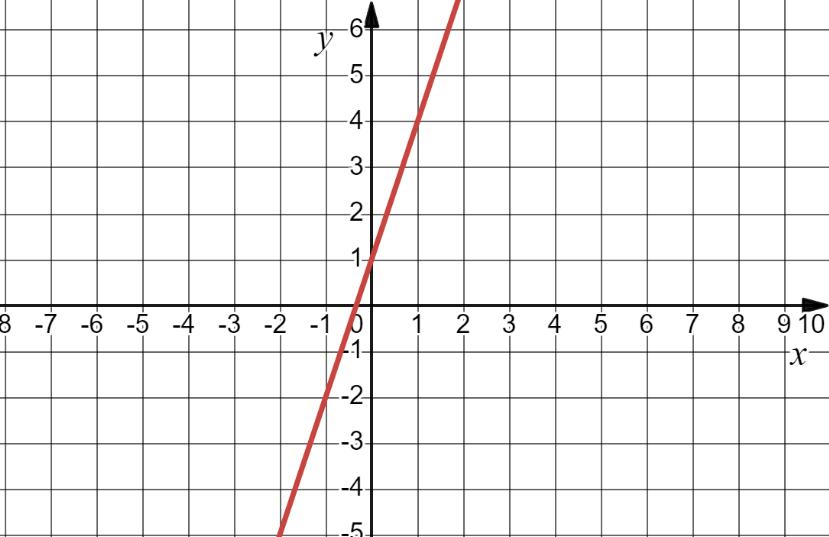
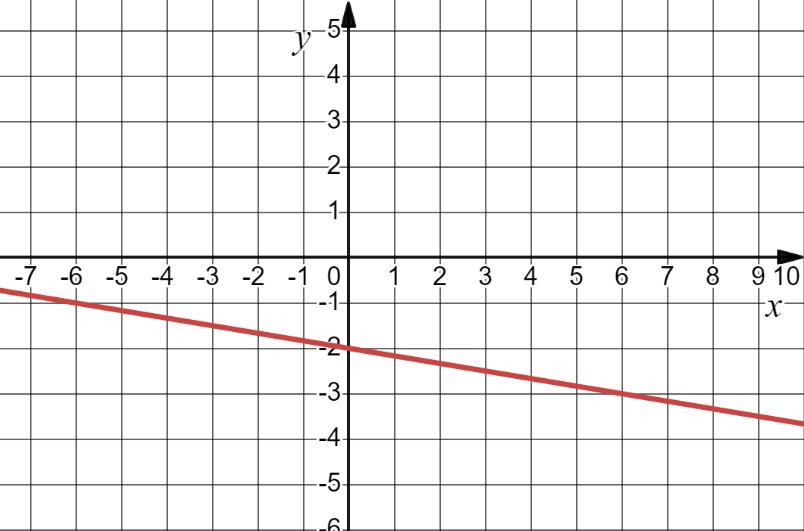
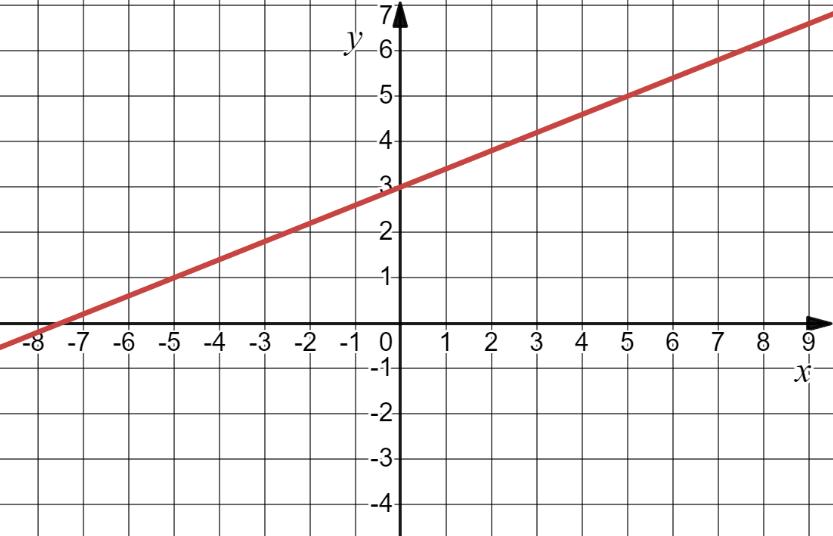
https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

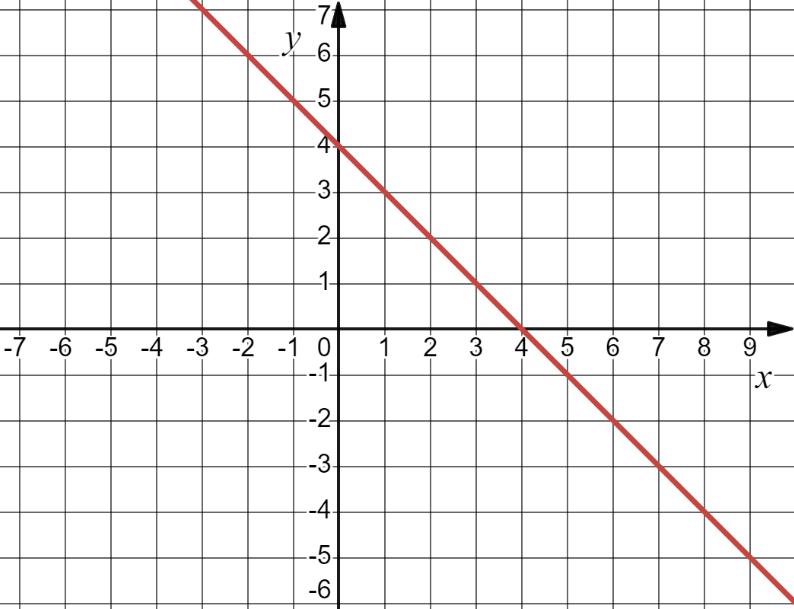
y = 1,2x.

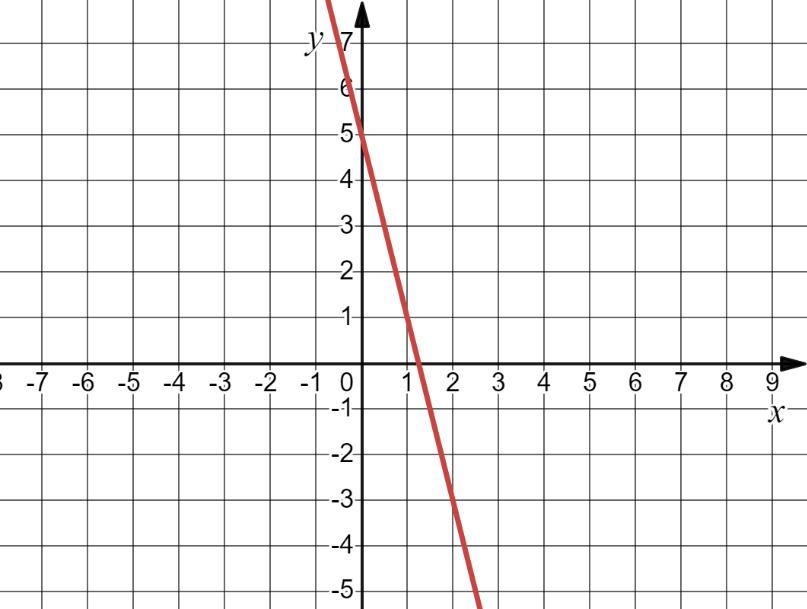
= –2; 1 3; 12. якщо у = –2, то: –2 = 1 3х; х = –6; якщо у = 1 3, то: 1 3 = 1 3

1) значення y, якщо x = 10; 0,6; –5; –4; Якщо х = 10, т о у= 1,2 ∙ 10= 12; якщо x = 0,6, то у = 1,2 ∙ 0 ,6 = 0,72; 2) значення x, при якому y = 3,6; –2,4; 6. якщо у = 3,6, то: 3,6 = 1,2x; х = 3; якщо у = –2,4, то: –2,4 = 1,2x; х = –2;

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

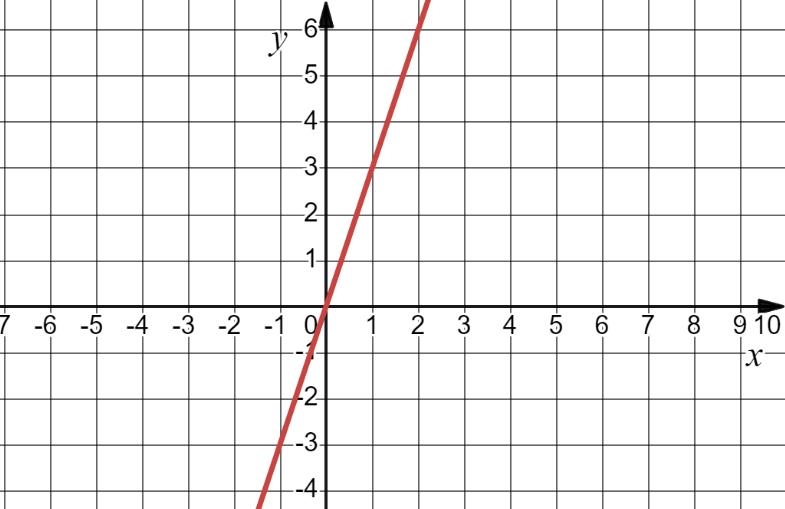
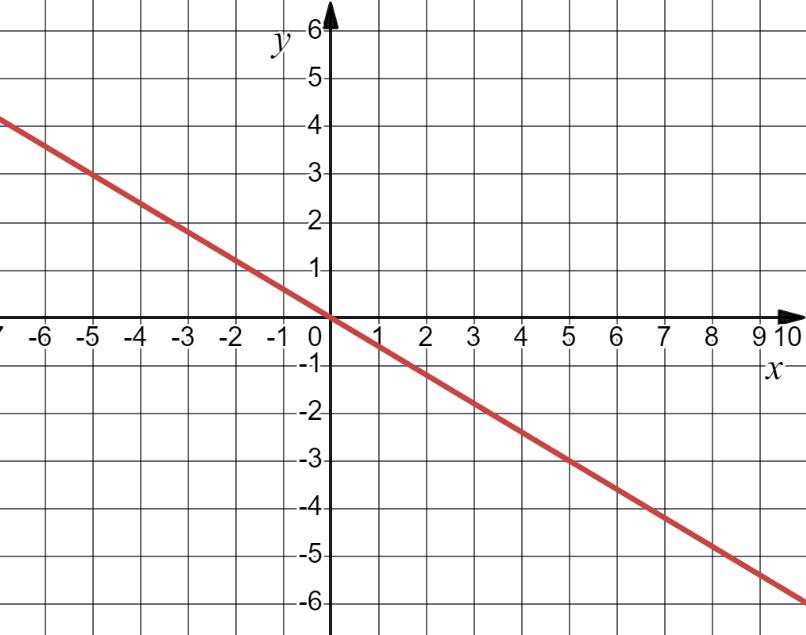
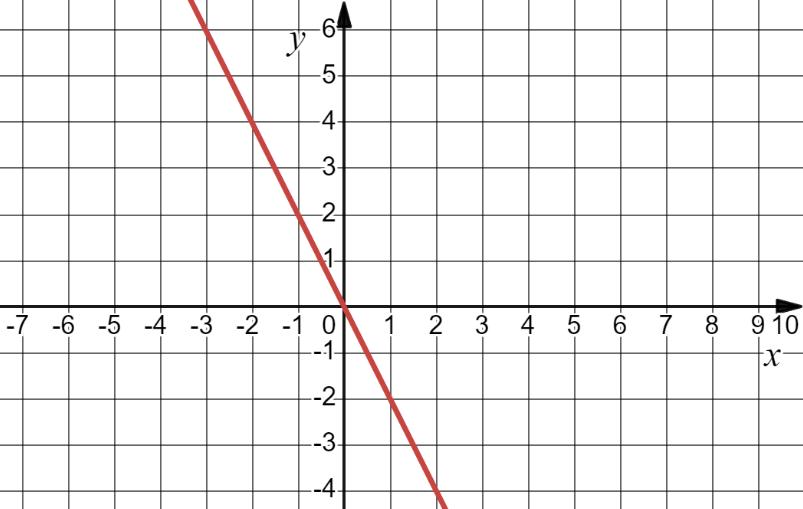
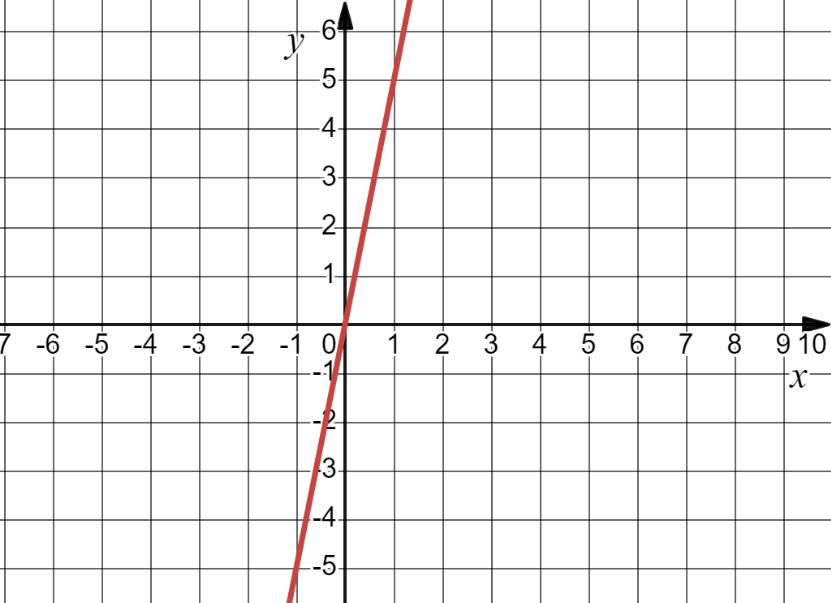
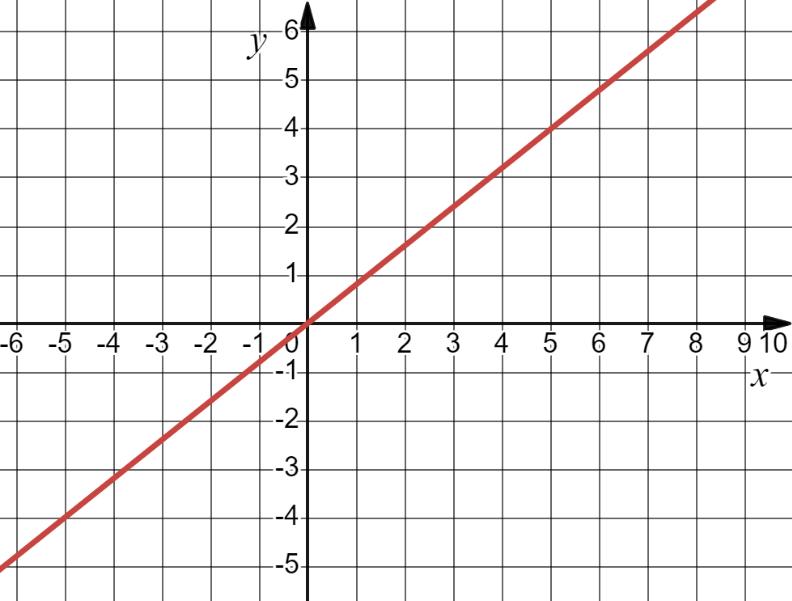
shkola.in.ua

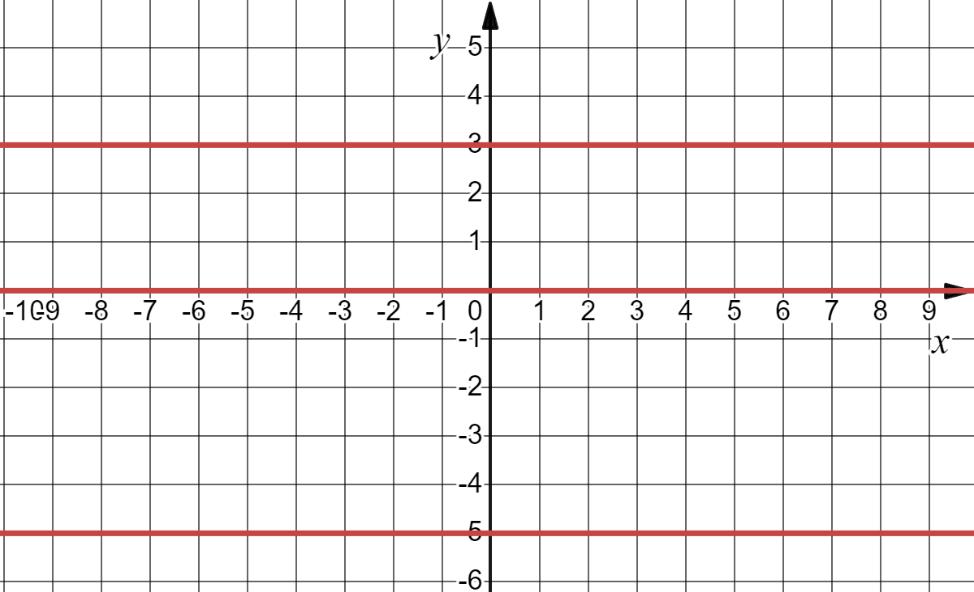
–6,6 = 1,8 ∙ (–2) – 3; –6,6 = –6,6 — правильна рівність.

Точка B(1; 1,2) не

1,2 = 1,8 ∙ 1 – 3; 1,2 = –1,2 — неправильна рівність.

Точка С(0;–3) належить графіку

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

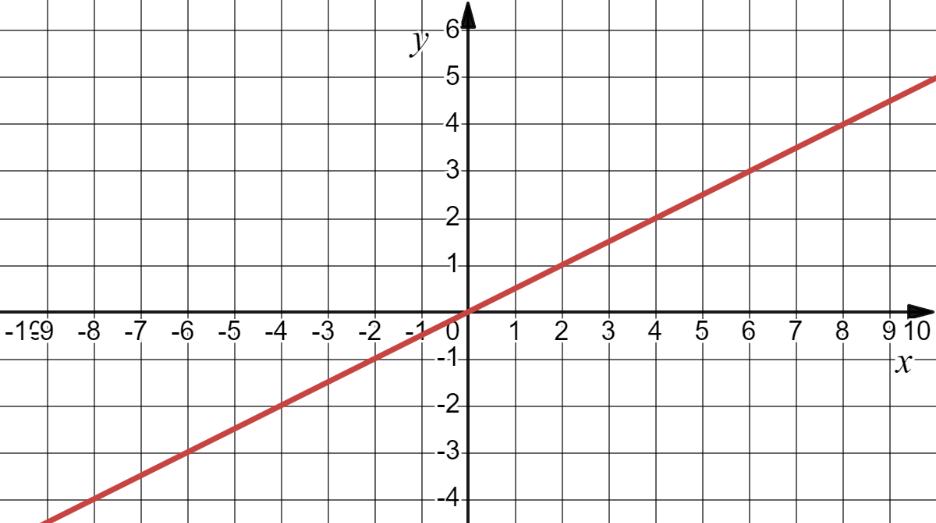
дорівнює: 1; –1; 0;

х 0 1 у -3 -1

1) Якщо х = 4,то у = 5;

якщо х = –1, то у = –5;

якщо х = 0,5, то у = –2;

2) якщо у = 1,то x = 2;

якщо y = –1, то x = 1; якщо у = 0, то х = 1,5; 3) функція

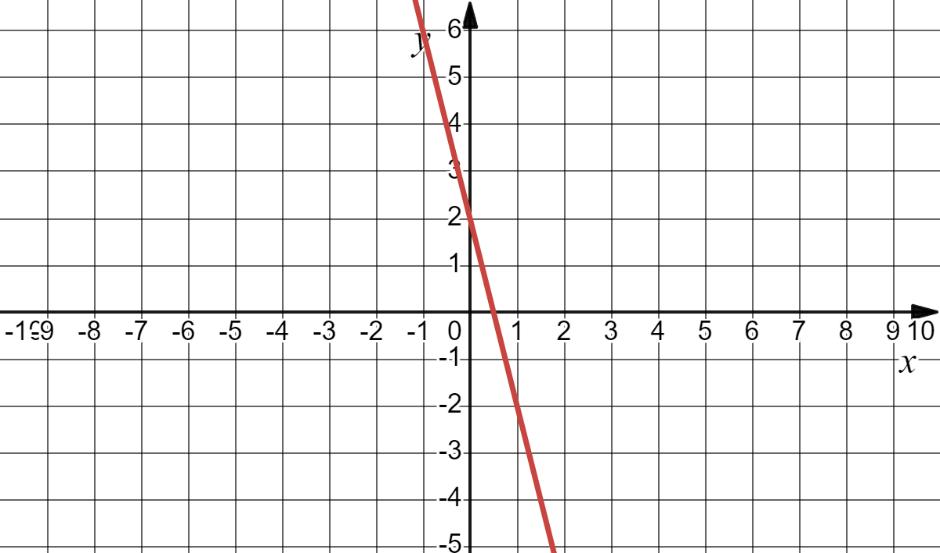
https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2,5; –2; 1; х 0 2

у 0 1

1) Якщо х = 4, то у = 2;

якщо х = –6, то у = –3; якщо х = 3, то у= 1,5;

2) якщо у = 2,5, то х = 5; якщо у = –2, то х = –4; якщо у= 1, то х = 2;

3) функція набуває від’ємних значень за усіх таких х, що х < 0.

973. Побудуйте графік функції y = –4x. Користуючись

х 0 0,5 у 0 -2

1) Якщо х = 2, то у = –8;

якщо х = –1, то у = 4; якщо х = 0,5, то у = –2;

2) якщо у = –4, то х = 1; якщо у = 2, то x = –0,5; 3) функція набуває додатних значень за усіх таких х, що х < 0.

у = х – 1

х 0 1

у -1 0 у = 1 4 х + 2

х 0 -4

у 2 1

(4; 3).

–

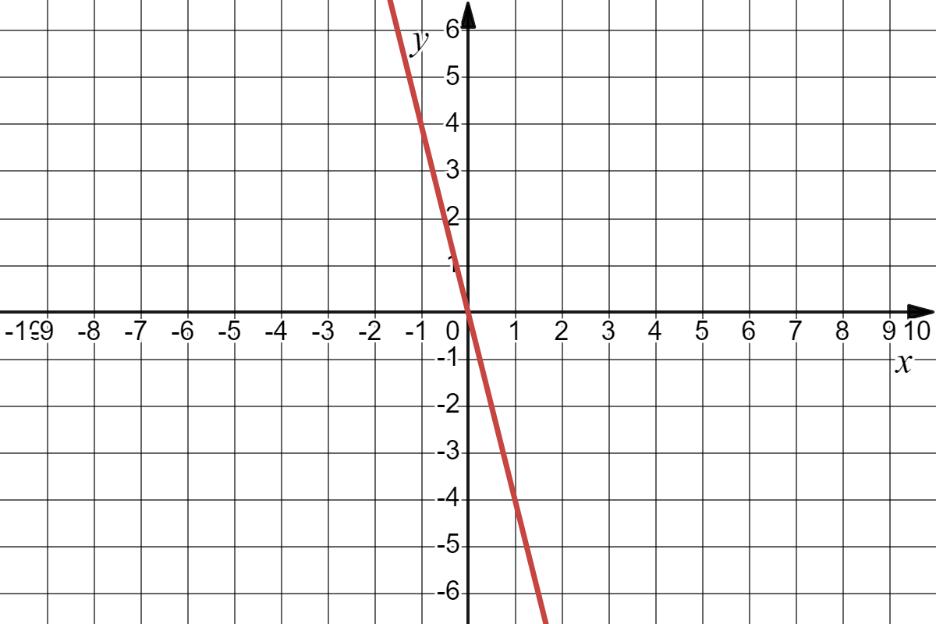
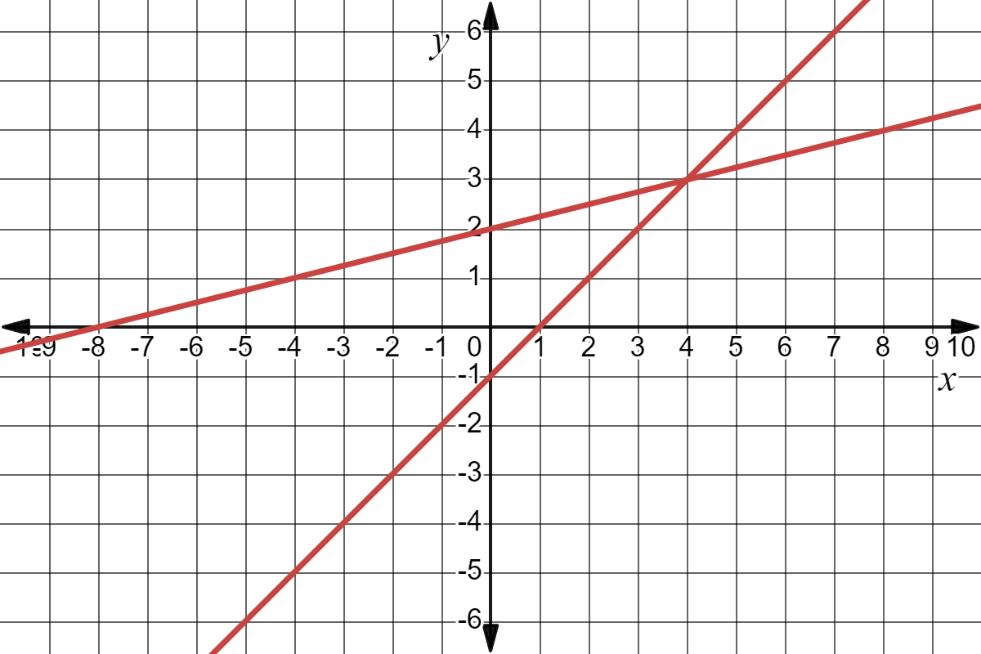
у = -2х + 1

х 0 1

у 1 -1

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Графіки перетинаються

(1; –1).

976.

функції:

1) у = 2,5х + 10.

а) 2,5х + 10 = 0; 2,5х = –10; х = –4.

б) 2,5 ∙ 0 + 10 = 10.

Координати

2) у = 6х – 4.

а) 6х – 4 = 0; 6х = 4; х = 2 3 .

Координати

б) 6 ∙ 0 – 4 = –4.

Координати

1) у = 2 3 х

б) 2 3 ∙ 0 –

2) у = 7 – 3х.

7 – 3х = 0; 3х = 7; х = 7 3 .

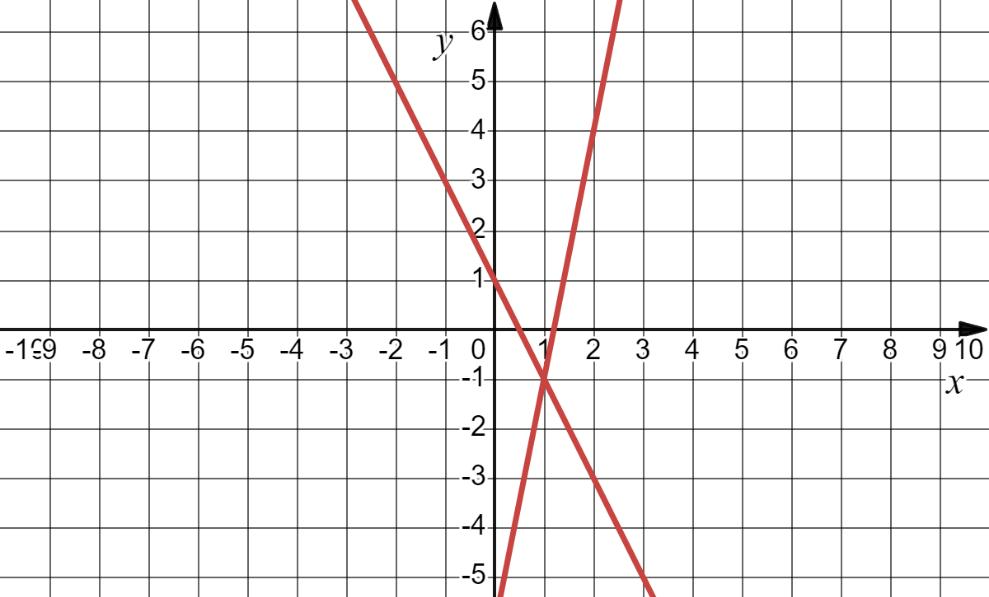
https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) 3,7x + 10= 1,4х – 13; 3,7х – 1,4х = –13 – 10; 2,3х = –23; х = –10; у = 1,4 ∙ (–10) – 13 = –27.

2) 4 –2 7 x = 2 7x + 26

28 – 2x = 9x + 182; –2x – 9x = 182 – 28; –11x = 154; x = –14; y = 9 7 ∙ (–14) + 26 = 8.

y = –2x + 11.

4х – 7 = –2x + 11; 6х = 18; x = 3; y = 4

x 0 1

ƒ(x) -3 1

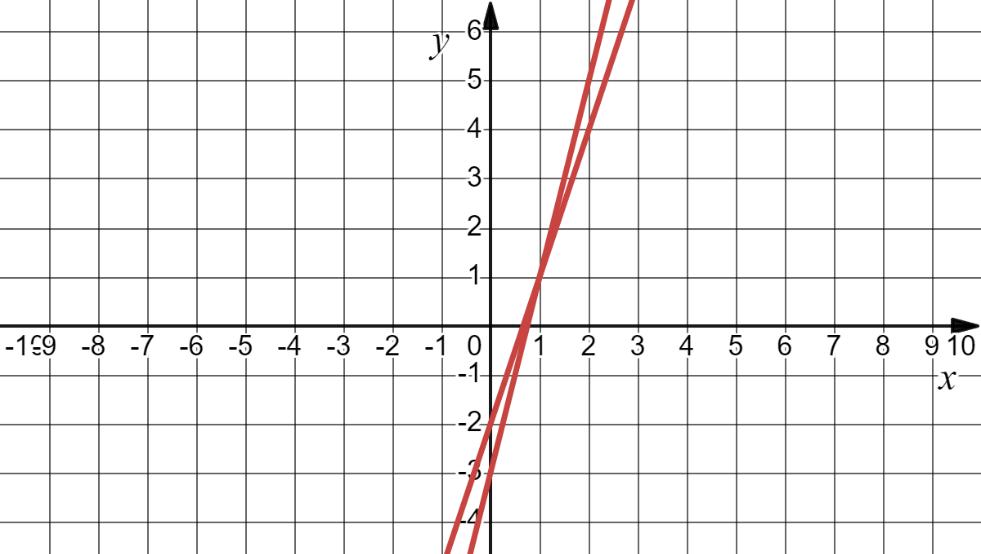
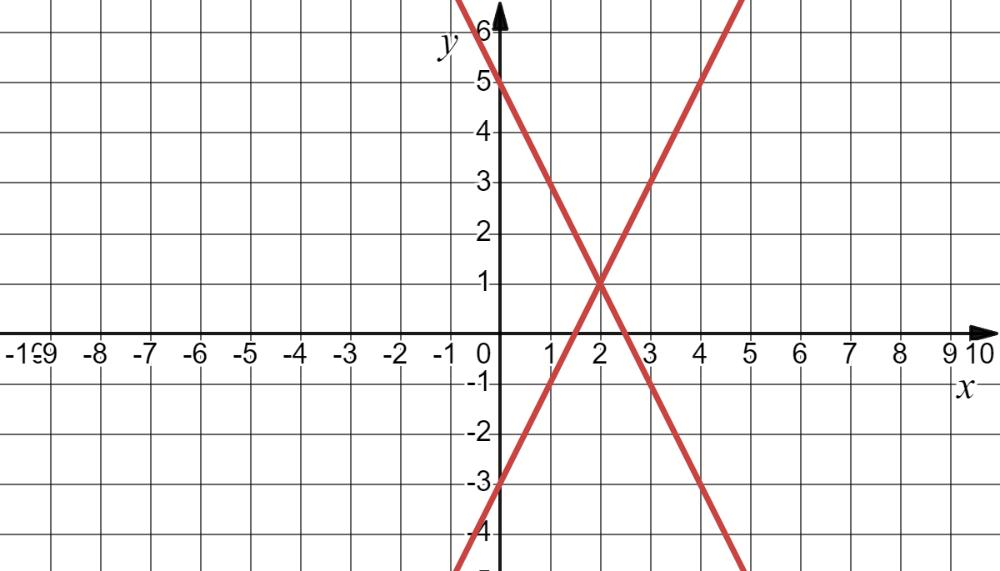
https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

M (2; –5).

985.

986.

–6 = k ∙ 3 – 15; 3k = –9; k = 3. 987. Графік функції y = kx + b

значення k і b. Якщо

функції у = kх + 4

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

функції у = kх + b проходить через точку (0; 50), то: 50 = k ∙ 0 + b; b = 50.

Якщо графік функції у = kх + 50 проходить через точку (10; 0), то: 0 = k ∙ 10 + 50; 10k = –50; k = –5. Формула залежності має вигляду = –5х + 50, де 0 ≤ х ≤ 10. Графік, зображений на рисунку б), є частиною

(0;

і (4; 20). Якщо

функції у = kx + b проходить через

у = kх + 10 проходить через точку (4; 20), то: 20 = k ∙ 4 + 10; 4k = 10; k = 2,5. Формула

3) графіком функції у = 1 4х на рисунку є

4) графіком функції у

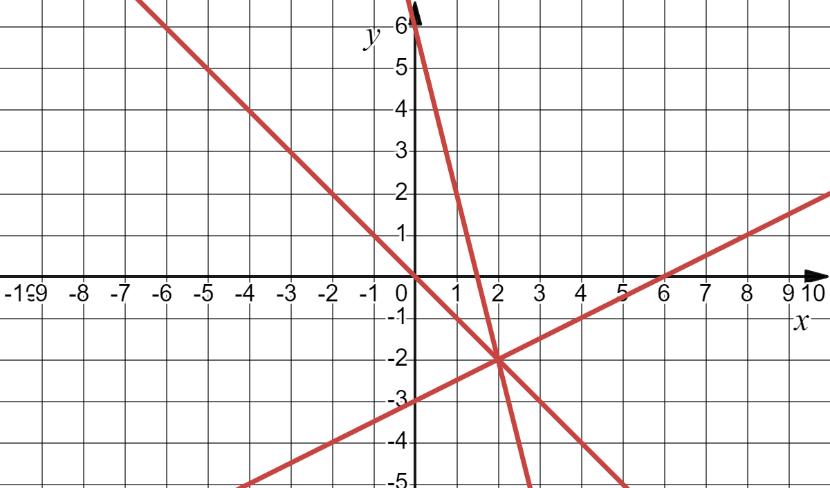
https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

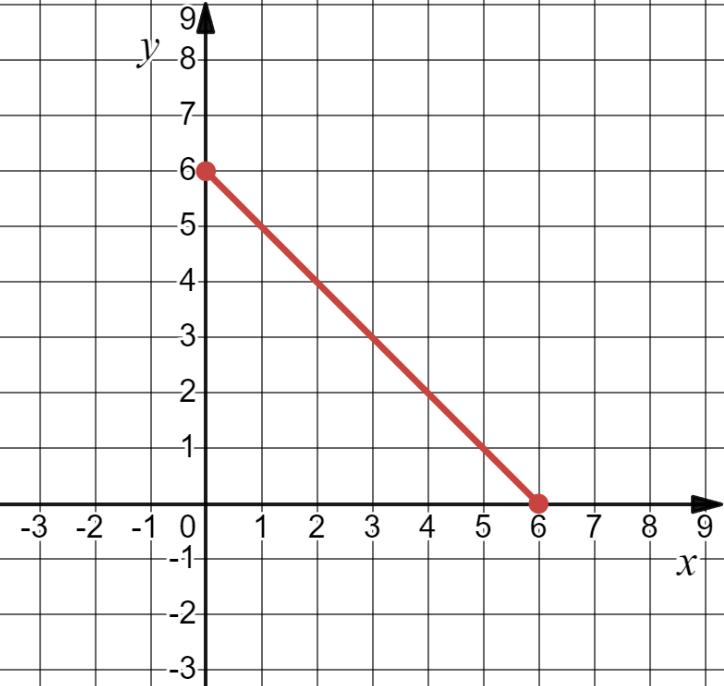
1) у = х – 4, х ≥ 0

х 0 2

у -4 -2

у = -2х – 4, х < 0

х -2 -1

у 0 -2

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2) у = 3х – 2, х ≤ 1

х -1 0 у -5 -2 у = 1, х > 1 х 1 2 у 1 1

3) у = 2, х ≠ 2

х -2 1

у 2 2

у = 3, х = 2

х 2 у 3

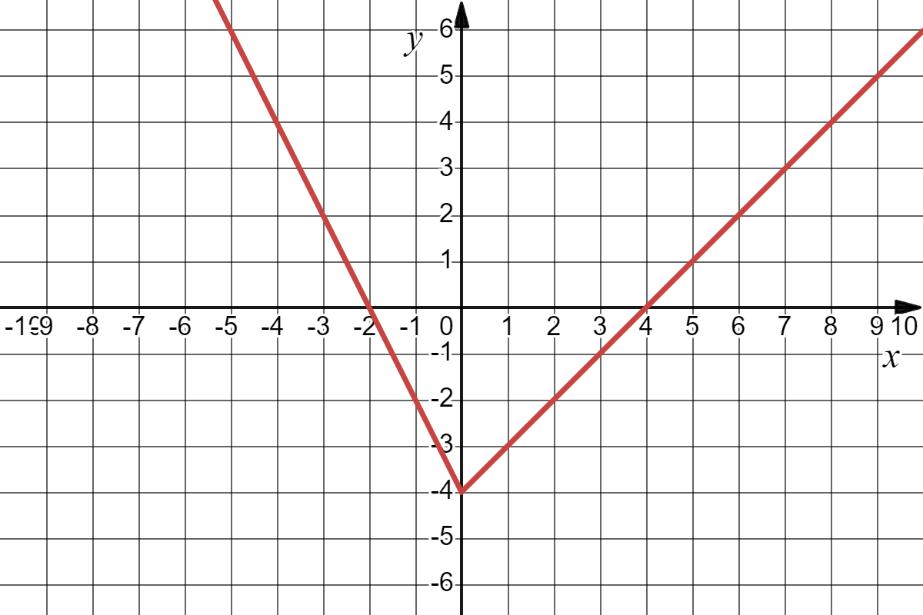
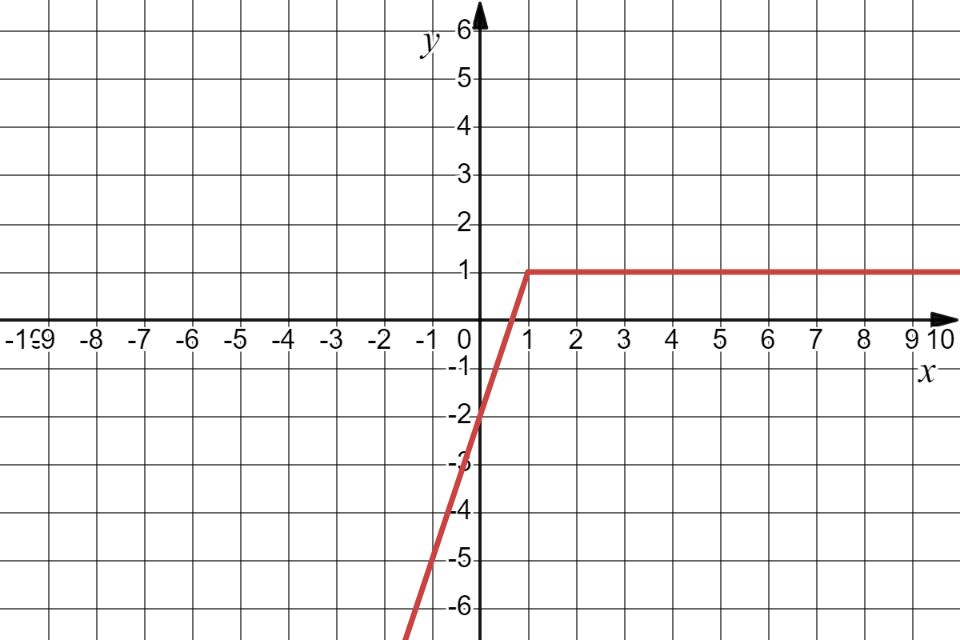
shkola.in.ua

у = 2х, х < -3

х -3 -2

у -6 -4

у = 1, х = -1

х -1

у 1

у = х + 3, х > -1

х 0 1 у 3 4

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

х -1,5 -1 у 4,5 3 у = 3, -1 < х < 1

х -0,5 0,5

у 3 3

shkola.in.ua

2) у = 5 – х, х ≤ 3

х 1 3

у 4 2

у = х + 1, х > 3

х 4 5

у 5 6

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1001. Побудуйте графік функції:

1) у = ǀхǀ. Скористаємось

означенням модуля:

у = �−х, якщо х <0, х, якщо х≥ 0.

у = -х, х < 0

х -2 -1

у 2 1

у = х, х ≥ 0

х 0 1

у 0 1

2) у = ǀхǀ + х. Скористаємось

означенням модуля:

у = �−х + х, якщо х <0, х + х, якщо х≥ 0;

у = � 0, якщо х <0, 2х, якщо х≥ 0.

у = 0, х < 0

х -2 -1

у 0 0

у = 2х, х ≥ 0

х 0 1

у 0 2

3) у = 4х - ǀхǀ + 2.

у = �4х

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

(−х) +2, якщо х <0, 4х −х +2, якщо х ≥ 0;

у = �5х +2, якщо х <0, 3х +2, якщо х≥ 0.

у = 5х + 2, х < 0

х -1,5 -1

у -5,5 -3

у = 3х + 2, х ≥ 0

х 0 1

у 2 5

1002. Побудуйте графік функції:

1) у = -ǀхǀ. Скористаємось

означенням модуля:

у = � (−х), якщо х <0, −х, якщо х≥ 0;

у = � х, якщо х <0, −х, якщо х≥ 0.

у = х, х < 0

х -4 -2

у -4 -2

у = -х, х ≥ 0

х 0 1

у 0 -1

2) у = х - ǀхǀ. Скористаємось

означенням модуля:

у = �х− (−х), якщо х <0, х−х, якщо х≥ 0;

у = �2х, якщо х <0, 0, якщо х≥ 0.

у = 2х, х < 0

х -2 -1

у -4 -2

у = 0, х ≥ 0

х 0 1

у 0 0

3) у = 3х + 2ǀхǀ.

Скористаємось

модуля:

у = �3х

у = �

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

+2(−х), якщо х <0, 3х + 2х, якщо х≥ 0;

х, якщо х <0, 5х, якщо х≥ 0.

у = х, х < 0

х -2 -1

у -2 -1

у = 5х, х ≥ 0

х 0 1

у 0 5

1003. Задайте

пряма a; 2) пряма b. 1) Пряма а, зображена на рисунку,

Якщо графік

Якщо графік функції у = kх + 3 проходить через

0 = k ∙ (–3) + 3; –3k = – 3; k = 1.

Формула функції має

у = x + 3.

2) пряма b, зображена на рисунку, проходить

Якщо графік лінійної функції у = kх + b

(–2; 0) і (0; –1).

точку (0; –1), то –1 = k ∙ 0 + b; b = –1 .

Якщо графік функції у = kх – 1

то: 0 = k ∙ (–2) – 1; 2k = –1; k = –0,5.

Формула функції має вигляд у = –0,5x – 1. 1004. Задайте формулою

пряма m; 2) пряма n. 1) Пряма m,

Якщо а = –1,5, то 26а = 26 ∙ (–1,5) = –39; 2) (3а + b)2 – (3а – b)2 = (3а + b – 3а + b)(3а + b +

Якщо a = –31 3, b = 0,3, то

1008. Розв’яжіть рівняння:

1) (5x + 1)(2х – 3) = (10х – 9)(х + 2); 10x2 – 15x + 2х – 3 = 10x2 + 20x – 9x – 18; 10x2 – 15x + 2x – 10x2 – 20x + 9x = –18 + 3; –24x = –15; x = 0,625.

Відповідь: 0,625; 2) (7x – 1)(х + 5) = (3 + 7x)(x + 3); 7x2 + 35x – x – 5 = 3x + 9 + 7x2 + 21x; 7x2 + 35x – x – 3x – 7х2 – 21x = 9 + 5; 10x = 14; x = 1,4.

Відповідь: 1,4.

1009. Доведіть,

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

shkola.in.ua

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

+ 4

у = –1,5х + 4, –2 = –1,5х + 4; –1,5х = –2 – 4; 1,5х = 6; х = 4.

Відповідь: А).

2. Серед наведених функцій укажіть

Відповідь: Г).

3. Яка з даних функцій не є

у = –2 х + 9. Відповідь: Б).

y(–3) = (–3)2 – 3 = 9 – 3 = 6. В(–3; 6).

Відповідь: Б).

5. Уранці

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

абсцисою –1?

у = mх + 2m – 5, А(–1;0);

у = 0, х = – 1;

m ∙ (–1 ) + 2m – 5 = 0;

–m + 2m = 5; m = 5.

Відповідь: А).

1016. Які з даних рівнянь є рівняннями з двома

Рівняннями з двома змінними є: 1) 2х + у = 8; 3) а2 – 3b = 8; 5) ху + 1 = 2; 6) 5m – 3n = 6; 8) х3 – 8у = 100; 9) х3 – 8ху = 100.

1017. Чи є пара чисел (–2; 3) розв’язком рівняння: 1) 4 ∙ (–2) + 3 ∙ 3 = – 8 + 9= 1. Пара чисел (–2; 3) є розв’язком рівняння 4х + 3у = 1; 2) (–2)2 + 5 = 32; 9 = 9. Пара чисел (–2; 3) є розв’язком рівняння х2 + 5 = у2; 3) –2 ∙ 3 = –6 ≠ 6. Пара чисел (–2; 3) не є розв’язком рівняння ху = 6. 1018. Які з пар чисел (0; 1), (5; –4), (0; 1,2), (–1; 1), (1; –1) є розв’язками рівняння: 1) х2 + 5у – 6 = 0; 02 + 5 ∙ 1 – 6 = –1 ≠ 0.

Пара чисел (0; 1) не є розв’язком рівняння

52 + 5 ∙ (–4) – 6 = 25 – 20 – 6 = –1 ≠ 0.

Пара чисел (5; –4) не є розв’язком рівняння

02 + 5 ∙ 1,2 – 6 = 6 – 6 = 0.

Пара чисел (0; 1,2) є розв’язком

(–1)2 + 5 ∙ 1 – 6 = 1 + 5 – 6 = 0.

Пара чисел (–1; 1) є розв’язком

12 + 5 ∙ (–1) – 6 = 1 – 5 – 6 = –10 ≠ 0.

Пара чисел (1; –1) не є розв’язком

2) ху + х = 0;

0 ∙ 1 + 0 = 0.

Пара чисел (0; 1) є розв’язком

5 ∙ (–4) + 5 = –20 + 5 = –15 ≠ 0.

Пара чисел (5; –4) не є

0 ∙ 1,2 + 0 = 0. Пара чисел (0; 1,2) є розв’язком

1 +

= 0; 1 ∙ (–1) + 1 = –1 + 1 = 0. Пара чисел (1; –1) є розв’язком рівняння

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

4) 2 ∙ (–1)2 – 4 + 1 = 2 – 4 + 1 = –1 ≠ 0.

Отже, точка D(–1; 4) не

1020. Доведіть, що графік рівняння xy – 12 = 0 не

2х2 – у + 1 = 0.

точку: 1) 3 ∙ (–4) – 12 = –12 – 12 = –24 ≠ 0.

Отже, графік рівняння ху – 12 = 0 не

через точку A(3; –4); 2) –2 ∙ 6 – 12 = –12 – 12 = –24 ≠ 0.

Отже, графік рівняння ху – 12 = 0 не проходить через точку В(–2; 6); 3) 7 ∙ 2 – 12 = 14 – 12 = 2 ≠ 0.

Отже, графік рівняння ху – 12 = 0 не проходить через точку С(7; 2).

1021. Чи проходить через початок координат графік рівняння: 1) 12 ∙ 0 + 17 ∙ 0 = 0.

Отже, графік рівняння 12х + 17у = 0 проходить через початок координат; 2) 02 – 0 ∙ 0 + 2 = 2 ≠ 0.

Отже, графік рівняння х2 – ху + 2 = 0 не проходить через початок координат;

3) 03 – 4 ∙ 0 = 02 + 3 ∙ 0; 0 = 0.

Отже, графік рівняння х3 – 4у = у2 + 3х проходить через

1022. Укажіть які–небудь три розв’язки рівняння:

1) Розв’язками рівняння х – у = 10 є, наприклад, пари чисел: (10; 0); (5;–5); (25; 15); 2) розв’язками рівняння х = 4у є, наприклад, пари чисел: (4; 1); (0; 0); (24; 6);

3) розв’язками рівняння 2х2 + у = 20 є, наприклад, пари чисел: (0; 20); (1; 18); (–1; 18). 1023. Укажіть які–небудь три розв’язки рівняння: 1) Розв’язками рівняння х + у = 1 є, наприклад, пари чисел: (1; 0), (2; –1), (0; 1); 2) розв’язками рівняння 5х – у = 2 є, наприклад, пари чисел: (1; 3), (2; 8), (0; –2).

1024. Графік рівняння 4x + 3y = 30 проходить через

4 ∙ 6 + 3 ∙ b = 30; 24 + 3b = 30; 3b = 6; b = 2. 1025. Графік рівняння 7x – 5y = 47

значення a?

7 ∙ а – 5 ∙ (–1) = 47; 7а + 5 = 47; 7а = 42; а = 6. 1026. Не виконуючи

A (6; b).

6; у = –2.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

чисел х = 1, у = 2 є розв’язком, наприклад,

2) пара чисел х = –3 ,у = 5 є розв’язком, наприклад, рівняння х2 + у = 14;

3) пара чисел х = 10, у = 0 є розв’язком, наприклад, рівняння х2 + у = 100. 1029. Складіть яке–небудь

точку:

1) Через точку А(–2; 2) проходить, наприклад,

2) через точку В(4; –1) проходить,

х + у = 3; 3) через точку С(0; 0) проходить,

x + у + 1= 1.

1030. Придумайте три рівняння,

Через точку М(6; –3) проходять,

1031.

3) 0 ∙ 0 = 0. Отже, рівняння ху = 0 має, наприклад, розв’язок (0; 0);

4) 32 + 42 = 25; 9 + 16 = 25. Отже, рівняння х2 + у2 = 25

наприклад, розв’язок (3; 4); 5) рівняння х2 + у2 = –25 не має розв’язків, бо сума

від’ємному числу.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

чисел (х + 2)2 + (у – 3)2

1036. Скільки розв’язків має рівняння:

1) Сума невід’ємних чисел х2 + (у

чисел (0; 2) — єдиний розв’язок рівняння

сума невід’ємних

пара чисел (–3; 1) є єдиним розв’язком рівняння (х + 3)2 + (у – 1)2 = 0;

3) сума невід’ємних чисел 9х2 + 16у2 може дорівнювати

дорівнюватиме нулю. Оскільки 02 + 02 = 0, то

рівняння 9x2 + 16у2 = 0; 4) рівняння (х2 + у2)у = 0 має безліч розв’язків, у

(0;

а y = 0; 5) рівняння ху = 2 має безліч розв’язків виду (а;2:а),

6) сума невід’ємних чисел |x + 1| + |у| може дорівнювати

дорівнюватиме

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

х = 2, то 22 + y2 = 5; y2 = 1; у = –1 або у = 1.

рівняння є: (–2; –1); (–2; 1); (–1; –2); (–1; 2); (1; –2); (1; 2); (2; –1); (2; 1). 1044.

2); 2) х2 + у2 + 2х – 6у + 10 = 0; (х

Розв’язком рівняння є (–1; 3);

3) х2 + y2 + х + у + 0,5 = 0; (х2 + х + 0,25) + (у2 + у + 0,25) = 0; (х +

Розв’язком рівняння є (–0,5; –0,5); 4) 9х

1047. Розв’яжіть рівняння: 1) х2 + 10у + 30 = 10х – у

(4х

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2) 150 + 90 = 240 (мл) —

3) 12 : 240 = 0,05 = 5% —

Відповідь: 5%.

1051. Знайдіть

��) 4х+1 5 2х 3 3 = х – 4|∙ 15;

3(4х + 1) – 5(2х – 3) = 15(х – 4); 12х + 3 – 10х + 15 = 15х – 60; 12х – 10х – 15х = –60 – 3 – 15; –13х = –78; х = 6.

Відповідь: 6;

км/год.

Рівняння: х 3,5 = 1,4(х−77) 3,5

3,5; x = 1,4(x – 77); x = 1,4x – 107,8; 0,4x = 107,8; x = 269,5.

Відповідь: 269,5 км. 1053. Чи

(5n + 10)2 – (2n + 4)2 = (5n + 10 –

3 = х + 9|∙ 12; 3(3х – 5) – 4(5х – 2) = 12(х + 9); 9х – 15 – 20х + 8 = 12х + 108; 9х – 20х – 12х = 108 + 15 – 8; –23х = 115; х = –5.

Відповідь: –5.

– 4)(5n + 10 + 2n + 4) = (3n + 6)(7n + 14) = = 3 ∙ 7 ∙ (n + 2)(n + 2) = 21(n + 2)2 .

Якщо n = 2k,

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1056.

є: 1) 7х + 11у = 36; 3) 12x – 17у = 0. 1057. Чи є

1) так; 2) ні; 3) ні; 4) так. 1058. Які з пар чисел (7; 1), (0; –2), (8; 2), (–7; –5), (10; 3) є розв’язками

14?

Пара чисел (7; 1) є розв’язком рівняння 3х

Пара чисел (0; –2) є розв’язком рівняння 3x

Пара чисел (8; 2) не є розв’язком

10 ≠ 14;

Пара чисел (–7; –5) є

Пара чисел (10; 3) не є розв’язком рівняння

9 ≠ 14. 1059. Розв’язком якого

2) пара чисел (3; –2) не є розв’язком рівняння

13 ≠ 5;

3) пара чисел (3; –2) є розв’язком рівняння,

0,2 ∙ 3 – 0,5 ∙ (–2) = 0,6 + 1 = 1,6.

1060. Чи є розв’язком рівняння 2x – 9y = 13

1) (2,5; 2) х = 2,5; у = 2 2 ∙ 2,5 – 9 ∙ 2 = 5 –

2) (10,5; 2) х = 10,5; у = 2 2 ∙ 10,5 – 9 ∙ 2 = 21 – 18 = 3 ≠ 13 не є розв’язком.

3) (5;–1 3) 2 ∙ 5 + 9 ∙ 1 3 = 10 + 3 = 13 є розв’язком.

4) (–7; –3) 2 ∙ (–7) – 9 ∙ (–3) = –14 + 27 = 13 є розв’язком. 1061. Відомо, що пара чисел (–5; y) є розв’язком рівняння 2x + 9y = 17. Знайдіть

значення y.

Якщо x = –5, то

2 ∙ (–5) + 9у = 17; –10 + 9у = 17; 9у = 27; у = 3.

1063. Відомо, що пара чисел (x; 2 3) є

1062. Відомо, що пара чисел (8; y) є розв’язком рівняння 2x – 3y = 4.

значення y. 2 ∙ (8) – 3у = 4; 16 – 3у = 4; –3у = 4 – 16; –3у = –12; у = 12 3 ; у = 4.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

(–3) + 10 = – 9 + 10 = 1 ≠ –1; 2)

розв’язки цього рівняння:

1) x + у = 12;

х = 12 – у.

Якщо у = 12, то х = 12 – 12 = 0.

Якщо у = 10, то х = 12 – 10 = 2.

Якщо у = 1, то х = 12 – 1 = 11.

Отже, пари чисел (0; 12), (2; 10), (11; 1) є

розв’язками рівняння;

3) 2х + 8у = 16;

х + 4у = 8;

х = 8 – 4у.

Якщо у = 0, то х = 8 – 0 = 8.

Якщо у = 1, то х = 8 – 4 = 4.

Якщо у = –1, то х = 8 + 4 = 12.

Отже, пари чисел (8; 0), (4; 1), (12; –1) є

розв’язками рівняння;

2) х – 7у = 5; х = 5 + 7у.

Якщо у = 0, то х = 5 + 0 = 5.

Якщо у = 1, то х = 5 + 7 = 12.

Якщо у = –1, то х = 5 – 7 = – 2.

Отже, пари чисел (5; 0), (12; 1), (–2; –1) є

розв’язками рівняння;

4) –6х + 5у = 18; –6х = 18 –5у; 6х = 5у – 18; х = 5у−18 6 .

у = 0, то х = 5∙0−18 6 = –3.

Якщо у = 6, то х = 5∙6−18 6 = 2. Якщо у = 12, то х = 5∙12−18 6 = 7.

пари чисел (–3; 0), (2; 6), (7; 12) є розв’язками рівняння. 1068. Виразіть із даного

у = 10. Якщо х = 0, то 0 – у = 10; у = –10. Якщо х = 5, то 5 – у = 10; у = –5. Якщо х = 10, то 10 – у = 10; у = 0. Отже, пари чисел (0; –10), (5;–5), (10; 0) є розв’язками рівняння; 2) 2у – 5х = 11. Якщо х = 0, то 2у – 0 = 11; у = 5,5. Якщо х = 1, то 2у – 5 = 11; 2у = 16; у = 8. Якщо х = –1, то 2у + 5 = 11; 2у = 6; у = 3. Отже, пари чисел (0; 5,5), (1; 8), (–1; 3) є розв’язками рівняння. 1070. Знайдіть які-небудь три розв’язки рівняння: 1) 6х + у = 7. Якщо х = 0, то 0 + у = 7; у = 7. Якщо х = 1, то 6 + у = 7; у = 1. Якщо х = 2, то 12 + у = 7; у = –5.

Отже, пари чисел (0; 7), (1; 1), (2; –5) є розв’язками рівняння; 2) 2х – 3у = –4. Якщо х = 1, то 2 – 3у = –4; –3у = –6; у = 2. Якщо х = 4, то 8 – 3у = –4; –3у = –12; у = 4. Якщо х = –2, то –4 – 3у = –4; –3у = 0; у = 0. Отже, пари чисел (1; 2), (4; 4), (–2; 0) є розв’язками рівняння.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1076. У якій точці

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

7y – 3x = 21 перетинає: 1) вісь x; 2) вісь y?

1) Якщо у = 0, то 0 – 3х = 21; х = –7.

Отже, пряма 7у – 3х = 21 перетинає вісь х у точці (–7; 0);

2) якщо х = 0, то 7у – 0 = 21; у = 3.

Отже, пряма 7у – 3х = 21 перетинає вісь у у точці (0; 3).

1077. Знайдіть координати точок перетину

1) Якщо у = 0, то 0,3х + 0 = 6; х = 20.

0,3x + 0,2y = 6 з

Отже, пряма 0,3х + 0,2у = 6 перетинає вісь х у точці (20; 0);

2) якщо х = 0, то 0 + 0,2у = 6; у = 30.

Отже, пряма 0,3х + 0,2у = 6

1078.

чисел (–2; 1).

Пара чисел (–2; 1) є розв’язком,

0,3х + у = 0,4.

1079. Складіть яке

чисел (3; 5).

Пара чисел (3; 5) є розв’язком,

3х + у = 14.

1080.

у у точці (0; 30).

7x + 8y = 30,

Якщо х = у, то: 7х + 8х = 30; 15х = 30; х = 2.

Розв’язком рівняння 7х + 8у = 30, який складається

(2; 2). 1081. Знайдіть розв’язок рівняння –12x + 17y = –87, який

чисел.

Якщо х = –у, то: –12(–у) + 17у = –87; 29у = –87; у = –3.

рівняння –

1085.

12 + 4

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

5 ∙ (–4) + b ∙ (–10) = 0; –10b = 20; b = –2; 2)

(0; 1), якщо: 5 ∙ 0 + b ∙ 1 = 0; b = 0; 3) графік рівняння 5x + bу = 0 не

точку К (–2; 0) бо, якщо: 5 ∙ (–2) + b ∙ 0 = 0; 0b = 10 і такого значення b не існує. 1088. Графіком яких рівнянь є та сама пряма, що й графік рівняння 2x – 5y = 3: Той же графік, що й графік рівняння 2х – 5у = 3, мають рівняння: 1) 4х – 10y = 6; 4) 5у – 2х = –3; 5) х – 2,5у =1,5. 1089. Складіть рівняння з двома змінними

і 3

1) 2х + 2у = 18; 2) 4х +

1) 2а + b = 32; 2) 7у – 6х = 32; 3) 0,14х – 0,18у = 1,2. 1091. Доведіть, що прямі 5y – x = 6 і 3x – 7y = 6 перетинаються в точці A (9; 3).

5 ∙ 3 – 9 = 6 — пряма 5у – х = 6 проходить через точку A(9; 3).

3 ∙ 9 – 7 ∙ 3 = 27 – 21 = 6 — пряма 3х – 7у = 6 проходить через точку A(9; 3). Отже, прямі 5у – х = 6 і 3х – 7у = 6 перетинаються

1096. При яких

0) і B (0; 12)?

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

ax + by = 24

Якщо х = –6, у = 0, то а ∙ (–6) + 0 = 24; –6а = 24; а = –4. Рівняння має вигляд: –4х + bу = 24.

Якщо х = 0,у = 12, то а ∙ 0 + b ∙ 12 = 24; b = 2.

Відповідь: –4; 2. 1097. На якому з рисунків 62, а–г зображено

рівняння x + y = 3?

Якщо у = 0, то х + 0 = 3; х = 3. Якщо х = 0, то 0 + у = 3; у = 3.

Отже, графік рівняння х + у = 3 проходить через точки (3; 0) і (0; 3).

Графік рівняння х + у = З зображено на рисунку в).

1098. На якому з рисунків 63, а–г зображено графік рівняння x – y = –5?

Якщо у = 0, то х – 0 = –5; х = –5. Якщо х = 0, то 0 – у = –5; у = 5.

Отже, графік рівняння х – у = –5 проходить через точки (–5; 0) і (0; 5).

Графік рівняння х – у = –5 зображено на рисунку в).

1099. Яка з прямих, зображених на рисунку 64, є графіком рівняння: 1) Графіком рівняння 0x + у = –3 є пряма d;

2) графіком рівняння 2х – у = 1 є пряма с;

3) графіком рівняння 3х + 0у = 6 є пряма b;

4) графіком рівняння х + 2у = 0 є пряма а.

1100. При якому значенні a

абсцис?

Якщо у = 0, то 2х – 0 = –6; х = –3.

Маємо: 4 ∙ (–3) + 0 = а; а = –12.

осі ординат?

Якщо х = 0, то 0 + 7у = 35; у = 5. Пряма

Маємо: 0 +

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Отже, рівняння має вид у = 0,6х

(6; 0) і K (0; 6).

Лінійне рівняння

0) і K(0; 6) можна записати у вигляді у = kх + b.

Якщо графік рівняння проходить через точку K(0; 6), то: 6 = 0k + b; b = 6.

Отже, рівняння має вид у = kх + 6.

Якщо графік рівняння проходить через точку М(6; 0), то: 0 = 6k + 6; 6k = –6; k = –1.

Отже, рівняння має виду = –х + 6. 1106. Складіть рівняння, графіки яких

Рівняння прямої m – х = –2.

рисунку 65.

Пряма d проходить через точки (0; 0) і (–1; 1). Рівняння прямої d

Маємо: –1 = k ∙ 1; k = –1. Отже, рівняння прямої

Пряма а проходить через точку (0; 3). Рівняння прямої

Маємо: 3 = k ∙ 0 + b; b = 3. Рівняння прямої а стало

Пряма а проходить через точку (–1; 0). Маємо: 0 = k

Рівняння прямої а стало у = 3х + 3.

Пряма с

через точку (0; –2).

Маємо: –2 = k ∙ 0 + b; b = –2. Рівняння прямої с стало у = kх –

Пряма с проходить через точку (4; 0).

kх + b.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Маг. «Смачно»: 2 ∙ 13 + 0,8 ∙ 140 + 0,5 ∙ 200 = 238 грн.

Знижка 5% 238 ∙ 0,95 = 226,10 (грн.).

«Апетит»: 2 ∙ 12 + 0,8 ∙ 135 + 0,5 ∙ 180 = 222 (грн).

«Свіжі продукти»: 2 ∙ 14 + 0,8 ∙ 155 ∙ 0,9 + 0,5 ∙ 240 ∙ 0,9 = 247,6 (грн).

Відповідь: найдешевше буде

Рівняння: 1,8х + х = 840; 2,8х = 840; х = 300.

Перша бригада виготовила 1,8 ∙ 300 = 540 (деталей).

Відповідь: 540 деталей, 300 деталей.

1111. Відомо, що 4 однакових екскаватори можуть

6 таких самих екскаваторів вириють 3 таких котловани?

12 ∙ 4 = 48 (год) — потрібно одному екскаватору, щоб вирити один котлован; 48 : 6 = 8 (год) — потрібно шести екскаваторам, щоб

8 ∙ 3 = 24 (год) — потрібно шести екскаваторам,

Відповідь: За 24 год. 1112. Доведіть, що

= 232

(16

2) 236 + 4100

= 232 ∙ (16 – 1) + 498

= 240 ∙ (228 + 496) — кратне числу 240.

1113. Розв’яжіть рівняння:

1) (х – 8)2 – (х – 4)(х + 4) = 0; x2 – 16х + 64 – х2 + 16 = 0; –16х + 80 = 0;

16х = 80;

х = 5.

Відповідь: 5; 2) (4х – 5)(4х + 5) – (4х – 1)2

8х + 2х =

10х = 35; х = 3,5.

Відповідь: 3,5.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

(1 + 100) + (2 + 99) + (3 + 98) + (4 + 97) +... + (50 + 51) = 101 ∙ 50 = 5050.

1118. Яка з пар чисел (–2; 1), (2; –1), (6; 4), (8; –4) є

8у = 14, є пара чисел (6;4), бо 4х + у = 28

3 ∙ 6 8 ∙ 4= 18 32 = 14, 4 ∙ 6+4= 24 +4= 28

1119. Чи є правильним твердження: 1) пара чисел (0; 0) не є розв'язком системи

рівнянь

= 53

�� +2�� =4

0 – 0 ≠ 5

0 + 0 ≠ 4

твердження правильне

3) пара

2(−1)

2(2) + 3(−1) = 4 – 3 = 1

правильне

5) �4�� +5�� =6 5�� +4�� =7 4 5 ≠ 5 7 система

2) пара чисел (-1; 2) є розв'язком системи рівнянь � �� + �� =1 3�� +2�� = 1 −1 + 2 = 1 3(−1) + 2(2) = −3 + 4 ≠ −1

твердження не є правильним

не є правильним

у = 1

х 0 1

у -1 0

х + 2у = 7

х 1 5

у 3 1

Графіки перетинаються в точкі (3; 2).

Розв’язком системи є

+ у = 0

х 0 1 у 0 -1

3х – у = 4

х 0 1 у -4 -1

Графіки перетинаються

чисел (3; 2);

х + у = -5

х 0 -5

у -5 0

4х

2х + у = 8

х 2 3

у 4 2

2х – у = 0

х 0 1

у 0 2

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Графіки перетинаються в точці (2; 4).

Розв’язком системи є пара чисел (2; 4);

х -2 -5 у 4 -3 у – 2х = 8 х -1 -4 у 6 0 Графіки

2х – 5у = 10

х 0 5

у -2 0

4х – у = 2

х 0 1

у -2 2

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

3��− 8�� = 7,

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

х = 3, у = 2 є,

4�� + �� = 14, бо �3 ∙ 3 8 ∙ 2=9 16 = 7, 4 ∙ 3+2= 12 +2= 14;

2) Пара значень змінних х = -4, у = 1 є, наприклад, розв’язком такої системи

рівнянь з двома змінними

3��− 8�� = 20, 4�� + �� = 15, бо �3 ∙ (−4) − 8 ∙ 1= −12 − 8= −20, 4 ∙ ( 4) +1= 16 +1= 15;

3) Пара значень змінних х = 5, у = 0 є, наприклад, розв’язком такої

рівнянь з двома змінними

3��− 8�� = 15,

4�� + �� = 20, бо �3 ∙ 5 8 ∙ 0= 15, 4 ∙ 5+0= 20. 1125. Складіть яку–небудь

(2; –2).

чисел (2; -2) є,

3��− 8�� = 22, 4�� + �� =5,

3 ∙ 2 − 8 ∙ (−2) =6+ 16 = 22, 4 ∙ 2+ ( 2) =8 2=6.

1126. Пара чисел (6; 4) є

1) Якщо пара чисел (6; 4) є розв’язком системи рівнянь

+2�� = 26, 4�� + �� = 14, то ��∙ 6+2 ∙ 4= 26, 4 ∙ 6+ ��∙ 4= 14; � 6�� = 18, 4�� = 10; � �� =3, �� = 2,5;

2) Якщо пара чисел (6; 4) є розв’язком системи рівнянь

5�� + �� =6, �� + �� =0, то � 5 ∙ 6+ ��∙ 4=6, 4 ∙ 6+ ��∙ 4=0; � 4�� = 24, 6�� +4�� =0; � �� = 6, 6�� + ( 24) =0; �� = −6. �� =4.

1127. При яких значеннях a і b пара чисел (–2; 3) є розв’язком системи рівнянь.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

3) Система рівнянь:

9�� +9�� = 18ǀ:9, �� + �� =2, �� + �� =2, �� + �� =2

1) Система рівнянь:

2��− 3�� =6, 3��−�� =5,

2) Система рівнянь:

2��− 3�� = 6ǀ ∙ 2, 2��− 3�� =6, �4��− 6�� = 12, 2��− 3�� =5

3) Система рівнянь:

2��− 3�� = 5ǀ ∙ 2, 2��− 3�� =6, �4��− 6�� = 10, 2��− 3�� =6 не має розв′ язків. 1131. До рівняння x – y = 2

рівнянь, яка: 1) має

1) Система рівнянь � ��−�� =2, 3��−�� =5, має єдиний розв′ язок;

2) Система рівнянь:

= 2ǀ ∙ 2, ��−�� =2, �2��− 2�� =4,

3) Система рівнянь:

= 3ǀ ∙ 2, ��−�� =2, �2��− 2�� =6, ��−�� =2,

При яких

рівнянь: �8�� +9�� =7, 8�� +9�� = �� ,

1133. При якому значення

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

3) Система рівнянь:

2�� = 3ǀ ∙ ( 2), �� +4�� = �� , � 2�� +4�� = 6, �� +4�� = ��

має розв’язків при а = -2, b ≠ -6. 1136. Підберіть такі значення m і n, при яких

єдиний розв’язок; 3) не має розв’язків.

1) Система рівнянь: �� + �� = 5ǀ ∙ 2, 3��− �� = ��, �3�� +3�� = 15, 3��− �� = ��

має безліч розв’язків при m = -3, n = 15; 2) Система рівнянь:

+ �� = 5ǀ ∙ 2,

3��− �� = ��, �3�� +3�� = 15, 3��− �� = ��

має один розв’язок, наприклад, при m = 1, n = 0; 3) Система рівнянь: �� + �� = 5ǀ ∙ 2, 3��− �� = ��, �3�� +3�� = 15, 3��− �� = ��

не має розв’язків при m = -3, n ≠ 15. 1137. Розв’яжіть графічно систему рівнянь: 1) Будуємо графік першого рівня.

х + у = 0, х ≥ 0

х 0 1

у 0 -1 -х + у = 0, х < 0

х -1 -2

у -1 -2

координат:

х + у = 2

х 0 2

у 2 0

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Графіки не перетинаються, тому система рівнянь розв’язку

4) Будуємо графік першого рівняння.

х 0 1

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

км/год.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

(32 60 + 1,2)x км,

Рівняння: (32 60 + 1,2)x + 1,2(x + 20) = 200│∙ 15;

(8 + 18)х + 18(х + 20) = 3000;

26х + 18х + 360 = 3000;

44х = 2640;

х = 60.

Відповідь: 60 км/год. 1142. Знайдіть

дорівнює 164.

Чотири послідовних

— 1,2(x + 20) км.

+ 1; 2n + 3. Рівняння: (2n – 3)2 + (2n – 1)2 + (2n + 1)2 + (2n + 3)2 = 164; 4n2 – 12n + 9 + 4n2 – 4n + 1 + 4n2 + 4n + 1 + 4n2 + 12n + 9 = 164; 16n2 + 20 = 164; 16n2 = 144; n2 = 9; n = 3. Шукані числа

2 ∙ 3 + 3 = 9.

Відповідь: 3; 5; 7; 9.

1143. Доведіть, що коли x + y = a – 1, то ax + x + ay + y + 1 = a2 .

ах + х + ау + у + 1 = х(а + 1) + у(а + 1) + 1 = (а + 1)(х + у) + 1.

Якщо x + у = а – 1, то (а + 1)(х + у) + 1 = (а + 1)(a – 1) + 1 = а2 – 1 +

(2; 5); 2)

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Відповідь: (48; 8); 4)

=2, �� =4.

Відповідь: (4; 2); 5) � 5��−�� =8, 5��− 4�� = 23; � �� =5��− 8, 5��− 4�� = 23;

=5��− 8, 21�� = 63; �� =5 ∙ 3 8, �� =3; �� =7, �� =3.

Відповідь: (7; 3); 6)

3�� +4�� =0, 2��− 5�� = 46; � 3�� +4�� =0, 2�� =5�� + 46; � 3�� +4�� =0, �� =2,5�� + 23; �3 ∙ (2,5�� + 23) +4�� =0, �� =2,5�� + 23;

7,5�� + 69 +4�� =0, �� =2,5�� + 23; � 11,5�� = 69, �� =2,5�� + 23; � �� = 6, �� =2,5 ∙ ( 6) + 23; �� = 6, �� =8.

Відповідь: (8; -6); 7)

15 −�� =2��, 4��− 3�� = 27; � �� = 15 2��, 4��− 3�� = 27; � �� = 15 − 2��, 4(15 2��) 3�� = 27; � �� = 15 2��, 60 8��− 3�� = 27; � �� = 15 − 2��, −11�� = −33; �� = 15 2 ∙ 3, �� =3; �� =9, �� =3. Відповідь: (9; 3);

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

5��−�� =6,2, 0,8�� +3�� = 13; � �� =5��− 6,2, 0,8�� +3�� = 13; � �� =5��− 6,2, 0,8�� +3(5��− 6,2) = 13; � �� =5��− 6,2, 0,8�� + 15��− 18,6= 13; � �� =5��− 6,2, 15,8�� = 31,6; �� =5 ∙ 2 − 6,2, �� =2; �� =3,8, �� =2.

Відповідь: (2; 3,8).

1148. Знайдіть розв’язок системи рівнянь: 1)

4�� + �� = 12, 7�� +2�� = 20; � �� = 12 4�� , 7�� +2�� = 20; � �� = 12 4�� , 7�� +2(12 4�� ) = 20; �

= 12 4�� , −�� = 4; �� = 12 4 ∙ 4, �� =4; �� = 4, �� =4.

Відповідь: (4; -4); 2)

��− 2�� =5, 3�� +8�� =1; � �� =2�� +5, 3�� +8�� =1; � �� =2�� +5,

=2 ∙ ( 1) +5, �� = −1; � �� =3, �� = 1.

Відповідь: (3; -1);

4��−�� = 11, 5��− 2�� = 17; � �� =4��− 11, 5��− 2�� = 17;

=4��− 11, 18�� = 72; �� =4 ∙ 4 11, �� =4; �� =5, �� =4.

Відповідь: (5; 4); 4)

6��−�� = 1, 2��− 3�� = 11; � �� =6�� +1, 2��− 3�� = 11;

=0,5; � �� =4, �� =0,5.

Відповідь: (0,5; 4); 5) � �� + �� =7, 9��− 2�� = −25; �

Відповідь: (3; 5). 1149. Розв’яжіть

Відповідь: (6; 3); 2)

(4; 2); 3)

Відповідь: (-5; 20); 2)

7�� +4�� =5, 3�� +2�� =3; �7�� +4�� =5, �� =1 2 3 �� ; �� = −1, �� =3.

Відповідь: (-1; 3). 3)

8�� 5�� = 11, 5�� 4�� = 6; � 8�� =5��− 11, 5�� 4��

5��−11 8 , 7�� =7;

Відповідь: (-2; -1); 4)

6��− 5�� = 38, 2��

(-3; 4).

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1,5��−3 3 + 7−3�� 8 = 3ǀ ∙ 24, 2,5��−2 3 2��+1 6 = ��− 0,5ǀ ∙ 6; � 8(1,5��− 3) +3(7 3��) = 72, 2(2,5��− 2) (2�� +1) =6��− 3;

12��− 24 + 21 9�� = 72, 5��− 4 2��− 1=6��− 3; �12��− 9�� = 75, −��− 2�� =2; �12(−2��− 2) − 9�� = 75, �� = −2��− 2; � 24��− 24 9�� = 75, �� = 2��− 2; � 33�� = 99, �� = 2��− 2; � �� = 3, �� = 2 ∙ ( 3) 2; �� = 3, �� =4.

Відповідь: (4; -3). 1152. Розв’яжіть систему рівнянь: 1)

6�� +3=5��− 4(5�� +4), 3(2��− 3��) 6�� =8 −��; �6�� +3=5��− 20��− 16, 6��− 9��− 6�� =8 −��; �6��− 5�� + 20�� = −16 − 3, 6��− 9��− 6�� + �� =8;

+ 20�� = 19, 8�� =8; �� + 20 ∙ ( 1) = 19, �� = 1; � �� =1, �� = 1.

Відповідь: (1; -1); 2)

2 ��−4 7 = 1ǀ ∙ 14, 6

Відповідь: (-2; 0,5); 3)

(14; 2).

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

(левів).

Рівняння: 8x – 56 = 0; 8х = 56; х = 7.

Відповідь: 7 левів.

1157.

проходить через точку A (4; –2)?

1158. Доведіть, що значення

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

7 + у = 6; у = -1.

Відповідь: (7; -1);

2) �

3�� + �� = 14, 5��−�� = 10.

Додамо почастинно ліві й праві частини

Підставимо у перше рівняння системи

9 + у = 14; у = 5.

Відповідь: (3; 5);

3) �2��− 9�� = 11, 7�� +9�� = 25.

Додамо почастинно ліві й

8 – 9у = 11; 9у = -3; у =1 3 .

Відповідь: (4;1 3);

4) � 6�� + �� = 16, 6�� +4�� = 34.

Додамо почастинно ліві й праві

-6х + 10 = 16; -6х = 6; х = -1.

Відповідь: (-1; 10).

х = 4 й

1167. Розв’яжіть систему рівнянь методом додавання:

1) �4��−�� = 20, 4�� + �� = 12.

16 – у = 20; у = -4.

Відповідь: (4; -4).

2) � 9�� + 17�� = 52, 26��− 17�� = 18. Додамо

Підставимо у

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

х = 2

18 + 17у = 52; 17у = 34; у = 2.

Відповідь: (2; 2); 1168. Розв’яжіть систему

1) �8�� + �� = 8ǀ ∙ ( 1), 12�� + �� =4; �−8��−�� = −8, 12�� + �� =4.

Додамо почастинно ліві й праві частини рівнянь: 4х = -4; х = -1.

Підставимо у друге рівняння системи значення х = -1 й одержимо: -12 + у = 4; у = 16.

Відповідь: (-1; 16);

2) �7��− 5�� = 29ǀ ∙ ( 1), 7�� +8�� = 10; � 7�� +5�� = 29, 7�� +8�� = 10.

Додамо почастинно ліві й праві частини рівнянь: 13у = -39; у = -3.

Підставимо у друге рівняння системи значення у = -3 й одержимо:

7х – 24 = - 10; 7х = 14; х = 2.

Відповідь: (2; -3);

3) ��− 3�� = 5ǀ ∙ 3, 4�� +9�� = 41; �3��− 9�� = 15, 4�� +9�� = 41.

Додамо почастинно ліві й праві частини рівнянь: 7х = 56; х = 8.

Підставимо у друге рівняння системи значення х = 8

32 + 9у = 41; 9у = 9; у = 1.

Відповідь: (8; 1);

4) �10�� +2�� = 23ǀ:2, 5�� +4�� = 6; � 5�� + �� =6, 5�� +4�� = 6.

Додамо почастинно ліві й праві частини рівнянь: 5у = 0; у = 0.

Підставимо у друге рівняння

-5х = -6; х = 1,2.

Відповідь: (1,2; 0);

5) �3��− 2�� = 1ǀ ∙ ( 4), 12�� +7�� = 26; � 12�� +8�� = 4, 12�� +7�� = 26.

Додамо почастинго ліві

Підставимо у

12х – 14 = -26; 12х = -12; х = -1.

Відповідь: (-1; -2);

рівнянь: 15у = -30; у = -2.

6) � 3�� +8�� = 13ǀ ∙ 2, 2��− 3�� = 17ǀ ∙ ( 3); � 6�� + 16�� = 26, 6�� +9�� = 51.

Додамо почастинно ліві й

2х + 3 = 17; 2х = 14; х = 7. Відповідь: (7; -1);

частини рівнянь: 25у = -25; у = -1.

7) � 3��− 4�� = 16ǀ ∙ 3, 5�� +6�� = 14ǀ ∙ 2; � 9��− 12�� = 48, 10�� + 12�� = 28.

20 + 6у = 14; 6у = -6; у = -1. Відповідь: (4; -1);

8) � 2�� +3�� = 6ǀ ∙ 3, 3�� +5�� = 8ǀ ∙ ( 2); � 6�� +9�� = 18, 6��− 10�� = 16

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

-у = 2; у = -2.

Підставимо

3х – 10 = 8; 3х = 18; х = 6.

Відповідь: (6; -2);

9) � 5�� +7�� = 24ǀ ∙ 7, 7�� +6�� = 2ǀ ∙ ( 5); � 35��− 49�� = 168, 35��− 30�� = 10.

Додамо почастинно ліві й праві частини рівнянь: -79v = 158; v = -2.

Підставимо у друге рівняння першої системи значення v = -2 й одержимо:

7u – 12 = 2; 7 u = 14; u = 2.

Відповідь: (2; -2).

10) �0,5�� +1,5�� = 10ǀ ∙ ( 2), 0,4��− 0,3�� =0,2; � 0,4��− 3�� = 20, 0,4��− 0,3�� =0,2.

Додамо почастинно ліві й праві частини рівнянь: -3,3у = -19,8; у = 6.

Підставимо у друге рівняння системи значення у = 6 й одержимо:

0,4х – 1,8 = 0,2; 0,4х = 2; х = 5.

Відповідь: (5; 6).

1169. Розв’яжіть систему рівнянь методом додавання:

1) � 5�� +7�� = 2ǀ ∙ ( 1), 8�� +7�� = 15; �5��− 7�� = 2, 8�� +7�� = 15.

Додамо почастинно ліві й праві частини рівнянь: 13х = 13; х = 1.

Підставимо у друге рівняння системи значення х = 1

8 + 7у = 15; 7у = 7; у = 1.

Відповідь: (1; 1);

2) �9��− 6�� = 24ǀ ∙ ( 1), 9�� +8�� = 10; � 9�� +6�� = 24, 9�� +8�� = 10.

Додамо почастинно ліві й праві

Підставимо у друге рівняння

9х – 8 = 10; 9х = 18; х = 2.

Відповідь: (2; -1);

3) �5�� + �� = 7ǀ ∙ 4, 7��− 4�� = 1; �20�� +4�� = 28, 7��− 4�� = 1.

Додамо почастинно

Підставимо у

7 – 4у = -1; -4у = -8; у = 2.

Відповідь: (1; 2);

4) � 6��− 5�� = 23, 2��− 7�� = 13ǀ ∙ ( 3); � 6��− 5�� = 23, 6�� + 21�� = 39.

6х + 5 = 23; 6х = 18; х = 3.

(3; -1);

5) � 5��− 2�� = 16ǀ ∙ 3, 8�� +3�� = 38ǀ ∙ 2; �15��− 6�� = 48, 16�� +6�� = 76.

32 + 3у = 38; 3у = 6; у = 2.

(4; 2);

14у = -14; у = -1.

у = -1

27х = 27; х = 1.

31х = 124; х = 4.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

6) � 5��− 4�� = 10ǀ ∙ 2, 2��− 3�� = 3ǀ ∙ ( 5); � 10��− 8�� = 20, 10�� + 15�� = 15.

Додамо почастинно ліві й праві частини рівнянь: 7у = 35; у = 5.

Підставимо у

рівняння першої системи

2х – 15 = -3; 2х = 12; х = 6.

Відповідь: (6; 5);

7) � 4��− 6�� = 9ǀ ∙ 3, 3��− 5�� = 2ǀ ∙ ( 4); � 12�� + 18�� = 27, 12�� + 20�� = 8.

у = 5 й одержимо:

Додамо почастинно ліві й праві частини рівнянь: 38b = 19; b = 0,5.

Підставимо у друге рівняння першої системи значення b = 0,5 й одержимо:

3а – 2,5 = 2; 3а = 4,5; а = 1,5.

Відповідь: (1,5; 0,5);

8) �9��− 13�� = 22ǀ ∙ ( 2), 2�� +3�� = −1ǀ ∙ 9; � 18�� + 26�� = 44, 18�� + 27�� = 9.

Додамо почастинно ліві й праві частини рівнянь: 53n = -53; n = -1.

Підставимо у друге рівняння першої системи

2m – 3 = -1; 2m = 2; m = 1.

Відповідь: (1; -1).

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

�9�� + �� = 3ǀ ∙ ( 3), 8�� +3�� = 10; � 27��− 3�� = 9, 8�� +3�� = 10

9 + у = 3; у = -6.

Відповідь:

1172. При яких значеннях а і b

В(2; -4)?

(1; -6).

Якщо графік рівняння ах + by = 8 проходить через точки А(1; 3) і

задовольняти систему: �� +3�� = 8ǀ ∙ ( 2), 2��− 4�� =8; � 2��− 6�� = 16, 2��− 4�� =8.

Додамо почастинно ліві у праві частини рівнянь: -10b = -8; b = 0,8.

Підставимо у перше рівняння першої системи

а + 2,4 = 8; а = 5,6.

Відповідь: а = 5,6, b = 0,8. 1173. При яких значеннях m і n графік

1) і D(-6; 5)?

Якщо

задовольняти систему: �2�� + �� = 6ǀ ∙ 5, 6��− 5�� =6; �10�� +5�� = 30, 6��− 5�� =6.

Додамо почастинно ліві й праві частини рівнянь: 4m – 36; m = 9.

Підставимо у перше рівняння першої системи

-4), то

m = 9 й одержимо: 18 + n = 6; n = -12.

Відповідь: m = 9; n = -12. 1174. Запишіть рівняння прямої y = kx + b, яка

системі: � 1 2�� + ��, 2= 3�� + ��ǀ∙ ( 1); � 2�� + �� =1, 3��−�� = 2.

Додамо почастинно

-0,4 + b = 1; b = 1,4.

у = -0,2х + 1,4;

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

-1,5 + b = 2; b = 3,5.

Відповідь: у = -0,5х + 3,5; 2) Якщо графік прямої у = kx + b проходить

задовольняти систему: � 3= 2�� + ��ǀ∙ ( 1), 6= �� + ��; �2��−�� =3, �� + �� =6.

Додамо почастинно ліві й праві частини рівнянь: 3k = 9; k = 3.

Підставимо у друге рівняння другої системи значення k = 3 й одержимо: 3 + b – 6; b = 3.

Відповідь: у = 3х + 3. 1176. Розв’яжіть систему рівнянь: 1) � 2(4��− 5) 3(3+4��) =5, 7(6��− 1) (4+3�� ) = 21��− 86; �

��− 86; � 8��− 12�� = 24ǀ:4, 3�� + 21�� = 75ǀ:3; � 2��− 3�� =6, −�� +7�� = 25ǀ ∙ 2; � 2��− 3�� =6, 2�� + 14�� = 50.

Додамо почастинно ліві й праві частини рівнянь: 11у = -44; у = -4.

Підставимо у

у = -4 й одержимо: 2х + 12 = 6; 2х = -6; х = -3.

Відповідь: (-3; -4); 2) � 2(2�� +1) +2,5=3(�� +2) 8�� , 8 − 5(4 −�� ) =6��− (5 −�� );

; � 4��− 3�� =5,5, 4��− 6�� = 7ǀ ∙ ( 1); � 4

почастинно ліві

(1; -0,5);

1) �0,2��− 0,3(2�� +1) =1,5, 3(�� +1) +3�� =2��− 2; �0,2��− 0,6��− 0,3=1,5 3�� +3+3�� =2��− 2; �0,2��− 0,6�� =1,8ǀ:0,2, 3�� + �� = 15ǀ ∙ 3; shkola.in.ua

11х = 22; х = 2.

4 – 3у = 10; -3у = 6; у = -2. Відповідь: (2; -2). 1177. Розв’яжіть

��− 3�� =9, 9�� +3�� = 15.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

-0,6 – 3у = 9; -3у – 9,6; у = -3,2. Відповідь: (-0,6; -3,2); 2)

4 + 3��+2�� 6 = 3ǀ ∙ 12, 3��+��

Додамо почастинно ліві й праві частини рівнянь: -192у = -576; у = 3.

Підставимо у друге рівняння

у = 3

: 3х + 33 = 36; 3х = 3; х = 1.

Відповідь: (1; 3).

1) � (��− 3)2 4�� = (�� +2)(

(1; 1);

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

�� 3 −�� 3 + 16�� + 20�� = 20 +8, 12�� + 15��− 8��− 12�� +2�� = 58 + 10; � 16�� + 20�� = 28ǀ:4, 15��− 6�� = 48ǀ:3; � 4�� +5�� = 7ǀ ∙ 2, 5��− 2�� = 16ǀ ∙ 5; � 8�� + 10�� = 14, 25��− 10�� = 80.

Додамо почастинно ліві й праві частини рівнянь: 33х = -66; х = -2.

Підставимо у друге рівняння передостанньої системи значення х = -2 й одержимо: -10 – 2у = -16; -2у = -6; у = 3.

Відповідь: (-2; 3).

1180. Чи має розв’язок система рівнянь: 1) � 2�� + �� =5, 3��− 4�� = 24, ��− 2�� =9.

Розв’яжемо спочатку систему

чи

�2�� + �� = 5ǀ ∙ 4, 3��− 4�� = 24; �8�� +4�� = 20, 3��− 4�� = 24.

Додамо почастинно ліві й праві частини рівнянь: 11х = 44; х = 4.

Підставимо у перше рівняння

8 + у = 5; у = -3.

Підставимо значення х = 4 і у = -3 у третє рівняння

рівність.

Отже, задача система не

розв’язку; 2) �2�� +3�� = −1, 3�� +5�� =1, 5�� +9�� =5.

Розв’яжемо систему

�2�� +3

-16 + 3у = -1; 3у = 15; у = 5. Підставимо значення

2) � ��− 2�� =1, 2�� + �� =7, 4�� + �� = 14.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Підставимо

1182. Запишіть систему

рисунку 73. 1) Одна пряма проходить через точки (0; 4) і (4;

kx + b повинні задовольняти систему: �4=0 ∙�� + ��, 0=4�� + �� ; � �� =4, 4�� +4=0;

2=0 ∙�� + ��, 0=2�� + ��; � �� = −2, 2��− 2=0; �� = 2, �� =1.

пряма проходить через точки (0; 4) і (2; 0), тому коефіцієнти

4=0 ∙�� + ��, 0=2�� + �� ; � �� =4, 2�� +4=0; � �� =4, �� = 2.

Отже, рівняння першої

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

(-3; 4) і (-2; 0),

4= 3�� + ��, 0= 2�� + ��ǀ∙ ( 1); �4= 3�� + ��, 0=2��−�� .

0 = 8 + b; b = -8.

рівняння

система буде: � �� +3�� =9, �� = 4��− 8.

1183. Запишіть систему лінійних

рисунку 74.

1) Перша пряма проходить через точки (0; 0) і (2; 3), тому коефіцієнт k її рівняння у = kx задовольняє рівнянню: 3 = 2k; k = 1,5. Отже, рівняння першої прямої у = 1,5х. Друга пряма проходить через точки (0; 3) і (1; 3), тому коефіцієнт b її рівняння у = b задовольняє рівнянню: 3 = 2k. Отже, рівняння другої

=1,5�� , �� =3, 2)

– kx + b повинні задовольняти системі:

3=0 ∙�� + ��, 0= −�� + �� ; � �� =3, −�� +3=0; �� =3, �� =3. Отже,

0), тому

k і b її

2=0 ∙�� + ��, 0=4�� + ��; � �� = −2, 4��− 2=0; �� = −2, �� =0,5.

2у = 24 системи.

якщо а = 2.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

(7; 5).

7а + 10 = 24; 7а = 14; а = 2.

1186. Розв’яжіть рівняння: 1) (х + у)2 + (х – 3)2 = 0. Сума квадратів

�� + �� =0, ��− 3=0; �3+ �� =0, �� =3; �� = 3, �� =3.

Відповідь: (3; -3); 2) (х + 2у – 3)2 + х2 – 4ху + 4у2 = 0; (х + 2у – 3)2 + (х – 2у)2 = 0.

Сума квадратів двох виразів дорівнює нулю лише тоді, коли вирази одночасно дорівнюють

нулю.

Отже, розв’язком даного рівняння є розв’язок системи: �� +2��− 3=0, ��− 2�� =0.

Додамо почастинно ліві й праві частини рівнянь: 2х – 3 = 0; х = 1,5.

Підставимо у друге рівняння системи значення х = 1,5

1,5 – 2у = 0; 2у = 1,5; у = 0,75. Розв’язком системи і рівняння є пара чисел (1,5; 0,75).

Відповідь: (1,5; 0,75); 3) ǀх – 3у – 6ǀ + (9х + 6у – 32)2 = 0. Сума

тоді, коли вирази одночасно

(4;2 3). 4) х2 + у2 + 10х – 12у +

нулю. Отже, розв’язком

�� +5=0, ��− 6=0; �� = 5, �� =6.

системи і

Відпоівдь: (-5; 6);

5) 25х2 + 10у2 – 30ху + 8у + 16 = 0; (25х2 – 30ху + 9у2) + (у2 + 8у + 16) = 0; (5х – 3у)2 + (у + 4)2 = 0. Сума

�5��− 3�� =0, �� +4=0; �5�� + 12 =0, �� = 4;

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2�� =0, ��− 5=0; ��− 10 =0, �� =5; �� = 10, �� =5.

Розв’язком системи і рівняння є пара чисел (10; 5).

Відповідь: (10; 5).

2) (4х + 2у – 5)2 + ǀ4х – 6у + 7ǀ = 0. Сума

коли

розв’язок системи: � ǀ4��− 6�� + 7ǀ =0, (4�� +2��− 5)2 =0; �4��− 6�� +7= 0ǀ ∙ (−1), 4�� +2��− 5=0; � 4�� +6��− 7=0, 4�� +2��− 5=0.

Додамо почастинно ліві й праві частини рівнянь: 8у – 12 = 0; у = 1,5.

Підставимо у перше рівняння другої системи значення у = 1,5 й одержимо: 4х – 9 + 7 = 0; 4х = 2; х = 0,5.

Розв’язком системи і рівняння є пара чисел (0,5; 1,5).

Відповідь: (0,5; 1,5).

3) 50х2 + 4у2 – 28ху + 16х + 64 = 0; (49х2 – 28ху + 4у2) + (х2 + 16х + 64) = 0; (7х – 2у)2 + (х + 8)2 = 0. Сума квадратів двох виразів

одночасно дорівнюють нулю. Отже, розв’язком

є розв’язок системи: �7��− 2�� =0, �� +8=0; � 56 2�� =0, �� = 8; �� = 28, �� = 8.

Розв’язком системи і рівняння є пара чисео (-8; -28).

Відповідь: (-8; -28).

1188. Розв’яжіть систему рівнянь:

1) �2 �� + 5 �� = 15; 3 �� + 8 �� = 23 Виконаємо

2�� +5�� = 15ǀ ∙ 3, 3�� +8�� = 23ǀ ∙ ( 2); � 6�� + 15�� = 45, 6��− 16�� = 46; -v = -1; v = 1. Із першого рівняння першої системи

до виконаної заміни:

1 �� =5, 1 �� =1; �� =0,2, �� =1.

(0,2; 1); 2) � 5 2��−3�� + 10 3��−2��

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2х + 3 = 5; 2х = 2; х = 1. Відповідь: (1; -1). 1189. Розв’яжіть систему рівнянь:

1 �� 7 �� =6, 2 �� + 3 �� = 46. Виконаємо заміну: 1 �� = �� , 1 �� = �� .

7�� = 6ǀ ∙ ( 2), 2�� +3�� = 46; � 2�� + 14�� = 12, 2�� +3�� = 46; 17v = 34; v = 2. Із першого рівняння

отримаємо: u – 14 = 6; u = 20. Повертаємося до виконаної зміни: 1 �� = 20, �� =0,05, 1 �� =2, �� =0,5. Відповідь: (0,05; 0,5); 2) � 9 ��+4�� 6 5��−�� = 2, 3 ��+4�� + 18 5��−�� =1. Виконаємо заміну:

9��− 6�� = 2ǀ ∙ 3, 3�� + 18�� =1; �27��− 18�� = −6, 3�� + 18

х – 8 = -6; х = 2.

Відповідь: (2; -2). 1190.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Рівняння: 5х – 3(12 – х) = 36; 5х – 36 + 3х = 36; 8х = 72;

х = 9.

Відповідь: 9 задач.

1194.

3, є кратною 3.

а) (3n – 1)2 – (3m – 1)2 = (3n – 1 – 3m + 1)(3n – 1 + 3m – 1) = (3n – 3m)(3n + 3m – 2) = = 3(n – m)(3n + 3m2) — кратне трьом; б) (3n – 2)2 – (3m – 2)2 = (3n – 2 – 3m + 2)(3n – 2 + 3m – 2) = (3n – 3m)(3n + 3m – 4) = = 3(n – m)(3n + 3m – 4) — кратне трьом. Якщо

(3n – 1)2 – (3m – 2)2 = (3n – 1 – 3m + 2)(3n – 1 + 3m – 2) = (3n – 3m + 1)(3n + 3m – 3) = = 3(3n – 3m + 1)(n + m – 1) — кратне трьом. 1196.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

� 5�� +5�� = 40, 3��− 2�� = 2ǀ ∙ 2; �5�� +4�� = 40, 6��− 4�� =4; 11�� = 44; �� =4.

Відповідь: набір олівців коштує 60 грн, а циркуль – 30 грн. 1207. За 11 однакових зошитів і 8 однакових ручок заплатили 245

1 зошит і скільки — 1 ручка, якщо 5

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

перший автомобіль проїхав (2,5 + 2)х = 4,5х (км), а другий – 2у (км). Система: � 4,5�� +2�� =563ǀ ∙ 3, 3��− 2�� = 69ǀ ∙ ( 2); �13,5+6�� = 1608, 4��− 6�� = 138; 17,5х = 1470; х = 84. З другого рівняння першої системи отримаємо: 3у – 168 = 69; 3у = 237; у = 79.

Відповідь: 84 км/год, 79 км/год.

1212. У двох бідонах

+9�� = 36; 100х = 1800; х = 18.

18 + 9у = 36; 9у = 18; у = 2.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

�20�� +8�� = 70, �� = 10��; �28�� = 70, �� = 10��; �� =2,5, �� = 25. Відповідь: 25 км/год, 2,5 км/год. 1216.

� �� + �� = 75, 0,6��− 0,5�� = 12ǀ ∙ 2; � �� + �� = 75, 1,2

Перше рівняння: 4х + 3у = 340.

грн. Друге рівняння: 2 ∙ 1,5х + 5

4�� +3�� = 340ǀ ∙ 4, 3�� +4�� = 360ǀ

0,8у = 360; 3х + 4у = 360. Система:

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

+ �� = 14000ǀ ∙ (−2), 4�� +6�� = 68000ǀ:2; � 2��− 2�� = 28000, 2�� +3�� = 34000; у = 6000.

+ у = 12000.

рівняння: 0,05х – 0,07у = 240; 5х – 7у = 24000. Система:

+ �� = 12000ǀ ∙ 7, 5��− 7�� = 24000; �7�� +7�� = 84000, 5��− 7�� = 24000. 12х = 108000; х = 9000.

З першого рівняння першої системи отримаємо: 9000 + у = 12000; у = 3000.

Відповідь: 9000 грн, 3000 грн. 1222. Маємо

0,09х + 0,3у = 0,23 ∙ 300; 9х + 30у = 6900. Система рівнянь:

�� + �� = 300ǀ ∙ ( 3), 9�� + 30�� = 6900ǀ:3; � 3��− 3�� = 900, 3�� + 10�� = 2300; 7у = 1400; у = 200.

рівняння першої системи отримаємо: х + 200 = 300; х = 100.

Відповідь: 100 кг, 200 кг. 1223.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Система рівнянь: � 2(�� + ��) = 28, (�� +6)(��− 2) �� = 24; � �� + �� = 14, �� 2�� +6��− 12 �� = 24; � �� + �� = 14, −2�� +6�� = 36; � �� + �� = 14, −�� +3�� = 18; 4у = 32; у = 8.

рівнянь:

= 45; х = 5.

рівняння передостанньої системи отримаємо: 5 + у = 12; у = 7.

Відповідь: 5 см, 7 см. 1227. Віслюк і мул ідуть

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

виїхав, на 1 год 15 хв = 1,25 год раніше,

велосипедист проїхав би 3,25х км, а пішохід

3,25х + 2у = 45. Система рівнянь:

+ �� = 15ǀ ∙ ( 2), 3,25�� +2�� = 45; � 2��− 2�� = 30, 3,25�� +2�� = 45; 1,25з = 15; х = 12.

12 км/год, 3 км/год. 1232. З пунктів A і B,

за 1,5 + 2 = 3,25

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

48 км/год, 60 км/год. 1236.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

10у + х. Система рівнянь: � ��−�� =2, (10�� + ��) (10��−�� ) = 18; � ��−�� =2, 9��− 9��

будь

другу. 1242. У рівності 4 (0,5x – 3) = 3x + * замініть

рівняння, яке: 1) не має коренів; 2)

4(0,5х – 3) = 3х + *; 2х – 12 = 3х + *; –х = 12 + *. 1) Щоб утворилося рівняння, яке не

виразом –х. Отримаємо рівняння: –х = 12 – х ; 0х = 12, яке

2) щоб утворилося рівняння, яке має безліч

х – 12. Отримаємо рівняння: –х = 12 – х – 12; 0х = 0, яке

коренів; 3) щоб утворилося рівняння, яке

виразом 0. Отримаємо рівняння:

shkola.in.ua

3) (0,5х + 2)2 – (0,5х – 1)(0,5х + 1) = 0,25х2 + 2х + 4

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

(а + 3b)2 – (a – 3b)2 = a2 + 6ab + 9b2 – a2 + 6ab – 9b2 = 12ab. Отже, 12ab = (а + 3b)2 – (а – 3b)2.

1247. Доведіть,

(а – bс)2 – 2(b2с2 – а2) +(bс + а)2 = (а

= (а – bс + а + bс)2 = (2а)2 = 4а2

2 +2(а – bс)(а + bс) + (а + bс)2

1249. Розкладіть на множники вираз: 1) 4kn + 6аk + 6аn + 9а2 = 2k(2n + 3а) + 3а(2n + 3а) = (2n + 3а)(2k + 3а); 2) b6 – 4b4 + 12b2 – 9 = b6 – (4b – 12b2 + 9) = b6 – (2b2 – 3)2 = (b32b2 + 3)(b3 + 2b2 – 3); 3) у4(х2 + 8x + 16) – а8 = у4(х + 4)2 – а8 = (y2(х + 4) – a4)(y2(x + 4) + а4) = = (ху2 + 4у2 – а4)(ху2 + 4у2 + а4); 4) 9x2 – 6x – 35 = 9x2 + 15x – 21х – 35 = 3х(3х + 5) – 7(3x + 5) = (3х + 5)(3x – 7).

1250. Відомо, що x + y = a, xy = b, x2 + y2 = c. Знайдіть

між a, b і c. x2 + у2 = x2 + 2ху + у2 – 2ху = (х + у)2 –

Якщо x + у = а, ху = b, х2 + у2 = с, то с = а2 – 2b. 1251. Точки A (2; 3) і B (5; a) належать прямій y = kx.

Якщо точка А(2; 3) належить прямій у = kx, то: 3 = 2х; k = 1,5.

Отже, рівняння прямої буде: у = 1,5x.

Якщо точка В(5;а) належить прямій у = 1,5x, то: а = 1,5 ∙ 5 = 7,5. Отже, а = 7,5. 1252. Знайдіть такі значення

5��− 4�� = 11, 2�� +4�� = 10; �5

Відповідь: А).

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

4. Розв’яжіть систему рівнянь:

15�� +2�� =7, 2��−�� =6; � 15�� +2

Відповідь: Б).

5. Нехай пара чисел (a; b) є розв’язком системи рівнянь. Знайдіть

�� + �� =1, 3��−�� =7; � 4�� =8, 3��−�� =7; � �� =2, 3 ∙ 2 −�� =7; � �� =2, �� = 1; ( 2; 1).

Тоді a2 – b2 = 22 – (-1)2 = 4 – 1 = 3.

Відповідь: В).

6. При якому значення а система рівнянт

3�� + �� =4, ��− �� = 6; 3 1 = 1 −�� ≠ 4 −6 ; �� = 1 3

Відповідь: Г).

7. При якому

Відповідь: А).

8. Графік

формулою. � 4=1 ∙�� + �� , 13

Б).

12. Розв’яжіть рівняння x2 + y2 + 12x – 2y + 37 = 0.

х2 + у2 + 12х – 2у + 37 = 0; (х2 + 12х + 36) + (у2 – 2у+ 1) = 0; (х + 6)2 + (у – 1)2 = 0;

х = –6, у = 1; (–6; 1).

Відповідь: Б).

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

3 – а2

а4 + а2 20 2 0,3125 0

2 20 1256. Подайте у вигляді степеня вираз:

1) (a8)4 = а32; 2) a8a4 = а12; 3) а5а5 = а10; 4) (а5)5 = а25; 5) а2а3а4 = а9; 6) (а2)3а4 = а6а4 = а10; 7) а6а6а6 = а18; 8) (а6а6)6 = (а12)6 = a72; 9) (а6)6а6 = а36а6 = а42; 10) (а4)5 : a7 = a20 : а7 = а13; 11) (a2)9: (а6)3 = а18 : а18 = 1; 12) (а8а7) : а14 = a15 : а14 = а.

1257. При якому значенні x є правильною рівність: 1) 5x ∙ 57 = 524; х + 7 = 24; x = 17; 2) (3m)x = 35m; хm = 5m; x = 5; 3) 2х ∙ 2m = 26m; х + m = 6m; х = 5m; 4) (4x)3m = 46��2 ; 3хm = 6m2; х = 2m.

1258. Чи є тотожно рівними вирази:

1) –а2 і (–а)2 = а2. Вирази –а2 і

2 не є тотожно рівними; 2) (–а)3 =

3) (а3)2 = а6. Вирази (а3)2 і а5 не є тотожно рівними;

4) 9а ∙ а2 = 9а3; (3а)2 ∙ а

5) (а4)3 = а12; (а2)6 = а12.

1259.

1) 81 ∙ 32 = 92 ∙ 9 = 93 = 729;

1260.

1) 155 ∙ 26 = 155 ∙ 25 ∙ 2; 25 ∙ 15

Отже, 25 ∙ 33 ∙ 54 > 24 ∙ 35

53 . 1261. Порівняйте значення виразів: 1) 1020 = (102)10 = 10010. Отже, 1020 < 10110; 2) 1015 = (103)5 = 10005. Отже, 1015 < 99905 1262. Спростіть вираз:

1) 4а ∙ (–3аb) = –12а2b; 2) –2m2 ∙ 0,1m4n ∙ (–5n3) = m6n4; 3) 0,3а2b4 ∙ 1,2а4b = 0,36а6b5; 4) –6х3у6 ∙ 1,5хy = –9х4y7; 5) –14b2с8d8 ∙ 12 7 b6d3 =

7) 3х6 ∙ (–4х2у)2 = 3х6 ∙ 16х4y2 = 48х10у2; 8) (–ху)3 ∙ (–2x2y2)4 = –х3у3 ∙ 16х8y8 = –16x11y11 1263.

1) А = a6b9 = (a2b3)3; 2) A = 32a10 = (2b2)5; 3) A = 81a2b4c8 = (9ab2c4)2; 4) A = –8a12b18 = (–2a4b6)3.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

4a3ab –

2) 11m2 ∙ 2mn – 9mn ∙ 6mn3 + 10mnm = 22m3n – 54m2n4 + 10m2n; 3) 8xx4x ∙ (–1 4xy) + 18xy ∙ 7 9yx5 = –2x7y + 14x6y2; 4) 9x3xy

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) 3х 1 6 –х 3 = 5 2х 9 │∙ 18;

3(3x – 1) – 6х = 2(5 – 2х);

9х – 3 – 6х = 10 – 4х;

9х – 6х + 4х = 10 + 3; 7x = 13;

х = 13 7 .

Відповідь: 13 7 ;

3) х+5 8 –1+х 2 = 2х+1 3 │∙ 24;

3(x + 5) – 12(1 + х) = 8(2х + 1);

3х + 15 – 12 – 12х = 16х + 8;

3х – 12х – 16х = 8 – 15 + 12; –25х = 5;

х = –0,2.

2) 3х+1 2 –5 4 = 3 2х 3 │∙ 12; 6(3х + 1) – 15х = 4(3 – 2х); 18 + 6 – 15х = 12 – 8х;

18х – 15х + 8х = 12 – 6; 11х = 6;

х = 6 11 .

Відповідь: 6 11;

Відповідь: –0,2; 4) 2х 3 –2х+1 6 = 3х 9 4 │∙ 12;

5) 9х 7 4 –9х+13 8 = 3 х 2 │∙ 8;

2(9х – 7) – (9х + 13) = 4(3 – х);

18х – 14 — 9х — 13 = 12 – 4х;

18х – 9х + 4х = 12 + 14 + 13;

13х = 39; х = 3.

8х – 2(2х + 1) = 3(3х – 9);

8х – 4х – 2 = 9х – 27;

8х – 4х – 9х = –27 + 2; –5х = –25; х = 5.

Відповідь: 5;

Відповідь: 3; 6) 6х+7 6 + 5х 8 9 = 3│∙ 18;

1273. Розв’яжіть рівняння:

1) 3х(4х – 1) – 6x(1,5 + 2х) = 4,8;

12х2 –3х – 9х – 12х2 = 4,8; –12х = 4,8;

х = –0,4.

Відповідь: –0,4;

3) х(9х – 4) – 3х(3х – 1) = 8 – х; 9x2 – 4х – 9х2 + 3х = 8 – х; –4х + 3х + х = 8; 0х = 8.

Відповідь: Коренів немає;

3(6х + 7) + 2(5х – 8) = 54;

18х + 21 + 10х – 16 = 54;

18х + 10х = 54 – 21 + 16; 28х = 49; х = 1,75.

Відповідь: 1,75.

2) 0,2х(5х – 8) + 3,6 = х(х – 0,7); х2 – 1,6х + 3,6 = х2 – 0,7х; –0,9х = –3,6; х = 4.

Відповідь: 4;

4) 18x2 – 6х(3х + 2) = –12х; 18х2 – 18х2 – 12х = –12х; –12х + 12х = 0; 0х = 0.

Відповідь: Будь-яке число. 1274. Доведіть тотожність: 1) –0,2x3(2,5х – 4)(6 – х2) = –0,2х3(15х – 2,5x3 – 24 + 4x2) = –3х4 + 0,5х6 + 4,8x3 – 0,8х5 = = 0,5х6 – 0,8х5 – 3х4 + 4,8х3 — тотожність доведена; 2) (а – 2)(a2 + 3а – 18) = (а – 2)((а2 – 3а) + (6а – 18)) = (а – 2)(а(а – 3) + 6(а – 3)) = = (а – 2)(a – 3)(a + 6) = (а – 3)((а

1277. Розкладіть

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1) 1 2 a6 –1 4 a2b = 1 4a2(1 4 a4 – b);

2) 5m2n3k4 + 35m4n3k2 = 5m2n3k2 (k2 + 7m2);

3) x3y2z5 – 2xy5z3 + 3x2y3z = xy2z(x2z4 – 2y3z2 + 3xy);

4) a2nb3n – anb4n = anb3n(an – bn).

1278. Обчисліть, використовуючи

многочлена:

1) a2 + 4,72a – 32,8 = a(a + 4,72) – 32,8.

Якщо a = 5,28, то: a(a + 4,72) – 32,8 = 5,28 ∙ (5,28 + 4,72) – 32,8 = = 5,28 ∙ 10 – 32,8 = 52,8 – 32,8 = 20; 2) 12,3x – 12,3y + 4,7 = 12,3(x – y) + 4,7.

Якщо x = 8,14, y = 8,04, то: 12,3(x – y) + 4,7 = 12,3 ∙ (8,14 – 8,04) + 4,7 = = 12,3 ∙ 0,1 + 4,7 = 1,23 + 4,7 = 5,93. 1279. Обчисліть, використовуючи

1) 2,49 ∙ 1,35 – 1,35 ∙ 1,84 + 1,352 = 1,35 ∙ (2,49 – 1,84 + 1,35) = 1,35 ∙ 2 = 2,7;

2) 0,252 ∙ 1,6 + 0,25 ∙ 1,62 – 0,25 ∙ 1,6 ∙ 0,85 = 0,25 ∙ 1,6 ∙ (0,25 + 1,6 – 0,85) = = 0,25 ∙ 1,6 ∙ 1 = 0,4;

3) 3,24 ∙ 18,7 – 3,24 ∙ 16,4 + 2,3

+ 2,3

6,76 = = 3,24 ∙ 2,3 + 2,3 ∙ 6,76 = 2,3 ∙ (3,24 + 6,76) = 2,3 ∙ 10 = 23;

4) 5,12 ∙ 9,76 + 5,12 ∙ 5,36 – 5,122 = 5,12 ∙ (9,76 + 5,36 – 5,12) = 5,12

1) 173 + 172 – 17= 17 ∙ (172 + 17

1) abba = 1000а +100b +10b +а =

2) aaabbb = 1000aaa + bbb = 1000 ∙ 111 ∙ a + 111b =

націло

на 7; 4) abab – baba = 100ab +

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

3) 9а – ab – 9 + b – а(9 – b) – (9 – b) = (9 – b)(a – 1);

4) а5 + а3 + 2а2 + 2 = а3(а2 + 1) + 2(а2 + 1) = (а2 + 1)(а3 + 2);

5) 6аb2 – 3b2 + 2a2b – ab = 3b2(2a – 1) + ab(2a – 1) = (2а – 1)(3b2 + ab) = b(2а – 1)(3b + а); 6) 2с3 – 5с2d – 4с + 10d = с2(2с – 5d) – 2(2с – 5d) = (2с – 5d)(с2 – 2);

7) х3y2 – х + х2у3 – у = х3у2 + х2y3 – х – у = х2у2(х +у) – (х + у) = (х +у)(х2у2 – 1) = = (х + у)(ху – 1)(ху + 1).

1285. Обчисліть значення виразу:

1) 1,662 + 1,66 ∙ 4,68 + 2,342 = 1,662 + 2 ∙ 1,66 ∙ 2,34 + 2,34

1286. При яких значеннях a, b, c і d виконується рівність аb ∙ сd = аd ∙ сd?

Якщо аb ∙ сd = аd ∙ сd, то: (10а + b)(10с + d) = (10а + d)(10с + b);

100ас + 10ad + 10bс + bd = 100aс + 10аb + 10сd + bd; 100ас + 10ad + 10bс + bd – 100ас – 10аb – 10сd – bd = 0; 10аd + 10bс – 10аb – 10сd = 0; 10(аd + bс – аb – сd) = 0; (d + b)(a – c) = 0; (аd – аb) + (bс – сd) = 0;

а(d – b) – с(d – b) = 0; (d – b)(а – с) = 0.

Отже, рівність аb ∙ сd = аd ∙ сb виконується, коли d = b

1287. Спростіть вираз: 1) 6х2 + (2у – 3х)(2у + 3х) = 6х2 + 4у2 – 9х2 = 4у

2) (а + 2)(а – 3) – (4 – а)(а + 4) = а

= 2а2 – а – 22; 3) (5 – 2х)(5 + 2х) – (3 – 2х)(4– 2х) = 25 – 4х2

4) (2аb + 1)(2аb – 1)(16а4b4 + 1)(4а2b2 + 1) = (4а

– 1)(4а2b2 + 1) ∙ (16а4b4 + 1) = = (16а4b4 – 1)(16а4b4 + 1) = 256а8b8 – 1. 1288. Обчисліть значення добутку,

1) 19 ∙ 21 = (20 – 1) ∙ (20 + 1) = 202 – 1 = 400 – 1 = 399; 2) 98 ∙ 102 = (100 – 2) ∙ (100 + 2) = 1002 – 22 = 10000 – 4 = 9996; 3) 22 3 ∙ 31 3 = (3 –1 3) ∙ (3 + 1 3) = 32 – (1 3)2 = 9 –

; 4) 7,9 ∙ 8,1 = (8 – 0,1) ∙ (8 + 0,1) = 82 – 0,12 = 64 – 0,01 = 63,99. 1289. Розв’яжіть рівняння:

1) 4х(7 + 9х) – (6х + 5)(6х – 5) = 39; 28х + 36х2 – 36х2 + 25 = 39; 28х = 14; х = 0,5.

Відповідь: 0,5; 2) (х – 8)(х + 10) – (х + 7)(х – 7) = 5х – 31; х2 + 10х – 8х – 80 – х2 + 49 = 5х – 31;

2х – 31 = 5х – 31;

2х – 5х = 0; х = 0.

Відповідь: 0. 1290. Доведіть, що

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

1293. Розв’яжіть рівняння:

1) 36х2 – (3х – 27)2 = 0;

(6х – 3х + 27)(6х + 3х – 27) = 0; (3х + 27)(9х – 27) = 0;

3х + 27 = 0 або 9х – 27 = 0;

3х = –27 або 9х = 27;

х = –9 або х = 3.

Відповідь: –9; 3;

1294. Доведіть, що при

–якому

2) (4х – 7)2 – (2х + 17)2 = 0;

(4х –7 – 2х –17)(4х – 7 + 2х + 17) = 0; (2х – 24)(6х + 10) = 0; 2х – 24 = 0 або 6х + 10 = 0;

2х = 24 або 6х = –10; х – 12 або х = –5 3 .

Відповідь: 12; –5 3

виразу: 1) (4n + 19)2 – (3n – 5)2 = (4n + 19 – 3n + 5)(4n + 19 + 3n – 5) = = (n + 24)(7n + 14) = 7(n + 24)(n + 2) — ділиться

на 7; 2) (2n + 5)2 – (2n – 3)2 = (2n + 5 – 2n + 3)(2n + 5 + 2n – 3) = 8(4n + 2) = = 16(2n + 1) — ділиться націло на 16. 1295. Доведіть, що

− n4 − 8n2 + 3n + 5 кратне 6. (n2 – 3n + 1)2 – n4 + 3n + 5 = (n2 – 3n

= n4 – 3n3 + n2 – 3n3 + 9n2 – 3n + n2

6, бо якщо,

+ 11n2 – 3n + 6 = –6

1296.

16n4

(4n2 −2n −1)2 + 8n +1 кратне 4. 16n4 – (4n2 – 2n – 1)2 + 8n + 1 = 16n4 – (4n2 – 2n – 1)(4n2 – 2n – 1) + 8n + 1 = = 16n4 – (16n4 – 8n3 – 4n2 – 8n3 + 4n2 + 2n – 4n2 + 2n + 1) + 8n + 1 = = 16n4 – 16n4 + 8n3 + 4n2 + 8n3 – 4n2 – 2n + 4n2 – 2n – 1

16n3 + 4n2 + 4n = = 4(4n3 + n2 + n) — кратне 4. 1297. При якому значенні a рівняння (a – 3) (a + 5) x = a2 – 9:

3) має один корінь? (а – 3)(а + 5)x = а2 – 9; (а – 3)(а + 5)х = (а – 3)(а + 3). 1) Якщо а = 3, то рівняння:

(70

2) 912 = (90

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

(2n

= 3(n2 – 2n – 6) — ділиться

n. 1302. Розв’яжіть рівняння:

1) 3(х – 7)2 – 2(х + 7)(х – 2) = (х + 11)(х – 4) + 101;

3x2 – 42x + 147 – 2x2 + 4х – 14х + 28 = х2 – 4х + 11x – 44 + 101; 3х2 – 42х – 2х2 + 4х – 14х – х2 + 4х – 11х = –44 + 101 – 147 – 28; –59х = –118;

х = 2.

Відповідь: 2;

2) 2х (х + 3)2 – 3х(х – 1)(х + 8) = х2(–х – 9) + 21;

2х(х2 + 6х + 9) – 3х(х2 + 8х – х – 8) = –x3 – 9x2 + 21;

2х3 + 12х2 + 18х – 3х3 – 24х2 + 3х2 + 24х + х3 + 9x2 = 21;

42х = 21; х = 0,5.

Відповідь: 0,5;

3) у(2у – 5)(2у + 5) – 4у(у + 6)2 = 13 – 48у2;

у(4у2 – 25) – 4у(y2 + 12у + 36) + 48y2 = 13; 4y3 – 25у – 4y3 – 48y2 – 144у + 48y2 = 13; –169у = 13; y = –1 13 .

Відповідь: –1 13 .

1303. Подайте у вигляді

1) (а + 4)2 – 2(а + 4) + 1 = ((а + 4) – 1)2 = (а + 3)2; 2) (3b + 2)2 + 4(3b + 2) + 4 = ((3b + 2) + 2)2 = (3b + 4)2; 3) (3у + 8)2 + (4у + 6)2 + 4у = 9y2 + 48у + 64 + 16y2 + 48у + 36 + 4у = = 25y2 + 100у + 100 = (5у+ 10)2; 4) (х – 5у)2 + (х + 12y)2 – х(х – 12у) = х2

= = х2 + 26ху + 169y2 = (х + 13у)2 .

1304. Суму

1) х2 – 8х + 18 = 0; (х2 – 8х + 16) + 2 = 0; (х – 4)2 + 2 = 0 — рівняння не має коренів; 2) x2 + x + 1 = 0; x2 + x + 1 4 –1 4 + 1 = 0; (x + 1 2)2 + 3 4 = 0 – рівняння не має коренів.

1306. Розкладіть на множники:

1) 1 64 a8 – b6 = (1 8 a4 – b3)( 1 8 a4 + b3);

2) а3b6с9 + 8 = (аb2с3)3 + 23 = (аb2с3 + 2)(а2b4с6 – 2аb2с3 + 4); 3) х21y4 – m12n15 = (x7y8)3 – (m4n5)3 = (х7y8 – m4n5)(x14y16 + x7y8m4n5 + m8n10);

4) а6b6 + 1 = (а2b2)3 + 13 = (а2b2 + 1)(a4b4 – a2b2 + 1).

1307. На скільки

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

27a3 + 4 – (9a2 – 3a + 1) (3a + 1) менше

числа 10? 10 – (27а3 + 4 – (9а2 – 3а + 1)(3а +1)) = 10 – 27а3 – 4 + (3а + 1)(9a2 – 3а + 1) = = 10 – 27а3 – 4 + 27а3 + 1 = 7.

Відповідь: на 7.

1308. Розв’яжіть рівняння: 1) (х – 2)(x2 + 2х + 4) = х3 + 24х;

х3 – 8 = х3 + 24х; 24х = –8;

х = –1 3 .

Відповідь: –1 3 . 2) (3 – 2х)(9 + 6х + 4х2) – 2х(5 – 2х)(5 + 2х) = 7; (3

27 – 8х3 – 50х + 8х3 = 7; –50х = –20; х = 0,4.

Відповідь: 0,4.

1309. Чи ділиться значення виразу 373 + 233 націло

1310.

1311. Розкладіть на множники: 1) (а – b)(a + b) – с(с

= (а – b + с)(а + b – c); 2) (b – с)(b + с) – а(а + 2с) =

= (b – а – с)(b + а + с).

1312. З

та розкладіть

1) 9mх – 6nх + 6mу – 4nу = 3х(3m – 2n) + 2y(3m – 2n) = (3m – 2n)

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

х + у = а,

= а4 – 4а2b + 2b2.

1319. Доведіть, що при будь–якому

(n + 1) (n + 2) (n + 3) + 1

n(n + 1)(n + 2)(n + 3) + 1 = (n(n + 3))((n + 1)(n + 2)) + 1 = (n2 + 3n)(n2 + 2n + n + 2) + 1 = = (n2 + 3n)(n2 + 3n + 2) + 1 = (n2 + 3n)2 + 2(n2 + 3n) + 1 = (n2 + 3n + 1)2.

1320. Доведіть, що

n (n + 2) (n + 4) (n + 6) + 16

n(n + 2)(n + 4)(n + 6) + 16 = (n(n + 6))((n + 2)(n + 4)) +16 = (n2 + 6n)(n2 + 4n + 2n + 8) + 16 = = (n2 + 6n)(n2 + 6n + 8) + 16 = (n2 + 6n)2

1321.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Якщо n = 5m – 2, то

n = 3m, то

n = 7m ± 2, або n = 7m ± 3.

Якщо n = 7m

7. Якщо

n = 7m ± 1, то

Отже, ƒ(0) = g(2); 3) ƒ(1) = 12 – 2 ∙ 1 = –1; g(1) = 1−2 1 = –1; –1 = –1. Отже, ƒ(1) = g(1).

2) якщо

30,

х + у = 30; х = 30 – у. З рівняння

у = 6(30 – у) – 5; у = 180 – 6у – 5; 7у = 175; у = 25.

Отже, х = 30 – 25 = 5 і

–2 = 3а – 8; 3а = 6; а = 2; 2) якщо

ƒ(x) = (x – 1)(x + 1) – х(х – 3);

ƒ(x) = х2 – 1 – x2 + x;

ƒ(x) = x – 1 – функція є лінійною.

1 2

0 1 2)

ƒ(x) = (2х – 3)2 – (х + 4) (х – 2);

ƒ(x) = 4х2 – 12x + 9 – x2 + 2x – 4x + 8;

ƒ(x) = 3x2 – 14х + 17 — функція не є

ƒ(х) = (х + 3)2 – х(х + 6);

ƒ(х) = х2 + 6х + 9 – х2 – 6х;

ƒ(х) = 9 — функція є лінійною.

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

функції y = 6x + 24.

х = 0, то у = 12 ∙ 0 – 6 = -6.

(0; -6).

Якщо у = 0, то 0 = 12х – 6; х = 0,5.

абсцис (0,5; 0);

2) Координати точки перетину

знайдемо з системи: � �� = 12��− 6, �� =6�� + 24ǀ ∙ ( 1); � �� = 12��− 6, −�� = 6��− 24; 6��− 30 =0; х = 5.

рівняння системи отримаємо: у = 12 ∙ 5 – 6 = 54.

у = ǀхǀ

3. у = -х – 3, х < 0;

х -3 -1

у 0 -2

у = х – 3, х 0;

х 0 3

у -3 0 2) у = ǀх - 3ǀ.

shkola.in.ua

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

чисел: 1) (1; 1); 2) (–3; 5). 1) Система двох

змінними, розв’язком якої

пара чисел (1; 1) може бути, наприклад, така: � 2��−�� =1, 3�� + �� = 4;

наприклад, така:

1) � 3�� +7�� =1, 6��− 5�� = 16; � 3�� +7�� = 1ǀ ∙ 5, −5�� +6�� = 16ǀ ∙ 3; � 15�� + 35�� =5, −15�� + 18�� = 48; 53у = 53; у =

З першого рівняння системи отримаємо:

3х + 7 = 1; х = -2.

Відповідь: (-2; 1);

2) �3��− 5�� = 19ǀ ∙ ( 2), 2�� +3�� = 0ǀ ∙ 3; � 6�� + 10�� = 38, 6�� +9�� =0; 19у = -38; у = -2. З першого рівняння системи отримаємо:

3х + 10 = 19; х = 3.

Відповідь: (3; -2); 3) � 3(2��− 1) +6(7 −�� ) = 51, 2(�� +6) 7(1+6�� ) = 49; � 6

3+ 42

2�� + 12 7 42�� = 49; � 6��− 6�� = 12, 2��− 42�� = 44; � ��−�� =2, ��− 21�� = 22; � ��−�� =2, 20�� = 20; � �� =1, �� = −1.

(1; -1); 4)

(4; 2).

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

2�� +3�� =2�� 2 12�� + 8ǀ ∙ 2, 3��− 2�� =3�� 2 +8�� + 12ǀ ∙ 3; � 4�� +6�� =4��2 24�� + 16, 9��− 6�� =9�� 2 + 24�� + 36; 13х = 13а2 + 52; х = а2 + 4. З першого рівняння першої системи отримаємо: 2(а2 + 4) + 3у = 2а2 – 12а + 8; 3у = 2а2 – 12а +

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

(ц) більше. Друге рівняння: 4х + 7у = 400.

�40�� + 35�� = 2600ǀ: ( 5), 4�� +7�� = 400; � 8��− 7�� = 520, 4�� +7�� = 400; -4х = -120; х = 30.

рівняння системи отримаємо: 120 + 7у = 400; 7у = 280; у = 40. Відповідь: 30 га, 40 га. 1347. З одного поля

https://shkola.in.ua/2211-hdz-alhebra-7-klas-merzliak-2015.html

Нехай більше число дорівнює х, а менше

рівнянь: � �� + �� = 28, �� 2 −�� 2 = 112; � �� + �� = 28, (��−��)(�� + ��) = 112; � �� + �� = 28, (��−��) ∙ 28 = 112; �� + �� = 28, ��−�� =4; 2х = 32; х = 16.

З першого рівняння системи отримаємо: 16 + у = 28; у = 12.

Відповідь: 16; 12. 1352. Розгадайте кросворд: По горизонталі: 5. Пропорційність. 6. Куб. 9. Визначення. 14. Функція. 15. Тотожність. 18. Многочлен. 20. Коефіцієнт. 21. Декарт. 23. Означення. 24. Хорезмі. По вертикалі: 1. Корінь. 2. Аргумент. 3. Групування. 4. Степінь. 7. Квадрат. 8. Пряма. 10. Графік. 11. Абсциса. 12. Ординат. 13. Основа. 16. Одночлен. 17. Алгоритм. 19. Показник. 22. Точка.