https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html






§2 №45-109
-185 §1 №1-44



на ст. 33-36


-246





-319

54-55 §4
на











8
-499

6
-382




9
-537 §7 №383-454 §11 №600-655
на ст. 74-77 Завдання на ст. 126-129
12
-700



10 №538-599 §14 №781-818
§13 №701-780


Завдання на ст. 170-174 §20 №1072-1155






17
-987


21 №1156-1225



-880






18
-1021

16
-934







19
-1071



№1226-1325 Завдання на ст. 221225



-1378


https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
1.
Тоді четвертий кут: 360° - 210° = 150°.
Відповідь: 150°.
2. Чи існує чотирикутник, який має три кути по 120°?
Сума внутрішніх кутів чотирикутника завжди дорівнює 360°.
Якщо три кути по 120°, то їхня сума: 120° + 120° + 120° = 360°.
Це означає, що для четвертого кута залишається: 360° - 360° = 0°. А кут у 0° неможливий у звичайному чотирикутнику. Висновок: такого чотирикутника не існує.
3. Чи існує чотирикутник,
внутрішніх кутів чотирикутника дорівнює 360°.
Тупий кут — це кут більше ніж 90°.
Сума трьох тупих кутів > 3 ⨯ 90° = 270°.
Отже, на четвертий кут залишиться: 360° - (сума трьох тупих кутів) < 90°.
Це означає, що четвертий кут буде гострим
Висновок: так, існує

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
a = P - 6,
b = P - 6,
c = P - 6,
d = P - 6.
Складаємо всі сторони:
a + b + c + d = 4(P - 6).
Але ліва частина — це сам периметр P, тому: P = 4(P - 6).
P = 4P - 24.
0 = 3P - 24
3P = 24
P = 8.
Тоді кожна сторона:
a = P - 6 = 8 - 6 = 2 (см).
Отже, всі сторони по 2 см.
Відповідь: чотирикутник зі сторонами по 2 см (квадрат).
7. Периметр чотирикутника дорівнює 20 м. Як він
збільшити на 1 м?
Чотирикутник має 4 сторони.
периметра буде:
∆P = 4 ⨯ 1 м = 4 (м).
Новий периметр: P = 20 м + 4 м = 24 м.
Відповідь: периметр стане 24 м (збільшиться на 4 м).
8. Периметр чотирикутника дорівнює 10
збільшити втричі?
Нехай сторони — a, b, c, d, тоді:
a + b + c + d = 10.
Якщо кожну сторону збільшити
Новий периметр: P = 3a + 3b + 3c + 3d = 3(a + b + c + d) = 3 ⨯ 10 = 30 (дм).
Відповідь: периметр
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

the
and one of the sides is twice as long as each of the others.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
3+5+ 16 = 24 >8;
3+8+ 16 = 27 >5;
5+8+ 16 = 29 >3. Оскільки

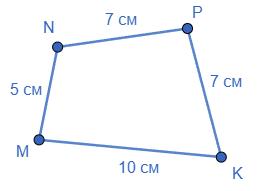
Периметр чотирикутника:
���� + ���� + ���� + ���� = 26 дм;
Периметри трикутників:
���� + ���� + ���� = 17 дм;
���� + ���� + ���� = 25 дм.
сторони:
Додаємо ці два рівняння: (���� + ���� + ���� )+(���� + ���� + ���� )= 17 + 25 = 42;
���� + ���� + ���� + ���� +2���� = 42.
Підставимо периметр чотирикутника: 26 +2���� = 42;
2���� = 42 26;
2���� = 16;
���� =8 дм.
протилежні кути
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
4���� +0= 360∘ ⇒���� = 90∘ .
Тоді:
1 −й кут: 90∘
�������� = ����
Toдi:
�������� = ���� +1; �������� = ���� +6; �������� =5 (за умовою).
Також відомо, що: �������� = �������� +
Toдi:
�������� =2; �������� =3; �������� =8; �������� =5.
Периметр:
18 см. 35. Одна зі
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
38. У чотирикутнику ���������������� �������� = �������� і
чотирикутника паралельні.
Дано:
у чотирикутнику ABCD сторони AB = CD і ∠BAC =
Довести:
AB‖CD i AD‖BC
Доведення:
1. Розглянемо трикутники △ ABC і △ CDA.
2. У цих трикутниках:
AB = CD (за умовою);
∠BAC = ∠DCA (за умовою);
Спільна сторона: AC = AC
3. Отже, за двома сторонами
трикутників).
4. Із рівності трикутників випливає,
, AC < CD + AD, BC < BC + CD, BC < AB + AD.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
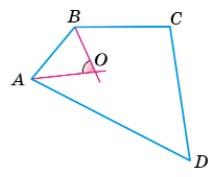
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
2���� +3���� = 180∘ ⇒ 5���� = 180∘ ⇒���� = 36∘ Тоді кути:
перший 2���� = 72∘
другий 3���� = 108∘
Відповідь: 72∘ і 108∘ .
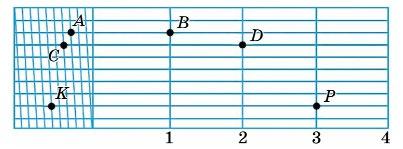
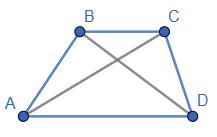
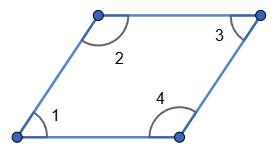
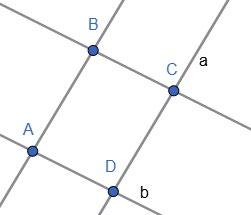
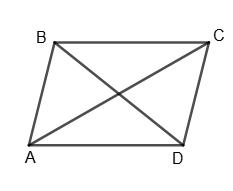
45. Які з фігур, зображених на малюнку, - паралелограми?

Відповідь: 1.
46. Сторони паралелограма завдовжки 3 см і 5 см. Знайди його периметр.
Р = (3 + 5) ∙ 2 = 8 ∙ 2 = 16 (см)
Відповідь: 16 см.
47. Периметр паралелограма
паралелограма. A. 50 см Б. 40 см B. 20 см Г. 10 см P = 2(a + b); 60 = 2(10 + b); 60 = 20 + 2b; 2b = 40; b = 20 (см).
Відповідь: 20 см.
48. Знайди периметр паралелограма,
дорівнює 3 м.
Середнє арифметичне всіх 4 сторін: ���� + ���� + ���� + ���� 4 = 2���� +2
Периметр паралелограма:
=2(���� + ���� ) =2 ⋅ 6= 12 м
Відповідь: 12 м.
49. Один із кутів паралелограма
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
360
Отже, один з кутів дорівнює 60°
паралелограмі
Тоді сума двох інших кутів:
360∘ 2 ⋅ 60∘ = 240∘
Відповідно, кожен із них:
240∘ 2 = 120∘
Відповідь: 60°, 120°, 60°, 120°.

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

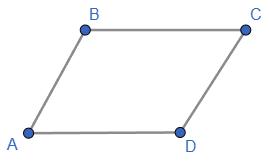
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

a) ∠B = 42∘ > ∠A. Нехай ∠A =x ∘ , тоді ∠B =x+ 42∘ . ∠A + ∠B = 180∘ - внутрішні
ABCD - паралелограм. Знайти: ∠A, ∠B, ∠C, ∠D.
x+x+ 42∘ = 180∘ , 2x = 180∘ 42∘ , 2x = 138∘ , ���� = 138∘ :2, x= 69∘ .
Отже, ∠A = ∠C = 69∘ ,
∠B + ∠D = 180∘ 69∘ = 111∘ .
б) ∠A y 3 p< ∠B.
Нехай ∠A =x ∘ , тоді ∠B = 3x, x+ 3x = 180∘ , 4x = 180∘ , x= 45∘ .
∠A = ∠C = 45∘ ;
∠B + ∠D =3 ⋅ 45∘ = 135∘ .
в) ∠A: ∠B =2:3.
∠A = 2x, ∠B = 3x. 2x + 3x = 180∘ , 5x = 180∘ , x= 180∘ :5, x= 36∘ .
∠A = ∠C = 36∘ ⋅ 2= 72∘ ; ∠B = ∠D = 36∘ ⋅ 3= 108∘ .
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
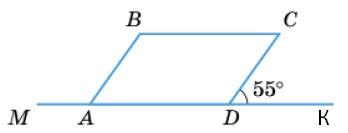
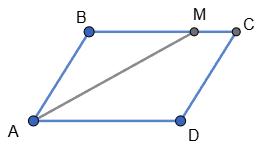
Дано: ABCD - паралелограм; ∠CDK = 55∘ .
Знайти: ∠MAB.
∠BAD = ∠CDK = 55∘ - як відповідні при AB‖CD і січні МК. ∠MAB + ∠BAD = 180∘ як суміжні → ∠MAB = 180∘ 55∘ = 125∘ .
Відповідь: ∠MAB = 125∘ .
62. Обчисли кути паралелограма ���������������� ,
якщо ∠������������ = 32∘ , ∠������������ = 37∘ .
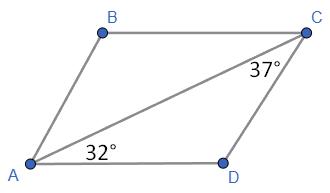
За умовою задачі ∠CAD = 32∘ , ∠ACD = 37∘
∠ACB = ∠CAD - як внутрішні різносторонні
прямими BC i AD. Зважаючи
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
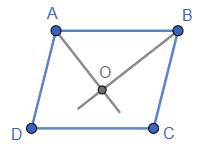
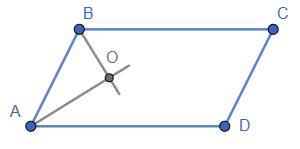
одній діагоналі.
Дано: ABCD - паралелограм; AB = BC = CD = AD = BD. Знайти: ∠A, ∠B, ∠C, ∠D.

За умовою AB = BD = AD →△ ABD - рівносторонній →∠A =
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
штампі.

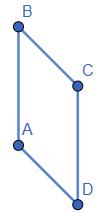
Дано: ABCD - паралелограм; PABCD = 4,8 см; AB =1,3 см.
Знайти: BC PABCD =4,8 см → PABCD =4,8 ∶ 2= 2,4 см - пів периметр (AB + BC).
Отже, AB + BC =2,4 см, AB =1,3 → BC =2,4 1,3=1,1 см.
Відповідь: BC =1,1 см.
а периметр трикутника ������������ становить 27 дм.
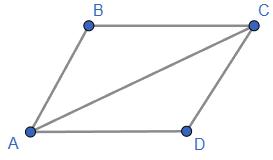
Згідно з умовою задачі 2 ⋅ (AB + BC)= 40, AB + BC + AC = 27.
Тоді AB + BC = 20, AC = 27 20 =7 (дм).
Відповідь: довжина діагоналі АС дорівнює 7 дм
70. Find the length of the diagonal �������� of parallelograм ���������������� if its periмeter is 30 см and the periмeter of triangle ������������ is 21 см.
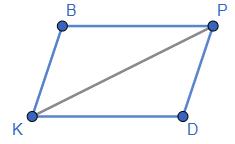
Дано: КВРD - паралелограм; PKВРD = 30 см; PKВР = 21 см
Знайти: КР.
Якщо PкВр = 30 см, то PKВРD = 30 ∶ 2= 15 см - пів периметр (КВ + BP).
Отже,
= 21 15 =6 см.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
P=2(a+b) → a+b= p 2 = 42 2 = 21(см)
a) Одна зі сторін на 5 см більша за другу.
Нехай коротша сторона - x , тоді інша x+5.
Складаємо рівняння: x+(x+5)= 21; 2x +5= 21; 2x = 16; x=8.
Отже, сторони паралелограма: 8 см і 13 см
б) Одна зі сторін у 2 рази більша за другу.
Нехай коротша сторона - x, тоді інша -2 x.
Складаємо рівняння:
x+ 2x = 21; 3x = 21; x=7.
Сторони паралелограма: 7 см i 14 см.
в) Різниця сторін дорівнюе 7 см.
Нехай коротша сторона -x , тоді інша -x+7.
Складаємо рівняння: x+(x+7)= 21; 2x +7= 21; 2x = 14; x=7.
Сторони паралелограма: 7 см i 14 см
г) Сторони відносяться як 3:4.
Нехай сторони - 3 x i 4 x.
Складаємо рівняння:
Складаємо рівняння: 3x + 4x = 21; 7x = 21; x=3.
Сторони паралелограма: 9 см і 12 см
Відповідь: а) 8
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
b = 5 ∙ 3 = 15 (см)
Перевірка:
2(a + b) = 2(9 + 15) = 2 ∙ 24 = 48 (см)
Відповідь: сторони — 9 см і 15 см.
в) Одна зі сторін на 6 см менша від другої
Нехай a = x, b = x + 6, тоді:
a + b = x + x + 6 = 2x + 6 = 24
2x = 18
x = 9
Отже:
a = 9 (см)
b = 15 (см)
Перевірка:
2(a + b) = 2(9 + 15) = 48 (см)
Відповідь: сторони — 9 см і 15 см.
прямі, паралельні
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

B.
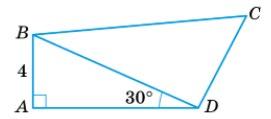
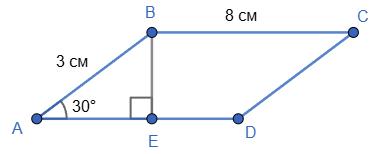
Дано: ABCD - паралелограм; AB = 3 см, BC =8 см; ∠A = 30∘
Знайти: BE . Розглянемо △ ABE (∠E = 90∘ ). BE - катет навпроти ∠A = 30∘ → BE = 1 2 AB, отже, BE =3 ∶ 2=1,5 см. Відповідь: BE = 1,5 см.
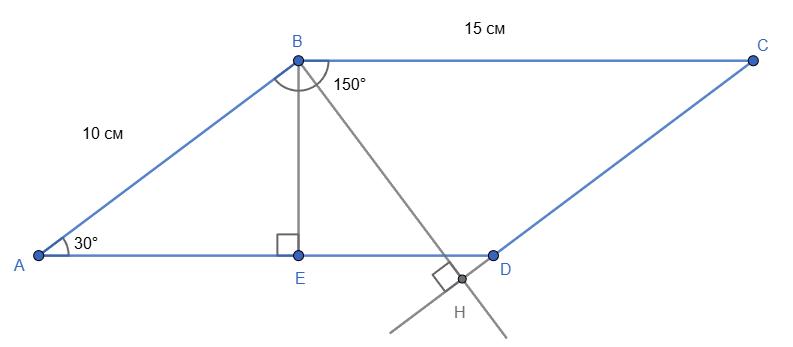
Дано: ABCD - паралелограм; AB = 10 см, BC = 15 см; ∠���� =150∘ .
Знайти: BE та BH .
∠A = 180° - ∠B = 180° - 150° = 30°. Оскільки в паралелограма протилежні
– прямокутний (∠E = 90°). BE – катет, що лежить навпроти кута 30°, отже BE = AB : 2 = 10 : 2 = 5 см.

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
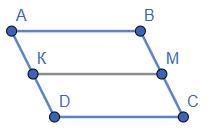
→ ABMK - паралелограм. Відповідь: АВМК - паралелограм. 78. Бісектриси
М і N відповідно. Доведи, що чотирикутник AМCN – паралелограм.
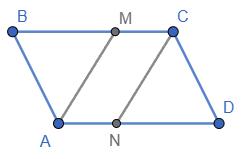
Дано: ABCD - паралелограм; AM - бісектриса ∠A; CN - бісектриса ∠C.
Довести: AMCN - паралелограм.
BC
Так як ABCD - паралелограм → BC‖AD, отже MC‖AN - лежать на паралельних прямих.
АМ - бісектриса ∠A→∠BAM = ∠MAN.
CN - бісектриса ∠C→ ∠MCN = ∠NCD
Т. як ABCD - паралелограм →∠A = ∠C, отже ∠BAM = ∠MAN = ∠MCN = ∠NCD.
BC‖AD → ∠MCN = ∠NCD - внутрішні рівносторонні
→∠CND = ∠MAN як відповідні → AM‖CN.
Отже, MC‖AN, AM‖CN → AMCN - паралелограм.
Відповідь: AMCN - паралелограм.
79. Точки ���� , ����, ���� , ���� - середини сторін паралелограма
паралелограм.
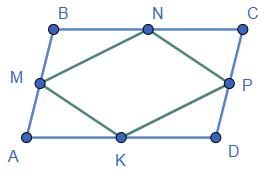
Дано: ABCD - паралелограм; M - середина AB; N - середина BC; P - середина CD; К - середина AD.
Довести: MNPK - паралелограм.
ABCD - паралелограм →∠A = ∠C; ∠B = ∠D.
ΔMBN = ΔKPD за I ознакою (за
1. MB = PD - як
2. BN = KD - як
3. ∠B = ∠D. → MN = KP.
ΔAMK = ΔNCP за I
1. АМ = СР - як
2. АК = NC - як половини рівних сторін.
3. ∠A = ∠C.
→ MK = NP.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
Отже, MN = KP, MK = NP → MNPK - паралелограм.
Відповідь: MNPK - паралелограм.
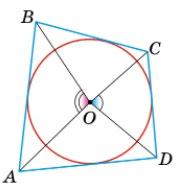
80. У колі проведено діаметри �������� і
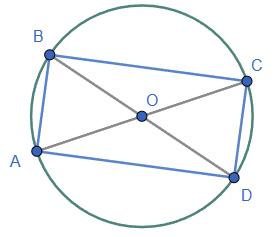
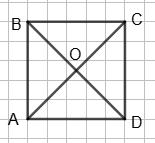
Дано: Коло з центром в точці O; AB i CD - діаметри.
Довести: ABCD - паралелограм.
CO = OD = OA = OB - радіуси кола.
ΔCOB = ΔAOD - за двома сторонами
1. CO = OD - як радіуси.
2. AO = OB - як радіуси.
3. ∠COB = ∠AOD вертикальні.
→ CB = AD.
Аналогічно: ΔCOA = ΔBOD - за двома сторонами
1. CO = OD - як радіуси.
2. AO = OB - як радіуси.
3. ∠COA = ∠BOD − вертикальні.
→ AC = BD
Отже, CB = AD, AC = BD → CABD - паралелограм.
Відповідь: CABD - паралелограм.
81. Які з наведених тверджень
I. Діагональ
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
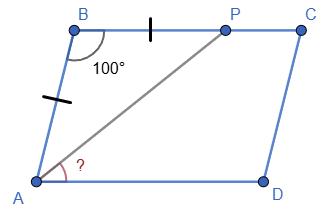
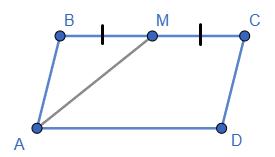
Згідно з умовою задачі �������� = �������� , ∠������������ = ∠������������ . Але ∠BMA = ∠MAD як
паралельними прямими BC та AD. Тому ΔABM - рівнобедрений. Отже, BM = AB =5. Тоді BC = 2BM = 10. Таким чином, периметр паралелограма ���� =2(�������� + �������� ) =2 ⋅ (5+ 10) = 30(см).
Відповідь: периметр паралелограма дорівнює 30 см 85. Бісектриса ∠���� ділить сторону
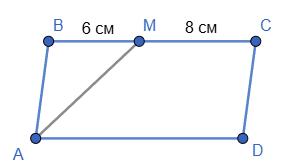
Дано: ABCD - паралелограм; AM - бісектриса ∠A; BM =6 см; MC =8 см.
Знайти: PABCD . AM - бісектриса ∠A→∠BAM = ∠MAD.
BC‖AD → ∠BMA = ∠MAD - як
∠BAM→
→△ ABM рівнобедрений → AB = BM =6 см.
Так як ABCD - паралелограм, то AB = CD =6 см.
BC = AD =6+8= 14 см.
Отже, PABCD =(6+ 14) ⋅ 2= 40 см.
Відповідь: PАВCD = 40 см.
86. Бісектриса ∠����
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
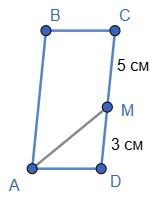
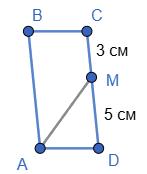
AD = MD =3 (см).
CD = СМ + MD =8 (см).
Отже, периметр P=2(AD + CD)=2 ⋅ (3+8)= 22 (см). Відповідь: периметр
22 см.
2-й випадок
AD = MD =5 (см).
CD = СМ + MD =8 (см).
Отже, периметр P=2(AD + CD)=2 ⋅ (5+8)= 26 (см).
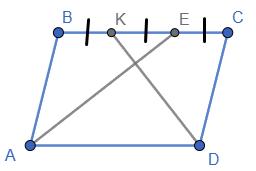
Дано: ABCD - паралелограм;
=
∠CKD =
AB = CD =2 ⋅ 4=8 см, BC = AD =3 ⋅ 4= 12 см.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
40 см.
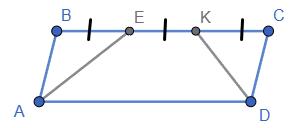
Дано: ABCD - паралелограм; AE - бісектриса ∠A; DK - бісектриса ∠D; PABCD = 40 см; BE = EK = KC.
Знайти: AB, BC, CD, AD.
Нехай BE = EK = КС =x.
AE - бісектриса ∠A→∠BAE = ∠EAD.
∠EAD = ∠BEA - як внутрішні різносторонні
BC‖AD і січній AE ,
отже, ∠BAE = ∠BEA →△ ABE рівнобедрений → BE = AB =x.
Аналогічно:
DK - бісектриса ∠D→ ∠ADK = ∠KDC. ∠ADK = ∠CKD− як внутрішні різносторонні
DK , отже, ∠CKD = ∠KDC →△КCD рівнобедрений →КС = CD =x.
BC = 3x PABCD = 40 см → pABCD = AB + BC = 40:2= 20 см (пів периметр).
3x +x= 20, 4x = 20,
���� = 20:4, x=5 см.
Отже, AB = CD =5 см,
BC = AD =3 ⋅ 5= 15 см.
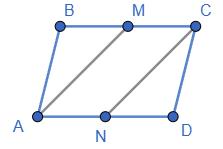
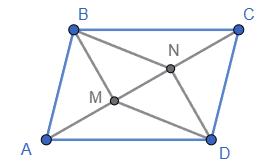
Відповідь: AB = CD =5 см, BC = AD = 15 см. 90. ���������������� - паралелограм, точки
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
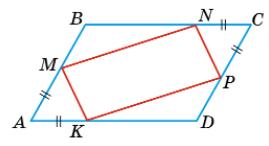
паралелограмі ABCDAM = AK = CN = CP. Крім того ∠A = ∠C як протилежні кути паралелограма. Отже, △ AMK =△ CNP, тобто MK = NP. З рівності AM = CN маємо MB = BN, а з рівності AK = CP маємо KD = DP. ∠B = ∠D як протилежні кути паралелограма, тому ΔMBN = ΔKDP, тобто MN = КР. В чотирикутнику MNPK протилежні сторони рівні
собою, тому
з теоремою 4 підручника MNPK - паралелограм. 93. Середини півдіагоналей
відрізками. Доведи, що чотирикутник ���������������� - паралелограм. В
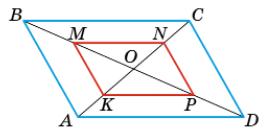


його кутів. Для будь-якого паралелограма бісектриси його
прямим кутом. Тому всі кути чотирикутника MNPK дорівнюють
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

97. Діагональ �������� паралелограма ���������������� є

Нехай ABCD
CD = 12 (дм).
а
AC є бісектрисою кута A, тобто ∠BAC = ∠CAD.
1) Доведемо рівність сусідніх сторін
CAD (між CA і AD).
Але ∠CAD = ∠BAC (бо AC — бісектриса). Отже, ∠BAC = ∠ACB.
= BC.
У паралелограмі ABCD маємо також BC = AD (протилежні сторони рівні). Звідси AB
2) Доведемо, що діагоналі
Нехай O — точка
діляться навпіл, тому AO = OC, BO = OD.
У ромбі AB = AD. Розглянемо
AO — спільна, BO = DO, AB = AD. Отже, ∆AOB = ∆AOD
BOA = ∠AOD.

→ CB = CD.
як ABCD - паралелограм → CB = AD, CD = BA → CB = CD = DA = AB.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
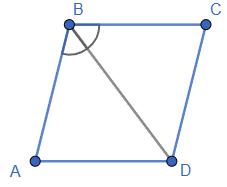
найменшим
всі кути рівні;
Б. сума протилежних кутів дорівнює 90




https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
24x = 72
x = 3
Сторони:
3 ⋅ 3 = 9; 5 ⋅ 3 = 15; 6 ⋅ 3 = 18; 10 ⋅ 3 = 30
Відповідь: 9 см, 15 см, 18 см, 30 см.
108. В опуклому чотирикутнику
чотирикутник паралельні сторони? У

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
Периметр квадрата: P = 4a
За умовою:
4a = a + 30
Звідси:
4����−���� = 30 ⇒ 3���� = 30 ⇒���� = 10 дм
Тоді
P = 4a = 4 ⋅ 10 = 40 дм = 400 см. Відповідь: периметр квадрата
β = 180∘ 40∘ = 140∘ ⇒ більший
ромбі (як у будь-якому паралелограмі)
(їхня сума дорівнює 180∘ ). Якщо взяти два протилежні
β = 180∘ 100∘ = 80∘ .
Отже, кути ромба: 100∘ , 80∘ , 100∘ , 80∘ .
Відповідь:

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
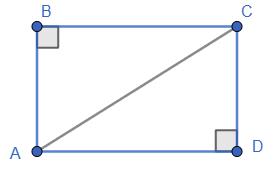
(наприклад, AB = CD).
△ABC і △ADC рівні.
Висновок: діагональ ділить
Знайдіть сторони прямокутника, якщо
Периметр прямокутника P = 48 см ⇒
2(���� + ���� ) = 48 ⇒���� + ���� = 24
а) Одна зі сторін 10 см
���� = 10 ⇒ ���� = 24 10 = 14.
Відповідь: 10 см і 14 см.
б) Одна зі сторін на 6 см більша за іншу
Нехай ���� = ���� +6. Тоді ���� + ���� = 24 ⇒���� + (
Відповідь: 9 см і 15 см.
в) Одна зі сторін у 3 рази більша за іншу
Нехай ���� =3���� . Тоді
����
Відповідь: 6 см і 18 см.
г) Сторони пропорційні числам 3 і 5
Нехай ���� =3���� ; ���� =5���� . Тоді ���� + ���� = 24 ⇒
Відповідь: 9 см і 15 см.
Відповідь: 12 см і 20 см.

48 см і:
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

перетинаються навпіл, тож AO = OC і BO = OD. 2. У трикутнику △AOB маємо рівні сторони AO = BO, а кут між ними ∠AOB = 60°. Отже це рівнобедрений трикутник з вершиною в O, тому ∠OAB =
AB = AO = BO.
Менша сторона прямокутника AB = CD = 7 см ⇒ AO = 7 см.
Діагональ дорівнює AC = 2 ∙ AO = 14 см.
Обидві діагоналі прямокутника рівні, тож AC = BD = 14 см.
Відповідь: діагоналі

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
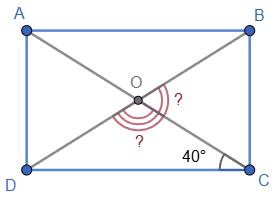
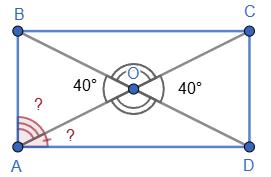
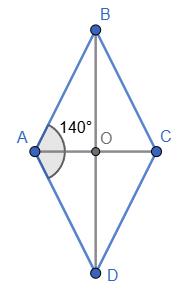
∠COB = 2 · 40° = 80°.
Кути ∠COB і ∠DOC — суміжні (при
∠DOC = 180° − 80° = 100°.
Відповідь: ∠COB = 80°, ∠DOC = 100°.
125. Діагональ
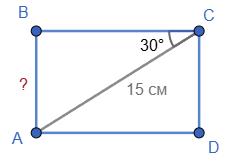
Нехай ABCD – заданий прямокутник.
трикутнику ABC: ∠ABC = 90° (прямокутний), AC = 15 см, ∠ACB = 30°.
гіпотенузи.

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
x + 2x = 90°; 3x = 90°; x = 30° (отже другий кут 60°).
Властивість: у прямокутному
проти кута 30°. Тому:
менша сторона = 5 : 2 = 2,5 дм.
Відповідь:
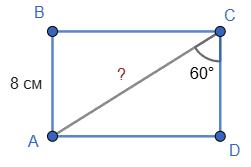
60°, тобто
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
Отже, ∠BCA = 30°, ∠ACD = 60°.
AC, тому
AB = AC : 2 ⇒ AC = 2 · 22 = 44 см.
Відповідь: AC = 44 см.
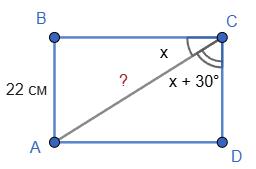
129. Діагоналі прямокутника
якщо
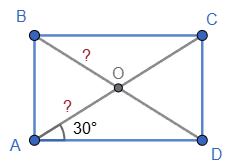
Розв’язок:
1. Властивість прямокутника: діагоналі рівні
CO = DO та AC = BD. Нехай AC = d. Тоді CO = DO = d/2.
2. Розглянемо трикутник ACD (прямий кут при D). Дано ∠CAD = 30°. Властивість:
що лежить проти кута 30°, дорівнює половині гіпотенузи ⇒ CD = AC/2 = d/2.
3. Периметр трикутника COD: CO + DO + CD = d/2 + d/2 + d/2 = 3d/2 = 12 ⇒ d = 8.
AC = BD = 8 см.

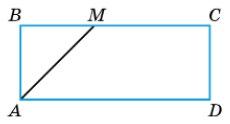

спільна). Отже, діагональ AC ділить паралелограм
за властивостями


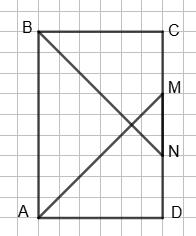
цьому CM = MN = ND = 3 см. Тоді AB = CD = 9 (см).
AМ
ABCD.
AD = MD = 6 (см).
P = 2(АВ + AD) = 2 • (9 + 6) = 30 (см). 142.

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
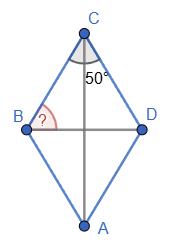
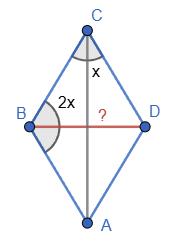
P = 40 м. Тоді 4ВС = 40, BС = 10 (м).
BC = BD = 10 (м).
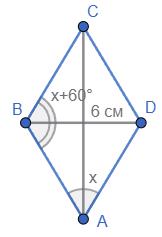
рівняння х + х + 60 = 180, звідки 2х = 180 – 60, 2х = 120, х = 60. Отже, кути ромба
60° і 120°. За умовою
BD = 6 см. Але ∠A = 60°, тому ∆ABD — правильний і AB = BD = 6 (см). Тоді шуканий
P = 4АВ = 24 (см).



158.

159.
64 см.
160. �������� and �������� are the bisectors of the angles ���� and ���� of the rectangle ���������������� , intersecting the side �������� at points ���� and ���� so that �������� = �������� = �������� . Find the sides of ���� rectangle if its periмeter is 32 см
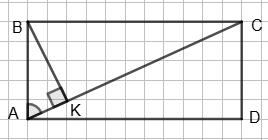
3а умовою BO ⊥ AC, O ∈ AC, AC = 12 см, ∠BAO = 60°. Потрібно
в 30°.
AK = х, тоді AB = 2х.
AB2 = AC • AK; 4х2 – 12 • х; 4x – 12; х = 3.
AK = 3 см; KC = 9 – 3 = 6 (см).
3 см; 6 см.

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
умовою BK ⊥ AC, K ∈ AC, AB = 6 см, ∠ABK : ∠KBC = 1 : 2. ∠ABK + ∠KBC = 90°,
∠ABK = 30°, ∠KBC = 60°.
У ∆ABK : AK = 1 2 АВ = 1 2 • 6 = 3 (см).
Позначимо KC = х, тоді AB2 = AC • AK;
36 = (х + 3) • 3; 3х = 27; х = 9.
Отже, KC = 9 см. AK : KC = 3 : 9 = 1 : 3.
Відповідь: 1 : 3.
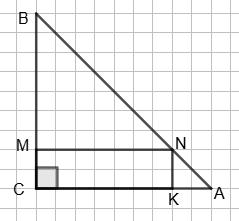
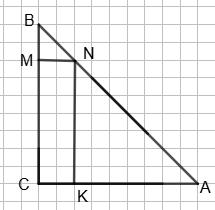
163. У прямокутний ∆ABC вписано прямокутник CKLM так, що
точка L — середина AB. Доведи, що KM = 1 2 АВ.

умовою у
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
4 = ∠BAO, тому ∠1 + ∠BAO = 90°, тобто ∠AOB = 180° –
ABCD – ромб. 168. Доведи, що чотирикутник, у якого
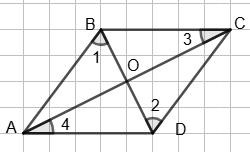
що згідно з теоремою 6 підручника
рівні, - ромб. За умовою AB = BC = CD = AD. Тоді ∆АОВ = ∆СОD (AB = CD за умовою,
=
= ∆AOD. Далі, ∠ABO = ∠CDO як різнобічні
собою. Тоді ABCD — паралелограм, у

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
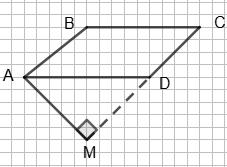
∠A + 5∠A = 180°, 6∠A = 180°, ∠A = 30°.
AB і CD.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
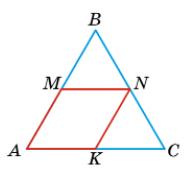
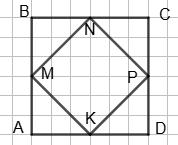
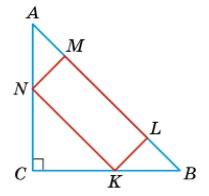
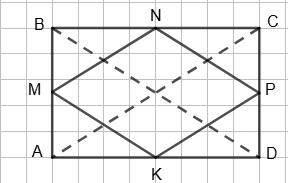
За умовою ∆АВС — правильний, AMNK — ромб, периметр якого дорівнює 16 см. P = 4MN, 4MN = 16, MN = 4 (см). MN ∥ AC, тобто ∆MBN також правильний, MN = MB. Але MN = AM як сторони ромба, тоді AM = MB і MN — середня лінія ∆ABC, AC = 2MN. Аналогічно, NK — середня лінія ∆АВС, AB = 2NK. Отже, сторони ∆ABC вдвічі
сторони ромба AMNK, AB = BC = AC = 2АМ = 2 • 4 = 8 (см). Таким чином,
∆ABC P = 3АВ = 3 • 8 = 24 (см).
176. 3 вершини

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
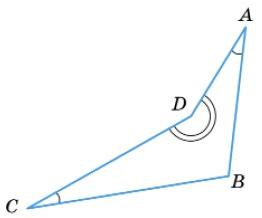
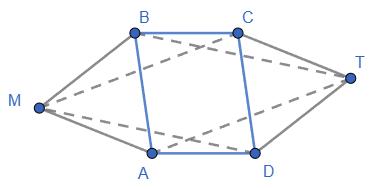
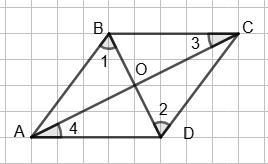
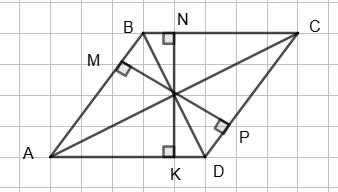
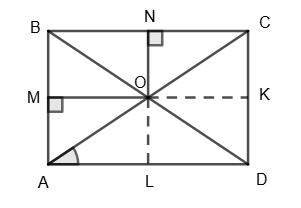
Сума внутрішніх кутів чотирикутника дорівнює 360°, тому
∠A + ∠B + ∠C + ∠D = 360°, 30° + ∠B + 30° + ∠D = 360°, ∠B + ∠D = 300°, ∠B + 2∠B = 300°, 3∠B = 300°, ∠B = 100°, ∠D = 2 • 100° = 200°.
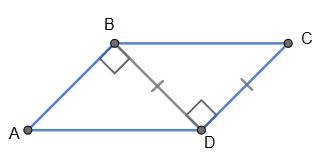
2. Дано: ▱ABCD, AB ⟂ BD, ∠ACD = 30°.
Довести: AO = BD.
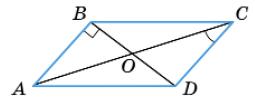
Потрібно довести, що: AO = BD. ∠BAO = ∠ACD = 30° як внутрішні
січній AC та паралельних прямих AB і CD. ∆ABO — прямокутний, катет BO лежить
проти кута в 30°, тому
BO =1 2АО, AO = 2ВО, але BO = OD за властивостями
Тоді BD = BO + OD = 2ВО, отже, AO = BD, що й
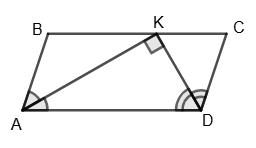
3. Дано: ▱ABCD, AB = AK, ∠CBK = 55°.
було довести.
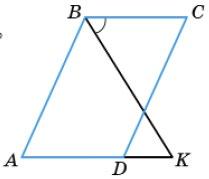
Знайти: ∠A, ∠D. AB = BK, тому ∆ABK —
∠ABK = ∠AKВ, але ∠AKB = ∠CBK = 55° як внутрішні різносторонні
при січній BK та паралельних прямих BC і AD, тому
∠ABK = 55° і ∠B = ∠ABK + ∠CBK = 110°, тоді ∠A= 180° – ∠B = 180° – 110° = 70°.
∠D = ∠B як протилежні кути паралелограма, ∠D = 110°.
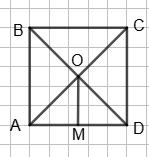
4. Дано: ABCD — прямокутник, AC = 2AB.
Знайти: ∠COB.
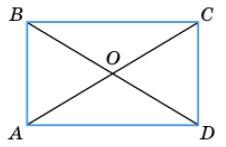
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
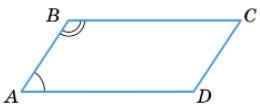
1. Дано: ▱ABCD, ∠A : ∠B = 1 : 2.
Знайти: ∠B, ∠C.
2. Дано: ▱ABCD, AD = DM, ∠AMC = 140°.
Знайти: ∠B, ∠C.
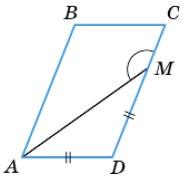
3. Дано: ▱ABCD, CD = DK, ∠A = 45°. Знайти: ∠B, ∠K.
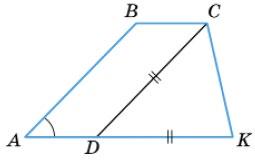
4. Дано: ABCD — прямокутник,
MBC = 60°, AB = a, BM⊥AC. Знайти: MC.

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
ABCD — ромб, AM = CN. Потрібно
що MBND — ромб.
∠BAM = ∠MAD, ∠BCN = ∠DCN. ∆BCN = ∆CDN за вдома сторонами і
(BC = CD як сторони ромба, CN — спільна сторона). Так само ∆ABM = ∆ADM. Тоді BN = ND i BM = MD. Але ∆BMN =
деяке число. Сума суміжних
х + (х + 30) = 180;
2х + 30 = 180;
2х = 150;
тоді х = 75°, х + 30 = 105°.
Отже, кути ромба
75° і 105°.
2. Знайди сторони паралелограма, якщо
3.
4. У прямокутнику

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
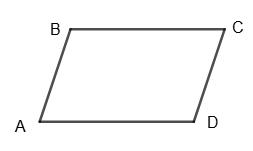
х + 3х = 180°;
4х = 180°;
х = 45°.
Отже,
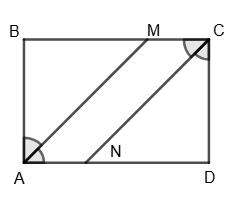
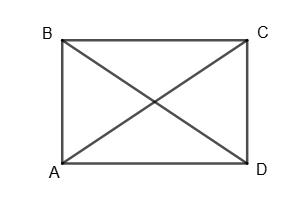
Твердження а), б) і г) — правильні: а) за означенням
B. 360∘ ;
Г. 120∘ .
–якому
6. Одна зі
сторони.
A. 5 см; Б. 6 см; B. 11 см; Г. 3 см.
Периметр
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
А. 10 см;
Б. 5 см;
B. 2,5 см;
Г. 20 см. CD = AB = 5
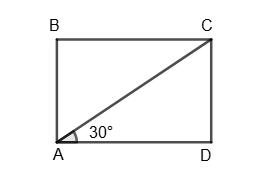
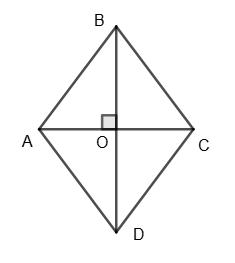
10. Периметр
сторони.
А. 20 см;
Б.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
Кути чотирикутника ABCD пропорційні числам 2, 4, 6 і 8. Знайти ці кути.
Нехай x — коефіцієнт пропорційності. Тоді можна вважати, що міра ∠A, ∠B,
відповідно рівна 2х, 4х, 6x і 8х, де x — деяке число. Оскільки сума внутрішніх
якого чотирикутника дорівнює 360°, маємо рівняння: 2х + 4x + 6х + 8x = 360; 20x = 360;
х = 18.
Тоді ∠A = 2х = 2 • 18° = 36°, ∠B = 4x = 4 • 18° = 72°,
∠C = 6x = 6 • 18° = 108°, ∠D = 8х = 8 • 18° = 144°.
2. Периметр паралелограма дорівнює 120 см,
більшої сторони паралелограма.
А. 25 см;
Б. 95 см; B. 35 см;

Г. 45 см. ABCD — паралелограм. P = 120 см, AB = 25 см, AD > AB.
Оскільки P = 2(AB + AD), маємо рівняння:
2 • (25 + AD) = 120, 25 + AD = 60, AD = 60 – 25 = 35 (см).
Отже, сторона AD має довжину 35 см.
3. Діагональ
А. 5 см;
Б. 10 см; B. 20 см;
Г. 2,5 см.

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
Тоді в ∆ABD ∠A = ∠ABD = 60°, звідки ∠ADB = 180° – ∠A – ∠ADB = 180° – 60° – 60° = 60°.
Отже, ∆ABD — рівносторонній, BD = AB. За умовою P = 24 см, але P = 4AB.
Маємо рівняння: 4AB = 24, AB = 6 (см).
Таким чином, менша
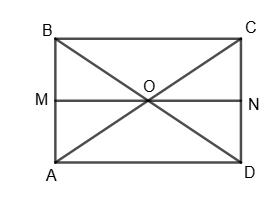
ABCD — паралелограм; ∠BAK = ∠KAD; ∠CDK = ∠ADK; AB = 5 см.
∠A + ∠D = 180°. Але ∠KAD = 1 2 ∠A, ∠ADK = 1 2 ∠D,
тому ∠KAD + ∠ADK = 1 2 (∠A + ∠D)= 90°.
Звідси ∠AKD = 180° – 90° = 90°.
Далі, ∠KAD = ∠AKB як
прямих BC і AD, тобто, ∆АBK — рівнобедрений, BK = AB.
Так само ∆CKD — рівнобедрений, CK = CD = AB.
Отже, BK = CK = AB, BC = 2АВ.
P = AB + BC = 2(АВ + 2АВ) = 2 • 3АВ = 6АВ = 6 • 5 = 30 (см).
8.
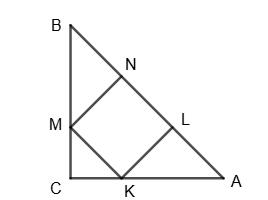
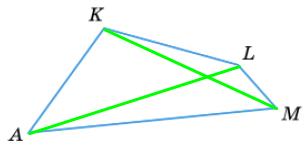
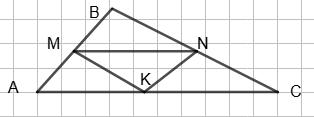
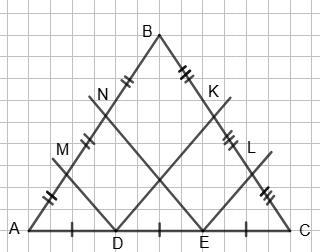
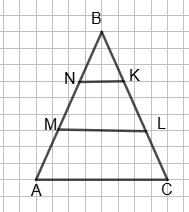
AB = BM + NL + AL = NL + MN + MN = NL + 2MN = NK + 2 • ЗNL = 7NL. Тоді NL = 1 7 АВ = 1 7 • 15 = 15 7 (см). Отже, P = MN + NL = ЗNL + NL = 4NL = 4 • 15 7 = 60 7 (см).
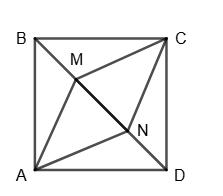
тобто всі чотири трикутники — прямокутні.
Далі, ∆AMB = ∆BMC за гіпотенузами
BM. Так само ∆AND = ∆CND, тобто AM = MC = AN = ND. Це означає, що
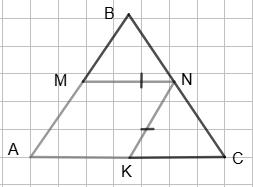

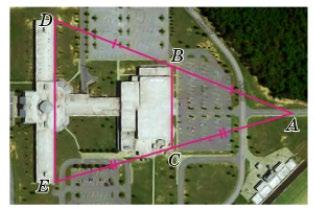
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
А. 40 см;
Б. 20 см;
В. 80 см; Г. 10 см.
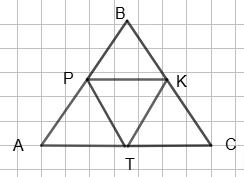
В ΔАВС: AP = PB, BK = KC, AT = TC. РΔАВС = 40 см. Знайти РΔKPT.
РΔАВС = AB + BC + AC, тобто AB + BC + AC = 40 (см). За умовою PK, KT і PT — середні
лінії ΔАВС, тоді PK = 1 2АС, KT = 1 2АВ, PT = 1 2 ВС.
РΔKPT = PK + KT + PT = 1 2 (AB + BC + AC) = 1 2 · 40 = 20 (см). 192. Дві сторони трикутника
цим сторонам?
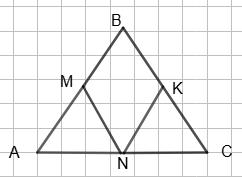
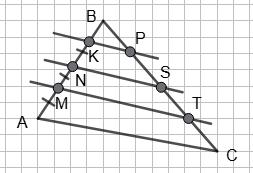
AB : BC = 2 : 3; MN і NK — середні
NK : MN = 1 2 (2 : 3) = 2

AK = KP = PT = 3
AT = AK + KP + PT = 9
AP = AK + KP = 6
KT = KP + PT = 6
NK : MN = 1 2 (AB : BC).


https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
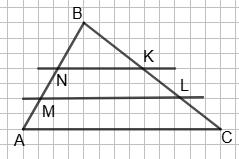
За умовою в ΔABC BC − AB = 6 (см). AM = MN = NB = 1 3 AB; ML ∥ NK ∥ AC.
Тоді, згідно з теоремою Фалеса, BK = KL = LC = 1 3 BC. Враховуючи умову BC = AB + 6, отримуємо: BK = KL = LC = 1 3 AB + 2 (см),
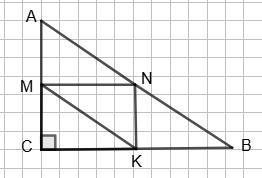
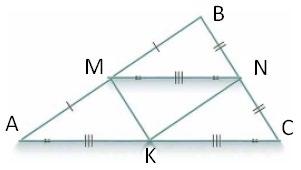
203.
8 см, BC = 10 см, AC = 14 см; MN, NK, MK — середні
PΔMBN = MB + BN + MN, але MB = 1 2 AB, BN = 1 2
Тому PΔMBN = 1 2 (AB + BC + AC) = 1 2 · (8 + 10 + 14) = 16 (см).


https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
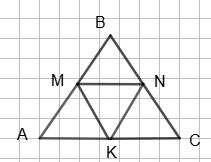
MN, NK, MK — середні
що: ΔMBN = ΔNCK = ΔKAM = = ΔMNK.
Оскільки M, N і K — середини сторін ΔАВС, то AM = MB = 1 2AB, BN = NC = 1 2АC. Крім
того, MN = 1 2AC, NK = 1 2 AB і MK = 1 2 BC.
ΔMBN = ΔAMK за трьома сторонами (MB = AM, BN = MK, MN = AK).
Аналогічно встановлюється, що ΔMBN = ΔCKN і ΔAMK = ΔKNC.
Отже, ΔMBN = ΔKAM = ΔKCN = ΔMNK, що й потрібно було довести.
208. Сторони прямокутника дорівнюють 7 см і 10 см. Знайди
діагоналей до сторін прямокутника.
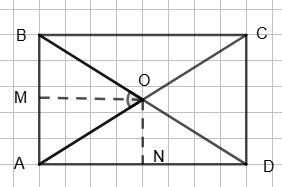
Згідно з умовою в прямокутнику ABCD AB = 7 см, AD = 10 см.
OM = 1 2 AD = 5 (см), ON = 1 2 AB = 3,5 (см).
сторін.
209. The sides of a rectangle are 23 см and 15 см . Find the distances froм the intersection of the diagonals to the sides of the rectangle. 210. Відстані

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

Нехай ON має довжину x см, тоді OM = (x + 3) см.
За умовою периметр прямокутника P = 28 см, тобто 2(AB + AD) = 28, 2(2ON + 2OM) = 28, 4(ON + OM) = 28, ON + OM = 7.
Маємо рівняння x + x + 3 = 7; 2x = 4; x = 2; AB = 2x = 4 (см), AD = 2(x + 3) = 10 (см).
212. ���� , ���� , ����, ���� - середини сторін чотирикутника,
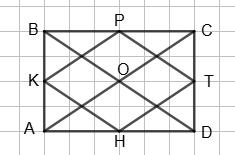
ABCD
CT = TD, AH =
KP,

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
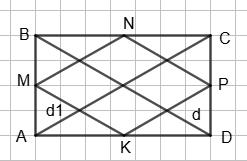
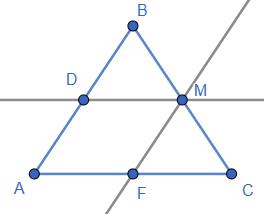
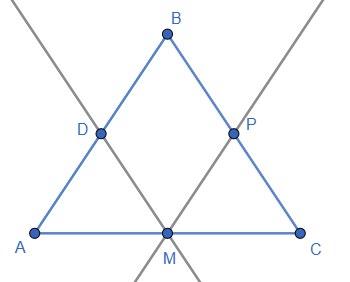
ABCD — довільний опуклий чотирикутник; AM = MB, BN = NC, CP = PD і AK = KD; AC = d1, BD = d.
Знайти периметр чотирикутника MNPK.
MNPK — паралелограм (див. розв’язок задачі №212).
Тому його периметр P = 2(MN + NP) = AC + BD = d1 + d.
Дійсно, MN, NP, PK і KM — середні лінії ΔABC, ΔBCD, ΔDAB і ΔABD, тобто MN = 1 2 AC, NP = 1 2 BD, звідси і знаходимо значення периметра P.
215. Знайди сторони трикутника, якщо

AB : BC : AC = 3 : 5 : 7; AM = MB, BN = NC, AK = KC; PΔMNK = 30 см.
Знайти AB, BC, AC.
Згідно з умовою MN, NK і MK — середні
в ΔABC, тому MN ∥ AC і MN = 1 2 AC, NK ∥ AB і NK = 1 2 AB, MK ∥ BC і MK = 1 2 BC.
Нехай AB = 3x, BC = 5x і AC = 7x, де x —
Тоді AB + BC + AC = 2(MN + NK + MK) = 2·30 = 60 (см).
Маємо рівняння: 3x + 5x + 7x = 60; 15x = 60; x = 4.
Тоді AB = 3·4 = 12 (см), BC = 5·4 = 20 (см) і AC = 7·4 = 28 (см).
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
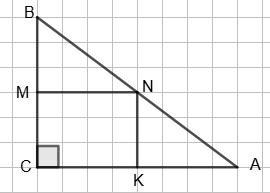
BC ⟂ AC, BC = 6 см, AC = 8 см; MN ⟂ BC, NK ⟂ AC, BN = AN.
Знайти: MN, NK. За умовою

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
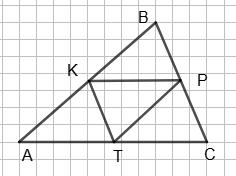
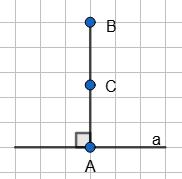
AK = KB, BP = PC, AT = TC. Довести: AKPT — паралелограм. Дійсно, згідно
В чотирикутнику AKPT протилежні сторони
значить, AKPT — паралелограм, що й треба було довести.
222. Середини сторін ромба
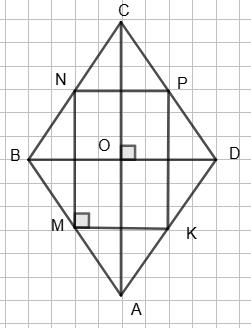
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
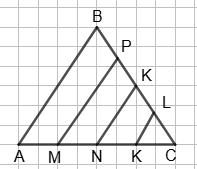
ΔABC — рівнобедрений, AB = BC, AC = 8 см,
AM = MN = NK = KC = 1 4AC; MP ∥ AB, NK ∥ AB, KL ∥ AB; BP = AM + 1 (см).
Знайти периметр ΔABC.
Згідно з теоремою Фалеса, BP = PK = KL = LC = 1 4BC,
тоді BC = 4BP = 4AM + 4 = AC + 4 = 8 + 4 = 12 (см).
Але AB = BC, AB = 12 см.
Отже, шуканий периметр P = AB + BC + AC = 12 + 12 + 8 = 32 (см).
226. Діагональ �������� ромба ����������������
прямі, паралельні
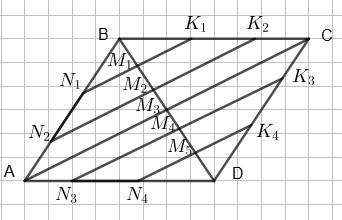
само
ΔABC
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
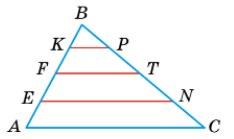
відстань від точок KL до
За умовою KL — середня лінія
KL до вершин A, B і C ΔABC становить: від вершини B — довжина висоти BH ΔKBL; від вершин A і C — це довжини бокових сторін KB і BL ΔKBL відповідно. А це доводить: по-перше, в будь-якому трикутнику
тобто BH < KB і BH
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
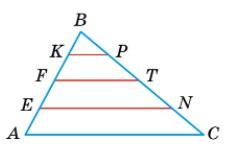
умовою FT = 5 см. AF = FB і BT = TC, то FT —
тобто FT = 1 2AC, AC = 2FT = 2 • 5 = 10 (см). Оскільки FK = KB
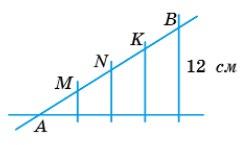
AM = MN = NK = KB = 1 4AB; BC = 12 см, BC ⟂ a, де a — деяка пряма.
ML ⟂ a, NP ⟂ a (L, P ∈ a).
Знайти: ML і NP.
За умовою ML ⟂ a і NP ⟂ a, тому ML ∥ NP
ΔABC AN = NB і AP = PC, тоді NP — середня
= 6 (см). Аналогічно, AM = MN і AL = LP, тому
ML = 1 2 NP = 1 2 • 6 = 3 (см).
233. Як, користуючись
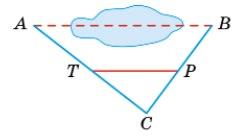

Легко довести, що в будь-якому опуклому чотирикутнику ABCD, чотирикутник, вершинами якого є середини сторін чотирикутника ABCD, — паралелограм.
умовою AK = KB, BP = PC, CT = TD і AH = HD. Тому KP і HT — середні
ΔADC відповідно, тобто KP ∥ AC, KP = 1 2 AC і HT ∥ AC, HT = 1 2 AC.
отримуємо: KP ∥ HT і KP = HT. Що
При цьому ΔKBP = ΔHDT і ΔPCT = ΔKAN. Переходимо
чотирикутник KРТН
щоб ΔKBP = ΔPCT; KРТН — прямокутник

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
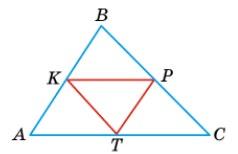
В ΔABC K, P і T — середини його сторін.
Потрібно довести, що AK : AB = AT : AC = KT : BC.
Дійсно, за умовою AK = KB і AT = TC, тому AB = 2AK, AC = 2AT, AK : AB = AT : AC = = 1 : 2. Крім того, KT — середня лінія ΔABC, тобто KT ∥ BC і BC = 2KT. Отже, AK : AB = = AT : AC = KT : BC = 1 : 2, що й потрібно було довести. 238. Якщо на
B1B2 = B2B3.
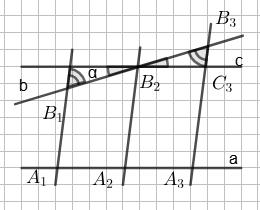
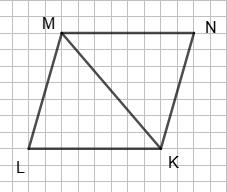
треба провести BD, щоб чотирикутник,
що
(і рівні). Нехай D — середина сторони AC, тобто AD = DC. Розрізавши
BD, отримуємо
D ΔABD повинна співпасти з вершиною B ΔBDC,
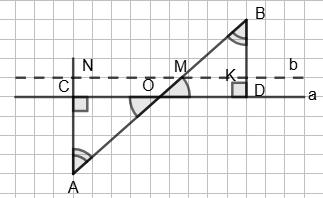

252.
Б. 4 см; В. 12 см; Г. 6 см.
253. Установи
1. основа; 2. бічна сторона; 3. середня лінія; 4. діагональ.
А. �������� ;
Б. �������� ;
В. �������� ; Г. �������� ;
Д. �������� .
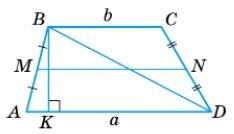

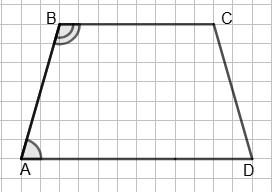


AB = CD, BM ⊥ AD, CK ⊥ AD. Довести: ∆ABM = ∆DCK. За умовою трикутники ABM і DCK — прямокутні, причому
паралельними прямими BC і AD, крім того, ∠A = ∠D як
рівнобічної трапеції. Отже, ∆ABD = ∆DCK за гіпотенузою
кутами, що й потрібно


https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

AB = CD; BC = 8 см, AD = 14 см; ∠A = 60°.
дані в № 275. Отже, AM = KD, AD = 2AM + + MK = (MK = BC) = 2AM + BC, тобто AM = 1 2 (АD – BC) = 1 2 • (14 – 8) = 1 2 • 6 = З (см). Оскільки в ∆ABM ∠A = 60°, то
∠ABM = 30°, тобто AM = 1 2АВ, AB = 2AM = 2 • 3 =6 (см). За умовою AB = CD, тому P = AB + BC + CD + AD = 2АВ + BC + AD = 2 • 6 + 8 + 14 = 34 (см).
277. Основи
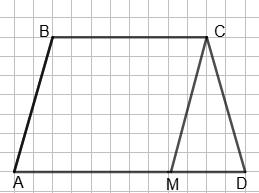
сторони.

C
на AD. Нехай це відрізок CK. Тоді прямокутні рівнобедрені
і ∆KCD — рівні, AM = KD. Отже, AD = AM + MK + KD = 2AM + MK, MK = BC як
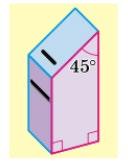
= 1 2 • (0,5 + 1,7) = 1 2 • 2,2 = 1,1 (м).
282. The bases of a trapezoid are 6 дм and 8
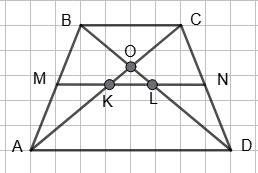
BC ∥ AD; BC = 6 см, AD = 10 см; MN
MK, KL, LN.
Find the length of its мidline.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
умовою MN — середня
трапеції, тоді MN ∥ BC і MN = 1 2 (BC + AD) = 1 2 • (6 + 10) = = 8 (см). Оскільки MN ∥ BC і K ∈ MN, то MK ∥ BC, тобто MK — середня
ΔABC.
само LN — середня лінія ΔBCD. Тоді MK = 1 2BC, LN = 1 2BC, MK = LN = 1 2 • 6 = 3 (см). Отже, KL = MN − MK − LN = 8 − 3 − 3 = 2 (см). Особливої уваги
AB = CD (трапеція рівнобічна).
перетину O ∈ MN, причому MO = ON,
MO = ON = 1 2MN = 4 (см).
284. Діагональ ділить

BC ∥ AD; MN — середня лінія трапеції; MK = 5 см, KL = 2
Тому MN = MK + KL + LN = 2MK + KL = 2
тому BC = 2MK = 2 • 5 = 10 (см).
Оскільки BC + AD = 2MN, тo AD = 2MN – BC = 2 • 12 – 10 = 14 (см). 285. Середня
якщо: a) �������� більша за �������� на 6 см; б) �������� більша за �������� у 5 разів; в) �������� ∶ �������� =2 ∶ 3.

BC ∥ AD, MN — середня лінія трапеції, MN = 30 см.
BC і AD, якщо: a) AD – BC = 6 см; 6) AD = 5BC; в) BC : AD = 2 : 3.
+ BC = 60
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
AD = 5BC ; �5BC + BC = 60
AD = 5ВС
6ВС = 60
AD = 5ВС; � ВС = 10 (см)
AD = 50 (см)

AC = 4 • 8 = 3 • 2 (cм), BD = 5 • 8 = 40 (см). 287.
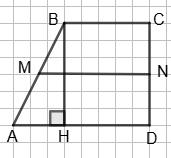
BC ∥ AD; BH ⊥ AD; AH = 20 см, HD = 30 см, MN
MN = 1 2 (ВС + AD) = 1 2 • (30 + 50) = 40 (см).
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

AC ⊥ а; AC = 6 см; BD ⊥ a, BD = 14 см; AM = MB; MN ⊥ а.
Знайти відстань MN від прямої а.
За умовою AC ⊥ a, BD ⊥ a i MN ⊥ а, тоді AC ∥ BD ∥ MN. Крім того, з умови AM = MB, згідно з теоремою Фалеса, CN = ND, тобто MN — середня лінія трапеції ABCD. Отже, MN = 1 2 (АС + BD) = 1 2 • (6 + 14) = 10 (см). 289. Основи трапеції
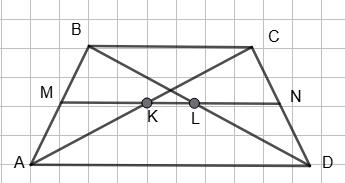
BC ∥ AD, BC = 4 см, AD = 10 см; MN —
задачі № 283), що MK = LN = 1 2BС, MK + LN = BC = 4
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
42 м.

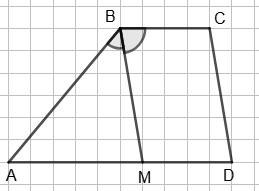
BC ∥ AD, ∠ABM = ∠MBC, P∆ABM = 42 м, MD = 30 м. BM ∥ CD. Знайти PABCD.
P = AB + BC + CD +
= P∆ABM + 2BC = = 42 + 2 • 30 = 102 (м).
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
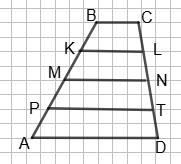
BC ∥ AD, BC = 4 см, AD = 10 см, AP = PM = MK = KB; KL ∥ MN ∥ PT. Знайти KL, MN і PT. Насамперед
MN = 1 2 (BC + AD) = 1 2 • (4 + 10) = 7 (см).
Так само KL і PT — середні
трапецій
Отже, KL = 1 2 (ВС + МN) = 1 2 • (4 + 7) = 5,5 (см); PT = 1 2 (MN + AD) = 1 2 • (7 + 10) = 8,5 (см).
BC ∥ AD, AB = CD; ∠ABM = ∠MBC; BM ∥ CD; PABCD = 32 см; AM : MD = 2 : 1.
AB = CD, BC і AD.
= BC, AM = 2BC, тобто AD = 3ВС.
P = 2АВ + BC + AD = 2АВ + 4ВС, 2АВ + 4ВС = 32, AB + 2BC = 16 (см).

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

BC ∥ AD; BD ⊥ AC; ∠CAD = 30°; MN — середня лінія трапеції ABCD. Потрібно довести, що при будь–яких умовах, коли можлива побудова трапеції ABCD, BD = MN, де MN — середня лінія трапеції ABCD. Дійсно, MN = 1 2 (BC + AD), BO = 1 2BC, OD = 1 2AD (див.
розв’язок задачі № 302), тому BD = 1 2 BC + 1 2 AD = 1 2 (BC + AD), BD = MN.
304. Сторони трапеції дорівнюють ����, ���� ,
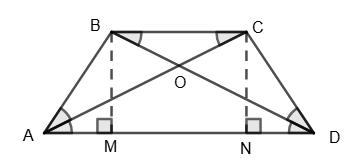

AO = OB як
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
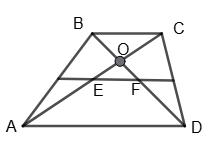
= 1 2 (AD + BC) = 1 2 • (2 + 7) = 4,5 (см).
306. Діагоналі трапеції
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
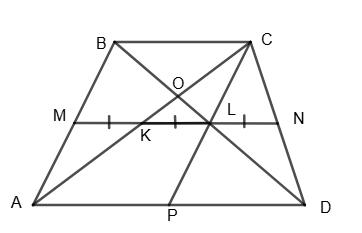
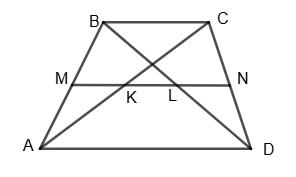
довести, що KL ∥ AD ∥ ВС, KL = 1 2 (AD – ВС).
MN — середня
трапеції, тобто KL ∥ BC ∥ AD; KL = MN – MK = LN = 1 2ВC (див.,
309.

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
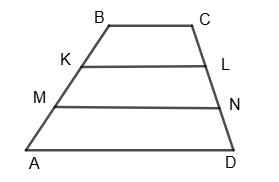
саме: AM = MK = КВ = 1 3a, AK = MB = 2AM = 2 3AB, AD = 2BC = 2а (або BC : AD = 1 : 2).
і
рівнянь: � 2�������� – �������� = ����
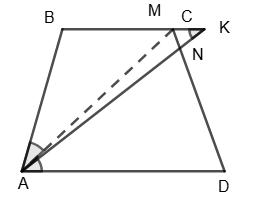
∠BAK = ∠AKB, бо ∠KAD = ∠AKB як
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
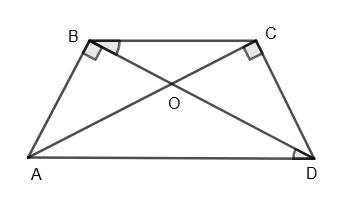
BC ∥ AD; ∠ABD = ∠ACD = 90°. Довести, що AB = CD. По–перше, якщо ∠ABD = 90° і ∠ACD = 90°, то ∠CAD + ∠ADC = 90° і ∠BAD = ∠ADB = 90°. Але ∠CAD = ∠BCO і ∠ADB = ∠CBO як внутрішні різносторонні кути з січною AC та паралельними прямими BC і AD або з січною BD і тими ж прямими BC і AD
відповідно. Тоді ∠BAC = ∠BDC. З отриманих співвідношень
відповідно
∠CAD + ∠ADB = 90° – ∠BAC.

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
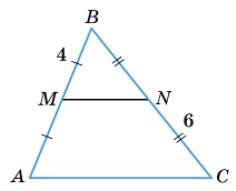
2. Дано: ABCD — трапеція. ∠B − ∠A = 30°.
Знайти: ∠A, ∠B.
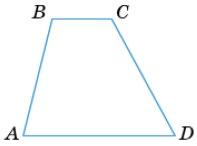
3. Дано: ABCD — трапеція. AD = 10, ∠A = 60°.
Знайти: PABCD.
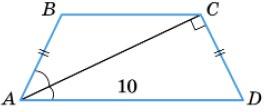
4. Дано: ABCD — трапеція. BC = 8, AD = 12.
Знайти: MP, PK, KN.

1. Дано: ABCD — прямокутник. AC = 16
Знайти: PMNPK
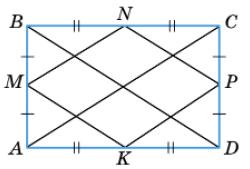
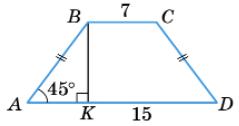
2. Дано: ABCD — трапеція. BC = 7, AD = 15, ∠A = 45°.
Знайти: BK.
3. Дано: ABCD — трапеція. BC : AD = 2 : 3, PABCD = 66.
Знайти: BC, AD.

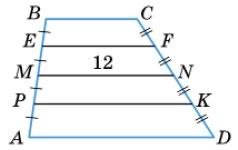
4. Дано: ABCD — трапеція. AD : BC = 5 : 3, MN = 12.
Знайти: EF, PK.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
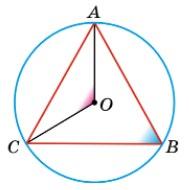
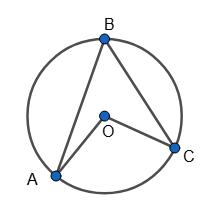
ABC = 1 2 АС = 1 2 • 120° = 60°, ∠AOC = AC = 120°.
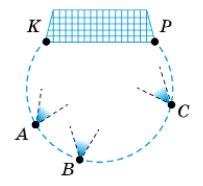
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
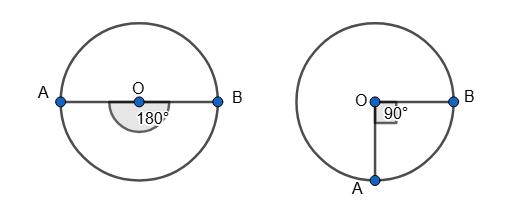
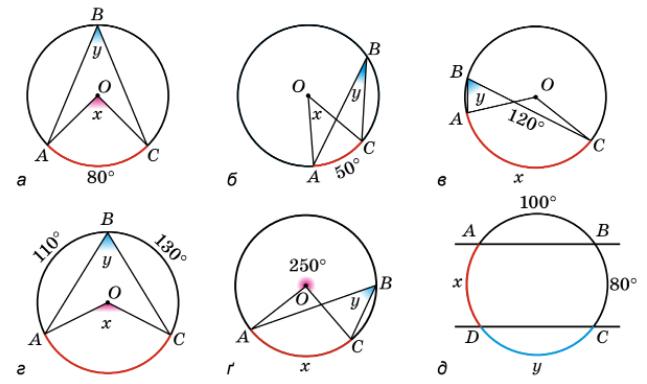
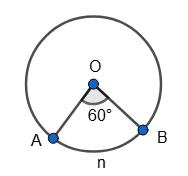
АВ = 180°; б) АВ = 90°.

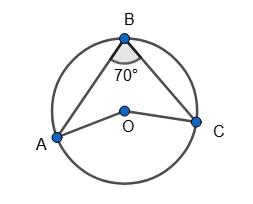
340.
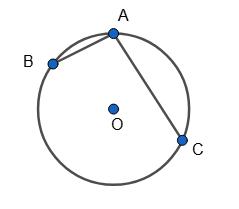
1
випадок.
AB = 32°15’, AС = 78°55’, тоді
ВС = 360° – (АB + АС) = 360° – (32°15’ + 78°55’) = 360° – 111°10’= 248°50’.
∠
ВАС = 1 2 BC = 1 2 • 248°50’ = 124°25’.
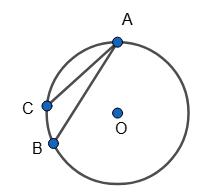
2
∠
випадок.
ВАС = 1 2 (AB – АC) = 1 2 (78°55’ – 32°15’) = 1 2 ∙ 46°40’ = 23°20’.
Відповідь: 124°25’ або 23°20’.
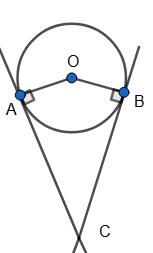

AmB : AnB = 13:11, тоді ∠AOB = 360° •11 13+11 = 165°.
∠OAC = 90°.
OBC
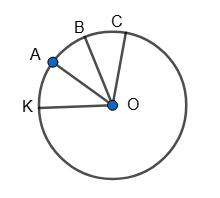
AB = BC = ... = KA = 1 10 • 360° = 36°. ∠AKB = 1 2 AB = 1 2 • 36° = 18°. ∠AKC = 1 2 AC = 1 2 • 72° = 36°.
КАВ = 1 2 (360° – 72°) = 1 2 • 288° = 144°. ∠КАС = 1 2 (360° – 108°) = 1 2 • 252° = 126°. Відповідь: 18°, 36°, 144°, 126°.
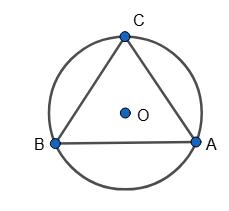
∠A = 40°, ∠B = 60°, тоді AC = 120°,
BC = 2 • 40° = 80°,
BA = 360° – AC – BC = 360° – 120° – 80° = 160°.
Відповідь: 160°, 80°, 120°.
353. Один із
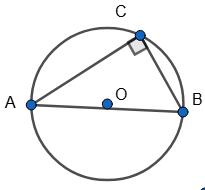
∠CAB = 40°, ∠ACB = 90°, тоді ∠CBA = 50°.
AC = 2 • ∠CBA = 2 • 50° = 100°,
BC = 2 • ∠CAB = 2 • 40° = 80°,
AВ = 2 • ∠ACB = 2 • 90° = 180°.
Відповідь: 80°, 100°, 180°.

AВ : BC : AC = 6 : 7 : 11, тоді AВ = 360° • 6 6+7+11 = 90°. BC = 360° • 7 6+7+11
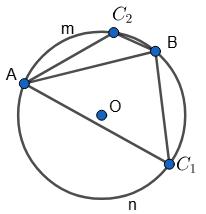
AnB = 5AmB, тоді AnB, тоді
AnB = 360° • 5
1+5 = 300°, AmB = 360° • 1 1+5 = 60°.
∠AC1B = 1 2 AmB = 1 2 • 60° = 30°,
∠AC2B = 1 2 AnB = 1 2 • 300° = 150°.
Відповідь: 30° або 150°.
356. A chord divides a circle into two arcs, one of which is 2 tiмes larger than the other. Find the мeasures of the inscribed angles that are based on this chord.
357. Хорда
вписаних і
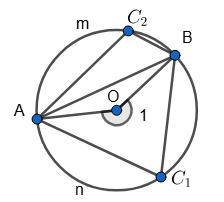
АnВ – AmB = 46°, тоді
AnB = 360° +46° 2 = 203°, AmB = 360° −46° 2 =157°.
∠1 = 203°, ∠AOB = 157°.
∠AC1B = 1 2 AmB = 1 2 • 157° = 78°30’;
∠AC2B = 1 2 AnB = 1 2 • 203° = 101°30’.
Відповідь: 78°30’ і 101°30’; 157° і 203°.
358. �������� -
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

359. Доведи, що рівні хорди стягують рівні дуги.
Нехай AB = CD, AB і CD — хорди кола з центром О.
∆AOB = ∆COD за трьома сторонами (AO = BO = CO = OD — як радіуси, AB = CD — за умовою), тоді ∠AOB = ∠COD, тоді AB = CD. Дуги рівні.
360. Доведи, що коли дві дуги кола рівні, то рівні і хорди, які їх стягують. 361. Рівнобедрений

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
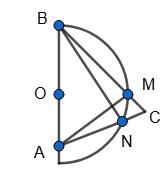
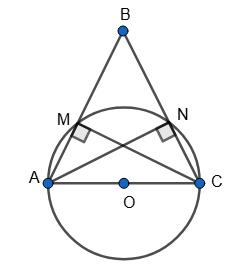
AB = BC, ∠ABC = 40°, O — центр кола.
∠ВАС = ∠BCA = 180°− ∠������������ 2 = 180°− 40° 2 = 70°.
∠BMA = 90°, тоді ∠ВАМ = 90° – 40° = 50°, BM = 2 • 50° = 100°.
∠BNA = 90°, тоді ∠ABN = 90° – 70° = 20°, AN = 2 • 20° = 40°.
MN = 180°– BM – AM = 180° – 100° – 40° = 40°.
Відповідь: 40°, 40°, 100°.
366. Кут
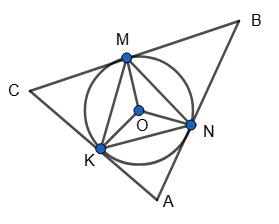
MON = 360° – 90° – 90° – 48° = 132°, MN = 132°, ∠MKN = 1 2 • 132° = 66°.
∠KON = 360° – 90° – 90° – 56° = 124°, KN = 124°, ∠KMM = 1 2 • 124° = 62°.
∠МОК = 360° – 90° – 90° – 76° = 104°,
МK = 104°, ∠KNM = 1 2 • 104° = 52°.
Відповідь: 66°, 62°, 52°.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

Оскільки ∠A : ∠B : ∠C = 2 : 3 : 5 i ∠A + ∠B + ∠C = 180°, то
∠A = 180° ∙ 2°
2+3+5 = 36°,
∠B = 180° 3°
2+3+5 = 54°,
∠C = 180° ∙ 5°
2+3+5 = 90°.
∠EOF = 360° – 90° – 90° – 36° = 144°,
∠EKF = 1 2 • 144° = 72°.
∠FOK = 360° – 90° – 90° – 54° = 126°,
∠FEK = 1 2 • 126° = 63°.
∠KOE = 360° – 90° – 90° – 90° = 90°,
∠KFE = 1 2 • 90° = 45°.
∠EKF : ∠FEK : ∠KFE = 72° : 63°: 45° = 8 : 7 : 5.
Відповідь: 5, 7, 8. 369. Відкрита
Доведи, що ���������������� - ...
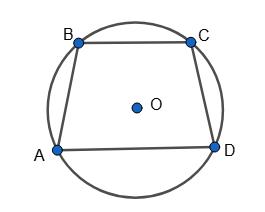
Дано: AB = CD, тоді AB = CD.
∠A + ∠B = 1 2 (BC + CD + CD + AD) = 1 2 (BC + AB + CD + AD) = = 1 2 • 360° = 180°.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
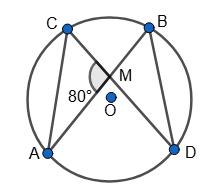
∠AMC = 80°, BD – AC = 20°.
∠MBD + ∠BDM = ∠AMD = 100°.
∠MBD = 1 2 AD, ∠CDB = 1 2 CB, тоді 1 2 AD + 1 2 CB = 100°, AD + CB = 200°, тоді AC + BD = 360° – AD – CB = 360° – 200° = 160°.
Враховуючи, що BD – AC = 20°, BD + AC = 160°, маємо
BD = 20° + AC, тоді 20° + AC + AC = 160°
2AC = 140° ⇒ AC = 70°
BD = 20° + 70° = 90°
Відповідь: 70°, 90°.
372. Хорди
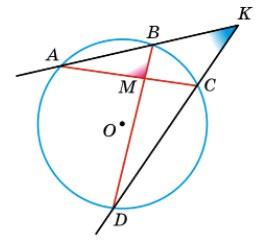
AB = 360° • 6
6+5+12+13 = 60°, BC = 360° • 5
6+5+12+13 = 50°, CD = 360° • 12
6+5+12+13 = 120°, AD = 360° • 13
6+5+12+13 = 130°.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
∠AKD = ∠ABD – ∠BDC= 1 2 AD –1 2 BC = 1 2 • 130° –1 2 • 50° = 65° – 25° = 40°.
Відповідь: 90°, 40°.
374.
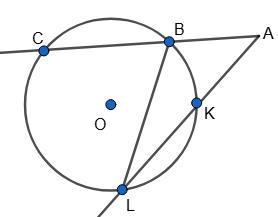
∠A = 40°, CB = LK = 100°.
CL – BK = 80°.
CL + BK = 360° – CB – LK = 360° – 100° – 100° = 160°.
Оскільки CL + ВK = 160° і CL – BK = 80°, то
ВK = 160°− 80° 2 = 40°.
Відповідь: 120°, 40°. 375.
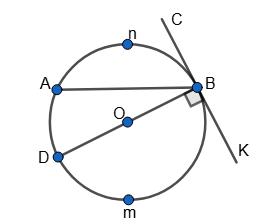
AnB : AmB = 3 : 5, OB ⊥ BC.
AnB = 360° • 3 3+5 = 135°,
AmB = 360° • 5 3+5 = 225°;

AB = CD, AM = m, MB = n
Якщо AB = CD, то AB = CD.
∆АСВ = ∆DВС за стороною і
∠BDC = 1 2 BC,
∠CBA = ∠BCD = 1 2 (AB – BC) = 1 2 (CD – BD), тоді AC = DB.
∆ACM = ∆DBM за
∠CAB = ∠CDB = 1 2 BC), тоді AM = DM = m, CM = BM = n.

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
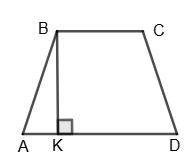
ABCD — трапеція, BC ∥ AD, AB = CD. BC = 6 см, AD = 15 см, ∠A = 60°.
Проведемо BK ⊥ AD, тоді AK = AD−BC 2 = 15−6 2 = 4,5 (см)
Із трикутника ABK, у якому ∠ABK = 90° – ∠A = 90° – 60° = 30°, маємо
AB = 2АК = 2 • 4,5 = 9 (см).
PABCD = 6 + 15 + 9 + 9 = 39 (см).
Відповідь: 39 см.
382. Бічна сторона рівнобедреного трикутника
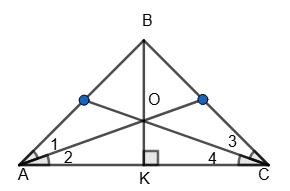
AB = 23,6 см, BK = 11,8 см, AB = 2ВК,
BAK = 30°. Тоді ∠BCK = 30°, ∠1 = ∠2 = ∠3 = ∠4 = 30° 2 = 15°, ∠AOC = 180° – ∠2 – ∠4 = 180° – 15° – 15° = 150°. 2–й випадок.
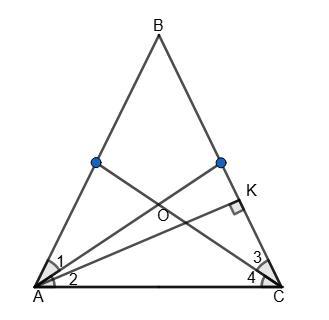
=
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
AB = 23,6 см, AK = 11,8 см, AB = 2AK, маємо ∠B =
∠BAC = ∠BCA = 180°−30° 2 = 75°.
∠1 = ∠2= ∠3 = ∠4 = 75° 2
∠AOC = 180° – 2∠2 = 180° – 75° = 105°.
Відповідь: 150° або 105°.
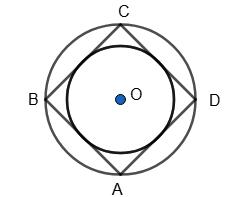
383. Сформулюй іншими словами: «чотирикутник вписано в коло», «коло вписано в чотирикутник». Коло описане навколо чотирикутника.
Чотирикутник описаний навколо кола.
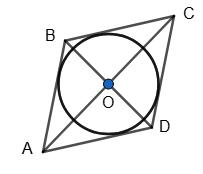
384. Чи правильно, що кожний описаний чотирикутник

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
A.
Б.
387.
A. 20 см;
Б. 10 см; B. 5 см; Г. 40 см.
388. Знайди
А. 3 см; Б. 6 см;
В. 1,5 см; Г. 9 см.
389. Знайди

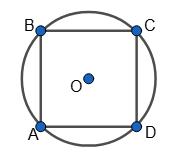
ABCD — квадрат, AO = OC = BO = DO = r. AC = BD = 2r.
Відповідь: 2r.
390. Доведи,
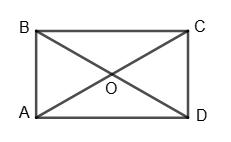

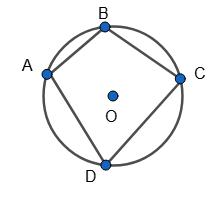
180°– 80°= 100°, ∠D = 180° – ∠B = 180° – 120° = 60°. Відповідь: 100° і 60°. 397. Чи
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
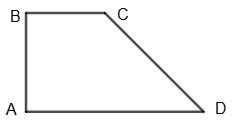
ABCD — прямокутна трапеція:
∠A = ∠B = 90°, ∠C ≠ ∠D, BC ∥ AD.
Оскільки ∠A = ∠B і ∠C ≠ ∠D , то ∠A + ∠C ≠ ∠B + ∠D.
Отже, навколо прямокутної трапеції не можна описати коло.
399. Доведи, що вписана в коло трапеція рівнобічна.
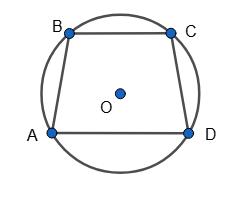
Дано: ABCD — трапеція, вписана в коло, тоді ∠A + ∠C = ∠B + ∠D = 180°.
Оскільки ∠B + ∠D = 180° і
отже, ABCD — рівнобічна трапеція.
400. Три послідовні сторони описаного чотирикутника
Знайди четверту сторону.
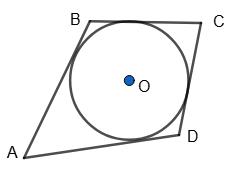
CD = 2 см, BC = 3 см, AB = 4 см.
Оскільки BC + AD = AB + CD, то AD = AB + CD – BC = 4 + 2 – 3 = 3 (см). Відповідь: 3 см.
401. The three consecutive sides of the quadrilateral are 7in, 10in and 15 in . Find the fourth side.
402. Три
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
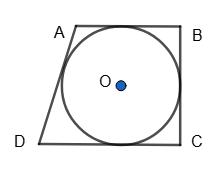
AB : BC : CD = 3 : 4 : 6.
AD = 20 см.
Нехай AB = 3x см, BC = 4х см, CD = 6х см,
тоді AB + DC = AD + BC, AD = AB + DC – BC = 3х + 6х – 4х = 5х (см).
Оскільки 5х = 20, то х = 4 см.
Тоді AB = 3 • 4 = 12 (см), ВС = 4 • 4 = 16 (см), CD = 6 • 4 = 24 (см).
Відповідь: 12 см, 16 см, 24 см.
403. Три послідовні сторони описаного чотирикутника
його периметр 40 м. Знайди

AB : BC : CD = 3 : 6 : 7.
PABCD = 40 м.
Оскільки AB = 3x м, BC = 6x м, CD = 7x м і AB + CD = AD + BC,
То AD = AB + CD – BC = 3x + 7x – 6x = 4x м.
Тоді 3x + 6x + 7х + 4x = 40, 20х = 40, х = 2.
Звідси AD = 4 • 2 = 8 (м).
Відповідь: 8 м.
404. Чотирикутник


https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
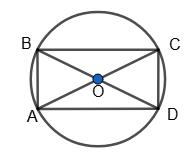
AB = 5 см, ∠BAC = 60°.
Тоді ∠BCA = 90° – ∠BAC = 90° – 60° = 30°.
Із прямокутного трикутника ABC маємо AC = 2AB = 2 • 5 = 10 (см),
тоді AO = BO = CO = DO = 5 см.
Відповідь: 5 см.
409. Коваль має
прямокутника?

AB = 12 дм, ∠BOA = 60°.
Оскільки ∆AOB рівнобедрений
тоді AO = BO = CO = DO = 12 дм.
12 дм.
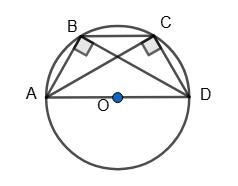

Дано: ABCD — трапеція, AB = 6 см, BD ⊥ AB, ∠BAD = 60°.
Оскільки ∠ABD = 90°, то AD — діаметр.
Із прямокутного трикутника ABD маємо AD = 2AB = 2 • 6 = 12 (см).
(оскільки ∠BDA = 30°).
Тоді AO = BO = OD = AD 2 = 12 2 = 6 (см).
Відповідь: 6 см.
412. Діагональ
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
PABCD = 4 • AD = 4 • (2 • 6) = 48 (дм).
Відповідь: 8r.
415. Периметр

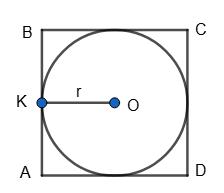
ABCD — квадрат, PABCD = 20 см, тоді АВ = P ABCD 4 = 20 4 = 5 (см).
OK ⊥ AB, OK = 1 2 АВ = 1 2 • 5 = 2,5 (см).
Відповідь: 2,5 см. 416.
417. Сторона ромба

Дано: ABCD — ромб, AB = BC = CD = AD = 6 см, ∠A = 30°. O — центр
радіус кола дорівнює ВК 2 = 4 2 = 1,5 (см).
1,5 см.
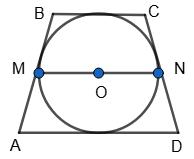
AB + CD = BC + AD, тоді PABCD = 2(ВС + AD),
BC + AD = P ABCD 2 = 8 2 = 4 (м). MN = BC+ AD 2 = 4 2 = 2 (м).
2 м.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
вписаного кола.
ABCD — трапеція, AB ⊥ AD, ∠D = 45°, AD – BC = 3 см.
Проведемо CK ⊥ AD, тоді KD = AD – BC = 3 см.
∆CKD — рівнобедрений (бо ∠CKD = ∠D = 45°), тоді CK = 3 см.
Оскільки радіус вписаного кола дорівнює
трапеції, то OF = 1 2 СК = 1 2 • 3 = 1,5 (см).
Відповідь: 1,5 см.
420. Знайди радіус
421.
із її
18 см , а кути
30∘ .

Дано: ABCD — трапеція, AB ⊥ AD, OF = 5 см, OF ⊥ AD, ∠D = 30°. AB = 2ОF = 10 см.
Проведемо CK ⊥ AD, тоді CK = AB = 10 см.
Із прямокутного трикутника CKD маємо CD = 2СК = 2 • 10 = 20 см.
Оскільки BC + AD = AB + CD то PABCD = 2(AB + CD) = 2(10 + 20) = 2 • 30 = 60 (см).
Відповідь: 60 см.
422. Радіус кола, вписаного
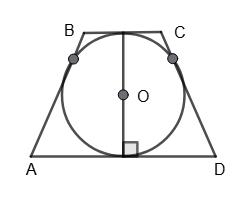
ABCD — трапеція, AB = CD = 18 дм, BC : AD = 2 : 7, O
в
Оскільки AB + CD = BC + AD і AB = CD = 18, то BC + AD = 2 • 18 = 36 (дм). Тоді BC = 36•2 2+7 = 8 (дм), AD = 36•7 2+7 = 28 (дм).
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
Відповідь: 8 дм і 28 дм.

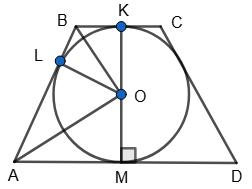
ABCD — трапеція, MN — середня лінія трапеції, MN = 20 см.
O — центр кола, вписаного в трапецію.
Оскільки ВС + AD = 2MN = 2 • 20 = 40 (см) і
то PABCD = 40 + 40 = 80 (см). Відповідь: 80 см.

Якщо
429. Які з наведених тверджень є правильними? І. У будь-який трикутник можна вписати коло. II. У будь-який прямокутник можна вписати коло.

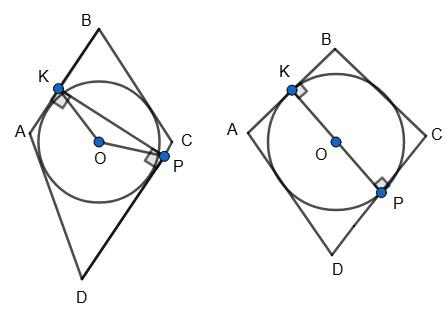
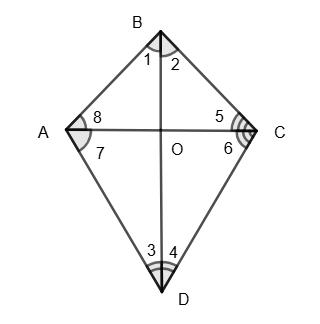
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
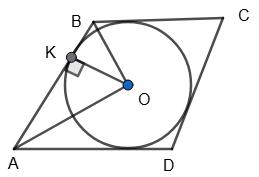
ABCD — ромб, ∠A = 60°, AB = BC = CD = AD = 8 см.
∠AOB = 90° (оскільки AO і BO — бісектриси
та ∠AOB = 180° –1 2 ∠A –1 2 ∠B = 180° –1 2 (∠A + ∠B ) = 180° –1 2 • 180° = 180° – 90° = 90°),
тоді ∠BAO = 30° і BO = 1 2 AB = 1 2 • 8 = 4(см). OK ⊥ AB.
Із трикутника KBO (у якому ∠BOK = 90° – ∠KBO = 90° – 60° = 30°)
маємо BK = 1 2 BO = 1 2 • 4 = 2 (см).
Отже. BK = 2 см, АK = AB – BK = 8 – 2 = 6 (см).
Відповідь: 2 см і 6 см. 440. У
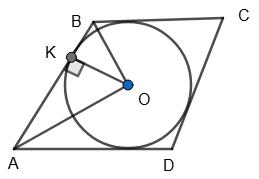
— ромб,
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
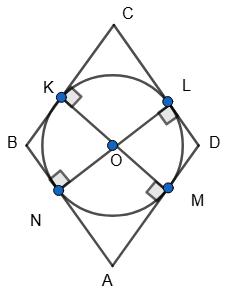
ABCD — ромб, O — центр кола, вписаного в ромб; К, L, М, N — точки дотику, ∠B – ∠A = 46°.
∠A = 180°−46° 2 = 134° 2 = 67°, ∠B = 180° – 67° = 113°.
Із чотирикутника KBLO маємо ∠KOL = 360° –
Із чотирикутника AKON маємо ∠KON = 360° –
–
Отже, KL = 67°, LM = 113°, MN = 67°, KN = 113°.
Відповідь: 67°, 113°, 67°, 113°. 442. У квадрат, периметр якого

– 113° = 67°. ∠MON = 67°.
= 113°.
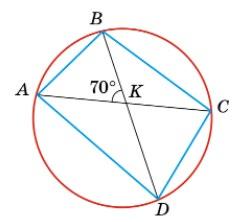
∠AKD = 180° – ∠AKB = 180° – 70° = 110°. ∠AKD —
∠AKD = ∠KCD + ∠KDC = 1 2 AD + 1 2 ВC ̅, 1 2 AD + 1 2 BC = 110°, AD + BC = 220°. Оскільки AD + BC = 220° і AD – BC = 60°,
то AD = 220°+60° 2 = 140°, BC = 220°−60° 2 = 80°.
Відповідь: 140° і 80°.
444.

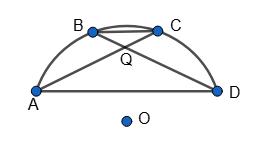
AB = CD,
DCK,
AB = 30°. Тоді AD = AB + BC + CD = 100°+ 30° = 130°. Оскільки AD = 130°, то
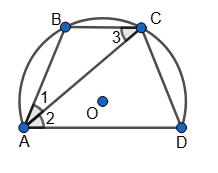
ABCD — трапеція, ∠B = 100°, ∠1 = ∠2.
∠BAD = 180° – ∠B = 180° – 100° = 80°, тоді ∠1 = ∠2 = 40°, ∠3 = ∠2 = 40°.
Тоді AD = AB + BC + CD = 2 • 40°+ 2 • 40° + 2 • 40° = 240°.
Оскільки AD = 240° > 180°, то центр
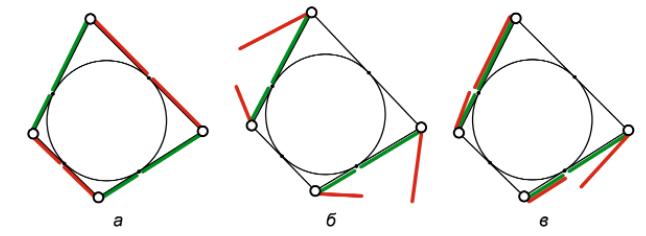
447. Доведи, що коли три
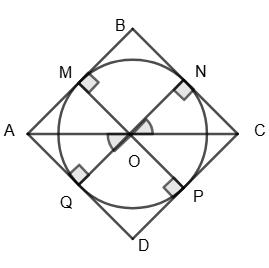
AB = AM + MB = AQ + BN = NC + BN = BC, AD = AQ + QD = AQ + DP = NC + DP = CP +
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
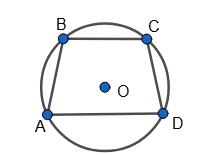
б) Нехай AB = BC = CD, тоді AB = BC = CD = α.
∠A = 1 2 (BC + CD ̅) = 1 2 • 2α = α, ∠D = 1 2 (АB + ВC ̅) = 1 2 • 2α = α.
Оскільки ∠В + ∠D = 180°, то маємо ∠B + ∠D = ∠B + α = ∠B + ∠A = 180°.
Оскільки ∠B + ∠A = 180°, а кути A і В —
січній AB, то BC ∥ AD. Отже, ABCD — рівнобічна трапеція.
в) описаний чотирикутник, три сторони
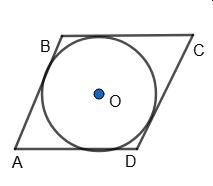
в) Нехай AB = BC = CD.
Оскільки AB + CD = BC + AD, то AD = BC.
Тоді AB = BC = CD = AD, тобто
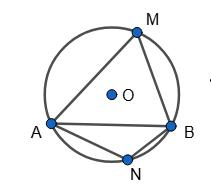
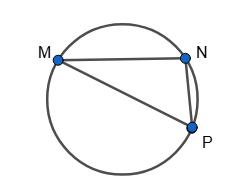
MN : NP : MP = 2 : 5 : 11.
MN = 360°•2
2+5+11 = 40°,
NP = 360°• 5 18 = 100°,
MP = 360°•11 18 = 220°.
∠P = 1
Відповідь: 20°, 50°, 110°. 454.
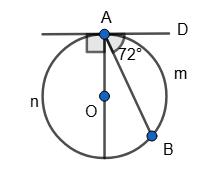
OA ⊥ AD, ∠DAB = 72°.
∠CAB = 90° – 72° = 18°, тоді BC = 2 • 18° = 36°, Am B =
An B = 360° – Am B = 360° – 144° = 216°.
Відповідь: 144° і 216°.
1. Дано: ∠AOB = 130°.
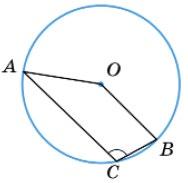
Знайти: ∠ACB. ������������ � = 130°, ∠ACB = 1 2 (360° – ������������ � ) = 1 2 (360° – 130°) = 1 2 • 230° = 115°.
Відповідь: 115°.
2. Дано: �������� � ∶ �������� � =4 ∶ 3, ∠ABC = 70°.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
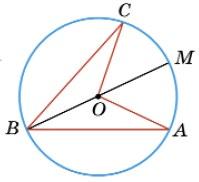
������������ � = 2∠ABC = 2 • 70° = 140°,
�������� � = 140°+4
4+3 = 80°,
�������� � = 140° •3
4+3 = 60°.
∠ABM = 1 2 �������� � = 1 2 • 80° = 40°,
∠A = ∠ABM = 40°,
∠MBC = 1 2 �������� � = 1 2 • 60° = 30°,
∠C = ∠MBC = 30°.
Відповідь: 40° і 30°.
3. Дано: ABCD — прямокутник, ∠2 − ∠1 = 30°, CD = 5.
Знайти: R.
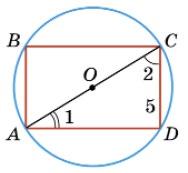
Оскільки ∠2 – ∠1 = 30°, ∠1 + ∠2 = 90°, то ∠2 = 90°+30° 2 = 60°, ∠1 = 90°−30° 2 = 30°.
Із прямокутного трикутника ACD маємо AC = 2 • CD = 2 • 5 = 10. R = 1 2 AС = 1 2 • 10 = 5.
Відповідь: 5.
4. Дано: ABCD — трапеція, MN = 9, ∠D = 30°.
Знайти: AB, CD.
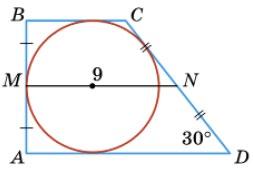
Оскільки MN = 9, то BC + AD = 18, тоді AB + CD = 18, AB = 1 2CD, тобто CD = 2АВ, тоді
АВ = 18 •1 1+2 = 6, CD = 18 •2 1+2 = 12.
Відповідь: 6 і 12.
1. Дано: AB = CD. Довести: BK = KC.
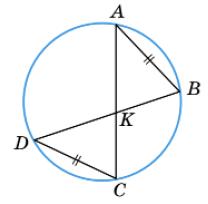
Оскільки AB = CD, ∠ABD = ∠ACD = 1 2 �������� � , ∠CAB = ∠BDC = 1 2 �������� � ,
2. Дано: ∠B = 50°.

�������� � , �������� � . ∠A = 90° – ∠B = 90° – 50° = 40°, �������� � = 2∠A = 2 • 40° = 80°. �������� � = 180° – �������� � = 180° – 80° = 100°.
100° і 80°.
3. Дано: ABCD — трапеція, CD = 7,
R.
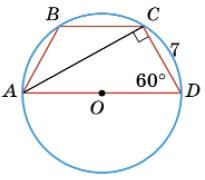
CAD = 90° – ∠D = 90° – 60° = 30°.
ACD
AD = 2 • CD = 2 • 7 = 14. R = 1 2 AD = 1 2 • 14 = 7.
7.
4.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
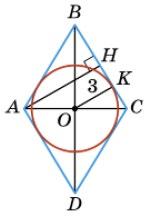
∠ABC = 180° •1 1+5 = 30°, ∠BCD = 180° •5 1+5 = 150°.
AH = 2OК = 2 • 3 = 6.
Із трикутника ABH маємо AB = 2АН = 2 • 6 = 12.
Відповідь: 12.
1. Два послідовні

ABCD — трапеція,
∠A = 70°, ∠D = 80°, тоді
∠B = 180° – ∠A = 180° – 70° = 110°,
∠C = 180° – ∠D = 180° – 80° = 100°.
Відповідь: 100° і 110°.
2.
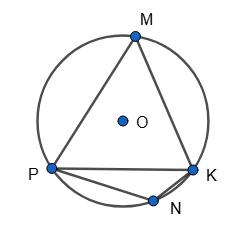
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
∠PMK = 1 2 ������������ � = 1 2 • 80° = 40°,
3.
4.
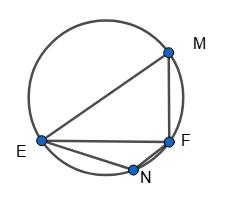
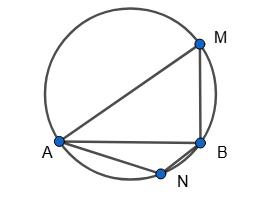
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
∠AMB = 1 2
3.

2.
Г. 6 см. Відповідь:
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
A. 14 см;
Б. 6 см;
B. 3 см;
Г. 7 см.
Відповідь: Г.
4. Центральний кут
A. 18∘ ;
Б. 36∘ ;
B. 72∘ ;
Г. 12∘ .
Відповідь: А.
5. Бічна сторона рівнобічної
довжину середньої лінії.
A. 7 см;
Б. 14 см;
B. 3,5 см;
Г. 21 см.
Відповідь: А.
6. Знайди
4 см, а кут між діагоналями 60∘ .
A. 8 см;
Б. 2 см;
B. 4 см;
Г. 6 см.
Відповідь: В.
7. Радіус
належать основи трапеції.
A. ���� 2;
Б. ���� ;
B. 2����;
Г. не можна встановити.
Відповідь: В.
8. Периметр
А. 10 см; Б. 2,5 см; B. 5 см; Г. 7,5 см.
9. Радіус
A. 10 см;
Б. 2,5 см;
B. 5 см;
Г. 7,5 см.
Відповідь: В.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
1. Середня лінія рівнобедреного трикутника дорівнює 7
периметр трикутника.
A. 20 см;
Б. 27 см;
B. 34 см;
Г. 38 см.
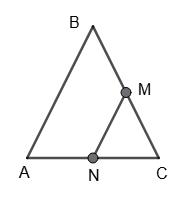
І випадок.
MN — середня лінія, MN = 7 см, AC = 10 см,
тоді AB = BC = 2MN = 2 • 7 = 14 (см).
Р∆АВС = 14 + 14 + 10 = 38 (см).
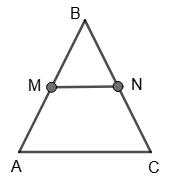
II випадок.
MN — середня лінія, MN = 7 см, AC = 2 • MN = 2 • 7 = 14 см,
тоді AB = BC = 10 (см).
Р∆АВС = 10 + 10 + 14 = 34 (см).
Відповідь: 34 см або 38 см.
2. △
A. 80∘ ; Б. 160∘ ; B. 40∘ ; Г. 120∘ .
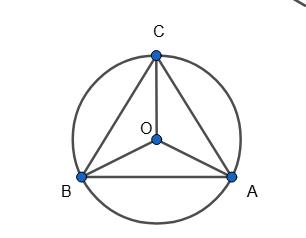
∠A = 40°, ∠B = 2∠A = 2 • 40° = 80°. AС = 2∠B = 2 • 80° = 160°, ∠AOC = AС = 160°.
Відповідь: 160°.
3. Менша
A. 4 см; Б. 8 см; B. 16 см; Г. 24 см.
4. У △ ������������∠����
1.
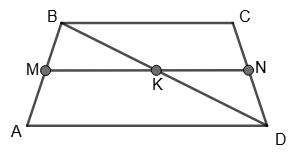
2 = 23 2 = 11,5 (см).
KN = 15−8 2 = 7 2 = 3,5 (см).
AD = 2МК = 2 • 11,5 = 23 (см), BC = 2KN = 2 • 3,5 = 7 (см).
23 см і 7 см. 6.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
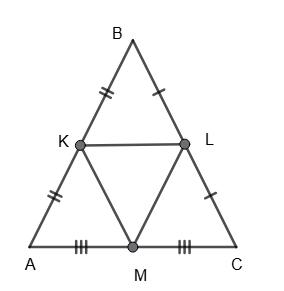
Якщо P∆KLM = 15 см, то P∆ABC = 30 см.
Нехай АВ = х см, тоді AC = (x + 2) см, BC = 2х см,
тоді х + х + 2 + 2x = 30, 4x = 28, x = 7.
Тоді AB = 7 см, AC = 9 см, BC = 14 см.
Відповідь: 7 см, 9 см, 14 см.
8. Знайди периметр рівнобічної
120
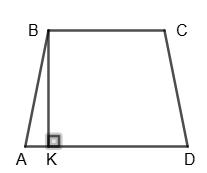
- 6
— рівнобічна трапеція, BC : AD = 2 : 5, ∠B = ∠C = 120°, AB = CD = 6 см. Проведемо
BK ⊥ AD, ∠ABK = 2ABC –
AK = 1 2 AB = 1 2 • 6 см = 3 см.
Нехай BC = 2х см, тоді AD = 5х см, AK = AD− BC 2 = 5x−2x
PABCD = 2AB + BC + AD = 2 • 6 + 4 + 10 = 26 (см).
Відповідь: 26 см. 9.
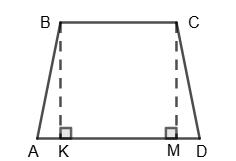
(см).
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

х + 2 х + 2х = 10,
5х = 10,
х = 2.
Відповідь: 2, 4, 4.
458. Стрічку
якому відношенні
А. 1 ∶ 5;
Б. 1 ∶ 4;
В. 1 ∶ 10;
Г. 1 ∶ 6.
х + 2 х + 2х = 20, 5х = 20,
х = 4.
Відповідь: 4 дм; 8 дм; 8 дм. 459.
A. 5 м;
Б. 6 м;
В. 22,5 м;
Г. 15 м.
3х = 9;
х = 3.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

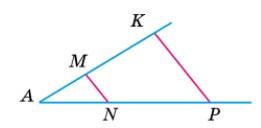
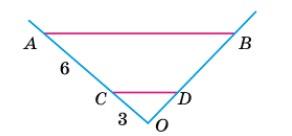
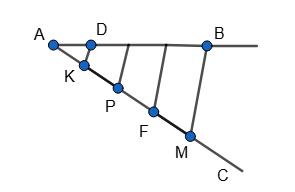
466. Точка

АМ : МВ = 7 : 2; AМ : АВ = 7 : 9; MB : AB = 2 : 9.
467. Гра.
2 : 5; б) CD : AD = 3 : 5; в) AC : АВ = 2 : 10 = 1 : 5; г) DB : AD = 5 : 5 = 1 : 1. 469.
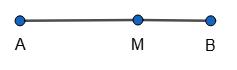
471.
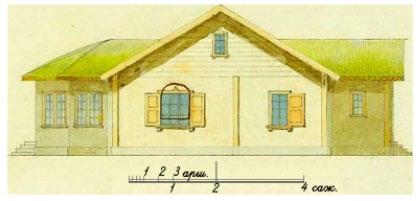
472.

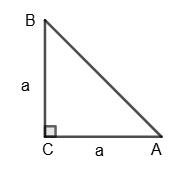
AC = BC = а;
AC : BC = а : а = 1 : 1.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
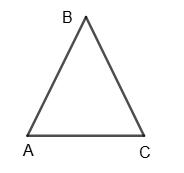
AC: AB = 2 : 3; P∆ABC = 2 + 3 + 3 = 8;
AC
P∆ABC = 2 8 = 1 4;
AB
P∆ABC = 3 8 .
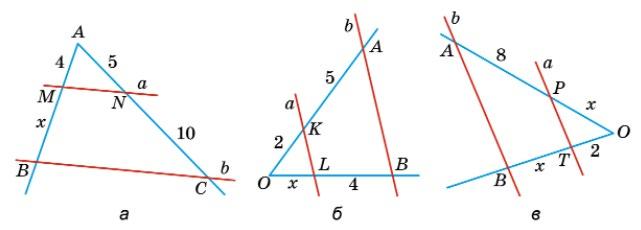
4
а)
х+4 = 5 15; 5x + 20 = 60; 5x = 40; x = 8.
х
б)
х+4 = 2 7; 7x = 2x + 8; 5x = 8; x = 1,6.
х
в)
х+8 = 2
х+2; x2 + 2x = 2x + 16; x2 = 16; x = 4.
476.
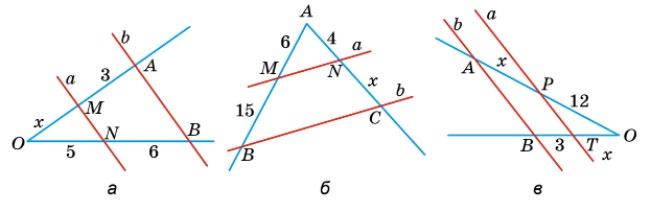
477.
479.
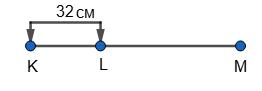
KM : KH = 9 : 4; 4х = 32;
x = 8 см;
KM = 9 • 8 = 72 см;
LM = 72 см – 32 см = 40 см.
Відповідь: 40 см.
480. На
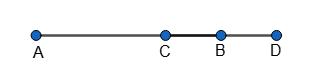
BC = 6 см – 3,6 см = 2,4 см.
AD : DB = AC : BC = 3,6 : 2,4 = 3 : 2
AB : BD = 5 : 2; AD : AB = 7 : 5.
2х + 3х + 4х + 5х = 7; 14х = 7; х = 0,5.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
5х + 1x + 4x = а; 10x = a; x = 0,1а.
Довжини частини: 0,5а; 0,1а; 0,4а.
484. A segмent of length ���� is divided into parts in the ratio ���� ∶���� . Find the lengths of the resulting parts.

mх + nх = а , х(m + n) = а, x = а m+n .
Довжини частин: ma m+n; na m+n
485. Чи пропорційні відрізки ���� , ���� , ���� , ���� , якщо: а) два перші відносяться як 2 ∶ 3, а два другі - як 3 ∶ 4; б) ���� ∶���� =2,4 ∶ 5,6; ���� ∶���� =9,1 ∶ 21,7 ?
a) 2 : 3 = 3 : 4, ні не пропорційні.
б)
2,4 : 5,6 = 9,1 : 21,7, ні не пропорційні.
Відношення цих
486.
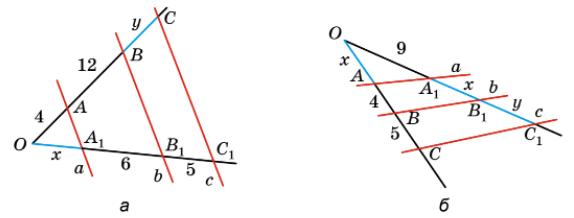
а) 16 4 = x+6 x ; 16x = 4x + 24; 12x = 24; 32 + 2y = 52; 16+y
4 = 13 2 ; 2y = 20; x = 2; y = 10; OA1 = 2; BC = 10.
Відповідь: 2; 10; б) 9 x+9 = x x+4; 9x + 36 = x2 + 9x; x2 = 36; 90 + 6y = 135; 15+y
9 = 15 6 ; 6y = 45; x = 6; y = 7,5.
Відповідь: 6; 7,5. 487. Користуючись
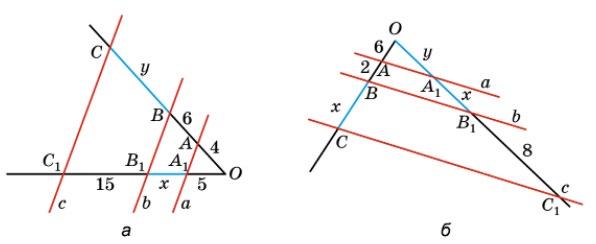
488. У трапеції ���������������� �������� = 10 см,
1. ��������;
2. C���� , якщо �������� =6 см;
3. �������� , якщо �������� =9 см.
А. 4 см;
Б. 6 см;
В. 9 см;
Г. 15 см;
Д. 30 см.
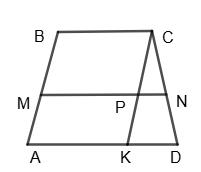
Нехай АМ = х , BM = х + 2; AB = 10 см;
х + х + 2 = 10 см;
2х + 2 = 10;
2х = 8;
х = 4;
AM = 4; BM = 6;
Проведемо СK ∥ AB; CP = BM = 6 см; PK = AM = 4 см; DN = 6 см;
Відрізок CN — четвертий пропорційний.
CP : СК = CD : CN, CN = y; CD = y + 6. 6 : 10 = (у + 6) : y; 10 6 = y+6 y ; 10y = 6y + 36; 4у = 36; у = 9; CN = 9 см; CD = 9 + 6 = 15 (см).
Відповідь: CD = 15 см. 489. �������� медіана △ ������������ �������� ∶ �������� =2 ∶ 3. Знайди
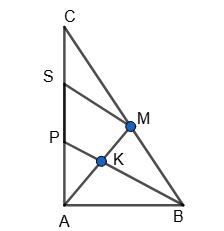
CM = MB, AK : KM = 2 : 3.
Проведемо SM ∥ PВ, тоді CS = PS. З іншого боку
AP : PS = AK : KM = 2 : 3,
АР : PS = 2 : (3 + 3) = 1 : 3,
AP : AC = 1 : 4.
Відповідь: 1 : 3, 1 : 4. 490. Точка

AM : MB = 3 : 2, BN : NC = 5 : 4.

Нехай BC = 6 см; AD = 10 см; AB = 5 см, CD = 8 см.
ВС ∥ AD, тому ∆BMC ~ ∆AMD, отже:
AM AD = BM BC ; BM = x; x+5 10 = x 6;
6х + 30 = 10х; 4х = 30; х = 7,5. BM = 7,5 см.
MC BC = MD AD , MD = y. y 6 = y+8 10 ; 10у = 6у + 48; 4у = 48; у = 12. MC = 12 см.
Відповідь: MC = 12 см; MB = 7,5 см.
492. На стороні �������� трикутника ������������ позначено точку
Побудуй відрізок, четвертий
(493, 494), якщо:
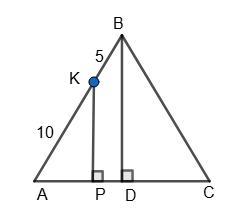
дано ∆АВС. AK = 10 см; BK = 5 см; PK ⊥ AC; BD ⊥ AC; тому PX ∥ BD. ∆APK ~ ∆ABD, з їх
2 3 .
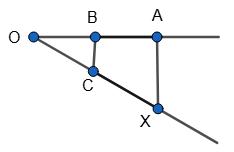
493. а) ���� =4 см; ���� =2 см; ���� =3 см; б) ���� =4,8 см; ���� =4 см; ���� =2,1 см; а) Дано: а = 4 см; b = 2 см; с = З см.
AK AB = PK BD = 10 15 = 2 3 .
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
: ОВ = ОС : ОХ;
4 : 2 = 3 : х;
4х = 6;
х = 1,5.
Відповідь: OX = 1,5 см.
б) 4,8 : 4 = 2,1 : х;
х = 4 •2,1 4,8 ; x = 1,75.
Відповідь: OX = 1,75 см.
494. а) ���� =4 см; ���� = 10 см; ���� =6 см; б) ���� =1,5 см; ���� =4,5 см; ���� =2 см.

а) 4 : 10 = 6 : х;
4х = 60;
х = 15.
Відповідь: OX = 15 см.
б) 1,5 : 4,5 = 2 : х;
1,5х = 4,5 • 2;
1,5х = 9;
х = 6.
Відповідь: OX = 6 см.
495. Накресли
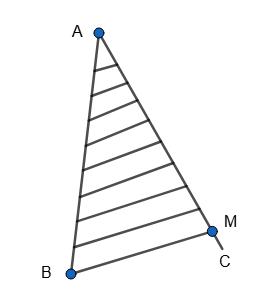
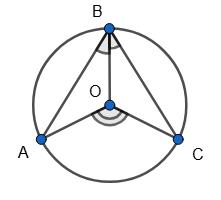
Нехай ∠ABO = x; ∠CBO = х + 15°.
AC � = 110°,
Вписаний ∠ABC = 1 2 ∠AOC; ∠ABC = 55°.
х + х + 15° = 55°, 2х = 40°,
х = 20°.
Відповідь: ∠ABO = 20°; ∠CBO = 35°. 498.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
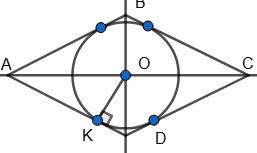
чотирикутника 360°.
∠1 : ∠2 : ∠3 : ∠4 = 2 : 3 : 5 : 8;
∠1 = 2x; ∠2 = 3х; ∠3 = 5x; ∠4 = 8x;
Складемо рівняння:
2х + 3х + 5х + 8х = 360°,
18х = 360°,
х = 20°,
∠1 = 40°; ∠2 = 60°; ∠3 = 100°; ∠4 = 160°.
Відповідь: 40°, 60°, 100°, 160°.

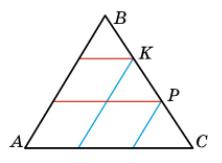
505.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
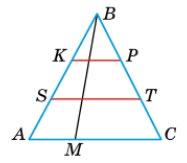
5

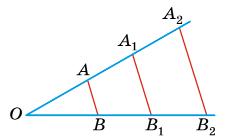
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
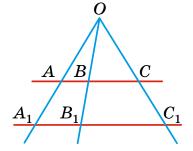
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
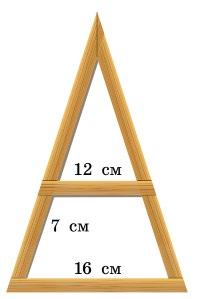
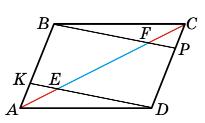
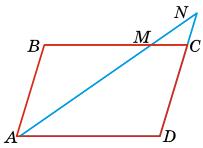
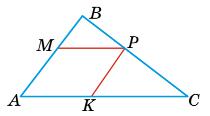

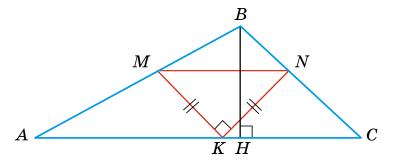




6 пар.
502.
503.
504.
Ні,
505.




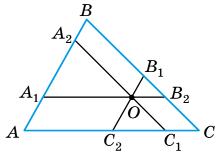
~ ∆OA1C1; ∆OAB ~ ∆OA1B1; ∆OBC ~ ∆OB1C1;
OB : OB1 = 2 : 3;
OC : OC1 = 2 : 3;
AB : A1B1 = 2 : 3;
OA : AA1 = 2 : 1;
AC : A1C1 = 2 : 1.

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
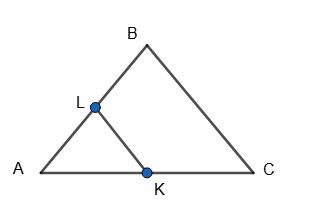
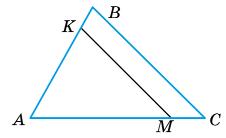
a) KL ∥ BC, отже за теоремою 15. ∆ALK ~ ∆ABC,
тому AK AC = ����K BC , 4 9 = ����K BC, LK = 4 27 9 = 12 (см).
б) AB = 30 cм; BC = 36 см, AC = 42 см; LK = 12 см; k = �������� LK = 36 12 = 3.
AL = 10 см; AK = 14 cм;
Р∆AKL = 10см + 14 cм + 12 см = 36 (cм).
Відповідь: 36 (см).
512. In triangle ������������ , a line parallel to side �������� is drawn through point ���� of side �������� to intersect with side �������� at point ���� . Find:
a) the segмent �������� , if �������� = 9ft and ��������: �������� =3:4;
b) the periмeter △ ������������, if


517.

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
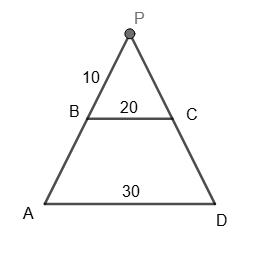
ABCD — трапеція, отже
BC ∥ AD, тому ∆BPC ~ ∆ADP.
AB = x; A���� AD = B���� BC ; x+10 30 = 10 20 ; 20x + 200 = 300; 20x = 100; x = 10, AB = 10 см.
Відповідь: AB = CD = 10 см.
521. У трапеції
522.

Нехай ABCD — трапеція; BC ∥ AD; BC = 12 см; AD = 16 см.
AB = CD = 7 см;
∆BCK ~ ∆AKD (BC ∥ AD).
ВК = КС = х;
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
AK = BC AD ; x x+7 = 12 16 ; 16x = 12x + 84; 4х = 84; х = 21.
Відповідь: 21 см.
523. Основи трапеції
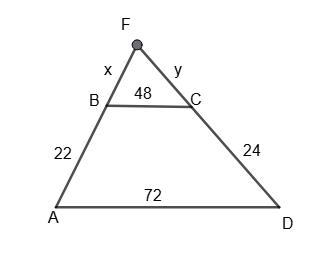
ABCD — трапеція; BC ∥ AD, BC = 48 см; AD = 72 см; AB = 22 см; CD = 24 см.
Необхідно знайти BF і FC.
∆FBC ~ ∆AFD, BC ∥ AD; BF AF = BC AD ; нехай BF = х; x x+ 22 = 48 72 ; x x+ 22 = 2 3 ; Зх = 2х + 44; х = 44; BF = 44.
Нехай FC = у; тоді FC FD = BC AD ; y y+24 = 2 3 ; 3y = 2y + 48; y = 48; FC = 48.
Відповідь: 44 см; 48 см. 524. На сторонах �������� і ��������
так, що ��������‖�������� , �������� = �������� , �������� =4 см, �������� =9 см, �������� =7

Нехай дано ∆ABC, MN ∥ AC, AM = BN,
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
MB = 4см; NC = 9 см, MN = 7 см.
∆MBN ~ ∆ABC за теоремою 15, (MN ∥ AC за умовою).
Нехай AM = BN = x; складемо рівняння:
MB
AB = BN BC ; 4 x+4 = x x+9 ; 4x + 36 = x2 + 4x; x2 = 36; х = 6.
Отже BN = 6 см.
Знайдемо AC:
AC MM = AB MB ; AC 7 –10 4 ;
AC = 10 ∙ 7 4 = 17,5.
Відповідь: MN = 7 см; AC = 17,5 см.
525. ���� і ���� - такі точки на сторонах
трикутники ������������
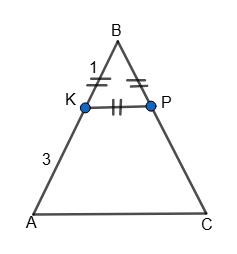
∆ABC ~ ∆KBP тому, що K P ∥ AC (теорема 15).
a) KB : AK = 1 : 2; BP : PC = 1 : 2; KP : AC = 1 : 2.
б) AK = KP = PB = 8 см; AK = 8 см; ВK = 4 см;
Р∆BKP = 4 + 8 + 8 = 20 (см).
Р∆ABC = 3 ∙ 20 = 60 (см).
Відповідь: 20 см; 60 см.
526. На сторонах �������� і ��������

AK = CP = 0,25 АВ = 1 4
AE : EF : FC = 1 : 4 : 1;
∆BCP = ∆DAK, з їх рівності BP ∥ KD.
∆AKE ~ ∆ABF, AK : KB = AE : EF = 1 : 4.
Аналогічно: CF : FE = 1 : 4.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
16 см.

AM : MN = 5 : 2; P∆AND – P∆MNC = 16см; ABCD — паралелограм, BC ∥ AD, тому MC ∥ AD.
Отже ∆AND ~ ∆MNC.
����∆AND
����∆MNC = AN MN = 7 2 .
Нехай P∆MNC = x; P∆AND = x + 16. x+ 16 x = 7 2 ;
2x + 32 = 7x; 5x = 32; x = 6,4.
Отже P∆AND = 6,4 + 16 = 22,4 (см).
P∆MNC = 6,4 см.
Відповідь: 22,4 см; 6,4 см.
528.



Нехай ∆MNK (∠N = 90°; NM = NK) вписано в ∆АВС.
MN ∥ AC, K ∈ AC. AC = ЗО см; BH = 10 см. MN ∥ AC, тому ∆MBN ~ ∆ABC.
MN
BP = AC BH ; MN BP = 30 10 =3.
BP : PH = 1 : 2.
FK ∥ PH. FK = PH.
∆FKN. ∠FNK = 45°;
∠F = 90°; ∠FKN = 45°. FN = FK; FK = 2 3

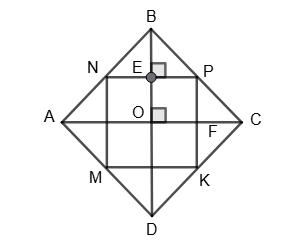
ABCD — ромб; MNPK — квадрат.
∆BOC — прямокутний (діагоналі ромба — перпендикулярні).
EP ⊥ OB, NP ∥ AC; ∆BEP ~ ∆BOC.
Нехай B���� BO = EP OC ;OE = OF = x;
BD = 8 см; ОВ = 4 см; AC = 12 см; ОС = 6 см;
4 –x
4 = x 6 ; 24 – 6x = 4x; 10x = 24; x = 2,4 см.
NP = 2x = 4,8 см.
Відповідь: сторона квадрата: 4,8 см. 533. На малюнку


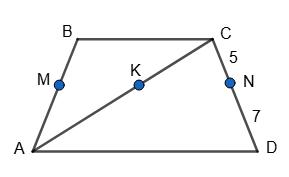
Нехай ABCD — трапеція. MN ∥ AD, AB = 24 см; CD : ND = 5 : 7.
Проведемо діагональ AC.
∆CKN ~ ∆CAD (KN ∥ AD).
CK
CA = CN CD = 5 12 ;
∆AMK ~ ∆ABC (MK ∥ KC).
AM
AB = AK AC = 7 12 ;
AM = 7x; MB = 5х
7х + 5х = 24; 12х = 24; х = 2; AM = 14 см; MB = 10 см.
536. Точка
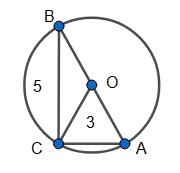
AB — гіпотенуза
OB

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
MN = 1 2 АС = 1 2 ∙ 14 = 7 (см);
∆DAC, KP — середня лінія, KP = 1 2АС = 7 см;
∆BDC, NP — середня лінія, NP = 1 2 BD = 1 2 ∙ 10 = 5 см;
∆BAD, MK — середня лінія, MK = 1 2 BD = 5 см.
Р∆MNPK = (7 + 5) ∙ 2 = 24 (см).
Відповідь: 24 см. §10. Ознаки подібності трикутників
538. Чи будь-які два рівносторонні трикутники подібні? Чому?
Будь–які 2 рівносторонніх трикутники


544.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
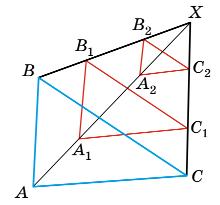
∆ABC — довільний. Х
XB2 = B2B1 = B1B; XA2 = A2A1 = A1A;
XC2 = C2C1 = C1C
545.
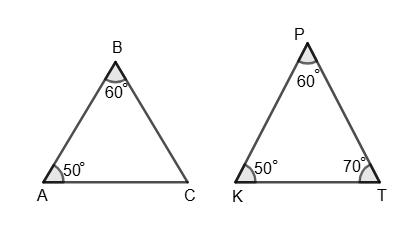

∠B = 42°; ∠A1 = 48°;
∠А = 90° – 42° = 48°;
∠А = ∠A1 = 48°.
Трикутники подібні тому, що у
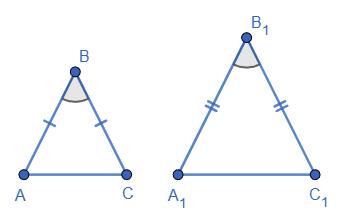
∠C = ∠C1 = 52°;
∠A = ∠В = (180° – 52°) : 2 = 64°;
∠A1 = ∠B1 = (180° –
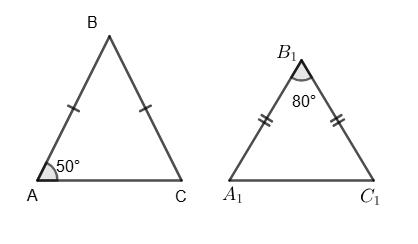
=
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
а) ∠A = ∠A1, ∠A = ∠C,
тоді ∠A1 = ∠C1, ∠C = ∠С1
∠B = 180° – (∠A + ∠C).
∠B1 = 180° – (∠A1 +∠C1) = 180° – (∠A + ∠C).
Отже, ∆ABC ~ ∆A1B1С1 тому, що у них
кути рівні (за теоремою 16). б) Якщо кути при вершинах у рівнобедрених трикутниках
будуть також рівні, отже трикутники подібні.
554. Чи подібні трикутники, утворені паралельними
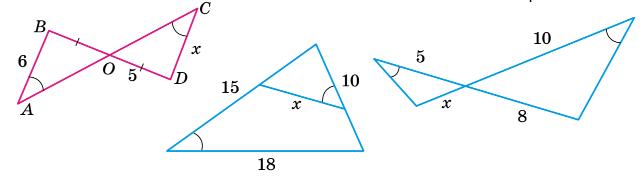
558.

Нехай ∆ABC — рівнобедрений.
AB = BC = 18 см; AC = 12 см.
∆ABC ~ ∆A1B1C1. A1B1 = B1C1 = 6 см. ��������
����1 ����1 = k; k = 18 6 = 3. ��������
����1 ����1 = 3; ����1 ����1 = 12 3 = 4. (см).
P∆A1B1C1 = 6 см + 6 см + 4 см = 16 см.
Відповідь: 16 см.
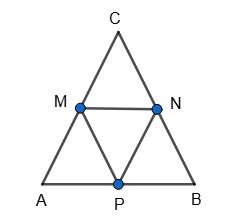
∆ABC; ∆MNP MN ∥ AB; PN ∥ AC; MP ∥ BC; ці трикутники подібні.
563. Дано ���������������� - паралелограм.
Доведи, що:
a) △ ������������ ∼△ ������������ ; б) △ ������������ ∼△ ������������ .
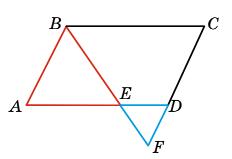
Нехай дано ABCD — паралелограм.
а) Доведемо, що ∆ABE ~ ∆DFE:
1. ∠BEA = ∠FED; (вертикальні кути).
2. ∠A = ∠C (протилежні кути паралеграма).
∠EDF = ∠BCD (відповіді кути, BC ∥ ED) тоді: ∠EDF = ∠BAE.
∆ABE ~ ∆DFE тому, що у них 2 кути рівні.
б) ∆BCF ~ ∆EAB (за двома кутами).
∠BAE = ∠BCF; ∠ABE = ∠BFC, внутрішні навхрест лежачі кути.
AB ∥ CF, BF — січна. 564. Дано ���������������� - паралелограм. Доведи, що: а) △ ������������ ∼△ ������������ ; б) △ ������������ ∼△ ������������; в) △ ������������ ∼△ ������������
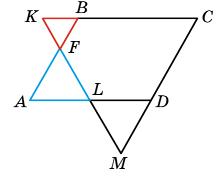
Нехай дано паралелограм ABCD.
a) ∆KBF ~ ∆LAF (за двома рівними кутами).
∠KFB = ∠LFA (вертикальні кути). ∠KBF = ∠FAL (внутрішні різносторонні кути).
KB ∥ AL, AB — січна.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
б) ∆KBF ~ ∆LDM (за двома рівними кутами).
∠1 = ∠2 (внутрішні різносторонні кути; KC ∥ AD).
∠2 = ∠3 (вертикальні кути), тоді ∠1 = ∠3.
∠4 = ∠5, кути суміжні рівним кутам паралелограма ∠ABC та ∠ADC.
в) ∆AFL ~ ∆CMK (за двома рівними кутами).
∠FAL = ∠KCM (протилежні кути паралелограма).
∠AFL = ∠XMC, внутрішні різносторонні кути.
AB ∥ CD, FM — січна.
565. Користуючись малюнком, доведи, що �������� ‖�������� .
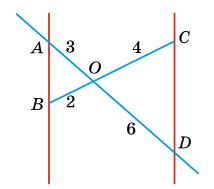
∆AOB ~ ∆DOC, за теоремою 17.
AO
OD = BO OC ; 3 6 = 2 4 = 1 2 ;
∠AOB = ∠DOC (вертикальні кути).
Отже, ∠BCD = ∠OBA, а це внутрішні
довести.
566. Дано трикутник
відрізок �������� = 15
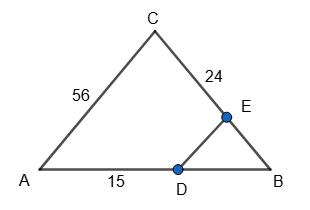
а) Нехай
∆ABC. AB = 40 см; AC = 56 см; ВС = 24 см. DE ∥ AC; DE ∥ AC, тому ∆DEB ~ ∆ACB.
DB = AB – AD = 40 – 15 = 25 см.
3 їх подібності маємо: AC
DE = AB BD ; 56 DE = 40 25 ; 40DE = 1400; DE = 35 см. б) BE BC = BD BA ; BE 24 = 25 40 ; 40BE = 600; ВЕ = 15 см.
567. У △ ������������ �������� = 15 см, �������� =9
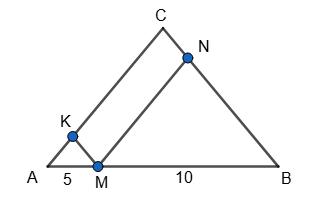
Нехай дано ∆ABC, AB = 15 см, BC = 9 cм; AC = 12 cм; MN ∥ AC, MK ∥ BC
AM = 5 cм. KM ∥ BC,
отже ∆AKM ~ ∆ACB, тоді AM
KM = AB BC ; 5 KM = 15 9 ; KM = 3 cм; MN ∥ AC,
отже, ∆MNB ~ ∆ACB, тоді MN
AC = MB AB ; MN 12 = 10 15 ; MN = 8 см; AK
AC = AM AB ; AK 12 = 5 15 ; MN = 4 см.
Відповідь:
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
366 – 14x = 18x, 32х = 336, x = 10,5.
OC = 10,5 см; OA = 13,5 см.
Відповідь: 10,5 см; 13,5 см.
571. На скільки
5 і 9?

Нехай ABCD трапеція. BC ∥ AD.
AB = 12 см; BC : AD = 5 9 .
∆BMC ~ ∆AMD. (BC ∥ AD).
BC AD = BM A���� , нехай BM = x, 5 9 = x x+12,
5х + 60 = 9х, 4х = 60, x = 15.
BM = 15 см.
Відповідь: 15 см.
572. У
Сторони трикутника, що утворюють
паралельні їм сторони паралелограма
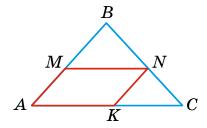
Нехай у ∆ABC вписано паралелограм.
AB = 6 см; AC = 9 см; NK : AK = 2 : 3.
∆MBN ~ ∆ABC (MN ∥ AC, ∠B — спільний)
Нехай AM = 2х, MN = 3x тоді
AB
AC = MB MN ; 6 9 = 6 2x 3x ; 36x = 54; x = 1,5;
Отже, AM = 3 (см); MN = 4,5 (см). Відповідь: 3 см і 4,5 см. 573. У трикутник
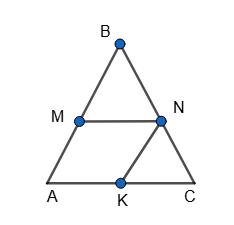
AB = 6 см; AC = 15 см; MN – NK = 8 см.
Нехай паралелограм AMNK вписано у трикутник ABC.
MN ∥ AC, ∆MBN ~ ∆ABC (∠B — спільний)
MB
MN = AB AC ; AM = х,
MN = х + 8; MB = 6 – x.
6 x
x+8 = 6 15 ;
90 – 15х = 6х + 48; 21x = 42; х = 2.
AM = 2 см; MN = 10 см.
Відповідь: 2 см і 10 см.
574. На сторонах
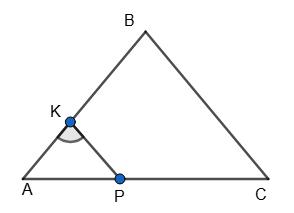

Проведемо DL ∥ BK,
тоді ∆AMB = ∆CND,
звідси AM = NC = 2 см.
Через точки поділу сторони AD
KD = 1 8 ;
тоді К ділить AD у відношенні 1 9; A����
MC = 1 9 ;
тоді AM = 1 10 ∙ AC;
AC = 10 ∙ AM = 10 ∙ 2 = 20 см.
Відповідь: 20 см.
578. On the �������� side of the parallelograм ���������������� , the point ���� is taken so that �������� : �������� =1: 10 Find �������� and �������� if �������� = 22 in.
579.
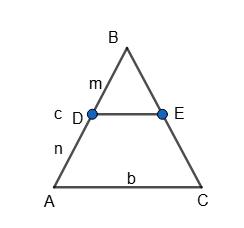

Нехай ABCD — трапеція, BC ∥ AD.
BC = 16 см; AD = 20 см; AC = 12 см; BD = 18 см.
∆BOC ~ ∆DOA (за двома кутами).
∠BOC = ∠DOA — вертикальні кути.
∠ACB = ∠CAD (внутрішні різносторонні кути, BC ∥ AD, AC — січна).
k = AD BC = 20 16 = 5 4 .
Отже, BO = 4x; OD = 5х; 4х + 5х = 18; 9х = 18, х = 2.
BO = 8 см; OD = 10 см; OC = 4y;
ОА = 5у: 45 + 5у = 12; 9у = 12; y = 12 9 = 4 3 ; OC = 4 ∙ 4 3 = 16 3 =5 1 3 см; O���� =5 ∙ 4 3 = 20 3 =6 2 3 см; Відповідь: 8 см і
см, а частина
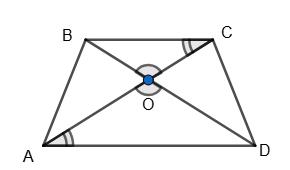
Нехай дано трапецію ABCD AO = 16 см; OC = 12 см; OD = 8 см. BC ∥ AD. ∆BOC ~ ∆DOA (за
OC
AO = OB OD ; 12 16 = x 8 ; OB = x = 6 см.
BD = BO + OD = 6 + 8 = 14 (см).
AD BC = AO OC ; 16 12 = 20 y ; y = 15 см. BC = 15 см.
Відповідь: 15 см; і 14 см. 583.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

BC = а; AD = b; ∆BOC ~ ∆DOA.
∠BOC = ∠DOА, вертикальні кути;
∠OBC = ∠ODА, внутрішні різносторонні кути;
BC
AD = OB OD = a b ;
Відповідь: a b .
584. Знайди за

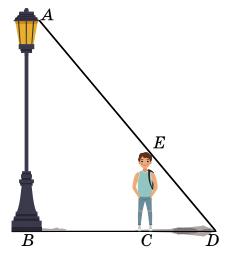
AС = 300 м, DC = 10 м, BC = 360 м, CF = 12 м, F = 13 м; ∆DCF ~ ∆ACB.
AC
DC = 300 10 = 30; BC CF = 360 12 = 30;
з подібності трикутників маємо: AB
DF = 30; �������� = 30 ∙ �������� = 30 ∙ 13 = 390.
Відповідь: 390 м.
585. У △ ������������ �������� = 10 см, �������� = 12
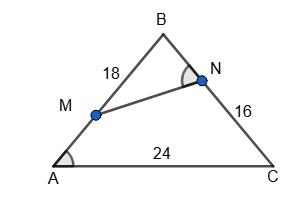
Нехай дано ∆ABC AB = 18 см, BC = 16 см; AC = 24 см; ∠MNB = ∠ВАС.
BN : NC = 3 : 5.
Знайдемо BN і NC. Зk + 5k = 16. 8k = 16. k = 2.
BN = 6 см; NC = 10 см. ∆MBN ~ ∆CBA за двома рівними кутами.
∠B — спільний, ∠MNP = ∠ВАС за умовою.
Маємо:
MN
AC = BN BA ; MN 24 = 6 18 ; MN = 8 см.
Відповідь: MN = 8 см.
587. У трапеції
588.
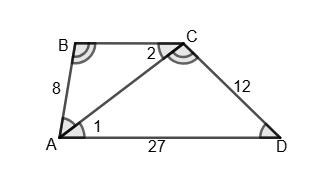
Нехай ABCD
∆ABC ~ ∆DCA (за умовою). 3 їх подібності маємо: CD
AD = AB AC ; 12 27 = 8 AC ; AC = 18 см.
BC
AB = AC CD ; BC 8 = 18 12 ; BC = 12 см.
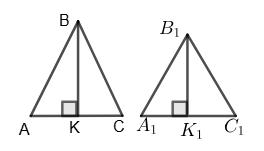
а) Нехай ∆ABC ~ ∆A1B1C1. ��������
����1 ����1 = ���� .
BK ⊥ AC; B1K1 ⊥ A1C1
∆ABK ~ ∆A1B1K1.
Отже �������� ����1 ����1 = �������� ����1 ����1 = ���� .

б) BM і B1M1 —
AM = MC; A1M1 = M1C1.
∆ABM ~ ∆A1B1M1
����1 = �������� ����1
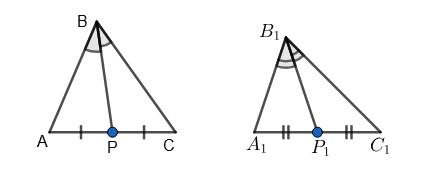
в) BP і B1P1
����1 ����1 = ���� ; ∠A = ∠A1; ∠ABP = ∠A1B1P1
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
591.
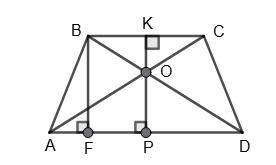
Нехай дано трапецію ABCD, BC ∥ AD. BF ⊥ AD, BF — висота трапеції.
BF = 15 см; BC = 8 см; AD = 12 см. OK ⊥ BC; OP ⊥ AD.
O — точка перетину діагоналей трапеції.
∆BOC ~ ∆DOA (за двома рівними кутами).
BC
AD =k= 8 12 = 2 3 ;
OK : OF = 2 : 3 – OK і OF — висоти даних трикутників.
KP = BF = 15.
2х + 3х = 15, 5х = 15, х = 3.
OK = 6 cм; OP = 9 см.
Відповідь: 6 см і 9 см.
592. У рівнобедрений △ ������������
Знайди периметр квадрата.
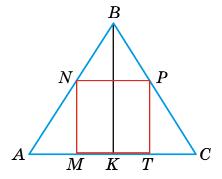
=6
Нехай дано ∆ABC — рівнобедрений AB = BC, AC = 10 см, BK ⊥ AC, BK = 6 см. MNPT — квадрат. ∆AMN ~ ∆АКВ, MN ∥ BK.
MK = х; MN = 2х; AK = 5 см; AM = 5 – х.
AM MN = AK BK ; 5 x 2x = 5 6 ; 30 – 6х = 10x; 16х = 30; х = 1,875. MN = NP = PT = MT = 2х = 3,75.
Відповідь: Pкв. = 15 см.
593.
=

∆FBP ~ ∆ABC; ∠В — спільний кут.
AC
BK = FP BM ; 27 30 = 9k x ;
BM = 10k.
BK = 10k + 5k = 15k; 15k = 30; k = 2.
FE = 10 см; FP = 18 см.
Відповідь: 10 см; і 18 см.
594. Пряма, що
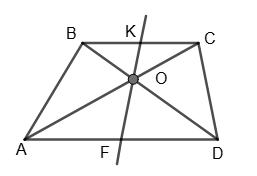
��������
K���� = m n ; AF FD = n m ;
595.
597.
598.
599.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
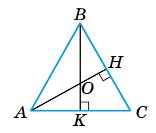
AO : OH = ВО : ОK = 2 : 1.
602. Чи
Ні, не можуть. 8 : 2 = 4 : 1; 10 : 5 = 1 : 2.
603.

604.
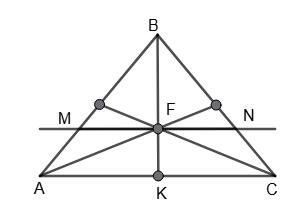
МN ∥ AC. ∆MBN ~ ∆ABC. FK : FD = 1 : 2.
AM : MB = 1 : 2.
CN : NB = 1 : 2.
605.
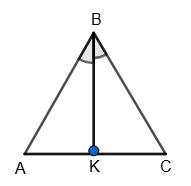
A. �������� < �������� ;
�������� > �������� ;
B. �������� = �������� ;
AB > BC, тоді AM > MC.
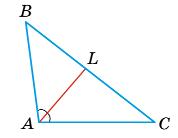
а) АВ = 8 cм; BC = 10 cм; AC = 12 см, за властивістю бісектриси кута трикутника: AB
AC = BL LC ; 8 12 = x 10 x ; 80 – 8х = 12х; 20х = 80; x = 4. BL = 4 cм; LC = 6 см.
б) AB = 16 cм; BL : LC = 4 : 5. 16
AC = 4 5 ;
4AC = 80; АС = 20; AC = 20 см.
в) BL = 3 см; CL = 5 см; AC – AB = 4 см;
АВ = х; AC = х + 4, x
x+4 = 3 5 ;
5х = 3х + 12; 2x = 12; х = 6; AB = 6 см; AC = 10 см;
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
Р∆ABC = 6 + 10 + 8 = 24 (см).
г) AB = 15 см; AC = 12 см, BL – CL = 2 см; CL = x; BL = х + 2; 15 12 = x+2 x ;
15х = 12х + 24;
Зх = 24; х = 8; CL = 8 см; BL = 10 см; BC = 18 см.
611. ��������

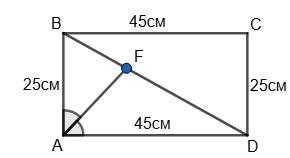
BF : FD = 5 : 9.
∆ABD. AF — бісектриса; AB A���� = BF FD = 5 9 ;
AB = 5х; AD = 9x; (5х + 9х) ∙ 2 = 140; 28х = 140; х = 5; AB = 25 см; AD = 45 см.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
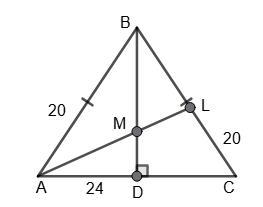
Нехай дано ∆ABC, AB = BC, AC = 24 см, AB = BC = 20 см. За
AB
AD = BM MF ; 20 12 = x 16 x ;
320 – 20x = 12x; 320 = 32х, х = 10; BM = 10 см; MD = 6 см.
Відповідь: BM = 10 см; MD = 6 см.
616. У рівнобедреному
якщо

AB = BC = 10 см, AC = 12 см, BH = 8 см; BH ⊥ AC AO — бісектриса. O — центр
AB
AH = BO OH ; 10 6 = x 8 x .
80 – 10х = 6х; 16х = 80;
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
х = 5; OB = 5 см; OH = 3 см.
Відповідь: 3 см.
617. У рівнобедреному

OH : ОВ = 5 : 12. AB = 36 см; AB AH = OB OH, за властивістю
36 AH = 12 5 ; AH = 36 ∙ 5 12 = 15 см;
AC = 30 см;
P∆ABC = 36 + 36 + 30 = 102 (см).
Відповідь: 102 см.
618.
кіл.
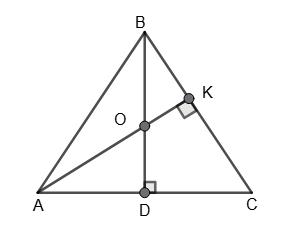
BD ⊥ AC, AK ⊥ BC. O
OD : BO = 1 : 2 (властивость медіан трикутника).
х + 2х = 12, 3х = 12, х = 4.
OD = 4 см; OB = 8 см.
Відповідь: 4 см; 8 см.
619.
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html

дано ∆ABC, AB = 12 см, BC = 15 см, AC = 21 см.
∆MBN ~ ∆ABC.
k = 2 3. OK : OB = 1 : 2 (властивість
MB = 12 ∙ 2 3 = 8 см, BN = 15 ∙ 2 3 = 10 см, MN = 21 ∙ 2 3 = 14 см.
Відповідь: 8 см; 10 см; 14 см. 624. Хорди �������� і
3 см, �������� =6 см
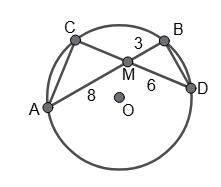
AM = 8 см; BM = 3 см; DM = 6 см. ∆CMA ~ ∆DMB
CMA =
MB
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
MD = CM AM ; CM =x; 3 6 = x 8, x = 4. CM = 4 см.
Відповідь: CM = 4 см.
625. Хорди �������� і �������� перетинаються
12 см. Знайдіть довжини хорд.

∆ACF ~ ∆DBF (див. попередню задачу).
FB – FC = 5; FC = x; FB = x + 5.
AF
CF = FD FB ; 10 x = 12 x+5 ,
10х + 50 = 12х,
2х = 50, х = 25,
CF = 25 см; FB = 30 см.
CD = CF + FD = 25 + 12 = 37 (см).
AB = AF + FB = 10 + 30 = 40 (см).
626. Хорди �������� і �������� перетинаються
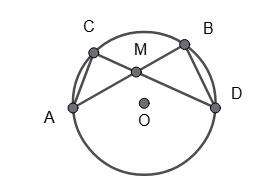
AM : MB = 1 : 3. CM = 9 см; DM = 12 см.
∆CMA ~ ∆BMD.
CM
AM = MB MD,
CM ∙ MD = AM ∙ MB, 9 ∙ 12 = х ∙ 3х.
Зх2 = 9 ∙ 12, x2 = 36, х = 6. AM = 6 см, MB = 18 см.
627. Хорди �������� і
AM = х, MB = 3х.
якщо �������� =4 см, �������� = 16 см.
.
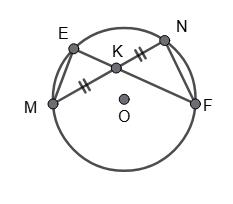
Нехай MK = KN = x,
∆AMEK ~ ∆FNK.
KE = 4 см, KF = 16 см. EK
MK = KN KF ,
EK ∙ KF = MK ∙ KN.
4 16 = x2, x2 = 64, х = 8.
MN = 2х = 16 см.
Відповідь: 16 см.
628. Із точки до кола
12 см, а зовнішня частина січної 8 см.
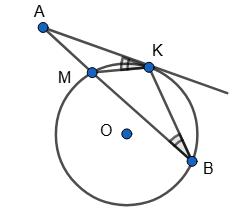
Нехай січна AB, AM = 8 см, AK = 12 см.
∆AMK ~ ∆AKB.
(∠A — спільний, ∠MKA = ∠ABK, рівні
їх подібності маємо: AM AK = AK AB , 8 12 = 12 x+8, МВ = х.
8х + 64 = 144, 8х = 80, x = 10. AB = AM + MB = 8 + 10 = 18 (см).
Відповідь: 18 см.
629. Із точки
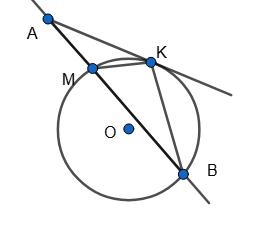
Нехай AK — дотична, AB — січна, MB = 9 см, AM = 16 см.
AM
AK = AK AB , 16 AK = AK 25 , AK2 = 16 ∙ 25, AK = 20 (см).
Відповідь: 20 см.
630.

Нехай AM : MB = 1 : 8.
AK = 12 см.
AM
AK = AK AB , x 12 = 12 9x , 9x2 = 144, x2 = 16, х = 4.
AM = 4 см; MB = 32 см; AB = 36 см. Відповідь: 36 см.
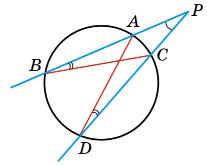
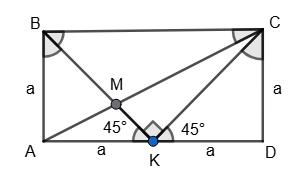
ABCD — прямокутник, BK і CK — бісектриси.
K ∈ AD AC — діагональ.
AC = 18 см, знайти: AM і MC.
∆ABK, ∠A = 90°,
∠B = 45°, ∠K = 45°,
АВ = АК = а;
∆KCD, CD = a, ∠K = ∠C = 45°, KD = а,
тому BC = 2а, BC = AD = 2а.
∆ABC за властивістю бісектриси маємо
AM
MC = AB BC = a 2a = 1 2 ,
АМ = х, MC = 2х; AC = Зх; 18 = 3х; х = 6 см.
Відповідь: 6 см і 12 см. 633. Користуючись умовою
що
���� і ����
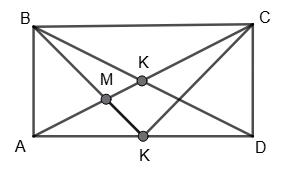
Доведемо, що AM = MK = KC. У попередній
що AB = а; BC = 2а.
AB : ВС = 1 : 2, тому
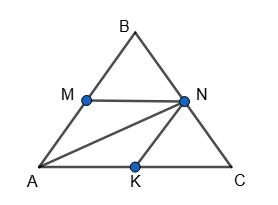
Нехай у ∆ABC вписано ромб AMNK N ∈ BC. AN — діагональ ромба, яка є бісектрисою
За властивістю бісектриси кута маємо:
AB
AC = BN BC ; 10 15 = x x+4 ; 10х + 40 = 15х; 5х = 40; х = 8.
Отже BN = 8 см; NC = 12 см.
Відповідь: BC = BN + NC = 8 + 12 = 20 (см).
636. Відкрита
1. AB;
2. BC;
3. AC.
A. 10 см; Б. 15 см;
B. 16 см;
24 см;
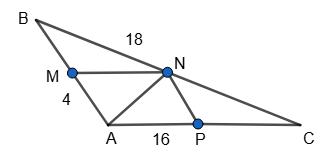
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
AB
AC = BN NC ; 4 16 = x 18 x ; 72 – 4x = 16x, 20x = 72, x = 3,6.
Відповідь: BN = 3,6 см; NC = 14,4 см.
639. ���� - середина дуги ��������
= 15 см, �������� = 18 см, �������� = 12 см.
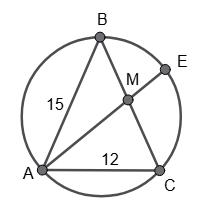
Нехай дано ∆ABC, AB = 15 см, BC = 18 см, AC = 12 см.
E — середина дуги BC.
∠BAE = ∠CAE— вписані кути рівні.
AE — бісектриса кута А.
За властивістю бісектриси кута:
AB
AC = BM MC ; 15 12 = 18 x x ;
15х = 216 – 12х, 27х = 216, х = 8.
MC = 8 см; BM = 10 см.
Відповідь: BM = 10 см, MC = 8 см.
640. У трикутник

https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
AB
BC = AO OC ; 10 x = 14 18 x ,
180 – 10x = 14x, x = 7,5.
AO = 7,5 cм; OC = 10,5 см.
Відповідь: AO = 7,5 см; OC = 10,5 см. 641. У рівнобедреному трикутнику, периметр якого 72 см, радіус
становить 5 18 висоти, проведеної до
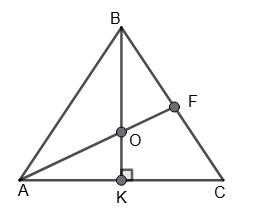
Нехай дано ∆АВС, AB = BC.
Р∆ABC = 72 см.
BK — бісектриса, AF — бісектриса.
OK — радіус вписаного кола. OK = 5 18 ВК.
Нехай OK = 5x, OB = 13x.
За властивістю бісектриси
AB
AK = BO OK = 15 5 ,
тоді AB = 13x, AK = 5x.
Складаємо рівняння: 13x + 10x + 13x = 72, 36x = 72, x = 2.
AB = 26 см; BC = 26 см; AC = 20 см.
Відповідь: AB = 26 см; BC = 26 см; AC = 20 см.
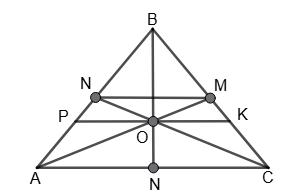
OB
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
PK = BN AC , OB BN = �������� AC ; 2 3 = �������� 8 ,
ЗРК = 16, PK = 16 3 , PK = 5 1 3 см.
Відповідь: 5 1 3 см.
643. Знайди
дорівнюють 26 см, 14 см і 18 см.
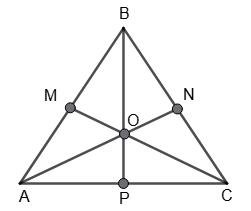
Нехай дано ∆ABC, CM, AN, BP — його медіани. O — точка їх перетину. OB = 26 см, OA = 14 см, OC = 18 см.
За властивістю медіан трикутника:
ОР : ОВ = 1 : 2, ON : AO = 1 : 2, OM : OC = 1 : 2, AN = 21 см, BP = 39 см, CM = 27 см.
Відповідь: 21 см, 39 см, 27 см. 644. Знайди довжини висот трикутника,
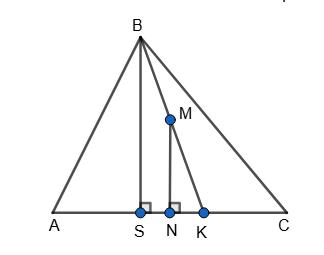
BK : MK = 3 : 1.
MN ⊥ AC, BS ⊥ AD,
AS : MN = 3 : 1.
15 см, 21 см, 24 см.
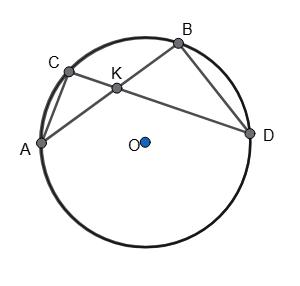
Нехай хорди AB і CD перетинаються в точці К.
AK = 18 см, CK = 20 см, KB + KD = 19.
∆САК ~ ∆DKB (за двома кутами).
∠CKA = ∠DKB — вертикальні кути, ∠ABD = ∠ACB —
З їх подібності маємо:
CK
AK = BK KD , 20 18 = ���� 19 x ; 18x = 380 – 20x, x = 10.
Отже, BK = 10 см, KD = 9 см.
CD = CK + KD = 20 + 9 = 29 см,
АК + ВК = 18 + 10 = 28 см.
Відповідь: 29 см, 28 см.
646. Точка
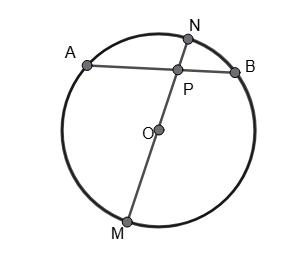
Нехай точка P ∈ AB, AP : PB = 3 : 2.
OM = ON = 11 см — радіуси кола.
OP = 5 см.
NP = 11 – 5 = 6 (см).
РМ = 11 + 5 = 16 (см).
За властивістю хорд маємо:
AP ∙ PB = NP ∙ PM.
3х ∙ 2х = 6 ∙ 16, x2 = 16, х = 4.
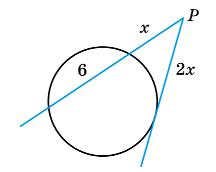


https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
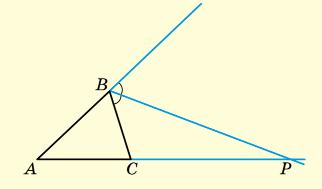
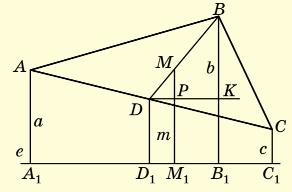

653.
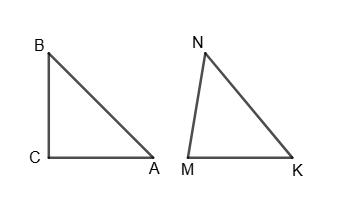
https://shkola.in.ua/3334-hdz-heometriia-8-klas-bevz.html
∠A : ∠B : ∠C = 3 : 5 : 10.
3х + 5х + 10х = 180°, 18x = 180°, x = 10°.
Кути ∆ABC: ∠A = 30°, ∠B = 50°, ∠C = 100°.
Кути ∆MNK : ∠M = x,
∠N = x – 20°, ∠K = x + 50°.
х + х – 20° + х + 50° = 180°, х = 50°.
∠M = 50°, ∠N = 30°, ∠K = 100°.
трикутники