1.
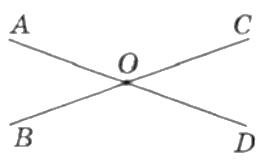
3. Знайдіть градусну
В. 132°.
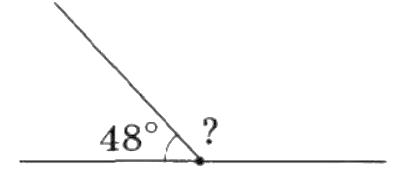
4. Знайдіть градусну міру
(мал. 3).

А. 123°. shkola.in.ua
5. Як зміниться кут, якщо вертикальний з ним
збільшити у 2 рази? Відповідь поясніть. Вертикальні кути — це пари кутів, які утворюються при перетині двох прямих і є рівними між собою. Це означає, що якщо один з вертикальних кутів змінюється, то інший кут також змінюється на стільки ж. Отже,
х = 80°
1.
В. 180° — 2α. shkola.in.ua
2. Який кут є

Б. ∠NOK.
3. Знайдіть градусну міру невідомого
(мал. 5).
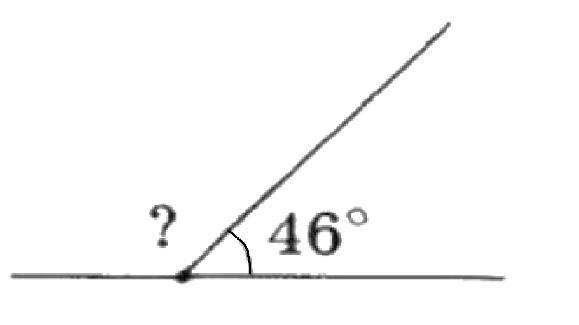
Б. 134°.
4. Знайдіть градусну міру невідомого кута (мал. 6).

Б. 26°. shkola.in.ua
5. Як зміниться кут, якщо вертикальний з ним кут зменшити в 3 рази? Відповідь поясніть. Вертикальні кути — це пари кутів, які утворюються при перетині двох прямих, і вони завжди рівні між собою. Отже, якщо один з вертикальних кутів зменшити в 3 рази, то інший кут також зменшиться в 3 рази, оскільки вертикальні кути завжди рівні.
6. Один із суміжних кутів менший від іншого на 40°. Знайдіть градусні міри обох кутів та побудуйте їх за допомогою транспортира. Нехай один із суміжних кутів дорівнює х, а інший — х + 40°.
х + (х + 40°) = 180°; 2х + 40° = 180°; 2х = 140°; shkola.in.ua
х = 70° — менший кут.
х + 40° = 70° + 40° = 110°.
1. На якому з малюнків а — г зображено паралельні прямі а і b (мал. 1)?

Б. в. shkola.in.ua
2. ∠1 = 25°, ∠3 = 135° (мал. 2). Знайдіть ∠2 і ∠4.
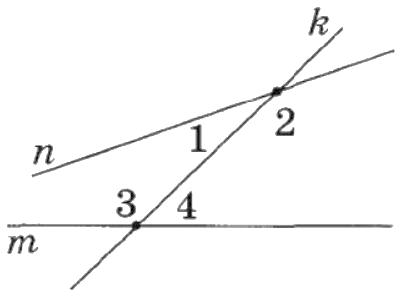
∠2 = 180° — 25° = 155°; ∠4 = 180° — 135° = 45°; Б. 155° і 45°.
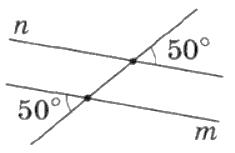
3 ∠1 = 25° (мал. 3). Яким повинен бути ∠3, щоб прямі n і m були паралельними?

180° — 25° = 155°.
Г. 155°
4. Знайдіть градусну міру невідомого кута, якщо n || m, a || b (мал. 4).

180° — 56° = 124°. shkola.in.ua А. 124°.
5. Січна с перетинає прямі а і b під кутом 75°. Виконайте малюнок і поясніть,
а і b.


1. На якому
паралельні
Б. в. shkola.in.ua
n i m (мал. 5)?
2 ∠1 = 36°, ∠4 = 35° (мал. 6). Знайдіть ∠2 і ∠3. ∠2 = 180° — 36° = 144°; ∠3 = 180° — 35° = 145°;
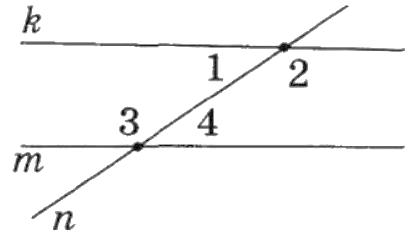
Г. 144° і 145°.
3 ∠3 = 146° (мал. 7). Яким повинен бути ∠1, щоб прямі n і m були паралельними? ∠1 = 180° — 146° = 34°.

Б. 34°.
4. Знайдіть градусну міру невідомого кута, якщо n || m, a || b (мал. 8).

180° — 146° = 34°. shkola.in.ua
А. 104°. Б. 86°. В. 76°. Г. 114°.
5. Січна с перетинає прямі a і b під кутом 55°. Виконайте малюнок і поясніть, як розміщені прямі a i b.

Якщо січна перетинає і пряму а, і пряму b під однаковим кутом 55°, тоді прямі а та b паралельні одна одній за рівними відповідними кутами. 6. Один із внутрішніх односторонніх кутів при двох прямих та січній на 40° менший від іншого. Які градусні міри повинні мати два інші внутрішні односторонні кути, щоб дані прямі були паралельними?

Щоб прямі були n || m, потрібно щоб ∠1 + ∠3 = 180°. shkola.in.ua
Тоді ∠1 = (180° — 40°) : 2 = 70°.
∠2 = 180° — 70° = 110°.
∠4 = 180° — 110° = 70°.
малюнках
(мал. 1)?

Б. а, г. shkola in ua
2. На малюнку 2 РΔ = ...
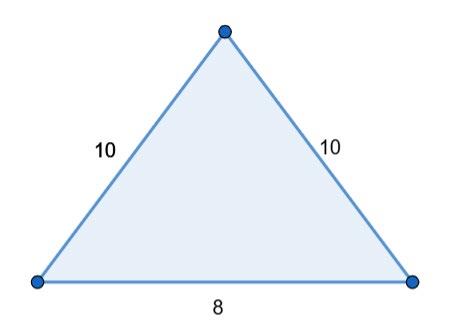
РΔ = 10 + 10 + 8 = 28. В. 28.
3. На малюнку 3 ∠C = ...

∠C = 180° — (70° + 38°) = 72°.
Б. 72°. shkola.in.ua
4. На малюнку 4 ∠BCM = ...

∠ACB = 180° — (75° + 42°) = 63°;
∠BCM = 180° — 63° = 117°.
А. 117°.
5. ВК – бісектриса трикутника ABC (мал. 5). ∠C =

∠ABK = 180° — (50° + 85°) = 45°;
∠ABK = ∠KBC = 45°.
∠BKC = 180° — 85° = 95°.
∠C = 180° — (45° + 45° + 50°) = 40°.
6. У трикутнику ABC ∠A = 60°, а кут В — у 4 рази менший від кута С. Знайдіть кути В і С. 1) Нехай кут В — х, тоді С — 4х. 60 + 4х + х = 180; 5х = 180 — 60; 5х = 120; shkola.in.ua х = 24° — кут В; 2) 24 • 4 = 96° — кут С.
1.
(мал. 6)?

Б. а, г. shkola in ua
2. На малюнку 7 PΔ = ...

PΔ = 8 + 8 + 5 = 21.
В. 21.
3. На малюнку 8 ∠A = ...

∠A = 180° (42° + 64°) = 74°.
Б. 74°. shkola.in.ua
4. На малюнку 9 ∠MAB = ...

∠BAC = 180° — (64° + 51°) = 65°;
∠MAB = 180° — 65° = 115°. A. 115°.
5. BN — бісектриса трикутника ABC (мал. 10). ∠A = ...
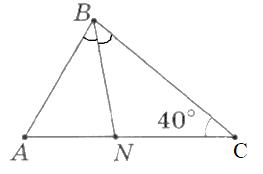
∠NBC = 180° — (40° + ∠BNC);
∠NBC = ∠ABN.
∠B = ∠NBC + ∠ABN.
∠A = 180° — (40° + ∠B).
6. У трикутнику ABC ∠B = 45°, а ∠C — на 35° більший за кут А. Знайдіть кути
і С. 1) Нехай кут А — х, тоді кут С — х + 35. 45 + х + х + 35 = 180; 2х = 180 — 80; 2х = 100; shkola.in.ua х = 50° — кут А; 2) 50 + 35 = 85° — кут С.
1. Доповніть речення.
ΔABC = ΔKMN за першою ознакою рівності трикутників. shkola.in.ua
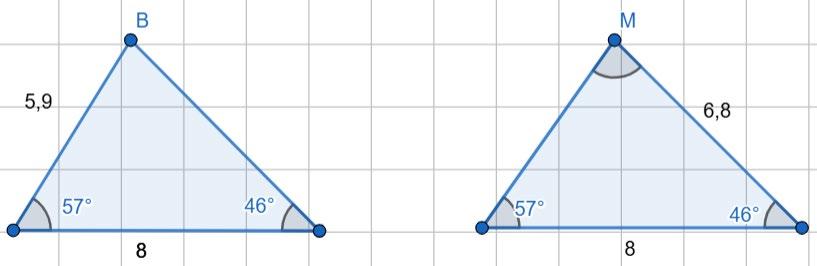
А. першою
2. KM = ...
A. 5,9.
3. ∠B = ...
∠B = 180° — (57° + 46°) = 77°. B. 77°.
4. Знайдіть периметр трикутника KMN.
5,9 + 6,8 + 8 = 20,7.
B. 20,7. shkola.in.ua
У задачах 5 – 6 доведіть рівність указаних трикутників.
5. ΔPON і ΔKOM (мал. 2).
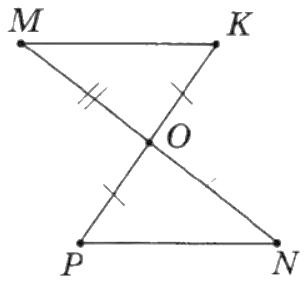
∠MOK = ∠PON; MO = ON; PO = OK.
ΔPON = ΔKOM за першою ознакою трикутника.
6. ΔNOA і ΔMOB (мал. 3).

NC = MC; ∠NCO = ∠MCO; CO — спільна. Тоді ΔNCO і ΔMCO. Звідси NO = MO. shkola.in.ua
∠NOA = ∠MOB як вертикальні; AO = BO; NO = MO. Тоді трикутники
ΔNOA = ΔMOB за першою ознакою.
1. Доповніть речення. shkola in ua

ΔABC = ΔKMN за другою
трикутників.
Б. другою.
2. AB = ...
Б. 6,1.
3. ∠M = ... 180° — (94° + 48°) = 38°.
B. 38°.
4. Знайдіть периметр трикутника АВС. 5 + 6,1 + 8,1 = 19,2.
A. 19,2 shkola.in.ua
5. ΔAOB і ΔCOD (мал. 5).

∠BOA = ∠COD як вертикальні; BO = OD; AO = OC. Тоді ΔAOB = ΔCOD за першою ознакою.
6. ΔBKC і ΔADC (мал. 6).

∠ACK = ∠DCK; ∠CAD = ∠CAK; CA — спільна. Тоді ΔDCA і ΔACK за другою ознакою. Звідси KA = DA = BK; CK = CD. shkola.in.ua
∠AKC = 180° — 90° = 90°.
∠BKC = ∠CDA; CK = CD; BK = DA. Тоді ΔBKC = ΔADC за першою ознакою.
1. Знайдіть радіус кола, якщо його діаметр дорівнює 5 см.
В. 2,5 см.
2. Точка В — центр кола, АО — дотична до кола (мал. 1). ∠АВО = ...

180° — (30° + 90°) = 60°. A. 60°. shkola.in.ua
3. Укажіть геометричне місце точок, рівновіддалених від вершин А і В трикутника АВС.
Б. Серединний перпендикуляр до відрізка АВ.
4. Точка О — центр кола, АС = а, ОС ⊥ АВ (мал. 2). АВ = ...

Б. 2а.
5. До кола проведено дотичні ВС, СА і AD (мал. 3). Точки В, М і D — точки дотику. СА = 6,2 см. Знайдіть ВС + DA.

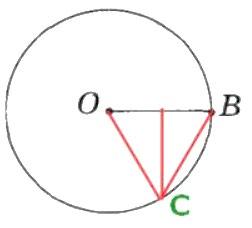
Дотичні, які провели до кола з однієї точки, рівні між собою: ВС = СМ; АМ = AD. АС = СМ + АМ = 6,2 см, АС = ВС + AD = 6,2 см. shkola in ua 6. Як на колі (мал. 4) знайти точки, рівновіддалені від кінців радіуса ОВ? Зробіть схематичний малюнок.
1. Знайдіть діаметр кола, якщо його радіус дорівнює 5 см.
Б. 10 см.
2. Точка В — центр кола, АО — дотична до кола (мал. 5). ∠АВО = ...

180° — (60° + 90°) = 30°. Б. 30°. shkola.in.ua
3. Укажіть геометричне місце точок, рівновіддалених від сторін АС і АВ трикутника АВС.
Г. Бісектриса кута САВ.
4. Точка О — центр кола, ОС ⊥
СВ = 13 см (мал. 6). АС = ...
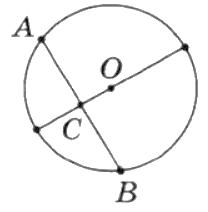
А. 13 см.
5. До кола (мал. 7) проведено дотичні СВ, СА і AD. Точки В, М і D — точки дотику. BC + DA = 25 см. Знайдіть СА.

Дотичні, які провели до кола з однієї точки, рівні між собою ВС = СМ; АМ = AD. shkola.in.ua
СА = СМ + АМ = ВС + AD = 25 см.
6. Як на даному колі (мал. 8) знайти точки, віддалені від точки А на відстань АО? Зробіть схематичний малюнок.

1. Відрізок АВ завдовжки 15 см точка С ділить у відношенні 2 : 3. Знайдіть довжини відрізків
СВ.
2х + 3х = 15; 5х = 15; х = 3 см.
АС = 2 • 3 = 6 см; СВ = 3 • 3 = 9 см.
Б. 6 см і 9 см.
2. Знайдіть площу квадрата, периметр якого дорівнює 12 см.
12 : 4 = 3 см – сторона квадрата;
3 • 3 = 9 (см2)
В. 9 см². shkola.in.ua
3. Знайдіть діаметр круга, площа якого дорівнює 28,26 см².
1) 28,26 : 3,14 = 9 – квадрат радіуса;
2) √9 = 3 (см) – радіус;
3) 3 • 2 = 6 см – діаметр.
В. 6 см.
4. Піцу розрізали на 6 рівних частин. Яка градусна міра кута кожної частини? 360° : 6 = 60°.
Г. 60°
5. Як зміниться об'єм коробки, що має форму прямокутного паралелепіпеда, якщо її довжину: зменшити на 10%, ширину збільшити на 20%, а висоту Не змінювати? На скільки відсотків зміниться 66 см? shkola.in.ua V= abc; a1 = а
дорівнює 50 мм, довжина другої сторони становить 3 5 довжини першої, а довжина третьої сторони становить 120% довжини другої. Знайдіть периметр іншого трикутника, кожна сторона якого на 20 % більша, ніж відповідна сторона даного трикутника. Відповідь запишіть у сантиметрах.
1) 5 : 5 • 3 = 3 (см) – друга сторона; 2) 3 • 1,2 = 3,6 (см) – третя сторона; 3) 5 • 1,2 = 6 (см) – перша сторона; 4) 3 • 1,2 = 3,6 (см) – друга сторона; 5) 3,6 • 1,2 = 4,32 (см) – третя сторона; 6) 6 + 3,6 + 4,32 = 13,92 (см). shkola.in.ua
2
1. Відрізок АВ завдовжки 21 см точка С ділить у відношенні 3 : 4. Знайдіть довжини відрізків
СВ.
3x + 4x = 21;
7x = 21; x = 3 (см).
АС = 3 • 3 = 9 (см);
СВ = 3 • 4 = 12 (см).
В. 9 см і 12 см.
2. Знайдіть периметр квадрата, площа якого дорівнює 36 см².
√36 = 6 (см) – сторона квадрата;
4 • 6 = 24 (см).
Б. 24 см. shkola.in.ua
3. Знайдіть площу круга, діаметр якого дорівнює 6 см.
1) 6 : 2 = 3 (см) – радіус; 2) 3,14 • 3² = 28,26 (см²).
Г. 28,26 см².
4. Круглий торт розрізали на 8 рівних частин. Яка градусна міра кута кожної частини?
360° : 8 = 45°.
В. 45°.
5. Як зміниться об'єм коробки, що має форму прямокутного паралелепіпеда, якщо
довжину збільшити на 25%, ширину не змінювати,
зменшити на 12
об’єм? shkola.in.ua
V= abс a1 =a (1+0,25) =1,25a; ����1=b (1 0,12) =0,88b;
іншого трикутника, кожна сторона якого на 20 % менша, ніж відповідна сторона даного трикутника. Відповідь запишіть у сантиметрах.
1) 2,4 : 8 • 5 = 1,5 (см) – друга сторона трикутника; 2) 1,5 • 1,1 = 1,65 (см) – третя сторона трикутника; 3) 2,4 • 0,8 = 1,92 (см) – перша сторона трикутника; 4) 1,5 • 0,8 = 1,2 (см) – друга сторона трикутника; 5) 1,65 • 0,8 = 1,32 (см) – третя сторона трикутника; shkola.in.ua
6) 1,92 + 1,2 + 1,32 = 4,44 (см) – периметр.
1. Назвіть промінь, доповняльний
(мал. 1).
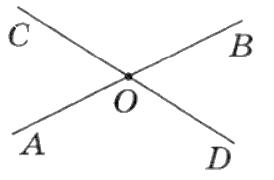
Г. OD.
2. Промінь ОА — бісектриса кута СОВ (мал. 2). ∠BOC = 40°.
∠BOA = ...

∠BOA = 40° : 2 = 20°. shkola.in.ua В. 20°.
3. Точка С належить відрізку АВ завдовжки 62 мм, АС = 22 мм.
СВ = ...
СВ = 62 — 22 = 40 мм = 4 см. Б. 4 см.
4. Точка А є серединою відрізка ВС, АВ = 16 см.
ВС = ...
ВС = 16 • 2 = 32 см.
В. 32 см.
5. Від променя ОВ відклали ∠BOA = 30° і ∠BOC = 40°. Знайдіть кут СОА. Скільки випадків треба розглянути?

І ВАРІАНТ:
∠COA = 40° — 30° = 10°; ІІ ВАРІАНТ:
∠COA = 40° + 30° = 70°.
6. На відрізку АВ = 12 см позначено точки О і Т так, що АО : ОТ : ТВ = 1 : 2 : 3. Знайдіть довжини цих відрізків.
x + 2x + 3x = 12; 6x = 12; shkola.in.ua
x = 2 (см) — АО; 2 • 2 = 4 (см) — ОТ; 2 • 3 = 6 (см) — ТВ.
6*. ∠ABD = ∠DBC (мал. 3). Обгрунтуйте, що промінь BD — бісектриса кута КВР.
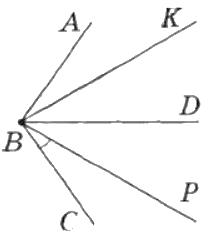
∠ABD = ∠DBC за умовою, та ∠ABK = ∠CBP за
малюнком.
∠ABD = ∠ABK + ∠KBD; ∠DBC = ∠CBP + ∠DBP. ∠ABD = ∠DBC за умовою, та ∠ABK = ∠CBP за малюнком. shkola in ua
Тоді: ∠ABK + ∠KBD = ∠CBP + ∠DBP; ∠CBP + ∠KBD = ∠CBP + ∠DBP, звідки випливає що ∠KBD = ∠DBP. Значить BD – бісектриса кута ∠KBP.
1. Назвіть промінь,
(мал. 4).

Г. ОD.
2. Промінь ОА — бісектриса кута СОВ (мал. 5).
∠COA = ...

∠COA = 90° : 2 = 45°. shkola.in.ua
В. 45°.
3. Точка В належить
7 см, АВ = 30 мм. СВ = ...
СВ = 70 – 30 = 40 мм.
А. 40 мм.
4. Точка С є серединою відрізка
АС = 20 см. АВ = ...
АВ = 20 • 2 = 40 см.
Г. 40 см.
5. На прямій ОВ від точки О відклали відрізки ОА = 3 см і ОС = 4 см. Знайдіть довжину
Скільки випадків треба розглянути?

І випадок: 4 – 3 = 1 (см) – АС;
ІІ випадок: 4 + 3 = 7 (см) – АС.
6. ∠DBC = 85°, ∠ABM = 40° (мал. 6). ∠NBC — ?

∠ABD = 40° : 2 = 20°; shkola.in.ua ∠DBM = ∠ABD = ∠MBN – за малюнком.
∠NBC = 85 – (20 + 20) = 85 – 40 = 45° 6*. Точки C i D ділять відрізок

