1.
виразу 4,8 : 12 - 2(3 5)
4,8 : 12 - 2(3 5) = 0,4 + 2,6 = -2,2;
Б. -2,2. shkola.in.ua
2.
4a−5 2 . А. а - будь-яке число.
3. Спростіть вираз 2,4(5 + 8a) - 6,4(3a - 5).
2,4(5 + 8a) - 6,4(3a - 5) = 12 + 19,2a - 19,2a + 32 = 44.
В. 44.
4. Винесіть спільний
-20x² + 8xy - 4xy². -20x² + 8xy - 4xy² = -4x(5x - 2y + y²).
В. -4x(5x - 2y + y²).
поїзда;
t + (t + 1) год.
2) шлях, пройдений поїздом зі
80 • t км. shkola.in.ua 3) шлях, пройдений
85 • (t + 1) км.
6. Відомо, що 2x + y = 0,3 і z
чення виразу −6x + 2z − 3y. 6x + 2z − 3y = −3(2x + y) + 2 • (−1,8) = −3 • 0,3 − 3,6 = −0,9 − 3,6 = −4,5.
Г. 1,8. 2.
9 – а = 0; а = 9; shkola.in.ua
Б. а ≠ 9. 3.
3,5(4 – 6с) – 4,2(5с + 10) = 14 – 21с – 21с – 42 = –42с – 28.
Б. –42с – 28.
аb – 4а.
–2а2b + ab – 4a = –a(2ab – b + 4).
Б. –а(2аb – b + 4).
2а2b +
t + (t − 1) год. 2) шлях, пройдений автомобілем зі швидкістю
Б. < 0.
2. 5 • 3² =...
5 • 3² = 5 • 9 = 45.
Г. 45. shkola.in.ua
3. 1⁵ + 0⁷ + 5² =...
1⁵ + 0⁷ + 5² = 1 + 0 + 25 = 26.
В. 26.
4. Запишіть вирази 0,5², (−3)³, 0⁵, (−1)⁷ у
збільшення їх значень.
А. (−3)³, (−1)⁷, 0⁵, 0,5².
5. Обчисліть подвоєну суму
рата числа 1,5.
2 • (2³ + 1,5²) = 2 • (8 + 2,25) = 2 • 10,25 = 20,5.
6. Розв'яжіть рівняння: 1) x − 2² • 2³ = 1²⁵; 2) (2 − 3x)⁶⁵ = 0.
1) x − 2² • 2³ = 1²⁵; x − 4 • 8 = 1; x − 32 = 1; x = 33. shkola.in.ua
2) (2 − 3x)⁶⁵ = 0; 2 − 3x = 0; 3x = 2; x = 2 3 .
А. > 0.
2. 3 • 2³ =...
3 • 2³ = 3 • 8 = 24.
В. 24.
3. 3¹ + 0¹¹ + 1⁹ =...
3¹ + 0¹¹ + 1⁹ = 3 + 0 + 1 = 4.
А. 4. shkola.in.ua
4. Запишіть вирази (−1)², 0⁷, (−5)², (−2)⁵ у
зменшення їх значень.
А. (−5)², (−1)², 0⁷, (−2)⁵.
5. Обчисліть подвоєну суму
куба числа 2.
2 • (1,1² + 2³) = 2 • (1,21 + 8) = 2 • 9,21 = 18,42.
6. Розв'яжіть рівняння: 1) 2x − 9 • 3² = 0²²; 2) (1 + 2x)⁴⁸ = 0.
1) 2x − 9 • 3² = 0²²; 2x − 9 • 9 = 0; 2x − 81 = 0; 2x = 81; x = 40,5. shkola.in.ua
2) (1 + 2x)⁴⁸ = 0;
1 + 2x = 0;
2x = -1; x = −0,5.
Г. са.
2. (−2d − 5) + (2d + 1) = ...
(−2d − 5) + (2d + 1) = −2d − 5 + 2d + 1 = −4.
Г. −4.
3. Знайдіть суму
2x² − x³ + x³ + 4x² = 6x².
Б. 6x². shkola.in.ua 4. Знайдіть різницю
a
7 і 2a
4. a − 7 − (2a − 4) = a − 7 − 2a + 4 = −a − 3.
А. a − 3.
5. Розв'яжіть рівняння: (3x + 5) − (8 − 7x) = 37. (3x + 5) − (8 − 7x) = 37; 3x + 5 − 8 + 7x = 37; 10x − 3 = 37; 10x = 34; x = 3,4. shkola.in.ua
b2 = 10b + 2; (де b — кількість десятків, а 2 — одиниці). 2b = 10 • 2 + b = 20 + b; (де 2 — кількість десятків, а b — одиниці).
(10b + 2) − (20 + b) = 10b + 2 − 20 − b = 9b − 18 = 9(b − 2); Отже, різниця 9(b − 2) ділиться на 9.
2. (–m + 3) + (2m – 3) = ... (–m + 3) + (2m – 3) = –m + 3 + 2m – 3 = m.
(−x − 12) + (2 − 9x) = 60; x − 12 + 2 − 9x =
1. (m + 0,2n)² = ...
Г. m² + 0,4mn + 0,04n².
2. (4p + t²)(4p - t²) = ...
(4p + t²)(4p - t²) = 16p² - 4pt² + 4pt² - t⁴ = 16p² - t⁴.
В. 16p² - t⁴.
3. (-2 - x)² = ...
A. 4 + 4x + x². shkola.in.ua
4. Який із
-20x + 25 + 4x² = 4x² - 20x + 25 = (2x - 5)².
B. -20x + 25 + 4x².
5. 49² - 47² = ...
49² - 47² = (49 - 47)(49 + 47) = 2 • 96 = 192.
6. Розв'яжіть рівняння: 1) 25x² - 36 = 0; 2) (2x - 5)² -
(4 - x)² = 0.
1) 25x² - 36 = 0;
(5x - 6)(5x + 6) = 0;
5x - 6 = 0;
5x = 6;
x = 1,2;
5x + 6 = 0;
5x = -6; shkola.in.ua
x = -1,2.
2) (2x - 5)² - (4 - x)² = 0;
(2x - 5 - 4 + x)(2x - 5 + 4 - x) = 0;
(3x - 9)(x - 1) = 0;
3x - 9 = 0;
x = 3;
x - 1 = 0;
x = 1.
1. (0,3c − b)² = ...
В. 0,9c² − 0,6bc + b².
2. (6c − b³)(6c + b³) = ...
Г. 36c² − b⁶.
3. (-6 + x)² = ... shkola.in.ua
A. 36 - 12x + x²
4. Який із виразів є повним квадратом?
B. 24x + 16 + 9x² = (3x + 4)²
5. 37² - 35² = ...
37² - 35² = (37 - 35)(37 + 35) = 2 • 72 = 144.
6. Розв'яжіть рівняння: 1) 64x² - 49 = 0; 2) (3x - 9)²(5 - x)² = 0.
1) 64x² - 49 = 0;
(8x - 7)(8x + 7) = 0;
8x - 7 = 0;
8x = 7; x = 7 8;
8x + 7 = 0;
8x = -7; shkola.in.ua
x =7 8 .
2) (3x - 9)² - (5 - x)² = 0;
(3x - 9 - 5 + x)(3x - 9 + 5 - x) = 0;
(4x - 14)(2x - 4) = 0;
4x - 14 = 0;
4x = 14;
х = 3,5
2x - 4 = 0;
2x = 4; x = 2.
1. Яка із точок A (-1; -1), B (-1; -4), C (-1; 2) чи D (1; -2) належить графіку функції y = 3x³ - 1? -4 = 3 • (-1)³ - 1; -4 = -3 - 1; -4 = -4. shkola.in.ua
Б. B.
2. У якій точці перетинає вісь
функції y = 4x - 8?
4x - 8 = 0; 4x = 8; x = 2.
В. (2; 0).
3. У якій точці перетинає вісь ординат графік функції y = 4x - 8? y = 4 • 0 - 8; y = -8.
А. (0; -8).
4. Скориставшись графіком функції,
ний на малюнку 1, знайдіть значення функції, яке відповідає значенню аргументу x = 5.
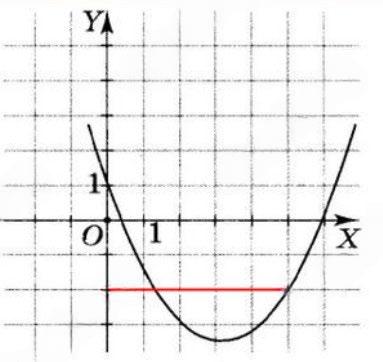
Б. -2. shkola.in.ua
5. Графік функції y = x² + 2a проходить через точку K (-2; 5). Знайдіть значення a. 5 = (-2)² + 2a; 5 = 4 + 2a; 2a = 1; a = 0,5.
6. Функцію задано формулою y = x² + 2. Заповніть таблицю 1. Таблиця 1
даної функції. shkola in ua
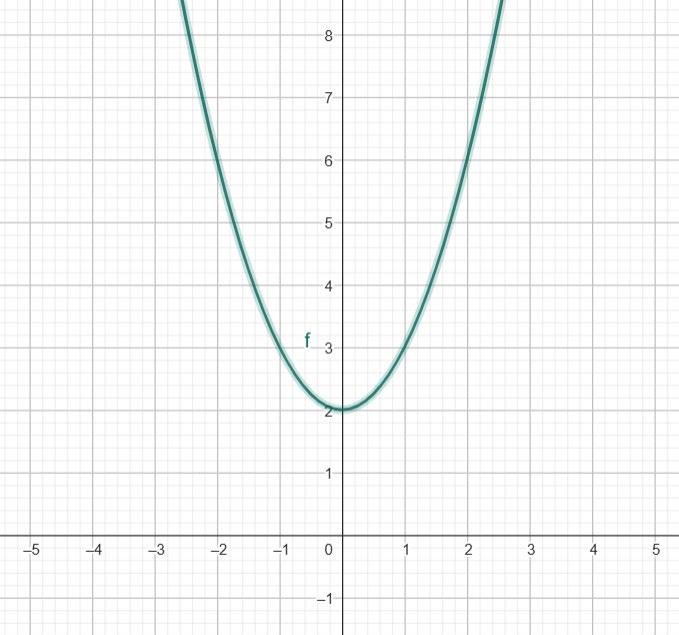
-5.
1. Яка із точок A (-1; -1), B (-1; -5), C (-1; 1) чи D (1; -1) належить графіку функції y = 2x³ + 3?
-1 = 2 • (-1)³ + 3; -1 = 2 • (-1) + 3; -1 = -2 + 3; -1 = 1. shkola.in.ua
В, С.
2. У якій точці перетинає вісь абсцис графік функції у = –х + 5?
0 = –х + 5;
х = –5;
х = 5.
Г. (5; 0).
3. У якій точці перетинає вісь ординат графік функції у = –х + 5?
у = 0 + 5;
у = 5.
Б. (0; 5).
4. Скориставшись графіком функції, що зображений на малюнку 2, знайдіть значення функції, яке відповідає значенню аргументу х = –1.
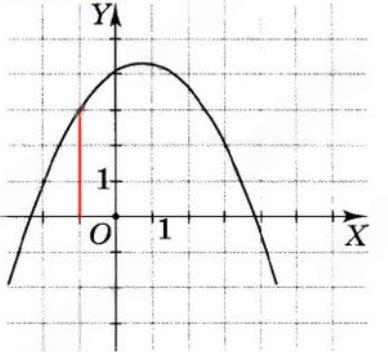
А. 3. shkola.in.ua
5. Графік функції у = х2 – 3b проходить через точку М (–1; –5). Знайдіть значення b.
5 = (–1)2 – 3b;
5 = 1 – 3b; 3b = 1 + 5; b = 2.
6. Функцію задано формулою y = x² - 1. Заповніть таблицю 2. Таблиця 2.
х -2 -1 0 1 2
У 3 0 -1 0 3 Скориставшись даними таблиці, побудуйте графік даної функції. shkola in ua

1. Рівняння 5y – 2 = 3 + 7y є рівносильним рівнянню...
5y - 2 = 3 + 7y;
5y - 7y - 3 - 2 = 0; 2y + 5 = 0.
Г. 2y + 5 = 0.
2. Яке із чисел є коренем рівняння 22 – 4x – 7 = 8x – 9?
22 - 4x - 7 = 8x - 9; -12x = -24; x = 2.
Б. 2. shkola.in.ua
3. Дано рівняння: 8x – 2y – 12 = 0. Запишіть його загальний розв'язок, виразивши змінну через змінну x.
8x - 2y - 12 = 0; -2y = -8x + 12; y = ( 8x + 12) −2 = 4x - 6.
В. (x; 4x - 6), де x — будь-яке число.
4. Точкою перетину графіка рівняння -x + 2y - 5 = 0 з віссю абсцис є точка: -x + 2 • 0 - 5 = 0; -x - 5 = 0; -x = 5;
x = -5.
В. (-5 ; 0).
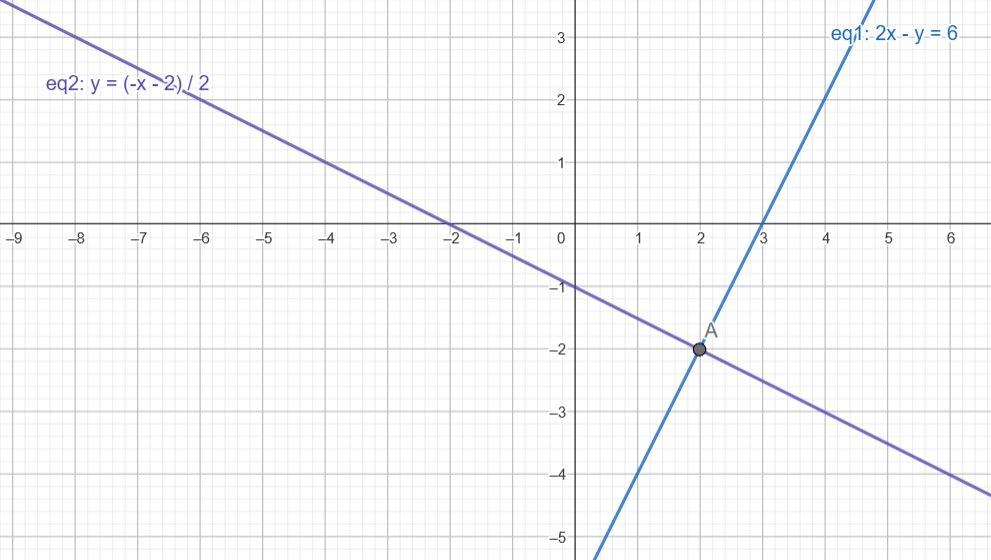
5. Побудуйте графіки рівнянь 5x - y + 1 = 0 і y = 3. Визначте координати точки перетину графіків.

А. (0,4; 3)
6. Серед розв’язків рівняння 4х + 3y + 1 = 0 є пара чисел (2; а). Знайдіть а.
4х + 3y + 1 = 0;
4 • 2 + 3а + 1 = 0; 8 + 3а + 1 = 0; 3а = –9;
а = –3. shkola.in.ua
1. Рівняння 2y + 3 = 8 – 4у є рівносильним рівнянню...
2y + 3 = 8 – 4у;
6у – 5 = 0.
В. 6у – 5 = 0.
2. Яке із чисел є коренем рівняння 15 + 12у – 9 = 9 + 15у?
15 + 12у – 9 = 9 + 15у; 12у – 15у = 9 + 9 – 15; –3у = 3;
у = –1.
Г. –1. shkola.in.ua
3. Дано рівняння: 6х + 2у – 10 = 0. Запишіть його загальний розв’язок, виразивши змінну через
змінну х.
2у = –6х + 10; у = ( 6х+10) 2 = –3х + 5.
Г. (х; –Зх + 5), де х — будь–яке число.
4. Точкою перетину графіка рівняння –2х + у + 7 = 0 з віссю ординат є точка: –2 • 0 + у + 7 = 0;
у = –7.
Г. (0; –7).
5. Побудуйте графіки рівнянь 3х + у + 1 = 0 і х = –1. Визначте координати точки перетину графіків.
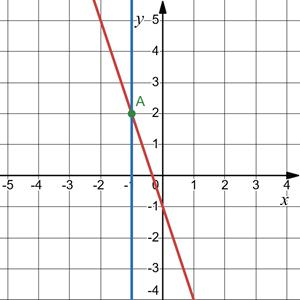
А (–1; 2)
6. Серед розв’язків рівняння Зх – 5у + 8 = 0 є пара чисел (2а; 1). Знайдіть а.
3х – 5у + 8 = 0;
3 • 2а – 5 • 1 + 8 = 0;
6а – 5 + 8 = 0;
6а + 3 = 0;
6а = –3; а = –0,5. shkola.in.ua
1. Число 50 збільшили на 20%. Яке число отримали?
50 • 1,2 = 60.
А. 60. shkola.in.ua
2. Знайдіть число, після зменшення якого на 30% отримано число 140.
140 : (1 – 0,3) = 140 : 0,7 = 200.
В. 200.
3. За перший день робітник виготовив 40 деталей, а за другий — 44. На скільки відсотків зросла продуктивність праці робітника?
1) 40 – 100%
44 – х%.
х = (44 • 100)/40 = 110%;
2) 110 – 100 = 10%.
Б. На 10%. shkola.in.ua
4. У сплаві 44% алюмінію, а решта — магній. Скільки грамів алюмінію треба взяти, щоб виготовити сплав, у якому міститься 280 г магнію?
1) 100% – 44% = 56% – вміст магнію;
2) 280 г – 56%;
х г – 44%.
х = 280 • 44 56 = 220 (г).
В. 220 г.
5. Кількість учнів у 7–А, 7–Б і 7–В класах пропорційна до чисел 7, 9 і 6. Скільки учнів навчається в кожному класі, якщо у 7–В класі — 24 учні? За отриманими даними побудуйте стовпчасту діаграму.
1) 24 : 6 = 4 – коефіцієнт пропорційності;
2) 4 • 7 = 28 (уч.) – в 7–А; 3) 4 • 9 = 36 (уч.)
1. Число 80 зменшили на 40%. Яке число отримали?
1) 80 • 0,4 = 32.
2) 80 – 32 = 48.
В. 48. shkola.in.ua
2. Знайдіть число, після збільшення якого на 20% отримано число 90. х + 0,2х = 90; 1,2х = 90; х = 90 : 1,2; х = 75.
В. 75.
3. У магазині ціну на товар зменшили з 300 гривень до 240 гривень. На скільки відсотків знизили ціну?
1) 300 грн – 100%; 240 грн – х%. х = (240•100) 300 = 80%;
2) 100% – 80% = 20%. shkola.in.ua А. На 20%.
4. У сплаві 24% міді, а решта — олово. Скільки грамів міді треба взяти, щоб виготовити сплав, у якому міститься 380 г олова?
1) 100% – 24% = 76% – олова; 380 г – 76%;
х г – 24%;
х = (380•24) 76 = 120 г.
Г. 120 г.
5. Кількість голосів на виборах президента школи розподілилась між трьома кандидатами у відношенні 6 : 9 : 3. Скільки учнів віддали свій голос за кожного з кандидатів, якщо всього в голосуванні взяли участь 270 учнів? За отриманими даними побудуйте стовпчасту діаграму.
1) 6х + 9х + 3х = 270; 18х = 270; х = 15 – коефіцієнт пропорційності; shkola.in.ua
2) 15 • 6 = 90 – І кандидат;
3) 15 • 9 = 135 – ІІ; 4) 15 • 3 = 45 – ІІІ.
6. Число збільшили на 50%, а потім зменшили на 20%. Як змінилося число.
1) х + 0,5х = 1,5х – збільшили на 50%; 2) 1,5х – 0,2 • 1,5х = 1,2х – зменшили на 20%; 3) 120% – 100% = 20% – збільшилося на 20%.
1. У їдальні є 5 других і
способами можна скласти
(першої і другої)?
Г. 15.
із двох
2. Андрію, Борису й Антону поталанило, вони купили 3 квитки на футбол на перше, друге і третє місця першого ряду стадіону. Скількома способами хлопці можуть зайняти ці місця? 3 • 2 • 1 = 6.
В. 6.
3. На столі лежать ручка, олівець і лінійка. Скількома способами із цих трьох предметів можна обрати два різні прилади? Можливі варіанти вибору двох предметів:
1. Ручка і олівець.
2. Ручка і лінійка.
3. Олівець і лінійка.
Отже, є 3 способи обрати два різні прилади. Б. 3. shkola.in.ua
4. Скільки чотирицифрових чисел, які закінчуються або цифрою З, або цифрою 5, можна скласти із цифр 3, 4, 7 і 5, якщо цифри в числі не повторюються?
1) 3 • 2 • 1 = 6 – число закінчується на 3; 2) 3 • 2 • 1 = 6 – число закінчується на 5; 3) 6 + 6 = 12. В. 12.
5. Які набори із трьох різних елементів можна скласти з букв Т, О, Н? Побудуйте дерево можливих варіантів.















1. Є 5 різних олівців і
способами
одного олівця?
5 • 7 = 35.
Г. 35.
2. Оксана, Тетяна та Ольга пішли на прогулянку. Було спекотно й вони вирішили купити морозиво. Скількома способами вони можуть вишукуватися в чергу за морозивом?
3 • 2 • 1 = 6.
В. 6.
3. На столі лежать яблуко, груша і слива. Скількома способами можна обрати два різних фрукти? Можливі варіанти
1. Яблуко і груша.
2. Яблуко і слива.
3. Груша і слива.
Отже, є 3 способи обрати
різних фрукти. Б. 3. shkola.in.ua
4. Скільки чотирицифрових чисел, які закінчуються або цифрою 9, або цифрою 7,
скласти із цифр 1, 9, 7 і 5, якщо цифри в числі не повторюються?
1) 3 • 2 • 1 = 6 – закінчується на 9; 2) 3 • 2 • 1 = 6 – закінчується на 7; 3) 6 + 6 = 12 – чисел. В. 12.
5. Які трицифрові числа можна скласти із цифр 2, 5, 8, якщо всі цифри в числі — різні? Побудуйте дерево можливих варіантів. Можливі комбінації трицифрових чисел такі: 258; 285; 528; 582; 825; 852.



6.












1. Обчисліть: 5,7 + (−4) • 1,8. 5,7 + (−4) • 1,8 = 5,7 − 7,2 = −1,5.
В. −1,5.
2. Знайдіть 24% числа 15. 15 • 0,24 = 3,6.
Б. 3,6. shkola.in.ua
3. Знайдіть невідомий член пропорції x : 4,2 = 9 : 10,8.
x = (4,2•9) 10,8 = 3,5.
А. 3,5.
4. Розв'яжіть рівняння: (1 2)(2 + 6x) + (4x - 1) • 3 = 10x - 12,5. (1 2)(2 + 6x) + (4x - 1) • 3 = 10x - 12,5; 1 + 3x + 12x - 3 = 10x - 12,5; 15x - 10x = 2 - 12,5; 5x = -10,5;
x = -2,1. shkola.in.ua
5. Задано координати трьох вершин прямокутника ABCD: А (2; 3); В (–5; 3); C (–5; –1). Побудуйте ці точки та знайдіть координати четвертої
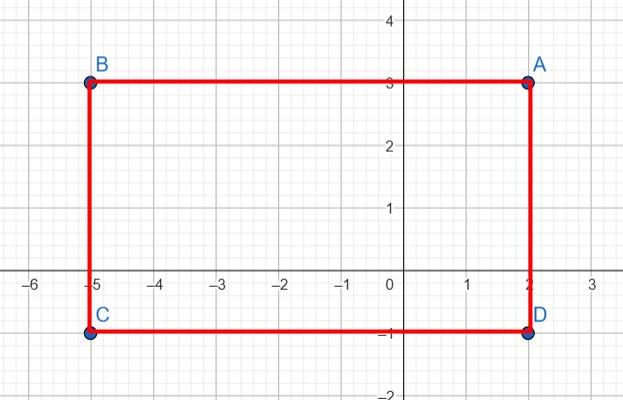
D (2; –1).
6. Петро на мотоциклі за 4,5 год проїжджає ту саму відстань, що й Ігор на автомобілі за 1 год 48 хв. Знайдіть швидкість руху Петра на мотоциклі і швидкість руху Ігоря на автомобілі, якщо швидкість автомобіля на 45 км/год більша, ніж швидкість мотоцикла.
1 год 48 хв = 1 год + 48 : 60 = 1 + 0,8 = 1,8 год.
1) 4,5х – 1,8(х + 45) = 0; 4,5х – 1,8х – 81 = 0; 2,7х = 81; shkola.in.ua х = 30 (км/год) – швидкість Петра; 2) 30 + 45 = 75 (км/год) – швидкість Ігоря.
1. Обчисліть: -7,4 + 8 • (-1,6). -7,4 + 8 • (-1,6) = -7,4 - 12,8 = -20,2.
В. -20,2.
2. Знайдіть число, 24% якого дорівнюють 96. 96 : 0,24 = 400.
Г. 400. shkola.in.ua
3. Знайдіть невідомий член пропорції 7 : 10,5 = х : 0,3.
х = (0,3•7) 10,5 = 0,2.
Б. 0,2.
4. Розв'яжіть рівняння: 1 3 (3y - 6) + (y - 5) • 2 = 5y16,8. 1 3 (3y - 6) + (y - 5) • 2 = 5y - 16,8;
у - 2 + 2у - 10 = 5у - 16,8; 3y - 5y = 12 - 16,8; -2y = -4,8; у = 2,4 shkola.in.ua
5. Задано координати трьох
ABCD:

C (-2; -4).
6.
стань,
5 год 6 хв = 5 год + 6 : 60 = 5,1 год. 1) 1,5(х + 12) - 5,1х = 0; 1,5х + 18 - 5,1х = 0 ; -3,6х = -18; shkola.in.ua х = 5 (км/год ) – швидкість туриста. 2) 5 + 12 = 17 (км/год) – велосипедиста.
1. Обчисліть 9 - 3² + 2⁵ • 1³. 9 - 9 + 32 = 32.
В. 32.
2. Обчисліть (36³ : 18³)². (363 183 )² = (36 18)³)² = (2³)² = 8² = 64.
А. 64. shkola.in.ua
3. Знайдіть значення виразу
) :
Б.5 54
4. Спростіть вираз 3(x - 2y) - 0,5(2y + 2x) - 4,5x. 3(x - 2y) - 0,5(2y + 2x) - 4,5x = 3x -
= -2,5x - 7y.
Г. -2,5x - 7y.
5. Доведіть тотожність: 1) 4(3 – 6а) – 7(3 – 4а) = 2(2а – 3) – 3; 4(3 – 6а) – 7(3 – 4а) = 12 – 24а – 21 + 28а = 4а – 9; 2(2а – 3) – 3 = 4а – 6 – 3 = 4а – 9; 4а – 9 = 4а – 9. 2) –4(3n – 0,4m) + 5(2,2m – 2n) – 10,2m = 2(1,2m –11n). shkola.in.ua –4(3n – 0,4m) + 5(2,2m – 2n) – 10,2m = –12n + 1,6m + 11m – 10n – 10,2m = –22n + 2,4m = 2,4m – 22n; 2(1,2m – 11n) = 2,4m – 22n; 2,4m – 22n = 2,4m – 22n.
6. Турист вирушив у триденну подорож. Першого дня він пройшов x км, другого — на 2
менше, аніж першого, а третього –2 3 того, що подолав першого і другого дня разом. Скільки кілометрів пройшов турист за три дні? Складіть вираз для розв’язування задачі, спростіть його і знайдіть його значення, якщо х = 10. х + (х – 2) + 2 3 (х + х – 2) = (2х – 2) • (1 + 2 3) = 5 3 (2х – 2) = 5 3 (20 – 2) = 5 3 • 18 = 30 км.
6*. Числа a і b дають однакову остачу
1. Обчисліть 16 + 2³ - 2⁴ • 1¹⁶. 16 + 2³ - 2⁴ • 1¹⁶ = 16 + 8 - 16 = 8. Г. 8.
2. Обчисліть (20² : 10²)³. (20² : 10²)³ = (202 102 )³ = (20 10)²·³ = (2²)³ = 4³ = 64. В. 64.
3. Знайдіть значення
1
�⋅ 10 63 = 3 10 −�21 42� =0,3 0,5 = 0,2.
B. 0,2
4. Спростіть вираз 6,5d 1,5(4c +5d) + 4(c 3d)
6,5d 1,5(4c +5d) + 4(c− 3d) =6,5d −6c− 7,5d+ 4c− 12d=
−2c− 13d. Г. −2c− 13 d
5. Доведіть тотожність:
1) 4(3 2x) 5(4x− 3) = 7(4x− 3) +6; 4(3 2x) 5(4x− 3) =12 8x 20x+15 =27 28x 7(4x− 3)+6= 28x+21+6 =27 28x; 27 28x=27 28x. shkola.in.ua ����) 3(2a 0,4b)+2(2,5b− 3a) 1,4b =12(0,4b− a); 3(2a 0,4b)+2(2,5b− 3a) 1,4b = 6a+1,2b + 5b− 6a 1,4b = 4,8b− 12a; 12(0,4b− a)= 4,8b− 12a; 4,8b− 12a= 4,8b− 12a.
6. Першого дня комбайн збирав пшеницю із продуктивністю а тонн за годину. Другого дня його продуктивність зросла на 10%, а
третього — зменшилася на 10% порівняно з попереднім днем.
Скільки тонн пшениці
третього дня?
Складіть вираз для розв'язування задачі, спростіть та знайдіть його значення, якщо а = 40. 0,9 • 1,1a = 0,9 • 1,1 • 40 = 39,6
ціле число. (2n) + (2n + 2) + (2n + 4) = 2n + 2n + 2 + 2n + 4 = 6n + 6 = 6(n + 1).
1. Знайдіть суму одночленів -32ac і 15ac. -32ac + 15ac = -17ac.
В. -17ac.
2. Знайдіть добуток одночленів 5k³ і 0,2k⁷x.
5k³ · 0,2k⁷x = k¹⁰x.
Б. k¹⁰x. shkola in ua
3. Піднесіть одночлен -pl3 до куба.
Г. -p³l9 .
4. (7y + 1)(2 - y) = ...
(7y + 1)(2 - y) = 14y - 7y² + 2 - y = 13y - 7y² + 2.
В. 13y - 7y² + 2.
5. Розв'яжіть рівняння:
1) (2y + 3) - (3y + 6) = 0;
2y + 3 - 3y - 6 = 0; -y = 3; y = -3. shkola.in.ua
2) 3(x + 2) - 2(x - 4) - 14 = 0;
3x + 6 - 2x + 8 - 14 = 0; x = 0.
3) (x² + 1)(x - 4) - (x - 5)(x² - 1) - 4x = x(-4 + x);
x³ - 4x² + x - 4 - x³ + x + 5x² - 5 - 4x = -4x + x²; x² - 2x - 9 + 4x - x² = 0;
2x = 9; x = 4,5.
6. Доведіть, що:
значення виразу (n + 1)(−n + 3) + n(n − 2) не залежить від значення n; n² + 3n − n + 3 + n² − 2n = 3.
вираз (4m + 1)(2m − 3) − (−m − 7)(m + 3) + 5 набуває додатних значень за будь-якого значення m. 8m² − 12m + 2m − 3 + m² + 3m + 7m + 21 + 5 = 9m² + 23 − при будь-якому значенні m, вираз буде додатнім, тому, що m² завжди додатнє число. 6*. 1. Доведіть, що різниця многочленів y² + 7y –35 і y² – 3y
y. 2. Знайдіть
= 384. shkola.in.ua
1. Знайдіть суму одночленів -24ху і 16ху.
А. -8ху.
2. Знайдіть добуток одночленів 3х² і 0,3x⁴y.
Б. 0,9x⁶y.
3. Піднесіть одночлен n4 m до куба. ( n4 m)3 = n12 m3 B. n12 m3 shkola.in.ua
4. (2l+1)(l-2) = (2I+1)(I 2)=2I 2
Б. 2l2 3l 2
5. Розв'яжіть рівняння:
1) x + 4 + (x + 8) - 9 = 0; 2x - 3 = 0; 2x = 3; x = 1,5.
2) y + 3 - 2(y - 5) = 13; y + 3 - 2y + 5 = 13; -y + 8 = 13; shkola.in.ua -y = 5; y = 5.
3) (2x² + 2)(x - 3) - (x - 4)(x² + 5) = x(x² - 2x + 4); 2x³ - 6x² + 2x - 6 - x³ + 4x² - 5x + 20 = x³ - 2x² + 4x; x³ - 2x² - 3x + 14 - x³ + 2x² - 4x = 0; -7x = -14; x = 2.
6. Доведіть, що:
1) значення виразу (2 + x)(x + 7) - x(x + 9) не залежить від значення х; (2 + x)(x + 7) - x(x + 9) = 2x + x² + 14 + 7x - x² - 9x = 14.
2) вираз m(m² + 2m - 1) - (2 + m²)(m - 2) + 3m набуває додатних значень за будь-якого значення m. m(m² + 2m - 1) - (2 + m²)(m - 2) + 3m = m³ + 2m²m - 2m + 4 - m³ + 2m² + 3m = 4m² + 4 – при будь якому значенні m, вираз буде додатнім, тому, що m² завжди додатне число. 6*. 1. Доведіть, що
a5n (b1+4n )2 c 6 , якщо
5n b2
1 2 b4n c 3 =1 ����) x² +9x 0,5+( x² 0,4) = x² +9x 0,5 x2 0,4 =9x 0,9= 9(x 0,1) - вираз кратний 9. ����) a5n (b1 + 4n)2 c 6 =a5n b2 b8n c 6 = 5 � 1 5 a5n b2 ��1 2 b4n c 2 �2 ⋅4 = 5 ⋅ 5 ⋅ 1 ⋅4 = 100. shkola.in.ua
1. Якщо 3ab + 2a²b³ = * • (3 + 2ab²), то * = ...
Б. ab. shkola.in.ua
2. Розкладіть на множники двочлен: x⁹ - 0,027.
x⁹ - 0,027 = (x³)³ - 0,3³ = (x³ - 0,3)(x⁶ + 0,3x³ + 0,09).
Б. (x³ - 0,3)(x⁶ + 0,3x³ + 0,09).
3. Якщо y⁴ - 10y³ + 25y² = y² • *, то * = ...
y⁴ - 10y³ + 25y² = y² • (y² - 10y + 25) = y² • (y - 5)².
Б. (y - 5)².
4. Спростіть вираз (-2 + 0,5x)(2 + 0,5x) + 4 та
діть його
для x = 4.
(-2 + 0,5x)(2 + 0,5x) + 4 = -4 + x – х + 0,25x² + 4 = 0,25x = 0,25 • 42 = 0,25 • 16 = 4.
В. 4. shkola.in.ua
5. Розкладіть на множники вираз: (x - 3)³ - x³.
(x - 3)3 - x³ = x³ - 3x²3 + 3x9 - 27 - x³ = -9x² + 27x27 = -9(x² - 3x + 3)
80 см². Знайдіть
1) x² – площа І квадрата, (x + 4)² –
рата.
(x + 4)² – x² = 80; x² + 8x + 16 – x² = 80; 8x = 64; x = 8 (см) – сторона І квадрата; 2) 8 + 4 = 12 (см) – сторона ІІ квадрата; 3) 4 • 8 = 32 (см) – периметр І квадрата.
4) 12 • 4 = 48 (см) – периметр
6*. Розкладіть на множники многочлен x⁴ + 7x² + 16. shkola.in.ua x⁴ + 7x² + 16 = x⁴ + 8x² + 16 – x² = (x² + 4)² – x² = (x² – x + 4)(x² + x + 4)
1. Якщо 3x²y + 7x³y² = * • (3 + 7xy), то * = ...
Г. x²y. shkola.in.ua
2. Розкладіть на множники: c¹² - 0,008.
c¹² - 0,008 = (c⁴)³ - 0,2³ = (c⁴ - 0,2)(c⁸ + 0,2c⁴ + 0,04).
В. (c⁴ - 0,2)(c⁸ + 0,2c⁴ + 0,04).
3. Якщо a³ - 6a² + 9a = a • *, то * = ...
a³ - 6a² + 9a = a(a² - 6a + 9) = a • (a - 3)²
A. (a - 3)².
4. Спростіть вираз (-3 - 0,1x)(3 - 0,1x) + 9 та знайдіть його значення для x = 10.
(-3 - 0,1x)(3 - 0,1x) + 9 = -9 + 0,3x - 0,3x + 0,01x² + 9 = 0,01x² =
0,01 • 100 = 1.
B. 1. shkola.in.ua
5. Розкладіть на множники вираз: (x + 2)³ - x³. (x + 2)³ - x³ = (x + 2 - x)((x + 2)² + (x + 2)x + x²) = 2(x² + 4x + 4 + x² + 2x + x²) = 2(3x² + 6x + 4). 6.
рони іншого
діть периметр
кожного квадрата. x2 – площа I квадрата; (x – 5)2 –
x2 – (x – 5)2 = 85;
x2 – x2 + 10x – 25 = 85; 10x = 110; x = 11 (см) – сторона І квадрата;
1) 11 – 5 = 6 (см) – сторона II квадрата; 2) 11 • 4 = 44 (см) – периметр І квадрата;
3) 6 • 4 = 24 (см) – периметр II квадрата.
6*. Розкладіть на множники многочлен: x⁴ + x² + 25. shkola.in.ua
x⁴ + x² + 25 = x⁴ + 10x² + 25 - 9x² = (x² + 5)² – (3x)² = (x² - 3x + 5)(x² + 3x + 5)
1. Укажіть область визначення функції у = 4х (3х+1)
3х + 1 ≠ 0; 3х ≠ –1;
х ≠ –1 3 shkola.in.ua
Г. х — будь–яке число, крім –1 3
2. Яка з даних лінійних функцій утворює гострий кут з додатним променем осі ОХ? k = 0,5 > 0. В. у = 0,5х + 2.
3. Графік функції у = kx + 5 перетинає вісь абсцис в точці (–2,5; 0). Знайдіть кутовий коефіцієнт. 0 = kx + 5; –2,5k + 5 = 0; –2,5k = –5; k = 2.
В. k = 2.
4. Яка з наведених формул задає функцію, графік якої зображено на малюнку 1? Функція має вигляд у = kх, тоді: 2 = k • 1; k = 2. shkola.in.ua Б. у = 2х.
5. Побудуйте графіки функцій у = 2х
одній системі координат і знайдіть координати їх точки перетину. у = 2х – 5; у

D (2; –1).
6. Функція задана формулою y = (2x - 1)² - (2x + 1)². 1) Доведіть, що задана функція є прямою пропорційністю. y = ((2x - 1) - (2x + 1))((2x - 1) + (2x + 1)) = (2x - 1 - 2x1)(2x - 1 + 2x + 1) = -2 • 4x = -8x. 2) Побудуйте її графік.
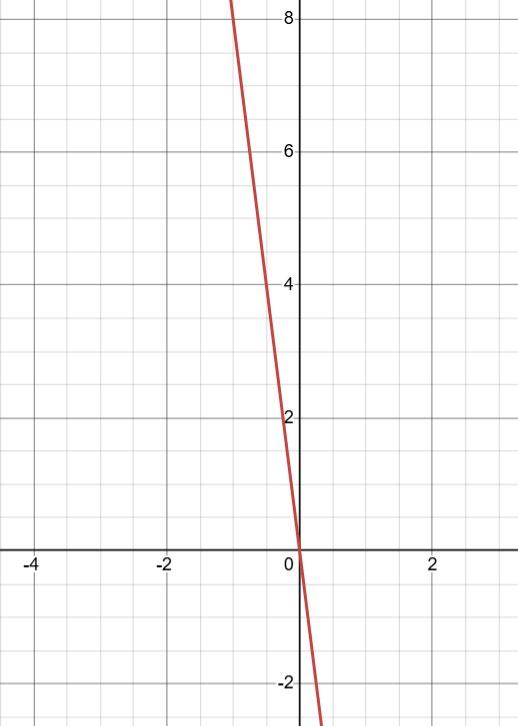
6*. Графік лінійної функції проходить через точки А (0;2) і В (6; 0). Задайте формулою функцію, яка є прямою пропорційністю, якщо її графік паралельний прямій АВ. Побудуйте графік отриманої функції. Рівняння прямої y = kx + b; k = (y2 − y1) (x2 − x1) = �0 − (−2)� (6 0) = 2 6 = 1 3 y = 1 3 x - 2. Оскільки графік функції паралельний прямій, то вони мають однаковий кутовий коефіцієнт, тоді рівняння функції y = 1 3 x. shkola in ua

-5.
1. Укажіть область визначення функції y = 3x 2−5x
2 5����≠ 0: 5x ≠ 2; x ≠ 2 5 shkola.in.ua
В. x будь-яке число, крім 2 5 2. Яка з даних лінійних функцій утворює тупий кут з додатним променем осі OX? Б. y=6 0,3x k = 0,3<0
3. Графік функції у = kx +3 перетинає вісь абсцис в ғочці ( 1,5;0 ). Знайдіть кутовий коефіцієнт. y= kx +3; 0=k 1,5 +3; k= 3 1,5 = 2.
Б. k= 2
4 Яка з наведених формул задає функцію, графік якої зображеніо на малюнку 2? Функція має вигляд y=kx 6 тоді: 1=k 2; k= 0,5. shkola in ua A. y= 0,5x
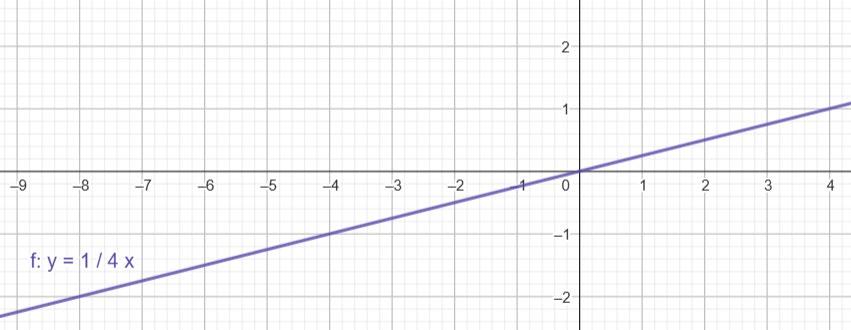
5. Побудуйте графіки функцій y = 2x +9 і y = x +3 в


1. Розв'яжіть рівняння 6х + 5 = 5х - 7(х - 3).
6х + 5 = 5х - 7(х - 3);
6х + 5 = 5х - 7х + 21;
6х - 5х + 7х = 21 - 5; 8х = 16 |:8; х = 2.
А. 2. shkola.in.ua
2. Дано систему: �x + y = 6 х у , Знайдіть у. �x + y = 6,+ х у
2x = 10 |:2; х = 5; 5 + у = 6; у = 6 – 5; у = 1
Г. 1.
3. Дано систему: �2x + 3y = 0, x y = 5 Знайдіть х.
2x + 3y = 0; х у =5 � y = x 5; 2x +3(x 5) =0; � y = x 5;
2х + 3х 15 = 0; 5x = 15 |:5; х = 3.
В. 3.
4. Серед розв'язків рівняння 2х - 5у + 1 = 0 є пара чисел (2а; а). Знайдіть а.
2х - 5у + 1 = 0; х = 2а; у = а; 2 • 2а - 5 • а + 1 = 0;
4а - 5а = -1; -1а = -1 |: (-1); а = 1; shkola.in.ua
В. 1
5. У 7-А класі навчається 22 учні. Якщо хлопцям роздати по 2 зошити, а дівчатам по 3 зошити, то знадобиться 56 зошитів. Скільки хлопців і скільки дівчат навчається в 7-А класі? Нехай хлопців - х, а дівчат - у, тоді:
x + y = 22; 2x + 3y = 56; => � x = 22 y; 2(22 y) + 3y = 56;
x = 22 y; 44 2y + 3y = 56; => � x = 22 y; У = 12; => �x = 22 12 У = 12 х = 10, y = 12. Відповідь: хлопців - 10, а дівчат - 12. 6. Розв'яжіть систему рівнянь:
2(3x 4y) 20 = 4(y+1), 3(x y) y= 16 (5x + 2y)
Розв'язання:
2(3x 4y) 20 = 4(y+1); 3(x y) y= 16 (5x + 2y);=>
6x 8y 20 = 4y + 4; 3x 3y y = 16 5x 2y;
6x 12y = 24 |:( 6); 8x 2y = 16; =>� x + 2y = −4; + 8x 2y = 16;
7x = 12 |: 7; 2y x = −4; =>� x = 12 7 ; 2y 12 7 = −4; 2y = -4 + 1 5 7 = -2 2 7; y =16 7 =8 7 shkola.in.ua
Відповідь: х = 12 7 ; y =8 7 6*. Розв'яжіть систему рівнянь із двома змінними х і у:
ax+y=a2 ; 4x + ay =2a2 + 4a 8; =>
y=a2 ax; 4х + а(a2 ax) =2а2 + 4а 8; =>� y=a2 ax; 4x +a3 a2 х =2a2 + 4a 8 x(4 - a²) = 2a² + 4a - 8 - a³; х = �2a(a+2)−�8+a3 �� �(2−a)(2+a)� = �2a(a+2) (2+a)�4−2a+a2 �� �(2−a)(2+a)� = �(a+2)�2a−4+2a−a2 �� �(2−a)(2+a)� = −�4−4a+a2 � 2−a = (2−a)2 (2−a) = -(2-a) = a-2. y = a² - a(a-2) = a² - a² + 2a = 2a.
Відповідь: x = a - 2; y = 2a.
-6.
1. Розв'яжіть рівняння 12 - 4у = 6у - 2(у - 2).
12 - 4у = 6у - 2(у - 2); 12 - 4у = 6у - 2у + 4; -4у - 4у = 4 - 12; -8y = -8|: (-8); y = 1.
Б. 1. shkola.in.ua
2. Дано систему: � x +y =7, x y = 1 Знайдіть y �x+y=7+; x y= 1; =>�2x=6|:2; x+y=7; =>�x=3; 3+y=7; �x=3 y= 4
Г. 4.
3. Дано систему: �3x 2y =0, x +y =5 Знайдіть x. �3x 2y=0; x+y=5; =>� y=5 x; 3x 2 (5 x) =0; => � y=5 x; 3x 10+2x=0; �y=5 x. 5x=10. x=2.
4. Серед розв'язків рівняння 3х - 2у + 9 = 0 є пара чисел (b; 3b). Знайдіть b.
3x - 2y + 9 = 0; x = b, y = 3b.
3b - 2 • 3b + 9 = 0; 3b - 6b = -9; -3b = -9|: (-3); b = 3. shkola.in.ua
Б. 3.
5. У шкільній їдальні два пиріжки і три булочки коштують 48 грн, а три пиріжки і чотири булочки коштують 68 грн. Скільки гривень коштує пиріжок і скільки гривень коштує булочка? Нехай ціна пиріжка - х грн, а булочки - у грн, тоді маємо систему рівнянь.
2x+3y= 48| 3; 3x+ 4y =68| ⋅ ( 2); =>� 6x+9y= 144+; 6x 8y= 136; =>
y=8; 2x+3 ⋅ 8= 48; => �y=8; 2x= 24|:2; =>� y=8. x=12.
Відповідь: пиріжок коштує 12 грн, а булочка 8 грн. 6. Розв'яжіть систему рівнянь:
15(3x 2) 8= 4(4y +1), 3(x y)+2=3x (5x y). =>
15(3x 2) 8= 4(4y +1); 3(x y)+2=3x (5x y); =>
45x− 30 8=16y+ 4; 3x 3y+2=3x 5x+y;
45x− 16y= 42; 5����−4���� = 2 ( 9); =>
45����− 16���� = 42; −45х + 36у =18 =>�45х−16у = 42; 20у =60
у =3; 45х− 16 ⋅ 3= 42 => � у =3; 45х =90; =>�у =3. х =2.
Відповідь: x = 2, y = 3 6*. Розв'яжіть систему рівнянь із
змінними х і у. shkola.in.ua ��������� + ���� = 2���� 2 ∣⋅ ( 3); ���� +3���� =3���� 2 1; � 3�������� 3���� =6���� 2 ���� +3���� =3���� 2 1; �����− 3�������� =9���� 2 1;1. ���� +3���� =3���� 2 1;2. 1 ⋅���� (1 3���� )=(3����− 1)(3���� +1); ���� = (3����− 1)(3���� +1) ( 1) (1 3���� ) ⋅ ( 1) = (3����− 1)(3���� +1) (3����− 1) = 3����− 1; 2 3����− 1+3���� =3���� 2 1;
3���� =3���� 2 +3���� ; 3���� =3(���� 2 + ���� ) ∣:3; ���� = ���� 2 + ���� .
Відповідь: x= (−3b− 1);y= b2 + b
1.
відсоток усіх завезених
Цибуля1 4; Картопля - 42%; Морква - ?%. 100% 4 = 25% - цибулі; shkola.in.ua 100% - (42% + 25%) = 100% - 67% = 33%.
В. морква становить 33% усіх овочів. 2. На дошці записані числа: 12; -8; -3; 25; 0; 16. Скількома способами можна вибрати два числа, добуток яких від'ємний? 12; -8; -3; 25; 0; 16.
Від'ємний добуток може бути при множенні від'ємного числа на додатне. Від'ємні числа: -8; -3. Кількість: 2. Додатні числа: 12; 25; 16. Кількість 3 При множині на 0, отримаємо – 0. Тому 2 • 3 = 6. Б. 6.
Відповідь: існує 6 способів. 3. У скриньці лежать 12 білих і 8 червоних однакових на дотик кульок. Вийнято навмання одну кульку. Яка ймовірність того, що вона НЕ біла?
Білих – 12 кульок; червоних – 8 кульок.
1) 12 + 8 = 20 (кульок) – всього; 2) «не біла», означає в даному випадку «червона», тому 8 20 = 2 5 shkola in ua
1) А. 2 5 2) - В. 2 5 4. Ділянка, що має форму квадрата зі стороною 2,8 м, на 70% засаджена полуницями. Яку площу займають полуниці?
1) 2,8 • 2,8 = 7,84 (м²) – площа квадрата. 2) 7,84 • 70% 100% = 7,84 • 0,7 = 5,488 (м²). Б.
Відповідь: полуниця займає 5,488 м².
5. Середнє арифметичне десяти чисел дорівнює 0,408, а середнє арифметичне інших шести чисел дорівнює 3,28. Знайдіть середнє арифметичне усіх шістнадцяти чисел. X₁₀ = �x1 +⋯+x10 � 10 = 0,408; х₁ + ... + х₁₀ = 10 • 0,408 = 4,08.
ȳ₆ = �y1 +⋯+y6 � 6 = 3,28; у₁ + ... + у6 = 6 • 3,28 = 19,68
n₁₆ = �x1 +⋯+x10 +y1 +⋯+y6 � 16 = (4,08 + 19,68) 16 = 23,76 16 = 1,485. Відповідь: середнє арифметичне 16 чисел дорівнює 1,485.
6. Сплав міді й цинку загальною масою 2 кг містить 75% міді. Скільки кілограмів цинку треба додати до цього сплаву, щоб одержати новий сплав, що містить 60% міді? shkola.in.ua
1) 2 кг – 100%; х = (2•75%) 100% = 1,5 (кг) – маса міді у сплаві; х кг – 75%.
2) у кг – 100%; y = (1,5•100) 60 = 2,5 (кг) – маса одержаного сплаву; 1,5 кг – 60%.
3) 2,5 – 2 = 0,5 (кг) – маса цинку, що додали до сплаву. Відповідь: треба додати 0,5
цинку. 6*. Скільки двоцифрових чисел із різними цифрами можна скласти із цифр 0, 1, 2, 3, 4, 5? Яка ймовірність того, що утворене число ділиться на 5? 0; 1; 2; 3; 4; 5. shkola.in.ua На першому місці може стояти одна з п'яти значущих цифр (1; 2; 3; 4; 5) – тобто 5 варіантів і на другому також п'ять, враховуючи 0 (одна з цифр вже
роботу на середньому рівні. Високий рівень: 100% 5 = 20%.
Середній рівень: 100% - (72% + 20%) = 100% - 92% = 8%. Б. 8%. shkola.in.ua
Відповідь: на середньому рівні написали 8% учнів.
2. На дошці записані числа: 28; -7; -5; 15; 12; 16; 30. Скількома способами можна вибрати два числа, добуток яких від'ємний?
Від'ємний добуток буде при множенні додатного та від'ємного числа. Додатних чисел: 5. Від'ємних чисел: 2. За правилом множення маємо: 5 • 2 = 10.
А. 10.
Відповідь: 10 способів. 3. У скриньці лежать 12 білих і 8 червоних однакових на дотик
кульок. Вийнято навмання одну кульку. Яка ймовірність того, що вона НЕ червона?
Білих – 12 кульок; червоних – 8 кульок. Якщо кулька не червона, то
вона біла 12 + 8 = 20 (к) – всього. 12 20 = 3 5 shkola.in.ua
Б. 3 5
4. Ділянка, що має форму прямокутника зі сторонами 2,8 м і 4,2 м, на 60% засаджена картоплею. Яку площу займає картопля? Знайдемо площу прямокутника: 2,8 • 4,2 = 11,76 (м²). 11,76 • 60% 100% = 11,76 • 0,6 = 7,056 (м²).
Г.
Відповідь: Картопля займає 7,056 м². 5. Середнє арифметичне п'яти чисел дорівнює 2,58 , а середнє арифметичне інших семи чисел дорівнює 4,56.
середнє арифметичне усіх дванадцяти чисел. ����5 = ����1 + ����2 …+ ����5
����12
=3,735 Відповідь: середнє арифметичне 12 чисел дорівнює 3,735. 6. Сплав магнію та алюмінію загальною масою 8 кг містить 25% магнію. Скільки кілограмів магнію треба додати до цього сплаву, щоб одержати новий сплав, що містить 60% магнію?
1) 8 кг 100%,x= 8⋅25% 100% =2 (кг) - маса магнію у сплаві; х кг - 25%. shkola.in.ua ����) 8 2=6 (кг) - маса алюмінію у сплаві сплаву; ����) 100% 60% = 40% алюмінію у повному сплаві. Маса алюмінію не змінюється.
4) у кг 100%; ���� = 6⋅100% 40% = 15(����г) маса нового сплаву; 6 кг 40%
5) 15 8=7 (кг) - різниця між масами сплавів. Відповідь: треба додати 7 кг магнію. 6*. Скільки двоцифрових чисел із різними цифрами можна скласти із цифр 0, 1, 2, 3, 4, 5? Яка ймовірність того, що утворене число непарне? На першому місці може стояти одна з п’яти значущих цифр (1; 2; 3; 4;5) - тобто 5 варіантів; на другому - також 5, враховуючи 0 (одна з цифр вже зайнята). Тоді за правилом множення: 5 5= 25 - двоцифрофих чисел можна отримати. Непарне число закінчується на непарну цифру. Перелічимо їх: 13; 15; 21; 23; 25; 31; 35; 41; 43; 45; 51; 53 - всього 12 чисел. shkola.in.ua Ймовірність того, що вибране число непарне: 12 25
1. b² - 16 = ...
b² - 16 = b² - 4² = (b - 4)(b + 4).
Г.
2. Розкладіть на множники вираз 3x + 3xy - 5 - 5y. 3x + 3xy - 5 - 5y = 3x(1 + y) - 5(1 + y) = (1 + y)(3x - 5).
Б.
3. Знайдіть значення функції y = -2x - 3, якщо значення аргументу дорівнює 4. у = -2х - 3; х = 4. у = -2 • 4 - 3 = -8 - 3 = -11.
Г.
4. Скільки різних двозначних кодів можна утворити з букв А, Б, В, Г і Д, якщо букви в коді можуть повторюватися? На першому місці може бути 5 літер, на другому теж 5 (букви можуть повторюватися). Тому за правилом множення маємо: 5 • 5 = 25.
5. Розв'яжіть рівняння: 1) (х - 1)(х + 5) = 0; shkola in ua х - 1 = 0 або х + 5 = 0; х = 1 х = -5.
2) (3х + 2)² + (-9х + 10)(4 + х) - 2 = 0; 9х² + 12х + 4 - 36х + 40 - 9х² + 10х - 2 = 0 -14х + 42 = 0; 14х = 42 ▏ : 14 х = 3.
6. Розв'яжіть систему рівнянь �x + 2y + 4 = 0, 3x + y = 3
1) �x + 2y + 4 = 0 3x + y = 3; ; ⇒ � y = 3 3x; x+2(3 3x) + 4 =0 ⇒
y = 3 3x; x + 6 6x + 4 = 0 ⇒ ⇒ � y = 3 3x 5x = 10|: ( 5);; ⇒ � x = 2; y = 3 3 • 2; ⇒
x = 2 y = 3.
2) �x + 2y + 4 = 0 3x + y = 3; ; ⇒ �y = (−4−x) 2 2; 1. y = 3 3x; 2.
Точки для 1. х = -4; у = 0. x = 2; y = -3. 2. х = 1; у = 0. x = 2; y = -3. shkola.in.ua
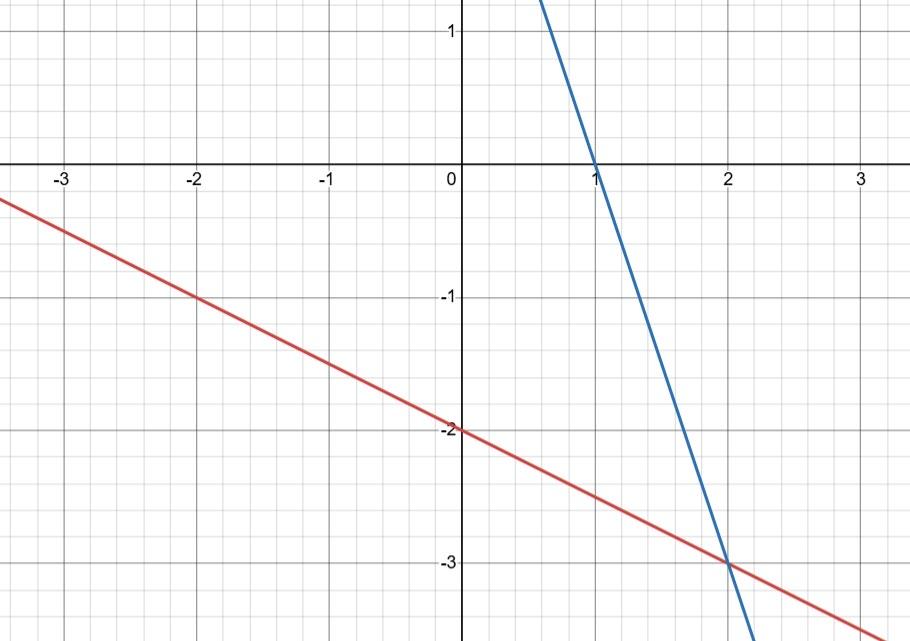
Відповідь: (2; -3).
6*. Є дві посудини, які відповідно містять 4 кг і 6 кг розчину солі різних концентрацій. Якщо обидва розчини змішати в новій посудині, то отримаємо 35 % -й розчин солі. Якщо з кожної посудини взяти по 2 кг розчину і змішати, то отримаємо 36% - й розчин солі. Скільки кілограмів солі в кожному розчині? 1) 4 + 6 = 10 (кг) – загальна маса розчинів; 2) 10 • 0,35 = 3,5 (кг) – маса солі загальна; 3) нехай у І розчині – х кг солі, а у другому – у кг 2 кг це 1 2 частина І розчину, та 1 3 – ІІ, тому і солі в повному розчині буде: ( х 2 + у 3) кг , загальна маса нового розчину 2 + 2 + 4 (кг) shkola in ua Маємо систему рівнянь:
x + y = 3,5 х 2 + у 3 = 4 • 0,36; ⇒ �x + y = 3,5| • ( 3); 3x + 2y = 8,64; ⇒
3x 3y = 10,5; + 3x + 2y = 8,64; ⇒ ⇒ � y = 1,86 x = 3,5 – 1,86 = 1,64 Відповідь: у першому розчині – 1,64 кг солі, а у другому – 1,86 кг.
КР-8. Повторення
2
1. (a - 4)² = ... (a - 4)² = a² - 2 • a • 4 + 4² = a² - 8a + 16. A.
2. Розкладіть на множники вираз 7m + 7mn - 2 - 2n. 7m + 7mn - 2 - 2n = 7m(1 + n) - 2(1 + n) = (1 + n)(7m - 2). B.
3. Знайдіть значення функції y = -2x + 1, якщо значення аргументу дорівнює 2. y = -2x + 1, x = 2. y = -2 • 2 + 1 = -4 + 1 = -3. shkola.in.ua Б.
4. Скільки різних двозначних кодів можна утворити з букв А, Б, В, Г і Д, якщо букви в коді мають бути різними? Першою може стояти одна з п'яти букв, а другою – 4 букви, тому що одна вже зайнята. За правилом множення маємо: 5 • 4 = 20.
В.
5. Розв'яжіть рівняння: 1) 9x² - 4x = 0; x(9x - 4) = 0; x = 0 або 9x - 4 = 0; 9x = 4|: 9; x = 4 9
Відповідь: 0 або 4 9 2) (3x - 5)(2x + 3) = (-6x + 1)(4 - x) + 5; 6x² - 10x + 9x - 15 = -24x + 6x² + 4 - x + 5; 24x = 24|: 24; x = 1.
Відповідь: 1.
6. Розв'яжіть систему рівнянь � 2���� −���� =6, ���� = 2���� 2 1) � 2����−���� =6; ���� = 2����− 2;; ⇒ �2( 2����− 2) −���� =6; ���� = 2����− 2; ⇒
=6; ���� = 2����− 2; ⇒ � 5���� = 10|:( 5), ���� = 2����− 2; ; ⇒
���� = 2; ���� =( 2) ( 2) 2; ⇒ ����� = 2. ���� =2.
Відповідь: x=2;y= 2 2) � 2����−���� =6; ���� = 2����− 2;
=2����− 6;1. ���� = −����−2 2 ;2. 1. ���� =0; ���� = 6; ���� =2, ���� = 2. 2. ���� =0; ���� = 1; ���� =2, ���� = 2. shkola.in.ua Відповідь: (2; 2). shkola.in.ua 6*.