13х - 5 = 3х + 15;
13х - 3х = 15 + 5;
10х = 20;
х = 2. (Б.) shkola in ua
2. Розв'яжіть рівняння
5у - 12 - (2у + 4) = 5;
5у - 12 - 2у - 4 = 5;
5у - 2у = 5 + 12 + 4;
3у = 21;
у = 7. (В.)
3. Знайдіть корінь рівняння
х 2 + 27 =2x 5 ;
х 2 + 2x 5 = -27;
5х 10 + 4х 10 = -27;
9х 10 = -27;
9x = -27 • 10;
9x = -270;
x = -30. shkola.in.ua
4. Розв'яжіть рівняння
6x - 2(x + 0,6) = -31 5;
6x - 2x - 1,2 = -3,2;
4x = -3,2 + 1,2;
4x = -2;
x = -0,5.
8x + 7 = 27 − 12x;
8x + 12x = 27 − 7;
20x = 20;
x = 1. (В.) shkola in ua
.
25 + 8y − (6y − 4) = 11;
25 + 8y − 6y + 4 = 11;
2y = 11 − 29;
2y = −18;
y = −9. (Г.)
217х 21 = 2; 9х - 7х = 2 · 21; 2х = 42; х = 21. shkola.in.ua
12х - 3(0,5 - х) = 131 2;
12х - 1,5 + 3х = 13,5;
15х = 13,5 + 1,5;
15х = 15;
х = 1.
ВАРІАНТ 1
1. Яку з наведених цифр
зірочки в записі 453* < 4535, щоб утворилася правильна нерівність? А. 4.
2. Знайдіть 2 5 числа 40. 40 : 5 • 2 = 8 • 2 = 16. (А.)
3. Периметр квадрата дорівнює 24 см. Обчисліть площу цього квадрата. shkola.in.ua 24 : 4 = 6 (см) – сторона квадрата;
6 • 6 = 36 (см²) – площа.
Г. 36 см².
4. Розв'яжіть рівняння: (85 – х) : 5 = 13;
85 – х = 13 • 5;
85 – х = 65;
х = 85 – 65;
х = 20.
5. Обчисліть: 10 : (1,5 • 2 – 0,5) + 14,7 = 10 : (3 – 0,5) + 14,7 = = 10 : 2,5 + 14,7 = 4 + 14,7 = 18,7. shkola in ua 5*. З
1. Яку з
зірочки в записі 453* > 4535, щоб утворилася правильна нерівність?
Г. 6.
2. Знайдіть 2 7 числа 42.
42 : 3 • 2 = 6 • 2 = 12. (А.)
3. Периметр прямокутника дорівнює 30 см, а одна з його сторін — 7 см. Обчисліть площу цього прямокутника. shkola in ua
30 : 2 – 7 = 8 (см) – інша сторона;
8 • 7 = 56 (см²) – площа. Г. 56 см².
4. Розв'яжіть рівняння:
72 : (52 – х) = 6;
52 – х = 72 : 6;
52 – х = 12; х = 52 – 12; х = 40.
5. Обчисліть: 14 : (2,5 • 3 – 0,5) + 16,2 = 14 : (7,5 – 0,5) + 16,2 = = 14 : 7 + 16,2 = 2 + 16,2 = 18,2. shkola in ua
1) 60 • 3 = 180 (км) –
3) 195 : 3 = 65 (км/год)
1.
А. 32. shkola in ua
2
В.
3.
В. 33.
4.
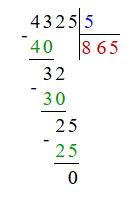
1.
В. 45. shkola in ua
2. Яке із чисел
Б. 42345.
3. Число
Б. 42.
4. Антоніна
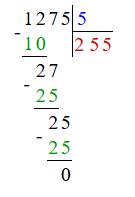
1. Великий рушник коштує 1332 5 грн, а маленький
— 33 7 20 грн. Скільки гривень коштують 15 маленьких рушників?
15 • 33 7 20 = 15 • 33 + 15 • 7 20 = 495 + 21 4 = 49521 4 = = 5001 4 грн. (Б.)
2. Великий рушник коштує 1332 5 грн, а маленький
— 33 7 20 грн. Скільки гривень коштують 3 великі рушники?
3 • 1332 5 = 3 • 133 + 3 • 2 5 = 399 + 6 5 = 3996 5 = = 4001 5 грн. (В.)
3. Великий рушник коштує 1332 5 грн, а маленький
— 33 7 20 грн. У скільки разів великий рушник дорожчий за маленький? shkola in ua 1332 5 : 33 7 20 = 667 5 : 667 20 = 667 5 • 20 667 = 4 (рази) (Г.)
4. Кут, градусною мірою 150°, поділили на 6 рівних частин, а потім кожну із цих частин поділили ще на 5 рівних частин.
у результаті всіх поділів.
1) 150 : 6 = 25° – міра одного
-5.
2
1. Маса ящика яблук становить 284 7 кг, а ящика
персиків — 4 16 21 кг. Яка маса трьох ящиків персиків?
3 • 4 16 21 = 3 • 4 + 3 • 16 21 = 12 + 16 7 = 12 16 7 = = 14 2 7 (кг). (А.)
2. Маса ящика яблук становить 28 4 7 кг, а ящика
персиків — 4 16 21 кг. Яка маса семи ящиків яблук? 7 • 28 4 7 = 7 • 28 + 7 • 4 7 = 196 + 4 = 200 (кг). (Б.)
3. Маса ящика яблук становить 28 4 7 кг, а ящика
персиків — 16 21 кг. У скільки разів ящик яблук
важчий за ящик персиків? shkola in ua 28 4 7 ÷ 4 16 21 = 200 7 ÷ 200 21 = 200 7 • 21 100 = 6 (разів).
Б. У 6 разів.
4. Кут, градусною мірою 180°, поділили на 12 рівних частин, а потім кожну з цих частин поділили ще на 3 рівні частини. Знайдіть
дорівнює семи частинам
у результаті всіх поділів.
1) 180° ÷ 12 = 15° — міра одного кута після
3) 5° • 7 = 35°.
5. Розв'яжіть рівняння:
1. Знайдіть невідомий член пропорції
18 : 9 = 30 : х.
х = (30 • 9) : 18 = 15. (В.)
2. Два числа відносяться як 2 : 7. Знайдіть менше із цих чисел, якщо їх сума дорівнює 36.
1) 2 + 7 = 9 – всього частин;
2) 36 : 9 = 4 – одна частина; 3) 2 • 4 = 8 – найменше число. (Г.)
3. Масштаб карти 1 : 500 000. Визначте відстань на місцевості, якщо на
зображена відрізком завдовжки 3 см.
3 • 500000 = 1500000 см = 15 км. (Г.)
4. Розв'яжіть пропорцію shkola.in.ua
1. Знайдіть невідомий член пропорції
40 : x = 15 : 3; (40 · 3) : 15 = 8.
Б. 8.
2. Два числа відносяться як 2 : 8. Знайдіть більше із цих чисел, якщо їх різниця дорівнює 30.
1) 8 – 2 = 6 – на стільки частин більше найбільше число;
2) 30 : 6 = 5 – одна частина;
3) 5 · 8 = 40 – більше число. (Б.)
3. Відстань між Донецьком і Харковом дорівнює близько 300 км. Чому дорівнює відстань між цими містами на карті, масштаб якої 1 : 20 000 000?
300 км : 20000000 см =
= 30 000 000 см : 20 000 000 см = 1,5 (см) (Г.)
4. Розв'яжіть пропорцію shkola in ua
1,7 х 8 1 2 = 4 1 2 0,9; 1,7x = 4,5 · 8,5 0,9 ; 1,7x = 5 · 8,5; x = 42,5 : 1,7; x = 25.
5. Відстань між Вінницею і Дніпром
км. За який час
1. Знайдіть довжину кола, радіус якого дорівнює 2 см.
l = 2πr = 2 • 3,14 • 2 = 12,56 (см). (Б.)
2. Знайдіть діаметр круга, площа якого дорівнює 28,26 см2.
S = πr²; r² = S : π = 28,26 : 3,14 = 9 см²; r = 3 см; d = 6 см. (В.) shkola in ua
3. У 6–А класі навчається 20 учнів, 12 із них — дівчата. Скільки відсотків учнів цього класу становлять хлопці?
20 - 12 = 8 - хлопців; 8 : 20 • 100 = 40%. (Г.)
4. У 6-А класі навчається 20 учнів, у 6-Б — 18 учнів, а в 6-В — 22 учні. За цими даними побудуйте кругову і стовпчасту діаграми.
20 + 18 + 22 = 60 — всього учнів;
17 : 60 = 20 60 = 10 30 — 6-А; 21 : 60 = 18 60 = 9 30 — 6-Б; 24 : 60 = 22 60 = 11 30 — 6-В.
5. У магазин привезли фрукти. Серед них 1000 кг яблук, що становить 40 % загальної кількості завезених фруктів, груш — на 500 кг менше, а решта — апельсини. Скільки кілограмів фруктів привезли до магазину? Знайдіть відсоткове відношення кількості апельсинів і груш.
1) 1000 : 40 • 100 = 2500 (кг) - всього фруктів; 2) 1000 - 500 = 500 (кг) - груши; 3) 2500 - 500 - 1000 = 1000 (кг) - апельсини; 4) 500 : 2500 • 100 = 20% - груши; 5) 1000 : 2500 • 100 = 40% - апельсини.
5*. Чи правильно, що площа прямокутника збільшиться на 30 %, якщо
1. Знайдіть
см.
S = πr² = 3,14 • (6 : 2)² = 3,14 • 9 = 28,26 (см²). (Г.) 2. Знайдіть радіус кола, довжина якого дорівнює 25,12 см.
l = 2πr; r = l : 2π = 25,12 : (3,14 • 2) = = 25,12 : 6,28 = 4 (см). (Б.) shkola in ua
3. У школі 112 учнів вивчають французьку мову, що становить 25 % загальної кількості учнів. Скільки учнів навчається в цій школі? 112 : 25 • 100 = 4,48 • 100 = 448 (учнів). (Г.)
4. У 6–А класі навчається 17 учнів, у 6–Б — 21 учень, а в 6–В — 24 учні. За цими даними побудуйте кругову і стовпчасту діаграми.
17 + 21 + 24 = 62 — всього учнів;
17 : 62 = 17 62 — 6-А; 21 : 62 = 21 62 — 6-Б; 24 : 62 = 24 62 — 6-В.
5. У першому цеху працює 600 робітників, що становить 25 % усіх робітників заводу. У другому цеху працює на 200 робітників більше, ніж у першому, а решта робітників працює в третьому цеху. Скільки всього робітників працює на заводі? Знайдіть відсоткове відношення робітників другого і третього цехів.
1) 600 : 25 • 100 = 2400 (р.) – в І цеху;
2) 600 + 200 = 800 (р.) – в ІІ цеху;
3) 2400 – 600 – 800 = 1000 (р.) – в ІІІ цеху; 4) 800 : 2400 • 100 = 33,33% – в ІІ цеху;
5) 1000 : 2400 • 100 = 41,67% – в
цеху. 5*. Чи правильно, що площа прямокутника
1. Число |-5,2| є меншим від числа...
А. |-6,01|
2. Дано числа: 3; 0,5; -4,5; 0. Яке із цих чисел є цілим, але не є натуральним?
Г. 0. shkola in ua
3. Дано числа 2 5; 5 2; -0,4; -5,2. Які із цих чисел є протилежними?
В. 2 5 і -0,4.
4. На карті селища Марійка побудувала координатну пряму вздовж прямолінійної вулиці, на якій вона проживає. Свій будинок обрала за початок відліку, одиничний відрізок — 20 метрів. Яку координату має будинок її подружки, якщо відстань від будинку Марійки до нього вздовж вулиці становить 80 метрів? Скільки розв'язків має задача?
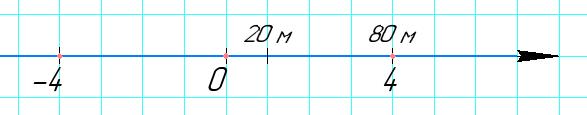
Координату 4 або -4. Задача має 2 розв’язки.
5. Знайдіть корені рівнянь:
а) |x| = 3,2; x = 3,2 або x = -3,2.
в) |x| = -7; немає коренів.
б) |x - 0,8| = 0; x - 0,8 = 0; x = 0,8.
г) -x = -|-3|; x = |-3|; x = 3.
Розташуйте отримані корені рівнянь у порядку збільшення. -3,2; 0,8; 3; 3,2. shkola in ua
5*. Позначте на координатній прямій усі цілі значення x, за яких правильною є нерівність -1,5 < x < |-5|. Знайдіть: а) найменше натуральне число, яке задовольняє дану нерівність; б) найбільше раціональне число, яке задовольняє дану нерівність; в) відстань між точкою A(-11) і точкою, що позначає найменше ціле число, що задовольняє дану нерівність.
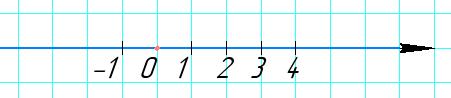
а) Натуральні числа з цієї множини: 1, 2, 3, 4.
Найменше — 1.
б) Найбільше раціональне не існує, бо можна брати числа, що наближаються до 5 зліва (наприклад, 4.9, 4.99, 4.999...).
в) Найменше ціле число в множині — −1. Відстань на координатній прямій: ∣ 11 (−1)∣ = ∣ 11 + 1∣ = ∣−10∣ = 10. shkola.in.ua
1. Число |-2,8| є більшим за число... В. 1.
2. Дано числа: 21 7 , 3 2 , -4; 0. Яке із цих чисел є раціональним, але не є цілим?
Б. 3 2 shkola in ua
3. Дано числа:5 4; 4 5; 0,25; 6 5; -11 5.
із цих чисел є протилежними? Б. 6 5 і -11 5
4. На карті селища Сергійко побудував координатну пряму вздовж прямолінійної вулиці, на якій він проживає. Свій будинок обрав за початок відліку, одиничний відрізок — 15 метрів. Яку координату має школа, якщо відстань від будинку Сергійка до школи вздовж вулиці становить 90 метрів? Скільки розв'язків має задача?

Координату 6 або -6. Задача має 2 розв’язки.
5. Знайдіть корені рівнянь:
а) |-x| = -21; Немає коренів.
в) |x| = 2,5; x = 2,5 або x = -2,5.
б) |2x – 9| = 0; 2x – 9 = 0; 2x = 9; x = 4,5.
г) x = -(-5); x = 5.
Розташуйте отримані корені рівнянь у порядку збільшення.
-2,5; 2,5; 4,5; 5. shkola in ua

5*. Позначте на координатній прямій усі цілі значення x, за яких правильною є нерівність -3 < x < ∣-2,2∣ Знайдіть: а) найбільше натуральне число, яке задовольняє дану нерівність; б) найменше раціональне число, яке задовольняє дану нерівність; в) відстань між точкою А(8) і точкою, що позначає найбільше ціле число, що задовольняє дану нерівність. а) Натуральні числа
1, 2. Найбільше — 2. б) Найменшого немає, бо можна взяти числа, що наближаються до −3 зліва: −2.9,−2.99,−2.999,….; в) Найбільше ціле число = 2. Відстань на координатній прямій: |8| – |2| = 6.
1
1. -13,5 + (-11,5) = -25. (В.)
2. shkola in ua -8 – (-76) = -8 + 76 = 68. (А.)
3. Розв'яжіть рівняння:
x + 32 3 = 11 5;
x = 11 5 - 32 3;
x = 18 1555 15;
x =37 15
x = -2 7 15. (Б.)
4. Обчисліть:
а)3 4- (-1,4) - 1,5 - (-1 2) + 0,75 = = -0,75 + 1,4 - 1,5 + 0,5 + 0,75 = 0,4. б) 3,75 - (-1 2) - |1 2| + 0,25 = 3,75 + 0,5 - 0,5 + 0,25 = 4.
5. Температуру повітря вимірювали кожний ранок о 8 год. У неділю вранці температура становила 24°С. Протягом п'яти днів температура знижувалася на 2°С, а потім три
підвищувалася відповідно на 3°С, 4°С, 1°С. Визначте, яка
вранці.
а) до суми чисел -7 3 14 і 2,6 додайте число -23 5; -7 3 14 + 2,6 + (-23
різницю чисел 3,5 і -11 5; (-14,7 - 2,9) - (3,5 - (-11 5)) = -17,6
8 відніміть модуль суми чисел -42 і 215 8 (633 4 - 567 8) - |-42 + 215 8| = (636 8 - 567 8) - |-418 8 + 215 8| = = (6214 8 - 567 8) - |-203 8| = 67 8 - 203 8 = -144 8 = -14,5.
Яке з отриманих значень є найменшим? Модуль якого з отриманих значень є найменшим?
Найменше -22,3. |-7 3 14| = 7 3 14
19,3 + (−13,7) = −33. (Б.)
2. shkola in ua
4,9 − (−7,1) = −4,9 + 7,1 = 2,2. (В.)
3. Розв'яжіть рівняння:
x + (−21 4) = −2 5;
x − 21 4 = − 2 5;
x = 21 4 − 2 5;
x = 2 5 20 − 8 20;
x = 125 20 − 8 20;
x = 117 20 (В.)
4. Обчисліть:
а) −43 4 − (−6,9) − 10,3 + (−1 8) + 0,125 = = 4,6 + 6,9 − 10,3 − 0,125 + 0,125 = = 14,9 + 6,9 = 8.
5. Температуру повітря вимірювали кожний ранок о 8 год. У
−9°С. Протягом
температура знижувалася на 1°С, а потім три дні поспіль підвищувалася
Визначте, яка температура була у четвер вранці. День Ср. Чт. Пт.
Четвер −10°С. shkola.in.ua 5*. Складіть вираз та знайдіть його значення: а) до суми чисел −50 і 32,2 додайте число −71 2; (−50 + 32,2) + (−71 2) = −17,8 − 7,5 = −25,3.
б) від різниці чисел −2,3 і −8,7 відніміть різницю чисел 12,05 і −21 1 100; (−2,3 − (−8,7)) − (12,05 − (−21 1 100)) = = 6,4 − (12,05 + 21,01) = 6,4 − 33,06 = −26,66. в)
7 і −91 4 (81 5 15 9 25) − |7 + (−91 4)| = (76 5 − 15 9
)
|6
− 91 4| = = (730 25 − 15 9 25) − |−33 4| = 821 25 − 33 4 = 8 84 100 − 3 75 100 = = 5 9 100 = 5,09.
1.
5 5 10 : (-5,5) = 5,5 · (-5,5) = -1. (В.)
2 shkola in ua
112,4 : (-122 5) = 112,4 : (-12,4) = 1. (A.)
3. Порівняйте: 12 : (1 2) і 0,5 : (-5). Який знак треба вставити між виразами?
12 : (1 2) = -6; 0,5 : (-5) = -0,1; -6 < -0,1. (А.)
4. Розв'яжіть рівняння: а) -12 : 5x = -6; 5x = -12 : (-6);
5x = 2.
x = 2 : 5;
x = 0,4.
в) 6x : (-24) = 0;
6x = 0 • (-24);
6x = 0;
x = 0 : 6;
x = 0.
б) -12 3 x = 14 5;
x = 14 5 : (-12 3);
x = 9 5 • (3 5);
x =27 25 = -1 2 25
г) 2 7 x = -1;
x = -1 : 2 7;
x = -1 • 7 2; x =7 2 = -31 2
5. Наталка і Сашко грали у
x : (–4,5) • 1,8 • (–0,5) = x : (–4,5) • (–0,9) = = x : 4,5 • 0,9 = x • 0,9 4,5 =
частки чисел 60136 і
1.
18,6 : (−3) = −6,2. (А.)
2. shkola in ua 3 5 : (−3) = 3 5 · (1 3) = 1 5 = 0,2. (Г.)
3. Порівняйте: −24 : (−1 6) і −0,18 : (−3). Який знак треба вставити між виразами?
−24 : (−1 6) = 24 · 6 1 = 144; −0,18 : (−3) = 0,06. 144 > 0,06. (А.)
4. Розв'яжіть рівняння: а) 46 : 5x = 23; 5x = −46 : 23; 5x = -2; x = -2 : 5; x = −0,4.
в) −234x : 66 = 0; 234x = 0 • 66; 234x = 0; x = 0 : (−234);
x = 0.
5. Наталка і Сашко грали
б) −34 5 x = 0,95; 3,8x = 0,95; x = 0,95 : (−3,8); x = −0,25.
г)3 8x = −2; x = −2 : (3 8);
x = 2 • 8 3;
x = 16 3 = 51 3
Наталка загадує число та виконує наступні
число на 2,4, а потім множить відповідно на −0,6 і на −8. Потім вона оголошує
число має поділити Сашко отримане Наталкою число, щоб назвати загадане? x : 2,4 • (−0,6) • (−8) = x : 2,4 • 4,8 = x
4,8 2,4 =
2. Наталка має поділити результат на 2. 5*. Складіть вираз і знайдіть його значення: а) до частки
1. Спростіть вираз 5(a − 2b) − 2(b + 2a) = 5a − 10b − 2b − 4a = a − 12b. (В.)
2. Розв'яжіть рівняння 30y + 16 = 11y − 22; 30y − 11y = −22 − 16; 19y = −38; y = −2. (В.)
3. Одне число в 4 рази більше за інше. Якщо від першого числа відняти 10, а до другого додати 5, то отримаємо рівні результати. Знайдіть задані числа. shkola in ua
1) 4x − 10 = x + 5; 4x − x = 5 + 10; 3x = 15; x = 5 − ІІ число; 2) 5 · 4 = 20 − І число.
A. 20 і 5.
4. Розв'яжіть рівняння
0,6(2x − 3) = 0,4(9 − x) − 0,2(2x + 17); 1,2x − 1,8 = 3,6 − 0,4x − 0,4x − 3,4; 1,2x + 0,4x + 0,4x = 0,2 + 1,8; 2x = 2; x = 1.
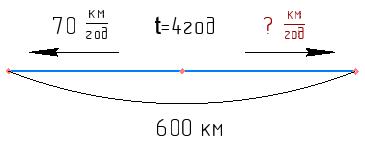
5 Два автобуси одночасно і в протилежних напрямках виїхали з міста. Швидкість першого автобуса на 10 км/год більша, ніж швидкість другого. Знайдіть швидкість кожного автобуса, якщо за 2 год другий автобус подолав 5 6 тієї відстані, яку подолав перший
автобус
1) (x + 10) • 2 = x • 2 : 5 6;
2x + 20 = 12 5 x;
2x12 5 x = -20; 10 5 x12 5 x = -20;2 5 x = -20;
x = 20 : 2 5;
x = 20 • 5 2; shkola in ua x = 50 (км/год) - швидкість II автобуса; 2) 50 + 10 = 60 (км/год) - швидкість I автобуса.
5*. Автомобіль виїхав із пункту А до пункту В. За першу годину він проїхав 1 3 всього шляху, за другу — 40 % решти, а за третю — останні 120 км. Знайдіть відстань між пунктами А і В. За яку годину автомобіль проїхав найбільшу відстань? Чи можна вважати, що за якусь із годин руху автомобіль подолав відстань,
1. Спростіть вираз 9(x − 2y) − 3(y + 2x) = 9x − 18y − 3y − 6x = = 3x − 21y. (В.)
2. Розв'яжіть рівняння 22x − 18 = 10x + 30; 22x − 10x = 30 + 18; 12x = 48; x = 48 : 12; x = 4. (В.)
3. Одне число в 3 рази більше за інше. Якщо від першого числа відняти 11, а до другого додати 3, то отримаємо рівні результати дій. Знайдіть задані числа. shkola in ua 1) 3x − 11 = x + 3; 3x − x = 3 + 11; 2x = 14; x = 7 - II число; 2) 3 • 7 = 21 - I число. (В.)
4. Розв'яжіть рівняння 0,3(4 − 2x) − 0,6(3x − 4) = 0,2(x + 5); 1,2 − 0,6x − 1,8x + 2,4 = 0,2x + 1; 2,4x − 0,2x = 1 − 2,4 − 1,2; 2,6x = −2,6; x = 1.
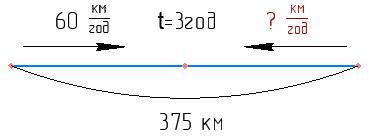
5. Два автобуси одночасно і назустріч один одному виїхали із двох міст. Швидкість першого автобуса на 5 км/год менша, ніж швидкість другого. Знайдіть швидкість кожного автобуса, якщо вони зустрілися через 2 год і перший автобус подолав 12 13 тієї відстані, яку подолав другий автобус.
1) (x + 5) • 2 = x • 2 • 12 13;
2x + 10 = 2 • 12 13 • x; 2x + 10 = 24 13 • x; 2x24 13 • x = -10; 11 6 • x13 6 • x = -10;2 6 • x = -10;
x = -10 : (2 6);
x = -10 • 6 2; shkola.in.ua
x = 30 (км/год) - швидкість І автобуса; 2) 30 + 5 = 35 (км/год) - швидкість ІІ автобуса. 5*. Потяг виїхав із пункту А до пункту В. За першу годину він проїхав 25 % усього шляху, за другу — 1 2 решти, а за третю — останні 180 км. Знайдіть відстань між пунктами А і В. За яку годину потяг
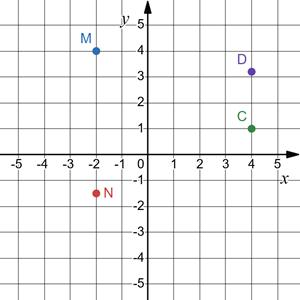
1. Яка з указаних точок
А. (-3; 4).
2. З пункту А в пункт В виїхали
тією самою трасою. На
руху. О котрій годині автобус і автомобіль зустрілися на трасі?
Б. О 13 год. shkola in ua
3. На скільки кілометрів більше проїхав автомобіль за перші 2 год руху, ніж автобус?
200 - 100 = 100 км. (Б.)
4. Дано точки: A(−1; 0), B(−2; 1), C(0; −2), D(4; −2). Накресліть систему координат та побудуйте в ній прямі AB і CD. Визначте координати точки перетину прямих AB і CD.
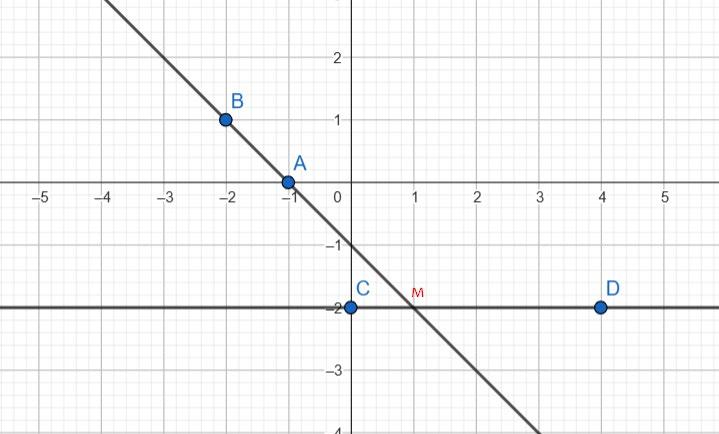
M(1; -2)
5. Точка A(−4; 6) — вершина квадрата ABCD. Відомо, що абсциса точки A дорівнює абсцисі точки B, ордината точки A удвічі більша за ординату точки B. Знайдіть координати вершин квадрата ABCD та побудуйте його. Скільки випадків треба розглянути? Треба розглянути два випадки: Ⅰ-й випадок: A(−4; 6), B(−4; 3), C(−1; 3), D(−1; 6) Ⅱ-й випадок: A(−4; 6), B(−4; 3), C1(−7; 3), D1(−7; 6)
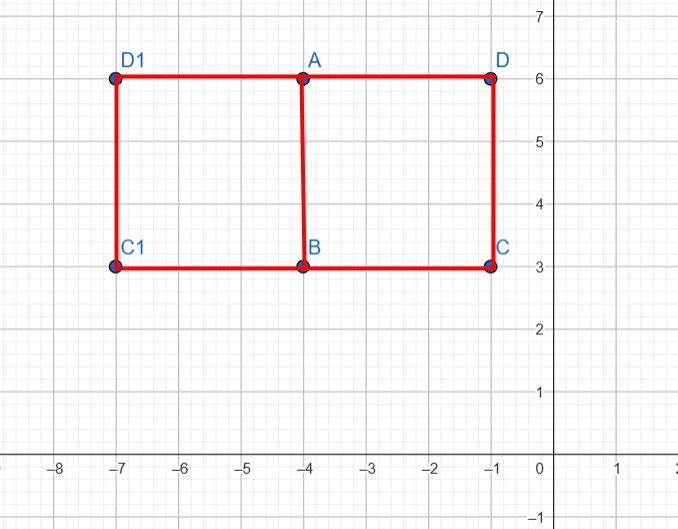
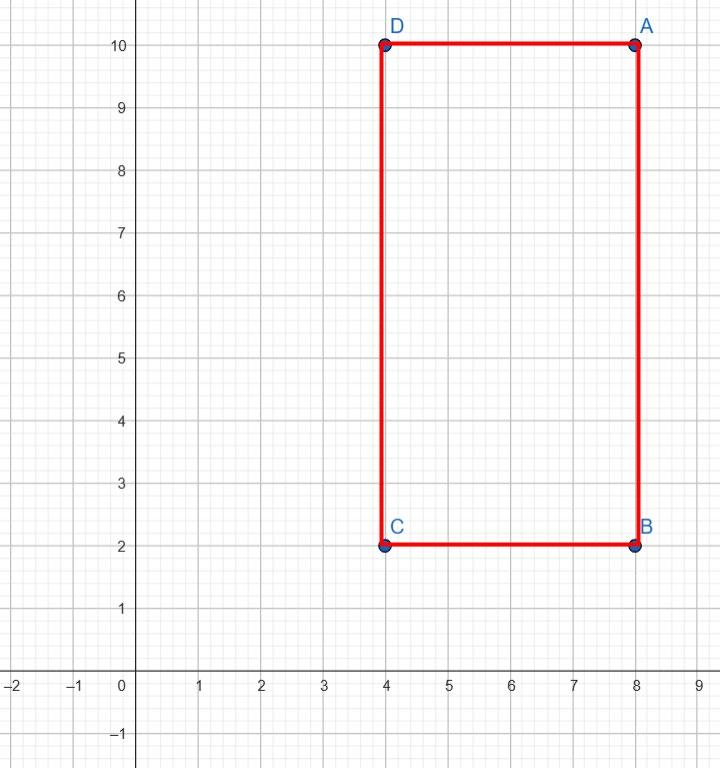
5*. Точка A(10; 8) — вершина прямокутника ABCD. Відомо, що абсциса точки В дорівнює абсцисі точки А, а її ордината становить 25 % ординати точки А; абсциса точки С на 50 % більша за абсцису точки А. Знайдіть координати вершин прямокутника ABCD та побудуйте його.
A(10; 8), B(10; 2), C(15; 2), D(15; 8)
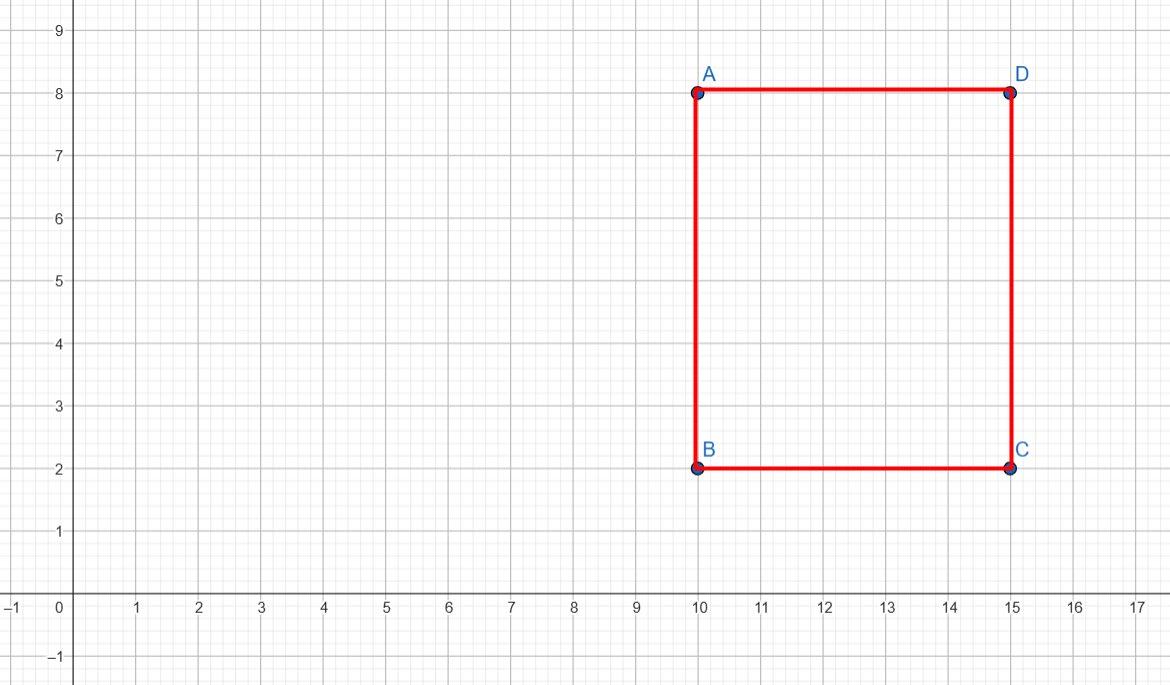
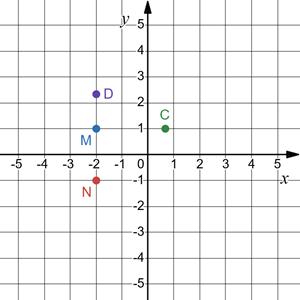
1.
чверті?
В. (−3; −4).
2 З пункту
руху. О
годині автобус і автомобіль зустрілися на трасі?
Г. О 15 год. shkola in ua
3. На скільки кілометрів більше проїхав автомобіль за перші 2 год руху, ніж автобус за перші 1 год руху?
100 − 50 = 50 км. (А.)
4. Дано точки: А(0; 2), В(2; 4), С(-3; 1), D(3; 1). Накресліть систему координат та побудуйте в ній прямі АВ і CD. Визначте координати точки перетину прямих АВ і CD.
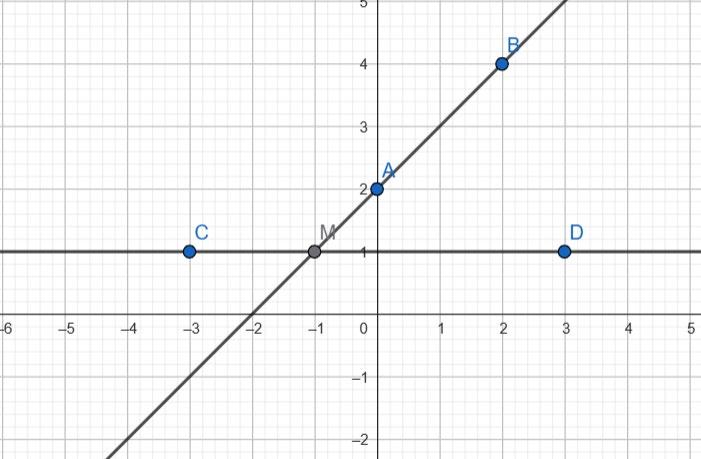
М(-1; 1)
5. Точка A(3; 2) — вершина квадрата ABCD. Абсциса точки B дорівнює абсцисі точки A, а її ордината — у 3 рази більша. Знайдіть координати вершин квадрата та побудуйте його. Скільки випадків
Треба розглянути два випадки: Ⅰ-й випадок: A(3; 2), B(3; 6), C(7; 6), D(7; 2) Ⅱ-й випадок: A(3; 2), B(3; 6), C1(-1; 6), D1(-1; 2)
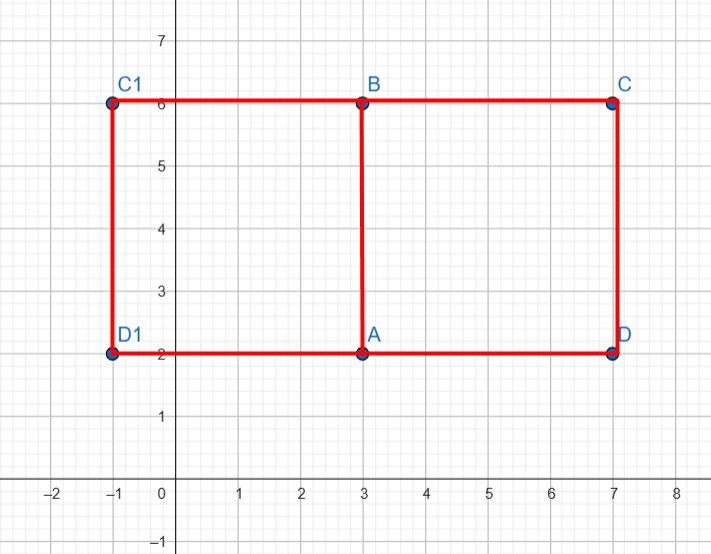
5*. Точка A(8; 10) — вершина прямокутника ABCD. Відомо, що абсциса точки B дорівнює абсцисі точки A, а її ордината становить 20 % ординати точки A; абсциса точки C на 50 % менша ніж абсциса точки A. Знайдіть координати вершин прямокутника ABCD та побудуйте його. A(8; 10), B(8; 2), C(4; 2), D(4; 10)
1. Знайдіть НСД (48; 84). 48 24 12 6 3
48 = 2 • 2 • 2 • 2 • 3; 84 = 2 • 2 • 3 • 7.
НСД(48; 84) = 2 • 2 • 3 = 12. (Б.) 2. Обчисліть: shkola.in.ua
-4,2 - (-2,7 + 5,6) • 2 = -4,2 - 2,9 • 2 = = -4,2 - 5,8 = -10. (Г.)
3. Не виконуючи побудови, з'ясуйте, у якій координатній чверті лежить точка A (x; y), якщо x = 3 7 + 5 14, y = -45 + 3,3 : 0,11. x = 3 7 + 5 14 = 6 14 + 5 14 = 11 14; y = -45 + 3,3 : 0,11 = -45 + 0,3 = -45,3. A(11 14; -45,3).
Г. У IV чверті.
4. У 6-А класі навчається 32 учні, з них 3 8 становлять
Який відсоток учнів класу становлять хлопці?
1) 32 : 8 • 3 = 12 - дівчат; 2) 32 - 12 = 20 - хлопців;
3) 20 : 32 • 100% = 63,5% - хлопців.
5. На обласних спортивних змаганнях з легкої атлетики найбільше призових місць зайняли три команди: «Лідер», «Олімп» і «Енергетик», які загалом вибороли 54 нагороди. Скільки нагород отримала кожна із цих команд, якщо нагороди були розподілені у відношенні 2 : 3 : 4?
1) 2 + 3 + 4 = 9 - всього частин;
2) 54 : 9 = 6 (н.) - в одній частині;
3) 6 • 2 = 12 (н.) - «Лідер»; 4) 6 • 3 = 18 (н.) - «Олімп»;
5) 6 • 4 = 24 (н.) - «Енергетик».
5*. Шості класи зібрали деяку кількість кілограмів макулатури. Половину всієї макулатури зібрав 6-А клас, третю решти зібрав 6-Б клас, а п'яту частину загальної кількості зібрав 6-В клас. Решта, яку зібрав 6-Г клас, на 3 кг більша за дванадцяту частину загальної маси макулатури. Скільки кілограмів макулатури зібрали всі шості класи?
всієї
(кг).
1. Знайдіть НСД (56; 84). 56 28 14 7 1 2 2 2 7
56 = 2 • 2 • 2 • 7; 84 = 2 • 2 • 3 • 7. НСД(56; 84) = 2 • 2 • 7 = 28. (Г.)
2. Обчисліть: shkola.in.ua -3,2 – (-3,3 – 5,1) : 3 = -3,2 – (-8,4) : 3 = = -3,2 + 8,4 : 3 = -3,2 + 2,8 = -0,4. (Б.)
3. Не виконуючи побудови, з'ясуйте, у якій координатній чверті лежить точка B (x; y), якщо x = 15 – 21: 0,7, y = 5 8 –5 24 . x = 15 – 21: 0,7 = 15 – 30 = -15; y = 5 8 –5 24 = 15 24 –5 24 = 10 24 = 5 12 B(-15; 5 12).
В. У ІІ чверті.
4. У 6–Б класі навчається 28 учнів, з них 1 7 становлять відмінники. Який відсоток учнів класу не є відмінниками? 1) 28 : 7 = 4 (уч.) – відмінники;
2) 28 – 4 = 24 (уч.) – не є відмінниками;
3) 24 : 28 • 100% = 86%
5. На обласному турнірі з латиноамериканських танців найбільше призових місць зайняли три танцювальних студії: «Метелик», «Едельвейс» і «Лілея», які загалом вибороли 48 нагород. Скільки нагород отримала кожна з цих студій, якщо нагороди були розподілені у відношенні 3 : 4 : 5?
1) 3 + 4 + 5 = 12 – всього частин; 2) 48 : 12 = 4 (н.) – в одній частині; 3) 4 • 3 = 12 (н.) – «Метелик»;
4) 4 • 4 = 16 (н.) – «Едельвейс»; 5) 4 • 5 = 20 (н.) – «Лілея».
5*. На новорічне свято в садочок привезли деяку кількість подарунків. Спочатку віддали третину подарунків в одну групу, потім третину решти подарунків віддали в другу групу, а потім четверта частина від залишку подарунків дісталися вихователям. У результаті
для третьої групи. Їх кількість на 21 більша від десятої частини початкової
