Oefeningen bij §1.3 en §1.4 B
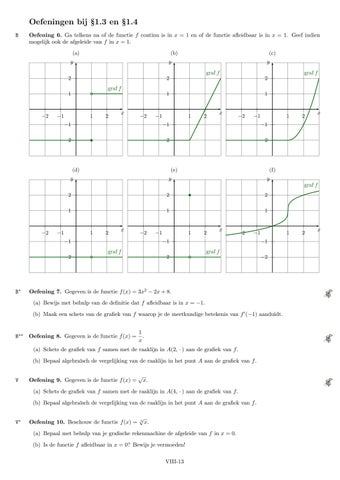
Oefening 6. Ga telkens na of de functie f continu is in x = 1 en of de functie afleidbaar is in x = 1. Geef indien mogelijk ook de afgeleide van f in x = 1. (a)
(b)
y
(c)
y
y graf f
2
graf f
2
2
1
1
graf f 1
−2
−1
1
2
x
−1
−2
−1
−2
1
2
x
−1
−2
−1
−2
(d)
1
x
−1 −2
(e)
y
2
(f)
y
y graf f
−2
−1
2
2
2
1
1
1
1
x
−1 −2
B⋆
2
−2
graf f
−1
1
2
x
−1 −2
−2
−1
graf f
1 −1 −2
Oefening 7. Gegeven is de functie f (x) = 3x2 − 2x + 8. (a) Bewijs met behulp van de definitie dat f afleidbaar is in x = −1. (b) Maak een schets van de grafiek van f waarop je de meetkundige betekenis van f ′ (−1) aanduidt.
B⋆⋆
Oefening 8. Gegeven is de functie f (x) =
1 . x
(a) Schets de grafiek van f samen met de raaklijn in A(2, · ) aan de grafiek van f . (b) Bepaal algebraı̈sch de vergelijking van de raaklijn in het punt A aan de grafiek van f .
V
Oefening 9. Gegeven is de functie f (x) =
√
x.
(a) Schets de grafiek van f samen met de raaklijn in A(4, · ) aan de grafiek van f . (b) Bepaal algebraı̈sch de vergelijking van de raaklijn in het punt A aan de grafiek van f . V⋆
Oefening 10. Beschouw de functie f (x) =
√ 3
x.
(a) Bepaal met behulp van je grafische rekenmachine de afgeleide van f in x = 0. (b) Is de functie f afleidbaar in x = 0? Bewijs je vermoeden! VIII-13
2
x