Kapitola4
Vícerozměrnálinearitaaneb lineárníalgebrapodruhé
Vprvnímdílutohototextujsmeseseznámiliselegantnídámou—lineárníalgebrou.Pomocíjejíchpravideljsmenejenřešilisoustavylineárníchrovnic,aletaképočítalismaticemi avektory.Zatímcooperacesmaticemi,akoneckoncůiřešenílineárníchrovnicpomocímatic, bychommohlichápatjakoužitečnouekvilibristikusčíselnýmisoubory,započítánímsvektory sezdálobýtpřecejenněcohlubšíhoazávažnějšího.Vázanévektorypronástotižbylyorientovanýmiúsečkamivtrojrozměrnémeuklidovskémprostoru,vněmžbylodefinovánoměření délekaúhlů.Volnévektorypakbylymnožinamistejněvelkýchasouhlasněrovnoběžnýchorientovanýchúseček.Jednalosetedyo geometrickéobjekty.Každývektorbylurčensvouvelikostí asměrem.Směrbylpřitomzadánnapříkladpomocíúhlůmezidanýmvektoremavybranými směry,kterébylypředempevnězvoleny.Mohlijsmesvektoryprovádětzákladníalgebraické operace,jimižjsousčítánívektorůanásobenívektoručíslem,podlepravidelzavedenýchpro (vtomtopřípaděřádkové)matice.Svektoryvtrojrozměrnémprostorujsmemohlivelmipohodlněpočítatjakostrojicemičísel.Nadruhéstranějsmevektoryvyjadřovalijakolineární kombinacejinýchvektorů,tvořícíchvprostoruvšechvektorů bázi.Koeficientylineárníkombinace,kterápředstavovalazápisdanéhovektoruvezvolenébázi,bylyjeho složkami vtéto bázi.Přizměněbázesezměnilysložkyvektoru,vektorsámvšaknikoliv.Vektorjestálesám sebou,jensevrůznýchbázíchjinaktváří—projevísejinoutrojicíčísel.Protožesevšakpři změněbázezměnísložkyvektorupřesnědefinovanýmzpůsobem(vzpomeňtenatransformační vztahy),dokážemejejvždyrozpoznat.Tutovlastnost, invariancivůčivolběbáze,majívšechny geometrickéobjekty.Ajetoprávěalgebra,kteránámumožňujetytoobjektyreprezentovat číselnýmisouboryatakétaksnimipočítat.Jde-linavícoobjektyřídícíselineárnímipravidly, jakýmijsounapříkladdistributivnízákony,jepočítánísnimi,vrámci lineárníalgebry,zvláště jednoduché.Ocenímetozejménavprostorechvyššídimenze,nežjenášběžnýeuklidovskýprostor.Připočítánísvektoryvtrojrozměrnémprostoru,kdeumímeměřitdélkyaúhlyakdeplatí trigonometrickápravidla,bychomsebezrutinníchalgebraickýchprocedurještětřebaobešli. Užalenapříkladvečtyřrozměrnémčasoprostoru,vněmžseodehrávajívšechnypřírodníjevy avněmžjetřebaformulovatfyzikálnízákony,všakproměřenídélekaúhlůplatíjinápravidla, nežjsouobvyklávběžném,tj.trojrozměrnémeuklidovském,prostoru.Napříkladtamneplatí
1
čtyřrozměrnáverzePythagorovyvěty.Aněkdyjepřírodadokoncetaknepřívětivá,ženásnutí pracovatisprostoryvícerozměrnými.Napříkladjednazvelmiúčinnýchteoriíprovýkladchováníelementárníchčástic,teoriestrun,jezaloženanageometriiprostorujedenáctirozměrného. Avtakovýchdimenzíchjsmeužsjakkolivynikajícígeometrickoupředstavivostívkoncích. Tehdysevděčněobracímekmetodámalgebry.Vtétokapitole,jakjejínázevnapovídá,půjde oalgebrulineární.
4.1 Prostorysvektory
Vkapitole1jsmepracovalisčíselnýmimaticemitypu m/n,tj.souboryčíseluspořádanýchv m řádcícha n sloupcích,azavedlijsmeproněoperacisoučtuanásobeníčíslem.Zjistilijsme, žeprosčítánímaticanásobenímaticečíslemplatíurčitápravidla.(Jejichsouhrnjeuveden vsamémzávěruodstavce1.3.3.)Vodstavci1.4jsmezasepočítalisvektory.Tymělyjednou konkrétnípodobu řádkovýchmaticspravidlyprojejichsčítáníanásobeníčíslem,podruhé, vtrojrozměrnémprostoru,naopak konkrétnípodobu orientovanýchúseček,resp.množin,které bylyorientovanýmiúsečkamivytvořeny,generovány.Zavedlijsmetenkrát konkrétnízpůsob sčítánívektorůanásobenívektoručíslempomocígeometrickýchoperací.Součetdvouvektorů u a v znamenal,žejsmepodlezcelaurčitéhopravidla,pravidlavektorovéhorovnoběžníka,přiřadiliuspořádanédvojici[u,v]třetívektor u+v,násobekvektoruačíslabylopětvektor αu,který jsmepřiřadilidvojici[α,u]tvořenéčíslemavektorem.Uvedlijsme,žepravidlaprotyto geometrické operacejsoushodnáspravidlypropočítánísmaticemialzejedokázatigeometrickými postupy.Množinuvolnýchvektorůgenerovanýchorientovanýmiúsečkamispolusuvedenými dvěmaoperacemijsmenazvali vektorovýmprostorem.Šlotedyozcelaodlišnémnožinyzákladníchobjektůazcelaodlišnýmzpůsobemdefinovanéoperace,prokterésevšakdaladokázat tatážpravidla.Nynísepodívámenaproblémdefinicevektorovéhoprostoruobecnějiaponěkud „opačně .Budemepracovats nosnoumnožinou V ,apřitomnebudepodstatné,jakkonkrétně vypadajíjejíprvky.Anijenebudemeoznačovatšipkami(ušipekzezvykuzůstanemepouze vpřípaděorientovanýchúsečekv R1 , R2 a R3,nebovektorůsfyzikálnímvýznamem).Dále přiberemedohrymnožinuvšechkomplexníchčísel C,popřípadějenmnožinuvšechreálných čísel R,adefinujemedvěoperace(zobrazení):
Prvek c nazýváme součet prvků a a b aznačímejej c = a + b,prvek d je α-násobek prvku a aznačíme d = αa.Zobrazeníuvedenávevztazích(4.1)všaknebudoumocibýtúplnělibovolná. Budemepožadovat,abymělaurčitévlastnosti,konkrétněty,kteréjsouuvedenypromaticena konciodstavce1.3.3.Teprvepakřekneme,žemnožina V spolusoperacemi(4.1)splňujícími potřebnépožadavkyjevektorovýmprostorem.Vidíme,žetaktonašeuvažovánívýrazněposunemenaabstraktníúroveň.Budelhostejné,cojsouprvkynosnémnožiny,budenepodstatné, jakkonkrétnějsoudefinoványoperacesčítáníprvkůanásobeníprvkučíslem.Důležitébudejen
2 KAPITOLA4.LINEÁRNÍALGEBRAPODRUHÉ
V × V [a,b] −→ c ∈ V, C × V [α,a] −→ d ∈ V. (4.1)
Prodané a jeurčenjednoznačně.Vpřípaděoperacenásobenímajívlastnosti(4.4)tvar
a G senazývá multiplikativnígrupou.Prvek eG jeopětuniverzálníprocelougrupuanazýváse neutrálníprvekgrupy neboli jednička,prvek a 1 je inverzníkprvku a Každáoperace(4.2)vmnožině G,kterásplňujevztahyasociativitytypu(4.3)avztahy specifikujícínuluaopačnýprvek,nebojedničkuainverzníprvektypu(4.4),nebo(4.5),představuje grupovouoperaci bezohledunato,podobá-lisespíšesčítání,nebospíšenásobení, čidokonceněčemujinému,napříkladskládánízobrazení.Má-ligrupakonečnýpočetprvků, nazývásetentopočetjejím řádem
Příklad4.1: Koliknulmá(aditivní)grupa?
Jakdokážeme,žemágrupaprávějednunulu?Cokdyžpředchozímutvrzenínebudemevěřit?Můžeme seojehopravdivostinějakpřesvědčit?Ten,kdomunevěří,simůžetřebapředstavit,žegrupamánulydvě.
Označmeje0G a0G.Vztah(4.4)platíprolibovolnýprvekgrupy,proto0G +0G =0G (tojsmebrali a =0G a0G považovalizanulu)asoučasně0G +0G =0G (nynízasebylprvek0G vrolinulya a =0G).Jevidět,že 0G =0G.Nulajetedyskutečnějenjedna.Podobnouúvahumůžemeprovéstprojedničkumultiplikativnígrupy.
Platítedytvrzení:
Neutrálníprvekgrupyjeurčenjednoznačně.
Stejnětakbychommohlimítpochybnostotom,žeopačnýprvekkdanému a ∈ G jejenjeden.Předpokládejme, že b a c jsoudvaopačnéprvkyk a.Platí a + b =0G.Přičtemektétorovnosti c zleva,tj. c + a + b = c.Protože však c + a =0G,dostáváme b = c,atedy:
Opačný(resp.inverzní)prvekklibovolnězvolenémuprvkugrupyjeurčenjednoznačně.
Vúvoduodstavcejsmesezmíniliotom,žemnožinyreálnýchakomplexníchčíselzískají zavedenímběžnýchoperacísčítáníanásobeníjistoualgebraickoustrukturu.Všimněmesijich nynípodrobněji.
Příklad4.2: Algebraickástrukturaakupecképočty
Uvažujmeomnožiněreálnýchčísel G = R tak,jakobychomjeumělipouzesčítat.Násobenísizatímnevšímejme.Sčítáníreálnýchčíseljezobrazenímtypuprvníhovztahuv(4.2),kterébezpochybysplňujepožadavky (4.3)i(4.4).Neutrálnímprvkem0R je„obyčejná nula,opačnýmprvkemkčíslu a ječíslo a,položenéna reálnéosesymetrickyk a vzhledemknule.Množinareálnýchčíselsoperacísčítáníjetedyaditivnígrupou.Pro operacisčítáníplatídokonceněconavíc—komutativnízákon
Grupuskomutativnímzákonemnazývámegrupou komutativní nebotaké abelovskou
Množinareálnýchčíselsoperacísčítáníjekomutativnígrupou.
Nynísemístonasčítánízaměřmenanásobeníreálnýchčíselaznovuposuďmevlastnostigrupy.Násobení reálnýchčíseljezobrazenímtypudruhéhovztahuv(4.2)asplňujepožadavekasociativnosti(4.3).Dálejezřejmé,
4 KAPITOLA4.LINEÁRNÍALGEBRAPODRUHÉ
a · eG = eG · a = a,a · a 1 = a 1 · a = eG (4.5)
a + b = b + a prolibovolné a,b ∈ R (4.6)
žečíslo eR =1(„obyčejná jednička)vyhovujeprvnímupožadavkuvevztazích(4.5).Potížjespožadavkem druhým.Inverzníprveknajdemejenknenulovýmčíslům.Nulainverzníprveknemá.Tatozdánlivádrobnostje příčinoutoho,žemnožinareálnýchčíselsoperacínásobenínenígrupou.
Příklad4.3: Algebraickástrukturanamnožiněkomplexníchčísel
Množina C komplexníchčíseljekartézskýmsoučinemreálnýchos, C = R×R,tedymnožinouuspořádaných dvojic[a,b]číselreálných.Značíme z =[a,b].Reálnéčíslo a =Re z je reálnou částíkomplexníhočísla z areálné číslo b =Im z částí imaginární.Operacesčítáníanásobeníkomplexníchčíseljsoudefinoványtakto:
Množinakomplexníchčíselsoperacísoučtujekomutativnígrupou.
Jejímneutrálnímprvkemječíslo0C =[0, 0],opačnýmprvkemkčíslu z =[a,b]je z =[ a, b].Přioperaci násobeníjeneutrálnímprvkemčíslo[1, 0],prvkeminverznímkčíslu z =[a,b]=0C je
Kčíslu0C všakinverzníprvekopětneexistuje.Množinakomplexníchčíselnenígrupouvzhledemknásobení.
Příklad4.4: Strukturaaditivnígrupynapodmnožináchreálnéosy
Některévýznamnépodmnožinyreálnéosymajísvázavedenáoznačení. N jemnožinapřirozenýchčísel, Z množinacelýchčísela Q množinaracionálníchčísel.Můžemesezajímatoto,zdapřizúženídefiničníhooboru operacesčítánína N × N, Z × Z,popřípadě Q × Q,budoutytomnožinystáleještěgrupami.Ihnedvidíme, žemnožinapřirozenýchčíselgrupounebude,neboťneobsahujenuluanizápornáčísla,kterájsouvgrupě R opačnýmiprvkykčíslůmkladným.Tímtonedostatkemnetrpímnožinycelýcharacionálníchčísel,kterétedy budougrupami.
Opodmnožině H ⊂ G grupy G soperacísčítánínebonásobenízúženouna H,kteráje samagrupou,hovořímejakoo podgrupě grupy G.Napříkladmnožinareálnýchčíselzapsaných vetvaru z =[a, 0]sesčítánímjepodgrupoumnožinykomplexníchčísel.
Kohogrupynebavíachceserychleprokousatkvektorovýmprostorům,kteréjsoukoneckoncůhlavnínáplnínašehopříběhuolineárníalgebře,můžezbytektohotoodstavcepřeskočit. Alebylabytoškoda,grupyjsouopravduzajímavé.
Příklad4.5: Grupyněkterýchčíselnýchobjektů
Komutativnígrupoujenapříkladmnožinačíselnýchmatictypu m/n (osazenýchreálnýminebokomplexními čísly)sobvyklýmsčítánímmatic.Nenídivu—sčítánímaticsedějepojednotlivýchprvcích,kteréjsoučísly. Komutativnígrupoujeimnožinavšechfunkcíreálnéproměnné F(R),vnížjesčítánídefinováno„bodpo bodu :
4.1.PROSTORYSVEKTORY 5
C × C [a1,b1], [a2,b2] −→ [a1,b1]+[a2,b2]=[a1 + a2,b1 + b2] ∈ C , C × C [a1,b1], [a2,b2] −→ [a1,b1] · [a2,b2]=[a1 · a2 b1 · b2,a1 · b2 + a2 · b1] ∈ C
z 1 = a a2 + b2 , b a2 + b2
F(R) ×F(R) [f,g] −→ f + g ∈F(R), kde(f + g)(x)= f (x)+ g(x)
prolibovolné x ∈ R.Vevýsledkujdetotižopětjenopočítánísčísly.Jezřejmé,žeproměnnábymohlabýt ikomplexní.Namnožiněvšechreálnýchfunkcíjednéreálnéproměnnésdefiničnímoborem R mámezkapitoly2 definovanouoperaciskládánífunkcí.Tatooperacejeasociativní,funkce f (x)= x (identita)hrajerolineutrálního prvku.Radostnámkazípouzetyfunkce,kekterýmneexistujefunkceinverznísdefiničnímoborem R,tj.funkce, kterénejsouprosténebojejichoboremhodnotnenícelé R.Vezmeme-livúvahupouzepodmnožinuprostých funkcísoboremhodnot R,vytvářínaníoperaceskládánístrukturu(nekomutativní)grupy.
Posuďmenyníalgebraickoustrukturumnožinyčtvercovýchmatictypu n/n soperacímaticovéhonásobení. Operacejezobrazením,kterémátvardruhéhovztahuv(4.2),asociativnízákon(4.3)rovněžplatí.Jednotková maticehrajeroliprvku eG,avšakinverzníprvekexistujepouzekregulárnímmaticím.Množinamatictypu n/n soperacímaticovéhonásobenítedynenígrupou.Pokudbychomsevšakomezilipouzenapodmnožinumatic regulárních,potížsinverznímprvkemodpadne.
Množinaregulárníchčtvercovýchmatictypu n/n soperacínásobeníje(nekomutativní)grupou.
Tatogrupa,kekterésepozdějiještěvrátíme,jevelmidůležitávefyzikálníchteoriích.
Příklad4.6: Grupynemusíbýttvořenyjenčísly
6 KAPITOLA4.LINEÁRNÍALGEBRAPODRUHÉ
σ3 σ2 σ1 A A B B C C D D A A B B C C D D σ2 M P O N vzor B B A A D D C C σ2 M P O N obraz
Obr.4.1Prvkysymetriekrychle—zrcadlení.
4.1.PROSTORYSVEKTORY 13 A A B B C C D D o4 3 vzor R Q U V D D C C B B A A R Q V U o4 3(90◦) o4 2 D C D C A B A B V U R Q o4 2(90◦) obraz A A B B C C D D vzor o4 2 U V Y X A D B C B C A D V U X Y obraz A D A D B C B C o4 3 V U Y X o4 3(90◦) o4 2(90◦)
vzor o4 3(90◦) obraz o4 2(90◦) vzor o4 2(90◦) obraz o4 3(90◦)
Obr.4.17Pořadípřemístěníkrychlenelzezaměňovat—kpříkladu4.6.
Obr.4.18Pořadípřemístěníkrychlenelzezaměňovat—kpříkladu4.6.
Homomorfismus,kterýjeprostýmzobrazenímgrupy H nagrupu G senazývá izomorfismus.
Grupy,mezikterýmilzedefinovatizomorfismus,jsouzhlediskaalgebrypovažoványzastejné. Jetotižúplnějedno,sekterouznichpočítáme,neboťpomocíizomorfismumůžemejasně definovanýmajednoznačnýmzpůsobemkdykolipřecházetodjednékdruhé.
Existencehomomorfismuvytvářívgrupěvzorůivgrupěobrazůdůležitépodmnožiny.Jsou jimi
Ker h = {a ∈ H|h(a)=0G}, Im h = {h(a) ∈ G|a ∈ H}
Prvníznich,zvaná jádro homomorfismu h,jemnožinouvšechvzorů,kterésezobrazilynaneutrálníprvekgrupy G.Druházoboumnožin, obraz homomorfismu h, jemnožinouvšechobrazů,kterévzniknouzevšechprvkůgrupy H.
Dokážetesepřesvědčitoplatnostinásledujícíhodůležitéhotvrzení?
Jádrolibovolnéhohomomorfismu h : H → G jepodgrupouvgrupě H,obrazje podgrupouvgrupě G.
Stačípoužíttoho,žehomomorfismus„přenáší grupovouoperaci.
Příklad4.9: Vžádnémtextuogrupáchnesmějíchybětzbytkovétřídy
Vpříkladu 4.4 jsmeviděli,žemnožinapřirozenýchčíselsoperacísčítánínenígrupou.Můžemejivšak použítkdefiniciurčitýchspeciálníchgrup,kterénámbudoumožnápřipadatponěkudzvláštní.Jejichprvky totižnebudoučísla,nýbržmnožinyčísel.Jakbychomalemohlidefinovatsčítánídvoumnožinčísel?Například takto:Zvolmelibovolnépřirozenéčíslo n.Budeme-likterékolipřirozenéčíslo q dělitdělitelem n,dostaneme částečnýpodíl p azbytek r,tj. q = pn + r.Zbytekmůženabývathodnotzmnožiny {0, 1,...,n 1}.Takto můžemepřirozenáčíslatříditdoskupinpodletoho,jakýzbytekdávajípřiděleníčíslem n.Tytoskupinyse nazývají zbytkovétřídymodulon.Napříkladpro n =3připadajívúvahuzbytky0,1,2.Dostávámetedytřídy Z0, Z1 a Z2.Třída Z0 obsahujevšechnapřirozenáčísla,kterájsoudělitelnátřemi,tj. Z0 = {3, 6, 9,..., 3k,... }, třídě Z1 náležíčísla,přijejichždělenítřemijezbytek1,tj. Z1 = {1, 4, 7,..., 3k 2,... },zbývajícípřirozená čísladávajípodělenítřemizbytek2análežítřídě Z2 = {2, 5, 8,..., 3k 1,... }.Číslo k nabýváhodnot1, 2, 3,... Všimněmesinynímožnázajímavé,alesamozřejmévěci:Sečteme-likterékolidvaprvkytřídy Z0,dostaneme opětprvektétotřídy.Sečtenímprvkutřídy Z0 sprvkemtřídy Z1 dostanemeprvektřídy Z1,sečtenímdvou prvkůtřídy Z1 dostanemeprvektřídy Z2,atakbychommohlipokračovat.Výsledektakovéhosčítánínezávisí nakonkrétníchprvcích,alepouzenajejichpříslušnostiktřídám.Každýprvektedyzastupuje„svou třídu rovnocennýmzpůsobem,aprotosenazývájejím reprezentantem.Výsledkyshrnujenásledujícítabulka.
16
KAPITOLA4.LINEÁRNÍALGEBRAPODRUHÉ
+ Z0 Z1 Z2 Z0 Z0 Z1 Z2 Z1 Z1 Z2 Z0 Z2 Z2 Z0 Z1
intervalutvoříjejí(samozřejměnormální)podgrupu C(a,b).Grupa C(a,b) jenormálnípodgrupoutakévpodgrupě F(a,b) všechfunkcí,kterémajínaintervalu(a,b)derivaciasloužítedyjakofunkceprimitivní.Faktorovágrupa Φ(a,b)/C(a,b) jetvořenatřídamifunkcílišícíchsenavzájemokonstantu,faktorovágrupa F(a,b)/C(a,b) paktřídami funkcíprimitivních.Kodstraněnívýšezmíněnýchnepřesnostístačí,abychomsedohodli,žesymbolneurčitého integrálu
f (x)dx ∈F(a,b)/C(a,b) znamenánikolijednotlivouprimitivnífunkci,aleceloutřídu,tj.prvekfaktorovégrupy.(Koneckoncůjsmetoani předtímjinaknemysleli.)Vztahyvevzorcích(2.30)pakneznamenajírovnostfunkcí,tj.prvkůpůvodnígrupy, nýbržrovnosttříd,tj.prvkůfaktorovégrupy.Vzorec(2.31)prometoduperpartesvšakmusímepoopravit takto:
u(x)v(x) = u (x)v(x)dx + u(x)v (x)dx,
kde u(x)v(x) jemnožinavšechfunkcí,lišícíchseod u(x)v(x)okonstantu,tj.třídafunkcí,prvekfaktorové grupy.(Funkce u(x)v(x)jereprezentantemtétotřídy,přičemžkaždájináfunkce,kteránáležídotétotřídy,je stejnědobrýmreprezentantem.)Obdobněsimůžetezkusitzpřesnitzápis(2.32)pronalezeníprimitivnífunkce substitučnímetodou.
4.1.2 Algebraickéstrukturysedvěmaoperacemi,hlavněpole
Příkladygrupipříkladymnožinsnějakouoperací,kterégrupaminebyly,jsmesičastoukazovali namnožináchčísel.Sčíslytotižumímepočítat,takžetakovépříkladyjsounázorné.Ukázky všakmělyjednunevýhodu.Grupyjsmesitotižoznačilijakostrukturysjednouoperací.Proto jsmevpříkladechsmnožinoureálnýchčíselajejímipodmnožinami,vnichžnaprostopřirozeně používámeoperacedvě,sčítáníanásobení,muselivždyjednuznichignorovat.Nynínaopak dobřevyužijemeobou.Předpokládejme,ževmnožině P jsouzadánydvěoperacetypu(4.2), prozápisjednéznichpoužijemeznaku„+ ,prodruhou„ .
Příklad4.13: Reálnáosajakoalgebraickástrukturasedvěmaoperacemi
Představmesi,ženosnoumnožinoujemnožinareálnýchčísel P = R s„obyčejnými operacemisčítání anásobení.Pokusmesepopsatconejvícevlastnostítěchtooperací.Prolibovolnáreálnáčísla a, b, c platí:
(1) Množina R sesčítánímjekomutativnígrupa,0R =0,
(2) (a b) c = a (b c),násobeníjeasociativní,
(3) (a + b) · c = a · c + b · c,a · (b + c)= a · b + a · c,platídistributivnízákony,
(4) a 1=1 a = a, existujeneutrálníprvekvzhledemknásobení,vtomtopřípadě1R =1,
(5) a b =0 ⇒ a =0nebo b =0, neexistujídělitelénuly,
(6) prokaždé a =0existujeprvek a 1 tak,že a · a 1 = a 1 · a =1,tj.kekaždémunenulovémuprvku existujeinverzníprvekvzhledemknásobení,
(7) a b = b a,násobeníjekomutativní.
Porovnejtetytovlastnostistěmi,kteréjsmesipromnožinureálnýchčíselvypsalijižvodstavci1.2.1.Kvlastnosti (1),kterápožaduje,abymnožina P sesčítánímbylakomutativnígrupou,přidávámevlastnostidalší,týkající senásobeníakombinacesčítánísnásobením.Pokudpřidámepouzevlastnosti(2)a(3),získámealgebraickou strukturu,kterásenazývá okruh.Nejjednoduššímpříklademokruhujemnožinaobsahujícípouzejedinýprvek r
4.1.PROSTORYSVEKTORY 19
Systémvektorů(a1,a2,...,ak)vektorovéhoprostoru V senazývá lineárnězávislý, jestližeexistujíčísla(skaláry) α1,α2,...,αk,znichžalespoňjednojenenulové,tak, že lineárníkombinace
Pokudnelzenulovoulineárníkombinacidanýchvektorůzískatjinaknežsnulovými koeficienty,říkáme,žesystémvektorůje lineárněnezávislý.
Předpokládejme,žesystém(a1,a2,...,ak)jelineárnězávislýaženapříkladzrovnačíslo α1 je nenulové.(Pokudbytomutaknebylo,stačívektorypřečíslovatajako a1 označitten,ukteréhoje právěvtélineárníkombinaci,jejímžvýsledkemjenulovývektor,nenulovýkoeficient.)Můžeme tedypsát
α 1 a1 + α 2 a2 + ··· + α k a
αj aj =0V ,α 1 =0
Vynásobíme-licelourovnostčíslem(α1) 1 (hnedjevidět,pročjsmepotřebovali,aby α1 bylo nenulové),můžemevektor a1 zapsatpomocíostatníchvektorůsystémujakojejichlineární kombinaci a1 = α2 α1 a2 + ··· + αk α1 ak
Prosystémtvořenýalespoňdvěmavektorytedyplatí:
Systémvektorůjelineárnězávislýprávětehdy,je-liněkterývektorzesystému lineárníkombinacíostatních.
Zdefinicelineárnízávislostijevidět,žesystémobsahujícíjedinývektorjezávislýprávěkdyž jetentovektornulový.
Jepřirozené,žesinyníklademeotázku,kolikvektorůprostoru V jenejméněpotřeba, abychompomocínichvyjádřilivšechnyostatní.Předpokládejme,ževevektorovémprostoru V existujelineárněnezávislýsystémvektorů(a1,a2,...,ak).Číslo k bymělobýtalespoň1. (Pro k =0byvektorovýprostormuselbýttvořenjedinýmprvkem,kterýbysoučasněplnil úlohuneutrálníhoprvkuiprvkusamaksoběopačného.Pakbyplatilo V = {0V }.Tentopřípad vektorovéhoprostorunenípřílišzajímavý,ikdyžionmánároknasvémístomezivektorovými prostory.)Přidejmeksystému(a1,a2,...,ak)dalšívektorazjišťujme,zdanovýsystémjelineárnězávislýčinezávislý.Pokudnajdemevektor ak+1 tak,žesystém(a1,a2,...,ak+1)bude lineárněnezávislý,pokračujemepřidánímdalšíhovektoru.Můžesestát,žeseproceduravjistém n-témkrokuzastaví,takženebudemeschopnisystém(a1,a2,...,an),stáleještělineárně nezávislý,doplnitdalšímnezávislýmvektorem.Budetoznamenat,žesystém(a1,a2,...,an,b) budelineárnězávislý,aťsesnažímesebevíc,tj.budezávislýprolibovolnězvolenývektor b ∈ V
4.1.PROSTORYSVEKTORY 23
α2a2
+ αkak dáváneutrálníprvekprostoru
,tj. α 1 a1 + α 2 a2 + ··· + α k ak =0V
α1a1 +
+
V
k
k =
j=1
KAPITOLA4.LINEÁRNÍALGEBRAPODRUHÉ
Určitěteďmátepodezření,žebudenutnésizopakovatzákladyřešenísoustavlineárníchrovniczkapitoly1. Tentoodhadjezcelasprávný.Zopakujemesipotřebnévlastnostisoustavlineárníchrovnicsouběžněsřešením našehoproblému.Mají-libýtvektory b1,b2,...,bm prvkynovébáze,musíbýtlineárněnezávislé.Jetedytřeba, abyvektorovárovnice
mělapouzetriviálnířešení(γ1,γ2,...,γm)=(0, 0,..., 0).Vímejižzpříkladu4.17,žekaždýzvektorů b1 až bm jelineárníkombinacívektorůbáze(a1,a2,...,an)sjednoznačněurčenýmikoeficienty.Dosadíme-litakto vyjádřenévektory b1 až bm dopředchozívektorovérovnice,dostanemelineárníkombinacivektorůbáze,která jeovšemnulovýmvektorem.Všechnykoeficientytétokombinacetedymusíbýtnulové.Vektorovárovnice(4.9) takpředstavujesoustavu n homogenníchlineárníchrovnico m neznámých γ1 až γm ,
Tatosoustavamářešenívždy,přinejmenšímtotriviální.Abyvšakmělapouzetriviálnířešeníažádnéjiné,jak požadujeme,jenutnéastačí,abymaticesoustavy
mělahodnostrovnoupočtuneznámých,tedy h(B)= m.Nutnoupodmínkouproto,abytentopožadavekmohl býtvůbecsplněn,je m ≤ n.Propřípad m>n bytotižhodnostmatice B nemohlapřekročithodnotu n,takže
26
o c = α1a1 + α2a2 = β1b1 + β2b2 a1 α1a1 a2 α2a2 b1 β1b1 b2 β2b2
Obr.4.19Rozkladvektoruvrovinědorůznýchbází.
γ 1b1 + γ 2b2 + ··· + γmbm =0V (4.9)
β1 1 γ 1 + β1 2 γ 2 + + β1 mγm =0 , β2 1 γ 1 + β2 2 γ 2 + ··· + β2 mγm =0 , .............................., βn 1 γ 1 + βn 2 γ 2 + + βn mγm =0 .
B = β1 1 β1 2 ...β1 m β2 1 β2 2 ...β2 m βn 1 βn 2 ...βn m
Zpříkladu4.24jstejižjistěusoudili,že:
Vektorovýmpodprostorem vektorovéhoprostoru Vn budemerozuměttakovoujeho podmnožinu L,ježmásamatakéstrukturuvektorovéhoprostoru.Tutostrukturu všaknanínevytvářímenově,nýbržprostřednictvímpůvodníchoperacísčítánívektorůajejichnásobenískalárem(tj. zúžením definičníhooborutěchtooperacína podmnožinu L).
Ajakpoznáme,žeurčitápodmnožina L ⊂ Vn jeopravduvektorovýmprostorem?Stačíse přesvědčit,zdajeuzavřenávzhledemkalgebraickýmoperacím,tj.zdaskaždýmidvěmavektory a,b ∈ L patřído L takéjejichsoučetaskaždýmvektorem a ∈ L takéjeholibovolnýskalární násobek.Ekvivalentníjedokázat,žeskaždýmidvěmavektory a,b ∈ L patřído L ijejich libovolnálineráníkombinace αa + βb.Pokudtomutakbude,nenítřebaprověřovatnicdalšího. Algebraickéoperacezúženímdefiničníhooborusvévlastnostineztratí.Množina L jižbude automatickyobsahovatnulu0Vn ,kterábudeplnitfunkcineutrálníhoprvkutakévpodprostoru L,atakéskaždýmsvýmprvkem a iprvekopačný, a.Nevěříte?Vezmeme-liprvek a ∈ L,pak 0Vn =0 a a a =( 1)a.Atojsouskalárnínásobkyvektoru a.
Vpříkladu4.24jsmegenerovali dvojrozměrný vektorovýpodprostor dvěma lineárněnezávislýmivektory.Jaktomuvšakbudevpřípadě,žepředemnevíme,zdajegenerujícísouborvektorů lineárněnezávislý?Budemnožinavšechjejichlineárníchkombinacíopětvektorovýmpodprostorempůvodníhoprostoru?Apokudano,jakýbudejehorozměr?Natytootázkyodpovíme obecněvnásledujícíchpříkladech.
Nechť(a1,a2,...,ak)jesystémvektorůve Vn
Příklad4.25: Jelineárníobalvektorovýmpodprostorem? Přesvědčímese,žeskaždýmidvěmavektory
+ + βk ak)=(αβ1)a1 + +(αβk)ak .
Zjistilijsme,ževektory b+d a αb jsouopětlineárnímikombinacemivektorůgenerujícíhosystému(a1,a2,...,ak).
Lineárníoballibovolnéhosystémuvektorůprostoru Vn jetedyvektorovýmpodprostorem Vn.
Příklad4.26: Ajakýmározměr?
Systémvektorů,kterýmgenerujemelineárníobal,musímenějakzadat.Nejčastějitodělámepomocíjejich
34 KAPITOLA4.LINEÁRNÍALGEBRAPODRUHÉ
=
1
k) = {γ 1 a1 + γ 2 a2 + ··· + γ k ak,γ 1 ,...,γ k ∈ C} nazýváme lineárnímobalem systému(a1,a2,...,ak).
.Množinu L
(a
,a2,...,a
b,d ∈ L, L = (a1,a2,...,ak) , b = β1a1 + + βk
b + d =(β1 a1 + ··· + βk ak)+(δ1 a1 + ··· + δk ak)=(β1 + δ1)a1 + ··· +(βk + δk)ak , αb = α(β1 a1
ak a d = δ1a1 + + δkak,patřído L ijejichsoučetaskaždýmvektorem b ∈ L jeholibovolnýnásobek:
Dimenzelineárníhoobaluvektorů(a1,a2,...,ak)jerovnahodnostimaticetvořenésložkamitěchto vektorů.
Hodnostzjistímeúpravounaschodovitýtvar.Jehonenulovéřádkypakobsahujísložkynovýchvektorů,které jsoujižlineárněnezávislé,avšakgenerujítýžpodprostoratvoříjehobázi.
Amohlobyněcobránitvolběvolnýchneznámýchpodlenávoduvpříkladu 4.26?Třeba nenímožnévždyvolitposledních d = kh neznámýchjakovolné.Itosemůžestát.Ukážeme tovdalšímpříkladu.
Příklad4.27: Jaktedyvolitvolnéneznámé?
Uvažujmeopodprostoru,kterýjegenerovánsouboremvektorův R4:
Abychomzjistilijehodimenzi,upravujmenynínaschodovitýtvarmaticihomogennísoustavy(4.14),kteráje tvořenasložkamizadanýchvektorůnaskládanýmidosloupců:
Vmaticizůstalytřinenulovéřádky,zadanévektorygenerujítrojrozměrnýpodprostorv R4.Řešenísoustavy 414budeobsahovatdvěvolnéneznámé.Obvyklejsmezatytovolnéneznámévoliliposlednídvě,tj. γ4 a γ5 Zpředposledníhořádkumaticevidíme,žetatovolbanenínynímožná,platítotiž γ5 =0.Pátáneznámáje pevněurčenaanemůžeprotohrátrolivolnéneznámé.Zostatníchneznámých γ1 , γ2 , γ3 a γ4 můžemejiž dvojicivolnýchneznámýchvybratlibovolně.
Čímtoje?Tentokráttotižnejsoulineárněnezávisléprvnítřivektory.Všimnětesi,žetřetívektorjesoučtem prvníhoadruhého.Čtvrtývektorjezaserozdílemprvníhoadruhého.Aťdělámecoděláme,zprvníčtveřice vektorůjsmeschopnivybratnejvýšedvanezávislé.Dobázepodprostorutedyvkaždémpřípaděmusímevzít poslední,pátývektor.Návodvpříkladu4.26bynámitentokrátdobře„fungoval ,alemuselibychomvhodně přeskládatpořadívektorů(vtomtopříkladuzařazenímposledníhovektorudoprvnítrojice).
Příklad4.28: Teďužzodpovímevšechnyotázkysoustavlineárníchrovnic
Pomocíprávěvyřešenéhopříkladusimůžemeuvědomitdalšídůležitouvlastnostřešenísoustavlineárních rovnic.Vodstavci1.1.2,konkrétněvevětě1.2,jsmeviděli,žeřešenísoustavy m lineárníchrovnico n neznámých,
prokteroujespolečnáhodnotahodnostimaticesoustavyamaticerozšířenérovna h,závisína d = n h volných neznámých,například γh+1,γh+2,...,γn.Zbývajícíneznámé γ1,γ2,...,γh jsouvpřípaděhomogennísoustavy,
36 KAPITOLA4.LINEÁRNÍALGEBRAPODRUHÉ
L = (1, 1, 0, 1), (1, 1, 0, 1), (1, 0, 0, 1), (0, 2, 0, 0), (1, 1, 1, 1)
11101 1 1021 00001 11101 ∼ 11101 0 2 120 00001 00000
(γ 1 γ 2 ...γn) a1 1 a2 1 ...am 1 a1 2 a2 2 ...am 2 a1 n a2 n ...am n = b1 b2 ...bm ,
Neznámou n-tici(β)=(β1 β2 ...βn)jsmenynízapsalijakořádkovoumatici(tj.jakovektor),stejnějako m-tici představujícívektorpravýchstranjednotlivýchrovnic.Matice A jetypu n/m,jednásetedyotransponovanou maticisoustavypodleterminologiezkapitoly1.Předpokládejme,že n-tice(γ)jeřešenímhomogennísoustavy (γ)A =(0),kde(0)jenulovámaticetypu1/m.Sečtenímobousoustavdostáváme
(γ)+(β) A =(b)
Zjišťujeme,žespoluskaždou n-ticí(β),kterájeřešenímnehomogennísoustavy,jeřešenímsoustavytaké n-tice (β)=(γ)+(β).Naopak,každédvě n-tice(β)a(β),kteréjsouřešenímnehomogennísoustavy,senutněliší o n-tici(γ),kterájeřešenímodpovídajícíhomogennísoustavyostejnématici A.Abychomnašlivšechnařešení nehomogennísoustavy,stačínajítobecnéřešenísoustavyhomogenníajedno(kterékoli)řešenísoustavynehomogenní,takzvané partikulárnířešení
.Jejichsoučetpakpopisujevšechnamožnářešenínehomogennísoustavy. Tentoalgebraickývýsledekmávelmijednoduchougeometrickouinterpretaci(vizobr.4.20).Správnépochopení
obrázku4.20vyžaduje,abychomsikaždou n-ticipředstavilijakosouborsouřadnicboduv n-rozměrnémeuklidovskémprostoru.Obrázekjekonstruovánpro n =3.„Základním bodemjepočátek(0, 0,..., 0),tj. n-tice, kterájeřešenímkaždéhomogennísoustavy.Ostatnířešeníhomogennísoustavysipředstavímejakokoncové bodyvázanýchvektorůumístěnýchvpočátku,jimžodpovídajívolnévektorynáležejícívektorovémupodprostorutvořenémuřešenímihomogennísoustavy.(Vobrázkuvytvoříkoncovébodytakovýchvázanýchvektorů rovinu γ.)Partikulárnířešenínehomogennísoustavyposouvátento„vázaný vektorovýpodprostordojiného boduosouřadnicích(β1,β2,...,βn)euklidovskéhoprostoru(vobrázkurovina β).
Výsledky,kekterýmjsmedospělivpředcházejícíchodstavcích,siformulujemevnásledující větě:
Věta4.1(Principsuperpozice): Množinavšechřešeníhomogennísoustavy m lineárníchrovnico n neznámýchtvoří (nh) rozměrnýpodprostorvevektorovém prostoruvšechuspořádaných n-tic(tj.v Rn),kde h jehodnostmaticesoustavy.
38 KAPITOLA4.LINEÁRNÍALGEBRAPODRUHÉ
(γ) (β) (β)=(β)+(γ) γ β (0) x y z
Obr.4.20Obecnéřešenínehomogennísoustavyrovnic.
Bezprostřednímdůsledkempředchozívětyjenásledujícítvrzení.
c) V P[6]:
L1 = |x +1,x2 +1, 2x2 2x| ,
L2 = |1,x2 + x,x3| ,
d) Vprostoručtvercovýchmaticřádu2:
L1 jepodmnožinavšechmaticsnulovoustopou(nulovýmsoučtemdiagonálníchprvků),
L2 jepodmnožinavšechdiagonálníchmatic.
13. Ukažte,žemnožina V = {x ∈ R|x> 0} soperacemi x ⊕ y = x y, t x = xt mástrukturuvektorového prostorunad R.Určetejehodimenzi d analeznětenějakýjehoizomorfismuss d-rozměrnýmprostorem Rd .
14. Ukažte,žezvlastnostíokruhuuvedenýchvpříkladu4.13vyplývá
• 0 a = a 0=0provšechna a,
• ( 1) a = a provšechna a
15. Ukažte,ževlibovolnémokruhuplatí:Existuje-likekaždémunenulovémuprvkuprvekinverzní,pakokruh nemádělitelenuly.Tj.vlastnost„neexistencedělitelůnuly (vpříkladu4.13označenáčíslem(5))jedůsledkemvlastnosti„existenceinverzníhoprvkukekaždémunenulovémuprvku (vpříkladu4.13označená číslem(6)).
16. Ukažte,ževdefinicivektorovéhoprostorumůžemeposlednízaxiomů( 1)a = a nahraditaxiomem1a = a (tj.definicestaktozaměněnýmaxiomembudeekvivalentníspůvodnídefinicí).
4.2 Lineárnízobrazenívektorovýchprostorů
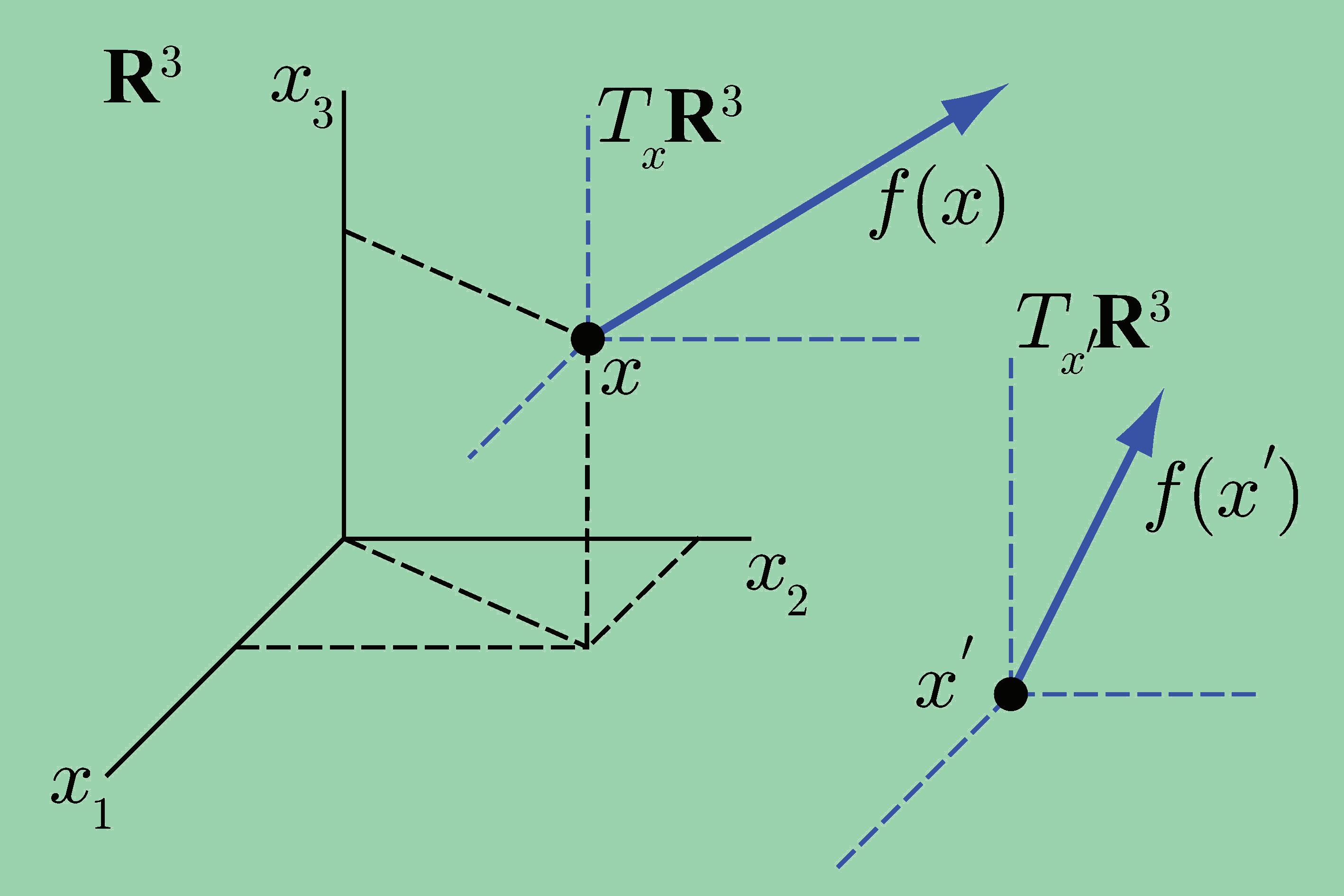
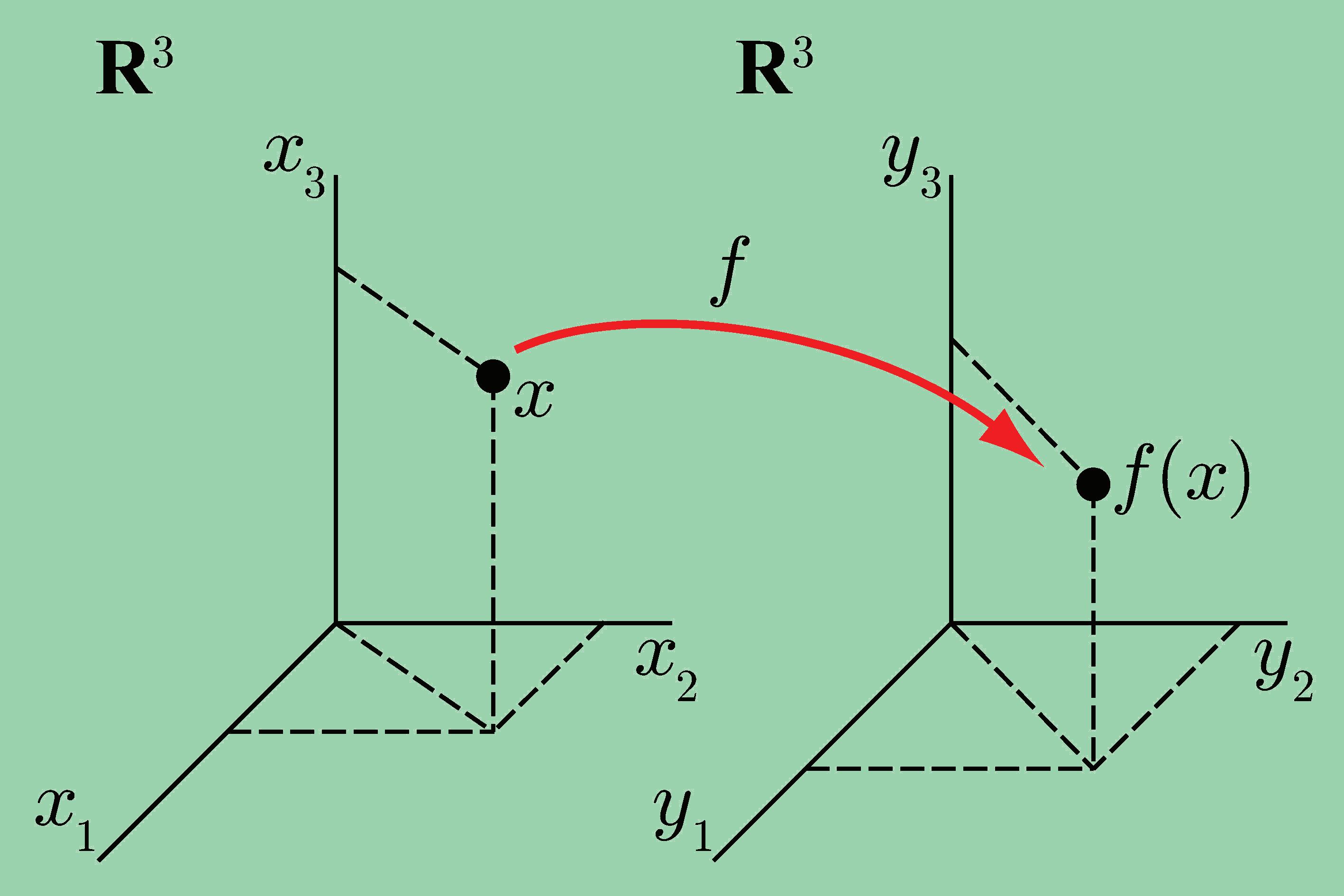
Spojmemzobrazeníjsmesesetkalijižvícekrát.Protosiumímepředstavit,ocopřizobrazování vektorovýchprostorůpůjde.Vzorům—vektorůmjednohovektorovéhoprostoru,řekněme Vn, budemezobrazením ϕ přiřazovatobrazy—vektoryobecnějinéhovektorovéhoprostoru,třeba Wm.Vespeciálních,alepraktickyvelmidůležitýchpřípadechmůžebýt Wm = Vn.Jaksivšak mámepředstavit,žezobrazení
ϕ
jelineární?Izdejižjakousipředstavumáme.Vzpomeňmetřebanalineárnífunkci,zobrazení f : R x → f (x)= kx ∈ R.Jednáseopřímouúměru,prokterousnadnoověříme,žeplatí
x
+ x
Ještělepšípředstavaolinearitějegeometrická.Podívejtesenaobrázek4.22.Jenaněmčtvercovámřížka(vzor)arůznéjejíobrazy,kterépodleníjakopředlohynamalovalirůznímalíři. Zkusteříci,kterýznichzobrazujemřížkulineárně,tj.jaksi„úměrně ?Snadnousoudíme,že prvnídvaurčitěano,třetíačtvrtýurčitěne.Jakjsmetopoznali?Jistěnámpřitompomohla určitágeometrickáintuice,kteroukaždýzískávázezkušenosti.Linearituobrazumřížkyvšak dokážemevystihnoutipřesněji.Všimnětesi,žeobrazyprvýchdvoumalířůponechávají všechny
48 KAPITOLA4.LINEÁRNÍALGEBRAPODRUHÉ
: Vn a −→ ϕ(a) ∈ Wm (4.20)
f (
1
2)= k(x1 + x2)= kx1 + kx2 = f (x1)+ f (x2) , f (αx)= k(αx)= α(kx)= αf (x)
4.2.1 Lineárnízobrazeníalgebraicky
Znovusiuvědomme,želinearitaznamenáúměru.Případyúměryvšakmohoubýtjaktynejjednodušší,takiobecnější,unichžsitřebaanihnedneuvědomíme,žeseoúměrujedná.Vydejme setedyzaúměramidooblastifyziky.
Příkladúměryskalárníchveličin: Protakovýpříkladnemusímechoditdaleko. Dokoncestačísevrátitkodstavci1.1,kdejsmemluvilioOhmovězákonu(viztéžobr.
1.3).Budeme-liměnitnapětímezikoncikovovéhodrátu,zjistíme(nebude-linapětípříliš velké,abysedrátmocnezahříval),žečímvětšíjenapětí,tímvětšítečedrátemproud. Jednáseolineárnízávislost(úměru)tvaru I = I(U )= R 1U ,konstantouúměrnostije převrácenáhodnotaelektrickéhoodporudrátu.Změníme-linapětízhodnoty
Speciálnípříkladúměryvektorovýchveličin: Přizkoumánírotačníhopohybu soustavyčásticčitělesasespojitěrozloženouhmotnostípracujemesmomentemhybnosti L tétosoustavyčitělesa,jehožderivacepodlečasujeurčenavýslednýmmomentemvnějšíchsil(druháimpulzovávěta).Pokudsejednáospeciálnípřípadtělesa,tělesotuhé, aspeciálnípřípadrotačníhopohybu,rotacikolempevnéosy,souvisímomenthybnostijednoduchýmvztahemskinematickouveličinoupopisujícítutorotaci,totižúhlovourychlostí ω.Jestližejehmotnosttělesarozloženavůčirotačníosesymetricky,jetentovztahzvlášť jednoduchý,mátvarúměry L = Joω,kde Jo jemomentsetrvačnostitělesa vzhledemkose rotaceo.Obdobnývztahplatíimezivektorovýmiveličinamivjinýchoblastechfyziky.
Napříkladvztah P = χE určuje,jaksebudepolarizovatdielektricképrostředí,vložíme-li jedoelektrickéhopoleointenzitě E.Vektor P senazývá polarizace,veličina χ = ε0χr jecharakteristikouprostředí,zvanou polarizovatelnost nebotéž dielektrickásusceptibilita. (Známějšíveličinoujetakzvaná permitivita,určenávztahem ε = ε0(1+ χr),kterápopisuje
úměrumezivektoremelektrickéindukceavektoremelektrickéintenzity, D = εE, ε0 je permitivitavakua.)Promagnetickéveličinyjetoanalogické, B = µH, µ je magnetická permeabilita.Opětsivšimněme,žeprozávislostmomentuhybnostinaúhlovérychlosti L(ω)(apodobněprozávislosti P (E), D(E), B(H))platí
50 KAPITOLA4.LINEÁRNÍALGEBRAPODRUHÉ
U ,přiníž tečedrátemproud I = R 1U , ohodnotu ∆U ,potečedrátemproud I(U +∆U )= R 1(U +∆U )= R 1U + R 1∆U = I(U )+ I(∆U ) , tedyproudzměněný ohodnotu ∆I = R 1∆U .Změníme-linapětí α-krát,změníseproud také α-krát, I(αU )= R 1(αU )= αR 1U = αI(U ) . Neboobecněji I(U1 + U2)= I(U1)+ I(U2),I(αU )= αI(U ) .
L(ω 1 +ω 2)= Jo(ω 1 +ω 2)= Joω 1 + Joω 2 = L(ω 1)+ L(ω 2) ,
jaktakovýpředpismůževypadat.Ukážeme,žedokoncebudestačit,abychompředepsali,jak sezobrazujívektoryalespoňjedné(libovolnězvolené)báze.Apakuždokážemenajítobraz jakéhokolivektoru.Vyřešímesoučasněipraktickouotázku:Jakvypočítatsložkyobrazuve zvolenébázivektorovéhoprostoru Wm,známe-lisložkyvzoruvjistébázivektorovéhoprostoru
Připosledníúpravějsmevyužilipředpokládanélinearityzobrazení ϕ.Označme ci = ϕ(ei) obrazyvektorůbáze.Okamžitěvidíme,žepokudpředemřekneme,jaksezobrazením ϕ zobrazí vektorybáze,můžemezapsatobrazkteréhokolivektoru a ∈
Pozor!Vektory c1, c2,...,
Symbolem c ∼ (γ1 ...γm)=(γ)opětvyznačujemeskutečnost,ževektor c jevezvolenébázi reprezentován m-ticí(γ).Abychommohlipočítatsvektory,kterépředstavujíobrazyvektorů bázeprostoru
56 KAPITOLA4.LINEÁRNÍALGEBRAPODRUHÉ
Vn. Zvolmevevektorovémprostoruvzorů Vn bázi(e1,e2,...,en)avprostoruobrazů Wm bázi (f1,f2,...,fm).Předpokládejme,že ϕ : Vn → Wm jelineárnízobrazení.Zobrazmevektor a = α 1 e1 + α 2 e2 + ··· + αnen = n i=1 α i ei,a ∼ (α 1 ...αn)=(α) . ϕ(a)= ϕ n i=1 α i ei = n i=1 α i ϕ(ei) .
ϕ(a)= α 1 c1 + α 2 c2 + ··· + αncn . (4.23)
Vn,
cn jsousiceprvkyprostoruobrazů Wm,alenemusívněmtvořitbázi. Každýznichjevšakzcelaurčitělineárníkombinacívektorůbáze(f1,f2,...,fm),tj. c1 = γ 1 1 f1 + γ 2 1 f2 + ··· + γm 1 fm = m β=1 γβ 1 fβ ,c1 ∼ (γ 1 1 ...γm 1 )=(γ1) , c2 = γ 1 2 f1 + γ 2 2 f2 + ··· + γm 2 fm = m β=1 γβ 2 fβ ,c2 ∼ (γ 1 2 ...γm 2 )=(γ2) , .................................................................., cn = γ 1 nf1 + γ 2 nf2 + ··· + γm n fm = m β=1 γβ n fβ ,cn ∼ (γ 1 n ...γm n )=(γn)
Vn,musímezadatjejichsložkyvbáziprostoru Wm.Tyvytvořímatici ϕ ∼ A = γ1 1 γ2 1 ...γm 1 γ1 2 γ2 2 ...γm 2 γ1 n γ2 n ...γm n .
Matice A reprezentujelineárnízobrazení ϕ v bázích (e1,e2,...,en)prostoru Vn a(f1,f2,...,fm) prostoru Wm.Podobně,jakojsmepřipočítánísesložkamivektorůmuseliuvádětinformaci,ke kterébázisetytosložkyvztahují(vjinébáziměltýžvektorjinésložky),musímetakévpřípadě číselnéreprezentacelineárníhozobrazeníspecifikovatbáze.Vpřípadězobrazení Vn → Wm je přirozeněnutnéurčitbázev obou vektorovýchprostorech.
Dosaďmenynívektory c1 až cn dovyjádřeníobrazu ϕ(a)vztahem(4.23):
Avehřejsouopětmatice!Zadáme-libázevprostorech Vn (prostorvzorů)a Wm (prostor možnýchobrazů),stačívzítjakoukolimaticitypu n/m amámejistotu,žetatomaticebude reprezentovatjistélineárnízobrazení ϕ : Vn → Wm.Připomeňmesi,žeřádkytétomatice obsahujísložkyobrazůvektorůbáze e1, e2, ..., en vyjádřenýchvbázi(f1,f2,...,fm).Coje všaktřebaověřit,jejednoznačnosttakovéhozpůsobuzadánílineárníhozobrazení.Představme si,žezvolímeve Wm vektory c1, c2, , cn ařekneme:„Totojsouobrazyvektorů e1, e2, , en tvořícíchbáziprostoru Vn prolineárnízobrazení ϕ. Skutečně,jednotakovélineárnízobrazení jižsestrojitumíme: ϕ(a)= α1c1 + α2c2 + ··· + αncn prolibovolnývzor a = α1e1 + α2e2 + + ··· + αnen.Dosadíme-litotiž a = ej ,dostanemeskutečně ϕ(ej )= cj .Cokdyžvšakexistuje ještějinélineárnízobrazení,třeba ψ,kterézobrazujevektorybáze ej rovněžnavektory cj ,tj. ψ(ej )= cj provšechna j ∈{1,...,n},avšakproněkterývektor a můžedávatjinýobraznež zobrazení ϕ,tj. ϕ(a)= ψ(a)?Předpokládejme,žetomutakskutečněje.Pak
4.2.LINEÁRNÍZOBRAZENÍVEKTOROVÝCHPROSTORŮ 57
ϕ(a)= n i=1 α i ci = n i=1 α i m β=1 γβ i fβ = = m β=1 n i=1 α i γβ i fβ =⇒ ϕ(a)= m β=1 αβ fβ ,αβ = n i=1 α i γβ i , vmaticovémzápisu a ∼ (α),ϕ(a) ∼ (¯ α), (¯ α)=(α)A, tj. (¯ α 1 α 2 ...αm)=(α 1 α 2 ...αn) γ1 1 γ2 1 ...γm 1 γ1 2 γ2 2 ...γm 2 γ1 n γ2 n ...γm n . (4.24)
ϕ(a)= ϕ n i=1 α i ei = n i=1 α i ϕ(ei)= n i=1 α i ci , ψ(a)= ψ n i=1 α i ei = n i=1 α iψ(ei)= n i=1 α i ci .
Jevidět,že ϕ(a)= ψ(a)prolibovolnývektor a,tedy ϕ = ψ.
Výsledky,kekterýmjsmeprávědospěli,jsouprozadávánílineárníchzobrazenínatolik důležité,žejevyjádřímeformoumatematickévěty:
Věta4.2: Každélineárnízobrazení ϕ : Vn → Wm jejednoznačněurčenoobrazy libovolnébázeprostoru Vn.
Příklad4.41: Geometrickápředstavivostaalgebraickýzápis
Abychomsizvyklinaalgebraickýpopisgeometrickýchobjektů,jimižvektorovéprostoryalineárnízobrazení mezinimijsou,porovnámealgebraickéřešeníúlohysgeometrickýmpropřípady,kdyještěmůžemeuplatnit představivost.Tojedobřemožnévprostorechjedno-,dvou-atrojrozměrných,jakdokumentujenapříklad ilustrativníobrázek4.27,znázorňujícípromítání.Prokonkrétnívýpočetzvolímejakozobrazení ϕ promítání
vektorůprostoru V3 = |e1, e2, e3| nad R
,
2 = e3.Abychom mohlidobřeuplatnitpředstavivost,předpokládejme,ževektory e1, e2, e3 jsoujednotkovéanavzájemkolmé. Abychomvěděli,jakmámepromítat,musímezadatdoplněk L vektorovéhopodprostoru L (vizpříklad4.39).
Zvolíme-li L = |e1 e2| ,představímesisituacivelmidobře,neboťpůjdeokolmépromítání,kterédobře známez„obyčejné geometrie(vizobrázek4.28).
Pozn.: Kolmostíadélkouvektorůzalgebraickéhohlediskasesicebudemezabývatažpozději,vodstavci oskalárnímsoučinuvektorů,zatímvšakmůžemevyužítznalostígeometrických.
Konkrétněpromítnemevektor a ∈ V3 znázorněnýnaobrázku.Ihnedvidíme,že
Vektor a ∈ V3 mátedyvbázi(e1, e2, e3)prostoru V3 složky(α)=(011),jehoobrazmávtéžebázisložky (¯ α)=( 1 2 1 2 1).
Nyníověřímetentovýsledek,kterýjsmenazákladěgeometricképředstavyzískaliokamžitě,algebraickým postupempomocívěty4.2.Podleobrázkuurčímeobrazybáze(e1, e1, e3)amaticizobrazení.
58 KAPITOLA4.LINEÁRNÍALGEBRAPODRUHÉ
o a b ϕ(a) ϕ(b) a + b ϕ(a)+ ϕ(b)= ϕ(a + b) o ϕ(ka)= kϕ(a) ϕ(a) ka a Obr.4.27Promítánínázorně.
f
f
,kde f1 = e1 + e2
dopodprostoru L = |
1,
2|
f
2 f
3
a = e2 + e3,ϕ(a)=1
1 + f2 = 1 2 e1 + 1 2 e2 + e
Obr.4.29Maticelineárníhozobrazenívrůznýchbázích.
Vztah(4.25)simůžemesnadnozapamatovatpomocídiagramunaobrázku 4.29.Všimněme sivztahu(4.25)vespeciálnímpřípadě,kdyzobrazení ϕ zobrazujevektoryzpětdoprostoru vzorů,tj. m = n, Wm = Vn.Vtakovémpřípaděhovořímeolineárnímzobrazeníprostoru Vn do sebe.Prozápisvesložkáchbudemepochopitelněvolitjednuatutéžbáziprovyjádřenívzorů iobrazů,tj. fi = ei a fi = ei provšechnyhodnotyindexu i =1, 2,...,n.Pak M = T a
A = TAT 1,A = T 1AT = SAS 1 . (4.26)
Matice A,A ,reprezentujícílineárnízobrazení ϕ : Vn → Vn prostoruvzorůdosebe,jsou podobné.Vztah(4.26)senazývá podobnostnítransformace.
4.2.3 Vektorovépodprostoryspjatéslineárnímzobrazením
Skaždýmlineárnímzobrazením ϕ : Vn → Wm jsouautomatickyspojenyurčitévektorové podprostoryvprostoruvzorůavprostoruobrazů, jádro a obraz lineárníhozobrazení.Nežje obecnědefinujeme,osvětlímesisituacipomocívýsledkůpříkladu4.41.
Příklad4.42: Jádroaobrazlineárníhozobrazení
Interpretujmepromítánízpříkladu4.41 napříkladjakolineárnízobrazeníprostoru V3 dosebe.Popišme nejprvevšechnyvektory,kterévzniknoujakoobrazyvšechvektorůprostoru V3 lineárnímzobrazením ϕ,tj. množinuprůmětůvšechvektorůz
4.2.LINEÁRNÍZOBRAZENÍVEKTOROVÝCHPROSTORŮ 61 (e1,...,en) (e1,...,en) T (α1,...,αn) (α1 ,...,αn ) T 1 T (¯ α1 ,..., αm) (¯ α1 ,..., αm ) M 1 M (f1,...,fm) (f1,...,fn) M A ϕ Vn Wm A A = TAM 1 A = T 1A M
3 dopodprostoru L = |f1, f2|
e1, e2, e3) složky (¯ α)= α1 α2 α3 A = α1 α2 α3 1 2 1 2 0 1 2 1 2 0 001 = 1 2 (α1 + α2) 1 2 (α1 + α2) α3 , α1 , α2 , α3 mohounabývatlibovolnýchhodnot,obrazyjsouurčenydvěmanezávislýmiproměnnými β = 1 2 (α1 + + α2)a γ = α3.Všechnyobrazymajítvar β(e1 + e2)+ γe3 (β, γ jsoulibovolné)avyplňujítedydvojrozměrný vektorovýpodprostorve V3 L =Im ϕ = |e1 + e2, e3|
V
.Každýtakovýprůmětmávbázi(
Pokusmesenynípopsatvšechnyvzory,kterésepřipromítání ϕ promítnounanulovývektor.Splňujípodmínku
Odtud α1 + α2 =0, α3 =0.Hledanévzorymajítvar
L =Ker ϕ = |e1 e2| .
(e
e2)agenerujíjednorozměrný vektorovýpodprostorve V3
Podprostor L je obrazem lineárníhozobrazení ϕ a L jeho jádrem.Všimnětesi,ževektorovépodprostory L = =Im ϕ a L =Ker ϕ jsounavzájemdoplňkové,tedy L + L = V3 a L ∩ L = {o}.Doplňkovéjsoutedyijejich dimenze,dim L +dim L =3.
Definujemenynípojemobrazuajádraobecně,propřípadlineárníhozobrazení ϕ : Vn → Wm. Prostorvzorůaprostor,vněmžležíjejichobrazy,jsoutedyobecněodlišné.
MnožinyIm ϕ ⊂ Wm,resp.Ker ϕ ⊂ Vn,definovanétakto:
) ∈ Wm | a ∈ Vn}, Ker ϕ = {a ∈ Vn | ϕ(a)=0Wm } , (4.27)
nazýváme obrazem,resp. jádrem lineárníhozobrazení ϕ
Jádrolibovolnéholineárníhozobrazení ϕ : Vn → Wm jevektorovýmpodprostorem ve Vn,obrazjevektorovýmpodprostoremve Wm.
Jakprověříme,žeseopravdujednáovektorovépodprostory?Snadno.Vímejiž,žestačíověřit uzavřenostzkoumanýchpodmnožinvzhledemkalgebraickýmoperacím,tj.vzhledemksčítání vektorůanásobenívektoruskalárem.Předpokládejmetedy,ževektory b1 a b2 jsouprvkyIm ϕ.
Potomkekaždémuznichexistujevprostoru Vn alespoňjedenvzor,tj. b1 = ϕ(a1)a b2 = ϕ(a2) projistévektory a1,a2 ∈ Vn.Prolibovolnéskaláry β1 a β2 dostaneme: β1b1 + β2b2 = β1 ϕ(a1)+ β2 ϕ(a2)= ϕ(β1 a1 + β2 a2) ∈ Im ϕ.
Spolusvektory b1 a b2 tedydoIm ϕ patříijejichlibovolnálineárníkombinace.Dokázali jsmetak,žeIm ϕ ⊂ Wm jepodmnožinaprostoru Wm uzavřenávzhledemkoperacím,jetedy vektorovýmpodprostoremve Wm.Obdobněpostupujemevpřípadějádra.Zvolmelibovolné vektory a1,a2 ∈ Ker ϕ alibovolnéskaláry α1 a α2.Zobrazmepomocí ϕ lineárníkombinaci α1a1 + α2a2:
Jakovždyvpřípaděvektorovýchprostorůvznikáinyníotázka,jakjetosdimenzemiIm ϕ aKer ϕ.Budemezinimivůbecnějakývztah?Vždyťsepřecejednáopodprostoryrůzných vektorovýchprostorů!
62
KAPITOLA4.LINEÁRNÍALGEBRAPODRUHÉ
1 2(α 1 + α 2) 1 2(α 1 + α 2) α 3 =(000)
.
α1e1 α1e2 +0e3 = α1
1
Im ϕ = {ϕ(a
ϕ(α 1 a1 + α 2 a2)= α 1 ϕ(a1)+ α 2 ϕ(a2)=0Wm , neboť ϕ(a1)= ϕ(a2)=0Wm .Odtud α1a1 + α2a2 ∈ Ker ϕ
.Uvědomtesi,nakterýchmístech výpočtujsmevyužililinearityzobrazení ϕ
Pozn.: Obecněselineárnízobrazení ϕ : Vn → Vn nazývá nilpotentní,jestližeexistujepřirozené číslo m takové,že
jenulovézobrazení.
4.2.4 Projekce
Projekcejsouzvláštnímtypemlineárníchzobrazenívektorovéhoprostoru Vn dosebe.Jejich typickévlastnostijsmesijižmohlivšimnoutvpříkladu4.41,kdejsmesezabývalispeciálním případemprojekce.Vraťmesektomutopříkladu.
Příklad4.46: Opakovanépromítání
Zkusmeještějednoupromítnoutobrazvektoru a.Díkygeometricképředstavě,kterávtrojrozměrném prostoruještěneselhává,očekáváme,žedalšípromítáníjižsjednoupromítnutýmvektoremnicnovéhoneudělá.
Předchozívlastnostpředstavujeobecnoudefiničnípodmínkuproprojekci:
Všimněmesiblíževlastnostíprojekce.Projejímatici A vlibovolnébáziplatí AA = A.Je-li ϕ regulární,dostáváme A = En (zdůvodněte).Jedinouregulárníprojekcíjeidentita.
Jakoukaždéholineárníhozobrazeníbudemeiuprojekcístudovatjádroaobraz.Vpříkladu 4.45 jsmeviděli,žejádroaobrazmohoumítspolečnéprvky.Jakjetomuuprojekce?Vpříkladu4.41,kdysejednalooprojekci,bylyjádroaobraznavzájemdoplňkovýmivektorovými podprostoryve Vn,jejichjedinýmspolečnýmprvkemtedybylnulovývektor.Platítentozávěr obecně?Předpokládejme,že c ∈ Im ϕ ∩ Ker ϕ.Zpředpokladu c ∈ Im ϕ plyneexistencevzoru a,prokterý ϕ(a)= c.Odtud ϕ(c)= ϕ2(a)= ϕ(a)= c.Avšaksoučasněje c ∈ Ker ϕ,tj. ϕ(c)=0Vn .Protoje c =0Vn .Jádroaobrazprojekcemajíjedinýspolečnýprvek,nulovývektor. Zvětyodimenzijepakjižzřejmé,žejsounavzájemdoplňkovýmivektorovýmipodprostoryve Vn,tj.
4.2.LINEÁRNÍZOBRAZENÍVEKTOROVÝCHPROSTORŮ 67
ϕm = ϕ ◦ ... ◦ ϕ m
Skutečně, ϕ(a) ∼ (α 1 α 2 α 3) 1 2 1 2 0 1 2 1 2 0 001 = 1 2(α 1 + α 2) 1 2(α 1 + α 2) α 3 , ϕ ϕ a ∼ 1 2(α 1 + α 2) 1 2(α 1 + α 2) α 3 1 2 1 2 0 1 2 1 2 0 001 = 1 2(α 1 + α 2) 1 2(α 1 + α 2) α 3 ∼ ϕ(a) Prozobrazenízpříkladu4.41tedyopravduplatí ϕ2 = ϕ ◦ ϕ = ϕ
Lineárnízobrazení ϕ : Vn
Vn
projekce
, jestližeplatí ϕ 2 = ϕ, tj.ϕ ◦ ϕ(a)= ϕ(a)prolibovolné a ∈ Vn . (4.30)
→
senazývá
neboli idempotentnízobrazení