Electric Circuits 10th Edition Nilsson Solutions Manual Visit to Download in Full: https://testbankdeal.com/download/electric-circuits-10th-editi on-nilsson-solutions-manual/
2 CircuitElements
a AssessmentProblems
AP2.1
[a]Notethatthecurrent ib isinthesamecircuitbranchasthe8Acurrent source;however, ib isdefinedintheoppositedirectionofthecurrent source.Therefore,
ib = 8A
Next,notethatthedependentvoltagesourceandtheindependent voltagesourceareinparallelwiththesamepolarity.Therefore,their voltagesareequal,and
vg = ib 4 = 8 4 = 2 V
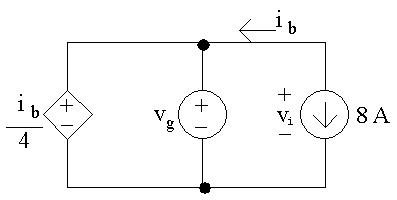
[b]Tofindthepowerassociatedwiththe8Asource,weneedtofindthe voltagedropacrossthesource, vi.Notethatthetwoindependentsources areinparallel,andthatthevoltages vg and v1 havethesamepolarities, sothesevoltagesareequal:
vi = vg = 2V
Usingthepassivesignconvention, ps =(8A)(vi)=(8A)( 2V)= 16W
Thusthecurrentsourcegenerated16Wofpower.
2–1 © 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458. Electric Circuits 10th Edition Nilsson Solutions Manual Visit TestBankDeal.com to get complete for all chapters
AP2.2
AP2.3
[a]Notefromthecircuitthat vx = 25V.Tofind α notethatthetwo currentsourcesareinthesamebranchofthecircuitbuttheircurrents flowinoppositedirections.Therefore
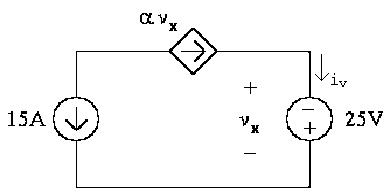
αvx = 15A
Solvetheaboveequationfor α andsubstitutefor vx,
α = 15A vx = 15A 25V =0.6A/V
[b]Tofindthepowerassociatedwiththevoltagesourceweneedtoknowthe current, iv .Notethatthiscurrentisinthesamebranchofthecircuitas thedependentcurrentsourceandthesetwocurrentsflowinthesame direction.Therefore,thecurrent iv isthesameasthecurrentofthe dependentsource:
iv = αvx =(0.6)( 25)= 15A
Usingthepassivesignconvention, ps = (iv )(25V)= ( 15A)(25V)=375W
Thusthevoltagesourcedissipates375W.
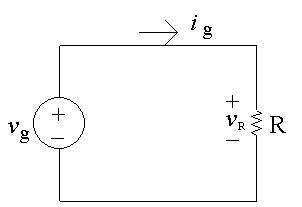
[a]Theresistorandthevoltagesourceareinparallelandtheresistorvoltage andthevoltagesourcehavethesamepolarities.Thereforethesetwo voltagesarethesame:
vR = vg =1kV
2–2 CHAPTER2.CircuitElements
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
AP2.4
Notefromthecircuitthatthecurrentthroughtheresistoris ig =5mA. UseOhm’slawtocalculatethevalueoftheresistor:
R = vR ig = 1 kV 5mA = 200kΩ
Usingthepassivesignconventiontocalculatethepowerintheresistor,
pR =(vR)(ig)=(1kV)(5mA)=5W Theresistorisdissipating5Wofpower.
[b]Notefrompart(a)the vR = vg and iR = ig .Thepowerdeliveredbythe sourceisthus
psource = vgig so vg = psource ig = 3 W 75mA = 40V
Sincewenowhavethevalueofboththevoltageandthecurrentforthe resistor,wecanuseOhm’slawtocalculatetheresistorvalue:
R = vg ig = 40V 75mA = 533 33Ω
Thepowerabsorbedbytheresistormustequalthepowergeneratedby thesource.Thus,
pR = psource = ( 3W)=3W
[c]Again,notethe iR = ig.Thepowerdissipatedbytheresistorcanbe determinedfromtheresistor’scurrent:
pR = R(iR)2 = R(ig )2
Solvingfor ig ,
i2 g = pr R = 480mW 300Ω = 0.0016so ig = √0.0016=0.04A=40mA
Then,since vR = vg
vR = RiR = Rig =(300Ω)(40mA)=12Vso vg =12V
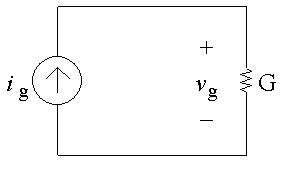
[a]Notefromthecircuitthatthecurrentthroughtheconductance G is ig , flowingfromtoptobottom,becausethecurrentsourceandthe
Problems 2–3
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
conductanceareinthesamebranchofthecircuitsomusthavethesame current.Thevoltagedropacrossthecurrentsourceis vg,positiveatthe top,becausethecurrentsourceandtheconductancearealsoinparallel somusthavethesamevoltage.FromaversionofOhm’slaw,
vg = ig G = 0 5 A 50mS = 10V
Nowthatweknowthevoltagedropacrossthecurrentsource,wecan findthepowerdeliveredbythissource:
psource = vgig = (10)(0.5)= 5W
Thusthecurrentsourcedelivers5Wtothecircuit.
[b]Wecanfindthevalueoftheconductanceusingthepower,andthevalue ofthecurrentusingOhm’slawandtheconductancevalue:
[c]Wecanfindthevoltagefromthepowerandtheconductance,andthen usethevoltagevalueinOhm’slawtofindthecurrent:
= 40,000=200V
AP2.5 [a] Redrawthecircuitwithallofthevoltagesandcurrentslabeledforevery circuitelement.
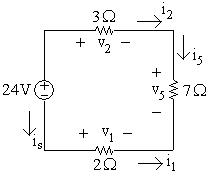
WriteaKVLequationclockwisearoundthecircuit,startingbelowthe voltagesource:
24V+ v2 + v5 v1 =0
Next,useOhm’slawtocalculatethethreeunknownvoltagesfromthe threecurrents:
2–4 CHAPTER2.CircuitElements
pg
g so G = pg v2 g = 9 152 = 0.04S=40mS i
g =(40mS)(15V)=0.6A
= Gv2
g = Gv
pg
Gv2 g so v 2 g = pg G = 8 W 200 µS = 40,000
=
Thus vg
ig = Gvg =(200 µS)(200V)=0 04A=40mA
v2 =3i2; v5 =7i5; v1 =2i1 © 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
AKCLequationattheupperrightnodegives i2 = i5;aKCLequationat thebottomrightnodegives i5 = i1;aKCLequationattheupperleft nodegives is = i2.Nowreplacethecurrents i1 and i2 intheOhm’slaw equationswith i5:
v2 =3i2 =3i5; v5 =7i5; v1 =2i1 = 2i5
Nowsubstitutetheseexpressionsforthethreevoltagesintothefirst equation:
24= v2 + v5 v1 =3i5 +7i5 ( 2i5)=12i5 Therefore i5 =24/12=2A
[b] v1 = 2i5 = 2(2)= 4V
[c] v2 =3i5 =3(2)=6V
[d] v5 =7i5 =7(2)=14V
[e]
AKCLequationatthelowerleftnodegives is = i1.Since i1 = i5, is = 2A.Wecannowcomputethepowerassociatedwiththevoltage source:
p24 =(24)is =(24)( 2)= 48W
Therefore24Vsourceisdelivering48W.
AP2.6Redrawthecircuitlabelingallvoltagesandcurrents:
Wecanfindthevalueoftheunknownresistorifwecanfindthevalueofits voltageanditscurrent.Tostart,writeaKVLequationclockwisearoundthe rightloop,startingbelowthe24Ωresistor:
120V+ v3 =0
UseOhm’slawtocalculatethevoltageacrossthe8Ωresistorintermsofits current:
v3 =8i3
Substitutetheexpressionfor v3 intothefirstequation:
120V+8i3 =0so i3 = 120 8 = 15A
Problems 2–5
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
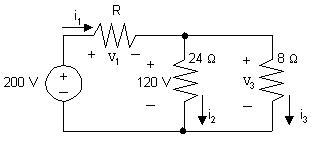
AlsouseOhm’slawtocalculatethevalueofthecurrentthroughthe24Ω resistor:
i2 = 120V 24Ω = 5A
NowwriteaKCLequationatthetopmiddlenode,summingthecurrents leaving:
i1 + i2 + i3 =0so i1 = i2 + i3 =5+15=20A
WriteaKVLequationclockwisearoundtheleftloop,startingbelowthe voltagesource:
200V+ v1 +120V=0so v1 =200 120=80V
Nowthatweknowthevaluesofboththevoltageandthecurrentforthe unknownresistor,wecanuseOhm’slawtocalculatetheresistance:
R= v1 i1 = 80 20 = 4Ω
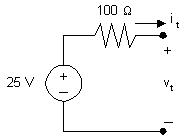
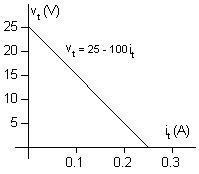
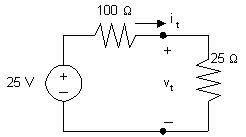
AP2.7 [a] Plottingagraphof vt versus it gives
Notethatwhen it = 0, vt =25V;thereforethevoltagesourcemustbe25 V.Sincetheplotisastraightline,itsslopecanbeusedtocalculatethe valueofresistance:
R = ∆v ∆i = 25 0 0 25 0 = 25 0 25 =100Ω
Acircuitmodelhavingthesame v i characteristicisa25Vsourcein serieswitha100Ωresistor,asshownbelow:
2–6 CHAPTER2.CircuitElements
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
AP2.8 [a]
Drawthecircuitmodelfrompart(a)andattacha25Ωresistor:
Tofindthepowerdeliveredtothe25Ωresistorwemustcalculatethe currentthroughthe25Ωresistor.DothisbyfirstusingKCLtorecognize thatthecurrentineachofthecomponentsis it,flowinginaclockwise direction.WriteaKVLequationintheclockwisedirection,starting belowthevoltagesource,andusingOhm’slawtoexpressthevoltage dropacrosstheresistorsinthedirectionofthecurrent it flowingthrough theresistors:
25V+100it +25it =0so125it =25so it = 25 125 = 0 2A
Thus,thepowerdeliveredtothe25Ωresistoris
p25 =(25)i2 t =(25)(0.2)2 =1W.
FromthegraphinAssessmentProblem2.7(a),weseethatwhen vt =0, it =0.25A.Thereforethecurrentsourcemustbe0.25A.Sincetheplot isastraightline,itsslopecanbeusedtocalculatethevalueofresistance:
R = ∆v ∆i = 25 0 0.25 0 = 25 0.25 =100Ω
Acircuitmodelhavingthesame v i characteristicisa0.25Acurrent sourceinparallelwitha100Ωresistor,asshownbelow: [b]
Drawthecircuitmodelfrompart(a)andattacha25Ωresistor:
NotethatbywritingaKVLequationaroundtherightloopweseethat thevoltagedropacrossbothresistorsis vt.WriteaKCLequationatthe topcenternode,summingthecurrentsleavingthenode.UseOhm’slaw
Problems 2–7
[b]
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
tospecifythecurrentsthroughtheresistorsintermsofthevoltagedrop acrosstheresistorsandthevalueoftheresistors.
0.25+ vt 100 + vt 25 = 0, so5vt =25, thus vt =5V
p25 = v2 t 25 = 1W
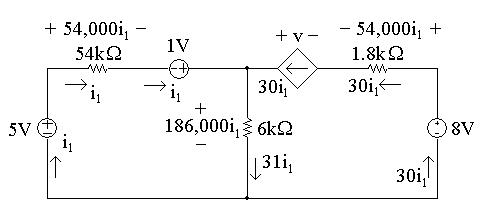
AP2.9Firstnotethatweknowthecurrentthroughallelementsinthecircuitexcept the6kΩresistor(thecurrentinthethreeelementstotheleftofthe6kΩ resistoris i1;thecurrentinthethreeelementstotherightofthe6kΩresistor is30i1).Tofindthecurrentinthe6kΩresistor,writeaKCLequationatthe topnode:
i1 +30i1 = i6k =31i1
WecanthenuseOhm’slawtofindthevoltagesacrosseachresistorinterms of i1.Theresultsareshowninthefigurebelow:
[a] Tofind i1,writeaKVLequationaroundtheleft-handloop,summing voltagesinaclockwisedirectionstartingbelowthe5Vsource:
5V+54,000i1 1V+186,000i1 =0
Solvingfor i1
54,000i1 +186,000i1 =6Vso240,000i1 =6V
Thus, i1 = 6 240,000 =25 µA
[b] Nowthatwehavethevalueof i1,wecancalculatethevoltageforeach componentexceptthedependentsource.ThenwecanwriteaKVL equationfortheright-handlooptofindthevoltage v ofthedependent source.Sumthevoltagesintheclockwisedirection,startingtotheleftof thedependentsource:
+v 54,000i1 +8V 186,000i1 =0
2–8 CHAPTER2.CircuitElements
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Wenowknowthevaluesofvoltageandcurrentforeverycircuitelement. Let’sconstructapowertable:
[c] Thetotalpowergeneratedinthecircuitisthesumofthenegativepower valuesinthepowertable:
Thus,thetotalpowergeneratedinthecircuitis6150 µW.
[d] Thetotalpowerabsorbedinthecircuitisthesumofthepositivepower valuesinthepowertable:
Thus,thetotalpowerabsorbedinthecircuitis6150 µW.
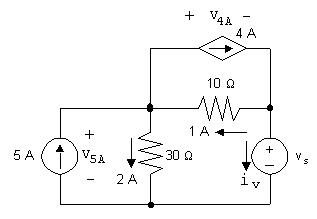
AP2.10Giventhat iφ =2A,weknowthecurrentinthedependentsourceis 2iφ =4A.WecanwriteaKCLequationattheleftnodetofindthecurrentin the10Ωresistor.Summingthecurrentsleavingthenode,
5A+2A+4A+ i10Ω =0so i10Ω =5A 2A 4A= 1A
Thus,thecurrentinthe10Ωresistoris1A,flowingrighttoleft,asseenin thecircuitbelow.
Problems 2–9
v =240,000i1 8V=240,000(25 × 10 6 ) 8V=6V 8V= 2V
Thus,
Element Current Voltage Power Power (µA) (V) Equation (µW) 5V 25 5 p = vi 125 54kΩ 25 1 35 p = Ri2 33 75 1V 25 1 p = vi 25 6kΩ 775 4.65 p = Ri2 3603.75 Dep.source 750 2 p = vi 1500 1.8 kΩ 750 1.35 p = Ri2 1012.5 8V 750 8 p = vi 6000
125 µW+ 25 µW+ 6000 µW= 6150 µW
µW+1500 µW+1012 5 µW=6150
33 75 µW+3603 75
µW
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
[a] Tofind vs,writeaKVLequation,summingthevoltagescounter-clockwise aroundthelowerrightloop.Startbelowthevoltagesource.
vs +(1A)(10Ω)+(2A)(30Ω)=0so vs =10V+60V=70V
[b] ThecurrentinthevoltagesourcecanbefoundbywritingaKCLequation attheright-handnode.Sumthecurrentsleavingthenode
4A+1A+ iv =0so iv =4A 1A=3A
Thecurrentinthevoltagesourceis3A,flowingtoptobottom.The powerassociatedwiththissourceis
p = vi =(70V)(3A)=210W
Thus,210Wareabsorbedbythevoltagesource.
[c] Thevoltagedropacrosstheindependentcurrentsourcecanbefoundby writingaKVLequationaroundtheleftloopinaclockwisedirection:
v5A +(2A)(30Ω)=0so v5A =60V
Thepowerassociatedwiththissourceis
p = v5Ai = (60V)(5A)= 300W
Thissourcethusdelivers300Wofpowertothecircuit.
[d] Thevoltageacrossthecontrolledcurrentsourcecanbefoundbywritinga KVLequationaroundtheupperrightloopinaclockwisedirection:
+v4A +(10Ω)(1A)=0so v4A = 10V
Thepowerassociatedwiththissourceis
p = v4Ai =( 10V)(4A)= 40W
Thissourcethusdelivers40Wofpowertothecircuit.
[e] Thetotalpowerdissipatedbytheresistorsisgivenby (i30Ω)2(30Ω)+(i10Ω)2(10Ω)=(2)2(30Ω)+(1)2(10Ω)=120+10=130W
2–10 CHAPTER2.CircuitElements
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ
07458.
Problems
P2.1 [a] Yes,independentvoltagesourcescancarrythe5Acurrentrequiredbythe connection;independentcurrentsourcecansupportanyvoltagerequired bytheconnection,inthiscase5V,positiveatthebottom.
[b] 20Vsource:absorbing
15Vsource:developing(delivering)
5Asource:developing(delivering)
[c] P20V =(20)(5)=100W(abs)
P15V = (15)(5)= 75W(dev/del)
P5A = (5)(5)= 25W(dev/del)
Pabs = Pdel =100W
[d] Theinterconnectionisvalid,butinthiscircuitthevoltagedropacrossthe 5Acurrentsourceis35V,positiveatthetop;20Vsourceisdeveloping (delivering),the15Vsourceisdeveloping(delivering),andthe5A sourceisabsorbing:
P20V = (20)(5)= 100W(dev/del)
P15V = (15)(5)= 75W(dev/del)
P5A =(35)(5)=175W(abs)
Pabs = Pdel =175W
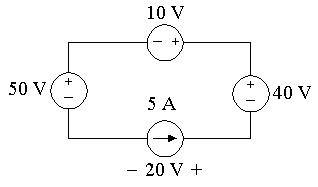
P2.2Theinterconnectisvalidsincethevoltagesourcescanallcarry5Aofcurrent suppliedbythecurrentsource,andthecurrentsourcecancarrythevoltage droprequiredbytheinterconnection.Notethatthebranchcontainingthe10 V,40V,and5Asourcesmusthavethesamevoltagedropasthebranch containingthe50Vsource,sothe5Acurrentsourcemusthaveavoltage dropof20V,positiveattheright.Thevoltagesandcurrentsaresummarize inthecircuitbelow:
Problems 2–11
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
P50V =(50)(5)=250W(abs)
P10V =(10)(5)=50W(abs)
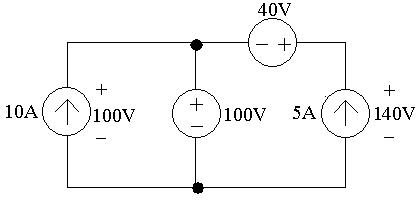
P40V = (40)(5)= 200W(dev)
P5A = (20)(5)= 100W(dev)
Pdev =300W
P2.3Theinterconnectionisvalid.The10Acurrentsourcehasavoltagedropof 100V,positiveatthetop,becausethe100Vsourcesuppliesitsvoltagedrop acrossapairofterminalssharedbythe10Acurrentsource.Therighthand branchofthecircuitmustalsohaveavoltagedropof100Vfromtheleft terminalofthe40Vsourcetothebottomterminalofthe5Acurrentsource, becausethisbranchsharesthesameterminalsasthe100Vsource.This meansthatthevoltagedropacrossthe5Acurrentsourceis140V,positiveat thetop.Also,thetwovoltagesourcescancarrythecurrentrequiredofthe interconnection.Thisissummarizedinthefigurebelow:
Fromthevaluesofvoltageandcurrentinthefigure,thepowersuppliedbythe currentsourcesiscalculatedasfollows:
P10A = (100)(10)= 1000W(1000Wsupplied)
P5A = (140)(5)= 700W(700Wsupplied)
Pdev =1700W
P2.4Theinterconnectionisnotvalid.Notethatthe3Aand4Asourcesareboth connectedinthesamebranchofthecircuit.Avalidinterconnectionwould requirethesetwocurrentsourcestosupplythesamecurrentinthesame direction,whichtheydonot.
P2.5Theinterconnectionisvalid,sincethevoltagesourcescancarrythecurrents suppliedbythe2Aand3Acurrentsources,andthecurrentsourcescan carrywhatevervoltagedropfromthetopnodetothebottomnodeisrequired bytheinterconnection.Inparticular,notethethevoltagedropbetweenthe topandbottomnodesintherighthandbranchmustbethesameasthe voltagedropbetweenthetopandbottomnodesinthelefthandbranch.In particular,thismeansthat
2–12 CHAPTER2.CircuitElements
v1 +8V=12V+ v2 © 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Henceanycombinationof v1 and v2 suchthat v1 + v2 = 4Visavalid solution.
P2.6 [a] Becausebothcurrentsourcesareinthesamebranchofthecircuit,their valuesmustbethesame.Therefore,
v1 50 = 0 4 → v1 =0 4(50)=20V
[b]
p = v1(0 4)=(20)(0 4)=8W(absorbed)
P2.7 [a] Thevoltagedropfromthetopnodetothebottomnodeinthiscircuit mustbethesameforeverypathfromthetoptothebottom.Therefore, thevoltagesofthetwovoltagesourcesareequal:
αi∆ =6
Also,thecurrent i∆ isinthesamebranchasthe15mAcurrentsource, butintheoppositedirection,so
i∆ = 0.015
Substituting,
α( 0.015)=6 → α = 6 0 015 =400 Theinterconnectionisvalidif α =400V/A.
[b] Thevoltageacrossthecurrentsourcemustequalthevoltageacrossthe6 Vsource,sincebothareconnectedbetweenthetopandbottomnodes. Usingthepassivesignconvention,
p = vi =(6)(0.015)=0.09=90mW
[c] Sincethepowerispositive,thecurrentsourceisabsorbingpower.
P2.8 [a] Yes,eachofthevoltagesourcescancarrythecurrentrequiredbythe interconnection,andeachofthecurrentsourcescancarrythevoltage droprequiredbytheinterconnection.(Notethat i1 =50mA.)
[b] No,becausethevoltagedropbetweenthetopterminalandthebottom terminalcannotbedetermined.Forexample,define v1, v2,and v3 as shown:
Problems 2–13
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Thevoltagedropacrosstheleftbranch,thecenterbranch,andtheright branchmustbethesame,sincethesebranchesareconnectedatthesame twoterminals.Thisrequiresthat
v1 20= v2 = v3 +30
Butthisequationhasthreeunknownvoltages,sotheindividualvoltages cannotbedetermined,andthusthepowerofthesourcescannotbe determined.
P2.9Theinterconnectionisinvalid.Inthemiddlebranch,thevalueofthecurrent ix mustbe50mA,sincethe50mAcurrentsourcesuppliescurrentinthis branchinthesamedirectionasthecurrent ix.Therefore,thevoltagesupplied bythedependentvoltagesourceintherighthandbranchis1800(0 05)=90
V.Thisgivesavoltagedropfromthetopterminaltothebottomterminalin therighthandbranchof90+60=150V.Butthevoltagedropbetweenthese sameterminalsinthelefthandbranchis30V,duetothevoltagesourcein thatbranch.Therefore,theinterconnectionisinvalid.
P2.10
First,10va = 5V,so va =0.5V.Thenrecognizethateachofthethree branchesisconnectedbetweenthesametwonodes,soeachofthesebranches musthavethesamevoltagedrop.Thevoltagedropacrossthemiddlebranch is5V,andsince va =0.5V, vg =0.5 5= 4.5V.Also,thevoltagedrop acrosstheleftbranchis5V,so20+ v9A =5V,and v9A = 15V,where v9A ispositiveatthetop.Notethatthecurrentthroughthe20Vsourcemustbe 9A,flowingfromtoptobottom,andthecurrentthroughthe vg is6Aflowing fromtoptobottom.Let’sfindthepowerassociatedwiththeleftandmiddle branches:
p9A =(9)( 15)= 135W
p20V =(9)(20)=180W
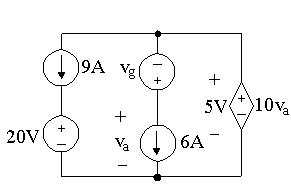
pvg = (6)( 4.5)=27W
p6A =(6)(0.5)=3W
Sincethereisonlyonecomponentleft,wecanfindthetotalpower:
ptotal = 135+180+27+3+ pds =75+ pds =0
so pds mustequal 75W.
Therefore,
2–14 CHAPTER2.CircuitElements
Pdev = Pabs =210W © 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
P2.11 [a] UsingthepassivesignconventionandOhm’slaw, v = Ri =(3000)(0 015)=45V
[b] PR = v2 R = 452 3000 = 0 675=675mW
[c] Usingthepassivesignconventionwiththecurrentdirectionreversed, v = Ri = (3000)(0.015)= 45V
PR = v2 R = 452 3000 = 0 675=675mW
P2.12 [a] UsingthepassivesignconventionandOhm’slaw, i = v R = 40 2500 = 0.016= 16mA
[b] PR = Ri2 =(2500)( 0.016)2 =0.64=640mW
[c] Usingthepassivesignconventionwiththevoltagepolarityreversed, i = v R = 40 2500 = 0.016=16mA
PR = Ri2 =(2500)(0 016)2 =0 64=640mW
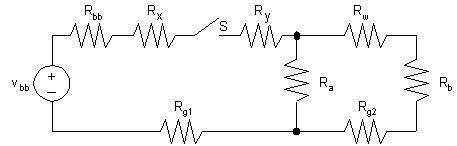
P2.13 [a]
[b] Vbb =no-loadvoltageofbattery
Rbb =internalresistanceofbattery
Rx =resistanceofwirebetweenbatteryandswitch
Ry =resistanceofwirebetweenswitchandlampA
Ra =resistanceoflampA
Rb =resistanceoflampB
Rw =resistanceofwirebetweenlampAandlampB
Rg1 =resistanceofframebetweenbatteryandlampA
Rg2 =resistanceofframebetweenlampAandlampB
S =switch
Problems 2–15
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
P2.14Sinceweknowthedeviceisaresistor,wecanuseOhm’slawtocalculatethe resistance.FromFig.P2.14(a),
P2.15Sinceweknowthedeviceisaresistor,wecanusethepowerequation.From
P2.16Theresistorvalueistheratioofthepowertothesquareofthecurrent:
P2.17Labeltheunknownresistorcurrentsandvoltages:
2–16 CHAPTER2.CircuitElements
v = Ri so R = v i UsingthevaluesinthetableofFig.P2.14(b), R = 7200 6 = 3600 3 = 3600 3 = 7200 6 = 10,800 9 = 1 2kΩ NotethatthisvalueisfoundinAppendixH.
p = vi = v2 R so R = v2 p UsingthevaluesinthetableofFig.P2.13(b) R = ( 8)2 640 × 10 3 = ( 4)2 160 × 10 3 = (4)2 160 × 10 3 = (8)2 640 × 10 3 = (12)2 1440 × 10 3 = (16)2 2560 × 10 3 =100Ω NotethatthisvalueisfoundinAppendixH.
Fig.P2.15(a),
R = p i2 . UsingthevaluesforpowerandcurrentinFig.P2.16(b), 8 25 × 10 3 (0 5 × 10 3 )2 = 33 × 10 3 (1 × 10 3)2 = 74 25 × 10 3 (1 5 × 10 3 )2 = 132 × 10 3 (2 × 10 3 )2 = 206.25 × 10 3 (2.5 × 10 3 )2 = 297 × 10 3 (3 × 10 3 )2 =33kΩ NotethatthisisavaluefromAppendixH.
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
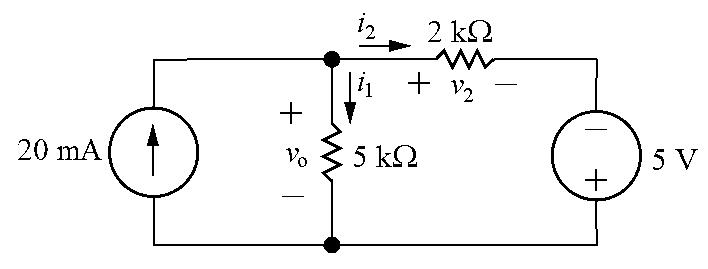
[a]
KCLatthetopnode:0 02= i1 + i2
KVLaroundtherightloop: vo + v2 5=0
UseOhm’slawtowritetheresistorvoltagesinthepreviousequationin termsoftheresistorcurrents:
MultiplytheKCLequationby
Solving,
1 = 35 7000 =0.005=5mA Therefore,
Problems 2–17
5=0
5000i1 +2000i2
→−5000i1 +2000i2 =5
2: 2000(i1 + i2)+( 5000i1 +2000i2 )= 2000(0.02)+5 →−7000i1 = 35
vo
[b] p20mA = (0.02)vo = (0.02)(25)= 0.5W i2 =0 02 i1 =0 02 0 005=0 015A p5V = (5)i2 = (5)(0.015)= 0.075W p5k =5000i2 1 =5000(0 005)2 =0 125W p2k =2000i2 2 =2000(0.015)2 =0.45W ptotal = p20mA + p5V + p5k + p2k = 0 5 0 075+0 125+0 45=0 Thusthepowerinthecircuitbalances. P2.18 [a] 20ia = 80ib ig = ia + ib =5ib ia =4ib 50=4ig +80ib =20ib +80ib =100ib ib =0.5A,therefore, ia =2Aand ig =2.5A [b] ib =0.5A [c] vo =80ib =40V © 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
2000andaddittotheKVLequationto eliminate i
i
= Ri1 =(5000)(0 005)=25V
P2.19
[d] p4Ω = i2 g (4)=6.25(4)=25W
p20Ω = i2 a(20)=(4)(20)=80W
p80Ω = i2 b(80)=0 25(80)=20W
[e] p50V (delivered)=50ig =125W
Check:
Pdis =25+80+20=125W
Pdel =125W
[a] WriteaKCLequationatthetopnode:
1.5+ i1 + i2 =0so i1 + i2 =1.5
WriteaKVLequationaroundtherightloop:
v1 + v2 + v3 =0
FromOhm’slaw,
v1 =100i1 ,v2 =150i2,v3 =250i2 Substituting, 100i1 +150i2 +250i2 =0so 100i1 +400i2 =0
Solvingthetwoequationsfor i1 and i2 simultaneously, i1 =1 2Aand i2 =0 3A
[b] WriteaKVLequationclockwisearoundtheleftloop:
vo + v1 =0but v1 =100i1 =100(1.2)=120V
So vo = v1 =120V
[c] Calculatepowerusing p = vi forthesourceand p = Ri2 fortheresistors:
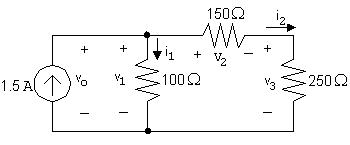
psource = vo(1 5)= (120)(1 5)= 180W
p100Ω =1 22(100)=144W
p150Ω =0 32(150)=13 5W
p250Ω =0.32(250)=22.5W
Pdev =180W Pabs =144+13 5+22 5=180W
2–18 CHAPTER2.CircuitElements
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
P2.20Labeltheunknownresistorvoltagesandcurrents:
[a] ia = 3.5 175 = 0 02A(Ohm’slaw)
i1 = ia =0.02A(KCL)
[b] vb =200i1 =200(0.02)=4V(Ohm’slaw)
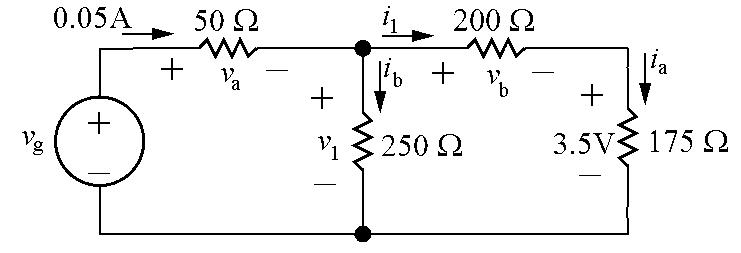
v1 + vb +3.5=0so v1 =3.5+ vb =3.5+4=7.5V(KVL)
[c] va =0.05(50)=2.5V(Ohm’slaw)
vg + va + v1 =0so vg = va + v1 =2 5+7 5=10V(KVL)
[d] pg = vg(0 05)=10(0 05)=0 5W
P2.21 [a] UseKVLfortherightlooptocalculatethevoltagedropacrossthe right-handbranch vo.Thisisalsothevoltagedropacrossthemiddle branch,soonce vo isknown,useOhm’slawtocalculate io:
vo =1000ia +4000ia +3000ia =8000ia =8000(0 002)=16V
16=2000io
io = 16 2000 = 8mA
[b] KCLatthetopnode: ig = ia + io =0.002+0.008=0.010A=10mA.
[c] Thevoltagedropacrossthesourceis v0,seenbywritingaKVLequation fortheleftloop.Thus,
pg = voig = (16)(0.01)= 0.160W= 160mW. Thusthesourcedelivers160mW.
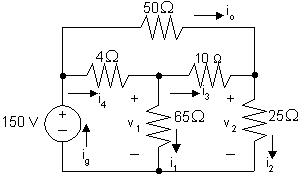
v2 = 150 50(1)=100V
Problems 2–19
P2.22 [a]
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
i2 = v2 25 = 4A
i3 +1= i2,i3 =4 1=3A
v1 =10i3 +25i2 =10(3)+25(4)=130V
i1 = v1 65 = 130 65 = 2A
Notealsothat
i4 = i1 + i3 =2+3=5A
ig = i4 + io =5+1=6A
[b] p4Ω =52(4)=100W
p50Ω =12(50)=50W
p65Ω =22(65)=260W
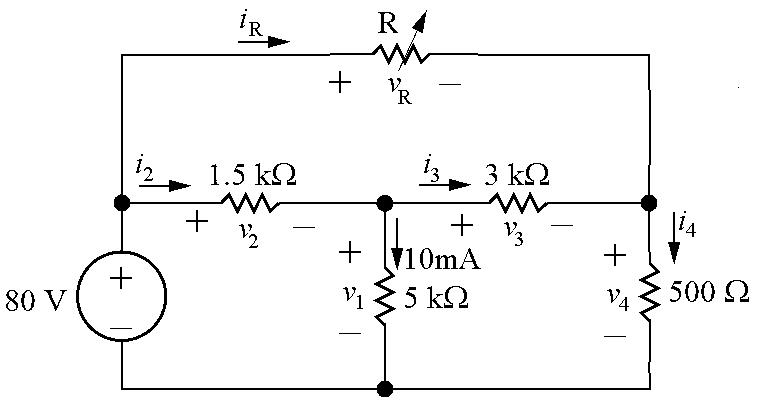
p10Ω =32(10)=90W
p25Ω =42(25)=400W
[c] Pdis =100+50+260+90+400=900W
Pdev =150ig =150(6)=900W
P2.23Labelallunknownresistorvoltagesandcurrents:
2–20 CHAPTER2.CircuitElements
Ohms’lawfor5kΩresistor: v1 = (0.01)(5000)=50V KVLforlowerleftloop: 80+ v2 +50=0 → v2 =80 50=30V Ohm’slawfor1.5kΩresistor: i2 = v2/1500=30/1500=20mA KCLatcenternode: i2 = i3 +0.01 → i3 = i2 0.01=0.02 0.01=0.01=10mA Ohm’slawfor3kΩresistor v3 =3000i3 =3000(0 01)=30V KVLforlowerrightloop: v1 + v3 + v4 =0 → v4 = v1 v3 =50 30=20V © 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Ohm’slawfor500Ωresistor: i4 = v4/500=20/500=0 04=40mA
KCLforrightnode:
i3 + iR = i4 → iR = i4 i3 =0 04 0 01=0 03=30mA
KVLforouterloop:
80+ vR + v4 =0 → vR =80 v4 =80 20=60V
Therefore, R = vR iR = 60 0.03 =2000=2kΩ
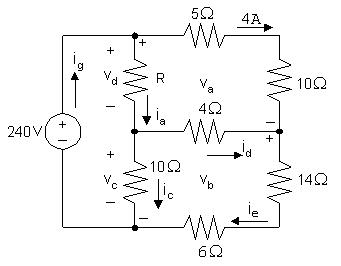
P2.24 [a]
va = (5+10)(4)=60V
240+ va + vb =0so vb =240 va =240 60=180V
ie = vb/(14+6)=180/20=9A
id = ie 4=9 4=5A
vc =4id + vb =4(5)+180=200V
ic = vc/10=200/10=20A
vd =240 vc =240 200=40V
ia = id + ic =5+20=25A
R = vd/ia =40/25=1.6Ω
[b] ig = ia +4=25+4=29A pg (supplied)=(240)(29)=6960W
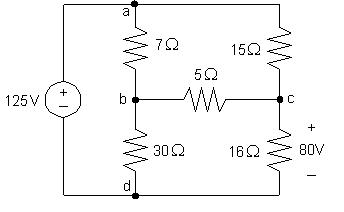
P2.25 [a]
icd =80/16=5A
vac =125 80=45so iac =45/15=3A
Problems 2–21
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
iac + ibc = icd so ibc =5 3=2A
vab =15iac 5ibc =15(3) 5(2)=35Vso iab =35/7=5A
ibd = iab ibc =5 2=3A
Calculatethepowerdissipatedbytheresistorsusingtheequation
pR = Ri2 R:
p7Ω =(7)(5)2 =175W p30Ω =(30)(3)2 =270W
p15Ω =(15)(3)2 =135W p16Ω =(16)(5)2 =400W
p5Ω =(5)(2)2 =20W
[b] Calculatethecurrentthroughthevoltagesource:
iad = iab iac = 5 3= 8A
Nowthatwehaveboththevoltageandthecurrentforthesource,wecan calculatethepowersuppliedbythesource:
pg =125( 8)= 1000Wthus pg (supplied)=1000W
[c] Pdis =175+270+135+400+20=1000W
Therefore, Psupp = Pdis
P2.26 [a] v2 = 100+4(15)=160V; v1 =160 (9+11+10)(2)=100V
2–22 CHAPTER2.CircuitElements
i1 = v1 4+16 =
20 = 5A; i3 = i1 2=5 2=3A vg = v1 +30i3 =100+30(3)=190V
4
4
3
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
100
i
=2+4=6A ig = i
i
= 6 3= 9A
[b] Calculatepowerusingtheformula p = Ri2:
p9Ω =(9)(2)2 =36W; p11Ω =(11)(2)2 =44W
p10Ω =(10)(2)2 =40W; p5Ω =(5)(6)2 =180W
p30Ω =(30)(3)2 =270W; p4Ω =(4)(5)2 =100W
p16Ω =(16)(5)2 =400W; p15Ω =(15)(4)2 =240W
[c] vg =190V
[d] Sumthepowerdissipatedbytheresistors:
pdiss =36+44+40+180+270+100+400+240=1310W
Thepowerassociatedwiththesourcesis
pvolt source =(100)(4)=400W
pcurr source = vg ig =(190)( 9)= 1710W
Thusthetotalpowerdissipatedis1310+400=1710Wandthetotal powerdevelopedis1710W,sothepowerbalances.
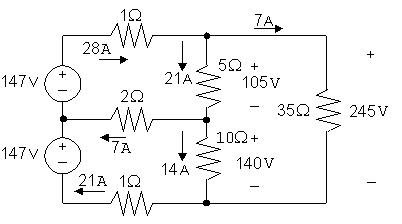
P2.27 [a]
Startbycalculatingthevoltagedropsduetothecurrents i1 and i2.Then useKVLtocalculatethevoltagedropacrossand35Ωresistor,and Ohm’slawtofindthecurrentinthe35Ωresistor.Finally,KCLateach ofthemiddlethreenodesyieldsthecurrentsinthetwosourcesandthe currentinthemiddle2Ωresistor.Thesecalculationsaresummarizedin thefigurebelow:
p147(top) = (147)(28)= 4116W
p147(bottom) = (147)(21)= 3087W
Thereforethetopsourcesupplies4116Wofpowerandthebottom sourcesupplies3087Wofpower. [b]
Psup =4116+3087=7203W
Therefore, Pdis = Psup =7203W
Problems 2–23
Pdis =(28)2 (1)+(7)2(2)+(21)2(1)+(21)2 (5)+(14)2 (10)+(7)2(35) =784+98+441+2205+1960+1715=7203W
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
P2.28 [a] Plotthe v i characteristic
Fromtheplot: R = ∆v ∆i = (130 50) (10 0) =8Ω
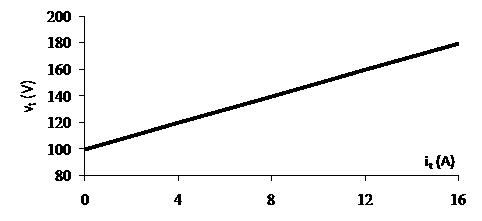
When it =0, vt =50V;thereforetheidealvoltagesourcehasavoltage of50V.
When vt = 0,it = 50 8 = 6 25A
Notethatthisresultcanalsobeobtainedbyextrapolatingthe v i characteristicto vt =0.
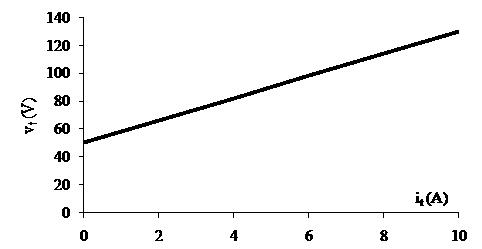
P2.29 [a] Plotthe v i characteristic:
2–24 CHAPTER2.CircuitElements
[b]
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Problems 2–25
Fromtheplot:
R = ∆v ∆i = (180 100) (16 0) =5Ω
When it =0, vt =100V;thereforetheidealcurrentsourcemusthavea currentof100/5=20A
[b]
Weattacha20Ωresistortothedevicemodeldevelopedinpart(a):
WriteaKCLequationatthetopnode:
20+ it = i1
WriteaKVLequationfortherightloop,inthedirectionofthetwo currents,usingOhm’slaw:
5i1 +20it =0
Combiningthetwoequationsandsolving, 5(20+ it)+20it =0so25it = 100;thus it = 4A
Nowcalculatethepowerdissipatedbytheresistor:
p20Ω =20i2 t =20( 4)2 =320W
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
P2.30 [a]
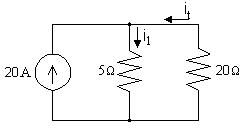
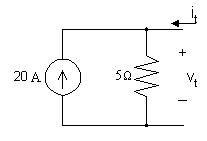
[b] ∆v =25V;∆i =2.5mA; R = ∆v ∆i = 10kΩ
[c] 10,000i1 =2500is ,i1 =0.25is 0.02= i1 + is =1.25is,is =16mA
[d] vs(opencircuit)=(20 × 10 3)(10 × 103 )=200V
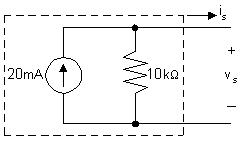
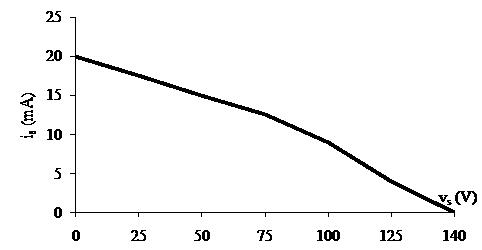
[e] Theopencircuitvoltagecanbefoundinthetableofvalues(orfromthe plot)asthevalueofthevoltage vs whenthecurrent is =0.Thus, vs(opencircuit)=140V(fromthetable)
[f] Linearmodelcannotpredictthenonlinearbehaviorofthepractical currentsource.
P2.31 [a] Beginbyconstructingaplotofvoltageversuscurrent:
[b] Sincetheplotislinearfor0 ≤ is ≤ 24mAamdsince R =∆v/∆i,wecan calculate R fromtheplottedvaluesasfollows:
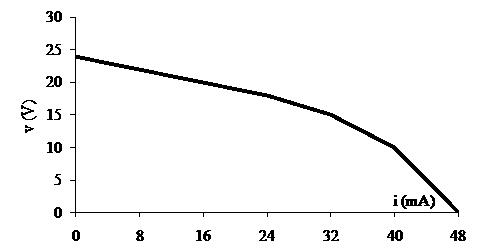
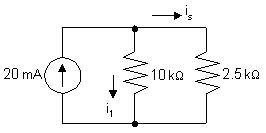
R = ∆v ∆i = 24 18 0.024 0 = 6 0.024 =250Ω
Wecandeterminethevalueoftheidealvoltagesourcebyconsideringthe valueof vs when is =0.Whenthereisnocurrent,thereisnovoltage dropacrosstheresistor,soallofthevoltagedropattheoutputisdueto thevoltagesource.Thusthevalueofthevoltagesourcemustbe24V.
Themodel,validfor0 ≤ is ≤ 24mA,isshownbelow:
2–26 CHAPTER2.CircuitElements
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
[c]
Thecircuitisshownbelow:
[d]
WriteaKVLequationintheclockwisedirection,startingbelowthe voltagesource.UseOhm’slawtoexpressthevoltagedropacrossthe resistorsintermsofthecurrent i:
24V+250i +1000i =0so1250i =24V
Thus, i = 24V 1250Ω = 19.2mA
Thecircuitisshownbelow:
[e]
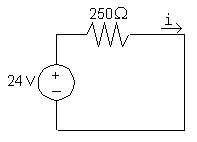
WriteaKVLequationintheclockwisedirection,startingbelowthe voltagesource.UseOhm’slawtoexpressthevoltagedropacrossthe resistorsintermsofthecurrent i: 24V+250i =0so250i =24V
Thus, i = 24V 250Ω = 96mA
Theshortcircuitcurrentcanbefoundinthetableofvalues(orfromthe plot)asthevalueofthecurrent is whenthevoltage vs =0.Thus, isc =48mA(fromtable)
[f]
Theplotofvoltageversuscurrentconstructedinpart(a)isnotlinear(it ispiecewiselinear,butnotlinearforallvaluesof is).Sincetheproposed circuitmodelisalinearmodel,itcannotbeusedtopredictthenonlinear behaviorexhibitedbytheplotteddata.
Problems 2–27
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
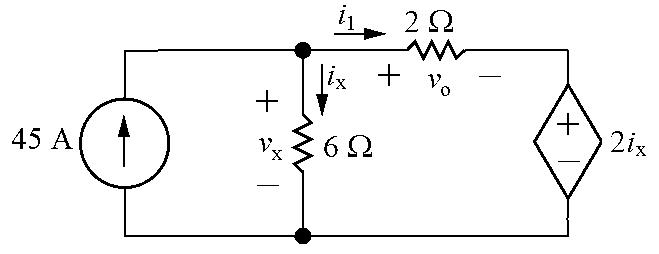
P2.32Labelunknownvoltageandcurrent:
vx + vo + 2ix =0(KVL)
vx =6ix (Ohm’slaw)
Therefore 6ix + vo +2ix =0so vo =4ix
Thus ix = vo 4 Also, i1 = vo 2 (Ohm’slaw)
45= ix + i1 (KCL)
Substitutingforthecurrents ix and i1:
45= vo 4 + vo 2 = 3vo 4
Thus vo =45 4 3 = 60V
Theonlytwocircuitelementsthatcouldsupplypowerarethetwosources,so calculatethepowerforeachsource:
vx =6ix =6 vo 4 = 6(60/4)=90V
p45V = 45vx = 45(90)= 4050W
pd s =(2ix)i1 =2(vo/4)(vo/2)=2(60/4)(60/2)=900W
Onlytheindependentvoltagesourceissupplyingpower,sothetotalpower suppliedis4050W.
2–28 CHAPTER2.CircuitElements
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
P2.33Labelunknowncurrent:
1 = (4000)(0.01)=40V(Ohm’slaw)
Problems 2–29
vx
vo =300 v
p20V = 20i = 20(0.0333)= 0.667W pd s = vo vx 100 = (15)(5/100)= 0.75W p450 =450i2 =450(0 033)2 =0 5W p150 =150i2 =150(0 033)2 =0 1667W p300 = v2 o 300 = 152 300 = 0 75W Thusthetotalpowerabsorbedis pabs =0 5+0 1667+0 75=1 4167W P2.34Thecircuit: v
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
20+450i +150i =0(KVLandOhm’slaw) so600i =20 → i =33.33mA
=150i =150(0.0333)=5V(Ohm’slaw)
x 100 = 300(5/100)=15V(Ohm’slaw) Calculatethepowerforallcomponents:
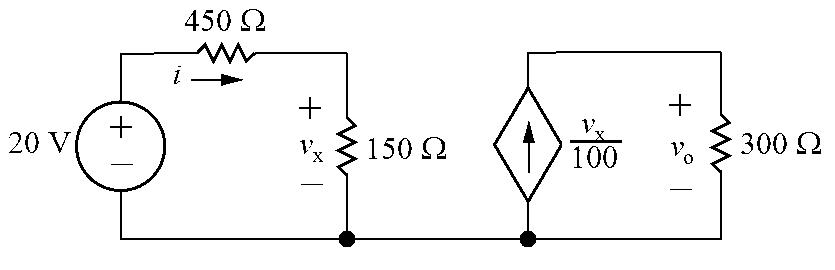
v1 2 = 2000io +6000io =8000io (KVL)
Thus,
Calculatethepowerforallcomponents:
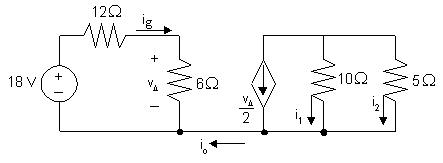
Thusthepowerinthecircuitbalances. P2.35 [a] io =0becausenocurrentcanexistinasingleconductorconnectingtwo partsofacircuit.
2–30 CHAPTER2.CircuitElements
io
= v1/2 8000 = 40/2 8000 = 0.0025=2.5mA
p10mA = (0.01)v1 = (0.01)(40)= 0.4W pd.s. = (v1/2)io = (40/2)(2 5 × 10 3 )= 0 05W p4k = v2 1 4000 = 402 4000 = 0 4W p2k =2000i2 o =2000(2 5 × 10 3 )2 =0 0125W p6k =6000i2 o =6000(2 5 × 10 3 )2 =0 0375W
ptotal = 0 4 0 05+0 4+0 0125+0 0375=0
Therefore,
[b] 18=(12+6)ig ig = 1A v∆ =6ig =6V v∆/2=3A 10i1 =5i2, so i1 +2i1 = 3A;therefore, i1 = 1A [c] i2 =2i1 = 2A. © 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
P2.36 [a]
Therefore,
vo =40iσ =80V
[b] ig =currentoutofthepositiveterminalofthe50Vsource
( 0 015625)=0; i1 =3 125mA
vg =60i1 +260i1 =320i1
Therefore, vg =1V
P2.38 iE iB iC =0
therefore
Problems 2–31
50 20iσ +18i∆ =0 18i∆ +5iσ +40iσ =0so18i∆ =45iσ
50 20iσ +45iσ =0, so iσ =2A
18i∆ =45iσ =90;so i∆ =5A
vd =voltagedropacrossthe8i∆ source
i∆
i∆
σ
ig = i∆ + iσ +8
=9
+ i
=47A
ig +20iσ ig =50(47)+20(2)(47)=4230W
diss
i2 ∆ +5iσ (ig i∆)+40i2 σ +8i∆vd +8i∆(20)
vd =80 20=60V Pgen =50
P
=18
=(18)(25)+10(47 5)+4(40)+40(60)+40(20) =4230W;Therefore, Pgen = Pdiss =4230W P2.3740i2 + 5 40 + 5 10 = 0; i2 = 15 625mA v1 =80i2 = 1.25V 25i1 + ( 1.25) 20 +
i2 = iB + i1 Vo + iE RE (i1 iB )R2 =0 i1R1 + VCC (i1 iB )R2 =0or i1 = VCC + iB R2 R1 + R2 © 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
iC = βiB
iE =(1+ β)iB
P2.39HereisEquation2.25:
2–32 CHAPTER2.CircuitElements Vo
E RE + iB R2 VCC + iB R2 R1 + R2 R2 = 0
iB
Vo (1+ β
E + R1R2/(R1 + R2)
+ i
Nowreplace iE by(1+ β)iB andsolvefor iB.Thus
= [VCC R2/(R1 + R2)]
)R
iB
VCC R2)/(R1 + R2) V0 (R1
2
1
2
β)RE V
1
=6V
1
=24kΩ iB
6 0
6
= 5.4 30,000 =0.18mA iC
iE
v
vbd
Vo + v3d
i2 = vbd R2
i1
iCC = iC + i1
v
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
= (
R
)/(R
+ R
)+(1+
CC R2 R
+ R2 = (10)(60,000) 100,000
R1R2 R
+ R2 = (40,000)(60,000) 100,000
=
.
24,000+50(120)
= βiB =(49)(0 18)=8 82mA
= iC + iB =8 82+0 18=9mA
3d =(0 009)(120)=1 08V
=
=1.68V
= 1.68 60,000 =28 µA
= i2 + iB =28+180=208 µA vab =40,000(208 × 10 6 )=8 32V
=8 82+0 208=9 028mA v13 +(8 82 × 10 3)(750)+1 08=10V
13 =2.305V
Therearethreeradiators,sothetotalpowerforthisheatingsystemis
Problems 2–33 P2.40 [a] [b]
WriteaKVLequationforeachofthethreeloops: 240+48i1 =0 → i1 = 240 48 = 5A 48i1 +48i2 =0 → i2 = i1 =5A 48i2 +48i3 =0 → i3 = i2 =5A
radiatoris prad = Ri
P2.41Eachradiatorismodeledasa48Ωresistor:
Therefore,thecurrentthrougheachradiatoris5Aandthepowerforeach
2 =48(5)2 =1200W
ptotal =3
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
prad =3(1200)=3600W
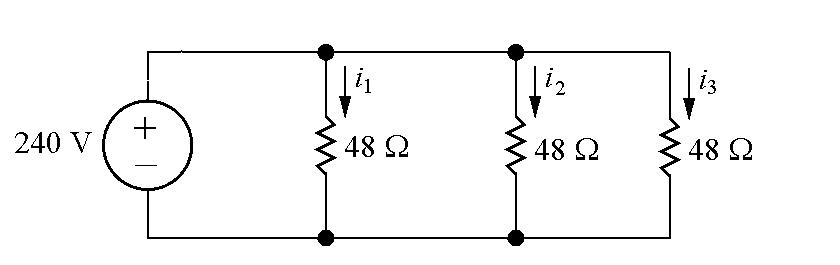
P2.42Eachradiatorismodeledasa48Ωresistor:
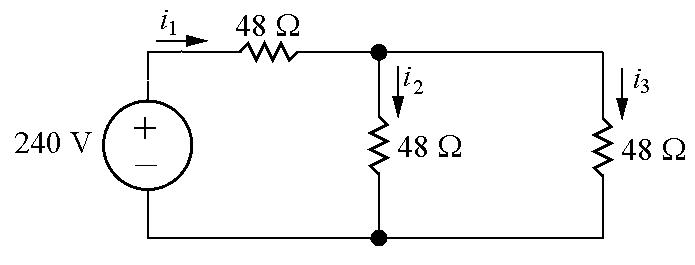
WriteaKVLequationfortheleftandrightloops: 240+48i1 =0 → i1 = 240 48 = 5A 48i1 +48i2 +48i2 =0 → i2 = i1 2 = 5 2 = 2 5A
Thepowerforthecenterradiatoris
pcen =48i2 1 =48(5)2 =1200W
Thepowerforeachoftheradiatorsontherightis
pright =48i2 2 =48(2 5)2 =300W
Thusthetotalpowerforthisheatingsystemis
ptotal = pcen +2pright =1200+2(300)=1800W
Thecenterradiatorproduces1200W,justlikethethreeradiatorsinProblem 2.41.Buttheothertworadiatorsproduceonly300Weach,whichis1/4thof thepoweroftheradiatorsinProblem2.41.Thetotalpowerofthis configurationis1/2ofthetotalpowerinFig.2.41.
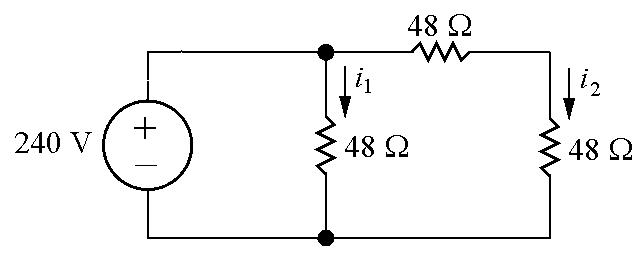
P2.43Eachradiatorismodeledasa48Ωresistor:
WriteaKVLequationfortheleftandrightloops: 240+48i1 +48i2 =0
2–34 CHAPTER2.CircuitElements
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Calculatethepowerforeachradiatorusingthecurrentforeachradiator:
Thusthetotalpowerforthisheatingsystemis
Allradiatorsinthisconfigurationhavemuchlesspowerthantheir counterpartsinFig.2.41.Thetotalpowerforthisconfigurationisonly22 2% ofthetotalpowerfortheheatingsysteminFig.2.41.
P2.44Eachradiatorismodeledasa48Ωresistor:
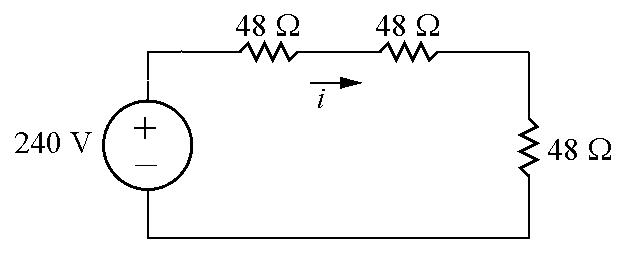
WriteaKVLequationforthisloop:
Calculatethepowerforeachradiator:
Calculatethetotalpowerforthisheatingsystem:
EachradiatorhasmuchlesspowerthantheradiatorsinFig.2.41,andthe totalpowerofthisconfigurationisjust1/9thofthetotalpowerinFig.2.41.
Problems 2–35 48i2 +48i3 =0 → i2 = i3
i1 = i2 + i3 → i1 = i2 + i2 =2i2
240+48(2i2)+48i2 =0 → i2 = 240 3(48) = 1 67A Solveforthecurrents i1 and i3: i3 = i2 =1.67A; i1 =2i2 =2(1.67)=3.33A
WriteaKCLequationatthetopnode:
SubstitutingintothefirstKVLequationgives
pleft =48i2 1 =48(3.33)2 =533.33W pmiddle = pright =48i2 2 =48(1 67)2 =133
33W
ptotal = pleft + pmiddle + pright =533
33+133 33+133 33=800W
240+48i
i =0
i =
+48i +48
→
240 3(48) = 1.67A
p
rad =48i2 =48(1 67)2 =133 33W
ptotal =3prad =3(133.33)=400W
© 2015 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458. Electric Circuits 10th Edition Nilsson Solutions Manual Visit TestBankDeal.com to get complete for all chapters