Nou Biaix, 49

Revista de la FEEMCAT i de la SCM

Desembre 2022

bia x uno i

número 49

sumari

Consell de redacció:

Marianna Bosch / Carlos Giménez (coords.)

Montserrat Alsina

Joan Carles Ferrer

Joan Miralles

Manuel Udina

© dels articles, els seus autors

Coediten:

Federació dEntitats per a lEnsenyament de les Matemàtiques (FEEMC AT ) Campus de Montilivi, edifici P-IV 17071 Girona feemcat.org

Societat Catalana de Matemàtiques (SCM) filial de l’Institut d’Estudis Catalans Carme, 47 08001 Barcelona scm.iec.cat noubiaix@gmail.com

Pol Albarrán Sánchez al Periodicitat: semestr Nombre dexemplars: 1.700 ’

Fotografia de la coberta: Noves perspectives de Barcelona a través d'una esfera

ISSN: 2014-2021

Dipòsit legal: B-22.314-2012

Impressió: Gráficas Rey

Edicions

de la Universitat de Barcelona

Adolf Florensa, s/n 08028 Barcelona

Tel.: 934 035 430 comercial.edicions@ub.edu www.edicions.ub.edu

Editorial 1 6 16 31 45 62 76

articles

Com dividir quan no nhi ha prou per a tothom? El problema de les emissions de CO ’

José Manuel Giménez-Gómez

CoriVilella-Bach

Dissenyar un tipi. Una activitat competencial per treballar la geometria amb el GeoGebra

Èdgar Ribot-Llobet

Neus Heras Navarro

Com ho farem? Descripció d’un taller amb diverses ac tivitats artístiques i matemàtiques per desenvolupar la creativitat en alumnes de primària

QueraltViladevallValldeperas

Salvador Linares Mustarós

Joan Carles Ferrer Comalat

Els mons impossibles de M. C. Escher

Toni Sellarès

Per què entonen bé les guitarres amb trasts no paral·lels?

Miquel Albertí Palmer

Les mates al billar i una situació d’exploració per treballar a l’aula de matemàtiques 2

Guillem Bonet Carb ó

88 93 seccions

Per pensar dun minut a una hora ’

Jordi Deulofeu

Aprendre matemàtiques amb jocs de taula ’

Jocs de taula per a laula de matemàtiques: per què? ’

SET, Grup de Jocs dABEAM

Enstrobemdavantd’unnounúmerodelarevista NouBiaix,el49,enelqualhemdonat protagonismeaaportacionsquesituenlesmatemàtiquescomaelementclauencontextos diversos:elrepartimentderecursos,eldisseny,l’art,lamúsicaieljoc.Aquestscontextosestanmoltpresentsenlavidasocialipodendonarrespostaalademandadesituacionsd’aprenentatgeriques,variadesirellevantsperal’alumnat.

Delalecturaatentadelsarticlespresentsenaquestvolum,elsilesdocentsenpodranextreuretantideesgeneralsquepodranconcretarenfunciódelescondicionsd’implementaciói delasevapròpiaexperiència,comexemplescomplets prêt-à-porter quehauriendepoder incorporarsensegairedificultat idebensegurambmoltbonsresultats alasevapràctica al’aula.

Enrelacióambl’articleambelqualobrimaquestnounúmerodelarevista NouBiaix,«Com dividirquannon’hihaprouperatothom?ElproblemadelesemissionsdeCO2 »,cal,en primerlloc,presentarlesnostresdisculpesméssincerestantalsseusautors,CoriVilellaiJosé ManuelGómez,comatotselsnostreslectorsilectores.Acausad’unaerradaimperdonable enelprocésd’edició,elseuarticle,totihaverestatrevisat,acceptatiressenyatenl’editorial, peralgunacausaincomprensibleva«desaparèixer»delaversióimpresa.Unaerradaqueés nomésnostracomaresponsablesfinalsdel’ediciódelarevistaiperlaqualreiteremlanostra peticiódedisculpes.

Recuperem,arasí,l’articleenqüestióienreproduïmaquílaressenyaquejafiguravaenelnúmeroanterior.Enelseuarticle,CoriVilellaiJoséManuelGómezposenfilal’agullaperaportar unenfocamentmatemàticamentrigorósaunproblemapràcticforçahabitual,conegutcom elproblemadelafallida,enelqualestractad’establirelmecanismemésjustperrepartir unacertaquantitatd’unrecursconcret(herència,embargament,quota pesquera,etc.)entre totselsagentsqueeldemanen,quanlaquantitattotaldelesdemandessuperalaquantitat disponibledelrecursques’haderepartir.Espresentenquatremecanismesdiferentsaplicats habitualmentenaquestessituacionsiescomparenelsresultatsqueassignacadascund’ells acadaagentdemandant,intentantestablirdemaneraqualitativaelgraudejustíciapresent

encadacas,apartirdelcomplimentonodefinsacincreglesrelativesal’equitatenelrepartiment.L’exempleconcretalquals’apliquenelsmecanismesindicats,eldelesemissionsde CO2 ,degranactualitatisummaimportància,ésidealperil¨lustrarelguanydequalitatenla presadedecisionsquecomportaincorporarcriterismatemàticspersobred’altresdetipus polític.

Elsegonarticlepresentaunaactivitatdeclassesobreeldissenyd’untipiperaunaclassede segond’ESOambmaterialsielGeoGebra.ÈdgarRibot-LlobetiNeusHerasfanunacontribuciómagníficaalanecessitat,nosemprebenentesa,depresentaralnostrealumnatactivitats realmentcompetencials,enlesqualsesparteixd’unasituacióproblemàticacontextualitzada enunentornconegutpelsalumnesperòencarapocdeterminada.Aixòpromoulanecessitatdeformularnovesqüestionsperabordarel problema,ferestimacionsperconcretarles mesuresdelproductequeesvoldissenyar,utilitzarunconjuntdeconeixementsihabilitats adquiritsprèviamentidesenvolupar-nedenousambl’ajudadelprofessorat,etc.Sensdubte, exemplescomaquestpodenserviramoltsdocentsperdecidir-seadesenvoluparlesseves pròpiessituacionsd’aprenentatge,quetannecessàrieshaurandeserambelnoucurrículum.

Enelseuarticlesobretallersdecreativitatperaalumnesdeprimària,QueraltViladevall,SalvadorLinaresiJoanCarlesFerrerposenelfocusenunaqualitatquemassasovintelsistema educatiutendeixasoterrarambelpesdelaprecisió,elformalismeielrigormalentesos,de maneramésomenysactivaidecididaopassivainovolguda.

Enspresentenunaexperiènciajaexperimentadaiambproudetallsirecursosperserdirectamentimplementadaalesaules.Enaquestaexperiència,lesmatemàtiquesapareixenal costatd’activitatsdiverses,comlalecturad’unconte,eltreballambdibuixosiil lustracionsi l’assaigierror,dinsd’untreballespecíficdedesenvolupamentdelacreativitatilaproducció d’ideesdisruptives.

Segueixunarticletambésobrelacreacióartísticailesmatemàtiques,onToniSellarèsens obsequiaambunaaproximaciómoltentenedora alsmonsimpossiblesd’Escher,disseccionantgeomètricamentelselementsquel’artistaneerlandèsutilitzavacomabasedelesseves obres.Aixípodemaconseguirpresentardemaneraracionalallòqueaqualsevolobservador noentrenatgeomètricamentlisemblasimplementimpossible.Debensegurquetenima lesnostresaulesforçaestudiantsquepodranaproximar-sed’unamaneramoltmésclarai precisaal’obrad’aquestartistapeculiarieixamplaranaixílasevaconcepciódelageometria. Amés,podremtreballarelproblemadelarepresentacióplanadelarealitatespacial,amb elsartificisqueaportenlesmatemàtiquesperabordar-lailesargúciesvisualsqueaquests artificispermeten.

Delapinturapassemalamúsicaenelquartarticled’aquestnúmero.MiquelAlbertíens mostraunnouiinteressantexempledelarelacióentrelamúsica,lafísicailesmatemàtiques enunestudioriginalsobrel’afinacióenlesguitarresambtrastsnoparal¨lels.Mostraralnostre alumnatcontextostandiversoscomsiguipossibleonlesmatemàtiquesexpliquinimodelitzinallòqueveiem(o,enaquestcas,sentim)éssensdubteunamaneramoltinteressant deposarenvalorlanecessitatdelsconeixementsmatemàticsenàmbitsprofessionalsmolt diversos,unfetnosemprebenentèsperlanostrasocietat.

GuillemBonetencetaambelseuarticleunapetitasèriesobrelesmatemàtiquesalbillar.Un copmés,estemdavantd’unestudiinteressantsobreunasituaciólúdica oesportiva que espotexperimentarambobjectesmaterialsoambsimuladorsvirtuals.L’autorfamalabars ambunaseqüènciadeqüestionsdecinemàtica,geometriaidivisibilitat,imostraunprocés moltricdematemàtiquesexperimentalsones modelitzensituacionsfísiquesambmodels geomètricsiconfiguracionsgeomètriquesambsèriesdelletresitaulesdenombres,finsa arribaraunainversiótotalonlestaulesdebillars’utilitzencomamodelspercalcularelmínimcomúmúltiplededosnombresilasumadefraccions.Esperemambdelitlesentregues següentsd’aquestasèrie.

Tanquenelnúmerodosarticlesdel’apartat«Seccions».Unanovapropostadeproblemesper pensard’unminutaunahoradeJordiDeulofeu,sensdubteundelsnostrescol¨laboradors mésfideliregular.Tambéinauguremlanovasecció«Aprendrematemàtiquesambjocsde taula»,acàrrecdeSET,GrupdeJocsd’ABEAM,ques’estrenaprecisamentpresentant-nosel jocSET,quedonanomalgrup.

AmbaquestSETalquadrattanquemelnúmero49,esperantqueusresultitaninteressant comenshohasemblatanosaltres.Quedemalesportesdelpropernúmero50,quearribarà ambl’any 2023encetatiambmésdetrentaanysdevidapercelebrar,vintdelsqualsambel formatactualcoma NouBiaix !

articles articles

Comdividirquannon’hiha prouperatothom? Elproblemadeles emissionsdeCO2

JoséManuelGiménez-GómeziCoriVilella-Bach

Departamentd’EconomiaiDepartamentdeGestiód’Empreses

ECO-SOS,UniversitatRoviraiVirgili

Resum Abstract

Ensituacionsenquèelsrecursosdisponibles nosónsuficientspersatisferlesdemandesde tothom,lateoriadelsproblemesdedemanda tractad’introduircertaobjectivitatijustíciaen ladistribuciódelsrecursos.Aleshores,es defineixendiferentsmaneres(regles)de repartirlaquantitatdisponiblederecursosi l’aplicaciódelesreglesesdefensanopel repartimentfinaldelrecurs,sinóperla filosofiadelrepartiment(axiomes).Aquest articlesecentraenl’aplicaciódelrepartiment d’emissionsdeCO2 permostrarcomfunciona l’artderepartirrecursosescassos.

1.Introducció

Insituationswheretheavailableresourcesare notsufficienttosatisfyalldemands,the conflictingclaimstheoryseekstointroduce someobjectivityandfairnessintotheir distribution.Thus,differentwaysofdistributing theavailablequantities(rules)aredefined,and theirapplicationisupheld,notbythefinal distributionoftheresource,butbythe philosophyofallocation(axioms).Thisarticle focusesontheapplicationofCO2 emission sharingtoshowhowtheartofallocatingscarce resourcesworks.

Elcanviclimàticespotveurecomelresultatd’unafallidapressupostàriadecarbonisense resoldre.LimitarelCO2 acumulatglobala 1.440 gigatonelades(Gt),durantelperíode 20002050 produiriaunaprobabilitatdel50 %desuperarels 2 ˝ Cdetemperaturamitjanaper sobredelsnivellspreindustrials[11].Totiaixí,s’estimaquelesemissionsacumuladesmundialsperalperíodeenqüestióoscil·laranentre 1.758i 2.736Gt[13].Enconseqüència,lagovernançaambientalestrobaràenunasituaciódefallidadelcarboni:siseguimactuantcom finsara,l’any 2050 elspaïsoshauranreclamatmésemissionsacumulades(1.758-2.736Gt) delesquehihadisponibles.

Situacionscomaquestaesconeixencomaproblemesdedemanda,elsqueesdonenquan ungrupdepersonesreclamenuncertdretsobreunbécomúilaquantitatdelbéques’hade repartirnoéssuficientpersatisferlademandadetotselsagents.Aquesttipusdeproblemes hanpreocupatlasocietatdesdefasegles.Al’èpocad’Aristòtiljahihaviadocumentsque parlavend’aquesttemaielsexemplesprocedentsdelTalmud,l’antigalleidelsjueus,deMaimònides,quedescriuremmésendavant,tambéensónunexempledel’èpocamedieval.No obstantaixò,elprimertreballformalsobreaquestaproblemàticaésl’articledeBarryO’Neill (1982)[14].

Coms’hauranderepartirelsrecursosquetenim?Utilitzaremreglesderepartimentqueassocienacadaproblemadedemandaunrepartimentdelsrecursosquetenimentreelsagents. Elnostreobjectiuéstrobarunaregladerepartimentques’adaptitanbécomsiguipossiblea cadasituació.Peraquestmotiu,analitzaremalgunesdelesreglesmésimportantsques’han estudiatenlabibliografiasobreaquesttemaiformularemalgunespropietats,anomenades axiomes,quevoldremquelesreglessatisfacin.Volemcompararlesreglesamblespropietats quesatisfanibuscarlesreglesquesatisfanlespropietatsdesitjadesencadasituació.Elcas mésconegutd’aquesttipusdeproblemaéseld’unaempresaquefafallida,conegutenla literaturacomun bankruptcyproblem,ielseuvalordeliquidaciónoéssuficientperassumir lesdemandesdelsseuscreditors.Noobstantaixò,aquestmodelespotaplicaramoltsaltres casos,compodrienserelrepartimentdepressupostosperpartdelBancMundialalsdiferents països,elrepartimentd’ajuthumanitariperpartdelaCreuRojaensituacionsdeguerrao dedesastresnaturals.També,enelmarcuniversitari,quanelsdiferentsgrupsderecerca demanemdinersal’AgènciadeGestiód’AjutsUniversitarisideRecerca(AGAUR)peralsnostresprojectesderecerca,coms’handerepartir?Tambés’haaplicataquestametodologiaa diferentstemesambientals,comaralareducciódelesquotesdepesca[9],elrepartimentde lespossiblesemissionsdeCO2 quepodenferelspaïsos[5]i[4]iladistribuciódelpressupost desanitatdelaGeneralitatdeCatalunya[16].Lareglamésconegudaipotserfinsitotla mésutilitzadaéslareglaproporcional,onelsrecursosesreparteixenproporcionalmenta lademandadecadaagent.AquestareglajavaserutilitzadaperAristòtilisempres’hafet servirmoltdemaneranatural.Peròhihamotiusperpensarqueaquestaéslamillor?De fet,apartd’Aristòtil,hihaliteraturamoltantiga,enparticularelTalmud,onespodentrobar exemplesnumèricsenelsqualsposteriorments’haninspiratdiversesreglesderepartiment quedifereixendelaproporcional.

EnaquestarticleexpliquemladistribuciódelesemissionsdeCO2 entrediferentsregions mitjançantaquestateoria.Concretament,ladotació(elsrecursosques’handedistribuir) éselpressupostdecarbonidisponible.Utilitzemelmodelprobabilísticde[11],onesproporcionendiferentspressupostosdecarboniambdiferentsriscosassociatsperalperíode 2000-2050.Enaquestcas,elsagentsquereclamenelsrecursosestanrepresentatspelspaïsos emissorsielpressupostdecarbonidisponiblenopotsatisferplenamentlasumadelesseves demandesglobals.Lesdemandesdelspaïsoss’aproximenalesprojeccionsd’emissionsfetes pelGrupIntergovernamentalsobreelCanviClimàtic(IntergovernmentalPanelonClimate Change,IPCC)peradiferentsregionsdelmón[13]:concretament,suposemqueelcomportamentmésnaturaldelspaïsos,enunmarcdefallidadelcarboni,seriareclamarlesseves emissionsmàximes(peramésinformació,vegeu[5]).

2.ElproblemadelesdemandesdeCO2

Formalment,almodeldelsproblemesdedemandatenimunaquantitat E P R` d’unrecurs infinitamentdivisible(endowment).1 Aquestéselrecursdelqualdisposemiquevolemrepartirentreungrupde N “t1,...,nu agentsquetenenunesdemandessobreaquestrecurs (claims): ci P R` éslademandadel’agent i P N .Caldestacarqueelsagentsnopodenreclamarlaquantitatdelrecursquevulguin:lesdemandeshandeserjustificadesohihad’haver unsdretsadquiritspercadaagent,quegeneralmenthand’estaravalatsperdocumentslegals.Percompletarelmodelhemdedirquela quantitatdelrecursdequèdisposemnoés suficientpersatisfertoteslesdemandesdelsagents,jaque,encascontrari,sitinguéssimrecursossuficientspersatisferatothom,elrepartimentesresoldriatrivialment.Pertant,podem definirunproblemadedemandacomunparell pc,E qP RN` ˆ R` talque n ř i“1 ci ě E . 2 Alguns delstreballsreferentsdeproblemesdedemandasón[17]i[18].Enelcasdedosagents,el problemaespotrepresentardemaneramoltsenzillaipodemidentificarencadacas,segons lesdemandesdecadaun,quinsserienelspossiblespagamentsquepodríemfer.Peramés detalls,espotconsultar[6].

Enl’aplicaciódelmodelanterioralrepartimentdelCO2 ,elpressupostdecarbonidisponible s’obtédeltreballde[11].Concretament,consideremtrespressupostosdiferentsdecarboni peralperíode 2000-2050: aq 1.440 GtdeCO2 ,quecorresponenaunaprobabilitatdel50 %de superarelllindarde 2 ˝ C; bq 1.000 GtdeCO2 ,quecorresponenaunaprobabilitatdel 25%,i cq 745GtdeCO2 ,quecorresponenaunaprobabilitat 0 desuperarelllindar.Pertant,elrecurs ques’hadedividirentreelsagentséslaquantitatdediòxiddecarboni.

1.Enelnostrecas,consideremqueelrecursques’hadedividirésperfectamentdivisibleihomogeni.No obstantaixò,hihamoltessituacionsrealsenlesqualstantelrecursques’haderepartircomlesdemandessón unitatsidèntiquesiindivisibles.Pertant,enaquestscasoslesregleshand’assignarunnombred’unitatsenteres d’aquestrecursacadaagent.Podempensar,perexemple,enladistribuciódelesllistesd’esperaperacirurgiesals hospitals,enladistribuciódevisatsperalsimmigrantso,comenstrobemrecentment,enladistribuciódevaccins entrelapoblacióenunmomentdepandèmia.Enaquestscasoss’apliquenmodelsdeprioritat.Peramesinformació, podeuconsultarelstreballsde[12],[8]i[2].

2.Observemquepermetemlaigualtat n ř i“1 ci “ E ,totiqueenaquestcastoteslesdemandespodrienser satisfetes.

Figura1.Agrupaciódelspaïsosenquatreregions.

Elconjuntdedemandants(elsagents)estàformatpelsquatregrupsmundialsdel’IPCSpecial ReportonEmissionsScenario,SRESquenormalmentesconsiderenenmodelsclimàtics:païsosdel’OrganitzacióperalaCooperacióielDesenvolupamentEconòmics(OECD)del 1990 (OECD90),Àsia(ASIA),ÀfricaiAmèricaLlatina(ALM)ipaïsosencursdecanviseconòmics (REF).Podemveurelesagrupacionsdelspaïsosalafigura 1.

PerdefinirlesdemandesdelsagentsutilitzaremlesdadesdelfuturacumulatdeCO2 projectatqueespodentrobaralSRES[13]comavaloraciódelquepodenreclamarelspaïsos.Concretament,enssituemenl’escenarionelspaïsosreclamenelmàximquepoden.En aquestcas,lesemissionsacumuladesmundialsascendirana 2.736GtdeCO2 el 2050 (una xifrasuperioraqualsevoldelstrespossiblesescenarisprevistos).

Compodemobservaralataula 1,lasumadelesdemandesdelsquatrepaïsosésde 2.736 GtdeCO2 .Entotstresescenarisaquestaxifrasuperalaquantitatques’haderepartir, E .Per tant,tenimunproblemadedemanadaenelstresescenarisconsiderats.

Taula1.ElproblemadelesdemandesdeCO2 acumulades. Laprimerafilamostraelstrespossiblesescenarisi, entreparèntesi,lesprobabilitatsd’excedirelsdosgrausencadascund’ells.Alasegonailatercerafilestenimels quatregrupsdepaïsosamblessevesdemandescorresponents.

3.Comespotrepartir?Regles

Unavegadatenimidentificadestoteslespartsdelproblemaderepartiment(recursdisponibleidemandesdelsagents),s’hadedecidircoms’hadeferladistribuciód’aquestrecurs entreelsdemandants.Enaquestsentit,hihaliteraturamoltantiga,enparticularelTalmud (antigalleidelsjueus),onjaespodentrobarexemplesnumèricsenelsqualsposteriorment s’haninspiratdiversesreglesderepartiment.

Formalment,una regla assignaacadaproblemadedemanda pc,E q unvectorderepartiment ϕ pc,E qP Rn talquehadeverificarduescondicions:

‚ Cadacomponenthadeseracotadaperlademandadecadaagent, i.e. 0 ď ϕj pc,E qď cj , @j “ 1,...,n.

‚ Sereficient, i.e. řj ϕj pc,E q“ E .

D’entretoteslesreglesproposadesenlaliteratura,lesmésanalitzadessón:laproporcional, laigualitàriaenguanysrestringida,laigualitàriaenpèrduesrestringidailaTalmud[7].

Lareglamésconeguda,japroposadaperAristòtilisempremoltutilitzadademaneranatural, éslaproporcional.AquestareglarecomanaunrepartimentdelesemissionsdeCO2 proporcionalalademandadecadaagent.Formalment,la reglaproporcional,P,assignaacada problemadedemanda pc,E q elvector Ppc,E q talqueperacadaagent i P N , Pi pc,E q” E ř cj ci

Unaaltrareglabastantnaturalseriarepartirdemaneraigualitàrialesemissionstotalsde CO2 atotselsagents,peròenaquestcaslareglaignorarialesdemandesdelsagentsiels tractariaatotsdemaneraigual;éselques’anomenaregladedivisióigualitària.Noobstant això,elproblemaambaquestareglasorgeix quanelsagentsnotenenlamateixademanda. Notemque,entrealtresmotius,aplicantaquestprincipipodríemassignaraalgunagentuna quantitatsuperioralquedemanaiaixònosatisfarialadefiniciódelaregla.Aleshoreses defineixlareglaigualitàriaenguanysrestringida[10],queproposaunrepartimentigualitari delesemissionsdeCO2 acadaagentsensequeningúpuguirebremésdelquedemana. Formalment,la reglaigualitàriaenguanysrestringida (CEA,del’anglès constrainedequal awards),assignaacadaproblemadedemanda pc,E q unvector CEApc,E q talqueperacada agent i P N , CEAi pc,E q” m´ıntci ,bu,on b ésescollitpertalque ř m´ıntci ,bu“ E .Delamateixa definiciópodemdeduirqueaquestareglaafavoreixelsagentsquetenenunademandamés petita.

Unareglarelacionadaambl’anterioréslareglaigualitàriaenpèrduesrestringida.Aquesta reglatambétél’objectiudeserigualitària,però,enaquestcas,enllocdebasar-nosenel repartimentigualitaridelesemissionstotalsdeCO2 ,enscentraremenelrepartimentigualitaridelespèrdues,ésadir,laquantitatd’emissionsdeCO2 quecadademandantdeixa derebredelquereclama.Sivolempèrduesigualitàriesperatots,aixòpotdonarllocque algunsagentsrebinquantitatsnegativesiaixòseriaincompatibleamblanociódelaregla, querequereixqueelsrepartimentssiguinnonegatius.Pertant,lareglaproposaràpèrdues màximamentigualitàriessensequeningúpuguitenirunpagamentnegatiu.Formalment, la reglaigualitàriaenpèrduesrestringida (CEL,del’anglès constrainedequallosses)assignaacadaproblemadedemanda pc,E q unvector CELpc,E q talqueperacadaagent i P N , CELi pc,E q” m´axtci b,0u,on b ésescollitpertalque ř m´axtci b,0u“ E .

Observemque,adiferènciadelaCEA,aquestareglaafavoreixelsagentsambdemandesmés grans.

L’últimareglaqueaplicaremaaquestcaséslaregladelTalmud.Aquestareglacombinales duesanteriors,laCEAilaCEL.Concretament,prenlameitatdelesdemandesagregades comapuntdereferència.Silameitatdeltotaldelesdemandesésinferioralaquantitat disponibled’emissionstotalsdeCO2 ,s’aplicalaCEAalesdemandesmitjanes;mentreque,en cascontrari,cadaregióreplameitatdelessevesdemandesméslaquantitatrecomanadaper laCEL.Formalment,la regladelTalmud,T,[1]recomanaperacadaproblemadedemanda pc,E q unvector T pc,E q talqueperacadaagent i P N , Ti pc,E q” CEAi pc{2,E q si E ď C {2;o Ti pc,E q” ci {2 ` CELi pc{2,E C {2q si E ě C {2.

Lataula 2 resumeixlacomparacióentrelesreglesproposadespercadaundelstresescenaris decarboniconsiderats.Talcomhemesmentat,hemconsideratquatreregionsdepaïsosi l’emissiódeCO2 peraunperíodedecinquantaanysentresescenarisdiferents.

Taula2.AssignaciódelesemissionstotalsdeCO2 . Alaprimeracolumnatenimelstresescenarisconsideratsi, entreparèntesis,laprobabilitatd’excedirelllindarde 2 ˝ C[11].Larestadecolumnesmostrenlesassignacionsrecomanadespercadareglaencadascundelspossiblesescenaris.Lesfilesproporcionenlesassignacionsrecomanades peracadascunadelesregionsconsiderades.

Demandes:REF=300,36;ALM=618,78;OECD90 =768,47;ASIA= 1.048,57

EmissionsCO2 Regions

E= 1.440 Gt (50 %)

E= 1.000 Gt (25%)

Amésamés,perafavorirlainterpretaciód’aquestresultatslafigura 2 proporcionalarepresentaciódecadaassignacióenfunciódelesdemandesdecadaregió.

Figura2.Representaciódebarresdelesassignacionsrebudespercadaregióamb E =1.440, E =1.000i E =745. Lesbarresblanques(lesmésamples)representenlesdemandesdecadaregió.Lesbarresmésestretes mostrenlaquantitatd’emissionsdeCO2 recomanadapercadascunadelesreglesintroduïdes:P(gris),CEA(groc), CEL(verd),T(marró).Elspercentatgesindiquenl’importrelatiudelesdemandessatisfetespercadaregla.

4.Coms’haderepartir?Principissocialmentadmissibles

Existeixenenlaliteraturaunagranquantitatd’axiomesopropietatsperal’anàlisiaxiomàtica delesreglesesmentadesanteriorment.L’objectiuprincipald’aquestaanàlisiésidentificar cadareglaambunconjuntdepropietatsbendefinides,demaneraqueseleccionarunaregla significaresoldreelproblemaaplicantaquestsprincipisd’equitatioperatius,quetradueixen uncertvalordejudicisobreelsresultatsdistributius(vegeu[7]).

Acontinuacióintroduïmalgunesdelespropietatsmésconsideradesifàcilmentadmissibles. Perobtenirmésdetallsiunconjuntcompletdelesdefinicionsmatemàtiquesdelsprincipis d’equitatilessevesimplicacions,vegeu[15].

Igualtractamentd’iguals.Implicaquelesregionsambdemandesigualshanderebrela mateixaassignaciódeCO2 .Formalment,peracadaproblemadedemanda pc,E q icadaagent ti,j uĎ N ,si ci “ cj ,llavors ϕi pc,E q“ ϕj pc,E q.

Anonimat.IndicaquelaquantitatdeCO2 rebudaperunaregióhadedependrenomésde lasevademanda,inodelasevaidentitat.Formalment,peracada pc,E q,cada π P ΠN icada agent i P N , ϕπpiq ppcπpiq qiPN ,E q“ ϕi pc,E q, onΠN éselconjuntdetoteslespermutacionsde N

Preservaciódel’ordre [1].Aquestapropietatrequereixrespectarl’ordredelesdemandes, ésadir,silademandad’unaregió i ésalmenystangrancomlad’unaaltraregió j ,laregió i hauriaderebreiperdrealmenystantcomlaregió j .Formalment,peracada pc,E q icada agent i,j P N talque ci ě cj ,llavors ϕi pc,E qě ϕj pc,E q i ci ϕi pc,E qě cj ϕj pc,E q

Autodualitat [1].Implicaqueelproblemadedividir«lesemissionsdeCO2 disponibles»o«les emissionsdeCO2 quenoespodenfer»hauriadedonarelsmateixosrepartiments.Formalment,peracadaproblemadedemanda pc,E q icadaagent i P N , ϕi pc,E q“ ci ϕi pc, řiPN ci E q.Penseu,perexemple,en E “ 1.440,demaneraque L “ 2.736,18-1.440 = 1 296,18.Després, Ppc,Lq“p142,29; 293,13;364,04;496,73q,demaneraquel’assignacióproposadas’obtindriarestantlespèrduessofertesdelesdemandes, c Ppc,Lq“p300,36;618,78;768,47; 1.048,57q´p142,29; 293,13;364,04;496,73q“p158,07;325,65;404,43;551,84q,quecoincideixambel P proposatperalrepartiment(vegeulataula 2).Laconveniènciad’aquestprincipi provédelfetqueelspaïsospodrienconsiderarl’assignaciódecarbonicomunpremi(CO2 quepodenemetre)ocomunapèrdua(CO2 quenopodenemetre).Enambdóscasos,tant siesnegocienadjudicacionscomsiesprodueixenpèrdues,elresultatéselmateixperales reglesquecompleixenaquestprincipi.Enuncontextdenegociacionsinternacionalsaquest principiresultamoltconvenientperfacilitaracords.Amés,aquestapropietatimplicaquecap regiórebràmésdelameitatdelquereclamasilarestaderegionsencaranohanrebutlaseva.

Invariànciarespectedelesdemandestruncades [3].Aquestapropietatfareferènciaal llindarsuperiordelesemissionsdeCO2 peracadaregió.EnsdiuquelesdemandesquesuperenelpressupostmundialdeCO2 nohauriendeserconsiderades.Pertant,l’assignacióno hauriadedependred’aquestexcésdedemanda queéssuperioralaquantitattotalques’ha dedividir.Formalment,peracadaproblemadedemanda pc,E q icadaagent i P N , ϕi pc,E q“ ϕi pm´ın tci ,E uiPN ,E q.Pertaldeveurequèimplicaaquestapropietatenelnostreproblema, podemanalitzarlesreglesproposadesalataula 2 endoscasosdiferents.Tingueuencompte quequanelpressupostésde 1.000 GtdeCO2 ,eltruncamentdelesdemandesimplicaque

sia redueixlasevademandade 1.048,57a 1.000.Sotaaquestsupòsitobtenimlataula3.Com podeuobservar,nohihagranscanvis,peròtoteslesregionsaugmentenlessevesassignacionsunamica,excepte sia,quedisminueixlaquantitatquereppertoteslesregles,excepte amblaCEAilaT.Aixídoncs,aquestapropietatajudaelsagentsatenirunaconnexiómés estretaamblacapacitatd’enfonsamentdel’atmosfera.

Taula3.Invariànciarespectedelesdemandestruncadesamb E =1.000.

Demandesinicials:REF=300,36;ALM=618,78;OECD90 =768,47;ASIA= 1.048,57

Perinvariànciarespectedelesdemandestruncades:

Demandesajustades:REF=300,36;ALM=618,78;OECD90 =768,47;ASIA=

Lataula4ensmostraquinsdelsprincipisesm entatsprèviamentescompleixenperales reglesproposades.Compodemveurealataula4,elTalmudésl’únicareglaquecompleix toteslespropietatsdesitjades.3

Taula4.Propietatsiregles. Lataulamostraelsprincipisquecompleixenlesreglesconsiderades.Cadacolumna corresponaunaregla,mentrequecadafilacorresponaunprincipiproposat.Elsresultatsd’aquestataulaespoden trobara[18].

Propietats/reglesPCEACELT Igualtractamentd’igualsSíSíSiSi AnonimitatSíSíSíSí Preservarl’ordreSíSiSíSí AutodualitatSíNoNoSí InvariànciarespectedelesdemandestruncadesNoSíNoSí

3.Aquestresultatespottrobara[18].

5.Conclusions

Aquesttreballproporcionaunaintroduccióalproblemaderepartirrecursosescassosmitjançantelcasdel’assignaciód’emissionsdeCO2 .Ensituacionsenquèlaquantitatquehi hadisponibled’unrecursnoéssuficientpersatisferlesdemandesdetothom,lateoriadels problemesdedemandatractad’introduircertaobjectivitatijustíciaenladistribuciódels recursos.

Aleshores,esdefineixendiferentsmaneresderepartirlaquantitatdisponibleilessevesregles,il’aplicaciódelesreglesesdefensanopelrepartimentfinaldelrecurs,sinóperlafilosofiadelrepartiment,elsaxiomes.Amésdel’enfocamentaxiomàticd’aquesttipusdeproblemesquehemplantejataquí,laliteraturaproposatambéaltresaproximacions,comara l’anàlisimitjançantlateoriadejocso,mésrecentment,l’estudidexarxes.

Referències

[1]Aumann,R.J.;Maschler,M.(1985).«GameTheoreticAnalysisofabankruptcyfromthe Talmud». JournalofEconomicTheory,36, 195-213.

[2]Chen,S.(2015).«Systematicfavorabilityinclaimsproblemswithindivisibilities». Social ChoiceandWelfare,44(2), 283-300.

[3]Dagan,N.;Volij,O.(1993).«Thebankruptcyproblem:acooperativebargainingapproach». MathematicalSocialSciences, 26, 287-287.

[4]Duro,J.A.;Giménez-Gómez,J.-M.;Vilella,C.(2020).«TheallocationofCO2 emissionsasa claimsproblem». EnergyEconomics,86(C), 104652.

[5]Giménez-Gómez,J.M.;Teixidó-Figueras,J.;Vilella,C.(2016).«Theglobalcarbonbudget: aconflictingclaimsproblem». ClimaticChange, 1-11.

[6]Giménez-Gómez,J.M.;Vilella-Bach,C.(2021).«L’artderepartirrecursosescassos», MaterialsMatemàtics, 1, 14.

[7]Herrero,C.;Villar,A.(2001).«Thethreemusketeers:fourclassicalsolutionstobankruptcy problems». MathematicalSocialSciences,42(3),307-328.

[8]Herrero,C.;Martínez,R.(2004).«Egalitarianrulesinclaimsproblemswithindivisiblegoods». SocialChoiceandWelfare, 20, 261-273.

[9]Iñarra,E.;Skonhoft,A.(2008).«Restoringafishstock:adynamicbankruptcyproblem». LandEconomics,84(2):327-339.

[10]Maimonides,M.(200). BookofJudgements (trad.deRabbiElihahuTouger).NovaYork: MoznaimPublishingCorporation.

[11]Meinshausen,M.;Meinshausen,N.;Hare,W.;Raper,S.C.;Frieler,K.;Knutti,R.;Frame,D.J.; Allen,M.R.(2009).«Greenhouse-gasemissiontargetsforlimitingglobalwarmingto 2 C». Nature,458(7242), 1158-1162.

[12]Moulin,H.(2000).«PriorityRulesandOtherAsymmetricRationingMethods». Econometrica,68(3),643-684.

[13]Nakicenovic,N.;Alcamo,J.;Davis,G.:Vries,B.de;Fenhann,J.;Gaffin,S.;Gregory,K.;Grubler,A.;Jung,T.;Kram,T., etal. (2000).Specialreportonemissionsscenarios.Cambridge: CambridgeUniversityPress.

[14]O’Neill,B.(1982).«AproblemofrightsarbitrationfromtheTalmud». MathematicalSocial Sciences, 2(4),345-371.

[15]Rose,A.;Stevens,B.;Edmonds,J.;Wise,M.(1998).«Internationalequityanddifferentiation inglobalwarmingpolicy». EnvironmentalandResourceEconomics, 12(1), 25-51

[16]Solís-Baltodano,M.J.;Vilella,C.;Giménez-Gómez,J.M.(2019).«TheCatalanhealthbudget:aconflictingclaimsapproach». HaciendaPúblicaEspañola, 228,35-53.

[17]Thomson,W.(2003).«Axiomaticandgame-theoreticanalysisofbankruptcyandtaxation problems:asurvey». MathematicalSocialSciences,45(3), 249-297.

[18]Thomson,W.(2019). HowtoDivideWhenThereIsn’tEnough:FromAristotle,theTalmud,and MaimonidestotheAxiomaticsofResourceAllocation(EconometricSocietyMonographs). Cambridge:CambridgeUniversityPress.

Dissenyaruntipi. Unaactivitatcompetencial pertreballarlageometria ambelGeoGebra

ÈdgarRibot-Llobet InstitutValldeLlémena eribot3@xtec.cat NeusHerasNavarro InstitutValldeLlémena nheras@xtec.cat

Resum Abstract

L’objectiud’aquestarticleésexplicarel desenvolupamentil’avaluaciód’unaactivitat d’aulacompetencialenlaqualelsalumnes haurand’utilitzarelsseusconeixementsde geometriaperresoldreunproblemaenun contextnomatemàticambelsuport delGeoGebra.

1.Fitxatècnica

‚ Nivell: 2nd’ESO.

Theaimofthisarticleistoexplainthe developmentandtheevaluationofa competency-basedclassroomlearningactivity inwhichstudentsarerequiredtousetheir knowledgeofgeometrytosolveaproblemina non-mathematicalcontextusingGeoGebra.

‚ Agrupament:grupscooperatiusde3-4alumnes.

‚ Temps:3hores.

‚ Recursos:dispositiudigitalambconnexióaInternet,GeoGebra,cilindreicondeplàstic, cartolina,escuradents.

‚ Contingutsdel’àmbitmatemàtictreballats:càlculdesuperfíciesdecossosgeomètrics, càlculdevolums,teoremadePitàgores,canvisd’unitats,estimaciódemesures,representaciódefiguresicàlculdemagnitudsamblacalculadora3DdelGeoGebra.

‚ Competènciesespecífiquesdel’àmbitmatemàtic(CEM)avaluades:CEM1 (traduirun problemaallenguatgematemàticoaunarepresentaciómatemàticautilitzantvaria-

bles,símbols,diagramesimodelsadequats)iCEM6(emprarelraonamentmatemàtic enentornsnomatemàtics).

2.Introducció

Elsresultatsdel’últimaprovadecompetènciesbàsiquespublicadesenelnúmero46de Quadernsd’Avaluació (ConsellSuperiord’AvaluaciódelSistemaEducatiu, 2020)posendemanifest,unanymés,queladimensiómatemàticaambunnivelld’assolimentmenoréslad’espai, formaimesura;ésadir,ladimensiórelacionadaamblageometria.Inosolamentaixò,sinó que,enaquestaspecte,gairebélameitatdelsalumnesdeCatalunyatenenunnivellbaixo mitjàbaix.Calrecordarquelesprovesdecompetènciesbàsiquesnosónunconjuntd’activitats detipusreproductiui/omemorístic,sinóquepersegueixenlaresoluciódecertessituacions mésomenyscomplexesicontextualitzadesapartirdeconeixementsquepodenimplicar diferentsàmbits.

Elsmotiuspelsqualselsalumnesanyrereanymostrendificultatsenlageometria,peròen canvimostrenunaltdominidelanumeracióielcàlcul,podensermúltiples.Unmotiu,tal comcomentaDamiàSabatéenelseullibre Lageometriaasecundària (Sabaté, 2005),pot sertansenzillcomlasimplereproduccióperpartdelprofessoratd’allòquevarebrecoma alumneenelseumoment.TalcomdiuSabater,elsplansd’educacióanticsvanpotenciarper sobredetoteldominidel’àlgebraielcàlcul;percontra,lageometriaquedavarelegadaaun segonpla.

Aixídoncs,noéscasualitatqueavuiendias’acabireproduintalesaules,moltsovintper inèrcia,elques’hafetsempre.Pertant,noésestranyque,mentrequelacompetènciaespai, formaimesuratéunnivelld’assolimentbaix,lacompetènciadenumeracióicàlculestigui quinzepuntspercentualspersobre.

Mésenllàdeparlardequinaimportànciaesdonaalageometriapersobredelcàlculales classesdematemàtiques,calcentrarelfocusencomestreballalageometriaal’aula.Sil’únic queesdemanaalsalumnesésquememoritzinfórmulespercalcularàreesivolums,noensha d’estranyarquequanse’lspresentiunproblemacomplexaldavant,tinguinmoltesdificultats al’horaderesoldre’l.Ésperaixòqueexisteixlanecessitatdetreballarlageometriamésenllà delapròpiadisciplina,relacionant-laambdiferentsàreesdelamatemàticaiambaltresàmbitsdeconeixement,idotant-lad’unsentitpertalqueelsalumneslapercebincomapropera.

Enaquestsentit,elsdarrersanyss’hancomençataferpassosimportantsenaquestadirecció iundelsmàximsexponentshaestatAntonAubanell,queambelseullibre Orientacionspràctiquesperalamilloradelageometria (Aubanell, 2010)reflexionasobrelescausesd’aquesta situació,quedivideixenduescategories:per unabanda,eldesequilibrienlaimplementació pràcticadelcurrículum;perl’altra,lametodologiadeltreballgeomètrical’aula.Tenintaixò present,proposatreslíniesbàsiquesdemillora:

1.augmentarlapresènciadelageometriaimoderarladelcàlcul;

2.integrareneltreballgeomètricactivitatsmésriquescompetencialment;

3.incorporarmésgeometriairaonamentvisualatotselsblocsdecontinguts.

Aquestarticlepresentaunaactivitatcentradaenelsegonpuntdelalíniad’actuacióque proposaAubanell.Elsalumneshaurandetransferirelsconeixementsadquiritsalllargd’una unitatdidàcticadegeometria,aldissenyd’untipideformacònica,delqualhaurandefixar lesdimensionsoportunesdonadesunescondicionsdedisseny.

3.Metodologia

3.1. El treball en grup

Aquestaactivitatesduràatermeengrupscooperatiusheterogenis.Elsgrupselsvadissenyar elprofessortenintencomptelesdiferentshabilitatsdelsalumnesdelgrupclasse,aixícom laparitat.Cadaalumnetéundelsrolssegüentssegonsquinasiguilasevahabilitat:

‚ Tècnicdissenyador:mostraunahabilitatgràficaicreativa.

‚ Matemàtic:téhabilitatsmatemàtiquescomaraelcàlcul,lageometriaielllenguatge algebraic.

‚ Redactor:téunaaltacapacitatcomunicativa,tantoralcomenlectoescriptura.

‚ Coordinador:técapacitatorganitzativaidelideratge.Enaquestrol,l’alumnes’had’assegurarquelestasquesesfaneneltempsestablert,hadecontrolarqueeltodeveudel grupnoexcedeixieldesitjableihademoderarelsdebatsinterns,entrealtrescoses.

D’aquestamanera,assegurant queungrupestàformatperalumnesambdiferentsperfils ihabilitats,s’aconsegueixunenriquimentmutumitjançantl’aprenentatgeentreiguals.Cal remarcar,però,queelsrolsnoimpliquenquel’alumneenqüestióhagidefertotalafeinarelacionadaambelseucamp;ésadir,elmatemàticnonomésésl’encarregatdeferelscàlculs, sinóqueéselresponsablequeelscàlculspertinentsesfacin,queesfacinbéi,amés,que totselsmembresdelgruphoentenguinicol laborin.

Peraconseguirl’èxitdeltreballcooperatiués indispensablequeexisteixiunveritableaprenentatgeentreiguals.Ambaquestobjectiu,s’hadetenirencomptequeelsalumnesque formenelgrupnopodentenirnivellsd’assolimentiritmesd’aprenentatgemoltdiferents,ja quesiaixòpassa,noexistiràunllenguatgeentreigualsniunaveritablecomunicacióentre ells.Aquestasituaciósolabocarl’alumnatamb mésdificultatsanoparticiparplenamentenla resoluciódel’activitatilaresta,aqueixar-se’n.Lafracturadelgrup impedeixques’estableixi unacooperacióreal,cosaquepropiciaràquenoexisteixiuntreballcooperatiu.

3.2. Atenció a la diversitat

Comesveuràenl’apartatsegüent,aquestaactivitats’estructuraalvoltantdelcon,uncos geomètricquepotesdevenircomplexdetreballarenunaactivitatcomaquestaperauna partdel’alumnat.Ambl’objectiuquepuguinferl’activitat,esproposendiferentsmecanismesqueespodenpresentarperseparatoconjuntament,depenentdelnivelld’adaptació desitjada:

‚ Proporcionarunmodel,quecontindràtotselspassosques’handeseguir,algunes ajudesperpoderferbonesestimacions,lesequacionsnecessàriesperferelscàlculsi, finsitot,algunaactivitatsemblantd’anysanteriors.

‚ Treballarambcossosméssenzills:unapiràmidedebasequadradaorectangular,en unprimernivelld’adaptació,iunortoedredebasequadradaofinsitotuncub,pera casosmésextrems.

3.3. Riquesa competencial

Unadelescaracterístiquesd’unaactivitatcompetencialésquel’alumnehadepoderproduir unasoluciónovaapartirdetotelquehaaprèsal’aula.Ésadir,nos’hadelimitaraferuna merareproducciódelsconeixementsiprocedimentsadquirits,sinóquehadesercapaçde traslladar-hoasituacionsinnovadores,diferents,complexesiinesperades.

Altrescaracterístiquesdelesactivitatscompetencialsques’hantingutmoltencompteenla propostad’activitatqueespresentasón:

‚ L’alumnehadecrearapartird’unespremissesocondicionsestablertes.

‚ Noesproporcionendadesqueespodensuposar,estimaropredirapartirdelcontext. D’aquestamanera,l’estudianthaderaonarsobrelasituacióproposadaihad’aplicarlaalarealitat.

‚ Esfomental’estimaciódemesuresiresultatsis’incentivalapresadedecisions.

‚ Esdemanaiesvaloralajustificaciódelesdecisionspreses.

‚ Lasolucióòptimasorgeixquanescomparteixenlesideesielsarguments.

Enaquestcas,esdemanaalsalumnesqueestiminlesdadesinicialsdelproblema(elradii l’alçada)apartird’unesrestriccionsqueprovenendelcontextdel’activitat,iquejustifiquin toteslesdecisionspreses:l’estimaciódedades,lessuposicions,lesaproximacionsilautilitzaciód’equacions.Calquel’estudiantexpliquicadapasquefacienelproblemairaoniels resultats.

4.Presentaciódel’activitat

Dinsd’unaunitatdidàcticadegeometriaidesprésd’havertreballatlesfiguresplanes,les àrees,lessuperfíciesielsvolumsdelscossosgeomètrics,aixícomelteoremadePitàgoresper afiguresicossos,esdemanaalsalumnesquedissenyinunatendadecampanya.L’enunciat diu:

Perfihaarribatl’estiuituitresamicsmésdecidiuquevoleuanarapassarunasetmanaenun campamentdesupervivènciaenmigdelanaturaques’organitzadesdelvostregrupd’esplai. Enarribar,elsmonitorsusexpliquenquedurantelspròximsdieshaureud’aprendreaviureamb elsrecursosqueusofereixelboscihaureud’elaborarelsvostrespropisutensilisielmenjar.La primeranecessitatquehaureudecobrirseràel llocondormireu.Elsmonitorsusdiuenqueheude dissenyarunatendadecampanyaqueusserveixiperpassartoteslesnits.

Pertaldeferl’activitat,s’imposenlessegüentscondicionssobreeldissenydelatenda:

‚ Hadetenircapacitatperatrespersones.

‚ Hihandecabreestirades(perdormir).

‚ Hihadecabreunapersonadretaalcentre.

‚ Hadeserenformadetipi.

‚ Hadetenirunvolummínimde4m3 (perassegurarquehihaprouaireperpassarla nit).

‚ Lasuperfíciemàximadetelahadeserde40 m2 (perassegurarquehihaproutelaper atotselsparticipants).

‚ Elspalsolescanyesquedonenrigidesaalatendas’hand’obtenirdel’entorn.

‚ Esdisposaràdecordesipiquetespersubjectarlatendaalterra.

Arribatsaaquestpunt,espotdecidirguiarmésomenysl’activitat,iaixòfinsitotespotanar decidintamesuraqueavancil’activitatiespuguindetectarlesdificultatsdel’alumnat.Les guiesqueesproposensónlessegüents:

a)Buscarinformaciósobrequèésuntipiicomesconstrueix.

b)Estudiarbéeldissenyd’untipi:aquintipusdecosgeomètrics’aproxima,quinésel seudesplegamentiquinessónlessevesequacionsdesuperfícieivolum.

c)Definirl’àreadelabasenecessàriaperquèhipuguindormirtrespersones.

d )Fixarl’alçadadeltipidemaneraqueunapersonapuguiestardretaalcentre.

e)Assegurarquetéelvolummínim.

f )Calcularlallargadaquehaurandetenirelspalsquesostindraneltipi.

g)Calcularelsmetresquadratsderoba quecaldrand’acordambeldisseny.

h)CreareldissenyambelGeoGebraicomprovarquetoteslesmidesielscàlculscoincideixen.

5.Desenvolupamentdel’activitat

a) Buscarinformaciósobrequèésuntipiicomesconstrueix

Ésmoltprobablequepocsalumnessàpiguenquèésuntipi.Pertant,elprimerpunt seràbuscarquèés.Aquestprimerpuntésforçaràpidiquanelsalumnesveuenuna fotografiadeseguidasabendequèestracta.Horelacionenrelativamentràpidamb lesconstruccionstradicionalsdelsnadiusamericansifinsitotalgunalumnerecorda haver-netingutundepetit.

b) Estudiarbéeldissenyd’untipi:aquintipusdecosgeomètrics’aproxima,quinéselseu desplegamentiquinessónlessevesequacionsdesuperfícieivolum.

Objectius:identificarcossosgeomètricsenentornsnomatemàtics,deduirequacions devolumisuperfície(avançat),fereldesplegamentdecossosgeomètrics.

Unavegadahanbuscatinformaciósobrequèésuntipi,observemquel’alumnatfa duesaproximacions:

‚ Uncon(ladesitjada).

‚ Unapiràmidequetéperbaseunpolígonregularde n costats,on n éselnombre depals(arestes)quesubjectenlatela.

Enaquestpuntse’nsplantegenduesopcions.Laprimeraésdeixarqueelsalumnes triïnl’opcióquedesitginilasegona,encarar-loscapal’opcióqueensinteressi.En aquestcas,s’optaperencaminar-loscapalcon,pelfetquenohaestattreballatprè-

viament,adiferènciadetotselsaltrescossos.Laideaésquel’alumnattransfereixi elsaprenentatgesdegeometriaadquiritsal’aula,auncasparticularquenohaestat estudiatprèviamental’aula.Aixòcomportaquehaurandededuirlesequacionsde superfícieivolum.

Peresbrinarl’equaciódevolumesduràatermelapràcticadecomparaciódevolums entreelcilindreielcon.Esproporcionaalsalumnesuncilindre(quehanestudiat prèviamental’aula)iunconamblesmateixesbaseialtura,talcomesveuenlaimatge:

Hand’omplird’aiguaelsdoscossosiposteriormentmesurar-neelvolum,d’aquesta manerapodrancomprovarqueelvolumdelconésunterçdeldelcilindre.Comque sabenl’equaciódevolumd’uncilindre:

elsseràsenzilldeduirl’equaciódevolumd’uncon:

Arribaral’equaciódevolumnopresentagairesdificultatsgràciesalapràcticaamb materialmanipulatiu,ial’horadecalcular-lotampocnopresentacapdificultatjaque solamentdepèndeduesmagnitudsprouconegudes:l’alturaielradi.Ambdueses fixaranenelspròximspassos.

Noobstantaixò,l’equacióperalcàlculdelasuperfícieelsresultaméscomplicada. Fàcilmentveuen,apartirdeldesplegament,quelasuperfíciedelconhadeserigual alasumadelabase(circumferència)ilacaracorba(sectorcircular).Sihihaalguna dificultatenaquestsentit,espotfacilitaralsalumnesquehonecessitinunconde cartolinapertalqueenfacineldesplegamentmanipulatiu:

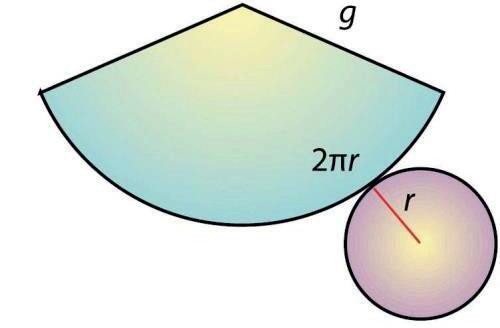
Figura2.Desplegamentplad’uncilindre.

Figura1.Cilindreiconperferlapràcticadevolums.

Elproblemaapareixjustamentamblacaracorba:quintipusdefiguraés?,comes calculalasevaàrea?Sibéelssectorscircularss’estudienencursosanteriors,noésun tipusdefiguraqueapareguisovinti,pertant,s’enténladificultatdegranpartde l’alumnataidentificar-la.Perdeduirl’equacióhaurandecomprovarquel’arcdelsector ésigualalperímetredelacircumferènciadelabase.Novament,espotutilitzaruncon decartolinaperfacilitarlacomprensió.Elraonamentésparal lelpertrobarundels costatsdelrectangledeldesplegamentdelcilindre.L’àreadelsectorcircular,sabentla longituddel’arc(Lq ielseuradi(Rq,és:

Enaquestcasconcretitalcomespotveurealafigura 2,elradidelsectorcircularés igualalageneratriudelcon:

i,finalment,lalongituddel’arccorresponalalongituddelacircumferènciadelabase:

Substituinteq.5al’eq.4obtenimfinalmentl’àreadelsectorcirculardelnostretipi:

Ésmoltprobablequealgunsdelsalumnesnoarribinacomprendrelademostració del’àreadelsectorcircular.Enaquestcas,esprioritzaràsolamentlacomprensióque aquestaàreadepèndelradidelabaseilageneratriudelcon.

S’introdueixunnouconcepte:lageneratriu.Unagranpartdelsalumnesn’intueixel significatapartirdelarepresentacióplanadelconidelstreballsprevisques’hanfet amblacreaciódecossosderevolució.S’adonenquel’altura,elradidelabaseila generatriuconformenuntrianglerectangle(raonamentquenecessitaremmésendavant),iqueelradiil’alturasónelscatetsilageneratriuéslahipotenusa.Alhora,és unabonaoportunitatperrecordaralsalumnesqueelscossosderevolucióesformen apartirdelarevoluciód’unafigurageomètricaalvoltantd’uneixique,enelcasdel con,ésjustamentlarevoluciód’aquesttrianglerectangle(figura3).Novament,elma-

terialmanipulableenspotresultarútilpermostrarlarevoluciód’aquesttriangle.Per fer-ho,necessitemuntrianglerectangledecartolina,unescuradentsicintaadhesiva. Finalment,solsquedafer-logirar.Espotgravarambundispositiumòbiliobservar-ne elresultat.

c) Definirl’àreadelabasenecessària perquèhipuguindormirtrespersones

Objectiu:calcularl’àread’unacircumferènciafixantundiàmetreapartird’unarestricció.

Elprimerqueraonenelsalumnesésque,perquèhipuguindormirtrespersones,la basehadeteniruna«llargada»quevedeterminadaperl’alturadelespersones.Una bonasuposiciód’alçadesestrobaràentreunmarged’entre 1,5i 2 metres.D’altrabanda,handetenirencomptequecadapersonatambéocupaunaampladadeterminada. Unabonasuposicióestaràalvoltantd’1 m(figura4).

Figura4.Espaiqueocupaunapersonaquandorm.

Així,unavegadadefinitl’espaiqueocupaunapersonaquandorm,espotdeterminar elqueocupentrespersones.Talcomespotveurealafigura4,espotassimilaraun rectanglede3 ˆ 2 m.

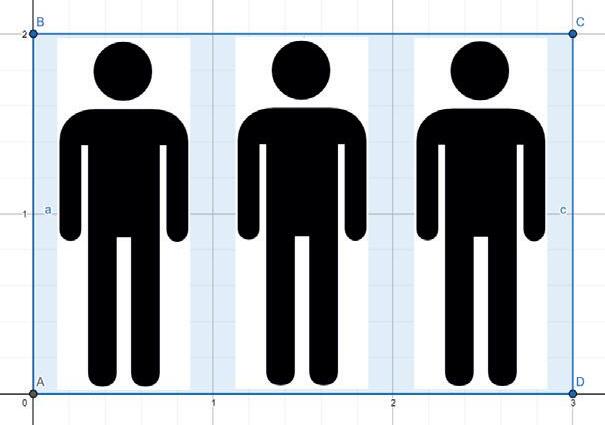
Figura5.Espaiqueocupentrespersonesquandormen.

Peracabardedeterminarlabaseésnecessaritrobarunacircumferènciaqueinscrigui elrectangleanterior.Perfer-ho,espotdeduirqueeldiàmetrehadeserigualala diagonaldelrectanglei,pertrobar-ho,aplicarelteoremadePitàgores.Enaquestcas, tenimuntriangleambunscatetsde 2 mi3miunahipotenusade3,6m;pertant, lacircumferènciatindràunradid’1,8m.TambéespotutilitzarnovamentelGeoGebrapercomprovarelcàlculiveureque,efectivament,elrectangleestàinscritenla circumferènciaiaquestapassapelsvèrtexsdelrectangle.

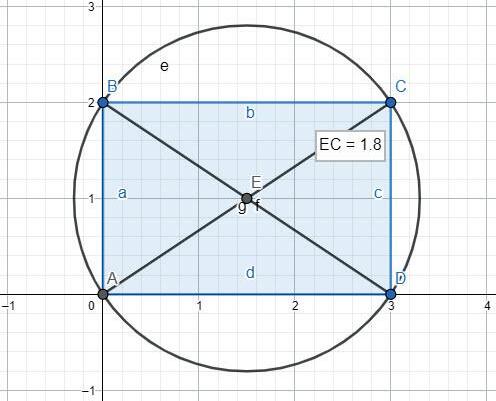
Éspossiblequealgunsalumnessuposinunaàreadelabasedirectament,sensepassar pelraonamentdel’alçada.Enaquestcas,se’lshadeferveurequenos’hanassegurat quehicàpiguentrespersones;pertant,tenenduesopcions:oseguirelspassosdescritsanteriorment,obé,apartirdel’àreasuposada,calculareldiàmetreicomprovarsi hicabenpersones.

d ) Fixarl’alçadadeltipidemaneraqueunapersonapuguiestardretaalcentre

Objectiu:fixarunadadaapartird’unarestricció.

Enl’apartatanteriorjas’hasuposatl’alçadail’ampladad’unapersona.Pertant,elrectanglequefixaràl’alçadaseràd’1 × 2 m.Amés,tenintencomptequeeldiàmetrede labaseésde3,6m,centrantelrectanglealabaseiintroduinttotesaquestesdadesal GeoGebras’obtél’esquemadelafigura7:

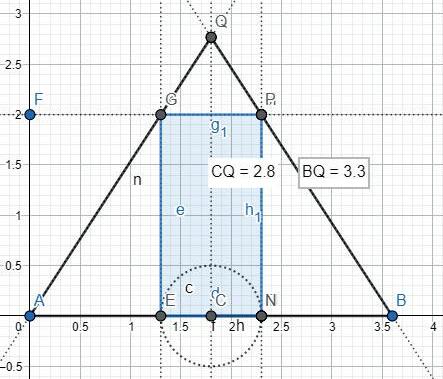
Figura7.Esquemadel’alçatdelconaplicantlescondicionsdedisseny.

Figura6.Esquemadelabasecirculardeltipi.

Apartirdelaintersecciódelssegments AQ i BQ espottrobarl’alçada CQ de 2,8m,així comlageneratriuBQde3,3m.

e) Assegurarquetéelvolummínim

Objectiu:calcularelvolumd’un conapartirdedadesfixades.

Uncopfixatelradidelabaseil’alturadeltipi,espotcalcularelvolumd’aireicomprovarquecompleixlacondicióimposadaal’enunciat.Elsalumneshaurand’aplicarla fórmuladevolumdel’equació 2,juntamentambl’alçadatrobadaal’apartatanteriori elradifixatenl’apartat c

Comqueelradidelabasefixatal’apartat c ésd’1,8mil’alçadacalculadaambel GeoGebraal’apartat d ésde 2,8m,elvolumésde 9,5m3 .Comque 9,5 ą 4,escompleix lacondiciódedisseny.

Encasqueelvolumfosméspetitque4,elsalumneshauriendetornarobéal’apartat c obéal d iaugmentar-nelesdimensions.

f ) Calcularlallargadaquehaurandetenirelspalsquesostindraneltipi

Objectiu:calcularlageneratriud’unconmitjançantelteoremadePitàgores

Comqueenl’apartat d elsalumnesjahanmesuratlageneratriuambelGeoGebra, se’lspotdemanarquecomprovinodemostrinqueelvalorobtingutéscorrecte.Per fer-ho,haurandecalcularlahipotenusadeltrianglerectangleformatpelradidela baseil’alçadadelcon,queseranelcatets.

Algunsalumnesvancomentarquesielspalsfessinexactamentlalongituddelageneratriu,quedarienunamicacurts,jaqueunapartesnecessitaràperfixareltipialterra i,peraltrabanda,seriaboquesobresortissinunxicperlapartdedaltpertaldelligar-los.Pertant,als3,3mdelageneratrius’hipodenafegir 20 cm,demaneraquela llargadatotaldelspalsnecessarisseràde3,5m.Enqualsevolcas,ésimportantque veginquenoconvéquemesurinexactamentelmateixquelageneratriuperpoderfer unabonaconstrucció.

g) Calcularelsmetresquadratsderobaquecaldran

Objectiu:calcularlasuperfícied’uncon.

Arribatsaaquestapartat,elsalumnesjadisposendetoteslesdadesnecessàriesper calcularlasuperfíciedelcon:elradidelabaseilageneratriu.Haurandecomprovar quelasuperfícienosuperielsmetresquadrat sfixatsal’enunciat.Caldirqueaquesta dadaestàsobredimensionadairealmentésmoltdifícilqueelsalumnessuperinels40 m2 ,ienelcasquehofacinvoldirquealgunadelesdadesquehanfixatnoésrealista i,pertant,handetornaralsapartats c i d

Enaquestapartat,algunsalumnesvanexposareldubtesieranecessaricomptarla superfíciedelabase,ésadir,sieranecessariposartelaalterra.Enaquestsentit,esva donarllibertatdedecisióenfunciódelpropicriteriiladisponibilitatdetela.

Enaquestcas,tenintencomptequeelradidelabaseésd’1,8milageneratriuésde 3,3m,siapliqueml’equació6lasuperfícieresultantésde 18,7m2 .Si,amés,esdesitja posartelaalterra,s’hauràdecalcularl’àreadelabasedelconresultant: 10,2 m2 .Sise

sumenambduesàrees,s’obtéunaàreatotaldelconde 28,9 m2 .Comque 28,9 <40,es compleixlacondiciódedisseny.

h) CreareldissenyambelGeoGebraicomprovarquetoteslesmidesielscàlculscoincideixen Objectius:utilitzarelGeoGebraperrepresentarunafiguraen3D.Comprovarelsvalors delageneratriu,lasuperfícieielvolumcalculats.

Independentmentquel’alumnatestigui mésomenysacostumatatreballarambel GeoGebra,dibuixarunconésrelativamentfàciliintuïtiufinsitotperaprincipiants. Solamenthaurand’introduirelpuntdelcentredelabase(recomanemutilitzarl’origen decoordenades),l’alçadai,finalment,elradi.Uncopintroduït,apareixeràeltipiipodrancalcular-nel’àreailasuperfícieamblesfuncionalitatsdelGeoGebra,perpoder-ho compararambelsseuspropisresultats.

6.Avaluació

Unaspecteimprescindibleiqueavegadesquedaoblidatpermancadetempso,finsitot, perlamalacreençaqueésunaspectesecundari,ésl’avaluació.Sienfinalitzarunaactivitat competencialcomaquestanoesdedicaeltempssuficientperquèelsalumnesreflexionin sobreelquehanfet,l’aprenentatgequedaincomplet.Ésperaixòquelapropostad’avaluació peraaquestaactivitatésunasessiód’unahoraonesfaràunacoavaluació.

Ésmoltrecomanableferservirlarúbricad’unsolpunt,pertalquepuguinreflexionarmés profundamentsobrelatascaavaluada.Aquestarúbricahadepartirdelsindicadorsd’avaluació, peròs’had’adequaralvocabularidel’alumnatpertalquelafacinseva.Calquesiguinels mateixosalumneselquiproposinelsítemsquehand’aparèixeralarúbrica.Noobstantaixò, eldocenthadetenirunapropostaquenohadecompartirambl’alumnat,sinóqueelsha deferbonespreguntesielshademostrarelsmodelsnecessarisperquèsiguinellselsque arribinaformularunsindicadorsalineatsamb elsdesitjats.Lataulasegüentpresentauna possibleproposta.

Figura8.Esquemafinaldeltipiamblessevesdimensions.

Criterisde realització

Interpretació delproblema

Resoluciódel problema

Mesures iunitats

Aplicaciódels aprenentatges previs

Identificació delscossos geomètrics

Representació decossos geomètrics

Úsdel Geogebra

Interèsper l’aprenentatge ilamillora

Elements destacats: «Etfelicito per...»

Disseny

Úsdela llengua

Criterisd’avaluació

Enquèemfixaré?

Tradueixunproblemageomètrica llenguatgematemàticielaborauna estratègiaderesoluciócorrecta,clara ibenexplicada.

Aplical’estratègiaproposadapercalcular àreesivolumsdefiguresgeomètriques. Utilitzavariables,símbols,diagramesi modelstreballatsin’elaboradepropis. Justificalesdecisionspreses.

Esculllesunitatsdemesuraadequadesen cadasituació,ienjustificairaonaels motius.Éscapaçdeferlaconversió d’unitatsdelongitud,àreaivolum.

ConeixelteoremadePitàgoresil’aplica correctamentutilitzantelsdiagramesi càlculsadequats.Sapjustificar-nel’ús.

Éscapaçd’identificarcossosgeomètricsa partirdeladescomposiciód’imatgesde contextosrealscomplexos.Coneixles propietatsdelscossosgeomètrics ilesaplicaperresoldreelproblema.

Representaelcosgeomètricenun contextrealcomplexmitjançant qualsevoldelestècniquestreballades: desenvolupamentpla,representació plana.Aixòlipermetresoldreqüestions directamentlligadesalproblema proposat.

Faúsdelesfuncionsestàndardi complexescomasuportperresoldre irepresentarproblemesdegeometria. Éscapaçd’aprendrepersimateix funcionalitatsnotreballadesal’aulai d’explicar-lesalscompanys.

Manifestainterèspelproblemais’esforça pertrobarlamillorsoluciódemanera continuada.Falestasquesambinterès iconstància.Reconeixelserrorsiestà disposataesmenar-los.

Eldissenydeltreballésordenat iequilibrat.Lesimatgestenenpeu. Ladistribuciódelsapartatsielformat millorenlasevacomprensió.

Laredacciódeltextésentenedora.Ellèxic utilitzatésespecíficdeltematreballatila sintaxi,ambfrasescurtesicompletes,és l’adequada.Nohihafaltesd’ortografia.

Elementsper millorar: «Etsuggereixo que...»

Ésimportantremarcarquelacoavaluaciónotéencapcasunaqualificaciónumèrica,sinó queésunretornenformad’avaluacióreguladora.Pertant,l’objectiuésquefacinunsbons comentarisambl’objectiudemillorarl’activitatrealitzadapelseucompany.Unavegadahan rebutdetornadalarúbricadecoavaluació,disposendemitjahoraperintroduirlesmillores proposadespelsseuscompanysqueconsiderin.

Enlarúbricad’avaluaciódelprofessorbasadaenlescompetènciesespecífiquesdel’àmbit matemàtic(CEM)ielscriterisd’avaluació(CA)associats,s’especifiquenelsobjectiusd’aprenentatgeconcretsd’aquestaactivitat,aixícomelsindicadorsperpoderobtenirlaqualificació finaldel’activitat.

Nivell 3 (assoliment excel·lent)

Indicadors d’avaluació

Nivell 2 (assoliment notable)

Tradueix un problema geomètric a llenguatge matemàtic i elabora una estratègia de resolució amb l’objectiu de calcular àrees i volums de figures geomètriques. Utilitza les variables, els símbols, els diagrames i els models treballats i n’elabora de propis, i en justifica l’adequació en cada cas.

Tradueix un problema geomètric a llenguatge matemàtic amb l’objectiu de calcular àrees i volums de figures geomètriques. Utilitza les variables, els símbols, els diagrames i els models treballats i adequats en cada cas.

Nivell 1 (assoliment satisfactori)

Objectius d’aprenentatge

Tradueix un problema de geometria senzill a llenguatge matemàtic per calcular àrees i volums de figures geomètriques bàsiques.

O1. Calcular longituds, àrees i volums mitjançant la traducció del problema a llenguatge matemàtic i utilitzant variables, símbols, diagrames i models adequats.

Criteris d’avaluació competencials

Competències específiques de l’àmbit matemàtic

Escull les unitats de mesura adequades en cada situació i en justifica i raona els motius. És capaç de fer tot tipus de conversió d’unitats (longitud, àrea i volum) en qualsevol escala mitjançant factors de conversió.

Escull les unitats de mesura adequades en cada situació. És capaç de fer conversions d’unitats (longitud, àrea i volum) mitjançant factors de conversió.

Escull les unitats de mesura adequades en contextos senzills. És capaç de fer conversions d’unitats bàsiques de longitud, àrea i volum.

O2. Escollir les unitats de mesura més adequades en cada situació. Canviar i relacionar les diferents unitats de la geometria (longitud, àrea i volum).

CA1.1 Interpretar problemes matemàtics organitzant la informació donada i comprenent les preguntes formulades.

CEM1 Interpretar, modelitzar i resoldre situacions de la vida quotidiana, pròpies de les matemàtiques i d’altres àmbits del coneixement aplicant diferents estratègies i formes de raonament per explorar procediments i obtenir solucions.

Coneix el teorema de Pitàgores i l’aplica en tot tipus de contextos reals utilitzant els diagrames i càlculs adequats. Sap justificar el seu ús en cada context.

Coneix el teorema de Pitàgores i l’aplica en diferents tipus de contextos reals utilitzant els diagrames i càlculs adequats.

Coneix el teorema de Pitàgores i l’aplica en casos senzills i concrets

O3. Conèixer i aplicar el teorema de Pitàgores en la resolució de problemes en diferents contextos.

És capaç d’identificar cossos geomètrics a partir de la descomposició d’imatges de contextos reals complexes. Coneix les propietats dels cossos geomètrics i els classifica adequadament per descriure el món físic.

És capaç d’identificar cossos geomètrics a partir de la descomposició d’imatges de contextos reals. Coneix les propietats dels cossos geomètrics i els classifica adequadament per descriure el món físic.

És capaç d’identificar cossos geomètrics a partir de la descomposició d’imatges de contextos reals senzills. Coneix les propietats bàsiques dels cossos geomètrics i els classifica adequadament per descriure el món físic

O4. Identificar figures i cossos geomètrics en contextos no matemàtics i utilitzar el coneixement sobre les seves propietats i la seva classificació per descriure el món físic

Representa tot tipus de cossos geomètrics en un context real complex mitjançant qualsevol de les tècniques treballades: desenvolupament pla, representació plana i construcció i deconstrucció de cossos.

Representa tot tipus de cossos geomètrics en un context real mitjançant qualsevol de les tècniques treballades: desenvolupament pla, representació plana i construcció i deconstrucció de cossos.

Representa cossos geomètrics bàsics en un context real mitjançant alguna de les tècniques treballades: desenvolupament pla, representació plana i construcció i deconstrucció de cossos

O5. Representar cossos geomètrics en contextos reals mitjançant les tècniques del desenvolupament pla, la representació plana i la construcció i deconstrucció de cossos.

Reconèixer i utilitzar les matemàtiques presents en la vida quotidiana usant els processos inherents a la investigació científica i matemàtica: inferir, mesurar, comunicar, classificar, predir…, en situacions susceptibles de ser abordades en termes matemàtics

CA6.1

Vincular i contextualitzar les matemàtiques amb altres àrees de coneixement, interrelacionant conceptes i procediments, per resoldre problemes i desenvolupar la capacitat crítica, creativa i innovadora en situacions diverses.

CEM6

7.Possiblescontinuacions

Aquestaactivitattéunaduraciótotalde3hores:unahorai45minutsperelaborarl’activitat, 15minutsperacordarlarúbricad’unsolpuntambelsalumnes,mitjahoraperalacoavaluacióimitjahoramésperintroduirlesmilloresproposades.Noobstantaixò,éspossible continuartreballantalvoltantd’aquestcontexticonnectarlaactivitataaltresàmbitstalcom esproposaacontinuació:

‚ Construirunamaquetadeltipiaescala.D’aquestamaneraestreballenlaproporcionalitatielsmaterialsilestècniquesdeconstrucciódesdelatecnologia.

‚ Construireltipiquehagiestatmésbendissenyatiescollitpertotalaclasse.Elsmaterialsnecessarissón:canyes,robaicorda.Posteriormentespodriacediraalgunaescola pròxima.

‚ Preguntainvestigabledel’àmbitcientífic:quinsfactorshemdetenirencompteper calcularelvolummínimdeltipi?S’handetenirencompteelsfactorssegüents:

•Biològics:respiració,necessitatd’oxigen,paperdelCO2 .

•Químics:concentracionsdegas.

•Matemàtics:percentatgesperalesconcentracions.

8.Conclusions

Elsalumnesesvanendinsarenunproblemasensedadesiaixòvacomportaralgunesdificultatsal’horadecomençarl’activitat.Unavegadasuperataquestescull,però,vansercapaços defixardadesdemaneraraonadaperaundissenycorrected’acordamblesrestriccions.La granmajoriadelsalumnesvansercapaçosdetransferirelsconeixementsadquiritsaclassea uncasquenohavientreballatprèviament.Vantrobarútill’úsdelGeoGebraenlarealització del’activitatperquèvanveureunúspràcticd’aquestaaplicació.Vanvalorarpositivament poderferunacoavaluació,jaqueposteriormentelsvapermetremillorarelseutreballi,així, obtenirmillorsresultats.

9.Referències

Aubanell,A.«Orientacionspràctiquesperalamilloradelageometria». Quadernsd’Avaluació, núm.31 (2015):63-137.

ConsellSuperiord’AvaluaciódelSistemaEducatiu, 2020 L’avaluaciódequartd’ESO2020 http://csda.gencat.cat/ca/arees-actuacio/avaluacions-consell/avaluacio-quart-eso/

Sabaté,D. Lageometriaasecundària. Barcelona:UniversitatPolitècnicadeCatalunya, 2005.

Comhofarem?Descripció d’untallerambdiverses activitatsartístiques imatemàtiquesper

desenvoluparlacreativitat enalumnesdeprimària

QueraltViladevallValldeperas

ProfessoradeMultimèdiaalaUOCiestudiantdelDoctoratenEducaciódelaUdG qviladevall@uoc.edu

SalvadorLinaresMustarós

ProfessordeMatemàtiquesdelaUdGimembredel’equipdirectiu delaCàtedradeJovesEmprenedorsdelaUdG salvador.linares@udg.edu

JoanCarlesFerrerComalat

ProfessordeMatemàtiquesdelaUdGimàsterenDidàcticadelesMatemàtiques joancarles.ferrer@udg.edu

Resum Abstract

Aquesttreballpresentalesdiferents activitatsd’untallerartísticimatemàticque técomaobjectiul’exercicidelacreativitat enelcicleinicialdeprimària.Peraconseguir aquestpropòsiteltallerestàdividiten quatreparts.Laprimeraestàcentradaenla lecturad’unconte.Lasegonapresenta diversosexemplesensituacionsrealsde cercadesolucions.Laterceraconsisteixa exercitarlacreativitatpersonalmitjançant lacercademúltiplessolucionsenactivitats artístiques.Laquartaconsisteixaexercitar lacreativitatpersonalmitjançantlacercade múltiplesmaneresdesolucionaractivitats logicomatemàtiques.

Thisarticlepresentsthedifferentactivities proposedinamathematicalartworkshop aimedatexercisingcreativityintheinitial cycleofprimaryschool.Toachievethisend, theworkshopisdividedintofourparts.The firstfocusesonreadingastory.Thesecond presentsseveralexamplesoffindingsolutions inrealsituations.Thethirdisaimedat exercisingpersonalcreativitybyfinding multiplesolutionsinartisticactivities.The fourthconsistsinexercisingpersonal creativitybylookingformultiplewaystosolve logical-mathematicalactivities.

1.Introducció

Desdel’any 2018,promogutatravésdel’OrganitzaciódelesNacionsUnides,cada 21 d’abril secelebrademaneraoficialelDiaMundialdelaCreativitatilaInnovacióambl’objectiude fomentarideesoriginalsperanimarapensartenintencomptenovespossibilitatsiutilitzant viesdesoluciónovesicreatives.Estractadepromoureenàmbitsdiversoselpensament creatiu,quepotabastarlacreativitatentesatantdesdelpuntdevistadelacreacióartística comdesdelaresoluciódeproblemes.Ambaquestpuntdepartidacomaobjectiu,hem dissenyatidutalapràcticaeltallerquepresentemenaquestarticle,amblaideaque,amb lesmodificacionsquecalgui,puguiinspirariserútilalsensenyants.

Totiquelaparaulacreativitatsuggereixinterpretacionsàmplies,segonsalgunsautorsla creativitatéslacapacitatdegeneraralgunacosanovai,igualquequalsevolaltrahabilitat, espotexercitardesquesompetits(Medina etal., 2017).Lesinvestigacionsenelcampdela creativitatsuggereixenqueaquestaésunpotencialquetenentoteslespersonesiqueelseu desenvolupamentdepèndelesoportunitatsqueofereixelcontext(Elisondo etal., 2012).Per aixònoespotdesaprofitarcapoportunitatamblaqualpotenciar-la,sobretotsitenimen comptelesnecessitatsactualsdelmón,onelsavençosenciènciaitecnologiahanfetque passemd’unasocietatdeproducciómassivad’objectes,aunadeserveisid’informacióonel motorsónlesideesilacreativitat.

Exercitarlacreativitatatravésdelarealitzaciód’activitatsartístiquesésunaopciópopularmentbenacceptada,jaquesempres’haassociatelmónartísticamblacreaciód’obres. Contràriament,enmatemàtiqueslacercadesolucionsdelessevesactivitatsnosolserpercebudacomunatascacreativa,sinómecànica,deseguimentd’unsprocessosespecíficssegons elproblemaplantejat.Aquestapercepcióéscompletamenterròniaperquèenlarecercade lasolucióaunproblemasemprehihapresentunafasedecreativitat(Hadamard, 1945;Polya, 1965).Consegüentment,semblaraonablesuggerir queperpotenciarlacreativitatsiguiideal quedavantdequalsevolproblematinguemunaactitudobertaenverslarecercadetotesles possiblesmaneresdesolucionar-lo.

DesdelDepartamentd’EmpresadelaUniversitatdeGironaesvainiciarunprojectedins delProgramaPilotdeSuportaIniciativesiActivitatsenelsàmbitsdelaDivulgaciódela RecercaidelCompromísSocialdelaUniversitatdeGirona,consistentacrearuntallerper aalumnesdeprimàriaqueoferístreballarl’habilitatdelacreativitatapartird’activitatstant matemàtiquescomartístiques,amblaideaque l’associacióentreelsdosmonspermetésque lacreativitatfospercebudaenlesmatemàtiquessimilarmentacomhoésenl’art.Laintenció delpresenttreballésmostrarambdetenimentcadascunadelesquatrepartsdeltaller.La primeraestàcentradaenlalecturad’uncontequefomentalacercademúltiplessolucions. Lasegonapresentadiversosexemplesdesituacionsrealsdecercadesolucions.Latercera consisteixaexercitarlacreativitatpersonalmitjançantlacercademúltiplessolucionsenactivitatsartístiques.Ladarreraconsisteixaexercitarlacreativitatpersonalmitjançantlacerca dediferentsmaneresdesolucionarproblemeslogicomatemàtics.Enaquestaparttambées tenenencompteelsexercicisquepodentenirmaneresdesoluciódisruptivesobtingudesen modificarlesreglesimplícitesdelsproblemesplantejats.Finalment,eltreballofereixalguns consellsderivatsdelarealitzaciód’aquesttallerentresgrupsdiferentsd’alumnesdelprimer cicledeprimària.

2.Eltaller,pasapas

Eltallers’iniciaamblalecturad’uncontequetéperobjectiuposardemanifestelsavantatges quetétrobardiferentsviesdesolucióaunmateixproblema.Elconte Comhofarem?,adreçat aalumnesdelcicled’infantilidelprimercicledeprimària,vaserescritexpressamentamb aquestpropòsit.1 Lahistòriatécomalíniaargumentallesdiferentsmaneresdesolucióque plantegenunconjuntdepersonatgesd’animalsdavantdelreptecomúd’assolirunraïmdeplàtanssituataunaalturaconsiderable.Alafigura 1 podemveurerecollidesalgunesdelesestratègiesdesolucióassajadespelsdiversosprotagonistes.Lalliçóqueil lustraelconteésqueal finalelsnenscoprotagonistes,totihaverestatelsprimersadescobrirelsplàtans,esqueden sensepelfetdenohaverpensatenaltresviesdesolucióméseficients,jaquehantrigat massaaaplicarlasevapropostaialtresanimalsse’lshanavançatambmaneresqueells tambépodrienhaverdutaterme.

Lasegonapartdel’activitattéperobjectiumostrarquelacreativitatpotestarassociadaala idead’assaigierrorenlacercad’unamaneradesolucionarunproblema.Peraquestaraóes vacrearlasegonapartdel’activitat,consistentaveureunconjuntdevídeosonesresolen, desprésdediversosintents,totdeproblemesensituacionsdelavidareal.Lagràciad’aquesta

1.Perfer-neunalecturacompletaiprojectar-loal’aula,elconteespotdescarregardel’adreçaweb https://dugi-doc.udg.edu/handle/10256/19568.

Figura1.Imatgesdelconte Comhofarem? Il¨¨lustracionsdeQueraltViladevall.

partdeltallerésquelespropostesdesoluciólestrobendiferentsespèciesd’animalsno humans.Algunsexemplesdevídeosqueespodenprojectarenaquestapartdeltalleres trobenalsenllaçossegüents:

‚ www.youtube.com/watch?v=nLsR3xj3d70

‚ (Orangutanicacauet).

‚ www.youtube.com/watch?v=KLK4kh39Jwg(Corbinou).

‚ www.youtube.com/watch?v=seRBI-LkoSE&t=166s(Porquetipilotadegolf).

Enelprimerenllaç,representatalafigura 2,s’observendiferentsintentsdesolució,perpart d’ungrupdepersones,pertreureuncacauetdelfonsd’untubdevidrellarg,primitancat pelfons.Eltubestàenganxatalataulaperquènoespuguitombarilataulaestàclavadaa terrapelmateixmotiu.Elvídeomostramúltiplesintentsinfructuosos,comarabufar,intentar arribaralcacauetdirectamentambelsditsointentartombareltubolataulaperquèelcacauetcaigui.Finalment,unpetitorangutanmostraunabonaestratègiadesolució:omplir-se labocad’aiguaibuidar-laaltubpertalqueelcacauetsuriipuguiagafar-loambelsdits.

Elsegondelsvídeos(figura3)presentalesestratègiesdesoluciód’uncorbdavantdelproblemadetrencarunanou.Esmostracomintentatrencar-lallançant-ladesdel’aireicom hoaconsegueixfinalmentdeixant-lacauresobreunacarreteraperquèl’esclafinlesrodes d’uncotxequanhipassapersobre.Lapartmés divertidadelvídeoésobservarqueelcorb s’esperaqueelsemàfordevianantsestiguiverdperarribaralanoutrencada,perevitarser atropellatpelscotxesquecirculenperlacarretera.

Finalment,eltercervídeo(figura4)mostraduesestratègiesdesolucióqueunporquetexecutaperintroduirunapilotadegolfdinsd’uncercledeplàsticqueimitaelforatdel green.En primerlloc,l’empenyambelmorrofinsalforat,peròpermoltquehointentanoaconsegueix ferpujarlapilotaperlavoraverdadelplàstic.Aleshoresagafaelplàsticamblaboca,l’aixeca persobredelapilotaielsituadetalmaneraqueaconsegueixquelapilotahiquediadins.La solucióinnovadoraqueaportaelporquetensmostraunamaneramoltcreativad’introduirla pilotaalforat.

Figura2.Escenesdelprimervídeosobrel’obtenciód’uncacauet.

Figura3.Escenesdelsegonvídeo,delcorbquevoltrencarunanou.

Latercerapartdeltallertéperobjectiuexercitarlacreativitatmitjançantlestrestasques artístiquessegüents:

Tasca1:completaril¨¨lustracions

Laprimeratascaconsisteixacompletaril lustracionsapartird’unafigurageomètrica,com arauncercle,unael¨lipse,unquadratountriangle.Així,perexemple,apartird’uncercle,els alumnespodencrearlacarad’unlleó,unarodaounsol.Aquestatascaajudaaintroduirla ideaenelsalumnesquetotasolucióéscorrectaiqueencreativitattoteslespropostesde soluciósónbenvingudes.

Tasca2:endevinareldibuixfinal

Enlamateixalínia,lasegonatascaconsisteixaproposaralsalumnescomacabarienunaimatgequemostraunfragmentd’unafiguramoltconeguda.Aquestaactivitatsegueixreforçant laideaquedavantd’unproblemapothaver-hiunagranquantitatdesolucionsdiferentsique potsermoltdivertitintentartrobar-ned’altres.Alafigura5podemveurealgunsexemples defiguresperacabar.Siesdesitgenmésil¨lustracionsd’aquestestil,espotescriureenel cercadoreltext«finishthepicture».

Tasca3:trobaranimalsocults

Laterceratascadel’activitatconsisteixatrobarelsanimalsocultsdinsunpaisatge.Lafigura6ésunbonexempled’imatgeidealperaaquestaactivitat.Siesdesitgenmésil¨lustracions d’aquestestilambdiversosanimalsamagats,espotescriureenelcercadoreltext«hidden animals».Aquestatascaconsolidalaideaque unproblemanoespotconsiderarenllestitsi noesmiradetrobartoteslessolucionspossibles.

Figura4.Escenesdeltercervídeo,delporquetqueintrodueixlapilotadegolfalforat.

Figura5.Dibuixosquecalacabar.Il¨¨lustracionsdeQueraltViladevall.

Finalment,laquartaidarrerapartdeltallerconsisteixatreballarlacreativitatapartirde trobarmúltiplesviesdesolucióaproblemesdetipuslogicomatemàtic.Alawebespottrobar ungrannombred’exercicisperaaquestpropòsit.Perexemple,elsexercicisméssenzillsde lesprovesCangur.Vegemacontinuaciótresexemplesinspiratsenexercicisdelesproves Cangurdecinquèdeprimària.

Problemalogicomatemàtic1

Eneldibuixhihaalgunesestrellesde5,6i7puntes.Quantespuntestenenentretotes?

Observemqueunaprimeramaneraderesoldre’léscomptartoteslespuntesques’intueixen quehihaaldibuix.Unasegonaésveurequehiha3estrellesde5puntes,unade6iunade7,i aleshoresfer5 ` 5 ` 5 ` 6 ` 7.Unaterceraéstreure 1 puntadelade6i 2 delade7.Aleshores tindrem5estrellesde5puntesi3puntessoltes.Pertant,tenen5 ` 5 ` 5 ` 5 ` 5 ` 3 “ 28 puntes.

Figura6.Animalsocults.Il¨lustraciódeQueraltViladevall.

Problemalogicomatemàtic2

Enaquestgratacelhihaquatreescalesdeseguretatcontraincendis.L’alturadelesescales estàmarcadaalapartsuperiordecadascunad’elles.Quinaésl’alturadel’escalamarcada ambl’interrogant?

Unaprimeramaneraderesoldreaquestproblemaésrestarlallargadadel’escala 9 ala 12 i desprésrestaraquestvalorobtingutala8.Enaquestcas,tindríem 12 9 “ 3i,aleshores, 8 3seriaiguala5.Unasegonaéstreureal’escala 12 lamidadel’escala8.Aleshores,sia l’escala 9 lirestemaquestvalor,obtindríeml’alturadel’escalamarcadaambl’interrogant.En aquestcas,tindríem 12 8 “ 4isia 9 lirestem4,obtenimtambéelvalor5.Finalment,una terceramaneraderesoldreaquestexerciciéssumarllargadadel’escala8iladela 9.Com queenaquestasumasumeml’alçadadel’interrogantduesvegades,totelqueenspassem de 12 ésl’alçadacercada.Enaquestcas,8 ` 9 “ 17iobservemqueenspassem5de 12. Aleshores,l’alçadamarcadaésde5.

Problemalogicomatemàtic3

Elcangurpuja3escalonscadavegadaqueelconillenbaixa 2.Enquinescalóestrobaran?

Unaprimeramaneraderesoldreelproblemaésanartrobantenquinescalóestrobenelsdos animalssegonasegon.

Escalóonestrobaelcangur Escalóonestrobaelconill

Veiemque,passatsquatresegons,totsdosanimalsestrobenal’escaló 12 i,pertant,ésen aquestescalóons’hantrobat.Unasegonamaneraésadonar-sequelasumadel’escalóon estrobenelsdosanimalshadecomplirques’hipuguiarribarsaltantde3en3i,alavegada,

s’hipuguiarribarsaltantde 2 en 2 (=hadeseralavegadaunmúltiplede3ide 2),ique,a més,hadeserunnombremajorde 10,jaque,comqueelcangurvamésràpidqueelconill, s’handetrobarpassadalameitat,imenorde 18,jaquesegurquetriguenmésd’unsegona trobar-se.Lasolució 12 compleixaquestacondiciói,pertant,hadeserlasolució.Unatercera opcióésadonar-sequetotsdosanimalscadasegons’apropenentreells5escalons.Comque inicialmentestanseparatsper 20 escalons,haurandepassar4segonspertrobar-se.

Finalment,volemcomentarqueenaquestapartdeltalleréspossibleescollirexercicisamb solucionsquepodríemanomenardisruptives,enelsentitquetrenquenelsistemadecreencesestablert.Acontinuaciódetallaremtresexercicismésperacabardecomprendrel’essència d’aquesttipusdeproblemes.

Problemalogicomatemàtic4:unirnoupuntsamb4líniessenseaixecarelllapis

Lasituacióespotpresentarprimeramentmitjançantunaimatgedequatrepuntssituatsen formadematriu 2 ˆ 2,comesveualaimatgeesquerradelafigura7.

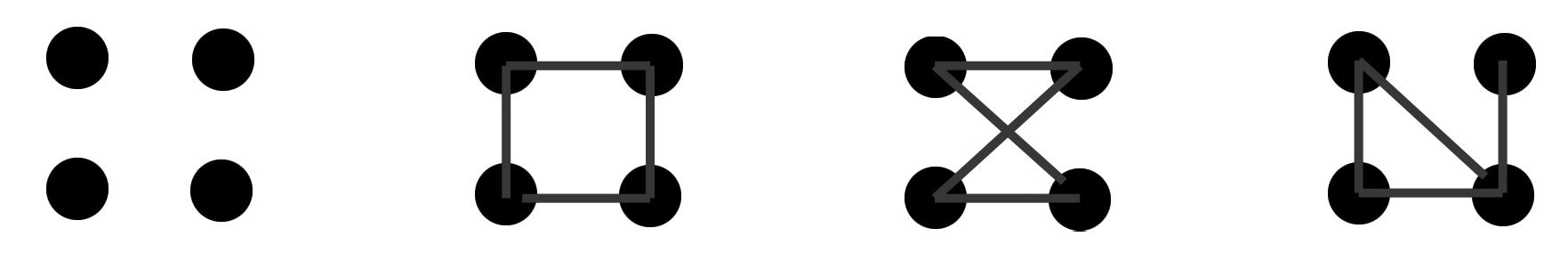
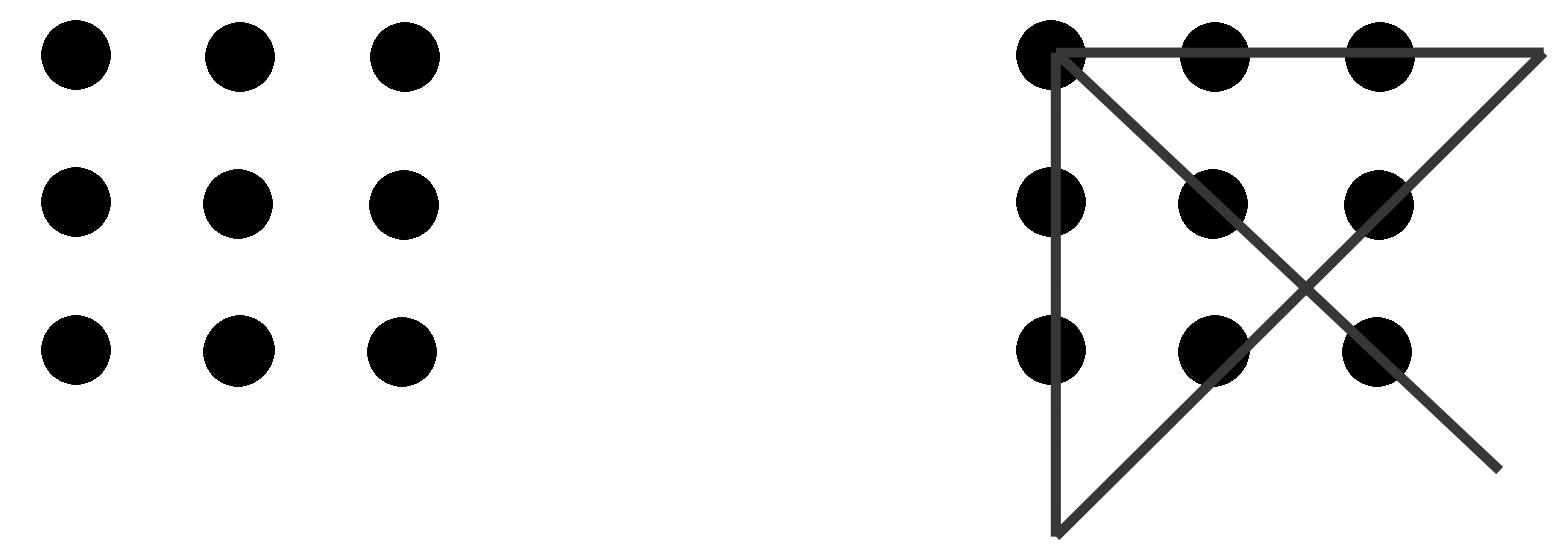
Enprimerlloc,espotdemanaralsalumnesquetracinquatrelíniessenseaixecarelllapisni repetirrecorregutdemaneraquetotselspuntsestiguinalmenysenunadeleslínies.Un copcomprovatqueéspossibleresoldreelproblemaiquehihadiversesmaneresdefer-ho, espresentaunanovaimatgedenoupuntssituatsenformadematriu3 ˆ 3,comlaquees presentaal’esquerradelafigura8,ise’lsdemanaquetorninatraçarquatrelíniessenseaixecarelllapisnirepetirrecorregutdemaneraquetotselspuntsestiguinalmenysenunade leslínies.

Comqueaquestproblemaéscomplicat,sialcapd’unaestonanohihapropostesdesolució espotmostrarunasoluciógairebéacabadaiesperarqueelsalumnesl’enllesteixin.Posteriormentjase’lsfaràveurequenopassaressisesurtdelquadratimaginariformatpelspunts, jaquel’enunciatnodiuquenoespuguisortirdelquadrat.Alapartdretadelafigura8es presentaunexempledesoluciódelproblema.Lògicament,uncoptrobadaunasolucióésfàcilquen’apareguinmés,siescomençaperunaltrepunt.

Figura7.Presentaciódelproblemadelsquatrepuntsambdiferentspossiblessolucions.

Figura8.Presentaciódelproblemadelsquatrepuntsambunapossiblesolució.

Problemalogicomatemàtic5:trobaruncamíentreunpuntdesortidaiund’arribada

Lasegonasituacióques’haderesoldreconsisteixacrearuncamíperalaformigadesdela posiciódesortida,situatalapartinferioresquerrad’unlaberint,finsalaposiciód’arribada, representadaambplàtans.Lafigura 9 permetvisualitzarlaimatgedelproblemajuntament ambunapossiblesoluciódisruptiva.

Problemalogicomatemàtic6:trobarlasolucióperescapardelperill

Enaquestsupòsitesproposaunasituaciódelaqualcalescapar-se.Lafigura 10 presentala imatgedel’enunciatdelproblema.Lafigura suggereixqueestemenunasituacióperillosa completamentindefensos:penjatsd’unarbrepelspeusambunacorda.Unaespelmaestà cremantlacordaqueenslligamentreunlleóesperaperdevorar-nos.Esdemanenmaneres possiblesd’escapar-sed’aquestasituació.Aquílacreativitatpotesdevenirfonamental.Per exemple,algúpotimaginarquetéunanavallaalabutxacaamblaqualpotalliberar-sei despréspujaralabrancaperlacorda.Lasoluciódisruptivaqueespotpresentaréscantar Per moltsanys allleóperquèbufil’espelmaiaixíevitemcaurealseuabastiqueensdevori.

Figura10.Atrapatsiapuntdeserdevorats.Il¨lustraciódeQueraltViladevall.

Figura9.Elrecorregutfinsalsplàtans.Il¨¨lustraciódeQueraltViladevall.

3.Eltalleralapràctica.Encertsierrors

Eltaller Comhofarem? esvaposarenpràcticadurantlaSetmanadelaCiènciadel 2018a laBibliotecaMunicipalCanRoscada,deVilobíd’Onyar,ambalumnesdeprimerisegonde primàriadel’EscolaJosepMadrenysdelmateixpoble.Lesfigures 11 i 12 mostrenl’ambient detreball.Totselsmenorstenienunespissarretesambretoladorsesborrablesambquèvan poderelaborarlessevespròpiespropostesdesolució.Larealitzaciódeltallerenunambient detreballdiferentdeldelesaulesiambmaterialsdetreballtambédiferentsdelshabituals vaserunencert,jaquevapredisposarl’alumnatapercebreeltemadeltallercomunacosaexcepcionalqueelsvacridarl’atenció.Totselsalumnesvanmostrarinterèsentotesles activitatsivanproposarmoltessolucions.

Figura11.Alumnesfenttasquesartístiques.

Figura12.Alumnesfenttasquesdetipuslogicomatemàtic

Elsresultatsobservatsencadapartdeltallervanserelssegüents:

‚ Enlaprimerapartdel’activitatesvaevidenciarqueelscontessónunrecursexcel¨lent perintroduirlesactivitatsposteriors,jaquelaimplicaciódel’alumnatvaserplenai satisfactòriaiaixòanimaaperseverarambaquestrecurstambéaprimària,seguinten lalíniadelstreballsdeSaá(2002),Molina(2012),Alsina(2019)iLópez(2021).

‚ Laintroducciódevídeosderesoluciódeproblemestambévaserunencert,jaque,a mésdesatisferlacuriositatdelsassistents,vaajudarafermésrical’activitatperquè vapresentar-selatemàticadeltallermitjançantdiferentsrecursos,talcomaconsella Alsina(2010)amblapiràmidedel’educaciómatemàtica.

‚ Elseguimentdelestasquesartístiquesvasermoltsatisfactori.Totl’alumnatesvaabocarentotmomentamostrarlessevespropostesdesolucióiesvacrearunclimade participaciómoltmotivador,fetquetestificaquel’educacióartísticaésenaquestes edatsunaopciómoltbenacceptadapertothomique,pertant,espotutilitzarper despertarinterèsenaltresassignaturescurriculars.

‚ Atèsquenomésesvadisposarde45minutsperfereltaller,esvadecidirfernomésels problemeslogicomatemàtics4,5i6,jaquesónelsproblemesquepermetenintroduir solucionsdisruptives.Entotestressessionsesvaconstatarunclarrebuigd’algunesde lespropostesdesoluciódisruptivesplantejades,jaqueelsmenorsvanmostrarreticènciesatrencaralgunesnormesimplícitespertald’acceptarlessolucionsproposades. Concretament,enelproblemadellaberint,algunsalumnesvanconsiderarqueelcamí directesensepassarperdinsdellaberintnoeraunarespostavàlidaperquènocomplia la«norma»deferunatascadetipuslaberint.Quanse’lsvarecordarqueencapmoment nos’haviaditques’haviadepassarpellaberint,noesvaacceptaraquestaexplicaciói majoritàriamentvanseguirconsiderantqueelcamídelasolucióhaviad’entrar-hi.De manerasimilar,enelproblemadellleó,quanse’lsvaproposarlasoluciódecantar Per moltsanys allleóperquèaquestbufésl’espelmaafiques’apaguésiaixínocaiguéssim aterraifóssimdevorats,unabonapartdel’alumnatnovaconsiderar-lavàlida,toti comentarqueningúhaviaditqueellleófosrealiquepodíemestarenunrelatde dibuixosanimatsonaquestescosespassen.

4.Conclusionsidarrersconsells

Malgratelsproblemestrobatsenladarrerapartdeltaller,creiemquesen’hademantenir l’estructurainicialtotiquecalfermodificacionslleugeresperònecessàriesenalgunesdeles parts.Lesnostrespropostess’exposenacontinuació.

Enprimerlloc,proposemseguirenlasevatotalitatlaprimerapartdeltaller,jaquelalectura delcontepermetpresentardemaneraamenalatemàticadelasessióal’alumnat,relaxar l’ambienticrearuncontextmoltfavorableperaltreballposterior.

Ensegonlloc,proposemcontinuarambelvisionamentdelsvídeos,jaqueagradaisorprèn elsparticipantsidefineixperfectamentlaideaquetothomposseeixlacapacitatderaonar pertrobarlasoluciód’unproblemaiquenorendir-seésessencialperaaquestfi,emprant exemplesd’aplicaciórealquemostrenquefinsitotelsanimalssóntenaçoscercantlasolució aproblemesqueenunprimermomentnoacabendetrobar.

Entercerlloc,aconsellemseguiramblestasquesartístiques,jaquesónseguidespertotsels alumnesdemaneraapassionada,atèsqueelsfansentirprotagonistesdelsseusdibuixosiaixòfaqueesmostrinansiososdecaptarl’atenciódelsmonitorsdeltallerperensenyar-los-els, fetqueelsanimaapassaralasegüentpartdeltalleriarebrelapartmésmatemàticaamb il¨lusió.Recordemqueésenaquestesedatsquanenalgunscasosescomençaateniruna mancadepredisposicióenversl’assignaturadematemàtiques.Totselsesforçosperevitar aquestatendènciahandeserbenvinguts.

Enquartlloc,aconsellemmantenirladarrerapartdel’activitatperòvigilant-necertsaspectes.Sialapartartísticanohihasolucionsdisruptives,ésmillornoposar-nealapartmatemàtica,pertalquenoespercebinelsexercicisdelapartmatemàticacomaméscomplicatsque elsdelapartartística.Enelcasquerealmentesvulguitreballarexercicislogicomatemàtics disruptius,s’aconsella,amésdededicarcomamínimunahoradetempsaltaller,introduir tambéactivitatsdisruptivesenproblemesartístics,com,perexemple,algunexercicirelacionatambcomelscubistesvanintroduirdiferentsperspectivesenlessevesobrespercaptar millorlarealitat,ocomDalívaintroduirescenessurrealistesimpossiblesdecreure,comara ladelselefantsambpotesfines,perrepresentarelmóndelssomnis.Aixòpermetriacrearde nouunasimetriarespectealnivelldelsexercicisdelapartartísticailapartmatemàtica.

Finalment,encasqueesfacialgundelstresproblemesdisruptiusproposatsenaquesttreball,esrecomanafercanvisenlapresentaciódelestasquesdellaberintidelproblemad’escapar-sedeserdevoratpellleó.Enprimerlloc,esproposamodificarelsdosdibuixosdepresentacióperfacilitarencaraméslacercadesolucions;ensegonlloc,modificarlaformadels dibuixospertaldesercoherentsamblapropostadePiaget(1983)delesfasesdemoralitat enelsnens,quesuggereixquecapalssetanyselsnensconsiderenlesreglesdeljocsagradesiesneguenacanviar-les.Enaquestadirecció,recomanemqueperaconseguirque lessolucionsdelsdosproblemessiguinconsideradesvàlidespertotl’alumnat,estinguin tambéencomptealtresnormesassociadesalestasquesques’handerealitzarpertalque lessolucionsdisruptivesnorepresentinunconflictemoralperal’alumnat.Pertotaixòes pot,perexemple,evitaresmentarlaparaulalaberintenlatascadellaberint,endemanar quetrobintotselspossiblescaminsqueportinlaformigafinsalsplàtans,isepararunamica eldibuixdellaberintdelspuntsdesortidaifinal,perallunyar-seunamicadelesimatges habitualsdelslaberints.Tambérecomanemqueellleódelatascadelparanyestiguiapeu dret,alamanerahumana,ovestitcomunapersona,pertalquesemblimésunasituació d’unapel¨lículadedibuixosanimats,jaqueenaquestcontextlesnormesmoralsdelsmenors noprohibeixenqueellleóentenguielspersonatgesipuguiferaccionspròpiesdelshumans. Enlesfigures 13i 14deixemdosexemplesdepossiblesimatgesrelacionadesambaquestes duesdarrerestasquespertaldefacilitarla comprensiódetoteslesideesproposades.

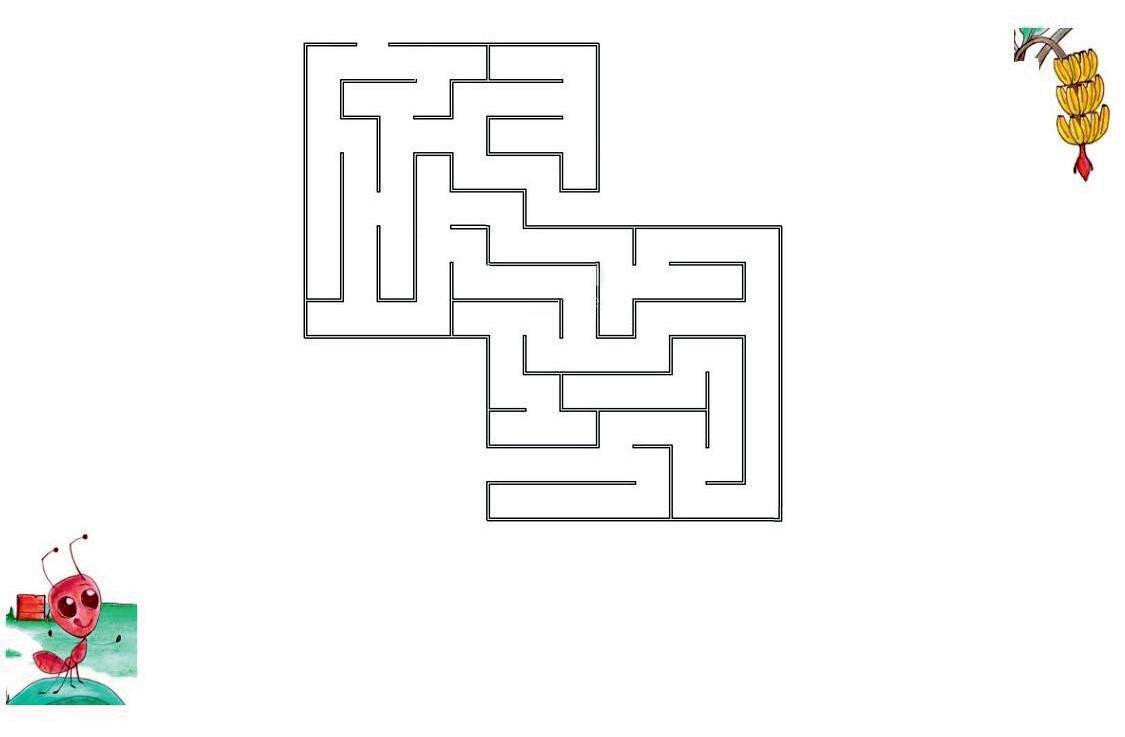
Figura13.Novail¨lustraciódelproblemadetrobarcaminsentredospunts.Il¨ lustraciódeQueraltViladevall.

Figura14.Novail lustraciódelproblemadellleó.Il lustraciódeQueraltViladevall.

Agraïments

AquesttreballhaestatpossiblegràciesalProgramaPilotdeSuportaIniciativesiActivitatsen elsàmbitsdelaDivulgaciódelaRecercaidelCompromísSocialdelaUniversitatdeGirona.

ElsautorstambévolenagrairalaFundacióMonal’atenciórebudadurantelcursd’estiu Intel¨ligènciaicogniciódeprimats,queaquestaentitatimparteixalasevaseudeRiudellots delaSelva,apropdeGirona.Sensecapmenadedubte,elcontingutdelcursilesagra-

dablesconversessobreintel ligènciaanimalmantingudesdurantelsdescansosambMiquel LlorenteEspino,directordelmàsterenPrimatologiacoorganitzatperlaFundacióMonaila FundacióUniversitatdeGirona:InnovacióiFormació,vanresultaressencialsperaconseguir unesactivitatsmésfidedignes.

Finalment,elsautorsagraeixenlacol laboraciódelaBibliotecaMunicipalCanRoscada,de Vilobíd’Onyar,del’EscolaJosepMadrenys,delamateixalocalitat,idelaFundacióCatalana delaRecercailaInnovació(FCRI).

9.Referències

Alsina,À.(2010).«La«pirámidedelaeducaciónmatemática»:unaherramientaparaayudara desarrollarlacompetenciamatemàtica». AuladeInnovaciónEducativa, 189, 12-16.

Alsina,À.(2019). Itinerariosdidácticosparalaenseñanzadelasmatemáticas(6-12años).Barcelona:Graó.

Elisondo,R.C.;Danolo,D.;Rinaudo,M.C.(2012).«Espacioscomunitarioscotidianos.Elartecomooportunidadparaser,crearytransformar». ASRI:ArteySociedad.RevistadeInvestigación, 1, 21-9.

Hadamard,J.(1945). Anessayonthepsychologyofinventioninthemathematicalfield.Nova York:PrincetonUniversityPress.

López,P.(2021). Taller:Elcuentocomorecursoparatrabajarlasmatemáticas.www.youtube. com/watch?v=yexwMc24pyQ[consulta: 28dedesembre 2022]

MedinaSánchez,N.;Tejeda,V.;Míriam,E.;Alhuay-Quispe,J.;AguirreChávez,F.(2017).«La creatividadenlosniñosdeprescolar,unretodelaeducacióncontemporània». REICE:Revista ElectrónicaIberoamericanasobreCalidad,EficaciayCambioenEducación, 15(2), 1-29.

Molina,E.(2012).«Narracióndeuntallerderesolucióndeproblemasaritméticosconniños de4años». Edma0-6:EducaciónMatemáticaenlaInfancia, 1(1),63-79.

Piaget,J.(1983). Elcriteriomoralenelniño.Barcelona:Fontanella.

Polya,G.(1965). Cómoplantearyresolverproblemas.CiutatdeMèxic:Trillas.

SaáRojo,M.D.(2002). Lasmatemáticasdeloscuentosylascanciones.Madrid:EOS.

Elsmonsimpossibles deM.C.Escher

ToniSellarès

ProfessorjubilatdelDepartamentd’Informàtica,MatemàticaAplicada iEstadísticadelaUniversitatdeGirona

Resum Abstract

Aquestarticlecomençaambunabreu introduccióalsconceptesde perspectiva, imatgeambigua i objecteimpossible,que desprésesfanservirperanalitzartresdeles obresdeM.C.Escherquerepresenten «monsimpossibles»: Relativitat, Convex iCòncau i Cascada

Thisarticlebeginswithabriefintroductionto theconceptsofperspective,ambiguous image,andimpossibleobject,whicharethen usedtoanalyzethreeworksbyM.C.Escher representing‘‘impossibleworlds’’: Relativity, ConvexandConcave and Waterfall.

M.C.Eschervacrearespaisarquitectònicsqueaprimeravistapercebemcomarealsperòque quanelsanalitzemambdetenimentcomprovemquesónmonsimpossibles.Hovapoderfer gràciesalasevahabilitatartística,aldominidelaperspectivaialconeixementdelesimatges ambigüesidelsobjectesimpossibles.Podeutrobarunabiografiad’Eschera[1]ilamajoria delessevesobresa[2].

Aquestarticleestàestructuratenquatreapartatsque,desdelpuntdevistadelageometria, ajudenaentendrelamaneracomEschervadissenyarelsseusmonsimpossibles:«Imatges

MonsimpossiblesdeM.C.Escher: Relativitat (1953), Convexicòncau (1955)i Cascada (1961).

enperspectiva»,«Imatgesambigüesenprofunditat»,«Objectesimpossibles»i«ElsmonsimpossiblesdeM.C.Escher»,ons’analitzenlesobres Relativitat, Convexicòncau i Cascada

Imatgesenperspectiva

Una imatge éslarepresentaciód’unobjecteounaescenatridimensionalenunsuportbidimensional(dibuix,pintura,fotografia...).La perspectiva ésunatècnicapergenerarimatges quepermetrecrearlaformailadisposiciódelsobjectesd’unaescena.D’entreelsdiversos tipusdeperspectivaexistents,Eschervaferservirenlesobresanalitzadeslaperspectiva paral¨lelaortogonalilaperspectivacentral.

Laperspectiva paral¨lela representaunaescenatridimensionalsobreelpladeldibuixmitjançantlautilitzacióderectesprojectantsparal lelesentresi.Dueslíniesparal lelesal’espai sóntambéparal¨lelesenlasevarepresentacióalpladeldibuix.Unaperspectivaparal¨lela és ortogonal silesrectesprojectantssónperpendicularsalpladeldibuix.Alesimatgesfetesambperspectivaparal lelaortogonal,l’escenaques’haderepresentaresposicionade maneraquecapdelessevestresdireccionsprincipalssiguiparal¨lelaalpladeldibuix.Una delesdireccionsprincipalssesolrepresentarverticalment,mentrequelesrepresentacionsde lesaltresduesdireccionsformenambl’horitzontalangles α i β ,enfunciódelsqualsesclassifiquenelsdiferentstipusdeperspectivaparal lelaortogonal.

Laperspectivaesdiuqueés isomètrica si α i β “ 30˝ iés dimètrica si α i β ‰ 30˝ .

Laperspectiva central representaunaescenatridimensionalsobreelpladeldibuixmitjançantlautilitzacióderectesprojectantsquepassenpelpuntdevistadesdelqualmiral’observador.Permetreconstituirmentalmentlaformailaprofunditatdelsobjectesrepresentats ilasevaposiciórelativa.La líniadelnivelldel’ull (LNU)éslarectahoritzontaldelpladeldibuix situadaalnivelldelpuntdevista.Un puntdefuga (PF)ésaquellenelqualconvergeixenles projeccionsd’ungrupderectesparal lelesdel’escenaques’haderepresentarquenosón paral¨lelesalpladeldibuix.Cadaconjuntderectesparal¨lelesdel’escenatéelseupropipunt defuga.Laposiciódelpuntdevistailadelpladeldibuixrespectedel’escenadeterminen trestipusdeperspectivacentral:d’un,dedosidetrespuntsdefuga.

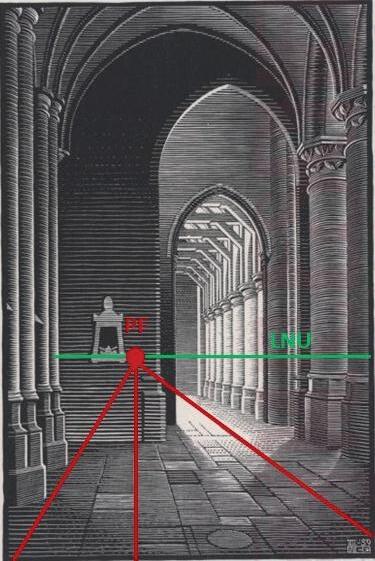
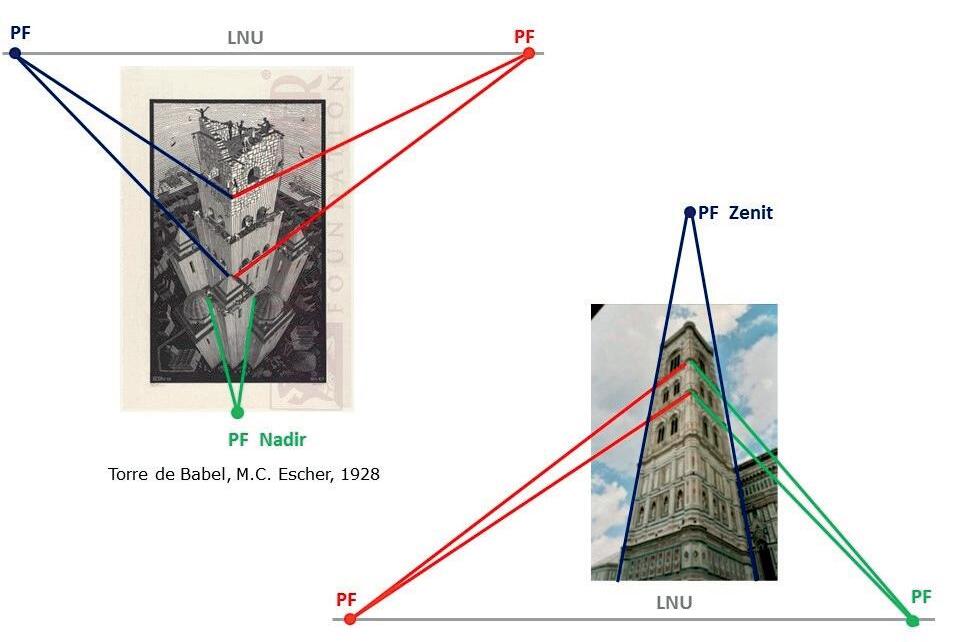
Perspectiva de tres punts de fuga.

Perspectiva d‘un punt de fuga

Església Nieuwe de Delft. M. C. Escher, 1939.

Perspectiva de dos punts de fuga Mirador. M. C. Escher, 1958.

Dinslaimatgeanterior«TorredeBabel.M.C.Escher, 1928»,lesarestesverticalsesrepresentenpermitjàdesegmentslaprolongaciódelsqualsconvergeixenunpuntdefugaanomenat zenit o nadir segonssil’observadormiracapamuntocapavall.

Lesimatgesobtingudesambperspectivacentralrepresentenlarealitatambmésfidelitat quelesobtingudesambperspectivaparal¨lelaortogonal.Laperspectivaparal¨lelaortogonal esfaservirperrepresentarimatgesambigüesiobjectesimpossibles.Laperspectivacentralés especialmentútilperrepresentardemanera realistaescenesonhihalíniesrectesparal¨leles, com,perexemple,lamajoriadevistesd’exteriorsiinteriorsd’edificis.

Imatgesambigüesenprofunditat

Unaimatgeés ambigua [3]sielquerepresentaespotinterpretardediversesmaneres.Durantl’observaciód’unaimatgeambigua,lesdiferentsinterpretacionsnoespercebenmai simultàniamentipodenrevertir-seinstantàniamentsensequehopuguemcontrolar.

Escala o motllura?Columna o motllura de columna? Cavitat o protuberància?

Exemples d’imatges ambigües que Escher fa servir a Convex i còncau.

Ésdifícilqueunobservadorpuguirevertirunaimatgeambiguaavoluntat,peròdesprésde mostrar-lilesversionsinequívoquesdelaimatgeésmoltmésprobablequesiguicapaçdepercebrelessevesduespossiblesinterpretacions.

ColumnaMotllura de columna Columna o motllura de columna?

Motllura

Escala

Motllura o escala?

Ambigüitatenprofunditat

Laprofunditatésladistànciapercebudaperl’observadorentreelfrontielfonsdel’objecte ol’escenarepresentada.

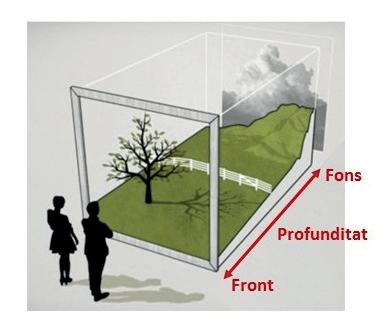
Unaimatgeésambiguaen profunditat quans’inverteixenespontàniamentlespartsquepercebemcomaproperesicomaallunyadesacausadelamancadereferènciessobrelaseva profunditat.Pertant,podemveureduesorientacionsdiferentsdel’objecteol’escena.

Peralarepresentaciód’imatgesambigüesenprofunditatgeneralmentesfaservirperspectivaparal¨lelaortogonalperquè:leslíniesisuperfíciesparal¨lelesesrepresentenpermitjà delíniesisuperfíciesparal lelesidèntiques;elsobjectesdelamateixamidaesrepresenten tambédelamateixamida.Peraixò,quanobservemunaimatgerepresentadaenperspectiva paral lelaortogonalnoquedaclarquinespartssónmésproperesiquinessónmésallunyades,demaneraquelespodempercebredelesduesformessensequelaimatgeperdi coherènciaenlasevainterpretaciótridimensional.L’atencióselectivacapaunadelesparts mésproperesd’unobjecterepresentatenuna imatgeambiguaenprofunditatafavoreixla percepciód’unadelesduespossiblesinterpretacionsdel’objecte.Siensfixemalternativamentenlesduespartsdel’objecteescollidescomamésproperes,llavorsaugmentala probabilitatd’unainversióentrelesduesinterpretacionspossibles.

Cavitat

Cavitat o protuberància? Protuberància

Part central més propera: columna

Columna o motllura de columna?

Parts laterals més properes: motllura de columna

Siafegiminformacióalaimatgeambigua,augmentalaprobabilitatdepercebreunadeles duesinterpretacionspossibles.

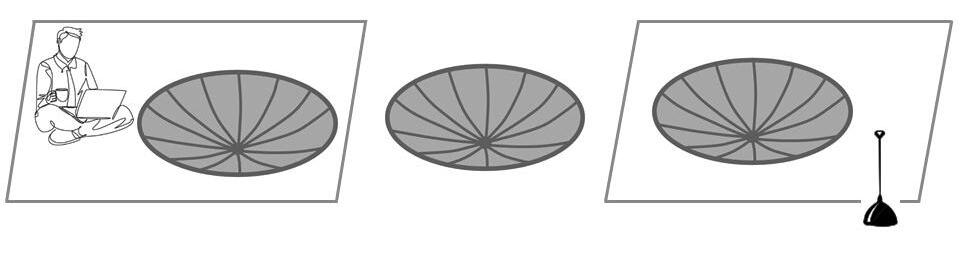
Cavitat

Cavitat o protuberància?

Protuberància

Anemaraonarperquèenlaimatgedel’ambigüitatqueespotinterpretarcomunacolumna olamotllurad’unacolumnasónpossibleslesduespercepcions.

Sidibuixemlesduesorientacionspossiblesd’un cilindreambigu,l’unvistdesdesobreil’altre vistdesdesota,veiemquelapartposteriordelcilindrevistadesdesobreilafrontalvistades desotasónidèntiques.

PeralarestadelesambigüitatsenprofunditatquevaferservirEschertambéhiharaonamentsgeomètricsqueexpliquenperquèsónpossibleslesduespercepcions(vegeu[3]).

Objectesimpossibles

Un objecte esdiuqueés impossible siespotrepresentarenunaimatgedemaneraquea primeravistal’observadorelpercepcomarealtotiquefísicamentnoespotconstruir.Cada partd’unobjecteimpossibleésplausible,peròlafalsapercepciódelaprofunditatrelativa entrelespartsfaquel’estructuraglobaldel’objectesiguiinconsistent.

Exemples dobjectes impossibles

Hihaobjectestridimensionalsquerepresentatsfentservirlaperspectivaparal lelaortogonaldesd’undeterminatpuntdevistacreenlail¨lusióquecoincideixenamblaimatged’un objecteimpossible.

Aixòpassaperquènoésclarquinespartssónmésproperesiquinessónmésallunyades,de maneraqueespodenpercebrecomaunidespartsqueenlarealitatnohoestan.Siescanvia elpuntdevista,estrencalail¨lusió.

Objecte tridimensional que representat des d‘un determinat punt de vista crea la il·lusió d‘un triangle de Penrose.

‘

Cub impossibleTriangle de PenroseEscala de Penrose

ElsmonsimpossiblesdeM.C.Escher

Enaquestapartatanalitzemtresdelesobresd’Escherquerepresentenmonsimpossibles:

Relativitat, Convexicòncau i Cascada.

Relativitat

A Relativitat,Eschermostraunespaiquerepresental’interiord’unedificiambescales,balconades,portesiarcadesquedeixenveureunapartdel’exterior.Lamajoriadelespersones quehihaal’espaiestanenposicionsquedesafienelsentitdelaforçadelagravetat.En mirarlaimatgeperprimeravegada,lanostra reaccióésdesorpresaidesconcertdavantla representaciód’unespaiimpossible!

Relativitat,M.C.Escher,1953.

Eschervadibuixar Relativitat dividintl’espaiques’haderepresentarentressubespaisqueen lasegüentfiguraesmostrendediferentscolors.

Girantlaimatgesubdivididaseixantagrausensentitantihorariiseixantagrausensentit horariveiemqueencadascundelstressubespaishihaunsolsentitdelaforçadelagravetat: el«correcte»(capavall).L’espaiglobal,uniódetressubespaispossibles,ésimpossibleperquè hihapresentstressentitsdelaforçadelagravetat.

girada 60º en sentit antihorari

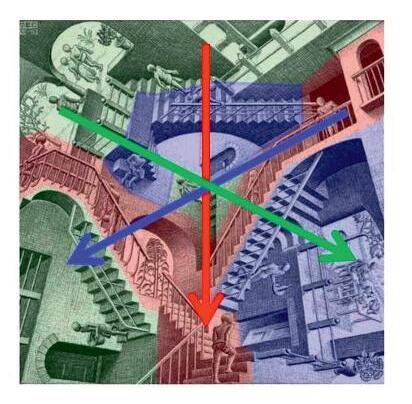
girada 60º en sentit horari

Perrepresentarcadascundelstressubespaisde Relativitat Eschervaferservirlaperspectiva centraldetrespuntsdefuga.Enlestresperspectiveselspuntsdefugasónelsvèrtexsdel mateixtriangleequilàterdebasehoritzontal.Comqueeltrianglequedeterminaelspunts defugaésequilàter,capdelestresperspectivesdistorsionaelssubespaisrepresentats.

Imatge

Imatge

Imatge original

Unadelesperspectivestécomalíniadenivelldel’ulllabasedeltriangleequilàtericoma zenit,elvèrtexsuperior.Elpuntdevistaésbaix.Lesaltresduesperspectivess’obtenengirant laimatgealvoltantdelcentredeltriangle60°ensentitshorariiantihorari,demaneraqueels altresdoscostatsdeltrianglepassenaserlíniesdenivelldel’ullielsvèrtexsoposatsnadirs.

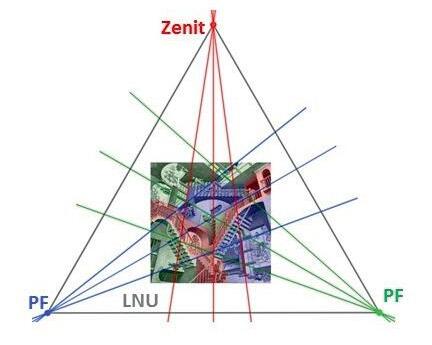
L’anàliside Relativitat permetpassardelasorpresaieldesconcertinicialsdavantlarepresentaciód’unespaiimpossible,aveurequeaquestespaiéselresultatdelauniódetres subespaisquesónpossiblesmiratsdesdediferentspuntsdevista.Talcompossiblement Eschervoliafernotar,lanostrapercepciódel’espaiés relativa.

Convex i còncau

A Convexicòncau Eschermostraunespaiambelementsarquitectònicsrepresentatsdemaneraambigua:columnes,escales,voltes...Inevitablement,elcanviinvoluntarientrelesdues possiblespercepcionsdelselementsambigussorprènl’observador.

Convexicòncau M.C.Escher,1955.Litografia.

Amésamés,alapartcentraldel’obraEschercombinahàbilmentelselementsarquitectònics ambigusperrepresentarunaestructuraqueés impossibleenlarealitat,cosaquedesconcertaeljasorprèsobservador:

‚ Elterraonhihaunnoiassegutéstambéelsostredelqualpenjaunornament.

‚ Si,comladonaambelcistellalamà,baixeml’escaladel’esquerra,creuemelreplà centralipugeml’escaladeladreta,desobtedescobriremqueestemalapartdesota d’unaarcada.

‚ Lavoltaqueuneixlaparetquetéunafinestraambuntest,amblaparetquetéuna finestraambunagerra,alapartesquerraéselsostred’untemplet,mentrequeala partdretaéselsotad’unagaleria.

‚ Lavoltaqueuneixlesduesparetsonhihadoshomestocantelclarinetdesdela finestra,alapartesquerraéselsostred’untemplet,mentrequealapartdretaésel sotad’unvoladísqueprotegeixlafinestra.

Alapartsuperiordretade Convexicòncau hihaunabanderaambunconjuntdecubsadjacents,conegutscoma«cubsreversibles».Elscubsestandibuixatsenperspectivaparal¨lela ortogonaldimètrica,demaneraquepodempercebrequeelsmiremtantdesdesobrecom desdesota.Lainterpretaciódepèndesipercebemelsrombesgrisoscomlacarasuperioro lacarainferiordelscubs.

Cubsreversibles.

Ambaquestabanderaquemostraunscubsreversibles,probablementEschervavolersuggerirquesidividiml’obraverticalmentenduespartsperlameitatdelacolumnacentral,la partesquerrade Convexicòncau ésvistadesdesobreiladreta,desdesota.Lapartcentral de Convexicòncau,onconvergeixenlapartvistadesdesobreilapartvistadesdesota,és unarepresentacióqueenlarealitatésimpossible.

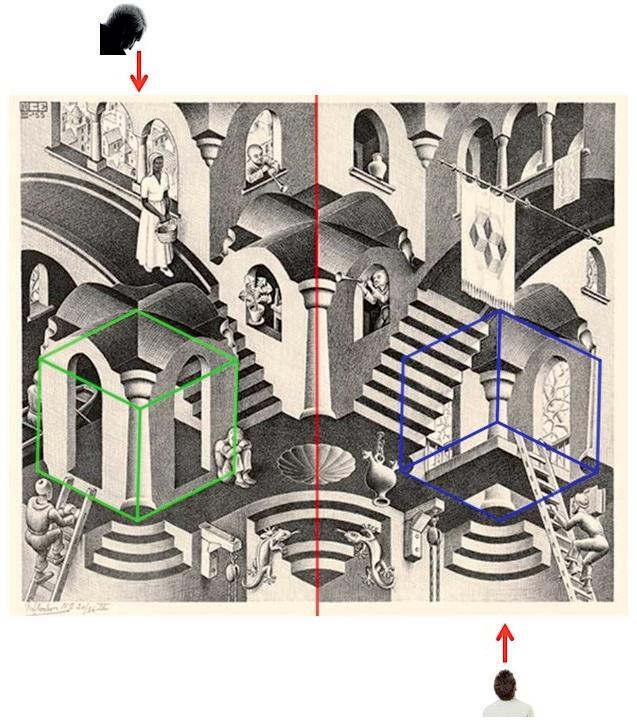
Perrepresentarcadascunadelesduespartsde Convexicòncau Eschervaferservirlaperspectivaparal lelaortogonaldimètricai,pertant,larepresentaciódelesduesdireccionsprincipals noverticalsformaambl’horitzontalanglesigualsidiferentsde30˝ .Amésamés,Escher vaferqueenlesduespartsdel’obralarepresentaciódelesduesdireccionsprincipalsno verticalscoincidís.

Gràciesaferservirlaperspectivadimètrica,Eschervapoderrepresentarelementsarquitectònicsambigusenprofunditat.Totseguit,per aalgunsd’aquestselementsambigusmostrem duesimatgesinequívoquesdel’objecterepresentat,pertalqueaugmentilaprobabilitatque l’observadorsiguicapaçdepercebrelessevesduespossiblesinterpretacions.

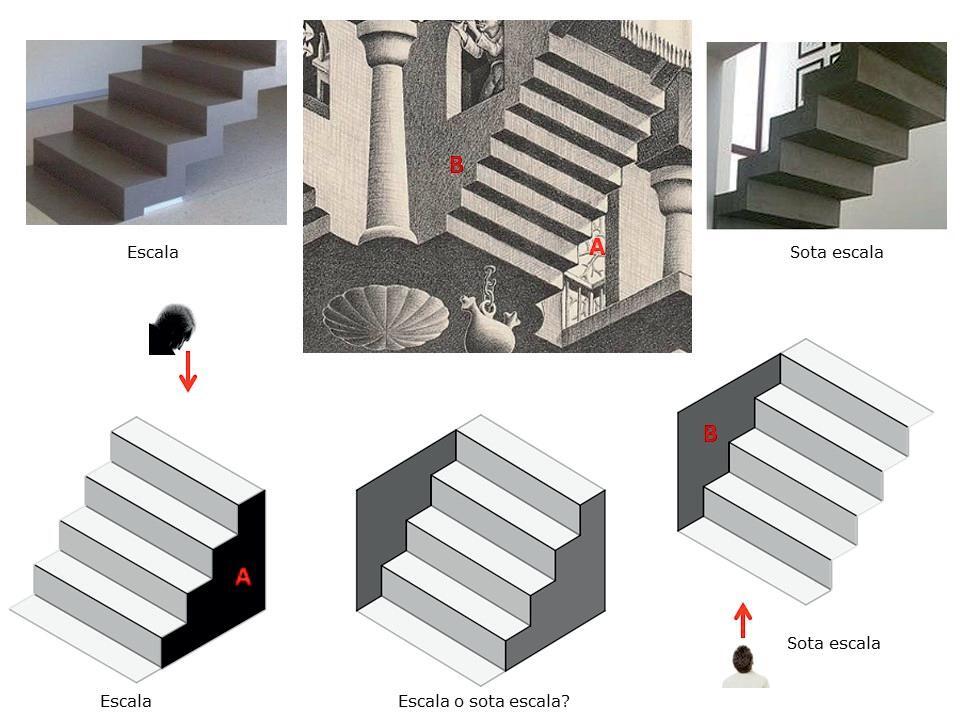
Sobreosotadevolta.

Escalaosotaescala.

Sobreosotadevoltes.

A Convexicòncau Eschercreaunespaiarquitectònicqueensdesconcertaquanobservem perprimeravegada.Sidividiml’obraverticalmentenduespartsperlameitatdelacolumna central,lapartesquerraésvistadesdesobreiladreta,desdesota,mentrequelapartcentral onconvergeixenlesduesvistes ésunaconstruccióimpossibleenlarealitat.Amés,Escher combinahàbilmentdiversoselementsarquitectònicsambigusenprofunditat,demanera quequanfixeml’atencióenund’aquestselements,percebemconfosos,alternativamentide manerainvoluntària,lessevesduespossiblesinterpretacions.

Cascada

A Cascada Eschermostraunaestructuraarquitectònicaenlaqualdestaquenunaqüeducte enformadeziga-zaga,unasíniaiunacascada.Enmirarl’obraperprimeravegadanoveiem resestrany,peròenanalitzar-laambmésdetenimentveiemquel’aiguaflueixdelasínia, baixapellleugerpendentdel’aqüeductefinsaarribaralapartsuperiordelacascadaiesprecipitasobrelasíniaonhacomençatelrecorregut.Confosos,ensadonemdelaimpossibilitat quel’aiguabaixiperpètuament.

Perrepresentar Cascada,Eschervaferservirlaperspectivacentraldedospuntsdefuga.El puntdevista,situatal’alçadadelalíniadenivelldel’ull,ésmoltaltielsdospuntsdefugaes trobenmoltallunyatsdelaimatgerepresentada.

Cascada.M.C.Escher,1961.Litografia.

Percrearl’aqüeducte,lapartméssorprenentde Cascada,Escheresvabasareneltrianglede Penrose.Encomptesderepresentareltrianglefentservirlaperspectivaparal lelaortogonal, talcomesfahabitualment,hovaferamblaperspectivacentraldedospuntsdefuga.En col locarelsdospuntsdefugamoltallunyatsdelaimatgesesegueixcreantlail lusiód’un triangleimpossible.

Perspectiva paral·lelaPerspectiva central amb dos punts de fuga molt allunyats

Eschervarepresentarl’aqüeductede Cascada combinanttrestrianglesdePenrose,ambla qualcosavacrearunnouobjecteimpossible.Labaixadadel’aiguaenziga-zagaperl’aqüeducte ilacascadasemblaperfectamentnatural.

Totiquesiguemconscientsquelarepresentacióqueveiema Cascada noéspossibleenel mónreal,elfetqueEscherhibarregielementsimpossiblesambaltresdenormalsfamés difícilqueensqüestionemlasevaimpossibilitat.

Comentarisfinals

L’anàlisiquehemfetde Relativitat, Convexicòncau i Cascada mostraquelageometriaajuda aentendreelsaspectesméssorprenentsidesconcertantsd’aquestesobresd’Escher.Eltipus d’anàlisigeomètricautilitzadaperestudiarlestresobrespresentadesespotestendreaaltresdelsmonsimpossiblescreatsperEscher(vegeuhttps://sellamonsimpossiblesmcescher. blogspot.com/p/mons-impossibles-de-mc-escher.html).

Desdelpuntdevistadidàctic,elsmonsimpossiblesd’Escherilasevavinculacióamblaperspectiva,lesimatgesambigüesielsobjectesimpossibles,proporcionenunmarcdiferentde l’habitualperincentivarl’interèsdelsestudiantsperlageometria.

Vullexpressarelmeuagraïmental’amicCarlesBarcelópelsseuscomentarisisuggeriments, quehanajudatamillorarelcontingutd’aquestarticle.

Referències

[1] BiografiadeM.C.Escher.https://ca.wikipedia.org/wiki/Maurits_Cornelis_Escher.

[2] ObresdeM.C.Escher.https://mcescher.com/gallery/most-popular/. [3] Imatgesambigües.https://sellamonsimpossiblesmcescher.blogspot.com/p/imatges-am bigues.html.

Perquèentonenbéles guitarresambtrasts noparal·lels?

MiquelAlbertíPalmer Alberti.miquel@gmail.com

Resum Abstract

Lesguitarrestradicionalstenenelstrasts paral¨lels.ElteoremadeTalesjustificalaseva bonaentonaciódesd’unaperspectiva geomètricagràciesalsistemaderectes paral¨lelesitransversalscompostpelstrastsi lescordes.Peròjafaunsanysquelesguitarres sensetrastsparal¨lelss’hanfetpopulars.Sense paral¨lelismedecordesnidetrasts,quina causajustificalasevabonaentonació?La respostaésunteoremageomètricsobrela conservaciódelaproporcionalitatmalgrat l’absènciadeparal¨lelismes.Totplegatté implicacionsrellevantsperalarecerca matemàticaenunàmbitlaboraliartesàcom éseldelalutieriaiperal’educació,fentdela guitarraunrecursd’aprenentatgematemàtic atravésdelqualparlalageometria.

Traditionalguitarsarebuiltwithparallelfrets. Fromageometricperspective,Thales’theorem explainstheirintonationthankstotheparallel andtransversestraightlinescomposedbythe fretsandstrings.Butsinceseveralyearsago, guitarswithoutparallelfretshavebecomequite popular.Withoutparallelismofstringsorfrets, howistheircorrectintonationexplained?The answerisageometrictheoremconcerningthe conservationofproportionalitydespitethelack ofanyparallelism.Allthishasimportant implicationsformathematicalresearchina labourandartisanalfieldsuchaslutherieand foreducation,makingtheguitara mathematicallearningresourcethroughwhich geometryspeaks.

D’unsanysençà,lesguitarresambtrastsnoparal lelss’hanfetpopulars.Sónlesanomenades guitarresd’escalamúltipleodetrastsenventall.Esdiuenaixíperquèelstrastssemblenles varetesd’unventall,totique,adiferènciadelquepassaenaquestobjecte,lesprolongacionsdelstrastsd’aquestesguitarresnoconvergeixenenunpunt.Elstrastsdelesguitarres d’escalaúnica,quesónparal¨lels,síqueconvergeixenenunpunt:eldel’infinit.

Lesguitarresd’escalamúltipleesdiuenaixíperquèleslongitudsvibrantsdelescordessón totesdiferents.Aixònovoldirqueleslongitudsvibrantsdelescordesenguitarresd’escala

únicasiguinidèntiques,sinóquelalongitudd’escala,ésadir,lalongitudvibrantdelescordes,vedeterminadaperladistànciaentreeltrastzero(celleta)ieltrastinfinit(celletadel pont)(figura 1).Comqueenlesguitarresd’escalaúnicaambduescelletessónparal¨leles,la distànciaquelesseparaésl’escaladelaguitarra.Leslongitudsvibrantsdelessiscordessón lleugeramentdiferents,jaqueaquestessíques’obrenenventall,atesalamajorseparació alpontquealacelleta.Laretículaqueformenlescordesielstrastsd’unaguitarrad’escala únicaéstrapezoidal.Encanvi,laretículadelesguitarresd’escalamúltiplenoéstrapezoidal, sinóquadrilàtera(notrapezoidal).Lesanomenaremretículessonores.

Desd’unaperspectivageomètrica,veuremqueelteoremadeTalessobrelaproporcionalitat desegmentsjustificalabonaentonaciódelesguitarresambtrastsparal lels,perallòqueel paral¨lelismeajudaaconservarlesproporcionsdeleslongituds.Peròalesguitarressense trastsparal lels,senseparal lelismedecordesnidetrasts,quinteoremapotjustificarlaseva bonaentonació?Atèsquelasevaretículanocontécapparelldesegmentsparal¨lels,noes potaplicarelteoremadeTales.I,malgrattot,larealitatésqueaquestesguitarresentonen correctament.Hihad’haverunacausamatemàticadelfenomen.Unfenomenrealinspirala cercad’unfenomenmatemàtic.

Unaguitarraentonabésilaintersecciódecadatrastambtoteslescordesdeterminalamateixafraccióvibrantdelescordesqueintercepta.S’entreveuque,gràciesalsistemadesegmentsparal¨lels(elstrasts)itransversals(lescordes),elteoremadeTalesjustificaràlaconservaciódelesproporcions.Elquenoéstanclard’entradaéscomespodenjustificarles proporcionalitatsenunsistemaabsentdequalsevolparal¨lelisme.Però,abansd’encetarla qüestió,convéfamiliaritzar-seamblespartsprincipalsd’unaguitarra(figura 1).

Figura1.Partsprincipalsd’unaguitarraconstruïdapellutier AntonioManjónMartínaSantAdriàdeBesòs(Barcelona).

Elstrastsnosónequidistants

Elsorígensdel’escalamusicalestrobenalacordatensadaquePitàgoresvaestudiar,elsode laqualcanviavasegonslasevalongitud.Méscurta,somésagut;mésllarga,somésgreu.El savigrecobservàtambéquealgunesfraccionsdelacordaproduïensonsmésagradablesa l’oïdaimésafinsambeldelacordasencera,sobretotlescorresponentsalameitat,elquarti elterç(Boyer, 1986).Aixínaixerenlesanomenadesconsonànciessonores.Sis’escurçalacor-

daalameitat,sonal’octava(8a);sis’escurçaunaquartapart,sonalaquarta(4a);siesredueix unterç,sonalaquinta(5a).ElquenovadeterminarPitàgoresforenlescausesfísiquesdel fenomen,lesqualsesconeixerienmil¨lennisdesprésambl’estudidelesfreqüènciessonores.

Eltod’unsoesquantificaambciclespersegon,fetqueenunacordavibrantequivalalaseva freqüènciadevibració.Enreduirlalongitudalameitat,lafreqüènciaesduplica;enreduir-la a 2{3,lafreqüènciaesmultiplicaper3{2.Enreduirlalongitudvibrantalafracció a{b de lalongitud,lafreqüènciadevibracióesmultiplicaper b{a.

Durantelssegles XVII i XVIII esconcretarenlesbasesdelesfreqüènciesquedefinirienelsistemamusicaloccidentalconegutcomasistematemperat.Fouunprocéscomplexqueva concloureambladivisiódel’octavaendotzeintervalsequidistantspelquefaallursfreqüènciesdevibració.Cadascund’aquestsdotzeintervalss’anomenasemitò.Si r ésl’augmentde freqüènciad’unanotaalsemitòimmediatsuperi or,fanfaltadotzeascensos,ésadir,multiplicardotzevegadesconsecutivesper r lafreqüènciadepartida,finsaarribaral’octava,la notacorresponentaladuplicaciódelafreqüènciaoriginal.Aixòvoldirquepujarunsemitò equivalamultiplicarlafreqüènciaper 1.059: r ¨ r ¨ cdots12 vegades ¨¨¨¨

Idotzepujadessuccessivesdesemitòequivalenaunapujadadirectad’unaoctava,lafreqüènciaduplicada:

L’escalaúnicaméscorrentavuidiaenlesguitarreséslade650 mm.Peròjas’haditqueles cordesnoesdisposenparal¨leles,sinóquevanseparant-seregularment,comunventall,des delacelletafinsalpont.Alacelletalaseparacióacostumaaserde8mmialpont,d’uns 11 mm.Comaconseqüència,lespartsvibrantsdelescordesnotenenexactamentlesmateixeslongituds.Leslongitudsvibrantsdelescordesprimeraisisenasóniguals.Tambésón iguals,peròunxicméscurtes,lesdelasegonailacinquena.Tambésóniguals,peròencara unamicaméscurtes,lesdelatercerailaquarta.

Alataula 1 esmostrenlesposicionsdelstrastsparal lelsd’unaguitarraquanadaptemles freqüènciesaunaescalade650 mm.Nosónequidistantsilesseparacionsesvanreduinta mesuraques’apropenalpont,lafreqüènciasonoraaugmentaielsoesfamésagut.

Taula1.Posicionsdelsdotzeprimerstrastsparal¨ lelsd’unaguitarra(m:menor,M:major,+:augmentada).

Escalade 650mm Relació Freqüència Interval musical Retalldelongitudvibrant decorda(mm) Separacióentretrasts consecutius

Teoremadel’entonacióperaguitarresambtrastsparal

¨ lels

Laguitarraclàssicailessevescosinesacústiquesielèctriquestradicionalsesconstrueixen ambtrastsparal¨lelsiseparatstalcoms’exposaenlataula 1.Tambécomparteixenl’equidistànciadecordesalacelletaialpont.Totesaquestesmidessónunxicinferiorsenlesguitarres ambcordesd’acerqueenlesquetenencordesdeniló.Unacordaaltrast VII,perexemple, redueixlasevalongitudvibrantals 2{3.Qualsevolaltracordaenelmateixtrasthadereduir lasevalongitudvibrantalsseus 2{3.Coms’asseguraaixò?

Jas’haditqueelstrastsilescordesd’unaguitarra,desdelacelletafinsalacelletadelpont, componenunaretículatrapezoidalques’anomenaretículasonora.Gràciesalparal¨lelisme entreambduescelletesielstrasts,lescel lesd’aquestaretículatambésóntotestrapezoidals (figura 2).

Amésd’això,l’equidistànciadelescordesenpassarperlacelletaiperlacelletadelpontfa queinterceptinelstrastsencincpartsiguals.Alataula 2 esmostrenlesseccionscorresponentsenunaguitarrahipotèticade n cordes.

Figura2.Trapezisonordelaguitarra.

Taula2.Seccionsprovocadesenelstrastsperl’equidistànciadelescordes.

Corda Secciócreadaperlacorda

1a 0{pn 1q 2a 1{pn 1q 3a 2{pn 1q enèsima pn 1q{pn 1q

Elsvalorsde n sóndiscretsinaturals.Peròsitenimencomptequeelstrastsnosónequidistantsique,pertant,lesseccionsquealescordesprovoquenlessevesintercepcionsnoes corresponenambvalorsenters,elteoremaque necessitemespotplantejarambvalorsreals:

Teorema1(d’entonaciódelesguitarresambtrastsparal¨lels).Enuntrapezi ABCD decostats paral lels AB i CD,sigui P sobre AC talque AC {AP “ k .Aleshores,laparal lelaalscostats AB i CD traçadaper P determinaunpunt Q sobre BD queeldivideixenlamateixaproporció: BD{BQ “ k (figura3).

Figura3.Teoremad’entonacióambtrastsparal lels.

AB i CD vindrienaserlacelletailacelletadelpontdelaguitarra,i PQ,qualsevoltrastintermedientreelles. AC i BD representenqualsevolparelldecordes.Aquestteoremaevoca elconegutcomateoremadelaparal lelamitjana,laproposició 2 delllibre VI dels Elements (Euclides, 1991):

Teorema2(delaparal lelamitjana).Elsegmentqueuneixelspuntsmitjansdedoscostats d’untriangleésparal¨lelaltercercostatilasevalongitudéslameitatd’aquest.

Elteorema 1 ésunageneralitzaciódelrecíprocd’aquestteorema 2.Nofareferènciaalspunts mitjans,sinóalspuntsquedivideixenelscostatsenqualsevolraó k .Tampocnoeslimitaal triangle,sinóaltrapezi.Comencemveientlageneralitzaciódelrecíprocdelteorema 2 (dela paral¨lelamitjana)altriangle:

Teorema3(generalitzaciódelrecíprocdelaparal¨lelamitjana).Enuntriangle ABC ,sigui P sobre AC talque AC {AP “ k .Aleshores,elpunt Q quelaparal lela r a BC traçadaper P determina sobre AB,eldivideixenlamateixaproporció: AB{AQ “ k (figura4).

Figura4.Generalitzaciódelteoremadelaparal lelamitjanaaunasecció k qualsevol.

Si PQ i BC sónparal lels, APQ i ABC sóntrianglessemblants.PelteoremadeTales,elsseus costatssónproporcionalsilaproporcióentre AC i AP éslamateixaquelaquehihaentre AQ i AB.Pertant, AB{AN “ k .Demostrateneltriangle,demostraremaralageneralitzacióenun paral¨lelogram.

Teorema4(generalitzaciódelteorema3alparal lelogram).Enunparal lelogram ABCD,prenem unpunt P sobre AC talque AC {AP “ k .Aleshores,elpunt Q quelaparal¨lelaa BC traçadaper P determinasobre BD,eldivideixenlamateixaproporció: BD{BQ “ r (figura5).

Figura5.Generalitzacióalparal lelogram.

Sitracemladiagonal AD delparal¨lelogram,obtenim P1 ,elpuntdetallde PQ amb AD (figura6).

Figura6.Ladiagonald’unparal¨ lelogrameldivideixendostrianglesiguals.

Siapliquemelteorema3altriangle ACD,tenimque P1 divideix AD enlamateixaproporció que P divideix AC ,ésadir: AD{AP1 “ k .Sirepliquemelprocésaltriangle DAB,també Q divideix DB enlamateixaproporcióque P1 divideix DA : BD{AP1 “ BD{BQ “ k .

Perdemostrarelteorema 1,lageneralitzaciód’aquestúltimteoremaaltrapezi,sigui ABCD untrapezienelqual P divideix AC enunaraó k .Veuremquelaparal lelaa CD traçadaper P divideixl’altrecostat BD delamateixamanera(figura7):

Figura7.Generalitzacióaqualsevolfracciódelrecíprocdelaparal¨ lelamitjana.

Sitracemper A unaparal lelaa BD,obtenimdospuntsdetall: D1 sobre CD i P1 sobre PQ (figura 8).D’aquestamanera,eltrapeziquedadescompostenuntriangle ACD1 ienunparal¨lelogram ABDD1 .

Figura8.Trapezidividitenuntriangleiunparal¨¨ lelogram.

Siapliquemelteorema3altriangle ACD1 ,obtenimunpunt P1 quedivideix AD1 enlamateixa proporcióque P divideix AC .Siapliquemelteorema4alparal lelogram ABDD1 ,tenimque Q divideix BD enlamateixaproporcióque P1 divideix AD1 iqueés,enconseqüència,lamateixa enlaqual P dividia AC .Aixíquedademostratelteorema 1 sobrel’entonacióenguitarresamb trastsparal¨lelsi,perextensió,eninstrumentsdecordaambtrastsd’aquesttipus.Talcom intuíem,elteoremadeproporcionalitatdeTalesn’éselrerefons.

Valadirqueelteoremanoobligaaobservarl’equidistànciadecordesalacelletaiala celletadelpont.Siambduessónparal lelesielstrastssónparal lels,qualsevoltrastiqualsevol parelldecordesformaràsempreamblacelletadelpontuntrapezi(figura 9)quepermetrà l’aplicaciódelteorema 1,il’instrumententonaràcorrectament.

Figura9.L’equidistànciadecordesnoésnecessària.

Elteorema 1 noésaltrequeelrecíprocdelteoremadelpuntmitjàdeltrapezireferitperDe Villiers(2013)iquerepresentaunageneralitzaciódelteoremadelabimediana:

Teorema4(bimediana).Siguin MN i PQ lesmedianesdelscostatsoposatsd’untrapezi ABCD enelqualelscostats AB i CD sónparal¨lels.Aleshores, PQ i MN estallenpelsseuspuntsmitjans.

Atèsqueenelteorema 1 lesdivisionsdelscostatsoposatsdeltrapezivanmésenllàdelsseus puntsmitjans,aquestaésunageneralitzaciódelteoremadelabimediana.

Teoremad’entonacióperaguitarressensetrastsparal¨¨lels

Avuidiaesconstrueixentottipusdeguitarresd’escalamúltiple(figura 10):clàssiques,acústiques,elèctriques...Elsmotiusprincipalssón dos:d’unabanda,s’aconsegueixaugmentarel nombredecordessensequelesmésgreushagindesermassagruixudespertaldemantenir unatensióiunsoequilibratambelsdelesrestants,ésperaixòquelamajoriadeguitarres d’escalamúltipleacostumenatenirmésdesiscordes;d’altrabanda,elstrastsnoparal¨lels permetenunaccésiunaposiciódelcanelldelamàesquerramésnaturalenelsprimersi últimstrastsdeldiapasó.

Comesmostraalafigura 10,laretículasonoralimitadaperlacelleta,lacelletadelponti lescordesprimeraisisenajanoéstrapezoidal,sinóquenoméstéformadequadrilàter.Les sevescel lestampocjanosóntrapezoidals.Sensecapparal lelisme,elsteoremesempratsfins aranosónaplicables.

Lacaracterísticacomunaentreaquestesguitarresilesd’escalaúnicaésl’equidistànciadeles cordes.Aixòfaquelescordesdivideixindoscostatsoposatsdelquadrilàterenpartsiguals.I atèsquetambéaracadascundelstrastshad’interceptartoteslescordesenpuntscorresponentsalamateixaproporció,elteoremaquejustifiquilabonaentonaciódel’instrumentve aserlageneralitzacióúltimadelteoremadelaparal lelamitjana,tantpelquefaalpolígon d’aplicació(quadrilàter)compelquefaalaràtiodelesseccionsdelscostats(qualssevol). L’anomenaremteoremadelesdivisòries.

Figura10.Guitarradenoucordesd’escalamúltipleconstruïdaperDanielZucali(Haag,Àustria).

Teorema5(delesdivisòriesd’unquadrilàter).Enunquadrilàter ABCD esprenenquatrepunts M, N , P i Q sobrecadascundelscostats,demaneraque AC {AP “ BD{BQ “ r i AB{AM “

CD{CN “ s (figura 11).De PQ i MN endiremlesdivisòriesdelquadrilàter.Aleshores,elpunt O d’intersecciódelesduesdivisòriesverificaque MN {MO “ r i PQ{PO “ s

Nohihacapparelldesegmentsparal¨lelsalafigura 11,peròelspodemcrearpermirar d’aplicarlarecomanaciódePolya(1988):adaptarlaresoluciód’unproblemasenzillaunde méscomplex.Sitracemparal¨lelesalesdivisòries PQ i MN pelsseuspuntsdetallambels costatsdelquadrilàteripelsquatrevèrtexsd’aquest,aconseguiremsuperposarunaretícula deparal¨lelogramsdamuntdel quadrilàter(figura 12).

Figura12.Retículadeparal lelogramsgeneradaperlesdivisòries PQ i MN.

Siapliquemelteorema4altrapezi AM2 N 2 C ,tenimque M2 N 2 {M2 O “ AC {AP “ r (figura 13).

Elmateixteoremaaplicataltrapezi M1 BDN 1 permetassegurarque M1 N 1 {M1 O “ BD{BQ “ r .

Figura13.Lesdivisionsd’AC i BD espropaguena M2 N2 i M1 N1 .

Figura11.Teoremadelesdivisòries.

Fixem-nosaraenelstriangles ABA1 i CDD1 (figura 14). AMM2 i ABA1 sóntrianglessemblantsperquètenenelscostatsparal lelsiperquèlaproporcióentreelsseuscostats,laque hihaentre AM i AB,és s.PelteoremadeTales, BA1 “ s ¨ MM2 .Però BA1 “ M1 M2 i,pertant, M1 M2 “ s MM2 ,Demaneraanàloga,eneltriangle CDD1 trobemque N 1 N 2 “ s NN 2

Figura14.Elstriangles ABA1 i CDD2 .

Enbeneficidelaclaredatd’exposició,diremque x “ MM2 , y “ NN 2 i z “ M2 O,iescriurem elssegments M1 N 1 i BD1 enaqueststermes: M1 N 1 “ M1 M2 ` M2 N 2 ` N 2 N 1 “ s ¨ MM2 ` r ¨ M2 O ` s ¨ NN 2 “ s ¨ x ` r ¨ z ` s ¨ y BD1 “ r M1 O “ r ¨pM1 M2 ` M2 Oq“ r ¨ps MM2 ` M2 Oq“ r ¨ps x ` z q

Atèsque M1 N 1 “ BD1 : sx ` rz ` sy “ r ¨psx ` z q sx ` rz ` sy “ rsx ` rz

Aixòpermetdescompondre MN iobtenirlaconclusió: MN “ x ` rz ` y “ rz ` rx “ r ¨px ` z q“ r MO

Siapliquemelmateixprocedimentaladivisòria PQ,arribaremaunresultatanàleg: PQ “ s ¨ OP.Comesvoliademostrar,elpunt O divideixcadadivisòriaenlesmateixesraons enlesqualscadadivisòriadivideixelscostatsoposatsdelquadrilàter.

Elteoremaésfalssilesdivisòriesnoseccionenelscostatsoposatsqueconnectenenlamateixaraó,comesposademanifestalafigura 15.Eltrast XII divideixperlameitatlescordes c1 i c3 Perònofaelmateixamblacorda c2 : x1 ą x2 .Aixòvoldirquesilesguitarresd’escalamúltiple noesfessinambequidistànciadecordesenlacelletaienlacelletadelpont,l’entonació esdevindriaimpossible.

Matemàtiques,treballartesàiaprenentatge

AlaxarxaInternethomtrobamolteswebsonlutiersd’arreuexpliquencomconstrueixen guitarresd’escalamúltipleambtrastsnoparal¨lels.Hihaguitarresenlesqualseltrastperpendicularalamediatriudeldiapasóésel VII;end’altres,encanvi,ésel XII.Segonsescriuen elslutiers,aixòdepèntantdelguitarristacomde lesescales(longitudsvibrantsdelescordes) idelnombredecordesquetindràlaguitarra.Larecercasobrelajustificaciógeomètricadela bonaentonaciónovaproduircapresultat.

Elsorígensd’aquestesguitarressóndelsegle XVI,quanaEuropaesvaconstruiruninstrument anomenat bandora quenoteniaelstrastsparal¨lels.Tresseglesdesprés,Novak(1988)va patentaralsEstatsUnitsunaguitarrad’escalamúltiple.Eneldocumentderegistreexplica comfunciona,peròtampocnoofereixcapjustificaciódelasevaentonaciócorrecta.

Aquesttreballs’haredactatpensantendiapasonsplans.Lesguitarresacústiquesielèctriques esfanambdiapasonscorbats,peròlescordeses disposensobreellsobservantl’equidistància pròpiadelsdiapasonsplans.Pertant,totselsteoremesdesenvolupatssónaplicablestambé aaquesttipusdediapasons.Lasituacióespotil¨lustrarimpriminteldiapasód’unaguitarrai desprésenrotllar-loenformadetub.Eldiapasóesdevéunasuperfíciecilíndricaambtrasts circulars,mentrequelescordescontinuenessentrectilínies.

Delesdiversesrelacionsentrelesmatemàtiquesil’entorn,esdestacaaquíqueunfenomen del’entorninspiraeldesenvolupamentdeconeixementmatemàtic.Estractad’untipusde relaciójaassenyaladaenunestudisobrel’úsde lesmatemàtiquesenl’àmbitlaboral(Albertí, 2009 i 2022).Enaquestaocasió,elproducted’untreballartesàcomeldelalutieriahainspirat elteoremadelesdivisòriesambelqualespotjustificargeomètricamentlabonaentonació delesguitarres,ambosensetrastsparal¨lels.I,perextensió,ladelsinstrumentsdecorda ambtrasts.Aixòinvitaapensarenlapossibilitatdetrobarmésqüestionsrellevantsperales matemàtiquesenaquestaactivitatartesana.

Pensem,perexemple,enelfetquel’equidistànciadecordesnosiguinecessàriaenlesguitarresd’escalaúnica(ambtrastsparal¨lels),peròesdevinguiessencialenlesd’escalamúltiple (ambtrastsnoparal lels).Uncopsituadeslaprimerailasisenacordes,lesinstruccionsd’un lutierdeguitarresambcordesd’acer,perposarlesrestantssón:«[...]espaiarlesquatre cordesinteriorsdemaneraqueequidistinl’unadel’altra.L’espaiequidistants’hauriadedeterminar entre (sic)lescordes,inodesdelsseuscentres»(Benedetto, 1994: 187).Aquest

Figura15.Sensel’equidistànciadecordeslesguitarresd’escalamúltiplenoentornarien.

«entre»destacatpellutiervoldirquelesequidistànciess’handeprendredesdelsperfilsde lescordes,inodesdelsseuscentres.Ladiferèncianoésgaireimportantenguitarresamb cordesdenilóperquètotselsseusgruixossónforçasemblants,jaquenomésoscil¨lenentre 0,7mmi 1,1 mm.Encanvi,enlesguitarresambcordesd’acer,ladiferènciadegruixentrela primeracorda(0,28mm)ilasisena(1,32 mm)superaelmil¨límetre.Siambcordessemblants l’equidistànciaesprendesdelscentres,laseparacióentreelsperfilsdelacinquenailasisena cordespodriasuperarenmésd’1 mmlaseparacióentreelsperfilsdelaprimerailasegona. Massadiferènciapernoafectarl’execució.PerònocaliaqueBenedettoespreocupésper l’entonació,jaquelesguitarresdeles qualsparlavatenienelstrastsparal¨lelsi,coms’ha demostrat,l’equidistàncianoésessencialperpreservarl’entonació.I,això,tenintencompte queenelsmodelsgeomètricsutilitzatshempresunacordacomunsegmentsensegruix. LesinstruccionsdeBenedettopotsernosón,doncs,lesmésapropiadesperaaquesttipus d’instruments.

Aixòplantejaunaqüestióessencialsobrelalutieria:¿l’equidistànciadelescordesalacelletaialacelletadelpontenlesguitarresd’escalamúltipleésdecisiódellutierperpreservarl’entonaciódel’instrumentoésunadecisióinconscientquetraslladaautomàticamenta aquestesguitarreslamaneraambquèesconstrueixenlesguitarresd’escalaúnica?Valdria esbrinar-hodirectamentdelsprofessionalsdelalutieria.Enbeneficiseuienbeneficideles matemàtiques,seriaboferunainterpretaciómatemàticasituadad’aquestoficibasadaen lestresfasesenlesqualsespotdividirunaactivitatartesana:l’obraacabada,l’obraencurs il’obraenprojecte(Albertí, 2007).Elsteoremesdesenvolupatsinterpretenmatemàticament unaspectedel’obraacabadain’estableixenlescausesdesd’unaperspectivamatemàtica. Analitzarl’obraencursil’obraprojectadapassariaperveurequèfanelslutiersiquèresponen quanse’lsinterpel¨lasobreelquevolenfer.

Amés,lalutierianohauriad’ignorarlesconseqüènciesquedeterminatsfetsi,possiblement, determinatscostumspodentenirenlasevafeina.Enaquestsentit,lacol¨laboracióentre matemàtiquesiartesaniaenriquiriaambduesactivitats.Demaneranaturalestemparlant d’aprenentatge.Ilesimplicacionsperal’aprenentatgeacadèmicespodenadreçaradues qüestionsprincipals:

a)D’unabanda,lamodelitzaciómatemàticadefenòmensdel’entorn.Elsentornssocial, culturalinaturalescomponendemultituddefenòmensquemassasovint,totiser extraordinàriamentquotidians,enspassendesapercebuts.És,defet,lasevaquotidianitatlaqueensimpedeixmirar-nos-elsdesd’unaperspectivadiferent.Laguitarraésun delsinstrumentsmusicalsméspopulars.Peròraramentparemesmentenelseupotencialcomarecursd’aprenentatgematemàtic.Nohiharesmésimportantenqualsevol instrumentmusicalquel’entonaciócorrecta.Totplegatfadel’entonacióuntemaper tractarmatemàticamental’educaciósecundària.Elcasdelesguitarresd’escalaúnica ésforçaabordableatesalasevarelacióambelteoremadeTales.Alhora,n’eixampla l’àmbittradicionald’aplicació.ArasabemqueelteoremadeTalestambéserveixper explicarl’eficàciadelesretículessonoresdelesguitarres.Elcasdelesguitarresd’escala múltiplenecessitaunconeixementmésprofunddels Elements d’Euclidesquerarament espottractaral’educaciósecundària.

b)D’altrabanda,lademostraciómatemàtica.Lamodelitzaciódigitalpermetabordarla qüestiódel’entonaciódelesguitarresd’escalamúltipledemaneramésdirecta,sense

haverd’aprofundirgaireenlageometriaeuclidiana.SiduematermeunadinamitzaciódigitalambGeoGebra,podemconfirmar elteoremadelesdivisòries.Sabremque elteoremaéscert.SegonsCarrillo(2012),l’haurem«demostrat»(sic).PeròGeoGebra raramentdemostra.GeoGebraconfirmaorefusa.Isiconfirmalacertesasenseque acabemd’entendre-la,esfaràclarquen’hauremdecontinuarbuscantlescauses.Això potimplicarcréixermésculturalment.Ésadir,aprendreperentendre.Lacomprensió definitivanoarribaràmentrenodemostremelteoremaamblametodologiapròpiade l’àmbitenelqualfouplantejat:eldelageometriaeuclidiana.

Tots’hadesenvolupatenelplabidimensional,peròelsoesprodueixenunespaitridimensionalons’hauriendeconsiderarmésvariables.Elsmaterialsdelescordes,els seusdiàmetres,lesalturessobreelstrasts,totaixòafectalleugerament,peròafecta, l’entonació.Larealitatdellutierésquetotinstrumentesdissenyasobrepapersiplantillesplanes,onelstrastssesituenaldiapasórespectantlesdistànciesdescrites.Un copacabatl’instrument,larealitatentraenjocis’handeferajustamentsperrestablir labonaentonacióplanejadasobreelpaper.Sovintcaldesplaçaroesmolarunxicla celletadelpont(unesdècimesdemm)ousarcordeslleugeramentmésprimesomés gruixudes.Enfer-ho,ellutiertornaalageometriadel’instrumentallòquelarealitatli haviatret.

Agraïment

VullferarribarelmeuagraïmentaAntonioManjónMartín,lutierdeSantAdriàdeBesòs (Barcelona),iaDanielZucali,lutierdeHaag(Àustria),percedirlesfotografiesdelesseves guitarresqueil lustrenaquestarticle.

Bibliografia

Albertí,M.(2007). Interpretaciómatemàticasituadad’unapràcticaartesanal.TesidoctoraldirigidaperNúriaGorgorióiSolà.Bellaterra:UniversitatAutònomadeBarcelona.

Albertí,M.(2009). Activitatmatemàticaenl’àmbitlaboralal’inicidelsegle XXI:Implicacionsper alcurrículumdel’ESO.Memòriadelprojectederecercaperalallicènciaretribuïdaconcedida pelDepartamentd’EnsenyamentdelaGeneralitatdeCatalunya.

Albertí,M.(2022). Laretículamatemática:Usoyrecursomásalládelespaciobidimensional. Madrid:Catarata(MiradasMatemáticas).

Benedetto,R.(1994), MakinganArchtopguitar:Thedefinitiveworkonthedesignandconstructionofanacousticarchtopguitar.CenterstreamPublishingCA.USA.

Boyer,C.B.(1986). Historiadelamatemática. Madrid:Alianza.

Carrillo,A.(2012).«DemostracióndeteoremasconGeoGebra,?‘esposible?». Épsilon:Revista deEducaciónMatemática,vol. 29(3),núm.82,79-87.

DeVilliers,M.(2013).«Atrapeziumtheoremgeneralized». AtRightAngles [AzimPremjiUniversity],vol. 2,n.3.

Euclides(1991). Elementos.TraducciódeMaríaLuisaPuertas Castaños.Barcelona:Gredos.

Novak,R.(1988). Fingerboardforastringedinstrument.Patent4852450.USA.

Polya,G.(1988). Howtosolveit:Anewaspectofmathematicalmethod.NewJersey:Princeton ScienceLibrary/UniversityPress.[reed.del’originalde 1945].

Lesmatesalbillariuna situaciód’exploracióper treballaral’aulade matemàtiques

GuillemBonetCarbó

InstitutdeSantaColomadeFarners gbonet2@xtec.cat

Resum Abstract

Totasituaciódesconegudaperal’alumne requereixunprocésdefamiliaritzacióiuna investigacióposteriorperconèixer-neles propietatsprincipals,queservirandeguiaper traçaruncamíqueensportiasolucionarun problemaconcret.Enaquestcas,elnostre problemaenspassejaràpelmóndelbillar,un mónambquèengeneralelsalumnesde l’ensenyamentsecundariobligatori(ESO)no estanfamiliaritzats.Atravésd’unprocés d’investigacióelsdonarempautesieinesamb laideaqueellsacabinconstruintlaseva maneraderesoldreelproblema.

Introducció

Everyunknownsituationforstudentsrequiresa processoffamiliarizationandsubsequent researchtolearnaboutitsmainproperties.This processwillguidetheminthedesignofa roadmapforsolvingaparticularproblem.Inour case,theproblemwilltakeusintotheworldof billiards,whichsecondaryschoolstudentsare notexpectedtobefamiliarwith.Throughguided investigationstudentswillbeprovidedwith guidelinesandtoolswiththeaimofthembeing abletodeveloptheirownwayofsolvingthe problem.

Aquestéselprimerdetresarticlesencaratsadescobriralgunespropietatsmatemàtiques quepodemtrobareneljocdelbillar.Ditaixò,elqueespreténenaquestmodestescrit noéstantdonarunesbasessòlidessobrelesgranspropietatsmatemàtiquesifísiquesque s’amaguenalmóndelbillar,sinóoferiralprofessoratideesmatemàtiquessenzillesiquepodenserexploradesianalitzadesal’auladematemàtiquesd’educaciósecundàriai,potser també,oferirunespaid’investigacióabatxillerat.

Ambaquestespropostesesvolferl’ulletalaidead’investigarlesmatemàtiquesenuncontextdeterminatatravésdelaresoluciódeproblemes.Sí,espreténqueelsalumnessiguin capaçosderesoldrelessituacionsproposadesatravésdelraonamentidel’experimentació, unaexperimentacióqueestreballainicialmentambmaterialsrudimentaris,comaraboles defusta,iposteriormentambaplicacionsdeGeoGebrajacreadesperaconseguirqueels alumnespuguincomprovarelresultatdelessevesdeduccionsentaulellsdebillar.

Unproblemaperanarfentboca...

Jafatemps,el 29 defebrerde 2020,vaigtrobaralesxarxessocialsunproblemasignatper l’usuarideTwitter@brilliantorgonesdemanavaresoldrematemàticamentunasituaciócontextualitzadaenelmóndelbillar.Elproblemaenqüestió,il¨lustratambl’esquemadelbillar quedibuixavalasituació,deiaelsegüent:

Tenimunbillarrectangulardedimensions 14 ˆ 6.Piquemunabolaqueestrobaenuna cantonadaseguintlabisectriud’aquesta.Sisuposemquelabolamainos’atura,podrem prediraquinforataniràapararlabolaencasquefinalmentcaiguienalgun?

Imatge1.Esquemadelasituacióproposadaalproblemade@Brilliantorg.

Elproblema,totiquequedaunxicllunydelarealitatsiensfixemenlesdimensionsdel billarenqüestió,permetexploraralgunespropietatsdeljocquepodenserconnectadesràpidamentambconceptesmatemàtics.Apart,permetmodificar-nefàcilmentlescondicions inicialsi,d’aquestamanera,obrir-loperaconseguirnonomésresoldre’l,sinótrobarresultats mésgenerals.

Elproblema,enelqualusconvidemapensarabansquecontinueullegintaquestarticle,té unpotenciald’exploracióincreïblealdarrere.Perexemple,enspodemplantejarcomvariarà lasoluciósimodifiquemelscostatsdelrectangleinicial.Suposantquelallargadadelataula sigui36m,quinamidahadetenirl’ampladaperaconseguirquelabolaacabienunforato enunaltre?Podriaserquemaiacabésencapforat?Isimodifiqueml’angledellançament?

Toteslespreguntesqueesfacinelsnostresalumnesperampliaraquestasituacióinicialde bensegurqueenriquiranelnostreproblemai aconseguiranqueelnivelld’aprenentatge decadascuns’ajustialessevesnecessitats.

Unparèntesienlaresoluciódelproblema

Perresoldreaquestexerciciensésimprescindibleentendreelfuncionamentd’alguneslleis delbillar;perexemple,elsrebotsaunabanda.

Sitiremlabolacontraunpuntconcretd’unabandasensecapefecte,1 comfaremapartir d’araentotselsexercicisd’aquestarticle,veuremquelabolanorebotademaneraaleatòria contralabanda,sinóquesempresegueixunmateixcamí.Enaquestcas,elcamíquesegueix desprésdelrebotmantécontralabandaelmateixanglequel’hihaportat.

angled’incidència “ anglederebot

Imatge2.Rebotsdebillard’unabolacontraunabanda.

Perconstataraquestfetpodemferalgunsllançamentsal’aulaambbolesdefusta,perexemple,fent-lesrebotarcontraunmur.Sienfilmemelmovimentdesd’unacàmerazenital,podemcaptarlatrajectòriadelabolai,posteriorment,analitzarl’angled’incidènciaidesortida. Aixímateix,desprésd’haverfetalgunaprovaamblesbolesdefustatambépodemusaralgunaaplicaciódegeometriadinàmica,comaraelGeoGebra,ianalitzarelmovimentdela bola.

Respostaaunapreguntaqueensobrelaportaaméspreguntes

Uncopentèselmovimentderebotd’unabolacontralabanda,elprocésdecercadela soluciósemblabensenzill.Noméscalprolongarelcamíquesegueixlabolaquansurtdel foratsuperiordretambunanglede45˝ ifinsatrobaraquinacantonadaacabaràananta parar.

Aprimercopd’ull,elprocésdecercadelarespostanohaestatespecialmentcomplicat: calanarbuscantelsrebotsdelabolacadacopquetocaunabandaigarantintquel’angle d’incidènciacoincideixiambl’angledesortida.Comquel’angleésde45˝ ielpuntdesortida inicial(hemescollitelpunt Oq ésunvèrtexdelatauladebillar,eltraçdelabolaseguiràel camímarcatperlabisectriud’aquestacantonada,rebotantcontralesbandessempreamb l’anglede45˝ ,iarribaràalpunt B,elvèrtexdelataulamésallunyatdelpuntdesortida, O.

1.Enaquestsexerciciséspreferibletreballarsenseefectesdelabolaperrestringirelscàlculsamodels lineals.

Imatge3.Camídelabolaambunllançamentde45˝ ˝ ˝ .

Nota:enl’aplicaciód’aquestaactivitatal’aulaésinteressantquel’alumnatdelaprimeraetapad’ESOtreballilamesuraengraususanteltransportadord’angles.Peraquestmotiu,serà convenientqueenaquestaprimeratascanolifacilitemelfullquadriculat.Encanvi,sielsvolemfacilitarlafeinaentasquesrepetitivesposteriors,elspodemdonareltaulellquadriculat ambquadratsunitaris;enaquestcas,elrecorregutdelabolamarcaràdiagonalsd’alguns d’aquestsquadrats.

Fet!Jahemdonatrespostaalproblemainicial.Sillancemunabolaambunanglede45˝ des d’undelsvèrtexsdelataula,acabaràarribantalacantonadamésallunyadad’aquestvèrtex desortida.

Fet?Nidebontros!Quèenshaaportatdemomentaquestpetitexercici?Benpocacosa.Hem deferunpasmés!Quinespreguntesenspodemferperampliarelproblema?Perexemple,si lesdimensionsdeltaulellfossinunesaltres, hauríemarribatalmateixpunt?Isimodifiquem l’angledesortida?Comvariaelnombrederebotsenfunciódelesdimensionsdelataula?Uf, quantespreguntes!Posem-nosainvestigar!

Primerspassoscapaunadescoberta

Totprocésdedescobertaexigeix,abansqueaquestaesprodueixi,unainvestigacióinicial delaqualhemdetenirdefinitsmoltbéquinsseranelsparàmetresdecerca.Enaquestcas, aniremvariantlesdimensionsdelatauladebillarianotaremelnombrederebotsielforat enquèacabalabolallançadaambunanglede45˝ sempredesdelcostatinferioresquerre, elnostreorigendecoordenades,queanomenaremvèrtex O.

Femunesquantesproves.Quinsresultatsapareixensihointentemperalstaulellsdedimensions3

3?Vegem-ho!

Imatge4.Camídelabolaambunllançamentde45˝ ˝ alstaulellsdedimensions3

Enunprincipi,aquestprimerintentnomésenshaservitpercomençarapenetrardinsel problema.Veiemaprimercopd’ullqueelsresultatsqueenssurtensónunxicdispars.Pel quefaalvèrtexd’arribada,elsresultatshanestat B, C , B i C .Falasensacióque,almenysals taulellsenquèlasegonadimensióés3,elsforats B i C esvanalternant,demaneraquecau enel B quanlaprimeradimensióésparellicauenel C quanéssenar.Pelquefaalnombrede tocsaunabanda(comptareml’entradaaldarrervèrtexcomaund’aqueststocs),elsresultats són 1,6,7i 2.Nosemblaquesesegueixicapordre.

Imatge5.AplicacióBillard’IgnacioLarrosa,www.geogebra.org/m/gzF2CrHS.

Elqueseriamoltrecomanablepercontinuarambl’exploraciódelproblemaseriacomençar ambcasosméssenzills.Perexemple,ambtaulellsenquèuncostatés 1 o 2.Desprésdeveure comvarienelsparàmetresestudiatsenelscasosméssenzills,podemanaraugmentantla dimensióperintentartrobarunanormaqueensserveixipertrobarunageneralitzaciódel nostrecas.

Aquestaestratègiadecercainductivadelasolucióésmoltbonaperòcostosa.Costosaenel sentitque,perdur-laaterme,hauremderepresentarmoltestaulesdebillarambelrecorre-

gutdelabolainclòs.Perfacilitar-noslafeina,ésaconsellableusaralgunaaplicaciójamuntadadeGeoGebra,com,perexemple,ladeJosepIglésias(www.geogebra.org/m/x9fkpj7b)o laproposadaperIgnacioLarrosa(imatge5),que enspermetvisualitzarlatrajectòriad’una bolaenuntaulelldedimensióvariableiambunaposicióinicialdelabolaiunanglede llançamentapeticiódelconsumidor.

Tantsis’usal’aplicaciócomsino,ésimportantmanteniralavistaqualsevolresultatque anemtraient,delamaneramésordenadapossible,usant,perexemple,unataula.D’aquesta manerapodremidentificarqualsevoltendènciaquesegueixinelsdiferentscamins.

Imatge6.Caminsd’unllançamenta45˝ ˝ ˝ endiferentstaulells.

Uncoprepresentatsiordenats(valadirquejon’hehagutdedibuixarunsquantsmésabans depodertreurecapmenadeconclusió),escomencenaveurealgunespropietats.Com,per exemple,queesdistingeixunamenad’antisimetriaentreelstaulells n ˆ m i m ˆ n.També,i ésmésqueevidentqueentaulellsquadrats n×n labolacauràsemprealvèrtex B,ennomes unabanda(lad’arribada).

Imatge7.Caminsd’unllançamenta45˝ ˝ ˝ endiferentstaulellsproporcionals.

Unaaltrapropietatcuriosaquepodemveurenomésambelsgràficsésentaulellsambla forma pk nqˆpk mq.Enelstaulellsqueesgenerend’aquestamanera,mantenint n i m i variantelvalorde k ,podemveurequeelscaminsseguitsperlabolatenenlamateixaforma (imatge7).Aquestapropietatespotentendredividintcadacostatdelsquadratsunitatsen k partsiguals;d’aquestaformageneraríemunaaltraretículamésfinaquemantindriaelcamí delabolatambéeneltaulelldedimensió pk nqˆpk mq

Enquèmésenspodemfixar?Observemalataula 1 elvèrtexd’arribada:

Taula1.Relaciódelvèrtexonvaapararlabolasegonsladimensiódelatauladebillar.

Enaquestataulas’acabadeconstatarl’antisimetriaqueintuíemabans.Observemquesial taulelldedimensió n ˆ m elrecorregutdelabolaacabaalvèrtex A,altaulell m ˆ n acabarà alvèrtex C .Encanvi,siundelsdosacabaalvèrtex B,l’altretambé.

Nosemblapossibleacabaralmateixvèrtex O enquèhemcomençat.Simiremqualsevoldels recorregutsquetenimrepresentats,comprendremperquèésimpossiblequelabolahitorni. Perarribaralvèrtexdesortida, O,labolahauràderebotarenalgunmomentaunabandai retornarpelmateixcamíqueacabadefer,iaixònopodràserperquèelcamíqueseguirà desprésdelrebotseràperpendicularalcamíquel’hihaportatenestarenviadaambangles de45˝ .

Elstaulellsdeltipus pk ¨ nqˆpk ¨ mq i pp ¨ nqˆpp ¨ mq haurand’acabarenelmateixvèrtex,ja que,coms’hacomentatal’apartatanterior,elsdoscaminstindranlamateixaforma.

Tambéobservemunacertaregularitatenelstaulellsonlaprimeradimensióéssenar, p2k ` 1qˆ m.Enaqueststaulells,labolacaualternativamentalvèrtex A o B segonssilasegonadimensióésparellosenar.

Unaltrefetcurióséselqueveiemquanunadimensióésunapotènciade 2.Siestudiemels taulellsdelaforma 2k ˆ m,veiemqueapareixensuccessionsde k 1C seguidesd’una B

Totesaquestesobservacionsensportenalaideaquelasoluciógeneralhad’estarrelacionada amblaparitat.Peranalitzarelsdiferentscasos,discriminaremelstipusdetaulellssegonssi contenenalgunadimensiósenarono.Imarcaremelspuntspossiblesperonpotpassarla bola(enelsqualslesduescoordenadesdelpuntsuminparell).

Imatge8.Caminsd’unllançamenta45˝

endiferentstaulells,marcatssegonslaparitat.

Així,elspuntsdelatauladebillarensquedendiferenciatscomlescasellesenuntaulell d’escacs:elspuntsperonpotpassarlabola,marcatsambunarodonaielspuntsperonno podràpassar,marcatsambunacreu.

Taulellsambduesdimensionssenars:quedamarcatnomésel B,apartdelvèrtexde sortida, O.Alsvèrtexs A i C labolanohicauràmai.Pertant,elcamíacabaràalpunt B.

Taulellsamblaprimeradimensiósenaril’altraparell:nomésestàmarcatelpunt A iel camíacabaràalvèrtex A;sigiremlesdimensions,nomésestaràmarcatel C ielcamí acabaràal C .

Taulellsambduesdimensionsparells:estanmarcatstotselsvèrtexsilabolapodria acabarenqualsevold’ellsmenysaldesortida.Perdescobrirenquinvèrtexcau,dividiremlesduesdimensions m i n perMCD pn,mq iaixícauremenunadelessituacions anteriors.2

Fixem-nosaraenelnombrederebotsquefalabolacontralesbandesdelatauladebillar:

Taula2.Relaciódelnombrederebotsquefalabolasegonsladimensiódelatauladebillar.

Quanobservemlataula,hiveiemunasimetriaabsoluta,iésquearanoméstenimencompte elnombrederebots.Siensfixemenlaimatge6,ensadonaremque,quangiremlataulade billaripassemd’untaulelldedimensió n ˆ m aundedimensió m ˆ n,elcamítambé«gira» (defet,esprodueixunasimetriarespectealabisectriudelvèrtexdesortida);encanvi,el nombrederebotsesmanté.

2.El 1961 A.ZavrotskyvapatentarunaparellòpticbasatenaquestateoriapertrobarelMCDdedos nombres.

Destaquemtambéelsuns(1)aladiagonalprincipal,iduesaltresdiagonalsquehihaurà ambdosos(2),oduesmésambtresos(3)...Engeneral,veuremquelesduesdiagonalsamb valors k ‰ 1 contindrantaulells n ˆ m, onMCDpn,mq“ k .

Quèpassa,doncs,ambelsaltresvalors?Siobservemlesdiagonalsquetallenperpendicularmentladiagonalformadanomésperuns(1),veiemunsquantsresultatsrepetitsnomésamb valorsparells;perexemple,ladiagonalambnomésquatres(4)querepresentaelstaulells 1 ˆ 4, 2 ˆ 3,3 ˆ 2 i4 ˆ 1.Tambén’hihaunaaltraambsisos(6).Ara,lareglaquepodríemtrobar peraquestsnombresparellss’estroncaambladiagonaldevuits(8),quecontédosdosos(2).

Ambunestudidetingutsobreelsvalorsquevanapareixent,acabemtrobantlafórmulaque generalitzaelnombredebandesenuntaulelldedimensió n ˆ m:

bandes “ n ` m MCDpn,mq MCDpn,mq

Unadarreracosa.Uncopcomparatselscamins,elnombrederebotsielvèrtexonacabala bola,encaraensquedaperinvestigarlarelacióentrelalongituddelcamíseguitilalongitud delscostatsdelatauladebillar.

Vegem-netresexemplesqueensserviranperextrapolarlapropietatalcasgeneral:

Imatge9.Exempledecaminsendiferentstaulellspercalcular-nelalongitud.

Enaquestscasoshemvistquelalongituddelcamíésunmúltipled’arrelde 2;defet,aquest coincideixambelnombredequadratsunitats pelsqualspassaelcamí.Sicomprovemaquestapropietatperalsaltresexemples,veiemquetambéfunciona.Deixarélademostraciócom aexercici,amblaintenciódedonar-nelaclauenunsegonarticle.

Conclusions

Alllargd’aquestarticleheminvestigatsobrelespeculiaritatsdelscaminsqueprenunabola debillarllançadadesd’unabandaambunanglede45˝ segonssieltaulellésd’unamidaod’unaaltra.Hemofertideesperconvertirunproblemacomaquestenunasituació d’investigacióal’auladematemàtiques.Hemintentatdonarrespostaaalgunesdelespreguntesqueenshemanatfentiara,quanescricaquesteslínies,m’adonoquealguneshan quedatsenserespostaiqueme’nvenenmoltesaltresalcap.Quèpassariasiundelscostats fosunnombreracional?I,sifosirracional,podríemarribarmaiacolarlabolaenalguna cantonada?

Epíleg:unpasmésenllàdelproblemainicial

El7dejuliolde 2022 emvasorprendreuntuitdeRobertoSantos(@rober_fun)enelqual explicavademaneravisualcomcalcularunasumadefraccionsambelsrebotsenunataula debillar.

Imatge10.ExempledelmètodedecàlculproposatperRobertoSantos.

Elmètodepercalcular a n ` b m consistiaaagafaruntaulelldebillardedimensió n ˆ m illançar unabolaambunanglede45˝ .Uncopfetelllançament,calcomptarelnombrederebotsals costatsdeltaulellquemesuren m,alsqualsdonemunvalorde a,ielnombrederebots alscostatsquemesurin n,alsqualsdonemelvalorde b.Elvèrtexd’arribadatocaambdós tipusdecostats,pertant,sumem a i b.Lasumadetotesles a iles b representaelnumerador delafracció,mentrequeeldenominadoréselnombredequadratsunitarisperonhapassat labola.

Aquestdarrermètodel’hetrobatfascinantipotarribaraserdemoltautilitatpertancar l’exerciciinicialambunasíntesidetotselspetitsresultatsquehemacabattrobanticonnectar lasumadeduesfraccionsambelllançamentd’unaboladebillar.

seccions seccions

rcions

JordiDeulofeu

DepartamentdeDidàcticadelesMatemàtiques ilesCiències

UniversitatAutònomadeBarcelona jordi.deulofeu@uab.cat

Somal’estiudel 2022,l’anydelsdosos,iescricaquestarticleambelrecordbenviudel’extraordinàriaponència,aixícomdeltaller,queelprofessorCharlieGilderdaleensvaoferirrecentmentalesXXJornadesperal’Aprenentatgeil’EnsenyançadelesMatemátiques(JAEM), celebradesaValènciaelsprimersdiesdejuliol.Comtotsvosaltres,coneciutilitzosovint,de fatemps,lamagníficapàginawebdelprojecteNRICH(nrich.maths.org),fontinesgotable deproblemesiactivitatsperal’auladematemàtiques,tantdeprimàriacomdesecundària. PeròarahetingutelgoigdeconèixerenCharlie,undelsseusprincipalscreadors,igaudir delessevessessions.Aelllidedicoaquestarticleiaprofitoperrecomanar-voslesseves magnífiquespropostesd’activitatsperal’auladematemàtiques,demoltsnivellsdiferents.

§ Problema1.Primersconsecutius

ComençaréambunproblemaqueensvaproposarenCharlie(eraelqueestavapensant aquellsdiesaValència)sobrenombresprimers.Preneudosnombresprimersconsecutius, majorsque 2,isumeu-los.Demostreuqueelresultatseràunnombrecompostqueenlaseva descomposicióenfactorsprimersté,almenys,tresfactors(quepodenserrepetits).

Perexemple,triemlaprimeraparella:3i5.Lasuma,8,és 2 2 2;ésadir,tétresfactors.Un altrecaspotser 11 i 13.Lasumaés 24,queés 2 ¨ 2 ¨ 2 ¨ 3;enaquestcas,téquatrefactors. S’enténquesónprimersconsecutiusaquells quesillistemordenadamenttotselsprimers (enl’On-lineencyclopediaofintegersequences ’OEIS,https://oeis.org/,éslasuccessióA00040), ocupendosllocsseguitsenaquestasuccessió.Nocal,doncs,quesiguinprimersbessons (aquellsladiferènciadelsqualsés 2),quesónuncasparticulardeprimersconsecutius.

Sitenimencomptequeelsnombresquenoméstenendosfactorsprimerss’anomenen semiprimers (també biprimers o quasiprimers),elproblemaespodriaformularaixí:lasumade dosprimersconsecutiusmajorsque 2 noésmaiunsemiprimer.Demaneraequivalent,tambépodríemdirquelasumadedosprimersconsecutiusmajorsque 2 éselproductededos primers.

Lademostraciónoésgairedifícil,peròsíqueté undetallbeninteressantquepermetconclourela.Quanelvaigtrobar,vaigtenirelgoigqueestéquanhomdescobreixunresultatbonici se’mvaescaparaquellaexpressióquetanbécaracteritzaaquestsmoments:eureka!

PodeutrobarinformaciósobrelaponènciaieltallerquevaimpartirenCharliea:https://nrich. maths.org/jaem2022.Elprimerquehitrobareusónlesdiapositivesquevautilitzari,acontinuació,lesdiferentsactivitatsqueexemplifiquenelssetpuntsqueva tractarenlaponènciai queempermetorecordar:

Despertarlacuriositatdelsalumnes.

Matemàtiquesinclusives:activitatsdeterrabaixisostrealt.

Tempsperexplorarenunaculturaons’acceptenelserrors.

Oferirbastidesperquèelsalumnessegueixinexploranticonstruint.

Laimportànciadelacol laboracióieldiàlegperconvèncer.

Valorardiferentsestratègiesidiferentsrepresentacions.

Descobrirpatrons,conjecturar,generalitzariprovar.

Delsmoltsexemplesquevaposar,empermetoreproduir-neunqueemsemblarepresentatiu(finsallàonpotser-hounúnicproblema)delasevaproposta.Ésunpetitjocd’estratègia peradosjugadors(jaconeixeulamevadebilitatperaquesttipusdeproblemes)quepodeu trobaripracticarenlínia(ambindicaciódelspossibleserrors)a:https://nrich.maths.org/5468.

§ Problema2.Eljocdelsmúltiplesielsdivisors

Disposemdelatauladelscentprimersnombresnaturals.Elprimerjugadorseleccionaun nombredelataula(menorque50);perexemple,el 25.Elsegonjugadortriaunnombreque siguiunmúltipleoundivisorde 25;perexemple,el5.Araelprimerhadeseleccionarun nombremúltipleodivisorde5senserepetircapdelsnombresjautilitzats;ésadir,pottriar l’1,el 10,el50 oel75(entremoltsd’altres),perònoel 25oel5.Esvaformantunasuccessió denombrestotsdiferents;perexemple:50, 25,75,5, 1,47...Elprimerjugadorquenopot jugarperdlapartida.

Unavegadapracticateljoc,espotenfocarenduesdireccionscomplementàries:trobaruna estratègiaperguanyareljoc(ésadir,impedirquel’altrepuguijugar)obéconsiderar-locom unaactivitatcol¨laborativapertaldetrobar,apartird’unnombreinicialdonat,quinaésla cadenamésllargapossible(tambélaméscurta).Enambdóscasosteniualdavantautèntics problemesdematemàtiquesque,sielsproposeu al’aula,uspermetrantractarelsconceptes demúltipleidivisord’unamaneranovaioriginal.Nocaldirque,abansdeportar-loala classe,caldedicarunabonaestonaaanalitzarlesnombrosessubtilitatsd’aquestmagnífic jocd’estratègia.

Totiquejam’agradariaseguirproposant-vosproblemesd’enCharlie,hodeixaréaquíperquè elspodeutrobaralsmaterialsjaesmentatsi,demanerageneral,alapàginadel’NRICH. Tanmateix,continuarél’articleproposant-vosalgunaltreproblemadenombres,queextrec delaxerradaorganitzadapelMuseudeMatemàtiquesdeCatalunya(MMACA)quevaigfer alaFacultatdeMatemàtiquesiEstadística(FME)delaUniversitatPolitècnicadeCatalunya (UPC)enunadataassenyalada:el 22-2-22.Enlafiguramostrol’anuncidelaxerrada,que enspermetveurequeladata,amésdesercapicua,siésescritaconvenientment,tésimetria central.

Enlaconferènciavaigparlardenombresformatsperunasolaxifra,datescurioses,capicuesi altrescuriositatsambnombresenters.Unadelesideesquevaigdesenvoluparésl’operació «girarunnombre»,queconsisteixainvertirl’ordredelessevesxifres.Elsinvariantsd’aquesta operaciósónprecisamentnombrescapicua.Combinantaquestaoperacióambd’altres,es generenproblemesinteressants,algunsdesenzillsiconeguts,d’altresmésdifícils,finsitot encaranoresolts.

§ Problema3.Sempres’acabaenuncapicua?

Tornemal’operació«invertirl’ordredelesxifres».Consideremunnombreielqueresulta d’invertir-nelesxifresisumemelsdosnombres:obtindremuncapicua?Sihoés,hemacabat. Sinohoés,repetiml’operació.Podemassegurarquesemprearribaremauncapicuaambun nombrefinitdepassos?

Exemple(I):54;sil’invertim,tenim45;sumem:54 ` 45 “ 99,capicua(1 pas).

Exemple(II):73;sil’invertim,tenim37;sumem:73 ` 37 “ 110.Horepetim: 110 ` 011 “ 121 (2 passos).

Exemple(III):78;sil’invertim,tenim87;sumem:78 ` 87 “

“ 1.353; 1.353 ` 3.531 “ 4.884(4passos).

Unaprovaempíricapermetassegurarquesielnombretéduesxifres,sempreacabemenun capicua.Tanmateix,elfetquejaperaalguns nombresdeduesxifreslaquantitatdepassos siguimoltelevada,fapensarquequanelnombredexifresaugmenti,elproblemaesdevindrà difícil.Concretament,elnombre89 requereix 24passos,eldarrerdelsqualsdonauncapicua de 13xifres:

L’estudiperalsnombresdetresxifresresultaapassionanticomplex.Unnombreesdiuqueés deLychrel(nomproposatperWadevanLandingham)si,quanrepetimlaseqüènciaanterior (invertirisumar),maiobtenimuncapicua.Jaambnombresdetresxifrestrobem«ferms» candidatsasernombresdeLychrel,elmenordelsqualsés 196.S’hanfetmésde700 milions d’iteracionsis’haarribatanombresdemésde300 milionsdexifressenseobtenircapcapicua!Altrescandidatsambtresxifressón: 295,394,493,592,689,691,788,790,879,887, 978 i 986(ielsinversoscorresponents).

Sibéenbase 10 encaranos’hademostratqueexisteixennombresdeLychrel,síques’ha aconseguitenaltresbasesdenumeració.Enparticular,elnombre 10.110,debase 2 (curio-

sament, 22 endecimal),ésunnombredeLychrel.Tambén’hihaenaltresbasesquesón potènciesde 2

Sivoleuentretenir-vosestudiantaquestsnombres,usaconselloquevisiteul’OEIS,aquest fantàsticllocontrobareuunaquantitatenormedesuccessionsilessevespropietats.

Enconcret,perestudiarelsnombresdeLychrelfixeu-vosenlessuccessions:

OEISA056964(n ` nombreobtingutinvertintlesxifresde nq

OEISA023108(successiódelscandidatsenbase 10 anombresdeLychrel).

OEISA060382 (successió an quedonaelmenorcandidatenbase n aserunnombrede Lychrel).

§ Problema4.Méscuriositatssobrenombrescapicua

Delamateixmaneraquetotnombreéslasumadetresnombrestriangularsoquatrequadrats,totnombreespotexpressarcomlasumadetrescapicues(excepteenbase 2,on,per exemple, 176escritenbase 2 ennecessitaquatre).

Perexemple: 2.022 “ 1.001 ` 999 ` 22 itambé 2.002 ` 11 ` 9.Proveuambaltresnombres imireud’indentificaralgunpatróqueuspermetitrobarlesdescomposicionsensumade capicues.

Unexemplemagníficéselsegüent(prenemcomaenterelnombreformatpels 21 primers decimalsdelnúmeropi):

314159265358979323846 “ 210100100111001001012 ` 98639929400492993689 ` 5419235847485329145

Unadelespropietatsquemésm’agradadetoteslesqueconecsobrenombrescapicuaésla quepermettrobar,ambuncàlculsenzill,elllocqueocupauncapicuaenlasuccessiódetots elscapicues,queexposoacontinuació.

Sielnombredexifresdelcapicuaésparell,preneulameitatdelesxifresiafegiu-hi 1 davant. Perexemple,elcapicua347743ocupaellloc 1347.Encanvi,sielnombredexifreséssenar, sumeu 1 alaprimeraxifraialdarrereposeu-hilarestadexifresfinsalameitat(inclosala xifracentral).Perexemple,elcapicua3.471.743ocupaellloc4.471.Proveuambaltresnombres(podeucomprovarqueelllocobtingutéselcorrecteconsultantlasuccessióA002113 del’OEIS.Ésbonic,oi?

§ Problema5.Productedequatrenombresconsecutius

Acabarél’articleambundarrerproblemadenombresqueemvaproposarXavierVallsique, sensdubte,podriaformarpartdelacol lecciódeproblemesdel’NRICH.Lasevaformulació éstansenzillacombonicéselproblema:quèpodemdirdelproductedequatrenombres naturalsconsecutius?

L’expressió«quèpodemdir»ésvolgudamentobertaienspermetpensarenlesduesvessants delsproblemesdematemàtiques:lesconjectures(plausibles)ilesdemostracions.Aprofitant queéseldarrerproblemad’avui,usdonarébenpoquespistessobreelseuabordatge(seguramenteltancarienmassaràpidament),iencaramenyssobrelasevaresoluciócompleta. Analitzeulasituacióicerqueupatronsdemaneralliure.I,quanussembliquesónconjectures sòlides,mireudeprovar-les.Sielporteuaclasse,tindreu,amésamés,pràcticaproductiva assegurada.

Gaudiuamblessituacionsielsproblemesd’avuii,semprequepugueu,feugaudirelvostre alumnat!

Bibliografia

ConwayH.J.;Guy,R.(1996). Thebookofnumbers.NovaYork:Springer.

Deulofeu,J.(2019). Lamagiadelosnúmeros. Barcelona:Gedisa.

Gilderdale,Ch.(2022).Enriquecerlasmatemáticas:?‘qué podemosofreceranuestrosalumnossiqueremosqueseconviertanenpersonassegurasdesímismasyconrecursospararesolverproblemas?Conferènciaplenàriaitallerales 20JAEM.València,juliolde 2022, https://nrich.maths.org/jaem2022 [consulta: 28desembre 2022].

Gilderdale,Ch.(2022). Factorsandmultiplesgame,https://nrich.maths.org/5468[consulta: 28 desembre 2022].

OEISFoundation. Theon-lineencyclopediaofintegersequences. OEIS,https://oeis.org/[consulta: 28desembre 2022].

aprendre matemàtiques amb jocs de taula

aprendre

SET,GrupdeJocsd’ABEAM(*)

(*)L’equiporganitzadordelgrupSET,responsabled’aquestasecció, estàformatper:LuisCros,MaríaBellés,MónicaRosado,TeresaLongueira, JordiDeulofeu,MònicaCasas,JoséMiguelMaimó,LauraLópez, AransaGonzález,AlexVideiPolSan.

Jocsdetaulaperal’auladematemàtiques:perquè?

Objectiusdelasecció

ElgrupSET,del’associacióABEAM,ésungrup deprofessorsiprofessoresdediferentsnivellseducatius(d’educacióinfantilalauniversitat)ambunobjectiucomú:emprarelsjocsde taulaperensenyarmatemàtiquesatotselsnivells.Totselsqueformemelgrupsomgrans aficionatsajugariabansdeproposaractivitatsd’aprenentatgebasadesenjocsdediquemun tempsapracticarlliurementelsjocsqueseleccionemi,posteriorment,aanalitzar-losdesdel puntdevistadel’aprenentatgedelesmatemàtiques,senseperdredevistaquelaprimera característicad’unbonjocéslaseva rejugabilitat,ésadir,quetinguemganesdetornara jugar-hiunavegadahemacabatunapartida,condiciófonamentalpermobilitzaremocions positivesafavoridoresdel’aprenentatge.

Desdefacincanyselsqueformemelgrup,desprésdeprovarunagranquantitatdejocs lamajoriadelsqualsdecreaciórecent hemanatelaborantunallistadejocspertreballar lesmatemàtiquesal’aula,amblaintenciódecobrirelsdiferentsblocsdecontingutsdel currículumdesdelprimercursd’educacióinfantilfinsalsegondebatxillerat.Moltsdelsjocs seleccionatselshempresentatentallersaescoles tantperamestrescomperafamílies ienjornadessobrel’ensenyamentdelesmatemàtiques(XIXJornadesperal’Aprenentatgei l’EnsenyamentdelesMatemàtiques[XIXJAEM]aLaCoruña,XXJAEMaValència,SegonCongrésCatalàd’EducacióMatemàtica,etc.).Tambépubliquemlafitxad’unjocacadanúmero delbutlletí ABEAMfamílies.

Iniciemaraal NouBiaix unaseccióenlaqualvolemaproparelsjocsdetaulaatotelprofessoratimostrarqueconstitueixenuncontextmagníficperaprendrematemàtiquesenels diferentsnivellseducatius.Comenaltrescontextos,darrerelapràcticad’unjocsovinttrobem elementsmatemàtics,tantconceptualscomprocedimentalsi,sobretot,competencials,per

laqualcosaelsjocsdetaulaconstitueixenunafontmagníficad’activitatsmatemàtiques.Per tant,mostrarunaselecciódejocsdetaulaadequatsalsdiferentsnivells,juntamentambel conjuntd’activitatsd’aprenentatgeassociades,ésl’objectiuprincipald’aquestasecció.

Enaquestarticleinicialtractaremdejustificarperquèestemconvençutsqueelsjocsdetaula preferentmentelscontemporaniscomercialitzats,peròtambéd’altresfàcilmentconstruïblesperal’aula hauriendeserpresentsalesclassesdematemàtiques.Tambépresentarem unjoc,elSET,queéselquedonanomalgrup,idiferentsactivitatsiproblemesdematemàtiquesrelacionatsambaquestjoc.

Perquècalutilitzarjocsal’aula?

Lapràcticadejocsdetaula,unadelesactivitatsquecaracteritzaelshumans,téduescaracterístiquesprincipals:diversióiaprenentatge.Enlapràcticad’unjoctrobemmoltíssimes coses,entred’altres:diversió,il¨lusió,relaciósocial,comunicació,repteintel¨lectual,ganes demillorar,competició,negociació,col laboració,treballenequip,imaginació,creativitat, habilitatsmentalsimanuals,interpretació,memòria,resoluciódeproblemes,presadedecisions,coneixements,competències,seduccióifinsitotpetitsenganys canvisderol D’altrabanda,quanunjuga,mostralessevescapacitatsilasevamaneradeserenaspectes cognitius,emocionals,socialsidecomportament,apartirdelesdecisionsquepren(diferentsmaneresdejugar):siésarriscatoconservador,competitiuocol¨laborador,negociadoro intransigent,empàticoindividualista.Perquèunjocés,quasisempre,unasimulació,més omenyspropera,d’unasituaciódelavidaodelmónenquèvivim.Endefinitiva,jugant s’aprènaviure,aconviureiacompartir.Elsjugadorssónelsactorsprincipals:senseellsres notésentitiambellslapràcticad’unjocpotesdevenirunaactivitatrellevant,unafontde plaerid’aprenentatgessignificatius,tantdesdelpuntdevistadelsqueeljuguencomdes delquevolemqueaprenguin.

Jocsdetaulaimatemàtiques

Encaraqueelsjocsdetaulaespodenemprarenlamajoriad’assignatures,moltsjocstenenunafortarelacióambdiferentsaspectes delesmatemàtiques,tantcompetencialscom tambéconceptualsiprocedimentals.

Desdelpuntdevistacompetencialcalcomençardestacantqueajudenaprendredecisions fonamentades,unacompetènciaqueconsideremfonamental,encaraquepoquesvegades s’explicitaenelcurrículumdematemàtiques. Tanmateix,entrelescompetènciesrellevants, laresoluciódeproblemesésseguramentlaquemésclaraments’identificaenelprocésde lapràcticad’unjocienmoltesdelesactivitatsassociadesalsjocs.Defet,aquestprocésila recercad’estratègiesguanyadoresode«bones»maneresdejugarqueaugmentinlaprobabilitatdeguanyar,segonselscasos,espodenanalitzarseguintunspassosmoltsimilarsales conegudesfasesdePolya.Així,éspossibleestablirunparal¨lelismeentreambdósprocessos: lacomprensiódelproblema(elqueensdemana,lesdadesqueensdonailasevarelació) escorresponamblacomprensiódeljoc(delseuobjectiuidelesregles).Eldissenyd’un pladeresoluciódelproblematérelacióambladeterminaciód’estratègies(entesescoma maneresdejugartenintencompteelquefanelsaltres)perintentaraconseguirl’objectiu

deljoc.L’execuciódelplaescorresponamblaimplementaciódelesestratègies(aplicacióen partidesconcretes)i,finalment,lavisióretrospectiva(validaciódelasoluciódelproblemaide lesestratègiesdissenyadesiimplementades,iplantejamentdegeneralitzacions)éssemblant alavalidaciódel’estratègiaguanyadora,que éslaqueresoleljociquepotteniruncaràcter mésinductiu,sil’apliquemanovespartidesiobservemelresultatobtingut,omésdeductiu, siraonemlasevavalidesademanerageneral.

Larestadecompetènciessóntambépresentsenlapràcticadejocsdetaula,enparticularles relacionadesambelraonamentmatemàticitambélescomunicatives.

Pelquefaalscontinguts,elsjocsespodenrelacionarambelsdiferentsblocsdelcurrículumdematemàtiques:elnumèric(especialment,sentitnumèricicàlcul),elgeomètric(sentit geomètric,relació3D-2D),elprobabilístic(idead’atzar,espaimostral,equiprobabilitat),elde lamesura(percepció,estimacióimesuraefectivadediferentsmagnituds)ielderelacionsi canvis(identificaciódepatrons,generalització,tipusdecanvis).

Dequinsjocsparlemicomelspodemportaral’aula

Al’horad’escollirjocsperportaral’aulahihaunasèried’aspectesquecaltenirencompte:les particularitatsdelsjocstriats,lesfinalitatsdelasevaintroduccióilescaracterístiquesconcretesdel’accióal’aula.Així,calevitarjocsquetinguininstruccionspocclaresomoltllarguesi feixugues,elsquetinguinmoltselementsidemidapetita,iaquellsenquèeltempsdejocsiguitanampliquenopermetipoderferdiversespartidesperreflexionarsobrel’estratègiadel jocipoderveureaixílesmatemàtiquesques’hantreballatenunamateixasessió(omàxim dues).

D’acordambaixòanterior,aconsellemelsjocsqueanomenem5-10-15:

5minutspercomprendrelesinstruccions.Uncops’estiguijugantaljoc,calrevisarque esjugademaneracorrectai,sis’hadecidit feralguncanvi,quenomodifiquil’objectiu pedagògicdeljoc.Unamaneradedinamitzarlacomprensiódelesinstruccionsésfer arribaral’alumnatlesinstruccionsatravésdetutorialsenvídeo,demaneraqueal’aula simplements’haginderesoldredubtesconcretsiposar-seajugar.Tambéésunabonasolucióutilitzarjocsqueelsalumnesjaconeixenperquèhihanjugatencursos anteriorsoacasaseva.

10 minutsdejoc(màxim 15),perpoderjugardiversespartidesitreballaractivitatsque permetinferaflorarlesmatemàtiquespresentseneljoc.

15eurosdepreu(omenys).Elsjocscomercialitzatss’handecomprarielspressupostos sempresónmigrats.

Unaaltracosaquehemdetenirencompteal’horadeseleccionarunjocperal’aula,talcom jahemcomentatal’inici,éslarejugabilitat,lesganesdejugarunanovapartidaquann’hem acabatuna.Sienacabarunjocnotenimganesdetornar-hiajugar,nocompleixlaideabàsica d’emocionari,pertant,encaraquesiguimatemàticamentpotent,noaconseguiràconsolidar elsconeixementstreballats.

Lagestiód’unaactivitatdejocal’aula

Al’horadeportareljocal’aula,comenqualsevolactivitat,ésfonamentaldissenyarunabona gestiódelaclasse,enparticularl’organitzaciódeltemps.

Sipensemensessionsde50-55minuts,podemdestinar:

Alvoltantde 10-15minutsperalapreparacióinicial:organitzacióespacialdel’aula, agrupaciódelsalumnes,repartimentdelsjocs,preparaciódeljocicomprensiódeles reglesdeljocperpartdetotselsjugadors.

Alvoltantde 20-25minutsperjugaraljoc,procurantqueespuguifermésd’unapartida.

Alvoltantde 15-20 minutspermostrarlesmatemàtiquesques’hantreballatdurantel joc,aportantpreguntesque permetinferunareflexiósobrequinesmatemàtiqueshan emergit,comleshemutilitzat,comlespodemconnectarambeljocicomlespodem representar.Tambéésrellevantqueapareguinelementsmetacognitius sovintrelacionatsamblesmaneresdejugar ,aixícomqueespuguiferunavaloraciódelasessió idelsjocsproposats.

Enelcasdejocsquetenenimplíciteslesmatemàtiques,odejocsqueespresentenadaptats perquèsorgeixinunesdeterminadesmatemàt iques,iaquestesesdesenvolupenclarament enlapràcticadeljoc,tésentitallargarelperíodedejocireduireldeferpresentslesmatemàtiques.D’altrabanda,enelcasdelsjocsals qualsesdecideixidedicarmésd’unasessió,és imprescindiblequeesfacipresentquelasessióhaestatd’aprenentatgeatravésd’unjoci nonomésunasessiódejoc.Quanl’alumnatsurt delasessióamblasensació«d’avuiaclasse hemjugat»(iresmés),esperdelsentitpedagògicdelasessióidifícilments’assoleixenels objectiusestablerts.

Pelquefaal’agrupamentdel’alumnat,dependràdelnombred’alumnesidelnombred’exemplarsdeljocdequèesdisposi.Perdecidirelnombredejugadorsperjocenspodemorientar perlarecomanacióqueesfaenelmateixjoc,tenintencomptequeunjugadorpotestarformatperunpetitgrupd’alumnes,cosaquemilloraràlainteraccióentreiguals.Elsgrupshan deserpetits,dedosotresalumnes,jaquequansónquatreacostumaasercomplicat,imés noésaconsellable.Fentaixòestreballal’úsd’informaciócompartida,esmilloral’atencióper prendredecisions,esfomentaeldebatd’ideesidepropostesi,endefinitiva,esdesenvolupa eltreballcol¨laboratiu.Aquestplantejamentésmoltadequatperalsjocssolitaris,demanera que,benorganitzats,sónunabonapropostapertreballarengrupscooperatius.

D’altrabanda,calanalitzarelquefa(ohadefer)cadajugadordesques’acabaelseutorn finsquelitornaatocarjugar:algunsjocsfomentenlaconcentracióielsjugadorshand’estar atentsalquefanelsaltres,jaqueinflueixenelseupropitorn,obéestractadejocsonnohi haunordredetorniespotparticiparenqualsevolmoment.Aquestsjocssón,segurament, elsmillorsperaunabonadinàmicaal’aula,mentrequeelsjocsenquèelsjugadors,desque acabenelseutornfinsqueelstornaatocar,nohand’estaratents opassamoltdetemps perquèaixíhorequereixladinàmicadeljoc,nosóngaireadequatsperal’aula.Algunsjocs podenestardissenyatsperaunnombremoltgrandejugadors,perònosaltrespodemlimitar aquestaquantitatenfunciódelsnostresobjectiusilesnostresnecessitats.

Isinodisposemdeprouexemplarsd’unmateixjoc?

Enelcasquedisposemdepocsexemplarsdelmateixjoc,usproposemalgunespossibilitats perorganitzarl’aulaipoderusarelsjocs,

Podeucreardinàmiquesambdiversosjocs quetreballinelmateixconcepteifer-losrotar entreelsdiferentsgrupsdejoc.Perfer-hocaltenirpresentque,pertalquelesrotacions funcioninbé,eltempsdejochadesersimilar,demaneraquelesdiferentspartidesila reflexiócorresponentsobrecadajocespuguinacabarabansdeferlarotació.Mainoésuna bonaopcióacabareljocsensearribaral’objectiupretès.Peral’alumnatésfrustranthaver dissenyatunaestratègiaguanyadorainopoder-necomprovarlavalidesa.Enaquestscasos, unabonaopcióésseleccionarjocsenquèespuguiadaptarelnombrederondesquecalper finalitzarunapartida.

Tambépodeuestablirespaisdetreballdiferenciat,demaneraquetinguemunracóamb alumnestreballantambunjoc,unaltreambalumnestreballantambmaterialmanipulatiu iunaltreambungruptreballantamblaformalitzaciód’unconcepte,ofentunasessióde dubtesod’explicacióentreexperts...Espodenfertantsespaiscomesconsideriadequat, peròhadequedarclaralasevafeinaencadaespaiiladuradahadesersimilar.Desprésde diversessessions,totselsalumneshand’haverpassatpertotselsespais.

Sobrel’avaluaciódelesactivitatsdejoc

Lespossibilitatsd’avaluació,aixícomelsinstrumentsperobtenirdadesrellevants,sónmúltiples.Desdelpuntdevistadeldocenticomsucceeixamblarestad’activitats,elprimerque calanalitzaréssis’hanaconseguitelsobjectiusques’havienplantejat.Aixòespotferatravés d’alguntipusdeprova aposteriori perexemple,plantejantunanovaactivitatquereculli elementsclaudeltreballfetambeljoc obéatravésd’unarúbricad’observació.Tambés’ha devalorarsieldissenydelasessióhaestatadequatis’hadeferunllistatdelsaspectesque calmillorarenlesproperesimplementacionsdeljoc.Tambéespotobtenirunaqualificació valorantlesfitxesdetreballques’hanfetservirdurantlasessió.

Desdelpuntdevistadel’alumnat,elprimerpuntquehemdeconèixeréselvalorquedonen alsjocsilasevarelacióamblesmatemàtiques.Lacomparacióderespostesalespreguntes «perquèjuguesajocsdetaula?»o«perquèfasmatemàtiques?»ensproporcionaràinformaciódecoml’alumnatveuaquestesduesactivitats.Alprincipi,engeneraltrobaremrespostes moltdiferentsifinsitotcontraposades.Enfunciód’aquestasituacióinicialcaldràajudar l’alumnat,ambmajoromenorintensitat,aestablirrelacionsiparal lelismesentrelapràcticai l’anàlisidejocsieltreballenmatemàtiques.

Unavegadafetaunasessiódejocsal’aula,ounaseqüència,caldràdemanaralsalumnes unavaloraciódel’activitatperdeterminarfinsaquinpunts’hancomplertlesexpectatives creadesisivoldrientornaraferunasessiódetreballsimilar.Aixímateix,hauriendeferuna valoraciócríticadelquehanaprèsdurantlasessió,destriantelselementscompetencials,els conceptualsielsprocedimentals.D’altrabanda,peravaluarelsaprenentatgesadquirits,tant siesvolferunavaloracióambfinalitatsqualificativescomanalítiques,recomanemutilitzar rúbriquesespecífiques,quepermetendisposardevaloracionsdetalladesiquepodenser valoradesambunacertaobjectivitat.

Utilitzarjocsdetaulacomacontextperensenyarmatemàtiquestémúltiplesavantatges, peròcaldissenyarigestionarlesactivitatsbasadesenjocspertalqueesdevinguinunaeina rellevantperal’aprenentatgedelesmatemàtiquesdetotselsnoisilesnoiesdetotsels nivellseducatius.Unprimerpas,eldel’interès,acostumaaaconseguir-semésfàcilmentque enaltrescontextos,peròaixòésnomésl’inici.Calseleccionarbéelsjocs,dissenyaractivitats iseqüènciesdidàctiquesapartird’aquestsi gestionaradequadamentl’aulaenlalíniaque hemtractatd’exposar,pertald’aprofitaraquestapredisposicióinicialitransformar-laenun aprenentatgereal.

Esperemquelespropostesqueaniremplantejantenaquestaseccióproporcioninideesal professoraticontribueixinaaquestobjectiu.

Comhemditalfinaldelprimerpunt,acabaremaquestprimerarticleambl’explicaciódeljoc SET,queésclaramentrepresentatiudelsjocs queensagradaportaral’aulaiqueespottreballarennivellsmoltdiferentssegonslesactivitatsqueacompanyinlasevapràctica.Potser peraixò,elgruptéprecisamentelnomd’aquestmagníficjoc.

ElSET,unmagníficjocdecartes

AquestjocvasercreatperMarshaFalco(1974)ielvapublicarinicialmentSetEnterprisesel 1991.Laideadeljocprovédelsistemadecodificacióquelasevacreadoraestavautilitzant enelseutreballcomagenetista.Actualmentse’npottrobarunaediciódel’editorialDevir.

Títol SET

Edat Apartirde6anys.

Jugadors 1 a8jugadors

Tempsd’unapartida Alvoltantde 15minuts

Resum

Entreteniment

ElSETésunjocdelògicaipercepcióvisualqueespotjugardemanera individualoengrup.Estàformatper81 cartesquecaldràbarrejarbéi, després,col¨locar-ne 12 decapperamuntformantunrectanglede3 ˆ 4. Larestaesdeixendecapperavallenunapila.

H

Cadacartatéquatrecaracterístiques:

H

Símbol:oval,onaorombe.

Color:vermell,verdolila.

Quantitat:un,dosotressímbols.

Fons:l’interiordelssímbolspotsertotalmentacolorit,ratllatoblanc.

H

L’objectiudeljocésidentificarconjunts(sets enanglès).Un set sóntres cartes,demaneraquecadascunadelesquatrecaracterístiques,avaluades perseparat,sónigualsenlestrescartesodiferentsentoteselles.Ésadir, siduescartessónigualsenalgunadelescaracterístiquesil’altracartaés diferent,llavorsnoésun set

H

Aquíusmostremcincexemplesdiferentsde sets:

H H

Alprincipisemblacomplicatidentificar-los,peròamesuraquehianeu jugant,lavelocitatd’identificaciócreixeràràpidament.

Complexitat

Preu

Competències/ habilitatsmatemàtiques

Tutorialsalaxarxa

Ambaquestjocestreballenhabilitatsdepercepcióvisualidelògica (atributsigualsodiferents),amésamésdelarapidesa,laconcentració il’anticipació.

H

Quanunjugadortrobaun set,calquehodiguiielmostrialarestade jugadors,elsqualsl’handevalidar.Siéscorrecte,eljugadoresqueda lestrescartes;sinohoés,haderetornartrescartessevesalapila. D’aquestamaneraestreballalacompetènciacomunicativai,alhora, s’habituaatotselsjugadorsaavaluarunresultatobtingut,fetprou importantenlaresoluciódeproblemes.Quans’hafetun set,esposen trescartesdelapilaalllocdeixatperlescartesretiradesieljocsegueix finsques’esgotentoteslescartes.

ComjugaralSET:https://youtu.be/fPdVrmCYtJw. SETenlínia:http://www.setgame.com/set/puzzle. App:https://goo.gl/Nm0wlr.

Activitats,preguntesiproblemes

Aquestésunjocexcel lentperportaral’aula.Apartirdeljocpodemplantejardiferentsqüestionsiproblemespertaldetreballarprincipalmentaspectesdelrecompteitambédela probabilitat.Encaraqueeljocespotportaraprimària,onespodendesenvoluparhabilitats depercepcióvisualidelògica,ésasecundàriaifinsitotalbatxilleratonpodemplantejarproblemesdematemàtiquesinteressantsirelacionatsambelcurrículum,tantdecombinatòria comdeprobabilitat.

Aquíenteniudeuexemples,peròsegurqueenpodreutrobarmoltsmés:

Quantescartestéeljocsisabemqueapareixentoteslespossibles(amblesquatre característiquesilestrespossibilitatsperacadacaracterística)sensecaprepetició?

Si,enllocdequatrecaracterístiques,nomésn’hihaguéstres,peròcadascunatingués quatrepossibilitatsi,comabans,hihaguéstoteslescartespossiblessenserepeticions, hihauriaméscartesaraalapila?Generalitzaelnombredecartesdelapilaper n característiquesi m possibilitatsperacadascuna.

Sitenimduescartes,quantes carteshihauràquefacinun set ambelles?Isitenimuna carta?

Dequantesmaneresdiferentsespodenposarles 12 primerescartesformantunrectanglede3×4?

Fixemelvalord’unavariable.Perexemple,ensquedemtoteslescartesdecolorblaui descartemlaresta.Quantescartestindrem?

Quantescarteshihasifixemelvalordeduesvariables?Ésadir,compodemcalcularla quantitatdecartesquesónrombesdecolorblau,perexemple?

Quants sets diferentspodemtrobarsiensquedemlescartesquesónrombesblaus?I siensquedemlesquesónblaves?

Sijuguemambles81 cartes,quants sets hihademaneraquelescartesnocomparteixin elvalordecapcaracterística?Iquants sets diferentshihaentotal?

Sitraiemtrescartesdelapilaal’atzar,quinaéslaprobabilitatquefacinun set ?

Quinaéslaprobabilitatdenoformarun set ambles 12 primerescartes?

Elsamicsd’Exploriumhanproposatlesactivitatssegüents:https://goo.gl/Z6682w.

Enl’articledela Wikipedia «Set (cardgame)»,https://en.wikipedia.org/wiki/Set_(card_game), espodentrobaralgunsproblemesdemajorcomplexitat,com,perexemple,quinéselmajor nombredecartesquepodemtrobardemaneraquenoespuguiformarcap set ?

Unreptefinal: sabríeutrobar6 sets diferentsenaquestes 12 cartes?

Bibliografia

Badillo,E.;Edo,M.;Deulofeu,J.(2012).«L’adquisiciódecompetènciesmatemàtiquesd’alumnes deprimàriaencontextosdejocsdetaulairesoluciódeproblemes». Noubiaix,31, 29-43.

Comas,O.(2021). Unmondedejeux. Vol. 1.París:YNNIS.

Corbalán,F.(1994). Juegosmatemáticosparasecundariaybachillerato. Madrid:Síntesis.

Corbalán,F.(1996).«Estrategiasutilizadasporlosalumnosdesecundariaenlaresoluciónde juegos». SUMA, 23, 21-32.

Corbalán,F.;Deulofeu,J.(1998).«Losjuegos,lasmatemáticasysuenseñanza». Uno:Revista deDidácticadelasMatemáticas, 18, Monogràfic:Jocsimatemàtiques,5-8.

Deulofeu,J.(2016).«Juegosdemesaparaaprendermatemáticas». Uno:RevistadeDidáctica delasMatematicas,74, Monogràfic:Jocsmatemàtics,7-13.

Edo,M.;Baeza,M.;Deulofeu,J.;Badillo,E.(2008).«Estudiodelparalelismoentrelasfasesde resolucióndeunjuegoylasfasesderesolucióndeunproblema». UNIÓN, 14,61-75.

Gairín,J.M.(1990).«Efectosdelautilizacióndejuegoseducativosenlaenseñanzadelas matemáticas». Educar, 17, 105-118.

Gairín,J.;Muñoz,J.M.(2006).«Moviendofichashaciaelpensamientomatemático». SUMA, 51, 15-29

GarcíaAzcárate,A.(2010). Pasatiemposyjuegosenclasedematemáticas:Númerosyálgebra. Madrid:Aviraneta.

GarcíaAzcárate,A.(2013). Pasatiemposyjuegosenclasedematemáticas:Geometría. Madrid: Aviraneta.

Guzmán,M.(1989).Juegosymatemáticas. SUMA,4,61-64.

Guzmán,M.de(2004).«Juegosmatemáticosenlaenseñanza». Números,59,5-38.

Lorenzo,E.;Deulofeu,J.(2021).«Analysisandclassificationofinappropriatestrategiesused bystudentstofindthewinningstrategyincatchtheFrogandDaisygames».A The11th InternationalConferenceonEUropeanTransnationalEducational:(ICEUTE2020). NovaYork: Springer, 21-29

Navarro,A.;Deulofeu,J.(2016).«Aprendiendoaresolverproblemasenuncontextodejuegos deestrategia». SUMA,82, 9-17.

Normes per a la presentació de contribucions

1. La revista NouBiaix acceptaper alasevapublicació contribucionsoriginalsrelacionadesamb experiències didàctiques, activitats d’ensenyamen ti aprenentatge,escritsd’opinió,dedivulgaci ói d’investigació enel camp dela matemàtica ielseuensenyamentenqualsevol nivell educatiu

2. Les contribucionsrebudesseran avaluadesprèviamentper dosespecialistesreconeguts. La decisiópresa pelConsell deredacciósobrel’acceptació dela publicació serànotificadadirectamentals autors ambuna indicaci ódeladataaproximadadepublicaci ói el possiblerequeriment d’introduir modificacionseneltext.

3. Pera lapresentaci ódetreballsoriginals, elsautorstrametran al’adreçanoubiaix@gmail.com un arxiu, en Word oenLaTeX.Els gràfics, elsdiagrames iles figureshaurandeser originals(no fotocopiats). Els arxius gràficsespresentaran en format epso tif.

4. La contribució hauràd’incorpora reltítol,elnom de l’autoro autors,lasevaadreçapostalprofessional completai la sevaadreça electròn ica.S’adjuntaràunresum només llarg de 300 paraules en català ianglès. Al finaldel document s’inclouràobligatòriamen tlabibliografiaper ordrealfabètic de cognoms,d’acordamb la normativaAPA, com enelsexemplessegüents:

Articles

Albertí, M. (2002).Les matemàtiquesdesd’unaperspectivacultural:Etnomatemàtiques Biaix, 20,6-25.

Llibres

Godino,J., Font,V.(2003) Razonamiento algebraicoparamaestros.Granada :Universidad de Granada. Capítols dellibres

Edo,M.,Revelles, S. (2004).Situacionesmatemática spotencialmentesignificativas. Dins M. Antóni B. Moll (ed.), Educación Infantil.Orientacionesy Recursos (0-6 años) (p.410/103-410/179).Barcelona:Praxis.

Actesdecongressos

Morales, M.,Font, V.,Planas, N. (2004).Estudiomicroetnográfico en tornoa un conocimiento matemático situado. Dins A.Franzé ialtres(ed.), ActasdelaI ReuniónCientíficaInternacional sobreEtnografía y Educación (CD-ROM).València: Germanía,Polis Paideia.

Pàginesweb

Geogebra pera Infantil iPrimària. https://www.geogebra.org/m/tkdC27m f

5. Els contingutsde NouBiaix estansubjectes llevatque s’indiquiel contrarieneltext, en lesfotografies oenaltresil.lustracions— auna llicència de Reconeixement-No comercial-Sense obra derivada 3.0deCreativeCommons,eltext completdela qual es pot consultar ahttp://creativecommons.org/ licenses/by-nc-nd/3.0/es/deed.ca. Així,doncs,s’autoritza el públic en generala reproduir,distribuir i comunicarl’obra,sempreque es reconegui l’autoriai l’entita tquela publica, inose’nfaciunús comercial ni se’n difongui capobraderivada.

6. Elsarticlesespublicara nen llenguacatalana.Només es traduiranalcatalàles contribucions acceptadesd’autorsnoresidents alsPaïsosCatalans.

7. Elsautorsesresponsabilitzarandel complimen tdeles normes establertesper al’autoritzaciódela reproducciódematerialprocedent d’altres fontsbibliogràfiques

8. Elsarticlestindran unaextensiómàximade 8000 paraules,inclosesles notesa peudepàgina,però s’acceptenarticles méscurts,d’entre 2000 i 4000 paraules

9. Femnotar queenaquesta publicació s’utilitza preferentmen telpuntper separardecimals, en lloc dela comarecomanadaper l’IEC, pertal defacilitarla comprensi ódeles expressionsmatemàtiques.