Nou Biaix, 48 by Institut d'Estudis Catalans

Revista de la FEEMCAT i de la SCM

bia x uno i

número 48

sumari

Consell de redacció:

Marianna Bosch / Carlos Giménez (coords.)

Montserrat Alsina

Joan Carles Ferrer

Joan Miralles

Manuel Udina

Coediten:

, © dels articles, els seus autors

Federació dEntitats per a lEnsenyament de les Matemàtiques (FEEMC AT ) Campus de Montilivi, edifici P-IV 17071 Girona feemcat.org

Societat Catalana de Matemàtiques (SCM) filial de l’Institut d’Estudis Catalans Carme, 47 08001 Barcelona scm.iec.cat

noubiaix@gmail.com

Fotografia de la coberta: Localitzada al pla Ber ta Piqué al Periodicitat: semestr Nombre dexemplars: 1.700 ’

ISSN: 2014-2021

Dipòsit legal: B-22.314-2012

Impressió: Gráficas Rey

Edicions

de la Universitat de Barcelona

Adolf Florensa, s/n 08028 Barcelona

Tel.: 934 035 430 comercial.edicions@ub.edu www.edicions.ub.edu

Editorial 1 4 14 37 49 62 78

Com fer ser vir l’estadística com a eina STE(A)M

Lourdes Rodero de Lamo

«El soroll i com afectala nostra salut». L’estadística per projectes a secundària

Maria Josep Freixanet

Descobrint el teorema de Pick

Mireia Vinyoles Serra

Apor tacions matemàtiques alt- empordaneses del segle XX articles

Lluís Sabater Anticó

seccions

El racó de l’oriflèxia

Cubs d’ocellets, de molinets i de vaixells

Jaume Coll Guerrero

Guillem Bonet Carb ó CarmeVicens Andrés Els problemes del Fem Matemàtiques com a recurs daula Treballant els problemes del Fem Mates fora de concurs ’

Aquestnúmero48queteniualesmansarribaambmoltderetardireculltreballsescritsel 2020 iel 2021,sotaelsefectesd’unapandèmiaquenoensdeixatreballaralritmed’abansia laqualensresistimaacostumar-nos.Peròelsarticlesques’hanrecollitaquítenenunagran diversitatdesaborsiaromes,propisdelesmengesques’hancuitafoclent.Lamesurade magnitudsil’estadísticahitenenunpapercentral,aixícomunavisiódelesmatemàtiques moltcentradaenlasevacapacitatperajudar-nosaprendredecisionsdifícils,comaradividir quantitatsméspetitesquelesdemanadesosabersielsorollafectalanostrasalut.També s’hipodenveurelespersonesquehihadarreredelesactivitatsmatemàtiques,jasiguiper crear-les,jasiguiperdesenvolupar-les,jasiguiperdifondre-les.

Enelseuarticle,CoriVilellaiJoséManuelGómezposenfilal’agullaperaportarunenfocamentmatemàticamentrigorósaunproblemapràcticforçahabitual,conegutcomelproblemadelafallida,enelqualestractad’establirelmecanismemésjustperrepartirunacerta quantitatd’unrecursconcret(herència,embargament,quotapesquera,etc.)entretotsels agentsqueeldemanen,quanlaquantitattotaldelesdemandessuperalaquantitatdisponibledelrecursques’haderepartir.Espresentenquatremecanismesdiferentsaplicats habitualmentenaquestessituacionsiescomparenelsresultatsqueassignacadascund’ells acadaagentdemandant,intentantestablirdemaneraqualitativaelgraudejustíciapresent encadacas,apartirdelcomplimentonodefinsacincreglesrelativesal’equitatenelrepartiment.L’exempleconcretalquals’apliquenelsmecanismesindicats,eldelesemissions deCO2 ,degranactualitatisummaimportància,ésidealperil¨lustrarelguanydequalitaten lapresadedecisionsquesignificaincorporarcriterismatemàticspersobred’altresdetipus polític.

ElsarticlesdeLourdesRoderoiMariaJosepFreixanetensintrodueixenenelmóndelsconcursosdeprojectesd’estadísticaques’hanimplementatarreudel’Estatsotal’auspicideles societatsd’estadísticaiquevaintroduiraCatalunyaPedroDelicado.LourdesRoderoensexplicalahistòriadelconcursPlanterdeSondeigsiExperimentsiil lustra,atravésd’exemples detreballsguanyadors,diferentsmaneresdepotenciarl’ensenyamentdel’estadísticacoma einaexperimentalid’investigació.MariaJosepFreixanetésprecisamentunadelesprofes-

soresquehapresentatalumnesalconcursiensexplicalasevaexperiènciad’aquestúltim curs,jaqueelseugrupd’alumnesvaguanyarelconcurscatalàilafinalespanyoladela sevamodalitat.Podem,doncs,gaudirdelesduesvisionsdel’aventuraiveureelsdetallsde l’organitzaciód’unensenyamentdel’estadísticabasatenprojectes,aixícomlesdificultats quesorgeixeniquerequereixencanvismésenllàdelradid’acciódelprofessorat.

Enunestilmoltàgil,MireiaVinyolesexplicaenelseuarticleunaexperiènciadeclassecentradaenelteoremadePickquepermetcalcularl’àread’unpoliedrereticularsimpleapartir delnombredepuntsfronteraipuntsinteriors.Estractad’unproblemafàcildeformular,que inclouunadimensiómanipulativaenl’exploraciódelsdiferentstriangles,aixícomladeducciódelafórmuladel’àreaapartirdelaconstrucciód’algunscasosconcrets,suposantque l’àreaésunacombinaciólinealdelnombredepuntsfronteraieldepuntsinteriors.L’autora endescriuunapossibleimplementacióal’educaciósecundàriaobligatòriaoalbatxilleratien valoralesqualitatsperintroduirelsalumnesenelmóndelaconjecturailaprova,totrelacionantlageometriaambl’aritmètica,l’àlgebra,lesfuncionsielssistemesd’equacions.

L’últimarticled’aquestnúmeropresentaunadobleoriginalitat,tantpeltemaqueaborda comperlamaneraenquèhaestatescrit.Enspresentaunconjuntdematemàticsipersonatgesrelacionatsambmatemàticsdel’AltEmpordàilarodalia,tandiversoscomdiferentment interessants.Amés,eltextcorresponaunaversióenformatarticlequefaLluísSabaterdel treballderecercadebatxilleratdelasevafilla,RosaSabater,ambelqualaconsegueixuna maneraexcel lentdedifondreelseucontingutalpúblicde NouBiaix.Esperemqueserveixiperanimaraltresprofessoresiprofessorsapublicarencol¨laboracióambelsestudiants, treballsdebatxillerat,degrauodemàsterquehagindirigit.

Enresum,compodeuveure,estractad’unnounúmerode NouBiaix quepreténserfidelal seuesperitdesempre:varietatdetemes,rigormatemàticimoltadidàctica.Estemconvençutsquehitrobareuelementsaplicablesalavostratascadocent.

articles articles

Comferservirl’estadística comaeinaSTE(A)M

LourdesRoderodeLamo

Departamentd’EstadísticaiInvestigacióOperativa UniversitatPolitècnicadeCatalunya lourdes.rodero@upc.edu

Resum Abstract

L’any 2010 elprofessorPedroDelicadova importarunconcursd’estadísticaprovinent delaUniversitatComplutensedeMadrid.En principi,l’objectiudelconcursera promocionarl’estadísticaenl‘àmbitdela secundàriaielbatxilleratpertald’apropar ladisciplinaiferconèixerelsalumnesdela carrerad’Estadística.Benaviatesvademostrar queelconcursanavamésenllà,molts professorsdesecundàriaibatxilleratvan adonar-sedelapotènciadel’einaies vancomençaraveuretreballsonescreuaven disciplinesiesfeiaservirl’estadísticacoma einamultidisciplinària. L’any 2016l’organitzaciódelconcursvapassar alesmansdelaprofessoraLourdesRodero, quehacontinuattreballant-hifinsal’actualitat intentantquecadacopmésaquestconcurses vegicomunaeinaSTE(A)M,acrònimanglès queenglobalesdisciplineseducatives següents:Science(ciència),Technology(tecnologia),Engineering(enginyeria),Art(art) iMathematics(matemàtiques)peralfoment del’úsdel’estadísticacomaeina interdisciplinàriaalesaules. Enaquestdocumentesmostraranexemples d’experiènciesd’aplicaciódel’estadísticacom aeinaSTE(A)Mquepodenservird’inspiració peraplicar-lesal’aulatotfentde l’aprenentatgedel’estadísticaunatasca divertidaiambutilitatquanesbarrejaamb altresdisciplines.

In2010,ProfessorPedroDelicadointroduceda statisticscompetitionfromtheComplutense UniversityofMadrid.Originally,theaimofthe competitionwastopromotestatisticsin secondaryandhighschooltobringthe disciplinecloserforthesestudents.Itsoon provedthatthecompetitionwentfurther,and manyhighschoolteacherssoonrealizedthe powerofthetoolandbegantoworkintopics whereotherdisciplinesappliedstatisticsasa multidisciplinarytool.

In2016ProfessorLourdesRoderosucceeded Pedrointheorganizationofthecontest,who carriedonthedevelopmentoftheevent.Today thiscontestisbeingpositionedasaSTE(A)Mtool fortheuseofstatisticsasaninterdisciplinary toolinclassroomsaroundthecountry. Thispaperwillshowexamplesofexperiencesof applyingstatisticsasaSTE(A)Mtoolthatcan serveasinspirationtoapplytheminthe classroombymakinglearningstatisticsafun andusefultaskwhenmixedwithother disciplines.

1.Introducció

L’estadísticaésunaciènciainterdisciplinàriaquetécomaobjectiusprincipalsplanificarla recollidadedadesadientsperrespondreauna determinadaqüestióitransformaraquestesdadeseninformacióperalapresadedecisions,enconcretperdonarrespostaales preguntesformuladesinicialment.

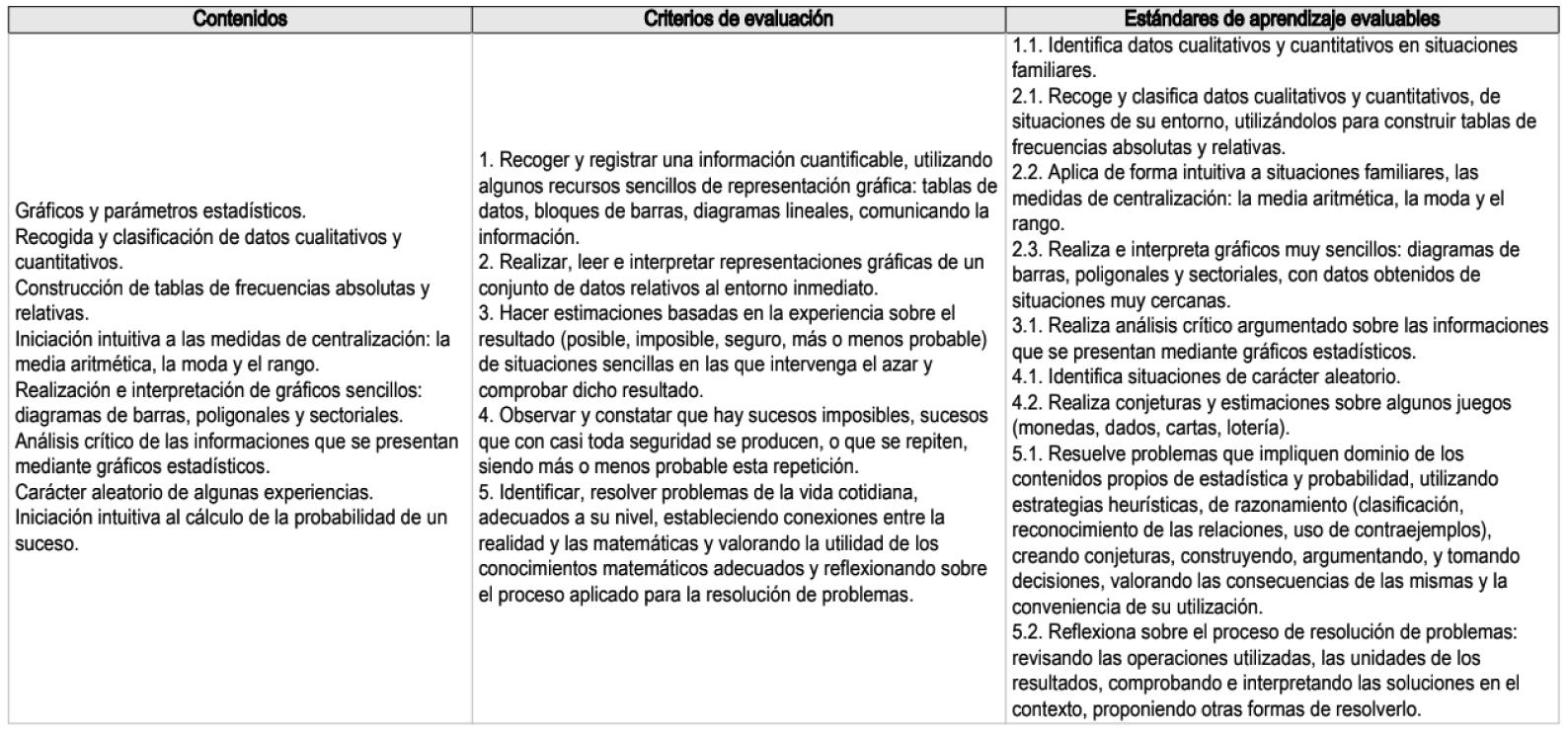
L’estudidel’estadísticaestàbreumentincorporadaalcurrículumdesecundària(tambépodríemtrobar-laenelcurrículumdebatxillerat),especialmentlapartdeprobabilitatiladefiniciód’estadísticsdescriptius.Moltesvegadesaquestapartésmenystingudaenlesescoles perquèéslapartdelfinaldeltemariimoltesaltrevegadeshoésperlafaltad’ideesdels docentssobrecomexplicaraquesttemaal’aula.

Taula1.Partdelcurrículumdesecundàriaambreferènciaalaprobabilitatil’estadística.

Peròespotarribaraassolirelsobjectiusproposatsdemaneradivertidaiinclúsaprofitarper ensenyarl’estadísticacomunaeinainterdisciplinàriai,pertant,connectadaamblametodologiaSTE(A)M?

Aixòfariaque,amés,esveiésl’estadísticacomunaeinaútilperdonarrespostaaqüestions relacionadesambelmónreali,sobretot,queesveiéscomunatècnicadelmètodecientífic, comespotveurealafigura 1.Comesdiua[1],l’estadísticatéelpotencialperfacilitarla integraciódelesdiferentsdisciplinesinclosesenelconcepteSTE(A)M.

L’acrònimSTEM(Science,Technology,EngineeringandMathematics)ésutilitzatperprimera vegadaperlaFundacióNacionaldeCiènciesdelsEstatsUnitsd’Amèrica[2][3][4].Ladefinicióexactadelscampsqueestaninclososenaquestadisciplinavariaentrelesdiferents organitzacions,peròincloulesmatemàtiquesi,sobretot,l’estadísticailessevesaplicacions. Quanparlemd’educacióSTE(A)M(afegint-hilaAenreferènciaal’art),estemparlantdedesenvoluparcompetènciesrelacionadesamblaciència,latecnologia,l’enginyeria,l’artiles matemàtiquesil’estadísticaentreelsjovesambl‘objectiud‘incrementarlesseveshabilitatsi elseugustperaquestscamps.

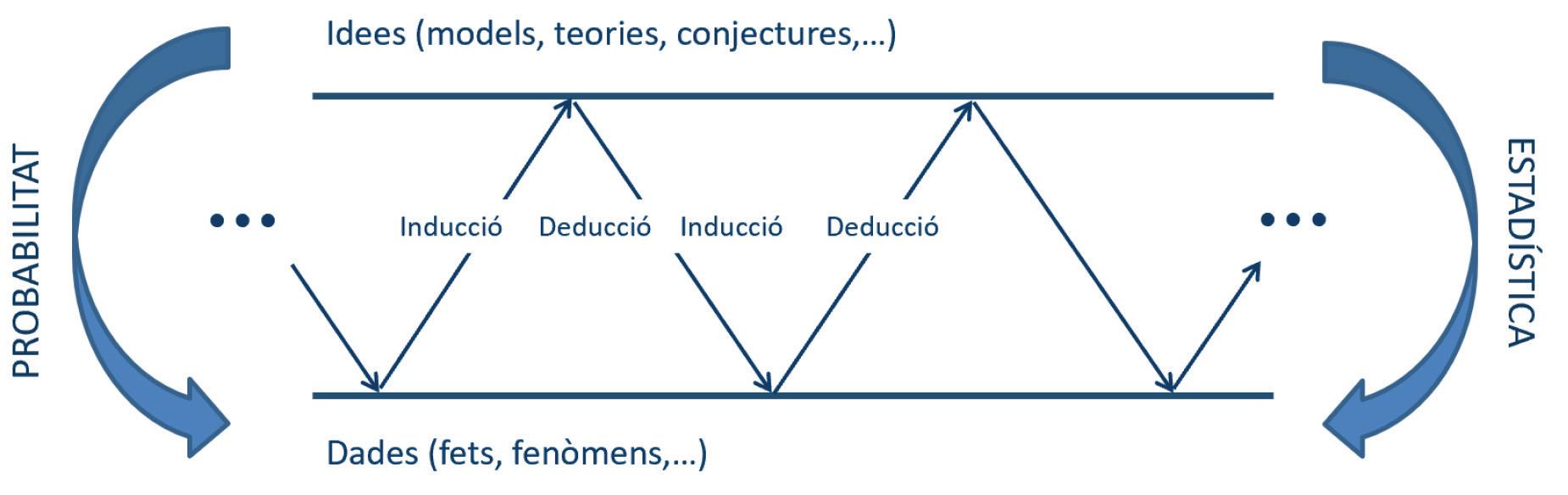
Figura1.L’estadísticailaprobabilitatcomatècnicadelmètodecientífic.

AcontinuaciópresentemexperiènciesdesenvolupadesenelmarcdelconcursPlanteriSondeigd’Experimentsquepodenservird’inspiracióal’horadeconstruircasosd’úspropion estreballenconceptesestadísticsal’entornd’unproblemarealquesovintestàrelacionat tambéambunaaltradisciplina.

2.ElconcursPlanterdeSondeigsiExperiments

Desdelcurs 2006-2007l’EscolaUniversitàriad’EstadísticadelaUniversitatComplutensede MadridconvocaelCertamenIncubadoradeSondeos,amblaprofessoraMaríaJoséNarros alcapdavant.Hiparticipengrupsd’estudiantsd’ensenyamentsecundariambtreballsque consisteixenenl’elaboraciód’unaenquestasobreuntemad’actualitat,l’anàlisidelesdadesobtingudesilapresentaciódelsresultats.Lesconvocatòrieshanaconseguitunèxitde participació,tantpelnombredetreballspresentatscompelnombred’estudiantsinvolucrats.

Durantelcurs 2009-2010 alaFacultatdeMatemàtiquesiEstadísticadelaUniversitatPolitècnicadeCatalunyaesvaconsideraroportúconvocaraCatalunyaunconcursambunes característiquessimilarsiésperaixòqueesvaposarenmarxaelprimerconcursPlanter deSondeigsiExperimentssotal’organitzaciódelprofessorPedroDelicado.Idesdelcurs 2010-2011 vanorganitzarelPlanterdeSondeigsiExperimentsdemaneraconjuntalestres facultatsdeCatalunyaqueofereixenestudisdegraud’estadística:laFacultatdeMatemàtiquesiEstadística(FME)delaUPC,laFacultatd’EconomiaiEmpresadelaUBilaFacultatde CiènciesdelaUAB.

Aquestconcurstécomaobjectiuprincipaldespertarenelsalumneslacuriositatperl’estadística comaeinafonamentalderecerca,tantenciènciesexperimentalscomenciènciessocials,i tambéincentivarlatascaeducativaenaquestaàreadeconeixementqueesportaatermeen elscentresdesecundària.

Jan’hemfetdotzeedicionsihihaenmarxaladel’any 2022.Elnombredetreballspresentats estàentreels50 (ediciómarcadaperlapandèmia)iels 180,iimpliquenentre 20 i40 centres d’arreudelterritori,queaportenlaparticipaciód’entre 150 a500 estudiantsid’entre 20 a60 professors.

3.Larelacióentreelconcursil’einaSTE(A)M

EspotcopsarqueelstreballsqueespresentenalconcursPlanteriSondeigd’Experiments podenservistoscomunaeinaSTE(A)Mperintroduirl’estadísticailaprobabilitatdemanera amenaidivertidai,enmoltscasos,apropant-seaaltresdisciplines,jaqueclaramentésuna einatransversal.

Enaquestarticleveuremalgunsexemplesdetreballsguanyadorsdelconcursquepoderser consideratscomaexemplesmotivadorsperseraplicatsalesaulesobédirectamentobé ambalgunaadaptació.

Comjahemvistalataula 1,elcurrículumdesecundària,perexemple,tocadiferentsaspectes delaprobabilitatil’estadística.Estracta, doncs,deveurecompodemtreballaraqueststemesdemaneradivertidaiamena.

Aquestsexemplesmostrenelprocedimentobservatalafigura 1 ienspodenservird’inspiracióa l’horadeprepararalgunaactivitatsimilarqueajudi,perexemple,aentendreelsconceptes probabilístics (deduccióestadística),aixícoml’anàlisid’enquestesilarecollidadedadesque portenaprocediments estadísticsinductius,quefanúsd’einesdescriptives,del’estimació deparàmetresiderepresentacionsdiverses.

També,encasd’emprarelcamí experimental,espotcreuarambdisciplinestècniquesipot ajudartambéacomprendreresultatsdelafísica,laquímica,labiologia,etc.

I,peracabar,espodenutilitzardadesjarecollidesenl’àmbitdel’estadísticaoficial.

4.Experiènciesguanyadoresenelconcurs

4.1. Exemple d’aplicació per tractar conceptes probabilístics

Eltreballmostratalafigura 2 vasereltreballguanyadoralacategoriadeBatxillerativa aconseguirunamencióalafasenacionaldelconcurs.ElvaferRondaSalavertielseututor vaserJordiNavazo,del’IESMiquelCrusafontiPairó,deSabadell.

Laideadeltreballésinvestigarsiéspossibletrobarunmètodeguanyadorperguanyaren uncasino.Elpuntdepartidaéslapel lícula LosPelayos,queensmostracomunafamíliava trobarlamanerad’enriquir-seamblaruleta.

L’activitatespotiniciarambelvisionamentdelapel lículapercomentartantlametodologia empradacomelscàlculsprobabilísticsquecaldriaferpercalcular-nelesprobabilitatsde guany,comespotveurealataula 2.

Taula2.Càlculdeprobabilitatsenl’entornd’unaruleta.

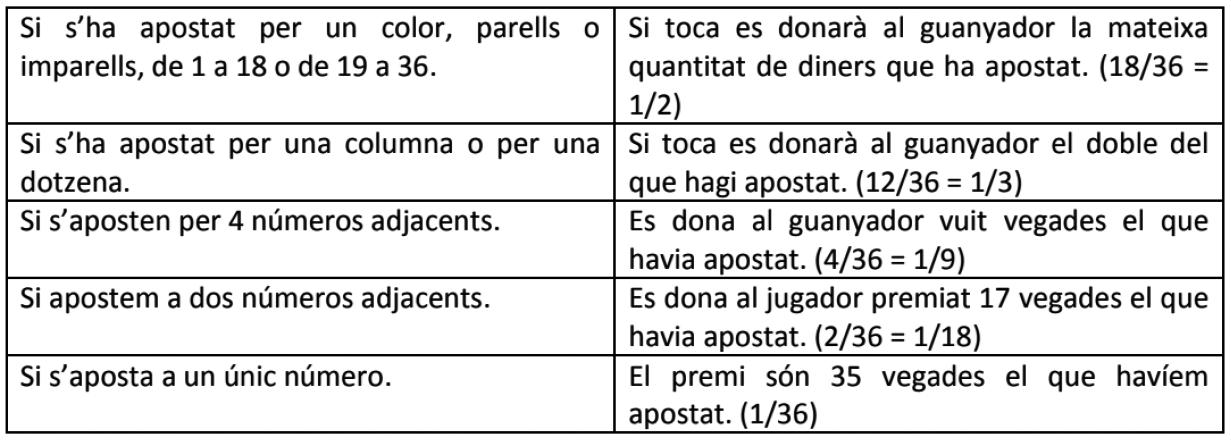
Desprésdetreballarelsconceptesprobabilístics,enaquestexempleesvadecidirresoldreel problemasimulantelsresultatsdeljocapartird’unaestratègiad’apostesdonada.Aquesta estratègia,tambéconegudacoma estratègiamartingala,consistiaacomençarajugaramb 1.000 =C iapartird’unaprimeraapostade 100 =C anardoblantlaquantitatquecaliaapostar finsa,obétornaratenirelsdinersinicials, 1.000 =C,obéperdre-hotot.

Perdefinirelprogramadesimulaciócaliaestablirexactamentelsconceptesdejugada,partida,èxit,fracàs,beneficiipreuperpartida,aixícomconstruirunarbreprobabilísticdepossibilitats.Enaquestcas,elprogramaesvaformularambelprogramariR,perlaqualcosa,a més,esvapodertreballarl’aprenentatged’aquestaeina.Esvansimularfinsa 10.000.000 de partidesalaruleta.

Quèaprènl’estudiant?

Conceptesprobabilístics,conceptedesimulacióidediferentsescenaris oestratègies.Valoresperatdeguany(benefici).Execuciódesimulacions. ProgramariR.Aplicaciód’unasimulacióperalapresadedecisions(surta comptejugar?).

Quenosurtacompte,jugarenuncasino!

4.2. Exemple d’aplicació per respondre preguntes partint de dades

Elsvideojocsindependents,guanyadorl’any2017.

Eltreballmostratalafigura3vaserelguanyadoralacategoriade3ri4td’educaciósecundàriaobligatòria(ESO)l’any 2017.ElvaferPauM.ValènciailasevatutoravaserMariadel PilarMenoyo,del’IESJuanManuelZafra,que actualmentesdenominaIESCaterinaAlbert, deBarcelona.

Enaquesttreballlaideaésdonarrespostaaunapregunta:tenencabudaenelmercatels videojocsindependentsdavantelsaltres?Aquestapreguntavaplantejar-lal’estudiant,que teniaungraninterèseneltemaperquèvoliaencaminarelseufuturcapaaquestadisciplina: laprogramaciódevideojocs.

Comespotrespondrealapregunta?Partintdedades.Hihaduespossibilitatsal’horad’obtenir dades:

1.ConsultarunabasededadessobrevideojocsSTREAMSPY,moltconegudaenelcamp delsvideojocs.

2.Construirunapròpiabasededadesapartird’enquestesrealitzadesagentdel’entorn.

AmblesdadesjaexistentsdelabasededadesSTREAMSPYesvapoderrespondreapreguntessobreelpercentatgedepropietarisdevideojocsindependents,aixícomsobrelesvendes eneurosdecadascund’ellsilesplataformesmésempradesperjugaraaquesttipusdejocs. Esvanferservirindicadorsestadísticscomlamitjanailesdesviacionstipus,elspercentatgesi tambégràficsdescriptiuscomelsdiagramesdebarresodesectorsperresumirlainformació idonarrespostaalespreguntesplantejades.

Perconstruirlabasededadespròpia,enprimerlloccalcalcularelnombred’enquestesque s’handeduraterme.Esfaservirlateoriadelmostreigestadísticpercalcularquinamidamostralcalperpoderferlesestimacionspertinentsambundeterminatmarged’error.Apartir d’aquíesdissenyaunqüestionariiespassaalnombredepersonesdeterminatpelscàlculs. Amblesdadesrecollidesesvapoderrespondreapreguntessobreelconeixementdelpúblic generalsobreelsvideojocsindependents,fentservirlesmateixeseinesestadístiquesqueen l’apartatanterior.

Figura3.Treball

Quèaprènl’estudiant?

Estadísticsdescriptiusbàsics:percentatges,mitjanes,desviacionstipus. Gràficsdescriptiusdebarresidesectors.Càlculsdelesmidesmostrals, representativitatdelamostra,construcciódeformularisirecollidade dades.

Quehihafutur,enlacreaciódevideojocsindependents!

4.3. Exemple d’aplicació emprant una estratègia experimental

Figura4.Treball Cargolssilvestresversuscargolsdegranja,guanyadorl’any2018.

Eltreballmostratalafigura4vasereltreballguanyadoralacategoriade 1ri 2nd’ESOl’any 2018ivasertambéguanyadoralafasenacional delconcurs.ElvanferQueraltSantacreu, RaquelMartín,PauBuscalliAranCapdevilailasevatutoravaserSílviaSalvador,del’Institut SerradeNoet,deBerga.Entrobareuunadescripcióalnúmero47de NouBiaix [5].

Enaquesttreballesvanunirconceptesdetresassignaturesdiferents: ciències,ons’estava estudiantlafuncióderelacióenelséssersvius,enconcretcomresponienelscargolsdavant dediferentsestímuls; física,ons’estavatreballanteltemadelacinemàtica,i matemàtiques, ontocavacomençaraferestadística.D’aqueststresconceptesvasortirlaideadeferun estudiestadísticexperimentalsobrelavelocitatdedesplaçamentdelscargolsdavantunestímul(enciam).

Elprimerqueesvafervaserdefinirunprocedimentexperimentalconsistenta:

1.Buscarcargolssilvestresicargolsdegranjaietiquetar-losconvenientment.

2.Pesarelscargolspersaber-ne«lamida».

3.Posarelscargolsdelsdostipusenunasafatadavantl’estímul(enciam).

4.Cronometrareltempsquetrigacadacargolaarribaral’enciam.

5.Calcularlavelocitatdelcargol.

Figura5.Procedimentexperimentalderecollidadedadesdelscargols.

Enaquestprocedimentexperimental,queespotveurealafigura5,vacaldrereflexionar sobrecoms’haviademesurarladistànciarecorregudapelscargolseneltempsdeterminat(punt5delprocediment),jaqueelscargolsnoanavenellíniarecta,iesvaarribarala conclusióqueesresseguiriaambagullesdecapiuncordilllababadeixadapelscargols.

Uncoprecollideslesdades,esvaintentarverificarunasèried’hipòtesis;enconcret,queels cargolssilvestressónmésràpids,mésgransiqueresponentotsal’estímul,adiferència delscargolsdegranja.Hihaalguneshipòtesisquenoesvanpodervalidar,com,perexemple, queelpesdelcargolsnodeterminasisónmésomenysràpids.

Percontrastarleshipòtesisplantejadesesvancalcularestadísticsdescriptiusbàsicsperala velocitatdelscargols,comaralamitjana,lamediana,lamoda,ladesviaciótipus,elcoeficient devariacióielrangperalsdostipusdecargols.

Quèaprènl’estudiant?

Construcciód’unexperimentdesdezeroperprendredadesqueserveixin pervalidarcerteshipòtesisplantejades.Quemesurarnoésfàciliques’han depensarprocedimentstanobjectiuscomsiguipossibleperrecollirles dadesnecessàries.Estadísticsdescriptiusbàsics:percentatges,mitjanes, medianes,modes,desviacionstipus,rangsicoeficientsdevariació.

Queelscargolssilvestressónmésràpidspermenjar-sel’enciamqueelsde granja!

4.4.

Exemple

d’aplicació per a l’anàlisi de dades oﬁcials

Figura6.Treball Elnomdels1000cognoms,guanyadorl’any2013.

Eltreballmostratalafigura6vaserelguanyadoralacategoriaIDESCAT.Vaserfetper NeusBock,MeritxellHeras,SaraTrabadoiMiquelParerailasevatutoravaserLucíaBayo,de l’InstitutSantQuirzedelVallès.

Enaquesttreballespresental’anàlisid’unabasededadesd’estadísticaoficialprovinentobé del’Institutd’EstadísticadeCatalunya(IDESCAT)obédel’InstitutoNacionaldeEstadística (INE).Enconcret,enaquesttreballesvoliaconèixersiladistribuciódelsnomsicognoms enunpobleerasimilaronoaladeCatalunya,establintunprocedimentpertrobarpobles «ambdistribucionsatípiquesdecognoms»respectealamitjanacatalana.Esvanemprar diagramesdebarresidesectorsitambéestadísticsdescriptiusbàsicsipercentatgesperfer lescomparatives.

Quèaprènl’estudiant?

Consultarianalitzarbasesdedadesoficialsqueespodendescarregar desdelespàgineswebdelsinstitutsd’estadística(IDESCATiINE).Estadísticsdescriptiusbàsics:percentatges,mitjanes,desviacionstipus.Gràfics descriptiusdebarresidesectors.

QueaSantQuirzeelscognomsnosóntandiferentsdelsdeCatalunya!

5.Conclusions

Espodenplantejartreballsinterdisciplinarisquecobreixinlescompetènciesespecificadesen elcurrículumd’ESOfentquel’assolimentdelsconceptesestadísticssiguidivertitiaportant unavisiórealistadel’úsdel’estadística.Enmoltesocasionsespodentreballartambéaltres disciplines.Aixòfad’aqueststreballsunsbonsexemplesd’einesambmetodologiaSTE(A)M.

Elstreballsespodenplantejardesd’unavessantmésexperimental,desdel’anàlisid’unabase dedadesoinclúsamblarecollidadedadesmitjançanteldissenyd’unqüestionaripropi.Es podentractartambétemesprobabilísticsifer-losigualmentdivertits.

Calfomentarl’estadísticacomapartimportantdelconeixementcientíficiveure-lacomuna einainterdisciplinàriaquedonarespostaaproblemesreals.

Sivoleumésinformaciósobreelconcursitambémésexperiènciesguanyadores,consulteu [5].

Bibliografia

[1]Watson,J.;Fitzallen,N.;Chick,H.(2020).«WhatIstheRoleofStatisticsinIntegratingSTEM Education?».A:Anderson,J.;Li,Y.(eds.). IntegratedApproachestoSTEMEducation.AdvancesinSTEMEducation.NovaYork:Springer.

[2]PàginawebdelaNationalScienceFoundation:www.nsf.gov.

[3]White,D.W.(2014).«WhatIsSTEMEducationandWhyIsItImportant?», FloridaAssociationofTeacherEducatorsJournal, 1(14), 1-9.

[4]Smith,C.;Fitzallen,N.;Watson,J.;Wright,S.(2019).«ThePracticeofStatisticsforSTEM:PrimaryStudentsandPre-ServicePrimaryTeachersExploringVariationinSeedDispersal», TeachingScience,65(1),38-47.

[5]Argerich,I.;Salvador,S.(2020).«Il’estadística,què?», NouBiaix,47,4-18.

[6]PàginawebdelconcursPlanterdeSondeigiExperiments:fme.upc.edu/ca/concurs_Planter.

«Elsorollicomafecta lanostrasalut».

L’estadísticaperprojectes asecundària

MariaJosepFreixanet

DepartamentdeMatemàtiques

EscolaPolitècnicaSuperiord’EnginyeriadeManresa UniversitatPolitècnicadeCatalunya(EPSEM-UPC) iEscolaReginaCarmelideRubí

Resum Abstract

Aquestarticleexplicaeldissenyila implementacióal’auladelprojecte d’estadística«Elsorollicomafectalanostra salut»,guanyadordedospremis:enl’àmbit autonòmic,dinselconcursPlanterde SondeigsiExperiments,ienlafasenacional delconcursIncubadoradeSondeosy Experimentos.Explicatambélamotivació quevadurelprofessoratamodificarles classesmagistralsiaevolucionar-lescapal treballperprojectesenl’àread’estadística alsegoncicledel’educaciósecundària obligatòria(ESO),aixícoml’evolucióque s’haanatfenteneldissenyila implementaciód’aquestsprojectesal’aula amesuraquen’hemanatdesenvolupant anyrereany.

Thisarticleexplainsthedesignand implementationoftheStatisticalProject«The noiseandhowitafectsourhealth»,winnerof twoawards:thefirstprizeintheCatalan contestPlanterdeSondeigsiExperimentsand thesecondintheSpanishnationalphase ConcursoLaIncubadoradeSondeosy Experimentos.Italsoexplainsthemotivation oftheteacherstomodifythetraditional lecturesandchangethemintolearning throughprojectswithintheareaofstatisticsin secondaryschool(grades9-10),aswellasthe evolutionofthedesignandimplementation oftheprojectsduringthesepastyears.

Introducció

Partintdelapregunta«Rubíésunaciutatsorollosa?»,elsalumnesde3rd’ESOdel’Escola ReginaCarmelideRubívanelaboraruntreballqueelsvaportaraguanyarelprimerpremi delacategoria3r-4td’ESOdelconcursPlanterdeSondeigsiExperiments,organitzatper

laFacultatdeMatemàtiquesiEstadísticadelaUPC,laFacultatd’EconomiaiEmpresadela UniversitatdeBarcelonailaFacultatdeCiènciesdelaUniversitatAutònomadeBarcelona, amblacol¨laboraciódel’Institutd’EstadísticadeCatalunya(IDESCAT),laSocietatCatalana deMatemàtiquesilaSocietatCatalanad’Estadística.Seguidamentidesprésd’haverguanyat aquestpremi,eltreballvapassaralafaseespanyola,anomenada FaseNacionaldelConcursoIncubadoradeSondeosyExperimentos iorganitzadaperlaSociedaddeEstadísticae InvestigaciónOperativa(SEIO),enlaqualtambévarebreelprimerpremienlasevacategoria.

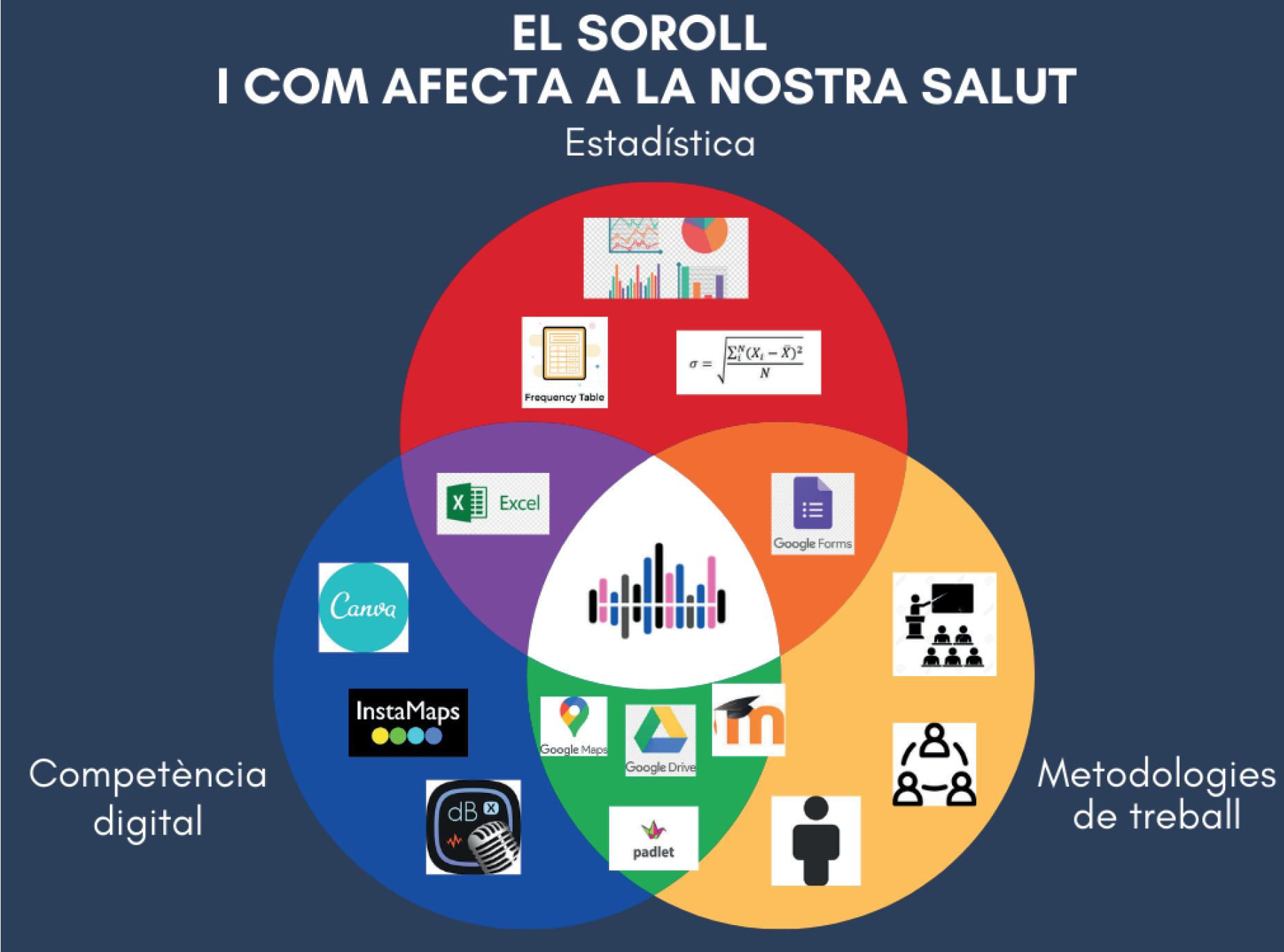
Enaquestarticlepresentaremtantlapreparaciódelprojectecomlasevaorganitzacióiel desenvolupamental’aula.S’adjuntaal’annex 2 unainfografiaquemostraelstreseixosprincipalsapartirdelsqualss’hatreballatelprojecte:

1.Estadística

2.Competènciesdigitals

3.Metodologiesdetreballal’aula

Espotveurequeentreelstreseixostambéhihaconvergències.Prèviament,però,explicarem l’evoluciódel’aprenentatgedel’estadísticadinselcentreenelsnivellsde3ri4td’ESOiles raonsquevanmotivarlaimplementaciódeltreball.

1.L’evoluciódel’aprenentatgedel’estadísticaal’aula

Podemdistingirquatreetapesenlamaneraenquès’haanattreballantl’estadísticaperprojectesalCol¨legiReginaCarmelideRubí(figura 1).

Cursos 2015-16 i 2016-17

Primeres exploracions del treball per projectes en Estadística

Curs 2017-18

Concurs El Planter de Sondeigs i Experiments

Cursos 2018-20

Normalitzant el treball per projectes

Curs 2020-21

Noves condicions

Figura 1. Evolució de la implementació del treball per projectes en estadística al Col·legi Regina Carmeli de Rubí. Figura1.Evoluciódelaimplementaciódeltreballperprojectesenestadística alCol¨ legiReginaCarmelideRubí.

Etapa 1. Primeres exploracions

Fasisanys(curs 2015-2016)vaigcomençaratreballarl’estadísticacomaprojectedinsl’assignaturadematemàtiquesa3rd’ESO.Al’escola,apartirde3rd’ESOlesmatemàtiquesestreballavenpergrupsdenivell.Deduesclassesde30 alumnes,se’nfeientresgrupsde 20 alumnes cadascuniseseparavenpernivellstenintencomptelessevescapacitatsielsresultatsobtingutsentre 1ri 2nd’ESO.Aquestcanvienlamaneradetreballarl’estadísticaa3rd’ESO comaprojectevasorgirarrand’haverd’impartirl’assignaturaaungrup3moltdesmotivat icomaideapergeneraruninterèsalsalumnespertalquepoguessinveureunautilitat realalqueestavenaprenent.Laprimeravegadavaigexplicarelsconceptesestadístics,vam dissenyarunaenquestaambunatemàticaqueinteressavaalsalumnes lesxarxessocials , elsmateixosalumneslavanpassarperlesaltresaulesivanelaborarunestudiestadístic bàsicdelsresultats:taulesdefreqüències,mesuresdecentralitzacióigràfics.L’experiència varesultarpositiva.Elsalumnesvanestarmotivatsivanaprendreconceptesbàsicsamb unaactituddiferent.Totiquevaserunaexperiènciapositiva,encaranoesvaimplementar deltotal’escolaieraunacosanomésdelsgrupsqueimpartiajomateixa.Alcurssegüent, 2016-2017,vaigtornar-hoaposarenpràcticaambungrup 1 (elsquetenienmésfacilitaten l’aprenentatgedelesmatemàtiques)de3rd’ESO,ambresultatsmoltpositiustambépelque faal’aprenentatgeilaimplicaciódelsalumnes.

Etapa 2. Concurs Planter de Sondeigs i Experiments

Enelcurs 2017-2018vamtenirconeixementdelconcursPlanterdeSondeigsiExperiments i,enexposar-loalsmateixosalumnesdelcursanterior,quearaestavena4td’ESO,esvan engrescarivandecidirparticipar-hi.Noestavaplanificattreballarl’estadísticaperprojectes aquellcurs,peròvaigconsiderarqueelfetd’haver-hiunconcurseramésmotivadorivaliala penaferunamodificaciódelaprogramació.Vamformargrupsdetresalumnes,cadagrup vatriaruntemaperestudiarqueelsinteressava,vanelaborarelsqüestionaris,elsvanpassar al’escola(al’ESOialsciclesformatius),envan ferl’estudi(taulesdefreqüències,gràfics, mesuresdecentralitzacióidispersió)ienvan treureunesconclusions.Vampresentarcinc treballsalconcurs.Vamguanyarelpremiala«professoranovellambméstreballspresentats».Finsllavors,nohavíemfetestudisprevisnihavíemestablertuneshipòtesis,nihavíem fetelcontrastd’hipòtesis.Enassistiralacerimòniadepremisdelconcursiveureelstreballs presentats,vamcomençaraintroduiraquestsconceptesenelsnostrestreballsposteriors.

Etapa 3. Normalitzant el treball amb projectes

Apartirdelcurssegüent(2018-2019)vamdecidircontinuarimplementantaquestamanera detreballaralsgrups 1 i 2 de3rd’ESO.Laprofessoraqueimpartiaelgrup3vadecidirno treballarl’estadísticad’aquestamanera.Vamferuntreballconjuntambl’InstitutSerrade Noet,deBerga.Elnostretreballs’anomenava«Educationalcentres:miniaturesocieties?»i consistiaacomprovarsielscentreseducatiusespodienconsiderarsocietatsenminiatura comparantlesdadespublicadesal’IDESCATsobrelesnostresciutats(RubíiBerga)iunes enquestesquevamdissenyarivamferalsnostrescentresrespectius.Unasegonapartdel treballcomparavaelsdoscentresiestudiavalesdiferènciesentrel’alumnatilesfamílies

quehihaviaencadascund’ells.Finalment,vamcompararelsnostrescentresamblesdadesdeCatalunya.Percomunicar-nosicompartirinformació,hovamfermitjançantunaeina queproporcionalaUnióEuropeaanomenadaeTwinning,laqualespromouperfertreballs col laboratiusambaltrescentresd’Europa.Aquesttreballtambéelvampresentaraconcurs ivamguanyarelPremiIDESCAT.

L’anysegüent(curs 2019-2020)vamampliareltreballperprojectesd’estadísticaa4td’ESOi aquellanyjaenshivamimplicarelstresprofessorsqueimpartíeml’assignatura,peròigualmentesvadecidircontinuarfent-honomésalsgrups 1 i 2.Elsprofessorsqueimpartienels grups3vanconsiderarnodur-loaterme.Elsalumnesde3rd’ESOvandecidirelaborarel treballapartirdelapregunta«lallunainflueixenelcreixementdelcabell?».Elsalumnesde4t ESOvanestard’acordambeltemaqueelsvaserproposatperpartdelprofessorat:estudiarsi lesfaçanesdelsedificisonvivienrebienunnivelldesorollmassaelevatisil’interiordelessevesvivendesteniaunsorollacceptableperalasalutdelespersonesquehivivien.Elstreballs esvancomençaraduratermedemanerahabitual:esvaferunestudiprevi,esvanestablir uneshipòtesis,esvanprendremesuresiesvaelaborarl’estudiestadístic.Malauradament, quanvaarribarlapandèmiaesvadecidirabandonareltreballideixar-lotalcomestava.

Etapa 4. Noves condicions

Elcurs 2020-2021,acausadelesmesuresadoptadesalscentreseducatiusperlapandèmia,es vadecidirnofergrupsdenivelliesvanimpartirlesmatemàtiquesambtotelgrupclasse,de trentaalumnes.Esvaassignarunahoraalasetmanaa3rd’ESOAiunaaltraa3rd’ESOBper podertreballarl’estadísticaperprojectes.Iambaquestesnovescondicionsvaigcomençarel projecteenqüestió.

2.Dissenydel’experiència

Laidead’aquestprojectevasorgircomunavariantdelprojectequenos’haviapoguttancar elcursanterior(2019-2020)ambelsalumnesde4td’ESOacausadelapandèmia.Elprojecte previvoliamesurarelgraudesorolldelesfaçanesidelsinteriorsdelsedificisonvivienels alumnesicomparar-loamblesdadesproporcionadesenladocumentaciópublicadaendocumentsdelaGeneralitatdeCatalunya.Aquest nouprojectehavolgutmesurarelsorolldels carrersdeRubíicomafectalasalutdelsseushabitants.

Laideainicialdelprojectehaviasorgitparlantambaltreprofessoratdelcentresobrequin estudipodríemduratermeenelprojected’estadística.Vanaparèixerideescomlacontaminacióacústicailacontaminaciólumínica.Vaigferunarecercaprèviaivaigcomprovarquehi haviaforçainformaciósobrelacontaminacióacústica:

‚ LaLleideprotecciócontralacontaminacióacústica(DiariOficialdelaGeneralitatde Catalunya (DOGC),núm.3675,d’11 dejuliolde 2002).

‚ ElmapadelsorolldeRubí,publicatalwebdel’AjuntamentdeRubí.

‚ Elpledel’AjuntamentdeRubídedata31 degenerde 2014,enelqual,entrealtres coses,esvaaprovarinicialmentlamodificaciódelmapadecapacitatacústicamunicipal adaptant-loalscanvislegislatiussofertsenmatèriadecontaminacióacústica.

‚ LapàginawebdelDepartamentdeMediAmbientiSostenibilitatdelaGeneralitatde Catalunya,enlaquals’explicaquèsónelsoroll,lacontaminacióacústicaielsefectes peralasalut,iunaeinaanomenadaMOBIACUSTICquecalculal’estimaciódel’impacte acústicdeltrànsitviarialesfaçanesdelsedificisperal’elaboraciódelsplansdemobilitat,entred’altres.1

‚ Undocumentons’especificavaelsorollmàximquehihauriad’haveral’interiord’una vivendasegonseltipusd’estances(entrealtrainformació),elaboratperl’Oficinade ConsultoriaTècnicadelaDiputaciódeGironajuntamentambelCol legid’Arquitectes deCatalunya(demarcaciódeGirona)ambdatafebrerdel 2002.

‚ Altresestudisfetsperuniversitatscatalanes.

Vaigconsiderarquese’npodriaferunbontreball,queeraunatemàticapocconegudaentre elsalumnesiquepodriaajudaraconscienciar-lossobreunproblemareal.

Enaquestnouprojecte,vaigtornarautilitzarpartd’aquestainformació,perònotota.Vaig reutilitzarelmapadelsorolldeRubíiinformaciótrobadaalwebdelDepartamentdeMedi Ambient,laqualvaigsintetitzaragafantlainformaciómésrellevantperaltreball,peròno vaigreutilitzarelDOGCenelqualesparlavasobrel’actuaciódelaGeneralitatentermes decontaminacióacústica,tenintencomptequeelcursanterioresvaferdifícildellegiri sintetitzariqueelprojecteespodiaduratermedemaneramésreeixidadonantinformació mésconcreta.Tampocnovamutilitzarladocumentaciórelacionadaambelsorollal’interior delsedificisnil’aplicacióMOBIACUSTIC.

Vamdecidirmodificarlatemàticadeltreballperquèvolíemferunestudidiferentienllaçarhoamblasalut,jaqueerauntemadelqualesparlavamoltenladocumentaciótrobada. Unaideainicialquemésendavantnoesvaduratermeeraferelprojectejuntamentamb altrescentres,uncentredeCatalunya(enaquestcas,l’InstitutSerradeNoet,deBerga)ialtres centresd’arreud’Europa,perpodercompararelsnivellsdesorollentrelesciutats.Esvoliafer mitjançantl’einaeTwinning,quepermetcompartirinformacióentreelscentresparticipants iferprojectescol¨laboratius.Finalment,aquestaideaesvadescartarperquèesvapreveure queseriaunanycomplicatamblapandèmia.

Vaigdecidirduratermeelprojectedurantelsdosprimerstrimestresdel’any,estudiantuna fasedelprojecteencadatrimestre.Eltercertrimestreeldedicaríemalacombinatòriailaprobabilitat.Disposavad’unahorasetmanalambcadagrup.Lesaltrestreshoreslesimpartiaun altreprofessor,elqualdonarialarestadelcurrículumdematemàtiquesde3rd’ESO.Durant laimplementaciódelprojecte,eltreballal’aulanoteniacomaobjectiuprincipalpresentar eltreballalconcurs,totiqueeraunapossibilitatfinal.Defet,elprojecteesvaferambtot l’alumnat.

3.Organitzaciódeltreball(aclasseiforadeclasse)

Totalainformaciódelaqualvaigferrecercai quevaigprepararperalprojecte,lavaigpublicarenuncursdeMoodlecreatperalprojecteienunacarpetadeDrivecompartidaamb 1.http://mediambient.gencat.cat/ca/05_ambits_dactuacio/atmosfera/contaminacio_acustica/.

elsalumnesonjopodiaanarseguintlestasquesdel’alumnat.Aquestacarpetateniadues subcarpetes,unaperacadafasedeltreball.Comquealgunespartsdeltreballesvanferen grups,cadagrupvacrearunasubcarpetadins d’aquestessubcarpetesivaanartreballant allà.

Enquèconsistiaeltreballicomesvaanarreformulantamesuraqueestrobavalainformació?

Eltreballestavaestructuratenduesfasesque corresponienalesduesqüestionsderecerca següents:

1.Rubíésunaciutatsorollosa?

2.Comafectaelsorollalanostrasalut?

Cadascunad’aquestesfasesestavapensadapersertreballadadurantuntrimestre.Latemporitzacióinicialdelprojectes’adjuntaal’«Annex 2».Alllargdelprojectehivahaveralguncanvi enlaplanificacióinicialqueesjustificaalllargdel’explicació.Esvanagruparelsalumnesen grupsdequatreocincperalesfeinesquehaviendeferdemaneragrupal.Vaigfergrups diferentsperacadafase.

Acontinuaciós’explicacadafasemésdetalladament.

Fase1.Rubíésunaciutatsorollosa?

Estudiitreballprevi

Abansdecomençararecollirdades,elsalumneshaviendetenirinformacióprèviaperpoderformularuneshipòtesisbenfonamentades.Peraquestaraó,vaigprepararelmaterial següent,elvaigpresentaraclasseielvaigdeixardisponibleenelcursdeMoodlecreatper alprojecte.Esvaestudiarelsegüentiesvadesenvoluparenlessessions 1-5:

‚ Presentació«Quèéselsoroll?».

‚ Mapadelsorollquel’AjuntamentdeRubí tédisponiblealasevaweb,ambdatade novembredel 2012.

‚ Creaciód’unmapaaGoogleMapsanomenat«MapadelsorolldeRubí»(figura 2).L’aplicacióGoogleMapspermetcrearelteupropimapaicompartir-loamblespersonesque vulguisieditar-loentretotes.Cadaalumnehivasituarelseudomiciliihivaescriureel colorcorresponentalafranjadedecibels tantdediacomdenitques’indicavaenelmapadelsorolldeRubí.Vampodercorroborarqueentretotselsalumnesescobrialaciutat inoquedavenconcentratsenunasolazona.Vegeuwww.google.com/maps/d/edit?mid =1ZoxA1Pj048ySYWGvTVAP4OO-nVNlFbXm&ll=41.50657590517241%2C2 017894199 99999&z=13.

‚ Dissenyd’unqüestionariperestudiarl’entorndecadadomiciliambqüestionsquepodienafectardirectamentelsnivellsdesoroll:comesviviaenunazonadevianants,el nombredecarrilsdelavia,lapresènciadezonesescolarsidecomerços,ilestipologies decomerços,entred’altres.Lesdadesd’aquestqüestionarivanseremmagatzemades enunfulldecàlculqueesvadesaralacarpetacompartidadeDrive.Cadagrupva fer-neunacòpia,lavadesaralasevasubcarpetaivaanalitzarunadelesqüestionsdel qüestionariqueelsvaigassignar(vegeul’«Annex3»).

Formulaciód’hipòtesis

Laformulaciód’hipòtesisesvaduratermealasessió6.Esvapresentarl’estudifetpercada grupal’aulai,pergrups,elsalumnesvandiscutirleshipòtesisqueconsideraveninteressants ilesvamposarencomúescrivint-lesalapissarra.Lamajoriaesrepetienoerenmoltsimilars. Vamseleccionaraquellesenquè lamajoriaestavad’acord.

Recollidadedades

Larecollidadedadesesvafermitjançant:

‚ L’aplicaciómòbilDecibelX,quetotselsalumnesvaninstal lar-sealmòbil,amblaqual mesuravenelsdecibelsipodienenregistrarunafotografia(figura3).Perobteniruna mesuramésfiable,elsalumneshaviendetenirl’aplicacióenmarxadurantunminuti recollirladadamitjanaquelamateixaaplicacióelsproporcionava.Finalment,enfeien unafotografia(onapareixenlamitjanadedecibelsil’adreçad’onesprenlamesura, entrealtresdades),laqualadjuntavenalqüestionarique s’explicaacontinuació.

Figura2.MapadelsorolldeRubí.

Figura3.AplicaciómòbilDecibelX.

‚ UnqüestionarideGoogleonelsalumnesinserienelnivelldesorollquehavienmesurat ambl’aplicacióiadjuntavenlafotografia(figura4).

Figura4.FormularideGoogleperrecollirlesmesuresdesoroll.

Larecollidadedadesesvaferdurantduessetmanes,del5al 18d’octubrede 2021 (inclosos elscapsdesetmana),ielsalumnesprenienlesmesuresenunhorarideterminat:entreles 7.00 iles8.00 h,entreles 17.00 iles 21 00 h,entreles 21 00 iles 23.00 h,iapartirdeles 23.00 h.Lestresprimeresfrangescorresponienalafranjadiürnail’últimacorresponiaalafranjade nit.

Anàlisidelesdadesrecollides

Mentreelsalumnesrecollienlesdades,aclasse vamexplicarlesmesuresdecentralització idispersió,icomcalcular-lesenelsfullsdecàlcul(sessions7i8).Enacabarl’explicacióila recollidadedades,vanprocediraanalitzar-les.Vamdescarregarelfulldecàlculgenerata partirdelformularideGoogleienvamferunacòpiaperacadagrup.Treballantambels mateixosgrupsanteriors,cadaalumnevacalcularlamitjanaaritmètica,ladesviaciótípicaiel coeficientdevariacióenelmateixfulldecàlcul,ivaelaborarelsgràficsdelesmesurespreses durantlesduessetmanes(sessió 9).Enpodeuveureunexemplealafigura5.

AnàlisicorresponentalcentredeRubí

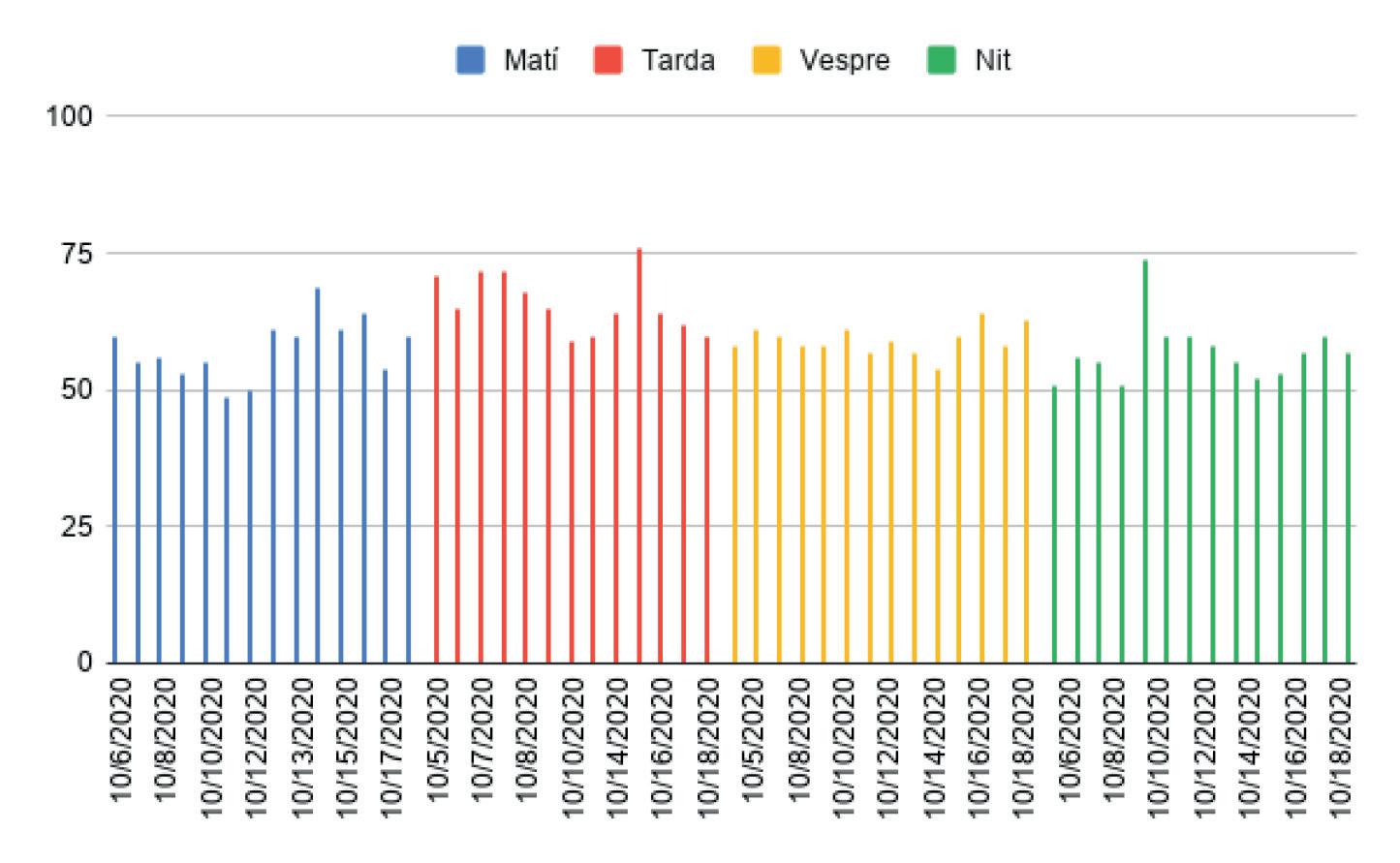
AnàlisicorresponentaCastellnou,Can’OrioliCanRosés

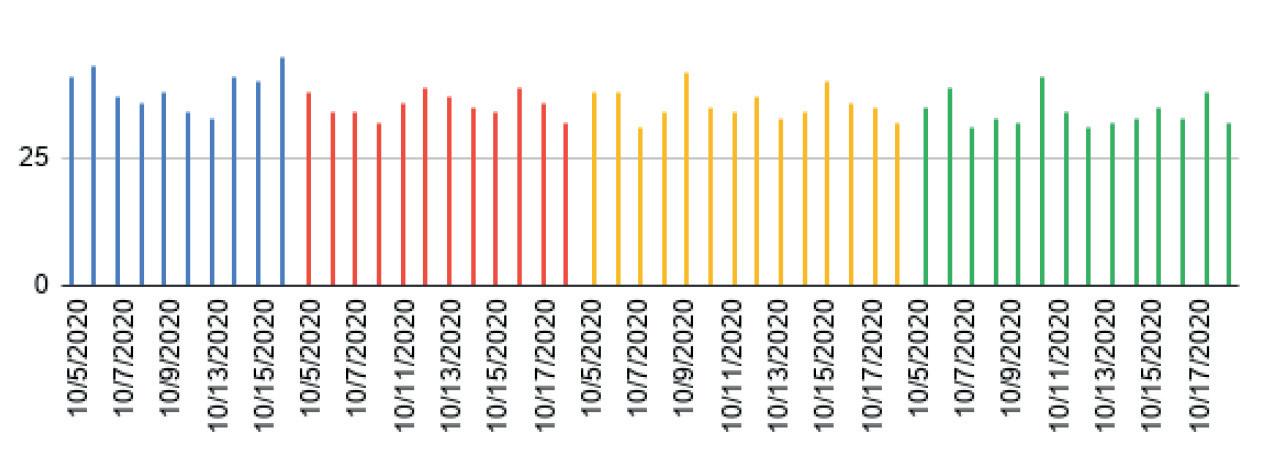
Figura5.Resumdelesdadesrecollides:decibelsmesurats.

Contrastdeleshipòtesisiconclusions

Elcontrastdeleshipòtesisilesconclusionsvanseguirl’esquemasegüent:

1.Individualment:cadaalumnevareflexionarsobresilesdadeserenhomogèniesiles vacontrastaramblesdadesdelmapadel’AjuntamentdeRubíiambleshipòtesisque haviaredactat.Envaescriureunesconclusions.

2.Engrupspetits,hovanposarencomú.Vanarribaraunesconclusionsgrupals(sessió 10).

3.Grupclasse:hovamposarencomúaclasse ivamarribaraunesconclusionsgenerals (sessions 11-14).Vamcontrastarlesdiferentshipòtesis.Quanvamposarlesdadesen comú,vampoderconstatarquehihaviaunadiferènciadenivelldesorollentreel centredeRubí,quevamanomenarzonavermella,ielsbarrismésperifèrics(Can’Oriol, CanRosésiCastellnou),quevamanomenarzonaverda.

Algunesdeleshipòtesisfetesnovanpodersercontrastadespermancad’informació,d’altres escomplienamblesdadesquehavíemrecollit.Tambévamveurequeapareixiennousfactorsquenohavíemtingutencompteinicialmental’horadeferlesnostreshipòtesis,com l’existènciadeparcsinfantils,elsqualsvamconstatarqueafectavendirectamentl’increment delsorollenlesmesuresdetardaalasortidadel’escola.

Elqueensvasobtarésquelesmesurespresesestavenpersotadelquemostravaelmapade Rubí.Vamsuposarque,desdel 2012 finsavui,s’haviarestringitlacirculaciódevehiclesenles zonesafectadesiaquestaenpodiaserlacausa.Perònovamanarmésenllà.

Dificultatsquevamtrobarenlaprimerafase

Acontinuacióesmentarélesdificultatstrobadesdurantlaprimerafase:

‚ Nomésvuitdelsalumnesvanrecollirmésdel70 %delesdades.Larestad’alumnesen vanrecollirmenys.Peraquestaraó,novamincloureaquestesmesureseneltreballfinal inovampoderarribaraunesconclusionsdeterminants.

‚ Algunalumnevaprendretanpoquesmesuresquenoenpodiaferunaanàlisiinteressant.Vahaverdeferl’anàlisidelesmesuresd’uncompanyounacompanya.

‚ Nohivahavertempsdefertoteslestasquesenlessessionsprogramades,perlaqual cosalessessions 12 (avaluacióindividualidelsaltresmembresdelgrup)i 13(inserció delesdadesal’Instamaps unaeinacreadaperl’Institut CartogràficdeCatalunyaque permetcrearmapesdigitalsambinformació ,feinaqueesvaferquanespreparavael treballperpresentar-loalconcurs)noesvanpoderduraterme.

‚ Algunalumneambpocinterèsenelprojectealentiaeltreballdelgrupielbonfuncionamentdelaclasse.

Fase2.Comafectaelsorollalanostrasalut?

Lasegonafasedel’estuditeniacomaobjectiuveuresielsorollafectavalasalutdelespersones(concretament,elsciutadansdeRubí)idequinamanerahofeia.Inicialment,esvolia enquestarlapoblaciódeRubísensefercapdistinció.Enveure,alaprimerafase,quepodíem distingirdueszonesdinsdeRubí(lazonavermella,méssorollosa,ilazonaverda,menys sorollosa),vamdecidirferaquestestudiales dueszones.Aquestvaseruncanviquevaigfer sobreeltreballpensatinicialment.

Estudiitreballprevi

L’estudipreviconsistiaenduespartsiesvaduratermeenlessessions 15-19:

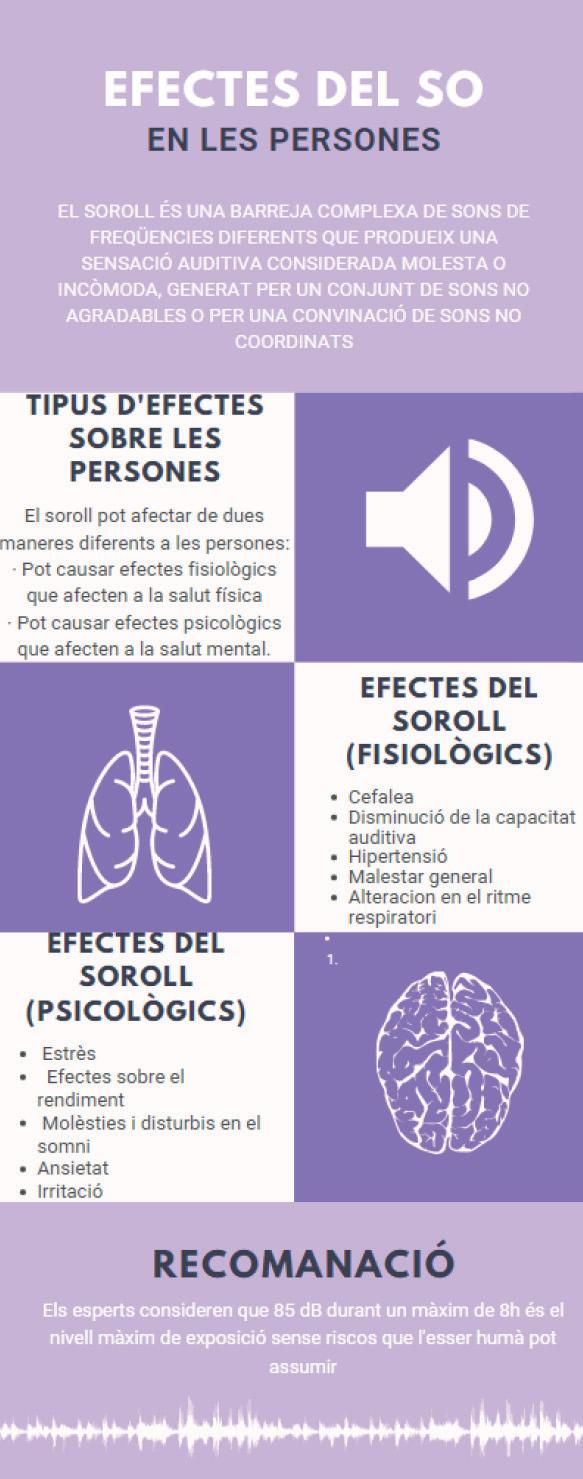
1.Recercasobrecomelsorollafectavalasalut:engrupsdequatreocincalumnes(diferentsdeltrimestreanterior),vanferlarecercailavansintetitzarenformad’infografia, laqualvanmostraripresentaralaclasse.Lafigura6enmostraunexemple:

Figura6.Infografiasobrecomelsorollafectaalasalut.

2.Elaboraciódelespreguntesdelqüestionariquedesprésfarienalapoblació.Ambels mateixosgrups,elsalumnesvanpensarquinespreguntesespodrienposarenunqüestionaripertaldepoderrespondrealapreguntaprincipal.VancompartirtoteslespreguntesenunmuraldigitalenlíniaPadlet(figura7);veg.https://padlet.com/mjosep_frei xane/vkyus3d8ap66m2wu:

Vaigcomentaralgunadelespreguntesfetesaclasse:elnivelldeconcreciódelespreguntesi respostes,siescobrientoteslespossiblesrespostes,silespossiblesafectacionsquedavencobertes,etc.Finalment,desprésd’aquestesreflexionsvamseleccionarlesquevamcreuremés

Figura7.Possiblespreguntesperaunqüestionarisobresorollisalut.

adientsilesvamposarenunformularideGooglequevaserenviatacadaalumne.Elqüestionarifinalespottrobaral’enllaçsegüentitambéenl’«Annex4»:https://forms.gle/pvaNYEdWe JfznkYo9.

Formulaciód’hipòtesis

Amblainformaciórecollidaalesinfografiesvamelaborarleshipòtesis(sessió 17).Lesmés destacadesvanser:

‚ AlcentredeRubílespersonespateixenméselsefectesqueprovocaelsorollquea Castellnou,Can’OrioliCanRosés.

‚ D’entretotselsefectesquepotprovocarelsoroll,elsmésfreqüentssóndel’àmbit psicològic,comaraestrès,ansietat,irritació,etc.

Recollidadedades

Eltreballderecollidadedadesesvaduratermeal’aulaenlessessions 20 i 21 ilesenquestes esvanferforadel’horariescolar.Vaigrepartirelscarrersdelazonaverdailazonavermella pertramsentretotselsalumnesicadascund’ellsesvafercàrrecd’entrevistarpersonesque treballessinovisquessinalazonaqueelshaviaestatassignada.Vamcalcularlagrandàriade lamostraassumintunerrordel5%ihaviendefer398entrevistes.

Vamcalcularlagrandàriadelamostraaclassedelamanerasegüent.LapoblaciódeRubí, segonsl’IDESCAT,ésde78.591 habitants.Pertant,comquetémenysde 100.000 habitants, lapoblacióesconsiderafinita.Vamcalcularlamostrapernivellsdeconfiança.Comqueno coneixíemlaprobabilitat p,vamsuposarlamàximadispersiópossible.Pertant, p “ 0,5i q “ 1 p “ 0,5.Vamferelscàlculsentretotsalapissarra:

Pertant,lamidadelamostraquenecessitàvemerade398enquestes.Vamfer-ne435,més delesesperades.

Desprésdeferaquestcàlcul,novamtenirencompteelnombrededonesohomesdeRubí, nilesdiferentsfrangesd’edat,iaquestésunaspectequeeljuratdelafasenacionaldel concursvadestacarcomamillorableenfuturstreballs,jaquevamafirmareneltreballque havíemobtingutunamostrarepresentativadelaciutatdeRubíi,ennotenirencompteles frangesd’edat,elsexe,etc.,aquestaafirmaciónoeracorrecta.Elquevamtenirencompteés sivivienotreballavenalazonaonestàvemfentlesenquestes.

Anàlisidelesdades

Comenlaprimerafase,vaigdescarregarlesenquestesenunfulldecàlcul,envaigferuna còpiaperacadagrupd’alumnes,icadascunvaanalitzarunadelespreguntes,distingint entrezonaverdaizonavermella.Lafigura8mostradosexemplesdepreguntes:

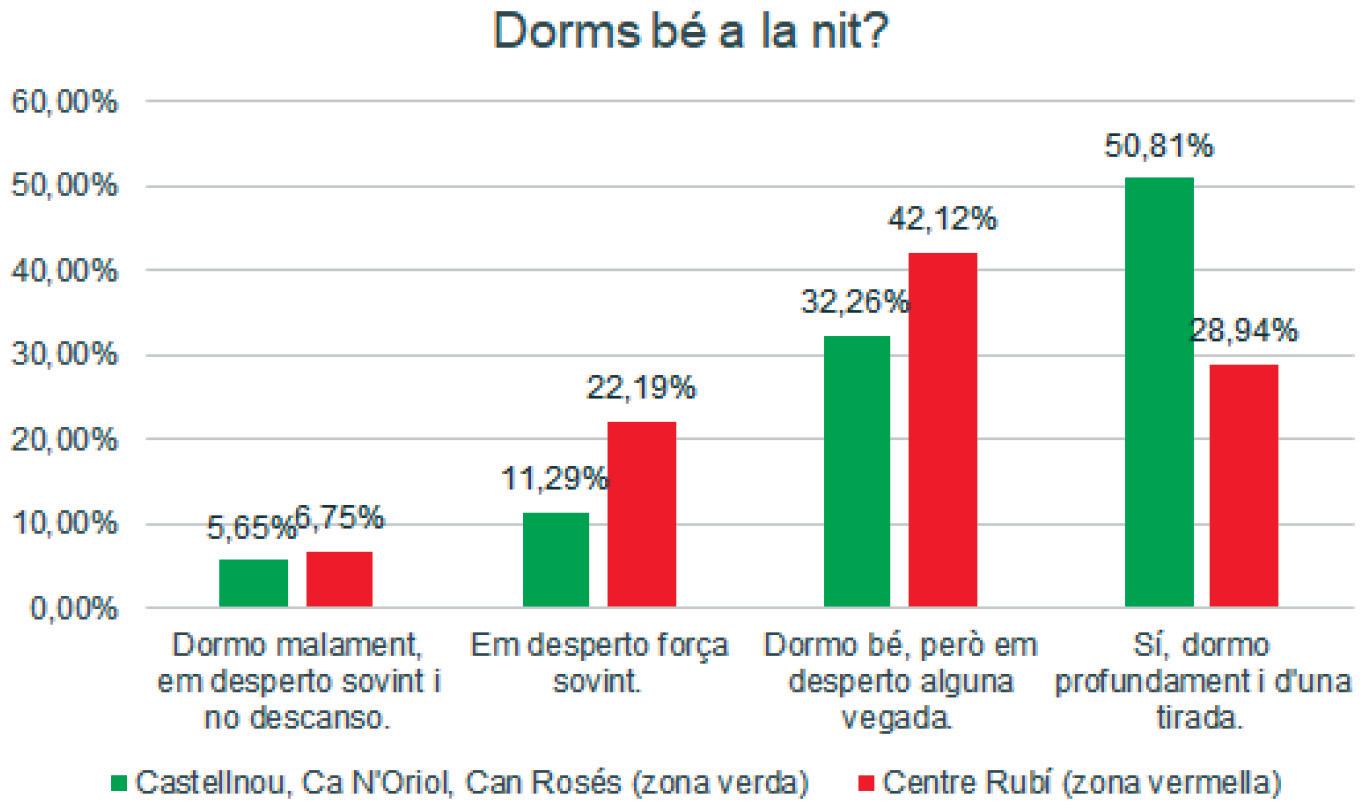
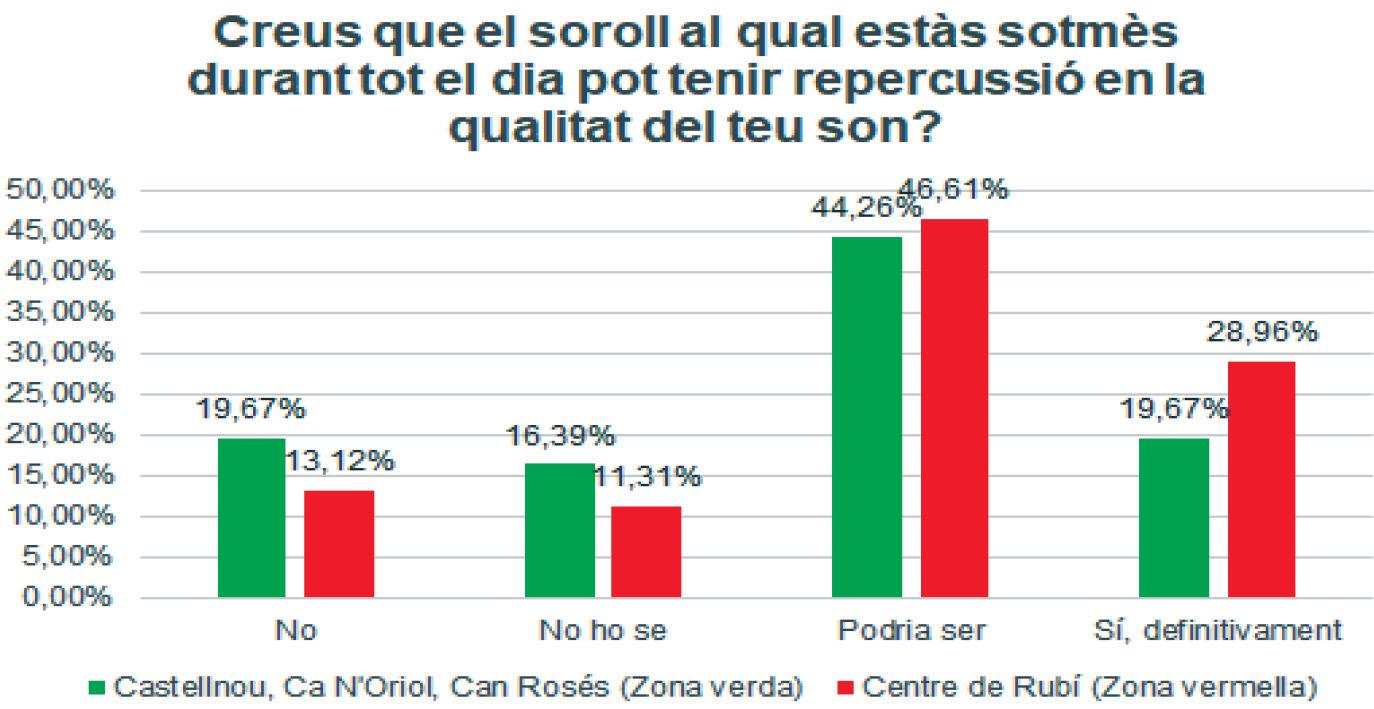
Figura8.Exemplesderesumsdelesrespostesaduespreguntes.

Contrastdeleshipòtesisiconclusions

Vamprojectaralapissarraelsgràficsfetsivamcontrastarlesnostreshipòtesis.Lesconclusionsprincipalsqueenvamextreuresónlessegüents:

‚ Lamajoriadelapoblaciótéconeixementssobreelsoroll,estàconscienciadaqueinflueixenelseubenestariassociaambelsorollalgunsdelsproblemesdesalutque pateix.

‚ Vampoderobservarque,comhavíemditenlesnostreshipòtesis,elcentredeRubíés onlespersonespateixenméselsproblemesquepodenserprovocatspelsoroll,toti quenohihaunagrandiferènciaamblespersonesqueviuenaCastellnou.

‚ Vamconstatarquetambéhavíemencertatal’horadedirquehihauriamésproblemespsicològicsquenopasfísics.ElquemésdestacavaeraquealcentredeRubíles personestenienmésproblemesal’horadedormiriestavenmésirritablesenalguns momentsdeldia.

Enferlaposadaencomú,ensvamadonarquehavíemd’haverfiltratlesdadesdelasegona preguntadelafigura7segonslesrespostesdelaprimera.

Dificultatsqueensvamtrobarenlasegonafase

Aquestasegonafasevafuncionarambforçaagilitat.Laprincipaldificultatvaser,comenla primera,quealgunalumneambpocinterèsenelprojectealentiaeltreballdegrupielbon funcionamentdelaclasse.

Propostesperdisminuirelnivelldesoroll

Finalment,ensvamatreviraferunespropostespertaldedisminuirelnivelldesorollala nostraciutat.Vamintentarposar-nosencontacteambl’Ajuntament,perònovaserpossible.Comaalternativa,hempublicatlapresentaciódelnostretreballalblogdel’escola.Les propostessónlessegüents:

1.Posarsenyalitzacionsaleszonesperavianantspersensibilitzarlapoblació.

2.Instal larpavimentsporosos,jaquelasevafuncióésabsorbirunapartconsiderablede l’onaacústica.

3.Ampliarl’illadevianantsielscaminsescolarsperrestringireltrànsitdevehicles.

4.FerservirRàdioRubí,el DiarideRubí ilarevista TotRubí perconscienciarlapoblació delsefectesdelacontaminacióacústicaidonarrecomanacionsperreduir-la.

5.Organitzarxerrades/tallersalesescolesperconscienciarelsnensenmatèriadecontaminacióacústica.

6.Incorporarcriterisacústicsenelplanejamentd’obresalaviapública.

7.Establircriterisdebonapràctica,pelquefaalsoroll,enl’organitzaciód’actesfestiusi culturalsal’airelliure.

Desprésd’haverguanyatelconcurscatalà,vaigpensarquepodríempresentareltreballiles propostesal’AjuntamentdeRubí.Perònoensvaserpossibleacausadelapreparaciódel treballperalafasenacionalilarectafinaldelcurs.

4.Presentacióalconcurs

Enelmomentenquèesdecideixpresentareltreballalconcurs,esfaunaselecciódelsalumnesquel’handepresentarseguintcriterisdedisposició,treballiinterèsdelsmateixos alumnesal’auladuranttotelprojecte.Ellímitd’alumnesvedonatperlesbasesdelconcursi malauradamentnoméspodenserunmàximdecinc.Finalment,elsalumnesseleccionatsvan ser:LauraAlbert,VíctorPinedo,MarGonzález,IreneGonzáleziEmmaOrtiz.Unavegadafeta laselecció,laredacciódeltreballques’haviadepresentaralconcurs,aixícomlesconclusions ireflexionsfinalsilapresentació,esvanfer foradel’horariescolar.Vamcrearungrupde Whatsapppercomunicar-nosdemaneramésefectivairàpida,vamcompartirunacarpeta deDrive,elsalumnesvantreballaracasaienalgunaaltrahoraqueelsvaigdeixardeles matèriesquefeienambmi,iensvamreuniral’escolaforadel’horariescolarentrecinciset vegadesperresoldredubtesiacabardedonarformaaltreball.

Durantlaredacciódeltreball, vamtenirencompteelsegüent:

‚ Fase 1:vamseleccionarlesdadesdelsalumnesquehavienrecollitmésdel70 %deles mesures.Vamrepresentaraquestesdadesenl’Instamapsque,comhemditabans,permetcrearmapesdigitalsambinformació.Perinserirdadesal’Instamaps,calfer-hoatravésd’unfulldecàlculExceloncalespecificarendiferentscolumneslaubicacióexactai lesdadesqueesvolenrepresentar(enllaçalgràficidadesengeneral).Apartirdel’eina, espodenimportaraquestesdades.Vamsituar-hielspuntsdelsalumnesseleccionats i,cadapuntconteniaelgràficdelsdecibelsmesurats(ambuncolordiferent,segonsla franjahoràriailesmesuresestadístiquescalculades);veg.www.instamaps.cat/visor.html? businessid=b099e4b7093f76d5bf574d1e26dc4893&3D=false:

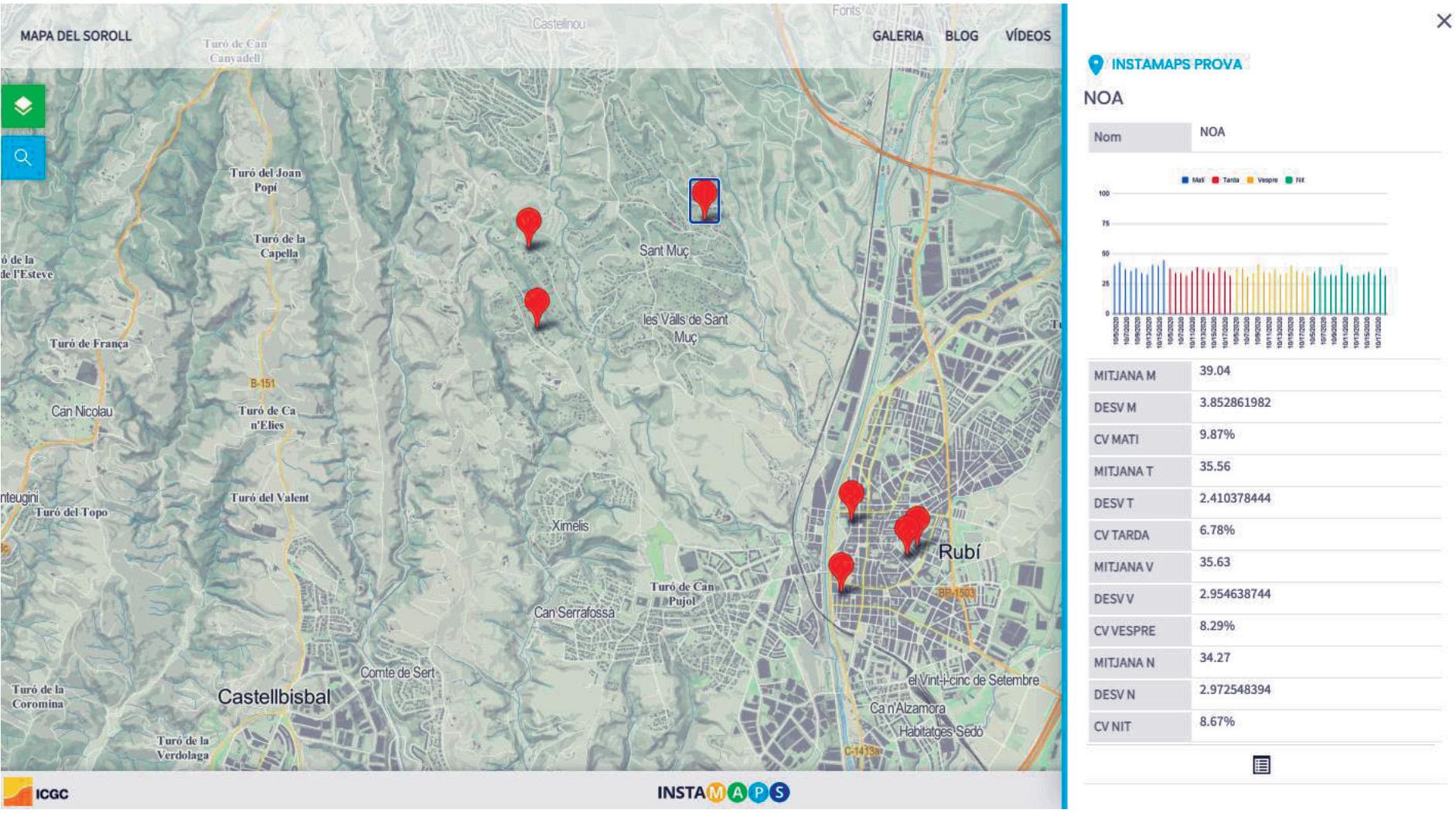
Figura9.Mapadigitalambleszonesestudiadesilesdadesrecollides.

‚ Fase 2:vamreferelsgràficsdelasegonapreguntaenfunciódelespersonesquehavien respostpositivamentalaprimerapregunta,cosaquevamobservarenlaposadaen comúenelmomentdeferelcontrastd’hipòtesisilesconclusions.

Elsalumnesvanrespondremoltpositivamentaaquestrepteis’hivanimplicarambmolta il¨lusió,totiquehivahavermomentsd’estrès.

EnelmomentdeguanyarelprimerpremidelPlanter,vamhaverdetraduireltreballalcastellàiprepararunvídeoqueexpliquéselprojecte.Elsalumnesesvandividirlafeinaihovan fertotforadel’horariescolar.LacomunicaciócontinuavasentperWhatsappivamferun parelldetrobadespervideoconferènciaperferelseguimentdeltreballiresoldredubtes,ja quetotsells,amés,vanestarconfinatspercontacteestretambmalaltsdeCOVID-19.

5.Unasorpresainesperada

Eltreballperprojectespotresultartanmotivadorquealgunsalumnespodenanarmoltmés enllàdel’esperat.Tantésaixíquetresdelesalumnesguanyadoresdelpremi,MarGonzález, EmmaOrtiziIreneGonzález,vansentirlanecessitatdecontinuartreballantenelprojectei crearunawebqueaniméslapoblacióengeneralaprendreconsciènciadelacontaminació acústica,prendremesuresdelsorolldelasevazona,fer-neunestudiestadísticdescriptiui publicaraquestainformacióenunmapa.Enaquestawebs’inclouenvídeosexplicatiusde coms’hadefercadapas.Usanimematotsaseguirelprojectealesvostresaules,acasa,amb elsamics,amblafamília...Aquíusdeixol’enllaçdelweb:https://soundedapp.wixsite.com/web site/tu-turno!

6.Conclusions

Elfetdetreballarl’estadísticamitjançantun projecterealfaquel’aprenentatgecobrimés sentitilidonaunvalorafegit.Ésfàciladonar-sequel’estadísticaésmoltmésquefergràfics ocalcularmitjanes.Enparticular,endestacariaelsavantatgessegüents:

‚ Ésunaprenentatgedinàmic,interdisciplinari,transversalicontextualitzat.

‚ Elsalumnesaprenenafer-sepreguntes,araonar,aferrecerca,aexplicarlainformació ilaimportànciademostrarlainformaciódemaneracorrecta,iautilitzareinesperferho.

‚ Elsalumnesaprenenaferservireinesdigitals.

‚ Elsalumnesaprenenatreballarengrup,aorganitzar-seiatreballarcol laborativament.

Arabé,calmillorarcertsaspectesperpodercontinuartreballantd’aquestamanera.Lescondicionsd’aquestcursnohanestatlesidònies,inonomésacausadelapandèmia.Engeneral, podemconclourequeestractad’unaestratègiadocentdifícildesosteniripoceficient.Algunsdelsaspectesqueenpodrienmillorarlescondicionsd’implementaciósónelssegüents:

‚ Treballarambgrupsreduïtsd’unnombrealvoltantdevintalumnes,otreballaramb trentaalumnesidosprofessorsal’aula.Ésmoltdifícilferunprojecteambtrentaalumnesal’aulaambdiferentsnivellsiunsolprofessor,quenopotatendretoteslesnecessitatsniassegurar-sequetotsassoleixinelsconeixementsmínims.Aixòvarepresentar undesgastimportantperpodertirarendavantelprojecte.

‚ Disposard’ordinadorsperacadaalumne,o disposardelasalad’ordinadors,iambuna bonaconnexióaInternet.

‚ Duratermeelprojectetotunequipdeprofessoratpercompartirl’excésdefeinaque significa,especialmentsiespresentaaconcurs.

Òbviament,aquestesmilloresrequereixenelsuportdeladirecciódelcentre.Enelmeucas,la satisfaccióésgranacausadelsresultatsobtinguts.Desprésdetotsaquestsanysduentatermeaquestsprojectes,peralpropercurshaquedatinstauradaunahorad’estadísticaacada grupde4td’ESOiladisponibilitatd’unaaulad’informàtica.Elqueencaranos’haaconseguit ésunareducciódelsgrupsicontinuemtreballantambtrentaalumnesal’aula.Tambévala dirqueelfetdepresentareltreballalconcurshasignificatunainversiód’horesiunesforç personalmoltimportant,ipotsernosempreestéladisponibilitatolavoluntatdefer-ho.Tot iaixò,continuodefensanteltreballperprojectesperquèpensoqueésmoltenriquidorper alsalumnes.Però,delamateixamanera,crecques’handemodificarlescondicionsambles qualsesfa.

Annex1.Infografiadelametodologiadelprojecte

Annex2.Planificaciódelessessions

Sessió

Descripciódelesactivitats

‚ Presentardeltreball,comtreballaremicoms’avaluarà

‚ MostrarelcursdeMoodleonhihauràtotelmaterialdisponible

‚ Presentarquèéselsoroll

‚ VisualitzarelmapadelsorolldeRubí

‚ Situar-sesobreelmapadeGoogleMapscreatespecíficamentperal projecteicompartitambtotselsalumnesatravésdeMoodle

‚ Trobar,cadascú,elpropicarrerianotarelnivelldesorollquemostra aquestmapaalpuntcorresponentdelGoogleMapsdissenyatperal projecte

‚ Respondreaunqüestionarisobrel’entornonviuen.

‚ Explicarlestaulesdefreqüènciesielsdiferentstipusdegràfics

‚ Instal larl’aplicaciómòbilDecibelX,explicar-neelfuncionamenti visualitzarelqüestionariquehand’ompliramblesmesurespreses

‚ ExplicarcomesfaungràficambExcel

‚ Iniciar,pergrups,l’estudid’unadelespreguntesdelqüestionari

Org.grup

Grupclasse

Grupclasse, treballindividual

Grupclasse, engrups

5 ‚ Acabarelsgràficsiposar-losencomú ‚ Formularhipòtesis Engrups

6 ‚ Explicarlesmesuresdecentralitzacióicomcalcular-lesambExcel Grupclasse, treballindividual

7 ‚ Explicarlesmesuresdedispersióicomcalcular-lesambExcel Grupclasse, treballindividual

8 ‚ Explicarcomsónlesdades,quantesn’hiha,quinserrorsconteneni comprovar-les Grupclasse

9 ‚ Treballindividualcadascúamblessevesdades Individual

10 ‚ Posarencomúelsresultatsambl’equipdetreballiarribaraunes conclusions Engrups

11 ‚ Posarencomúamblarestadelaclasse

12 ‚ Compararhipòtesisiarribaraunesconclusions

Engrups, grupclasse

13 ‚ Ferrecercasobrelesafectacionsdelsorollenlasalut.Ferhipòtesis delquesortiràalanostraciutat Individual, engrups

14 ‚ Prepararundocumentcompartitamblainformaciócercada. Engrups

15 ‚ Ferlapresentacióaclasseiformularhipòtesis

Engrups, grupclasse 16 ‚ Pensarpossiblespreguntesperal’enquestaicompartir-lesalPadlet Engrups

‚ Discutirsobrelespreguntesproposadesaclasseitriarlespreguntesi respostesques’inclouranenelqüestionari Grupclasse

‚ Repartirleszonesenlesqualscadaalumnehadeferlesenquestes

‚ Enviarl’enquestapercorreuelectrònic

‚ Calcularlagrandàriadelamostra

Grupclasse

19 ‚ Ferelgràficdelapreguntaquehaestatassignadaalgrup Engrups

20 ‚ Posareltreballencomúaclasse

21 ‚ Elaborarlesconclusions

Engrups, grupclasse

22 ‚ Elaborarpropostesperreduirelsnivellsaltsdesorollalanostra ciutat Engrups

Annex3.FormularisobreelnivelldesorollaRubí

https://forms.gle/RWdPELiEqxqVAXko9

Annex4.Qüestionari:elsorollafectalanostrasalut?

MireiaVinyolesSerra AulaEscolaEuropea

Av.MaredeDéudeLorda,34 08034Barcelona

mvinyoles@aula-ee.com

Resum Abstract

ElteoremadePickésunafórmulasenzilla quepermettreballarlageometria,la descobertaielgustperlesmatemàtiquesa primercopd’ull.L’activitatpreténfer descobriral’alumnatqueprovant,juganti conjecturantespodendescobrirpropietats taninteressantscomaralafórmuladel càlculdel’àreadepolígons(simples, reticulars),ipotenciaraixíladescobertaen lesnostresclassesdematemàtiques.El teoremadePickésunexempleperfectede simplicitat,d’apropamentaunes matemàtiquesque,sónboniques, agradablesidebontracte,nonomésperla sevasenzillesa.L’activitatconsisteixa deduirlafórmuladelteoremabuscant primerunpatróapartird’exemplesi desprésconnectantambsistemes d’equacionspertaldededuirlafórmula. Finalment,hihaunapetitareflexiósobre quèésunademostracióisobreelcamíque s’hadeseguirenlarecercad’unafórmula.

Pick’stheoremisasimpleresultthatallowsus toworkongeometry,researchaswellas enjoyingMathematicsataglance.Theaimof theactivityistomakestudentsdiscoverthat bytrying,playingandguessing,theycan exploresuchinterestingpropertiesasthe formulaforcalculatingtheareaofsimple reticularpolygonsinourMathclasses.Pick’s Theoremisaperfectexampleofsimplicityand beautyallowingeveryonetoexplore Mathematicsinaverypleasantway.The activityconsistsofdeducingthePick’s theoremformula.Firstly,bylookingfora patternusingexamplesandsecondly, connectingwithsystemsofequationsinorder todeducetheformula.Finally,weendupwith asmallreflectionaboutwhataproofisand whichpathhastobefollowedinorder tofindit.

1.Introducció

Quèvoldirbellesaenmatemàtiques?Quandiemqueunresultatésbell?Hardy[7][ 12]deia queelsentitdelabellesave,almenysenpart,delsentitdelasorpresa.Podemestar-hid’acordono,

peròlacaradesorpresaisatisfacciód’unalumnequandescobreixquelcom(enmatemàtiques,ésclar)notépreu!

Poincaré,d’altrabanda,deiaque«elcientíficnoestudialanaturaperquèésútildefer-ho, l’estudiaperquètrobaplaerafer-hoihitrobaplaerperquèésbell»[11].

Labellesanodeixadesersubjectiva,peròseguramenttotesitotsestaremd’acordqueel teoremadePickésundelsenunciatsméssimples,propersibonicsquehihaenlaliteraturamatemàtica,cosaqueelfairresistibleal’horadeprepararactivitatsal’aula.Amésde permetre’nstreballarladescobertad’unamaneramanipulativa,elteoremaenspermetactivarelpensamentmatemàticbuscantsolucions,formulantpreguntesipotenciantelcicle experimentació-conjecturació-generalització.Almateixtemps,enspermetconnectaramb diferentsconceptesestudiatsenelcurrículumtantdel’educaciósecundàriaobligatòria(ESO) comdelbatxillerat.

2.Oniquandescobrirelteorema

Elmomentoportúperferunaactivitatpotserunelementclaual’horad’aprofitarmillorel queelsalumnesenpodentreureoaprendre,jasiguiatalld’introducció,jasiguicomareforç d’algunconcepte,comaaplicacióocomaconclusiópertancaruntema.Comaprofessorat, nosaltreshemdedecidirsimostrarl’activitatiusar-lacomarecursenfunciódecomcreguem quepotsermésútilalsnostresalumnes.L’activitat(basadaenl’originaldelprojecteNrich [9])estàpensadacomaclausuradeltemadelssistemesd’equacions.L’alumnatnoconeix elteoremadePickiaixòhauriadepermetreenfrontar-nos-hisenseporiambganes,i,per tant,ladescobertaestàservida.Alhora,enspermetobrirnouscaminsdereflexió,com, perexemple,aprendreadiscernirentreelsconceptesdedemostracióidededucciód’un resultat.

Siformuleml’enunciatcomapregunta,podríemcomençar,perexemple,peraquesta: podem calcularl’àread’unpolígonsimplementcomptantpunts?

3.L’activitatpasapas

Primerdefinireml’espaiontreballarempertenirclarquintipusdepolígonsusarem,jaque nototssónvàlids.PresentemelmaterialobédemaneravirtualambGeogebra,obéde maneramanualambpaperillapis,obémanipulativamentambungeoplà,siésquedisposemd’aquestmaterialal’escola. Elprofessorattriacomferlapartd’experimentacióal’inici del’activitat.Històricament,nosaltreshemtreballatambpaperillapisenlaprimerasessió idespréshemintroduïtlatecnologia.Abordarunproblemaplasmantsobreunpaperquè estemfent,comestemtreballantionvolemarribar,ajudaaentendremillorl’activitatpera desprésserméseficientsal’horad’usarlatecnologia.Araéselmomentdeferelsgrupsde treballidesprésjapodremcomençar.Elnombred’alumnespergrupdependràdeladensitat delaclasse(habitualmentnosaltreshemtreballatambgrupsdetresoquatrealumnes).

Donadaunamalladepunts,tenimun polígon reticularsimplesipodemsituartotselsseusvèrtexsencoordenadesenteres(reticular)ielsseus costatsnos’intersequen,demaneraquedivi-

deixenelplaennomésduesregions,senseforats(simple).Aquestspolígonstenenpunts pPq en lasevavora(puntsperimetrals)isovinttenentambépuntsinteriors pIq.Lesfiguresespoden descriuredonant-neelspunts pP,Iq.Perexempleitalcommostralafigura1,elquadratvermellté comapunts pP,Iq“p4, 0q;eltrianglegris, p3, 1q;eltriangleverd, p5, 0q,il’hexàgonblau, p6, 4q

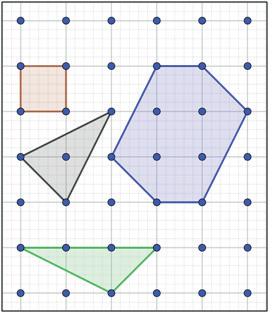
Elnostreobjectiuseràdescobrirunafórmulaquecalculil’àrea pAq d’aquestspolígonsusant elspuntsperimetrals pPq ielspuntsinteriors pIq.Peraixònecessitemprimerestudiaruna micaelproblemaianarreflexionantsobrecompodemtrobar-nelasolució.Aradeduiremla fórmuladelteoremadePick.

1. Reprodueixenungeoplàoambpaperillapis, elspolígonsdelafiguraifes-nedenous.

Comtotproblema,primers’had’analitzar,provar,jugarideixarquel’alumneesfamiliaritzi ambelquevolemestudiar.Engrups,podenreproduirelspolígonsquemostralafigura 1 i fer-nedenoustalcomveiemenlafigura 2.

Enlespreguntessegüentsespreténqueelsalumnesjuguinambelsconeixementsqueja tenenicalculinlesàreesdelamaneraquecreguinmésconvenient.Entenenprouambsaber calcularl’àread’unrectangleil’àread’untriangle.Nocalquehaginfetàreesdepolígons regulars,siestemenuncursdesecundària.Peralsalumnesdebatxillerat,hauriadeserbufar

Figura1.Polígonsreticularssimples.

Figura2.Alumnestreballantal’aula.

iferampolles.Perexemple,enl’hexàgonblaudelafigura 1,podencalcularl’àreadelquadratqueelcontéirestar-hil’àreadelsquatretrianglesdelavora.Perpoderferelscàlculs necessitensaberenquinesunitatstreballemilamidadelagraelladepunts.Femunaposada encomúiacordemqueladistànciaentredospuntshoritzontalmentoverticalmentésd’1 unitat.

Amés,potenciemunamaneraeficientdemostrarelsresultatsobtingutsusantunataulade valors(taula 1)perpoderferl’anàlisipertinent.

Taula1.Tauladevalorsdelsdiferentspolígonsusats.

Quadrat 401 Triangle 503/2

2. Cadafiguraenglobaunaàrea pAq delagraelladepunts.Calculal’àreadelesquatrefigures explicantelmètodequeuses.

3. Dibuixaunaretículaambméspolígonsienunatauladevalorsapunta’nelspuntsperimetrals pPq,elspuntsinteriors pIq ilesàrees pAq

Recordemqueelsalumnesestantreballantengrups.Aquíelprofessoratpotmoderarl’activitat i,perexemple,suggerirquecadagrupsecentrienuntipusdepolígon:elgrup 1 treballaambdiferentstriangles,elgrup 2 treballaambdiferentsquadrilàters,elgrup3treballa ambdiferentspentàgonsiaixísuccessivamentdepenentdelsgrupsquetinguem.Aixòfarà quealprincipiesconcentrinnomésenunafiguraqueelsmotiviielsdonaràseguretatper amésendavant,quanhagindecol laborarentreelsgrupspertaldecontinuarconstruint coneixement.

Abansdeseguiravançant,lapreguntanúmero4preténserunaparadasaludableperferque elsalumnesraoninsobrecomhemconstruïtelspolígonsi,sihohanfetaleatòriament,intentinbuscaralgoritmespercrearnousexemples,jaquedesprésentretotselsgrupshaurem deferunatriadequinsexemplesdepolígonssónmésconvenientspertreure’nconclusions iseguirinvestigant:

4. Reflexionemarasobrequintipusdepolígonshemusatiperquè.Hohasfetdemanera aleatòria?Haspensatalgunaestratègia?Suggeriments:

a) Sideixemelspuntsreticularsfixos pPq iincrementemen `1 elspuntsinteriors pI ` 1q, comcanvial’àrea pAq?

b) Siaugmentemelspuntsreticulars pP ` 1q ideixemfixoselspuntsinteriors pIq,com canvial’àrea pAq?

c) Quantesfiguresdiferentstenenlamateixaàrea?(Posadaencomú).

d) Feslestevespròpiespreguntes.

Figura P I A

Engeneral,alsalumneselscostaferunareflexiósobrelafeinafeta.Noestanacostumatsa pararipensarsielqueestanfentésadientono.Peraixò,aquestaésunapartdel’activitat queelscostaiquenosabengairecomabordar.Aquíelpaperdelprofessorattornaaser crucialperajudar-losaaprendreaaprendreiaserautocríticsamblapròpiafeina,aixícom perposarencomúlafeinadelarestadecompanys.

5. Trobalarelacióquehihaentrelestres magnituds:A,PiI.

a) Comcreusquehadeser?

b) Creusquel’àrea pAq ésuna funció quedepèndelspuntsinteriors pIq idelspuntsreticulars pPq?Perquè?

Enaquestapreguntajacomencemausartemesexplicatsaclasse,comaralaideadefunció ilademagnitud.Quèesperemcomarespostaalaprimerapregunta?Doncsqueresponguin«unarelacióocombinaciólinealdelestresmagnituds».Se’lshad’incentivarperquè conjecturin,perquès’arrisquinadonarunarespostasenseimportarsiéslacorrectaono, perquèintentin,ambelsexemplescalculatsalataula,deduiralgunpatróoalgunarelació entrel’àreaielsdiferentspunts.Uncophanfetunaconjectura,handecomprovar-laperals valorsdelataula,isovintpassaquehihaalgunvalorquenolacompleix.Aquíésimportant recordarquearaestanfentd’investigadorsiquenopassaressinolaveuen.Elqueésrealmentrellevantésquehointentinicol laborinentreells.Ésindispensablequeelsdiferents grupsd’investigaciófacinunaposadaencomúpercomprovarsilasevafórmulaéscertao noperalsexemplesd’unaltregrup.Recordemquecadagruphatriatpolígonsdiferentsi quesibusquemunafórmula,hadesercertaperaqualsevoltipusdepolígonsemprequees compleixinlescondicionsditesalprincipidel’activitat.

Segonselconeixementprevidelsalumnes,lasevarespostaacostumaaserdeltipus A “ aP ` bI is’oblidendeposarquehipothaverunaconstantsumantalfinal.Aquítornaaentrar enjocelprofessorat.Quèésunarelaciólinealentrevariables?Quanunarelaciónoéslineal? Quinpaperhitéla c?Uncophemtrobatquelarelaciótélaforma A “ aP ` bI ` c,arahem detrobarelscoeficients ab i c.

6. Usantlesdadestrobadesanteriormentalestaules,intentemaconseguirtrobara,bic.

a) Quinmètodeestudiataclassepodemusar?

b) Quinesdadesobtingudesenspodenserútils?

Normalment,ungrupnombrósd’alumnesresponenaaquestapreguntafentlaconnexió ambsistemesd’equacions,isovints’emocionenpensantquehantrobatlamanera!D’altres senzillamentsegueixenelspassosdelsmésaventurersihiestand’acord.Calferunaposada encomúialtrecoprumiarsobrequantesequacionsnecessitemicomhemdetriar-lesper podertrobarlasolució.

Podemaprofitaraquestpuntperaprofundireneltemaiestablirladiferènciaentre paràmetres i variables.Filosofantunamica,encaraquenoméssiguiatallintroductori,podem aprofitarperexplicar-neladiferència;ésadir,elscoeficientsfixosperòdesconeguts abi csón elsquerelacionenlavariabledependentA(àrea)amblesvariablesindependents P i I.Amés, podemajudaraassimilarlaideadefunciórecordantqueacadapolígon,i,pertant,acada parell pPIq,licorresponunaúnicaàrea.

Taula2.Paràmetresivariables.

Paràmetres

ab i c A P,I

Ensserveixenperrelacionarlesvariables ElseuvalordepèndePiI Elsdonemelvalorquevolem

Tambépodemaprofitaraquíperparlarquenotot,nienlavidanienlesmatemàtiques,té unasolucióúnica:devegadesentémoltesidevegades,finsitot,noenté.Inopassares.Així posemlallavorperquè,quanarribinalbatxillerat,puguintreballarladiscussiódesistemes d’equacions(compatiblesdeterminats,compatiblesindeterminatsiincompatibles).

7. Escriuelsistemad’equacionsiresol-lousantelmètodequecreguismésconvenient.

Uncopcadagruphatriatlessevesequacions(nohandeserlesmateixesperatotselsgrups), japodemusarelquehemaprèsaclasseiresoldreelsistematrobantelsvalorsquevolíem peralafórmula.Tambépodemusartotslesmateixes,peròésmésinteressantferlareflexió que,encaraquenousemlesmateixesequacions, lasoluciódelsistemapotserlamateixa. Perexemple,dosgrupsdiferents vantriarlesequacionssegüents: Grup 1:3 “ 6a ` 1b ` c; 2 “ 4a ` 1

Evidentment,ambdósvanarribaralamateixasolucióperalsparàmetres.Ésimportantque cadagruptriïiqüestioniquindelsmètodesexplicatsperresoldresistemesliésmésútilper alseusistema.Normalment,lesvegadesque hemusataquestaactivitatasecundàriaera ambalumnesquenoméshavientreballatsistemesdeduesequacionsambduesincògnites i,pertant,elprimerdilemaera:comhofaremaraqueentenimtres?Éshabitualquese lesempesquintotssolsperresoldre-hosihandutatermeunabonatriadelesequacions delsistema.Aquestanovarevelacióelsencoratjaaseguirendavant.Aquestéselmoment d’empoderar-losiferquesesentininvestigadors,quegaudeixindeladescoberta.Evidentment,nototselsalumnesreaccionenigual,peròaalgunsse’lsil¨luminalamirada,comdient «Eureka,hemdescobertunafórmula!».D’altresesquedenpassiusis’hoprenencomuna activitatmés:«Miraquebé,unaaltrafórmulaperaprendre!».Enambdóscasos,però,queda unamiquetadesatisfacció.

Enaquestpuntdel’activitat,quanjahandescobertlafórmula,podemserunamicamés formalsienunciarelteoremadonantpesalacomunicaciómatemàtica.

8. ArajapodemenunciarelteoremadePick :

Teorema(Pick,G.) SiguiPunpolígonreticularsimpleambvèrtexsquetenencoordenadesenteres.SiPéselnombredepuntsentersquehihaalavoraiIéselnombredepuntsentersquehiha al’interiordelpolígon,llavorsl’àreadelpolígon,A,espotcalcularamblafórmulasegüent:

Unteoremaésunaparaulaqueenmatemàtiquesusemmoltesvegades,peròelsnostres alumnesdevegadesnotenengaireclarquèsignifica.Quèésunteorema?Qualsevolenunciatmatemàticpotserunteorema?Aleshorescomhodistingim?Sinotédemostració,no ésunteorema?Habitualmentesdiuqueenmatemàtiquesnoestemsatisfetsd’unresultat finsquenotrobemunademostracióqueelcertifica.Nosaltreshemfetunademostració,una comprovacióounadeducció?Nohadeferporintroduirlaideadequèéselquehemfetiaixí poderenllaçaramblanecessitatd’unademostracióqueverifiquiquelapropietatenunciada pelSr.Pickéscertaperatotpolígonreticularsimple.Podemaprofitarperbuscarinformació aInternetsobrequèésunteorema(proposicióquehadeserdemostradademaneralògicaa partird’unaxiomaod’altresteoremes)isobreperquès’anomenaaixí.Aixòpotdonarpeua, mésendavant,podercontinuarambaquestteoremaiferlademostracióenunaaltraactivitat usant,perexemple,lasumad’anglesinteriors[4].

9. Reflexionem:

a) Qualsevoldadahaservitperresoldreelproblema?

b) Quinéselnombremínimd’equacionsquehasnecessitat?

c) Creusqueaixòésunademostraciódelteorema?Fesunacercadelsignificatdeteorema.

d) Creusqueésunresultatbonic?

Finalment,atalldeclausuradiscutimsobrelesreflexionsquehemanatfentalllargdel’activitati sobrecomhohemanatfent.Aixòenspermetconvergircapalaideaquelesmatemàtiques podensersorprenents,divertidesiboniques.

4.L’activitatal’auladesecundària

Passardelateoriaalapràcticaéssemprerefrescant.L’activitatestàpensadaperserfetaen duessessionsobéenunasessiódedueshores.Enlaprimerapart,mésjuganera,elsalumness’organitzenengrupsdetreball,busquenelspolígonsqueensservirand’exempleivan prenentlesdadesquese’lsdemanen.Usantaquestaactivitat,tambéelshemproposatque comencinaescriure-hoenundocumentcompartitielsexpliquemcominserirequacions, imatgesitauleseneldocument.Peralamajoriaéslaprimeravegadaquefanuntreballde matemàtiquesambordinador,fetqueelsmotivaaseguirambl’activitat.Històricament,hem arribatnomésfinsalapregunta5,demaneraquequedaensuspens,entresessions,quinaés lafórmulaquerelacional’àreaielspunts.Algungrupjacomençaaferlessevesconjecturesi abuscarmésdadesentreelscompanysperpoderveureunpatró.

Lasegonapart,mésdedescobertaireflexió,ésonfemlaposadaencomúideduïmlafórmula delteoremadePick.Aprofitemperincidirenlesconnexionsquehemhagutdeferservir entrediferentscontingutsdel’assignatura,comaraelsconceptesdefunció,equació,variable,paràmetreisistemad’equacions.Amés,tambéincidimenladimensiódecomunicació irepresentació,jaqueelfetd’haverd’escriurel’activitatenundocumentdigitalcomporta implícitintentarcomunicardemaneracorrectaelquehemanatdescobrint,jasiguinles fórmules,jasiguinlesexplicacionsdelraonamentseguitperarribaralresultatfinal.

L’últimapreguntasurtgairebésensevoler:heutrobatbonicaquestresultat?Lesmatemàtiquespodenserboniques?Iaquíeldebatestàservit.Lamajorianos’hanplantejatmaiabans silesmatemàtiquespodenonoserboniques:sóniprou.Acabem,doncs,reflexionantsobre labellesa.

5.L’activitatal’auladebatxillerat

Engeneral,lamateixaactivitatespotportaraunaauladebatxilleratsensehaverdecanviar gairecoses.Sí,però,queeltempsdedicatal’activitatesredueixdràsticamentielsobjectius internscanvien.Arapodemanarmésenllàiusarl’activitatcomaexerciciintroductoridel treballderecercaicomençaraplantejarpreguntessobreperquèfuncionaunafórmulaoper aqui(enaquestcas,peraquinspolígons)funciona.Ladeducciódelteoremaés,engeneral, moltmésràpidainormalmentaprofitenelmètodedereducciódeGaussperresoldreel sistema.Aquísíquepodemferèmfasienelsignificatdesistemacompatibledeterminat, sistemacompatibleindeterminatisistemaincompatible,al’horad’escollirquinesequacions usem.Nosaltresvolemquesiguicompatibledeterminat;pertant,novolemdependències entrelesequacions.Amés,podemreflexionarsobreelsdiferentssistemesd’equacionsquan apareixenalaclasseiveurequeelssistemessónequivalentsencaraquenousemexactamentequacionsidèntiques.UsantelmètodereducciódeGauss-Jordanpodemdemostrar quediferentssistemessónequivalents; ésadir,quetenenlamateixasolució.

Uncopformalitzemelteorema,podemderivar-locapatemesderecercadiferents.Perexemple,enladiscussiósobrequèésunademostració,podemveurequinstipusdedemostració hiha(directes,percontradicció,perinducció...)iambquinsconceptesiideesexplicadesen l’assignatura,onoexplicades,espotrelacionar.Lapreguntaésinevitable:potserviraixòper auntreballderecerca?Doncspotsersí.

Araéselmomentdepotenciarlarecercad’informaciósobreeltematractatireflexionar sobrequinesreferènciespodenservàlidesonoperauntreballd’investigació.Aquíentra enjoclabibliografiaadjuntadaalfinaldel’activitat,queelsalumnespodenconsultaratall introductori.L’excusapotserbuscarmaneresdiferentsdedemostrarelteorema.Evidentment,notrobaranenllocalgúresolentunsistemad’equacions,jaquenosaltresnohemfet capdemostració.Però,perexemple,enl’article[12]hitrobaranduesmaneresdiferentsde l’habitualdedemostrarelteorema.Laprimeranomésusaelsanglesdelpolígonilasegona jahorelacionaamblateoriadegrafs.

Aixòenspermetrelacionaruntemaque apriori nosemblacomplicatambmoltesaltresbranquesdelamatemàtica,fetquedonaràllocanovespreguntesianovesinvestigacions,com arasielteorematambééscertsiusemaltrestipusderetícules,compodrienserlatriangular ol’hexagonal.

Perexemple,podemtrobarrelacionsambeltemadelessuccessions,comaralessuccessions deFarey[2],ambpolígonsdeJordanilafórmuladeltopògrafdescobertaperGauss,on s’usentambédeterminantspercalcularàreesdepolígons[8],oelteoremadeMinkowski,per quisiguimésteòric[6].

Figura3.ArbrerelacionaldePick.

Aquestapodriaserlaprimeraexcusaperveurecoms’hadetriareltemadeltreballderecerca. Ésinteressantmostrarlesnovesbranquesenformadeconnexions(figura3)perdescobrir quepodensorgirdelaideaoriginaldelteoremadePickiferveureal’alumnatqued’una ideaparticulariconegudase’npottreuremoltdesuc.Tambépodemensenyarunexemple detreball,comara[5].

Fentúsd’unadelesfrasescitadesa[1],aquíéson«unprofessordonaunamà[...]obreuna ment[...]itocauncor».Potserenl’activitattenimunaprobabilitataltadepodertocaraquest coriferquel’alumnedescobreixilabellesaquehihaenaquestresultatmatemàtic,obrir-lila portapergaudirdelesmatemàtiquesiguiar-loperferunabonainvestigació.

6.Unamicad’història

Acostumaasermoltenriquidorperalsalumnesconèixerunamicalahistòriadelteoremai delapersonaqueelvadescobrir.Unapetitaexplicació quenormalmentfemdemanera oral sobrelapocaimportànciaqueesvadonard’entradaalteoremadePickensserveixper veureque,devegades,investigacionsquemésendavanthanestatimportants,alprincipivan serpocvalorades.Aixòacostumaapassarenelmóndelesmatemàtiques,onaportacions quesemblaquenoportinenlloc,ambelsanysesdevenencrucialsperamoltesbranques, disciplinesiaplicacions(ono)enlavidaquotidiana.

Algunsexemplesd’aplicacionsdelteoremadePickpodenser:calculardemaneraràpida l’àread’unaregiódebosccremadaapartird’imatgesviasatèl¨lit,oveurequeésimpossible construiruntriangleequilàterenunagraelladepuntsenters.

Pelquefaalasevavida,segonsConnor[3],GeorgAlexanderPickvanéixerenunafamília juevael 1859 aViena(Àustria).Vaentraralauniversitatambsetzeanysiesvagraduaren EstudisdeMatemàtiquesiFísicaalaUniversitatdeViena.Uncopfetelseudoctorat,va anaraPraga,onexercídeprofessor.Vaferrecercaendiferentsàreesdelesmatemàtiques, comaraàlgebralineal,geometria,funcionsambvariablecomplexaogeometriadiferencial, entred’altres.AquívaconèixerAlbertEinsteinivaviurefinsqueelsnazis,quanjatenia vuitanta-dosanys,elvanempresonaridestinaralcampdeconcentraciódeTheresienstadt, onvamorir.

El«famós»teoremavaserpublicatperprimercopel 1900 enundiaritxec,dinsl’articletitulat «GeometrischeszurZahlenlehre»(«Resultatsgeomètricssobrelateoriadenombres»)[10]. Ningú,però,novafer-necasinovaserfinsal 1969 queunmatemàticpolonès,H.Steinhaus, enelseullibre MathematicalSnapshots [13],vaesmentar-loidescobrir-loatotalacomunitat iesvapopularitzar.

7.Anàlisidel’activitat

Hebasatl’anàlisienlespreguntesquepodenservird’indicadorsdelnivellderiquesacompetenciald’unaactivitat[14].LadescobertadelafórmuladelteoremadePickenspermetusar coneixementsjaadquirits,comaralaresoluciódesistemesd’equacions,enuncontextque apriori nosemblaquetinguicapmenaderelació.Ensajudaarelacionarcampsdiferentsde

lamatemàticausantalhoraelsconceptesdefunció,variableimagnituddinsd’unproblema meramentgeomètriccoméseldelesàreesdelspolígons.L’activitatespotdesenvoluparde diferentsmaneres:usantlatecnologia(GeoGebra)ousantmaterialmanipulatiucomarael geoplà,cosaquefal’activitatmoltatractivaperal’alumnat.

Pelquefaaestimularlacuriositatdelsalumnes,calqueelprofessorats’impliquienl’activitat ielsguiï.Altrament,esdesanimenquansesentenperdutsinosabencomseguir.Elpuntclau del’activitatésaconseguirquetriïnbéelsexemplesiqueellsmateixos,totdiscutint,facinla connexióambelssistemesd’equacions.Aleshoresésquansesentensatisfetsitenenganes d’arribarfinsalfinal.Elfetd’haverdecompartirdadesentreelsgrupsid’haverdeferuna posadaencomúpertirarendavant ésunacosaquetambéelsmotiva.

Hand’entregarundocumentdigitalamblesrespostesalespreguntesfetesdurantl’activitat ionhand’aprendreainserirequacions,taulesifigures.Tambéhihad’haveralgunapetita explicacióoreflexiósobrecomhananatresolentlesqüestionsproposades.

Enelcasdelbatxillerat,hand’aprendre,amés,abuscarinformació,acitar-lacorrectament iaanalitzarcomescriuredemaneraadientunarticlecientífic.Lafidel’activitatpreténser l’inicidelarecercad’untemadematemàtiquescomatreballderecercaperalquihiestigui interessat,ésclar.

Percompletarl’activitat,potserseriaboqueelsmateixosalumness’autoavaluessinseguint unarúbricafixadapelprofessorat.Normalment,quanenunaactivitatellsmateixos(engrup) s’hand’avaluar,acostumenaserfinsitotméscríticsqueelquehopodríemsernosaltres,iés aleshoresquans’adonendecomhanfetlescosesiacabendeconsolidarelsconeixements adquiritsobédescobreixenquèéselquenoacabend’entendre.Enambdóscasos,aquest seriaunbonfinalperalsalumnes.Eltemps,però,moltesvegadesésor,iaixòimplicariauna tercerasessióquenotenim.

Nopodiaacabarsenseferreferènciaalasorpresaquerepresentaperal’alumnatelfetde descobrirquelesmatemàtiquestambéespodenadjectivarcomaboniques.Elsresultats matemàtics,comelsdelspintors,elsmúsicsoelspoetes,podenserbonics;lesidees,comles notes,elscolorsolesparaules,espodencombinardemaneraharmoniosapercrearbellesa. Enelnostrecas,hempogutgaudirdelabellesamatemàticaencriptadaenlafórmuladel teoremadePick.

Referències

[1]Alsina,C.;Aubanell,A.;Burgués,C.(2019). Tresprofessorsdematemàtiques:Comferestimariaprendrebélesmatemàtiques.Col¨leccióReferents.Barcelona:RosaSensat.

[2]Amen,J.(2006).FareySequences,FordCirclesandPick’sTheorem.Lincoln:Universityof Nebraska(MATExamExpositoryPapers, 2).https://digitalcommons.unl.edu/mathmidex ppap/2 .

[3]O’Connor,J.J.;Robertson,E.F.(2005). GeorgAlexanderPick.https://mathshistory.st-an drews.ac.uk/Biographies/Pick/.

[4]O’Connor,J.J.;Robertson,E.F.(2013). TheHistoryBehindPick’sTheorem.SchoolofMathematicsandStatistics.SaintAndrews(Escòcia):UniversityofSt.Andrews.

[5]Conover,B.;Marlow,C.;Neff,J.;Spung,A.(2013). Pick’sTheorem. Math445Spring.Projectefinaldecarrera.

[6]Garbett,J.(2010). LatticePointGeometry:Pick’sTheoremandMinkowski’sTheorem. Senior ExerciseinMathematics.https://web.archive.org/web/20170829044759/http://docu ments.kenyon.edu/math/GarbettJSenEx2011.pdf.

[7]Hardy,G.H.(1940). Apologíadeunmatemático.Cambridge:CambridgeUniversityPress.

[8]Kowalski,J.M.(2017). RecurrentThemeofPick’sTheorem. arXivpreprintarXiv:1707.04808. [9]Nrich. Pick’stheorem. UniversityofCambridge.https://nrich.maths.org/1867.

[10]Pick,G.A.(1900).«GeometrischeszurZahlenlehre(Geometricresultsonnumbertheory)». SitzungsberichtedesDeutschenNaturwissenschaftlich-MedizinischenVereinsfürBöhmen «Lotos»inPrag 19 (1899),S.311-319.

[11]Poincaré,H.(1952). Scienceandmethod. NovaYork:Dover.

[12]RamanSundström,M.;Öhman,L.-D.(2011).«TwobeautifulproofsofPick’stheorem». A: ProceedingsofSeventhCongressofEuropeanResearchinMathematicsEducation.Rzeszow:UniversityofRzeszow,p. 224-232.http://urn.kb.se/resolve?urn=urn:nbn:se:umu:di va-38363.

[13]Steinhaus,H.(1969). MathematicalSnapshots.Oxford:OxfordUniversityPress.

[14] Creamat.Preguntesquepodenservird’indicadorsdelnivellderiquesacompetenciald’una activitat. Barcelona:GeneralitatdeCatalunya,Departamentd’Educació.http://xtec.gen cat.cat/web/.content/alfresco/d/d/workspace/SpacesStore/0039/25c246d5-835c-427f9f87-68bdfc9d78a3/indicadors_competencials.pdf.

Aportacionsmatemàtiques alt-empordaneses delsegle XX1

LluísSabaterAnticó

Professordematemàtiquesal’InstitutdeLlançà lsabate1@xtec.cat

Resum Abstract

Siduranttotalahistòriafinsalsegle XX és difíciltrobarnomsiobradematemàtics catalansdestacats,alsegle XX hihahagut, ambeldesenvolupamentdelsmitjansde comunicació,lesnovestecnologiesiels canvissocials,moltamésactivitat matemàticaaCatalunyai,concretament,a l’AltEmpordà.Així,enelmóndeles matemàtiquessónreconeguts internacionalmentFerranSunyeriBalaguer iEduardoCasas-Alvero,itambéalmónde l’ensenyamentaCatalunyaésreconegut SimóBoschEstany,ial’AltEmpordàés reconegutFredericMacauiVilar.Enaquest articleesparlad’aquestsquatre alt-empordanesosilessevesaportacions,i d’altresquetambéhantingutimportància enlasocietatalt-empordanesadelsegle XX.

Introducció

Throughouthistory,untilthe20thcentury,itis difficulttofindnamesofprominentCatalan mathematiciansandtheirwork.However,in the20thcentury,withthedevelopmentofthe media,newtechnologiesandsocialchanges, therehasbeenmuchmoremathematical activityinCatalonia,andspecificallyintheAlt Empordà.Thus,FerranSunyeriBalaguerand EduardoCasasAlveroareinternationally recognizedintheworldofmathematics,and SimóBoschEstanyisalsorecognizedinthe worldofeducationinCatalonia,andintheAlt EmpordàisrecognizedFredericMacauiVilar. ThisarticletalksaboutthesefourAltEmpordà peopleandtheircontributions,andothers thathavealsobeenimportantintheAlt Empordàsocietyofthe20thcentury.

Lamatemàticaésunadisciplinatradicionalmentpocapreciadaentrelagent,quelatroba difíciliavorrida.Nomésunsquantsentremoltshitrobenunabellesaounautilitatquefaque hidediquinbonapartdelasevavida,delasevaactivitatquotidiana.Aixòpassaarreudel mónitambé,concretament,al’AltEmpordà.

1.BasatenelTreballdeRecercadeBatxilleratdelasevafillaRosaSabaterRojas.

Aquestfetesveufinsitotenlatriadelstreballsderecerca(TdR)delsalumnesdebatxillerat, jaquesónpocselsqueescullenuntemarelacionatamblesmatemàtiques.Aquestarticle esbasaenelTdRambelmateixtítolfetperRosaSabaterRojas,estudiantdesegondela dobletitulaciódebatxilleri baccalauréat (Batxibac)del’InstitutLlançà,enelquals’hafetun estudid’aquestsalt-empordanesosdelsegle XX ilessevesaportacions(nonomésenelmón delesmatemàtiques,sinó,comveurem,tambéenlasocietatalt-empordanesa)totseguint elfildelllibre Santaló,Sunyer,DouiTeixidor:quatredestacatsmatemàticsgironinsdeladècada 1911-1920 (Reventós etal., 2012).

Aquestarticlenopretén(nitampocelTdResmentat)analitzarmatemàticamentambtotsels pèlsisenyalslesaportacionsd’aquestsalt-empordanesos(entrealtrescosesperquèelseu estudiilasevaanàlisijaestanfetsenllibres i/orevistesmatemàtiques),sinónomésdonar-les aconèixeridestacarlasevaimportànciaiutilitat,alhoraquetambéesvoldestacarlafaçana humanad’aquestspersonatges,lesrelacionsentreellsiamblasocietat,lasevainfluència.

PerferelTdR,l’autoravaentrevistarEduardoCasasAlvero,l’únicqueencaraésviu,ialtres matemàticsqueelshaguessinpogutconèixer oqueenconeguessinlavidaiobra,iquesón elssegüents: ManelCastelletiSolanes (nascutaBarcelonael 1943,directordelaFundació FerranSunyeriBalaguer,catedràticemèritdelaUniversitatAutònomadeBarcelona,Creu deSantJordi 2006,MedallaNarcísMonturiol 1991), AntonAubanellPou (nascutaBlanes el 1954,catedràticdesecundàriaimembredelCentredeRecursosperEnsenyariAprendre Matemàtiques[CREAMAT],harebutelreconeixementLaDonaMarineradel’Ajuntamentde LloretdeMaritambédiversospremisd’àmbit europeu,ivaconèixeripresentarambSimó Boschl’activitatMatemàgiques,organitzadapelbiòleginaturalistaJosepMariaDacostasobrelafórmuladeSimóBoschielteoremadel’EmpordàdeFredericMacau), SebastiàXambó Descamps (nascutaVilallongadeTerel 1945,catedràticemèritdelaUniversitatPolitècnica deCatalunya,comissaridel’exposició«Imaginari»del 2011 al 2013,medalladelaReialSocietatMatemàticaEspanyolael 2019 iMedallaNarcísMonturiolel 2020,entrealtresmèrits,ha estatcompanydefeinad’EduardoCasasAlveroijuntshanescritllibresdegeometria)i Josep MariaLluchLuis (nascutalaSeud’Urgellel 1956,secretariiprofessordel’InstitutRamon Muntaner,onhatreballatmésdetrentaanysionvacoincidirambSimóBosch).

Breuressenyahistòricadelesmatemàtiquesfinsabansdelsegle XX als PaïsosCatalans

RebuscantperInternet,lesdadesquetenimsobreaportacionscatalanesalesmatemàtiques finsabansdelsegle XX sónbenpoques:

‚ AbrahamBarHiyya(s. XII),barcelonítambéconegutcomaSavasorda,fouautordenombrosostractatsiobresmatemàtiquesquecontribuïrenaladifusiódelesmatemàtiques al’Europamedieval.Treballàsobretotl’àlgebraitambévaescriureelllibre Geometria pràctica.

‚ AbrahamCresques(s. XIV),mallorquí,fouuncartògrafque vacalcularlacircumferència delaTerraambunerrordenomés4.000 kml’any 1375.

‚ FrancescSantcliment(s. XV),barceloní,fouautorel 1482 delmanual Aritmèticamercantil delmón,elsegonqueesvaimprimiralmón,desprésdeldeTreviso.

‚ JosepChaix(s. XVIII),nascutaXàtiva,col laboràl’any 1793enlamesuradelmeridià terrestre.Treballàsobretotelcàlculdiferencialiintegral.

‚ FrancescAragó(s. XIX),rossellonès,vacontinuarambla mesuradelmeridiàterrestre.La sevaobravatenirinfluènciaprincipalmentenlafísica(electromagnetisme,velocitatde lallum...).Comaanècdota,calconèixerquequanesvaexaminaraParísdematemàtiques(perLegendre),nolireconeixienquefosfrancèsiellvadirqueeradelaCatalunya Nord(vaaprovarl’examenresolenttotselsexercicis).

Però,arribatsalsegle XX,laproducciómatemàticacatalanaaugmenta.Defet,aixòésconseqüènciadelsavençossocials,entreelsqualshihaelderecolliriemmagatzemarlaproducció mitjançantllibresiescritsinicialmentiambelsordinadorsmésendavant,iaixòpassano nomésaCatalunya,sinóarreudelmón.

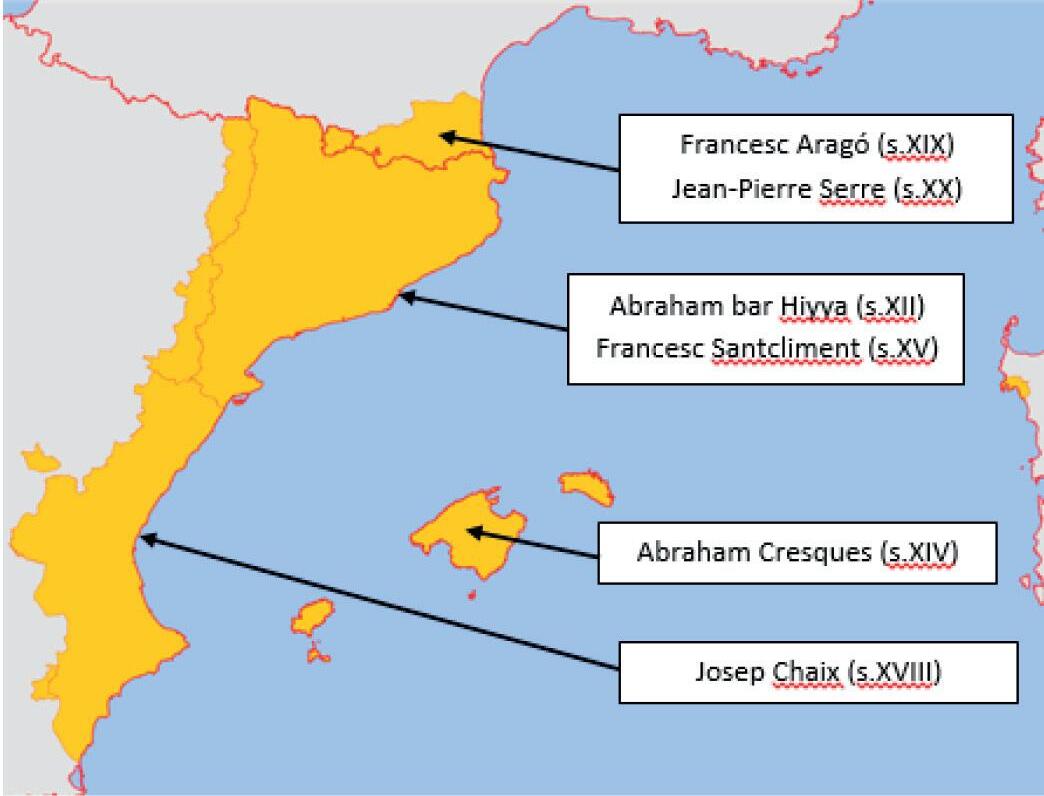
Francesc Aragó (s.) XIX

Jean-Pierre Serre (s.) XX

Abraham bar Hiyya (s.) XII

Francesc Santcliment (s.) XV Abraham Cresques (s.) XIV

Josep Chaix (s.) XVIII

Figura1.MapadelsPaïsosCatalansonhihasituatselsprimersmatemàticscatalansconeguts.

Així,ésdestacabletambéJean-PierreSerre(BagesdeRosselló, 1926),guanyadorl’any 1954 delaMedallaFieldsiel 2003delPremiAbel,elsdospremismésimportantsdinsdelesmatemàtiques,enaquestaressenyahistòricadematemàticsdelsPaïsosCatalans.

Peròhihaunpersonatgedelsegle X quenos’hamencionatperquènoeranicatalànimatemàtic,peròquevatenirunainfluènciaexcepcionalenladifusiódelesmatemàtiquesarreu d’Europa,iques’had’esmentarperquèaixòvasucceirmentreelleraalaprovínciadeGirona, aRipoll:

‚ Gerbertd’Orlhac(Aquitània, 938 Roma, 1003)fouunmonjofrancèsqueenunaestadaquevaferalmonestirdeSantaMariadeRipollvaconèixerelsistemadecimaliel nombrezerogràciesalsconeixementsquehihavienportatelsjueusexpulsatsdelsregnesdeCastella,LleóiAragó,iaixòl’impulsàainiciar-seenlesmatemàtiquesil’astronomia. Elsseusllibresilessevestraduccionsvantenirunaàmpliadifusióentrelacristiandati, pertant,pertotEuropa,quanaquestmonjovaesdevenirpapa(SilvestreII,del 999 al 1003).

Primersvintanysdelsegle XX al’AltEmpordà

HemvistqueenlaressenyahistòricadematemàticsdelsPaïsosCatalansfinsalsegle XX nohihacapgironí:jas’hacomentatenlaintroduccióqueelpuntdepartidadelainvestigaciósobrelesaportacionsmatemàtiquesalt-empordaneseseraelllibre Santaló,Sunyer, DouiTeixidor:quatredestacatsmatemàticsgironinsdeladècada1911-1920 (Reventós etal., 2012).Ésadir,alsegle XX jatenimreferenciatsaquestsquatrematemàtics,totsellsnascuts enelsprimersvintanysdelsegleitotsellsambunprestigiinternacionalreconegut,atès quevanrebrediversesdistincionsipremisivanconèixeritreballarambgranspersonatges delesmatemàtiquesdel’època,comaraB.Eckmann,W.Blaschke,M.H.Stone,A.Einstein iJ.Hadamard.Tambévanparticiparenprojectesinternacionalsimportants,comeldisseny delsprogramesdematemàtiquesdesecundàriad’Argentina,uncontracteamblaMarinadelsEstatsUnits(USNavy),elprogramaApol lodel’AdministracióNacionald’Aeronàutica idel’Espaiamericana(NationalAeronauticsandSpaceAdminsitration,NASA)iladescodificaciódelpapir7Q5,entred’altres.L’enumeraciódetalladadelsseusmèrits,treballsipremis allargariaexcessivamentaquestarticlei espotconsultarenelllibredeReventós etal.(2012).

Dosdelsmatemàticsesmentatsnosóndel’AltEmpordà:

AlbertDouiMasdeXexàs (Olot, 1915 SantCugatdelVallès, 2009)ocupàlaCàtedra d’EquacionsDiferencialsdelaFacultatdeCiènciesdelaUniversitatdeMadrid.Fourector delaUniversitatdeDeustoidel’escolad’enginyeriadelaUniversitatPontifíciadeComillas(InstitutCatòlicd’ArtsiIndústries-InstitutCatòlicd’AdministracióiDirecciód’Empreses, ICAI-ICADE).Exercíelsdarrersanysd’activitatacadèmicaalaUniversitatAutònomadeBarcelonacomaprofessord’històriadelesmatemàtiques.Rebénombrososreconeixements, entreelsqualsdestaquenlaGranCreudel’Orded’AlfonsXelSavi,lamedallad’ordelCol legi d’EnginyersdeCamins,CanalsiPorts,ielsdoctoratshonoriscausaperlesuniversitatspontifíciesdeComillasideMàlaga.Desdel 1963fouacadèmicnumeraridelaReialAcadèmiade Ciències.

LluísAntoniSantalóiSors (Girona, 1911 BuenosAires, 2001)esveiéobligataexiliar-se desprésdeformarpartdel’exèrcitrepublicà(fouamicdeJulioReyPastorid’ÉlieCartan,que l’ajudarenenaquestsmomentscrítics)ivadesenvoluparelseutreballal’Argentina,tant

Figura2.AlbertDouiMasdeXexàs. Figura3.LluísAntoniSantalóiSors.

alauniversitatcomassessorant enelsprogramesdesecundària.Quantornàdel’exili,va rebreelreconeixementmerescut:varebreeltítoldedoctorhonoriscausaperlaUniversitat PolitècnicadeCatalunyael 1977iperladeSevillael 1990;varebrelaMedalladelaUniversitatdeValènciael 1993ivaseracadèmicdelaReialAcadèmiadeCiènciesExactes,Físiquesi NaturalsdeMadridel 1955.L’any 2000 laUniversitatdeGironacreàlaCàtedraLluísSantaló.

Elsaltresdosmatemàticssíquesóndel’AltEmpordà,itambéenfaremunresumapartirdel llibreesmentat:

JosepTeixidoriBatlle (Llers, 1920 Figueres, 1989)foupresidentdelaSocietatCatalanade CiènciesFísiques,QuímiquesiMatemàtiquesdel 1968al 1973itresorerdel’Institutd’Estudis Catalans(IEC)del 1979 al 1983.Vaintroduirlatopologiaalesuniversitatsespanyolesireformàelsmètodesdelageometriail’anàlisi.VaajudaraladifusiódelafeinadeFerranSunyer. L’IECofereixdesdel 1979 elPremiJosepTeixidoralamillortesidoctoralotreballderecerca sobrematemàtiques.

FerranSunyeriBalaguer (Figueres, 1912 1967)vanéixerambunadiscapacitatfísicagairebétotalinovaanaral’escola,peròvaaprendreallegirsoli,gràciesaleslliçonsdelaseva mareialsllibresdelsseuscosins,vainteressar-seenl’astronomia,lafísicailesmatemàtiques, finsatalpuntquevaarribarapublicararticlesenrevistestanprestigiosescom Comptes Rendus,del’AcadèmiadeCiènciesdeParís,ivacartejar-seambmatemàticstanimportants comHadamardoMandelbrot.AlgunsdelsdiversospremisqueFerranSunyervaobteniral llargdelasevavidasónelPremiAgelldel’AcadèmiadeCiènciesiArtsdeBarcelona(1948),el PremiPratdelaRibadel’Institutd’EstudisCatalans(1949),elPremidel’AcadèmiadeCiències deSaragossa(1950),elspremisTorresQuevedoiFranciscoFrancodelCSIC(1956),dospremisdel’AcadèmiadeCiènciesdeMadrid(1954i 1957)ielPremiMartíd’Ardenyadel’Institut d’EstudisCatalans(1966).L’any 1963vasignaruncontracteperalaMarinadelsEstatsUnitsi apartird’aquellmomentelsseusresultatsderecercaforenmésrespectats.El 9 dedesembre de 1967,divuitdiesabansdelasevamort,founomenatinvestigadorcientíficdelaDivisióde CiènciesMatemàtiques,MèdiquesidelaNaturadelCSIC,eltítold’investigadorcientíficque tantdesitjava.

Figura4.JosepTeixidoriBatlle.

Figura5.FerranSunyeriBalaguer.

HisvaluetotheprestigeoftheSpanishScientificcommunitywasoutstanding andhisworkinmathematicswasofasteadyexcellencethatmakeshislossdifficulttoaccept.2

TeoremadeSunyer-Corominas3 (SunyeriCorominas,1954)

Siunafuncióf px q derivableindefinidamentenl’interval ra,bs compleixqueperacadavalorx entreaib(itambéperaaib)existeixunenterpositiun(quedependràdex)talquef pnqpx q“ 0 aleshoresaquestafuncióésunpolinomi.

Peròhihaunaltrealt-empordanèsd’aquestsprimersvintanysdelsegle XX destacableper unainteressantaportacióquevaferalesm atemàtiques,totiqueellnoerapròpiament matemàtic:

FredericMacauiVilar (Figueres, 1917 Barcelona, 1970)fouenginyerdecaminsigeòleg itreballàcomaprofessoralaCàtedradeGeologiadel’escolad’enginyersdecaminsde Madrid.VaserdelegatprovincialdelMinisterid’ObresPúbliquesienginyerencapdelaprefecturaprovincialdecarreteresdeGirona,onplantejàlamodernitzaciódelsprincipalsvials.

L’AjuntamentdeFiguereseldistingícoma«ConcejalHonorario»el 1970.Foudirectortècnic del’ediciódelmapalitològicd’Espanya,encol¨laboracióambelCSIC,ivaserdurantl’estudi delgolfdeRosesquanvaenunciarlapropietatqueellvaanomenar«teoremadel’Empordà», jaquenoteniaconeixençaques’haguésdescobertabans.ElvapublicarEl 1964,aixícomla sevademostraciógràficaialgebraica,als Annalsdel’Institutd’EstudisEmpordanesos (Macau, 1964).

Aixímateix,amésdelapropietatpuramentmatemàtica,ellhiveiéunaaltravessant,enamoratcomestavadelpaisatgealt-empordanès:segonsFredericMacau,algolfdeRosess’hi podenimaginarduesel¨lipseselscentresdelesqualssónalaprolongaciódelsriusMuga iFluvià,ilsesemieixosmajorsdelesqualsfan 13,9 kmdelagrani8,6kmeldelapetita,i resultaquesiesdivideixenaquestsdosnombress’obté 1,616279...,quegairebécoincideix

2.«Elseuvalorperalprestigidelacomunitatcientíficaespanyolaeraexcepcionalielseutreballen matemàtiquesvaserunaexcel lènciaconstantquefalasevapèrduadifícild’acceptar».CartadecondoldeT.B. Owen,almiralldelaMarinadelsEstatsUnits.

3.ErnestCorominasiVigneaux(Barcelona, 1913 Lió, 1992)vaserunmatemàticquevacol laboraramb FerranSunyerenlademostraciódelteoremailadifusiódelsseustreballs.

Figura6.FredericMacauiVilar.

ambelnombred’or ϕ “ 1,6180339 ...,ielsgrecstenientanarrelataquestnombrealaseva vidaque,inconscientment,laplatjaelsvasemblartanbellaqueesvaninstal laraRosesi Empúries.Defet,aquestargumentesvaferservirl’any 2012 enlacandidaturadelabadiade Rosesperserinclosaalclubdelesbadiesmésbellesdelmón.

Teoremadel’Empordà(Macau,1964): Donadesduesfamíliesd’el lipsestangentsenunpunt D italsquellurratlladelscentressiguiparal¨lelaalatangentcomuna,cadaundelsaltresdos puntsd’intersecciódecadaparelld’el¨lipses E1 i E2 ,ielpunt D,determinenduesrectessobre lesqualsestallenelsparellsdetangentsalesel¨lipses,paral¨lelesalsdiàmetresquepassenpel punt D.

Aportacionsmatemàtiquesalt-empordanesesapartirdel1920

SimóBoschEstany (Figueres, 1946 2018)vaserprofessordel’InstitutRamonMuntaner del 1974al 1993(ienvaserdirectorelcurs 1988-1989),inspectord’ensenyamentdel 1993al 2001 i,després,professoral’InstitutdeLlançàfinsal 2006(comvadirA.Aubanell,ésun«dels pocsquedesprésdeserinspectortornenaserprofessors»).

Lapropietatqueindiquemmésavallvaaparèixerenlesrevistes Biaix (núm. 28-29)i Suma (núm.62),escritaambelseupermísielseuvistiplauperLluísSabaterAnticó4 (Sabater, 2008i 2009).PeròSimóBoschjal’haviaexplicatenpetitcomitèmoltsanysabans.Vasorgirquanera joveiambelsseusavisdeLladócomentavenquedesdelaMaredeDéudelMónesveienset Bisbats:dosdefrancesos,NarbonaiPerpinyà-Elna,icincdecatalans,Vic,Barcelona,Girona, laSeud’UrgelliSolsona.Llavorsellesvainteressartambéperlasuperfíciequeesveia.

Encomentaremdosexemples:desdeSantPeredeRodes,a500 md’altitud,espodenveure 20.000 km2 desuperfície(unaextensióquasitangrancomCatalunya[32.000 km2 ])ifinsa

4.CompanydefeinadeSimóBoschal’InstitutdeLlançàianteriormentalumneseual’InstitutRamon Muntaner.

Figura7.SimóBoschEstany.

80 kmdedistància(mésenllàdeGirona,sinohihaguessinaltresmuntanyespelmig),ides deMontserratespotveureMallorca(laserradeTramuntana)elsdiesclars.Valadirqueen navegaciós’usavalafórmula d “ 2,0778 ¨ ?h perferelcàlculdelesmillesnàutiques(1 mn = 1.852 m)finsonesveudesdelapartmésaltad’unvaixell, h,enmetres,iqueperavalors petitsde L (valorspetitsdel’altura)(L)enkms’assemblamoltalresultatques’obtéaplicant d “ 80 ?2Lkm.Aquestapropietatvadespertarcuriositatenelmónmatemàticcatalàiel 2009 LluísSabater(tambéambelvistiplaudeSimóBosch)envaferunaponènciaal’IECen elmarcdelaVIJornadad’EnsenyamentdelesMatemàtiques.

Fórmula/propietatdeSimóBosch(1990): Lasuperfíciequeesveudesd’uncimd’alturaL(en km)és,aproximadament, 40 000 L pkm2 q

EduardCasasAlvero (Figueres, 1948)ésdesdel 1983catedràticdeGeometriaalaUB(actualmentn’ésprofessoremèrit),onhaestatdirectordelsdepartamentsdeGeometriaid’ÀlgebraiGeometria.Especialitzatenl’estudidesingularitats,haescritdiversosllibresiarticles degeometriaalgebraica.

Enund’aquestsarticlesvanecessitaraplicar lapropietatques’enunciamésavall,pensant enunprimermomentqueeraunacosatrivial, evident.Peròquanvahaverd’escriure’nla demostració(enmatemàtiques,resnoésvàlidsinoespotdemostrar,tretdelsaxiomes), esvaadonarquenoeratanevident.Aleshores,enmatemàtiques,quanunapropietatse suposacertaisemblaser-ho,jaquenose’ntrobencontraexemplesperònosesapdemostrar, s’anomenaconjectura.5 Així,desdel 2001 diversosinvestigadorsn’hanbuscatlademostració demomentsenseèxit,iperaixòcontinuaanomenant-seconjecturadeCasas-Alvero.

5.Exposemacontinuacióunsquantsexemplesdeconjecturesfamoses.ConjecturadeGoldbach:tot nombreentermajorque 2 espotescriurecomlasumadedosnombresprimers.ConjecturadePoincaré:formulada el 1904perH.Poincaré,novaserdemostradafinsal 2003perG.Perelmaniaras’anomenateoremadePoincaréPerelman.DarrerteoremadeFermat:formulatl’any 1642,vaserresoltperA.Wilesel 1994(352 anysdesprés!)iara s’anomenateoremadeFermat-Wiles.

Figura8.EduardCasasAlvero.

Relacionatsambaquestaconjectura,s’anomenenpolinomisdeCasas-Alveroelspolinomis lesderivadesdelsqualscomparteixenalgunaarrelambelpolinomi(i,aleshores,laconjectura tambépotenunciar-sedientque«elspolinomisdeCasas-Alverosóndelaforma a ¨px bqn ».

ConjecturadeCasas-Alvero(2001): SiguifunpolinomidegraunsobreuncosKdecaracterística 0.Siftéunfactorencomúambtoteslessevesderivades,f piq ,i “ 1,...,n 1,aleshoresf hadeserpotènciad’unfactorlineal,f px q“ a ¨px bqn .

(Atenció:elfactorencomúpotserdiferentperacadaderivada.)

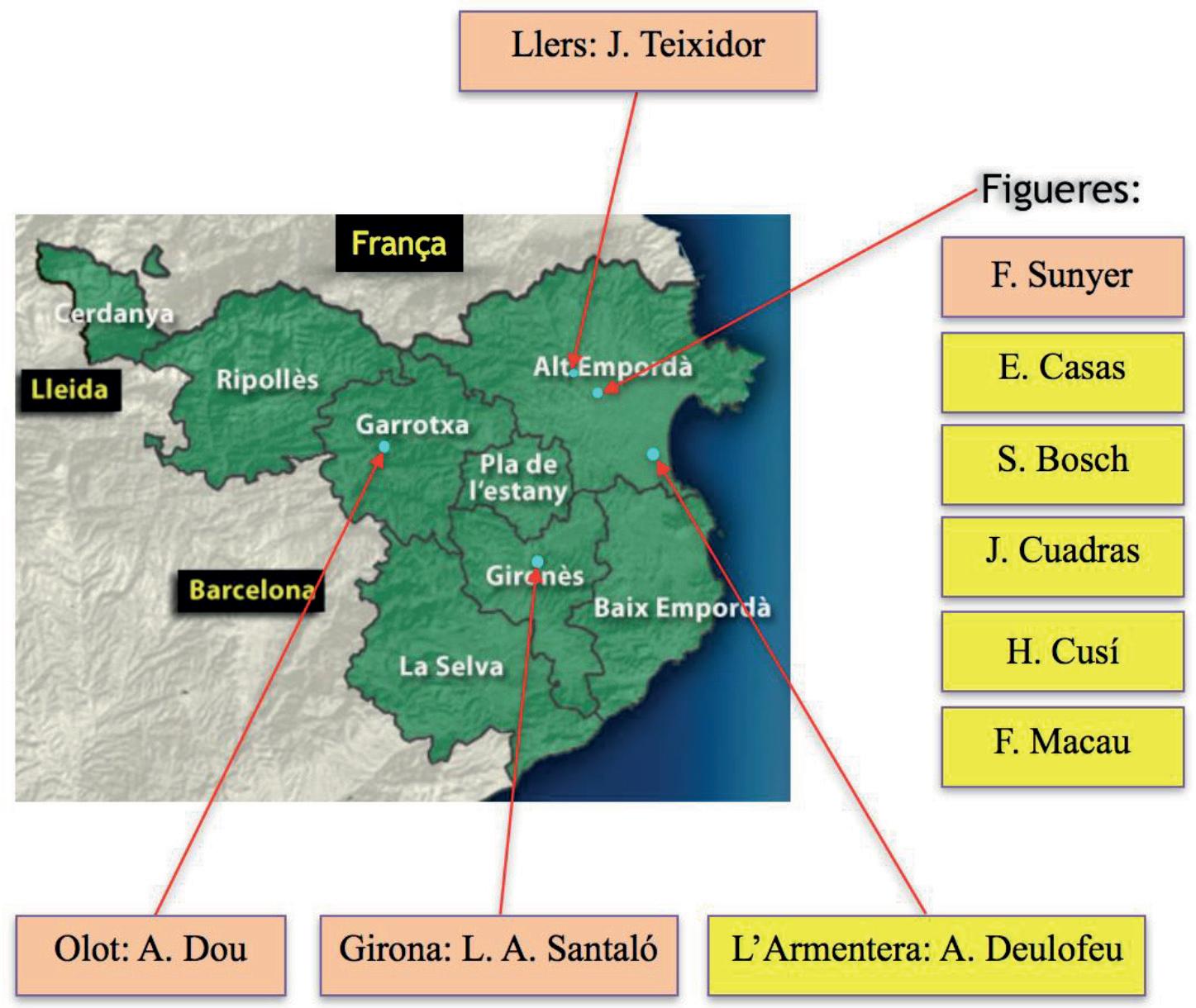
Figura9.MapadelaprovínciadeGirona.

Altrespersonatgesalt-empordanesosdelsegle XX

D’altrabanda,hihatrespersonatgesmésquemereixenserdestacatsperlessevesaportacionsalasocietatalt-empordanesadurantelsegle XX,relacionadestambéamblesmatemàtiques:

AlexandreDeulofeuiTorres (l’Armentera, 1903 Figueres, 1978)vaserprofessordel’InstitutRamonMuntanerdeFigueresidesprésdelaGuerraCivilesvaexiliaraFrançafinsal 1947 (haviaestatalcaldedeFigueresel 1937),ientornaresdedicàalafarmàciaiaescriure.Enla sevaobra Lamatemàticadelahistòria explicaquelesgranscivilitzacionss’assemblenenel fetquepassensemprepertresetapesenunespaidetempsde5.100 anys,iapartird’això faunesprediccions(pèrduadelescolòniesfranceses,desintegraciódeIugoslàviaideRússia capal 2000,desintegraciód’Espanyacapal 2029...).

JosepCuadrasPlanas (SantPeredeRibes, 1911 Figueres, 1990)vaserdistingitcomafill adoptiudelaciutatdeFigueresel 1988.Vacomençaratreballargratuïtamentfinsqueel

1940 obtinguéelprimersoui,perladificultatdel’època,vahaverdetreballarsimultàniamentendiversosllocsifentclassesparticulars.Atèsquenoméshihaviauninstitutpúblic, l’InstitutRamonMuntaner,ésdifíciltrobara lacomarcaalgúmajordeseixantaanysquehagi estudiatinohagiestatalumneseu(E.Casas,S. Xambó,J.M.LluchiH.Cusíhanestatalumnes seus).ElsseusfillsJosepMariaiCarlesMariavanseguirelsseuspassosenlesmatemàtiquesi enl’ensenyament.

HelenaCusíiMoner (Figueres, 1956 2015)vaserprofessoraal’InstitutAlexandreDeulofeu,deRoses,ial’InstitutRamonMuntaner,deFigueres,ivaserunadelesfundadores delMuseudeMatemàtiquesdeCatalunya(MMACA)idelJugamat(grupdetreballdeprofessorsdesecundàriaibatxilleratdel’Empordàquecol laboraiorganitzaactivitatscomara exposicionsdetreballsdelsalumnes,provescangur,materialperaprofessors,concursosper Internet...).Enl’exposicióaFigueresdelMMACAdel 2015selivaferl’homenatgedeprojectar lasevaimatgeambombresxineses.Abandadelesmatemàtiques,lessevesaltrespassions erenelteatre(foudirectoradel’AuladeTeatreMunicipaldeFigueresdel 1997al 2000 i eramembredeLaFuncionalTeatre)iladansa,ivacol¨laborarambdiferentsassociacions culturalsfiguerenques.

Figura10. AlexandreDeulofeuiTorres.

Figura11. JosepCuadrasPlanas.

Figura12. HelenaCusíiMoner. Figura13.Relacionsentreelsmatemàticsinclososenl’articlenascutsal’AltEmpordàdurantelsegle

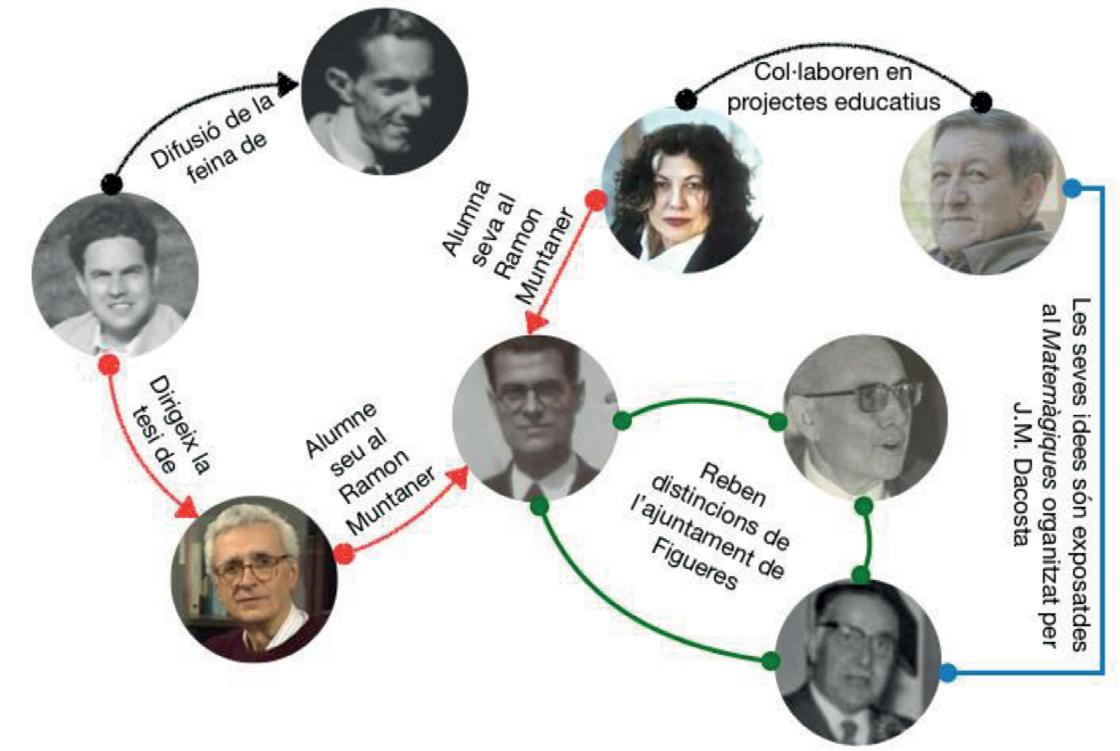
Remarquemunparellderelacionsentreaquestspersonatges(figura 13):

‚ JosepTeixidorvadirigirlatesidoctorald’EduardCasas,que,amés,vaseralumnede JosepCuadrasicompanyd’estudisalacarreradeJosepMariaCuadras,filldeJosep Cuadras.

‚ SimóBoschvapublicartambéunarticleals Annalsdel’Institutd’EstudisEmpordanesos (sibénodecairematemàtic,sinóhistòric:elllinatgedelsBiuredel’Empordà),com FredericMacau,ivasercompanydefeinadeJosepMariaCuadrasal’InstitutRamon Muntaner,deFigueres(unaltrepuntdeconnexióentrequasitots).

Totique,comdiuAntoniMalet6 aldocumental FerranSunyeriBalaguer.Històriad’unexili interior (FundacióFerranSunyeriBalaguer etal., 2016),enmorirFerranSunyernoselivafer capreconeixementinstitucionalperpartdelaUniversitatdeBarcelona,actualmentserveix comaprincipalpuntdeconnexióentreells,iésquetothomelconeixiaiadmiravaelseu treball,coms’hapogutveurealtreballderecercaenquèesbasaaquestarticleapartirdeles entrevistesiopinionsdelsentrevistats(Sabater, 2020).

Referències

Corominas,E.(1954).«Condicionesparaqueunafuncióninfinitamentederivableseaunpolinomio», RevistaMatemáticaHispanoamericana, 14, 1-2.

FundacióF.SunyeriBalaguer;BenecéProduccions,SL;TelevisiódeCatalunya(2016). Ferran SunyeriBalaguer.Històriad’unexiliinterior.Documental.Disponible awww.ccma.cat/tv3/alacar ta/33-i-ciencia/ferran-sunyer-i-balaguer-historia-dun-exili-interior/coleccio/7310/4545916/.

Macau,F.(1964).«L’AltEmpordàgeometritzatperlaTramontana», Annalsdel’Institutd’Estudis Empordanesos,5, 20-39.https://raco.cat/index.php/AnnalsEmpordanesos/article/view/116 598/168766.

Reventós,A.;Malet,A.;García,M.;Teixidor,M.(2012). Santaló,Sunyer,DouiTeixidor:quatre destacatsmatemàticsgironinsdeladècada1911-1920.Girona:UniversitatdeGirona.

Sabater,L.(2009).«Lasuperfíciequeabarcalavistadesdelacimadeunmonte», SUMA:RevistasobreEnseñanzayAprendizajedelasMatemáticas,62,7-9.

Sabater,L.(2010).«L’àreaqueespotveuredesd’uncimd’alturaLés,gairebé,40000 ¨ L», Biaix, 28-29,44-47.

Sabater,R.(2020). Aportacionsmatemàtiquesalt-empordanesesdelsegle XX.Treballderecerca debatxillerat.Llançà:InstitutdeLlançà.

6.Catedràticd’HistòriadelaCiènciadelDepartamentd’HumanitatsdelaUniversitatPompeuFabra.

Fontsdelesfotografiesiesquemes

‚ Figura 1:MapadelsPaïsosCatalanssituant-hielsprimersmatemàticscatalansconeguts.[Fotografiamodificada].(s.d.).Recuperatel5d’agostde 2019 dehttps://blocs.mesvi laweb.cat/vicent/?p=268581

‚ Figura 2:AlbertDouiMasdeXexàs.[Fotografia].(1964).Recuperatel6demarçde 2019 dehttps://scbcientifics.iec.cat/ca/cientifics/dou-mas-de-xexas-albert.html

‚ Figura3:LluísAntoniSantalóiSors[Fotografia]dehttps://ciaem-iacme.org/luis-santalo/

‚ Figura4:JosepTeixidoriBatlle.(Gener 2019).Recuperatel8demarçde 2019 dehttps://ca. wikipedia.org/wiki/Josep_Teixidor_i_Batlle

‚ Figura5:FerranSunyeriBalaguer.(31 d’agost 2019).Recuperatl’1 dejuliolde 2019 de https://ca.wikipedia.org/wiki/Ferran_Sunyer_i_Balaguer

‚ Figura6:FredericMacauiVilar.[Fotografia].(s.d.).Recuperatel 25demaigde 2019 de 3&europeana_query=Tráfico&europeana_cursor=AoQhVH70kfS84AIGAAAAAD8dLzIw MjQ5MTQvcGhvdG9ncmFwaHlfUHJvdmlkZWRDSE9fQWp1bnRhbWVudF9kZV9HaXJvb mFfNjUwMjY2&europeana_prev_cursor=%2A&dpla_nav_start=2&obcnt=151

‚ Figura7:SimóBoschEstany.[FotografiadeJosepMariaDacosta].(2010).

‚ Figura8:EduardCasasAlvero.[Fotografiad’autoriapròpia].(2019).

‚ Figura 9:MapadelaprovínciadeGirona.[Fotografiamodificada].(s.d.).Recuperatel 8d’agostde 2019 dehttps://www.fortiseguridad.com/servicio-tEcnico-de-cajas-fuertes -engirona-n-28-es

‚ Figura 10:AlexandreDeulofeuiTorres.[Fotografia].(s.d.).Recuperatel5demaigde 2019 dehttp://www.deulofeu.org/alexandre-deulofeu-portada//

‚ Figura 11:JosepCuadrasPlanas. [Fotografiadel’InstitutRamonMuntaner].(anys50).

‚ Figura 12:HelenaCusíiMoner.[Fotografia].(s.d.).Recuperatel6dejuliolde 2019 de http://m.tramuntana.tv.com/news/la-dama-del-teatre-un-musical-dhomenatge-a-he lena-cusi/

‚ Figura 13:Relacionsentreelsmatemàticsinclososenl’articlenascutsal’AltEmpordà durantelsegle XX.[Esquemad’elaboraciópròpia].(2019).

seccions seccions rcions

oriflèxia el racó de l’oriflèxia

Cubsd’ocellets,demolinetsidevaixells

JaumeCollGuerrero CFARafaelFarré(MolinsdeRei) UniversitatAutònomadeBarcelona

DepartamentdeMatemàtiques Professorassociat

1.Unahistòriadel’ocelldepaper

Quan,oniquivaserlaprimerapersonaquevaferunocelldepaper?Diversesraonsfan pensarquerespondreaaquestesenigmàtiquespreguntesésforçadifícil.Laprimeradificultatésqueelmaterialambquèesfanaquestesfiguresésmoltefímer,perlaqualcosa noesconservenocelletsdepaperfísicsantics.Unasegonadificultatésquenoestroben gairesdocumentsescritsd’èpocaquefacinreferènciaaaquestsobjectes;elfetquefossin jocsinfantilshadeterminatquenose’lshagidonatgaireimportànciaiqueambeltemps s’hagicreatl’expressiócastellana hacerpajaritas olacatalana ferocellets,quesónsinònimes depèrduadetemps,comesreflecteixenelpoemasatíricsegüent,publicataldiari ElGlobo el 1883:

Eltrabajomemolesta, mefatigaymeimportuna, – deciaáDonJuanGinesta elcorregidordeOsuna. Docehoraspaso durmiendo,roncandocomo unlebrel; seisholgando,yseishaciendo pajaritasdepapel.

Aixídoncs,nointentodonarunarespostadefinitivaaaquestestrespreguntes,peròpodem apropar-nos-hianalitzantelrastredel’ocelletdepaperalllargdeltempsendiversesdisciplinesartístiques,comlapintura,l’escultura,l’arquitectura,elcinema,lamúsicaoelteatre,o endiferentstipusdedocumentsescritsigràfics,comelcòmic,lafotografia,lapremsaola literatura.

Cadascunad’aquestesfontstéelseupropilímittemporal.Elsetèarts’iniciàel 1895ambla projecciódelapel lícula Lasortiedel’uineLumièreàLyon,delsgermansLumière.Apocsmetresd’onesvanrodaraquestesprimeresimatges,actualmentespotvisitarelMuseuLumière. Enaquestscentvint-i-cincanys,l’ocelldepapers’hadeixatveureendiferentspel lícules, com,perexemple,enelsbitlletsdebancdelapel¨lícula Uchronia (2016). Uchronia (delgrec oυ =«no», κρ óνoς =«temps»)ésunaparaulacreadapelfilòsofiescriptorfrancèsCharles Renouvier(Montpeller, 1815 PradadeConflent, 1903)perdesignarquelcomqueestàfora detemps,enanalogiaambutopia(oυ =«no», τóπoς =«lloc»).Nopodemlocalitzarellloc nisituareneltempsonvanéixerl’ocelletdepaper;etimològicamentenstrobemdavant d’unautopiaucrònicaal’horadedonarrespostaalespreguntesinicials.Altrespel lícules onapareixl’ocelletdepapersón ManolitoGafotas (1999); ElBar (2017),d’ÀlexdelaIglesia; lapel¨lículad’acció Fast & Furious8 (2017),o Laisladelviento (2015),onesdescriul’exilidel papiroflectaMigueldeUnamunoal’illadeFuerteventuraperlasevaoposicióaladictadura dePrimodeRivera.El 1965esvanrodarelscurtmetratgesd’animaciócubans Cotorama i El GallitodePapel (aquestésunaltrenomambquèesconeixl’ocelldepaper,especialmenta l’AmèricadelSud).

Aprincipisdelsegle XX s’estrenalapel¨lícula IlFuoco (1915),basadaenl’obraliteràriade Gabrieled’Annunzioienlesdarreresescenes delaqualapareixendiversosocellsdepaper. Unsanysabans,elcineastaSegundodeChomón(Terol, 1871 París, 1929)vaestrenarla pel lículadeproducciófrancesa Lescocottesenpapier (1908),uncurtd’unscincminutson apareixendesenesd’ocelletsdediferentsmides;enunadelesescenesesconstrueixelcosde l’ocelletambdosquadrats,ielcap,elbec,lespotesilacuaesfanambquatretrianglesrectanglesisòsceles.Elmateixany,elfrancèsÉmileCohlvarodarlapel lícula Lecerceaumagique, onespotveurecomunpaperquadratdinsd’uncercleesvaplegantfinsatransformar-seen unocelldepaperquefinalmentdesapareixacompanyatperunsaltresvintocellsméspetits.

ÉmileCohlvaserdeixebledelcaricaturistaAndréGill,quevacol¨laborarendiferentspublicacionsperiòdiques,com LaLune, LaLuneRosse, L’Eclipse, LeCharivari o LaRue.Avegadesels personatgescontemporanisquecaricaturitzavaapareixienambocellsdepaper:Alexandre Dumasfill(LaLune, 21 demarçde 1867),elnovel listaArsèneHoussaye(L’Eclipse, 28de junyde 1868),elperiodistaAugustVillemot(L’Eclipse, 15denovembrede 1868).Enaquella època,tambéaltrescaricaturistesutilitzaven aquestrecursenaquesttipusdepublicacions.

Figura 1. Uchronia (2016).Figura 2. Les cocottes en papier (1908).

L’il lustradorPaulHadolvadibuixar,acompanyatd’unsocellsdepaper,l’autorteatralÉmile Augier(LeCharivari, 9 d’abrilde 1866).DelmateixdibuixantesconservaalMuseuCarnavalet deParísl’obra Lescocottesexpulséesdescafés,onelsocelletsestandeformats.Aixòeraforça habitualenimatgesdelsegle XIX:perexemple,sóndeformatselsquatreocelletspublicats aldiari LeCharivari l’agostde 1833.Elmateixanyl’il¨lustradorMichelDelaportevaferuna litografiadeBarthélemyProsperEnfantin,reformadorsocialiundelsimpulsorsdelcanal deSuez(LaCharge, 24defebrerde 1833),ambcincocellsdepaper.Elgenerde 1832 el setmanari LaCaricature vapublicarlalitografia ArmesdugrandPoulot,onapareixunocellet depaperdarrered’ungranbarretdepaper.

L’ocelldepaperestàmoltrepresentatenlespublicacionsdelcaricaturistaJ.J.Grandville, pseudònimdeJeanIgnaceIsidoreGérard(Nancy, 1803 Vanves, 1847).D’aquestautorcal destacarelsgravats RondoAllegrettoconBrio i MoyensCoercitifs,publicatseldesembrede 1832 alsetmanarisatíric LaCaricature.Enlapartcentraldelprimergravathihaunmonument ambunainscripcióquecommemoralafuturavictòriadel’armadafrancesasobreelsholandesos.Elmonumentestàcoronatperunsoldatdejoguina,uncanóisisocelletsdepaper,i alvoltantdelmonòlitballenenrotllanaelsmembresdelgovernfrancès und’ellsportaun barretdepaper alsodelapopularcançóinfantil LaTourprendsgarde.Enelsegongravates denuncialaparticipaciódeFrançaenelsetgedelaciutatbelgad’Anvers,is’hiveuenquatre personatgesjugantalaguerraambvaixellsde paperivuitocellets.Aquestgravattambées trobaalllibre Histoiredesjouets (1902),d’HenryRenéd’Allemagne.

Peròésl’artdelapinturaelquearaperaraensproporcionalesimatgesmésantiguesque esconeixend’unocelldepaper.El 1862 l’italiàGioacchinoTomavapintarelquadre Ipiccoli patrioti,queactualmentestrobaenunacol¨leccióparticular,onesveuentresnensjuganta laguerra.Und’ells,ambunbarretdepaper,estàdavantd’unpetitcanódejoguinaientrefiguretesdesoldatsapareixendosocelletsdepaper,quepossiblementrepresentenlesforces decavalleria.

Moltsolisonapareixl’ocelldepaperforenrealitzatsperdonespintores.Enlamajoria,l’ocell depaperestàdamuntd’unataula,acompanyatd’alguninfant.Esdesconeixeneltítolil’any enquèesvapintarelquadreonespodenveuresetocellsdepapersobreunatauladavant d’unanoiaambunllibre,delapintorafrancesaÉtienneAdolphePiotiquevasersubhastat perlacasaSotheby’sel 2015.Éssemblantelquadre Noiambunllibre (ca. 1855),dePavel Petrov,queesconservaalagaleriaTetryakovdeMoscouionunnoientotsolat,assegut enunataula,téentrelesmansunllibreialadreta,unapilotaiunocelletdepaper.Així mateix,enelquadre Lebonnetd’âne (ca. 1880),delapintoraAngèleDubos(1844 -1916)i queactualmentestrobaalMuseuAndréMalrauxdeLeHavre,s’hipodenveuretresnoies estudiant,unadelesqualss’haquedatadormida,alvoltantd’unataulaonhihatresocellets depaper.LouisGaillac(1849-1934)tambévapintarassegudaenunataulaunaballarina ambunvestitdecolorrosaquedescansajugant ambsisocelletsdepaper.Noesconeixcap imatged’ocelletdepaperenlesdècadesde 1810 i 1820.

Actualmentlescincimatgesmésantiguesd’unocelletdepaperespodenveureentresquadresd’èpocanapoleònica.El 1807Louis-LéopoldBoilly(LaBassée, 1761 París, 1845)va pintarl’oli ReadingoftheBulletinoftheGrandArmy,exposatactualmentalMuseud’Artde SaintLouis(EstatsUnits).Mentreelsadultsmirenunmapaiesmostrenpreocupatsperun

jovefamiliarquehaanatcomasoldatalfrontalemanyenlesguerresnapoleòniques,els infantsjuguenaterraambcartesitresocellsdepaper.Aquestpintortambévaferel 1821 unalitografiadelmatemàticAugustinLouisCauchy.

ElsaltresdosquadressóndelapintoraJeanne-ÉlisabethChaudet-Hausson.Elprimer,de 1806,estitula MariaLaetitiaportantunbustedeNapoleon ipertanyalacol lecciódelMuseuFesch,delaciutatcorsad’Ajaccio,onvanéixerl’emperadordelsfrancesos.Hiapareixla princesaMarieLaetitiaMurat,filladeCaroli neBonaparteidelmariscalMurat,quevaserel responsabledelsafusellamentsdel3demaigaMadrid,pintatsunsanysméstardperGoya. Alcostatd’unocelldepaper,laprincesaportaunbustdelseuoncle,Napoleó.Existeixuna còpiad’aquestquadrealMuseudeNapoleó 1r,alcastelldeFontainebleau,queésdipòsitdel MuseuNacionaldelCastelldeVersalles.El segonquadred’aquestamateixapintoraés del 1801 iactualmentpertanyalfonsd’unacol leccióprivadadelsEstatsUnits.Enaquest quadreesveuunanenaquemiral’espectador iassenyalaenungranllibreobertunail¨lustració deCupido,eldéudel’amor.Aterra,entrealtres objectes,hihaunocelldepaper.Aquestaés, araperara,laimatgemésantigaqueesconeixd’unocelldepaper.

2.L’ocelldepaperaCatalunya

Passejantpelcarrerd’AragódeBarcelonapodreuveurequatreesculturesdelsanomenats ocelletsanarquistesdelClot,duesal’alturadel’avingudadelaMeridianaiduesal’altura delcarrerdeLasNavasdeTolosa.AquestesesculturessónunarèplicadelafontdeLasPajaricasdelparcMiguelServetd’Osca,dissenyadapeldibuixant,pintor,escultoriperiodista anarcosindicalistaRamónArsenioAcínAquiluéel 1928.L’anysegüentaquestartistalesva exposaralesGaleriesDalmaudelaCiutatComtalenunamaquetadecartró.Unacinquena esculturadeferroambaquestmotiu,d’unsdosmetresimigd’alçària,estàsituadaal’entrada delMuseudeVestitsdePaper,aMollerussa(Plad’Urgell).Unaesculturadepapermoltmés petitarealitzadapelrellotgeripapiroflectacentellencLluísValldeneuiBiguesvaassolirel

Oli de Boilly (1807).

Oli de Chaudet (1801).

1993unrècordGuinness:plegantunpaperquadratdedimensions 0,4mm ˆ 0,4mmvafer l’ocelletadepaperméspetitadelmón,de 0,3mm ˆ 0,3mm.

Antiguesimatgesdel’efímerocelldepaperespodentrobarendiferentsmuseusdelageografiacatalana.ElMuseuNacionald’ArtdeCatalunya(MNAC)téendipòsitl’obra Nenamb ocell (1877),del’escultorVenanciVallmitjana.Peròaquestapetitatalladeterracotanoconserval’ocelldepaperqueestavaentrelesmansdelnen,comespotveureenunalitografia del’arxiumunicipaldel’AjuntamentdeBurgos.ElMNACtambétéendipòsitunaimatgede 1927ambunocelldepaper,delfotògrafEmiliGodesHurtado(1895-1970).Enaquestmuseu actualments’exposaelgravatlitogràfic L’estratega (1936),deRamónPuyolRomán(Algesires, 1907-1981),onunpensatiuguàrdiacivildibuixaunatrajectòriaenunmapasobreunataula alcostatd’unocelliambunvaixelldepaperdinsungot.

Enl’eclècticiimpressionantMuseuFredericMarès(MFM)espodenveurediversespecesamb ocellsdepaper.Unaprimeraimatgequehihaenunacol¨lecciódepersonatgeséselcos d’unocelletdepaperambelcapd’unhomebarbut.Aquesttipusd’imatgeshíbrideseren habitualsenil¨lustracionsdefinalsdelsegle XIX iprincipisdel XX.Enunsegonapeça,unnoi, unanoiaiunocelldepaperobrenlaprimeraescenadel’auca Juegosdelainfancia amb elrodolí«entrejuegosplacenterospasanlosañosprimeros».Aquestaediciódel’aucafou publicadadurantelprimerquartdelsegle XX perlallibreriaSucesoresdeHernandoaMadrid; hihaedicionsmésantiguesd’aquestamateixaauca,publicadesaValènciael 1857.Untercer objectedelMFMésunguarnimentdellautóambdosocellsdepaperqueformavapartd’una carrossaquevaparticiparenunacavalcadaorganitzadael 1891 oel 1892 perl’entitatrecreativabarceloninaloNiuGuerrer(1874-1936).Gràciesalesnotíciesdelapremsapublicadesa finalsdelsegle XIX iprincipisdel XX sabemquel’ocelletdepapereraforçapopularentrela poblacióiques’utilitzavaenballsdedisfressesoperguarnircarrossesperalcarnestoltes.

Enelsdosmuseusempordanesossobrelajogui na,l’unaFigueres(AltEmpordà)il’altre aSantFeliudeGuíxols(BaixEmpordà),trobemestablesdejoguinadelcomençamentdel segle XX (ca. 1915),deprocedènciaanglesaiambunsquantsocellsdepaperdibuixatsales parets; hobbyhorse éselnomambquèconeixenelsanglesosl’ocelldepaper.ASalvadorDalí, l’empordanèsuniversal,noliagradavenelsocellsdepaper,comvaconfessaraAntoniPitxot, elseuamicitambépintor,mentreaquestplegavaunpaper:lirecordavenelssaltamartins, alsqualsteniafòbia.Totiaixí,enunadelessalesdelacasamuseudePortlligatespotveure unenigmàticocelletdepaperdemetall.

Aprincipisdelsegle XX podemtrobarl’empremtadel’ocelldepaperendiferentsedificis modernistesbarcelonins,comelsmosaicsdelrebedordelescasesdeMiquelSoleriJoan Chillida(1915)alcarrerdeFloridablancadelbarrideSantAntoni,obradel’arquitecteJosep MasdeuiPuigdemasa,lesportesdefustadel’entradadelacasadeBaldomerRovira(1900), alcarrerdelRossellódelbarridel’AntigaEsquerradel’Eixample,construïtperl’arquitecte AndreuAudetiPuig,oelsmosaicsde l’escaladelacasaJosepSabadell(1904),delmateix arquitecte,alarambladePratdelbarrideGràcia.Dinselmodernismenobarceloní,l’ocell depaperéspresentendiferentsmosaicsexteriorsrealitzatspelceramistaLluísBruiSalelles queenvoltenlacasaotorreMauri(1907),queactualmentésl’edificidelaCasadelaVilade laPobladeSegur(PallarsJussà).

Variatsdocumentshistòricsdediferentsdisciplinesenspermetenconèixerelnomconcret d’algunspapiroflectescatalans.El 1957elbarceloníFelipSaguésBadiavaaconseguiraRoma unprimerpremienelXXConcursInternacionaldeCinemaAmateur,organitzatperlaUnió InternacionaldeCinemad’Aficionats(UNICA),ambeldocumental Hybris,fantasiadidàctica protagonitzadaperocellsdepaperdecolorsdiferentsqueviuenenunmóndejoguinaisón regitsmetafòricamentperleslleisdeMendel.El 1933esvaformaraIgualada(Anoia)lacobla orquestraTheNightingaleBoys,elscomponentsdelaqualesreunienal’avuidesaparegut cafèGoya.Elsímbold’aquestaorquestraeraunlogotipambunocelldepapercreatper l’animador,director,trompetistaivioloncel¨listaJoanXausiOlivé,elqualsempreteniaun ocelletdepaperalatauladetreball.L’any 1935elgrupesvaescindiriesvacrearelgrupThe BirdBoys,ambunnomnouamericanitzatqueenfinalitzarlaGuerraCivilel 1939 vancanviar peldeCobla-OrquestraTriunfal.Aqueststresgrupsmusicalsigualadinsquevanactuarper lageografiacatalanautilitzavenl’ocelldepapercomasímbolidentificatiu.Enlesprimeres dècadesdelsegle XX,elfundadordelaLligaRegionalistaipapiroflectabaixempordanèsFrancescCambóiBatlle(Verges, 1876 BuenosAires, 1947)vaserdoscopsministreidiputatal Congrésendiferentslegislatures.L’ArxiuNacionaldeCatalunyaconservaunafotografiade 1930 deGabrielCasesiGalobardesambocellsde paperfetsperFrancescCambóiperRamon d’AbadaldurantunareuniódelaLligaRegionalista.Aquestspolíticstambéfeienocelletsde paperenlessessionsdelarlament,cosaqueelsretreialapremsadel’època.

L’ocelldepaperésforçapresentenmoltesobrespictòriquesd’algunspintorscatalans.Enel segonquartdelsegle XX caldestacarl’existènciademésdevintobresambaquestatemàtica del’artistavilanovíEnricCristòforRicartiNin.Podeuveurelasevaobra FantasiaCubista (1925)alaBibliotecaMuseuVíctorBalaguer.LamajoriadelesobrespictòriquesdeChantal Ripol,artistadelMasnou(Maresme)queactualmentresideixaBrussel¨les,estanhabitades perdospersonatgesrecurrents:lafemeninaocelletadepaperielmasculívaixelldepaper. Aquestesfiguretesdepaperlesfeiaelseuparei,enparaulesdel’artista,sónreminiscències delainfànciaquerecordenlafragilitatdelescoses,aixícomelcostatlúdicirefrescantd’una infànciafeliç.

Lo Gall de Paper (1870).c/ Floridablanca, 108, Barcelona (1915).

UnapinturamésantigaésalasegonaplantadelMuseudel’Empordà,aFigueres,onespot veureelquadreceditpelMuseudelPrado Elcaminodelagloriaartística (1855),delpintor JoséGonzálezBande.Finsfapoc,aquestaeralaimatgemésantigad’unocelldepaperquees coneixiaaCatalunya.Aquestadatahaestat desbancadaperlalitografiadeGrandville Rondo AllegrettoconBrio (1832),quepertanyalacol¨lecciód’unparticulardelBaixLlobregat.

Caricatura de Cambó (1933). Olga Cortadellas,(2020). L'aprenent de vol

Pelquefaalapremsacatalanadefinalsdelsegle XIX,l’ocelldepaperapareixdediferentsmaneres.Enaquellaèpocalesauqueserenmoltpopularsienalguneshihaviadibuixatsocells depaper,comenl’auca Vidayhechosdelfederal oenl’Aucadelsborbons,publicadesper La CampanadeGràcia el 1872 iel 1874,respectivament.Enduesvinyetesd’aquestasegonaauca hihadibuixateljovereiAlfonsXIIambalgunsocellsdepaper.El seufill,AlfonsXIII,vaserun granaficionataplegarocelletsdepaper.Entre 1896i 1907eldiari LaPublicidad proposava resoldreocelletsnumèricsdediferentsmidesiformesenlasevasecciódepassatemps.Enles respostesdelslectors,undelsencertantssignavaambelpseudònimPajaritadePapel.Del setmanari LoGalldePaper (1870),queteniaalacapçaleraunocelldepaper,únicamentse’n vanferduesedicions.Aquestaésfinsaralail¨lustraciómésantigaqueesconeixd’unocellde papercatalà.

L’ocelldepaperestàpresentenlesobresdediversosdibuixantsbarcelonins,comRomà BonetSintes(1886-1967),mésconegutambelpseudònim BON,ManuelUrdaMarín(18881974),JosepBartolíGuiu(1910-1995)oelmolinencJuliàSerraiRiu(1921-2006),aixícom enleshistorietesdelspersonatgesMortadel loiFilemóoPepeGoteraiOtilio,deltambé barceloníFranciscoIbáñezTalavera.Altrespersonatgesdeficciódelabarceloninaeditorial Bruguera,comSuperlópez,deJan,oelparedelaFamiliaCebolleta,deVázquez,sónuns gransaficionatsaplegarocellets.L’ocelldepaperfoudibuixatpeltambébarceloníApel¨les Mestresenelsdotzequadernsdevuitpàginestitulats Granizada (1880),quesónconsiderats comundelsprimerscòmics.

3.Apel¨ lesMestres

Apel¨lesMestresiOñósvanéixermentretocavenlesdotzecampanadesentreelsdies 29 i30 d’octubrede 1854,enlajadesaparegudaCasaVelladel’actualplaçadeSantFelipNeride l’aleshoresemmuralladaciutatdeBarcelona.Enunlaterald’aquestaplaçaespotveureun modernianònimocelldepaperdeceràmicafetamblatècnicadeltrencadísiqueestàformat pervuittrianglesrectanglesisòsceles.Moltaprop,mésdequinzedesapercebutsocellets semblantsestandispersosiamagatsperdiferentscarrersdelbarriGòtic.L’obradelpolifacètic Apeles,talcomelldeiaques’escriviaelseunom,contradientlanormativadePompeu Fabra,estàformadapercançons,partituresmusicals,poemes,narracions,obresdeteatrei mésdequarantamildibuixosquevapublicarcomacol laboradorendiferentssetmanaris, comara LaCampanadeGràcia o L’EsquelladelaTorratxa,ocomail¨lustradordellibres.Els seusbiògrafseldescriuenosecentrenendiferentsaspectesdelasevavidacomapoeta, escriptor,dramaturg,contista,folklorista,floricultor,músic,cançoner,compositor,dibuixant, il¨lustradorograncol¨leccionista,peròtotsellspassenperaltlasevafacetacomapapiroflecta.L’obrad’Apel lesMestresestàplenadefiguresplegades,entrelesqualsdestacal’ocellde paper,peralqualvacompondreunacançóique,comvaobservarJuanGimeno,historiadori investigadorsevillàdelapapiroflèxia,avegadessubstitueixlalletra A enelmonogramadela sevasignatura.L’ocelldepaperapareixdibuixatmésdevintcopsenelscincvolumsdelmai publicat LlibreVert (1874-1895),conservatal’ArxiuMunicipaldelaCiutatdeBarcelona;en algunsd’aquestsdibuixosl’anomenagall.L’ocelldepaperéselprotagonistadelahistorieta Cuentodepapel dibuixadaalvolumtercerdel LlibreVert,el 1883,ipublicadaunquartde segleméstardalsetmanarihumorístic LaCampanaCatalana ambeltítol«Fantasies,idil¨li depaper».Enaquestahistòriad’amorentreunocelletiunaocelletadepaperapareixenonze figuresmésdepapiroflèxia:unataula,unacadira,unsofà,unmirall,unacarretel la,uncalaix, unallanxa,unavaixellambsoterrani,untauró,uncuciunaoreneta.Aprincipisdelsegle XXI aquestahistòriafourepresentadapel cocotòleg ititellairebarceloníPepGómez.

Il·lustracions d'Apel·les Mestres (1877 i 1879).

Moltsocellsdepaperialtresfiguresplegadesapareixenendibuixosd’Apel lesMestresde diferentspublicacionsperiòdiquesenlesqualscol¨laboravaoenil¨lustracionsdediversos

llibres.El 1877Mestresil lustràlaportadadel’obradeBalzac Losdosobreros,onesveuen cincnensjugantambunocelletdepaperenorme.ElpapiroflectaBenitoPérezGaldósvaser acasad’Apel¨lesMestresperencarregar-liunesil¨lustracionsd’unadelesprimeresedicions dels Episodiosnacionales.UntercerpapiroflectacontemporanidelsanteriorsfouMiguelde Unamuno,quemanteniacorrespondènciaambGaldós.Encaraquecompartienl’aficiódela papiroflèxia,noesconeixcaprelacióentre MestresiUnamuno,totiqueaquestúltimva visitarfreqüentmentlaciutatdeBarcelona,onelseucosí,eltambépapiroflectaTelesforo AranzadiUnamuno,eracatedràticdeBotànicai AntropologiaalaUniversitatdeBarcelona. Unamuno,GaldósiMestres(Unam-1,Gal-2 iMes-3)vansertrespapiroflectesacavalldels segles XIX i XX.

Apel¨lesMestresvamorirel 19 dejuliolde 1936,l’endemàquecomencéslaGuerraCivil Espanyola.Comquevamorirsensedescendència,unapartdelseupatrimoniesvarepartir entreelsseusnebots,amicsiminyones.Larestad’aquestgranpatrimoniesvadeixaralaciutatdeBarcelonaivaquedardispersentrediferentsmuseusiinstitucionscatalanes.Després delasevamortesvaferuninventaridelsseusobjectespersonals,entreelsqualshihaviauna capsetadecartróambocellsdepaperqueesvatrobarenelprimercalaixdelnínxolllibreria situatalsalódelacasaonresidia,alnúmero 14delpassatgedePermanyerdeBarcelona.

4.Diagramadel’ocelldepaper

Combinantaquestsmateixosdotzeplecselementalsquehemfetfinsalpas4perobtenir elmolinet,espodenferaltresfigures,com,perexemple,diferentstipusdevaixells,unpeix, unataula,unacasaambteulada....

Fareml’ocelldepaperambtrespassosmésapartirdelafiguradelmolinet,modificantels diagramesdelapapirolanúmero4delprimervolumdelacol¨lecciódenoullibrets Figuras depapel,delpolifacèticmierencGuillermoÁlvarezRoces.

Pas 7Pas 8Pas 9

Ocellet de paper

Perobtenirl’ocelletdepapercalqueenelpas8plegueuenmuntanyalescapesdedarrerei enelpas 9 invertiulesduescapesdelsdostrianglessuperiors;perferaixòcalobrirunamica lafigura.

5.Cubd’ocellets

Algunscreadorspapiroflecteshanproposatdiferentsmodelsmodularsdecubsd’ocellets: VicentePalacios(1983),JuanGimeno(2003)iRobertLang(2013).Elmodelqueesproposaa continuacióésmoltsemblantaldeJuanGimeno.

Perferuncubmodulard’ocelletsutilitzaremsispapersbicolorsquadrats,unperacadacara delcub.Situemlacaradecoloraldavantilacarablancaaldarrere.

Enaquestsquatreprimerspassosdoblegueuidesdoblegueuenvallpelssegmentsindicats.Enelpas 2 feulesmarquesdelesmeitatsdelscostatslateralsienelpas3éssuficient ferlesmarquesenlesdiagonalsdelquadrat;defet,éssuficientferunadelesquatremarques.Ambaquestsplecsaconseguimdividircadacostatdelquadratentrespartsiguals.En efecte,unintelsextremsdelcostatinferiordelquadratambelpuntd’intersecciódelesdiagonalsplegadesenelpas 2 ielssegmentsinferiorsobtingutsenelsplecsdelpas3,obtenim trianglesambanglesde30˝ ,45˝ i 105˝ .

Observemque b “ h perquèsónelscatetsd’untrianglerectangleambanglesde45˝ i a “ 2h perquèsónelscatetsd’untrianglerectangleambanglesde30˝ i60˝ .Aixídoncs, a ` b “ 3h ésadir,l’alçàriad’aquesttriangleés latercerapartdelcostatdelquadrat.

Araconstruïmdostipusdemòdulsdiferents. Cadascund’aquestsmòdulsesfaambdosplecs mésapartirdelpas 12

Perobtenirelcubd’ocellets,unimtresmòdulsdelprimertipus(pas 14.1)ambtresmòduls delsegontipus(pas 14.2)segonseldiagramasegüent.

6.Cubdemolinets

Fentpetitesmodificacionsapartirdelpas5delsdiagramesanteriorsespodenobtenircubs ambaltresmotius.Acontinuaciós’explicitenelspassosperferuncubdemolinets.

Segon mòdul

Cub d‘ocellets Vista frontal

Cub d‘ocellets Vista posterior

Pas 5Pas 6Pas 7Pas 8

Pas 9Pas 10

Pas 13Pas 14 Cub de molinets dextrogir

Sicanviemelplecdelpas5perunplecenelvèrtexsuperioresquerre(pas5’)irepetim elspassossuccessius,aleshoresobtindremuncubdemolinetslevogirqueésunaimatge especulardel’anterior. Pas 5'

1.(a)Quantstrianglesveusenaquestocelldepaper? a b c

(b)Comprovaquel’àread’aquestafiguracoincideixambeldobledelquadratdela base pbq,ambelquadratdelacuadel’ocellet pcq iamblameitatdelquadratde lasevaalçària paq:

(c)Comprovaqueelseuperímetreval:

(d)Comprovaquegenèricament Qpaq“ Qpbq‰ Qpcq.

(e)Trobaalgunsvalorsalgebraics a,b,c P R quecompleixin Qpaq“ Qpbq“ Qpcq.

2.Resoll’ocelletnumèricsegüent,publicatel7d’agostde 1896alasecciódepassatemps del’ediciódenitdeldiaribarceloní LaPublicidad :

Suggeriment:espotprogramarambunfulldecàlculcomaraExceloCalc.

3.Plegatoteslesfiguresqueapareixenenlahistòria Idil lidepaper,d’Apel lesMestres:

4.Modificaelsmòdulsdelcubd’ocelletsidelcubdemolinetsiconstrueixelcubmultimodularsegüentambocellets,molinetsivaixells:

Bibliografia

[1]ÁlvarezRoces,G.(1984). Figurasdepapel. 9 llibrets.Madrid:Sena.

[2]CanoCió,M.(2019). Apel lesmestres(1854-1936),artistaicol leccionistapolifacètic.Tesis UAB.

[3]Coll,J.(2020). PajariticumPapiroflexicum,volum I.Tesidoctoral.CerdanyoladelVallès: UniversitatAutònomadeBarcelona.

[4]FuenteRíos,T.dela. Lainagotablepajarita.3volsAutoeditat.

[5]Gimeno,J.(2003).«Cuboconpajaritas», Pajarita,82.

[6]GrupoRiglos(1988). Ellibrodelaspajaritasdepapel.Madrid:Alianza.

[7]Mestres,A.(1874-1895). LlibreVert

[8]Palacios,V.(2008). Historiadelapajarita,siglo XI.Barcelona:Salvatella.

[9] Pasatiempos,juguetesdepapel.Barcelona:MuntañolaS.A.

[10]Roca,A.;Márquez,A.(2006). L’ocelleta.Olot:EsplaisdelaGarrotxa.

[11]Sotillos,E.;Pascual,M.(1969). Elpájarodepapel.Madrid:Toray.

VullferarribarelmeuagraïmentaMinervaCiruelaperintroduir-meenelmóndelapapiroflèxia,aJosepRamisperlescorreccionsdecatalài,especialment,almeuamicimestre historiadorpapiroflectaJuanManuelGimenoViguera,delGrupoRiglos,perlesconverses quehemtingutsobreeltema.

L’autordel’articleambelgravat RondoAllegrettoconBrio, 1832

federació dentitats per a lensenyament ’’ de les matemàtiques a Catalunya

feemcat

ElsproblemesdelFemMatemàtiques comarecursd’aula

TreballantelsproblemesdelFemMatesforadeconcurs

GuillemBonetCarbóiCarmeVicensAndrés GrupdeResoluciódeProblemesFemMatemàtiques

Resum Abstract

ElFemMatemàtiques1 noésnomésun concursderesoluciódeproblemes,sinó quetambépreténserunbancderecursos onmestresiprofessorstrobinmaterialsútils alesaulesiqueajudiatreballartotesles competènciesielsprocessosmatemàtics d’unamaneraintegrada.Enaquestarticle femunapinzelladasobrelesvirtutsdel treballatravésdelaresoluciódeproblemes iensendinsemdepleenunúnicproblema perveurequeapartird’unaproposta senzillapodemaconseguirdiferents activitatsriquesiquedonenmoltjoca l’aula.

Introducció

FemMatemàtiques1 isnotonlya problem-solvingcompetitionbutalsoa resourcebankwhereteachersfinduseful materialsintheclassroomandhelpworkon allmathskillsandprocessesinanintegrated way.Inthisarticlewegiveaglimpseatthe virtuesofworkingthroughproblemsolving anddelveintoasingleproblemtoseehow, fromasimpleproposal,wecanachieve differentrichactivitiesthatcanbe productivelyusedintheclassroom.

HeuintentatferelsproblemesdelaprimerafasedelFemMatemàtiques?Sihoheufet,sabreuquenosónderespostaimmediata,sinóque exigeixenuncerttreballdelproblema perpoderarribaradonar-hisolució.Tambéalsadults,quanelsvolemtreballar,enscomportenunsmomentsdededicació,activitatmatemàticaireflexió,iunprocésdedescoberta d’algunapropietatamagada.

Precisament,elsproblemesestanplantejatsperdonaraccésalsnostresalumnesaladescobertad’unaideaclau(concepte,propietat,relació,procediment...),cosaquefacilital’accés alaresolucióalsalumnesambmésdificultatsialhoradonaunespaiperal’ampliacióalsmés avantatjats.Peraquestmotiu,pensemqueelsproblemesdelaprimerafasedelconcurssón

idealspertreballar-loscomaactivitatd’auladinsiforadelconcursambl’objectiudetreballar elsprocessosielpensamentmatemàticmitjançantlaresoluciódeproblemes.

Perquèlaresoluciódeproblemes?

L’educaciómatemàticasovints’haconfósambunasèried’exercicisambrespostesfàcilment assolibles,ambunentrenamentdesprésdelquall’aprenenttélafalsasensaciód’haverarribatal’objectiu.Encanvi,s’haquedatenunestadimoltinicialsensesaber-ho,jaquetéuna llistad’einesenuncalaix...,perònoleshautilitzatmai!

Laresoluciódeproblemes(enendavant,RP)ésmoltmésprofunda.L’alumne,perpoderresoldreproblemes,necessitaleseinesanteriors:tantcontingutscomestratègiesquel’ajudin aanarmésenllàiapensarmatemàticament,però,sobretot,unesriquesicontinuadesexperiències.

Enelcamí,laRPajudaelsalumnesaacceptarriscos,aserresilientsiperseverants.Enaquest sentit,al’horad’enfrontar-nosalproblemaésimportantelpaperdelespròpiescreencesi actituds,peròunbonentrenamentensportaràareforçaractitudscomlamotivació,l’interès, laconfiança,elgustperassumirriscos...El nivelldeprofunditatquerequereixresoldre problemescomplexosestransfereixafuturescarreresdecampsSTEM(STEMésl’acrònimanglèsqueenglobalesdisciplineseducatives:Science(ciència),Technology(tecnologia),Engineering(enginyeria),Art(art)iMathematics(matemàtiques)(Andreescu, 2020).

Amés,treballaratravésdelaRPincideixenelqueensfaméshumans:lacreativitat.Maino hihaunaúnicaaproximacióalproblema,sinóquemoltscaminssónpossiblesperarribara lasolucióolessolucions nohadeserúnica! .Al’aula,sideixemmargealacreativitat, éshabitualquen’apareguindiversos,decamins,icaldonar-losvaloratots:mésllargs,més curts,mésoriginalsoméselegants,quanesposenencomútotsaportenbonesestratègies queensenriqueixenperemprendrenousreptes.

Caltenirencompteque,malgratquel’alumnatestiguicentratadonarsolucióalproblema, lanostraintencióeducativahadesercrearaprenentatge:elsprocessosmatemàtics,leseines ilesestratègiesqueposemenmarxa,lacapacitatderepresentaricomunicarelsraonaments seguitsielsresultatsobtinguts,lacapacitatdeplantejar-senovespreguntesolesconnexions internes(dinslesmateixesmatemàtiques)oexternesquepuguinsorgir.Si,amés,femaixò engrup,totesaquesteshabilitats o,sivoleu,competències esmultipliquen.Sivolemun treballtotalmentcompetencial,aquítenimunamoltbonaopció.

Peròcomsónelsveritablesproblemes?SegonsAntoniVilaiM.LuzCallejo(VilaiCallejo, 2005),unproblemanoésnibonidolent perse,sinóqueaixòdependràdelselementsdel problemaidelasevaformulació,peròtambédel’alumne(idelsseusconeixementsiafectes), delesnostresintencionseducatives,del’organitzaciódelatascaidelagestióqueenfem comamestresal’aula.Lanostracomesa,llunydedictarsentènciasobresiuncamíésboo dolent,seràacompanyarelsalumnesatravésdebonespreguntesquefomentinlaconversa matemàticaobéelsfacindubtarireplantejar-selessevesestratègiesielsseusresultatsquan s’intueixinincorrectesobéelsportinmésenllàenlessevesinvestigacionsquanlalíniaque estanseguintsemblibona.

Totiaixò,segonslaComissióperal’ImpulsdelesConclusionsdelCongrésCatalàdeMatemàtiques(C2 EM) 2016,hihaproblemesquetenenmés«ingredients»pertriomfarenelnostre propòsit.Algunsd’aquestsingredientssón: quesiguiaccessible,ésadir,elqueanomenem «dellindarbaix»,pertalquetotselsalumnespuguincomençar;queadmetimúltiplesenfocamentsirepresentacions;quesiguisignificatiuperalsaprenentsisiguicapaçdemantenir elrepteil’interès;quesiguimatemàticamentrellevantiimpliquiideesicontingutsclau,obé facilitilaconstrucciódenousconeixementsiladeconnexions;queactivielpensamentiels processosmatemàtics;quefomentilacol laboracióiladiscussióentreelsaprenents;ique siguiextensible,ésadir,quepermetiamplitudiprofunditatenelsobjectesd’aprenentatge perpodersaciarlacuriositatdelsqueaprenenmésràpidament.

ElsproblemesdelaprimerafasedelFemMatemàtiquesestanpensatsdemaneraquetinguin elmàximnombrepossibled’aquestescaracterístiques.

Totseguitpresentemcomaexempleunproblemaquehemadaptatapartird’unaproposta senzillaiquepensemquetémoltesdelescaracterístiquesdescritesanteriorment.Aprofundintenlaideadel’extensibilitat,proposemalgunespossibilitatsquepermetenanarmés enllàienriquirencaramésl’activitat.Enaquest tipusdeproblemeséshabitualtreballartotes ogairebétoteslescompetènciesdelcurrículum,peròenaquestarticledestaquemnomés lesmésrellevants.

Problema1:plegantpaper

Imaginemunatirallargadepaper.Dobleguem-laperlameitatfentcoincidirelsdosextremscurts l’unsobrel’altre.Quanlatornemaobrir,observaremalmigunamarcadedoblec.Sienllocde doblegar-launavegadahofemduesvegades,sempreperlameitatienelmateixsentit,quanla tornemaobrirobservaremtresmarquesdedoblec.Quantesmarquesobservaríemsiféssimaixò deuvegadesentotal?

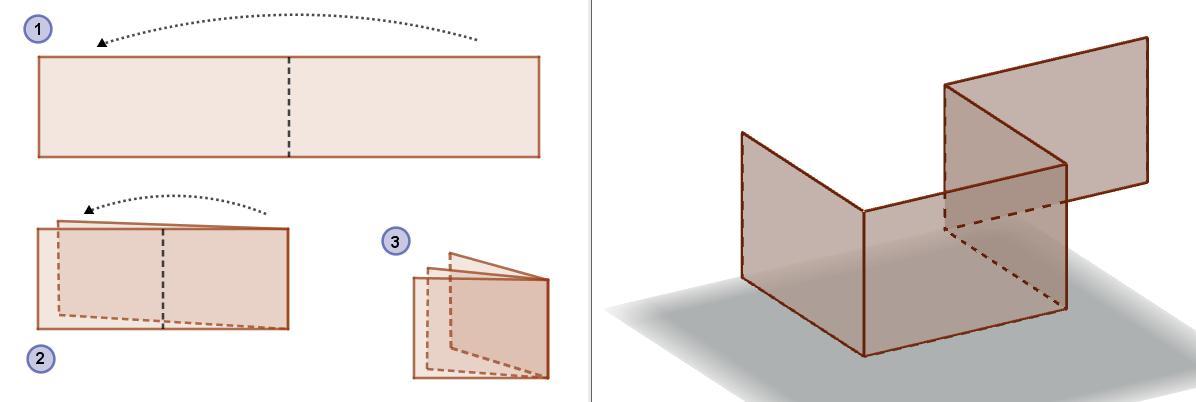
Imatge1.Tiradepaperdoblegadaduesvegadesilamateixatiradesplegadaaladreta.

Treballemelproblema?

Ésunproblemadelsqueesconeixencomdellindarbaixisostrealt: enpodermanipular,tothompotcomençar,jaquenocomencemenabstracte.Quancomencemadoblegar,intuiremcompodematacarelproblema.

Observemquelapreguntaésmoltconcreta,peròenrealitatensestàdemanantunageneralització,jaquenoéspossibleplegarfísicamentdeuvegadeslatiradepaper.

L’alumnatcomençaràamanipulariaferlesseveshipòtesis.Éshabitualquedeseguidaapareguilaproporcionalitat.Pensen:«sidoblegantduesvegadesobtinctresmarques,doblegantquatrevegadesn’obtindrésis».Nosaltres,docentsqueestemgestionantl’activitat,no hauríemdedir-lossiaixòésonocorrecte,peròsíquepodemguiar-losperdescobrirque nohoés.

Com?Doncsfentbonespreguntes.Perexemple:

‚ Elspodemdemanarquinesdadeshantrobatfinsalmomentisuggerir-losquehocomprovinambalgunesquecompleixinlescondicions.

‚ Quantesmarqueshihaambundobleciamb dos(oambdosiquatredoblecs)?Sónel doblel’unadel’altra?

‚ Enquantespartsquedadivididalacintadepaperdesprésdedoblegar-latresvegades?

D’aquestamanera,seranellsmateixoselsquehodescobriran.

Perbuscarlasolucióhauremdecomençaraplegari,demaneraordenada,anaranotantels resultatsqueobtenim.Ésimportantinsistira anarregistrantelprocésperpoderferunbon informealfinal.

Enspodemanarfixant,també,enlesdiferentsmaneresderepresentarelsresultatsquevanobtenint.Això,juntamentambl’elaboraciódel’informe,ensdonaràinformaciósobreelnivelld’assolimentdelescompetènciesdecomunicacióirepresentació,quesovintcostenmésd’avaluar.Sitreballemelproblemaforadeconcurs, podemaprofitarperposarencomúlesdiferentsmaneresderepresentar,peraixítenirmodelsianaromplintelcalaixdenoves eines.

Sienscentremenlesmarques,talcomdemanaelproblema,laseqüènciaqueobtenimnoensdonagairespistes...Peraixòseràbo afegirelnombredepartsenquèestàdivididalacinta.

Enaquestcas,ambunamicadetreballdescobriremunarelacióentreelnombrededoblecsi elnombredepartsgenerat,quesempreésunapotènciade 2 (sempre?,resultaadiental’aula buscarl’explicaciód’aquestaafirmació),iencararesultaméssenzillrelacionarelnombrede marquesambelnombredeparts,quesempreésunamenys.Peraixò,jaestemconvençuts quelarespostaalapreguntaqueenshanfetés: 210 1 “ 1.023.

Comhemcomentatambanterioritat,elsproblemessolentenirdiferentsviesd’aproximació.Ésrecomanablerepensarelproblema dediferentsmaneresperestarprevingutsdeperonesmouranels alumnesiambquinesdificultats estrobaran.Peraquestmotiués interessantqueensfemaquestapregunta:compodemtrobarel nombredemarquessensepassarpelnombredeparts?

Observemelprocésdecreaciódemarquesiensfixemenelmomentenquèvaapareixent cadascuna.

Imatge2.Tiradepaperdoblegadaquatrevegadesiamblesmarquesaconseguides.

Comencemmanipulantunacintanovadepaperimarquemambcadadobleclesmarques novesqueapareixen.Podemanotarelsresultatsobtingutsenunataulacomlaquehemfet abans:

Peròpodempredirquantsdoblecsnousenssortiransijahemdoblegatunesquantesvegades?

Suposemquehemdoblegatlacintatresvegadesiqueestemapuntdedoblegaruncop més.Podemobservarquelacintaquedaràdoblegadajustpelmigdelrectangleplegaten quèse’nshaconvertitlacintainicial.

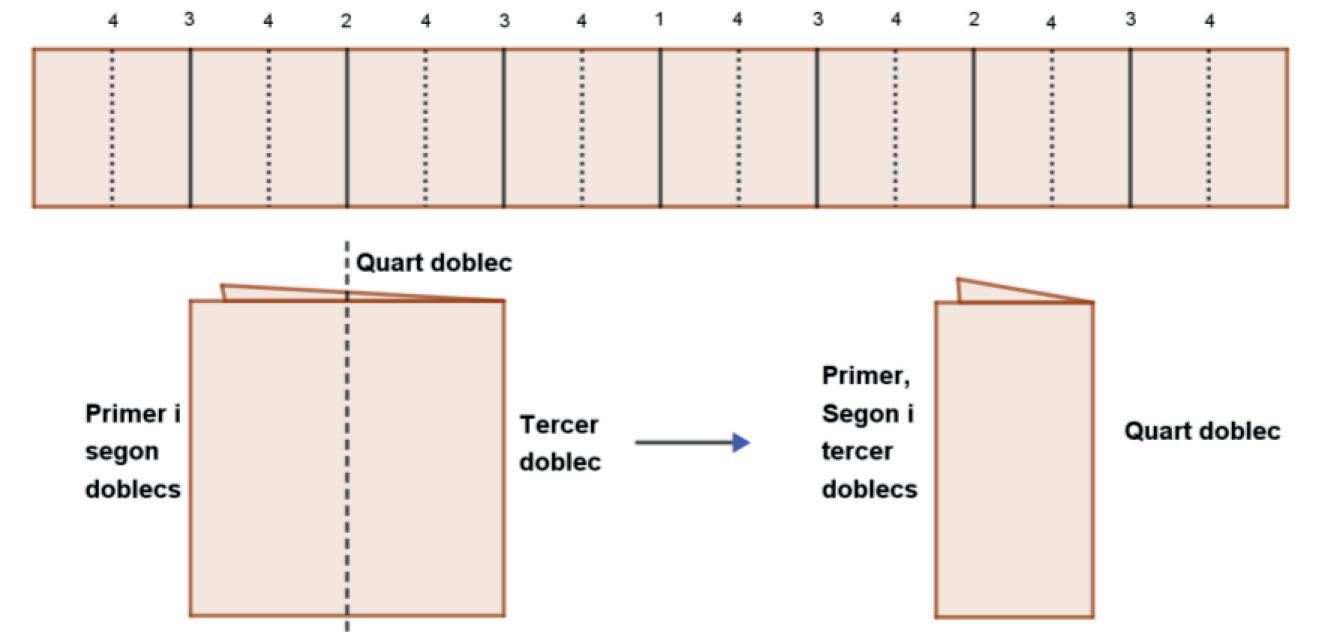
Imatge3.Tiradepaperdoblegadaquatrevegadesiamblesmarquesaconseguides.

Pertant,elnombrenoudemarquesqueapareixeranenaquestquartdoblecéselmateix queelnombretotaldepartsquehihaviafinsara.Apart,comquehemanatdoblegantla cintasempreperlameitat,aquestnombretotaldepartsseràunapotènciade 2!

Aquestraonamentseràmoltmésricsiaconseguimquesiguinells quieltrobin.Perfer-hoseràimprescindiblequeelsexpliquemmolt béquèéselquevolemiquecomencinabuscarlainterpretaciódel nombrededoblecsmanipulant.En aquestasituació,elsalumnes trobaranlainterpretacióquebusquenresponentalespreguntes adequades.Encasqueelsajudemnosaltres,hemdevigilarque aquestesnoportinimplícitalaresposta.

Arribaelmomentdeposarencomúelsresultatsobtingutsfinsal momentpelsdiferentsgrupsd’alumnes.Aquestmomentésimportantperdiversosmotius:donavaloralquehanestatfent,elsproporcionanoveseinesapartirdelesideesdelscompanysi,devegades,finsitotelspermetdescobrirpropietatsinteressants.Enaquest cas,ésmoltprobablequehihagidiferentsmaneresdepensarel problemaidebuscar-nelasolució,perònosaltresjaenshemasseguratquen’apareguincomamínimdues,que,pertant,handeser equivalents:

Aquestaideaésunaoportunitatal’aulapertrobarconjuntament unageneralitzaciódelaigualtat:

Quanproposemaquestaigualtat,elsalumness’acostumenapreguntarsiaixòpassasempre. Larespostatornaaestarenlatiradepaper.

Agafemlatiradepaperambquatredoblecs.Aquestaestàdivididaen 24 “ 16parts.Sieliminemunad’aquestesparts,obtenim

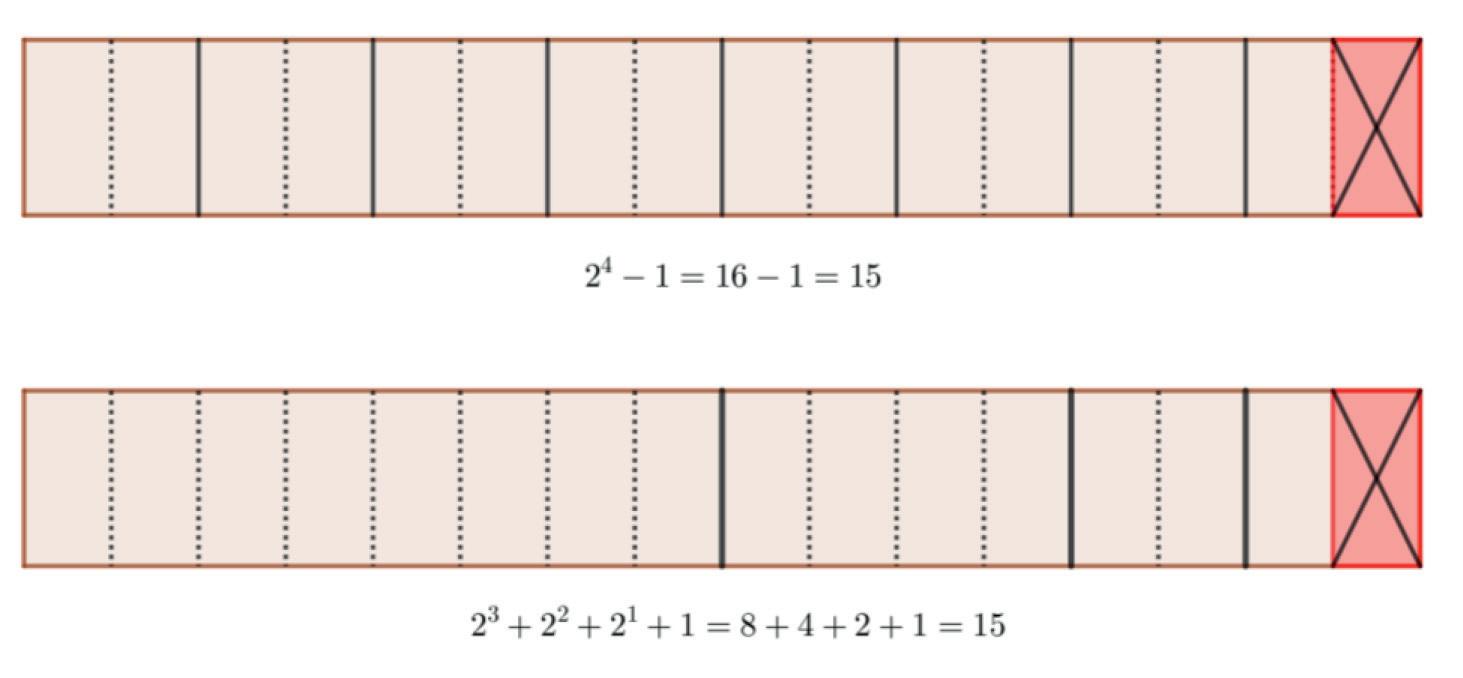
Agrupemaraaquestesquinzepartsrestantsensumadepotènciesde 2 icomprovemquehi haelmateixnombredeparts.

Lapropostadevisualitzacióésbonica,malgratquelademostracióésunpuntmenysvisual:

Espotargumentarque,d’unamaneramésomenysllarga,podemarribaralmateixresultat ambqualsevolaltrevalorde n,iaixíobtenimlageneralitzacióperatotnombrenatural n.

Primeraextensió

Malauradament,algunsalumneshauranestatcapaçosdedonarsolucióalproblemasense veureaquestesrelacionsi,pertant,perdent-separtdelabellesaqueamaga.Altresalumnes, mésavantatjats,hihaurandonatsoluciósatisfactòriamentielscalméscarburantpercontinuartreballant.Enambdóscasoselspodemferpreguntesperaconseguirquerepensinel problema,totiquelespreguntesnoseranlesmateixesperatots.

Enaquestapartathemreformulatcomareptesduesd’aquestes preguntes,enlesqualsobligueml’alumneareplantejarelproblemafixant-senonomésenelresultatnumèric,sinóenqüestions comaralaparitatonod’unresultat.Lioferimunaeinapertreballar elproblemadesd’unaltrepuntdevistaseguramentmoltdiferent delquehatrobatinicialmentilidoneml’oportunitatdetreballarel raonamentbuscantunarelacióintrínsecaentreelsdiferentsresultatsquevansorgint.

Repte1.1.Quinéselnombremínimdecopsquehemdedoblegarlacintaperaconseguirqueel nombredemarquessiguiunnombreparell?

Jahohemrespostambanterioritat:comqueelnombredepartssempreseràparell,elnombredemarquessemprehauràdesersenari,pertant,noseràmaiparell.

Repte1.2.Ambquantsdoblecsaconseguimunnombreprimerdemarques?

Enaquestcas,comencemambunaexploracióexhaustivadelsprimersvalorsdelessolucions imarquemelsvalorsqueensdonen unnombreprimerdemarques.

Doblecs Marques Doblecs Marques

Siensfixemenelsresultatsnumèricsobtinguts,comencemaintuirqueapareixeràunnombreprimerdemarquesquanelnombrededoblecstambésiguiprimer.Ambaquestatasca aconseguimaproparal’alumneelsnombresprimersde Mersenne.

Arabé,siensquedemenelsvalorsdelataula, podemarribaraunaconclusióequivocada. Semblaquesielnombrededoblecsésprimer,elnombredemarquestambéhohadeser.

Provemambelsegüentnombreprimer?Ambonzedoblecsapareixunnombredemarques iguala:

quenoésprimer.Lateoria,encanvi,tornaafuncionarperalsnombresdedoblecs 13, 17, 19...Elqueensquedaclarésquelaimplicaciónoésdirecta.Tambépodemarribararaonar quesielnombredemarquesésunnombreprimer,elnombrededoblecstambéhoserà.Per aaixòcaldràuncàlculalgebraicméspotent:

Queda,doncs,provatqueambunnombrecompostdedoblecsaconseguiremunnombre compostdemarques.

Segonaextensió

Aquestanovaextensióésmoltinteressantperacabardereforçarelsconeixementsapresos, justenelmomentposterioralaposadaencomú.

Repte2.Suposemquehemdoblegatlacintadepapertresvegades.Uncopdoblegada,ensqueda unamenadellibretenformaderectangle.Ambunestisorestallemelllibrethoritzontalmenti verticalment.Enquantstrossosensquedaràtalladalacinta?

Evidentment,elrepteésbuscarlarespostasensemanipularlacinta,sensetallarlacinta físicament.

Perrespondreaaquestapregunta,recordemquelacintadepaperestavadoblegadaenel momentdeferelsdostalls(horitzontalivertical).

Després,fixem-nosqueelprimertallenhoritzontaltallaràlacintainicialenduespartsiguals (semprequeaquesttallsiguiperpendicularalsentitdeldoblec).

Encanvi,eltallverticaltallaràcadapàginadelllibretendues,peròestaranunidesperun plec!Demaneraqueesrespectaranelnombrededoblecs.Tots?No!Enaquestcas,pera cadameitatdecintaenssortirantantstallscomdoblecshihagiméselsdosdelsextrems.

Aixòésfàcildeveuresiensfixemencomquedalacintaenelmomentprevialtall:

Imatge5.Visualitzaciódelacintaabansdelstalls.

Observemquecadatallverticalestrobaentredosplecsconsecutiusi,pertant,

parts “ 2 ¨pn ` 2q ,

on n éselnombredemarquesqueenshasortit(enelnostrecas, n

Terceraextensió

Latercerailaquartaextensióqueproposemestanformuladescoma divertimento,comun problemaperpensarsensemés.Aquestamenadeproblemesacostumemaplantejar-losa l’aulacomareptes(noobligatoris)peratots,ambl’esperançaqueelsalumnesmésmotivats s’animinatreballar-los.

Repte3.1.Fixeu-vosque,quandobleguem,algunesmarquesquedencapamuntid’altres,cap avall.Lesprimereslesanomenarempics(P)ilessegones,valls(V).Podríeutrobaralgunpatróen laseqüènciadepicsivalls?2

(Recordeuquedobleguemsempreenelmateixsentit)

Manipulantlacintafísicamentianotantpicsivallsacadaiteraciódelprocés,podemrecollir elsprimerspassosenunataulaiintentarbuscarpatronsnumèricsovisuals.Enpodemtrobar algunsapartirdelsnombresdepics,vallsitotal:elspicsilesvallssempredifereixend’una unitat,obéqueelnombredepicscoincideixambelnombretotaldeplecsenlaiteració anterior.

2..Extensióproposadaa[2].

Peròésquen’hihamés!Usheufixatenlasimetriadelasolució?Siensfixemenlaseqüència depicsivalls,mirantalcentreveuremqueesrepeteixdemanerasimètricaperòambelvalor contrari:sicomençaambduesvalls,acabaambdospics,iaixíanarfent.

Sivolemestudiarmillorcomevolucionalafreqüència,podemmirarlasèried’iteracionsdiferenciantelsplecsnousdelsantics.

Uncopentradalamarcadelesiteracionsanteriors,siensfixemnomésenlesnovesveiem queesvanalternant:comencenambunavalliesvaalternant,aravall,arapic.

Iésquetémoltsentitqueesvaginalternant.Simiremcomtenimlatiradepaperdoblegada endosdoblecs,perfer-homéssenzill ,veuremquelesmarquesquehihaenelsegon doblecsónunpiciunavallqueescomplementen,ésadir,quel’unaencaixadinsl’altra,ijust entreaquestesdueshihaunavallquelesencadena.

Alternantlamanipulació,lareflexióil’anotaciócorrectadelsresultatsaconseguimdonar respostaaunproblemacomplexqueinicialmentsenblavasenzill.

Perònoacabemaquíifemunpasmés.Usproposemunpetitsegonreptedinsaquestapartat.

Repte3.2.Hemportatal’aulaelreptedelspicsilesvallsdoblegantunacintadepaper.Unalumne enscomentapreocupatquenolihasortitlamateixaseqüènciadepicsivallsdoblegantquatre copslacinta.Lasevaseqüènciaés:V-P-P-V-V-V-P-V-V-P-P-P-V-V-P.Quèpothaverpassat?Podem detectarons’haequivocat?

Quartaextensió

Aquestadarreraextensióespassejaperunavessantmésartísticaquelesanteriors,peròal mateixtempsnoexemptaderaonamentmatemàtic.

Repte4.1.Despleguemlestiresdepaperdemaneraquecadaplecformiunanglerecte.Sihofem ambdiversesiteracions,quintipusdefiguraobtenim?

Imatge6.Primeresiteracionsdelacinta.

Sianalitzemlaterceraiteració,perexemple, observaremquecontéduesvegadeslasegonai quatrevegadeslaprimera.Sifemelmateixamblaquarta,veiemquepassaelmateix:conté duesvegadeslatercera,quatrevegadeslasegonaivuitlaprimera.

Semblaquehemdescobertunpatróisospitemquelafiguraqueobtindremésunfractal... Comprovem-ho,creem-lonosaltresmateixos!Percomençar,ésrecomanableconstruirles primeresiteracionsenpaperimanipular-lesperentendrebédequinamaneracadaiteració contélesanteriors.Totseguitpodemprovardedibuixar-nealgunesenpaperquadriculat, peròpertaldefacilitarlatascausproposemquedeixeuelpaperquadriculatcomabasei utilitzeuunfulldepapervegetalodeplàstictransparentperacadascunadelesiteracions. D’aquestamaneraresultaràméssenzillcanviarcadasegmentperlaiteració 1 o 2 (sihofem ambla 2,avançaremmésràpidamentenlaconstrucciódelfractal).Tambéenshauremde fixarenelfetquel’orientacióvacanviant.

Hemdescobertelfractalanomenat corbadeldrac. Enpodeuvisualitzarlaconstruccióen l’aplicaciósegüentdeGeoGebra(www.geogebra.org/m/qpuk5wck):

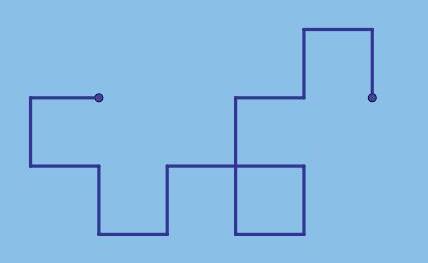
Imatge7.Iteracions4,6,8i10delfractalcorbadeldrac.3

3.AplicacióambGeoGebracreadaperGuillemBonet: www.geogebra.org/m/qpuk5wck.(consulta:3d’abril de 2022).

Repte4.2.Podeuomplirelplaambnomésunadelesiteracionsanteriors?

Enaquestcas,estractanomésd’unentretenimentalqualpodemjugarmanipulanttiresde paperobéambpaperquadriculatillapisdecolors,perexemple.Triemunadelesiteracions il’anemposant/dibuixantambdiferentscolors,modificantl’orientacióilasimetriadetota lapeça,siensconvé.Elrepteconsisteixabuscarunarutinaqueenrajolielplaamblapeça escollida.

Conclusions

Hemvistqueunsolproblemapotdonarmoltjoc.Ésclarquenopodempresentartotesles propostesalsalumnes,sinóquetriaremlesquesiguinmésadequades,tenintencompteque nocalquetotelgrupfacilesmateixes.

Elsalumnesdelscursossuperiorsdeprimàriapodrantrobarelspatronsdecreixementdel nombredepartsidemarques,sobretotsijaconeixenelconceptedepotènciaihantreballat prèviamentlespotènciesde 2.Elfetquenoconeguinelllenguatgealgebraicnoimpedeix quepuguinarribarageneralitzarelresultat:estractad’unabonaocasiópertreballarladimensiódecomunicacióirepresentació,aixícomladeraonamentiprova.Pensemqueen aquestsnivellstambéespotadaptarelproblemaalsalumnesafegintalgunaextensió,que podentreballar comasecundària! ambelsuportdematerialmanipulatiu.

Enqualsevolcas,pensemqueelsproblemesnohandeserrígidsiinamovibles,sinóque elspodem(ihemde)adaptaralesnecessitatsdelsnostresalumnesenfunciódelesseves característiques,delsseusconeixementsprevisidelsobjectiusdidàcticsqueensplantegem assolir.

Peracabar,usconvidemaconsultarelBancdeRecursosdelFemMatemàtiques,4 ontrobareu exemplesdeproblemesquehanaparegutalconcurs,juntamentamblessevespropostesi anàlisisdidàctiques.

Referències

[1]Andreescu,T.;Cordeiro,K.;Andreescu,A.(2020). AwesomeMath.Teachingmathematics withproblembasedlearning.Hoboken(NJ):Jossey-Bass.

[2]ShellCenterforMathematicalEducation(1984). Problemasconpautasynúmeros. UniversitatdeNottingham.

[3]Vila,A.;Callejo,M.L.(2005). Matemáticasparaaprenderapensar:Elpapeldelascreencias enlaresolucióndeproblemas. Madrid:Narcea.

[4]Vila,A. etal.(2018). Activitatsdereferència:Comissió peral’impulsdelesconclusionsdel C2EM2016. https://c2em.feemcat.org/cic-c2em-comissio-per-a-limpuls-de-les-conclu sions-del-congres-catala- deducacio-matematica/activitats-de-referencia/.

4.BancderecursosdelFemMatemàtiques:https://bancfm.blogspot.com/.(consulta:3d’abrilde 2022)

Normes per a la presentació de contribucions

1. La revista NouBiaix acceptaper alasevapublicació contribucionsoriginalsrelacionadesamb experiències didàctiques, activitats d’ensenyamen ti aprenentatge,escritsd’opinió,dedivulgaci ói d’investigació enel camp dela matemàtica ielseuensenyamentenqualsevol nivell educatiu

2. Les contribucionsrebudesseran avaluadesprèviamentper dosespecialistesreconeguts. La decisiópresa pelConsell deredacciósobrel’acceptació dela publicació serànotificadadirectamentals autors ambuna indicaci ódeladataaproximadadepublicaci ói el possiblerequeriment d’introduir modificacionseneltext.

3. Pera lapresentaci ódetreballsoriginals, elsautorstrametran al’adreçanoubiaix@gmail.com un arxiu, en Word oenLaTeX.Els gràfics, elsdiagrames iles figureshaurandeser originals(no fotocopiats). Els arxius gràficsespresentaran en format epso tif.

4. La contribució hauràd’incorpora reltítol,elnom de l’autoro autors,lasevaadreçapostalprofessional completai la sevaadreça electròn ica.S’adjuntaràunresum només llarg de 300 paraules en català ianglès. Al finaldel document s’inclouràobligatòriamen tlabibliografiaper ordrealfabètic de cognoms,d’acordamb la normativaAPA, com enelsexemplessegüents:

Articles

Albertí, M. (2002).Les matemàtiquesdesd’unaperspectivacultural:Etnomatemàtiques Biaix, 20,6-25.

Llibres

Godino,J., Font,V.(2003) Razonamiento algebraicoparamaestros.Granada :Universidad de Granada. Capítols dellibres

Edo,M.,Revelles, S. (2004).Situacionesmatemática spotencialmentesignificativas. Dins M. Antóni B. Moll (ed.), Educación Infantil.Orientacionesy Recursos (0-6 años) (p.410/103-410/179).Barcelona:Praxis.

Actesdecongressos

Morales, M.,Font, V.,Planas, N. (2004).Estudiomicroetnográfico en tornoa un conocimiento matemático situado. Dins A.Franzé ialtres(ed.), ActasdelaI ReuniónCientíficaInternacional sobreEtnografía y Educación (CD-ROM).València: Germanía,Polis Paideia.

Pàginesweb

Geogebra pera Infantil iPrimària. https://www.geogebra.org/m/tkdC27m f

5. Els contingutsde NouBiaix estansubjectes llevatque s’indiquiel contrarieneltext, en lesfotografies oenaltresil.lustracions— auna llicència de Reconeixement-No comercial-Sense obra derivada 3.0deCreativeCommons,eltext completdela qual es pot consultar ahttp://creativecommons.org/ licenses/by-nc-nd/3.0/es/deed.ca. Així,doncs,s’autoritza el públic en generala reproduir,distribuir i comunicarl’obra,sempreque es reconegui l’autoriai l’entita tquela publica, inose’nfaciunús comercial ni se’n difongui capobraderivada.

6. Elsarticlesespublicara nen llenguacatalana.Només es traduiranalcatalàles contribucions acceptadesd’autorsnoresidents alsPaïsosCatalans.

7. Elsautorsesresponsabilitzarandel complimen tdeles normes establertesper al’autoritzaciódela reproducciódematerialprocedent d’altres fontsbibliogràfiques

8. Elsarticlestindran unaextensiómàximade 8000 paraules,inclosesles notesa peudepàgina,però s’acceptenarticles méscurts,d’entre 2000 i 4000 paraules

9. Femnotar queenaquesta publicació s’utilitza preferentmen telpuntper separardecimals, en lloc dela comarecomanadaper l’IEC, pertal defacilitarla comprensi ódeles expressionsmatemàtiques.