Nou Biaix, 47

Revista

bia x uno i

Desembre 2020

de la FEEMCAT i de la SCM

número 47

sumari

Consell de redacció:

Marianna Bosch / Carlos Giménez (coords.)

Montserrat Alsina

Joan Carles Ferrer

Joan Miralles

Manuel Udina

Coediten:

Federació dEntitats per a lEnsenyament de les Matemàtiques (FEEMC AT ) Campus de Montilivi, edifici P- IV 17071 Girona feemcat.org

’’ , © dels articles, els seus autors

Societat Catalana de Matemàtiques (SCM ) filial de l’Institut d’Estudis Catalans Carme, 47 08001 Barcelona scm.iec.cat noubiaix@gmail.com

articles

Imma Casas Argerich

Sílvia Salvador Fàbregas

Criptografia a batxillerat: aplicacions de les matrius i implementació amb TAC

Víctor Ranera i Martín

Continguts didàctics del curs d’Aritmètica

Social del físic català Aragó

Gabriel Ruiz-Garzón

Jaime Ruiz-Zapatero

Coneixement, arguments i magnituds

Pedro Nicolás Zaragoza

seccions

Nombre dexemplars: 1.700 ’

Fotografia de la coberta:

Cinc quar tes parts

Pau Pérez Argemí al Periodicitat: semestr

ISSN : 2014-2021

Dipòsit legal: B-22.314-2012

Impressió: Gráficas Rey

Edicions

de la Universitat de Barcelona

Adolf Florensa, s/n 08028 Barcelona

Tel.: 934 035 430 comercial.edicions@ub.edu www.edicions.ub.edu

Editorial 1 4 19 35 46 68 82 I l’estadística, què?

El racó de l’oriflèxia

Tóng xn fng shèng: infinites cartes d'amor īā

Jaume Coll Guerrero

Xi oxián Huáng

Per pensar d’un minut a una hora

Jordi Deulofeu ă

Comencemambaquestnúmerounanovaetapadel NouBiaix,jaques’haproduïtundoble relleuenlacoordinaciódelConselldeRedacció,onMariannaBoschsubstitueixJosepLluís SoléperpartdelaSocietatCatalanadeMatemàtiques(SCM)iCarlosGiménezprenelrelleu deLluísMoraperpartdelaFederaciód’Entitatsperal’EnsenyamentdelesMatemàtiquesa Catalunya(FEEMCAT).

Siguin,doncs,lesnostresprimeresparaulesd’agraïmentsincerperalatascadelsnostres predecessors,quehanportateltimód’aquestanauambdecisióicoratgeihanaconseguit mantenirelnivelldel NouBiaix allàonlipertocacomareferentenladivulgaciódel’activitat deladidàcticadelesmatemàtiquesdetotselsnivellseducatiusaCatalunya.

Entomemaquestrepteamblafermavoluntatd’aconseguir,simésno,mantenirl’esperit quesemprehainspiratel NouBiaix.Malgratelstempsconvulsosqueensestàtocantviure, creiemmésquemaiquecaleniniciatives,comaquestadel NouBiaix,perpartdetotes lesassociacionsimplicadesenelmóndel’educaciómatemàticaacasanostra.Sempreens trobareudefensantaquestaidea.

Elnúmeroqueteniualesmanscontéquatrearticlessobretemàtiquesvariadesidiferents nivellseducatius.

ImmaCasasiSílviaSalvadorenspresentenenel seuarticle«Il’estadística,què?»elplantejamentintegralquefanalseucentre,l’InstitutSerradeNoet,pertaldedignificarl’ensenyament del’estadísticaal’educaciósecundàriaobligatòria(ESO),massasovintoblidadapelfetdeno ocupar,aparentment,unaposiciócentralen elcurrículumdematemàtiquesd’aquestaetapa educativa.Veuremdiferentsexemplesdeprojectesrealitzatspelseualumnatquetenencom adenominadorcomúpermetrequepuguinveurel’estadísticacom«laciènciaquetractala recollida,l’organitzacióieltractamentdelesdadesambl’objectiud’extreure’nconclusions queenspermetinfergeneralitzacionsambcriterismatemàtics».

VíctorRaneraensregalaenelseuarticle«Criptografiaabatxillerat»unaguiallestaperser utilitzadasobrecomaplicarelcàlculmatricialqueestreballaasegondebatxillerataunmón

quesempreresultaengrescadorperal’alumnat:eldelacriptografiaocodificaciódelainformació.Faunrepàsdelesprincipalstècniquesdexifratgequeespodenaplicaramissatgesde textilesidentificaambelcàlculmatricialassociat,totincloent -hielcodinecessariperpoder automatitzarelsprocessosdexifrat-desxifratutilitzantl’entorndeprogramacióOctave.

Enl’article«Contingutsdidàcticsdelcursd’aritmèticasocialdelfísiccatalàAragó»,Gabriel Ruiz-GarzóniJaimeRuiz-Zapaterodescriuenunaspectedelahistòriadelesmatemàtiques quesovintdonempersabut:eldel’origendel’organitzaciódelscontingutsqueavuis’ensenyen.Enaquestcas,estractadelcàlculdeprobabilitats,queoriginàriamentesvaestructurar entorndeproblemesd’interèssocial,d’especulacionscomercials,taulesdemortalitatijocs d’atzar.Elsautorsensenmostrenl’origenatravésdelabiografiadelfísicd’origencatalà FrancescAragó,quevasucceirGasparMongeenlaprestigiosaÉcolePolytechniquedeParís ivasereldissenyadordel’assignaturad’aritmèticasocialenelnouplad’estudisdel 1816 dirigitperPierre-SimonLaplace.

Enelquartarticled’aquestvolum,«Coneixement,argumentsimagnituds»,PedroNicolás enspresentaunaanàlisiepistemològicaididàcticasobreeltractamentdelesmagnituds enl’ensenyamentdelesmatemàtiques.Aquesttreballsorgeixdepreguntar-sequèsón lesmagnituds,comespodendefiniriquinpapertenenenlamatemàticaescolar.Perquè lesmagnitudstenenuntractamentmoltambiguenl’ensenyamentdelesmatemàtiques, especialmentasecundàriaialauniversitat,semprepresentsperòsempredesotamà.Nicolás abordaaquesttemadifícildes d’unaperspectivadidàctica. Enlaprimerapartdel’article desenvolupaunareflexiógeneralsobreelsprocessosdetransmissiódeconeixementiels supòsitsenquèesfonamenten,iexaminaelstipusd’argumentsqueutilitzemperjustificar lesnostresafirmacionsoproposicions.Enlasegonapartjas’endinsaenl’universdeles magnitudsiensproposaunmodelepistemològicdereferènciaqueenshauriad’ajudara plantejariabordarelproblema.

Enlapartdelescol laboracionsregulars,«Elracódel’oriflèxia»ensreservaunasorpresa relacionadaamblaXina,lescartesd’amor,elpaper,elsplecsilessevesequacions.I,com sempre,JordiDeulofeu,enlasecció«Perpensard’unminutaunahora»,ensobsequiaamb unaselecciómoltequilibradadereptesmatemàticsdedificultatitemàticadiversa,quede bensegurresultaranatractiusperalamajoriadelectorsilectoresdel NouBiaix.Usdesitgem moltasortambelsproblemes!

Usdesitgematotsitotesunamoltbonalecturaiesperemtambélesvostrescol laboracions perquè NouBiaix puguianarcreixentievolucionantcomhofanelstemps.

articles articles

Il’estadística,què?

ImmaCasasArgerichi SílviaSalvadorFàbregas

DepartamentdeMatemàtiquesdel’InstitutSerradeNoet

Resum Abstract

Aquestarticlepresentaelplantejament integralqueesfaal’InstitutSerradeNoet deBergapertaldedignificarl’ensenyament del’estadísticaal’ESO,massasovint oblidadapelfetdenoocupar,aparentment, unaposiciócentralenelcurrículumde matemàtiquesd’aquestaetapaeducativa. Veuremdiferentsexemplesdeprojectes realitzatspelseualumnatquetenencoma denominadorcomúpermetrequepuguin veurel’estadísticacom«laciènciaquetracta larecollida,l’organitzacióieltractamentde lesdadesambl’objectiud’extreure’n conclusionsqueenspermetinfer generalitzacionsambcriterismatemàtics».

Thisarticlepresentsthecomprehensive approachtakenatthesecondaryschool InstitutSerradeNoetinBerga,tohighlightthe teachingofstatisticsingrades7-10.The subjectofstatisticsisoftenneglectedatthis educationallevel,becauseitdoesnotoccupy acentralpositioninthemathematics curriculum.Differentexamplesofprojects carriedoutbythestudentsareused,whose commondenominatoristoallowthemtosee statisticsas«thesciencethatdealswiththe collection,organisationandprocessingof datatodrawconclusionsandgeneralisations withmathematicalcriteria».

L’estadísticaésunadisciplinafonamentalperatotselsestudiantsquedecideixenfercarreres científiques.Algunsd’ellsesdedicaranalarecercaiunadelesseveseinesbàsiquesserà l’estadística.D’altrabanda,l’estadísticaprenunaimportànciarellevantendiversosàmbits, tantcientíficscomsocials,iéspresentenels mitjansdecomunicaciódemaneraconstant.És peraixòqueelprofessoratdematemàtiquesdel’InstitutSerradeNoetdeBergavamacordar treballar-ladesdel’ESOid’aquestamaneraimpulsargeneracionsfuturesamillorarlarecerca enlaciència,aixícomapotenciarelseuesperitcrític.

Apartirdel’anàlisidelsresultatsdelsnostresalumnes,tantenrelacióambl’avaluacióinterna comamblesprovesdecompetènciesbàsiques,elsmembresdelDepartamentdeMatemàtiquesdel’InstitutSerradeNoetensvamadonar,jafaunacollad’anys,quehihaviacertsblocs temàticsquequedavendescuidatsiqueelnostre alumnatnohaviaassolitcorrectamenten acabarl’ESO.Aixòensvaportaraferunestudienprofunditatdelcurrículumd’aquestaetapa educativa,apartirdelqualvamdecidirreordenar-loiplantejarlaprogramaciódelcentrede maneraquecapblocquedésoblidat.

Abandadelamodificacióireordenaciódelcurrículum,aquestareflexiótambéensva portaraoptarperunaltreenfocamentmetodològical’horadeplantejarlesclassesde matemàtiquesalesnostresaules:ensvamadonarquelanostramanerad’ensenyarinduïa algunsdelsnostresalumnesaveurelesmatemàtiquescomunasimplerepeticiód’algoritmes i,enconseqüència,al’horaderesoldreproblemesosituacionsaplicadesaplicavenlacercai repeticiód’unpatróaprèssenseentendreelsprocedimentsqueestavenduentaterme.Això elsduiaaoblidarràpidamentelsaprenentatgesassolitsilessevesaplicacionsiaaprendre elsconceptescomsifossinbolets,ésadir,aïllatsisensetenircapmenadecontinuïtatdins elseuprocésd’aprenentatge.Aixímateix,ensvamadonarquemoltesvegadesnosabien aplicarelsconeixementsadquiritsdavantd’uncontextconcret.Vamferèmfasienelfet queelsnostresalumneshaviendesercompetencialsihaviendepoderaplicardemanera naturaliambnormalitatallòquefèiemal’aulaalasevavidaquotidiana.Aixídoncs,ensvam proposarl’objectiudecanviarlasevamiradadelmónidelesmatemàtiques,peralaqualcosa haviend’entendrequelesmatemàtiquesnosón receptes,sinóqueenspermetenadquirir lacapacitatdecrearsolucionsitrobarrespostesaproblemesipreguntesquese’nsgeneren enelnostrediaadia.Aixídoncsvampassaracanviarl’enfocamentdelamatèriabuscant diferentsmaneresd’introduircadablocapartirdelraonamentiladeducció.Volíemensenyar alsnostresalumnesautilitzarlesmatemàtiquescomunaeinaperpotenciarelraonamenti elpensamentcrític.

Undelsblocsquevamvolermillorar,ionteníemmésfeinaperfer,eraelblocd’estadística iprobabilitat.Ensvamplantejardueslíniesdemillora:canviarlatemporitzacióirevisarels objectiusd’aprenentatgeafiqueelsaprenentatgesd’aquestblocfossincompetencials.Ésa dir,transferibles,queespoguessinutilitzarenaltrescontextos;significatius,queperduressin eneltemps;productius,quepermetessinrealitzaractivitatsquenofossinexclusivament reproductivesorepetitives;ifuncionals, quepermetessinresoldreproblemesdelavida quotidiana,propersalcontextdelsnostresalumnes.Enaquestnoumarcdetreballvam decidirincorporarlestecnologiesdelainformacióilacomunicació(TIC)comaeinaessencial del’aprenentatgeentoteslespartsdelprocésestadístic:recollidad’informacióenwebs oficialsomitjançantqüestionarisgeneratsambl’einadeGoogle,recollidadedades,càlcul deparàmetresestadísticsmitjançantfullsdecàlculielaboraciódegràficsperextreure conclusions.

Ensvamproposarpresentarl’estadísticaalsnostresalumnescomlaciènciaquetractala recollida,l’organitzacióieltractamentdelesdadesambl’objectiud’extreure’nconclusions queenspermetinfergeneralitzacionsambcri terismatemàtics,ivamveurelanecessitat d’anarmésenllàdelfetd’ensenyarafertaules defreqüències,gràficsicalcularalgunes mesuresestadístiques.Vamcreurequeseriaunabonaideatreballarelblocd’estadística iprobabilitatatravésdeprojectesambtemàtiquesdiversesqueenspermetessinobrir canalsd’investigacióendiferentstemesd’interèsperalsalumnesiqueenglobessinàmbits d’aprenentatgediversos:vidasaludable,reciclatge,comportamentdelséssersviusdavant diferentsestímuls,característiquessocioeconòmiquesdelesnostresciutats,genètica...

Cadascund’aquestsprojectessegueixl’estructurasegüent:

Dissenyiinvestigació

1. Quèvolemestudiar? Escollireltema:calescolliruntemaperinvestigarquecridi l’atenciódelalumnes.

2. Dequihovolemestudiar? Caldeterminarlapoblació/individusquevolemestudiar.

3. Quinescaracterístiquesvolemestudiar? Enaquestpuntdefinimleshipòtesisiels objectiusdelnostreprojecte.Calexplicaralsalumnesquèsónleshipòtesisicoms’han deformular.L’objectiudelprojecteéscontrastarleshipòtesisformulades,ésadir, determinarsileshipòtesisielsobjectiusqueenshemplantejatescompleixenono desprésd’haverfetl’estudiestadístic.Perferunesboneshipòtesiscalpensarquines sónlescaracterístiquesquepodemobservarimesurardelanostramostra.Ésmolt importantqueelsalumnesparticipindemaneraactivaenlasevaformulacióiper fer-hocompartimundocumentalGoogleDriveoncadagrupd’alumnesescriules seveshipòtesis;acontinuaciólesposemencomúal’aulaientretotsescollimlesque formaranpartdelprojecte.

4. Quinesdadeshemderecollir?Comleshemderecollir?Comd’importantésla recollidadelesdadesperferunbonestudi? Apartirdeleshipòtesisielsobjectius escollitscaldecidirquinesdadess’handerecolliriquinesvariablesestadístiquess’han dedefinirperdespréspodercontrastar-les.Depenentdeltipusd’estudis’estableixel procedimentperrecolliraquestesdadesise’ndeterminenlamostrailadimensió.

a)Enunplaexperimental,larecollidadedadesesbasaenl’observacióil’experimentació.Aquestesdadespodenprendre’sfentúsd’instrumentsdemesura,allaboratori oenelmedionesdesenvolupal’experiment.

b) Podemrecollirdadesenbasesdedadesoficials:Idesctat,INE,MinisterideSanitat, Conselleriad’Educació...

c) Podemrecollirdadesatravésd’unaenquesta.

Estudiestadístic

Enaquestapartcalorganitzarlesdadesrecollidespertald’extreure’nlainformaciórellevant peralnostreestudi.Treballaremduesbranquesdel’estadística:

1 L’estadísticadescriptiva,ques’ocupad’organitzarlesdadesquehemrecollitentaules igràficsperestablirrelacionsiobservarlainformaciód’aquestesdades.

2. L’estadísticainferencial,queextreuconclusionssobretotaunapoblació,peròl’estudi s’hafetrealmentd’unapetitapartd’aquesta:lamostra.Perferlapartd’inferència norealitzemtestsd’hipòtesisdedistribucionsdeprobabilitat,jaqueenelsnivellsde l’ESOaquestscontingutsencaranos’estudien,peròsíquefemmoltd’èmfasienelfet quelamostrapresasiguiraonablementsignificativadelapoblació;ésadir,donem importànciaalvalorquetéelprocésderecollidadelesdades.Silesdadesrepresenten lapoblació,aleshorespodremferunabonainferència;sino,lesconclusionsseran errònies.Peralcàlculdelvolummostralintroduïmunaaplicacióenlíniaquecalcula quantsindividushadetenirlanostramostrasegonslagrandàriadelapoblacióque volemestudiar.

Perferl’estudiestadísticcal:

‚ Definirlesvariables,qualitatives/quantitatives.

‚ Construirlestaulesdefreqüènciesperacadavariable.

‚ Dibuixarelsgràficsmésadequatsperacadavariableicompararaquestsgràfics.

‚ Calcularlesmesuresestadístiquesdecentralitzacióidispersiódelesvariables.

‚ Ferinferènciesiprediccions.

Contrastemhipòtesisiextraiemconclusions

Elsprimerscursos,quanvamcomençaratreballar,vamdecidirconcentrarelblocd’estadísticaalprimertrimestredetercerd’ESO,dissenyatdemaneraquehiapareguessintots elscontingutsd’estadísticadelblocd’estadísticaiatzardelcurrículumdematemàtiques desecundària.Aquestsprimersanyserenelsestudiantselsqueproposavenelstemesdels projectesquevolientreballar.Apartird’aquíiseguintunapautadetreballdelsprojectes,eren elsalumneselsquedonavenformaalsseuspropisprojectes:escollienuntema,formulaven hipòtesis,definienobjectius,recolliendades, generavenlestaules,dibuixavenelsgràfics, calculavenmesuresestadístiques,extreienlesconclusionsipresentavenelsprojectes.Però aixònovaacabardefuncionarperquèensvam trobarambtemesmoltdisparsal’aulai aixòensdificultavapoderduratermeunabonaavaluacióformadoraenrelacióambtotsels temesquenosaltresvolíemtreballarestadísticament.Aquestaprimeraexperiènciaensva servirperadonar-nosquehihaviapuntsquehavíemdemillorar:caliainsistirsobretotenla importànciadelarecollidadelesdades,puntclauperferunbonestudi,enelformatdels gràficsienlalecturail’anàlisidelsresultats.

Caliadonar-hiduesvoltesmés.Caliapensarcomhopodíemmillorar.Aixívasercomvam decidirferdoscanvisimportants.D’unabanda,treballaríemunprojecteúnicieltemael proposariaelprofessorat,sempretenintencompteelqueelsalumnestreballenenaltres matèries,l’actualitat,elsinteressosdel’alumnat...Aixòfacilitarial’organitzaciódelprojecte pertalqueelsalumnesassolissinelsobjectiusd’aprenentatgedelbloc.D’altrabanda, treballaríeml’estadísticaendosnivellsidefiniríemunprojectepernivell:unprojecteentre primerisegond’ESO,quecomençaalllargdeltercertrimestredeprimeriacabadurantel segontrimestredesegonobéenl’optativatallerdematemàtiques;iunprojecteentretercer iquartd’ESO,quecomençaelprimertrimestredeterceriacabaafinalsdelsegontrimestre dequart.Durantelprimercursdecadaprojecte primerotercerd’ESO plantegemla ideadelprojectealsnostresalumnes,formulemleshipòtesis,marquemelsobjectiusque volemassolir,recollimlesdades,lesendrecementaules,definimlesvariablesidibuixemels gràfics.Alllargdelsegoncurs segonoquartd’ESO calculemelsparàmetresestadístics, interpretemelsgràfics,relacionemelsresultatsiextraiemlesconclusions,escriviml’informe delnostreestudiielaboremunapresentació.Elsalumnesexposenlessevesconclusions davantdelsseuscompanysi,finalment,presentemeltreballmésboalconcursPlanteri Sondeigd’Experimentslaqualcosadonaunamotivacióextraalsalumnesperintentarfer millorelseutreball.

Pertalquequedimésclaralamaneradetreballar,acontinuacióusmostremtresprojectes quehemdutatermeambelsnostresalumnesenaqueststresúltimscursos.

Cargolssilvestresvs.cargolsdegranja

‚ Projectetreballatambelsalumnesdeprimerisegond’ESO.Perpreparariduraterme aquestprojectevancol¨laborarambnosaltreslesàreesdeBiologiaiFísicaiQuímica. Aquestprojecteésunplaexperimentalenelqualescomparenlesrespostesdedos grupsdecargolsdavantl’estímuldelmenjar,elscargolssilvestresielscargolsdegranja, ambdósdelamateixaespèciedecargols, Helixaspersa ocargolcomúdejardí.

Dissenyiinvestigació

‚ Quèvolemestudiar? Enaquestprojectevamdecidirinvestigarquinscargolserenmés ràpids,elssilvestresoelsdegranja,silasevarapidesadepeniadelseupesonoiquins erenmésgrossos.

‚ Dequihovolemestudiar? Enelnostreprojectelapoblacióéselgrupdelscargols comuns, Helixaspersa.

‚ Quinescaracterístiquesvolem estudiard’aquestscargols? Vamformularleshipòtesissegüents:

Hipòtesi1:elscargolsdegranjapesenmésqueelscargolssilvestres.

Hipòtesi2:elscargolssilvestressónmésràpids.

Hipòtesi3:elscargolsmésràpidssónelsmésgrans.

Estudiestadístic

‚ Recollidadedades. Estractad’unplaexperimental.Larecollidadedadeslavamferal laboratoriivamanotarlesdadesenunfulldecàlcul.Vamseguirelspassossegüents:

Identificarlamostra.Vametiquetarelscargolsambgomets enumeratsdecolorsverd(cargolssilvestres)irosa(cargolsde granja).Lanostramostraestavaformadaperdostipusdecargols:elsquevamanarabuscarielsqueensvaportard’una granjadecargolslaprofessoradebiologia.Ladimensiódela mostraerade48cargols.Els individus delamostraeren 27 cargolssilvestresi 21 cargolsdegranja. Pesarelscargols.

Mesurarl’espairecorregutieltempsquetrigacadacargoldesdelpuntde sortidafinsalafullad’enciam. Permesurarl’espaivamferservirlabavaque haviendeixatalsfullsdecel¨lulosa.Ambunfiliagullesdecapvamanarresseguint latrajectòriadelabava.Uncoprecoberttotelrecorregutdelabavaambelfil,vam treurelesagullesivammesurarlalongituddeltrosdefil.Ambuncronòmetrevam mesurareltempsquecadacargolinvertiaarecórrerlatrajectòria.Totseguitvam anotarlesduesdadesenelfulldecàlcul.

Calcularlavelocitatmitjanadelscargols.

Vmitjana “ espairecorregut temps .

Esparladevelocitatmitjanaperquèevidentmentelcargolnoseguiràunmoviment rectiliniuniforme(MRU),ésadir,noaniràavelocitatconstantnienlíniarecta.Per tant,lavelocitatescalculaapartirdel’espaitotalrecorregutdelatrajectòriaseguida ieltempstotalinvertitarecórrer-la.Vamcalcularaquestesvelocitatsamblesdades recollidesenelfulldecàlcul.

Definirlesvariables.

‚ Variable«tipusdecargol». Ensserviràperdefinircoméslamostra.Ésuna variablequalitativaambduescategories:cargolssilvestresicargolsdegranja.

‚ Variable«pesdelscargols». Ésunavariablequantitativacontínua.Enaquesta variableagrupemelspesosenintervalsd’1,5grams.

‚ Variable«velocitatdelscargols». Ésunavariablequantitativacontínuaenla qualagrupemlesvelocitatsenintervalsde5cm/minut.

Construirlestaulesdefreqüènciesper cadavariable.Dibuixaricompararels gràficsmésadequatsperacadavariable.

‚ Variable«tipusdecargol». Diagramadesectors%.

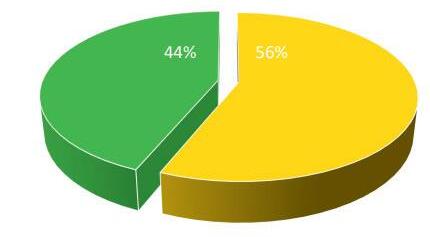
Tipusdemostra Nombredecargols % Graudelsector

Cargolssilvestres

,5

‚ Variable«pesivelocitatdelscargols». Diagramesdebarres%.

‚ Variable«pesrespectealavariablevelocitat». Núvoldepunts(pesdelcargols, velocitatdelscargols).

Calcularlesmesuresdecentralitzacióidispersiódelesvariables«pes»i «velocitat».

Contrastemhipòtesisiextraiemconclusions

‚ Observantl’estudiestadísticfet,comprovemleshipòtesisiextraiemconclusions. Elresultatd’aquestprojectevasereltreballd’estadísticaguanyadordelanovena ediciódelconcursPlanteriSondeigd’Experimentsl’any 2018.Ielmateixanytambé vaserguanyadordelconcursd’estadísticaaescalanacional«IncubadoradeSondeosy Experimentos».Siteniuinterèsallegireltreballcomplet,elpodeutrobaraquí:

CARGOLSSILVESTRESvsCARGOLSDEGRANJA

Lesfamíliestenensexe?

‚ Aquestprojectel’hemtreballataterceri quartd’ESOjuntamentambl’assignaturade Biologia.Enelprojecteenshemplantejatestudiarladeterminaciódelsexeenles famíliesdelanostracomarca,elBerguedà.Enaquestestudihemseguitdueslínies detreball:unaprimeralíniaenlaqualestudiemelsexeenlesfamílies tipusde família,sexedelsgermansisexedelgermàmésgran,pergeneracions unasegona líniaenlaqualhemvolgutobservar,entermesgenerals,sidinsd’unamateixafamília existeixrelacióentreeltipusdefamíliadel’enquestat,elsseusantecedentsielsseus descendents.Perferaquestestudihemfetúsdel’estructuradelsarbresgenealògics.

Cargols de granja

Cargols silvestres

Dissenyiinvestigació

‚ Quèvolemestudiar? Enaquestprojecteenspreguntemsiéspossibledeterminarel sexedelesfamíliesdelBerguedàpartintdel’arbregenealògicdecadafamíliaisihiha relacióentreelsexedelesfamíliesdediferentsgeneracions.

‚ Dequihovolemestudiar? Lapoblaciódel’estudiestadísticésladelacomarcadel Berguedà,unacomarcaambunabaixadensitatdepoblacióconcentradaenlaseva capital:Berga.Segonslesdadesdel’IDESCAT(dadesIDESCATrecollidesel 2019),el 2019 lapoblacióalacomarcadelBerguedàerade39.446habitants, 19.748homesi 19.698 dones.

‚ Quinescaracterístiquesvolemestudiardelanostrapoblació? Formularhipòtesis. Aquestprojecteté quatrehipòtesis:

Hipòtesi1:hihamésfamíliesd’homesquededones. Ambaquestestudivolem determinarsihihafamíliesenlesqualspredomininelshomes,famíliesenlesquals predomininlesdonesifamíliesenlesqualselnombred’homesielnombrededones siguielmateix,ienquinaproporcióencadageneració.Perfer-hoestudiemlavariable «Tipusdefamíliapergeneracions».

Hipòtesi2:eltipusdefamíliad’unageneracióestàrelacionatambeltipusde famíliadelparedelageneracióanterior. Ambaquestahipòtesivolemcomprovarsi labrancamasculinadelafamíliaéslaquemanasobreeltipusdefamíliadelageneració següent.Perferl’anàlisienscentraremenlapartmasculinadelabrancapaternai buscaremquinessónlesrelacionssegüents:«tipusdefamíliaenquestat»vs.«tipusde famíliapare»,«tipusdefamíliapare»vs.«tipusdefamíliaavipatern».Descriuremles relacionsambtaulesbivariadesimostraremelsresultatsengràficsitaules.

Hipòtesi3:larelacióentreeltipusdefamíliadel’enquestatieltipusdefamíliesde lasevabrancamasculinaesmantéenlageneraciósegüent. Ambaquestahipòtesi descriuremlarelacióquehihaentreeltipus defamíliadel’enquestatdesexemasculíi eltipusdefamíliadelsseusfills.Aquestarelaciólacompararemambladelageneració passada,ésadir,amblarelacióentreelstipusdefamíliesdel’enquestatidelseupare, quejahemdescritenlahipòtesi 2.

Hipòtesi4:lamajoriadegermansgranssóndelsexemasculí. Ambaquestahipòtesiestudiaremsielsexemasculídelgermàgranpredominasobreelfemeníacada generació.Perfer-hoestudiaremlavariable«Sexedelgermàgran»pergeneracions.

‚ Recollidadedades. Elsalumnesdetercerd’ESOvanduratermelarecollidadedades. Enaquestprojectevamprepararunesenquestessobrelafamília(progenitors,germans, descendents...)ambl’ajudadel’estructurad’unarbregenealògic.Fetaixò,elsalumnes vansortiraferlesenquestesalseupoble.Pertald’escollirlespersonesquehavien d’enquestarhaviendeseguirelscriterissegüents:

Nopodienformarpartdelamateixafamília.

Cadaalumne/ahaviad’enquestarcomamínimunindividudecadafranjad’edat següents:

‚ de 9 a 17anys

‚ de 18a 27anys

‚ de 28a37anys

‚ de38a47anys

‚ de48a57anys

‚ mésde57anys

Lameitatdelsenquestatshaviendeserhomesil’altrameitat,dones.

Estudiestadístic

‚ Coméslamostra:dimensiódelamostra. D’acordamblesdadesoficialsutilitzemla pàginaSurveymonkeypercalcularqueambunadimensiódelamostrade381 individus obtindremunmarged’errord’un5%iunnivelldeconfiançadel 95%.Seguintelscriteris

anteriorsiamblacol laboraciódetotselsalumnesvamaconseguirunmostrade 234 individus.

‚ Definimlavariable. Acontinuacióvamdefinirunavariablequalitativa,quetéquatre categories:H,homes;D,dones;HD,mixta;NI,noenteniminformació.Vamcomptabilitzarelnombred’homesidedonespergeneracions:primerl’enquestat,desprésels seusascendents primerageneració:ladelsseuspares;segonageneració:ladelsseus avis i,enelcasquetinguésfills,elsseusdescendents.Uncopdeterminatelnombre d’homesidedonesacadageneració,vamdefinirlavariable«tipusdefamília»talcom usindiquem:

Famíliesd’homes(H):sónlesfamíliesenquèelnombred’homeséssuperioral nombrededones.

Famíliesdedones(D): sónlesfamíliesenlesquèelnombrededoneséssuperior alnombred’homes.

Famíliesmixtes(HD): sónlesfamíliesenquèelnombred’homesielnombrede donesesreparteixendemaneraequilibrada.

Famíliessenseinformació(NI): sónlesfamíliesdelesqualsnoesdisposad’informació.

Desdelnostrepuntdevista,aquestésundelspuntsques’hadevalorard’aquestprojecte,jaquecentremtotl’estudienelcomportamentd’aquestavariablequeacabem dedefinir.Ladistribuciód’aquestavariableéslasegüent:

TIPUSFAMÍLIA

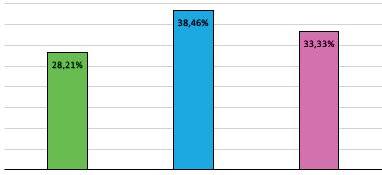
‚ Construïmlestaulesdefreqüènciesperacadavariable.Dibuixemicomparemels gràficsmésadequatsperacadavariable. Enaquestestudiprincipalmentfemúsde diagramesdesectorsidiagramesdebarres,jaqueestudiemproporcionsipercentatges. Pelquefaal’estudiestadístic,envolemdestacarl’úsd’algunarelacióbidimensional, compodriaserentrelesvariables«nombredegermans»i«nombredegermanes». D’aquestavariablevolemobservarque,totiqueprenelsvalorsmésgrans,segueixla mateixalíniaquedelarestademembresestudiats.Elquevolemremarcarésquela modaésNI:hiha56enquestatsquenorecordenalgunesdelespreguntesquese’ls hafetsobrelasevaàviapaterna.Observemquelamitjanadelnombredegermansi germanesés3,6,superioraladelesgeneracionsanteriors.Itambéfeml’úsdetaules dedobleentrada,queenspermetencreuardadesperextreureinformacions,lesquals ensajudensobretotatreureinformaciódeleshipòtesis 2 i3,talcompodeuveureen lesimatgesanteriors.

Contrastemhipòtesisiextraiemconclusions

Ambaquestestudi,entrealtrescoses,vampoder concloureque,efectivament,lesfamílies enquestadestenensexe.Isiestractadefamíliesdesexemasculí,latipologiadefamíliaes mantétantenlesgeneracionsanteriorscomenlesposteriors.

Elresultatd’aquestprojecteéseltreballd’estadísticaguanyadordel’onzenaediciódel concursPlanteriSondeigd’Experimentsdel’any 2020 enlacategoriadeterceriquartd’ESO. Aquíteniul’enllaçpersihivoleuferunaullada:

https://drive.google.com/file/d/17mSSNLj8rB9LHthp5X1cRQE0vyNjfxZE/view?usp=sharing.

Dissenyiinvestigació

Educationalcenters:miniaturesocieties? Aquestprojecte elvamtreballarambalumnesdequartd’ESOdelnostre centreconjuntamentambalumnesdetercerd’ESOdel Col¨legiReginaCarmelideRubímitjançantlaplataforma eTwinning.AquesttreballvaguanyarelpremiIdescatenla desenaediciódelconcursPlanteriSondeigsd’Experiments del’any 2019.Estractad’unestudisocioeconòmicones comparenelsnostrescentres,l’InstitutSerradeNoetde BergaielCol legiReginaCarmelideRubí,amblesnostres ciutatsrespectives,BergaiRubí,entreellsiambCatalunya, ambl’objectiudecomprovarsielscentreseducatiussón bonsrepresentantsaescalasocioeconòmicadelesciutats onpertanyenideCatalunya.L’anglèsvaserlallengua vehiculard’aquestprojecte.

‚ Escollimeltema. AquestprojecteelvamferconjuntamentambelCol legiRegina CarmelideRubí.Caliaescolliruntemaqueenspermetéstreballardemaneraconjunta desdelsdoscentresiqueresultésproperiinteressantperalsalumnesdeBergaiperals

deRubí.Vamdecidircentraraquesttreballenelsnostrescentresienlesnostresciutats. Vamestudiarenquinsaspecteslarealitatsocioeconòmicadelnostrescentress’acostai s’allunyamésdelarealitatdelesnostresciutatsidelconjuntdeCatalunya.Tambévam estudiarenquinsaspectess’assemblavenidiferienméselscentresentreells.

‚ Població,mostra,dimensió delamostraiindividus. Elsindividussónelshabitants deBerga,Rubí,Catalunyaielsalumnesd’ESOdelsnostrescentresquehancontestat l’enquesta.Perdefinirlapoblaciód’aquestestudihemdetenirencomptequeaquest projectetétresparts:

Unaprimerapartenlaqualfeml’estudidelesnostresciutats:lapoblacióéslade BergailadeRubí.

Unasegonapartenlaqualfeml’estudidelsnostrescentres:lapoblacióéselconjunt delsalumnesd’ESOdelsnostrescentres.

UnatercerapartenlaqualfemlacomparacióambCatalunya:lapoblacióéslade Berga,RubíiCatalunya.

‚ Formularleshipòtesis. Leshipòtesisd’aquestprojecteesbasenenl’estructurasocioeconòmicadelscentres.Cadacentrevaformularunseguitd’hipòtesisdel’àmbit socioeconòmicsobre:

elseucentre;

l’altrecentre,desprésd’havervistelsvídeosqueelsseuscompanyshavieneditat ions’explicaonsesituenlessevesciutatsgeogràficamentiquinessónlesseves característiquessocioeconòmiques.

‚ Recollidadedades. Perrecollirlesdadesd’aquestprojectevamseguirdoscamins:

Fontsoficials.Vamprendredadesdel’IdescatdeBerga,RubíiCatalunyasobre:el sexe,elllocdenaixement,lanacionalitat,elnivelld’estudis,lapoblacióactivaono, elsectoreconòmicontreballenelspares,elsconeixementsdecatalà,l’habitatge depropietatodelloguer ,elnombredepersonesqueformenelnuclifamiliari eltipusdevehiclequetécadafamília.

Enquesta.Perpoderferl’estudidelsnostrescentresvamcrearunaenquestaila vampassaratotselsalumnesd’ESOdelcentre.

Estudiestadístic

‚ Definimlesvariables

Pelquefaal’alumne/aenquestat

‚ Sexe

‚ Edat

‚ Llocdenaixement

‚ Nacionalitat

‚ Tipusdefamília

‚ Nombredepersonesqueviuenacasa

‚ Nombredecotxes

‚ Nombredemotocicletes

‚ Tipusd’habitatge

‚ Llenguaqueparlaacasa.

‚ Llenguaqueparlaambelsamics.

‚ Extraescolarsquefa.

Pelquefaalpare/maredel’alumne/aenquestat

‚ Llocdenaixement

‚ Nacionalitat

‚ Nivelld’estudis

‚ Situaciólaboral

‚ Sectoreconòmicontreballa

‚ Règimdetinençadel’habitatge

‚ Coneixementdecatalà

‚ Construïmlestaulesdefreqüènciesperacadavariable

Perrepresentarlesdadesd’aquestprojecteutilitzeminfografiesbasadesenels percentatges comsifóssim 100,talcomensmostrenlesimatgessegüents:

‚ Contrastemhipòtesisiextraiemconclusions. Siesteuinteressatsaferunaulladaal resultatd’aquestprojecte,hopodeuferal’enllaçsegüent:

Educationalcenters:miniaturesocieties?

https://drive.google.com/file/d/1thNGqJ-8AtRZOXnApKB7UhwT1QkSJDgQ/view

Peracabar,elquemostraremésque,talcomtreballeml’estadística,cobrimpràcticament totelblocd’estadísticaiatzardelcurrículumdematemàtiquesdesecundària.Enlataula següentveiemremarcatselscontingutstreballatsenelsprojectesd’estadísticaalllargde total’etapaiamblletradecolorblauescrivimelscontingutsclaudel’àmbitdigitalquetambé estreballenenaquestprojectes:

CursosContinguts clauContinguts

Estudis estadístics (CC13, CC14)

Primer

CC13. Sentit de l’estadística

CC14. Dades de les taules i gràfics estadístics

CD13. Fonts d’informació digital: selecció i valoració

CD22. Entorns de treball i aprenentatge col·laboratiu

CC14. Dades de les taules i gràfics estadístics

CD9. Eines d’edició de documents de text, presentacions multimèdia i processament de dades numèriques

CD16.Tractament de la informació

CC15. Mètodes estadístics d’anàlisi de dades

CD9. Eines d’edició de documents de text, presentacions multimèdia i processament de dades numèriques

CD10. Llenguatge audiovisual: imatge fixa, so i vídeo

CC13. Sentit de l’estadística

CC14. Dades de les taules i gràfics estadístics

CD9. Eines d’edició de documents de text, presentacions multimèdia i processament de dades numèriques

CD13. Fonts d’informació digital: selecció i valoració

CD22. Entorns de treball i aprenentatge col·laboratiu

CC14. Dades de les taules i gràfics estadístics

CD9. Eines d’edició de documents de text, presentacions multimèdia i processament de dades numèriques

CC15. Mètodes estadístics d’anàlisi de dades

CD10. Llenguatge audiovisual: imatge fixa, so i vídeo

Disseny d’investigacions

Recollida de dades: observacions, enquestes i experiments

Dades qualitatives i dades quantitatives

Entorn col·laboratiu: Drive.

Gràfics estadístics (CC14)

Diagrames de punts, de barres i de sectors

Característiques i classificació

Full de càlcul i recursos TAC (Tecnologies de l’aprenentatge i els coneixement)

Eines d’anàlisi de dades (CC15)

Full de càlcul i recursos TAC

Mesures de centralització: mitjana, mediana i moda

Edició d’una presentació i/o un vídeo del projecte

Estudis estadístics

Disseny d’investigacions i recollida de dades

Població i individu, mostra i variables estadístiques

Taules, freqüències absolutes i relatives, ordinàries i acumulades.

Entorn col·laboratiu: Drive

Gràfics estadístics

Diagrames de barres, de línies i de sectors

Full de càlcul i eines TAC

Eines d’anàlisi de dades (CC15)

Mesures de centralització: mitjana, mediana i moda

Mesures de dispersió: valor màxim, mínim i rang

Edició d’una presentació i/o un vídeo del projecte

Segon

CursosContinguts clauContinguts

CC13. Sentit de l’estadística

CC14. Dades de les taules i gràfics

Tercer

CD22. Entorns de treball i aprenentatge col·laboratiu

CC14. Dades de les taules i gràfics

CC15. Mètodes estadístics d’anàlisi de dades

CD9. Eines d’edició de documents de text, presentacions multimèdia i processament de dades numèriques

CD10. Llenguatge audiovisual: imatge fixa, so i vídeo

Estudis estadístics (CC13, CC14)

Mostres

Variables discretes i contínues

Agrupació de dades en intervals

Entorn col·laboratiu: Drive

Gràfiques estadístiques (CC14)

Histogrames i polígons de freqüències

Eines d’anàlisi de dades (CC15)

Mesures de centralització: mitjana, moda, quartil i mediana

Mesures de dispersió: rang i desviació típica

Full de càlcul i recursos TAC

Edició d’una presentació i/o un vídeo del projecte

Estudis estadístics (CC13, CC14)

CC13. Sentit de l'estadística

CC14. Dades i gràfics

CD22. Entorns de treball i aprenentatge col·laboratiu

Quart

CC14. Dades de les taules i gràfics

CD9. Eines d’edició de documents de text, presentacions multimèdia i processament de dades numèriques

CC15. Mètodes estadístics d’anàlisi de dades

CD9. Eines d’edició de documents de text, presentacions multimèdia i processament de dades numèriques

CD10. Llenguatge audiovisual: imatge fixa, so i vídeo

Disseny, mostres i aleatorietat de les respostes i els experiments

Dades quantitatives i qualitatives, unidimensionals i bidimensionals

Història de l’estadística aplicada a les ciències socials

Entorn col·laboratiu: Drive

Gràfics estadístics (CC14)

Histogrames, diagrames de caixa, núvols de punts, coeficients de correlació

Eines d’anàlisi de dades (CC15)

Mesures de centralització i de dispersió

Full de càlcul i recursos digitals per a l’estadística (CCD24)

Inferència i predicció Edició d’una presentació i/o un vídeo del projecte

Criptografiaabatxillerat: aplicacionsdelesmatriusi implementacióambTAC

VíctorRaneraiMartín EscolaJoanPelegrí vranera@joanpelegri.cat

Resum Abstract

Enaquesttreballesdescriucoms’ha d’aplicarl’àlgebradematriusqueforma partdelscontingutscurricularsdeles matemàtiquesdebatxilleratala criptografia.Enaquestsentit,empraremla sumaielproductedematriusielcàlculde lamatriuinversapelmètodedelsadjunts. Finalment,implementaremtotelprocésde codificació,xifratge,desxifratgei descodificacióambl’entornOctave,un llenguatgedeprogramaciópensat essencialmentperalacomputació numèrica.

Objectiu

Thisarticleexplainshowtoapplymatrix algebra includedintheuppersecondary mathematicscurriculum tocryptography. Tothisend,wewillusethesumandthe productofmatricesandthecalculationofthe inversematrixbythemethodofadjoints. Finally,wewillimplementtheentireprocess ofcoding,encrypting,decryptingand decodingusingOctave,softwarefeaturinga high-levelprogramminglanguage,primarily intendedfornumericalcomputations.

Enaquestaactivitatesproposaemprarl’àlgebra lineali,enparticular,lestransformacions ambmatriusperxifraridesxifrartextos.Enconcret,esproposaemprarmatriusde3files comaclauperxifraridesxifrariunalfabetde 28símbols.Noesdetallalaversiógeneral delssistemesdexifratge,sinóques’havolgutanardirectamentalesparticularitatsdeles adaptacionsdelsmodelsproposats.

L’objectiuprincipaléstreballarelxifratgedeHill,malgratques’exposaranelsxifratgesper permutacióideCèsarcomaintroductoris.Tambéesfaranalgunesobservacionssobre seguretatdelssistemesemprats,peròseràmés atítolinformatiuiamblafinalitatdepensar estratègiesdemillora.

Elsprocedimentsdecàlculaquíexposatsespodenduratermeambpaperillapisamb alumnatdebatxillerat,peròtambédetallaremunapropostad’implementacióambl’entorn GNUOctave,einaessencialmentcompatibleambMatlab.

Introducció

Lacriptografiaésl’estudidelestècniquesd’escriuremissatgesdemanerasecretapertalque nomésunreceptorautoritzatsiguicapaçdellegir-los[1].Elseuorigenetimològics’hade buscarenlesparaulesgregues kriptos («ocult»)i grafos («escriptura»).Elseudesenvolupament alllargdelahistòriatéduesetapes:laprecientíficailamoderna[2][3].Laprimeravadesdela Grèciaclàssicafinsalaintroducciódelsordinadors,capalfinaldelaSegonaGuerraMundial. Lasegonacomprènelperíodeenquèlacomputaciótéunpapercabdal,especialmentper lasevacapacitatdegestionargransquantitatsd’informacióifermoltíssimesoperacionsde càlcul.Avuidialacriptografiaésunabrancadelesmatemàtiquesambaplicacionsencamps comlaseguretat,laintegritatol’autenticitatdelesdades,lescomunicacions...

Quanunemissorvoltransmetreuntextounmissatgeaunreceptor,hofaviauncanalon aquestpotserinterceptat.Perevitarquepuguisercomprèsencasd’arribaramansdequi nos’esperaqueelrebi,s’enviaunaversiómodificadadeltext.Elprocésdemodificaciódel texts’anomenaxifratgeihadepermetrequeunreceptoramblainformaciósuficientpugui recuperareltextoriginal.Enaquestsentit,caldistingir:

‚ Elmètodedexifratge:éselconjuntdetècniquessegonslesqualsesmodificaeltext originalperobtenireltextxifrat.

‚ Elmètodededesxifratge:éselconjuntdetècniquessegonslesqualsesrecuperaeltext originalapartirdeltextxifrat.

‚ Laclau:ésunodiversosvalorsnumèricssenseelsqualsnoespotaplicarelmètodede xifratge[4].Unmateixmètodedexifratgesoltenirmúltiplesclaus.Laclaudexifratgei desxifratgepotserlamateixaono,ifinsitotnohadeserfàcilmentdeduïblel’unaa partirdel’altra.

Elsmètodesqueaquís’exposenpertanyenal’èpocaprecientíficainomésl’emissoriel receptorpodenconèixerlaclau:éselqueesconeixcomaclauprivada.Encasqueaquesta clausiguiconegudaperquiinterceptaelmissatgexifrat,llavorspodriarecuperareltext originalsisapquinhaestatelmètodedexifratge.Aixòesdeualfetqueelsmètodesde xifratgeidesxifratgesónl’unl’inversdel’altreilaclauéslamateixaol’unas’obtédel’altra demanerasenzilla.Pertant,laclaus’hadetransmetreperuncanalsegurihad’estarben custodiada.

Codificació

Sivolemtreballarambtextosdesd’unpuntdevistaalgebraic,elprimerquehemdeferabans dexifrar-loséscodificar-los.Ésadir,hemdetransformarleslletresielssímbolsalfanumèrics ennúmeros.D’aquestamanera,elprocésd’emissióirecepciód’untextsegueixl’esquema següent:

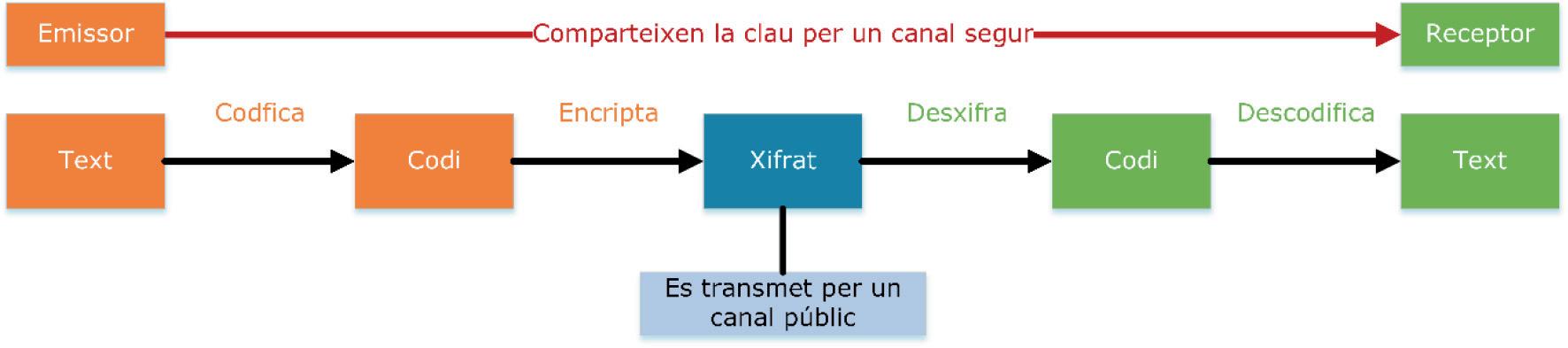
Durantaquestaactivitatempraremunalfabetdevint-i-vuitcaràcters(leslletresmajúscules senseaccentuar,elpuntil’espaienblanc)ifaremlacodificaciósegüent:

Símbol Codi

A 0

B 1

C 2

D 3

E 4 F 5 G 6

Símbol Codi

7

Símbol Codi

Així,perexemple,codificaremalgunes paraulesotextdelamanerasegüent:

Ñ 15 020

Ñ

Peròaquestatirallongadexifreshadedisposar-sed’algunamanera pertaldepoder-la gestionar.Enaquestaactivitatproposemquesiguienformadematriuiaixípodremrecórrer alestècniquesdel’àlgebralineal.Enparticular,hofaremenmatriusdetresfilesperquèsón lesqueméscomunamentmanipulemalbatxillerat.

Així,col¨locaremelcodienunamatriu C ambtresfilesitantescolumnescomcalguiianirem situantelscodisalescolumnes(omplint,sical,ambelcodicorresponental’espaienblanc, lesposicionsfinalsquepuguinquedarbuides).Perexemple:

Hompodriainterpretarlacodificaciócomunamenadexifratge,jaqueeltext,uncop codificat,ésdifícilmentcomprensible.Totiaixò,consideremqueenaquestafasenoes preténocultarcapinformaciói,pertant,nopodemconsiderar-lapròpiamentunxifratge[1].

Text1 “ «PAU» ÑC1 “

Text2 “ «JOANPELEGRI» ÑC2 “

Text3 “ «BONDIA»ÑC3 “

Hihaforçamètodesclàssics,conegutscomaxifratgedesubstitució,quetenencomaclau unataulapercanviarelscaràctersperalgunaaltrarepresentaciósimbòlica[2].

Araaltextcodificatliaplicaremunatransformaciómitjançantelqueconeixemcomaclau, demaneraqueeltextresultantsiguidifícilmentreconeixible.Aixòéselquehemanomenat xifratge.Aquíestudiaremtressistemesdexifratgeenquèlaclauésunamatriuis’empren operacionsbàsiquesd’àlgebralineal:

‚ Xifratgeperpermutacions

‚ XifratgedeCèsar

‚ XifratgepelmètodedeHill

Xifratgeperpermutacions

Aquestatècnicaésunadelesméssenzillesiconsisteixaalterarl’ordredeleslletresd’untext: cadagrupdetreslletres,lesreordenemsegonsuncertcriteri.

Perexemple,sivolemquelaprimerapassialllocdelasegona,lasegonaaldelaterceraila terceraaldelaprimera,elxifratgeserà:

Text1 “ «PAU» codificació ÝÑ C

Text2 “ «JOANPELEGRI» codificació ÝÑ

Text3 “ «BONDIA» codificació ÝÑ C3 “

xifratge ÝÑ X3 “

Pertant,sialgúinterceptéselmissatgexifrat,llegiriaunacol lecciódenúmeros,quesi descodifiquésdonarienllocalstextossegüents:

Aquestxifratgeespotferambmatriusdelamanerasegüent:

1.Partimd’unamatriuidentitatd’ordre3: I3 “ ¨ ˝ 1 00 0 1 0 00 1 ˛ ‚ .

2.Reordenemlesfilesd’acordambelcriteriquevolemreordenarelsgrupsde3lletresi obtenim P.

3.Codifiquemfent X “ P C .

Aixídoncs,laclaudexifratgeés P.

Seguintambl’exempleanterior,onhemfetquelaprimerapassialllocdelasegona,lasegona aldelatercerailaterceraaldelaprimera,lamatriu A serà:

Fixem-nosque,aplicadaacadascunadelesmatrius C delcodi,dona:

Perdesxifrarelmissatgecaltenirencomptequesi X “ P ¨ C ,llavors P 1 ¨ X “ P 1 ¨ P ¨ C “ C ésadir: C “ P 1

Laclauperdesxifrarés P 1 .

Enelcasanterior, P

Tornematenirlesmatriuscodificadesoriginals,ésadir:

XifratgedeCèsar

Aquestmètodedexifratgeconsisteixadesplaçarlacodificaciódelscaràctersalfanumèrics b posicions.Ésadir,perxifrarsesuma b acadascundelscodisenquèhemconvertiteltext.Per tant,laclautantperxifrarcomperdesxifrarés b,enuncasfentundesplaçamentendavanti enl’altrefent-loenrere.

Siquandesplacemuncodi b posicionsenspassemde 27,llavorstornemacomençar,ésa dir,lirestem 28.Aixòéselquealgebraicamentesconeixcoml’aritmèticamòdulis’expressa mitjançant ”.

Atèsqueelnostreobjectiuéstreballarambmatrius,empraremunamatriu B ambles característiquessegüents:

‚ 3files.

‚ Tantescolumnescomelcodirequereixi.

‚ Toteslesentradesamb b.

Així,perexemple,siprenem b “ 12 peralscasosdelsexemplesanteriors: Text1 “ «PAU» codificació ÝÑ

Text3 “ «BONDIA» codificació ÝÑ

Elquefaràelmètodededesxifratgeésrestar b atotselscodis.Comhemdit,laclauésla mateixa b:generaremunamatriu B,comabans,iperdesxifrarrestarem b atotselselements. Tornaremaaplicarl’aritmèticamòdul 28,enaquestcassumant 28alspossiblesnegatius.

Seguintambl’exemple: X1 “

13 1112 26 15 11 25 20 11

Tornematenirlesmatriuscodificadesoriginals,ésadir:

XifratgedeHill

ElxifratgedeHillvaserideatperLesterS.Hill[5].Aquíespresentaunaversióambalgunes variacionspertalqueelscàlculsespuguinferambpaperillapisenunaauladebatxillerat comaaplicacionsdelesmatrius.

Bàsicament,aquestxifratgeconsisteixaobtenirunamatriu A amblescaracterístiques següents:

‚ Quesiguiinvertible,ésadir,queexisteixi A 1 .

‚ Quelessevesentradessiguinenters.

‚ Queelseudeterminantnosiguimúltiplede 2 nide7(quesónelsdivisorsprimersde 28q

Xifraremfent X “ A ¨ C tenintencomptequepotserquealgundelstermesde X tingui coeficientsmajorsque 27omenorsque.Enaquestscasos,sumaríemorestaríemtantes vegades 28comcalgués(buscaríemunvalorcongruentmòdul 28,quedenotemamb l’operador ”q acadascunadelesentradesperquèelresultatestiguésentrei 27.Malgrat quel’aritmèticamòdul 28noformipartdelcurrículumdel’ensenyamentpreuniversitari, ésfàcilmentexplicableal’alumnatperquè l’alfabetquetenimtéaquestamidaicalfer reduccionsacodisentrei 27.

Perexemple,siprenem

dexifratgeserà:

Eldesxifratgeesfamitjançant A 1 ,ésadir,laclauperdesxifraréslamatriuinversadelaclau dexifrar:

Enl’exemplequeacabemdeveures’haproduïtlacircumstànciaque det pAq“ 1,laqual cosaenshafacilitatelcàlculdelamatriuinversa.Peròsi det pAq‰˘1,llavorshauremde recórreralcàlculdelamatriuinversavia

Tenintencompteque 1 det pAq hadeserl’inversmòdul 28de detpAq.O,elqueéselmateix,cal buscarunvalor u entertalque

pAq¨ u “ 1 ` k ¨ 28 peralgunk P Z.

Ditd’unaaltramanera,calcercar u queverifiqui

L’existènciade u ésconegudaapartirdelaidentitatdeBézout:

Elmètodeperobtenir u s’escapadel’objectiuqueaquíensplantegem,peròespotrecórrer aeinesinformàtiqueso,nomésperaalgunscasos,alataulasegüentperobtenir-lo:

Pertant,laclauperdesxifrarserà

idesxifraríemvia:

OperacionsambmatriusaOctave

Octaveésunprogramarilliurequeenspermetunagestióàgildelsprocedimentsdecàlcul queaquínecessitem.Totiaixò,hemdefinitalgunesfuncionsquefacilitenlacomprensiódels càlculs.

Vegeualgunesfuncionsilasintaxibàsicad’Octavequenecessitem:

‚ Introduirunamatriu A 3ˆ3perfiles: A=[[a11a12a13];[a21a22a23];[a31a32a33]].

‚ Introduirunamatriu A 3ˆ3percolumnes: A=[[a11;a12;a13][a12;a22;a32][a13;a23;a33]].

‚ Calcularlamatriutransposadadelamatriu A: traspostaA=A1

‚ Calculareldeterminantdelamatriu A: a=det(A).

‚ Calcularlamatriuinversadelamatriu A: invA=inv(A).

‚ Determinarelnombredefilesicolumnesd’unamatriu A: m=rows(A) n=columns(A).

‚ Generarlamatriuidentitatd’ordre3, I3 : I=eye(3).

‚ Generarunamatriude m filesi n columnesamb 1 atoteslesentrades: A=ones(m,n).

‚ Generarunamatriude m filesi n columnesambnombresal’atzarentre 0 i 1 segonsuna distribucióuniformeatoteslesentrades: A=rand(m,n)

‚ Calcularelmàximcomúdivisor d de p i q iobtenirelscoeficientsdelaidentitatde Bézout (p*u+q*v=d): [d,u,v]=gcd(p,q).

‚ Obtenirelresidudeladivisióde p per m: r=mod(p,m).

‚ Convertirunadadaenunenterde8o 16bits: n=int8(x) n=int16(x).

‚ Perrecuperareldarrercàlculdutatermetenimans.

Amés,hemdefinittresfuncions:

‚ Codificarenunamatriuuntextd’acordambl’alfabetilametodologiadefinitsenaquest article: C=codifica(text).

‚ Descodificardemanerainversaacomhofalafunció codifica: text=descodifica(C)

‚ Calcularlamatriuadjuntadelamatriu A: adjuntaA=adj(A).

Aquestesfuncionssónal bucket https://octave-online.net/bucket~NQzX4rncyNJxKFDYdWc2m, esmostrenalapartfinald’aquestarticleiespodendescarregarde:https://drive.google.com/file/ d/1oc4rTk99DS78ZNnsVTky7Be6rBO_RrB6/view?usp=sharing.

AplicacióambOctave

Podemproposaralnostrealumnatqueduguiatermemanualmentelsexercicissegüents,i altresquese’nspuguinacudir,idesprésseguirelprocedimentambOctave.Aquís’optaper laversióenlíniad’Octave,peròtambéespotemprarlaversióques’instal laal’ordinador,la qualestàdisponibleperadiversossistemesoperatius.

Xifratgeperpermutacions

Procedimentmatemàtic

Xifraremmitjançantelxifratgeperpermutacionstotcanviant la 1afilaperla3aideixantla 2acomestà: P “

00 1 0 1 0 1 00

ImplementacióambOctave

Accedimal bucket delaversióenlínia d’Octave:https://octave-online.net/ bucket~NQzX4rncyNJxKFDYdWc2m

I=eye(3) P([13],:)=I([31],:)

Volemtransmetreeltext«PLOUIFASOL».Calcodificar-loala matriu C C=codifica("PLOUIFASOL")

Encriptemeltextcodificat: X “ P ¨ C X=P*C

Aquestseriaelmissatgequehauríemdetransmetre.Sialgú l’interceptéssembladifícilqueenpoguésferres.Provemde descodificar-lo.

descodifica(X)

Trobemlaclauperdesxifrar: P 1 inv(P)

Desxifrem X . ans*X

Descodifiquemiobtenimelmissatgeoriginal. descodifica(ans)

XifratgedeCèsar

Procedimentmatemàtic

ImplementacióambOctave

Accedimal bucket delaversióenlínia d’Octave:https://octave-online.net/ bucket~NQzX4rncyNJxKFDYdWc2m

XifraremmitjançantelmètodedeCèsarilaclaués b “ 17. b=17

Volemtransmetreeltext PLOUIFASOL.Calcodificar-loala matriu C . C=codifica("PLOUIFASOL")

Creemunamatriu B amblesmateixesmidesquelamatriu C delcodi.Lamatriu B tindràtoteslesentradesigualsa b. ones(rows(C),columns(C)) B=b*ans

Encriptemeltextcodificat: X “ C ` B. X=C+B

Reduïmlesentradesavalorsentrei 27. X=mod(X,28)

Aquestseriaelmissatgequehauríemdetransmetre.Sialgú l’interceptéssembladifícilqueenpoguésferres.Provemde descodificar-lo. descodifica(X)

Desxifrem X X-B

Reduïmlesentradesavalorsentrei 27. mod(ans,28)

Descodifiquemiobtenimelmissatgeoriginal. descodifica(ans)

XifratgedeHill

Procedimentmatemàtic

ImplementacióambOctave

Accedimal bucket delaversióenlínia d’Octave:https://octave-online.net/ bucket~NQzX4rncyNJxKFDYdWc2m

XifraremmitjançantelmètodedeHillilaclaués A “ ˜ 1 1 0 02 1 1 2 1 ¸ A=[[1-10];[021];[1-21]]

Volemtransmetreeltext PLOUIFASOL.Calcodificar-loala matriu C C=codifica("PLOUIFASOL")

Encriptemeltextcodificat: X “ A ¨ C . X=A*C

Femquelesentradesdelamatriuambeltextxifratestiguin entrei 27. X=mod(X,28)

Aquestseriaelmissatgequehauríemdetransmetre.Sialgú l’interceptés,sembladifícilqueenpoguésferres.Provemde descodificar-lo. descodifica(X)

Observemqueeldeterminantdelamatriudelaclaudexifratge és3. det(A)

Cerquem u talque detpAq¨ u ” 1. [g,u,v]=gcd(det(A),28)

Trobemlaclauperdesxifrar u ¨ adj pAq T ilireduïmlesentrades avalorsentrei 27.

u*adj(A)1 mod(ans)

Desxifrem X ans*X

Reduïmlesentradesavalorsentrei 27. mod(ans,28)

Descodifiquemiobtenimelmissatgeoriginal. descodifica(ans)

Observacionsfinalssobreseguretat

SegonselprincipideKerckhoffs,laseguretatdelssistemescriptogràficsnoesbasaaocultar elsistemadexifratge,sinóenla dificultatd’aconseguirlaclau [6].Enconseqüència,disposar d’unampliventalldeclausfaràquesiguimenysprobablequel’enemicl’encertioque,a còpiad’anarprovant,latrobi.

Lallenguaenlaqualpotestarescriteltextquevolemtransmetre,liconfereixunescaracterístiquescomaralafreqüènciadecadascunadeleslletresodecertesparaulesenelstextos quenototselssistemesdexifratgeoculten.D’aquíneixlacriptoanàlisi,ésadir,elconjuntde tècniquesperanalitzareltextxifratiintentardeduir-nelaclau[3].

Xifratgeperpermutacions

Aquestmètode,talcoml’hemplantejat,reordenalestresfilesdelamatriu.Pertant,eltotal declauspossibleséselnombredepermutacionsdetreselements,ésadir3! “ 6.Aixòelfa moltinsegurdavantd’algúquevagiprovantclaus.

XifratgedeCèsar

Talcoms’haplantejataquí,hihatantespossiblesclauscomdesplaçamentsespuguinfer,és adir, 28.Tampocnosemblaunbonsistema,peròseriafàcilmentmillorable.Perexemple, podríemferelconegutcomamètodedexifratgeafí,queaplicaacadascundelscodis c una transformaciódeltipus x “ a ¨ c ` b.Matricialment,hopodemescriurecom:

X “ A ¨ C ` B

on A ésunamatriudiagonal.Lamatriu B podríemdefinir-ladediversesmaneres,però proposaríemfer-hocom:

D’aquestamanera,laclauseria ` a11 a

Comqueelsistemahadeserinvertible,lesentradesd’A handesercoprimeresamb lamidadel’alfabet,ésadir, 28.Així, taii u3 i“1 podràserqualsevoldelselementsde 3, 5, 9, 11, 13, 15, 17, 19, 23, 35, 27u.Pera B nohihacapmenaderestricció[4].Pertant, elnombrepossibledeclausserà 113 ¨ 283 “ 29218112.

XifratgedeHill

ElxifratgedeHillpresentaunproblemadeseguretatperaltresmotius.Elfetquelamatriu A dexifratgeté 28possiblesentradesencadascunadelessevesposicionsi,pertant,per forçabrutaespodriaprovarambles 289 “ 10.578.455.953.408clauspossiblesiesperar que,desprésdedesxifrarelmissatge,alguna d’ellesproduísuntextcomprensible.Hemde

reduiraquestnombretenintencompteque,d’aquestespossiblesclaus,forçatindrienel determinantambvalormúltiplede 2 o7.Algunesalternativespodrienseraugmentarlamida del’alfabetoqueaquestasiguiunnombreprimerprougran[7][8].

Peròelriscmésimportantésquealgúconeguieltextpla C ielxifratged’aquest, X .Comque X “ A C ,llavorspodriasaberlaclaufent A “ X C 1 .Pertalquelamatriu C siguiinvertible, espotprendreunmenorqualsevol3 ˆ 3de C quetinguiaquestapropietat.

UnamaneradeferfrontaaquestproblemadeseguretatésafegirunatransformaciódeCèsar afí,ésadir,triarunamatriu B3ˆn demaneraqueelxifratgesigui:

ilaclauestariaformadaperlesmatrius

Conclusions

Elconjuntdepropostespresentadesaquíenshaservitperil•lustraral’alumnatdesegon debatxilleratlespossiblesaplicacionsdelesmatrius.Cadavegadasónmésfreqüentsla contextualitzaciódelscontingutsd’aprenentatgeil’aprenentatgebasatenproblemes.L’alumnatnosolconèixergairesaplicacionsdelesmatemàtiquesmésenllàd’emprar-lesen altresmatèries,fetqueredueixlaconcepcióquealgunsdelsestudiantspodentenird’ellesa quelcompuramentacadèmic.

Enaquestsentit,nosesolenexposaraplicacionsdelesmatriusmésenllàdel’estudide sistemesd’equacionslinealsilacriptografiaensdonaunexempled’aplicaciódelesmatemàtiques.Elproblemaprincipalqueenspodemtrobarambelnostrealumnatéslamanca d’experiènciaprèviaencriptografiaiseguretati,pertant,l’esforçaddicionalquecalferper situarl’objected’estudiilasevaterminologia.

Elprincipalrepteques’albiraésplantejareltemadel’estudidelesmatriuscomunaprenentatgebasatenproblemes(ABP).Ésadir,podemcrearlaunitatdidàcticadelesmatriustot plantejantelreptedexifraridesxifrartextosianarfentexercicisd’operacionsdematrius, càlculdedeterminantirang,deducciódelainversa,resoluciódesistemesd’equacions...,tot utilitzantelsdiferentsmètodesdexifratgeexposatsaquí.

Finalment,malgratqueelstresmètodesdexifratgepresentatsaquípodennoserprousegurs nieficientsdesdelpuntdevistadelesoperacionsdecàlculqueimpliquen,hemgauditd’una experiènciad’aplicaciódel’àlgebralineal.

Annex.Elcodifontqueensajudaatreballar

Perfermésàgiliclareldesenvolupamentd’aquestaactivitats’handefinitalgunesfuncions enunfitxerdescriptsd’Octave.TotseguithihaelscodisQRperaccedir-hiodescarregar-los iesdonalatranscripciódelesfuncionsdesenvolupades.

Bibliografia

[1]Juher,D.(2004). L’artdelacomunicaciósecreta.Elllenguatgedelacriptografia.Barcelona: Llibresdel’Índex.

[2]Taranilla,C.(2017). Loslenguajessecretosalolargodelahistoria.Còrdova:Guadalmazán.

[3]DomingoFerrer,J.,HerreraJoancomartí,J.(1999). Criptografiaperalsserveistelemàticsi elcomerçelectrònic.Barcelona:EdicionsdelaUniversitatObertadeCatalunya.

[4]Koblitz,N.(1987). ACourseinNumberTheoryandCryptography.NovaYork:Springer.

[5]Hill,L.S.(1929).CryptographyinanAlgebraicAlphabet. TheAmericanMathematical Monthly,36,6,juny-juliol,306-312.

[6]Kerckhoffs,A.(1883).Lacryptographiemilitaire. JournaldesSciencesMilitaires,ix,5-38.

[7]Toorani,M.,Falahati,A.(2009).Asecurecryptosystembasedonaffine[enlínia], 14 setembre 2009.A:https://onlinelibrary.wiley.com/doi/pdf/10.1002/sec.137.

[8]Saxena,A.,Iohiya,H.,Patidar,K.(2017).ANovelTechniqueofHillCipherforEvaluation ofNon-invertiblekeymatrix. InternationalJournalofAdvanceResearchinScienceand Engineering,6, 1,p.856-862.

[9]Sharma,N.,Chirgaiya,S.(2013).«AReviewofModernHillCipherTechniques». InternationalJournalforScientificResearch&Development, 1, 10,ISSN(online): 2321-0613.

1

GabrielRuiz-Garzón

UniversidaddeCádiz gabriel.ruiz@uca.es

JaimeRuiz-Zapatero

OxfordUniversity jaime.ruiz-zapatero@stx.ox.ac.uk

Resum Abstract

L’objectiud’aquesttreballésmostrar l’origendelscontingutsdidàcticsimpartits pelfísiccatalàFrancescAragó,entre 1808i 1830,al’ÉcolePolytechniquedeParís,enel cursd’AritmèticaSocial.Aquesta assignaturatécomaantecedents l’aritmèticapolíticadePetty,l’aritmètica moraldeBuffonilamatemàticasocialde Condorcet,iéslaprecursoradelcàlculde probabilitatsactual.

Biografiad’Aragó

Theaimofthisworkistotracetheoriginsof theteachingcontentsoftheCatalanphysicist FrancescArago’scourseinSocialArithmetic, whichhetaughtduringhistimeattheÉcole PolytechniqueinParisbetween1808and 1830.Thissubjectiscomparedhereto precedingcoursesPoliticalArithmeticby Petty,Buffon’sMoralArithmetic,andSocial MathematicsbyCondorcet.Furthermore,our studyshowstherelevanceofArago’scourse asoneofthevitalprecursorsofthecurrent CalculusofProbability.

FrancescJoanDomènecAragó(FrançoisArago)vanéixerel 1786aEstagell,unavilaadivuit quilòmetresdePerpinyà,alRossellófrancès,ivamorirel 2 d’octubrede 1853aParís(vegeula figura 1).Elseupare,BonaventuraAragó,ilaseva mare,MariaRoig,conformavenunafamília catalanoparlantdecamperolsacomodats.Francesceraelgrandelscincgermanshomesdels onzefillsquevantenirelsseuspares.Elsseusaltresgermanseren:Jean,quevasergeneral

1.Traduccióalcatalàd’ÀnniaBoschiCasabò.

del’exèrcitmexicà;Jacques,quevaserexplorador,dibuixantiescriptor(entrealtresobres, d’unatitulada Curieuxvoyageautourdumonde,onnoutilitzalalletra a acausad’unaaposta quevafer);Victor,quevaocuparelcàrrecd’oficialdel’armadafrancesa;Joseph,quevaser coroneldel’exèrcitmexicà,iÉtienne,quevaaconseguirelllocdediputatialcaldedeParís,a mésdeserdramaturgidirectord’unteatreparisenc.

Francesc,desprésd’estudiaral’InstitutMunicipaldePerpinyà,vapreparardurantl’any 1802 l’ingrésal’ÉcolePolytechnique,estudiant,entrealtresmanuals,elssegüents: Introduction àl’analyseinfinitésimale,d’Euler, Résolutiondeséquationsnumériques, Théoriedesfonctions analytiques, Mécaniqueanalytique,deJosephLouisLagrange, MécaniqueCeleste,dePierre SimonLaplace,i MémoiresurlamanièrededistinguerlesMaximadesMinimadansleCalculdes Variations i MémoiresurlesIntégrationspararcsd’ellipse,ambdósd’AdrienMarieLegendre. L’examend’ingréselvarealitzaraTolosaielseuexaminadorvaserLouisMonge,germàdel matemàticidirectordel’ÉcolePolytechniqueGasparMonge,iel 1803hivaseradmèsamb unadelessismillorsnotesdetotFrança.

Però,comdesprésveurem,lasevavidaestàmoltmarcadaperladel’astrònomfrancèsPierre Méchain(1744-1804),quealcostatdeJeanDelambre(1749-1822)haviaparticipatenel mesuramentdelmeridiàdesdeDunkerquefinsaBarcelona,entre 1792 i 1798,mitjançant latècnicadelatriangulació.Aquestatècnicaconsisteixadissenyarunamalladetriangles adjacentsonelsvèrtexssesituenalternativamentaunapartial’altradel’arcABdelmeridià queesvolmesurar.ElprimertrianglehadetenirunvèrtexenelpuntAil’últimtriangleen B.Apartirdelamesurad’uncostatdelprimertriangleidedosdelsseusanglesespoden determinar,pertrigonometria,totselscostatsdetotselstriangles.Abatentlesalturesdels trianglessobreelsegmentABespotcalcularladistànciaABdel’arc.Lamesuradel’arcdel meridiàterrestretambétenialautilitatdesabersilaTerraestavaaplanadapelspolsoper l’equador,amésdepoderdefinirambprecisióelmetrecomaunitatdelongitud.

Figura1.FrancescAragó.

AbansqueDelambreiMéchainacabessinlasevamissió,el7d’abrilde 1795laConvenció Nacionalfrancesavadefinirelmetreapartirdedadesantiguesproporcionadesperaquests dosastrònoms,sensecomptarambelsnouscàlculsquepodriaaportarMéchainenfinalitzar lasevavisitaaEspanya.El 10 dedesembrede 1799 NapoleóBonapartevasignarl’actade naixementdelmetre,definitcomladeumilionèsimapartdelquadrantdelmeridiàterrestre. Mentrestant,el 1795MéchainestrobavaaBarcelonaefectuantelsúltimsmesuramentsde l’arcdelmeridiàquanl’inicidelaguerrafrancoespanyolaelvaobligaraexiliar-seaItàlia. Desgraciadament,repassantelsseuscàlculss’adonàquehihaviaunadiferènciadetres segonsdegrauperaunmateixpuntdeBarcelonaidecidíocultarelseuerror,ialhora demanàqueselipermetéstornaraEspanyaireprendreelcàlculdelmeridià,estenent-lodes deBarcelonafinsalesBalearsambl’objectiusoterratdetornaraferelscàlculs.

Perfi,elsetembrede 1801 elBureaudesLongitudesencomanàaPierreMéchainl’extensióde lesmesuresdelmeridiàdesdelsuddeBarcelonafinsaFormentera.L’abrilde 1803Méchain vatornarcapaEspanyaitriangulàlacostacatalanailamallorquina.EnelseupasperEspanya s’allotjàalacasadelpared’Aragó.Méchainva conèixerFrancescAragó,queenaquellaèpoca tansolsteniavuitanys.Elseuparevademanarconsellal’astrònomsobrelabondatdela sevaprofessióperalseufill.Méchaincontestà(Bayard, 2007,p.40;latraduccióésnostra):

Ésuncamímoltdifícilderecórreri,tretqueestinguiunavocaciómoltespecial,elvostre fillnoméstrobaràdecepcions.

Elsetembrede 1804MéchaincaiguémalaltdefebregrogaimoríaCastellódelaPlana,sense arribaraadonar-sequenohaviacomèscaperror,jaquelesdiscrepànciesobservadeseren fruitdel’acumulaciódepetitserrorsinstrumentals,larefracciódelesestrelles,etc.

ElfetluctuósdelamortdePierreMéchaintornàamarcarlavidad’Aragópersegonavegada, jaqueAugustinMéchain,filldePierreMéchai n,presentàlasevadimissiócomasecretaride l’ObservatorideParís.LaplacepreguntàaPoissonquipodriaocuparelllocvacantiaquest esrecordàd’unveí,FrancescAragó,queaméseraalumneseu,quepodriaocuparelllocde secretari.Almateixtemps,liencomanarencontinuaramblamissiódelcàlculdelmeridiàdes deBarcelonafinsalesBalears(vegeulafigura 2).

El 1806AragómarxàcapaEspanyaambJean-BaptisteBiot(1774-1862),professordefísica delCollègedeFranceimembredel’InstitutdesSciences.Totsdoscomptavenambnou instrumentalperefectuarelscàlculs,comelcerclerepetidordeBorda.Elsacompanyarenen latascadosespanyols,JoséRodríguez(1770-1824),alumnetambédel’ÉcolePolytechnique, iJoséChaix(1765-1809).Apartird’aquí,lavidad’Aragóésdignad’unanovel laounguió cinematogràfic.

El 1808començàlaGuerrad’IndependènciaespanyolaiAragó,queestrobavaaMallorcafent lessevestasquesdetriangulació,vaseracusatd’espia.Lestasquesdetriangulaciórequerien larealitzaciódefocsisenyalslluminosospertalqueelspuntsfossinalbirats,devegades,des demésdecentquilòmetresdedistància.Aquestsfocsforeninterpretatspelsvilatanscom asenyalsquepodrienafavorireldesembarcamentdepiratesitropesestrangeres.Aragó, davantlapossibilitatdeserlinxatperlamultitud,demanàingressaralapresódelcastellde BellverdeMallorca.

Unmatí,davantelsrumorsdelasevapròximaexecució,decidíescaparenunvaixellcapa Algèriaambl’ajudadelgovernadordel’illa,quesabiaqueelsseustreballscientíficseren aliensaaltresmotiusqueelspròpiamentcientífics.

El 16d’agostde 1808sortícapaMarsellaenunvaixellqueportavaunregalsingulardel dei,ogovernantd’Algèria,aNapoleó:doslleons!Peròelvaixellfoucapturatperuncorsari espanyoliAragófouempresonataRoses.Sorprenentment,elposarenenllibertat.Lacausa calbuscar-laenlacartaqueAragóvaescriurealdeid’Algèriaperainformar-lodelamortd’un delsseuslleons.EldeivaamenaçarEspanyad’entrarenguerrasinodeixavenenllibertatels tripulantsdelvaixell.

El 28denovembrede 1808AragóembarcàcapaMarsella,peròunagrantempestaels obligàaretrocedirnovamentfinsaAlgèria.Founovamentcapturatifingíconvertir-sea l’islamismepersalvarlasevavidaiaconseguirembarcar-seenunaltrevaixell,pertercera vegada,novamentcapaMarsella,onperfiarribàel 2 dejuliolde 1809 ambelseuquadern denotesdetriangulacióamagatentrelapellilacamisa.AParís,comacompensacióperla sevagesta,founomenatmembredel’AcadèmiadeCiènciesal’edatdevint-i-tresanys.

El 1809 fouelegitmembredel’AcadèmiadeCiències,primercomasecretariperpetuidesprés comapresident.Vaserdirectordel’ObservatoireRoyaldeParísde 1813a 1846,ciutatonva residirfinsalasevamort.Aragó,comafísic,ajudatpelseucompanydetriangulacióBiot, vadescobrirlataxaderefraccióatravésdediversosgasos,elcromatismeilapolarització rotatòriadelallum.

Figura2.TriangulaciódeBarcelonaiBalears.

Col laboràambFresnel(1788-1827)enlaconfirmaciódelateoriaondulatòriadelallum, jaqueeraméslentaenelsmitjansmésdensos,ienlacomprovaciódelasevavelocitat, juntamentambFizeau(1819-1896)iFoucault(1819-1868).Vadescobrirquelavelocitatdela llumeralamateixaentoteslesdireccionsieraindependentdel’estrellaquel’emetia.També ésseuelconceptedecromosferadelsol.Vainvestigarleslleisdel’electromagnetismeamb Ampère(1775-1836),ambquivaconstruirl’electroimant,inventquevaobrirlesportesal telèfonialtelègraf.Vaestudiarlatemperaturadelesaigüesdelsoceans,elcorrentdelGolfi laderivadelscontinents.El 1845vaproposaraUrbainLeVerrier(1811-1877)l’estudideles anomaliesdetectadesaUrà,laqualcosaportariaaaquestúltimadescobrirl’existènciad’un nouplaneta:Neptú.

Aragóvaobrirl’Acadèmiaalsperiodistesialpúblicengeneral.Vanserfamososelsseus programesdeconferènciesonestractaventemesd’astronomiaperalpúblicgeneral.

Comapolític,el 23d’abrilde 1848founomenatministredelaGuerra,laMarinailesColònies, ivaproclamarlaRepúblicadavantdelpobledeParís.Vaarribarasernomenatprimerministre el 10 demaigde 1848ivadimitireljunyd’aquellmateixany,aclaparatperlesinsurreccions populars.

Entrelestasquesmésrellevantsquevadesenvolupardestacaelfetquevaimpulsarl’abolició del’esclavitudalescolòniesfrancesesidelscàstigscorporalsalamarina.Tambévabuscar finançamentperaactivitatstandiversescomeldesenvolupamentdelferrocarril,eltelègraf, eldaguerreotip,comaprecursordelafotografia,ilapublicaciódelesobresdeLaplacei Fermat.Peramésdetallsbiogràficshemdeconsultarl’obradeJacques(2017).

EncaraquedeFrancescAragóésmésconegudalasevafacetadefísic,enaquestarticle mostraremlasevacaramenysconegudadeprofessor,entre 1808i 1830,al’ÉcolePolytechnique,onimpartial’assignaturad’AritmèticaSocial.Enl’apartatsegüentenscentrarema mostrarquinscontingutsotemesconteniaaquestaassignaturacomaprecursoradelscursos posteriorsdecàlculdeprobabilitats.

Antecedentsdelcursd’AritmèticaSocial

Elscontingutsqueimpartimactualmentenqualsevolcursbàsicd’estadísticas’hananat conformantatravésdelssegles.Entreelsseusantecedentstrobeml’aritmèticasociald’Aragó i,aquesta,alseutorn,téelsantecedentsenl’aritmèticapolítica.

Aritmètica política

Sotaelterme aritmèticapolítica s’agrupenunasèried’operacionsútilsperalgoverndels pobles,comaraelcàlculdelnombred’homesquehabitenunpaís,laquantitatd’aliments quehandeconsumir,etc.Eltermeenqüestióprovédel’obra PoliticalArithmetik,delcientífic anglèsWilliamPetty(1623-1687)ipublicadael 1691.

Pettyvaexercirdemetge,vaserresponsabledelcadastreiagrimensorenelrepartimentde terresd’Irlanda,onfouordenatperCromwelld’acordambelsresultatsdelaguerraentre catòlicsiprotestants.L’objectiudePettyvaserelcàlculdelariquesailapoblaciódeles

illesBritàniquesidemostrarqueAnglaterraeraméspuixantqueFrança.Enaquestsentit,va proporcionartresmètodesperestimarlapoblaciódeLondres:

1.Multiplicarelnombrededefuncionsper30.

2.Multiplicarelnombredellarsper8,nombremitjàdecomponentsd’unallarenaquelles dates.

3.Prendrecomabaseelnombredellarsd’altresllocs,comDublínoBristol,iprocedira unaestimació.

Petty,enelsúltimsanysdelasevavida,vaescriureunaaltrasèried’assajosquetambéva anomenard’aritmèticapolíticadedicatsacompararelshabitantsdeLondres,ParísielsPaïsos Baixos(vegeuReungoat, 2004).Després,sotalaterminologia políticaaritmètica s’agruparen fonamentalmentcontingutsdecàlculsitaulesdemogràfiques.

Aritmètica moral

Eltermesegüentéseld’aritmèticamoral. ElvaencunyarelnaturalistainoblefrancèsGeorges LouisLeclerc,comtedeBuffon(1707-1788).DesdelseullocdesupervisordelJardinduRoi, vaemprendrelaredacciódelasevaobracabdal,laseva Històrianatural,enundelsúltims tomsdelaqualhitrobemambunsuplementtitulat Essaid’ArithmétiqueMorale.

Buffonvaserunfermobservadordetotselséssersdelanaturalesa,dinslaqualconsiderava l’homecomunintegrantaquilicaliaestudiarnosolsdesd’unpuntdevistafisiològic,sinó tambéenelseuesperit,amblessevesesperances,lessevesporsilessevespassions,per aixòvaafegiralnomdeladisciplinal’adjectiu moral.Enelseu Essaid’ArhitmétiqueMorale es tractendosproblemesmoltimportantsenlahistòriadel’estadística.Elprimerésl’anomenat problemadel’agulla,lasolució delqualtéaveureambelnombre π (vegeuRuiz-Garzón, 2001,p.71;latraduccióésnostra):

Suposemqueenunahabitacióelsòls’hagidividitenlíniesparal leles.Estiraunpali undelsjugadorsapostaperquèelpalnotallaràcapdelesparal¨lelesdelsòl.L’altre, percontra,apostaperquèelpaltallaràalgunad’aquesteslínies.Espreguntasobreles probabilitatsdetotsdosjugadors.Éspossiblejugaraquestjocambunaagulladecosiro unaagullasensecap.

Ielsegonésl’anomenadaparadoxadeSantPetersburg(vegeuRuiz-Garzón, 1999,p.7):

Perellençaunamonedaal’airetantesvegadescomsiguinecessaripertreurecara.Siaixò passaalaprimeratirada,hadedonaraPauunducat;sipassaalasegona, 2;sipassaa latercera,4;sipassaalacambra,8,iaixísuccessivament,duplicantelnombrededucats acadajugadaquecalefectuar.Quinaésl’esperançadeguanyarcorresponentaPau?En altresparaules,quinéselpreujustquePauhadepagarperaquestjoc?

PerepagaaPau 2n 1 ducatssilamonedasurtcaraperprimeravegadaenl’enèsimllançament, ambunaprobabilitat p1{2qn ;aixíl’esperançadePaués:

Ésadir,Pauhauriadepagarunpreuinfinitperparticipareneljociacanvinomésrebria unpagamentfinitencadallançament.Elresultatsemblaqueestiguiencontradiccióambel sentitcomú,però,malgrattot,éscert,aquestaéslaparadoxa.

Buffonproposamenysprearlesprobabilitatspetites,concretamentlesmenorsque 1/10.000, jaque,segonslessevestaulesdemortalitat,laprobabilitatqueunhomede56anysmorien eltranscursdeldiaerad’1/10.189;isi,peraunhomed’aquestaedat,aquestaprobabilitat nolicausatemorilisemblapetita,ambigualmotiuhoserà 1/10.000 enelnostreproblema. Ambaquestespremisses,comque

perparticiparenlaparadoxadeSantPetersburgserà:

Desprésdelconcepted’aritmèticapolíticadePettyid’aritmèticamoraldeBuffon,queja involucravaconceptesdeprobabilitatiesperançamatemàtica,envindriaundenouque encunyariaCondorcet.

Matemàtica social

SegonsCondorcet(1743-1794),sotaelterme matemàticasocial estroben:

[...]totesaquestesaplicacionsquesónimmediatamentrelativesalsinteressossocials[...]. Lamatemàticasocialpottenirperobjecteelshomes,lescosesoalhoraelshomesiles coses.(Crepel, 1989a,p.1;latraduccióésnostra)

Condorcetteniacomaobjectiulallibertat,laigualtatielbenestarmaterialdetotsels ciutadans,iperaaixòcomptavaambelprogramareflectitenlamatemàticasocial.

Condorcethaviapublicatel 1805unllibretitulat Élémensducalculdesprobabilitésetson applicationauxjeuxdehasard,àlaloterieetauxjugemensdeshommes.Dinsdelvolum figuravencontingutsd’aritmètica,geometria,mecànicaicàlculdeprobabilitats,ques’havien d’impartirdurantvint-i-cincsetmanes,enclassesdedueshores,distribuïtsensettemes:

1.L’interèsdeldiner

2.Unmètodeperformartaules

3.Principisfonamentalsdelcàlculdeprobabilitats

4.Lanaturalesadelesveritatsalesqualspotconduirelcàlculdeprobabilitats

5.Lamaneradecompararsuccessosdeprobabilitatsdiferents:problemadelspuntsi paradoxadeSantPetersburg

6.Aplicacionsdelcàlculdeprobabilitats:especulacionscomercialsitaulesdemortalitat

7.Aplicacionsdelateoriadelescombinacionsalsjocsd’atzar.

Comveiem,Condorcethaviadissenyatuncursd’estadísticaambelementsdecàlculde probabilitatsidematemàtiquesfinanceres.No oblidemqueostentavaelcàrrecd’inspector generaldelaMoneda.

Elcursd’AritmèticaSocial

Aritmètica social

I,perfi,eltermesegüentéseld’aritmèticasocial,ques’encunyariaal’ÉcolePolytechniquei técomaprotagonistaelnostreFrancescAragó.L’objectiuqueesperseguiaamblacreació del’ÉcolePolytechniqueeraformarelsenginyerscivilsimilitarsnecessarisperalanació itransmetreconeixementatravésdelnivellcientíficd’unainstitucióelsprofessorsdela qualestriarienentrelesmillorsmentsdelmoment.Ambtansolsvintanys,Aragóeraun d’aquestscapsifoutriatperformarpartdelplanterdeprofessorsdel’ÉcolePolytechnique, concretamentpersucceirGaspardMongeenelDepartamentdeGeometriaAnalítica.Laseva missióconsistíaimpartircontingutsdegeodèsiaimecànicaaritmèticadesdelcurs 1809-18

finsal 1830,dinsdelamatèriatituladaAnàlisiAplicadaalaGeometria.Paradoxalment,mai novaimpartirnifísicaniastronomia,matèriesperlesquals,noobstantaixò,ésmésconegut. El 1812 Aragóvaascendirderangivasernomenatprofessoradjunt.

El4desetembrede 1816esvareformarelplad’estudisdel’École.Lacomissióquevaelaborar elnouplad’estudisestavapresididaperLaplaceiesproposàcrearuncursd’AritmèticaSocial sobrelabasedelsmotiussegüents(Crepel, 1989a,p. 15;latraduccióésnostra):

Elcursd’AritmèticaSocial,adequatperajudarelsalumnesaraonar,habituar-losalscàlculs del’altaadministracióioferir-losunaaplicacióinteressantdelsseusconeixements,és susceptibledeserintroduïtal’ÉcolePolytechnique,onespotincorporarfàcilmentalcurs d’AnàlisiAplicadaalaGeometria.Unnombrepetitdelliçonsbastaràperaaquestnou objected’estudi,quenoexigiràcapdespesaaddicional.Aquestsmotiushandeterminat lacomissióaproposarlaintroducciód’uncursd’AritmèticaSocialjuntamentambla partteòricadelageodèsiaenelcursd’AnàlisiAplicadaalaGeometriadeCorbesiala GeometriadeTresDimensions.

Gràciesalesnotesd’unalumnequevaassistir alesclassesd’Aragó,HippolyteRenaud,els dies7, 9, 11, 14i 16dejuliolde 1825,enshanarribatelsepígrafsqueAragóvaimpartir (Crepel, 1989b)(vegeulafigura3).

1.Probabilitaticertitud.Definiciódelaprobabilitat.Esdevenimentcontrari.Esdevenimentscomposts.Independència.ObjeccionsdeD’Alembert.Repeticions.

2.Probabilitatscompostesenelcasnoindependent.Desigualtatsdesconegudesquepodenexistirentreprobabilitatsquesesuposeniguals.Parelloimparell.Probabilitatsde lescauses.Esperançamatemàtica.Problema deSantPetersburg:esperançamatemàtica iesperançamoral.

3.Problemadelspunts.LoteriadeFrança.Taulesdemortalitat:vidaprobable,vidamitjana.

4.Estimacionsdelapoblació,multiplicadoruniversal.Inoculació.Proporcionsdenaixementsmasculinsifemenins.Qüestionsd’interèsdeldiner:caixesdepréstecs,rendes viatgeres,anualitats,tontines,casesd’empenyorament,assegurancesdevida,assegurancesmarítimes,assegurancesmútuesicompanyies.

5.Rudimentsrelatiusalesoperacionsbancàries:canvi,preusdeldiner,bitlletsdebanc, papermoneda,lletresdecanvi.Errorsd’observació,mètodedemínimsquadrats.

Comapreciem,aquestcursd’Aragó,finsitotbasant-seeneldeCondorcet,significavaun incrementdelnombredetemestractats.

Figura3.Anotacionsd’HippolyteRenauddelaclassed’Aragó.

Desprésdelcursd’AritmèticaSocial

Alterme aritmèticasocial d’Aragóelvaseguirelde físicasocial.

Física social

Elterme físicasocial tambéapareixenunaobra,concretamentenlatitulada Surl’hommeet ledéveloppementdesesfacultés,ouEssaidephysiquesociale,publicadael 1835perAdolphe Quetelet(1796-1874).NascutaGant,vaserenviataParísel 1823periniciar-seenlapràctica del’astronomiaalcostatd’AragóienelcàlculdeprobabilitatsalcostatdeLaplace(17491827)iPoisson(1781-1840).L’objectiueraencarregar-sedeladirecciód’unnouobservatori astronòmicquehaviadeconstruir-seaBèlgica.Elseusomniesmaterialitzàel 1830,anyen quèvasernomenatprimerdirectordel’ObservatorideBrussel•les.Vaserallíonesvacelebrar, el 1853,unaconferènciaquevaserelgermendelqueserial’OrganitzacióMeteorològica Internacional.VaserelpresidentdelPrimerCongrésInternacionald’Estadística.

Elseu Physiquesociale estàconsagratadesenvoluparlesqualitatsfísiquesimoralsdel’home, elqueellvaanomenarl’homefísicisocial.Nosolsestudiaelsatributsfísicshumans,com l’alturaoelpesd’unapersona,sinóelsseusatributsmorals,comlestaxesdesuïcidi,decriminalitat,etc.Desenvolupalateoriadel’home mitjà,quenoésnomésunateoriamatemàtica, sinótambésocial.LamitjanaeraperaQueteletl’expressiódel’equilibri.L’homemitjàera larepresentaciód’unapoblaciódiversail’homeidealsesituavaenelpuntmitjà.Segonsles sevesparaules(Quetelet, 1869,p.491;latraduccióésnostra):

L’homequeconsideroésdinsdelasocietatl’anàlegdelcentredegravetatdinsdelcos; éslamitjanaalvoltantdelaqualoscil¨lenelselementssocials.

Quetelet,perdefensarl’existènciadelseuhomemitjà,seserviadelalleidelsgransnombres quevaformularPoisson, queveniaadirquelespetitesanomaliesenlaconstrucciódeles monedesdesapareixiensil’experiènciaesrepetiaunnombreprougrandevegades.D’igual manera,lesdiferènciesentreunapersonaiunaaltradesapareixien,iapareixial’homemitjà.

El càlcul de probabilitats

Desde 1831 ifinsa 1838SavarysubstitueixAragóal’ÉcolePolytechniqueiafegeixel teoremadeBernoulliielproblemadel’agulladeBuffonalprogramadelcursd’Aragó.El curs 1834-1835elcursd’AritmèticaSocialpassaadir-seElementsdeCàlculdeProbabilitats iAritmèticaSocial.Elcurs 1838-1839 lescinclliçonsdeprobabilitatproposadesperAragó seranimpartidesperJean-MarieConstantDuhamel(1797-1872).Desdelcurs 1841,seran elsmatemàticsJosephLiouville(1809-1882)iCharlesFrancescSturm(1803-1855)elsque s’encarregarand’impartir-loalternadament,ieliminaranalgunscontingutsd’aritmèticacomercial,elpuntquetractadelamitjanaentrediversesobservacions,elteoremadeBernoulli ilaprobabilitatdelsesdevenimentsqueprovédel’observaciód’esdevenimentsanteriorsde lamateixanaturalesa.

EnmorirAragó,ladirecciódel’ÉcolePolytechniquefouperaUrbainLeverrier.Aquest vaproposardonarprioritatalesaplicacionspràctiquesperalageodèsia,lacartografiai l’artilleria,enllocdelsconceptesteòrics.Aixòportàasuprimirlademostraciódelteoremade Bernoullioatraslladarl’explicaciódelmètodedemínimsquadratsdinsdelageodèsia.

Enlataulasegüentiamaneraderesum,figurenelsdiferentscontingutsestadísticsiels científicsqueesvanimpartirenlaprimerameitatdelsegle XIX,totconsolidantlatendènciaa separarelqueavuianomenaríemestadísticadelesmatemàtiquescomercials.

Taula1.Contingutsestadísticsicientíficsqueelsvanimpartir.

Continguts

Probabilitat

Estimaciódelapoblació. Inoculació

Interessosdeldiner. Assegurances

TeoremadeBernoulli

TeoremadeBayes

Condorcet (1805)

Aragó (1809-1830)

Savary (1831-1838)

LiouvilleiSturm (1841-1853)

Conclusions

Enaquestarticlehemvistunesfacetespocconegudesdelavidail’obradelfísiccatalà FrancescAragó,comaralasevaaportacióal’estadística,atravésdelscontingutsdidàcticsdel seucursd’AritmèticaSocial.HireculltemestractatsperPetty,BuffonoCondorcetiinflueix enlaconformaciódelcurrículumdelscursosdecàlculdeprobabilitatsdefinalsdelsegle XIX deLiouville,SturmoposteriormentCournot.Comvadirl’historiadorcatalànascutaFrança iMedallad’OrdelaGeneralitatdeCatalunyaPierreVilar,«calcomprendreelpassatper entendreelpresent».

L’obrailavidadeltambécatalàFrancescAragóésunabonaexcusaperfer-ho.

Referències

Bayard,P.(2007). LaméridiennedeFranceetl’aventurede saprolongationjusqu’auxBaléares. París:L’Harmattan.

Crepel,P.(1989a).DeCondorcetàArago:l’enseignementdesprobabilitésenFrancede 1786 à 1830 BulletindelaSabix,4, 29-55.

Crepel,P.(1989b).Lecoursd’ArithmetiquesocialedeFrancescAragoàl’Écolepolytechnique (1825).Transcritpiondesnotesprisesparl’élèveHippolyteRenaud. BulletindelaSabix,4, 56-73.

Jacques,G.(2017). FrancescArago:l’oublié. París:NouveauMonde.

Quetelet,A.(1869). PhysiqueSocialouEssaisurledéveloppementdesfacultésdel’homme. Brussel¨les:Muquardt.

Reungoat,S.(2004). WilliamPetty,Observateurdesîlesbritanniques. París:InstitutNational d’ÉtudesDémographiques.

Ruiz-Garzón,G.(1999).LaparadojadeSanPetersburgo:unareivindicacióndidáctica. Suma: RevistasobreEnseñanzayAprendizajedelasMatemáticas,32,5-9

Ruiz-Garzón,G.(2001).Sobrelautilidaddelageometríaenlaenseñanzadelaprobabilidad. Suma:RevistasobreEnseñanzayAprendizajedelasMatemáticas,37,67-74.

Coneixement,argumentsi magnituds

PedroNicolásZaragoza

UniversitatdeMúrcia,Facultatd’Educació

Resum Abstract

Enaquesttreballdefensemquetansols fonamentantl’estudidelesmatemàtiques enl’estudidelesmagnituds,estaremen condicionsdecomplirundelspropòsitsde l’educació,asaber,l’ampliaciódelnostre coneixementdelmón.

1.Introducció

Inthiswork,wearguethatonlybybasingthe studyofmathematicsonquantitieswillwebe abletoaccomplishoneoftheeducational purposes,namelythebroadeningofour knowledgeabouttheworld.

ComesmostraaBoschiChevallard(2000b),l’expulsiódel’estudisistemàticdelesmagnituds del’ensenyamentdelesmatemàtiques,portadaatermesotalainfluènciadelmoviment reformadordel’ensenyamentdelesmatemàtiquesanomenat newmaths,originatalsEstats Unitsalasegonameitatdelsegle XX iqueaEspanyaesvaanomenar matemàticamoderna perquèvaarribaratravésdelaversiófrancesa mathématiquemoderne,vadonarlloca diversosfenòmensdidàctics«indesitjables»queencarasemblaqueperduren.Enaquest treballmostraremque,amés,nofonamentarl’estudidelesmatemàtiquesenl’estudide lesmagnitudsimpedeixlaconsecuciód’unadelesfinalitatsbàsiquesdelesinstitucions educatives:latransmissiód’uncerttipusessencialdeconeixement.

AGascóniNicolás(2017, 2019a)defensemferexplícitaambtotselsdetallslafinalitatde l’educació,queespressuposaquehauriadeserunapràcticaméshabitualenelstreballs dedidàcticadelesmatemàtiques.Nomésaixíespodentransformarelsjudicisdevalor ilesprescripcionsnormatives,tanabundantsencaraenaquestadisciplina,enenunciats objectiussobrel’eficàciad’algunsmitjansperassoliraquestesfinalitats.Comencem,doncs,a l’apartat 2,analitzantunadelesfinalitatsdel’educaciódelaqualtractaremenaquesttreball: latransmissiódeconeixement.Unapartd’aquestaanàlisiinclouconsideracionssobreels diferentstipusdeconeixementisobrequès’enténper coneixementproposicional,eltipusde coneixementqueensinteressaaquí.

Laconstrucciódeconeixementproposicional,perlasevamateixadefinició,requereixla presènciad’argumentsracionalsqueapuntalinelquediemconèixer.Al’apartat3explorem diferentstipusd’arguments,ambunaatencióespecialals argumentsdeductius pelseupaper essencialenlapràcticadelacomunitatmatemàtica.

Al’apartat4mostremcomlacrisidelsfonamentsdelesmatemàtiquesvaferques’organitzessinalvoltantd’axiomesiargumentsdeductiusivaometredeldiscursexplícitioficiall’ús dequalsevolaltretipusd’argument.Comexposem,senselapresènciad’aquestaltretipus d’argumentsésimpossibleconcebrelesafirmacionsmatemàtiquescomaenunciatsque expressenunautènticconeixementproposicionalsobreelmón.Això,alseutorn,dificultala consecuciódelatransmissiód’aquesttipusdeconeixementpermitjàdel’ensenyamentde lesmatemàtiques,totiqueaquestaésunadelesfinalitatseducativesessencials.

Al’apartat5exploremunaorganitzaciódelesmatemàtiquesalternativaalaques’exposa alaseccióanterior.Així,encomptedeguiar-nospercriterisqueprovenendelalògica deductiva,consideremlapossibilitatd’oferirunadescripciódiacrònicadelesmatemàtiques quemostricomneixenievolucionenparal¨lelamental’afanyhumàdedominarunmedi materialobjectiu.

Al’apartat6esbossemaquestaorganitzacióalternativadelesmatemàtiques,quesitualaraó deserdelsobjectesmatemàticsbàsicsenlaconsideracióil’intentderesoluciód’algunstipus detasquesrelacionadesambdiferentstipusdemagnitudsiambcontextosquecombinen mésd’unamagnitud.

Finalment,al’apartat7ensreferimbreumentaalgunstreballsque,enelmarcdelateoriaantropològicadeldidàctic,desenvolupenambmésomenysdetallalgunespartsdel’esquema presentatalaseccióanterior.

2.Latransmissiódeconeixement

Unadelesfinalitatsdelesinstitucionseducativeséslatransmissiódeconeixement.Aquesta tascaésdifícildesubestimari,comassenyalaDewey(1916-2004),lasubsistènciadelessocietatsdepèntantdelatransmissiód’informacióbiològica(quetípicamentesportaaterme mitjançantlaprocreació)comdelatransmissiód’informacióculturalodeconeixement.De fet,talcomexplicaEverett(2018),alsegle XIX unacomunitatd’esquimalsdelnord-oestde Groenlàndiagairebévadesaparèixerdesprésqueunaepidèmiamatéselsmésvells,queeren elsúnicscustodisdelsconeixementsquepermetienfabricararmesialtreseinesclauperala supervivència.Lacomunitatvasobreviureperquèesvatrobarambunaaltracomunitatque livatransmetreelsconeixementsnecessaris.Aquestaanècdotamostralaimportànciaqueté peraunasocietatpreservarelconeixementtransmetent-loalesgeneracionsfutures.

Podemconsideraralmenysdostipusdeconeixement:elprocedimental(relacionatambl’ús detècniquesperresoldrecertstipusdetasques)ielproposicional(relacionatamblescreencesproposicionals).El coneixementprocedimental éselconeixementquealgútéquansapfer algunacosa(anarenbicicleta,cuinarunplatdeterminat,parlarunallengua).El coneixement proposicional éselqueesdonaquanalgúcreuqueunacertaproposicióésvertaderaipot justificarracionalmentaquestacreença.Aixòsesolresumir,seguintlafórmuladePlató,

dientqueconeixementproposicionalequivala creençavertaderajustificadaracionalment (IchikawaiSteup, 2018).Imposemlacondicióquelajustificaciósiguiracionalperquèalllarg delahistòrial’ésserhumàhaempratdiversostipusdemitjansperjustificarlasevacreença encertesproposicionsinototsaquestsmitjansconvertienlajustificacióenracional.

Segonsqueexplical’historiadorFernández-Armesto(1997),eneldecursdediferentsèpoques iendiferentsculturess’hanempratfonamentalmentquatremodesdejustificarlacreençaen laveritatd’unaproposició.Aquestsmodeshanestatsemprepresents,competintocooperant dediversesmaneres.

Laveritatqueunsent. Segonselprimerd’aquestsmodes,unestariajustificatacreurequela proposició p ésvertaderasienperceplaveritatnoatravésdelssentitsodelaraó,sinóatravés delssentiments,comunacosaqueunsent.Aquestmètodedejustificaciódecreencesés propidesocietatspreliteràries,peròencaraperviuentrenosaltresjaqueenmoltessituacions escontinuadonantunarelacióestretaentresentimentsiveritat.Defet,llevatdel’activitat científica,perdetectarlaveritatd’algunacosaquese’nsdiunoacostumemaempraruna provamésexigentqueladelanostrareaccióemocional.Ielssentimentsquetenimen presènciadelquepercebemcomaveritatomentidatenenmoltencomúambemocions bàsiquescoml’amor,lapor,lapenaolaràbia,queesregistrenneurològicamentipodenser mesuradesperdetectorsdementides.

Laveritatquese’mdiu. D’acordambelsegond’aquestsmodes,unestariajustificatacreure quelaproposició p ésvertaderasiaixílihoharevelatunafontd’autoritat,quesegonsel contextpotserunoracle,unsacerdot,unendeví,unllibresagrat,unatradició,undiari, algunapersonaexpertaenlamatèriaenqüestió,etc.

Laveritatquejoperceboatravésdelsmeussentits. Malgratquesembladesentitcomúquehagi dedonarpervertaderelquepercebosensorialment(perexemple,laproposició«aquesta tassaésdamuntlataula»ésvertaderaperquèjo veigqueaquestatassaésdamuntlataula), unadelestroballesdeFernández-Armesto(1997)ésquelapreponderànciad’aquestmode dedetecciódeveritatsdavantd’altresésrelativamenttardana.Enqualsevolcas,l’abastde l’úsdelsmeussentitsperal’establimentdeveritatsésrealmentlimitat.

Laveritatquejoargumento. Aquestmodeconsisteixenl’úsdel’argumentacióperjustificar creences.Així,unestariajustificatacreurequeunaproposició p ésvertaderasihihaalgun argumentsatisfactoriafavorde p.Ésimprescindiblelapresènciad’unargumentsatisfactori perdistingirelconeixementproposicionaldelescreencesvertaderesqueresultendelamera especulacióodel’endevinament.Enefecte,sialgúcreuque p notécapargumentsatisfactori afavorde p iresultaque p ésvertadera,nodiremqueaquestalgú sap que p.

Al’efected’aquesttreball,anomenem justificacióracional alajustificaciód’unacreença mitjançantaquestsdosúltimsmodes:lapercepciósensorialil’elaboraciód’arguments satisfactoris.

3.Tipusd’argumentsracionals

Ensbasaremenladisciplinaespecialitzadaenl’assumpte,lalògica(ambunenfocament pragmàtic,siesvol),perveureambmésdetenimentquèésun argument iquès’hadecomplir perquèsigui satisfactori

Ambelllenguatge,elséssershumansnonomésexpressemproposicions,ésadir,nosolamentproposemsituacionspossiblesdelmóncomsucceeixenrealment.Tambéprometem, felicitem,inaugurem,preguem,instem...Expressarproposicions,felicitar,inaugurar,pregar, instar...totesaquestesaccionssónelqueanomenem actesdeparla,accionsquefemper mitjàdelesparaulesiqueescaracteritzenperla pretensió delparlantdeportaraterme unafinalitatdeterminada.LateoriadelsactesdeparlavaserinauguradapelfilòsofJohn LangshawAustinambunasèriedeconferènciesquevaferel 1955alaUniversitatdeHarvard iqueesvanpublicarpòstumamentel 1962 enunllibretitulat HowtoDoThingswithWords Unexempled’actedeparlaés argumentar. 1 Unargumentésunaseqüènciad’afirmacions caracteritzadaperlapretensió queunad’aquestes,queanomenarem conclusió,repsuport, s’infereix,sesegueix,etc.,delesrestants,queanomenarem premisses.

Elsactesdeparlaespodenferamb: èxit,quansatisfanlafinalitatpretesa,o fracàs,quannola satisfan.Així,perexemple,unactedeparlaconsistentaenunciarunaproposició(pretenent dirlaveritat)esrealitzaambèxitsilaproposicióésvertadera,iambfracàssiésfalsa.

Unactedeparlaconsistentaargumentar,presentarunargument,esfaamb:

‚ èxit(iparlemd’argument vàlid)siefectivamentlespremissesabonenlaconclusió; ‚ fracàs(iparlemd’argument invàlid)silespremissesnoabonenlaconclusió.

Observemquelavalidesad’unargumentnogaranteixperellamateixaqueestiguemjustificatsacreurelaveritatdelaconclusió,jaque potserquesiguiunargumentvàlidperòamb premisseslaveritatdelesqualsnoestàjustificada,oambpremissesfalses.Parlaremaleshores d’argument satisfactori perreferir-nosaunargumentvàlididetalmaneraquelaveritatdeles sevespremissesestàjustificada.Icomesjustificalaveritatd’aquestespremisses?Enmoltes ocasions,mostrantque,alseutorn,ellesmateixessónconclusionsd’argumentssatisfactoris. Afortunadament,aixònoensportaaunaregressióal’infinitperquèhihaproposicionsla veritatdelesqualsnoesjustificapermitjàd’unargument,sinóúnicamentpermitjàdel significatd’algunstermesinvolucratsenl’expressiódeladitaproposició.Perexemple,si desprésdefercoincidirelsextremsdedosbastonsdiemqueelquesobresurtés mésllarg quel’altre,estaremenunciantunaproposicióvertadera,iaixòésaixíúnicamentpelsignificat de«mésllarg».

Independentmentdesisónonosatisfactoris,hihauntipusd’arguments,queanomenarem argumentsdeductius,enelsqualselparlantpreténquenopotestarjustificatcreureenla veritatdelespremissessensecreureenlaveritatdelaconclusió.Així,elsargumentsdeductius

1.Hihaunsentitmésamplid’«argumentar»segonselqualelqueespreténéspersuadirl’audiènciaque formicertacreença,finsitotambmalesarts,comaramitjançantamenacesomitjançantelcarismadelparlant.Aquí reservemelterme«argument»perauntipusparticulardediscurspersuasiu,elqueprovendeconvèncerpermitjà deraons.

vàlids,ésadir,aquellsenquèescompleixlapretensiódelparlant,sónargumentsvàlids enelsentitmésfortpossible.Perexemple,unargumentcomelsegüent:«Totselshomes sónmortals.Sòcratesésunhome.Pertant,Sòcratesésmortal»,ésuncastípicd’argument deductiuvàlid,enelquallespremissessón«totselshomessónmortals»i«Sòcratesésun home»,ilaconclusióésque«Sòcratesésmortal».

La formalògica del’enunciat,ésadir,elquequedaquansubstituïmelstermesnològics(ésa dir,diferentsde«peratot»,«existeix»,«i»,«o»,«si...aleshores...»,etc.)perconstants,variables ipredicatsabstractes,és

on x ésunavariable, s ésunaconstant(enl’argumentoriginalera«Sòcrates»)i H i M sónpredicats 1-aris(enl’argumentoriginalerenelspredicats«serhome»i«sermortal»). Observemque,sensequeimportielsignificatquedonemalaconstant s ialspredicats H i M,nomésperlaformalògicadelespremissesilaconclusiójatenimunargumentdeductiu. Enefecte,unadelespremissesésquetotindividuquecompleixilapropietat H complirà forçosamentlapropietat M iunaaltradelespremissesésquel’individuconcret s compleixla propietat H;aleshores,siunacceptalespremisses,perforçahad’acceptartambélaconclusió, asaber,quel’individuconcret s compleixlapropietat M.

Espotdemostrarqueelquepassaambl’argumentdeductiuvàlidanteriorpassaengeneral ambtotselsargumentsdeductiusvàlids.Ésa dir,quequanunargumentdeductiuésvàlid, hoésgràciesalaformalògica,independentmentdelainterpretacióquefemdelstermesno lògics.Enaltresparaules,lavalidesad’unargumentdeductiuesdeualaseva sintaxi,inoala seva semàntica.

Perdescomptat,hihaaltrestipusd’arguments,perexempleinductius(DíeziMoulines, 2008), peròaquíenscentraremenelsdeductiusperquèsemblaquetenenunpaperessencialen lesmatemàtiquesactuals.

4.Lesmatemàtiquesorganitzadesalvoltantdelsargumentsdeductius

Alllargdelahistòria,l’argumentaciódutaatermeperlacomunitatmatemàticas’habasat enintuïcionsinocionsque,ambeltemps,hanestatfontdecontradiccionsiparadoxes preocupantsiquevandonarllocaunacrisidelsfonamentsdelesmatemàtiquesafinals delsegle XIX iprincipisdel XX.Vaserllavorsqueunapartdelacomunitatmatemàticai filosòficavacomençarunaintensaactivitatorientadaaestablirunsfonamentssòlidsperales afirmacionsassumidesperlacomunitatmatemàtica.Elsproblemesquevanmotivarlarevisió delsfonamentsesreferiennosolamentalanaturalesamateixadel’activitatmatemàtica quèfemquanfemmatemàtiques ,sinóalaqualitatdelsargumentsques’hidonaven quansónvàlids,quansónsatisfactoris.

Unadelespropostesdefonamentaciódeles matemàtiquesesvadeureaDavidHilberti esconeixambelnomde formalisme.Segonslaversióactuald’aquestaproposta,totesles assumpcionssubstantivesdelesmatemàtiqueshand’estarcodificadesenunasèried’afirmacions,els axiomes,mentrequetotsels teoremes handederivardelsaxiomesúnicament

tpp@x qpHx Ñ Mx qq,Hsu( Ms,

permitjàd’argumentsdeductiusvàlids.Així,nomésfemservirelsignificatdelstermesno lògicsenlatriadelsaxiomes,peròmaienl’elaboraciódelsargumentsqueensportendels axiomesalsteoremes.

Undelsavantatgesi,defet,lamotivacióprincipaldelformalisme,ésquel’úsexclusiudel tipusd’argumentvàlidmésfortaclareixqualsevoldubtesobrelesconclusionsobtingudes. Acanvi,perlamateixanaturalesadelsargumentsdeductius,estemobligatsapagar-neun preugensmenyspreable.Enefecte,encaraqueenlesmatemàtiquesesfanservirmoltstipus d’objectesdiferents(nombres,dinselsnombresdiferentstipusdenombres,funcions,dinsles funcionsdiferentstipusdefuncions,punts,segments,rectes,plans,hiperplans,superf ´ ícies, cossosgeomètrics,etc.),l’úsexclusiud’argumentsdeductiusensobliga,perraonsqueno explicaremaquí,aexpressartotsaquestsobjectesentermesd’unúnictipusd’objectes. L’adopciódelsconjuntscomaobjectesbàsicsapartirdelsqualsesconstruiriatotalarestaha estatundelspeatgesques’hahagutdepagar.Unaaltradelesconseqüènciesdelformalisme vaserlanecessitatd’expressarmitjançantaxiomesalgunesdelesconclusionsperalesquals teníemarguments,encaraque aquestsargumentsnofossindeductius.Perexemple,enla construccióactualde N dinslateoriadeconjunts,lapropietatdistributivadelproducte respectedelasumaestàcodificadaenunaxioma(elquedefineixelproductedenombres naturals)inoestàjustificada.Així,unaltredelspeatgesqueesvahaverdepagarvaserla desaparicióoficialdetotargumentquenofosdeductiu.

5.Organitzacióalternativadelesmatemàtiques

Comhemvistal’apartat 2,capcreenças’hadeconsiderarconeixementproposicionalsense unargumentsatisfactoriquelatinguicomaconclusió,llevatqueaquestacreençaprovingui directamentdelanostraexperiènciasensorial.Pertant,l’ocultaciód’algunsargumentsfaimpossiblequealgunesproposicions,lesconclusionsd’aquestsarguments,adquireixinestatus deconeixementproposicional.Algunesd’aquestesproposicionssón:

‚ Lapropietatassociativadelasumadenombresnaturals.

‚ Lapropietatdistributivadelproducterespectedelasumadenombresnaturals.

‚ Elmètodedelproductecreuatperdetectarequivalènciaentreduesfraccions.

‚ Elproductededuesfraccions, a b ¨ c d ,éslafracció a c b d .

‚ Ladivisiódeduesfraccions, a b : c d ,éslafracció a¨d b c

‚ Lapropietatdistributivadelproducterespectedelasumadenombresdecimals.

Sinodisposemd’argumentsquefonamentinaquestesproposicions,nopodemdirque sapiguemelqueaquestesproposicionsexpressen.Aixídesenzill.

Elquetenenencomútotesaquestesproposicionsésqueelsargumentsafavorseunosón deductius,sinóquerecolzensobreelsignificatdelstermesnològics,recolzensobreelfet queaqueststermesesrefereixenaquantitatsdemagnitud.

Vegemelcasdeladefiniciódelproductedefraccions.Segonsaquestadefinició,si a b i c d són duesfraccions,llavorselseuproducteés

Permoltqueaixòespresenticomadefinició,témoltsentitpreguntar-seperquèésveritat, quinésl’argumentqueavalaaquestaafirmació.Larespostaaaquestapreguntanola trobaremenlaconstrucciódelesfraccionsodelsnombresracionalsenelsidelateoriade conjunts.Aquí,precisament,aixòesdonacomadefinició,sensecapargumentafavorseu. Noméssiinterpretemlesfraccionscomquefanreferènciaaunaquantitatdemagnitud, podemcomençarajustificarracionalmentaquestaafirmació.Pensemenlesfraccions 2 3 i 4 5 fentreferènciaalongituds.Perexemple,pensemenunrectangleelscostatsdelqual mesuren 2 3 mi 4 5 m.Ésfàcilveurequel’àread’unrectangleelscostatsdelqualtenennombres naturalscomamesuresvedonadapelproducte d’aquestsnombresnaturals,amblaunitat demesuracorresponent.Així,perextensió,anomenaremtambé producte al’operacióque hemdeferamblesfraccions 2 3 i 4 5 perobtenirl’àreadelrectangle,mesuradaenm2 .Definint aixíelproducte,lafórmula

ensdiuquel’àread’unrectangleambcostatsde

.Arabé,perquèés veritat?Elprimerpasésconsideraraquestrectangledinsunmetrequadratdetalmaneraque undelsseuscostats(perexemple,elvertical)estàdividiten3partsigualsil’altrecostat(per exemple,l’horitzontal)estàdividiten5partsiguals.D’aquestamanera,elmetrequadratestà dividiten3 ¨ 5partsiguals(3filesper5columnes),ésadir, 15parts.Elnostrerectangleinicial estàformatper 2 vegades4(ésadir, 2 filesd’alçadaper4columnesd’amplada)d’aquestes 15 parts.D’aquestamanera,alafracció 2¨4 3¨5 m2 eldenominadorindicaelnombredepartsenles qualsesdivideixelmetrequadratielnumerador indicaquantesd’aquestespartsnecessitem percobrirexactamentelnostrerectangle.

Totiqueéscontrovertit,l’ocultaciód’aquesttipusd’argumentspotsercomprensibleeninstitucionseducativescomlesfacultatsdematemàtiques.Sónengeneralaquestesinstitucions lesquegaranteixenlarenovacióilapervivènciadelacomunitatmatemàtica.Així,pertalde deixarelsfutursprofessionalsencondicionsdecontinuarlatascadelsseusantecessors,les facultatsdematemàtiqueselstransmetenl’estatactualdeladisciplina,sinopelquefaa resultats,sípelquefaalaconceptualitzacióilametodologia.Laconceptualitzacióactualde lesmatemàtiques,comateoriaformalexpressadaenunllenguatgedeprimerordrequeha aportatrigoriclaredataunaactivitatquetrobavaseriososproblemesdefonamentació,s’ha decomunicaralsquil’handecontinuardesenvolupant.Aixònoobstant,aquestnoéselcas delsalumnesd’altresnivellseducatius.

Hauríemdedisposaraleshoresdemodesalternatiusdepresentarlesmatemàtiques,uns modesmésadequatsalspropòsitsdel’educacióprimària,l’educaciósecundàriaielbatxillerat.Und’aquestspropòsits,comdèiemal’apartat 2,éslatransmissiódeconeixement, inohihaconeixementsenseargumentsquel’avalin.Demaneraque,eneldecursdels processosd’estudidelesmatemàtiquesenaquestsnivellseducatius,s’hauriad’intentar evitarl’afirmaciódeproposicionssenseelsuportd’arguments.Enaquestsentit,s’haurien dereconstruirlesmatemàtiquesapartirdelesmagnitudsiadmetentl’úsd’argumentsno deductius.

Arabé,sielcriterilògicdeductiunoéselqueguiaràlapresentaciódelesobresmatemàtiques peralseuestudi,analitzantiintroduintprogressivamentlesdefinicionsilesdemostracions enfunciódelasevacomplexitatlògica,quinpodriaser-neelcriteri?Enllocdeseguirun criterianalític,podríemseguiruncriterievolucionista,queexpliquilesobresmatemàtiques comelresultatd’unprocésevolutiuiqueproporcioniinformaciósobrelasevahistòriacausal. Segonsaquestcriteri,serialavoluntatderesoluciód’algunstipusdetasqueslaqueimpulsariaeldesenvolupamentdedeterminadestècniquesil’elaboraciód’undiscursteòriccada vegadaméssofisticat.Sotaaquestprisma,lesmatemàtiquesespresentencomelresultat delacercadelamillorsolucióaalgunstipusdeproblemes,lacercadelamillorresposta aalgunstipusdepreguntes.Aquestacercano començatrobantjalasoluciódefinitiva, sinóqueconsisteixenunaexploraciósostingudaeneltemps,eneldecursdelaquales vanacumulanticomparanttècniques,noustipusdetasquesiconsideracionsteòriques. Aquesttipusdedescripciódiacrònicadeles matemàtiquesespotveuredesdel’enfocament conegutcom epistemologiaevolucionista (BradieiHarms, 2020),queproposaconsiderar eldesenvolupamentdelconeixementcomunarealitzacióconcretadelaideadarwinista abstractad’evolució.

Endidàcticadelesmatemàtiques,elprimeradesenvoluparsistemàticamentaquestenfocamentvaserGuyBrousseau,fundadordelateoriadelessituacionsdidàctiques(Brousseau, 1997)amblasevanocióde situació (Brousseau, 1986,apartat III).Aquestanocióneixsota lainfluènciad’algunsmodelsdelaconstrucció(noinstruccional)deconeixementicoma reaccióaaquests,elaboratsdesdelapsicologiacognitiva(BurrhusF.Skinner,JeanPiaget, PierreGréco,LevS.Vigotski,PatrickSuppes,etc.).EnparaulesdelmateixBrousseau,«Hem anomenat situació aunmodeld’interacciód’unsubjecteambundeterminatmedique determinaunconeixementdonatcomelrecursdequèdisposaelsubjecteperassoliro conservarunestatfavorableenaquestmedi.Algunesd’aquestes situacions requereixen l’adquisicióanteriordetotselsconeixementsiesquemesnecessaris,peròn’hihad’altres queofereixenunapossibilitatalsubjectedeconstruirperellmateixunconeixementnouen unprocés genètic»(Brousseau, 2000).Així,enaquestúltimtipusdesituacions,éspossiblela gènesidelconeixementcomasolucióaunproblemaqueunsubjecteexperimentaenlaseva relacióambunmedi.Enelconeixementqueesgeneraiesdesenvolupaapartird’activitats alvoltantdelesmagnituds,aquestmediésuncontextmaterialenelqualintervenenalguns objectesquevolemcompararrespected’algunamagnitud.

Unexempleclàssicdesituació(Briand, 1993)ésaquellenelqualunsubjectetédosconjunts d’objectes, A i B,ihad’esbrinarquinésmésgran.Elmediestàformatpelsconjuntsd’objectes iperlasevadisposicióespaciotemporal.Sitotsdosconjuntssónsimultàniamentaccessibles peralsubjecte,llavorspotutilitzarunatècnicaestàndarddecomparaciódirectadelsdos conjunts,ladel’aparellamentdirecte,queconsisteixaferparellesprenentunobjectede A iunaltrede B.Elprimerconjuntquequedisenseobjecteséselméspetit.Ambtot,si noespotaccediralsconjuntssimultàniament,perexempleperquèundiaelsubjecteté accésnomésa A il’altredianomésa B,aleshoresaquestatècnicadecomparaciódirecta janofunciona.S’hadeportaratermeunatècnicadecomparacióindirecta,l’aparellament indirecte,queconsisteixaferl’aparellamentdirecteentreelconjunt A (respectivament, B)i unconjuntauxiliar, μpAq (respectivament, μpBq),desímbolsquel’agentcrea,perexemple dibuixantpaletsenunpaper,iacontinuaciócomparar μpAq i μpBq mitjançantl’aparellament directe.Apareixaixíunobjectenou,unsistemadenumeracióprimitiu,comasolucióaun

tipusdeproblemaque,d’unaaltramanera,nohauriatingutunasoluciófàcil.Enaquestcas, lamagnitudenjocéslamagnitud cardinalitat

Desdeladidàcticadelesmatemàtiquesnos’afirmaqueaquestfosexactamentl’esquema quevaregirl’apariciódelaideadenombrenaturalodelprimersistemadenumeració. Aixònoobstant,ésunesquemaqueensserveixperaprendrelautilitatd’aquestsobjectes matemàtics,jaqueelsmostracomlamillorsolucióaunasituacióproblemàticahipotètica. Aquestesquemaespodriaveurecomuna històriacontrafàctica delnaixementdelsnombres naturals,ésadir,unahistòriaquedemana queesconsideriunasituacióproblemàtica imaginàriaenvistadelaqualespodràavaluarlaimportànciad’unesdevenimentoaltre.Així, elnostreesquemacontrafàcticenshail luminatsobrelanaturadelsnombresnaturals,sobre elseunaixement,sobrelasevaraódeser,ienshapermèsimaginarquintipusdeproblemes trobaríemsinodisposéssimdelsnombresnaturalsiquintipusdesolucionsaquestsnombres aporten.Noésestranyl’úsd’històriescontrafàctiquesperpartdelshistoriadors(Maar, 2014) ienaltresdisciplinesdelesciènciessocials(MorganiWinship, 2007;Elster, 1994),jaquela nocióde fetcontrafàctic haresultatútilenl’anàlisidelanocióde causalitat (MenziesiBeebee, 2020).

6.Modelepistemològicdereferènciageneral

Aixídoncs,elrepteconsisteix,donadaunaobramatemàtica O ,areconstruir-lamitjançant unahistòriacontrafàcticaquelapresenticomelresultatd’unprocésevolutiuenelqual unsubjecteagentidealcercadonarrespostaobjectivaadeterminatstipusdetasques problemàtiques.Cadaavençenaquestprocés haderespondrealanecessitatd’adaptar-sea unmediobjectiu,icadaafirmaciós’had’argumentarenfunciódelssignificatsqueelstermes nològicsdelnostrellenguatgeadquireixinmitjançantlarelaciódelsubjecteagentambel medienqüestió.

Enmoltstreballsdedidàcticadelesmatemàtiques,enelmarcdelateoriaantropològica deldidàctic(Bosch,Chevallard,GarcíaiMonaghan, 2019),aquesteshistòriescontrafàctiques rebenelnomde modelepistemològicdereferència (MER),perquè,enefecte,serveixende modeldereferènciaperal’estudidedeterminatsfenòmensdidàcticsenrelacióamblagènesi il’evoluciódelconeixement(GascóniNicolás, 2019b;Gascón, 2014).Enendavant,farem serviraquestaterminologia.

PresentemacontinuacióunMERgeneralquedescriulagènesidegranpartdelesmatemàtiqueselementals.Lesrealitzacionsparticularsd’algunesdelespartsserveixend’esquemes contrafàcticssobrel’origendediversosaspectesbàsicsdediferentsdominisdelesmatemàtiques(elssistemesdenumeració,lageometriaplana,lageometriaespacial,laprobabilitat, etc.).

6.1. Sistemes comparatius

L’esquemacomençaambunsubjecteagentilaconsideració,perpartd’aquestagent,d’una magnitud.Unamagnitudésun sistemacomparatiu,ésadir,unacertaclassed’objectesque comparementreellsrespected’unacaracterísticacomunadeterminadaqueespotdonar

enmésomenysgrau.Així,unsistemacomparatiuésunparell pΩ, ă , „q,on Ω éslaclasse d’objectesquecomparementreellsi ă i „ sónduesrelacionsbinàriesa Ω quecompleixen:

‚ x „ x

‚ px „ y qÑpy „ x q

‚ ppx „ y q^py „ z qqÑpx „ z q

‚ ppx ă y q^py ă z qqÑpx ă z q

‚ px ă y qÑ py ă x q

‚ px ă y q_px „ y q_py ă x q

Elssistemescomparatiusesreflecteixenen untretdelanostrallenguaquotidiana,queels gramàticsanomenengraucomparatiudelsadjectius.

Elssignificatsdeproposicionsdeltipus x „ y o x ă y ,ésadir,lescondicionsdeveritat,es fonamentenenunasèried’accionsquedefineixenelqueanomenem comparaciódirecta.

6.2. Exemple

Podempensarenunsistemacomparatiuquepodriatenirundominimoltampli,format virtualmentpertotselsobjectesdelmónioncomparemrespectedela massa.Diemque x ă y si,col locatstotsdosobjectesensenglesplatsd’unabalança,aquestaesdesequilibra enfavorde y ,idiemque x „ y silabalançanoafavoreixni x ni y .Laprovadelabalança constitueixelmètodeestàndardde comparaciódirecta enelcasdelamassa.

6.3. Exemple

Podempensarenelsistemacomparatiueldominidelqualestàformatpelsconjuntsfinitsi oncomparemrespectedela cardinalitat.Diemque x ă y si,enferparellesambunobjecte de x iunaltrede y ,s’acabenabanselsobjectesde x .Diemque x „ y si,enferparelles ambunobjectede x iunaltrede y ,ambdósconjuntss’exhaureixenalmateixtemps.Aquest aparellamentdirecteésla comparaciódirecta enelcasdelacardinalitat.

Moltsdelssistemescomparatiusques’estudienal’educacióprimàriail’educaciósecundària (comaracardinalitat,massa,temps,longitud, àrea,volum)tenen,amés,unpredicattriàdic, ˝,queserveixpercombinarobjectesienunciarcosesdeltipus a ˝ b “ c.

6.4. Exemple

Enelcasde:

‚ lacardinalitat, ˝ fareferènciaalauniódisjunta,

‚ lamassa, ˝ fareferènciaal’acciódeposardosobjectesalmateixplatdelabalança, ‚ lalongitud, ˝ fareferènciaalacoalineaciódeduesbarres.

Típicament,elsignificatatribuïtaaquestpredicatfaquelessentènciessegüentssiguin vertaderes:

‚ p@x,y qppx ă x ˝ y q^py ă x ˝ y qq

‚ p@x,y,z qpppx ˝ y q˝ z q„px ˝py ˝ z qqq

‚ p@x,y,z qppx ă y qØpx ˝ z ă y ˝ z qq

‚ p@x,y,z qppx ă y qØpz ˝ x ă z ˝ y qq

‚ ...

Laprimerad’aquestespropietatsinspiraqueaquestesmagnitudsosistemescomparatius s’anomenin extensius.

6.5. Comparació indirecta mitjançant mesurament directe: nombres

Acausadelimitacionsmaterials,enlamajoriad’ocasionslacomparaciódirectanoespotdur aterme.

Elnostreagentcreaaleshoresla comparacióindirecta.Aquestanoconsisteixacomparar directamentelsobjectes a i b,sinóindirectament,atravésdelacomparaciódirectadedos conjuntsdesímbols(anomenats nombres), μpaq i μpbq,queatribuïmalsconjunts a i b.En aquestpuntdelnostreesquemageneral,l’atribucióde μpaq de a ésun mesuramentdirecte, queesportatermefentúsdeles unitatsdemesura.D’aquestamaneraapareixenelssistemes mètrics.

Un sistemamètric ésunacosadiferentd’unsistemacomparatiu.Elssistemesmètricsnotenen correspondènciaenelllenguatgeordinari.Alcontrari,sónunacreaciódel’activitatcientífica, característicadelsestadismésavançatsdelaciència.Larevoluciócientíficavaconsistiren granpartenlaintroduccióil’ússistemàticdelssistemesmètrics.

Elssistemesmètricsamplienelllenguatge quefemservirenelssistemescomparatiusmitjançantlaintroducciódenombres,vectorsotensors.Enl’educaciósecundàriaielbatxillerat noméss’estudienexplícitamentelsnombresielsvectors.

Laintroducciód’un sistemamètric significa:

‚ l’ampliaciódelnostreuniversintroduintunconjunt M denousobjectes,els nombres,

‚ laintroducciódelsconegutspredicatsdiàdics, ă i “,referitsalsnombres,

‚ laintroducciód’unafunció μ : Ω ÝÑ M quefacorrespondreunnombreaunobjecte. Enlasentència μpaq“ m diemque m ésla mesura de a

Amés,s’hadecomplirquelessentènciessegüentssiguinvertaderes:

p@x,y qppx ă y qØpμpx qă μpy qqq

p@x,y qppx „ y qØpμpx q“ μpy qqq

Donatunsistemacomparatiu,la metrització implicaampliar-neelllenguatgeperintroduir tambéenlanostraactivitatunsistemamètric.Lametritzaciód’unsistemacomparatiuconsisteixadefinirunafunció μ.Calnoconfondre metrització amb mesurament,queconsisteix, donatunsistemacomparatiujametritzatidonatunobjecte a,atrobarelvalor μpaq.En l’ensenyamentobligatorilaconstrucciódemesuresésunaactivitatmoltmarginal.Encanvi, enl’àmbitdelesciènciessocialsidel’estadísticaésunaactivitatimportant.Perexemple,un qüestionariespotconsideraruna μ (ounprojectede μ)permesuraropinions,creences,etc.

Hihadeterminatssistemescomparatiusque,demoment,noméstenen metritzacionsordinals, queeslimitenaassignarnombresaobjectesrespectantl’ordredelsistemacomparatiu(per exemple,l’escaladeRichterperalaintensitatdelsterratrèmols,ladeBeaufortperaladels vents,ladeMohsperaladuresadelsmineralsoladeLikertenlesopcionsderespostaa unqüestionari).Afortunadament,hihasistemescomparatiusquetenen metritzacionsproporcionals,quenonomésensdiuenquanunobjecteésmésomenysqueunaltrerespecte d’algunacaracterística,sinóqueensdiuenenquinaproporciól’unésmésomenysquel’altre. Aquesttipusdemetritzacióéspossibleambalgunssistemescomparatiusextensius.Pera això,esfixaunaclassed’equivalènciad’objectes rus respectedelarelaciód’equivalència „ . Aquestaclassed’equivalènciaesdirà unitatdemesura.Acontinuació,donatunobjecte a, trobemelnombre m demaneraque

„ u ˝ m vegades ... ˝ u, on u ésunrepresentantdelaunitatdemesura.Llavorsestablim μpaq“ m.Silacomprovació del’equivalència

a „ u ˝ m vegades ... ˝ u

s’hafetmitjançantcomparaciódirecta,aleshoresdiemqueelmesuramentde a haestatun mesuramentdirecte.Elmesuramentdirecteambeltreballdelamagnitud cardinalitat dona lloc,enprimerainstància,alsnombresnaturals.Quanesconsiderenaltresmagnituds,per exemplela longitud ola massa,apareixlanecessitatd’ampliarelconjuntnumèricperincloure elsnombresdecimalspositiusfinitsilesfraccionspositives,iapareixenlesnocionsde fracció equivalent i nombreracional,ielpasdedecimalafraccióiviceversa.

Lametritzacióproporcionalenspermetsovintargumentarafavordesentènciescom pa ă bq o pa „ bq.Enefecte,apartirdelespremisses μpaq“ n, μpbq“ m i n ă m,podemelaborar unargumentquetinguiperconclusió a ă b.Enaquestcas,diemquehemdutatermeuna comparacióindirecta.

6.6. Comparació indirecta mitjançant mesurament indirecte: operacions numèriques

Desafortunadament,devegadeselmesuramentdirectenoéspossible.Totiaixò,enmoltes ocasionselnostreagentpotduratermelacomparacióindirectamitjançantel mesurament indirecte.Elmesuramentindirecteésunmesurament(ésadir,trobarelvalor μpaq pera undeterminat a),perònoesfacomparantdirectament a ambdiversosrepresentantsdela unitatdemesura.Vegemcomespotduratermeaquestmesuramentindirecte.

Lametritzacióquesolemintroduirenelssistemescomparatiusextensiusampliaelnostre llenguatgemitjançantlaintroducciódelconegutpredicatdiàdicsuma, `,referitanombres, ifavertaderalasentènciasegüent:

Vegemcomespodriaferservirlasumaperduratermeaquestmesuramentindirecte. Imaginemquevolemmesurarl’objecte a iquenoesdonenlescondicionsmaterialsperfer unmesuramentdirecte.Unaalternativaseriaverificarlessentències a “ b ˝ c, μpbq“ n i μpcq“ m.Illavors,ambaquestespremisses,podemelaborarunargumentquetinguicoma conclusiólasentència μpaq“ n ` m.

Aixídoncs,segonselnostreesquemacontrafàctic,lesoperacionsenmatemàtiques(no noméslasuma)entrenombresnaturals,fraccionspositivesinombresdecimalspositiusfinits apareixenpertalqueelnostreagentpuguiduratermemesuramentsindirectes.Observem queladivisióentrenombresdecimalsfinitspotdonarllocanombresdecimalsinfinits,però, entotcas,seranracionals.

Aixònoobstant,elmesuramentindirecte(perexemple,delahipotenusad’untriangle rectangleodelalongituddelacircumferènciafentservircomaunitatdemesuraeldiàmetre)provocal’apariciódecerts nombresirracionals.Aquestsnombresescorresponenamb nombresdecimalsinfinitsenquèlapartdecimalnoofereixunpatrórecurrent.

Lesoperacionsnonomésserveixenpermesurarindirectament,sinótambéperdefiniraltres magnituds(comara velocitatmitjana i acceleració).

L’estudiperdiferentsautors(desdelesmatemàtiques,lafilosofiaolapsicologia)delsdiferentstipusdemagnituds(nonoméslesextensives),lespossiblesmetritzacionsilesrelacions entreaquestesmetritzacions,hadonatllocalqueesconeixcomlateoriadelamesura.El naixementilesprincipalsfitesd’aquestateoriafinsaladarreriadelsegle XX estanrecollitsa Díez(1997a, 1997b)iunagranpartd’aquestateorias’explicasistemàticamentaKrantz,Luce, SuppesiTversky(1971, 1989, 1990).

6.7. Sistemes de variació de magnituds: proporcionalitat, equacions i funcions

Hihaocasionsenquèelnostreagentconsideraràcontextosenquèintervenenduesmagnitudsques’afectenmútuament;perexempl e,quanconsideriunobjecteambmoviment uniformerecorrentunadeterminadalongitudfixaiespregunticomesrelacionenenaquest contextlesmagnituds velocitat i temps.Parlemenaquestcasd’un sistemadevariacióde magnituds (SVM).QuanenunSVMunaquantitatdemagnitudcorresponunívocamentauna altraquantitatdemagnitud,diemqueésunSVM determinista

AquestsSVMdeterministesespodenferintel¨ligiblespermitjàde relacionsdeproporcionalitat (directaoinversa),d’equacions ide funcions queelsgovernen.

6.8. Sistemes de variació de magnituds: derivades

Enocasions,enelsSVMdeterministeselnostreagentvolduratermeunestudidela covariació,ésadir,decomvariaunamagnitudapartirdevariacionsdel’altramagnitud involucrada.S’estudiaranperaaixòels intervalsdecreixement o decreixement.Aixòdonapeu alesnocionsde derivadad’unafuncióenunpunt i funcióderivada,definidesapartirdetaxes devariaciómitjanacalculadesenunintervald’amplitudmenorqueelnostre graudeprecisió enelmaneigdelesmagnitudsinvolucrades.Mitjançantmanipulacionsalgebraiquesespot calcularladerivadadequalsevolfuncióracional.

6.9. Sistemes de variació de magnituds: límits

Ambtot,aquestesmanipulacions,aquestscàlculs,noespodenduratermeambunaltretipus defuncions(perexemple,exponencialsotrigonomètriques).Ésaleshoresqueapareixenles nocionsde límit ide continuïtat (importantsperalcàlculdelímits,jaqueenlesfuncions contínueselcàlculdelímitsésespecialmentfàcil).

Lanocióde pasallímit tambéapareixcomunatècnicademesuramentindirecteengeometria idonallocalqueesconeixcoma càlculintegral.

6.10. Probabilitat

ElsSVMdeterministesestanrelacionatsambels experimentsdeterministes,ésadir,aquellsen elsqualslarepeticiódel’experimentencondicionssimilarsdonapeualmateixresultat.En contraposició,hihatambéels experimentsaleatoris,ésadir,aquellsenelsqualslarepetició del’experimentencondicionssimilarspotdonarpeuaresultatsdiferents.

Enlamagnitud probabilitat escomparen successos,ésadir,tipusderesultatsd’experiments aleatorisrespectedelasevafreqüènciarelativaallargtermini.Larepeticiósuccessivade l’experimentielrecomptedefreqüènciesrelativeséselmètodedecomparaciódirectaen elcasdelamagnitud probabilitat.LafórmuladeLaplace(mitjançantelrecomptedecasos favorablesidecasospossibles,peralaqualcosaésmoltútilla combinatòria)ialtresmètodes queinvolucrenlaprobabilitatcondicionadasóntècniquesdemesuramentindirectedela probabilitat.

7.Algunstreballssobrelesmagnituds

Acontinuacióemreferirébreumentaalgunstreballsquehanabordatambdeteniment algunespartsdel’esquemaanteriorendidàcticadelesmatemàtiquesi,mésespecíficament, enlateoriaantropològicadeldidàctic.

Lesactivitatshumanesdecomparaciódirectadedosobjectesrespected’unamagnitud extensiva,elseumesuramentdirecteielseumesuramentindirecte(permitjàd’operacions matemàtiques),donenllocal’esquemasegüent:

pΩ, ă , „ ,˝q

pM, ă , “ ,`q

pΩ{„ , ă , “ ,`q

on pΩ, ă , „ ,˝q éselquehemanomenat sistemacomparatiu, pM, ă , “ ,`q ésel sistema numèric,unconjuntdenombresambl’ordre ă ilasuma ` habituals,i μ ésl’aplicació mesura, quesatisfà:

‚ p@x,y P Ωqppx ă y qØpμpx qă μpy qqq

‚ p@x,y P Ωqppx „ y qØpμpx q“ μpy qqq

‚ p@x,y P Ωqpμpx ˝ y q“ μpx q` μpy qq

L’aplicació π éslaprojeccióde Ω enelconjunt Ω{„ declassesd’equivalència,alesquals anomenarem quantitatsdemagnitud.Perdiferenciarelsobjectesdelesquantitatsdemagnitud,pensemenlanociód’unitatdemesura.Avegades,s’hafixatunobjectepatróperdefinir unaunitatdemesura,peròlaunitatdemesura,enrealitat,noésunúnicobjecte,sinómés aviattotalaclassed’equivalènciadel’objectepatrócorresponent.ANicolás(2014a)esfan algunesconsideracionsdidàctiquesalvoltantdelfetque,enaquestconjuntquocient,la relaciódecomparació ă estransformaenunarelaciód’ordre ă ,ilarelaciód’equivalència „ , enigualtat.L’aplicació˜μ,induïdaper μ,esdefineixcomsegueix:˜μprasq“ μpaq.

UnaquantitatconsiderabledelstreballsdeBrousseauielsseuscol laboradorssecentren enlacomparaciód’objectesrespectededeterminadesmagnitudsextensives(apartat6.1)i enlaconstrucciódelsistemanumèriccorresponent(apartat6.5).Unagranpartdelesseves investigacionss’exposensistemàticamentaBrousseau(2002).

DesdelainiciativapioneradeHölder(1901),hanestatdiversoselstreballsquehanestudiat condicionssuficientsperquè˜μ estableixiunisomorfismeentrelesquantitatsdemagnitud iuncertsubconjuntdelsnombresrealsnonegatius, R` .Enaquestatradicióiinspiratsper Bourbaki(1963,apartat V.2.)iWhitney(1968),BoschiChevallarddesenvolupenaBoschi Chevallard(2000a)unateoriaaxiomàticasobrequantitatsdemagnitudsextensivesilaseva connexióambelsistemanumèricd’arribada,i considerenpossiblesampliacionsd’aquest (apartat6.6)enfunciódelesnecessitatsquesorgeixenapartirdelesactivitatsdutesaterme enelsistemacomparatiudepartida.

Analitzantelstreballsdel’entorndeBrousseau,aBolea etal. (2000, 2002, 2005)escomença aelaborarunmodelepistemològicdereferènciaalvoltantdelamesurademagnituds extensives,queescompletaaSierra(2006).Enaquestesquemaesfanconsideracionssobre lanecessitatdel’ampliaciódelconjuntdelsnaturals,peròesdonapersuposadal’existència d’aquestsnombresnaturals,quenoesmostrencomaresultatdel’estudidelamagnitud extensivafonamental,asaber,la cardinalitat.Undelsèxitsd’aquestmodelésquemostra demanerageneral(peramagnitudsextensivesarbitràries)imésomenysdetalladauna cosaquejaapareixia(peròparticularitzatenmagnitudsespecífiquesisensetantsdetalls)en treballsdeBrousseau.

ALópeziNicolás(2016)esfanalgunesconsideracionsenrelacióamblaraódeserdels nombresdecimals.

ANicolás(2014b)i,posteriorment,aGarcíaiSierra(2015)s’ampliaelmodeldeSierra(2006) perinclourelamagnitud cardinalitat ielsnombresnaturalsdinsd’aquestesquema.Imés endavant,aLicera(2017),escontinuaampliantpermostrarlaraódeserdelsnombres irracionals.

AGarcía(2005)esdissenyaunmodelepistemològicdereferènciasobreelques’exposaa l’apartat6.7,enquèesconnectal’estudidelaproporcionalitatambl’estudidefuncionsen contextosenquèconcorrenduesmagnitudsextensivesquecovarien.

AAbellán(2016)iBochaca,GascóniNicolás(2020)esdissenyaunmodelepistemològicde referènciadel’inicidelcàlculdiferencialquesitualasevaraódeserenlalimitaciódeles tècniquesalgebraiquesperal’estudidelacovariaciódeduesmagnituds(apartats6.8,6.9).

8.Perspectives

ElMERexposatal’apartat6ésnomésunesbósdelques’hafetimoltesdelespartsencara s’handerefinaridesenvoluparpertaldeguanyarpoderexplicatiu.Mésencara,unagranpart delesmatemàtiquesd’infantil,deprimària,desecundàriaidelauniversitatnoestannitan solsprevistesencaraenaquestesquema.

Amésisegonselqueesdefensaaquí,nohihatransmissiódeconeixementproposicionalsensetransmissiód’argumentsielMER semblaqueesbossal’entornadequatperala consideraciódelsdiferentstipusd’arguments(nosolamentelsdeductius)sobreelsquals esfonamentaelconeixementmatemàticdelmón.Peròencaracalduratermeunaanàlisi detalladadelatipologiad’aquestsargumentsidelsmomentsenquèapareixen.

Potserunllenguatgeapropiatperaaquestaempresasiguieldelateoriadejocs,extensament utilitzatenlesciènciessocials.2 Enefecte,elnostre agent seriaundelsjugadors,el medi seriaunaltredelsjugadorsieljoccomençariaambcertstipusdetasquesqueelnostre agenthauriadeportaraterme,oambdeterminadespreguntesalesqualsl’agenthauriade respondre.L’agentguanyaquanhagitrobatunaestratègiaperresoldreelstipusdetasques operrespondrelespreguntesinicials.Pertaldeconsiderarqueund’aquestsjocsexplica proul’obramatemàtica O ,s’hademostrarquecompleixalmenysduescondicions: 1)una condicióde necessitat,ésadir,perelaborarunaestratègiaguanyadoral’agenthanecessitat construirtotselselementsde O ques’handeciditestudiar,3 2)unacondicióde possibilitat,

2.Brousseau,potserinspiratpertreballsdel’estildeSuppes(1969),javaformalitzarlasevanocióde situació mitjançantlaideade joc formal,(Brousseau, 1986,apartat III)ivaapuntarl’interèsd’aquestaformalització enlaconsideraciódelespossiblesestratègiesdelsalumnes,perònovaferunússistemàticd’aquestaformalització.

3.Aixóimplica,enparticular,quel’agentexploraràdiferentstipusdetècniquesperabordarlestasques, quecompararàaquestestècniques,queenmenysprearàunesienprivilegiaràl’estudid’altres,demaneraque, finalment,totiqueengranmesuraesquedésnomésambelselementsquetradicionalmentformenpartde O , l’agents’hauràvistobligatainspeccionardiferentselementsque,típicament,noformenpartdelaversióoficial de O ;enaltresparaules,l’agentenriquiràmoltlasevapraximatemàticamitjançantunaexploracióreflexivadeles diferentspossibilitatsd’acció.

ésadir,ambtotsaquestselementsamà,al’agentliresultapossibleelaborarunaestratègia guanyadora.

Unapartd’aquestenfocamenthaestatconsiderataGascóniNicolás(2018),inspiratper l’anomenat modelinterrogatiud’indagació deHintikka(Hintikka,HaloneniMutanen, 2002). Aquestenfocamentnonomésretcomptedelcaràcterdinàmic,evolutiuiadaptatiudela construcciódelconeixement,sinóquetambéexplicitacomesconstrueixaquestconeixement,il’elaboraciód’argumentsésundelsmovimentsdelsqualsl’agents’hadevalerper guanyareljoc.

Agraïments

AgraeixoaAriadnaMartínSirarolslasevatraduccióalcatalà.

Referències

Abellán,V.(2016). Cálculodiferencial.Treballdefidemàster.Múrcia:UniversidaddeMúrcia.

Bochaca,P.,Gascón,J.,Nicolás,P.(2020).Juegosdidácticosdeindagaciónentornoala covariacióndedosmagnitudes. CaminhosdaEducaçãoMatemática,enpremsa.

Bolea,P.,Bosch,M.,García,J.,Gascón,J.,Ruiz,L.,Sierra,T.(2000).Análisisdidácticodelartículo «Elpesodelrecipiente.EstudiodelosproblemasdelamediciónenCM»enelmarcodela teoríaantropológica. BoletínSI-IDM, 10.https://www.ugr.es/jgodino/siidm/boletin10.htm

Bolea,P.,Bosch,M.,García,J.,Gascón,J.,Ruiz,L.,Sierra,T.(2002).Analysedespraxeologies mathématiquesautourdelamesuredesgrandeurs.Dins ActesdelaXIÉcoled’étédeDidactique desMathématiques (p.369-374).Grenoble:LaPenséeSauvage.

Bolea,P.,Bosch,M.,García,J.,Gascón,J.,Ruiz,L.,Sierra,T.(2005).Analysede«Lemesureen CM1»d’aprèslaThéorieAnthropologiqueduDidactique.DinsP.C.M.H.SaliniB.Sarrazy (eds.), SurlaThéoriedesSituationsDidactiques.HommageàGuyBrousseau (p. 153-166). Grenoble:LaPenséeSauvage.

Bosch,M.,Chevallard,Y.(2000a).LesgrandeursenMathématiquesaucollège.PartieII. Mathématisations. Petitx,59,43-76.

Bosch,M.,Chevallard,Y.(2000b).LesgrandeursenMathématiquesaucollège.PartieI.Une Atlantideoubliée. Petitx,55,5-32.

Bosch,M.,Chevallard,Y.,García,F.J.,Monaghan,J.(2019). WorkingwiththeAnthropological TheoryoftheDidacticinMathematicsEducation.Londres:Routledge.

Bourbaki,N.(1963). Élémentsdemathématique.LivreIII.Topologiegénérale,chapitres5à8. París:Hermann.

Bradie,M.,Harms,W.(2020).EvolutionaryEpistemology.DinsE.N.Zalta(ed.). TheStanford EncyclopediaofPhilosophy.Stanford.MetaphysicsResearchLab,StanfordUniversity.Disponible enlíniaa:https://plato.stanford.edu/archives/spr2020/entries/epistemology-evolutionary/.

Briand,J.(1993). L’énumérationdanslemesuragedes collections.Undysfonctionnement danslatranspositiondidactique.Tesidoctoral,UniversitéBordeaux 1.Disponibleenlíniaa: https://tel.archives-ouvertes.fr/tel-00494623

Brousseau,G.(1986). Théorisationdesphénomènesd’EnseignementdesMathématiques.Tesi doctoral,UniversitéBordeaux 1.Disponibleenlíniaa:https://tel.archives-ouvertes.fr/file/index/ docid/509225/filename/TheseetAnnexesGBA.pdf.

Brousseau,G.(1997). TheoryofDidacticalSituationsinMathematics.Didactiquedesmathématiques,1970-1990.Dordrecht:KluwerAcademicPublishers.

Brousseau,G.(2000).Educaciónydidácticadelasmatemáticas. EducaciónMatemática, 12(1), 5-38.

Brousseau,G.(2002).Lesgrandeursdanslascolaritéobligatoire.DinsJ.-L.Dorier,M.Artaud,M. Artigue,R.BerthelotiR.Floris(eds.). Actesdela11eecoled’etédedidactiquedesmathématiques (p.331-348).Grenoble:LaPenséeSauvage.

Dewey,J.(1916/2004). Democraciayeducación.Madrid:Morata.

Díez,J.A.(1997a).AHundredYearsofNumbers.AnHistoricalIntroductiontoMeasurement Theory 1887-1990.PartI:SuppesandtheMatureTheory. StudiesinHistoryandPhilosophyof Science, 28(2), 237-265.

Díez,J.A.(1997b).AHundredYearsofNumbers.AnHistoricalIntroductiontoMeasurement Theory 1887-1990.PartII:TheFormationPeriod. StudiesinHistoryandPhilosophyofScience, 28(1), 167-185.

Díez,J.A.,Moulines,C.U.(2008). Fundamentosdefilosofíadelaciencia.Barcelona:Ariel.

Elster,J.(1994). Lógicaysociedad.Contradiccionesymundosposibles.Barcelona:Gedisa.

Everett,C.(2018). Losnúmerosnoshicieroncomosomos.Barcelona:Crítica.

Fernández-Armesto,F.(1997). Truth.Ahistoryandaguidefortheperplexed.NovaYork:St. Martin’sPress.

García,F.J.(2005). Lamodelizacióncomoherramientadearticulacióndelamatemáticaescolar. Delaproporcionalidadalasrelacionesfuncionales.Tesidoctoral.Jaén:UniversidaddeJaén.

García,F.J.iSierra,T.A.(2015).Modelosepistemológicosdereferenciaenelanálisisdela actividadmatemáticaenlibrosdetexto:elcasodelnúmeroenlaescuelainfantil.DinsC. Fernández,M.MolinaiN.Planas(eds.). InvestigacióneneducaciónmatemáticaXIX (p. 299-307). Alicante:SEIEM.

Gascón,J.(2014).Losmodelosepistemológicosdereferenciacomoinstrumentosdeemancipacióndeladidácticaylahistoriadelasmatemáticas. EducaciónMatemática,25años(número especial), 99-123.

Gascón,J.,Nicolás,P.(2017).Candidacticssayhowtoteach?Thebeginningofadialogue betweentheAnthropologicalTheoryoftheDidacticandotherapproaches. FortheLearning ofMathematics,37(3), 9-13.

Gascón,J.,Nicolás,P.(2018).Inquiry-basedlearningandpre-serviceteacherseducation. DinsS.G.V.Durand-Guerrier,R.HochmuthiN.M.Hogstad(eds.), Secondconferenceofthe internationalnetworkfordidacticresearchinuniversitymathematics (p.412-421).Proceedings ofINDRUM.

Gascón,J.,Nicolás,P.(2019a).Economía,ecologíaynormatividadenlateoríaantropológica delodidáctico. EducaçaoMatemáticaPesquisa, 21(4),36-52.

Gascón,J.,Nicolás,P.(2019b).ResearchendsandteachingendsintheAnthropological TheoryoftheDidactic. FortheLearningofMathematics,39(2),42-47.

Hintikka,J.,Halonen,I.,Mutanen,A.(2002).InterrogativeLogicasaGeneralTheoryofReasoning.DinsD.M.Gabbay,R.H.Johnson,H.J.OhlbachiJ.Woods(eds.), HandbookoftheLogicof ArgumentandInference,vol.1 (p. 295-337).Amsterdam:Elsevier.

Hölder,O.(1901).DieAxiomederQuantitätunddieLehrevomMass. BerichteüberdieVerhhandlungenderköniglichesächsischenAkademiederWissenschaftenzuLepzigMathematical PhysicsClasse,53, 1-64.

Ichikawa,J.J.,Steup,M.(2018).TheAnalysisofKnowledge.DinsE.N.Zalta(ed.), TheStanford EncyclopediaofPhilosophy.Stanford:MetaphysicsResearchLab,StanfordUniversity.Disponibleenlíniaa:https://plato.stanford.edu/archives/sum2018/entries/knowledge-analysis/.

Krantz,D.,Luce,D.,Suppes,P.,Tversky,A.(1971). FoundationsofMeasurement,Vol.1.Nova York:AcademicPress.

Krantz,D.,Luce,D.,Suppes,P.,Tversky,A.(1989). FoundationsofMeasurement,Vol.2.Nova York:AcademicPress.

Krantz,D.,Luce,D.,Suppes,P.,Tversky,A.(1990). FoundationsofMeasurement,Vol.3.Nova York:AcademicPress.

Licera,R.(2017). Economíayecologíadelosnúmerosrealesenlaenseñanzasecundariayla formacióndelprofesorado.Tesidoctoral.Valparaíso(Xile):PontificiaUniversidadCatólicade Valparaíso.

López,M.P.,Nicolás,P.(2016).Razóndeserdelosnúmerosdecimales.Dins Librodeactas delIVCongresoInternacionaldeInvestigacióneInnovaciónenEducaciónInfantilyEducación Primaria (p. 156-159).Múrcia:UniversidaddeMúrcia.

Maar,A.(2014).PossibleUsesofCounterfactualThoughtExperimentsinHistory. Principia, 18(1),87-113.

Menzies,P.,Beebee,H.(2020).CounterfactualTheoriesofCausation.DinsE.N.Zalta(ed.), The StanfordEncyclopediaofPhilosophy.MetaphysicsResearchLab,StanfordUniversity.Disponibleenlíniaa:https://plato.stanford.edu/archives/sum2020/entries/causation-counterfactual/.

Morgan,S.L.,Winship,C.(2007). CounterfactualsandCausalInference.MethodsandPrinciples ofSocialResearch.Cambridge:CambridgeUniversityPress.

Nicolás,P.(2014a).Eliniciodelamedidademagnitudesenlaeducaciónprimaria:delas relacionesdecomparaciónalasrelacionesdeorden.DinsM.Sánchez,A.B.MireteiN.Orcajada (eds.), Investigacióneducativaenlasaulasdeprimaria (p.337-348).Múrcia:Universidadde Múrcia.

Nicolás,P.(2014b).Lacantidad:unamagnitudcardinaleneducaciónintantilyeducación primaria.DinsP.Miralles,M.B.AlfagemeiR.A.Rodríguez(eds.), Investigacióneinnovaciónen educacióninfantil (p. 199-206).Múrcia:UniversidaddeMúrcia.

Sierra,T.Á.(2006). Lomatemáticoeneldiseñoyanálisisdeorganizacionesdidácticas.Lossistemas denumeraciónylamedidademagnitudes.Tesidoctoral.Madrid:UniversidadComplutense deMadrid.

Suppes,P.(1969).Stimulus-ResponseTheoryofFiniteAutomata. JournalofMathematical Psychology,6(3),327-355.

Whitney,H.(1968).TheMathematicsofPhysicalQuantities:PartII:QuantityStructuresand DimensionalAnalysis. TheAmericanMathematicalMonthly,75(3), 227-256.Disponibleenlínia a:http://www.jstor.org/stable/2314953

seccions seccions

rcions

oriflèxia el racó de l’oriflèxia

Tóng xīn fāng shèng: infinites cartes d’amor

JaumeCollGuerrero MolinsdeRei(Barcelona)

XiˇaoxiánHuáng (黄晓娴)

Nanjing(provínciadeJiangsu)

1.ElplegatalaXina

Totelqueésexòticensatrau.Und’aquestsexotismeséslaculturaxinesa,que,situadaa l’altreextremdelsupercontinenteurasiàticiambunscincmilanysd’història,moltmésque qualsevolcivilitzacióoccidental,vaserdurantmoltsseglesunagrandesconegudaacausade lasevallunyaniaielseucomplexalfabetpictogràfic.Unapartd’aquestdesconeixementes produeixenlahistòriadelpaperplegat,unahistòriaqueencaraestàperescriure.AOccident ésbenconegutiacceptatqueelpapervaserinventatalaXinaalvoltantdel’any 100 dCper CaiLunenelperíodedeladinastiaHandel’Est(21 dC-221 dC).Totiaixí,recentments’ha trobataYumen,provínciadeGansu,unfragmentdepaperambcaràctersxinesosfetamb fibradelliquehaestatdatatal’any8aC,dinsdelperíodedeladinastiaHandel’Oest(202 aC-8dC).Aixídoncs,espotdirqueCaiLun(63dC-121 dC)vaferunamillorasignificativa enlatecnologiadel’elaboraciódelpaper,queésconsideradacomunadelesquatregrans creacionsdel’antigaXina.Undelsproblemesal’horad’escriureaquestahistòriaésquenoes conservengairesobresoriginalsperquèelpaperésunmaterialmoltefímer.Així,lesmostres depaperplegatitallatmésantiguesques’hantrobatfinsarasóndelsegle VI dC(dinastiaWei del’Oest).Juntamentambundocumentquecontenialadata541 dC,vanserdescobertesel 1959 alatombanúmero306,aljacimentarqueològicd’Astana,propdelaciutatdeTurpan, situadaal’antigarutadelaseda,alaregióautònomauygurdeXinjiang,alnordoestdela Xina.Sóndospapersdeformacircularplegatsiretallats.Elprimerpapertéretallatstriangles imotiusromboidalsrepetitsambvuitsimetriesaxialsicentrals.Delsegonpapernomésse’n conservauntrosenquèapareixentresmotiusanimalssimètrics,moltpossiblementcavalls. Lesbasesdelespotesdedosd’aquestsmotiusanimalsformenunanglede 135graus,d’ones potintuirquelapeçaoriginalteniaformaoctogonalambvuitsimetriesaxialsicentrals.Així doncs,lesfiguresrepresentadesenaquestsdospaperstenenungrupdesimetriesdiedral D2¨8 .Alatomba303esvantrobardosfullsdepapersemblantsambmotiusgeomètricsi ornamentalsamb 16simetriesaxialsicentrals,unfullambquatrefigureshumanesretallades perpendicularmentambunainscripciócal ligràficaiundocumentambdatadel551 dC.

Astana,tomba306.Astana,tomba303.

ActualmentaquestsanticspapersestanexposatsalMuseuProvincialdeXinjiang,alaciutat d’Urumqi.AvuidiaatotalaXinaencaraesconservaaquestatradiciódelpaperplegatitallat.

EnaquellaèpocaelpaperencaranohaviaarribataEuropa.L’elaboraciódelseusecretva passaralsàrabsdelaciutatdeSamarcandal’any751;lesfontsescritesensdiuenquedos xinesoscaptiusalabatalladeTulaselsvantransmetreaquestconeixement.Elsàrabsvan introduirelpaperaEuropapelsuddelapenínsulaIbèricaalsegle X iràpidamentesva expandirperl’arcmediterranifinsaarribaralarestad’EuropaiposteriormentaAmèrica. Segonselgeògrafal-Idrissí,l’any 1150 esproduïaunpaperdemoltbonaqualitataXàtiva. LesprimeresreferènciesdemolinspaperersalaciutatdeBarcelonasóndelsegle XV.Uns seglesméstardesconstrueixenmoltsmolinspaperersal’interiordeCatalunya.Unadeles poblacionsonesfabricavaméspapereraCapellades(Anoia),quealsegle XVIII teniadisset molinspaperers;elmésimportanteraelmolídelavila,actualMuseuMolíPaperer,quedata del’any 1700.

Unsobjectesmoltsorprenentsfetsambpapersónels zhenxianbao,quepodríemtraduir percaixesdecosturera.Lesméscomunessónestructuresformadesperunaprogressió geomètricadecaixesquadradesirectangularsdediferentsmidesdisposadesensuccessius nivells;totiaixí,tambéhihaaltresformesmoltcreativesambcombinacionsirregulars. Enelsdiferentsnivellss’alternencaixesquadradesambcaixesrectangulars;lescaixesd’un nivellinferiorteneneldobled’àreaquelesdelnivellsuperior.Aquestsconjuntsdecaixes, normalmentforçapolicromadesambdiferentsmotius,s’utilitzavenperdesarpetitescoses comarafils,agullesoretallsderoba.Els zhenxianbao esfeienatotalaXina,peròtambés’han trobataaltrespaïsosasiàtics.AltempleReikan-jideKyotoesconservaunaluxosacapsade fustaambestrisperalacerimòniadel’encensquepertanyiaal’esposadelsh¯ogunIemoto Tokugawa.Aquestacapsa,queesvaferabansdel 1779,contédeu zhenxianbao d’unnivell. Encaraavuidiaaquesttipusdeplegats’utilitzaalJapóenalgunescerimòniesdel’encens. Tresmoderns zhenxianbao delsegle XX,possiblementdeprocedènciacoreana,unambtres nivellsdecaixesielsaltresdosambunúnicnivell,pertanyenalacol lecciódelMatsumoto FolkCraftMuseum.L’historiadoriinvestigadordelplegatJoanSallasvatrobaraFrançauna capsaqueconteniaun zhenxianbao decincnivellsiunacartaescritaenfrancèsixinèsdel 1866.Aquestinvestigadoréselpropietariiconservadordel’arxiuPaDoRe(Paper-folding DocumentationandResearch),quecontélacol¨lecciómésimportantde zhenxianbao.Fa unsanysaquestacol leccióestrobavaalaciutatalemanyadeWeimar,peròactualment

Zhen xian bao (1866).Recipientmodular(provínciadeShanxi).

ésaBadalona.Alamateixacol¨leccióhihaquatreanticsrecipientsmodulars.Algunsd’ells provenendelaprovínciadeShanxi,alnorddelaXina,estanfetsambcartesantiguesitenen probablementmésd’unsegled’antiguitat,peròésdifícildatar-losambprecisió.

AltresformesdepaperplegatalaXina,ambreferènciesliteràriesdesdelsegle XIV finsals nostresdies,sónels tóngx¯ınf¯angshèng.

2. Tóngx¯ınf¯angshèng

Sovintelsanglesosutilitzencomasinònimderombelaparaula diamant.Aquestaparaula tambédesignaundelsquatrepalsdeljocdelpòquerenlescartesdelabarallafrancesa. D’altrabanda,unquadratespotinterpretarcomunrombeenquèelsquatreanglestenen 90 graus. Tóngx¯ınf¯angshèng ésunaformageomètricaformadaperdosdiamantsodos quadratsparcialmentsolapatsentresi.Desdel’antiguitataquestpatróestrobamoltsovint enlavidadiàriaalaXina,perexempleenampollesdeporcellana,petitessafatesdejade pernetejarpinzellsd’escriure,ornamentsd’orperadones,caixesdelaca,nusos,patronsen finestresdefusta,etc.

Aquestconceptetambéespottrobarescritcom tóngx¯ınf¯angshèng’r 同 心 方 胜 儿, f¯ang shèng 方 胜 o f¯angshèng’r 方 胜 儿.Cadacaràcterxinèstéunsignificatprecís. Tóng 同 significa «elmateix»; x¯ın, 心 «cor»o«centre»,perquèelcorespotconsiderarcomelcentredelcos.Els caràcters tóngx¯ın 同心 juntsespodenentendrecom:ambuncor,concèntric,desigcomúo apreciaelsmateixosidealsisegueixelmateixcamí.Aquí,l’úsde 同心 ésunaexpressióambun significatdoble:notansolsdescriuelsdosquadratsodiamantssolapatsquecomparteixen

uncentregeomètric,sinóquetambésignificaqueduespersonescomparteixenunmateix cor(opinió,sentiment,emoció,etc.),ésadir,escomprenenl’unaal’altra.

F¯ang 方 significa«quadrat»,peròperalsqueno sónxinesosespotentendrecomuna famíliadeparal¨lelogramsenunsentitmésgeneral.Enl’idiomaxinès,quadratesdiu 正方 zhèngf¯ang,quadratestàndard;rectangleesdiu 长方 chángf¯ang,quadratllarg;elsdiamants (rombes)ialtresparal¨lelogramsesdiuen 斜方 xiéf¯ang,quadratinclinat.Així,elsquadratsiels diamantsespodenanomenar f¯ang engeneral. Shèng 胜 (勝)espotescriureambdoscaràcters diferentsambelmateixsignificat.Peralsxinesosmoderns, 胜 s’utilitzamajoritàriamentpera victòria,peròenaquestcontext 胜 significaunantictipusd’ornamentperadonesquesolien posar-sealscabells.Perexemple,unornamentfetenformadeflors’anomena 花 胜 hu¯a shèng,ornamentfloral;fetenformadefigurahumanas’anomena 人胜 rénshèng;fetd’ores diu 金胜 j¯ınshèng,ornamentdaurat;fetambunabonicateladesedaesdiu 彩 胜 cˇaishèng, ornamentdesedadecolors;l’ocellpuputambplomesdecolorsalcaps’anomena 戴 胜 dài shèng,queportaornaments,etc. 方 胜 f¯angshèng juntsignificaornamentquasiquadrat,amb laformaqueesdescriumésamunt. 同 心 方 胜 tóngx¯ınf¯angshèng juntsignificadosquadrats odiamantsquecomparteixenuncentregeomètric.Comqueelsdos quadratsodiamants representendosamants,tambésignificaunparelld’amantsquecomparteixenelmateixcor, ésadir,ques’estimen.

方 胜 ensindicalaformageomètricadel 同 心 方 胜,aixíque 同 心 方 胜 ésnoméselnom completde 方 胜;pertant 同 心 方 胜 espotescriurecom 方 胜 perabreujar. 儿 (兒) ér de vegadesapareixalfinalde 同 心 方 胜 odelasevaexpressióabreujada, 方 胜.Amésde shèng 胜 (勝), ér 儿 (兒)tétambéduesmaneresdiferentsd’escriure’sambelmateixsignificat. 勝,兒 sónlesversionstradicionalsiméscomplicadesques’utilitzavenenl’antiguitat,mentre queelscaràcters 胜, 儿 sónlesversionssimplificadesque s’utilitzenmésfreqüentmenten elsnostresdies. 儿 persimateixvoldirfillonen,peròenaquestcontextaquestcaràcter ésutilitzatalesregionsdelnorddelaXina,comalacapital,Pequín,onelsdialectestenen unamaneradeparlarambaccentròtic.Quan 儿 s’utilitzasimplementalfinald’unnomoun adjectiu,notéunsignificatespecial,simplementespronunciais’escriucom r.Pertant, 同 心 方 胜 儿 és tóngx¯ınf¯angshèngr i 方 胜 儿 és f¯angshèngr.Generalment,espotconsiderar simplementqueaquesthàbitdeparlarésdelnorddelaXina,ésadir, 同 心 方 胜 儿 obé 方 胜 儿 s’utilitzamésfreqüentmentalnordi 同心 方 胜 obé 方 胜 s’utilitzaalsud.

3.Cartesd’amoralaliteraturaxinesa

Laformageomètrica tóngx¯ınf¯angshèng 同心 方 胜 tambés’hautilitzatalllargdelsseglesen undissenytradicionalxinèsdepaperplegatperaunacartad’amoriencaraesplegaavuidia alaXinamoderna.Enelsdarrersanysdiferentsautorsxinesoshanescritsobreaquestantic model.L’any 2012 l’escriptora 洪颖 HongYingvapublicarunanticdiaripersonalambdata 10 dejuliolde 1994quetépertítol Plegarlacartalleugerament,enquèesrecullunacol¨lecció decartesescritesperlessevesamistatsambdiferentstipusdeplecs.Unad’aquestescartes télaformade tóngx¯ınf¯angshèng.Unanyméstard,l’escriptora 木 子 琴 缘 MuZiQinYuan vapublicarl’article Recordaaquellacartaplenadepols,enquèdescriuquelasevaamiga 梅 Meivatrobarunacartaescritacatorzeanysabansenformade tóngx¯ınf¯angshèng,lava desplegar,lavallegirivaaconseguirtornar-laaplegarambelsanticsplecs.Enaquestacarta apareixenelstrescaràcters 心连心 x¯ınliánx¯ın,quesignificaelcoresconnectaambelcor.

El 1981 ellingüista,educador,traductoripoetaxinès 王力 WangLi(1900-1986)vapublicar l’article Parlantd’escriureunacartaambelsjovescamarades eneldiari DailyChinaYouth,en quècriticavaelfenomenqueelsjovespleguessinlescartesamblaformade tóngx¯ınf¯ang shèng ambmassafreqüència,fosquinafoslasituació:«Alfinal,percert,moltagentdesprés d’escriureunacartalaplegaenformade fangsheng,crecquenoésrealmentnecessari. Fang sheng ésunornamentquadratquelesdonesportavenal’antiguitat,fetensedadecolorso altresmaterials,formatperdosrombes(quadratsinclinats)parcialmentsobreposats.Aquest erauncostumenlasocietatfeudal.Alprincipiesfeiaperpresentarl’amor.A ElRomançdela CambraOccidental esdiu:Enpocaestona,vaplegarelfullfloriten tóngx¯ınf¯angshèngr formant unbrocatambelsbellscaràctersescritsamà.Desprésd’obrirelsobreencaranecessitotemps perdesplegarel FangSheng,llavorspuccomençarallegirlacarta.Aixòésuninconvenient peralreceptor.Esperoqueelsvostreshomespuguincorregiraquesthàbit».

LainvestigadoradelahistòriadelplegatXiˇaoxiánHuánghatrobatreferènciesd’aquestmodel deplegatenmésdequarantaobresdiferentsdelaliteraturaxinesa,ienmésdeseixantasi tenimencomptelesdiferentsversionsdecadaobra;tambéhatrobatunestrentaversions onnos’esmentaelplegat tóngx¯ınf¯angshèng.Lamajoriad’aquestesobresnos’hantraduït acapllenguaoccidentalipossiblementcapd’ellesalcatalà.Moltsdocumentsanticsxinesos s’handigitalitzat,espodencercaraInternetianalitzarintroduintdiferentscombinacionsde lesparaulesclaudescritesenl’apartatanterior.

Comqueelnom 同 心 方 胜 ésuntipusdeformainonomésunmodeldecartadepaper, ésnecessariintroduiraltresparaulesclauper distingirsiquanapareixaquestacombinació decaràctersrealmentesrefereixaaquestmodeldepaperplegat.Persort, 同 心 方 胜 no ésunnomcomú,aixíquequanapareixelnom,hi afegimundeterminatverbounmaterial ipodemconfirmarqueaquestdocumentesmentavaaquestmodel.Elsmotsclauinclouen: verbsrelacionatsambelplegat,com zhé 折 doblegar, dié 叠 superposar-se, zhédié 折 叠 plegar;elsmaterialsques’utilitzenperplegar, zhˇ ı 纸 paper, xìn 信 carta, ji¯an 笺 paperde notes, xìnji¯an 信笺 paperdecarta, hu¯aji¯an 花笺 paperdenotesflorejat;elnomdelmodel 同 心 方 胜 tóngx¯ınf¯angshèng, 方 胜 f¯angshèng,idiferentscombinacionsd’aquestesparaules.

Entreaquestesquarantareferènciesliteràries,lamajoriasónhistòriesd’amor.Observemque hihaalgunesregularitats:apareixenalgunsverbsrelacionatsambeldesplegat,comara ch¯ai 拆 desplegar-se, zhˇan 展 estendre’s, dˇak¯ai 打 开 obert;elscontingutsdelmodelde paperplegatsónmissatgesopoemes,principalmentsobreamor,citacionsoalgunsecret;

CartesdeHongYing.

Tóng xīn fāng shèng deMei.

elmodeldepaperplegatsempreesdonadela personaAdemaneraindirectaalapersona B,generalmentelmissatges’enviaatravésd’unatercerapersona,C,perquèelmodeles bloquejamoltbéiaixòésunabonamaneradeguardarelsecret.Sinòlegsdelsegle XIX van traduiralgunesd’aquestesobresliteràries;aixòenspermetveurequineraelconeixement quetenienelsnoxinesosd’aquestmodelenaquelltemps.Unad’aquestesobresés IU-KIAO-LI („ 1644),traduïdaalfrancèspelsinòlegJean-PierreAbel-Rémusatambeltítol Lesdeux cousins el 1826.L’anysegüentesvanferadaptacionsd’aquestaobraal’anglèsial’alemany. Enaquestesversions, tóngx¯ınf¯angshèng esvatraduirper unplegatenquadrat.D’aquesta mateixaobraexisteixunasegonatraduccióalfrancèsdelsinòlegStanislasJuliendel 1864. Unasegonaobraés WangKeaouLwan,traduïdael 1839 al’anglèsperRobertThomia l’alemanyel 1846perAdolfRottger.

LesobresliteràriesmésantiguestrobadesperXiˇaoxiánHuángenquèesfareferènciaal modeldeplegat tóngx¯ınf¯angshèng sóntresobresdeteatredeladinastiaYuan(1271-1368), duesdelesqualssóndelgènere zaju iunaésdelgènere sanqu.Lamésfamosaésel Xi XiangJi o Històriadel’AlaOest,deldramaturgWangShifu.Aquestaobrahaestattraduïda adiversesllengüeseuropees(alemany,anglès,castellà,francès,italià,portuguès,rus);toti així,enmoltesd’aquestestraduccionsnoapareixlaformadelacarta f¯angshèng oapareix traduïdacom doscorsunits.

Ruyi's Royal Love in the Palace (capítol43).

Aprincipisdelsegle XIX elmonjobudistaTooyamaKat¯o(1795-1831)vaferunesanotacions enjaponèsaltextoriginalenxinèsdel XiXiangJi.Alcostatdel’expressióxinesa 方 胜 儿 fangshengr vaescriurelaparaulajaponesa worikata,quesignificaformadeplegar. Worikata i orikata erenlesparaulesquefaunsdos-centsanyss’utilitzavenalJapóabansdelaparaula origami perdesignarlesfiguresdepapiroflèxia.

Lamajoriadelavintenad’obresdeladinastiaMing(1368-1644)enquès’esmentaelplegat tóngx¯ınf¯angshèng sóndelesprovínciessituadesalacostaoriental:Shandong,Jiangsui Zhejiang.Enaquestperíodecaldestacarquatrehistòriesdel’escriptorFengMenglong,de Jiangsu(1574-1645);moltesdelessevesobressónrecopilacionsdenarracionsdedinasties anteriors.Molttraduïdaaaltresidiomesés l’obraeròticadelaprovínciadeShandong Florde

pruneraengerrodaurat,tambéconegudaambelnomd’Ellotusdaurat o JinPingMei,signada ambelpseudònimdeLanlingXiaoxiaoSheng,quevoldirl’eruditbromistadeLangling.La carta f¯angshèng tambéapareixenversionsposteriorsd’aquestamateixaobra,comaraenla TerceracontinuaciódelLotusDaurat,signadaambelpseudònimNeYinJuShi,quesignifica l’eremitaqueparlararament.Defet,unaquartapartdelesobresdelesdinastiesMingiQing estansignadesambpseudònimsialgunespermonjostaoistes.

RespectealadinastiaQing(1644-1911),tambétrobemmésd’unavintenad’obresons’esmentaelplegat tóngx¯ınf¯angshèng.Elstítolsd’aquestesobresielsnomsdelsseusautorsno sóngaireconegutsaOccident.Unad’aquestesobresésel RomançdelesdinastiesSuiiTang, del’escriptorChuRenhuo,delaprovínciadeJiangsu.Enaquestaobraundelspersonatgesés l’heroïnaMulan,moltconegudaaOccidentperlapel¨lículad’animaciódelafactoriaDisney. Unasegonaobramolttraduïdaésel Somnialacambravermella,deCaoXueqin.Enaquesta obranoapareixaquestplegat,peròsíqueapareixenduesdelessevesversionsescrites posteriorment:enl’obraanònima Somnideprimaveraenlacambravermella ien Continuació delsomnidelacambravermella,publicadael 1821.

Els tóngx¯ınf¯angshèng tambéapareixenenobresliteràriesdelsdarrersperíodesnodinàstics. EnelperíodedelaRepúblicaXinesa(1912-1949)l’escriptorCaiDongfanvarecopilarendiversosvolumshistòriesdelesdiferentsèpoquesdinàstiques.Els tóngx¯ınf¯angshèng apareixen enduesdelessevesobres: ElromançpopulardeladinastiaSong i Elromançpopulardeles duesdinastiesJin.

Finalment,enl’actualperíodecorresponentalaRepúblicaPopulardelaXina(desde 1949), aquestplegats’esmentaendiferentsobres.Apareixenelllibre Elcérvolielcalderó,deJin Yong,pseudònimdeLouisCha,escriptor,historiadoriperiodistadelaprovínciadeZhejiang ambnacionalitatbritànica.Aquestaobraesvapublicarenentreguesperiòdiquesentre 1969 i 1972 enundiarideHongKong.Tambéapareixenelllibre EljoveMarshal,del’escriptora deXangaienllenguaanglesaEileenChang.El 2012 lajoveescriptoraWuXuelanvapublicar sotaelpseudònimLiuLianZil’obra ElsamorsreialsdeRuyienelpalau.D’aquestllibrese’nva ferl’any 2018unasèrieperalatelevisióxinesa.Enelcapítol43d’aquestasèrieespotveure comesdesplegaunacartaambplegat tóngx¯ınf¯angshèng;eneldarrerdesplegamentlacarta esdesplegaperlameitat,laqualcosaésunavariantd’unprimerpasquenoconsideremen elsdiagramesdelasecció5.

EneldiagramadeXiˇaoxiánHuángesrelacionenlesdiferentsobresliteràriesxineseson apareixlacartaplegada tóngx¯ınf¯angshèng desdelsegle XIV finsalsegle XXI.Enlesversions anteriorsd’aquestesobresdelesdinastiesTang(618-907)iSong(960-1279)nos’hatrobatcap obraenquèapareguiaquestplegat.Enaquestdiagramas’utilitzenlesnotacionssegüents: 1 peral’obra XiXiangJi deWangShifu(„ 1300);6peraJinPingMei(„ 1600);4h,7a,8ei 9 per alesobresdeFengMenglong(„ 1600); 11aperl’obraonapareixl’heroïnaMulan(„ 1650); 7, 25, 26perlesversionsdel SomnidelaCambraVermella („ 1800); 1β Tperal XiXiangJi amb l’anotaciójaponesa worikata („ 1830); 13αA, 13β A, 13γA, 13δ Jperalesversionsfrancesa, anglesaialemanyade Lesdeuxcousins („ 1830);8αT,8β Bperalestraduccionsal’anglès il’alemanydel’obra WangKeauLwan („ 1840);40,41 peralsromançospopularsdeCai Dongfan(„ 1920);42TYMperal’obra EljoveMarshal („ 1960);43pera Elcérvolielcalderó („ 1970).

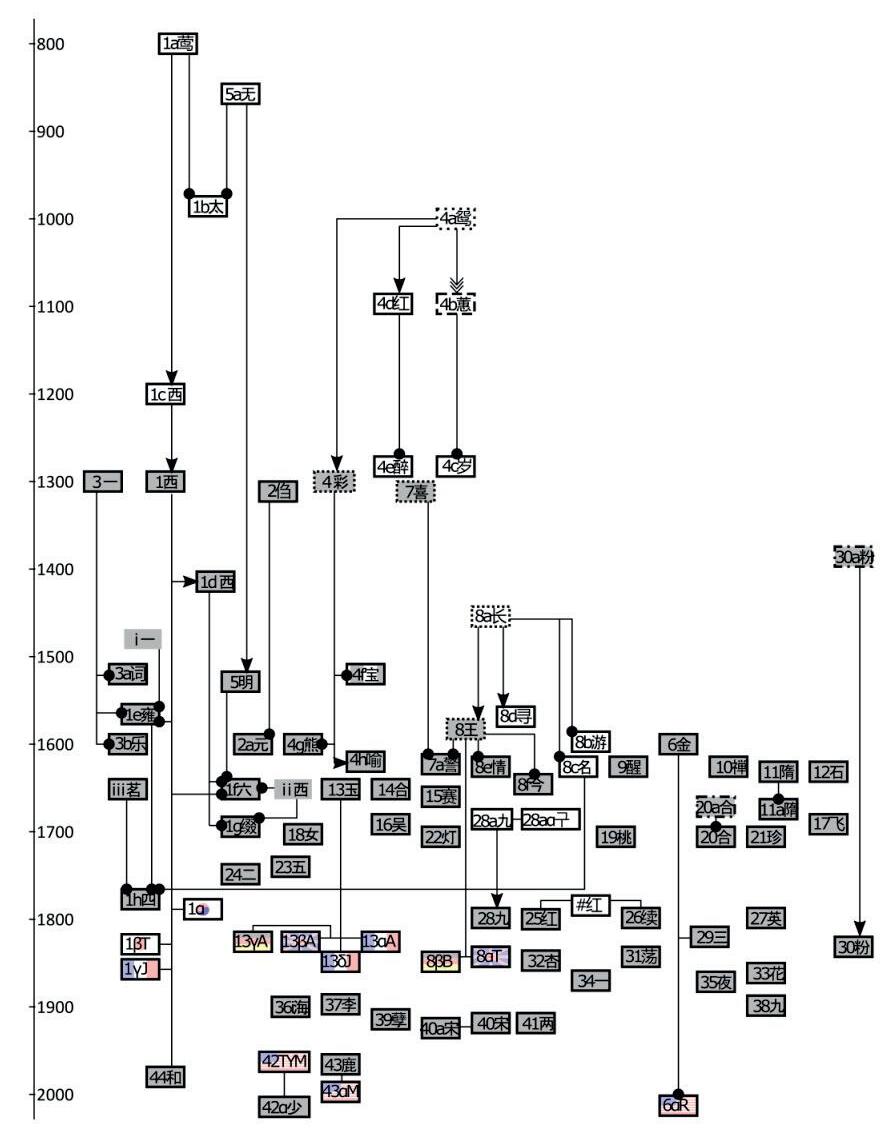
4.Formatsdepaper

Avuidiaelformatdepapermésutilitzatés elDINA4.EnelsistemaDINA,acrònimde DeutschesInstitutfürNormung,esproposaunacol¨lecciódeformatsdepaperrectangulars DINAn.Cadatipusdeformats’obtédel’anteriordividintelpaperperlameitat,detalmanera quel’alçadailabasedelnouformat phn ,bn q coincideixenrespectivamentamblabaseila meitatdel’alçadadelformatanterior. hn “ bn 1 ,bn “ hn 1 {2, @n ě 1 (1)

DiagramadeXiˇaoxiánHuáng.

PerdefinirrigorosamentelsformatsDINAn calimposarduescondicions.Laprimeracondició ésquel’àrea A0 delformatinicialDINA0 ésd’unmetrequadrat,ipertant,l’àrea An delformat DINAn ésunasuccessiódevalorsdecreixentsdemesura 1{2n metresquadrats.

Lasegonacondicióésquecadaformatéssemblantalsegüenti,pertant,larelacióentre l’alçadailabaseésconstantencadaformat.

D’aquestesigualtatsdeduïmqueaquestaconstantés ?2 iaplicantelteoremadePitàgores veiemqueladiagonald’aquestsrectanglesval ?3bn .

De(2)i(3)obtenimelstermesgeneralsdelsvalorsenmetresdelesbasesilesalçades d’aquestsrectangles.

d’ondeduïmquelesmesuresdelformatDINA0 sónaproximadament841 mm ˆ 1189 mmi lesdelsméshabituals 210 mm ˆ 297mmperalDINA4i 297mm ˆ 420 mmperalDINA3. Observemqueelsvalorsexactespertanyenalcos Qp 4 ?2q.

Unasegonamaneradeferaquestcàlculésescriurematricialmentlarecurrència(1).

Elpolinomicaracterísticdelamatriuval x 2 1{2,ambvalorspropis λ “˘1{?2 ivectorspropis #» v 1 “p?2,1q i #» v 2 “p´?2,1q,respectivament.Fentuncanvidebaseespotdiagonalitzar lamatriu

iobtenirlesdimensionsdelsformatsDINAn enfunciódelesdimensionsdelformatDINA0

Anàlogament,elsistemaDINBesdefineiximposantlacondicióqueelformatinicialDINB0 tinguiàrea ?2 i,pertant,dimensionsaproximadesde 1000 mm ˆ 1414mm.Peraquest sistemaelsformatsDINBn tenendimensionsexactesalcos Qp?2q.

UntercertipusdeformatmenysconegutéselsistemaDINC,enquèlesdimensionsdels formatsDINCn esdefineixencomlamitjanageomètricadelesdimensionsdelsformatsdels sistemesanteriorsDINAn iDINBn.

,hn

PeraquestsistemalesdimensionsaproximadesdelformatDINC0 són 917mm ˆ 1297mmi lesdimensionsexactesdelsformatsDINCn sónelementsdelcos Qp 8 ?2q

5.Papiroflèxiade tóngx¯ınf¯angshèng generalitzats

PrenemunfullDINA4.Prèviament(pas 0)pleguemidespleguemenvallperlesbisectrius delsdosanglessuperiorsiacontinuaciópleguemidespleguemenmuntanyaperlesdues bisectriusdelsdosanglesinferiors.Enelspassos 1 a4pleguemenvallperlesbisectrius indicades.

Pas0Pas1Pas2Pas3 Q1 Q2 Q3

Pas4Pas5FigurafinalTotselsplecs

Finalment,enelpas5plegaremenvallelsdostrianglessuperiorsienmuntanyaelsdos inferiorsiamagaremelsquatrevèrtexsperobtenirlacarta-sobre tóngx¯ınf¯angshèng.La figurafinalésunoctàgoncòncauformatperlauniódedosdiamantsamblamateixaàrea(Q1

i Q2 )queintersequenenuntercerquadratméspetit, Q3 .Sidespleguemlafiguraiobservem totselsplecs,deduïmquelesdiagonalsdelsdiamants Q1 i Q2 mesurenlameitatdelabase delfulli,pertant,ladiagonaldelquadratintersecció Q3 mesuraladiferènciaentrel’alçadai labasedelfullinicial.

Elprocésanteriorespotgeneralitzarperobteniraltresformesde f¯angshèng canviantla proporcióentrel’alçadailabasedelfullinicial.Sienllocd’unfullDINA4femtotselsplecsen unfullqualsevold’alçada h ibase b,prenent h ě b,aleshoresleslíniesrectesperonesfan elsplecstallenenunnombrevariabledepuntsquedepèndelaproporció r “ h{b.

13punts 26punts18punts22punts18punts20punts 6plecs ÐÝ 8plecs ÝÑ

Comhemvistenl’apartatanterior,ladiagonaldelsdiamantsnodepèndel’alçadadelfull

Eldarrervalorésmínimsil’alçadacoincideixamblabase;enaquestcas,elfullinicialésun quadrat r “ 1 ilafiguranoespottancar.Iésmàximsiladiagonaldelquadratintersecció coincideixambladiagonaldelsdiamantsgrans, h b “ b{2;ésadir,pera r “ 3{2.Pervalors delaproporció r superiorsa 1,5lafiguratampoctanca.Aixídoncs,els f¯angshèng espoden realitzarpelsinfinitsvalorsdel’intervalsemiobert

r Pp1,1.5s

Toteslesrectesperonesfanelsplecstenenpendent m “˘1 ilessevesequacionsfixant unseixoscartesiansamborigenalcentredelfullrectangularsón y “˘x ˘ h b 2 ,y “˘x ˘ h 2

Juntamentamblesequacionsdelesrectesquelimitenelscostatsdelfull y “˘h{2,x “˘b{2 espodendeterminarlescoordenadesdetotselspuntsd’intersecció.

Enlesfiguressegüentsdelpas5observemqueelssegmentsverticalss’allunyendelcentre quandecreixelvalorde r “ h{b

D’aquestamaneraespodendiferenciarsissituacionsdiferents.Pera r “ 3{2 lafigurafinalés unquadratformatperdosdiamantsquesesobreposen.Al’interval4{3 ď r ă 3{2 s’obtéun octàgoncòncau;quandisminueixelvalordelaproporcióenaquestinterval,elsdiamantsse separenfinsaassolirunaseparaciómàximapera r “ 4{3.Al’interval5{4 ă r ă 4{3lafigura finalésundecàgoncòncauformatpelsdosdiamantsidostriangleslateralsipera r “ 5{4, unhexàgonconvex.Finalment,al’intervalobert 1 ă r ă 5{4tambés’obtéunhexàgon,però ambpentàgonsenelslaterals.

DelamateixamaneraqueelsformatsDIN,elsanticspapersxinesosons’escrivienlescartes d’amorambplegat tóngx¯ınf¯angshèng hauriendetenirunaproporció4{3 ď r ď 3{2.

6.Equacionsd’unplec

Senseperdregeneralitatconsideraremque,enllocdeferplecsenunfullfinit,femelsplecs enunplainfinit.Enferunplecenunplaperunarecta,cadapunt P d’unsemiplàsesobreposa sobreelseupuntsimètric P1 respecteaaquestarecta L

Elpuntmitjàd’aquestsdospuntspertanyalarectaielsegmentqueelsuneix PP1 és perpendicularalarecta:

on #» v “ k pA,Bq ésunvectorperpendicularalarecta L.D’aquestamaneraobtenimles coordenadesdelpunt P1 “px 1 ,y 1 q enfunciódelescoordenadesdelpunt P “px0 ,y0 q iels coeficientsdel’equaciógeneraldelarecta L : Ax ` By ` C “ 0:

Aquestesequacionsensperm etencalcularlaposiciódecadapuntquanesfanelsplecs successius.EspodenprogramarenunmanipuladoralgebraiccomMathematicaoMaple pertrobarlescoordenadesexactesoaproximacionsnumèriquesimplementant-lesenC, PythonofinsitotenunfulldecàlculcomExceloCalc.Comqueestreballaambun fulldedimensionsfinites,lesequacionsespodenafinarambexpressionsméscomplexes afegintdominisiparàmetrespercontrolarlescapes.Deixemcomaexerciciperallectorles afirmacionssegüents:

1.Àreadelsdiamants: b2 {8

2.Àreadelquadratd’intersecció:

2 {2

3.Distànciaentreelscentresdelsdiamants:

4.Àreadel tóngx¯ınf¯angshèng:

5.Perímetredel tóngx¯ınf¯angshèng: ppb,hq“

6.Lesfuncionsdefinidesatrossosdeduesvariables Apb,hq i ppb,hq sóncontínuesenel seudominidedefinició, D “tpb,hqP R2 | b ą 0,h ą 0,b ă h ď 1 5bu

Referències

[1]Corrigan,G.,Smith,R.(2012). ALittleKnownChineseFolkArt:ZhenXianBao. [2]GayosoCarreira,G.(1994). HistoriadelpapelenEspaña,DiputaciónProvincialdeLugo.

[3]Huáng,X.(2018). Tóngx¯ınf¯angshèng,BritishOrigamiSocietyConvention. [4]Huáng,X.(2019). Chineseloveletter,MouvementFrançaisdesPlieursdePapier/Colmar.

[5]LanlingXiaoxiaoSheng(2010). Eleruditodelascarcajadas,EditorialAtalanta.

[6]Menglong,F.(2002). Sanyan:unatria,PublicacionsUAB.

[7]PlaiCarrera,J.(2009). LiuHui.Nuevecapítulosdelamatemáticachina,Nivola.

[8]Shifu,W.(2008). Historiadelalaoeste(Tresdramaschinos) ,Gredos.

[9]Shifu,W.(2008). Elpabellóndelalaoeste,EditorialPonentMon.

[10]Soong,M.(2004). Papiroflexiachinaparaprincipiantes,JoseJ.deOlañeta.

[11]Xueqin,C.(2017). Sueñoenelpabellónrojo,GalaxiaGutenberg.

Agraïments: aenJoanSallaspercedir-noslesfotografiesdel’arxiuPaDoReiorganitzarles jornadesdelplegatFALTIKaFriburgdeBrisgòviaiAPLECaBadalona,onesvaexposargran partdelcontingutd’aquestarticle,iaen JosepRamisperlescorreccionsdecatalà.

Els autors d'aquest article al Matsumoto Folk Craft Museum.

JordiDeulofeu

DepartamentdeDidàcticadelesMatemàtiques ilesCiències

UniversitatAutònomadeBarcelona jordi.deulofeu@uab.cat

Escricaquestarticledurantl’estiudel 2020,aquestanytanestranyacausadelaCOVID19 i totelqueestàcomportantaquestapandèmia.Tanmateix,eltempsdeconfinamenthaestat propici,peratotselsquehemtingutlasortdegaudirdesalut,peridear,descobrir,plantejar iresoldreproblemes.Peraixòaquestarticleésunpetitreculld’algunsdelsproblemesque heconegutitreballatdurantelsdarrersmesos.Almateixtemps,constitueixelmeupetit homenatgeatotselsquedurantaqueststemps difícilsenshandeixat,desdelgranJohn Conwayfinsal’amicPepBujosa.

§ Problema1.Posantnombresalesanellesolímpiques

Observeulafiguraamblescincanellesolímpiquesentrellaçades:totesellesdeterminen nouregionstancades.Estractadeposarencadascunad’ellesunnombredel’1 al 9 (sense repetir-necap)demaneraquelasumadelsnombresquehihadinsdecadacerclesiguila mateixaperatotselscercles.

Abansdecomençaraprovarambdiferentsnombres,penseucomespotsaberquinaserà lasumaencadacercle.Aviattrobareuquenoméshihacincpossibilitats(penseuquehiha quatrenombresquepertanyenadoscerclesielsaltrescinc,anomésun).Tingueuencompte que,quantingueulescincsumespossibles,noperatoteshihaunasolució,peròsíquen’hi haperamésd’una.

§ Problema2.Elcalendariielsnombresprimers

El 23demarç(23-3),quanfeiatansolsdeudiesquehavíemcomençatelconfinament,vaig constatarqueeraunadatabenrelacionadaambelsnombresprimers.Nonomesperquè tantel3comel 23sónprimers,sinóperquèestractadeldia83del’anyienfalten 283per acabar-lo(compte,somenunanydetraspàs),itantel83comel 283sónprimers.Hideu haveraltresdiesenrelacióambelsqualstantladata(diaimes)comelsdiestranscorregutsi elsquefaltenperacabarl’anysiguintotsprimers?

Ràpidamentdescobrireuqueenunany«normal»aixònopotpassar,jaquesil’any«normal» té365dies,llavorsundelsdosnombres,eldelsdiestranscorregutsoeldelsdiesquefalten, hadeserparell(isiés 2,l’únicparellprimer,resultaque363nohoés).Pertant,sin’hiha d’altres,haurandecorrespondreaunanydetraspàscomel 2020.

Elsegüentproblemame’lvaproposarJoanGómez,professordelaUPC,col¨legadelmàster deprofessoratdesecundàriadematemàtiquesiamic.Emsemblauninteressantproblema degeometriaquetéunabonicasolucióutilitzantúnicamentlageometriasintètica,moltmés ràpidaielegantquelaques’obtéaplicantàlgebra.

§ Problema3.Divisiód’unquadratiàread’unquadrilàter

Observeulafigura,quehemobtingutdelamanerasegüent:prenemunpuntinteriorqualsevold’unquadratil’unimambelspuntsmitjansdelsquatrecostatsdelquadrat.Esformen quatrefiguresquesónquadrilàteres.Siconeixeml’àreadetresd’elles,quinaseràl’àreadela quarta?

Nomésusdiréquenocalfergransitediososcàlculsalgebraics,jaqueaplicantelementsde geometriaespotresoldreelproblemademaneraelegant.

Quanl’hagueuresolt,penseuenunapossiblegeneralització,ésadir,peraquinsaltres quadrilàters,amésdelquadrat,repetintelmateixprocésseràpossibletrobarl’àread’unade lesparts,conegudeslesaltrestres?

Iencaraunageneralitzaciómésgran:preneuunpolígonregulariuniuunpuntinterior qualsevolambelspuntsmitjansdelscostats.Obtindreuquatrequadrilàters.Quinarelació

additivapotestablir-seentrelesàreesdetotselsquadrilàters?Calqueelpolígonsiguiregular on’hihaprouambunaaltracondiciómenysforta?

Sinoushasortitelproblemautilitzantmètodesgeomètricsperalcasdelquadratinecessiteu unapista,usproposoqueresoleuaquestaltreproblema,unamicamésfàcilialmateixtemps útilperresoldreelnostre:enunquadratprenemunpuntinterioril’unimambelsquatre vèrtexs,demaneraqueesformenquatretriangles.Quèpodemdirdelasumadelesàreesde dostrianglesoposatspelvèrtex?AquestproblemaéselquePolyaanomenariaunestrepper resoldrel’altreiespotobteniremprantunadelesheurístiquesqueensproposavaelgran mestre:coneixesunproblemasimilarperòméssenzillqueetpuguiajudararesoldreelteu problema?

JaqueheparlatdePolyaitenintencompteque aquestasecciótécomaobjectiuprincipal proposarproblemes,empermetorecordar-vosunapetitallistad’heurístiquesquem’han estatútilsquanunproblemase’mresisteix.HeelaborataquestllistatambAbrahamdela Fuenteperalasessiósobreresoluciódeproblemes,dinsdelcursActivitatsRiquesiCompetènciesMatemàtiquesal’AuladeSecundària.Noméspresentounallista,sensecomentaris (fer-hoimplicariaunaltrearticle!),permostrarlariquesaivarietatdelesheurístiques:

‚ Visualitzarrelacions(ambdibuixos,i/oesquemes).

‚ Organitzarlesdades(ambtaules)i/oelaborardiagrames(arbre,altres).

‚ Triarunllenguatgeadequati/ounacodificació.

‚ Realitzarproves,experimentaramblesdadesilescondicions.

‚ Emprarassaigierror.

‚ Realitzaruntreballsistemàtic.

‚ Cercarpautesoregularitats.

‚ Estudiarcasosparticulars/particularització:simplificaciódedades.

‚ Generalitzar/estudiarunproblemamésgeneral.

‚ Dividirelproblemaenparts/subdivisiódelsobjectius.

‚ Procedirperanalogia/relacionarelproblemaambund’anàlegconegut.

‚ Introduirelementsauxiliars/graonsintermedis.

‚ Començarpelfinal/suposarelproblemaresolt.

‚ Emprarideesmatemàtiquesespecials,comlaparitat,lasimetria,elprincipidelcolomar...

Elsegüentproblemaéselmeupetithomenatgeenaquestaseccióalgranmatemàtici creadordejocsdeLiverpoolJohnHortonConway(1937-2020),queelpassat 11 d’abrilva moriraPrinceton,NewJersey,acausadelaCovid19.Elseuimmensllegatromandràdurant moltdetempsiensmostraràelgenid’aquestgrancreador.

Estractadetrobarlalleideformaciódeduessuccessions.Laprimeraésextretadelfantàstic llibre TheBookofNumbers,lalecturadelqualusrecomanomolt,mentrequelasegona,més senzilla,térelacióambunadelessuccessionsmésfamosesdelesmatemàtiques,elnomde laqualrecordaaunimportantmatemàticmedieval.

§ Problema4.Lasuccessió«audioactiva». Considereulasuccessiótalqueelsseusprimers termessón:

Estractadedescobrircomesformacadatermeapartirdel’anterior.Sivoleupensar-ho unaestona,noseguiullegint.Quanelresoleu ous«rendiu»(enaquestcas,estractad’una endevinalladifícil),podeullegirelcomentarisegüent,que,ambtotaseguretat,uspermetrà resoldre’lsinohohavíeufetencara.

L’endevinallaamaga,almeuparer,unanotabledificultatpelfetqueundígitpottenirdos significats:comaobjecteicomapropietatque expressalaquantitatd’objectes.Ambaquesta ideaitenintencomptequeelseunomés audioactiva,tracteude«llegir»cadascundels númerosperdescobrirlalleideformació.

Arausproposounaaltrasuccessió,pertalquetrobeueltermesegüentieltermegeneral. Esticsegurque,totiqueésigualdebonica,trobarlarecurrèncianoseràtandifícilcomenel casanterior.

Uspodeuferaltrespreguntesinteressantssobreaquestasuccessió,comaraquantesxifres técadaterme,obéquinaéslasumadelesxifresdecadaterme.Finalment,comqueés possiblequehagueutrobatunarecurrènciaquerequereixihaverfixatelsdosprimerstermes, usproposoquetrobeulalleideformacióquannomésconeixeuelprimerterme.

Acabarél’articled’avuiambunproblemadenombresunamicamésdifícilqueelsanteriors. Me’lvaproposarRamónVillanueva,alqual,al seutorn,l’hihaviaproposatJaumeParadís, totsdosprofessorsdematemàtiquesdelaUniversitatPompeuFabra,ielcertésqueemva tenirforçatempsentretingut.

§ Problema5.Diferènciadequadrats

Observeuqueelnúmero7espotescriurecomadiferènciadedosquadrats,jaque7 “ 16 9. Estractadetrobarquinssónelsnombresenterspositiusquepodenexpressar-secoma

diferènciadedosquadratsiprovarqueperatotsaquestshihaalmenys unasolució,mentre queperalarestanohihasoluciópossible.

Uncophagueutrobatquinssónaquestsnombres,tracteudedeterminardequantesmaneres diferentsundeterminatnombreespotexpressarcomadiferènciadequadrats.Perexemple, 7nomésadmetunadiferència(16 9,queésladonadaenl’exempleanterior)mentreque 9 espotexpressarcom 25 16itambécoma 9 0.

Aixòéstot.Desitjoque,quanllegiuaquestarticle,lescoseshaginmilloratmolt,especialment pelquefaalasanitat,peròtambéal’economiaialesproblemàtiqueseducativesderivades delapandèmia,queensfamoltafalta,i,en particular,quegaudiudemoltasalut.

Bibliografia

ConwayH.J.,Guy,R.(1996). TheBookofNumbers.NovaYork:Springer.

Deulofeu,J.(2019). Lamagiadelosnúmeros. Barcelona:Gedisa.

Deulofeu,J.(2020). Relojes,medidasycalendarios. Barcelona:Gedisa.

Normes per a la presentació de contribucions

1. La revista NouBiaix acceptaper alasevapublicació contribucionsoriginalsrelacionadesamb experiències didàctiques, activitats d’ensenyamen ti aprenentatge,escritsd’opinió,dedivulgaci ói d’investigació enel camp dela matemàtica ielseuensenyamentenqualsevol nivell educatiu

2. Les contribucionsrebudesseran avaluadesprèviamentper dosespecialistesreconeguts. La decisiópresa pelConsell deredacciósobrel’acceptació dela publicació serànotificadadirectamentals autors ambuna indicaci ódeladataaproximadadepublicaci ói el possiblerequeriment d’introduir modificacionseneltext.

3. Pera lapresentaci ódetreballsoriginals, elsautorstrametran al’adreçanoubiaix@gmail.com un arxiu, en Word oenLaTeX.Els gràfics, elsdiagrames iles figureshaurandeser originals(no fotocopiats). Els arxius gràficsespresentaran en format epso tif.

4. La contribució hauràd’incorpora reltítol,elnom de l’autoro autors,lasevaadreçapostalprofessional completai la sevaadreça electròn ica.S’adjuntaràunresum només llarg de 300 paraules en català ianglès. Al finaldel document s’inclouràobligatòriamen tlabibliografiaper ordrealfabètic de cognoms,d’acordamb la normativaAPA, com enelsexemplessegüents:

Articles

Albertí, M. (2002).Les matemàtiquesdesd’unaperspectivacultural:Etnomatemàtiques Biaix, 20,6-25.

Llibres

Godino,J., Font,V.(2003) Razonamiento algebraicoparamaestros.Granada :Universidad de Granada. Capítols dellibres

Edo,M.,Revelles, S. (2004).Situacionesmatemática spotencialmentesignificativas. Dins M. Antóni B. Moll (ed.), Educación Infantil.Orientacionesy Recursos (0-6 años) (p.410/103-410/179).Barcelona:Praxis.

Actesdecongressos

Morales, M.,Font, V.,Planas, N. (2004).Estudiomicroetnográfico en tornoa un conocimiento matemático situado. Dins A.Franzé ialtres(ed.), ActasdelaI ReuniónCientíficaInternacional sobreEtnografía y Educación (CD-ROM).València: Germanía,Polis Paideia.

Pàginesweb

Geogebra pera Infantil iPrimària. https://www.geogebra.org/m/tkdC27m f

5. Els contingutsde NouBiaix estansubjectes llevatque s’indiquiel contrarieneltext, en lesfotografies oenaltresil.lustracions— auna llicència de Reconeixement-No comercial-Sense obra derivada 3.0deCreativeCommons,eltext completdela qual es pot consultar ahttp://creativecommons.org/ licenses/by-nc-nd/3.0/es/deed.ca. Així,doncs,s’autoritza el públic en generala reproduir,distribuir i comunicarl’obra,sempreque es reconegui l’autoriai l’entita tquela publica, inose’nfaciunús comercial ni se’n difongui capobraderivada.

6. Elsarticlesespublicara nen llenguacatalana.Només es traduiranalcatalàles contribucions acceptadesd’autorsnoresidents alsPaïsosCatalans.

7. Elsautorsesresponsabilitzarandel complimen tdeles normes establertesper al’autoritzaciódela reproducciódematerialprocedent d’altres fontsbibliogràfiques

8. Elsarticlestindran unaextensiómàximade 8000 paraules,inclosesles notesa peudepàgina,però s’acceptenarticles méscurts,d’entre 2000 i 4000 paraules

9. Femnotar queenaquesta publicació s’utilitza preferentmen telpuntper separardecimals, en lloc dela comarecomanadaper l’IEC, pertal defacilitarla comprensi ódeles expressionsmatemàtiques.