Nou Biaix, 37

Revista de la FEEMCAT i de la SCM

Desembre 2015

biaix

número 37

sumari

Consell de Redacció:

Manel Sol / Josep Lluís Solé (coords.)

Marianna Bosch

Joan Carles Ferrer

Joan Miralles

Josep Pla

Romà Pujol

Manuel Udina

Juanjo Cárdenas (responsable pàgina web)

© dels autors dels ar ticles

Coediten:

Federació dEntitats per a ’’lEnsenyament de les Matemàtiques (FEEMC AT ) Campus de Montilivi, edifici P-IV 17071 Girona feemcat.org

Societat Catalana de Matemàtiques (SCM) filial de l’Institut d’Estudis Catalans Carme, 47 08001 Barcelona scm.iec.cat noubiaix@gmail.com sites.google.com/site/noubiaix

al Periodicitat: semestr Nombre d‘exemplars: 1.700

Fotografia de la coberta: Perfec ta geometria ennuvolada

Erola Pons Wendenburg IES Santa Coloma de Farners 16 anys. 1r de Batxillerat

ISSN: 2014-2021

Dipòsit legal: B-22.314-2012

Impressió: Gráficas Rey

Publicacions i Edicions de la Universitat de Barcelona

Adolf Florensa, s/n 08028 Barcelona

Tel.: 934 035 430

Fax: 934 035 531 comercial.edicions@ub.edu www.publicacions.ub.edu

Editorial

Congrés Català d’Educació Matemàtic 3 5

8 29 41 51 65

articles

El problema de Dido, abelles, billars i principis de màxims i mínims

José G. Llorente

La descober ta matemàtica en l’entorn. La reflexió i el raonament dins el treball d’investigació, base de l’aprenentatge matemàtic

Carme Alemany Miralpeix

Bones ac tivitats per a la transició entre primària i secundària

David Barba Uriach i Cecilia Calvo Pesce

La resolució de problemes complexos per parelles d’alumnes amb TDHA i sense TDHA a la secundària

Yolanda Colom i Núria Rosich

Estrelles a la Sagrada Família de Gaudí: un contex t nou per a estudiar poliedres

María de los Desamparados López de Briñas Ferragut

seccions

90 97 104 87 Per pensar d’un minut a una hora

Jordi Deulofeu

Construint matemàtiques

Anton Aubanell

El racó del MMAC A Enric Brasó

El racó del Cesire- Creamat

La FEEMCAT organitza perals propers 11, 12 i13dejuliolde 2016el2nCongrés d’Educació MatemàticadeCatalunya.És unacontinuació del quees vacelebrar el 2000 aMataró ambmotiudel’AnyInternacional delaMatemàtica. Volserunespai peracompartiridescobrirrecursosper alamilloradelanostrafeinaal’auladematemàtiques a totsels nivellseducatius. Ales primeres planesdela revista trobareuuna presentaciód’aquestesdeveniment.Desdel NouBiaix volem animartots elsmestres iels professors aparticipar-hi.

Enaquest número us presentem unarticledeJoséG. Llorenteenelqual l’autorensproposa unatractiu recorregutper preguntesclàssiques relacionades ambqüestionsdemàxims i mínims,comelproblema d’Heród’Alexandria,lallegenda del aprincesaDidoila fundació de Cartago, que ensportaals problemesisoperimètrics,alsegontreball d’Hèrcules i,finalment, alajustificaciódelasagacitatde lesabelles.Aquestarticleésunaversióimpresa delque trobareu alarevistaelectrònica MaterialsMatemàtics.Elseditorsdel NouBiaix usrecomanen, sense capvacil ·lació, visitaramb freqüèncialasevaweb, quereuneixunseguitd’articles matemàtics,engeneral magníficsi moltinteressants,decairedivulgatiu idediversos nivells

Al’articlesegüent, CarmeAlemany ensfaalgunes propostes perexperimentar iinvestigar ambmaterialsmanipulables,ambl’objectiu que els alumnes deprimària redescobreixin i construeixinles matemàtiques.

DavidBarbaiCecilia Calvoexpliquen unapropostaoriginalper a millorarels processos matemàtics enlatransiciódeprimàriaasecundària.Enspresententres activitats centrades en la resoluciódeproblemes, enlacerca de patronsi en promoure eltreball sistemàtic, més que en unscontingutsespecífics.Estandirigides aalumnes definaldeprimària,així comals dels primerscursos d’ESO.Elsautorsposen enrelleu elpaperactiu iflexibledel mestrei el professor peral bondesenvolupament deles tasques.

L’atenciódels alumnesamb dèficitd’atencióihiperactivitat(TDHA) asecundàrianoésfàcil. Yolanda ColomiNúria Rosich enspresenten partdels resultats quehan obtingutenuna recerca sobre la resoluciódeproblemes complexosproposatsaaquest tipus d’alumnat.Enel seutreball podreutrob ar-hisuggeriments i idees pera la vostraactivitat.

LaprofessoraAmpar Lópezenspresentapart detreball derecercaquehaportat aterme, durant mésdedosanysde treballintens,alvoltant delaSagrada FamíliadeBarcelona.

L’interèsdelseu treballésdoble:d’unabanda, ensdescobreix algunsdelsaspectes més desconeguts del’obradeGaudí, coml’existènciadels poliedresestrellats. D’unaaltrabanda, fa unainterpretació benraonadadeperquè creu quehovafera la SagradaFamília.Així ens acosta acomprendremillor lesideesquel’arquitecteens volia transmetrea travésdelaseva

obra iposaenevidència,unavegada més, l’abast delgenideGaudí.Finalment,enssuggereix algunes activitatsper al’auladematemàtiques.

JordiDeulofeuensproposa,enlasevasecció,uns quantsproblemesinteressantsamb algunessorpreses. Passeu-vos-hobéambells.

Elsresultatsdelesprovesdecompetènciesbàsiquesa quartd’ESO,publicatsl’abrilde 2015, posendemanifestunassoliment molt baixenel blocEspai,Formai Mesura. Talcomes desprèn delesdades,noes tracta d’unfet puntual,sinód’una tendènciadelsdarrersanys. ElConsell Superior d’Avaluació delSistema Educatiu hapublicat el document«Orientacions pràctiques per alamillora delageometria».L’An tonAubanell ha estatun col·laborador rellevant enl’elaboraciódel documenti ensl’explica enlasevasecciófixa «Construint Matemàtiques». Hipodreutrobarreflexionsipropostes interessantsper portar alesaules.

ElCesire-Creamatensnarrauna petitahistòriaalvoltantd’unproblema que es vacomençar en unseminariambl’A. Arcavi l’any 2008, però queva continuar molt mésenllà. A més de l’interèsque téintrínsecament el problema itotesles seves variacions,l’articleenstransmet la passióquegenera la resoluciód’unproblema enelsmatemàtics.

Per a acabar, enl’habitual «Racódel Museu», EnricBrasóensmostraquatremòdulsdelMuseu que podenajudara treballari entendreconceptes nointuïtius,iavoltes paradoxals, relacionatsamblateoria de la probabilitat il’estadística.

Esperemquegaudiud’aquestnúmerodel No uBiaix i, comsempre,els editors usanimemque ensenvieu articles exposantles vostresexperiències,recerques iactivitats,perquèpuguin ser conegudes icompartides perlacomunitat, apesardetotesles dificultats,benentusiasta, delsensenyants de matemàtiques.

Congrés Catalàd’EducacióMatemàtica

L’educaciómatemàtica juga un paper clauenqualsevol societat moderna. Des defamolts anys,mestres iprofessors delnostre paístreballen permillorarlaqualitatdelseu ensenyament. D’aquest treball ensóntestimonil’esforç queesfacadadia dins de les aulesper promoureunaprenentatge més significatiu ifuncional,elpotent associacionisme que hihaentre elsensenyants, l’abundantquantitat de concursos,tallers, fires... adreçats al’alumnatil’elevatnombre dejornadesi trobades de mestres i professorsper compartir idifondreexperiències.

Recollint aquestesforç, sembla unbon momentper impulsarunespaidetrobadade lacomunitat d’ensenyants de matemàtiques. Peraquesta raó, laFederació d’Entitatsper a l’Ensenyament de les Matemàtiquesa Catalunya(FEEMCAT) esproposal’organització delCongrés Catalàd’Educació Matemàtica (c2 em).

Antecedents

Els mestres ielsprofessors de matemàtiques de Catalunya,dinselmarc de les sevesrespectives associacions,hananatorganitzanttrobadesd’educaciómatemàtica:

• Jornades anuals de lesdiversesassociacions:APMCM,ADEMGI,APaMMs,ABEAM iLleimat.

• JornadaconjuntadelaFEEMCAT,laSocietatCatalanadeMatemàtiques,laSocietatBalearde MatemàtiquesXeix ilaSocietatd’Educació Matemàtica delaComunitat Valenciana Al-Khwarizmi.

• Jornadesespecífiques organitzadesper les universitatscatalanes.

• Jornadadel’AssociacióCatalana de GeoGebra iactivitatsdel MMACA adreçadesalprofessorat.

• Accionsimpulsadesdes delCESIRECREAMAT (Departament d’Ensenyament).

• Trobades de grupsdetreball.

Abandad’aquestes activitatsde caireanual,s’han celebratdurantelsdarrers anystres granscongressos:

• Congrésd’EducacióMatemàtica, cem(Mataró 2000).

• Jornadas parael aprendizaje yenseñanzadelasMatemáticas,JAEM(Girona 2009).

• Jornades de Didàctica deles Matemàtiques alescomarquesmeridionals (Tarragona 2012).

Potserfruitdetotes aquestes accionsenstrobemen un moment de canvienl’ensenyament de la nostramatèria enelqualcaldriareflexionarsobreel què,elcomi elperquè ensenyemmatemàtiques. Peraquesta raós’hapensata organitzar elCongrésCatalàd’EducacióMatemàtica.

ElCongrés Catalàd’EducacióMatemàtica

DesdelaFEEMCAT,ambelsuportd’altres entitatsi institucions, s’està organitzantelCongrés Català d’Educació Matemàtica (c2 em) que,abastanttotselsnivellseducatius,secelebraràeljuliolde 2016 amblavoluntatque espuguianarrepetint cadaquatre anys.

Els objectiusd’aquestcongrés,pendentsencara d’acabarde perfilar,són:

• Identificari impulsar línies de milloraenl’educaciómatemàtica

• Promourelaposada encomú d’experiències docents innovadores.

• Contribuir al’enriquiment de lapràcticaprofessionaldelsensenyants de matemàtiques.

• Arribara idees de consens que puguincontribuir amillorarlanostra educació matemàtica.

• Acostar lesmatemàtiques al’entornfamiliarialasocietat.

• Promourel’atenció als valorsenl’educaciómatemàtica

Enlalínia d’aquests objectius, d’unamanera provisional,hem adoptatcomalema delcongrés:

Unesmatemàtiquesobertes i per a tothom

Compartimper construir

Fins aquestmoment, s’handesenvolupat treballs d’organitzaciógeneralindispensables pertenir un punt de partidasòlid queenspermeti començara caminar.Així, s’ha establert queelcongréssecelebri els dies 11, 12 i13dejuliolde 2016a laFacultatdeMatemàtiques de laUniversitatdeBarcelona.Les conferènciesplenàries previstestindran llocalseuparanimf.

S’hainiciatlaformació dels grups queimpulsaranels diferents àmbits organitzatius(comitè científic, tresoreria,relacionsinstitucionals, mitjans de comunicació, cerca depatrocinis, activitatssatèl·lit, voluntariat...).Tenimperdavantuncamíenelqual ens agradariacomptaramblacol laboració detotes les institucions i entitats queesmouenenelcamp de l’educaciómatemàtica acasa nostra. La tasca és tanàmplia com engrescadora:

• Identificargransblocstemàtics entornals qualscentrar lareflexió.

• Cercar maneres àgils ieficients de comunicar, debatre,contrastaricompartir opinions.

• Ferpossibleque,tantenlainauguraciócomenlacloendadelcongrés,espugui comptar ambaportacionspotents i innovadores depersones deprestigi internacional enelcamp de l’ensenyament delesmatemàtiques.

• Dissenyarun programa d’actes que resulti atractiu per amestres iprofessors ieficaçper afer possible l’intercanvid’idees.

• Cercarelmajorressò de l’esdevenimentenelsmitjans i, mitjançantactivitatsparal·leles,contribuir adonar presència sociala les matemàtiques.

Per fer això,i moltmés,caldranmitjans ivoluntats, complicitatsi entusiasme, temps ifeina...Aquests materialsque fanpossible construirprojectes iobrir camins demillora.

És unainiciativaoberta a totes lesidees ilesmaneres defer ideser de mestres i professors quevol projectar-secapalfutur enimpulsosd’innovació i recerca educativa.

Barcelona, 20 de maig de 2015 Comitè organitzadordel c2 em

articles articles

ElproblemadeDido, abelles,billarsiprincipis demàximsimínims1

JoséG.Llorente

Departament deMatemàtiques

Universitat Autònoma deBarcelona

Resum Abstract

Alavidaquotidianaesplanteja constantment el reptedetreure elmàxim profit possiblea partir d’unsrecursos donats. Nombrososexemplesmostren que laNatura tambésegueixunamenade principid’economia quel’empenya maximitzarel rendimentambels recursos disponibles.Matemàticament,elmarc adientperabordaraquestesqüestionssón elsanomenats problemes d’optimització o problemesdemàxims i mínims. Enaquest articlefaremun breu recorregut peralguns problemes famososdemàxims imínims quetenenencomúunmarcatsabor geomètric.

1.Introducció

Everydaylife oftenpresentsuswiththe challengeofgetting themostout of limited resources.There are manyexamples showingthatNaturealso followssomesort of economy principle,whereby itmaximizes theutility ofthe materialsathand. Mathematicallyspeaking,therightcontext forsuchquestionsaretheso-called optimization problems orproblems of maxima andminima.Thisarticleprovidesa briefoverviewofsomefamous problemsof maxima andminima thatsharea remarkable geometricalflavour.

Natura,tuetslamevadeessa,ialatevalleicenyeixoelsmeusserveis. (W. SHAKESPEARE, ElreiLear,acte I,escena II).

Per quèdeterminades formesgeomètriques apareixen reiteradamentalmón natural?En virtutdequins principislanatura triacertes configuracionsino d’altrestambépossibles? Aquesta mena depreguntesvan impulsar elnaixementde lesmatemàtiques familers d’anys.

1. Aquestarticle ésunaversióimpresadel que trobareua larevistaelectrònica MaterialsMatemàtics (Mat2 ) al’adreçahttp://mat.uab.cat/matmat.Elseditorsdel NouBiaix usrecomanen,sensecapvacil lació, visitarambfreqüèncialaweb indicada,quereuneixunseguitd’articlesmatemàtics,engeneralmagníficsimoltinteressants, de caire divulgatiui dediversos nivells

Unadeles funcionsbàsiques del coneixementmatemàticalllarg dela història ha estat la interpretacióila comprensió delmón natural. Laconvicció que la natura es regeix peruna menade principid’economia ha estat unapeçaclauenaquest procés, nonomésdes d’un puntdevistaestètic,sinótambéperquèestracta d’una idea quecombinal’eficiènciaila senzillesa.

Unsegmentrectilini éseltrajectemés curtentre dos puntsdel pla. Unarc de cerclemàxim éseltrajectemés curtentre dos puntsdelasuperfícied’unaesfera.Detotes les corbes tancadesde perímetrefix, la queenvolta mésàreaésla circumferència. Qüestions d’aquest estil elsanomenats problemesdemàxims i mínims ja van interessar elsmatemàtics grecs ides d’aleshoresnonomés han contribuïtd’una maneradecisivaaldesenvolupamentdeles matemàtiques,sinó tambédelafísica, les ciències delavida, l’economia il’art.Lanostravida diària plantejaconstantmentproblemes querequereixen maximitzar o minimitzar alguna quantitat,enelsentit detreureelmàxim profit d’unadeterminadasituació apartir d’uns mitjans donats.Per què la naturas’hauria decomportard’una maneradiferent?A partir del segle XVII iparal lelament aldesenvolupamentdel càlculdiferencial,els problemesde màxims imínims han proporcionateinesfonamentals perdonarsentital principi d’economia de mitjans de quèparlàvemabans i aprofundir en la comprensió del mónfísic.

Enaquestanotafaremunbreurecorregut,necessàriament parcial iincomplet,peralguns dels problemes demàxims i mínimsmés rellevantsdelahistòriai les sevesimplicacions en qüestionsdelmón natural.

2.El problema d’Heró d’Alexandria,lareflexiódela llum ielbillar

Undels problemes demínims més antics està relacionatamblageometriadela reflexiódela llumi s’atribueixalmatemàtic,enginyer iinventorHeród’Alexandria.Nosesap gairesobre lavidad’Heró; s’especulaquevaviure durant elprimersegle desprésdeCrist i queva escriurediversostractatsòptics,geomètricsi mecànics[9].Enund’ells, Catoptrica,vaestudiarles propietatsde reflexiódelallum i l’ús pràctic demiralls. La llei fonamentaldelareflexió de lallum diuque quan un raigdellum ésreflectitperunasuperfícieplana, l’angled’incidènciai dereflexiósón iguals iprobablementjaeraconegudaperEuclidesquatre-centsanys abans. L’observació fonamental d’Heró ésquelallei dereflexióespodia deduir d’unpri ncipi més general:lallum viatjadetal manera queel temps delrecorregut és mínim.

Acontinuació deduiremlallei dereflexió apartir delprincipidetemps mínimseguint l’argument d’Heró.Suposem(fig. 1)queunraigdellumquesurtdelpunt P es reflecteixen

unalínia L itornaa Q.Onhad’estarsituatelpuntdecontacte R pertalqueelcamí PRQ sigui òptim d’acordambelprincipidetemps mínim? Com quela velocitatdela llum nocanvia amblareflexió,tempsmínimequivaladistànciamínima.Pertant, R hadesertalquela suma de les distàncies PR + RQ sigui mínima.Podemplantejar elmateix problemamatemàtic adaptata diferentssituacions dela«vida real».Per exemple, suposemquesom alpunt P,casa nostra ésel punt Q ilarecta L representaunriu.Enaquestcontext,la preguntaés:quinésel camí òptimdetornada acasa sivolemfer abansuna parada alriu?Unaaltrainterpretació, méslúdica, téaveureambtrajectòriesen billars.Unabolasurtde P,xocaenlarecta L (una deles parets delataulade billar) enun punt R itornaa Q. Comquela bolaseguiràelcamí més curt,el problemaésidèntic aldel raigdellum i,pertant,la llei bàsicadel billar éstambé laigualtat entreels anglesd’incidència idereflexió. Tornarem alsbillarsalasecció9.

La soluciódel problemad’Heró es basaenunargument desimetriatan simplecomelegant. Sigui Q∗ el punt simètricde Q respecte de la recta L (fig. 2).

2

Comque RQ = RQ∗ ,elproblemaespotreplantejaraixí:quinéselpunt R sobrelarecta L de manera quela suma de les distàncies PR + RQ∗ siguimínima?Araésgeomètricamentobvi queaquesta suma ésmínima quan R ésel punt d’intersecciódelsegment PQ∗ amblarecta L (fig. 3).

Figura 3

Figura

Tornanta la preguntaoriginal,elraonamentd’Heró implicanonomés que els angles d’incidència idereflexió del camíòptim sóniguals(fig. 4)sinóque tambéproporciona unmètodeconstructiu.AquestargumentprobablementjaeraconegutperArquímedes. Trobaremmés aplicacions del problema d’Heróenlesseccionssegüents.

3.Lallegendadela princesaDido

Res millorqueacudira L’Eneida de Virgiliper explicarlallegendadelaprincesaDido.Laversió de Virgili diu que Dido,princesafenícia de la ciutatde Tir,esvaveure obligada afugir-nequan elseu germà Pigmalió vaassassinar elmarit de Dido. Aleshoresvaemprendreuna travessia pel Mediterranique la vaportarfins alaciutatde Cartago, alacosta nordde l’actualTunísia,ones vavoler establir amblaseva gent.Vanegociar ambelcap local,Jarbes,quili vaproposar el tracte següent:tot elterreny que poguéstancar ambunapell debrauseriaseu. Potser Jarbes nocomptava ambl’astúciadeDido,queva fertallar lapell entiresmolt primes perdesprésunir-les i formaruna cordatancadaque envoltava unafiguraambl’àrea màximapossible.

Elproblemamatemàtic al qualesvaenfrontar Dido(problemaisoperimètric)éselsegüent: entre totes les corbes tancadesdelongitudfixa, quinaenvolta unaàrea màxima? Éslegítim pensarque Didova trobar la soluciócorrecta: lacircumferència.

Teorema isoperimètric. Detotes les corbestancadesdelongitudfixa,lacircumferènciaésla que envoltamésàrea.2

2.Elproblemaisoperimètric dual preguntaperlacorbatancadadeperímetremínimentrelesquetenen àrea donada. Elsdosproblemessón equivalents. Considerarem laformulaciódualalasecció 8.

Figura 4

De fet,Didopodria havertretencara més partit de la situació aprofitant lalíniadecosta, que sesuposa recta(fig.5): ambla cordasensetancar,esformaunarcsemicircular elsextrems delqualsóndospuntsdelacosta.Enaquestcas, el problemamatemàtic corresponent de fet,equivalent al’anterior és: detotesles corbesdelongitud fixaquetenenelsextrems sobreunarectadonada,quina éslaqueenvolta mésàrea? Laresposta ésunarc semicircular.

Paral·lelament, L’Eneida relatala històriad’Eneesde Troia.Enees, juntament amb ungrupde supervivents de la batalla contra els grecs,esdirigia capa Itàlia perfundarunanovaciutat. Unatempesta vadesviarelvaixell cap aCartago,onDido els vaacollir i,perobra deVenus,es vaenamorard’Enees. Hermes,enviat perZeus,vaordenarEneesqueabandonésDido,que, desesperada,esvasuïcidar. Dant vacondemnar Didoals inferns i,en claumusical, Purcell varecuperar lahistòriaenl’òpera Dido iEnees.LahistòriadeDidovaacabartràgicamenti Cartagovadesaparèixerfamolt, peròelproblemadeDidohaesdevingutundelsclàssicsde lesmatemàtiquesi durantsegles hacontinuat sentunafontd’inspiraciótantdintrecomfora deles matemàtiques pures. 3

4.Breu històriadelproblemaisoperimètric

Laconfusióentreàreaiperímetreestavamolt estesaa l’antiguitat.Al llibre4deles Històries, l’historiador grecPolibi(ca. 200-118aC),enunfragmentambtítol Càlculdela midadeles ciutats,diu:

Molta gentjutja lamidadeles ciutatssimplementpelseu perímetre. Quanhom diu queMegalopolisfacinquanta estadis deperímetrei Espartanomés quaranta vuit, però queEspartaésdues vegadesmésgrossaqueMegalopolis,l’afirmació elssemblaincreïble...Hearribat a feraquestesobservacionsperquènonomésels homesordinaris,sinótambéaquells quiaspirenalpoder polítici alcomandament delsexèrcits, sónignorantsd’aquestes coses.

Dos segles méstard,elfilòsof Procle(alprimerllibredels Elements d’Euclides)tambéfeia reflexionssemblants.Perexemple, lafigura6 mostradostriangles A i B dela m ateixaàrea (tenenlamateixa base i lamateixa alçada), peròelperímetre de B és claramentmésgran.

3. Alllibre Amathematician’sapology,G.H.Hardyfaunadeliciosa reivindicaciódel caràcterestèticdeles matemàtiques i, entred’altresobservacionssucoses, deixa anar l’afirmaciósegüent,quecertamentnocontribueixa enfortir elsponts entrematemàtiquesiliteratura:«Arquímedesseràrecordat quan Èsquil siguioblidat,perquèles llengüesmoren iles idees matemàtiques no».

Figura 5

Una observacióprèviaés que, uncopassumida l’existència d’unacorbatancadaqueés soluciódel problemaisoperimètric, l’aproximaciódelacorbaperpoligonals mostra que podemreduir-nosalcasdepolígons (fig.7).

Aquestmètodevaserempratpelsgrecs,quejaconeixien lasolució delproblema isoperimètric,malgrat la confusióentreàreaiperímetreesmentadaabans.Possiblementelprimer atacseriósalproblemaisoperimètricvaaparèixeral tractat Deles figuresisomètriques del matemàtic grecZenodor.Sabem pocacosade la vidadeZenodor,peròescreuquevaviure al segle II aC,poctempsdesprésd’Arquimedes. Lesreferènciesals seus treballsenshanarribat pels comentarisde Teód’Alexandria4 idePappus d’Alexandria.Entreels resultatsdemostrats perZenodor,hihaelssegüents:

1.L’àread’un polígon regular de n costatsésmésgranquel’àreadequalsevolaltre polígonde n costatsambelmateix perímetre.

2.Donats dos polígonsregulars del mateix perímetreicostats m<n,l’àreadelpolígon de n cost atsésmésgranqueladelpolígonde m costats.

3.Uncercletémés àreaquequalsevol polígon regularamb elmateix perímetre.

Delsqualses potdeduir, perargumentsd’aproximació,quelasoluciódel problema isoperimètricéslacircumferència(que es potconsiderarunpolígon regulard’infinits costats). LesdemostracionsdeZenodorerenincompletes:enel primer resultatassumia que el polígon òptimexisteix, afirmació querequereix una justificació.Defet,laqüestió de l’existènciadesolucióalproblema isoperimètric no vaser objected’atencióseriosa finsben entratelsegle XIX.Elmatemàtic suísJakobSteiner (1796-1863)vadonarcinc«demostracions»

4.Teó era elparedelafilòsofaimatemàticaHipàtia.

Figura 6

Figura 7

del teoremaisoperimètric[2], però tot i queels argumentsdeSteinersónveritables joies perlasevaelegància isimplicitat,unpuntrestavasenseaclarir:entotesles demostracions donava perfetqueexistia solució(bàsicament,lasevaestratègiasempre és partird’una figuraqueno és uncercleimillorar lasevaàrea).Elmatemàtic alemany Peter Dirichlet, contemporanideSteiner, li vafernotarque lesdemostracions estaven incompletes perquè pressuposaven l’existènciadesolució.GràciesalsesforçosdeDirichlet, Weierstrass iHilbert, entred’altres, les qüestionsd’existènciaes van anar incorporantcomunapartnecessàriade les resolucions matemàtiques als problemes demàxims i mínims.

5.El problema isoperimètricpertriangles

Coms’hacomentat a laseccióanterior, éssuficientresoldreelproblema isoperimètric per polígons.Enaquesta seccióanalitzaremel primerteorema deZenodor pertriangles, cas que ja és prouinteressanticontéels principals elementsdel casgeneral. Elsarguments que s’exposaran a continuacióestan basats enlasoluciódel problemad’Heróienconsideracions geomètriques elementals.Vegeu [2,3,14]peralcasgeneralienparticular[9]per al’argument originaldeZenodor.

Es tracta dedemostrar que, entre totsels triangles deperímetredonat,eltriangle equilàter éseld’àreamàxima. Prescindiremdelajustificaciód’existènciai,donantper fet que hiha un triangleòptim, demostrarem queésl’equilàter.Suposemqueeltriangle PRQ té doscostats diferents,per exemple PR = RQ (fig. 8). L’estratègia consisteix aprovarque existeix unaltre triangledel mateix perímetre quetémés àrea.

8

Sigui L la rectaparal·lela a PQ que passa per R.Triemunpunt S sobre L demaneraqueel triangle PSQ sigui isòsceles(fig.9).

Figura 9

Pelteoremad’Heró discutit alasegonasecció,tenim PR + RQ >PS + SQ.D’altrabanda, les àreesde PRQ ide PSQ són igualsperquèsón trianglesde lamateixabase ilamateixaalçada.

Figura

Ara (fig. 10)apugemelpunt S iconstruïmunaltretriangleisòsceles PTQ deformaque PT + TQ = PR + RQ.Comquehem augmentat l’alçada,l’àreade PTQ ésmés granquelade PRQ,peròelperímetre éselmateix.

Pertant (fig. 11),lasuposicióque PRQ té doscostats diferentsimplica que hiha un altre triangle (PTQ) quetéelmateix perímetreperòmésàrea. Laconclusióésqueeltrianglede més àreaentre totselsquetenenelmateix perímetreha deser equilàter

6. La sagacitat delesabelles(I)

Construeixo casa meva segons leslleisd’una arquitectura severa; ielmateix Euclidess’instruiria admirantlageometriadels meus alvèols.

(Les miliunanits. Cantdel’abella.Nit934)

Lesabelles i les seves construccionshanatretl’atencióde científics,literats i artistesalllarg dela història.Virgilien parlaal llibre IV deles Geòrgiques idesde Kepler finsaDarwinmolts hanelogiat les seves habilitatsgeomètriques. Alvoltant del’any36aC, Marc Terenci Varró, enelseullibred’agricultura[18],vaescriure sobre la formahexagonalde lescel les deles abelles.Elsmatemàticsdel’èpocasecundaven lateoria que la formahexagonals’explicava apartirdeprincipis d’optimització.L’origendela qüestióésincert,peròVarrós’hivareferir molt abansquePappus d’Alexandria,undelsgrans geòmetresde l’antiguitat, incloguésel problemaenlaseva gran obra,la Col lecció.Pappus,quevaviureafinalsdelsegle III dC, va escriure un prefacial llibre V dela Col·lecció ambeltítol Delasagacitatdelesabelles.Alcapítol dedicat a Pappusdelllibre Ahistoryofgreek mathematics [9], Heath escriuapropòsitdel’estil ieltema del prefaci:

Figura10

Figura11

És característic dels grans matemàtics grecs que,quan estavenlliuresdeles restriccionsdelllenguatge tècnicmatemàtic,com perexemplequan tenien l’ocasiód’escriure un prefaci,eren capaçosd’escriureenun llenguatge delamés altaqualitatliterària,comparableambel dels filòsofs,historiadorsipoetes...El temaéstal quequalsevolescriptor ambgustiimaginacióeltrobariaatractiu:la intel ligència pràcticaque mostren lesabellesentriar la formahexagonalper les cel les deles bresques. Pappusnoens decep; el fragment éstan atractiu comel tema...

Acontinuació,alguns fragments deltextoriginal dePappusquecorroborenles paraules de Heath:

[...]primer recol·lectenelsucredeles florsmés bellesque creixen sobre laterrai construeixen,per al’emmagatzematgedelamel, cel lesiguals,contigüesentre sí,deforma hexagonal. Perforçadeuenhaver pensatque lesfigures han deser contigüesentresi,ésa dir,han detenir costatscomuns demaneraquecap matèriaestranya pugui entrarpelsintersticisi corrompreaixíla puresadelseu producte.Només tresfigures rectilínies complirien lacondició, vull dirfigures regulars equilàteresiequiangulars (trianglesequilàters,quadratsi hexàgonsregulars).

D’aquestestres figures,les abelles trien,d’acord amb laseva saviesainstintiva, lafiguraamb mésangles perquè imaginenqueconté mésmelquequalsevol deles altres dues.Les abelles, pertant,coneixenaquestfetqueels ésútil,que l’hexàgon ésmésgranqueeltriangle equilàterielquadraticontindràmésmel amblamateixa despesa dematerialutilitzada enlaconstrucció.

Pappusdescriuadmirablementperquèles abelles trienla configuració hexagonal.Un tessel lat ésunaparticiódel plaenpolígonsdisjunts(aexcepciódels costats).Eltessel lates diu regular siestà fetamb polígonscongruents iregulars.

L’explicaciódela formahexagonaldepèndels dos fetssegüents:

1.Noméshihatrespolígonsregularsquetessel·len elpla:trianglesequilàters, quadratsi hexàgonsregulars (fig.12).

2.Donatsuntriangleequilàter,unquadrat iunhexàgon regular delmateix perímetre, l’hexàgon ésel quetémés àrea.

Figura12

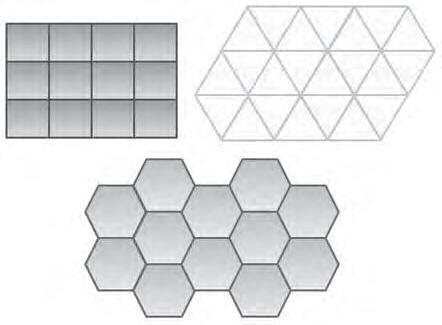
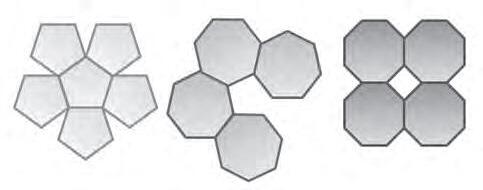
La segona afirmacióesdedueixdel segonteorema deZenodor iconfirma quel’estructura hexagonalresponaunprincipi isoperimètricdemínims.Pelquefaalaprimera,probablement ja eraconeguda pels pitagòrics. Perexemple, lafigura13mostragràficament laimpossibilitat detessel ·lar elplaamb pentàgons,heptàgonsioctàgonsregulars.

La demostraciógeneralés, defet, elemental. Suposemqueeltessel latésper n-polígons regulars itriem unpuntquesiguiunvèrtexcomúd’exactament m polígons delsque formen el tessel lat.Un càlculsenzill mostraquecadaangleinternd’un n-polígon regularésigual a π(n 2) n .Pertant,s’hadecomplir m π(n 2) n =2π o,equivalentment,

(m 2)(n 2)=4. (1)

L’equació(1)nomésadmet lessolucionsenteres (n, m)= (3, 6), (4, 4) i(6, 3)que corresponen alscasosdelstriangles equilàters, quadratsihexàgonsregulars.L’anàlisi anteriortambé permet considerarlasituacióenquè hiha vèrtexs d’unpolígonsobreelcostat d’unpolígon contigu.Enaquestcas,siunpuntdelcostatd’unpolígonés amésunvèrtex comúd’altres m polígons,tenim: π + m π(n 2) n =2π o,equivalentment:

(m 1)(n 2)= 2,

quetéles solucionsenteres (n, m)= (3, 3) i(4, 2).Aquestcas nomésoriginatrianglesequilàters i quadrats.Siguicomsigui, noapareixennous valors de n.

Elfetqueeltessel·latper hexàgonsregulars ésòptim des delpuntdevistaisoperimètric finsitotquanespermetentessel latsmoltgenerals,formats perregionsnonecessàriamentpoligonals (ni tan sols convexes)és part dela Honeycombconjecture o Conjectura deles cel·lesd’abella.L’origen,comespot suposar, ésmolt antic,però la demostració, de T.Hales,és forçarecent[8], la qual cosa ensconfirmaqueels nostresavantpassatssovint s’interessavenperproblemesgenstrivials!

Tornaremalsaspectesmatemàticsdelescel·les deles abelles desd’un punt de vista tridimensional ala secció8.

7. Latercera labord’Hèrcules,elvold’ocellsialtres qüestions pràctiques

Hèrcules, elmés famós dels herois grecs,erafilldeZeus id’Alcmena.Enunatac debogeria induïtperladeessaHera,Hèrculesvaassassinarelsseusfillsi,comapenitència,esvaposar

Figura13

alesordresd’Eristeus, reideMicenes,quilivaordenar realitzardotze treballsquerequerien una forçasobrehumana.Enunoriginal intentd’acostarmatemàtiques imitologia, l’autordel llibre Mythemathics [11]explica les dotzelabors d’Hèrcules ambl’ajutd’einesmatemàtiques.

La terceralabord’Hèrcules consistia a atraparlacérvolasagrada deCirenea,5 quesegonsla llegendatenia banyesd’or ipeülles debronze. Hèrcules havia estat perseguint-ladurant un any sencer ila sevaúnicaopció era atrapar-laquan hagués decreuar elriu Ladon,venintdel montArtemisius(punt A alafigura14)endireccióalbosc d’Arcàdia(punt B alafigura14).

Hèrculeshauria d’esbrinar a quinpunt delaribasuperior arribarialacérvola perpoder-la atrapartotsortintdel riu,abans quetingués temps d’emprendrelarestadel recorregut corrent enterra,onseriamoltmés difícild’atrapar. Evidentment, hiha moltestrajectòries per arribar des de A fins a B creuantelriu. Perexemple,latrajectòriadirecta AB és certamentla més curta, però tél’inconvenientquetot eltrajectes’hadeferal’aigua,enquèlavelocitat ésmés petitaquesobreterra.D’altrabanda,siestrialatrajectòria ACB,eltrajectesobre aigua AC éselmés curtpossible, però després CB s’hadefersobre terrailadistànciatotal recorreguda AC + CB és mésgranqueamb qualsevolaltratrajectòria arbitrària APB.

Museum.Berlín.

Figura14

100 5km/h 8km/h

Iaquíésonentraelproblema matemàtic:siesconeixen lesvelocitatsdela cérvola nedant sobreelriu icorrentsobreterra,l’ampladadelriu(distància AC )i tambéladistància CB, quin seràelrecorregut òptim APB?Mésconcretament:quinseràelpunt P triatperla cérvola assumintqueel temps total del recorregut hadeser mínim?Suposem, perexemple,quela velocitata l’aigua ésde5km/h, sobreterra ésde 8km/h, l’ampladadel riuésde 100 mi ladistància CB ésde 1.000m.Siintroduïm com avariablel’angle α que formenels segments AP i AC (fig. 15), eltemps total del recorregut APB (en funciód’α)és

T (α)= 100 5cos α + 1000 100 tan α 8

Determinar el punt P òptimésequivalent adeterminar l’angle α òptim.Ésunexercici elemental encàlculdiferencial comprovarquela funció T ,definidaal’interval[0, arctan (10)], assoleixel seumínimglobalquan α =arcsin( 5 8 )(fig.16). Uncàlculsenzillmostra queen aquestcasladistància CP ésde 100 √39 m. Pertant, Hèrcules hauriad’esperarlacérvola a 100 √39 m delpunt C de l’altrecostatdelaribaenfrontdelmontArtemisius.S’observaràque l’angle òptim només depèndelaraó entreles velocitatsenl’aigua i enterrainopasde les distàncies AC o CB.

0 arcsin(5/ 8)arctan (10)

Figura16

Aquesttipusdeproblema espresentasempre queensproposem determinarel temps mínim d’unrecorregutenuncontexton hiha diferentsmitjans.Elsexemplessegüentssón variacions del mateix problema:

Figura15

• Refracció dela llum. La llei deSnellsobrelarefracciódela llum també es potdeduir apartir d’unprincipidemínims.Unraig de llumpassad’un mitjàenquè la velocitatés v1 aunaltre enquèés v2 .Latrajectòriadel raig ésunapoligonalformada perdoslínies rectes, una en cadamitjà.Siels angles dels rajosamb lanormal alpuntdecanvisón θ1 i θ2 (fig. 17), la llei deSnelldiuque

sin θ1 sin θ2 = v1 v2 .

Es potdeduir la llei deSnell apartir del Principidetemps mínim de Fermat.Siunraigde llumsurtd’unpunt A delprimermitjà, arriba enlíniarecta finsalpunt P ones refracta idesprés continuaenlíniarecta finsaarribara B,dintredelsegon aleshoreseltemps totaldel recorregut APB ha deser mínim. Quan s’interpreta elproblema entermes dela funciódetempsi s’imposala condiciódemínim,s’obtélallei deSnell(vegeu [12]pera la resolucióicomentaris històricsdel problema).

1

2

• Vold’ocells. Està comprovat experimentalment queels ocellsvolen méslent sobre aiguaquesobreterra;pertant,ladeterminaciódelatrajectòriaòptimad’unocellque ha devolarsobreuna gran extensiód’aigua originaelmateix tipusdeproblema que l’exempled’Hèrcules.

• Conduccionssotal’aigua. Unaversió pràcticadelmateix problemaes presentaquan s’hadeportaruna conduccióelèctricad’unpunt A aunaltrepunt B al’altraribad’unriu. Elpreu permetrede la conducciósotal’aigua éslògicament méscarquesobre terra; pertant,estracta delmateix tipus deproblema,en quèles velocitatssón substituïdes pels preus.

• Ramificació vascular. Laresistènciadelasang quan viatjaperunvas sanguinidepèn de la secciódelvas.Siunvas sanguiniprincipalesramificaper crearunvas secundari, les seccionsvarien i,pertant,les resistènciestambé.Unmodel simplificatdel problema consisteixadeterminar l’angle deramificació que minimitzalaresistènciatotalalllarg del recorregut (vegeu [1], secció9.7).

Figura17

8.Lasagacitatdelesabelles(II)

Abandonantaquellaterravam arribar deseguida a unaaltraonlesabellesielsocellssónmatemàtics detantgeniierudicióquedonenlliçonscientífiquesde geometria alssavis del’imperi. (E.A.Poe, ElcontemilidosdeScherezade)

Alasecció6 analitzàvem l’estructura hexagonalde lescel·les deles abelles enclaubidimensional. Peròdesd’un punt devistatridimensional,els hexàgonssónnoméslesentrades deles cel les,mentre quel’estudidel fonsdeles cel les ésposterior,més complex,més interessantimenysconegut.Enun principi,espodriapensarqueles cel·les sónsimplement prismesrecteshexagonalsamb baseobertaitapa tancada (fig.18),

peròdefets’observaquelaterminaciónoésplana,sinóqueésunamenadepiràmideamb tres rombesen formadediedre(fig. 19).

Figura19

Amés, les cel les encaixen perfectamentenunsistemadedues capes:quan trescel les es col loquen juntes enlamateixaorientaciódeixenunforatonunaquartacel la col locadaen l’orientació contràriaencaixa perfectament (fig. 20). Pertant,les cel·les , seguintaquestsistema dedoblecapa, omplen perfectament l’espai entredosplansparal lelssensedeixarforats.

Figura18

Figura20

Alllibre Ongrowth and form [17],Thompsonofereix unadescripcióexhaustivasobre l’evolució històricadel’estudidelfonsdelescel les.Aparentment,l’estructura geomètrica dels rombes que formenlatapa deles cel·les javaser reconeguda perKepler,però elseu descobriment va passar desapercebutfins quel’astrònomMaraldi,6 cap al1712,vamesurarels angles del rombe: 109◦ 28 7 i70◦ 32 ilainclinaciódelestapesromboïdals: 35◦ 16 .

La idea que els principis de màxim i mínimexplicarien certsdissenysdelanaturajacirculava entreelsambients científics del’època.El físic Réaumurvaser possiblementdels primersa afirmarqueunprincipidemínimspodriaserlaclaudelaqüestióique,delamateixamanera quepassaambeltessel·lathexagonalalpla,elsanglesobservats per Maraldifarienque la cel la necessités elmínim desuperfície perunvolumdonat. Enparaules de Réaumur:

Convençut queles abelles prefereixenel fonspiramidal, he sospitat quela raó, o unadeles raons,queles haviamotivat era l’estalvi decera;queentreles cel les de lamateixacapacitat idefons piramidal,la quepodiaestarconstruïdaamb menysceraera aquellatalqueels rombestenien dosanglesd’aproximadament 110◦ idosd’aproximadament 70◦ .

Anys méstard,Réaumurlivaenviarelproblemaaljove matemàtic suís S.Koenig,8 queelva resoldre,toti queperunerrornumèric va obtenirelvalor 109◦ 26 .Elmètodedelaprova deKoeniges desconeix, peròprobablementvautilitzartècniquesdecàlculinfinitesimal. Koenig afirmavaque les abelles havien resolt unproblema foradel’àmbit de lageometria clàssica, que requerienels mètodesde Newton iLeibniz.Tanmateix,capal 1743,el matemàtic escocèsColinMcLaurinesva proposar resoldre el problema fent servir capgeometriamés avançadaque laqueconeixien els antics ihovaaconseguir.L’argumentdeMacLaurin(vegeu [17], p. 533)ésunamicamésllarg,peròefectivamentarriba al resultatdeMaraldi utilitzant només geometriaelemental.

Acontinuacióveuremunaversió 2-dimensional més senzilla delproblema quecontéels principalsingredients.Perenunciar-la,tornaremala formulació delproblemaisoperimètric queconsisteix afixar el perímetrei maximitzarl’àrea. Suposemquevolem ferobresenuna habitaciórectangular oberta per uncantó(fig. 21).

6. Nebotdel famósastrònomCassini.

7. Angledistingit,ara anomenatangledeMaraldi. Apareix al dodecaedreromboïdalitambé ésl’angleque formenelssegmentsqueuneixenelcentred’untetraedreregularambdosdels vèrtexs.

8. DeixebledeJohann Bernouilli.

Figura21

La modificacióconsistiràa substituirel costatdel fonsperdos segmentssimètrics en forma depunxa(fig. 22)ambla condició que mantinguemel perímetretotalde l’habitació.

Siintroduïm com avariable α l’angled’inclinaciódelsdos noussegments respecte de l’horitzontal,enspodem plantejarles preguntes següents:és possibletriarangles α de manera quel’àreadel’habitaciónovasiguimés gran quel’àreadel’habitacióvella?I si fosaixí, quin ésl’angleòptim?Un càlculelemental mostraqueelguanyd’àreaaconseguitambuna modificaciód’angle α és:

on a és l’amplada del’habitació.Uncàlcul elementalambladerivada de G mostranonomés queelmàximde G éspositiu,sinóques’assoleixquan α = π 6 (lagràficade G esveu a la fig. 23).

(α)

/ 6

Figura23

Per tant, si,mantenintelperímetre,volemmodificar l’habitacióperaconseguir àrea màxima, hauríemdetriarunangled’inclinacióde30◦ .Elproblema deles cel·les d’abella només és unaversió tridimensional,tècnicamentmés complicada, d’aquest problemaenquèl’angle d’inclinacióòptim resulta serde35◦ 16 (vegeu [1], [17]).No caldir que,tot iladificultatpràctica demesurarels anglesinvolucratsenles cel les reals, els valors observatss’acosten forçaals teòrics.Enparaules de Fontanelle,secretaride l’AcadémieFrançaisedurant laprimera meitat del segle XVIII,lesabelles estaven utilitzantcegamentlesméselevadesmatemàtiquesperordre

Figura22

iguia divina.D’Arcy Thompson pensavaque teniaméssentit suposarque laregularitatdeles obres arquitectòniques del’abelles obeeix a algunainteraccióautomàticadelesforcesfísiques quenopasadmetreque l’abella buscaintencionadament unmètode d’economitzar cera.Sigui comsigui,aquestamanifestaciód’unprincipidemínims a la naturacontinuaprovocant-nos fascinació.

Semblaqueestem admetentqueles abelles hanconstruïtles bresquesperfectes,peròaixò,és realmentaixí?Dit d’una altra manera, espot utilitzarunaltredissenypolièdricper alfonsde maneraqueles cel les omplin l’espai sensedeixarforatsi quela proporcióentre laquantitat decerade la superfície ilacapacitatde la cel·la siguimésavantatjosa?Laresposta ésque sí.El 1964,enunarticleambelsuggestiutítol «Whatthebeesknowandwhattheydonot know» [6],elmatemàtic hongarès Fejes Tóthvatrobar un disseny millor,ambunfons format perdos hexàgonsidos rombesen comptes detresrombes(fig. 24)

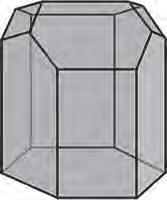
Encara esdesconeix silaconfiguraciódeFejes Tóthéslamillor possible.

9.El problema de Fagnanoielsbillars

Alasegonaseccióintroduíem la llei fonamentalque regeixlageometriadel billar comuna aplicaciódel problemad’Heró:els anglesque formenles trajectòries d’entrada idesortida amblanormala la paretsóniguals. Limitarem aquíladiscussió alcas de billarsambformade polígonsconvexos.

Hihanombrosespreguntesinteressantssobrebillars, algunes de les quals sónmoltfàcilsde formular,peròmolt difícils deresoldre.Unad’elles ésl’existènciadetrajectòries periòdiques. Donat n ∈ N, n ≥ 2,diremqueunatrajectòriaés n-periòdicasisurtd’unpuntenalgun delscostatsitorna alpunt desortidadesprés de n xocs.Una trajectòriaésperiòdica siés nperiòdicaper algun n ≥ 2.Perexemple,qualsevolsegmentperpendicularsimultàniamenta doscostatsésunatrajectòria 2-periòdica.Enel casd’unrectangleéstrivial obtenirtrajectòries 2-periòdiquesi4-periòdiques:qualsevoltrajectòria queconnectiperpendicularmentdos costatsparal·lelsés 2-periòdicailatrajectòria queconnectaels puntsmitjansdels costatsés 4-periòdica.

El casdels triangles ja és prouinteressant.Quan eltriangle ésacutangle, l’existènciadetrajectòries periòdiquesestàestretamentrelacionada amb undels problemesmés fascinants de minimitzaciógeomètrica:elproblema de Fagnano, que deuelnom al matemàtics italians Giulio Carlo Toschi deFagnano(1682-1766) ielseu fill,Giovanni FrancescoFagnano(1715-1797).

Figura24

Donat untriangleacutangle,elproblemaconsisteixa determinarun triangleinscritde perímetre mínim ambunvèrtex encadacostatdeltriangle donat. Comentem, primer detot, la connexió entre el problemadeFagnanoi els billars.Suposemque DEF éseltrianglede perímetremíniminscritaltriangle acutangle ABC ,on D ∈ BC , E ∈ AC i F ∈ AB.Fixats E i F , latrajectòria EDF ésunasoluciódel problema d’Heróambdades els punts E , F ilarecta BC . Pertant,els angles d’incidènciai de reflexióen D són iguals i EDF compleixelrequisitd’una trajectòriadebillar Evidentment,elmateixargument aplicatalsaltresvèrtexs diuqueel triangleinscrit DEF ésunatrajectòria 3-periòdicaalbillar ABC .

Queda com aexerciciperallector comprovarqueenel casdetriangles rectangles i obtusangles elmínimdels perímetresdelstriangles inscrits ésdues vegadesl’altura més petita, perònohihatriangle òptim(degeneraenl’alturacomptada dues vegades). Pel que faalestrajectòries periòdiques, la situacióésmoltmés complicadai interessant.Discutirem sobreaquestproblemaalfinaldelasecció.

La soluciódel problemadeFagnanoésl’anomenat triangle òrtic:eltrianglequetécoma vèrtexselspeusdelestresaltures(fig.25).

Des delaprova originalde J.F.Fagnano[5], queutilitzava tècniquesdecàlculdiferencial, s’hantrobatdiverses demostracions del teoremadeFagnanoambsabormésgeomètric, entrelesqualsles més famoses sónles deFéjer iSchwarz [3,10, 12,15].Laprovaqueveurem acontinuacióésladeFéjeri està basadaenel problemad’Heró discutit alasegonasecció. Suposemque ABC és un triangle acutanglearbitrari.Arribaremala conclusió que eltriangle òrtic éslasoluciódel problema deFagnano enduesetapes. Primer,fixem unpunt D alcostat BC i, de totsels trianglesinscrits DEF amb E ∈ AC i F ∈ AB,volemdeterminarelde perímetre mínim. Lafigura següentsuggereixlasolució.9

Siguin D , D els punts reflectits de D respectedelscostats AB, AC respectivament.Aleshores, el perímetredeltriangle EDF coincideix amblalongituddelapoligonal D FED queésmínima

9.Lesfigures26i 27s’han reproduïtpercortesiadel professorParisPamfilos(Universitat deCreta),de la sevaweb personal http://www.math.uoc.gr/~pamfilos/eGallery/Gallery.html,que conté informació sobre molts problemesgeomètricsinteresants,incloent-hiel problemadeFagnano.

Figura25

quan E = E , F = F ,els puntsd’intersecciódelarecta D D ambels costats AB, AC .Pertant, fixat D,eltriangle DE F éslasoluciód’aquesta primera etapadel problemadeFagnano.

Figura27

Lasegonaetapaconsisteixatriarelpunt D de maneraque el perímetrede DE F (o equivalentment lalongitud |D D |)siguimínim.Inspeccionantlafigura26s’observa:i) |AD | = |AD | = |AD| i, per tant, elstriangles D AD sónisòsceles,ii)quel’anglealvèrtex A és independentdel’elecciódel punt D icoincideixamb2α,on α ésl’angle deltriangleoriginal ABC alvèrtex A.Comque |D D | =2|AD | sin α =2|AD| sin α,elmillor D éselqueminimitza |AD|:elpeudel’alturadesdelpunt A (fig 27).

Com quel’elecciódel costat BC ha estatarbitrària, elmateix argumentdonaria que eltriangle òrtic ésla solucióalproblemadeFagnano iproporcionauna trajectòria3-periòdicaenun billartriangularacutangle.

Figura26

Pera triangles rectangles i obtusangles, laqüestió de l’existència de trajectòries periòdiques resulta molt més complicada.Coms’hacomentatabans,lasoluciódel problemadeFagnano ésdegeneradaenaquest cas,d’onesdesprén que nohiha trajectòries 3-periòdiques. Tanmateix, podemplantejar-nossiexisteixen altrestrajectòries periòdiques.Pera triangles rectangles, laresposta éspositiva (la figura28mostrauna trajectòria6-periòdica), però, per sorprenent quesembli, enelcasobtusangleel problemaencara estàobert: només esconeix l’existènciadetrajectòries periòdiques per acertes classes detrianglesobtusangles.Vegeu [16] perainformaciógeneral sobre lageometriadelsbillars i, perexemple[4,7,9], [13, pàg.440], peralprobl ema delestrajectòries periòdiques i altresqüestions geomètriques interessantsrelacionadesamb billars.

Ambladiscussiódel problema de Fagnano,en quèconflueixen els principisdeminimització, lageometriaelemental iels billars, acabemaquestbreu recorregutpelsproblemes de màxims imínims, totassenyalant unavegada méslacapacitat inesgotabledeles matemàtiques per connectar territorisaparentment independentsiposar-hisentitiperspectiva.

Referències

[1]Batschelet,E.(1975). Matemáticasbásicas para biocientíficos.Springer Verlag.

[2]Blåsjö,V.(2005). The IsoperimetricProblem. American Math.Monthly,vol. 112,6,526-566.

[3]Courant,R.,Robins, H.(1979). Qué eslaMatemática.Aguilar.

[4] DeTemple,D.,Robertson,J.(1981).Abilliard pathcharacterizationofregularpolygons. MathematicsMagazine,vol.54, 2,73-75.

[5]Fagnano,J.F.(1755;aparegut 1779). ActaErud.,281-303.

[6] Fejes Tóth,L.(1964).What thebees know and what theydonot know. Bull.Amer.Math. Soc.,70, 468-481.

[7] Gutkin, E. (1997). Twoapplicationsof Calculustotriangular billiards,vol. 104,7, 618-622

[8] Hales, T.(2001). The honeycomb conjecture. DiscreteComput.Geom.,25, 1-22.

[9]Heath,T.(1981). Ahistoryofgreek mathematics.Dover.

Figura28

[10]Hildebrandt,S.,Tromba, A.(1989). Matemática yformasóptimas.BibliotecaScientific American.PremsaCientífica.

[11]Huber,M.(2009). Mythematics.PrincetonUniversity Press.

[12]Nahin,P.J.(2007). Whenleast is best.PrincetonUniversity Press.

[13] Pickover,C.A.(2009). ElLibrodelas Matemáticas.Librero.

[14] Polya,G. (1954). Mathematicsandplausible reasoning.PrincetonUniversity Press.

[15]Rademacher,H.,Toeplitz, O.(1994). The enjoymentof Mathematics.PrincetonUniversity Press. (Traduït de l’edició alemanyade 1933).

[16]Tabachnikov,S. (2005). GeometryandBilliards.AmericanmathematicalSociety.

[17] Thompson,D.(1942). Ongrowth and form,vol. II.CambridgeUniversity Press.

[18]Varró,M.T.(1934). On Agriculture.LoebClassical Library.

[19]Vorobets,Y.B.,Galperin, G.A.,Stepin, A.M. (1992). Periodic billiardtrajectories inpolygons: generating mechanisms. RussianMath.Surveys, 47,3, 5-80.

Ladescobertamatemàtica enl’entorn.Lareflexióiel raonamentdinseltreball d’investigació,basede l’aprenentatgematemàtic

Carme Alemany Miralpeix Mestrad’educació

Resum Abstract

Considerocom aobjectiu prioritaride l’escola, en qualsevoldeles sevesetapes, la descobertadelplaerd’aprendre apartirde lainvestigació ilainterpretació delmón. L’experimentacióilainvestigaciósónla formanaturald’acostar-nosal coneixementdel’entorn.L’entorn, global i complex,ensparlamatemàticament i, al mateixtemps, lamatemàtica és necessària peralasevadescoberta.Ésapartirdel treballd’investigacióques’adquireixno solsel coneixement,sinó tambéel procedimentd’aprendre.Us presento exemplesde propostes enaquest context.

primària

Ibelievethatthepleasureoflearningfrom observationandresearch has tobeoneof themaingoalsofthe school. Experimentationand researcharethe natural ways wegainknowledge ofthe environment. The world aroundus is complexandglobal,and itspeaksto us mathematicallysowe needmathsto understand it. Fromresearchwe obtain not onlyknowledgebutalsotheabilitytolearn. This articleintroducessomeexample proposalsrelated totheseideas.

Undelsobjectiusdel’ensenyamentaprenentatge,sobretotenlesetapes d’infantiliprimària, ha deser ladescobertadelmón partint del’entorn quotidià.

Aquestaafirmació,peròbvia,sovintésanalitzadad’una manera superficial iinsuficient. Comésl’entorn, elmónque habitem?Ensreferim només a l’entornnaturalmés proper? Considerementorn tambéels fets culturals?Form en part d’aquestentorn els objectes més quotidians, lesjoguines, leseines...?Lesmanifestacionsdelmónfísic que ensafecten cadadia poden sermotiu profund d’estudi? Qualsevolelement, ielmateix entornenelseu conjunt,

és complex, divers, ple d’estímuls,ple decontingut, d’informació,derecursos...,però és intel ligible. Caluna miradaatenta,analitzant, reflexiva, que connectiicoordini tot elnostre saber,queprovoquipreguntesiensposienacciópertrobar possibles respostesqueens ajudin acomprendre.

Comprendresignificafer connexions,relacionarnousconeixements ambd’altresjaconeguts. Comprendre,entendre,noéselmateixqueobservar,peròcontél’observació ieldiàleg entotes lesseves formes:eldiàlegamb unmateix(la reflexióindividual),amb elfet ol’objecte (manipulació, experimentació,intervenció), ambels altres(conversa, reflexió conjunta, presa dedecisions).

L’entornno està parcel lat enàrees idifícilmentpodem comprendre’lentota laseva plenitud apartir delasimplificació querepresentalamiradaparciali en un tempsprefixat,talcom pretenenels horarisescolarshabituals.És desd’aquestpuntdevistaqueparteixo,nodel treballexclusiual’horade matemàtiques,sinódel fetdecom lamatemàticaensajuda a comprendre la realitat enqualsevolmomentien qualsevoltema.

Enprincipi,isobretotenl’educacióinfantil iprimària(tambéenels primerscursosd’ESO),és important observar larealitattalcom esmanifesta.Lacreació derealitatsvirtualssovintéstotalmentadaptada a les respostesquevolem obtenir.Noésmillor sortir a observarelmón queportaruna part del mónal’aula?Davant ladicotomia entrecreença irealitat,la realitat éselque preval. Elsllibres, les pel ·lícules,els programesd’ordinador...representen larealitat, però la realitatparlasolailesrepresentacionssónnomésinterpretacions.Parteixo,doncs, del treball ambmaterials ifetsque parlin perellssols.

D’acordambelqueexpressaJorgeWagensbergenelseullibre Elgozointelectual (Wagensberg, 2007), «las tresfasesdetodo conocer...fases sucesivas, peronodisjuntas. Enlaprimera predominaelestímulo peronecesariamentepreexiste ya algunaformadeconversación y de comprensión; enla segunda predomina la conversación peroanimada porestímulosymanejandocomprensiones previas¸yenlatercerapredominalacomprensiónquesedaenel extremo dealgunaclasede conversación»(Wagensberg,J. 2007),jon’hi afegiriaunaquarta, queserial’aplicació delcomprès,aaccionsirealitzacionscreatives pròpies.

L’estímul la motivació és perellmateixunafontdesatisfacció.Éselqueenspermet activar,dirigirimantenir una conductaadequadaper tald’aconseguir unobjectiu concret, que possiblementnoéscompartit pertotsels nens iles nenesd’ungrupclasseodela mateixa edat. La mevapropostatampoc no es concretaenl’agrupacióperedatsopergrups d’infantsmés omenyshomogenisenels coneixementstal comes fa enlamajoriad’escoles, sinó eneltreball d’investigació que prové del’interèsd’un,o d’ungrupde nensinenes. Està pensatperportar-loatermeambgrupsheterogenis,quemanifestininteressosoestímuls comuns,enhorarislliures ioberts,ambl’acompanyamentde mestres que valorin l’autonomia delsinfantsila seva totalimplicacióenelseu procés d’aprenentatge, quenoprefixinels continguts concrets aaprendre,que admetin ladiversitatdeprocedimentsper arribaral coneixement,queactuïn coma guies mésque coma «ensenyants».

Lesmatemàtiques són presentsalmón i tot ens pot parlarmatemàticament. L’aprenentatge matemàtic,sobretot ainfantil iprimària,had’aportarcapacitatsque ajudin ainteractuar d’una manera eficaç i constructivaambl’entorn.L’activitatmatemàtica,entesaaixí,ajuda a

desenvoluparcapacitats associadesalpensament lògicidereflexiói raonament, al mateix temps queeducalapercepció de l’espai,estimulal’actitud crítica,aguditza laintuïciói fomentalacreativitatilapresadedecisions. Lesmatemàtiques treballen ambidees, idees d’espai, de temps,denombres,derelacions...L’abstracciónoésunacaracterística exclusiva de lesmatemàtiques,com tampoc nohosónaltresprocessos cognitiuscom l’anàlisi,la generalització,lasíntesi,lademostració...,però lesmatemàtiques reforcen totsaquests aspectesenrelacióambla realitat

Quinaés,doncs, la proposta de treballmatemàtic?Enprimerlloc,prioritzaraquells procediments queafavoreixenels aprenentatgesexperimentalsiinductius itambéelsdeles tècniques d’expressió, de llenguatge matemàtic.Proposo estructurareltreballmatemàtic al’escola apartir dedos aspectessimultanis:d’una banda, ladescobertamatemàticadela realitat,talcom heanat dient,i de l’altra,el treball puramentdedescobertadel’estructura matemàtica enellamateixa,deleslleisquegovernenels nombres, lesoperacions,les formes, lestransformacions, lalògica...sempreque siguipossiblepartintdelanecessitatqueel coneixementdelarealitat provoqui.

Aquestesdues formesdetreball vanabsolutament lligades i l’unaprovoca l’altra. Ésinteressant que la descoberta purament matemàticaparteixi d’interrogantsprovocats perles realitatsde l’entorn iespuguirealitzardinsd’un grup una micanombrós,divers, amb participació de tots, sense por de l’error,afavorinti construintconjuntament l’estructuraciódel pe nsament. On la conversa, lainvestigacióconjunta, la comunicació delsraonamentsindividuals,laconstrucció d’idees pròpies apartir de les aportacionsdels companys,l’extracciódeconclusions,laseva expressió en llenguatge matemàtic... siguinla base ielfonamentdel procésd’aprenentatge.

Quinhadeserelnostre paper, elpaper delmestre,enaquest treball?

Elmestre,lamestra,comamediadors,femquelanostrarelacióambelsabersiguimolt important. Elfetdemantenirunarelaciódogmàticaodesinteressadaambels coneixements faquenoconvidiels alumnesal’aprenentatge;alcontrari,llunydecrearintel·ligència, fomentales actituds més puramentestratègiques isòrdides.Encanvi,sielnostrediscurs expressa, inclús ambincorreccionsi dubtes,una exigènciainterior d’exactitud, deprecisió, derigor,podemesperarfercompartir unadinàmica, implicar els altresa més denosaltres mateixos capalsaber.

Calteniren compteque, pergarantirl’aprenentatge, ésnecessàrialavoluntat dels alumnes, icalqueels mestreslasapiguem provocar através delanostraactitud respectealsaber, al coneixement.És necessari quetransmetemvalentia, il lusió,esforç,interès, motivació, capacitat dereconèixer elserrorsiderefereltreball amb constància...

Cal queels mestresaportem possiblesestímuls pergenerarmotivacióicrear interès i necessitat deconèixer. Aquesta aportació, sempreacompanyadadeles diferents formesde conversa, pot produir-se atravésdesortidesal’entornnatural,museus...,portant al’espai de l’escolaelements atraientsper qualsevol dels seusaspectes(moviment, bellesa, funció...), suggerintatravés delaconversamotius d’estudi, presentantnotícies ofets realsquegenerin preguntes aresoldre... Ésdes d’aquesta miradaque presentounsdeterminats fets omaterials que podensermotiu d’estudides delpuntdevista de lamatemàtica,peròenrealitat

qualsevoltemaqueel neno la nenaproposin contématemàticaoprecisa delamatemàtica percomprendre’l.Ésla nostra intervencióla que potajudar l’infanta descobrir-ho.

Hemdeseguirdemoltaproplesactivitatsdelsalumnespertaldeservir-los deguia i de motor; de la nostra implicació, endependràmolt l’èxit del’experiència.Hem d’estarmolt atentsal que va succeintenelgrup,pertald’aprofitartotallòque creguem convenient, perrepassar continguts ja treballats,per anar introduintconceptes nousque potser nos’aprofundiran en aquellmoment, peròqueservirande pòsitper quanarribi l’ocasió, perorientarposteriors treballs oinvestigacions, perressaltar les aportacionsconcretes,perencaminar el procés... Per ajudar cada nen:

• Aformular-sepreguntes.

• Aanticipar possiblesrespostes.

• Adur aterme petites investigacions.

• Aconfeccionarmodels.

• Aproposarsolucionsiestratègiespròpiessense pordeser censurats encasd’equivocar-se.

• Autilitzar l’error comuna font valuosad’aprenentatge.

• Aaplicar conceptes iprocedimentsapresos.

• Abuscar informacióendiversesfonts.

• Acontrastarlesinformacions trobades.

• Atreure conclusions.

• Aexpressar oralment,perescrit, ambsignes, símbols,esquemes...lesconclusionsdels treballs.

• Avalorarel procés il’esforçfettantcomelresultat aconseguit.

Quin éselpaper del grup?

Dins el procés d’aprenentatge,també ésmoltinteressantpodercomptarambelsuporti l’ajutdels companys ilescompanyes; es tracta d’avançar d’una maneracol·lectiva,partint delsencertsi delserrors detots imantenint eldiàleg ilaconfrontaciód’experiències com una forma enriquidorad’anarendavant

Caltambé lainterioritzaciópersonali el raonament individual peracabard’assumirtotelque ambelgrups’haanatdescobrint.És,doncs,moltimportantafavorir aquestesduessituacions ideixarqueesdonin.

Algunespropostes concretes

Presentomaterials diversos ipropostes d’activitats realitzades al’escolaqueensofereixenla possibilitatdeconèixer,comprendre iaprendre conceptesmatemàtics apartirdel’entorn proper i queensajuden aformarel pensamentabstracte, aplicable anous contexts ia

creacionspròpies.Novol dir ques’hagindeproposardirectamentaquestes activitats i esperar unresultatconcret coma correcte, sinóquecal tenir-les presentspersuggerir-les enelmomentconvenient,dinsdeltreball d’investigació queun omésinfantsfacindins d’un context adient.Són nomésexemplesque podenprovocar altrespropostes, quepoden suggerircaminsdedescobertarelacionats ambelconeixement matemàtic.

Amb ampolles de diverses formes, mides, colors...

• Observació,classificaciói ordenacióespontàniaper partdels infants.Cadascú,segons elseu procésdereflexió i elseu momentmaduratiu, trobarà els criterisdeclassificació quesiguicapaçdeportar aterme.

• Ordenació,quan siguielmoment, delesampollessegons laseva capacitat.Realitzar primer hipòtesis, comprovar posteriorment,ordenar ireflexionarsobrelarelacióentre la forma, l’alçada ilacapacitat

• Fer hipòtesis, comprovar ireflexionarsobre quantesvegades elcontingutd’unadeles ampollescapdinsd’una altra. Reflexionar itrobar lamanera decomunicarqueuna és tantes vegadesl’altra i que l’altraésunadeterminada part delaprimera.

• Elmateixqueenel punt anterior,peròapartird’untercer flascó queserveixid’unitat per alesaltresdues omésampolles.Comparació,ordenacióicomunicació dels resultats ambllenguatgematemàtic.

• Utilitzaciódels comptagotes perflasconso ampolles petites, seguint el procediment del punt anterior.

• Presentaciódelaunitat decapacitat convencionalqueenssembliadequada, probablementelmil lilitreo el centilitre.Presentar-loatravésd’unaprovetagraduada, experimentar ireflexionarsobrequantes vegadesaquestaunitatcapdinsd’un litre.

• Provarquants mil lilitres ocentilitres cabendinsd’una deles ampolles.

• Fer hipòtesis sobreels centilitresi/omil·lilitresque cabendinsd’unesdeterminades ampolles, relacionant-lesambl’ampolla quehemprovat Comprovar i reflexionar sobre els resultatsobtinguts.

• Fer hipòtesis iposteriorscomprovacions sobre quantesvegades cabrà el contingut d’unaxeringa oampollagraduadadins d’unaaltraampolladelaqualjasesap la capacitat.

• Ferhipòtesissobrequantpesaunlitred’aigua.Comprovar-ho.

• Apartirdelque pesaunlitre d’aigua,reflexionaricomprovarquanpesarien undecilitre, uncentilitreiunmil lilitre.

• Reflexionar sobrecompodem saberla quantitatd’aiguad’unaampolla sense mesurar lasevacapacitat, sinóelseu pes. Ferhipòtesisiposteriorscomprovacions.

• Fer hipòtesis sobre quinvolumocupaunlitred’unlíquid.Comprovar-ho.

• Apartirdelvolumqueocupaunlitredelíquid,reflexionaricomprovarquinvolum ocuparien undecilitre,uncentilitreiun mil lilitre.

• Reflexionarsobrecompodemsaberelvolumdel’interiord’unaampolla apartir del líquidquepotcontenir.

• Apartirdesaberquinaés la capacitatd’unaampolla,ferhipòtesisi comprovarquinés elseu voluminterior i quin seràelpesdel’aiguaque potcontenir. Reflexionarsobre els resultatsobtinguts.

• Fer hipòtesis icomprovarsobre què fapujarelvolumdel’aigua d’undeterminatrecipient enintroduir-hiunsòlid,elseuvolumoelseupes.Comprovar-ho amb pecesd’igual volum ipesdiferent(ésinteressant queaquestes peces siguincubsd’un centímetre de costat idematerials dediferentsdensitats).

• Comprovarqueunobjecte d’un centímetre cúbic semprefaaugmentar unmil·lilitre. Reflexionarsobre lamesura indirectadesòlidsdeformes diverses.

• Aportantuncubellodipòsit,delqualsabemlacapacitat, ferhipòtesis icomprovarquantesvegadeshicabrà ellíquidd’unadeterminada ampolla.Expressar matemàticament la relacióentre un recipienti l’altre,tant d’unamaneradirecta cominversa.

• Amb ampolles i/o recipientsenl’etiquetadelsqualses puguillegir lasevacapacitat, reflexionar,ferhipòtesis icomprovar relacionsentre aquesta i altresampolles deles qualstambésabemla capacitat.

Daus de diverses formes, tant regulars com irregulars

• Observació,classificaciói ordenacióespontàniaper partdels infants.Cadascú,segons elseu procésdereflexió i elseu momentmaduratiu, trobarà els criterisdeclassificació quesiguicapaçdeportar aterme.

• Ordenaciói classificaciódeles diferentsformespolièdriques que tenenels daus.

• Totamenade treballsobre el volum i la forma.

• Observació dedausregulars iirregulars. Preguntar-sesiundauirregularpotserequiprobable. Comprovar-ho tirant-lomoltes vegades, anotantels resultatsifent elgràfic perveure latendència quevatenintamesura queaugmentael nombre detirades.

• Ferjocsdeprobabilitati atzaronentri el raonamentsobrepossibilitat, probabilitat i seguretato certesa.

• Crear diferents jocs ques’hagin dejugarutilitzant dausdiferents.

• Utilitzarels dausperfer càlcul mental,donant funcions diverses a cadascundelsdaus emprats.

Col·lecció de caixes

Lescaixes ofereixenunamultitud dedescobertesmatemàtiques i,alhora,sin’hemdefer per embolcallaro guardaralgunobjecte, precisemdemultitudde coneixementsmatemàtics pertalqueensquedincorrectes.

Amb les caixes, podemtreballar també totalainformacióescrita alesseves cares(contingut: pesnetipes brut,composiciódel producteiexcipients, caducitat, codidebarres, preu), que segurque contémolts aspectesmatemàtics:mesures,tants percent, nombresdecimals, fraccionaris...

Contenentambéuna grandoside creativitat pertal deseduir elcomprador(forma, color, eslògans,imatges,tipologiagràfica...) quetampoc no estàexemptadematemàtica.

Laformadeles caixesenspermet treballar els poliedres,elseu volum, lesseves parts...A més deser,uncopmuntades, poliedresmés o menyssimples, sovintcontenencomplexes pestanyesque permetenmuntar-les i quees mantinguin sòlides.Eldesenvolupament plade lescaixesésmoltinteressantdesdel punt devista matemàtic

Laconstrucciódecaixesper contenirobjectes concretsensajuda aaplicard’una manera creativaels conceptesassolitsenl’observacióde col·leccionsdecaixesdiverses.

Una càmera de retratar des de dins

Consisteixainvestigari descobrir quèpassa atravésdel forat d’unacaixafoscaquan l’observadorés adins.

Femla caixa (oaprofitemuna caixad’embalatge de nevera)

Si fem lacaixa,activitatquepermetunamultitud detreballmatemàtic,hemdepensar que hadeserprougran per cabre-hidins.

Lafaremnegraperdins,quenohi entrigensdellum. Compremlàmines decartró,folrem un delsseus plans amb paperd’embalarnegre,dissenyemeldesplegament dela caixa i, finalment, ajuntem totesles parts completant-la.

Quanja latenimfeta,fem unforat molt petitenundelslaterals, aunaalçadasuficient perquèelcap de quisigui dins,assegut aterra, noeltapi.Alaparetdedavantdel forat iaproximadament alamateixaalçada hienganxarem unfullDINA3blancqueserviràde pantalla.

Ja hipodem entrar. Segurament,als primersmomentstot serànegre,però, apoc apoc,la nostravista s’adaptaràa la foscor iveuremalgunaimatge a la pantalla blanca.Potserque haguemde retocaruna mica el foratpertal dedonar-liladimensió adequada

Eldescobriment

Si el foratésl’adequati l’interior de la caixa ésproufosc,seguramentsentiremel crit d’emoció del’observadorque hi ésdins quans’adoni de comesveulaimatge alapantalla.Veurà la imatge encolor,peròs’adonaràquenohihares alseu lloc, totestàgirat,el queés aladreta esveu a l’esquerra;eldedalt, abaix...

Convéquequiésadinsnocomuniquielqueveufins quetots hagin fetl’observació; sihofa, lamàgiadeladescobertas’esvairà.

Però...què passa i perquè passa?

Quèpassaentrelaimatge real i la reflectidaal fons dela caixa?

Ésevidentquehasofertuna transformació,peròquina iperquè?

Esveulaimatgegirada,eldedaltésabaix;eldeladreta,al’esquerra...Nomésunpuntes mantéalmateixlloc, el punt del centre.

La imatge ha giratalvoltant del punt. Hafetungirde 180◦ .Perquè?

S’haproduïtunasimetria,peròonésl’eix oelpla desimetria?

Partintdelaideaque lallumviatjaenlínia recta,siposéssimunfilenganxat en cadascundels puntsdel’objecte real ielféssimpassar pelforat mantenint-lo benrecte,arribaríem just on veiem laseva imatge.

Quan femuna simetriaenel plarespected’uneix, totesles rectesqueuneixen unpuntde la figura original ielseusimètricsón perpendicularsa un amateixa recta,queésl’eix desimetria. Quan femunasimetriad’unobjecteenl’espairespected’unpla, totesles líniesque uneixen unpuntdel’objecteamb elseusimètric són perpendiculars a unmateixpla queés el pladesimetria. Totes les rectesquevan desd’un punt delaimatge real fins almateix punt reflectitdinslacaixa passen pelforat delacaixa.Éselforatde la caixaunpunt desimetria?

Podríem analitzar sientrel’objecte realielreflectitdins la caixa esconservenleslleis bàsiques delasimetria:

• Esconservalaforma.

• Si esguarda lamateixa distància desdelafigurarealfinsalpuntdesimetriaidelpunt desimetriaalaimatgevirtual,lesdimensionsdelesduesimatgessóniguals.Ladedins la caixa esveumés petita perquèapropemelplaenquèes reflecteix.

• Sifemunaaltrasimetriadelaimatge virtual quetenimdinslacaixa,sembla que doni la figura inicial, però en un lloc diferent: hasofertunatranslació. Lasuccessiódediverses simetriesnoésigual alafigurainicial.

Leslleis bàsiquesdelasimetria, lescompleix; pertant, podemconsiderar quela caixaprovoca unaimatge simètrica del’espaiexterior situat davantdel forat.

Provemdefer unafotografia

• Hemdeportarelpaper fotogràfic bentapatperquènose’ns veliabansdefer-loservir, per aixòelposaremdinsd’una caixa fosca petita.

• Taparemelforatde la caixagran iensassegurarem queno entrallumperenlloc.

• Uncop dinslacaixagran, trauremelpaper fotogràfici,ambl’ajutd’una llanterna tapada ambpaper vermell,la col·locaremsobre la pantalla blanca dedins la caixa i la fixarem ambuntros decinta adhesiva.

• Tancaremlallanterna.

• Destaparemuns segons elforatde la caixagran i el tornarem atapar.

• Desenganxarem elpaperfotogràfic,elposarem dins la caixafoscapetitaianirema revelarelpaper.

Com que possiblementlaprimerafotografia no enssortiràprou bé,caldràinvestigar eltemps d’exposiciónecessari perquènosurtinigaire fosca nigaireclara.Espot ferunassaig amb un fullde paperfotogràfic, tapant la part que novolemquees veli ambuntrosdecartolina negra.Aniremexposantadiferentstempspetiteszonesdel paperfotogràfic. Anotaremel tempsd’exposicióen cadascunadeles proves. Obtindremaixíunseguitde provesqueens ajudaranadecidireltempsd’exposiciómés adient.

Pilota de futbol

• Formada per polígonsregulars. Quins? Quants?Qualsevolpolígonla podria formar? Podria fer-seambnoméspentàgons? Inomésambhexàgons?Quin paper fanelspentàgons enla formaciódel’esfera?Podríem continuartreballant els angles enels polígons, els polígonsregulars,els girs,les simetries, elsmosaics...

• Podríemdescobrir comcalcular-ne la superfície apartir deladels polígonsque la formen.Podríem percebre el pesdel’airepesant-la abans i després d’inflar-la.

• Si handescobert el nombrepi,podríem calcularelseu cerclemàximendiferents momentsdel procés d’inflar-la

• Podríemtreballarlapressióilasevamesura,eninflar-la.Améspressió,botamés?Quina ésla pressió ideal?

• Podríemxutar.Quinefectefaelmovimentdelapilotasegonselpuntonesxuta?Comi onxutar perdirigir lapilota a l’objectiudesitjat?

• Podríem ferla nostrapilotade futbolamb robaocartolina, amb unglobusdintreper poder-lainflar...

Bastons

Serveixqualsevol pal,millor mésd’un idiferents,iconvéquealgunsiguiprouirregular.

• Posemelditíndexdecadamàunasotadecadaextremdelpaliprovemdefer-los lliscarcapalmigdelpal,quèpassa?Perquè?

• Passa ambtots els palsigual?Entotss’ajunten elsdits alpunt mig del pal?

• Provemdefer unabalança debraços,ambunpal llisi ambunpaldesigual.Onhede lligar elfil encada palperquès’equilibri?

• Puc provar d’equilibrar lesbalances amb pesosdiversos.Existeix algunarelacióentre els pesos iladistànciaons’handeposar perquès’equilibrilabalança?

• Podem treballar relacions entremesuresde pes.

• Podem treballarlaromana, la bàscula...

Nombre pi

Mesurant el perímetreiel diàmetredediferentscossos rodons. Quantes vegadeslalongitud deldiàmetrecapdinslalongituddelperímetre?

Podemfertaules peranotarresultats iferlamitjanaentre totsels resultatsobtinguts.

Podem ajuntarels nostres resultats ambels d’altrescompanysicompanyesiferdesprésla mitjana.

Amb elsinstrumentsdelsqualsdisposem, podem fermesuresexactes? Amésdades,més aproximacióalresultat exacte? Per quèenspotservirel nombrepi?

Mesura del radi de laTerra imitant el procediment que va seguir Eratòstenes el primer dia destiu ’

• Descobertadelasemblançadetriangles, comprovacionspràctiques delaconservació del’amplituddelsseusangles.

• Activitats perdescobrirque dospals,situatsdeforma verticalal terra,provoquen, conjuntamentamblasevaombra,triangles semblants.

• Activitats perdescobrirla proporcionalitatdels costats homòlegs dedostriangles semblants: mesurad’alçadesd’arbres,fanals,cases...mesurant,enelmateixmoment, lessevesombres il’ombrad’unpal d’un metred’alçadaclavatverticalmental terra.

• Activitats perobservarl’alçadadel’eclípticaal llargde l’any.

• Buscarlesdadesnecessàriesperalanostra medició:situaciógeogràfica exacta i lloc exacteoncoincideixen elmeridià del lloc i eltròpic deCàncer iladistànciaen quilòmetresdes dellloc onens trobem finsaaquest punt.

• Practicar sobrediversesesferessituadesalallumdel Soli ambla«terraparal·lela»els procediments necessarisperefectuar correctamenteltreball.

• Realitzaciódel’activitat el dia 21de junyicàlculdels resultatsdelamesura.

Velocitatdels movimentsdelaTerra

• Apartir delesdescobertes fetesamb la«terra paral lela»sobre els movimentsdel planeta i sabent eldiàmetre dela TerrailadistànciamitjanaalSol, podem calcularla velocitat aproximada delseu movimentderotació idetranslació.

Trobem matemàtiques passejant per lentorn exterior ’

«Comomuchosmatemáticos,extraigomiinspiración de la naturaleza.Quizála naturaleza noparezcamuymatemática:unonovesumasescritasenlos árboles.Pero lamatemáticano tratarealmente desumas.Tratadepautasy porquésedan.Las pautasenlanaturalezason a la vezbellase inagotables»(Stewwart, 2006).

• Passejarpel poble,el barri,laciutat,els entornsnaturals... trobantelementsmatemàtics.

• Descobrirlestransformacionsgeomètriquesqueesmostrenenlescases,elmobiliari urbà,elsvehicles, les plantes i els arbres...

• Fotografiar iposteriormentdebatre els aspectes matemàticsdecada descoberta, classificar-los,aprofundirenels conceptes, iniciartreballsmatemàticsprovocats pel debati els estímuls recollits...

Sistema solar a escala

• Recollidadedades:distànciadeNeptú al Sol,diàmetresdels planetes i del Sol.

• Treballarorepassarelconcepted’escala.

• Adonar-seque, perencabira igual escala dediàmetres idistàncies totelsistema enun lloc reduït,els planetes hauriendetenirdiàmetresmicroscòpics. Cal,pertant,buscar unespaimolt granper poder veure els planetes. Ha deser a l’exterior,enentorns molt amplis.

• Sies potfer pujant unturóouna muntanya,podemaprofitar pertreballar elteorema dePitàgoresper saberladistànciaenla pujadaapartir deladistància horitzontal que enspotdonarelGoogleMapsil’alçada delturó.

• Buscar materials esfèrics(pilotes,llavors...)quetinguineldiàmetrenecessariper representar els planetesenl’escalaque hemdecidit.

• Sortir amesurarladistànciaen què hemdeposarels diferents cossos.

• Adonar-nos que, desd’on hemsituat elSol, nopodemveuretots els planetes aprimera vista.

Altres objectes propers que ens poden portar a la descoberta matemàtica

• Baldufes

• Esferesdediàmetres diversos

• Joguines ijocs

• Fruites

• Utensilis domèstics

• Pedres

• El nostrepropicos...

Totl’entornensparlamatemàticamenti des del’escola hopodemdescobrirambgoig.

Siprovoquemqueaquestamiradamatemàticaesprodueixi, capinfant es preguntaràper quèserveixen lesmatemàtiques.

Ialmateix temps provocarem, senseadonar-nos-en, que aquests infants creixin coneixent amb més plenitudelmónque habitem.

Bibliografia

Alsina,C.(2000). Estimarles matemàtiques.BarcelonaColumnaAssaig, Eines4.

Alsina,C.(2011). Lasmilcarasdelabellezageométrica.Barcelona:RBALibros.

Canals,M.A.(2009). ElsdossiersdelaM.AntòniaCanals.Barcelona: Associació de mestres Rosa Sensat.

Charpak,G.,Léna,P.iQuéré,Y.(2006). Losniñosylaciencia.Madrid:Sigloveintiuno.

Stewwart,I.(2006). Cartas aunajoven matemática.Barcelona: Drakontos. Wagensberg,J.(2007). Elgozointelectual.Barcelona:Tusquets.Metatemas.

Bonesactivitatsperala transició entreprimària i secundària

DavidBarba Uriach

Facultatd’Educació.UniversitatAutònoma deBarcelona davidbarbauriach@gmail.com

Cecilia CalvoPesce

Escola Sadako ccalvopesce@gmail.com

Resum Abstract

Enaquestarticleproposem tres activitats que creiemque poden servir demodelde treballa l’aula perajudarels alumnesenel seuaprenentatge delesmatemàtiques durant latransicióentreaquestes dues etapesdel’ensenyamentobligatori.

Aquestes activitats promouenla resolució de problemes,la cercadepatronsi regularitatsieltreball sistemàtic coma valorsfonamentalsperaaprendre matemàtiques.

Introducció

Inthis article wesuggestthreeactivities that webelieve could serveas amodelfor mathematics classes for pupilsmaking the transitionbetweenthetwokeystagesof compulsory education.Theactivities promoteproblem solving, therecognitionof patterns andorder and systematicworkas thebasis forlearningmathematics.

Creiemque, perajudarels alumnesenelseu aprenentatge delesmatemàtiques durantla transicióentre el ciclesuperiordeprimàriaiel primer cicledel’ESO, noestractatant deposar l’atencióenaquestcontingut o enaquellaltrecomdedonaralsalumnesd’aquestesduesetapesoportunitats dedesenvoluparprocessosqueels apropin aunveritabletreball matemàtic al’aula.Aquestesoportunitats s’handebrindar entot moment, desdelaintroducciódels conceptesfinsal’avaluació,peròcreiemquesón principalment importants en lesmol tes estonesdedicades alapràcticademecàniques.Elmotiu pelqual destaquem aquestmoment de lesclasses dematemàtiques éslapreocupant afirmació deJesús Goñi (2000):«No esnada exagerado afirmarquemás del75%del tiempoescolarse reduce alentrenamientodelos alumnos enlaaplicaciónmecánicadelosalgoritmos».

Tres característiques fonamentalsdel tipusde feina que proposemdurant les estonesde classededicada alapràcticademecàniquessón:

• Laresoluciódeproblemes coma ambient.EnVandenHeuvel-Panhuizen(2001)trobem la nocióde«pràcticaproductiva»quecreiemquereculll’essència delquevolem dir: la necessàriapràcticademecàniques que handedur atermeels alumnes per automatitzar-lesi poderaplicar-les ensituacionsdeveritableinterèsmatemàtices pot ferd’una manerareproductiva (comla quehemvistmilersdecopsenllibres de text oen quadernsd’exercitació clàssics)o envoltadad’unafinalitatmésenllàdelamera pràctica.

• La cercadepatrons iregularitats.Enreiteradesoportunitats, en Burguési Sarramona (2013)esdestacalaimportànciaqueels alumnesactuïn al’aula com averitables detectiusmatemàtics: identifiquinpatrons, facin conjectures ilesrebatinojustifiquin.

• El costumdetreballar d’una manerasistemàtica.Aquestamaneradetreballarintrínsecament lligada alafeina del matemàtic,peròútil per alaresoluciódequalsevoltipus de problemaalqual hemde ferfront,hadeserapresa(Woodham, 2013) ihihamoltes activitatsque podemproposarenles nostresclasses quetenenaquest treballsistemàtic coma objectiuexplícit.

Perexemplificar eltipusde treballal qual fem referència,comentaremtresactivitats que poden ser proposadestantafinals deprimàriacom aprincipidel’ESOenlesqualses promou. Però, abansd’entrarenladescripció d’aquestsexemples,cal dir quel’ajuda alsalumnes enla transiciónopotacabaren latria d’unesbones tasques,sinóquehem deconsiderar l’actituddel mestre (siguideprimària odesecundària)durantlasevaproposta.Esnecessitaunprofessor queconvidiels seusalumnesatreballard’una maneraplena,que elsanimi ambpreguntes adequades,quesiguicapaçdemodificarelseupladeclassequanunaintervenciód’unalumne hofarecomanablei queels organitzienelmomentdecomunicaridiscutirles troballes.El granproblema d’aquestademandacap aldocent és que, mentre quelatria de l’activitatentra dintrede la planificació, l’atenció de la contingència desprésque l’activitatésproposada nopotser planificada i requereixun professorflexiblei benpreparat (Rowland, 2006).

Activitat 1.Cadenadedivisors

Si comparemaquestestrestasques:diguessi 7ésdivisorde 28,diguesalguns divisors de36, diguestotsels divisorsde60,veiemque, mentre que perexecutar laprimera tascasolament calentendreladefinició dedivisor,pera la segona posem enjocl’úsde propietats (per exemple:totsels nombressón divisibles entre1,si a és un divisor de b llavors b/ a éstambé undivisorde b,etc.) iper al’últimanecessitemdonarunpas endavant eneltipusde treball que posem enjoc(comenshofarem perano deixar-nos capdivisor?).Aquestasofisticació en la demanda decada tascaés moltimportant plantejar-lagradualmenticreiemoportú proposar-laals alumnesamb freqüènciaidesquesón petits.Aquestaexercitació, enelcas detrobartotsels divisorsd’unnombre,s’acostuma aferd’unamanera reproductiva (es dóna al’alumneuna sèriedenombres iesdemana quetrobitots elsseusdivisors), peròhiha altres possibilitats defer-ho.

Pensemquèpodriapassarsiproposemaungrup d’alumneslapreguntasegüent:«Quinés el nombrededuesxifres que témés divisors?».Aquestaactivitat implicacalcular els divisors denorantanombres;pertant,convida aplantejarun treballdecol laboracióen quècada

subgrupd’alumness’encarregui d’uns quants(cadascúfalamateixa feina queenla proposta reproductiva,peròaraaquestafeinatéunafinalitat:forma partd’una investigacióproposada atota laclasse). La dinàmicacreada permetgenerarpreguntes oplantejar reptes, com per exemple:«El grupdelaJoanaha trobatun nombre amb 8 divisors:el24,quèlipassaràal nombre48?entindràmés?perquè?».Idesprésd’aquestadiscussióespotproposar:«Com podemfer servirel descobrimentqueunnombre té sempre menys divisors que el seudoble peralatascadetrobar elnombre deduesxifresambmés divisors?Calquefem l’estudi dels divisors de34si ja sabem queel68entindrà més?».

Unadelesmotivacionsquepodemoferiralsalumnesper amillorarlesseves estratègiesde cercaexhaustivadedivisorsd’unnombreés eljocFactorsand Multiples Game,tretdela fantàsticapàgina del ProjecteNRICH (http://nrich.maths.org/5468).

Descripció de l’activitat

Donema dos jugadorsuna llista dels nombresdel’1 al 100;elprimerjugador ratlla un nombrealasevaelecciódelaprimera llistaicomençaamb aquestnombre unasegona llista; alternativament, cadajugador varatllantunnombrede la primera llistail’afegeixalfinalde lasegona,detalmanera queel nombre afegitésdivisor del’anterior o l’anteriorésundels seusdivisors.Perdaquelljugadorqueesquedasensejugadapossible.

La imatge1mostrauna partidaacabada jugada sobreel«tauler»queens ofereixla versió del NRICH abans esmentada.

Imatge 1

Comentaris

Reflexionantsobre eljoc,poden plantejar-sepreguntescom:«Quèpassasicomencemper 1?». Hauríemd’arribara laconclusió quenoseriauna bona idea, ja quesil’altre jugadortria un nombreprimermés gran que 50perdríem. «Compodemutilitzar aquesta reflexió pertrobar una estratègiaguanyadora?».Sicomencéssimnosaltresambunnombre primersuperiora 50,obligaríem l’altrejugador aratllarl’1 iaixípodríemguanyar.

Però enla nostra experiència,aquest joctémoltamés gràciasielplantegem comunsolitarien quèl’objectiuésintentar quelasegona llista sigui commésllargamillor.Perposar en pràctica aquesta versió del joc, ensharesultat interessant l’úsd’unasegonaaplicaciódel NRICH (http://nrich.maths.org/content/id/5468/100square.swf)quepermetseguirla«història»del jocdistingintper colors: elprimernombre triat el pintadegroci cadascundels següentsels pintadeverdsisóndivisors del’anterior odevermellsiensón múltiples. A laimatge 2 es pot veure unacadena llarguíssima(setanta-quatrenombres!)aconseguida sobre aquestsegon «tauler».

Imatge 2

Vallapenaesmentarqueunaaltraversió d’aquestjoc(http://www.transum.org/Software/sw/ Starter_of_the_day/Starter_May7.asp,que apareixalaimatge 3)ens hadonat molt bons resultatsaclasse. Elfetquela primera llista siguide 24nombres permetals alumnesentendre moltmillor ladinàmicadel joci explicarperquè 20 éselmàximllarg d’unacadenaenla qual queden exclosos nombrescom 13, 17,19 o23.

3

Imatge

Activitat 2.Sumadefraccions

Undels contingutsqueestà presentenelpasde primària asecundàriasónles fraccionsi,en aquestàmbit,la pràcticaassociada ala realitzaciód’operacions,enlesqualscal adquirirun bondomini.Aquesta preocupació portaalgunsmestres aplantejarals seus alumnes pàgines senceres d’exercitaciód’operacions.Perònosaltrescreiem queaquestanecessàriapràcticaes potportar a termeenlaforma productivaqueesmentaven al’activitat 1 italcomhoproposa Don Stewardalseublog Medianenunaactivitat que anomena«Four digits,twofractions» (http://donsteward.blogspot.com.es/2011/04/four-digits-two-fractions.html).

Descripció de l’activitat

Donem a unalumnequatretargetesencadascunade les quals apareixunnombre: 2,3,4 i5. Demanem a l’alumnequeles col·loquienl’esquemadela imatge 4formant dues fraccionsi quedoni el resultatde la sumaen formadefraccióirreductible.

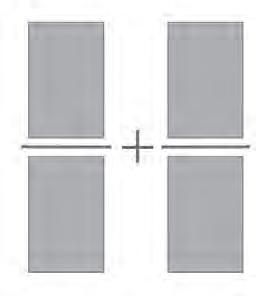
Imatge 4

Compots disposar lestargetes perobtenir coma suma:

• Unafracciódedenominador10?

• El resultat mésgran (oelmés petit) possible?

• Una fracció quenosiguiimpròpia?

• Elresultatmésproperpossiblea3(oa2)?

Fes unpetitinformeque expliqui comhohaspensat.

Unamanerad’atacaraquest problemaés feruna llista delesdotze distribucionspossiblesde les targetes,sumar-les i triarels resultats que compleixinles condicionsdelestres preguntes (la commutativitatdelasuma fainnecessarianalitzarles altres dotze possibilitatsenquèles dues fraccionsintercanvien elseulloc enlasuma).

Peròsegur que aclasse tindremalumnes quenovoldran fer aquest tipus detreballipreferiran fermenys sumes acanvid’unareflexió prèvia alacol locaciódelestargetes.

Enaquestcas, la resposta alaprimerapreguntainvolucramolts components:

• Quines fraccionshandetriar perquèel resultattinguidenominador10?Laprimera idea que poden tenirels alumneséslimitar-seals casosenquèuna delesfraccions hade tenirdenominador 2il’altra 5, però tambépodriapassarqueuna tingués denominador 4,l’altre5i queel resultattingués denominador10 després d’unasimplificació.

• Desprésdetriatsels possibles denominadors,handeposarenjocun procés de treball exhaustiu: si les fraccionsdepartida tenendenominadors2 i5,podenfer 3/ 2 + 4/ 5 o 4/ 2 + 3/ 5,peròcaldràferles sumes percomprovarque compleixenamb els requeriments dela pregunta(això els farà descartaruna deles dues possibilitats, ja queel resultat simplificattédenominador5). Si les fraccionsdepartidatenendenominadors4i5, tambétenendues possiblessumes 3/ 4 + 2/ 5 i 3/ 5 + 2/ 4,perònomésunaelsdóna un resultat dedenominador 10

Pertrobarlasumamésgran,elprimerquehandepensar és queles dues fraccions handeser impròpies(sialgunanohofos, intercanviant elnumerador ieldenominadores podriaobtenir unresultat mésgran),però aixòels deixarà encara tres sumesper analitzar: 5/ 2 + 4/ 3 = 23/ 6, 5/ 3 + 4/ 2 = 11/ 3 i 5/ 4 + 3/ 2 = 11/ 4.Persaberquinéselmajordelstresresultatspodranexpressar-los comfraccionsdelmateixdenominador,podranexpressar elstres resultats ennotaciómixta otrobar lasevaexpressiódecimal.Elraonamentseriaanàlegpertrobar la sumamínimai,en trobarque 11/ 10 ésel resultatmínim,queda respostalatercerapregunta:sielmenorresultat possibleésmajorque1 tots ho serani,pertant,ésimpossiblecol·locarlestargetesdemanera queelresultatnosiguiunafraccióimpròpia.

Enla cercadelasuma més properaa3interessariaanardescartantalgunesdistribucionsde les targetes (perexemple: sihan sumat 3/ 2 + 4/ 5 = 23/ 10, queésmenorque3,nocalquesumin 2/ 3 + 4/ 5,ja queseràunnombre menori,pertant,més allunyatdel3), però en aquestapregunta el procésdedescartnorepresentarealmentuna manera d’evitar fermoltes sumes iels alumnes acaben complintambl’objectiu depràcticaambel quehavíemproposat l’activitat. Quan tinguin les sumes candidates a tenirelresultatmés proper a3,tornarananecessitar compararfraccions i descobriranquehihadosresultatsqueestanigualmentpropers:31/ 4 i23/ 4,sitreballen amb notaciómixta,o2,75i3,25, sihofan amb notaciódecimal.Aquesta comparacióésmoltmés rica quantrobemles dues fraccions quemés s’aproximen al2,ja quesón 23/ 12 (perdefecte) i 13/ 6 (perexcés). Lanotaciómixta permet veure amb unafacilitat relativa queles distàncies al2 són d’1/ 12 i 1/ 6 i, pertant,la segona ésméspropera. Peròtreballar ambexpressionsdecimalspotposarenalgun compromísalguns alumnes, ja quehaurande comparar lesdistànciesal2dedosnombresdecimalsperiòdics:1,9166... i2,166...

Comentaris

Unadeles característiques principalsdel plantejamentd’activitats depràcticaproductiva ésel canvi radicalenel«contracte didàctic».Quan proposemals alumnesunapàginad’operacions, les realitzen,lesentreguen i,posteriorment,escorregeixen; algunes poden estar bé,d’altres no,peròelfetde fer-nealgunade malamentno és realmentdeterminant, jaquepothaver sigutunadistracció,il’objectiuerapracticar lamecànicai això s’hafet. Encanvi,enincorporar coma objectiula resoluciód’unproblema, ferbélesoperacions ésunapartimprescindible

perdonar la resposta correcta.Això portaalfet que elsalumnes,treballant en petitsgrups, «vigilin»ocomparinels resultats quevanobtenintambels seuscompanys.

Endescriurel’activitat, hemesmentatla possibilitatqueels alumnes considerin coma estratègia plantejartotesles sumes possibles icalcular-les.Davant d’aquesta opciódetreball, enshemtrobatque, enuninici,elsalumnesacostumen acomençarfentsumes al’atzar, sensesentir lanecessitat deferuntreball sistemàtic queels doni laseguretatquehan trobat totes lessumes possibles i que non’hanrepetit cap(enuntreball sistemàtic podrien,per exemple, fixar laposiciód’unadelestargetes imoure les altresexhaurint totes les possibilitats abansdemoure la primeratargeta).Els mestres, ambles nostresintervencions,els hemde ferconscientsdels beneficisdeteniruna estratègia davant d’aquesta mena desituacions.

Tambéhem comentat la possibilitat quealgunsalumnestrobinpertinentutilitzarl’expressió decimald’unafraccióperrespondre algunesde lespreguntesplantejades.Enaquestscas, podem valorarsiens interessaallunyar-nosdel’objectiuinicialdepràcticadesumesa canvi deconnectarfraccionsi decimalsireflexionarsobre els beneficisd’aquestes connexionsper facilitarlaresoluciód’unproblema.

Una ampliacióaaquestaactivitatés la deplantejar elmateixproblemaamb restes (o multiplicacionsodivisions)i,enaquestsentit, l’únicapreguntaqueofereix una situació qualitativamentdiferentrespecte alasuma ésladetrobarelresultatmésgranimés petit, ja queara noestractademaximitzarels sumands,sinóde trobar lesfraccions mésallunyades possibles.

La demandad’unpetitinformesobre la resolució del problemaes basaenel nostre convencimentque tanimportantcomtrobar lasolucióés saber-laexplicarojustificar.

Activitat 3.Quadrilàters enungeoplàde3 × × × 3

Deles moltes propostesque podem feramb ungeoplà(segurament elmés famósdels materialsmanipulatiusrelacionats ambeltreball ambgeometria plana i,sortosament,força presentenles nostresescoles), hemtriataquesta enconcret perlaseva història. Laprimera

Imatge 5

referència que tenimd’aquestaactivitat ésl’articleescritper MariaRigon Grandesso,de l’escolaelemental deCartigliano,aparegut a la revista L’insegnamentodellaMatemàticae dellescienzeintegrate,vol.2,núm.3,i traduïtperFrancescEstevaperalarevista L’Escaire,la primerarevista dedidàcticadelesmatemàtiques publicada en català,arafa trenta-cincanys (https://sites.google.com/site/espaijordiesteve2/lescaire.pdf).

Descripció de l’activitat

Esdemana als alumnesquetrobintotselsquadrilàterspossiblesquees poden obtenirenun geoplàde 9 punts.

Alaimatge 6 tenimalguns exemples d’aquests quadrilàtersi unamaneradedesenvolupar aquestatasca: fent servirgeoplans digitals(enaquest cas,els geoplanssónelsque proposa el projecte«CountMe in Too»ahttp://www.curriculumsupport.education.nsw.gov.au/count mein/children_geoboard.html, peròse’npodentrobar molts d’altres,talcomesveua http://appletspuntmat.blogspot.com.es/2013/09/geoplans.html). Peròaquestatascaespot fer sobre geoplans materials(enaquestscas,les diferentssolucionsquevan trobant els alumnesespoden recollir mitjançantfotografies)osobre geoplans que podendibuixarels alumnesenunpaperquadriculatoquepodemlliurarimpresos.

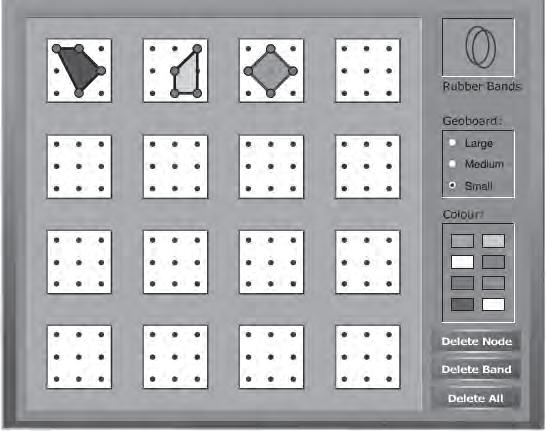
Imatge 6

Creiemqueésunabonaactivitat perquèels alumnestreballin engrupsipuguin donar-se suport entreells no sols al’horadecercarmoltes solucions,sinóenassegurar-sequenoen repeteixencap.Perquèaquesttreballexhaustiu quedemanem alsalumnespuguitenirlloc, hauríem d’administrarambcurainformacionstalscom dir-losquantessolucionsdiferents hi ha abans queellss’enfrontin a la pregunta«els he trobattots?»(perexemple,sidonemunfull amb geoplansimpresos perquè hirepresentin lessolucions, convé que hihagimés desetze geoplanspernodonarpistes d’unamaneraprematura). Però trobar totselsquadrilàtersno és fàcil; pertant, arribarà elmomentquehaurem d’intervenir donant informació dosificada: «us falta un trapezi»,«non’heutrobat capdecòncau?»,«esteusegursqueheutrobat tots elsp aral lelogramspossibles?», etc.D’aquesta manera, l’úsdels nomsdeles figurestéun sentitil’alumneexperimentael beneficide la classificacióde quadrilàterscomaeinade comunicació.

Trobartotes lessolucionspossiblesensdónal’oportunitatde convidar-los a treballard’una manerasistemàtica.Hihaurà alumnes queseguramentho tindran encompte, peròd’altres necessitaran les nostrespreguntes peradonar-sequeanarrevisantles sevessolucions per tipusdequadrilàters:quadrats,rectangles, paral lelograms,trapezis, etc.ésunabona estratègia, molt pròpiadelesmatemàtiques.D’altrabanda,quan posemendubtel’afirmació d’unalumnequediuquenoméshihadosquadratsentre lessolucions, l’estem animant a no restringirlessevessolucionsalesposicionsméstípiquesd’aquestesfigures(perexemple,els quadratspodenno tenirels seuscostatsparal ·lels ales bandesdel geoplà).

Una altra maneraque elmestre intervinguienlarecercade totesles solucionsésproposant aungrupquehatrobatunquadrilàterd’aquellsquemés costatrobarque passi alapissarra i el representi peralsseus companys (si esdisposad’unapissarra digital espoden ferservir les aplicacionssobre geoplans digitalsabansesm entades). Larestadegrupsbuscaranentre els quejahantrobatsiaquest«jaeltenen»osiésun denou.Aquestafeina ésmoltinteressant, jaquelaposiciódeldelapissarranotéperquèserlamateixaquelaquehandibuixatenel seugrupijustificarperquèdosquadrilàterssóniguals,malgratlasevaposició,ensacostaal món deles simetries i els girsipromouunús de vocabulari ipropietats geomètriquesque moltesvegades aprenend’unamaneradescontextualitzadade la sevafinalitatcomunicativa (perexemple, poden refutarlaigualtatentredosquadrilàters dientqueel primertéunangle rectei elsegon noo queenunels costatsoposats sóniguals ienl’altreno,e tc.).

Comentaris

Podríem pensarque nohacanviat resentrenta-cincanys,perònoésaixí.L’activitatque proposaval’any 1979 éslamateixaque femactualment, però el procésde presentacióés moltdiferent.Sidoneuun copd’ull al’articledeRigon (teniul’enllaçmés amunt), veureu que l’activitat que presentem ésl’onzena(de tretze de proposades),estàestructuradaseguintla filosofiadedescobrimentdirigit pròpia de l’època(és adir,vaproposant tasquesambles quals vaavançant apetitspassos capalconeixementgeneralquevolqueadquireixinels seus alumnes) ielprocésestàmoltpautat, fins itotel nombrede geoplansqueapareixensota cadapreguntaindica lessolucionspossibles:primertrobar elsquatrepolígonsnoconvexos, després elstresquadrats,despréslesaltres tresfiguresque tenen els costatsparal·lels 2a2, etc.

En lamentalitatactual,l’activitatde trobar tots els quadrilàters possiblescontinuasent perfectament vàlida, peròlapresentemenunambientderesolucióde problemes enel qual desapareix qualsevolcamí pautat.

Cloenda

Amb elsexemplesdescrits icomentats, hemintentattransmetre algunesideesque creiem bàsiques perajudarels alumnesenelseu aprenentatge delesmatemàtiques durantla transicióentreprimàriaisecundària.

• La importànciadedissenyaractivitatsmolt flexibles quepermetin que, davant d’un mateixenunciat que plantegem a totsels alumnesquetenima l’aula, siguinellselsqui

determininelgraud’aprofundimentdelatasca queels plantegem. Aquestaprofundiment,atesaladiversitatdel’alumnat, dependrà mésdeles possibilitats decadaalumne quedelcursenquèestà.

• La importànciad’unificar una maneradefermatemàtiques a les aules, jasiguinde primàriaosecundària, méscentrada eneltipusde pràctiquesqueenels continguts matemàticsalvoltantdelsqualsgirenaquestespràctiques.Creiemqueelquehauria dediferenciareltreball d’un mateix alumne en una etapa ienl’altrano ésel contingut matemàtic dels problemesqueli proposem, sinóelseu progrésenl’actitudambquè afrontaaquests problemes: augment delasevadisposició perfer conjectures,dels elementsdequèdisposa per justificar-les i del’eficiènciaenel pensamentexhaustiu queli permettreballarsistemàticament.

Referències

BurguésC.i Sarramona, J.(coord.) (2013a). Competènciesbàsiquesdel’àmbit matemàtic Identificaciói desplegament a l’educacióprimària.Barcelona: GeneralitatdeCatalunya. (2013b). Competènciesbàsiquesdel’àmbit matemàtic.Identificaciói desplegament a l’educaciósecundària obligatòria.Barcelona: GeneralitatdeCatalunya.

Goñi,J.M.(coord.)(2000). Elcurrículum dematemáticas enlosinicios del siglo XXI.Barcelona: Graó.

Rowland, T.(2006). TheKnowledge Quartet: A tool fordevelopingmathematics teaching. ConferènciaplenàriadelaFourthMediterranean Conference onMathematicsEducation,Palerm,Sicília,http://www.maths-ed.org.uk/skima/Rowland%20Palermo%20paper.pdf [2015, 2 de maig]

Van den Heuvel-Panhuizen,M.(ed.)(2001). Childrenlearn mathematics.Utrecht:Freudenthal Institute.

Woodham, L.(2013).EncouragingPrimary ChildrentoWorkSystematically.NRICHProject: UniversitatdeCambridge, ahttp://nrich.maths.org/9776 [2015, 2 de maig]

Laresoluciódeproblemes complexosperparelles d’alumnesambTDHAi

senseTDHAalasecundària

YolandaColom

Universitatd’Andorra

NúriaRosich

Universitat deBarcelona

Resum Abstract

Enles últimesdècades,l’educació matemàticahafetèmfasienlaresolució deproblemesmatemàtics(NCTM, 2000).

Amblaintroducciódel’aprenentatge matemàtic per competències(Generalitat deCatalunya, 2013)encara s’ha donatmés valor aaquest tipusd’activitat.D’altra banda, sabem, desd’unenfocament sociocognitiu,que la construccióde coneixements al’aula esprodueix enla interaccióambelsaltres.Alnostre estudi investiguemlaresolució dels problemes complexos dels alumnesamb dèficit

d’atenciói hiperactivitat (TDHA) a secundària.Els resultatsmostren comels estudiants ambTDHAtreballantambuna parellamillorenlasevacompetència matemàtica enla resoluciódeproblemes entreballar deforma cooperativa.

Introducció

In recentdecades, mathematics education has emphasized mathematicalproblem solving(NCTM, 2000), and withthe introductionofskill-basedlearningfor mathematics (Serramona,Burgués,2013) thistypeofactivityhasgainedevenmore importance.Ontheother hand,from a socio-cognitiveapproach, weknow that knowledge inthe classroom comesfrom the interactionwithotherpupils.Inourstudywe investigatehow secondary studentswith attentiondeficithyperactivitydisorder (ADHD)solvecomplexproblems.Theresults show that studentswithADHDimprovetheir mathematical competence inproblem solvingwhenworking inpairs.

Estudis deladècada dels anysnorantadel segle passat vanmostrar quela construcciósocial del coneixement (Cobb, Yackel iWood,1995)en bonapart esdu aterme apartir deles interaccionsengrup o perparelles.

Sabem que, per alaconstrucciódeconeixements,els alumnes handedonarunsignificat personalalscontingutsquese’lspresenten al’aulai ser capaçosd’aplicar-los endiferents situacions. Autors deladidàcticade lesmatemàtiques comBranco, Angelinoi César (Branco, AngelinoiCésar, 1995;1995,1998) hanutilitzatel coneixementsociocognitiuesmentat per Vigoski enlaconstrucciódel coneixement.Sfard(2008) consideralaconceptualitzaciódel pensament comuncas particulardelacomunicació,entreun mateixiamb altrespersones. La construcciódel coneixementdesd’aquesta perspectiva comunicativa només tésentit enel contextdelainteracciósocial. Així,Sfard (2008) iKrummheuer (2011)veuenenl’aprenentatge uncas particulardelaparticipacióenlapràcticasocial.

Elsreferents del’estudi

Alsúltimsanyssóndiverseslespolítiques educativesquesuggereixenfomentarladiscussió matemàticaal’aula (Sfard, 2008;Webb, 1991),tot i queelsol fetdediscutiren parelles no garanteixl’èxitdela qualitatdeles argumentacions (Sfard iKieran, 2001).Enunestudisobre parellesvanobservarquefaltava comunicació efectiva perserproductivaper a l’aprenentatge encara quetreballessin enparella;aquest fetelsvainduirapensarqueunaltreaspectea considerar eraeltipusdefeina.

Algunsautorshan ressenyat laimportànciadelasituacióen quèesduen atermelestasques (Abreu, 1998; Carraher,Carraheri Schliemann, 1989),sobretotaquellesquesón delavida quotidiana enfrontde lesdelaboratori, encara que siguin d’estructuressemblants.

César (1998)ensdónadosexemplesde parelles asimètriques analitzantcadascundels comportamentsdels membresdela parella i ens mostra elvalor pedagògicquetéla promociódeles interaccionsenl’aprenentatgematemàtic,enl’adquisiciód’habilitatsi en lamillora del’èxitescolar Elvalor deltreball per parelles éslanecessitat d’enfrontarels alumnesa diferentstipusd’argumentacions iintentarcol·locar-seenlloc del’altreperseguir elsraonaments, la qual cosaportarà elsalumnes aunaprenentatge més reflexiu.

Alnostre estudivolemidentificarquinesinteraccionss’estableixen quan els alumnesresolen un problemaen parelles formades perunalumneamb TDHAi unsense.És peraixò queens hemcentratenels estudisduts atermeinicialmentper Cobo(1998),queanalitza idefineix conceptesque nosaltrestambé utilitzarem. Lesdiferentstipologiesd’interaccions quemostra són lessegüents:

• Intervenció. Hemdetenir present queenuntorn de paraula hipot haver diverses intervencionsi que el canvi detorndeparaula potimplicar uncanvi d’intervenció. SegonsCalsamiglia ialtres (1997)es potdistingirentre:

Intervencionsproblematitzades:són lesque converteixeneltemaenobjectede debat

Intervencions noproblematitzades:són lesquenoaportenresal tema dediscussió.

• Intercanvi. Ésquan esprodueix unareacció.S’entén com areacciólaresposta a un estímul,és adir,a una acció.Per aquestmotiu, podem distingir les situacions següents.

Existeixuna referència implícita o explícita a la intervenciód’A

Intervenció del subjecte A

No prenla paraula i continua elsubjecte A

Però el subjecteB prenla paraula

Produeix una reacció en el subjecte B

No existeix cap referència implícita o explícita a la intervenciód’A

Però el subjecteB prenla paraula

No produeixcap reacció enelsubjecte B

Però el subjecteB prenla paraula

No prenla paraula i continua elsubjecte A

Imatge1. Quadre de les interacciones d’intervencions.

No prenla paraula i continua elsubjecte A

Envoler ferl’anàlisi seguint aquestes categoriesamb les nostres parelles d’alumnes(de TDHA isense),enshemtrobatqueenscaliaintroduir-ne de noves perexpressarelselementsd’intercanvi quetenenlloc ambaquests alumnes i que no eren presentsenla bibliografia revisada. Per aquestmotiu,vam crearunsistema decodis d’interaccionsambalgunescategoriesnoves, relacionadesamb les presentades enl’estudi deChico(2014) itambépresentsdins elmarc teòric imetodològicdel treballde Cobo(1998).Elscodisques’hanaplicatsónelsd’aportar, compartir,dubtar, iniciar,rebutjari donarsuportdonadesperChico,(2014) inosaltres hem afegitlescategories:desconnectar, interrompre ipreguntar,quan els alumnes comencen aresoldre els problemes mirantacadamembre dela parellade formaind ividual.Després queels alumnes jahan llegitel problema i estanen ple procésde resolució, hem tinguten compteles interaccionsentre els dosmembresde la parella iels codis utilitzatshan estat elssegüents:d’aclariment, ampliació, qüestionament,clarificació, dubte,exposició,opinió, perífrasi, refutaciói síntesis,donatsper(Chico, 2014).

Lesnostres aportacionss’hancentraten lesinteraccionsd’atenció(CA)/desatenció (CD)de la parellad’alumnes.Són lessegüents:

• Externes: quan hihaaltresalumnesque captenlasevaatenció(CAE) ocausen desatenció (CDE).

• Internes: quan l’alumne,sensecapinfluència, atén (CAI) odesatén(CDI).

Dissenydelainvestigació

L’estudideles interaccions,elvan dur atermeeneltranscursd’untaller matemàticsobre el geoplà. Entre els diferentsobjectius d’aquesttaller,hihaviaelsdeveuresiun materialdidàctic

(enelnostrecas,elgeoplà)podiaajudara fixarl’atenció dels alumnesamb TDHA isieltreball ambparelles contribuïa a lamillora dela resoluciódeproblemes ambaquesttipusd’alumnat. Partíem delahipòtesiqueels materialsdidàcticspodenajudar alaresolucióde problemes amb parelles,especialment enels alumnesamb dèficitd’atenció. Tambévolíem veure si els tipusd’interaccions queexisteixenentreelsalumnes(amb TDHAi sense) col·laborena resoldre els problemes. Espretenia queels alumnes construïssin estratègies conjuntes enla resoluciódeproblemes,jaquehandenegociarels significatsi mantenir relacionssocials entreells perresoldreelproblema (Wertsch, 1991).

El taller disposavad’unes activitats prèvies per atots els alumnesperquè totstinguessinels mateixos coneixements. També teniaactivitats d’aprenentatge,queeren fonamentalment problemes deconnexió(problemesquenosón d’aplicacióimmediata,sinóque impliquen relacionardiferentsconceptes), perquèvolíemque fossinunacontinuaciódeles activitats queesfeienal’aula.Alhora,volíemqueaquestsproblemes fossin complexos irealistes, perquè consideremquesón precisament elsqueenspodenmostrarmésles competències. I,finalment, hihaviaunesactivitatsd’avaluació perveure elsconeixementsapresos.

Població

La mostrade l’estudi,lavanconstituirtotsels alumnes de tercer cursd’educació secundària del’escolad’Ordinod’Andorra. Vanformarpartdel taller dematemàtiques untotalde48 alumnesi,peraltreball per parelles,esvatriar unalumneamb TDHAiunaltre senseprocurant quehihagués una bonaentesaentre ells,ja que l’objectiuera que poguessin resoldreels problemes.El totaldeles parelles d’alumnesambTDHAi sense vaserdesis.

Enaquestarticlemostrem, a talld’exemple, unabreudescripciódetalladad’unadeles parelles del’estudi ilaresolució d’un problema.Aquímostreml’anomenadaparella C.Les característiques decada membredelaparellasón lessegüents:

• Alumne 1. Va néixeraAndorra. Té15anys.Laseva mare té estudissecundaris. Té germans iésl’únicmembrede la família que té dictaminatTDHA. A casaparlen diferents idiomes (català icastellà).Du aterme activitatsextraescolarsesportivesunescinchores setmanals.Sesentsegurquanfales activitatsmatemàtiquesqueell coneix icreuque no necessitaajuda enlaresolució de problemes.Ésunalumneque,totitenir diagnosticat TDHA,noesdistreu ambfacilitat (creiem que és comaconseqüència de lamedicació), tot i quesís’evadeix delesexplicacions,però quan està atentcaptalesexplicacionsi proporcionasolucions als problemes. Aquestalumne assoleixel nivellde curs tant en els conceptes comenels procedimentsdel’àreadematemàtiques ambunanota de5,5.

• Alumne 2. Parella sense TDHA. Va néixeraAndorra. Té14anys.Ésunalumneal qualagradenlesmatemàtiques,ambunbonrendimentacadèmiciunbonnivellde llenguatge. Parlaamb correccióelcatalà,el castellà, elfrancès il’anglès.Els seus pares tenenestudis universitaris.Aquestalumne téintenció decursarunbatxilleratcientífic, segons elsqüestionarisd’orientacióacadèmica.Elseu rendimentacadèmic téuna mitjanade8.

Aquímostreml esinteraccions quees produeixenenl’anomenat problemadel’Antàrtida, queésundels problemes d’aprenentatge.

Anàlisis iresultats

Superfícied’uncontinent

Acontinuació,espresentaunmapa deL’Antàrtida.

ANTÀR TIDA

kilomètres

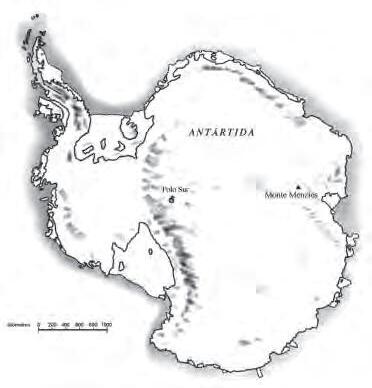
L’enunciatdiu:«Estimal’àrea del’Antàrtidautilitzant l’escala queacompanya elmapa.Mostra comhasfetels càlculsiexplicacom has fetlateva estimació(pots dibuixar sobre elmapa, si t’ésútil perferlaestimació)».

El procésde resolucióseguit perla parellaéselqueesmostraacontinuació:

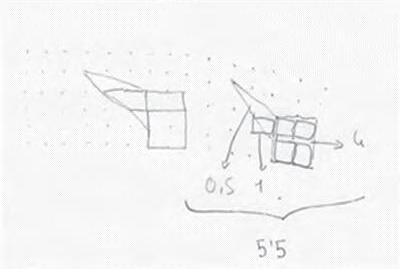
1.1. Primer realitzen el dibuix en un paper

1.2. Seguidament, ho presenten en el geoplà

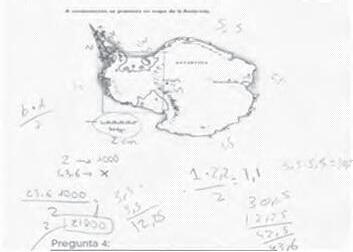
1.3. Finalment ho passen a l'enunciat

Imatge2. Esquemadetreball. Durantlaresolució, podem assenyalarcom unmomentinteressant eldiàlegques’estableix utilitzant elgeoplà.Enunprincipi,l’alumnesenseTDHAfalalecturadelproblema i,sobre unfulltabulat(geoplà ambpaper), faeldibuix aproximatdel’Antàrtida (imatge1.1). Llavors, l’alumneambTDHA(sembla quehaentèsbéelproblema)agafa elmapa del’Antàrtida ihorepresentaamb elgeoplà(imatge 1.2)i,seguidament,faeldibuixa sobre l’enunciat(imatge 1.3).

Pol Sud Mont Menzies

Mostrempartdeldiàlegentreelsdos alumnes, perveurecom plantegen elproblema i les argumentacionsqueutilitzen.

Alumne 1(senseTDHA): Potserésaixí. Ensenya aquestdibuix. Ésunabona estimació.

Alumne2(ambTDHA): Síques’hiassembla.

Imatge3.Fotografiarepresentació delproblemaamb elgeoplà.

Alumne2(ambTDHA): Ara hemde trobarl’àrea.

Alumne 1: Sí.

Alumne 2: D’acord. Doncs, l’àread’això és 1 quadrat, 2 quadrats, 3 quadrats, 4 quadrats, ésquatre.

Alumne 2: Doncs,quèés?Ésdos.

Alumne 2: Iaquíhihaunquadrat, ésa dir,aixòésunquadrat.

Alumne 1: Iunacosarara.

Alumne 2: Iaixò, comhofem, ésmig.

Alumne 1: És mig.

Alumne 2: Iaixòés0,5.D’acord.

Demanaunreglealscompanysisegueixenladiscussiósobrelamesura:

Alumne 1: Vinga, elmesurem.

Alumne 1: Aixòésellímit.Mesuremapartird’aquí.

Alumne 2: No.Perquèapartird’aquí?Primermesuremaixò, desprésaixò idesprésaixò.

Alumne 2: Aixòés5,5,aproximat. Iaixò també mesurasiésunquadrat.Ésaproximat.Això siésunquadrattot aixòfa4.Vingamolt bé.

Alumne 2: Noséquèfaremambaixò.

Alumne 1: Iaixò ésuntriangle. Sí,això ésuntriangle.

Alumne 2: Llavors,quèfem?

Alumne 2: No. Fes-ho tu.

Segueix mésdiàleg i llavors arribena:

Alumne 1: 3,5per3,5,seran?

Alumne 2: Seran 12,25.

Alumne 1: D’acord.Araels sumem. Suma’ls.Quesón 42,5.

Alumne 2: Sí,42,5.

Alumne 1: D’acord.Com calculeml’àrea del triangle?

Alumne 1: Ésqueésaixò. Deuser.Li sumem 1,1,queésl’àreadeltriangle.Pelqueindiquen queserà 43,6.

Iposteriormentfane lcàlculde 43,6 per 1.000 idivideixen entre2.Ambel quedonenuna resposta final de 21.800 cm2 .Lasolució no és correcta, peròha estat interessant veure queel procedimentseguit sí que ho és. Ladificultat quetenenésquenointerpretenbél’escalaino sen’adonen nivalorenelresultat.

Acontinuació,mostrem l’assignació de lescategoriesper l’anàlisidelproblema.

Per ferlareducciódelesdades,s’ha passat primerlatranscripcióenforma de taulaper poder detectar,analitzaricomentarels diferentsinstantsi motiusque provoquen uncanvid’actitud enla resoluciói lainteraccióentre els integrantsdelaparella.

Observacions

Aïllat Pregunta-resposta Pregunta Cooperatiu

Llegeixtotelproblemainodiures més. Llavors fan un dibuix aproximat de l’Antàrtida en el paper. Com mostrem a continuació.

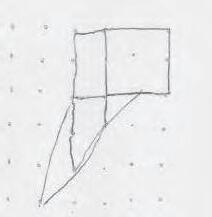
Alumne1(ambTDHA) Alumne2 (senseTDHA)

Aixòes faaixí. ’hi

Ontenimel mapa. Creusques assembla? Què estàs fent?

Aveurel’àrea, si ho fem a partir d’això: 1, 2, 3, 4, 5, 6.

Volsdir? Sí, no. í Un,dos, tres, quatre; això fa 6.

00.00 02.00 03.09

Ho fan tenint present el geoplà, ja que realitzen l’entramat.Veiem que tots dos dirigeixen la interpretació de l’enunciat. L’alumne sense TDHAmotiva el que téTDHA.

Cooperatiu Pregunta-resposta Validació

Agafenel mapai hi assenyalen els passos que creuen que són correctes.

Però, és clar, a partir de l’escala. Jotampoc.

03.17 Quina escala? L’escala. Això no és cap escala. Jo no entenc res.

L’alumne ambTDHApregunta com calcular la superfície de l’Antàrtida al company.

Resposta Interrupció Cooperatiu Pregunta Resposta Interrupció

L’alumne senseTDHAfa una pregnta i dóna la resposta. L’alumne senseTDHA li dóna la raó. Inicialment, sense reẃexionar, encara que després observem que reẃexiona, el fa pensar i intenta arribar a les seves pròpies conclusions.

Què vol dir que d’aquí a aquí hi ha 1.000. Potser. Novoldirqueaixòés 1.000. No, a veure. Necessitem un regle. No vol dir que aquí hi ha 1.000. És a dir 1.000, 2.000. I això vol dir que això és 2.000. No? Necessitem un regle. I això vol dir que això fa 2.000.

Taula 1.Transcripció del problema i assignació de categories de la parella

Unavegada s’hacategoritzat elproblema, passema comptabilitzarcadascundelsdiferents tipusd’interaccions queenspermetin compararels resultatsamb altres parelles. Iamblataula comptabilitzemel nombredevegades ques’han donat lesinteraccionsinicialsenfuncióde siles haproduïtl’alumneambTDHA(1)ol’alumnesense TDHA(2).

Interaccióinicial Amb TDHA SenseTDHA Totalnúm.

Taula 2.Taularesum delesinteraccionsinicials del problemanúm. 1, activitatnúm.1,parellanúm. 3.

Acontinuació, comentem elstipusd’interaccions que hansorgit del’anàlisideles dades, així comelstipus que apareixen eneltranscurs dela resoluciód’aquest problema.

• Aportar. Observemquel’alumnesenseTDHAentresocasionsaportai introdueix diferentsideesmatemàtiques:l’escala, lamesura, la realitzaciód’undibuixi,tot seguit, ambelgeoplàfísic,aclareixl’enunciat. L’alumneambTDHAtambéfa tresaportacions diferents:l’escala,elconceptedel càlculdel’àread’untriangle id’un quadrat.Aquestes aportacionspodenaclarirlaresoluciódel problema. Toti queles aportacionsno tenen per quèser correctes, generalmentprovoquen unintercanvid’informaciói indueixen aladiscussió.Peraquestmotiu, aportar es considerauna interacciópositiva,jaque té coma implicacióla discussiómatemàticaquesensdubteensportaràa la comprensió del’enunciatia la resoluciódel problema plantejat.

• Compartir. Aquestasituacióescreaquanelsdosalumnes comparteixenel concepte matemàtic, lametodologia deresolució il’explicació. Elsdosmembresdelaparella actuen conjuntament enla resoluciódel problema, cosaque creaunacomplicitat queresultaeficientperalaresoluciódequalsevol problemàtica.Enlaresoluciódel problema,elsalumneshancompartitdinouvegadeslamateixaidea.Peraquestmotiu, tambéhoconsideremuna interacciópositivaenuntreball perparelles

• Desconnectar. Ésquan undels dosalumnesnoestà centratenla resoluciódel problema, ja sigui per causesexternes, ésa dir,perl’accióolaintromissiód’unaltrealumne,objecte osimplementperunadistraccióalienaalasituaciódel problema, opercauses internes, ésadir,quanéselmateixalumnequis’evadeix delarealitat.Això potprovocar que

posteriormentelseu companytambé desconnectidelasituaciódel problema com hempogutcomprovar.Hemobservatquel’alumneambTDHAs’ha desconnectat tres vegades(la primeraa l’inicidelaresolució delproblema i les successivespermotius generalment derecercade material)i això haprovocatque l’alumnesense TDHA,alseu torn, hagidesconnectatuna vegada, tambébuscantel materialsol ·licitatperl’alumne ambTDHA.

• Dubtar. Observem que l’alumneambTDHAdubta respecte de lainterpretaciódel concepted’escala. Encanvi, l’alumnesense TDHA dubtasobre l’escala, sobre el resultat queha trobat isobre la correcciódelscàlculs realitzats.Lainteracciódel dubtemoltes vegades comportaunapreguntaqueellsmateixosesveuen enlanecessitat derespondreperpoder arribar a unaresolució del problema.Per tant, aquestainteracció que apriori podríemcreurequenoésbona,siimplica unaresolució posterior,creiemque no éstan perjudicial.

• Iniciar. Éslaintroduccióa la resoluciódel problema.Observem quel’alumneambTDHA indica apartird’ons’ha demesurarperferel càlculcorrectedel’àreadel’Antàrtida. Encanvi,l’alumnesense TDHAiniciales argumentacions. Comença la resoluciódel problema realitzantundibuix aclaridoracompanyat posteriormentperlarepresentació engeoplàdel’alumneambTDHAi introduintl’enumeraciódelsquadrats.

• Interrompre. La interrupcióenl’explicacióenla resoluciód’unproblema sensemotiu aparentésuna acció queladu atermegeneralmentl’alumneamb TDHA;ésuna acció queva mésenllà de la desconnexió. Enaquest cas, tenimuna interrupció perpart de l’alumneamb TDHA queestàmotivada perlanecessitat detenirun regle i,encanvi, tenim quatreinterrupcionsdelseu companysenseTDHA tambépelmateixmotiu.

• Rebutjari donarsuport. Sóndues interaccions que, al llarg dela resolució,s’hanmanifestatsis vegadesentotal. Totsdos rebutgenlesmesuresdel’escalaqueestableixen. No estan d’acord enel concepted’escala ienlaseva mesura. L’alumne amb TDHAdiuque el càlculqueestan fentésl’àreadel’Antàrtida iafirma que l’argumentació realitzadaen la resoluciódel problema ha servit. Encanvi,l’alumnesense TDHA dóna suportalaidea del càlculdel’àreadeltriangle contestant la preguntadel seu company.

• Preguntar. L’alumnefa unapreguntasobre l’enunciat, lainterpretació olaresolució. Aquestaacciócreaun diàlegentre elsalumnes, comportalanecessitat depensar i respondrea les inquietuds manifestades perlaseva parella. Les preguntesque fa l’alumne amb TDHAsóndetipusaclaridor iconceptual:«I comsapsaixò?»,«Comes calcula l’àreadeltriangle?». Encanvi, l’alumnesense TDHAfapreguntes perestar segur queelseu company entén el queestàdienti li potaclarirels dubtesqueseli presenten; perexemple: «Perquè apartird’aquí?», «Llavors,quèfem?»,«Quèfem?».

Acontinuació, mostremelgràfic resum delesinteraccionsinicialsque hanaparegut enla resoluciódel problema:

AportarCompartirDesconnectarDubtar IniciarInterrompreRefusarDonarsuport Preguntar

Imatge4. Gràfic quemostralesinteraccionsinicials entrelaparellanúm. 3 enlaresolució del problema de l’Antàrtida.

Iamblataula comptabilitzem elnombredevegadesques’handonatles interaccionsper parellesenfunciódesileshaprovocat l’alumneambTDHA(1)ol’alumnesense TDHA(2).

Intervencióparelles Amb TDHA SenseTDHA Totalnúm.

Aclariment

Taula 3.Taularesum delaintervenció de les parelles.

Els dosalumnes llegeixen bé l’enunciat, amb fluïdesa. Peròlesseves argumentacionssón incompletes,ja que no interpreten correctamentl’escalaino tenenencomptelesunitats demesura.I això provoca queel resultatobtingutnosiguicorrecte,toti quefan unabona interpretaciógràficade l’Antàrtida.Iutilitzenelgeoplà perraonari establir conclusions, encaraquesiguinerrònies.

Iamblataula comptabilitzem elnombredevegadesques’hadonat CA-CD:

Taula 4.Taularesum delesinteraccionsatenció/desatenció.

Observemqueaquestscodisensinformensobre el nombredevegades ques’haproduïtuna desatencióoatenció.L’alumneamb TDHAdesconnectaduesvegades percausesinternes durant la realitzaciódel’exercici. Ésadir,untotaldedosminutssenseprestaratenció. Això provoca que l’alumnesense TDHAdesconnectiduesvegadesitorni aprestaratenciódos cops més.El temps que desatén l’alumnesenseTDHA ésmenora unminut.

Conclusions i orientacionsdidàctiques

Elcasquehemmostratésunaparellaenlaquall’alumneamb TDHA ésun alumne medicat que té bonasintonia ambelseu company.Nohembuscat elmilloralumneamb TDHAni la millor parella,sinó que hempresentat un casestàndard.

L’alumneambTDHA quehem presentathaestatcapaçdeseguirlesargumentacions del seucompany iarribar finsalfinal,malgrat lesseves desconnexions(que tampoc nohan sigut moltes siles comparemamb lesaltres parelles). Elsdos alumnes hancaptat l’enunciat correctament,és adir,sabenqueel problematractade conèixerquant mesura lasuperfíciede l’Antàrtida.Perònohan interpretatcorrectamentelconcepted’escalaitampoc nohan tingut en compteel pasdecentímetres a quilòmetres. Peròhanestat capaçosdetrobarestratègies peraresoldre el problemad’unamaneraconjunta, hangenerat preguntes i argumentacions matemàtiques ihanplantejatel problemaamb elgeoplà. Hanutilitzatles diferents relacions implicadesque hiha enel problema, comsón lesàrees, lamesura,etc.peranalitzarsituacions iper raonar.Elgeoplàhaestatelmitjàperestablirel fullde rutadel problema.

Dels resultats que hem anatobservantal llarg del’estudide cadascunadeles parelles, podem dirqueaquestespresentenforçavariabilitat, ja que no són homogènies entre elles. Apriori, aixòsemblaevident, però enshemtrobatqueaquesta diversitat ésmolt mésgrandelque nosaltresesperàvem, ja que, a més delapersonalitat decadascú,entrenenjoc factorspropis del dèficit(el graud’afectació, elmomentdedetecció,lamedicació,elseguimentmèdic i familiar,lesestratègies decontroladquirides,etc.)a més dediferènciesqueesdonenentre parelles (disponibilitatdetreball amb parella, coneixements,motivació,etc.),encara queen el nostre estudihemtrobat elementscomuns entre elles.Hemvist queaquestaforma de treballgrupal per parelleshapropiciatque,enlamajoriadecasos,toselsalumnesamb TDHA, malgrat lesdiferentsinterrupcions, hanacabat ( enmés omenys temps)resolentels problemes,cosaqueno passaquan eltreballés individual, ja quemoltesvegades elsdeixen alameitat.

El treballperparelles,especialmentambalumnes ambTDHA, generaunpuntdeparticipaciói atencióper part delsdos alumnes. Hemobservatqueels alumness’impliquen més, cadascun enlaseva mesura,enlarealitzaciódels problemes. Iellsmateixos, a l’enquestaque hem passat, hanmanifestatque la utilitzaciódematerials didàcticsels permet visualitzarmésla interpretaciódels enunciats iels ajudaafer un treballmés participatiu.

Referències

Abreu,G. (1998). StudyingSocialRepresentations of MathematicsLearninginMultiethnic PrimarySchools:Work in Progress. Papers onSocial Representations,7(1-2), 1-20.

Branco,J., Angelino,N.iCésar, M.(1995). Ensinocooperativo:trabalho em díade vs.individual. Dins ActasdoProfMat 95 (p. 175-181). Lisboa:Associaçãode ProfessoresdeMatemática.

Calsamiglia i altres(1997). Laparla com aespectacle:una anàlisi de«Lavidaenunxip». Barcelona:Publicacionsde la UniversitatAutònoma.

Carraher,T.Carraher, D. iSchliemann, A.(1989). Navidadez, naescola zero.SãoPaulo:Cortez.

César, M.(1995). Factorespsico-sociais eequações. Dins ActasdoProfMat 94 (p 82-92). Lisboa: AssociaçãodeProfessores deMatemática.

(1997). Investigação,interacçõesentreparese matemática.Dins ActasdoVIII. Seminário de Investigaçãoem Educação Matemática (p.7-33).Lisboa:AssociaçãodeProfessores de Matemática.

(1998a).¿Ysiaprendocontigo? Interaccionesentreparejasenelauladematemáticas. Uno:RevistadeDidáctica de la sMatemáticas, 16,11-23.

(1998b). Socialinteractions andmathematics learning.Dins MEAS1Proceedings (p. 110-119). Nottingham:NottinghamUniversity.

Chico,J.(2014). Impactodelainteracciónengrupo enlaconstruccióndeargumentación colectiva enclasedematemáticas.Tesi doctoral.Universitat Autònoma deBarcelona.

Cobb,P.,Yackel,E. iWood, T.(1995). The teaching experimentclassroom. DinsP.CobbiH. Bauersfeld(ed.). The emergence of mathematical meaning: interactioninclassroom cultures (p. 17-24). Hillsdale, NJ: Lawrence Erlbaum Associates.

Cobo,P.(1998). Análisisdelosprocesoscognitivosy delasinteraccionessocialesentre alumnos (16-17)enlaresolucióndeproblemasquecomparanáreas desuperficiesplanas. Unestudiode casos.Tesi doctoral.Universitat Autònoma deBarcelona.

Generalitat deCatalunya (2013). Competènciesbàsiquesdel’àmbit matemàtic.Identificació i desplegament a l’educaciósecundària obligatòria.Barcelona: DireccióGenerald’Educació Secundària ObligatòriaiBatxillerat. Servei deComunicacióiPublicacions.

Krummheuer,G.(2011). Representation ofthenotion«learning-as-participation»ineveryday situationsof mathematicsclasses.ZDM. The International Journal onMathematicsEducation, 43(172),81-90.

National CouncilofTeachersofMathematics.(2000). Principles and standardsforschool mathematics.Reston,VA:National CouncilofTeachersofMathematics.

Sfard,A.(2008). Thinkingas communicating. Humandevelopment,thegrowth ofdiscourses, and mathematizing.Cambridge,MA:CambridgeUniversityPress.

Sfard,A. iKieran,C. (2001). Cognitionas communication:rethinkinglearning-by-talking through multi-faceted analysisof students’mathematicalinteractions . Mind, Culture, and activity,8(1),42-76.

Vigoski, L.S.(1988). Pensament illenguatge.Barcelona: Eumo,DiputaciódeBarcelona.

Webb, N. M. (1991). Task-Related VerbalInteration and MathematicsLearninginSmallGroups. Journal forReserchinMathematicsEducation, 22,5, 366-389.

WertschJ.V.(1991).Voicesofthemind.HarvardUniversity Press.

EstrellesalaSagradaFamília deGaudí:uncontextnou peraestudiarpoliedres

María delos Desamparados López deBriñasFerragut

InstitutEl Til ler (LesFranqueses delVallès-Barcelona) GrupVilatzara (ICE-UAB) mlope453@xtec.cat

Resum Abstract

Tradicionalment,s’hasostingutque pràcticamentnohihapoliedresal’obrade Gaudí.

Però unaullada adeterminatsindrets dela façanadelNaixementde la Sagrada Família permet entreveurel’existènciade diversostipusdepoliedres. Enconcret, poliedresestrellats querepresenten estrelles amb significatsdiversos. Lavarietatdepoliedresestrellats que trobemserveix demarcperaprofundiren algunes delesseves característiques, alhora que proporcionaunnou context ambquètreballar-los a l’aula

Traditionallyithas been maintainedthat there arevirtually nopolyhedra tobefound inGaudi’swork.Buta glance at certain points of theNativityfacade oftheSagrada Familiahintsattheexistenceofdifferent types of polyhedra. Specifically, stellated polyhedra that representstars with different meanings.Thevarietyofstellatedpolyhedra found provides aframeworkfor further investigationintosomeoftheir characteristics, and a new context with whichtostudythemintheclassroom.

Introducció

Tradicionalment,els poliedres s’hanestudiatenobjectes delavidaquotidiana, enl’àmbit científic(estructurade la cobertad’alguns virus, estructura deminerals...) ifinsitotenobres escultòriquesopictòriquesoenl’arquitectura.

Peròuna revisió dedeterminatsindrets delafaçanadel NaixementdelaSagrada Família de Barcelonapermet ent reveurel’existènciademés poliedres.En concret, poliedresestrellats representant estrelles ambsignificats diversos i queensproporcionenunnou contextquees potportara l’aula perestudiar-los.

L’estrelladeBetlem

Estàsituadaasobred’unacolumna,justalmig delafaçanadel Naixement,aldamunt de l’escenadelNaixement isotaladel’Anunciació(figura 1).

Figura1. Detall delportaldelaCaritat.L’estrella de Betlemésalcentre de laimatge, adalt, just asobre de la columnaquedivideixlaimatge en dues partsiguals.1

Figura2. (esquerra).Vistafrontalampliada. Figura3.(dreta).Les piràmidesespiralssesituen alcentre de cada cinc piràmidestriangulars.

1.Totes lesfotografies,aexcepciód’aquellesque s’indica el contrari, sóndel’autora

Figura4. Agrupem lespiràmidesformantpentàgonsambelcentreenuna piràmideenespiral(esquerra). En repetirelprocés per tota l’estrella obtenim l’estructura dodecaèdricasubjacent (dreta).

Unaimatge ampliada(figura2)enspermetobservar la simetriailaregularitaten la distribució deles puntes.Aquestdetallapuntacap a la possibilitatclarad’unadistribució basada en una estructurapolièdrica. D’altrabanda, observem piràmidestriangulars ipiràmidesenespiral. Aquestes darreresestansituades alcentre,rodejades percincpiràmidestriangulars,com podemobservar alesfigures2,3i4.

Siagrupemles puntestriangularsformantpentàgonspertotal’estrella, obtenimlaimatge dela figura 4. Clarament,ladistribuciódepuntes del’estrellade Betlemsegueix ladisposició delsvèrtexs d’undodecaedre.Als centresdeles cares d’aquestdodecaedre subjacentsesitua una piràmideenespiralpentagonal.

Models teòrics a partir del dodecaedre

Sivolem buscarunmodelteòricde poliedre queexpliquila majorpartdels detalls del’estrella, enshauremdebasarenl’estructura dodecaèdrica.Els poliedres quelisón associats sónalguns arquimedians,coml’icosidodecaedre,l’icosaedre truncat,el petitrombicosidodecaedre oel dodecaedre truncat.

Per tald’esbrinarquinéselmodel teòric possible, hemd’aconseguiruna imatge d’aquests poliedres que hemesmentat abans,peròestrellats percomplet. Aquestesimatges espoden obtenirgràcies al’AppletdelaUniversitat Brasilera FederalFluminense,laUFF,ques’anomena «A Plethora of Polyhedra» (http://www.uff.br/cdme/pdp/pdp-html/pdp-en.html).

D’aqueststres candidats,eldarrer,eldodecaedre truncat,éselquedescartem desd’un principi,jaque les piràmidestriangularsobtingudessónmassapetites comparadesamb les altresial’estrellade Betlemtenenuna mida forçasimilar.A més,són decagonalsino pentagonals.

L’icosaedre truncatquedadescartat, perquè la posiciódelesarestes deles piràmides hexagonals nocoincideix.

Elpetitrombicosidodecaedrequedadescartatenpresentarcaresquadrades,quanal’estrella deBetlem nohihapiràmides quadrangulars iéspocprobablequeaquestescaresdel’arquimedià nos’estrellin i la resta sí.

Finalment,ens quedal’icosidodecaedre, perònovament la posiciódelesarestes deles piràmides triangularsnocoincideix ambladelesdel’estrelladeBetlem.

Pertant,tots aquestscandidatsquedendescartats(figura 5).

Els delgrupde poliedresdeJohnson(aquells poliedresconvexos les caresdelsqualssón polígonsregulars, perònosón platònics,niarquimedians,niprismes,niantiprismes) també queden descartats, ja que nopresenten laregularitat,nilasimetria,ni l’esfericitatenla distribuciódelesseves caresdelamateixa manera queesveu a l’estrella.

Elsque presenten esfericitat contenen cares quadrades otriangularscontigües perles arestes, dos detalls quetampoc no apareixen a l’estrellade Betlem.

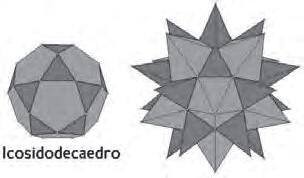
Icosidodecaedre

Icosidodecaedre totalment estrellat

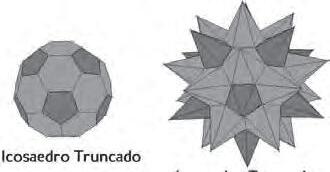
Icosaedre truncat

Icosaedre truncat totalment estrellat

Figura5. Comparació de l’icosaedre truncat ide l’icosidodecaedreestrellat ambl’estrella de Betlem. En ambdós casos, tots els detallsreferentsalnombre,la distribució i l’orientació de les piràmidesno queden explicats, fetpel qualaquestsmodels teòricsnosónvàlids.

Model teòric final

Uncopdescartatstotsaquestscandidats,encaraensquedaunapossibilitatquepugui aportar unmodelteòricvàlid perexplicarlamajorpartdels detallsdel’estrellade Betlem: és la composició dedospoliedres.

Delamateixa manera quel’Stella Octangula espotentendrecomunoctaedreestrellatocom unaintersecciódedostetraedres, existeix unapossibilitat perexplicarl’estrellade Betlem perunprocedimentsimilar.

Quinspoliedreses podrien intersecarpertal d’explicar-la?

L’agrupacióenpiràmidestriangulars il’estructuradodecaèdricasubjacentsón característiques d’undels poliedresde Kepler-Poinsot. Concretament,delgrandodecaedre estrellat de Kepler.Espotentendrecomunicosaedre estrellat ocomuna intersecciódedotze pentagrames (estrelles decincpuntes)sobrelesdotze seccions pentagonalsquees poden realitzarenunicosaedre.

Unacomparacióambl’estrellade Betlem(figura6)enspermet comprovar lacoincidènciadel nombre,ladistribucióil’orientaciódeles piràmidestriangulars delmodelteòric ambles de l’estrella.Pertant,seriaundels poliedres quela componen.

Figura6. Comparació de l’estrella de Betlemamb elmodel delgran dodecaedreestrellat deKepler.2

Alafigura6podem observar leslletres Ecorresponents a«espiral».

Jaqueles vintpuntes delmodel teòricestanagrupades demanera queels seus vèrtexs estansituats justsobre elsvèrtexsd’un dodecaedre i quealcentredecadagrupdecinc piràmidestriangularssesituaunapiràmidepentagonal espiral, aquestes piràmidesespirals estandistribuïdessobrelescaresd’undodecaedre.

2.Totes lesinfografies depoliedres, aexcepciódelesque apareixenalesfigures 7i 8, hansigutobtingudes mitjançant APlethoraofPolyhedra.

Pertant,serienles puntes d’undodecaedreestrellat depiràmidesespirals. I aquestseria l’altrepoliedre que formal’estrella.Lesespiralsfanqueles puntes nosiguinpoliedres. Les considerem comapart del’ornamentacióafegida aundodecaedreestrellat.

És adir,l’estrellade Betlemes potexplicarmitjançantlacomposiciód’ungrandodecaedre estrellat deKepler ambundodecaedre estrellat depiràmidesenespiral.

Alafigura 7 podemveureuna imatged’aquest modelteòricproposat, resultatdecompondre dos poliedresestrellats. Engroc, elgrandodecaedre estrellat deKepler. Envermell,un dodecaedre estrellat. Lespiràmidesenespiralserien una ornamentacióafegida.

Alafigura8podem compararl’estrelladeBetlemamb elmodelteòric proposatenlamateixa posició,observantlacoincidènciadetoteslespuntes dels dos poliedrescompostosamb les del’escultura,excepted’una,lanúmero3,unapuntaenespiral.

3.

Figura7.Infografia: Jaume SerraNogués.3

Figura8. Vistafrontal de l’estrella icomparació ambelmodelteòric.Infografia: JaumeSerraNogués.

JaumeSerra Noguésésprofessordematemàtiquesal’Institut VilatzaradeVilassar deMar(Barcelona).

Unafotografiaampliadadelapartposteriordel’estrella(figura9)enspermet constatar que aquesta puntaenespiralnoestà enlaposició correcta, potser perlesdificultats enelmoment d’assegurar-la ifixar-la alaparetdela façana.Pertant,elmodelteòricseriacorrecte.

Elspinaclesdelsbalconsdelestorres delafaçanadelNaixement

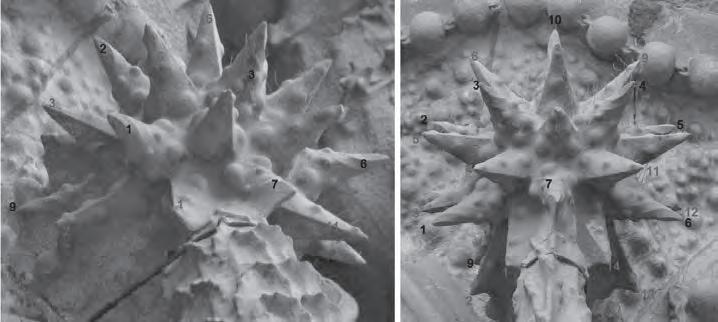
En cadascundels balconsdelestorresdelafaçanadelNaixementhihaunpinacleque constitueix l’extremdecoratiusuperiordel’estàtuadel’apòstol a quivadedicadacada torre. Cada pinacleestà format perestrelles representantuncelestrellat a sobredel’apòstol. En trobem cinc tipusdiferents iper acadascunahiha unmodel teòricdepoliedreestrellatque explicaelsdetallsque hiapareixen (figura 10).

Figura10. Elsdostipus depinacles estrellatsales torres delafaçana delNaixement.

Figura9. Vistadelapart posteriorde l’estrella, ambles puntesnumeradescoma la figura8.

Lapunta3 noestà ben situada.

Models teòrics proposats

Alaprimera estrella(figura 11)podemobservaronze puntesvisibles,quesón piràmides pentagonalsestilitzades i ambpuntesi arestessuavitzades. Cincestandisposadesalvoltant d’una queesdirigeix capa l’espectador in’hihacincmésqueapareixen perdarrere,just entrecadascuna deles cinc quesón enprimer pla. Laseva disposiciói elseu nombrees corresponen alsd’un dodecaedre estrellat(figura 11).

Unasegonaestrellaésladela figura 12.Comqueles puntes del’estrellasón piràmides quadrades,enveiemcinciestandisposadesde manera ortogonallesunesamb lesaltres; el modelteòricproposat éseld’un cub estrellat peragregaciódepiràmides.

Figura11. Estrellaimodel teòricproposat.

Figura12. Estrellaimodel teòricproposat.

Perals altrestrestipusd’estrelles (figures13, 14i 15), nomésapareixen piràmides hexagonals en unnombreiunadisposició quecoincideixen ambels dels següentsmodels proposatsde poliedres arquimedians parcialmentestrellats.

Figura13.Icosaedre truncat estrellat perles careshexagonals.

Figura14. Octaedre truncat estrellat perles careshexagonals.

Figura15. Tetraedre truncat estrellat perles careshexagonals.

Peròsifem unaanàlisimésdetalladacomparant-los elsunsambels altres, podem observar que el nombre,eltipusiladistribució de les piràmidescoincideixen,perònolasevaorientació.

Alafigura15esveu clarament queles arestesdeles piràmides hexagonals contigües tenen dos i trescostats encomú,fetqueés impossiblesinoés que lespiràmidesestanparal leles les unesa les altreso enelmateix pla, peròno ésel cas. Id’altrabanda,observemquetres arestes convergeixen enunúnicpunt,un detallque al modelteòricdeladreta,tambéala figura 15, no es compleix.

Elmateix podem observar enlesimatges deles figures13i 14.Lespiràmidesapareixen girades 30◦ respecte alesdel poliedreproposat.

Toti això,éspossibletrobar unmodelqueexpliquiaquestdetall i, alhora, mantinguiels anteriors,referentsalessimilituds amb algunsarquimedians. Alafigura 16quedail lustrat pera und’ells:

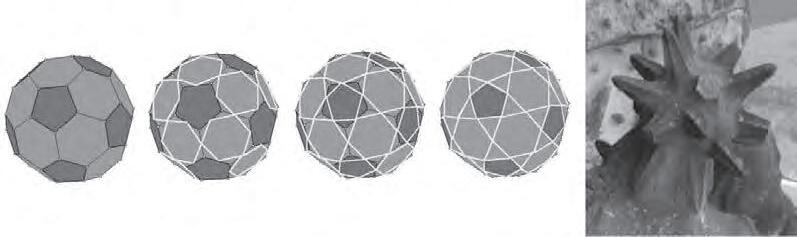
El procésseguit pera generaraquestestresestrelles éselsegüent:

• Partimd’un poliedreplatònic(tetraedre,octaedreo icosaedre)que convertim en arquimediàmitjançant untruncament pelspuntsmitjans.

• Acontinuaciótornematruncar l’arquimedià,novamentpels puntsmitjansde totesles sevesarestes,igeneremnoves carestriangularsquenosónequilàteres.

• Finalment,estrellem elpoliedreagregant-hipiràmides, perònomésperlescares hexagonals.

Nombre i distribució d’estrelles a cada pinacle

Hihemd’afegir undetall més, i ésqueels pinacles detotesles torresnosóniguals. N’hiha dedos tipus, estandistribuïtsd’una maneraasimètrica alafaçanai,amés,ladiferènciaentre l’un il’altre estàenel nombre d’estrelles (enun,n’hihauna demés) ienlaseva distribució, tal com podem comprovar ales figures 10 i17.

Alafigura 10,esquerra,tenimel pinacledelestorresdeSantSimó i Sant Mateu.Elde ladreta correspon alestorresdeSantBernabéiSantJudes Tadeu. Atots dos hiha dos cubs estrellats,dos dodecaedresestrellats,unúnicicosaedre truncatestrellat, dosoctaedres

Figura16

truncatsestrellats idostetraedrestruncatsestrellats(aqueststresdarrers models,estrellats de lamaneraquehemexplicat prèviament).

Però,amés,alpinacledelestorresdeSant Simói SantMateuhihauntetraedre truncat estrellatdemés, situata la partfrontal.

És adir,Gaudíes basaenels cincplatònicsientruncamentsd’alguns d’ells peraconstruir cinc tipusd’estrelles diferents, peragregaciódepiràmides.

Lesestrellesdeles constel· · ·lacions a l’escenadel’Anunciació

Figura18.Imatgedel’arc delesConstel lacions,asobre de l’escena de l’Anunciació.

Eltercerindretdela façana del Naixement enquètrobemestrelles està situat just a sobre del’estrellade Betlem. Estractadel’arc deles Constel·lacions,queemmarca l’escena de l’Anunciació,enla qual l’arcàngelGabriel comunicaalaVergequeseràlamaredeJesús.

Figura17

Enaquestarcesrepresentensisdelesconstel·lacionszodiacals presentsal celnocturn enel momentdelnaixementde Jesús.Són: Verge, Lleó,Cranc, Bessons, Taure iÀries.

En cadascunad’elles esrepresentendiferentstipusd’estrelles.Apareixen menys definides queles estudiades alsdos indretsanteriors, jaquehiha poques arestes icaresclarament identificables, peròelnombrei ladistribuciódeles puntesque presenten fan possible assignarun poliedreconcret a cadascuna.

Models teòrics proposats

Els cincpoliedresamb elsqualses corresponenaquestesestrelles són poliedresestrellats obtinguts directamentapartir dels cincplatònics.A les figures 19 a23lesmostremunaper unaambelmodel teòricenlamateixa posició.

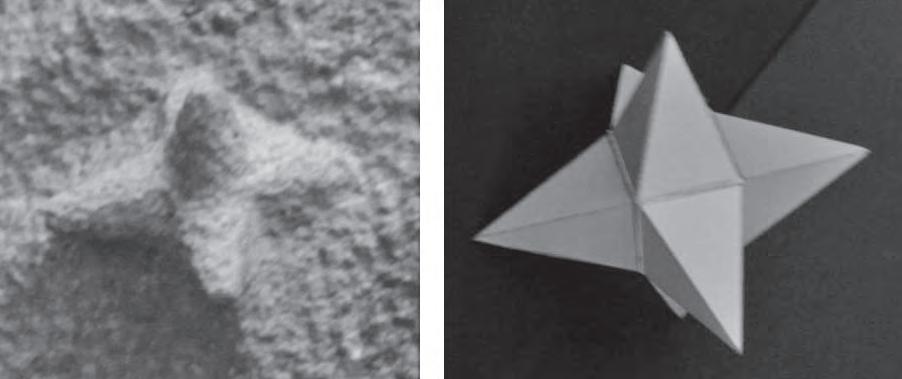
4. Lafotografiadel’estrelladelaimatgeesquerra és d’AlexanderMenzinsky.

5. Lafotografiadel’estrelladelaimatgeesquerra és d’AlexanderMenzinsky.

Figura19. Estrella tetraèdricaimodel teòricproposat.4

Figura20. Estrellacúbicaimodel teòricproposat.5

Figura21. Estrella imodel teòric de l’octaedreestrellat.

Figura22. Estrella imodel teòric deldodecaedreestrellat.

Figura23. Estrella imodel teòric de l’icosaedreestrellat.6

6. Lafotografiadel’estrelladelaimatgeesquerra és d’AlexanderMenzinsky.

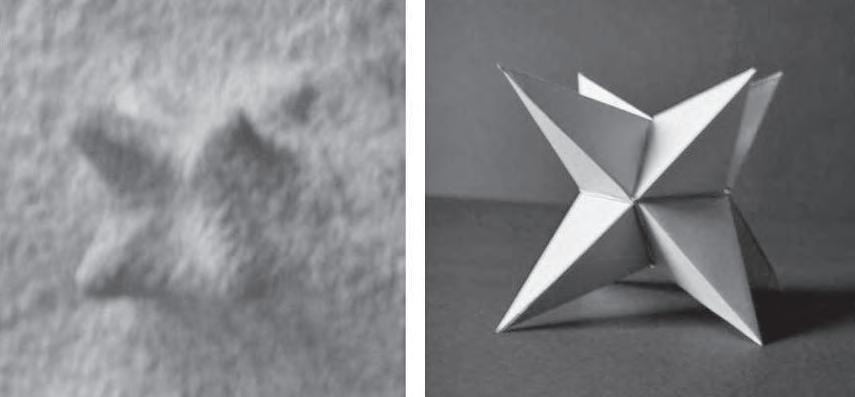
Els quatreprimers, del 19 al 22,tenen piràmides en quèles careslateralssón trianglesauris. Encanvi, alafigura23,elmodel escollit noéselgrandodecaedreestrellat deKepler (un icosaedreestrellat les piràmides delqual tenen careslateralsquesón trianglesauris), sinó unaaltradelescinquanta-nouformes possiblesd’aconseguirunicosaedreestrellat i que presentamés similitudambelque observem al’arc.

Els estrellaments 19 al 21 s’aconsegueixenmitjançant agregació depiràmides alpoliedre platònicoriginal.Elmodel 22éseldel petitdodecaedre estrellat deKepler i s’aconsegueix obéallargantlesarestes deldodecaedrefins queestallen obéperintersecciódedotze pentagrames o estrelles decincpuntes.El model23s’aconsegueix perextensió dels plans quecontenenlescaresdel’icosaedrefinsques’intersequen.

Relació entre els poliedres i les estrelles

La utilitzaciódecincpoliedresdiferentsper arepresentarestrelles té,enaquesta casdeles constel·lacions,unsignificataddicional.

Siacadaestrelladeles constel·lacionsrepresentadessituemunainicialindicant el poliedre platònic corresponenta l’estrellat (T, tetraedre; C,cub;O, octaedre;D,dodecaedre;I,icosaedre) icompareml’esculturaambunmapa estel·lar actual (enaquest cas, prenem comareferència elsdelaUnióAstronòmicaInternacional),trobem quehihauna gran similitud entreles unes ilesaltres, essentpossiblereproduirlamateixa estructuradelínies traçades alsmapes estel·lars (iquees fanservir per areconèixer laconstel·lacióalcel real)enl’escultura, com podemobservar enles figures24a 30.

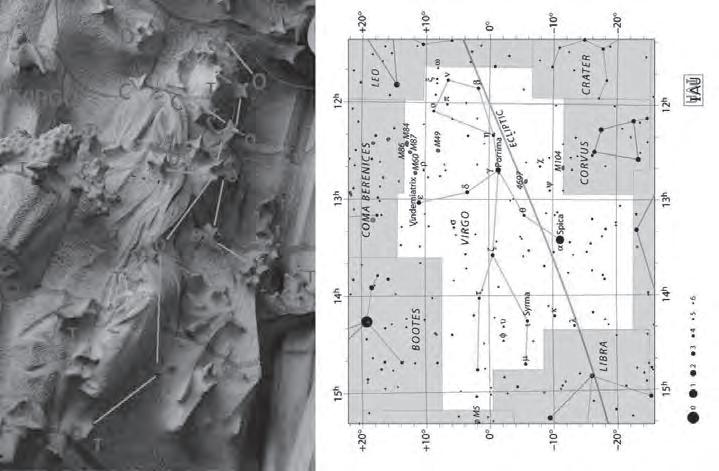
·lació deVerge.7

7. Lafotografiadela constel lació deVerge (imatgeesquerra)ésd’Alexander Menzinsky.

Figura24.Comparaciódelaconstel

lació deLleó.

Figura26.Comparaciódelaconstel lació deCranc.

Figura25.Comparaciódelaconstel

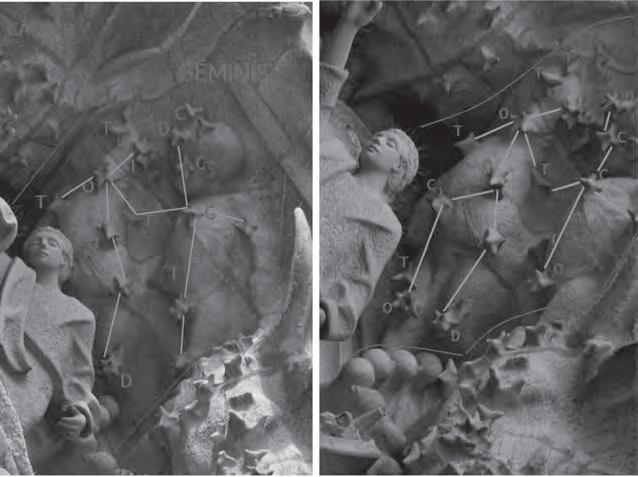
Figura27.Comparaciódelaconstel··lació deBessons.8

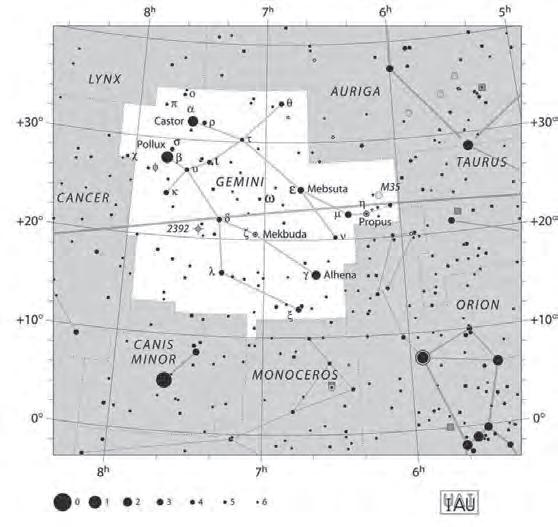
Figura28. Mapaestel laractualdelaconstel llació deBessons.9

8. Lafotografiadela constel laciódeBessons(imatgeesquerra)ésd’Alexander Menzinsky. 9.Totes lesimatges delsmapesestel larsdelaIAU (UnióAstronòmica Internacional)s’han obtingutdela Viquimèdia

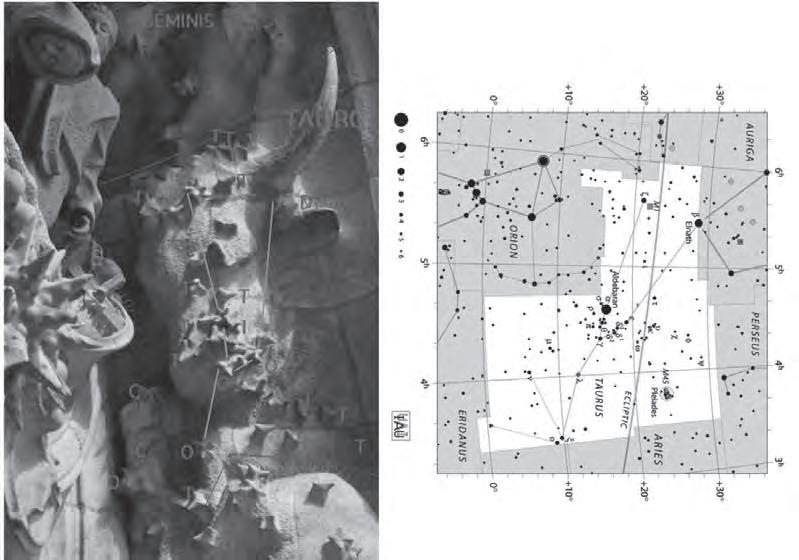
··lació deTaure.

Figura30.Comparaciódelaconstel lació d’Àries.10

10.Lafotografia delaconstel lació d’Àries (imatgeesquerra)ésd’Alexander Menzinsky.

Figura29.Comparaciódelaconstel

Aquestasimilitudpermetestablir unarelació directaentre lamagnitudaparentdel’estrella (és a dir,la brillantorquetéquan ésobservadadesdelaTerra)ieltipusdepoliedreestrellat quees fa servir pera laseva representacióenl’arc deles Constel·lacions.

Unaanàlisidels valors demagnituds visualsdeles 49 estrelles identificables alsmapes(del totalde136 representades a les sis constel·lacions,incloentaquellesmésdesdibuixadesque es prestena classificacióerrònia) ensduu aestablir l’assignaciómagnitudipoliedreestrellat següent:

Magnitudvisual Poliedreestrellat

0,98-1,35 Icosaedre(20 p.)

1,93-2,61 Dodecaedre (12 p.)

2,64-4,35 Octaedre(8 p.)

3,52-4,50 Cub (6p.)

3,57-5,35 Tetraedre (4p.)

Figura31.Font:Dades de magnitudvisual delPrograma CartesduCiel.

Aquesta correspondènciaenspermet afirmarqueGaudí vaferservirels cincpoliedres platònicsestrellats pera crearuna escala debrillantor basada enel nombredepuntes de cadascun,demanera quelamés brillant (menormagnitudvisual) estaria representada per unicosaedreestrellat. Pera lasegüent,menysbrillant,esfariaservirundodecaedre estrellat... iaixí finsa lamenysbrillant,representadaperuntetraedreestrellat.

Lesdiferènciesde brillantor ja es representaven alsmapesestel·larsantics, mitjançant dibuixosdiferentsperacadatipusd’estrella.Però, alaSagradaFamília,aquest procediment es realitza fentservir figuresentresdimensionscom sónels poliedresestrellats.

Aplicacionsdidàctiques

La varietatde poliedresestrellatsquees fa servir ielseu context ens serveixen demarcper a estudiar aspectesdeduesdisciplinescomlageometriai l’astronomia, així com pera entendre lavisiópersonaldeGaudísobreelnaixementdeJesús.

Alguns aspectesenelsquals podem aprofundir són:

• Conèixermaneresdeconstruir unpoliedre/sòlidestrellatapartird’un poliedre qualsevol: perextensió dels plans que contenenles cares, o deles arestes; peragregació depiràmides; perintersecciódepolígons,i percomposiciódediversospoliedres.

• Conèixer possiblesestrellamentsdels poliedres platònics.

• Identificardiferentstipusdepoliedresestrellatsmitjançant:

la utilitzaciódediversesvistes; el recompted’elements característicscomles caresdeles piràmides,les arestes iels vèrtexs,i la representaciód’elementsgeomètricssuperposatsen fotografies digitals.

• Conèixer comesgenerendos dels poliedresde Kepler-Poinsot:elgrandodecaedre estrellat deKepler i el petit dodecaedreestrellat deKepler.

• Reconèixerquanuntruncamentd’unpoliedregeneraunpoliedrearquimediàiquan no.

• Conèixerel concepte debrillantoromagnitudaparentd’una estrella.

• Conèixerla representaciódesis constel lacionszodiacals,tant l’artísticaclàssicacomla utilitzadaalsmanuals d’astronomia actuals,així com ladissenyada perGaudí.

• Utilitzarelconceptededualitatdels poliedres pera identificarels poliedresplatònics estrellats ales constel·lacions.

seccions seccions rcions

pensar p

er pensar d’un minut a una hora

JordiDeulofeu

Departament deDidàcticade lesMatemàtiques ideles CiènciesExperimentals Universitat Autònoma deBarcelona jordi.deulofeu@uab.cat

Quanemtroboacabant aquestarticle, he tingut coneixement queel propermes dejuliol de 2016se celebraràaBarcelonaelCongrés Catalàd’EducacióMatemàtica,ellogotipdelqual contél’expressióc2 em,queensrecordala coneguda fórmula d’Einstein. Des d’aquí, animo atots elslectorsdel Noubiaix aprepararles sevescontribucionsiaparticiparactivamental congrés,pelbédel’educaciómatemàticadel nostrepaís.

Ipensant enel2016m’adono queésunmúltiplede 4i,pertant,any detraspàs.Desprésde tresanys esfènics (lesdescomposicionsenfactorsprimersde 2013,2014 i 2015tenentots els exponentsiguals a 1), ladescomposicióde 2016 no semblagaireespecial, però enspodem adonarràpidame ntque és unnombreambunaquantitatnotablededivisorsi abundant (la sumadelsseusdivisorssuperaeldobledelnombre).Iaquestfetempermetsuggerir-vosun petit problema periniciarl’article.

Problema 1. És possibleexpressar2016 coma sumad’alguns delsseusdivisors (llevat del propide 2016)? Quantessolucionsdiferents hiha?Quina éslaqueutilitzamenysdivisors? Ila quen’utilitzamés?

Quan trobeula solucióqueutilitzamenysdivisorsiconstateu que el nombrededivisors empratséselmenor possible, nousserà gairedifíciltrobar la condició quehadeverificarun nombre enter pertalquees pugui expressar d’una manerasimilar, ésadir,sumant elmenornombre possiblededivisorspropis.Apartird’aquí,uspodeue mbrancar perterrenys força més complexos:n’hihaprou deconsiderarnomésels nombressenars i fer-sepreguntes similars.

Problema 2. Trobeuelmenornombresenarquees pugui expressar com a suma d’alguns delsseusdivisorspropis.Quinéselmínim nombrededivisorsnecessari?

Parlant denombresenters idivisibilitat,ala darreraprovadeseleccióper formarpart d’Estalmat, elprograma per al’estímuldel talentmatemàtic,celebradael 6dejunyde 2015, esva plantejarunproblema l’enunciat delqual éselsegüent:

Problema 3. Formarun nombre de10xifres, totesdiferents,és adir,utilitzantcada xifra unasolavegada,demaneraque,quanposemlaprimeraxifra,elnombresigui múltiple de 1; quan posemlasegona xifra, aladretadela primera,el nombre deduesxifres resultantsigui múltiple de 2; quanposemlaterceraxifra,elnombresigui múltiple de 3, iaixí finsaposarla darrera xifra,queensdonaràunnombrededeuxifresque hauràdesermúltiplede10. Per exemple:123654 podriaser unboninici, ja que 1ésmúltiplede1,12hoésde2, 123de3, 1236de4,12365ésmúltiplede 5i 123654ésmúltiplede6.

Tanmateix,aquest iniciprometedorqueda bloquejatquanintentemposarlasetenaxifra,de manera quelasolució,queexisteix, nocomençaperaquestesxifres. Siteniuen compteels criteris dedivisibilitat,les possibilitatses redueixen molt inoméscal feralgunes proves(moltes menysdelesque potsemblar)pertrobarunasolució.Quan l’hagueu trobat,determineusi és únicao bén’hihaalguna més.

Totique el problema nosemblagairedifícil, als nois inoies quevolien formarpartd’Estalmat elsvacostarmoltresoldre’l i podem dir quecap d’ells vaser capaçd’arribar finsalfinal. Algunsalumnesvanarribar finsa sisxifresi van establir que la novenapodiaser qualsevol xifra, perquèladesenahavia deserel0,demanera queesvan encallar enhaverde posar la setenailavuitenaxifra.Caldirquenopodienemprarlacalculadora,inocalqueusdiguique recordar, o deduir,elcriteridedivisibilitatper 7noésunacosaelemental per aalumnesd’11 anys, encaraque tinguintalent per alesmatemàtiques,coméselcas.

Seguintambelsnombresentersipassantalterrenydelessuccessions,segurquemoltsde vosaltresconeixeu lasuccessió els primerstermes dela qual són:1, 11,21,1211,111221, 312211,13112221,etc.Certament,trobareltermesegüent, queequival aconèixerla regla de formació, ésmolt difícil pelfet que combinaduesinterpretacionsde les xifresqueformenels nombres.Per aquellsquinolaconeixeu, usdiré quedinsdecadanombre, d’esquerra adreta, esvanalternantnombresqueindiquenlaquantitatdevegadesque es repeteix unaxifra,i aquesta xifra,enelnombreanterior. Així, desprésdel’1tenim11,queindica:un1.Després vindrà el21,queindica dos uns,i després 1211,quellegiremaixí:un 2i dos 1.Lasuccessió creix ràpidament: perexemple, elterme16té ja més de 100xifres, amb predominid’unsi presènciadedosos itresos.Sabríeu demostrarque, entota lasuccessió, només apareixenles xifres1, 2i 3?

Alllibre The MathBook,deClifford A. Pickover(versió encastellà: Ellibro delasmatemáticas), hetrobatqueaquestasuccessió, id’altresamb lleis deformació similars,vaser àmpliament estudiada pelgranmatemàtic JohnH.Conway(1937),queles vaanomenarsuccessions «audioactives».Undels resultats sorprenentsés queeltermeenèsimtendeix a C n ,onCés l’anomenada constant deConway (C =1,30357 ), queaparentment notérelació ambla successió.

Problema 4. El primerstermes d’una successió són: 123,111213,411213,14311213... Tenint en compte que té una llei deformaciósimilaraladelasuccessióanterior,sabríeu trobarels termes següents?El creixement d’aquestasuccessióéssimilaral’anterior obé passaalgunacosaquefaqueesredueixi?

Perunavegada, enllocd’acabar l’article ambunproblema,hofaréambunacuriositat d’aquellesquedeixa meravellat qualsevolque apreciïla bellesadels nombresenters.El

professor icompanyd’Estalmat GuillermoPérezemva ferconèixer unnombrede 100xifres que m’hadeixatabsolutamentfascinat.Elnombre és:

31399719737866347113914486515772694858917594191229 38744591877656925789747974914319422889611373939731

Estractad’un nombreprimerque, a més,ésun primer reversible, com ho són 37i 73.Aixòvol dir queelnombre:

13793937311698822491341947974798752965677819544783 92219149571985849627751568441931174366873791799313

que es formaa partir de l’anterior,peròllegitdedretaaesquerra, també és primer.Lahistòria d’aquestnombrefascinant nos’acaba aquí,sinó quetot just comença. Sifragmentem el nombre en10 nombresde10xifrescadascun,ielsdisposemenunataula comlasegüent:

3139971973 7866347113 9144865157 7269485891 7594191229 3874459187 7656925789 7479749143 1942288961 1373939731

resulta que tots sónprimers, i si invertiml’ordre delesxifres,els altres10 nombresobtinguts tambésón primers.Però,siconsideremels nombres queresulten decadacolumna, tenim elmateix: 10nombres primersreversibles. I encara,siformem lesdiagonals,seguimtrobant nombresprimersreversibles.Total, que el nostrenombre inicialde100xifresenshagenerat unapila denombres primersreversiblesquequasi fa venirmalde cap!Quetingueuun bon curs 2015-2016 iensretrobemal proper número.

Bibliografia

Pickover,CliffordA.(2011). Ellibro delasmatemáticas.Madrid:IlusBooks,S.L.

AntonAubanell

claudio.alsina@upc.edu

Perintentarobjectivarlarealitateducativa,finsalpunt que això sigui possibleisense menystenirlaimportànciadels estudis decasos,semblafonamentallarecercad’einesque hofacilitin.Laquantificacióenla descripció dels fenòmensnaturalsisocials ha estatun avençgensfàcili,entermes relatius, forçarecent.Lamesura(enunsentitampli)d’una realitatésel primer pasper poder conèixer-lai,si cal,modificar-la. Éscert queels instruments ilesunitats demesuracondicionensovint el resultatdel’amidament(enun pladiferent, peròbenproperal’aula,novoldria deixarderecomanar elvídeo Lalongituddepèndela unitatambquèes mesura queels estudiantsdel’institut Martíl’Humà deMontblanc,sotala direcci ódel professor Ramon Bergadà,varenpresentaralvídeoMat 2014) i això encaraésmés notable quan estractademesuraraspectes complexos comésel casdelacompetènciade l’alumnat. Tanmateixunaavaluacióobjectivas’hadefonamentarnecessàriamentendades quantitatives, enmesures. L’avaluacióésunartcomplicat, peròimprescindible.

Elmes d’abril passat,elDepartamentd’Ensenyament va ferpúblics els resultatsdeles proves d’avaluaciódel’educaciósecundàriaobligatòria corresponents al’any 2015,aplicades a alumnatde quart d’ESO. Entreles competènciesavaluades enaquestes proves, hihala competènciamatemàtica,ques’articula enquatreblocs: numeracióicàlcul; espai, formai mesura; canvi irelacions, i estadística.Tantper alglobal delamatèria com per acadascun delsquatreblocss’aporten dostipusdedades:

• Les puntuacions mitjanessobre100dels resultatsobtinguts

• Elspercentatges d’alumnes agrupatsenquatretrams segons les puntuacions obtingudes:nivell baix,nivellmitjà-baix, nivellmitjà-alti nivell alt. Elnivell baixmostrael percentatge d’alumnesque no assoleixenla competència.

La taula 1presentaels resultatsobtinguts tot assenyalant lesdades corresponents albloc geomètric(espai, formai mesura) que cridenespecialment l’atenció:

Percentatge d’alumnat ambnivelld’assoliment... Bloc avaluat Mitjana ...baix ...mitjà-baix ...mitjà-alt ...alt

Taula1

Aquests resultats posen enevidència,d’unamanera molt clara,una dificultatimportanten el blocd’espai, formai mesura.Lamitjana de52,2puntsés, demolt,lamés baixadels quatreblocsavaluats,el41,3% d’alumnat mostraunnivelld’assolimentbaix(unpercentatge molt persobre del15,7%d’alumnat que presentaun nivelld’assolimentbaixenelglobal delamatèria) itansolsel14,5%d’alumnatmostraunnivell d’assoliment alt (més de14 puntspercentuals persota del28,8%quemostra un nivelld’assoliment alt enelglobaldela matèria).

Malauradament,aquestesdades segueixen(i accentuen) lamateixatendència quejas’observavaenels resultatsdeles proves d’avaluaciódelsanys 2014 i 2013 ideixen també unatraça claramentobservableenelsdeles proves PISA2012 i 2003quevarenavaluar prioritàriament l’àmbitmatemàtic.Espotampliaraquestainformacióestadísticaenelsdocument s del web delConsellSuperiord’Avaluaciódel SistemaEducatiu.

Larotunditatilapersistènciad’aquestes dadesdifícilmentpodenser atribuïdes abiaixos incidentals. L’evidència quantitativa i elseu manteniment eneltempsdeixen pocsdubtes sobreelfetqueenstrobemdavantd’una dificultat important enl’ensenyamentde la geometriaa secundària quenecessàriamentenshadeportar afer una reflexiósobre les causes iles possibleslíniesdemillora.Enaquest sentit,elConsellSuperiord’Avaluaciódel Sistema Educatiu delDepartamentd’Ensenyamenthapublicateldocument «Orientacions pràctiques per alamillora delageometria», 11 ques’amplia,pelquefa ales proposes concretes, enl’espai web http://www.xtec.cat/web/curriculum/eso/orientacionsgeometria. Quisignaaquestaseccióhatingutl’oportunitat de treballarenaquestsdocumentsquetenen lavoluntatde plantejarunareflexióoberta icompromesa sobre la presènciai eltractament delageometriaenlanostraeducaciósecundàriai de poder serútilal professoratenles seves classes.Cal assenyalarqueles observacionsquecontenenaquestsdocuments,així commoltes deles propostesques’hipresenten,permetenlecturesadaptades a l’etapade primària.Eltreballté dues parts:

• Unaprimerapart enlaqual esfauna anàlisi depossibles causes iesplantegen possibles líniesdesolució.

11. ConsellSuperiord’AvaluaciódelSistemaEducatiu,Departament d’Ensenyament (2015), Orientacionspràctiquesperalamilloradela geometria, Quadernsd’Avaluació, 31,abril,disponibleahttp://csda.gencat. cat/ca/arees_d_actuacio/publicacions/quaderns_avaluacio/Quaderns-davaluacio-31.

• Unasegonapartenla qual esdesenvolupenaquesteslíniesdesoluciómitjançant reflexions específiques i,sobretot, proposantactivitats concretes perportar a l’aula. Es proposen seixanta activitats,trentadelesqualsestan descritesamb molt detall.

Acontinuacióintentarem ferunasíntesid’aquestdocument totposant unaatencióespecial enles propostes pràctiques.

Entrelescausesdeladificultatques’observaengeometria, s’assenyala undesequilibrien laimplementaciópràcticadel currículum.Eltempsescolarésun bépreuat ilimitat. Quan dediquem untempsdesproporcionat a una partdelamatèria, necessàriamentn’estem sacrificant unaaltra.Sovints’hadonat moltméstempsala numeraciói alcàlcul (aritmètic ialgebraic) que alageometria il’estadística.Mésenllàdela pràctica d’aula, aquestésun fetobservableennopocs llibresdetextquedeixenaquests blocs enunaposiciódesegon ordreamb pocespaiialfinal.Un grupdemestres iprofessoratdeGironatitulava«Estadística, tema13»untaller d’estadísticaiprobabilitat adreçat adocents. Probablement,lageometria s’haressentitmésquel’estadísticad’aquestsdesequilibris.Potsercomençarperdiversos blocscurriculars elsdiferents cursos de l’ESO podriaevitar-ho,talcomesproposa enel nou currículum dematemàtiques delDepartamentd’Ensenyament.

Sovint,lamancade tempshaprovocatqueel professorathagués deferunenfocament delageometriamolt centratenel reconeixementdeformes i l’aplicaciódefórmules peral càlculdelongituds,àrees ivolums. Potserunapresentaciómés experimental delageometria plantejantsituacions mésobertesquecomportinexploració,amb materialsiamb programes de geometriadinàmica,percepcióespacialiraonamentvisual, moviment,orientació, ubicació, construcció, connexió...resultariamés motivadorai aportariamés benefici educatiu. Enaquest sentit, eldocument que comentem fapropostes endues vessants: respectealtreball dinsdels blocsgeomètrics(mesuraiespaiiforma)irespectealapresènciadelageometriadins dels blocs noestrictament geomètrics(numeraciói càlcul,canvi irelacions iestadística iatzar).

Pelquefaal treballdinsdelsblocs geomètrics, esproposaavançar en quatredireccions:

• Impulsarlapresència enlesclasses d’activitats quepermetinviure,enprimera persona,l’experiènciadeconstruirconeixement geomètric.Entreaquestesactivitats,poden serespecialmentútilslesque comportenquatreetapessobre lesquals no insistirem perquèjahan estatobjected’un altrecomentari enaquestasecció: experimentació,descoberta,conceptuació i formalitzacióodemostració(sical!).Una metodologiad’aquesttipusésunmarc idonipertreballar,perexemple,laproporcionalitatgeomètrica(teorema deTales),la suma d’angles d’untriangle, les propietats mètriques detriangles rectangles(teoremesdePitàgores, del’alturai del catet),el teorema deViviani...

• Emprarmés material manipulableenl’ensenyament delageometria.Persubratllar laimportànciad’aquesta menaderecurs,manllevem les paraulesde PerePuigAdam al pròlegdel seullibre Geometríaintuitiva (Madrid,1928): «Aquíet presentem,estimat lector,elsqui handeserels teus companysdetreball:unestisores,un cabdell,un regle, un parell d’escaires,unpilómoltgran defulls depaper. Niunsoldia has decomençar lalliçó degeometriasenseteniralcostataqueststeus bons companys,niacabar d’estudiar-la sensedeixar lateva taula materialmentplenaderetalls idepapersamb

figures...».Actualment,disposem d’unaesplèndidaofertadematerialsquepodenser moltútils:desdelsclàssicsgeoplans,tangrams,modelsdefustaodeplàstic(alguns peromplird’aigua)...finsalsconegutsLokon,Polydron,Creator..., oelsmésmoderns Zometool, Geomag, Polydronmagnètic...Tanmateix elsmillors materialssempreseran elsque cadamestre esvagi construintoconvidi aconstruirels seus alumnes. El professoratdetecnologia potser unmagníficaliatenaquesta tasca tot generant sinergiesentre lesduesmatèries.

• Donar méspresència alGeoGebra oaaltres programesdegeometria dinàmica TenimlafortunadecomptarambunaAssociació CatalanadelGeoGebramolt activa queestàtreballant de fermperaconseguir més presènciad’aquesta einaenles classes dematemàtiques engeneral idegeometriaen particular.Les facilitats queofereix per a ferconstruccionsdefiguresgeomètriques iexploracionsdinàmiquessón una invitació inajornablea repensar afons notansolsla metodologia,sinó tambéels contingutsque estreballen aclassedegeometria.Aquíésobligat citarunajoia deles construccions gràfiquesambGeoGebra:Euclid:TheGame. Es tracta d’unamenadejocque planteja successivesconstruccionsgràfiquesamb reglei compàs. S’inicial’aventura amb un menú d’einesmolt petitqueesvaaugmentantamesura queesvan passantnivells, fent les construccionsreptesquees proposen.Així,demica enmica,esvaconstruintl’edifici de lageometriaeuclidiana...comsires!Totuntresor:http://euclidthegame.com/

• Cercarunmajorsuportdels contextos.Lageometriaensenvolta icalaprofitartotes lesoportunitatspossibles perdescobrir-laiexplorar-la: un objectematerial(desd’un llapisfinsa unenvàs,des d’una llaunadebeguda finsa unmosaic),unespaidel’escola (desd’unarbredel pati finsaleslíniesdel camp debàsquet,des d’unplànolfins aunpassadís),l’entornquotidiàdel’alumnat(lacol lecciópermanentdelvídeoMat, http://www.videomat.cat/?page_id=435,contéabundants exemplesd’activitats escolarsd’aquestamena)...Elsconcursos defotografiamatemàtica tambésónunainvitació alamirada matemàticai,enmolts casos, adescobrirgeometria.

Malgratquehihauns blocscurricularsdecairemésgeomètric, es potfergeometria quan estreballaqualsevol dels altres blocs.La matemàtica téun cosdeconeixement únicque a vegades escompartimenta artificialment.Cadacop,entre el professoratdematemàtiques, ésmés compartitel criteri que hauríem decercarelmajor nombrepossibledeconnexions internes(siguitreballantprojectes transversals,sigui fentreferències creuades, sigui programant enespiral...). La integració d’activitats decairegeomètricquanestreballen els blocsde numeraciói càlcul,decanvi irelacions id’estadística iatzar obresuggeridoresoportunitats d’enllaç que, d’unabanda, estenenlapresènciadelageometriai,del’altra,aportenla potència didàcticadelainterpretaciógràficai la visualització. Aldocumentquecomentem hiha moltes propostesenaquestsentit,comles ques’assenyalenacontinuació:

• Elsnombres figuratsiles sevespropietatssón unpuntde trobada entre la numeració ielcàlcul ilageometria.Les demostracions geomètriquesdepropietatsaritmètiques són tanelegants com didàcticamentpotents.En la figura 1sobren paraules:

1

1+3+5 + ··· +(2n 1) = n2

• Descobriri expressar algebraicamentels patronsdeconstrucciódefiguresgeomètriques ésunaactivitat molt bonicapertreballarel llenguatge simbòlic iperintroduirles successionsi les relacionsfuncionals. Dosexemples:

Patronsenfigurespolicúbiques: donadaunasèriedefigurespolicúbiquescomlesde la figura 2,esbrinarel nombre de cubetsqueles formen enfunciód’unparàmetre com,en aquestcas, l’alçadade latorre.

2

Patronsenestructures: donadauna estructura de«tubs iconnectors»comles de la figura 3,trobarl’expressió del nombre detubsiladel nombre de connectorsen funciódelnombredetubsdelabase.

3

Figura

Figura

Figura

• Deduir,amb criterisgeomètrics, laprobabilitat queuna monedallançada sobredeterminadestrames(figura 4)toqui onouna línia.

Cadascunadeles activitatsque s’hanesmentattantpertreballar mésexperimentalment els blocsd’espai iforma idemesuracom perintegrargeometriaenels altresblocscurriculars estàdescrita(algunesmoltàmpliament)enl’espai webdelaXTEC que jaha estat referenciat: http://www.xtec.cat/web/curriculum/eso/orientacionsgeometria.

Malgrat queeltreballquees comentaestà especialmentadreçat al’etapa desecundària, les ideesgeneralsques’exposen i les possibleslíniesdemillora ques’apunten són aplicables al’educacióprimària.Aixímateix, moltes deles propostes concretesquees fanpermeten lectures benadients pera aquesta etapa;sempreéslamirada delmestre laqueadaptael recurs,perquè, afortunadament,les fronteresentreetapessónmés difusesdelque avegades esdibuixa.

Elsresultatsquecomentàvema l’inicid’aquestescritilapròpiapràcticaprofessional ens plantegenun repte seriósalqual calrespondre repensantafonslapresènciadelageometria (tantpelque fa als continguts com alametodologia)entotesles etapeseducatives,donant-li uncaràctermés experimentalifuncionali integrant-la entots els blocscurriculars.Això, d’un costat, permetria construir coneixement directamentaplicable alarealitat més propera al’alumnei,del’altre,contribuiriaa desenvolupar qualitatsmoltgenuïnesdel pensament matemàtic comla percepcióespacialo el raonamentvisual enferdeduccionssobrefigures geomètriques.

Figura 4

No estracta d’unreptefàcil.Calen canvisiels canvis sempreprovoquenincerteses.Peròhiha molta feinafeta desdel’esforçi la creativitatdemoltsmestresiprofessors:les activitats de l’ARC(AplicaciódeRecursosalCurrículum)en sónuna mostra. Tant debo que el document ilespropostesquehemcomentatpuguincontribuiraaquestesforçperferpossibleuna millorade l’aprenentatge d’idees id’habilitats geomètriques per partdelsalumnes i,en definitiva, undesenvolupament més sòliddelaseva competènciamatemàtica.

VoldriaagrairalDepartamentd’Ensenyamentquehagiimpulsat la realitzacióila difusió d’aquest treballi voldriaagrairtambé la col laboraciódelaIolandaGuevara,enSergiMuria ienLluísMora enla revisió d’aquests materialsquedesitjaríem que poguessinserútilsa mestres iprofessorat enlaseva tascade construirmatemàtiques!

mmaca el racó del mma

Elsmòdulsdeprobabilitati

estadística delMMACA

EnricBrasó(MMACA)

Toti queels conceptes ileseinesd’aquesta brancadelesmatemàtiques sóndelsmés utilitzats directamentenlanostravida quotidiana, la sevapresènciaenelsmuseus de matemàtiques ésescassa.

Un treball,aparer nostre,reeixit, ha estatl’exposició«Big Bang Data» que es vaveure al CCCB l’any 2014 ien quèl’aparell tecnològic darrere delsmòdulseramolt important.

AlMMACA,ambunespossibilitatsmésmodestes,hemconstruït ienaquestarticle usels presentem unsquantsmòdulsenquèintentemsorprendre ifer reflexionar sobrealguns aspectes d’aquesttema d’unamanerasimpleimanipulativa.

Les pedres ol’extracciódemostres

Lapropostad’aquestmòdul consisteix a extraureipesarunamostrade10pedresentre una poblacióde100còdolsdediferentsmides.

Observemque, enelsdiversos intentsquefan elsvisitants,lespedresmésvisiblesqueden normalmentsobrerepresentadesil’estimació delpesmitjàqueda,enlamajoriadelsvisitants, persobredelreal.

Apartird’aquestaconstatació és interessantla reflexiósobrelanecessitat d’un procedimentaleatori, lliurede qualsevol subjectivitat, pertald’aconseguirquelamostrasigui representativa.

Figura1. El mòduldelespedres ol’extracció demostres.

L’atzar noésregular

Prèviament aexplicar en quèconsisteix aquestmòdul,us proposemunexperiment.

Demaneu a algúque ompliduesfiles de20caselles delamanera següent:

Una s’ha d’omplirambzeros iunssegonselresultatdelllançament imaginari d’una moneda. L’altres’had’omplirsegonselresultatde20llançamentsreals.

Noushadedir quinaéslaseqüència real iquina éslaimaginada.

Sinoésqueestemmolt«contaminats»per lanostraformaciómatemàtica,ens ésdifícil posar caradesprésde3oméscares.Aixíque,alaseqüència,difícilmenthitrobarem 4omésdígits iguals seguits.Compareu,però, amblafigura2:

Les220 seqüències de20dígits binaris ordenades segonselnombremàxim dedígitsigualsseguits

x =4,66

Figura2.Ladistribució deles 220 seqüènciessegonselmàximdedígitsiguals seguits.

Figura3.Les pilotes de ping-pongdelmòdul«L’atzar noésregular».

Deles 1.048.576(220 )possiblesseqüències,un77% contenen 4o més dígits iguals seguits.

Tendim arepartir mentalmentlasuccessió decares icreusamb més regularitat delque hofa l’atzar.

El mòduldel MMACAreprodueix unasituaciósimilarambduesdimensions. Dinsunacaixa transparenthiha 120 boles deping-pong6delesqualssón taronges i la resta blanques.

Unsenzill mecanisme permet fer-les saltar pertal d’anarvariant laseva col ·locacióaleatòria. S’observa quesempre apareixen agrupacionsizones buides. Sidemanéssim lacol locació aleatòriadeles bolesd’una manera manual,hofaríemmés regularment.

Lano-afectació d’algunsbarrisals bombardeigsdeLondresalaSegonaGuerraMundial ol’acumulaciódedeterminades malaltiesenunentorn són casosenquèes buscauna explicació casualquan podenser explicats simplementpel comportament del’atzar.

Dausintransitius

Consideremelllançamentdedosdausespecials en quèguanya quiobtéla puntuaciómés alta.Conegudeslescaracterístiquesdelsdaus,éssenzill calcularles probabilitatsi,pertant, establir«el dauguanyador».Sorprenentment,aquesta relació no éstransitiva.

Esconeixen diferentsexemplesd’aquestfetambdauscúbics(2).Enaquestmòdul, però, hem anat abuscar unasituació al méssimplepossible, il’hem trobatambelstresdaus tetraèdrics 4-4-4-1,5-5-2-2 i 3-3-3-6.

Figura4. Elsdaus intransitius.

És fàcilcomprovarqueeldau guanyadoren cadaunadelestres confrontacions ésdiferent. Però lasumadeles caresde cadadau és 13,14 i 15,aixíquetenimunaformaalternativa clara d’establir unarelació d’ordre. Éspossiblemodificar la puntuaciópertalque la suma de les puntuacionsdeles 4caressigui lamateixa? Hodeixem obertpersivoleuentretenir-vos.

El bombo,lesmostresielsintervalsdeconfiança

Aquest mòdulconsisteix enuncilindregiratoritransparentquecontéaproximadament2.500 boletesdedos colors. Unapeçaposadaal llargpermet recollir, acada gir,una mostrade 50 boletes.Així, lamostraespot repetir iacumularfàcilment.

Resulta clar peral públicqueel percentatge debolesde co lor delamostranotéper què coincidirambel percentatge delapoblació.Unapeça lliscantmostraelsintervalsde confiançaicomesredueixen amesura queaugmentalamidadelamostra.

Elconcepte d’intervaldeconfiança nos’explicafinsalscursosd’estadísticadenivell universitari.Així,enstrobemque aquestaeinamatemàticad’úsgeneralitzatésòbviament moltmal entesa.

Ambaquestbomboaldavant noésgens complicatcomprovar ientendreque la repeticiód’extraccionsdemostressegueix unespautes. Conèixeraquestes pautesenspermet quantificar la probabilitatqueelresultat mostral estigui llunydel valorde la població.

Figura5. El bombo i ellliscador amb elsintervals deconfiança.

De fet,aquestmòdul nomésésunamaneradevisualitzarinicialmentelconcepte.Amb un senzill full decàlcul(3)es potsimular fàcilmentl’extracciódecentenars demostresi amb els resultatsmarcar empíricament elslímits delsintervalsdeconfiança.

Creiem, doncs, quel’argument deladificultat de l’aparell teòricnojustifica la no-inclusió d’aquesttemaalcurrículum desecundària.

Les coincidències

Aquest mòdul ésunaplasmaciódelconegutproblema(oparadoxa)de l’aniversari:

Enqualsevolreuniódemésde50persones,laprobabilitatquen’hihagiduesquecelebrin l’aniversari elmateixdia éspràcticament1.

Mésexactament,les probabilitats són:

Persones 20 30 40 50 60

Probabilitatquehihagiunaparella nascudaelmateix dia del’any

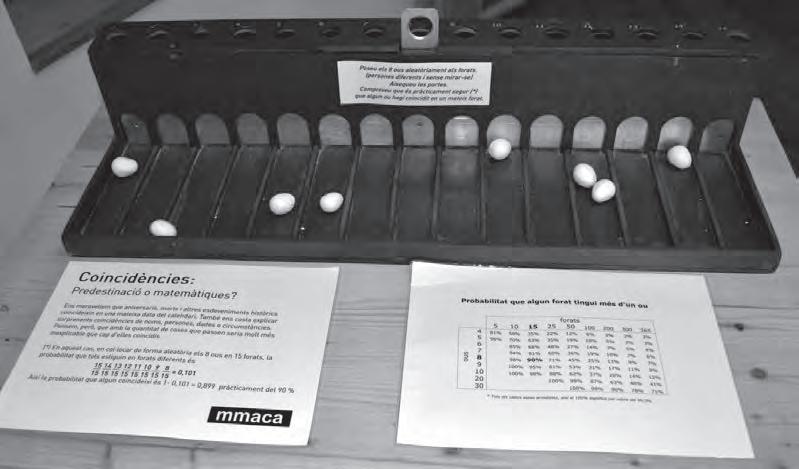
Mòdul delescoincidències.

Al’aparell que tenimalMMACA,invitem 8visitants aagafar,cadascund’ells,unoui,sense havervistonhancol locatelsous els anteriorsparticipants, posar-loenundels15 forats del mòdul. Uncopfet,s’aixequen les portesdels15forats iespotcomprovarsihihahagut coincidències.

Figura6.

Hemconvertit, pertant,elsdiesen forats iles personesenous (uep!)buscant unacombinació delsdosvalorsenlaqualelresultatsiguiproucontundent aquíel90% iels valorsprou petits pera unobjectemanipulable.

Comheuvist, ambels nostresmòduls, intentem presentard’unamaneraplàsticaaspectes propersa la realitat quotidianai tangible, aspectesque potser s’ignorenenunaformació acadèmicaen quèes prioritzi l’aspecte formal.

Peracabar,reiterematothoml’ofertadecol laboracióper portar alapràcticaidees de possiblesnousmaterials.

Bibliografia

Blastland,M. iDilnot,A.(2009). Eltigrequenoestà (p 51-68). Madrid: Turner

Gardner, M.(1985). Ruedas,vida yotrasdiversiones matemáticas (p. 44-54). Barcelona:Labor. MMACA. Elbombo il’extracciódemostres.http://www.mmaca.cat/images/mmaca/moduls/ bombo_mostres[Consultat elset.2015]

creamat el racó del cesire-creamat

Unapetitahistòriaapartird’unproblemaaparentmentpetit

Elmes demaig del2008vam gaudir delapresènciaal nostrepaísd’AbrahamArcavi.Ensva venira parlardevisualitzaciói resoluciódeproblemes. Desdel Creamatvam poderorganitzar unaconferència iunseminaridetressessions queensvandeixarunsrecordsmoltespecials. Podeuveure l’enregistramentde laxerrada («Lo queentraporlos ojos»,http://goo.gl/rhk1UF) idescarregarelsmaterialsdel seminari (http://goo.gl/PVICWm) desdel nostreweb.Però en aquestarticle,mésqueparlardelasevavisita,volem recuperarunapetita històriaque va sorgirdela resoluciód’undels problemesqueesvan treballar alseminari.

El problemaen concretesvapresentar alasegonasessió i elseu autor éselgran creador de trencaclosques americà Sam Loyd(1841-1911).

El problemadel segador

Quina ampladahadetenir labanda?

Elspagesos sense coneixementsmatemàticsparticularssovintresolend’una manera pràcticaalgunsproblemesmoltdifícils. Vull assenyalaralsnostresaficionatsl’astuta formaen quèdosgrangersvanarreglar elsseusafers.

UnranxerdeTexas,queposseïamés terradelaquepodiasembrar,vacedirla meitatd’un camp aunveí. Elcamptenia 2.000iardesdellargi1.000d’amplada, però acausad’algunes zonesde mala terra queeltravessaven, esvadecidir ques’obtindriaunadivisiómésjustasi sesegavauna bandaalvoltant delcamp en comptes dedividir-lo perlameitat.

Suposo queels nostres aficionats no trobaran unagrandificultat adeterminar l’ampladad’una bandaquerecorri tota la perifèriai quecontinguiexactamentlameitatdelacollita.Hihaunareglasimpleque és aplicablea qualsevol camp rectangular.

Al’article d’Abraham Arcavi «Generatingproblemesfromproblemsandsolutionsfrom solutions» (http://goo.gl/PnmqRs)s’analitzen amb amplitudles característiques del problema. Entot cas, comenmolts altresreptes d’aquestestil, podem consideraranecdòtiques les dades concretes iinteressar-nosmés perinvestigarunasoluciógeneral.Actuantaixí,entre moltesaltres coses, podem posardemanifestles relacions entrelesdades departida iles solucionsobtingudes.Aquestesrelacionsenspoden servir per atrobarunafórmula o un mètodequeensajudi aresoldretots els problemes semblants obé, iaquestaspecteésmés remarcable, a descobrirles possiblementinteressantspropietatsmatemàtiquesque, d’una altramanera,queden amagades. Amés, Loyd mateixensconvidaa fer-hoquan diu que«hi ha unareglasimplequeés aplicablea qualsevol camp rectangular».

En el cas d’aquestproblema,l’abordatge algèbricensporta alsorprenentdescobrimentque unadelesmesures que caracteritzen laresposta éslalongitud deladiagonaldel rectangle. L’aparició d’aquestasobtadarelacióremourà en nosaltreslanecessitatd’una investigació mésprofunda i ambunaorientacióméspurament geomètrica, mésbasada enlavisualització, quedemostri,per una altravia, el resultat obtingut en primerainstància.Lapetita història d’aquesta resolucióencara guanya enters observantl’esperit cooperatiudels resultorsi resolutores del talleri com lapetitainsatisfacciódenohaveracabat la sessióamb una solució prousenzilla ivisual vaferque continuessin pensant enel problema.

Començarem perlasolucióalgebraica.L’esquemasegüentésuna representaciógràfica del problema:

A

Una equaciódesegongrau, anomenant a i b els costats delrectangle, ensresolelproblema: (a 2x ) · (b 2x )= a · b 2 .

Ambunspetits càlculs, obtenimlasolució següent, vàlidapera la x : x = a + b √a2 + b2 4

Aquítrobemla primerasorpresa del problema: siinterpretemalgebraicament lasolució, veuremqueaquestaésunquartdeladiferènciaentrelasuma dels dos costats (el semi -

perímetre)i lalongituddeladiagonal del rectangledesortida. De fet,éslasolució queens proporciona SamLoyd, sensejustificar-la,ambeltextsegüent:

«[...] elssegadors[...] vanseguir una regla simple:‘‘Unquartde la diferènciaentreladrecera passantpel mig del campi elcamí quecircumda’’.Elsmatemàticshocomprendran millor sidiem:delasumadelsdoscostats,resteu-neladiagonaldel camp idividiuel resultat perquatre».

Alseminari es vacontinuar discutintsobre possiblessolucionsgràfiquesdelproblema derivadesd’aquestadescobertaalgèbrica.

Lasegonasorpresa la descobreix Pili Royo en continuar treballantambelproblemaun copacabat eltaller(la petitainsatisfacció quenodeixadescansar el cervell,l’emotivitat despertadaperlaimplicacióviscuda enel procé s deresolució del problema...).

Lasevaaportacióéslasegüent:sianomenem m i n els costats delrectanglemeitat,podem calcularalgebraicamentelsseus costatsi quinéselvalorde la sevasuma:

Elsemiperímetredelrectanglequeesbusca,que tinguilameitat del’àreadel’originali que equidisti dels costats, ésigualaladiagonaldel rectangle gran!

PiliRoyo envia laseva solució al’AntonAubanell,queencara està pensantpelseu compte enel problema ibusca algun tipusdesoluciógeomètrica. L’Anton se’nvaadormir,però, commolt béhanexplicat científicscomPoincaréoKekulé,el cervell continuatreballant tambéd’una manera inconscient.Dematinada, l’Antontrobal’enllaçentre lesdiferentsidees inopotevitarferunaprimeratranscripció. Aquestaversióqueexpliquemaraésunaversió reelaborada senseles urgènciesdelamatinada(suposemquel’Anton ensperdonaràla revelaciópúblicad’aquestes intimitatsnocturnes).

Observemaquestgràficquetornaarepresentarelproblemaienel qual tenimla diagonal representada:

Apliquem una translació alrectangleperajustar-lo ambelvèrtexinferiordelrectanglegran.

CampA

CampB d b a

Sabem queles àreesdel rectangle idelafiguraenforma deLsóniguals perquè ésla condició queensimposa elproblema.

Repetim aquesta construcciótresvegadesmés aplicantconvenientmentgirssuccessiusde 90◦ :

Fem araalgunesobservacions:

• Elquadrilàter ABCD ésunquadrat, perquèelsquatre costatssón ladiagonaldel rectangle gran girada90◦ cadavegada.

• Elquadrilàter A B C D tambéésun quadrat.Totsquatrecostatstenenuna longitud iguala la suma dels doscostats delrectangle petit (el semiperímetre) ielsquatreangles sónrectes.

• L’àreadelquadrat ABCD éslasumadelquadradetcentralidelsquatretriangles rectanglesformatsper la diagonal iels costatsdelrectanglegran,és adir, quatre «mitges àrees» del rectangle granmésladelquadrat petit.

• L’àreadelquadrat A B C D éslasumadelsquatrerectangles petits i ladelquadradet petit.Si recordemqueel rectangle petittélameitatdel’àreadel gran, trobemquela sevaàreaéstambé quatre«mitgesàrees» del rectangle granmésladelquadrat petit.

Laconclusióés quetots dos quadratstenenlamateixa àreai,pertant,elmateix costat. Ditd’unaaltramanera: la diagonaldel rectanglegran (elCampA )ésigualalsemiperímetre delrectangle petit (el CampB ). Hemtrobat unademostracióvisual clara ielegantd’aquesta igualtat.Podem sentir-nos bensatisfets.I el plural està benutilitzatperquè, tot i queel problemaés capaçdegenerarmolts estímuls,encara són mésgranselsqueesgenerende lasevadiscussiócol·lectiva dinselmarcdeltaller enla qual intervenenmés personesdeles duesques’esmentenenaquesta resolució. Lasolucióés«una mica detothom».

Nomésquedaundetall perresoldreelproblema original: calcular ladistànciadeseparació entreels camps. Pecataminuta:tornema observarel primerdibuix:

Tenim que:

• Elsemiperímetredel rectanglegran és a + b.

• Tambéaquestsemiperímetreés(m +2x )+ (n +2x )=(m + n)+4x .

• Sabem que m + n ésigual a d ,ladiagonaldel rectangle gran.

Amb lestres premisses podem plantejaruna senzillaequació: a + b = d +4x .

Delaqual deduïmfinalmentque x = a + b d 4

La implicació personalilacol·lectivapoden parar? Encarano... El problema vapassantdeboca aorella.Eldarrercapítol,finsara, ens el vaaportarManuel Sada deNavarra (eltrencaclosques

de Loyd anava fent quilòmetres) ambunabella construccióinteractivaamb GeoGebra que permetiavisualitzar lessolucionsperdiferentsrectangles.Enaquestenllaç,podeu veure una construccióinspiradaenlaseva (http://tube.geogebra.org/student/m1238301).

Combéhaureuvist...unbonproblema,una bona«visualitzacióalgebraica»,unabonica demostracióvisual i un gran iagradabletreballenequip.Una gran petitahistòria.