Nou Biaix, 35

Revista de la FEEMCAT i de la SCM

Desembre 2014

ubiaixno

número 35

Consell de Redacció:

Manel Sol / Josep Lluís Solé (coords.)

Marianna Bosch

Joan Carles Ferrer

Joan Miralles

Josep Pla

Romà Pujol

Manuel Udina

Juanjo Cárdenas (responsable pàgina web)

© dels autors dels articles

Coediten:

Federació dEntitats per a ’’lEnsenyament de les Matemàtiques (FEEMC AT )

Campus de Montilivi, edifici P-IV 17071 Girona feemcat.org

Societat Catalana de Matemàtiques (SCM) filial de l’Institut d’Estudis Catalans Carme, 47 08001 Barcelona scm.iec.cat noubiaix@gmail.com sites.google.com/site/noubiaix

al Periodicitat: semestr

Preu d‘exemplar ordinari: 12 €

Nombre d‘exemplars: 1.700

Fotografia de la coberta:

On, discretament, prega Gauss

Marta Adán Gómez

Oak House School de Barcelona

Concurs del curs 2013-2014

Fotografia guanyadora

Categoria de professor

ISSN: 2014-2021

Dipòsit legal: B-22.314-2012

Impressió: Gráficas Rey

Publicacions i Edicions de la Universitat de Barcelona

Adolf Florensa, s/n 08028 Barcelona

Tel.: 934 035 430

Fax: 934 035 531 comercial.edicions@ub.edu www.publicacions.ub.edu

sumari

90 109 3

Editorial 6 39 52 68 79

articles

Gauss i el polígon de 17 costats

Agustí Reventós

A classe... amb corbata!

Pedro Cobo Lozano

Parlar i enraonar per aprendre matemàtiques a educació infantil

MontserratTorra Bitlloch

Descobrir i mostrar matemàtiques amb fotografie s

Roser Codina Pascual i Carme Burgués Flamarich

El teorema de l’Empordà (de F. Macau) vist amb el GeoGebra

Lluís Sabater Anticó

Joan Vinyoli i la recerca del cercle convincent

Pep Solà

Matemàtiques amb eines digitals

Lluís Mora Cañellas

cròniques

seccions

Per pensar d’un minut a una hora

Jordi Deulofeu

Construint matemàtiques

Anton Aubanell

El racó del MMAC A

Josep Rey i Manuel Udina

El racó del Cesire- Creamat

Quantingueuaquestnúmerodel NouBiaix alesmansjafaràuntempsqueelcurs hauràcomençat.Uncursenquèlaprincipalnovetatseràl’estrenadelapolèmicallei Werta1r,3ri5èdeprimària.

Elpassat1demarçesvapublicaralBOEelDecret126/2014enquès’estableixel currículumbàsicdel’educacióprimària.Quanescrivimaquesteslínies,elDepartament d’EnsenyamentdelaGeneralitatencaranohafetpúbliceldecretpropiperordenar elsensenyamentsenaquestaetapaaCatalunya.Mentrecontinuïaquestasituació,el marcnormatiuvigentéselqueestableixeldecretesmentat.Aparentmentconserva l’ensenyamentpercompetències,perònos’hiveuunadescripciód’aquestesdarreres, totiquehihacanvisrespectealaformulacióactual,nitampoccapreferènciaacom espotcontribuiraldesenvolupamentcompetencialdesdecadamatèria.I,onesfan elscanvismésnotablesésalallistadecontinguts,ienespecialalscriterisd’avaluació i«losestándaresdeaprendizajeevaluables».Enaquestsúltims,espresentenbarrejats algunscriterisenfocatsaldesenvolupamentdelescompetènciesiunsaltresque notenencapreferentaaquestaorientació.Interpretemqueaixòrepresentaunpas enrererespectealmodelactual.

Amésamés,s’hadetenirpresentqueelGoverncentralesreservaenexclusivaeldreta determinarelscriterisd’avaluacióilescaracterístiquesgeneralsdelesprovesfinalsd’etapa, amblaqualcosalimitamoltelqueespuguidirenelcurrículumquedesenvolupilaGeneralitat deCatalunya.

Enaquestnúmeropubliquemunbongrapatd’articlesqueesperemqueresultindel’interès delslectorsdel NouBiaix.Enprimerlloc,l’AgustíReventósensexplicaelscelebratstreballs deGausssobrelaconstrucciódelpolígonregulardedissetcostatsambreglaicompàsque estrobenalesdarrerespàginesdeles DisquisitionesArithmeticae.Aquestescritdel’Agustí téelseuorigenenunaxerradaiuntallersobreaquesttema,queellorganitzà,adreçatsals estudiantsdebatxillerat.L’hareorientatperadirigir-loalsprofessorsdematemàtiques.Per seguiralgunesprovescalposar-s’hibéiseure,peròcreiemquese’npotgaudiramoltsnivells diferentsiquetothoms’hopassaràbé.

EnPedroCoboenspresentaunproblemaimaginatiupertreballaraclassealvoltantdela corbata,preguntant-sequantsnusosespodenfersegonselnombredemoviments.

LaMontserratTorraenspresentadiferentsexperiènciesd’aulaenquès’utilitzalaparlapera aprendrematemàtiquesenunaclassed’infantil.Eltemaésdemoltaactualitat,ise’npoden ferextrapolacionsaaltresnivellseducatius.Peraixòcreiemquelasevalecturaseràd’interès peralsprofessorsdetotselsnivells.

LaCarmeBurguésilaRoserCodinaenspresentenunrecursinnovador coméslafotografia perintroduirsituacionsrealsdel’entornal’auladeprimària.Hitrobareubonsexemplesper relacionarmatemàtiquesirealitatquetambéespodenextrapolaraaltresnivellseducatius.

Elteoremadel’Empordà,quevaenunciarFredericMacau,ensl’explicaenLluísSabater.És unapropostaatractivaquereconeixelementsmatemàticsalageografiadelgolfdeRoses.

Unaoriginalcontribuciódesdelesmatemàtiquesal’anyVinyolilafaenPepSolà.Al’article ensdestacalapresènciadelesmatemàtiquesenalgunsdelspoemesdeVinyoli.

Unesreflexionssobrel’úsdeleseinesTICal’auladesecundària,lestrobemal’articled’en LluísMora.Inclourecursosdisponiblesperal’aula,metodologiesdetreballil’avaluació.Es completaeltreballexposantunaexperiènciad’aulaanivelld’ESO.

Tambépresentemunacrònicadelesjornadesquehancelebratelscompanysd’Ademgii Apammsidel’olimpíadaestatalqueesvaferaBarcelonaelmesdejunypassatambla participaciód’alumnesde2nd’ESOdetotl’Estatespanyol.

Comsempre,tenimlesseccionshabitualsd’enJordiDeulofeu,l’AntonAubanell,elCREAMAT, ielMMACA,alsqualselshoagraïmmoltsincerament.

DesdelaFEEMCAT

AlajuntaextraordinàriadelaFEEMCATdeldia5dejuny,laFederacióvaaprovarlaincorporaciódelleiMATcomanoumembre.

Dono,ennompropiidetotalajuntadegovern,labenvingudapúblicaal’associació d’ensenyantsdematemàtiquesdelescomarquesdeLleidaiagraeixolasevaconfiançaenla FEEMCATilasevacol laboracióactualifuturaenelsseusprojectes.

Ambl’associaciódeLleidahemampliatl’àmbitdelaFEEMCATatotCatalunyaiarasíque enspodemdirdeveritatFederaciód’Entitatsperal’EnsenyamentdelesMatemàtiquesa Catalunya.

Benvingutsiunafortaabraçada!

VictòriaOliu PresidentadelaFEEMCAT

articles articles rticles

Gaussielpolígon de 17costats

AgustíReventós1 DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona 08193Bellaterra(CerdanyoladelVallès) agusti@mat.uab.cat

Resum Abstract

Enaquestarticlevolemposardemanifestla importànciahistòricadelaconstruccióambreglei compàsdelpolígonde17costats,problemaal qualGaussdedicàelprimertreballqueva publicar.Veuremcomelmateixprocediment seguitenaquestcas,queconsisteixaagruparles arrelsd’unpolinomidegrau17 1 = 16endos grupsdevuitarrels,iaquestsdosgrupstornar-los adividirendos,iterantelprocedimentfinsarribar avuitgrupsdedosarrelscadascun,espot generalitzaralaconstrucciódepolígonsregulars de n costatssempreque n 1siguiuna potènciadedos.Apartird’aquíesveufàcilment quesialadescomposicióenfactorsprimersde n nomésapareixenpotènciesdedosoprimersde Fermat,elpolígonregularde n costatsespot construirambregleicompàs. Elrecíproc,queGaussdónasensedemostració,és coneixavuidiacomateoremadeWantzel.Enun apèndixdonemunademostraciód’aquest teoremaonapareixenextensionsdecossosi polinomismínims,dosdelsingredientsbàsicsde lateoriadeGalois.

1.Introduccióhistòrica

Inthisarticlewehighlightthehistoricalimportance ofthe constructionofthe17-sidedregularpolygon, problematwhichGaussdevotedthefirstworkthat hepublished.We’llseehowthesameprocedure followedinthiscase,whichinvolvesgroupingthe rootsofapolynomialofdegree17 1 = 16 intwogroupsofeightrootseach,andwedivide againeachofthesegroupsintwogroups,upto arrivetoeightgroupsoftworootseach,canbe generalizedtoconstructthe n-sizedregularpolygon when n 1isapoweroftwo.Fromthisitiseasily seenthatifintheprimefactordecomposition of n itappearsonlypowersoftwoandFermatprime numbers,thentheregularpolygonof n sidescanbe constructedwithrulerandcompas. Thereciprocalofthistheorem,givenbyGauss withoutproof,isknowntodayasWantzeltheorem. Inanappendixwegiveaproofofthistheoremusing fieldextensionsandminimalpolynomials,twoofthe basicingredientsofGaloistheory.

ComencemreproduintlesparaulesqueGaussutilitzaenunacartaalseuamicGerling,el6de generde1819,perexplicar-licomvadescobrirlapossibilitatdeconstruirelpolígonregular dedissetcostatsambregleicompàs.Esveuclarament,enaquestaredacció,lamoltaestima enquèGaussteniaaquestresultat,elprimerdelsseusquevaveurepublicat.

1.Notabasadaenlaconferènciapronunciadadinselmarcdel«DissabteTransfontererdelesMatemàtiques al’AltEmpordà»,organitzatperlesFundacionsPríncepd’AstúriesiFerranSunyeriBalaguer,Figueres,1defebrer de2014.

Lahistòriad’aquestdescobrimentnol’heexplicatenllocfinsara,peròpucindicar-la exactament.

Vaserel29demarçde1796,ilacasualitatnohivatenirresaveure.Totestavaendividir lesarrelsdel’equació

endosgrups[...]

Apartird’esforçadesmeditacionsentrelesconnexionsdelesarrelsielsfonaments del’aritmètica,feliçperunesvacancesaBraunschweig,elmatíd’aquelldia,abansde llevar-me,vaigtenirlasortdeveureambgranclaredattotaaquestacorrelació,demaneraqueallàmateixiimmediatamentvaigaplicaral’heptadecàgonlacorresponent confirmaciónumèrica.

Elresultatvaserenunciatalacolumna NeueEntdeckungen (Nousdescobriments)de IntellegenzblattderallgemeinenLitteraturzeitung,l’1dejunyde1796,perA.W.Zimmermann, professordeGaussalCollegiumCarolinumdeBraunschweig.Reproduïml’escritdeGaussi lapresentaciódeZimmermann.

Comtotprincipiantengeometriasap,hihadiversospolígonsregulars,perexemple, eltriangle,tetràgon,pentàgon,15-gon,iaquellsques’obtenendoblantelnombrede costatsd’algund’ells,quesóngeomètricamentconstruïbles.

Aixòjasesabiadesdeltempsd’Euclides,isemblaques’haditdesdellavorsqueel campdelageometriaelementalnovamésenllà:almenysjonoconeccapintentreeixit d’estendreelsseuslímitsenaquestadirecció.

Ambmésraó,eldescobrimentmereixatenció...queapartd’aquellspolígonsregulars n’hihad’altres,perexempleel17-gon,queespodenconstruirgeomètricament.Aquest descobrimentés,enrealitat,nomésuncasespeciald’unateoriamésgeneral,encarano completada,iqueespresentaràalpúblictanbonpunthosigui.2

CARL FRIEDRICH GAUSS

EstudiantdeMatemàtiquesaGöttingen

ÉsimportantremarcarqueelSr.Gausstéara18anys,iesdedicaaquíaBraunschweig ambigualèxitalafilosofiaialaliteraturaclàssicaaixícomal’altamatemàtica.

18d’abrilde1796

E.A.W.ZIMMERMANN,Prof.

Justl’endemàdelseudescobriment,el30demarçde1796,Gausscomençaelseufamós diari.Laprimeraentrada(figura2)diu:«Elsprincipisdelsqualsdepènladivisiódelcercle,ila sevadivisibilitatgeomètricaendissetparts,etc».

2.Gausscompleixlasevaparaulaicincanysméstard,el1801,publicales DisquisitionesArithmeticae,on, entremoltesaltrescoses,respontotalmentlapreguntadequinspolígonsregularsespodenconstruirambreglei compàs.

Figura2.Diari.

Diulallegendaque,aixícomalatombad’Arquimedeshi haviadibuixatsunaesferaiuncilindre,aGausslihauria agradatquealasevatombahifigurésl’heptadecàgon.A l’estàtuadelseupoblenatal,Braunschweig,síquehifigura aquestpolígon.Alatomba,aGöttingen,no(almenysabans quehipassésl’autord’aquestesnotes).

2.Construccionsgeomètriquesambregleicompàs

Concretemprimeramentquèentenemper construirambregleicompàs.Suposaremsempre donats(oconstruïts)dospunts A, B.

Diremque unarectaestàconstruïda siestanconstruïtsdosdelsseuspunts.Pertant,de momenttansolsestàconstruïdalarecta AB.

Figura1.Braunschweig.

Figura3.Göttingen.

Diremque unacircumferènciaestàconstruïda sielcentreielradiestanconstruïts.Construir elradivoldirconstruirdospunts,jaqueelradiésllavorselsegmentdeterminatperaquests dospunts.Pertant,demomenttansolspodemconstruirlacircumferènciadecentre A iradi AB iladecentre B iradi BA

Diremque unpuntestàconstruït siésinterseccióderectesocircumferènciesjaconstruïdes. Perexemple,podemconstruirelsegonpuntd’intersecciódelarecta AB amblacircumferència decentre A iradi AB.

Donemacontinuacióalgunesconstruccionselementalsqueutilitzaremmésendavantpera laconstrucciódelspolígonsregulars.

Transport de segments i dangles ’

LestresprimeresProposicionsdels Elements d’Euclidesestandedicadesaveurequesitenim construïtsunsegment AB iunasemirectad’origen P,podemconstruirambregleicompàs unpunt Q sobreaquestasemirectademaneraque AB = PQ.

Laideaésconstruiruntriangleequilàterdecostat AP i,ambcentre A,girarelsegment AB sobrelasemirecta OA;acontinuació,ambcentre O,girar-losobrelasemirecta OP;idesprés, ambcentre P,girar-losobrelasemirectadonada(figura4).

Figura5.Transportd’angles.

Transportaranglesésunamicamésdifícil.Pertransportarl’angle BAC (construïm C demanera que AB = AC)sobrelasemirecta PQ,construïmlacircumferènciadecentre P iradi AB ila circumferènciadecentre Q iradi BC (figura5).Si R éselpuntd’intersecciód’aquestesdues

Figura4.Transportdesegments.

circumferències,elstriangles ABC i PQR sóniguals(criteri3 CCC)i,pertant,l’angle ∠BAC és igualal’angle ∠QPR

Apartird’aquestesduesconstruccionsquehemfet,transportdesegmentsitransports d’angles,quedaclarque ambregleicompàspodemsumarirestarsegmentsipodemsumari restarangles.

Mediatriu

Suposemconstruïtelsegment AB.Per construirlasevamediatriuintersequemlacircumferènciadecentre A iradi AB amblacircumferènciadecentre B iradi AB (figura6).Larecta determinadapelspunts A′ i B′ queaixíobteniméslamediatriubuscada.

Figura6.Mediatriu.

Enefecte,elstriangles △ABA′ i △ABB′ sóniguals(criteriCCC)i,pertant, ∠A′AO = ∠OAB′ , enquè O éselpuntd’intersecciódelesrectes AB i A′B′ (i,pertant,construït).Aplicantarael criteri4 CACalstriangles △A′AO i △B′AO,obtenimquel’angle ∠A′OA ésrecte.Tambéesveu fàcilmentque O éselpuntmigdelsegment AB,i,pertant, A′B′ éslamediatriubuscada.

Bisectriu

Donatunangledevèrtex O construïm unacircumferènciadecentre O iradiarbitrari,que tallaràelscostatsdel’angleenpuntsrespectius A i B (figura7).

Observemqueelradiarbitrarihadeserunradiconstruïtprèviament.

3.CriteriCCC(costat-costat-costat)voldirquedostrianglesambelscostatscorresponentsigualssón iguals.Ésadir,queelsanglescorresponentstambésóniguals.Podeuveureelpuntdevistaaxiomàtica[10].

4.CriteriCAC(costat-angle-costat)voldirquedostriangles,ambdoscostatscorresponentsigualsiamb l’anglecomprèsentreaquestsdoscostatstambéigual,sóniguals.

Llavorslescircumferènciesdecentres A i B iradi OA estallenenelpunt O ienunaltrepunt O′.Comqueelstriangles △AOO′ i △BOO′ sóniguals(CCC),lasemirecta OO′ éslabisectriu buscada.

Perpendicular

◮ Perpendiculardesd’unpuntexterior. Sigui A unpunt quenopertanyalarecta r.Prenemdos puntsarbitraris P i Q de r (figura8).Perexemple,elsquehanservitperconstruir-la.Construïm unangle ∠A′PQ iguala ∠APQ talque A i A′ estiguinsituatsacostatsdiferentsrespecte r,ital que AP = A′P.Perferaixòconstruïmlacircumferènciadecentre P iradi PA,quetalla r enun certpunt B.Lacircumferènciadecentre B iradi BA tallal’anteriorcircumferènciaenelpunt A′ buscat,jaque,pelcriteri CCC aplicatalstriangles △APQ i △A′PQ,elsangles ∠A′PQ i ∠APQ sóniguals.Aplicantaraelcriteri CAC alstriangles △APR i △A′PR veiemquelarecta AA′ és perpendiculara r.

Figura7.Bisectriu.

◮ Perpendicularperunpuntdelamateixarecta. Estractadeconstruirunaperpendicular a r quepassiperunpuntdonat P de r.Construïmunpuntarbitrari A forade r (figura9). Construïmlacircumferència C decentre P iradi PA.Sigui A′ l’altrapuntenquè C tallalarecta PA.Construïmlaperpendiculara r desde A′,quetalla C enunsegonpunt A′′.Lamediatriu delsegment AA′′ éslaperpendicularbuscada.

Paral·lela

Araésfàcil,construïdaunarectaiunpuntexterior,construirlaparal·lelaalarectaperaquest punt.Enefecte,éssuficientconstruirlaperpendicularalarectadesdelpuntiacontinuació construirlaperpendicularaaquestarectapelpunt.

Arrel quadrada d’un segment

Perconstruirl’arrelquadradad’unsegmentdelongitud a només hemdecol locarlaunitat demesuraacontinuaciód’aquestsegmenticonstruirlacircumferènciadediàmetre a + 1 (figura10).Laperpendicularaaquestdiàmetreenl’extremdelsegmenttélongitud h = √a. Enefecte,pelteoremadel’altura,tenimque h a = 1 h

1 h = √a

Figura10.Arrelquadrada.

Figura9.Perpendicular.

Invers d’un segment

Donatunsegmentdelongitud a,volemconstruirunsegmentdelongitud1/a.Prenemdues semirectesarbitràriesamborigencomú O.Sobreunad’ellesprenempunts A i A′ talsque OA = a, AA′ = 1i A estiguientremigde O i A′ (figura11).Sobrel’altraprenemunpunt B tal que OB = 1.Llavorslaparal·lelaa AB per A′ tallalarecta OB enunpunt B′ talque BB′ = 1/a. Enefecte,siapliquemelteoremadeTalesalstriangles △OAB i △OA′B′,obtenim

Figura11.Invers.

Observemque,comquesabemconstruirinversosisumes,sitenimconstruïtunsegmentde longitud1llavorssabemconstruirunsegmentdelongitud r peratot r ∈ Q.Concretament, si r = p/q,noméshemdesumar p copsl’inversde q.Ésadir, elsnombresracionalssón construïbles.

3.Pentàgonregular

Enaquestasecciódonaremduesconstruccionsdelpentàgonregular.Unad’ellesperquèés lamésràpidaisenzillail’altraperquèensil lustraràelmètodequedesprésutilitzaràGauss perconstruirl’heptadecàgon.5

◮ Primeraconstrucció. Perexplicaraquestaconstrucció,suposemquelacircumferènciadela figura12éslacircumferènciadecentre O = (0,0)6 iradi1.Sigui A = (0, 1/2)i B = (1,0).Amb centre A iradi AB tracemunacircumferènciaquetallal’eixdeles y′s enelpunt C = 0, √5 1 2 . Elpuntdetalldelacircumferènciainicialamblacircumferènciadecentre B iradi BC ésel primervèrtexdelpentàgon.

5.LaideaqueGaussesvainspirarenelpentàgonperresoldrel’heptadecàgonésnomésunaconjecturameva.

6.Nocalintroduircoordenades,noméshofempercomoditat.

Lajustificacióésclarasisabemqueelcostatdelpentàgonregularinscritalacircumferència deradi1val L = 5 √5 2 .

Aixòes demostrafàcilmentobservantprimerque

L = 2sin π 5

iobservantacontinuacióquelaraód’or τ val

τ = 2cos π 5 .

Aquestarelacióentrelaraód’or τ ielcos π 5 esdedueixdeltriangleauri △AOB queapareixen dibuixareldecàgonregulardecostat AB inscritenlacircumferènciadecentre O (figura13). Esconstrueixelpunt B′,intersecciódelabisectriudel’angleenelvèrtex B ambelcostat OA. Elstriangles △AOB i △B′BA delafigurasónsemblants.

Pertant,

Figura12.Pentàgon.

Figura13.Decàgon.

Equivalentment,

queimplicaqueelquocient OA/AB ésarreldel’equació x2 x 1 = 0,iéspertantlaraó d’or.Ésadir, τ = OA AB . D’altrabanda,considerantl’alturadesde O veiemque

Aplicant aralafórmuladel’angledobleobtenim τ = 2cos(π/5).Així,

◮ Segonaconstrucció. Situem-nosenelplacomplex.Lesarrelsdelpolinomiciclotòmic

són w,w2,w3 , w4 amb w = e2πi/5 . Observemque1,w,w2,w3,w4 sónelsvèrtexsdelpentàgon quevolemconstruir.Observemtambéque w

Aquestaagrupaciós’hafetperquèelsdosnúmeros w + w4 i w2 + w3,queGaussanomena períodes,sónnúmerosreals.Elseuproducteserà,doncs,tambéreal.Defet,tenim

Elsdosperíodessumen 1ielseuproducteés 1;pertant,sónarrelsdel’equaciódesegon grau

Tenintencompteelssignesveiemquehadeser

on τ ésla raód’or.Multiplicantper w laprimerad’aquestesequacionstenim

+ 1 = 1 τ w, igualtat queensdiuque w ésarreldelpolinomidesegongrau

2 1 τ x + 1, quetécoeficientsquesónracionalsicoeficientsquesónextensionsquadràtiquesde racionals.Així,

Comquel’arrelésnegativa,lapartreald’aquestnombrecomplexés1/2τ,ésadir, cos 2π 5 = 1 2τ .

Comque τ és unirracionalquadràticisabemconstruirsumes,productes,arrelsquadradesi inversos,sabemconstruircos 2π 5 ,ipertant,elpentàgon.

4.Heptadecàgonregular

Elmètodeseguitalasegonaconstrucciódelpentàgonespotrepetirquasiexactamentpera l’heptadecàgon.

Enaquestcas,lesarrelsdelpolinomiciclotòmic z17 1 z 1 = z16 + z15 + ··· + z2 + z + 1,

són1,w,w2 , ,w16 amb w = e2πi/17 Observemque1,w,w2 , ,w16 sónelsvèrtexsdel heptadecàgonquevolemconstruir.7 Denotarem wk = wk .Elscàlculsquevénenacontinuació apareixenjaenel DisquisitionesArithmeticae [6],peròelspodeutrobartambé,perexemple, a[3].

Agrupem8 lesarrelsenelsdosprimersperíodes

Estanformatspervuitarrelscadascunisónnombresreals.Enparticular,elseuproducteés unnombrereal.Esveudeseguidaque

2 = 4, jaque

iaquestaexpressiónoésmésquelasumadevuitperíodestalsquedosadossumen 1.

Lamaneradeconstruir-losésordenarelselementsde Z/17diferentsdezerod’acordamb lespotènciesde3(mòdul17).9 Concretament,

7.Comquenosaltresentindríemprousabentconstruirlapartrealde w,espresentaaquíunapregunta interessantqueéslasegüent:si w ésarreldelciclotòmic,quinpolinomisatisfàlapartrealde w?Ésunapreguntaqueenspodemferengeneral(ésadir,encaraqueelpolinominosiguiciclotòmic)iquesembladifícil.Elscàlculs deGaussquevénenacontinuaciósónlarespostaaaquestapreguntaenelcasparticulardel’heptadecàgon.

8.JustamentaaquestaagrupacióesrefereixGaussenlasevacartaaGerlingcomentadaalapàgina7quan diu:«Totestavaendividirlesarrelsdel’equació[...]endosgrups».

9.Aquestapropietatextraordinàriaquefaquelespotènciesde3generin Z/(17)ésconseqüènciadel teoremadelgeneradoroteoremadel’elementprimitiu,quediu(vegeu,perexemple,[9],p.342): Teorema. Elgrupmultiplicatiude Z/(p),ambpprimer,éscíclic.

Aixòvoldirquehihaunelement g a Z/(p),anomenatelement primitiu,talque Z/(p) = {0,g,g2 , ,gp 1}

n 0123456789101112131415

3n 13910135151116148741226

Llavors u1 haestatlasumadelespotènciesde3parellsi u2 haestatlasumadelespotències de3imparells.

Així, u1 i u2 sóndosnombresrealsquesumen 1itenenproducte4.Aixòvoldirquesón soluciódel’equaciódesegongrau

Són,doncs,irracionalsquadràtics.Ara,decadaperíodeenfemdos.

1 = w1 + w13 + w16 + w4,

Estanformatsperquatrearrelscadascunisónnombresreals.Mirem,comabans,lesseves sumesiproductes.Tenim v1 + v2 = u1 (obvi)i v1 · v2 = 1(càlculdirecte).Pertant, v1 i v2 són soluciódel’equaciódesegongrau

Anàlogament, v3 i v4 sónsoluciódel’equaciódesegongrau

2 u2x 1 = 0

Pertant, elsperíodesd’ordre 4,v1 iv2,sónarrelsd’equacionsdesegongrauquetenencoeficients racionalsicoeficientsquesónperíodesd’ordre 8.

Novament,decadaperíodeenfemdos wk + w17 k = 2cos(2kπ/17),k = 1, ... , 8

Estanformatsperduesarrelscadascunisónnombresreals.Mirem,comabans,lesseves sumesiproducte.Perexemple, (w1 + w16) + (w4 + w13) = v1 i

(w1 + w16) (w4 + w13) = w5 + w14 + w3 + w12 = v3.

Així, w1 + w16 = 2cos θ ,i w4 + w13 = 2cos4θ sónarrelsdel’equaciódesegongrau x2 v1x + v3 = 0 (4)

Jahemvistcomlespotènciesde3generentotselselementnonulsde Z/(17).Unaltreexempleserienlespotències de3a Z/(7):1, 3, 2, 6, 4 ,5 Encanvi,perexemple,alasuccessiódepotènciesde2a Z/(7),quesón1,2,4,nohi apareixentotselselementsnonulsde Z/(7).S’intueix,doncs,quetotiqueelteoremaensdiuquehihaunelement primitiu potserdifíciltrobar-lo.

Pertant, elsperíodesd’ordre 2, 2 cos θ i 2 cos 5θ ,sónarrelsd’equacionsdesegongrauquetenen coeficientsracionalsicoeficientsquesónperíodesd’ordre 4.

Resolentlesequacions(1),(2),(3)i(4),obtenimsuccessivament

Substituint al’últimaelsvalorsobtingutsalesanteriors,obtenim

Comquesabemconstruirsumes,productes,arrelsquadradesiinversos,sabemconstruir cos 2π 17 ,ipertant,elheptadecàgon.Però,aixòsí,ambmoltsméscopsdecompàsqueambla construccióquevadonarRichmond(figura14)moltsanysméstard(1893).

Figura14.Heptadecàgon.

Expliquem lasorprenentconstrucciódeRichmondsensejustificar-la(vegeu[3],pàgina62). Totselspuntsqueintroduïmacontinuacióespodenconstruirambregleicompàsapartirde O,I.

1.Construïm A demaneraque A = (0, 1/4).

2.Construïm B demaneraque ∠OAB = 1 4 ∠OAI.

3.Construïm C demaneraque ∠CAB = π 4

4.Construïm D comelpuntd’intersecciódel’eixdeles y′s amblacircumferènciade diàmetre CI

5.Construïm P3 i P5 comelspuntsd’interseccióambl’eixdeles x′s delacircumferència decentre B iradi BD.

6.Construïm M3 i M5 comelspuntsd’interseccióamblacircumferènciainicialdeles perpendicularsal’eixdeles x′s per P3 i P5,respectivament. M3 i M5 sónelsvèrtexs3i5 del’heptàdecàgon.

7.Construïm M4 comlainterseccióamblacircumferènciainicialdelamediatriude M3M5. M4 éselquartvèrtexdel’heptadecàgon,quetécostat,doncs, M3M4.

5.Polígonsregulars.Lacondiciósuficientdeconstructibilitat

Enel DisquisitionesArithmeticae [6],Gaussdemostraque,sielnúmeronatural n ésproducte depotènciesdedosperprimersdeFermatdiferents(vegeuladefiniciódeprimerde Fermatalapàgina23),llavorselpolígonregularde n costatsespotconstruirambreglei compàs,ienunciasensedemostracióqueelrecíprocéstambécert.Lafórmulaexplícitaper alcos(2π/17),quedemostraquel’heptadecàgonespotconstruir,apareixalasecció365 (lapenúltimadel DisquisitionesArithmeticae),ontambéenunciasensedemostracióqueel polígonde p costatsamb p primeri p 1nopotènciade2noespotconstruir(enparticular, l’heptàgonnoespotconstruir).10 Aquestresultatfoudemostratel1837perWantzel[12].Ala secció366iúltimadel DisquisitionesArithmeticae demostraquelespotènciesdeprimersno espodenconstruiriacabaamblallistadelspolígonsconstruïblesambmenysdetres-cents costats.

DonemaralaideadelademostraciódeGauss.Recomanem[11].

◮ Primerpas. Suposem n dela forma n = 2k · p amb p senar.Comquesabembisecarl’angle, sisabemconstruirelpolígonregularde p costatssabremconstruirtambéelpolígonregular de2k · p costats.Irecíprocament,sisabemconstruirelpolígonregularde2k · p costatssabrem construirunintelsvèrtexsde2k en2k ,elpolígonregularde p costats.Ésadir,elpolígon

10.Gaussdiu(lesmajúsculessónseves;lanegreta,del’editordel NouBiax):«PODEMDEMOSTRARAMBTOT RIGORQUEAQUESTESEQUACIONSELEVADESNOESPODENNIEVITARNIREDUIRDECAPMANERAAINFERIORS, encaraqueelslímitsd’aquestaobranopermetintransmetreaquíaquestademostració;cosa,però,quehem consideratques’had’advertirperquèningúnoespericonduiraconstruccionsgeomètriquesencaraaltresseccions exceptelesquelanostrateoriasuggereix,ésadir,lesseccionsen7, 11, 13, 19,etc.,parts,i consumeixieltemps inútilment».

regular de n = 2k · p espotconstruirsiinoméssielpolígonregularde p costatsespot construir.Aixòredueixelproblemadelaconstrucciódepolígonsregularsalcasenquèel númerodecostatsésproductedepotènciesdeprimersdiferentsde2.

◮ Segonpas.Suposem n dela forma n = p · q amb p i q primersentreells.Sisabemconstruir elpolígonregularde p costatsielpolígonregularde q costatssabemconstruirpolígons regularsde n = p q costats.

Enefecte,perlaidentitatdeBézout,existeixenenters r,s talsque qr + ps = 1

Dividintper pq imultiplicantper2π tenim

Aixòimplicaquesisabemconstruirelsangles

sabremconstruir,sumant-loso restant-los(r i s tenensignesoposats),l’angle 2π pq ,ipertant,elpolígonregularde p · q costats. Perexemple,comquesabemconstruireltriangleequilàterielpentàgonregular,sabem construirelpolígonregulardequinzecostats,jaqueatesalaigualtat

Figura15.Pentadecàgon.

només hemdesumarduesvegadesl’anglecentraldelpentàgonirestar-liunavegadal’angle centraldeltriangleequilàterpertenirl’anglecentraldelpentadecàgon.

Alafigura15esveucomelcostat E1P2,formatpelprimervèrtexdeltriangleequilàteriel segonvèrtexdelpentàgon,dónaelcostatdelpentadecàgon.

Notemdepassadaquevalelrecíproc,ésadir,quesisabemconstruirelpolígonregularde p · q costatssabemconstruirelpolígonregularde p costats,simplementunintelsvèrtexs de q en q,ielde q costatsunintelsvèrtexsde p en p.

◮ Tercerpas.Comquetotnombre n descomponcom

amb pi primersimparellsdiferents,iateseslesobservacionsanteriors,elproblemadesaber sipodemconstruirelpolígonregularde n costatsesredueixasabersisabemconstruirels polígonsregularsde pαi i costats.

◮ Quartpas.Polígonsambunnombreprimerdecostats. Pelsmateixoscomentarisfetsen estudiarelpentàgonil’heptadecàgon,sabemqueelsvèrtexsdelpolígonquevolemconstruir, pensatscomnombrescomplexos,sónelnúmero1 ∈ C ilesarrelsdelpolinomiciclotòmicde grau p 1,enquè p éselnombreprimerdecostats.L’observacióqueelmètodeseguitpera l’heptadecàgonespotgeneralitzarestàrecollidaenelteoremasegüent(vegeu[6]o[4]).

Teorema5.1. Sipésunnombreprimerdelaformap = 2

+ 1,l’equació

espotresoldreperradicalsquadràtics(extracciósuccessivad’arrelsquadrades),ipertant,el polígondepcostatsespotconstruirambregleicompàs.

Demostració. Consideremelciclotòmic

ilessevesarrels

Sigui g unnúmeromenorque p talque

doninresidu1, 2, ... ,p 1enserdividitsper p (aquestelement g existeixpelteoremade l’elementprimitiu,quehemrecordatalpeudepàgina9,pàgina16).Llavors,

reordenatsespodenescriurecom

Posemara

Iacontinuació

Observemaraqueconeixemlasumaielproductede η1 i

2.Enefecte,

amb1 ≤ r,s,t ≤ p,jaqueelproducted’arrelsésunaarrel.

Siacadatermedelsumatoricanviem ω per ωg elvalortotalnocanvia,jaqueaquestcanvi transforma η1 en η2 i η2 en η1.Aixòvoldirquecadaarrelapareixenelsumatorielmateix nombredevegadesi,pertant,

amb ν ∈ N

Pertant, η1 i η2 sónarrelsde x2 + x ν = 0.

Argumentssimilarsensdiuenque η11 i η12 sónarrelsde x2 η1x + (ν1η1 + ν2η2) = 0, amb ν1, ν2 ∈ N;vegeu,perexemple,[5].Ielmateixpassaamb η21 i η22

Quan p 1éspotènciade2,aquestprocedimentensportaqueelsperíodesd’ordre1,ésa dir,lesarrels,espodencalcularresolentunaequaciódesegongrauambcoeficientsperíodes d’ordre2,elsqualsespodencalcularresolentunaequaciódesegongrauambcoeficients períodesd’ordre4,etc.

◮ Cinquèiúltimpas.Polígonsambunnombrearbitraridecostats.

Corol·lari5.2. Sin = 2α · p1 · ... · pr ambpi primersitalsquepi = 2k1 + 1,elpolígonregular dencostatsespotconstruirambregleicompàs.

Demostració. Conseqüènciadelteorema5.1ielscomentarisanteriors.

Proposició5.3. Si 2k + 1 ésprimer,llavorsk = 2a,amba ∈ N.

Demostració.Enefecte,suposemque k fosdivisibleperunnúmeroimparell.Tindríem k = (2m + 1)r.Llavors, p = 2k + 1 = 2(2m+1)r + 1 = (2r )2m+1 + 1.

Aixòvoldirque2r ésarreldelpolinomi x2m+1 + 1

Comqueaquestpolinomiadmetl’arrel x = 1,tenim x2m+1 + 1 = (x + 1)q(x)

perauncertpolinomi q(x).Enparticular, p = (2r )2m+1 + 1

i p noseriaprimer.Pertant, k nomésésdivisibleper2,ésadir, k = 2a amb a ∈ N

Corol·lari5.4. Sin = 2α p1 ... pr ambpi primersitalsquepi = 22ai + 1,ambai ∈ N,el polígonregulardencostatsespotconstruirambregleicompàs.

Demostració. Conseqüènciadelcorol lari5.2ilaproposició5.3.

Elsnombresprimers p ques’escriuendelaforma p = 22k + 1,k ∈ N,

esdiuen primersdeFermat.Perònototselsnombresd’aquestaformasónprimers.Defet, nomésesconeixencincprimersdeFermat,elsquecorresponena k = 0, 1, 2, 3, 4,ésadir, p = 3, 5, 17, 257, 65537.

Gausscomentaenel DisquisitionesArithmeticae quel’il·lustreEulerjaesvaadonarqueelsisè nombredeFermatnoésprimer.Concretament, 225 + 1 = 232 + 1 = 4294967297 = 641 · 6700417.

Elcorol·lari5.4ensdiuqueelspolígonsconstruïblesambmenysdetres-centscostatssónelsde 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272 costats.11

11.Comhemditabans,el DisquisitionesArithmeticae acabajustamentambaquestallistadelstrenta-vuit polígonsregularsconstruïblesambmenysdetres-centscostats.Aixòdónaunaideadelaimportànciaquedonava Gaussaaquestresultat.

6.Lacondiciónecessàriadeconstructibilitat

PeraaquestapartnecessitemelqueesconeixcomaTeoremadeWantzelperòquejaera benconegutperGauss,comesveullegintlasecció365del DisquisitionesArithmeticae (vegeu elpeudepàginanúmero10delapàgina19),totiquenose’nvadonarunademostració rigorosafinsaltreballdeWantzelde1837.

Hemutilitzat,entred’altres,l’articledeH.S.Carslaw[4],elqualestàbasatenl’articled’Enriques «Sulleequazionialgebricherisolubiliperradicaliquadraticiesullaconstruibilitàdeipoligoni regolari»,capítol17,p.263-305,delllibre[5].NiCarslawniEnriquesciteneltreballdeWantzel, quevapassardesapercebutdurantquasicentanys.TambérecomanemeltreballdeD.Kuh [1].Alasecció8,teorema8.4,demostraremelresultatsegüent.

Teorema6.1(Wantzel).12 SuposemqueelpuntPdelplaeuclidiàambcoordenadescartesianes (a,b) haestatconstruït.Llavorselpolinomidegrauméspetitqueadmeta(ob)comaarrelté graupotènciade 2.

Larelacióentrecoordenadescartesianesipuntsconstruïtséslasegüent(vegeu,perexemple, [3]).Denotem O,I elspuntsambelsqualsiniciemelprocésdeconstrucció.Construïmun tercerpunt I′ comlaintersecciódelarecta OI (pertant,construïda)idelacircumferència C decentre O iradi OI (tambéconstruïda).Construïmacontinuaciólamediatriudelsegment II′.Denotem J elpuntd’intersecciód’aquestamediatriuamblacircumferència C.Prenem comareferènciaortonormaldelplalareferència {O; −→ OI, −→ OJ},ésadir,lareferènciad’origen O ibase −→ OI, −→ OJ.Sobrelarecta OI agafemcomaunitatdemesuraelsegment OI isobrelarecta OJ agafemcomaunitatdemesuraelsegment OJ.Elspuntsdelarecta OI adistància x de O elsdenotem(x, 0)ielspuntsdelarecta OJ adistància y de O elsdenotem(0,y).Esdiullavors queunpunt P delplatécoordenades(x,y)silesrectesortogonalsalseixos OI i OJ per P els tallenenelspunts(x, 0)i(0,y),respectivament.

Apartirdelteorema6.1,Wantzeldemostralaimpossibilitatdelatrisecciódel’angleide laduplicaciódelcub,essencialmentcomleshemreproduïtmésendavant,alasecció7 d’aquestesnotes.Tambédiu13 queespotprovarlaimpossibilitatdeconstruirunpolígon regularambunnombredecostatsigualalapotènciad’unprimer,jaqueespotprovar, modificantlleugeramentlademostraciódeGauss,queelpolinomiciclotòmiccorresponent ésirreductible.Comqueaquesta‘demostració’noésgairesatisfactòria,14 nosaltresen donaremunad’aquestaimpossibilitatapartird’unaversióunamicadiferentdelteorema6.1. Concretament,identificantcoméshabitualelplaeuclidiàambelplacomplex,demostrarem elresultatsegüent.

12.L’enunciatoriginaldeWantzeldiu:«L’equationdudegree2n,f (x) = 0,quidonnetouteslessolutions d’unproblèmesusceptibled’ètrerésoluaumoyende n équationsduseconddegré,estnécessairementirréductible». Vegeu[12].

13.«Onpeutprouver,enmodifiantlégèrementladémonstrationdeM.Gaussquel’equationdedegree (a 1)aα 1,obtenueenégalantàzérolequotientde xaα 1par xaα 1 1,estirréductible;ilfaudraitdonc que(a 1)aα 1 fûtdelaforme2k enmêmetempsque a 1,cequiestimpossibleàmoinsque a = 2».

14.Wantzel,enelseuarticle,treballaambequacionsalgèbriquesdelesqualsnoespecificasilesvariables sónrealsocomplexes.Peròquanpensemelspuntsdelplaeuclidiàcomcomplexos z = (x,y),ésclarqueles circumferènciestenenequacionsquadràtiquesen x i y,perònoen z

Teorema6.2. Suposemqueelpuntzdelplacomplex,amb |z| = 1,haestatconstruït.Llavorsel polinomidegrauméspetitqueadmetzcomaarreltégraupotènciade 2

Pernoanarparlantsempredelpolinomidegrauméspetits’introdueixelconceptede polinomimínim

Definició6.3. El polinomimínim sobre Q dea ∈ C éselpolinomimònicdegrauméspetit,amb coeficientsa Q,quetéacomaarrel.

Proposició6.4. Totpolinomimòniciirreductiblesobre Q éselpolinomimínimdelesseves arrels.

Demostració. Sigui P(x) ∈ Q[x] mòniciirreductiblesobre Q isuposem P(a) = 0.Si P(x)no foselpolinomimínimde a hihauriaunpolinomimònic m(x) ∈ Q[x] degrauméspetitque elgraude P(x)italque m(a) = 0.Peròllavorselresidu R(x)deladivisióde P(x)entre m(x) compliria R(a) = 0icomque R(x)tégrauméspetitqueelgraude m(x)hadeser R(x) = 0i, pertant, P(x) = m(x) · q(x),contradiccióambser P(x)irreductiblesobre Q.

Teorema6.5. Elpolinomiciclotòmic

ambpprimer,ésirreductiblesobre Q.

Demostració. Posant z = x + 1elciclotòmics’escriucom

Elcriterid’Eisenstein15 ensdiuqueaquestpolinomiésirreductiblesobre Q,jaque p divideix totselscoeficients(excepteelde xp 1)i p2 nodivideixeltermeindependent.

Nombre de costats igual a un primer no de Fermat

ArajapodemdemostrarelrecíprocdelTeorema5.1.

Teorema6.6. Elpolígonregulardepcostats,ambpunnombreprimernodeFermat,noespot construir.

Demostració. Comqueelpolinomiciclotòmiccorresponentésirreductiblesobre Q,ésel polinomimínimdelessevesarrels(teorema6.5iproposició6.4).Pertant,pelteorema6.2, perquèaquestesarrelsespuguinconstruirelgraudelpolinomiciclotòmichadeserpotència de2,ipertant, p hadeserprimerdeFermat.

Corol·lari6.7. Sialadescomposicióenfactorsprimersdenhihaunprimerpdiferentde 2 ino deFermat,llavorselpolígonregulardencostatsnoespotconstruir.

Demostració. Siespoguésconstruirelpolígonregularde n costatsamb n = p q,unintels vèrtexsde q en q tindríemconstruïtunpolígonregularde p costats,cosaquenopotser.

15. Criterid’Eisenstein. SiguiP(x) = a0 + a1x + a2x2 + + anxn ∈ Z[x],isiguip ∈ N unnombreprimer talquep | a0,p | a1, ,p | an 1,p ∤ an,p2 ∤ a0.LlavorsP(x) ésirreductiblesobre Q.Vegeu,perexemple,[9],p.220.

Nombre de costats igual a la potència d’un primer

UtilitzantelteoremadeWantzelcomplex,teorema6.2,podemveureque elspolígonsamb unnombredecostatsigualalapotènciad’unprimernoespodenconstruir.Concretament tenim:

Teorema6.8. Elpolígondepa costats,ambpprimerdiferentde 2 ia = 1,noespotconstruir.16

Demostració. Sabemqueconstruirlesarrelsd’aquestpolinomiequivalaconstruirlesarrels delpolinomiciclotòmic

Però

Observem quelafracciódel’esquerrailaprimeradeladretasónelspolinomisciclotòmics delgraucorresponent.Ilasegonafracciódeladretaésunpolinomi(elsdospolinomisque apareixensóndivisibles)queespotescriurecomelciclotòmic

Perexemple,si p = 5i a = 2(polígonde25costats),tenim z25 1 z 1

Engeneral,fentelcanvidevariablehabitual z = y + 1queesfaquanesvolaplicarelcriteri d’Eisenstein,tenim

Eltermeindependentés p,jaqueéslasumade p uns.Pertant, p2 nodivideixelterme independentiencanvi p síquedivideixtotselscoeficientsexcepteeldemajorgrauqueés1. Aixòespotveureaplicantlafórmuladelbinomialssumandsdel’expressióanteriorirecordant lespropietatsdelsnúmeroscombinatoris.Peròesdedueixdirectamentdel’expressió

zpa 1 zpa 1 1 =

enquè p voldirmúltiplede p

Pertant,pelcriterid’Eisenstein,aquestpolinomiésirreductiblesobre Q,iperlaproposició6.4,éselpolinomimínimdelessevesarrels.

16.Alasecció366del DisquisitionesArithmeticae,Gaussdiu:«Sielcercles’hadeseccionaren aα parts,en què a designaunnombreprimer,aixòespotfer,evidentment,geomètricament,quan a = 2,perònoperacapaltra valorde a,suposatque α > 1;enefecte,llavors,apartdelesequacionsqueesrequereixenperalaseccióen a parts, encaraenconvindràresoldrenecessàriamentunesaltres α 1degrau a;itampocaquestesnoespodenresoldre nievitarnirebaixardecapmanera.Així,elsgrausdelesequacionsnecessàriesespodenconèixerengeneralapartir delsfactorsprimersdelnombre(a 1)aα 1».

Aixídoncs,sipoguéssimconstruirlesarrelsde

zpa 1 zpa 1 1 ,

elgraud’aquestpolinomihauriadeserunapotènciade2,ésadir, pa pa 1 = pa 1(p 1) = 2k ,

peraalgun k ∈ N.Comqueestemsuposant a = 1,hadeserque p divideixia2,icomque p ésprimerhadeser p = 2.Resumint,elsúnicspolígonsconstruïblesamb pa costats,amb p primeri a = 1,sónelsquecorresponenalcas p = 2.

Corol·lari6.9. Sialadescomposicióenfactorsprimersdenhihalapotènciad’unprimerdiferent de 2,llavorselpolígonregulardencostatsnoespotconstruir.

Demostració. Siespoguésconstruirelpolígonregularde n costatsamb n = pα · q,unintels vèrtexsde q en q podríemconstruirelpolígonde pα costats,cosaquenopotser.

Resumim,finalment,totelquehemditfinsaquíenelteoremasegüent.

Teorema6.10(Gauss). Elpolígonregulardencostatsespotconstruirambregleicompàssii noméssintéunadescomposicióenfactorsprimersdelaforma

enquè α1,α2, , αk sónentersdiferentsentreells.

Demostració. Lacondiciósuficientéselcorol lari5.4ilacondiciónecessàriaésconseqüència delscorol·laris6.7i6.9.

Comquelafunció ϕ d’Eulerqueassociaacada n ∈ N elnúmerodecoprimersamb n,menors que n,espotcalcularapartirdeladescomposicióenfactorsprimersde n = pα1 1 ··· p α

k perla fórmula(vegeu,perexemple,[9]) ϕ(n) = n k i=1 1 1 pi ,

noésdifícilveurequel’anteriorteoremaespotenunciardientque elpolígonregularden costatsespotconstruirambregleicompàssiinoméssi ϕ(n) éspotènciade 2.

6.1. L’heptàgon regular

Totiquejasabemquel’heptàgonregularnoespotconstruir(teorema6.6),donem-neuna demostraciódirectaqueenspermetnorecórreralcriterid’Eisenstein.

Teorema6.11. L’heptàgonregularnoespotconstruirambregleicompàs.

Demostració. Jahemcomentatqueequivalaconstruirelpunt

Peròaquest puntpensatcomanombrecomplexésunaarrelsetenadelaunitat,ésadir, soluciódelpolinomi z7 1.Aquestpolinomitésetarrels,peròunad’ellesés z = 1,demanera queelproblemaquetenimésconstruirunaarreldelpolinomiciclotòmic

Elfet que z ∈ C siguiarreld’aquestpolinomiensdiusilasevapartrealéssoluciód’un polinomisimilar?Compodemtrobarunpolinomiquetinguicomaarrellapartrealde z (sent z soluciódelciclotòmic)?17 Doncs,moltsenzill,noméshemd’estudiarlespotènciesde z + z = 2R(z).Observemquecomlesarrelsdelciclotòmictenenmòdul1, z = 1

Equivalentment,

i,pertant,denotant w = z + z,

Ésadir,elnombrereal w = 2R(z)ésarreldelpolinomi x3 + x2 2x 1,

demaneraquesiespoguésconstruirl’heptàgonpodríemconstruir R(z),ipertant2R(z),és adir,podríemconstruirl’arreld’aquestpolinomi.

Però x3 + 3x2 2x 1ésirreductiblesobre Q.Lessevesarrelstenenpolinomimínimdegrau 3,quenoéspotènciade2,ipertant,noespodenconstruir.

7.Elstresproblemesclàssics

Duplicació del cub

Estractadeconstruir,ambregleicompàs,uncubdevolumdobled’uncubdonat. Podemsuposar queelcubdonattévolum1.Tenirdonatelcubvoldirtenirconstruïdalasevaaresta,que podemsuposar,doncs,queésl’intervalunitat OI amb O = (0, 0)i I = (1, 0).

Construiraraelcubdevolum2equivalaconstruirelpunt(α, 0)amb α3 = 2.Siaquest puntfosconstruïble,pelteoremadeWantzel,elpolinomimínimde α sobre Q tindriagrau potènciade2.

17.Jaenshemfetaquestapreguntaenelpeudepàgina7,pàgina16.

Peròel polinomimínimde α sobre Q és x3 2.Enefecte,ésclarque α ésarreld’aquest polinomi.Iamés,aquestpolinomiésirreductiblesobre Q (ipertant,perlaproposició6.4,és elpolinomimínimdelessevesarrels).

Perveureque x3 2ésirreductiblesobre Q pensemquesiespoguésescriurecomaproducte dedospolinomisdegrausméspetits,und’ellstindriagrau1i,pertant, x3 2tindriaunaarrel racional.Siaquestnombreracionall’escrivimcom p/q amb p i q primersentreells,tindríem p3 = 2q3 d’ondeduiríemprimeramentque p ésparelli,simplificantun2,que q ésparell,elqueésuna contradicció.

Trisecció de l’angle

Estractadeconstruir,ambregleicompàs,unangleigualalatercera partd’unangledonat. Demostraremquel’anglede π/3deradian,queésconstruïble,noespottrisecar.Defet, veuremquel’angle π/9noespotconstruir.

Suposemcomsempredonatselspunts O = (0, 0),I = (1, 0).Observemprimeramentque laconstrucciódel’angle π/9ésequivalentaconstruirelpunt(c, 0)amb c = cos π 9 .La perpendicularper(c, 0)alarecta OI tallalacircumferènciadecentre(0, 0)iradi1enunpunt C talquel’angle ∠COI mesura π 9 .

Arabé,si aquestpuntfosconstruïble,tambéhoseriaelpunt(β , 0)amb β = 2c.

Utilitzantque cos3θ = 4cos3θ 3cos θ tenim 1 2 = cos π 3 = 4cos3 π 9 3cos π

ésadir,

Comqueelpolinomi x3 3x 1ésmòniciirreductiblesobre Q,éselpolinomimínimde β . Pertant, β noespotconstruir.Tampocnoespotconstruir,doncs, β /2 = cos π 9 .

Perveureque x3 3x 1ésirreductiblesobre Q pensemquesiespoguésescriurecoma productededospolinomisdegrausméspetits,und’ellstindriagrau1i,pertant, x3 3x 1 tindriaunaarrelracional.Siaquestnombreracionall’escrivimcom p/q amb p i q primers entreells,tindríem p3 3pq2 = q3

d’ondeduiríemque p divideix q3,i q2 divideix p3.Aixòimplica p = q = ±1,però ±1noés arreldelpolinomi.

Observemenparticularquecapdelsangles π/180, π/90, 2π/90, π/36, π/18(1-2-4-5-10 graus)ésconstruïbleambregleicompàs,jaquesiund’ellshofos,podríemconstruir,sumantlorepetidament,l’angle π/9(20graus).Noobstantaixò, π/60(3graus)ésconstruïble,jaque

pelteorema6.10,elpolígonde120costatsésconstruïble,jaque120 = 23 · 3 · 5i3i5són primersdeFermat.Resumint,l’anglede m grausespotconstruirsiinoméssi m ≡ 0(mod3).

Quadratura del cercle

Estractadeconstruir,ambregleicompàs,uncercled’àreaiguala l’àread’unquadratdonat Podemsuposarqueelcostatdelquadratdonat,ésadir,construït,estàformatpelspunts O = (0, 0),I = (1, 0),demaneraquehemdeconstruirunradi R talque πR2 = 1.Construirel radi R voldirconstruirunsegmentdemesura R,oequivalentmentconstruirelpunt (R, 0) = 1

, 0 .

Però,comquesabemconstruirinversosielevaralquadrat,sabríemconstruirelpunt(π, 0)a partirde O i I.

Aixòvoldriadirque π ésarreld’unpolinomidegraupotènciade2.Però,comvademostrar Lindemana[7], π noésarreldecappolinomi.

8.Apèndix.DemostraciódelteoremadeWantzel

EnaquestasecciódonemunademostracióoriginaldelteoremadeWantzelvolgudament preartiniana.18 Enpodeutrobarunademostraciómoltbenexplicadapelsmètodeshabituals al’articledeJosepPla[8].

Vegemcomsónlescoordenadesdelspuntsqueanemconstruintambregleicompàsapartir delareferènciaortonormal O,I,J construïdaalapàgina24.

Perexemple,construïmunprimerpunt P tallantlacircumferència C decentre I iradi IO amb larecta OI.Clarament P = (2, 0),ipodemdir,enparticular,quelescoordenadesde P són nombresenters.Ambunprocedimentsemblantpodemconstruirtotselspunts(m, 0)amb m ∈ Z.

Perconstruirunpunt Q foradelarecta OI tallem,perexemple,l’anteriorcircumferència C amblacircumferènciadecentre O iradi OI

18.El1942EmilArtinvareformularlateoriadeGaloisqueesconeixiaenelseudiaenllenguatged’espais vectorials;vegeu[2].Peròelpreuqueesvapagarvaserunelevatgraud’abstraccióiunadificultatperalsestudiants, queperdienl’origenilamotivació.Amés,algunspuntsmoltimportantscomlaresolventdeLagrangeolaresolvent delpropiGaloisquedavenamagats.Enparticular,nohevolgututilitzarlafórmuladelsgraus,laquediuquesi K ⊂ L ⊂ M sóntrescossosllavors [M : K]=[M : L][L : K] (recordemque [M : K] voldirladimensióde M com a K-espaivectorial).Siaquestscossosprovenende K adjuntantprimerl’arreld’unpolinomiambcoeficientsa K, L = K(α),iadjuntantacontinuaciól’arrel β d’unpolinomiacoeficients K(α), M = K(α)(β )lafórmuladelsgrausens diuqueelgraudelpolinomimínimde β sobre K, P(x),éselproductedelgraudelpolinomimínimde β sobre K(α) pelgraudelpolinomimínimde α sobre K,perònoensdiuquiéselpolinomi P(x).Vegeulaproposició8.3iels teoremesposteriors.

Resolentelsistema

x2 + y2 = 1 (x 1)2 + y2 = 1

obtenim Q = 1 2 , √3 2 .

Lescoordenadesde Q janosónnombresenters.Laprimeracoordenadaésracional,però lasegonano.Podríemdirsimplementquelasegonacoordenadaésunnombrereal, peròseremunamicamésprecisosidiremquelescoordenadesde Q pertanyenaunconjunt queestàentre Q i R,quedenotem Q(√3),iqueestàformatpertotselsnombresrealsque espodenescriurecom

Q(√3) = {p + q√3,p,q ∈ Q}.

Dónalacasualitatquequansumemomultipliquemelementsde Q(√3)obtenimelements de Q(√3).Enefecte,si a,b,c,d ∈ Q, (a + b√3) · (c + d√3) = ac + 3bd + (ad + bc)√3,ac + 3bd,ad + bc ∈ Q,

Ique l’inversd’unelementde Q(√3)éstambéunelementde Q(√3).Enefecte,multiplicant pel‘conjugat’tenim, 1 a + b√3 = a b√

Peraixò esdiuque Q(√3)ésuncos,omésconcretamentqueésunsubcosde R.

Observem quetotselselementsde Q(√3)espodenconstruirambregleicompàs.Enefecte, jahem vistqueelsracionalsi √3sónconstruïblesiperconstruirelproducte(p/q)√3només hemde saberdividirunsegmentconstruït(enaquestcas √3)en q partsiguals.Aixòésfàcil deferutilitzantelteoremadeTales.

Observemfinalmentqueelpaperjugatper √3potserjugatperqualsevolaltrenúmeroreal quesiguiarreld’unaequaciódesegongrau.Concretament,si α ∈ R tépolinomimínimde grau2sobre Q,podemconsiderarelsubcosde R formatpelconjuntd’expressions a + bα, amb a,b ∈ Q,ambelproducteinduïtpelpolinomimínimde α.Ésadir,sielpolinomimínim de α és x2 + px + q = 0,amb p,q ∈ Q,llavors

(a + bα)(c + dα) = ac + (ad + bc)α + bd( pα q)

Aquestcos,eldenotaremper Q(α).

8.1. Cos associat a un conjunt de punts construïts

Generalitzeml’exempleanterioralaconstrucciódediversospunts.

Sigui C0 unconjuntdepuntsdelplaconstruïtsambregleicompàs.Associema C0 elsubcòs K0 de R generatperlescoordenades,tantla x comla y,detotselspuntsde C0.Quandiem

«subcòsgenerat»volemdirelconjuntformatpertotselsnúmerosrealsquepodemobtenir sumant,multiplicant,ifentinversosamblescoordenadesdelspuntsde C0

Perexemple,siconsideremque C0 éselconjuntformatúnicamentpelspunts O = (0, 0)i I = (1, 0),llavors K0 = Q,jaqueel0il’1,persumes,productesiinversosgeneren Q.

Siconsideremque C0 éselconjuntformatpelspunts O,I,Q del’exempleanterior,llavors K0 = Q(√3),jaqueel0,l’1,i √3persumes,productesiinversosgeneren Q(√3).

Definició8.1. DiremqueunpuntP = (x1,y1) és construïbleenunpasapartirde C0 siespot obtenirperintersecciódefigures(rectesocircumferències)construïdesambelspuntsdeC0.

Lesrectesquepodemconstruirsónlesdeterminadesperdospuntsde C0,ilescircumferències lesquetenencentreenunpuntde C0 iradiunsegmentformatperdospuntsde C0.

Uncopelconjunt C0 haquedatampliatamblaconstrucciód’unnoupunt P,elcosassociatal nouconjunt C1 = C0 ∪ P éstambéunaampliaciódelcos K0,obtingudaafegintalselements de K0 lescoordenadesde P itoteslessumes,productesiinversosnecessarisperobtenirun cos.Aquestnoucos,elméspetitqueconté K0,x1,y1 esdenotaper K1 = K0(x1,y1).Observem que K1 podriaeventualmentcoincidiramb K0.

Aixídefiniminductivamentcossos

Ki = Ki 1(xi,yi)

quecorresponenalprocésd’adjuntara Ki 1 lescoordenadesd’unpuntconstruïtenunpas apartirde Ci 1.

Proposició8.2. Lescoordenadesxi iyi d’unpuntconstruïtenunpasapartirdeCi 1 sónzeros depolinomislinealsoquadràticsacoeficients Ki 1.

Demostració. Estudiemprimeramentelcas recta ∩ circumferència,jaqueelcas recta ∩ recta ésmoltsimple.Siguin A,B,C puntsdecoordenades(p,q),(r,s),(t,u)jaconstruïts,ésadir, delconjunt Ci 1.Perdefinició,lescoordenadespertanyena Ki 1.Tallarlarecta AB ambla circumferènciadecentre C iradi ρ,donatperladistànciaentrepuntsde Ci 1,equivala resoldreelsistema x p r p = y q s q , (x t)2 + (y u)2 = ρ2 .

Aïllant y a laprimeraequacióisubstituintalasegona,tenim (x t)2 + s q r p (x p) + q u 2 = ρ2 . (5)

Com que ρ ésladistànciaentrepuntsde Ci 1,tenimque ρ2 ∈ Ki 1,ipertant x (itambé y,ja quedepènlinealmentde x)észerod’unpolinomidegrau2acoeficients Ki 1.

Estudiem araelcas circumferència ∩ circumferència.Perlesmateixesconsideracionsque anteriormenthemderesoldreunsistemadeltipus

s,t,u,v, ρ

Aïllant19 y alaprimeraequacióisubstituintalasegona,tenim

Equivalentment,

Ielquefaqueles«cosesfuncionin»ésjustamentqueelterme x2 d’aquestaequació desapareix,demaneraqueaquestaequacióespotescriurecom

Elevantalquadrat

tenimelresultat,ésadir, x észerod’unpolinomiquadràticambcoeficientsa Ki 1

Observemquesi v = u,aquestadarrerafórmulaensdiuque y depèn Ki 1-linealmentde x, concretament

demaneraque Ki 1(x,y) = Ki 1(x).Si v = u, x ésunzerod’unpolinomilinealacoeficients Ki 1 ipertant x ∈ Ki 1,i Ki 1(x,y) = K(y).Aixòvoldirqueencadapas,ésadir,peracada puntqueesconstrueix,elcosampliatésunaextensiósimpledelcosanteriorobtinguda adjuntantl’abscissa x ol’ordenada y delpuntconstruït.

8.2. Punts construïts en dos passos

Suposemqueapartird’unconjuntdepuntsconstruïts Ci 1 hempassat, perunpas,aun conjuntdepuntsconstruïts Ci,iquenovamentperunpashempassataunconjuntdepunts construïts Ci+1.Aixòenshadonatllocalstrescossos

Ki 1 ⊆ Ki ⊆ Ki+1, generatsperlescoordenadesdelspuntsconstruïts.

Jahemvistquepodemconsiderarqueaquestesextensionssónsimples,ésadir,

Ki = Ki 1(αi 1)i Ki+1 = Ki(αi),

19.Restantlesduesequacionsdelescircumferències,aquestcasesredueixal’anterior.

enquè αi 1 ésl’abscissaol’ordenadadelprimerpuntconstruïti αi l’abscissaol’ordenada delsegonpuntconstruït.Isabemqueelpolinomimínimde αi sobre Ki tégrau1o2.

Proposició8.3. Sigui K elcosassociataunconjuntCdepuntsconstruïtsambregleicompàs. Sigui α l’abscissaol’ordenadad’unpuntAconstruïtapartirdeCenunpas.Sigui β l’abscissao l’ordenadad’unpuntBconstruïtapartirdeC ∪ Aenunpas.Llavorselpolinomimínimde β sobre K tégraupotènciade 2 (1, 2 o 4).

Demostració. 20 Sabemqueelpolinomimínimde α sobre K tégrau1o2.Isabemtambéque elpolinomimínimde β sobre K(α)tégrau1o2.

Estudiemúnicamentelcasenquètotsdospolinomismínimstenengrau2.Elsaltrescasos sónsimilars.

Sigui

P(x) = x2 + (a + bα)x + (c + dα),a,b,c,d ∈ K, elpolinomimínimde β sobre K(α).L’escrivimcom

P(x) = P2(x) + αP1(x), amb

P2(x) = x2 + ax + c ∈ K[x],P1(x) = bx + d ∈ K[x]

Podemsuposarque P1(x)noéselpolinomizero,jaquellavors P(x) ∈ K[x],ipertant,el polinomimínimde β sobre K tégrau2ihemacabat.Suposarem,doncs,apartird’ara,que b o d sóndiferentsdezero.

Sigui α′ lasegonaarreldelpolinomimínim x2 + px + q de α sobre K.Ésadir, α + α′ = p, α · α′ = q.Elfetdeser α / ∈ K implica α = α′.Denotem P′(x) = P2(x) + α′P1(x).

Afirmemqueelpolinomimínimde β sobre K és

P4(x) = P(x)P′(x). Enefecte,hemdeveurequeaquestpolinomicompleixtrescoses:queadmet β comaarrel, queelsseuscoeficientsestana K,iqueésirreductiblesobre K.

1. P4(x) admet β comaarrel.Aixòésevident,jaque P(β ) = 0.

2. ElscoeficientsdeP4(x) pertanyena K,i.e. P4(x) ∈ K[x].Aixòesveudirectament,jaque enefectuarelproductede P(x)per P′(x)obtenim

P4(x) = P2(x)2 pP2(x) P1(x) + qP1(x)2

i p,q ∈ K.Observem,doncs,que P4(x) ésunpolinomide K[x] queésproductededos polinomisde K(α)[x].

20.Ésunademostraciódirecta,senseusarelllenguatgeartiniàd’espaisvectorials,delafórmuladelsgraus [K(α, β ) : K]=[K(α, β ) : K(α)][K(α) : K] ons’explicitenelspolinomismínims.

3. P4(x)ésirreductiblesobre K.Perveureaixòsuposem,perl’absurd,que P4(x)fosreductible. Llavorstindríem

P4(x) = A(x) · B(x),A(x),B(x) ∈ K[x],

ambni A(x)ni B(x)constants,i β hauriadeserarreld’und’aquestspolinomis.Suposem quehoésde A(x),i.e. A(β ) = 0.

Comque K ⊂ K(α),podempensarquetant A(x)com P(x)sónpolinomisacoeficients K(α).Comque P(x)éselmínimde β sobre K(α),hadeser

jaque siunpolinomitéunaarrelencomúambelpolinomimínimésunmúltipled’aquest.

Sigui β ′ l’arrelde P′(x)ques’obtécanviantformalmentenl’expressióquadràticade β , α per α′.Concretament,si

llavors,

Comqueestemsuposant b o d diferentsdezero,espotveureque β = β ′.Observemque P′(x)éselpolinomimínimde β ′ sobre K(α).Aixòimplicaque P(β ′) = 0,jaquesi β ′ fosarrel de P(x)aquestseriamúltiplede P′(x),cosaquenopotser.

Comque P4(β ′) = 0,tenimdoscasossegons β ′ siguiarrelde A(x)ode B(x):

◮ Primercas. β ′ ésarrelde B(x).Llavors, B(x) = λ(x)P′(x)perser P′(x)elpolinomimínimde β ′.Peròllavorstindríem

P(x)

laqualcosaimplicaque µ(x) = λ(x) = 1,ésadir, A(x) = P(x),cosaquenopotser,jaque P(x) / ∈ K[x].

◮ Segoncas. β ′ ésarrelde A(x).Llavors,hadeser µ(β ′) = 0.Aixòimplica,comabans,que µ(x) = ν(x)P′(x).Peròllavorstindríem

P(x)P′(x) = A(x)B(x) = ν(x)P′(x)P(x)B(x),

laqualcosaimplicaque ν(x) · B(x) = 1,contradicció,jaquegrau B(x) ≥ 1.

Comqueenelsdoscasoshemarribatacontradicció,aixòvoldirque P4(x)ésirreductiblesobre K.Pertant,éselpolinomimínimdelessevesarrels.Ésadir,elpolinomimínimde β sobre K tégrau4,comvolíemdemostrar.

8.3. Punts construïts enpassos k

Denotem K0 = Q elcos associatalconjunt C0 = {(0, 0), (1, 0)},idefiniminductivament cossos Ki+1 = Ki(αi)adjuntantacadacos Ki l’abscissaol’ordenada αi ∈ R d’unpunt

construït apartirde Ci perunpas.Recordemqueelcosestèsambl’abscissail’ordenada delpuntconstruïtcoincideixambelcosestèsambl’abscissaol’ordenadadelpunt.Ésadir, semprepodempensarquetenimextensionssimples.

Observemquetota αj ésunaexpressió«racionalquadràtica»de α0, α1, , αj 1.Ésadir,una expressióformadapersumes,productesiradicalsquadràticsd’expressions Q-linealsenles αl anteriors.

Teorema8.4(Wantzel). Sigui αj+k l’abscissaol’ordenadad’unpuntconstruïtenk + jpassosa partirdeC0 = {(0, 0), (1, 0)}.

Peratotj ∈ N,iperatotk ∈ N, αj+k tépolinomimínimdegraupotènciade 2 sobre Kj

Enparticular,prenentj = 0,veiemqueelpolinomimínimsobre Q,tantdel’abscissacomde l’ordenadad’unpuntconstruïtenkpassosapartirde C0,tégraupotènciade 2.

Demostració.Perinducciósobre k.Si k = 0hemdedemostrarqueperatot j ∈ N, αj té polinomimínimdegraupotènciade2sobre Kj,laqualcosaéscertaperladefiniciód’αj.

Suposem,perhipòtesid’inducció,elresultatcertfinsa k.

Volemdemostrarqueperatot j ∈ N, αj+k+1 tépolinomimínimdegraupotènciade2sobre Kj .

Apliquemlahipòtesid’inducciópera j + 1.Aixòvoldirque αj+1+k tépolinomimínimdegrau potènciade2sobre Kj+1.Denotemaquestpolinomiper

P(x) = x2k+1 + Σar xr ,ar ∈ Kj+1 = Kj(αj).

Iaral’escrivimcom

P(

, simplementtenintencompteque ar = br + cr αj,amb br ,cr ∈ Kj.

Afirmemqueelpolinomimínimde αj+k+1 sobre Kj és

R(x) = (P2(x) + αjP1(x)) (P2(x) + α ′ j P1(x)).

Enefecte,hemdeveurequeaquestpolinomicompleixtrescoses:queadmet αj+k+1 coma arrel,queelsseuscoeficientsestana Kj,iqueésirreductiblesobre Kj.

1. R(x) admet αj+k+1 comaarrel.Aixòésevident,jaque P(αj+k+1) = 0.

2. ElscoeficientsdeR(x) pertanyena Kj,i.e. R(x) ∈ Kj[x].Aixòesveudirectament,jaqueen efectuarelproducteindicatobtenim R(x) = P2(x)2 pP2(x)P1(x) + qP1(x)P1(x) ∈ Kj[x], amb

p = αj + α ′ j ∈ Kj,q = αjα ′ j ∈ Kj.

Observem,doncs,que R(x) ésunpolinomide Kj[x] queésproductededospolinomisde Kj+1[x].

3. R(x) ésirreductiblesobre K.Mateixosargumentsquealademostraciódelaproposició 8.3.

Com R(x)tégraupotènciade2,hemacabat.

Finalmentdonemlaideadelademostraciódelteorema6.2,quehemanomenatTeoremade Wantzelcomplex.

Teorema8.5. Suposemqueelpuntzdelplacomplex,amb |z| = 1,haestatconstruït.Llavorsel polinomidegrauméspetitqueadmetzcomarreltégraupotènciade 2.

Demostració. Posem z = a + bi.Sihemconstruït z tambépodemconstruir a i,pelteorema deWantzel, a ésarreld’unpolinomi P(x) ∈ Q[x] degrau m igualapotènciade2.Observem que z ésarreldelpolinomi

Siguin a = r1,r2, ,rm lesarrelsde P(x).Llavors,elpolinomi

tégrau2m,pertant,potènciade2,admet z comaarrel,iésirreductiblesobre Q (aixòs’ha deprovar,peroésessencialmentelmateixraonamentquealademostraciódelaproposició 8.3).Pertant,éselpolinomimínimde z sobre Q.

Que S(x) ∈ Q[x],ésadir,queelsseuscoeficientssónracionals,ésconseqüènciadelfetque enefectuarelsproductesindicatsvanapareixentlesfuncionssimètriqueselementalsdeles ri,quepertanyena Q,jaquesónelscoeficientsde P(x).

Perexemple,si m = 2,posant M = M(x) = x2 + 1 ∈

tenim

jaque r1 + r2 i r1r2 sónracionals.

ObservemqueelteoremadeWantzelnodiuquelesarrelsdepolinomisdegraupotènciade2 icoeficientsracionalsespuguinconstruir.Perexemple,espotveuresensegairedificultatque elpolinomi x4 x 1téalmenysunaarrelrealnoconstruïble;vegeu,perexemple,[3]o[8].

Agraïments. EsticmoltagraïtaRosaCampsperlesmoltesimoltútilsconversesalvoltantde lateoriadeGaloisquehemmantingutdurantlapreparaciód’aquesttreball.ItambéaEduard Gallego,JuditAbardiaiFerranCedóperhaver-nefetunaprimeralectura.

Referències

[1]Kuh,D.(2013).Constructibleregular n-gons. SeniorProjectArchive2013.EUA:Withman College,1-36.

[2]Artin,E.(1970). LaTeoriadeGalois.Barcelona:Vicens-Vives.Primeraedició(1942):Galois Theory.LecturesDeliveredattheUniversityofNotreDame. NotreDameMathematicalLectures,2.

[3]Carrega,J.C.(1981). ThéoriedesCorps.LarègleetleCompas.París:Hermann.

[4]Carslaw,H.S.(1909).Gauss’sTheoremontheRegularPolygonswhichcanbeconstructed byEuclid’sMethod. ProceedingsoftheEdinburgMathematicalSociety,121-128.

[5]Enriques,F.(1900). QuestioniriguardantilaGeometriaElementare.Bolònia:NicolaZanichelli.FederigoEnriquesésl’editoriautord’algunsdelscapítolsd’aquestaobraendos volums.Hiparticipen,entred’altres,U.Amaldi,E.Baroni,R.Bonola,B.Calò,G.Castelnuovo, A.Conti,E.Daniele,A.Giacomini,A.GuarducciiG.Vitale.

[6]Gauss,C.F.(1801). DisquisitionesArithmeticae.Lipsiae,Gerh.Fleisher.Traducciócatalana acàrrecdeGriseldaPascualXufré; DisquisicionsAritmètiques.Barcelona:SocietatCatalanade Matemàtiques(1996).

[7]Lindeman,F.(1882).ÚberdieZahl π. MathematischeAnnalen,20,213-225.

[8]Pla,J.(2006).L’àlgebradelapapiroflexia. ButlletídelaSocietatCatalanadeMatemàtiques, 21,81-155.

[9]Antoine,R.,Camps,R.iMoncasi,J.(2007). Introduccióal’ÀlgebraAbstracta.ManualsUAB, vol.46.

[10]Reventós,A.(1993). GeometriaAxiomàtica.Barcelona:Institutd’EstudisCatalans,vol. CVI SegonaedicióacàrrecdelaSocietatCatalanadeMatemàtiques(2010),vol.5.

[11]Stewart,I.(2004). GaloisTheory.ChapmanandHall.Terceraedició.Primeraedició:1973.

[12]Wantzel,P.L.(1837).RecherchessurlemoyensdereconnaîtresiunProblèmedeGéométriepeutserésoudreaveclarègleetlecompas. J.deMathématiquesPuresetAppliquées, 366-372.

Aclasse...ambcorbata!

PedroCoboLozano UniversitatRoviraiVirgili

Resum Abstract

Enaquestarticlemostremcomels alumnesresolenunproblemaproduintles sevespròpiesrepresentacionsdel procedimentdeconstruirunnusde corbata.Elsalumnesfanserviraquestes representacionsperagenerarnousnusosi peracalcularelnombredenusosde corbataenfunciódelsmoviments necessarisperconstruir-los.Totaixòdinsel marcd’unametodologiaqueafavoreixels processoscomunicatiusal’aula.

1.Introducció

Thispapershowshowstudentssolvea problemcreatingtheirownrepresentations oftheprocessofdoingatieknot.Students usetheserepresentationstogenerate newknotsandtocalculatethenumberoftie knotsdependingontherequiredmovements totiethem.Thisisdoneinthecontextofa methodologythatbenefitsthe communicationprocessintheclassroom.

Undiad’estiu,passejantpelcarrerLaugavegurdeReykjavík,vamveureunafotografiagran (figura1)enlaquals’esquematitzava,mitjançantimatges,laformadeferdiversosnusosde corbata.

Ensvamdemanarsiseriapossible,sotadeterminadescondicions,queelsnostresalumnes arribessinaresoldreelsproblemesdeconstruirigenerarnousnusosdecorbataiacalcular elnombredenusosdecorbataenfunciódelnombredemovimentsutilitzatsperalaseva construcció.

Pensemquepersolucionaraquestsproblemeshemdeproposaralsalumnestasquesque afavoreixinlaintegraciódetrescompetènciesmatemàtiquesprincipalment,comsónla representació,lamodelitzacióilacomunicació.L’associaciódeprofessorsdematemàtiques delsEstatsUnits(NCTM,2003)resumeixaquestaintegraciódelaforma:«Lesrepresentacions hauriendetractar-secomaelementsessencialspersustentarlacomprensiódelsconceptesirelacionsmatemàtiques,perquèelsalumnescomuniquinelsseusenfocaments,argumentsiconeixements,perreconèixerlesconnexionsentreconceptesmatemàticsiper aplicarlesmatemàtiquesaproblemesrealsatravésdelamodelització»(p.71).

Fig.1.Reproducciódelafigurad’uncarrerdeReykjavíkenlaqual es mostrenlesconstruccionsdetresnusosdecorbata.

Concretemacontinuacióelsaspectesdelarepresentacióilamodelitzacióqueconsiderem enaquesttreballilamaneradepotenciarlacomunicacióal’aula.

Pelquefaalarepresentació,Duval(1995)identificatresactivitatscognitivesrelacionadesamb elssistemesderepresentaciósemiòtica:laformaciód’unarepresentació,elseutractamenti laconversióentrerepresentacions.Iressaltaduesideesperquèhihagiaprenentatge: a)elfet quehemd’aconseguirqueelsalumnesdiferenciïnentreunobjecteilasevarepresentació,i b)laimportànciaquetéobservarianalitzarlesrepresentacionsgeneradespelsalumnesper taldefomentarlaconversióentreellesenelcontextdeconstrucciósocialdeconeixements enlesclassesdematemàtiques(Hitt,2013).

Aquestaconversióentrerepresentacionsesfacilitaràatravésdelsprocessoscomunicatius al’aulaienspermetrà,siplantegemlestasquesdeformaadient,quesiguinelsmateixos alumnes,ambl’ajutdelprofessor,elsquifacinlestransicionsdelessevesrepresentacions espontàniescaparepresentacionsmésinstitucionalitzades(formals).

Consideremqueésimportanttrobarelsigneadientquerepresentielconcepteoprocediment, peròtambéhoésressaltarelsprocessossocialsqueportencapalsigne(Radford,2003).En aquestsentit,enlapràcticaquemostremaniremdescrivintl’evoluciódelesrepresentacions espontàniesdelsalumnes.

Entenemlamodelitzaciócomunprocéscíclicquetécomapuntdepartidaid’arribadaun dominiextramatemàtic.Elprocéscomportariapassossuccessiuscom:seleccionarvariables icaracterístiquesqueesconsiderinrepresentativesdelqueesvolestudiar,dinsdeldomini extramatemàtic;expressar-lesentermesmatemàtics;extreureconclusionsmatemàtiques,i traslladaraquestesconclusionsaldominiinicial.Arabé,aquestaideademodelitzacióens interessasilafemservirambintencionsdemillorarlamotivaciódelsalumnesid’ajudar-losa consolidarlaformaciódeconceptesilaresoluciódeproblemes(Niss,2012).

CastroiCastro(2000)tambéressaltenlaimportànciadel’úsdemodelsmatemàticspera potenciarl’ensenyamentdelesmatemàtiquescomaeinesheurístiquesquesón,jaqueel quefanéstraslladarelproblemaqueesvolresoldre«alstermesespecíficsdelmodelia travésd’aquests’hadetrobarlasoluciófentservirnoméslessevespròpiesreglesielements» (p.111).

Pelquefaalacomunicacióal’aula,lesrepresentacionsespontàniesdelsalumnessónles quelafacilitaran,inicialmentforad’unllenguatgeformal,ipossibilitaranl’evoluciódela verbalitzaciócapal’úsdelllenguatgenumèricigràficfinsaarribaralautilitzaciódelllenguatgesimbòlic(DOGC,2007).

Hihaduesideesbàsiquesenlamanerad’ensenyarqueseguimalesnostresaulesquevolem ressaltariqueincideixenenlacomunicació:

• Pensemquelamaneradepotenciarelsprocessoscomunicatiusal’aulaéscrearun entornenelqualelsalumnessiguinelsprotagonistesprincipalsdelseuaprenentatge i,pertant,elsquiconstrueixinelseuspropisconeixements,quehandesersocialment compartits.Ésadir,hemdetenircomareferentlateoriadelconstructivismesocialen cadamomentdelprocésd’ensenyament-aprenentatge.

• Elsproblemesqueproposemhandeserricsenelsentitde:generarenelsalumnes actitudsdecuriositatid’interès;serobertsperapermetrepoderabordar-losdediferentsmaneres;facilitarlautilitzaciódediversossistemesderepresentacióperquèels alumnespuguincomunicarelquevolenexpressar,ipermetreestablirconnexionsentre contingutsmatemàticsdistints(CoboiMolina,2014).

Peracabaraquestaintroducció,concretemelsdosobjectiusquepretenemqueelsalumnes assoleixinenaquesttreball:

• Establirsistemesderepresentaciópropisperalaconstrucciódenusosdecorbata,amb lafinalitatqueelspermetinmodelitzarelprocéspertaldegenerarnousnusos.

• Utilitzaraquestmodelperidentificarprocedimentsqueelspermetincalcularelnombre denusosdecorbataenfunciódelsmovimentsnecessarisperconstruir-los.

2.Què s’haescritsobreeltemadelsnusosdecorbates

Hemtrobatmoltaliteraturasobrelahistòriailaconstrucciódenusosdecorbata,però hihaduesreferènciesqueenshansemblatlesmésrepresentativesiquecomentarema continuació:FinkiMao(1999)iHirschialtres(2014).

FinkiMao(1999)fanunestudihistòricdel’evoluciódelsnusosdecorbata,modelitzenel procedimentdeconstrucciódenusosdecorbataiarribenarepresentarelsvuitanta-cinc nusosdecorbataqueidentifiquenambmenysdedeumoviments.

Aquestsautorsimposentotunseguitdecondicionsperconstruirnusosdecorbata.Per exemple,considerenlacorbatadivididaenduesparts:lapartampla(oactiva),queésl’única queesmoualvoltantdelapartestreta(opassiva),pertaldegenerarunnusquesiguiescorredorsobreaquestapartestreta(figura2).Parteixentambéd’unacorbataque,mirada decara,tinguilapartamplaaladreta(figura2),pertant,elprimermovimentdelapartactivade lacorbatanoméséspossiblequesiguicapal’esquerra.

FinkiMao(1999)divideixenelplaentresregions:esquerra(L),dreta(R)icentre(C)(figura3),alesqualsespotmourelapartactivadelacorbata.Tambéindiquenambelssubíndexs «∗»i«o»ladirecciódelmoviment,ésadir,silapartactivapassapersobreopersota, respectivament,delapartpassiva.Així,perexemple,L∗ seriaelmovimentdelapartactiva delacorbatacapal’esquerraipersobredelapartpassiva.

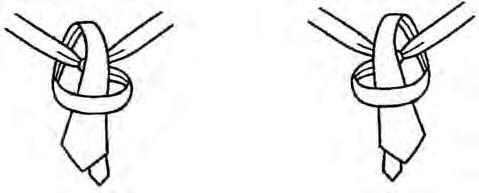
Ambaquestescondicions,defineixenunnusdecorbata«comunaseqüènciademoviments triatsdelconjunt{Ro,R∗,Lo,L∗,CoiC∗}començantperLooL∗ iacabantper...RoL∗ CoTo... LoR∗CoT»(p.55).IndiquenperTelfetquelapartactivafinalmentesficafrontalmentatravés delllaçconstruïtperl’últimmoviment,ielconsiderencomunamaneraestèticad’acabarel nus(figura4),sempredelamateixamanera;pertant,noelconsiderencomunmoviment.

Alafigura4mostremlesduesformesd’acabarunnussegonsFinkiMaoielpasfinaldeficar lapartampladelacorbatasotaelplecanterior.

Comressaltenelsautors,laformadedefinirunnuscondicionaelfetquedosmoviments consecutiusnopodenanaralamateixaregió(nopodenserRRoLLoCC),nienlamateixa direcció(nopodenser ∗∗ nioo).

Figura2

Figura3

Apartd’aquestesnormesperconstruirnusosdecorbata,FinkiMao(1999)defineixen paràmetrescomlagrandària,laforma,lasimetriaielbalançd’unnusperadeterminar-ne l’estètica.

Percalcularelnombredenusosqueespodenconstruiramblescondicionsestablertes,Fink iMao(1999)representenelsnusoscomaseqüènciesdecaminsaleatorissobreunamalla triangular(figura5,enlaqualesrepresentaelnus:L∗ RoL∗ CoT).Enaquestamalla,elseixos → r , → l i → c corresponenalsmovimentssobrelesregionsR,LiC,respectivament,ienlesque ometenlesnotacionsdireccionals«∗»i«o»perquèesvanalternantielnussempreacabaen Co;pertant,ésfàcildeduirlaseqüènciadireccional.

FinkiMao(1999)arribenaobtenirl’expressiósegüentdelnombredenusos(K)enfunciódel nombredemoviments:

icalculenelnombretotaldenusosambcomamàximnoumovimentsdelaforma:

enquè K(1) = K(2) = 0.

Perlasevapart,Hirschialtres(2014)considerenqueelquefanFinkiMaoésconstruirun llenguatgesobreelsnusosdecorbata.Unllenguatgequetéunalfabet{Ro,R∗,Lo,L∗,Co, C∗ iT}iqueésunsubconjuntAdelconjuntMformatpertoteslesseqüènciesdequalsevol

Figura4

Figura5

longituddelletresdel’alfabet.Qualsevolllenguatgetéunagramàtica,que,enaquestcas, sónlesnormesqueestableixenFinkiMaoperalaconstrucciódenusos.

JaquelesregionsestablertesperFinkiMao(L,RiC)noespodenrepetirdeformaconsecutiva ilesdireccions ∗ io(persobreipersota)s’hand’alternarenlaconstrucciód’unnus,Hirschi altres(2014)afirmenque:«lallistaderegionsésmenysimportantqueladirecciódetransició: qualsevoltransicióvàlidaesfaoenelsentitdelmovimentdelesbusquesdelrellotgeoen sentitcontrari»(p.4).Irepresentenlestransicionsdelamanerasegüent(figura6):

• T:comeldesplaçamentdel’extremdelacorbataenelsentitdelmovimentdeles busquesd’unrellotge.Ésadir,lestransicionsRL,LCiCResrepresentarienperT.

• W:comeldesplaçamentdel’extremdelacorbataenelsentitdelmovimentcontrarial delesbusquesd’unrellotge.Ésadir,lestransicionsLR,RCiCLesrepresentarienperW.

• U:eldesplaçamentdel’extremdelacorbatasotaelplecanterior.

D’aquestamanera,Hirschialtres(2014)eliminenlescondicionsqueimposavenFinkiMao. Així,d’unabanda,considerenquelapartestretadelacorbataéstambépartactiva,laqual cosasuposaqueelnusnosiguiescorredor;i,del’altra,quel’extremdelacorbatapot ficar-se,enunmateixnus,diversesvegadesperl’últimplec,ésadir,aquestatransicióno necessàriamentsuposalafidelnus.

Hirschialtresarribenadeduirquecombinantfinsaonzetransicionsespodengenerar 177.147nusosdecorbata;naturalment,lamajoriad’ellsambunaestèticaunamicarara.

3.Comarribenelsalumnesamodelitzarlaconstrucciódenusos decorbates

Latascaqueproposemformapartd’unaseqüènciadidàcticacontextualitzadaeneldesenvolupamentdeprocessoscomlacomunicació,larepresentació,lamodelitzacióilaresolució deproblemes.Esduuatermedurantaproximadamenttreshoresdeclasse.

Latascas’implementaenungrupnormalde4td’ESO,enelqualseguimunametodologia quefomentalaparticipaciódelsalumnes,quealternentreballindividual,engrupspetitsi

Figura6

posades encomúenelgrup-classe(Cobo,2004iCoboiMolina,2014),moltsemblantala queHittiMorasse(2009)anomenen«metodologiad’ACODESA».

Elsalumneshantreballatnormalmentambrepresentacionsdeconceptesiprocedimentsmatemàticsquesónintroduïtspelprofessoriquesónelsquefanservirhabitualmentpercomunicarlessevesideesmatemàtiques.

a) Presentaciódelatasca. Elprofessorcomençafentunbreurepàshistòricdelsnusos decorbata.Abansdeplantejarl’objectiudelatasca,tambéexplicaalgunsexemplesde representacionsdeconceptesiprocedimentsqueesfanservirenmatemàtiques(funcions, nombres...)iambelsqualselsalumnesjaestanfamiliaritzats.Ressaltalaimportància d’utilitzardiferentsrepresentacionsd’unmateixcontingutmatemàtic.Finalment,al mateixtempsquefaunnusd’unacorbata,plantejal’objectiudelatasca,animant,en unprimermoment,elsalumnesatrobarrepresentacionsdelprocedimentdeconstruir nusosdecorbata.

Pertractard’unificarisimplificarelprocés,considerem,comfanFinkiMao(1999),quela posicióinicialdelacorbataéslaquemostremalafigura2,enlaqualensveiemlacorbata decaraamblapartamplaaladreta.Amés,tenimencomptequenomésaquestapart amplaéslapartactivaperconstruirelnus,ésadir,l’únicaquepodemmourealvoltant delapartestreta(passiva).Tambéconsideremquelesúniquesposicionsfinals(pertalde conservarl’estètica)d’unnusdecorbatasónlesdelafigura4.

b) Evoluciódelesrepresentacionsdelsalumnes. Alprincipi,elsalumnescomencenexperimentantlaformadeconstruirnusosamblacorbataquecadascúhaportataclasse. Quanjahanfetunnus,intentenrepresentarelprocésdeconstrucció.Lesprimeres representacionssóndibuixoscompletsdelacorbataidelprocés,seguitsd’explicacions escritesenllenguatgeordinari.Deseguida,hihagrupsd’alumnesquesimplifiquenla representació,fentservirlíniesicapsdefletxesperrepresentarlescorbates(figura7).

Abansd’acabarlaprimerahoradeclasse,pràcticamentcadagrupd’alumneshaaconseguit unarepresentaciócomlesquemostrem.LestresprimeressónsimilarsalesdeFinkiMao (1999)ilaquartaésunintentderepresentaciómésalgèbrica:

Ungrupd’alumnesrepresentaper D ← elmovimentdelapartactivadelacorbatacapa l’esquerraiperdaltdelapartpassiva.Iper ← B elmovimentdelapartactivadelacorbata

Figura7

capal’esquerraiperbaixdelapartpassiva.Igualment,representenper D →→ B els movimentscapaladretaperdaltiperbaix,respectivament.I,finalment,representen per ↓D iper ↓B,elsmovimentscapalcentre,endavantienrere,respectivament.

Unaltregrupd’alumnes,evitalesfletxes,dibuixantnoméselseuscapçals,ambla qualcosatrobem:

< D, < B:movimentscapal’esquerraperdaltiperbaix,respectivament.

> D, > B:movimentscapaladretaperdaltiperbaix,respectivament.

VD,VB:movimentscalalcentre,endavantienrere,respectivament.

Unsaltresrepresentenelsmovimentsdirectamentamblletres:

∗, E!, D∗, D!, C∗ i C!:movimentscapal’esquerra(adaltiabaix),capaladreta (adaltiabaix)icapalcentre(endavantienrere),respectivament.

AquestestresrepresentacionsacabensempreelnusambunaFqueindicaelfetdeficar lapartampladelacorbataenelplecanterioriquesempreéselmateixperacabarelnus i,pertant,noelconsiderencomunmoviment(figura4).

Finalment,ungrupd’alumnesintentaferunarepresentaciógraficosimbòlica,dibuixant líniesquesimuleneixostridimensionalspositiusinegatius,commostremalafigura8.

+x → capadreta

x → capaesquerra

+y → capdalt

y → capbaix

+z → persobre

z → persota

dinsnus

Cadagrupexplicaalaclasselasevarepresentacióiesdiscuteixenlessemblancesi diferènciesentreelles.

c) Familiaritzacióamblesrepresentacionsielaboraciódenormesperconstruirnusos.Generació denousnusosdecorbata. Enaquestafasedefamiliaritzacióamblesrepresentacionsque cadagruphaelaborat,presentemalsalumnes,enfigures(tretesdeFinkiMao,1999),el procésdeconstrucciódequatrenusosdecorbata,comveiemalafigura9(enlaqual mostremtambélarepresentacióassociadad’undelsgrupsd’alumnes)ielsdemanemque:

Elsrepresentinsegonselllenguatgequeellshantrobat. Observinlesnormesqueregeixenperalaconstrucciódenusos.

Figura8

Associatsacadafigura,elsalumnesfanlasevarepresentació(figura9).

Desprésdeferlatraducciócompleta,arribenaresumirlesnormessegüentsperala construcciódenusos,queungrupd’alumnesescriuendelamanerasegüent:

Elprimermovimentsemprehauràdesercapal’esquerra( ← B , D ← ).

Unmovimentmainoespodràrepetir;així,perexemple,desprésd’unmovimentcap al’esquerraelsegüenthauràdeser: ↓D , ↓B, D → o → B .

Lesdireccions B i D esvanalternant.

Elnusacabaràambunmovimentcapabaix: ↓B. Lesduesúniquesmaneresd’acabarunnussón:( → B D ←↓B F)o( ← B D →↓B F).

Apartird’aquestmoment,elsalumnesacabendemodelitzarelprocedimentdela construcciódenusosdecorbataicomencenagenerarnousnusos,quevanconstruint simultàniamentamblasevacorbata.Ésatravésd’aquestmodel,fentservirlessevesregles ielements,queelsalumnescomencenatrobarlasoluciódelsproblemesdegenerarnous nusosdecorbataidecalcularelnombredenusos.

Aquestafaseéslaméscreativa,perquèelsalumnesinventennusosnous,elsconstrueixen amblacorbataiexpliquenfàcilmentid’unamaneraentenedoraelprocedimentde construccióalsseuscompanys.

4.Comcalculenelsalumneselnombredenusosdecorbata

Proposemalsalumnescalcularelnombredenusosdecorbataqueespodrienfer,partintde lesformesdecomençariacabarunnusquehemconsiderat(apartat3a)idelesnormesque hantrobatperal’elaboraciódenusos(apartat3c).

Figura9

Desprésdediferentsintents,elsalumnescomencendesdelfinalitreballencapenrere. Elaborendiagramesenarbre,partintdelesduesposicionsfinalspossibles,alesqualsvan afegintmovimentssuccessius(figura10)iratllantlespossibilitatsquenosóncorrectes perquènocompleixenlesnormesdeconstrucció,perexemplelesquenocomencenambun movimentcapal’esquerra.Alafigura10mostremelsdiagramesenarbrequefanelsalumnesperconstruirnusosdecorbataambsismoviments.

Observen que3éselnombremínimdemovimentsquecalenperconstruirunnusiconstrueixentaulesquedonenelnombredenusosdecorbataenfunciódelsmoviments necessarisperconstruir-los(figura11).

Observantlestaulesconstruïdes,elsalumnesarribenaduesformesrecursivesdegeneralització.Enlaprimera(figura12),nomésfanunadescripció(representacióescritaenllenguatge ordinari)delaformadegenerarcadanombredenusosenfunciódel’anterior.

Sielnombredemovimentsésimparell,esfaeldobledelnombredenusos +1; siésparell,eldobledelnombredenusos 1idónaelnombredenusossegüent.

Figura12

L’expressió simbòlicaformaldelqueelsalumnesescriuenseria:

Figura10

Figura11

associaciómoltsemblantaFibonacci

Figura13

Enlasegona(figura13),ungrupd’alumnesjamostradirectamentl’expressióalgèbrica (representacióformal)iafegeixlaindicacióquemostralasevasemblançaamblasuccessió deFibonacci.

Enaquestmomentacabeml’activitat,sentconscientsquepodríemhaver-lacontinuat,com fèiemaCoboiMolina(2014)ambelsproblemesqueproposàvem.

Hihamoltesformesdecontinuarl’activitat.Laquesemblamésevidentserialadetrobaruna altrarepresentació(expressióexplícita)quenosiguirecurrentper

itractardejustificarqueésequivalental’expressiótrobadaperFinkiMao(1999):

Aixòs’aconsegueixbuscantl’equaciócaracterísticadel’expressiórecurrent,queenaquests casseria:

2 t 2 = 0; resolent-laitrobantl’expressióexplícita,queseriadelaforma:

icomprovantqueaquestailadeFinkiMaosónequivalents.

Altrespossiblescontinuacionsdel’activitattindrienaveureamblacomparaciódelasuccessió obtingudaambladeFibonacci.

5.Reflexionsfinals

Pensemqueactualmentesfomentapocalesnostresaulesqueelsalumnesgenerinlesseves pròpiesrepresentacionsperquèhihaunatendènciacapaconstruirlesmatemàtiquesdirectamentsobrerepresentacionsinstitucionalitzadesdeconceptesiprocedimentsintroduïts directamentpelprofessor.Nitansolesfansemblanceshistòriquesdelsprocessosculturals quehanfacilitatl’evoluciód’aquestesrepresentacionsinstitucionalitzades.ComindicaHitt (2013),unadelesformesdefomentarenelsalumneslageneracióderepresentacions espontàniesésplantejantiresolentproblemes.

Elplantejamentdeproblemesquegenerinactitudsdecuriositatenelsalumnesiquefacilitin l’úsdediferentssistemesderepresentaciódeconceptesiprocedimentsafavoreixenels

processoscomunicatiusal’auladematemàtiquesielpasderepresentacionsespontànies capalesmésinstitucionalitzades.

Enelnostrecas,hemmostratcomevolucionenlesrepresentacionsdelsalumnessobre elprocedimentdeconstruirnusosdecorbatesicomarribenaobtenirlesnormesque modelitzenaquestprocediment;ocomfanunarepresentacióendiagramad’arbreper analitzarpossibilitats,quedesprésrepresentenenunatauladevalors,perarribar,finalment, aobtenirelnombretotaldenusosdecorbatademaneraformalmitjançantunaexpressió semblantaladeFibonacci.

Elsprocessoscomunicatiustambéesfomentensielsalumnesparticipend’unametodologia detreballenlaqualsónprotagonistesprincipalsenlaconstrucciódelseuconeixement,que hadesersocialmentcompartit.Ésperaixòquepensemque,enaquestametodologia,hem decombinarmomentsdereflexióindividual,queenmoltscasosserveixenperreactivarels processosderesolució,ambmomentsdetreballenpetitgrupiambreflexionsconjuntesen elgrup-classe,queserviranperinstitucionalitzarelconeixementcompartit.

Amés,laconstrucciódenusosdecorbataielcàlculdelnombredenusosenfunciódels movimentsnecessarisperalasevaconstrucciósónproblemesquehemobservatque interessenalsalumnes,malgratquelacorbatasiguiunapeçadevestirquesemblacada copmenysutilitzadasocialment.Ambaquestsproblemes,elsalumneshanpogutreflexionar conjuntamentdinsdelgrup-classesobrelesaportacionsdecontingutsmatemàticsque hanfet,relacionades,perexemple,ambelsprocessosd’induccióigeneralització,lacreació iutilitzaciódemodels,larealitzaciódetaules,lautilitzaciódediferentssistemesderepresentació,l’anàlisidepossibilitats,l’úsd’expressionsalgebraiques,elprocedimentde començarpelfinalitreballarcapenrere,etc.

6.Bibliografia

CastroE.iCastro,E.(2000).RepresentacionesyModelización.AL.Rico(coord.). LaEducación MatemáticaenlaEnseñanzaSecundaria.Barcelona:Horsori.

Cobo,P.(2004).Experienciassobreenseñanzaderesolucióndeproblemasdematemáticas. AGiménez,SantosidaPonte(coords.). Laactividadmatemáticaenelaula.HomenajeaPaulo Abrantes.Barcelona:Graó,p.127-136.

Cobo,P.iMolina,M.A.(2014).¿Puedennuestrosestudiantesconstruirconocimientosmatemáticos? Números.RevistadeDidácticadelasMatemáticas 85,49-73. (http://www.sinewton.org/numeros).

DOGC(2007).Ordenaciódelsensenyamentsdel’EducacióSecundàriaObligatòria. DiariOficial delaGeneralitatdeCatalunya.Decret143/2007.

Duval,R.(1995). Sémiosisetpenséehumaine.Registressémiotiquesetappretissatgesintellectuals. Berna:PeterLang.

Fink,T. iMao,Y.(1999). The85Waystotieatie.TheScienceandAestheticsofTieKnots.Londres: FourthEstateLimited.

Hirsch,D.,Patterson,M.L.,Sandberg,A.iVejdemo-Johansson,M.(2014). MoreTiesthanwe Thought.(http://arxiv.org/abs/1401.8242v1).

Hitt,F.(2013).Theoriedel’activité,interactionnismeetsocioconstructivisme.Quelcadrethéoriqueautourdesreprésentationsdanslaconstructiondesconnaissancesmathématiques? AnnalesdeDidactiqueetdeSciencesCognitives,18,9-27.

Hitt,FiMorasse,C.(2009).Dévoloppementduconceptdecovariationetfonctionen3ème secondairedansuncontextedemodélisationmathématiqueetderésolutiondesituations problemes.ActesdeCIEAEM-61,Montréal,Quebéc,Canadà,Juliol26-31,2009. Quaderni diRecercainDidattica(ScienzeMatematiche) ofG.R.I.M.Suplement2,núm.19.Palerm. (http://math.unipa.it/~grim/cieaem/quaderno19_suppl_2.htm)

NCTM(2003). PrincipiosyestándaresparalaeducaciónMatemática.TheNationalCouncilof TeachersofMathematics,Inc.Sevilla:SociedadAndaluzadeEducaciónMatemáticaThales (ediciócastellana).

Niss,M.(2012).ModelsandModellinginMathematicsEducation. NewsletterofEuropean MathematicalSociety,86,49-52.

Radford,L.(2003).Gestures,SpeechandtheSproutingofSigns:ASemiotic-CulturalApproach toStudents’TypesofGeneralization. MathematicalThinkingandLearning,5(1),37-70.

Parlarienraonarper aprendre matemàtiquesa educacióinfantil

MontserratTorraBitlloch

MestraimembredelCesire-Creamat

Resum Abstract

Enaquestarticleespresentendiverses pràctiquesd’aulaenlesqualsesparlaper aprendrematemàtiques.S’analitzenles situacionsperveurequèaportaelfetde parlardelques’estàaprenenties reflexionasobrecomavançarcapaunús mésfreqüentiméseficientdelllenguatge.

Inthispaperweprovideseveralclassroom practiceswherestudentsspeaktolearn mathematics.Thesituationsareanalyzedto checkhowthefactofspeakingaboutwhat theylearncontributestotheirlearningand thereissomereflectiononhowtomove towardsamorefrequentandefficientuseof language.

Larelacióentrellenguatgeipensamentnoésuntemanou,ésundelsmésestudiatsen psicologiadel’aprenentatge.Tanmateixenaquestsmoments,enquèl’objectiufinalde l’aprenentatgeéspoderferunúscompetentd’allòques’aprènielsdocumentscurriculars assenyalenlacomunicacióil’úsdelllenguatgecomundelsaspectesprincipalsperaconseguirho,s’harenovatl’interèspeltema.

L’etimologiadelverb«parlar»expressamoltclaramentelsignificatdel’acciósobrelaquales volreflexionar: Parlar,expressarallòquehompensamitjançantelllenguatgearticulat.1 Tractaremdeveurecomelfetdeparlard’allòqueespensaquans’estanaprenentmatemàtiques, ajudaaanarmésafonsenaquestaprenentatge.Enlanostrallengua,amés,tenimunaltre verb: Enraonar,parlaralternativamentduesoméspersonesentreelles, 2 quefareferènciaal’ús delaparlaperacompartir.Aquestésunaltredelsaspectessobreelqualreflexionarem.

Enscentraremaveurequèaportaelfetdeparlard’allòques’estàaprenentidecomelfet deparlar-neajudaaaprendre.Reflexionarementornacompodemavançarcapaunúsmés freqüentiméseficientdelllenguatgedesd’educacióinfantil,iveuremcomaquestaopció metodològicavamésenllàdel’aprenentatgedelscontingutsimplicats.

1.Definicióde‘parlar’alDIEC2,Diccionaridelallenguacatalanadel’Institutd’EstudisCatalans.

2.Definiciód’‘enraonar’alDIEC2,Diccionaridelallenguacatalanadel’Institutd’EstudisCatalans.

Presentem,enprimerlloc,unreculldepràctiquesd’aula.Sónpràctiquesquemostren situacionsenlesqualsesparlaperaprendre.Compartir-lesensserviràpertenirunsreferents comunsal’horadeparlardecomsorgeixen,quèaprenenicoms’hancreaticonduït lessituacionsienspotajudaraveurecomespotanarmésenllà.Lespràctiquesespresenten organitzadesendiversosgrups:intervencionsespontànies,aprenentatgesconceptuals, situacionsderesoluciódeproblemesisituacionsenlesqualscalcercaracords.

Reculldepràctiquesd’aula

1.Intervencionsespontànies

Enaquestgrupesrelacionensituacionsenlesqualsestractadecaptarexpressionsverbals quesorgeixendemaneraespontània,demanarl’atenciódelgrupicompartir-lesicomplementar-lesentretots.Vegem-nealgunessituacions:

◮ Aquestmesempaten

EnNick,de4anys,mirantelcalendariielregistredeltempsqueesfeiacadadiad’escola,va exclamar:«sielsdosdiesquefaltenfasol,aquestmesempaten!»Elgràficdeltemps(figura1) mostravaencolorgrocelsdiesdesol,engriselsdenúvolsienblauelsdeplujaiestavajust alcostatdelcalendarionanavenratllantidescomptantelsdiesquequedavendelmes.

Demanar alNickqueexpliquésatotalaclasseperquèhodeiavarepresentarperaellun reconeixement,perònolivaserfàcil.Assenyalavael27i28ilesduescasellesbuidesala columnadelsdiesdesolideia:«Hoveus?».Erabenclarquesabiaelquevoliadir.Construirel relatvaserunafeinadegrupquefinalmentvaquedarcomsegueix: faltendosdiesperacabar elmes;sitotsdosdiesfasol,aquestmeshihauràtantsdiesdesolcomdenúvols. Lacapacitatde comprensiódelasituació,enaquestcas,eraclaramentmésgranquelad’expressióverbal; latascarealitzadavacontribuiracercarl’equilibri.

Figura1

◮ Mira,sónelsmateixos

Unacosasemblantvapassarunaltremes,ambelmateixgrup.Cadadiaesdeienelsnoms delsnúmerosdelsdiesdelmesquejahavienpassat;algundia,amés,s’escrivienalapissarra pertald’anarrepetintelsnoms,localitzar-losirecordar-los.Undelsdiesesvanescriureen filesde10,comesveualaimatge.EnMouadvaassenyalarlapissarraambelditfentun movimentverticalidient:«Mira,sónelsmateixos!»Indicavalafiladelsnombres3,13i23 (figura2).

1-2-3-4-5-6-7-8-9

10-11-12 -13-14-15-16-17-18-19

20-21-22-23-24

Esvademanarl’atenciódetotsiesvapreguntaralMouadperquèdeiaque«erenels mateixos».Demicaenmicaesvaanarprecisant,ambdiversesaportacions,quetotselsnúmerosd’aquellacolumnatenienun3:el3alaprimerafilaestavasol,alasegonaeraaldarrere del’1ialatercera,aldarreredel2.

Laintervenciód’enMouadvatenirunefectecrida.Immediatament,laFirdaus,vadir:«Mira,i aquítambé!»Moventelditenaquestcasenhoritzontalidientmentreassenyalavalasegona fila:«Totstenenun1!»(figura3).Elgruplavaajudaraconcretarque,enaquestcas,l’1 sempreeraaldavant.Unaclaramostrad’aplicaciódelquehavienaprèselaborantlaprimera explicació.

1-2-3-4-5-6-7-8-9 10-11-12 -13-14-15-16-17-18-19 20-21-22-23-24

Lasituació vaportaraobservarquealafilahihaviamésnombresquealacolumnaivan demanarques’ampliéslataula.Enaugmentarlataulafinsal39,vanpoderobservarenles columnesdel7,8i9laregularitatenelsnomsdelsnombres(set,disset,vint-i-set,trenta-set... vuit,divuit,vint-i-vuit,trenta-vuit,etc.).Captarregularitatsenelsnombresibuscarmaneres d’explicar-lesserveixperanarcomprenentelsnombresielsistemadenumeració.Ésuncontingutimportantquevasorgirdemaneraespontània.

◮ Sicamines,noestanca

Ensituacionsd’exploraciótambéesprodueixenintervencionsespontàniesinteressants.Ésel casd’unaclassedecincanysonjahavientreballatlaidentificaciódelcercle,l’havienretallat perposarl’atencióenelcontorn,ésadir,enlacircumferència,ilamestraelsvaproposar sortiralpatiambgalledesd’aiguaipalsdefregarperdibuixar-ne,detalmaneraqueells fossinelcentreielpaldefregarelradi(figura4).Eneltranscursdelasessió,unanenavadir aunacompanya:«Nocaminis!Sicaminesnoestanca».

Figura2

Figura3

Elgrupesvaasseureaterrapervalorarl’observaciófetailaconversavaportaraconstatar que,efectivament,perquèestanquéslalíniacaliarodargirantelspeussensedesplaçar-se.Es vanadonartambéqueeraimportantnomourelesmans,perquèsilesapropaveniallunyaven delcoslalíniatampocnoestancava.

◮ Sóniguals

Enunasituaciódetreballdedescobertaambmaterialestructuratesvaproduirunadiscussió beninteressant.LaSouhailaesvaadonarqueambsistrianglespodiaconstruirunhexàgon (figura5);l’haviaconstruïtambtrianglesdecolorverditeniaalcostatunhexàgond’unasola peçaquetambéeradecolorverdideiacontentaisorpresa:«Sóniguals!».Sobrelataulahihavia

Figura4

Figura5

diversos hexàgonsformatsapartirdetrianglesdediferentscolors,cosaquevapermetrea lamestraferlapregunta:«N’hihaalgunaltrequesiguiigualqueaquest?».Elscompanysde taulavanintervenirindicantunaltrehexàgonverdsensedubtarqueaquelltambéeraigual. Eninsistirenlapreguntadesiencaran’hihaviamésd’igualsvanassenyalar,enaquestcas sensetantconvenciment,l’hexàgonfetambtrianglesgrocs.

Llavorslapreguntavacanviar;lamestravademanar:«Perquècreieuquesóniguals?».La Souhailavadir:«Perquètambén’hihasis»,assenyalantelssistrianglesgrocsielssisverds. Larespostavaportarlamestraaacostarundelshexàgonsambelstrianglesdediversos colorsidir:«Aquesttambéentésis»,iacontinuaciómostrarl’hexàgonverdd’unasolapeçai dir:«Iencanviaquestnomésentéuna».Lacomparacióvaportaraprecisarmés,ilaresposta vaser:«Peròtenenlamateixaforma».

Elfetquetotselstrianglesfossindelmateixcolorelsfacilitavaveurequelaformaera lamateixa;encanvi,lescomposicionsdetrianglesdecolorsdiferentsnoelsajudavena veure-ho.Superposarlesduesfiguresinicialselsvaajudaraadonar-sequecompartienla formaiacontinuacióhovananarfentamblarestadecomposicionspercomprovar-ho.

Elscasosbasatsenintervencionsespontàniescomelsexposatstenenunpuntdemàgia. L’espontaneïtatdequifal’aportacióacostumaaestarimpregnadad’emoció,del’emoció queprovocacomprendredesobteunacosa,veurequelcomquefinsenaquellmoment nos’haviadetectat.L’alegria,lasorpresa,ladescobertadesercapaç...acompanyenmoltes vegadesaquestessituacionsis’encomanenalgrup.Són,amés,moltcomprensiblesperals companys,tantperquèestanexpressadesambllenguatgequotidià,sovintacompanyatper gestos,comperquèelgrupcomparteixmoltsdelsreferentsquehanprovocatladescoberta. Enelprocésdetreballposterior,quihohaaportatéselprotagonistaisesentacompanyat pertotelgrup,ialhora,elgrupesfaseuunconeixementquenovedelmestre,sinód’un igual,iaixòtambéensenya.

2.Aprenentatgesconceptuals

Ensituacionsd’aprenentatgeplanificadesésimportanttenirbenclarquèesvolensenyar iconcretarquèesvolquel’alumnataprengui,jaqueresultad’unagranajudaperfer intervencionsitrobarmaneresdereconduirlesrespostescapal’objectiufixat.Vegem-ne tambéalgunexemple.

◮ Fesunquadrat

Quanlamainadajareconeixelsquadratsiesvolferunpasmésportant-losaconstruir-ne un,caldecidirelmaterialquese’lsposaràal’abastilespreguntesquese’lsfaranpertalde modularladificultatiavançarcapasituacionsprogressivamentméscomplexes.

Ensproposemenaquestprimerexemplequeinterioritzinqueelsquadratstenenquatre costatsigualsiqueelspuguincol·locardeformaqueelscostatssiguinparal·lelsdosados, coincideixinenelsvèrtexidelimitinunasuperfícietancada.

Sabemdeladificultatquerepresentaperaellstraçarlíniesrectes,unadificultatquenofa aconsellabledemanarqueeldibuixin.Pertant,planifiquemqueconstrueixinelsquadrats

ambunestiresdecartolinaquerepresentaranelscostats.Posaremal’abastdelsnensun nombresuficientdetiresdecartolina,totesdelmateixcolorimida,ielsdemanaremque pensinquantestiresnecessitenperferunquadrat,lesagafinielfacindamuntlataula.Tenir elsobjectiusclarsajudaaintervenirquanesdonensituacionscomlesqueesdescriuenies veuenalesimatges.

EnFernandovacol locarlestirescomesveualaimatge(figura6)iendemanavamés.

«Vullméstires,me’nfalten».Larespostavaser:«Quantscostatstéelquadrat?».«Quatre», vadir:«Iquantestireshasagafat?».«Quatre»,vacontestar.«Llavorsnote’nfalten,oi?Pensa comleshasdeposar...».Comquelicostavareferlafiguraselivasuggerir:«Isitornesacomençar?».Iaixílivasermésfàcil.

LaSandradeiaquejahoteniafet,peròundelsobjectiusfixats,queelscostatscoincideixin enelsvèrtex,noescomplia(figura7).Lamestralivademanarqueesfixésenelquehaviafet elseucompanydetaulaimiréscomerenlescantonadesillavorslivapreguntar:«Perones toquenelscostats?».«Perlapunta»,varespondrelaSandra,ihovapoderarreglar.

Figura6

Figura7

LaYasminetambéconsideravaquehaviafetelquadratdemaneracorrectai,encanvi,havia posatelscostatsdemaneraquelespuntesnoestocaven(figura8);nodelimitaven,pertant, unasuperfícietancada.LamestralivarecordarlarespostaquehaviadonatlaSandra,«els costatsestoquenperlapunta»,perquèajustésméslafigura.

Lasituaciómésinteressant,però,vavenirquanl’Alketnoaconseguiaformarelseuquadrat. Haviaposatlestiresenladisposicióqueesveualafigura9i,malgratquealasevataulala restadecompanystenienelquadratfetiellse’lsmirava,nose’nsortiadefer-lo.

Lamestraanavapassantilipreguntava:«Ésunquadratelquèhasfet?».Iellresponia:«No». «Peròtensquatretires,provadeferunquadrat...»,ilasituaciónoesdesencallava.Finalment, uncanvidepreguntailaintervenciód’uncompanyvandesbloquejarlasituació.Lamestraliva preguntar:«Peròaveure,perquènoésunquadrat?».Inoell,sinól’Ismaelqueseiaalseucostat, varespondre:«Perquènotédintre!»L’Alketvaentendredeseguidaonhihaviaelproblema,va

Figura8

Figura9

treureimmediatamentlesduestiresenformadecreuqueocupavenl’espaiinterioriles vaposardemaneraquecompletessinelquadrat.Sorprèn,enaquestasituació,larapidesa acomprendrel’aportacióquelifaelcompany,probablementdegudaaunaactitudreceptiva, d’escolta,decercaactivad’unasolucióperpartdel’Alketidel’úsd’unaexpressióplanerai entenedoraperpartdel’Ismael.

Ladescripciódel’Ismael,«noésunquadratsinotédintre»,ésadir,sinoésunasuperfície tancada,suposaunagranaportació.Defet,estàdientqueunquadratésunasuperfícietancadaihodiuambparaulesquetothompotentendre.Noés,però,unaintervenciódeltot espontània,sinósorgidaenunasituaciódetreballenlaqualfeiaestonaquelespreguntes delamestraanavendirigidesaparlarsobrecomhadeserunquadrat,ilesintervencionsen elscasosenquènos’aconseguiaesparlavenambtotelgrup.

Enunanovasessióamblamateixaactivitat,objectiusimaterials,esvapoderobservar progréstantenlarealitzaciócomenlesrespostesverbalsalespreguntes.Llavorsesvaafegir unnourepte:«Iara,podríeuferuntriangle?».Larealitzaciónovaserdifícililarespostaa lapregunta«quèpassasifasuntriangle?»vasorgirambfacilitat:«Sobraunatira,perquèel triangletétrescostats».

Lasituacióesdevéméscomplexasis’ofereixengrupsdetiresambmidesdiferentsihande triar-nequatred’igualsperferelquadrat.Quanesvanconstruintelsquadratss’observaque nototselsquadratssóniguals,perquèencaraquelesquatretiresd’unquadratsiguinde lamateixamida,nototselsquadratsques’hanobtinguttenenlamateixamida.L’ocasióés perfectaperpreguntar:«Totssónquadrats?Comhosaps?»,ilesexperiènciesensessions anteriorsajudenaconcretarquesónquadratsperquètotstenenquatrecostats,elscostats estoquenperlespuntesitanquenlafigura.

Aquestespropostestenenunobjectiuclar:treballarfiguresgeomètriquesmésenllàdela simpleidentificació.Perfer-hoesposaenjocl’accióiesdisposadematerialmanipulable, perònoesdónaperacabadal’activitatenelmomentquel’acciófinalitza.Enelcasqueel resultatnosiguiprousatisfactoriesparlaiesrectifica,iquans’aconsegueixelresultatbuscat esdemanaquevaginmésenllà,queexpliquinquèhanfetiperquèsabenqueésunquadrat. S’aconsegueixaixíunconeixementméssòlid,perquèésmésconscient.

3.Situacionsderesoluciódeproblemes

Lessituacionsderesoluciódeproblemessónunterrenyadobatperparlardematemàtiques. Siesdeixenlespropostesprouobertesperquèhihagidiversesinterpretacionsiesrespecten lesiniciativesquevaginsorgint,esdonensituacionsqueportenaexposarelsdiferentspunts devistaiaconsensuari/oaacceptarsolucionsdiverses.Algunsproblemesquereuneixen aquestescondicionssónelssegüents:

◮ Repartimgaletes

Tenim cincgaletesisomdosamics.Enslesvolemrepartir,comhopodemfer?

Calvalorar,enprimerlloc,siesdónaalgunarepresentaciódelescincgaletes.Espodenrepartir,perexemplecinccerclesdepaperi,acontinuació,s’esperaquecomencinasortir respostesquehaurand’explicarijustificar.

Éspossible quealgúdigui:«Se’ndonenduesacadascúiensobrauna».Tambéquealgú proposi:«Aunn’hidonemtresial’altredues».Encapmoments’haditqueelsdosamics hagindetenirlamateixaquantitatdegaletesi,pertant,totesduespropostesseriencorrectes iespodriademanaralsautorsqueexpliquessinquèhanpensatenprendreladecisió.És importantques’adoninquehanfetunaopció,iquelasolucióquehanpreséscorrecta,però quenoésl’única.Veurequeuncompanyhapresunadecisiódiferentiquetambéexplica lesraonsquel’hanportatafer-hopotportaracanviarlapròpiaopcióobéamantenir-lai argumentar-la.Finsitot,abuscarsientrobenunaquetinguiaspectesdelesdues.

Desprésd’haveracceptatcomaboneslesdiversessolucionsquehaginsorgit,espotoptar perferunanovapregunta:«Podríemtrobarunamaneraqueelsdosamicstinguessinla mateixaquantitatdegaletesinoensobréscap?».Elfetdedisposard’unarepresentacióen paperdelesgaletespotafavorirqueenparteixinunaperlameitatiendoninduesimitjaa cadascú,peròconvédeixartempsperquèsiguinellsmateixosquehodescobreixin.Sis’arriba aaquestasolucióconvéquenosiguielfinaldelatasca.Explicarquèhanfeticomse’lsha acuditlasolucióelsportaràaprendre’nconsciènciaiverbalitzarqueamblasoluciótrobada escompleixenlesduescondicionsqueesdemanaven:elsdosamicsentenenlamateixa quantitatinoensobracap.Ésungranavençencapacitatderesoluciódeproblemes.

Enunaltremomentespotferunapropostasemblantrepartintlescincgaletesentre quatreamics.Fer-hoplantejaunasituacióqueespotrelacionarambl’anterioradaptant-la convenientment,ésadir,fentunúsestratègicdelconeixementadquirit.Parlardelque hanfetipensat,enaquestcas,seràmoltmésfàcilqueenlaprimeraocasióireforçaràles estructurescreadesanteriorment.

◮ Expliquemhistòries

L’objectiu,enaquestcas,éspresentarsituacionsdecàlculpermostrardiversossignificatsde lesoperacionsilasevarepresentació.Enaquestasituació,l’úsdelaparlajugaunpaperdeprimerordre.

Enl’activitatBearsintheHouseandintheParkexposadaaNCTM(2003)esproporcionaa cadanenonenaunfullonhihadibuixadaunacasaambdospisosiduesestancesclarament caracteritzadesacadapis,iunnombred’ossetsdepaper(entresisidotzeenfunciódel’edat enlaqualesfal’activitat).

Elprimerobjectiuésqueescoltiniinterpretincorrectamentlaformulacióquefalamestra, col·locantelsossetscorrectament.

Hihadosóssosalacuina Hihatresóssosalasalad’estar Quantsóssoshihaalaplantabaixa?

Enaquestcas,comquetantlacuinacomlasalad’estarsónalaplantabaixa,calsumar-losi respondre:cinc.

Hihavuitóssosal’estudi Dosóssosse’nvanadormir Quantsóssosquedenal’estudiara?

Enaquestcasesplantejaunarestailarespostaés:sis.

Elsnensilesnenesajuntenoseparenelsóssosdepaperidonenlaresposta.Amés,desprésque tothomhadonatlaresposta,s’hadiscutitsieraonocorrectaicoms’hihaarribat,esdemana aunnenonenaquerepeteixielquehaditlamestra,i,ambmésomenysajuda,repeteixenel textdelproblema,preparantaixíunadelespropostesqueesfaranposteriorment.

Unaltrenivelldetreballmésavançat,dinselmarcdelamateixaactivitat,ésdemanarque inventinunproblemaques’assemblialques’acabadeformular,ésadir,queelprenguide model.Aixídoncs,elprimerproblema,canviantelnombred’óssosilesestancesdelaplanta baixaperlesdelprimerpis,espodriaconvertiren:

Hihadosóssosalacuina

Hihatresóssosal’estudi

Hihatresóssosalasalad’estarHihaquatreóssosaldormitori

Quantsóssoshihaalaplantabaixa?Quantsóssoshihaalprimerpis?

Laconnexióllengua-matemàtiquesenaquestapropostaésmoltclara.Esrecreaunasituació queimplicaquantitat,situacióal’espaiiconcrecióenlapreguntaiesformulaenfrasesben construïdesiencadenadescorrectament.

Unaltrepasesfaquanespresentaal’alumnatunnoucontext:undibuixd’unparcinfantil onhihagronxadors,tobogans,sorral,bancs...,iesdemanaquecadascúcreïunahistòriaen laqualelsóssosestiguinjugantdistribuïtspelparc,l’escriguinutilitzantelsnúmerosentre1 i6ifacinservirelssignes:+, i=perexplicar-la.Ésdesprésd’haverutilitzatelllenguatge matemàticdenombresisignesqueexpliquenverbalmentlahistòriaquehancreat.Lamestra, acontinuació,demanasialgúpodriaexplicarunahistòriadiferentqueespoguésescriure ambelsmateixosnombresisignes.

Comveiemenaquestaactivitat,larelacióentrematemàticaillenguaésmoltestreta.Enprimer lloc,esdemanacomprensióiunainterpretacióprecisadelasituació,cosaqueescomprova amblacorrecciódelresultatnumèric.Enunsegonmoment,lallenguaajudaamodelar,és adir,amantenirl’estructuramatemàticadelahistòriacanviant-neaspectesformalsatravés delllenguatge.Ifinalment,encrearunahistòriaquecalescriureenllenguatgematemàticia continuacióexplicar-laverbalment,esreforçaelpaperdellenguatgedelsnombresisignes matemàtics.

Podeutrobarunaadaptaciód’aquestaactivitatal’ARCqueportapertítol: Nensinenesala casa nensinenesalparci .

4.Cercantacords

Treballarenparellesperferunatascaobligaaparlar,aprovardeconvènceral’altreexposant lespròpiesraons,amirarlescosesdesd’unaltrepuntdevistapercomprendrelesaportacions delcompanyianarteixintaixíelconsensnecessariperrealitzarlatascaencomanada.Ésuna activitatengrescadora,quecreaunagrancomplicitatentreelsquilarealitzenienlaquales parlad’unaformamésdistesaiàgilquequanhihamésintervenciód’unadult.Potsemblar queésunapropostamassacomplexaperfer-laanensinenesdeparvulari,tanmateixnomés calprovar-hopervalorarsiensóncapaçosono,comveuremenelsexemplessegüents.

◮ Classifiquemanimals

Classificar ajudaaorganitzarelpensamentisabemproubéqueunmateixmaterialés possibleclassificar-lodemaneresdiferents.Justamentaquestaéslaraóquefainteressant l’activitatques’explicaacontinuació.

Seleccionemunnombredeterminatd’imatgesd’animalstriantlaquantitatilescaracterístiquesenfunciódel’edatil’experiènciadelsnensinenesalsqualsesproposa.Seleccionem tambéunaparellad’alumnes,enlaqualnohihagiundelsmembresquedominisobrel’altre iqueconsideremquesóncapaçosdecol·laborar.Elsdemanemqueagrupinelsanimalsque s’assemblenenalgunacosaique,després,ensdiguinenquès’assemblenelsanimalsde cadaundelsgrupsquehanfet.

Enregistrarelprocésmostrafinsaquinpuntésricaaquestasituació.Espotveureclarament compensament,accióillenguatgeescombinenpergenerarconeixement.L’anàlisidel procésmostraseqüènciesenlesqualsespotobservarcomlanecessitatdefer-seentendre pelcompany/ailadecomprendrequinescaracterístiquessónlesqueestàtenintencompte l’altre,fanqueelsgrupsd’animalsesvaginfentidesfentperadaptar-seconstantmentals noussupòsits.

Unadelesparelles,laformadaperl’IvanienQuetzal,haanatcol locantelsanimalscomesveu alafigura10.Encaraelsenquedenalgunspercol·locarielconsens,finsenaquestmoment, ésagrupar,comellsdiuen:«elsquesónd’aigua,elsquevolen,elsques’arrosseguen...». Quedentresfilesmésquenoestantandefinides.Unadelesquals,segonsdiuen,és«la delsquetenenquatrepotes».Desobte,l’Ivanpreguntaperl’ós:«Iaquest,perquènoel posesaquí?»,lidiualseucompanymostrantlafiladelsdequatrepotes.EnQuetzalcontesta: «Perquènomésentédues.Quènohoveus?».L’Ivancontinuapreguntant:«Iaquestaaltrafila quèsón?»,assenyalantlaquehihaelximpanzéil’esquirol,ienQuetzalrespon:«Sónelsque

Figura10

vanpels arbres».Immediatament,l’Ivanadmetaquestanovacategoria,quelisolucionael problemad’onposarlaserpquetéalesmans.«Ah,doncsmira,laserptambévapelsarbres, laposoaquí...ilapantera,eltigreiellleótambé»,ielscanviadefila.EnQuetzal,però,nohi estàd’acordidiu:«Mira,aquests mostrantelximpanzéil’esquirol noméstenendues potes, ilapantera,eltigreiellleóentenenquatre».Respostadel’Ivan:«Entenenquatre coml’ós.Araperquèestanasseguts,peròquanvolencaminar...què?Eh?».Aquestargument convençimmediatamentelQuetzal,quenos’haadonatquel’óstéquatrepotesfinsque l’Ivanlihaofertlapossibilitatd’imaginar-locaminant.Llavorsproposadeixarl’elefantil’ósen unafiladient:«Aquestsnoméspodenanarperterra,perquèpesenmolt,iaquestsaltres(el ximpanzél’esquirol,eltigre,lapanteraiellleó)podenanarperterraipelsarbres».«Val»,diu l’Ivan,«ilaserpil’aranyatambépodenanarperterraipelsarbres;elsdeixemaquítambé...»i encaracontinuenfentidesfentunaestonamés.

Algunscompanysseusambmenysdominidelllenguatges’ajudenambelgestielscosta mésd’explicarlesraonsperlesqualshanfetunsgrupsinounsaltresperòentotselscasos espalpaungraninterèsafer-seentendreipercomprendrelesraonsqueportenelcompany aferelquefa.Bensegurqueambaquestaactitudfaranprogressos.

◮ Construïmunelefant

Unasituaciósemblantesvadonarenungrupquejahaviaconstruïtdeformaindividualuna girafaambpecesdeconstrucció(figura11).Unprocésquevasermoltviscutienelqualesva prendreconsciènciaquecaliaferquatrecolumnesdepecesdelamateixaalçada,perferles potes,relligar-les,performarelcos,construiruncollllargicol·locar-loenunextremdelcosi posarasobreuncappetit.Ambaquestaexperiènciaprèviaesvademanarqueconstruïssin unelefantiesvaorganitzarperquèhofessinenparelles.

Figura11

Figura12

Elscomentaris,enaquestcas,anavenmoltadreçatsatrobarlamaneradereflectirles diferènciesentreunaconstruccióil’altra,esfeiencomentariscomara:«lespoteshandeser mésgruixudesilapanxamésgran...moltmésgran...elcollbencurt,enganxatalcos,iles orelles,hihad’haverorellesitrompa»isecercavenlespecesquepodienajudaramarcar aquestesdiferencies.Finsitotelcolor,queenlagirafareflectialestaques,enelcasde l’elefant,totiquealcomençamentnohotenienencompte,vaacabaressentelgris(figura12).

Parlardelques’aprènésaprendre

Enelreculldepropostesmostrathempogutobservarquelesintervencionsespontànies,en moltscasos,esprodueixenenmomentsqueescaptaunaestructuraies«veuen»semblances iregularitatsquefinsenaquellmomentpassavendesapercebudes.Entoteslessituacions mostradeshihaunadescoberta.Enelcasdelatauladelsnombress’observalaregularitaten lesfilesilescolumnes;eneldelaconstrucciód’hexàgons,lasemblançaentrel’hexàgonila composiciódelamateixafiguraapartirdesistriangles;enladelcalendariesdescobreix larelacióentreelgràficdeltempsielcalendari;eneldibuixdelcercle,lacondicióque calcomplirperquèestanqui.Sónmostresdeconnexions,realitzadesdeformaespontània icompartidespermitjàdelllenguatge,queportenelconeixementmésenllàd’onhavia arribatapartirdel’acció.Calnooblidarque,amés,passendeserdescobertesindividualsa col·lectives,ambl’enriquimentdetotelgrupqueaixòsuposa.

Enelsaprenentatgesconceptuals,parlardelqueesfairespondrelespreguntesperconcretar iprecisarelques’hafetobéperrectificarelquenos’acabad’ajustaralaproposta, portaaferunpasmésenlaconceptualització,unpasquel’acciónosempreassegura. Alhora,dónaelementspercontinuaraprenentconceptesqueimpliquenungrauméselevat decomplexitat.Enl’exempledelaconstrucciódelquadrat,elgraudeconceptualització aconseguitserviràdebaseperveure,enunaaltreocasió,queladiferènciaambeltriangleno ésenelfetdeserunasuperfícietancada,aspectequecomparteixen,sinóquesecentraenel nombredecostatsienelfetque,enelcasdeltriangle,nocalquesiguintotsdelamateixa mida.

Enlaresoluciódeproblemeselconeixementcreixdemaneraexponencialalparlar-ne. Compartirlesformesderesoldreunproblemaposademanifestquehihadiferentsmaneres deveure’l,queespotfermésd’unainterpretaciócorrecta,queprobablementhihamés d’unasolucióvàlida...portaaprecisarlescondicionsdelapreguntaiadesenvolupardiverses estratègiesderesolució.Aquestariquesaesperdsiesplantejacomunatascapersonali silenciosa.D’altrabanda,elfetd’exposarelpuntdevistaolainterpretaciópersonalobligaa cadascúafer-se’nconscient,aorganitzareldiscursiaintentarjustificarimirardeconvèncer elsaltresdelasevaopció.Entotcas,alfinaldelprocéss’haaprèsnosolselcontingut matemàticimplicatenelproblema,sinótambé,iespecialment,sobrecomplantejari resoldreproblemes.

Realitzarunaactivitatenparellaicercarl’acorddelsdosmembresperportar-laatermeés donaralfetdeparlarid’enraonarelpaperprincipalenl’aprenentatge.Ésunatascaambpoca intervenciódelmestre,enlaqualelprocéséselquetéimportànciaielresultatúnicament ésunaconstatacióqueelprocéss’hadutatermeambèxit,ésadir,quehanaconseguit

combinar elsdospuntsdevistaperrealitzarunatasca.Comprendreelquel’altrevoldir,ser capaçd’intervenir,deproposar,decorregir,desuggerir,d’acceptarlesaportacionsdel’altre... ésunaprenentatgeperellmateixquedonaremperbosiesdesenvolupaambtranquil·litat, s’arribaarealitzarlatascaiespotexplicaralgunacosadelprocés.

Avançardecididamentcapa parlarperaprendre

Parlarienraonarportaaaprendre,perquèobligaaorganitzarelpensament,acontrastar,a donarraonsquejustifiquinelquehemdit,ienfer-ho,elconeixementguanyaenprofunditati solidesa.Hauríemdereflexionar,doncs,sobrecomespotavançarcapaunúsmésfreqüent iméseficientdelllenguatgeambaquestafinalitat.

Coms’havistenlespràctiquesexposades,elolamestratéunpaperdeprimerordreen promouresituacionsenlesqualsparlarésmotord’aprenentatge.Defet,ésquicrealessituacionsifalespropostes,estàatentalesintervencionsespontànies,lesaprofitaoenpromoui lescondueixilestancafentpreguntesadients.

Calfer-seconscientdecomn’ésdedeterminantqueelolamestraaconsegueixiquesiguin elsnensilesneneselsqueparlin.Sónellselsquihandeparlar,elsquihandetrobarla paraulaol’expressióadequada,elsquihand’explicarelquehanentèsomanifestarelque noveuencomelsaltres,perquèésaixòelqueelsfaaprendre.Laprincipaleinaquetéelola mestraperaconseguir-hoéslapregunta.Ésperaixòquesaberalgunacosaméssobrecom formularpreguntespotmillorarclaramentlasevaactuació.

Unadelesdarrerespublicacionsdel’NCTM(2014)dónaorientacionsinteressantssobrel’ús delespreguntes.Assenyalaquecaltenirpresentl’objectiudelapreguntaisaberquines respostesespodenesperar,pertald’estarpreparatperseguirencaminantl’aprenentatge.

• Enunscasos,lapreguntatéunobjectiuconceptual.Seràquanespregunta:«Quinaés aquestafigura?»,iesperemqueensresponguin:«Unquadrat».Obéquanpreguntem directament:«Aquestafiguraésunquadrat?»,iesperemqueresponguin:«Sí»o«No». Sónpreguntescurtes,ambrespostacurtaiconceptual.

• Enaltrescasossónpreguntesqueportenaindagar,comquanlamestradelasituació explicadaanteriormentvadeixarpalsdefregarigalledesambaiguaielsvademanar: «Podeufercerclesaterrautilitzantelpaldefregarmoll?Proveu-ho».Sónpreguntes quesuggereixenacció,comprovació...idemanenunarespostaméscomplexaqueun síobéunno.Calpreveure,enaquestscasos,comesconstruiràlarespostaentretots, partintdelqueellsaportin,iaixònoméséspossiblesiestémoltclarquineral’objectiu del’activitat.

• Tambés’hadecontemplarl’úsdepreguntesperreconduirunasituació.Éselcasde laintervencióenlacomparaciódel’hexàgonambaltreshexàgonsformatspersis triangles.Davantdelaconfusióentrelasemblançadelesfiguresperlaformaopel color,quecomhemvistinterferiaclaramentenlacomparació,calestarpreparatperfer unapreguntaqueencaminiunarespostaaclaridora.Unaaltramostrad’aquestamena d’intervencióéselcanvidepreguntaqueesvaferiquevapermetresuperarl’atzucac

enquees trobaval’Alket.Deixardepreguntar:«Ésunquadrat?»ipassarapreguntar: «Perquènoésunquadrat?»,vaencaminaralasolució.

• Tambécalconsiderarlespreguntesqueobrennousfrontsiqueportenaanarmésenllà delques’estàtreballantenunmomentdeterminat.Uncasaixíéselqueesmostraquan, desprésdeferelquadratamblesquatretiresdecartolina,espreguntasitambées podriaferuntriangle.Aquesttipusdepreguntaésmoltútilensituacionsderesolució deproblemes.Enelmomentenquès’haarribataunasolucióespotvalorarsiés convenientpreguntar:«Podriesresoldre-hod’unaaltramanera?».Obé,«Podriestrobar unasoluciódiferent?».Contribuïmaixíadonarelmissatgequesovinthihamésd’una maneraresoldreimésd’unasoluciócorrecta.

Avançarpassapertenirbenassumitqueparlardelques’aprènés,defet,aprendre,ique elconeixementques’elaboraambl’úsdelllenguatgecomplementaelqueespothaver aconseguitambl’acció.Lespreguntessónlaprincipaleinaquetéelprofessoratperconduir aquestessituacions.

Unaopciómetodològica

Parlarperaprendreésunaopciómetodològicaque,mésenllàdelesmilloresquehem vistqueaportaalaconstrucciódeconeixement,transmetunadeterminadaconcepcióde l’aprenentatge:

• Ésoptarpernopensarquejan’hihaproudefer-hobéiquenopassaressinosaben explicar-ho.Éscreurequetotsse’npodensortiridesdebenaviatiajudar-losafer-ho.

• Transmetacadascundelsnensonenesunmissatgeclar:elqueellsdiuenésimportant iinteressa.Elconeixementnovenomésdelmestre;entretotsesvaconstruinti estructurantiensónprotagonistes

• Elsacostumaaexposarlesraons,ajustificarlesdecisionspresesielsdónaeinesper fer-ho.Ensenyaquelescosesnopassenperatzar:hihaunesraonsdarreredelquepassa iaquestesraonsespodenconèixer.

• Presentaelconeixementsensediferenciar-loenmatèries.Encaraquelanaturalesadel coneixementsiguidiferent,calfer-sepreguntes,observar,recollirdadesievidències, relacionar,raonarijustificarlesafirmacionsiparlarensajudaafer-hoiacompartir-ho ambelsaltres.

L.S.Vigotskidiua Pensamentillenguatge (1985):«Larelacióentrepensamentiparaulanoés unfetsinóunprocés,unanarivenircontínuamentdelpensamentalaparaulaidelaparaula alpensament(...)ielpensamentnos’expressasimplementenparaules,sinóqueexisteixa travésd’elles».

Bibliografia

Alsina,A.(2011). Aprendreausarlesmatemàtiques.Elsprocessosmatemàticsperal’Educació. Vic:Eumo.

Jorba,J.ialtres(1998). Parlariescriureperaprendre.Barcelona:ICE;UAB.

Vigotski,L.S.(1998). Pensamentillenguatge. Vic:Eumo.

Serra,T.(2011). Parlantdematemàtiquesperaprendre’n.Barcelona:RosaSensat.

Greenes,C.E.(2003). NavigatingthroughProblemSolvingandReasoninginPrekindergardenKindergarden.Reston:NationalCouncilofTheachersofMathematics.

NationalCouncilofTheachersofMathematics(2014). PrinciplestoActions:EnsuringMathematicalSuccessforAll.Reston:NationalCouncilofTheachersofMathematics.

RoserCodinaPascual rosercodina@ub.edu

CarmeBurguésFlamarich

DepartamentdeDidàcticadelesCCEEilaMatemàtica UniversitatdeBarcelona cburgues@ub.edu

Resum Abstract

Lesdemandesactualsdeconeixement matemàticidel’úsquesen’hadefer obrenlanecessitatdeconnectarrealitati matemàtiques,persabercomaplicar-les perresoldreoanalitzarsituacionsiper trobarexemplesquepuguinil·lustraridees matemàtiques.Tanmateix,sabermirarla realitatambullsmatemàticsnecessita entrenamentimotivació. Enl’articleesdescriul’úsdelafotografia ambtalfinalitat,posantalgunsexemples d’activitatsperalaclassed’educació primària.Alhora,esdonenindicacionsper promoureelraonamentilacomprensió delsconceptesilesrelacionspresentsen lesimatges.

Thecurrentdemandsonmathematical knowledgeanditsuse,opentheneedof connectinrealityandmathematics,toknow howtoapplythemtosolveoranalize situationsandfindexampleswhichmay illustratemathematicalidees.Buttoknow howtoperciverealitywithmathematical eyesneedstrainingandmotivation. Inthispaperwedescribetheuseof photographyforsuchpurposes,givingsome examplesofactivitiesfortheclassroomof ElementaryEducation.Atthesametimewe giveindicationsonhowtopromote reasoningandtheunderstandingof conceptsandrelationswhicharepresentin thepictures.

Unamiradaalssuccessiuscurrículumsdematemàtiquesdel’ensenyamentobligatoriensfa veurecomhananatevolucionant.Desdefixarcomaobjectiusconeixementsmemorístics finsalademandad’unsabermésprofundquepermetiaplicarlesmatemàtiquesalarealitat quotidianapersonal.

L’afirmació quecadacopesdemanamenysnivelldeconeixemental’alumnatnoéspascerta, almenysdesdelsobjectiusfixatsenl’actualitatperlesadministracionseducativesnacionalsi internacionals.Conèixeriaplicarreglesifórmulesésunestadideconeixementmoltinferior alderesoldreproblemesianalitzarsituacionsquotidianesfentúsdelesmatemàtiques.

Amblapublicaciódelsdocuments«Competènciesbàsiquesdel’àmbitmatemàtic»del’educacióprimàriaidel’ESOperpartdelaGeneralitatdeCatalunya,s’hancompletatelscurrículumsvigentsafegintunallistadetalladadelescompetènciesquel’alumnehadedominar enuncertgrauenfinalitzarl’etapaeducativa.

Lescompetències,estructuradesapartirdelsprocessosmatemàticsquejaerenpartessencial delcurrículumactual,recullend’unamanerarellevantqueresoldreproblemes,raonarmatemàticament,ferconnexionsicomunicarmatemàtiquesésunsaberdesitjableperatothom, nosolsperals«afortunats»quetenenfacilitatperlesmatemàtiques.

Enaquestarticlevolempresentar-vos,apartirdelesnostresexperiències,elpaperquepot jugarlafotografiaenl’aprenentatgematemàtical’educacióprimària.Desprésdemésdeset anysd’usaraquestrecursambestudiantsdemestredeprimària,mirantdedesenvoluparel seuaprenentatgematemàticididàctic,hempogutadonar-nosdelsavantatgesd’introduir aquestrecurscomunmésdinsdelventalldepossibilitatsdequèdisposenelsmestres.

Siensatenimalespropostesdelesadministracionseducatives,delsinvestigadorsidemestresexperts,ésclarquecalintroduircontextosrealsalesnostresescoles.Nomésdesdela pràcticareiteradadetreballmatemàticapartirdelarealitatpodemdemanaral’alumnat deprimàriaquedesenvolupilacapacitatdeveure,analitzariexemplificarmatemàtiquesen situacionsquotidianes.

D’altrabanda,enelprocésd’aprendredelesmatemàtiquesésessencialanardesenvolupant lacapacitatderepresentarlesideesmatemàtiques.Perfer-ho,espodenusarobjectes,com materialsmanipulablesoquotidians;imatgescomdibuixos,fotografies,vídeosopòsters,i símbolsabstractescomaranombres,taules,gràfics,signes,vocabularimatemàticilletres.

Arabé,elsmaterialsconcretsilesimatgessóndecisiusperanarconstruintelsconceptesiles relacionsmatemàtiques,perexpressarideesiraonaments,perplantejariresoldreproblemes, etc.Aixòsí,apocapochauriendesersubstituïtsperrepresentacionsméssimbòliques.

Ésclarquelesdiversesrepresentacionsimpliquendiferentsnivellsd’abstracció.Lesmenys abstractesapareixenenlaintroducciódenousconceptesorelacionsilesméssimbòliques noméss’usenespontàniamentquanl’aprenentsesentseguricomprènelquevolendir.

Doncsbé,creiemqueenaquestsdoscampslafotografiaenspotferunbonservei.D’una banda,enspermetcaptariobservardetingudamentenun«moment»determinatun«bocí» derealitat.Del’altra,potservirperaexemplificarconceptesirelacionsmatemàtiquesamb unsignificatconcretqueestàmoltrelacionatambelcontext.

Enelprimercashemdetenirencomptequequan«estudiem»matemàticamentlafotografia ensreferirem,sobretot,alquehifigura.Moltscops,elsaprenentsvanmésenllàipensenen elcontextensi,ensentitglobal.Perexemple,suposemquetenimunafotografiad’unestoig

desisous, onenfaltendos.Amésdeplantejar-seqüestionscom:quantsousenscalenper completarl’estoig,dequantesmanerespodríemcol locarelsquatreousquehiha,etc.,que estandirectamentrelacionadesamblaimatge,espodrienplantejarpreguntescomquantsestoigscaldrienperacincdotzenesd’ousquejauseninformacióquenoestrobaenlaimatge, peròquepertanyenalcontextmésglobaldelavendad’ous.

Pelquefaacomlafotografiarepresentaunconcepteorelació,hemdetenirpresentque unconceptepottenirdiversesmaneresdeserentès,elqueanomenemsignificats.Restar ésunaoperaciómatemàticaquepotserentesasegonselcontextcomaseparar;afegir, percompletar,comparar,etc.Elssignificatsdiferentscorresponenasituacionsdiferentsical aprofitar-hoperconnectar-lesambelconceptederestar.

Acontinuacióoferimexemplesd’activitatsqueespodenduralapràcticaal’auladeprimàriai comentaremcompresentar-les,gestionar-lesivalorar-les.Tambéintentaremfer-vosavinents consellsquedesdelanostrapràcticaireflexióconsideremútils.

Il·lustrarunlema

Unaprimeraactivitatqueusproposeméslad’aparellarunafotografiaiunconcepteorelació matemàticaquedestaquienlaimatge.Lafrasequedescriulaideamatemàticaéselqueanomenem lema.Unaltrenompotsereslògan matemàtic,ésclar! ,siussemblamésadient.

Percomençar,mostraremunafotografiaidemanaremalsalumnesqueexpressinlesidees matemàtiquesquehivegin.Seràmoltimportantqueesjustifiquion,com...espotpercebre laidea.Aquestaactivitatd’escalfamentenspotmostrarquinstipusdeconceptesirelacions sóncapaçosde«veure»icomlesjustifiquen.

Figura1

Ésinteressantques’adoninquehipothavermoltesideesimplicadesidediferentstipus.Posem,perexemple,lafotografiadelafigura1(originalment,lafotografiamostravaunconjunt dequinzebolesdebillaramblamateixaestructuraipropietatsmatemàtiquesexplícites.Va serbaixadad’Internetinoespotreproduirenl’articleperqüestionsdequalitatd’imatge). Formesesfèriques,disposició«entriangle»delesboles,sèriesnumèriquesinombrestriangulars,patrons...sónevidentsenlaimatge.Discutirsobresiladisposicióformaonoun veritabletriangleensportaarevisar-neladefinició.Tambésilesformesquepercebemcom aesferes,hosónonoenlaimatge.

Lesdiferentssèriesques’hipodenapreciar(1,2,3,4...14,15;1,3,6,10,15;i1,2,4,7,11;...) provoquenladiscussiódepatronsnumèricsdiversos(sumar1acadatermeperobtenirel següent;sumar2alprimerterme,3alsegon,4alterceri5alquart;ienlatercerasèrie,sumar 1,2,3o4perobtenirelsdiferentstermes).

Unasegonaactivitat,dedificultatmajor,ésquefacinelmateix,peròlafotografial’han d’aportarells.Ésmésdifícilperquèimplicatriarlaimatgeintencionalment.Handecreure quetéelementsmatemàticsielshandejustificar.D’altrabanda,ladiscussiósobreles contribucionsnoespotferambtotalaclasse,especialmentsielsalumnessóndeprimercicle. Unaopcióésqueelmestrelesagrupiperfacilitarladiscussióenpetitsgrups.Lapregunta essencialseriasobresiellemaescorresponamblafotografia.

Desprésd’aquestalecturamatemàticadelafotografia,espotencarregarl’activitatbàsica queésjustamentlainversadelaprimera: donatunlema,ferocercarunafotografiaque l’exemplifiqui.L’objectiuprincipalésladiscussiódelsignificatdellemail’argumentació matemàticadelacoherènciaentrefotografiailema.Aixòesdóna,sobretot,durantelprocés derecercaiselecciódelaimatge.

Fetl’encàrrecdelatasca, fotoijustificació,elsgrupsdetreballhandetenirproutempsper ferlarecercaoferellslesfotosidiscutir-nelavalidesa.Ameitatdelperíodeassignatespot plantejarunapresentacióatotelgrupclassedelesfotosseleccionadesprovisionalment.

Enlasessiódediscussió,tothompotaportarideesdemillora,discutirlavalidesad’alguna imatgeoferveurequelafotocontéaltresideesmésrellevantsqueellemaproposat.El mestrepotparticiparactivamentposanten«crisi»algunesimatgespocadientsidemanant justificacionsal’alumnat.

Elresultatdelatascapotrecollir-seenunapresentacióppt(oaltra),unpòster,ferunàlbum amblesdetotalaclasse,penjarunaexposiciórealal’escolaovirtual,etc.Elreculldeles propostesespotusarperaplantejaractivitatsposteriorspertald’aprofundirenelsconceptes implicats.

Tantlafotografiadel’activitatinicialdelecturamatemàticacomellemadelapropostahan detriar-sesegonsl’edatdelsalumnesielsconceptestreballatsoques’estiguintreballant.És evidentquetotplegathad’anarpreceditd’unestudidelmestreperassegurar-sequelatria ésprouricaperproduirresultatsenelsalumnes.

Aquestaactivitatpermettreballarprocessosdeconnexió(entreconceptes,entrematemàtica irealitat)deraonament(trobantpatrons,argumentant)iderepresentacióicomunicació

(exemplificantconceptesirelacionsmatemàtiquesatravésd’imatgesreals)ielmateix plantejamentdel’activitatamblaresoluciódeproblemes.Pelquefaalscontinguts,depèn dellematriat.

Usmostremalgunesfotografiestriadesperevidenciarellema «Entretotsfanunmetre».En lafigura2,podeuapreciarcomestàpresentlaidead’unitatdemaneradirectaenlesdues imatges.Enuncasestractademansienl’altre,decalçat.S’evidencialarepeticiódelpatró, sensedeixarespaientremig.Ienlafigura3s’usal’ombradelarepeticiódelpatró,unpot dellauna,peròésenl’ombraontrobemelmetre,corroboratperunaindicacióexplícita.Es tractadereflectirproporcionalitatgeomètrica,quenoésunconceptedel’educacióprimària. Ésclar,doncs,queunmateixlemapotproduirdiferentsnivellsdecomplexitat,totsegonsels coneixementsdel’alumnat.

Lestresactivitatsdescritesesbasenenaparellarfotografiesilemes,ésadir,enconnectarmatemàtiquesirealitat.Elfetqueestractid’unafotopermetacotarlarealitatiaixíconcentrar-se enalgunsaspectesconcrets,fetquecomportaaprofundirenelconcepteorelació.

Figura2

Figura3

Proposar problemes

Resoldreproblemesésunprocéscomplex,peròproposar-neencaratémésdificultat. Provocarqueelsnensinenesplanteginpreguntesenquècalguiusarlesmatemàtiquesper respondre-lesésessencial.Unbonrecursperfer-hoésusarfotografiesdesituacionsreals.

Podemcomençarpermostrarunafotografiaiferpreguntessobreallòques’himostra.Les pregunteshandeserpertinentsenrelacióamblaimatge;novalqualsevolpregunta,han d’estarrelacionadesambelfetdevoleraconseguirmésinformaciósobreelcontextiusar lesmatemàtiquesperfer-ho.Resolteslesqüestionscaldràjustificarcoms’hausatlafoto perresoldre-les.Perexemple,enlafigura4,elsalumnesplantejavenpreguntessobrepreus dequantitatsdepesdeterminades,unitatsdefruitaquecaliaperaunpesconcret,canvia tornarperunacompra...elquevaportaradiscutirsobreestimaciódepesos,comparacióde volums,etc.Desprésdeltreballcomúse’lsvaproposarunproblemaméscomplex:«Compres possiblesamb25euros(amb5cèntimsdemarge)ihaventdecontenirproductesdiversos».

Enunasegonafaseespotdonarunafotografiaiesdemanaràqueellsproposinpreguntes oproblemesielsresolguin.Abansdeprocediralaresoluciódelsproblemesplantejatscal ferunadiscussióconjuntadelgrupclassesobrelespreguntesqueteneniquinessónmés interessantsderesoldre.

Elveritablerepteéslaproposta,perpartdelsalumnes,defotosiproblemes.Tantenles activitatsprèviescomenaquestaésrellevanteltreballengrup.Ladiscussiódelesidees implicadesésfructíferaquanelsalumnesnotenenpord’errarialhoraveuenlanecessitat d’argumentarlessevesafirmacionsiintuïcions.

Figura4

Perexemple,enlafigura5,mostremunapropostadefotografiaielproblemadedues alumnesdelgrupclasse:

Lesformesdelestrescapsesdebombons,quètenenencomú?

L’arestabàsicadelaprimeramesura10cmil’alçada5cm;l’arestabàsicadelasegona, 6cmil’alçada3cm;l’arestadelatriangularmesura18cmil’alçada10cm.Suposantque elsbombonstenenformad’esferade3cmdediàmetre,calcularaproximadamentels bombonsquecabranacadascunadelescapses

Al’horaderesoldre’lproposenl’úsdemodelsperesbrinareltipusdefiguresielquetenenen comú.Lesreconeixencomaprismesicitenlescareslateralscomarectangles.Usenunitats demesuradelongitud,àreaicapacitaticalculenvolumsapartirdefórmules.Calferús d’aproximacionsenteres.

Caldeixarproutempsperalarealitzaciódelesactivitats;ésimportant«madurar»elsarguments,quelesinteraccionsentreelsgrupsprovoquinnovesideesiques’entenguiqueun problemaounafotografiapodenestar«vius»encaraquesemblinfinalitzats.

Algunsexemplesdefotografiesiproblemesespodenveureenlesfigures6i7.

ElMiquelil’AnnahanmarxataIrlandadeviatge.Hansortitambmoltsdinersdecasa.Però, esvangastar 1/5 partdelqueportavenpercomprarelsbitlletsperalvaixell.Enarribar, vanllogaruncotxequevacostarlameitatdelrestant.Amés,uncopagafatelcotxevan haver-lideposar50eurosdebenzina.Després,vananarpagantmenjarihotels;aixòels vacostar 2/3 partsdelrestant.Uncoppagattotaixò,vananaraveureunesmuntanyesonvan haverdepagar4eurosperpersona.Peracabar,l’Annaesvagastar20eurosenregalsien Miquelunsaltres17euros.Hantornatacasanomésamb5euros.Quantsdinerstenien abansdemarxar?

Figura5

Mirant lafotografia,consideral’estrellaformadaperunhexàgonielssistrianglesque l’envolten.Quinseriaelseuperímetreusantelcostatdeltrianglecomaunitat?Ilaseva àrea?

Mirantelconjuntdelmosaic,diguesquinspolígonss’hipodenveure.Dibuixa’lsiposael seunom.

Reflexionsfinals

L’úsdelesfotografiescomarecursd’aprenentatgematemàticcontribueixaconnectar realitatimatemàtiques,aspecteessencialperdesenvoluparlescompetènciesbàsiques matemàtiquesdel’etapa.Aquestaconnexióesfaquanesbusquenlesideesmatemàtiques queunafotografiacontéitambéalainversa,quans’estableixunacorrespondènciaentre

Figura6

Figura7

diverses imatgesiunaideamatemàticadeterminada.Totplegatésessencialperresoldre problemesplantejatsencontextosquotidians.

Recollirun«boci»derealitatmitjançantunvídeotambéésunamaneradefacilitarla connexióentrerealitatimatemàtiques.LesexperiènciesdelVideomatqueesproposendes delCreamatsónunexempled’activitatsdeconnexió.Tanmateixcaldistingirentrevídeoi fotografia.Elvídeo,perlessevescaracterístiquesderapidesadelesaccions,noéstanidoni comlafotografiaperrepresentarelsmomentsclaud’unprocés.Perexemple,enelcasde representarunatransformaciód’uncubenunaltrepoliedre,unaseqüènciadefotografies potmostrarelsmomentsielscanvisrellevantsdelafigura.Unvídeoquemostrielprocés «noobliga»atriarijustificarelsmomentsclau.

Comenqualsevolaltrerecurs,elprogrésenelmaneigilatriad’imatgess’aconsegueixabase deproposarperiòdiquesidiversessituacionsenquèlafotografiatinguiunpaperprincipal. Igualmentimportantssónlesdiscussionsiargumentacionssobrecomlafoto«mostra»un concepteounarelació.

Unaltreaspectequeenspotserútiléscomamitjàd’avaluaciódelgraudecomprensióde l’alumnat.Quanelqueescaptasónsenzillamentnombresofiguresexplícitsalafotografia estemdavantd’unnivellmésbaixquesiesveuenrelacionsentrenombresoentreformes. Otambésisóncapaçosdetrobarrelacionsentreduesimatgesquerepresentinlesmateixes idees;perexemple,enelplaienl’espai.

Lanostraexperiènciaenshamostratcoml’alumnatestàmoltmotivatperlesactivitatsamb fotografies,malgratqueestractienrealitatd’investigacionsoproblemesd’altnivell.Trobar unaimatgequereflecteixiunlemaésunveritableproblema,ielmateixenelcasinvers.

Moltsalumnesmostrenbenaviatuncomportamentmésindependent:usenlafotografiaper prendreapuntsiperil·lustrarprocessos,totcombinant-hoambnotesescritesoesquemes. Diuentambéqueelrecursdelesfotoselshafocalitzatl’atencióihanesdevingutobservadors matemàticsdelarealitat.

Espodenproposartambétasquesenquèlafotografianomésserveixipercomunicarresultats derecerques.Perexemple,perexplicarelprocésseguitperobtenirdesenvolupamentsplans d’untetraedrequenoestiguinformatsexclusivamentperlauniódetrianglesequilàters.Es tractadefotografiarelspassosseguitsiseleccionarlesimatgesfinsatenirunaseqüènciadel procésqueuncompanypuguireproduirsensecapinformaciócomplementària.

Al’horadepensarquinstemessónmésidonisperproposaractivitatsambfotografies,ésclar queelstemesgeomètricshosón.Perexemple,figures(objectesdeformesdiferents),generaciódeformes(uncilindreenformaderotlledepaperodecordillcargolat),propietats geomètriques(mostrardesenvolupamentsplans,paral lelismedecaresoarestes),propietatscomunesaduesformes(simetries,nombred’elements...).

Peròsiestéencomptequemoltesideesnumèriquesespodenrepresentarvisualment, aleshoreselblocdenombresioperacionsdelcurrículumtambépermetplantejaractivitats interessants.Perexemple,l’estimaciódequantitats(comptargent,objectespetitsengrans quantitats...),representaciódenombrescomamultiplicació(rajolesdexocolata,ousenuna

ouera...),nombresparellsisenars(cosesquevanenparellescomaramitjons,sabates...)i moltesaltres.

Al’horad’obtenirlesimatgespodemrecórrerafonsd’imatgesd’Internet,concursosde fotografiaqueesfandesdelesassociacionsdeprofessorsdematemàtiques,arxiuspersonals ofer-lesexpressament!

Lanostraexperiènciaenshafetveurequeelsalumnestendeixena«fabricar»elsseus escenaris.Jaenssemblabé,doncs,ladiscussióqueimplicala«definició»delqueesvol;és altamentproductivadeconeixementmatemàticd’altnivell.

Elqueésevidentésqueavuiésmoltfàciltenirunacàmeradigital(telèfons,tauletes...),que podemferunagranquantitatd’imatgesiquedar-nosamblesqueinteressen,passar-lesauna pantallaidiscutirsobreelseucontingutmatemàtic.Comsempre,elquecomptaésinteressar elsalumnesenunaprenentatgeprofunddelesmatemàtiquesisercapaçosd’afrontartasques complexes.

Usanimemaproposaractivitatsdefotografiaimatemàtiquesquepromoguinelgustperfer matemàtiques.

Referències

Alsina,C.,Nelsen,R.(2006). Mathmadevisual:CreatingImagesforUnderstandingMathematics. Washington,DC:TheMathematicalAssociationofAmerica,Col.ClassroomResources Materials.

Añón,E.,Martín,O.,Morales,L.(2011). MatemáticasenImágenes.Eloeditoras

Borrás,E.,Moreno,P.,Nomdedeu,X.,Albalat,A.(2002). RITMOSmatemáticaseimágenes. Madrid:Nivola.

«Competènciesbàsiquesdel’àmbitmatemàtic»del’EducacióPrimàriaidel’ESO.(2013).GeneralitatdeCatalunya,Departamentd’Ensenyament.

«iMÁTgen» secciónde SUMA,desde2003finsa2012.

«MathematicalLens» seccióde MathematicsTeacher,apartirde2004.

Vilches,S.,Cubas,C.(2009). DiezañosdeconcursodeFotografíaMatemáticaenCataluña.Actas XIVJAEM,Girona.

Websd’interès

DivulgaMATCentroVirtualdeDivulgacióndelasMatemáticas.ExposicionesVirtuales. http://www.divulgamat.net

Enrichingmath

https://www.westsussex.gov.uk/learning.aspx

Matemáticasentumundo

http://catedu.es/matematicas_mundo/FOTOGRAFIAS/fotografia.htm

Matemáticasyfotografía.MEC.

http://ntic.educacion.es/w3//eos/MaterialesEducativos/mem2000/matefoto/libro/index.htm

Problempictures

http://www.problempictures.co.uk

Elteoremadel’Empordà (de F.Macau)vistambel

GeoGebra

LluísSabaterAnticó ProfessordeMatemàtiques INSdeLlançà lsabate1@xtec.cat

Resum Abstract

El14desetembrede2012,labadiade Rosesvaserinclosaalclubdelesbadies mésbellesdelmón,unadistincióde caràcterturísticanivellmundialavalada perlaUnesco. Amésdelesevidènciespaisatgístiques, culturals...,unarticledeFredericMacau, publicatl’any1964als Annalsdel’Institut d’EstudisEmpordanesos sobrelageometria delabadia,vaajudartambéal’acceptació delacandidatura.

Actualment,igràciesaeinescomel GeoGebra,lesrevistes,Internet, elGeoGebraTube...,estemencondicions deferunamésàmpliadifusiódelque F.Macauvaanomenarteoremade l’Empordà,aixícomdel’explicacióque donavadelfetqueelsgrecss’instal lessina Empúries.

OnSeptember14th2012,RosesBayjoined theMostBeautifulBaysintheWorldClub,a worldwidetourismdistinctionthatcarries theendorsementoftheUnesco. Amongthelandscapeandculturalevidences thatsupportedRosesBay’candidacy,there wasanarticlebyFredericMacau,published in1964intheAnnalsdel’Institutd’Estudis Empordanesos,abouttheGeometryofthe Bay.

Today,thankstotoolssuchasGeoGebra,the differentmagazines,theInternet, GeoGebraTube,...,weareabletoprovidea widerdiffusionofwhatMrMacaucalled Theoremofl’Empordàaswellasofthe explanationheprovidedforthefactthatthe GreekssettledinEmpúries.

Als Annalsdel’Institutd’EstudisEmpordanesos,alvolum5,any1964,hitrobeml’articlede FredericMacauiVilar(Figueres,1917 Barcelona,1970)1 «L’AltEmpordàgeometritzatperla tramuntana».

1.ElsenyorFredericMacau,enginyerdecaminsigeòleg,foufinsalasevamortundelsprofessorsdela càtedradeGeologiaal’Escolad’EnginyersdeCaminsdeMadrid,icomadirectordeCarreteresdeGironahiplanejà lamodernitzaciódelsprincipalsvials.EntrelessevesobrestrobemunestudidelacostadelgolfdeRoses: Geología, vientoygeometría (1966).

Enaquestarticle,hitrobemduespropostesatenirencompte,ambduesreferidesalfetque algolfdeRoses«podemveure-hiduesel lipses:unadepetitacapaRoses,iunadegrancap al’Escala.Elseixospetitsd’aquestesel·lipsesdelgolfdeRosescoincideixenambladirecció delatramuntanailacontinuïtatcapadinsdelmardeladireccióqueportenelsriusMugai Fluvià»,compodemveurealafigura1.

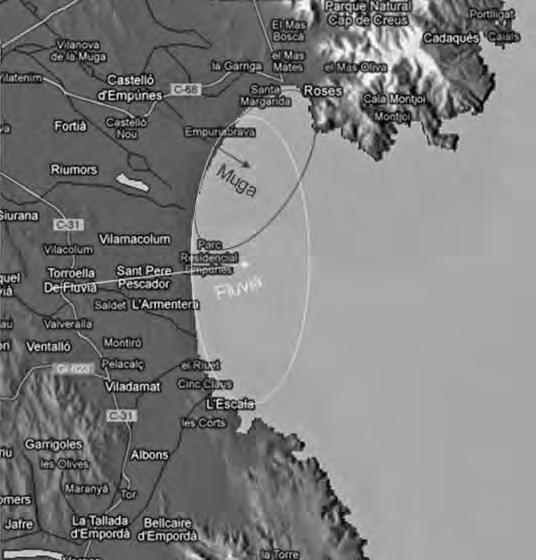
Figura1.MapadelabadiadeRoses.

Enprimer lloc,queelsgrecsesvareninstal laraRosesiEmpúriesperlabellesadelaplatja,i ensegonlloc,elqueellvaanomenarcomateoremadeL’Empordà,2 quediu: donadesduesfamíliesd’el lipses,tangentsenunpunt P,italsquellurratlla delscentressiguiparal lelaalatangentcomuna,cadaundelsaltresdospunts d’intersecciódecadaparelld’el lipses F i E ielpunt P determinenduesrectessobre lesqualsestallenelsparellsdetangentsalesel lipses,paral lelesalsdiàmetresque passenpelpunt P.

Ambduespropostesestrobenperfectamentjustificadesal’article.

Peralaprimera,elsgrecsesvareninstal·laraEmpúriesperlainfluènciasobreelseu subconscientdelnombred’or,jaqueelresultatdeladivisióentreleslongitudsdels semieixosmajorsdelesduesel lipses(el lipsegran:13,9km,el lipsepetita:8,6km)ésgairebé elnombred’or:

2.Livadonaraquestnomperquèvaconstatarquenofiguravaenlabibliografiaquevaconsultariperquè ningúaquihodemanava(matemàtics,s’entén)elconeixia.

Iaquestéselmotiudel’extraordinàriabellesadelgolfdeRosesidelfetqueelsgrecs decidissininstal·lar-s’hi.

Caltenirpresentprecisamentqueelnom ϕ queesdónaalnombred’oréslainicialde l’escultor,arquitecteipintorgrecFídies(segle V aC),iqueelsgrecsbuscavenlamàxima perfeccióibellesaenlessevesobres,tantenl’artcomenlesconstruccionsoficials...iaixòho haviendetenirmoltinterioritzat.

Siesvol,ésunajustificaciósentimental(l’amoralapàtria),peròtambéfonamentadamatemàticamentpelnombred’or.

Però,peralasegonaproposta,elsenyorFredericMacaufaservireinesmatemàtiquespotents:

Lademostració3 queenfa(enunapèndixdel’article)esbasaenl’equaciódelescòniques delfeixformatperlescòniquesquepassenperdospunts A i B (quedeterminenunarecta r)i lestangentsencadaund’ells(tA i tB)ialeshoresl’equacióés

Iencaramés:hifaunaaltrademostracióusantafinitats.

ComdiuJosepPlaa ElmeuPaís:«...elsestudisdelsenyorMacauhandonatunasíntesi científicadel’Empordà,literalmentexcepcional».

Laintenciód’aquestarticleéslad’aportarunacomprovaciógràfica,ambl’ajudadelGeoGebra, del«teoremadel’Empordà»:

AlGeoGebraTubehihalaconstrucció Teoremadel’Empordà(bellesanaturaldelaBadiade Roses) (escriviualcercadorencastellà«macau»,«roses»,«empordà»o«sabater»)4 (darrera visita,25-11-2013),enlaqualmoventelspuntslliscantspodementrardiversesparelles d’el lipsesdelesfamílies (y mx)2 + α · (y 2a) · y = 0i(y nx)2 + β · (y 2a) · y = 0 (amb m i n diferentsiamb a, m i n diferentsde0).

Perexemple,iperafermésentenedorelgràfic,prenem m = 1 > 0i n = 1 < 0iprenem lesel lipsesdelesfamíliescorresponentsa α = 2i β = 1iambcentresaalturaa = 2: ǫ1 : (y x)2 + 2 · (y 4) · y = 0i ǫ2 : (y + x)2 + (y 4) · y = 0

Talcommostralafigura2,obtindremduesel lipses,unad’orientadacapaladretail’altra capal’esquerra,tangentsenunpunt(s’observamillorapropant-nosalaimatge).

3.Consulteua Annalsdel’Institutd’EstudisEmpordanesos,alvolum5,any1964,l’article«L’AltEmpordà geometritzatperlatramuntana».

4.Tambéhotrobareudirectamentahttp://www.geogebratube.org/student/m46316

Alturadelscentres

Primerael·lipse ǫ1

Segonael·lipse ǫ2

= 2

= 1

= 2

= 1 β = 1

Tangentscomunes

Eixosd’afinitat

Interseccióde ǫ1 i ǫ2 P

Figura2.Representaciódeduesel·lipsesdelesfamíliesambelGeoGebra.

Observemquetenenduesrectestangentsparal·leles(ladistànciaentrelesqualsésenaquest cas2a = 4):

Alturadelscentres

Primerael lipse ǫ1

Segonael lipse ǫ2

= 2

= 1

= 2

= 1 β = 1

Eixosd’afinitat

Interseccióde ǫ1 i ǫ2

Figura3.Representaciódelesduesrectestangents.

ContinuaremarafentunaconstruccióambelGeoGebra,entrantalalíniad’ordresles equacionsdelesduesel lipses, ǫ1 i ǫ2,peraveureambmésdetallelprocés:

Lesduesel lipsess’intersequenentrespunts A, B i D (aquestéselpuntdoble,onambdues sóntangents),quedeterminenelsdoseixosd’afinitat:

2

A B D

Figura4.Puntsd’interseccióentrelesduesel·lipsesieixosd’afinitat.

Siprenema = 2, m = 1, n = 2, α = 2,i β = 2obtenimlafigura5,onesveuenmillorels eixosd’afinitatilesinterseccionsitangènciaentrelesel lipses:

Figura5.Puntsd’interseccióentrelesduesel·lipsesieixosd’afinitat.

Aleshores,agafantunpunt P sobrelaprimerael·lipseiconsiderantlarecta r quepassaper P i ésparal lelaalestangentscomunes,aquestarectatallal’el lipse ǫ1 enunaltrepunt Q itambé tallal’eixd’afinitat1enunpunt M il’el·lipse ǫ2 enelsafinsde P i Q, P′ i Q′,demaneraque

MP′ = MQ MQ′ ialeshoreslesrectestangentsalesel·lipsespelspunts P i P′ estallensobrel’eixd’afinitatcom esveualafigura6:

Figura6.Puntafíde P, P′ ,irectestangentsper P i P′ intersecant-sesobrel’eixd’afinitat1.

Inaturalmenttambéamblestangentspelspunts Q i Q′ (figura7):

Figura7.Puntafíde Q, Q′ ,irectestangentsper Q i Q′ intersecant-sesobrel’eixd’afinitat1.

Isiconsideremelpuntdetall N delarecta r ambl’eixd’afinitat2,demaneraqueara NP NQ′ = NQ NP′

resultarà quetambélesrectestangentsalesel·lipsespelspunts P i Q′ estallensobrel’eix d’afinitat(ara, Q′ ésl’afíde P i P′ ésl’afíde Q)comesveualafigura8:

Figura8.Puntafíde P, Q′ ,irectestangentsper P i Q′ intersecant-sesobrel’eixd’afinitat2.

Inaturalment,tambéamblestangentspelspunts P′ i Q (figura9):

Figura9.Puntafíde Q, P′ ,irectestangentsper Q i P′ intersecant-sesobrel’eixd’afinitat2.

Siesvolenprovaraltresvalorsfinsaobtenirelsdiàmetresquefanquelasevaraósiguiel nombred’or,caldràferunanovaconstruccióambelGeoGebra,jaqueelsvalorsdonatsals paràmetres a, m, n, α i β delaconstrucciódelGeoGebraTube«Teoremadel’Empordà(bellesa naturaldelaBadiadeRoses)»nohopermeten.

Aixímateix,caldestacarquenoespodendonardeterminatsvalorsa α i/o β ,jaqueenlloc d’el·lipsesapareixerienhipèrboles(perexemple,si β = 1

ǫ : (y + x)2 (y 2) · y = 0).

Totaixòquedaperaunapossibleampliaciódelessevesutilitatsdidàctiques.

Aixímateix,seriainteressantestudiar-neunústurístic(promociódeRoses,l’Escala-Empúries, SantPerePescadoriCastellód’Empúries-Empuriabrava),5 comfanperiòdicamentelsdiaris comarcals(DiarideGirona, HoraNova...),iméssitenimencomptequeelpassat14de setembrede2012labadiadeRosesvarebreeldiploma,corroboratperlaUnesco,quela incloualclubdelesbadiesmésbellesdelmón.

5.Visiteulapàginahttp://santpere.net/content/la-badia-de-roses-entra-al-club-de-les-badies-m%C3% 83%C2%A9s-belles-del-m%C3%83%C2%B3niusn’acabareudeconvèncer!(darreravisita,25-11-2013).

Bibliografia

L’AltEmpordàgeometritzatperlatramuntana. Annalsdel’Institutd’EstudisEmpordanesos, vol.5,any1964.

UniversitatdelaCorunya,DepartamentodeMétodosMatemáticosydeRepresentación: caminos.udc.es/info/asignaturas/101/pdfs/teoria18.pdf(darreravisita,25-11-2013).

Granenciclopèdiacatalana:http://www.enciclopedia.cat/enciclop%C3%A8dies/granenciclop%C3%A8dia-catalana/EC-GEC-0038897.xml#.UpB_Cax_hP0 (darreravisita,25-11-2013).

JosepPla. Obracompleta,vol.7, Elmeupaís.Barcelona:Destino.

JoanVinyoliila recercadel cercleconvincent

PepSolà

INSdeSantaColomadeFarners

Autorde Labastidadelssomnis.VidaiobradeJoanVinyoli

Resum Abstract

L’article mostracomenlapoesiadeJoan Vinyoli,undelsgranspoetescatalans,de quiaquestanysecelebraelcentenaridel naixement,hitrobemalgunselementsque enspermetenconsiderarunacerta presènciadelpensamentmatemàticen algunsdelsseuspoemes.Ésespecialment interessantelcasdel Llibred’amic,enel qualVinyolivolguéacompanyarelsseus poemesambil·lustracionsd’untractatde geometria.

ThearticleshowshowinJoanVinyoli’s poetry,oneofthegreatestCatalanpoetsfor whomthisyearwecelebratetheone hundredyearcentenaryofhisbirth,wecan findsomeelementswhichallowusto consideracertainpresenceofmathematical thinkinginsomeofhispoems.Especially interestingisthecaseofthebooktitled Llibre d’amic,wherethepoetdecidedto accompanythepoemswithvaried geometricalillustrations.

JoanVinyoli(1914-1970)ésundelsgranspoetesde laliteraturauniversal.Perlaimportànciaiprofunditatdelasevaobra,laConselleriadeCulturadela GeneralitatdeCatalunyavadecidircommemorarel seucentenarideclarantl’any2014AnyVinyoli.La sevaobracomprèndissetllibres desde Primer desenllaç (1937)finsa Passeigd’aniversari (1984) queinclouenmésdecinc-centspoemes.

Lapoesia deVinyoliéslarespostalíricad’unhomea unaexperiènciavitalmoltintensaentotselsordres: l’amor,lamort,lasolitud,elssomnis,elsrecords... Lasevadivisa«Hedeferalgunacosadelameva indigència»enspermetentendreelsentitprofund delasevaobra:haviadeferalgunacosaperdonar sentitalavidaiprovard’assolirunestatespiritual superior,unavidamésalta,ielquevafervaser, justament,poesia.

JoanVinyoli. FotografiadeJordiNebot,1978.

EneltrajectelíricdeVinyolitrobemalmenystresmomentsbrillantsenelsqualselpoetafa unaaproximació,mésomenysconscient,alamatemàtica.Elprimerd’aquestsmoments,el trobemenelpoema«L’esfera»,publicatl’any1975enelllibre Araqueéstard.Laimportància d’aquestpoemarauenelfetdetrobarenelsdarrersversoselquepodemconsiderarlasíntesi delseupensamentlíric:

unsomnival:Només unsomnival: unsomnival:AmoriMort.

AquestssónelsdosgranstemesdelapoesiadeVinyoli l’amorilamort ,elsqualssón tractats entotl’espectredepossibilitats.Enelcasdel’amor,enelsseuspoemestrobemdes del’amormésterrenalieroticosensualfinsal’amorenunsentitextremamentespiritual, passantperl’amorcomaformadeconeixementitambéd’alteritat possibilitatdeseren l’altre .Defet,lasevapoesiapotinterpretar-secoml’intentdeconciliaraquestesdues forcesoposadesquesónl’amorilamort:«Lespersoness’hauriendemorird’amorinopasde malaltiesabsurdes»,vaescriureelpoeta.

Elsegond’aquestsmoments,eltrobemenel Llibred’amic,publicatl’any1977.Estracta d’unllibredetemàticamisticoamorosa.Podemdirqueésunaversiócontemporàniadela tradicióqueensvedeRamonLlull,JoandelaCreu,SantaTeresa...Éselfruitd’unaprofunda experiènciaafectivaenlaqualelsamantshanpretèsassolirunarelacióunitivaperfecta,tant físicacomespiritual.Inclouquinzepoemesbreuscomaraaquest:

VIII.VÀREMEMPRENDREUNLLARG, DIFÍCIL,PERILLÓSCAMÍ.

Vàrememprendreunllarg,difícil, perillóscamí.Iestimàvemlescoses fossinneuofang, rosadao constel·lació. Ilesfèiemnostrespercausa del’amorqueenshaviaensenyatcomanostrar-les.

Elcuriósd’aquestllibreésqueelpoetavavolerqueelspoemess’acompanyessindegravats extretsd’unllibredelmatemàticfrancèsSébastienLeClerc,delsegle XVII.Perquèhovafer?, podempreguntar-nos.Jodiriaquehovaferperquèvatrobarenlamatemàticaunmodel deperfeccióqueliserviaperacompanyarl’anhelil’enyorançadeperfeccióamorosaque traspuenaquestspoemes.Estracta,ésclar,d’unavisióplatònicadelaforçaamorosa.D’altra banda,ésinnegablequeaquesthomequeapareixenlail lustracióiques’adreçacapalfons

deles muntanyesésunaimatgealtamentsuggestivaperaunpoetaquevatransitarpertots elsviaranys,sovintdramàtics,quelivaoferirlavida.

Ifinalment,trobemuntercermomentenelllibre Cercles,publicatl’any1979.Elprimerpoema d’aquestllibreestitulatambé«Cercles»iVinyolihifaunafiguracióenlaqualesprojectaell mateixcomunhomequellençapedresal’aigua,lesqualsgenerarancerclesconcèntrics, finsaobtenir,siésqueéspossible,elcercleconvincent.Osigui,l’homequepassaeltemps obstinatenlarecercad’unarespostaalsmisterisdelavida,anhelantlasaviesaiassedegatde coneixementdelescosesprofundes.

CERCLES

Unaltrecopvolsagitarlesaigües delllac.

delllac.Estàbé,peròpensa quenoserveixderestirarunasolapedra, quehasd’estaraquídesdelamatinada finsalaposta,desqueneixlanit finsalllevant finsalllevant tindràslacompanyia deles estrelles,podràsveurel’ocellassa delanitnegracovantl’oudelallum deldianou , deldianou ,assajantsemprecercles, persial capdemoltsanys,totaunavida,etsembla imaipotsernon’estaràssegur quehasassolitelcercleconvincent.

VersdeVinyolienelsapuntsdematemàtiquesdel’alumnaAnnaCufí, de4td’ESOdel’InstitutdeSantaColomadeFarners.

Sóntresmomentsenelsqualsgràciesalpoetapodemvincularl’experiènciapoèticaambla matemàtica,podemtravessarunpontqueenriqueixambduesexperiènciesilesprojectaen ladireccióqueensapropaal’harmonia,labellesaielconeixement.

Matemàtiquesamb einesdigitals

LluísMoraCañellas

Cesire-Creamat

DepartamentdeDidàcticadelesMatemàtiques UniversitatdeBarcelona

Resum Abstract

Abansd’utilitzarleseinesdigitalspertalde treballarlesmatemàtiques,oqualsevol altraassignatura,hemdedecidirquines matemàtiquesvolemtreballar.Però aquestadecisióhad’anaracompanyada delaselecciódelametodologiaque utilitzarempertreballar-lesal’aula.Amb elscontingutsilametodologianon’hiha prou,hemdetenirencompteuntercer element:l’avaluaciód’aquestscontinguts. Uncopestablertsaquestselementsprevis podremdecidirlautilitzaciódeleseines digitalsqueconsideremnecessàriespera desenvolupareltreballquevolemrealitzar. Enl’articlemostrarem,fruitdeltreballcom aprofessorenuninstitut,queaquestes einesespodenclassificardedues maneres: a)einesútilsperadesenvolupar eltreballmatemàtic,i b)einesútilspera contenirlesactivitatsmatemàtiquesque hemdesenvolupat. Finalitzareml’articlemostrantunaactivitat realitzadaenunaclassede3rd’ESOdel’IES Llavaneresqueintentaconjugartotsels elementsmostratsanteriorment.

Beforeusingdigitaltoolsinthemath classroomwemustdecidewhatkindofmath wewanttoteach.Thisdecisionmustbe accompaniedbythechoiceofwhat classroommethodologywehavetousein thistask.Butcontentandmethodologyis notenough,wehavetoconsiderathird element:thestudentsassessmentrelated withthekindofmathandhismethodology. Oncetheseelementsaredeterminedwe havetochoosethedigitaltoolsthat weconsidernecessarytocarryout.

Asateacherandaresearcher,thepaper showsthatthesetoolscanbeclassifiedin twoways: a) toolstodevelopthe mathematicalwork,and b) usefultoolsto containthemathematicalactivities. Attheendthearticle,weshowanactivity performedin3rdESOmathclassroomatthe INSLlavaneres,wherewetryingtocombine someoftheelementslistedabove.

1.Introducció

Enlesclassesdematemàtiquessempres’hanpogututilitzarelsmitjanstecnològics:àbacs, reglesdecàlcul,calculadores,...uncordilliunpalperdibuixaraterra.Enelsdarrersanys, aquestsmitjanstecnològicss’hananatdesenvolupantexponencialmentambelsordinadors, demaneraquemoltesdeles«antigues»einestecnològiqueshantrobatelseuequivalent digitalinstal latenelsordinadorsoenelstelèfonsdigitalsquepràcticamenttothomtéalseu abast.Ésclar,doncs,quequanparlemdenovestecnologiesensestemreferintatecnologies digitals,o«numèriques»,comdiuenelsfrancesos,definicióquepersonalmentprefereixoatès querepresentamilloreltipusdetecnologiaalqualensestemreferint.

Aquestúsmassiudeleseinesdigitalshadecomportarcanvisenelfuncionamentdeles aulesienelsmaterialsambquèhaurandetreballarelsnostresalumnes.Mitra(1999)mostra quelaintroducciód’ordinadorspotferqueelsestudiantspuguinserelsquicondueixin l’adquisiciódelsseusaprenentatges.LeadbeateriWong(2010)ensmostrenqueeltreball ambordinadorspotinduirl’aprenentatreballardemaneraméscreativaicol laborativa,i portar,pertant,aunensenyamentméspersonalitzat.

Peròpenso,comAdell(2011),queallòrealmentimportantnoéslatecnologia,sinóelque elsnostresestudiantspodenferambella.Elcordillielpalerenimportants,atèsqueeldibuix d’uncercle,od’unael lipse,eraútilperalgunpropòsitprevi.Primerhihaunaideailes einesenshandepermetreassolir-la;ditd’unaaltramanera,leseineshand’estaralservei delquevolemfer.Nopodemoblidar,comensrecordaBates(2014),quelatecnologianoés neutral;perlaqualcosanol’hemdeposardavantdelesidees.Elsmitjansnohandesermés importantsquelestasquesarealitzarilescompetènciesaassolir.Allòimportantseranles tasquesqueelsestudiantsdesenvolupin.

Apartird’aquestesideesparlaremprimerdelaformaciómatemàticaquehauríemdedonar alsnostresestudiants.Enaquestbloc,tindremencomptetresaspectes:primerdetot,els contingutsmatemàticsquecaltreballar;ensegonlloc,lamaneracomhemdetreballar aquestscontingutsalesnostresaules,iperfinalitzaraquestprimerapartat,comavaluaremaquesttreballmatemàticquehemdesenvolupat.

Uncopestablertaquestpuntdepartida,enscaldecidirquinessónleseinesdigitalsque utilitzarempertaldeferelnostretreball.Isempretenintpresentquehandesereines queensajudinatreballarelscontingutsmatemàticsamblametodologiaproposadaia fer-nel’avaluació,ambl’objectiuqueelsestudiantsassoleixinlacompetènciamatemàtica. Enaquestsentit,entenemquepodemclassificarleseinesdigitalsendostipus: a)Einesque donaransuportalscontinguts,i b)Einesquedonaransuportal’organitzaciódelestasquesi elscontinguts.

2.Formaciómatemàtica

Seguintlesideesexposadesenl’apartatanterior,elprimerquehemdeferésplantejar-nos quinaformaciómatemàtica(general)volemdonaralsnostresestudiants.Aquíhauremde tenirencomptetantelscontingutscomlametodologiail’avaluació.

2.1. Quines matemàtiques?

Latesidel’articleésques’hand’ensenyarelscontingutsmatemàticsatravésdelaresolució deproblemes.Iaquestprocésnohad’estarsubordinatalscontingutsqueestreballin.Seguint lalíniaindicadaperSantalóquandiu:

Ensenyarmatemàtiqueshadeserequivalentaensenyararesoldreproblemes. Estudiarmatemàtiquesnohadeserresmésquepensarenlasoluciódeproblemes.

OelqueensdiuJohnMason:

Volemqueelsnostresestudiantstinguinprouconfiançaicapacitatperreproduir problemesanticsi,sobretot,pertreballarambnousproblemes.

OelqueensdiuHalmos(1980):

Lamatemàticaseguramentnoexistiriasensetotsaquestsingredients(axiomes, teoremes,postulats,conceptes,definicions,teories,fórmules,mètodes);totssón essencials.Peròcapd’ellséselcordeladisciplina,jaquelaprincipalraód’existir d’unmatemàticésresoldreproblemesi,pertant,enelquerealmentconsisteixla matemàticaésen[plantejar]problemesi[trobarlesseves]solucions(p.519).

Tenimmoltesreferènciessobreelqueentenemperproblemesilasevaresolució;podem anaralNCTM,mirarelcurrículumcatalàdel2007tantdeprimàriacomdesecundària,peròes potentendrequeunproblemavalligataunasituacióqueensportaaenfrontar-nosaunnou repte,situatenuncontextiperalqualnodisposemd’unarespostaimmediataiestàndard. Pertant,aquestprocésensrequeriràentendrelainformaciórebuda,reflexionar-hi,prendre decisions,dissenyarestratègiesicomunicarelsresultats.Unaaltrareferènciaateniren compteésladeWolfram(2010)enlaconferènciaquevaferaTED,«Teachingkidsrealmath withcomputers»,onrelacionaclarament(esquema1)quèvoldirfermatemàtiquesambel procésderesoluciódeproblemes.

Plantejar bones preguntes en el món real Trobar la solució matemàtica

matemàticament Comparar amb el món real

Poden serexemplesdeproblemeslessituacionssegüentsadiferentsnivellseducatius.

Unelefanthad’entrarisortird’unlaberint.Alseuinteriorhiha molteshabitacions.Dins deleshabitacionshihaplàtans(elnúmeroquehihaacadahabitaciórepresentael nombredeplàtansquehihaal’habitació).Cadavegadaquepassaperunahabitació recullelsplàtansquetroba.Nopotpassarperleshabitacionsmésd’unavegada.Amb quantsplàtanspotsortir?

O,perexemple,l’activitatsegüentproposadaalconcurs+MATESl’any2010:

Sumescurioses(+Mates10)

Observeu lessumessegüents.

Podeuescriurelareglageneral?Comlapodeujustificar?

Ésimportantassenyalarqueuntreballmatemàticd’aquestamenaafavoreixl’assolimentper partdelsestudiantsdelsprocessosques’intentenpotenciarambl’actualcurrículum.Aquests processossón:resoluciódeproblemes,raonamentiprova,comunicacióirepresentacióiconnexions.EnelsdocumentseditatspelDepartamentd’Ensenyament(2013),«Competències bàsiquesenl’àmbitmatemàtic»,tantpelquefaaprimàriacomasecundària,aixòesmostra clarament.

Sianalitzemelcurrículumactual,veuremqueestàclaramentorientataprocessos,enfront decurrículumsanteriorsmésorientatsaobjectius.Enlataulasegüentenpodemveure claramentlesdiferènciesentreelsdostipusdecurrículum.

Orientataprocessos

Orientataobjectius

Elsobjectiussónflexibles. Objectiusgeneralsformulatsambprecisió. Modeldedescobriment.Mètodecientífic. Estransmetenfonamentalmentideesalvoltant detècniques.

Participacióactivadeprofessorsiestudiants. Activitatstancadesirepetitives. Esvaloraelprocésd’adquisiciódeconeixements. Importànciadelesdestreses.

Produirresultatsdeconeixementquantificablesi normalitzables.

Eltipusdetreballqueespotdesenvoluparenuncurrículumguiatperobjectiuss’orientaala transmissiódeconeixementsialtreballd’habilitatsenfrontdeltreballenfocatalaresolució deproblemes,oalaindagacióquepermetl’orientataprocessos.Aquestadiferència,Flowers (2012),éslamateixaquelaquehihaentreinstrucció(objectius)ieducació(processos).

Ibelievethateducationandtrainingaredifferent.Tome,training isanessential commoditythatwillcertainlybeoutsourcedtodigitalsystemsandbedramatically improvedintheprocess.Educationismuchmoresubtleandcomplexandislikely tobeaccomplishedthroughmentorshiporapprentice-likeinteractionsbetweena learnerandanexpert.

2.2. Com volem treballar-les?

Laresoluciódeproblemeséslabasedeltreballmatemàticquevolemdesenvolupar,peròval adirque,amblleugeresdiferències,aquítambéhipodemincloureeltreballperprojectes, laindagació,etc.Enscalprecisarunametodologiad’acordambaquesttreball.Enaquest aspecte,hemdeserinnovadorsiescoltarelsgegants,tantPuigAdam(1958)comPolya (1967),enelsseusdecàlegssobreeltreballmatemàtic.Apartird’aquestesidees,eltreball matemàticnecessitaunametodologiad’aula-taller,delaboratori,onestreballiseguintles etapessegüents:

a)Unaintroduccióalesactivitatsquedesenvoluparem.Onespresentaranelsobjectius quevolemassolir.

b)Presentarlesinvestigacions,elsproblemesielsprojectes.

c)Treballenpetitgrup.

d)Discussióicontrastengrangrup.

e)Isiescau,realitzaciód’altresactivitatsrelacionades,querecullentambéAlsina,Burgués iFortuny(1988).

2.3. Com volem avaluar-les?

Aquestaspecteseguramentéselmésdifícilalqualenshemd’enfrontarsivolemavaluarles matemàtiquesqueenshemproposattreballaridelamaneraquevolemfer-ho.

Peròtenimreferentsqueensorientenenaquestprocés.DeLange(1999)n’ésun.Aldocument «FrameworkforclassroomassessmentinMathematics»ensestableixundecàlegdeprincipis del’avaluacióaclasse.Apartird’aquestsprincipisensproposemelsaspectessegüentspera realitzarunaavaluacióequilibrada:

a)Toteslesactivitatsquerealitzemhandeseravaluables.

b)Caltreballardiversostipusd’activitats:orals,escrites,individuals,engrup,pràctiques, teòriques...

c)Elsestudiantshandepoderdisposardetotalainformacióqueesgenerienelprocés d’avaluació.

d)Calestablirmecanismesd’autoavaluació.Enelsentitqueelsestudiantssiguinconscientsdelsseugraud’aprenentatge.

DeLangetambéensdiucomhand’estarconstituïdeslesproves,detotamena,queenshan deservirperrecollirlainformaciópertald’avaluard’unamaneraadequada.

Aquestainformacióesresumeixenlafigura1.

connections

LevelIII analysis

Assessment

Pyramid

Over time, assessment questions should“ ll“ the pyramid.

DomainsofMathematics

Figura1.DeLangePyramidforassessment.

Ensíntesi,creiemquepodemafegirquehemdeprocurarque,entoteslesactivitatsquerealitzem,siguind’avaluacióono:

a)Had’haver-hielementsdelsdiversosblocsdecontingutmatemàticdelcurrículum, ambdiversosgrausdedificultat,i

b)Handepredominarlesactivitatsdelnivellde«reproducció»,peròtambén’hihad’haver, enmenormesura,delnivelldeconnexionsidelnivelldereflexió(anàlisi).

Ambaquestesduesdarreresreflexionsielsquatrecriterisesmentatspodemavaluareltreball delsestudiants.Uncopestablertelquehemdefer,comfer-hoicomavaluar-ho,enscal buscarlesmillorseinesinformàtiquespertaldepoderrealitzarlatasca.Aixòéselquefarem alsapartatssegüents.

3.Dequinsmitjansdigitalspodemdisposarperdesenvolupar-les?

Quèvolemdelsmitjansdigitals?

Quèpodemaconseguirdelsmitjansdigitals?

Comelspodemutilitzarpercanviarcoms’aprenenlesmatemàtiques?

Leseinesquepodemutilitzarperadesenvolupareltreballmatemàtic,lespodemclassificar endostipus:aquellesqueenspermetendirectamenteltreballmatemàtic,unadelesquals podriaserelGeoGebra,iaquellesqueactuencomacontenidorsdelestasquesmatemàtiques quevolemtreballar,entrelesquals,s’inclouenaquelleseinesqueensajudeneneltreball;el Moodleenpodriaserunexemple,entred’altres.Peròabansdeveurequineseinespodem incloureencadascundelsdosapartats,enscalestabliralgunscriterisperveurequines, delgranventalld’einesdisponibles,podenserlesmésinteressants,atèsquevolemque elsnostresestudiantsassoleixinlacompetènciamatemàtica,peròtambécalquesiguin competentsdigitalment.Enaquestapartatdel’articleveurem,doncs,tresaspectes:

a)Quinescaracterístiquesvolemquetinguinlesnostreseinesdigitals,tantperalsestudiantscomperalsprofessors.Quèvolemd’aquestsmitjansdigitals?

b)Quineseinespodemconsiderarquedonenunbonsuportalscontinguts.

c)Quineseinesdonensuportal’organitzacióialapresentaciódelestasquesadesenvolupar.

3.1. Què volem d’aquests mitjans digitals?

Elsmitjansdigitalsqueutilitzaremal’aulas’adreçaranaestudiantsiprofessors.Pertant, enshemdeplantejarquinescaracterístiquesvolemquepotenciïnenambdóscol·lectius. Comenmoltsaltresaspectesjatenimreferentsenaquestapartat.Podemveurecoml’ISTE (InternationalSocietyforTechnologyinEducation),delamateixamaneraquel’NCTM,ha elaboratunseguitd’estàndardsreferitsalsmitjansdigitalsadreçatsaprofessorsialumnes.

Estàndardsreferitsaestudiants

Volemqueleseinesdigitalsqueutilitzemal’aulapermetinalsestudiants:

• Demostrarcreativitatiinnovació.

• Comunicaricol laborar.

• Duratermeinvestigacionsiutilitzarinformació.

• Pensarcríticament,resoldreproblemesiprendredecisions.

• Utilitzarlatecnologiademaneraeficaçiproductiva.

Ésimportantassenyalarlasemblançaquehihaentreaquestsdarrersaspectesambeltipus dematemàtiquesquehemproposatques’handetreballaral’aula.

Peròleseinesdigitalstambéseranutilitzadespelprofessorat;pertant,tambéhihad’haver unsestàndardsadreçatsaaquestespersones.Defet,elweb2.0preveuuncanviderol d’estudiantsiprofessorsalesaules.Had’augmentarlainteracció,isobretot,deixarandeser usuarisperconvertir-seencreadors.

Estàndardsreferitsaprofessors

Volemquepermetinalsprofessors:

• Disposardematerialsperfacilitarl’aprenentatgedelsestudiants.

• Facilitatd’integracióambaltreseines.

• Dissenyar idesenvoluparescenarisd’aprenentatgeiavaluació.

• Recollirinformaciódelstreballsrealitzatspelsestudiants.

• Compartirinformacióambelsestudiantsiambaltresprofessors.

Aquestsestàndardsensdonencriterisperdecidirsiunaeinadigitalésadequadaperala tascaquevolemferono.Així,podemutilitzarlataula1pervalorarlespotencialitatsilesdebilitatsdeleseinesdigitals.

Peralsestudiants

Demostrarcreativitatiinnovació.

Comunicaricol·laborar.

Duratermeinvestigacionsiutilitzarinformació. Pensarcríticament,resoldreproblemesiprendre decisions.

Utilitzarlatecnologiademaneraeficaçiproductiva.

Peralsprofessors

Disposardematerialsperfacilitarl’aprenentatge delsestudiants.

Facilitatd’integracióambaltreseines.

Dissenyaridesenvoluparescenarisd’aprenentatgeiavaluació.

Recollirinformaciódelstreballsrealitzatspels estudiants.

Compartirinformacióambelsestudiantsiamb altres professors.

Possibilitatsqueofereix

Possibilitatsqueofereix

Taula1.Potencialitatsidebilitatsdeleseinesdigitals.

L’úsd’aquestataulaperrevisarelsestàndardsquepermetassolironounadeterminadaeina digitalenspermetràsaber,entred’altrescoses,siaquestaeinaespotutilitzard’unamanera individualocalqueelseuúsescomplementiambaltreseines.Així,perexemple,sianalitzem unaeinadigital,jamencionadaanteriorment,elGeoGebra,amblataulaanteriorobtenimel resultatsegüent:

Peralsestudiants

Possibilitatsqueofereix

Demostrarcreativitatiinnovació. Permetcreardibuixos,macrosperpersonalitzar treballs.

Comunicaricol laborar.

Ésunaeinadetreballindividual,totiquepermetqueambuntreballdeterminathipuguin interactuarambaltrespersones.

Duratermeinvestigacionsiutilitzarinformació. Permetl’avaluaciódediversessituacionsfent canvis enlescondicionsdelsproblemesplantejats.

Peralsestudiants

Pensarcríticament,resoldreproblemesiprendre decisions.

Utilitzarlatecnologiademaneraeficaçiproductiva.

Peralsprofessors

Disposardematerialsperfacilitarl’aprenentatge delsestudiants.

Facilitatd’integracióambaltreseines.

Dissenyaridesenvoluparescenarisd’aprenentatgeiavaluació.

Recollirinformaciódelstreballsrealitzatspels estudiants.

Compartirinformacióambelsestudiantsiamb altres professors.

Possibilitatsqueofereix

Espodenresoldreproblemesgeomètrics,ien elmomentquepodemcanviarlasituació,ens potajudaraprendredecisions.

Segurquesí.

Possibilitatsqueofereix

LesassociacionsdeGeoGebraiprofessorsposenadisposiciódelsprofessorsmultitudde materialsperaltreballambaquestaeina.

Espodeninserirelstreballscreatsenblogs, pàgines weboaltres.

Hihamoltsexemples.

Nopermetfer-ho.

Lainformacióespotcompartir,perònopermet lainteracció.Éscomparteixl’ús.

Taula2.ValoracióGeoGebra.

Encaraque ambelGeoGebradisposemd’unaeinamoltcomplerta,elsaspectesquefan referènciaarecollirinformaciódeltreballdelsestudiantsicompartiraquestainformació podensermillorables.Handeserutilitzadesconjuntamentambaltreseinesdigitals.

3.2. Eines que donen un bon suport als continguts de matemàtiques

JahemcomentatqueelGeoGebra,segonscoms’utilitzi,potserunaeinamoltcomplerta peraltreballmatemàtic.Ésinteressantcomentarque,atèseldesenvolupamentques’està donantenlaweb,hihamolteseinesqueenglobendiversosaspectes.Pertant,laseva classificaciópotvariar.

Altreseinesútilsperadesenvolupareltreballmatemàticlestrobemenlataula3.

Einesútils

Adreçaweb

GeoGebra http://acgeogebra.cat/joomla Geometriadinàmica.

WolframAlpha http://www.wolframalpha.com Cercadorcomputacionali creador deginys.

Illuminations http://illuminations.nctm.org Fontderecursosdiversos. Lliçons, activitatsdigitals.

Nrich http://nrich.maths.org/frontpage Fontdeproblemes,alguns ambrecursosdigitals.Desde p3finsa18anys.

Einesútils Adreçaweb

ARDORA6 http://webardora.net

Creaciódecontinguts escolars.

WEBQUEST https://sites.google.com/site/webquestcathome Metodologiadetreballamb suportdigital.

Estadística paratodos

http://www.estadisticaparatodos.es

eduteka http://www.eduteka.org

Scratch http://scratch.mit.edu

Úsd’applets idel fulldecàlcul.

Portaleducatiuqueinclou diversosapartats.Totsútils.

Einadeprogramació.

Taula3.Einesdigitalspertreballarlesmatemàtiques.

Moltesd’aquestesactivitatstambétenenespaiswebscol·laboratiusenquèlespersonesque elsutilitzenhiacostumenapenjarlesactivitatsquedesenvolupen.

Hemdeserconscientsquehihamolteseinesdigitals.Semblaclarquetotselsprofessors hemd’experimentar,provar,aquelleseinesques’acostinalanostramaneradetreballar.Si aquestaeinas’hiadaptacalaprofundirenelseuús,isino,calbuscar-nealgunadenova,que debensegurexisteix.

Einesútils Adreçaweb

GoogleDocs https://drive.google.com

Wix http://es.wix.com

EXELearning http://exelearning.net

Wikispaces https://www.wikispaces.com

CMAPTools http://cmap.ihmc.us

CoolToolsfor Schools

https://cooltoolsforschools.wikispaces.com

Paquetintegratqueinclou processador detextos,fullde càlcul,espaiweb,formularis. Multiplicitatdefuncionalitats.

Creadord’espaisweb.

Dissenyadord’activitatsque permet eldissenyd’espais webaixícomd’activitats SCORM.

Espaiwebquepermet organitzardocuments, enllaçosialtrestasques.

Dissenydemapes conceptuals,itambéens permetdissenyarespaisweb quefacilitenl’accésales activitatsdigitalsdissenyades.

Espaiwikiquerecullunagran quantitatd’einesquepodem utilitzarperapresentarles tasques.

Taula4.Einesqueajudenaorganitzarlesactivitats.

3.3. Eines que donen suport a lorganització i a la presentació de les tasques

Aquesteseinessónlesqueensajudaranapresentaridonarformaalestasquesque pretenemquefacinelsnostresestudiants.Lesquehemescollitperutilitzarentenemquesón lesques’adaptenaltipusdetreballmatemàticquevolendesenvolupariquecompleixenels estàndardsperaltreballdigital.Valadirquepoqueseines,pernodircap,compleixentots elsestàndardsdigitals.Pertant,ésimprescindibleutilitzar-neunacombinació.Alataula4en veiemunrecull.

Lesdarreresversionsdemoltesd’aquesteseinespresentenunacaracterísticamoltimportant: permeteneltreballcol·laboratiusensehaverdecompartirordinadorsoespaifísic.També caltenirpresentqueenlestasquesquetreballemnoutilitzaremsempretotesleseines digitalsdisponibles;nomésutilitzaremaquellesqueenssiguininteressantspertaldepoder desenvolupareltreballmatemàticconcretqueenshemproposat.Semprecal,perpartdel professorat,unaselecciódeleseinesquehemd’utilitzar.

Podemtrobaraltreseinesqueenspodenpermetrearribaralsmateixosresultats.Nohiha einesmillorsopitjors;hihaeinesútilsperaprofessorsiestudiantsoeinesnotanútils,i tothomhadetrobarlesqueelfacinsentirméscòmode.

4.Unexemple:lestruitesalllac

Mostraremaracompodemaplicarelquehemproposatenelsapartatsanteriorsdel’article aunaactivitatpertalquepuguisertreballadaambmitjansdigitals.Permostrar-ho,hem seleccionatunaactivitatanomenada«Lestruitesalllac»iqueespottreballaral’aulaapartir de3rd’ESO.

Inicialment,l’enunciatd’aquestaactivitatés:

Cadaprimavera,unestanyésrepoblatambtruites.Ésadir,lapoblaciódisminueix cadaanypercausesnaturals,peròalfinaldecadaanys’afegeixenméspeixos.Les dadesqueenscalsabersón:

• Actualmenthiha3.000truitesal’estany.

• Acausadelapesca,lamortnaturaloaltrescircumstàncies,lapoblaciódisminueix enun20%cadaany,independentmentdelareposició.

• Alfinaldecadaany,miltruitess’afegeixenalallacuna.

A.Quantestruiteshihadesprésdelprimeranydecomençarelprocésal’estany? Ialfinaldelsegonany,quantestruiteshitindrem?

B.Comcreieuquelapoblaciócanviaràeneltempssielsparàmetresinicialscanvien?Ésadir,quèsucceiràsiesrealitzauncanvienelnombreinicialdepeixos, enlavelocitatalaquallapoblaciódisminueixoenelnombredetruitesque esreposacadaany?

Pertalderealitzarlaconversiódigital,hemutilitzatcomabaseel programaEXELearningamb formularisrealitzatsambl’einagoogledocs.Iatèsqueesfaunademandarelativaainvestigar comcanviaranunsdeterminatsparàmetresambeltempsheminclòslapossibilitatdetre-

ballarambunfulldecàlculoambun applet,enllaçatenelwebIlluminationspertald’experimentaramblesdadesqueensplantejaelproblema.Tambéutilitzemeltractamentde textosdegoogledocsperalapresentaciód’informes.

Laideadeltreballdigitalqueensvamproposareraqueelsestudiantsfessinúsdeleseines anteriorspertalderealitzartoteslestasques.Espodriahaverpensatl’activitatdemanera queelsestudiantsrealitzessinundossierenformatpdfil’enviessinviacorreuelectrònic.Però aquestanoeralaidea.Pertant,vamhaverdeferunaadaptaciódel’activitat.Aixòvavolerdir modificarunamical’estructuradel’activitat,enbasealtipusdematemàtiquesquevolíem treballarialamaneradetreballar-les.

Podeutrobarlaversiódigitald’aquestaactivitata:

http://walipi.webatu.com/nous_projectes/lestany_truites/index.html

iunaversióambladocumentacióenformatpdfowordenelrepositoridelDepartment d’EnsenyamentARC,al’adreça:

http://apliense.xtec.cat/arc/node/1773.

4.1. L’estany de les truites digital

Aquestespantallesestanextretesdel’espaiwebonestrobaallotjadal’activitat.Ilesutilitzarem permostrarlaconversiódigitaldel’activitat.

Imatge1.Objectiusdel’activitat.

Laimatge1mostraelsobjectiusdel’activitat;esdónainformaciórellevantdelproblemaies demanalaformulaciód’unahipòtesi,quequedaràrecollidaenunformulari.

Imatge2.Subactivitats.

Alaimatge2,hipodemveuretresactivitatsdiferents.Laprimeraésunexercicid’aplicació directad’uncàlcul.Alsestudiants,se’lsdonendiversespossiblesrespostesiellshauran d’assenyalaraquellaqueconsiderinadequada.Quanresponenapareixunaretroalimentació queelsinformadelavalidesadelasevaresposta.Aquestapartdel’activitatfinalitzaamb duesactivitatsdereflexió.Primer,araquejahantreballatamblesdadesdelproblema,hande ferunaprediccióallargterminidelnombredetruitesquehihauràal’estany.Ienlasegona, se’lsdemanaquetrobinunafórmuladerecurrènciaqueelspermetiobtenirelnombrede truitesenunanyconcretapartirdelestruitesquehihavial’anyanterior.

Alaimatge3esmostralapartdel’activitatenquèutilitzaremunfulldecàlcul.S’had’utilitzar perelaborarunatauladelnombredetruitesenfunciódelsanysiungràficquerepresenti aquestesdades.Ambaquestainformaciós’hadevalidarlahipòtesiformuladaiintentar raonarsiésadequadaono.Podemutilitzarduesversionsdelfulldecàlcul;enuna,els estudiantshand’elaborarlafórmuladerecurrènciaperdeterminarelnombredetruitesal llac,ienlasegonaespotdonaraquestainformacióalsestudiants.

Finalment,esdemanadescriureelgràficquehanobtingutamblaideaderelacionar-loamb lafórmulatrobada.

Imatge3.Activitatenquèutilitzemunfulldecàlcul.

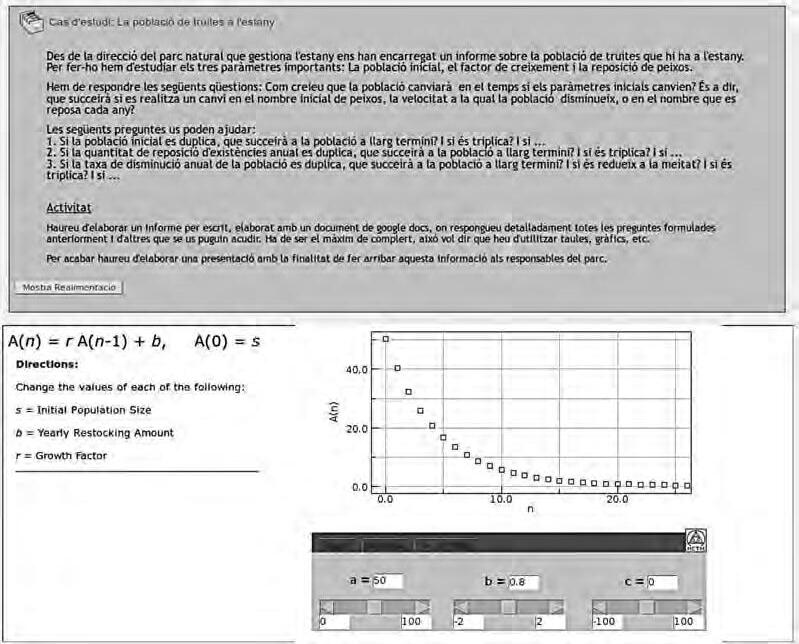
Imatge4.Casd’estudiiúsd’un applet.

Alaimatge4esmostracoml’activitatesplantejacomunapetitarecerca.Calelaborarun informeons’expliquicompotevolucionarelnombredetruitesal’estanyenfunciódels tresparàmetresquepodenanarvariant.Sempreestudiant-losd’unenun.Podremcanviarla poblacióinicial,laquantitatdetruitesquereposemielfactordecreixement.Perfer-hopodran disposard’un applet pertaldepoderferelscanvisquenecessitenperobtenirrespostes. També,sihoprefereixen,podenutilitzarelfulldecàlculques’hadissenyat.L’informeper escrits’hadeferenundocumentdetextcreatambelGoogledocsques’hauràdecompartir ambelprofessor.

Iperfinalitzar,alaimatge5veiemqueenl’activitatnomésrestaintentartrobarunafórmula queexpliquiladistribuciódetruitesalllargdeltempsenfunciódelstresfactors,il’elaboració d’uninformeonesrecullinlesdescobertesialtresaspectesalvoltantdelatascarealitzada. Aquestinformes’haderealitzarenundocumentdetextapartirdelGoogledocs.

4.2. Resultat del treball dels estudiants

Cadascunadeleseinesutilitzadestéfuncionsdiferents.EXELearningenshapermèscrear unespaiwebamigablepertalqueelsestudiantsesplanteginlespreguntesiquinaresposta volendonaracadascuna.Aquestatascaésfeinadelprofessor.

ElsformularisdeGoogleenspermetenrecollirlesrespostesdelsestudiantsalesactivitats enunfulldecàlcul.Ambunavantatgeimportantrespectealtreballalallibreta.Ielpodem veureenlaimatgesegüent:

Imatge5.Fórmulageneraliconclusions.

Escriuelteunom Hasd’explicarsi creusque creixerà indefinidament, creixeràfinsa arribaraunlímit, olapoblació anirà augmentanti disminuint alternativament, osianirà disminuintfinsa desaparèixer.

TM Lapoblacióanirà augmentanti disminuint alternativament.

Explicaels motius dela respostaanterior.

Éspossiblepredir lapoblaciódela llacunadesprés d’unnombre determinat d’anys, cinquanta,per exemple?

Sihascontestat quesí, explica comcreusquees podriafer.Isihas contestatqueno, explica’nels motius.

Creusqueés possiblepredirla poblacióde truitesdela llacunadesprés d’unnombre determinat d’anys, cinquanta,per exemple?

pmlbr Lapoblacióanirà augmentanti disminuint alternativament.

Acausadela pesca, la poblacióanirà disminuint,però comqueles truitestambées reprodueixen, creixen.Anirà seguintla seqüència augmentanti disminuint.

Perquècadaany selirestaunvint percentiseli sumamil;per tant,arribaràun puntenquèel vintpercentserà mésquemil.

No.

Perquèpot haver-hiuna temporadade pescamoltgrani queesquedi sensegaire peixosoes podenreproduir moltitambé creixeràmolt.

Sí.

Sí,calculantla població d’aquestany augmentai treureelvintper centpermil truitespercada any(anant intercalant«20 percent/més mil»).

Imatge6.Mostraderespostesd’estudiants.

No.

Sí.

Alaimatge6podemveurelarespostaaalgunadelesqüestionsproposadesperpartdedos grupsdetreball.Iacontinuacióhihaurialesrespostesdelarestadegrupsdetreball.Aquest aspecteésimportantal’horaderealitzarunarevisiódelatascaengrangrup.Podemveureles respostesdetotselsgrupsdetreballalespreguntesproposadesirealitzar-neladiscussió.Els estudiantspodenteniraccésaaquestdocumentpertalderevisard’unamaneraindividual lasevafeina,ambpossibilitatd’edicióonomésderevisió,acriteridelprofessorresponsable.

Elfulldecàlculd’aquestmateixaplicatiuenspermetexperimentar,delamateixamanera quel’applet,ambelnombredetruites,larepoblacióielpercentatgedemortalitat.

Alaimatge7hopodemveure.

Disposemdeduesversionsd’aquestfulldecàlcul:una,laqueesmostra,amblafórmulade recurrènciaintroduïda,ilasegonasenseaquestafórmula.

Població inicial Factor de creixement

Quantitat restituïda

Imatge7.Úsdelfulldecàlculperalarealitzaciódelarecerca.

Enelprimercas,elsestudiantshand’experimentarambelsvalorsdepoblacióinicial,factorde creixementiquantitatrestituïdapertaldedonarrespostaalarecercaquese’lshaproposat.El fulldecàlculs’encarregaderealitzarelscàlculsielgràficcorresponent.Elprofessorpotoptar, enfunciódelsestudiants,perdonarmésomenysinformacióenaquestfulldecàlcul.L’applet téexactamentlesmateixesfuncionalitatsqueelfulldecàlcul.Espotoptarperutilitzarol’un ol’altre,sempreacriteridelprofessor.Espotcrearunginyquefaciunafeinasemblantamb l’einaWolframAlpha.

LadarreraeinaqueutilitzareméseltractamentdetextosdeGoogledocs.Elsestudiants, d’unamaneracol·laborativa,handepresentarduestasques.Uninformeonrecullinlarecerca realitzadaiunaltreondesenvolupinlessevesconclusionssobrelatascarealitzada.Unsol documentpergrupdetreballques’hauràdecompartirambelprofessorpertalderealitzar-ne l’avaluaciócorresponent.Enaquestinformes’haurand’integrarelsgràfics,lagraelladelfull decàlculitotsaquellselementsqueajudinelsestudiantsacompletarl’informe.

Enladarreratasca,elsestudiantshauran,d’unamaneraindividual,depresentarlesconclusions alvoltantdelatascarealitzada.Pretenemqueenaquestdarrerdocumentvalorinduescoses: 1)l’activitat,i2)elseutreball.

5.Reflexionsfinals

a)Leseinesdigitalshandeseruninstrumentalserveidel’aprenentatgedelesmatemàtiquesperpartdelsestudiants.Hemdetenirmoltclarquinesmatemàtiquesvolem treballar,comvolemfer-hoicomlesavaluarem.Uncoptenimclarsaquestsaspectes, podremdecidirquineseinesdigitalsutilitzarempertaldedonarunvalorafegita aquellesactivitats.Siunaeinadigitalnoaportaaquestvalorafegital’activitat,ésmillor noutilitzar-laicontinuartreballantcomsemprefinsatrobarunaeinaqueensaporti aquestvalor.

b)D’eines,n’hihademoltstipusicontínuamentn’apareixeniendesapareixen.Penso quehihatresnivellsd’usuaris:1)elsqueutilitzenleseines;2)elsquesóncapaços demodificarunaeinaperadaptar-laalqueelsinteressa,i3)elsquesóncapaçosde

Variació del nombre de truites a l’estany

dissenyar l’einaquenecessiten.Pertant,enshemdepermetrecol·locarenelnivell d’usuariquevulguem;nocalserexpertentotselsprogramesquevaginapareixent nidelessevesdarreresversions.Enscalutilitzarleseinesdigitalsdelamaneramés eficientpossibleperal’objectiuqueperseguim,queésqueelsnostresestudiants aprenguinmatemàtiques.

c)Hemd’aprofitarelsavantatgesdeconnectivitatqueensofereixlaxarxa.Hihamoltes associacionsdemestresiprofessors,d’usuarisdeprogrames;hihaeinesquepermeten eltreballcol laboratiu.Calqueestiguemconnectatsitreballemcol laborativament, nomésaixípodremarribarmoltméslluny.

d)Iperfinalitzar,diversifiquemleseinesqueutilitzem,lesmetodologiesdetreballa l’aula,lesd’avaluació,etc.;seràlamaneracomnosaltresielsnostresestudiantsestarem preparatsperafrontarelmónd’incertesesenelqualestemvivint.

Referències

Adell,J.(2011).http://elbonia.cent.uji.es/jordi/2011/05/08/lo-importante-no-es-la-tecnologia-sino-lo-que-tus-alumnos-pueden-hacer-con-ella (Darreraconsulta:abril2014).

Alsina,C.,Burgués,C.iFortuny,J.M.(1988). Construirlageometria.Madrid:Síntesis.

Bates,T.(2014).http://www.tonybates.ca/2014/04/15/time-to-retire-from-online-learning (Darreraconsulta:abril2014).

Currículum2007.Departamentd’Ensenyament,http://www.xtec.cat/alfresco/d/d/workspace/ SpacesStore/c8437f7a-6a8a-476a-813c-0f897525d119/matematiques_eso.pdf (Darreraconsulta:abril2014).

DeLange,J.(1999). Aframeworkforclassroomassessmentinmathematics.(Unpublished manuscript).Madison,WI:NationalCenterforImprovingStudentLearningandAchievement inMathematicsandScience,AssessmentStudyGroup.

Departamentd’Ensenyament,«Competènciesbàsiquesdel’àmbitmatemàtic» http://srvcnpbs.xtec.cat/creamat/joomla/index.php/suport-curricular/73-documents-de-suport-curricular/1121-competencies-basiques-de-lambit-matematic (Darreraconsulta:abril2014).

Flowers,W.http://web.mit.edu/fnl/volume/243/flowers.html (Darreraconsulta:abril2014).

Halmos,P.(1980).Theheartofthemathematics.Washington: AmericanMathematicalMonthly, 87,519-524.

http://mellbreak.lboro.ac.uk/problemsolving/pathways(Darreraconsulta:abril2014).

InternationalSocietyforTechnologyinEducation(ISTE)https://www.iste.org (Darreraconsulta:maig2014).

Leadbeater,Ch.(2010).http://www.ted.com/talks/charles_leadbeater_on_education#t-97371 (Darreraconsulta:abril2014).

Leadbeater,C.,Wong,A.(2010). Learningfromtheextremes.http://www.cisco.com/web/ about/citizenship/socio-economics/docs/LearningfromExtremes_WhitePaper.pdf (Darreraconsulta:abril2012).

Mason,J.,L.BurtonandStacey,K.(2010). ThinkingMathematically (2aed.).PearsonEducation Limited.

MathematicalProblem-SolvingProjectforHESTEMTeachingProblemSolvinginundergraduateMathematics.http://mellbreak.lboro.ac.uk/problemsolving/sites/default/files/guide/ Guide.pdf

Mitra,S.(1999).http://www.ted.com/talks/sugata_mitra_the_child_driven_education (Darreraconsulta:abril2014).

Mora,Ll.(2012).«L’activitatmatemàticaal’aulavirtualipresencial.Estudicomparatiua1r cicled’ESO».PhD.Tesis.UniversitatdeBarcelona.

NCTM.http://www.nctm.org/standards/content.aspx?id=26860 (Darreraconsulta:abril2014).

Polya,G.(1967). Ladécouvertedesmathématiques (2vols.).París:Dunod.

PuigAdam,P.(1955).Decálogodeladidácticamatemáticamedia. GacetaMatemática, 1asèrie,7,5-6.Madrid:InstitutoJorgeJuandeMatemáticasiRealSociedadMatemática Española.

Wolfram,C.(2010).TED,«Teachingkidsrealmathwithcomputers»https://www.ted.com/ talks/conrad_wolfram_teaching_kids_real_math_with_computers#t-213860 (Darreraconsulta:abril2014).

cròniques cròniques riques s

XXVOlimpíada MatemàticaEspanyola

Catalunya2014

LuisaAlmazán CoordinadoraOlimpíadaMatemàticaperCatalunya lalmazanster@gmail.com

Aquestmesdejuny,CatalunyavatornaraorganitzarunaOlimpíadaMatemàtica,després decatorzeanysdesdel’últimavegada.Desdeldia25finsal29,vamrebreseixanta-un alumnesivint-i-dosprofessorsdetoteslescomunitatsdel’Estat.Latrobadaesvaproduir dinselmarcdel’albergMaredeDéudeMontserratdeBarcelona.Lasingularitatdel’edifici, unaconstrucciómodernistacombinadaambestilneomoresc,ambungranvalorhistòrici arquitectònic,enshapermèsgaudird’unsdiesenunentornprivilegiatiamblatranquil litat necessàriaperdesenvoluparcadaunadelesactivitatsquehavíemprevist.

Primerdia:Pertrencarelgel

Laprimeranitvaserintensa.Percomençar,uncopvamdeixarlesmaletesivamberenar,vam prepararelprimertaller:POLIEDRES.Demanerainformaliambentusiasme,elsalumnesvan construircadascundelspoliedresregularsfentservirdiferentstècniques:cubs,tetraedres, octaedres,dodecaedresiicosaedres.Aquestspoliedresserienelssímbolsquealllargdela setmanaservirienperanar-seagrupantperfercadaunadelesactivitatsprevistes.

Algunesdinàmiquesdegrupalpatidel’albergelsvanpermetreconèixer-seunamicamillor icomençarafernousamicsiamigues.

Segondia:Inauguracióoficial,provaindividual,sincrotróAlbaiSagrada Família

Desprésd’esmorzarensvamdirigiralaFacultatdeMatemàtiquesiEstadísticadelaUPCper solucionarelsproblemesdelaprovaindividual,queesvarealitzarambinterèsiambl’enginy propid’aquestsalumnes.

Uncopfinalitzadalaprovaesvaduratermelainauguracióoficialdela25aOlimpíada MatemàticaenlapròpiaFacultatiacontinuacióensvamdirigircapaCerdanyoladelVallèsa visitarelsincrotróAlba.

Albaésl’únicafontdellumdesincrotróqueexisteixal’Estatespanyol.Estractad’uncomplex d’acceleradorsd’electronsquepermetanalitzarl’estructuraatòmicadelamatèriailesseves propietats.Lesseveslíniesd’investigacióvandesd’aplicacionsenlesciènciesdelavidafins alamedicina,laciènciadematerials,lesciènciesambientalsilafísicaolaquímica.

DesprésdedinarvamtornaraBarcelonaiensvamdirigircapalaSagradaFamília,on elsalumnesvanrealitzarunstallersmatemàtics,preparatspelGrupVilatzara,queelsvan permetreentendremilloralgunsdelstretsquefandiferentaquestaobraarquitectònicadel segle XX.Unavisitaal’interiordelabasílicavadonarperfinalitzadal’activitativamtornarcap al’alberg.

Desprésdesopar,elsalumnesvandiscutirengrupsobreelsproblemesindividualsivan contrastarambelprofessorJordiDeulofeulessolucionsilesestratègiesquehavienfetservir encadascundelproblemesproposats.

Figura2.UndelstallersrealitzatsalaSagradaFamília.

Tercerdia:SerradeCollserola,MMACA,ParkGüell,GeoGebraiobservació astronòmica

UnautocarensvaportaralaserradeCollserola,alportelldeValldaura,onelsalumnesvan anarpujantfinsalTibidaborealitzantdiferentsactivitatsdetriangulaciósobreelterreny preparadespelprofessorJaumeSerra.Uncopacabadal’activitat,l’autocarensvaportarcap aCornellàdeLlobregat,onvamvisitarl’exposiciópermanentdelMuseudeMatemàtiquesde Catalunyaivamexperimentarambcadascunadelespropostesquepresentavacadamòdul: corbes,miralls,mosaics,mesuraimoltsaltresmaterialsquepodemtrobar-hi.

DesprésdedinarvamanaralParkGüell,onelshavíempreparatunagimcanaambproves matemàtiquesquevanresoldreràpidament.Seguidament,vamtornaral’albergpersopar.

Jaalanit,vamanaral’aulad’informàtica,onvanexperimentarambelprogramaGeoGebra ivanresoldrealgunsproblemesqueelsvaproposarelprofessorRaülFernàndez.Uncop acabadalasessió,elsalumnesvananaralasalad’actesivanaprendreconceptesastronòmics queposteriormentelsvanajudarainterpretaralgunesdelesobservacionsquevamferal patiambelstelescopis.

QuartdiaaLloretdeMar:Activitatscientífiquesiesportives,Jardinsde SantaClotilde,concursfotogràficirevetllaalbarridePescadors

Desprésdedosdiesplensd’activitats,professorsialumnesesvanprepararperaunajornada mésrelaxadaalaplatjadeLloretdeMar.Totiaixò,elsalumnesvanpodergaudird’activitats científiquesiesportivesalaplatjadeFenalsmentreelsprofessorspassejavenpelsJardinsde SantaClotilde.

DesprésdedinarvampujaralvaixellperferunrecorregutfinsaarribaraBlanes,onels alumnesvandisposardetempsperbanyar-se.Alatornadavamanarlacasa-museudeCan Saragossa,onvanfermésprovesd’equipsivanacabardeseleccionarlestresmillorsimatges peralconcursdefotografiamatemàtica.

DesprésdesoparvamdisposardetempslliurepelpasseigdeLloret,quemoltsvanaprofitar perbanyar-se.EnacabatvamanarderevetllaalbarridePescadors,ambcocaihavaneres,i finalmentvamtornaral’alberg.

Últimdia:Visitamedieval,actedeclausura

Esmorzem,agafemlesmaletes,lespugemal’autocariensdirigimcapalPalaudelaGeneralitat,onlesdeixaremfinsalfinaldelaclausuradela25aOlimpíadaMatemàtica.A continuació,enshemdirigitcapalaplaçadelaCatedralpercomençarunitineraripelsracons mésinteressantsdelaBarcelonamedieval.

Alesonze,puntualment,vacomençarl’actedeclausurapresiditperlaconsellerad’Ensenyament,IreneRigau.Desprésdelabenvigudadelaconselleravamcomençarambunes paraulesperpartdelapresidentadeFEEMCAT,senyoraVictoriaOliu,iacontinuacióvaser elsenyorOnofreMonzó,presidentdelaFESPM,quivadirigirunesparaulesalsassistents.

Desprésvamgaudirdelaconferència-talleracàrrecdelprofessorAntonAubanell«Geometría conpompasdejabón».

Seguidament,laconselleravadonarpasal’actecorresponentdelliuramentdediplomesals alumnesassistentsialesmencionshonorífiquesalsalumnesquevandestacarenlesdiferents provesrealitzadesdurantl’Olimpíada.Abansdellliuramentdelesmencionsd’honor,dos representantsdelsalumnesidosrepresentantsdelprofessoratvanexplicar-noscomhavien viscutellsl’Olimpíada.

Finalment,laconselleraIreneRigauvatancarl’acteambunesparaulesvalorantmolt positivamentlafeinafetaperlesdiferentsassociacionsdematemàtiques.

Figura3.Cloenda.

XIJornadad’EducacióMatemàticad’APaMMs

LuisaAlmazán CoordinadoraOlimpíadaMatemàticaperCatalunya lalmazanster@gmail.com

LaXIJornadad’EducacióMatemàticad’APaMMs,dutaatermeal’InstitutVilatzaradeVilassar deMarel15demarç,vatenirmésdevuitantaassistents,principalmentdelMaresme.Ens vammourealvoltantdeltema«Modelitzacióal’auladematemàtiques»ivamobrirunanova viadeparticipació.

Defeiatempsqueensplantejàvemlaparticipaciódelsalumnesenlanostrajornadacom unaviadecomunicaciódirectaideparticipacióactivadelsprotagonistesdelfeteducatiu. Peraixòvamdecidirreprendrelaideaifer-larealitat.Vamconvidarelssocisaportar-nosla sevaaulaalajornada,isihocreienoportú...tambéelsseusalumnes.Desprésd’unsilenci inicial,ensvanarribaralgunespropostesitambéalgunespreguntes:elspetitspodienvenir «virtualment»?Reflexionantsobreeltemavamobrirlespresentacionsaclipsifotografies d’aulaenquèl’activitatdutaatermepelsalumnesfosprotagonista.Iaixívamaconseguir finsadeupresentacions,tresambalumnesd’ESOpresentsal’acteilarestaconsistentsen presentacionsfetespelsmestresqueleshaviendutaterme.

Però,anemapams...

EnManelSolensvaintroduiraltemafentunaclaraexposiciósobre«Modelitzacióal’aulade matemàtiques»,enquèvanquedarclareslesprincipalsideessobrequèsóniquèimpliquen lesactivitatsquepromouenlamodelitzacióal’auladematemàtiques.

Acontinuacióesvaobrirlaprimerarondadepresentacions,quevaoferir-nosexemples departicipacióimodelatgeperpartd’alumnesd’ESOalsd’Inicialdel’EscolaFonlladosade Malgrat.ElsalumnesilatutoraAnnaManriquevanexposarcomduratermeactivitatsd’espai iformaalcarrer.

LaMartaArmengol,del’AngeletaFerrerdeMataró,ensvamostrarelsnensinenesde2n d’infantilactuantireflexionantsobreeltemadeladistànciailavelocitata«Rampesitorres». Elclipil lustratiuvaposarenevidènciacomésd’importantcomptarambmestresqueinvestiguinal’aulapertaldemillorarlasevapràctica.

Enlamateixalínia,l’IngridTena,delMasMariadeCabrils,vamostrarexemplesd’activitats enquèelsalumnesinvestiguensobreunapremissadonadaalvoltantdelaideade«doble» fentservirmiralls.Alhora,ensvaquedarmoltclarqueelsalumnessolenarribarmésllunydel queelrepteinicialplanteja.

Lapresentaciódelsalumnesde5èdel’EscolaSantLlorençdelMuntdeTerrassavaserun al·licientmés,unplusperatotsiseguramenttambéperaellsilessevesfamílies,quevan

poder-losescoltarparlardematesambclaretat,entusiasmeitocsartísticstotexposantel quehavienfetperadissenyarelseuhortescolar.ElsacompanyavenelsseusmestresJuanjo CárdenasiLoliMoreno.

Peracabarlaprimerapartdelamatinalvamtenirelsalumnesde3rd’ESOdelVilatzara exposantelseuestudisobre«Quinatarifademòbilésl’adientperacadaperfild’usuari?».

Desprésdelapausa,queesconverteixcadaanyenunaltrepuntd’intercanvi,vamseguir veientunexempled’unamateixaactivitatdutaatermeperalumnesde2nd’infantili2nde primàriadel’escolaMaria-MercèMarçaldeMataró.LesmestresDolorsDuraniTxonVidal ensvanmostrarelsresultatsdel’activitat«Enrajolem»,enquèesposademanifestcomuna activitatpotentpotsertreballadaadiferentsedatsidonarpeuaobservarlaprogressióen elsresultatsques’obtenen.

LesvaseguirlaMontseCanet,quevainformar-nossobrecomferfraccionsambelsesmorzars ocomfraccionarelsesmorzarssegonselsdesitjosdecadacompanydeclasse.Elmés interessantvaserveurecomlesfraccionsteniensignificacióperalsnensinenesquelesfeien servir.

LaMartaPou,fentestadísticaambelsseusalumnesde2nd’infantildelMasMaria,vamostrar comferservirl’estadísticaperaendreçar,ordenariinterpretardadesalsquatreanys.

EnRubenFabri,del’escolaPallaresadeSantaColomadeGramenet,ensvapresentaruns problemesmoltespecialsquefanballarelcapalsnensdecicleinicialalhoraqueensfan adonardelanecessitatd’apujarelllistódelsreptesqueplantegemal’aula.

EnJordiFont,del’InstitutBaixaMardeVilanovailaGeltrú,juntamentambalumnesd’ESO, «virtuals»,ensvaintroduirenlatrigonometriaamblapreguntasegüent:Quinaésl’alçada delfardeVilanova?Aquestprojecteconstavadediferentsfases,entrelesquals,l’elaboració detaulestrigonomètriquesilaconstrucciód’ungoniòmetre.

Lesvaloracionspositivesd’aquestnouformatdejornadaensportenaseguiranimantels nostressocisacomunicarlessevesexperiènciescomaformadeconeixementcompartit.

VJornadesd’ADEMGI

GuillemBonetCarbó Vicepresidentd’ADEMGI

Lesjornadesqueanualmentorganitzal’Associaciód’EnsenyantsdeMatemàtiquesdeles ComarquesGironines(ADEMGI)tenenlafinalitatdedifondrelamatemàticaperaladocència entoteslesetapeseducatives,ferdivulgacióentreelsnostressocisdelesnovespràctiques educatives,icrearunambientdedebatiparticipacióambelssocisino-socisqueparticipin enaquestesjornades.Ambaquestesjornades,espreténsobretotquelesmatemàtiques traspassinlafronteradelsnostressocisiarribinalsnostresalumnesialasocietat.

Lesdarreresjornadesd’ADEMGIvarentenirlloceldissabtedia26d’octubreal’Escola PolitècnicaSuperiordelaUniversitatdeGirona,al’edificiP-IVdelamateixafacultat.

Enaquestesjornadesesvarenplanificarunstallersdeprobabilitatiestadísticaquebuscaven queelssocisparticipessinposant-semomentàniamentenlapelldelsalumnesiresolent algunsdelsproblemesprobabilísticsqueelgrupMATGIelsproposava.

D’altrabanda,tambéesvaplanificarunaconferència-col·loquisobrelahistòriadelcalendari acàrrecd’AntonAubanellambl’objectiudedivulgarlamatemàticaques’amagadarrereel nostrecalendariidonaralgunapropostad’aplicacióal’aulaperaprofessorsimestresdetots elsnivellseducatius.

Finalment,aprofitàvemaquestatrobadaambelssocisperferentregadelspremisdelconcurs defotografiamatemàticaiinformar-losdelesdiferentsactivitatsalesqualspodrienparticipar durantelcurs.

Tallersdeprobabilitatiestadística-GrupMATGI

ElGrupMatGIésungrupdeprofessorsimestresdelescomarquesgironinesqueestroba regularmentperreplantejarladocènciamatemàtica,buscantexperiènciespràctiquespera l’aulaiposant-lesal’abastdelprofessorat.

Enaquestaocasió,elGrupMatGIensplantejalanecessitatdetreballarelstemesdeprobabilitatiestadísticaalsnivellsdeprimària,secundàriaibatxillerat.Tambéconsiderala possibilitatqueaqueststemessiguintractatspelprofessoratd’unaformanoúnicament calculísticaialgorítmica.Exposa,doncs,lanecessitatdecanviarelroldel’alumneal’aula tambéenaquesttemaiproposadiversesactivitats,oexperiènciesd’aula,enriquidoresi competencialsqueplanteginautènticsreptesalsalumnesiqueiniciïnunadiscussióal’aula atravésdel’experimentació,l’anàlisidedadesielraonament.

Exposem acontinuacióalgunesdelesexperiènciesqueproposaMatGI:

◮ Experiència1:Cursadecamellsicavalls

Esproposa convertirl’aulaenunaautènticacursadecamells,comlesqueacostumema trobaralesfires.Aquestavegada,però,elsmovimentsdelscamellsvindrandonatspel resultatdelllançamentd’undau.Perquincamellvolemapostar?

Enaquestaactivitat,elsestudiants,apartird’unjocd’atzarambdaus,recollirandades,les representaranentaulesigràfics;aixòelsportaràaunaprimeraintroduccióal’assignacióde probabilitatsalsfetspossiblesdinsunesdeveniment.Desprésassignaremteòricamentvalors alesprobabilitatsdelsfets.

◮ Experiència2:Cursad’obstacles

Conjunt dejocsenelsqualscalrealitzardiversosexperimentsiobservar-neelsresultatsper intuirquealgunssónmésprobablesqued’altres.Elsalumnesjuguenihandereflexionarsobre laprobabilitat,raonantquinessónlesopcionsmésprobablesencadaundelsexperiments realitzats.Encursossuperiorsespodriademanartambéquecalculinlesprobabilitats.

Aquestaactivitatesplantejacomunacursad’obstaclesqueenfrontadosalumnesrivals.

◮

Experiència3:Nusos

Enuncertpaísexisteixunritualquecadaparellaqueesvolcasarhadesuperar.Enaquest ritual,elsacerdotagafasistrossosdecordillsigualsambunamà,demaneraqueperlapart superiordelpunylisurtensiscapsdecordilliperlapartinferior,siscapsmés.

Enaquestsmoments,l’aspirantanuvinuaràdedosendoselscapsdecordillsdelapart superior,fent-netresnusos,unperparella.Lanúvia,perlasevabanda,acabarànuantels capsdelapartinferiortambéperparelles.

Laparellanomésespodràcasarsielsresultaunúniccordillambsisnusosformantuncercle.

Quinacreieuqueéslaprobabilitatqueespuguincasar?Creieuqueéspocomoltprobable?

◮ Experiència4:Mesureml’error

Esproposenunseguitd’efectesòpticsconstruïtsambGeoGebraperRaülFernàndez.En aquestsexperiments,elsalumnesaniranprovantlasevaperíciaperdetectarl’efecteòptici l’ordinadoraniràanotantl’errord’aproximacióquecometen.Automàticament,elsalumnes podrananarveientladificultatd’encertarencadaexerciciatravésdelesdadesaportadesi extreure’nconclusions.

◮ Experiència5:Quantstaxishiha?

Femla propostasegüent:seiemenunbancdelaplaçaUrquinaonadurantunaestonetaiens apuntemelnúmerodellicènciadecadaundelstaxisqueveiempassar;suposemqueaquests

són:332,125,052,387,212,431,038i142.Esdemanatrobarunaaproximacióacuradadel nombretotaldetaxisquehihaalaciutat.

Perrealitzaraquestaactivitats’extreuenaleatòriamentd’unaurnaelstaxisqueveuelvianant. AquestaurnahadecontenirelmateixnombredetaxisNqueproposemquetinguilaciutat numeratsdel’1al’N.L’alumnehad’apropar-seaaquestvalorN.

Espottrobarmésinformaciósobreaquestesexperiències,aixícomlesfitxesdelprofessoro del’alumneialtresactivitatsproposadespelgrupMatGI,al’adreçasegüent:http://ademgi. feemcat.org/materials/tema13

Unapassejadaperlahistòriadelnostrecalendaritotpensanteneducació matemàtica;AntonAubanell

Enaquestaocasió,l’AntonAubanellutilitzalahistòriadelnostrecalendariperparlar-nos deladificultatd’aconseguirmesurarunfenomenfísic,comésaraladuraciódelmovimentde translaciódelnostreplanetaalvoltantdelSol.Resposta:unany,fàcil,peròaquestconcepte aparentmenttansenzilldecomprendreenséstanhabitualquenosomconscientsdel’esforç quehacalgutperanar-loajustantprogressivament.

Desdelsinicisdelahumanitat,aquestamesurahaestatmoltnecessàriaperal’homea l’horad’organitzareltemps,depreveurel’èpocadelesriuades,lesèpoquesdemassafredo massasol,organitzarlessembresilescollites.Ijadesdelprincipiaquestcàlculs’harealitzat observantelscanvisenlanaturalesailaposiciódelesconstel·lacionsalcel.Elsmaiesfinsi totaconseguienpreveurequindiaeraelsolsticid’estiusegonssielraigdesolqueescolava perunafinestradeltempleanavaapararaunespaiconcretdelaparetoposada.

Aquestesobservacionsenshandonataproximacionsmoltraonablesdelqueéslamesura del’any.Enaquestsmomentssabemqueladuradadel’any2000vaserde365,242199 dies;aquestadadaésrelativamentactualinitansolscinc-centsanysenrerenoestenia coneixementdeladuradadel’anyambaquestaprecisió.Mésencara,siensmovemalllarg demil lennis,veiemqueeltercerdecimalvaria,iaixòésdegutalleugeresoscil lacionsde l’eixterrestre.Defet,elprincipalproblemadelsnostresavantpassatseraajustarl’anycivil al’anyreal.Pertant,lasevaprincipalpreocupacióeralamesurad’unanyrealmitjançant unnombresencerdedies.Enveurepetitsdesajustamentsdelespropostesinicialsesvan començaraintroduirdies,afabricaranysbixestsamb366diesperreajustarcadaquatre anyseldesajustamentproduïtperlainexactituddelapropostainicialde365diesperany. Siensfixemenlamesuradel’anyproposada,seriaarade365,25diesdesajustadaperuna centèsimaipocmés.Alcalendarigregorià(querepaquestnomenhonordelpapaGregoriXIII)esprodueixunnoucanvipercorregirelsdeudiesderetardques’havienproduïtdesde lapromulgaciódelcalendarijulià(aquestenhonoraJuliCèsar)i,percorregiraquesterror,es decideixafegirundiaatotselsanysmúltiplesdequatreexceptuantelsmúltiplesdecentque nohosiguindequatre-cents.Ambaixòs’eliminentresanysbixestscadaquatre-centsanys is’aconsegueixajustarundecimalmés.Amés,pereliminarelsdeudiesdedesajustament acumulatsfinsllavors,eldijous4d’octubrede1582fouseguitpeldivendres15d’ocubrede 1582.

Enaquestsentit,parlantdelcanvialcalendarigregorià,l’Antonenscomentalacuriositat observadaenlesactesdelcapítoldelacatedraldeGironacorresponentsalmesd’octubre de1582:nis’esmentaelcanviiespassa,sensemés,delareuniódedimecres3d’octubrealade divendres15d’octubre.Enaltrescasos,elcanvivadonarllocaanècdotescurioses...

Resumint,l’Antonensportapertotselspetitscanvisisobretotpelsmotiusqueelshan provocatenelnostrecalendarifinsalmodeldelcalendariactual,perseguintdecimala decimalianotantelsdesajustamentsilesanècdotesquehanprovocat.

Reflexionantsobrel’exposiciódel’Anton,eldocentpottrobarenlahistòriadelcalendari moltesoportunitatspertreballarlesmatemàtiquesatotselsnivellseducatius:organització del’anyenmesos,elsmúltiplesdequatre,l’estudidel’error...totunmuntd’ideesqueben enfocadespeldocentpodenresultarexperiènciesd’aulamoltimoltmaques.

MATEMÀTIQUES EN JOC

Exposició temporal al Museu del Joguet de Catalunya

Figueres

Des de finals d’octubre fins al desembre de 2014

Comissària:Maria Bras-Amorós,doctora en matemàtiques,URV

L’exposició«Matemàtiquesenjoc»ésunainvitacióaferunamiradamatemàticaaljocial joguetengeneral.Mestresiprofessorsdematemàtiquesrepetimsovintqueles matemàtiquessónpresentsenlesnostresvides.Sinoenshifixem,però,enspoden passardesapercebudes.Eljocieljoguetnoensónunaexcepció.ElMuseudelJoguet deCatalunyaésunmarcidoniperapoder-nosfixarbéenlapresènciadeles matemàtiques,devegadesméssubtilisovintbenevident.L’exposicióvolserun subratllatd'aquestapresència.

Lamostratindràunavarietatdejoguetsijocsenquèsónpresentslalògica,lanumeració ielcàlcul,lageometriailamesura.Tambédisposaràd’unasecciódellibresanticssobrejocs,enginysientretenimentsmatemàtics.Enparal·lelal’exposició,hihauràunes quantesactivitatsprogramadesdirigidesafamíliesitambéaprofessionalsdel’educació.

El paper de les matemàtiques en el joc.

El paper del joc en les matemàtiques

Si a més de fixar-nos bé en les matemàtiques que ens envolten, hiinvolucrem el pensa- « ment, utilitzant paraules de MariaAntònia » Canals, el joc pot tenir un paper complementari en l’aprenentatge de les matemàtiques. Volem parlar sobre aquest paper en una taula rodona amb MariaAntònia Canals, referent a Catalunya en la Didàctica de les Matemàtiques i responsable del gabinet de materials Gamar; Mequè Edo, doctora de la Universitat Autònoma de Barcelona i investigadora en joc i matemàtiques, i Helena Cusí, representant del Museu de Matemàtiques de Catalunya.

Els números canten

Hi haurà animació musical amb cançons tradicionals i algunes d’autor, de la mà del doctor en pedagogia i cantant professionalToni Giménez. Es tracta de presentar el treballEls números canten , en què « » s’ha volgut recalcar el paper que les cançons poden tenir per complementar el treball d’elaboració de la seqüència numèrica, l’aproximació als diferents significats del nombre i unes primeres pràctiques de càlcul mental.

Mésinformació:MuseudelJoguetdeCatalunya,info@mjc.cat,972504585.

seccions seccions rcions

pensar perpensard’unminut

JordiDeulofeu

DepartamentdeDidàcticadelesMatemàtiques idelesCiènciesExperimentals UniversitatAutònomadeBarcelona

jordi.deulofeu@uab.cat

Ladiversitatd’activitatsperfergaudirdelesmatemàtiquesalsnostresalumnesquetrobem avuialnostreentornnoparadecréixer.Alsjaconeguts,iquasipodríemdirtradicionals, concursosdelCangur,Femmatemàtiques,Problemesal’esprint,l’Olimpíadamatemàticaper petitsigrans,ielsconcursosdedibuixosidefotografiamatemàtica,percitarelsprimers queemvénenalcap,juntamentambaltresactivitatsextraescolarscomEstalmat,queja hasuperatlesdeupromocions,oelmésrecentAnempermésmates,podemafegir-hila recentestrenadaCopaCangur,undivertitiinteressantconcursques’hacelebratenguany perprimeravegadaacasanostra.Tosells,malgratlasevadiversitat,tenenunpuntencomúi ésqueensproporcionenunainacabablecol·lecciódeproblemesinteressantsperadiferents nivellsidedificultatmoltdiversa.

L’articled’avuiéselmeupetithomenatgeatotsaquellsqueambelvostreenginy,anyrere any,aneutrobant,ideantiproposantproblemesmatemàticsamblafinalitatdefergaudir elsnostresalumnesdelreptequesuposaresoldreunproblema,unjoc,unenigma,altemps quemostremlavarietat,tantpelquefaalatemàticacomalnivelldedificultat,delanostra ciència.

SegurquemoltsdevosaltresrecordeuunproblemadelCangurdefaalguntempsenel qualesdonavaunrectangleiunpuntinteriorunitambelsdiferentsvèrtexsdelrectangle, demaneraqueesdeterminenquatretriangles.Conegudeslesàreesdetresdelstriangles, estractadetrobarelquart.Sinoelrecordeu,nouscostaràgaireresoldre’l,permètodes elementals.

Fapocsdies,laLourdesFigueirasemvaproposarunproblemasemblant.Araelqueconeixem sóntresdistànciesivolemtrobarlaquarta.

◮ Problema1. Tenimun rectangleiunpuntinterioriconeixemlesdistànciesd’aquestpunt atresdelsvèrtexdelrectangle.Trobarladistànciaalquartvèrtex.Conegudaaquesta,què podemdirdeleslongitudsdelscostatsdelrectangle?

Resoldreelproblemaemprantequacionsésforçasenzill;fer-hopermètodesgeomètricsno hoéstantiésunrepteconsiderable.

Deixemlageometriaperanaralsjocsd’estratègia,quejasabeuqueésunadelesmeves aficions.AlVIISeminarideprofessorsdelesdiferentsseusd’Estalmat,ques’hacelebrat aBarcelonaelpassatmesd’abril,ienunasessiósobreactivitatsrelacionadesambla paritattitulada«Paridadymagia»,elprofessorAntonioArroyo,d’EstalmatCastillayLeón,va presentareljocsegüentquecorresponalsanomenatspetitsjocsd’estratègia.Ésunjocde tipusNimqueintrodueixunaideaoriginal,ipochabitual,iquetérelacióambelfetdepoder convertirlesfitxesd’uncolorenfitxesdel’altrecolor.

Laideadelareversibilitatdelesfitxesapareguéperprimeravegadaafinalsdelsegle XIX quan esvaformularperprimercopelmagníficjocd’estratègiaconegutambelnomdeReversi (tambés’anomenaOthelloi,enalgunsllocs,Yang).L’enunciatdeljocéselsegüent:

◮ Problema2. Jocd’estratègiaperadosjugadors.Tenim2013fitxesreversibles(unacara blancail’altranegra)ienlaposicióinicial m fitxesmostrenlacarablancai2013 m lacaranegra(m, n > 1).Alseutorn,unjugadorpotferunadelesduescosessegüents:A)retirar toteslesfitxesquevulguid’unmateixcolor(mínim1).B)girartoteslesfitxesquevulgui d’uncolordemaneraquepassinaserdel’altrecolor.Eljugadorqueaconsegueixiretirar l’últimafitxaéselguanyadordelapartida.Peraquindelsdosjugadorshihaunaestratègia guanyadora?Comhadejugaraquestjugadorperguanyarsempre?L’estratègiadepèndels valorsde m i n?Idelnombretotaldefitxes?

Podeutrobaraquestjoc,aixícomlarestadeponènciesd’aquestseminari,al’adreça: https://sites.google.com/site/reunionestalmatcat

Ijaqueparlemdejocs,heretrobatunanticjocd’estratègiadelsditsjocsdeconnexió, anomenat Sprouts (literalment,brots),creatperConwayiPatersonel1967,darreredelqual hihaunmuntdematemàtiques.Avegadessorprènqueapartird’unenunciattansenzill comaquests’hiamaguiunproblematancomplex.Defet,crecquesibéhihaunaconjectura sobrequinéseljugadorquetéunaestratègiaguanyadorasegonslaposicióinicial,estracta d’unproblemaobert,jaqueaquestaconjecturaencaranoestàdemostrada.

◮ Problema3. Sprouts,jocd’estratègiaperadosjugadors.Dibuixemuncertnombrede puntsenunpaper.Alseutorn,cadajugadoruneixdospuntsambunalínia(nonecessàriament recta)amblescondicionssegüents:A)lalínianopottallarcapaltralíniajadibuixada:B)de cadapuntnoméspodensortirtreslínies.Percompletarlajugada,unavegadadibuixadala líniaesmarcaunnoupuntsobreaquesta.Eljugadorquenopotdibuixarunalíniaambles condicionsanteriors,perdlapartida.Éspossiblequeunalíniacomenciiacabienelmateix punt.

Ésinteressantanalitzarelscasosambpocspuntsinicials(entredosicinc)quesónelsque permetenveure«cosesinteressants»sensecomplicargairelespartides.Desprésdejugar unamica,espotcomençarperveurequeeljocésefectivamentfinit,despréstrobarquinés elmàximielmínimnombredejugadesd’unapartidaifinalmentintentarconjecturarqui guanyaenaquestsprimerscasos.

Imatge1.Unapartidade Sprouts iniciadaambnomésdospunts.

Aquíguanyaelprimerjugador,peròsielsegonjugad’unamaneradiferent,semprepotguanyar.

Sieljocusagradaienvoleusabermés,laxarxan’ésplenad’informació(perexemplea: http://nrich.maths.org/2413,ambpropostapertreballar-loaclasse)itambétrobareuuna curiosavariant(BrusselsSprouts-colsdeBrussel·les)queinicialmentsemblaméscomplexa (araenllocdepuntsdibuixemcreus,demaneraquepodensortirquatrelíniesdecadapunt, peròaquestesestanprèviamentfixadespeldibuixdelescreus),peròqueenrealitatnoho és.Enefecte,podeucomprovarqueenaquestcaselnombredejugadesquedadeterminat pelnombreinicialdecreus,sensequeelsjugadorspuguinferrespervariar-lo,perlaqual cosadiemqueestractad’unpseudojoc,ésadir,unjocdeterminatperlescondicionsinicials.

Bensegurquel’anàlisideljocussuggerirànombrosesrelacionsambelsgrafs,entreles qualslafórmulad’Eulerenelpla,aquellaquediuquelasumadelnombrederegionside vèrtexsequivalalnombredecostatsmés2(sinoméscomptemlesregionstancadesés1).

L’aplicaciód’aquestafórmulapermetresoldreaquestsegonjoc,itrobaremqueelnombre demovimentsestàdeterminatpelnombredepuntsinicials,demaneraque,siaquestés n, elnombredemovimentsés5n 2.

L’interèsperaquestjocésmoltgran,comconfirmenlesnombrosesreferènciesalaxarxa.Existeixfinsitotunaassociaciódedicadaaljoc,WorldGameofSproutsAssociation, http://www.wgosa.orginombrosespàgines.Enunad’elles,delauniversitatdeUtah, http://www.math.utah.edu/~alfeld/Sprouts,espotdescarregarunprogrametperjugara l’Sprouts;enunaaltra,http://gameofsprouts.com/refs.html,hitrobareuunaextensabibliografia.

Acabarél’articleambunbonicproblemad’optimitzacióqueemvaproposarl’amicLluís Bibilonijafauncerttemps,queencaranohaviatingutocasiódeproposariambqui, juntamentambenXavierValls,hetingutl’ocasiódecomentaridiscutirllargament,al voltantd’unataula,diversesmaneresdetrobar-nelasolució.Unavegadaméselsproblemes geomètricsdemàximsimínimsapareixenenaquestasecció,fruit,sensdubte,del’interès que,almeuparer,tenenaquesttipusdeproblemesperlabellesaisovinttambélasorpresade lessevessolucions,comtindreuocasiódecomprovarsiusendinseuenlaresoluciód’aquest problemaquearamateixusproposo.

◮ Problema4. Dibuixeuunacircumferència,unpuntexteriorilesduestangentsala circumferènciaquepassenperaquestpunt.EscolliuunpuntPsobrel’arcmenordeterminat enlacircumferènciaitraceulatangentquepassaperaquestpunt.Lestrestangents dibuixadesdeterminenuntriangle.QuinhadeserelpuntPpertalquel’àreadeltriangle siguimàxima?Quèpodeudirdelperímetred’aquestafamíliadetriangles?

Encaraquelasoluciódelproblemapuguiserl’esperada,estractadetrobarunargument quelavalidiempranttansolsgeometriaelemental.Encanvi,noéstanesperadalasolució alasegonapreguntadelproblema quanlavaigdescobriraixím’hovasemblar iésa aquestaa laqualemreferiaabans.Sitrobeularespostaemprantreiteradamentunaúnicai benconegudapropietatdelestangentsaunacircumferència,esperoqueentendreulameva fascinacióperaquestasolucióilareferènciaquehefetalabellesaquesovinttrobemdarrere lessolucionselementals quenosemprevoldirsenzilles d’aquesttipusdeproblemes.

Quegaudiu amblaresoluciód’aquestsialtresproblemesdematemàtiques,tantcomhofaig jotriant-lositractantderesoldre’ls,ifinsaunaproperaocasió.

Bibliografia

Berlekamp,E.,ConwayiJ.Guy,R.(1992), WinningWaysforyourMathematicalPlays.AK Peters/CRCPress.

TheCompleteListofReferencesfortheGameofSprouts,http://gameofsprouts.com/refs.html, WorldGameofSproutsAssociation,http://www.wgosa.org

TheUniversityofUtah,TheGameofSproutshttp://www.math.utah.edu/~alfeld/Sprouts

L’edificidelamatemàtica,sensecapdubte,téunaenormebellesa.Enell,lamiradaavesada, hiobservaharmonia,coherència,completesa...Éselresultatdeseglesiseglesd’esforçhumà percrearuncosformidabledeconeixement.Tanmateixnoésunedificiacabat,hihapaletes ifustersquevantreballantperfer-lomésamplipertald’acollirnovesidees,méspotentper respondreanovesnecessitats,mésbenfonamentatperassegurar-nelasolidesa...Ésuncos viuencontínuaconstrucció.Iaixòliatorgaencaramésencant!

Avegades,lapersonaqueensenyamatemàtiquesactuacomunguiaquevamostrantalseu alumnatlesestancesd’aquestedifici,netesiacabades,ambmiradameravelladaperòamb pocespaiperaladescoberta,ambmagnífiquesexplicacionssobrecomesvaconstruirperò sensegaireoportunitatperal’experiènciapersonaldeconstrucció...

Sirecordemelsnostresanysescolarsouniversitarispotserse’nsfaranpresentsaquelles exposicionsquecomençavenperunesdefinicionsprecisesdelsconceptesquemanejaríem, seguienperl’establimentd’axiomesodepropietatselementals,continuavenenunciant proposicionsméscomplexesquesovinterenmoltlaboriosesdedemostrar,teoremesque culminavenlaconstrucciói,avegades,corol·larisqueacabavend’arrodonirl’edifici.Ami, deixeu-meserfranc,emseduïaiemcontinuaseduintaquestaperfectaconstrucció,l’encaix detoteslesidees,l’encadenamentdelsraonaments,labellesaconjunta...Probablement moltesdelespersonesquellegiuaquesteslíniestambéusheuenamoratunamicad’aquesta harmoniainternadelamatemàticaques’hadesentiriviureenprimerapersona.Tanmateix hemdereconèixerquesentiriviurelesmatemàtiquesenprimerapersonanosempreha estatpresentenl’experiènciaescolardemoltsdelsnostresconciutadansd’unamaneratan intensacomseriadesitjable.

Sovintl’educaciómatemàticaescolar,reproduintlapròpiaformaciódemestresiprofessorat, haestatmésunavisitaguiadaal’edificimatemàticqueunadescobertapersonal,viscudai

emocionantdecadascundelsseusracons.Senseoblidarelsvalorspositiusquetéunguiatge amatentiordenat,capaçd’estructurarbéelconeixement,detransmetreideesclaresiben seqüenciades...hauríemd’admetrequeseriaimportantaconseguirunamajorpresènciaales classesdematemàtiquesd’activitatsqueimpliquinexploració,reptepersonal,descobertai constataciódelautilitatrealdelconeixement.

Actualment,entremestresiprofessoratdematemàtiques,s’observaunesforçdecidit peraccentuarlapresènciad’aquestenfocamentmésvivencialiaplicatenlesclassesde matemàtiques.Potserenshihaportatunaevoluciódelaculturaprofessionalqueanem construinticompartint,potserlaperspectivacompetencialquetéunapresènciacadacop mésclaraenelsistemaeducatiu,potserlanecessitatd’unamajoradaptacióaunalumnat immergitenunmónmoltdinàmiciinteractiu,potserelfetdedisposard’einespotents associadesalestecnologiesidematerialsmanipulablesatractius.Elfetésquecadacop mésescomparteixl’interèsdocentperquè,enelnostreguiatgeperl’edificimatemàtic,no tansolsesdescriguiniesgaudeixidelsespaisjaconstruïts,sinóqueesvisquipersonalment l’experiènciadelaconstrucció.Itenimlasortqueferdescobertesésmoltemocionanten matemàtiques.Permeteu-mequepresentitotseguitunexempled’experiènciad’aquest tipusques’emmarcaenelsblocsdemesuraod’espaiiformade3ro4td’ESOiqueespot estendrediversesclasses.

Arribemal’aulaambunmuntdefotocòpiesenlesqualssimplementhihadibuixatungran triangleequilàterienrepartimunaperacadaalumne/atotdemanantqueassenyaliunpunt enelseuinterior,elquevulgui.Alaclasseanteriorjaelsvàremindicarqueportessinunregle, unescaireiuncompàs.

Acontinuacióelsconvidematraçarlesrectesperpendicularsdesdelpuntescollitacada costat(ambelregleielcompàsol’escaire,peròconvéfer-hoambcura)iquemesurinles distànciesdesdelpuntacadascundelscostats.Tothomobtémesuresdiferents,naturalment!

Arademanemquesuminlestresmesuresiqueposinencomúelsresultatsobtinguts. Sorpresa!Atothomlidónaigual(llevatdepetitesdiferènciesdegudesaerrorsdemesura) ambindependènciadelpuntques’hagiescollit!

Aixòproposaunanovapreguntaquehauremd’investigar:Téalgunacosad’especialaquest nombrequeenshasortit?Téalgunarelacióambeltriangle?Elsalumnescomencena mesurar.D’entrada,mesurenelscostatsinohiveuenrelació.Finalment,algúamidal’altura deltriangle(novamentcaldràtenircuraeneltraçatdelaperpendicular)iobservaamb sorpresaquelalongituddel’alturacoincideixamblasumadelestresdistànciesquehavíem obtingut.Tothomhovaprovantiladescobertaescomparteix.

Realment,aquesttriangleequilàterdeusermoltespecialsicompleixaixò!Potserque provéssimambaltestriangles!Convidemque,formantparelles(aixíhand’anarverbalitzant elquefan),construeixinelsseuspropistrianglesequilàters,escullinunpuntinterior,calculin lestresdistànciesalscostats,lessuminicomprovinqueelresultatobtingutésigualal’altura deltriangle.Llevatdepetitserrorsdemesura,tothomaniràfentaquestacomprovació. Meravellós!Aquellapropietatquehavíemdescobertperaltriangledelfullfotocopiattambé escompleixperacadascundelsnostrestriangles!

Totaixò quehemfetsobrepaper,ambregleicompàs,arahopodemfermésfàcilmentamb GeoGebra.Resultamoltinstructiuferlaconstruccióiemprarleseinesquetéperprendre mesuresicomprovarlaigualtatobservada(ambmoltamésprecisió!).Lespossibilitats dinàmiquesdelGeoGebraenspermetenmoureelpuntescollitocanviareltriangleequilàter icontinuarobservantquelapropietatesmanté.

Araseriaelmomentde«prendreconsciència»delanostradescoberta,deperfilarbéla regularitatquehemobservat.Ambaquestpropòsitdemanemquecadaparellaescriguien unpaper,delamaneramésclarapossible,elques’hadescobert.Noestractadedescriureel procésexperimentalquehemfet,sinósimplementlapropietatobservada.Desprésanirem compartintelquehemescriti,conjuntament,construiremunafrasequeresumeixilanostra descoberta.L’escriuremalapissarra.Seràinteressantanarcomentantlaterminologiaila lògicadeltextpertalquedescriguifidelmentlaideaquevolemexpressar.Potsersortiràuna frasesemblantalasegüent:

Enqualsevoltriangleequilàter,lasumadelesdistànciesdesd’unpuntinterioracadascun delsseuscostatséssempreigualal’alturadeltriangle.

Acabemd’anunciarenunafraseelnostredescobriment!Lescomprovacionsquehemfetens mostren moltsdecasosenquèescompleix,peròno demostren l’afirmaciófeta.Peraraestracta,doncs,d’unaconjectura.Tansolsarribaràaserunteoremasihoaconseguimdemostrar!

Hodemostrem?Probablemententrel’alumnathihauràinterèsademostrarelqueacabende descobrir.Hihaduespossibilitatsatractives:

1.Lademostracióclàssica,queesbasaenestablirunaigualtatentreàrees.Sieltriangle és ABC ianomenem P alpuntinterior,ésevidentquel’àreadeltriangle ABC coincideix amblasumadelesàreesdelstriangles APB, BPC i CPA.Sianomenem h i l l’alturaiel costat,respectivament,deltriangleequilàteri h1, h2 i h3 lesalturesrespectivesdels triangles APB, BPC i CPA quepassendelpunt P icauensobreelsrespectiuscostats, igualantàreestindrem:

Simplificant 1 2 l obtindremlaigualtat h = h1 + h2 + h3.Tenintencompteque h1, h2 i h3 sónlesdistànciesdelpunt P alstrescostats,elteoremaquedademostrat.

2.Unademostracióvisualmoltbonicabasadaenunmaterialmanipulableformatper trestrianglesequilàtersinstal·latsunsobrel’altredemaneraque,atravésdedosgirs, lestresdistàncies«recobreixen»exactamentl’alturadeltrianglegran:

Lapropostaespotconsultaral’ARC:http://apliense.xtec.cat/arc/node/1282.Agraeixo alprofessorQuimTarradaslaconstrucciódelmagníficmodelqueapareixalesimatges.

Arasíquelanostradescobertahadeixatdeserunaconjecturais’haconvertitenunteorema! Defet,apartdeserelnostreteorema,éselteoremadeViviani,queportaaquestnomen honoralseuprimerdescobridor,VincenzoViviani(Florència,1622-1703),undeixeblede Galileu.

Arribatsaquí,potseralgunsalumnesoalgunesalumnespodenampliarencaraunamicamés aquestaexploracióifer-senovespreguntesqueimpulsarannovesexperimentacions(aquí,el GeoGebraenspotsermoltútil!),novesdescobertesi,sical,novesdemostracions:Tambées compliriaaquestapropietatsiprenemelpuntsobrealgundelscostatsoalgundelsvèrtexs deltriangle?Espodriaformularunapropietatsemblantperauntriangleisòscelesenquèels costatsigualsfossineldobledellargsqueelcostatdiferent?Espodriareformularperaalgun tipusdetrianglesescalens?Espodriapensarenunageneralitzacióa3Dperatetraedres regulars?

EsvaproposarunaaplicaciócontextualitzadadelteoremadeVivianienundels«desafíos matemáticos»queesvarenplantejaraldiari ElPaís enocasiódelcentenaridelaRealSociedadMatemáticaEspañola.ElproblemavaserpresentatiresoltpelprofessorDavidObrador atravésdedosvídeosinteressantsperportaraclasseiqueespodenconsultaralweb: http://goo.gl/Uj2xWH

Analitzantaquestexempleobservemcomhemseguitunprocésenquatreetapesque permetenviure,enprimerapersona,l’experiènciadeconstruirconeixementmatemàtic:

◮ Experimentació: S’explora,s’estableixcontacteamblesideesqueestanenjoc,estempteja,esfanproves,esprenenmesures,esfancomparacions...Enl’exempleques’hapresentat (comentantsd’altres),elGeoGebraenspotajudarmoltenaquestaetapa!

◮ Descoberta:S’observaunaregularitatexperimental,sovintsorprenent,queapareix repetidamentensuccessivesproves.Noestractad’unconeixementqueensvedefora,sinó d’unadescobertapersonal,resultatdelanostraexperiència!

◮ Conceptualització:Ésimportantposarencomúallòquehemdescobert,perfilarbé laidea,sentir-lapròpia,esforçar-seenexpressar-lacorrectament,arribaraunaformulació compartidaqueneixidel’experiènciaviscuda.Noestractadedescriureelprocésrealitzat, sinólaregularitatdescoberta.

◮ Demostracióoformalització(sical!): Finsaquítenimunaconjecturaques’ha mostrat experimentalmentenmoltsdecasos,peròquenos’ha demostrat apartird’unraonament lògicqueliatorgageneralitat(aquestadistincióésinteressantperaproparelsalumnesala metodologiamatemàtica).Avegadesseràconvenientferlademostració,d’altrespotserno caldràarribarademostrar-ho(finsitotperquènosiguipossibleambleseinesdequèes disposa),unesaltreslademostracióseràrequeridapelspropisalumnes...

Lapossibilitatd’emprarunametodologiad’aquestamenanoésexcepcional.Sónmoltes lesocasionsenquètenimoportunitatdeferuntrajecte Experimentació → Descoberta → Conceptualització → Demostracióoformalització(sical) perconstruirideesmatemàtiques. Enaquestasecció,queprecisamentportapertítol«construintmatemàtiques»,intentarem presentarmésexemplesqueusanimemaportaraclasse!

elracódelmmaca

Epicicloides,hipocicloidesiengranatges

JosepRey,ManuelUdina

Entreelsmòdulsqueesproposenenl’exposició«Experiènciesmatemàtiques»n’hihaque sónméspròximsatemàtiquesdelcurrículumdel’ensenyamentobligatoriid’altresque,tot inoser-hotant,permetenferreferènciaaaspectesquepodenserd’interèstransversal.Les corbesdefinidesapartirdemoviments,comatracesd’algunpuntdel’objectemòbil,tenen unaforçaemotivaquepotajudaralareflexiósobreaspectesmatemàticsiquefacilitala conversasobrealgunspuntsd’interès.

Elsmòdulsd’engranatgessónmoltsuggerents,perquèpermetenvisualitzarunasèriede corbesinosolsvisualitzar-les,sinótambé«seguir-lesambelmovimentdelamà»tot experimentantcomesgeneren.Partimd’unacircumferènciafixa(circumferènciabase) formadaperpiusquepermetranengranar-hicircumferènciesmòbils(rodetes)perfervoltes perfora(totdescrivintepicicloides)operl’interior(generanthipocicloides).Enelcasdeles epicicloides,espotcomprovarqueelgestquefemquanlesresseguimés«natural»,perquè elsdosmoviments(degiriderotació)tenenelmateixsentit.Enelcasdeleshipocicloides, quanmovemlarodetaesprodueixalgunmomentdedubte,perquèelsdosmovimentsvan ensentitoposat.Enelsdoscasos,l’experiènciaensajudaràaentendrequelavariacióde l’angled’unradidelacircumferènciamòbiléslasumadelesvariacionsdelsanglesderotació idegir.

◮ Cicloide.Sifemrodar(senselliscar)unacircumferènciaalllargd’unalíniarectaqualsevol puntde lacircumferènciadescriuunacicloide.Presentemunmòdulquepermetvisualitzar diversescicloidesambrodesdentadesdediferentsradistotsituant-lesenunapistaengranatgeambpiusquepermetelmoviment«senselliscar»delesrodetes.

Elmòdulespresentaalcostatd’unacicloideenformade tobogan alcostatd’unapistarecta peronpodenbaixarduesbolesionésfàcilexplicariexperimentaralgunespropietatsdela cicloide:ésbraquistòcrona(corbaderecorregutmésràpidentredospunts)itautòcrona(el tempsnecessariperarribaralpuntmésbaixnodepèndel’alçadadelpuntdesd’onesdeixa anar).Totilasevasenzillesa,elmòdulprovocaunimpactefortenelvisitant,perquèconeixi potparlardelespropietatstotexperimentant-lesfinsacertpunt.D’altrabanda,permetfer referènciaaaspecteshistòricsial’aportaciódeGalileu,Newton,elsgermansBernouilli,etc.

◮ Hipocicloidesiepicicloides.Quanfem rodar,senselliscar,circumferènciesderadimés petitperdins(operfora)d’unacircumferènciafixamésgran,qualsevolpuntdelacircumferènciainteriordescriuunahipocicloide(ounaepicicloide).Enelmòdulhemoptatper assenyalarlatraçad’unpuntielvisitantpotcomprovarcom,totfentelmovimentdegir alvoltantdelacircumferènciafixa(iderotaciódelapetita),elpuntassenyalatvaseguint latraça.Segonslarelacióentreelsradisdelesduescircumferències,lestracesprodueixen diferentstipusdecorbes.Destaquementreleshipocicloides,ladeltoideil’astroide(quan elradidelacircumferènciamòbilés 1/3 o 1/4 delradidelafixa),ientrelesepicicloides,la cardioideilanefroide(radidelacircumferènciamòbil 1/2 oigualqueeldelafixa).

Ésclarqueelnombredebaguesdelescorbesgeneradesdepèndelarelacióentreels radisenjoc.Elmòdulpresentarelacionssenzilles,perquèpermetenentendreqüestionsde divisibilitat.Defet,hihauncertparal·lelismeentreelspolígonsestrellatsileshipocicloides(en elsentitquetenenelmateixnombredevèrtexsicanvienelscostatsperarcsd’hipocicloide).

Enlarealitzaciófísicadelmòdul,lacircumferènciafixaesconfigurapartirdelspiusdemanera quelesrodetesfuncionentantperdinscomperforatotpermetentenlamateixabasel’estudi delesepiileshipocicloides.Amés,laconfiguracióambelpiusfacilitaunacertamesuradel perímetredelacircumferència,delamateixamaneraqueelnombrededentsdelesrodetes s’adiuambelseuperímetre.Esdisposadeduesbasesambcircumferènciesfixesde60i40 pius,is’hihanassenyalatlestracesquesegueixendiversesrodetesqueesmanipulenambel suportsituatalcentredelcolordelatraçaaseguir.

Unapropietatadestacarenleshipocicloidesiqueésfàcildecomprovarexperimentalment enaquestmòdul,endisposardelestracesdibuixades,ésqueperrodetescomplementàries, ésadir,rodetestalsquelasumadelsradissiguielradidelacircumferènciabase,lestraces coincideixen(totiquesóndescritesensentitscontraris).Aixòvoldir,perexemple,que l’astroidepotsergeneradatantperunacircumferènciaderadi 1/4 delacircumferènciabase comperladeradi 3/4 delamateixacircumferència.

Cicloide.

Hipocicloidesiepicicloides.

Unaltre elementdesorpresaqueincorporaelmòduléselfetque,sifemgiraralavegada duesrodetesperl’interioriperl’exteriordelacircumferènciafixa,elmovimentderotacióde l’exteriorésmoltmésràpidqueeldelainterior.Ésunfenomenques’explicapelfetquela variaciódel’angleenlacircumferènciamòbiléslasumadelesvariacionsdel’angledegiri derotaciói,enelcasdelesepicicloides,elsdosangles(degiriderotació)tenenelmateix sentit,ienleshipocicloides,sóndesentitcontrari.

◮ Pentàgonatrapat.Ensbasemenelfetqueperaunahipocicloideambrelaciódelsradis2:1 latrajectòriadequalsevolpuntdelacircumferènciainteriorésunalíniarecta.Simarquemcinc puntsdelacircumferènciamòbilinteriorqueforminunpentàgonregular,podremveurecom aquestpentàgongiraperdinsdelacircumferènciademaneraquelestrajectòriesdelsvèrtexs sóncincdiàmetresdelacircumferènciagran(elfetqueelrodamentsiguisenselliscament esrealitzafísicamentambelsengranatges).Enelmòdulquepresentaaquestfenomen,la circumferènciagranestàformadaperunengranatgeambcinquantadentsilainterior,de diàmetrelameitat,tévint-i-cincdents.Perestabilitzarelmoviments’hafetunarasaperon esmouelcentredelacircumferènciamòbil(quedisposad’unpiuqueencaixaenlarasa).

Arapodemdualitzarencertsentitelmòdul:siobliguemelscincvèrtexsdelpentàgona mantenir-seenelscincdiàmetrescitats(aralesrasesdelabasecorresponenaaquests segments,ielpentàgonmòbiltéunspiusqueelforçaranamantenir-s’hi),elmoviment delpentàgonéselmateixqueabans:elpentàgonvadonantvoltesperl’interiordelacircumferènciacomsiestiguéslligatalsengranatges,peròelqueabanseratrajectòriaaraés lligamiviceversa.Aquíjanocalmostrarlacircumferènciafixail’impactedelmoviment permetfer-sepreguntesicausaunefectesorprenent.

Fotodelmòdul.

◮ El·lipsògrafs.Enl’apartatanteriorhemconsideratunahipocicloideamblarelaciódels radis2:1 ihemobservatquelatrajectòriadequalsevolpuntdelacircumferènciainterior ésunsegmentdelíniarecta.Araobservemquelestrajectòriesd’altrespuntsd’aquesta circumferènciaolligatsaella(lesanomenadeshipotrocoides)sónel lipses.

Dibuixosel·lipseshipotrocoides.

Aixícomenelspentàgonsatrapatsconsideràvemcincpuntsdelacircumferènciainterior,ara nomésenconsideremdosdediametralmentoposatsquedelimitenunsegmentiquelliguem aunesrasesqueescorresponenambelsseustrajectes.Ensoblidemdelescircumferències igràciesaaquestslligamsobtenimelmateixefecte.Elsextremsdelsegmentestanforçats aseguirrectes,elpuntmigsegueixunacircumferència(el lipsedegenerada)itotselsaltres puntsdelsegmentodelasevaprolongaciósegueixenel·lipses.

Aquesttipusd’el lipsògraf(atribuïtaArquímedes)haestatmoltutilitzat.Espodriaanomenar el·lipsògrafdelfuster,jaqueenaquestoficil’utilitzentotposantunafresadoramanualallloc deltraçque,enllocdedibuixar,talla.

El·lipsògrafMMACA.

El·lipsògraf.

◮ Movimentterra-sol.Unaaltraaplicaciód’aquestmòdulésquepermetferunaanalogia ambelmovimentterra-solenquèhihaunmovimentdegiriunmovimentderotació.En ungircomplet(corresponentaun«any»),elnombredepuntsenquèlarodetamiracapal centredelacircumferènciafixafinsquetornaalaposicióinicialcorrespondriaal«nombre dediesdel’any»(perexemple,siutilitzemlarodetadevintdentsenlabasedeseixanta pius,diríemque unanytétresdies).Peròsiensfixemenquantesvegadeselradiassenyalat miraenladireccióinicial,veuremquesónquatre(quecorrespondrienals«diessideris»).La senzillesadelmaterialfísicfaràqueaquestfenomenenspermetientendrelarespostaalapregunta«quantesvoltesfalaterrasobreellamateixaenunany?».Enaquestsentit,elmòdul serveixperaferunaanalogiadeladiferènciaentrediasolaridiasideriipermetveurecom enunanyde n dieselsatèl·lithauràfet n+1rotacions(diessideris).(Sis’objectésqueenel movimentdelsastresnohihaengranatgesni«no-lliscament»,podríemrespondrequeles lleisdeNewtonsónlesquecreenlesrestriccionsalmoviment,iqueentotcas,l’analogiaés fontdeconeixement).

Epicicloidessiderals.

Unade lessatisfaccionsquehemtingutéscomprovarcom,moltesvegadesdesprésd’haver comentatambalgunvisitantalgundelsaspectesesmentats,sovintveiemquealcapd’una estonaquiabansensescoltavaarafalesexplicacionsauntercer.Éselqueendiem «s’encomanenlesganesd’explicar».Endefinitiva,elquepretenemambaquestmòdulés atraurel’interèsdelvisitantquepotaproximar-s’hiadiferentsnivells:simplementgaudintde laregularitatd’unmovimentcomplex,intentantanticiparquinescorbescorresponenaquines rodetes,buscantlesrelacionsdedivisibilitatimplícites,etc.Entotcas,ésunbonexemple decomespotinduirelsvisitantsaparlardeisobrematemàtiques.

Notes

1.Undels applets cinderellapresentatenl’exposicióimaginary.org(http://www.imaginary. org/program/cinderella-applets)enquèespresentaunpentàgonquegiratotmantenintelsvèrtexsenunssegments(quesóndiàmetresdelacircumferènciaperongira elpentàgon)ensvasuggerirlapossibilitatderealitzarfísicamentaquestfenomen.

2.Tambéespodrienestudiartrajectòriesdepuntslligatsalacircumferènciamòbil.Defet, eljocmoltconegut spirograph permetdibuixarmoltesd’aquestescorbesiferfigures quetenenunatractiuquehansabutexplotarelscreadorsdeljoc.Lescorbesquees produeixenesdiuenepiihipotrocoides,perquèpeldissenydeljocnoespodenutilizar puntsdelperímetredelesrodetes.

3.Hihamoltsprogramesquepermetengenerardigitalmentaquesttipusdecorbes.En l’apartat«Descàrregues»delawebdelMMACAenpodeutrobaralgunsproposatsper JosepRey.

creamat elracódelcesire-creamat

Matemàtiquesalallengua

Sommolteslespersonesalesqualsensagradenlesmatemàtiques,nosomnomés quatre gats.Enun tresinores usfem cinccèntims deperquèhodiem.D’entrada,caldirque somgentnormal:ni venemdurosaquatrepessetes,nisomtan aguts o quadriculats com esdiu,peròtampoctan obtusos.Procuremtreballarambels cincsentits iamb mésdedos ditsdefront.Busquem solucionsrodones alsproblemesinointentemenvala quadratura delcercle.Noensagrada buscartrespeusalgatinnecessàriament,procuremno caurede quatrepotes alesprimeresdecanvi,elquenosignificaquenoensquedemamb unpam denas,detantentant,quanveiemquenosemprelescosessóntanclarescomque dos idosfanquatre oquenoens quadren deltot.Encaraquefemunbon cercled’amics,si calens cantemlasquaranta.Però,engeneral,solemserpersonesacollidores:nopensem que tressiguinmultitud nivolemquealgúsesenticom unzeroal’esquerra o méssolquela una.Tampocnoexigimquetothomvagisemprede vint-i-unbotons.Enaquest sentit,ens agradamés sumar que restar.

Aquestpetittext-jocl’hemconstruïtapartird’algunesdelescontribucionsquehemrebut alblogobertpelCreamat«Matemàtiquesalallengua».Peròencaraesperemrebre’nmés. Sensedonar-himés voltes,ushoexpliquemen quatre paraules.

Sovinthemditosentitalestrobadesdemestresiprofessorsquecalfervisiblelamatemàtica amagadaalnostreentorn.Ésundelsgransrepteseducatius.Unadelesrespostesalclàssic «iaixòperaquèserveix»ésmostrarquelesmatemàtiquesrealmentsíquesónútils.No ésl’únicaresposta,peròn’ésuna.I,alavegadaquelesmatemàtiquessónensimateixes unllenguatge,tambécontribueixenaenriquirlesnostresformesd’expressióenllenguatge oraloescrit.Tambétenenaquestautilitat.Elfetquelesmatemàtiquessiguintanpresents enelnostreentornquotidià,perquèenscalelseuúsenmoltesdelesnostresactivitats diàries(complirhoraris,comprarovendre,mesurar,orientar-nos...),hafetquelallenguahagi incorporatconceptesitermesmatemàticsperconstruiroformarpartd’expressions,frases fetesodites.Sónmoltfàcilsdetrobarlesexpressionsqueinclouennúmeros(onperexemple quatre éssovint«poc»),formesgeomètriquessenzilles,mesures(onun pam éssovint«molt») o,finsitot,algèbriques(«t’hodicper enèsima vegada»,«repetimelprocés x vegades»).Com espotveure,lallenguaquedaimpregnadaperlesideesmatemàtiques.

Peròalainversatambépassa.Ésmoltfreqüentquealsnousconceptesmatemàtics, especialmentateoriesmésomenyscompletes,selesanomeniambsubstantiustretsdel llenguatgecorrentqueil·lustrenambdiversafortunaelseutemadetreball.Finsitot,devegadesl’èxitd’unateoriahaestatlligadaaaquestnom.Aixíhaestatambla Teoriadeca-

tàstrofes plantejadaperRenéThomalsanyscinquantadelseglepassatola Teoriadelcaos. Notanafortunat,perexemple,haestateltítolde Teoriadejocs que,enrealitat,estudiala presadedecisions.Sovinttenim,amés,termesduals.Lescòniquesensónunexemple,jaque el lipse,hipèrbolaoparàbolatambésónfiguresliteràries.Hihaunfamósacuditquejuga ambaquestaambivalènciaiqueexplicaqueJesús,al’ÚltimSopar,vadiralsseusapòstols «enveritatusdicque y ésiguala x2»;davantdelacaradedesconcertdelsseusdeixebles,el mateixJesúsvaafegir«nosigueuximplets,queésunaparàbola!».

Unaltreaspecteinteressantderelacióentrellenguaimatemàticaésestudiarl’etimologia delstermesmatemàtics(punt vedel punctum llatíquesignifica‘picadura’, onze del‘undecim tambéllatíquevaperdreunasíl laba...),peròsobreaquesttemajafruïmd’unamagnífica seccióenaquestamateixarevista.

Deixemperunaaltraocasiólesrelacionsentrematemàtiquesiliteratura.

Entotcas,desdelCreamatensvamplantejaral’inicidelcurs2013-2014prendrealguna iniciativapertreballaraquestesconnexions.Ensvasemblarqueunadelesformesmés claresconsistiaarealitzarunaconvocatòriaobertaalscentresdemaneraque,apartird’uns temesproposats,espoguéstraslladaralesaulesaquestaindagaciólingüística.Elformat proposatconsisteix(ipassemaltempsverbaldelpresentperquèlainvitacióencaraestà oberta)aomplirunasenzillafitxaamblafrase,elsignificat,unexempled’úsialgunaimatge d’elaboraciópròpiail·lustrativa.Tambévamcontemplarunpetitaspectemulticulturalperquè lapropostaanimaaenviarfrasesenqualsevolllenguaqueesparlialscentresoperlesfamílies del’alumnat,afegint,enaquestcas,latraducció.Així,perexemple,hemsabutqueaEuskadi quanalgúabusad’unaltrediuen«aixòésdonar-neunaiagafar-nedues»(batemanetabi hartu).Lesfitxesquerebemsónpublicadesposteriormentalwebcreatespecialmentper recollir-les:

Matemàtiquesalallengua:http://matesalallengua.blogspot.com.es

Elsprimerstemesproposatshanestat«nombresdel0al5»,«polígons»i«mesura».Usanimemavisitarelblogi,sobretot,aparticipar-hiambelvostrealumnatianar-hiafegint aquellesexpressionsqueencaranoveieurecollides.Noésque onhicabentrestambéhicaben quatre,ésquevolemarribar al’infinitimésenllà